Systems of Equations and Inequalities
|
|
|
- Millicent Lindsey
- 5 years ago
- Views:
Transcription
1 Sstems of Equations and Inequalities 7 7. Linear and Nonlinear Sstems of Equations 7. Two-Variable Linear Sstems 7.3 Multivariable Linear Sstems 7. Partial Fractions 7.5 Sstems of Inequalities 7.6 Linear Programming In Mathematics You can use a sstem of equations to solve a problem involving two or more equations. In Real Life Sstems of equations and inequalities are used to determine the correct amounts to use in making an acid miture, how much to invest in different funds, a break-even point for a business, and man other real-life applications. Sstems of equations are also used to find least squares regression parabolas. For instance, a wildlife management team can use a sstem to model the reproduction rates of deer. (See Eercise 8, page 58.) Krzsztof Wiktor/Shutterstock IN CAREERS There are man careers that use sstems of equations and inequalities. Several are listed below. Economist Eercise 7, page 503 Investor Eercises 53 and 5, page 55 Dietitian Eample 9, page 5 Concert Promoter Eercise 78, page 56 93
2 9 Chapter 7 Sstems of Equations and Inequalities 7. LINEAR AND NONLINEAR SYSTEMS OF EQUATIONS ML Sinibaldi/Corbis What ou should learn Use the method of substitution to solve sstems of linear equations in two variables. Use the method of substitution to solve sstems of nonlinear equations in two variables. Use a graphical approach to solve sstems of equations in two variables. Use sstems of equations to model and solve real-life problems. Wh ou should learn it Graphs of sstems of equations help ou solve real-life problems. For instance, in Eercise 75 on page 503, ou can use the graph of a sstem of equations to approimate when the consumption of wind energ surpassed the consumption of solar energ. The Method of Substitution Up to this point in the tet, most problems have involved either a function of one variable or a single equation in two variables. However, man problems in science, business, and engineering involve two or more equations in two or more variables. To solve such problems, ou need to find solutions of a sstem of equations. Here is an eample of a sstem of two equations in two unknowns. 5 Equation 3 Equation A solution of this sstem is an ordered pair that satisfies each equation in the sstem. Finding the set of all solutions is called solving the sstem of equations. For instance, the ordered pair, is a solution of this sstem. To check this, ou can substitute for and for in each equation. Check (, ) in Equation and Equation : 5? ? 6 Write Equation. Substitute for and for. checks in Equation. Write Equation. Substitute for and for. checks in Equation. In this chapter, ou will stud four was to solve sstems of equations, beginning with the method of substitution. Method Section Tpe of Sstem. Substitution 7. Linear or nonlinear, two variables. Graphical method 7. Linear or nonlinear, two variables 3. Elimination 7. Linear, two variables. Gaussian elimination 7.3 Linear, three or more variables Method of Substitution. Solve one of the equations for one variable in terms of the other.. Substitute the epression found in Step into the other equation to obtain an equation in one variable. 3. Solve the equation obtained in Step.. Back-substitute the value obtained in Step 3 into the epression obtained in Step to find the value of the other variable. 5. Check that the solution satisfies each of the original equations.
3 Section 7. Linear and Nonlinear Sstems of Equations 95 Eample Solving a Sstem of Equations b Substitution You can review the techniques for solving different tpes of equations in Appendi A.5. WARNING / CAUTION Because man steps are required to solve a sstem of equations, it is ver eas to make errors in arithmetic. So, ou should alwas check our solution b substituting it into each equation in the original sstem. Solve the sstem of equations. Begin b solving for in Equation. Solve for in Equation. Net, substitute this epression for into Equation and solve the resulting singlevariable equation for. Write Equation. Substitute for. Distributive Propert Combine like terms. Divide each side b. Finall, ou can solve for b back-substituting 3 into the equation, to obtain Write revised Equation. Substitute 3 for. Solve for. The solution is the ordered pair 3,. You can check this solution as follows. Check 3. Substitute 3, into Equation : 3? Substitute 3, into Equation : 3? 6 3 Equation Equation Write Equation. Substitute for and. checks in Equation. Write Equation. Substitute for and. checks in Equation. Because 3, satisfies both equations in the sstem, it is a solution of the sstem of equations. Now tr Eercise. The term back-substitution implies that ou work backwards. First ou solve for one of the variables, and then ou substitute that value back into one of the equations in the sstem to find the value of the other variable.
4 96 Chapter 7 Sstems of Equations and Inequalities Eample Solving a Sstem b Substitution A total of $,000 is invested in two funds paing 5% and 3% simple interest. (Recall that the formula for simple interest is I Prt, where P is the principal, r is the annual interest rate, and t is the time.) The earl interest is $500. How much is invested at each rate? Verbal Model: 5% fund 5% interest 3% fund 3% interest Total investment Total interest When using the method of substitution, it does not matter which variable ou choose to solve for first. Whether ou solve for first or first, ou will obtain the same solution. When making our choice, ou should choose the variable and equation that are easier to work with. For instance, in Eample, solving for in Equation is easier than solving for in Equation. TECHNOLOGY One wa to check the answers ou obtain in this section is to use a graphing utilit. For instance, enter the two equations in Eample, and find an appropriate viewing window that shows where the two lines intersect. Then use the intersect feature or the zoom and trace features to find the point of intersection. Does this point agree with the solution obtained at the right? Labels: Amount in 5% fund Interest for 5% fund 0.05 Amount in 3% fund Interest for 3% fund 0.03 Total investment,000 Total interest 500 Sstem: (dollars) (dollars) (dollars) (dollars) (dollars) (dollars) To begin, it is convenient to multipl each side of Equation b 00. This eliminates the need to work with decimals To solve this sstem, ou can solve for in Equation.,000 Multipl each side b 00. Revised Equation Revised Equation Then, substitute this epression for into revised Equation and solve the resulting equation for. 5, ,000 60, ,000 Net, back-substitute the value 5000 to solve for.,000, , , ,000 0, Write revised Equation. Substitute,000 for. Distributive Propert Combine like terms. Divide each side b. Write revised Equation. Substitute 5000 for. Simplif. The solution is 7000, So, $7000 is invested at 5% and $5000 is invested at 3%. Check this in the original sstem. Now tr Eercise 5. Equation Equation
5 Section 7. Linear and Nonlinear Sstems of Equations 97 Nonlinear Sstems of Equations The equations in Eamples and are linear. The method of substitution can also be used to solve sstems in which one or both of the equations are nonlinear. Eample 3 Substitution: Two- Case You can review the techniques for factoring in Appendi A.3. Solve the sstem of equations. 3 Begin b solving for in Equation to obtain. Net, substitute this epression for into Equation and solve for Equation Equation Substitute for in Equation. Simplif. Write in general form. Factor. 3, Solve for. Back-substituting these values of to solve for the corresponding values of produces the solutions 3, and, 3. Check these in the original sstem. 3 Now tr Eercise 3. When using the method of substitution, ou ma encounter an equation that has no solution, as shown in Eample. Eample Substitution: No-Real- Case Solve the sstem of equations. 3 Begin b solving for in Equation to obtain. Net, substitute this epression for into Equation and solve for. 3 0 ± 3 Substitute for in Equation. Simplif. Use the Quadratic Formula. Because the discriminant is negative, the equation 0 has no (real) solution. So, the original sstem has no (real) solution. Now tr Eercise 33. Equation Equation
6 98 Chapter 7 Sstems of Equations and Inequalities TECHNOLOGY Most graphing utilities have built-in features that approimate the point(s) of intersection of two graphs. Tpicall, ou must enter the equations of the graphs and visuall locate a point of intersection before using the intersect feature. Use this feature to find the points of intersection of the graphs in Figures 7. to 7.3. Be sure to adjust our viewing window so that ou see all the points of intersection. Graphical Approach to Finding s From Eamples, 3, and, ou can see that a sstem of two equations in two unknowns can have eactl one solution, more than one solution, or no solution. B using a graphical method, ou can gain insight about the number of solutions and the location(s) of the solution(s) of a sstem of equations b graphing each of the equations in the same coordinate plane. The solutions of the sstem correspond to the points of intersection of the graphs. For instance, the two equations in Figure 7. graph as two lines with a single point of intersection; the two equations in Figure 7. graph as a parabola and a line with two points of intersection; and the two equations in Figure 7.3 graph as a line and a parabola that have no points of intersection. (, 0) + 3 = = 3 = (, ) = 3 (0, ) + = = 3 You can review the techniques for graphing equations in Section.. FIGURE 7. + = (, 0) = ln One intersection point Two intersection points No intersection points FIGURE 7. FIGURE 7. FIGURE 7.3 Eample 5 Solve the sstem of equations. Solving a Sstem of Equations Graphicall Sketch the graphs of the two equations. From the graphs of these equations, it is clear that there is onl one point of intersection and that, 0 is the solution point (see Figure 7.). You can check this solution as follows. Check (, 0) in Equation : ln 0 ln 0 0 ln Check (, 0) in Equation : 0 Equation Equation Write Equation. Substitute for and. checks in Equation. Write Equation. Substitute for and. Now tr Eercise 39. checks in Equation. Eample 5 shows the value of a graphical approach to solving sstems of equations in two variables. Notice what would happen if ou tried onl the substitution method in Eample 5. You would obtain the equation ln. It would be difficult to solve this equation for using standard algebraic techniques.
7 Section 7. Linear and Nonlinear Sstems of Equations 99 Applications The total cost C of producing units of a product tpicall has two components the initial cost and the cost per unit. When enough units have been sold so that the total revenue R equals the total cost C, the sales are said to have reached the break-even point. You will find that the break-even point corresponds to the point of intersection of the cost and revenue curves. Eample 6 Break-Even Analsis A shoe compan invests $300,000 in equipment to produce a new line of athletic footwear. Each pair of shoes costs $5 to produce and is sold for $60. How man pairs of shoes must be sold before the business breaks even? Algebraic The total cost of producing units is Total cost Equation The revenue obtained b selling units is Total revenue Equation Because the break-even point occurs when R C, ou have C 60, and the sstem of equations to solve is C 5 300,000. R 60. C 5 300,000. C 60 Solve b substitution , , Cost per unit Price per unit Number of units Number of units Subtract 5 from each side. Divide each side b 55. So, the compan must sell about 555 pairs of shoes to break even. Substitute 60 for C in Equation. Initial cost Graphical The total cost of producing units is Total cost Equation The revenue obtained b selling units is Equation Because the break-even point occurs when R C, ou have C 60, and the sstem of equations to solve is Total revenue Cost per unit R 60. Price per unit C 5 300,000. C 60 C 5 300,000. Use a graphing utilit to graph 5 300,000 and 60 in the same viewing window. Use the intersect feature or the zoom and trace features of the graphing utilit to approimate the point of intersection of the graphs. The point of intersection (break-even point) occurs at 555, as shown in Figure 7.5. So, the compan must sell about 555 pairs of shoes to break even. 600,000 Number of units Number of units C = ,000 Initial cost C = 60 Now tr Eercise FIGURE 7.5 0,000 Another wa to view the solution in Eample 6 is to consider the profit function P R C. The break-even point occurs when the profit is 0, which is the same as saing that R C.
8 500 Chapter 7 Eample 7 Sstems of Equations and Inequalities Movie Ticket Sales The weekl ticket sales for a new comed movie decreased each week. At the same time, the weekl ticket sales for a new drama movie increased each week. Models that approimate the weekl ticket sales S (in millions of dollars) for each movie are S 60 8 S 0.5 Comed Drama where represents the number of weeks each movie was in theaters, with 0 corresponding to the ticket sales during the opening weekend. After how man weeks will the ticket sales for the two movies be equal? Algebraic Numerical Because the second equation has alread been solved for S in terms of, substitute this value into the first equation and solve for, as follows. You can create a table of values for each model to determine when the ticket sales for the two movies will be equal Substitute for S in Equation Add 8 and 0 to each side Combine like terms. Divide each side b.5. So, the weekl ticket sales for the two movies will be equal after weeks. Number of weeks, Sales, S (comed) Sales, S (drama) So, from the table above, ou can see that the weekl ticket sales for the two movies will be equal after weeks. Now tr Eercise 69. CLASSROOM DISCUSSION Interpreting Points of Intersection You plan to rent a -foot truck for a two-da local move. At truck rental agenc A, ou can rent a truck for $9.95 per da plus $0.9 per mile. At agenc B, ou can rent a truck for $50 per da plus $0.5 per mile. a. Write a total cost equation in terms of and for the total cost of renting the truck from each agenc. b. Use a graphing utilit to graph the two equations in the same viewing window and find the point of intersection. Interpret the meaning of the point of intersection in the contet of the problem. c. Which agenc should ou choose if ou plan to travel a total of 00 miles during the two-da move? Wh? d. How does the situation change if ou plan to drive 00 miles during the two-da move?
9 Section 7. Linear and Nonlinear Sstems of Equations EXERCISES VOCABULARY: Fill in the blanks. See for worked-out solutions to odd-numbered eercises.. A set of two or more equations in two or more variables is called a of.. A of a sstem of equations is an ordered pair that satisfies each equation in the sstem. 3. Finding the set of all solutions to a sstem of equations is called the sstem of equations.. The first step in solving a sstem of equations b the method of is to solve one of the equations for one variable in terms of the other variable. 5. Graphicall, the solution of a sstem of two equations is the of of the graphs of the two equations. 6. In business applications, the point at which the revenue equals costs is called the point. SKILLS AND APPLICATIONS In Eercises 7 0, determine whether each ordered pair is a solution of the sstem of equations. 7. (a) 0, (b), (c) (d), 5 3, 8. (a), 3 (b), 9 3 (c) 3 (d) 7, 3 3, e (a), 0 (b) 0, 7 (c) 0, (d), 3 0. log 3 (a) 9, 37 9 (b) 0, (c), 3 (d), In Eercises 0, solve the sstem b the method of substitution. Check our solution(s) graphicall In Eercises 3, solve the sstem b the method of substitution
10 50 Chapter 7 Sstems of Equations and Inequalities BREAK-EVEN ANALYSIS In Eercises 65 and 66, find the sales necessar to break even R C for the cost C of producing units and the revenue R obtained b selling units. (Round to the nearest whole unit.) C ,000, C 5.5 0,000, 3 3 R 9950 R 3.9 In Eercises 35 8, solve the sstem graphicall In Eercises 9 5, use a graphing utilit to solve the sstem of equations. Find the solution(s) accurate to two decimal places. 9. e log In Eercises 55 6, solve the sstem graphicall or algebraicall. Eplain our choice of method e ln ln e e BREAK-EVEN ANALYSIS A small software compan invests $5,000 to produce a software package that will sell for $ Each unit can be produced for $5.5. (a) How man units must be sold to break even? (b) How man units must be sold to make a profit of $00,000? 68. BREAK-EVEN ANALYSIS A small fast-food restaurant invests $0,000 to produce a new food item that will sell for $3.99. Each item can be produced for $.90. (a) How man items must be sold to break even? (b) How man items must be sold to make a profit of $,000? 69. DVD RENTALS The weekl rentals for a newl released DVD of an animated film at a local video store decreased each week. At the same time, the weekl rentals for a newl released DVD of a horror film increased each week. Models that approimate the weekl rentals R for each DVD are R R where represents the number of weeks each DVD was in the store, with corresponding to the first week. (a) After how man weeks will the rentals for the two movies be equal? (b) Use a table to solve the sstem of equations numericall. Compare our result with that of part (a). 70. SALES The total weekl sales for a newl released portable media plaer (PMP) increased each week. At the same time, the total weekl sales for another newl released PMP decreased each week. Models that approimate the total weekl sales S (in thousands of units) for each PMP are S 5 50 S 0 90 Animated film Horror film PMP PMP where represents the number of weeks each PMP was in stores, with 0 corresponding to the PMP sales on the da each PMP was first released in stores.
11 Section 7. Linear and Nonlinear Sstems of Equations 503 (a) After how man weeks will the sales for the two PMPs be equal? (b) Use a table to solve the sstem of equations numericall. Compare our result with that of part (a). 7. CHOICE OF TWO JOBS You are offered two jobs selling dental supplies. One compan offers a straight commission of 6% of sales. The other compan offers a salar of $500 per week plus 3% of sales. How much would ou have to sell in a week in order to make the straight commission offer better? 7. SUPPLY AND DEMAND The suppl and demand curves for a business dealing with wheat are Suppl: Demand: p p where p is the price in dollars per bushel and is the quantit in bushels per da. Use a graphing utilit to graph the suppl and demand equations and find the market equilibrium. (The market equilibrium is the point of intersection of the graphs for > 0. ) 73. INVESTMENT PORTFOLIO A total of $5,000 is invested in two funds paing 6% and 8.5% simple interest. (The 6% investment has a lower risk.) The investor wants a earl interest income of $000 from the two investments. (a) Write a sstem of equations in which one equation represents the total amount invested and the other equation represents the $000 required in interest. Let and represent the amounts invested at 6% and 8.5%, respectivel. (b) Use a graphing utilit to graph the two equations in the same viewing window. As the amount invested at 6% increases, how does the amount invested at 8.5% change? How does the amount of interest income change? Eplain. (c) What amount should be invested at 6% to meet the requirement of $000 per ear in interest? 7. LOG VOLUME You are offered two different rules for estimating the number of board feet in a 6-foot log. (A board foot is a unit of measure for lumber equal to a board foot square and inch thick.) The first rule is the Dole Log Rule and is modeled b V D, 5 D 0, and the other is the Scribner Log Rule and is modeled b V 0.79D D, 5 D 0, where D is the diameter (in inches) of the log and V is its volume (in board feet). (a) Use a graphing utilit to graph the two log rules in the same viewing window. (b) For what diameter do the two scales agree? (c) You are selling large logs b the board foot. Which scale would ou use? Eplain our reasoning. 75. DATA ANALYSIS: RENEWABLE ENERGY The table shows the consumption C (in trillions of Btus) of solar energ and wind energ in the United States from 998 through 006. (Source: Energ Information Administration) Year Solar, C Wind, C (a) Use the regression feature of a graphing utilit to find a cubic model for the solar energ consumption data and a quadratic model for the wind energ consumption data. Let t represent the ear, with t 8 corresponding to 998. (b) Use a graphing utilit to graph the data and the two models in the same viewing window. (c) Use the graph from part (b) to approimate the point of intersection of the graphs of the models. Interpret our answer in the contet of the problem. (d) Describe the behavior of each model. Do ou think the models can be used to predict consumption of solar energ and wind energ in the United States for future ears? Eplain. (e) Use our school s librar, the Internet, or some other reference source to research the advantages and disadvantages of using renewable energ. 76. DATA ANALYSIS: POPULATION The table shows the populations P (in millions) of Georgia, New Jerse, and North Carolina from 00 through 007. (Source: U.S. Census Bureau) Year Georgia, G New Jerse, J North Carolina, N
12 50 Chapter 7 Sstems of Equations and Inequalities (a) Use the regression feature of a graphing utilit to find linear models for each set of data. Let t represent the ear, with t corresponding to 00. (b) Use a graphing utilit to graph the data and the models in the same viewing window. (c) Use the graph from part (b) to approimate an points of intersection of the graphs of the models. Interpret the points of intersection in the contet of the problem. (d) Verif our answers from part (c) algebraicall. 77. DATA ANALYSIS: TUITION The table shows the average costs (in dollars) of one ear s tuition for public and private universities in the United States from 000 through 006. (Source: U.S. National Center for Education Statistics) Year Public universities Private universities,08 5,000 5,7 6,383 7,37 8,5 8,86 (a) Use the regression feature of a graphing utilit to find a quadratic model T for tuition at public universities and a linear model T for tuition at private universities. Let t represent the ear, with t 0 corresponding to 000. (b) Use a graphing utilit to graph the data and the two models in the same viewing window. (c) Use the graph from part (b) to determine the ear after 006 in which tuition at public universities will eceed tuition at private universities. (d) Verif our answer from part (c) algebraicall. GEOMETRY In Eercises 78 8, find the dimensions of the rectangle meeting the specified conditions. 78. The perimeter is 56 meters and the length is meters greater than the width. 79. The perimeter is 80 centimeters and the width is 0 centimeters less than the length. 80. The perimeter is inches and the width is threefourths the length. 8. The perimeter is 8 feet and the length is times the width. 8. The perimeter is 30.6 millimeters and the length is. times the width. 83. GEOMETRY What are the dimensions of a rectangular tract of land if its perimeter is kilometers and its area is 0 square kilometers? 8. GEOMETRY What are the dimensions of an isosceles right triangle with a two-inch hpotenuse and an area of square inch? EXPLORATION TRUE OR FALSE? In Eercises 85 and 86, determine whether the statement is true or false. Justif our answer. 85. In order to solve a sstem of equations b substitution, ou must alwas solve for in one of the two equations and then back-substitute. 86. If a sstem consists of a parabola and a circle, then the sstem can have at most two solutions. 87. GRAPHICAL REASONING Use a graphing utilit to graph and in the same viewing window. Use the zoom and trace features to find the coordinates of the point of intersection. What is the relationship between the point of intersection and the solution found in Eample? 88. GRAPHICAL REASONING Use a graphing utilit to graph the two equations in Eample 3, 3 7 and, in the same viewing window. How man solutions do ou think this sstem has? Repeat this eperiment for the equations in Eample. How man solutions does this sstem have? Eplain our reasoning. 89. THINK ABOUT IT When solving a sstem of equations b substitution, how do ou recognize that the sstem has no solution? 90. CAPSTONE Consider the sstem of equations a b c d e f. (a) Find values for a, b, c, d, e, and f so that the sstem has one distinct solution. (There is more than one correct answer.) (b) Eplain how to solve the sstem in part (a) b the method of substitution and graphicall. (c) Write a brief paragraph describing an advantages of the method of substitution over the graphical method of solving a sstem of equations. 9. Find equations of lines whose graphs intersect the graph of the parabola at (a) two points, (b) one point, and (c) no points. (There is more than one correct answer.) Use graphs to support our answers.
13 Section 7. Two-Variable Linear Sstems TWO-VARIABLE LINEAR SYSTEMS Bill Stormont/Corbis What ou should learn Use the method of elimination to solve sstems of linear equations in two variables. Interpret graphicall the numbers of solutions of sstems of linear equations in two variables. Use sstems of linear equations in two variables to model and solve real-life problems. Wh ou should learn it You can use sstems of equations in two variables to model and solve real-life problems. For instance, in Eercise 6 on page 55, ou will solve a sstem of equations to find a linear model that represents the relationship between wheat ield and amount of fertilizer applied. The Method of Elimination In Section 7., ou studied two methods for solving a sstem of equations: substitution and graphing. Now ou will stud the method of elimination. The ke step in this method is to obtain, for one of the variables, coefficients that differ onl in sign so that adding the equations eliminates the variable. Equation Equation Add equations. Note that b adding the two equations, ou eliminate the -terms and obtain a single equation in. Solving this equation for produces, which ou can then backsubstitute into one of the original equations to solve for. Solving a Sstem of Equations b Elimination Solve the sstem of linear equations Eample Because the coefficients of differ onl in sign, ou can eliminate the -terms b adding the two equations Write Equation. Write Equation. Add equations. Solve for. B back-substituting into Equation, ou can solve for Equation Equation Write Equation. Substitute for. Simplif. Solve for. The solution is,. Check this in the original sstem, as follows. Check 3? 6 5? 0 Now tr Eercise 3. Substitute into Equation. Equation checks. Substitute into Equation. Equation checks.
14 506 Chapter 7 Sstems of Equations and Inequalities Method of Elimination To use the method of elimination to solve a sstem of two linear equations in and, perform the following steps.. Obtain coefficients for (or ) that differ onl in sign b multipling all terms of one or both equations b suitabl chosen constants.. Add the equations to eliminate one variable. 3. Solve the equation obtained in Step.. Back-substitute the value obtained in Step 3 into either of the original equations and solve for the other variable. 5. Check that the solution satisfies each of the original equations. Eample Solving a Sstem of Equations b Elimination Solve the sstem of linear equations. 7 5 Equation Equation For this sstem, ou can obtain coefficients that differ onl in sign b multipling Equation b. Write Equation. Multipl Equation b. Add equations. Solve for. B back-substituting into Equation, ou can solve for. Write Equation. Substitute for. Combine like terms. Solve for. The solution is, 3. Check this in the original sstem, as follows. Check ? ? 5 3 Now tr Eercise Write original Equation. Substitute into Equation. Equation checks. Write original Equation. Substitute into Equation. Equation checks.
15 Section 7. Two-Variable Linear Sstems 507 In Eample, the two sstems of linear equations (the original sstem and the sstem obtained b multipling b constants) 7 5 and 7 0 are called equivalent sstems because the have precisel the same solution set. The operations that can be performed on a sstem of linear equations to produce an equivalent sstem are () interchanging an two equations, () multipling an equation b a nonzero constant, and (3) adding a multiple of one equation to an other equation in the sstem. Eample 3 Solving the Sstem of Equations b Elimination Solve the sstem of linear equations Equation Equation Algebraic You can obtain coefficients that differ onl in sign b multipling Equation b and multipling Equation b Multipl Equation b. Multipl Equation b 3. Add equations. Solve for. B back-substituting 3 into Equation, ou can solve for Write Equation. Substitute 3 for. Combine like terms. Solve for. The solution is 3,. Check this in the original sstem. Graphical Solve each equation for. Then use a graphing utilit to graph and in the same viewing window. Use the intersect feature or the zoom and trace features to approimate the point of intersection of the graphs. From the graph in Figure 7.6, ou can see that the point of intersection is 3,. You can determine that this is the eact solution b checking 3, in both equations. 3 5 = = 7 Now tr Eercise 7. FIGURE You can check the solution from Eample 3 as follows. 53 3? ? 6 8 Substitute 3 for and for in Equation. Equation checks. Substitute 3 for and for in Equation. Equation checks. Keep in mind that the terminolog and methods discussed in this section appl onl to sstems of linear equations.
16 508 Chapter 7 Sstems of Equations and Inequalities Graphical Interpretations of s Graphical Interpretation of s It is possible for a general sstem of equations to have eactl one solution, two or more solutions, or no solution. If a sstem of linear equations has two different solutions, it must have an infinite number of solutions. For a sstem of two linear equations in two variables, the number of solutions is one of the following. Number of s Graphical Interpretation Slopes of Lines. Eactl one solution The two lines intersect at one point. The slopes of the two lines are not equal.. Infinitel man solutions The two lines coincide (are identical). The slopes of the two lines are equal. 3. No solution The two lines are parallel. The slopes of the two lines are equal. A sstem of linear equations is consistent if it has at least one solution. A consistent sstem with eactl one solution is independent, whereas a consistent sstem with infinitel man solutions is dependent. A sstem is inconsistent if it has no solution. Eample Recognizing Graphs of Linear Sstems Match each sstem of linear equations with its graph in Figure 7.7. Describe the number of solutions and state whether the sstem is consistent or inconsistent. a. 3 3 b. 3 3 c. 6 6 i. ii. iii FIGURE 7.7 A comparison of the slopes of two lines gives useful information about the number of solutions of the corresponding sstem of equations. To solve a sstem of equations graphicall, it helps to begin b writing the equations in slope-intercept form. Tr doing this for the sstems in Eample. a. The graph of sstem (a) is a pair of parallel lines (ii). The lines have no point of intersection, so the sstem has no solution. The sstem is inconsistent. b. The graph of sstem (b) is a pair of intersecting lines (iii). The lines have one point of intersection, so the sstem has eactl one solution. The sstem is consistent. c. The graph of sstem (c) is a pair of lines that coincide (i). The lines have infinitel man points of intersection, so the sstem has infinitel man solutions. The sstem is consistent. Now tr Eercises 3 3.
17 Section 7. Two-Variable Linear Sstems 509 In Eamples 5 and 6, note how ou can use the method of elimination to determine that a sstem of linear equations has no solution or infinitel man solutions. Eample 5 No- Case: Method of Elimination Solve the sstem of linear equations. + = 3 Equation Equation To obtain coefficients that differ onl in sign, ou can multipl Equation b. 3 = Multipl Equation b. Write Equation False statement FIGURE 7.8 Because there are no values of and for which 0 7, ou can conclude that the sstem is inconsistent and has no solution. The lines corresponding to the two equations in this sstem are shown in Figure 7.8. Note that the two lines are parallel and therefore have no point of intersection. Now tr Eercise. In Eample 5, note that the occurrence of a false statement, such as 0 7, indicates that the sstem has no solution. In the net eample, note that the occurrence of a statement that is true for all values of the variables, such as 0 0, indicates that the sstem has infinitel man solutions. Eample 6 Man- Case: Method of Elimination Solve the sstem of linear equations. Equation Equation 3 (, 3) To obtain coefficients that differ onl in sign, ou can multipl Equation b. = Multipl Equation b. Write Equation. (, ) Add equations. Because the two equations are equivalent (have the same solution set), ou can conclude that the sstem has infinitel man solutions. The solution set consists of all points, ling on the line, as shown in Figure 7.9. Letting a, where a is an real number, ou can see that the solutions of the sstem are a, a. FIGURE 7.9 Now tr Eercise 3.
18 Eample 7 illustrates a strateg for solving a sstem of linear equations that has decimal coefficients. A Linear Sstem Having Decimal Coefficients Solve the sstem of linear equations. Because the coefficients in this sstem have two decimal places, ou can begin b multipling each equation b 00. This produces a sstem in which the coefficients are all integers. Now, to obtain coefficients that differ onl in sign, multipl Equation b 3 and multipl Equation b Multipl Equation b Multipl Equation b. Add equations. So, ou can conclude that 3 3. Back-substituting into revised Equation produces the following The solution is 6,. Write revised Equation. Substitute for. Combine like terms. Solve for. Check this in the original sstem, as follows. Check ? ? Write original Equation. Substitute into Equation. Equation checks. Write original Equation. Substitute into Equation. Equation checks. Now tr Eercise 5.
19 Section 7. Two-Variable Linear Sstems 5 Applications At this point, ou ma be asking the question How can I tell which application problems can be solved using a sstem of linear equations? The answer comes from the following considerations.. Does the problem involve more than one unknown quantit?. Are there two (or more) equations or conditions to be satisfied? If one or both of these situations occur, the appropriate mathematical model for the problem ma be a sstem of linear equations. Eample 8 An Application of a Linear Sstem WIND FIGURE 7.0 Original flight r r Return flight WIND r + r An airplane fling into a headwind travels the 000-mile fling distance between Chicopee, Massachusetts and Salt Lake Cit, Utah in hours and minutes. On the return flight, the same distance is traveled in hours. Find the airspeed of the plane and the speed of the wind, assuming that both remain constant. The two unknown quantities are the speeds of the wind and the plane. If r is the speed of the plane and r is the speed of the wind, then r r speed of the plane against the wind r r speed of the plane with the wind as shown in Figure 7.0. Using the formula distance ratetime for these two speeds, ou obtain the following equations. 000 r r r r These two equations simplif as follows r r 500 r r To solve this sstem b elimination, multipl Equation b. Equation Equation 5000 r r 500 r r 5000 r r 5500 r r Write Equation. Multipl Equation b. So, and r 0, r Check this solution in the original statement of the problem. Now tr Eercise 3. 0,500 r 77.7 miles per hour.73 miles per hour. Add equations. Speed of plane Speed of wind
20 5 Chapter 7 Sstems of Equations and Inequalities In a free market, the demands for man products are related to the prices of the products. As the prices decrease, the demands b consumers increase and the amounts that producers are able or willing to suppl decrease. Eample 9 Finding the Equilibrium Point Price per unit (in dollars) Equilibrium p (3,000,000, 0) 50 Demand 5 00 Suppl ,000,000 3,000,000 Number of units FIGURE 7. The demand and suppl equations for a new tpe of personal digital assistant are where p is the price in dollars and represents the number of units. Find the equilibrium point for this market. The equilibrium point is the price p and number of units that satisf both the demand and suppl equations. Because p is written in terms of, begin b substituting the value of p given in the suppl equation into the demand equation. Write demand equation. Substitute for p. Combine like terms. Solve for. So, the equilibrium point occurs when the demand and suppl are each 3 million units. (See Figure 7..) The price that corresponds to this -value is obtained b backsubstituting 3,000,000 into either of the original equations. For instance, backsubstituting into the demand equation produces The solution is 3,000,000, 0. You can check this as follows. Check p p p ,000, $0. Substitute 3,000,000, 0 into the demand equation. p ? ,000, Substitute 3,000,000, 0 into the suppl equation. p ? ,000, p ,000,000 Now tr Eercise 5. Demand equation Suppl equation Write demand equation. Substitute 0 for p and 3,000,000 for. checks in demand equation. Write suppl equation. Substitute 0 for p and 3,000,000 for. checks in suppl equation.
21 Section 7. Two-Variable Linear Sstems EXERCISES VOCABULARY: Fill in the blanks. See for worked-out solutions to odd-numbered eercises.. The first step in solving a sstem of equations b the method of is to obtain coefficients for (or ) that differ onl in sign.. Two sstems of equations that have the same solution set are called sstems. 3. A sstem of linear equations that has at least one solution is called, whereas a sstem of linear equations that has no solution is called.. In business applications, the is defined as the price p and the number of units that satisf both the demand and suppl equations. SKILLS AND APPLICATIONS In Eercises 5, solve the sstem b the method of elimination. Label each line with its equation. To print an enlarged cop of the graph, go to the website In Eercises 3 30, solve the sstem b the method of elimination and check an solutions algebraicall u 6v 0. 3u 5v b 3m b m r s 5 6r 50s
22 5 Chapter 7 Sstems of Equations and Inequalities In Eercises 3 3, match the sstem of linear equations with its graph. Describe the number of solutions and state whether the sstem is consistent or inconsistent. [The graphs are labeled (a), (b), (c) and (d).] (a) (c) (b) (d) In Eercises 35, use an method to solve the sstem AIRPLANE SPEED An airplane fling into a headwind travels the 800-mile fling distance between Pittsburgh, Pennslvania and Phoeni, Arizona in 3 hours and 36 minutes. On the return flight, the distance is traveled in 3 hours. Find the airspeed of the plane and the speed of the wind, assuming that both remain constant.. AIRPLANE SPEED Two planes start from Los Angeles International Airport and fl in opposite directions. The second plane starts hour after the first plane, but its speed is 80 kilometers per hour faster. Find the airspeed of each plane if hours after the first plane departs the planes are 300 kilometers apart SUPPLY AND DEMAND In Eercises 5 8, find the equilibrium point of the demand and suppl equations. The equilibrium point is the price p and number of units that satisf both the demand and suppl equations Demand p p p p Suppl p p 5 0. p p NUTRITION Two cheeseburgers and one small order of French fries from a fast-food restaurant contain a total of 830 calories. Three cheeseburgers and two small orders of French fries contain a total of 360 calories. Find the caloric content of each item. 50. NUTRITION One eight-ounce glass of apple juice and one eight-ounce glass of orange juice contain a total of 77. milligrams of vitamin C. Two eight-ounce glasses of apple juice and three eight-ounce glasses of orange juice contain a total of 36.7 milligrams of vitamin C. How much vitamin C is in an eight-ounce glass of each tpe of juice? 5. ACID MIXTURE Thirt liters of a 0% acid solution is obtained b miing a 5% solution with a 50% solution. (a) Write a sstem of equations in which one equation represents the amount of final miture required and the other represents the percent of acid in the final miture. Let and represent the amounts of the 5% and 50% solutions, respectivel. (b) Use a graphing utilit to graph the two equations in part (a) in the same viewing window. As the amount of the 5% solution increases, how does the amount of the 50% solution change? (c) How much of each solution is required to obtain the specified concentration of the final miture? 5. FUEL MIXTURE Five hundred gallons of 89-octane gasoline is obtained b miing 87-octane gasoline with 9-octane gasoline. (a) Write a sstem of equations in which one equation represents the amount of final miture required and the other represents the amounts of 87- and 9-octane gasolines in the final miture. Let and represent the numbers of gallons of 87-octane and 9-octane gasolines, respectivel. (b) Use a graphing utilit to graph the two equations in part (a) in the same viewing window. As the amount of 87-octane gasoline increases, how does the amount of 9-octane gasoline change? (c) How much of each tpe of gasoline is required to obtain the 500 gallons of 89-octane gasoline?
23 Section 7. Two-Variable Linear Sstems INVESTMENT PORTFOLIO A total of $,000 is invested in two corporate bonds that pa 3.5% and 5% simple interest. The investor wants an annual interest income of $930 from the investments. What amount should be invested in the 3.5% bond? 5. INVESTMENT PORTFOLIO A total of $3,000 is invested in two municipal bonds that pa 5.75% and 6.5% simple interest. The investor wants an annual interest income of $900 from the investments. What amount should be invested in the 5.75% bond? 55. PRESCRIPTIONS The numbers of prescriptions P (in thousands) filled at two pharmacies from 006 through 00 are shown in the table. Year Pharmac A Pharmac B (a) Use a graphing utilit to create a scatter plot of the data for pharmac A and use the regression feature to find a linear model. Let t represent the ear, with t 6 corresponding to 006. Repeat the procedure for pharmac B. (b) Assuming the numbers for the given five ears are representative of future ears, will the number of prescriptions filled at pharmac A ever eceed the number of prescriptions filled at pharmac B? If so, when? 56. DATA ANALYSIS A store manager wants to know the demand for a product as a function of the price. The dail sales for different prices of the product are shown in the table. Price, $.00 $.0 $ (a) Find the least squares regression line a b for the data b solving the sstem for a and b. 3.00b 3.70a b.69a 3.90 Demand, (b) Use the regression feature of a graphing utilit to confirm the result in part (a). (c) Use the graphing utilit to plot the data and graph the linear model from part (a) in the same viewing window. (d) Use the linear model from part (a) to predict the demand when the price is $.75. FITTING A LINE TO DATA In Eercises 57 60, find the least squares regression line a b for the points,,,,..., n, n b solving the sstem for a and b. n i i b n i a n i i Then use a graphing utilit to confirm the result. (If ou are unfamiliar with summation notation, look at the discussion in Section 9. or in Appendi B at the website for this tet at academic.cengage.com.) (, 5.8) nb n i (3, 5.) (,.) (,.9) (0,.) 3 5 i a n 0, 8,, 6,,, 3,, 0.0,,., 3,.3,, 3.8, 5,.0, 6, 5.5, 7, 6.7, 8, 6.9 i i i 6. DATA ANALYSIS An agricultural scientist used four test plots to determine the relationship between wheat ield (in bushels per acre) and the amount of fertilizer (in hundreds of pounds per acre). The results are shown in the table. Fertilizer, i (a) Use the technique demonstrated in Eercises to set up a sstem of equations for the data and to find the least squares regression line a b. (b) Use the linear model to predict the ield for a fertilizer application of 60 pounds per acre. 8 (0, 5.) (,.8) (3, 3.5) (5,.5) (,.3) (, 3.) Yield,
24 56 Chapter 7 Sstems of Equations and Inequalities 6. DEFENSE DEPARTMENT OUTLAYS The table shows the total national outlas for defense functions (in billions of dollars) for the ears 000 through 007. (Source: U.S. Office of Management and Budget) (a) Use the technique demonstrated in Eercises to set up a sstem of equations for the data and to find the least squares regression line at b. Let t represent the ear, with t 0 corresponding to 000. (b) Use the regression feature of a graphing utilit to find a linear model for the data. How does this model compare with the model obtained in part (a)? (c) Use the linear model to create a table of estimated values of. Compare the estimated values with the actual data. (d) Use the linear model to estimate the total national outla for 008. (e) Use the Internet, our school s librar, or some other reference source to find the total national outla for 008. How does this value compare with our answer in part (d)? (f) Is the linear model valid for long-term predictions of total national outlas? Eplain. EXPLORATION Year Outlas, TRUE OR FALSE? In Eercises 63 and 6, determine whether the statement is true or false. Justif our answer. 63. If two lines do not have eactl one point of intersection, then the must be parallel. 6. Solving a sstem of equations graphicall will alwas give an eact solution. 65. WRITING Briefl eplain whether or not it is possible for a consistent sstem of linear equations to have eactl two solutions. 66. THINK ABOUT IT Give eamples of a sstem of linear equations that has (a) no solution and (b) an infinite number of solutions. 67. COMPARING METHODS Use the method of substitution to solve the sstem in Eample. Is the method of substitution or the method of elimination easier? Eplain. 68. CAPSTONE Rewrite each sstem of equations in slope-intercept form and sketch the graph of each sstem. What is the relationship among the slopes of the two lines, the number of points of intersection, and the number of solutions? THINK ABOUT IT In Eercises 69 and 70, the graphs of the two equations appear to be parallel. Yet, when the sstem is solved algebraicall, ou find that the sstem does have a solution. Find the solution and eplain wh it does not appear on the portion of the graph that is shown In Eercises 7 and 7, find the value of k such that the sstem of linear equations is inconsistent ADVANCED APPLICATIONS In Eercises 73 and 7, solve the sstem of equations for u and v. While solving for these variables, consider the transcendental functions as constants. (Sstems of this tpe are found in a course in differential equations.) (a) (c) u sin v cos u cos v sin k 6 u cos v sin 0 u sin v cos csc (b) PROJECT: COLLEGE EXPENSES To work an etended application analzing the average undergraduate tuition, room, and board charges at private degree-granting institutions in the United States from 990 through 007, visit this tet s website at academic.cengage.com. (Data Source: U.S. Dept. of Education) 0 sec k 9
25 Section 7.3 Multivariable Linear Sstems MULTIVARIABLE LINEAR SYSTEMS What ou should learn Use back-substitution to solve linear sstems in row-echelon form. Use Gaussian elimination to solve sstems of linear equations. Solve nonsquare sstems of linear equations. Use sstems of linear equations in three or more variables to model and solve real-life problems. Wh ou should learn it Sstems of linear equations in three or more variables can be used to model and solve real-life problems. For instance, in Eercise 83 on page 59, a sstem of equations can be used to determine the combination of scoring plas in Super Bowl XLIII. Row-Echelon Form and Back-Substitution The method of elimination can be applied to a sstem of linear equations in more than two variables. In fact, this method easil adapts to computer use for solving linear sstems with dozens of variables. When elimination is used to solve a sstem of linear equations, the goal is to rewrite the sstem in a form to which back-substitution can be applied. To see how this works, consider the following two sstems of linear equations. Sstem of Three Linear Equations in Three Variables: (See Eample 3.) 3z z 7 Equivalent Sstem in Row-Echelon Form: (See Eample.) 3z 9 3z 5 z The second sstem is said to be in row-echelon form, which means that it has a stair-step pattern with leading coefficients of. After comparing the two sstems, it should be clear that it is easier to solve the sstem in row-echelon form, using back-substitution. Eample Using Back-Substitution in Row-Echelon Form Solve the sstem of linear equations. Harr E. Walker/MCT/Landov 3z 9 3z 5 z From Equation 3, ou know the value of z. To solve for, substitute z into Equation to obtain 3 5. Substitute for z. Solve for. Then substitute and z into Equation to obtain 3 9. Substitute for and for z. Solve for. The solution is,, and z, which can be written as the ordered triple,,. Check this in the original sstem of equations. Now tr Eercise. Equation Equation Equation 3
26 58 Chapter 7 Sstems of Equations and Inequalities Christopher Lui/China Stock HISTORICAL NOTE One of the most influential Chinese mathematics books was the Chui-chang suan-shu or Nine Chapters on the Mathematical Art (written in approimatel 50 B.C.). Chapter Eight of the Nine Chapters contained solutions of sstems of linear equations using positive and negative numbers. One such sstem was as follows. 3 z 39 3 z 3 3z 6 This sstem was solved using column operations on a matri. Matrices (plural for matri) will be discussed in the net chapter. Gaussian Elimination Two sstems of equations are equivalent if the have the same solution set. To solve a sstem that is not in row-echelon form, first convert it to an equivalent sstem that is in row-echelon form b using the following operations. Operations That Produce Equivalent Sstems Each of the following row operations on a sstem of linear equations produces an equivalent sstem of linear equations.. Interchange two equations.. Multipl one of the equations b a nonzero constant. 3. Add a multiple of one of the equations to another equation to replace the latter equation. To see how this is done, take another look at the method of elimination, as applied to a sstem of two linear equations. Eample Using Gaussian Elimination to Solve a Sstem Solve the sstem of linear equations. 3 0 There are two strategies that seem reasonable: eliminate the variable or eliminate the variable. The following steps show how to use the first strateg Interchange the two equations in the sstem. Multipl the first equation b 3. Add the multiple of the first equation to the second equation to obtain a new second equation. New sstem in row-echelon form Notice in the first step that interchanging rows is an eas wa of obtaining a leading coefficient of. Now back-substitute into Equation and solve for Equation Equation Substitute for. Solve for. The solution is and, which can be written as the ordered pair,. Now tr Eercise 9.
27 Section 7.3 Multivariable Linear Sstems 59 Rewriting a sstem of linear equations in row-echelon form usuall involves a chain of equivalent sstems, each of which is obtained b using one of the three basic row operations listed on the previous page. This process is called Gaussian elimination, after the German mathematician Carl Friedrich Gauss ( ). Eample 3 Using Gaussian Elimination to Solve a Sstem WARNING / CAUTION Arithmetic errors are often made when performing elementar row operations. You should note the operation performed in each step so that ou can go back and check our work. Solve the sstem of linear equations. 3z z 7 Because the leading coefficient of the first equation is, ou can begin b saving the at the upper left and eliminating the other -terms from the first column. 3z 9 3 3z 5 3z 9 3z 5 5 5z 7 6z 8 5 5z 7 z 3z 9 3z 5 z Write Equation. Write Equation. Add Equation to Equation. Multipl Equation b. Write Equation 3. Add revised Equation to Equation 3. Now that all but the first have been eliminated from the first column, go to work on the second column. (You need to eliminate from the third equation.) 3z 9 Adding the second equation to 3z 5 the third equation produces z a new third equation. Finall, ou need a coefficient of for z in the third equation. 3z 9 Multipling the third equation 3z 5 b produces a new third z equation. This is the same sstem that was solved in Eample, and, as in that eample, ou can conclude that the solution is,, and Now tr Eercise. Equation Equation Equation 3 Adding the first equation to the second equation produces a new second equation. Adding times the first equation to the third equation produces a new third equation. z.
28 50 Chapter 7 Sstems of Equations and Inequalities The net eample involves an inconsistent sstem one that has no solution. The ke to recognizing an inconsistent sstem is that at some stage in the elimination process ou obtain a false statement such as 0. Eample An Inconsistent Sstem Solve the sstem of linear equations. Equation Equation 3 z z 3z Equation 3 : one point FIGURE 7. : one line FIGURE 7.3 : one plane FIGURE 7. 3 z 5 z 0 3z 3 z 5 z 0 5 z 3 z 5 z 0 0 Because 0 is a false statement, ou can conclude that this sstem is inconsistent and has no solution. Moreover, because this sstem is equivalent to the original sstem, ou can conclude that the original sstem also has no solution. Now tr Eercise 5. Adding times the first equation to the second equation produces a new second equation. Adding times the first equation to the third equation produces a new third equation. Adding times the second equation to the third equation produces a new third equation. As with a sstem of linear equations in two variables, the solution(s) of a sstem of linear equations in more than two variables must fall into one of three categories. : none FIGURE 7.5 The Number of s of a Linear Sstem For a sstem of linear equations, eactl one of the following is true.. There is eactl one solution.. There are infinitel man solutions. 3. There is no solution. : none FIGURE 7.6 In Section 7., ou learned that a sstem of two linear equations in two variables can be represented graphicall as a pair of lines that are intersecting, coincident, or parallel. A sstem of three linear equations in three variables has a similar graphical representation it can be represented as three planes in space that intersect in one point (eactl one solution) [see Figure 7.], intersect in a line or a plane (infinitel man solutions) [see Figures 7.3 and 7.], or have no points common to all three planes (no solution) [see Figures 7.5 and 7.6].
29 Section 7.3 Multivariable Linear Sstems 5 Eample 5 A Sstem with Infinitel Man s Solve the sstem of linear equations. 3z z 0 3z z 0 3 3z 0 3z z Equation Equation Equation 3 Adding the first equation to the third equation produces a new third equation. Adding 3 times the second equation to the third equation produces a new third equation. In Eample 5, and are solved in terms of the third variable z. To write the correct form of the solution to the sstem that does not use an of the three variables of the sstem, let a represent an real number and let z a. Then solve for and. The solution can then be written in terms of a, which is not one of the variables of the sstem. When comparing descriptions of an infinite solution set, keep in mind that there is more than one wa to describe the set. This result means that Equation 3 depends on Equations and in the sense that it gives no additional information about the variables. Because 0 0 is a true statement, ou can conclude that this sstem will have infinitel man solutions. However, it is incorrect to sa simpl that the solution is infinite. You must also specif the correct form of the solution. So, the original sstem is equivalent to the sstem 3z z 0. In the last equation, solve for in terms of z to obtain z. Back-substituting z in the first equation produces z. Finall, letting z a, where a is a real number, the solutions to the given sstem are all of the form a, a, and z a. So, ever ordered triple of the form a, a, a is a solution of the sstem. Now tr Eercise 9. a is a real number. In Eample 5, there are other was to write the same infinite set of solutions. For instance, letting b, the solutions could have been written as b, b, b. b is a real number. To convince ourself that this description produces the same set of solutions, consider the following. Substitution a 0 b a b a b 3 0, 0, 0, 0, 0,,, 0, 0,,,,,,,,,, 3,, 3, 3, 3 3,, Same solution Same solution Same solution
30 5 Chapter 7 Sstems of Equations and Inequalities Nonsquare Sstems So far, each sstem of linear equations ou have looked at has been square, which means that the number of equations is equal to the number of variables. In a nonsquare sstem, the number of equations differs from the number of variables. A sstem of linear equations cannot have a unique solution unless there are at least as man equations as there are variables in the sstem. Eample 6 A Sstem with Fewer Equations than Variables Solve the sstem of linear equations. z z Begin b rewriting the sstem in row-echelon form. z 3 3z 3 z z Solve for in terms of z, to obtain z. B back-substituting z into Equation, ou can solve for, as follows. z z z z Write Equation. Substitute z for in Equation. Distributive Propert Solve for. Finall, b letting z a, where a is a real number, ou have the solution a, z and So, ever ordered triple of the form a, a, a z a, a is a real number. is a solution of the sstem. Because there were originall three variables and onl two equations, the sstem cannot have a unique solution. Now tr Eercise 33. Equation Equation Adding times the first equation to the second equation produces a new second equation. Multipling the second equation b 3 produces a new second equation. z a. In Eample 6, tr choosing some values of a to obtain different solutions of the sstem, such as, 0,,,,, and 3,, 3. Then check each of the solutions in the original sstem to verif that the are solutions of the original sstem.
31 Section 7.3 Multivariable Linear Sstems 53 Applications Eample 7 Vertical Motion s t = t = t = 3 t = 0 FIGURE 7.7 The height at time t of an object that is moving in a (vertical) line with constant acceleration a is given b the position equation s at v 0 t s 0. The height s is measured in feet, the acceleration a is measured in feet per second squared, t is measured in seconds, v 0 is the initial velocit (at t 0), and s 0 is the initial height. Find the values of a, v 0, and s 0 if s 5 at t, s 5 at t, and s 0 at t 3, and interpret the result. (See Figure 7.7.) B substituting the three values of t and s into the position equation, ou can obtain three linear equations in a, v 0, and. When t : When t : When t 3: This produces the following sstem of linear equations. a v 0 s 0 0 a v 0 s 0 5 9a 6v 0 s 0 0 a a v 0 v 0 v 0 v 0 v 0 a v 0 v 0 a v 0 s 0 5 a v 0 s 0 5 a3 v 0 3 s 0 0 s 0 3s 0 6s 0 s 0 3s 0 s 0 s 0 3 s 0 s s 0 a v 0 s 0 0 a v 0 s 0 5 9a 6v 0 s 0 0 Now solve the sstem using Gaussian elimination. a v 0 s 0 0 Adding times the first equation to the second equation pro- v 0 3s a 6v 0 s 0 0 duces a new second equation. Adding 9 times the first equation to the third equation produces a new third equation. Adding 6 times the second equation to the third equation produces a new third equation. Multipling the second equation b produces a new second equation and multipling the third equation b produces a new third equation. So, the solution of this sstem is a 3, v 0 8, and s 0 0, which can be written as 3, 8, 0. This solution results in a position equation of s 6t 8t 0 and implies that the object was thrown upward at a velocit of 8 feet per second from a height of 0 feet. Now tr Eercise 5.
32 5 Chapter 7 Sstems of Equations and Inequalities Eample 8 Data Analsis: Curve-Fitting = 6 (, 6) 5 (, 3) 3 (, ) 3 3 FIGURE 7.8 Find a quadratic equation a b c whose graph passes through the points, 3,,, and, 6. Because the graph of a b c passes through the points, 3,,, and, 6, ou can write the following. When, 3: a b c 3 When, : a b c When, 6: a b c 6 This produces the following sstem of linear equations. Equation Equation a b c 3 a b c a b c 6 Equation 3 The solution of this sstem is a, b, and c 0. So, the equation of the parabola is, as shown in Figure 7.8. Now tr Eercise 9. Eample 9 Investment Analsis An inheritance of $,000 was invested among three funds: a mone-market fund that paid 3% annuall, municipal bonds that paid % annuall, and mutual funds that paid 7% annuall. The amount invested in mutual funds was $000 more than the amount invested in municipal bonds. The total interest earned during the first ear was $670. How much was invested in each tpe of fund? Let,, and z represent the amounts invested in the mone-market fund, municipal bonds, and mutual funds, respectivel. From the given information, ou can write the following equations. z,000 z z 670 Rewriting this sstem in standard form without decimals produces the following. Equation Equation z,000 z, z 67,000 Equation 3 Using Gaussian elimination to solve this sstem ields 000, 3000, and z So, $000 was invested in the mone-market fund, $3000 was invested in municipal bonds, and $7000 was invested in mutual funds. Now tr Eercise 6. Equation Equation Equation 3
33 Section 7.3 Multivariable Linear Sstems EXERCISES VOCABULARY: Fill in the blanks. See for worked-out solutions to odd-numbered eercises.. A sstem of equations that is in form has a stair-step pattern with leading coefficients of.. A solution to a sstem of three linear equations in three unknowns can be written as an, which has the form,, z. 3. The process used to write a sstem of linear equations in row-echelon form is called elimination.. Interchanging two equations of a sstem of linear equations is a that produces an equivalent sstem. 5. A sstem of equations is called if the number of equations differs from the number of variables in the sstem. 6. The equation s at v 0 t s 0 is called the equation, and it models the height s of an object at time t that is moving in a vertical line with a constant acceleration a. SKILLS AND APPLICATIONS In Eercises 7 0, determine whether each ordered triple is a solution of the sstem of equations z 3z 9 5z 5 (a), 0, (b) 3, 0, 5 (c) 0,, (d), 0, z 7 5 z 3 7z (a) 3,, (b), 3, (c),, 3 (d),, 9. z z 7 3 (a) (b) (c) (d) 0. 8z 6 z (a) (c),, 3 7,, 3 5,, 8,, 9 (b) (d) In Eercises 6, use back-substitution to solve the sstem of linear equations... 5z z 6 z z 0 z z, 3 5, 5, 6, 3 33, 0, 0,, 3 z 6 5z 8 z z 3 8z 9 z z 8 z z In Eercises 7 and 8, perform the row operation and write the equivalent sstem. 7. Add Equation to Equation. Equation Equation 3z 5 3 5z 3z 0 Equation 3 What did this operation accomplish? 8. Add times Equation to Equation 3. Equation Equation 3z 5 3 5z 3z 0 Equation 3 What did this operation accomplish? 5 8z 3 5z 0 z In Eercises 9, solve the sstem of linear equations and check an solution algebraicall z 5 z 3 z 7 z 9 3 z 0 3 z 3.. z 3z z z z 3. 6 z. z 7 z z 0 z z 3 z 7 z 7 z 9 3 z 5 z 3
34 56 Chapter 7 Sstems of Equations and Inequalities z 5 3z 0 7 3z z z z z 0z 0 z z z 0 z z z w w w w 3. 5 z 0. 3 z VERTICAL MOTION In Eercises 5 8, an object moving verticall is at the given heights at the specified times. Find the position equation s at v 0 t s 0 for the object. 5. At t second, s 8 feet At t seconds, s 80 feet At t 3 seconds, s 0 feet 6. At t second, s 3 feet At t seconds, s 3 feet At t 3 seconds, s 0 feet z z 3w w w 0 5 3z 6 8z z z z 0 3 3z z 5 3 z 3 3 6z 6 z z 7 6 5z z 8 5z z z z z 7 8 5z 6z 3 6z 5z 3 3 7z 0 5 z 0 9z 0 z 0 6 z 7. At t second, s 35 feet At t seconds, s 7 feet At t 3 seconds, s 60 feet 8. At t second, s 3 feet At t seconds, s 00 feet At t 3 seconds, s 36 feet In Eercises 9 5, find the equation of the parabola a b c that passes through the points. To verif our result, use a graphing utilit to plot the points and graph the parabola. 9. 0, 0,,,, , 3,,,, 3 5., 0, 3,,, 0 5., 3,,, 3, ,,, 3,, 3, 3,, 0,, 3 In Eercises 55 58, find the equation of the circle D E F 0 that passes through the points. To verif our result, use a graphing utilit to plot the points and graph the circle , 0, 5, 5, 0, 0 0, 0, 0, 6, 3, 3 3,,,, 6, 8 0, 0, 0,, 3, SPORTS In Super Bowl I, on Januar 5, 967, the Green Ba Packers defeated the Kansas Cit Chiefs b a score of 35 to 0. The total points scored came from 3 different scoring plas, which were a combination of touchdowns, etra-point kicks, and field goals, worth 6,, and 3 points, respectivel. The same number of touchdowns and etra-point kicks were scored. There were si times as man touchdowns as field goals. How man touchdowns, etra-point kicks, and field goals were scored during the game? (Source: Super Bowl.com) 60. SPORTS In the 008 Women s NCAA Final Four Championship game, the Universit of Tennessee Lad Volunteers defeated the Universit of Stanford Cardinal b a score of 6 to 8. The Lad Volunteers won b scoring a combination of two-point baskets, three-point baskets, and one-point free throws. The number of two-point baskets was two more than the number of free throws. The number of free throws was two more than five times the number of three-point baskets. What combination of scoring accounted for the Lad Volunteers 6 points? (Source: National Collegiate Athletic Association)
35 Section 7.3 Multivariable Linear Sstems FINANCE A small corporation borrowed $775,000 to epand its clothing line. Some of the mone was borrowed at 8%, some at 9%, and some at 0%. How much was borrowed at each rate if the annual interest owed was $67,500 and the amount borrowed at 8% was four times the amount borrowed at 0%? 6. FINANCE A small corporation borrowed $800,000 to epand its line of tos. Some of the mone was borrowed at 8%, some at 9%, and some at 0%. How much was borrowed at each rate if the annual interest owed was $67,000 and the amount borrowed at 8% was five times the amount borrowed at 0%? INVESTMENT PORTFOLIO In Eercises 63 and 6, consider an investor with a portfolio totaling $500,000 that is invested in certificates of deposit, municipal bonds, blue-chip stocks, and growth or speculative stocks. How much is invested in each tpe of investment? 63. The certificates of deposit pa 3% annuall, and the municipal bonds pa 5% annuall. Over a five-ear period, the investor epects the blue-chip stocks to return 8% annuall and the growth stocks to return 0% annuall. The investor wants a combined annual return of 5% and also wants to have onl one-fourth of the portfolio invested in stocks. 6. The certificates of deposit pa % annuall, and the municipal bonds pa % annuall. Over a five-ear period, the investor epects the blue-chip stocks to return 0% annuall and the growth stocks to return % annuall. The investor wants a combined annual return of 6% and also wants to have onl one-fourth of the portfolio invested in stocks. 65. AGRICULTURE A miture of 5 pounds of fertilizer A, 3 pounds of fertilizer B, and pounds of fertilizer C provides the optimal nutrients for a plant. Commercial brand X contains equal parts of fertilizer B and fertilizer C. Commercial brand Y contains one part of fertilizer A and two parts of fertilizer B. Commercial brand Z contains two parts of fertilizer A, five parts of fertilizer B, and two parts of fertilizer C. How much of each fertilizer brand is needed to obtain the desired miture? 66. AGRICULTURE A miture of liters of chemical A, 6 liters of chemical B, and 6 liters of chemical C is required to kill a destructive crop insect. Commercial spra X contains,, and parts, respectivel, of these chemicals. Commercial spra Y contains onl chemical C. Commercial spra Z contains onl chemicals A and B in equal amounts. How much of each tpe of commercial spra is needed to get the desired miture? 67. GEOMETRY The perimeter of a triangle is 0 feet. The longest side of the triangle is feet longer than the shortest side. The sum of the lengths of the two shorter sides is feet more than the length of the longest side. Find the lengths of the sides of the triangle. 68. GEOMETRY The perimeter of a triangle is 80 feet. The longest side of the triangle is 9 feet shorter than twice the shortest side. The sum of the lengths of the two shorter sides is 30 feet more than the length of the longest side. Find the lengths of the sides of the triangle. In Eercises 69 and 70, find the values of,, and z in the figure z ( + 7) ( 7) z (.5z + 3) (.5z ) 7. ADVERTISING A health insurance compan advertises on television, on radio, and in the local newspaper. The marketing department has an advertising budget of $,000 per month. A television ad costs $000, a radio ad costs $00, and a newspaper ad costs $500. The department wants to run 60 ads per month, and have as man television ads as radio and newspaper ads combined. How man of each tpe of ad can the department run each month? 7. RADIO You work as a disc jocke at our college radio station. You are supposed to pla 3 songs within two hours. You are to choose the songs from the latest rock, dance, and pop albums. You want to pla twice as man rock songs as pop songs and four more pop songs than dance songs. How man of each tpe of song will ou pla? 73. ACID MIXTURE A chemist needs 0 liters of a 5% acid solution. The solution is to be mied from three solutions whose concentrations are 0%, 0%, and 50%. How man liters of each solution will satisf each condition? (a) Use liters of the 50% solution. (b) Use as little as possible of the 50% solution. (c) Use as much as possible of the 50% solution. 7. ACID MIXTURE A chemist needs gallons of a 0% acid solution. The solution is to be mied from three solutions whose concentrations are 0%, 5%, and 5%. How man gallons of each solution will satisf each condition? (a) Use gallons of the 5% solution. (b) Use as little as possible of the 5% solution. (c) Use as much as possible of the 5% solution.
36 58 Chapter 7 Sstems of Equations and Inequalities 75. ELECTRICAL NETWORK Appling Kirchhoff s Laws to the electrical network in the figure, the currents I, I, and I 3 are the solution of the sstem I I I 3 0 3I I 7 I I 3 8 find the currents. 3Ω 76. PULLEY SYSTEM A sstem of pulles is loaded with 8-pound and 3-pound weights (see figure). The tensions t and t in the ropes and the acceleration a of the 3-pound weight are found b solving the sstem of equations t t t t where t and t are measured in pounds and a is measured in feet per second squared. (a) Solve this sstem. (b) The 3-pound weight in the pulle sstem is replaced b a 6-pound weight. The new pulle sstem will be modeled b the following sstem of equations. t t t I a a t t I lb a a Ω 8 lb Solve this sstem and use our answer for the acceleration to describe what (if anthing) is happening in the pulle sstem. I 3 t Ω 7 volts 8 volts FITTING A PARABOLA In Eercises 77 80, find the least squares regression parabola a b c for the points,,,..., n, n b solving the following sstem of linear equations for a, b, and c. Then use the regression feature of a graphing utilit to confirm the result. (If ou are unfamiliar with summation notation, look at the discussion in Section 9. or in Appendi B at the website for this tet at academic.cengage.com.) n i i c n i b n i 3 a n i i i i i n i c n i 3 b n i a n i i i i i i (, 6) (, 5) (0, 0) nc n 8 6 (, ) i (, 6) (, ) (3, 6) (, ) 6 i b n 8 i i a n (, 0) 8 6 (, 0) 8. DATA ANALYSIS: WILDLIFE A wildlife management team studied the reproduction rates of deer in three tracts of a wildlife preserve. Each tract contained 5 acres. In each tract, the number of females, and the percent of females that had offspring the following ear, were recorded. The results are shown in the table. Number, i i (a) Use the technique demonstrated in Eercises to set up a sstem of equations for the data and to find a least squares regression parabola that models the data. (b) Use a graphing utilit to graph the parabola and the data in the same viewing window. (0, 0) (, 9) (, ) (0, ) Percent, (, 6) (3, 0) (, 5) 6 8
37 Section 7.3 Multivariable Linear Sstems 59 (c) Use the model to create a table of estimated values of. Compare the estimated values with the actual data. (d) Use the model to estimate the percent of females that had offspring when there were 70 females. (e) Use the model to estimate the number of females when 0% of the females had offspring. 8. DATA ANALYSIS: STOPPING DISTANCE In testing a new automobile braking sstem, the speed (in miles per hour) and the stopping distance (in feet) were recorded in the table. Speed, Stopping distance, (a) Use the technique demonstrated in Eercises to set up a sstem of equations for the data and to find a least squares regression parabola that models the data. (b) Graph the parabola and the data on the same set of aes. (c) Use the model to estimate the stopping distance when the speed is 70 miles per hour. 83. SPORTS In Super Bowl XLIII, on Februar, 009, the Pittsburgh Steelers defeated the Arizona Cardinals b a score of 7 to 3. The total points scored came from 5 different scoring plas, which were a combination of touchdowns, etra-point kicks, field goals, and safeties, worth 6,, 3, and points, respectivel. There were three times as man touchdowns as field goals, and the number of etra-point kicks was equal to the number of touchdowns. How man touchdowns, etra-point kicks, field goals, and safeties were scored during the game? (Source: National Football League) 8. SPORTS In the 008 Armed Forces Bowl, the Universit of Houston defeated the Air Force Academ b a score of 3 to 8. The total points scored came from 8 different scoring plas, which were a combination of touchdowns, etra-point kicks, field goals, and two-point conversions, worth 6,, 3, and points, respectivel. The number of touchdowns was one more than the number of etra-point kicks, and there were four times as man field goals as two-point conversions. How man touchdowns, etra-point kicks, field goals, and two-point conversions were scored during the game? (Source: ESPN.com) ADVANCED APPLICATIONS In Eercises 85 88, find values of,, and that satisf the sstem. These sstems arise in certain optimization problems in calculus, and is called a Lagrange multiplier EXPLORATION TRUE OR FALSE? In Eercises 89 and 90, determine whether the statement is true or false. Justif our answer. 89. The sstem 3 6z 6 z z 3 is in row-echelon form. 90. If a sstem of three linear equations is inconsistent, then its graph has no points common to all three equations. 9. THINK ABOUT IT Are the following two sstems of equations equivalent? Give reasons for our answer. 3 z 6 7 z 3 z 6 z 3 z 7 z 6 In Eercises 93 96, find two sstems of linear equations that have the ordered triple as a solution. (There are man correct answers.) 93. 3,, ,, ,,,, PROJECT: EARNINGS PER SHARE To work an etended application analzing the earnings per share for Wal-Mart Stores, Inc. from 99 through 007, visit this tet s website at academic.cengage.com. (Data Source: Wal-Mart Stores, Inc.) CAPSTONE Find values of a, b, and c (if possible) such that the sstem of linear equations has (a) a unique solution, (b) no solution, and (c) an infinite number of solutions. a b z z cz 0
38 530 Chapter 7 Sstems of Equations and Inequalities 7. PARTIAL FRACTIONS What ou should learn Recognize partial fraction decompositions of rational epressions. Find partial fraction decompositions of rational epressions. Wh ou should learn it Partial fractions can help ou analze the behavior of a rational function. For instance, in Eercise 6 on page 537, ou can analze the ehaust temperatures of a diesel engine using partial fractions. Introduction In this section, ou will learn to write a rational epression as the sum of two or more simpler rational epressions. For eample, the rational epression 7 6 can be written as the sum of two fractions with first-degree denominators. That is, Partial fraction decomposition 7 of Michael Rosenfeld/Gett Images You can review how to find the degree of a polnomial (such as 3 and ) in Appendi A.3. Appendi A. shows ou how to combine epressions such as 3 The method of partial fraction decomposition shows ou how to reverse this process and write Partial fraction Partial fraction Each fraction on the right side of the equation is a partial fraction, and together the make up the partial fraction decomposition of the left side. Decomposition of N/D into Partial Fractions. Divide if improper: If ND is an improper fraction degree of N degree of D, divide the denominator into the numerator to obtain N D polnomial N D and appl Steps, 3, and below to the proper rational epression N D. Note that N is the remainder from the division of N b D.. Factor the denominator: Completel factor the denominator into factors of the form p q m and a b c n where a b c is irreducible. 3. Linear factors: For each factor of the form p q m, the partial fraction decomposition must include the following sum of m fractions. A p q A p q... A m p q m. Quadratic factors: For each factor of the form a b c n, the partial fraction decomposition must include the following sum of n fractions. B C a b c B C a b c B... n C n a b c n
39 Section 7. Partial Fractions 53 Partial Fraction Decomposition Algebraic techniques for determining the constants in the numerators of partial fractions are demonstrated in the eamples that follow. Note that the techniques var slightl, depending on the tpe of factors of the denominator: linear or quadratic, distinct or repeated. Eample Distinct Linear Factors Write the partial fraction decomposition of 7 6. TECHNOLOGY You can use a graphing utilit to check the decomposition found in Eample. To do this, graph and in the same viewing window. The graphs should be identical, as shown below The epression is proper, so be sure to factor the denominator. Because 6 3, ou should include one partial fraction with a constant numerator for each linear factor of the denominator. Write the form of the decomposition as follows. 7 6 Write form of decomposition. Multipling each side of this equation b the least common denominator, 3, leads to the basic equation 7 A B 3. Basic equation Because this equation is true for all, ou can substitute an convenient values of that will help determine the constants A and B. Values of that are especiall convenient are ones that make the factors and 3 equal to zero. For instance, let. Then 7 A B 3 5 A0 B5 5 5B B. To solve for A, let 3 and obtain 3 7 A3 B3 3 0 A5 B0 0 5A A. A 3 B So, the partial fraction decomposition is Substitute for. Substitute 3 for. Check this result b combining the two partial fractions on the right side of the equation, or b using our graphing utilit. Now tr Eercise 3.
40 53 Chapter 7 Sstems of Equations and Inequalities The net eample shows how to find the partial fraction decomposition of a rational epression whose denominator has a repeated linear factor. Eample Repeated Linear Factors Write the partial fraction decomposition of You can review long division of polnomials in Section.3. You can review factoring of polnomials in Appendi A.3. WARNING / CAUTION To obtain the basic equation, be sure to multipl each fraction in the form of the decomposition b the LCD. This rational epression is improper, so ou should begin b dividing the numerator b the denominator to obtain Because the denominator of the remainder factors as 3 ou should include one partial fraction with a constant numerator for each power of and and write the form of the decomposition as follows A B C Multipling b the LCD,, leads to the basic equation A B C. Letting eliminates the A- and B-terms and ields C Letting 0 eliminates the B- and C-terms and ields A0 B00 C0 6 A A. Write form of decomposition. Basic equation A B C At this point, ou have ehausted the most convenient choices for, so to find the value of B, use an other value for along with the known values of A and C. So, using, A 6, and C 9, B B 9 B B. C 9. So, the partial fraction decomposition is Now tr Eercise
41 Section 7. Partial Fractions 533 The procedure used to solve for the constants in Eamples and works well when the factors of the denominator are linear. However, when the denominator contains irreducible quadratic factors, ou should use a different procedure, which involves writing the right side of the basic equation in polnomial form and equating the coefficients of like terms. Then ou can use a sstem of equations to solve for the coefficients. Eample 3 Distinct Linear and Quadratic Factors HISTORICAL NOTE The Granger Collection John Bernoulli (667 78), a Swiss mathematician, introduced the method of partial fractions and was instrumental in the earl development of calculus. Bernoulli was a professor at the Universit of Basel and taught man outstanding students, the most famous of whom was Leonhard Euler. Write the partial fraction decomposition of 3 3 This epression is proper, so factor the denominator. Because the denominator factors as 3 ou should include one partial fraction with a constant numerator and one partial fraction with a linear numerator and write the form of the decomposition as follows A B C Multipling b the LCD,, ields the basic equation 3 A B C. Write form of decomposition. Basic equation Epanding this basic equation and collecting like terms produces 3 A A B C A B C A. Polnomial form Finall, because two polnomials are equal if and onl if the coefficients of like terms are equal, ou can equate the coefficients of like terms on opposite sides of the equation. 3 A B C A Equate coefficients of like terms. You can now write the following sstem of linear equations. Equation Equation A B 3 C A Equation 3 From this sstem ou can see that A and C. Moreover, substituting A into Equation ields B 3 B. So, the partial fraction decomposition is 3 3. Now tr Eercise 33.
42 53 Chapter 7 Sstems of Equations and Inequalities The net eample shows how to find the partial fraction decomposition of a rational epression whose denominator has a repeated quadratic factor. Eample Repeated Quadratic Factors Write the partial fraction decomposition of Include one partial fraction with a linear numerator for each power of A B C D Write form of decomposition. Multipling b the LCD,, ields the basic equation A B C D Basic equation A 3 A B B C D A 3 B A C B D. Polnomial form Equating coefficients of like terms on opposite sides of the equation A 3 B A C B D produces the following sstem of linear equations. A B A C B D Equation Equation Equation 3 Equation Finall, use the values A 8 and B 0 to obtain the following. 8 C 3 Substitute 8 for A in Equation 3. C 3 0 D 0 Substitute 0 for B in Equation. D 0 So, using A 8, B 0, C 3, and D 0, the partial fraction decomposition is Check this result b combining the two partial fractions on the right side of the equation, or b using our graphing utilit. Now tr Eercise 55.
43 Section 7. Partial Fractions 535 Guidelines for Solving the Basic Equation Linear Factors. Substitute the zeros of the distinct linear factors into the basic equation.. For repeated linear factors, use the coefficients determined in Step to rewrite the basic equation. Then substitute other convenient values of and solve for the remaining coefficients. Quadratic Factors. Epand the basic equation.. Collect terms according to powers of. 3. Equate the coefficients of like terms to obtain equations involving A, B, C, and so on.. Use a sstem of linear equations to solve for A, B, C,.... Keep in mind that for improper rational epressions such as N D ou must first divide before appling partial fraction decomposition. CLASSROOM DISCUSSION Error Analsis You are tutoring a student in algebra. In tring to find a partial fraction decomposition, the student writes the following.! # # $ A B! #! # A # B! # #! A# # $! B Basic equation B substituting 0 and into the basic equation, the student concludes that A # and B. However, in checking this solution, the student obtains the following. ##$# # $! #$ # # $ #! #! # # $ $ What is wrong?! # # $
44 536 Chapter 7 Sstems of Equations and Inequalities 7. EXERCISES VOCABULARY: Fill in the blanks. See for worked-out solutions to odd-numbered eercises.. The process of writing a rational epression as the sum or difference of two or more simpler rational epressions is called.. If the degree of the numerator of a rational epression is greater than or equal to the degree of the denominator, then the fraction is called. 3. Each fraction on the right side of the equation is a The is obtained after multipling each side of the partial fraction decomposition form b the least common denominator. SKILLS AND APPLICATIONS In Eercises 5 8, match the rational epression with the form of its decomposition. [The decompositions are labeled (a), (b), (c), and (d).] (a) (c) A B C A B C (b) (d) In Eercises 9 8, write the form of the partial fraction decomposition of the rational epression. Do not solve for the constants In Eercises 9, write the partial fraction decomposition of the rational epression. Check our result algebraicall A B A B C In Eercises 3 50, write the partial fraction decomposition of the improper rational epression
45 Section 7. Partial Fractions 537 In Eercises 5 58, write the partial fraction decomposition of the rational epression. Use a graphing utilit to check our result GRAPHICAL ANALYSIS In Eercises 59 and 60, (a) write the partial fraction decomposition of the rational function, (b) identif the graph of the rational function and the graph of each term of its decomposition, and (c) state an relationship between the vertical asmptotes of the graph of the rational function and the vertical asmptotes of the graphs of the terms of the decomposition. To print an enlarged cop of the graph, go to the website 6. ENVIRONMENT The predicted cost C (in thousands of dollars) for a compan to remove p% of a chemical from its waste water is given b the model C Write the partial fraction decomposition for the rational function. Verif our result b using the table feature of a graphing utilit to create a table comparing the original function with the partial fractions. 6. THERMODYNAMICS The magnitude of the range R of ehaust temperatures (in degrees Fahrenheit) in an eperimental diesel engine is approimated b the model R p 0,000 p, 0 p < , < where is the relative load (in foot-pounds). 8 (a) Write the partial fraction decomposition of the equation. 8 (b) The decomposition in part (a) is the difference of two fractions. The absolute values of the terms give the epected maimum and minimum temperatures of the ehaust gases for different loads. Write the equations for Yma and Ymin. (c) Use a graphing utilit to graph each equation from part (b) in the same viewing window. (d) Determine the epected maimum and minimum temperatures for a relative load of 0.5. EXPLORATION Yma st term TRUE OR FALSE? In Eercises 63 65, determine whether the statement is true or false. Justif our answer. 63. For the rational epression the 0 0, partial fraction decomposition is of the form A 0 B For the rational epression the partial fraction decomposition is of the form, A B C D. 65. When writing the partial fraction decomposition of the epression 3 the first step is to divide the 5, numerator b the denominator. In Eercises 67 70, write the partial fraction decomposition of the rational epression. Check our result algebraicall. Then assign a value to the constant a to check the result graphicall a a Ymin nd term 66. CAPSTONE Eplain the similarities and differences in finding the partial fraction decompositions of proper rational epressions whose denominators factor into (a) distinct linear factors, (b) distinct quadratic factors, (c) repeated factors, and (d) linear and quadratic factors. a a 7. WRITING Describe two was of solving for the constants in a partial fraction decomposition.
46 538 Chapter 7 Sstems of Equations and Inequalities 7.5 SYSTEMS OF INEQUALITIES What ou should learn Sketch the graphs of inequalities in two variables. Solve sstems of inequalities. Use sstems of inequalities in two variables to model and solve real-life problems. Wh ou should learn it You can use sstems of inequalities in two variables to model and solve real-life problems. For instance, in Eercise 83 on page 57, ou will use a sstem of inequalities to analze the retail sales of prescription drugs. The Graph of an Inequalit The statements 3 < 6 and 3 6 are inequalities in two variables. An ordered pair a, b is a solution of an inequalit in and if the inequalit is true when a and b are substituted for and, respectivel. The graph of an inequalit is the collection of all solutions of the inequalit. To sketch the graph of an inequalit, begin b sketching the graph of the corresponding equation. The graph of the equation will normall separate the plane into two or more regions. In each such region, one of the following must be true.. All points in the region are solutions of the inequalit.. No point in the region is a solution of the inequalit. So, ou can determine whether the points in an entire region satisf the inequalit b simpl testing one point in the region. Sketching the Graph of an Inequalit in Two Variables. Replace the inequalit sign b an equal sign, and sketch the graph of the resulting equation. (Use a dashed line for < or > and a solid line for or.). Test one point in each of the regions formed b the graph in Step. If the point satisfies the inequalit, shade the entire region to denote that ever point in the region satisfies the inequalit. Jon Feingersh/Masterfile Eample Sketching the Graph of an Inequalit Sketch the graph of. Begin b graphing the corresponding equation, which is a parabola, as shown in Figure 7.9. B testing a point above the parabola 0, 0 and a point below the parabola 0,, ou can see that the points that satisf the inequalit are those ling above (or on) the parabola. = WARNING / CAUTION Be careful when ou are sketching the graph of an inequalit in two variables. A dashed line means that all points on the line or curve are not solutions of the inequalit. A solid line means that all points on the line or curve are solutions of the inequalit. FIGURE 7.9 Now tr Eercise 7. (0, 0) Test point Test point above parabola below parabola (0, )
47 Section 7.5 Sstems of Inequalities 539 You can review the properties of inequalities in Appendi A.6. The inequalit in Eample is a nonlinear inequalit in two variables. Most of the following eamples involve linear inequalities such as a b < c ( a and b are not both zero). The graph of a linear inequalit is a half-plane ling on one side of the line a b c. Eample Sketching the Graph of a Linear Inequalit Sketch the graph of each linear inequalit. a. > b. 3 TECHNOLOGY A graphing utilit can be used to graph an inequalit or a sstem of inequalities. For instance, to graph, enter and use the shade feature of the graphing utilit to shade the correct part of the graph. You should obtain the graph below. Consult the user s guide for our graphing utilit for specific kestrokes. 0 a. The graph of the corresponding equation is a vertical line. The points that satisf the inequalit > are those ling to the right of this line, as shown in Figure 7.0. b. The graph of the corresponding equation 3 is a horizontal line. The points that satisf the inequalit 3 are those ling below (or on) this line, as shown in Figure 7.. > = 3 3 = FIGURE 7.0 FIGURE 7. Now tr Eercise 9. Eample 3 Sketching the Graph of a Linear Inequalit Sketch the graph of <. (0, 0) < The graph of the corresponding equation is a line, as shown in Figure 7.. Because the origin 0, 0 satisfies the inequalit, the graph consists of the half-plane ling above the line. (Tr checking a point below the line. Regardless of which point ou choose, ou will see that it does not satisf the inequalit.) Now tr Eercise 5. = To graph a linear inequalit, it can help to write the inequalit in slope-intercept form. For instance, b writing < in the form > FIGURE 7. ou can see that the solution points lie above the line or, as shown in Figure 7..
48 50 Chapter 7 Sstems of Equations and Inequalities Sstems of Inequalities Man practical problems in business, science, and engineering involve sstems of linear inequalities. A solution of a sstem of inequalities in and is a point, that satisfies each inequalit in the sstem. To sketch the graph of a sstem of inequalities in two variables, first sketch the graph of each individual inequalit (on the same coordinate sstem) and then find the region that is common to ever graph in the sstem. This region represents the solution set of the sstem. For sstems of linear inequalities, it is helpful to find the vertices of the solution region. Eample Solving a Sstem of Inequalities Sketch the graph (and label the vertices) of the solution set of the sstem. Inequalit Inequalit < > 3 Inequalit 3 Using different colored pencils to shade the solution of each inequalit in a sstem will make identifing the solution of the sstem of inequalities easier. The graphs of these inequalities are shown in Figures 7., 7.0, and 7., respectivel, on page 539. The triangular region common to all three graphs can be found b superimposing the graphs on the same coordinate sstem, as shown in Figure 7.3. To find the vertices of the region, solve the three sstems of corresponding equations obtained b taking pairs of equations representing the boundaries of the individual regions. Verte A:, Verte B: 5, 3 Verte C:, = = 3 C(, 3) B(5, 3) = 3 set A(, ) FIGURE 7.3 Note in Figure 7.3 that the vertices of the region are represented b open dots. This means that the vertices are not solutions of the sstem of inequalities. Now tr Eercise.
49 Section 7.5 Sstems of Inequalities 5 For the triangular region shown in Figure 7.3, each point of intersection of a pair of boundar lines corresponds to a verte. With more complicated regions, two border lines can sometimes intersect at a point that is not a verte of the region, as shown in Figure 7.. To keep track of which points of intersection are actuall vertices of the region, ou should sketch the region and refer to our sketch as ou find each point of intersection. Not a verte FIGURE 7. Eample 5 Solving a Sstem of Inequalities = = + (, 3) 3 (, 0) FIGURE 7.5 Sketch the region containing all points that satisf the sstem of inequalities. As shown in Figure 7.5, the points that satisf the inequalit Inequalit are the points ling above (or on) the parabola given b. Parabola The points satisfing the inequalit Inequalit are the points ling below (or on) the line given b. Line To find the points of intersection of the parabola and the line, solve the sstem of corresponding equations. Inequalit Inequalit Using the method of substitution, ou can find the solutions to be, 0 and, 3. So, the region containing all points that satisf the sstem is indicated b the shaded region in Figure 7.5. Now tr Eercise 3.
50 5 Chapter 7 Sstems of Equations and Inequalities When solving a sstem of inequalities, ou should be aware that the sstem might have no solution or it might be represented b an unbounded region in the plane. These two possibilities are shown in Eamples 6 and 7. Eample 6 A Sstem with No Sketch the solution set of the sstem of inequalities. > 3 < Inequalit Inequalit From the wa the sstem is written, it is clear that the sstem has no solution, because the quantit cannot be both less than and greater than 3. Graphicall, the inequalit > 3 is represented b the half-plane ling above the line 3, and the inequalit < is represented b the half-plane ling below the line, as shown in Figure 7.6. These two half-planes have no points in common. So, the sstem of inequalities has no solution. + > < FIGURE 7.6 Now tr Eercise 5. Eample 7 An Unbounded Set 3 + = 3 + = 3 (3, 0) 3 FIGURE 7.7 Sketch the solution set of the sstem of inequalities. < 3 > 3 Inequalit Inequalit The graph of the inequalit < 3 is the half-plane that lies below the line 3, as shown in Figure 7.7. The graph of the inequalit > 3 is the halfplane that lies above the line 3. The intersection of these two half-planes is an infinite wedge that has a verte at 3, 0. So, the solution set of the sstem of inequalities is unbounded. Now tr Eercise 7.
51 Section 7.5 Sstems of Inequalities 53 Price p Consumer surplus Producer surplus FIGURE 7.8 Demand curve Number of units Equilibrium point Suppl curve Applications Eample 9 in Section 7. discussed the equilibrium point for a sstem of demand and suppl equations. The net eample discusses two related concepts that economists call consumer surplus and producer surplus. As shown in Figure 7.8, the consumer surplus is defined as the area of the region that lies below the demand curve, above the horizontal line passing through the equilibrium point, and to the right of the p-ais. Similarl, the producer surplus is defined as the area of the region that lies above the suppl curve, below the horizontal line passing through the equilibrium point, and to the right of the p-ais. The consumer surplus is a measure of the amount that consumers would have been willing to pa above what the actuall paid, whereas the producer surplus is a measure of the amount that producers would have been willing to receive below what the actuall received. Eample 8 Consumer Surplus and Producer Surplus The demand and suppl equations for a new tpe of personal digital assistant are given b p p Demand equation Suppl equation where p is the price (in dollars) and represents the number of units. Find the consumer surplus and producer surplus for these two equations. Price per unit (in dollars) p FIGURE 7.9 Suppl vs. Demand p = Consumer surplus Producer surplus p = 0 p = ,000,000 3,000,000 Number of units Begin b finding the equilibrium point (when suppl and demand are equal) b solving the equation In Eample 9 in Section 7., ou saw that the solution is 3,000,000 units, which corresponds to an equilibrium price of p $0. So, the consumer surplus and producer surplus are the areas of the following triangular regions. Consumer Surplus p p 0 0 Producer Surplus p p 0 0 In Figure 7.9, ou can see that the consumer and producer surpluses are defined as the areas of the shaded triangles. Consumer surplus (base)(height) $5,000,000 3,000,00030 Producer surplus (base)(height) $90,000,000 3,000,00060 Now tr Eercise 7.
52 5 Chapter 7 Sstems of Equations and Inequalities Eample 9 Nutrition The liquid portion of a diet is to provide at least 300 calories, 36 units of vitamin A, and 90 units of vitamin C. A cup of dietar drink X provides 60 calories, units of vitamin A, and 0 units of vitamin C. A cup of dietar drink Y provides 60 calories, 6 units of vitamin A, and 30 units of vitamin C. Set up a sstem of linear inequalities that describes how man cups of each drink should be consumed each da to meet or eceed the minimum dail requirements for calories and vitamins. Begin b letting and represent the following. number of cups of dietar drink X number of cups of dietar drink Y To meet or eceed the minimum dail requirements, the following inequalities must be satisfied Calories Vitamin A Vitamin C The last two inequalities are included because and cannot be negative. The graph of this sstem of inequalities is shown in Figure (More is said about this application in Eample 6 in Section 7.6.) 8 6 (0, 6) (, ) (3, ) (9, 0) FIGURE Now tr Eercise 75. CLASSROOM DISCUSSION Creating a Sstem of Inequalities Plot the points 0, 0!,, 0!, 3,!, and 0,! in a coordinate plane. Draw the quadrilateral that has these four points as its vertices. Write a sstem of linear inequalities that has the quadrilateral as its solution. Eplain how ou found the sstem of inequalities.
53 Section 7.5 Sstems of Inequalities EXERCISES See for worked-out solutions to odd-numbered eercises. VOCABULARY: Fill in the blanks.. An ordered pair a, b is a of an inequalit in and if the inequalit is true when a and b are substituted for and, respectivel.. The of an inequalit is the collection of all solutions of the inequalit. 3. The graph of a inequalit is a half-plane ling on one side of the line a b c.. A of a sstem of inequalities in and is a point, that satisfies each inequalit in the sstem. 5. A of a sstem of inequalities in two variables is the region common to the graphs of ever inequalit in the sstem. 6. The area of the region that lies below the demand curve, above the horizontal line passing through the equilibrium point, to the right of the p-ais is called the. SKILLS AND APPLICATIONS In Eercises 7 0, sketch the graph of the inequalit. 7. < 5 8. < <. > <. > < 9 > > In Eercises 3, use a graphing utilit to graph the inequalit. 5 In Eercises 33 36, write an inequalit for the shaded region shown in the figure < ln. ln 3 3. < < > < In Eercises 37 0, determine whether each ordered pair is a solution of the sstem of linear inequalities > < < 7 In Eercises 5, sketch the graph and label the vertices of the solution set of the sstem of inequalities > 5 > (a) (c) (a) (c) (a) (c) 0, 0, 0 0, 8, 0, 0, 9 (a), 7 (c) 6, < > 0 > (b), 3 (d) 3, (b) 6, (d) 3, (b) 0, (d), 6 (b) 5, (d), 8
54 56 Chapter 7 Sstems of Equations and Inequalities 5. > 6. 7 > 6 3 < 5 > 6 5 > < 6 > < > < In Eercises 55 60, use a graphing utilit to graph the solution set of the sstem of inequalities In Eercises 6 70, derive a set of inequalities to describe the region < < 3 > < > 0 > 3 < 0 < < 3 > 3 e ( 8, 8) < > Rectangle: vertices at, 3, 9, 3, 9, 9,, Parallelogram: vertices at 0, 0,, 0,,, 5, 69. Triangle: vertices at 0, 0, 6, 0,, Triangle: vertices at, 0,, 0, 0, SUPPLY AND DEMAND In Eercises 7 7, (a) graph the sstems representing the consumer surplus and producer surplus for the suppl and demand equations and (b) find the consumer surplus and producer surplus Demand p p p p Suppl p 0.5 p 5 0. p p PRODUCTION A furniture compan can sell all the tables and chairs it produces. Each table requires hour in the assembl center and hours in the finishing center. Each chair requires 3 hours in the assembl center and hours in the finishing center. The compan s assembl center is available hours per da, and its finishing center is available 5 hours per da. Find and graph a sstem of inequalities describing all possible production levels. 76. INVENTORY A store sells two models of laptop computers. Because of the demand, the store stocks at least twice as man units of model A as of model B. The costs to the store for the two models are $800 and $00, respectivel. The management does not want more than $0,000 in computer inventor at an one time, and it wants at least four model A laptop computers and two model B laptop computers in inventor at all times. Find and graph a sstem of inequalities describing all possible inventor levels. 77. INVESTMENT ANALYSIS A person plans to invest up to $0,000 in two different interest-bearing accounts. Each account is to contain at least $5000. Moreover, the amount in one account should be at least twice the amount in the other account. Find and graph a sstem of inequalities to describe the various amounts that can be deposited in each account. 78. TICKET SALES For a concert event, there are $30 reserved seat tickets and $0 general admission tickets. There are 000 reserved seats available, and fire regulations limit the number of paid ticket holders to The promoter must take in at least $75,000 in ticket sales. Find and graph a sstem of inequalities describing the different numbers of tickets that can be sold.
55 Section 7.5 Sstems of Inequalities SHIPPING A warehouse supervisor is told to ship at least 50 packages of gravel that weigh 55 pounds each and at least 0 bags of stone that weigh 70 pounds each. The maimum weight capacit of the truck to be used is 7500 pounds. Find and graph a sstem of inequalities describing the numbers of bags of stone and gravel that can be shipped. 80. TRUCK SCHEDULING A small compan that manufactures two models of eercise machines has an order for 5 units of the standard model and 6 units of the delue model. The compan has trucks of two different sizes that can haul the products, as shown in the table. Truck Standard Delue Large Medium Find and graph a sstem of inequalities describing the numbers of trucks of each size that are needed to deliver the order. 8. NUTRITION A dietitian is asked to design a special dietar supplement using two different foods. Each ounce of food X contains 0 units of calcium, 5 units of iron, and 0 units of vitamin B. Each ounce of food Y contains 0 units of calcium, 0 units of iron, and 0 units of vitamin B. The minimum dail requirements of the diet are 300 units of calcium, 50 units of iron, and 00 units of vitamin B. (a) Write a sstem of inequalities describing the different amounts of food X and food Y that can be used. (b) Sketch a graph of the region corresponding to the sstem in part (a). (c) Find two solutions of the sstem and interpret their meanings in the contet of the problem. 8. HEALTH A person s maimum heart rate is 0, where is the person s age in ears for When a person eercises, it is recommended that the person strive for a heart rate that is at least 50% of the maimum and at most 75% of the maimum. (Source: American Heart Association) (a) Write a sstem of inequalities that describes the eercise target heart rate region. (b) Sketch a graph of the region in part (a). (c) Find two solutions to the sstem and interpret their meanings in the contet of the problem. 83. DATA ANALYSIS: PRESCRIPTION DRUGS The table shows the retail sales (in billions of dollars) of prescription drugs in the United States from 000 through 007. (Source: National Association of Chain Drug Stores) Year (a) Use the regression feature of a graphing utilit to find a linear model for the data. Let t represent the ear, with t 0 corresponding to 000. (b) The total retail sales of prescription drugs in the United States during this eight-ear period can be approimated b finding the area of the trapezoid bounded b the linear model ou found in part (a) and the lines 0,t 0.5, and t 7.5. Use a graphing utilit to graph this region. (c) Use the formula for the area of a trapezoid to approimate the total retail sales of prescription drugs. 8. DATA ANALYSIS: MERCHANDISE The table shows the retail sales (in millions of dollars) for Aeropostale, Inc. from 000 through 007. (Source: Aeropostale, Inc.) Year Retail sales, Retail sales, (a) Use the regression feature of a graphing utilit to find a linear model for the data. Let t represent the ear, with t 0 corresponding to 000. (b) The total retail sales for Aeropostale during this eight-ear period can be approimated b finding the area of the trapezoid bounded b the linear model ou found in part (a) and the lines 0, t 0.5, and t 7.5. Use a graphing utilit to graph this region. (c) Use the formula for the area of a trapezoid to approimate the total retail sales for Aeropostale.
56 58 Chapter 7 Sstems of Equations and Inequalities 85. PHYSICAL FITNESS FACILITY An indoor running track is to be constructed with a space for eercise equipment inside the track (see figure). The track must be at least 5 meters long, and the eercise space must have an area of at least 500 square meters. (a) Find a sstem of inequalities describing the requirements of the facilit. (b) Graph the sstem from part (a). EXPLORATION TRUE OR FALSE? In Eercises 86 and 87, determine whether the statement is true or false. Justif our answer. 86. The area of the figure defined b the sstem is 99 square units. 87. The graph below shows the solution of the sstem > 6. 3 Eercise equipment GRAPHICAL REASONING Two concentric circles have radii and, where >. The area between the circles must be at least 0 square units. (a) Find a sstem of inequalities describing the constraints on the circles. (b) Use a graphing utilit to graph the sstem of inequalities in part (a). Graph the line in the same viewing window. (c) Identif the graph of the line in relation to the boundar of the inequalit. Eplain its meaning in the contet of the problem. 90. The graph of the solution of the inequalit < 6 is shown in the figure. Describe how the solution set would change for each of the following. (a) (b) In Eercises 9 9, match the sstem of inequalities with the graph of its solution. [The graphs are labeled (a), (b), (c), and (d).] (a) (c) 6 > (b) (d) CAPSTONE (a) Eplain the difference between the graphs of the inequalit 5 on the real number line and on the rectangular coordinate sstem. (b) After graphing the boundar of the inequalit < 3, eplain how ou decide on which side of the boundar the solution set of the inequalit lies
57 Section 7.6 Linear Programming LINEAR PROGRAMMING What ou should learn Solve linear programming problems. Use linear programming to model and solve real-life problems. Wh ou should learn it Linear programming is often useful in making real-life economic decisions. For eample, Eercise on page 557 shows how ou can determine the optimal cost of a blend of gasoline and compare it with the national average. Linear Programming: A Graphical Approach Man applications in business and economics involve a process called optimization, in which ou are asked to find the minimum or maimum value of a quantit. In this section, ou will stud an optimization strateg called linear programming. A two-dimensional linear programming problem consists of a linear objective function and a sstem of linear inequalities called constraints. The objective function gives the quantit that is to be maimized (or minimized), and the constraints determine the set of feasible solutions. For eample, suppose ou are asked to maimize the value of z a b Objective function subject to a set of constraints that determines the shaded region in Figure 7.3. Feasible solutions FIGURE 7.3 Tim Bole/Gett Images Because ever point in the shaded region satisfies each constraint, it is not clear how ou should find the point that ields a maimum value of z. Fortunatel, it can be shown that if there is an optimal solution, it must occur at one of the vertices. This means that ou can find the maimum value of z b testing z at each of the vertices. Optimal of a Linear Programming Problem If a linear programming problem has a solution, it must occur at a verte of the set of feasible solutions. If there is more than one solution, at least one of them must occur at such a verte. In either case, the value of the objective function is unique. Some guidelines for solving a linear programming problem in two variables are listed at the top of the net page.
58 550 Chapter 7 Sstems of Equations and Inequalities Solving a Linear Programming Problem. Sketch the region corresponding to the sstem of constraints. (The points inside or on the boundar of the region are feasible solutions.). Find the vertices of the region. 3. Test the objective function at each of the vertices and select the values of the variables that optimize the objective function. For a bounded region, both a minimum and a maimum value will eist. (For an unbounded region, if an optimal solution eists, it will occur at a verte.) Eample Solving a Linear Programming Problem 3 (0, ) = 0 + = (, ) = (, 0) (0, 0) = 0 3 FIGURE Find the maimum value of z 3 subject to the following constraints. 0 0 Objective function Constraints The constraints form the region shown in Figure 7.3. At the four vertices of this region, the objective function has the following values. At 0, 0: At 0, : At, : At, 0: z z 30 z 3 8 z Maimum value of z So, the maimum value of z is 8, and this occurs when and. Now tr Eercise 9. In Eample, tr testing some of the interior points in the region. You will see that the corresponding values of z are less than 8. Here are some eamples. At, : z 3 5 At, 3 : z To see wh the maimum value of the objective function in Eample must occur at a verte, consider writing the objective function in slope-intercept form 3 z Famil of lines FIGURE z = z = z = 6 z = 8 where z is the -intercept of the objective function. This equation represents a famil of lines, each of slope. 3 Of these infinitel man lines, ou want the one that has the largest z-value while still intersecting the region determined b the constraints. In other words, of all the lines whose slope is, 3 ou want the one that has the largest -intercept and intersects the given region, as shown in Figure From the graph, ou can see that such a line will pass through one (or more) of the vertices of the region.
59 Section 7.6 Linear Programming 55 The net eample shows that the same basic procedure can be used to solve a problem in which the objective function is to be minimized. Eample Minimizing an Objective Function 5 (, 5) (0, ) (6, 3) 3 (0, ) (3, 0) (5, 0) FIGURE 7.3 Find the minimum value of z 5 7 Objective function where 0 and 0, subject to the following constraints Constraints The region bounded b the constraints is shown in Figure 7.3. B testing the objective function at each verte, ou obtain the following. At 0, : At 0, : At, 5: At 6, 3: At 5, 0: At 3, 0: z 50 7 z z z z z Minimum value of z So, the minimum value of z is, and this occurs when 0 and. Now tr Eercise. HISTORICAL NOTE Eample 3 Maimizing an Objective Function Edward W. Souza/News Services/ Stanford Universit George Dantzig (9 005) was the first to propose the simple method, or linear programming, in 97. This technique defined the steps needed to find the optimal solution to a comple multivariable problem. Find the maimum value of z 5 7 Objective function where 0 and 0, subject to the following constraints Constraints This linear programming problem is identical to that given in Eample above, ecept that the objective function is maimized instead of minimized. Using the values of z at the vertices shown above, ou can conclude that the maimum value of z is z and occurs when 6 and 3. Now tr Eercise 3.
Linear and Nonlinear Systems of Equations. The Method of Substitution. Equation 1 Equation 2. Check (2, 1) in Equation 1 and Equation 2: 2x y 5?
 3330_070.qd 96 /5/05 Chapter 7 7. 9:39 AM Page 96 Sstems of Equations and Inequalities Linear and Nonlinear Sstems of Equations What ou should learn Use the method of substitution to solve sstems of linear
3330_070.qd 96 /5/05 Chapter 7 7. 9:39 AM Page 96 Sstems of Equations and Inequalities Linear and Nonlinear Sstems of Equations What ou should learn Use the method of substitution to solve sstems of linear
Systems of Equations and Inequalities
 Sstems of Equations and Inequalities 7. Linear and Nonlinear Sstems of Equations 7. Two-Variable Linear Sstems 7.3 Multivariable Linear Sstems 7. Partial Fractions 7.5 Sstems of Inequalities 7.6 Linear
Sstems of Equations and Inequalities 7. Linear and Nonlinear Sstems of Equations 7. Two-Variable Linear Sstems 7.3 Multivariable Linear Sstems 7. Partial Fractions 7.5 Sstems of Inequalities 7.6 Linear
14.1 Systems of Linear Equations in Two Variables
 86 Chapter 1 Sstems of Equations and Matrices 1.1 Sstems of Linear Equations in Two Variables Use the method of substitution to solve sstems of equations in two variables. Use the method of elimination
86 Chapter 1 Sstems of Equations and Matrices 1.1 Sstems of Linear Equations in Two Variables Use the method of substitution to solve sstems of equations in two variables. Use the method of elimination
1.5. Analyzing Graphs of Functions. The Graph of a Function. What you should learn. Why you should learn it. 54 Chapter 1 Functions and Their Graphs
 0_005.qd /7/05 8: AM Page 5 5 Chapter Functions and Their Graphs.5 Analzing Graphs of Functions What ou should learn Use the Vertical Line Test for functions. Find the zeros of functions. Determine intervals
0_005.qd /7/05 8: AM Page 5 5 Chapter Functions and Their Graphs.5 Analzing Graphs of Functions What ou should learn Use the Vertical Line Test for functions. Find the zeros of functions. Determine intervals
Chapter 5: Systems of Equations
 Chapter : Sstems of Equations Section.: Sstems in Two Variables... 0 Section. Eercises... 9 Section.: Sstems in Three Variables... Section. Eercises... Section.: Linear Inequalities... Section.: Eercises.
Chapter : Sstems of Equations Section.: Sstems in Two Variables... 0 Section. Eercises... 9 Section.: Sstems in Three Variables... Section. Eercises... Section.: Linear Inequalities... Section.: Eercises.
1.7 Inverse Functions
 71_0107.qd 1/7/0 10: AM Page 17 Section 1.7 Inverse Functions 17 1.7 Inverse Functions Inverse Functions Recall from Section 1. that a function can be represented b a set of ordered pairs. For instance,
71_0107.qd 1/7/0 10: AM Page 17 Section 1.7 Inverse Functions 17 1.7 Inverse Functions Inverse Functions Recall from Section 1. that a function can be represented b a set of ordered pairs. For instance,
P.4 Lines in the Plane
 28 CHAPTER P Prerequisites P.4 Lines in the Plane What ou ll learn about Slope of a Line Point-Slope Form Equation of a Line Slope-Intercept Form Equation of a Line Graphing Linear Equations in Two Variables
28 CHAPTER P Prerequisites P.4 Lines in the Plane What ou ll learn about Slope of a Line Point-Slope Form Equation of a Line Slope-Intercept Form Equation of a Line Graphing Linear Equations in Two Variables
The Method of Substitution. Linear and Nonlinear Systems of Equations. The Method of Substitution. The Method of Substitution. Example 2.
 The Method of Substitution Linear and Nonlinear Systems of Equations Precalculus 7.1 Here is an example of a system of two equations in two unknowns. Equation 1 x + y = 5 Equation 3x y = 4 A solution of
The Method of Substitution Linear and Nonlinear Systems of Equations Precalculus 7.1 Here is an example of a system of two equations in two unknowns. Equation 1 x + y = 5 Equation 3x y = 4 A solution of
Maintaining Mathematical Proficiency
 Name Date Chapter 5 Maintaining Mathematical Proficienc Graph the equation. 1. + =. = 3 3. 5 + = 10. 3 = 5. 3 = 6. 3 + = 1 Solve the inequalit. Graph the solution. 7. a 3 > 8. c 9. d 5 < 3 10. 8 3r 5 r
Name Date Chapter 5 Maintaining Mathematical Proficienc Graph the equation. 1. + =. = 3 3. 5 + = 10. 3 = 5. 3 = 6. 3 + = 1 Solve the inequalit. Graph the solution. 7. a 3 > 8. c 9. d 5 < 3 10. 8 3r 5 r
Introduction Direct Variation Rates of Change Scatter Plots. Introduction. EXAMPLE 1 A Mathematical Model
 APPENDIX B Mathematical Modeling B1 Appendi B Mathematical Modeling B.1 Modeling Data with Linear Functions Introduction Direct Variation Rates of Change Scatter Plots Introduction The primar objective
APPENDIX B Mathematical Modeling B1 Appendi B Mathematical Modeling B.1 Modeling Data with Linear Functions Introduction Direct Variation Rates of Change Scatter Plots Introduction The primar objective
3.2 LOGARITHMIC FUNCTIONS AND THEIR GRAPHS
 Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
LESSON #12 - FORMS OF A LINE COMMON CORE ALGEBRA II
 LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
LESSON #11 - FORMS OF A LINE COMMON CORE ALGEBRA II
 LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
Chapter 1: Linear Equations and Functions
 Chapter : Linear Equations and Functions Eercise.. 7 8+ 7+ 7 8 8+ + 7 8. + 8 8( + ) + 8 8+ 8 8 8 8 7 0 0. 8( ) ( ) 8 8 8 8 + 0 8 8 0 7. ( ) 8. 8. ( 7) ( + ) + + +. 7 7 7 7 7 7 ( ). 8 8 0 0 7. + + + 8 +
Chapter : Linear Equations and Functions Eercise.. 7 8+ 7+ 7 8 8+ + 7 8. + 8 8( + ) + 8 8+ 8 8 8 8 7 0 0. 8( ) ( ) 8 8 8 8 + 0 8 8 0 7. ( ) 8. 8. ( 7) ( + ) + + +. 7 7 7 7 7 7 ( ). 8 8 0 0 7. + + + 8 +
Can a system of linear equations have no solution? Can a system of linear equations have many solutions?
 5. Solving Special Sstems of Linear Equations Can a sstem of linear equations have no solution? Can a sstem of linear equations have man solutions? ACTIVITY: Writing a Sstem of Linear Equations Work with
5. Solving Special Sstems of Linear Equations Can a sstem of linear equations have no solution? Can a sstem of linear equations have man solutions? ACTIVITY: Writing a Sstem of Linear Equations Work with
3-1. Solving Systems Using Tables and Graphs. Concept Summary. Graphical Solutions of Linear Systems VOCABULARY TEKS FOCUS ESSENTIAL UNDERSTANDING
 3- Solving Sstems Using Tables and Graphs TEKS FOCUS VOCABULARY Foundational to TEKS (3)(A) Formulate sstems of equations, including sstems consisting of three linear equations in three variables and sstems
3- Solving Sstems Using Tables and Graphs TEKS FOCUS VOCABULARY Foundational to TEKS (3)(A) Formulate sstems of equations, including sstems consisting of three linear equations in three variables and sstems
Infinite Limits. Let f be the function given by. f x 3 x 2.
 0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
Solve each system by graphing. Check your solution. y =-3x x + y = 5 y =-7
 Practice Solving Sstems b Graphing Solve each sstem b graphing. Check our solution. 1. =- + 3 = - (1, ). = 1 - (, 1) =-3 + 5 3. = 3 + + = 1 (, 3). =-5 = - 7. = 3-5 3 - = 0 (1, 5) 5. -3 + = 5 =-7 (, 7).
Practice Solving Sstems b Graphing Solve each sstem b graphing. Check our solution. 1. =- + 3 = - (1, ). = 1 - (, 1) =-3 + 5 3. = 3 + + = 1 (, 3). =-5 = - 7. = 3-5 3 - = 0 (1, 5) 5. -3 + = 5 =-7 (, 7).
The Natural Base e. ( 1, e 1 ) 220 Chapter 3 Exponential and Logarithmic Functions. Example 6 Evaluating the Natural Exponential Function.
 0 Chapter Eponential and Logarithmic Functions (, e) f() = e (, e ) (0, ) (, e ) FIGURE.9 The Natural Base e In man applications, the most convenient choice for a base is the irrational number e.78888....
0 Chapter Eponential and Logarithmic Functions (, e) f() = e (, e ) (0, ) (, e ) FIGURE.9 The Natural Base e In man applications, the most convenient choice for a base is the irrational number e.78888....
What Did You Learn? Key Terms. Key Concepts. 158 Chapter 1 Functions and Their Graphs
 333371_010R.qxp 12/27/0 10:37 AM Page 158 158 Chapter 1 Functions and Their Graphs Ke Terms What Did You Learn? equation, p. 77 solution point, p. 77 intercepts, p. 78 slope, p. 88 point-slope form, p.
333371_010R.qxp 12/27/0 10:37 AM Page 158 158 Chapter 1 Functions and Their Graphs Ke Terms What Did You Learn? equation, p. 77 solution point, p. 77 intercepts, p. 78 slope, p. 88 point-slope form, p.
LESSON #24 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
6.2. TWO-VARIABLE LINEAR SYSTEMS
 6.2. TWO-VARIABLE LINEAR SYSTEMS What You Should Learn Use the method of elimination to solve systems of linear equations in two variables. Interpret graphically the numbers of solutions of systems of
6.2. TWO-VARIABLE LINEAR SYSTEMS What You Should Learn Use the method of elimination to solve systems of linear equations in two variables. Interpret graphically the numbers of solutions of systems of
x. 4. 2x 10 4x. 10 x
 CCGPS UNIT Semester 1 COORDINATE ALGEBRA Page 1 of Reasoning with Equations and Quantities Name: Date: Understand solving equations as a process of reasoning and eplain the reasoning MCC9-1.A.REI.1 Eplain
CCGPS UNIT Semester 1 COORDINATE ALGEBRA Page 1 of Reasoning with Equations and Quantities Name: Date: Understand solving equations as a process of reasoning and eplain the reasoning MCC9-1.A.REI.1 Eplain
Systems and Matrices CHAPTER 7
 CHAPTER 7 Systems and Matrices 7.1 Solving Systems of Two Equations 7.2 Matrix Algebra 7.3 Multivariate Linear Systems and Row Operations 7.4 Partial Fractions 7.5 Systems of Inequalities in Two Variables
CHAPTER 7 Systems and Matrices 7.1 Solving Systems of Two Equations 7.2 Matrix Algebra 7.3 Multivariate Linear Systems and Row Operations 7.4 Partial Fractions 7.5 Systems of Inequalities in Two Variables
LESSON #28 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #8 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #8 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
Fair Game Review. Chapter 2. and y = 5. Evaluate the expression when x = xy 2. 4x. Evaluate the expression when a = 9 and b = 4.
 Name Date Chapter Fair Game Review Evaluate the epression when = and =.... 0 +. 8( ) Evaluate the epression when a = 9 and b =.. ab. a ( b + ) 7. b b 7 8. 7b + ( ab ) 9. You go to the movies with five
Name Date Chapter Fair Game Review Evaluate the epression when = and =.... 0 +. 8( ) Evaluate the epression when a = 9 and b =.. ab. a ( b + ) 7. b b 7 8. 7b + ( ab ) 9. You go to the movies with five
Chapter 4. Chapter 4 Opener. Section 4.1. Big Ideas Math Blue Worked-Out Solutions. x 2. Try It Yourself (p. 147) x 0 1. y ( ) x 2
 Chapter Chapter Opener Tr It Yourself (p. 7). As the input decreases b, the output increases b.. Input As the input increases b, the output increases b.. As the input decreases b, the output decreases
Chapter Chapter Opener Tr It Yourself (p. 7). As the input decreases b, the output increases b.. Input As the input increases b, the output increases b.. As the input decreases b, the output decreases
Properties of Limits
 33460_003qd //04 :3 PM Page 59 SECTION 3 Evaluating Limits Analticall 59 Section 3 Evaluating Limits Analticall Evaluate a it using properties of its Develop and use a strateg for finding its Evaluate
33460_003qd //04 :3 PM Page 59 SECTION 3 Evaluating Limits Analticall 59 Section 3 Evaluating Limits Analticall Evaluate a it using properties of its Develop and use a strateg for finding its Evaluate
Systems of Linear Equations
 Sstems of Linear Equations Monetar Sstems Overload Lesson 3-1 Learning Targets: Use graphing, substitution, and elimination to solve sstems of linear equations in two variables. Formulate sstems of linear
Sstems of Linear Equations Monetar Sstems Overload Lesson 3-1 Learning Targets: Use graphing, substitution, and elimination to solve sstems of linear equations in two variables. Formulate sstems of linear
PRECALCULUS FINAL EXAM REVIEW
 PRECALCULUS FINAL EXAM REVIEW Evaluate the function at the indicated value of. Round our result to three decimal places.. f () 4(5 ); 0.8. f () e ; 0.78 Use the graph of f to describe the transformation
PRECALCULUS FINAL EXAM REVIEW Evaluate the function at the indicated value of. Round our result to three decimal places.. f () 4(5 ); 0.8. f () e ; 0.78 Use the graph of f to describe the transformation
10.3 Solving Nonlinear Systems of Equations
 60 CHAPTER 0 Conic Sections Identif whether each equation, when graphed, will be a parabola, circle, ellipse, or hperbola. Then graph each equation.. - 7 + - =. = +. = + + 6. + 9 =. 9-9 = 6. 6 - = 7. 6
60 CHAPTER 0 Conic Sections Identif whether each equation, when graphed, will be a parabola, circle, ellipse, or hperbola. Then graph each equation.. - 7 + - =. = +. = + + 6. + 9 =. 9-9 = 6. 6 - = 7. 6
Ready To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions
 Read To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions Find these vocabular words in Lesson 5-1 and the Multilingual Glossar. Vocabular quadratic function parabola verte
Read To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions Find these vocabular words in Lesson 5-1 and the Multilingual Glossar. Vocabular quadratic function parabola verte
Module 3, Section 4 Analytic Geometry II
 Principles of Mathematics 11 Section, Introduction 01 Introduction, Section Analtic Geometr II As the lesson titles show, this section etends what ou have learned about Analtic Geometr to several related
Principles of Mathematics 11 Section, Introduction 01 Introduction, Section Analtic Geometr II As the lesson titles show, this section etends what ou have learned about Analtic Geometr to several related
3.2 Introduction to Functions
 8 CHAPTER Graphs and Functions Write each statement as an equation in two variables. Then graph each equation. 97. The -value is more than three times the -value. 98. The -value is - decreased b twice
8 CHAPTER Graphs and Functions Write each statement as an equation in two variables. Then graph each equation. 97. The -value is more than three times the -value. 98. The -value is - decreased b twice
8.4. If we let x denote the number of gallons pumped, then the price y in dollars can $ $1.70 $ $1.70 $ $1.70 $ $1.
 8.4 An Introduction to Functions: Linear Functions, Applications, and Models We often describe one quantit in terms of another; for eample, the growth of a plant is related to the amount of light it receives,
8.4 An Introduction to Functions: Linear Functions, Applications, and Models We often describe one quantit in terms of another; for eample, the growth of a plant is related to the amount of light it receives,
Essential Question How can you use a quadratic function to model a real-life situation?
 3. TEXAS ESSENTIAL KNOWLEDGE AND SKILLS A..A A..E A..A A..B A..C Modeling with Quadratic Functions Essential Question How can ou use a quadratic function to model a real-life situation? Work with a partner.
3. TEXAS ESSENTIAL KNOWLEDGE AND SKILLS A..A A..E A..A A..B A..C Modeling with Quadratic Functions Essential Question How can ou use a quadratic function to model a real-life situation? Work with a partner.
Systems of Linear and Quadratic Equations. Check Skills You ll Need. y x. Solve by Graphing. Solve the following system by graphing.
 NY- Learning Standards for Mathematics A.A. Solve a sstem of one linear and one quadratic equation in two variables, where onl factoring is required. A.G.9 Solve sstems of linear and quadratic equations
NY- Learning Standards for Mathematics A.A. Solve a sstem of one linear and one quadratic equation in two variables, where onl factoring is required. A.G.9 Solve sstems of linear and quadratic equations
a. In the statement "Height is a function of weight," which is the independent variable and which is the dependent variable?
 1. The weights and heights of si mathematics students are given in the table. Answer parts a through e. Weight (lb.) Height (cm) 157 19 11 155 1 11 175 17 157 15 17 17 a. In the statement "Height is a
1. The weights and heights of si mathematics students are given in the table. Answer parts a through e. Weight (lb.) Height (cm) 157 19 11 155 1 11 175 17 157 15 17 17 a. In the statement "Height is a
Solving Systems of Linear Equations
 5 Solving Sstems of Linear Equations 5. Solving Sstems of Linear Equations b Graphing 5. Solving Sstems of Linear Equations b Substitution 5.3 Solving Sstems of Linear Equations b Elimination 5. Solving
5 Solving Sstems of Linear Equations 5. Solving Sstems of Linear Equations b Graphing 5. Solving Sstems of Linear Equations b Substitution 5.3 Solving Sstems of Linear Equations b Elimination 5. Solving
Chapter 1: Linear Equations and Functions
 Chapter : Answers to Eercises Chapter : Linear Equations and Functions Eercise.. 7= 8+ 7+ 7 8 = 8+ + 7 8 = 9. + 8= 8( + ). + 8= 8+ 8 8 = 8 8 7 = 0 = 0 9 = = = () = 96 = 7. ( 7) = ( + ) 9.. = + + = + =
Chapter : Answers to Eercises Chapter : Linear Equations and Functions Eercise.. 7= 8+ 7+ 7 8 = 8+ + 7 8 = 9. + 8= 8( + ). + 8= 8+ 8 8 = 8 8 7 = 0 = 0 9 = = = () = 96 = 7. ( 7) = ( + ) 9.. = + + = + =
CHAPTER 2 Solving Equations and Inequalities
 CHAPTER Solving Equations and Inequalities Section. Linear Equations and Problem Solving........... 8 Section. Solving Equations Graphically............... 89 Section. Comple Numbers......................
CHAPTER Solving Equations and Inequalities Section. Linear Equations and Problem Solving........... 8 Section. Solving Equations Graphically............... 89 Section. Comple Numbers......................
Mini-Lecture 8.1 Solving Quadratic Equations by Completing the Square
 Mini-Lecture 8.1 Solving Quadratic Equations b Completing the Square Learning Objectives: 1. Use the square root propert to solve quadratic equations.. Solve quadratic equations b completing the square.
Mini-Lecture 8.1 Solving Quadratic Equations b Completing the Square Learning Objectives: 1. Use the square root propert to solve quadratic equations.. Solve quadratic equations b completing the square.
Systems of Linear Equations
 Sstems of Linear Equations Monetar Sstems Overload Lesson 3-1 Learning Targets: Use graphing, substitution, and elimination to solve sstems of linear equations in two variables. Formulate sstems of linear
Sstems of Linear Equations Monetar Sstems Overload Lesson 3-1 Learning Targets: Use graphing, substitution, and elimination to solve sstems of linear equations in two variables. Formulate sstems of linear
Systems of Linear Equations: Solving by Graphing
 8.1 Sstems of Linear Equations: Solving b Graphing 8.1 OBJECTIVE 1. Find the solution(s) for a set of linear equations b graphing NOTE There is no other ordered pair that satisfies both equations. From
8.1 Sstems of Linear Equations: Solving b Graphing 8.1 OBJECTIVE 1. Find the solution(s) for a set of linear equations b graphing NOTE There is no other ordered pair that satisfies both equations. From
Solving Linear Systems
 1.4 Solving Linear Sstems Essential Question How can ou determine the number of solutions of a linear sstem? A linear sstem is consistent when it has at least one solution. A linear sstem is inconsistent
1.4 Solving Linear Sstems Essential Question How can ou determine the number of solutions of a linear sstem? A linear sstem is consistent when it has at least one solution. A linear sstem is inconsistent
Lecture Guide. Math 90 - Intermediate Algebra. Stephen Toner. Intermediate Algebra, 2nd edition. Miller, O'Neill, & Hyde. Victor Valley College
 Lecture Guide Math 90 - Intermediate Algebra to accompan Intermediate Algebra, 2nd edition Miller, O'Neill, & Hde Prepared b Stephen Toner Victor Valle College Last updated: 11/24/10 0 1.1 Sets of Numbers
Lecture Guide Math 90 - Intermediate Algebra to accompan Intermediate Algebra, 2nd edition Miller, O'Neill, & Hde Prepared b Stephen Toner Victor Valle College Last updated: 11/24/10 0 1.1 Sets of Numbers
Fair Game Review. Chapter 9. Find the square root(s) ± Find the side length of the square. 7. Simplify Simplify 63.
 Name Date Chapter 9 Find the square root(s). Fair Game Review... 9. ±. Find the side length of the square.. s. s s Area = 9 ft s Area = 0. m 7. Simplif 0. 8. Simplif. 9. Simplif 08. 0. Simplif 88. Copright
Name Date Chapter 9 Find the square root(s). Fair Game Review... 9. ±. Find the side length of the square.. s. s s Area = 9 ft s Area = 0. m 7. Simplif 0. 8. Simplif. 9. Simplif 08. 0. Simplif 88. Copright
Name: Period: QVMS GTA FALL FINAL EXAM REVIEW PRE-AP ALGEBRA 1
 Name: Period: QVMS GTA FALL FINAL EXAM REVIEW PRE-AP ALGEBRA ) When simplifing an epression, ou perform operations inside grouping smbols first. a. alwas b. sometimes c. never ) The opposite of a negative
Name: Period: QVMS GTA FALL FINAL EXAM REVIEW PRE-AP ALGEBRA ) When simplifing an epression, ou perform operations inside grouping smbols first. a. alwas b. sometimes c. never ) The opposite of a negative
Identify the domain and the range of the relation from the graph. 8)
 INTERMEDIATE ALGEBRA REVIEW FOR TEST Use the given conditions to write an equation for the line. 1) a) Passing through (, -) and parallel to = - +. b) Passing through (, 7) and parallel to - 3 = 10 c)
INTERMEDIATE ALGEBRA REVIEW FOR TEST Use the given conditions to write an equation for the line. 1) a) Passing through (, -) and parallel to = - +. b) Passing through (, 7) and parallel to - 3 = 10 c)
Intermediate Algebra. Exam 1 Review (Chapters 1, 2, and 3)
 Eam Review (Chapters,, and ) Intermediate Algebra Name. Epress the set in roster form. { N and 7}. Epress the set in set builder form. {-, 0,,,, }. Epress in set builder notation each set of numbers that
Eam Review (Chapters,, and ) Intermediate Algebra Name. Epress the set in roster form. { N and 7}. Epress the set in set builder form. {-, 0,,,, }. Epress in set builder notation each set of numbers that
Intermediate Algebra / MAT 135 Spring 2017 Master ( Master Templates)
 Test 1 Review #1 Intermediate Algebra / MAT 135 Spring 017 Master ( Master Templates) Student Name/ID: 1. Solve for. = 8 18. Solve for. = + a b 3. Solve for. a b = L 30. Two trains leave stations miles
Test 1 Review #1 Intermediate Algebra / MAT 135 Spring 017 Master ( Master Templates) Student Name/ID: 1. Solve for. = 8 18. Solve for. = + a b 3. Solve for. a b = L 30. Two trains leave stations miles
Bridge-Thickness Experiment. Student 2
 Applications 1. Below are some results from the bridge-thickness eperiment. Bridge-Thickness Eperiment Thickness (laers) Breaking Weight (pennies) 15 5 5 a. Plot the (thickness, breaking weight) data.
Applications 1. Below are some results from the bridge-thickness eperiment. Bridge-Thickness Eperiment Thickness (laers) Breaking Weight (pennies) 15 5 5 a. Plot the (thickness, breaking weight) data.
Linear Equations and Arithmetic Sequences
 CONDENSED LESSON.1 Linear Equations and Arithmetic Sequences In this lesson, ou Write eplicit formulas for arithmetic sequences Write linear equations in intercept form You learned about recursive formulas
CONDENSED LESSON.1 Linear Equations and Arithmetic Sequences In this lesson, ou Write eplicit formulas for arithmetic sequences Write linear equations in intercept form You learned about recursive formulas
13.1 2X2 Systems of Equations
 . X Sstems of Equations In this section we want to spend some time reviewing sstems of equations. Recall there are two basic techniques we use for solving a sstem of equations: Elimination and Substitution.
. X Sstems of Equations In this section we want to spend some time reviewing sstems of equations. Recall there are two basic techniques we use for solving a sstem of equations: Elimination and Substitution.
Exponential and Logarithmic Functions
 7 Eponential and Logarithmic Functions In this chapter ou will stud two tpes of nonalgebraic functions eponential functions and logarithmic functions. Eponential and logarithmic functions are widel used
7 Eponential and Logarithmic Functions In this chapter ou will stud two tpes of nonalgebraic functions eponential functions and logarithmic functions. Eponential and logarithmic functions are widel used
Exercises. Bottled Water Consumption. U. S. Paper Recycling
 Eercises Use the graph of each function to estimate the indicated function values. Then confirm the estimate algebraicall. Round to the nearest hundredth, if necessar. (Eample 1) 1.. 36 g() = -5 + 5 16
Eercises Use the graph of each function to estimate the indicated function values. Then confirm the estimate algebraicall. Round to the nearest hundredth, if necessar. (Eample 1) 1.. 36 g() = -5 + 5 16
2.4 Library of Functions; Piecewise-defined Functions. 1 Graph the Functions Listed in the Library of Functions
 80 CHAPTER Functions and Their Graphs Problems 8 88 require the following discussion of a secant line. The slope of the secant line containing the two points, f and + h, f + h on the graph of a function
80 CHAPTER Functions and Their Graphs Problems 8 88 require the following discussion of a secant line. The slope of the secant line containing the two points, f and + h, f + h on the graph of a function
Exponential and Logarithmic Functions
 Eponential and Logarithmic Functions. Eponential Functions and Their Graphs. Logarithmic Functions and Their Graphs. Properties of Logarithms. Eponential and Logarithmic Equations.5 Eponential and Logarithmic
Eponential and Logarithmic Functions. Eponential Functions and Their Graphs. Logarithmic Functions and Their Graphs. Properties of Logarithms. Eponential and Logarithmic Equations.5 Eponential and Logarithmic
3.2 Logarithmic Functions and Their Graphs
 96 Chapter 3 Eponential and Logarithmic Functions 3.2 Logarithmic Functions and Their Graphs Logarithmic Functions In Section.6, you studied the concept of an inverse function. There, you learned that
96 Chapter 3 Eponential and Logarithmic Functions 3.2 Logarithmic Functions and Their Graphs Logarithmic Functions In Section.6, you studied the concept of an inverse function. There, you learned that
Functions and Their Graphs
 Functions and Their Graphs. Rectangular Coordinates. Graphs of Equations. Linear Equations in Two Variables. Functions. Analzing Graphs of Functions. A Librar of Parent Functions.7 Transformations of Functions.9
Functions and Their Graphs. Rectangular Coordinates. Graphs of Equations. Linear Equations in Two Variables. Functions. Analzing Graphs of Functions. A Librar of Parent Functions.7 Transformations of Functions.9
CONSUMER CHOICES Madison is thinking about leasing a car for. Example 1 Solve the system of equations by graphing.
 2-1 BJECTIVES Solve sstems of equations graphicall. Solve sstems of equations algebraicall. Solving Sstems of Equations in Two Variables CNSUMER CHICES Madison is thinking about leasing a car for two ears.
2-1 BJECTIVES Solve sstems of equations graphicall. Solve sstems of equations algebraicall. Solving Sstems of Equations in Two Variables CNSUMER CHICES Madison is thinking about leasing a car for two ears.
9 (0, 3) and solve equations to earn full credit.
 Math 0 Intermediate Algebra II Final Eam Review Page of Instructions: (6, ) Use our own paper for the review questions. For the final eam, show all work on the eam. (-6, ) This is an algebra class do not
Math 0 Intermediate Algebra II Final Eam Review Page of Instructions: (6, ) Use our own paper for the review questions. For the final eam, show all work on the eam. (-6, ) This is an algebra class do not
Name Date. and y = 5.
 Name Date Chapter Fair Game Review Evaluate the epression when = and =.... 0 +. 8( ) Evaluate the epression when a = 9 and b =.. ab. a ( b + ) 7. b b 7 8. 7b + ( ab ) 9. You go to the movies with five
Name Date Chapter Fair Game Review Evaluate the epression when = and =.... 0 +. 8( ) Evaluate the epression when a = 9 and b =.. ab. a ( b + ) 7. b b 7 8. 7b + ( ab ) 9. You go to the movies with five
6. Graph each of the following functions. What do you notice? What happens when x = 2 on the graph of b?
 Pre Calculus Worksheet 1. Da 1 1. The relation described b the set of points {(-,5,0,5,,8,,9 ) ( ) ( ) ( )} is NOT a function. Eplain wh. For questions - 4, use the graph at the right.. Eplain wh the graph
Pre Calculus Worksheet 1. Da 1 1. The relation described b the set of points {(-,5,0,5,,8,,9 ) ( ) ( ) ( )} is NOT a function. Eplain wh. For questions - 4, use the graph at the right.. Eplain wh the graph
3.1 Graph Quadratic Functions
 3. Graph Quadratic Functions in Standard Form Georgia Performance Standard(s) MMA3b, MMA3c Goal p Use intervals of increase and decrease to understand average rates of change of quadratic functions. Your
3. Graph Quadratic Functions in Standard Form Georgia Performance Standard(s) MMA3b, MMA3c Goal p Use intervals of increase and decrease to understand average rates of change of quadratic functions. Your
12.1 Systems of Linear equations: Substitution and Elimination
 . Sstems of Linear equations: Substitution and Elimination Sstems of two linear equations in two variables A sstem of equations is a collection of two or more equations. A solution of a sstem in two variables
. Sstems of Linear equations: Substitution and Elimination Sstems of two linear equations in two variables A sstem of equations is a collection of two or more equations. A solution of a sstem in two variables
5.3 Polynomials and Polynomial Functions
 70 CHAPTER 5 Eponents, Polnomials, and Polnomial Functions 5. Polnomials and Polnomial Functions S Identif Term, Constant, Polnomial, Monomial, Binomial, Trinomial, and the Degree of a Term and of a Polnomial.
70 CHAPTER 5 Eponents, Polnomials, and Polnomial Functions 5. Polnomials and Polnomial Functions S Identif Term, Constant, Polnomial, Monomial, Binomial, Trinomial, and the Degree of a Term and of a Polnomial.
Algebra I. Slide 1 / 176 Slide 2 / 176. Slide 3 / 176. Slide 4 / 176. Slide 6 / 176. Slide 5 / 176. System of Linear Equations.
 Slide 1 / 176 Slide 2 / 176 Algebra I Sstem of Linear Equations 21-11-2 www.njctl.org Slide 3 / 176 Slide 4 / 176 Table of Contents Solving Sstems b Graphing Solving Sstems b Substitution Solving Sstems
Slide 1 / 176 Slide 2 / 176 Algebra I Sstem of Linear Equations 21-11-2 www.njctl.org Slide 3 / 176 Slide 4 / 176 Table of Contents Solving Sstems b Graphing Solving Sstems b Substitution Solving Sstems
Name Class Date. Solving by Graphing and Algebraically
 Name Class Date 16-4 Nonlinear Sstems Going Deeper Essential question: How can ou solve a sstem of equations when one equation is linear and the other is quadratic? To estimate the solution to a sstem
Name Class Date 16-4 Nonlinear Sstems Going Deeper Essential question: How can ou solve a sstem of equations when one equation is linear and the other is quadratic? To estimate the solution to a sstem
6-1 Study Guide and Intervention
 NAME DATE PERID 6- Stud Guide and Intervention Graphing Sstems of Equations Possible Number of Solutions Two or more linear equations involving the same variables form a sstem of equations. A solution
NAME DATE PERID 6- Stud Guide and Intervention Graphing Sstems of Equations Possible Number of Solutions Two or more linear equations involving the same variables form a sstem of equations. A solution
6.4 graphs OF logarithmic FUnCTIOnS
 SECTION 6. graphs of logarithmic functions 9 9 learning ObjeCTIveS In this section, ou will: Identif the domain of a logarithmic function. Graph logarithmic functions. 6. graphs OF logarithmic FUnCTIOnS
SECTION 6. graphs of logarithmic functions 9 9 learning ObjeCTIveS In this section, ou will: Identif the domain of a logarithmic function. Graph logarithmic functions. 6. graphs OF logarithmic FUnCTIOnS
Finding Limits Graphically and Numerically. An Introduction to Limits
 8 CHAPTER Limits and Their Properties Section Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach Learn different was that a it can fail to eist Stud and use
8 CHAPTER Limits and Their Properties Section Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach Learn different was that a it can fail to eist Stud and use
REVIEW PACKET FOR END OF COURSE EXAM
 Math H REVIEW PACKET FOR END OF COURSE EXAM DO NOT WRITE ON PACKET! Do on binder paper, show support work. On this packet leave all fractional answers in improper fractional form (ecept where appropriate
Math H REVIEW PACKET FOR END OF COURSE EXAM DO NOT WRITE ON PACKET! Do on binder paper, show support work. On this packet leave all fractional answers in improper fractional form (ecept where appropriate
Answer Explanations. The SAT Subject Tests. Mathematics Level 1 & 2 TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE
 The SAT Subject Tests Answer Eplanations TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE Mathematics Level & Visit sat.org/stpractice to get more practice and stud tips for the Subject Test
The SAT Subject Tests Answer Eplanations TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE Mathematics Level & Visit sat.org/stpractice to get more practice and stud tips for the Subject Test
Essential Question How can you determine the number of solutions of a linear system?
 .1 TEXAS ESSENTIAL KNOWLEDGE AND SKILLS A.3.A A.3.B Solving Linear Sstems Using Substitution Essential Question How can ou determine the number of solutions of a linear sstem? A linear sstem is consistent
.1 TEXAS ESSENTIAL KNOWLEDGE AND SKILLS A.3.A A.3.B Solving Linear Sstems Using Substitution Essential Question How can ou determine the number of solutions of a linear sstem? A linear sstem is consistent
3.7 InveRSe FUnCTIOnS
 CHAPTER functions learning ObjeCTIveS In this section, ou will: Verif inverse functions. Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
CHAPTER functions learning ObjeCTIveS In this section, ou will: Verif inverse functions. Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
Study Guide and Intervention
 6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
Systems of Linear Equations Monetary Systems Overload
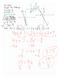 Sstems of Linear Equations SUGGESTED LEARNING STRATEGIES: Shared Reading, Close Reading, Interactive Word Wall Have ou ever noticed that when an item is popular and man people want to bu it, the price
Sstems of Linear Equations SUGGESTED LEARNING STRATEGIES: Shared Reading, Close Reading, Interactive Word Wall Have ou ever noticed that when an item is popular and man people want to bu it, the price
Coached Instruction Supplement
 Practice Coach PLUS Coached Instruction Supplement Mathematics 8 Practice Coach PLUS, Coached Instruction Supplement, Mathematics, Grade 8 679NASP Triumph Learning Triumph Learning, LLC. All rights reserved.
Practice Coach PLUS Coached Instruction Supplement Mathematics 8 Practice Coach PLUS, Coached Instruction Supplement, Mathematics, Grade 8 679NASP Triumph Learning Triumph Learning, LLC. All rights reserved.
LESSON #48 - INTEGER EXPONENTS COMMON CORE ALGEBRA II
 LESSON #8 - INTEGER EXPONENTS COMMON CORE ALGEBRA II We just finished our review of linear functions. Linear functions are those that grow b equal differences for equal intervals. In this unit we will
LESSON #8 - INTEGER EXPONENTS COMMON CORE ALGEBRA II We just finished our review of linear functions. Linear functions are those that grow b equal differences for equal intervals. In this unit we will
CHAPTER 3 Graphs and Functions
 CHAPTER Graphs and Functions Section. The Rectangular Coordinate Sstem............ Section. Graphs of Equations..................... 7 Section. Slope and Graphs of Linear Equations........... 7 Section.
CHAPTER Graphs and Functions Section. The Rectangular Coordinate Sstem............ Section. Graphs of Equations..................... 7 Section. Slope and Graphs of Linear Equations........... 7 Section.
M122 College Algebra Review for Final Exam
 M1 College Algebra Review for Final Eam Revised Fall 017 for College Algebra - Beecher All answers should include our work (this could be a written eplanation of the result, a graph with the relevant feature
M1 College Algebra Review for Final Eam Revised Fall 017 for College Algebra - Beecher All answers should include our work (this could be a written eplanation of the result, a graph with the relevant feature
Practice A ( 1, 3 ( 0, 1. Match the function with its graph. 3 x. Explain how the graph of g can be obtained from the graph of f. 5 x.
 8. Practice A For use with pages 65 7 Match the function with its graph.. f. f.. f 5. f 6. f f Lesson 8. A. B. C. (, 6) (0, ) (, ) (0, ) ( 0, ) (, ) D. E. F. (0, ) (, 6) ( 0, ) (, ) (, ) (0, ) Eplain how
8. Practice A For use with pages 65 7 Match the function with its graph.. f. f.. f 5. f 6. f f Lesson 8. A. B. C. (, 6) (0, ) (, ) (0, ) ( 0, ) (, ) D. E. F. (0, ) (, 6) ( 0, ) (, ) (, ) (0, ) Eplain how
[ ] 4. Math 70 Intermediate Algebra II Final Exam Review Page 1 of 19. Instructions:
![[ ] 4. Math 70 Intermediate Algebra II Final Exam Review Page 1 of 19. Instructions: [ ] 4. Math 70 Intermediate Algebra II Final Exam Review Page 1 of 19. Instructions:](/thumbs/80/81204581.jpg) Math Intermediate Algebra II Final Eam Review Page of 9 Instructions: Use our own paper for the review questions. For the final eam, show all work on the eam. This is an algebra class do not guess! Write
Math Intermediate Algebra II Final Eam Review Page of 9 Instructions: Use our own paper for the review questions. For the final eam, show all work on the eam. This is an algebra class do not guess! Write
Math098 Practice Final Test
 Math098 Practice Final Test Find an equation of the line that contains the points listed in the table. 1) 0-6 1-2 -4 3-3 4-2 Find an equation of the line. 2) 10-10 - 10 - -10 Solve. 3) 2 = 3 + 4 Find the
Math098 Practice Final Test Find an equation of the line that contains the points listed in the table. 1) 0-6 1-2 -4 3-3 4-2 Find an equation of the line. 2) 10-10 - 10 - -10 Solve. 3) 2 = 3 + 4 Find the
7.1 Guided Practice (p. 401) 1. to find an ordered pair that satisfies each of the equations in the system. solution of the system.
 CHAPTER 7 Think and Discuss (p. 9). 6,00,000 units. 0,00,000 6,00,000 4,400,000 renters Skill Review (p. 96) 9r 4r 6r. 8.. 0.d.d d 4. w 4 w 4 w 4 w 4 w. 6. 7 g g 9 g 7 g 6 g 0 7 8 40 40 40 7. 6 8. 8 9....
CHAPTER 7 Think and Discuss (p. 9). 6,00,000 units. 0,00,000 6,00,000 4,400,000 renters Skill Review (p. 96) 9r 4r 6r. 8.. 0.d.d d 4. w 4 w 4 w 4 w 4 w. 6. 7 g g 9 g 7 g 6 g 0 7 8 40 40 40 7. 6 8. 8 9....
11.1 Solving Linear Systems by Graphing
 Name Class Date 11.1 Solving Linear Sstems b Graphing Essential Question: How can ou find the solution of a sstem of linear equations b graphing? Resource Locker Eplore Tpes of Sstems of Linear Equations
Name Class Date 11.1 Solving Linear Sstems b Graphing Essential Question: How can ou find the solution of a sstem of linear equations b graphing? Resource Locker Eplore Tpes of Sstems of Linear Equations
Nonlinear Systems. No solution One solution Two solutions. Solve the system by graphing. Check your answer.
 8-10 Nonlinear Sstems CC.9-1.A.REI.7 Solve a simple sstem consisting of a linear equation and a quadratic equation in two variables algebraicall and graphicall. Objective Solve sstems of equations in two
8-10 Nonlinear Sstems CC.9-1.A.REI.7 Solve a simple sstem consisting of a linear equation and a quadratic equation in two variables algebraicall and graphicall. Objective Solve sstems of equations in two
Section 3.1 Solving Linear Systems by Graphing
 Section 3.1 Solving Linear Sstems b Graphing Name: Period: Objective(s): Solve a sstem of linear equations in two variables using graphing. Essential Question: Eplain how to tell from a graph of a sstem
Section 3.1 Solving Linear Sstems b Graphing Name: Period: Objective(s): Solve a sstem of linear equations in two variables using graphing. Essential Question: Eplain how to tell from a graph of a sstem
MA 15800, Summer 2016 Lesson 25 Notes Solving a System of Equations by substitution (or elimination) Matrices. 2 A System of Equations
 MA 800, Summer 06 Lesson Notes Solving a Sstem of Equations b substitution (or elimination) Matrices Consider the graphs of the two equations below. A Sstem of Equations From our mathematics eperience,
MA 800, Summer 06 Lesson Notes Solving a Sstem of Equations b substitution (or elimination) Matrices Consider the graphs of the two equations below. A Sstem of Equations From our mathematics eperience,
Solving Systems Using Tables and Graphs
 3-1 Solving Sstems Using Tables and Graphs Vocabular Review 1. Cross out the equation that is NOT in slope-intercept form. 1 5 7 r 5 s a 5!3b 1 5 3 1 7 5 13 Vocabular Builder linear sstem (noun) LIN ee
3-1 Solving Sstems Using Tables and Graphs Vocabular Review 1. Cross out the equation that is NOT in slope-intercept form. 1 5 7 r 5 s a 5!3b 1 5 3 1 7 5 13 Vocabular Builder linear sstem (noun) LIN ee
MATH 1710 College Algebra Final Exam Review
 MATH 7 College Algebra Final Eam Review MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. ) There were 80 people at a pla. The admission price was $
MATH 7 College Algebra Final Eam Review MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. ) There were 80 people at a pla. The admission price was $
Final Exam Review. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Final Eam Review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Determine whether or not the relationship shown in the table is a function.
Final Eam Review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Determine whether or not the relationship shown in the table is a function.
Functions. Introduction
 Functions,00 P,000 00 0 70 7 80 8 0 000 00 00 Figure Standard and Poor s Inde with dividends reinvested (credit "bull": modification of work b Praitno Hadinata; credit "graph": modification of work b MeasuringWorth)
Functions,00 P,000 00 0 70 7 80 8 0 000 00 00 Figure Standard and Poor s Inde with dividends reinvested (credit "bull": modification of work b Praitno Hadinata; credit "graph": modification of work b MeasuringWorth)
A.5. Solving Equations. Equations and Solutions of Equations. Linear Equations in One Variable. What you should learn. Why you should learn it
 A46 Appendi A Review of Fundamental Concepts of Algebra A.5 Solving Equations What you should learn Identify different types of equations. Solve linear equations in one variable and equations that lead
A46 Appendi A Review of Fundamental Concepts of Algebra A.5 Solving Equations What you should learn Identify different types of equations. Solve linear equations in one variable and equations that lead
Summary and Vocabulary
 Chapter Chapter Summar and Vocabular Equations involving percents ma be written in the form p q = r, where p is the decimal form of the percent, q is the initial quantit, and r is the resulting quantit.
Chapter Chapter Summar and Vocabular Equations involving percents ma be written in the form p q = r, where p is the decimal form of the percent, q is the initial quantit, and r is the resulting quantit.
LESSON #1 - BASIC ALGEBRAIC PROPERTIES COMMON CORE ALGEBRA II
 1 LESSON #1 - BASIC ALGEBRAIC PROPERTIES COMMON CORE ALGEBRA II Mathematics has developed a language all to itself in order to clarif concepts and remove ambiguit from the analsis of problems. To achieve
1 LESSON #1 - BASIC ALGEBRAIC PROPERTIES COMMON CORE ALGEBRA II Mathematics has developed a language all to itself in order to clarif concepts and remove ambiguit from the analsis of problems. To achieve
Math 154A Elementary Algebra Fall 2014 Final Exam Study Guide
 Math A Elementar Algebra Fall 0 Final Eam Stud Guide The eam is on Tuesda, December 6 th from 6:00pm 8:0pm. You are allowed a scientific calculator and a " b 6" inde card for notes. On our inde card be
Math A Elementar Algebra Fall 0 Final Eam Stud Guide The eam is on Tuesda, December 6 th from 6:00pm 8:0pm. You are allowed a scientific calculator and a " b 6" inde card for notes. On our inde card be
Determinants. We said in Section 3.3 that a 2 2 matrix a b. Determinant of an n n Matrix
 3.6 Determinants We said in Section 3.3 that a 2 2 matri a b is invertible if and onl if its c d erminant, ad bc, is nonzero, and we saw the erminant used in the formula for the inverse of a 2 2 matri.
3.6 Determinants We said in Section 3.3 that a 2 2 matri a b is invertible if and onl if its c d erminant, ad bc, is nonzero, and we saw the erminant used in the formula for the inverse of a 2 2 matri.
Assessment Readiness. 28 Unit 1 MIXED REVIEW. 1. Look at each number. Is the number between 2π and
 MODULE 1 1. Look at each number. Is the number between π and 5? Select or for epressions A C. A. 6 _ 3 5π B. C. 3 5. Consider the number - 11 15. A. The number is rational. True False B. The number can
MODULE 1 1. Look at each number. Is the number between π and 5? Select or for epressions A C. A. 6 _ 3 5π B. C. 3 5. Consider the number - 11 15. A. The number is rational. True False B. The number can
