LATTICE POINTS ON THE PLANE AND THE DIOPHANTINE SYSTEM. By Konstantine Hermes Zelator. Page 1 of 27
|
|
|
- Madeleine Garrett
- 6 years ago
- Views:
Transcription
1 LATTICE POINTS ON THE PLANE AN THE IOPHANTINE SYSTEM B Konstntine Heres Zeltor Pge of 7
2 Lttie Points on the plne n the liner iophntine sste Introution In lost ever introutor nuer theor ook there is setion evote to the tretent of the liner iophntine eqution in two unknowns or vriles n n with integer oeffiients n.the wor iophntine refers to equtions to e solve in the set of integers usull enote Z. Also the se wor iophntine hs its histori erivtion in the ne of iophntos Greek thetiin (estite to hve live in the perio 5A-5A who live in Alenri Egpt. iophntos tkle rel life proles whose solution relie on the solution of ertin equtions to e solve in integers.the ooks Eleentr Nuer Theor with Applitions (see [] Kenneth Rosen n Clssil Alger (see[] Willi J.Gilert n Sott A.Vnstone re eellent ourses for the stuent who is unfilir with the ove liner iophntine eqution; the re replete with interesting eerises not onl on this topi ut throughout n the ephsie the oputtionl spets of nuer theor in ler n onise nner. As with ever other tetook wiih ontins presenttion of the ove eqution the oplete solution set is presente (pretri solutions in ters of n integer-vlue preter long with the relevnt onitions n fts. Fro geoetri perspetive when one tries to solve the iophntine eqution one hs the ojetive of eterining ll the lttie points if n tht lie on the stright line esrie the eqution.in given oorinte plne with oorinte es n lttie point ( is sipl point in whih oth oorintes n re integers. Lter on in this pper we will ke use of the pretri solution to the ove liner iophntine eqution. Now let us turn our ttention to three-iensionl spe equippe with oorinte sste of three utull perpeniulr or orthogonl es n ; n igine for oent lttie points ( in spe; tht woul e point with the rel nuers tull eing integers. The prole of eterining the set of ll lttie points tht lie on given plne esrie the eqution (with eing integers is tntount to fining ll integer solutions to the ove eqution. This eqution often rises in prtil proles s well. Onl rrel oes n Pge of 7
3 introutor nuer theor ook evote setion to this eqution. Even ore rrel oes it ontin setion on the sste of two (siultneous liner iophntine equtions Geoetrill speking we woul seek to fin the set of ll the lttie points whih lie on the intersetion line of two plnes. Of ourse there e not line of intersetion (prllel plnes or if there is one it not ontin n lttie points. This is then the i of this rtile: to present (in step--step nner the pretri solutions to the ove three-vrile iophntine eqution s well s the sste of the two three-vrile iophntine equtions; long with interesting oputtionl eples. The orgnition of this pper in sequentil setions is s follows:. Terinolog. Review: Solving the iophntine eqution 3. The Four For uls 4. Eples 5. Eplntions n Proofs 6. Chrt of Speil Cses. Terinolog A nottion of the for ( kl n e interprete three ws: s point in the oorinte plne (with es n ; seonl s the gretest oon ivisor of two integers k n l.an thirl s solution to the iophntine eqution (here we eep t the open intervl nottion. S n hve three enings: s point in spe (equippe with n oorinte sste s the gretest oon ivisor of three integers k l r or (thir ening s solution to the liner iophntine eqution or the iophntine sste iilrl nottion of the for ( k l r ( It will lws e ler fro the tet whether for eple k l r refers to the gretest oon ivisor of the integers k l r ; or to point in spe or solution to the ove tree vrile iophntine eqution or sste. Note tht the ifferene etween the enings of the triple ( k l r s point or s solution to the ove eqution (or sste is onl senti; for ll prtil purposes we regr the frist n the thir enings s inistinguishle. Thus the onl istintion tht nees to e e ler is tht etween Pge 3 of 7
4 ( k l rs point (or solution n s gretest oon ivisor of k l r we will e writing ( k l r or soe other letter. With regr to the nottion Z whih pper on osion throughout this pper it sipl ens elongs to the set Z or is eer of the set Z (in plin lnguge is n integer. Finll the onjuntive e use etween stteents whih sipl ens n. An one ore lrifition. If we stte tht the integer k ivies the integer l we will en tht k etl ivies l ; tht is k t l for soe t Z. The se ening we will ttriute to the epression k is ivisor of l. The nottion n lso e eploe k l ens k ivies l ".. Review: Solving the iophntine eqution First ssue tht oth n re nonero integers.the speil se (n the geoetri interprettion of (i.e. ( ( or ( is isusse in the speil ses setion.(setion 6 The grph esrie the eqution is slnt (stright line whose slope is equl to. The eqution hs solutions in the set of integers Z if n onl if the gretest oon ivisor ( is lso ivisor of : (. If oes not ivie then the set of solutions is the ept set (no solutions We hve ; the lst iophntine eqution is equivlent to the originl one; tht is the hve the se solution set. The two reue integers n re reltivel prie or oprie nother w of sing tht their gretest oon ivisor is equl to : iophntine eqution then ll the solutions re given. If ( is prtiulr solution to the ove liner Solution set S: ( (For further etils proof et see either of the two referenes [] or [] Where is n integer preter; in other wors n tke n integer vlue; we n sipl write Z.Thus for eh speifi integer vlue of new prtiulr solution is proue. Pge 4 of 7
5 So for ( (. Thus if we know one speifi or prtiulr solution ll the rest n e foun. But how oes one eterine prtiulr solution (? Soeties it is es to fin one inspetion or short tril n error proess espeill if the oeffiients n re sll in solutel vlue. But there is fil proof proeure tht works in ll ses lthough it severl steps in orer to rrive t prtiulr solution (.Essentill this proess is wht is known s the Eulien Algorith. We n eplin how it works without eoing unul theoretil. For sipliit let us put ;(.We hve the eqution. If or we re one; for eple s (i.e. or - n suppose.we solve for to otin. So the solution set S is given S: ( ( Z. A siilr piture eerges in the ses or. Now suppose tht > n >. Beuse of the onition ( it follows tht n ust e istint positive integers: either > or <. For the ske of isussion suppose tht < : we solve the eqution for (if it were > we woul solve for : We perfor the ivisions n ; we hve q r Q R : : Where qq re the quotients of the ivisions n r R the two reiners. As we know for the ivision theore r < n R <. We fin tht q ( q r ( Q R r R Q Oviousl for to e n integer the rtio r R r R. r R ust e n integer; s Pge 5 of 7
6 Note tht in the lst eqution R R <. Thus setting we n repet the proess solving for the vrile (whih is one tht hs the sller in solute vlue oeffiient. The Eulien Algorith ensures us tht the proess ust terinte fter finite nuer of steps otining in the lst stge n eqution of the for kn n μ whih hs the integer solution ( μ.b k sustitution we n tre prtiulr solution ( to eqution. Let us illustrte this with n eple. Consier the liner iophntine eqution 4 38 We hve 4 38; ( ( 4 ; n 59. The originl eqution is equivlent to Oviousl 5 5 < 7 7 so we solve for : The ivisions 59:5 n 7:5 iel 59(3(56 n 7((59. Therefore [(( 3 5 6] [(( 5 9] ; Net we set n liner iophntine eqution with unknowns 5 n ; we otin 5 9 6; 9 9 < 5 5so we solve for : ( Agin we set liner iophntine eqution in the unknowns n : 9 we hve ; note tht 3 3 < 9 6 n so solve for : Pge 6 of 7
7 ( ( 3 We oul ontinue for few ore steps till we get n eqution of the for k μ (whih hs the integer solution (μ ; ut it is not rell neessr for the n n lst iophntine eqution hs n ovious prtiulr solution: n. Tring k we fin n 3 3 ( 3 Thus ( ( 3 is prtiulr solution to the iophntine eqution n hene the originl one. All the solutions re given ; Solution set S((--735 Z In the Eples Setion in ll the eples (eept for one the prtiulr solutions re esil foun inspetion. However we wnte to give n illustrtion to the reer of how this proess works in less thn ovious ses. 3. The Four Foruls In foruls n 3 elow ssue tht the oeffiients re nonero (for the ses in whih see the Speil Cses Setion. Forul If t lest on of the positive integers is equl to (i.e. ± or ± or ± ll the solutions to the iophntine eqution n e otine erel solving for the orresponing vrile. For eple if solution set S : ( ( n n where n n re integer- vlue preters. While in the se - S : n n with n Z Solution set ( ( The net forul pertins to the se in whih > > > n t lest one of the gretest oon ivisors ((( is equl to. First oserve tht the iophntine eqution will hve solutions if n onl if the nuer ( is ivisor of. Otherwise if oes not ivie the eqution hs no integer solutions. If the given iophntine eqution is equivlent to Pge 7 of 7
8 ; n Beuse of the ove reution in Foruls n 3 we strt with n eqution whih is lre reue; ( Forul Assue ( > n t lest one of ( ( ( eing equl to. If ( ll the solutions to the iophntine eqution re given ( n ( n with n eing integervlue preters n ( eing solution to the liner iophntine eqution L ikewise if ( ll the solution n e epresse the two-preter foruls ( n ( n with ( eing solution to the eqution. S iilrl if ( ll the solutions n e given ( n with eing solution to ( n ( The net forul Forul 3 els with the ses in whih not onl eh of the three oeffiient is greter thn in solute vlue; ut lso eh of the gretest oon is greter thn (so we n not use Forul. ivisors ( ( ( There is ft fro nuer theor tht is use in Forul 3 nel (( ( for n nonero integers. We leve this s n eerise for the r eer to show. In our se ( (( Pge 8 of 7
9 Forul 3 Assue > n ( ( ( > n let ( All the solutions to the iophntine eqution re given the foruls n n ( t ( t Where n re integer-vlue preters ( is solution to the liner iophntine eqution ; iophntine eqution t. n ( t is solution to the liner To finish this setion we stt Forul 4 whih pertins to the iophntine sste entione in the introution. Forul 4 ssue tht t ost one of the si integers onsier the liner iophntine sste A is ero n here n re lso integers. i. If ε ε ε where ε or - then the ove eqution hs solutions if n onl if ε ; tht is if ε the solution set is the ept set; while for ε the solution set to the ove sste is equl to the solution set of the liner iophntine eqution whih n e solve with the i of Foruls or 3; provie tht ( is ivisor of (otherwise there re no solutions; if one of or hppens to e ero refer to the Speil Cses setion. W Pge 9 of 7
10 ii. Assue tht t lest one of the onitions ε ε ε hols true s well s ( (. Let 3 e the eterinnts respetivel of the tries : 3 n. n 3 n not oth e ero (see Eplntions n Proofs setion n so we n efine ( 3 3 n 3 Uner the onition (see notes n elow. The ove iophntine sste will hve solutions (i.e. nonept solution set onl if oth onitions stte elow re stisfie: Conition : The integer ivies (or is ivisor of the integer 3 Conition : is ivisor of the integer for n solution ( to the liner iophntine eqution 3 (see note 3. If oth onitions re et the solution set to the ove sste n e esrie λ λ λ 3 3 where λ is n integer-vlue preter n ( is solution to the liner iophntine eqution 3 (whih will hve solutions onition. Note : Note tht the nuer-frtion is inee n integer: n es 3 oputtion shows tht Oviousl oth n 3 re integers sine is the gretest oon ivisor of n 3.Siilrl the nuers n re 3 oth integers the ver efinition of the integer. Pge of 7
11 Note : We ssue sine if it were ; hpothesis we know tht t ost one of the oeffiient is ero n so neessit we woul hve.we n sipl rene the oeffiients: eoe n onversel. Note 3: With regr to Conition : It will either hol for ever solution none; this will eoe evient in the Eplntions n Proof setion. ( or for When one is fe with speifi liner iophntine eqution (or sste of two three or ore vriles one solve it without ppling n ssteti generl etho or foruls; ut if one follows ifferent pth for solving the ver se sste one en up with ifferent set of pretri foruls esriing the se solution set. Assuing tht no error ourre in the proess oth sets of pretri foruls woul e orret; the woul e equivlent: one oul in finite nuer of lgeri steps erive one fro the other. We ke this rerk in light of the possiilit tht soe reers wnt to eperient n iprovise with speifi liner iophntine equtions or sstes n isover this ft in their own eperiene. 4. Eples Below we present seven eples. Eple i. Fin the solutions to the iophntine eqution 3 4 ii. eterine the lttie points tht lie on the plne esrie the ove eqution n whih lso lie in the interior of or on the ounr of (sphere the ll whose enter is the origin ( n whose rius is R. Solution i We re in the siplest of ses nel those elt with Froul. We solve for to otin 3 4 ; solution set S : 3 4n where n re integer-vlue preters. ( ( n ii For point ( to lie insie or on the given ll it is neessr n suffiient tht its istne fro the enter not eee R; sine the enter is the point ( we ust hve 4 It follows tht 4 ( ( Pge of 7
12 These onitions re neessr ut not suffiient for point ( to lie in or on the given ll.the lous tht the lst three inequlities esrie is the set of ll points in spe whih lie insie or on the retngulr o whose ounr surfe is ue entere t ( n whose eges hve length The given ll is insrie in tht o. Appling prt (i we rrive t the neessr onitions ( 3 4n n. A quik serh n e one sstetill piking vlue of (-- n heking to see whether there re vlues of n stisfing the first n the thir inequlities. Seven points re proues: (-- (- (- ( (-- (-- n (-. However onl three lie in or the given ll (tull ll three lie insie the ll: (- ( (-- Eple In how n ws n person p the ount of 8 ents using onl ies nikels or qurters? Solution If is the nuer of ies the nuer of nikels n the nuer of qurters we ust hve We re seeking the nuer of nonnegtive solutions to the lst iophntine eqution; we ust hve whih le to the onstrints This is Forul se solving the eqution iels 6 5n n where n n re integer-vlue preters. Appling the onstrins iplies 8 5n 6 n 3 A serh proues etl twent solutions; the triples (6((6(3(4(9(4((7((3 (35(3(48(43(56(5(64(7 n (8 Therefore there re etl twent ws of ping the given ount. Eple 3 i Fin the integer solutions to the eqution ii Fin those lttie points tht lie on the plne esrie the eqution of prt (i n in the interior spe oune or on the ue whih is esrie the inequlities Pge of 7
13 Solution i. Sine (3 (37 (7 we n ppl Forul with ore thn one hoie; we ppl it with ( (3 ; in our se 3 7 n 3. All the solutions n e esrie ( n ( 3 7 n where n Z re the two preters n is n integer solution to the eqution 3. ( B inspetion ( ( is solution. Hene Solution set S : ( ( 3 7 3n3 7 n. ii. We ppl the onstrins to the solutions we foun: ( n n n 6 7 n ( A serh shows tht onl n 3 iel vlues of n tht stisf the first n seon inequlities. Speifill for we otin n -3 n n -4; while for the vlues of n re onl n -6; n for 3 those vlues of n re n - n n. Going k to the pretri foruls for n we otin etl five points. ( (3 (3 (4 ( 3 (-3 The thir point in the list lies in the interior spe oune the ue wheres the other four lie on the ue itself. Eple 4 Fin the solutions to the iophntine eqution Solution We hve thus (. Sine > 3 > 5 > n ( > the relevnt forul to use is Forul 3. ( ( First we nee to fin n integer solution ( where ( 3. to the liner eqution B inspetion the eqution 5 hs solution ( ( integer solution ( t ( Forul 3 we otin 3. Net we fin n is solution. Appling the pretri foruls in Solution set S:( (-6-3 5n - n 3 with n Z Chek: 6 (-6 3 5n -5 (- n ( 3 4 Pge 3 of 7
14 Eple Fin the solutions to the liner iophntine sste Solution We hve Note tht ( ( n ll the oeffiients re nonero. Also oviousl the requireent tht ± or ± or 3 ± 3 is stisfie so we n ppl Forul 4 prt (ii. We opute the four eterinnts to fin Also 3 3 ( 3 ( n ((3 ( We hek the two onitions: Conition : 3 oviousl ivies -35. So this onition is lso stisfie. Conition : First we fin solution ( to the eqution ; ( (53 is solution. We opute stisfie. whih is ivisile 3; so the onition is Thus the sste hs solutions. To fin the we ust fin solution ( eqution 3 ( ; to the liner ; n ovious solution is ( (4. Appling this together with the other infortion we lre hve to the foruls in Forul 4. we fin Solution set S : ( (5 λ 3 λ 4 48λ; λ Z Chek: 6 ( 5 λ 4( 3 λ 3( 4 48λ 3 An 3 ( 5 λ 6 ( 3 λ ( 4 48λ 5 Pge 4 of 7
15 Eple 6 Solve the iophntine sste Solution Oserve tht this sste flls in the tegor of the Speil Cses setion sine two of the si oeffiients re ero nel n. We n solve this sste first fining the generl solution to the seon eqution n sustituting (for into the first eqution. B inspetion is solution to the seon eqution. The generl solution n e given 7λ 5λ; λ Z Sustituting into the first eqution gives ( 5λ λ To fin solution ( λ to the lst eqution we solve for : we hve 55 λ 3λ 4λ λ Let t 3t λ 4t 3 t An ovious solution to the lst eqution is t λ 3λ 3 Thus 4λ We onlue tht ( λ ( is solution to the liner iophntine eqution 3 55λ. Hene ll integer solutions to the lst eqution re given -(-55 n λ 3. We sustitute for λ in the previous equtions for n to fin. Solution set S: ( ( Chek: 3(55 ( n -5 (-5-9 7( Eple 7 Let p e positive integer. i esrie the set of ll triples ( with the two properties. The su of the three integers is equl to p n. The integers (in tht orer re suessive ters of n ritheti progression. Pge 5 of 7
16 ii Wht onition ust p stisf in orer tht e positive integers? iii Fin the sllest vlue of p for whih re positive integers. iv Wht onitions ust p stisf in orer tht e the sie lengths of tringle? v For p 85 fin those triples ( with >. Whih of those triples orrespon to tringle with eing the sie lengths? Solution i if the nuers re onseutive ters of n ritheti progression the ile ter ust e the verge of the other two. Thus we otin the iophntine sste p p ( ( p ( p ( 7 p 4 3 3p 3[ ( ] 3p In the lst sste we solve the seon eqution for to otin 3 ; lerl 4 ( ( 9 p 3p is solution n so ll the solutions to the seon liner iophntine eqution re given 9 p 3 n 3p 4 where is n integer-vlue preter. Sustituting k in the first eqution (of the lst sste ove for we fin tht Solution set S ( ( 9 p 33 p 4 p 7 : Z ii Setting ( > > > ( 9 p 3 > 3p 4 > p 7 > 9 p 3p p < < < p 9 p sin e p > n < < < < is the neessr n suffiient onition for n to e positive integers. Wht this rell ss is tht in orer for n to e positive integers it is neessr n suffiient tht the open intervl p 9 l p p (here we use stnr prelulus/ 7 3 lulus nottion ontin t lest one integer. For eh suh vlue of the preter positive integer triple ( will e generte. Pge 6 of 7
17 iii iv An es lultion show tht p 3 is the sllest vlue of the (positive integer p for whih the intervl l p ontins n integer. For p l p l3 ; is the onl integer tht flls in l 3. For p 3 n 7 3 the foruls prt (i proue ( (. If ( orrespons to tringle the three tringle inequlities ust e stisfie: ( > > >. Note tht these three inequlities lone ipl > > > ( for eple the first two inequlities eer wise to otin >. This ens tht we shoul otin n intervl (tht epens on p whih ust ontin t lest one integer n whih is suintervl of the intervl otine in prt (ii. Inee using the ove three tringles inequlities n pretri foruls for ( in prt (i we now hve ( p 7 < p 7 8 p 3 > 9 p 3 p 4 > 3p 4 3p 7 p 5p > > > p 3p sin e p > n < < < We see tht the neessr n suffiient onition for ( to orrespon to 7 p 3p tringle is tht the open intervl J p ontin n integer No te s epete tht sine < < < the intervl J p lies entirel within (the intervl in prt (ii. l p v For p 85 l85 n J 85. Also sine we see tht the internl l ontins three integers; the integers ; wheres the intervl 85 J 85 ontins two integers nel Sustituting for p 85 n in the foruls in prt (i we fin tht ( (3737 (4734 (35 Pge 7 of 7
18 The first two triples orrespon to tringle ut the thir one oes not sine 3 34 is in ft less thn 5; this is s epete virtue of the ft tht the integer 58 oes not lie within the intervl J 85. Also note tht in prt (iii where we foun tht for p 3 there is one positive integer triple ( nel ( (; we see tht p 3 is lso the sllest vlue of p for whih triple ( orrespons to tringle; whih for p 3 is the equilterl tringle of sie lengthe. 5. Eplntions n Proofs. Of Forul Not uh to show here one sipl solves for the vrile whose oeffiient is or -.. Of forul We onl nee eplin the erivtion of Forul in the se (. Sine ( the liner iophntine eqution hs solutions let ( e prtiulr solution. We hve. We put where n e n integer; so tht [( ] [ ( ] (( whih shows tht the pir ( is solution to the liner iophntine eqution. Consequentl ll the integer solutions of the lst eqution re given ( n ( n n Z. But the initil iophntine eqution is oviousl equivlent to ( Z. Hene ll the solutions to the initil eqution re given ( n ( n where n re integervlue preters. We re one. 3. Of Forul 3 The iophntine eqution is equivlent to. Sine is the gretest oon ivisor of n we ust hve n where the integers n re reltivel prie; tht is. We see tht Clerl the lst eqution will hve solutions if n onl if is ivisor of -. Evientl the originl eqution is equivlent to the sste of iophntine equtions Pge 8 of 7
19 t t t t ( ( the vriles eing n t. Oserve tht eh eqution in the lst sste hs solutions: the first hs solutions sine. The seon eqution hs solutions s well virtue of ( (( ( whih is true hpothesis. If ( is n integer solution then oviousl ( t t t Z is solution to eqution (. Furtherore let ( t e prtiulr solution to (; then ll the integer solutions to eqution ( re given t t Z But for given integer vlue of t ( t t is prtiulr solution to eqution (; therefore ll the integer solutions to eqution ( while ( lso ho ls true n e esrie t n t n; where n Z n t t. We onlue tht the solution set to the originl eqution n e esrie ; ( t n ( t n Where n re integer-vlue preters ( iophntine eqution 4.. Of Forul 4 is prtiulr solution to the liner t prtiulr solution to t. n ( i This prt is ovious it is self-eplntor. ii First note tht the integers n 3 n not e oth ero: for if tht were the se we woul hve ; then none of oul e ero sine if one the were ero nother woul lso hve to e ero (for eple if then whih is not llowe hpothesis sine t ost one of the si oeffiients n e ero. Thus ll si oeffiients woul e nonero n so we woul hve Pge 9 of 7
20 ; ut lso ( where n re reltivel prie ( ( ( integers (i.e. n is the gretest oon ivisor of n ; thus whih iplies (see rerk ( μ μ λ λ for soe integers μ n λ ; we see tht μ λ ( n in view of the ssuptio n tht gretest oon ivisor of n is equl to we onlue or -; Likewise the hpothesis ( iplies or -. Oviousl there re four ointions of vlues of n ut in ll ses ε where ε or -. Consequentl ( ε ε ε ε Contrr to the ssuption of prt (ii. It is now ler tht t lest one of 3 ust e nonero n therefore their gretest oon ivisor 3 eists n is of ourse positive integer. We hve sine st n ( ties eq.plus 3 (3 (4 We see tht in orer for eqution (4 to hve integer solutions it is neessr n suffiient t ht 3 ( 3 e ivisor of in other wors onition ust hol true. Pge of 7
21 If is n integer solution to eqution (4 then ll integer solutions to (4 re given ( Z (5 Sustituting for n in eqution (4 iels ( n sine the quntit in the rkets in equl to 3 (see note we rrive t ( 3 (6 It is ler tht the originl iophntine sste is equivlent to the pir of equtions (5 n (6 in the vriles n. For eqution (6 to hve integer solutions it is neessr n suffiient tht 3 e ivisor of the integer ( ; in other wors onition ust hol true. The integer solutions to (6 given 3 λ λ where λ is n integer-vlue preter n prtiulr solution to (6. Sustituting for n in (5 we fin ( 3 3 λ λ 3 λ Pge of 7
22 Rerk. Note the ssuption ( (. Oviousl if we re given sste of two liner iophntine equtions in three vriles the first thing to o woul e hek whether the gretest oon evisor of the oeffiients of the unknowns in eh eqution ivies the orresponing onstnt ( or on the other sie of the eqution. If either eqution fils the test sste hs no integer solutions. If on the other hn oth eqution pss the test we reue eh eqution the ( iviing oth sies with so tht we hve ( for i i i i i Rerk. In the eplntions of forul 4 we e use of the following ft fro α γ nuer theor: if four non ero integers α β γ stisf the onitions n β α γ ( γ then ( α k γ β k for soe nonero integer k. Inee iplies β α βγ ; sine γ is reltivel prie to n γ ivies the proutα it ust ivie α ;this ft fro nuer theor is tpill overe in the first or 3 weeks of n introutor ourse in eleentr nuer theor. We hve α kγ for soe non ero integer k ; n froα βγ ( k γ βγ (sineγ β k. 6. Chrt of Speil Cses A. The liner iophntine eqution with. i If n then the eqution hs no solution if is not ivisor of. If on the other hn is evisor of then the solution set onsists of ll pirs of the for where Z(ll lttie points on the horiontl line. ii If n there re no solutions if is not ivisor of ; otherwise (if ivies solution set S : ( ( Z (ll lttie points on the vertil line iii If there re no solutions unless in whih se the solution set onsist of ll lttie points on the plne. Nel S : ( ( n n Z B. The liner iophntine eqution with. Let [ ] e the tri of the oeffiients. In eh group elow we onl present the solution for the first (s viewe fro left to right tri (of the oeffiients in the group. The others re trete siilrl. Pge of 7
23 i Group : Etl one of the oeffiients is ero. Possile tries re[ ]. [ ] [ ] [ : The eqution esries plne whih is prllel to or ontins the -is. If oes not ivie there re no solutions. If on the other hn ] ( ( ivies the solution set is given n n n S ; ( : Z n solution to (. ii Group : Two of the oeffiients re ero. The thir non ero [ ] [ ][ ] [ ]: If is not ivisor of there re no solutions. If oes ivie solution set n n S ; ( : Z. The eqution esries plne prllel or oinient to the - plne. iii Group 3: [ ] There re no solutions unless in whih se λ λ ( ( : n n S Z (ll lttie points in spe. C. The liner iophntine sste with t lest two of the oeffiients eing ero. Mtri of oeffiients is. Etl two of the si oeffiients re ero i Group: Two eros in olun. : Eh eqution esries plne tht is prllel to or ontins the -is. If or equivlentl ; then the sste hs no solutions unless in whih se the proleis reue to the single eqution with (see prt B se (i. Pge 3 of 7
24 If there re no solutions unless the integer ( is oon ivisor of the integers ( n ( ;if tht is the se solution set S ( : Z. ii Group : Two eros in row. : The first eqution esries plne prllel to of oinient with plne. If is not ivisor of the sste hs no integer solutions. If is ivisor of the sste will hve solutions onl if ( is ivisor of the integer ; in tht se ll the solutions re given ( : S where is solution to (. iii Group 3: Two eros not oth on the se row or olun. : If ( is not ivisor of the sste will hve no solutions.if is ivisor of the sste will hve solutions onl if is ivisor of the integer where n e n prtiulr solution to ; if tht is the se the solution set to the sste n e esrie ( λ : S n Pge 4 of 7
25 λ where is solution to ( n λ is n integer-vlue preter.. Etl three of the si oeffiients re ero i The two of the three eros re on the se olun n two ong the lie on the se row. Possile tries: : The first eqution esries plne prllel to or oinient with -plne; the seon eqution esries plne prllel to or ontining the - is. The sste will hve no solutions onl if not ivisor of. If on the other hn the sste will hve solutions onl if is ivisor of the integer. In tht se Solution set ( : S ii Two ong the three eros lies on the se row ut no two lie on the se olun. Possile tries: : The first eqution esries plne prllel to or oinient with the plne; the seon eqution esries plne prllel to or ontining the -is. If is not ivisor of there re no solutions. If on the other hn the sste will hve solutions onl if (. If tht is the se the solution set n e esrie Pge 5 of 7
26 S ( : Z; where is solution to (. iii Three eros on the row. : If there re no solutions while if the sste is reue to with whih hs lre een overe Foruls or Etl four of the si oeffiients re ero i Group : : There re solutions onl if n ; if so there re solutions onl if ; if tht is the se Solution set ( : n S where n Z (lttie points on the plne. ii Group : : The first eqution esrie plne prllel to or oinient with the plne while the seon eqution esries plne prllel to or oinient with -plne. There re solutions onl if n in whih se solution set ( : S ; Z iii Group 3: Pge 6 of 7
27 : If there re no solutions. If the se reues to prt B(i. iv Etl five of the si oeffiients re ero : If there re no solutions. If the se reues to prt B(ii. 5. All oeffiients re ero : If either or is non ero there re no solutions. If solution set S : ( ( n k ; n k in other wors eh lttie point in spe is solution. Referenes [] Kenneth Rosen Eleentr Nuer Theor with Applitions n eition Prentie Hll. [] Willi J. Gilert & Sott A. Vnstone Clssil Alger Wterloo Universit Press. Pge 7 of 7
Section 2.3. Matrix Inverses
 Mtri lger Mtri nverses Setion.. Mtri nverses hree si opertions on mtries, ition, multiplition, n sutrtion, re nlogues for mtries of the sme opertions for numers. n this setion we introue the mtri nlogue
Mtri lger Mtri nverses Setion.. Mtri nverses hree si opertions on mtries, ition, multiplition, n sutrtion, re nlogues for mtries of the sme opertions for numers. n this setion we introue the mtri nlogue
CS 491G Combinatorial Optimization Lecture Notes
 CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
Numbers and indices. 1.1 Fractions. GCSE C Example 1. Handy hint. Key point
 GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
MCH T 111 Handout Triangle Review Page 1 of 3
 Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
mywbut.com Lesson 13 Representation of Sinusoidal Signal by a Phasor and Solution of Current in R-L-C Series Circuits
 wut.co Lesson 3 Representtion of Sinusoil Signl Phsor n Solution of Current in R-L-C Series Circuits wut.co In the lst lesson, two points were escrie:. How sinusoil voltge wvefor (c) is generte?. How the
wut.co Lesson 3 Representtion of Sinusoil Signl Phsor n Solution of Current in R-L-C Series Circuits wut.co In the lst lesson, two points were escrie:. How sinusoil voltge wvefor (c) is generte?. How the
Factorising FACTORISING.
 Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
A Primer on Continuous-time Economic Dynamics
 Eonomis 205A Fll 2008 K Kletzer A Primer on Continuous-time Eonomi Dnmis A Liner Differentil Eqution Sstems (i) Simplest se We egin with the simple liner first-orer ifferentil eqution The generl solution
Eonomis 205A Fll 2008 K Kletzer A Primer on Continuous-time Eonomi Dnmis A Liner Differentil Eqution Sstems (i) Simplest se We egin with the simple liner first-orer ifferentil eqution The generl solution
for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx
![for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx](/thumbs/74/70408252.jpg) Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Vibration with more (than one) degrees of freedom (DOF) a) longitudinal vibration with 3 DOF. b) rotational (torsional) vibration with 3 DOF
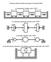 irtion with ore (thn one) degrees of freedo (DOF) ) longitudinl irtion with DOF ) rottionl (torsionl) irtion with DOF ) ending irtion with DOF d) the D (plnr) irtion of the fleil supported rigid od with
irtion with ore (thn one) degrees of freedo (DOF) ) longitudinl irtion with DOF ) rottionl (torsionl) irtion with DOF ) ending irtion with DOF d) the D (plnr) irtion of the fleil supported rigid od with
Mid-Term Examination - Spring 2014 Mathematical Programming with Applications to Economics Total Score: 45; Time: 3 hours
 Mi-Term Exmintion - Spring 0 Mthemtil Progrmming with Applitions to Eonomis Totl Sore: 5; Time: hours. Let G = (N, E) e irete grph. Define the inegree of vertex i N s the numer of eges tht re oming into
Mi-Term Exmintion - Spring 0 Mthemtil Progrmming with Applitions to Eonomis Totl Sore: 5; Time: hours. Let G = (N, E) e irete grph. Define the inegree of vertex i N s the numer of eges tht re oming into
Lecture 6: Coding theory
 Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
APPENDIX. Precalculus Review D.1. Real Numbers and the Real Number Line
 APPENDIX D Preclculus Review APPENDIX D.1 Rel Numers n the Rel Numer Line Rel Numers n the Rel Numer Line Orer n Inequlities Asolute Vlue n Distnce Rel Numers n the Rel Numer Line Rel numers cn e represente
APPENDIX D Preclculus Review APPENDIX D.1 Rel Numers n the Rel Numer Line Rel Numers n the Rel Numer Line Orer n Inequlities Asolute Vlue n Distnce Rel Numers n the Rel Numer Line Rel numers cn e represente
SIMPLE NONLINEAR GRAPHS
 S i m p l e N o n l i n e r G r p h s SIMPLE NONLINEAR GRAPHS www.mthletis.om.u Simple SIMPLE Nonliner NONLINEAR Grphs GRAPHS Liner equtions hve the form = m+ where the power of (n ) is lws. The re lle
S i m p l e N o n l i n e r G r p h s SIMPLE NONLINEAR GRAPHS www.mthletis.om.u Simple SIMPLE Nonliner NONLINEAR Grphs GRAPHS Liner equtions hve the form = m+ where the power of (n ) is lws. The re lle
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
50 AMC Lectures Problem Book 2 (36) Substitution Method
 0 AMC Letures Prolem Book Sustitution Metho PROBLEMS Prolem : Solve for rel : 9 + 99 + 9 = Prolem : Solve for rel : 0 9 8 8 Prolem : Show tht if 8 Prolem : Show tht + + if rel numers,, n stisf + + = Prolem
0 AMC Letures Prolem Book Sustitution Metho PROBLEMS Prolem : Solve for rel : 9 + 99 + 9 = Prolem : Solve for rel : 0 9 8 8 Prolem : Show tht if 8 Prolem : Show tht + + if rel numers,, n stisf + + = Prolem
EXTENSION OF THE GCD STAR OF DAVID THEOREM TO MORE THAN TWO GCDS CALVIN LONG AND EDWARD KORNTVED
 EXTENSION OF THE GCD STAR OF DAVID THEOREM TO MORE THAN TWO GCDS CALVIN LONG AND EDWARD KORNTVED Astrt. The GCD Str of Dvi Theorem n the numerous ppers relte to it hve lrgel een evote to shoing the equlit
EXTENSION OF THE GCD STAR OF DAVID THEOREM TO MORE THAN TWO GCDS CALVIN LONG AND EDWARD KORNTVED Astrt. The GCD Str of Dvi Theorem n the numerous ppers relte to it hve lrgel een evote to shoing the equlit
18.06 Problem Set 4 Due Wednesday, Oct. 11, 2006 at 4:00 p.m. in 2-106
 8. Problem Set Due Wenesy, Ot., t : p.m. in - Problem Mony / Consier the eight vetors 5, 5, 5,..., () List ll of the one-element, linerly epenent sets forme from these. (b) Wht re the two-element, linerly
8. Problem Set Due Wenesy, Ot., t : p.m. in - Problem Mony / Consier the eight vetors 5, 5, 5,..., () List ll of the one-element, linerly epenent sets forme from these. (b) Wht re the two-element, linerly
I 3 2 = I I 4 = 2A
 ECE 210 Eletril Ciruit Anlysis University of llinois t Chigo 2.13 We re ske to use KCL to fin urrents 1 4. The key point in pplying KCL in this prolem is to strt with noe where only one of the urrents
ECE 210 Eletril Ciruit Anlysis University of llinois t Chigo 2.13 We re ske to use KCL to fin urrents 1 4. The key point in pplying KCL in this prolem is to strt with noe where only one of the urrents
Counting Paths Between Vertices. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs
 Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
Solids of Revolution
 Solis of Revolution Solis of revolution re rete tking n re n revolving it roun n is of rottion. There re two methos to etermine the volume of the soli of revolution: the isk metho n the shell metho. Disk
Solis of Revolution Solis of revolution re rete tking n re n revolving it roun n is of rottion. There re two methos to etermine the volume of the soli of revolution: the isk metho n the shell metho. Disk
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
a) Read over steps (1)- (4) below and sketch the path of the cycle on a P V plot on the graph below. Label all appropriate points.
 Prole 3: Crnot Cyle of n Idel Gs In this prole, the strting pressure P nd volue of n idel gs in stte, re given he rtio R = / > of the volues of the sttes nd is given Finlly onstnt γ = 5/3 is given You
Prole 3: Crnot Cyle of n Idel Gs In this prole, the strting pressure P nd volue of n idel gs in stte, re given he rtio R = / > of the volues of the sttes nd is given Finlly onstnt γ = 5/3 is given You
m m m m m m m m P m P m ( ) m m P( ) ( ). The o-ordinte of the point P( ) dividing the line segment joining the two points ( ) nd ( ) eternll in the r
 CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
Algebra 2 Semester 1 Practice Final
 Alger 2 Semester Prtie Finl Multiple Choie Ientify the hoie tht est ompletes the sttement or nswers the question. To whih set of numers oes the numer elong?. 2 5 integers rtionl numers irrtionl numers
Alger 2 Semester Prtie Finl Multiple Choie Ientify the hoie tht est ompletes the sttement or nswers the question. To whih set of numers oes the numer elong?. 2 5 integers rtionl numers irrtionl numers
Differentiation of Polynomials
 C H A P T E R 9 Differentition of Polnomils Ojetives To unerstn te onept of it. To unerstn te efinition of ifferentition. To unerstn n use te nottion for te erivtive of polnomil funtion. To e le to fin
C H A P T E R 9 Differentition of Polnomils Ojetives To unerstn te onept of it. To unerstn te efinition of ifferentition. To unerstn n use te nottion for te erivtive of polnomil funtion. To e le to fin
Solutions for HW9. Bipartite: put the red vertices in V 1 and the black in V 2. Not bipartite!
 Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS
 Bull. Koren Mth. So. 35 (998), No., pp. 53 6 POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS YOUNG BAE JUN*, YANG XU AND KEYUN QIN ABSTRACT. We introue the onepts of positive
Bull. Koren Mth. So. 35 (998), No., pp. 53 6 POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS YOUNG BAE JUN*, YANG XU AND KEYUN QIN ABSTRACT. We introue the onepts of positive
1. Extend QR downwards to meet the x-axis at U(6, 0). y
 In the digrm, two stright lines re to be drwn through so tht the lines divide the figure OPQRST into pieces of equl re Find the sum of the slopes of the lines R(6, ) S(, ) T(, 0) Determine ll liner functions
In the digrm, two stright lines re to be drwn through so tht the lines divide the figure OPQRST into pieces of equl re Find the sum of the slopes of the lines R(6, ) S(, ) T(, 0) Determine ll liner functions
Let s divide up the interval [ ab, ] into n subintervals with the same length, so we have
![Let s divide up the interval [ ab, ] into n subintervals with the same length, so we have Let s divide up the interval [ ab, ] into n subintervals with the same length, so we have](/thumbs/79/79376941.jpg) III. INTEGRATION Eonomists seem muh more intereste in mrginl effets n ifferentition thn in integrtion. Integrtion is importnt for fining the epete vlue n vrine of rnom vriles, whih is use in eonometris
III. INTEGRATION Eonomists seem muh more intereste in mrginl effets n ifferentition thn in integrtion. Integrtion is importnt for fining the epete vlue n vrine of rnom vriles, whih is use in eonometris
Calculus Cheat Sheet. Integrals Definitions. where F( x ) is an anti-derivative of f ( x ). Fundamental Theorem of Calculus. dx = f x dx g x dx
 Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
CIT 596 Theory of Computation 1. Graphs and Digraphs
 CIT 596 Theory of Computtion 1 A grph G = (V (G), E(G)) onsists of two finite sets: V (G), the vertex set of the grph, often enote y just V, whih is nonempty set of elements lle verties, n E(G), the ege
CIT 596 Theory of Computtion 1 A grph G = (V (G), E(G)) onsists of two finite sets: V (G), the vertex set of the grph, often enote y just V, whih is nonempty set of elements lle verties, n E(G), the ege
Eigenvectors and Eigenvalues
 MTB 050 1 ORIGIN 1 Eigenvets n Eigenvlues This wksheet esries the lger use to lulte "prinipl" "hrteristi" iretions lle Eigenvets n the "prinipl" "hrteristi" vlues lle Eigenvlues ssoite with these iretions.
MTB 050 1 ORIGIN 1 Eigenvets n Eigenvlues This wksheet esries the lger use to lulte "prinipl" "hrteristi" iretions lle Eigenvets n the "prinipl" "hrteristi" vlues lle Eigenvlues ssoite with these iretions.
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Now we must transform the original model so we can use the new parameters. = S max. Recruits
 MODEL FOR VARIABLE RECRUITMENT (ontinue) Alterntive Prmeteriztions of the pwner-reruit Moels We n write ny moel in numerous ifferent ut equivlent forms. Uner ertin irumstnes it is onvenient to work with
MODEL FOR VARIABLE RECRUITMENT (ontinue) Alterntive Prmeteriztions of the pwner-reruit Moels We n write ny moel in numerous ifferent ut equivlent forms. Uner ertin irumstnes it is onvenient to work with
Exercise sheet 6: Solutions
 Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
H (2a, a) (u 2a) 2 (E) Show that u v 4a. Explain why this implies that u v 4a, with equality if and only u a if u v 2a.
 Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
( ) { } [ ] { } [ ) { } ( ] { }
![( ) { } [ ] { } [ ) { } ( ] { } ( ) { } [ ] { } [ ) { } ( ] { }](/thumbs/96/129291861.jpg) Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Basic Derivative Properties
 Bsic Derivtive Properties Let s strt this section by remining ourselves tht the erivtive is the slope of function Wht is the slope of constnt function? c FACT 2 Let f () =c, where c is constnt Then f 0
Bsic Derivtive Properties Let s strt this section by remining ourselves tht the erivtive is the slope of function Wht is the slope of constnt function? c FACT 2 Let f () =c, where c is constnt Then f 0
Necessary and sucient conditions for some two. Abstract. Further we show that the necessary conditions for the existence of an OD(44 s 1 s 2 )
 Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
22: Union Find. CS 473u - Algorithms - Spring April 14, We want to maintain a collection of sets, under the operations of:
 22: Union Fin CS 473u - Algorithms - Spring 2005 April 14, 2005 1 Union-Fin We wnt to mintin olletion of sets, uner the opertions of: 1. MkeSet(x) - rete set tht ontins the single element x. 2. Fin(x)
22: Union Fin CS 473u - Algorithms - Spring 2005 April 14, 2005 1 Union-Fin We wnt to mintin olletion of sets, uner the opertions of: 1. MkeSet(x) - rete set tht ontins the single element x. 2. Fin(x)
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
Mathematics SKE: STRAND F. F1.1 Using Formulae. F1.2 Construct and Use Simple Formulae. F1.3 Revision of Negative Numbers
 Mthemtis SKE: STRAND F UNIT F1 Formule: Tet STRAND F: Alger F1 Formule Tet Contents Setion F1.1 Using Formule F1. Construt nd Use Simple Formule F1.3 Revision of Negtive Numers F1.4 Sustitution into Formule
Mthemtis SKE: STRAND F UNIT F1 Formule: Tet STRAND F: Alger F1 Formule Tet Contents Setion F1.1 Using Formule F1. Construt nd Use Simple Formule F1.3 Revision of Negtive Numers F1.4 Sustitution into Formule
Data Structures LECTURE 10. Huffman coding. Example. Coding: problem definition
 Dt Strutures, Spring 24 L. Joskowiz Dt Strutures LEURE Humn oing Motivtion Uniquel eipherle oes Prei oes Humn oe onstrution Etensions n pplitions hpter 6.3 pp 385 392 in tetook Motivtion Suppose we wnt
Dt Strutures, Spring 24 L. Joskowiz Dt Strutures LEURE Humn oing Motivtion Uniquel eipherle oes Prei oes Humn oe onstrution Etensions n pplitions hpter 6.3 pp 385 392 in tetook Motivtion Suppose we wnt
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
CS 2204 DIGITAL LOGIC & STATE MACHINE DESIGN SPRING 2014
 S 224 DIGITAL LOGI & STATE MAHINE DESIGN SPRING 214 DUE : Mrh 27, 214 HOMEWORK III READ : Relte portions of hpters VII n VIII ASSIGNMENT : There re three questions. Solve ll homework n exm prolems s shown
S 224 DIGITAL LOGI & STATE MAHINE DESIGN SPRING 214 DUE : Mrh 27, 214 HOMEWORK III READ : Relte portions of hpters VII n VIII ASSIGNMENT : There re three questions. Solve ll homework n exm prolems s shown
Math 211A Homework. Edward Burkard. = tan (2x + z)
 Mth A Homework Ewr Burkr Eercises 5-C Eercise 8 Show tht the utonomous system: 5 Plne Autonomous Systems = e sin 3y + sin cos + e z, y = sin ( + 3y, z = tn ( + z hs n unstble criticl point t = y = z =
Mth A Homework Ewr Burkr Eercises 5-C Eercise 8 Show tht the utonomous system: 5 Plne Autonomous Systems = e sin 3y + sin cos + e z, y = sin ( + 3y, z = tn ( + z hs n unstble criticl point t = y = z =
THREE DIMENSIONAL GEOMETRY
 MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
CARLETON UNIVERSITY. 1.0 Problems and Most Solutions, Sect B, 2005
 RLETON UNIVERSIT eprtment of Eletronis ELE 2607 Swithing iruits erury 28, 05; 0 pm.0 Prolems n Most Solutions, Set, 2005 Jn. 2, #8 n #0; Simplify, Prove Prolem. #8 Simplify + + + Reue to four letters (literls).
RLETON UNIVERSIT eprtment of Eletronis ELE 2607 Swithing iruits erury 28, 05; 0 pm.0 Prolems n Most Solutions, Set, 2005 Jn. 2, #8 n #0; Simplify, Prove Prolem. #8 Simplify + + + Reue to four letters (literls).
y z A left-handed system can be rotated to look like the following. z
 Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
Lecture 2: Cayley Graphs
 Mth 137B Professor: Pri Brtlett Leture 2: Cyley Grphs Week 3 UCSB 2014 (Relevnt soure mteril: Setion VIII.1 of Bollos s Moern Grph Theory; 3.7 of Gosil n Royle s Algeri Grph Theory; vrious ppers I ve re
Mth 137B Professor: Pri Brtlett Leture 2: Cyley Grphs Week 3 UCSB 2014 (Relevnt soure mteril: Setion VIII.1 of Bollos s Moern Grph Theory; 3.7 of Gosil n Royle s Algeri Grph Theory; vrious ppers I ve re
Reflection Property of a Hyperbola
 Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
Section 10.2 Angles and Triangles
 117 Ojective #1: Section 10.2 nges n Tringes Unerstning efinitions of ifferent types of nges. In the intersection of two ines, the nges tht re cttycorner fro ech other re vertic nges. Vertic nges wi hve
117 Ojective #1: Section 10.2 nges n Tringes Unerstning efinitions of ifferent types of nges. In the intersection of two ines, the nges tht re cttycorner fro ech other re vertic nges. Vertic nges wi hve
Mathematical Proofs Table of Contents
 Mthemtil Proofs Tle of Contents Proof Stnr Pge(s) Are of Trpezoi 7MG. Geometry 8.0 Are of Cirle 6MG., 9 6MG. 7MG. Geometry 8.0 Volume of Right Cirulr Cyliner 6MG. 4 7MG. Geometry 8.0 Volume of Sphere Geometry
Mthemtil Proofs Tle of Contents Proof Stnr Pge(s) Are of Trpezoi 7MG. Geometry 8.0 Are of Cirle 6MG., 9 6MG. 7MG. Geometry 8.0 Volume of Right Cirulr Cyliner 6MG. 4 7MG. Geometry 8.0 Volume of Sphere Geometry
Linear Algebra Introduction
 Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Logic, Set Theory and Computability [M. Coppenbarger]
![Logic, Set Theory and Computability [M. Coppenbarger] Logic, Set Theory and Computability [M. Coppenbarger]](/thumbs/90/103901048.jpg) 14 Orer (Hnout) Definition 7-11: A reltion is qusi-orering (or preorer) if it is reflexive n trnsitive. A quisi-orering tht is symmetri is n equivlene reltion. A qusi-orering tht is nti-symmetri is n orer
14 Orer (Hnout) Definition 7-11: A reltion is qusi-orering (or preorer) if it is reflexive n trnsitive. A quisi-orering tht is symmetri is n equivlene reltion. A qusi-orering tht is nti-symmetri is n orer
Introduction to Algebra - Part 2
 Alger Module A Introduction to Alger - Prt Copright This puliction The Northern Alert Institute of Technolog 00. All Rights Reserved. LAST REVISED Oct., 008 Introduction to Alger - Prt Sttement of Prerequisite
Alger Module A Introduction to Alger - Prt Copright This puliction The Northern Alert Institute of Technolog 00. All Rights Reserved. LAST REVISED Oct., 008 Introduction to Alger - Prt Sttement of Prerequisite
are coplanar. ˆ ˆ ˆ and iˆ
 SML QUSTION Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor ii The question pper onsists of 6 questions divided into three Setions, B nd C iii Question No
SML QUSTION Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor ii The question pper onsists of 6 questions divided into three Setions, B nd C iii Question No
21.1 Using Formulae Construct and Use Simple Formulae Revision of Negative Numbers Substitution into Formulae
 MEP Jmi: STRAND G UNIT 1 Formule: Student Tet Contents STRAND G: Alger Unit 1 Formule Student Tet Contents Setion 1.1 Using Formule 1. Construt nd Use Simple Formule 1.3 Revision of Negtive Numers 1.4
MEP Jmi: STRAND G UNIT 1 Formule: Student Tet Contents STRAND G: Alger Unit 1 Formule Student Tet Contents Setion 1.1 Using Formule 1. Construt nd Use Simple Formule 1.3 Revision of Negtive Numers 1.4
M344 - ADVANCED ENGINEERING MATHEMATICS
 M3 - ADVANCED ENGINEERING MATHEMATICS Lecture 18: Lplce s Eqution, Anltic nd Numericl Solution Our emple of n elliptic prtil differentil eqution is Lplce s eqution, lso clled the Diffusion Eqution. If
M3 - ADVANCED ENGINEERING MATHEMATICS Lecture 18: Lplce s Eqution, Anltic nd Numericl Solution Our emple of n elliptic prtil differentil eqution is Lplce s eqution, lso clled the Diffusion Eqution. If
Surds and Indices. Surds and Indices. Curriculum Ready ACMNA: 233,
 Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Matrices SCHOOL OF ENGINEERING & BUILT ENVIRONMENT. Mathematics (c) 1. Definition of a Matrix
 tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
2.4 Theoretical Foundations
 2 Progrmming Lnguge Syntx 2.4 Theoretil Fountions As note in the min text, snners n prsers re se on the finite utomt n pushown utomt tht form the ottom two levels of the Chomsky lnguge hierrhy. At eh level
2 Progrmming Lnguge Syntx 2.4 Theoretil Fountions As note in the min text, snners n prsers re se on the finite utomt n pushown utomt tht form the ottom two levels of the Chomsky lnguge hierrhy. At eh level
Particle Physics. Michaelmas Term 2011 Prof Mark Thomson. Handout 3 : Interaction by Particle Exchange and QED. Recap
 Prtile Physis Mihelms Term 2011 Prof Mrk Thomson g X g X g g Hnout 3 : Intertion y Prtile Exhnge n QED Prof. M.A. Thomson Mihelms 2011 101 Rep Working towrs proper lultion of ey n sttering proesses lnitilly
Prtile Physis Mihelms Term 2011 Prof Mrk Thomson g X g X g g Hnout 3 : Intertion y Prtile Exhnge n QED Prof. M.A. Thomson Mihelms 2011 101 Rep Working towrs proper lultion of ey n sttering proesses lnitilly
Integration. antidifferentiation
 9 Integrtion 9A Antidifferentition 9B Integrtion of e, sin ( ) nd os ( ) 9C Integrtion reognition 9D Approimting res enlosed funtions 9E The fundmentl theorem of integrl lulus 9F Signed res 9G Further
9 Integrtion 9A Antidifferentition 9B Integrtion of e, sin ( ) nd os ( ) 9C Integrtion reognition 9D Approimting res enlosed funtions 9E The fundmentl theorem of integrl lulus 9F Signed res 9G Further
Section - 2 MORE PROPERTIES
 LOCUS Section - MORE PROPERTES n section -, we delt with some sic properties tht definite integrls stisf. This section continues with the development of some more properties tht re not so trivil, nd, when
LOCUS Section - MORE PROPERTES n section -, we delt with some sic properties tht definite integrls stisf. This section continues with the development of some more properties tht re not so trivil, nd, when
R(3, 8) P( 3, 0) Q( 2, 2) S(5, 3) Q(2, 32) P(0, 8) Higher Mathematics Objective Test Practice Book. 1 The diagram shows a sketch of part of
 Higher Mthemtics Ojective Test Prctice ook The digrm shows sketch of prt of the grph of f ( ). The digrm shows sketch of the cuic f ( ). R(, 8) f ( ) f ( ) P(, ) Q(, ) S(, ) Wht re the domin nd rnge of
Higher Mthemtics Ojective Test Prctice ook The digrm shows sketch of prt of the grph of f ( ). The digrm shows sketch of the cuic f ( ). R(, 8) f ( ) f ( ) P(, ) Q(, ) S(, ) Wht re the domin nd rnge of
MATH 122, Final Exam
 MATH, Finl Exm Winter Nme: Setion: You must show ll of your work on the exm pper, legily n in etil, to reeive reit. A formul sheet is tthe.. (7 pts eh) Evlute the following integrls. () 3x + x x Solution.
MATH, Finl Exm Winter Nme: Setion: You must show ll of your work on the exm pper, legily n in etil, to reeive reit. A formul sheet is tthe.. (7 pts eh) Evlute the following integrls. () 3x + x x Solution.
Section 6.3 The Fundamental Theorem, Part I
 Section 6.3 The Funmentl Theorem, Prt I (3//8) Overview: The Funmentl Theorem of Clculus shows tht ifferentition n integrtion re, in sense, inverse opertions. It is presente in two prts. We previewe Prt
Section 6.3 The Funmentl Theorem, Prt I (3//8) Overview: The Funmentl Theorem of Clculus shows tht ifferentition n integrtion re, in sense, inverse opertions. It is presente in two prts. We previewe Prt
y = c 2 MULTIPLE CHOICE QUESTIONS (MCQ's) (Each question carries one mark) is...
 . Liner Equtions in Two Vriles C h p t e r t G l n e. Generl form of liner eqution in two vriles is x + y + 0, where 0. When we onsier system of two liner equtions in two vriles, then suh equtions re lle
. Liner Equtions in Two Vriles C h p t e r t G l n e. Generl form of liner eqution in two vriles is x + y + 0, where 0. When we onsier system of two liner equtions in two vriles, then suh equtions re lle
5.3 The Fundamental Theorem of Calculus
 CHAPTER 5. THE DEFINITE INTEGRAL 35 5.3 The Funmentl Theorem of Clculus Emple. Let f(t) t +. () Fin the re of the region below f(t), bove the t-is, n between t n t. (You my wnt to look up the re formul
CHAPTER 5. THE DEFINITE INTEGRAL 35 5.3 The Funmentl Theorem of Clculus Emple. Let f(t) t +. () Fin the re of the region below f(t), bove the t-is, n between t n t. (You my wnt to look up the re formul
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
SEMI-EXCIRCLE OF QUADRILATERAL
 JP Journl of Mthemtil Sienes Volume 5, Issue &, 05, Pges - 05 Ishn Pulishing House This pper is ville online t http://wwwiphsiom SEMI-EXCIRCLE OF QUADRILATERAL MASHADI, SRI GEMAWATI, HASRIATI AND HESY
JP Journl of Mthemtil Sienes Volume 5, Issue &, 05, Pges - 05 Ishn Pulishing House This pper is ville online t http://wwwiphsiom SEMI-EXCIRCLE OF QUADRILATERAL MASHADI, SRI GEMAWATI, HASRIATI AND HESY
Inspiration and formalism
 Inspirtion n formlism Answers Skills hek P(, ) Q(, ) PQ + ( ) PQ A(, ) (, ) grient ( ) + Eerise A opposite sies of regulr hegon re equl n prllel A ED i FC n ED ii AD, DA, E, E n FC No, sies of pentgon
Inspirtion n formlism Answers Skills hek P(, ) Q(, ) PQ + ( ) PQ A(, ) (, ) grient ( ) + Eerise A opposite sies of regulr hegon re equl n prllel A ED i FC n ED ii AD, DA, E, E n FC No, sies of pentgon
Here we consider the matrix transformation for a square matrix from a geometric point of view.
 Section. he Mgnifiction Fctor In Section.5 we iscusse the mtri trnsformtion etermine mtri A. For n m n mtri A the function f(c) = Ac provies corresponence etween vectors in R n n R m. Here we consier the
Section. he Mgnifiction Fctor In Section.5 we iscusse the mtri trnsformtion etermine mtri A. For n m n mtri A the function f(c) = Ac provies corresponence etween vectors in R n n R m. Here we consier the
Solutions to Problem Set #1
 CSE 233 Spring, 2016 Solutions to Prolem Set #1 1. The movie tse onsists of the following two reltions movie: title, iretor, tor sheule: theter, title The first reltion provies titles, iretors, n tors
CSE 233 Spring, 2016 Solutions to Prolem Set #1 1. The movie tse onsists of the following two reltions movie: title, iretor, tor sheule: theter, title The first reltion provies titles, iretors, n tors
Solutions to Assignment 1
 MTHE 237 Fll 2015 Solutions to Assignment 1 Problem 1 Find the order of the differentil eqution: t d3 y dt 3 +t2 y = os(t. Is the differentil eqution liner? Is the eqution homogeneous? b Repet the bove
MTHE 237 Fll 2015 Solutions to Assignment 1 Problem 1 Find the order of the differentil eqution: t d3 y dt 3 +t2 y = os(t. Is the differentil eqution liner? Is the eqution homogeneous? b Repet the bove
The Ellipse. is larger than the other.
 The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
The Legacy of Pythagoras Theorem
 Prol Volue 39, Issue 1(2003) The Legy of Pythgors Theore Peter G.rown 1 When sked wht thetil result they reeer fro High Shool, the verge person would proly reply with Pythgors Theore. In ny right tringle,
Prol Volue 39, Issue 1(2003) The Legy of Pythgors Theore Peter G.rown 1 When sked wht thetil result they reeer fro High Shool, the verge person would proly reply with Pythgors Theore. In ny right tringle,
If we have a function f(x) which is well-defined for some a x b, its integral over those two values is defined as
 Y. D. Chong (26) MH28: Complex Methos for the Sciences 2. Integrls If we hve function f(x) which is well-efine for some x, its integrl over those two vlues is efine s N ( ) f(x) = lim x f(x n ) where x
Y. D. Chong (26) MH28: Complex Methos for the Sciences 2. Integrls If we hve function f(x) which is well-efine for some x, its integrl over those two vlues is efine s N ( ) f(x) = lim x f(x n ) where x
2.4 Linear Inequalities and Interval Notation
 .4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
.4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
Section 4: Integration ECO4112F 2011
 Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
Reference : Croft & Davison, Chapter 12, Blocks 1,2. A matrix ti is a rectangular array or block of numbers usually enclosed in brackets.
 I MATRIX ALGEBRA INTRODUCTION TO MATRICES Referene : Croft & Dvison, Chpter, Blos, A mtri ti is retngulr rr or lo of numers usull enlosed in rets. A m n mtri hs m rows nd n olumns. Mtri Alger Pge If the
I MATRIX ALGEBRA INTRODUCTION TO MATRICES Referene : Croft & Dvison, Chpter, Blos, A mtri ti is retngulr rr or lo of numers usull enlosed in rets. A m n mtri hs m rows nd n olumns. Mtri Alger Pge If the
For a, b, c, d positive if a b and. ac bd. Reciprocal relations for a and b positive. If a > b then a ab > b. then
 Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
, MATHS H.O.D.: SUHAG R.KARIYA, BHOPAL, CONIC SECTION PART 8 OF
 DOWNLOAD FREE FROM www.tekoclsses.com, PH.: 0 903 903 7779, 98930 5888 Some questions (Assertion Reson tpe) re given elow. Ech question contins Sttement (Assertion) nd Sttement (Reson). Ech question hs
DOWNLOAD FREE FROM www.tekoclsses.com, PH.: 0 903 903 7779, 98930 5888 Some questions (Assertion Reson tpe) re given elow. Ech question contins Sttement (Assertion) nd Sttement (Reson). Ech question hs
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
ON AN INEQUALITY FOR THE MEDIANS OF A TRIANGLE
 Journl of Siene nd Arts Yer, No. (9), pp. 7-6, OIGINAL PAPE ON AN INEQUALITY FO THE MEDIANS OF A TIANGLE JIAN LIU Mnusript reeived:.5.; Aepted pper:.5.; Pulished online: 5.6.. Astrt. In this pper, we give
Journl of Siene nd Arts Yer, No. (9), pp. 7-6, OIGINAL PAPE ON AN INEQUALITY FO THE MEDIANS OF A TIANGLE JIAN LIU Mnusript reeived:.5.; Aepted pper:.5.; Pulished online: 5.6.. Astrt. In this pper, we give
Counting intersections of spirals on a torus
 Counting intersections of spirls on torus 1 The problem Consider unit squre with opposite sides identified. For emple, if we leve the centre of the squre trveling long line of slope 2 (s shown in the first
Counting intersections of spirls on torus 1 The problem Consider unit squre with opposite sides identified. For emple, if we leve the centre of the squre trveling long line of slope 2 (s shown in the first
3 Angle Geometry. 3.1 Measuring Angles. 1. Using a protractor, measure the marked angles.
 3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
LINEAR ALGEBRA APPLIED
 5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
Section 2.1 Special Right Triangles
 Se..1 Speil Rigt Tringles 49 Te --90 Tringle Setion.1 Speil Rigt Tringles Te --90 tringle (or just 0-60-90) is so nme euse of its ngle mesures. Te lengts of te sies, toug, ve very speifi pttern to tem
Se..1 Speil Rigt Tringles 49 Te --90 Tringle Setion.1 Speil Rigt Tringles Te --90 tringle (or just 0-60-90) is so nme euse of its ngle mesures. Te lengts of te sies, toug, ve very speifi pttern to tem
Chapter17. Congruence and transformations. Contents: A Transformations B Congruent figures C Congruent triangles D Proof using congruence
 hpter17 ongruene nd trnsfortions ontents: Trnsfortions ongruent figures ongruent tringles Proof using ongruene 352 ONGRUENE N TRNSFORMTIONS (hpter 17) Opening prole Jne ut two tringulr slies of heeseke,
hpter17 ongruene nd trnsfortions ontents: Trnsfortions ongruent figures ongruent tringles Proof using ongruene 352 ONGRUENE N TRNSFORMTIONS (hpter 17) Opening prole Jne ut two tringulr slies of heeseke,
Matrix- System of rows and columns each position in a matrix has a purpose. 5 Ex: 5. Ex:
 Mtries Prelulus Mtri- Sstem of rows n olumns eh position in mtri hs purpose. Element- Eh vlue in the mtri mens the element in the n row, r olumn Dimensions- How mn rows b number of olumns Ientif the element:
Mtries Prelulus Mtri- Sstem of rows n olumns eh position in mtri hs purpose. Element- Eh vlue in the mtri mens the element in the n row, r olumn Dimensions- How mn rows b number of olumns Ientif the element:
Calculus Module C21. Areas by Integration. Copyright This publication The Northern Alberta Institute of Technology All Rights Reserved.
 Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
Applications of Definite Integral
 Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
List all of the possible rational roots of each equation. Then find all solutions (both real and imaginary) of the equation. 1.
 Mth Anlysis CP WS 4.X- Section 4.-4.4 Review Complete ech question without the use of grphing clcultor.. Compre the mening of the words: roots, zeros nd fctors.. Determine whether - is root of 0. Show
Mth Anlysis CP WS 4.X- Section 4.-4.4 Review Complete ech question without the use of grphing clcultor.. Compre the mening of the words: roots, zeros nd fctors.. Determine whether - is root of 0. Show
F / x everywhere in some domain containing R. Then, + ). (10.4.1)
 0.4 Green's theorem in the plne Double integrls over plne region my be trnsforme into line integrls over the bounry of the region n onversely. This is of prtil interest beuse it my simplify the evlution
0.4 Green's theorem in the plne Double integrls over plne region my be trnsforme into line integrls over the bounry of the region n onversely. This is of prtil interest beuse it my simplify the evlution
