BENFORD'S LAW AND PSYCHOLOGICAL BARRIERS IN. CERTAIN ebay AUCTIONS
|
|
|
- Robyn Roberts
- 6 years ago
- Views:
Transcription
1 Eoomeris Workig Pper EWP0606 ISSN eprme of Eoomis BENFOR'S LAW AN PSYCHOLOGICAL BARRIERS IN CERTAIN eby AUCTIONS Oe F Lu & vid E. Giles* Asr eprme of Eoomis, Uiversiy of Viori Viori, B.C., Cd V8W Y Sepemer, 006 Usig geerlizios of Beford s Lw we es for he see of psyhologil rriers vrious prie levels i eby uios for professiol fooll ikes. Our empiril resuls idie h his hypohesis o e rejeed. Keywords: JEL Clssifiios: Psyhologil rriers, uio pries, Beford s lw C, C6, 44 * We re greful o Sophie Heslig for her ssise wih d olleio, d o o Ferguso for his helpful ommes.. Iroduio Auhor Co: vid Giles, ep. of Eoomis, Uiversiy of Viori, P.O. Box 700, STN CSC, Viori, B.C., Cd V8W Y; e-mil: dgiles@uvi.; FAX: (50) 7-64
2 . Iroduio Severl sudies hve ivesiged he possiiliy of psyhologil rriers or resise levels i fiil mrkes. os of hese sudies (e.g., oldso d Kim, 993; Ley d Vri, 994; Koedijk d Sork, 994; d Cyree e l., 999) ssume h he digis of he ssoied pries re uiformly disriued. However, e Ceuser e l. (997) use Beford s Lw o show h his ssumpio is ipproprie, d heir lysis quesios previous fidigs of suh rriers. I is url o sk wheher here re similr resise levels i oher mrkes, d uio prie d provides oe soure of iformio o ddress his quesio. Why wo eri idders go higher h some prie level? Wh re he hresholds for he ids? We lyze eby uio d for professiol fooll ikes d fid o sisil evidee of psyhologil rriers vriey of levels. The mehism ehid his reserh is o exr he sigifi digis of he uio pries o exmie wheher heir disriuios follow geerlized versios of Beford s Lw, whih re irodued i seio. Seio 3 desries our d d he use of -vlues defied y e Ceuser e l. (997) o pure iformio ou he relive proximiy o psyhologil rrier. Our empiril es resuls pper i seio 4, d some oludig remrks re give i seio 5.. Beford s Lw Beford (938) re-disovered Newom s (88) fidig h my urlly ourrig umeril d exhii speil feures wih regrd o he firs sigifi digi. He showed h he disriuio of firs sigifi digis is o-uiform. Beford s Lw idies h i umers from my rel-life d soures, he firs sigifi digi ours wih proiliy of lmos 3%, o.% (/9). The igger he digi, he less likely i is o our s he firs sigifi digi. Speifilly, le deoe he firs sigifi digi i umer N. If N = 95, he = 9; if N = , he = 4. Beford s Lw ses h Pr 0 k.[ = k] = log [ + (/ )] ; k =,,., 9. Wh is less well kow is h he joi disriuio for seod d higher sigifi digis is k i Pr.[ = d,..., k = dk ] = log0[ + ( di 0 ) ], k i=
3 for d {,,...,9} d d {0,,,...,9}, j >. So, he proiliy of he firs hree sigifi i j digis eig 5, d 8 is log 0 [ + ] = This disriuio is ivri o sle 58 (Pikhm, 96). Sok pries d x d (Geyer d Willimso, 004; Nigrii, 99; Nigrii d iermier 997) oey Beford s Lw, s do wiig ids for eri eby uios (Giles, 006). Beford s Lw provides foudio for esig for resise levels i mrkes. e Ceuser e l. (997) proposed es for psyhologil rriers usig ylil permuios of he oserved dily sok reurs d oluded h here ws o evidee of psyhologil rriers i vrious U.S., U.K. d Jpese sok mrke idies. Aggrwl d Luey (006) lysed gold pries i similr wy d foud evidee h psyhologil rriers he 00 s digis (prie levels suh s $00, $300, e.). 3. d -sisis Giles (006) hs show h he losig pries of suessful eby uios for pro-fooll gme ikes sisfy Beford s Lw, whih suggess he see of mrke ollusio mog idders or ierveio y sellers. Usig his d, our smple omprises ll,59 suessful uios for ikes for professiol U.S. fooll gmes i he eby eve ikes egory ewee 5 Novemer d eemer 004. As Beford s Lw is sisfied, we use hese d o osru sisis for esig for he exisee of vrious psyhologil rriers. We deoe he suessful uio pries s P, =,,, wih =,59. We osider poeil rriers he levels, 300, 400,, e. (oldso, 990; oldso d Kim, 993; Ley d Vri, 994; e Ceuser e l., 997), or: k 00, k =,,.., e. () I order o represe psyhologil rriers ll levels, we should osider rriers he levels, 0, 0,, 00, 00,,000, 0000,, e., for k 0, k =,,, 9; =, -, 0,, ; () or he more omprehesive se of levels, 0,,,, 00, 0,, 000, 00,, e., for k 0, k = 0,,, 99; =, -, 0,,. (3) We he eed o defie -vlues, whih re me o rry he iformio o he relive loseess o rrier. Correspodig o he ove levels defied i equio (), 3
4 = [ P]mod00, () where [P ] is he ieger pr of he pries, mod00 sds for modulo 00, d lerly, he vlues re mde up of he pir of rilig digis preedig he deiml poi. For rriers he levels defied y equio () d (3), he -vlues re (log p )mod [00 0 ]mod00 = (log P )mod [000 0 ]mod00 = (3) () seles he pir of digis i P preedig he deiml poi; seles he seod d hird sigifi digis; d piks he hird d fourh sigifi digis. y reserhers wrogly ssume h he -vlues re uiformly disriued i he see of psyhologil rrier, les i lrge smples. e Ceuser e l. (997) derived of he limi disriuios of he -vlues, whih we hve pplied i pr of he followig lysis: r + 0 limpr.( ) lim log i + + r = r k = k = L = (4) r i 00 = i= i = i + r = r k 9 i 0 + k + limpr.( = k) = log (5) i= i 0 + k i 0 + j 0 + k + limpr.( = k) = log. (6) 3 i= j = 0 i 0 + j 0 + k The limi proiliies i equios (4), (5) d (6) give us he relive frequeies over he smple =,,, of he -vlues whe here re o psyhologil rriers i he mrke, d he smple size eds o ifiiy. The frequeies for he -vlues i our d re expeed o e o-uiform for d, d uiform for. Alhough he uiformiy of seems o riolize he sdrd ssumpio of uiformiy esig for he presee of psyhologil rriers, oly pure psyhologil rriers he levels, 00, 300,, 3400, 3500,., e., d he series hose levels is o mulipliively regeerive (e Ceuser e l., 997). Therefore, resuls h re oied from ivesigig oly he he wrog olusio, d i is ruil h he d vlues ould led o vlues re lso osidered. 4
5 4. Tes resuls Firs, we es wheher our d exhii properies osise wih he limi disriuios i equios (4) (6). The ull hypohesis is h here re o psyhologil rriers i pries for pro-fooll ikes i he eby uio mrke. The Kolmogorov-Smirov (K-S) es d oher o-prmeri ess suh s iegred deviios ess of he Crmér-vo ises ype re o pproprie here euse of he irulr ure of our d (Giles, 006). Kuiper s es is similr o he fmilir K-S es, whih uses he differee sisis omies + d + d. Kuiper's es io oe sisi, mkig he es s sesiive i he ils s he medi, d mkig i ivri uder ylil d rsformios. If he empiril disriuio fuio for he smple is F (x), d he ull populio disriuio fuio is F ( ) 0 x, Kuiper s es sisi is: where V, + = + + = sup. ( F ( x) F0 ( x)) < x< = sup. ( F0 ( x) F ( x)) < x<. Aoher impor feure of Kuiper s es is h he ull disriuio of he es sisi is ivri o he hypohesized disriuio, for ll. Sephes (970) ules riil vlues for he ull disriuio of he rsformed sisi V / = V ( * /. ) The 0%, 5% d % riil vlues re.60,.747 d.00 respeively, for ll. Our vlues for, d re 0.947,.663 d 4.0 respeively. So, our vlues for d re osise wih he hypohesis of o psyhologil rriers, he 5% level, u our vlue for implies rejeio of his hypohesis gis he mos geerl of he lerive hypoheses osidered. * V Our goodess-of-fi ess re desiged o exmie wheher he empiril d hve hrerisis osise wih he limi disriuios for he -vlues disussed ove. e Ceuser e l. (997) 5
6 show h exremely lrge smple sizes re eeded for hese limi disriuios o e pplile, d he fiie-smple disriuios re d-depede. We follow e Ceuser e l. (998) d lso es for psyhologil rriers usig ylil permuios of he d. Psyhologil rriers geere ormlly low umer of -vlues i he 00 regio. Le Ψ e se of -vlues i he eighourhood of psyhologil rrier, suh s Ψ = {00}, Ψ = {99, 00, 0}, e. For some Ψ, he uio prie P is i eighourhood of psyhologil rrier if Ψ. Le I Ψ ( ) = i his se, zero oherwise, d defie ψ = = I Ψ ( ). For y d Ψ, suffiiely smll ψ sigls psyhologil rrier. The disriuio of ψ is d-speifi, u p-vlues for he hypohesis of o psyhologil rrier e oosrpped s he proporio of oosrpped ψ vlues less h he empiril ψ. Our experimel resuls, for 0,000 repeiios, pper i Tle. The ull hypohesis of o psyhologil rriers i he uio pries for fooll ikes o e rejeed. 5. Colusios Usig some geerlizios of Beford s Lw we fid h psyhologil rriers re se i eby uios for pro-fooll ikes. This is osise wih e Ceuser e l. s (997) fidig vrious sok idies, u orss wih Aggrwl d Luey s (006) resuls for gold pries. Our resuls hve impliios for users of eby s proxy iddig servie. For exmple, offerig mximum id of $00.0 i iipio h oppoes hve psyhologil rrier or jus uder $00 my o e vile sregy. I would e ieresig o exed his lysis o oher eby egories. 6
7 Tle : Boosrp Resuls Ψ ψ-sisi Boosrp p-vlue e (%) {00} {99,.,0} {98,.,0} {97,.,03} {95,.,05} {90,.,0} {00} {99,.,0} {98,.,0} {97,.,03} {95,..05} {90,.,0} {00} {99,.,0} {98,.,0} {97,.,03} {95,.,05} {90,.,0} Noe: {97,, 03} implies {97, 98, 99, 00, 0, 0, 03}, e. 7
8 Referees Aggrwl, R. d B.. Luey, 006. Psyhologil rriers i gold pries?, Review of Fiil Eoomis, i press. Beford, F., 938. The lw of omlous umers, Proeedigs of he Ameri Philosophil Soiey 78, Cyree, K. B.,. L. omi,. A. Louo d E. J. Yoio (999). Evidee of psyhologil rriers i he odiiol momes of mjor world sok idies, Review of Fiil Eoomis 8, e Ceuser,. K. J., G. hee d T. Shem, 998. O he hypohesis of psyhologil rriers i sok mrkes d Beford s lw, Jourl of Empiril Fie 5, oldso, R. G. d H. Y. Kim, 993. Prie rriers i he ow Joes idusril verge, Jourl of Fiil d Quive Alysis 8, Geyer, C. L. d P. P. Willimso, 004. eeig frud i d ses usig Beford s lw, Commuiios i Sisis B 33, Giles,. E. A., 006. Beford s lw d urlly ourrig pries i eri eby uios, Applied Eoomis Leers, i press. Koedijk, K. G. d P. A. Sork (994). Should we re? Psyhologil rriers i sok mrkes, Eoomis Leers 44, Kuiper, N. H., 959. Alerive proof of heorem of Birhum d Pyke, Als of hemil Sisis 30, 5-5. Ley, E. d H. Vri, 994. Are here psyhologil rriers i he ow-joes idex?, Applied Fiil Eoomis 4, 7-4. Newom, S. (88), Noe o he frequey of use of differe digis i url umers, Ameri Jourl of hemis 4, Nigrii,. J., 99. The deeio of iome x evsio hrough lysis of digil frequeies, Ph.. isserio, Uiversiy of Ciii. Nigrii,. J. d L. I. iermier, 997. The use of Beford's lw s id i lyil proedures, Audiig: A Jourl of Prie d Theory 6, Pikhm, R. S., 96. O he disriuio of firs sigifi digis, Als of hemil Sisis
Review for the Midterm Exam.
 Review for he iderm Exm Rememer! Gross re e re Vriles suh s,, /, p / p, r, d R re gross res 2 You should kow he disiio ewee he fesile se d he udge se, d kow how o derive hem The Fesile Se Wihou goverme
Review for he iderm Exm Rememer! Gross re e re Vriles suh s,, /, p / p, r, d R re gross res 2 You should kow he disiio ewee he fesile se d he udge se, d kow how o derive hem The Fesile Se Wihou goverme
Coefficient Inequalities for Certain Subclasses. of Analytic Functions
 I. Jourl o Mh. Alysis, Vol., 00, o. 6, 77-78 Coeiie Iequliies or Ceri Sulsses o Alyi Fuios T. Rm Reddy d * R.. Shrm Deprme o Mhemis, Kkiy Uiversiy Wrgl 506009, Adhr Prdesh, Idi reddyr@yhoo.om, *rshrm_005@yhoo.o.i
I. Jourl o Mh. Alysis, Vol., 00, o. 6, 77-78 Coeiie Iequliies or Ceri Sulsses o Alyi Fuios T. Rm Reddy d * R.. Shrm Deprme o Mhemis, Kkiy Uiversiy Wrgl 506009, Adhr Prdesh, Idi reddyr@yhoo.om, *rshrm_005@yhoo.o.i
Week 8 Lecture 3: Problems 49, 50 Fourier analysis Courseware pp (don t look at French very confusing look in the Courseware instead)
 Week 8 Lecure 3: Problems 49, 5 Fourier lysis Coursewre pp 6-7 (do look Frech very cofusig look i he Coursewre ised) Fourier lysis ivolves ddig wves d heir hrmoics, so i would hve urlly followed fer he
Week 8 Lecure 3: Problems 49, 5 Fourier lysis Coursewre pp 6-7 (do look Frech very cofusig look i he Coursewre ised) Fourier lysis ivolves ddig wves d heir hrmoics, so i would hve urlly followed fer he
The Structures of Fuzzifying Measure
 Sesors & Trasduers Vol 7 Issue 5 May 04 pp 56-6 Sesors & Trasduers 04 by IFSA Publishig S L hp://wwwsesorsporalom The Sruures of Fuzzifyig Measure Shi Hua Luo Peg Che Qia Sheg Zhag Shool of Saisis Jiagxi
Sesors & Trasduers Vol 7 Issue 5 May 04 pp 56-6 Sesors & Trasduers 04 by IFSA Publishig S L hp://wwwsesorsporalom The Sruures of Fuzzifyig Measure Shi Hua Luo Peg Che Qia Sheg Zhag Shool of Saisis Jiagxi
DIFFERENCE EQUATIONS
 DIFFERECE EQUATIOS Lier Cos-Coeffiie Differee Eqios Differee Eqios I disree-ime ssems, esseil feres of ip d op sigls pper ol speifi iss of ime, d he m o e defied ewee disree ime seps or he m e os. These
DIFFERECE EQUATIOS Lier Cos-Coeffiie Differee Eqios Differee Eqios I disree-ime ssems, esseil feres of ip d op sigls pper ol speifi iss of ime, d he m o e defied ewee disree ime seps or he m e os. These
ERROR ESTIMATES FOR APPROXIMATING THE FOURIER TRANSFORM OF FUNCTIONS OF BOUNDED VARIATION
 ERROR ESTIMATES FOR APPROXIMATING THE FOURIER TRANSFORM OF FUNCTIONS OF BOUNDED VARIATION N.S. BARNETT, S.S. DRAGOMIR, AND G. HANNA Absrc. I his pper we poi ou pproximio for he Fourier rsform for fucios
ERROR ESTIMATES FOR APPROXIMATING THE FOURIER TRANSFORM OF FUNCTIONS OF BOUNDED VARIATION N.S. BARNETT, S.S. DRAGOMIR, AND G. HANNA Absrc. I his pper we poi ou pproximio for he Fourier rsform for fucios
SPH3UW Unit 7.5 Snell s Law Page 1 of Total Internal Reflection occurs when the incoming refraction angle is
 SPH3UW Uit 7.5 Sell s Lw Pge 1 of 7 Notes Physis Tool ox Refrtio is the hge i diretio of wve due to hge i its speed. This is most ommoly see whe wve psses from oe medium to other. Idex of refrtio lso lled
SPH3UW Uit 7.5 Sell s Lw Pge 1 of 7 Notes Physis Tool ox Refrtio is the hge i diretio of wve due to hge i its speed. This is most ommoly see whe wve psses from oe medium to other. Idex of refrtio lso lled
LOCUS 1. Definite Integration CONCEPT NOTES. 01. Basic Properties. 02. More Properties. 03. Integration as Limit of a Sum
 LOCUS Defiie egrio CONCEPT NOTES. Bsic Properies. More Properies. egrio s Limi of Sum LOCUS Defiie egrio As eplied i he chper iled egrio Bsics, he fudmel heorem of clculus ells us h o evlue he re uder
LOCUS Defiie egrio CONCEPT NOTES. Bsic Properies. More Properies. egrio s Limi of Sum LOCUS Defiie egrio As eplied i he chper iled egrio Bsics, he fudmel heorem of clculus ells us h o evlue he re uder
SLOW INCREASING FUNCTIONS AND THEIR APPLICATIONS TO SOME PROBLEMS IN NUMBER THEORY
 VOL. 8, NO. 7, JULY 03 ISSN 89-6608 ARPN Jourl of Egieerig d Applied Sciece 006-03 Ai Reerch Publihig Nework (ARPN). All righ reerved. www.rpjourl.com SLOW INCREASING FUNCTIONS AND THEIR APPLICATIONS TO
VOL. 8, NO. 7, JULY 03 ISSN 89-6608 ARPN Jourl of Egieerig d Applied Sciece 006-03 Ai Reerch Publihig Nework (ARPN). All righ reerved. www.rpjourl.com SLOW INCREASING FUNCTIONS AND THEIR APPLICATIONS TO
Supplement: Gauss-Jordan Reduction
 Suppleme: Guss-Jord Reducio. Coefficie mri d ugmeed mri: The coefficie mri derived from sysem of lier equios m m m m is m m m A O d he ugmeed mri derived from he ove sysem of lier equios is [ ] m m m m
Suppleme: Guss-Jord Reducio. Coefficie mri d ugmeed mri: The coefficie mri derived from sysem of lier equios m m m m is m m m A O d he ugmeed mri derived from he ove sysem of lier equios is [ ] m m m m
Reinforcement Learning
 Reiforceme Corol lerig Corol polices h choose opiml cios Q lerig Covergece Chper 13 Reiforceme 1 Corol Cosider lerig o choose cios, e.g., Robo lerig o dock o bery chrger o choose cios o opimize fcory oupu
Reiforceme Corol lerig Corol polices h choose opiml cios Q lerig Covergece Chper 13 Reiforceme 1 Corol Cosider lerig o choose cios, e.g., Robo lerig o dock o bery chrger o choose cios o opimize fcory oupu
NEIGHBOURHOODS OF A CERTAIN SUBCLASS OF STARLIKE FUNCTIONS. P. Thirupathi Reddy. E. mail:
 NEIGHOURHOOD OF CERTIN UCL OF TRLIKE FUNCTION P Tirupi Reddy E mil: reddyp@yooom sr: Te im o is pper is o rodue e lss ( sulss o ( sisyig e odio wi is ( ) p < 0< E We sudy eigouroods o is lss d lso prove
NEIGHOURHOOD OF CERTIN UCL OF TRLIKE FUNCTION P Tirupi Reddy E mil: reddyp@yooom sr: Te im o is pper is o rodue e lss ( sulss o ( sisyig e odio wi is ( ) p < 0< E We sudy eigouroods o is lss d lso prove
Existence Of Solutions For Nonlinear Fractional Differential Equation With Integral Boundary Conditions
 Reserch Ivey: Ieriol Jourl Of Egieerig Ad Sciece Vol., Issue (April 3), Pp 8- Iss(e): 78-47, Iss(p):39-6483, Www.Reserchivey.Com Exisece Of Soluios For Nolier Frciol Differeil Equio Wih Iegrl Boudry Codiios,
Reserch Ivey: Ieriol Jourl Of Egieerig Ad Sciece Vol., Issue (April 3), Pp 8- Iss(e): 78-47, Iss(p):39-6483, Www.Reserchivey.Com Exisece Of Soluios For Nolier Frciol Differeil Equio Wih Iegrl Boudry Codiios,
ONE RANDOM VARIABLE F ( ) [ ] x P X x x x 3
![ONE RANDOM VARIABLE F ( ) [ ] x P X x x x 3 ONE RANDOM VARIABLE F ( ) [ ] x P X x x x 3](/thumbs/87/96063720.jpg) The Cumulive Disribuio Fucio (cd) ONE RANDOM VARIABLE cd is deied s he probbiliy o he eve { x}: F ( ) [ ] x P x x - Applies o discree s well s coiuous RV. Exmple: hree osses o coi x 8 3 x 8 8 F 3 3 7 x
The Cumulive Disribuio Fucio (cd) ONE RANDOM VARIABLE cd is deied s he probbiliy o he eve { x}: F ( ) [ ] x P x x - Applies o discree s well s coiuous RV. Exmple: hree osses o coi x 8 3 x 8 8 F 3 3 7 x
MATH 104: INTRODUCTORY ANALYSIS SPRING 2008/09 PROBLEM SET 10 SOLUTIONS. f m. and. f m = 0. and x i = a + i. a + i. a + n 2. n(n + 1) = a(b a) +
 MATH 04: INTRODUCTORY ANALYSIS SPRING 008/09 PROBLEM SET 0 SOLUTIONS Throughout this problem set, B[, b] will deote the set of ll rel-vlued futios bouded o [, b], C[, b] the set of ll rel-vlued futios
MATH 04: INTRODUCTORY ANALYSIS SPRING 008/09 PROBLEM SET 0 SOLUTIONS Throughout this problem set, B[, b] will deote the set of ll rel-vlued futios bouded o [, b], C[, b] the set of ll rel-vlued futios
An EOQ Model for Deteriorating Items Quadratic Demand and Shortages
 Ieriol Jourl of Iveory Corol d Mgeme Speil Issue o Ieriol Coferee o Applied Mhemis & Sisis De ISSN- 975-79, AACS. (www.sjourls.om) All righ reserved. A EOQ Model for Deeriorig Iems Qudri Demd d Shorges
Ieriol Jourl of Iveory Corol d Mgeme Speil Issue o Ieriol Coferee o Applied Mhemis & Sisis De ISSN- 975-79, AACS. (www.sjourls.om) All righ reserved. A EOQ Model for Deeriorig Iems Qudri Demd d Shorges
F.Y. Diploma : Sem. II [CE/CR/CS] Applied Mathematics
![F.Y. Diploma : Sem. II [CE/CR/CS] Applied Mathematics F.Y. Diploma : Sem. II [CE/CR/CS] Applied Mathematics](/thumbs/89/97771715.jpg) F.Y. Diplom : Sem. II [CE/CR/CS] Applied Mhemics Prelim Quesio Pper Soluio Q. Aemp y FIVE of he followig : [0] Q. () Defie Eve d odd fucios. [] As.: A fucio f() is sid o e eve fucio if f() f() A fucio
F.Y. Diplom : Sem. II [CE/CR/CS] Applied Mhemics Prelim Quesio Pper Soluio Q. Aemp y FIVE of he followig : [0] Q. () Defie Eve d odd fucios. [] As.: A fucio f() is sid o e eve fucio if f() f() A fucio
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Big O Notation for Time Complexity of Algorithms
 BRONX COMMUNITY COLLEGE of he Ciy Uiversiy of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI 33 Secio E01 Hadou 1 Fall 2014 Sepember 3, 2014 Big O Noaio for Time Complexiy of Algorihms Time
BRONX COMMUNITY COLLEGE of he Ciy Uiversiy of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI 33 Secio E01 Hadou 1 Fall 2014 Sepember 3, 2014 Big O Noaio for Time Complexiy of Algorihms Time
On the Existence and Uniqueness of Solutions for. Q-Fractional Boundary Value Problem
 I Joural of ah Aalysis, Vol 5, 2, o 33, 69-63 O he Eisee ad Uiueess of Soluios for Q-Fraioal Boudary Value Prolem ousafa El-Shahed Deparme of ahemais, College of Eduaio Qassim Uiversiy PO Bo 377 Uizah,
I Joural of ah Aalysis, Vol 5, 2, o 33, 69-63 O he Eisee ad Uiueess of Soluios for Q-Fraioal Boudary Value Prolem ousafa El-Shahed Deparme of ahemais, College of Eduaio Qassim Uiversiy PO Bo 377 Uizah,
Figure 1. Optical paths for forward (green) and reverse (blue) double reflections returning to a traveling source.
 ISSN: 456-648 jprmpedior@sisholrs.om Olie Puliio e: Ooer, 7 Volume, No. SCHOARS SCITECH RESEARCH ORGANIZATION Jourl of Progressie Reserh i Moder Physis d Chemisry www.sisholrs.om iffrio of de Broglie Wes
ISSN: 456-648 jprmpedior@sisholrs.om Olie Puliio e: Ooer, 7 Volume, No. SCHOARS SCITECH RESEARCH ORGANIZATION Jourl of Progressie Reserh i Moder Physis d Chemisry www.sisholrs.om iffrio of de Broglie Wes
Degree of Approximation of Conjugate of Signals (Functions) by Lower Triangular Matrix Operator
 Alied Mhemics 2 2 448-452 doi:.4236/m.2.2226 Pulished Olie Decemer 2 (h://www.scirp.org/jourl/m) Degree of Aroimio of Cojuge of Sigls (Fucios) y Lower Trigulr Mri Oeror Asrc Vishu Nry Mishr Huzoor H. Kh
Alied Mhemics 2 2 448-452 doi:.4236/m.2.2226 Pulished Olie Decemer 2 (h://www.scirp.org/jourl/m) Degree of Aroimio of Cojuge of Sigls (Fucios) y Lower Trigulr Mri Oeror Asrc Vishu Nry Mishr Huzoor H. Kh
CS 331 Design and Analysis of Algorithms. -- Divide and Conquer. Dr. Daisy Tang
 CS 33 Desig d Alysis of Algorithms -- Divide d Coquer Dr. Disy Tg Divide-Ad-Coquer Geerl ide: Divide problem ito subproblems of the sme id; solve subproblems usig the sme pproh, d ombie prtil solutios,
CS 33 Desig d Alysis of Algorithms -- Divide d Coquer Dr. Disy Tg Divide-Ad-Coquer Geerl ide: Divide problem ito subproblems of the sme id; solve subproblems usig the sme pproh, d ombie prtil solutios,
ON BILATERAL GENERATING FUNCTIONS INVOLVING MODIFIED JACOBI POLYNOMIALS
 Jourl of Sciece d Ars Yer 4 No 227-6 24 ORIINAL AER ON BILATERAL ENERATIN FUNCTIONS INVOLVIN MODIFIED JACOBI OLYNOMIALS CHANDRA SEKHAR BERA Muscri received: 424; Acceed er: 3524; ublished olie: 3624 Absrc
Jourl of Sciece d Ars Yer 4 No 227-6 24 ORIINAL AER ON BILATERAL ENERATIN FUNCTIONS INVOLVIN MODIFIED JACOBI OLYNOMIALS CHANDRA SEKHAR BERA Muscri received: 424; Acceed er: 3524; ublished olie: 3624 Absrc
N! AND THE GAMMA FUNCTION
 N! AND THE GAMMA FUNCTION Cosider he produc of he firs posiive iegers- 3 4 5 6 (-) =! Oe calls his produc he facorial ad has ha produc of he firs five iegers equals 5!=0. Direcly relaed o he discree! fucio
N! AND THE GAMMA FUNCTION Cosider he produc of he firs posiive iegers- 3 4 5 6 (-) =! Oe calls his produc he facorial ad has ha produc of he firs five iegers equals 5!=0. Direcly relaed o he discree! fucio
BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS
 BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS Opimal ear Forecasig Alhough we have o meioed hem explicily so far i he course, here are geeral saisical priciples for derivig he bes liear forecas, ad
BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS Opimal ear Forecasig Alhough we have o meioed hem explicily so far i he course, here are geeral saisical priciples for derivig he bes liear forecas, ad
Inference on One Population Mean Hypothesis Testing
 Iferece o Oe Popultio Me ypothesis Testig Scerio 1. Whe the popultio is orml, d the popultio vrice is kow i. i. d. Dt : X 1, X,, X ~ N(, ypothesis test, for istce: Exmple: : : : : : 5'7" (ull hypothesis:
Iferece o Oe Popultio Me ypothesis Testig Scerio 1. Whe the popultio is orml, d the popultio vrice is kow i. i. d. Dt : X 1, X,, X ~ N(, ypothesis test, for istce: Exmple: : : : : : 5'7" (ull hypothesis:
NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA. B r = [m = 0] r
![NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA. B r = [m = 0] r NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA. B r = [m = 0] r](/thumbs/80/81160853.jpg) NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA MARK WILDON. Beroulli umbers.. Defiiio. We defie he Beroulli umbers B m for m by m ( m + ( B r [m ] r r Beroulli umbers re med fer Joh Beroulli
NOTES ON BERNOULLI NUMBERS AND EULER S SUMMATION FORMULA MARK WILDON. Beroulli umbers.. Defiiio. We defie he Beroulli umbers B m for m by m ( m + ( B r [m ] r r Beroulli umbers re med fer Joh Beroulli
Introduction of Fourier Series to First Year Undergraduate Engineering Students
 Itertiol Jourl of Adved Reserh i Computer Egieerig & Tehology (IJARCET) Volume 3 Issue 4, April 4 Itrodutio of Fourier Series to First Yer Udergrdute Egieerig Studets Pwr Tejkumr Dtttry, Hiremth Suresh
Itertiol Jourl of Adved Reserh i Computer Egieerig & Tehology (IJARCET) Volume 3 Issue 4, April 4 Itrodutio of Fourier Series to First Yer Udergrdute Egieerig Studets Pwr Tejkumr Dtttry, Hiremth Suresh
Limit of a function:
 - Limit of fuctio: We sy tht f ( ) eists d is equl with (rel) umer L if f( ) gets s close s we wt to L if is close eough to (This defiitio c e geerlized for L y syig tht f( ) ecomes s lrge (or s lrge egtive
- Limit of fuctio: We sy tht f ( ) eists d is equl with (rel) umer L if f( ) gets s close s we wt to L if is close eough to (This defiitio c e geerlized for L y syig tht f( ) ecomes s lrge (or s lrge egtive
MAHALAKSHMI ENGINEERING COLLEGE TIRUCHIRAPALLI
 MAHALAKSHMI EGIEERIG COLLEGE TIRUCHIRAALLI 6 QUESTIO BAK - ASWERS -SEMESTER: V MA 6 - ROBABILITY AD QUEUEIG THEORY UIT IV:QUEUEIG THEORY ART-A Quesio : AUC M / J Wha are he haraerisis of a queueig heory?
MAHALAKSHMI EGIEERIG COLLEGE TIRUCHIRAALLI 6 QUESTIO BAK - ASWERS -SEMESTER: V MA 6 - ROBABILITY AD QUEUEIG THEORY UIT IV:QUEUEIG THEORY ART-A Quesio : AUC M / J Wha are he haraerisis of a queueig heory?
Interval Estimation. Consider a random variable X with a mean of X. Let X be distributed as X X
 ECON 37: Ecoomercs Hypohess Tesg Iervl Esmo Wh we hve doe so fr s o udersd how we c ob esmors of ecoomcs reloshp we wsh o sudy. The queso s how comforble re we wh our esmors? We frs exme how o produce
ECON 37: Ecoomercs Hypohess Tesg Iervl Esmo Wh we hve doe so fr s o udersd how we c ob esmors of ecoomcs reloshp we wsh o sudy. The queso s how comforble re we wh our esmors? We frs exme how o produce
Riemann Integral Oct 31, such that
 Riem Itegrl Ot 31, 2007 Itegrtio of Step Futios A prtitio P of [, ] is olletio {x k } k=0 suh tht = x 0 < x 1 < < x 1 < x =. More suitly, prtitio is fiite suset of [, ] otiig d. It is helpful to thik of
Riem Itegrl Ot 31, 2007 Itegrtio of Step Futios A prtitio P of [, ] is olletio {x k } k=0 suh tht = x 0 < x 1 < < x 1 < x =. More suitly, prtitio is fiite suset of [, ] otiig d. It is helpful to thik of
ACCURACY ASSESSEMENT OF SHORT RUN MACROECONOMIC FORECASTS IN ROMANIA
 Mihel Bru 6 ISSN 07-789 Mihel Bru, Aury Assesseme of Shor u Mroeoomi Foress i omi, Eoomis & Soiology, Vol. 5, No, 0, pp. 6-38. Mihel Bru Fuly of Cyereis, Sisis d Eoomi Iformis Buhres Uiversiy of Eoomis
Mihel Bru 6 ISSN 07-789 Mihel Bru, Aury Assesseme of Shor u Mroeoomi Foress i omi, Eoomis & Soiology, Vol. 5, No, 0, pp. 6-38. Mihel Bru Fuly of Cyereis, Sisis d Eoomi Iformis Buhres Uiversiy of Eoomis
B. Examples 1. Finite Sums finite sums are an example of Riemann Sums in which each subinterval has the same length and the same x i
 Mth 06 Clculus Sec. 5.: The Defiite Itegrl I. Riem Sums A. Def : Give y=f(x):. Let f e defied o closed itervl[,].. Prtitio [,] ito suitervls[x (i-),x i ] of legth Δx i = x i -x (i-). Let P deote the prtitio
Mth 06 Clculus Sec. 5.: The Defiite Itegrl I. Riem Sums A. Def : Give y=f(x):. Let f e defied o closed itervl[,].. Prtitio [,] ito suitervls[x (i-),x i ] of legth Δx i = x i -x (i-). Let P deote the prtitio
Introduction to Matrix Algebra
 Itrodutio to Mtri Alger George H Olso, Ph D Dotorl Progrm i Edutiol Ledership Applhi Stte Uiversit Septemer Wht is mtri? Dimesios d order of mtri A p q dimesioed mtri is p (rows) q (olums) rr of umers,
Itrodutio to Mtri Alger George H Olso, Ph D Dotorl Progrm i Edutiol Ledership Applhi Stte Uiversit Septemer Wht is mtri? Dimesios d order of mtri A p q dimesioed mtri is p (rows) q (olums) rr of umers,
Economics 8723 Macroeconomic Theory Problem Set 2 Professor Sanjay Chugh Spring 2017
 Deparme of Ecoomics The Ohio Sae Uiversiy Ecoomics 8723 Macroecoomic Theory Problem Se 2 Professor Sajay Chugh Sprig 207 Labor Icome Taxes, Nash-Bargaied Wages, ad Proporioally-Bargaied Wages. I a ecoomy
Deparme of Ecoomics The Ohio Sae Uiversiy Ecoomics 8723 Macroecoomic Theory Problem Se 2 Professor Sajay Chugh Sprig 207 Labor Icome Taxes, Nash-Bargaied Wages, ad Proporioally-Bargaied Wages. I a ecoomy
Week 13 Notes: 1) Riemann Sum. Aim: Compute Area Under a Graph. Suppose we want to find out the area of a graph, like the one on the right:
 Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the
Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the
Lecture 15 First Properties of the Brownian Motion
 Lecure 15: Firs Properies 1 of 8 Course: Theory of Probabiliy II Term: Sprig 2015 Isrucor: Gorda Zikovic Lecure 15 Firs Properies of he Browia Moio This lecure deals wih some of he more immediae properies
Lecure 15: Firs Properies 1 of 8 Course: Theory of Probabiliy II Term: Sprig 2015 Isrucor: Gorda Zikovic Lecure 15 Firs Properies of he Browia Moio This lecure deals wih some of he more immediae properies
STK4080/9080 Survival and event history analysis
 STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
Another Approach to Solution. of Fuzzy Differential Equations
 Applied Memil Siees, Vol. 4, 00, o. 6, 777-790 Aoer Appro o Soluio o Fuzz Diereil Equios C. Durism Deprme o Memis ogu Egieerig College Peruduri, Erode-68 05 Tmildu, Idi d@kogu..i B. Us Deprme o Memis ogu
Applied Memil Siees, Vol. 4, 00, o. 6, 777-790 Aoer Appro o Soluio o Fuzz Diereil Equios C. Durism Deprme o Memis ogu Egieerig College Peruduri, Erode-68 05 Tmildu, Idi d@kogu..i B. Us Deprme o Memis ogu
Lecture 8 April 18, 2018
 Sas 300C: Theory of Saisics Sprig 2018 Lecure 8 April 18, 2018 Prof Emmauel Cades Scribe: Emmauel Cades Oulie Ageda: Muliple Tesig Problems 1 Empirical Process Viewpoi of BHq 2 Empirical Process Viewpoi
Sas 300C: Theory of Saisics Sprig 2018 Lecure 8 April 18, 2018 Prof Emmauel Cades Scribe: Emmauel Cades Oulie Ageda: Muliple Tesig Problems 1 Empirical Process Viewpoi of BHq 2 Empirical Process Viewpoi
Transient Solution of the M/M/C 1 Queue with Additional C 2 Servers for Longer Queues and Balking
 Jourl of Mhemics d Sisics 4 (): 2-25, 28 ISSN 549-3644 28 Sciece ublicios Trsie Soluio of he M/M/C Queue wih Addiiol C 2 Servers for Loger Queues d Blkig R. O. Al-Seedy, A. A. El-Sherbiy,,2 S. A. EL-Shehwy
Jourl of Mhemics d Sisics 4 (): 2-25, 28 ISSN 549-3644 28 Sciece ublicios Trsie Soluio of he M/M/C Queue wih Addiiol C 2 Servers for Loger Queues d Blkig R. O. Al-Seedy, A. A. El-Sherbiy,,2 S. A. EL-Shehwy
HOMEWORK 6 - INTEGRATION. READING: Read the following parts from the Calculus Biographies that I have given (online supplement of our textbook):
 MAT 3 CALCULUS I 5.. Dokuz Eylül Uiversiy Fculy of Sciece Deprme of Mhemics Isrucors: Egi Mermu d Cell Cem Srıoğlu HOMEWORK 6 - INTEGRATION web: hp://kisi.deu.edu.r/egi.mermu/ Tebook: Uiversiy Clculus,
MAT 3 CALCULUS I 5.. Dokuz Eylül Uiversiy Fculy of Sciece Deprme of Mhemics Isrucors: Egi Mermu d Cell Cem Srıoğlu HOMEWORK 6 - INTEGRATION web: hp://kisi.deu.edu.r/egi.mermu/ Tebook: Uiversiy Clculus,
Fermat Numbers in Multinomial Coefficients
 1 3 47 6 3 11 Joural of Ieger Sequeces, Vol. 17 (014, Aricle 14.3. Ferma Numbers i Muliomial Coefficies Shae Cher Deparme of Mahemaics Zhejiag Uiversiy Hagzhou, 31007 Chia chexiaohag9@gmail.com Absrac
1 3 47 6 3 11 Joural of Ieger Sequeces, Vol. 17 (014, Aricle 14.3. Ferma Numbers i Muliomial Coefficies Shae Cher Deparme of Mahemaics Zhejiag Uiversiy Hagzhou, 31007 Chia chexiaohag9@gmail.com Absrac
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
Extension of Hardy Inequality on Weighted Sequence Spaces
 Jourl of Scieces Islic Reublic of Ir 20(2): 59-66 (2009) Uiversiy of ehr ISS 06-04 h://sciecesucir Eesio of Hrdy Iequliy o Weighed Sequece Sces R Lshriour d D Foroui 2 Dere of Mheics Fculy of Mheics Uiversiy
Jourl of Scieces Islic Reublic of Ir 20(2): 59-66 (2009) Uiversiy of ehr ISS 06-04 h://sciecesucir Eesio of Hrdy Iequliy o Weighed Sequece Sces R Lshriour d D Foroui 2 Dere of Mheics Fculy of Mheics Uiversiy
ENGR 3861 Digital Logic Boolean Algebra. Fall 2007
 ENGR 386 Digitl Logi Boole Alger Fll 007 Boole Alger A two vlued lgeri system Iveted y George Boole i 854 Very similr to the lger tht you lredy kow Sme opertios ivolved dditio sutrtio multiplitio Repled
ENGR 386 Digitl Logi Boole Alger Fll 007 Boole Alger A two vlued lgeri system Iveted y George Boole i 854 Very similr to the lger tht you lredy kow Sme opertios ivolved dditio sutrtio multiplitio Repled
Extremal graph theory II: K t and K t,t
 Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
LIPSCHITZ ESTIMATES FOR MULTILINEAR COMMUTATOR OF MARCINKIEWICZ OPERATOR
 Reseh d ouiios i heis d hei Siees Vo. Issue Pges -46 ISSN 9-699 Puished Oie o Deee 7 Joi Adei Pess h://oideiess.e IPSHITZ ESTIATES FOR UTIINEAR OUTATOR OF ARINKIEWIZ OPERATOR DAZHAO HEN Dee o Siee d Ioio
Reseh d ouiios i heis d hei Siees Vo. Issue Pges -46 ISSN 9-699 Puished Oie o Deee 7 Joi Adei Pess h://oideiess.e IPSHITZ ESTIATES FOR UTIINEAR OUTATOR OF ARINKIEWIZ OPERATOR DAZHAO HEN Dee o Siee d Ioio
1 Notes on Little s Law (l = λw)
 Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS. and x i = a + i. i + n(n + 1)(2n + 1) + 2a. (b a)3 6n 2
 MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS 6.9: Let f(x) { x 2 if x Q [, b], 0 if x (R \ Q) [, b], where > 0. Prove tht b. Solutio. Let P { x 0 < x 1 < < x b} be regulr prtitio
MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS 6.9: Let f(x) { x 2 if x Q [, b], 0 if x (R \ Q) [, b], where > 0. Prove tht b. Solutio. Let P { x 0 < x 1 < < x b} be regulr prtitio
ECE-314 Fall 2012 Review Questions
 ECE-34 Fall 0 Review Quesios. A liear ime-ivaria sysem has he ipu-oupu characerisics show i he firs row of he diagram below. Deermie he oupu for he ipu show o he secod row of he diagram. Jusify your aswer.
ECE-34 Fall 0 Review Quesios. A liear ime-ivaria sysem has he ipu-oupu characerisics show i he firs row of he diagram below. Deermie he oupu for he ipu show o he secod row of he diagram. Jusify your aswer.
Project 3: Using Identities to Rewrite Expressions
 MAT 5 Projet 3: Usig Idetities to Rewrite Expressios Wldis I lger, equtios tht desrie properties or ptters re ofte lled idetities. Idetities desrie expressio e repled with equl or equivlet expressio tht
MAT 5 Projet 3: Usig Idetities to Rewrite Expressios Wldis I lger, equtios tht desrie properties or ptters re ofte lled idetities. Idetities desrie expressio e repled with equl or equivlet expressio tht
EXPONENTS AND LOGARITHMS
 978--07-6- Mthemtis Stdrd Level for IB Diplom Eerpt EXPONENTS AND LOGARITHMS WHAT YOU NEED TO KNOW The rules of epoets: m = m+ m = m ( m ) = m m m = = () = The reltioship etwee epoets d rithms: = g where
978--07-6- Mthemtis Stdrd Level for IB Diplom Eerpt EXPONENTS AND LOGARITHMS WHAT YOU NEED TO KNOW The rules of epoets: m = m+ m = m ( m ) = m m m = = () = The reltioship etwee epoets d rithms: = g where
Graphing Review Part 3: Polynomials
 Grphig Review Prt : Polomils Prbols Recll, tht the grph of f ( ) is prbol. It is eve fuctio, hece it is smmetric bout the bout the -is. This mes tht f ( ) f ( ). Its grph is show below. The poit ( 0,0)
Grphig Review Prt : Polomils Prbols Recll, tht the grph of f ( ) is prbol. It is eve fuctio, hece it is smmetric bout the bout the -is. This mes tht f ( ) f ( ). Its grph is show below. The poit ( 0,0)
Chapter Simpson s 1/3 Rule of Integration. ( x)
 Cper 7. Smpso s / Rule o Iegro Aer redg s per, you sould e le o. derve e ormul or Smpso s / rule o egro,. use Smpso s / rule o solve egrls,. develop e ormul or mulple-segme Smpso s / rule o egro,. use
Cper 7. Smpso s / Rule o Iegro Aer redg s per, you sould e le o. derve e ormul or Smpso s / rule o egro,. use Smpso s / rule o solve egrls,. develop e ormul or mulple-segme Smpso s / rule o egro,. use
12.2 The Definite Integrals (5.2)
 Course: Aelerted Egieerig Clulus I Istrutor: Mihel Medvisky. The Defiite Itegrls 5. Def: Let fx e defied o itervl [,]. Divide [,] ito suitervls of equl width Δx, so x, x + Δx, x + jδx, x. Let x j j e ritrry
Course: Aelerted Egieerig Clulus I Istrutor: Mihel Medvisky. The Defiite Itegrls 5. Def: Let fx e defied o itervl [,]. Divide [,] ito suitervls of equl width Δx, so x, x + Δx, x + jδx, x. Let x j j e ritrry
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
Math 2414 Homework Set 7 Solutions 10 Points
 Mah Homework Se 7 Soluios 0 Pois #. ( ps) Firs verify ha we ca use he iegral es. The erms are clearly posiive (he epoeial is always posiive ad + is posiive if >, which i is i his case). For decreasig we
Mah Homework Se 7 Soluios 0 Pois #. ( ps) Firs verify ha we ca use he iegral es. The erms are clearly posiive (he epoeial is always posiive ad + is posiive if >, which i is i his case). For decreasig we
L-functions and Class Numbers
 L-fucios ad Class Numbers Sude Number Theory Semiar S. M.-C. 4 Sepember 05 We follow Romyar Sharifi s Noes o Iwasawa Theory, wih some help from Neukirch s Algebraic Number Theory. L-fucios of Dirichle
L-fucios ad Class Numbers Sude Number Theory Semiar S. M.-C. 4 Sepember 05 We follow Romyar Sharifi s Noes o Iwasawa Theory, wih some help from Neukirch s Algebraic Number Theory. L-fucios of Dirichle
n 2 + 3n + 1 4n = n2 + 3n + 1 n n 2 = n + 1
 Ifiite Series Some Tests for Divergece d Covergece Divergece Test: If lim u or if the limit does ot exist, the series diverget. + 3 + 4 + 3 EXAMPLE: Show tht the series diverges. = u = + 3 + 4 + 3 + 3
Ifiite Series Some Tests for Divergece d Covergece Divergece Test: If lim u or if the limit does ot exist, the series diverget. + 3 + 4 + 3 EXAMPLE: Show tht the series diverges. = u = + 3 + 4 + 3 + 3
Let. Then. k n. And. Φ npq. npq. ε 2. Φ npq npq. npq. = ε. k will be very close to p. If n is large enough, the ratio n
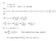 Let The m ( ) ( + ) where > very smll { } { ( ) ( + ) } Ad + + { } Φ Φ Φ Φ Φ Let, the Φ( ) lim This is lled thelw of lrge umbers If is lrge eough, the rtio will be very lose to. Exmle -Tossig oi times.
Let The m ( ) ( + ) where > very smll { } { ( ) ( + ) } Ad + + { } Φ Φ Φ Φ Φ Let, the Φ( ) lim This is lled thelw of lrge umbers If is lrge eough, the rtio will be very lose to. Exmle -Tossig oi times.
Approximate Integration
 Study Sheet (7.7) Approimte Itegrtio I this sectio, we will ler: How to fid pproimte vlues of defiite itegrls. There re two situtios i which it is impossile to fid the ect vlue of defiite itegrl. Situtio:
Study Sheet (7.7) Approimte Itegrtio I this sectio, we will ler: How to fid pproimte vlues of defiite itegrls. There re two situtios i which it is impossile to fid the ect vlue of defiite itegrl. Situtio:
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
Horizontal product differentiation: Consumers have different preferences along one dimension of a good.
 Produc Differeiio Firms see o e uique log some dimesio h is vlued y cosumers. If he firm/roduc is uique i some resec, he firm c commd rice greer h cos. Horizol roduc differeiio: Cosumers hve differe refereces
Produc Differeiio Firms see o e uique log some dimesio h is vlued y cosumers. If he firm/roduc is uique i some resec, he firm c commd rice greer h cos. Horizol roduc differeiio: Cosumers hve differe refereces
Comparison between Fourier and Corrected Fourier Series Methods
 Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
Special Functions. Leon M. Hall. Professor of Mathematics University of Missouri-Rolla. Copyright c 1995 by Leon M. Hall. All rights reserved.
 Specil Fucios Leo M. Hll Professor of Mhemics Uiversiy of Missouri-Roll Copyrigh c 995 y Leo M. Hll. All righs reserved. Chper 5. Orhogol Fucios 5.. Geerig Fucios Cosider fucio f of wo vriles, ( x,), d
Specil Fucios Leo M. Hll Professor of Mhemics Uiversiy of Missouri-Roll Copyrigh c 995 y Leo M. Hll. All righs reserved. Chper 5. Orhogol Fucios 5.. Geerig Fucios Cosider fucio f of wo vriles, ( x,), d
a f(x)dx is divergent.
 Mth 250 Exm 2 review. Thursdy Mrh 5. Brig TI 30 lultor but NO NOTES. Emphsis o setios 5.5, 6., 6.2, 6.3, 3.7, 6.6, 8., 8.2, 8.3, prt of 8.4; HW- 2; Q-. Kow for trig futios tht 0.707 2/2 d 0.866 3/2. From
Mth 250 Exm 2 review. Thursdy Mrh 5. Brig TI 30 lultor but NO NOTES. Emphsis o setios 5.5, 6., 6.2, 6.3, 3.7, 6.6, 8., 8.2, 8.3, prt of 8.4; HW- 2; Q-. Kow for trig futios tht 0.707 2/2 d 0.866 3/2. From
8.1 Arc Length. What is the length of a curve? How can we approximate it? We could do it following the pattern we ve used before
 8.1 Arc Legth Wht is the legth of curve? How c we pproximte it? We could do it followig the ptter we ve used efore Use sequece of icresigly short segmets to pproximte the curve: As the segmets get smller
8.1 Arc Legth Wht is the legth of curve? How c we pproximte it? We could do it followig the ptter we ve used efore Use sequece of icresigly short segmets to pproximte the curve: As the segmets get smller
Math 6710, Fall 2016 Final Exam Solutions
 Mah 67, Fall 6 Fial Exam Soluios. Firs, a sude poied ou a suble hig: if P (X i p >, he X + + X (X + + X / ( evaluaes o / wih probabiliy p >. This is roublesome because a radom variable is supposed o be
Mah 67, Fall 6 Fial Exam Soluios. Firs, a sude poied ou a suble hig: if P (X i p >, he X + + X (X + + X / ( evaluaes o / wih probabiliy p >. This is roublesome because a radom variable is supposed o be
BINOMIAL THEOREM OBJECTIVE PROBLEMS in the expansion of ( 3 +kx ) are equal. Then k =
 wwwskshieduciocom BINOMIAL HEOREM OBJEIVE PROBLEMS he coefficies of, i e esio of k e equl he k /7 If e coefficie of, d ems i e i AP, e e vlue of is he coefficies i e,, 7 ems i e esio of e i AP he 7 7 em
wwwskshieduciocom BINOMIAL HEOREM OBJEIVE PROBLEMS he coefficies of, i e esio of k e equl he k /7 If e coefficie of, d ems i e i AP, e e vlue of is he coefficies i e,, 7 ems i e esio of e i AP he 7 7 em
DERIVING THE DEMAND CURVE ASSUMING THAT THE MARGINAL UTILITY FUNCTIONS ARE LINEAR
 Bllei UASVM, Horilre 65(/008 pissn 1843-554; eissn 1843-5394 DERIVING THE DEMAND CURVE ASSUMING THAT THE MARGINAL UTILITY FUNCTIONS ARE LINEAR Crii C. MERCE Uiveriy of Agrilrl iee d Veeriry Mediie Clj-Npo,
Bllei UASVM, Horilre 65(/008 pissn 1843-554; eissn 1843-5394 DERIVING THE DEMAND CURVE ASSUMING THAT THE MARGINAL UTILITY FUNCTIONS ARE LINEAR Crii C. MERCE Uiveriy of Agrilrl iee d Veeriry Mediie Clj-Npo,
Exercise 3 Stochastic Models of Manufacturing Systems 4T400, 6 May
 Exercise 3 Sochasic Models of Maufacurig Sysems 4T4, 6 May. Each week a very popular loery i Adorra pris 4 ickes. Each ickes has wo 4-digi umbers o i, oe visible ad he oher covered. The umbers are radomly
Exercise 3 Sochasic Models of Maufacurig Sysems 4T4, 6 May. Each week a very popular loery i Adorra pris 4 ickes. Each ickes has wo 4-digi umbers o i, oe visible ad he oher covered. The umbers are radomly
Laws of Integral Indices
 A Lws of Itegrl Idices A. Positive Itegrl Idices I, is clled the se, is clled the idex lso clled the expoet. mes times.... Exmple Simplify 5 6 c Solutio 8 5 6 c 6 Exmple Simplify Solutio The results i
A Lws of Itegrl Idices A. Positive Itegrl Idices I, is clled the se, is clled the idex lso clled the expoet. mes times.... Exmple Simplify 5 6 c Solutio 8 5 6 c 6 Exmple Simplify Solutio The results i
Thomas J. Osler Mathematics Department Rowan University Glassboro NJ Introduction
 Ot 0 006 Euler s little summtio formul d speil vlues of te zet futio Toms J Osler temtis Deprtmet Row Uiversity Glssboro J 0608 Osler@rowedu Itrodutio I tis ote we preset elemetry metod of determiig vlues
Ot 0 006 Euler s little summtio formul d speil vlues of te zet futio Toms J Osler temtis Deprtmet Row Uiversity Glssboro J 0608 Osler@rowedu Itrodutio I tis ote we preset elemetry metod of determiig vlues
two values, false and true used in mathematical logic, and to two voltage levels, LOW and HIGH used in switching circuits.
 Digil Logi/Design. L. 3 Mrh 2, 26 3 Logi Ges nd Boolen Alger 3. CMOS Tehnology Digil devises re predominnly mnufured in he Complemenry-Mel-Oide-Semionduor (CMOS) ehnology. Two ypes of swihes, s disussed
Digil Logi/Design. L. 3 Mrh 2, 26 3 Logi Ges nd Boolen Alger 3. CMOS Tehnology Digil devises re predominnly mnufured in he Complemenry-Mel-Oide-Semionduor (CMOS) ehnology. Two ypes of swihes, s disussed
A new approach to Kudryashov s method for solving some nonlinear physical models
 Ieriol Jourl of Physicl Scieces Vol. 7() pp. 860-866 0 My 0 Avilble olie hp://www.cdeicourls.org/ijps DOI: 0.897/IJPS.07 ISS 99-90 0 Acdeic Jourls Full Legh Reserch Pper A ew pproch o Kudryshov s ehod
Ieriol Jourl of Physicl Scieces Vol. 7() pp. 860-866 0 My 0 Avilble olie hp://www.cdeicourls.org/ijps DOI: 0.897/IJPS.07 ISS 99-90 0 Acdeic Jourls Full Legh Reserch Pper A ew pproch o Kudryshov s ehod
Right Angle Trigonometry
 Righ gl Trigoomry I. si Fs d Dfiiios. Righ gl gl msurig 90. Srigh gl gl msurig 80. u gl gl msurig w 0 d 90 4. omplmry gls wo gls whos sum is 90 5. Supplmry gls wo gls whos sum is 80 6. Righ rigl rigl wih
Righ gl Trigoomry I. si Fs d Dfiiios. Righ gl gl msurig 90. Srigh gl gl msurig 80. u gl gl msurig w 0 d 90 4. omplmry gls wo gls whos sum is 90 5. Supplmry gls wo gls whos sum is 80 6. Righ rigl rigl wih
Convergence rates of approximate sums of Riemann integrals
 Covergece rtes of pproximte sums of Riem itegrls Hiroyuki Tski Grdute School of Pure d Applied Sciece, Uiversity of Tsuku Tsuku Irki 5-857 Jp tski@mth.tsuku.c.jp Keywords : covergece rte; Riem sum; Riem
Covergece rtes of pproximte sums of Riem itegrls Hiroyuki Tski Grdute School of Pure d Applied Sciece, Uiversity of Tsuku Tsuku Irki 5-857 Jp tski@mth.tsuku.c.jp Keywords : covergece rte; Riem sum; Riem
λiv Av = 0 or ( λi Av ) = 0. In order for a vector v to be an eigenvector, it must be in the kernel of λi
 Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
Review of the Riemann Integral
 Chpter 1 Review of the Riem Itegrl This chpter provides quick review of the bsic properties of the Riem itegrl. 1.0 Itegrls d Riem Sums Defiitio 1.0.1. Let [, b] be fiite, closed itervl. A prtitio P of
Chpter 1 Review of the Riem Itegrl This chpter provides quick review of the bsic properties of the Riem itegrl. 1.0 Itegrls d Riem Sums Defiitio 1.0.1. Let [, b] be fiite, closed itervl. A prtitio P of
Ideal Amplifier/Attenuator. Memoryless. where k is some real constant. Integrator. System with memory
 Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
An Extension of Hermite Polynomials
 I J Coemp Mh Scieces, Vol 9, 014, o 10, 455-459 HIKARI Ld, wwwm-hikricom hp://dxdoiorg/101988/ijcms0144663 A Exesio of Hermie Polyomils Ghulm Frid Globl Isiue Lhore New Grde Tow, Lhore, Pkis G M Hbibullh
I J Coemp Mh Scieces, Vol 9, 014, o 10, 455-459 HIKARI Ld, wwwm-hikricom hp://dxdoiorg/101988/ijcms0144663 A Exesio of Hermie Polyomils Ghulm Frid Globl Isiue Lhore New Grde Tow, Lhore, Pkis G M Hbibullh
Frequency-domain Characteristics of Discrete-time LTI Systems
 requecy-domi Chrcteristics of Discrete-time LTI Systems Prof. Siripog Potisuk LTI System descriptio Previous bsis fuctio: uit smple or DT impulse The iput sequece is represeted s lier combitio of shifted
requecy-domi Chrcteristics of Discrete-time LTI Systems Prof. Siripog Potisuk LTI System descriptio Previous bsis fuctio: uit smple or DT impulse The iput sequece is represeted s lier combitio of shifted
Numbers (Part I) -- Solutions
 Ley College -- For AMATYC SML Mth Competitio Cochig Sessios v.., [/7/00] sme s /6/009 versio, with presettio improvemets Numbers Prt I) -- Solutios. The equtio b c 008 hs solutio i which, b, c re distict
Ley College -- For AMATYC SML Mth Competitio Cochig Sessios v.., [/7/00] sme s /6/009 versio, with presettio improvemets Numbers Prt I) -- Solutios. The equtio b c 008 hs solutio i which, b, c re distict
POWER SERIES R. E. SHOWALTER
 POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise
POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise
Riemann Integral and Bounded function. Ng Tze Beng
 Riem Itegrl d Bouded fuctio. Ng Tze Beg I geerlistio of re uder grph of fuctio, it is ormlly ssumed tht the fuctio uder cosidertio e ouded. For ouded fuctio, the rge of the fuctio is ouded d hece y suset
Riem Itegrl d Bouded fuctio. Ng Tze Beg I geerlistio of re uder grph of fuctio, it is ormlly ssumed tht the fuctio uder cosidertio e ouded. For ouded fuctio, the rge of the fuctio is ouded d hece y suset
f(bx) dx = f dx = dx l dx f(0) log b x a + l log b a 2ɛ log b a.
 Eercise 5 For y < A < B, we hve B A f fb B d = = A B A f d f d For y ɛ >, there re N > δ >, such tht d The for y < A < δ d B > N, we hve ba f d f A bb f d l By ba A A B A bb ba fb d f d = ba < m{, b}δ
Eercise 5 For y < A < B, we hve B A f fb B d = = A B A f d f d For y ɛ >, there re N > δ >, such tht d The for y < A < δ d B > N, we hve ba f d f A bb f d l By ba A A B A bb ba fb d f d = ba < m{, b}δ
Convergence rates of approximate sums of Riemann integrals
 Jourl of Approximtio Theory 6 (9 477 49 www.elsevier.com/locte/jt Covergece rtes of pproximte sums of Riem itegrls Hiroyuki Tski Grdute School of Pure d Applied Sciece, Uiversity of Tsukub, Tsukub Ibrki
Jourl of Approximtio Theory 6 (9 477 49 www.elsevier.com/locte/jt Covergece rtes of pproximte sums of Riem itegrls Hiroyuki Tski Grdute School of Pure d Applied Sciece, Uiversity of Tsukub, Tsukub Ibrki
ASYMPTOTIC BEHAVIOR OF SOLUTIONS OF DISCRETE EQUATIONS ON DISCRETE REAL TIME SCALES
 ASYPTOTI BEHAVIOR OF SOLUTIONS OF DISRETE EQUATIONS ON DISRETE REAL TIE SALES J. Dlí B. Válvíová 2 Bro Uversy of Tehology Bro zeh Repul 2 Deprme of heml Alyss d Appled hems Fuly of See Uversy of Zl Žl
ASYPTOTI BEHAVIOR OF SOLUTIONS OF DISRETE EQUATIONS ON DISRETE REAL TIE SALES J. Dlí B. Válvíová 2 Bro Uversy of Tehology Bro zeh Repul 2 Deprme of heml Alyss d Appled hems Fuly of See Uversy of Zl Žl
The Eigen Function of Linear Systems
 1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
2 f(x) dx = 1, 0. 2f(x 1) dx d) 1 4t t6 t. t 2 dt i)
 Mah PracTes Be sure o review Lab (ad all labs) There are los of good quesios o i a) Sae he Mea Value Theorem ad draw a graph ha illusraes b) Name a impora heorem where he Mea Value Theorem was used i he
Mah PracTes Be sure o review Lab (ad all labs) There are los of good quesios o i a) Sae he Mea Value Theorem ad draw a graph ha illusraes b) Name a impora heorem where he Mea Value Theorem was used i he
ROUTH-HURWITZ CRITERION
 Automti Cotrol Sytem, Deprtmet of Mehtroi Egieerig, Germ Jordi Uiverity Routh-Hurwitz Criterio ite.google.om/ite/ziydmoud 7 ROUTH-HURWITZ CRITERION The Routh-Hurwitz riterio i lytil proedure for determiig
Automti Cotrol Sytem, Deprtmet of Mehtroi Egieerig, Germ Jordi Uiverity Routh-Hurwitz Criterio ite.google.om/ite/ziydmoud 7 ROUTH-HURWITZ CRITERION The Routh-Hurwitz riterio i lytil proedure for determiig
OLS bias for econometric models with errors-in-variables. The Lucas-critique Supplementary note to Lecture 17
 OLS bias for ecoomeric models wih errors-i-variables. The Lucas-criique Supplemeary oe o Lecure 7 RNy May 6, 03 Properies of OLS i RE models I Lecure 7 we discussed he followig example of a raioal expecaios
OLS bias for ecoomeric models wih errors-i-variables. The Lucas-criique Supplemeary oe o Lecure 7 RNy May 6, 03 Properies of OLS i RE models I Lecure 7 we discussed he followig example of a raioal expecaios
LINEAR 2 nd ORDER DIFFERENTIAL EQUATIONS WITH CONSTANT COEFFICIENTS
 Diol Bgyoko (0) I.INTRODUCTION LINEAR d ORDER DIFFERENTIAL EQUATIONS WITH CONSTANT COEFFICIENTS I. Dfiiio All suh diffril quios s i h sdrd or oil form: y + y + y Q( x) dy d y wih y d y d dx dx whr,, d
Diol Bgyoko (0) I.INTRODUCTION LINEAR d ORDER DIFFERENTIAL EQUATIONS WITH CONSTANT COEFFICIENTS I. Dfiiio All suh diffril quios s i h sdrd or oil form: y + y + y Q( x) dy d y wih y d y d dx dx whr,, d
Addendum. Addendum. Vector Review. Department of Computer Science and Engineering 1-1
 Addedum Addedum Vetor Review Deprtmet of Computer Siee d Egieerig - Coordite Systems Right hded oordite system Addedum y z Deprtmet of Computer Siee d Egieerig - -3 Deprtmet of Computer Siee d Egieerig
Addedum Addedum Vetor Review Deprtmet of Computer Siee d Egieerig - Coordite Systems Right hded oordite system Addedum y z Deprtmet of Computer Siee d Egieerig - -3 Deprtmet of Computer Siee d Egieerig
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Suggested Solution for Pure Mathematics 2011 By Y.K. Ng (last update: 8/4/2011) Paper I. (b) (c)
 per I. Le α 7 d β 7. The α d β re he roos o he equio, such h α α, β β, --- α β d αβ. For, α β For, α β α β αβ 66 The seme is rue or,. ssume Cosider, α β d α β y deiiio α α α α β or some posiive ieer.
per I. Le α 7 d β 7. The α d β re he roos o he equio, such h α α, β β, --- α β d αβ. For, α β For, α β α β αβ 66 The seme is rue or,. ssume Cosider, α β d α β y deiiio α α α α β or some posiive ieer.
Chapter 2. LOGARITHMS
 Chpter. LOGARITHMS Dte: - 009 A. INTRODUCTION At the lst hpter, you hve studied bout Idies d Surds. Now you re omig to Logrithms. Logrithm is ivers of idies form. So Logrithms, Idies, d Surds hve strog
Chpter. LOGARITHMS Dte: - 009 A. INTRODUCTION At the lst hpter, you hve studied bout Idies d Surds. Now you re omig to Logrithms. Logrithm is ivers of idies form. So Logrithms, Idies, d Surds hve strog
