ASYMPTOTIC BEHAVIOR OF SOLUTIONS OF DISCRETE EQUATIONS ON DISCRETE REAL TIME SCALES
|
|
|
- Sharleen Parrish
- 5 years ago
- Views:
Transcription
1 ASYPTOTI BEHAVIOR OF SOLUTIONS OF DISRETE EQUATIONS ON DISRETE REAL TIE SALES J. Dlí B. Válvíová 2 Bro Uversy of Tehology Bro zeh Repul 2 Deprme of heml Alyss d Appled hems Fuly of See Uversy of Zl Žl Slov Repul ABSTRAT. Ths oruo dels wh he vesgo of sympo ehvor of soluos of dsree equos o dsree rel me sles. Sysem of dsree equos u ( + ) = F ( u ( )) wh F : T R R s osdered o dsree rel me sle T. We develop geerl prple whh gves guree h he grph of les oe soluo sys presred dom. Exsee of ouded soluos of oler sysem s gve o llusre our resuls. Key words d phrses: Dsree equo sympo ehvor of soluo ouded soluo rero. hems Suje lssfos: 39A 39A. Iroduo. We use followg oo: for egers s q s q we defe q Zs := { ss + q } where possly s = or q = s dmed oo. Throughou q hs pper usg oo Z s or oher oe wh ouple of egers sq we suppose uomlly s q. We osder he sysem of dsree equos u ( + ) = F ( u ( )) () wh F : T R R u = ( u u ) where T = T( ) s rrry dsree me sle. e. T ( ) := { } wh R Z s eger d < + for y Z. We suppose h he mppg F s ouous wh respe o he seod rgume. We osder he l prolem () (2) where s u ( + s) = u R (2) wh fxed posve eger s. The exsee d uqueess of soluo of he l prolem () (2) o T ( + s) := { } Z + ss ovous. oreover due o ouy of he fuo F wh respe o he seod rgume hs l prolem depeds ouously o l d. The sequee {( u( ))} Z + ss lled he grph of soluo u = u( ) for Z + sof he l prolem () (2). We defe se Ω T R s Ω:= {( u) : T Z u ( )} where Ω ( ) s ope ouded d oeed se he spe 5-98
2 S ( ) {( ) u := u : u R } for every T. Ovously Ω= ( ) TΩ. The oudry Ω ( ) of Ω ( ) s defed he spe S ( ) orde wh usul defos. u Defo. We sy h po s he frs oseque po o po = ( u ) T R d we wre = [ ] f s frs oorde s shfed o + d he seod oe s he resul of he mppg of he po y mes of ().e. = [ ] = ( u( )) + + wh u ( + ) = F ( ). We sy h po s s he s -h oseque po of po = ( u ) T R f [ ] := = s where provded 2 s T R. Defo 2. A ouous fuo Vu ( ):[ ) R R s lled oeg fuo for he ses Ω ( ) T( ) f for every T( ) : Ω( ) {( u) : V( u) < }. Wh he d of he oeg fuo we defe he ses h wll e used he followg. Le oss α β R α < β e gve. We defe uxlry se Vαβ := {( u) : α β V( u) } wh oudry Vαβ :={( u) : α β V( u) = } d uxlry se Vα := {( u) : α < V( u) } wh oudry V :={( u) : α < V( u) = }. α Defo 3. If A B re y wo ses of opologl spe d π : B A s ouous mppg from B oo A suh h π ( p) = p for every p A he π s sd o e rero of B oo A. Whe here exss rero of B oo A A s lled rer of B. Prolem. Suppose h he ove uxlry supposos hold. We wll ry o fd suffe odos wh respe o he rgh-hd sde of he sysem () order o guree he exsee of les oe soluo u = u ( ) T Z ssfyg ( u ( )) Ω ( ) for every T. Exsee Resuls I hs seo we formule m resuls of he vesgo. Theorem. Suppose F : T R R s ouous wh respe o he seod rgume. oreover he ses Ω ( ) T d orrespodg oeg fuo Vu ( ) re gve suh h he followg properes hold:. The se s ovex for every T. V
3 2. For every T d Ω ( ) he le segme oeg po d s frs oseque po hs oly oe po of erseo wh he se mely he po self. 3. There exss rero π of he se The here exss soluo u u ( ) u for every T. V V + oo he se Ω ( ). = T of () ssfyg he relo ( ( )) Ω ( ) (3) PROOF. Le us suppose h he l d ( u ( )) ( ) geerg soluo u = u ( ) of he sysem () wh he propery (3) does o exs. Th mes o he oher hd for every = ( u ) ( ) here s rel umer Z + suh h for he orrespodg soluo u = u ( ) of he sysem () ssfyg he l odo u ( ) = u we hve ( u ( )) / ( ) d ( ) l + l l =. I mes h he ( )-h oseque po of he po does o elog o Ω ( ) u ll preedg oseque pos l = elog l o he orrespodg ses Ω ( ). oreover f = ( u ( )) Ω ( ) he + + ( ) ( ) + l / ( ). I hs wy we reformule hese resog: For y po = u here exss eger Z + suh h he orrespodg soluo u = u ( ) Z of he sysem () ssfyg he l odo u ( ) = u ssfes d for mddle oseque pos = ( u ( )) / ( ) (4) 2 l Z l ( ( )) ( ) l + l u + l + l = ( u ) wh = ( u ( )) ( ). (5) (f y) he relos = (6) hold. oreover le us remr h for u Ω ( ) (7) we hve Ω ( + ). Now we prove h uder ove desred properes here exss rero of he se Ω ( ) oo he se Ω ( ). I oher words hs suo ouous mppg-rero P of se (whh s opologlly equvle o losed -dmesol ll; our se - wh he se Ω ( )) oo s oudry ( our se - oo he se Ω ( ) ) for whh oudry pos re sory pos wll exs. Ths resuls ordo se well ow f ses h he oudry of -dmesol ll o e s rer. We wll osru suh rero P wh he d of wo uxlry mppgs P d P d he gve rero π. Le us defe mppg P of po = ( u ) wh u ( ) s 5-
4 P : ( u ( )) Ω ( ) where he vlue ws well defed ove y he relos d properes (4) (7). Ovously f u Ω ( ) he P ( ) =. Noe h he mppg P s ouous (due o ouous depedee o l d). Suppose = ( u ). The P( ) =. Le us defe mppg P : P ( ) = P ( P ( )) = wh eg he po of erseo of he le segme of he le oeg pos d d he se V. Le us show h due o he ovexy propery he po s defed uquely. Le hs o e he se. The here re les wo erseo pos d lyg o he le L oeg pos d he order ded (we suppose whou loss of geerly h s erer o h s). Se s he oudry po of he se V every s suffely smll eghourhood U( ) [ ) R os oempy se S ossg of exeror pos wh respe o V.e. for every s S we hve V. s Whou loss of geerly we wll suppose h S os ll exeror pos wh U( Δ ). Le us e po L V lyg ewee d d e suffely smll eghourhood U( Δ ) of suh h Δ U( ) U( ) =. Le us oe y po A U( Δ ) wh y le segme LA. Due o suffely smlless of eghourhood U( Δ ) we hve V. Bu o he oher hd here exss suh po A U( Δ ) h LA L Δ S. We ge ordo se S / V A. So d he uqueess of he po s proved. Le us prove he ouy of he ompose mppg P o P. I s ovous h P( P( )) = f Ω ( ). We show h due o he ouous depedee of soluo o he l d he ompose mppg P o P s ouous. There s o dou h P o P s ouous eghourhood of f Ω ( ). Suppose ow ( ) Ω. The P( P ( )) = d he resul of he mppg P( P( U( ))) where U( ) Ω ( ) s suffely smll eghourhood of he po gves smll eghourhood of he po V V due 2 o ouy of he mp F d ouous depedee of soluos o l d. Ths mes h he ompose mppg P o P s ouous. Defe he resulg rero wh he d of mppgs P P d π s 5-
5 P= π op o P. Ovously P:Ω( ) Ω ( ). As omposo of hree ouous mppgs P s ouous oo d P ( ) = f Ω ( ). So P s he desred rero. Ths f leds o ordom. Le uxlry fuos ( ) ( ): T( ) R = wh ( ) < ( ) e gve. We defe he fuos d he ses B ( u) := u + ( ) = ( u) := u ( ) = Ω :={( u) : T( ) B( u) = B B ( u) ( u) forll j s = d j } j s Ω :={( u) : T( ) ( u) = B j( u) s( u) forll j s = d s } for every =. Suppose h he se Ω s wre he form Ω= {( u) : T( ) B( u) < j( u) < j = }. (8) Followg resul s osequee of Theorem. We om s proof. Theorem 2. Le = e rel fuos defed o T ( ) suh h ( ) < ( ) d F : T( ) R R s ouous wh he respe o he seod rgume. If moreover he se Ω hs he form (8) F( u) < ( + ) for every = d every ( u) B F( u) > ( + ) for every = d every ( u) he here exss soluo u = u ( ) of he sysem () ssfyg he equles ( ) < u ( ) < ( ) for every T( ) d =. Exsee of Bouded Soluos of Noler Sysem Le us de suffe odos uder whh here exss ouded soluo of sysem of dsree equos u( + ) = μ( ) u( ) + ω( u( )) = (9) wh T( ) u = ( u u 2 u ) R μ = ( μ μ2 μ) : T( ) R d ω = ( ω ω2 ω) : T( ) R R. Bsed o Theorem 2 oe prove he followg Theorem 3. Le = e rel fuos defed o T ( ) suh h ( ) < ( ) ω : T ( ) Ω R wh Ω defed y (9) s ouous wh respe o he seod rgume. If moreover ( + ) μ( ) ( ) > ω( u) for every = d every ( u) d B 5-2
6 ( + ) μ( ) ( ) < ω( u) for every = d every ( u) he here exss soluo u = u ( ) of he sysem (2) ssfyg he equles ( ) < u ( ) < ( ) for every N( ) d =. Defo 4. Le posve umer δ e gve. We sy h soluo u = u( ) T( ) of he sysem (9) s δ -ouded f he equly u ( ) < δ wh u ( ) = mx = { u( ) } holds for every T( ). The ls heorem s osequee of Theorem 3. We om s proof. Theorem 4. Le posve umer δ e gve. Le ω : T ( ) R R s ouous wh respe o he seod rgume. If moreover + μ ( ) > ω ( u) / δ for every = d every ( u) d B μ ( ) < ω ( u) / δ for every = d every ( u) he here exss soluo u = u( ) N( ) of he sysem (2) ssfyg for every N( ). u ( ) < δ Aowledgme Ths wor ws suppored y he Gr /3238/6 of he Gr Agey of Slov Repul (VEGA). REFERENES:. WAŻEWSKI T. Sur u prpe opologque de l exme de l llure sympoque des égrles des équos dfféreelles ordres A. So. Polo. h. (947) BORSUK K. Theory of Rers PWN Wrsw DIBLÍK J. Dsree rer prple for sysems of dsree equos ompu. h. Appl. (2) DIBLÍK J. Asympo ehvour of soluos of sysems of dsree equos v Lypuov ype ehque ompu. h. Appl. (23)
TEACHERS ASSESS STUDENT S MATHEMATICAL CREATIVITY COMPETENCE IN HIGH SCHOOL
 Jourl o See d rs Yer 5, No., pp. 5-, 5 ORIGINL PPER TECHERS SSESS STUDENT S MTHEMTICL CRETIVITY COMPETENCE IN HIGH SCHOOL TRN TRUNG TINH Musrp reeved: 9..5; eped pper:..5; Pulsed ole:..5. sr. ssessme s
Jourl o See d rs Yer 5, No., pp. 5-, 5 ORIGINL PPER TECHERS SSESS STUDENT S MTHEMTICL CRETIVITY COMPETENCE IN HIGH SCHOOL TRN TRUNG TINH Musrp reeved: 9..5; eped pper:..5; Pulsed ole:..5. sr. ssessme s
Cyclically Interval Total Colorings of Cycles and Middle Graphs of Cycles
 Ope Joural of Dsree Mahemas 2017 7 200-217 hp://wwwsrporg/joural/ojdm ISSN Ole: 2161-7643 ISSN Pr: 2161-7635 Cylally Ierval Toal Colorgs of Cyles Mddle Graphs of Cyles Yogqag Zhao 1 Shju Su 2 1 Shool of
Ope Joural of Dsree Mahemas 2017 7 200-217 hp://wwwsrporg/joural/ojdm ISSN Ole: 2161-7643 ISSN Pr: 2161-7635 Cylally Ierval Toal Colorgs of Cyles Mddle Graphs of Cyles Yogqag Zhao 1 Shju Su 2 1 Shool of
On Metric Dimension of Two Constructed Families from Antiprism Graph
 Mah S Le 2, No, -7 203) Mahemaal Sees Leers A Ieraoal Joural @ 203 NSP Naural Sees Publhg Cor O Mer Dmeso of Two Cosrued Famles from Aprm Graph M Al,2, G Al,2 ad M T Rahm 2 Cere for Mahemaal Imagg Tehques
Mah S Le 2, No, -7 203) Mahemaal Sees Leers A Ieraoal Joural @ 203 NSP Naural Sees Publhg Cor O Mer Dmeso of Two Cosrued Famles from Aprm Graph M Al,2, G Al,2 ad M T Rahm 2 Cere for Mahemaal Imagg Tehques
Calculating Exact Transitive Closure for a Normalized Affine Integer Tuple Relation
 Clulg E Trsve Closure for Normlzed Affe Ieger Tuple elo W Bele*, T Klme*, KTrfuov** *Fuly of Compuer See, Tehl Uversy of Szze, lme@wpspl, bele@wpspl ** INIA Sly d Prs-Sud Uversy, ordrfuov@rfr Absr: A pproh
Clulg E Trsve Closure for Normlzed Affe Ieger Tuple elo W Bele*, T Klme*, KTrfuov** *Fuly of Compuer See, Tehl Uversy of Szze, lme@wpspl, bele@wpspl ** INIA Sly d Prs-Sud Uversy, ordrfuov@rfr Absr: A pproh
Integral Equations and their Relationship to Differential Equations with Initial Conditions
 Scece Refleco SR Vol 6 wwwscecereflecocom Geerl Leers Mhemcs GLM 6 3-3 Geerl Leers Mhemcs GLM Wese: hp://wwwscecereflecocom/geerl-leers--mhemcs/ Geerl Leers Mhemcs Scece Refleco Iegrl Equos d her Reloshp
Scece Refleco SR Vol 6 wwwscecereflecocom Geerl Leers Mhemcs GLM 6 3-3 Geerl Leers Mhemcs GLM Wese: hp://wwwscecereflecocom/geerl-leers--mhemcs/ Geerl Leers Mhemcs Scece Refleco Iegrl Equos d her Reloshp
ANSWERS TO ODD NUMBERED EXERCISES IN CHAPTER 2
 Joh Rley Novembe ANSWERS O ODD NUMBERED EXERCISES IN CHAPER Seo Eese -: asvy (a) Se y ad y z follows fom asvy ha z Ehe z o z We suppose he lae ad seek a oado he z Se y follows by asvy ha z y Bu hs oads
Joh Rley Novembe ANSWERS O ODD NUMBERED EXERCISES IN CHAPER Seo Eese -: asvy (a) Se y ad y z follows fom asvy ha z Ehe z o z We suppose he lae ad seek a oado he z Se y follows by asvy ha z y Bu hs oads
Chapter Trapezoidal Rule of Integration
 Cper 7 Trpezodl Rule o Iegro Aer redg s per, you sould e le o: derve e rpezodl rule o egro, use e rpezodl rule o egro o solve prolems, derve e mulple-segme rpezodl rule o egro, 4 use e mulple-segme rpezodl
Cper 7 Trpezodl Rule o Iegro Aer redg s per, you sould e le o: derve e rpezodl rule o egro, use e rpezodl rule o egro o solve prolems, derve e mulple-segme rpezodl rule o egro, 4 use e mulple-segme rpezodl
The Poisson Process Properties of the Poisson Process
 Posso Processes Summary The Posso Process Properes of he Posso Process Ierarrval mes Memoryless propery ad he resdual lfeme paradox Superposo of Posso processes Radom seleco of Posso Pos Bulk Arrvals ad
Posso Processes Summary The Posso Process Properes of he Posso Process Ierarrval mes Memoryless propery ad he resdual lfeme paradox Superposo of Posso processes Radom seleco of Posso Pos Bulk Arrvals ad
Solution. The straightforward approach is surprisingly difficult because one has to be careful about the limits.
 ose ad Varably Homewor # (8), aswers Q: Power spera of some smple oses A Posso ose A Posso ose () s a sequee of dela-fuo pulses, eah ourrg depedely, a some rae r (More formally, s a sum of pulses of wdh
ose ad Varably Homewor # (8), aswers Q: Power spera of some smple oses A Posso ose A Posso ose () s a sequee of dela-fuo pulses, eah ourrg depedely, a some rae r (More formally, s a sum of pulses of wdh
An Improvement on Disc Separation of the Schur Complement and Bounds for Determinants of Diagonally Dominant Matrices
 ISSN 746-7659, Egd, UK Jor of Iformo d Compg See Vo. 5, No. 3, 2, pp. 224-232 A Improveme o Ds Sepro of he Shr Compeme d Bods for Deerms of Dgoy Dom Mres Zhohog Hg, Tgzh Hg Shoo of Mhem Sees, Uversy of
ISSN 746-7659, Egd, UK Jor of Iformo d Compg See Vo. 5, No. 3, 2, pp. 224-232 A Improveme o Ds Sepro of he Shr Compeme d Bods for Deerms of Dgoy Dom Mres Zhohog Hg, Tgzh Hg Shoo of Mhem Sees, Uversy of
Laplace Transform. Definition of Laplace Transform: f(t) that satisfies The Laplace transform of f(t) is defined as.
 Lplce Trfor The Lplce Trfor oe of he hecl ool for olvg ordry ler dfferel equo. - The hoogeeou equo d he prculr Iegrl re olved oe opero. - The Lplce rfor cover he ODE o lgerc eq. σ j ple do. I he pole o
Lplce Trfor The Lplce Trfor oe of he hecl ool for olvg ordry ler dfferel equo. - The hoogeeou equo d he prculr Iegrl re olved oe opero. - The Lplce rfor cover he ODE o lgerc eq. σ j ple do. I he pole o
Collocation Method for Nonlinear Volterra-Fredholm Integral Equations
 Ope Joural of Appled Sees 5- do:436/oapps6 Publshed Ole Jue (hp://wwwsrporg/oural/oapps) Colloao Mehod for olear Volerra-Fredhol Iegral Equaos Jafar Ahad Shal Parvz Daraa Al Asgar Jodayree Akbarfa Depare
Ope Joural of Appled Sees 5- do:436/oapps6 Publshed Ole Jue (hp://wwwsrporg/oural/oapps) Colloao Mehod for olear Volerra-Fredhol Iegral Equaos Jafar Ahad Shal Parvz Daraa Al Asgar Jodayree Akbarfa Depare
Interval Estimation. Consider a random variable X with a mean of X. Let X be distributed as X X
 ECON 37: Ecoomercs Hypohess Tesg Iervl Esmo Wh we hve doe so fr s o udersd how we c ob esmors of ecoomcs reloshp we wsh o sudy. The queso s how comforble re we wh our esmors? We frs exme how o produce
ECON 37: Ecoomercs Hypohess Tesg Iervl Esmo Wh we hve doe so fr s o udersd how we c ob esmors of ecoomcs reloshp we wsh o sudy. The queso s how comforble re we wh our esmors? We frs exme how o produce
(1) Cov(, ) E[( E( ))( E( ))]
![(1) Cov(, ) E[( E( ))( E( ))] (1) Cov(, ) E[( E( ))( E( ))]](/thumbs/86/94405490.jpg) Impac of Auocorrelao o OLS Esmaes ECON 3033/Evas Cosder a smple bvarae me-seres model of he form: y 0 x The four key assumpos abou ε hs model are ) E(ε ) = E[ε x ]=0 ) Var(ε ) =Var(ε x ) = ) Cov(ε, ε )
Impac of Auocorrelao o OLS Esmaes ECON 3033/Evas Cosder a smple bvarae me-seres model of he form: y 0 x The four key assumpos abou ε hs model are ) E(ε ) = E[ε x ]=0 ) Var(ε ) =Var(ε x ) = ) Cov(ε, ε )
Representation of Solutions of Linear Homogeneous Caputo Fractional Differential Equations with Continuous Variable Coefficients
 Repor Nuber: KSU MATH 3 E R 6 Represeo o Souos o Ler Hoogeeous puo Fro ere Equos w ouous Vrbe oees Su-Ae PAK Mog-H KM d Hog-o O * Fu o Mes K Sug Uvers Pogg P R Kore * orrespodg uor e: oogo@ooo Absr We
Repor Nuber: KSU MATH 3 E R 6 Represeo o Souos o Ler Hoogeeous puo Fro ere Equos w ouous Vrbe oees Su-Ae PAK Mog-H KM d Hog-o O * Fu o Mes K Sug Uvers Pogg P R Kore * orrespodg uor e: oogo@ooo Absr We
A NEW FIVE-POINT BINARY SUBDIVISION SCHEME WITH A PARAMETER
 Jourl of ure d Appled Mhemcs: Advces d Applcos Volume 9 Numer ges -9 Avlle hp://scefcdvcesco DOI: hp://dxdoorg/6/ms_9 A NEW FIVE-OINT BINARY UBDIVIION CHEME WITH A ARAMETER YAN WANG * d HIMING LI chool
Jourl of ure d Appled Mhemcs: Advces d Applcos Volume 9 Numer ges -9 Avlle hp://scefcdvcesco DOI: hp://dxdoorg/6/ms_9 A NEW FIVE-OINT BINARY UBDIVIION CHEME WITH A ARAMETER YAN WANG * d HIMING LI chool
Chebyshev Polynomials for Solving a Class of Singular Integral Equations
 Appled Mahemas, 4, 5, 75-764 Publshed Ole Marh 4 SRes. hp://www.srp.org/joural/am hp://d.do.org/.46/am.4.547 Chebyshev Polyomals for Solvg a Class of Sgular Iegral Equaos Samah M. Dardery, Mohamed M. Alla
Appled Mahemas, 4, 5, 75-764 Publshed Ole Marh 4 SRes. hp://www.srp.org/joural/am hp://d.do.org/.46/am.4.547 Chebyshev Polyomals for Solvg a Class of Sgular Iegral Equaos Samah M. Dardery, Mohamed M. Alla
International Journal of Pure and Applied Sciences and Technology
 I J Pure Al S Teol, 04, 64-77 Ierol Jourl o Pure d Aled Sees d Teoloy ISSN 9-607 Avlle ole wwwjos Reser Per O New Clss o rmo Uvle Fuos Deed y Fox-r Geerled yereomer Fuo Adul Rm S Jum d Zrr,* Derme o Mems,
I J Pure Al S Teol, 04, 64-77 Ierol Jourl o Pure d Aled Sees d Teoloy ISSN 9-607 Avlle ole wwwjos Reser Per O New Clss o rmo Uvle Fuos Deed y Fox-r Geerled yereomer Fuo Adul Rm S Jum d Zrr,* Derme o Mems,
Chapter Simpson s 1/3 Rule of Integration. ( x)
 Cper 7. Smpso s / Rule o Iegro Aer redg s per, you sould e le o. derve e ormul or Smpso s / rule o egro,. use Smpso s / rule o solve egrls,. develop e ormul or mulple-segme Smpso s / rule o egro,. use
Cper 7. Smpso s / Rule o Iegro Aer redg s per, you sould e le o. derve e ormul or Smpso s / rule o egro,. use Smpso s / rule o solve egrls,. develop e ormul or mulple-segme Smpso s / rule o egro,. use
4.1 Schrödinger Equation in Spherical Coordinates
 Phs 34 Quu Mehs D 9 9 Mo./ Wed./ Thus /3 F./4 Mo., /7 Tues. / Wed., /9 F., /3 4.. -. Shodge Sphe: Sepo & gu (Q9.) 4..-.3 Shodge Sphe: gu & d(q9.) Copuo: Sphe Shodge s 4. Hdoge o (Q9.) 4.3 gu Moeu 4.4.-.
Phs 34 Quu Mehs D 9 9 Mo./ Wed./ Thus /3 F./4 Mo., /7 Tues. / Wed., /9 F., /3 4.. -. Shodge Sphe: Sepo & gu (Q9.) 4..-.3 Shodge Sphe: gu & d(q9.) Copuo: Sphe Shodge s 4. Hdoge o (Q9.) 4.3 gu Moeu 4.4.-.
INTERNATIONAL JOURNAL OF ENGINEERING SCIENCES & RESEARCH TECHNOLOGY
 [Mjuh, : Jury, 0] ISSN: -96 Scefc Jourl Impc Fcr: 9 ISRA, Impc Fcr: IJESRT INTERNATIONAL JOURNAL OF ENINEERIN SCIENCES & RESEARCH TECHNOLOY HAMILTONIAN LACEABILITY IN MIDDLE RAPHS Mjuh*, MurlR, B Shmukh
[Mjuh, : Jury, 0] ISSN: -96 Scefc Jourl Impc Fcr: 9 ISRA, Impc Fcr: IJESRT INTERNATIONAL JOURNAL OF ENINEERIN SCIENCES & RESEARCH TECHNOLOY HAMILTONIAN LACEABILITY IN MIDDLE RAPHS Mjuh*, MurlR, B Shmukh
Asymptotic Behavior of Solutions of Nonlinear Delay Differential Equations With Impulse
 P a g e Vol Issue7Ver,oveber Global Joural of Scece Froer Research Asypoc Behavor of Soluos of olear Delay Dffereal Equaos Wh Ipulse Zhag xog GJSFR Classfcao - F FOR 3 Absrac Ths paper sudes he asypoc
P a g e Vol Issue7Ver,oveber Global Joural of Scece Froer Research Asypoc Behavor of Soluos of olear Delay Dffereal Equaos Wh Ipulse Zhag xog GJSFR Classfcao - F FOR 3 Absrac Ths paper sudes he asypoc
Key words: Fractional difference equation, oscillatory solutions,
 OSCILLATION PROPERTIES OF SOLUTIONS OF FRACTIONAL DIFFERENCE EQUATIONS Musafa BAYRAM * ad Ayd SECER * Deparme of Compuer Egeerg, Isabul Gelsm Uversy Deparme of Mahemacal Egeerg, Yldz Techcal Uversy * Correspodg
OSCILLATION PROPERTIES OF SOLUTIONS OF FRACTIONAL DIFFERENCE EQUATIONS Musafa BAYRAM * ad Ayd SECER * Deparme of Compuer Egeerg, Isabul Gelsm Uversy Deparme of Mahemacal Egeerg, Yldz Techcal Uversy * Correspodg
CHAPTER 5 Vectors and Vector Space
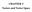 HAPTE 5 Vetors d Vetor Spe 5. Alger d eometry of Vetors. Vetor A ordered trple,,, where,, re rel umers. Symol:, B,, A mgtude d dreto.. Norm of vetor,, Norm =,, = = mgtude. Slr multplto Produt of slr d
HAPTE 5 Vetors d Vetor Spe 5. Alger d eometry of Vetors. Vetor A ordered trple,,, where,, re rel umers. Symol:, B,, A mgtude d dreto.. Norm of vetor,, Norm =,, = = mgtude. Slr multplto Produt of slr d
The University of Sheffield
 The Uversy of Sheffeld Deprme of uom Corol d Sysems Egeerg Sldg ode Corol of Noler Sysems Houm Dlll.S. Corol Sysems ugus 7 Supervsor: Professor Sephe P. Bks dssero submed prl fulflme of he requremes for
The Uversy of Sheffeld Deprme of uom Corol d Sysems Egeerg Sldg ode Corol of Noler Sysems Houm Dlll.S. Corol Sysems ugus 7 Supervsor: Professor Sephe P. Bks dssero submed prl fulflme of he requremes for
STOCHASTIC CALCULUS I STOCHASTIC DIFFERENTIAL EQUATION
 The Bk of Thld Fcl Isuos Polcy Group Que Models & Fcl Egeerg Tem Fcl Mhemcs Foudo Noe 8 STOCHASTIC CALCULUS I STOCHASTIC DIFFERENTIAL EQUATION. ก Through he use of ordry d/or prl deres, ODE/PDE c rele
The Bk of Thld Fcl Isuos Polcy Group Que Models & Fcl Egeerg Tem Fcl Mhemcs Foudo Noe 8 STOCHASTIC CALCULUS I STOCHASTIC DIFFERENTIAL EQUATION. ก Through he use of ordry d/or prl deres, ODE/PDE c rele
Isotropic Non-Heisenberg Magnet for Spin S=1
 Ierol Jourl of Physcs d Applcos. IN 974- Volume, Number (, pp. 7-4 Ierol Reserch Publco House hp://www.rphouse.com Isoropc No-Heseberg Mge for p = Y. Yousef d Kh. Kh. Mumov.U. Umrov Physcl-Techcl Isue
Ierol Jourl of Physcs d Applcos. IN 974- Volume, Number (, pp. 7-4 Ierol Reserch Publco House hp://www.rphouse.com Isoropc No-Heseberg Mge for p = Y. Yousef d Kh. Kh. Mumov.U. Umrov Physcl-Techcl Isue
Technical Appendix for Inventory Management for an Assembly System with Product or Component Returns, DeCroix and Zipkin, Management Science 2005.
 Techc Appedx fo Iveoy geme fo Assemy Sysem wh Poduc o Compoe eus ecox d Zp geme Scece 2005 Lemm µ µ s c Poof If J d µ > µ he ˆ 0 µ µ µ µ µ µ µ µ Sm gumes essh he esu f µ ˆ > µ > µ > µ o K ˆ If J he so
Techc Appedx fo Iveoy geme fo Assemy Sysem wh Poduc o Compoe eus ecox d Zp geme Scece 2005 Lemm µ µ s c Poof If J d µ > µ he ˆ 0 µ µ µ µ µ µ µ µ Sm gumes essh he esu f µ ˆ > µ > µ > µ o K ˆ If J he so
Solution 2. Since. 1. Sums and Products
 . Sus Prous I h, ver oe we hve soe eresg uers whh we woul le o her su or prou. elow we wll loo ew ehos or og hese operos. (Here we wll lso oser egrls whh we vew s sug uoul uers.) Prg Meho. Rell o S we
. Sus Prous I h, ver oe we hve soe eresg uers whh we woul le o her su or prou. elow we wll loo ew ehos or og hese operos. (Here we wll lso oser egrls whh we vew s sug uoul uers.) Prg Meho. Rell o S we
Suggested Solution for Pure Mathematics 2011 By Y.K. Ng (last update: 8/4/2011) Paper I. (b) (c)
 per I. Le α 7 d β 7. The α d β re he roos o he equio, such h α α, β β, --- α β d αβ. For, α β For, α β α β αβ 66 The seme is rue or,. ssume Cosider, α β d α β y deiiio α α α α β or some posiive ieer.
per I. Le α 7 d β 7. The α d β re he roos o he equio, such h α α, β β, --- α β d αβ. For, α β For, α β α β αβ 66 The seme is rue or,. ssume Cosider, α β d α β y deiiio α α α α β or some posiive ieer.
Learning of Graphical Models Parameter Estimation and Structure Learning
 Learg of Grahal Models Parameer Esmao ad Sruure Learg e Fukumzu he Isue of Sasal Mahemas Comuaoal Mehodology Sasal Iferee II Work wh Grahal Models Deermg sruure Sruure gve by modelg d e.g. Mxure model
Learg of Grahal Models Parameer Esmao ad Sruure Learg e Fukumzu he Isue of Sasal Mahemas Comuaoal Mehodology Sasal Iferee II Work wh Grahal Models Deermg sruure Sruure gve by modelg d e.g. Mxure model
Coefficient Inequalities for Certain Subclasses. of Analytic Functions
 I. Jourl o Mh. Alysis, Vol., 00, o. 6, 77-78 Coeiie Iequliies or Ceri Sulsses o Alyi Fuios T. Rm Reddy d * R.. Shrm Deprme o Mhemis, Kkiy Uiversiy Wrgl 506009, Adhr Prdesh, Idi reddyr@yhoo.om, *rshrm_005@yhoo.o.i
I. Jourl o Mh. Alysis, Vol., 00, o. 6, 77-78 Coeiie Iequliies or Ceri Sulsses o Alyi Fuios T. Rm Reddy d * R.. Shrm Deprme o Mhemis, Kkiy Uiversiy Wrgl 506009, Adhr Prdesh, Idi reddyr@yhoo.om, *rshrm_005@yhoo.o.i
Modified Taylor's Method and Nonlinear Mixed Integral Equation
 Uversl Jourl of Iegrl quos 4 (6), 9 wwwpperscecescom Modfed Tylor's Mehod d oler Mxed Iegrl quo R T Moog Fculy of Appled Scece, Umm Al Qurh Uversy Mkh, Kgdom of Sud Ar rmoog_777@yhoocom Asrc I hs pper,
Uversl Jourl of Iegrl quos 4 (6), 9 wwwpperscecescom Modfed Tylor's Mehod d oler Mxed Iegrl quo R T Moog Fculy of Appled Scece, Umm Al Qurh Uversy Mkh, Kgdom of Sud Ar rmoog_777@yhoocom Asrc I hs pper,
Modeling and Predicting Sequences: HMM and (may be) CRF. Amr Ahmed Feb 25
 Modelg d redcg Sequeces: HMM d m be CRF Amr Ahmed 070 Feb 25 Bg cure redcg Sgle Lbel Ipu : A se of feures: - Bg of words docume - Oupu : Clss lbel - Topc of he docume - redcg Sequece of Lbels Noo Noe:
Modelg d redcg Sequeces: HMM d m be CRF Amr Ahmed 070 Feb 25 Bg cure redcg Sgle Lbel Ipu : A se of feures: - Bg of words docume - Oupu : Clss lbel - Topc of he docume - redcg Sequece of Lbels Noo Noe:
14. Poisson Processes
 4. Posso Processes I Lecure 4 we roduced Posso arrvals as he lmg behavor of Bomal radom varables. Refer o Posso approxmao of Bomal radom varables. From he dscusso here see 4-6-4-8 Lecure 4 " arrvals occur
4. Posso Processes I Lecure 4 we roduced Posso arrvals as he lmg behavor of Bomal radom varables. Refer o Posso approxmao of Bomal radom varables. From he dscusso here see 4-6-4-8 Lecure 4 " arrvals occur
Eurasian International Center of Theoretical Physics, Eurasian National University, Astana , Kazakhstan
 Joul o Mhems d sem ee 8 8 87-95 do: 765/59-59/8 D DAVID PUBLIHIG E Loled oluos o he Geeled +-Dmesol Ldu-Lsh Equo Gulgssl ugmov Ao Mul d Zh gdullev Eus Ieol Cee o Theoel Phss Eus ol Uves As 8 Khs As: I
Joul o Mhems d sem ee 8 8 87-95 do: 765/59-59/8 D DAVID PUBLIHIG E Loled oluos o he Geeled +-Dmesol Ldu-Lsh Equo Gulgssl ugmov Ao Mul d Zh gdullev Eus Ieol Cee o Theoel Phss Eus ol Uves As 8 Khs As: I
Handout on. Crystal Symmetries and Energy Bands
 dou o Csl s d g Bds I hs lu ou wll l: Th loshp bw ss d g bds h bs of sp-ob ouplg Th loshp bw ss d g bds h ps of sp-ob ouplg C 7 pg 9 Fh Coll Uvs d g Bds gll hs oh Th sl pol ss ddo o h l slo s: Fo pl h
dou o Csl s d g Bds I hs lu ou wll l: Th loshp bw ss d g bds h bs of sp-ob ouplg Th loshp bw ss d g bds h ps of sp-ob ouplg C 7 pg 9 Fh Coll Uvs d g Bds gll hs oh Th sl pol ss ddo o h l slo s: Fo pl h
Chapter Gauss-Seidel Method
 Chpter 04.08 Guss-Sedel Method After redg ths hpter, you should be ble to:. solve set of equtos usg the Guss-Sedel method,. reogze the dvtges d ptflls of the Guss-Sedel method, d. determe uder wht odtos
Chpter 04.08 Guss-Sedel Method After redg ths hpter, you should be ble to:. solve set of equtos usg the Guss-Sedel method,. reogze the dvtges d ptflls of the Guss-Sedel method, d. determe uder wht odtos
The Properties of Probability of Normal Chain
 I. J. Coep. Mah. Sceces Vol. 8 23 o. 9 433-439 HIKARI Ld www.-hkar.co The Properes of Proaly of Noral Cha L Che School of Maheacs ad Sascs Zheghou Noral Uversy Zheghou Cy Hea Provce 4544 Cha cluu6697@sa.co
I. J. Coep. Mah. Sceces Vol. 8 23 o. 9 433-439 HIKARI Ld www.-hkar.co The Properes of Proaly of Noral Cha L Che School of Maheacs ad Sascs Zheghou Noral Uversy Zheghou Cy Hea Provce 4544 Cha cluu6697@sa.co
X-Ray Notes, Part III
 oll 6 X-y oe 3: Pe X-Ry oe, P III oe Deeo Coe oupu o x-y ye h look lke h: We efe ue of que lhly ffee efo h ue y ovk: Co: C ΔS S Sl o oe Ro: SR S Co o oe Ro: CR ΔS C SR Pevouly, we ee he SR fo ye hv pxel
oll 6 X-y oe 3: Pe X-Ry oe, P III oe Deeo Coe oupu o x-y ye h look lke h: We efe ue of que lhly ffee efo h ue y ovk: Co: C ΔS S Sl o oe Ro: SR S Co o oe Ro: CR ΔS C SR Pevouly, we ee he SR fo ye hv pxel
Mathematically, integration is just finding the area under a curve from one point to another. It is b
 Numerl Metods or Eg [ENGR 9] [Lyes KADEM 7] CHAPTER VI Numerl Itegrto Tops - Rem sums - Trpezodl rule - Smpso s rule - Rrdso s etrpolto - Guss qudrture rule Mtemtlly, tegrto s just dg te re uder urve rom
Numerl Metods or Eg [ENGR 9] [Lyes KADEM 7] CHAPTER VI Numerl Itegrto Tops - Rem sums - Trpezodl rule - Smpso s rule - Rrdso s etrpolto - Guss qudrture rule Mtemtlly, tegrto s just dg te re uder urve rom
Solution of Impulsive Differential Equations with Boundary Conditions in Terms of Integral Equations
 Joural of aheacs ad copuer Scece (4 39-38 Soluo of Ipulsve Dffereal Equaos wh Boudary Codos Ters of Iegral Equaos Arcle hsory: Receved Ocober 3 Acceped February 4 Avalable ole July 4 ohse Rabba Depare
Joural of aheacs ad copuer Scece (4 39-38 Soluo of Ipulsve Dffereal Equaos wh Boudary Codos Ters of Iegral Equaos Arcle hsory: Receved Ocober 3 Acceped February 4 Avalable ole July 4 ohse Rabba Depare
MTH 146 Class 7 Notes
 7.7- Approxmte Itegrto Motvto: MTH 46 Clss 7 Notes I secto 7.5 we lered tht some defte tegrls, lke x e dx, cot e wrtte terms of elemetry fuctos. So, good questo to sk would e: How c oe clculte somethg
7.7- Approxmte Itegrto Motvto: MTH 46 Clss 7 Notes I secto 7.5 we lered tht some defte tegrls, lke x e dx, cot e wrtte terms of elemetry fuctos. So, good questo to sk would e: How c oe clculte somethg
For the plane motion of a rigid body, an additional equation is needed to specify the state of rotation of the body.
 The kecs of rgd bodes reas he relaoshps bewee he exeral forces acg o a body ad he correspodg raslaoal ad roaoal moos of he body. he kecs of he parcle, we foud ha wo force equaos of moo were requred o defe
The kecs of rgd bodes reas he relaoshps bewee he exeral forces acg o a body ad he correspodg raslaoal ad roaoal moos of he body. he kecs of he parcle, we foud ha wo force equaos of moo were requred o defe
4. Runge-Kutta Formula For Differential Equations
 NCTU Deprme o Elecrcl d Compuer Egeerg 5 Sprg Course by Pro. Yo-Pg Ce. Ruge-Ku Formul For Derel Equos To solve e derel equos umerclly e mos useul ormul s clled Ruge-Ku ormul
NCTU Deprme o Elecrcl d Compuer Egeerg 5 Sprg Course by Pro. Yo-Pg Ce. Ruge-Ku Formul For Derel Equos To solve e derel equos umerclly e mos useul ormul s clled Ruge-Ku ormul
Least Squares Fitting (LSQF) with a complicated function Theexampleswehavelookedatsofarhavebeenlinearintheparameters
 Leas Squares Fg LSQF wh a complcaed fuco Theeampleswehavelookedasofarhavebeelearheparameers ha we have bee rg o deerme e.g. slope, ercep. For he case where he fuco s lear he parameers we ca fd a aalc soluo
Leas Squares Fg LSQF wh a complcaed fuco Theeampleswehavelookedasofarhavebeelearheparameers ha we have bee rg o deerme e.g. slope, ercep. For he case where he fuco s lear he parameers we ca fd a aalc soluo
Special Curves of 4D Galilean Space
 Irol Jourl of Mhml Egrg d S ISSN : 77-698 Volum Issu Mrh hp://www.jms.om/ hps://ss.googl.om/s/jmsjourl/ Spl Curvs of D ll Sp Mhm Bkş Mhmu Ergü Alpr Osm Öğrmş Fır Uvrsy Fuly of S Dprm of Mhms 9 Elzığ Türky
Irol Jourl of Mhml Egrg d S ISSN : 77-698 Volum Issu Mrh hp://www.jms.om/ hps://ss.googl.om/s/jmsjourl/ Spl Curvs of D ll Sp Mhm Bkş Mhmu Ergü Alpr Osm Öğrmş Fır Uvrsy Fuly of S Dprm of Mhms 9 Elzığ Türky
Review for the Midterm Exam.
 Review for he iderm Exm Rememer! Gross re e re Vriles suh s,, /, p / p, r, d R re gross res 2 You should kow he disiio ewee he fesile se d he udge se, d kow how o derive hem The Fesile Se Wihou goverme
Review for he iderm Exm Rememer! Gross re e re Vriles suh s,, /, p / p, r, d R re gross res 2 You should kow he disiio ewee he fesile se d he udge se, d kow how o derive hem The Fesile Se Wihou goverme
Decompression diagram sampler_src (source files and makefiles) bin (binary files) --- sh (sample shells) --- input (sample input files)
 . Iroduco Probblsc oe-moh forecs gudce s mde b 50 esemble members mproved b Model Oupu scs (MO). scl equo s mde b usg hdcs d d observo d. We selec some prmeers for modfg forecs o use mulple regresso formul.
. Iroduco Probblsc oe-moh forecs gudce s mde b 50 esemble members mproved b Model Oupu scs (MO). scl equo s mde b usg hdcs d d observo d. We selec some prmeers for modfg forecs o use mulple regresso formul.
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
Supporting information How to concatenate the local attractors of subnetworks in the HPFP
 n Effcen lgorh for Idenfyng Prry Phenoype rcors of Lrge-Scle Boolen Newor Sng-Mo Choo nd Kwng-Hyun Cho Depren of Mhecs Unversy of Ulsn Ulsn 446 Republc of Kore Depren of Bo nd Brn Engneerng Kore dvnced
n Effcen lgorh for Idenfyng Prry Phenoype rcors of Lrge-Scle Boolen Newor Sng-Mo Choo nd Kwng-Hyun Cho Depren of Mhecs Unversy of Ulsn Ulsn 446 Republc of Kore Depren of Bo nd Brn Engneerng Kore dvnced
4. Runge-Kutta Formula For Differential Equations. A. Euler Formula B. Runge-Kutta Formula C. An Example for Fourth-Order Runge-Kutta Formula
 NCTU Deprme o Elecrcl d Compuer Egeerg Seor Course By Pro. Yo-Pg Ce. Ruge-Ku Formul For Derel Equos A. Euler Formul B. Ruge-Ku Formul C. A Emple or Four-Order Ruge-Ku Formul
NCTU Deprme o Elecrcl d Compuer Egeerg Seor Course By Pro. Yo-Pg Ce. Ruge-Ku Formul For Derel Equos A. Euler Formul B. Ruge-Ku Formul C. A Emple or Four-Order Ruge-Ku Formul
Week 8 Lecture 3: Problems 49, 50 Fourier analysis Courseware pp (don t look at French very confusing look in the Courseware instead)
 Week 8 Lecure 3: Problems 49, 5 Fourier lysis Coursewre pp 6-7 (do look Frech very cofusig look i he Coursewre ised) Fourier lysis ivolves ddig wves d heir hrmoics, so i would hve urlly followed fer he
Week 8 Lecure 3: Problems 49, 5 Fourier lysis Coursewre pp 6-7 (do look Frech very cofusig look i he Coursewre ised) Fourier lysis ivolves ddig wves d heir hrmoics, so i would hve urlly followed fer he
The ray paths and travel times for multiple layers can be computed using ray-tracing, as demonstrated in Lab 3.
 C. Trael me cures for mulple reflecors The ray pahs ad rael mes for mulple layers ca be compued usg ray-racg, as demosraed Lab. MATLAB scrp reflec_layers_.m performs smple ray racg. (m) ref(ms) ref(ms)
C. Trael me cures for mulple reflecors The ray pahs ad rael mes for mulple layers ca be compued usg ray-racg, as demosraed Lab. MATLAB scrp reflec_layers_.m performs smple ray racg. (m) ref(ms) ref(ms)
Area and the Definite Integral. Area under Curve. The Partition. y f (x) We want to find the area under f (x) on [ a, b ]
![Area and the Definite Integral. Area under Curve. The Partition. y f (x) We want to find the area under f (x) on [ a, b ] Area and the Definite Integral. Area under Curve. The Partition. y f (x) We want to find the area under f (x) on [ a, b ]](/thumbs/83/87614710.jpg) Are d the Defte Itegrl 1 Are uder Curve We wt to fd the re uder f (x) o [, ] y f (x) x The Prtto We eg y prttog the tervl [, ] to smller su-tervls x 0 x 1 x x - x -1 x 1 The Bsc Ide We the crete rectgles
Are d the Defte Itegrl 1 Are uder Curve We wt to fd the re uder f (x) o [, ] y f (x) x The Prtto We eg y prttog the tervl [, ] to smller su-tervls x 0 x 1 x x - x -1 x 1 The Bsc Ide We the crete rectgles
The Products of Regularly Solvable Operators with Their Spectra in Direct Sum Spaces
 Advces Pure Mhemcs 3 3 45-49 h://dxdoorg/436/m3346 Pulshed Ole July 3 (h://wwwscrorg/ourl/m) he Producs of Regulrly Solvle Oerors wh her Secr Drec Sum Sces Sohy El-Syed Irhm Derme of Mhemcs Fculy of Scece
Advces Pure Mhemcs 3 3 45-49 h://dxdoorg/436/m3346 Pulshed Ole July 3 (h://wwwscrorg/ourl/m) he Producs of Regulrly Solvle Oerors wh her Secr Drec Sum Sces Sohy El-Syed Irhm Derme of Mhemcs Fculy of Scece
Available online through
 Avlble ole through wwwmfo FIXED POINTS FOR NON-SELF MAPPINGS ON CONEX ECTOR METRIC SPACES Susht Kumr Moht* Deprtmet of Mthemtcs West Begl Stte Uverst Brst 4 PrgsNorth) Kolt 76 West Begl Id E-ml: smwbes@yhoo
Avlble ole through wwwmfo FIXED POINTS FOR NON-SELF MAPPINGS ON CONEX ECTOR METRIC SPACES Susht Kumr Moht* Deprtmet of Mthemtcs West Begl Stte Uverst Brst 4 PrgsNorth) Kolt 76 West Begl Id E-ml: smwbes@yhoo
Application of Multiple Exp-Function Method to Obtain Multi-Soliton Solutions of (2 + 1)- and (3 + 1)-Dimensional Breaking Soliton Equations
 Amerc Jourl of Compuol Appled Mhemcs: ; (: 4-47 DOI:.593/j.jcm..8 Applco of Mulple Exp-Fuco Mehod o Ob Mul-Solo Soluos of ( + - (3 + -Dmesol Breg Solo Equos M. T. Drvsh,*, Mlheh Njf, Mohmmd Njf Deprme
Amerc Jourl of Compuol Appled Mhemcs: ; (: 4-47 DOI:.593/j.jcm..8 Applco of Mulple Exp-Fuco Mehod o Ob Mul-Solo Soluos of ( + - (3 + -Dmesol Breg Solo Equos M. T. Drvsh,*, Mlheh Njf, Mohmmd Njf Deprme
RAKE Receiver with Adaptive Interference Cancellers for a DS-CDMA System in Multipath Fading Channels
 AKE v wh Apv f Cs fo DS-CDMA Ss Muph Fg Chs JooHu Y Su M EEE JHog M EEE Shoo of E Egg Sou o Uvs Sh-og Gw-gu Sou 5-74 Ko E-: ohu@su As hs pp pv AKE v wh vs og s popos fo DS-CDMA ss uph fg hs h popos pv
AKE v wh Apv f Cs fo DS-CDMA Ss Muph Fg Chs JooHu Y Su M EEE JHog M EEE Shoo of E Egg Sou o Uvs Sh-og Gw-gu Sou 5-74 Ko E-: ohu@su As hs pp pv AKE v wh vs og s popos fo DS-CDMA ss uph fg hs h popos pv
On the Existence and uniqueness for solution of system Fractional Differential Equations
 OSR Jourl o Mhms OSR-JM SSN: 78-578. Volum 4 ssu 3 Nov. - D. PP -5 www.osrjourls.org O h Es d uquss or soluo o ssm rol Drl Equos Mh Ad Al-Wh Dprm o Appld S Uvrs o holog Bghdd- rq Asr: hs ppr w d horm o
OSR Jourl o Mhms OSR-JM SSN: 78-578. Volum 4 ssu 3 Nov. - D. PP -5 www.osrjourls.org O h Es d uquss or soluo o ssm rol Drl Equos Mh Ad Al-Wh Dprm o Appld S Uvrs o holog Bghdd- rq Asr: hs ppr w d horm o
An improved Bennett s inequality
 COMMUNICATIONS IN STATISTICS THEORY AND METHODS 017,VOL.0,NO.0,1 8 hps://do.org/10.1080/0361096.017.1367818 A mproved Bee s equly Sogfeg Zheg Deprme of Mhemcs, Mssour Se Uversy, Sprgfeld, MO, USA ABSTRACT
COMMUNICATIONS IN STATISTICS THEORY AND METHODS 017,VOL.0,NO.0,1 8 hps://do.org/10.1080/0361096.017.1367818 A mproved Bee s equly Sogfeg Zheg Deprme of Mhemcs, Mssour Se Uversy, Sprgfeld, MO, USA ABSTRACT
Partial Molar Properties of solutions
 Paral Molar Properes of soluos A soluo s a homogeeous mxure; ha s, a soluo s a oephase sysem wh more ha oe compoe. A homogeeous mxures of wo or more compoes he gas, lqud or sold phase The properes of a
Paral Molar Properes of soluos A soluo s a homogeeous mxure; ha s, a soluo s a oephase sysem wh more ha oe compoe. A homogeeous mxures of wo or more compoes he gas, lqud or sold phase The properes of a
QR factorization. Let P 1, P 2, P n-1, be matrices such that Pn 1Pn 2... PPA
 QR facorzao Ay x real marx ca be wre as AQR, where Q s orhogoal ad R s upper ragular. To oba Q ad R, we use he Householder rasformao as follows: Le P, P, P -, be marces such ha P P... PPA ( R s upper ragular.
QR facorzao Ay x real marx ca be wre as AQR, where Q s orhogoal ad R s upper ragular. To oba Q ad R, we use he Householder rasformao as follows: Le P, P, P -, be marces such ha P P... PPA ( R s upper ragular.
NONLINEAR SYSTEM OF SINGULAR PARTIAL DIFFERENTIAL EQUATIONS
 Jourl of Mhemcl Sceces: dvces d pplcos Volume 43, 27, Pges 3-53 vlble hp://scefcdvces.co. DOI: hp://d.do.org/.8642/ms_72748 OLIER SYSTEM OF SIGULR PRTIL DIFFERETIL EQUTIOS PTRICE POGÉRRD Mhemcs Lborory
Jourl of Mhemcl Sceces: dvces d pplcos Volume 43, 27, Pges 3-53 vlble hp://scefcdvces.co. DOI: hp://d.do.org/.8642/ms_72748 OLIER SYSTEM OF SIGULR PRTIL DIFFERETIL EQUTIOS PTRICE POGÉRRD Mhemcs Lborory
Problem Set 4 Solutions
 4 Eoom Altos of Gme Theory TA: Youg wg /08/0 - Ato se: A A { B, } S Prolem Set 4 Solutos - Tye Se: T { α }, T { β, β} Se Plyer hs o rte formto, we model ths so tht her tye tke oly oe lue Plyer kows tht
4 Eoom Altos of Gme Theory TA: Youg wg /08/0 - Ato se: A A { B, } S Prolem Set 4 Solutos - Tye Se: T { α }, T { β, β} Se Plyer hs o rte formto, we model ths so tht her tye tke oly oe lue Plyer kows tht
Cyclone. Anti-cyclone
 Adveco Cycloe A-cycloe Lorez (963) Low dmesoal aracors. Uclear f hey are a good aalogy o he rue clmae sysem, bu hey have some appealg characerscs. Dscusso Is he al codo balaced? Is here a al adjusme
Adveco Cycloe A-cycloe Lorez (963) Low dmesoal aracors. Uclear f hey are a good aalogy o he rue clmae sysem, bu hey have some appealg characerscs. Dscusso Is he al codo balaced? Is here a al adjusme
Matrix. Definition 1... a1 ... (i) where a. are real numbers. for i 1, 2,, m and j = 1, 2,, n (iii) A is called a square matrix if m n.
 Mtrx Defto () s lled order of m mtrx, umer of rows ( 橫行 ) umer of olums ( 直列 ) m m m where j re rel umers () B j j for,,, m d j =,,, () s lled squre mtrx f m (v) s lled zero mtrx f (v) s lled detty mtrx
Mtrx Defto () s lled order of m mtrx, umer of rows ( 橫行 ) umer of olums ( 直列 ) m m m where j re rel umers () B j j for,,, m d j =,,, () s lled squre mtrx f m (v) s lled zero mtrx f (v) s lled detty mtrx
Bethe-Salpeter Equation
 Behe-Slpee Equo No-elvs Fomlsm Behe-Slpee Equo: ouo o he op. Dgesso Seo Quzo. Dgesso: fs quzo s movo fo seo quzo. Quum Fel Theoel Hmlo Seo Quzo. Shöge Equo. Equo of Moo. Shöge Fomulo. Behe-Slpee Equo fo
Behe-Slpee Equo No-elvs Fomlsm Behe-Slpee Equo: ouo o he op. Dgesso Seo Quzo. Dgesso: fs quzo s movo fo seo quzo. Quum Fel Theoel Hmlo Seo Quzo. Shöge Equo. Equo of Moo. Shöge Fomulo. Behe-Slpee Equo fo
In Calculus I you learned an approximation method using a Riemann sum. Recall that the Riemann sum is
 Mth Sprg 08 L Approxmtg Dete Itegrls I Itroducto We hve studed severl methods tht llow us to d the exct vlues o dete tegrls However, there re some cses whch t s ot possle to evlute dete tegrl exctly I
Mth Sprg 08 L Approxmtg Dete Itegrls I Itroducto We hve studed severl methods tht llow us to d the exct vlues o dete tegrls However, there re some cses whch t s ot possle to evlute dete tegrl exctly I
Data Compression Techniques (Spring 2012) Model Solutions for Exercise 4
 58487 Dt Compressio Tehiques (Sprig 0) Moel Solutios for Exerise 4 If you hve y fee or orretios, plese ott jro.lo t s.helsii.fi.. Prolem: Let T = Σ = {,,, }. Eoe T usig ptive Huffm oig. Solutio: R 4 U
58487 Dt Compressio Tehiques (Sprig 0) Moel Solutios for Exerise 4 If you hve y fee or orretios, plese ott jro.lo t s.helsii.fi.. Prolem: Let T = Σ = {,,, }. Eoe T usig ptive Huffm oig. Solutio: R 4 U
Integration by Parts for D K
 Itertol OPEN ACCESS Jourl Of Moder Egeerg Reserc IJMER Itegrto y Prts for D K Itegrl T K Gr, S Ry 2 Deprtmet of Mtemtcs, Rgutpur College, Rgutpur-72333, Purul, West Begl, Id 2 Deprtmet of Mtemtcs, Ss Bv,
Itertol OPEN ACCESS Jourl Of Moder Egeerg Reserc IJMER Itegrto y Prts for D K Itegrl T K Gr, S Ry 2 Deprtmet of Mtemtcs, Rgutpur College, Rgutpur-72333, Purul, West Begl, Id 2 Deprtmet of Mtemtcs, Ss Bv,
The Existence and Uniqueness of Random Solution to Itô Stochastic Integral Equation
 Appled Mhemcs,, 3, 8-84 hp://dx.do.org/.436/m..379 Pulshed Ole July (hp://www.scrp.org/jourl/m) The Exsece d Uqueess of Rdom Soluo o Iô Sochsc Iegrl Equo Hmd Ahmed Alff, Csh Wg School of Mhemcs d Iformo
Appled Mhemcs,, 3, 8-84 hp://dx.do.org/.436/m..379 Pulshed Ole July (hp://www.scrp.org/jourl/m) The Exsece d Uqueess of Rdom Soluo o Iô Sochsc Iegrl Equo Hmd Ahmed Alff, Csh Wg School of Mhemcs d Iformo
Determination of Antoine Equation Parameters. December 4, 2012 PreFEED Corporation Yoshio Kumagae. Introduction
 refeed Soluos for R&D o Desg Deermao of oe Equao arameers Soluos for R&D o Desg December 4, 0 refeed orporao Yosho Kumagae refeed Iroduco hyscal propery daa s exremely mpora for performg process desg ad
refeed Soluos for R&D o Desg Deermao of oe Equao arameers Soluos for R&D o Desg December 4, 0 refeed orporao Yosho Kumagae refeed Iroduco hyscal propery daa s exremely mpora for performg process desg ad
8. Queueing systems lect08.ppt S Introduction to Teletraffic Theory - Fall
 8. Queueg sysems lec8. S-38.45 - Iroduco o Teleraffc Theory - Fall 8. Queueg sysems Coes Refresher: Smle eleraffc model M/M/ server wag laces M/M/ servers wag laces 8. Queueg sysems Smle eleraffc model
8. Queueg sysems lec8. S-38.45 - Iroduco o Teleraffc Theory - Fall 8. Queueg sysems Coes Refresher: Smle eleraffc model M/M/ server wag laces M/M/ servers wag laces 8. Queueg sysems Smle eleraffc model
Ruin Probability-Based Initial Capital of the Discrete-Time Surplus Process
 Ru Probablty-Based Ital Captal of the Dsrete-Tme Surplus Proess by Parote Sattayatham, Kat Sagaroo, ad Wathar Klogdee AbSTRACT Ths paper studes a surae model uder the regulato that the surae ompay has
Ru Probablty-Based Ital Captal of the Dsrete-Tme Surplus Proess by Parote Sattayatham, Kat Sagaroo, ad Wathar Klogdee AbSTRACT Ths paper studes a surae model uder the regulato that the surae ompay has
I I M O I S K J H G. b gb g. Chapter 8. Problem Solutions. Semiconductor Physics and Devices: Basic Principles, 3 rd edition Chapter 8
 emcouc hyscs evces: Bsc rcles, r eo Cher 8 oluos ul rolem oluos Cher 8 rolem oluos 8. he fwr s e ex f The e ex f e e f ex () () f f f f l G e f f ex f 59.9 m 60 m 0 9. m m 8. e ex we c wre hs s e ex h
emcouc hyscs evces: Bsc rcles, r eo Cher 8 oluos ul rolem oluos Cher 8 rolem oluos 8. he fwr s e ex f The e ex f e e f ex () () f f f f l G e f f ex f 59.9 m 60 m 0 9. m m 8. e ex we c wre hs s e ex h
Continuous Indexed Variable Systems
 Ieraoal Joural o Compuaoal cece ad Mahemacs. IN 0974-389 Volume 3, Number 4 (20), pp. 40-409 Ieraoal Research Publcao House hp://www.rphouse.com Couous Idexed Varable ysems. Pouhassa ad F. Mohammad ghjeh
Ieraoal Joural o Compuaoal cece ad Mahemacs. IN 0974-389 Volume 3, Number 4 (20), pp. 40-409 Ieraoal Research Publcao House hp://www.rphouse.com Couous Idexed Varable ysems. Pouhassa ad F. Mohammad ghjeh
Chapter 5 Transient Analysis
 hpr 5 rs Alyss Jsug Jg ompl rspos rs rspos y-s rspos m os rs orr co orr Dffrl Equo. rs Alyss h ffrc of lyss of crcus wh rgy sorg lms (ucors or cpcors) & m-ryg sgls wh rss crcus s h h quos rsulg from r
hpr 5 rs Alyss Jsug Jg ompl rspos rs rspos y-s rspos m os rs orr co orr Dffrl Equo. rs Alyss h ffrc of lyss of crcus wh rgy sorg lms (ucors or cpcors) & m-ryg sgls wh rss crcus s h h quos rsulg from r
this is the indefinite integral Since integration is the reverse of differentiation we can check the previous by [ ]
![this is the indefinite integral Since integration is the reverse of differentiation we can check the previous by [ ] this is the indefinite integral Since integration is the reverse of differentiation we can check the previous by [ ]](/thumbs/78/76749440.jpg) Atervtves The Itegrl Atervtves Ojectve: Use efte tegrl otto for tervtves. Use sc tegrto rules to f tervtves. Aother mportt questo clculus s gve ervtve f the fucto tht t cme from. Ths s the process kow
Atervtves The Itegrl Atervtves Ojectve: Use efte tegrl otto for tervtves. Use sc tegrto rules to f tervtves. Aother mportt questo clculus s gve ervtve f the fucto tht t cme from. Ths s the process kow
Numerical Methods using the Successive Approximations for the Solution of a Fredholm Integral Equation
 ece Advce Appled d eorecl ec uercl eod u e Succeve Approo or e Soluo o Fredol Ierl Equo AIA OBIŢOIU epre o ec d opuer Scece Uvery o Peroş Uvery Sree 6 Peroş OAIA rdorou@yoo.co Arc: pper pree wo eod or
ece Advce Appled d eorecl ec uercl eod u e Succeve Approo or e Soluo o Fredol Ierl Equo AIA OBIŢOIU epre o ec d opuer Scece Uvery o Peroş Uvery Sree 6 Peroş OAIA rdorou@yoo.co Arc: pper pree wo eod or
ICS141: Discrete Mathematics for Computer Science I
 Uversty o Hw ICS: Dscrete Mthemtcs or Computer Scece I Dept. Iormto & Computer Sc., Uversty o Hw J Stelovsy bsed o sldes by Dr. Be d Dr. Stll Orgls by Dr. M. P. Fr d Dr. J.L. Gross Provded by McGrw-Hll
Uversty o Hw ICS: Dscrete Mthemtcs or Computer Scece I Dept. Iormto & Computer Sc., Uversty o Hw J Stelovsy bsed o sldes by Dr. Be d Dr. Stll Orgls by Dr. M. P. Fr d Dr. J.L. Gross Provded by McGrw-Hll
under the curve in the first quadrant.
 NOTES 5: INTEGRALS Nme: Dte: Perod: LESSON 5. AREAS AND DISTANCES Are uder the curve Are uder f( ), ove the -s, o the dom., Prctce Prolems:. f ( ). Fd the re uder the fucto, ove the - s, etwee,.. f ( )
NOTES 5: INTEGRALS Nme: Dte: Perod: LESSON 5. AREAS AND DISTANCES Are uder the curve Are uder f( ), ove the -s, o the dom., Prctce Prolems:. f ( ). Fd the re uder the fucto, ove the - s, etwee,.. f ( )
NEIGHBOURHOODS OF A CERTAIN SUBCLASS OF STARLIKE FUNCTIONS. P. Thirupathi Reddy. E. mail:
 NEIGHOURHOOD OF CERTIN UCL OF TRLIKE FUNCTION P Tirupi Reddy E mil: reddyp@yooom sr: Te im o is pper is o rodue e lss ( sulss o ( sisyig e odio wi is ( ) p < 0< E We sudy eigouroods o is lss d lso prove
NEIGHOURHOOD OF CERTIN UCL OF TRLIKE FUNCTION P Tirupi Reddy E mil: reddyp@yooom sr: Te im o is pper is o rodue e lss ( sulss o ( sisyig e odio wi is ( ) p < 0< E We sudy eigouroods o is lss d lso prove
Example: MOSFET Amplifier Distortion
 4/25/2011 Example MSFET Amplfer Dsoron 1/9 Example: MSFET Amplfer Dsoron Recall hs crcu from a prevous handou: ( ) = I ( ) D D d 15.0 V RD = 5K v ( ) = V v ( ) D o v( ) - K = 2 0.25 ma/v V = 2.0 V 40V.
4/25/2011 Example MSFET Amplfer Dsoron 1/9 Example: MSFET Amplfer Dsoron Recall hs crcu from a prevous handou: ( ) = I ( ) D D d 15.0 V RD = 5K v ( ) = V v ( ) D o v( ) - K = 2 0.25 ma/v V = 2.0 V 40V.
1 4 6 is symmetric 3 SPECIAL MATRICES 3.1 SYMMETRIC MATRICES. Defn: A matrix A is symmetric if and only if A = A, i.e., a ij =a ji i, j. Example 3.1.
 SPECIAL MATRICES SYMMETRIC MATRICES Def: A mtr A s symmetr f d oly f A A, e,, Emple A s symmetr Def: A mtr A s skew symmetr f d oly f A A, e,, Emple A s skew symmetr Remrks: If A s symmetr or skew symmetr,
SPECIAL MATRICES SYMMETRIC MATRICES Def: A mtr A s symmetr f d oly f A A, e,, Emple A s symmetr Def: A mtr A s skew symmetr f d oly f A A, e,, Emple A s skew symmetr Remrks: If A s symmetr or skew symmetr,
FALL HOMEWORK NO. 6 - SOLUTION Problem 1.: Use the Storage-Indication Method to route the Input hydrograph tabulated below.
 Jorge A. Ramírez HOMEWORK NO. 6 - SOLUTION Problem 1.: Use he Sorage-Idcao Mehod o roue he Ipu hydrograph abulaed below. Tme (h) Ipu Hydrograph (m 3 /s) Tme (h) Ipu Hydrograph (m 3 /s) 0 0 90 450 6 50
Jorge A. Ramírez HOMEWORK NO. 6 - SOLUTION Problem 1.: Use he Sorage-Idcao Mehod o roue he Ipu hydrograph abulaed below. Tme (h) Ipu Hydrograph (m 3 /s) Tme (h) Ipu Hydrograph (m 3 /s) 0 0 90 450 6 50
Solution set Stat 471/Spring 06. Homework 2
 oluo se a 47/prg 06 Homework a Whe he upper ragular elemes are suppressed due o smmer b Le Y Y Y Y A weep o he frs colum o oba: A ˆ b chagg he oao eg ad ec YY weep o he secod colum o oba: Aˆ YY weep o
oluo se a 47/prg 06 Homework a Whe he upper ragular elemes are suppressed due o smmer b Le Y Y Y Y A weep o he frs colum o oba: A ˆ b chagg he oao eg ad ec YY weep o he secod colum o oba: Aˆ YY weep o
A note on Turán number Tk ( 1, kn, )
 A oe o Turá umber T (,, ) L A-Pg Beg 00085, P.R. Cha apl000@sa.com Absrac: Turá umber s oe of prmary opcs he combaorcs of fe ses, hs paper, we wll prese a ew upper boud for Turá umber T (,, ). . Iroduco
A oe o Turá umber T (,, ) L A-Pg Beg 00085, P.R. Cha apl000@sa.com Absrac: Turá umber s oe of prmary opcs he combaorcs of fe ses, hs paper, we wll prese a ew upper boud for Turá umber T (,, ). . Iroduco
12.2 The Definite Integrals (5.2)
 Course: Aelerted Egieerig Clulus I Istrutor: Mihel Medvisky. The Defiite Itegrls 5. Def: Let fx e defied o itervl [,]. Divide [,] ito suitervls of equl width Δx, so x, x + Δx, x + jδx, x. Let x j j e ritrry
Course: Aelerted Egieerig Clulus I Istrutor: Mihel Medvisky. The Defiite Itegrls 5. Def: Let fx e defied o itervl [,]. Divide [,] ito suitervls of equl width Δx, so x, x + Δx, x + jδx, x. Let x j j e ritrry
Chapter 1 - Free Vibration of Multi-Degree-of-Freedom Systems - I
 CEE49b Chaper - Free Vbrao of M-Degree-of-Freedo Syses - I Free Udaped Vbrao The basc ype of respose of -degree-of-freedo syses s free daped vbrao Aaogos o sge degree of freedo syses he aayss of free vbrao
CEE49b Chaper - Free Vbrao of M-Degree-of-Freedo Syses - I Free Udaped Vbrao The basc ype of respose of -degree-of-freedo syses s free daped vbrao Aaogos o sge degree of freedo syses he aayss of free vbrao
AML710 CAD LECTURE 12 CUBIC SPLINE CURVES. Cubic Splines Matrix formulation Normalised cubic splines Alternate end conditions Parabolic blending
 CUIC SLINE CURVES Cubc Sples Marx formulao Normalsed cubc sples Alerae ed codos arabolc bledg AML7 CAD LECTURE CUIC SLINE The ame sple comes from he physcal srume sple drafsme use o produce curves A geeral
CUIC SLINE CURVES Cubc Sples Marx formulao Normalsed cubc sples Alerae ed codos arabolc bledg AML7 CAD LECTURE CUIC SLINE The ame sple comes from he physcal srume sple drafsme use o produce curves A geeral
Unscented Transformation Unscented Kalman Filter
 Usceed rsformo Usceed Klm Fler Usceed rcle Fler Flerg roblem Geerl roblem Seme where s he se d s he observo Flerg s he problem of sequell esmg he ses (prmeers or hdde vrbles) of ssem s se of observos become
Usceed rsformo Usceed Klm Fler Usceed rcle Fler Flerg roblem Geerl roblem Seme where s he se d s he observo Flerg s he problem of sequell esmg he ses (prmeers or hdde vrbles) of ssem s se of observos become
Riemann Integral Oct 31, such that
 Riem Itegrl Ot 31, 2007 Itegrtio of Step Futios A prtitio P of [, ] is olletio {x k } k=0 suh tht = x 0 < x 1 < < x 1 < x =. More suitly, prtitio is fiite suset of [, ] otiig d. It is helpful to thik of
Riem Itegrl Ot 31, 2007 Itegrtio of Step Futios A prtitio P of [, ] is olletio {x k } k=0 suh tht = x 0 < x 1 < < x 1 < x =. More suitly, prtitio is fiite suset of [, ] otiig d. It is helpful to thik of
Supplement: Gauss-Jordan Reduction
 Suppleme: Guss-Jord Reducio. Coefficie mri d ugmeed mri: The coefficie mri derived from sysem of lier equios m m m m is m m m A O d he ugmeed mri derived from he ove sysem of lier equios is [ ] m m m m
Suppleme: Guss-Jord Reducio. Coefficie mri d ugmeed mri: The coefficie mri derived from sysem of lier equios m m m m is m m m A O d he ugmeed mri derived from he ove sysem of lier equios is [ ] m m m m
Some Probability Inequalities for Quadratic Forms of Negatively Dependent Subgaussian Random Variables
 Joural of Sceces Islamc epublc of Ira 6(: 63-67 (005 Uvers of ehra ISSN 06-04 hp://scecesuacr Some Probabl Iequales for Quadrac Forms of Negavel Depede Subgaussa adom Varables M Am A ozorga ad H Zare 3
Joural of Sceces Islamc epublc of Ira 6(: 63-67 (005 Uvers of ehra ISSN 06-04 hp://scecesuacr Some Probabl Iequales for Quadrac Forms of Negavel Depede Subgaussa adom Varables M Am A ozorga ad H Zare 3
10.2 Series. , we get. which is called an infinite series ( or just a series) and is denoted, for short, by the symbol. i i n
 0. Sere I th ecto, we wll troduce ere tht wll be dcug for the ret of th chpter. Wht ere? If we dd ll term of equece, we get whch clled fte ere ( or jut ere) d deoted, for hort, by the ymbol or Doe t mke
0. Sere I th ecto, we wll troduce ere tht wll be dcug for the ret of th chpter. Wht ere? If we dd ll term of equece, we get whch clled fte ere ( or jut ere) d deoted, for hort, by the ymbol or Doe t mke
ESTABILIZATION TIME FOR SUBCRITICAL SYSTEM WITH DIFFERENT EXTERNAL NEUTRON SOURCE
 03 Iero Nuer Coferee - INC 03 Refe PE Brz Noveer 4-9 03 OCIÇÃO BRILEIR E ENERGI NUCLER - BEN IBN: 978-85-994-05- ETBILIZTION TIE FOR UBCRITICL YTE WITH IFFERENT EXTERNL NEUTRON OURCE Bry. Fose Ferdo C.
03 Iero Nuer Coferee - INC 03 Refe PE Brz Noveer 4-9 03 OCIÇÃO BRILEIR E ENERGI NUCLER - BEN IBN: 978-85-994-05- ETBILIZTION TIE FOR UBCRITICL YTE WITH IFFERENT EXTERNL NEUTRON OURCE Bry. Fose Ferdo C.
6.6 Moments and Centers of Mass
 th 8 www.tetodre.co 6.6 oets d Ceters of ss Our ojectve here s to fd the pot P o whch th plte of gve shpe lces horzotll. Ths pot s clled the ceter of ss ( or ceter of grvt ) of the plte.. We frst cosder
th 8 www.tetodre.co 6.6 oets d Ceters of ss Our ojectve here s to fd the pot P o whch th plte of gve shpe lces horzotll. Ths pot s clled the ceter of ss ( or ceter of grvt ) of the plte.. We frst cosder
Design maintenanceand reliability of engineering systems: a probability based approach
 Desg mateaead relablty of egeerg systems: a probablty based approah CHPTER 2. BSIC SET THEORY 2.1 Bas deftos Sets are the bass o whh moder probablty theory s defed. set s a well-defed olleto of objets.
Desg mateaead relablty of egeerg systems: a probablty based approah CHPTER 2. BSIC SET THEORY 2.1 Bas deftos Sets are the bass o whh moder probablty theory s defed. set s a well-defed olleto of objets.
Posterior analysis of the compound truncated Weibull under different loss functions for censored data.
 INRNAIONA JOURNA OF MAHMAIC AND COMUR IN IMUAION Vou 6 oso yss of h oou u Wu u ff oss fuos fo so. Khw BOUDJRDA Ass CHADI Ho FAG. As I hs h Bys yss of gh u Wu suo s os u y II so. Bys sos osog ss hv v usg
INRNAIONA JOURNA OF MAHMAIC AND COMUR IN IMUAION Vou 6 oso yss of h oou u Wu u ff oss fuos fo so. Khw BOUDJRDA Ass CHADI Ho FAG. As I hs h Bys yss of gh u Wu suo s os u y II so. Bys sos osog ss hv v usg
