1.3 LECTURE 3. Vector Product
|
|
|
- Raymond Blankenship
- 6 years ago
- Views:
Transcription
1 12 CHAPTER 1. VECTOR ALGEBRA Example. Let L be a line x x 1 a = y y 1 b = z z 1 c passing through a point P 1 and parallel to the vector N = a i +b j +c k. The equation of the plane passing through the point P 0 orthogonal to the line L is a(x x 0 ) + b(y y 0 ) + c(z z 0 ) = LECTURE 3. Vector Product Vector Product Let { e 1, e 2 } be an orthonormal basis in the plane. We say that another basis { f 1, f 2 } is equivalent to the former basis (or has the same orientation) if it can be obtained from the first basis by a rotation and has the opposite orientation if it can be obtained from the first basis by a rotation and one reflection. We declare that the standard basis has positive (or right handed) orientation. Then there are just two types of bases, the ones with positive orientation (that have the same orientation as the standard one) and the one with negative (or left handed) orientation (that have the opposite orientation with the standard one). The orientation of the space is done similarly. We declare that the standard basis { i, j, k } has positive (or right-handed) orientation. Then all bases { e 1, e 2, e 3 } obtained by pure rotations from the standard one have positive orientation and those that need one reflection have negative orientation. Explain the right hand rule. The vector product (or cross product) of two non-zero vectors, A, B, is defined by B = A B sin θ n, vecanal332.tex; August 25, 2017; 16:29; p. 12
2 1.3. LECTURE 3. VECTOR PRODUCT 13 where n is the unit vector orthogonal to both vectors A and B and such that the triple { A, B, n } is right-handed. The magnitude of the cross product is equal to the area of the parallelogram formed by A and B. Properties A = 0, B = B A, 3. ( A + B ) C = C + B C, 4. (a A ) B = (a B ) = a( B ) 5. A B = 0 if and only if the vectors are zero or parallel, The vector product of orthogonal unit vectors, e 1, e 2, is a unit vector e 3 = e 1 e 2 such that the triple { e 1, e 2, e 3 } is a right-handed orthonormal triple. In particular, if { e 1, e 2, e 3 } is an right-handed orthonormal basis then e 1 e 2 = e 3, e 2 e 3 = e 1, e 3 e 1 = e 2. This can be written in the form e i e j = ε ki j e k, i, j = 1, 2, 3, k=1 where ε i jk is the Levi-Civita symbol defined by ε 123 = ε 231 = ε 312 = 1 ε 213 = ε 321 = ε 132 = 1 and all other components are zero. vecanal332.tex; August 25, 2017; 16:29; p. 13
3 14 CHAPTER 1. VECTOR ALGEBRA This can be written in the form +1, if (i, j, k) is an even permutation of (1, 2, 3) ε i jk = 1, if (i, j, k) is an odd permutation of (1, 2, 3) 0, otherwise (1.3.1) The Levi-Civita symbol is completely anti-symmetric, that is, it changes sign under the permutation of any two indices, ε i jk = ε jik = ε k ji = ε ik j and does not change sign under the cyclic permutation of indices ε i jk = ε jki = ε ki j. Vector Product in Cartesian Coordinates. In an orthonormal basis A B = A i e i = i=1 i, j,k=1 B j e j j=1 ε ki j A i B j e k (1.3.2) That is, ( B ) k = ε ki j A i B j i, j This can be written in the form of a formal determinant i j k A B = ε i jk A j B k e i = A 1 A 2 A 3 B 1 B 2 B 3 Intersecting Planes. Consider two planes with the normals N 1 and N 2. If the vectors N 1 and N 2 are parallel then the plane are parallel and do not intersect. If the normals are not parallel, then the vector N 1 N 2 is non-zero and is parallel to the line L of the intersection of these planes. vecanal332.tex; August 25, 2017; 16:29; p. 14
4 1.3. LECTURE 3. VECTOR PRODUCT 15 Then the parametric equation of the line L passing through the point P 0 is R = R 0 + t N 1 N 2. Angular Velocity. Consider a rigid body rotating about a fixed axis with a constant angular speed ω. Then the velocity of the particle at the point R is v = ω R where ω is the angular velocity directed along the axis of rotation and with the magnitude ω = ω. The speed of the particle is v = ω R sin θ, where θ is the angle between R and the axis of rotation. Orthogonal Decomposition. Let A and B be two nonzero vectors. Let n = A A be the unit vector in the direction of A. Then the vector B can be decomposed as the sum of two orthogonal vectors B = B + B, where B = n ( n B ) = n B cos θ is the signed projection of B onto A and B = B B = ( n B ) n is the orthogonal component. vecanal332.tex; August 25, 2017; 16:29; p. 15
5 16 CHAPTER 1. VECTOR ALGEBRA Triple Product The triple product of three vectors A, B and C is defined by In tensor notation it is A ( B C ) = [ A, B, C ] = A ( B C ) i, j,k=1 ε i jk A i B j C k = A 1 A 2 A 3 B 1 B 2 B 3 C 1 C 2 C 3 It is equal to the signed volume of a parallelepiped based on three vectors A i, B j, C k Properties. 1. [A, B, C] = [B, C, A] = [C, A, B] = [B, A, C] = [C, B, A] = [A, C, B], 2. [A, B, C] = 0 if and only if the vectors are coplanar, 3. [A, B, C] is linear in each argument, 4. for an orthonormal basis [ e 1, e 2, e 3 ] = LECTURE 4. Tensors and Vector Identities We will denote the Cartesian coordinates by x 1 = x, x 2 = y, x 3 = z and the unit vectors in the direction of positive axes (called the standard basis vectors) by e 1 = i, e 2 = j, e 3 = k This can be denoted simply by x i and e j, where i, j = 1, 2, 3. For the indices one usually uses the lowercase Latin letters i, j, k, l, m, n etc. (do not confuse with i, j, k). If you run out of letters, you can use any other letters. The convention is though that the indices are denoted by small (versus capital) Latin (versus Greek) letters, and take values 1, 2, 3. Greek indices are used in four-dimensional space-time in special relativity, where they take values 0, 1, 2, 3, with x 0 = t denoting time. vecanal332.tex; August 25, 2017; 16:29; p. 16
1.4 LECTURE 4. Tensors and Vector Identities
 16 CHAPTER 1. VECTOR ALGEBRA 1.3.2 Triple Product The triple product of three vectors A, B and C is defined by In tensor notation it is A ( B C ) = [ A, B, C ] = A ( B C ) i, j,k=1 ε i jk A i B j C k =
16 CHAPTER 1. VECTOR ALGEBRA 1.3.2 Triple Product The triple product of three vectors A, B and C is defined by In tensor notation it is A ( B C ) = [ A, B, C ] = A ( B C ) i, j,k=1 ε i jk A i B j C k =
Lecture Notes Introduction to Vector Analysis MATH 332
 Lecture Notes Introduction to Vector Analysis MATH 332 Instructor: Ivan Avramidi Textbook: H. F. Davis and A. D. Snider, (WCB Publishers, 1995) New Mexico Institute of Mining and Technology Socorro, NM
Lecture Notes Introduction to Vector Analysis MATH 332 Instructor: Ivan Avramidi Textbook: H. F. Davis and A. D. Snider, (WCB Publishers, 1995) New Mexico Institute of Mining and Technology Socorro, NM
1.2 LECTURE 2. Scalar Product
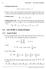 6 CHAPTER 1. VECTOR ALGEBRA Pythagean theem. cos 2 α 1 + cos 2 α 2 + cos 2 α 3 = 1 There is a one-to-one crespondence between the components of the vect on the one side and its magnitude and the direction
6 CHAPTER 1. VECTOR ALGEBRA Pythagean theem. cos 2 α 1 + cos 2 α 2 + cos 2 α 3 = 1 There is a one-to-one crespondence between the components of the vect on the one side and its magnitude and the direction
Math 241, Exam 1 Information.
 Math 241, Exam 1 Information. 2/13/13, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.2. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241sp13/241.html)
Math 241, Exam 1 Information. 2/13/13, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.2. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241sp13/241.html)
VECTOR AND TENSOR ALGEBRA
 PART I VECTOR AND TENSOR ALGEBRA Throughout this book: (i) Lightface Latin and Greek letters generally denote scalars. (ii) Boldface lowercase Latin and Greek letters generally denote vectors, but the
PART I VECTOR AND TENSOR ALGEBRA Throughout this book: (i) Lightface Latin and Greek letters generally denote scalars. (ii) Boldface lowercase Latin and Greek letters generally denote vectors, but the
FoMP: Vectors, Tensors and Fields
 FoMP: Vectors, Tensors and Fields 1 Contents 1 Vectors 6 1.1 Review of Vectors................................. 6 1.1.1 Physics Terminology (L1)........................ 6 1.1.2 Geometrical Approach..........................
FoMP: Vectors, Tensors and Fields 1 Contents 1 Vectors 6 1.1 Review of Vectors................................. 6 1.1.1 Physics Terminology (L1)........................ 6 1.1.2 Geometrical Approach..........................
MAT 1339-S14 Class 8
 MAT 1339-S14 Class 8 July 28, 2014 Contents 7.2 Review Dot Product........................... 2 7.3 Applications of the Dot Product..................... 4 7.4 Vectors in Three-Space.........................
MAT 1339-S14 Class 8 July 28, 2014 Contents 7.2 Review Dot Product........................... 2 7.3 Applications of the Dot Product..................... 4 7.4 Vectors in Three-Space.........................
Index Notation for Vector Calculus
 Index Notation for Vector Calculus by Ilan Ben-Yaacov and Francesc Roig Copyright c 2006 Index notation, also commonly known as subscript notation or tensor notation, is an extremely useful tool for performing
Index Notation for Vector Calculus by Ilan Ben-Yaacov and Francesc Roig Copyright c 2006 Index notation, also commonly known as subscript notation or tensor notation, is an extremely useful tool for performing
VECTORS, TENSORS AND INDEX NOTATION
 VECTORS, TENSORS AND INDEX NOTATION Enrico Nobile Dipartimento di Ingegneria e Architettura Università degli Studi di Trieste, 34127 TRIESTE March 5, 2018 Vectors & Tensors, E. Nobile March 5, 2018 1 /
VECTORS, TENSORS AND INDEX NOTATION Enrico Nobile Dipartimento di Ingegneria e Architettura Università degli Studi di Trieste, 34127 TRIESTE March 5, 2018 Vectors & Tensors, E. Nobile March 5, 2018 1 /
MAC Module 5 Vectors in 2-Space and 3-Space II
 MAC 2103 Module 5 Vectors in 2-Space and 3-Space II 1 Learning Objectives Upon completing this module, you should be able to: 1. Determine the cross product of a vector in R 3. 2. Determine a scalar triple
MAC 2103 Module 5 Vectors in 2-Space and 3-Space II 1 Learning Objectives Upon completing this module, you should be able to: 1. Determine the cross product of a vector in R 3. 2. Determine a scalar triple
The Cross Product. MATH 311, Calculus III. J. Robert Buchanan. Fall Department of Mathematics. J. Robert Buchanan The Cross Product
 The Cross Product MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Introduction Recall: the dot product of two vectors is a scalar. There is another binary operation on vectors
The Cross Product MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Introduction Recall: the dot product of two vectors is a scalar. There is another binary operation on vectors
Vectors. September 2, 2015
 Vectors September 2, 2015 Our basic notion of a vector is as a displacement, directed from one point of Euclidean space to another, and therefore having direction and magnitude. We will write vectors in
Vectors September 2, 2015 Our basic notion of a vector is as a displacement, directed from one point of Euclidean space to another, and therefore having direction and magnitude. We will write vectors in
Introduction to Vector Spaces
 1 CSUC Department of Physics Mechanics: Class Notes Introduction to Vector Spaces I. INTRODUCTION Modern mathematics often constructs logical systems by merely proposing a set of elements that obey a specific
1 CSUC Department of Physics Mechanics: Class Notes Introduction to Vector Spaces I. INTRODUCTION Modern mathematics often constructs logical systems by merely proposing a set of elements that obey a specific
Rotational motion of a rigid body spinning around a rotational axis ˆn;
 Physics 106a, Caltech 15 November, 2018 Lecture 14: Rotations The motion of solid bodies So far, we have been studying the motion of point particles, which are essentially just translational. Bodies with
Physics 106a, Caltech 15 November, 2018 Lecture 14: Rotations The motion of solid bodies So far, we have been studying the motion of point particles, which are essentially just translational. Bodies with
Distance Formula in 3-D Given any two points P 1 (x 1, y 1, z 1 ) and P 2 (x 2, y 2, z 2 ) the distance between them is ( ) ( ) ( )
 Vectors and the Geometry of Space Vector Space The 3-D coordinate system (rectangular coordinates ) is the intersection of three perpendicular (orthogonal) lines called coordinate axis: x, y, and z. Their
Vectors and the Geometry of Space Vector Space The 3-D coordinate system (rectangular coordinates ) is the intersection of three perpendicular (orthogonal) lines called coordinate axis: x, y, and z. Their
Course Name : Physics I Course # PHY 107
 Course Name : Physics I Course # PHY 107 Lecture-2 : Representation of Vectors and the Product Rules Abu Mohammad Khan Department of Mathematics and Physics North South University http://abukhan.weebly.com
Course Name : Physics I Course # PHY 107 Lecture-2 : Representation of Vectors and the Product Rules Abu Mohammad Khan Department of Mathematics and Physics North South University http://abukhan.weebly.com
Cartesian Tensors. e 2. e 1. General vector (formal definition to follow) denoted by components
 Cartesian Tensors Reference: Jeffreys Cartesian Tensors 1 Coordinates and Vectors z x 3 e 3 y x 2 e 2 e 1 x x 1 Coordinates x i, i 123,, Unit vectors: e i, i 123,, General vector (formal definition to
Cartesian Tensors Reference: Jeffreys Cartesian Tensors 1 Coordinates and Vectors z x 3 e 3 y x 2 e 2 e 1 x x 1 Coordinates x i, i 123,, Unit vectors: e i, i 123,, General vector (formal definition to
BSc (Hons) in Computer Games Development. vi Calculate the components a, b and c of a non-zero vector that is orthogonal to
 1 APPLIED MATHEMATICS INSTRUCTIONS Full marks will be awarded for the correct solutions to ANY FIVE QUESTIONS. This paper will be marked out of a TOTAL MAXIMUM MARK OF 100. Credit will be given for clearly
1 APPLIED MATHEMATICS INSTRUCTIONS Full marks will be awarded for the correct solutions to ANY FIVE QUESTIONS. This paper will be marked out of a TOTAL MAXIMUM MARK OF 100. Credit will be given for clearly
What you will learn today
 What you will learn today The Dot Product Equations of Vectors and the Geometry of Space 1/29 Direction angles and Direction cosines Projections Definitions: 1. a : a 1, a 2, a 3, b : b 1, b 2, b 3, a
What you will learn today The Dot Product Equations of Vectors and the Geometry of Space 1/29 Direction angles and Direction cosines Projections Definitions: 1. a : a 1, a 2, a 3, b : b 1, b 2, b 3, a
Calculus 1 for AE (WI1421LR) Lecture 1: 12.3 The dot product 12.4 The cross product
 Calculus 1 for AE (WI1421LR) : 12.3 The dot product 12.4 The cross product About this course Textbook James Stewart, Calculus, Early Transcendentals, 7th edition Course Coordinator Dr. Roelof Koekoek,
Calculus 1 for AE (WI1421LR) : 12.3 The dot product 12.4 The cross product About this course Textbook James Stewart, Calculus, Early Transcendentals, 7th edition Course Coordinator Dr. Roelof Koekoek,
MP2A: Vectors, Tensors and Fields
 MP2A: Vectors, Tensors and Fields [U3869 PHY-2-MP2A] Brian Pendleton (ourse Lecturer) email: bjp@ph.ed.ac.uk room: JMB 4413 telephone: 131-65-5241 web: http://www.ph.ed.ac.uk/ bjp/ March 26, 21 Abstract
MP2A: Vectors, Tensors and Fields [U3869 PHY-2-MP2A] Brian Pendleton (ourse Lecturer) email: bjp@ph.ed.ac.uk room: JMB 4413 telephone: 131-65-5241 web: http://www.ph.ed.ac.uk/ bjp/ March 26, 21 Abstract
Vectors Coordinate frames 2D implicit curves 2D parametric curves. Graphics 2008/2009, period 1. Lecture 2: vectors, curves, and surfaces
 Graphics 2008/2009, period 1 Lecture 2 Vectors, curves, and surfaces Computer graphics example: Pixar (source: http://www.pixar.com) Computer graphics example: Pixar (source: http://www.pixar.com) Computer
Graphics 2008/2009, period 1 Lecture 2 Vectors, curves, and surfaces Computer graphics example: Pixar (source: http://www.pixar.com) Computer graphics example: Pixar (source: http://www.pixar.com) Computer
Study guide for Exam 1. by William H. Meeks III October 26, 2012
 Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
CP3 REVISION LECTURES VECTORS AND MATRICES Lecture 1. Prof. N. Harnew University of Oxford TT 2013
 CP3 REVISION LECTURES VECTORS AND MATRICES Lecture 1 Prof. N. Harnew University of Oxford TT 2013 1 OUTLINE 1. Vector Algebra 2. Vector Geometry 3. Types of Matrices and Matrix Operations 4. Determinants
CP3 REVISION LECTURES VECTORS AND MATRICES Lecture 1 Prof. N. Harnew University of Oxford TT 2013 1 OUTLINE 1. Vector Algebra 2. Vector Geometry 3. Types of Matrices and Matrix Operations 4. Determinants
Course MA2C02, Hilary Term 2010 Section 4: Vectors and Quaternions
 Course MA2C02, Hilary Term 2010 Section 4: Vectors and Quaternions David R. Wilkins Copyright c David R. Wilkins 2000 2010 Contents 4 Vectors and Quaternions 47 4.1 Vectors...............................
Course MA2C02, Hilary Term 2010 Section 4: Vectors and Quaternions David R. Wilkins Copyright c David R. Wilkins 2000 2010 Contents 4 Vectors and Quaternions 47 4.1 Vectors...............................
Homework 2. Solutions T =
 Homework. s Let {e x, e y, e z } be an orthonormal basis in E. Consider the following ordered triples: a) {e x, e x + e y, 5e z }, b) {e y, e x, 5e z }, c) {e y, e x, e z }, d) {e y, e x, 5e z }, e) {
Homework. s Let {e x, e y, e z } be an orthonormal basis in E. Consider the following ordered triples: a) {e x, e x + e y, 5e z }, b) {e y, e x, 5e z }, c) {e y, e x, e z }, d) {e y, e x, 5e z }, e) {
The Cross Product. In this section, we will learn about: Cross products of vectors and their applications.
 The Cross Product In this section, we will learn about: Cross products of vectors and their applications. THE CROSS PRODUCT The cross product a x b of two vectors a and b, unlike the dot product, is a
The Cross Product In this section, we will learn about: Cross products of vectors and their applications. THE CROSS PRODUCT The cross product a x b of two vectors a and b, unlike the dot product, is a
Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors.
 Vectors summary Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors. AB is the position vector of B relative to A and is the vector
Vectors summary Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors. AB is the position vector of B relative to A and is the vector
Physics 6303 Lecture 2 August 22, 2018
 Physics 6303 Lecture 2 August 22, 2018 LAST TIME: Coordinate system construction, covariant and contravariant vector components, basics vector review, gradient, divergence, curl, and Laplacian operators
Physics 6303 Lecture 2 August 22, 2018 LAST TIME: Coordinate system construction, covariant and contravariant vector components, basics vector review, gradient, divergence, curl, and Laplacian operators
Elementary maths for GMT
 Elementary maths for GMT Linear Algebra Part 1: Vectors, Representations Algebra and Linear Algebra Algebra: numbers and operations on numbers 2 + 3 = 5 3 7 = 21 Linear Algebra: tuples, triples... of numbers
Elementary maths for GMT Linear Algebra Part 1: Vectors, Representations Algebra and Linear Algebra Algebra: numbers and operations on numbers 2 + 3 = 5 3 7 = 21 Linear Algebra: tuples, triples... of numbers
Chapter 2: Vector Geometry
 Chapter 2: Vector Geometry Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 2: Vector Geometry Semester 1 2018 1 / 32 Goals of this chapter In this chapter, we will answer the following geometric
Chapter 2: Vector Geometry Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 2: Vector Geometry Semester 1 2018 1 / 32 Goals of this chapter In this chapter, we will answer the following geometric
1 Vectors and Tensors
 PART 1: MATHEMATICAL PRELIMINARIES 1 Vectors and Tensors This chapter and the next are concerned with establishing some basic properties of vectors and tensors in real spaces. The first of these is specifically
PART 1: MATHEMATICAL PRELIMINARIES 1 Vectors and Tensors This chapter and the next are concerned with establishing some basic properties of vectors and tensors in real spaces. The first of these is specifically
12.1. Cartesian Space
 12.1. Cartesian Space In most of your previous math classes, we worked with functions on the xy-plane only meaning we were working only in 2D. Now we will be working in space, or rather 3D. Now we will
12.1. Cartesian Space In most of your previous math classes, we worked with functions on the xy-plane only meaning we were working only in 2D. Now we will be working in space, or rather 3D. Now we will
Department of Physics, Korea University
 Name: Department: Notice +2 ( 1) points per correct (incorrect) answer. No penalty for an unanswered question. Fill the blank ( ) with (8) if the statement is correct (incorrect).!!!: corrections to an
Name: Department: Notice +2 ( 1) points per correct (incorrect) answer. No penalty for an unanswered question. Fill the blank ( ) with (8) if the statement is correct (incorrect).!!!: corrections to an
The Geometry of R n. Supplemental Lecture Notes for Linear Algebra Courses at Georgia Tech
 The Geometry of R n Supplemental Lecture Notes for Linear Algebra Courses at Georgia Tech Contents Vectors in R n. Vectors....................................... The Length and Direction of a Vector......................3
The Geometry of R n Supplemental Lecture Notes for Linear Algebra Courses at Georgia Tech Contents Vectors in R n. Vectors....................................... The Length and Direction of a Vector......................3
MATH 19520/51 Class 2
 MATH 19520/51 Class 2 Minh-Tam Trinh University of Chicago 2017-09-27 1 Review dot product. 2 Angles between vectors and orthogonality. 3 Projection of one vector onto another. 4 Cross product and its
MATH 19520/51 Class 2 Minh-Tam Trinh University of Chicago 2017-09-27 1 Review dot product. 2 Angles between vectors and orthogonality. 3 Projection of one vector onto another. 4 Cross product and its
Cartesian Tensors. e 2. e 1. General vector (formal definition to follow) denoted by components
 Cartesian Tensors Reference: Jeffreys Cartesian Tensors 1 Coordinates and Vectors z x 3 e 3 y x 2 e 2 e 1 x x 1 Coordinates x i, i 123,, Unit vectors: e i, i 123,, General vector (formal definition to
Cartesian Tensors Reference: Jeffreys Cartesian Tensors 1 Coordinates and Vectors z x 3 e 3 y x 2 e 2 e 1 x x 1 Coordinates x i, i 123,, Unit vectors: e i, i 123,, General vector (formal definition to
GROUP THEORY PRIMER. New terms: tensor, rank k tensor, Young tableau, Young diagram, hook, hook length, factors over hooks rule
 GROUP THEORY PRIMER New terms: tensor, rank k tensor, Young tableau, Young diagram, hook, hook length, factors over hooks rule 1. Tensor methods for su(n) To study some aspects of representations of a
GROUP THEORY PRIMER New terms: tensor, rank k tensor, Young tableau, Young diagram, hook, hook length, factors over hooks rule 1. Tensor methods for su(n) To study some aspects of representations of a
How can we find the distance between a point and a plane in R 3? Between two lines in R 3? Between two planes? Between a plane and a line?
 Overview Yesterday we introduced equations to describe lines and planes in R 3 : r = r 0 + tv The vector equation for a line describes arbitrary points r in terms of a specific point r 0 and the direction
Overview Yesterday we introduced equations to describe lines and planes in R 3 : r = r 0 + tv The vector equation for a line describes arbitrary points r in terms of a specific point r 0 and the direction
Review of Coordinate Systems
 Vector in 2 R and 3 R Review of Coordinate Systems Used to describe the position of a point in space Common coordinate systems are: Cartesian Polar Cartesian Coordinate System Also called rectangular coordinate
Vector in 2 R and 3 R Review of Coordinate Systems Used to describe the position of a point in space Common coordinate systems are: Cartesian Polar Cartesian Coordinate System Also called rectangular coordinate
Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems
 To locate a point in a plane, two numbers are necessary. We know that any point in the plane can be represented as an ordered pair (a, b) of real numbers, where a is the x-coordinate and b is the y-coordinate.
To locate a point in a plane, two numbers are necessary. We know that any point in the plane can be represented as an ordered pair (a, b) of real numbers, where a is the x-coordinate and b is the y-coordinate.
The Matrix Representation of a Three-Dimensional Rotation Revisited
 Physics 116A Winter 2010 The Matrix Representation of a Three-Dimensional Rotation Revisited In a handout entitled The Matrix Representation of a Three-Dimensional Rotation, I provided a derivation of
Physics 116A Winter 2010 The Matrix Representation of a Three-Dimensional Rotation Revisited In a handout entitled The Matrix Representation of a Three-Dimensional Rotation, I provided a derivation of
Chapter 2 - Vector Algebra
 A spatial vector, or simply vector, is a concept characterized by a magnitude and a direction, and which sums with other vectors according to the Parallelogram Law. A vector can be thought of as an arrow
A spatial vector, or simply vector, is a concept characterized by a magnitude and a direction, and which sums with other vectors according to the Parallelogram Law. A vector can be thought of as an arrow
(arrows denote positive direction)
 12 Chapter 12 12.1 3-dimensional Coordinate System The 3-dimensional coordinate system we use are coordinates on R 3. The coordinate is presented as a triple of numbers: (a,b,c). In the Cartesian coordinate
12 Chapter 12 12.1 3-dimensional Coordinate System The 3-dimensional coordinate system we use are coordinates on R 3. The coordinate is presented as a triple of numbers: (a,b,c). In the Cartesian coordinate
Course 2BA1: Hilary Term 2007 Section 8: Quaternions and Rotations
 Course BA1: Hilary Term 007 Section 8: Quaternions and Rotations David R. Wilkins Copyright c David R. Wilkins 005 Contents 8 Quaternions and Rotations 1 8.1 Quaternions............................ 1 8.
Course BA1: Hilary Term 007 Section 8: Quaternions and Rotations David R. Wilkins Copyright c David R. Wilkins 005 Contents 8 Quaternions and Rotations 1 8.1 Quaternions............................ 1 8.
Objective 1. Lesson 87: The Cross Product of Vectors IBHL - SANTOWSKI FINDING THE CROSS PRODUCT OF TWO VECTORS
 Lesson 87: The Cross Product of Vectors IBHL - SANTOWSKI In this lesson you will learn how to find the cross product of two vectors how to find an orthogonal vector to a plane defined by two vectors how
Lesson 87: The Cross Product of Vectors IBHL - SANTOWSKI In this lesson you will learn how to find the cross product of two vectors how to find an orthogonal vector to a plane defined by two vectors how
X-MA2C01-1: Partial Worked Solutions
 X-MAC01-1: Partial Worked Solutions David R. Wilkins May 013 1. (a) Let A, B and C be sets. Prove that (A \ (B C)) (B \ C) = (A B) \ C. [Venn Diagrams, by themselves without an accompanying logical argument,
X-MAC01-1: Partial Worked Solutions David R. Wilkins May 013 1. (a) Let A, B and C be sets. Prove that (A \ (B C)) (B \ C) = (A B) \ C. [Venn Diagrams, by themselves without an accompanying logical argument,
Tensors, and differential forms - Lecture 2
 Tensors, and differential forms - Lecture 2 1 Introduction The concept of a tensor is derived from considering the properties of a function under a transformation of the coordinate system. A description
Tensors, and differential forms - Lecture 2 1 Introduction The concept of a tensor is derived from considering the properties of a function under a transformation of the coordinate system. A description
Formalism of the Tersoff potential
 Originally written in December 000 Translated to English in June 014 Formalism of the Tersoff potential 1 The original version (PRB 38 p.990, PRB 37 p.6991) Potential energy Φ = 1 u ij i (1) u ij = f ij
Originally written in December 000 Translated to English in June 014 Formalism of the Tersoff potential 1 The original version (PRB 38 p.990, PRB 37 p.6991) Potential energy Φ = 1 u ij i (1) u ij = f ij
Mathematical Preliminaries
 Mathematical Preliminaries Introductory Course on Multiphysics Modelling TOMAZ G. ZIELIŃKI bluebox.ippt.pan.pl/ tzielins/ Table of Contents Vectors, tensors, and index notation. Generalization of the concept
Mathematical Preliminaries Introductory Course on Multiphysics Modelling TOMAZ G. ZIELIŃKI bluebox.ippt.pan.pl/ tzielins/ Table of Contents Vectors, tensors, and index notation. Generalization of the concept
mathematical objects can be described via equations, functions, graphs, parameterization in R, R, and R.
 Multivariable Calculus Lecture # Notes This lecture completes the discussion of the cross product in R and addresses the variety of different ways that n mathematical objects can be described via equations,
Multivariable Calculus Lecture # Notes This lecture completes the discussion of the cross product in R and addresses the variety of different ways that n mathematical objects can be described via equations,
Lecture 1 Complex Numbers. 1 The field of complex numbers. 1.1 Arithmetic operations. 1.2 Field structure of C. MATH-GA Complex Variables
 Lecture Complex Numbers MATH-GA 245.00 Complex Variables The field of complex numbers. Arithmetic operations The field C of complex numbers is obtained by adjoining the imaginary unit i to the field R
Lecture Complex Numbers MATH-GA 245.00 Complex Variables The field of complex numbers. Arithmetic operations The field C of complex numbers is obtained by adjoining the imaginary unit i to the field R
11.1 Three-Dimensional Coordinate System
 11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
CHAPTER 3 : VECTORS. Definition 3.1 A vector is a quantity that has both magnitude and direction.
 EQT 101-Engineering Mathematics I Teaching Module CHAPTER 3 : VECTORS 3.1 Introduction Definition 3.1 A ector is a quantity that has both magnitude and direction. A ector is often represented by an arrow
EQT 101-Engineering Mathematics I Teaching Module CHAPTER 3 : VECTORS 3.1 Introduction Definition 3.1 A ector is a quantity that has both magnitude and direction. A ector is often represented by an arrow
Supplementary Notes on Mathematics. Part I: Linear Algebra
 J. Broida UCSD Fall 2009 Phys 130B QM II Supplementary Notes on Mathematics Part I: Linear Algebra 1 Linear Transformations Let me very briefly review some basic properties of linear transformations and
J. Broida UCSD Fall 2009 Phys 130B QM II Supplementary Notes on Mathematics Part I: Linear Algebra 1 Linear Transformations Let me very briefly review some basic properties of linear transformations and
Remark 3.2. The cross product only makes sense in R 3.
 3. Cross product Definition 3.1. Let v and w be two vectors in R 3. The cross product of v and w, denoted v w, is the vector defined as follows: the length of v w is the area of the parallelogram with
3. Cross product Definition 3.1. Let v and w be two vectors in R 3. The cross product of v and w, denoted v w, is the vector defined as follows: the length of v w is the area of the parallelogram with
R n : The Cross Product
 A FIRST COURSE IN LINEAR ALGEBRA An Open Text by Ken Kuttler R n : The Cross Product Lecture Notes by Karen Seyffarth Adapted by LYRYX SERVICE COURSE SOLUTION Attribution-NonCommercial-ShareAlike (CC BY-NC-SA)
A FIRST COURSE IN LINEAR ALGEBRA An Open Text by Ken Kuttler R n : The Cross Product Lecture Notes by Karen Seyffarth Adapted by LYRYX SERVICE COURSE SOLUTION Attribution-NonCommercial-ShareAlike (CC BY-NC-SA)
vand v 3. Find the area of a parallelogram that has the given vectors as adjacent sides.
 Name: Date: 1. Given the vectors u and v, find u vand v v. u= 8,6,2, v = 6, 3, 4 u v v v 2. Given the vectors u nd v, find the cross product and determine whether it is orthogonal to both u and v. u= 1,8,
Name: Date: 1. Given the vectors u and v, find u vand v v. u= 8,6,2, v = 6, 3, 4 u v v v 2. Given the vectors u nd v, find the cross product and determine whether it is orthogonal to both u and v. u= 1,8,
Lecture 2: Vector-Vector Operations
 Lecture 2: Vector-Vector Operations Vector-Vector Operations Addition of two vectors Geometric representation of addition and subtraction of vectors Vectors and points Dot product of two vectors Geometric
Lecture 2: Vector-Vector Operations Vector-Vector Operations Addition of two vectors Geometric representation of addition and subtraction of vectors Vectors and points Dot product of two vectors Geometric
Contents. D. R. Wilkins. Copyright c David R. Wilkins
 MA232A Euclidean and Non-Euclidean Geometry School of Mathematics, Trinity College Michaelmas Term 2017 Section 5: Vector Algebra and Spherical Trigonometry D. R. Wilkins Copyright c David R. Wilkins 2015
MA232A Euclidean and Non-Euclidean Geometry School of Mathematics, Trinity College Michaelmas Term 2017 Section 5: Vector Algebra and Spherical Trigonometry D. R. Wilkins Copyright c David R. Wilkins 2015
12.5 Equations of Lines and Planes
 12.5 Equations of Lines and Planes Equation of Lines Vector Equation of Lines Parametric Equation of Lines Symmetric Equation of Lines Relation Between Two Lines Equations of Planes Vector Equation of
12.5 Equations of Lines and Planes Equation of Lines Vector Equation of Lines Parametric Equation of Lines Symmetric Equation of Lines Relation Between Two Lines Equations of Planes Vector Equation of
5. Vector Algebra and Spherical Trigonometry (continued)
 MA232A Euclidean and Non-Euclidean Geometry School of Mathematics, Trinity College Michaelmas Term 2017 Section 5: Vector Algebra and Spherical Trigonometry David R. Wilkins 5.1. Vectors in Three-Dimensional
MA232A Euclidean and Non-Euclidean Geometry School of Mathematics, Trinity College Michaelmas Term 2017 Section 5: Vector Algebra and Spherical Trigonometry David R. Wilkins 5.1. Vectors in Three-Dimensional
Last week we presented the following expression for the angles between two vectors u and v in R n ( ) θ = cos 1 u v
 Orthogonality (I) Last week we presented the following expression for the angles between two vectors u and v in R n ( ) θ = cos 1 u v u v which brings us to the fact that θ = π/2 u v = 0. Definition (Orthogonality).
Orthogonality (I) Last week we presented the following expression for the angles between two vectors u and v in R n ( ) θ = cos 1 u v u v which brings us to the fact that θ = π/2 u v = 0. Definition (Orthogonality).
Week 3: Differential Geometry of Curves
 Week 3: Differential Geometry of Curves Introduction We now know how to differentiate and integrate along curves. This week we explore some of the geometrical properties of curves that can be addressed
Week 3: Differential Geometry of Curves Introduction We now know how to differentiate and integrate along curves. This week we explore some of the geometrical properties of curves that can be addressed
Lecture 19 (Nov. 15, 2017)
 Lecture 19 8.31 Quantum Theory I, Fall 017 8 Lecture 19 Nov. 15, 017) 19.1 Rotations Recall that rotations are transformations of the form x i R ij x j using Einstein summation notation), where R is an
Lecture 19 8.31 Quantum Theory I, Fall 017 8 Lecture 19 Nov. 15, 017) 19.1 Rotations Recall that rotations are transformations of the form x i R ij x j using Einstein summation notation), where R is an
Semester University of Sheffield. School of Mathematics and Statistics
 University of Sheffield School of Mathematics and Statistics MAS140: Mathematics (Chemical) MAS152: Civil Engineering Mathematics MAS152: Essential Mathematical Skills & Techniques MAS156: Mathematics
University of Sheffield School of Mathematics and Statistics MAS140: Mathematics (Chemical) MAS152: Civil Engineering Mathematics MAS152: Essential Mathematical Skills & Techniques MAS156: Mathematics
Kevin James. MTHSC 206 Section 12.5 Equations of Lines and Planes
 MTHSC 206 Section 12.5 Equations of Lines and Planes Definition A line in R 3 can be described by a point and a direction vector. Given the point r 0 and the direction vector v. Any point r on the line
MTHSC 206 Section 12.5 Equations of Lines and Planes Definition A line in R 3 can be described by a point and a direction vector. Given the point r 0 and the direction vector v. Any point r on the line
Vectors and Matrices Notes.
 Vectors and Matrices Notes Jonathan Coulthard JonathanCoulthard@physicsoxacuk 1 Index Notation Index notation may seem quite intimidating at first, but once you get used to it, it will allow us to prove
Vectors and Matrices Notes Jonathan Coulthard JonathanCoulthard@physicsoxacuk 1 Index Notation Index notation may seem quite intimidating at first, but once you get used to it, it will allow us to prove
Lecture «Robot Dynamics»: Kinematics 2
 Lecture «Robot Dynamics»: Kinematics 2 151-0851-00 V lecture: CAB G11 Tuesday 10:15 12:00, every week exercise: HG E1.2 Wednesday 8:15 10:00, according to schedule (about every 2nd week) Marco Hutter,
Lecture «Robot Dynamics»: Kinematics 2 151-0851-00 V lecture: CAB G11 Tuesday 10:15 12:00, every week exercise: HG E1.2 Wednesday 8:15 10:00, according to schedule (about every 2nd week) Marco Hutter,
Mathematics 2203, Test 1 - Solutions
 Mathematics 220, Test 1 - Solutions F, 2010 Philippe B. Laval Name 1. Determine if each statement below is True or False. If it is true, explain why (cite theorem, rule, property). If it is false, explain
Mathematics 220, Test 1 - Solutions F, 2010 Philippe B. Laval Name 1. Determine if each statement below is True or False. If it is true, explain why (cite theorem, rule, property). If it is false, explain
A Brief Introduction to Tensor
 Gonit Sora Article 1-13 Downloaded from Gonit Sora Gonit Sora: http://gonitsora.com Introductory Article Rupam Haloi Department of Mathematical Sciences, Tezpur University, Napaam - 784028, India. Abstract:
Gonit Sora Article 1-13 Downloaded from Gonit Sora Gonit Sora: http://gonitsora.com Introductory Article Rupam Haloi Department of Mathematical Sciences, Tezpur University, Napaam - 784028, India. Abstract:
5. Orthogonal matrices
 L Vandenberghe EE133A (Spring 2017) 5 Orthogonal matrices matrices with orthonormal columns orthogonal matrices tall matrices with orthonormal columns complex matrices with orthonormal columns 5-1 Orthonormal
L Vandenberghe EE133A (Spring 2017) 5 Orthogonal matrices matrices with orthonormal columns orthogonal matrices tall matrices with orthonormal columns complex matrices with orthonormal columns 5-1 Orthonormal
Intro Vectors 2D implicit curves 2D parametric curves. Graphics 2011/2012, 4th quarter. Lecture 2: vectors, curves, and surfaces
 Lecture 2, curves, and surfaces Organizational remarks Tutorials: Tutorial 1 will be online later today TA sessions for questions start next week Practicals: Exams: Make sure to find a team partner very
Lecture 2, curves, and surfaces Organizational remarks Tutorials: Tutorial 1 will be online later today TA sessions for questions start next week Practicals: Exams: Make sure to find a team partner very
CE-570 Advanced Structural Mechanics - Arun Prakash
 Ch1-Intro Page 1 CE-570 Advanced Structural Mechanics - Arun Prakash The BIG Picture What is Mechanics? Mechanics is study of how things work: how anything works, how the world works! People ask: "Do you
Ch1-Intro Page 1 CE-570 Advanced Structural Mechanics - Arun Prakash The BIG Picture What is Mechanics? Mechanics is study of how things work: how anything works, how the world works! People ask: "Do you
Brief Review of Vector Algebra
 APPENDIX Brief Review of Vector Algebra A.0 Introduction Vector algebra is used extensively in computational mechanics. The student must thus understand the concepts associated with this subject. The current
APPENDIX Brief Review of Vector Algebra A.0 Introduction Vector algebra is used extensively in computational mechanics. The student must thus understand the concepts associated with this subject. The current
Linear Algebra and Dirac Notation, Pt. 3
 Linear Algebra and Dirac Notation, Pt. 3 PHYS 500 - Southern Illinois University February 1, 2017 PHYS 500 - Southern Illinois University Linear Algebra and Dirac Notation, Pt. 3 February 1, 2017 1 / 16
Linear Algebra and Dirac Notation, Pt. 3 PHYS 500 - Southern Illinois University February 1, 2017 PHYS 500 - Southern Illinois University Linear Algebra and Dirac Notation, Pt. 3 February 1, 2017 1 / 16
Introduction to tensors and dyadics
 1 Introduction to tensors and dyadics 1.1 Introduction Tensors play a fundamental role in theoretical physics. The reason for this is that physical laws written in tensor form are independent of the coordinate
1 Introduction to tensors and dyadics 1.1 Introduction Tensors play a fundamental role in theoretical physics. The reason for this is that physical laws written in tensor form are independent of the coordinate
NIU PHYS 500, Fall 2006 Classical Mechanics Solutions for HW6. Solutions
 NIU PHYS 500, Fall 006 Classical Mechanics Solutions for HW6 Assignment: HW6 [40 points] Assigned: 006/11/10 Due: 006/11/17 Solutions P6.1 [4 + 3 + 3 = 10 points] Consider a particle of mass m moving in
NIU PHYS 500, Fall 006 Classical Mechanics Solutions for HW6 Assignment: HW6 [40 points] Assigned: 006/11/10 Due: 006/11/17 Solutions P6.1 [4 + 3 + 3 = 10 points] Consider a particle of mass m moving in
Euler Characteristic of Two-Dimensional Manifolds
 Euler Characteristic of Two-Dimensional Manifolds M. Hafiz Khusyairi August 2008 In this work we will discuss an important notion from topology, namely Euler Characteristic and we will discuss several
Euler Characteristic of Two-Dimensional Manifolds M. Hafiz Khusyairi August 2008 In this work we will discuss an important notion from topology, namely Euler Characteristic and we will discuss several
1. Matrix multiplication and Pauli Matrices: Pauli matrices are the 2 2 matrices. 1 0 i 0. 0 i
 Problems in basic linear algebra Science Academies Lecture Workshop at PSGRK College Coimbatore, June 22-24, 2016 Govind S. Krishnaswami, Chennai Mathematical Institute http://www.cmi.ac.in/~govind/teaching,
Problems in basic linear algebra Science Academies Lecture Workshop at PSGRK College Coimbatore, June 22-24, 2016 Govind S. Krishnaswami, Chennai Mathematical Institute http://www.cmi.ac.in/~govind/teaching,
NOTES ON DIFFERENTIAL FORMS. PART 3: TENSORS
 NOTES ON DIFFERENTIAL FORMS. PART 3: TENSORS 1. What is a tensor? Let V be a finite-dimensional vector space. 1 It could be R n, it could be the tangent space to a manifold at a point, or it could just
NOTES ON DIFFERENTIAL FORMS. PART 3: TENSORS 1. What is a tensor? Let V be a finite-dimensional vector space. 1 It could be R n, it could be the tangent space to a manifold at a point, or it could just
Lecture 10: Vector Algebra: Orthogonal Basis
 Lecture 0: Vector Algebra: Orthogonal Basis Orthogonal Basis of a subspace Computing an orthogonal basis for a subspace using Gram-Schmidt Orthogonalization Process Orthogonal Set Any set of vectors that
Lecture 0: Vector Algebra: Orthogonal Basis Orthogonal Basis of a subspace Computing an orthogonal basis for a subspace using Gram-Schmidt Orthogonalization Process Orthogonal Set Any set of vectors that
Lecture 10: A (Brief) Introduction to Group Theory (See Chapter 3.13 in Boas, 3rd Edition)
 Lecture 0: A (Brief) Introduction to Group heory (See Chapter 3.3 in Boas, 3rd Edition) Having gained some new experience with matrices, which provide us with representations of groups, and because symmetries
Lecture 0: A (Brief) Introduction to Group heory (See Chapter 3.3 in Boas, 3rd Edition) Having gained some new experience with matrices, which provide us with representations of groups, and because symmetries
Linear Algebra I for Science (NYC)
 Element No. 1: To express concrete problems as linear equations. To solve systems of linear equations using matrices. Topic: MATRICES 1.1 Give the definition of a matrix, identify the elements and the
Element No. 1: To express concrete problems as linear equations. To solve systems of linear equations using matrices. Topic: MATRICES 1.1 Give the definition of a matrix, identify the elements and the
The Cross Product. Philippe B. Laval. Spring 2012 KSU. Philippe B. Laval (KSU) The Cross Product Spring /
 The Cross Product Philippe B Laval KSU Spring 2012 Philippe B Laval (KSU) The Cross Product Spring 2012 1 / 15 Introduction The cross product is the second multiplication operation between vectors we will
The Cross Product Philippe B Laval KSU Spring 2012 Philippe B Laval (KSU) The Cross Product Spring 2012 1 / 15 Introduction The cross product is the second multiplication operation between vectors we will
Exam 1 Review SOLUTIONS
 1. True or False (and give a short reason): Exam 1 Review SOLUTIONS (a) If the parametric curve x = f(t), y = g(t) satisfies g (1) = 0, then it has a horizontal tangent line when t = 1. FALSE: To make
1. True or False (and give a short reason): Exam 1 Review SOLUTIONS (a) If the parametric curve x = f(t), y = g(t) satisfies g (1) = 0, then it has a horizontal tangent line when t = 1. FALSE: To make
Vectors. The standard geometric definition of vector is as something which has direction and magnitude but not position.
 Vectors The standard geometric definition of vector is as something which has direction and magnitude but not position. Since vectors have no position we may place them wherever is convenient. Vectors
Vectors The standard geometric definition of vector is as something which has direction and magnitude but not position. Since vectors have no position we may place them wherever is convenient. Vectors
. D CR Nomenclature D 1
 . D CR Nomenclature D 1 Appendix D: CR NOMENCLATURE D 2 The notation used by different investigators working in CR formulations has not coalesced, since the topic is in flux. This Appendix identifies the
. D CR Nomenclature D 1 Appendix D: CR NOMENCLATURE D 2 The notation used by different investigators working in CR formulations has not coalesced, since the topic is in flux. This Appendix identifies the
Mathematics for the Theory of Materials: Lectures 1 13
 Imperial College London Department of Physics Mathematics for the Theory of Materials: Lectures 1 13 Dr Arash Mostofi Comments and corrections to a.mostofi@imperial.ac.uk Lecture notes may be found on
Imperial College London Department of Physics Mathematics for the Theory of Materials: Lectures 1 13 Dr Arash Mostofi Comments and corrections to a.mostofi@imperial.ac.uk Lecture notes may be found on
Square 2-designs/1. 1 Definition
 Square 2-designs Square 2-designs are variously known as symmetric designs, symmetric BIBDs, and projective designs. The definition does not imply any symmetry of the design, and the term projective designs,
Square 2-designs Square 2-designs are variously known as symmetric designs, symmetric BIBDs, and projective designs. The definition does not imply any symmetry of the design, and the term projective designs,
Course Notes Math 275 Boise State University. Shari Ultman
 Course Notes Math 275 Boise State University Shari Ultman Fall 2017 Contents 1 Vectors 1 1.1 Introduction to 3-Space & Vectors.............. 3 1.2 Working With Vectors.................... 7 1.3 Introduction
Course Notes Math 275 Boise State University Shari Ultman Fall 2017 Contents 1 Vectors 1 1.1 Introduction to 3-Space & Vectors.............. 3 1.2 Working With Vectors.................... 7 1.3 Introduction
1 More on the Bloch Sphere (10 points)
 Ph15c Spring 017 Prof. Sean Carroll seancarroll@gmail.com Homework - 1 Solutions Assigned TA: Ashmeet Singh ashmeet@caltech.edu 1 More on the Bloch Sphere 10 points a. The state Ψ is parametrized on the
Ph15c Spring 017 Prof. Sean Carroll seancarroll@gmail.com Homework - 1 Solutions Assigned TA: Ashmeet Singh ashmeet@caltech.edu 1 More on the Bloch Sphere 10 points a. The state Ψ is parametrized on the
10.4 The Cross Product
 Math 172 Chapter 10B notes Page 1 of 9 10.4 The Cross Product The cross product, or vector product, is defined in 3 dimensions only. Let aa = aa 1, aa 2, aa 3 bb = bb 1, bb 2, bb 3 then aa bb = aa 2 bb
Math 172 Chapter 10B notes Page 1 of 9 10.4 The Cross Product The cross product, or vector product, is defined in 3 dimensions only. Let aa = aa 1, aa 2, aa 3 bb = bb 1, bb 2, bb 3 then aa bb = aa 2 bb
,, rectilinear,, spherical,, cylindrical. (6.1)
 Lecture 6 Review of Vectors Physics in more than one dimension (See Chapter 3 in Boas, but we try to take a more general approach and in a slightly different order) Recall that in the previous two lectures
Lecture 6 Review of Vectors Physics in more than one dimension (See Chapter 3 in Boas, but we try to take a more general approach and in a slightly different order) Recall that in the previous two lectures
Linear Algebra and Dirac Notation, Pt. 1
 Linear Algebra and Dirac Notation, Pt. 1 PHYS 500 - Southern Illinois University February 1, 2017 PHYS 500 - Southern Illinois University Linear Algebra and Dirac Notation, Pt. 1 February 1, 2017 1 / 13
Linear Algebra and Dirac Notation, Pt. 1 PHYS 500 - Southern Illinois University February 1, 2017 PHYS 500 - Southern Illinois University Linear Algebra and Dirac Notation, Pt. 1 February 1, 2017 1 / 13
Tensors and Special Relativity
 Tensors and Special Relativity Lecture 6 1 Introduction and review of tensor algebra While you have probably used tensors of rank 1, i.e vectors, in special relativity, relativity is most efficiently expressed
Tensors and Special Relativity Lecture 6 1 Introduction and review of tensor algebra While you have probably used tensors of rank 1, i.e vectors, in special relativity, relativity is most efficiently expressed
Linear Algebra. Paul Yiu. 6D: 2-planes in R 4. Department of Mathematics Florida Atlantic University. Fall 2011
 Linear Algebra Paul Yiu Department of Mathematics Florida Atlantic University Fall 2011 6D: 2-planes in R 4 The angle between a vector and a plane The angle between a vector v R n and a subspace V is the
Linear Algebra Paul Yiu Department of Mathematics Florida Atlantic University Fall 2011 6D: 2-planes in R 4 The angle between a vector and a plane The angle between a vector v R n and a subspace V is the
Dr. Allen Back. Sep. 8, 2014
 in R 3 Dr. Allen Back Sep. 8, 2014 in R 3 in R 3 Def: For f (x, y), the partial derivative with respect to x at p 0 = (x 0, y 0 ) is f x = lim f (x 0 + h, y 0 ) f (x 0, y 0 ) h 0 h or f x = lim f (p 0
in R 3 Dr. Allen Back Sep. 8, 2014 in R 3 in R 3 Def: For f (x, y), the partial derivative with respect to x at p 0 = (x 0, y 0 ) is f x = lim f (x 0 + h, y 0 ) f (x 0, y 0 ) h 0 h or f x = lim f (p 0
CALCULUS III. prepared by
 EXAMINATION 1 CALCULUS III REVIEW PROBLEMS prepared by Antony Foster Department of Mathematics (office: NAC 6-73) The City College of The City University of New York Convent Avenue At 138th Street New
EXAMINATION 1 CALCULUS III REVIEW PROBLEMS prepared by Antony Foster Department of Mathematics (office: NAC 6-73) The City College of The City University of New York Convent Avenue At 138th Street New
1.1 Bound and Free Vectors. 1.2 Vector Operations
 1 Vectors Vectors are used when both the magnitude and the direction of some physical quantity are required. Examples of such quantities are velocity, acceleration, force, electric and magnetic fields.
1 Vectors Vectors are used when both the magnitude and the direction of some physical quantity are required. Examples of such quantities are velocity, acceleration, force, electric and magnetic fields.
