CHAPTER 3 : VECTORS. Definition 3.1 A vector is a quantity that has both magnitude and direction.
|
|
|
- Jeffery West
- 5 years ago
- Views:
Transcription
1 EQT 101-Engineering Mathematics I Teaching Module CHAPTER 3 : VECTORS 3.1 Introduction Definition 3.1 A ector is a quantity that has both magnitude and direction. A ector is often represented by an arrow or a directed line segment. The length of the arrow represents the magnitude of the ector and the arrow points in the direction of the ector. For example, force, elocity, acceleration, etc are quantity that has magnitude and direction. Definition 3. A scalar is a quantity that has magnitud only. Length, area, olume, mass, time, etc are types of scalar that has magnitude only. 3. Vector Representation Suppose a particle moes along a line segment from point P to point Q. The corresponding displacement ector, shown in figure below, has initial point P (the tail) and the point Q is referred as its head and we indicate this by writing PQ. Notice that the ector QP has the same length but it is in the opposite direction. Q Q PQ QP P P
2 A ector could be written as a, b, u, and w. The magnitude of the ector, is denoted by. Note that would represent a ector of the same magnitude but with opposite direction. Q Q P P 3.3 Two Equal Vectors Definition 3.3 Two ectors u and are said to be equal if and only if they hae the same magnitude and the same direction Example 1 : w u u = and w = x 3.4 Addition of Vectors x Definition 3.4 If u and are ectors, then the addition of u and can be written as u +. i) The Triangle Law If u and are ectors, we connect the initial point of with the terminal point of u, then the sum u + is the ector from the initial point of u to the terminal point of. 41
3 Example : u u u + ii) The Parallelogram Law In figure below, we start with the same ectors u and as in figure aboe and we draw another copy of with the same initial point as u. Completing the parallelogram, we could see that u + = + u. This also gie another way to construct the sum : if we place u and so they start at the same point, then u + lies along the diagonal of the parallelogram with u and as sides. Example 3 : u u + iii) The Sum of a Number of Vectors u The sum of all ectors is gien by the single ector joining the start of the first to the end of last. Example 4: a x b c 1. a + b = x. a + b + c = w u w Note: Addition of ector is satisfied u + = + u (commutatie law) 4
4 3.5 Subtraction of Vectors Definition 3.5 If u and are ectors, then u - can be written as u + ( ) Example 5: u u Note: Subtraction of ectors is not satisfied the commutatie law, but their magnitudes are still the same een though the direction is opposite. 3.6 Scalar Multiplication of Vectors Definition 3.6 If is a ector and α is a scalar, then the scalar multiplication α is a ector whose length is α times the length of and whose direction is the same as if α > 0 and is opposite to if α < 0. Example 6 : Parallel Vectors Definition 3.7 Two ectors u and are said to be parallel if they are in the same direction or opposite direction and is equialent to αu. 43
5 Example 7: u -u αu = αu = 3.8 Components of Vectors in Terms of Unit Vectors If we place the initial point of a ector r at the origin of a rectangular coordinate system, then the terminal point of r has coordinate of the form x, y, z. These coordinates are called the components of r and we write r = xi + y j + zk Where, i, j and k are unit ectors in the x, y and z-axes, respectiely. Unit ectors i, j, k. i = 1,0, 0 to be a unit ector in the ox direction (x-axis) j = 0,1, 0 to be a unit ector in the oy direction (y-axis) k = 0,0, 1 to be a unit ector in the oz direction (z-axis) Vectors in Two Dimension (R ) Two unit ectors along ox and oy direction are denoted by the symbol i and j respectiely. Example 8 : u = 3 i + 4 j 44
6 3.8. Vectors in Three Dimension (R 3 ) Three unit ectors along ox, oy and oz direction are denoted by the symbol i, j and k respectiely. Example 9 : u = i + 3 j + 5k 3.9 Position Vectors Definition 3.8 If r represents the ector from the origin to the point P(a, b, c) in R 3, then the position ector of P can be defined by r = OP = (a, b, c) (0, 0, 0) = a, b, c Example 10 Two forces D and E are acts from the origin point O. If D = 46N, θ D = 0 o and E = 17N, θ E = 90 o. Find the resultant force. Solution 45
7 3.10 Components of Vectors Definition 3.9 If P and Q are two points in R 3 where P(a, b, c) and Q(x, y, z), then the components ector P and Q can be defined by PQ = OQ OP = ( x, y, z) ( a, b, c) = x a, y b, z c Example 11 Gien P(5,, 1) and Q(6, 1, 7) are two points in R 3. Find the components ector of PQ. Solution 3.11 Magnitude (Length) of Vectors Definition 3.10 If u is a ector with the components a, b, c, then the magnitude of ector u can be written as u = a + b + c Example 1 Find the magnitude of the following ectors: i) u = 5, =5i+j ii) u = 5,, 1 =5i+j+k Solutions 46
8 Definition 3.11 If P and Q are two points with coordinate (a, b, c) and (x, y, z), respectiely, then the length from P to Q can be written as PQ = ( x a) + ( y b) + ( z c ) Example 13 If P(5,, 1) and Q(6, 1, 7) in R 3. Find the length from P to Q. Solution 3.1 Unit Vectors Definition 3.1 If u is a ector, then the unit ector u is defined by u = u = 1. A unit ector is a ector whose length is 1. Normally, the symbol ^ is used to represent the unit ector. In general, if u 0, then the unit ector that has the same direction as u is, u u, where In order to erify this, let 1 u u = u = u u 1 c =. Then u = cu u and c is a positie scalar, so u has the same direction as u. Also 1 u = cu = c u = u = 1 u 47
9 Example 14 Find the unit ector in the direction of the ector u = 3i + 4j + k. Solutions 3.13 Direction Angles and Direction Cosines z P O y x The direction angles of a ector OP = xi + y j + zk are the angles α, β and γ that OP makes with the positie x-, y- and z-axes. The cosines of these direction angles, cos α, cos β and cos γ are called the direction cosines of the ector OP and defined by cos α = x OP, cos β = y OP, cos γ = z OP. [0 α, β, γ ] Example 15 Find the direction angles of the ector u = 6i -5j + 8k Solution 48
10 3.14 Operations of Vectors by Components Definition 3.13 If u = u 1, u, u 3, = 1,, 3 and k is a scalar, then i) u + = u 1 + 1, u +, u ii) u - = u 1-1, u -, u 3-3 iii) ku = ku 1, ku, ku 3 Example 16 Gien u =, -1, 1 and = 1, 3, -. Find i) u + ii) u iii) u i) 3u ) 4 Solutions i) ii) iii) i) Properties of A Vectors If a, b, and c are ectors, k and t are scalar, then i) a + b = b + a ii) a + (b + c) = (a + b) + c iii) a + 0 = 0 + a = a i) a + (-a) = (-a) + a = 0 ) k(a + b) = ka + kb i) (k + t)a = ka + ta ii) k(tb) = (kt)b iii) 0c = 0 ix) 1a = a x) -1b = -b 49
11 3.15 Product of Two Vectors Definition 3.14 (The Dot/Scalar Product) If u = u 1 i + u j + u 3 k and = 1 i + j + 3 k are ectors in R 3, then the dot product of u and can be written as u = u u + u 3 3 Teorem 1 If θ is the angle between the ectors u and, then cos θ = u u ; 0 < θ < π Example 17 Find the angle between the ectors u = 4i 5j k and = i + j + 3k. Solution 50
12 Properties of the Dot Product i) u. =. u ii) u. ( + w ) = u. + u. w iii) ( u + ). ( w + z ) = u. w +. w + u. z +. z i) If k is a scalar, then k(u. ) = (ku). = u. (k) ) i.i = j.j = k.k = 1 i) If u and are orthogonal, then u. = 0 ii) i. j = j. k = k. i = 0 iii) u. u = u Definition 3.15 (The Cross Product) If u = u 1, u, u 3 and = 1,, 3 are ectors, then the cross product of u and is the ector u = i j k u1 u u3 = ( u3 u3 ) i ( u13 u31) j + ( u1 u1) k 1 3 Example 18 If u = 3i + 6j + k and = 4i + 5j k. Find i) u ii) u Solutions 51
13 Theorem If u = u 1, u, u 3 and = 1,, 3 are ectors in R 3, then u x = u sin θ ^ n where θ is the angle between the ectors u and and normal unit ector that perpendicular to both u and. ^ n is a u ^ n θ ^ n θ u u x x u Note that: u x = u sin θ ^ n u x = u sin θ ^ n u x = u sin θ = Area of the parallelogram determined by u and. Example 19 Find the angle between the ectors u = 4i + 5j 3k and = i + j. Solution 5
14 Properties of the Cross Product If u,, w are ectors and k is a scalar, then i) u x = - x u ii) u x + w = u x + u x w iii) u x k = (ku) x = k u x i) u x 0 = 0 x u = 0 ) u x = 0 if and only if u // i) u x = u sin θ ii) i x i = j x j = k x k = 0 iii) i x j = k ; j x k = i ; k x i = j ix) j x i = -k ; ; k x j = -i ; i x k = -j 3.16 Applications of the Dot Product and Cross Product i) Projections Figure below shows representations PQ and PR of two ectors a and b with the same initial point P. If S is the foot of the perpendicular from R to the lines containing PQ, then the ector with representation PS is called the ector projection of b onto a and is denoted by proj a b. b R P proj a b S a Q The scalar projection of b onto a (also called the component of b along a) is defined to be magnitude of the ector projection, which is the number b cos θ, where θ is the angle between a and b. This is denoted by comp a b. The equation a b = a b cosθ 53
15 shows that the dot product of a and b can be interpreted as the length of a times the scalar projection of b onto a. Since b cosθ = a b a = b a a the component of b along a can be computed by taking the dot product of b with the unit ector in the direction of a. Theorem 3 Scalar projection of b onto a: Vector projection of b onto a: a b comp a b = a a b a a b proj a b = = a a a a Example 0 Gien b = i + j + k and a = -i + 3j + k. Find the scalar projection and ector projection of b onto a. Solution ii) The Area of Triangle and Parallelogram A C a θ O b B 54
16 Area of triangle OBC = ½ a b sin θ = ½ a x b Area of parallelogram OBCA = a b sin θ = a x b Example 1 Find the area of triangle and parallelogram with A(1,-1, 0), B(, 1, -1) and C(-1, 1, ). Solution i) The Volume of Parallelepiped and Tetrahedron Parallelepiped determined by three ectors a, b and c. 55
17 The olume of the parallelepiped determined by the ectors a, b and c is the magnitude of their scalar triple product Notice that: V = a. ( b x c ) i) a. (b x c) = (a x b). c a. (b x c) if a = a1, a, a3, b = b1, b, b3 and c = c1, c, c3 so a. (b x c)= a b c a b c a b c ii) If a. (b x c) = 0, then the all ectors on a same plane. A a b B O c C The olume of the tetrahedron by the ectors a, b and c is 6 1 of the olume of parallelepiped, that is V = 6 1 a. (b x c). i) Equations of Planes n = a, b, c P 1 = (x 1, y 1, z 1 ) S P = (x, y, z) 56
18 Let P(x, y, z) a point on the plane S and n is normal ector to the plane S. If P 1 (x 1, y 1, z 1 ) is an arbitrary point in the plane S, then P 1 P. n = 0 x x 1, y y 1, z z 1. a, b, c = 0 a(x x 1 ) + b(y y 1 ) + c(z z 1 ) = 0 So that, the equation of the plane is gien by ax + by + cz + k = 0; where k = ax 1 by 1 cz 1 Example Find an equation of the plane through the point P(3,-1,7) with normal ector n = 4,, 5. Solution ) Parametric Equations of A Line in R 3 l B(x, y, z) A(x 1, y 1, z 1 ) a,b,c 57
19 A line l in three-dimensional space is determined when we know a point A(x 1, y 1, z 1 ) on l and the direction of l. The direction of line is coneniently described by a ector, so we let be a ector parallel to l. If B(x, y, z) be an arbitrary point on l, then AB = t. ; t is a scalar become x x 1, y y 1, z z 1 = t. a, b, c = ta, tb, tc So that, the parametric equations of a line can be written as or x = x 1 + ta y = y 1 + tb z = z 1 + tc x x1 a y = y + 1 t b z z1 c These equations can be described in terms of Cartesian equations when we eliminate the parameter of t from parametric equations. Therefore, we obtain x x a y y b z z c t = = =, a, b, c 0. Example 3 a) Find a parametric equations of the line that passes through the point P(1,, 3) and is parallel to the ector = 1, -1,. b) From the result of (a), state the parametric equations to the Cartesian equations. Solutions 58
20 i) Distance from a Point to the Plane P 1 b n D P 0 Let P 0 (x 0, y 0, z 0 ) be any point in the gien plane and let b be the ector corresponding to P 0P1, then b = x x0, y y0, z z0 From figure aboe, we can se that the distance D from P 1 to the plane is equal to the absolute alue of the ector projection of b onto the normal ector n = a, b, c. Thus D = W 1 = = n b n n n b n 59
21 = = a( x x 0 ) + b( y y0 ) + c( z z0 ) a + b + c ( ax + by + cz) ( ax + by a + b cz0 ) + c Since P 0 (x 0, y 0, z 0 ) lies in the plane, its coordinates satisfy the equation of the plane and so we hae ax0 + by0 + cz0 = d. Thus, the formula for D can be written as D = ax + by + cz + d a + b + c Example 4 Find the distance between the parallel planes 10 x + y z = 5 and 5 x + y z = 1. Solution 60
6.1.1 Angle between Two Lines Intersection of Two lines Shortest Distance from a Point to a Line
 CHAPTER 6 : VECTORS 6. Lines in Space 6.. Angle between Two Lines 6.. Intersection of Two lines 6..3 Shortest Distance from a Point to a Line 6. Planes in Space 6.. Intersection of Two Planes 6.. Angle
CHAPTER 6 : VECTORS 6. Lines in Space 6.. Angle between Two Lines 6.. Intersection of Two lines 6..3 Shortest Distance from a Point to a Line 6. Planes in Space 6.. Intersection of Two Planes 6.. Angle
different formulas, depending on whether or not the vector is in two dimensions or three dimensions.
 ectors The word ector comes from the Latin word ectus which means carried. It is best to think of a ector as the displacement from an initial point P to a terminal point Q. Such a ector is expressed as
ectors The word ector comes from the Latin word ectus which means carried. It is best to think of a ector as the displacement from an initial point P to a terminal point Q. Such a ector is expressed as
Review of Coordinate Systems
 Vector in 2 R and 3 R Review of Coordinate Systems Used to describe the position of a point in space Common coordinate systems are: Cartesian Polar Cartesian Coordinate System Also called rectangular coordinate
Vector in 2 R and 3 R Review of Coordinate Systems Used to describe the position of a point in space Common coordinate systems are: Cartesian Polar Cartesian Coordinate System Also called rectangular coordinate
Unit 11: Vectors in the Plane
 135 Unit 11: Vectors in the Plane Vectors in the Plane The term ector is used to indicate a quantity (such as force or elocity) that has both length and direction. For instance, suppose a particle moes
135 Unit 11: Vectors in the Plane Vectors in the Plane The term ector is used to indicate a quantity (such as force or elocity) that has both length and direction. For instance, suppose a particle moes
8.0 Definition and the concept of a vector:
 Chapter 8: Vectors In this chapter, we will study: 80 Definition and the concept of a ector 81 Representation of ectors in two dimensions (2D) 82 Representation of ectors in three dimensions (3D) 83 Operations
Chapter 8: Vectors In this chapter, we will study: 80 Definition and the concept of a ector 81 Representation of ectors in two dimensions (2D) 82 Representation of ectors in three dimensions (3D) 83 Operations
Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors.
 Vectors summary Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors. AB is the position vector of B relative to A and is the vector
Vectors summary Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors. AB is the position vector of B relative to A and is the vector
A vector in the plane is directed line segment. The directed line segment AB
 Vector: A ector is a matrix that has only one row then we call the matrix a row ector or only one column then we call it a column ector. A row ector is of the form: a a a... A column ector is of the form:
Vector: A ector is a matrix that has only one row then we call the matrix a row ector or only one column then we call it a column ector. A row ector is of the form: a a a... A column ector is of the form:
Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems
 To locate a point in a plane, two numbers are necessary. We know that any point in the plane can be represented as an ordered pair (a, b) of real numbers, where a is the x-coordinate and b is the y-coordinate.
To locate a point in a plane, two numbers are necessary. We know that any point in the plane can be represented as an ordered pair (a, b) of real numbers, where a is the x-coordinate and b is the y-coordinate.
Vectors in R n. P. Danziger
 1 Vectors in R n P. Danziger 1 Vectors The standard geometric definition of ector is as something which has direction and magnitude but not position. Since ectors hae no position we may place them whereer
1 Vectors in R n P. Danziger 1 Vectors The standard geometric definition of ector is as something which has direction and magnitude but not position. Since ectors hae no position we may place them whereer
Chapter 8 Vectors and Scalars
 Chapter 8 193 Vectors and Scalars Chapter 8 Vectors and Scalars 8.1 Introduction: In this chapter we shall use the ideas of the plane to develop a new mathematical concept, vector. If you have studied
Chapter 8 193 Vectors and Scalars Chapter 8 Vectors and Scalars 8.1 Introduction: In this chapter we shall use the ideas of the plane to develop a new mathematical concept, vector. If you have studied
UNIT NUMBER 8.2. VECTORS 2 (Vectors in component form) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 8.2 VECTORS 2 (Vectors in component form) by A.J.Hobson 8.2.1 The components of a vector 8.2.2 The magnitude of a vector in component form 8.2.3 The sum and difference of vectors
JUST THE MATHS UNIT NUMBER 8.2 VECTORS 2 (Vectors in component form) by A.J.Hobson 8.2.1 The components of a vector 8.2.2 The magnitude of a vector in component form 8.2.3 The sum and difference of vectors
Math 425 Lecture 1: Vectors in R 3, R n
 Math 425 Lecture 1: Vectors in R 3, R n Motiating Questions, Problems 1. Find the coordinates of a regular tetrahedron with center at the origin and sides of length 1. 2. What is the angle between the
Math 425 Lecture 1: Vectors in R 3, R n Motiating Questions, Problems 1. Find the coordinates of a regular tetrahedron with center at the origin and sides of length 1. 2. What is the angle between the
What you will learn today
 What you will learn today The Dot Product Equations of Vectors and the Geometry of Space 1/29 Direction angles and Direction cosines Projections Definitions: 1. a : a 1, a 2, a 3, b : b 1, b 2, b 3, a
What you will learn today The Dot Product Equations of Vectors and the Geometry of Space 1/29 Direction angles and Direction cosines Projections Definitions: 1. a : a 1, a 2, a 3, b : b 1, b 2, b 3, a
12.1 Three Dimensional Coordinate Systems (Review) Equation of a sphere
 12.2 Vectors 12.1 Three Dimensional Coordinate Systems (Reiew) Equation of a sphere x a 2 + y b 2 + (z c) 2 = r 2 Center (a,b,c) radius r 12.2 Vectors Quantities like displacement, elocity, and force inole
12.2 Vectors 12.1 Three Dimensional Coordinate Systems (Reiew) Equation of a sphere x a 2 + y b 2 + (z c) 2 = r 2 Center (a,b,c) radius r 12.2 Vectors Quantities like displacement, elocity, and force inole
MAC Module 5 Vectors in 2-Space and 3-Space II
 MAC 2103 Module 5 Vectors in 2-Space and 3-Space II 1 Learning Objectives Upon completing this module, you should be able to: 1. Determine the cross product of a vector in R 3. 2. Determine a scalar triple
MAC 2103 Module 5 Vectors in 2-Space and 3-Space II 1 Learning Objectives Upon completing this module, you should be able to: 1. Determine the cross product of a vector in R 3. 2. Determine a scalar triple
(1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3
 Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
VECTORS IN 2-SPACE AND 3-SPACE GEOMETRIC VECTORS VECTORS OPERATIONS DOT PRODUCT; PROJECTIONS CROSS PRODUCT
 VECTORS IN -SPACE AND 3-SPACE GEOMETRIC VECTORS VECTORS OPERATIONS DOT PRODUCT; PROJECTIONS CROSS PRODUCT GEOMETRIC VECTORS Vectors can represented geometrically as directed line segments or arrows in
VECTORS IN -SPACE AND 3-SPACE GEOMETRIC VECTORS VECTORS OPERATIONS DOT PRODUCT; PROJECTIONS CROSS PRODUCT GEOMETRIC VECTORS Vectors can represented geometrically as directed line segments or arrows in
Lecture 2: Vector-Vector Operations
 Lecture 2: Vector-Vector Operations Vector-Vector Operations Addition of two vectors Geometric representation of addition and subtraction of vectors Vectors and points Dot product of two vectors Geometric
Lecture 2: Vector-Vector Operations Vector-Vector Operations Addition of two vectors Geometric representation of addition and subtraction of vectors Vectors and points Dot product of two vectors Geometric
Math 144 Activity #9 Introduction to Vectors
 144 p 1 Math 144 ctiity #9 Introduction to Vectors Often times you hear people use the words speed and elocity. Is there a difference between the two? If so, what is the difference? Discuss this with your
144 p 1 Math 144 ctiity #9 Introduction to Vectors Often times you hear people use the words speed and elocity. Is there a difference between the two? If so, what is the difference? Discuss this with your
12.5 Equations of Lines and Planes
 12.5 Equations of Lines and Planes Equation of Lines Vector Equation of Lines Parametric Equation of Lines Symmetric Equation of Lines Relation Between Two Lines Equations of Planes Vector Equation of
12.5 Equations of Lines and Planes Equation of Lines Vector Equation of Lines Parametric Equation of Lines Symmetric Equation of Lines Relation Between Two Lines Equations of Planes Vector Equation of
MAT 1339-S14 Class 8
 MAT 1339-S14 Class 8 July 28, 2014 Contents 7.2 Review Dot Product........................... 2 7.3 Applications of the Dot Product..................... 4 7.4 Vectors in Three-Space.........................
MAT 1339-S14 Class 8 July 28, 2014 Contents 7.2 Review Dot Product........................... 2 7.3 Applications of the Dot Product..................... 4 7.4 Vectors in Three-Space.........................
VECTORS AND THE GEOMETRY OF SPACE
 VECTORS AND THE GEOMETRY OF SPACE VECTORS AND THE GEOMETRY OF SPACE A line in the xy-plane is determined when a point on the line and the direction of the line (its slope or angle of inclination) are given.
VECTORS AND THE GEOMETRY OF SPACE VECTORS AND THE GEOMETRY OF SPACE A line in the xy-plane is determined when a point on the line and the direction of the line (its slope or angle of inclination) are given.
The Dot Product Pg. 377 # 6ace, 7bdf, 9, 11, 14 Pg. 385 # 2, 3, 4, 6bd, 7, 9b, 10, 14 Sept. 25
 UNIT 2 - APPLICATIONS OF VECTORS Date Lesson TOPIC Homework Sept. 19 2.1 (11) 7.1 Vectors as Forces Pg. 362 # 2, 5a, 6, 8, 10 13, 16, 17 Sept. 21 2.2 (12) 7.2 Velocity as Vectors Pg. 369 # 2,3, 4, 6, 7,
UNIT 2 - APPLICATIONS OF VECTORS Date Lesson TOPIC Homework Sept. 19 2.1 (11) 7.1 Vectors as Forces Pg. 362 # 2, 5a, 6, 8, 10 13, 16, 17 Sept. 21 2.2 (12) 7.2 Velocity as Vectors Pg. 369 # 2,3, 4, 6, 7,
1.1 Bound and Free Vectors. 1.2 Vector Operations
 1 Vectors Vectors are used when both the magnitude and the direction of some physical quantity are required. Examples of such quantities are velocity, acceleration, force, electric and magnetic fields.
1 Vectors Vectors are used when both the magnitude and the direction of some physical quantity are required. Examples of such quantities are velocity, acceleration, force, electric and magnetic fields.
Prepared by: M. S. KumarSwamy, TGT(Maths) Page
 Prepared by: M S KumarSwamy, TGT(Maths) Page - 119 - CHAPTER 10: VECTOR ALGEBRA QUICK REVISION (Important Concepts & Formulae) MARKS WEIGHTAGE 06 marks Vector The line l to the line segment AB, then a
Prepared by: M S KumarSwamy, TGT(Maths) Page - 119 - CHAPTER 10: VECTOR ALGEBRA QUICK REVISION (Important Concepts & Formulae) MARKS WEIGHTAGE 06 marks Vector The line l to the line segment AB, then a
10.1 Vectors. c Kun Wang. Math 150, Fall 2017
 10.1 Vectors Definition. A vector is a quantity that has both magnitude and direction. A vector is often represented graphically as an arrow where the direction is the direction of the arrow, and the magnitude
10.1 Vectors Definition. A vector is a quantity that has both magnitude and direction. A vector is often represented graphically as an arrow where the direction is the direction of the arrow, and the magnitude
DATE: MATH ANALYSIS 2 CHAPTER 12: VECTORS & DETERMINANTS
 NAME: PERIOD: DATE: MATH ANALYSIS 2 MR. MELLINA CHAPTER 12: VECTORS & DETERMINANTS Sections: v 12.1 Geometric Representation of Vectors v 12.2 Algebraic Representation of Vectors v 12.3 Vector and Parametric
NAME: PERIOD: DATE: MATH ANALYSIS 2 MR. MELLINA CHAPTER 12: VECTORS & DETERMINANTS Sections: v 12.1 Geometric Representation of Vectors v 12.2 Algebraic Representation of Vectors v 12.3 Vector and Parametric
UNDERSTAND MOTION IN ONE AND TWO DIMENSIONS
 SUBAREA I. COMPETENCY 1.0 UNDERSTAND MOTION IN ONE AND TWO DIMENSIONS MECHANICS Skill 1.1 Calculating displacement, aerage elocity, instantaneous elocity, and acceleration in a gien frame of reference
SUBAREA I. COMPETENCY 1.0 UNDERSTAND MOTION IN ONE AND TWO DIMENSIONS MECHANICS Skill 1.1 Calculating displacement, aerage elocity, instantaneous elocity, and acceleration in a gien frame of reference
Kinematics on oblique axes
 Bolina 1 Kinematics on oblique axes arxi:physics/01111951 [physics.ed-ph] 27 No 2001 Oscar Bolina Departamento de Física-Matemática Uniersidade de São Paulo Caixa Postal 66318 São Paulo 05315-970 Brasil
Bolina 1 Kinematics on oblique axes arxi:physics/01111951 [physics.ed-ph] 27 No 2001 Oscar Bolina Departamento de Física-Matemática Uniersidade de São Paulo Caixa Postal 66318 São Paulo 05315-970 Brasil
Distance Formula in 3-D Given any two points P 1 (x 1, y 1, z 1 ) and P 2 (x 2, y 2, z 2 ) the distance between them is ( ) ( ) ( )
 Vectors and the Geometry of Space Vector Space The 3-D coordinate system (rectangular coordinates ) is the intersection of three perpendicular (orthogonal) lines called coordinate axis: x, y, and z. Their
Vectors and the Geometry of Space Vector Space The 3-D coordinate system (rectangular coordinates ) is the intersection of three perpendicular (orthogonal) lines called coordinate axis: x, y, and z. Their
Math 241, Exam 1 Information.
 Math 241, Exam 1 Information. 2/13/13, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.2. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241sp13/241.html)
Math 241, Exam 1 Information. 2/13/13, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.2. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241sp13/241.html)
UNIT 1 VECTORS INTRODUCTION 1.1 OBJECTIVES. Stucture
 UNIT 1 VECTORS 1 Stucture 1.0 Introduction 1.1 Objectives 1.2 Vectors and Scalars 1.3 Components of a Vector 1.4 Section Formula 1.5 nswers to Check Your Progress 1.6 Summary 1.0 INTRODUCTION In this unit,
UNIT 1 VECTORS 1 Stucture 1.0 Introduction 1.1 Objectives 1.2 Vectors and Scalars 1.3 Components of a Vector 1.4 Section Formula 1.5 nswers to Check Your Progress 1.6 Summary 1.0 INTRODUCTION In this unit,
CHAPTER 4 VECTORS. Before we go any further, we must talk about vectors. They are such a useful tool for
 CHAPTER 4 VECTORS Before we go any further, we must talk about vectors. They are such a useful tool for the things to come. The concept of a vector is deeply rooted in the understanding of physical mechanics
CHAPTER 4 VECTORS Before we go any further, we must talk about vectors. They are such a useful tool for the things to come. The concept of a vector is deeply rooted in the understanding of physical mechanics
Detailed objectives are given in each of the sections listed below. 1. Cartesian Space Coordinates. 2. Displacements, Forces, Velocities and Vectors
 Unit 1 Vectors In this unit, we introduce vectors, vector operations, and equations of lines and planes. Note: Unit 1 is based on Chapter 12 of the textbook, Salas and Hille s Calculus: Several Variables,
Unit 1 Vectors In this unit, we introduce vectors, vector operations, and equations of lines and planes. Note: Unit 1 is based on Chapter 12 of the textbook, Salas and Hille s Calculus: Several Variables,
4.1 Distance and Length
 Chapter Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at vectors
Chapter Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at vectors
Vectors and the Geometry of Space
 Vectors and the Geometry of Space Many quantities in geometry and physics, such as area, volume, temperature, mass, and time, can be characterized by a single real number scaled to appropriate units of
Vectors and the Geometry of Space Many quantities in geometry and physics, such as area, volume, temperature, mass, and time, can be characterized by a single real number scaled to appropriate units of
CHAPTER 10 VECTORS POINTS TO REMEMBER
 For more important questions visit : www4onocom CHAPTER 10 VECTORS POINTS TO REMEMBER A quantity that has magnitude as well as direction is called a vector It is denoted by a directed line segment Two
For more important questions visit : www4onocom CHAPTER 10 VECTORS POINTS TO REMEMBER A quantity that has magnitude as well as direction is called a vector It is denoted by a directed line segment Two
MAT1035 Analytic Geometry
 MAT1035 Analytic Geometry Lecture Notes R.A. Sabri Kaan Gürbüzer Dokuz Eylül University 2016 2 Contents 1 Review of Trigonometry 5 2 Polar Coordinates 7 3 Vectors in R n 9 3.1 Located Vectors..............................................
MAT1035 Analytic Geometry Lecture Notes R.A. Sabri Kaan Gürbüzer Dokuz Eylül University 2016 2 Contents 1 Review of Trigonometry 5 2 Polar Coordinates 7 3 Vectors in R n 9 3.1 Located Vectors..............................................
Vectors. The standard geometric definition of vector is as something which has direction and magnitude but not position.
 Vectors The standard geometric definition of vector is as something which has direction and magnitude but not position. Since vectors have no position we may place them wherever is convenient. Vectors
Vectors The standard geometric definition of vector is as something which has direction and magnitude but not position. Since vectors have no position we may place them wherever is convenient. Vectors
(arrows denote positive direction)
 12 Chapter 12 12.1 3-dimensional Coordinate System The 3-dimensional coordinate system we use are coordinates on R 3. The coordinate is presented as a triple of numbers: (a,b,c). In the Cartesian coordinate
12 Chapter 12 12.1 3-dimensional Coordinate System The 3-dimensional coordinate system we use are coordinates on R 3. The coordinate is presented as a triple of numbers: (a,b,c). In the Cartesian coordinate
Department of Physics, Korea University
 Name: Department: Notice +2 ( 1) points per correct (incorrect) answer. No penalty for an unanswered question. Fill the blank ( ) with (8) if the statement is correct (incorrect).!!!: corrections to an
Name: Department: Notice +2 ( 1) points per correct (incorrect) answer. No penalty for an unanswered question. Fill the blank ( ) with (8) if the statement is correct (incorrect).!!!: corrections to an
Culminating Review for Vectors
 Culminating Review for Vectors 0011 0010 1010 1101 0001 0100 1011 An Introduction to Vectors Applications of Vectors Equations of Lines and Planes 4 12 Relationships between Points, Lines and Planes An
Culminating Review for Vectors 0011 0010 1010 1101 0001 0100 1011 An Introduction to Vectors Applications of Vectors Equations of Lines and Planes 4 12 Relationships between Points, Lines and Planes An
Course Notes Math 275 Boise State University. Shari Ultman
 Course Notes Math 275 Boise State University Shari Ultman Fall 2017 Contents 1 Vectors 1 1.1 Introduction to 3-Space & Vectors.............. 3 1.2 Working With Vectors.................... 7 1.3 Introduction
Course Notes Math 275 Boise State University Shari Ultman Fall 2017 Contents 1 Vectors 1 1.1 Introduction to 3-Space & Vectors.............. 3 1.2 Working With Vectors.................... 7 1.3 Introduction
Vector Geometry. Chapter 5
 Chapter 5 Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at
Chapter 5 Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at
1 Vectors. c Kun Wang. Math 151, Fall Vector Supplement
 Vector Supplement 1 Vectors A vector is a quantity that has both magnitude and direction. Vectors are drawn as directed line segments and are denoted by boldface letters a or by a. The magnitude of a vector
Vector Supplement 1 Vectors A vector is a quantity that has both magnitude and direction. Vectors are drawn as directed line segments and are denoted by boldface letters a or by a. The magnitude of a vector
Last week we presented the following expression for the angles between two vectors u and v in R n ( ) θ = cos 1 u v
 Orthogonality (I) Last week we presented the following expression for the angles between two vectors u and v in R n ( ) θ = cos 1 u v u v which brings us to the fact that θ = π/2 u v = 0. Definition (Orthogonality).
Orthogonality (I) Last week we presented the following expression for the angles between two vectors u and v in R n ( ) θ = cos 1 u v u v which brings us to the fact that θ = π/2 u v = 0. Definition (Orthogonality).
1.1 Single Variable Calculus versus Multivariable Calculus Rectangular Coordinate Systems... 4
 MATH2202 Notebook 1 Fall 2015/2016 prepared by Professor Jenny Baglivo Contents 1 MATH2202 Notebook 1 3 1.1 Single Variable Calculus versus Multivariable Calculus................... 3 1.2 Rectangular Coordinate
MATH2202 Notebook 1 Fall 2015/2016 prepared by Professor Jenny Baglivo Contents 1 MATH2202 Notebook 1 3 1.1 Single Variable Calculus versus Multivariable Calculus................... 3 1.2 Rectangular Coordinate
LECTURE 2: CROSS PRODUCTS, MULTILINEARITY, AND AREAS OF PARALLELOGRAMS
 LECTURE : CROSS PRODUCTS, MULTILINEARITY, AND AREAS OF PARALLELOGRAMS MA1111: LINEAR ALGEBRA I, MICHAELMAS 016 1. Finishing up dot products Last time we stated the following theorem, for which I owe you
LECTURE : CROSS PRODUCTS, MULTILINEARITY, AND AREAS OF PARALLELOGRAMS MA1111: LINEAR ALGEBRA I, MICHAELMAS 016 1. Finishing up dot products Last time we stated the following theorem, for which I owe you
Study guide for Exam 1. by William H. Meeks III October 26, 2012
 Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
Chapter 2 - Vector Algebra
 A spatial vector, or simply vector, is a concept characterized by a magnitude and a direction, and which sums with other vectors according to the Parallelogram Law. A vector can be thought of as an arrow
A spatial vector, or simply vector, is a concept characterized by a magnitude and a direction, and which sums with other vectors according to the Parallelogram Law. A vector can be thought of as an arrow
Mathematics Revision Guides Vectors Page 1 of 19 Author: Mark Kudlowski M.K. HOME TUITION. Mathematics Revision Guides Level: GCSE Higher Tier VECTORS
 Mathematics Revision Guides Vectors Page of 9 M.K. HOME TUITION Mathematics Revision Guides Level: GCSE Higher Tier VECTORS Version:.4 Date: 05-0-05 Mathematics Revision Guides Vectors Page of 9 VECTORS
Mathematics Revision Guides Vectors Page of 9 M.K. HOME TUITION Mathematics Revision Guides Level: GCSE Higher Tier VECTORS Version:.4 Date: 05-0-05 Mathematics Revision Guides Vectors Page of 9 VECTORS
12.1. Cartesian Space
 12.1. Cartesian Space In most of your previous math classes, we worked with functions on the xy-plane only meaning we were working only in 2D. Now we will be working in space, or rather 3D. Now we will
12.1. Cartesian Space In most of your previous math classes, we worked with functions on the xy-plane only meaning we were working only in 2D. Now we will be working in space, or rather 3D. Now we will
Math 234. What you should know on day one. August 28, You should be able to use general principles like. x = cos t, y = sin t, 0 t π.
 Math 234 What you should know on day one August 28, 2001 1 You should be able to use general principles like Length = ds, Area = da, Volume = dv For example the length of the semi circle x = cos t, y =
Math 234 What you should know on day one August 28, 2001 1 You should be able to use general principles like Length = ds, Area = da, Volume = dv For example the length of the semi circle x = cos t, y =
Chapter 8: Polar Coordinates and Vectors
 Chapter 8: Polar Coordinates and Vectors 8.1 Polar Coordinates This is another way (in addition to the x-y system) of specifying the position of a point in the plane. We give the distance r of the point
Chapter 8: Polar Coordinates and Vectors 8.1 Polar Coordinates This is another way (in addition to the x-y system) of specifying the position of a point in the plane. We give the distance r of the point
VECTORS IN COMPONENT FORM
 VECTORS IN COMPONENT FORM In Cartesian coordinates any D vector a can be written as a = a x i + a y j + a z k a x a y a x a y a z a z where i, j and k are unit vectors in x, y and z directions. i = j =
VECTORS IN COMPONENT FORM In Cartesian coordinates any D vector a can be written as a = a x i + a y j + a z k a x a y a x a y a z a z where i, j and k are unit vectors in x, y and z directions. i = j =
MATH 151 Engineering Mathematics I
 MATH 151 Engineering Mathematics I Spring 2018, WEEK 1 JoungDong Kim Week 1 Vectors, The Dot Product, Vector Functions and Parametric Curves. Section 1.1 Vectors Definition. A Vector is a quantity that
MATH 151 Engineering Mathematics I Spring 2018, WEEK 1 JoungDong Kim Week 1 Vectors, The Dot Product, Vector Functions and Parametric Curves. Section 1.1 Vectors Definition. A Vector is a quantity that
Give a geometric description of the set of points in space whose coordinates satisfy the given pair of equations.
 1. Give a geometric description of the set of points in space whose coordinates satisfy the given pair of equations. x + y = 5, z = 4 Choose the correct description. A. The circle with center (0,0, 4)
1. Give a geometric description of the set of points in space whose coordinates satisfy the given pair of equations. x + y = 5, z = 4 Choose the correct description. A. The circle with center (0,0, 4)
Euclidean Spaces. Euclidean Spaces. Chapter 10 -S&B
 Chapter 10 -S&B The Real Line: every real number is represented by exactly one point on the line. The plane (i.e., consumption bundles): Pairs of numbers have a geometric representation Cartesian plane
Chapter 10 -S&B The Real Line: every real number is represented by exactly one point on the line. The plane (i.e., consumption bundles): Pairs of numbers have a geometric representation Cartesian plane
MATH 255 Applied Honors Calculus III Winter Midterm 1 Review Solutions
 MATH 55 Applied Honors Calculus III Winter 11 Midterm 1 Review Solutions 11.1: #19 Particle starts at point ( 1,, traces out a semicircle in the counterclockwise direction, ending at the point (1,. 11.1:
MATH 55 Applied Honors Calculus III Winter 11 Midterm 1 Review Solutions 11.1: #19 Particle starts at point ( 1,, traces out a semicircle in the counterclockwise direction, ending at the point (1,. 11.1:
LINEAR ALGEBRA - CHAPTER 1: VECTORS
 LINEAR ALGEBRA - CHAPTER 1: VECTORS A game to introduce Linear Algebra In measurement, there are many quantities whose description entirely rely on magnitude, i.e., length, area, volume, mass and temperature.
LINEAR ALGEBRA - CHAPTER 1: VECTORS A game to introduce Linear Algebra In measurement, there are many quantities whose description entirely rely on magnitude, i.e., length, area, volume, mass and temperature.
Roberto s Notes on Linear Algebra Chapter 1: Geometric vectors Section 8. The dot product
 Roberto s Notes on Linear Algebra Chapter 1: Geometric ectors Section 8 The dot product What you need to know already: What a linear combination of ectors is. What you can learn here: How to use two ectors
Roberto s Notes on Linear Algebra Chapter 1: Geometric ectors Section 8 The dot product What you need to know already: What a linear combination of ectors is. What you can learn here: How to use two ectors
A Geometric Review of Linear Algebra
 A Geometric Reiew of Linear Algebra The following is a compact reiew of the primary concepts of linear algebra. The order of presentation is unconentional, with emphasis on geometric intuition rather than
A Geometric Reiew of Linear Algebra The following is a compact reiew of the primary concepts of linear algebra. The order of presentation is unconentional, with emphasis on geometric intuition rather than
How can we find the distance between a point and a plane in R 3? Between two lines in R 3? Between two planes? Between a plane and a line?
 Overview Yesterday we introduced equations to describe lines and planes in R 3 : r = r 0 + tv The vector equation for a line describes arbitrary points r in terms of a specific point r 0 and the direction
Overview Yesterday we introduced equations to describe lines and planes in R 3 : r = r 0 + tv The vector equation for a line describes arbitrary points r in terms of a specific point r 0 and the direction
Vector Algebra August 2013
 Vector Algebra 12.1 12.2 28 August 2013 What is a Vector? A vector (denoted or v) is a mathematical object possessing both: direction and magnitude also called length (denoted ). Vectors are often represented
Vector Algebra 12.1 12.2 28 August 2013 What is a Vector? A vector (denoted or v) is a mathematical object possessing both: direction and magnitude also called length (denoted ). Vectors are often represented
Course Name : Physics I Course # PHY 107
 Course Name : Physics I Course # PHY 107 Lecture-2 : Representation of Vectors and the Product Rules Abu Mohammad Khan Department of Mathematics and Physics North South University http://abukhan.weebly.com
Course Name : Physics I Course # PHY 107 Lecture-2 : Representation of Vectors and the Product Rules Abu Mohammad Khan Department of Mathematics and Physics North South University http://abukhan.weebly.com
11.1 Three-Dimensional Coordinate System
 11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
2.1 Scalars and Vectors
 2.1 Scalars and Vectors Scalar A quantity characterized by a positive or negative number Indicated by letters in italic such as A e.g. Mass, volume and length 2.1 Scalars and Vectors Vector A quantity
2.1 Scalars and Vectors Scalar A quantity characterized by a positive or negative number Indicated by letters in italic such as A e.g. Mass, volume and length 2.1 Scalars and Vectors Vector A quantity
2) If a=<2,-1> and b=<3,2>, what is a b and what is the angle between the vectors?
 CMCS427 Dot product reiew Computing the dot product The dot product can be computed ia a) Cosine rule a b = a b cos q b) Coordinate-wise a b = ax * bx + ay * by 1) If a b, a and b all equal 1, what s the
CMCS427 Dot product reiew Computing the dot product The dot product can be computed ia a) Cosine rule a b = a b cos q b) Coordinate-wise a b = ax * bx + ay * by 1) If a b, a and b all equal 1, what s the
Overview of vector calculus. Coordinate systems in space. Distance formula. (Sec. 12.1)
 Math 20C Multivariable Calculus Lecture 1 1 Coordinates in space Slide 1 Overview of vector calculus. Coordinate systems in space. Distance formula. (Sec. 12.1) Vector calculus studies derivatives and
Math 20C Multivariable Calculus Lecture 1 1 Coordinates in space Slide 1 Overview of vector calculus. Coordinate systems in space. Distance formula. (Sec. 12.1) Vector calculus studies derivatives and
Definition 6.1. A vector is a quantity with both a magnitude (size) and direction. Figure 6.1: Some vectors.
 Chapter 6 Vectors 6.1 Introduction Definition 6.1. A vector is a quantity with both a magnitude (size) and direction. Many quantities in engineering applications can be described by vectors, e.g. force,
Chapter 6 Vectors 6.1 Introduction Definition 6.1. A vector is a quantity with both a magnitude (size) and direction. Many quantities in engineering applications can be described by vectors, e.g. force,
Vectors and Plane Geometry
 Vectors and Plane Geometry Karl Heinz Dovermann Professor of Mathematics University of Hawaii January 7, 0 Preface During the first week of the semester it is difficult to get started with the course
Vectors and Plane Geometry Karl Heinz Dovermann Professor of Mathematics University of Hawaii January 7, 0 Preface During the first week of the semester it is difficult to get started with the course
2- Scalars and Vectors
 2- Scalars and Vectors Scalars : have magnitude only : Length, time, mass, speed and volume is example of scalar. v Vectors : have magnitude and direction. v The magnitude of is written v v Position, displacement,
2- Scalars and Vectors Scalars : have magnitude only : Length, time, mass, speed and volume is example of scalar. v Vectors : have magnitude and direction. v The magnitude of is written v v Position, displacement,
Linear Algebra Homework and Study Guide
 Linear Algebra Homework and Study Guide Phil R. Smith, Ph.D. February 28, 20 Homework Problem Sets Organized by Learning Outcomes Test I: Systems of Linear Equations; Matrices Lesson. Give examples of
Linear Algebra Homework and Study Guide Phil R. Smith, Ph.D. February 28, 20 Homework Problem Sets Organized by Learning Outcomes Test I: Systems of Linear Equations; Matrices Lesson. Give examples of
6.3 Vectors in a Plane
 6.3 Vectors in a Plane Plan: Represent ectors as directed line segments. Write the component form of ectors. Perform basic ector operations and represent ectors graphically. Find the direction angles of
6.3 Vectors in a Plane Plan: Represent ectors as directed line segments. Write the component form of ectors. Perform basic ector operations and represent ectors graphically. Find the direction angles of
1.2 LECTURE 2. Scalar Product
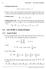 6 CHAPTER 1. VECTOR ALGEBRA Pythagean theem. cos 2 α 1 + cos 2 α 2 + cos 2 α 3 = 1 There is a one-to-one crespondence between the components of the vect on the one side and its magnitude and the direction
6 CHAPTER 1. VECTOR ALGEBRA Pythagean theem. cos 2 α 1 + cos 2 α 2 + cos 2 α 3 = 1 There is a one-to-one crespondence between the components of the vect on the one side and its magnitude and the direction
1. Vectors and Matrices
 E. 8.02 Exercises. Vectors and Matrices A. Vectors Definition. A direction is just a unit vector. The direction of A is defined by dir A = A, (A 0); A it is the unit vector lying along A and pointed like
E. 8.02 Exercises. Vectors and Matrices A. Vectors Definition. A direction is just a unit vector. The direction of A is defined by dir A = A, (A 0); A it is the unit vector lying along A and pointed like
The geometry of least squares
 The geometry of least squares We can think of a vector as a point in space, where the elements of the vector are the coordinates of the point. Consider for example, the following vector s: t = ( 4, 0),
The geometry of least squares We can think of a vector as a point in space, where the elements of the vector are the coordinates of the point. Consider for example, the following vector s: t = ( 4, 0),
Semester University of Sheffield. School of Mathematics and Statistics
 University of Sheffield School of Mathematics and Statistics MAS140: Mathematics (Chemical) MAS152: Civil Engineering Mathematics MAS152: Essential Mathematical Skills & Techniques MAS156: Mathematics
University of Sheffield School of Mathematics and Statistics MAS140: Mathematics (Chemical) MAS152: Civil Engineering Mathematics MAS152: Essential Mathematical Skills & Techniques MAS156: Mathematics
The Geometry of R n. Supplemental Lecture Notes for Linear Algebra Courses at Georgia Tech
 The Geometry of R n Supplemental Lecture Notes for Linear Algebra Courses at Georgia Tech Contents Vectors in R n. Vectors....................................... The Length and Direction of a Vector......................3
The Geometry of R n Supplemental Lecture Notes for Linear Algebra Courses at Georgia Tech Contents Vectors in R n. Vectors....................................... The Length and Direction of a Vector......................3
Mechanics: Scalars and Vectors
 Mechanics: Scalars and Vectors Scalar Onl magnitude is associated with it Vector e.g., time, volume, densit, speed, energ, mass etc. Possess direction as well as magnitude Parallelogram law of addition
Mechanics: Scalars and Vectors Scalar Onl magnitude is associated with it Vector e.g., time, volume, densit, speed, energ, mass etc. Possess direction as well as magnitude Parallelogram law of addition
Motion In Two Dimensions. Vectors in Physics
 Motion In Two Dimensions RENE DESCARTES (1736-1806) GALILEO GALILEI (1564-1642) Vectors in Physics All physical quantities are either scalars or ectors Scalars A scalar quantity has only magnitude. In
Motion In Two Dimensions RENE DESCARTES (1736-1806) GALILEO GALILEI (1564-1642) Vectors in Physics All physical quantities are either scalars or ectors Scalars A scalar quantity has only magnitude. In
Chapter Objectives. Copyright 2011 Pearson Education South Asia Pte Ltd
 Chapter Objectives To show how to add forces and resolve them into components using the Parallelogram Law. To express force and position in Cartesian vector form and explain how to determine the vector
Chapter Objectives To show how to add forces and resolve them into components using the Parallelogram Law. To express force and position in Cartesian vector form and explain how to determine the vector
10.2,3,4. Vectors in 3D, Dot products and Cross Products
 Name: Section: 10.2,3,4. Vectors in 3D, Dot products and Cross Products 1. Sketch the plane parallel to the xy-plane through (2, 4, 2) 2. For the given vectors u and v, evaluate the following expressions.
Name: Section: 10.2,3,4. Vectors in 3D, Dot products and Cross Products 1. Sketch the plane parallel to the xy-plane through (2, 4, 2) 2. For the given vectors u and v, evaluate the following expressions.
The Dot Product
 The Dot Product 1-9-017 If = ( 1,, 3 ) and = ( 1,, 3 ) are ectors, the dot product of and is defined algebraically as = 1 1 + + 3 3. Example. (a) Compute the dot product (,3, 7) ( 3,,0). (b) Compute the
The Dot Product 1-9-017 If = ( 1,, 3 ) and = ( 1,, 3 ) are ectors, the dot product of and is defined algebraically as = 1 1 + + 3 3. Example. (a) Compute the dot product (,3, 7) ( 3,,0). (b) Compute the
Regent College. Maths Department. Core Mathematics 4. Vectors
 Regent College Maths Department Core Mathematics 4 Vectors Page 1 Vectors By the end of this unit you should be able to find: a unit vector in the direction of a. the distance between two points (x 1,
Regent College Maths Department Core Mathematics 4 Vectors Page 1 Vectors By the end of this unit you should be able to find: a unit vector in the direction of a. the distance between two points (x 1,
Chapter 13: Vectors and the Geometry of Space
 Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
Chapter 13: Vectors and the Geometry of Space
 Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
1. Vectors in the Plane
 CHAPTER 10 Vectors and the Geometry of Space 1. Vectors in the Plane We denote the directed line segment from the point P (initial point) to the!! point Q (terminal point) as P Q. The length of P Q is
CHAPTER 10 Vectors and the Geometry of Space 1. Vectors in the Plane We denote the directed line segment from the point P (initial point) to the!! point Q (terminal point) as P Q. The length of P Q is
Mon Apr dot product, length, orthogonality, projection onto the span of a single vector. Announcements: Warm-up Exercise:
 Math 2270-004 Week 2 notes We will not necessarily finish the material from a gien day's notes on that day. We may also add or subtract some material as the week progresses, but these notes represent an
Math 2270-004 Week 2 notes We will not necessarily finish the material from a gien day's notes on that day. We may also add or subtract some material as the week progresses, but these notes represent an
scalar and - vector - - presentation SCALAR AND VECTOR
 http://www.slideshare.net/fikrifadzal/chapter-14scalar-and-vector- and presentation SCLR ND VECTOR Scalars Scalars are quantities which have magnitude without directioni Examples of scalars temperaturere
http://www.slideshare.net/fikrifadzal/chapter-14scalar-and-vector- and presentation SCLR ND VECTOR Scalars Scalars are quantities which have magnitude without directioni Examples of scalars temperaturere
11.1 Vectors in the plane
 11.1 Vectors in the plane What is a vector? It is an object having direction and length. Geometric way to represent vectors It is represented by an arrow. The direction of the arrow is the direction of
11.1 Vectors in the plane What is a vector? It is an object having direction and length. Geometric way to represent vectors It is represented by an arrow. The direction of the arrow is the direction of
Exam 1 Review SOLUTIONS
 1. True or False (and give a short reason): Exam 1 Review SOLUTIONS (a) If the parametric curve x = f(t), y = g(t) satisfies g (1) = 0, then it has a horizontal tangent line when t = 1. FALSE: To make
1. True or False (and give a short reason): Exam 1 Review SOLUTIONS (a) If the parametric curve x = f(t), y = g(t) satisfies g (1) = 0, then it has a horizontal tangent line when t = 1. FALSE: To make
Extra Problems for Math 2050 Linear Algebra I
 Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
MATH 19520/51 Class 2
 MATH 19520/51 Class 2 Minh-Tam Trinh University of Chicago 2017-09-27 1 Review dot product. 2 Angles between vectors and orthogonality. 3 Projection of one vector onto another. 4 Cross product and its
MATH 19520/51 Class 2 Minh-Tam Trinh University of Chicago 2017-09-27 1 Review dot product. 2 Angles between vectors and orthogonality. 3 Projection of one vector onto another. 4 Cross product and its
VIII - Geometric Vectors
 MTHEMTIS 0-NY-05 Vectors and Matrices Martin Huard Fall 07 VIII - Geometric Vectors. Find all ectors in the following parallelepiped that are equialent to the gien ectors. E F H G a) b) c) d) E e) f) F
MTHEMTIS 0-NY-05 Vectors and Matrices Martin Huard Fall 07 VIII - Geometric Vectors. Find all ectors in the following parallelepiped that are equialent to the gien ectors. E F H G a) b) c) d) E e) f) F
MOTION IN 2-DIMENSION (Projectile & Circular motion And Vectors)
 MOTION IN -DIMENSION (Projectile & Circular motion nd Vectors) INTRODUCTION The motion of an object is called two dimensional, if two of the three co-ordinates required to specif the position of the object
MOTION IN -DIMENSION (Projectile & Circular motion nd Vectors) INTRODUCTION The motion of an object is called two dimensional, if two of the three co-ordinates required to specif the position of the object
Motion in Two and Three Dimensions
 PH 1-1D Spring 013 Motion in Two and Three Dimensions Lectures 5,6,7 Chapter 4 (Halliday/Resnick/Walker, Fundamentals of Physics 9 th edition) 1 Chapter 4 Motion in Two and Three Dimensions In this chapter
PH 1-1D Spring 013 Motion in Two and Three Dimensions Lectures 5,6,7 Chapter 4 (Halliday/Resnick/Walker, Fundamentals of Physics 9 th edition) 1 Chapter 4 Motion in Two and Three Dimensions In this chapter
EGR2013 Tutorial 8. Linear Algebra. Powers of a Matrix and Matrix Polynomial
 EGR1 Tutorial 8 Linear Algebra Outline Powers of a Matrix and Matrix Polynomial Vector Algebra Vector Spaces Powers of a Matrix and Matrix Polynomial If A is a square matrix, then we define the nonnegative
EGR1 Tutorial 8 Linear Algebra Outline Powers of a Matrix and Matrix Polynomial Vector Algebra Vector Spaces Powers of a Matrix and Matrix Polynomial If A is a square matrix, then we define the nonnegative
Chapter 2: Force Vectors
 Chapter 2: Force Vectors Chapter Objectives To show how to add forces and resolve them into components using the Parallelogram Law. To express force and position in Cartesian vector form and explain how
Chapter 2: Force Vectors Chapter Objectives To show how to add forces and resolve them into components using the Parallelogram Law. To express force and position in Cartesian vector form and explain how
Exercise Solutions for Introduction to 3D Game Programming with DirectX 10
 Exercise Solutions for Introduction to 3D Game Programming with DirectX 10 Frank Luna, September 6, 009 Solutions to Part I Chapter 1 1. Let u = 1, and v = 3, 4. Perform the following computations and
Exercise Solutions for Introduction to 3D Game Programming with DirectX 10 Frank Luna, September 6, 009 Solutions to Part I Chapter 1 1. Let u = 1, and v = 3, 4. Perform the following computations and
