1. Vectors in the Plane
|
|
|
- Patrick McCormick
- 6 years ago
- Views:
Transcription
1 CHAPTER 10 Vectors and the Geometry of Space 1. Vectors in the Plane We denote the directed line segment from the point P (initial point) to the!! point Q (terminal point) as P Q. The length of P Q is its magnitude, denoted k P! Qk. Definition. A vector is the equivalence class of all directed line segments (or arrows) having the same magnitude and the same direction (an arrow and its parallel translates). Any arrow in the class may be used to name the vector. Example. a = b = c since a, b, c name the same vector. 1
2 2 10. VECTORS AND THE GEOMETRY OF SPACE Definition. A position vector is the arrow in each class with tail (initial point) at the origin. If the tip (terminal point) is at the point A(a 1, a 2 ), we write a = OA! = ha 1, a 2 i. In ha 1, a 2 i, a 1 and a 2 are called the components of a a 1 is the first component, a 2 the second component. From the Pythagorean Theorem, kak = kha 1, a 2 ik = q a a2 2. Note. The magnitude of a is often called the norm or 2-norm of a, and is sometimes denoted kak 2. For a =! OA = ha 1, a 2 i and b =! OB = hb 1, b 2 i, a = b () A = B () a 1 = b 1 and a 2 = b 2. () means if and only if (=) is only if and (= is if ).
3 Basic Operations Addition: 1. VECTORS IN THE PLANE 3 ha 1, a 2 i + hb 1, b 2 i = ha 1 + b 1, a 2 + b 2 i. This is the tip-to-tail or parallelogram law. The sum a+b is called the resultant. Example. h4, 3i + h 1, 4i = h3, 7i
4 4 10. VECTORS AND THE GEOMETRY OF SPACE Subtraction: ha 1, a 2 i hb 1, b 2 i = ha 1 b 1, a 2 b 2 i. For direction of di erence vector, make sure b + (a b) = a. Zero vector: 0 = h0, 0i k0k = 0 and the zero vector has all directions. Scalar multiplication: Thus ca is a vector and ca = cha 1, a 2 i = hca 1, ca 2 i kcak = khca 1, ca 2 ik = p q (ca 1 ) 2 + (ca 2 ) 2 = c 2 a c2 a 2 2 qc = 2 (a 21 + a22 ) = p q c 2 a a2 2 = c kak.
5 1. VECTORS IN THE PLANE 5 Vectors are parallel if one is a scalar multiple of the other. ca k a, in the same direction for c 0, the opposite direction for c apple 0. Additive inverse: hx, yi x, y 2 R, the set of all two-dimensional posi- Definition. V 2 = tion vectors. a = ha 1, a 2 i = ( 1)ha 1, a 2 i = h a 1, a 2 i k ak = k( 1)ha 1, a 2 ik = 1 kha 1, a 2 ik = kak Definition. A vector space is a set of vectors with the same dimension and a set of scalars (real or complex numbers) with addition and scalar multiplication such that for any vectors u, v, and w, and any scalars and, (1) v + w = w + v (2) (u + v) + w = u + (v + w) (3) ( v) = ( )v (4) ( + )v = v + v (5) (v + w) = v + w (6) 1v = v (7) 0v = 0 (8) v + 0 = v (9) For each v there is v such that v + ( v) = 0
6 6 10. VECTORS AND THE GEOMETRY OF SPACE Theorem (1.1). V 2 is a vector space. Proof. (of (2)) (u + v) + w = (hu 1, u 2 i + hv 1, v 2 i) + hw 1, w 2 i = hu 1 + v 1, u 2 + v 2 i + hw 1, w 2 i = h(u 1 + v 1 ) + w 1, (u 2 + v 2 ) + w 2 i = hu 1 + (v 1 + w 1 ), u 2 + (v 2 + w 2 )i = hu 1, u 2 i + hv 1 + w 1, v 2 + w 2 i = hu 1, u 2 i + (hv 1, v 2 i + hw 1, w 2 i) = u + (v + w) Note. For any two distinct points A(x 1, y 1 ) and B(x 2, y 2 ), to the position vector hx 2 x 1, y 2 y 1 i. Any vector can be written in terms of the standard basis vectors For any a 2 V 2, i = h1, 0i and j = h0, 1i.! AB corresponds a = ha 1, a 2 i = ha 1, 0i + h0, a 2 i = a 1 h1, 0i + a 2 h0, 1i = a 1 i + a 2 j. We call a 1 and a 2 the horizontal and vertical components of a Note. kik = kjk = 1. A unit vector is a vector a where kak = 1. Theorem (1.2). For any nonzero vector a, a unit vector having the same direction as a is u = 1 kak a. Proof. a 6= 0 =) kak > 0 =) u is a positive scalar multiple of a =) u has the same direction as a. kuk = 1 kak a = 1 kak kak = 1 kak kak = 1.
7 1. VECTORS IN THE PLANE 7 Example. Find a unit vector in the same directioin as a = h6, 8i. Therefore kak = kh6, 8ik = p = p 100 = 10. u = 1 10 h6, 8i = h3 5, 4 5 i. Resolving a vector a into horizontal and vertical components: a = kak cos i + kak sin j = kak(cos i + sin j) = kakhcos, sin i Note. khcos, sin ik = 1.
8 8 10. VECTORS AND THE GEOMETRY OF SPACE Example. A plane is flying at 500 km/hr. The wind is blowing at 60 km/hr toward the SE. In what direction should the plane head to go due east? What is the plane s speed relative to the ground? Solution Let p = the motion vector for the plane and w = the wind vector. Find and kp + wk. w = kwk cos( 45 )i + kwk sin( 45 )j p p 2 2 = 60 2 i 60 2 j = 30p 2 i 30 p 2 j = 42.43i 42.43j. Since the j-component of p + w is 0, p = xi + 30 p 2j where x is the i-component of p. Since kpk = 500, q 500 = x 2 + (30 p 2) 2 =) = x =) Thus x 2 = 250, = 248, 200 =) x p = i j =) tan = =.085 =) = arctan.085 = 4.86, and since p + w = i + 0j, kp + wk = km/hr.
9 2. VECTORS IN SPACE 9 Maple. See vectorsinplane(10.1).mw or vectorsinplane(10.1).pdf 2. Vectors in Space We use a right-handed coordinate system. The coordinate system has 8 octants. The first octant has x > 0, y > 0, z > 0. Distance Formula d (x 1, y 1, z 1 ), (x 2, y 2, z 2 )} = p (x 2 x 1 ) 2 + (y 2 y 1 ) 2 + (z 2 z 1 ) 2. Vectors in R 3 These are similar to vectors in R 2, with one more dimension. V 3 = hx, y, zi x, y, z 2 R is a vector space with a + b = ha 1, a 2, a 3 i + hb 1, b 2, b 3 i = ha 1 + b 1, a 2 + b 2, a 3 + b 3 i, ca = cha 1, a 2, a 3 i = hca 1, ca 2, ca 3 i, and a b = ha 1, a 2, a 3 i hb 1, b 2, b 3 i = ha 1 b 1, a 2 b 2, a 3 b 3 i,
10 VECTORS AND THE GEOMETRY OF SPACE Also, so kak = kha 1, a 2, a 3 ik = q a a2 2 + a2 3, kcak = c kak, 0 = h0, 0, 0i, and a = h a 1, a 2, a 3 i Note. The vector with initial point P (a 1, a 2, a 3 ) and terminal point Q(b 1, b 2, b 3 ) corresponds to the position vector! P Q = hb 1 a 1, b 2 a 2, b 3 a 3 i. The standard basis consists of i = h1, 0, 0, i, j = h0, 1, 0i, k = h0, 0, 1i with kik = kjk = kkk = 1. For any vector a = ha 1, a 2, a 3 i, a = a 1 i + a 2 j + a 3 k. Also, for any vector a = ha 1, a 2, a 3 i 6= 0, a unit vector u in the same direction as a is u = 1 kak a. The sphere of radius r centered at (a, b, c) consists of all points (x, y, z) such that d (x, y, z), (a, b, c)} = p (x a) 2 + (y b) 2 + (z c) 2 or (x a) 2 + (y b) 2 + (z c) 2 = r 2, the standard form of the equation of a sphere.
11 2. VECTORS IN SPACE 11 Problem (Page 711 #28). Identify the geometric shape given by Solution Rewrite as x 2 + x + y 2 y + z 2 = 7 2. (x 2 + x ) + (y 2 y ) + z 2 = 7 2. Complete squares: x 2 + x y 2 y z 2 = =) x y + z 2 = Thus we have the sphere of radius 2 centered at 2, 1 2., 0 Problem (Page 711 #20). Find a vector of magnitude 3 in the same direction as v = 3i + 3j k. Solution Thus kvk = p ( 1) 2 = p 19 u = 1 p 19 v is a unit vector in the same direction of v, so 3u = p 3 v = p 9 i + p 9 j p 19 k has magnitude 3 in the same direction as v. Problem (Page 711 #40). An equation for the x-axis is y 2 + z 2 = 0 or y = z = 0.
12 VECTORS AND THE GEOMETRY OF SPACE Problem (Page 712 #62). Three ropes are attached to a 300-pound crate. Rope A exerts a force of h10, 130, 200i pounds on the crate, and rope B exerts a force of h 20, 180, 160i pounds on the crate. What force must rope C exert on the crate to move it up and to the right with a constant force of h0, 30, 20i pounds. Solution Force of rope A is a = h10, 130, 200i, rope B is b = h 20, 180, 160i, rope C is c = hc 1, c 2, c 3 i, and the weight is w = h0, 0, 300i. We want the net force a + b + c + w = h0, 30, 20i =) h 10 + c 1, 50 + c 2, 60 + c 3 i = h0, 30, 20i =) c 1 = 10, c 2 = 20, c 3 = 40 =) c = h10, 20, 40i =) kck Thus rope C exerts a force of about 45.8 pounds in the direction h1, 2 4i. Maple. See vectorsinspace(10.2).mw or vectorsinspace(10.2).pdf 3. The Dot Product This is also often referred to as the scalar product. In V 2 : In V 3 : a b = ha 1, a 2 i hb 1, b 2 i = a 1 b 1 + a 2 b 2 a b = ha 1, a 2, a 3 i hb 1, b 2, b 3 i = a 1 b 1 + a 2 b 2 + a 3 b 3 Example. If a = h 3, 2, 5i and b = h3, 5, 6i, a b = h 3, 2, 5i h3, 5, 6i = ( 3)(3) + 2(5) + 5( 6) = = 29
13 Note. (1) The dot product of two vectors is a number. 3. THE DOT PRODUCT 13 (2) A vector ha, bi in V 2 can be thought of a vector ha, b, 0i in V 3, so results we prove for V 3 also hold for V 2. Theorem (3.1). For vectors a, b, c and any scalar d, (1) a b = b a (2) a (b + c) = a b + a c (3) (da) b = d(a b) = a (db) (4) 0 a = 0 (5) a a = kak 2 Proof. (2) a (b + c) = ha 1, a 2, a 3 i hb 1, b 2, b 3 i + hc 1, c 2, c 3 i = ha 1, a 2, a 3 i hb 1 + c 1, b 2 + c 2, b 3 + c 3 i = a 1 (b 1 + c 1 ) + a 2 (b 2 + c 2 ) + a 3 (b 3 + c 3 ) = a 1 b 1 + a 1 c 1 + a 2 b 2 + a 2 c 2 + a 3 b 3 + a 3 c 3 = a 1 b 1 + a 2 b 2 + a 3 b 3 + a 1 c 1 + a 2 c 2 + a 3 c 3 = ha 1, a 2, a 3 i hb 1, b 2, b 3 i + ha 1, a 2, a 3 i hc 1, c 2, c 3 i = a b + a c. (5) a a = ha 1, a 2, a 3 i ha 1, a 2, a 3 i = a a a 2 3 = kha 1, a 2, a 3 ik 2 = kak 2. Note. a b = 0 does not imply a = 0 or b = 0, so this di ers from our usual multiplication.
14 VECTORS AND THE GEOMETRY OF SPACE For a 6= 0 and b 6= 0 in V 3, the angle (0 apple apple ) between a and b is the smaller of the two angles in the plane formed by giving both vectors the same initial point. If a and b have the same direction, = 0. If a and b have the opposite direction, =. a and b are orthogonal (or perpendicular) if = 2. We say 0 is orthogonal to every vector. Law of Cosines ka bk 2 = kak 2 + kbk 2 2kakkbk cos Theorem (3.2). Let be the angle between nonzero vectors a and b. Then a b = kakkbk cos. Corollary. For nonzero vectors a and b, cos = a b kakkbk. Example. Find the angle between a = h2, 3, 6i and b = h 2, 1, 4i. 2( 2) + 3(1) + 6(4) cos = p p = p 21 =) 23 = arccos 7 p.7713 R
15 or 3. THE DOT PRODUCT 15 Corollary. a and b are orthogonal (a? b) () a b = 0. Theorem (3.3 Cauchy-Schwarz Inequality). For any vectors a and b, Proof. a 1 b 1 + a 2 b 2 + a 3 b 3 apple a b apple kakkbk q q a a2 2 + a2 3 b b2 2 + b2 3. a b = kakkbk cos = kakkbk cos apple kakkbk. Theorem (3.4 Triangle Inequality). For any vectors a and b, ka + bk apple kak + kbk. Proof. ka + bk 2 = (a + b) (a + b) = a a + a b + b a + b b = kak 2 + 2a b + kbk 2 apple kak 2 + 2kakkbk + kbk 2 = (kak + kbk) 2 Taking square roots then gives the result.
16 VECTORS AND THE GEOMETRY OF SPACE Component of a along b comp b a 0 < < 2 -comp b a 2 < < Note. cos( ) = cos comp b a = kak cos = kakkbk kbk cos = 1 1 kakkbk cos = kbk kbk a b =) comp b a = a b kbk is a number, a directed length, that depends on the length of a since unit vector. b kbk is a
17 Projection of a onto b 3. THE DOT PRODUCT 17 This is a force vector parallel to b having the same component along b as a. proj b a is a vector. 0 < < 2 proj b a = comp b a b kbk = proj b a = a b kbk proj b a! a b kbk b kbk! 2 < < b kbk =)
18 VECTORS AND THE GEOMETRY OF SPACE Problem (Page 721 #63b). Find the component of the weight vector along the road vector for a 2500-pound car on a 15 bank. Let b be the direction of the banked road with kbk = 1. b = hcos 15, sin 15 i. The weight w = h0, 2500i. The component of w in the direction of b is comp b w = w b = h0, 2500i hcos 15, sin 15 i = 2500 sin 15 = 647. kbk Thus the force is to the inside of the track, allowing the car to turn. Problem (Page 720 #56). The orthogonal projection of a vector a along a vector b is defined as orth b a = a proj b a. Sketch a picture showing a, b, proj b a, and orth b a, and explain what is orthogonal about orth b a. Maple. See dotprod(10.3).mw or dotprod(10.3).pdf
19 4. THE CROSS PRODUCT The Cross Product This is a product that exists only in 3 dimensions. We fist need an introduction to determinants for computational purposes. apple a1 a Definition. For a 2 2 ( 2 by 2 ) matrix M = 2, the determinant b 1 b 2 of M is M = a 1 a 2 = a b 1 b 1 b 2 a 2 b 1. 2 Definition. The determinant of a 3 3 matrix M is M = Example. a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 = a 1 b 2 b 3 c 2 c 3 a 2 b 1 b 3 c 1 c 3 + a 3 b 1 b 2 c 1 c 2 = a 1 b 2 c 3 a 1 b 3 c 2 + a 2 b 3 c 1 a 2 b 1 c 3 + a 3 b 1 c 2 a 3 b 2 c = = 1 Area of the Parallelogram formed by a and b Area = (base) (height) = kakkbk sin
20 VECTORS AND THE GEOMETRY OF SPACE Definition. The cross product a b is the vector orthogonal to a and b by the right-hand rule, whose magnitude is the area of the parallelogram determined by the vectors a and b, i.e., ka bk = kakkbk sin. Theorem (4.4). For nonzero vectors a and b in V 3, if is the angle between a and b (0 < < ), then ka bk = kakkbk sin. Theorem (4.2). For any vectors a and b in V 3, a b? a and a b? b. Definition (Algebraic Definition of Cross Product). a b = i j k a 1 a 2 a 3 b 1 b 2 b 3 = a 2 a 3 b 2 b 3 i a 1 a 3 b 1 b 3 j + a 1 a 2 b 1 b 2 k.
21 Example. h5, 1, 2i h 1, 3, 4i = 4. THE CROSS PRODUCT 21 i j k = (4 + 6)i + (2 20)j + (15 + 1)k = h10, 18, 16i kh10, 18, 16ik = p = p 680 = 2 p Theorem (4.1). For any vector a in V 3, a a = 0 and a 0 = 0. Example. i j k i j = but i j k j i = so the cross product is not commutative. = k, = k, i j = k j i = k j k = i k j = i k i = j i k = j
22 VECTORS AND THE GEOMETRY OF SPACE Theorem (4.3). For any a, b, c 2 V 3, and any scalar d, (1) a b = (b a) (anti-commutativity) (2) (da) b = d(a b) = a (db) (3) a (b + c) = a b + a c (4) (a + b) c = a c + b c (5) a (b c) = (a b) c (scalar triple product) (6) a (b c) = (a c)b (a b)c (vector triple product) Corollary (to Theorem 4.4). Two nonzero vectors a and b in V 3 are parallel if and only if a b = 0. Proof. a k b () (\ between a and b) = 0 or = () sin = 0 () ka bk = kakkbk sin = 0 () a b = 0. Volume of a Parallelepiped having noncoplanar vectors a, b, c as adjacent edges. Volume = (area of base) altitude = ka bk comp a b c = ka bk the absolute value of a scalar triple product. c (a b) ka bk = c (a b)
23 4. THE CROSS PRODUCT 23 Corollary (to Theorem 4.3). The scalar triple product of a, b, c is Note. a (b c) = a a (b c) = b (c a) = c (a b). i j k b 1 b 2 b 3 c 1 c 2 c 3 = ha 1, a 2, a 3 i b 2 b 3 c 2 c 3 i = a 1 b 2 b 3 c 2 c 3 a 2 b 1 b 3 c 1 c 3 + a 3 b 1 b 2 c 1 c 2 = a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 b 1 b 3 c 1 c 3 j + b 1 b 2 c 1 c 2 k Example. Find the volume of the parallelepiped with 3 adjacent edges formed by h 2, 1, 2i, h1, 1, 2i, and h2, 1, 3i. V = = = 15!
24 VECTORS AND THE GEOMETRY OF SPACE Example. Find the distance from a point Q to the line through P and R. k! P Q! P Rk = k! P Qkk! P Rk sin = d = k P! Q P! Rk k P! Rk {z} d=k! P Qk sin k! P Rk d =) Problem (Page 732 #20). Find the distance from the point Q = (1, 3, 1) to the line through P = (1, 3, 2) and R = (1, 0, 2).!! P Q = h0, 0, 3i and P R = h0, 3, 0i =) d = kh0, 0, 3i h0, 3, 0ik kh0, 3, 0ik = 1 3 k i j k k = 1 3 k9ik = 1 (9) = 3. 3
25 4. THE CROSS PRODUCT 25 Example (Torque applied by a wrench). F = force applied at end of handle. = torque applied to the bolt. r = position vector for handle. Then = r F =) k k = kr Fk = krkkfk sin Problem (Page 732 #28). If you apply a force of magnitude 40 pounds at the end of an eighteen-inch-long wrench at an angle of to the wrench, find 3 the magnitude of the torqe applied to the wrench. kfk = 40, krk = 18, = 3 =) k k = sin 3 = 720 p 3 2 = 360p Maple. See crossprod(10.4).mw or crossprod(10.4).pdf.
26 VECTORS AND THE GEOMETRY OF SPACE 5. Lines and Planes in Space Lines in 3-space: (1) Vector equation specified by two points or a point and a direction. P = OP! 1 + ta = hx 1, y 1, z 1 i + tha 1, a 2, a 3 i = hx 1 + ta 1, y 1 + ta 2, z 1 + ta 3 i or! P 1 P k a =) P! 1 P = ta =) hx x 1, y y 1, z z 1 i = tha 1, a 2, a 3 i Note. If given two points, use one point with the direction vector determined by the two points. (2) Parametric equations x = x 1 + ta 1, y = y 1 + ta 2, z = z 1 + ta 3 or x x 1 = ta 1, y y 1 = ta 2, z z 1 = ta 3 (3) Symmetric equations (solve for t in the three equations above, and equate the results). x x 1 = y y 1 = z z 1 a 1 a 2 a 3
27 5. LINES AND PLANES IN SPACE 27 Problem (Page 740 #8). Find the vector, parametric and symmetric equations of the line through ( 3, 1, 0) and perpendicular to both h0, 3, 1i and h4, 2, 1i. h0, 3, 1i h4, 2, 1i = i j k = h1, 4, 12i is perpendicular to bothh0, 3, 1i and h4, 2, 1i. Then the vector equation is the parametric equations are hx + 3, y 1, zi = th1, 4, 12i, x + 3 = t, y 1 = 4t, z = 12t, and the symmetric equations are x + 3 = y 1 = z For t = 3, x = 0, y = 13, and z = 36, so (0, 13, 36) is on this line and each quotient of the symmetric equations is 3. Definition. Let l 1 and l 2 be two lines in R 3, with parallel (or direction) vectors a and b, respectively, and let be the angle between a and b. (1) l 1 and l 2 are parallel whenever a and b are parallel. (2) If l 1 and l 2 intersect, then (a) the angle between l 1 and l 2 is. (b) l 1 and l 2 are orthogonal whenever a and b are orthogonal. (3) Nonparallel, nonintersecting lines are called skew lines.
28 VECTORS AND THE GEOMETRY OF SPACE Problem (Page 740 #14). Determine whether the following lines are parallel, skew, or intersect: 8 8 >< x = 1 2t >< x = 3 + 2s y = 2t y = 2 >: z = 5 t >: z = 3 + 2s We have hx 1, y, z 5i = th 2, 2, 1i and hx 3, y + 2, z 3i = sh2, 0, 2i. Since h 2, 2, 1i 6= ch2, 0, 2i, lines are not k. Do lines intersect? Equate x s: Equate y s and substitute: 1 2t = 3 + 2s =) 2t = 2s 2. 2t = 2 =) 2 = 2s 2 =) s = 0 and t = 1. Substitute into z s: = 3 + 0, so the lines do not intersect, and thus we have skew lines.
29 Planes in R 3 5. LINES AND PLANES IN SPACE 29 A plane in space is determined by a vector a = ha 1, a 2, a 3 i that is normal to the plane and a point P 1 (x 1, y 1, z 1 ) lying in the plane. A vector is normal to a plane if it is orthogonal to every vector in the plane. (1) Linear equation: a! P 1 P = ha 1, a 2, a 3 i hx x 1, y y 1, z z 1 i = Simplifying, every equation of the form a 1 (x x 1 ) + a 2 (y y 1 ) + a 3 (z z 1 ) = 0 {z } linear equation for the plane ax + by + cz + d = 0 is the equation of a plane with normal vector ha, b, ci 6= 0. (2) Vector equation: a! P 1 P = 0 Definition. Two planes are parallel when their normal vectors are parallel, and orthogonal when their normal vectors are orthogonal.
30 VECTORS AND THE GEOMETRY OF SPACE Example. Three noncollinear points determine a plane. Find the plane containing P ( 1, 3, 0), Q(3, 2, 4), and R(1, 1, 5). We first find two vectors in the plane by using the points given.!! P Q = h4, 1, 4i and QR = h 2, 3, 1i. We then find a normal vector n by taking their cross product.! P Q QR! = Therefore, the equation is or i j k = h11, 12, 14i. 11(x + 1) 12(y 3) 14(z 0) = 0 11x 12y 14z + 47 = 0. Intercepts are x = 47 11, y = 47 12, z =
31 5. LINES AND PLANES IN SPACE 31 Problem (Page 740 #24). Find the plane containing the point (3, 0, 1) and? to the planes x + 2y z = 2 and 2x z = 1. Normal vectors to the two given planes are n 1 = h1, 2, 1i and n 2 = h2, 0, 1i. Then a normal vector to the sought plane is Then the equation is or n = n 1 n 2 = i j k = h 2, 1, 4i. 2(x 3) y 4(z + 1) = 0 2x + y + 4z = 2.
32 VECTORS AND THE GEOMETRY OF SPACE Distance from a point P 0 to a plane ax + by + cz + d = 0 We measure the distance orthogonal to the plane. (1) Choose any point P 1 in the plane. (2) a = ha, b, ci is a normal vector to the plane. (3) The distance d is then 2. d = comp a! P1 P 0. Problem (Page 741 #40). Find the distance from (1, 3, 0) to 3x+y 5z = P 0 = (1, 3, 0), a normal vector is h3, 1, 5i, and we choose P 1 = (0, 2, 0) since! it satisfies the equation. Then P 1 P 0 = h1, 1, 0i, and d = comp h3,1, 5i h1, 1, 0i = h1, 1, 0i h3, 1, 5i kh3, 1, 5ik = 4 p 35 = 4 p 35 Note. You can see the derivation of the distance formula on page 739 of the text.
33 5. LINES AND PLANES IN SPACE 33 Problem (Page 740 #36 Finding the intersection of 2 planes). Find the intersection of 3x + y z = 2 and 2x 3y + z = 1. (1) Possibilities are that the intersection is a line, a plane, or does not exist (the planes are parallel. Since normal vectors to the planes, h3, 1, 1i and h2, 3, 1i, are not parallel, the intersection here is a line. (2) Solve each equation for the same variable z seems easiest here. (3) Set these equal to each other. z = 3x + y 2 and z = 2x + 3y 1 3x + y 2 = 2x + 3y 1 (4) Solve for a second variable we choose y. 2y = 5x 1 =) y = 5 2 x 1 2 (5) Substitute this into either first equation. 5 z = 3x + 2 x 1 2 =) z = x 5 2 or 5 z = 2x x 1 1 =) z = x 5 2 (6) Set the third variable equal to a parameter t. x = t (7) Then parametric equations for the line are 8 >< x = t y = 5 2 >: t 1 2 z = 11 2 t 5 2 Note. Compare this problem to Example 5.8 on page 738.
34 VECTORS AND THE GEOMETRY OF SPACE Maple. See Lines and Planes(10.5).mw or Lines and Planes(10.5).pdf Also see Matching Lines. 6. Sufaces in Space Maple. See surfaces(10.6).mw or surfaces(10.6).pdf Also see Drawing Surfaces, Drawing 3D Surfaces, and Matching Quadric Surfaces.
Chapter 13: Vectors and the Geometry of Space
 Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
Chapter 13: Vectors and the Geometry of Space
 Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
What you will learn today
 What you will learn today The Dot Product Equations of Vectors and the Geometry of Space 1/29 Direction angles and Direction cosines Projections Definitions: 1. a : a 1, a 2, a 3, b : b 1, b 2, b 3, a
What you will learn today The Dot Product Equations of Vectors and the Geometry of Space 1/29 Direction angles and Direction cosines Projections Definitions: 1. a : a 1, a 2, a 3, b : b 1, b 2, b 3, a
Math 241, Exam 1 Information.
 Math 241, Exam 1 Information. 2/13/13, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.2. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241sp13/241.html)
Math 241, Exam 1 Information. 2/13/13, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.2. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241sp13/241.html)
12.1. Cartesian Space
 12.1. Cartesian Space In most of your previous math classes, we worked with functions on the xy-plane only meaning we were working only in 2D. Now we will be working in space, or rather 3D. Now we will
12.1. Cartesian Space In most of your previous math classes, we worked with functions on the xy-plane only meaning we were working only in 2D. Now we will be working in space, or rather 3D. Now we will
Detailed objectives are given in each of the sections listed below. 1. Cartesian Space Coordinates. 2. Displacements, Forces, Velocities and Vectors
 Unit 1 Vectors In this unit, we introduce vectors, vector operations, and equations of lines and planes. Note: Unit 1 is based on Chapter 12 of the textbook, Salas and Hille s Calculus: Several Variables,
Unit 1 Vectors In this unit, we introduce vectors, vector operations, and equations of lines and planes. Note: Unit 1 is based on Chapter 12 of the textbook, Salas and Hille s Calculus: Several Variables,
Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors.
 Vectors summary Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors. AB is the position vector of B relative to A and is the vector
Vectors summary Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors. AB is the position vector of B relative to A and is the vector
Review of Coordinate Systems
 Vector in 2 R and 3 R Review of Coordinate Systems Used to describe the position of a point in space Common coordinate systems are: Cartesian Polar Cartesian Coordinate System Also called rectangular coordinate
Vector in 2 R and 3 R Review of Coordinate Systems Used to describe the position of a point in space Common coordinate systems are: Cartesian Polar Cartesian Coordinate System Also called rectangular coordinate
(arrows denote positive direction)
 12 Chapter 12 12.1 3-dimensional Coordinate System The 3-dimensional coordinate system we use are coordinates on R 3. The coordinate is presented as a triple of numbers: (a,b,c). In the Cartesian coordinate
12 Chapter 12 12.1 3-dimensional Coordinate System The 3-dimensional coordinate system we use are coordinates on R 3. The coordinate is presented as a triple of numbers: (a,b,c). In the Cartesian coordinate
VECTORS AND THE GEOMETRY OF SPACE
 VECTORS AND THE GEOMETRY OF SPACE VECTORS AND THE GEOMETRY OF SPACE A line in the xy-plane is determined when a point on the line and the direction of the line (its slope or angle of inclination) are given.
VECTORS AND THE GEOMETRY OF SPACE VECTORS AND THE GEOMETRY OF SPACE A line in the xy-plane is determined when a point on the line and the direction of the line (its slope or angle of inclination) are given.
MATH 1020 WORKSHEET 12.1 & 12.2 Vectors in the Plane
 MATH 100 WORKSHEET 1.1 & 1. Vectors in the Plane Find the vector v where u =, 1 and w = 1, given the equation v = u w. Solution. v = u w =, 1 1, =, 1 +, 4 =, 1 4 = 0, 5 Find the magnitude of v = 4, 3 Solution.
MATH 100 WORKSHEET 1.1 & 1. Vectors in the Plane Find the vector v where u =, 1 and w = 1, given the equation v = u w. Solution. v = u w =, 1 1, =, 1 +, 4 =, 1 4 = 0, 5 Find the magnitude of v = 4, 3 Solution.
Vectors and the Geometry of Space
 Vectors and the Geometry of Space Many quantities in geometry and physics, such as area, volume, temperature, mass, and time, can be characterized by a single real number scaled to appropriate units of
Vectors and the Geometry of Space Many quantities in geometry and physics, such as area, volume, temperature, mass, and time, can be characterized by a single real number scaled to appropriate units of
The Cross Product. In this section, we will learn about: Cross products of vectors and their applications.
 The Cross Product In this section, we will learn about: Cross products of vectors and their applications. THE CROSS PRODUCT The cross product a x b of two vectors a and b, unlike the dot product, is a
The Cross Product In this section, we will learn about: Cross products of vectors and their applications. THE CROSS PRODUCT The cross product a x b of two vectors a and b, unlike the dot product, is a
DATE: MATH ANALYSIS 2 CHAPTER 12: VECTORS & DETERMINANTS
 NAME: PERIOD: DATE: MATH ANALYSIS 2 MR. MELLINA CHAPTER 12: VECTORS & DETERMINANTS Sections: v 12.1 Geometric Representation of Vectors v 12.2 Algebraic Representation of Vectors v 12.3 Vector and Parametric
NAME: PERIOD: DATE: MATH ANALYSIS 2 MR. MELLINA CHAPTER 12: VECTORS & DETERMINANTS Sections: v 12.1 Geometric Representation of Vectors v 12.2 Algebraic Representation of Vectors v 12.3 Vector and Parametric
Midterm 1 Review. Distance = (x 1 x 0 ) 2 + (y 1 y 0 ) 2.
 Midterm 1 Review Comments about the midterm The midterm will consist of five questions and will test on material from the first seven lectures the material given below. No calculus either single variable
Midterm 1 Review Comments about the midterm The midterm will consist of five questions and will test on material from the first seven lectures the material given below. No calculus either single variable
1.1 Single Variable Calculus versus Multivariable Calculus Rectangular Coordinate Systems... 4
 MATH2202 Notebook 1 Fall 2015/2016 prepared by Professor Jenny Baglivo Contents 1 MATH2202 Notebook 1 3 1.1 Single Variable Calculus versus Multivariable Calculus................... 3 1.2 Rectangular Coordinate
MATH2202 Notebook 1 Fall 2015/2016 prepared by Professor Jenny Baglivo Contents 1 MATH2202 Notebook 1 3 1.1 Single Variable Calculus versus Multivariable Calculus................... 3 1.2 Rectangular Coordinate
12.5 Equations of Lines and Planes
 12.5 Equations of Lines and Planes Equation of Lines Vector Equation of Lines Parametric Equation of Lines Symmetric Equation of Lines Relation Between Two Lines Equations of Planes Vector Equation of
12.5 Equations of Lines and Planes Equation of Lines Vector Equation of Lines Parametric Equation of Lines Symmetric Equation of Lines Relation Between Two Lines Equations of Planes Vector Equation of
Chapter 8: Polar Coordinates and Vectors
 Chapter 8: Polar Coordinates and Vectors 8.1 Polar Coordinates This is another way (in addition to the x-y system) of specifying the position of a point in the plane. We give the distance r of the point
Chapter 8: Polar Coordinates and Vectors 8.1 Polar Coordinates This is another way (in addition to the x-y system) of specifying the position of a point in the plane. We give the distance r of the point
CHAPTER 3 : VECTORS. Definition 3.1 A vector is a quantity that has both magnitude and direction.
 EQT 101-Engineering Mathematics I Teaching Module CHAPTER 3 : VECTORS 3.1 Introduction Definition 3.1 A ector is a quantity that has both magnitude and direction. A ector is often represented by an arrow
EQT 101-Engineering Mathematics I Teaching Module CHAPTER 3 : VECTORS 3.1 Introduction Definition 3.1 A ector is a quantity that has both magnitude and direction. A ector is often represented by an arrow
10.2,3,4. Vectors in 3D, Dot products and Cross Products
 Name: Section: 10.2,3,4. Vectors in 3D, Dot products and Cross Products 1. Sketch the plane parallel to the xy-plane through (2, 4, 2) 2. For the given vectors u and v, evaluate the following expressions.
Name: Section: 10.2,3,4. Vectors in 3D, Dot products and Cross Products 1. Sketch the plane parallel to the xy-plane through (2, 4, 2) 2. For the given vectors u and v, evaluate the following expressions.
The Cross Product. MATH 311, Calculus III. J. Robert Buchanan. Fall Department of Mathematics. J. Robert Buchanan The Cross Product
 The Cross Product MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Introduction Recall: the dot product of two vectors is a scalar. There is another binary operation on vectors
The Cross Product MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Introduction Recall: the dot product of two vectors is a scalar. There is another binary operation on vectors
Study guide for Exam 1. by William H. Meeks III October 26, 2012
 Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
45. The Parallelogram Law states that. product of a and b is the vector a b a 2 b 3 a 3 b 2, a 3 b 1 a 1 b 3, a 1 b 2 a 2 b 1. a c. a 1. b 1.
 SECTION 10.4 THE CROSS PRODUCT 537 42. Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular. 43.
SECTION 10.4 THE CROSS PRODUCT 537 42. Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular. 43.
CHAPTER 10 VECTORS POINTS TO REMEMBER
 For more important questions visit : www4onocom CHAPTER 10 VECTORS POINTS TO REMEMBER A quantity that has magnitude as well as direction is called a vector It is denoted by a directed line segment Two
For more important questions visit : www4onocom CHAPTER 10 VECTORS POINTS TO REMEMBER A quantity that has magnitude as well as direction is called a vector It is denoted by a directed line segment Two
Course Notes Math 275 Boise State University. Shari Ultman
 Course Notes Math 275 Boise State University Shari Ultman Fall 2017 Contents 1 Vectors 1 1.1 Introduction to 3-Space & Vectors.............. 3 1.2 Working With Vectors.................... 7 1.3 Introduction
Course Notes Math 275 Boise State University Shari Ultman Fall 2017 Contents 1 Vectors 1 1.1 Introduction to 3-Space & Vectors.............. 3 1.2 Working With Vectors.................... 7 1.3 Introduction
Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems
 To locate a point in a plane, two numbers are necessary. We know that any point in the plane can be represented as an ordered pair (a, b) of real numbers, where a is the x-coordinate and b is the y-coordinate.
To locate a point in a plane, two numbers are necessary. We know that any point in the plane can be represented as an ordered pair (a, b) of real numbers, where a is the x-coordinate and b is the y-coordinate.
Geometric Interpretation of Vectors
 Math 36 "Fall 08" 7.4 "Vectors" Skills Objectives: * Represent vectors geometrically and algebraically * Find the magnitude and direction of a vector * Add and subtract vectors * Perform scalar multiplication
Math 36 "Fall 08" 7.4 "Vectors" Skills Objectives: * Represent vectors geometrically and algebraically * Find the magnitude and direction of a vector * Add and subtract vectors * Perform scalar multiplication
CALCULUS III. prepared by
 EXAMINATION 1 CALCULUS III REVIEW PROBLEMS prepared by Antony Foster Department of Mathematics (office: NAC 6-73) The City College of The City University of New York Convent Avenue At 138th Street New
EXAMINATION 1 CALCULUS III REVIEW PROBLEMS prepared by Antony Foster Department of Mathematics (office: NAC 6-73) The City College of The City University of New York Convent Avenue At 138th Street New
MAT1035 Analytic Geometry
 MAT1035 Analytic Geometry Lecture Notes R.A. Sabri Kaan Gürbüzer Dokuz Eylül University 2016 2 Contents 1 Review of Trigonometry 5 2 Polar Coordinates 7 3 Vectors in R n 9 3.1 Located Vectors..............................................
MAT1035 Analytic Geometry Lecture Notes R.A. Sabri Kaan Gürbüzer Dokuz Eylül University 2016 2 Contents 1 Review of Trigonometry 5 2 Polar Coordinates 7 3 Vectors in R n 9 3.1 Located Vectors..............................................
Brief Review of Exam Topics
 Math 32A Discussion Session Week 3 Notes October 17 and 19, 2017 We ll use this week s discussion session to prepare for the first midterm. We ll start with a quick rundown of the relevant topics, and
Math 32A Discussion Session Week 3 Notes October 17 and 19, 2017 We ll use this week s discussion session to prepare for the first midterm. We ll start with a quick rundown of the relevant topics, and
Chapter 2: Vector Geometry
 Chapter 2: Vector Geometry Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 2: Vector Geometry Semester 1 2018 1 / 32 Goals of this chapter In this chapter, we will answer the following geometric
Chapter 2: Vector Geometry Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 2: Vector Geometry Semester 1 2018 1 / 32 Goals of this chapter In this chapter, we will answer the following geometric
Quiz 2 Practice Problems
 Quiz Practice Problems Practice problems are similar, both in difficulty and in scope, to the type of problems you will see on the quiz. Problems marked with a are for your entertainment and are not essential.
Quiz Practice Problems Practice problems are similar, both in difficulty and in scope, to the type of problems you will see on the quiz. Problems marked with a are for your entertainment and are not essential.
5. A triangle has sides represented by the vectors (1, 2) and (5, 6). Determine the vector representing the third side.
 Vectors EXAM review Problem 1 = 8 and = 1 a) Find the net force, assume that points North, and points East b) Find the equilibrant force 2 = 15, = 7, and the angle between and is 60 What is the magnitude
Vectors EXAM review Problem 1 = 8 and = 1 a) Find the net force, assume that points North, and points East b) Find the equilibrant force 2 = 15, = 7, and the angle between and is 60 What is the magnitude
MATH 255 Applied Honors Calculus III Winter Midterm 1 Review Solutions
 MATH 55 Applied Honors Calculus III Winter 11 Midterm 1 Review Solutions 11.1: #19 Particle starts at point ( 1,, traces out a semicircle in the counterclockwise direction, ending at the point (1,. 11.1:
MATH 55 Applied Honors Calculus III Winter 11 Midterm 1 Review Solutions 11.1: #19 Particle starts at point ( 1,, traces out a semicircle in the counterclockwise direction, ending at the point (1,. 11.1:
Department of Mathematical and Statistical Sciences University of Alberta
 MATH 214 (R1) Winter 2008 Intermediate Calculus I Solutions to Problem Set #8 Completion Date: Friday March 14, 2008 Department of Mathematical and Statistical Sciences University of Alberta Question 1.
MATH 214 (R1) Winter 2008 Intermediate Calculus I Solutions to Problem Set #8 Completion Date: Friday March 14, 2008 Department of Mathematical and Statistical Sciences University of Alberta Question 1.
11.4 Dot Product Contemporary Calculus 1
 11.4 Dot Product Contemporary Calculus 1 11.4 DOT PRODUCT In the previous sections we looked at the meaning of vectors in two and three dimensions, but the only operations we used were addition and subtraction
11.4 Dot Product Contemporary Calculus 1 11.4 DOT PRODUCT In the previous sections we looked at the meaning of vectors in two and three dimensions, but the only operations we used were addition and subtraction
Solutions to Assignment #01. (a) Use tail-to-head addition and the Parallelogram Law to nd the resultant, (a + b) = (b + a) :
 Solutions to Assignment # Puhalskii/Kawai Section 8. (I) Demonstrate the vector sums/di erences on separate aes on the graph paper side of our engineering pad. Let a = h; i = i j and b = h; i = i + j:
Solutions to Assignment # Puhalskii/Kawai Section 8. (I) Demonstrate the vector sums/di erences on separate aes on the graph paper side of our engineering pad. Let a = h; i = i j and b = h; i = i + j:
Vector Geometry. Chapter 5
 Chapter 5 Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at
Chapter 5 Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at
DEPARTMENT OF MATHEMATICS AND STATISTICS UNIVERSITY OF MASSACHUSETTS. MATH 233 SOME SOLUTIONS TO EXAM 1 Fall 2018
 DEPARTMENT OF MATHEMATICS AND STATISTICS UNIVERSITY OF MASSACHUSETTS MATH SOME SOLUTIONS TO EXAM 1 Fall 018 Version A refers to the regular exam and Version B to the make-up 1. Version A. Find the center
DEPARTMENT OF MATHEMATICS AND STATISTICS UNIVERSITY OF MASSACHUSETTS MATH SOME SOLUTIONS TO EXAM 1 Fall 018 Version A refers to the regular exam and Version B to the make-up 1. Version A. Find the center
4.1 Distance and Length
 Chapter Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at vectors
Chapter Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at vectors
MAT 1339-S14 Class 8
 MAT 1339-S14 Class 8 July 28, 2014 Contents 7.2 Review Dot Product........................... 2 7.3 Applications of the Dot Product..................... 4 7.4 Vectors in Three-Space.........................
MAT 1339-S14 Class 8 July 28, 2014 Contents 7.2 Review Dot Product........................... 2 7.3 Applications of the Dot Product..................... 4 7.4 Vectors in Three-Space.........................
12.1 Three Dimensional Coordinate Systems (Review) Equation of a sphere
 12.2 Vectors 12.1 Three Dimensional Coordinate Systems (Reiew) Equation of a sphere x a 2 + y b 2 + (z c) 2 = r 2 Center (a,b,c) radius r 12.2 Vectors Quantities like displacement, elocity, and force inole
12.2 Vectors 12.1 Three Dimensional Coordinate Systems (Reiew) Equation of a sphere x a 2 + y b 2 + (z c) 2 = r 2 Center (a,b,c) radius r 12.2 Vectors Quantities like displacement, elocity, and force inole
Introduction to Vectors Pg. 279 # 1 6, 8, 9, 10 OR WS 1.1 Sept. 7. Vector Addition Pg. 290 # 3, 4, 6, 7, OR WS 1.2 Sept. 8
 UNIT 1 INTRODUCTION TO VECTORS Lesson TOPIC Suggested Work Sept. 5 1.0 Review of Pre-requisite Skills Pg. 273 # 1 9 OR WS 1.0 Fill in Info sheet and get permission sheet signed. Bring in $3 for lesson
UNIT 1 INTRODUCTION TO VECTORS Lesson TOPIC Suggested Work Sept. 5 1.0 Review of Pre-requisite Skills Pg. 273 # 1 9 OR WS 1.0 Fill in Info sheet and get permission sheet signed. Bring in $3 for lesson
Unit #17: Spring Trig Unit. A. First Quadrant Notice how the x-values decrease by while the y-values increase by that same amount.
 Name Unit #17: Spring Trig Unit Notes #1: Basic Trig Review I. Unit Circle A circle with center point and radius. A. First Quadrant Notice how the x-values decrease by while the y-values increase by that
Name Unit #17: Spring Trig Unit Notes #1: Basic Trig Review I. Unit Circle A circle with center point and radius. A. First Quadrant Notice how the x-values decrease by while the y-values increase by that
LINEAR ALGEBRA - CHAPTER 1: VECTORS
 LINEAR ALGEBRA - CHAPTER 1: VECTORS A game to introduce Linear Algebra In measurement, there are many quantities whose description entirely rely on magnitude, i.e., length, area, volume, mass and temperature.
LINEAR ALGEBRA - CHAPTER 1: VECTORS A game to introduce Linear Algebra In measurement, there are many quantities whose description entirely rely on magnitude, i.e., length, area, volume, mass and temperature.
10.1 Three Dimensional Space
 Math 172 Chapter 10A notes Page 1 of 12 10.1 Three Dimensional Space 2D space 0 xx.. xx-, 0 yy yy-, PP(xx, yy) [Fig. 1] Point PP represented by (xx, yy), an ordered pair of real nos. Set of all ordered
Math 172 Chapter 10A notes Page 1 of 12 10.1 Three Dimensional Space 2D space 0 xx.. xx-, 0 yy yy-, PP(xx, yy) [Fig. 1] Point PP represented by (xx, yy), an ordered pair of real nos. Set of all ordered
58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that
![58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that 58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that](/thumbs/86/94310732.jpg) 786 CAPTER 12 VECTORS AND TE GEOETRY OF SPACE 0, 0, 1, and 1, 1, 1 as shown in the figure. Then the centroid is. ( 1 2, 1 2, 1 2 ) ] x z C 54. If c a a, where a,, and c are all nonzero vectors, show that
786 CAPTER 12 VECTORS AND TE GEOETRY OF SPACE 0, 0, 1, and 1, 1, 1 as shown in the figure. Then the centroid is. ( 1 2, 1 2, 1 2 ) ] x z C 54. If c a a, where a,, and c are all nonzero vectors, show that
Main Ideas in Class Today
 Main Ideas in Class Today After today, you should be able to: Understand vector notation Use basic trigonometry in order to find the x and y components of a vector (only right triangles) Add and subtract
Main Ideas in Class Today After today, you should be able to: Understand vector notation Use basic trigonometry in order to find the x and y components of a vector (only right triangles) Add and subtract
If the pull is downward (Fig. 1), we want C to point into the page. If the pull is upward (Fig. 2), we want C to point out of the page.
 11.5 Cross Product Contemporary Calculus 1 11.5 CROSS PRODUCT This section is the final one about the arithmetic of vectors, and it introduces a second type of vector vector multiplication called the cross
11.5 Cross Product Contemporary Calculus 1 11.5 CROSS PRODUCT This section is the final one about the arithmetic of vectors, and it introduces a second type of vector vector multiplication called the cross
Prepared by: M. S. KumarSwamy, TGT(Maths) Page
 Prepared by: M S KumarSwamy, TGT(Maths) Page - 119 - CHAPTER 10: VECTOR ALGEBRA QUICK REVISION (Important Concepts & Formulae) MARKS WEIGHTAGE 06 marks Vector The line l to the line segment AB, then a
Prepared by: M S KumarSwamy, TGT(Maths) Page - 119 - CHAPTER 10: VECTOR ALGEBRA QUICK REVISION (Important Concepts & Formulae) MARKS WEIGHTAGE 06 marks Vector The line l to the line segment AB, then a
Distance Formula in 3-D Given any two points P 1 (x 1, y 1, z 1 ) and P 2 (x 2, y 2, z 2 ) the distance between them is ( ) ( ) ( )
 Vectors and the Geometry of Space Vector Space The 3-D coordinate system (rectangular coordinates ) is the intersection of three perpendicular (orthogonal) lines called coordinate axis: x, y, and z. Their
Vectors and the Geometry of Space Vector Space The 3-D coordinate system (rectangular coordinates ) is the intersection of three perpendicular (orthogonal) lines called coordinate axis: x, y, and z. Their
Give a geometric description of the set of points in space whose coordinates satisfy the given pair of equations.
 1. Give a geometric description of the set of points in space whose coordinates satisfy the given pair of equations. x + y = 5, z = 4 Choose the correct description. A. The circle with center (0,0, 4)
1. Give a geometric description of the set of points in space whose coordinates satisfy the given pair of equations. x + y = 5, z = 4 Choose the correct description. A. The circle with center (0,0, 4)
Congruence Axioms. Data Required for Solving Oblique Triangles
 Math 335 Trigonometry Sec 7.1: Oblique Triangles and the Law of Sines In section 2.4, we solved right triangles. We now extend the concept to all triangles. Congruence Axioms Side-Angle-Side SAS Angle-Side-Angle
Math 335 Trigonometry Sec 7.1: Oblique Triangles and the Law of Sines In section 2.4, we solved right triangles. We now extend the concept to all triangles. Congruence Axioms Side-Angle-Side SAS Angle-Side-Angle
Calculus Vector Principia Mathematica. Lynne Ryan Associate Professor Mathematics Blue Ridge Community College
 Calculus Vector Principia Mathematica Lynne Ryan Associate Professor Mathematics Blue Ridge Community College Defining a vector Vectors in the plane A scalar is a quantity that can be represented by a
Calculus Vector Principia Mathematica Lynne Ryan Associate Professor Mathematics Blue Ridge Community College Defining a vector Vectors in the plane A scalar is a quantity that can be represented by a
CHAPTER 4 VECTORS. Before we go any further, we must talk about vectors. They are such a useful tool for
 CHAPTER 4 VECTORS Before we go any further, we must talk about vectors. They are such a useful tool for the things to come. The concept of a vector is deeply rooted in the understanding of physical mechanics
CHAPTER 4 VECTORS Before we go any further, we must talk about vectors. They are such a useful tool for the things to come. The concept of a vector is deeply rooted in the understanding of physical mechanics
Culminating Review for Vectors
 Culminating Review for Vectors 0011 0010 1010 1101 0001 0100 1011 An Introduction to Vectors Applications of Vectors Equations of Lines and Planes 4 12 Relationships between Points, Lines and Planes An
Culminating Review for Vectors 0011 0010 1010 1101 0001 0100 1011 An Introduction to Vectors Applications of Vectors Equations of Lines and Planes 4 12 Relationships between Points, Lines and Planes An
Workbook. MAT 397: Calculus III
 Workbook MAT 397: Calculus III Instructor: Caleb McWhorter Name: Summer 217 Contents Preface..................................................... 2 1 Spatial Geometry & Vectors 3 1.1 Basic n Euclidean
Workbook MAT 397: Calculus III Instructor: Caleb McWhorter Name: Summer 217 Contents Preface..................................................... 2 1 Spatial Geometry & Vectors 3 1.1 Basic n Euclidean
The geometry of least squares
 The geometry of least squares We can think of a vector as a point in space, where the elements of the vector are the coordinates of the point. Consider for example, the following vector s: t = ( 4, 0),
The geometry of least squares We can think of a vector as a point in space, where the elements of the vector are the coordinates of the point. Consider for example, the following vector s: t = ( 4, 0),
Lecture 2: Vector-Vector Operations
 Lecture 2: Vector-Vector Operations Vector-Vector Operations Addition of two vectors Geometric representation of addition and subtraction of vectors Vectors and points Dot product of two vectors Geometric
Lecture 2: Vector-Vector Operations Vector-Vector Operations Addition of two vectors Geometric representation of addition and subtraction of vectors Vectors and points Dot product of two vectors Geometric
6. Vectors. Given two points, P 0 = (x 0, y 0 ) and P 1 = (x 1, y 1 ), a vector can be drawn with its foot at P 0 and
 6. Vectors For purposes of applications in calculus and physics, a vector has both a direction and a magnitude (length), and is usually represented as an arrow. The start of the arrow is the vector s foot,
6. Vectors For purposes of applications in calculus and physics, a vector has both a direction and a magnitude (length), and is usually represented as an arrow. The start of the arrow is the vector s foot,
The Cross Product -(10.4)
 The Cross Product -(10.4) Questions: What is the definition of the cross product of two vectors? Is it a scalar or vector? What can you say about vectors u and v (all possibilities) if the cross product
The Cross Product -(10.4) Questions: What is the definition of the cross product of two vectors? Is it a scalar or vector? What can you say about vectors u and v (all possibilities) if the cross product
10.1 Vectors. c Kun Wang. Math 150, Fall 2017
 10.1 Vectors Definition. A vector is a quantity that has both magnitude and direction. A vector is often represented graphically as an arrow where the direction is the direction of the arrow, and the magnitude
10.1 Vectors Definition. A vector is a quantity that has both magnitude and direction. A vector is often represented graphically as an arrow where the direction is the direction of the arrow, and the magnitude
Linear Algebra. 1.1 Introduction to vectors 1.2 Lengths and dot products. January 28th, 2013 Math 301. Monday, January 28, 13
 Linear Algebra 1.1 Introduction to vectors 1.2 Lengths and dot products January 28th, 2013 Math 301 Notation for linear systems 12w +4x + 23y +9z =0 2u + v +5w 2x +2y +8z =1 5u + v 6w +2x +4y z =6 8u 4v
Linear Algebra 1.1 Introduction to vectors 1.2 Lengths and dot products January 28th, 2013 Math 301 Notation for linear systems 12w +4x + 23y +9z =0 2u + v +5w 2x +2y +8z =1 5u + v 6w +2x +4y z =6 8u 4v
11.1 Three-Dimensional Coordinate System
 11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
Vectors and Plane Geometry
 Vectors and Plane Geometry Karl Heinz Dovermann Professor of Mathematics University of Hawaii January 7, 0 Preface During the first week of the semester it is difficult to get started with the course
Vectors and Plane Geometry Karl Heinz Dovermann Professor of Mathematics University of Hawaii January 7, 0 Preface During the first week of the semester it is difficult to get started with the course
Chapter 8 Vectors and Scalars
 Chapter 8 193 Vectors and Scalars Chapter 8 Vectors and Scalars 8.1 Introduction: In this chapter we shall use the ideas of the plane to develop a new mathematical concept, vector. If you have studied
Chapter 8 193 Vectors and Scalars Chapter 8 Vectors and Scalars 8.1 Introduction: In this chapter we shall use the ideas of the plane to develop a new mathematical concept, vector. If you have studied
Calculus 1 for AE (WI1421LR) Lecture 1: 12.3 The dot product 12.4 The cross product
 Calculus 1 for AE (WI1421LR) : 12.3 The dot product 12.4 The cross product About this course Textbook James Stewart, Calculus, Early Transcendentals, 7th edition Course Coordinator Dr. Roelof Koekoek,
Calculus 1 for AE (WI1421LR) : 12.3 The dot product 12.4 The cross product About this course Textbook James Stewart, Calculus, Early Transcendentals, 7th edition Course Coordinator Dr. Roelof Koekoek,
Vectors in the Plane
 Vectors in the Plane MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Vectors vs. Scalars scalar quantity having only a magnitude (e.g. temperature, volume, length, area) and
Vectors in the Plane MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Vectors vs. Scalars scalar quantity having only a magnitude (e.g. temperature, volume, length, area) and
Extra Problems for Math 2050 Linear Algebra I
 Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
1 Vectors. c Kun Wang. Math 151, Fall Vector Supplement
 Vector Supplement 1 Vectors A vector is a quantity that has both magnitude and direction. Vectors are drawn as directed line segments and are denoted by boldface letters a or by a. The magnitude of a vector
Vector Supplement 1 Vectors A vector is a quantity that has both magnitude and direction. Vectors are drawn as directed line segments and are denoted by boldface letters a or by a. The magnitude of a vector
3. Interpret the graph of x = 1 in the contexts of (a) a number line (b) 2-space (c) 3-space
 MA2: Prepared by Dr. Archara Pacheenburawana Exercise Chapter 3 Exercise 3.. A cube of side 4 has its geometric center at the origin and its faces parallel to the coordinate planes. Sketch the cube and
MA2: Prepared by Dr. Archara Pacheenburawana Exercise Chapter 3 Exercise 3.. A cube of side 4 has its geometric center at the origin and its faces parallel to the coordinate planes. Sketch the cube and
LB 220 Homework 1 (due Monday, 01/14/13)
 LB 220 Homework 1 (due Monday, 01/14/13) Directions. Please solve the problems below. Your solutions must begin with a clear statement (or re-statement in your own words) of the problem. You solutions
LB 220 Homework 1 (due Monday, 01/14/13) Directions. Please solve the problems below. Your solutions must begin with a clear statement (or re-statement in your own words) of the problem. You solutions
Objective 1. Lesson 87: The Cross Product of Vectors IBHL - SANTOWSKI FINDING THE CROSS PRODUCT OF TWO VECTORS
 Lesson 87: The Cross Product of Vectors IBHL - SANTOWSKI In this lesson you will learn how to find the cross product of two vectors how to find an orthogonal vector to a plane defined by two vectors how
Lesson 87: The Cross Product of Vectors IBHL - SANTOWSKI In this lesson you will learn how to find the cross product of two vectors how to find an orthogonal vector to a plane defined by two vectors how
VECTORS vectors & scalars vector direction magnitude scalar only magnitude
 VECTORS Physical quantities are classified in two big classes: vectors & scalars. A vector is a physical quantity which is completely defined once we know precisely its direction and magnitude (for example:
VECTORS Physical quantities are classified in two big classes: vectors & scalars. A vector is a physical quantity which is completely defined once we know precisely its direction and magnitude (for example:
6.1.1 Angle between Two Lines Intersection of Two lines Shortest Distance from a Point to a Line
 CHAPTER 6 : VECTORS 6. Lines in Space 6.. Angle between Two Lines 6.. Intersection of Two lines 6..3 Shortest Distance from a Point to a Line 6. Planes in Space 6.. Intersection of Two Planes 6.. Angle
CHAPTER 6 : VECTORS 6. Lines in Space 6.. Angle between Two Lines 6.. Intersection of Two lines 6..3 Shortest Distance from a Point to a Line 6. Planes in Space 6.. Intersection of Two Planes 6.. Angle
1.2 LECTURE 2. Scalar Product
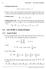 6 CHAPTER 1. VECTOR ALGEBRA Pythagean theem. cos 2 α 1 + cos 2 α 2 + cos 2 α 3 = 1 There is a one-to-one crespondence between the components of the vect on the one side and its magnitude and the direction
6 CHAPTER 1. VECTOR ALGEBRA Pythagean theem. cos 2 α 1 + cos 2 α 2 + cos 2 α 3 = 1 There is a one-to-one crespondence between the components of the vect on the one side and its magnitude and the direction
EUCLIDEAN SPACES AND VECTORS
 EUCLIDEAN SPACES AND VECTORS PAUL L. BAILEY 1. Introduction Our ultimate goal is to apply the techniques of calculus to higher dimensions. We begin by discussing what mathematical concepts describe these
EUCLIDEAN SPACES AND VECTORS PAUL L. BAILEY 1. Introduction Our ultimate goal is to apply the techniques of calculus to higher dimensions. We begin by discussing what mathematical concepts describe these
SUPPLEMENT I. Example. Graph the vector 4, 3. Definition. Given two points A(x 1, y 1 ) and B(x 2, y 2 ), the vector represented by # AB is # AB =,
 SUPPLEMENT I 1. Vectors Definition. A vector is a quantity that has both a magnitude and a direction. A twodimensional vector is an ordered pair a = a 1, a 2 of real numbers. The numbers a 1 and a 2 are
SUPPLEMENT I 1. Vectors Definition. A vector is a quantity that has both a magnitude and a direction. A twodimensional vector is an ordered pair a = a 1, a 2 of real numbers. The numbers a 1 and a 2 are
Ch. 7.3, 7.4: Vectors and Complex Numbers
 Ch. 7.3, 7.4: Vectors and Complex Numbers Johns Hopkins University Fall 2014 (Johns Hopkins University) Ch. 7.3, 7.4: Vectors and Complex Numbers Fall 2014 1 / 38 Vectors(1) Definition (Vector) A vector
Ch. 7.3, 7.4: Vectors and Complex Numbers Johns Hopkins University Fall 2014 (Johns Hopkins University) Ch. 7.3, 7.4: Vectors and Complex Numbers Fall 2014 1 / 38 Vectors(1) Definition (Vector) A vector
1. Vectors and Matrices
 E. 8.02 Exercises. Vectors and Matrices A. Vectors Definition. A direction is just a unit vector. The direction of A is defined by dir A = A, (A 0); A it is the unit vector lying along A and pointed like
E. 8.02 Exercises. Vectors and Matrices A. Vectors Definition. A direction is just a unit vector. The direction of A is defined by dir A = A, (A 0); A it is the unit vector lying along A and pointed like
OpenStax-CNX module: m Vectors. OpenStax College. Abstract
 OpenStax-CNX module: m49412 1 Vectors OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 4.0 In this section you will: Abstract View vectors
OpenStax-CNX module: m49412 1 Vectors OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 4.0 In this section you will: Abstract View vectors
Exam 1 Review SOLUTIONS
 1. True or False (and give a short reason): Exam 1 Review SOLUTIONS (a) If the parametric curve x = f(t), y = g(t) satisfies g (1) = 0, then it has a horizontal tangent line when t = 1. FALSE: To make
1. True or False (and give a short reason): Exam 1 Review SOLUTIONS (a) If the parametric curve x = f(t), y = g(t) satisfies g (1) = 0, then it has a horizontal tangent line when t = 1. FALSE: To make
(1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3
 Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
Linear Algebra. Alvin Lin. August December 2017
 Linear Algebra Alvin Lin August 207 - December 207 Linear Algebra The study of linear algebra is about two basic things. We study vector spaces and structure preserving maps between vector spaces. A vector
Linear Algebra Alvin Lin August 207 - December 207 Linear Algebra The study of linear algebra is about two basic things. We study vector spaces and structure preserving maps between vector spaces. A vector
Math 3c Solutions: Exam 1 Fall Graph by eliiminating the parameter; be sure to write the equation you get when you eliminate the parameter.
 Math c Solutions: Exam 1 Fall 16 1. Graph by eliiminating the parameter; be sure to write the equation you get when you eliminate the parameter. x tan t x tan t y sec t y sec t t π 4 To eliminate the parameter,
Math c Solutions: Exam 1 Fall 16 1. Graph by eliiminating the parameter; be sure to write the equation you get when you eliminate the parameter. x tan t x tan t y sec t y sec t t π 4 To eliminate the parameter,
Department of Physics, Korea University
 Name: Department: Notice +2 ( 1) points per correct (incorrect) answer. No penalty for an unanswered question. Fill the blank ( ) with (8) if the statement is correct (incorrect).!!!: corrections to an
Name: Department: Notice +2 ( 1) points per correct (incorrect) answer. No penalty for an unanswered question. Fill the blank ( ) with (8) if the statement is correct (incorrect).!!!: corrections to an
1 Geometry of R Conic Sections Parametric Equations More Parametric Equations Polar Coordinates...
 Contents 1 Geometry of R 1.1 Conic Sections............................................ 1. Parametric Equations........................................ 3 1.3 More Parametric Equations.....................................
Contents 1 Geometry of R 1.1 Conic Sections............................................ 1. Parametric Equations........................................ 3 1.3 More Parametric Equations.....................................
BELLWORK feet
 BELLWORK 1 A hot air balloon is being held in place by two people holding ropes and standing 35 feet apart. The angle formed between the ground and the rope held by each person is 40. Determine the length
BELLWORK 1 A hot air balloon is being held in place by two people holding ropes and standing 35 feet apart. The angle formed between the ground and the rope held by each person is 40. Determine the length
REVIEW - Vectors. Vectors. Vector Algebra. Multiplication by a scalar
 J. Peraire Dynamics 16.07 Fall 2004 Version 1.1 REVIEW - Vectors By using vectors and defining appropriate operations between them, physical laws can often be written in a simple form. Since we will making
J. Peraire Dynamics 16.07 Fall 2004 Version 1.1 REVIEW - Vectors By using vectors and defining appropriate operations between them, physical laws can often be written in a simple form. Since we will making
3 Scalar Product. 3.0 The Dot Product. ~v ~w := v 1 w 1 + v 2 w v n w n.
 3 Scalar Product Copyright 2017, Gregory G. Smith 28 September 2017 Although vector products on R n are rare, every coordinate space R n is equipped with a binary operation that sends two vectors to a
3 Scalar Product Copyright 2017, Gregory G. Smith 28 September 2017 Although vector products on R n are rare, every coordinate space R n is equipped with a binary operation that sends two vectors to a
This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication.
 This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication. Copyright Pearson Canada Inc. All rights reserved. Copyright Pearson
This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication. Copyright Pearson Canada Inc. All rights reserved. Copyright Pearson
CALC 3 CONCEPT PACKET Complete
 CALC 3 CONCEPT PACKET Complete Written by Jeremy Robinson, Head Instructor Find Out More +Private Instruction +Review Sessions WWW.GRADEPEAK.COM Need Help? Online Private Instruction Anytime, Anywhere
CALC 3 CONCEPT PACKET Complete Written by Jeremy Robinson, Head Instructor Find Out More +Private Instruction +Review Sessions WWW.GRADEPEAK.COM Need Help? Online Private Instruction Anytime, Anywhere
BC VECTOR PROBLEMS. 13. Find the area of the parallelogram having AB and AC as adjacent sides: A(2,1,3), B(1,4,2), C( 3,2,7) 14.
 For problems 9 use: u (,3) v (3, 4) s (, 7). w =. 3u v = 3. t = 4. 7u = u w (,3,5) 5. wt = t (,, 4) 6. Find the measure of the angle between w and t to the nearest degree. 7. Find the unit vector having
For problems 9 use: u (,3) v (3, 4) s (, 7). w =. 3u v = 3. t = 4. 7u = u w (,3,5) 5. wt = t (,, 4) 6. Find the measure of the angle between w and t to the nearest degree. 7. Find the unit vector having
Math 153 Calculus III Notes
 Math 153 Calculus III Notes 10.1 Parametric Functions A parametric function is a where x and y are described by a function in terms of the parameter t: Example 1 (x, y) = {x(t), y(t)}, or x = f(t); y =
Math 153 Calculus III Notes 10.1 Parametric Functions A parametric function is a where x and y are described by a function in terms of the parameter t: Example 1 (x, y) = {x(t), y(t)}, or x = f(t); y =
Introduction. Law of Sines. Introduction. Introduction. Example 2. Example 1 11/18/2014. Precalculus 6.1
 Introduction Law of Sines Precalculus 6.1 In this section, we will solve oblique triangles triangles that have no right angles. As standard notation, the angles of a triangle are labeled A, B, and C, and
Introduction Law of Sines Precalculus 6.1 In this section, we will solve oblique triangles triangles that have no right angles. As standard notation, the angles of a triangle are labeled A, B, and C, and
Linear Algebra Homework and Study Guide
 Linear Algebra Homework and Study Guide Phil R. Smith, Ph.D. February 28, 20 Homework Problem Sets Organized by Learning Outcomes Test I: Systems of Linear Equations; Matrices Lesson. Give examples of
Linear Algebra Homework and Study Guide Phil R. Smith, Ph.D. February 28, 20 Homework Problem Sets Organized by Learning Outcomes Test I: Systems of Linear Equations; Matrices Lesson. Give examples of
b) The trend is for the average slope at x = 1 to decrease. The slope at x = 1 is 1.
 Chapters 1 to 8 Course Review Chapters 1 to 8 Course Review Question 1 Page 509 a) i) ii) [2(16) 12 + 4][2 3+ 4] 4 1 [2(2.25) 4.5+ 4][2 3+ 4] 1.51 = 21 3 = 7 = 1 0.5 = 2 [2(1.21) 3.3+ 4][2 3+ 4] iii) =
Chapters 1 to 8 Course Review Chapters 1 to 8 Course Review Question 1 Page 509 a) i) ii) [2(16) 12 + 4][2 3+ 4] 4 1 [2(2.25) 4.5+ 4][2 3+ 4] 1.51 = 21 3 = 7 = 1 0.5 = 2 [2(1.21) 3.3+ 4][2 3+ 4] iii) =
Vectors are used to represent quantities such as force and velocity which have both. and. The magnitude of a vector corresponds to its.
 Fry Texas A&M University Fall 2016 Math 150 Notes Chapter 9 Page 248 Chapter 9 -- Vectors Remember that is the set of real numbers, often represented by the number line, 2 is the notation for the 2-dimensional
Fry Texas A&M University Fall 2016 Math 150 Notes Chapter 9 Page 248 Chapter 9 -- Vectors Remember that is the set of real numbers, often represented by the number line, 2 is the notation for the 2-dimensional
Math 302 Outcome Statements Winter 2013
 Math 302 Outcome Statements Winter 2013 1 Rectangular Space Coordinates; Vectors in the Three-Dimensional Space (a) Cartesian coordinates of a point (b) sphere (c) symmetry about a point, a line, and a
Math 302 Outcome Statements Winter 2013 1 Rectangular Space Coordinates; Vectors in the Three-Dimensional Space (a) Cartesian coordinates of a point (b) sphere (c) symmetry about a point, a line, and a
Pre-Calculus Vectors
 Slide 1 / 159 Slide 2 / 159 Pre-Calculus Vectors 2015-03-24 www.njctl.org Slide 3 / 159 Table of Contents Intro to Vectors Converting Rectangular and Polar Forms Operations with Vectors Scalar Multiples
Slide 1 / 159 Slide 2 / 159 Pre-Calculus Vectors 2015-03-24 www.njctl.org Slide 3 / 159 Table of Contents Intro to Vectors Converting Rectangular and Polar Forms Operations with Vectors Scalar Multiples
