Remark 3.2. The cross product only makes sense in R 3.
|
|
|
- Victoria Phillips
- 5 years ago
- Views:
Transcription
1 3. Cross product Definition 3.1. Let v and w be two vectors in R 3. The cross product of v and w, denoted v w, is the vector defined as follows: the length of v w is the area of the parallelogram with sides v and w, that is, v w sin θ. v w is orthogonal to both v and w. the three vectors v, w and v w form a right-handed set of vectors. Remark 3.2. The cross product only makes sense in R 3. Example 3.3. We have By contrast ˆı j ˆ = k, ˆ j ˆ k ˆ = î and kˆ ˆı = ĵ. ĵ ˆı = ˆ k, k ˆ j ˆ = ˆı and î kˆ = ˆ j. Theorem 3.4. Let u, v and w be three vectors in R 3 and let λ be a scalar. (1) v w = w v. (2) u ( v + w ) = u v + u w. (3) ( u + v) w = u w + v w. (4) λ( v w ) = (λ v) w = v (λ w). Before we prove (3.4), let s draw some conclusions from these properties. Remark 3.5. Note that (1) of (3.4) is what really distinguishes the cross product (the cross product is skew commutative). Consider computing the cross product of î, î and ĵ. On the one hand, On the other hand, (î î) ĵ = 0 j = 0. î (î ĵ) = î kˆ = j. ˆ In other words, the order in which we compute the cross product is important (the cross product is not associative). Note that if v and w are parallel, then the cross product is the zero vector. One can see this directly from the formula; the area of the parallelogram is zero and the only vector of zero length is the zero 1
2 vector. On the other hand, we know that w = λ v. In this case, v w = v (λ v) = λ v v = λ v v. To get from the second to the third line, we just switched the factors. But the only vector which is equal to its inverse is the zero vector. Let s try to compute the cross product using (3.4). If v = (v 1, v 2, v 3 ) and w = (w 1, w 2, w 3 ), then v w = (v 1 î + v 2 ĵ + v 3 kˆ) (w 1 î + w 2 ĵ + w 3 kˆ) = v 1 w 1 (î î) + v 1 w 2 (î ĵ) + v 1 w 3 (î kˆ) + v 2 w 1 (ĵ î) + v 2 w 2 (ĵ ĵ) + v 2 w 3 (ĵ kˆ) + v 3 w 1 (kˆ î) + v 3 w 2 (kˆ ĵ) + v 3 w 3 (kˆ kˆ) = (v 2 w 3 v 3 w 2 )î + (v 3 w 1 v 1 w 3 )ˆ j + (v 1 w 2 v 2 w 1 )ˆ k. Definition 3.6. A matrix A = (a ij ) is a rectangular array of numbers, where a ij is in the i row and jth column. If A has m rows and n columns, then we say that A is a m n matrix. Example 3.7. ( ) ( ) a A = = 11 a 12 a 13, a 21 a 22 a 23 is a 2 3 matrix. a 23 = 4. Definition 3.8. If ( ) a b A = c d is a 2 2 matrix, then the determinant of A is the scalar a b = ad bc. c d If a b c A = d e f g h i is a 3 3 matrix, then the determinant of A is the scalar a b c e f d f d e d e f = a b + c h i g i g h. g h i 2
3 Note that the cross product of v and w is the (formal) determinant î ĵ kˆ v 1 v 2 v 3. w 1 w 2 w 3 Let s now turn to the proof of (3.4). Definition 3.9. Let u, v and w be three vectors in R 3. The triple scalar product is ( u v) w. The triple scalar product is the signed volume of the parallelepiped formed using the three vectors, u, v and w. Indeed, the volume of the parallelepiped is the area of the base times the height. For the base, we take the parallelogram with sides u and v. The magnitude of u v is the area of this parallelogram. The height of the parallelepiped, up to sign, is the length of w times the cosine of the angle, let s call this φ, between u v and w. The sign is positive, if u, v and w form a right-handed set and negative if they form a left-handed set. Lemma If u = (u 1, u 2, u 3 ), v = (v 1, v 2, v 3 ) and w = (w 1, w 2, w 3 ) are three vectors in R 3, then u 1 u 2 u 3 ( u v) w = v 1 v 2 v 3. w 1 w 2 w 3 Proof. We have already seen that î ĵ kˆ u v = u 1 u 2 u 3. v 1 v 2 v 3 If one expands this determinant and dots with w, this is the same as replacing the top row by (w 1, w 2, w 3 ), w 1 w 2 w 3 ( u v) w = u 1 u 2 u 3. v 1 v 2 v 3 Finally, if we switch the first row and the second row, and then the second row and the third row, the sign changes twice (which makes no change at all): ( u v) w = u 1 u 2 u 3 v 1 v 2 v 3. w 1 w 2 w 3 3
4 Example The scalar triple product of î, ĵ and kˆ is one. One way to see this is geometrically; the parallelepiped determined by these three vectors is the unit cube, which has volume 1, and these vectors form a right-handed set, so that the sign is positive. Another way to see this is to compute directly (î ĵ) kˆ = kˆ kˆ = 1. Finally one can use determinants, (î ĵ) kˆ = = Lemma Let u, v and w be three vectors in R 3. Then ( u v) w = ( v w ) u = ( w u) v. Proof. In fact all three numbers have the same absolute value, namely the volume of the parallelepiped with sides u, v and w. On the other hand, if u, v, and w is a right-handed set, then so is v, w and u and vice-versa, so all three numbers have the same sign as well. Lemma Let v and w be two vectors in R 3. Then v = w if and only if v x = w x, for every vector x in R 3. Proof. One direction is clear; if v = w, then v x = w x for any vector x. So, suppose that we know that v x = w x, for every vector x. Suppose that v = (v 1, v 2, v 3 ) and w = (w 1, w 2, w 3 ). If we take x = î, then we see that v 1 = v î = w î = w 1. Similarly, if we take x = ĵ and x = kˆ, then we also get and v 2 = v ĵ = w ĵ = w 2, v 3 = v kˆ = w kˆ = w 3. But then v = w as they have the same components. Proof of (3.4). We first prove (1). Both sides have the same magnitude, namely the area of the parallelogram with sides v and w. Further both sides are orthogonal to v and w, so the only thing to check is the change in sign. 4
5 As v, w and v w form a right-handed triple, it follows that w, v and v w form a left-handed triple. But then w, v and v w form a right-handed triple. It follows that This is (1). To check (2), we check that w v = v w. ( u ( v + w )) x = ( u v + u w ) x, for an arbitrary vector x. We first attack the LHS. By (3.12), we have We now attack the RHS. ( u ( v + w )) x = ( x u) ( v + w ) = ( x u) v + ( x u) w = ( u v) x + ( u w ) x. ( u v + u w ) x = ( u v) x + ( u v) x. It follows that both sides are equal. This is (2). We could check (3) by a similar argument. Here is another way. ( u + v) w = w ( u + v) = w u w v = u w + v w. This is (3). To prove (4), it suffices to prove the first equality, since the fact that the first term is equal to the third term follows by a similar derivation. If λ = 0, then both sides are the zero vector, and there is nothing to prove. So we may assume that λ = 0. Note first that the magnitude of both sides is the area of the parallelogram with sides λ v and w. If λ > 0, then v and λ v point in the same direction. Similarly v w and λ( v w ) point in the same direction. As v, w and v w for a right-handed set, then so do λ v, w and λ( v w ). But then λ( v w ) is the cross product of λ v and w, that is, (λ v) w = λ( v w ). If λ < 0, then v and λ v point in the opposite direction. Similarly v w and λ( v w ) point in the opposite direction. But then λ v, w and λ( v w ) still form a right-handed set. This is (4). 5
6 MIT OpenCourseWare Calculus of Several Variables Fall 2010 For information about citing these materials or our Terms of Use, visit:
CHAPTER 10 VECTORS POINTS TO REMEMBER
 For more important questions visit : www4onocom CHAPTER 10 VECTORS POINTS TO REMEMBER A quantity that has magnitude as well as direction is called a vector It is denoted by a directed line segment Two
For more important questions visit : www4onocom CHAPTER 10 VECTORS POINTS TO REMEMBER A quantity that has magnitude as well as direction is called a vector It is denoted by a directed line segment Two
Lecture 2: Vector-Vector Operations
 Lecture 2: Vector-Vector Operations Vector-Vector Operations Addition of two vectors Geometric representation of addition and subtraction of vectors Vectors and points Dot product of two vectors Geometric
Lecture 2: Vector-Vector Operations Vector-Vector Operations Addition of two vectors Geometric representation of addition and subtraction of vectors Vectors and points Dot product of two vectors Geometric
Figure 17.1 The center of mass of a thrown rigid rod follows a parabolic trajectory while the rod rotates about the center of mass.
 17.1 Introduction A body is called a rigid body if the distance between any two points in the body does not change in time. Rigid bodies, unlike point masses, can have forces applied at different points
17.1 Introduction A body is called a rigid body if the distance between any two points in the body does not change in time. Rigid bodies, unlike point masses, can have forces applied at different points
MODEL ANSWERS TO HWK #1
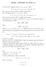 MODEL ANSWERS TO HWK #1 1.1.20. (a) 0. Suppose that a = (a 1, a 2, a 3 ). Then 0 a = (0 a 1, 0 a 2, 0 a 3 ) = (0, 0, 0) = 0. The case of a vector in R 2 is similar (and easier). (b) a. Suppose that a =
MODEL ANSWERS TO HWK #1 1.1.20. (a) 0. Suppose that a = (a 1, a 2, a 3 ). Then 0 a = (0 a 1, 0 a 2, 0 a 3 ) = (0, 0, 0) = 0. The case of a vector in R 2 is similar (and easier). (b) a. Suppose that a =
The Cross Product. Philippe B. Laval. Spring 2012 KSU. Philippe B. Laval (KSU) The Cross Product Spring /
 The Cross Product Philippe B Laval KSU Spring 2012 Philippe B Laval (KSU) The Cross Product Spring 2012 1 / 15 Introduction The cross product is the second multiplication operation between vectors we will
The Cross Product Philippe B Laval KSU Spring 2012 Philippe B Laval (KSU) The Cross Product Spring 2012 1 / 15 Introduction The cross product is the second multiplication operation between vectors we will
Module 02: Math Review
 Module 02: Math Review 1 Module 02: Math Review: Outline Vector Review (Dot, Cross Products) Review of 1D Calculus Scalar Functions in higher dimensions Vector Functions Differentials Purpose: Provide
Module 02: Math Review 1 Module 02: Math Review: Outline Vector Review (Dot, Cross Products) Review of 1D Calculus Scalar Functions in higher dimensions Vector Functions Differentials Purpose: Provide
Worksheet 1.3: Introduction to the Dot and Cross Products
 Boise State Math 275 (Ultman Worksheet 1.3: Introduction to the Dot and Cross Products From the Toolbox (what you need from previous classes Trigonometry: Sine and cosine functions. Vectors: Know what
Boise State Math 275 (Ultman Worksheet 1.3: Introduction to the Dot and Cross Products From the Toolbox (what you need from previous classes Trigonometry: Sine and cosine functions. Vectors: Know what
12.3 Dot Products, 12.4 Cross Products
 12.3 Dot Products, 12.4 Cross Products How do we multiply vectors? How to multiply vectors is not at all obvious, and in fact, there are two different ways to make sense of vector multiplication, each
12.3 Dot Products, 12.4 Cross Products How do we multiply vectors? How to multiply vectors is not at all obvious, and in fact, there are two different ways to make sense of vector multiplication, each
The Cross Product. MATH 311, Calculus III. J. Robert Buchanan. Fall Department of Mathematics. J. Robert Buchanan The Cross Product
 The Cross Product MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Introduction Recall: the dot product of two vectors is a scalar. There is another binary operation on vectors
The Cross Product MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Introduction Recall: the dot product of two vectors is a scalar. There is another binary operation on vectors
Chapter 2: Vector Geometry
 Chapter 2: Vector Geometry Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 2: Vector Geometry Semester 1 2018 1 / 32 Goals of this chapter In this chapter, we will answer the following geometric
Chapter 2: Vector Geometry Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 2: Vector Geometry Semester 1 2018 1 / 32 Goals of this chapter In this chapter, we will answer the following geometric
Math 241, Exam 1 Information.
 Math 241, Exam 1 Information. 2/13/13, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.2. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241sp13/241.html)
Math 241, Exam 1 Information. 2/13/13, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.2. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241sp13/241.html)
Vectors. J.R. Wilson. September 27, 2018
 Vectors J.R. Wilson September 27, 2018 This chapter introduces vectors that are used in many areas of physics (needed for classical physics this year). One complication is that a number of different forms
Vectors J.R. Wilson September 27, 2018 This chapter introduces vectors that are used in many areas of physics (needed for classical physics this year). One complication is that a number of different forms
CHAPTER 4 VECTORS. Before we go any further, we must talk about vectors. They are such a useful tool for
 CHAPTER 4 VECTORS Before we go any further, we must talk about vectors. They are such a useful tool for the things to come. The concept of a vector is deeply rooted in the understanding of physical mechanics
CHAPTER 4 VECTORS Before we go any further, we must talk about vectors. They are such a useful tool for the things to come. The concept of a vector is deeply rooted in the understanding of physical mechanics
The Cross Product of Two Vectors
 The Cross roduct of Two Vectors In proving some statements involving surface integrals, there will be a need to approximate areas of segments of the surface by areas of parallelograms. Therefore it is
The Cross roduct of Two Vectors In proving some statements involving surface integrals, there will be a need to approximate areas of segments of the surface by areas of parallelograms. Therefore it is
The Cross Product The cross product of v = (v 1,v 2,v 3 ) and w = (w 1,w 2,w 3 ) is
 The Cross Product 1-1-2018 The cross product of v = (v 1,v 2,v 3 ) and w = (w 1,w 2,w 3 ) is v w = (v 2 w 3 v 3 w 2 )î+(v 3 w 1 v 1 w 3 )ĵ+(v 1 w 2 v 2 w 1 )ˆk = v 1 v 2 v 3 w 1 w 2 w 3. Strictly speaking,
The Cross Product 1-1-2018 The cross product of v = (v 1,v 2,v 3 ) and w = (w 1,w 2,w 3 ) is v w = (v 2 w 3 v 3 w 2 )î+(v 3 w 1 v 1 w 3 )ĵ+(v 1 w 2 v 2 w 1 )ˆk = v 1 v 2 v 3 w 1 w 2 w 3. Strictly speaking,
MAT 1339-S14 Class 8
 MAT 1339-S14 Class 8 July 28, 2014 Contents 7.2 Review Dot Product........................... 2 7.3 Applications of the Dot Product..................... 4 7.4 Vectors in Three-Space.........................
MAT 1339-S14 Class 8 July 28, 2014 Contents 7.2 Review Dot Product........................... 2 7.3 Applications of the Dot Product..................... 4 7.4 Vectors in Three-Space.........................
Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors.
 Vectors summary Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors. AB is the position vector of B relative to A and is the vector
Vectors summary Quantities which have only magnitude are called scalars. Quantities which have magnitude and direction are called vectors. AB is the position vector of B relative to A and is the vector
The Cross Product. In this section, we will learn about: Cross products of vectors and their applications.
 The Cross Product In this section, we will learn about: Cross products of vectors and their applications. THE CROSS PRODUCT The cross product a x b of two vectors a and b, unlike the dot product, is a
The Cross Product In this section, we will learn about: Cross products of vectors and their applications. THE CROSS PRODUCT The cross product a x b of two vectors a and b, unlike the dot product, is a
Elementary maths for GMT
 Elementary maths for GMT Linear Algebra Part 1: Vectors, Representations Algebra and Linear Algebra Algebra: numbers and operations on numbers 2 + 3 = 5 3 7 = 21 Linear Algebra: tuples, triples... of numbers
Elementary maths for GMT Linear Algebra Part 1: Vectors, Representations Algebra and Linear Algebra Algebra: numbers and operations on numbers 2 + 3 = 5 3 7 = 21 Linear Algebra: tuples, triples... of numbers
Vector Algebra August 2013
 Vector Algebra 12.1 12.2 28 August 2013 What is a Vector? A vector (denoted or v) is a mathematical object possessing both: direction and magnitude also called length (denoted ). Vectors are often represented
Vector Algebra 12.1 12.2 28 August 2013 What is a Vector? A vector (denoted or v) is a mathematical object possessing both: direction and magnitude also called length (denoted ). Vectors are often represented
Math Review Night: Work and the Dot Product
 Math Review Night: Work and the Dot Product Dot Product A scalar quantity Magnitude: A B = A B cosθ The dot product can be positive, zero, or negative Two types of projections: the dot product is the parallel
Math Review Night: Work and the Dot Product Dot Product A scalar quantity Magnitude: A B = A B cosθ The dot product can be positive, zero, or negative Two types of projections: the dot product is the parallel
Chapter 3 Vectors. 3.1 Vector Analysis
 Chapter 3 Vectors 3.1 Vector nalysis... 1 3.1.1 Introduction to Vectors... 1 3.1.2 Properties of Vectors... 1 3.2 Coordinate Systems... 6 3.2.1 Cartesian Coordinate System... 6 3.2.2 Cylindrical Coordinate
Chapter 3 Vectors 3.1 Vector nalysis... 1 3.1.1 Introduction to Vectors... 1 3.1.2 Properties of Vectors... 1 3.2 Coordinate Systems... 6 3.2.1 Cartesian Coordinate System... 6 3.2.2 Cylindrical Coordinate
Worksheet 1.4: Geometry of the Dot and Cross Products
 Boise State Math 275 (Ultman) Worksheet 1.4: Geometry of the Dot and Cross Products From the Toolbox (what you need from previous classes): Basic algebra and trigonometry: be able to solve quadratic equations,
Boise State Math 275 (Ultman) Worksheet 1.4: Geometry of the Dot and Cross Products From the Toolbox (what you need from previous classes): Basic algebra and trigonometry: be able to solve quadratic equations,
Module 3: Cartesian Coordinates and Vectors
 Module 3: Cartesian Coordinates and Vectors Philosophy is written in this grand book, the universe which stands continually open to our gaze. But the book cannot be understood unless one first learns to
Module 3: Cartesian Coordinates and Vectors Philosophy is written in this grand book, the universe which stands continually open to our gaze. But the book cannot be understood unless one first learns to
CSC 470 Introduction to Computer Graphics. Mathematical Foundations Part 2
 CSC 47 Introduction to Computer Graphics Mathematical Foundations Part 2 Vector Magnitude and Unit Vectors The magnitude (length, size) of n-vector w is written w 2 2 2 w = w + w2 + + w n Example: the
CSC 47 Introduction to Computer Graphics Mathematical Foundations Part 2 Vector Magnitude and Unit Vectors The magnitude (length, size) of n-vector w is written w 2 2 2 w = w + w2 + + w n Example: the
Vectors. September 2, 2015
 Vectors September 2, 2015 Our basic notion of a vector is as a displacement, directed from one point of Euclidean space to another, and therefore having direction and magnitude. We will write vectors in
Vectors September 2, 2015 Our basic notion of a vector is as a displacement, directed from one point of Euclidean space to another, and therefore having direction and magnitude. We will write vectors in
Vectors. The standard geometric definition of vector is as something which has direction and magnitude but not position.
 Vectors The standard geometric definition of vector is as something which has direction and magnitude but not position. Since vectors have no position we may place them wherever is convenient. Vectors
Vectors The standard geometric definition of vector is as something which has direction and magnitude but not position. Since vectors have no position we may place them wherever is convenient. Vectors
Section 13.4 The Cross Product
 Section 13.4 The Cross Product Multiplying Vectors 2 In this section we consider the more technical multiplication which can be defined on vectors in 3-space (but not vectors in 2-space). 1. Basic Definitions
Section 13.4 The Cross Product Multiplying Vectors 2 In this section we consider the more technical multiplication which can be defined on vectors in 3-space (but not vectors in 2-space). 1. Basic Definitions
(arrows denote positive direction)
 12 Chapter 12 12.1 3-dimensional Coordinate System The 3-dimensional coordinate system we use are coordinates on R 3. The coordinate is presented as a triple of numbers: (a,b,c). In the Cartesian coordinate
12 Chapter 12 12.1 3-dimensional Coordinate System The 3-dimensional coordinate system we use are coordinates on R 3. The coordinate is presented as a triple of numbers: (a,b,c). In the Cartesian coordinate
Review of Linear Algebra
 Review of Linear Algebra Definitions An m n (read "m by n") matrix, is a rectangular array of entries, where m is the number of rows and n the number of columns. 2 Definitions (Con t) A is square if m=
Review of Linear Algebra Definitions An m n (read "m by n") matrix, is a rectangular array of entries, where m is the number of rows and n the number of columns. 2 Definitions (Con t) A is square if m=
18.02 Multivariable Calculus Fall 2007
 MIT OpenCourseWare http://ocw.mit.edu 18.02 Multivariable Calculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.02 Problem Set 1 Due Thursday
MIT OpenCourseWare http://ocw.mit.edu 18.02 Multivariable Calculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.02 Problem Set 1 Due Thursday
Vector Operations. Vector Operations. Graphical Operations. Component Operations. ( ) ˆk
 Vector Operations Vector Operations ME 202 Multiplication by a scalar Addition/subtraction Scalar multiplication (dot product) Vector multiplication (cross product) 1 2 Graphical Operations Component Operations
Vector Operations Vector Operations ME 202 Multiplication by a scalar Addition/subtraction Scalar multiplication (dot product) Vector multiplication (cross product) 1 2 Graphical Operations Component Operations
Vectors. Introduction
 Chapter 3 Vectors Vectors Vector quantities Physical quantities that have both numerical and directional properties Mathematical operations of vectors in this chapter Addition Subtraction Introduction
Chapter 3 Vectors Vectors Vector quantities Physical quantities that have both numerical and directional properties Mathematical operations of vectors in this chapter Addition Subtraction Introduction
Vector calculus background
 Vector calculus background Jiří Lebl January 18, 2017 This class is really the vector calculus that you haven t really gotten to in Calc III. Let us start with a very quick review of the concepts from
Vector calculus background Jiří Lebl January 18, 2017 This class is really the vector calculus that you haven t really gotten to in Calc III. Let us start with a very quick review of the concepts from
What you will learn today
 What you will learn today The Dot Product Equations of Vectors and the Geometry of Space 1/29 Direction angles and Direction cosines Projections Definitions: 1. a : a 1, a 2, a 3, b : b 1, b 2, b 3, a
What you will learn today The Dot Product Equations of Vectors and the Geometry of Space 1/29 Direction angles and Direction cosines Projections Definitions: 1. a : a 1, a 2, a 3, b : b 1, b 2, b 3, a
18.02 Multivariable Calculus Fall 2007
 MIT OpenCourseWare http://ocw.mit.edu 18.02 Multivariable Calculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. M. Matrices and Linear Algebra
MIT OpenCourseWare http://ocw.mit.edu 18.02 Multivariable Calculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. M. Matrices and Linear Algebra
Dot Product August 2013
 Dot Product 12.3 30 August 2013 Dot product. v = v 1, v 2,..., v n, w = w 1, w 2,..., w n The dot product v w is v w = v 1 w 1 + v 2 w 2 + + v n w n n = v i w i. i=1 Example: 1, 4, 5 2, 8, 0 = 1 2 + 4
Dot Product 12.3 30 August 2013 Dot product. v = v 1, v 2,..., v n, w = w 1, w 2,..., w n The dot product v w is v w = v 1 w 1 + v 2 w 2 + + v n w n n = v i w i. i=1 Example: 1, 4, 5 2, 8, 0 = 1 2 + 4
Module 24: Angular Momentum of a Point Particle
 24.1 Introduction Module 24: Angular Momentum of a Point Particle When we consider a system of objects, we have shown that the external force, acting at the center of mass of the system, is equal to the
24.1 Introduction Module 24: Angular Momentum of a Point Particle When we consider a system of objects, we have shown that the external force, acting at the center of mass of the system, is equal to the
Chapter 3. The Scalar Product. 3.1 The scalar product using coördinates
 Chapter The Scalar Product The scalar product is a way of multiplying two vectors to produce a scalar (real number) Let u and v be nonzero vectors represented by AB and AC C v A θ u B We define the angle
Chapter The Scalar Product The scalar product is a way of multiplying two vectors to produce a scalar (real number) Let u and v be nonzero vectors represented by AB and AC C v A θ u B We define the angle
Physics 40 Chapter 3: Vectors
 Physics 40 Chapter 3: Vectors Cartesian Coordinate System Also called rectangular coordinate system x-and y- axes intersect at the origin Points are labeled (x,y) Polar Coordinate System Origin and reference
Physics 40 Chapter 3: Vectors Cartesian Coordinate System Also called rectangular coordinate system x-and y- axes intersect at the origin Points are labeled (x,y) Polar Coordinate System Origin and reference
6.1.1 Angle between Two Lines Intersection of Two lines Shortest Distance from a Point to a Line
 CHAPTER 6 : VECTORS 6. Lines in Space 6.. Angle between Two Lines 6.. Intersection of Two lines 6..3 Shortest Distance from a Point to a Line 6. Planes in Space 6.. Intersection of Two Planes 6.. Angle
CHAPTER 6 : VECTORS 6. Lines in Space 6.. Angle between Two Lines 6.. Intersection of Two lines 6..3 Shortest Distance from a Point to a Line 6. Planes in Space 6.. Intersection of Two Planes 6.. Angle
12.1. Cartesian Space
 12.1. Cartesian Space In most of your previous math classes, we worked with functions on the xy-plane only meaning we were working only in 2D. Now we will be working in space, or rather 3D. Now we will
12.1. Cartesian Space In most of your previous math classes, we worked with functions on the xy-plane only meaning we were working only in 2D. Now we will be working in space, or rather 3D. Now we will
MATH 1020 WORKSHEET 12.1 & 12.2 Vectors in the Plane
 MATH 100 WORKSHEET 1.1 & 1. Vectors in the Plane Find the vector v where u =, 1 and w = 1, given the equation v = u w. Solution. v = u w =, 1 1, =, 1 +, 4 =, 1 4 = 0, 5 Find the magnitude of v = 4, 3 Solution.
MATH 100 WORKSHEET 1.1 & 1. Vectors in the Plane Find the vector v where u =, 1 and w = 1, given the equation v = u w. Solution. v = u w =, 1 1, =, 1 +, 4 =, 1 4 = 0, 5 Find the magnitude of v = 4, 3 Solution.
Section 10.7 The Cross Product
 44 Section 10.7 The Cross Product Objective #0: Evaluating Determinants. Recall the following definition for determinants: Determinants a The determinant for matrix 1 b 1 is denoted as a 1 b 1 a b a b
44 Section 10.7 The Cross Product Objective #0: Evaluating Determinants. Recall the following definition for determinants: Determinants a The determinant for matrix 1 b 1 is denoted as a 1 b 1 a b a b
Exercise Solutions for Introduction to 3D Game Programming with DirectX 10
 Exercise Solutions for Introduction to 3D Game Programming with DirectX 10 Frank Luna, September 6, 009 Solutions to Part I Chapter 1 1. Let u = 1, and v = 3, 4. Perform the following computations and
Exercise Solutions for Introduction to 3D Game Programming with DirectX 10 Frank Luna, September 6, 009 Solutions to Part I Chapter 1 1. Let u = 1, and v = 3, 4. Perform the following computations and
6. Vectors. Given two points, P 0 = (x 0, y 0 ) and P 1 = (x 1, y 1 ), a vector can be drawn with its foot at P 0 and
 6. Vectors For purposes of applications in calculus and physics, a vector has both a direction and a magnitude (length), and is usually represented as an arrow. The start of the arrow is the vector s foot,
6. Vectors For purposes of applications in calculus and physics, a vector has both a direction and a magnitude (length), and is usually represented as an arrow. The start of the arrow is the vector s foot,
11.1 Three-Dimensional Coordinate System
 11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
Vectors. Introduction. Prof Dr Ahmet ATAÇ
 Chapter 3 Vectors Vectors Vector quantities Physical quantities that have both n u m e r i c a l a n d d i r e c t i o n a l properties Mathematical operations of vectors in this chapter A d d i t i o
Chapter 3 Vectors Vectors Vector quantities Physical quantities that have both n u m e r i c a l a n d d i r e c t i o n a l properties Mathematical operations of vectors in this chapter A d d i t i o
Dr. Allen Back. Sep. 8, 2014
 in R 3 Dr. Allen Back Sep. 8, 2014 in R 3 in R 3 Def: For f (x, y), the partial derivative with respect to x at p 0 = (x 0, y 0 ) is f x = lim f (x 0 + h, y 0 ) f (x 0, y 0 ) h 0 h or f x = lim f (p 0
in R 3 Dr. Allen Back Sep. 8, 2014 in R 3 in R 3 Def: For f (x, y), the partial derivative with respect to x at p 0 = (x 0, y 0 ) is f x = lim f (x 0 + h, y 0 ) f (x 0, y 0 ) h 0 h or f x = lim f (p 0
Detailed objectives are given in each of the sections listed below. 1. Cartesian Space Coordinates. 2. Displacements, Forces, Velocities and Vectors
 Unit 1 Vectors In this unit, we introduce vectors, vector operations, and equations of lines and planes. Note: Unit 1 is based on Chapter 12 of the textbook, Salas and Hille s Calculus: Several Variables,
Unit 1 Vectors In this unit, we introduce vectors, vector operations, and equations of lines and planes. Note: Unit 1 is based on Chapter 12 of the textbook, Salas and Hille s Calculus: Several Variables,
Math Vector Calculus II
 Math 255 - Vector Calculus II Review Notes Vectors We assume the reader is familiar with all the basic concepts regarding vectors and vector arithmetic, such as addition/subtraction of vectors in R n,
Math 255 - Vector Calculus II Review Notes Vectors We assume the reader is familiar with all the basic concepts regarding vectors and vector arithmetic, such as addition/subtraction of vectors in R n,
Vectors Coordinate frames 2D implicit curves 2D parametric curves. Graphics 2008/2009, period 1. Lecture 2: vectors, curves, and surfaces
 Graphics 2008/2009, period 1 Lecture 2 Vectors, curves, and surfaces Computer graphics example: Pixar (source: http://www.pixar.com) Computer graphics example: Pixar (source: http://www.pixar.com) Computer
Graphics 2008/2009, period 1 Lecture 2 Vectors, curves, and surfaces Computer graphics example: Pixar (source: http://www.pixar.com) Computer graphics example: Pixar (source: http://www.pixar.com) Computer
An overview of key ideas
 An overview of key ideas This is an overview of linear algebra given at the start of a course on the mathematics of engineering. Linear algebra progresses from vectors to matrices to subspaces. Vectors
An overview of key ideas This is an overview of linear algebra given at the start of a course on the mathematics of engineering. Linear algebra progresses from vectors to matrices to subspaces. Vectors
Matrices. Chapter Definitions and Notations
 Chapter 3 Matrices 3. Definitions and Notations Matrices are yet another mathematical object. Learning about matrices means learning what they are, how they are represented, the types of operations which
Chapter 3 Matrices 3. Definitions and Notations Matrices are yet another mathematical object. Learning about matrices means learning what they are, how they are represented, the types of operations which
Vectors. J.R. Wilson. September 28, 2017
 Vectors J.R. Wilson September 28, 2017 This chapter introduces vectors that are used in many areas of physics (needed for classical physics this year). One complication is that a number of different forms
Vectors J.R. Wilson September 28, 2017 This chapter introduces vectors that are used in many areas of physics (needed for classical physics this year). One complication is that a number of different forms
Module 12: Work and the Scalar Product
 Module 1: Work and the Scalar Product 1.1 Scalar Product (Dot Product) We shall introduce a vector operation, called the dot product or scalar product that takes any two vectors and generates a scalar
Module 1: Work and the Scalar Product 1.1 Scalar Product (Dot Product) We shall introduce a vector operation, called the dot product or scalar product that takes any two vectors and generates a scalar
Study guide for Exam 1. by William H. Meeks III October 26, 2012
 Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
1.1 Single Variable Calculus versus Multivariable Calculus Rectangular Coordinate Systems... 4
 MATH2202 Notebook 1 Fall 2015/2016 prepared by Professor Jenny Baglivo Contents 1 MATH2202 Notebook 1 3 1.1 Single Variable Calculus versus Multivariable Calculus................... 3 1.2 Rectangular Coordinate
MATH2202 Notebook 1 Fall 2015/2016 prepared by Professor Jenny Baglivo Contents 1 MATH2202 Notebook 1 3 1.1 Single Variable Calculus versus Multivariable Calculus................... 3 1.2 Rectangular Coordinate
22m:033 Notes: 1.3 Vector Equations
 m:0 Notes: Vector Equations Dennis Roseman University of Iowa Iowa City, IA http://wwwmathuiowaedu/ roseman January 7, 00 Algebra and Geometry We think of geometric things as subsets of the plane or of
m:0 Notes: Vector Equations Dennis Roseman University of Iowa Iowa City, IA http://wwwmathuiowaedu/ roseman January 7, 00 Algebra and Geometry We think of geometric things as subsets of the plane or of
VECTORS vectors & scalars vector direction magnitude scalar only magnitude
 VECTORS Physical quantities are classified in two big classes: vectors & scalars. A vector is a physical quantity which is completely defined once we know precisely its direction and magnitude (for example:
VECTORS Physical quantities are classified in two big classes: vectors & scalars. A vector is a physical quantity which is completely defined once we know precisely its direction and magnitude (for example:
Section 1.6. M N = [a ij b ij ], (1.6.2)
![Section 1.6. M N = [a ij b ij ], (1.6.2) Section 1.6. M N = [a ij b ij ], (1.6.2)](/thumbs/78/77913520.jpg) The Calculus of Functions of Several Variables Section 16 Operations with Matrices In the previous section we saw the important connection between linear functions and matrices In this section we will
The Calculus of Functions of Several Variables Section 16 Operations with Matrices In the previous section we saw the important connection between linear functions and matrices In this section we will
Calculus 1 for AE (WI1421LR) Lecture 1: 12.3 The dot product 12.4 The cross product
 Calculus 1 for AE (WI1421LR) : 12.3 The dot product 12.4 The cross product About this course Textbook James Stewart, Calculus, Early Transcendentals, 7th edition Course Coordinator Dr. Roelof Koekoek,
Calculus 1 for AE (WI1421LR) : 12.3 The dot product 12.4 The cross product About this course Textbook James Stewart, Calculus, Early Transcendentals, 7th edition Course Coordinator Dr. Roelof Koekoek,
Vectors. Teaching Learning Point. Ç, where OP. l m n
 Vectors 9 Teaching Learning Point l A quantity that has magnitude as well as direction is called is called a vector. l A directed line segment represents a vector and is denoted y AB Å or a Æ. l Position
Vectors 9 Teaching Learning Point l A quantity that has magnitude as well as direction is called is called a vector. l A directed line segment represents a vector and is denoted y AB Å or a Æ. l Position
Lecture 3: Matrix and Matrix Operations
 Lecture 3: Matrix and Matrix Operations Representation, row vector, column vector, element of a matrix. Examples of matrix representations Tables and spreadsheets Scalar-Matrix operation: Scaling a matrix
Lecture 3: Matrix and Matrix Operations Representation, row vector, column vector, element of a matrix. Examples of matrix representations Tables and spreadsheets Scalar-Matrix operation: Scaling a matrix
Last week we presented the following expression for the angles between two vectors u and v in R n ( ) θ = cos 1 u v
 Orthogonality (I) Last week we presented the following expression for the angles between two vectors u and v in R n ( ) θ = cos 1 u v u v which brings us to the fact that θ = π/2 u v = 0. Definition (Orthogonality).
Orthogonality (I) Last week we presented the following expression for the angles between two vectors u and v in R n ( ) θ = cos 1 u v u v which brings us to the fact that θ = π/2 u v = 0. Definition (Orthogonality).
CHAPTER 3 : VECTORS. Definition 3.1 A vector is a quantity that has both magnitude and direction.
 EQT 101-Engineering Mathematics I Teaching Module CHAPTER 3 : VECTORS 3.1 Introduction Definition 3.1 A ector is a quantity that has both magnitude and direction. A ector is often represented by an arrow
EQT 101-Engineering Mathematics I Teaching Module CHAPTER 3 : VECTORS 3.1 Introduction Definition 3.1 A ector is a quantity that has both magnitude and direction. A ector is often represented by an arrow
D(f/g)(P ) = D(f)(P )g(p ) f(p )D(g)(P ). g 2 (P )
 We first record a very useful: 11. Higher derivatives Theorem 11.1. Let A R n be an open subset. Let f : A R m and g : A R m be two functions and suppose that P A. Let λ A be a scalar. If f and g are differentiable
We first record a very useful: 11. Higher derivatives Theorem 11.1. Let A R n be an open subset. Let f : A R m and g : A R m be two functions and suppose that P A. Let λ A be a scalar. If f and g are differentiable
University of Alabama Department of Physics and Astronomy. PH 125 / LeClair Spring A Short Math Guide. Cartesian (x, y) Polar (r, θ)
 University of Alabama Department of Physics and Astronomy PH 125 / LeClair Spring 2009 A Short Math Guide 1 Definition of coordinates Relationship between 2D cartesian (, y) and polar (r, θ) coordinates.
University of Alabama Department of Physics and Astronomy PH 125 / LeClair Spring 2009 A Short Math Guide 1 Definition of coordinates Relationship between 2D cartesian (, y) and polar (r, θ) coordinates.
Homework 2. Solutions T =
 Homework. s Let {e x, e y, e z } be an orthonormal basis in E. Consider the following ordered triples: a) {e x, e x + e y, 5e z }, b) {e y, e x, 5e z }, c) {e y, e x, e z }, d) {e y, e x, 5e z }, e) {
Homework. s Let {e x, e y, e z } be an orthonormal basis in E. Consider the following ordered triples: a) {e x, e x + e y, 5e z }, b) {e y, e x, 5e z }, c) {e y, e x, e z }, d) {e y, e x, 5e z }, e) {
D. Determinants. a b c d e f
 D. Determinants Given a square array of numers, we associate with it a numer called the determinant of, and written either det(), or. For 2 2 and 3 3 arrays, the numer is defined y () a c d = ad c; a c
D. Determinants Given a square array of numers, we associate with it a numer called the determinant of, and written either det(), or. For 2 2 and 3 3 arrays, the numer is defined y () a c d = ad c; a c
Department of Physics, Korea University
 Name: Department: Notice +2 ( 1) points per correct (incorrect) answer. No penalty for an unanswered question. Fill the blank ( ) with (8) if the statement is correct (incorrect).!!!: corrections to an
Name: Department: Notice +2 ( 1) points per correct (incorrect) answer. No penalty for an unanswered question. Fill the blank ( ) with (8) if the statement is correct (incorrect).!!!: corrections to an
Objective 1. Lesson 87: The Cross Product of Vectors IBHL - SANTOWSKI FINDING THE CROSS PRODUCT OF TWO VECTORS
 Lesson 87: The Cross Product of Vectors IBHL - SANTOWSKI In this lesson you will learn how to find the cross product of two vectors how to find an orthogonal vector to a plane defined by two vectors how
Lesson 87: The Cross Product of Vectors IBHL - SANTOWSKI In this lesson you will learn how to find the cross product of two vectors how to find an orthogonal vector to a plane defined by two vectors how
Vectors for Physics. AP Physics C
 Vectors for Physics AP Physics C A Vector is a quantity that has a magnitude (size) AND a direction. can be in one-dimension, two-dimensions, or even three-dimensions can be represented using a magnitude
Vectors for Physics AP Physics C A Vector is a quantity that has a magnitude (size) AND a direction. can be in one-dimension, two-dimensions, or even three-dimensions can be represented using a magnitude
Answers in blue. If you have questions or spot an error, let me know. 1. Find all matrices that commute with A =. 4 3
 Answers in blue. If you have questions or spot an error, let me know. 3 4. Find all matrices that commute with A =. 4 3 a b If we set B = and set AB = BA, we see that 3a + 4b = 3a 4c, 4a + 3b = 3b 4d,
Answers in blue. If you have questions or spot an error, let me know. 3 4. Find all matrices that commute with A =. 4 3 a b If we set B = and set AB = BA, we see that 3a + 4b = 3a 4c, 4a + 3b = 3b 4d,
Vectors and 2D Kinematics. AIT AP Physics C
 Vectors and 2D Kinematics Coordinate Systems Used to describe the position of a point in space Coordinate system consists of a fixed reference point called the origin specific axes with scales and labels
Vectors and 2D Kinematics Coordinate Systems Used to describe the position of a point in space Coordinate system consists of a fixed reference point called the origin specific axes with scales and labels
Vectors and Fields. Vectors versus scalars
 C H A P T E R 1 Vectors and Fields Electromagnetics deals with the study of electric and magnetic fields. It is at once apparent that we need to familiarize ourselves with the concept of a field, and in
C H A P T E R 1 Vectors and Fields Electromagnetics deals with the study of electric and magnetic fields. It is at once apparent that we need to familiarize ourselves with the concept of a field, and in
Chapter 1. Units, Physical Quantities, and Vectors
 Chapter 1 Units, Physical Quantities, and Vectors 1.3 Standards and Units The metric system is also known as the S I system of units. (S I! Syst me International). A. Length The unit of length in the metric
Chapter 1 Units, Physical Quantities, and Vectors 1.3 Standards and Units The metric system is also known as the S I system of units. (S I! Syst me International). A. Length The unit of length in the metric
THE IMPORTANCE OF GEOMETRIC REASONING
 THE IMPORTANCE OF GEOMETRIC REASONING Tevian Dray & Corinne Manogue Oregon State University I: Mathematics Physics II: The Bridge Project III: Geometric Visualization QUESTIONS I: Suppose T (x, y) = k(x
THE IMPORTANCE OF GEOMETRIC REASONING Tevian Dray & Corinne Manogue Oregon State University I: Mathematics Physics II: The Bridge Project III: Geometric Visualization QUESTIONS I: Suppose T (x, y) = k(x
CURRENT MATERIAL: Vector Calculus.
 Math 275, section 002 (Ultman) Spring 2012 FINAL EXAM REVIEW The final exam will be held on Wednesday 9 May from 8:00 10:00am in our regular classroom. You will be allowed both sides of two 8.5 11 sheets
Math 275, section 002 (Ultman) Spring 2012 FINAL EXAM REVIEW The final exam will be held on Wednesday 9 May from 8:00 10:00am in our regular classroom. You will be allowed both sides of two 8.5 11 sheets
Matrix Basic Concepts
 Matrix Basic Concepts Topics: What is a matrix? Matrix terminology Elements or entries Diagonal entries Address/location of entries Rows and columns Size of a matrix A column matrix; vectors Special types
Matrix Basic Concepts Topics: What is a matrix? Matrix terminology Elements or entries Diagonal entries Address/location of entries Rows and columns Size of a matrix A column matrix; vectors Special types
3. Vector spaces 3.1 Linear dependence and independence 3.2 Basis and dimension. 5. Extreme points and basic feasible solutions
 A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
Review of Coordinate Systems
 Vector in 2 R and 3 R Review of Coordinate Systems Used to describe the position of a point in space Common coordinate systems are: Cartesian Polar Cartesian Coordinate System Also called rectangular coordinate
Vector in 2 R and 3 R Review of Coordinate Systems Used to describe the position of a point in space Common coordinate systems are: Cartesian Polar Cartesian Coordinate System Also called rectangular coordinate
22A-2 SUMMER 2014 LECTURE Agenda
 22A-2 SUMMER 204 LECTURE 2 NATHANIEL GALLUP The Dot Product Continued Matrices Group Work Vectors and Linear Equations Agenda 2 Dot Product Continued Angles between vectors Given two 2-dimensional vectors
22A-2 SUMMER 204 LECTURE 2 NATHANIEL GALLUP The Dot Product Continued Matrices Group Work Vectors and Linear Equations Agenda 2 Dot Product Continued Angles between vectors Given two 2-dimensional vectors
REVIEW - Vectors. Vectors. Vector Algebra. Multiplication by a scalar
 J. Peraire Dynamics 16.07 Fall 2004 Version 1.1 REVIEW - Vectors By using vectors and defining appropriate operations between them, physical laws can often be written in a simple form. Since we will making
J. Peraire Dynamics 16.07 Fall 2004 Version 1.1 REVIEW - Vectors By using vectors and defining appropriate operations between them, physical laws can often be written in a simple form. Since we will making
Course Notes Math 275 Boise State University. Shari Ultman
 Course Notes Math 275 Boise State University Shari Ultman Fall 2017 Contents 1 Vectors 1 1.1 Introduction to 3-Space & Vectors.............. 3 1.2 Working With Vectors.................... 7 1.3 Introduction
Course Notes Math 275 Boise State University Shari Ultman Fall 2017 Contents 1 Vectors 1 1.1 Introduction to 3-Space & Vectors.............. 3 1.2 Working With Vectors.................... 7 1.3 Introduction
The Geometry of R n. Supplemental Lecture Notes for Linear Algebra Courses at Georgia Tech
 The Geometry of R n Supplemental Lecture Notes for Linear Algebra Courses at Georgia Tech Contents Vectors in R n. Vectors....................................... The Length and Direction of a Vector......................3
The Geometry of R n Supplemental Lecture Notes for Linear Algebra Courses at Georgia Tech Contents Vectors in R n. Vectors....................................... The Length and Direction of a Vector......................3
vand v 3. Find the area of a parallelogram that has the given vectors as adjacent sides.
 Name: Date: 1. Given the vectors u and v, find u vand v v. u= 8,6,2, v = 6, 3, 4 u v v v 2. Given the vectors u nd v, find the cross product and determine whether it is orthogonal to both u and v. u= 1,8,
Name: Date: 1. Given the vectors u and v, find u vand v v. u= 8,6,2, v = 6, 3, 4 u v v v 2. Given the vectors u nd v, find the cross product and determine whether it is orthogonal to both u and v. u= 1,8,
Solutions to Selected Questions from Denis Sevee s Vector Geometry. (Updated )
 Solutions to Selected Questions from Denis Sevee s Vector Geometry. (Updated 24--27) Denis Sevee s Vector Geometry notes appear as Chapter 5 in the current custom textbook used at John Abbott College for
Solutions to Selected Questions from Denis Sevee s Vector Geometry. (Updated 24--27) Denis Sevee s Vector Geometry notes appear as Chapter 5 in the current custom textbook used at John Abbott College for
MATH 19520/51 Class 2
 MATH 19520/51 Class 2 Minh-Tam Trinh University of Chicago 2017-09-27 1 Review dot product. 2 Angles between vectors and orthogonality. 3 Projection of one vector onto another. 4 Cross product and its
MATH 19520/51 Class 2 Minh-Tam Trinh University of Chicago 2017-09-27 1 Review dot product. 2 Angles between vectors and orthogonality. 3 Projection of one vector onto another. 4 Cross product and its
v = ( 2)
 Chapter : Introduction to Vectors.. Vectors and linear combinations Let s begin by saying what vectors are: They are lists of numbers. If there are numbers in the list, there is a natural correspondence
Chapter : Introduction to Vectors.. Vectors and linear combinations Let s begin by saying what vectors are: They are lists of numbers. If there are numbers in the list, there is a natural correspondence
MATH Topics in Applied Mathematics Lecture 12: Evaluation of determinants. Cross product.
 MATH 311-504 Topics in Applied Mathematics Lecture 12: Evaluation of determinants. Cross product. Determinant is a scalar assigned to each square matrix. Notation. The determinant of a matrix A = (a ij
MATH 311-504 Topics in Applied Mathematics Lecture 12: Evaluation of determinants. Cross product. Determinant is a scalar assigned to each square matrix. Notation. The determinant of a matrix A = (a ij
Engineering Mechanics: Statics
 Engineering Mechanics: Statics Chapter 2: Force Systems Part A: Two Dimensional Force Systems Force Force = an action of one body on another Vector quantity External and Internal forces Mechanics of Rigid
Engineering Mechanics: Statics Chapter 2: Force Systems Part A: Two Dimensional Force Systems Force Force = an action of one body on another Vector quantity External and Internal forces Mechanics of Rigid
Graphics (INFOGR), , Block IV, lecture 8 Deb Panja. Today: Matrices. Welcome
 Graphics (INFOGR), 2017-18, Block IV, lecture 8 Deb Panja Today: Matrices Welcome 1 Today Matrices: why and what? Matrix operations Determinants Adjoint/adjugate and inverse of matrices Geometric interpretation
Graphics (INFOGR), 2017-18, Block IV, lecture 8 Deb Panja Today: Matrices Welcome 1 Today Matrices: why and what? Matrix operations Determinants Adjoint/adjugate and inverse of matrices Geometric interpretation
,, rectilinear,, spherical,, cylindrical. (6.1)
 Lecture 6 Review of Vectors Physics in more than one dimension (See Chapter 3 in Boas, but we try to take a more general approach and in a slightly different order) Recall that in the previous two lectures
Lecture 6 Review of Vectors Physics in more than one dimension (See Chapter 3 in Boas, but we try to take a more general approach and in a slightly different order) Recall that in the previous two lectures
22m:033 Notes: 6.1 Inner Product, Length and Orthogonality
 m:033 Notes: 6. Inner Product, Length and Orthogonality Dennis Roseman University of Iowa Iowa City, IA http://www.math.uiowa.edu/ roseman April, 00 The inner product Arithmetic is based on addition and
m:033 Notes: 6. Inner Product, Length and Orthogonality Dennis Roseman University of Iowa Iowa City, IA http://www.math.uiowa.edu/ roseman April, 00 The inner product Arithmetic is based on addition and
LS.1 Review of Linear Algebra
 LS. LINEAR SYSTEMS LS.1 Review of Linear Algebra In these notes, we will investigate a way of handling a linear system of ODE s directly, instead of using elimination to reduce it to a single higher-order
LS. LINEAR SYSTEMS LS.1 Review of Linear Algebra In these notes, we will investigate a way of handling a linear system of ODE s directly, instead of using elimination to reduce it to a single higher-order
MODEL ANSWERS TO HWK #1
 MODEL ANSWERS TO HWK # Part B (a The four vertices are (,,, (,,, (,, and (,, The distance between the first two vertices is, since two coordinates differ by There are six edges, corresponding to the choice
MODEL ANSWERS TO HWK # Part B (a The four vertices are (,,, (,,, (,, and (,, The distance between the first two vertices is, since two coordinates differ by There are six edges, corresponding to the choice
18.06 Quiz 2 April 7, 2010 Professor Strang
 18.06 Quiz 2 April 7, 2010 Professor Strang Your PRINTED name is: 1. Your recitation number or instructor is 2. 3. 1. (33 points) (a) Find the matrix P that projects every vector b in R 3 onto the line
18.06 Quiz 2 April 7, 2010 Professor Strang Your PRINTED name is: 1. Your recitation number or instructor is 2. 3. 1. (33 points) (a) Find the matrix P that projects every vector b in R 3 onto the line
DS-GA 1002 Lecture notes 0 Fall Linear Algebra. These notes provide a review of basic concepts in linear algebra.
 DS-GA 1002 Lecture notes 0 Fall 2016 Linear Algebra These notes provide a review of basic concepts in linear algebra. 1 Vector spaces You are no doubt familiar with vectors in R 2 or R 3, i.e. [ ] 1.1
DS-GA 1002 Lecture notes 0 Fall 2016 Linear Algebra These notes provide a review of basic concepts in linear algebra. 1 Vector spaces You are no doubt familiar with vectors in R 2 or R 3, i.e. [ ] 1.1
Introduction. Introduction (2) Easy Problems for Vectors 7/13/2011. Chapter 4. Vector Tools for Graphics
 Introduction Chapter 4. Vector Tools for Graphics In computer graphics, we work with objects defined in a three dimensional world (with 2D objects and worlds being just special cases). All objects to be
Introduction Chapter 4. Vector Tools for Graphics In computer graphics, we work with objects defined in a three dimensional world (with 2D objects and worlds being just special cases). All objects to be
