dt dx dy dz dtdx dtdy dtdz dxdy dxdz dydz dxdydz dtdydz dtdxdz dtdxdy dtdxdydz
|
|
|
- Leonard Williamson
- 6 years ago
- Views:
Transcription
1 DIFFERENTIAL FORMS ON R 4 Thomas Wieting, 20 Differential Forms 0 One locates Events (t, x, y, z) in Time/Space by specifying a coordinate t for time and Cartesian coordinates x, y, andz for position. One measures t, x, y, andz in meters. In one meter of time, light travels one meter. In these units, the speed of light is one. 02 On R 4, one introduces the following sixteen monomials: dt dx dy dz dtdx dtdy dtdz dxdy dxdz dydz dxdydz dtdydz dtdxdz dtdxdy dtdxdydz In terms of these monomials, one defines Differential Forms on R 4 as follows: 0forms: f = f. forms: ρdt + udx + vdy + wdz 2forms: adtdx + bdtdy + cdtdz αdydz + βdxdz γdxdy 3forms: σdxdydz + pdtdydz qdtdxdz + rdtdxdy 4forms: gdtdxdydz where: f, ρ, u, v, w, a, b, c, α, β, γ, σ, p, q, r, g are real valued functions of t, x, y, andz. 03 For a given k form φ, one refers to k as the degree of φ. 04 Such forms compose an algebra, let it be F. One adds them in the manner expected but one multiplies them by invoking antisymmetry: dtdt =0,dtdx= dxdt,...,dydz = dzdy, dzdz =0 For instance: udx cdtdz = ucdtdxdz
2 05 One can easily check that, for any k form φ and for any l form ψ: The Star Operator ψφ =( ) kl φψ 06 One computes the Star Operator on a k form φ by applying the following relations: =+dtdxdydz dt = +dxdydz, dx = +dtdydz, dy = dtdxdz, dz = +dtdxdy dxdydz = +dt, dtdydz = +dx, dtdxdz = dy, dtdxdy = +dz dtdx = dydz, dtdy =+dxdz, dtdz = dxdy dydz = +dtdx, dxdz = dtdy, dxdy = +dtdz dtdxdydz = For instance: (ρdt + βdxdz) =ρdxdydz βdtdy 07 Clearly, if the degree of φ is k then the degree of φ is 4 k. Moreover: φ =( ) k+ φ 08 Let us describe the rhyme which underlies the foregoing operation. To that end, we supply the algebra F with an (indefinite) Inner Product:, by declaring the family of monomials to be orthonormal. We determine the signsbycounting the numberofoccurrencesofdx, dy, anddz in the monomial. For instance: dz, dz =, dtdxdz, dtdxdz =+, dtdxdydz, dtdxdydz = Now, for any monomial m, we identify the monomial n for which: mn = ± m, m dtdxdydz Matching signs, we then declare m to be ± n. For instance: dy dtdxdz = dy, dy dtdxdydz = dy = dtdxdz 2
3 The Exterior Derivative 09 One defines the Exterior Derivative dφ of a k form φ as follows: (k =0) df = f t dt + f x dx + f y dy + f z dz (k =) d(ρdt + udx + vdy + wdz) =dρ dt + du dx + dv dy + dw dz (k =2) d(adtdx + bdtdy + cdtdz αdydz + βdxdz γdxdy) = da dtdx + db dtdy + dc dtdz dα dydz + dβ dxdz dγ dxdy (k =3) d(σdxdydz + pdtdydz qdtdxdz + rdtdxdy) = dσ dxdydz + dp dtdydz dq dtdxdz + dr dtdxdy (k =4) d(gdtdxdydz) =dg dtdxdydz =0 Note that d increases the degree of φ by. One finds that dd =0. 0 One can easily check that, for any k form φ and for any l form ψ: d(φψ) =dφ ψ +( ) k φdψ Divergence One defines the Divergence δφ of a k form φ as follows: δφ = d φ Note that d decreases the degree of φ by. Moreover, δδ =0. Maxwell s Equations 2 In studies of ElectroDynamics, one represents the electric charge density as a time-dependent scalar field: ρ and the electric current density, the electric field, and the magnetic field as time-dependent vector fields: J =(u, v, w), E =(a, b, c), B =(α, β, γ) 3
4 These representations lead to the following forms: j = ρdt udx vdy wdz φ = adtdx + bdtdy + cdtdz αdydz + βdxdz γdxdy They are the Electric Current Form and the ElectroMagnetic Field Form. Now Maxwell s Equations stand as follows: (M) δφ = j, dφ =0 3 Let us show that the equations just stated are consistent with the four classical Equations of Maxwell. First, we note that dφ is the sum of the following four forms: Consequently, dφ =0iff: (α x + β y + γ z )dxdydz ( α t + b z c y )dtdydz (β t + a z c x )dtdxdz ( γ t + a y b x )dtdxdy B =0, B t + E =0 These are two of the four classical Equations of Maxwell. 4 Second, we note that: φ = αdtdx βdtdy γdtdz adydz + bdxdz cdxdy Hence, d φ is the sum of the following four forms: (a x + b y + c z )dxdydz ( a t β z + γ y )dtdydz (b t α z + γ x )dtdxdz ( c t α y + β x )dtdxdy Third, we note that δφ = j iff d φ = j. Moreover: Consequently, δφ = j iff: j = ρdxdydz udtdydz + vdtdxdz wdtdxdy E = ρ, E t + B = J These are the other two of the four classical Equations of Maxwell. 4
5 The Continuity Equation 5 From the first of Maxwell s Equations (M), we obtain the Continuity Equation for the current form: (C) δj =0 For later reference, let us compute δj explicitly: δj =( d )(ρdt udx vdy wdz) = d(ρdxdydz udtdydz + vdtdxdz wdtdxdy) = (ρ t dtdxdydz u x dxdtdydz + v y dydtdxdz w z dzdtdxdy) = (ρ t + u x + v y + w z )dtdxdydz Consequently: δj = ρ t + u x + v y + w z Hence, the classical form of the Continuity Equation stands as follows: ρ t + J =0 Apology 6 We acknowledge that, in our presentation of Maxwell s Equations, we have stripped from all relations the common constants which usually figure in them. We have achieved this effect by adopting suitable, admittedly obscure units of measurement for the fields involved, regarding the common constants as conversion factors. Of such a practice one might say that the analysis is agreeable but the application, troublesome. The Wave Operator 7 At this point, let us introduce the Wave Operator : =(δ + d) 2 = δd + dδ For functions f, wehaveδf = 0. Hence: so that: f = δdf = δ(f t dt + f x dx + f y dy + f z dz) f = f tt f xx f yy f zz 5
6 See article 5. For forms in general, one can readily check that coefficient by coefficient. For instance: operates (adtdx + bdtdy + cdtdz) =( a)dtdx +( b)dtdy +( c)dtdz The Lorentz Gauge Condition 8 Given Maxwell s Equations, one may apply Poincaré s Lemma to define aformψ such that dψ = φ. One refers to the form ψ as a Potential for the field form φ. One says that ψ satisfies the Lorentz Gauge Condition (that is, the LGC) iff δψ = 0. Such potentials do exist. In fact, for any potential ψ for the field form φ, wemayintroduceasolutionf of the following instance of the Inhomogeneous Wave Equation: (W ) f = δψ Then: d(ψ + df) =φ and δ(ψ + df) =0 Hence, ψ + df is a potential for φ which satisfies the LGC. Let us hasten to note that there are standard procedures for solving equation (W ). 9 Let ψ and ψ be potentials for φ which satisfy the LGC. That is, dψ = φ, δψ =0,dψ = φ, andδψ = 0. Let us define ψ ψ ψ. We find that dψ =0andδψ = 0. By Poincaré s Lemma, we may define a function f such that df = ψ. We find that: f = δdf = δψ =0 Conversely, let ψ be a potential for φ which satisfies the LGC and let f be a function for which f = 0. Let us define ψ ψ + df. Clearly, ψ is also a potential for φ which satisfies the LGC. We conclude that potentials for the field form φ which satisfy the LGC are unique within solutions of the Homogeneous Wave Equation: Maxwell s Equations Redux f =0 20 Let j be the current form. Of course, δj = 0. We contend that Maxwell s Equations can be presented in the following alternate form: (N) ψ = j, δψ =0 6
7 Indeed, let ψ satisfy equations (N). Define φ = dψ. Thendφ = 0 and: δφ = δdψ =(δd + dδ)ψ = ψ = j so that φ satisfies equations (M). In turn, let φ satisfy equations (M). Introduce ψ such that dψ = φ and δψ = 0. Then: so that ψ satisfies equations (N). Retarded Potentials ψ =(δd + dδ)ψ = δdψ = δφ = j 2 Let us apply the theory of the Inhomogeneous Wave Equation to design a procedure for solving equations (N), hence for solving Maxwell s Equations (M) as well. We begin with the current form j: j = ρdt udx vdy wdz Of necessity, it satisfies the Continuity Equation: δj = ρ t + u x + v y + w z =0 We introduce the form ψ as follows: ψ = ρ dt u dx v dy w dz The functions ρ, u, v,andw are the retarded potentials defined by ρ, u, v, andw, respectively: (R) ρ (t, x, y, z) = 4π u (t, x, y, z) = 4π v (t, x, y, z) = 4π w (t, x, y, z) = 4π R s 3 R s 3 R s 3 ρ(t s, x + u, y + v, z + w)dudvdw u(t s, x + u, y + v, z + w)dudvdw v(t s, x + u, y + v, z + w)dudvdw w(t s, x + u, y + v, z + w)dudvdw R s 3 where: s = u 2 + v 2 + w 2 7
8 By the theory of the Inhomogeneous Wave Equation: Consequently: ρ = ρ, u = u, v = v, w = w (ρ dt u dx v dy w dz) =( ρ )dt ( u )dx ( v )dy ( w )dz = ρdt udx vdy wdz Hence: ψ = j Obviously: [ ] ρ t + u x + v y + w z (t, x, y, z) = [ ] ρt + u x + v y + w z (t s, x + u, y + v, z + w)dudvdw 4π R s 3 By the Continuity Equation, ψ satisfies the LGC: δψ =0 Hence, ψ satisfies equations (N). In turn, φ dψ satisfies Maxwell s Equations (M). 22 One refers to ψ as the Retarded Potential for the field form φ, defined by the current form j. Indeed, we find the values of ρ, u, v,andw at (t, x, y, z) by computing certain integrals of the functions ρ, u, v, andw over the past light cone for (t, x, y, z), which consists of the events: where 0 <sand s 2 = u 2 + v 2 + w 2. The General Solution (t s, x + u, y + v, z + w) 23 The field form φ, just described, is a Particular Solution of Maxwell s Equations (M). The General Solution φ of (M) stands as follows: φ = φ + φ where φ is any solution of the Homogeneous Form of Maxwell s Equations: (M ) δφ =0, dφ =0 Let us describe all such solutions.... 8
9 Radiation 24 Let j be the current form and φ the field form underlying Maxwell s Equations (M). Obviously: φ =(δd + dδ)φ = dj It may happen that dj =0. Insuchacase: 0= φ =( a)dtdx +( b)dtdy +( c)dtdz ( γ)dxdy +( β)dxdz ( α)dydz so that: a =0, b =0, c =0, α =0, β =0, γ =0 The theory of the Homogeneous Wave Equation insures that, in this context, the components of the field form propagate at speed through space. That is, the electric and magnetic fields radiate. 25 By Poincaré s Lemma, dj = 0 iff there is a function f such that df = j. Since δj =0,weinferthat: f =0 so that f is a solution of the Homogeneous Wave Equation. Conversely, every such solution f defines a current form: for which δj =0anddj =0. Helmholtz Theorem j df 26 Let l be an integer for which 0 <l<4. Let λ be an l formonr 4 for which δλ =0andletν be an l +form onr 4 for which dν =0. We contend that there is an l form µ on R 4 such that: (H) λ = δµ, dµ = ν Schematically: 0 δ λ δ µ d ν d 0 This contention is the substance of Helmholtz Theorem. require certain preparations. To prove it, we 9
10 27 The members of F stand as follows: µ = µ 0 + µ + µ 2 + µ 3 + µ 4 where, for each index l, µ l is an l form on R 4. The operators d,, δ, and act on F as follows: dµ = dµ 0 + dµ + dµ 2 + dµ 3 + dµ 4 µ = µ 0 + µ + µ 2 + µ 3 + µ 4 δµ = δµ 0 + δµ + δµ 2 + δµ 3 + δµ 4 and: µ = µ 0 + µ + µ 2 + µ 3 + µ 4 Of course, dµ 4 =0andδµ 0 =0. 28 With reference to article 9, let us introduce the Retarded Potential Operator. To that end, let f be a function of t, x, y, andz. Let f be the retarded potential defined by f, as follows: ( f)(t, x, y, z) = f(t s, x + u, y + v, z + w)dudvdw 4π R s 3 where s = u 2 + v 2 + w 2. In turn, let l be an integer for which 0 l 4and let µ be an l form on R 4. Let µ be the l form on R 4 defined by applying to µ coefficient by coefficient. For instance: (adtdx + bdtdy + cdtdz) =( a)dtdx +( b)dtdy +( c)dtdz Finally, let µ an arbitrary differential form in F: µ = µ 0 + µ + µ 2 + µ 3 + µ 4 Let µ be defined as follows: µ = µ 0 + µ + µ 2 + µ 3 + µ 4 One can easily check that is a right inverse for : (P ) µ = µ See article 9. 0
11 29 Remarkably, commutes with d,, andδ: d = d, =, δ = δ Of course, the last relation follows from the first two. Let us defend the first two relations by presenting particular cases: ( d)(adtdx) = (d(adtdx)) = (da dtdx) = (a y dydtdx + a z dzdtdx) =( a y )dydtdx +( a z )dzdtdx =( a) y dydtdx +( a) z dzdtdx = d(( a)dtdx) = d( (adtdx)) =(d )(adtdx) ( )(σdxdydz) = ( (σdxdydz)) = (σ( dxdydz)) = (σdt) =( σ)dt = (( σ)dxdydz) = ( (σdxdydz)) =( )(σdxdydz) 30 Now let us prove Helmholtz Theorem. We must design an l form µ on R 4 such that λ = δµ and dµ = ν. Thatis: (δ + d)µ = λ + ν With the foregoing preparation, we may produce µ very easily: µ (dλ + δν) Clearly, µ is an l form on R 4.Sinceδλ =0anddν = 0, we find that: (δ + d)µ =(δ + d) (δ + d)(λ + ν) = (λ + ν) =λ + ν The proof is complete. Rigor (Incomplete)
12 3 We have been cavalier in our treatment of the operators and. In particular, we have failed to specify precisely the domains on which they act. Our failure leads to a preposterous conclusion. Since commutes with d and δ, it must commute with. It would follow that, for any solution f of the Homogeneous Wave Equation: which is absurd. 0= f = f = f The Question of Uniqueness (Incomplete) Magnetic Monopoles (Incomplete) 34 Let j be the Electric Current Form and let κ be the Magnetic Current Form: j = ρdt udx vdy wdz κ = (σdt pdx qdy rdz) = σdxdydz pdtdydz + qdtdxdz rdtdxdy One may propose the following generalization of Maxwell s Equations: ( M) δφ = j, dφ = κ Of course, one must first set the Continuity Equations: δj =0, dκ = The Dirac Operator (Incomplete) 36 The sixteen dimensional algebra F introduced in article 4 proves to be an alter ego of the Dirac Algebra and the operators d and δ combine to define the Dirac Operator
AE/ME 339. Computational Fluid Dynamics (CFD) K. M. Isaac. Momentum equation. Computational Fluid Dynamics (AE/ME 339) MAEEM Dept.
 AE/ME 339 Computational Fluid Dynamics (CFD) 9//005 Topic7_NS_ F0 1 Momentum equation 9//005 Topic7_NS_ F0 1 Consider the moving fluid element model shown in Figure.b Basis is Newton s nd Law which says
AE/ME 339 Computational Fluid Dynamics (CFD) 9//005 Topic7_NS_ F0 1 Momentum equation 9//005 Topic7_NS_ F0 1 Consider the moving fluid element model shown in Figure.b Basis is Newton s nd Law which says
SUPPLEMENTARY READING FOR MATH 53: DIFFERENTIAL FORMS AND THE GENERAL STOKES FORMULA
 SUPPLEMENTARY READING FOR MATH 53: DIFFERENTIAL FORMS AND THE GENERAL STOKES FORMULA EDWARD FRENKEL, UC BERKELEY The purpose of these notes is to outline briefly a general formalism which allows for a
SUPPLEMENTARY READING FOR MATH 53: DIFFERENTIAL FORMS AND THE GENERAL STOKES FORMULA EDWARD FRENKEL, UC BERKELEY The purpose of these notes is to outline briefly a general formalism which allows for a
AE/ME 339. K. M. Isaac. 9/22/2005 Topic 6 FluidFlowEquations_Introduction. Computational Fluid Dynamics (AE/ME 339) MAEEM Dept.
 AE/ME 339 Computational Fluid Dynamics (CFD) 1...in the phrase computational fluid dynamics the word computational is simply an adjective to fluid dynamics.... -John D. Anderson 2 1 Equations of Fluid
AE/ME 339 Computational Fluid Dynamics (CFD) 1...in the phrase computational fluid dynamics the word computational is simply an adjective to fluid dynamics.... -John D. Anderson 2 1 Equations of Fluid
Part 8. Differential Forms. Overview. Contents. 1 Introduction to Differential Forms
 Part 8 Differential Forms Printed version of the lecture Differential Geometry on 25. September 2009 Tommy R. Jensen, Department of Mathematics, KNU 8.1 Overview Contents 1 Introduction to Differential
Part 8 Differential Forms Printed version of the lecture Differential Geometry on 25. September 2009 Tommy R. Jensen, Department of Mathematics, KNU 8.1 Overview Contents 1 Introduction to Differential
Caltech Ph106 Fall 2001
 Caltech h106 Fall 2001 ath for physicists: differential forms Disclaimer: this is a first draft, so a few signs might be off. 1 Basic properties Differential forms come up in various parts of theoretical
Caltech h106 Fall 2001 ath for physicists: differential forms Disclaimer: this is a first draft, so a few signs might be off. 1 Basic properties Differential forms come up in various parts of theoretical
Solutions of M3-4A16 Assessed Problems # 3 [#1] Exercises in exterior calculus operations
![Solutions of M3-4A16 Assessed Problems # 3 [#1] Exercises in exterior calculus operations Solutions of M3-4A16 Assessed Problems # 3 [#1] Exercises in exterior calculus operations](/thumbs/87/96222240.jpg) D. D. Holm Solutions to M3-4A16 Assessed Problems # 3 15 Dec 2010 1 Solutions of M3-4A16 Assessed Problems # 3 [#1] Exercises in exterior calculus operations Vector notation for differential basis elements:
D. D. Holm Solutions to M3-4A16 Assessed Problems # 3 15 Dec 2010 1 Solutions of M3-4A16 Assessed Problems # 3 [#1] Exercises in exterior calculus operations Vector notation for differential basis elements:
APPM 2350 Final Exam points Monday December 17, 7:30am 10am, 2018
 APPM 2 Final Exam 28 points Monday December 7, 7:am am, 28 ON THE FONT OF YOU BLUEBOOK write: () your name, (2) your student ID number, () lecture section/time (4) your instructor s name, and () a grading
APPM 2 Final Exam 28 points Monday December 7, 7:am am, 28 ON THE FONT OF YOU BLUEBOOK write: () your name, (2) your student ID number, () lecture section/time (4) your instructor s name, and () a grading
3. The Theorems of Green and Stokes
 3. The Theorems of Green and tokes Consider a 1-form ω = P (x, y)dx + Q(x, y)dy on the rectangle R = [a, b] [c, d], which consists of points (x, y) satisfying a x b and c y d. The boundary R of R have
3. The Theorems of Green and tokes Consider a 1-form ω = P (x, y)dx + Q(x, y)dy on the rectangle R = [a, b] [c, d], which consists of points (x, y) satisfying a x b and c y d. The boundary R of R have
Vacuum Spacetimes with a Constant Weyl Eigenvalue
 Vacuum Spacetimes with a Constant Weyl Eigenvalue Alan Barnes School of Engineering and Applied Science Aston University, Birmingham UK Gent Meeting, Tuesday 8th April 2014 1/28 The Problems Vacuum spacetimes
Vacuum Spacetimes with a Constant Weyl Eigenvalue Alan Barnes School of Engineering and Applied Science Aston University, Birmingham UK Gent Meeting, Tuesday 8th April 2014 1/28 The Problems Vacuum spacetimes
Stochastic Calculus. Kevin Sinclair. August 2, 2016
 Stochastic Calculus Kevin Sinclair August, 16 1 Background Suppose we have a Brownian motion W. This is a process, and the value of W at a particular time T (which we write W T ) is a normally distributed
Stochastic Calculus Kevin Sinclair August, 16 1 Background Suppose we have a Brownian motion W. This is a process, and the value of W at a particular time T (which we write W T ) is a normally distributed
Electromagnetic Wave Propagation Lecture 1: Maxwell s equations
 Electromagnetic Wave Propagation Lecture 1: Maxwell s equations Daniel Sjöberg Department of Electrical and Information Technology September 2, 2014 Outline 1 Maxwell s equations 2 Vector analysis 3 Boundary
Electromagnetic Wave Propagation Lecture 1: Maxwell s equations Daniel Sjöberg Department of Electrical and Information Technology September 2, 2014 Outline 1 Maxwell s equations 2 Vector analysis 3 Boundary
Hertz potentials in curvilinear coordinates
 Hertz potentials in curvilinear coordinates Jeff Bouas Texas A&M University July 9, 2010 Quantum Vacuum Workshop Jeff Bouas (Texas A&M University) Hertz potentials in curvilinear coordinates July 9, 2010
Hertz potentials in curvilinear coordinates Jeff Bouas Texas A&M University July 9, 2010 Quantum Vacuum Workshop Jeff Bouas (Texas A&M University) Hertz potentials in curvilinear coordinates July 9, 2010
NOTES ON DIFFERENTIAL FORMS. PART 1: FORMS ON R n
 NOTES ON DIFFERENTIAL FORMS. PART 1: FORMS ON R n 1. What is a form? Since we re not following the development in Guillemin and Pollack, I d better write up an alternate approach. In this approach, we
NOTES ON DIFFERENTIAL FORMS. PART 1: FORMS ON R n 1. What is a form? Since we re not following the development in Guillemin and Pollack, I d better write up an alternate approach. In this approach, we
Advanced Electrodynamics Exercise 11 Guides
 Advanced Electrodynamics Exercise 11 Guides Here we will calculate in a very general manner the modes of light in a waveguide with perfect conductor boundary-conditions. Our derivations are widely independent
Advanced Electrodynamics Exercise 11 Guides Here we will calculate in a very general manner the modes of light in a waveguide with perfect conductor boundary-conditions. Our derivations are widely independent
Divergence Theorem and Its Application in Characterizing
 Divergence Theorem and Its Application in Characterizing Fluid Flow Let v be the velocity of flow of a fluid element and ρ(x, y, z, t) be the mass density of fluid at a point (x, y, z) at time t. Thus,
Divergence Theorem and Its Application in Characterizing Fluid Flow Let v be the velocity of flow of a fluid element and ρ(x, y, z, t) be the mass density of fluid at a point (x, y, z) at time t. Thus,
ENERGY IN ELECTROSTATICS
 ENERGY IN ELECTROSTATICS We now turn to the question of energy in electrostatics. The first question to consider is whether or not the force is conservative. You will recall from last semester that a conservative
ENERGY IN ELECTROSTATICS We now turn to the question of energy in electrostatics. The first question to consider is whether or not the force is conservative. You will recall from last semester that a conservative
Maxwell s equations in Carnot groups
 Maxwell s equations in Carnot groups B. Franchi (U. Bologna) INDAM Meeting on Geometric Control and sub-riemannian Geometry Cortona, May 21-25, 2012 in honor of Andrey Agrachev s 60th birthday Researches
Maxwell s equations in Carnot groups B. Franchi (U. Bologna) INDAM Meeting on Geometric Control and sub-riemannian Geometry Cortona, May 21-25, 2012 in honor of Andrey Agrachev s 60th birthday Researches
New Transformation Equations and the Electric Field Four-vector
 New Transformation Equations and the Electric Field Four-vector Copyright c 1999 2008 David E. Rutherford All Rights Reserved E-mail: drutherford@softcom.net http://www.softcom.net/users/der555/newtransform.pdf
New Transformation Equations and the Electric Field Four-vector Copyright c 1999 2008 David E. Rutherford All Rights Reserved E-mail: drutherford@softcom.net http://www.softcom.net/users/der555/newtransform.pdf
Chapter 1. Vector Analysis
 Chapter 1. Vector Analysis Hayt; 8/31/2009; 1-1 1.1 Scalars and Vectors Scalar : Vector: A quantity represented by a single real number Distance, time, temperature, voltage, etc Magnitude and direction
Chapter 1. Vector Analysis Hayt; 8/31/2009; 1-1 1.1 Scalars and Vectors Scalar : Vector: A quantity represented by a single real number Distance, time, temperature, voltage, etc Magnitude and direction
GEOMETRICAL TOOLS FOR PDES ON A SURFACE WITH ROTATING SHALLOW WATER EQUATIONS ON A SPHERE
 GEOETRICAL TOOLS FOR PDES ON A SURFACE WITH ROTATING SHALLOW WATER EQUATIONS ON A SPHERE BIN CHENG Abstract. This is an excerpt from my paper with A. ahalov [1]. PDE theories with Riemannian geometry are
GEOETRICAL TOOLS FOR PDES ON A SURFACE WITH ROTATING SHALLOW WATER EQUATIONS ON A SPHERE BIN CHENG Abstract. This is an excerpt from my paper with A. ahalov [1]. PDE theories with Riemannian geometry are
Special Theory of Relativity
 June 17, 2008 1 1 J.D.Jackson, Classical Electrodynamics, 3rd Edition, Chapter 11 Introduction Einstein s theory of special relativity is based on the assumption (which might be a deep-rooted superstition
June 17, 2008 1 1 J.D.Jackson, Classical Electrodynamics, 3rd Edition, Chapter 11 Introduction Einstein s theory of special relativity is based on the assumption (which might be a deep-rooted superstition
examples of equations: what and why intrinsic view, physical origin, probability, geometry
 Lecture 1 Introduction examples of equations: what and why intrinsic view, physical origin, probability, geometry Intrinsic/abstract F ( x, Du, D u, D 3 u, = 0 Recall algebraic equations such as linear
Lecture 1 Introduction examples of equations: what and why intrinsic view, physical origin, probability, geometry Intrinsic/abstract F ( x, Du, D u, D 3 u, = 0 Recall algebraic equations such as linear
Physics 4183 Electricity and Magnetism II. Covariant Formulation of Electrodynamics-1
 Physics 4183 Electricity and Magnetism II Covariant Formulation of Electrodynamics 1 Introduction Having briefly discussed the origins of relativity, the Lorentz transformations, 4-vectors and tensors,
Physics 4183 Electricity and Magnetism II Covariant Formulation of Electrodynamics 1 Introduction Having briefly discussed the origins of relativity, the Lorentz transformations, 4-vectors and tensors,
Solution to Problem Set 4
 Solution to Problem Set 4 October 017 Pb 1. 0 pts. There are many ways of doing this problem but the easiest would be â α =â ˆD(α) 0 = â exp ( αâ α â ) 0 = â e α α/ e αâ 0 = α + α e α α/ e αâ 0 = α + α
Solution to Problem Set 4 October 017 Pb 1. 0 pts. There are many ways of doing this problem but the easiest would be â α =â ˆD(α) 0 = â exp ( αâ α â ) 0 = â e α α/ e αâ 0 = α + α e α α/ e αâ 0 = α + α
New Transformation Equations and the Electric Field Four-vector
 New Transformation Equations and the Electric Field Four-vector c Copyright 1999 2003 David E. Rutherford All Rights Reserved E-mail: drutherford@softcom.net http://www.softcom.net/users/der555/newtransform.pdf
New Transformation Equations and the Electric Field Four-vector c Copyright 1999 2003 David E. Rutherford All Rights Reserved E-mail: drutherford@softcom.net http://www.softcom.net/users/der555/newtransform.pdf
Dierential geometry for Physicists
 Dierential geometry for Physicists (What we discussed in the course of lectures) Marián Fecko Comenius University, Bratislava Syllabus of lectures delivered at University of Regensburg in June and July
Dierential geometry for Physicists (What we discussed in the course of lectures) Marián Fecko Comenius University, Bratislava Syllabus of lectures delivered at University of Regensburg in June and July
K N O T S A N D E L E C T R O M A G N E T I S M
 a.j.j.m. de klerk K N O T S A N D E L E C T R O M A G N E T I S M bachelor s thesis supervised by dr. R.I. van der Veen, dr. J.W. Dalhuisen, and prof. dr. D. Bouwmeester 25 june 2016 Mathematical Institute
a.j.j.m. de klerk K N O T S A N D E L E C T R O M A G N E T I S M bachelor s thesis supervised by dr. R.I. van der Veen, dr. J.W. Dalhuisen, and prof. dr. D. Bouwmeester 25 june 2016 Mathematical Institute
Math 304, Differential Forms, Lecture 1 May 26, 2011
 Math 304, Differential Forms, Lecture 1 May 26, 2011 Differential forms were developed and applied to vector fields in a decisive way by the French Mathematician Élie artan (1869 1951) in the first quarter
Math 304, Differential Forms, Lecture 1 May 26, 2011 Differential forms were developed and applied to vector fields in a decisive way by the French Mathematician Élie artan (1869 1951) in the first quarter
Electromagnetic. G. A. Krafft Jefferson Lab Jefferson Lab Professor of Physics Old Dominion University TAADI Electromagnetic Theory
 TAAD1 Electromagnetic Theory G. A. Krafft Jefferson Lab Jefferson Lab Professor of Physics Old Dominion University 8-31-12 Classical Electrodynamics A main physics discovery of the last half of the 2 th
TAAD1 Electromagnetic Theory G. A. Krafft Jefferson Lab Jefferson Lab Professor of Physics Old Dominion University 8-31-12 Classical Electrodynamics A main physics discovery of the last half of the 2 th
2 Feynman rules, decay widths and cross sections
 2 Feynman rules, decay widths and cross sections 2.1 Feynman rules Normalization In non-relativistic quantum mechanics, wave functions of free particles are normalized so that there is one particle in
2 Feynman rules, decay widths and cross sections 2.1 Feynman rules Normalization In non-relativistic quantum mechanics, wave functions of free particles are normalized so that there is one particle in
Electromagnetic Waves Retarded potentials 2. Energy and the Poynting vector 3. Wave equations for E and B 4. Plane EM waves in free space
 Electromagnetic Waves 1 1. Retarded potentials 2. Energy and the Poynting vector 3. Wave equations for E and B 4. Plane EM waves in free space 1 Retarded Potentials For volume charge & current = 1 4πε
Electromagnetic Waves 1 1. Retarded potentials 2. Energy and the Poynting vector 3. Wave equations for E and B 4. Plane EM waves in free space 1 Retarded Potentials For volume charge & current = 1 4πε
Euler E842: An Introduction to Natural Science, Establishing the Fundamentals..., from his Opera Postuma. Translated from German by E.
 95 On the laws of equilibrium in liquid substances. 147. A liquid substance, the particles of which are not subject to any forces other than the pressure due to adjacent particles, can, whatever it density
95 On the laws of equilibrium in liquid substances. 147. A liquid substance, the particles of which are not subject to any forces other than the pressure due to adjacent particles, can, whatever it density
Introduction to supersymmetry
 Introduction to supersymmetry Vicente Cortés Institut Élie Cartan Université Henri Poincaré - Nancy I cortes@iecn.u-nancy.fr August 31, 2005 Outline of the lecture The free supersymmetric scalar field
Introduction to supersymmetry Vicente Cortés Institut Élie Cartan Université Henri Poincaré - Nancy I cortes@iecn.u-nancy.fr August 31, 2005 Outline of the lecture The free supersymmetric scalar field
Exercise 1 (Formula for connection 1-forms) Using the first structure equation, show that
 1 Stokes s Theorem Let D R 2 be a connected compact smooth domain, so that D is a smooth embedded circle. Given a smooth function f : D R, define fdx dy fdxdy, D where the left-hand side is the integral
1 Stokes s Theorem Let D R 2 be a connected compact smooth domain, so that D is a smooth embedded circle. Given a smooth function f : D R, define fdx dy fdxdy, D where the left-hand side is the integral
Chemistry. Lecture 10 Maxwell Relations. NC State University
 Chemistry Lecture 10 Maxwell Relations NC State University Thermodynamic state functions expressed in differential form We have seen that the internal energy is conserved and depends on mechanical (dw)
Chemistry Lecture 10 Maxwell Relations NC State University Thermodynamic state functions expressed in differential form We have seen that the internal energy is conserved and depends on mechanical (dw)
A Practical Introduction to Differential Forms. Alexia E. Schulz. William C. Schulz
 A Practical Introduction to Differential Forms Alexia E. Schulz and William C. Schulz December 2, 204 Transgalactic Publishing Company Flagstaff, Vienna, Cosmopolis ii c 202 by Alexia E. Schulz and William
A Practical Introduction to Differential Forms Alexia E. Schulz and William C. Schulz December 2, 204 Transgalactic Publishing Company Flagstaff, Vienna, Cosmopolis ii c 202 by Alexia E. Schulz and William
Introduction. Statistical physics: microscopic foundation of thermodynamics degrees of freedom 2 3 state variables!
 Introduction Thermodynamics: phenomenological description of equilibrium bulk properties of matter in terms of only a few state variables and thermodynamical laws. Statistical physics: microscopic foundation
Introduction Thermodynamics: phenomenological description of equilibrium bulk properties of matter in terms of only a few state variables and thermodynamical laws. Statistical physics: microscopic foundation
611: Electromagnetic Theory II
 611: Electromagnetic Theory II CONTENTS Special relativity; Lorentz covariance of Maxwell equations Scalar and vector potentials, and gauge invariance Relativistic motion of charged particles Action principle
611: Electromagnetic Theory II CONTENTS Special relativity; Lorentz covariance of Maxwell equations Scalar and vector potentials, and gauge invariance Relativistic motion of charged particles Action principle
The heat equation in time dependent domains with Neumann boundary conditions
 The heat equation in time dependent domains with Neumann boundary conditions Chris Burdzy Zhen-Qing Chen John Sylvester Abstract We study the heat equation in domains in R n with insulated fast moving
The heat equation in time dependent domains with Neumann boundary conditions Chris Burdzy Zhen-Qing Chen John Sylvester Abstract We study the heat equation in domains in R n with insulated fast moving
Module 2: Governing Equations and Hypersonic Relations
 Module 2: Governing Equations and Hypersonic Relations Lecture -2: Mass Conservation Equation 2.1 The Differential Equation for mass conservation: Let consider an infinitely small elemental control volume
Module 2: Governing Equations and Hypersonic Relations Lecture -2: Mass Conservation Equation 2.1 The Differential Equation for mass conservation: Let consider an infinitely small elemental control volume
Mathematical Concepts & Notation
 Mathematical Concepts & Notation Appendix A: Notation x, δx: a small change in x t : the partial derivative with respect to t holding the other variables fixed d : the time derivative of a quantity that
Mathematical Concepts & Notation Appendix A: Notation x, δx: a small change in x t : the partial derivative with respect to t holding the other variables fixed d : the time derivative of a quantity that
Gravitation: Tensor Calculus
 An Introduction to General Relativity Center for Relativistic Astrophysics School of Physics Georgia Institute of Technology Notes based on textbook: Spacetime and Geometry by S.M. Carroll Spring 2013
An Introduction to General Relativity Center for Relativistic Astrophysics School of Physics Georgia Institute of Technology Notes based on textbook: Spacetime and Geometry by S.M. Carroll Spring 2013
Jim Lambers MAT 280 Summer Semester Practice Final Exam Solution. dy + xz dz = x(t)y(t) dt. t 3 (4t 3 ) + e t2 (2t) + t 7 (3t 2 ) dt
 Jim Lambers MAT 28 ummer emester 212-1 Practice Final Exam olution 1. Evaluate the line integral xy dx + e y dy + xz dz, where is given by r(t) t 4, t 2, t, t 1. olution From r (t) 4t, 2t, t 2, we obtain
Jim Lambers MAT 28 ummer emester 212-1 Practice Final Exam olution 1. Evaluate the line integral xy dx + e y dy + xz dz, where is given by r(t) t 4, t 2, t, t 1. olution From r (t) 4t, 2t, t 2, we obtain
Electromagnetism HW 1 math review
 Electromagnetism HW math review Problems -5 due Mon 7th Sep, 6- due Mon 4th Sep Exercise. The Levi-Civita symbol, ɛ ijk, also known as the completely antisymmetric rank-3 tensor, has the following properties:
Electromagnetism HW math review Problems -5 due Mon 7th Sep, 6- due Mon 4th Sep Exercise. The Levi-Civita symbol, ɛ ijk, also known as the completely antisymmetric rank-3 tensor, has the following properties:
Chapter 1 Mathematical Foundations
 Computational Electromagnetics; Chapter 1 1 Chapter 1 Mathematical Foundations 1.1 Maxwell s Equations Electromagnetic phenomena can be described by the electric field E, the electric induction D, the
Computational Electromagnetics; Chapter 1 1 Chapter 1 Mathematical Foundations 1.1 Maxwell s Equations Electromagnetic phenomena can be described by the electric field E, the electric induction D, the
Section 2. Basic formulas and identities in Riemannian geometry
 Section 2. Basic formulas and identities in Riemannian geometry Weimin Sheng and 1. Bianchi identities The first and second Bianchi identities are R ijkl + R iklj + R iljk = 0 R ijkl,m + R ijlm,k + R ijmk,l
Section 2. Basic formulas and identities in Riemannian geometry Weimin Sheng and 1. Bianchi identities The first and second Bianchi identities are R ijkl + R iklj + R iljk = 0 R ijkl,m + R ijlm,k + R ijmk,l
An Undergraduate View of a Second Year Course in Physics
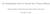 An Undergraduate View of a Second Year Course in Physics Josuan Calderon, Sruthi Narayanan, Farid Salazar, Pedro Soto November 1, 2015 Contents Foreword 4 Preface 7 1 Electromagnetism and the Wave Equation
An Undergraduate View of a Second Year Course in Physics Josuan Calderon, Sruthi Narayanan, Farid Salazar, Pedro Soto November 1, 2015 Contents Foreword 4 Preface 7 1 Electromagnetism and the Wave Equation
Lecturer: Bengt E W Nilsson
 2009 05 07 Lecturer: Bengt E W Nilsson From the previous lecture: Example 3 Figure 1. Some x µ s will have ND or DN boundary condition half integer mode expansions! Recall also: Half integer mode expansions
2009 05 07 Lecturer: Bengt E W Nilsson From the previous lecture: Example 3 Figure 1. Some x µ s will have ND or DN boundary condition half integer mode expansions! Recall also: Half integer mode expansions
The integrating factor method (Sect. 1.1)
 The integrating factor method (Sect. 1.1) Overview of differential equations. Linear Ordinary Differential Equations. The integrating factor method. Constant coefficients. The Initial Value Problem. Overview
The integrating factor method (Sect. 1.1) Overview of differential equations. Linear Ordinary Differential Equations. The integrating factor method. Constant coefficients. The Initial Value Problem. Overview
Covariant electrodynamics
 Lecture 9 Covariant electrodynamics WS2010/11: Introduction to Nuclear and Particle Physics 1 Consider Lorentz transformations pseudo-orthogonal transformations in 4-dimentional vector space (Minkowski
Lecture 9 Covariant electrodynamics WS2010/11: Introduction to Nuclear and Particle Physics 1 Consider Lorentz transformations pseudo-orthogonal transformations in 4-dimentional vector space (Minkowski
ORDINARY DIFFERENTIAL EQUATIONS
 ORDINARY DIFFERENTIAL EQUATIONS GABRIEL NAGY Mathematics Department, Michigan State University, East Lansing, MI, 48824. JANUARY 3, 25 Summary. This is an introduction to ordinary differential equations.
ORDINARY DIFFERENTIAL EQUATIONS GABRIEL NAGY Mathematics Department, Michigan State University, East Lansing, MI, 48824. JANUARY 3, 25 Summary. This is an introduction to ordinary differential equations.
Worked Examples Set 2
 Worked Examples Set 2 Q.1. Application of Maxwell s eqns. [Griffiths Problem 7.42] In a perfect conductor the conductivity σ is infinite, so from Ohm s law J = σe, E = 0. Any net charge must be on the
Worked Examples Set 2 Q.1. Application of Maxwell s eqns. [Griffiths Problem 7.42] In a perfect conductor the conductivity σ is infinite, so from Ohm s law J = σe, E = 0. Any net charge must be on the
Single Particle Motion
 Single Particle Motion C ontents Uniform E and B E = - guiding centers Definition of guiding center E gravitation Non Uniform B 'grad B' drift, B B Curvature drift Grad -B drift, B B invariance of µ. Magnetic
Single Particle Motion C ontents Uniform E and B E = - guiding centers Definition of guiding center E gravitation Non Uniform B 'grad B' drift, B B Curvature drift Grad -B drift, B B invariance of µ. Magnetic
Solving Einstein s Equation Numerically III
 Solving Einstein s Equation Numerically III Lee Lindblom Center for Astrophysics and Space Sciences University of California at San Diego Mathematical Sciences Center Lecture Series Tsinghua University
Solving Einstein s Equation Numerically III Lee Lindblom Center for Astrophysics and Space Sciences University of California at San Diego Mathematical Sciences Center Lecture Series Tsinghua University
Introduction and Review Lecture 1
 Introduction and Review Lecture 1 1 Fields 1.1 Introduction This class deals with classical electrodynamics. Classical electrodynamics is the exposition of electromagnetic interactions between the develoment
Introduction and Review Lecture 1 1 Fields 1.1 Introduction This class deals with classical electrodynamics. Classical electrodynamics is the exposition of electromagnetic interactions between the develoment
Covariant Formulation of Electrodynamics
 Chapter 7. Covariant Formulation of Electrodynamics Notes: Most of the material presented in this chapter is taken from Jackson, Chap. 11, and Rybicki and Lightman, Chap. 4. Starting with this chapter,
Chapter 7. Covariant Formulation of Electrodynamics Notes: Most of the material presented in this chapter is taken from Jackson, Chap. 11, and Rybicki and Lightman, Chap. 4. Starting with this chapter,
Exact Solutions of the Einstein Equations
 Notes from phz 6607, Special and General Relativity University of Florida, Fall 2004, Detweiler Exact Solutions of the Einstein Equations These notes are not a substitute in any manner for class lectures.
Notes from phz 6607, Special and General Relativity University of Florida, Fall 2004, Detweiler Exact Solutions of the Einstein Equations These notes are not a substitute in any manner for class lectures.
Radiation Integrals and Auxiliary Potential Functions
 Radiation Integrals and Auxiliary Potential Functions Ranga Rodrigo June 23, 2010 Lecture notes are fully based on Balanis [?]. Some diagrams and text are directly from the books. Contents 1 The Vector
Radiation Integrals and Auxiliary Potential Functions Ranga Rodrigo June 23, 2010 Lecture notes are fully based on Balanis [?]. Some diagrams and text are directly from the books. Contents 1 The Vector
Joel A. Shapiro January 20, 2011
 Joel A. shapiro@physics.rutgers.edu January 20, 2011 Course Information Instructor: Joel Serin 325 5-5500 X 3886, shapiro@physics Book: Jackson: Classical Electrodynamics (3rd Ed.) Web home page: www.physics.rutgers.edu/grad/504
Joel A. shapiro@physics.rutgers.edu January 20, 2011 Course Information Instructor: Joel Serin 325 5-5500 X 3886, shapiro@physics Book: Jackson: Classical Electrodynamics (3rd Ed.) Web home page: www.physics.rutgers.edu/grad/504
Maxwell s equations. based on S-54. electric field charge density. current density
 Maxwell s equations based on S-54 Our next task is to find a quantum field theory description of spin-1 particles, e.g. photons. Classical electrodynamics is governed by Maxwell s equations: electric field
Maxwell s equations based on S-54 Our next task is to find a quantum field theory description of spin-1 particles, e.g. photons. Classical electrodynamics is governed by Maxwell s equations: electric field
Metrics and Curvature
 Metrics and Curvature How to measure curvature? Metrics Euclidian/Minkowski Curved spaces General 4 dimensional space Cosmological principle Homogeneity and isotropy: evidence Robertson-Walker metrics
Metrics and Curvature How to measure curvature? Metrics Euclidian/Minkowski Curved spaces General 4 dimensional space Cosmological principle Homogeneity and isotropy: evidence Robertson-Walker metrics
CANONICAL EQUATIONS. Application to the study of the equilibrium of flexible filaments and brachistochrone curves. By A.
 Équations canoniques. Application a la recherche de l équilibre des fils flexibles et des courbes brachystochrones, Mem. Acad. Sci de Toulouse (8) 7 (885), 545-570. CANONICAL EQUATIONS Application to the
Équations canoniques. Application a la recherche de l équilibre des fils flexibles et des courbes brachystochrones, Mem. Acad. Sci de Toulouse (8) 7 (885), 545-570. CANONICAL EQUATIONS Application to the
Coordinate systems and vectors in three spatial dimensions
 PHYS2796 Introduction to Modern Physics (Spring 2015) Notes on Mathematics Prerequisites Jim Napolitano, Department of Physics, Temple University January 7, 2015 This is a brief summary of material on
PHYS2796 Introduction to Modern Physics (Spring 2015) Notes on Mathematics Prerequisites Jim Napolitano, Department of Physics, Temple University January 7, 2015 This is a brief summary of material on
Hertz Potentials in Cylindrical Coordinates
 Introduction 26 June 2009 Motivation Introduction Motivation Differential Forms and the Hodge Star Motivation 1 To extend Hertz Potentials to general curvilinear coordinates. 2 To explore the usefulness
Introduction 26 June 2009 Motivation Introduction Motivation Differential Forms and the Hodge Star Motivation 1 To extend Hertz Potentials to general curvilinear coordinates. 2 To explore the usefulness
Lecture No 1 Introduction to Diffusion equations The heat equat
 Lecture No 1 Introduction to Diffusion equations The heat equation Columbia University IAS summer program June, 2009 Outline of the lectures We will discuss some basic models of diffusion equations and
Lecture No 1 Introduction to Diffusion equations The heat equation Columbia University IAS summer program June, 2009 Outline of the lectures We will discuss some basic models of diffusion equations and
Global properties of solutions to the Einstein-matter equations
 Global properties of solutions to the Einstein-matter equations Makoto Narita Okinawa National College of Technology 12/Nov./2012 @JGRG22, Tokyo Singularity theorems and two conjectures Theorem 1 (Penrose)
Global properties of solutions to the Einstein-matter equations Makoto Narita Okinawa National College of Technology 12/Nov./2012 @JGRG22, Tokyo Singularity theorems and two conjectures Theorem 1 (Penrose)
NOTES ON DIFFERENTIAL FORMS. PART 5: DE RHAM COHOMOLOGY
 NOTES ON DIFFERENTIAL FORMS. PART 5: DE RHAM COHOMOLOGY 1. Closed and exact forms Let X be a n-manifold (not necessarily oriented), and let α be a k-form on X. We say that α is closed if dα = 0 and say
NOTES ON DIFFERENTIAL FORMS. PART 5: DE RHAM COHOMOLOGY 1. Closed and exact forms Let X be a n-manifold (not necessarily oriented), and let α be a k-form on X. We say that α is closed if dα = 0 and say
Lecture 9: RR-sector and D-branes
 Lecture 9: RR-sector and D-branes José D. Edelstein University of Santiago de Compostela STRING THEORY Santiago de Compostela, March 6, 2013 José D. Edelstein (USC) Lecture 9: RR-sector and D-branes 6-mar-2013
Lecture 9: RR-sector and D-branes José D. Edelstein University of Santiago de Compostela STRING THEORY Santiago de Compostela, March 6, 2013 José D. Edelstein (USC) Lecture 9: RR-sector and D-branes 6-mar-2013
Math 225B: Differential Geometry, Final
 Math 225B: Differential Geometry, Final Ian Coley March 5, 204 Problem Spring 20,. Show that if X is a smooth vector field on a (smooth) manifold of dimension n and if X p is nonzero for some point of
Math 225B: Differential Geometry, Final Ian Coley March 5, 204 Problem Spring 20,. Show that if X is a smooth vector field on a (smooth) manifold of dimension n and if X p is nonzero for some point of
Solitons and point particles
 Solitons and point particles Martin Speight University of Leeds July 28, 2009 What are topological solitons? Smooth, spatially localized solutions of nonlinear relativistic classical field theories Stable;
Solitons and point particles Martin Speight University of Leeds July 28, 2009 What are topological solitons? Smooth, spatially localized solutions of nonlinear relativistic classical field theories Stable;
E & M Qualifier. August 16, To insure that the your work is graded correctly you MUST: 5. number every page starting with 1 for each problem,
 E & M Qualifier August 16, 2012 To insure that the your work is graded correctly you MUST: 1. use only the blank answer paper provided, 2. write only on one side of the page, 3. put your alias on every
E & M Qualifier August 16, 2012 To insure that the your work is graded correctly you MUST: 1. use only the blank answer paper provided, 2. write only on one side of the page, 3. put your alias on every
Lecturer: Bengt E W Nilsson
 9 3 19 Lecturer: Bengt E W Nilsson Last time: Relativistic physics in any dimension. Light-cone coordinates, light-cone stuff. Extra dimensions compact extra dimensions (here we talked about fundamental
9 3 19 Lecturer: Bengt E W Nilsson Last time: Relativistic physics in any dimension. Light-cone coordinates, light-cone stuff. Extra dimensions compact extra dimensions (here we talked about fundamental
Numerical Heat and Mass Transfer
 Master degree in Mechanical Engineering Numerical Heat and Mass Transfer 02-Transient Conduction Fausto Arpino f.arpino@unicas.it Outline Introduction Conduction ü Heat conduction equation ü Boundary conditions
Master degree in Mechanical Engineering Numerical Heat and Mass Transfer 02-Transient Conduction Fausto Arpino f.arpino@unicas.it Outline Introduction Conduction ü Heat conduction equation ü Boundary conditions
MULTIVARIABLE INTEGRATION
 MULTIVARIABLE INTEGRATION (PLANE & CYLINDRICAL POLAR COORDINATES) PLANE POLAR COORDINATES Question 1 The finite region on the x-y plane satisfies 1 x + y 4, y 0. Find, in terms of π, the value of I. I
MULTIVARIABLE INTEGRATION (PLANE & CYLINDRICAL POLAR COORDINATES) PLANE POLAR COORDINATES Question 1 The finite region on the x-y plane satisfies 1 x + y 4, y 0. Find, in terms of π, the value of I. I
Relativistic Quantum Mechanics
 Physics 342 Lecture 34 Relativistic Quantum Mechanics Lecture 34 Physics 342 Quantum Mechanics I Wednesday, April 30th, 2008 We know that the Schrödinger equation logically replaces Newton s second law
Physics 342 Lecture 34 Relativistic Quantum Mechanics Lecture 34 Physics 342 Quantum Mechanics I Wednesday, April 30th, 2008 We know that the Schrödinger equation logically replaces Newton s second law
Thermodynamic Variables and Relations
 MME 231: Lecture 10 Thermodynamic Variables and Relations A. K. M. B. Rashid Professor, Department of MME BUET, Dhaka Today s Topics Thermodynamic relations derived from the Laws of Thermodynamics Definitions
MME 231: Lecture 10 Thermodynamic Variables and Relations A. K. M. B. Rashid Professor, Department of MME BUET, Dhaka Today s Topics Thermodynamic relations derived from the Laws of Thermodynamics Definitions
1 The postulates of quantum mechanics
 1 The postulates of quantum mechanics The postulates of quantum mechanics were derived after a long process of trial and error. These postulates provide a connection between the physical world and the
1 The postulates of quantum mechanics The postulates of quantum mechanics were derived after a long process of trial and error. These postulates provide a connection between the physical world and the
Black Hole Universe with Rotation Chan Park KAIST
 Black Hole Universe with Rotation 2016.01.02. Chan Park KAIST Motivation FLRW cosmology Highly symmetric assumption : spatial homogeneity and isotropy Metric ds 2 = dt 2 + a 2 t a t : scale factor Friedmann
Black Hole Universe with Rotation 2016.01.02. Chan Park KAIST Motivation FLRW cosmology Highly symmetric assumption : spatial homogeneity and isotropy Metric ds 2 = dt 2 + a 2 t a t : scale factor Friedmann
First-Order Ordinary Differntial Equations: Classification and Linear Equations. David Levermore Department of Mathematics University of Maryland
 First-Order Ordinary Differntial Equations: Classification and Linear Equations David Levermore Department of Mathematics University of Maryland 1 February 2009 These notes cover some of the material that
First-Order Ordinary Differntial Equations: Classification and Linear Equations David Levermore Department of Mathematics University of Maryland 1 February 2009 These notes cover some of the material that
752 Final. April 16, Fadeev Popov Ghosts and Non-Abelian Gauge Fields. Tim Wendler BYU Physics and Astronomy. The standard model Lagrangian
 752 Final April 16, 2010 Tim Wendler BYU Physics and Astronomy Fadeev Popov Ghosts and Non-Abelian Gauge Fields The standard model Lagrangian L SM = L Y M + L W D + L Y u + L H The rst term, the Yang Mills
752 Final April 16, 2010 Tim Wendler BYU Physics and Astronomy Fadeev Popov Ghosts and Non-Abelian Gauge Fields The standard model Lagrangian L SM = L Y M + L W D + L Y u + L H The rst term, the Yang Mills
On the existence of magnetic monopoles
 On the existence of magnetic monopoles Ali R. Hadjesfandiari Department of Mechanical and Aerospace Engineering State University of New York at Buffalo Buffalo, NY 146 USA ah@buffalo.edu September 4, 13
On the existence of magnetic monopoles Ali R. Hadjesfandiari Department of Mechanical and Aerospace Engineering State University of New York at Buffalo Buffalo, NY 146 USA ah@buffalo.edu September 4, 13
1. (a) (5 points) Find the unit tangent and unit normal vectors T and N to the curve. r (t) = 3 cos t, 0, 3 sin t, r ( 3π
 1. a) 5 points) Find the unit tangent and unit normal vectors T and N to the curve at the point P 3, 3π, r t) 3 cos t, 4t, 3 sin t 3 ). b) 5 points) Find curvature of the curve at the point P. olution:
1. a) 5 points) Find the unit tangent and unit normal vectors T and N to the curve at the point P 3, 3π, r t) 3 cos t, 4t, 3 sin t 3 ). b) 5 points) Find curvature of the curve at the point P. olution:
7-7 Multiplying Polynomials
 Example 1: Multiplying Monomials A. (6y 3 )(3y 5 ) (6y 3 )(3y 5 ) (6 3)(y 3 y 5 ) 18y 8 Group factors with like bases together. B. (3mn 2 ) (9m 2 n) Example 1C: Multiplying Monomials Group factors with
Example 1: Multiplying Monomials A. (6y 3 )(3y 5 ) (6y 3 )(3y 5 ) (6 3)(y 3 y 5 ) 18y 8 Group factors with like bases together. B. (3mn 2 ) (9m 2 n) Example 1C: Multiplying Monomials Group factors with
Sec. 1.1: Basics of Vectors
 Sec. 1.1: Basics of Vectors Notation for Euclidean space R n : all points (x 1, x 2,..., x n ) in n-dimensional space. Examples: 1. R 1 : all points on the real number line. 2. R 2 : all points (x 1, x
Sec. 1.1: Basics of Vectors Notation for Euclidean space R n : all points (x 1, x 2,..., x n ) in n-dimensional space. Examples: 1. R 1 : all points on the real number line. 2. R 2 : all points (x 1, x
29.3. Integral Vector Theorems. Introduction. Prerequisites. Learning Outcomes
 Integral ector Theorems 9. Introduction arious theorems exist relating integrals involving vectors. Those involving line, surface and volume integrals are introduced here. They are the multivariable calculus
Integral ector Theorems 9. Introduction arious theorems exist relating integrals involving vectors. Those involving line, surface and volume integrals are introduced here. They are the multivariable calculus
MAS 4156 Lecture Notes Differential Forms
 MAS 4156 Lecture Notes Differentil Forms Definitions Differentil forms re objects tht re defined on mnifolds. For this clss, the only mnifold we will put forms on is R 3. The full definition is: Definition:
MAS 4156 Lecture Notes Differentil Forms Definitions Differentil forms re objects tht re defined on mnifolds. For this clss, the only mnifold we will put forms on is R 3. The full definition is: Definition:
2.4 Parity transformation
 2.4 Parity transformation An extremely simple group is one that has only two elements: {e, P }. Obviously, P 1 = P, so P 2 = e, with e represented by the unit n n matrix in an n- dimensional representation.
2.4 Parity transformation An extremely simple group is one that has only two elements: {e, P }. Obviously, P 1 = P, so P 2 = e, with e represented by the unit n n matrix in an n- dimensional representation.
Summary: Curvilinear Coordinates
 Physics 2460 Electricity and Magnetism I, Fall 2007, Lecture 10 1 Summary: Curvilinear Coordinates 1. Summary of Integral Theorems 2. Generalized Coordinates 3. Cartesian Coordinates: Surfaces of Constant
Physics 2460 Electricity and Magnetism I, Fall 2007, Lecture 10 1 Summary: Curvilinear Coordinates 1. Summary of Integral Theorems 2. Generalized Coordinates 3. Cartesian Coordinates: Surfaces of Constant
Note: Each problem is worth 14 points except numbers 5 and 6 which are 15 points. = 3 2
 Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
arxiv: v2 [physics.gen-ph] 20 Mar 2013
![arxiv: v2 [physics.gen-ph] 20 Mar 2013 arxiv: v2 [physics.gen-ph] 20 Mar 2013](/thumbs/96/127587291.jpg) arxiv:129.3449v2 [physics.gen-ph] 2 Mar 213 Potential Theory in Classical Electrodynamics W. Engelhardt 1, retired from: Max-Planck-Institut für Plasmaphysik, D-85741 Garching, Germany Abstract In Maxwell
arxiv:129.3449v2 [physics.gen-ph] 2 Mar 213 Potential Theory in Classical Electrodynamics W. Engelhardt 1, retired from: Max-Planck-Institut für Plasmaphysik, D-85741 Garching, Germany Abstract In Maxwell
Astronomy 9620a / Physics 9302a - 1st Problem List and Assignment
 Astronomy 9620a / Physics 9302a - st Problem List and Assignment Your solution to problems 4, 7, 3, and 6 has to be handed in on Thursday, Oct. 7, 203.. Prove the following relations (going from the left-
Astronomy 9620a / Physics 9302a - st Problem List and Assignment Your solution to problems 4, 7, 3, and 6 has to be handed in on Thursday, Oct. 7, 203.. Prove the following relations (going from the left-
2.20 Fall 2018 Math Review
 2.20 Fall 2018 Math Review September 10, 2018 These notes are to help you through the math used in this class. This is just a refresher, so if you never learned one of these topics you should look more
2.20 Fall 2018 Math Review September 10, 2018 These notes are to help you through the math used in this class. This is just a refresher, so if you never learned one of these topics you should look more
So far we have derived two electrostatic equations E = 0 (6.2) B = 0 (6.3) which are to be modified due to Faraday s observation,
 Chapter 6 Maxwell Equations 6.1 Maxwell equations So far we have derived two electrostatic equations and two magnetostatics equations E = ρ ɛ 0 (6.1) E = 0 (6.2) B = 0 (6.3) B = µ 0 J (6.4) which are to
Chapter 6 Maxwell Equations 6.1 Maxwell equations So far we have derived two electrostatic equations and two magnetostatics equations E = ρ ɛ 0 (6.1) E = 0 (6.2) B = 0 (6.3) B = µ 0 J (6.4) which are to
3: Mathematics Review
 3: Mathematics Review B. Rouben McMaster University Course EP 4D03/6D03 Nuclear Reactor Analysis (Reactor Physics) 015 Sept.-Dec. 015 September 1 Review of: Table of Contents Co-ordinate systems (Cartesian,
3: Mathematics Review B. Rouben McMaster University Course EP 4D03/6D03 Nuclear Reactor Analysis (Reactor Physics) 015 Sept.-Dec. 015 September 1 Review of: Table of Contents Co-ordinate systems (Cartesian,
Comment about Didactical formulation of the
 Comment about Didactical formulation of the Ampère law Hendrik van Hees Institute for Theoretical Physics, Goethe University Frankfurt, Max-von-Laue-Str. 1, D-60438 Frankfurt, Germany Frankfurt Institute
Comment about Didactical formulation of the Ampère law Hendrik van Hees Institute for Theoretical Physics, Goethe University Frankfurt, Max-von-Laue-Str. 1, D-60438 Frankfurt, Germany Frankfurt Institute
Antenna Theory (Engineering 9816) Course Notes. Winter 2016
 Antenna Theory (Engineering 9816) Course Notes Winter 2016 by E.W. Gill, Ph.D., P.Eng. Unit 1 Electromagnetics Review (Mostly) 1.1 Introduction Antennas act as transducers associated with the region of
Antenna Theory (Engineering 9816) Course Notes Winter 2016 by E.W. Gill, Ph.D., P.Eng. Unit 1 Electromagnetics Review (Mostly) 1.1 Introduction Antennas act as transducers associated with the region of
ALL SPECIAL RELATIVITY EQUATIONS OBTAINED WITH GALILEAN TRANSFORMATION
 ALL SPECIAL RELATIVITY EQUATIONS OBTAINED WITH GALILEAN TRANSFORMATION Sergio Garcia Chimeno Abstract Demonstration how to do the light velocity c it to be the same independently of the velocity of observer
ALL SPECIAL RELATIVITY EQUATIONS OBTAINED WITH GALILEAN TRANSFORMATION Sergio Garcia Chimeno Abstract Demonstration how to do the light velocity c it to be the same independently of the velocity of observer
Physics 209 Fall 2002 Notes 5 Thomas Precession
 Physics 209 Fall 2002 Notes 5 Thomas Precession Jackson s discussion of Thomas precession is based on Thomas s original treatment, and on the later paper by Bargmann, Michel, and Telegdi. The alternative
Physics 209 Fall 2002 Notes 5 Thomas Precession Jackson s discussion of Thomas precession is based on Thomas s original treatment, and on the later paper by Bargmann, Michel, and Telegdi. The alternative
NLControl - package for modelling, analysis and synthesis of nonlinear control systems
 NLControl - package for modelling, analysis and synthesis of nonlinear control systems Maris Tõnso Institute of Cybernetics Tallinn University of Technology Estonia maris@cc.ioc.ee May, 2013 Contents 1
NLControl - package for modelling, analysis and synthesis of nonlinear control systems Maris Tõnso Institute of Cybernetics Tallinn University of Technology Estonia maris@cc.ioc.ee May, 2013 Contents 1
The linear equations can be classificed into the following cases, from easier to more difficult: 1. Linear: u y. u x
 Week 02 : Method of C haracteristics From now on we will stu one by one classical techniques of obtaining solution formulas for PDEs. The first one is the method of characteristics, which is particularly
Week 02 : Method of C haracteristics From now on we will stu one by one classical techniques of obtaining solution formulas for PDEs. The first one is the method of characteristics, which is particularly
