Boundary-Value Problems: Part II
|
|
|
- Scarlett Todd
- 6 years ago
- Views:
Transcription
1 Chapter 3 Boundary-Value Problems: Part II Problem Set #3: 3., 3.3, 3.7 Due Monday March. th 3. Spherical Coordinates Spherical coordinates are used when boundary conditions have spherical symmetry. The Laplace equation in spherical coordinates takes the following form, Φ= r r rφ + sin θ Φ Φ + r sin θ θ θ r sin =. 3. θ φ To use the separation of variables method we can plug in the following ansatz Φr, θ, φ = Ur P θqφ 3. r into 3. toyield P θqφ d r dr Ur+Ur d Qφ sin θ ddθ r r sin θ dθ P θ + Ur d P θ r r sin Qφ = θ dφ 3.3 r or after multiplying by 3 sin θ, UrP θqφ r sin θ d U dr U + sin θ d sin θ ddθ P dθ P = d Q. 3.4 Q dφ Since the right hand side depends only on φ and the left hand side does not there must be some constant m such that d Q dφ Q = m
2 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 5 and r sin θ d U dr U + sin θ d sin θ ddθ P dθ P = m 3.6 Equation 3.5 hassolutions Q = C m e imφ 3.7 where m must be an integer for Q to be single valued. Similarly we can separate variables θ and r in 3.6 toget r d U dr U = m sin θ d sin θ ddθ P sin θ dθ P 3.8 or r d U = ll U dr and m sin θ d sin θ ddθ P sin θ dθ P = ll + 3. for some constant ll +. These two equation can be rewritten as d dr U = ll +U 3. r and d sin θ ddθ m sin θ dθ P = sin ll + P 3. θ Equation 3. canbesolveusingpolynomialansatz where or U r α 3.3 αα = ll α = { l + Thus, the most general solution of 3. isgivenby l 3.5 U = A l r l+ + B l r l. 3.6 To determine l we switch to 3. rewrittenintermsofx =cosθ, d x d m dx dx P l = ll + P x l. 3.7 This is the generalized Legendre equation whose solutions are the associated Legendre functions.
3 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 6 3. Legendre polynomials For starters let us consider a special case m =corresponding to the ordinary Legendre equation d x d dx dx P l + ll +P l = 3.8 If we assume the following expansion of where a,thenweobtain + P l x =x α j= a j x j 3.9 [ α + jα + j aj x α+j α + jα + j + l l +a j x α+j] =3. j= αα a x α ++ααa x α + [α + j +α + j +a j+ α + jα + j + l l +a j ] x α+j =. j= Since the coefficient of all of the powers of x have to vanish separately, we find and a j+ = α α = for a α α + = for a 3. α + jα + j + l l + a j. 3. α + j +α + j + The two equation 3. areredundantandtheonlyconditionthatfollows from them is α =or. Then the expansion 3.9 haseitheroddfor α =orevenforα =powersofx. One can show that the series expansion converges for x =only if it terminates. Since α and j are positive integers or zero the relation 3. terminates only if l is a positive integer or zero. Then only one of the two series terminates when { j max + αj max + α + ll + j max = l for α = = j max + α +j max + α + j max = l for α = 3.3
4 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 7 Thus, { l/ j P l x = a jx j where a j+ = jj+ ll+ a j+j+ j for even l l / j a j x j+ where a j+ = j+j+ ll+ a j+3j+ j for odd l. 3.4 For example, if we set P l =, then P x = P x = x P x = +3x P 3 x = 3x +5x We note without proving that the Legendre Polynomial have the following properties P l x = P l+ x = P l x = P l x P l x = d l l l! dx l x l Rodrigues Formula 3.6 l + l + P lx l l + P l x Recurrence Relation # 3.7 d l +dx l+x P l x Recurrence Relation # 3.8 l + δ ll Orthogonality condition 3.9 The last property implies that the Legendre polynomials formacomplete set of orthogonal function on the interval, and any function can be expanded as fx = A l P l x where A l = l + fxp l xdx. 3.3 Then the general solution of the Laplace equation in spherical coordinates for the case of azimuthal symmetry i.e. m =isgivenby Φr, θ, φ = A l r l + B l r l P l cos θ Azimuthal symmetry Consider a sphere of radius a with potential V θ on its surface.to find the potential everywhere inside the sphere we note that the potential should not
5 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 8 blow up at r =and thus the B l s in 3.3 mustvanish. Thenourproblem reduces to finding the appropriate coefficients in Φr, θ, φ = A l r l P l cos θ 3.3 for boundary conditions V θ = A l a l P l cos θ Multiplying both sides of 3.33byP l cos θ sin θ and integrating over θ leads to or π V θp l cos θ sin θdθ = π A l a l P l cos θp l cos θ sin θdθ = A l a l A l = l + a l P l xp l xdx = A l a l l V θp l cos θ sin θdθ For instance the potential inside of two hemispherical shells of radius a held at different potentials, i.e. { +V for θ<π/ V θ = 3.36 V for π/ <θ π, can be estimated from [ 3 r Φr, θ =V a P cos θ 7 r 8 a 3 P3 cos θ+ r 5 P5 cos θ...]. 6 a 3.37 For the potential outside of the sphere r/a l would be replaced by r/a l+. In fact this solution could have been obtained from an alreadyknownsolution.9 forθ =.Since Φr, = A l r l + B l r l 3.38
6 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 9 and Φr, = V r a r = V r + a π we get Φr, θ = V π j= j= j j Γ j a j j! r 3.39 j j Γ j a j Pj cos θ 3.4 j! r which can be shown to be equivalent to Another important problem with azimuthal symmetry that can be solved by the same method is the potential due to a unit point charge at x placed anywhere on z axis. Then, the Taylor series expansion for x also on the z axis is given by x x = r r = r< l 3.4 r > where r < or r > isthesmallerorlargerofr and r,andthus, x x = r< l r> l+ 3.4 Fields in a Conical Hole r l > P l cos θ. 3.4 Consider a conical hole in a conductor that has angle β relative z axis. To find the potential inside the hole we are restricted to the region of interest in spherical coordinates: <θ<βand <φ<π. The problem has an azimuthal symmetry, but the solutions arenot given by Legendre polynomials since we can no longer expand around θ = π/ or x =in 3.8. For this particular problem it makes sense to look for an expansion around θ =or x =in 3.8, and thus it is convenient to change variables d dy in 3.8 torewritetheequationas y y d dy P ν d dy y = x 3.43 = d dx νν +P ν =. 3.45
7 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 3 We have switched from subscript l to ν to emphasize the fact that the functions P ν y are not Legendre polynomials. Just like before we can plug in a series expansion P ν y =y α j= a j y j 3.46 into 3.45 todeducethatvanishingofacoefficientofthelowestpowerof y requires α =and the recursion relation between successive coefficients is a j+ = j νj + ν + j + a j Moreover, if we choose a normalization corresponding to a then we obtain our final solution or P ν y =+ νν + y +!! νν + P ν x =+!! x ν ν +ν +ν + y !! ν ν +ν +ν + +!! x These are the so-called Legendre functions of the first kind and order ν, where ν sarenotnecessarilyintegers.theirvaluesaredeterminedfrom the boundary conditions Φθ = β = corresponding to and the most general solution is given by Φr, θ, φ =A + P ν cos β =, 3.5 A n r ν k P νk cos θ where P νk cos β =. 3.5 n= Deep inside the hole r ofagroundedconductora =onlythe leading term would dominate, i.e. Φr, θ, φ =Ar ν P ν cos θ, 3.5 where ν = {.45 β for small β ln for large β. π β 3.53
8 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II Spherical Harmonics Let us now consider the Laplace equation in spherical coordinates without azimuthal symmetry which boils down to solving the generalized Legendre equation for m d dx x d dx P l m = ll + x P l It can be shown that for the equation to be finite between and the parameter l must be positive integer and Then the solution of 3.54 aregivenby m = { l, l +,..., l,l} P m l x = { m x m/ dm P dx m l x for m m l m! l+m! lx for m< 3.56 Another definition of P m l s is obtained from the Rodrigues formula 3.6 and is valid for positive as well as negative m, P m l x = m l l! x m/ dl+m dx l+m x l The associated Legendre function form a set of orthogonal functions on the interval,, Pl m xpl m xdx = δ ll l + l + m! l m! It is now convenient to define a set of orthonormal functions l +l m! Y lm θ, φ = 4π l + m! P l m cos θe imφ 3.59 with Y l, m θ, φ = m Ylm θ, φ. 3.6 which also satisfy the orthogonality and normalization conditions π π dφ dθ sin θy l m θ, φylm θ, φ =δ ll δ mm 3.6
9 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 3 and the completeness relation l m= l Y lmθ,φ Y lm θ, φ =δφ φ δcos θ cos θ. 3.6 These function are known as spherical harmonics as they represent the angulardependent part of the solutions of the Laplace equation in spherical coordinates θ, φ. For example, Y = 4π 3 Y = sin θeiφ 8π 3 Y = 8π cos θ 3 Y, = 8π sin θe iφ, 3.63 Note that for m =the spherical harmonic reduce to the Legendre polynomials l + Y l θ, φ = 4π P lcos θ 3.64 and for m = l Y mm θ, φ = m m +m! e imφ sin m θ m m! 4π Since the spherical harmonics form a complete orthonormal set of function, an arbitrary square-integrable function on a unit sphere can be expanded as, l gθ, φ = A lm Y lm θ, φ, 3.66 m= l where the coefficients are given by A lm = dωylmθ, φgθ, φ, 3.67 and the most general solution to the Laplace equation can also beexpanded in spherical harmonics as Φr, θ, φ = l Alm r l + B lm r l+ Y lm θ, φ m= l
10 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 33 It will be useful to prove the so-called addition theorem for spherical harmonics which expresses a Legendre polynomial of order l and angle γ in terms of spherical harmonics of angles θ, φ and θ,φ where cos γ =cosθ cos θ + sin θ sin θ cosφ φ Clearly, the expansion 3.66 implies that P l cos γ = l = m= l A l mθ,φ Y l mθ, φ. 3.7 If θ =,correspondingtoθ,φ lying on the z axis, then cos γ =cosθ and then P l cos γ must satisfy d sin θ d sin θ dθ dθ P lcos γ + ll +P l cos γ = 3.7 and, since the Laplacian operator ψ = d r sin θ dθ sin θ d ψ is a scalar which dθ must be invariant under rotations, we have P l cos γ+ ll + r P l cos γ = 3.7 for arbitrary θ.thereforep l cos γ must be expressible in terms of spherical harmonics of order l, i.e. with coefficients A m θ,φ = P l cos γ = l m= l dω Y lm θ, φp lcos γ = A m θ,φ Y lm θ, φ π l + Y lm θ,φ in agreement with the addition theorem for spherical harmonics P l cos γ = 4π l + l m= l Y lm θ,φ Y lm θ, φ This result can, for example, be used to express the potential atx due to a unit point charge at x.bysubstituting3.75 into3.4 weobtain x x =4π l m= l l + r< l r> l+ Y lm θ,φ Y lm θ, φ. 3.76
11 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II Bessel functions The cylindrical coordinates ρ, φ, z are used when the boundary surface has a cylindrical symmetry, but the boundary conditions are not uniform along the z axis. The Laplace equation in cylindrical coordinates takes thefollowing form Φ= ρ ρ ρ ρ Φ + Φ ρ φ + Φ = z As usual we apply the separation of variables technique and substitute Φρ, φ, z =RρQφZz 3.78 to obtain the three ordinary differential equations d R dρ + dr ρ dρ + d Z dz k Z = 3.79 d Q dφ + ν Q = 3.8 R =. 3.8 k ν ρ Solutions of the first two equations 3.79 and3.8 aregivenby { Zz = A { A + B z for k = k e kz + B k e kz for k Qφ = C + D φ for ν = C ν e iνφ + D ν e iνφ for ν and the solutions of 3.8 willbederivedusingseriesexpansion. Aswewill see shortly that by choosing a real k the solutions will be given in terms of Bessel function, when a chose of imaginary k would have led to solutions in terms of modified Bessel functions. In terms of variable x = kρ equation 3.8 takestheformofthebessel equation d x dx If we substitute expansion x drx + dx ν x Rx = Rx = a j x j+α, 3.85 j=
12 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 35 where a,into3.84 then a j x j+α j + α ν + a j x j+α = j= Since coefficient of every power of x must vanish independently we get and a recursive relation It follows that and If we choose j= a α ν = 3.87 a + α ν = 3.88 a j+ = j ++α ν a j α = ±ν 3.9 a j+ = 3.9 a j = 4jj + α a j. 3.9 α = α Γα + then the recursion relation leads to th following solutions J ν x = J ν x = x ν j= x ν j= 3.93 j x j 3.94 j!γj + ν + j x j 3.95 j!γj ν + known as Bessel functions of the first kind of order ±ν. Thesetwosolutions are linearly independent only when ν is not an integer and otherwise J ν x = ν J ν x In either case one can construct another linearly independent solutions using the Neumann function or Bessel function of the second kind N ν x J νxcosνπ J ν x sinνx
13 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 36 Alternatively, one can use the Hankel functions or Bessel function of the third kind defined as linear combinations of Bessel and Neumann functions, H ν x J ν x+in ν x 3.98 H ν x J ν x in ν x 3.99 which also form a fundamental set of solutions to the Bessel equation We note that all of these functions, i.e. Ω ν = J ν,n ν,h ν or H ν satisfy very useful recursion formulas, Ω ν x+ω ν+ x = ν x Ω νx 3. Ω ν x Ω ν+ x = d dx Ω νx. 3. One can use Bessel function to expand an arbitrary function on theinterval ρ a into Fourier-Bessel series where x νn are the roots of and A νn = fρ = n= a J ν+ x νn A νn J ν x νn ρ a 3. J ν x = 3.3 a ρ ρfρj ν x νn. 3.4 a Although the expansion in terms of ρ ρj ν x νn is very useful for homogeneous Dirichlet boundary conditions an alternative expansion in terms of a ρ ρjν y νn,wherey a νn are the roots of d dx J νx =, 3.5 is useful for homogeneous Neumann boundary conditions. Some otherex- pansions are given by a n J ν+n x = Neumann series 3.6 n= a n J ν+n ν + nx = Kapteyn series 3.7 n= a n J ν n + x = Schlomilch series. 3.8 n=
14 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II Cylindrical Coordinates By summing over all of the solutions to the Laplace equation of theform 3.78 weobtain Φρ, φ, z = A + B zc + D φe + F log ρ ν A ν + B ν zc ν e iνφ + D ν e iνφ E ν ρ ν + F ν ρ ν + + k A k e kz + B k e kz C k + D k φe k J kρ+f k N kρ + + k A νk e kz + B νk e kz C νk e iνφ + D νk e iνφ E νk J ν kρ+f νk N ν kρ. ν As an example we can consider a cylinder with radius a and height L with boundary conditions for ρ = a Φρ, φ, z = for z = 3. V ρ, φ for z = L. If we are to solve the Laplace equation for the interior of the cylinder, then the solutions which blow up at ρ =must vanish. Moreover the solutions must be matched at φ =and φ =π. Thisleadsto Φρ, φ, z = A + B z ν A ν + B ν zc ν e iνφ + D ν e iνφ ρ ν + + k A k e kz + B k e kz C k + D k φj kρ+ + k A νk e kz + B νk e kz C νk e iνφ + D νk e iνφ J ν kρ. ν The boundary condition Φρ, φ, z ==implies that = A ν A ν C ν e iνφ + D ν e iνφ ρ ν + + k A k + B k C k + D k φj kρ+ + k A νk + B νk C νk e iνφ + D νk e iνφ J ν kρ, ν
15 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 38 or A = 3.3 A v = A k = B k A νk = B νk and Φρ, φ, z = B z zc ν e iνφ + D ν e iνφ ρ ν + ν + k e kz e kz C k + D k φj kρ+ + e kz e kz C νk e iνφ + D νk e iνφ J ν kρ k ν = zc ν e iνφ + D ν e iνφ ρ ν ν sinhkzc νk e iνφ + D νk e iνφ J ν kρ k ν The boundary condition Φρ = a, φ, z =implies that or = zc ν e iνφ + D ν e iνφ a ν 3.5 ν + sinhkzc νk e iνφ + D νk e iνφ J ν ka k ν C ν = 3.6 D ν = and if J m k mn a= 3.7 defines k mn s from its roots k mn a then Φρ, φ, z = sinhkza mn sinmφ+b mn cosmφj ν k mn ρ. m= n= 3.8
16 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 39 The remaining boundary condition fixes the coefficients A mn and B mn using.4 and3.4, A mn = B mn = sinhk mn Lπa J m+k mn a sinhk mn Lπa J m+k mn a π π dφ dφ a a with a correction B n B n due to coefficient in.4. How would the solution 3.8 changeifa? dρ ρv ρ, φj m k mn ρ sinmφ 3.9 dρ ρv ρ, φj m k mn ρcosmφ Spherical expansion of Green s functions If the problem involves the distributions of charges AND boundary conditions, then it is important to be able to express the Green functions using expansion appropriate for the boundary conditions. For example, consider asphereofradiusa, withaspecifiedpotentialv φ, θ at its surface, and a point charge. This problem was already solved using the method of Green s functions, Φx = 4πɛ ρx G D d 3 x 4π such that G D =at the surface of the sphere, i.e. rˆx r ˆx = G D x, x = It was already shown 3.76 that { 4π l m= l 4π l m= l Φ n G Dda, 3. rˆx r ˆx r r ˆx aˆx a. 3. r l Y l+ r l+ r l Y l+ r l+ lm θ,φ Y lm θ, φ for r<r lm θ,φ Y lm θ, φ for r <r 3.3 and the expansion of 3. insphericalharmonicsisgiveby, 4π l r l G D x, x m= l al+ Y l+ r = l+ rr l+ lm θ,φ Y lm θ, φ for r<r 4π l r l m= l al+ Y l+ r l+ rr l+ lm θ,φ Y lm θ, φ for r <r, 3.4 for the exterior of the sphere and 4π l r l G D x, x m= l rr l Y l+ r = l+ a l+ lm θ,φ Y lm θ, φ for r<r 4π l r l m= l rr l Y l+ r l+ a l+ lm θ,φ Y lm θ, φ for r <r. 3.5
17 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 4 for the interior of the sphere. For illustration let us find potential inside a sphere of radius b at potential V θ, φ and a charge Q on a uniformly charged ring of radius a<bin the xy plane with center at x = y =,i.e. ρx = Q πa δr aδcos θ. 3.6 From 3.4 G D n = [ ] GD r r =b = 4π and the second term in 3. is Φ l 4π n G Dda = m= l l m= l r l b l+ Y lm θ,φ Y lm θ, φ 3.7 r l b Y lmθ, φ l+ dω V θ,φ Y lm θ,φ. 3.8 To calculate the first term in 3. wealsousetheexpansion3.4 and 3.6 4πɛ ρx G D d 3 x = Q πa ɛ π dφ l m= l l + r< l r r >r < l l+ > b l+ 3.9 where r < or r > isthesmallerorlargerofr and a. But because of the azimuthal symmetry of the potential due to the ring only m =terms would survive, 4πɛ Y lm π/,φ Y lm θ, φ ρx G D d 3 x = = dφ r< l l + r r >r < l Y l+ > b l+ l π/,φ Y l θ, φ Q r< l = 4πa ɛ r r >r < l P l+ > b l+ l P l cos θ 3.3 and the final answer is Φx = 3.3 Q r< l = 4πa ɛ r r >r < l P l+ > b l+ l P l cos θ+ l r l + b Y lmθ, φ dω V θ,φ Y l+ lm θ,φ. 3.3 m= l
18 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II Cylindrical expansion of Green s functions For the boundary value problems with cylindrical symmetry it is useful to expand the Green s function in cylindrical coordinates. This corresponds to solving the Laplace equation in cylindrical coordinates, i.e. Gx, x = 4π ρ δρ ρ δφ φ δz z, 3.33 where δz z = dk e ikz z = dk coskz z 3.34 π π δφ φ = e imφ φ π m= The Green s function can be expanded as Gx, x = π m= dk e imφ φ coskz z g m k, ρ, ρ, 3.36 where the functions g m k, ρ, ρ must satisfy d ρ dg m k + m = 4π ρ dρ dρ ρ ρ δρ ρ 3.37 For ρ ρ the solutions of 3.37 arethemodifiedbesselfunctions I m kρ i m J m ikρ 3.38 K m kρ π iν+ H m ikρ Then the most general solution is a linear combination of 3.38 and3.39, ψ kρ = ai m kρ+bk m kρ satisfies b.c. for ρ<ρ 3.4 ψ kρ = a I m kρ+b K m kρ satisfies b.c. for ρ <ρ 3.4 but due to symmetry ρ ρ wemusthave g m k, ρ, ρ =ψ kρ < ψ kρ >. 3.4
19 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 4 Then 3.37 givesus ρ +ɛ d ρ dg m dρ ρ ɛ ρ +ɛ ρ ɛ [ ] dgm dρ ρ=ρ +ɛ k ρ + m [ ρ dg m dρ [ dgm dρ ρ ] ρ=ρ +ɛ ] ρ=ρ ɛ ρ=ρ ɛ = 4π = 4π = 4π ρ k ψ kρ ψ kρ ψ kρ ψ kρ = 4π ρ ρ +ɛ ρ ɛ δ ρ ρ dρ kw[ψ kρ,ψ kρ ] = 4π ρ 3.43 where W [ψ,ψ ] is the Woronskian of ψ and ψ. As an aside, consider the Sturm-Liouville equation [ d px dyx ] +qx+λrx yx = 3.44 dx dx with two solutions y x and y x from some λ. Then, and thus d dx [pxw y,y ] = d dx [pxy xy x y xy x] = 3.45 = y xpxy x y xpxy x =3.46 In our problem p = ρ and W y,y px W ψ kρ,ψ kρ = 4π kρ 3.48 for all ρ.for the solution g m k, ρ, ρ to be finite at ρ =and to vanish at ρ = ψ kρ = AI m kρ 3.49 ψ kρ = K m kρ 3.5 and the constant A =4π determined from 3.48 since W I m,k m = x. 3.5
20 CHAPTER 3. BOUNDARY-VALUE PROBLEMS: PART II 43 Therefore the expansion of the Green s function in cylindrical coordinates is given by = dk e imφ φ coskz z I x x m kρ < K m kρ > 3.5 π m= = 4 dk coskz z π I kρ < K kρ > + cosmφ φ I m kρ < K m kρ > If we let x, thenonlym =term is finite and ρ + z = π m= coskzk kρdk 3.53 If we let z then the Green s function can be obtain by two methods. We can either replace ρ R = ρ + ρ ρρ cosφ φ in 3.53 or we can derive it directly from 3.5. By equating the integrands of both expressions we obtain, K k ρ + ρ ρρ cosφ φ = I kρ < K kρ > + cosmφ φ I m kρ < K m kρ > 3.54 which must hold for all z. Then one can show by expanding around k that in polar coordinates the Green s function is given by log ρ + ρ ρρ cosφ φ = log ρ > + m= m= m ρ< ρ > m cosmφ φ For example, the potential of a line of charge with linear charge density λ is Φx = ρ e x Gx, x d 3 x = π + λδρ dφ dz dρ 4πɛ 4πɛ πρ λ + = dz dk coskz z π ɛ I K kρ λ + = dk dz coskz K π kρ ɛ λ = dk δk K kρ πɛ λ kρ = lim log k πɛ = Gx, x λ log ρ πɛ + const. 3.56
Classical Field Theory: Electrostatics-Magnetostatics
 Classical Field Theory: Electrostatics-Magnetostatics April 27, 2010 1 1 J.D.Jackson, Classical Electrodynamics, 2nd Edition, Section 1-5 Electrostatics The behavior of an electrostatic field can be described
Classical Field Theory: Electrostatics-Magnetostatics April 27, 2010 1 1 J.D.Jackson, Classical Electrodynamics, 2nd Edition, Section 1-5 Electrostatics The behavior of an electrostatic field can be described
Electrodynamics I Midterm - Part A - Closed Book KSU 2005/10/17 Electro Dynamic
 Electrodynamics I Midterm - Part A - Closed Book KSU 5//7 Name Electro Dynamic. () Write Gauss Law in differential form. E( r) =ρ( r)/ɛ, or D = ρ, E= electricfield,ρ=volume charge density, ɛ =permittivity
Electrodynamics I Midterm - Part A - Closed Book KSU 5//7 Name Electro Dynamic. () Write Gauss Law in differential form. E( r) =ρ( r)/ɛ, or D = ρ, E= electricfield,ρ=volume charge density, ɛ =permittivity
Solutions to Laplace s Equation in Cylindrical Coordinates and Numerical solutions. ρ + (1/ρ) 2 V
 Solutions to Laplace s Equation in Cylindrical Coordinates and Numerical solutions Lecture 8 1 Introduction Solutions to Laplace s equation can be obtained using separation of variables in Cartesian and
Solutions to Laplace s Equation in Cylindrical Coordinates and Numerical solutions Lecture 8 1 Introduction Solutions to Laplace s equation can be obtained using separation of variables in Cartesian and
Expansion of 1/r potential in Legendre polynomials
 Expansion of 1/r potential in Legendre polynomials In electrostatics and gravitation, we see scalar potentials of the form V = K d Take d = R r = R 2 2Rr cos θ + r 2 = R 1 2 r R cos θ + r R )2 Use h =
Expansion of 1/r potential in Legendre polynomials In electrostatics and gravitation, we see scalar potentials of the form V = K d Take d = R r = R 2 2Rr cos θ + r 2 = R 1 2 r R cos θ + r R )2 Use h =
Physics 505 Fall 2003
 Physics 505 Fall 2003 G. Raithel December 8, 2003 Disclaimer: The purpose of these notes is to provide you with a general list of topics that were covered in class. The notes are not a substitute for reading
Physics 505 Fall 2003 G. Raithel December 8, 2003 Disclaimer: The purpose of these notes is to provide you with a general list of topics that were covered in class. The notes are not a substitute for reading
Electromagnetism HW 1 math review
 Electromagnetism HW math review Problems -5 due Mon 7th Sep, 6- due Mon 4th Sep Exercise. The Levi-Civita symbol, ɛ ijk, also known as the completely antisymmetric rank-3 tensor, has the following properties:
Electromagnetism HW math review Problems -5 due Mon 7th Sep, 6- due Mon 4th Sep Exercise. The Levi-Civita symbol, ɛ ijk, also known as the completely antisymmetric rank-3 tensor, has the following properties:
l=0 The expansion coefficients can be determined, for example, by finding the potential on the z-axis and expanding that result in z.
 Electrodynamics I Exam - Part A - Closed Book KSU 15/11/6 Name Electrodynamic Score = 14 / 14 points Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try
Electrodynamics I Exam - Part A - Closed Book KSU 15/11/6 Name Electrodynamic Score = 14 / 14 points Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try
Spherical Coordinates and Legendre Functions
 Spherical Coordinates and Legendre Functions Spherical coordinates Let s adopt the notation for spherical coordinates that is standard in physics: φ = longitude or azimuth, θ = colatitude ( π 2 latitude)
Spherical Coordinates and Legendre Functions Spherical coordinates Let s adopt the notation for spherical coordinates that is standard in physics: φ = longitude or azimuth, θ = colatitude ( π 2 latitude)
LEGENDRE POLYNOMIALS AND APPLICATIONS. We construct Legendre polynomials and apply them to solve Dirichlet problems in spherical coordinates.
 LEGENDRE POLYNOMIALS AND APPLICATIONS We construct Legendre polynomials and apply them to solve Dirichlet problems in spherical coordinates.. Legendre equation: series solutions The Legendre equation is
LEGENDRE POLYNOMIALS AND APPLICATIONS We construct Legendre polynomials and apply them to solve Dirichlet problems in spherical coordinates.. Legendre equation: series solutions The Legendre equation is
Survival Guide to Bessel Functions
 Survival Guide to Bessel Functions December, 13 1 The Problem (Original by Mike Herman; edits and additions by Paul A.) For cylindrical boundary conditions, Laplace s equation is: [ 1 s Φ ] + 1 Φ s s s
Survival Guide to Bessel Functions December, 13 1 The Problem (Original by Mike Herman; edits and additions by Paul A.) For cylindrical boundary conditions, Laplace s equation is: [ 1 s Φ ] + 1 Φ s s s
Connection to Laplacian in spherical coordinates (Chapter 13)
 Connection to Laplacian in spherical coordinates (Chapter 13) We might often encounter the Laplace equation and spherical coordinates might be the most convenient 2 u(r, θ, φ) = 0 We already saw in Chapter
Connection to Laplacian in spherical coordinates (Chapter 13) We might often encounter the Laplace equation and spherical coordinates might be the most convenient 2 u(r, θ, φ) = 0 We already saw in Chapter
FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 2017
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II November 5, 207 Prof. Alan Guth FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 207 A few items below are marked
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II November 5, 207 Prof. Alan Guth FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 207 A few items below are marked
1. (3) Write Gauss Law in differential form. Explain the physical meaning.
 Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Electro Dynamic Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about
Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Electro Dynamic Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about
Notes: Most of the material presented in this chapter is taken from Jackson, Chap. 2, 3, and 4, and Di Bartolo, Chap. 2. 2π nx i a. ( ) = G n.
 Chapter. Electrostatic II Notes: Most of the material presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartolo, Chap... Mathematical Considerations.. The Fourier series and the Fourier
Chapter. Electrostatic II Notes: Most of the material presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartolo, Chap... Mathematical Considerations.. The Fourier series and the Fourier
Problem Set #4: 4.1,4.7,4.9 (Due Monday, March 25th)
 Chapter 4 Multipoles, Dielectrics Problem Set #4: 4.,4.7,4.9 (Due Monday, March 5th 4. Multipole expansion Consider a localized distribution of charges described by ρ(x contained entirely in a sphere of
Chapter 4 Multipoles, Dielectrics Problem Set #4: 4.,4.7,4.9 (Due Monday, March 5th 4. Multipole expansion Consider a localized distribution of charges described by ρ(x contained entirely in a sphere of
PHYS 404 Lecture 1: Legendre Functions
 PHYS 404 Lecture 1: Legendre Functions Dr. Vasileios Lempesis PHYS 404 - LECTURE 1 DR. V. LEMPESIS 1 Legendre Functions physical justification Legendre functions or Legendre polynomials are the solutions
PHYS 404 Lecture 1: Legendre Functions Dr. Vasileios Lempesis PHYS 404 - LECTURE 1 DR. V. LEMPESIS 1 Legendre Functions physical justification Legendre functions or Legendre polynomials are the solutions
Two special equations: Bessel s and Legendre s equations. p Fourier-Bessel and Fourier-Legendre series. p
 LECTURE 1 Table of Contents Two special equations: Bessel s and Legendre s equations. p. 259-268. Fourier-Bessel and Fourier-Legendre series. p. 453-460. Boundary value problems in other coordinate system.
LECTURE 1 Table of Contents Two special equations: Bessel s and Legendre s equations. p. 259-268. Fourier-Bessel and Fourier-Legendre series. p. 453-460. Boundary value problems in other coordinate system.
Spherical Harmonics on S 2
 7 August 00 1 Spherical Harmonics on 1 The Laplace-Beltrami Operator In what follows, we describe points on using the parametrization x = cos ϕ sin θ, y = sin ϕ sin θ, z = cos θ, where θ is the colatitude
7 August 00 1 Spherical Harmonics on 1 The Laplace-Beltrami Operator In what follows, we describe points on using the parametrization x = cos ϕ sin θ, y = sin ϕ sin θ, z = cos θ, where θ is the colatitude
d 1 µ 2 Θ = 0. (4.1) consider first the case of m = 0 where there is no azimuthal dependence on the angle φ.
 4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
Chapter 4 Boundary Value Problems in Spherical and Cylindrical Coordinates
 Chapter 4 Boundary Value Problems in Spherical and Cylindrical Coordinates 4. Laplace s Equation in spherical coordinates Laplace s equation in spherical coordinates, (r, θ, φ), has the form where r r
Chapter 4 Boundary Value Problems in Spherical and Cylindrical Coordinates 4. Laplace s Equation in spherical coordinates Laplace s equation in spherical coordinates, (r, θ, φ), has the form where r r
Boundary Value Problems in Cylindrical Coordinates
 Boundary Value Problems in Cylindrical Coordinates 29 Outline Differential Operators in Various Coordinate Systems Laplace Equation in Cylindrical Coordinates Systems Bessel Functions Wave Equation the
Boundary Value Problems in Cylindrical Coordinates 29 Outline Differential Operators in Various Coordinate Systems Laplace Equation in Cylindrical Coordinates Systems Bessel Functions Wave Equation the
Separation of Variables in Polar and Spherical Coordinates
 Separation of Variables in Polar and Spherical Coordinates Polar Coordinates Suppose we are given the potential on the inside surface of an infinitely long cylindrical cavity, and we want to find the potential
Separation of Variables in Polar and Spherical Coordinates Polar Coordinates Suppose we are given the potential on the inside surface of an infinitely long cylindrical cavity, and we want to find the potential
Legendre s Equation. PHYS Southern Illinois University. October 13, 2016
 PHYS 500 - Southern Illinois University October 13, 2016 PHYS 500 - Southern Illinois University Legendre s Equation October 13, 2016 1 / 10 The Laplacian in Spherical Coordinates The Laplacian is given
PHYS 500 - Southern Illinois University October 13, 2016 PHYS 500 - Southern Illinois University Legendre s Equation October 13, 2016 1 / 10 The Laplacian in Spherical Coordinates The Laplacian is given
Power Series Solutions to the Legendre Equation
 Department of Mathematics IIT Guwahati The Legendre equation The equation (1 x 2 )y 2xy + α(α + 1)y = 0, (1) where α is any real constant, is called Legendre s equation. When α Z +, the equation has polynomial
Department of Mathematics IIT Guwahati The Legendre equation The equation (1 x 2 )y 2xy + α(α + 1)y = 0, (1) where α is any real constant, is called Legendre s equation. When α Z +, the equation has polynomial
Solutions to Problems in Jackson, Classical Electrodynamics, Third Edition. Chapter 2: Problems 11-20
 Solutions to Problems in Jackson, Classical Electrodynamics, Third Edition Homer Reid December 8, 999 Chapter : Problems - Problem A line charge with linear charge density τ is placed parallel to, and
Solutions to Problems in Jackson, Classical Electrodynamics, Third Edition Homer Reid December 8, 999 Chapter : Problems - Problem A line charge with linear charge density τ is placed parallel to, and
Physics 4617/5617: Quantum Physics Course Lecture Notes
 Physics 467/567: Quantum Physics Course Lecture Notes Dr. Donald G. Luttermoser East Tennessee State University Edition 5. Abstract These class notes are designed for use of the instructor and students
Physics 467/567: Quantum Physics Course Lecture Notes Dr. Donald G. Luttermoser East Tennessee State University Edition 5. Abstract These class notes are designed for use of the instructor and students
Math 4263 Homework Set 1
 Homework Set 1 1. Solve the following PDE/BVP 2. Solve the following PDE/BVP 2u t + 3u x = 0 u (x, 0) = sin (x) u x + e x u y = 0 u (0, y) = y 2 3. (a) Find the curves γ : t (x (t), y (t)) such that that
Homework Set 1 1. Solve the following PDE/BVP 2. Solve the following PDE/BVP 2u t + 3u x = 0 u (x, 0) = sin (x) u x + e x u y = 0 u (0, y) = y 2 3. (a) Find the curves γ : t (x (t), y (t)) such that that
The 3 dimensional Schrödinger Equation
 Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Spherical Waves. Daniel S. Weile. Department of Electrical and Computer Engineering University of Delaware. ELEG 648 Spherical Coordinates
 Spherical Waves Daniel S. Weile Department of Electrical and Computer Engineering University of Delaware ELEG 648 Spherical Coordinates Outline Wave Functions 1 Wave Functions Outline Wave Functions 1
Spherical Waves Daniel S. Weile Department of Electrical and Computer Engineering University of Delaware ELEG 648 Spherical Coordinates Outline Wave Functions 1 Wave Functions Outline Wave Functions 1
CHAPTER 3 POTENTIALS 10/13/2016. Outlines. 1. Laplace s equation. 2. The Method of Images. 3. Separation of Variables. 4. Multipole Expansion
 CHAPTER 3 POTENTIALS Lee Chow Department of Physics University of Central Florida Orlando, FL 32816 Outlines 1. Laplace s equation 2. The Method of Images 3. Separation of Variables 4. Multipole Expansion
CHAPTER 3 POTENTIALS Lee Chow Department of Physics University of Central Florida Orlando, FL 32816 Outlines 1. Laplace s equation 2. The Method of Images 3. Separation of Variables 4. Multipole Expansion
Physics 116C Solutions to the Practice Final Exam Fall The method of Frobenius fails because it works only for Fuchsian equations, of the type
 Physics 6C Solutions to the Practice Final Exam Fall 2 Consider the differential equation x y +x(x+)y y = () (a) Explain why the method of Frobenius method fails for this problem. The method of Frobenius
Physics 6C Solutions to the Practice Final Exam Fall 2 Consider the differential equation x y +x(x+)y y = () (a) Explain why the method of Frobenius method fails for this problem. The method of Frobenius
Virtual current density in magnetic flow meter
 Virtual current density in magnetic flow meter Problem presented by Claus Nygaard Rasmussen Siemens Flow Instruments Background Siemens Flow Instruments submits this problem for the 51st European Study
Virtual current density in magnetic flow meter Problem presented by Claus Nygaard Rasmussen Siemens Flow Instruments Background Siemens Flow Instruments submits this problem for the 51st European Study
Quantum Mechanics in Three Dimensions
 Physics 342 Lecture 21 Quantum Mechanics in Three Dimensions Lecture 21 Physics 342 Quantum Mechanics I Monday, March 22nd, 21 We are used to the temporal separation that gives, for example, the timeindependent
Physics 342 Lecture 21 Quantum Mechanics in Three Dimensions Lecture 21 Physics 342 Quantum Mechanics I Monday, March 22nd, 21 We are used to the temporal separation that gives, for example, the timeindependent
Spherical Coordinates
 Spherical Coordinates Bo E. Sernelius 4:6 SPHERICAL COORDINATES Φ = 1 Φ + 1 Φ + 1 Φ = 0 r r r θ sin r r sinθ θ θ r sin θ ϕ ( ) = ( ) ( ) ( ) Φ r, θϕ, R r P θq ϕ 1 d 1 1 0 r R dr r dr d dp d Q dr + sinθ
Spherical Coordinates Bo E. Sernelius 4:6 SPHERICAL COORDINATES Φ = 1 Φ + 1 Φ + 1 Φ = 0 r r r θ sin r r sinθ θ θ r sin θ ϕ ( ) = ( ) ( ) ( ) Φ r, θϕ, R r P θq ϕ 1 d 1 1 0 r R dr r dr d dp d Q dr + sinθ
PHYS 502 Lecture 8: Legendre Functions. Dr. Vasileios Lempesis
 PHYS 502 Lecture 8: Legendre Functions Dr. Vasileios Lempesis Introduction Legendre functions or Legendre polynomials are the solutions of Legendre s differential equation that appear when we separate
PHYS 502 Lecture 8: Legendre Functions Dr. Vasileios Lempesis Introduction Legendre functions or Legendre polynomials are the solutions of Legendre s differential equation that appear when we separate
Physics 6303 Lecture 11 September 24, LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation
 Physics 6303 Lecture September 24, 208 LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation, l l l l l l. Consider problems that are no axisymmetric; i.e., the potential depends
Physics 6303 Lecture September 24, 208 LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation, l l l l l l. Consider problems that are no axisymmetric; i.e., the potential depends
Note: Each problem is worth 14 points except numbers 5 and 6 which are 15 points. = 3 2
 Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
SOLUTIONS TO SELECTED PROBLEMS FROM ASSIGNMENTS 3, 4
 SOLUTIONS TO SELECTED POBLEMS FOM ASSIGNMENTS 3, 4 Problem 5 from Assignment 3 Statement. Let be an n-dimensional bounded domain with smooth boundary. Show that the eigenvalues of the Laplacian on with
SOLUTIONS TO SELECTED POBLEMS FOM ASSIGNMENTS 3, 4 Problem 5 from Assignment 3 Statement. Let be an n-dimensional bounded domain with smooth boundary. Show that the eigenvalues of the Laplacian on with
Bessel Functions - Lecture 7
 1 Introduction We study the ode; Bessel Functions - Lecture 7 x 2 f ν + xf ν + (x2 ν 2 )f ν = This is a Sturm-Liouville problem where we look for solutions as the variable ν is changed. The equation has
1 Introduction We study the ode; Bessel Functions - Lecture 7 x 2 f ν + xf ν + (x2 ν 2 )f ν = This is a Sturm-Liouville problem where we look for solutions as the variable ν is changed. The equation has
Final Examination Solutions
 Math. 42 Fulling) 4 December 25 Final Examination Solutions Calculators may be used for simple arithmetic operations only! Laplacian operator in polar coordinates: Some possibly useful information 2 u
Math. 42 Fulling) 4 December 25 Final Examination Solutions Calculators may be used for simple arithmetic operations only! Laplacian operator in polar coordinates: Some possibly useful information 2 u
Electrodynamics PHY712. Lecture 4 Electrostatic potentials and fields. Reference: Chap. 1 & 2 in J. D. Jackson s textbook.
 Electrodynamics PHY712 Lecture 4 Electrostatic potentials and fields Reference: Chap. 1 & 2 in J. D. Jackson s textbook. 1. Complete proof of Green s Theorem 2. Proof of mean value theorem for electrostatic
Electrodynamics PHY712 Lecture 4 Electrostatic potentials and fields Reference: Chap. 1 & 2 in J. D. Jackson s textbook. 1. Complete proof of Green s Theorem 2. Proof of mean value theorem for electrostatic
(b) Show that the charged induced on the hemisphere is: Q = E o a 2 3π (1)
 Problem. Defects This problem will study defects in parallel plate capacitors. A parallel plate capacitor has area, A, and separation, D, and is maintained at the potential difference, V = E o D. There
Problem. Defects This problem will study defects in parallel plate capacitors. A parallel plate capacitor has area, A, and separation, D, and is maintained at the potential difference, V = E o D. There
Electromagnetic Theory I
 Electromagnetic Theory I Final Examination 18 December 2009, 12:30-2:30 pm Instructions: Answer the following 10 questions, each of which is worth 10 points. Explain your reasoning in each case. Use SI
Electromagnetic Theory I Final Examination 18 December 2009, 12:30-2:30 pm Instructions: Answer the following 10 questions, each of which is worth 10 points. Explain your reasoning in each case. Use SI
Lecture Notes for MAE 3100: Introduction to Applied Mathematics
 ecture Notes for MAE 31: Introduction to Applied Mathematics Richard H. Rand Cornell University Ithaca NY 14853 rhr2@cornell.edu http://audiophile.tam.cornell.edu/randdocs/ version 17 Copyright 215 by
ecture Notes for MAE 31: Introduction to Applied Mathematics Richard H. Rand Cornell University Ithaca NY 14853 rhr2@cornell.edu http://audiophile.tam.cornell.edu/randdocs/ version 17 Copyright 215 by
Quantum Mechanics in 3-Dimensions
 Quantum Mechanics in 3-Dimensions Pavithran S Iyer, 2nd yr BSc Physics, Chennai Mathematical Institute Email: pavithra@cmi.ac.in August 28 th, 2009 1 Schrodinger equation in Spherical Coordinates 1.1 Transforming
Quantum Mechanics in 3-Dimensions Pavithran S Iyer, 2nd yr BSc Physics, Chennai Mathematical Institute Email: pavithra@cmi.ac.in August 28 th, 2009 1 Schrodinger equation in Spherical Coordinates 1.1 Transforming
SUMMARY PHYSICS 707 Electrostatics. E(x) = 4πρ(x) and E(x) = 0 (1)
 SUMMARY PHYSICS 707 Electrostatics The basic differential equations of electrostatics are E(x) = 4πρ(x) and E(x) = 0 (1) where E(x) is the electric field and ρ(x) is the electric charge density. The field
SUMMARY PHYSICS 707 Electrostatics The basic differential equations of electrostatics are E(x) = 4πρ(x) and E(x) = 0 (1) where E(x) is the electric field and ρ(x) is the electric charge density. The field
Physics 505 Fall 2005 Homework Assignment #8 Solutions
 Physics 55 Fall 5 Homework Assignment #8 Solutions Textbook problems: Ch. 5: 5., 5.4, 5.7, 5.9 5. A circular current loop of radius a carrying a current I lies in the x-y plane with its center at the origin.
Physics 55 Fall 5 Homework Assignment #8 Solutions Textbook problems: Ch. 5: 5., 5.4, 5.7, 5.9 5. A circular current loop of radius a carrying a current I lies in the x-y plane with its center at the origin.
21 Laplace s Equation and Harmonic Functions
 2 Laplace s Equation and Harmonic Functions 2. Introductory Remarks on the Laplacian operator Given a domain Ω R d, then 2 u = div(grad u) = in Ω () is Laplace s equation defined in Ω. If d = 2, in cartesian
2 Laplace s Equation and Harmonic Functions 2. Introductory Remarks on the Laplacian operator Given a domain Ω R d, then 2 u = div(grad u) = in Ω () is Laplace s equation defined in Ω. If d = 2, in cartesian
23 Elements of analytic ODE theory. Bessel s functions
 23 Elements of analytic ODE theory. Bessel s functions Recall I am changing the variables) that we need to solve the so-called Bessel s equation 23. Elements of analytic ODE theory Let x 2 u + xu + x 2
23 Elements of analytic ODE theory. Bessel s functions Recall I am changing the variables) that we need to solve the so-called Bessel s equation 23. Elements of analytic ODE theory Let x 2 u + xu + x 2
Physics 342 Lecture 23. Radial Separation. Lecture 23. Physics 342 Quantum Mechanics I
 Physics 342 Lecture 23 Radial Separation Lecture 23 Physics 342 Quantum Mechanics I Friday, March 26th, 2010 We begin our spherical solutions with the simplest possible case zero potential. Aside from
Physics 342 Lecture 23 Radial Separation Lecture 23 Physics 342 Quantum Mechanics I Friday, March 26th, 2010 We begin our spherical solutions with the simplest possible case zero potential. Aside from
BOUNDARY PROBLEMS IN HIGHER DIMENSIONS. kt = X X = λ, and the series solutions have the form (for λ n 0):
 BOUNDARY PROBLEMS IN HIGHER DIMENSIONS Time-space separation To solve the wave and diffusion equations u tt = c u or u t = k u in a bounded domain D with one of the three classical BCs (Dirichlet, Neumann,
BOUNDARY PROBLEMS IN HIGHER DIMENSIONS Time-space separation To solve the wave and diffusion equations u tt = c u or u t = k u in a bounded domain D with one of the three classical BCs (Dirichlet, Neumann,
1. (3) Write Gauss Law in differential form. Explain the physical meaning.
 Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about the physics involved,
Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about the physics involved,
Orthogonal functions
 Orthogonl functions Given rel vrible over the intervl (, b nd set of rel or complex functions U n (ξ, n =, 2,..., which re squre integrble nd orthonorml b U n(ξu m (ξdξ = δ n,m ( if the set of of functions
Orthogonl functions Given rel vrible over the intervl (, b nd set of rel or complex functions U n (ξ, n =, 2,..., which re squre integrble nd orthonorml b U n(ξu m (ξdξ = δ n,m ( if the set of of functions
On an Eigenvalue Problem Involving Legendre Functions by Nicholas J. Rose North Carolina State University
 On an Eigenvalue Problem Involving Legendre Functions by Nicholas J. Rose North Carolina State University njrose@math.ncsu.edu 1. INTRODUCTION. The classical eigenvalue problem for the Legendre Polynomials
On an Eigenvalue Problem Involving Legendre Functions by Nicholas J. Rose North Carolina State University njrose@math.ncsu.edu 1. INTRODUCTION. The classical eigenvalue problem for the Legendre Polynomials
Astronomy 9620a / Physics 9302a - 1st Problem List and Assignment
 Astronomy 9620a / Physics 9302a - st Problem List and Assignment Your solution to problems 4, 7, 3, and 6 has to be handed in on Thursday, Oct. 7, 203.. Prove the following relations (going from the left-
Astronomy 9620a / Physics 9302a - st Problem List and Assignment Your solution to problems 4, 7, 3, and 6 has to be handed in on Thursday, Oct. 7, 203.. Prove the following relations (going from the left-
Power Series Solutions to the Legendre Equation
 Power Series Solutions to the Legendre Equation Department of Mathematics IIT Guwahati The Legendre equation The equation (1 x 2 )y 2xy + α(α + 1)y = 0, (1) where α is any real constant, is called Legendre
Power Series Solutions to the Legendre Equation Department of Mathematics IIT Guwahati The Legendre equation The equation (1 x 2 )y 2xy + α(α + 1)y = 0, (1) where α is any real constant, is called Legendre
The Spherical Harmonics
 Physics 6C Fall 202 The Spherical Harmonics. Solution to Laplace s equation in spherical coordinates In spherical coordinates, the Laplacian is given by 2 = ( r 2 ) ( + r 2 r r r 2 sin 2 sinθ ) + θ θ θ
Physics 6C Fall 202 The Spherical Harmonics. Solution to Laplace s equation in spherical coordinates In spherical coordinates, the Laplacian is given by 2 = ( r 2 ) ( + r 2 r r r 2 sin 2 sinθ ) + θ θ θ
(a) Determine the general solution for φ(ρ) near ρ = 0 for arbitary values E. (b) Show that the regular solution at ρ = 0 has the series expansion
 Problem 1. Curious Wave Functions The eigenfunctions of a D7 brane in a curved geometry lead to the following eigenvalue equation of the Sturm Liouville type ρ ρ 3 ρ φ n (ρ) = E n w(ρ)φ n (ρ) w(ρ) = where
Problem 1. Curious Wave Functions The eigenfunctions of a D7 brane in a curved geometry lead to the following eigenvalue equation of the Sturm Liouville type ρ ρ 3 ρ φ n (ρ) = E n w(ρ)φ n (ρ) w(ρ) = where
does not change the dynamics of the system, i.e. that it leaves the Schrödinger equation invariant,
 FYST5 Quantum Mechanics II 9..212 1. intermediate eam (1. välikoe): 4 problems, 4 hours 1. As you remember, the Hamilton operator for a charged particle interacting with an electromagentic field can be
FYST5 Quantum Mechanics II 9..212 1. intermediate eam (1. välikoe): 4 problems, 4 hours 1. As you remember, the Hamilton operator for a charged particle interacting with an electromagentic field can be
1 Solutions in cylindrical coordinates: Bessel functions
 1 Solutions in cylindrical coordinates: Bessel functions 1.1 Bessel functions Bessel functions arise as solutions of potential problems in cylindrical coordinates. Laplace s equation in cylindrical coordinates
1 Solutions in cylindrical coordinates: Bessel functions 1.1 Bessel functions Bessel functions arise as solutions of potential problems in cylindrical coordinates. Laplace s equation in cylindrical coordinates
Background and Definitions...2. Legendre s Equation, Functions and Polynomials...4 Legendre s Associated Equation and Functions...
 Legendre Polynomials and Functions Reading Problems Outline Background and Definitions...2 Definitions...3 Theory...4 Legendre s Equation, Functions and Polynomials...4 Legendre s Associated Equation and
Legendre Polynomials and Functions Reading Problems Outline Background and Definitions...2 Definitions...3 Theory...4 Legendre s Equation, Functions and Polynomials...4 Legendre s Associated Equation and
Angular Momentum. Classically the orbital angular momentum with respect to a fixed origin is. L = r p. = yp z. L x. zp y L y. = zp x. xpz L z.
 Angular momentum is an important concept in quantum theory, necessary for analyzing motion in 3D as well as intrinsic properties such as spin Classically the orbital angular momentum with respect to a
Angular momentum is an important concept in quantum theory, necessary for analyzing motion in 3D as well as intrinsic properties such as spin Classically the orbital angular momentum with respect to a
Electrodynamics Exam Solutions
 Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Physics 221A Fall 1996 Notes 12 Orbital Angular Momentum and Spherical Harmonics
 Physics 221A Fall 1996 Notes 12 Orbital Angular Momentum and Spherical Harmonics We now consider the spatial degrees of freedom of a particle moving in 3-dimensional space, which of course is an important
Physics 221A Fall 1996 Notes 12 Orbital Angular Momentum and Spherical Harmonics We now consider the spatial degrees of freedom of a particle moving in 3-dimensional space, which of course is an important
Math Homework 2
 Math 73 Homework Due: September 8, 6 Suppose that f is holomorphic in a region Ω, ie an open connected set Prove that in any of the following cases (a) R(f) is constant; (b) I(f) is constant; (c) f is
Math 73 Homework Due: September 8, 6 Suppose that f is holomorphic in a region Ω, ie an open connected set Prove that in any of the following cases (a) R(f) is constant; (b) I(f) is constant; (c) f is
The Hydrogen atom. Chapter The Schrödinger Equation. 2.2 Angular momentum
 Chapter 2 The Hydrogen atom In the previous chapter we gave a quick overview of the Bohr model, which is only really valid in the semiclassical limit. cf. section 1.7.) We now begin our task in earnest
Chapter 2 The Hydrogen atom In the previous chapter we gave a quick overview of the Bohr model, which is only really valid in the semiclassical limit. cf. section 1.7.) We now begin our task in earnest
In this chapter we study elliptical PDEs. That is, PDEs of the form. 2 u = lots,
 Chapter 8 Elliptic PDEs In this chapter we study elliptical PDEs. That is, PDEs of the form 2 u = lots, where lots means lower-order terms (u x, u y,..., u, f). Here are some ways to think about the physical
Chapter 8 Elliptic PDEs In this chapter we study elliptical PDEs. That is, PDEs of the form 2 u = lots, where lots means lower-order terms (u x, u y,..., u, f). Here are some ways to think about the physical
Eigenfunctions on the surface of a sphere. In spherical coordinates, the Laplacian is. u = u rr + 2 r u r + 1 r 2. sin 2 (θ) + 1
 Eigenfunctions on the surface of a sphere In spherical coordinates, the Laplacian is u = u rr + 2 r u r + 1 r 2 [ uφφ sin 2 (θ) + 1 sin θ (sin θ u θ) θ ]. Eigenfunctions on the surface of a sphere In spherical
Eigenfunctions on the surface of a sphere In spherical coordinates, the Laplacian is u = u rr + 2 r u r + 1 r 2 [ uφφ sin 2 (θ) + 1 sin θ (sin θ u θ) θ ]. Eigenfunctions on the surface of a sphere In spherical
Steady and unsteady diffusion
 Chapter 5 Steady and unsteady diffusion In this chapter, we solve the diffusion and forced convection equations, in which it is necessary to evaluate the temperature or concentration fields when the velocity
Chapter 5 Steady and unsteady diffusion In this chapter, we solve the diffusion and forced convection equations, in which it is necessary to evaluate the temperature or concentration fields when the velocity
Summary: angular momentum derivation
 Summary: angular momentum derivation L = r p L x = yp z zp y, etc. [x, p y ] = 0, etc. (-) (-) (-3) Angular momentum commutation relations [L x, L y ] = i hl z (-4) [L i, L j ] = i hɛ ijk L k (-5) Levi-Civita
Summary: angular momentum derivation L = r p L x = yp z zp y, etc. [x, p y ] = 0, etc. (-) (-) (-3) Angular momentum commutation relations [L x, L y ] = i hl z (-4) [L i, L j ] = i hɛ ijk L k (-5) Levi-Civita
Solutions VI. MAE294A/SIO203A: Methods in Applied Mechanics Fall Quarter
 MAE94A/SIO3A: Methods in Applied Mechanics Fall Quarter 17 http://web.eng.ucsd.edu/~sgls/mae94a_17/ Solutions VI 1 We let Tx, t) = Xx)τt). We have two homogeneous conditions in x, so let X = λ X to obtain
MAE94A/SIO3A: Methods in Applied Mechanics Fall Quarter 17 http://web.eng.ucsd.edu/~sgls/mae94a_17/ Solutions VI 1 We let Tx, t) = Xx)τt). We have two homogeneous conditions in x, so let X = λ X to obtain
Methods of Theoretical Physics: I
 Methods of Theoretical Physics: I ABSTRACT First-order and second-order differential equations; Wronskian; series solutions; ordinary and singular points. Orthogonal eigenfunctions and Sturm-Liouville
Methods of Theoretical Physics: I ABSTRACT First-order and second-order differential equations; Wronskian; series solutions; ordinary and singular points. Orthogonal eigenfunctions and Sturm-Liouville
More on Bessel functions. Infinite domain, δ-function normalization
 More on Bessel functions Infinite domain, δ-function normalization Consider Bessel s equation on the domain < ρ < as R ½ Bessel s equation, (375) or (393), says ρ d ρ dj ν(kρ) + k 2 ν 2 ρ 2 J ν (kρ) =
More on Bessel functions Infinite domain, δ-function normalization Consider Bessel s equation on the domain < ρ < as R ½ Bessel s equation, (375) or (393), says ρ d ρ dj ν(kρ) + k 2 ν 2 ρ 2 J ν (kρ) =
Week 2 Notes, Math 865, Tanveer
 Week 2 Notes, Math 865, Tanveer 1. Incompressible constant density equations in different forms Recall we derived the Navier-Stokes equation for incompressible constant density, i.e. homogeneous flows:
Week 2 Notes, Math 865, Tanveer 1. Incompressible constant density equations in different forms Recall we derived the Navier-Stokes equation for incompressible constant density, i.e. homogeneous flows:
Problem Set #5: 5.7,5.9,5.13 (Due Monday, April 8th)
 Chapter 5 Magnetostatics Problem Set #5: 5.7,5.9,5.13 (Due Monday, April 8th) 5.1 Biot-Savart Law So far we were concerned with static configuration of charges known as electrostatics. We now switch to
Chapter 5 Magnetostatics Problem Set #5: 5.7,5.9,5.13 (Due Monday, April 8th) 5.1 Biot-Savart Law So far we were concerned with static configuration of charges known as electrostatics. We now switch to
Series Solution of Linear Ordinary Differential Equations
 Series Solution of Linear Ordinary Differential Equations Department of Mathematics IIT Guwahati Aim: To study methods for determining series expansions for solutions to linear ODE with variable coefficients.
Series Solution of Linear Ordinary Differential Equations Department of Mathematics IIT Guwahati Aim: To study methods for determining series expansions for solutions to linear ODE with variable coefficients.
Curvilinear coordinates
 C Curvilinear coordinates The distance between two points Euclidean space takes the simplest form (2-4) in Cartesian coordinates. The geometry of concrete physical problems may make non-cartesian coordinates
C Curvilinear coordinates The distance between two points Euclidean space takes the simplest form (2-4) in Cartesian coordinates. The geometry of concrete physical problems may make non-cartesian coordinates
LAPLACE EQUATION. = 2 is call the Laplacian or del-square operator. In two dimensions, the expression of in rectangular and polar coordinates are
 LAPLACE EQUATION If a diffusion or wave problem is stationary (time independent), the pde reduces to the Laplace equation u = u =, an archetype of second order elliptic pde. = 2 is call the Laplacian or
LAPLACE EQUATION If a diffusion or wave problem is stationary (time independent), the pde reduces to the Laplace equation u = u =, an archetype of second order elliptic pde. = 2 is call the Laplacian or
Qualification Exam: Mathematical Methods
 Qualification Exam: Mathematical Methods Name:, QEID#41534189: August, 218 Qualification Exam QEID#41534189 2 1 Mathematical Methods I Problem 1. ID:MM-1-2 Solve the differential equation dy + y = sin
Qualification Exam: Mathematical Methods Name:, QEID#41534189: August, 218 Qualification Exam QEID#41534189 2 1 Mathematical Methods I Problem 1. ID:MM-1-2 Solve the differential equation dy + y = sin
The purpose of this lecture is to present a few applications of conformal mappings in problems which arise in physics and engineering.
 Lecture 16 Applications of Conformal Mapping MATH-GA 451.001 Complex Variables The purpose of this lecture is to present a few applications of conformal mappings in problems which arise in physics and
Lecture 16 Applications of Conformal Mapping MATH-GA 451.001 Complex Variables The purpose of this lecture is to present a few applications of conformal mappings in problems which arise in physics and
Review of Electrostatics. Define the gradient operation on a field F = F(x, y, z) by;
 Review of Electrostatics 1 Gradient Define the gradient operation on a field F = F(x, y, z) by; F = ˆx F x + ŷ F y + ẑ F z This operation forms a vector as may be shown by its transformation properties
Review of Electrostatics 1 Gradient Define the gradient operation on a field F = F(x, y, z) by; F = ˆx F x + ŷ F y + ẑ F z This operation forms a vector as may be shown by its transformation properties
lim = F F = F x x + F y y + F z
 Physics 361 Summary of Results from Lecture Physics 361 Derivatives of Scalar and Vector Fields The gradient of a scalar field f( r) is given by g = f. coordinates f g = ê x x + ê f y y + ê f z z Expressed
Physics 361 Summary of Results from Lecture Physics 361 Derivatives of Scalar and Vector Fields The gradient of a scalar field f( r) is given by g = f. coordinates f g = ê x x + ê f y y + ê f z z Expressed
G( x x, t) = 1 (2π) 3. d 3 k e k2 t/µσ e i k ( x x ) A( k, t)e k x d 3 k. A( x, t) = 1
 Physics 505 Fall 2005 Homework Assignment #10 Solutions Textbook problems: Ch. 6: 6.3, 6.4, 6.14, 6.18 6.3 The homogeneous diffusion equation (5.160) for the vector potential for quasi-static fields in
Physics 505 Fall 2005 Homework Assignment #10 Solutions Textbook problems: Ch. 6: 6.3, 6.4, 6.14, 6.18 6.3 The homogeneous diffusion equation (5.160) for the vector potential for quasi-static fields in
Final Examination Solutions
 Math. 42 Fulling) December 22 Final Examination Solutions Calculators may be used for simple arithmetic operations only! Laplacian operator in polar coordinates: Some possibly useful information 2 u =
Math. 42 Fulling) December 22 Final Examination Solutions Calculators may be used for simple arithmetic operations only! Laplacian operator in polar coordinates: Some possibly useful information 2 u =
DO NOT WRITE YOUR NAME OR STUDENT NUMBER ON ANY SHEET!
 tatistical Mechanics ubject Exam, Wednesday, May 3, 2017 DO NOT WRITE YOUR NAME OR TUDENT NUMBER ON ANY HEET! a ( b c) = b( a c) c( a b), a ( b c) = b ( c a) = c ( a b), ( a b) ( c d) = ( a c)( b d) (
tatistical Mechanics ubject Exam, Wednesday, May 3, 2017 DO NOT WRITE YOUR NAME OR TUDENT NUMBER ON ANY HEET! a ( b c) = b( a c) c( a b), a ( b c) = b ( c a) = c ( a b), ( a b) ( c d) = ( a c)( b d) (
Physics 228 Today: Ch 41: 1-3: 3D quantum mechanics, hydrogen atom
 Physics 228 Today: Ch 41: 1-3: 3D quantum mechanics, hydrogen atom Website: Sakai 01:750:228 or www.physics.rutgers.edu/ugrad/228 Happy April Fools Day Example / Worked Problems What is the ratio of the
Physics 228 Today: Ch 41: 1-3: 3D quantum mechanics, hydrogen atom Website: Sakai 01:750:228 or www.physics.rutgers.edu/ugrad/228 Happy April Fools Day Example / Worked Problems What is the ratio of the
Math Review for Exam Compute the second degree Taylor polynomials about (0, 0) of the following functions: (a) f(x, y) = e 2x 3y.
 Math 35 - Review for Exam 1. Compute the second degree Taylor polynomial of f e x+3y about (, ). Solution. A computation shows that f x(, ), f y(, ) 3, f xx(, ) 4, f yy(, ) 9, f xy(, ) 6. The second degree
Math 35 - Review for Exam 1. Compute the second degree Taylor polynomial of f e x+3y about (, ). Solution. A computation shows that f x(, ), f y(, ) 3, f xx(, ) 4, f yy(, ) 9, f xy(, ) 6. The second degree
Using Green s functions with inhomogeneous BCs
 Using Green s functions with inhomogeneous BCs Using Green s functions with inhomogeneous BCs Surprise: Although Green s functions satisfy homogeneous boundary conditions, they can be used for problems
Using Green s functions with inhomogeneous BCs Using Green s functions with inhomogeneous BCs Surprise: Although Green s functions satisfy homogeneous boundary conditions, they can be used for problems
Electromagnetism Answers to Problem Set 8 Spring Jackson Prob. 4.1: Multipole expansion for various charge distributions
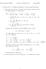 Electromagnetism 76 Answers to Problem Set 8 Spring 6. Jackson Prob. 4.: Multipole expansion for various charge distributions (a) In the first case, we have 4 charges in the xy plane at distance a from
Electromagnetism 76 Answers to Problem Set 8 Spring 6. Jackson Prob. 4.: Multipole expansion for various charge distributions (a) In the first case, we have 4 charges in the xy plane at distance a from
Electric fields in matter
 Electric fields in matter November 2, 25 Suppose we apply a constant electric field to a block of material. Then the charges that make up the matter are no longer in equilibrium: the electrons tend to
Electric fields in matter November 2, 25 Suppose we apply a constant electric field to a block of material. Then the charges that make up the matter are no longer in equilibrium: the electrons tend to
Multipole moments. November 9, 2015
 Multipole moments November 9, 5 The far field expansion Suppose we have a localized charge distribution, confined to a region near the origin with r < R. Then for values of r > R, the electric field must
Multipole moments November 9, 5 The far field expansion Suppose we have a localized charge distribution, confined to a region near the origin with r < R. Then for values of r > R, the electric field must
Solutions to Laplace s Equations- II
 Solutions to Laplace s Equations- II Lecture 15: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Laplace s Equation in Spherical Coordinates : In spherical coordinates
Solutions to Laplace s Equations- II Lecture 15: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Laplace s Equation in Spherical Coordinates : In spherical coordinates
Computation of the scattering amplitude in the spheroidal coordinates
 Computation of the scattering amplitude in the spheroidal coordinates Takuya MINE Kyoto Institute of Technology 12 October 2015 Lab Seminar at Kochi University of Technology Takuya MINE (KIT) Spheroidal
Computation of the scattering amplitude in the spheroidal coordinates Takuya MINE Kyoto Institute of Technology 12 October 2015 Lab Seminar at Kochi University of Technology Takuya MINE (KIT) Spheroidal
PHY752, Fall 2016, Assigned Problems
 PHY752, Fall 26, Assigned Problems For clarification or to point out a typo (or worse! please send email to curtright@miami.edu [] Find the URL for the course webpage and email it to curtright@miami.edu
PHY752, Fall 26, Assigned Problems For clarification or to point out a typo (or worse! please send email to curtright@miami.edu [] Find the URL for the course webpage and email it to curtright@miami.edu
6 Wave equation in spherical polar coordinates
 6 Wave equation in spherical polar coorinates We now look at solving problems involving the Laplacian in spherical polar coorinates. The angular epenence of the solutions will be escribe by spherical harmonics.
6 Wave equation in spherical polar coorinates We now look at solving problems involving the Laplacian in spherical polar coorinates. The angular epenence of the solutions will be escribe by spherical harmonics.
Math 210, Final Exam, Spring 2012 Problem 1 Solution. (a) Find an equation of the plane passing through the tips of u, v, and w.
 Math, Final Exam, Spring Problem Solution. Consider three position vectors (tails are the origin): u,, v 4,, w,, (a) Find an equation of the plane passing through the tips of u, v, and w. (b) Find an equation
Math, Final Exam, Spring Problem Solution. Consider three position vectors (tails are the origin): u,, v 4,, w,, (a) Find an equation of the plane passing through the tips of u, v, and w. (b) Find an equation
Chapter 4. Series Solutions. 4.1 Introduction to Power Series
 Series Solutions Chapter 4 In most sciences one generation tears down what another has built and what one has established another undoes. In mathematics alone each generation adds a new story to the old
Series Solutions Chapter 4 In most sciences one generation tears down what another has built and what one has established another undoes. In mathematics alone each generation adds a new story to the old
1. (a) (5 points) Find the unit tangent and unit normal vectors T and N to the curve. r (t) = 3 cos t, 0, 3 sin t, r ( 3π
 1. a) 5 points) Find the unit tangent and unit normal vectors T and N to the curve at the point P 3, 3π, r t) 3 cos t, 4t, 3 sin t 3 ). b) 5 points) Find curvature of the curve at the point P. olution:
1. a) 5 points) Find the unit tangent and unit normal vectors T and N to the curve at the point P 3, 3π, r t) 3 cos t, 4t, 3 sin t 3 ). b) 5 points) Find curvature of the curve at the point P. olution:
Electromagnetism: Worked Examples. University of Oxford Second Year, Part A2
 Electromagnetism: Worked Examples University of Oxford Second Year, Part A2 Caroline Terquem Department of Physics caroline.terquem@physics.ox.ac.uk Michaelmas Term 2017 2 Contents 1 Potentials 5 1.1 Potential
Electromagnetism: Worked Examples University of Oxford Second Year, Part A2 Caroline Terquem Department of Physics caroline.terquem@physics.ox.ac.uk Michaelmas Term 2017 2 Contents 1 Potentials 5 1.1 Potential
Math221: HW# 7 solutions
 Math22: HW# 7 solutions Andy Royston November 7, 25.3.3 let x = e u. Then ln x = u, x2 = e 2u, and dx = e 2u du. Furthermore, when x =, u, and when x =, u =. Hence x 2 ln x) 3 dx = e 2u u 3 e u du) = e
Math22: HW# 7 solutions Andy Royston November 7, 25.3.3 let x = e u. Then ln x = u, x2 = e 2u, and dx = e 2u du. Furthermore, when x =, u, and when x =, u =. Hence x 2 ln x) 3 dx = e 2u u 3 e u du) = e
