Chapter 4 Boundary Value Problems in Spherical and Cylindrical Coordinates
|
|
|
- Adam Harper
- 5 years ago
- Views:
Transcription
1 Chapter 4 Boundary Value Problems in Spherical and Cylindrical Coordinates 4. Laplace s Equation in spherical coordinates Laplace s equation in spherical coordinates, (r, θ, φ), has the form where r r Φ (r, θ, φ) r r L LΦ (r, θ, φ). (4.) r L L sin θ sin θ Φ (r, θ, φ) + θ θ sin θ φ (4.) Multiplying Eq. 4. by r,dividing by Φ (r, θ, φ)r (r) Y (θ, φ) and rewriting, r R(r) R r r L L Y (θ, φ). (4.3) Y This equation must be satisfied for all (r, θ, φ) As r, θ, φ are independent variables, Eq. 4.3 can only be satisfied if both sides equal a constant which we choose this constant to be ( +).Then, and L LY (θ, φ) ( +)Y (θ, φ) (4.4) d r R(r) ( +)R(r) (4.5) dr ddr Eq. 4.4 can be further separated using Y (θ, φ) V (θ)w (φ): V (θ) sin θ sin θ V (θ) + θ θ V (θ) sin θ( +)V (θ) W φ W (4.6) Again, since θ,φ are independent variables both sides must equal a constant (the second separation constant) which we take to be m φ W (φ) m W (φ) or (4.7a) and sin θ θ sin θ W m (φ) A m e imφ + B m e imφ (4.7b) θ V (θ) +[sin θ( +) m ]V (θ) (4.8) 73
2 Substituting x cosθ Eq. 4.8 becomes the associated Legendre equation: d ( x ) d dx dx F (x) +[ ( +) m ]F (x).; x cosθ (4.9) x with two linearly independent solutions called the associated Legendre functions of the first, P m (x), and second kind, Q m (x). F, m (x) A, m P m (x)+b, m Q m (x) (4.) One can show that:the P m (cos θ) canbemadetoconvergeforall θ π if : <m m,,. > P m (cos θ) converge.. The Q m (cos θ), howeverdivergeatcos θ for the above conditions on m and. The Q m (cos θ) are possible solutions when cos θ <. In our problem we expect the functions to be well behaved for all x cos θ. A special case is found when m and these solutions, P (x) P (x)are called Legende functions or Legendre polynomials. The P (x) are normalized so that: P (x) (4.) P (x) x P (x) 3x P 3 (x) x 5x 3 P 4 (x) 35x 4 3x +3 8 The associated Legendre polynomials, P m Legendre polynomials by (x) P m (x), of degree and order m. are related to the P m (x) x m/ d m P (x),m ; (4.) dxm P m (x) ( ) m P m (x),m< This particular sign convention is just one possibility. Clearly these are only non-zero when m. FinallywenotethatatP () (by definition), P ( ) ( ), and, if m 6,P m symmetry of these functions for x xis P m ( x) ( ) +m P m (x) (±). The general Legendre s functions of the second kind Q (x), have singularities at x ±. This solution would be one of the set known as Legendre functions of the second kind. The first two Legendre functions of the second kind are, for x, 74
3 Section 4. Spherical harmonics Q (x) µ +x ln tanh (x) (4.3) x Q (x) x µ +x ln x We note the logarithmic divergences for Q n (x) at x ±. In general, the associated Legendre functions can be written in terms of the hypergeometric function, F (a, b, c : z) an infinite series which terminates for a (or b) equal to a negative integer. The termination of the series for a m produces the convergence of the, P m (x): Q m (x) constant m/ x + F (, +, m; x ) (4.4) x P m (x) constant x + x m/ µ x m F (m, + m +,m+; x ) (4.5) where (Handbook of Mathematical Functions, M. Abramowitz and I. Stegun, NBS ) F (a, b, c; z) Γ( c) Γ(a)Γ(b) Σ Γ(a + n)γ(b + n) n z n n!γ(c + n) (4.6) Γ(a) (a )! 4. Spherical harmonics Laplace s and Poisson s equation in spherical coordinates are encountered in a wide range of problems (E&M, thermodynamics, mechanics of continuous media, and quantum mechanics). As might be expected the solutions of these equations have been well studied. The solutions to the angular part of the equation are the spherical harmonics. Theseare the appropriately normalized products of the associated Legendre polynomials in cos θ and the exp (imφ) Y m (θ, φ) ( ) m s +( m)! ( + m)! P m (cos (θ)) e imφ (4.7) The Y m (θ, φ) are solutions to Eq. 4.3: and Some useful properties are: L z Y m L L Y m l ( +)Y m my m ; where L z ẑ L Y m (θ, φ) ( ) m Y m (θ, φ) (4.8a) 75
4 Section 4.3 Poisson s equation with point charge in (r, θ, φ) Y m (π θ, π φ) ( ) Y m (θ, φ) (4.8b) The orthonormality condition: Z π Z π Y m (θ, φ) Y m (θ, φ)sinθdθdφ δ δ mm (4.9) (Y m,ym ) δ δ mm and the completeness condition: X m Y θ,φ Y m (θ, φ) δ φ φ δ cos θ cos θ (4.) 3 Y (θ, φ) 3 Y (θ, φ) Y (θ, φ) / 5 Y (θ, φ) / cos θ Y (θ, φ) / sin θe iφ Y (θ, φ) / 3 cos θ / 5 sin θ cos θe iφ 8π / 5 sin θe iφ (4.) Y 3 (θ, φ) Y 3 (θ, φ) 4 Y 3 (θ, φ) 4 Y 3 3 (θ, φ) 4 / 7 5 cos3 θ 3 cos θ / sin θ 5cos θ e iφ / 5 sin θ cos θe iφ π 35 / sin 3 θe i3φ (4.) 4.3 Poisson s equation with point charge in (r, θ, φ) We will now re-examine the solution to Poisson s equation with a point charge q. Let the charge lie at coordinates r,θ,φ and let the observation point have coordinates (r, θ, φ). The solution will be a Green s function and we consider the dependence on r,θ,φ and on (r, θ, φ) The charge density is ρ (r, θ, φ) qδ(r r ) Gaussian units (4.3) q r δ (r r ) δ cos θ cos θ δ φ φ 76
5 Section 4.3 Poisson s equation with point charge in (r, θ, φ) and Poisson s equation is Φ (r, θ, φ) k ρ (r, θ, φ) (4.4) δ(r r ). Gaussian units (4.4) Φ (r, θ, φ) ρ (r, θ, φ) S.I. units We look for a solution of the form Φ (r, θ, φ) X m Inserting this into Poisson s equation we obtain (using Gaussian units) r X m X X m f m r; r,θ,φ Y m (θ, φ) (4.5) f m r; r,θ,φ Y m (θ, φ) q r δ (r r ) δ cos θ cos θ δ φ φ (4.6) µ d r d dr dr f m ( +)f m Y m (θ, φ) q r δ (r r ) δ cos θ cos θ δ φ φ Multiply both sides by Y m (θ, φ) and integrate over RR d(cos θ)dφ Using the orthonormality of the spherical harmonics one finds: ZZ X µ d r r d dr dr f m ( +)f m Y m m (θ, φ) Y (θ, φ) d(cos θ)dφ r X m X m d dr q r δ (r r ) µr ddr f m ( +)f m δ δ m m ZZ δ φ φ δ cos θ cos θ Y m (θ, φ) d(cos θ)dφ d µr ddr r dr f m ( +)f m q r δ (r r ) Y m θ,φ (4.7) Thus the angular dependence of f m r; r,θ,φ is given by Y m θ,φ and we define The functions g (r; r ) satisfy f m r; r,θ,φ g (r; r ) Y m θ,φ. (4.8) µ d r r d dr dr g ( +)g q r δ (r r ) (4.9) These equations are solved by : () obtaining the solutions to the homogeneous equations for r<r and r>r, () making g (r; r ) continuous at r r, and (3) satisfying the condition placed on g (r; r ) obtained by integrating Eq. 4.9 from r r ε to r r + ε. 77
6 Section 4.3 Poisson s equation with point charge in (r, θ, φ) The solution to the homogeneous equation in r has the general form g (r; r )α (r ) r + β (r ) r. (4.3) For r<r g (r; r )α (r ) r and for r>r g (r; r )β (r ) r. Continuity at r r requires that Integrating Eq. 4.9 from r r ε to r r + ε we obtain Z r +ε r ε g (r; r ) a r r +,r<r (4.3) g (r; r r ) a,r>r r+ µ d r r d dr dr g ( +)g dr q r Z r +ε r ε δ (r r ) dr Z r +ε r ε µ d r r d dr dr g ( +)g dr q r The second term on the left is continuous at r r and drops out of the equation. Z r +ε r ε µ d r r d dr dr g dr q r Integrating by parts twice, µ r r d dr g rr +ε Z r +ε rr ε + r ε r d dr g dr q r µ r r d dr g rr +ε rr ε + r g rr +ε Only the first term on the left is non-zero at r r so Z r +ε rr ε + r ε " µdg r (r; r µ ) dg (r; r ) dr rr +ε dr Now use the specificformsforg (r; r ): r a " µ d dr r µ d r + rr +ε dr r g dr rr ε r # r + q rr ε q r # q (4.3) Thus r r r a[ ( +) ]a[ ( +) ] a( +) r+ r + a q + 78 (4.33)
7 Section 4.4 The Coulomb potential in spherical coordinates 4.4 The Coulomb potential in spherical coordinates Using Eq we have the expansion of a point charge coulomb potential given by, X r< Φ (r, θ, φ) q +r + Y m (θ, φ) Y θ,φ. (4.33b) m > Φ (r, θ, φ) qδ(r r ) Gaussian units where the point charge is at r and r < min(r, r ) and r > max(r, r ). Since the position of the point charge is provided in this simple example, one considers r r a constant vector and qδ(r r ) is only a function of.r However, if wehaveachargedensity,ρ(r) q f(r, θ, ϕ) it is clear that ρ(r) is a function of r, andisspecified by f(r, θ, ϕ). The latter includes any dependence on known vectors such as r. 4.5 Green s Function and Expansion of r r Note that the Green s function for Laplace s equation (for V all space) satisfies the following: Thus. r r δ(r r ) G(r, r ) X r< +r + m > G(r, r ) δ(r r ) Gaussian units Recall that the G(r, r ) can also be written as follows: Y m (θ, φ) Y θ,φ. (4.34a) G(r, r ) r r (4.34b) The Green s function differs from the Φ (r) (ineq4.33)asφ(r) describes the electrostatic potential due to a point charge, q at a given point, r r. In contrast, G(r, r ) represents a unit point charge at r, which is as yet unspecified.. Equations 4.34 yield a convenient expansion for r r in spherical harmonics r r X X m + and provides a convenient way to evaluate integrals of the form: r< r> + Y m (θ, φ) Y θ,φ (4.35) ZZZ ρ(r ZZZ ) r r dv 79 ρ(r )G(r, r )dv
8 Section 4.4 The Coulomb potential in spherical coordinates Example: Determine the electrostatic potential due to the following distribution of charge (a spherical shell of charge with a cos θ angular dependence); ρ(r) Q cos θδ(r a) a assuming that the potential like as r r Solution: We use the Green s function for all of space (Eq. 4.34a) as follows in S.I. units: φ (r) ε ZZZ all space ZZ [ ρ (r )]G (r, r ) d 3 r + φ (r) ε r ZZZ ZZ φ (r s) G (r, r s) ds G (r, r s) φ (r s) ds r r >a since the surface integrals vanish like r as r. (seepage59). φ (r) ε ε ZZZ ZZZ Q ε a all space all space m ρ (r ) X ρ (r ) G (r, r ) d 3 r r r d3 r (note r dependence of ρ) SI units Q a cos θ δ(r a) Z + Y m (θ, φ) X m r< r> + + r< r> + Y m r δ(r a)dr ZZ Next, we use the expansion of cos θ in spherical harmonics: r cos θ 3 Y (θ,φ ) φ (r) φ (r) φ (r) ε Q ε a Q ε a X m X m Q a + Q 3εa r cos θ Q a 3 3εa r cos θ Z + Y m (θ, φ) Z + Y m (θ, φ) r 3 Y (θ, φ) if r<a if r>a r< r> + Note that the final angular dependence of φ (r) is r< r> + r< r> + r ZZ r δ(r a)dr 3 r δ(r a)dr (θ, φ) Y θ,φ d 3 r r 3 δ δ m r δ(r a)dr Q 3εa cos θ r < of radius a and falls off like outside the sphere. Continuity at r a is preserved r cos θ Y θ,φ d(cos θ )dϕ Y (θ,φ )Y θ,φ d(cos θ )dϕ r> + a r 3 Y (θ, φ) cosθ.and the r dependence is linear inside the sphere 8
9 Section 4.6 Addition Theorem for Spherical Harmonics 4.6 Addition Theorem for Spherical Harmonics Suppose in the expansion of r r X X m + r< r> + Y m (θ, φ) Y θ,φ (see 4.33) we let r r ẑ.sothat θ. Then only the m terms will appear in the su Y m,φ if m 6.Inthiscase, using the expression for Y m (θ, φ) in Eq. 4.7 and P () r r ẑ r r ẑ [r r r r cos θ+r ] / r< +r> + r< +r> + r< P (cos θ) r + > r< r + > P (cos θ) Y (θ, φ) Y,φ r r + + P (cos θ) P () The angular dependence of this expression depends only on the angle, γ, between the vector locating the charge, r,and the vector locating the observation point, r. That is, r r rr cos γ. So [r r r r cos γ+r ] / r< r + > X m P (cos γ) + Thus, one obtains the addition theorem for spherical harmonics: r< r> + Y m (θ, φ) Y θ,φ P (cos γ) X + Y m (θ, φ) Y θ,φ m ˆr ˆr cos γ sinθ sin θ [cos φ cos φ +sinφsin φ ]+cosθcos θ sinθ sin θ cos φ φ +cosθ cos θ (4.36) 4.7 Problems with azimuthal symmetry The angular dependence of systems in which the boundary conditions and the charge densities have axial symmetry, i.e., 8
10 Section 4.6 Addition Theorem for Spherical Harmonics they are independent of φ,is given by the Legendre functions P ν (cos θ). The potential will have the general form Φ (r, θ) f n (r) P νn (cos θ) (4.37) n Problems with θ π If the range of θ is from zero to π then the condition that Φ (r, θ) be non-singular requires that ν n n (an integer). In this case the sum will be over Legendre polynomials. The potential is then given by Φ (r, θ) αn r n + β n r n P n (cos θ). (4.38) n To evaluate the coefficients we need the orthogonality condition for the Legendre polynomials δ mn n + Z π Z π P m (cos θ) P n (cos θ)sinθdθ (4.39) P m (cos θ) P n (cos θ) d(cos θ). Specifying the potential at r a and at r b>athe coefficients satisfy the equations Φ (a, θ) Φ (b, θ) αn a n + β n a n P n (cos θ) I n (a) P n (cos θ) n n αn b n + β n b n P n (cos θ) I n (b) P n (cos θ) n n Mulitply each side byp n (cos θ) and integrate over θ: αn a n + β n a n µ n + Z π P n (cos θ) Φ (a, θ)sinθdθ I n (a) (4.4) αn b n + β n b n µ n + Z π P n (cos θ) Φ (b, θ)sinθdθ I n (b) which have solutions α n an+ I n (a) b n+ I n (b) a n+ b n+ (4.4) β n (ab) n+ b n I n (a) a n I n (b) a n+ b n+ In the limit that a we have that α n b n I n (b) and β n, while if b we have α n and β n a n+ I n (a). Problems with θ θ m <π If we require that the solution of Legendre s equation be zero at θ θ m andthatitbefinite for θ θ m the most general solution will be a Legendre function of the first kind, P ν (cos θ) where ν 6 integer (See Abramowitz & Stegun, pp33, 556). Legendre functions of the second kind, which diverges at cos θ,are excluded. The P ν (cos θ) are generally expressed in terms of the hypergeometric functions, F (a, b, c; w) (See Eqs. 4.5 and 4.6) where we set a ν, b +ν, 8
11 c and w cos θ series. Section 4.6 Addition Theorem for Spherical Harmonics sin θ.whenν 6 integer ( a is not a negative integer) the F ( ν,+ν;,w) is an infinite P ν (cos θ) P υ (x) F µ µ θ ν,+ν;, sin with the function (z) n given by [sin (θ/)] n ( ν) n (ν +) n n! n (z) n z (z +)(z +)... (z + n ). (z + n )! (z )! For a given angle, θ β, the Legendre functions can be plotted as a function of ν to determine the values of ν which yield P ν (cos β). The figure below illustrates the approach with β π/6, π/3, and π/. In the case that β π/ we note that the appropriate functions will be the Legendre polynomials of odd order. Plot versus order.63 Legendre function order 9 deg. 3 deg. 6 deg.fig. 4. Example: the fields near the point of a cone The results of the last section can be applied to the problem of determining the fields and surface charge density near the tip of a conical conductor. In the region of interest the surface of the cone makes an angle β with the z axis. For β<π/ the region of interest is inside the cone while for β>π/ the region is outside the conical surface. If we take the cone to be at zero potential then the leading term in the potential will be where ν is determined by the condition that cos β is the first zero of P ν (cos θ). 83 Φ (r, θ, φ) Φ r ν P ν (cos θ) (4.43)
12 Section 4.8 Green s function in a spherical shell For example if β π/6 then ν 4 (see Fig. 4.). Near the tip of the cone the electric field will have components E r (r, θ) Φ ν r ν P ν (cos θ) E θ (r, θ) r θ Φ r ν P ν (cos θ) Φ r ν sin θpν (cos θ) and the surface charge density will be given by ˆn E σ (r) where ˆn is normal to the conical surface defined by θ π/6. Thatis, ˆn ˆθ. σ (r) () Φ r ν sin βp ν (cos β). (4.45) We first consider the case with β<π/. For this system ν > and the fields and surface charge vanish as r. The geometry of this system would correspond to a conical hole in a conductor. As expected the field does not readily penetrate a hole in a conductor. The alternate case has β>π/. From Fig. we deduce that ν <. Clearly the fields and surface charge diverge as one approaches the point of the cone. This is confirmation of the folk-lore that the fields are strong at pointed regions of a charged conductor. 4.8 Green s function in a spherical shell To illustrate the Green s function techniques we consider systems which lie in a spherical shell a r b bounded by conducting (segmented?) spherical shells. In this case the potentials on the conductors are generally specified and the Dirichlet green s function is required. Excluding the value r r gives two homogeneous equations, one for a r<r and the other for r <r b. The solutions for the r and r dependence are of the form in Eq To make the g (r; r ) at the surfaces of the conductor we set " # g (r; r ) α (r r ) r + a+ (rr ) +, a r<r (4.46) at r " a # g (r; r ) β (r ) (rr ) b + + r r +,r <r b at r b Continuity of g (r; r ) at r r requires that " # " # α (r ) r a+ (r ) + β (r ) (r ) b + + r (4.47) while to satisfy the differential equation, Eq. 4.9, one needs to carry out the procedure in Eq 4.3. (That is one needs to integrate the differential equation, O Φ(r, r ) δ(r r ) from r r to r r + ). The procedure (in Gaussian units) results in the following equation: α (r ( +)a+ r ) + r r + + β (r ( +) ) + b+ r r (4.48) 84
13 Section 4.8 Green s function in a spherical shell The solution to these equations is α (r ) β (r ) (r /b) + + (a/b) + (3-49) (a/r ) + + (a/b) + giving the result Φ (r; r ) G (r; r ) b + R> + R + < a + ( +)(b + a + )(rr ) + X+ m b + R> + R + < a + ( +)(b + a + )(rr ) + R < min(r, r ), R > max(r, r ) Y m X+ m (θ, φ) Y θ,φ, (4.5) Y m (θ, φ) Y θ,φ If a this gives the Green s function for the system confined to lie inside a spherical shell of radius b while if b this is the Green s function for the system confined to lie outside a spherical shell of radius a. Example : Uniformly charged annulus in θ π/ plane As an application for the Green s function of the last section we consider the system consisting of grounded concentric spheres, radii a<b,separated by a uniformly charged annulus (ring) with total charge Q. The problem is to determine the total charges on the spherical surfaces r a and r b. The surface charge density on the ring between the spheres is (4.6) the charge density is σ Q π (b a ), ρ (r) σ δ (z) σ δ (cos θ), a r b r and the boundary conditions are Φ (a, θ, φ) Φ (b, θ, φ). Solution: With the given boundary conditions and the azimuthal symmetry The charge on the inner sphere is ZZZ Φ (r, θ, φ) G (r; r )[ ρ (r )]d 3 r Gaussian units a r b X Z P (cos θ) P () b b πσ (b + a + r + R + > R + < a + ) a (rr ) + dr Q a ZZ ra πσ a b a ZZ σ(r)r dω Z b a ra E r r dω a (b r ) dr πσ a (b a) 85 ZZ Φ (r, θ, φ) r dω ra
14 Section 4.9 Laplace s equation in cylindrical coordinates and on the inner surface of the outer sphere ZZ Φ Q b b (r, θ, φ) r πσ Z b b b a a where we have used the orthogonality of the Legendre polynomials Z dω rb (r a) dr πσ b (b a) P (x) dx δ. (4.5) As a variation on this problem we relax the condition that the two spheres are at the same potential. Instead we require that the inner sphere be neutral and determine the potential of the inner sphere minus the potential of the outer sphere. The result can be readily obtained using the superposition principle. The inner sphere is made neutral by distributing a charge πσ a (b a) uniformly over its surface. The inner surface of the outer sphere will then have a total charge of π b a σ. Applying the superposition principle yields that Φ (a) Φ (b) πσ (b a) b Q (b a) b (b + a) Example : Inner sphere potential is Φ P (cos θ), outer sphere is grounded To demonstrate another application of the Green s function we consider a boundary value problem. Again the system consists of concentric spheres, radii a<b.the boundary conditions are Φ (a, θ, φ) Φ cos θ, Φ (b, θ, φ). The green s function solution to this problem is given by ZZ Φ (r, θ, φ) a Φ cos θ r G (r; r ) dω r a Using the orthogonality of the Legendre polynomials this reduces to Ã Φ (r, θ, φ) a 3 Φ cos θ b 3 r 3 r 3 a 3! r (b 3 a 3 )(rr ) a Φ cos θ b 3 r 3 r (b 3 a 3 ) This result illustrates the general result that the boundary value problems. The boundary conditions are expanded in spherical harmonics and the boundary value problem is solved for each coefficient in the expansion. The solution of the problem is then given by the superposition principle r a 4.9 Laplace s equation in cylindrical coordinates Problems in which the system is confined to cylindrical volumes are best analyzed in cylindrical coordinates. In cylindrical coordinates Laplace s equation is ρ ρ z) ρ ρ Φ (ρ, ϕ, + ρ Φ (ρ, ϕ, z)+ Φ (ρ, ϕ, z). (4.5) ϕ z 86
15 Section 4.9 Laplace s equation in cylindrical coordinates As in the case of spherical coordinates, this equation is solved by a series expansion in terms of products of functions of the individual cylindrical coordinates. That is, we use separation of variables. Φ (ρ, ϕ, z) X α lmn U l (ρ) V m (ϕ) W k (z). (4.53) l,m,n Substituting Φ lmk (ρ, ϕ, z) U l (ρ) V m (ϕ) W k (z).into Eq 4.5 and dividing by Φ lmk (ρ, ϕ, z), we can sequentially separate all the variable.dependence: d U l ρ dρ ρ d dρ U l + d V m ρ dϕ V m d W n dz W k ±k (4.54) ρ d ρ d U l dρ dρ U l ρ k d V m dϕ V m ±m (4.55) These functions satisfy the Eqs. 4.54, 4.55 and 4.56: d W k (z) dz λ z W k (z) ; λ z k (4.54a) W k (z) A k e kz + B k e kz (4.54b) Note that k can be complex, pure imaginary or real. d dϕ V m (ϕ) λ ϕ V m (ϕ) ; λ ϕ m (4.55) V m (ϕ) C m e imϕ + D m e imϕ (4.55b) Note that m could be non-integer and/or complex ρ d dρ U (ρ)+ρ d dρ U (ρ)+ k ρ m U (ρ) (4.56) (kρ) d d(kρ) U d m (kρ)+kρ d(kρ) U m (kρ)+ (kρ) m U m (kρ) U m (kρ) a m J m (kρ)+b m N m (kρ) (4.56b) wherenowthelabelonu m (kρ) becomes m and the J m and.n m are called Bessel functions of the first and second kind, respectively. [Note that one could also use Hankel functions, H m(kρ) ± J m (kρ) ± in m (kρ), rather than J m (kρ) and N m (kρ).] The boundary conditions on the system determine the allowed values of k and m. Typically the system fills the region from ϕ to ϕ π. In this case the continuity of V m (ϕ) and Vm (ϕ) requires that m be an integer. We consider these systems first. The values of k are determined by boundary conditions requiring solutions to be periodic in z ( k must be pure imaginary, k ±i k ) or exponential in z ( k ± k ). 87
16 Section 4.9 Laplace s equation in cylindrical coordinates 4.9. Potential is zero at ρ a, ρ b In the case that the potential on the cylindrical surfaces are zero, Eq determines the allowed values for k. The appropriate solutions, U (ρ), will be the Bessel functions of the first and second kind, J m (kρ) and N m (kρ) (see Abramowitz & Stegun, Chapts. 9-) which can be made equal to zero at.ka and kb. We can obtain the small ρ dependence of the solutions by neglecting the term k ρ in the differential equation. In this case, if m 6, U (ρ) J m (kρ) (kρ/)m Γ (m +) U (ρ) N m (kρ) Γ (p)(kρ/) m /π. (4.57) If m,we find that U (ρ) or U (ρ) (/π)lnρ. For real m the non-singular solutions are Bessel functions of the first kind, J m (kρ), and the singular solutions are Bessel functions of the second kind, N p (kρ). For large values of kρ the asymptotic behavior of these functions is J m (kρ) N m (kρ) r ³ πkρ cos kρ mπ π 4 r ³ πkρ sin kρ mπ π 4, (4.58). Note: Either of these approximations (4.57 and 4.58) can be used to determine the normalization of the functions for the Green s function. Also, the N m (kρ) has already been made linearly independent of J m (kρ) for integer m. The n th root, in order of magnitude, of the equation J m (x) is given by (see Hildebrand, Advance Calculus for Engineers, Prentice-Hall 949, p ) where µ x n nπ + m c 4n k 4c 3k 3 3c 3... (4.59) 5k5 k π (m +4n ), q 4m, (4.59b) c q, c (q ) (7q 3), c 3 (q ) 83q 98q n m m m m 3 m 4 m Some values for x n are It is often useful to have the zeros of Jm (x). The n th root, in order of magnitude, of the equation Jm (x) is given by µ m + x n nπ + c 4n k 4c 3k 3 3c k5 (4.6) where k π (m +4n +), q 4m, (4.6b) c q +3, c 7q +8q 9, c 3 83q q 339q
17 Section 4. Expansion of the Green s function in cylindrical coordinates The reference also gives formulae for the solutions of J m (x) N m (ax) J m (ax) N m (x) (a>) (4.6) Jm (x) Nm (ax) Jm (ax) Nm (x) (a>) If the system is contained in a cylinder of radius a and length L, a boundary value problem has the potential given on the end caps. In this case the solutions are Bessel functions of the first kind which satisfy the condition J m (ka). This requirement determines values of k, k n with n,,...these functions satisfy the orthogonality relationship Z a ρj m (k n ρ) J m (k n ρ) dρ.5 δ n n [aj m+ (k n a)]. (4.6) For a given value of m we can assume that these functions form a complete set of orthogonal functions on the interval ρ a. Finally, if a the orthogonality condition is ρj m (kρ) J m (k ρ) dρ k δ (k k ). (4.63) 4.9. Potential is zero at z z,z z With the potential equal to zero on the end-caps of the cylindrical region Eq provides the eigenvalue problem for λ z. The required solutions would be a superposition of cos ( k z) and sin ( k z) and λ z (ik) k. Theρ dependence is given by the modified Bessel functions, I m ( k ρ) i m J m (i k ρ) and K m ( k ρ) π im+ H + m(i k ρ) The solutions to Bessel s equation would be the associated Bessel functions I m ( k z) and K m ( k z). For k z these functions behave as µ m k z I m ( k z) (4.64) Γ (m +) K m ( k z) Γ (m) µ m, m 6 k z µ k z ln, m and for large kz these functions have the asymptotic form I m (kz) (π k z) / exp ( k z) (4.65) µ / π K m (kz) exp ( k z). k z A general cylindrical problem would expected to involve both types of solutions. 4. Expansion of the Green s function in cylindrical coordinates The following steps illustrate the general procedure for finding a Green s function expansion...in cylindrical coordinates the Green s function satisfies G (r; r )δ (r r ) ρ δ (ρ ρ ) δ (z z ) δ (ϕ ϕ ) (4.66). Note that there are three representations of delta functions, useful for cylindrical problems: δ (z z ) π e ik(z z ) dk π 89 cos [k (z z )] dk,, (4.67a)
18 Section 4. Expansion of the Green s function in cylindrical coordinates δ (ϕ ϕ ) π m e im(ϕ ϕ ) π {+cos[m (ϕ ϕ )]} (4.67b) δ (ρ ρ )ρ kj p (kρ) J p (kρ ) dk. (4.67c) 3.Making use of the orthogonal functions appearing in the delta function expansions, write a general form for G (r; r ) leaving one set of variables (in this case z and z ) in terms of an unknown function, g m (z; z ): G (r; r ) π m e im(ϕ ϕ ) kg m (z; z ) J m (kρ) J m (kρ ) dk. (4.68) 4. Apply to the general form forg (r; r ) and set the result equal to δ (r r ): G (r; r ) [ ρ ρ ρ + ρ ρ ϕ + z ] π kg m (z; z ) J m (kρ) J m (kρ ) dk m e im(ϕ ϕ ) m e im(ϕ ϕ ) kj m (kρ ) J m (kρ) π [g m (z; z ) ρj m (kρ) ρ + m g m (z; z ) ρ + g m (z; z ) z ] ρ J m (kρ) ρ m e im(ϕ ϕ ) kj m (kρ ) J m (kρ) π [(m ρ k + m ρ )g m (z; z )+ g m (z; z ) z ]dk e im(ϕ ϕ ) kj m (kρ ) J m (kρ) π [ k g m (z; z )+ g m (z; z ) z ]dk m δ (ρ ρ ) δ (z z ) δ (ϕ ϕ ) ρ 9
19 Section 4. Expansion of the Green s function in cylindrical coordinates 5. Multiply both sides by R π dϕe im ϕ R Z π π m + g m (z; z ) z ]dk Z π dϕ e i(m m)ϕ e imϕ dϕ e im (ϕ ) Jm (k ρ ) δ (z z ) ρj m (k ρ) dρ and integrate over dϕ and dρ : kj m (kρ )[ dρδ (ρ ρ ) δ (z z ) δ (ϕ ϕ ) e im (ϕ) J m (k ρ) ρj m (kρ) J m (k ρ) dρ][ k g m (z; z ) R π 6. On the left hand side, use the orthogonality condition, π e imϕ e imϕ dϕ δ mm to reduce the sum over m to a single term with m m, and the integral, R ρj m (kρ) J m (k ρ) dρ k δ (k k ) to carry out the integration over k. e im (ϕ ) kj m (kρ ) k δ (k k )[ k g m (z; z )+ g m (z; z ) z ]dk e im (ϕ ) Jm (k ρ ) [ k g m (z; z )+ g m (z; z ) z ]e im (ϕ ) Jm (k ρ ) δ (z z ) 7. Finally, extract the differential equation for, g m (z; z ), which in this case must satisfy The Dirac delta function on the right hand side indicates d dz g m (z; z ) k g m (z; z )δ (z z ). (4.69) that dg m dz has a discontinuity at zz. 8.To determine the overall normalization constant for g m integrate both sides of 4.69 over R z + z dz Z z + z [ d dz g m (z; z ) k g m (z; z )]dz Z z + z δ (z z ).dz Z z + z d dz g m (z; z ) dz Z z + z k g m (z; z ) dz Z z + z δ (z z ).dz Z z + z d dz [ d dz g m (z; z )]dz d dz g m (z; z ) z + z 9. Assume a general form for g m (z; z ) in terms of the functions given in step.and evaluate the limit in step 8. g m (z; z )C m exp(kz < )exp( kz > ) d dz g m (z; z ) z + z C m[exp(kz ) d dz exp( k(z + )) d dz exp(kz)exp( kz ) C m [exp(kz )( k)exp( k(z + )) k exp(k(z )exp( kz ) 9
20 Section 4. Expansion of r r and the Coulomb potential: As, C m [ k exp(kz kz ) C m k. Put the function, g m (z; z ) k exp(kz < kz >) into the expansion for the Greens function: G (r; r ) π m G (r; r ) e im(ϕ ϕ ) m r r z > max(z,z ), z < min(z, z ) k k exp(kz <)exp( kz > )J m (kρ) J m (kρ ) dk. e im(ϕ ϕ ) exp(kz < )exp( kz > )J m (kρ) J m (kρ ) dk. (4.7) 4. Expansion of r r and the Coulomb potential: Thus by comparing G (r; r ) with its compact form, r r, the expansion of r r is obtained r r X e im(ϕ ϕ ) exp [ k (z > z < )] J m (kρ) J m (kρ ) dk (4.7) m and the Coulomb potential (with unit charge) in cylindrical coordinates can be written q r r q P ) R m eim(ϕ ϕ exp [ k (z > z < )]J m (kρ)j m (kρ )dk (4.7b) If we set ρ and z we can obtain the Laplace transform of J (t) from p ρ + z +s e kz J (kρ) dk or (4.7) e st J (t) dt You should refer to Jackson to review the expansion of the Green s function in terms of the modified Bessel functions. 4. Eigenfunction expansions for the Green s function We consider a system in a volume Ω. A property of the system satisfies the differential equation ψ (r)+[f (r)+λ] ψ (r) (4.73) 9
21 Section 4.3 Green s function in orthogonal functions of spherical coordinates which with appropriate boundary conditions on ψ (r) becomes an eigenvalue equation for λ. Let λ n and ψ n (r) be the eigenvalues and corresponding eigenfunctions. The {ψ n (r)} can be assumed to provide a complete set of functions for describing the property of the system and, since the ψ n satisfy an eigenvalue problem in a finite volume, they form an orthogonal set and Z ψ n (r) ψ m (r) d 3 r δ mn. (4.74) Completeness implies that for r, r in Ω. We now use the functions {ψ n (r)} to expand the Green s function solution to Ω X ψ n (r) ψ n (r )δ(r r ) (4.75) n G (r; r )+[f (r)+λ] G (r; r ) δ (r r ) (4.76) X ψ n (r) ψ n (r ) n The solution is In the case that λ we have G (r; r ) X n G (r; r ) X n ψ n (r) ψ n (r ) λ λ n ψ n (r) ψ n (r ) λ n (4.77a) (4.77b) This is a common form for the Green s function. 4.3 Green s function in orthogonal functions of spherical coordinates We consider an infinite system, the eigenfunctions are taken to be zero on a sphere of radius R and then R istakentoinfinity. The eigenvalue problem is from which we immediately extract the angular dependence obtaining The radial dependence satisfies ψ (r) ψ (r)+k ψ (r) (4.78) lx l m l R l (r) Y m l (θ, φ). (4.79) r d dr R l (r)+r d dr R l (r) l (l +)R l (r)+k r R l (r). (4.8) For small r the solutions behave as r l and r l. Requiring that the solution is regular at the origin we pick the solution which varies as r l for small r. These solutions are the spherical Bessel functions. r π j l (kr) kr J l+ (kr) (4.8) 93
22 Section 4.4 Simple application: point charge at origin The first few spherical Bessel functions are l l j l (z) z sin z z sin z z cos z 3z 3 z sin z 3z cos z The eigenfunctions satisfy the orthogonality condition ( Cohen-Tannoudji, Du, and Laloë, Qunatum Mechanics, Vol. II, p. 95) ZZ r j l (kr) j l (k r) dr Yl m (θ, φ) Yl m (θ, φ) dω π kk δ (k k ) δ ll δ mm. (4.8) The (assumed) completeness relationship is given by lx k j l (kr) j l (kr ) dk Yl m (θ, φ) Yl θ,φ π δ (r r ) (4.83) m l For reference a plane wave can be written as exp (ik r) X lm i l j l (kr) Yl m (θ r,φ r ) Yl m (θ k,φ k ) (4.84) Assuming that the Green s function has the form G (r, r ) X lm we find that g l (k) 8k. It follows that k g l (k) j l (kr) j l (kr ) Y m l (θ, φ) Yl θ,φ (4.85) r r 8X lm j l (kr) j l (kr ) dk Y m l (θ, φ) Yl θ,φ (4.86) This can be compared to the expansion in terms of plane waves r r ZZZ exp [ik (r r )] π k d 3 k (4.87) Comparing Eq.?? with Eq.?? (taking a and b ) we find that j l (kr) j l (kr π ) dk (l +) r< l r> l+ (4.88) 4.4 Simple application: point charge at origin To illustrate the application of this Green s function expansion we consider a point charge q locatedonthezaxisatz a. The potential will be evaluated for a. The charge density for this system is ρ (r) q a δ (r a) δ cos θ δ φ φ. (4.89) 94
23 Section 4.5 Multipole expansion of charge distributions In terms of the Green s function, expanded in the spherical Bessel functions and spherical harmonics, the potential is Φ (r) 4q ZZZ µ r dr d cos θ dφ δ (r a) δ cos θ (4.9) π a X j l (kr) j l (kr ) dk Yl m (θ, φ) Y l θ,φ lm The spatial integration over the delta functions can be performed to obtain Φ (r) q π (l +)P l (cos θ) l Since j l () for l 6 and j (), if a Φ (r) q π j (kr) dk q πr j l (kr) j l (ka) dk (4.9) sin (kr) dk q k r It is obvious that the expansion of the Green s function for Poisson s equation in terms of spherical Bessel function is not as convenient as the expansion in terms of powers of r. Expansions of Green s functions in terms of orthogonal functions is more commonly used when differential equations are converted into integral equations. In that case the solutions are often expanded in a set of orthogonal functions automatically leading to the expansion of the Green s function in orthogonal functions. (4.9) 4.5 Multipole expansion of charge distributions In the case that the charge is restricted to a finite volume, say a sphere of radius R, then the potential outside of this volume is obtained using the form of the Green s function given in Eq.?? Φ (r) lx l m l l + Yl m ZZZ (θ, φ) r l+ ρ (r ) r l Yl θ,φ d 3 r (4.93) The integral in this expression defines the multipole moments of the charge distribution because of the relationship Y m l (θ, φ) ( ) m Yl m (θ, φ) it follows that q l m ( ) m qlm. In terms of the multipole moments of the charge distribution the potential for r>ris Φ (r) lx l m l i q lm l + Y m l (θ, φ) r l+. (4.95) The set of elements {q lm ; m l,..., l,l} form a spherical tensor of rank l. There are two common representations of tensors, the familiar rectilinear representation and the spherical representation. For comparison we consider the charge dipole moment. In rectilinear representation 3X ZZZ p p i e i r ρ (r) d 3 r p i ZZZ or {p i ; i,, 3}. In the spherical representation we find that r i ρ (r) d 3 r q ± q r 3 8π [±p ip ] (4.96) r 3 p 3. 95
24 Section 4.6 Multipole expansion of the energy of a charge distribution in an external field 4.6 Multipole expansion of the energy of a charge distribution in an external field Consider a charge distribution contained in a volume of radius R. Let there be a potential Φ (r) in this region due to charges external to the volume. The potential energy of the charge distribution is ZZZ W ρ (r) Φ (r) d 3 r (4.97) For convenience we can chose the origin of the coordinate system to be at the middle of the charge distribution. Since the sources of the potential are external to the volume containing the charge, the electric potential can be expanded in a Taylor series. 3X Φ (r ) Φ (r) Φ () + r i ri (4.98) + The potential energy has the expansion ZZZ W Φ () " + 3X i, j 3X i, j i r i r j " Φ (r ) r i r j r # ZZZ ρ (r) d 3 r E () # Φ (r ) r i r j r ZZZ r +... rρ (r) d 3 r (4.99) r i r j ρ (r) d 3 r +... The first term is a kind of average potential energy, the second is the interaction of the electric dipole distribution with the applied electric field, and the third term gives the interaction of the quadrupole moment of the charge distribution with the gradient of the electric field. The quadrupole moment of the charge distribution, which transforms as a second rank tensor under rotations, is Q ij ZZZ 3ri r j δ ij r ρ (r) d 3 r. (4.) The additional diagonal term, which is invariant under rotations, does not contribute to the potential energy. Since the quadrupole moment of the charge distribution is a symmetric, traceless second rank tensor. It is therefore specified by five parameters. These parameters for this rectilinear tensor are related to the five parameters of the spherical tensor q m, The simplest relationship occurs for q and Q 33 This simplicity is obtained because the spherical tensors we are using have taken the z or 3 axis as a preferred axis. 4.7 Boundary value problems, conclusions We have developed the solutions of Laplace s and Poisson s equations in rectilinear, cylindrical, and spherical coordinates. Most problems which we encounter are most readily solved in one of these coordinate systems. 3 i, j δ ij Φ (r) r i r j r Φ (r) r 96
25 Section 4.6 Multipole expansion of the energy of a charge distribution in an external field The solutions of Laplace s equation were obtained by taking a superposition of potentials. Each solution matched the given boundary conditions on a different segment of the bounding surface and was zero on the rest of the surfaces. The solutions to Poisson s equation, and to Laplace s equation, were obtained in terms of Green s functions. We found that given the Green s function for a given boundary geometry the solution to a potential problem with this boundary was reduced to integration. A number of Green s functions, in various forms, for rectangular, cylindrical, and spherical volumes were obtained. Finally, we have found that the potential generated by a charge distribution is a superposition of potentials due to the multipole moments of the charge distribution. 97
Electrodynamics I Midterm - Part A - Closed Book KSU 2005/10/17 Electro Dynamic
 Electrodynamics I Midterm - Part A - Closed Book KSU 5//7 Name Electro Dynamic. () Write Gauss Law in differential form. E( r) =ρ( r)/ɛ, or D = ρ, E= electricfield,ρ=volume charge density, ɛ =permittivity
Electrodynamics I Midterm - Part A - Closed Book KSU 5//7 Name Electro Dynamic. () Write Gauss Law in differential form. E( r) =ρ( r)/ɛ, or D = ρ, E= electricfield,ρ=volume charge density, ɛ =permittivity
Classical Field Theory: Electrostatics-Magnetostatics
 Classical Field Theory: Electrostatics-Magnetostatics April 27, 2010 1 1 J.D.Jackson, Classical Electrodynamics, 2nd Edition, Section 1-5 Electrostatics The behavior of an electrostatic field can be described
Classical Field Theory: Electrostatics-Magnetostatics April 27, 2010 1 1 J.D.Jackson, Classical Electrodynamics, 2nd Edition, Section 1-5 Electrostatics The behavior of an electrostatic field can be described
Notes: Most of the material presented in this chapter is taken from Jackson, Chap. 2, 3, and 4, and Di Bartolo, Chap. 2. 2π nx i a. ( ) = G n.
 Chapter. Electrostatic II Notes: Most of the material presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartolo, Chap... Mathematical Considerations.. The Fourier series and the Fourier
Chapter. Electrostatic II Notes: Most of the material presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartolo, Chap... Mathematical Considerations.. The Fourier series and the Fourier
Solutions to Laplace s Equation in Cylindrical Coordinates and Numerical solutions. ρ + (1/ρ) 2 V
 Solutions to Laplace s Equation in Cylindrical Coordinates and Numerical solutions Lecture 8 1 Introduction Solutions to Laplace s equation can be obtained using separation of variables in Cartesian and
Solutions to Laplace s Equation in Cylindrical Coordinates and Numerical solutions Lecture 8 1 Introduction Solutions to Laplace s equation can be obtained using separation of variables in Cartesian and
Spherical Coordinates and Legendre Functions
 Spherical Coordinates and Legendre Functions Spherical coordinates Let s adopt the notation for spherical coordinates that is standard in physics: φ = longitude or azimuth, θ = colatitude ( π 2 latitude)
Spherical Coordinates and Legendre Functions Spherical coordinates Let s adopt the notation for spherical coordinates that is standard in physics: φ = longitude or azimuth, θ = colatitude ( π 2 latitude)
l=0 The expansion coefficients can be determined, for example, by finding the potential on the z-axis and expanding that result in z.
 Electrodynamics I Exam - Part A - Closed Book KSU 15/11/6 Name Electrodynamic Score = 14 / 14 points Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try
Electrodynamics I Exam - Part A - Closed Book KSU 15/11/6 Name Electrodynamic Score = 14 / 14 points Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try
FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 2017
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II November 5, 207 Prof. Alan Guth FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 207 A few items below are marked
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II November 5, 207 Prof. Alan Guth FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 207 A few items below are marked
PHY752, Fall 2016, Assigned Problems
 PHY752, Fall 26, Assigned Problems For clarification or to point out a typo (or worse! please send email to curtright@miami.edu [] Find the URL for the course webpage and email it to curtright@miami.edu
PHY752, Fall 26, Assigned Problems For clarification or to point out a typo (or worse! please send email to curtright@miami.edu [] Find the URL for the course webpage and email it to curtright@miami.edu
d 1 µ 2 Θ = 0. (4.1) consider first the case of m = 0 where there is no azimuthal dependence on the angle φ.
 4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
Expansion of 1/r potential in Legendre polynomials
 Expansion of 1/r potential in Legendre polynomials In electrostatics and gravitation, we see scalar potentials of the form V = K d Take d = R r = R 2 2Rr cos θ + r 2 = R 1 2 r R cos θ + r R )2 Use h =
Expansion of 1/r potential in Legendre polynomials In electrostatics and gravitation, we see scalar potentials of the form V = K d Take d = R r = R 2 2Rr cos θ + r 2 = R 1 2 r R cos θ + r R )2 Use h =
Separation of Variables in Polar and Spherical Coordinates
 Separation of Variables in Polar and Spherical Coordinates Polar Coordinates Suppose we are given the potential on the inside surface of an infinitely long cylindrical cavity, and we want to find the potential
Separation of Variables in Polar and Spherical Coordinates Polar Coordinates Suppose we are given the potential on the inside surface of an infinitely long cylindrical cavity, and we want to find the potential
Electrodynamics PHY712. Lecture 4 Electrostatic potentials and fields. Reference: Chap. 1 & 2 in J. D. Jackson s textbook.
 Electrodynamics PHY712 Lecture 4 Electrostatic potentials and fields Reference: Chap. 1 & 2 in J. D. Jackson s textbook. 1. Complete proof of Green s Theorem 2. Proof of mean value theorem for electrostatic
Electrodynamics PHY712 Lecture 4 Electrostatic potentials and fields Reference: Chap. 1 & 2 in J. D. Jackson s textbook. 1. Complete proof of Green s Theorem 2. Proof of mean value theorem for electrostatic
Boundary-Value Problems: Part II
 Chapter 3 Boundary-Value Problems: Part II Problem Set #3: 3., 3.3, 3.7 Due Monday March. th 3. Spherical Coordinates Spherical coordinates are used when boundary conditions have spherical symmetry. The
Chapter 3 Boundary-Value Problems: Part II Problem Set #3: 3., 3.3, 3.7 Due Monday March. th 3. Spherical Coordinates Spherical coordinates are used when boundary conditions have spherical symmetry. The
Electrodynamics Exam Solutions
 Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Multipole moments. November 9, 2015
 Multipole moments November 9, 5 The far field expansion Suppose we have a localized charge distribution, confined to a region near the origin with r < R. Then for values of r > R, the electric field must
Multipole moments November 9, 5 The far field expansion Suppose we have a localized charge distribution, confined to a region near the origin with r < R. Then for values of r > R, the electric field must
Lecture 13: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay. Poisson s and Laplace s Equations
 Poisson s and Laplace s Equations Lecture 13: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay We will spend some time in looking at the mathematical foundations of electrostatics.
Poisson s and Laplace s Equations Lecture 13: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay We will spend some time in looking at the mathematical foundations of electrostatics.
1 Solutions in cylindrical coordinates: Bessel functions
 1 Solutions in cylindrical coordinates: Bessel functions 1.1 Bessel functions Bessel functions arise as solutions of potential problems in cylindrical coordinates. Laplace s equation in cylindrical coordinates
1 Solutions in cylindrical coordinates: Bessel functions 1.1 Bessel functions Bessel functions arise as solutions of potential problems in cylindrical coordinates. Laplace s equation in cylindrical coordinates
Problem Set #4: 4.1,4.7,4.9 (Due Monday, March 25th)
 Chapter 4 Multipoles, Dielectrics Problem Set #4: 4.,4.7,4.9 (Due Monday, March 5th 4. Multipole expansion Consider a localized distribution of charges described by ρ(x contained entirely in a sphere of
Chapter 4 Multipoles, Dielectrics Problem Set #4: 4.,4.7,4.9 (Due Monday, March 5th 4. Multipole expansion Consider a localized distribution of charges described by ρ(x contained entirely in a sphere of
Review of Electrostatics. Define the gradient operation on a field F = F(x, y, z) by;
 Review of Electrostatics 1 Gradient Define the gradient operation on a field F = F(x, y, z) by; F = ˆx F x + ŷ F y + ẑ F z This operation forms a vector as may be shown by its transformation properties
Review of Electrostatics 1 Gradient Define the gradient operation on a field F = F(x, y, z) by; F = ˆx F x + ŷ F y + ẑ F z This operation forms a vector as may be shown by its transformation properties
Electromagnetism HW 1 math review
 Electromagnetism HW math review Problems -5 due Mon 7th Sep, 6- due Mon 4th Sep Exercise. The Levi-Civita symbol, ɛ ijk, also known as the completely antisymmetric rank-3 tensor, has the following properties:
Electromagnetism HW math review Problems -5 due Mon 7th Sep, 6- due Mon 4th Sep Exercise. The Levi-Civita symbol, ɛ ijk, also known as the completely antisymmetric rank-3 tensor, has the following properties:
Angular Momentum. Classically the orbital angular momentum with respect to a fixed origin is. L = r p. = yp z. L x. zp y L y. = zp x. xpz L z.
 Angular momentum is an important concept in quantum theory, necessary for analyzing motion in 3D as well as intrinsic properties such as spin Classically the orbital angular momentum with respect to a
Angular momentum is an important concept in quantum theory, necessary for analyzing motion in 3D as well as intrinsic properties such as spin Classically the orbital angular momentum with respect to a
Electromagnetic Theory I
 Electromagnetic Theory I Final Examination 18 December 2009, 12:30-2:30 pm Instructions: Answer the following 10 questions, each of which is worth 10 points. Explain your reasoning in each case. Use SI
Electromagnetic Theory I Final Examination 18 December 2009, 12:30-2:30 pm Instructions: Answer the following 10 questions, each of which is worth 10 points. Explain your reasoning in each case. Use SI
1. (3) Write Gauss Law in differential form. Explain the physical meaning.
 Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about the physics involved,
Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about the physics involved,
Physics 221A Fall 1996 Notes 12 Orbital Angular Momentum and Spherical Harmonics
 Physics 221A Fall 1996 Notes 12 Orbital Angular Momentum and Spherical Harmonics We now consider the spatial degrees of freedom of a particle moving in 3-dimensional space, which of course is an important
Physics 221A Fall 1996 Notes 12 Orbital Angular Momentum and Spherical Harmonics We now consider the spatial degrees of freedom of a particle moving in 3-dimensional space, which of course is an important
Electric fields in matter
 Electric fields in matter November 2, 25 Suppose we apply a constant electric field to a block of material. Then the charges that make up the matter are no longer in equilibrium: the electrons tend to
Electric fields in matter November 2, 25 Suppose we apply a constant electric field to a block of material. Then the charges that make up the matter are no longer in equilibrium: the electrons tend to
Astronomy 9620a / Physics 9302a - 1st Problem List and Assignment
 Astronomy 9620a / Physics 9302a - st Problem List and Assignment Your solution to problems 4, 7, 3, and 6 has to be handed in on Thursday, Oct. 7, 203.. Prove the following relations (going from the left-
Astronomy 9620a / Physics 9302a - st Problem List and Assignment Your solution to problems 4, 7, 3, and 6 has to be handed in on Thursday, Oct. 7, 203.. Prove the following relations (going from the left-
Review of Electrostatics
 Review of Electrostatics 1 Gradient Define the gradient operation on a field F = F(x, y, z) by; F = ˆx F x + ŷ F y + ẑ F z This operation forms a vector as may be shown by its transformation properties
Review of Electrostatics 1 Gradient Define the gradient operation on a field F = F(x, y, z) by; F = ˆx F x + ŷ F y + ẑ F z This operation forms a vector as may be shown by its transformation properties
(b) Show that the charged induced on the hemisphere is: Q = E o a 2 3π (1)
 Problem. Defects This problem will study defects in parallel plate capacitors. A parallel plate capacitor has area, A, and separation, D, and is maintained at the potential difference, V = E o D. There
Problem. Defects This problem will study defects in parallel plate capacitors. A parallel plate capacitor has area, A, and separation, D, and is maintained at the potential difference, V = E o D. There
The 3 dimensional Schrödinger Equation
 Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Spherical Coordinates
 Spherical Coordinates Bo E. Sernelius 4:6 SPHERICAL COORDINATES Φ = 1 Φ + 1 Φ + 1 Φ = 0 r r r θ sin r r sinθ θ θ r sin θ ϕ ( ) = ( ) ( ) ( ) Φ r, θϕ, R r P θq ϕ 1 d 1 1 0 r R dr r dr d dp d Q dr + sinθ
Spherical Coordinates Bo E. Sernelius 4:6 SPHERICAL COORDINATES Φ = 1 Φ + 1 Φ + 1 Φ = 0 r r r θ sin r r sinθ θ θ r sin θ ϕ ( ) = ( ) ( ) ( ) Φ r, θϕ, R r P θq ϕ 1 d 1 1 0 r R dr r dr d dp d Q dr + sinθ
1. (3) Write Gauss Law in differential form. Explain the physical meaning.
 Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Electro Dynamic Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about
Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Electro Dynamic Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about
1. Poisson-Boltzmann 1.1. Poisson equation. We consider the Laplacian. which is given in spherical coordinates by (2)
 1. Poisson-Boltzmann 1.1. Poisson equation. We consider the Laplacian operator (1) 2 = 2 x + 2 2 y + 2 2 z 2 which is given in spherical coordinates by (2) 2 = 1 ( r 2 ) + 1 r 2 r r r 2 sin θ θ and in
1. Poisson-Boltzmann 1.1. Poisson equation. We consider the Laplacian operator (1) 2 = 2 x + 2 2 y + 2 2 z 2 which is given in spherical coordinates by (2) 2 = 1 ( r 2 ) + 1 r 2 r r r 2 sin θ θ and in
Steady and unsteady diffusion
 Chapter 5 Steady and unsteady diffusion In this chapter, we solve the diffusion and forced convection equations, in which it is necessary to evaluate the temperature or concentration fields when the velocity
Chapter 5 Steady and unsteady diffusion In this chapter, we solve the diffusion and forced convection equations, in which it is necessary to evaluate the temperature or concentration fields when the velocity
Connection to Laplacian in spherical coordinates (Chapter 13)
 Connection to Laplacian in spherical coordinates (Chapter 13) We might often encounter the Laplace equation and spherical coordinates might be the most convenient 2 u(r, θ, φ) = 0 We already saw in Chapter
Connection to Laplacian in spherical coordinates (Chapter 13) We might often encounter the Laplace equation and spherical coordinates might be the most convenient 2 u(r, θ, φ) = 0 We already saw in Chapter
which implies that we can take solutions which are simultaneous eigen functions of
 Module 1 : Quantum Mechanics Chapter 6 : Quantum mechanics in 3-D Quantum mechanics in 3-D For most physical systems, the dynamics is in 3-D. The solutions to the general 3-d problem are quite complicated,
Module 1 : Quantum Mechanics Chapter 6 : Quantum mechanics in 3-D Quantum mechanics in 3-D For most physical systems, the dynamics is in 3-D. The solutions to the general 3-d problem are quite complicated,
4 Power Series Solutions: Frobenius Method
 4 Power Series Solutions: Frobenius Method Now the ODE adventure takes us to series solutions for ODEs, a technique A & W, that is often viable, valuable and informative. These can be readily applied Sec.
4 Power Series Solutions: Frobenius Method Now the ODE adventure takes us to series solutions for ODEs, a technique A & W, that is often viable, valuable and informative. These can be readily applied Sec.
20 The Hydrogen Atom. Ze2 r R (20.1) H( r, R) = h2 2m 2 r h2 2M 2 R
 20 The Hydrogen Atom 1. We want to solve the time independent Schrödinger Equation for the hydrogen atom. 2. There are two particles in the system, an electron and a nucleus, and so we can write the Hamiltonian
20 The Hydrogen Atom 1. We want to solve the time independent Schrödinger Equation for the hydrogen atom. 2. There are two particles in the system, an electron and a nucleus, and so we can write the Hamiltonian
Phys. 505 Electricity and Magnetism Fall 2003 Prof. G. Raithel Problem Set 1
 Phys. 505 Electricity and Magnetism Fall 2003 Prof. G. Raithel Problem Set Problem.3 a): By symmetry, the solution must be of the form ρ(x) = ρ(r) = Qδ(r R)f, with a constant f to be specified by the condition
Phys. 505 Electricity and Magnetism Fall 2003 Prof. G. Raithel Problem Set Problem.3 a): By symmetry, the solution must be of the form ρ(x) = ρ(r) = Qδ(r R)f, with a constant f to be specified by the condition
PHYS 404 Lecture 1: Legendre Functions
 PHYS 404 Lecture 1: Legendre Functions Dr. Vasileios Lempesis PHYS 404 - LECTURE 1 DR. V. LEMPESIS 1 Legendre Functions physical justification Legendre functions or Legendre polynomials are the solutions
PHYS 404 Lecture 1: Legendre Functions Dr. Vasileios Lempesis PHYS 404 - LECTURE 1 DR. V. LEMPESIS 1 Legendre Functions physical justification Legendre functions or Legendre polynomials are the solutions
3 Chapter. Gauss s Law
 3 Chapter Gauss s Law 3.1 Electric Flux... 3-2 3.2 Gauss s Law (see also Gauss s Law Simulation in Section 3.10)... 3-4 Example 3.1: Infinitely Long Rod of Uniform Charge Density... 3-9 Example 3.2: Infinite
3 Chapter Gauss s Law 3.1 Electric Flux... 3-2 3.2 Gauss s Law (see also Gauss s Law Simulation in Section 3.10)... 3-4 Example 3.1: Infinitely Long Rod of Uniform Charge Density... 3-9 Example 3.2: Infinite
Additional Mathematical Tools: Detail
 Additional Mathematical Tools: Detail September 9, 25 The material here is not required, but gives more detail on the additional mathmatical tools: coordinate systems, rotations, the Dirac delta function
Additional Mathematical Tools: Detail September 9, 25 The material here is not required, but gives more detail on the additional mathmatical tools: coordinate systems, rotations, the Dirac delta function
Survival Guide to Bessel Functions
 Survival Guide to Bessel Functions December, 13 1 The Problem (Original by Mike Herman; edits and additions by Paul A.) For cylindrical boundary conditions, Laplace s equation is: [ 1 s Φ ] + 1 Φ s s s
Survival Guide to Bessel Functions December, 13 1 The Problem (Original by Mike Herman; edits and additions by Paul A.) For cylindrical boundary conditions, Laplace s equation is: [ 1 s Φ ] + 1 Φ s s s
University of Illinois at Chicago Department of Physics. Electricity & Magnetism Qualifying Examination
 University of Illinois at Chicago Department of Physics Electricity & Magnetism Qualifying Examination January 7, 28 9. am 12: pm Full credit can be achieved from completely correct answers to 4 questions.
University of Illinois at Chicago Department of Physics Electricity & Magnetism Qualifying Examination January 7, 28 9. am 12: pm Full credit can be achieved from completely correct answers to 4 questions.
Multipole Expansion for Radiation;Vector Spherical Harmonics
 Multipole Expansion for Radiation;Vector Spherical Harmonics Michael Dine Department of Physics University of California, Santa Cruz February 2013 We seek a more systematic treatment of the multipole expansion
Multipole Expansion for Radiation;Vector Spherical Harmonics Michael Dine Department of Physics University of California, Santa Cruz February 2013 We seek a more systematic treatment of the multipole expansion
Dielectrics. Lecture 20: Electromagnetic Theory. Professor D. K. Ghosh, Physics Department, I.I.T., Bombay
 What are dielectrics? Dielectrics Lecture 20: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay So far we have been discussing electrostatics in either vacuum or in a conductor.
What are dielectrics? Dielectrics Lecture 20: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay So far we have been discussing electrostatics in either vacuum or in a conductor.
(a) Determine the general solution for φ(ρ) near ρ = 0 for arbitary values E. (b) Show that the regular solution at ρ = 0 has the series expansion
 Problem 1. Curious Wave Functions The eigenfunctions of a D7 brane in a curved geometry lead to the following eigenvalue equation of the Sturm Liouville type ρ ρ 3 ρ φ n (ρ) = E n w(ρ)φ n (ρ) w(ρ) = where
Problem 1. Curious Wave Functions The eigenfunctions of a D7 brane in a curved geometry lead to the following eigenvalue equation of the Sturm Liouville type ρ ρ 3 ρ φ n (ρ) = E n w(ρ)φ n (ρ) w(ρ) = where
Legendre s Equation. PHYS Southern Illinois University. October 13, 2016
 PHYS 500 - Southern Illinois University October 13, 2016 PHYS 500 - Southern Illinois University Legendre s Equation October 13, 2016 1 / 10 The Laplacian in Spherical Coordinates The Laplacian is given
PHYS 500 - Southern Illinois University October 13, 2016 PHYS 500 - Southern Illinois University Legendre s Equation October 13, 2016 1 / 10 The Laplacian in Spherical Coordinates The Laplacian is given
CHAPTER 3 POTENTIALS 10/13/2016. Outlines. 1. Laplace s equation. 2. The Method of Images. 3. Separation of Variables. 4. Multipole Expansion
 CHAPTER 3 POTENTIALS Lee Chow Department of Physics University of Central Florida Orlando, FL 32816 Outlines 1. Laplace s equation 2. The Method of Images 3. Separation of Variables 4. Multipole Expansion
CHAPTER 3 POTENTIALS Lee Chow Department of Physics University of Central Florida Orlando, FL 32816 Outlines 1. Laplace s equation 2. The Method of Images 3. Separation of Variables 4. Multipole Expansion
Maxwell s equations for electrostatics
 Maxwell s equations for electrostatics October 6, 5 The differential form of Gauss s law Starting from the integral form of Gauss s law, we treat the charge as a continuous distribution, ρ x. Then, letting
Maxwell s equations for electrostatics October 6, 5 The differential form of Gauss s law Starting from the integral form of Gauss s law, we treat the charge as a continuous distribution, ρ x. Then, letting
The Spherical Harmonics
 Physics 6C Fall 202 The Spherical Harmonics. Solution to Laplace s equation in spherical coordinates In spherical coordinates, the Laplacian is given by 2 = ( r 2 ) ( + r 2 r r r 2 sin 2 sinθ ) + θ θ θ
Physics 6C Fall 202 The Spherical Harmonics. Solution to Laplace s equation in spherical coordinates In spherical coordinates, the Laplacian is given by 2 = ( r 2 ) ( + r 2 r r r 2 sin 2 sinθ ) + θ θ θ
Quantum Mechanics in 3-Dimensions
 Quantum Mechanics in 3-Dimensions Pavithran S Iyer, 2nd yr BSc Physics, Chennai Mathematical Institute Email: pavithra@cmi.ac.in August 28 th, 2009 1 Schrodinger equation in Spherical Coordinates 1.1 Transforming
Quantum Mechanics in 3-Dimensions Pavithran S Iyer, 2nd yr BSc Physics, Chennai Mathematical Institute Email: pavithra@cmi.ac.in August 28 th, 2009 1 Schrodinger equation in Spherical Coordinates 1.1 Transforming
Fun With Carbon Monoxide. p. 1/2
 Fun With Carbon Monoxide p. 1/2 p. 1/2 Fun With Carbon Monoxide E = 0.25 ± 0.05 ev Electron beam results p. 1/2 Fun With Carbon Monoxide E = 0.25 ± 0.05 ev Electron beam results C V (J/K-mole) 35 30 25
Fun With Carbon Monoxide p. 1/2 p. 1/2 Fun With Carbon Monoxide E = 0.25 ± 0.05 ev Electron beam results p. 1/2 Fun With Carbon Monoxide E = 0.25 ± 0.05 ev Electron beam results C V (J/K-mole) 35 30 25
Physics 505 Fall 2005 Homework Assignment #8 Solutions
 Physics 55 Fall 5 Homework Assignment #8 Solutions Textbook problems: Ch. 5: 5., 5.4, 5.7, 5.9 5. A circular current loop of radius a carrying a current I lies in the x-y plane with its center at the origin.
Physics 55 Fall 5 Homework Assignment #8 Solutions Textbook problems: Ch. 5: 5., 5.4, 5.7, 5.9 5. A circular current loop of radius a carrying a current I lies in the x-y plane with its center at the origin.
Two special equations: Bessel s and Legendre s equations. p Fourier-Bessel and Fourier-Legendre series. p
 LECTURE 1 Table of Contents Two special equations: Bessel s and Legendre s equations. p. 259-268. Fourier-Bessel and Fourier-Legendre series. p. 453-460. Boundary value problems in other coordinate system.
LECTURE 1 Table of Contents Two special equations: Bessel s and Legendre s equations. p. 259-268. Fourier-Bessel and Fourier-Legendre series. p. 453-460. Boundary value problems in other coordinate system.
Field Theory exam II Solutions
 Field Theory exam II Solutions Problem 1 (a) Consider point charges, one with charge q located at x 1 = (1, 0, 1), and the other one with charge q at x = (1, 0, 1). Compute the multipole moments q lm in
Field Theory exam II Solutions Problem 1 (a) Consider point charges, one with charge q located at x 1 = (1, 0, 1), and the other one with charge q at x = (1, 0, 1). Compute the multipole moments q lm in
Physics 4617/5617: Quantum Physics Course Lecture Notes
 Physics 467/567: Quantum Physics Course Lecture Notes Dr. Donald G. Luttermoser East Tennessee State University Edition 5. Abstract These class notes are designed for use of the instructor and students
Physics 467/567: Quantum Physics Course Lecture Notes Dr. Donald G. Luttermoser East Tennessee State University Edition 5. Abstract These class notes are designed for use of the instructor and students
Solutions to Problems in Jackson, Classical Electrodynamics, Third Edition. Chapter 2: Problems 11-20
 Solutions to Problems in Jackson, Classical Electrodynamics, Third Edition Homer Reid December 8, 999 Chapter : Problems - Problem A line charge with linear charge density τ is placed parallel to, and
Solutions to Problems in Jackson, Classical Electrodynamics, Third Edition Homer Reid December 8, 999 Chapter : Problems - Problem A line charge with linear charge density τ is placed parallel to, and
Solutions to Laplace s Equations- II
 Solutions to Laplace s Equations- II Lecture 15: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Laplace s Equation in Spherical Coordinates : In spherical coordinates
Solutions to Laplace s Equations- II Lecture 15: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Laplace s Equation in Spherical Coordinates : In spherical coordinates
Solutions to PS 2 Physics 201
 Solutions to PS Physics 1 1. ke dq E = i (1) r = i = i k eλ = i k eλ = i k eλ k e λ xdx () (x x) (x x )dx (x x ) + x dx () (x x ) x ln + x x + x x (4) x + x ln + x (5) x + x To find the field for x, we
Solutions to PS Physics 1 1. ke dq E = i (1) r = i = i k eλ = i k eλ = i k eλ k e λ xdx () (x x) (x x )dx (x x ) + x dx () (x x ) x ln + x x + x x (4) x + x ln + x (5) x + x To find the field for x, we
PHYS 3327 PRELIM 1. Prof. Itai Cohen, Fall 2010 Friday, 10/15/10. Name: Read all of the following information before starting the exam:
 PHYS 3327 PRELIM 1 Prof. Itai Cohen, Fall 2010 Friday, 10/15/10 Name: Read all of the following information before starting the exam: Put your name on the exam now. Show all work, clearly and in order,
PHYS 3327 PRELIM 1 Prof. Itai Cohen, Fall 2010 Friday, 10/15/10 Name: Read all of the following information before starting the exam: Put your name on the exam now. Show all work, clearly and in order,
Equations of linear stellar oscillations
 Chapter 4 Equations of linear stellar oscillations In the present chapter the equations governing small oscillations around a spherical equilibrium state are derived. The general equations were presented
Chapter 4 Equations of linear stellar oscillations In the present chapter the equations governing small oscillations around a spherical equilibrium state are derived. The general equations were presented
Boundary value problems
 1 Introduction Boundary value problems Lecture 5 We have found that the electric potential is a solution of the partial differential equation; 2 V = ρ/ǫ 0 The above is Poisson s equation where ρ is the
1 Introduction Boundary value problems Lecture 5 We have found that the electric potential is a solution of the partial differential equation; 2 V = ρ/ǫ 0 The above is Poisson s equation where ρ is the
(a) Show that electric field and magnetic field have units (force)/area or energy/volume.
 Problem. Units (a) how that electric field and magnetic field have units (force)/area or energy/volume. (b) A rule of thumb that you may need in the lab is that coaxial cable has a capcitance of 2 pf/foot.
Problem. Units (a) how that electric field and magnetic field have units (force)/area or energy/volume. (b) A rule of thumb that you may need in the lab is that coaxial cable has a capcitance of 2 pf/foot.
A cylinder in a magnetic field (Jackson)
 Problem 1. A cylinder in a magnetic field (Jackson) A very long hollow cylinder of inner radius a and outer radius b of permeability µ is placed in an initially uniform magnetic field B o at right angles
Problem 1. A cylinder in a magnetic field (Jackson) A very long hollow cylinder of inner radius a and outer radius b of permeability µ is placed in an initially uniform magnetic field B o at right angles
The Hydrogen atom. Chapter The Schrödinger Equation. 2.2 Angular momentum
 Chapter 2 The Hydrogen atom In the previous chapter we gave a quick overview of the Bohr model, which is only really valid in the semiclassical limit. cf. section 1.7.) We now begin our task in earnest
Chapter 2 The Hydrogen atom In the previous chapter we gave a quick overview of the Bohr model, which is only really valid in the semiclassical limit. cf. section 1.7.) We now begin our task in earnest
Computation of the scattering amplitude in the spheroidal coordinates
 Computation of the scattering amplitude in the spheroidal coordinates Takuya MINE Kyoto Institute of Technology 12 October 2015 Lab Seminar at Kochi University of Technology Takuya MINE (KIT) Spheroidal
Computation of the scattering amplitude in the spheroidal coordinates Takuya MINE Kyoto Institute of Technology 12 October 2015 Lab Seminar at Kochi University of Technology Takuya MINE (KIT) Spheroidal
More on Bessel functions. Infinite domain, δ-function normalization
 More on Bessel functions Infinite domain, δ-function normalization Consider Bessel s equation on the domain < ρ < as R ½ Bessel s equation, (375) or (393), says ρ d ρ dj ν(kρ) + k 2 ν 2 ρ 2 J ν (kρ) =
More on Bessel functions Infinite domain, δ-function normalization Consider Bessel s equation on the domain < ρ < as R ½ Bessel s equation, (375) or (393), says ρ d ρ dj ν(kρ) + k 2 ν 2 ρ 2 J ν (kρ) =
(b) Show that electric field and magnetic field (in Heavyside Lorentz) have units (force)/area or energy/volume.
 Problem. Units (a) The Gaussian unit system (or cgs) is often used in Quantum mechanics. Look it up on the internet, and write down the Coulomb and Biot Savart laws in this system of units. (i) What is
Problem. Units (a) The Gaussian unit system (or cgs) is often used in Quantum mechanics. Look it up on the internet, and write down the Coulomb and Biot Savart laws in this system of units. (i) What is
Physics 342 Lecture 23. Radial Separation. Lecture 23. Physics 342 Quantum Mechanics I
 Physics 342 Lecture 23 Radial Separation Lecture 23 Physics 342 Quantum Mechanics I Friday, March 26th, 2010 We begin our spherical solutions with the simplest possible case zero potential. Aside from
Physics 342 Lecture 23 Radial Separation Lecture 23 Physics 342 Quantum Mechanics I Friday, March 26th, 2010 We begin our spherical solutions with the simplest possible case zero potential. Aside from
lim = F F = F x x + F y y + F z
 Physics 361 Summary of Results from Lecture Physics 361 Derivatives of Scalar and Vector Fields The gradient of a scalar field f( r) is given by g = f. coordinates f g = ê x x + ê f y y + ê f z z Expressed
Physics 361 Summary of Results from Lecture Physics 361 Derivatives of Scalar and Vector Fields The gradient of a scalar field f( r) is given by g = f. coordinates f g = ê x x + ê f y y + ê f z z Expressed
Physics 505 Fall 2003
 Physics 505 Fall 2003 G. Raithel December 8, 2003 Disclaimer: The purpose of these notes is to provide you with a general list of topics that were covered in class. The notes are not a substitute for reading
Physics 505 Fall 2003 G. Raithel December 8, 2003 Disclaimer: The purpose of these notes is to provide you with a general list of topics that were covered in class. The notes are not a substitute for reading
Physics 116C Solutions to the Practice Final Exam Fall The method of Frobenius fails because it works only for Fuchsian equations, of the type
 Physics 6C Solutions to the Practice Final Exam Fall 2 Consider the differential equation x y +x(x+)y y = () (a) Explain why the method of Frobenius method fails for this problem. The method of Frobenius
Physics 6C Solutions to the Practice Final Exam Fall 2 Consider the differential equation x y +x(x+)y y = () (a) Explain why the method of Frobenius method fails for this problem. The method of Frobenius
Appendix A Vector Analysis
 Appendix A Vector Analysis A.1 Orthogonal Coordinate Systems A.1.1 Cartesian (Rectangular Coordinate System The unit vectors are denoted by x, ŷ, ẑ in the Cartesian system. By convention, ( x, ŷ, ẑ triplet
Appendix A Vector Analysis A.1 Orthogonal Coordinate Systems A.1.1 Cartesian (Rectangular Coordinate System The unit vectors are denoted by x, ŷ, ẑ in the Cartesian system. By convention, ( x, ŷ, ẑ triplet
Units without the 4π in the Maxwell equations such as Heavyside Lorentz and SI (but with the 4π in the Coulomb law) are called rationalized.
 Problem. Units (a) The Gaussian unit system (or cgs) is often used in Quantum mechanics. Look it up on the internet, and write down the Coulomb and Biot Savart laws in this system of units. (i) What is
Problem. Units (a) The Gaussian unit system (or cgs) is often used in Quantum mechanics. Look it up on the internet, and write down the Coulomb and Biot Savart laws in this system of units. (i) What is
Sheet 06.6: Curvilinear Integration, Matrices I
 Fakultät für Physik R: Rechenmethoden für Physiker, WiSe 5/6 Doent: Jan von Delft Übungen: Benedikt Bruognolo, Dennis Schimmel, Frauke Schwar, Lukas Weidinger http://homepages.physik.uni-muenchen.de/~vondelft/lehre/5r/
Fakultät für Physik R: Rechenmethoden für Physiker, WiSe 5/6 Doent: Jan von Delft Übungen: Benedikt Bruognolo, Dennis Schimmel, Frauke Schwar, Lukas Weidinger http://homepages.physik.uni-muenchen.de/~vondelft/lehre/5r/
Eigenfunctions on the surface of a sphere. In spherical coordinates, the Laplacian is. u = u rr + 2 r u r + 1 r 2. sin 2 (θ) + 1
 Eigenfunctions on the surface of a sphere In spherical coordinates, the Laplacian is u = u rr + 2 r u r + 1 r 2 [ uφφ sin 2 (θ) + 1 sin θ (sin θ u θ) θ ]. Eigenfunctions on the surface of a sphere In spherical
Eigenfunctions on the surface of a sphere In spherical coordinates, the Laplacian is u = u rr + 2 r u r + 1 r 2 [ uφφ sin 2 (θ) + 1 sin θ (sin θ u θ) θ ]. Eigenfunctions on the surface of a sphere In spherical
Electromagnetism Answers to Problem Set 8 Spring Jackson Prob. 4.1: Multipole expansion for various charge distributions
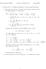 Electromagnetism 76 Answers to Problem Set 8 Spring 6. Jackson Prob. 4.: Multipole expansion for various charge distributions (a) In the first case, we have 4 charges in the xy plane at distance a from
Electromagnetism 76 Answers to Problem Set 8 Spring 6. Jackson Prob. 4.: Multipole expansion for various charge distributions (a) In the first case, we have 4 charges in the xy plane at distance a from
Chapter 21: Gauss law Tuesday September 13 th. Gauss law and conductors Electrostatic potential energy (more likely on Thu.)
 Chapter 21: Gauss law Tuesday September 13 th LABS START THIS WEEK Quick review of Gauss law The flux of a vector field The shell theorem Gauss law for other symmetries A uniformly charged sheet A uniformly
Chapter 21: Gauss law Tuesday September 13 th LABS START THIS WEEK Quick review of Gauss law The flux of a vector field The shell theorem Gauss law for other symmetries A uniformly charged sheet A uniformly
ONE AND MANY ELECTRON ATOMS Chapter 15
 See Week 8 lecture notes. This is exactly the same as the Hamiltonian for nonrigid rotation. In Week 8 lecture notes it was shown that this is the operator for Lˆ 2, the square of the angular momentum.
See Week 8 lecture notes. This is exactly the same as the Hamiltonian for nonrigid rotation. In Week 8 lecture notes it was shown that this is the operator for Lˆ 2, the square of the angular momentum.
Problem Set #3: 2.11, 2.15, 2.21, 2.26, 2.40, 2.42, 2.43, 2.46 (Due Thursday Feb. 27th)
 Chapter Electrostatics Problem Set #3:.,.5,.,.6,.40,.4,.43,.46 (Due Thursday Feb. 7th). Coulomb s Law Coulomb showed experimentally that for two point charges the force is - proportional to each of the
Chapter Electrostatics Problem Set #3:.,.5,.,.6,.40,.4,.43,.46 (Due Thursday Feb. 7th). Coulomb s Law Coulomb showed experimentally that for two point charges the force is - proportional to each of the
IV. Electronic Spectroscopy, Angular Momentum, and Magnetic Resonance
 IV. Electronic Spectroscopy, Angular Momentum, and Magnetic Resonance The foundation of electronic spectroscopy is the exact solution of the time-independent Schrodinger equation for the hydrogen atom.
IV. Electronic Spectroscopy, Angular Momentum, and Magnetic Resonance The foundation of electronic spectroscopy is the exact solution of the time-independent Schrodinger equation for the hydrogen atom.
Electromagnetism: Worked Examples. University of Oxford Second Year, Part A2
 Electromagnetism: Worked Examples University of Oxford Second Year, Part A2 Caroline Terquem Department of Physics caroline.terquem@physics.ox.ac.uk Michaelmas Term 2017 2 Contents 1 Potentials 5 1.1 Potential
Electromagnetism: Worked Examples University of Oxford Second Year, Part A2 Caroline Terquem Department of Physics caroline.terquem@physics.ox.ac.uk Michaelmas Term 2017 2 Contents 1 Potentials 5 1.1 Potential
Summary: Curvilinear Coordinates
 Physics 2460 Electricity and Magnetism I, Fall 2007, Lecture 10 1 Summary: Curvilinear Coordinates 1. Summary of Integral Theorems 2. Generalized Coordinates 3. Cartesian Coordinates: Surfaces of Constant
Physics 2460 Electricity and Magnetism I, Fall 2007, Lecture 10 1 Summary: Curvilinear Coordinates 1. Summary of Integral Theorems 2. Generalized Coordinates 3. Cartesian Coordinates: Surfaces of Constant
A A + B. ra + A + 1. We now want to solve the Einstein equations in the following cases:
 Lecture 29: Cosmology Cosmology Reading: Weinberg, Ch A metric tensor appropriate to infalling matter In general (see, eg, Weinberg, Ch ) we may write a spherically symmetric, time-dependent metric in
Lecture 29: Cosmology Cosmology Reading: Weinberg, Ch A metric tensor appropriate to infalling matter In general (see, eg, Weinberg, Ch ) we may write a spherically symmetric, time-dependent metric in
Introduction to Spherical Harmonics
 Introduction to Spherical Harmonics Lawrence Liu 3 June 4 Possibly useful information. Legendre polynomials. Rodrigues formula:. Generating function: d n P n x = x n n! dx n n. wx, t = xt t = P n xt n,
Introduction to Spherical Harmonics Lawrence Liu 3 June 4 Possibly useful information. Legendre polynomials. Rodrigues formula:. Generating function: d n P n x = x n n! dx n n. wx, t = xt t = P n xt n,
Analysis of eddy currents in a gradient coil
 Analysis of eddy currents in a gradient coil J.M.B. Kroot Eindhoven University of Technology P.O.Box 53; 56 MB Eindhoven, The Netherlands Abstract To model the z-coil of an MRI-scanner, a set of circular
Analysis of eddy currents in a gradient coil J.M.B. Kroot Eindhoven University of Technology P.O.Box 53; 56 MB Eindhoven, The Netherlands Abstract To model the z-coil of an MRI-scanner, a set of circular
Indiana University Physics P331: Theory of Electromagnetism Review Problems #3
 Indiana University Physics P331: Theory of Electromagnetism Review Problems #3 Note: The final exam (Friday 1/14 8:00-10:00 AM will be comprehensive, covering lecture and homework material pertaining to
Indiana University Physics P331: Theory of Electromagnetism Review Problems #3 Note: The final exam (Friday 1/14 8:00-10:00 AM will be comprehensive, covering lecture and homework material pertaining to
Physics 6303 Lecture 11 September 24, LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation
 Physics 6303 Lecture September 24, 208 LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation, l l l l l l. Consider problems that are no axisymmetric; i.e., the potential depends
Physics 6303 Lecture September 24, 208 LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation, l l l l l l. Consider problems that are no axisymmetric; i.e., the potential depends
Physics 228 Today: Ch 41: 1-3: 3D quantum mechanics, hydrogen atom
 Physics 228 Today: Ch 41: 1-3: 3D quantum mechanics, hydrogen atom Website: Sakai 01:750:228 or www.physics.rutgers.edu/ugrad/228 Happy April Fools Day Example / Worked Problems What is the ratio of the
Physics 228 Today: Ch 41: 1-3: 3D quantum mechanics, hydrogen atom Website: Sakai 01:750:228 or www.physics.rutgers.edu/ugrad/228 Happy April Fools Day Example / Worked Problems What is the ratio of the
Jackson 6.4 Homework Problem Solution Dr. Christopher S. Baird University of Massachusetts Lowell
 Jackson 6.4 Homework Problem Solution Dr. Christopher S. Baird University of Massachusetts Lowell PROBLEM: A uniformly magnetized and conducting sphere of radius R and total magnetic moment m = 4πMR 3
Jackson 6.4 Homework Problem Solution Dr. Christopher S. Baird University of Massachusetts Lowell PROBLEM: A uniformly magnetized and conducting sphere of radius R and total magnetic moment m = 4πMR 3
University of Illinois at Chicago Department of Physics
 University of Illinois at Chicago Department of Physics Electromagnetism Qualifying Examination January 4, 2017 9.00 am - 12.00 pm Full credit can be achieved from completely correct answers to 4 questions.
University of Illinois at Chicago Department of Physics Electromagnetism Qualifying Examination January 4, 2017 9.00 am - 12.00 pm Full credit can be achieved from completely correct answers to 4 questions.
Scattering cross-section (µm 2 )
 Supplementary Figures Scattering cross-section (µm 2 ).16.14.12.1.8.6.4.2 Total scattering Electric dipole, a E (1,1) Magnetic dipole, a M (1,1) Magnetic quardupole, a M (2,1). 44 48 52 56 Wavelength (nm)
Supplementary Figures Scattering cross-section (µm 2 ).16.14.12.1.8.6.4.2 Total scattering Electric dipole, a E (1,1) Magnetic dipole, a M (1,1) Magnetic quardupole, a M (2,1). 44 48 52 56 Wavelength (nm)
1 Introduction. Green s function notes 2018
 Green s function notes 8 Introduction Back in the "formal" notes, we derived the potential in terms of the Green s function. Dirichlet problem: Equation (7) in "formal" notes is Φ () Z ( ) ( ) 3 Z Φ (
Green s function notes 8 Introduction Back in the "formal" notes, we derived the potential in terms of the Green s function. Dirichlet problem: Equation (7) in "formal" notes is Φ () Z ( ) ( ) 3 Z Φ (
Boundary Value Problems in Cylindrical Coordinates
 Boundary Value Problems in Cylindrical Coordinates 29 Outline Differential Operators in Various Coordinate Systems Laplace Equation in Cylindrical Coordinates Systems Bessel Functions Wave Equation the
Boundary Value Problems in Cylindrical Coordinates 29 Outline Differential Operators in Various Coordinate Systems Laplace Equation in Cylindrical Coordinates Systems Bessel Functions Wave Equation the
free space (vacuum) permittivity [ F/m]
![free space (vacuum) permittivity [ F/m] free space (vacuum) permittivity [ F/m]](/thumbs/79/79624275.jpg) Electrostatic Fields Electrostatic fields are static (time-invariant) electric fields produced by static (stationary) charge distributions. The mathematical definition of the electrostatic field is derived
Electrostatic Fields Electrostatic fields are static (time-invariant) electric fields produced by static (stationary) charge distributions. The mathematical definition of the electrostatic field is derived
BOUNDARY PROBLEMS IN HIGHER DIMENSIONS. kt = X X = λ, and the series solutions have the form (for λ n 0):
 BOUNDARY PROBLEMS IN HIGHER DIMENSIONS Time-space separation To solve the wave and diffusion equations u tt = c u or u t = k u in a bounded domain D with one of the three classical BCs (Dirichlet, Neumann,
BOUNDARY PROBLEMS IN HIGHER DIMENSIONS Time-space separation To solve the wave and diffusion equations u tt = c u or u t = k u in a bounded domain D with one of the three classical BCs (Dirichlet, Neumann,
PHYS 502 Lecture 8: Legendre Functions. Dr. Vasileios Lempesis
 PHYS 502 Lecture 8: Legendre Functions Dr. Vasileios Lempesis Introduction Legendre functions or Legendre polynomials are the solutions of Legendre s differential equation that appear when we separate
PHYS 502 Lecture 8: Legendre Functions Dr. Vasileios Lempesis Introduction Legendre functions or Legendre polynomials are the solutions of Legendre s differential equation that appear when we separate
Solutions VI. MAE294A/SIO203A: Methods in Applied Mechanics Fall Quarter
 MAE94A/SIO3A: Methods in Applied Mechanics Fall Quarter 17 http://web.eng.ucsd.edu/~sgls/mae94a_17/ Solutions VI 1 We let Tx, t) = Xx)τt). We have two homogeneous conditions in x, so let X = λ X to obtain
MAE94A/SIO3A: Methods in Applied Mechanics Fall Quarter 17 http://web.eng.ucsd.edu/~sgls/mae94a_17/ Solutions VI 1 We let Tx, t) = Xx)τt). We have two homogeneous conditions in x, so let X = λ X to obtain
Topic 7. Electric flux Gauss s Law Divergence of E Application of Gauss Law Curl of E
 Topic 7 Electric flux Gauss s Law Divergence of E Application of Gauss Law Curl of E urface enclosing an electric dipole. urface enclosing charges 2q and q. Electric flux Flux density : The number of field
Topic 7 Electric flux Gauss s Law Divergence of E Application of Gauss Law Curl of E urface enclosing an electric dipole. urface enclosing charges 2q and q. Electric flux Flux density : The number of field
Phys 622 Problems Chapter 6
 1 Problem 1 Elastic scattering Phys 622 Problems Chapter 6 A heavy scatterer interacts with a fast electron with a potential V (r) = V e r/r. (a) Find the differential cross section dσ dω = f(θ) 2 in the
1 Problem 1 Elastic scattering Phys 622 Problems Chapter 6 A heavy scatterer interacts with a fast electron with a potential V (r) = V e r/r. (a) Find the differential cross section dσ dω = f(θ) 2 in the
