G( x x, t) = 1 (2π) 3. d 3 k e k2 t/µσ e i k ( x x ) A( k, t)e k x d 3 k. A( x, t) = 1
|
|
|
- Joleen Townsend
- 6 years ago
- Views:
Transcription
1 Physics 505 Fall 2005 Homework Assignment #10 Solutions Textbook problems: Ch. 6: 6.3, 6.4, 6.14, The homogeneous diffusion equation (5.160) for the vector potential for quasi-static fields in unbounded conducting media has a solution to the initial value problem of the form A( x, t) = d 3 x G( x x, t) A( x, 0) where A( x, 0) describes the initial field configuration and G is an appropriate kernel. a) Solve the initial value problem by use of a three-dimensional Fourier transform in space for A( x, t). With the usual assumption on intrchange of orders of integration, show that the Green function has the Fourier representation G( x x, t) = 1 (2π) 3 d 3 k e k2 t/µσ e i k ( x x ) and it is assumed that t > 0. We define the Fourier transform by A( x, t) = 1 (2π) 3 A( k, t)e k x d 3 k In this case, the diffusion equation 2 A = µσ A/ t becomes i k 2 A = µσ t A t A = k2 µσ A This equation is first order in time, and is easily solved to yield A( k, t) = A( k, 0)e k2 t/µσ ) Note that we have written the solution in terms of initial conditions specified as A( k, 0) at time t = 0. This is essentially the answer in momentum space. All we have to do is to invert the transform. The inverse transform gives A( x, t) = 1 (2π) 3 A( k, 0)e k2 t/µσ e i k x d 3 k where A( k, 0) = A( x, 0)e i k x d 3 x
2 The result is A( x, 0) = 1 A( x (2π) 3, 0)e k2t/µσ e i k ( x x ) d 3 k d 3 x = G( x x, t) A( x, 0) d 3 x with the Greens function G( x x, t) = 1 (2π) 3 e k2 t/µσ e i k ( x x ) d 3 k Alternatively, we could have noted directly from ) that the solution in momentum space is a product of e k2 t/µσ with A( k, 0). As a result, the ordinary space solution is a convolution as indicated. b) By introducing a Fourier decomposition in both space and time, and performing the frequency integral in the complex ω plane to recover the result of part a), show that G( x x, t) is the diffusion Green function that satisfies the inhomogeneous equation G t 1 µσ 2 G = δ (3) ( x x )δ(t) and vanishes for t < 0. Introducing the Fourier transform G( x, t) = 1 (2π) 4 the above inhomogeneous equation becomes which gives the Greens function G( k, ω)e i( k x ωt) d 3 k dω [( iω) 2 i k 2 /µσ]g = e i k x G( k, ω) = e i k x k 2 /µσ iω We may invert the transform by first performing the ω integral. We have G( k, t) = 1 G( 2π k, ω)e iωt dω = ie i k x 2π e iωt ω + ik 2 /µσ dω This may be performed by contour integration. For t > 0, Jordan s lemma tells us to close the contour in the lower-half plane. As a result, we pick up the residue at ω = ik 2 /µσ. The result is G( k, t) = ( 2πi) ie i k x e k2t/µσ = e k2t/µσ e i k x 2π
3 On the other hand, for t < 0, we close the contour in the upper-half plane and end up with G = 0 as there are no enclosed poles. Finally, writing out the momentum space Fourier transform gives G( x x, t) = Θ(t) (2π) 3 e k2 t/µσ e i k ( x x ) d 3 k (2) c) Show that if σ is uniform throughout all space, the Green function is ( µσ ) ( 3/2 µσ x x G( x, t; x 2 ), 0) = Θ(t) exp 4πt 4t Actually, we must take both µ and σ to be uniform in all space. In this case, the momentum integration in (2) may be performed by completing the square G( x x, t) = Θ(t) (2π) 3 e µσ x x 2 /4t e t k iµσ( x x )/2t 2 /µσ d 3 k = Θ(t) ( πµσ ) 3/2 e µσ x x 2 /4t (3) (2π) 3 t ( µσ ) 3/2 = Θ(t) e µσ x x 2 /4t 4πt d) Suppose that at time t = 0, the initial vector potential A( x, 0) is nonvanishing only in a localized region of linear extent d around the origin. The time dependence of the fields is observed at a point P far from the origin, i.e., x = r d. Show that there are three regimes of time, 0 < t T 1, T 1 t T 2, and t T 2. Give plausible definitions of T 1 and T 2, and describe qualitatively the time dependence at P. Show that in the last regime, the vector potential is proportional to the volume integral of A( x, 0) times t 3/2, assuming that integral exists. Relate your discussion to those of Section 5.18.B and Problems 5.35 and For a local disturbance near the origin, physical intuition tells us that it will take some time before the observer at point P will manage to observe it. For a diffusion problem, this time is essentially the timescale for diffusion, set by the diffusion coefficient D = 1/µσ, where the diffusion equation is of the form ρ/ t = (D ρ). To be specific, the field at point P is given by the convolution A( x, t) = G( x x, t) A( x, 0) d 3 x ( µσ ) 3/2 = Θ(t) A( x, 0)e µσ x x 2 /4t d 3 x 4πt Assuming x = r d, we may approximate the integral by simply taking x x 2 d 2. This gives ( ) 3/2 µσd A(r, t) Θ(t) e µσr2 /4t A 4πt t=0 (4)
4 where A is the spatial average of A in the nonvanishing region. Defining τ 1 = µσr 2 /4 and τ 2 = µσd/4π, the behavior of the vector potential is then ( τ2 A(r, t) Θ(t) t ) 3/2 e τ 1 /t At short times, t τ 1, the exponential is highly suppressed, and there is no signal at point P. After time τ 1, however, the exponential becomes of order O). The initial vector potential has now diffused to P. However, because of the (τ 2 /t) 3/2 prefactor, the signal dies away at long times. For a rough estimate, we take T 1 = τ 1 = µσr 2 /4 T 2 = 2T 1 Then for t < T 1 the vector potential at point P is essentially zero. Between T 1 and T 2, the vector potential is non-zero, and at long times after T 2, everything has diffused away. Finally, noting that the volume integral of A( x, 0) is simply d 3 A, the expression in (4) demonstrates that at late times (when the exponential is essentially unity) the vector potential is indeed proportional to this volume integral times t 3/ A uniformly magnetized and conducting sphere of radius R and total magnetic moment m = 4πMR 3 /3 rotates about its magnetization axis with angular speed ω. In the steady state no current flows in the conductor. The motion is nonrelativistic; the sphere has no excess charge on it. a) By considering Ohm s law in the moving conductor, show that the motion induces an electric field and a uniform volume charge density in the conductor, ρ = mω/πc 2 R 3. We assume the sphere is magnetized and spinning along the ẑ axis. Since the magnetic moment is m = M V where V = 4 3 πr3 is the volume of the sphere, we see that the magnetization is simply M = Mẑ. As demonstrated earlier, a uniformly magnetized sphere has a uniform magnetic induction B = 2 3 µ 0 M in its interior. In terms of m, this is B = 2 3 µ 0 ( ) 3 4πR 3 mẑ = µ 0m 2πR 3 ẑ We now observe that the electric field E in the rotating frame of the sphere may be related to lab quantities by E = E + v B. Ohm s law in the rotating reference frame is then J = σ E = σ( E + v B). Since no current flows in the steady state ( J = 0), this motion must induce an electric field E = v B. Using ω = ωẑ and v = ω r, we obtain E = ( ω r) B = µ 0mω 2πR 3 (ẑ r) ẑ = µ 0mω ( r ẑ(ẑ r)) 2πR3
5 The vector structure is essentially a projection of r into the horizontal plane perpendicular to the ẑ axis. In cylindrical coordinates, this indicates that E ρ = µ 0mωρ 2πR 3 (5) It is then a simple matter of applying Gauss law to recover the volume charge density. However, before we do so, we note that this is a cylindrically symmetric electric field (pointed horizontally inward towards the ẑ axis). It may at first be somewhat surprising that a sphere will give a cylindrical electric field. However, rotation about an axis is actually a cylindrical process. So from this point of view, the electric field is quite natural. Using ρ = ɛ 0 E we obtain a uniform volume charge density ρ = ɛ 0 E ρ ρ = µ 0ɛ 0 mω 2πR 3 = mω 2πc 2 R 3 It is important to note that, while the charge density is uniform inside the sphere, the electric field is not radial. The discrepancy between a uniform spherical charge distribution and the cylindrical electric field must then arise due to a surface charge. This then provides a hint as to how to approach the remainder of this problem. b) Because the sphere is electrically neutral, there is no monopole electric field outside. Use symmetry arguments to show that the lowest possible electric multipolarity is quadrupole. Show that only a quadrupole field exists outside and that the quadrupole moment tensor has nonvanishing components, Q 33 = 4mωR 2 /3c 2, Q 11 = Q 22 = Q 33 /2. No charge resides outside the sphere. As a result, the exterior field may be described through the multipole expansion. As indicated, charge neutrality guarantees the vanishing of the monopole (l = 0) moment. Furthermore, the odd moments vanish due to symmetry of the electric field (5) under the parity transformation z z. (That is of course the internal field; however we may see that the external field must necessarily respect the symmetry of the internal one.) Thus a simple symmetry argument demonstrates that the lowest possible multipole is the quadrupole (l = 2). Symmetry along will not preclude higher even moments. However an explicit calculation will. Without knowing the surface charge, we cannot directly calculate the electric multipoles. However, we note that the interior electric field (5) can be integrated to obtain the interior electrostatic potential Φ(ρ) = E dl = Converted back to spherical coordinates, this gives E ρ dρ = Φ 0 + µ 0mωρ 2 4πR 3 Φ(r, θ) = Φ 0 + µ 0mω 4πR 3 r2 sin 2 θ = Φ 0 + µ 0mω 6πR 3 r2 [P 0 (cos θ) P 2 (cos θ)]
6 where we have converted sin 2 θ into Legendre polynomials. This can be written explicitly as a Legendre expansion ( Φ(r, θ) = Φ 0 + µ 0mω 6πR 3 r2) P 0 (cos θ) µ 0mω 6πR 3 r2 P 2 (cos θ) so that in particular the potential at the surface of the sphere is ( Φ(R, θ) = Φ 0 + µ ) 0mω P 0 (cos θ) µ 0mω 6πR 6πR P 2(cos θ) We may now solve for the exterior potential by treating this as an electrostatic boundary value problem. We recall that, given a sphere with azimuthally symmetric potential V (θ) = l α lp l (cos θ) on the surface, the exterior solution has the form Φ(r, θ) = l α l(r/r) l+1 P l (cos θ). Furthermore, charge neutrality in the present case forces the monopole (l = 0) term to vanish. Hence we find that Φ 0 = µ 0 mω/6πr, and that the external potential is Φ(r, θ) = µ 0mωR 2 6πr 3 P 2 (cos θ) (6) Incidentally, we could write an expression valid both in the interior and the exterior as Φ(r, θ) = µ [( ) ] 0mω r 2 6πR R 2 1 Θ(R r)p 0 (cos θ) R r2 < r> 3 P 2 (cos θ) (7) Note that this potential is only harmonic outside the sphere; inside the sphere the r 2 /R 2 term multiplying P 0 (cos θ) is not of the right (A l r l + B l r l 1 )P l (cos θ) form to be harmonic. However, this is present precisely because of the uniform volume charge density, which acts as a l = 0 source. In any case, we are essentially done, as the exterior potential (6) clearly has only a quadrupole term 4π µ 0 mωr 2 Y 2,0 (θ, φ) Φ = 5 6π r 3 Comparing this with the multipole expansion gives Φ = 1 4π 4πɛ 0 2l + 1 q Y l,m (θ, φ) l,m r l+1 l,m 5 µ 0 mωr 2 q 2,0 = 4πɛ 0 4π 6π 5 2mωR 2 = 4π 3c 2 Converting to cartesian tensors yields 4π Q 33 = 2 5 q 2,0 = 4mωR2 3c 2, Q 11 = Q 22 = 1 2 Q 33
7 c) By considering the radial electric fields inside and outside the sphere, show that the necessary surface-chrage density σ(θ) is σ(θ) = 1 [ 4mω 4πR 2 3c ] 2 P 2(cos θ) The surface charge may be computed by first obtaining the jump in the normal component of the electric field at the surface of the sphere. Working in spherical components, and taking the gradient of the potential (7), we find E out r = µ 0mωR 2 2πr 4 P 2 (cos θ) E in r = µ 0mωr 3πR 3 [P 0(cos θ) P 2 (cos θ)] The surface charge is then computed as σ = ɛ 0 (Er out Er in ) = µ 0ɛ 0 mω r=r 3πR 2 [ 3 2 P 2(cos θ) (P 0 (cos θ) P 2 (cos θ))] = mω 3πc 2 R 2 [P 0(cos θ) 5 2 P 2(cos θ)] d) The rotating sphere serves as a unipolar induction device if a stationary circuit is attached by a slip ring to the pole and a sliding contact to the equator. Show that the line integral of the electric field from the equator contact to the pole contact by any path) is E = µ 0 mω/4πr. Although the sphere is rotating, both the electric and the magnetic field are static. Hence the line integral of the electric field gives simply the electrostatic potential. In this case E = pole equator E d l = Φ equator Φ pole = Φ(θ = π 2 ) Φ(θ = 0) Using (6) or (7) evaluated on the surface, this becomes E = µ 0mω 6πR [P 2(0) P 2 )] = µ 0mω 4πR 6.14 An ideal circular parallel plate capacitor of radius a and plate separation d a is connected to a current source by axial leads, as shown in the sketch. The current in the wire is I(t) = I 0 cos ωt. a) Calculate the electric and magnetic fields between the plates to second order in powers of the frequency (or wave number), neglecting the effects of fringing fields. We begin with an observation that this problem is cylindrically symmetric. For a static circular parallel plate capacitor, the electric field is in the axial direction
8 (which we take to be ẑ). If this were to vary in time, it would induce an azimuthal magnetic field. Hence we are concerned with finding the cylindrical coordinate components E z (ρ, t) and B φ (ρ, t), at least if we were to neglect fringing. Note that, in this case, both E = 0 and B = 0 are automatically satisfied, and we are left with Faraday s law and the Ampère-Maxwell law. One method to approach this problem is to expand in powers of frequency. Working with complex quantities, a current I(t) = I 0 e iωt results in a charge q = I dt = (ii 0 /ω)e iωt. At lowest order in frequency, we essentially have an electrostatic problem. Thus the charge q = ii 0 /ω gives rise to a surface charge density σ = q/πa 2 = ii 0 /πa 2 ω. The resulting electric field is E (0) z = σ ɛ 0 = ii 0 ɛ 0 πa 2 ω (where we have hidden the e iωt behavior). By the Ampère-Maxwell law, this induces a magnetic field B ) = 1 c 2 ( iω) E (0) = µ 0I 0 πa 2 ẑ Working in cylindrical coordinates, we solve to obtain ( B ) ) z = 1 ρ ρρb ) φ = µ 0I 0 πa 2 B ) φ = µ 0I 0 ρ 2πa 2 Note that a possible integration constant was dropped to avoid an unphysical 1/ρ singularity in the magnetic induction. Proceeding in a similar fashion, this oscillating magnetic field will induce an electric field by Faraday s law This integrates to ρ E (2) z = ( E (2) ) φ = iωb ) φ = iωi 0ρ 2πɛ 0 a 2 c 2 E (2) z = ii 0ρ 2 ω 4πɛ 0 a 2 c 2 Note that this time we have chosen to drop a possible constant of integration since any such ρ independent constant can be absorbed in E z (0) by suitable redefinition of I 0. This does indicate to us, however, that we may need to reexamine the assumed boundary condition that was used to relate E z (0) to the current specified by I 0. Ignoring this for the moment, we proceed once more with the Ampère- Maxwell law to obtain B (3) φ = µ 0Iρ 3 ω 2 16πa 2 c 2
9 Putting the above expressions together gives and restoring the time dependence gives E z = ii 0 πɛ 0 a 2 ρ2 ω 2 ) ω 4c 2 + B φ = µ 0I 0 ρ 2πa 2 ρ2 ω 2 ) (8) 8c 2 + E z = I 0 πɛ 0 a 2 ρ2 ω 2 ) ω 4c 2 + sin ωt B φ = µ 0I 0 ρ 2πa 2 ρ2 ω 2 ) 8c 2 + cos ωt A more formal method for solving this problem is to develop a series expansion in ω of the form E z = n= 1 e n (ρ)ω n, B φ = b n (ρ)ω n and to substitute this into the component Faraday and Ampère-Maxwell equations 1 ρ ρρb φ = iω c 2 E z, ρ E z = iωb φ (9) Collecting the resulting powers of ω of course reduces to the same expressions that we solved one at a time to arrive at (8) above. Of course, we could also be more clever, and simply manipulate (9) to obtain the second order equations which may be rewritten as n=0 1 ρ ρρ ρ E z = ω2 c 2 E z, ρ 1 ρ ρρb φ = ω2 c 2 B φ ζ 2 E z (ζ)+ζe z(ζ)+(ζ 2 0)E z (ζ) = 0, ζ 2 Bφ (ζ)+ζb φ(ζ)+(ζ 2 1)B φ (ρ) = 0 where ζ = ωρ/c. These may be recognized as Bessel s equations, with solution E z (ρ) = E 0 zj 0 (ωρ/c), B φ (ρ) = B 0 φj 1 (ωρ/c) (We have avoided the Neumann functions since they blow up at ρ = 0.) Note, however, that the first order equations (9) tie together E 0 z and B 0 φ. Using B φ = i ω ρe z = i c ζe z = ie0 z c J 0(ζ) = ie0 z c J 1(ζ)
10 (since J 0 = J 1 by the Bessel recursion relations), we see that B 0 φ = ie0 z/c. Since J 0 (ζ) 1 for small argument, ζ 0, the above above boundary conditions are satisfied by taking E z = I 0 πɛ 0 a 2 ω J 0(ωρ/c) sin ωt, B φ = µ 0I 0 c πa 2 ω J 1(ωρ/c) cos ωt 0) b) Calculate the volume integrals of w e and w m that enter the definition of the reactance X, (6.140), to second order in ω. Show that in terms of the input current I i, defined by I i = iωq, where Q is the total charge on one plate, these energies are w e d 3 x = 1 I i 2 d 4πɛ 0 ω 2 a 2, w m d 3 x = µ 0 I i 2 d + ω2 a 2 ) 4π 8 12c 2 Working with the series expansion, (8), the small signal energy densities are given by w e = 1 4E D = ɛ 0 4 E 2 I 0 2 = 4π 2 ɛ 0 a 4 ω 2 ρ2 ω 2 ) 2c 2 + w m = 1 4B H = 1 B 4µ 2 = I 0 2 ρ π 2 ɛ 0 a 4 c 2 ρ2 ω 2 ) 4c 2 + Integrating over the volume of the capacitor with a d 3 x = 2πd ρdρ 0 gives w e d 3 x = I 0 2 d 4πɛ 0 a 2 ω 2 a2 ω 2 ) 4c 2 + w m d 3 x = µ 0 I 0 2 d a2 ω 2 ) 1) 32π 6c 2 + These do not seem to agree with the expected results. However, we have used the constant I 0 to describe the current, whereas I i = iωq, defined by the total charge on one plate, may differ from I 0 due to frequency dependent effects. To compute the total charge Q, we may first use Gauss law to obtain the surface charge density σ and then integrate σ over the plate. For E z given in (8), this gives simply σ = ɛ 0 ( E z ) = ii 0 πa 2 ρ2 ω 2 ) ω 4c 2 + (where the extra sign comes from taking the charge on the top plate) so that a Q = 2π σ(ρ) ρdρ = 2iI ( 0 a 2 0 a 2 ω 2 a4 ω 4 ) 16c 2 + = ii 0 a2 ω 2 ) ω 8c 2 +
11 This yields the relation between I 0 and I i ( I i = iωq = I 0 1 a2 ω 2 ) 8c 2 + so that ( I i 2 = I a2 ω 2 ) 4c 2 + Substituting this into 1) finally results in w e d 3 x = I i 2 d 4πɛ 0 a 2 ω 2, w m d 3 x = µ 0 I i 2 d 32π at least to the order that we are working at. + a2 ω 2 ) c) Show that the equivalent series circuit has C πɛ 0 a 2 /d, L µ 0 d/8π, and that an estimate for the resonant frequency of the system is ω res 2 2c/a. Compare with the first root of J 0 (x). The reactance is given by X 4ω I 2 (w m w e ) d 3 x 4ω I 2 = µ 0d 8π ω 12c 2 ( µ0 I 2 ) d 32π I 2 d 4πɛ 0 a 2 ω 2 ( πɛ0 a 2 ) 1 ω d Since the reactance of an inductor is X = Lω and a capacitor is X = 1/(Cω), we see that the equivalent series circuit has C πɛ 0 a 2 /d and L µ 0 d/8π as indicated. The resonant frequency of a LC circuit is then ω res = 1 LC 8 µ 0 ɛ 0 a 2 = 2 The reason we may compare this with the first zero of the Bessel function J 0 (x) is that the exact expression for the electric field in 0) involves J 0 (ωρ/c). The assumption of no fringing outside the capacitor demands that the electric field vanish at ρ = a. This occurs when ωa/c = x 0,1 where x 0,1 2.4 is the first zero of J 0. The value we have computed, , differs from x 0,1 by more than 15%. Nevertheless, it is at least of the correct magnitude Consider the Dirac expression A( x ) = g d l ( x x ) 4π L x x 3 for the vector potential of a magnetic monopole and its associated string L. Suppose for definiteness that the monopole is located at the origin and the string along the negative z axis. 2c a
12 a) Calculate A explicitly and show that in spherical coordinates it has components A r = 0, A θ = 0, A φ = g cos θ) 4πr sin θ = ( g ) tan θ 4πr 2 Taking the Dirac string along the negative ẑ axis, we write x = z ẑ and d l = ẑdz. Hence Dirac s expression is A( x ) = g 0 4π = g 4π 0 = g (ẑ x) 4π dz ẑ ( x z ẑ) x z ẑ 3 dz ẑ x [ρ 2 + (z z ) 2 ] 3/2 z du (ρ 2 + u 2 ) 3/2 This integral is easily performed by trig substitution. The result is A( x ) = g ẑ x 4π ρ 2 z ) r where ρ 2 = x 2 + y 2 and r 2 = x 2 + y 2 + z 2. Noting that ẑ x = ρ ˆφ = r sin θ ˆφ, and converting to spherical coordinates, we obtain A( x ) = g r z 4π r 2 sin θ ˆφ = g 1 cos θ 4π r sin θ ˆφ b) Verify that B = A is the Coulomb-like field of a point charge, except perhaps at θ = π. Note that the vector potential blows up on the negative ẑ axis. (The positive ẑ axis is safe, as a Taylor or l Hopital expansion near θ = 0 will demonstrate.) Away from this point, we have B = A 1 = ˆr r sin θ θ(sin θa φ ) ˆθ 1 r r(ra φ ) ( ) 1 g = ˆr r sin θ 1 cos θ ( g ) θ = ˆr 4π r 4πr 2 which is the expected field of a magnetic monopole. c) With the B determined in part b), evaluate the total magnetic flux passing through the circular loop of radius R sin θ shown in the figure. Consider θ < π/2 and θ > π/2 spearately, but always calculate the upward flux.
13 Assuming B = gˆr/4πr 2 everywhere, the flux through a circular loop of radius R sin θ is Φ = B ˆn da = B z da = g z ρdρ dφ 4π (ρ 2 + z 2 ) 3/2 = gz (R sin θ) 2 (R sin θ) du gz 1 2 = 4 0 (u + z 2 ) 3/2 2 u + z 2 0 ( gr cos θ 1 = 2 R cos θ 1 ) = g ( ) sgn(cos θ) cos θ R 2 where we have used z = R cos θ. For θ < π/2 (the top hemisphere) we find Φ top = g 2 cos θ), while for θ > π/2 we find Φ bottom = g 2 ( 1 cos θ). Note that the (upward) flux so calculated is discontinuous as we pass through the plane of the monopole. d) From A d L around the loop, determine the total magnetic flux through the loop. Compare the result with that found in part c). Show that they are equal for 0 < θ < π/2, but have a constant difference for π/2 < θ < π. Interpret this difference. By Stokes theorem, the line integral of the vector potential gives the magnetic flux. We find A d l = 0 2π A φ (R, θ) R sin θ dφ = g 1 cos θ 4π R sin θ (2πR sin θ) = g cos θ) 2 Thus A d l = Φ top = Φ bottom + g What has happened in this case is that the computation of part c) did not take into account the flux of the Dirac string. For a positively charged monopole, the Dirac string carries upward magnetic flux. So the total flux of the monopole plus string is really Φ bottom + g. This is fully accounted for by taking the line integral of the vector potential (which is after all the vector potential due to the Dirac string). Of course, an honest magnetic monopole will have a magnetic field B = gˆr/4πr 2 everywhere in space. In this case, the flux calculation of part c) is the correct one. Every calculation involving the vector potential must then be treated with care, and in particular the location of the Dirac string may have to be moved by gauge transformation when working with A in the southern hemisphere. In the modern language of differential geometry (fiber bundles), we have to introduce separate coordinate patches for the northern and southern hemisphere, with an overlap region around the equator. We then define differentiable transition functions (essentially gauge transformations) connecting the different sections of the bundle in the overlap region. The Dirac string can then be avoided by working with the fiber bundle itself.
Jackson 6.4 Homework Problem Solution Dr. Christopher S. Baird University of Massachusetts Lowell
 Jackson 6.4 Homework Problem Solution Dr. Christopher S. Baird University of Massachusetts Lowell PROBLEM: A uniformly magnetized and conducting sphere of radius R and total magnetic moment m = 4πMR 3
Jackson 6.4 Homework Problem Solution Dr. Christopher S. Baird University of Massachusetts Lowell PROBLEM: A uniformly magnetized and conducting sphere of radius R and total magnetic moment m = 4πMR 3
Physics 505 Fall 2005 Homework Assignment #7 Solutions
 Physics 505 Fall 005 Homework Assignment #7 Solutions Textbook problems: Ch. 4: 4.10 Ch. 5: 5.3, 5.6, 5.7 4.10 Two concentric conducting spheres of inner and outer radii a and b, respectively, carry charges
Physics 505 Fall 005 Homework Assignment #7 Solutions Textbook problems: Ch. 4: 4.10 Ch. 5: 5.3, 5.6, 5.7 4.10 Two concentric conducting spheres of inner and outer radii a and b, respectively, carry charges
Physics 505 Fall Homework Assignment #9 Solutions
 Physics 55 Fall 25 Textbook problems: Ch. 5: 5.2, 5.22, 5.26 Ch. 6: 6.1 Homework Assignment #9 olutions 5.2 a) tarting from the force equation (5.12) and the fact that a magnetization M inside a volume
Physics 55 Fall 25 Textbook problems: Ch. 5: 5.2, 5.22, 5.26 Ch. 6: 6.1 Homework Assignment #9 olutions 5.2 a) tarting from the force equation (5.12) and the fact that a magnetization M inside a volume
Electrodynamics Exam Solutions
 Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Physics 506 Winter 2008 Homework Assignment #4 Solutions. Textbook problems: Ch. 9: 9.6, 9.11, 9.16, 9.17
 Physics 56 Winter 28 Homework Assignment #4 Solutions Textbook problems: Ch. 9: 9.6, 9., 9.6, 9.7 9.6 a) Starting from the general expression (9.2) for A and the corresponding expression for Φ, expand
Physics 56 Winter 28 Homework Assignment #4 Solutions Textbook problems: Ch. 9: 9.6, 9., 9.6, 9.7 9.6 a) Starting from the general expression (9.2) for A and the corresponding expression for Φ, expand
Classical Mechanics/Electricity and Magnetism. Preliminary Exam. August 20, :00-15:00 in P-121
 Classical Mechanics/Electricity and Magnetism Preliminary Exam August 20, 2008 09:00-15:00 in P-121 Answer THREE (3) questions from each of the TWO (2) sections A and B for a total of SIX (6) solutions.
Classical Mechanics/Electricity and Magnetism Preliminary Exam August 20, 2008 09:00-15:00 in P-121 Answer THREE (3) questions from each of the TWO (2) sections A and B for a total of SIX (6) solutions.
Classical Field Theory: Electrostatics-Magnetostatics
 Classical Field Theory: Electrostatics-Magnetostatics April 27, 2010 1 1 J.D.Jackson, Classical Electrodynamics, 2nd Edition, Section 1-5 Electrostatics The behavior of an electrostatic field can be described
Classical Field Theory: Electrostatics-Magnetostatics April 27, 2010 1 1 J.D.Jackson, Classical Electrodynamics, 2nd Edition, Section 1-5 Electrostatics The behavior of an electrostatic field can be described
Worked Examples Set 2
 Worked Examples Set 2 Q.1. Application of Maxwell s eqns. [Griffiths Problem 7.42] In a perfect conductor the conductivity σ is infinite, so from Ohm s law J = σe, E = 0. Any net charge must be on the
Worked Examples Set 2 Q.1. Application of Maxwell s eqns. [Griffiths Problem 7.42] In a perfect conductor the conductivity σ is infinite, so from Ohm s law J = σe, E = 0. Any net charge must be on the
Electromagnetism: Worked Examples. University of Oxford Second Year, Part A2
 Electromagnetism: Worked Examples University of Oxford Second Year, Part A2 Caroline Terquem Department of Physics caroline.terquem@physics.ox.ac.uk Michaelmas Term 2017 2 Contents 1 Potentials 5 1.1 Potential
Electromagnetism: Worked Examples University of Oxford Second Year, Part A2 Caroline Terquem Department of Physics caroline.terquem@physics.ox.ac.uk Michaelmas Term 2017 2 Contents 1 Potentials 5 1.1 Potential
2nd Year Electromagnetism 2012:.Exam Practice
 2nd Year Electromagnetism 2012:.Exam Practice These are sample questions of the type of question that will be set in the exam. They haven t been checked the way exam questions are checked so there may
2nd Year Electromagnetism 2012:.Exam Practice These are sample questions of the type of question that will be set in the exam. They haven t been checked the way exam questions are checked so there may
Electric fields in matter
 Electric fields in matter November 2, 25 Suppose we apply a constant electric field to a block of material. Then the charges that make up the matter are no longer in equilibrium: the electrons tend to
Electric fields in matter November 2, 25 Suppose we apply a constant electric field to a block of material. Then the charges that make up the matter are no longer in equilibrium: the electrons tend to
AP Physics C. Magnetism - Term 4
 AP Physics C Magnetism - Term 4 Interest Packet Term Introduction: AP Physics has been specifically designed to build on physics knowledge previously acquired for a more in depth understanding of the world
AP Physics C Magnetism - Term 4 Interest Packet Term Introduction: AP Physics has been specifically designed to build on physics knowledge previously acquired for a more in depth understanding of the world
Consider a ring of radius a lying flat in the xy plane. Take the current in the ring to be I(t) = I 0 cos(ωt).
 Problem 1. A rotating magnet Consider a ring of radius a lying flat in the xy plane. Take the current in the ring to be I(t) = I 0 cos(ωt). (a) Determine the electric field close z axis for z a using the
Problem 1. A rotating magnet Consider a ring of radius a lying flat in the xy plane. Take the current in the ring to be I(t) = I 0 cos(ωt). (a) Determine the electric field close z axis for z a using the
Solutions to PS 2 Physics 201
 Solutions to PS Physics 1 1. ke dq E = i (1) r = i = i k eλ = i k eλ = i k eλ k e λ xdx () (x x) (x x )dx (x x ) + x dx () (x x ) x ln + x x + x x (4) x + x ln + x (5) x + x To find the field for x, we
Solutions to PS Physics 1 1. ke dq E = i (1) r = i = i k eλ = i k eλ = i k eλ k e λ xdx () (x x) (x x )dx (x x ) + x dx () (x x ) x ln + x x + x x (4) x + x ln + x (5) x + x To find the field for x, we
EM radiation - Lecture 14
 EM radiation - Lecture 14 1 Review Begin with a review of the potentials, fields, and Poynting vector for a point charge in accelerated motion. The retarded potential forms are given below. The source
EM radiation - Lecture 14 1 Review Begin with a review of the potentials, fields, and Poynting vector for a point charge in accelerated motion. The retarded potential forms are given below. The source
l=0 The expansion coefficients can be determined, for example, by finding the potential on the z-axis and expanding that result in z.
 Electrodynamics I Exam - Part A - Closed Book KSU 15/11/6 Name Electrodynamic Score = 14 / 14 points Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try
Electrodynamics I Exam - Part A - Closed Book KSU 15/11/6 Name Electrodynamic Score = 14 / 14 points Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try
For the magnetic field B called magnetic induction (unfortunately) M called magnetization is the induced field H called magnetic field H =
 To review, in our original presentation of Maxwell s equations, ρ all J all represented all charges, both free bound. Upon separating them, free from bound, we have (dropping quadripole terms): For the
To review, in our original presentation of Maxwell s equations, ρ all J all represented all charges, both free bound. Upon separating them, free from bound, we have (dropping quadripole terms): For the
Solution Set Eight. 1 Problem #1: Toroidal Electromagnet with Gap Problem #4: Self-Inductance of a Long Solenoid. 9
 : Solution Set Eight Northwestern University, Electrodynamics I Wednesday, March 9, 6 Contents Problem #: Toroidal Electromagnet with Gap. Problem #: Electromagnetic Momentum. 3 3 Problem #3: Type I Superconductor.
: Solution Set Eight Northwestern University, Electrodynamics I Wednesday, March 9, 6 Contents Problem #: Toroidal Electromagnet with Gap. Problem #: Electromagnetic Momentum. 3 3 Problem #3: Type I Superconductor.
Indiana University Physics P331: Theory of Electromagnetism Review Problems #3
 Indiana University Physics P331: Theory of Electromagnetism Review Problems #3 Note: The final exam (Friday 1/14 8:00-10:00 AM will be comprehensive, covering lecture and homework material pertaining to
Indiana University Physics P331: Theory of Electromagnetism Review Problems #3 Note: The final exam (Friday 1/14 8:00-10:00 AM will be comprehensive, covering lecture and homework material pertaining to
Maxwell s equations for electrostatics
 Maxwell s equations for electrostatics October 6, 5 The differential form of Gauss s law Starting from the integral form of Gauss s law, we treat the charge as a continuous distribution, ρ x. Then, letting
Maxwell s equations for electrostatics October 6, 5 The differential form of Gauss s law Starting from the integral form of Gauss s law, we treat the charge as a continuous distribution, ρ x. Then, letting
Solutions: Homework 5
 Ex. 5.1: Capacitor Solutions: Homework 5 (a) Consider a parallel plate capacitor with large circular plates, radius a, a distance d apart, with a d. Choose cylindrical coordinates (r,φ,z) and let the z
Ex. 5.1: Capacitor Solutions: Homework 5 (a) Consider a parallel plate capacitor with large circular plates, radius a, a distance d apart, with a d. Choose cylindrical coordinates (r,φ,z) and let the z
Physics 342 Lecture 23. Radial Separation. Lecture 23. Physics 342 Quantum Mechanics I
 Physics 342 Lecture 23 Radial Separation Lecture 23 Physics 342 Quantum Mechanics I Friday, March 26th, 2010 We begin our spherical solutions with the simplest possible case zero potential. Aside from
Physics 342 Lecture 23 Radial Separation Lecture 23 Physics 342 Quantum Mechanics I Friday, March 26th, 2010 We begin our spherical solutions with the simplest possible case zero potential. Aside from
PHYS 110B - HW #4 Spring 2004, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased
 PHYS 11B - HW #4 Spring 4, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased [1.] Problem 8. from Griffiths Reference problem 7.31 figure 7.43. a Let
PHYS 11B - HW #4 Spring 4, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased [1.] Problem 8. from Griffiths Reference problem 7.31 figure 7.43. a Let
Problem Set #3: 2.11, 2.15, 2.21, 2.26, 2.40, 2.42, 2.43, 2.46 (Due Thursday Feb. 27th)
 Chapter Electrostatics Problem Set #3:.,.5,.,.6,.40,.4,.43,.46 (Due Thursday Feb. 7th). Coulomb s Law Coulomb showed experimentally that for two point charges the force is - proportional to each of the
Chapter Electrostatics Problem Set #3:.,.5,.,.6,.40,.4,.43,.46 (Due Thursday Feb. 7th). Coulomb s Law Coulomb showed experimentally that for two point charges the force is - proportional to each of the
A cylinder in a magnetic field (Jackson)
 Problem 1. A cylinder in a magnetic field (Jackson) A very long hollow cylinder of inner radius a and outer radius b of permeability µ is placed in an initially uniform magnetic field B o at right angles
Problem 1. A cylinder in a magnetic field (Jackson) A very long hollow cylinder of inner radius a and outer radius b of permeability µ is placed in an initially uniform magnetic field B o at right angles
Physics GRE: Electromagnetism. G. J. Loges 1. University of Rochester Dept. of Physics & Astronomy. xkcd.com/567/
 Physics GRE: Electromagnetism G. J. Loges University of Rochester Dept. of Physics & stronomy xkcd.com/567/ c Gregory Loges, 206 Contents Electrostatics 2 Magnetostatics 2 3 Method of Images 3 4 Lorentz
Physics GRE: Electromagnetism G. J. Loges University of Rochester Dept. of Physics & stronomy xkcd.com/567/ c Gregory Loges, 206 Contents Electrostatics 2 Magnetostatics 2 3 Method of Images 3 4 Lorentz
Mansfield Independent School District AP Physics C: Electricity and Magnetism Year at a Glance
 Mansfield Independent School District AP Physics C: Electricity and Magnetism Year at a Glance First Six-Weeks Second Six-Weeks Third Six-Weeks Lab safety Lab practices and ethical practices Math and Calculus
Mansfield Independent School District AP Physics C: Electricity and Magnetism Year at a Glance First Six-Weeks Second Six-Weeks Third Six-Weeks Lab safety Lab practices and ethical practices Math and Calculus
ECE 3209 Electromagnetic Fields Final Exam Example. University of Virginia Solutions
 ECE 3209 Electromagnetic Fields Final Exam Example University of Virginia Solutions (print name above) This exam is closed book and closed notes. Please perform all work on the exam sheets in a neat and
ECE 3209 Electromagnetic Fields Final Exam Example University of Virginia Solutions (print name above) This exam is closed book and closed notes. Please perform all work on the exam sheets in a neat and
Inductance. thevectorpotentialforthemagneticfield, B 1. ] d l 2. 4π I 1. φ 12 M 12 I 1. 1 Definition of Inductance. r 12
![Inductance. thevectorpotentialforthemagneticfield, B 1. ] d l 2. 4π I 1. φ 12 M 12 I 1. 1 Definition of Inductance. r 12 Inductance. thevectorpotentialforthemagneticfield, B 1. ] d l 2. 4π I 1. φ 12 M 12 I 1. 1 Definition of Inductance. r 12](/thumbs/72/67161747.jpg) Inductance 1 Definition of Inductance When electric potentials are placed on a system of conductors, charges move to cancel the electric field parallel to the conducting surfaces of the conductors. We
Inductance 1 Definition of Inductance When electric potentials are placed on a system of conductors, charges move to cancel the electric field parallel to the conducting surfaces of the conductors. We
1. (3) Write Gauss Law in differential form. Explain the physical meaning.
 Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Electro Dynamic Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about
Electrodynamics I Midterm Exam - Part A - Closed Book KSU 204/0/23 Name Electro Dynamic Instructions: Use SI units. Where appropriate, define all variables or symbols you use, in words. Try to tell about
The Helmholtz theorem at last!
 Problem. The Helmholtz theorem at last! Recall in class the Helmholtz theorem that says that if if E =0 then E can be written as E = φ () if B =0 then B can be written as B = A (2) (a) Let n be a unit
Problem. The Helmholtz theorem at last! Recall in class the Helmholtz theorem that says that if if E =0 then E can be written as E = φ () if B =0 then B can be written as B = A (2) (a) Let n be a unit
Summary: Applications of Gauss Law
 Physics 2460 Electricity and Magnetism I, Fall 2006, Lecture 15 1 Summary: Applications of Gauss Law 1. Field outside of a uniformly charged sphere of radius a: 2. An infinite, uniformly charged plane
Physics 2460 Electricity and Magnetism I, Fall 2006, Lecture 15 1 Summary: Applications of Gauss Law 1. Field outside of a uniformly charged sphere of radius a: 2. An infinite, uniformly charged plane
Problem Set #4: 4.1,4.7,4.9 (Due Monday, March 25th)
 Chapter 4 Multipoles, Dielectrics Problem Set #4: 4.,4.7,4.9 (Due Monday, March 5th 4. Multipole expansion Consider a localized distribution of charges described by ρ(x contained entirely in a sphere of
Chapter 4 Multipoles, Dielectrics Problem Set #4: 4.,4.7,4.9 (Due Monday, March 5th 4. Multipole expansion Consider a localized distribution of charges described by ρ(x contained entirely in a sphere of
E&M. 1 Capacitors. January 2009
 E&M January 2009 1 Capacitors Consider a spherical capacitor which has the space between its plates filled with a dielectric of permittivity ɛ. The inner sphere has radius r 1 and the outer sphere has
E&M January 2009 1 Capacitors Consider a spherical capacitor which has the space between its plates filled with a dielectric of permittivity ɛ. The inner sphere has radius r 1 and the outer sphere has
AP Physics C Mechanics Objectives
 AP Physics C Mechanics Objectives I. KINEMATICS A. Motion in One Dimension 1. The relationships among position, velocity and acceleration a. Given a graph of position vs. time, identify or sketch a graph
AP Physics C Mechanics Objectives I. KINEMATICS A. Motion in One Dimension 1. The relationships among position, velocity and acceleration a. Given a graph of position vs. time, identify or sketch a graph
Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Electro Dynamic
 Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Name Electro Dynamic Instructions: Use SI units. Short answers! No derivations here, just state your responses clearly. 1. (2) Write an
Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Name Electro Dynamic Instructions: Use SI units. Short answers! No derivations here, just state your responses clearly. 1. (2) Write an
Theory of Electromagnetic Fields
 Theory of Electromagnetic Fields Andrzej Wolski University of Liverpool, and the Cockcroft Institute, UK Abstract We discuss the theory of electromagnetic fields, with an emphasis on aspects relevant to
Theory of Electromagnetic Fields Andrzej Wolski University of Liverpool, and the Cockcroft Institute, UK Abstract We discuss the theory of electromagnetic fields, with an emphasis on aspects relevant to
Lecture notes for ELECTRODYNAMICS.
 Lecture notes for 640-343 ELECTRODYNAMICS. 1 Summary of Electrostatics 1.1 Coulomb s Law Force between two point charges F 12 = 1 4πɛ 0 Q 1 Q 2ˆr 12 r 1 r 2 2 (1.1.1) 1.2 Electric Field For a charge distribution:
Lecture notes for 640-343 ELECTRODYNAMICS. 1 Summary of Electrostatics 1.1 Coulomb s Law Force between two point charges F 12 = 1 4πɛ 0 Q 1 Q 2ˆr 12 r 1 r 2 2 (1.1.1) 1.2 Electric Field For a charge distribution:
Electromagnetism Answers to Problem Set 9 Spring 2006
 Electromagnetism 70006 Answers to Problem et 9 pring 006. Jackson Prob. 5.: Reformulate the Biot-avart law in terms of the solid angle subtended at the point of observation by the current-carrying circuit.
Electromagnetism 70006 Answers to Problem et 9 pring 006. Jackson Prob. 5.: Reformulate the Biot-avart law in terms of the solid angle subtended at the point of observation by the current-carrying circuit.
week 3 chapter 28 - Gauss s Law
 week 3 chapter 28 - Gauss s Law Here is the central idea: recall field lines... + + q 2q q (a) (b) (c) q + + q q + +q q/2 + q (d) (e) (f) The number of electric field lines emerging from minus the number
week 3 chapter 28 - Gauss s Law Here is the central idea: recall field lines... + + q 2q q (a) (b) (c) q + + q q + +q q/2 + q (d) (e) (f) The number of electric field lines emerging from minus the number
Problem Set 10 Solutions
 Massachusetts Institute of Technology Department of Physics Physics 87 Fall 25 Problem Set 1 Solutions Problem 1: EM Waves in a Plasma a Transverse electromagnetic waves have, by definition, E = Taking
Massachusetts Institute of Technology Department of Physics Physics 87 Fall 25 Problem Set 1 Solutions Problem 1: EM Waves in a Plasma a Transverse electromagnetic waves have, by definition, E = Taking
Currents (1) Line charge λ (C/m) with velocity v : in time t, This constitutes a current I = λv (vector). Magnetic force on a segment of length dl is
 Magnetostatics 1. Currents 2. Relativistic origin of magnetic field 3. Biot-Savart law 4. Magnetic force between currents 5. Applications of Biot-Savart law 6. Ampere s law in differential form 7. Magnetic
Magnetostatics 1. Currents 2. Relativistic origin of magnetic field 3. Biot-Savart law 4. Magnetic force between currents 5. Applications of Biot-Savart law 6. Ampere s law in differential form 7. Magnetic
Electrodynamics I Midterm - Part A - Closed Book KSU 2005/10/17 Electro Dynamic
 Electrodynamics I Midterm - Part A - Closed Book KSU 5//7 Name Electro Dynamic. () Write Gauss Law in differential form. E( r) =ρ( r)/ɛ, or D = ρ, E= electricfield,ρ=volume charge density, ɛ =permittivity
Electrodynamics I Midterm - Part A - Closed Book KSU 5//7 Name Electro Dynamic. () Write Gauss Law in differential form. E( r) =ρ( r)/ɛ, or D = ρ, E= electricfield,ρ=volume charge density, ɛ =permittivity
Physics 6303 Lecture 11 September 24, LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation
 Physics 6303 Lecture September 24, 208 LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation, l l l l l l. Consider problems that are no axisymmetric; i.e., the potential depends
Physics 6303 Lecture September 24, 208 LAST TIME: Cylindrical coordinates, spherical coordinates, and Legendre s equation, l l l l l l. Consider problems that are no axisymmetric; i.e., the potential depends
Problem Set 7: Solutions
 UNIVERSITY OF ALABAMA Department of Physics and Astronomy PH 126 / LeClair Fall 2009 Problem Set 7: Solutions 1. A thin ring of radius a carries a static charge q. This ring is in a magnetic field of strength
UNIVERSITY OF ALABAMA Department of Physics and Astronomy PH 126 / LeClair Fall 2009 Problem Set 7: Solutions 1. A thin ring of radius a carries a static charge q. This ring is in a magnetic field of strength
AP Physics C. Electricity - Term 3
 AP Physics C Electricity - Term 3 Interest Packet Term Introduction: AP Physics has been specifically designed to build on physics knowledge previously acquired for a more in depth understanding of the
AP Physics C Electricity - Term 3 Interest Packet Term Introduction: AP Physics has been specifically designed to build on physics knowledge previously acquired for a more in depth understanding of the
where the last equality follows from the divergence theorem. Now since we did this for an arbitrary volume τ, it must hold locally:
 8 Electrodynamics Read: Boas Ch. 6, particularly sec. 10 and 11. 8.1 Maxwell equations Some of you may have seen Maxwell s equations on t-shirts or encountered them briefly in electromagnetism courses.
8 Electrodynamics Read: Boas Ch. 6, particularly sec. 10 and 11. 8.1 Maxwell equations Some of you may have seen Maxwell s equations on t-shirts or encountered them briefly in electromagnetism courses.
NIU Ph.D. Candidacy Examination Fall 2018 (8/21/2018) Electricity and Magnetism
 NIU Ph.D. Candidacy Examination Fall 2018 (8/21/2018) Electricity and Magnetism You may solve ALL FOUR problems if you choose. The points of the best three problems will be counted towards your final score
NIU Ph.D. Candidacy Examination Fall 2018 (8/21/2018) Electricity and Magnetism You may solve ALL FOUR problems if you choose. The points of the best three problems will be counted towards your final score
Inductance - Lecture 3
 Inductance - Lecture 3 1 Further Discussion of Faraday s Law In Lecture 2 Faraday s law was developed using the Lorentz force on a charge within a moving, conducting loop with the magnetic field is at
Inductance - Lecture 3 1 Further Discussion of Faraday s Law In Lecture 2 Faraday s law was developed using the Lorentz force on a charge within a moving, conducting loop with the magnetic field is at
Solution Set Two. 1 Problem #1: Projectile Motion Cartesian Coordinates Polar Coordinates... 3
 : Solution Set Two Northwestern University, Classical Mechanics Classical Mechanics, Third Ed.- Goldstein October 7, 2015 Contents 1 Problem #1: Projectile Motion. 2 1.1 Cartesian Coordinates....................................
: Solution Set Two Northwestern University, Classical Mechanics Classical Mechanics, Third Ed.- Goldstein October 7, 2015 Contents 1 Problem #1: Projectile Motion. 2 1.1 Cartesian Coordinates....................................
EXAM 3: SOLUTIONS. B = B. A 2 = BA 2 cos 0 o = BA 2. =Φ(2) B A 2 = A 1 cos 60 o = A 1 2 =0.5m2
 EXAM : S Q.The normal to a certain m area makes an angle of 6 o with a uniform magnetic field. The magnetic flux through this area is the same as the flux through a second area that is perpendicular to
EXAM : S Q.The normal to a certain m area makes an angle of 6 o with a uniform magnetic field. The magnetic flux through this area is the same as the flux through a second area that is perpendicular to
PHYS 110B - HW #4 Fall 2005, Solutions by David Pace Equations referenced as EQ. # are from Griffiths Problem statements are paraphrased
 PHYS B - HW #4 Fall 5, Solutions by David Pace Equations referenced as EQ. # are from Griffiths Problem statements are paraphrased [.] Problem 8. from Griffiths Reference problem 7.3 figure 7.43. a Let
PHYS B - HW #4 Fall 5, Solutions by David Pace Equations referenced as EQ. # are from Griffiths Problem statements are paraphrased [.] Problem 8. from Griffiths Reference problem 7.3 figure 7.43. a Let
Physics 208, Spring 2016 Exam #3
 Physics 208, Spring 206 Exam #3 A Name (Last, First): ID #: Section #: You have 75 minutes to complete the exam. Formulae are provided on an attached sheet. You may NOT use any other formula sheet. You
Physics 208, Spring 206 Exam #3 A Name (Last, First): ID #: Section #: You have 75 minutes to complete the exam. Formulae are provided on an attached sheet. You may NOT use any other formula sheet. You
(a) Write down the total Hamiltonian of this system, including the spin degree of freedom of the electron, but neglecting spin-orbit interactions.
 1. Quantum Mechanics (Spring 2007) Consider a hydrogen atom in a weak uniform magnetic field B = Bê z. (a) Write down the total Hamiltonian of this system, including the spin degree of freedom of the electron,
1. Quantum Mechanics (Spring 2007) Consider a hydrogen atom in a weak uniform magnetic field B = Bê z. (a) Write down the total Hamiltonian of this system, including the spin degree of freedom of the electron,
Chapter 5. Shallow Water Equations. 5.1 Derivation of shallow water equations
 Chapter 5 Shallow Water Equations So far we have concentrated on the dynamics of small-scale disturbances in the atmosphere and ocean with relatively simple background flows. In these analyses we have
Chapter 5 Shallow Water Equations So far we have concentrated on the dynamics of small-scale disturbances in the atmosphere and ocean with relatively simple background flows. In these analyses we have
Lecture 13: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay. Poisson s and Laplace s Equations
 Poisson s and Laplace s Equations Lecture 13: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay We will spend some time in looking at the mathematical foundations of electrostatics.
Poisson s and Laplace s Equations Lecture 13: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay We will spend some time in looking at the mathematical foundations of electrostatics.
University of Illinois at Chicago Department of Physics. Electricity and Magnetism PhD Qualifying Examination
 University of Illinois at Chicago Department of Physics Electricity and Magnetism PhD Qualifying Examination January 8, 216 (Friday) 9: am - 12: noon Full credit can be achieved from completely correct
University of Illinois at Chicago Department of Physics Electricity and Magnetism PhD Qualifying Examination January 8, 216 (Friday) 9: am - 12: noon Full credit can be achieved from completely correct
Circular motion. Aug. 22, 2017
 Circular motion Aug. 22, 2017 Until now, we have been observers to Newtonian physics through inertial reference frames. From our discussion of Newton s laws, these are frames which obey Newton s first
Circular motion Aug. 22, 2017 Until now, we have been observers to Newtonian physics through inertial reference frames. From our discussion of Newton s laws, these are frames which obey Newton s first
1 Fundamentals. 1.1 Overview. 1.2 Units: Physics 704 Spring 2018
 Physics 704 Spring 2018 1 Fundamentals 1.1 Overview The objective of this course is: to determine and fields in various physical systems and the forces and/or torques resulting from them. The domain of
Physics 704 Spring 2018 1 Fundamentals 1.1 Overview The objective of this course is: to determine and fields in various physical systems and the forces and/or torques resulting from them. The domain of
Multipole Fields in the Vacuum Gauge. June 26, 2016
 Multipole Fields in the Vacuum Gauge June 26, 2016 Whatever you call them rubber bands, or Poincaré stresses, or something else there have to be other forces in nature to make a consistent theory of this
Multipole Fields in the Vacuum Gauge June 26, 2016 Whatever you call them rubber bands, or Poincaré stresses, or something else there have to be other forces in nature to make a consistent theory of this
Multipole moments. November 9, 2015
 Multipole moments November 9, 5 The far field expansion Suppose we have a localized charge distribution, confined to a region near the origin with r < R. Then for values of r > R, the electric field must
Multipole moments November 9, 5 The far field expansion Suppose we have a localized charge distribution, confined to a region near the origin with r < R. Then for values of r > R, the electric field must
University of Illinois at Chicago Department of Physics
 University of Illinois at Chicago Department of Physics Electromagnetism Qualifying Examination January 4, 2017 9.00 am - 12.00 pm Full credit can be achieved from completely correct answers to 4 questions.
University of Illinois at Chicago Department of Physics Electromagnetism Qualifying Examination January 4, 2017 9.00 am - 12.00 pm Full credit can be achieved from completely correct answers to 4 questions.
Azimuthal eddy currents in a wire
 Problem 1. Azimuthal eddy currents in a wire A longitudinal AC magnetic field B(t) = ẑb o cos(ωt) is driven through the interior of a (solid) ohmic tube with length L and radius R L, drawn rather schematically
Problem 1. Azimuthal eddy currents in a wire A longitudinal AC magnetic field B(t) = ẑb o cos(ωt) is driven through the interior of a (solid) ohmic tube with length L and radius R L, drawn rather schematically
CHAPTER 8 CONSERVATION LAWS
 CHAPTER 8 CONSERVATION LAWS Outlines 1. Charge and Energy 2. The Poynting s Theorem 3. Momentum 4. Angular Momentum 2 Conservation of charge and energy The net amount of charges in a volume V is given
CHAPTER 8 CONSERVATION LAWS Outlines 1. Charge and Energy 2. The Poynting s Theorem 3. Momentum 4. Angular Momentum 2 Conservation of charge and energy The net amount of charges in a volume V is given
Homework Assignment 4 Solution Set
 Homework Assignment 4 Solution Set PHYCS 442 7 February, 24 Problem (Griffiths 2.37 If the plates are sufficiently large the field near them does not depend on d. The field between the plates is zero (the
Homework Assignment 4 Solution Set PHYCS 442 7 February, 24 Problem (Griffiths 2.37 If the plates are sufficiently large the field near them does not depend on d. The field between the plates is zero (the
Evaluating this approximately uniform field at the little loop s center which happens to lie on the big loop s axis we find
 PHY 35 K. Solutions for problem set #1. Problem 7.: a) We assume the small loop is so much smaller than the big loop or the distance between the loops that the magnetic field of the big loop is approximately
PHY 35 K. Solutions for problem set #1. Problem 7.: a) We assume the small loop is so much smaller than the big loop or the distance between the loops that the magnetic field of the big loop is approximately
Vector Potential for the Magnetic Field
 Vector Potential for the Magnetic Field Let me start with two two theorems of Vector Calculus: Theorem 1: If a vector field has zero curl everywhere in space, then that field is a gradient of some scalar
Vector Potential for the Magnetic Field Let me start with two two theorems of Vector Calculus: Theorem 1: If a vector field has zero curl everywhere in space, then that field is a gradient of some scalar
Exam 3 Topics. Displacement Current Poynting Vector. Faraday s Law Self Inductance. Circuits. Energy Stored in Inductor/Magnetic Field
 Exam 3 Topics Faraday s Law Self Inductance Energy Stored in Inductor/Magnetic Field Circuits LR Circuits Undriven (R)LC Circuits Driven RLC Circuits Displacement Current Poynting Vector NO: B Materials,
Exam 3 Topics Faraday s Law Self Inductance Energy Stored in Inductor/Magnetic Field Circuits LR Circuits Undriven (R)LC Circuits Driven RLC Circuits Displacement Current Poynting Vector NO: B Materials,
Supporting Information
 Supporting Information A: Calculation of radial distribution functions To get an effective propagator in one dimension, we first transform 1) into spherical coordinates: x a = ρ sin θ cos φ, y = ρ sin
Supporting Information A: Calculation of radial distribution functions To get an effective propagator in one dimension, we first transform 1) into spherical coordinates: x a = ρ sin θ cos φ, y = ρ sin
PHY481 - Outline of solutions to Homework 3
 1 PHY481 - Outline of solutions to Homework 3 Problem 3.8: We consider a charge outside a conducting sphere that is neutral. In order that the sphere be neutral, we have to introduce a new image charge
1 PHY481 - Outline of solutions to Homework 3 Problem 3.8: We consider a charge outside a conducting sphere that is neutral. In order that the sphere be neutral, we have to introduce a new image charge
CHAPTER 7 ELECTRODYNAMICS
 CHAPTER 7 ELECTRODYNAMICS Outlines 1. Electromotive Force 2. Electromagnetic Induction 3. Maxwell s Equations Michael Faraday James C. Maxwell 2 Summary of Electrostatics and Magnetostatics ρ/ε This semester,
CHAPTER 7 ELECTRODYNAMICS Outlines 1. Electromotive Force 2. Electromagnetic Induction 3. Maxwell s Equations Michael Faraday James C. Maxwell 2 Summary of Electrostatics and Magnetostatics ρ/ε This semester,
r r 1 r r 1 2 = q 1 p = qd and it points from the negative charge to the positive charge.
 MP204, Important Equations page 1 Below is a list of important equations that we meet in our study of Electromagnetism in the MP204 module. For your exam, you are expected to understand all of these, and
MP204, Important Equations page 1 Below is a list of important equations that we meet in our study of Electromagnetism in the MP204 module. For your exam, you are expected to understand all of these, and
Electromagnetism. Christopher R Prior. ASTeC Intense Beams Group Rutherford Appleton Laboratory
 lectromagnetism Christopher R Prior Fellow and Tutor in Mathematics Trinity College, Oxford ASTeC Intense Beams Group Rutherford Appleton Laboratory Contents Review of Maxwell s equations and Lorentz Force
lectromagnetism Christopher R Prior Fellow and Tutor in Mathematics Trinity College, Oxford ASTeC Intense Beams Group Rutherford Appleton Laboratory Contents Review of Maxwell s equations and Lorentz Force
The 3 dimensional Schrödinger Equation
 Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS 110A. Homework #7. Benjamin Stahl. March 3, 2015
 UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS A Homework #7 Benjamin Stahl March 3, 5 GRIFFITHS, 5.34 It will be shown that the magnetic field of a dipole can written in the following
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS A Homework #7 Benjamin Stahl March 3, 5 GRIFFITHS, 5.34 It will be shown that the magnetic field of a dipole can written in the following
(b) For the system in question, the electric field E, the displacement D, and the polarization P = D ɛ 0 E are as follows. r2 0 inside the sphere,
 PHY 35 K. Solutions for the second midterm exam. Problem 1: a The boundary conditions at the oil-air interface are air side E oil side = E and D air side oil side = D = E air side oil side = ɛ = 1+χ E.
PHY 35 K. Solutions for the second midterm exam. Problem 1: a The boundary conditions at the oil-air interface are air side E oil side = E and D air side oil side = D = E air side oil side = ɛ = 1+χ E.
University of California, Berkeley Physics H7B Spring 1999 (Strovink) SOLUTION TO PROBLEM SET 11 Solutions by P. Pebler
 University of California Berkeley Physics H7B Spring 999 (Strovink) SOLUTION TO PROBLEM SET Solutions by P. Pebler Purcell 7.2 A solenoid of radius a and length b is located inside a longer solenoid of
University of California Berkeley Physics H7B Spring 999 (Strovink) SOLUTION TO PROBLEM SET Solutions by P. Pebler Purcell 7.2 A solenoid of radius a and length b is located inside a longer solenoid of
Yell if you have any questions
 Class 31: Outline Hour 1: Concept Review / Overview PRS Questions possible exam questions Hour : Sample Exam Yell if you have any questions P31 1 Exam 3 Topics Faraday s Law Self Inductance Energy Stored
Class 31: Outline Hour 1: Concept Review / Overview PRS Questions possible exam questions Hour : Sample Exam Yell if you have any questions P31 1 Exam 3 Topics Faraday s Law Self Inductance Energy Stored
Magnetostatics and the vector potential
 Magnetostatics and the vector potential December 8, 2015 1 The divergence of the magnetic field Starting with the general form of the Biot-Savart law, B (x 0 ) we take the divergence of both sides with
Magnetostatics and the vector potential December 8, 2015 1 The divergence of the magnetic field Starting with the general form of the Biot-Savart law, B (x 0 ) we take the divergence of both sides with
Physics 505 Fall 2005 Homework Assignment #8 Solutions
 Physics 55 Fall 5 Homework Assignment #8 Solutions Textbook problems: Ch. 5: 5., 5.4, 5.7, 5.9 5. A circular current loop of radius a carrying a current I lies in the x-y plane with its center at the origin.
Physics 55 Fall 5 Homework Assignment #8 Solutions Textbook problems: Ch. 5: 5., 5.4, 5.7, 5.9 5. A circular current loop of radius a carrying a current I lies in the x-y plane with its center at the origin.
Conductors and Insulators
 Conductors and Insulators Lecture 11: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Self Energy of a Charge Distribution : In Lecture 1 we briefly discussed what we called
Conductors and Insulators Lecture 11: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Self Energy of a Charge Distribution : In Lecture 1 we briefly discussed what we called
Complex Analysis MATH 6300 Fall 2013 Homework 4
 Complex Analysis MATH 6300 Fall 2013 Homework 4 Due Wednesday, December 11 at 5 PM Note that to get full credit on any problem in this class, you must solve the problems in an efficient and elegant manner,
Complex Analysis MATH 6300 Fall 2013 Homework 4 Due Wednesday, December 11 at 5 PM Note that to get full credit on any problem in this class, you must solve the problems in an efficient and elegant manner,
Joel A. Shapiro January 20, 2011
 Joel A. shapiro@physics.rutgers.edu January 20, 2011 Course Information Instructor: Joel Serin 325 5-5500 X 3886, shapiro@physics Book: Jackson: Classical Electrodynamics (3rd Ed.) Web home page: www.physics.rutgers.edu/grad/504
Joel A. shapiro@physics.rutgers.edu January 20, 2011 Course Information Instructor: Joel Serin 325 5-5500 X 3886, shapiro@physics Book: Jackson: Classical Electrodynamics (3rd Ed.) Web home page: www.physics.rutgers.edu/grad/504
Electromagnetism Answers to Problem Set 8 Spring Jackson Prob. 4.1: Multipole expansion for various charge distributions
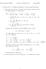 Electromagnetism 76 Answers to Problem Set 8 Spring 6. Jackson Prob. 4.: Multipole expansion for various charge distributions (a) In the first case, we have 4 charges in the xy plane at distance a from
Electromagnetism 76 Answers to Problem Set 8 Spring 6. Jackson Prob. 4.: Multipole expansion for various charge distributions (a) In the first case, we have 4 charges in the xy plane at distance a from
Calculus Relationships in AP Physics C: Electricity and Magnetism
 C: Electricity This chapter focuses on some of the quantitative skills that are important in your C: Mechanics course. These are not all of the skills that you will learn, practice, and apply during the
C: Electricity This chapter focuses on some of the quantitative skills that are important in your C: Mechanics course. These are not all of the skills that you will learn, practice, and apply during the
Problem Set #5: 5.7,5.9,5.13 (Due Monday, April 8th)
 Chapter 5 Magnetostatics Problem Set #5: 5.7,5.9,5.13 (Due Monday, April 8th) 5.1 Biot-Savart Law So far we were concerned with static configuration of charges known as electrostatics. We now switch to
Chapter 5 Magnetostatics Problem Set #5: 5.7,5.9,5.13 (Due Monday, April 8th) 5.1 Biot-Savart Law So far we were concerned with static configuration of charges known as electrostatics. We now switch to
Electrodynamics Qualifier Examination
 Electrodynamics Qualifier Examination August 15, 2007 General Instructions: In all cases, be sure to state your system of units. Show all your work, write only on one side of the designated paper, and
Electrodynamics Qualifier Examination August 15, 2007 General Instructions: In all cases, be sure to state your system of units. Show all your work, write only on one side of the designated paper, and
A half submerged metal sphere (UIC comprehensive
 Problem 1. exam) A half submerged metal sphere (UIC comprehensive A very light neutral hollow metal spherical shell of mass m and radius a is slightly submerged by a distance b a below the surface of a
Problem 1. exam) A half submerged metal sphere (UIC comprehensive A very light neutral hollow metal spherical shell of mass m and radius a is slightly submerged by a distance b a below the surface of a
Physics for Scientists and Engineers 4th Edition 2017
 A Correlation and Narrative Summary of Physics for Scientists and Engineers 4th Edition 2017 To the AP Physics C: Electricity and Magnetism Course Description AP is a trademark registered and/or owned
A Correlation and Narrative Summary of Physics for Scientists and Engineers 4th Edition 2017 To the AP Physics C: Electricity and Magnetism Course Description AP is a trademark registered and/or owned
3 Chapter. Gauss s Law
 3 Chapter Gauss s Law 3.1 Electric Flux... 3-2 3.2 Gauss s Law (see also Gauss s Law Simulation in Section 3.10)... 3-4 Example 3.1: Infinitely Long Rod of Uniform Charge Density... 3-9 Example 3.2: Infinite
3 Chapter Gauss s Law 3.1 Electric Flux... 3-2 3.2 Gauss s Law (see also Gauss s Law Simulation in Section 3.10)... 3-4 Example 3.1: Infinitely Long Rod of Uniform Charge Density... 3-9 Example 3.2: Infinite
There are four questions on this exam. All are of equal value but not necessarily of equal difficulty. Answer all four questions
 Electricity and Magnetism (PHYS2016) Second Semester Final Exam 2015 There are four questions on this exam. All are of equal value but not necessarily of equal difficulty. Answer all four questions You
Electricity and Magnetism (PHYS2016) Second Semester Final Exam 2015 There are four questions on this exam. All are of equal value but not necessarily of equal difficulty. Answer all four questions You
University of Illinois at Chicago Department of Physics. Electricity & Magnetism Qualifying Examination
 University of Illinois at Chicago Department of Physics Electricity & Magnetism Qualifying Examination January 7, 28 9. am 12: pm Full credit can be achieved from completely correct answers to 4 questions.
University of Illinois at Chicago Department of Physics Electricity & Magnetism Qualifying Examination January 7, 28 9. am 12: pm Full credit can be achieved from completely correct answers to 4 questions.
Physics 9 Spring 2012 Midterm 1 Solutions
 Physics 9 Spring 22 NAME: TA: Physics 9 Spring 22 Midterm s For the midterm, you may use one sheet of notes with whatever you want to put on it, front and back. Please sit every other seat, and please
Physics 9 Spring 22 NAME: TA: Physics 9 Spring 22 Midterm s For the midterm, you may use one sheet of notes with whatever you want to put on it, front and back. Please sit every other seat, and please
Problem Set 8: Solutions
 UNIVRSITY OF ALABAMA Department of Physics and Astronomy PH 106-4 / LeClair Fall 2008 Problem Set 8: Solutions 1. (Purcell 7.22 A thin ring of radius a carries a static charge q. This ring is in a magnetic
UNIVRSITY OF ALABAMA Department of Physics and Astronomy PH 106-4 / LeClair Fall 2008 Problem Set 8: Solutions 1. (Purcell 7.22 A thin ring of radius a carries a static charge q. This ring is in a magnetic
Unit-1 Electrostatics-1
 1. Describe about Co-ordinate Systems. Co-ordinate Systems Unit-1 Electrostatics-1 In order to describe the spatial variations of the quantities, we require using appropriate coordinate system. A point
1. Describe about Co-ordinate Systems. Co-ordinate Systems Unit-1 Electrostatics-1 In order to describe the spatial variations of the quantities, we require using appropriate coordinate system. A point
Additional Mathematical Tools: Detail
 Additional Mathematical Tools: Detail September 9, 25 The material here is not required, but gives more detail on the additional mathmatical tools: coordinate systems, rotations, the Dirac delta function
Additional Mathematical Tools: Detail September 9, 25 The material here is not required, but gives more detail on the additional mathmatical tools: coordinate systems, rotations, the Dirac delta function
Field Theory exam II Solutions
 Field Theory exam II Solutions Problem 1 (a) Consider point charges, one with charge q located at x 1 = (1, 0, 1), and the other one with charge q at x = (1, 0, 1). Compute the multipole moments q lm in
Field Theory exam II Solutions Problem 1 (a) Consider point charges, one with charge q located at x 1 = (1, 0, 1), and the other one with charge q at x = (1, 0, 1). Compute the multipole moments q lm in
NIU Ph.D. Candidacy Examination Fall 2017 (8/22/2017) Electricity and Magnetism
 NIU Ph.D. Candidacy Examination Fall 2017 (8/22/2017) Electricity and Magnetism You may solve ALL FOUR problems if you choose. The points of the best three problems will be counted towards your final score
NIU Ph.D. Candidacy Examination Fall 2017 (8/22/2017) Electricity and Magnetism You may solve ALL FOUR problems if you choose. The points of the best three problems will be counted towards your final score
Physics Lecture 40: FRI3 DEC
 Physics 3 Physics 3 Lecture 4: FRI3 DEC Review of concepts for the final exam Electric Fields Electric field E at some point in space is defined as the force divided by the electric charge. Force on charge
Physics 3 Physics 3 Lecture 4: FRI3 DEC Review of concepts for the final exam Electric Fields Electric field E at some point in space is defined as the force divided by the electric charge. Force on charge
Übungen zur Elektrodynamik (T3)
 Arnold Sommerfeld Center Ludwig Maximilians Universität München Prof. Dr. vo Sachs SoSe 8 Übungen zur Elektrodynamik T3 Übungsblatt Bearbeitung: Juni - Juli 3, 8 Conservation of Angular Momentum Consider
Arnold Sommerfeld Center Ludwig Maximilians Universität München Prof. Dr. vo Sachs SoSe 8 Übungen zur Elektrodynamik T3 Übungsblatt Bearbeitung: Juni - Juli 3, 8 Conservation of Angular Momentum Consider
