Lesson 14: An Axiom System for Geometry
|
|
|
- Wesley Moody
- 6 years ago
- Views:
Transcription
1 219 Lesson 14: n xiom System for Geometry We are now ready to present an axiomatic development of geometry. This means that we will list a set of axioms for geometry. These axioms will be simple fundamental facts about geometry which we will assume to be true. We will not require further justification for the axioms. The statements of the axioms will involve certain basic geometric words like point and line. We will not define these words; we will assume that you have an intuitive idea of their meaning. Your intuitive understanding of these words may help you to visualize the concepts they represent; however, all the hard information you will need about these words is expressed in the axioms. You do not need to bring any extra information about these geometric words to the process of developing geometry from its axioms. In fact, it would be wrong to bring any information to this task that is not contained in the axioms or their logical consequences. In addition to these basic words, we will find it convenient to introduce other geometric words which we will define in terms of the basic words. Finally, we will state and prove a number of theorems of geometry. theorem is a true geometric statement that is not an axiom. The axioms are foundational statements that we assume to be true without proof. However, the theorems require proof to establish their truth. For each theorem that we state, we will either present its complete proof or present a partial proof or present no proof and leave some aspect of the proof or all of the proof as a class activity or homework problem. Of course, many geometric statements are false. There is no hope of proving such statements. If we suspect that a statement is false, we need a technique for demonstrating its falsity. The usual method for showing that a geometric statement is false is to present a counterexample to the statement. counterexample to a geometric statement is a description or picture of a situation in which all the axioms of geometry are true, but the statement in question is false. To summarize: in an axiomatic development of geometry, a true geometric statement or theorem is shown to be true by presenting a proof of it from the axioms or from previously proved theorems. false geometric statement is shown to be false by presenting a counterexample in which the statement is false but all the axioms are true. Historically, the earliest known axiomatic development of geometry is the book The Elements by the Greek mathematician Euclid. Euclid lived in lexandria, Egypt about Egypt was conquered by lexander the Great in He created the city of lexandria and made it the capital of Egypt. When lexander died at age 33 in 323.., his empire was divided among his generals. The name of the general who took control of Egypt was Ptolemy. Ptolemy and his descendants ruled Egypt until it
2 220 was conquered by the Romans in 80.. (The last member of the Ptolemaic dynasty to rule Egypt was leopatra.) lexander and his general Ptolemy who were of Greek heritage made lexandria the primary center of Greek culture and learning, and the greatest Greek thinkers of that era found their way to lexandria, including Euclid. In writing The Elements, Euclid codified the previous three centuries of work of Greek mathematicians including Thales, Pythagorus and Plato. (Thales first learned of geometry in Egypt and brought it to ancient Greece around 600..) The contribution of these mathematicians was to view geometry as a subject to be developed axiomatically. They did not view geometry as it had been seen by earlier cultures as simply a large collection of related facts that are useful for measurement and design. They realized that all the facts of geometry can be proved logically from a few basic assumptions or axioms, and they regarded this observation as a powerful approach to the subject that allowed them to organize it and generate new geometric facts in a very efficient way. Euclid brought together in one book his own geometric discoveries as well as those of his predecessors and organized them into an axiomatic system. In subsequent centuries, The Elements became the primary model for the organization of knowledge in science, philosophy and many other areas of human thought, and has persisted in this role to the present day. In The Elements Euclid based geometry on only five axioms or postulates. Our development of geometry is much less efficient than Euclid s; we will base our axiomatic approach to geometry on 14 axioms. The basic reason that we tolerate this glut of axioms is to save time. We could pare our list of axioms down to a much smaller list and then use the axioms on the smaller list to prove all the others. ut this would be a complicated undertaking that would consume much thought and time and would be inappropriate for this course. lso with a larger list of axioms, it becomes easier to prove theorems. We have chosen for our axioms statements that are reasonably familiar and self-evident and which are numerous enough to lead to relatively straightforward, short and transparent proofs of the theorems we want to establish. We begin our axiomatic development of geometry by introducing the basic geometric terms point, line, plane and space (meaning 3-dimensional space). We assume that you know the meaning of these terms. We will not define them. 1 We also assume that you understand that for any two points in space, there is a distance between the two points that is a specific number which is 0. 1 In every mathematical theory, there must be some undefined terms. This is because every defined term has a definition which explains the term by relating it to terms that are already understood. So the very first terms of a subject can t be defined because there are no previously understood terms to which they can be related. Point, line, plane and space are some of the undefined terms in our development of geometry.
3 221 We recall two logical concepts that are useful in all areas of mathematics, not just geometry. Two objects are distinct if they are not identical. Thus, and are distinct if. n object is the unique object with certain properties, if the object has the properties and it is the only object that has these properties. Now we state our first axiom for geometry. The Incidence xiom. ny two distinct points in space lie on a unique line. In other words, if and are distinct points in space ( ), then there is one and only one line that passes through both and. Sometimes we paraphrase this principle by saying that any two distinct points in space determine a unique line. Here, the line determined by the two distinct points is the unique line that passes through the two points. 2 We will use the same basic notation for lines, line segments, rays and distance that we introduced earlier. Notation. Let and be points in space. If, let denote the unique line determined by and. Let denote the line segment with endpoints and. Thus, consists of all the points of the line that lie between and, together with the points and themselves. If, let denote the ray that emanates from and passes through. Thus, consists of all the points of the line that lie either between and or on the opposite side of from, together with the points and themselves. Let denote the distance between and. 2 The Incidence xiom which we have just stated is sufficient for a development of 2-dimensional or plane geometry. We are going to concentrate on 2-dimensional geometry in this axiomatic development of geometry. So this Incidence xiom is all we need. However, if we were going to pursue an axiomatic development of 3-dimensional geometry, we would require the following three additional Incidence xioms. Incidence xiom 2. ny three points in space that do not lie on a single line lie in a unique plane. Incidence xiom 3. If two distinct points in space lie in the plane P in space, then the line determined by the two points also lies in the plane P. Incidence xiom 4. If two distinct planes in space intersect, then their intersection is a line.
4 222 We recall our earlier observations about this notation. First note that if and are points in space, then is a number which is 0, while, and are sets in space. Indeed, is the length of. Warning: Don t write one of these notations when you mean the other. lso, we recall that distance has the following three properties: 0, = 0 if and only if =, and =. Definition. Let, and be three points in a plane or in space. If, and all lie on the same line, we say they are collinear. If, and do not lie on a single line, then we say they are noncollinear. Here is our second axiom for geometry. The Length ddition xiom. If, and are collinear points and lies between and, then = +. Next we recall the definition of angle. Definition. Let, and be three points in space such that and. The union of the two rays and is called the angle with vertex and sides and. This angle can be denoted either or.
5 223 We assume that you understand that every angle has a measure that is a number between 0 and 180. The measure of the angle is denoted m( ). To indicate that angles are being measured in degrees, we attach the symbol º to the numerical measure of each angle. Thus, 0º m( ) 180º. We observe that if is an angle in space, then is a set in space, while m( ) is a number between 0º and 180º. Warning: Don t write one of these notations when you mean the other. Here is our third axiom for geometry. The ngle ddition xiom. If D is a point that lies in the interior of the angle, then m( ) = m( D) + m( D). D We remark that the equation m( ) = m( D) + m( D) makes sense because m( ), m( D) and m( D) are numbers and we know how to add numbers. On the other hand, the equation = D + D does not make sense because, D and D are sets in space, and, in general, we don t know how to add sets. (We observe that a similar remark applies to the two equations: = + and = +. The first equation makes sense because we know how to add numbers, but the second equation doesn t make sense because, in general, we don t know how to add sets.)
6 224 We recall some geometry terminology about angles. If, and are collinear points, and lies between and, then the angle is often called a straight angle. We now state our fourth axiom for geometry. The Straight ngle xiom. If, and collinear points and is between and, then m( ) = 180º. Up to this point we have stated four axioms of geometry. We have assumed that these four statements are true. Hopefully, their truth is obvious to you. We now come to our first theorem. In other words, the truth of the following geometric statement will not simply be assumed. It will be demonstrated by proving it from the previously stated axioms. efore stating this theorem, we need to introduce the concept of vertical angles. Definition. If lines and D intersect at a point E such that E lies between and on line and E lies between and D on line D, then the angles E and ED are called vertical angles or opposite angles. The angles ED and E are also called vertical angles or opposite angles. E D Theorem 1: The Vertical ngles Theorem. Vertical angles have equal measures. In other words, if and D are lines that intersect at a point E such that E lies between and on line and E lies between and D on line D, then m( E) = m( ED). (lso m( ED) = m( E).)
7 225 ctivity 1. The class as a whole should carry out the following activity. proof of Theorem 1 is given below. However, in seven lines of the proof there are blanks where the name of one of the previously stated axioms or the numbers of earlier lines of the proof need to be entered to justify the line. Fill in the name of an appropriate axiom or the appropriate line numbers to justify each of the seven lines of the proof in which a blank occurs. Proof of the Vertical ngles Theorem. 1) m( E) = m( E) + m( E) by the xiom. 2) m( E) = 180º by the xiom. 3) Therefore, m( E) + m( E) = 180º by lines. 4) m( ED) = m( E) + m( ED) by the xiom. 5) m( ED) = 180º by the xiom. 6) Therefore, m( E) + m( ED) = 180º by lines. 7) Hence, m( E) + m( E) = m( E) + m( ED) by lines. 8) Subtracting m( E) from both sides of the equation in line 7) gives: m( E) = m( ED). The proof that m( ED) = m( E) is similar. This completes the proof of the Vertical ngles Theorem. We continue our axiomatic development of geometry with a review of two of the most important concepts of the subject: rigid motion and congruence. Recall: Definition. rigid motion of a plane is a motion of points of the plane to other points of the plane that preserves the distance between any two points. Thus, M is a rigid motion of a plane P if: M moves each point of the plane P to another point M() of the plane P, and if and are any two points of the plane P, then the distance from to equals the distance from M() to M(). (In terms of our notation: = M()M().) rigid motion of space can be defined similarly. It is a distance preserving motion of the points of space. Recall that we have identified four different types of rigid motions of a plane: translations, rotations, reflections and glide reflections. Furthermore, according to the
8 226 lassification Theorem for Rigid Motions of a Plane, every rigid motion of a plane is of one of these for types. Once we have introduced the notion of a rigid motion, we are in a position to define the most important idea in geometry: congruence. Definition. Two geometric figures in a plane are congruent if and only if there is a rigid motion of the plane that moves one figure to the other. We remark that we can similarly define the relation of congruence for two geometric figures in space. Two geometric figures in space are congruent if there is a rigid motion of space that moves one figure to the other. Notation. If S and T are geometric figures in a plane, then we will write S " T to indicate that S is congruent to T. Thus, S " T means there is a rigid motion of the plane containing S and T that moves S to T. Here are our first two axioms involving the notion of congruence. The ongruence xiom for Line Segments. Two line segments are congruent if and only if they have the same length. Thus, " D if and only if = D. The ongruence xiom for ngles. Two angles are congruent if and only if they have the same measures. Thus, " DEF if and only if m( ) = m( DEF). Observe that each of these ongruence xioms is an if and only if statement. Thus, each of these axioms breaks into two separate assertions which convey independent information. For example, the ongruence xiom for Line Segments implies the two assertions: 1) If " D, then = D. 2) If = D, then " D. ssertion 1) says that if there is a rigid motion that moves to D, then = D. This assertion isn t surprising because rigid motions preserve distance. ssertion 2) says that if the distances and D are equal, then there must exist a rigid motion that moves to D. This assertion 2) is a more substantial claim because it promises the existence of a rigid motion based only on the equality of two distances. Similarly, the ongruence xiom for ngles breaks into two independent assertions. One assertion says that if there is a rigid motion moving angle to angle DEF, then these two angles have the same measure. The other assertion says
9 227 that if the two angles have the same measure, then there must exist a rigid motion that moves one angle to the other. gain the second assertion is more substantial. One of the simplest types of geometric objects is a triangle. We will study the congruence of triangles extensively. We begin by defining this class of geometric objects. Definition. Let, and be three points in space. The union of the three line segments, and is called a triangle. We denote this triangle by Δ. (Observe that the same triangle can also be denoted by writing Δ, Δ, Δ, Δ and Δ.) The points, and are called the vertices of the triangle. The line segments, and are called the sides of the triangle. We write, and as abbreviations for the three angles, and of the triangle. Observe that if the two triangles Δ and ΔDEF that lie in the same plane are congruent, then there is a rigid motion of the plane that moves Δ to ΔDEF. This rigid motion will move the vertices, and of the triangle Δ to the vertices D, E and F of the triangle ΔDEF. There are potentially six different ways that a rigid motion can create a correspondence between the vertices,, and the vertices D, E, F: D, E, F, D, F, E, E, F, D, E, D, F, F, D, E, and F, E, D. So the assertion that Δ is congruent to ΔDEF tells us only that there are possibly as many as six different rigid motions that move triangle Δ to triangle ΔDEF. It does not tell us which of these six possibilities is actually realized by a rigid motion that moves Δ to ΔDEF. We now enrich definition of congruence and the notation " to overcome this failing.
10 228 Definition. When we use the notation " with triangles, we will endow it with extra meaning. If Δ and ΔDEF are triangles in a plane, then the writing Δ " ΔDEF will mean more than just that the two triangles Δ and ΔDEF are congruent. Δ " ΔDEF will mean that there is a rigid motion of the plane that moves vertex to vertex D, vertex to vertex E, and vertex to vertex F. Such a rigid motion will then necessarily move edge to edge DE, edge to edge EF, and edge to edge DF. The rigid motion will also move angle to angle D, angle to angle E, and angle to angle F. Furthermore, when Δ " ΔDEF, we will say that Δ is congruent to ΔDEF via a rigid motion that extends the vertex correspondence D, E, F. The two triangles Δ and ΔDEF pictured below are congruent via a rigid motion that extends the vertex correspondence E, F, D. ccording to the prescription just stated for the use of the notation ", all of the following three statements about these two triangles are also true: Δ " ΔEFD, Δ " ΔFED, and Δ " ΔDEF. On the other hand, each of the following three statements is false: Δ " ΔDEF, Δ " ΔFED and Δ " ΔFDE. (These are not the only true and false statements expressing congruence relations between these two triangles. For example, Δ " ΔDFE is true and Δ " ΔDEF is false. ) D E F We now state four congruence axioms for triangles. y declaring these statements to be axioms, we assume that they are true. We do not require proofs to establish their truth. The four congruence axioms stated next tell us that to demonstrate that triangles T and T are congruent, it is sufficient to match up three appropriately chosen measurements on T to three corresponding measurements on T.
11 229 The Side-ngle-Side xiom (SS). If T and T are triangles and there is a correspondence between the vertices of T and the vertices of T so that: two of the sides of T are congruent to the corresponding sides of T, and the included angle between these two sides of T is congruent to the corresponding angle of T, then T and T are congruent via a rigid motion that extends the given vertex correspondence. T T The ngle-side-ngle xiom (S). If T and T are triangles and there is a correspondence between the vertices of T and the vertices of T so that: two of the angles of T are congruent to the corresponding angles of T, and the included side between these two angles of T is congruent to the corresponding side of T, then T and T are congruent via a rigid motion that extends the given vertex correspondence. T T
12 230 The Side-Side-Side xiom (SSS). If T and T are triangles and there is a correspondence between the vertices of T and the vertices of T so that each side of T is congruent to the corresponding side of T, then T and T are congruent via a rigid motion that extends the given vertex correspondence. T T Recall the measures of the three angles of a triangle add up to 180º. Hence, if two angles of a triangle T are congruent to two angles of the triangle T, then the third angle of T must be congruent to the third angle of T! It follows that the S xiom can be strengthened: the side doesn't have to be included between the two angles. The ngle-ngle-side xiom (S). If T and T are triangles and there is a correspondence between the vertices of T and the vertices of T so that: two of the angles of T are congruent to the corresponding angles of T, and one of the sides of T is congruent to the corresponding side of T, then T and T are congruent via a rigid motion that extends the given vertex correspondence. (The selected side of T does not have to be included between the two selected angles of T.) T T
13 231 Warning. Unlike the S Principle, the SS Principle does not generalize. In other words, there is no SS principle. This is because it is possible for two triangles T and T to be non-congruent and yet have two sides and a non-included angle of T congruent to the corresponding two sides and non-included angle of T. T T Observe that we have not bothered to formulate the four preceding congruence axioms for triangles as if and only if statements. This is because it is obvious that the converses of these four axioms are true, and it is unnecessary to include the assertion of the truth of the converse in the statement of the axiom. Indeed, if the triangles T and T are congruent, then there is a rigid motion that carries T to T. This rigid motion will carry each side or angle of T to the corresponding side or angle of T. Therefore, the existence of this rigid motion automatically implies that each side or angle of T is congruent to the corresponding side or angle of T. We have just stated four congruence principles as axioms. We could have taken a more economical approach: we could have stated only one congruence axiom and proved the other three principles as theorems from this axiom. This is the approach Euclid took in The Elements where he stated the SS principle as an axiom and proved the S, SSS and S principles from it. We avoid this more economical approach here because the process of proving three congruence principles from one is long and complicated and is not consistent with the focus of this course. We prefer to assume all four congruence principles as axioms and have the immediate use of them to give simple proofs of other theorems. We now use the congruence axioms to prove a fundamental geometric theorem. First we need a definition.
14 232 Definition. triangle is isosceles if two of its sides are congruent. Theorem 2: The Isosceles Triangle Theorem. Let Δ be a triangle. Then is congruent to if and only if is congruent to. Remark. This theorem asserts an if and only if statement. Recall that such statements break into two separate assertions each of which conveys independent information. The two assertions conveyed by this statement are: 1) if is congruent to, then is congruent to, and 2) if is congruent to, then is congruent to. To prove this theorem, we will prove assertions 1) and 2) separately. We will present two different proofs of this theorem, one here and another as Homework Problem 3. Either proof alone is enough to establish the theorem. There are several reasons for presenting two different proofs. One reason is simply to demonstrate that different proofs are possible. nother reason is that different proofs give different insights into the meaning of the theorem. The proof we give here is short but subtle, and perhaps a little hard to understand. The second proof which is appears in Homework Problem 3 is longer but perhaps more obvious. Students may find that it is easier to imagine how someone could come up with the idea for the second proof. ctivity 2. The class as a whole should carry out the following activity. Proofs of parts 1) and 2) of Theorem 2 are given below. However, in one line of each proof there is a blank where the name of one of the previously stated axioms needs to be entered to justify the line. Fill in the name of an appropriate axiom to justify the line of the proof in which a blank occurs.
1) If AB is congruent to AC, then B is congruent to C.
 233 1) If is congruent to, then is congruent to. Proof of 1). 1) ssume ". (We must prove that ".) 2) ", because the identity is a rigid motion that moves to. 3) Therefore, Δ " Δ by the xiom. (The correspondence
233 1) If is congruent to, then is congruent to. Proof of 1). 1) ssume ". (We must prove that ".) 2) ", because the identity is a rigid motion that moves to. 3) Therefore, Δ " Δ by the xiom. (The correspondence
Neutral Geometry. October 25, c 2009 Charles Delman
 Neutral Geometry October 25, 2009 c 2009 Charles Delman Taking Stock: where we have been; where we are going Set Theory & Logic Terms of Geometry: points, lines, incidence, betweenness, congruence. Incidence
Neutral Geometry October 25, 2009 c 2009 Charles Delman Taking Stock: where we have been; where we are going Set Theory & Logic Terms of Geometry: points, lines, incidence, betweenness, congruence. Incidence
MAT 3271: Selected solutions to problem set 7
 MT 3271: Selected solutions to problem set 7 Chapter 3, Exercises: 16. Consider the Real ffine Plane (that is what the text means by the usual Euclidean model ), which is a model of incidence geometry.
MT 3271: Selected solutions to problem set 7 Chapter 3, Exercises: 16. Consider the Real ffine Plane (that is what the text means by the usual Euclidean model ), which is a model of incidence geometry.
Please note that, as always, these notes are really not complete without diagrams. I have included a few, but the others are up to you.
 Mathematics 3210 Spring Semester, 2005 Homework notes, part 6 March 18, 2005 lease note that, as always, these notes are really not complete without diagrams. I have included a few, but the others are
Mathematics 3210 Spring Semester, 2005 Homework notes, part 6 March 18, 2005 lease note that, as always, these notes are really not complete without diagrams. I have included a few, but the others are
DISCOVERING GEOMETRY Over 6000 years ago, geometry consisted primarily of practical rules for measuring land and for
 Name Period GEOMETRY Chapter One BASICS OF GEOMETRY Geometry, like much of mathematics and science, developed when people began recognizing and describing patterns. In this course, you will study many
Name Period GEOMETRY Chapter One BASICS OF GEOMETRY Geometry, like much of mathematics and science, developed when people began recognizing and describing patterns. In this course, you will study many
Course Notes for MA 460. Version 5.
 ourse Notes for M 460. Version 5. Jim Mclure 1 Definitions and asic Facts. The goal of this course is to help you become expert in geometry, so that you can teach it with confidence and pleasure. We begin
ourse Notes for M 460. Version 5. Jim Mclure 1 Definitions and asic Facts. The goal of this course is to help you become expert in geometry, so that you can teach it with confidence and pleasure. We begin
Q1: Lesson 6 Parallel Lines Handouts Page 1
 6.1 Warmup Per ate Instructions: Justify each statement using your Vocab/Theorems ook. If!! =!! and!! = 50, then!! = 50. P F S If!" is rotated 180 around point F, then!"!" If!!"# +!!"# = 180, then!"# is
6.1 Warmup Per ate Instructions: Justify each statement using your Vocab/Theorems ook. If!! =!! and!! = 50, then!! = 50. P F S If!" is rotated 180 around point F, then!"!" If!!"# +!!"# = 180, then!"# is
Unit 1: Introduction to Proof
 Unit 1: Introduction to Proof Prove geometric theorems both formally and informally using a variety of methods. G.CO.9 Prove and apply theorems about lines and angles. Theorems include but are not restricted
Unit 1: Introduction to Proof Prove geometric theorems both formally and informally using a variety of methods. G.CO.9 Prove and apply theorems about lines and angles. Theorems include but are not restricted
Chapter 3. Betweenness (ordering) A system satisfying the incidence and betweenness axioms is an ordered incidence plane (p. 118).
 Chapter 3 Betweenness (ordering) Point B is between point A and point C is a fundamental, undefined concept. It is abbreviated A B C. A system satisfying the incidence and betweenness axioms is an ordered
Chapter 3 Betweenness (ordering) Point B is between point A and point C is a fundamental, undefined concept. It is abbreviated A B C. A system satisfying the incidence and betweenness axioms is an ordered
CMA Geometry Unit 1 Introduction Week 2 Notes
 CMA Geometry Unit 1 Introduction Week 2 Notes Assignment: 9. Defined Terms: Definitions betweenness of points collinear points coplanar points space bisector of a segment length of a segment line segment
CMA Geometry Unit 1 Introduction Week 2 Notes Assignment: 9. Defined Terms: Definitions betweenness of points collinear points coplanar points space bisector of a segment length of a segment line segment
Angle-Side-Angle Congruence Theorem
 ngle to the Left of Me, ngle to the Right of Me ngle-side-ngle ongruence Theorem. Learning Goals In this lesson, you will: Explore the ngle-side-ngle ongruence Theorem using constructions. Explore the
ngle to the Left of Me, ngle to the Right of Me ngle-side-ngle ongruence Theorem. Learning Goals In this lesson, you will: Explore the ngle-side-ngle ongruence Theorem using constructions. Explore the
Solutions to Exercises in Chapter 1
 Solutions to Exercises in hapter 1 1.6.1 heck that the formula 1 a c b d works for rectangles but not for 4 parallelograms. b a c a d d b c FIGURE S1.1: Exercise 1.6.1. rectangle and a parallelogram For
Solutions to Exercises in hapter 1 1.6.1 heck that the formula 1 a c b d works for rectangles but not for 4 parallelograms. b a c a d d b c FIGURE S1.1: Exercise 1.6.1. rectangle and a parallelogram For
2 Homework. Dr. Franz Rothe February 21, 2015 All3181\3181_spr15h2.tex
 Math 3181 Dr. Franz Rothe February 21, 2015 All3181\3181_spr15h2.tex Name: Homework has to be turned in this handout. For extra space, use the back pages, or blank pages between. The homework can be done
Math 3181 Dr. Franz Rothe February 21, 2015 All3181\3181_spr15h2.tex Name: Homework has to be turned in this handout. For extra space, use the back pages, or blank pages between. The homework can be done
Mathematics 3210 Spring Semester, 2005 Homework notes, part 8 April 15, 2005
 Mathematics 3210 Spring Semester, 2005 Homework notes, part 8 April 15, 2005 The underlying assumption for all problems is that all points, lines, etc., are taken within the Poincaré plane (or Poincaré
Mathematics 3210 Spring Semester, 2005 Homework notes, part 8 April 15, 2005 The underlying assumption for all problems is that all points, lines, etc., are taken within the Poincaré plane (or Poincaré
Greece In 700 BC, Greece consisted of a collection of independent city-states covering a large area including modern day Greece, Turkey, and a multitu
 Chapter 3 Greeks Greece In 700 BC, Greece consisted of a collection of independent city-states covering a large area including modern day Greece, Turkey, and a multitude of Mediterranean islands. The Greeks
Chapter 3 Greeks Greece In 700 BC, Greece consisted of a collection of independent city-states covering a large area including modern day Greece, Turkey, and a multitude of Mediterranean islands. The Greeks
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg
 Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg Undefined Terms: Point, Line, Incident, Between, Congruent. Incidence Axioms:
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg Undefined Terms: Point, Line, Incident, Between, Congruent. Incidence Axioms:
Math 1230, Notes 2. Aug. 28, Math 1230, Notes 2 Aug. 28, / 17
 Math 1230, Notes 2 Aug. 28, 2014 Math 1230, Notes 2 Aug. 28, 2014 1 / 17 This fills in some material between pages 10 and 11 of notes 1. We first discuss the relation between geometry and the quadratic
Math 1230, Notes 2 Aug. 28, 2014 Math 1230, Notes 2 Aug. 28, 2014 1 / 17 This fills in some material between pages 10 and 11 of notes 1. We first discuss the relation between geometry and the quadratic
Name Geometry Common Core Regents Review Packet - 3. Topic 1 : Equation of a circle
 Name Geometry Common Core Regents Review Packet - 3 Topic 1 : Equation of a circle Equation with center (0,0) and radius r Equation with center (h,k) and radius r ( ) ( ) 1. The endpoints of a diameter
Name Geometry Common Core Regents Review Packet - 3 Topic 1 : Equation of a circle Equation with center (0,0) and radius r Equation with center (h,k) and radius r ( ) ( ) 1. The endpoints of a diameter
Chapter 03 Test. 1 Complete the congruence statement. A B C D. 2 Complete the congruence statement. A B C D
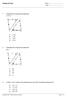 hapter 03 Test Name: ate: 1 omplete the congruence statement. 2 omplete the congruence statement. 3 If, which of the following can you NOT conclude as being true? opyright 2005-2006 by Pearson Education
hapter 03 Test Name: ate: 1 omplete the congruence statement. 2 omplete the congruence statement. 3 If, which of the following can you NOT conclude as being true? opyright 2005-2006 by Pearson Education
UCLA Curtis Center: March 5, 2016
 Transformations in High-School Geometry: A Workable Interpretation of Common Core UCLA Curtis Center: March 5, 2016 John Sarli, Professor Emeritus of Mathematics, CSUSB MDTP Workgroup Chair Abstract. Previous
Transformations in High-School Geometry: A Workable Interpretation of Common Core UCLA Curtis Center: March 5, 2016 John Sarli, Professor Emeritus of Mathematics, CSUSB MDTP Workgroup Chair Abstract. Previous
EUCLID S AXIOMS A-1 A-2 A-3 A-4 A-5 CN-1 CN-2 CN-3 CN-4 CN-5
 EUCLID S AXIOMS In addition to the great practical value of Euclidean Geometry, the ancient Greeks also found great aesthetic value in the study of geometry. Much as children assemble a few kinds blocks
EUCLID S AXIOMS In addition to the great practical value of Euclidean Geometry, the ancient Greeks also found great aesthetic value in the study of geometry. Much as children assemble a few kinds blocks
Logic, Proof, Axiom Systems
 Logic, Proof, Axiom Systems MA 341 Topics in Geometry Lecture 03 29-Aug-2011 MA 341 001 2 Rules of Reasoning A tautology is a sentence which is true no matter what the truth value of its constituent parts.
Logic, Proof, Axiom Systems MA 341 Topics in Geometry Lecture 03 29-Aug-2011 MA 341 001 2 Rules of Reasoning A tautology is a sentence which is true no matter what the truth value of its constituent parts.
P1-763.PDF Why Proofs?
 P1-763.PDF Why Proofs? During the Iron Age men finally started questioning mathematics which eventually lead to the creating of proofs. People wanted to know how and why is math true, rather than just
P1-763.PDF Why Proofs? During the Iron Age men finally started questioning mathematics which eventually lead to the creating of proofs. People wanted to know how and why is math true, rather than just
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg ( )
 Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2005-02-16) Logic Rules (Greenberg): Logic Rule 1 Allowable justifications.
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2005-02-16) Logic Rules (Greenberg): Logic Rule 1 Allowable justifications.
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg ( )
 Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2009-03-26) Logic Rule 0 No unstated assumptions may be used in a proof.
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2009-03-26) Logic Rule 0 No unstated assumptions may be used in a proof.
Geometry and axiomatic Method
 Chapter 1 Geometry and axiomatic Method 1.1 Origin of Geometry The word geometry has its roots in the Greek word geometrein, which means earth measuring. Before the time of recorded history, geometry originated
Chapter 1 Geometry and axiomatic Method 1.1 Origin of Geometry The word geometry has its roots in the Greek word geometrein, which means earth measuring. Before the time of recorded history, geometry originated
Euclid Geometry And Non-Euclid Geometry. Have you ever asked yourself why is it that if you walk to a specific place from
 Hu1 Haotian Hu Dr. Boman Math 475W 9 November 2016 Euclid Geometry And Non-Euclid Geometry Have you ever asked yourself why is it that if you walk to a specific place from somewhere, you will always find
Hu1 Haotian Hu Dr. Boman Math 475W 9 November 2016 Euclid Geometry And Non-Euclid Geometry Have you ever asked yourself why is it that if you walk to a specific place from somewhere, you will always find
Math Number 842 Professor R. Roybal MATH History of Mathematics 24th October, Project 1 - Proofs
 Math Number 842 Professor R. Roybal MATH 331 - History of Mathematics 24th October, 2017 Project 1 - Proofs Mathematical proofs are an important concept that was integral to the development of modern mathematics.
Math Number 842 Professor R. Roybal MATH 331 - History of Mathematics 24th October, 2017 Project 1 - Proofs Mathematical proofs are an important concept that was integral to the development of modern mathematics.
35 Chapter CHAPTER 4: Mathematical Proof
 35 Chapter 4 35 CHAPTER 4: Mathematical Proof Faith is different from proof; the one is human, the other is a gift of God. Justus ex fide vivit. It is this faith that God Himself puts into the heart. 21
35 Chapter 4 35 CHAPTER 4: Mathematical Proof Faith is different from proof; the one is human, the other is a gift of God. Justus ex fide vivit. It is this faith that God Himself puts into the heart. 21
NAME DATE PER. 1. ; 1 and ; 6 and ; 10 and 11
 SECOND SIX WEEKS REVIEW PG. 1 NME DTE PER SECOND SIX WEEKS REVIEW Using the figure below, identify the special angle pair. Then write C for congruent, S for supplementary, or N for neither. d 1. ; 1 and
SECOND SIX WEEKS REVIEW PG. 1 NME DTE PER SECOND SIX WEEKS REVIEW Using the figure below, identify the special angle pair. Then write C for congruent, S for supplementary, or N for neither. d 1. ; 1 and
Math 103 Finite Math with a Special Emphasis on Math & Art by Lun-Yi Tsai, Spring 2010, University of Miami
 Math 103 Finite Math with a Special Emphasis on Math & rt by Lun-Yi Tsai, Spring 2010, University of Miami 1 Geometry notes 1.1 ngles and Parallel Lines efinition 1.1. We defined the complement of an acute
Math 103 Finite Math with a Special Emphasis on Math & rt by Lun-Yi Tsai, Spring 2010, University of Miami 1 Geometry notes 1.1 ngles and Parallel Lines efinition 1.1. We defined the complement of an acute
MA 460 Supplement: Analytic geometry
 M 460 Supplement: nalytic geometry Donu rapura In the 1600 s Descartes introduced cartesian coordinates which changed the way we now do geometry. This also paved for subsequent developments such as calculus.
M 460 Supplement: nalytic geometry Donu rapura In the 1600 s Descartes introduced cartesian coordinates which changed the way we now do geometry. This also paved for subsequent developments such as calculus.
9. TRANSFORMING TOOL #2 (the Multiplication Property of Equality)
 9 TRANSFORMING TOOL # (the Multiplication Property of Equality) a second transforming tool THEOREM Multiplication Property of Equality In the previous section, we learned that adding/subtracting the same
9 TRANSFORMING TOOL # (the Multiplication Property of Equality) a second transforming tool THEOREM Multiplication Property of Equality In the previous section, we learned that adding/subtracting the same
If two sides of a triangle are congruent, then it is an isosceles triangle.
 1. What is the hypothesis of the conditional statement If two sides of a triangle are congruent, then it is an isosceles triangle. two sides of a triangle are congruent it is an isosceles triangle If two
1. What is the hypothesis of the conditional statement If two sides of a triangle are congruent, then it is an isosceles triangle. two sides of a triangle are congruent it is an isosceles triangle If two
October 16, Geometry, the Common Core, and Proof. John T. Baldwin, Andreas Mueller. The motivating problem. Euclidean Axioms and Diagrams
 October 16, 2012 Outline 1 2 3 4 5 Agenda 1 G-C0-1 Context. 2 Activity: Divide a line into n pieces -with string; via construction 3 Reflection activity (geometry/ proof/definition/ common core) 4 mini-lecture
October 16, 2012 Outline 1 2 3 4 5 Agenda 1 G-C0-1 Context. 2 Activity: Divide a line into n pieces -with string; via construction 3 Reflection activity (geometry/ proof/definition/ common core) 4 mini-lecture
1.4 Reasoning and Proof
 Name Class Date 1.4 Reasoning and Proof Essential Question: How do you go about proving a statement? Explore Exploring Inductive and Deductive Reasoning Resource Locker A conjecture is a statement that
Name Class Date 1.4 Reasoning and Proof Essential Question: How do you go about proving a statement? Explore Exploring Inductive and Deductive Reasoning Resource Locker A conjecture is a statement that
Triangle Geometry. Often we can use one letter (capitalised) to name an angle.
 1) Naming angles Triangle Geometry Often we can use one letter (capitalised) to name an angle. A C B When more than two lines meet at a vertex, then we must use three letters to name an angle. Q X P T
1) Naming angles Triangle Geometry Often we can use one letter (capitalised) to name an angle. A C B When more than two lines meet at a vertex, then we must use three letters to name an angle. Q X P T
Chapter 2 Review. Short Answer Determine whether the biconditional statement about the diagram is true or false.
 Chapter 2 Review Short Answer Determine whether the biconditional statement about the diagram is true or false. 1. are supplementary if and only if they form a linear pair. 2. are congruent if and only
Chapter 2 Review Short Answer Determine whether the biconditional statement about the diagram is true or false. 1. are supplementary if and only if they form a linear pair. 2. are congruent if and only
TOPICS IN GEOMETRY: THE GEOMETRY OF THE EUCLIDEAN PLANE. 1. Introduction
 TOPIS IN GEOMETRY: THE GEOMETRY OF THE EULIEN PLNE TUGHT Y PIOTR PRZYTYKI. NOTES Y YLN NT. Note. These course notes are based on a course taught by Piotr Przytycki at McGill University in the fall of 2016.
TOPIS IN GEOMETRY: THE GEOMETRY OF THE EULIEN PLNE TUGHT Y PIOTR PRZYTYKI. NOTES Y YLN NT. Note. These course notes are based on a course taught by Piotr Przytycki at McGill University in the fall of 2016.
Foundations of Neutral Geometry
 C H A P T E R 12 Foundations of Neutral Geometry The play is independent of the pages on which it is printed, and pure geometries are independent of lecture rooms, or of any other detail of the physical
C H A P T E R 12 Foundations of Neutral Geometry The play is independent of the pages on which it is printed, and pure geometries are independent of lecture rooms, or of any other detail of the physical
Euclidean Geometry Proofs
 Euclidean Geometry Proofs History Thales (600 BC) First to turn geometry into a logical discipline. Described as the first Greek philosopher and the father of geometry as a deductive study. Relied on rational
Euclidean Geometry Proofs History Thales (600 BC) First to turn geometry into a logical discipline. Described as the first Greek philosopher and the father of geometry as a deductive study. Relied on rational
Contact. Emina. Office: East Hall 1825 Phone:
 to Contact Emina Email: eminaa@umich.edu Office: East Hall 1825 Phone: 734 647 5518 About me Born in Bosnia: Real home Utah Family Your turn Please fill out the questionnaire Back to business Class website
to Contact Emina Email: eminaa@umich.edu Office: East Hall 1825 Phone: 734 647 5518 About me Born in Bosnia: Real home Utah Family Your turn Please fill out the questionnaire Back to business Class website
Honors 213 / Math 300. Second Hour Exam. Name
 Honors 213 / Math 300 Second Hour Exam Name Monday, March 6, 2006 95 points (will be adjusted to 100 pts in the gradebook) Page 1 I. Some definitions (5 points each). Give formal definitions of the following:
Honors 213 / Math 300 Second Hour Exam Name Monday, March 6, 2006 95 points (will be adjusted to 100 pts in the gradebook) Page 1 I. Some definitions (5 points each). Give formal definitions of the following:
INTRODUCTION TO LOGIC
 INTRODUCTION TO LOGIC L. MARIZZA A. BAILEY 1. The beginning of Modern Mathematics Before Euclid, there were many mathematicians that made great progress in the knowledge of numbers, algebra and geometry.
INTRODUCTION TO LOGIC L. MARIZZA A. BAILEY 1. The beginning of Modern Mathematics Before Euclid, there were many mathematicians that made great progress in the knowledge of numbers, algebra and geometry.
Geometry Triangles
 1 Geometry Triangles 2015-12-08 www.njctl.org 2 Table of Contents Click on the topic to go to that section Triangles Triangle Sum Theorem Exterior Angle Theorem Inequalities in Triangles Similar Triangles
1 Geometry Triangles 2015-12-08 www.njctl.org 2 Table of Contents Click on the topic to go to that section Triangles Triangle Sum Theorem Exterior Angle Theorem Inequalities in Triangles Similar Triangles
CHAPTER 5 INTRODUCTION TO EUCLID S GEOMETRY. 5.1 Introduction
 78 MATHEMATICS INTRODUCTION TO EUCLID S GEOMETRY CHAPTER 5 5.1 Introduction The word geometry comes form the Greek words geo, meaning the earth, and metrein, meaning to measure. Geometry appears to have
78 MATHEMATICS INTRODUCTION TO EUCLID S GEOMETRY CHAPTER 5 5.1 Introduction The word geometry comes form the Greek words geo, meaning the earth, and metrein, meaning to measure. Geometry appears to have
Teaching fractions and geometry according to the CCSSM
 Teaching fractions and geometry according to the CCSSM Selden, NY April 25, 2015 H. Wu Part 1. Definition and the addition of fractions. Part 2. Congruence and similarity (geometry of grade 8 and high
Teaching fractions and geometry according to the CCSSM Selden, NY April 25, 2015 H. Wu Part 1. Definition and the addition of fractions. Part 2. Congruence and similarity (geometry of grade 8 and high
Introduction to Proofs
 Introduction to Proofs Many times in economics we will need to prove theorems to show that our theories can be supported by speci c assumptions. While economics is an observational science, we use mathematics
Introduction to Proofs Many times in economics we will need to prove theorems to show that our theories can be supported by speci c assumptions. While economics is an observational science, we use mathematics
Geometry Unit 1 Practice
 Lesson 1-1 1. Persevere in solving problems. Identify each figure. hen give all possible names for the figure. a. S Geometry Unit 1 Practice e. P S G Q. What is a correct name for this plane? W R Z X b..
Lesson 1-1 1. Persevere in solving problems. Identify each figure. hen give all possible names for the figure. a. S Geometry Unit 1 Practice e. P S G Q. What is a correct name for this plane? W R Z X b..
Section 2-1. Chapter 2. Make Conjectures. Example 1. Reasoning and Proof. Inductive Reasoning and Conjecture
 Chapter 2 Reasoning and Proof Section 2-1 Inductive Reasoning and Conjecture Make Conjectures Inductive reasoning - reasoning that uses a number of specific examples to arrive at a conclusion Conjecture
Chapter 2 Reasoning and Proof Section 2-1 Inductive Reasoning and Conjecture Make Conjectures Inductive reasoning - reasoning that uses a number of specific examples to arrive at a conclusion Conjecture
This handout gives a summary of topics and definitions in Chapter
 MA341 071125 Notes on Chapter 6 This handout gives a summary of topics and definitions in Chapter 6. 1 Definitions. In the following, we assume that we have a Protractor Geometry (which means we have a
MA341 071125 Notes on Chapter 6 This handout gives a summary of topics and definitions in Chapter 6. 1 Definitions. In the following, we assume that we have a Protractor Geometry (which means we have a
MATH 115 Concepts in Mathematics
 South Central College MATH 115 Concepts in Mathematics Course Outcome Summary Course Information Description Total Credits 4.00 Total Hours 64.00 Concepts in Mathematics is a general education survey course
South Central College MATH 115 Concepts in Mathematics Course Outcome Summary Course Information Description Total Credits 4.00 Total Hours 64.00 Concepts in Mathematics is a general education survey course
2) Are all linear pairs supplementary angles? Are all supplementary angles linear pairs? Explain.
 1) Explain what it means to bisect a segment. Why is it impossible to bisect a line? 2) Are all linear pairs supplementary angles? Are all supplementary angles linear pairs? Explain. 3) Explain why a four-legged
1) Explain what it means to bisect a segment. Why is it impossible to bisect a line? 2) Are all linear pairs supplementary angles? Are all supplementary angles linear pairs? Explain. 3) Explain why a four-legged
Introduction to Geometry
 Introduction to Geometry What is Geometry Why do we use Geometry What is Geometry? Geometry is a branch of mathematics that concerns itself with the questions of shape, size, position of figures, and the
Introduction to Geometry What is Geometry Why do we use Geometry What is Geometry? Geometry is a branch of mathematics that concerns itself with the questions of shape, size, position of figures, and the
EC and AB because AIA are congruent Substituting into the first equation above
 4.1 Triangles Sum onjectures uxillary line: an extra line or segment that helps you with your proof. Page 202 Paragraph proof explaining why the Triangle Sum onjecture is true. onjecture: The sum of the
4.1 Triangles Sum onjectures uxillary line: an extra line or segment that helps you with your proof. Page 202 Paragraph proof explaining why the Triangle Sum onjecture is true. onjecture: The sum of the
UNIT 1. Basics of Geometry. What is a pattern? Aug 20 11:14 AM. Jun 8 2:09 PM. Aug 20 10:46 AM. Aug 20 11:08 AM. 1.1 Finding and Describing Patterns
 UNIT 1 Basics of Geometry 1.1 Finding and Describing Patterns What is a pattern? Jun 8 2:09 PM Aug 20 11:00 AM Aug 20 10:46 AM Aug 20 11:04 AM Let's Practice! Making predictions! Describe a pattern. 3.
UNIT 1 Basics of Geometry 1.1 Finding and Describing Patterns What is a pattern? Jun 8 2:09 PM Aug 20 11:00 AM Aug 20 10:46 AM Aug 20 11:04 AM Let's Practice! Making predictions! Describe a pattern. 3.
Introduction to Logic
 Introduction to Logic L. Marizza A. Bailey June 21, 2014 The beginning of Modern Mathematics Before Euclid, there were many mathematicians that made great progress in the knowledge of numbers, algebra
Introduction to Logic L. Marizza A. Bailey June 21, 2014 The beginning of Modern Mathematics Before Euclid, there were many mathematicians that made great progress in the knowledge of numbers, algebra
Chapter 2. Reasoning and Proof
 Chapter 2 Reasoning and Proof 2.1 Use Inductive Reasoning Objective: Describe patterns and use deductive reasoning. Essential Question: How do you use inductive reasoning in mathematics? Common Core: CC.9-12.G.CO.9
Chapter 2 Reasoning and Proof 2.1 Use Inductive Reasoning Objective: Describe patterns and use deductive reasoning. Essential Question: How do you use inductive reasoning in mathematics? Common Core: CC.9-12.G.CO.9
31. TRANSFORMING TOOL #2 (the Multiplication Property of Equality)
 3 TRANSFORMING TOOL # (the Multiplication Property of Equality) a second transforming tool THEOREM Multiplication Property of Equality In the previous section, we learned that adding/subtracting the same
3 TRANSFORMING TOOL # (the Multiplication Property of Equality) a second transforming tool THEOREM Multiplication Property of Equality In the previous section, we learned that adding/subtracting the same
Semester 1 Cumulative Summative Review Teacher: Date: B
 GOMTRY Name: 2016-2017 Semester 1 umulative Summative Review Teacher: ate: To be prepared for your midterm, you will need to PRTI PROLMS and STUY TRMS from the following chapters. Use this guide to help
GOMTRY Name: 2016-2017 Semester 1 umulative Summative Review Teacher: ate: To be prepared for your midterm, you will need to PRTI PROLMS and STUY TRMS from the following chapters. Use this guide to help
MATHE 4800C FOUNDATIONS OF ALGEBRA AND GEOMETRY CLASS NOTES FALL 2011
 MATHE 4800C FOUNDATIONS OF ALGEBRA AND GEOMETRY CLASS NOTES FALL 2011 MATTHEW AUTH, LECTURER OF MATHEMATICS 1. Foundations of Euclidean Geometry (Week 1) During the first weeks of the semester we will
MATHE 4800C FOUNDATIONS OF ALGEBRA AND GEOMETRY CLASS NOTES FALL 2011 MATTHEW AUTH, LECTURER OF MATHEMATICS 1. Foundations of Euclidean Geometry (Week 1) During the first weeks of the semester we will
Affine Planes: An Introduction to Axiomatic Geometry
 Affine Planes: An Introduction to Axiomatic Geometry Here we use Euclidean plane geometry as an opportunity to introduce axiomatic systems. Keep in mind that the axiomatic approach is not the only approach
Affine Planes: An Introduction to Axiomatic Geometry Here we use Euclidean plane geometry as an opportunity to introduce axiomatic systems. Keep in mind that the axiomatic approach is not the only approach
The Crossbar Theorem and Coordinates for Rays
 The Crossbar Theorem and Coordinates for Rays Theorem (The Crossbar Theorem: If a point D lies in the interior of pc, then ray Dmeets segment C at some point G interior to C. Note: This is the first of
The Crossbar Theorem and Coordinates for Rays Theorem (The Crossbar Theorem: If a point D lies in the interior of pc, then ray Dmeets segment C at some point G interior to C. Note: This is the first of
Math 309 Notes and Homework for Days 4-6
 Math 309 Notes and Homework for Days 4-6 Day 4 Read Section 1.2 and the notes below. The following is the main definition of the course. Definition. A vector space is a set V (whose elements are called
Math 309 Notes and Homework for Days 4-6 Day 4 Read Section 1.2 and the notes below. The following is the main definition of the course. Definition. A vector space is a set V (whose elements are called
Congruence. Chapter The Three Points Theorem
 Chapter 2 Congruence In this chapter we use isometries to study congruence. We shall prove the Fundamental Theorem of Transformational Plane Geometry, which states that two plane figures are congruent
Chapter 2 Congruence In this chapter we use isometries to study congruence. We shall prove the Fundamental Theorem of Transformational Plane Geometry, which states that two plane figures are congruent
LESSON 2 5 CHAPTER 2 OBJECTIVES
 LESSON 2 5 CHAPTER 2 OBJECTIVES POSTULATE a statement that describes a fundamental relationship between the basic terms of geometry. THEOREM a statement that can be proved true. PROOF a logical argument
LESSON 2 5 CHAPTER 2 OBJECTIVES POSTULATE a statement that describes a fundamental relationship between the basic terms of geometry. THEOREM a statement that can be proved true. PROOF a logical argument
Lecture 1: Axioms and Models
 Lecture 1: Axioms and Models 1.1 Geometry Although the study of geometry dates back at least to the early Babylonian and Egyptian societies, our modern systematic approach to the subject originates in
Lecture 1: Axioms and Models 1.1 Geometry Although the study of geometry dates back at least to the early Babylonian and Egyptian societies, our modern systematic approach to the subject originates in
#785 Dr. Roger Roybal MATH October 2017 Project 1 A proof is a deliberate process where a mathematical concept is proven to be true using a
 #785 Dr. Roger Roybal MATH 331-02 24 October 2017 Project 1 A proof is a deliberate process where a mathematical concept is proven to be true using a step-by-step explanation and a lettered diagram. The
#785 Dr. Roger Roybal MATH 331-02 24 October 2017 Project 1 A proof is a deliberate process where a mathematical concept is proven to be true using a step-by-step explanation and a lettered diagram. The
0.G. Notational conventions for elementary geometry
 0.G. Notational conventions for elementary geometry Since concepts from elementary geometry play an important role in any account of the history of mathematics, we shall frequently discuss various geometrical
0.G. Notational conventions for elementary geometry Since concepts from elementary geometry play an important role in any account of the history of mathematics, we shall frequently discuss various geometrical
Geometry: A Complete Course
 Geometry: omplete ourse (with Trigonometry) Module Progress Tests Written by: Larry E. ollins Geometry: omplete ourse (with Trigonometry) Module - Progress Tests opyright 2014 by VideotextInteractive Send
Geometry: omplete ourse (with Trigonometry) Module Progress Tests Written by: Larry E. ollins Geometry: omplete ourse (with Trigonometry) Module - Progress Tests opyright 2014 by VideotextInteractive Send
Math 016 Lessons Wimayra LUY
 Math 016 Lessons Wimayra LUY wluy@ccp.edu MATH 016 Lessons LESSON 1 Natural Numbers The set of natural numbers is given by N = {0, 1, 2, 3, 4...}. Natural numbers are used for two main reasons: 1. counting,
Math 016 Lessons Wimayra LUY wluy@ccp.edu MATH 016 Lessons LESSON 1 Natural Numbers The set of natural numbers is given by N = {0, 1, 2, 3, 4...}. Natural numbers are used for two main reasons: 1. counting,
B C. You try: What is the definition of an angle bisector?
 US Geometry 1 What is the definition of a midpoint? The midpoint of a line segment is the point that divides the segment into two congruent segments. That is, M is the midpoint of if M is on and M M. 1
US Geometry 1 What is the definition of a midpoint? The midpoint of a line segment is the point that divides the segment into two congruent segments. That is, M is the midpoint of if M is on and M M. 1
Chapter 2. Reasoning and Proof
 Chapter 2 Reasoning and Proof 2.1 Use Inductive Reasoning Objective: Describe patterns and use deductive reasoning. Essential Question: How do you use inductive reasoning in mathematics? Common Core: CC.9-12.G.CO.9
Chapter 2 Reasoning and Proof 2.1 Use Inductive Reasoning Objective: Describe patterns and use deductive reasoning. Essential Question: How do you use inductive reasoning in mathematics? Common Core: CC.9-12.G.CO.9
Euclid s Elements Part II
 Euclid s Elements Part II The discovery of incommensurable magnitudes steered the ancient Greeks away from the study of number and towards the development of geometry. s a result, geometry was pushed in
Euclid s Elements Part II The discovery of incommensurable magnitudes steered the ancient Greeks away from the study of number and towards the development of geometry. s a result, geometry was pushed in
MTH 05. Basic Concepts of Mathematics I
 MTH 05. Basic Concepts of Mathematics I Uma N. Iyer With Appendices by Sharon Persinger and Anthony Weaver Department of Mathematics and Computer Science Bronx Community College ii To my parents and teachers
MTH 05. Basic Concepts of Mathematics I Uma N. Iyer With Appendices by Sharon Persinger and Anthony Weaver Department of Mathematics and Computer Science Bronx Community College ii To my parents and teachers
Higher Geometry Problems
 Higher Geometry Problems (1) Look up Eucidean Geometry on Wikipedia, and write down the English translation given of each of the first four postulates of Euclid. Rewrite each postulate as a clear statement
Higher Geometry Problems (1) Look up Eucidean Geometry on Wikipedia, and write down the English translation given of each of the first four postulates of Euclid. Rewrite each postulate as a clear statement
16 circles. what goes around...
 16 circles. what goes around... 2 lesson 16 this is the first of two lessons dealing with circles. this lesson gives some basic definitions and some elementary theorems, the most important of which is
16 circles. what goes around... 2 lesson 16 this is the first of two lessons dealing with circles. this lesson gives some basic definitions and some elementary theorems, the most important of which is
2-6 Geometric Proof. Warm Up Lesson Presentation Lesson Quiz. Holt Geometry
 2-6 Geometric Proof Warm Up Lesson Presentation Lesson Quiz Warm Up Determine whether each statement is true or false. If false, give a counterexample. 1. It two angles are complementary, then they are
2-6 Geometric Proof Warm Up Lesson Presentation Lesson Quiz Warm Up Determine whether each statement is true or false. If false, give a counterexample. 1. It two angles are complementary, then they are
Warm Up Lesson Presentation Lesson Quiz. Holt McDougal Geometry
 2-4 Warm Up Lesson Presentation Lesson Quiz Geometry Warm Up Write a conditional statement from each of the following. 1. The intersection of two lines is a point. If two lines intersect, then they intersect
2-4 Warm Up Lesson Presentation Lesson Quiz Geometry Warm Up Write a conditional statement from each of the following. 1. The intersection of two lines is a point. If two lines intersect, then they intersect
Chapter 1. Theorems of Ceva and Menelaus
 hapter 1 Theorems of eva and Menelaus We start these lectures by proving some of the most basic theorems in the geometry of a planar triangle. Let,, be the vertices of the triangle and,, be any points
hapter 1 Theorems of eva and Menelaus We start these lectures by proving some of the most basic theorems in the geometry of a planar triangle. Let,, be the vertices of the triangle and,, be any points
Euclidean Geometry Rediscovered
 Euclidean Geometry Rediscovered Presenter: John C. Mayer Assistants: William Bond & David Cosper University of Alabama at Birmingham Greater Birmingham Mathematics Partnership Supported by NSF EHR-0632522
Euclidean Geometry Rediscovered Presenter: John C. Mayer Assistants: William Bond & David Cosper University of Alabama at Birmingham Greater Birmingham Mathematics Partnership Supported by NSF EHR-0632522
triangles in neutral geometry three theorems of measurement
 lesson 10 triangles in neutral geometry three theorems of measurement 112 lesson 10 in this lesson we are going to take our newly created measurement systems, our rulers and our protractors, and see what
lesson 10 triangles in neutral geometry three theorems of measurement 112 lesson 10 in this lesson we are going to take our newly created measurement systems, our rulers and our protractors, and see what
Ready to Go On? Skills Intervention 2-1 Using Inductive Reasoning to Make Conjectures
 Ready to Go On? Skills Intervention 2-1 Using Inductive Reasoning to Make Conjectures Find these vocabulary words in Lesson 2-1 and the Multilingual Glossary. Vocabulary inductive reasoning conjecture
Ready to Go On? Skills Intervention 2-1 Using Inductive Reasoning to Make Conjectures Find these vocabulary words in Lesson 2-1 and the Multilingual Glossary. Vocabulary inductive reasoning conjecture
ACTIVITY 12 Continued. TEACHER to TEACHER. Lesson 12-3 PLAN TEACH
 Learning Targets: pply the Segment ddition Postulate to find lengths of segments. Use the definition of midpoint to find lengths of segments. SUESTED LERNIN STRTEIES: Close Reading, Look for a Pattern,
Learning Targets: pply the Segment ddition Postulate to find lengths of segments. Use the definition of midpoint to find lengths of segments. SUESTED LERNIN STRTEIES: Close Reading, Look for a Pattern,
7. m JHI = ( ) and m GHI = ( ) and m JHG = 65. Find m JHI and m GHI.
 1. Name three points in the diagram that are not collinear. 2. If RS = 44 and QS = 68, find QR. 3. R, S, and T are collinear. S is between R and T. RS = 2w + 1, ST = w 1, and RT = 18. Use the Segment Addition
1. Name three points in the diagram that are not collinear. 2. If RS = 44 and QS = 68, find QR. 3. R, S, and T are collinear. S is between R and T. RS = 2w + 1, ST = w 1, and RT = 18. Use the Segment Addition
8. TRANSFORMING TOOL #1 (the Addition Property of Equality)
 8 TRANSFORMING TOOL #1 (the Addition Property of Equality) sentences that look different, but always have the same truth values What can you DO to a sentence that will make it LOOK different, but not change
8 TRANSFORMING TOOL #1 (the Addition Property of Equality) sentences that look different, but always have the same truth values What can you DO to a sentence that will make it LOOK different, but not change
EUCLIDEAN AND HYPERBOLIC CONDITIONS
 EUCLIDEAN AND HYPERBOLIC CONDITIONS MATH 410. SPRING 2007. INSTRUCTOR: PROFESSOR AITKEN The first goal of this handout is to show that, in Neutral Geometry, Euclid s Fifth Postulate is equivalent to the
EUCLIDEAN AND HYPERBOLIC CONDITIONS MATH 410. SPRING 2007. INSTRUCTOR: PROFESSOR AITKEN The first goal of this handout is to show that, in Neutral Geometry, Euclid s Fifth Postulate is equivalent to the
Geometry: A Complete Course
 Geometry: omplete ourse (with Trigonometry) Module - Student WorkText Written by: Thomas E. lark Larry E. ollins Geometry: omplete ourse (with Trigonometry) Module Student Worktext opyright 2014 by VideotextInteractive
Geometry: omplete ourse (with Trigonometry) Module - Student WorkText Written by: Thomas E. lark Larry E. ollins Geometry: omplete ourse (with Trigonometry) Module Student Worktext opyright 2014 by VideotextInteractive
Chapter 1 The Real Numbers
 Chapter 1 The Real Numbers In a beginning course in calculus, the emphasis is on introducing the techniques of the subject;i.e., differentiation and integration and their applications. An advanced calculus
Chapter 1 The Real Numbers In a beginning course in calculus, the emphasis is on introducing the techniques of the subject;i.e., differentiation and integration and their applications. An advanced calculus
3.C. Further comments on axioms for geometry
 3.C. Further comments on axioms for geometry One important feature of the Elements is that it develops geometry from a very short list of assumptions. Although axiom systems like Hilbert s (or G. D. Birkhoff
3.C. Further comments on axioms for geometry One important feature of the Elements is that it develops geometry from a very short list of assumptions. Although axiom systems like Hilbert s (or G. D. Birkhoff
Homework 10: p.147: 17-41, 45
 2-4B: Writing Proofs Homework 10: p.147: 17-41, 45 Learning Objectives: Analyze figures to identify and use postulates about points, lines and planes Analyze and construct viable arguments in several proof
2-4B: Writing Proofs Homework 10: p.147: 17-41, 45 Learning Objectives: Analyze figures to identify and use postulates about points, lines and planes Analyze and construct viable arguments in several proof
Chapter 2: Reasoning and Proof
 Name: Chapter 2: Reasoning and Proof Guided Notes Geometry Fall Semester 2.1 Use Inductive Reasoning CH. 2 Guided Notes, page 2 Term Definition Example conjecture An unproven statement that is based on
Name: Chapter 2: Reasoning and Proof Guided Notes Geometry Fall Semester 2.1 Use Inductive Reasoning CH. 2 Guided Notes, page 2 Term Definition Example conjecture An unproven statement that is based on
Theorem 1.2 (Converse of Pythagoras theorem). If the lengths of the sides of ABC satisfy a 2 + b 2 = c 2, then the triangle has a right angle at C.
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
Russell s logicism. Jeff Speaks. September 26, 2007
 Russell s logicism Jeff Speaks September 26, 2007 1 Russell s definition of number............................ 2 2 The idea of reducing one theory to another.................... 4 2.1 Axioms and theories.............................
Russell s logicism Jeff Speaks September 26, 2007 1 Russell s definition of number............................ 2 2 The idea of reducing one theory to another.................... 4 2.1 Axioms and theories.............................
Predicates, Quantifiers and Nested Quantifiers
 Predicates, Quantifiers and Nested Quantifiers Predicates Recall the example of a non-proposition in our first presentation: 2x=1. Let us call this expression P(x). P(x) is not a proposition because x
Predicates, Quantifiers and Nested Quantifiers Predicates Recall the example of a non-proposition in our first presentation: 2x=1. Let us call this expression P(x). P(x) is not a proposition because x
MATHEMATICS (IX-X) (CODE NO. 041) Session
 MATHEMATICS (IX-X) (CODE NO. 041) Session 2018-19 The Syllabus in the subject of Mathematics has undergone changes from time to time in accordance with growth of the subject and emerging needs of the society.
MATHEMATICS (IX-X) (CODE NO. 041) Session 2018-19 The Syllabus in the subject of Mathematics has undergone changes from time to time in accordance with growth of the subject and emerging needs of the society.
30. TRANSFORMING TOOL #1 (the Addition Property of Equality)
 30 TRANSFORMING TOOL #1 (the Addition Property of Equality) sentences that look different, but always have the same truth values What can you DO to a sentence that will make it LOOK different, but not
30 TRANSFORMING TOOL #1 (the Addition Property of Equality) sentences that look different, but always have the same truth values What can you DO to a sentence that will make it LOOK different, but not
5.3 It s All In Your Head A Solidify Understanding Task
 16 5.3 It s All In Your Head A Solidify Understanding Task In the previous task you were asked to justify some claims by writing paragraphs explaining how various figures were constructed and how those
16 5.3 It s All In Your Head A Solidify Understanding Task In the previous task you were asked to justify some claims by writing paragraphs explaining how various figures were constructed and how those
Geometry First Semester Exam Review
 Geometry First Semester Exam Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Name three points that are collinear. a. points T, Q, and R c. points
Geometry First Semester Exam Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Name three points that are collinear. a. points T, Q, and R c. points
MORE EXERCISES FOR SECTIONS II.1 AND II.2. There are drawings on the next two pages to accompany the starred ( ) exercises.
 Math 133 Winter 2013 MORE EXERCISES FOR SECTIONS II.1 AND II.2 There are drawings on the next two pages to accompany the starred ( ) exercises. B1. Let L be a line in R 3, and let x be a point which does
Math 133 Winter 2013 MORE EXERCISES FOR SECTIONS II.1 AND II.2 There are drawings on the next two pages to accompany the starred ( ) exercises. B1. Let L be a line in R 3, and let x be a point which does
