1) If AB is congruent to AC, then B is congruent to C.
|
|
|
- Sheena Harrell
- 5 years ago
- Views:
Transcription
1 233 1) If is congruent to, then is congruent to. Proof of 1). 1) ssume ". (We must prove that ".) 2) ", because the identity is a rigid motion that moves to. 3) Therefore, Δ " Δ by the xiom. (The correspondence between the vertices of Δ and the vertices of Δ that we are using here is:,,.) 4) The rigid motion that moves Δ to Δ, moves to. Hence, ". This completes the proof of 1). Remark. The congruence relation Δ " Δ which is established in this proof is associated with a correspondence between the vertices of Δ and the vertices of Δ. This correspondence sends vertex to itself and interchanges vertices and. Thus, although the two triangles Δ and Δ are identical, the correspondence between their vertices is not the identity correspondence. In proving the congruence relation Δ " Δ, we are tacitly demonstrating that there is a rigid motion of the plane containing Δ that keeps point fixed and interchanges points and, although the existence of this rigid motion doesn t arise explicitly in the proof. Since this rigid motion fixes while interchanging and, then it can t be the identity and, in fact, must be a reflection in the perpendicular bisector of the line segment. 2) If is congruent to, then is congruent to. Proof of 2). 1) ssume ". (We must prove ".) 2) ", because the identity is a rigid motion that moves to itself. 3) Therefore, Δ " Δ by the xiom. (The correspondence between the vertices of Δ and the vertices of Δ that we are using here is:,,.) 4) The rigid motion that moves Δ to Δ, moves to. Hence, ". This completes the proof of 2). Remark. In this proof, as in the previous proof, when we establish the congruence relation Δ " Δ, we are tacitly (but not explicitly) demonstrating the existence of a rigid motion of the plane containing Δ that fixes vertex and interchanges vertices and. This rigid motion must be the reflection in the perpendicular bisector of the line segment.
2 234 Our final group of axioms for geometry involve the concept of parallel lines and some related ideas. We now define these notions. Definition. Two lines in space are parallel if they both lie in a plane and don t intersect. Two lines in space which don t lie in a single plane are called skew lines. Parallel Lines Skew Lines Definition. Let L, M and T be lines in the same plane such that T intersects both L and M, as in the picture below. Then line T is called a transversal to lines L and M. In the figure below, the pair of angles labeled a and a are called corresponding angles. (The pair of angles labeled b and b are also called corresponding angles, as are the pair c and c and the pair d and d.) lso in this figure, the pair of angles labeled c and a are called alternate interior angles or simply alternate angles. (The pair of angles labeled b and d are also called alternate interior angles.) lso in this figure the pair of angles labeled b and a are called supplementary angles. (The pair of angles labeled c and d are also called supplementary angles.) T L a d L b c a d M b c M T
3 235 We now state four basic axioms about parallel lines. gain we assume these axioms to be true. The Parallel Postulate. If L is a line and P is a point not on L, then there is exactly one line that passes through P and is parallel to L. The orresponding ngles xiom. Let L, M and T be lines in the same plane such that T intersects both L and M, as in the figure above. Then L and M are parallel if and only if a pair of corresponding angles are congruent. The lternate Interior ngles xiom. Let L, M and T be lines in the same plane such that T intersects both L and M, as in the figure above. Then L and M are parallel if and only if a pair of alternate interior angles are congruent. The Supplementary ngles xiom. Let L, M and T be lines in the same plane such that T intersects both L and M, as in the figure above. Then L and M are parallel if and only if the angle measures of a pair of supplementary angles add up to 180º. We have just stated four parallel line principles as axioms. s with the congruence axioms, we could have taken a more economical approach: we could have stated only one parallel line axiom and proved the other three principles as theorems from this axiom. Indeed, Euclid took this approach in The Elements where he stated a single parallel line principle as an axiom and proved the other parallel line principles from it. (Euclid s basic parallel line axiom was similar to the Supplementary ngles xiom.) s we did with the congruence axioms, we avoid this more economical approach because the process of proving three parallel line principles from one is long and complicated and is not consistent with the goals of this course. We prefer to assume all four parallel line principles as axioms and have the immediate use of them to give simple proofs of other theorems We now use the axioms we have assumed so far to prove two very important theorems of geometry.
4 236 Theorem 3: The Exterior ngle Theorem. In a triangle, the measure of the exterior angle at a vertex equals the sum of the measures of the interior angles at the other two vertices. In other words, in triangle Δ pictured below, m( D) = m( ) + m( ). D ctivity 3. The class as a whole should carry out the following activity. proof of the Exterior ngle Theorem is given below. However, in six lines of the proof there are blanks where the name of one of the previously stated axioms or the numbers of earlier lines of the proof need to be entered to justify the line. Fill in the name of an appropriate axiom or the appropriate line numbers to justify each of the six lines of the proof in which a blank occurs. Proof of the Exterior ngle Theorem. 1) Draw a ray E emanating from the point parallel to the line so that E is interior to the angle D, as in the figure below. (This ray exists by the Parallel Postulate.) D E 2) m( D) = m( DE) + m( E), by. 3) is congruent to DE by. 4) Therefore, m( ) = m( DE) by. 5) is congruent to E by.
5 237 6) Therefore, m( ) = m( E) by. 7) Hence, m( D) = m( ) + m( ), by lines. This completes the proof. We now introduce some well known terminology that will be used in the homework problems. Definition. The midpoint of a line segment is a point on such that ". Thus, the ongruence xiom for Line Segments implies that is the midpoint of if and only if is a point on such that =. Definition. Let S be a line segment and let L be a line or a ray or a line segment. We say that L bisects S and we call L a bisector of S if L crosses S at the midpoint of S. Definition. n angle is a right angle if its angle measure is 90º. Definition. Two lines L and M are perpendicular if they intersect and if any of the four angles between the two lines is a right angle. L M
6 238 Definition. line L is a perpendicular bisector of a line segment if L bisects (i.e., L crosses at the midpoint of ) and L is perpendicular to the line. L L Definition. Let be an angle and let D be a ray originating at the point. We say that the ray D bisects the angle and we call D the bisector of if the point D lies in the interior of the angle and D " D. Thus, the ongruence xiom for ngles implies that D is the bisector of if and only if the point D lies in the interior of the angle and m( D) = m( D). D We close this lesson with: Some General Remarks on the Philosophy of Proof. The method of establishing geometric facts by proof from axioms is also known as the axiomatic method. It is a completely reliable procedure for growing our geometric knowledge. It is completely reliable because it starts from basic axioms that we know are true (along with some basic terms and definitions), and it accepts new statements as true only if their truth can be argued logically from the basic axioms or from other previously proved truths. This procedure is very conservative. It does not allow a statement to be
7 239 asserted on a line of a proof simply because it looks like its true in all the pictures that you can draw or because you think you remember the truth of a similar statement being asserted in another class. statement is acceptable as a line in a proof only if it follows logically from an axiom or a previously proved statement. The very restrictiveness of the procedure is what guarantees its reliability. It prevents the process of accumulating geometric facts from being contaminated by dubious statements. metaphor for the process of proving new geometric facts from the axioms is the growth of a tree. The roots represent the basic terms, definitions and axioms that we assume to be true. Moving to a new fact through proof is like growing a new branch of the tree. Moving from one step of a proof to the next is like growing a new twig out of a joint or node of the tree. The new twig can grow only if it is securely founded on the part of the tree that lies beneath it: the roots together with the joints of the tree that lie between the new twig and the roots. The roots represent the axioms that we assume to be true, and the joints of the tree between the new twig and the roots represent previously proved facts. Like a new twig of a tree, each new step in a proof must be securely based on the structure beneath it. The roots of this structure are, as we said earlier, the axioms we have assumed to be true. The nodes of the structure between the axioms and the new step of the proof consist of previously proved truths that either occur in earlier theorems or appear on lines of the proof that precede the new step. To be justified, each new line in a proof must be related to the mathematical structure that precedes it (axioms, previously proved theorems, and earlier lines of the proof) in a specific way. Namely, the new line of the proof must fall into one of the following five categories. It is a logical or mathematical truth like x + y = y + x. It is one of basic principles or axioms that we have assumed to be true. It is a previously proved theorem. It is a hypothesis (the if part) of an if, then statement that you are trying to prove. It follows logically from previous lines in the proof. When you write a proof, you should check that each line of your proof falls into one of these five categories.
8 240 Homework Problem 1. In parts a) j) of this problem, decide whether the two given triangles must necessarily be congruent. If they must be congruent, express this by writing a correct equation of the form Δ " ΔDEF, and write down the acronym for the congruence axiom (SS, S, SSS or S) that justifies your conclusion. If they are not necessarily congruent, then write not congruent. a) 2.3 cm F 3.5 cm 110º 110º E 3.5 cm D 2.3 cm b) G L 6 cm J 60º 12 cm 4 cm H 60º M 8 cm K c) In ΔNPQ, m( N) = 80º, m( P) = 60º and m( Q) = 40º. In ΔRST, m( R) = 60º, m( S) = 80º and m( T) = 40º. d) U 10 in X 120º 40º 120º 40º V W Y 10 in Z
9 241 e) In Δ, m( ) = 55º, m( ) = 81º and = 4 cm. In ΔXYZ, m( X) = 81º, m( Y) = 55º and XY = 4 cm. f) In ΔDEF, m( E) = 105º, m( F) = 39º and EF = 12 in. In ΔUVW, m( W) = 39º, UW = 12 in and m( U) = 105º. g) G S 2 cm 3 cm J 4 cm H 6 cm 9 cm T 12 cm R h) In ΔKLM, LM = 25 cm, m( L) = 21º and KM = 14 cm. In ΔNPQ, m( Q) = 21º, NP = 14 cm and NQ = 25 cm. i) In ΔE, = 23 in, E = 38 in and E = 19 in. In ΔDF, D = 19 in, F = 23 in and DF = 38 in. j) J K 7 cm 55º 45º 7 cm 45º G L 55º H M
10 242 Homework Problem 2. Theorem 4 The ngle Sum Theorem is stated below, and a proof is given. However, on five lines of the proof there are blanks where the name of an axiom or a previously proved theorem or the numbers of earlier lines of the proof need to be entered to justify the line. In each of these blanks, fill in the name of the appropriate axiom or theorem or the appropriate line numbers. Theorem 4: The ngle Sum Theorem. The measures of the angles of a triangle add up to 180º. In other words, in triangle Δ pictured below, m( ) + m( ) + m( ) = 180º. Proof of the ngle Sum Theorem. 1) Extend the line segment to a ray D as in the figure below. D 2) Then m( D) = 180º by. 3) m( D) = m( D) + m( ) by. 4) Therefore, m( D) + m( ) = 180º, by lines. 5) m( D) = m( ) + m( ) by. 6) Therefore, m( ) + m( ) + m ) = 180º, by lines. This completes the proof.
11 243 Homework Problem 3. Here we present an alternative proof of Theorem 2: The Isosceles Triangle Theorem. Let Δ be a triangle. Then is congruent to if and only if is congruent to. Recall that because this theorem asserts an if and only if statement, then it splits into two separate assertions each of which conveys independent information and each of which must be proved separately. The two assertions conveyed by this statement are: 1) if is congruent to, then is congruent to, and 2) if is congruent to, then is congruent to. The proofs of assertions 1) and 2) which are given below contain blanks. Each blank must filled in with the name of an axiom or a statement to justify the line in which the blank appears. Fill in each blank with the appropriate statement or axiom name. Proof of 1). 1) ssume ". (We must prove that ".) 2) Let D be the ray emanating from the point that bisects, and let E be the point where the ray D intersects the line segment. E D 3) Then E " E. (This is what D bisects means.) 4) E " E because. 5) Therefore, ΔE " ΔE by the xiom. 6) The rigid motion that moves ΔE to ΔE, moves to. Hence, ". This completes the proof of 1).
12 244 Proof of 2). 1) ssume that ". (We must prove ".) 2) Let D be the ray emanating from the point that bisects, and let E be the point where the ray D intersects the line segment. E D 3) Then E " E. (This is what D bisects means.) 4) E " E because. 5) Therefore, ΔE " ΔE by the xiom. 6) The rigid motion that moves ΔE to ΔE, moves to. Hence, ". This completes the proof of 2).
13 245 Homework Problem 4. Theorem 5 is stated below, and a proof is given. However, there are blanks in several lines of the proof where the name of an axiom or a previously proved theorem or the numbers of earlier lines of the proof or a statement need to be entered to justify the line. Fill in the name of the appropriate axiom or theorem or the appropriate line numbers or the appropriate statement in each of these blanks. Theorem 5. Let Δ be an isosceles triangle with congruent to, and let D be a point of. Then D bisects if and only if D is perpendicular to. D Remark. Since this theorem asserts an if and only if statement, then it splits into two separate assertions each of which conveys independent information and each of which must be proved separately. The two assertions conveyed by this statement are: 1) if D bisects, then D is perpendicular to, and 2) if D is perpendicular to, then D bisects. Proof of 1): 1) y hypothesis, ", and D is a point of. 2) ssume that D bisects. 3) Then D is the midpoint of. 4) Thus, D " D. 5) Hence, ΔD " ΔD by. 6) Therefore, D " D, because. 7) Hence, m( D) = m( D) by. 8) Since, D and are collinear and D is between and, then m( D) = 180º, by.
14 246 9) m( D) = m( D) + m( D) by. 10) Therefore, m( D) + m( D) = 180º by. 11) Thus, 2m( D) = 180º by. 12) Dividing both sides of the equation in line 11) by 2 gives: m( D) = 90º. 13) Therefore, D is a right angle. 14) Hence, if D is perpendicular to. This completes the proof of 1). Proof of 2). 1) y hypothesis, ", and D is a point of. 2) ssume D is perpendicular to. 3) Therefore, D and D are right angles. 4) Hence, m( D) = 90º = m( D). 5) Thus, D " D by. 6) Since Δ is an isosceles triangle with congruent to, then " by. 7) Therefore, ΔD " ΔD by. 8) Hence, D " D, because. 9) Thus, D is the midpoint of. 10) Therefore, D bisects. This completes the proof 2).
Lesson 14: An Axiom System for Geometry
 219 Lesson 14: n xiom System for Geometry We are now ready to present an axiomatic development of geometry. This means that we will list a set of axioms for geometry. These axioms will be simple fundamental
219 Lesson 14: n xiom System for Geometry We are now ready to present an axiomatic development of geometry. This means that we will list a set of axioms for geometry. These axioms will be simple fundamental
B C. You try: What is the definition of an angle bisector?
 US Geometry 1 What is the definition of a midpoint? The midpoint of a line segment is the point that divides the segment into two congruent segments. That is, M is the midpoint of if M is on and M M. 1
US Geometry 1 What is the definition of a midpoint? The midpoint of a line segment is the point that divides the segment into two congruent segments. That is, M is the midpoint of if M is on and M M. 1
Unit 1: Introduction to Proof
 Unit 1: Introduction to Proof Prove geometric theorems both formally and informally using a variety of methods. G.CO.9 Prove and apply theorems about lines and angles. Theorems include but are not restricted
Unit 1: Introduction to Proof Prove geometric theorems both formally and informally using a variety of methods. G.CO.9 Prove and apply theorems about lines and angles. Theorems include but are not restricted
right angle an angle whose measure is exactly 90ᴼ
 right angle an angle whose measure is exactly 90ᴼ m B = 90ᴼ B two angles that share a common ray A D C B Vertical Angles A D C B E two angles that are opposite of each other and share a common vertex two
right angle an angle whose measure is exactly 90ᴼ m B = 90ᴼ B two angles that share a common ray A D C B Vertical Angles A D C B E two angles that are opposite of each other and share a common vertex two
Q1: Lesson 6 Parallel Lines Handouts Page 1
 6.1 Warmup Per ate Instructions: Justify each statement using your Vocab/Theorems ook. If!! =!! and!! = 50, then!! = 50. P F S If!" is rotated 180 around point F, then!"!" If!!"# +!!"# = 180, then!"# is
6.1 Warmup Per ate Instructions: Justify each statement using your Vocab/Theorems ook. If!! =!! and!! = 50, then!! = 50. P F S If!" is rotated 180 around point F, then!"!" If!!"# +!!"# = 180, then!"# is
Course Notes for MA 460. Version 5.
 ourse Notes for M 460. Version 5. Jim Mclure 1 Definitions and asic Facts. The goal of this course is to help you become expert in geometry, so that you can teach it with confidence and pleasure. We begin
ourse Notes for M 460. Version 5. Jim Mclure 1 Definitions and asic Facts. The goal of this course is to help you become expert in geometry, so that you can teach it with confidence and pleasure. We begin
Geometry GENERAL GEOMETRY
 Geometry GENERAL GEOMETRY Essential Vocabulary: point, line, plane, segment, segment bisector, midpoint, congruence I can use the distance formula to determine the area and perimeters of triangles and
Geometry GENERAL GEOMETRY Essential Vocabulary: point, line, plane, segment, segment bisector, midpoint, congruence I can use the distance formula to determine the area and perimeters of triangles and
7. m JHI = ( ) and m GHI = ( ) and m JHG = 65. Find m JHI and m GHI.
 1. Name three points in the diagram that are not collinear. 2. If RS = 44 and QS = 68, find QR. 3. R, S, and T are collinear. S is between R and T. RS = 2w + 1, ST = w 1, and RT = 18. Use the Segment Addition
1. Name three points in the diagram that are not collinear. 2. If RS = 44 and QS = 68, find QR. 3. R, S, and T are collinear. S is between R and T. RS = 2w + 1, ST = w 1, and RT = 18. Use the Segment Addition
Name: Date: Period: 1. In the diagram below,. [G.CO.6] 2. The diagram below shows a pair of congruent triangles, with and. [G.CO.
![Name: Date: Period: 1. In the diagram below,. [G.CO.6] 2. The diagram below shows a pair of congruent triangles, with and. [G.CO. Name: Date: Period: 1. In the diagram below,. [G.CO.6] 2. The diagram below shows a pair of congruent triangles, with and. [G.CO.](/thumbs/78/77420594.jpg) Name: Date: Period: Directions: Read each question carefully and choose the best answer for each question. You must show LL of your work to receive credit. 1. In the diagram below,. [G.CO.6] Which statement
Name: Date: Period: Directions: Read each question carefully and choose the best answer for each question. You must show LL of your work to receive credit. 1. In the diagram below,. [G.CO.6] Which statement
Chapter 03 Test. 1 Complete the congruence statement. A B C D. 2 Complete the congruence statement. A B C D
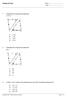 hapter 03 Test Name: ate: 1 omplete the congruence statement. 2 omplete the congruence statement. 3 If, which of the following can you NOT conclude as being true? opyright 2005-2006 by Pearson Education
hapter 03 Test Name: ate: 1 omplete the congruence statement. 2 omplete the congruence statement. 3 If, which of the following can you NOT conclude as being true? opyright 2005-2006 by Pearson Education
Please note that, as always, these notes are really not complete without diagrams. I have included a few, but the others are up to you.
 Mathematics 3210 Spring Semester, 2005 Homework notes, part 6 March 18, 2005 lease note that, as always, these notes are really not complete without diagrams. I have included a few, but the others are
Mathematics 3210 Spring Semester, 2005 Homework notes, part 6 March 18, 2005 lease note that, as always, these notes are really not complete without diagrams. I have included a few, but the others are
Exterior Angle Inequality
 xterior ngle Inequality efinition: Given Î, the angles p, p, and p are called interior angles of the triangle. ny angle that forms a linear pair with an interior angle is called an exterior angle. In the
xterior ngle Inequality efinition: Given Î, the angles p, p, and p are called interior angles of the triangle. ny angle that forms a linear pair with an interior angle is called an exterior angle. In the
MAT 3271: Selected solutions to problem set 7
 MT 3271: Selected solutions to problem set 7 Chapter 3, Exercises: 16. Consider the Real ffine Plane (that is what the text means by the usual Euclidean model ), which is a model of incidence geometry.
MT 3271: Selected solutions to problem set 7 Chapter 3, Exercises: 16. Consider the Real ffine Plane (that is what the text means by the usual Euclidean model ), which is a model of incidence geometry.
Unit 5: Congruency. Part 1 of 3: Intro to Congruency & Proof Pieces. Lessons 5-1 through 5-4
 Name: Geometry Period Unit 5: Congruency Part 1 of 3: Intro to Congruency & Proof Pieces Lessons 5-1 through 5-4 In this unit you must bring the following materials with you to class every day: Please
Name: Geometry Period Unit 5: Congruency Part 1 of 3: Intro to Congruency & Proof Pieces Lessons 5-1 through 5-4 In this unit you must bring the following materials with you to class every day: Please
A Theorem of Hilbert. Mat 3271 Class
 Theorem of Hilbert Mat 3271 lass Theorem (Hilbert) ssume that there exists lines l and l parallel such that l is not asymptotic to l. Then there exists a unique common perpendicular to the given lines.
Theorem of Hilbert Mat 3271 lass Theorem (Hilbert) ssume that there exists lines l and l parallel such that l is not asymptotic to l. Then there exists a unique common perpendicular to the given lines.
UNIT 1: SIMILARITY, CONGRUENCE, AND PROOFS. 1) Figure A'B'C'D'F' is a dilation of figure ABCDF by a scale factor of 1. 2 centered at ( 4, 1).
 1) Figure A'B'C'D'F' is a dilation of figure ABCDF by a scale factor of 1. 2 centered at ( 4, 1). The dilation is Which statement is true? A. B. C. D. AB B' C' A' B' BC AB BC A' B' B' C' AB BC A' B' D'
1) Figure A'B'C'D'F' is a dilation of figure ABCDF by a scale factor of 1. 2 centered at ( 4, 1). The dilation is Which statement is true? A. B. C. D. AB B' C' A' B' BC AB BC A' B' B' C' AB BC A' B' D'
Geometry Advanced Fall Semester Exam Review Packet -- CHAPTER 1
 Name: Class: Date: Geometry Advanced Fall Semester Exam Review Packet -- CHAPTER 1 Multiple Choice. Identify the choice that best completes the statement or answers the question. 1. Which statement(s)
Name: Class: Date: Geometry Advanced Fall Semester Exam Review Packet -- CHAPTER 1 Multiple Choice. Identify the choice that best completes the statement or answers the question. 1. Which statement(s)
Geometry Unit 1 Practice
 Lesson 1-1 1. Persevere in solving problems. Identify each figure. hen give all possible names for the figure. a. S Geometry Unit 1 Practice e. P S G Q. What is a correct name for this plane? W R Z X b..
Lesson 1-1 1. Persevere in solving problems. Identify each figure. hen give all possible names for the figure. a. S Geometry Unit 1 Practice e. P S G Q. What is a correct name for this plane? W R Z X b..
Geometry: A Complete Course
 Geometry: omplete ourse (with Trigonometry) Module - Student WorkText Written by: Thomas E. lark Larry E. ollins Geometry: omplete ourse (with Trigonometry) Module Student Worktext opyright 2014 by VideotextInteractive
Geometry: omplete ourse (with Trigonometry) Module - Student WorkText Written by: Thomas E. lark Larry E. ollins Geometry: omplete ourse (with Trigonometry) Module Student Worktext opyright 2014 by VideotextInteractive
Chapter 3. Betweenness (ordering) A system satisfying the incidence and betweenness axioms is an ordered incidence plane (p. 118).
 Chapter 3 Betweenness (ordering) Point B is between point A and point C is a fundamental, undefined concept. It is abbreviated A B C. A system satisfying the incidence and betweenness axioms is an ordered
Chapter 3 Betweenness (ordering) Point B is between point A and point C is a fundamental, undefined concept. It is abbreviated A B C. A system satisfying the incidence and betweenness axioms is an ordered
Semester 1 Cumulative Summative Review Teacher: Date: B
 GOMTRY Name: 2016-2017 Semester 1 umulative Summative Review Teacher: ate: To be prepared for your midterm, you will need to PRTI PROLMS and STUY TRMS from the following chapters. Use this guide to help
GOMTRY Name: 2016-2017 Semester 1 umulative Summative Review Teacher: ate: To be prepared for your midterm, you will need to PRTI PROLMS and STUY TRMS from the following chapters. Use this guide to help
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg
 Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg Undefined Terms: Point, Line, Incident, Between, Congruent. Incidence Axioms:
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg Undefined Terms: Point, Line, Incident, Between, Congruent. Incidence Axioms:
Section 5-1: Special Segments in Triangles
 Section 5-1: Special Segments in Triangles Objectives: Identify medians, altitudes, angle bisectors, and perpendicular bisectors. perpendicular bisector C median altitude Vocabulary: A B Perpendicular
Section 5-1: Special Segments in Triangles Objectives: Identify medians, altitudes, angle bisectors, and perpendicular bisectors. perpendicular bisector C median altitude Vocabulary: A B Perpendicular
Int. Geometry Units 1-6 Review 1
 Int. Geometry Units 1-6 Review 1 Things to note about this review and the Unit 1-6 Test: 1. This review packet covers major ideas of the first six units, but it does not show examples of all types of problems..
Int. Geometry Units 1-6 Review 1 Things to note about this review and the Unit 1-6 Test: 1. This review packet covers major ideas of the first six units, but it does not show examples of all types of problems..
Geometry Note Cards EXAMPLE:
 Geometry Note Cards EXAMPLE: Lined Side Word and Explanation Blank Side Picture with Statements Sections 12-4 through 12-5 1) Theorem 12-3 (p. 790) 2) Theorem 12-14 (p. 790) 3) Theorem 12-15 (p. 793) 4)
Geometry Note Cards EXAMPLE: Lined Side Word and Explanation Blank Side Picture with Statements Sections 12-4 through 12-5 1) Theorem 12-3 (p. 790) 2) Theorem 12-14 (p. 790) 3) Theorem 12-15 (p. 793) 4)
Geometry: CBA-I Review
 Name: Period: ate: Geometry: 2013-2014 -I Review 1. Identify each construction. X 1 2 2. Identify the converse, inverse, contrapositive, and bi-conditional form of the statement given below. If a triangle
Name: Period: ate: Geometry: 2013-2014 -I Review 1. Identify each construction. X 1 2 2. Identify the converse, inverse, contrapositive, and bi-conditional form of the statement given below. If a triangle
Unit 2 Review. Determine the scale factor of the dilation below.
 Unit 2 Review 1. oes the graph below represent a dilation? Why or why not? y 10 9 8 7 (0, 7) 6 5 4 3 (0, 3.5) 2 1 (5, 7) (5, 3.5) -10-9 -8-7 -6-5 -4-3 -2-1 0 1 2 3 4 5 6 7 8 9 10-1 F -2 (5, 0) -3-4 -5-6
Unit 2 Review 1. oes the graph below represent a dilation? Why or why not? y 10 9 8 7 (0, 7) 6 5 4 3 (0, 3.5) 2 1 (5, 7) (5, 3.5) -10-9 -8-7 -6-5 -4-3 -2-1 0 1 2 3 4 5 6 7 8 9 10-1 F -2 (5, 0) -3-4 -5-6
Angle-Side-Angle Congruence Theorem
 ngle to the Left of Me, ngle to the Right of Me ngle-side-ngle ongruence Theorem. Learning Goals In this lesson, you will: Explore the ngle-side-ngle ongruence Theorem using constructions. Explore the
ngle to the Left of Me, ngle to the Right of Me ngle-side-ngle ongruence Theorem. Learning Goals In this lesson, you will: Explore the ngle-side-ngle ongruence Theorem using constructions. Explore the
1. Based on the pattern, what are the next two terms of the sequence?,... A. C. B. D.
 Semester Exam I / Review Integrated Math II 1. Based on the pattern, what are the next two terms of the sequence?,... B. D. 2. Alfred is practicing typing. The first time he tested himself, he could type
Semester Exam I / Review Integrated Math II 1. Based on the pattern, what are the next two terms of the sequence?,... B. D. 2. Alfred is practicing typing. The first time he tested himself, he could type
Segment Measurement, Midpoints, & Congruence
 Lesson 2 Lesson 2, page 1 Glencoe Geometry Chapter 1.4 & 1.5 Segment Measurement, Midpoints, & Congruence Last time, we looked at points, lines, and planes. Today we are going to further investigate lines,
Lesson 2 Lesson 2, page 1 Glencoe Geometry Chapter 1.4 & 1.5 Segment Measurement, Midpoints, & Congruence Last time, we looked at points, lines, and planes. Today we are going to further investigate lines,
Geometry First Semester Exam Review
 Geometry First Semester Exam Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Name three points that are collinear. a. points T, Q, and R c. points
Geometry First Semester Exam Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Name three points that are collinear. a. points T, Q, and R c. points
Triangle Congruence and Similarity Review. Show all work for full credit. 5. In the drawing, what is the measure of angle y?
 Triangle Congruence and Similarity Review Score Name: Date: Show all work for full credit. 1. In a plane, lines that never meet are called. 5. In the drawing, what is the measure of angle y? A. parallel
Triangle Congruence and Similarity Review Score Name: Date: Show all work for full credit. 1. In a plane, lines that never meet are called. 5. In the drawing, what is the measure of angle y? A. parallel
Chapter 2. Reasoning and Proof
 Chapter 2 Reasoning and Proof 2.1 Use Inductive Reasoning Objective: Describe patterns and use deductive reasoning. Essential Question: How do you use inductive reasoning in mathematics? Common Core: CC.9-12.G.CO.9
Chapter 2 Reasoning and Proof 2.1 Use Inductive Reasoning Objective: Describe patterns and use deductive reasoning. Essential Question: How do you use inductive reasoning in mathematics? Common Core: CC.9-12.G.CO.9
If two sides of a triangle are congruent, then it is an isosceles triangle.
 1. What is the hypothesis of the conditional statement If two sides of a triangle are congruent, then it is an isosceles triangle. two sides of a triangle are congruent it is an isosceles triangle If two
1. What is the hypothesis of the conditional statement If two sides of a triangle are congruent, then it is an isosceles triangle. two sides of a triangle are congruent it is an isosceles triangle If two
UNIT 1: SIMILARITY, CONGRUENCE, AND PROOFS. 1) Figure A'B'C'D'F' is a dilation of figure ABCDF by a scale factor of 1. 2 centered at ( 4, 1).
 EOCT Practice Items 1) Figure A'B'C'D'F' is a dilation of figure ABCDF by a scale factor of 1. 2 centered at ( 4, 1). The dilation is Which statement is true? A. B. C. D. AB B' C' A' B' BC AB BC A' B'
EOCT Practice Items 1) Figure A'B'C'D'F' is a dilation of figure ABCDF by a scale factor of 1. 2 centered at ( 4, 1). The dilation is Which statement is true? A. B. C. D. AB B' C' A' B' BC AB BC A' B'
Triangle Geometry. Often we can use one letter (capitalised) to name an angle.
 1) Naming angles Triangle Geometry Often we can use one letter (capitalised) to name an angle. A C B When more than two lines meet at a vertex, then we must use three letters to name an angle. Q X P T
1) Naming angles Triangle Geometry Often we can use one letter (capitalised) to name an angle. A C B When more than two lines meet at a vertex, then we must use three letters to name an angle. Q X P T
Postulates, Definitions, and Theorems (Chapter 4)
 Postulates, Definitions, and Theorems (Chapter 4) Segment Addition Postulate (SAP) All segments AB and BC have unique real number measures AB and BC such that: ABCBC = AC if and only if B is between A
Postulates, Definitions, and Theorems (Chapter 4) Segment Addition Postulate (SAP) All segments AB and BC have unique real number measures AB and BC such that: ABCBC = AC if and only if B is between A
Name: Jan 2016 Semester1 Review Block: Date:
 GOMTRY Name: Jan 2016 Semester1 Review lock: ate: To be prepared for your midterm, you will need to PRTI PROLMS and STUY TRMS from the following chapters. Use this guide to help you practice. Unit 1 (1.1
GOMTRY Name: Jan 2016 Semester1 Review lock: ate: To be prepared for your midterm, you will need to PRTI PROLMS and STUY TRMS from the following chapters. Use this guide to help you practice. Unit 1 (1.1
Segment Measurement, Midpoints, & Congruence
 Lesson 2 Lesson 2, page 1 Glencoe Geometry Chapter 1.4 & 1.5 Segment Measurement, Midpoints, & Congruence Last time, we looked at points, lines, and planes. Today we are going to further investigate lines,
Lesson 2 Lesson 2, page 1 Glencoe Geometry Chapter 1.4 & 1.5 Segment Measurement, Midpoints, & Congruence Last time, we looked at points, lines, and planes. Today we are going to further investigate lines,
Neutral Geometry. October 25, c 2009 Charles Delman
 Neutral Geometry October 25, 2009 c 2009 Charles Delman Taking Stock: where we have been; where we are going Set Theory & Logic Terms of Geometry: points, lines, incidence, betweenness, congruence. Incidence
Neutral Geometry October 25, 2009 c 2009 Charles Delman Taking Stock: where we have been; where we are going Set Theory & Logic Terms of Geometry: points, lines, incidence, betweenness, congruence. Incidence
Exercises for Unit I I (Vector algebra and Euclidean geometry)
 Exercises for Unit I I (Vector algebra and Euclidean geometry) I I.1 : Approaches to Euclidean geometry Ryan : pp. 5 15 1. What is the minimum number of planes containing three concurrent noncoplanar lines
Exercises for Unit I I (Vector algebra and Euclidean geometry) I I.1 : Approaches to Euclidean geometry Ryan : pp. 5 15 1. What is the minimum number of planes containing three concurrent noncoplanar lines
Name Geometry Common Core Regents Review Packet - 3. Topic 1 : Equation of a circle
 Name Geometry Common Core Regents Review Packet - 3 Topic 1 : Equation of a circle Equation with center (0,0) and radius r Equation with center (h,k) and radius r ( ) ( ) 1. The endpoints of a diameter
Name Geometry Common Core Regents Review Packet - 3 Topic 1 : Equation of a circle Equation with center (0,0) and radius r Equation with center (h,k) and radius r ( ) ( ) 1. The endpoints of a diameter
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg ( )
 Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2005-02-16) Logic Rules (Greenberg): Logic Rule 1 Allowable justifications.
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2005-02-16) Logic Rules (Greenberg): Logic Rule 1 Allowable justifications.
2) Are all linear pairs supplementary angles? Are all supplementary angles linear pairs? Explain.
 1) Explain what it means to bisect a segment. Why is it impossible to bisect a line? 2) Are all linear pairs supplementary angles? Are all supplementary angles linear pairs? Explain. 3) Explain why a four-legged
1) Explain what it means to bisect a segment. Why is it impossible to bisect a line? 2) Are all linear pairs supplementary angles? Are all supplementary angles linear pairs? Explain. 3) Explain why a four-legged
MA 460 Supplement: Analytic geometry
 M 460 Supplement: nalytic geometry Donu rapura In the 1600 s Descartes introduced cartesian coordinates which changed the way we now do geometry. This also paved for subsequent developments such as calculus.
M 460 Supplement: nalytic geometry Donu rapura In the 1600 s Descartes introduced cartesian coordinates which changed the way we now do geometry. This also paved for subsequent developments such as calculus.
Theorem 1.2 (Converse of Pythagoras theorem). If the lengths of the sides of ABC satisfy a 2 + b 2 = c 2, then the triangle has a right angle at C.
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
Geometry Midterm Review Packet
 Name: ate: lock: 2012 2013 Geometry Midterm Review Packet ue: 1/7/13 (for +5 on packet) 1/8/13 (for +3 on packet) 1/9/13 (for +2 on packet) 1/10/13 ( ay lasses) 1/11/13 ( ay lasses) The midterm will be
Name: ate: lock: 2012 2013 Geometry Midterm Review Packet ue: 1/7/13 (for +5 on packet) 1/8/13 (for +3 on packet) 1/9/13 (for +2 on packet) 1/10/13 ( ay lasses) 1/11/13 ( ay lasses) The midterm will be
NAME DATE PER. 1. ; 1 and ; 6 and ; 10 and 11
 SECOND SIX WEEKS REVIEW PG. 1 NME DTE PER SECOND SIX WEEKS REVIEW Using the figure below, identify the special angle pair. Then write C for congruent, S for supplementary, or N for neither. d 1. ; 1 and
SECOND SIX WEEKS REVIEW PG. 1 NME DTE PER SECOND SIX WEEKS REVIEW Using the figure below, identify the special angle pair. Then write C for congruent, S for supplementary, or N for neither. d 1. ; 1 and
Lesson 9.1 Skills Practice
 Lesson 9.1 Skills Practice Name Date Earth Measure Introduction to Geometry and Geometric Constructions Vocabulary Write the term that best completes the statement. 1. means to have the same size, shape,
Lesson 9.1 Skills Practice Name Date Earth Measure Introduction to Geometry and Geometric Constructions Vocabulary Write the term that best completes the statement. 1. means to have the same size, shape,
You must show your work to receive full credit! Write your final answer on the blank provided.
 1 st Semester Final xam Review Name: Geometry ate: lock: You must show your work to receive full credit! Write your final answer on the blank provided. Topic #1 (Foundations of Geometry) 1) Multiple hoice:
1 st Semester Final xam Review Name: Geometry ate: lock: You must show your work to receive full credit! Write your final answer on the blank provided. Topic #1 (Foundations of Geometry) 1) Multiple hoice:
12.1 Triangle Proportionality Theorem
 Name lass Date 12.1 Triangle Proportionality Theorem ssential Question: When a line parallel to one side of a triangle intersects the other two sides, how does it divide those sides? Resource Locker xplore
Name lass Date 12.1 Triangle Proportionality Theorem ssential Question: When a line parallel to one side of a triangle intersects the other two sides, how does it divide those sides? Resource Locker xplore
UNIT 1 SIMILARITY, CONGRUENCE, AND PROOFS Lesson 9: Proving Theorems About Triangles Instruction
 Prerequisite Skills This lesson requires the use of the following skills: identifying and using vertical angles, supplementary angles, and complementary angles to find unknown angle measures recognizing
Prerequisite Skills This lesson requires the use of the following skills: identifying and using vertical angles, supplementary angles, and complementary angles to find unknown angle measures recognizing
Writing: Answer each question with complete sentences. 1) Explain what it means to bisect a segment. Why is it impossible to bisect a line?
 Writing: Answer each question with complete sentences. 1) Explain what it means to bisect a segment. Why is it impossible to bisect a line? 2) Are all linear pairs supplementary angles? Are all supplementary
Writing: Answer each question with complete sentences. 1) Explain what it means to bisect a segment. Why is it impossible to bisect a line? 2) Are all linear pairs supplementary angles? Are all supplementary
Solutions to Exercises in Chapter 1
 Solutions to Exercises in hapter 1 1.6.1 heck that the formula 1 a c b d works for rectangles but not for 4 parallelograms. b a c a d d b c FIGURE S1.1: Exercise 1.6.1. rectangle and a parallelogram For
Solutions to Exercises in hapter 1 1.6.1 heck that the formula 1 a c b d works for rectangles but not for 4 parallelograms. b a c a d d b c FIGURE S1.1: Exercise 1.6.1. rectangle and a parallelogram For
TOPIC-1 Rational Numbers
 TOPI- Rational Numbers Unit -I : Number System hapter - : Real Numbers Rational Number : number r is called a rational number, if it can be written in the form p/q, where p and q are integers and q 0,
TOPI- Rational Numbers Unit -I : Number System hapter - : Real Numbers Rational Number : number r is called a rational number, if it can be written in the form p/q, where p and q are integers and q 0,
Name: Date: Period: ID: REVIEW CH 1 TEST REVIEW. 1. Sketch and label an example of each statement. b. A B. a. HG. d. M is the midpoint of PQ. c.
 Name: Date: Period: ID: REVIEW CH 1 TEST REVIEW 1 Sketch and label an example of each statement a HG b A B c ST UV d M is the midpoint of PQ e Angles 1 and 2 are vertical angles f Angle C is a right angle
Name: Date: Period: ID: REVIEW CH 1 TEST REVIEW 1 Sketch and label an example of each statement a HG b A B c ST UV d M is the midpoint of PQ e Angles 1 and 2 are vertical angles f Angle C is a right angle
Exercises for Unit V (Introduction to non Euclidean geometry)
 Exercises for Unit V (Introduction to non Euclidean geometry) V.1 : Facts from spherical geometry Ryan : pp. 84 123 [ Note : Hints for the first two exercises are given in math133f07update08.pdf. ] 1.
Exercises for Unit V (Introduction to non Euclidean geometry) V.1 : Facts from spherical geometry Ryan : pp. 84 123 [ Note : Hints for the first two exercises are given in math133f07update08.pdf. ] 1.
Question 1 (3 points) Find the midpoint of the line segment connecting the pair of points (3, -10) and (3, 6).
 Geometry Semester Final Exam Practice Select the best answer Question (3 points) Find the midpoint of the line segment connecting the pair of points (3, -0) and (3, 6). A) (3, -) C) (3, -) B) (3, 4.5)
Geometry Semester Final Exam Practice Select the best answer Question (3 points) Find the midpoint of the line segment connecting the pair of points (3, -0) and (3, 6). A) (3, -) C) (3, -) B) (3, 4.5)
Integrated Math 3 Math 3 Course Description:
 Course Description: Integrated Math 3 Math 3 Course Description: Integrated strands include algebra, functions, geometry, trigonometry, statistics, probability and discrete math. Scope and sequence includes
Course Description: Integrated Math 3 Math 3 Course Description: Integrated strands include algebra, functions, geometry, trigonometry, statistics, probability and discrete math. Scope and sequence includes
Geometry: A Complete Course
 Geometry: omplete ourse (with Trigonometry) Module Progress Tests Written by: Larry E. ollins Geometry: omplete ourse (with Trigonometry) Module - Progress Tests opyright 2014 by VideotextInteractive Send
Geometry: omplete ourse (with Trigonometry) Module Progress Tests Written by: Larry E. ollins Geometry: omplete ourse (with Trigonometry) Module - Progress Tests opyright 2014 by VideotextInteractive Send
Geometry Final Review. Chapter 1. Name: Per: Vocab. Example Problems
 Geometry Final Review Name: Per: Vocab Word Acute angle Adjacent angles Angle bisector Collinear Line Linear pair Midpoint Obtuse angle Plane Pythagorean theorem Ray Right angle Supplementary angles Complementary
Geometry Final Review Name: Per: Vocab Word Acute angle Adjacent angles Angle bisector Collinear Line Linear pair Midpoint Obtuse angle Plane Pythagorean theorem Ray Right angle Supplementary angles Complementary
3.2. Parallel Lines and Transversals
 . Parallel Lines and Transversals Essential Question When two parallel lines are cut by a transversal, which of the resulting pairs of angles are congruent? Exploring Parallel Lines Work with a partner.
. Parallel Lines and Transversals Essential Question When two parallel lines are cut by a transversal, which of the resulting pairs of angles are congruent? Exploring Parallel Lines Work with a partner.
Geometry A Exam Review, Chapters 1-6 Final Exam Review Name
 Final Exam Review Name Hr. Final Exam Information: The Final Exam consists of a Multiple-Choice Section and an Open-Response Section. You may not use notes of any kind on the Final Exam. This Exam Review
Final Exam Review Name Hr. Final Exam Information: The Final Exam consists of a Multiple-Choice Section and an Open-Response Section. You may not use notes of any kind on the Final Exam. This Exam Review
3.2. Parallel Lines and Transversals
 . Parallel Lines and Transversals COMMON CORE Learning Standard HSG-CO.C.9 Essential Question When two parallel lines are cut by a transversal, which of the resulting pairs of angles are congruent? Work
. Parallel Lines and Transversals COMMON CORE Learning Standard HSG-CO.C.9 Essential Question When two parallel lines are cut by a transversal, which of the resulting pairs of angles are congruent? Work
Geometry 1 st Semester review Name
 Geometry 1 st Semester review Name 1. What are the next three numbers in this sequence? 0, 3, 9, 18, For xercises 2 4, refer to the figure to the right. j k 2. Name the point(s) collinear to points H and
Geometry 1 st Semester review Name 1. What are the next three numbers in this sequence? 0, 3, 9, 18, For xercises 2 4, refer to the figure to the right. j k 2. Name the point(s) collinear to points H and
Geometry Honors Review for Midterm Exam
 Geometry Honors Review for Midterm Exam Format of Midterm Exam: Scantron Sheet: Always/Sometimes/Never and Multiple Choice 40 Questions @ 1 point each = 40 pts. Free Response: Show all work and write answers
Geometry Honors Review for Midterm Exam Format of Midterm Exam: Scantron Sheet: Always/Sometimes/Never and Multiple Choice 40 Questions @ 1 point each = 40 pts. Free Response: Show all work and write answers
2 Homework. Dr. Franz Rothe February 21, 2015 All3181\3181_spr15h2.tex
 Math 3181 Dr. Franz Rothe February 21, 2015 All3181\3181_spr15h2.tex Name: Homework has to be turned in this handout. For extra space, use the back pages, or blank pages between. The homework can be done
Math 3181 Dr. Franz Rothe February 21, 2015 All3181\3181_spr15h2.tex Name: Homework has to be turned in this handout. For extra space, use the back pages, or blank pages between. The homework can be done
North Carolina Math 2 Transition Edition Unit 4 Assessment: Similarity and Congruence
 Name: Class: _ Date: _ North Carolina Math 2 Transition Edition Unit 4 Assessment: Similarity and Congruence Multiple Choice Identify the choice that best completes the statement or answers the question.
Name: Class: _ Date: _ North Carolina Math 2 Transition Edition Unit 4 Assessment: Similarity and Congruence Multiple Choice Identify the choice that best completes the statement or answers the question.
Activity Sheet 1: Constructions
 Name ctivity Sheet 1: Constructions Date 1. Constructing a line segment congruent to a given line segment: Given a line segment B, B a. Use a straightedge to draw a line, choose a point on the line, and
Name ctivity Sheet 1: Constructions Date 1. Constructing a line segment congruent to a given line segment: Given a line segment B, B a. Use a straightedge to draw a line, choose a point on the line, and
Geometry/Trig Name: Date: Lesson 1-11 Writing the Equation of a Perpendicular Bisector
 Name: Date: Lesson 1-11 Writing the Equation of a Perpendicular Bisector Learning Goals: #14: How do I write the equation of a perpendicular bisector? Warm-up What is the equation of a line that passes
Name: Date: Lesson 1-11 Writing the Equation of a Perpendicular Bisector Learning Goals: #14: How do I write the equation of a perpendicular bisector? Warm-up What is the equation of a line that passes
EC and AB because AIA are congruent Substituting into the first equation above
 4.1 Triangles Sum onjectures uxillary line: an extra line or segment that helps you with your proof. Page 202 Paragraph proof explaining why the Triangle Sum onjecture is true. onjecture: The sum of the
4.1 Triangles Sum onjectures uxillary line: an extra line or segment that helps you with your proof. Page 202 Paragraph proof explaining why the Triangle Sum onjecture is true. onjecture: The sum of the
Honors Geometry Mid-Term Exam Review
 Class: Date: Honors Geometry Mid-Term Exam Review Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. 1. Classify the triangle by its sides. The
Class: Date: Honors Geometry Mid-Term Exam Review Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. 1. Classify the triangle by its sides. The
2.4 Algebraic and Congruence Properties
 2.4 Algebraic and Congruence Properties Learning Objectives Understand basic properties of equality and congruence. Solve equations and justify each step in the solution. Use a 2-column format to prove
2.4 Algebraic and Congruence Properties Learning Objectives Understand basic properties of equality and congruence. Solve equations and justify each step in the solution. Use a 2-column format to prove
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg ( )
 Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2009-03-26) Logic Rule 0 No unstated assumptions may be used in a proof.
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2009-03-26) Logic Rule 0 No unstated assumptions may be used in a proof.
1.2 Perpendicular Lines
 Name lass ate 1.2 erpendicular Lines Essential Question: What are the key ideas about perpendicular bisectors of a segment? 1 Explore onstructing erpendicular isectors and erpendicular Lines You can construct
Name lass ate 1.2 erpendicular Lines Essential Question: What are the key ideas about perpendicular bisectors of a segment? 1 Explore onstructing erpendicular isectors and erpendicular Lines You can construct
Nozha Directorate of Education Form : 2 nd Prep. Nozha Language Schools Ismailia Road Branch
 Cairo Governorate Department : Maths Nozha Directorate of Education Form : 2 nd Prep. Nozha Language Schools Sheet Ismailia Road Branch Sheet ( 1) 1-Complete 1. in the parallelogram, each two opposite
Cairo Governorate Department : Maths Nozha Directorate of Education Form : 2 nd Prep. Nozha Language Schools Sheet Ismailia Road Branch Sheet ( 1) 1-Complete 1. in the parallelogram, each two opposite
Geometry: A Complete Course
 Geometry: omplete ourse (with Trigonometry) Module - Student WorkText Written by: Thomas. lark Larry. ollins RRT 4/2010 6. In the figure below, and share the common segment. Prove the following conditional
Geometry: omplete ourse (with Trigonometry) Module - Student WorkText Written by: Thomas. lark Larry. ollins RRT 4/2010 6. In the figure below, and share the common segment. Prove the following conditional
Chapter 2-Reasoning and Proof
 Chapter 2-Reasoning and Proof Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Identify the hypothesis and conclusion of this conditional statement: If
Chapter 2-Reasoning and Proof Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Identify the hypothesis and conclusion of this conditional statement: If
Chapter 1. Some Basic Theorems. 1.1 The Pythagorean Theorem
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a 2 + b 2 = c 2. roof. b a a 3 2 b 2 b 4 b a b
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a 2 + b 2 = c 2. roof. b a a 3 2 b 2 b 4 b a b
Instructional Goal Terminal Objective Assessment Item Students will generate twocolumn
 eport Two Objectives Instructional Goal Terminal Objective ssessment Item Students will generate twocolumn geometric proofs. PS Given a statement to be proven, a diagram, and a given statement student
eport Two Objectives Instructional Goal Terminal Objective ssessment Item Students will generate twocolumn geometric proofs. PS Given a statement to be proven, a diagram, and a given statement student
Chapter 6. Worked-Out Solutions. Chapter 6 Maintaining Mathematical Proficiency (p. 299)
 hapter 6 hapter 6 Maintaining Mathematical Proficiency (p. 99) 1. Slope perpendicular to y = 1 x 5 is. y = x + b 1 = + b 1 = 9 + b 10 = b n equation of the line is y = x + 10.. Slope perpendicular to y
hapter 6 hapter 6 Maintaining Mathematical Proficiency (p. 99) 1. Slope perpendicular to y = 1 x 5 is. y = x + b 1 = + b 1 = 9 + b 10 = b n equation of the line is y = x + 10.. Slope perpendicular to y
Geometry Triangles
 1 Geometry Triangles 2015-12-08 www.njctl.org 2 Table of Contents Click on the topic to go to that section Triangles Triangle Sum Theorem Exterior Angle Theorem Inequalities in Triangles Similar Triangles
1 Geometry Triangles 2015-12-08 www.njctl.org 2 Table of Contents Click on the topic to go to that section Triangles Triangle Sum Theorem Exterior Angle Theorem Inequalities in Triangles Similar Triangles
Lesson. Warm Up deductive 2. D. 3. I will go to the store; Law of Detachment. Lesson Practice 31
 Warm Up 1. deductive 2. D b. a and b intersect 1 and 2 are supplementary 2 and 3 are supplementary 3. I will go to the store; Law of Detachment Lesson Practice a. 1. 1 and 2 are. 2. 1 and 3 are. 3. m 1
Warm Up 1. deductive 2. D b. a and b intersect 1 and 2 are supplementary 2 and 3 are supplementary 3. I will go to the store; Law of Detachment Lesson Practice a. 1. 1 and 2 are. 2. 1 and 3 are. 3. m 1
DISCOVERING GEOMETRY Over 6000 years ago, geometry consisted primarily of practical rules for measuring land and for
 Name Period GEOMETRY Chapter One BASICS OF GEOMETRY Geometry, like much of mathematics and science, developed when people began recognizing and describing patterns. In this course, you will study many
Name Period GEOMETRY Chapter One BASICS OF GEOMETRY Geometry, like much of mathematics and science, developed when people began recognizing and describing patterns. In this course, you will study many
1-2 Measuring and Constructing Segments
 1-2 Measuring and Constructing Segments Warm Up Lesson Presentation Lesson Quiz Objectives Use length and midpoint of a segment. Construct midpoints and congruent segments. Vocabulary coordinate midpoint
1-2 Measuring and Constructing Segments Warm Up Lesson Presentation Lesson Quiz Objectives Use length and midpoint of a segment. Construct midpoints and congruent segments. Vocabulary coordinate midpoint
MATHEMATICS (IX-X) (CODE NO. 041) Session
 MATHEMATICS (IX-X) (CODE NO. 041) Session 2018-19 The Syllabus in the subject of Mathematics has undergone changes from time to time in accordance with growth of the subject and emerging needs of the society.
MATHEMATICS (IX-X) (CODE NO. 041) Session 2018-19 The Syllabus in the subject of Mathematics has undergone changes from time to time in accordance with growth of the subject and emerging needs of the society.
Exercise. and 13x. We know that, sum of angles of a quadrilateral = x = 360 x = (Common in both triangles) and AC = BD
 9 Exercise 9.1 Question 1. The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral. Solution Given, the ratio of the angles of quadrilateral are 3 : 5 : 9
9 Exercise 9.1 Question 1. The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral. Solution Given, the ratio of the angles of quadrilateral are 3 : 5 : 9
Plane geometry Circles: Problems with some Solutions
 The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
8-6. a: 110 b: 70 c: 48 d: a: no b: yes c: no d: yes e: no f: yes g: yes h: no
 Lesson 8.1.1 8-6. a: 110 b: 70 c: 48 d: 108 8-7. a: no b: yes c: no d: yes e: no f: yes g: yes h: no 8-8. b: The measure of an exterior angle of a triangle equals the sum of the measures of its remote
Lesson 8.1.1 8-6. a: 110 b: 70 c: 48 d: 108 8-7. a: no b: yes c: no d: yes e: no f: yes g: yes h: no 8-8. b: The measure of an exterior angle of a triangle equals the sum of the measures of its remote
Honors Geometry Semester Review Packet
 Honors Geometry Semester Review Packet 1) Explain what it means to bisect a segment. Why is it impossible to bisect a line? 2) Are all linear pairs supplementary angles? Are all supplementary angles linear
Honors Geometry Semester Review Packet 1) Explain what it means to bisect a segment. Why is it impossible to bisect a line? 2) Are all linear pairs supplementary angles? Are all supplementary angles linear
1.4 Midpoints and Bisectors
 www.ck12.org Chapter 1. Basics of Geometry 1.4 Midpoints and Bisectors Learning Objectives Identify the midpoint of line segments. Identify the bisector of a line segment. Understand and the Angle Bisector
www.ck12.org Chapter 1. Basics of Geometry 1.4 Midpoints and Bisectors Learning Objectives Identify the midpoint of line segments. Identify the bisector of a line segment. Understand and the Angle Bisector
Integrated Math II. IM2.1.2 Interpret given situations as functions in graphs, formulas, and words.
 Standard 1: Algebra and Functions Students graph linear inequalities in two variables and quadratics. They model data with linear equations. IM2.1.1 Graph a linear inequality in two variables. IM2.1.2
Standard 1: Algebra and Functions Students graph linear inequalities in two variables and quadratics. They model data with linear equations. IM2.1.1 Graph a linear inequality in two variables. IM2.1.2
IMPORTANT VOCABULARY. Scalene Triangle. Triangle. SSS ASA SAS AAS sides/angles
 1 Pre-AP Geometry Chapter 5 Test Review Standards/Goals: C.1.f.: I can prove that two triangles are congruent by applying the SSS, SAS, ASA, and AAS congruence statements. C.1.g. I can use the principle
1 Pre-AP Geometry Chapter 5 Test Review Standards/Goals: C.1.f.: I can prove that two triangles are congruent by applying the SSS, SAS, ASA, and AAS congruence statements. C.1.g. I can use the principle
2013 ACTM Regional Geometry Exam
 2013 TM Regional Geometry Exam In each of the following choose the EST answer and record your choice on the answer sheet provided. To insure correct scoring, be sure to make all erasures completely. The
2013 TM Regional Geometry Exam In each of the following choose the EST answer and record your choice on the answer sheet provided. To insure correct scoring, be sure to make all erasures completely. The
UCLA Curtis Center: March 5, 2016
 Transformations in High-School Geometry: A Workable Interpretation of Common Core UCLA Curtis Center: March 5, 2016 John Sarli, Professor Emeritus of Mathematics, CSUSB MDTP Workgroup Chair Abstract. Previous
Transformations in High-School Geometry: A Workable Interpretation of Common Core UCLA Curtis Center: March 5, 2016 John Sarli, Professor Emeritus of Mathematics, CSUSB MDTP Workgroup Chair Abstract. Previous
8-6. a: 110 b: 70 c: 48 d: a: no b: yes c: no d: yes e: no f: yes g: yes h: no
 Lesson 8.1.1 8-6. a: 110 b: 70 c: 48 d: 108 8-7. a: no b: yes c: no d: yes e: no f: yes g: yes h: no 8-8. b: The measure of an exterior angle of a triangle equals the sum of the measures of its remote
Lesson 8.1.1 8-6. a: 110 b: 70 c: 48 d: 108 8-7. a: no b: yes c: no d: yes e: no f: yes g: yes h: no 8-8. b: The measure of an exterior angle of a triangle equals the sum of the measures of its remote
CBSE Class IX Syllabus. Mathematics Class 9 Syllabus
 Mathematics Class 9 Syllabus Course Structure First Term Units Unit Marks I Number System 17 II Algebra 25 III Geometry 37 IV Co-ordinate Geometry 6 V Mensuration 5 Total 90 Second Term Units Unit Marks
Mathematics Class 9 Syllabus Course Structure First Term Units Unit Marks I Number System 17 II Algebra 25 III Geometry 37 IV Co-ordinate Geometry 6 V Mensuration 5 Total 90 Second Term Units Unit Marks
Chapter 2. Reasoning and Proof
 Chapter 2 Reasoning and Proof 2.1 Use Inductive Reasoning Objective: Describe patterns and use deductive reasoning. Essential Question: How do you use inductive reasoning in mathematics? Common Core: CC.9-12.G.CO.9
Chapter 2 Reasoning and Proof 2.1 Use Inductive Reasoning Objective: Describe patterns and use deductive reasoning. Essential Question: How do you use inductive reasoning in mathematics? Common Core: CC.9-12.G.CO.9
REVIEW PACKET January 2012
 NME: REVIEW PKET January 2012 My PERIOD DTE of my EXM TIME of my EXM **THERE RE 10 PROBLEMS IN THIS REVIEW PKET THT RE IDENTIL TO 10 OF THE PROBLEMS ON THE MIDTERM EXM!!!** Your exam is on hapters 1 6
NME: REVIEW PKET January 2012 My PERIOD DTE of my EXM TIME of my EXM **THERE RE 10 PROBLEMS IN THIS REVIEW PKET THT RE IDENTIL TO 10 OF THE PROBLEMS ON THE MIDTERM EXM!!!** Your exam is on hapters 1 6
Euclidean Geometry Rediscovered
 Euclidean Geometry Rediscovered Presenter: John C. Mayer Assistants: William Bond & David Cosper University of Alabama at Birmingham Greater Birmingham Mathematics Partnership Supported by NSF EHR-0632522
Euclidean Geometry Rediscovered Presenter: John C. Mayer Assistants: William Bond & David Cosper University of Alabama at Birmingham Greater Birmingham Mathematics Partnership Supported by NSF EHR-0632522
