Brownian Motion An Introduction to Stochastic Processes de Gruyter Graduate, Berlin 2012 ISBN:
|
|
|
- Ira Bryan
- 6 years ago
- Views:
Transcription
1 Browia Moio A Iroducio o Sochasic Processes de Gruyer Graduae, Berli 22 ISBN: Soluio Maual Reé L. Schillig & Lohar Parzsch Dresde, May 23
2 R.L. Schillig, L. Parzsch: Browia Moio Ackowledgeme. We are graeful o Björ Böcher, Kaharia Fischer, Fraziska Küh, Julia Holleder, Felix Lider ad Michael Schwarzeberger who suppored us i he preparaio of his soluio maual. Daiel Tillich poied ou quie a few mispris ad mior errors. Dresde, May 23 Reé Schillig Lohar Parzsch 2
3 Coes Rober Brow s New Thig 5 2 Browia moio as a Gaussia process 3 3 Cosrucios of Browia Moio 25 4 The Caoical Model 3 5 Browia Moio as a Marigale 35 6 Browia Moio as a Markov Process 45 7 Browia Moio ad Trasiio Semigroups 55 8 The PDE Coecio 7 9 The Variaio of Browia Pahs 79 Regulariy of Browia Pahs 89 The Growh of Browia Pahs 95 2 Srasse s Fucioal Law of he Ieraed Logarihm 99 3 Skorokhod Represeaio 7 4 Sochasic Iegrals: L 2 Theory 9 5 Sochasic Iegrals: Beyod L 2 T 9 6 Iô s Formula 2 7 Applicaios of Iô s Formula 29 8 Sochasic Differeial Equaios 39 9 O Diffusios 53 3
4
5 Rober Brow s New Thig Problem. (Soluio) a) We show he resul for R d -valued radom variables. Le ξ, η R d. By assumpio, lim E exp [i (ξ η ), (X ) ] E exp [i ( ξ Y η ), (X Y ) ] lim E exp [i ξ, X + i η, Y ] E exp [i ξ, X + i η, Y ] If we ake ξ ad η, respecively, we see ha Sice X Y we fid lim E exp [i η, Y d ] E exp [i η, Y ] or Y Y lim E exp [i ξ, X ] E exp [i ξ, X ] or X d X. E exp [i ξ, X + i η, Y ] lim E exp [i ξ, X + i η, Y ] ad his shows ha X Y. b) We have Y X X X + lim E exp [i ξ, X ] E exp [i η, Y ] lim E exp [i ξ, X ] lim E exp [i η, Y ] E exp [i ξ, X ] E exp [i η, Y ] almos surely d X X X almos surely d X X Y X X + Y almos surely d X + Y. A simple direc calculaio shows ha X 2 (δ + δ ) Y. Thus, X d X, Y d Y X, X + Y d. Assume ha (X, Y ) d (X, Y ). Sice X Y, we fid for he disribuio of X + Y : X + Y 2 (δ + δ ) 2 (δ + δ ) 4 (δ δ + 2δ δ + δ δ ) 4 (δ + 2δ + δ 2 ). Thus, X + Y / δ lim (X + Y ) ad his shows ha we cao have ha (X, Y ) d (X, Y ). 5
6 R.L. Schillig, L. Parzsch: Browia Moio c) If X Y ad X Y, he we have X + Y d X + Y : his follows sice we have for all ξ R: lim E eiξ(x+y) lim E e iξx E e iξy lim E e iξx E e iξx E e iξy a) E [e iξx e iξy ] E e iξ(x+y ). lim E e iξy A similar (eve easier) argume works if (X, Y ) d (X, Y ). The we have f(x, y) e iξ(x+y) is bouded ad coiuous, i.e. we ge direcly lim E eiξ(x+y) lim E f(x, Y ) E f(x, Y ) E e iξ(x+y ). For a couerexample (if X ad Y are o idepede), see par b). Noice ha he idepedece ad d-covergece of he sequeces X, Y already implies X Y ad he d-covergece of he bivariae sequece (X, Y ). This is a cosequece of he followig Lemma. Le (X ) ad (Y ) be sequeces of radom variables (or radom vecors) o he same probabiliy space (Ω, A, P). If he (X, Y ) d X Y for all ad X X ad Y d Y, d (X, Y ) ad X Y. Proof. Wrie φ X, φ Y, φ X,Y (X, Y ). By assumpio for he characerisic fucios of X, Y ad he pair lim φ X (ξ) lim E e iξx E e iξx φ X (ξ). A similar saeme is rue for Y ad Y. For he pair we ge, because of idepedece lim φ X,Y (ξ, η) lim E e iξx+iηy lim E e iξx E e iηy lim E e iξx lim E e iηy E e iξx E e iηy φ X (ξ)φ Y (η). 6
7 Soluio Maual. Las updae Jue 2, 27 Thus, φ X,Y (ξ, η) h(ξ, η) φ X (ξ)φ Y (η). Sice h is coiuous a he origi (ξ, η) ad h(, ), we coclude from Lévy s coiuiy heorem ha h is a (bivariae) characerisic fucio ad ha (X, Y ) d (X, Y ). Moreover, h(ξ, η) φ X,Y (ξ, η) φ X (ξ)φ Y (η) which shows ha X Y. Problem.2 (Soluio) Usig he elemeary esimae e iz iz e ζ dζ sup e iy z z (*) y z we see ha he fucio e i ξ,, ξ, R d is locally Lipschiz coiuous: Thus, e i ξ, e i ξ,s e i ξ, s ξ, s ξ s for all ξ,, s R d, E e i ξ,y E [e i ξ,y X e i ξ,x ] E [(e i ξ,y X )e i ξ,x ] + E e i ξ,x. Sice lim E e i ξ,x E e i ξ,x, we are doe if we ca show ha he firs erm i he las lie of he displayed formula eds o zero. To see his, we use he Lipschiz coiuiy of he expoeial fucio. Fix ξ R d. E [(e i ξ,y X )e i ξ,x ] E (e i ξ,y X )e i ξ,x E e i ξ,y X Y X δ ei ξ,y X d P + Y X >δ ei ξ,y X d P (*) δ ξ + Y X >δ 2 d P δ ξ + 2 P ( Y X > δ) δ ξ, δ where we used i he las sep he fac ha X Y P. Problem.3 (Soluio) Recall ha Y d Y wih Y c a.s., i. e. where Y δc for some cosa c R. Sice he d-limi is rivial, his implies Y P Y. This meas ha boh is his sill rue -quesios ca be aswered i he affirmaive. We will show ha (X, Y ) d (X, c) holds wihou assumig ayhig o he joi disribuio of he radom vecor (X, Y ), i.e. we do o make assumpio o he correlaio srucure of X ad Y. Sice he maps x x + y ad x x y are coiuous, we see ha lim E f(x, Y ) E f(x, c) f C b (R R) 7
8 R.L. Schillig, L. Parzsch: Browia Moio implies boh ad This proves (a) ad (b). lim E g(x Y ) E g(xc) lim E h(x + Y ) E h(x + c) g C b (R) h C b (R). I order o show ha (X, Y ) coverges i disribuio, we use Lévy s characerizaio of disribuioal covergece, i.e. he poiwise covergece of he characerisic fucios. This meas ha we ake f(x, y) e i(ξx+ηy) for ay ξ, η R: E e i(ξx+ηy) E e i(ξx+ηc) E e i(ξx+ηy) E e i(ξx+ηc) + E e i(ξx+ηc) E e i(ξx+ηc) E e i(ξx+ηy) E e i(ξx+ηc) + E e i(ξx+ηc) E e i(ξx+ηc) E e iηy e iηc + E e iξx E e iξx. d The secod expressio o he righ-had side coverges o zero as X X. For fixed η we have ha y e iηy is uiformly coiuous. Therefore, he firs expressio o he righ-had side becomes, wih ay ɛ > ad a suiable choice of δ δ(ɛ) > E e iηy e iηc E [ e iηy e iηc { Y c >δ}] + E [ e iηy e iηc { Y c δ}] 2 E [ { Y c >δ}] + E [ɛ { Y c δ}] 2 P( Y c > δ) + ɛ P -covergece as δ,ɛ are fixed ɛ. ɛ Remark. The direc approach o (a) is possible bu relaively ugly. Par (b) has a relaively simple direc proof: Fix ξ R. E e iξ(x+y) E e iξx ( E e iξ(x+y) E e iξx ) + ( E e iξx E e iξx ) by d-covergece For he firs erm o he righ we fid wih he uiform-coiuiy argume from Problem..2 ad ay ɛ > ad suiable δ δ(ɛ, ξ) ha E e iξ(x+y) E e iξx E e iξx (e iξy ) E e iξy where we use P-covergece i he peulimae sep. ɛ + P ( Y > δ) ɛ fixed ɛ ɛ. 8
9 Soluio Maual. Las updae Jue 2, 27 Problem.4 (Soluio) Le ξ, η R ad oe ha f(x) e iξx ad g(y) e iηy are bouded ad coiuous fucios. Thus we ge ad we see ha (X, Y ) d (X, Y ). E e i (ξ η ), (X Y ) E e iξx e iηy E f(x)g(y ) lim E f(x )g(y ) lim E e iξx e iηy lim E e i (ξ ), (X η Y ) Assume ow ha X φ(y ) for some Borel fucio φ. Le f C b ad pick g f φ. Clearly, f φ B b ad we ge E f(x )f(x) E f(x )f(φ(y )) E f(x )g(y ) E f(x)g(y ) E f(x)f(x) E f 2 (X). Now observe ha f C b f 2 C b ad g B b. By assumpio Thus, i.e. f(x ) L2 f(x). E f 2 (X ) E f 2 (X). E ( f(x) f(x ) 2 ) E f 2 (X ) 2 E f(x )f(x) + E f 2 (X) E f 2 (X) 2 E f(x)f(x) + E f 2 (X), Now fix ɛ > ad R > ad se f(x) R x R. Clearly, f C b. The P( X X > ɛ) P( X X > ɛ, X R, X R) + P( X R) + P( X R) P( f(x ) f(x) > ɛ, X R, X R) + P( X R) + P( f(x ) R) P( f(x ) f(x) > ɛ) + P( X R) + P( f(x ) R) P( f(x ) f(x) > ɛ) + P( X R) + P( f(x) R/2) + P( f(x ) f(x) R/2) where we used ha { f(x ) R} { f(x) R/2} { f(x ) f(x) R/2} because of he riagle iequaliy: f(x ) f(x) + f(x) f(x ) P( f(x ) f(x) > ɛ) + P( X R/2) + P( X R/2) + P( f(x ) f(x) R/2) 9
10 R.L. Schillig, L. Parzsch: Browia Moio P( f(x ) f(x) > ɛ) + 2 P( X R/2) + P( f(x ) f(x) R/2) ( ɛ R 2 ) E ( f(x) f(x ) 2 ) + 2 P( X R/2) ɛ,r fixed ad ff R C b X is a.s. R-valued 2 P( X R/2). R Problem.5 (Soluio) Noe ha E δ j ad V δ j E δ 2 j. Thus, E S ad V S. a) We have, by he ceral limi heorem (CLT) S S CLT G where G N(, ), hece G G N(, ). b) Le s <. Sice he δ j are iid, we have, S S s S s, ad by he ceral limi heorem (CLT) S s s S s CLT s G G s. s If we kow ha he bivariae radom variable (S s, S S s ) coverges i disribuio, we do ge G G s +G s because of Problem.. Bu his follows agai from he lemma which we prove i par d). This lemma shows ha he limi has idepede coordiaes, see also par c). This is as close as we ca come o G G s G s, uless we have a realizaio of ALL he G o a good space. I is Browia moio which will achieve jus his. c) We kow ha he eries of he vecor (X m X m,..., X 2 X, X ) are idepede (hey deped o differe blocks of he δ j ad he δ j are iid) ad, by he oe-dimesioal argume of b) we see ha X k X k k k G k G k k k d for all k,..., m where he G k, k,..., m are sadard ormal radom vecors. By he lemma i par d) we eve see ha (X m X m,..., X 2 X, X ) d ( G,..., m m G m ) ad he G k, k,..., m are idepede. Thus, by he secod asserio of par b) ( G,..., m m G m ) (G,..., G m m m ) (G,..., G m G m ). d) We have he followig Lemma. Le (X ) ad (Y ) be sequeces of radom variables (or radom vecors) o he same probabiliy space (Ω, A, P). If he (X, Y ) d X Y for all ad X X ad Y d Y, d (X, Y ) ad X Y (for suiable versios of he rv s).
11 Soluio Maual. Las updae Jue 2, 27 Proof. Wrie φ X, φ Y, φ X,Y (X, Y ). By assumpio for he characerisic fucios of X, Y ad he pair lim φ X (ξ) lim E e iξx E e iξx φ X (ξ). A similar saeme is rue for Y ad Y. For he pair we ge, because of idepedece lim φ X,Y (ξ, η) lim E e iξx+iηy lim E e iξx E e iηy lim E e iξx lim E e iηy E e iξx E e iηy φ X (ξ)φ Y (η). Thus, φ X,Y (ξ, η) h(ξ, η) φ X (ξ)φ Y (η). Sice h is coiuous a he origi (ξ, η) ad h(, ), we coclude from Lévy s coiuiy heorem ha h is a (bivariae) characerisic fucio ad ha (X, Y ) d (X, Y ). Moreover, which shows ha X Y. h(ξ, η) φ X,Y (ξ, η) φ X (ξ)φ Y (η) Problem.6 (Soluio) Necessiy is clear. For sufficiecy wrie B() B(s) B() B( s+ 2 ) + s 2 s 2 B( s+ 2 ) B(s) s 2 2 (X + Y ). By assumpio X Y, X Y ad X 2 (X + Y ). This is already eough o guaraee ha X N(, ), cf. Réyi [8, Chaper VI.5, Theorem 2, pp ]. Aleraive Soluio: Fix s < ad defie j s + j ( s) for j,...,. The B B s B j B j s j j j j B j B j j j G j By assumpio, he radom variables (G j ) j, are ideically disribued (for all j, ) ad idepede (i j). Moreover, E(G j ) ad V(G j ). Applyig he ceral limi heorem (for riagular arrays) we obai G j where G N(, ). Thus, B B s N(, s). d G
12
13 2 Browia moio as a Gaussia process Problem 2. (Soluio) Le us check firs ha f(u, v) g(u)g(v)( si u si v) is ideed a probabiliy desiy. Clearly, f(u, v). Sice g(u) (2π) /2 e u2 /2 is eve ad si u is odd, we ge f(u, v) du dv g(u) du g(v) dv g(u) si u du g(v) si v dv. Moreover, he desiy f U (u) of U is f U (u) f(u, v) dv g(u) g(v) dv g(u) si u g(v) si v dv g(u). This, ad a aalogous argume show ha U, V N(, ). Le us show ha (U, V ) is o a ormal radom variable. Assume ha (U, V ) is ormal, he U + V N(, σ 2 ), i.e. O he oher had we calculae wih f(u, v) ha ad his coradics (*). E e iξ(u+v ) e 2 ξ2 σ 2. (*) E e iξ(u+v ) e iξu+iξv f(u, v) du dv 2 2 ( e iξu g(u) du) ( e iξu g(u) si u du) e ξ2 ( 2i e iξu (e iu e iu 2 )g(u) du) e ξ2 ( 2i (e i(ξ+)u e i(ξ )u 2 )g(u) du) e ξ2 ( 2i (e 2 (ξ+)2 e 2 2 (ξ )2 )) e ξ2 + 4 (e 2 (ξ+)2 e 2 (ξ )2 ) 2 e ξ2 + 4 e e ξ2 (e ξ e ξ ) 2, Problem 2.2 (Soluio) Le (ξ,..., ξ ) (,..., ) ad se. The we fid from (2.2) ( j k ) ξ j ξ k ( j j )(ξ j + + ξ ) 2. (2.) k > Equaliy ( ) occurs if, ad oly if, (ξ j + + ξ ) 2 for all j,...,. This implies ha ξ... ξ. 3
14 R.L. Schillig, L. Parzsch: Browia Moio Absrac aleraive: Le (X ) I be a real-valued sochasic process which has a secod mome (such ha he covariace is defied!), se µ E X. For ay fiie se S I we pick λ s C, s S. The Cov(X s, X )λ s λ E ((X s µ s )(X µ ))λ s λ s, S s, S E (X s µ s )λ s (X µ )λ s, S E ((X s µ s )λ s(x µ )λ ) s S S E s S(X s µ s )λ s 2. Remark: Noe ha his aleraive does o prove ha he covariace is sricly posiive defiie. A sadard couerexample is o ake X s X. Problem 2.3 (Soluio) These are direc & sraighforward calculaios. Problem 2.4 (Soluio) Le e i (,...,,,...) R be he ih sadard ui vecor. The i a ii Ae i, e i Be i, e i b ii. Moreover, for i j, we ge by he symmery of A ad B ad which shows ha a ij b ij. Thus, A B. We have A(e i + e j ), e i + e j a ii + a jj + 2b ij B(e i + e j ), e i + e j b ii + b jj + 2b ij Le A, B R be symmeric marices. If Ax, x Bx, x for all x R, he A B. Problem 2.5 (Soluio) a) X 2B /4 is a BM : scalig propery wih c /4, cf b) Y B 2 B is o a BM, he idepede icremes is clearly violaed: E(Y 2 Y )Y E(Y 2 Y ) E Y 2 E(B 4 B 2 )(B 2 B ) E(B 2 B ) 2 (B) E(B 4 B 2 ) E(B 2 B ) E(B 2 B ) 2 (B) E(B 2 ). c) Z B is o a BM, he idepede icremes propery is violaed: E(Z Z s )Z s ( s) s E B 2 ( s) s. 4
15 Soluio Maual. Las updae Jue 2, 27 Problem 2.6 (Soluio) We use formula (2.b). a) f B(s),B() (x, y) 2π s( s) exp [ (y 2 (x2 x)2 + s s )]. b) Deoe by f B() he desiy of B(). The we have f B(s),B() B() (x, y B() z) f B(s),B(),B()(x, y, z) f B() (z) Thus, (2π) 3/2 s( s)( ) exp [ (y 2 (x2 x)2 + + s s f B(s),B() B() (x, y B() ) Noe ha x 2 s + (y x)2 s Therefore, (z y)2 )] (2π) /2 exp [ z2 2 ]. 2π s( s)( ) exp [ (y 2 (x2 x)2 + + y2 s s )]. + y2 s( s) (x s 2 y) + y2 + y2 s( s) (x s 2 y) y 2 + ( ). E(B(s)B() B() ) c) I aalogy o par b) we ge xyf B(s),B() B() (x, y B() ) dx dy 2π s( s)( ) y y exp [ 2 y 2 ( ) ] x exp [ x 2 s( s) (x s 2 y) ] dx dy 2π ( ) s ( ) s( ). s( s) s y y2 f B(2 ),B( 3 ) B( ),B( 4 )(x, y B( ) u, B( 4 ) z) f B( ),B( 2 ),B( 3 ),B( 4 )(u, x, y, z) f B( ),B( 4 )(u, z) 2π s y exp [ 2 y 2 ( ) ] dy 2π [ ( 4 ) ( 2 )( 3 2 )( 4 3 ) ] 2 (x exp [ 2 (u2 u)2 (y x)2 (z y) )] Thus, exp [ (z 2 (u2 u)2 + )]. 4 f B(2 ),B( 3 ) B( ),B( 4 )(x, y B( ) B( 4 ) ) 5
16 R.L. Schillig, L. Parzsch: Browia Moio 2π [ ( 4 ) ( 2 )( 3 2 )( 4 3 ) ] 2 exp [ 2 ( x2 (y x)2 + + y2 )] Observe ha x 2 (y x)2 + + y ( 2 )( 3 2 ) (x 2 2 y) ( 3 )( 4 3 ) y2. Therefore, we ge (usig physiciss oaio: dy h(y) h(y) dy for easier readabiliy) xy f B(2 ),B( 3 ) B( ),B( 4 )(x, y B( ) B( 4 ) ) dx dy 2π( 4 3 ) y dy exp [ 2 4 ( 3 )( 4 3 ) y2 ] y 2π(2 )( 3 2 ) x exp [ x 2 (x y) 3 ( 2 )( 3 2 ) ] dx y ( 4 3 )( 3 ) 4 ( 2 )( 4 3 ) 4. Problem 2.7 (Soluio) Le s. The C(s, ) E(X s X ) E(B 2 s s)(b 2 ) E(B 2 s s)([b B s + B s ] 2 ) E(B 2 s s)(b B s ) E(B 2 s s)b s (B B s ) + E(B 2 s s)b 2 s E(B 2 s s) (B) E(B 2 s s) E(B B s ) E(B 2 s s)b s E(B B s ) + E(B 2 s s)b 2 s E(B 2 s s) ( s) + 2 E(B 2 s s)b s + E B 4 s s E B 2 s 2s 2 2(s 2 2 ) 2(s ) 2. Problem 2.8 (Soluio) a) We have for s, m() E X e α/2 E B e α. C(s, ) E(X s X ) e α 2 (s+) E B e αsb e α e α 2 (s+) (e αs e α ) e α 2 s. b) We have P(X( ) x,..., X( ) x ) P (B(e α ) e α /2 x,..., B(e α ) e α/2 x ) Thus, he desiy is f X( ),...,X( )(x,..., x ) k e α k/2 f B(e α ),...,B(e α)(e α /2 x,..., e α/2 x ) 6
17 k e αk/2 (2π) /2 ( k (2π) /2 ( ( e α( k k ) )) k /2 (e α k e α k )) (we use he coveio ad x ). Soluio Maual. Las updae Jue 2, 27 e 2 k (eα k /2 x k e α k /2 x k ) 2 /(e α k e α k ) /2 e 2 k (x k e α( k k )/2 x k ) 2 /( e α( k k ) ) Remark: he form of he desiy shows ha he Orsei Uhlebeck is sricly saioary, i.e. (X( + h),..., X( + h) (X( ),..., X( )) h >. Problem 2.9 (Soluio) Assume ha we have (B). Observe ha he family of ses σ(b u,..., B u ) u u s, is a -sable family. This meas ha i is eough o show ha By (B) we kow ha B B s (B u,..., B u ) for all s. B B s (B u, B u2 B u,..., B u B u ) ad so... B u... B u2 B u B B s... B u3 B u2... B u B u B u B u2 B u3 B u Le < 2 <... < <,. The we fid for all ξ,..., ξ R d E (e i k ξ k, B( k ) B( k ) ) E (e i ξ, B() B( ) e i ) F mble., hece B( ) B( ) k ξ k, B( k ) B( k ) E (e i ξ, B() B( ) ) E (e i k ξ k, B( k ) B( k ) ) This shows (B). k E (e i ξ k, B( k ) B( k ) ). Problem 2. (Soluio) Reflecio ivariace of BM, cf. 2.8, shows τ a if{s B s a} if{s B s a} if{s B s a} τ a. The scalig propery 2.2 of BM shows for c /a 2 τ a if{s B s a} if{s ab s/a 2 a} if{a 2 r ab r a} a 2 if{r B r } a 2 τ. 7
18 R.L. Schillig, L. Parzsch: Browia Moio Problem 2. (Soluio) a) No saioary: E W 2 C(, ) E(B 2 ) 2 E(B 4 2B ) cos. b) Saioary. We have E X ad E X s X e α(+s)/2 E B e αsb e α e α(+s)/2 (e αs e α ) e α s /2, i.e. i is saioary wih g(r) e α r /2. c) Saioary. We have E Y. Le s. The we use E B s B s o ge E Y s Y E(B s+h B s )(B +h B ) E B s+h B +h E B s+h B E B s B +h + E B s B (s + h) ( + h) (s + h) s ( + h) + s, if > s + h h < s (s + h) (s + h) h ( s), if s + h h s. Swappig he roles of s ad fially gives: he process is saioary wih g() (h ) + (h ). d) No saioary. Noe ha E Z 2 E Be 2 e cos. Problem 2.2 (Soluio) Clearly, W is coiuous for. If we ge ad his proves coiuiy for. lim W (ω) W (ω) B (ω) lim W (ω) B (ω) lim β / (ω) β (ω) B (ω); Le us check ha W is a Gaussia process wih E W ad E W s W s. Corollary 2.7, W is a BM. By Pick ad < <... <. Case : If, here is ohig o show sice (B ) [,] is a BM. Case 2: Assume ha >. The we have W W 2 W 2 3 B β / β / β 8
19 Soluio Maual. Las updae Jue 2, 27 ad sice B (β /,..., β /, β ) are boh Gaussia, we see ha (W,..., W ) is Gaussia. Furher, le ad i < j : E W E B + E β / E β E W i W j E(B + i β /i β )(B + j β /j β ) + i j j i i j j + i i j. Case 3: Assume ha < <... < k < k+ <... <. The we have W W 2 W k W k+ k+2 B B k B β /k+ β / β. Sice (B,..., B k, B ) (β /k+,..., β /, β ) are Gaussia vecors, (W,..., W ) is also Gaussia ad we fid E W E W i W j E B i (B + j β /j β ) i i j for i k < j. Problem 2.3 (Soluio) The process X() B(e ) has o memory sice (cf. Problem 2.9) σ(b(s) s e a ) σ(b(s) B(e a ) s e a ) ad, herefore, σ(x() a) σ(b(s) s e a ) σ(b(e a+s ) B(e a ) s ) σ(x( + a) X(a) ). The process X() e /2 B(e ) is o memoryless. For example, X(a + a) X(a) is o idepede of X(a): E(X(2a) X(a))X(a) E (e a B(e 2a ) e a/2 B(e a ))e a/2 B(e a ) e 3a/2 e a e a e a. 9
20 R.L. Schillig, L. Parzsch: Browia Moio Problem 2.4 (Soluio) The process W B a B a, a clearly saisfies (B) ad (B4). For s a we fid W W s B a B a s B a s B a B s N(, ( s) id) ad his shows (B2) ad (B3). For < <... < a we have W j W j B a j B a j B a j B a j j ad his proves ha W iheris (B) from B. Problem 2.5 (Soluio) We kow from Paragraph 2.3 ha Moreover, B(s) lim B(/) lim a.s. s s E ( B(s) 2 ) s s s 2 s i.e. we ge also covergece i mea square. s Remark: a direc proof of he SLLN is a bi more ricky. Of course we have by he classical SLLN ha B (B j B j ) SLLN a.s. Bu he we have o make sure ha B s /s coverges. This ca be doe i he followig way: fix s >. The here is a uique ierval (, + ] such ha s (, + ]. Thus, B s s B s B + + B + s + + sup s + B s B s B ad we have o show ha he expressio wih he sup eds o zero. This ca be doe by showig, e.g., ha he L 2 -limi of his expressio goes o zero (usig he reflecio priciple) ad wih a subsequece argume. Problem 2.6 (Soluio) Se Clearly, Σ σ(b() J) J [,), J couable σ(b ) Σ σ(b ) def F B (*) The firs iclusio follows from he fac ha each B is measurable wih respec o Σ. Le us show ha Σ is a σ-algebra. Obviously, Σ ad F Σ F c Σ. 2
21 Soluio Maual. Las updae Jue 2, 27 Le (A ) Σ. The, for every here is a couable se J such ha A σ(b() J ). Sice J J is sill couable we see ha A σ(b() J) for all. Sice he laer family is a σ-algebra, we fid A σ(b() J) Σ. Sice σ(b ) Σ, we ge oe: F B is, by defiiio, he smalles σ-algebra for which all B are measurable ha This shows ha Σ F B. F B Σ. Problem 2.7 (Soluio) Assume ha he idices,..., m ad s,..., s are give. Le {u,..., u p } {s,..., s } {,..., m }. By assumpio, (X(u ),..., X(u p )) (Y (u ),..., Y (u p )). Thus, we may hi ou he idices o each side wihou edagerig idepedece: {s,..., s } {u,..., u p } ad {,..., m } {u,..., u p }, ad so (X(s ),..., X(s )) (Y ( ),..., Y ( m )). Problem 2.8 (Soluio) Sice F F ad G G i is clear ha F G F G. Coversely, sice (F ) ad (G ) are filraios we fid F F, G G, F F, G G. By assumpio: P(F G) P(F ) P(G). Thus, F G. Sice he families F ad G are -sable (use agai he argume ha we have filraios o fid for F, F F some wih F, F F ec.), he σ-algebras geeraed by hese families are idepede: F σ ( F ) σ ( G ) G. Problem 2.9 (Soluio) Le U R d d be a orhogoal marix: UU id ad se X UB for a BM d (B ). The E exp i ξ j, X( j ) X( j ) E exp i ξ j, UB( j ) UB( j ) 2
22 R.L. Schillig, L. Parzsch: Browia Moio E exp i U ξ j, B( j ) B( j ) exp 2 ( j j ) U ξ j, U ξ j exp 2 ( j j ) ξ j 2. (Observe U ξ j, U ξ j UU ξ j, ξ j ξ j, ξ j ξ j 2 ). The claim follows. Problem 2.2 (Soluio) Noe ha he coordiae processes b ad β are idepede BM. a) Sice b β, he process W (b + β )/ 2 is a Gaussia process wih coiuous sample pahs. We deermie is mea ad covariace fucios: E W 2 (E b + E β ) ; Cov(W s, W ) E(W s W ) 2 E(b s + β s )(b + β ) 2 ( E b sb + E β s b + E b s β + E β s β ) (s s ) s 2 where we used ha, by idepedece, E b u β v E b u E β v. Now he claim follows from Corollary 2.7. b) The process X (W, β ) has he followig properies W ad β are BM E(W b ) 2 /2 E(b + β )β 2 /2 (E b E β + E β 2 ) / 2, i.e. W ad β are NOT idepede. This meas ha X is o a BM 2, as is coordiaes are o idepede. The process Y ca be wrie as b + β 2 b β U b β b 2 β. Clearly, UU id, i.e. Problem 2.9 shows ha (Y ) is a BM 2. Problem 2.2 (Soluio) Observe ha b β sice B is a BM 2. Sice E X Cov(X, X s ) E X X s E(λb s + µβ s )(λb + µβ ) λ 2 E b s b + λµ E b s β + λµ E b β s + µ 2 β s β 22
23 Soluio Maual. Las updae Jue 2, 27 λ 2 E b s b + λµ E b s E β + λµ E b E β s + µ 2 E β s β λ 2 (s ) µ 2 s (λ 2 + µ 2 )(s ). Thus, by Corollary 2.7, X is a BM if, ad oly if, λ 2 + µ 2. Problem 2.22 (Soluio) X (b, β s β ), s, is NOT a Browia moio: X (, β s ) (, ). O he oher had, Y (b, β s β s ), s, IS a Browia moio, sice b ad β s β s are idepede BM, cf. Time iversio 2. ad Theorem 2.6. Problem 2.23 (Soluio) We have W UB cos α si α si α b cos α β. The marix U is a roaio, hece orhogoal ad we see from Problem 2.9 ha W is a Browia moio. Geeralizaio: ake U orhogoal. Problem 2.24 (Soluio) If G N(, Q) he Q is he covariace marix, i.e. Cov(G j, G k ) q jk. Thus, we ge for s < The characerisic fucio is Cov(X j s, X k ) E(X j sx k ) E X j s(x k X k s ) + E(X j sx k s ) E X j s E(X k X k s ) + sq jk (s )q jk. E e i ξ,x E e i Σ ξ,b e 2 Σ ξ 2 e 2 ξ,σσ ξ, ad he rasiio probabiliy is, if Q is o-degeerae, f Q (x) (2π) de Q exp ( x, Qx ). 2 If Q is degeerae, here is a orhogoal marix U R such ha UX (Y,..., Y k,,..., k ) where k < is he rak of Q. disribuio i R k. The k-dimesioal vecor has a odegeerae ormal 23
24
25 3 Cosrucios of Browia Moio Problem 3. (Soluio) The parial sums W N (, ω) N G (ω)s (), [, ], coverge as N P-a.s. uiformly for owards B(, ω), [, ] cf. Problem 3.2. Therefore, he radom variables W N() d N G S () d P -a.s. X N B() d. This shows ha W N() d is he sum of idepede N(, )-radom variables, hece iself ormal ad so is is limi X. From he defiiio of he Schauder fucios (cf. Figure 3.2) we fid ad his shows S () d 2 S 2 j +k() d j, k,,..., 2 j, j. W 2 +() d 2 G + 4 j 2 j j G 2 j +l. l Cosequely, sice he G j are iid N(, ) radom variables, This meas ha E W 2 +() d, V W 2 +() d X 2 G + j j 2 3j l j 2 2j j (+) j 2 j l G 2 j +l N(,2 j ) where he series coverges P-a.s. ad i mea square, ad X N(, 3 ). 25
26 R.L. Schillig, L. Parzsch: Browia Moio Problem 3.2 (Soluio) [, ], we fid a) From he defiiio of he Schauder fucios S (),, S (), S 2 j +k() S 2 j +k((2k + )/2 j+ ) 2 j/2 /2 j+ 2 2 j/2 j, k, 2 j S 2 j +k() k 2 2 j/2 (disjoi suppors!) By assumpio, C >, ɛ (, 2 ), a C ɛ. Thus, we fid a S () a + j a + j a + (The series is coverge sice ɛ < /2). j 2 j a 2 j +k S 2 j +k() k 2 j C (2 j+ ) ɛ S 2 j +k() k C 2 (j+)ɛ 2 2 j <. This shows ha a S () coverges absoluely ad uiformly for [, ]. b) For C > 2 we fid from P ( G > log ) 2 π C log e 2 C2 log 2 π C C2 /2 3 ha he followig series coverges: P ( G > log ) <. By he Borel Caelli Lemma we fid ha G (ω) O( log ) for almos all ω, hus G (ω) O( ɛ ) for ay ɛ (, /2). From par a) we kow ha he series G (ω)s () coverges a.s. uiformly for [, ]. Problem 3.3 (Soluio) Se f p ( E f p ) /p Soluio : We observe ha he space L p (Ω, A, P; S) {X X S, d(x, ) p < } is complee ad ha he codiio saed i he problem jus says ha (X ) is a Cauchy sequece i he space L p (Ω, A, P; S). A good referece for his is, for example, he moograph by F. Trèves [3, Chaper 46]. You will fid he pedesria approach as Soluio 2 below. 26
27 Soluio Maual. Las updae Jue 2, 27 Soluio 2: By assumpio k N k sup m N k d(x Nk, X m ) p 2 k. Wihou loss of geeraliy we ca assume ha N k N k+. I paricular d(x Nk, X Nk+ ) p 2 k l l>k d(x Nk, X Nl ) p jk 2 j 2 2 k. Fix m. The we see ha d(x Nk, X m ) d(x Nl, X m ) p d(x Nk, X Nl ) p k,l. This meas ha ha (d(x Nk, X m )) k is a Cauchy sequece i L p (P; R). By he compleeess of he space L p (P; R) here is some f m L p (P; R) such ha d(x Nk, X m ) ad, for a subsequece ( k ) (N k ) k we fid d(x k, X m ) The subsequece k may also deped o m. i Lp f m k almos surely f m. k Sice ( k (m)) k is sill a subsequece of (N k ), we sill have d(x k (m), X m+ ) f m+ i L p, hece we ca fid a subsequece ( k (m + )) k ( k (m)) k such ha d(x k (m+), X m+ ) f m+ a.s. Ieraig his we see ha we ca assume ha ( k ) k does o deped o m. I paricular, we have almos surely Moreover, ɛ > L L(ɛ) k L d(x k, X m ) f m ɛ. lim f m p lim lim d(x k, X m ) p lim lim d(x k, X m ) p m m k m k lim sup d(x k, X m ) p. m k k Thus, f m i L p ad, for a subsequece m k we ge Therefore, ɛ > K K(ɛ) r K f mr ɛ. d(x k, X l ) d(x k, X mr ) + d(x k, X mr ) d(x k, X mr ) f mr + d(x k, X mr ) f mr + 2 f mr. Fix ɛ > ad pick r > K. The le k, l. This gives d(x k, X l ) d(x k, X mr ) f mr + d(x k, X mr ) f mr + 2ɛ 4ɛ k, l L(ɛ). 27
28 R.L. Schillig, L. Parzsch: Browia Moio Sice S is complee, his proves ha (X k ) k coverges o some X S almos surely. Remark: If we replace he codiio of he Problem by higs become MUCH simpler: lim E (sup d p (X, X m )) m This codiio says ha he sequece d sup m d p (X, X m ) coverges i L p (P; R) o zero. Hece here is a subsequece ( k ) k such ha lim sup d(x k, X m ) k m k almos surely. This shows ha d(x k, X l ) as k, l, i.e. we fid by he compleeess of he space S ha X k X. Problem 3.4 (Soluio) Fix,... ad Borel ses A,..., A. By assumpio, we kow ha P(X Y ) P(X j Y j j,..., ) P {X j Y j }. Thus, P {X j A j } P {X j A j } {X j Y j } P {X j A j } {X j Y j } P {Y j A j } {X j Y j } P {Y j A j }. Problem 3.5 (Soluio) idisiguishable modificaio: P(X Y ) P(X Y ). modificaio equivale: see he previous Problem 3.4 Now assume ha I is couable or X, Y are (lef- or righ-)coiuous. modificaio idisiquishable: By assumpio, P(X Y ) for ay I. Le D I be ay couable dese subse. The P q D{X q Y q } P(X q Y q ) q D 28
29 Soluio Maual. Las updae Jue 2, 27 which meas ha P(X q Y q q D). If I is couable, we are doe. I he oher case we have, by he desiy of D, P(X Y I) P (lim D q X q lim D q Y q I) P (X q Y q q D). equivale / modificaio: To see his le (B ) ad (W ) be wo idepede oe-dimesioal Browia moios defied o he same probabiliy space. Clearly, hese processes have he same fiie-dimesioal disribuios, i.e. hey are equivale. O he oher had, for ay > P(B W ) P(B y) P(W dy) P(W dy). Problem 3.6 (Soluio) Sice (B q ) q Q [,) is uiformly coiuous, here exiss a uique process (B ) such ha B lim q B q ad B is coiuous. We use he characerizaio from Lemma 2.4. Is proof shows ha we ca derive (2.7) E exp i j, X qj X qj + i ξ, X q ξ exp 2 o he basis of (B) (B3) for (B q ) q Q [,) ad q,..., q Q [, ). ξ j 2 (q j q j ) Now se q ad pick,..., R ad approximae each j by a raioal sequece, k. Sice (2.7) holds for q (k), j,..., ad every k, we ca easily perform q (k) j j he limi k o boh sides (o he lef we use domiaed covergece!) sice B is coiuous. This proves (2.7) for (B ), ad sice (B ) has coiuous pahs, Lemma 2.4 proves ha (B ) is a BM. Problem 3.7 (Soluio) The joi desiy of (W ( ), W (), W ( )) is f,, (x, x, x ) (2π) 3/2 exp ( ( )( ) 2 [(x x) 2 + (x x ) 2 + x2 ]) while he joi desiy of (W ( ), W ( )) is f, (x, x ) (2π) exp ( ( ) 2 [(x x ) 2 + x2 ]). The codiioal desiy of W () give (W ( ), W ( )) is f, (x x, x 2 ) f,, (x, x, x ) f, (x, x ) (2π) 3/2 exp ( ( )( ) 2 [ (x x) 2 + (x x ) 2 + x2 ]) (2π) exp ( ( ) 2 [ (x x ) 2 + x2 ]) 29
30 R.L. Schillig, L. Parzsch: Browia Moio ( ) 2π ( )( ) exp ( 2 [(x x) 2 + (x x ) 2 (x x ) 2 ]) ( ) 2π ( )( ) exp ( 2 [( )(x x) 2 + ( )(x x ) 2 (x x ) 2 ]) ( )( ) Now cosider he argume i he square brackes [ ] of he exp-fucio [ ( )(x x) 2 + ( )(x x ) 2 ( )( ) (x x ) 2 ] ( ) ( )( ) [ (x x) 2 + (x x ) 2 ( )( ) ( ) 2 (x x ) 2 ] ( ) ( )( ) [ ( + ) x 2 + ( ( )( ) ( ) 2 ) x 2 + ( ( )( ) ( ) 2 ) x 2 2 x x 2 xx + 2 ( )( ) ( ) 2 x x ] ( ) ( )( ) [x2 + ( ) 2 ( ) 2 x2 + ( ) 2 ( ) 2 x2 2 x x 2 xx + 2 ( )( ) ( ) 2 x x ] ( ) ( )( ) [x x 2 x ] ( ) ( )( ) [x ( x + 2 x )]. Se σ 2 ( )( ) ( ) ad m x + x he our calculaio shows ha f, (x x, x 2 ) (x m)2 exp ( 2π σ 2σ 2 ). 3
31 4 The Caoical Model Problem 4. (Soluio) Le F R [, ] be a disribuio fucio. We begi wih a geeral lemma: F has a uique geeralized moooe icreasig righ-coiuous iverse: F (u) G(u) if{x F (x) > u} [ sup{x F (x) u}]. (4.) We have F (G(u)) u if F () is coiuous i G(u), oherwise, F (G(u)) u. Ideed: For hose where F is sricly icreasig ad coiuous, here is ohig o show. Le us look a he wo problem cases: F jumps ad F is fla. F () G(u) w + w w v u G(u) G(v ) G(v) G(w) u Figure 4.: A illusraio of he problem cases If F () jumps, we have G(w) G(w + ) G(w ) ad if F () is fla, we ake he righ edpoi of he flaess ierval [G(v ), G(v)] o defie G (his leads o righ-coiuiy of G) a) Le (Ω, A, P) ([, ], B[, ], du) (du sads for Lebesgue measure) ad defie X G (G F as before). The P({ω Ω X(ω) x}) λ({u [, ] G(u) x}) (he discoiuiies of F are couable, i.e. a Lebesgue ull se) 3
32 R.L. Schillig, L. Parzsch: Browia Moio λ({ [, ] F (x)}) λ([, F (x)]) F (x). Measurabiliy is clear because of moooiciy. b) Use he produc cosrucio ad par a). To be precise, we do he cosrucio for wo radom variables. Le X Ω R ad Y Ω R be wo iid copies. We defie o he produc space (Ω Ω, A A, P P ) he ew radom variables ξ(ω, ω ) X(ω) ad η(ω, ω ) Y (ω ). The we have ξ, η live o he same probabiliy space ξ X, η Y P P (ξ A) P P ({(ω, ω ) Ω Ω ξ(ω, ω ) A}) P P ({(ω, ω ) Ω Ω X(ω) A}) P P ({ω Ω X(ω) A} Ω ) P({ω Ω X(ω) A}) P(X A). ad a similar argume works for η. ξ η P P (ξ A, η B) P P ({(ω, ω ) Ω Ω ξ(ω, ω ) A, η(ω, ω ) B}) P P ({(ω, ω ) Ω Ω X(ω) A, Y (ω ) B}) P P ({ω Ω X(ω) A} {ω Ω Y (ω ) B}) P({ω Ω X(ω) A}) P ({ω Ω Y (ω ) B}) P(X A) P(Y B) P P (ξ A) P P (η B) The same ype of argume works for arbirary producs, sice idepedece is always defied for ay fiie-dimesioal subfamily. I he ifiie case, we have o ivoke he heorem o he exisece of ifiie produc measures (which are cosruced via heir fiie margials) ad which ca be see as a paricular case of Kolmogorov s heorem, cf. Theorem 4.8 ad Theorem A.2 i he appedix. c) The saemes are he same if oe uses he same cosrucio as above. A difficuly is o ideify a mulidimesioal disribuio fucio F (x). Roughly speakig, hese are fucios of he form F (x) P (X (, x ] (, x ]) where X (X,..., X ) ad x (x,..., x ), i.e. x is he upper righ edpoi of a ifiie recacle. A absrac characerisaio is he followig 32
33 Soluio Maual. Las updae Jue 2, 27 F R [, ] x j F (x) is moooe icreasig x j F (x) is righ coiuous F (x) if a leas oe ery x j F (x) if all eries x j + ( ) k ɛ k F (ɛ a +( ɛ )b,..., ɛ a +( ɛ )b ) where < a j < b j < ad where he ouer sum rus over all uples (ɛ,..., ɛ ) {, } The las propery is equivale o () h () h F (x) h,..., h where (k) h F (x) F (x + he k) F (x) ad e k is he kh sadard ui vecor of R. I priciple we ca cosruc such a mulidimesioal F from is margials usig he heory of copulas, i paricular, Sklar s heorem ec. ec. ec. Aoher way would be o ake (Ω, A, P) (R, B(R ), µ) where µ is he probabiliy measure iduced by F (x). The he radom variables X are jus he ideiy maps! The idepede copies are he obaied by he usual produc cosrucio. Problem 4.2 (Soluio) Sep : Le us firs show ha P(lim s X s exiss) <. Sice X r X s ad X s X s we ge Thus, X r X s X r + X s N(, s + r) s + r N(, ). P( X r X s > ɛ) P ( X > ɛ ) P ( X > ɛ ). s + r r,s 2 This proves ha X s is o a Cauchy sequece i probabiliy, i. e. i does o eve coverge i probabiliy owards a limi, so a.e. covergece is impossible. I fac we have {ω lim X s (ω) does o exis} { sup X s X r > } s k s,r [ /k,+/k] ad so we fid wih he above calculaio P ( lim X s does o exis) lim P ( sup X s X r > ) P ( X > ɛ ) s k s,r [ /k,+/k] 2 This shows, i paricular ha for ay sequece we have P ( lim X exiss) < q <. where q q() (bu idepede of he sequece). Sep 2: Fix >, fix a sequece ( ) wih, ad se A {ω Ω lim s X s (ω) exiss} ad A( ) {ω Ω lim X (ω) exiss}. 33
34 R.L. Schillig, L. Parzsch: Browia Moio Clearly, A A( ) for ay such sequece. Moreover, ake wo sequeces (s ), ( ) such ha s ad ad which have o pois i commo; he we ge by idepedece ad sep (X s, X s2, X s3...) (X, X 2, X 3...) A( ) A(s ) ad so, P(A) P(A(s ) A( )) P(A(s )) P(A( )) q 2. By Sep, q <. Sice here are ifiiely may sequeces havig all o pois i commo, we ge P(A) lim k q k. 34
35 5 Browia Moio as a Marigale Problem 5. (Soluio) a) We have F B σ(σ(x), F B ) σ(x, B s s ) F. Le s. The σ(b B s ), F B s ad σ(x) are idepede, hus σ(b B s ) is idepede of σ(σ(x), F B ) F. This shows ha F B (B ). b) Se N {N M A such ha N M, P(M) }. The we have F B σ(f B, N) F B. is a admissible filraio for From measure heory we kow ha (Ω, A, P) ca be compleed o (Ω, A, P ) where We fid for all A B(R d ), F F s, N N A {A N A A, N N}, P (A ) P(A) for A A N A. P ({B B s A} (F N)) P (({B B s A} F ) ({B B s A} N) ) A N P({B B s A} F ) P(B B s A) P(F ) P (B B s A) P (F N). Therefore F B is admissible. Problem 5.2 (Soluio) Le <... <, ad cosider he radom variables B( ) B( ),..., B( ) B( ). Usig he argume of Problem 2.9 we see for ay F F E (e i k ξ k, B( k ) B( k ) F ) E (e i ξ, B() B( ) e i k ξ k, B( k ) B( k ) F ) F mble., hece B( ) B( ) E (e i ξ, B() B( ) ) E (e i k ξ k, B( k ) B( k ) F ) 35
36 R.L. Schillig, L. Parzsch: Browia Moio k E (e i ξ k, B( k ) B( k ) ) E F. This shows ha he icremes are idepede amog hemselves (use F Ω) ad ha hey are all ogeher idepede of F (use he above calculaio ad he fac ha he icremes are amog hemselves idepede o combie agai he expeced value) uder he Thus, F σ(b( k ) B( k ) k,..., ) Therefore he saeme is implied by F < <...< σ(b( k ) B() k,..., ). Problem 5.3 (Soluio) a) i) E X <, sice he expecaio does o deped o he filraio. ii) X is F measurable ad F F. Thus X is F measurable. iii) Le N deoe he se of all ses which are subses of P-ull ses. Deoe by P he measure of he compleio of (Ω, A, P) (compare wih he soluio o Exercise 5..b)). Le s. For all F F s here exis F F s, N N such ha F F N ad F X s d P F X s d P F X d P F X d P. Sice F is arbirary his implies ha E(X F s ) X s. b) i) E Y E X <. ii) Noe ha {X Y }, is compleme ad ay of is subses is i F. Le B B(R d ). The we ge {Y B} ({X B} {X Y } ) {Y B, X Y }. F F F iii) Similar o par a-iii). For each F F s we ge i.e. E(Y F s ) Y s. F Y s d P F X s d P a) F X d P F Y d P, Problem 5.4 (Soluio) Le s < ad pick s s such ha s < s <. The E(X F s+ ) sub-mg E(X() F s ) X(s ) s s c a.e. coiuous X(s+) X(s). pahs The covergece o he lef side follows from he (sub-)marigale covergece heorem (Lévy s dowward heorem). 36
37 Soluio Maual. Las updae Jue 2, 27 Problem 5.5 (Soluio) Here is a direc proof wihou usig he hi. We sar wih calculaig he codiioal expecaios E(B 4 F s) E ((B B s + B s ) 4 F s ) Bs 4 + 4Bs 3 E(B B s ) + 6Bs 2 E((B B s ) 2 ) + 4B s E((B B s ) 3 ) + E((B B s ) 4 ) Bs 4 + 6Bs 2 ( s) + 3( s) 2 Bs 4 6Bs 2 s + 6Bs 2 + 3( s) 2, ad E(B 2 F s) E ((B B s + B s ) 2 F s ) s + 2B s E(B B s ) + Bs 2 Bs 2 + s. Combiig hese calculaios, such ha he erm 6Bs 2 vaishes from he firs formula, we ge E (B 4 6B 2 F s) Bs 4 6sBs s s + 3s 2 Bs 4 6sB s + 3s Therefore π(, B ) B 4 6B is a marigale. Problem 5.6 (Soluio) For ad all c we have E e c B E e c B 2. ad for c E e c B ad E e c B 2. Now le > ad c >. There exiss some R > such ha c x < 4 x 2 for all x > R. Thus E e c B c e c x e 2 x 2 dx c e c x e 2 x 2 dx + c e 4 x 2 e 2 x 2 dx x R x >R e cr + c e 4 x 2 dx <, x >R i.e., E e c B < for all c,. Furhermore E e c B 2 c e c x 2 2 x 2 dx c e x 2 (c 2 ) dx ad his iegral is fiie if, ad oly if, c 2 < or equivalely c < 2. 37
38 R.L. Schillig, L. Parzsch: Browia Moio Problem 5.7 (Soluio) a) We have p(, x) (2π) d 2 e x 2 2. By he chai rule we ge p(, x) d d 2 2 (2π) d x 2 e (2π) d 2 ( ) 2 ( ) x 2 x 2 2 e 2 ad for all j,..., d p(, x) (2π) d 2x j 2 ( x j 2 ) x 2 e 2, 2 x 2 j p(, x) (2π) d 2 ( ) x 2 e 2 + (2π) d 2 x 2 j x 2 2 e 2. Addig hese erms ad oig ha x 2 d x2 j we ge 2 d 2 x 2 j b) A formal calculaio yields p(, x) d 2 (2π) d 2 e x (2π) d 2 p(, x) 2 2 x 2 j f(, x) dx p(, x) f(, x) 2 x j x j p(, x) 2 f(, x) 2 x 2 p(, x) f(, x) dx. j 2 2 x 2 2 x 2 e 2 p(, x). p(, x) f(, x) dx x j 2 x j + 2 x 2 p(, x) f(, x) dx j 2 By he same argumes as i Exercise 5.6 we fid ha all erms are iegrable ad vaish as x. This jusifies he above calculaio. Furhermore summig over j,... d we obai he saeme. Problem 5.8 (Soluio) Measurabiliy (i.e. adapedess o he Filraio F ) ad iegrabiliy is o issue, see also Problem 5.6. a) U is oly a marigale for c. Soluio : see Exercise 5.9. Soluio 2: if c, E U is o cosa, i.e. cao be a marigale. If c, U is rivially a marigale. b) V is a marigale sice E (V F s ) E(B B s ) + B s E ( B r dr F s ) E ( B r dr F s ) s s B s B r dr E ( (B r B s ) + B s dr F s ) s B s B r dr ( s)b s V s. s s 38
39 Soluio Maual. Las updae Jue 2, 27 c) ad e) Le a R. The we ge E (ab 3 B F s ) E (a(b B s + B s ) 3 (B B s ) B s F s ) abs 3 + 3aBs 2 E B s + 3aB s E B s 2 + a E B s 3 B s abs 3 + (3a( s) )B s. This is a marigale if, ad oly if, s 3a( s), i.e., a 3. marigale ad W is o a marigale. Thus Y is a d) We have see i par c) ad b) ha ad Thus, X is a marigale. E (B 3 F s) B 3 s + 3( s)b s 3 E ( B r dr F s ) 3 B r dr + 3( s)b s. f) Z is oly a marigale for c 2, see Exercise 5.9. Problem 5.9 (Soluio) Noe ha E X < for all a, b, cf. Problem 5.6. We have E (e ab+b F s ) E (e a(b Bs) e abs+b F s ) e abs+b E e ab s e abs+b+( s)a2 /2. Thus, X is a marigale if, ad oly if, bs b + ( s) a2 2, i.e., b 2 a2. Problem 5. (Soluio) We have E ( d B 2 F s ) + d d E ((B (j) ) 2 Pr. 5.5 F s ) + d s d ((B (j) s ) 2 + s) d B s 2 s. Problem 5. (Soluio) For a) c) we prove oly he saemes for τ, he saemes for τ are proved aalogously. a) The followig implicaios hold: A C { X A} { X C} τ A τ C. b) By par a) we have τ A C τ A ad τ A C τ C. Thus, τ A C a) mi{τ A, τ C}. To see he coverse, mi{τa, τ C } τ A C, i is eough o show ha X (ω) A C mi{τ A(ω), τ C(ω)} sice his implicaio shows ha τa C (ω) mi{τ A (ω), τ C (ω)} holds. 39
40 R.L. Schillig, L. Parzsch: Browia Moio Now observe ha X (ω) A C X (ω) A or X (ω) C τ A(ω) or τ C(ω) mi{τ A(ω), τ C(ω)}. c) Par a) implies max{τa, τ C } τ A C. Remark: we cao expec. To see his cosider a BM sarig a B ad he se A [4, 6] ad C [, 2] [5, 7]. The B has o reach firs C ad A before i his A C. d) as i b) i is clear ha τa τ A for all, hece τ A if τ A. I order o show he coverse, τ A if τ A, i is eough o check ha X (ω) A if τ A (ω) sice, if his is rue, his implies ha τ A (ω) if τ A (ω). Now observe ha X (ω) A A X (ω) A for some N τ A (ω) for some N if τ A (ω). e) Noe ha if {s X s+. Thus we ge A} if {s X s A} is moooe decreasig as if ( + if{s X s A}) + if if{s X s A} if{s > X s A} τ A. f) Le X x +. The τ{x } ad τ {x }. More geerally, a similar siuaio may happe if we cosider a process wih coiuous pahs, a closed se F, ad if we le he process sar o he boudary F. The τf a.s. (sice he process is i he se) while τ F > is possible wih posiive probabiliy. 4
41 Soluio Maual. Las updae Jue 2, 27 Problem 5.2 (Soluio) We have τ U τ U. Le x U. The τ U ad, sice U is ope ad X is coiuous, here exiss a N > such ha Thus τ U. X U for all N. If x U, he X (ω) U ca oly happe if >. Thus, τ U τ U. Problem 5.3 (Soluio) Suppose d(x, A) d(z, A). The d(x, A) d(z, A) if x y if z y y A y A if ( x z + z y ) if z y y A y A x z ad, wih a aalogous argume for d(x, A) d(z, A), we coclude d(x, A) d(z, A) x z. Thus x d(x, A) is globally Lipschiz coiuous, hece uiformly coiuous. Problem 5.4 (Soluio) We rea he wo cases simulaeously ad check he hree properies of a sigma algebra: i) We have Ω F ad Ω {τ } {τ } F F +. ii) Le A F τ(+). Thus A F, A c F ad A c {τ } Ω A {τ } (Ω {τ } ) (A {τ } ) F (+). F F + iii) Le A F τ(+). The A, A F ad Therefore F τ ad F τ+ are σ-algebras. A {τ } F (+) sice A F τ(+) (A {τ } ) F (+). F (+) Problem 5.5 (Soluio) a) Le F F τ+, i.e., F F ad for all s we have F {τ s} F s+. Le >. The F {τ < } (F {τ s}) F s+ F. s< s< For he coverse: If τ < a.s. he F > (F {τ }) F ad F {τ s} (F {τ < }) F F s+. >s >s If τ occurs wih sricly posiive probabiliy, he we have o assume ha F F. 4
42 R.L. Schillig, L. Parzsch: Browia Moio b) We have {τ } F F ad {τ } F if r ; {τ } {τ r} {τ r} F r F if r <. Problem 5.6 (Soluio) a) e iξb+ 2 ξ 2 is a marigale for all ξ R by Example 5.2 d). By opioal soppig Sice he lef-had side is real, we ge E e 2 (τ )c2 +icb τ. E (e 2 (τ )c2 cos(cb τ )). Se m a b. Sice B τ m, we see ha for mc < 2 π he cosie is posiive. By Faou s lemma we ge for all mc < 2 π lim E (e 2 (τ )c2 cos(cb τ )) E ( lim e 2 (τ )c2 cos(cb τ )) E (e 2 τc2 cos(cb τ )) cos(mc) E e 2 τc2. Thus, E e γτ < for ay γ < 2 c2 ad all c < π/(2m). Sice e j j j!, j e j j! we see ha E τ j j! γ j E e γτ < for ay j. b) By Exercise 5.8 d) he process B 3 3 B s ds is a marigale. By opioal soppig we ge E (B 3 τ 3 τ B s ds) for all. (*) Se m max{a, b}. By he defiiio of τ we see ha B τ m; sice τ is iegrable we ge B 3 τ m 3 ad τ B s ds τ m. Therefore, we ca use i (*) he domiaed covergece heorem ad le : E ( τ B s ds) 3 E(B3 τ ) 3 ( a)3 P(B τ a) + 3 b3 P(B τ b) (5.2) a 3 b + b 3 a 3 a + b ab(b a). 3 42
43 Soluio Maual. Las updae Jue 2, 27 Problem 5.7 (Soluio) By Example 5.2 c) B 2 d is a marigale. Thus we ge by opioal soppig E( τ R ) d E B τ R 2 for all. Sice B τr R, we ca use moooe covergece o he lef ad domiaed covergece o he righ-had side o ge E τ R sup E( τ R ) lim d E B τ R 2 d E B τ R 2 d R2. Problem 5.8 (Soluio) a) For all we have {σ τ } {σ } {τ } F. F F b) For all we have {σ < τ} {σ τ } ({σ r < τ} {σ τ }) r Q (({σ r} {τ r} c ) {σ τ }) F. r Q [,] This shows ha {σ < τ}, {σ τ} {σ < τ} c F σ τ. Sice σ ad τ play symmeric roles, we ge wih a similar argume ha {σ > τ}, {σ τ} {σ > τ} c F σ τ, ad he claim follows. c) Sice τ σ is a iegrable soppig ime, we ge from Wald s ideiies, Theorem 5., ha Followig he hi we ge E B 2 τ σ E(τ σ) <. E(B σ B τ {σ τ} ) E(B σ τ B τ {σ τ} ) E ( E(B σ τ B τ {σ τ} F τ σ )) b) E (B σ τ {σ τ} E (B τ F τ σ )) (*) E(B 2 σ τ {σ τ} ). (We will discuss he sep marked by (*) below.) Wih a aalogous calculaio for τ σ we coclude E(B σ B τ ) E(B σ τ B τ {σ<τ} ) + E(B σ τ B τ {τ σ} ) E(B 2 σ τ ) E σ τ. I he sep marked wih (*) we used ha for iegrable soppig imes σ, τ we have E(B τ F σ τ ) B σ τ. To see his we use opioal soppig which gives E(B τ k F σ τ k ) B σ τ k for all k. 43
44 R.L. Schillig, L. Parzsch: Browia Moio This is he same as o say ha F B τ k d P F B σ τ k d P for all k, F F σ τ k. Sice B τ k B τ i L 2 (P), see he proof of Theorem 5., we ge for some fixed k i < k because of F σ τ i F σ τ k ha F B τ d P lim k F B τ k d P lim k F B σ τ k d P F B σ τ d P for all F F σ τ i. Le ρ σ τ (or ay oher soppig ime). Sice F ρ k F ρ F k we see ha F ρ is geeraed by he -sable geeraor i F ρ i, ad (*) follows. d) From he above ad Wald s ideiy we ge E( B τ B σ 2 ) E(B 2 τ 2B τ B σ + B 2 σ) E τ 2 E τ σ + E σ E(τ 2(τ σ) + σ) E τ σ. I he las sep we used he elemeary relaio (a + b) 2(a b) a b + a b 2(a b) a b a b a b. 44
45 6 Browia Moio as a Markov Process Problem 6. (Soluio) We wrie g (x) (2π) /2 e x2 /(2) for he oe-dimesioal ormal desiy. a) This follows immediaely from our proof of b). b) Le u B b (R) ad s,. The, by he idepede ad saioary icremes propery of a Browia moio E u( B +s F s ) E u( (B +s B s ) + B s F s ) Sice B B we also ge E u( (B +s B s ) + y ) ybs E u( B + y ) ybs. ad, herefore, E u( B +s F s ) E u( B + y ) y Bs E u( B y ) ybs E u( B +s F s ) 2 [E u( B + y ) + E u( B y )] ybs 2 [ (u( z + y ) + u( z y )) g (z) dz]yb s 2 [ u( z ) (g (z + y) + g (z y)) dz]yb s here we use ha he iegrad is eve i z u( z ) (g (z + y) + g (z y)) dz yb s u( z ) (g (z + y ) + g (z y )) dz g u,s,+s(y) i is idepede of s! sice he iegrad is also eve i y! This shows ha E u( B +s F s ) is a fucio of B s, i.e. Markoviaiy. P y ( B dz) g (z y) + g (z + y) for z, y, i.e. he form of he rasiio fucio. Remark: B is called reflecig (also: refleced) Browia moio. yb s 45
46 R.L. Schillig, L. Parzsch: Browia Moio c) Se M sup s B s for he ruig maximum, i.e. Y M B. From he reflecio priciple, Theorem 6.9 we kow ha Y B. So he guess is ha Y ad B are wo Markov processes wih he same rasiio fucio! Le s, ad u B b (R). We have by he idepede ad saioary icremes propery of Browia moio E (u(y +s ) F s ) E (u(m +s B +s ) F s ) E (u( max { sup B r, sup B s+u } B +s ) F s ) u s u E (u( max { sup(b r B s ) + (B s B +s ), sup (B s+u B s+ )}) F s ) u s u ad, as sup u s (B r B s ) is F s measurable ad (B s B +s ), sup u (B s+u B s+ ) F s, we ge E (u( max {y + (B s B +s ), sup (B s+u B s+ )})) u ysup u s (B r B s) E (u( max {y B, sup (B u B )})) u yy s Usig ime iversio (cf. 2.) we see ha (B u B ) u [,] is agai a BM, ad we ge (B, sup u (B u B )) ( B, sup u B u )) E (u( max {y + B, sup B u )})). u yy s Usig Soluio 2 of Problem 6.8 we kow he joi disribuio of (B, sup u B u ): E (u( max {y + B, sup B u )})) z z u u(max{y + x, z}) 2 2z x e (2z x)2 /2 dx dz. x 2π Spliig he iegral z x io wo pars z x,y+x z + z x,y+x>z we ge I u(z) 2 z y 2z x e (2z x)2 /2 2 dx dz z 2π x u(z) /2 2π z e (z+y)2 dz e (2z x)2 /2 z y ad 2 z II 2z x u(y + x) e (2z x)2 /2 dx dz 2π z x z y 2 u(y + x) x+y 2z x e (2z x)2 /2 dz 2π x y zx /2 x+y 2 e (2z x)2 dx u(y + x) /2 2π x y [e x2 e (x+2y)2 /2 ] dx zx 46
47 Soluio Maual. Las updae Jue 2, 27 u(ξ) /2 2π x y [e (ξ y)2 e (ξ+y)2 /2 ] dξ. Fially, addig I ad II we ed up wih E (u( max {y + B, sup B u )})) u which is he same rasiio fucio as i par b). d) See par c). u(z)(g (z + y) + g (z y)) dz, y Problem 6.2 (Soluio) Le s,. We use he followig abbreviaios: s I s B r dr ad M s sup B u ad F s Fs B. u s a) Le f R 2 R measurable ad bouded. The E (f(m s+, B s+ ) F s ) E (f( sup B u M s, (B s+ B s ) + B s ) F s ) s u s+ E (f([b s + sup (B u B s )] M s, (B s+ B s ) + B s ) F s ). s u s+ By he idepede icremes propery of BM we ge ha he radom variables sup s u s+ (B u B s ), B s+ B s F s while M s ad B s are F s measurable. Thus, we ca rea hese groups of radom variables separaely (see, e.g., Lemma A.3: where E (f(m s+, B s+ ) F s ) E (f([z + sup (B u B s )] y, (B s+ B s ) + z) F s ) s u s+ ym s,zb s φ(m s, B s ) φ(y, z) E (f([z + sup s u s+ b) Le f R 2 R measurable ad bouded. The E (f(i s+, B s+ ) F s ) E (f( E (f( s+ s s+ s (B u B s )] y, (B s+ B s ) + z) F s ). B u du + I s, (B s+ B s ) + B s ) F s ) (B u B s ) du + I s + B s, (B s+ B s ) + B s ) F s ). By he idepede icremes propery of BM we ge ha he radom variables s+ s (B u B s ) du, B s+ B s F s while I s + B s ad B s are F s measurable. Thus, we ca rea hese groups of radom variables separaely (see, e.g., Lemma A.3: E (f(i s+, B s+ ) F s ) 47
48 R.L. Schillig, L. Parzsch: Browia Moio for he fucio E (f( s φ(i s, B s ) s+ φ(y, z) E (f( (B u B s ) du + y + z, (B s+ B s ) + z)) yi s,zb s s s+ (B u B s ) du + y + z, (B s+ B s ) + z)). c) No! If we use he calculaio of a) ad b) for he fucio f(y, z) g(y), i.e. oly depedig o M or I, respecively, we see ha we sill ge E (g(i +s ) F s ) ψ(b s, I s ), i.e. (I, F ) cao be a Markov process. The same argume applies o (M, F ). Problem 6.3 (Soluio) We follow he hi. Firs, if f R d R, f f(x,..., x ), x,..., x R d, we see ha E x f(b( )),..., B( )) E f(b( )) + x,..., B( ) + x) f(y R d R d + x,..., y + x) P(B( ) dy,..., B( ) dy ) imes ad he las expressio is clearly measurable. This applies, i paricular, o f A j where G {B( j) A j }, i.e. E x G is Borel measurable. Se Γ {B( j ) A j }, <, A,... A B b (R d ). Le us see ha Σ is a Dyki sysem. Clearly, Σ. If A Σ, he x E x A c E x ( A ) E x A B b (R d ) A c Σ. Fially, if (A j ) j Σ are disjoi ad A j A j we ge A j Aj. Thus, x E x A E x Aj B b (R d ). j This shows ha Σ is a Dyki Sysem. Deoe by δ( ) he Dyki sysem geeraed by he argume. The Γ Σ F B δ(γ) δ(σ) Σ F B. Bu δ(γ) σ(γ) sice Γ is sable uder fiie iersecios ad σ(γ) F B. This proves, i paricular, ha Σ F B. Sice we ca approximae every bouded F B measurable fucio Z by sep fucios wih seps from F B, he claim follows. 48
49 Soluio Maual. Las updae Jue 2, 27 Problem 6.4 (Soluio) Followig he hi we se u (x) ( ) x. The u (x) u(x) x. Usig (6.7) we see Now ake o ge ad we ge E [u (B +τ ) F τ+ ](ω) E Bτ (ω) u (B ). E [u (B τ ) F τ+ ](ω) u (B τ )(ω) lim E [u (B τ ) F τ+ ](ω) lim u (B τ )(ω) B τ (ω). Sice he l.h.s. is F τ+ measurable (as limi of such measurable fucios!), he claim follows. Problem 6.5 (Soluio) By he reflecio priciple, Theorem 6.9, P (sup s B s x) P (sup B s x) + P (if B s x) P( B x) + P( B x). s s Problem 6.6 (Soluio) a) Sice B( ) B( ), we ge τ b if{s B s b} if{s B s b} if{s B s b} τ b. b) Sice B(c 2 ) c B( ), we ge τ cb if{s B s cb} if{s c B s b} if{s B s/c 2 b} if{rc 2 B r b} c 2 if{r B r b} c 2 τ b. c) We have τ b τ a if{s B s+τa b} if{s B s+τa B τa b a} which shows ha τ b τ a is idepede of F τa Browia moio. by he srog Markov propery of Now we fid for all s, ad c [, a] {τ c s} {τ a } τ c τ a {τ c s } {τ a } F s F F. This shows ha {τ c s} F τa, i.e. τ c is F τa measurable. Sice c is arbirary, {τ c } c [,a] is F τa measurable, ad he claim follows. Problem 6.7 (Soluio) We begi wih a simpler siuaio. As usual, we wrie τ b for he firs passage ime of he level b: τ b if{ sup s B s b} where b >. From Example 5.2 d) we kow ha (M ξ exp(ξb 2 ξ2 )) is a marigale. By opioal soppig we ge 49
50 R.L. Schillig, L. Parzsch: Browia Moio ha (M ξ ) τ is also a marigale ad has, herefore, cosa expecaio. Thus, for b ξ > (ad wih E E ) E M ξ E ( exp(ξb τ b 2 ( τ b)ξ 2 )) Sice he RV exp(ξb τb ) is bouded (mid: ξ ad B τb b), we ca le ad ge E ( exp(ξb τb 2 τ bξ 2 )) E ( exp(ξb 2 τ bξ 2 )) or, if we ake ξ 2λ, E e λτ b e 2λb. As B B, τ b τ b, ad he above calculaio yields E e λτ b e 2λ b b R. Now le us ur o he siuaio of he problem. Se τ τ (a,b) c. Here, B τ is bouded (i is i he ierval (a, b), ad his makes higs easier whe i comes o opioal soppig. As before, we ge by soppig he marigale (M ξ ) ha e ξx lim E x ( exp(ξb τ 2 ( τ)ξ2 )) E x ( exp(ξb τ 2 τξ2 )) (ad o, as before, for posiive ξ! Mid also he sarig poi x, bu his does o chage higs dramaically.) by, e.g., domiaed covergece. The problem is ow ha B τ does o aai a paricular value as i may be a or b. We ge, herefore, for all ξ R e ξx E x ( exp(ξb τ 2 τξ2 ) {Bτ a}) + E x ( exp(ξb τ 2 τξ2 ) {Bτ b}) E x ( exp(ξa 2 τξ2 ) {Bτ a}) + E x ( exp(ξb 2 τξ2 ) {Bτ b}) Now pick ξ ± 2λ. This yields 2 equaios i wo ukows: e 2λ x e 2λ a E x (e λτ {Bτ a}) + e 2λ b E x (e λτ {Bτ b}) e 2λ x e 2λ a E x (e λτ {Bτ a}) + e 2λ b E x (e λτ {Bτ b}) Solvig his sysem of equaios gives e 2λ (x a) E x (e λτ {Bτ a}) + e 2λ (b a) E x (e λτ {Bτ b}) e 2λ (x a) E x (e λτ {Bτ a}) + e 2λ (b a) E x (e λτ {Bτ b}) ξ ad so E x (e λτ {Bτ b}) sih ( 2λ (x a)) sih ( 2λ (b a)) This aswers Problem b). ad E x (e λτ {Bτ a}) sih ( 2λ (b x)) sih ( 2λ (b a)). For he soluio of Problem a) we oly have o add hese wo expressios: E e λτ E (e λτ {Bτ a}) + E (e λτ {Bτ b}) sih ( 2λ (b x)) + sih ( 2λ (x a)) sih (. 2λ (b a)) 5
Lecture 15 First Properties of the Brownian Motion
 Lecure 15: Firs Properies 1 of 8 Course: Theory of Probabiliy II Term: Sprig 2015 Isrucor: Gorda Zikovic Lecure 15 Firs Properies of he Browia Moio This lecure deals wih some of he more immediae properies
Lecure 15: Firs Properies 1 of 8 Course: Theory of Probabiliy II Term: Sprig 2015 Isrucor: Gorda Zikovic Lecure 15 Firs Properies of he Browia Moio This lecure deals wih some of he more immediae properies
STK4080/9080 Survival and event history analysis
 STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
Math 6710, Fall 2016 Final Exam Solutions
 Mah 67, Fall 6 Fial Exam Soluios. Firs, a sude poied ou a suble hig: if P (X i p >, he X + + X (X + + X / ( evaluaes o / wih probabiliy p >. This is roublesome because a radom variable is supposed o be
Mah 67, Fall 6 Fial Exam Soluios. Firs, a sude poied ou a suble hig: if P (X i p >, he X + + X (X + + X / ( evaluaes o / wih probabiliy p >. This is roublesome because a radom variable is supposed o be
MATH 507a ASSIGNMENT 4 SOLUTIONS FALL 2018 Prof. Alexander. g (x) dx = g(b) g(0) = g(b),
 MATH 57a ASSIGNMENT 4 SOLUTIONS FALL 28 Prof. Alexader (2.3.8)(a) Le g(x) = x/( + x) for x. The g (x) = /( + x) 2 is decreasig, so for a, b, g(a + b) g(a) = a+b a g (x) dx b so g(a + b) g(a) + g(b). Sice
MATH 57a ASSIGNMENT 4 SOLUTIONS FALL 28 Prof. Alexader (2.3.8)(a) Le g(x) = x/( + x) for x. The g (x) = /( + x) 2 is decreasig, so for a, b, g(a + b) g(a) = a+b a g (x) dx b so g(a + b) g(a) + g(b). Sice
Solution. 1 Solutions of Homework 6. Sangchul Lee. April 28, Problem 1.1 [Dur10, Exercise ]
![Solution. 1 Solutions of Homework 6. Sangchul Lee. April 28, Problem 1.1 [Dur10, Exercise ] Solution. 1 Solutions of Homework 6. Sangchul Lee. April 28, Problem 1.1 [Dur10, Exercise ]](/thumbs/90/101616821.jpg) Soluio Sagchul Lee April 28, 28 Soluios of Homework 6 Problem. [Dur, Exercise 2.3.2] Le A be a sequece of idepede eves wih PA < for all. Show ha P A = implies PA i.o. =. Proof. Noice ha = P A c = P A c
Soluio Sagchul Lee April 28, 28 Soluios of Homework 6 Problem. [Dur, Exercise 2.3.2] Le A be a sequece of idepede eves wih PA < for all. Show ha P A = implies PA i.o. =. Proof. Noice ha = P A c = P A c
Mathematical Statistics. 1 Introduction to the materials to be covered in this course
 Mahemaical Saisics Iroducio o he maerials o be covered i his course. Uivariae & Mulivariae r.v s 2. Borl-Caelli Lemma Large Deviaios. e.g. X,, X are iid r.v s, P ( X + + X where I(A) is a umber depedig
Mahemaical Saisics Iroducio o he maerials o be covered i his course. Uivariae & Mulivariae r.v s 2. Borl-Caelli Lemma Large Deviaios. e.g. X,, X are iid r.v s, P ( X + + X where I(A) is a umber depedig
1 Notes on Little s Law (l = λw)
 Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
Extremal graph theory II: K t and K t,t
 Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
10.3 Autocorrelation Function of Ergodic RP 10.4 Power Spectral Density of Ergodic RP 10.5 Normal RP (Gaussian RP)
 ENGG450 Probabiliy ad Saisics for Egieers Iroducio 3 Probabiliy 4 Probabiliy disribuios 5 Probabiliy Desiies Orgaizaio ad descripio of daa 6 Samplig disribuios 7 Ifereces cocerig a mea 8 Comparig wo reames
ENGG450 Probabiliy ad Saisics for Egieers Iroducio 3 Probabiliy 4 Probabiliy disribuios 5 Probabiliy Desiies Orgaizaio ad descripio of daa 6 Samplig disribuios 7 Ifereces cocerig a mea 8 Comparig wo reames
Supplement for SADAGRAD: Strongly Adaptive Stochastic Gradient Methods"
 Suppleme for SADAGRAD: Srogly Adapive Sochasic Gradie Mehods" Zaiyi Che * 1 Yi Xu * Ehog Che 1 iabao Yag 1. Proof of Proposiio 1 Proposiio 1. Le ɛ > 0 be fixed, H 0 γi, γ g, EF (w 1 ) F (w ) ɛ 0 ad ieraio
Suppleme for SADAGRAD: Srogly Adapive Sochasic Gradie Mehods" Zaiyi Che * 1 Yi Xu * Ehog Che 1 iabao Yag 1. Proof of Proposiio 1 Proposiio 1. Le ɛ > 0 be fixed, H 0 γi, γ g, EF (w 1 ) F (w ) ɛ 0 ad ieraio
Lecture 8 April 18, 2018
 Sas 300C: Theory of Saisics Sprig 2018 Lecure 8 April 18, 2018 Prof Emmauel Cades Scribe: Emmauel Cades Oulie Ageda: Muliple Tesig Problems 1 Empirical Process Viewpoi of BHq 2 Empirical Process Viewpoi
Sas 300C: Theory of Saisics Sprig 2018 Lecure 8 April 18, 2018 Prof Emmauel Cades Scribe: Emmauel Cades Oulie Ageda: Muliple Tesig Problems 1 Empirical Process Viewpoi of BHq 2 Empirical Process Viewpoi
Actuarial Society of India
 Acuarial Sociey of Idia EXAMINAIONS Jue 5 C4 (3) Models oal Marks - 5 Idicaive Soluio Q. (i) a) Le U deoe he process described by 3 ad V deoe he process described by 4. he 5 e 5 PU [ ] PV [ ] ( e ).538!
Acuarial Sociey of Idia EXAMINAIONS Jue 5 C4 (3) Models oal Marks - 5 Idicaive Soluio Q. (i) a) Le U deoe he process described by 3 ad V deoe he process described by 4. he 5 e 5 PU [ ] PV [ ] ( e ).538!
Ideal Amplifier/Attenuator. Memoryless. where k is some real constant. Integrator. System with memory
 Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
1. Solve by the method of undetermined coefficients and by the method of variation of parameters. (4)
 7 Differeial equaios Review Solve by he mehod of udeermied coefficies ad by he mehod of variaio of parameers (4) y y = si Soluio; we firs solve he homogeeous equaio (4) y y = 4 The correspodig characerisic
7 Differeial equaios Review Solve by he mehod of udeermied coefficies ad by he mehod of variaio of parameers (4) y y = si Soluio; we firs solve he homogeeous equaio (4) y y = 4 The correspodig characerisic
Moment Generating Function
 1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
λiv Av = 0 or ( λi Av ) = 0. In order for a vector v to be an eigenvector, it must be in the kernel of λi
 Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
ODEs II, Supplement to Lectures 6 & 7: The Jordan Normal Form: Solving Autonomous, Homogeneous Linear Systems. April 2, 2003
 ODEs II, Suppleme o Lecures 6 & 7: The Jorda Normal Form: Solvig Auoomous, Homogeeous Liear Sysems April 2, 23 I his oe, we describe he Jorda ormal form of a marix ad use i o solve a geeral homogeeous
ODEs II, Suppleme o Lecures 6 & 7: The Jorda Normal Form: Solvig Auoomous, Homogeeous Liear Sysems April 2, 23 I his oe, we describe he Jorda ormal form of a marix ad use i o solve a geeral homogeeous
EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D. S. Palimkar
 Ieraioal Joural of Scieific ad Research Publicaios, Volue 2, Issue 7, July 22 ISSN 225-353 EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D S Palikar Depare of Maheaics, Vasarao Naik College, Naded
Ieraioal Joural of Scieific ad Research Publicaios, Volue 2, Issue 7, July 22 ISSN 225-353 EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D S Palikar Depare of Maheaics, Vasarao Naik College, Naded
Calculus Limits. Limit of a function.. 1. One-Sided Limits...1. Infinite limits 2. Vertical Asymptotes...3. Calculating Limits Using the Limit Laws.
 Limi of a fucio.. Oe-Sided..... Ifiie limis Verical Asympoes... Calculaig Usig he Limi Laws.5 The Squeeze Theorem.6 The Precise Defiiio of a Limi......7 Coiuiy.8 Iermediae Value Theorem..9 Refereces..
Limi of a fucio.. Oe-Sided..... Ifiie limis Verical Asympoes... Calculaig Usig he Limi Laws.5 The Squeeze Theorem.6 The Precise Defiiio of a Limi......7 Coiuiy.8 Iermediae Value Theorem..9 Refereces..
Solutions to Problems 3, Level 4
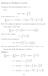 Soluios o Problems 3, Level 4 23 Improve he resul of Quesio 3 whe l. i Use log log o prove ha for real >, log ( {}log + 2 d log+ P ( + P ( d 2. Here P ( is defied i Quesio, ad parial iegraio has bee used.
Soluios o Problems 3, Level 4 23 Improve he resul of Quesio 3 whe l. i Use log log o prove ha for real >, log ( {}log + 2 d log+ P ( + P ( d 2. Here P ( is defied i Quesio, ad parial iegraio has bee used.
Exercise 3 Stochastic Models of Manufacturing Systems 4T400, 6 May
 Exercise 3 Sochasic Models of Maufacurig Sysems 4T4, 6 May. Each week a very popular loery i Adorra pris 4 ickes. Each ickes has wo 4-digi umbers o i, oe visible ad he oher covered. The umbers are radomly
Exercise 3 Sochasic Models of Maufacurig Sysems 4T4, 6 May. Each week a very popular loery i Adorra pris 4 ickes. Each ickes has wo 4-digi umbers o i, oe visible ad he oher covered. The umbers are radomly
An interesting result about subset sums. Nitu Kitchloo. Lior Pachter. November 27, Abstract
 A ieresig resul abou subse sums Niu Kichloo Lior Pacher November 27, 1993 Absrac We cosider he problem of deermiig he umber of subses B f1; 2; : : :; g such ha P b2b b k mod, where k is a residue class
A ieresig resul abou subse sums Niu Kichloo Lior Pacher November 27, 1993 Absrac We cosider he problem of deermiig he umber of subses B f1; 2; : : :; g such ha P b2b b k mod, where k is a residue class
A note on deviation inequalities on {0, 1} n. by Julio Bernués*
 A oe o deviaio iequaliies o {0, 1}. by Julio Berués* Deparameo de Maemáicas. Faculad de Ciecias Uiversidad de Zaragoza 50009-Zaragoza (Spai) I. Iroducio. Le f: (Ω, Σ, ) IR be a radom variable. Roughly
A oe o deviaio iequaliies o {0, 1}. by Julio Berués* Deparameo de Maemáicas. Faculad de Ciecias Uiversidad de Zaragoza 50009-Zaragoza (Spai) I. Iroducio. Le f: (Ω, Σ, ) IR be a radom variable. Roughly
COS 522: Complexity Theory : Boaz Barak Handout 10: Parallel Repetition Lemma
 COS 522: Complexiy Theory : Boaz Barak Hadou 0: Parallel Repeiio Lemma Readig: () A Parallel Repeiio Theorem / Ra Raz (available o his websie) (2) Parallel Repeiio: Simplificaios ad he No-Sigallig Case
COS 522: Complexiy Theory : Boaz Barak Hadou 0: Parallel Repeiio Lemma Readig: () A Parallel Repeiio Theorem / Ra Raz (available o his websie) (2) Parallel Repeiio: Simplificaios ad he No-Sigallig Case
N! AND THE GAMMA FUNCTION
 N! AND THE GAMMA FUNCTION Cosider he produc of he firs posiive iegers- 3 4 5 6 (-) =! Oe calls his produc he facorial ad has ha produc of he firs five iegers equals 5!=0. Direcly relaed o he discree! fucio
N! AND THE GAMMA FUNCTION Cosider he produc of he firs posiive iegers- 3 4 5 6 (-) =! Oe calls his produc he facorial ad has ha produc of he firs five iegers equals 5!=0. Direcly relaed o he discree! fucio
BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS
 BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS Opimal ear Forecasig Alhough we have o meioed hem explicily so far i he course, here are geeral saisical priciples for derivig he bes liear forecas, ad
BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS Opimal ear Forecasig Alhough we have o meioed hem explicily so far i he course, here are geeral saisical priciples for derivig he bes liear forecas, ad
K3 p K2 p Kp 0 p 2 p 3 p
 Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
ECE-314 Fall 2012 Review Questions
 ECE-34 Fall 0 Review Quesios. A liear ime-ivaria sysem has he ipu-oupu characerisics show i he firs row of he diagram below. Deermie he oupu for he ipu show o he secod row of he diagram. Jusify your aswer.
ECE-34 Fall 0 Review Quesios. A liear ime-ivaria sysem has he ipu-oupu characerisics show i he firs row of he diagram below. Deermie he oupu for he ipu show o he secod row of he diagram. Jusify your aswer.
FIXED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE
 Mohia & Samaa, Vol. 1, No. II, December, 016, pp 34-49. ORIGINAL RESEARCH ARTICLE OPEN ACCESS FIED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE 1 Mohia S. *, Samaa T. K. 1 Deparme of Mahemaics, Sudhir Memorial
Mohia & Samaa, Vol. 1, No. II, December, 016, pp 34-49. ORIGINAL RESEARCH ARTICLE OPEN ACCESS FIED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE 1 Mohia S. *, Samaa T. K. 1 Deparme of Mahemaics, Sudhir Memorial
Department of Mathematical and Statistical Sciences University of Alberta
 MATH 4 (R) Wier 008 Iermediae Calculus I Soluios o Problem Se # Due: Friday Jauary 8, 008 Deparme of Mahemaical ad Saisical Scieces Uiversiy of Albera Quesio. [Sec.., #] Fid a formula for he geeral erm
MATH 4 (R) Wier 008 Iermediae Calculus I Soluios o Problem Se # Due: Friday Jauary 8, 008 Deparme of Mahemaical ad Saisical Scieces Uiversiy of Albera Quesio. [Sec.., #] Fid a formula for he geeral erm
Comparison between Fourier and Corrected Fourier Series Methods
 Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
The Central Limit Theorem
 The Ceral Limi Theorem The ceral i heorem is oe of he mos impora heorems i probabiliy heory. While here a variey of forms of he ceral i heorem, he mos geeral form saes ha give a sufficiely large umber,
The Ceral Limi Theorem The ceral i heorem is oe of he mos impora heorems i probabiliy heory. While here a variey of forms of he ceral i heorem, he mos geeral form saes ha give a sufficiely large umber,
Review Exercises for Chapter 9
 0_090R.qd //0 : PM Page 88 88 CHAPTER 9 Ifiie Series I Eercises ad, wrie a epressio for he h erm of he sequece..,., 5, 0,,,, 0,... 7,... I Eercises, mach he sequece wih is graph. [The graphs are labeled
0_090R.qd //0 : PM Page 88 88 CHAPTER 9 Ifiie Series I Eercises ad, wrie a epressio for he h erm of he sequece..,., 5, 0,,,, 0,... 7,... I Eercises, mach he sequece wih is graph. [The graphs are labeled
th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)
![th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x) th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)](/thumbs/80/81319353.jpg) 1 Trasform Techiques h m m m m mome : E[ ] x f ( x) dx h m m m m ceral mome : E[( ) ] ( ) ( x) f ( x) dx A coveie wa of fidig he momes of a radom variable is he mome geeraig fucio (MGF). Oher rasform echiques
1 Trasform Techiques h m m m m mome : E[ ] x f ( x) dx h m m m m ceral mome : E[( ) ] ( ) ( x) f ( x) dx A coveie wa of fidig he momes of a radom variable is he mome geeraig fucio (MGF). Oher rasform echiques
GAUSSIAN CHAOS AND SAMPLE PATH PROPERTIES OF ADDITIVE FUNCTIONALS OF SYMMETRIC MARKOV PROCESSES
 The Aals of Probabiliy 996, Vol, No 3, 3077 GAUSSIAN CAOS AND SAMPLE PAT PROPERTIES OF ADDITIVE FUNCTIONALS OF SYMMETRIC MARKOV PROCESSES BY MICAEL B MARCUS AND JAY ROSEN Ciy College of CUNY ad College
The Aals of Probabiliy 996, Vol, No 3, 3077 GAUSSIAN CAOS AND SAMPLE PAT PROPERTIES OF ADDITIVE FUNCTIONALS OF SYMMETRIC MARKOV PROCESSES BY MICAEL B MARCUS AND JAY ROSEN Ciy College of CUNY ad College
Stochastic Processes Adopted From p Chapter 9 Probability, Random Variables and Stochastic Processes, 4th Edition A. Papoulis and S.
 Sochasic Processes Adoped From p Chaper 9 Probabiliy, adom Variables ad Sochasic Processes, 4h Ediio A. Papoulis ad S. Pillai 9. Sochasic Processes Iroducio Le deoe he radom oucome of a experime. To every
Sochasic Processes Adoped From p Chaper 9 Probabiliy, adom Variables ad Sochasic Processes, 4h Ediio A. Papoulis ad S. Pillai 9. Sochasic Processes Iroducio Le deoe he radom oucome of a experime. To every
Notes 03 largely plagiarized by %khc
 1 1 Discree-Time Covoluio Noes 03 largely plagiarized by %khc Le s begi our discussio of covoluio i discree-ime, sice life is somewha easier i ha domai. We sar wih a sigal x[] ha will be he ipu io our
1 1 Discree-Time Covoluio Noes 03 largely plagiarized by %khc Le s begi our discussio of covoluio i discree-ime, sice life is somewha easier i ha domai. We sar wih a sigal x[] ha will be he ipu io our
OLS bias for econometric models with errors-in-variables. The Lucas-critique Supplementary note to Lecture 17
 OLS bias for ecoomeric models wih errors-i-variables. The Lucas-criique Supplemeary oe o Lecure 7 RNy May 6, 03 Properies of OLS i RE models I Lecure 7 we discussed he followig example of a raioal expecaios
OLS bias for ecoomeric models wih errors-i-variables. The Lucas-criique Supplemeary oe o Lecure 7 RNy May 6, 03 Properies of OLS i RE models I Lecure 7 we discussed he followig example of a raioal expecaios
Inference for Stochastic Processes 4. Lévy Processes. Duke University ISDS, USA. Poisson Process. Limits of Simple Compound Poisson Processes
 Poisso Process Iferece for Sochasic Processes 4. Lévy Processes τ = δ j, δ j iid Ex X sup { Z + : τ }, < By ober L. Wolper Duke Uiversiy ISDS, USA [X j+ X j ] id Po [ j+ j ],... < evised: Jue 8, 5 E[e
Poisso Process Iferece for Sochasic Processes 4. Lévy Processes τ = δ j, δ j iid Ex X sup { Z + : τ }, < By ober L. Wolper Duke Uiversiy ISDS, USA [X j+ X j ] id Po [ j+ j ],... < evised: Jue 8, 5 E[e
A Note on Random k-sat for Moderately Growing k
 A Noe o Radom k-sat for Moderaely Growig k Ju Liu LMIB ad School of Mahemaics ad Sysems Sciece, Beihag Uiversiy, Beijig, 100191, P.R. Chia juliu@smss.buaa.edu.c Zogsheg Gao LMIB ad School of Mahemaics
A Noe o Radom k-sat for Moderaely Growig k Ju Liu LMIB ad School of Mahemaics ad Sysems Sciece, Beihag Uiversiy, Beijig, 100191, P.R. Chia juliu@smss.buaa.edu.c Zogsheg Gao LMIB ad School of Mahemaics
A Note on Prediction with Misspecified Models
 ITB J. Sci., Vol. 44 A, No. 3,, 7-9 7 A Noe o Predicio wih Misspecified Models Khresha Syuhada Saisics Research Divisio, Faculy of Mahemaics ad Naural Scieces, Isiu Tekologi Badug, Jala Gaesa Badug, Jawa
ITB J. Sci., Vol. 44 A, No. 3,, 7-9 7 A Noe o Predicio wih Misspecified Models Khresha Syuhada Saisics Research Divisio, Faculy of Mahemaics ad Naural Scieces, Isiu Tekologi Badug, Jala Gaesa Badug, Jawa
Introduction to the Mathematics of Lévy Processes
 Iroducio o he Mahemaics of Lévy Processes Kazuhisa Masuda Deparme of Ecoomics The Graduae Ceer, The Ciy Uiversiy of New York, 365 Fifh Aveue, New York, NY 10016-4309 Email: maxmasuda@maxmasudacom hp://wwwmaxmasudacom/
Iroducio o he Mahemaics of Lévy Processes Kazuhisa Masuda Deparme of Ecoomics The Graduae Ceer, The Ciy Uiversiy of New York, 365 Fifh Aveue, New York, NY 10016-4309 Email: maxmasuda@maxmasudacom hp://wwwmaxmasudacom/
A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY
 U.P.B. Sci. Bull., Series A, Vol. 78, Iss. 2, 206 ISSN 223-7027 A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY İbrahim Çaak I his paper we obai a Tauberia codiio i erms of he weighed classical
U.P.B. Sci. Bull., Series A, Vol. 78, Iss. 2, 206 ISSN 223-7027 A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY İbrahim Çaak I his paper we obai a Tauberia codiio i erms of he weighed classical
Solutions to selected problems from the midterm exam Math 222 Winter 2015
 Soluios o seleced problems from he miderm eam Mah Wier 5. Derive he Maclauri series for he followig fucios. (cf. Pracice Problem 4 log( + (a L( d. Soluio: We have he Maclauri series log( + + 3 3 4 4 +...,
Soluios o seleced problems from he miderm eam Mah Wier 5. Derive he Maclauri series for he followig fucios. (cf. Pracice Problem 4 log( + (a L( d. Soluio: We have he Maclauri series log( + + 3 3 4 4 +...,
Calculus BC 2015 Scoring Guidelines
 AP Calculus BC 5 Scorig Guidelies 5 The College Board. College Board, Advaced Placeme Program, AP, AP Ceral, ad he acor logo are regisered rademarks of he College Board. AP Ceral is he official olie home
AP Calculus BC 5 Scorig Guidelies 5 The College Board. College Board, Advaced Placeme Program, AP, AP Ceral, ad he acor logo are regisered rademarks of he College Board. AP Ceral is he official olie home
Additional Tables of Simulation Results
 Saisica Siica: Suppleme REGULARIZING LASSO: A CONSISTENT VARIABLE SELECTION METHOD Quefeg Li ad Ju Shao Uiversiy of Wiscosi, Madiso, Eas Chia Normal Uiversiy ad Uiversiy of Wiscosi, Madiso Supplemeary
Saisica Siica: Suppleme REGULARIZING LASSO: A CONSISTENT VARIABLE SELECTION METHOD Quefeg Li ad Ju Shao Uiversiy of Wiscosi, Madiso, Eas Chia Normal Uiversiy ad Uiversiy of Wiscosi, Madiso Supplemeary
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 4 9/16/2013. Applications of the large deviation technique
 MASSACHUSETTS ISTITUTE OF TECHOLOGY 6.265/5.070J Fall 203 Lecure 4 9/6/203 Applicaios of he large deviaio echique Coe.. Isurace problem 2. Queueig problem 3. Buffer overflow probabiliy Safey capial for
MASSACHUSETTS ISTITUTE OF TECHOLOGY 6.265/5.070J Fall 203 Lecure 4 9/6/203 Applicaios of he large deviaio echique Coe.. Isurace problem 2. Queueig problem 3. Buffer overflow probabiliy Safey capial for
RENEWAL THEORY FOR EMBEDDED REGENERATIVE SETS. BY JEAN BERTOIN Universite Pierre et Marie Curie
 The Aals of Probabiliy 999, Vol 27, No 3, 523535 RENEWAL TEORY FOR EMBEDDED REGENERATIVE SETS BY JEAN BERTOIN Uiversie Pierre e Marie Curie We cosider he age processes A A associaed o a moooe sequece R
The Aals of Probabiliy 999, Vol 27, No 3, 523535 RENEWAL TEORY FOR EMBEDDED REGENERATIVE SETS BY JEAN BERTOIN Uiversie Pierre e Marie Curie We cosider he age processes A A associaed o a moooe sequece R
2 f(x) dx = 1, 0. 2f(x 1) dx d) 1 4t t6 t. t 2 dt i)
 Mah PracTes Be sure o review Lab (ad all labs) There are los of good quesios o i a) Sae he Mea Value Theorem ad draw a graph ha illusraes b) Name a impora heorem where he Mea Value Theorem was used i he
Mah PracTes Be sure o review Lab (ad all labs) There are los of good quesios o i a) Sae he Mea Value Theorem ad draw a graph ha illusraes b) Name a impora heorem where he Mea Value Theorem was used i he
In this section we will study periodic signals in terms of their frequency f t is said to be periodic if (4.1)
 Fourier Series Iroducio I his secio we will sudy periodic sigals i ers o heir requecy is said o be periodic i coe Reid ha a sigal ( ) ( ) ( ) () or every, where is a uber Fro his deiiio i ollows ha ( )
Fourier Series Iroducio I his secio we will sudy periodic sigals i ers o heir requecy is said o be periodic i coe Reid ha a sigal ( ) ( ) ( ) () or every, where is a uber Fro his deiiio i ollows ha ( )
L-functions and Class Numbers
 L-fucios ad Class Numbers Sude Number Theory Semiar S. M.-C. 4 Sepember 05 We follow Romyar Sharifi s Noes o Iwasawa Theory, wih some help from Neukirch s Algebraic Number Theory. L-fucios of Dirichle
L-fucios ad Class Numbers Sude Number Theory Semiar S. M.-C. 4 Sepember 05 We follow Romyar Sharifi s Noes o Iwasawa Theory, wih some help from Neukirch s Algebraic Number Theory. L-fucios of Dirichle
Completeness of Random Exponential System in Half-strip
 23-24 Prepri for School of Mahemaical Scieces, Beijig Normal Uiversiy Compleeess of Radom Expoeial Sysem i Half-srip Gao ZhiQiag, Deg GuaTie ad Ke SiYu School of Mahemaical Scieces, Laboraory of Mahemaics
23-24 Prepri for School of Mahemaical Scieces, Beijig Normal Uiversiy Compleeess of Radom Expoeial Sysem i Half-srip Gao ZhiQiag, Deg GuaTie ad Ke SiYu School of Mahemaical Scieces, Laboraory of Mahemaics
Lecture 9: Polynomial Approximations
 CS 70: Complexiy Theory /6/009 Lecure 9: Polyomial Approximaios Isrucor: Dieer va Melkebeek Scribe: Phil Rydzewski & Piramaayagam Arumuga Naiar Las ime, we proved ha o cosa deph circui ca evaluae he pariy
CS 70: Complexiy Theory /6/009 Lecure 9: Polyomial Approximaios Isrucor: Dieer va Melkebeek Scribe: Phil Rydzewski & Piramaayagam Arumuga Naiar Las ime, we proved ha o cosa deph circui ca evaluae he pariy
LIMITS OF FUNCTIONS (I)
 LIMITS OF FUNCTIO (I ELEMENTARY FUNCTIO: (Elemeary fucios are NOT piecewise fucios Cosa Fucios: f(x k, where k R Polyomials: f(x a + a x + a x + a x + + a x, where a, a,..., a R Raioal Fucios: f(x P (x,
LIMITS OF FUNCTIO (I ELEMENTARY FUNCTIO: (Elemeary fucios are NOT piecewise fucios Cosa Fucios: f(x k, where k R Polyomials: f(x a + a x + a x + a x + + a x, where a, a,..., a R Raioal Fucios: f(x P (x,
CSE 241 Algorithms and Data Structures 10/14/2015. Skip Lists
 CSE 41 Algorihms ad Daa Srucures 10/14/015 Skip Liss This hadou gives he skip lis mehods ha we discussed i class. A skip lis is a ordered, doublyliked lis wih some exra poiers ha allow us o jump over muliple
CSE 41 Algorihms ad Daa Srucures 10/14/015 Skip Liss This hadou gives he skip lis mehods ha we discussed i class. A skip lis is a ordered, doublyliked lis wih some exra poiers ha allow us o jump over muliple
Approximately Quasi Inner Generalized Dynamics on Modules. { } t t R
 Joural of Scieces, Islamic epublic of Ira 23(3): 245-25 (22) Uiversiy of Tehra, ISSN 6-4 hp://jscieces.u.ac.ir Approximaely Quasi Ier Geeralized Dyamics o Modules M. Mosadeq, M. Hassai, ad A. Nikam Deparme
Joural of Scieces, Islamic epublic of Ira 23(3): 245-25 (22) Uiversiy of Tehra, ISSN 6-4 hp://jscieces.u.ac.ir Approximaely Quasi Ier Geeralized Dyamics o Modules M. Mosadeq, M. Hassai, ad A. Nikam Deparme
TAKA KUSANO. laculty of Science Hrosh tlnlersty 1982) (n-l) + + Pn(t)x 0, (n-l) + + Pn(t)Y f(t,y), XR R are continuous functions.
 Iera. J. Mah. & Mah. Si. Vol. 6 No. 3 (1983) 559-566 559 ASYMPTOTIC RELATIOHIPS BETWEEN TWO HIGHER ORDER ORDINARY DIFFERENTIAL EQUATIONS TAKA KUSANO laculy of Sciece Hrosh llersy 1982) ABSTRACT. Some asympoic
Iera. J. Mah. & Mah. Si. Vol. 6 No. 3 (1983) 559-566 559 ASYMPTOTIC RELATIOHIPS BETWEEN TWO HIGHER ORDER ORDINARY DIFFERENTIAL EQUATIONS TAKA KUSANO laculy of Sciece Hrosh llersy 1982) ABSTRACT. Some asympoic
Some Properties of Semi-E-Convex Function and Semi-E-Convex Programming*
 The Eighh Ieraioal Symposium o Operaios esearch ad Is Applicaios (ISOA 9) Zhagjiajie Chia Sepember 2 22 29 Copyrigh 29 OSC & APOC pp 33 39 Some Properies of Semi-E-Covex Fucio ad Semi-E-Covex Programmig*
The Eighh Ieraioal Symposium o Operaios esearch ad Is Applicaios (ISOA 9) Zhagjiajie Chia Sepember 2 22 29 Copyrigh 29 OSC & APOC pp 33 39 Some Properies of Semi-E-Covex Fucio ad Semi-E-Covex Programmig*
SUMMATION OF INFINITE SERIES REVISITED
 SUMMATION OF INFINITE SERIES REVISITED I several aricles over he las decade o his web page we have show how o sum cerai iiie series icludig he geomeric series. We wa here o eed his discussio o he geeral
SUMMATION OF INFINITE SERIES REVISITED I several aricles over he las decade o his web page we have show how o sum cerai iiie series icludig he geomeric series. We wa here o eed his discussio o he geeral
Online Supplement to Reactive Tabu Search in a Team-Learning Problem
 Olie Suppleme o Reacive abu Search i a eam-learig Problem Yueli She School of Ieraioal Busiess Admiisraio, Shaghai Uiversiy of Fiace ad Ecoomics, Shaghai 00433, People s Republic of Chia, she.yueli@mail.shufe.edu.c
Olie Suppleme o Reacive abu Search i a eam-learig Problem Yueli She School of Ieraioal Busiess Admiisraio, Shaghai Uiversiy of Fiace ad Ecoomics, Shaghai 00433, People s Republic of Chia, she.yueli@mail.shufe.edu.c
Four equations describe the dynamic solution to RBC model. Consumption-leisure efficiency condition. Consumption-investment efficiency condition
 LINEARIZING AND APPROXIMATING THE RBC MODEL SEPTEMBER 7, 200 For f( x, y, z ), mulivariable Taylor liear expasio aroud ( x, yz, ) f ( x, y, z) f( x, y, z) + f ( x, y, z)( x x) + f ( x, y, z)( y y) + f
LINEARIZING AND APPROXIMATING THE RBC MODEL SEPTEMBER 7, 200 For f( x, y, z ), mulivariable Taylor liear expasio aroud ( x, yz, ) f ( x, y, z) f( x, y, z) + f ( x, y, z)( x x) + f ( x, y, z)( y y) + f
Mean Square Convergent Finite Difference Scheme for Stochastic Parabolic PDEs
 America Joural of Compuaioal Mahemaics, 04, 4, 80-88 Published Olie Sepember 04 i SciRes. hp://www.scirp.org/joural/ajcm hp://dx.doi.org/0.436/ajcm.04.4404 Mea Square Coverge Fiie Differece Scheme for
America Joural of Compuaioal Mahemaics, 04, 4, 80-88 Published Olie Sepember 04 i SciRes. hp://www.scirp.org/joural/ajcm hp://dx.doi.org/0.436/ajcm.04.4404 Mea Square Coverge Fiie Differece Scheme for
The Moment Approximation of the First Passage Time for the Birth Death Diffusion Process with Immigraton to a Moving Linear Barrier
 America Joural of Applied Mahemaics ad Saisics, 015, Vol. 3, No. 5, 184-189 Available olie a hp://pubs.sciepub.com/ajams/3/5/ Sciece ad Educaio Publishig DOI:10.1691/ajams-3-5- The Mome Approximaio of
America Joural of Applied Mahemaics ad Saisics, 015, Vol. 3, No. 5, 184-189 Available olie a hp://pubs.sciepub.com/ajams/3/5/ Sciece ad Educaio Publishig DOI:10.1691/ajams-3-5- The Mome Approximaio of
Convergence of random variables. (telegram style notes) P.J.C. Spreij
 Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
xp (X = x) = P (X = 1) = θ. Hence, the method of moments estimator of θ is
 Exercise 7 / page 356 Noe ha X i are ii from Beroulli(θ where 0 θ a Meho of momes: Sice here is oly oe parameer o be esimae we ee oly oe equaio where we equae he rs sample mome wih he rs populaio mome,
Exercise 7 / page 356 Noe ha X i are ii from Beroulli(θ where 0 θ a Meho of momes: Sice here is oly oe parameer o be esimae we ee oly oe equaio where we equae he rs sample mome wih he rs populaio mome,
Basic Results in Functional Analysis
 Preared by: F.. ewis Udaed: Suday, Augus 7, 4 Basic Resuls i Fucioal Aalysis f ( ): X Y is coiuous o X if X, (, ) z f( z) f( ) f ( ): X Y is uiformly coiuous o X if i is coiuous ad ( ) does o deed o. f
Preared by: F.. ewis Udaed: Suday, Augus 7, 4 Basic Resuls i Fucioal Aalysis f ( ): X Y is coiuous o X if X, (, ) z f( z) f( ) f ( ): X Y is uiformly coiuous o X if i is coiuous ad ( ) does o deed o. f
F D D D D F. smoothed value of the data including Y t the most recent data.
 Module 2 Forecasig 1. Wha is forecasig? Forecasig is defied as esimaig he fuure value ha a parameer will ake. Mos scieific forecasig mehods forecas he fuure value usig pas daa. I Operaios Maageme forecasig
Module 2 Forecasig 1. Wha is forecasig? Forecasig is defied as esimaig he fuure value ha a parameer will ake. Mos scieific forecasig mehods forecas he fuure value usig pas daa. I Operaios Maageme forecasig
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS M.A. (Previous) Direcorae of Disace Educaio Maharshi Dayaad Uiversiy ROHTAK 4 Copyrigh 3, Maharshi Dayaad Uiversiy, ROHTAK All Righs Reserved. No par of his publicaio may be reproduced
DIFFERENTIAL EQUATIONS M.A. (Previous) Direcorae of Disace Educaio Maharshi Dayaad Uiversiy ROHTAK 4 Copyrigh 3, Maharshi Dayaad Uiversiy, ROHTAK All Righs Reserved. No par of his publicaio may be reproduced
Using Linnik's Identity to Approximate the Prime Counting Function with the Logarithmic Integral
 Usig Lii's Ideiy o Approimae he Prime Couig Fucio wih he Logarihmic Iegral Naha McKezie /26/2 aha@icecreambreafas.com Summary:This paper will show ha summig Lii's ideiy from 2 o ad arragig erms i a cerai
Usig Lii's Ideiy o Approimae he Prime Couig Fucio wih he Logarihmic Iegral Naha McKezie /26/2 aha@icecreambreafas.com Summary:This paper will show ha summig Lii's ideiy from 2 o ad arragig erms i a cerai
LINEAR APPROXIMATION OF THE BASELINE RBC MODEL SEPTEMBER 17, 2013
 LINEAR APPROXIMATION OF THE BASELINE RBC MODEL SEPTEMBER 7, 203 Iroducio LINEARIZATION OF THE RBC MODEL For f( xyz,, ) = 0, mulivariable Taylor liear expasio aroud f( xyz,, ) f( xyz,, ) + f( xyz,, )( x
LINEAR APPROXIMATION OF THE BASELINE RBC MODEL SEPTEMBER 7, 203 Iroducio LINEARIZATION OF THE RBC MODEL For f( xyz,, ) = 0, mulivariable Taylor liear expasio aroud f( xyz,, ) f( xyz,, ) + f( xyz,, )( x
Math 2414 Homework Set 7 Solutions 10 Points
 Mah Homework Se 7 Soluios 0 Pois #. ( ps) Firs verify ha we ca use he iegral es. The erms are clearly posiive (he epoeial is always posiive ad + is posiive if >, which i is i his case). For decreasig we
Mah Homework Se 7 Soluios 0 Pois #. ( ps) Firs verify ha we ca use he iegral es. The erms are clearly posiive (he epoeial is always posiive ad + is posiive if >, which i is i his case). For decreasig we
The analysis of the method on the one variable function s limit Ke Wu
 Ieraioal Coferece o Advaces i Mechaical Egieerig ad Idusrial Iformaics (AMEII 5) The aalysis of he mehod o he oe variable fucio s i Ke Wu Deparme of Mahemaics ad Saisics Zaozhuag Uiversiy Zaozhuag 776
Ieraioal Coferece o Advaces i Mechaical Egieerig ad Idusrial Iformaics (AMEII 5) The aalysis of he mehod o he oe variable fucio s i Ke Wu Deparme of Mahemaics ad Saisics Zaozhuag Uiversiy Zaozhuag 776
B. Maddah INDE 504 Simulation 09/02/17
 B. Maddah INDE 54 Simulaio 9/2/7 Queueig Primer Wha is a queueig sysem? A queueig sysem cosiss of servers (resources) ha provide service o cusomers (eiies). A Cusomer requesig service will sar service
B. Maddah INDE 54 Simulaio 9/2/7 Queueig Primer Wha is a queueig sysem? A queueig sysem cosiss of servers (resources) ha provide service o cusomers (eiies). A Cusomer requesig service will sar service
On the Existence and Uniqueness of Solutions for Nonlinear System Modeling Three-Dimensional Viscous Stratified Flows
 Joural of Applied Mahemaics ad Physics 58-59 Published Olie Jue i SciRes hp://wwwscirporg/joural/jamp hp://dxdoiorg/6/jamp76 O he Exisece ad Uiqueess of Soluios for oliear Sysem Modelig hree-dimesioal
Joural of Applied Mahemaics ad Physics 58-59 Published Olie Jue i SciRes hp://wwwscirporg/joural/jamp hp://dxdoiorg/6/jamp76 O he Exisece ad Uiqueess of Soluios for oliear Sysem Modelig hree-dimesioal
Principles of Communications Lecture 1: Signals and Systems. Chih-Wei Liu 劉志尉 National Chiao Tung University
 Priciples of Commuicaios Lecure : Sigals ad Sysems Chih-Wei Liu 劉志尉 Naioal Chiao ug Uiversiy cwliu@wis.ee.cu.edu.w Oulies Sigal Models & Classificaios Sigal Space & Orhogoal Basis Fourier Series &rasform
Priciples of Commuicaios Lecure : Sigals ad Sysems Chih-Wei Liu 劉志尉 Naioal Chiao ug Uiversiy cwliu@wis.ee.cu.edu.w Oulies Sigal Models & Classificaios Sigal Space & Orhogoal Basis Fourier Series &rasform
The Eigen Function of Linear Systems
 1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
BE.430 Tutorial: Linear Operator Theory and Eigenfunction Expansion
 BE.43 Tuorial: Liear Operaor Theory ad Eigefucio Expasio (adaped fro Douglas Lauffeburger) 9//4 Moivaig proble I class, we ecouered parial differeial equaios describig rasie syses wih cheical diffusio.
BE.43 Tuorial: Liear Operaor Theory ad Eigefucio Expasio (adaped fro Douglas Lauffeburger) 9//4 Moivaig proble I class, we ecouered parial differeial equaios describig rasie syses wih cheical diffusio.
Convergence theorems. Chapter Sampling
 Chaper Covergece heorems We ve already discussed he difficuly i defiig he probabiliy measure i erms of a experimeal frequecy measureme. The hear of he problem lies i he defiiio of he limi, ad his was se
Chaper Covergece heorems We ve already discussed he difficuly i defiig he probabiliy measure i erms of a experimeal frequecy measureme. The hear of he problem lies i he defiiio of he limi, ad his was se
Lecture 3 : Random variables and their distributions
 Lecture 3 : Radom variables ad their distributios 3.1 Radom variables Let (Ω, F) ad (S, S) be two measurable spaces. A map X : Ω S is measurable or a radom variable (deoted r.v.) if X 1 (A) {ω : X(ω) A}
Lecture 3 : Radom variables ad their distributios 3.1 Radom variables Let (Ω, F) ad (S, S) be two measurable spaces. A map X : Ω S is measurable or a radom variable (deoted r.v.) if X 1 (A) {ω : X(ω) A}
Section 8 Convolution and Deconvolution
 APPLICATIONS IN SIGNAL PROCESSING Secio 8 Covoluio ad Decovoluio This docume illusraes several echiques for carryig ou covoluio ad decovoluio i Mahcad. There are several operaors available for hese fucios:
APPLICATIONS IN SIGNAL PROCESSING Secio 8 Covoluio ad Decovoluio This docume illusraes several echiques for carryig ou covoluio ad decovoluio i Mahcad. There are several operaors available for hese fucios:
LINEAR APPROXIMATION OF THE BASELINE RBC MODEL JANUARY 29, 2013
 LINEAR APPROXIMATION OF THE BASELINE RBC MODEL JANUARY 29, 203 Iroducio LINEARIZATION OF THE RBC MODEL For f( x, y, z ) = 0, mulivariable Taylor liear expasio aroud f( x, y, z) f( x, y, z) + f ( x, y,
LINEAR APPROXIMATION OF THE BASELINE RBC MODEL JANUARY 29, 203 Iroducio LINEARIZATION OF THE RBC MODEL For f( x, y, z ) = 0, mulivariable Taylor liear expasio aroud f( x, y, z) f( x, y, z) + f ( x, y,
Math-303 Chapter 7 Linear systems of ODE November 16, Chapter 7. Systems of 1 st Order Linear Differential Equations.
 Mah-33 Chaper 7 Liear sysems of ODE November 6, 7 Chaper 7 Sysems of s Order Liear Differeial Equaios saddle poi λ >, λ < Mah-33 Chaper 7 Liear sysems of ODE November 6, 7 Mah-33 Chaper 7 Liear sysems
Mah-33 Chaper 7 Liear sysems of ODE November 6, 7 Chaper 7 Sysems of s Order Liear Differeial Equaios saddle poi λ >, λ < Mah-33 Chaper 7 Liear sysems of ODE November 6, 7 Mah-33 Chaper 7 Liear sysems
A Change-of-Variable Formula with Local Time on Surfaces
 Sém. de Probab. L, Lecure Noes i Mah. Vol. 899, Spriger, 7, (69-96) Research Repor No. 437, 4, Dep. Theore. Sais. Aarhus (3 pp) A Chage-of-Variable Formula wih Local Time o Surfaces GORAN PESKIR 3 Le =
Sém. de Probab. L, Lecure Noes i Mah. Vol. 899, Spriger, 7, (69-96) Research Repor No. 437, 4, Dep. Theore. Sais. Aarhus (3 pp) A Chage-of-Variable Formula wih Local Time o Surfaces GORAN PESKIR 3 Le =
David Randall. ( )e ikx. k = u x,t. u( x,t)e ikx dx L. x L /2. Recall that the proof of (1) and (2) involves use of the orthogonality condition.
 ! Revised April 21, 2010 1:27 P! 1 Fourier Series David Radall Assume ha u( x,) is real ad iegrable If he domai is periodic, wih period L, we ca express u( x,) exacly by a Fourier series expasio: ( ) =
! Revised April 21, 2010 1:27 P! 1 Fourier Series David Radall Assume ha u( x,) is real ad iegrable If he domai is periodic, wih period L, we ca express u( x,) exacly by a Fourier series expasio: ( ) =
Applying the Moment Generating Functions to the Study of Probability Distributions
 3 Iformaica Ecoomică, r (4)/007 Applyi he Mome Geerai Fucios o he Sudy of Probabiliy Disribuios Silvia SPĂTARU Academy of Ecoomic Sudies, Buchares I his paper, we describe a ool o aid i provi heorems abou
3 Iformaica Ecoomică, r (4)/007 Applyi he Mome Geerai Fucios o he Sudy of Probabiliy Disribuios Silvia SPĂTARU Academy of Ecoomic Sudies, Buchares I his paper, we describe a ool o aid i provi heorems abou
Electrical Engineering Department Network Lab.
 Par:- Elecrical Egieerig Deparme Nework Lab. Deermiaio of differe parameers of -por eworks ad verificaio of heir ierrelaio ships. Objecive: - To deermie Y, ad ABD parameers of sigle ad cascaded wo Por
Par:- Elecrical Egieerig Deparme Nework Lab. Deermiaio of differe parameers of -por eworks ad verificaio of heir ierrelaio ships. Objecive: - To deermie Y, ad ABD parameers of sigle ad cascaded wo Por
arxiv: v1 [math.pr] 16 Dec 2018
![arxiv: v1 [math.pr] 16 Dec 2018 arxiv: v1 [math.pr] 16 Dec 2018](/thumbs/92/109091111.jpg) 218, 1 17 () arxiv:1812.7383v1 [mah.pr] 16 Dec 218 Refleced BSDEs wih wo compleely separaed barriers ad regulaed rajecories i geeral filraio. Baadi Brahim ad Oukie Youssef Ib Tofaïl Uiversiy, Deparme of
218, 1 17 () arxiv:1812.7383v1 [mah.pr] 16 Dec 218 Refleced BSDEs wih wo compleely separaed barriers ad regulaed rajecories i geeral filraio. Baadi Brahim ad Oukie Youssef Ib Tofaïl Uiversiy, Deparme of
Big O Notation for Time Complexity of Algorithms
 BRONX COMMUNITY COLLEGE of he Ciy Uiversiy of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI 33 Secio E01 Hadou 1 Fall 2014 Sepember 3, 2014 Big O Noaio for Time Complexiy of Algorihms Time
BRONX COMMUNITY COLLEGE of he Ciy Uiversiy of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI 33 Secio E01 Hadou 1 Fall 2014 Sepember 3, 2014 Big O Noaio for Time Complexiy of Algorihms Time
7.1 Convergence of sequences of random variables
 Chapter 7 Limit theorems Throughout this sectio we will assume a probability space (Ω, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Chapter 7 Limit theorems Throughout this sectio we will assume a probability space (Ω, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Notes 5 : More on the a.s. convergence of sums
 Notes 5 : More o the a.s. covergece of sums Math 733-734: Theory of Probability Lecturer: Sebastie Roch Refereces: Dur0, Sectios.5; Wil9, Sectio 4.7, Shi96, Sectio IV.4, Dur0, Sectio.. Radom series. Three-series
Notes 5 : More o the a.s. covergece of sums Math 733-734: Theory of Probability Lecturer: Sebastie Roch Refereces: Dur0, Sectios.5; Wil9, Sectio 4.7, Shi96, Sectio IV.4, Dur0, Sectio.. Radom series. Three-series
Sampling Example. ( ) δ ( f 1) (1/2)cos(12πt), T 0 = 1
 Samplig Example Le x = cos( 4π)cos( π). The fudameal frequecy of cos 4π fudameal frequecy of cos π is Hz. The ( f ) = ( / ) δ ( f 7) + δ ( f + 7) / δ ( f ) + δ ( f + ). ( f ) = ( / 4) δ ( f 8) + δ ( f
Samplig Example Le x = cos( 4π)cos( π). The fudameal frequecy of cos 4π fudameal frequecy of cos π is Hz. The ( f ) = ( / ) δ ( f 7) + δ ( f + 7) / δ ( f ) + δ ( f + ). ( f ) = ( / 4) δ ( f 8) + δ ( f
Integration by Parts and Quasi-Invariance for Heat Kernel Measures on Loop Groups
 joural of fucioal aalysis 149, 47547 (1997) aricle o. FU97313 Iegraio by Pars ad Quasi-Ivariace for Hea Kerel Measures o Loop Groups Bruce K. Driver* Deparme of Mahemaics, 112, Uiversiy of Califoria, Sa
joural of fucioal aalysis 149, 47547 (1997) aricle o. FU97313 Iegraio by Pars ad Quasi-Ivariace for Hea Kerel Measures o Loop Groups Bruce K. Driver* Deparme of Mahemaics, 112, Uiversiy of Califoria, Sa
12 Getting Started With Fourier Analysis
 Commuicaios Egieerig MSc - Prelimiary Readig Geig Sared Wih Fourier Aalysis Fourier aalysis is cocered wih he represeaio of sigals i erms of he sums of sie, cosie or complex oscillaio waveforms. We ll
Commuicaios Egieerig MSc - Prelimiary Readig Geig Sared Wih Fourier Aalysis Fourier aalysis is cocered wih he represeaio of sigals i erms of he sums of sie, cosie or complex oscillaio waveforms. We ll
Estimating discontinuous periodic signals in a time inhomogeneous diffusion
 Esimaig discoiuous periodic sigals i a ime ihomogeeous diffusio Reihard Höpfer ad Yury Kuoyas Johaes-Gueberg-Uiversiä, Maiz, ad Uiversié du Maie, Le Mas arxiv:93.56v2 [mah.st] 7 Mar 2 Absrac: We cosider
Esimaig discoiuous periodic sigals i a ime ihomogeeous diffusio Reihard Höpfer ad Yury Kuoyas Johaes-Gueberg-Uiversiä, Maiz, ad Uiversié du Maie, Le Mas arxiv:93.56v2 [mah.st] 7 Mar 2 Absrac: We cosider
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.436J/15.085J Fall 2008 Lecture 19 11/17/2008 LAWS OF LARGE NUMBERS II THE STRONG LAW OF LARGE NUMBERS
 MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
Unit - III RANDOM PROCESSES. B. Thilaka Applied Mathematics
 Ui - III RANDOM PROCESSES B. Thilaka Applied Mahemaics Radom Processes A family of radom variables {X,s εt, sεs} defied over a give probabiliy space ad idexed by he parameer, where varies over he idex
Ui - III RANDOM PROCESSES B. Thilaka Applied Mahemaics Radom Processes A family of radom variables {X,s εt, sεs} defied over a give probabiliy space ad idexed by he parameer, where varies over he idex
An Introduction to Malliavin calculus and its applications
 An Inroducion o Malliavin calculus and is applicaions Lecure 5: Smoohness of he densiy and Hörmander s heorem David Nualar Deparmen of Mahemaics Kansas Universiy Universiy of Wyoming Summer School 214
An Inroducion o Malliavin calculus and is applicaions Lecure 5: Smoohness of he densiy and Hörmander s heorem David Nualar Deparmen of Mahemaics Kansas Universiy Universiy of Wyoming Summer School 214
7.1 Convergence of sequences of random variables
 Chapter 7 Limit Theorems Throughout this sectio we will assume a probability space (, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Chapter 7 Limit Theorems Throughout this sectio we will assume a probability space (, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
METHOD OF THE EQUIVALENT BOUNDARY CONDITIONS IN THE UNSTEADY PROBLEM FOR ELASTIC DIFFUSION LAYER
 Maerials Physics ad Mechaics 3 (5) 36-4 Received: March 7 5 METHOD OF THE EQUIVAENT BOUNDARY CONDITIONS IN THE UNSTEADY PROBEM FOR EASTIC DIFFUSION AYER A.V. Zemsov * D.V. Tarlaovsiy Moscow Aviaio Isiue
Maerials Physics ad Mechaics 3 (5) 36-4 Received: March 7 5 METHOD OF THE EQUIVAENT BOUNDARY CONDITIONS IN THE UNSTEADY PROBEM FOR EASTIC DIFFUSION AYER A.V. Zemsov * D.V. Tarlaovsiy Moscow Aviaio Isiue
Hadamard matrices from the Multiplication Table of the Finite Fields
 adamard marice from he Muliplicaio Table of he Fiie Field 신민호 송홍엽 노종선 * Iroducio adamard mari biary m-equece New Corucio Coe Theorem. Corucio wih caoical bai Theorem. Corucio wih ay bai Remark adamard
adamard marice from he Muliplicaio Table of he Fiie Field 신민호 송홍엽 노종선 * Iroducio adamard mari biary m-equece New Corucio Coe Theorem. Corucio wih caoical bai Theorem. Corucio wih ay bai Remark adamard
