Riding a Ferris Wheel
|
|
|
- Bryan Atkins
- 6 years ago
- Views:
Transcription
1 Lesson.1 Skills Practice Name ate iding a Ferris Wheel Introduction to ircles Vocabulary Identify an instance of each term in the diagram. 1. center of the circle 6. central angle T H I 2. chord 7. inscribed angle U V N P 3. secant of the circle 8. arc 4. tangent of the circle. major arc 5. point of tangency 10. minor arc 11. diameter 12. semicircle hapter Skills Practice 727
2 Lesson.1 Skills Practice page 2 Problem Set Identify the indicated part of each circle. xplain your answer NP H I N K P Point is the center of the circle. It is a point that is the same distance from each point on the circle F 5. H 6. N H L I K N P 728 hapter Skills Practice
3 Lesson.1 Skills Practice page 3 Name ate 7. SQ 8. TU Q T U S V W Identify each angle as an inscribed angle or a central angle.. U ngle U is an inscribed angle. 10. Z Z K 11. K U 12. ZKU 13. U 14. K hapter Skills Practice 72
4 Lesson.1 Skills Practice page 4 lassify each arc as a major arc, a minor arc, or a semicircle F rc is a minor arc. 17. FHI 18. L F H K I L 1. NPQ 20. TS N P S Q T U raw the part of a circle that is described. 21. raw chord. 22. raw radius. 730 hapter Skills Practice
5 Lesson.1 Skills Practice page 5 Name ate 23. raw secant H. 24. raw a tangent at point. 25. Label the point of tangency. 26. Label center. 27. raw inscribed angle F. 28. raw central angle HI. hapter Skills Practice 731
6 732 hapter Skills Practice
7 Lesson.2 Skills Practice Name ate Take the Wheel entral ngles, Inscribed ngles, and Intercepted rcs Vocabulary efine each term in your own words. 1. degree measure of a minor arc 2. adjacent arcs 3. rc ddition Postulate 4. intercepted arc 5. Inscribed ngle Theorem 6. Parallel Lines ongruent rcs Theorem hapter Skills Practice 733
8 Lesson.2 Skills Practice page 2 Problem Set etermine the measure of each minor arc The measure of is 0º. 3. F 4. H H F 5. I 6. KL 120 I K 85 L 734 hapter Skills Practice
9 Lesson.2 Skills Practice page 3 Name ate etermine the measure of each central angle. 7. m/yz 8. m/t P Y Z T m/yz m/lk 10. m/f 31 K N 72 L 30 8 F 11. m/kws 12. m/viq V 5 W S T K N 22 I Q hapter Skills Practice 735
10 Lesson.2 Skills Practice page 4 etermine the measure of each inscribed angle. 13. m YZ 14. m TU 150 Z T Q U 82 Y m YZ m/kls 16. m V V K L 112 S m Q 18. m SI Q 155 S 28 I 736 hapter Skills Practice
11 Lesson.2 Skills Practice page 5 Name ate etermine the measure of each intercepted arc. 1. m K K 20. m IU L m K L I U 21. m QW 22. m TV Q W T V 23. m m S S 0 P hapter Skills Practice 737
12 Lesson.2 Skills Practice page 6 alculate the measure of each angle. 25. The measure of is 62º. What is the measure of? 1 m 5 (m/) 5 62º 5 31º The measure of is 8º. What is the measure of? 27. The measure of / is 128º. What is the measure of /F? F 738 hapter Skills Practice
13 Lesson.2 Skills Practice page 7 Name ate 28. The measure of /H is 74º. What is the measure of /IH? H I 2. The measure of /K is 168º. What is the measure of /IK? I K 30. The measure of /KL is 148º. What is the measure of /KL? K L hapter Skills Practice 73
14 Lesson.2 Skills Practice page 8 Use the given information to answer each question. 31. In circle, m Z 5 86º. What is m WY? W Z Y m WY In circle, m W 5 102º. What is m YZ? W Y Z 33. In circle, m WZ 5 65º and m Z 5 38º. What is m W? Z W 740 hapter Skills Practice
15 Lesson.2 Skills Practice page Name ate 34. In circle, m W 5 105º. What is m WY? W Y 35. In circle, m WY 5 83º. What is m/z? W Z Y 36. In circle, m WY 5 50º and m YZ 5 30º. What is m WZ? W Z Y hapter Skills Practice 741
16 742 hapter Skills Practice
17 Lesson.3 Skills Practice Name ate anhole overs easuring ngles Inside and utside of ircles Vocabulary efine each theorem in your own words. 1. Interior ngles of a ircle Theorem 2. xterior ngles of a ircle Theorem 3. Tangent to a ircle Theorem Problem Set Write an expression for the measure of the given angle. 1. m P 2. m P N Q m P ( m 1 m QN ) hapter Skills Practice 743
18 Lesson.3 Skills Practice page 2 3. m NK 4. m UWV L N K U V W Y 5. m SWT 6. m HI S W T F V U H I List the intercepted arc(s) for the given angle. 7. Q 8. SU Q S T N P U P NP, Q 744 hapter Skills Practice
19 Lesson.3 Skills Practice page 3 Name ate. FH 10. ZW F I Y W H Z L Z Z K L Write an expression for the measure of the given angle. 13. m 14. m UY W Y m ( m 2 m ) U Z hapter Skills Practice 745
20 Lesson.3 Skills Practice page m ST 16. m F U F S V T H I 17. m 18. m LPN F H L N p Q 746 hapter Skills Practice
21 Lesson.3 Skills Practice page 5 Name ate reate a proof to prove each statement. 1. iven: hords and intersect at point. Prove: m ( m 1 m ) Statements easons 1. hords and intersect at 1. iven point. 2. raw chord 2. onstruction 3. m 1 5 m 1 m 3. xterior ngle Theorem 4. m 5 2 m 4. Inscribed ngle Theorem 1 5. m 5 2 m m 5 2 m 1 2 m 7. m ( m 1 m ) 5. Inscribed ngle Theorem 6. Substitution 7. istributive Property hapter Skills Practice 747
22 Lesson.3 Skills Practice page iven: Secant QT and tangent S intersect at point S. Prove: m QS 5 1 ( 2 m Q 2 m T ) Q P T S 748 hapter Skills Practice
23 Lesson.3 Skills Practice page 7 Name ate 21. iven: Tangents VY and Y intersect at point Y. Prove: m Y ( m VW 2 m V ) V Y W hapter Skills Practice 74
24 Lesson.3 Skills Practice page iven: hords FI and H intersect at point. Prove: m FH ( m FH 1 m I ) F H I 750 hapter Skills Practice
25 Lesson.3 Skills Practice page Name ate 23. iven: Secant L and tangent NL intersect at point L. Prove: m L ( m 2 m K ) K L N hapter Skills Practice 751
26 Lesson.3 Skills Practice page iven: Tangents S and U intersect at point. Prove: m ( m VTW 2 m VW ) T S U V W 752 hapter Skills Practice
27 Lesson.3 Skills Practice page 11 Name ate Use the diagram shown to determine the measure of each angle or arc. 25. etermine m FI. m/k 5 20 m 5 80 F K 26. etermine m KL. m K m N K I The measure 1 of arc FI is 120 degrees. m/k 5 2 (m FI 5 m ) (m FI 2 80) 40 5 m FI 2 80 m FI L N hapter Skills Practice 753
28 Lesson.3 Skills Practice page etermine m. m VW 5 50 m TU etermine m WY. m WUY W T U S U V W Y Z 754 hapter Skills Practice
29 Lesson.3 Skills Practice page 13 Name ate 2. etermine m S. m UV 5 30 m/ts 5 80 S 30. etermine m. m Z m 5 30 Z T U V hapter Skills Practice 755
30 756 hapter Skills Practice
31 Lesson.4 Skills Practice Name ate olor Theory hords Vocabulary atch each definition with its corresponding term. 1. iameter hord Theorem a. If two chords of the same circle or congruent circles are congruent, then their corresponding arcs are congruent. 2. quidistant hord Theorem b. The segments formed on a chord when two chords of a circle intersect 3. quidistant hord c. If two chords of the same circle or congruent onverse Theorem circles are congruent, then they are equidistant from the center of the circle. 4. ongruent hord ongruent d. If two arcs of the same circle or congruent rc Theorem circles are congruent, then their corresponding chords are congruent. 5. ongruent hord ongruent rc e. If two chords of the same circle or congruent onverse Theorem circles are equidistant from the center of the circle, then the chords are congruent. 6. segments of a chord f. If two chords of a circle intersect, then the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments in the second chord. 7. Segment hord Theorem g. If a diameter of a circle is perpendicular to a chord, then the diameter bisects the chord and bisects the arc determined by the chord. hapter Skills Practice 757
32 Lesson.4 Skills Practice page 2 Problem Set Use the given information to answer each question. xplain your answer. 1. If diameter bisects, what is the angle of intersection? The angle of intersection is 0º because diameters that bisect chords are perpendicular bisectors. 2. If diameter FH intersects at a right angle, how does the length of I compare to the length of I? F I H 3. How does the measure of KL and L compare? L N K 758 hapter Skills Practice
33 Lesson.4 Skills Practice page 3 Name ate 4. If KP > LN, how does the length of Q compare to the length of? K L Q P N 5. If Y > Z, what is the relationship between TU and V? S U Y T V Z W 6. If > H and diameter is perpendicular to both, what is the relationship between F and HK? I H F K hapter Skills Practice 75
34 Lesson.4 Skills Practice page 4 etermine each measurement. 7. If is a diameter, what is the length of? 5 cm cm 8. If the length of is 13 millimeters, what is the length of?. If the length of is 24 centimeters, what is the length of? 10. If the length of F is 32 inches, what is the length of H? F H 760 hapter Skills Practice
35 Lesson.4 Skills Practice page 5 Name ate 11. If the measure of 5 155º, what is the measure of? 12. If segment is a diameter, what is the measure of? ompare each measurement. xplain your answer. 13. If > F, how does the measure of and F compare? F The measure of is equal to the measure of F because the corresponding arcs of congruent chords are congruent. hapter Skills Practice 761
36 Lesson.4 Skills Practice page If K > L, how does the measure of L and K compare? K L 15. If Q > PS, how does the measure of QP and PS compare? Q P S 16. If > H, how does the measure of and H compare? F H 762 hapter Skills Practice
37 Lesson.4 Skills Practice page 7 Name ate 17. If >, what is the relationship between and? 18. If H > F, what is the relationship between H and F? H F Use each diagram and the Segment hord Theorem to write an equation involving the segments of the chords. 1. F 20. L Q P N H? 5 F? H hapter Skills Practice 763
38 Lesson.4 Skills Practice page T V 22. S K H V 23. I 24. Y U L V 764 hapter Skills Practice
39 Lesson.5 Skills Practice Name ate Solar clipses Tangents and Secants Vocabulary Write the term from the box that best completes each statement. external secant segment Secant Segment Theorem tangent segment secant segment Secant Tangent Theorem Tangent Segment Theorem 1. (n) is the segment that is formed from an exterior point of a circle to the point of tangency. 2. The states that if two tangent segments are drawn from the same point on the exterior of the circle, then the tangent segments are congruent. 3. When two secants intersect in the exterior of a circle, the segment that begins at the point of intersection, continues through the circle, and ends on the other side of the circle is called a(n). 4. When two secants intersect in the exterior of a circle, the segment that begins at the point of intersection and ends where the secant enters the circle is called a(n). 5. The states that if two secants intersect in the exterior of a circle, then the product of the lengths of the secant segment and its external secant segment is equal to the product of the lengths of the second secant segment and its external secant segment. 6. The states that if a tangent and a secant intersect in the exterior of a circle, then the product of the lengths of the secant segment and its external secant segment is equal to the square of the length of the tangent segment. hapter Skills Practice 765
40 Lesson.5 Skills Practice page 2 Problem Set alculate the measure of each angle. xplain your reasoning. 1. If is a radius, what is the measure of /? The measure of angle is 0 degrees because a tangent line and the radius that ends at the point of tangency are perpendicular. 2. If is a radius, what is the measure of /? 3. If Y is a radius, what is the measure of / Y? Y 766 hapter Skills Practice
41 Lesson.5 Skills Practice page 3 Name ate 4. If S is a tangent segment and S is a radius, what is the measure of /S? 35 S 5. If UT is a tangent segment and U is a radius, what is the measure of /TU? 23 T U hapter Skills Practice 767
42 Lesson.5 Skills Practice page 4 6. If V W is a tangent segment and V is a radius, what is the measure of /VW? V 72 W Write a statement to show the congruent segments. 7. and are tangent to circle. 8. Z and ZW are tangent to circle. Z W >. S and T are tangent to circle. 10. P and NP are tangent to circle. S N T P 768 hapter Skills Practice
43 Lesson.5 Skills Practice page 5 Name ate 11. and F are tangent to circle. 12. H and I are tangent to circle. H F I alculate the measure of each angle. xplain your reasoning. 13. If F and F are tangent segments, what is the measure of /F? F 64 The measure of angle F is 58 degrees. I know triangle F is isosceles and its base angles are congruent. Let x represent the measure of angle F and the measure of angle F. m/f 1 x 1 x x x x 5 58 hapter Skills Practice 76
44 Lesson.5 Skills Practice page If HI and I are tangent segments, what is the measure of /HI? H 48 I 15. If K and L are tangent segments, what is the measure of /KL? K L hapter Skills Practice
45 Lesson.5 Skills Practice page 7 Name ate 16. If NP and QP are tangent segments, what is the measure of /NPQ? P N 71 Q 17. If F and VF are tangent segments, what is the measure of / VF? V 22 F hapter Skills Practice 771
46 Lesson.5 Skills Practice page If T and T are tangent segments, what is the measure of /T? 33 T Name two secant segments and two external secant segments for circle. 1. P Q 20. T S Secant segments: PT and QT xternal secant segments: T and ST 21. U V W 22. L N P Y 772 hapter Skills Practice
47 Lesson.5 Skills Practice page Name ate 23. F 24. H N I K L Use each diagram and the Secant Segment Theorem to write an equation involving the secant segments. 25. S T U V 26. N Q S V? TV 5 SV? UV I H K L hapter Skills Practice 773
48 Lesson.5 Skills Practice page V F W Y Z Name a tangent segment, a secant segment, and an external secant segment for circle. 31. S T 32. I U H K Tangent segment: TU Secant segment: T xternal secant segment: ST 33. F 34. P Q S 774 hapter Skills Practice
49 Lesson.5 Skills Practice page 11 Name ate 35. H 36. W y F Z Use each diagram and the Secant Tangent Theorem to write an equation involving the secant and tangent segments Q W S V ( ) 2 5 Q? W 3. Z 40. T I hapter Skills Practice 775
50 Lesson.5 Skills Practice page U 42. V Q l W 776 hapter Skills Practice
Skills Practice Skills Practice for Lesson 11.1
Skills Practice Skills Practice for Lesson.1 Name ate Riding a Ferris Wheel Introduction to ircles Vocabulary Identify an instance of each term in the diagram. 1. circle X T 2. center of the circle H I
Riding a Ferris Wheel. Students should be able to answer these questions after Lesson 10.1:
.1 Riding a Ferris Wheel Introduction to ircles Students should be able to answer these questions after Lesson.1: What are the parts of a circle? How are the parts of a circle drawn? Read Question 1 and
Assignment. Riding a Ferris Wheel Introduction to Circles. 1. For each term, name all of the components of circle Y that are examples of the term.
ssignment ssignment for Lesson.1 Name Date Riding a Ferris Wheel Introduction to ircles 1. For each term, name all of the components of circle Y that are examples of the term. G R Y O T M a. hord GM, R,
radii: AP, PR, PB diameter: AB chords: AB, CD, AF secant: AG or AG tangent: semicircles: ACB, ARB minor arcs: AC, AR, RD, BC,
h 6 Note Sheets L Shortened Key Note Sheets hapter 6: iscovering and roving ircle roperties eview: ircles Vocabulary If you are having problems recalling the vocabulary, look back at your notes for Lesson
Ready To Go On? Skills Intervention 11-1 Lines That Intersect Circles
Name ate lass STION 11 Ready To Go On? Skills Intervention 11-1 Lines That Intersect ircles ind these vocabulary words in Lesson 11-1 and the Multilingual Glossary. Vocabulary interior of a circle exterior
Lesson 12.1 Skills Practice
Lesson 12.1 Skills Practice Introduction to ircles ircle, Radius, and iameter Vocabulary efine each term in your own words. 1. circle circle is a collection of points on the same plane equidistant from
2 Explain 1 Proving the Intersecting Chords Angle Measure Theorem
xplain 1 Proving the Intersecting hords ngle easure Theorem In the xplore section, you discovered the effects that line segments, such as chords and secants, have on angle measures and their intercepted
Study Guide. Exploring Circles. Example: Refer to S for Exercises 1 6.
9 1 Eploring ircles A circle is the set of all points in a plane that are a given distance from a given point in the plane called the center. Various parts of a circle are labeled in the figure at the
C=2πr C=πd. Chapter 10 Circles Circles and Circumference. Circumference: the distance around the circle
10.1 Circles and Circumference Chapter 10 Circles Circle the locus or set of all points in a plane that are A equidistant from a given point, called the center When naming a circle you always name it by
Review for Grade 9 Math Exam - Unit 8 - Circle Geometry
Name: Review for Grade 9 Math Exam - Unit 8 - ircle Geometry Date: Multiple hoice Identify the choice that best completes the statement or answers the question. 1. is the centre of this circle and point
Introduction Circle Some terms related with a circle
141 ircle Introduction In our day-to-day life, we come across many objects which are round in shape, such as dials of many clocks, wheels of a vehicle, bangles, key rings, coins of denomination ` 1, `
Assignment. Riding a Ferris Wheel Introduction to Circles. 1. For each term, name all of the components of circle Y that are examples of the term.
ssignment ssignment for Lesson.1 Name Date Riding a Ferris Wheel Introduction to Circles 1. For each term, name all of the components of circle Y that are examples of the term. G R Y O T M a. Chord b.
Chords and Arcs. Objectives To use congruent chords, arcs, and central angles To use perpendicular bisectors to chords
- hords and rcs ommon ore State Standards G-.. Identify and describe relationships among inscribed angles, radii, and chords. M, M bjectives To use congruent chords, arcs, and central angles To use perpendicular
UNIT OBJECTIVES. unit 9 CIRCLES 259
UNIT 9 ircles Look around whatever room you are in and notice all the circular shapes. Perhaps you see a clock with a circular face, the rim of a cup or glass, or the top of a fishbowl. ircles have perfect
Circles. II. Radius - a segment with one endpoint the center of a circle and the other endpoint on the circle.
Circles Circles and Basic Terminology I. Circle - the set of all points in a plane that are a given distance from a given point (called the center) in the plane. Circles are named by their center. II.
Replacement for a Carpenter s Square
Lesson.1 Skills Practice Name Date Replacement for a arpenter s Square Inscribed and ircumscribed Triangles and Quadrilaterals Vocabulary nswer each question. 1. How are inscribed polygons and circumscribed
10-1 Study Guide and Intervention
opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. NM I 10-1 tudy Guide and Intervention ircles and ircumference arts of ircles circle consists of all points in a plane that are
Geo - CH11 Practice Test
Geo - H11 Practice Test Multiple hoice Identify the choice that best completes the statement or answers the question. 1. Identify the secant that intersects ñ. a. c. b. l d. 2. satellite rotates 50 miles
Page 1 Central Angles & Arc Measures
Geometry/Trig Unit 8 ll bout ircles! Name: ate: Page 1 entral ngles & rc Measures Example 1: JK is a diameter of ircle. Name two examples for each: K Minor rc:, Major rc:, M Semicircle:, Name Pair of djacent
What is the longest chord?.
Section: 7-6 Topic: ircles and rcs Standard: 7 & 21 ircle Naming a ircle Name: lass: Geometry 1 Period: Date: In a plane, a circle is equidistant from a given point called the. circle is named by its.
Honors Geometry Circle Investigation - Instructions
Honors Geometry ircle Investigation - Instructions 1. On the first circle a. onnect points and O with a line segment. b. onnect points O and also. c. Measure O. d. Estimate the degree measure of by using
Solve problems involving tangents to a circle. Solve problems involving chords of a circle
8UNIT ircle Geometry What You ll Learn How to Solve problems involving tangents to a circle Solve problems involving chords of a circle Solve problems involving the measures of angles in a circle Why Is
Chapter 10. Properties of Circles
Chapter 10 Properties of Circles 10.1 Use Properties of Tangents Objective: Use properties of a tangent to a circle. Essential Question: how can you verify that a segment is tangent to a circle? Terminology:
SM2H Unit 6 Circle Notes
Name: Period: SM2H Unit 6 Circle Notes 6.1 Circle Vocabulary, Arc and Angle Measures Circle: All points in a plane that are the same distance from a given point, called the center of the circle. Chord:
Unit 10 Geometry Circles. NAME Period
Unit 10 Geometry Circles NAME Period 1 Geometry Chapter 10 Circles ***In order to get full credit for your assignments they must me done on time and you must SHOW ALL WORK. *** 1. (10-1) Circles and Circumference
Lesson 1.7 circles.notebook. September 19, Geometry Agenda:
Geometry genda: Warm-up 1.6(need to print of and make a word document) ircle Notes 1.7 Take Quiz if you were not in class on Friday Remember we are on 1.7 p.72 not lesson 1.8 1 Warm up 1.6 For Exercises
Using Chords. Essential Question What are two ways to determine when a chord is a diameter of a circle?
10.3 Using hords ssential uestion What are two ways to determine when a chord is a diameter of a circle? rawing iameters OOKI O UU o be proficient in math, you need to look closely to discern a pattern
Tangent Lines Unit 10 Lesson 1 Example 1: Tell how many common tangents the circles have and draw them.
Tangent Lines Unit 10 Lesson 1 EQ: How can you verify that a segment is tangent to a circle? Circle: Center: Radius: Chord: Diameter: Secant: Tangent: Tangent Lines Unit 10 Lesson 1 Example 1: Tell how
Chapter 1. Some Basic Theorems. 1.1 The Pythagorean Theorem
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a 2 + b 2 = c 2. roof. b a a 3 2 b 2 b 4 b a b
Using Properties of Segments that Intersect Circles
ig Idea 1 H UY I I Using roperties of egments that Intersect ircles or Your otebook You learned several relationships between tangents, secants, and chords. ome of these relationships can help you determine
Answers. Chapter10 A Start Thinking. and 4 2. Sample answer: no; It does not pass through the center.
hapter10 10.1 Start Thinking 6. no; is not a right triangle because the side lengths do not satisf the Pthagorean Theorem (Thm. 9.1). 1. (3, ) 7. es; is a right triangle because the side lengths satisf
Chapter 6. Worked-Out Solutions. Chapter 6 Maintaining Mathematical Proficiency (p. 299)
hapter 6 hapter 6 Maintaining Mathematical Proficiency (p. 99) 1. Slope perpendicular to y = 1 x 5 is. y = x + b 1 = + b 1 = 9 + b 10 = b n equation of the line is y = x + 10.. Slope perpendicular to y
MODULE. (40 + 8x) + (5x -16) = 180. STUDY GUIDE REVIEW Angles and Segments in Circles. Key Vocabulary
STUDY GUIDE REVIEW Angles and Segments in ircles ODULE 15 Essential Question: How can you use angles and segments in circles to solve real-world problems? EY EXALE (Lesson 15.1) Determine m DE, m BD, m
Chapter-wise questions
hapter-wise questions ircles 1. In the given figure, is circumscribing a circle. ind the length of. 3 15cm 5 2. In the given figure, is the center and. ind the radius of the circle if = 18 cm and = 3cm
Mth 076: Applied Geometry (Individualized Sections) MODULE FOUR STUDY GUIDE
Mth 076: pplied Geometry (Individualized Sections) MODULE FOUR STUDY GUIDE INTRODUTION TO GEOMETRY Pick up Geometric Formula Sheet (This sheet may be used while testing) ssignment Eleven: Problems Involving
Circles in Neutral Geometry
Everything we do in this set of notes is Neutral. Definitions: 10.1 - Circles in Neutral Geometry circle is the set of points in a plane which lie at a positive, fixed distance r from some fixed point.
If the measure ofaacb is less than 180, then A, B, and all the points on C that lie in the
age 1 of 7 11.3 rcs and entral ngles oal Use properties of arcs of circles. Key Words minor arc major arc semicircle congruent circles congruent arcs arc length ny two points and on a circle determine
Geometry: A Complete Course
eometry: omplete ourse with rigonometry) odule - tudent Worket Written by: homas. lark Larry. ollins 4/2010 or ercises 20 22, use the diagram below. 20. ssume is a rectangle. a) f is 6, find. b) f is,
4. 2 common tangents 5. 1 common tangent common tangents 7. CE 2 0 CD 2 1 DE 2
hapter 0 opright b Mcougal Littell, a division of Houghton Mifflin ompan. Prerequisite Skills (p. 648). Two similar triangles have congruent corresponding angles and proportional corresponding sides..
Int. Geometry Units 1-6 Review 1
Int. Geometry Units 1-6 Review 1 Things to note about this review and the Unit 1-6 Test: 1. This review packet covers major ideas of the first six units, but it does not show examples of all types of problems..
Theorem 1.2 (Converse of Pythagoras theorem). If the lengths of the sides of ABC satisfy a 2 + b 2 = c 2, then the triangle has a right angle at C.
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
15.5 Angle Relationships in Circles
ame lass ate 15.5 ngle Relationships in ircles ssential uestion: What are the relationships between angles formed by lines that intersect a circle? xplore xploring ngle Measures in ircles The sundial is
Objectives To find the measure of an inscribed angle To find the measure of an angle formed by a tangent and a chord
1-3 Inscribed ngles ommon ore State Standards G-.. Identify and describe relationships among inscribed angles, radii, and chords. lso G-..3, G-..4 M 1, M 3, M 4, M 6 bjectives To find the measure of an
1 = 1, b d and c d. Chapter 7. Worked-Out Solutions Chapter 7 Maintaining Mathematical Proficiency (p. 357) Slope of line b:
hapter 7 aintaining athematical Proficienc (p. 357) 1. (7 x) = 16 (7 x) = 16 7 x = 7 = 7 x = 3 x 1 = 3 1 x = 3. 7(1 x) + = 19 = 7(1 x) = 1 7(1 x) 7 = 1 7 1 x = 3 1 = 1 x = x 1 = 1 x = 3. 3(x 5) + 8(x 5)
MT - GEOMETRY - SEMI PRELIM - II : PAPER - 5
017 1100 MT MT - GEOMETRY - SEMI PRELIM - II : PPER - 5 Time : Hours Model nswer Paper Max. Marks : 40.1. ttempt NY FIVE of the following : (i) X In XYZ, ray YM bisects XYZ XY YZ XM MZ Y Z [Property of
10.3 Start Thinking Warm Up Cumulative Review Warm Up
10.3 tart hinking etermine if the statement is always true, sometimes true, or never true. plain your reasoning. 1. chord is a diameter. 2. diameter is a chord. 3. chord and a radius have the same measure.
Circles-Tangent Properties
15 ircles-tangent roperties onstruction of tangent at a point on the circle. onstruction of tangents when the angle between radii is given. Tangents from an external point - construction and proof Touching
MT EDUCARE LTD. MATHEMATICS SUBJECT : Q L M ICSE X. Geometry STEP UP ANSWERSHEET
IS X MT UR LT. SUJT : MTHMTIS Geometry ST U NSWRSHT 003 1. In QL and RM, LQ MR [Given] LQ RM [Given] QL ~ RM [y axiom of similarity] (i) Since, QL ~ RM QL M L RM QL RM L M (ii) In QL and RQ, we have Q
Evaluate: Homework and Practice
valuate: Homework and Practice Identify the chord (s), inscribed angle (s), and central angle (s) in the figure. The center of the circles in xercises 1, 2, and 4 is. Online Homework Hints and Help xtra
MT - MATHEMATICS (71) GEOMETRY - PRELIM II - PAPER - 1 (E)
04 00 eat No. MT - MTHEMTI (7) GEOMETY - PELIM II - PPE - (E) Time : Hours (Pages 3) Max. Marks : 40 Note : (i) ll questions are compulsory. Use of calculator is not allowed. Q.. olve NY FIVE of the following
Pre-Test. Use the following figure to answer Questions 1 through 6. B C. 1. What is the center of the circle? The center of the circle is point G.
Pre-Test Name Date Use the following figure to answer Questions 1 through 6. A B C F G E D 1. What is the center of the circle? The center of the circle is point G. 2. Name a radius of the circle. A radius
THEOREM 10.3 B C In the same circle, or in congruent circles, two minor arcs are congruent if and only if their corresponding chords are congruent.
10.3 Your Notes pply Properties of hords oal p Use relationships of arcs and chords in a circle. HOM 10.3 In the same circle, or in congruent circles, two minor arcs are congruent if and only if their
Arcs and Inscribed Angles of Circles
Arcs and Inscribed Angles of Circles Inscribed angles have: Vertex on the circle Sides are chords (Chords AB and BC) Angle ABC is inscribed in the circle AC is the intercepted arc because it is created
DO NOW #1. Please: Get a circle packet
irclengles.gsp pril 26, 2013 Please: Get a circle packet Reminders: R #10 due Friday Quiz Monday 4/29 Quiz Friday 5/3 Quiz Wednesday 5/8 Quiz Friday 5/10 Initial Test Monday 5/13 ctual Test Wednesday 5/15
Name Date Period. Notes - Tangents. 1. If a line is a tangent to a circle, then it is to the
Name ate Period Notes - Tangents efinition: tangent is a line in the plane of a circle that intersects the circle in eactly one point. There are 3 Theorems for Tangents. 1. If a line is a tangent to a
Circle-Chord properties
14 ircle-hord properties onstruction of a chord of given length. Equal chords are equidistant from the centre. ngles in a segment. ongrue nt circles and concentric circles. onstruction of congruent and
Use Properties of Tangents
6.1 Georgia Performance Standard(s) MM2G3a, MM2G3d Your Notes Use Properties of Tangents Goal p Use properties of a tangent to a circle. VOULRY ircle enter Radius hord iameter Secant Tangent Example 1
Click on a topic to go to that section. Euclid defined a circle and its center in this way: Euclid defined figures in this way:
lide 1 / 59 lide / 59 New Jersey enter for eaching and Learning Progressive Mathematics Initiative his material is made freely available at www.njctl.org and is intended for the non-commercial use of students
Geometry: A Complete Course
Geometry: omplete ourse (with Trigonometry) Module - Student WorkText Written by: Thomas E. lark Larry E. ollins Geometry: omplete ourse (with Trigonometry) Module Student Worktext opyright 2014 by VideotextInteractive
10.1 Tangents to Circles. Geometry Mrs. Spitz Spring 2005
10.1 Tangents to Circles Geometry Mrs. Spitz Spring 2005 Objectives/Assignment Identify segments and lines related to circles. Use properties of a tangent to a circle. Assignment: Chapter 10 Definitions
Practice For use with pages
Name ate ON 0. ractice For use with pages 678 686 se ( to draw the described part of the circle.. raw a diameter and label it }.. raw a tangent ra and label it ###$. 3. raw a secant and label it } F. 4.
Plane geometry Circles: Problems with some Solutions
The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
1. Draw and label a diagram to illustrate the property of a tangent to a circle.
Master 8.17 Extra Practice 1 Lesson 8.1 Properties of Tangents to a Circle 1. Draw and label a diagram to illustrate the property of a tangent to a circle. 2. Point O is the centre of the circle. Points
New Jersey Center for Teaching and Learning. Progressive Mathematics Initiative
Slide 1 / 150 New Jersey Center for Teaching and Learning Progressive Mathematics Initiative This material is made freely available at www.njctl.org and is intended for the non-commercial use of students
( ) Chapter 10 Review Question Answers. Find the value of x mhg. m B = 1 2 ( 80 - x) H x G. E 30 = 80 - x. x = 50. Find m AXB and m Y A D X 56
hapter 10 Review Question nswers 1. ( ) Find the value of mhg 30 m = 1 2 ( 30) = 15 F 80 m = 1 2 ( 80 - ) H G E 30 = 80 - = 50 2. Find m X and m Y m X = 1 120 + 56 2 ( ) = 88 120 X 56 Y m Y = 1 120-56
Example 1: Finding angle measures: I ll do one: We ll do one together: You try one: ML and MN are tangent to circle O. Find the value of x
Ch 1: Circles 1 1 Tangent Lines 1 Chords and Arcs 1 3 Inscribed Angles 1 4 Angle Measures and Segment Lengths 1 5 Circles in the coordinate plane 1 1 Tangent Lines Focused Learning Target: I will be able
Geometry: A Complete Course
Geometry: omplete ourse (with Trigonometry) Module - Student WorkText Written by: Thomas. lark Larry. ollins RRT 4/2010 6. In the figure below, and share the common segment. Prove the following conditional
0110ge. Geometry Regents Exam Which expression best describes the transformation shown in the diagram below?
0110ge 1 In the diagram below of trapezoid RSUT, RS TU, X is the midpoint of RT, and V is the midpoint of SU. 3 Which expression best describes the transformation shown in the diagram below? If RS = 30
Indicate whether the statement is true or false.
PRACTICE EXAM IV Sections 6.1, 6.2, 8.1 8.4 Indicate whether the statement is true or false. 1. For a circle, the constant ratio of the circumference C to length of diameter d is represented by the number.
Reteaching , or 37.5% 360. Geometric Probability. Name Date Class
Name ate lass Reteaching Geometric Probability INV 6 You have calculated probabilities of events that occur when coins are tossed and number cubes are rolled. Now you will learn about geometric probability.
Geometry Honors Homework
Geometry Honors Homework pg. 1 12-1 Practice Form G Tangent Lines Algebra Assume that lines that appear to be tangent are tangent. O is the center of each circle. What is the value of x? 1. 2. 3. The circle
MAHESH TUTORIALS. Time : 1 hr. 15 min. Q.1. Solve the following : 3
S.S.. MHESH TUTRILS Test - II atch : S Marks : 30 Date : GEMETRY hapter : 1,, 3 Time : 1 hr. 15 min..1. Solve the following : 3 The areas of two similar triangles are 18 cm and 3 cm respectively. What
11. Concentric Circles: Circles that lie in the same plane and have the same center.
Circles Definitions KNOW THESE TERMS 1. Circle: The set of all coplanar points equidistant from a given point. 2. Sphere: The set of all points equidistant from a given point. 3. Radius of a circle: The
C Given that angle BDC = 78 0 and DCA = Find angles BAC and DBA.
UNERSTNING IRLE THEREMS-PRT NE. ommon terms: (a) R- ny portion of a circumference of a circle. (b) HR- line that crosses a circle from one point to another. If this chord passes through the centre then
Mid-Chapter Quiz: Lessons 10-1 through Refer to. 1. Name the circle. SOLUTION: The center of the circle is A. Therefore, the circle is ANSWER:
Refer to. 1. Name the circle. The center of the circle is A. Therefore, the circle is 2. Name a diameter. ; since is a chord that passes through the center, it is a diameter. 3. Name a chord that is not
b. Find the measures of the two angles formed by the chord and the tangent line.
0.5 NI NOW N I.5... ngle Relationships in ircles ssential Question When a chord intersects a tangent line or another chord, what relationships exist aong the angles and arcs fored? ngles ored by a hord
B C. You try: What is the definition of an angle bisector?
US Geometry 1 What is the definition of a midpoint? The midpoint of a line segment is the point that divides the segment into two congruent segments. That is, M is the midpoint of if M is on and M M. 1
UNIT 3 CIRCLES AND VOLUME Lesson 1: Introducing Circles Instruction
Prerequisite Skills This lesson requires the use of the following skills: performing operations with fractions understanding slope, both algebraically and graphically understanding the relationship of
Chapter 10 Worksheet 1 Name: Honors Accelerated Geometry Hour:
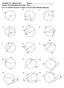hapter 10 Worksheet 1 Name: Honors ccelerated Geometry Hour: For 1-15, find the measure of angle in each of the following diagrams. 1. 2.. 258 84 140 40 4. 5. 6. 2 y 80 y 72 7. 8. 9. 50 X 40 140 4 y 10.
UNIT 1: SIMILARITY, CONGRUENCE, AND PROOFS. 1) Figure A'B'C'D'F' is a dilation of figure ABCDF by a scale factor of 1. 2 centered at ( 4, 1).
1) Figure A'B'C'D'F' is a dilation of figure ABCDF by a scale factor of 1. 2 centered at ( 4, 1). The dilation is Which statement is true? A. B. C. D. AB B' C' A' B' BC AB BC A' B' B' C' AB BC A' B' D'
Chapter 19 Exercise 19.1
hapter 9 xercise 9... (i) n axiom is a statement that is accepted but cannot be proven, e.g. x + 0 = x. (ii) statement that can be proven logically: for example, ythagoras Theorem. (iii) The logical steps
Student Exploration: Chords and Arcs
Name: ate: Student xploration: hords and rcs Vocabulary: arc, central angle, chord Prior nowledge Questions (o these BFOR using the Gizmo.) In circle to the right, and are central angles because their
Math 3 Quarter 4 Overview
Math 3 Quarter 4 Overview EO5 Rational Functions 13% EO6 Circles & Circular Functions 25% EO7 Inverse Functions 25% EO8 Normal Distribution 12% Q4 Final 10% EO5 Opp #1 Fri, Mar 24th Thu, Mar 23rd ML EO5
Lesson 7.1: Central Angles
Lesson 7.1: Central Angles Definition 5.1 Arc An arc is a part of a circle. Types of Arc 1. Minor Arc 2. Major Arc 3. Semicircle Figure 5.1 Definition 5.2 Central Angle A central angle of a circle is an
Chapter 12 Practice Test
hapter 12 Practice Test Multiple hoice Identify the choice that best completes the statement or answers the question. ssume that lines that appear to be tangent are tangent. is the center of the circle.
What You ll Learn. Why It s Important. We see circles in nature and in design. What do you already know about circles?
We see circles in nature and in design. What do you already know about circles? What You ll Learn ircle properties that relate: a tangent to a circle and the radius of the circle a chord in a circle, its
Common Core Readiness Assessment 4
ommon ore Readiness ssessment 4 1. Use the diagram and the information given to complete the missing element of the two-column proof. 2. Use the diagram and the information given to complete the missing
MT - GEOMETRY - SEMI PRELIM - II : PAPER - 4
017 1100 MT.1. ttempt NY FIVE of the following : (i) In STR, line l side TR S SQ T = RQ x 4.5 = 1.3 3.9 x = MT - GEOMETRY - SEMI RELIM - II : ER - 4 Time : Hours Model nswer aper Max. Marks : 40 4.5 1.3
Chapter 3. The angle bisectors. 3.1 The angle bisector theorem
hapter 3 The angle bisectors 3.1 The angle bisector theorem Theorem 3.1 (ngle bisector theorem). The bisectors of an angle of a triangle divide its opposite side in the ratio of the remaining sides. If
Geometry Arcs and Chords. Geometry Mr. Peebles Spring 2013
10.2 Arcs and Chords Geometry Mr. Peebles Spring 2013 Bell Ringer: Solve For r. B 16 ft. A r r 8 ft. C Bell Ringer B 16 ft. Answer A r r 8 ft. C c 2 = a 2 + b 2 Pythagorean Thm. (r + 8) 2 = r 2 + 16 2
MT - MATHEMATICS (71) GEOMETRY - PRELIM II - PAPER - 6 (E)
04 00 Seat No. MT - MTHEMTIS (7) GEOMETRY - PRELIM II - (E) Time : Hours (Pages 3) Max. Marks : 40 Note : ll questions are compulsory. Use of calculator is not allowed. Q.. Solve NY FIVE of the following
Chapter (Circle) * Circle - circle is locus of such points which are at equidistant from a fixed point in
Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
Name two radii in Circle E.
A C E B D Name two radii in Circle E. Unit 4: Prerequisite Terms A C E B D ECandED Unit 4: Prerequisite Terms A C E B D Name all chords in Circle E. Unit 4: Prerequisite Terms A C E B D AD, CD, AB Unit
0114ge. Geometry Regents Exam 0114
0114ge 1 The midpoint of AB is M(4, 2). If the coordinates of A are (6, 4), what are the coordinates of B? 1) (1, 3) 2) (2, 8) 3) (5, 1) 4) (14, 0) 2 Which diagram shows the construction of a 45 angle?
Answer Key. 9.1 Parts of Circles. Chapter 9 Circles. CK-12 Geometry Concepts 1. Answers. 1. diameter. 2. secant. 3. chord. 4.
9.1 Parts of Circles 1. diameter 2. secant 3. chord 4. point of tangency 5. common external tangent 6. common internal tangent 7. the center 8. radius 9. chord 10. The diameter is the longest chord in
Geometry Arcs and Chords. Geometry Mr. Austin
10.2 Arcs and Chords Mr. Austin Objectives/Assignment Use properties of arcs of circles, as applied. Use properties of chords of circles. Assignment: pp. 607-608 #3-47 Reminder Quiz after 10.3 and 10.5
SSC EXAMINATION GEOMETRY (SET-A)
GRND TEST SS EXMINTION GEOMETRY (SET-) SOLUTION Q. Solve any five sub-questions: [5M] ns. ns. 60 & D have equal height ( ) ( D) D D ( ) ( D) Slope of the line ns. 60 cos D [/M] [/M] tan tan 60 cos cos
Intermediate Math Circles Wednesday October Problem Set 3
The CETRE for EDUCTI in MTHEMTICS and CMPUTIG Intermediate Math Circles Wednesday ctober 24 2012 Problem Set 3.. Unless otherwise stated, any point labelled is assumed to represent the centre of the circle.
MAHESH TUTORIALS. GEOMETRY Chapter : 1, 2, 6. Time : 1 hr. 15 min. Q.1. Solve the following : 3
S.S.C. Test - III Batch : SB Marks : 0 Date : MHESH TUTORILS GEOMETRY Chapter : 1,, 6 Time : 1 hr. 15 min..1. Solve the following : (i) The dimensions of a cuboid are 5 cm, 4 cm and cm. Find its volume.
Chapter 6. Worked-Out Solutions AB 3.61 AC 5.10 BC = 5
27. onstruct a line ( DF ) with midpoint P parallel to and twice the length of QR. onstruct a line ( EF ) with midpoint R parallel to and twice the length of QP. onstruct a line ( DE ) with midpoint Q