Chapter-wise questions
|
|
|
- Ami McKinney
- 6 years ago
- Views:
Transcription
1 hapter-wise questions ircles 1. In the given figure, is circumscribing a circle. ind the length of. 3 15cm 5 2. In the given figure, is the center and. ind the radius of the circle if = 18 cm and = 3cm 3. and are two parallel chords of a circle. If = 24cm & = 18cm and distance between these chords is 21cm find the radius of the circle. 4. The radii of two concentric circles are 15cm and 41cm. The chord of larger circle cuts the smaller circle at and. ind the length of if = 24cm. 5. In the given figure and are two tangents. ind if = 49º 6. rom a point outside the circle with radius 8 cm the distance to the centre of the circle is 17cm. ind the the length of the tangent.
2 hapter-wise questions 7. Two concentric circles are of radii 6cm and 10 cm. ind the length of the chord of the larger circle which touches the smaller circle 8. In the figure and are tangents from external point. is a third tangent, 5cm touching the circle at. If = 17cm and = 5cm find. 9. In the figure is a chord of the large circle which touches the small circle at. = 8cm and radius of the small circle is 3cm find the diameter of the large circle. 10. In the figure = 84º. find. 11. In the given figure, two circles touch each other externally at. rove that the common tangent at bisects the other two common tangents. 12. In the given figure, a circle is inscribed L H in a quadrilateral in which = 90º. If = 23cm, = 29cm and = 5cm, find the radius of the circle. 13. point is 13cm from the center of the circle. The length of the tangents drawn from to the circle is 12cm. ind the radius of the circle. 14. In the given figure, X and X are tangents from to the circle with center. is a point on the circle. rove that X + = X +. X 15. how that the tangent lines drawn at the end points of the diameter of a circle are parallel.
3 hapter-wise questions 16. circle is inscribed in a triangle having sides 8cm, 10 cm and 12cm as shown in the figure. ind, and. 17. If,, are tangents in the given figure, X and = 5cm. ind the perimeter of. 18. In the given figure, is a right triangle right angled at such that = 6cm and = 8cm. ind the radius of its incircle. 19. In the given figure l and m are two parallel tangents at and. The tangent at makes an intercept between l and m. rove that = 90º l m 20. circle is touching the side of at and touching and produced at and respectively. rove that = 1 (erimeter of ) In the given figure, T = 6cm = 5cm. ind the length of. 6 cm T 5 cm rove that the lengths of the tangents drawn from an external point to a circle are equal. Using the above theorem, prove that: If quadrilateral is circumscribing a circle, then + = rove that the tangent at any point of a circle is perpendicular to the radius through the point of contact. Using the above, do the following: In the figure below, is the centre of the two concentric circles. is a chord of the larger circle touching the smaller circle at. rove that =.
4 hapter-wise questions 24. In the given figure = and = 20 find the measure of In the figure chords and of the circle intersect at 0. = 5cm, = 3cm, and = 2.5 cm. etermine length of. 26. rove that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle. Using the above, do the follwing rove that the angle formed by a chord in the major segment is acute. 27. rove that the sum of either pair of opposite angles of a cyclic quadrilateral is 180. Using the above, do the following: In figure 3, is a cyclic quadrilateral in which = (x+y+10), = (y+20), = (x+y 30) and = (x+y). ind x and y. igure In the given figure, is diameter of a circle with centre. If = 65, = 40, M = 50, find, and M M
5 hapter-wise questions 29. The sum of either pair of opposite angles of a cyclic quadrilateral is 180. rove Using the above result, in figure 2. is a cyclic quadrialteral. circle passing through and meets and in the points and respectively. rove that
Circles. Exercise 9.1
 9 uestion. Exercise 9. How many tangents can a circle have? Solution For every point of a circle, we can draw a tangent. Therefore, infinite tangents can be drawn. uestion. Fill in the blanks. (i) tangent
9 uestion. Exercise 9. How many tangents can a circle have? Solution For every point of a circle, we can draw a tangent. Therefore, infinite tangents can be drawn. uestion. Fill in the blanks. (i) tangent
Plane geometry Circles: Problems with some Solutions
 The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
Page 1
 Pacing Chart Unit Week Day CCSS Standards Objective I Can Statements 121 CCSS.MATH.CONTENT.HSG.C.A.1 Prove that all circles are similar. Prove that all circles are similar. I can prove that all circles
Pacing Chart Unit Week Day CCSS Standards Objective I Can Statements 121 CCSS.MATH.CONTENT.HSG.C.A.1 Prove that all circles are similar. Prove that all circles are similar. I can prove that all circles
LLT Education Services
 8. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle. (a) 4 cm (b) 3 cm (c) 6 cm (d) 5 cm 9. From a point P, 10 cm away from the
8. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle. (a) 4 cm (b) 3 cm (c) 6 cm (d) 5 cm 9. From a point P, 10 cm away from the
Circles. II. Radius - a segment with one endpoint the center of a circle and the other endpoint on the circle.
 Circles Circles and Basic Terminology I. Circle - the set of all points in a plane that are a given distance from a given point (called the center) in the plane. Circles are named by their center. II.
Circles Circles and Basic Terminology I. Circle - the set of all points in a plane that are a given distance from a given point (called the center) in the plane. Circles are named by their center. II.
MAHESH TUTORIALS. Time : 1 hr. 15 min. Q.1. Solve the following : 3
 S.S.. MHESH TUTRILS Test - II atch : S Marks : 30 Date : GEMETRY hapter : 1,, 3 Time : 1 hr. 15 min..1. Solve the following : 3 The areas of two similar triangles are 18 cm and 3 cm respectively. What
S.S.. MHESH TUTRILS Test - II atch : S Marks : 30 Date : GEMETRY hapter : 1,, 3 Time : 1 hr. 15 min..1. Solve the following : 3 The areas of two similar triangles are 18 cm and 3 cm respectively. What
Circles-Tangent Properties
 15 ircles-tangent roperties onstruction of tangent at a point on the circle. onstruction of tangents when the angle between radii is given. Tangents from an external point - construction and proof Touching
15 ircles-tangent roperties onstruction of tangent at a point on the circle. onstruction of tangents when the angle between radii is given. Tangents from an external point - construction and proof Touching
Chapter (Circle) * Circle - circle is locus of such points which are at equidistant from a fixed point in
 Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
C Given that angle BDC = 78 0 and DCA = Find angles BAC and DBA.
 UNERSTNING IRLE THEREMS-PRT NE. ommon terms: (a) R- ny portion of a circumference of a circle. (b) HR- line that crosses a circle from one point to another. If this chord passes through the centre then
UNERSTNING IRLE THEREMS-PRT NE. ommon terms: (a) R- ny portion of a circumference of a circle. (b) HR- line that crosses a circle from one point to another. If this chord passes through the centre then
Math & 8.7 Circle Properties 8.6 #1 AND #2 TANGENTS AND CHORDS
 Math 9 8.6 & 8.7 Circle Properties 8.6 #1 AND #2 TANGENTS AND CHORDS Property #1 Tangent Line A line that touches a circle only once is called a line. Tangent lines always meet the radius of a circle at
Math 9 8.6 & 8.7 Circle Properties 8.6 #1 AND #2 TANGENTS AND CHORDS Property #1 Tangent Line A line that touches a circle only once is called a line. Tangent lines always meet the radius of a circle at
Solve problems involving tangents to a circle. Solve problems involving chords of a circle
 8UNIT ircle Geometry What You ll Learn How to Solve problems involving tangents to a circle Solve problems involving chords of a circle Solve problems involving the measures of angles in a circle Why Is
8UNIT ircle Geometry What You ll Learn How to Solve problems involving tangents to a circle Solve problems involving chords of a circle Solve problems involving the measures of angles in a circle Why Is
Example 1: Finding angle measures: I ll do one: We ll do one together: You try one: ML and MN are tangent to circle O. Find the value of x
 Ch 1: Circles 1 1 Tangent Lines 1 Chords and Arcs 1 3 Inscribed Angles 1 4 Angle Measures and Segment Lengths 1 5 Circles in the coordinate plane 1 1 Tangent Lines Focused Learning Target: I will be able
Ch 1: Circles 1 1 Tangent Lines 1 Chords and Arcs 1 3 Inscribed Angles 1 4 Angle Measures and Segment Lengths 1 5 Circles in the coordinate plane 1 1 Tangent Lines Focused Learning Target: I will be able
Grade 9 Geometry-Overall
 ID : au-9-geometry-overall [1] Grade 9 Geometry-Overall For more such worksheets visit www.edugain.com Answer t he quest ions (1) A chord of a circle is equal to its radius. Find the angle subtended by
ID : au-9-geometry-overall [1] Grade 9 Geometry-Overall For more such worksheets visit www.edugain.com Answer t he quest ions (1) A chord of a circle is equal to its radius. Find the angle subtended by
SM2H Unit 6 Circle Notes
 Name: Period: SM2H Unit 6 Circle Notes 6.1 Circle Vocabulary, Arc and Angle Measures Circle: All points in a plane that are the same distance from a given point, called the center of the circle. Chord:
Name: Period: SM2H Unit 6 Circle Notes 6.1 Circle Vocabulary, Arc and Angle Measures Circle: All points in a plane that are the same distance from a given point, called the center of the circle. Chord:
VAISHALI EDUCATION POINT (QUALITY EDUCATION PROVIDER)
 BY:Prof. RAHUL MISHRA Class :- X QNo. VAISHALI EDUCATION POINT (QUALITY EDUCATION PROVIDER) CIRCLES Subject :- Maths General Instructions Questions M:9999907099,9818932244 1 In the adjoining figures, PQ
BY:Prof. RAHUL MISHRA Class :- X QNo. VAISHALI EDUCATION POINT (QUALITY EDUCATION PROVIDER) CIRCLES Subject :- Maths General Instructions Questions M:9999907099,9818932244 1 In the adjoining figures, PQ
Geometry: A Complete Course
 eometry: omplete ourse with rigonometry) odule - tudent Worket Written by: homas. lark Larry. ollins 4/2010 or ercises 20 22, use the diagram below. 20. ssume is a rectangle. a) f is 6, find. b) f is,
eometry: omplete ourse with rigonometry) odule - tudent Worket Written by: homas. lark Larry. ollins 4/2010 or ercises 20 22, use the diagram below. 20. ssume is a rectangle. a) f is 6, find. b) f is,
Grade 9 Circles. Answer t he quest ions. For more such worksheets visit
 ID : th-9-circles [1] Grade 9 Circles For more such worksheets visit www.edugain.com Answer t he quest ions (1) ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it
ID : th-9-circles [1] Grade 9 Circles For more such worksheets visit www.edugain.com Answer t he quest ions (1) ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it
Indicate whether the statement is true or false.
 PRACTICE EXAM IV Sections 6.1, 6.2, 8.1 8.4 Indicate whether the statement is true or false. 1. For a circle, the constant ratio of the circumference C to length of diameter d is represented by the number.
PRACTICE EXAM IV Sections 6.1, 6.2, 8.1 8.4 Indicate whether the statement is true or false. 1. For a circle, the constant ratio of the circumference C to length of diameter d is represented by the number.
1. Draw and label a diagram to illustrate the property of a tangent to a circle.
 Master 8.17 Extra Practice 1 Lesson 8.1 Properties of Tangents to a Circle 1. Draw and label a diagram to illustrate the property of a tangent to a circle. 2. Point O is the centre of the circle. Points
Master 8.17 Extra Practice 1 Lesson 8.1 Properties of Tangents to a Circle 1. Draw and label a diagram to illustrate the property of a tangent to a circle. 2. Point O is the centre of the circle. Points
CLASS IX GEOMETRY MOCK TEST PAPER
 Total time:3hrs darsha vidyalay hunashyal P. M.M=80 STION- 10 1=10 1) Name the point in a triangle that touches all sides of given triangle. Write its symbol of representation. 2) Where is thocenter of
Total time:3hrs darsha vidyalay hunashyal P. M.M=80 STION- 10 1=10 1) Name the point in a triangle that touches all sides of given triangle. Write its symbol of representation. 2) Where is thocenter of
radii: AP, PR, PB diameter: AB chords: AB, CD, AF secant: AG or AG tangent: semicircles: ACB, ARB minor arcs: AC, AR, RD, BC,
 h 6 Note Sheets L Shortened Key Note Sheets hapter 6: iscovering and roving ircle roperties eview: ircles Vocabulary If you are having problems recalling the vocabulary, look back at your notes for Lesson
h 6 Note Sheets L Shortened Key Note Sheets hapter 6: iscovering and roving ircle roperties eview: ircles Vocabulary If you are having problems recalling the vocabulary, look back at your notes for Lesson
C=2πr C=πd. Chapter 10 Circles Circles and Circumference. Circumference: the distance around the circle
 10.1 Circles and Circumference Chapter 10 Circles Circle the locus or set of all points in a plane that are A equidistant from a given point, called the center When naming a circle you always name it by
10.1 Circles and Circumference Chapter 10 Circles Circle the locus or set of all points in a plane that are A equidistant from a given point, called the center When naming a circle you always name it by
(D) (A) Q.3 To which of the following circles, the line y x + 3 = 0 is normal at the point ? 2 (A) 2
 CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
Objective Mathematics
 . In BC, if angles, B, C are in geometric seq- uence with common ratio, then is : b c a (a) (c) 0 (d) 6. If the angles of a triangle are in the ratio 4 : :, then the ratio of the longest side to the perimeter
. In BC, if angles, B, C are in geometric seq- uence with common ratio, then is : b c a (a) (c) 0 (d) 6. If the angles of a triangle are in the ratio 4 : :, then the ratio of the longest side to the perimeter
2. (i) Find the equation of the circle which passes through ( 7, 1) and has centre ( 4, 3).
 Circle 1. (i) Find the equation of the circle with centre ( 7, 3) and of radius 10. (ii) Find the centre of the circle 2x 2 + 2y 2 + 6x + 8y 1 = 0 (iii) What is the radius of the circle 3x 2 + 3y 2 + 5x
Circle 1. (i) Find the equation of the circle with centre ( 7, 3) and of radius 10. (ii) Find the centre of the circle 2x 2 + 2y 2 + 6x + 8y 1 = 0 (iii) What is the radius of the circle 3x 2 + 3y 2 + 5x
Prove that a + b = x + y. Join BD. In ABD, we have AOB = 180º AOB = 180º ( 1 + 2) AOB = 180º A
 bhilasha lasses lass- IX ate: 03- -7 SLUTIN (hap 8,9,0) 50 ob no.-947967444. The sides and of a quadrilateral are produced as shown in fig. rove that a + b = x + y. Join. In, we have y a + + = 80º = 80º
bhilasha lasses lass- IX ate: 03- -7 SLUTIN (hap 8,9,0) 50 ob no.-947967444. The sides and of a quadrilateral are produced as shown in fig. rove that a + b = x + y. Join. In, we have y a + + = 80º = 80º
10-1 Study Guide and Intervention
 opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. NM I 10-1 tudy Guide and Intervention ircles and ircumference arts of ircles circle consists of all points in a plane that are
opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. NM I 10-1 tudy Guide and Intervention ircles and ircumference arts of ircles circle consists of all points in a plane that are
Honors Geometry Circle Investigation - Instructions
 Honors Geometry ircle Investigation - Instructions 1. On the first circle a. onnect points and O with a line segment. b. onnect points O and also. c. Measure O. d. Estimate the degree measure of by using
Honors Geometry ircle Investigation - Instructions 1. On the first circle a. onnect points and O with a line segment. b. onnect points O and also. c. Measure O. d. Estimate the degree measure of by using
Study Guide. Exploring Circles. Example: Refer to S for Exercises 1 6.
 9 1 Eploring ircles A circle is the set of all points in a plane that are a given distance from a given point in the plane called the center. Various parts of a circle are labeled in the figure at the
9 1 Eploring ircles A circle is the set of all points in a plane that are a given distance from a given point in the plane called the center. Various parts of a circle are labeled in the figure at the
Mth 076: Applied Geometry (Individualized Sections) MODULE FOUR STUDY GUIDE
 Mth 076: pplied Geometry (Individualized Sections) MODULE FOUR STUDY GUIDE INTRODUTION TO GEOMETRY Pick up Geometric Formula Sheet (This sheet may be used while testing) ssignment Eleven: Problems Involving
Mth 076: pplied Geometry (Individualized Sections) MODULE FOUR STUDY GUIDE INTRODUTION TO GEOMETRY Pick up Geometric Formula Sheet (This sheet may be used while testing) ssignment Eleven: Problems Involving
UNIT 3 CIRCLES AND VOLUME Lesson 1: Introducing Circles Instruction
 Prerequisite Skills This lesson requires the use of the following skills: performing operations with fractions understanding slope, both algebraically and graphically understanding the relationship of
Prerequisite Skills This lesson requires the use of the following skills: performing operations with fractions understanding slope, both algebraically and graphically understanding the relationship of
Name. Chapter 12: Circles
 Name Chapter 12: Circles Chapter 12 Calendar Sun Mon Tue Wed Thu Fri Sat May 13 12.1 (Friday) 14 Chapter 10/11 Assessment 15 12.2 12.1 11W Due 16 12.3 12.2 HW Due 17 12.1-123 Review 12.3 HW Due 18 12.1-123
Name Chapter 12: Circles Chapter 12 Calendar Sun Mon Tue Wed Thu Fri Sat May 13 12.1 (Friday) 14 Chapter 10/11 Assessment 15 12.2 12.1 11W Due 16 12.3 12.2 HW Due 17 12.1-123 Review 12.3 HW Due 18 12.1-123
( ) Find the value of x mhg. H x G. Find m AXB and m Y A D X 56. Baroody Page 1 of 18
 1. ( ) Find the value of x mhg 30 F 80 H x G E 2. Find m X and m Y 120 X 56 Y aroody age 1 of 18 3. Find mq X 70 30 Y Q 4. Find the radius of a circle in which a 48 cm. chord is 8 cm closer to the center
1. ( ) Find the value of x mhg 30 F 80 H x G E 2. Find m X and m Y 120 X 56 Y aroody age 1 of 18 3. Find mq X 70 30 Y Q 4. Find the radius of a circle in which a 48 cm. chord is 8 cm closer to the center
Page 1 of 15. Website: Mobile:
 Exercise 10.2 Question 1: From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is (A) 7 cm (B) 12 cm (C) 15 cm (D) 24.5
Exercise 10.2 Question 1: From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is (A) 7 cm (B) 12 cm (C) 15 cm (D) 24.5
MAHESH TUTORIALS. GEOMETRY Chapter : 1, 2, 6. Time : 1 hr. 15 min. Q.1. Solve the following : 3
 S.S.C. Test - III Batch : SB Marks : 0 Date : MHESH TUTORILS GEOMETRY Chapter : 1,, 6 Time : 1 hr. 15 min..1. Solve the following : (i) The dimensions of a cuboid are 5 cm, 4 cm and cm. Find its volume.
S.S.C. Test - III Batch : SB Marks : 0 Date : MHESH TUTORILS GEOMETRY Chapter : 1,, 6 Time : 1 hr. 15 min..1. Solve the following : (i) The dimensions of a cuboid are 5 cm, 4 cm and cm. Find its volume.
(5) Find the resultant shape obtained by connecting points (0, 5) (0, 20) (25, 20) and (25, 5).
 ID : ww-9-olympiad [1] Grade 9 Olympiad For more such worksheets visit www.edugain.com Answer t he quest ions (1) If a cone and hemisphere stands on equal bases, and have the same height. Find the ratio
ID : ww-9-olympiad [1] Grade 9 Olympiad For more such worksheets visit www.edugain.com Answer t he quest ions (1) If a cone and hemisphere stands on equal bases, and have the same height. Find the ratio
+ 2gx + 2fy + c = 0 if S
 CIRCLE DEFINITIONS A circle is the locus of a point which moves in such a way that its distance from a fixed point, called the centre, is always a constant. The distance r from the centre is called the
CIRCLE DEFINITIONS A circle is the locus of a point which moves in such a way that its distance from a fixed point, called the centre, is always a constant. The distance r from the centre is called the
What is the longest chord?.
 Section: 7-6 Topic: ircles and rcs Standard: 7 & 21 ircle Naming a ircle Name: lass: Geometry 1 Period: Date: In a plane, a circle is equidistant from a given point called the. circle is named by its.
Section: 7-6 Topic: ircles and rcs Standard: 7 & 21 ircle Naming a ircle Name: lass: Geometry 1 Period: Date: In a plane, a circle is equidistant from a given point called the. circle is named by its.
MT - GEOMETRY - SEMI PRELIM - II : PAPER - 4
 017 1100 MT.1. ttempt NY FIVE of the following : (i) In STR, line l side TR S SQ T = RQ x 4.5 = 1.3 3.9 x = MT - GEOMETRY - SEMI RELIM - II : ER - 4 Time : Hours Model nswer aper Max. Marks : 40 4.5 1.3
017 1100 MT.1. ttempt NY FIVE of the following : (i) In STR, line l side TR S SQ T = RQ x 4.5 = 1.3 3.9 x = MT - GEOMETRY - SEMI RELIM - II : ER - 4 Time : Hours Model nswer aper Max. Marks : 40 4.5 1.3
CBSE Board Class X Summative Assessment II Mathematics
 CBSE Board Class X Summative Assessment II Mathematics Board Question Paper 2014 Set 2 Time: 3 hrs Max. Marks: 90 Note: Please check that this question paper contains 15 printed pages. Code number given
CBSE Board Class X Summative Assessment II Mathematics Board Question Paper 2014 Set 2 Time: 3 hrs Max. Marks: 90 Note: Please check that this question paper contains 15 printed pages. Code number given
( ) ( ) Geometry Team Solutions FAMAT Regional February = 5. = 24p.
 . A 6 6 The semi perimeter is so the perimeter is 6. The third side of the triangle is 7. Using Heron s formula to find the area ( )( )( ) 4 6 = 6 6. 5. B Draw the altitude from Q to RP. This forms a 454590
. A 6 6 The semi perimeter is so the perimeter is 6. The third side of the triangle is 7. Using Heron s formula to find the area ( )( )( ) 4 6 = 6 6. 5. B Draw the altitude from Q to RP. This forms a 454590
QUESTION BANK ON STRAIGHT LINE AND CIRCLE
 QUESTION BANK ON STRAIGHT LINE AND CIRCLE Select the correct alternative : (Only one is correct) Q. If the lines x + y + = 0 ; 4x + y + 4 = 0 and x + αy + β = 0, where α + β =, are concurrent then α =,
QUESTION BANK ON STRAIGHT LINE AND CIRCLE Select the correct alternative : (Only one is correct) Q. If the lines x + y + = 0 ; 4x + y + 4 = 0 and x + αy + β = 0, where α + β =, are concurrent then α =,
QUESTION BANK ON. CONIC SECTION (Parabola, Ellipse & Hyperbola)
 QUESTION BANK ON CONIC SECTION (Parabola, Ellipse & Hyperbola) Question bank on Parabola, Ellipse & Hyperbola Select the correct alternative : (Only one is correct) Q. Two mutually perpendicular tangents
QUESTION BANK ON CONIC SECTION (Parabola, Ellipse & Hyperbola) Question bank on Parabola, Ellipse & Hyperbola Select the correct alternative : (Only one is correct) Q. Two mutually perpendicular tangents
Grade 11 Pre-Calculus Mathematics (1999) Grade 11 Pre-Calculus Mathematics (2009)
 Use interval notation (A-1) Plot and describe data of quadratic form using appropriate scales (A-) Determine the following characteristics of a graph of a quadratic function: y a x p q Vertex Domain and
Use interval notation (A-1) Plot and describe data of quadratic form using appropriate scales (A-) Determine the following characteristics of a graph of a quadratic function: y a x p q Vertex Domain and
Circle geometry investigation: Student worksheet
 Circle geometry investigation: Student worksheet http://topdrawer.aamt.edu.au/geometric-reasoning/good-teaching/exploringcircles/explore-predict-confirm/circle-geometry-investigations About these activities
Circle geometry investigation: Student worksheet http://topdrawer.aamt.edu.au/geometric-reasoning/good-teaching/exploringcircles/explore-predict-confirm/circle-geometry-investigations About these activities
Chapter 1. Some Basic Theorems. 1.1 The Pythagorean Theorem
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a 2 + b 2 = c 2. roof. b a a 3 2 b 2 b 4 b a b
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a 2 + b 2 = c 2. roof. b a a 3 2 b 2 b 4 b a b
chapter 1 vector geometry solutions V Consider the parallelogram shown alongside. Which of the following statements are true?
 chapter vector geometry solutions V. Exercise A. For the shape shown, find a single vector which is equal to a)!!! " AB + BC AC b)! AD!!! " + DB AB c)! AC + CD AD d)! BC + CD!!! " + DA BA e) CD!!! " "
chapter vector geometry solutions V. Exercise A. For the shape shown, find a single vector which is equal to a)!!! " AB + BC AC b)! AD!!! " + DB AB c)! AC + CD AD d)! BC + CD!!! " + DA BA e) CD!!! " "
CIRCLES. ii) P lies in the circle S = 0 s 11 = 0
 CIRCLES 1 The set of points in a plane which are at a constant distance r ( 0) from a given point C is called a circle The fixed point C is called the centre and the constant distance r is called the radius
CIRCLES 1 The set of points in a plane which are at a constant distance r ( 0) from a given point C is called a circle The fixed point C is called the centre and the constant distance r is called the radius
9.7 Extension: Writing and Graphing the Equations
 www.ck12.org Chapter 9. Circles 9.7 Extension: Writing and Graphing the Equations of Circles Learning Objectives Graph a circle. Find the equation of a circle in the coordinate plane. Find the radius and
www.ck12.org Chapter 9. Circles 9.7 Extension: Writing and Graphing the Equations of Circles Learning Objectives Graph a circle. Find the equation of a circle in the coordinate plane. Find the radius and
( ) Chapter 10 Review Question Answers. Find the value of x mhg. m B = 1 2 ( 80 - x) H x G. E 30 = 80 - x. x = 50. Find m AXB and m Y A D X 56
 hapter 10 Review Question nswers 1. ( ) Find the value of mhg 30 m = 1 2 ( 30) = 15 F 80 m = 1 2 ( 80 - ) H G E 30 = 80 - = 50 2. Find m X and m Y m X = 1 120 + 56 2 ( ) = 88 120 X 56 Y m Y = 1 120-56
hapter 10 Review Question nswers 1. ( ) Find the value of mhg 30 m = 1 2 ( 30) = 15 F 80 m = 1 2 ( 80 - ) H G E 30 = 80 - = 50 2. Find m X and m Y m X = 1 120 + 56 2 ( ) = 88 120 X 56 Y m Y = 1 120-56
Ch 10 Review. Multiple Choice Identify the choice that best completes the statement or answers the question.
 Ch 10 Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. In the diagram shown, the measure of ADC is a. 55 b. 70 c. 90 d. 180 2. What is the measure
Ch 10 Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. In the diagram shown, the measure of ADC is a. 55 b. 70 c. 90 d. 180 2. What is the measure
Unit 10 Geometry Circles. NAME Period
 Unit 10 Geometry Circles NAME Period 1 Geometry Chapter 10 Circles ***In order to get full credit for your assignments they must me done on time and you must SHOW ALL WORK. *** 1. (10-1) Circles and Circumference
Unit 10 Geometry Circles NAME Period 1 Geometry Chapter 10 Circles ***In order to get full credit for your assignments they must me done on time and you must SHOW ALL WORK. *** 1. (10-1) Circles and Circumference
Circles. 1. In the accompanying figure, the measure of angle AOB is 50. Find the measure of inscribed angle ACB.
 ircles Name: Date: 1. In the accompanying figure, the measure of angle AOB is 50. Find the measure of inscribed angle AB. 4. In the accompanying diagram, P is tangent to circle at and PAB is a secant.
ircles Name: Date: 1. In the accompanying figure, the measure of angle AOB is 50. Find the measure of inscribed angle AB. 4. In the accompanying diagram, P is tangent to circle at and PAB is a secant.
Review for Grade 9 Math Exam - Unit 8 - Circle Geometry
 Name: Review for Grade 9 Math Exam - Unit 8 - ircle Geometry Date: Multiple hoice Identify the choice that best completes the statement or answers the question. 1. is the centre of this circle and point
Name: Review for Grade 9 Math Exam - Unit 8 - ircle Geometry Date: Multiple hoice Identify the choice that best completes the statement or answers the question. 1. is the centre of this circle and point
Chapter 19 Exercise 19.1
 hapter 9 xercise 9... (i) n axiom is a statement that is accepted but cannot be proven, e.g. x + 0 = x. (ii) statement that can be proven logically: for example, ythagoras Theorem. (iii) The logical steps
hapter 9 xercise 9... (i) n axiom is a statement that is accepted but cannot be proven, e.g. x + 0 = x. (ii) statement that can be proven logically: for example, ythagoras Theorem. (iii) The logical steps
MT EDUCARE LTD. MATHEMATICS SUBJECT : Q L M ICSE X. Geometry STEP UP ANSWERSHEET
 IS X MT UR LT. SUJT : MTHMTIS Geometry ST U NSWRSHT 003 1. In QL and RM, LQ MR [Given] LQ RM [Given] QL ~ RM [y axiom of similarity] (i) Since, QL ~ RM QL M L RM QL RM L M (ii) In QL and RQ, we have Q
IS X MT UR LT. SUJT : MTHMTIS Geometry ST U NSWRSHT 003 1. In QL and RM, LQ MR [Given] LQ RM [Given] QL ~ RM [y axiom of similarity] (i) Since, QL ~ RM QL M L RM QL RM L M (ii) In QL and RQ, we have Q
Circles Print Activity. Use the Explore It mode to answer the following questions. 1. Use the diagram below to answer the following questions:
 Name: Circles Print Activity Use the Explore It mode to answer the following questions. 1. Use the diagram below to answer the following questions: a. A is a/an angle. (central/inscribed) b. A is subtended
Name: Circles Print Activity Use the Explore It mode to answer the following questions. 1. Use the diagram below to answer the following questions: a. A is a/an angle. (central/inscribed) b. A is subtended
Secondary School Certificate Examination Syllabus MATHEMATICS. Class X examination in 2011 and onwards. SSC Part-II (Class X)
 Secondary School Certificate Examination Syllabus MATHEMATICS Class X examination in 2011 and onwards SSC Part-II (Class X) 15. Algebraic Manipulation: 15.1.1 Find highest common factor (H.C.F) and least
Secondary School Certificate Examination Syllabus MATHEMATICS Class X examination in 2011 and onwards SSC Part-II (Class X) 15. Algebraic Manipulation: 15.1.1 Find highest common factor (H.C.F) and least
MT - MATHEMATICS (71) GEOMETRY - PRELIM II - PAPER - 6 (E)
 04 00 Seat No. MT - MTHEMTIS (7) GEOMETRY - PRELIM II - (E) Time : Hours (Pages 3) Max. Marks : 40 Note : ll questions are compulsory. Use of calculator is not allowed. Q.. Solve NY FIVE of the following
04 00 Seat No. MT - MTHEMTIS (7) GEOMETRY - PRELIM II - (E) Time : Hours (Pages 3) Max. Marks : 40 Note : ll questions are compulsory. Use of calculator is not allowed. Q.. Solve NY FIVE of the following
Trans Web Educational Services Pvt. Ltd B 147,1st Floor, Sec-6, NOIDA, UP
 Solved Examples Example 1: Find the equation of the circle circumscribing the triangle formed by the lines x + y = 6, 2x + y = 4, x + 2y = 5. Method 1. Consider the equation (x + y 6) (2x + y 4) + λ 1
Solved Examples Example 1: Find the equation of the circle circumscribing the triangle formed by the lines x + y = 6, 2x + y = 4, x + 2y = 5. Method 1. Consider the equation (x + y 6) (2x + y 4) + λ 1
Unit 8 Circle Geometry Exploring Circle Geometry Properties. 1. Use the diagram below to answer the following questions:
 Unit 8 Circle Geometry Exploring Circle Geometry Properties Name: 1. Use the diagram below to answer the following questions: a. BAC is a/an angle. (central/inscribed) b. BAC is subtended by the red arc.
Unit 8 Circle Geometry Exploring Circle Geometry Properties Name: 1. Use the diagram below to answer the following questions: a. BAC is a/an angle. (central/inscribed) b. BAC is subtended by the red arc.
Chapter 12 Practice Test
 hapter 12 Practice Test Multiple hoice Identify the choice that best completes the statement or answers the question. ssume that lines that appear to be tangent are tangent. is the center of the circle.
hapter 12 Practice Test Multiple hoice Identify the choice that best completes the statement or answers the question. ssume that lines that appear to be tangent are tangent. is the center of the circle.
( 1 ) Find the co-ordinates of the focus, length of the latus-rectum and equation of the directrix of the parabola x 2 = - 8y.
 PROBLEMS 04 - PARABOLA Page 1 ( 1 ) Find the co-ordinates of the focus, length of the latus-rectum and equation of the directrix of the parabola x - 8. [ Ans: ( 0, - ), 8, ] ( ) If the line 3x 4 k 0 is
PROBLEMS 04 - PARABOLA Page 1 ( 1 ) Find the co-ordinates of the focus, length of the latus-rectum and equation of the directrix of the parabola x - 8. [ Ans: ( 0, - ), 8, ] ( ) If the line 3x 4 k 0 is
 = ( +1) BP AC = AP + (1+ )BP Proved UNIT-9 CIRCLES 1. Prove that the parallelogram circumscribing a circle is rhombus. Ans Given : ABCD is a parallelogram circumscribing a circle. To prove : - ABCD is
= ( +1) BP AC = AP + (1+ )BP Proved UNIT-9 CIRCLES 1. Prove that the parallelogram circumscribing a circle is rhombus. Ans Given : ABCD is a parallelogram circumscribing a circle. To prove : - ABCD is
11. Concentric Circles: Circles that lie in the same plane and have the same center.
 Circles Definitions KNOW THESE TERMS 1. Circle: The set of all coplanar points equidistant from a given point. 2. Sphere: The set of all points equidistant from a given point. 3. Radius of a circle: The
Circles Definitions KNOW THESE TERMS 1. Circle: The set of all coplanar points equidistant from a given point. 2. Sphere: The set of all points equidistant from a given point. 3. Radius of a circle: The
Mathematics. Single Correct Questions
 Mathematics Single Correct Questions +4 1.00 1. If and then 2. The number of solutions of, in the interval is : 3. If then equals : 4. A plane bisects the line segment joining the points and at right angles.
Mathematics Single Correct Questions +4 1.00 1. If and then 2. The number of solutions of, in the interval is : 3. If then equals : 4. A plane bisects the line segment joining the points and at right angles.
UNIT 6. BELL WORK: Draw 3 different sized circles, 1 must be at LEAST 15cm across! Cut out each circle. The Circle
 UNIT 6 BELL WORK: Draw 3 different sized circles, 1 must be at LEAST 15cm across! Cut out each circle The Circle 1 Questions How are perimeter and area related? How are the areas of polygons and circles
UNIT 6 BELL WORK: Draw 3 different sized circles, 1 must be at LEAST 15cm across! Cut out each circle The Circle 1 Questions How are perimeter and area related? How are the areas of polygons and circles
Theorem 1.2 (Converse of Pythagoras theorem). If the lengths of the sides of ABC satisfy a 2 + b 2 = c 2, then the triangle has a right angle at C.
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
Introduction Circle Some terms related with a circle
 141 ircle Introduction In our day-to-day life, we come across many objects which are round in shape, such as dials of many clocks, wheels of a vehicle, bangles, key rings, coins of denomination ` 1, `
141 ircle Introduction In our day-to-day life, we come across many objects which are round in shape, such as dials of many clocks, wheels of a vehicle, bangles, key rings, coins of denomination ` 1, `
AREA RELATED TO CIRCLES
 CHAPTER 11 AREA RELATED TO CIRCLES (A) Main Concepts and Results Perimeters and areas of simple closed figures. Circumference and area of a circle. Area of a circular path (i.e., ring). Sector of a circle
CHAPTER 11 AREA RELATED TO CIRCLES (A) Main Concepts and Results Perimeters and areas of simple closed figures. Circumference and area of a circle. Area of a circular path (i.e., ring). Sector of a circle
Chapter 10 Worksheet 1 Name: Honors Accelerated Geometry Hour:
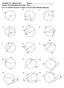 hapter 10 Worksheet 1 Name: Honors ccelerated Geometry Hour: For 1-15, find the measure of angle in each of the following diagrams. 1. 2.. 258 84 140 40 4. 5. 6. 2 y 80 y 72 7. 8. 9. 50 X 40 140 4 y 10.
hapter 10 Worksheet 1 Name: Honors ccelerated Geometry Hour: For 1-15, find the measure of angle in each of the following diagrams. 1. 2.. 258 84 140 40 4. 5. 6. 2 y 80 y 72 7. 8. 9. 50 X 40 140 4 y 10.
Riding a Ferris Wheel. Students should be able to answer these questions after Lesson 10.1:
 .1 Riding a Ferris Wheel Introduction to ircles Students should be able to answer these questions after Lesson.1: What are the parts of a circle? How are the parts of a circle drawn? Read Question 1 and
.1 Riding a Ferris Wheel Introduction to ircles Students should be able to answer these questions after Lesson.1: What are the parts of a circle? How are the parts of a circle drawn? Read Question 1 and
The gradient of the radius from the centre of the circle ( 1, 6) to (2, 3) is: ( 6)
 Circles 6E a (x + ) + (y + 6) = r, (, ) Substitute x = and y = into the equation (x + ) + (y + 6) = r + + + 6 = r ( ) ( ) 9 + 8 = r r = 90 = 0 b The line has equation x + y = 0 y = x + y = x + The gradient
Circles 6E a (x + ) + (y + 6) = r, (, ) Substitute x = and y = into the equation (x + ) + (y + 6) = r + + + 6 = r ( ) ( ) 9 + 8 = r r = 90 = 0 b The line has equation x + y = 0 y = x + y = x + The gradient
Objective Mathematics
 . A tangent to the ellipse is intersected by a b the tangents at the etremities of the major ais at 'P' and 'Q' circle on PQ as diameter always passes through : (a) one fied point two fied points (c) four
. A tangent to the ellipse is intersected by a b the tangents at the etremities of the major ais at 'P' and 'Q' circle on PQ as diameter always passes through : (a) one fied point two fied points (c) four
Geometry Honors Homework
 Geometry Honors Homework pg. 1 12-1 Practice Form G Tangent Lines Algebra Assume that lines that appear to be tangent are tangent. O is the center of each circle. What is the value of x? 1. 2. 3. The circle
Geometry Honors Homework pg. 1 12-1 Practice Form G Tangent Lines Algebra Assume that lines that appear to be tangent are tangent. O is the center of each circle. What is the value of x? 1. 2. 3. The circle
MT - GEOMETRY - SEMI PRELIM - II : PAPER - 5
 017 1100 MT MT - GEOMETRY - SEMI PRELIM - II : PPER - 5 Time : Hours Model nswer Paper Max. Marks : 40.1. ttempt NY FIVE of the following : (i) X In XYZ, ray YM bisects XYZ XY YZ XM MZ Y Z [Property of
017 1100 MT MT - GEOMETRY - SEMI PRELIM - II : PPER - 5 Time : Hours Model nswer Paper Max. Marks : 40.1. ttempt NY FIVE of the following : (i) X In XYZ, ray YM bisects XYZ XY YZ XM MZ Y Z [Property of
Objectives To find the measure of an inscribed angle To find the measure of an angle formed by a tangent and a chord
 1-3 Inscribed ngles ommon ore State Standards G-.. Identify and describe relationships among inscribed angles, radii, and chords. lso G-..3, G-..4 M 1, M 3, M 4, M 6 bjectives To find the measure of an
1-3 Inscribed ngles ommon ore State Standards G-.. Identify and describe relationships among inscribed angles, radii, and chords. lso G-..3, G-..4 M 1, M 3, M 4, M 6 bjectives To find the measure of an
Tangent Lines Unit 10 Lesson 1 Example 1: Tell how many common tangents the circles have and draw them.
 Tangent Lines Unit 10 Lesson 1 EQ: How can you verify that a segment is tangent to a circle? Circle: Center: Radius: Chord: Diameter: Secant: Tangent: Tangent Lines Unit 10 Lesson 1 Example 1: Tell how
Tangent Lines Unit 10 Lesson 1 EQ: How can you verify that a segment is tangent to a circle? Circle: Center: Radius: Chord: Diameter: Secant: Tangent: Tangent Lines Unit 10 Lesson 1 Example 1: Tell how
Conic section. Ans: c. Ans: a. Ans: c. Episode:43 Faculty: Prof. A. NAGARAJ. 1. A circle
 Episode:43 Faculty: Prof. A. NAGARAJ Conic section 1. A circle gx fy c 0 is said to be imaginary circle if a) g + f = c b) g + f > c c) g + f < c d) g = f. If (1,-3) is the centre of the circle x y ax
Episode:43 Faculty: Prof. A. NAGARAJ Conic section 1. A circle gx fy c 0 is said to be imaginary circle if a) g + f = c b) g + f > c c) g + f < c d) g = f. If (1,-3) is the centre of the circle x y ax
Integrated Math II. IM2.1.2 Interpret given situations as functions in graphs, formulas, and words.
 Standard 1: Algebra and Functions Students graph linear inequalities in two variables and quadratics. They model data with linear equations. IM2.1.1 Graph a linear inequality in two variables. IM2.1.2
Standard 1: Algebra and Functions Students graph linear inequalities in two variables and quadratics. They model data with linear equations. IM2.1.1 Graph a linear inequality in two variables. IM2.1.2
Replacement for a Carpenter s Square
 Lesson.1 Skills Practice Name Date Replacement for a arpenter s Square Inscribed and ircumscribed Triangles and Quadrilaterals Vocabulary nswer each question. 1. How are inscribed polygons and circumscribed
Lesson.1 Skills Practice Name Date Replacement for a arpenter s Square Inscribed and ircumscribed Triangles and Quadrilaterals Vocabulary nswer each question. 1. How are inscribed polygons and circumscribed
ACTM Regional Geometry Exam 2009
 TM Regional Geometry xam 009 In each of the following questions choose the best answer and bubble the corresponding letter on the answer sheet. Note: The geometric figures on this exam are not necessarily
TM Regional Geometry xam 009 In each of the following questions choose the best answer and bubble the corresponding letter on the answer sheet. Note: The geometric figures on this exam are not necessarily
Maharashtra Board Class X Mathematics - Geometry Board Paper 2014 Solution. Time: 2 hours Total Marks: 40
 Maharashtra Board Class X Mathematics - Geometry Board Paper 04 Solution Time: hours Total Marks: 40 Note: - () All questions are compulsory. () Use of calculator is not allowed.. i. Ratio of the areas
Maharashtra Board Class X Mathematics - Geometry Board Paper 04 Solution Time: hours Total Marks: 40 Note: - () All questions are compulsory. () Use of calculator is not allowed.. i. Ratio of the areas
CBSE X Mathematics 2012 Solution (SET 1) Section B
 CBSE X Mathematics 01 Solution (SET 1) Section B Q11. Find the value(s) of k so that the quadratic equation x kx + k = 0 has equal roots. Given equation is x kx k 0 For the given equation to have equal
CBSE X Mathematics 01 Solution (SET 1) Section B Q11. Find the value(s) of k so that the quadratic equation x kx + k = 0 has equal roots. Given equation is x kx k 0 For the given equation to have equal
SYSTEM OF CIRCLES OBJECTIVES (a) Touch each other internally (b) Touch each other externally
 SYSTEM OF CIRCLES OBJECTIVES. A circle passes through (0, 0) and (, 0) and touches the circle x + y = 9, then the centre of circle is (a) (c) 3,, (b) (d) 3,, ±. The equation of the circle having its centre
SYSTEM OF CIRCLES OBJECTIVES. A circle passes through (0, 0) and (, 0) and touches the circle x + y = 9, then the centre of circle is (a) (c) 3,, (b) (d) 3,, ±. The equation of the circle having its centre
Chapter 10. Properties of Circles
 Chapter 10 Properties of Circles 10.1 Use Properties of Tangents Objective: Use properties of a tangent to a circle. Essential Question: how can you verify that a segment is tangent to a circle? Terminology:
Chapter 10 Properties of Circles 10.1 Use Properties of Tangents Objective: Use properties of a tangent to a circle. Essential Question: how can you verify that a segment is tangent to a circle? Terminology:
Riding a Ferris Wheel
 Lesson.1 Skills Practice Name ate iding a Ferris Wheel Introduction to ircles Vocabulary Identify an instance of each term in the diagram. 1. center of the circle 6. central angle T H I 2. chord 7. inscribed
Lesson.1 Skills Practice Name ate iding a Ferris Wheel Introduction to ircles Vocabulary Identify an instance of each term in the diagram. 1. center of the circle 6. central angle T H I 2. chord 7. inscribed
WARM UP. Sunday, November 16, 2014
 WARM UP Sunday, November 16, 2014 1 2 3 4 5 6 7 8 9 10 Objectives Use properties of circles to derive the formula for sector area. Determine arc length and arc measure for given central and inscribed angle
WARM UP Sunday, November 16, 2014 1 2 3 4 5 6 7 8 9 10 Objectives Use properties of circles to derive the formula for sector area. Determine arc length and arc measure for given central and inscribed angle
King Fahd University of Petroleum and Minerals Prep-Year Math Program Math (001) - Term 181 Recitation (1.1)
 Recitation (1.1) Question 1: Find a point on the y-axis that is equidistant from the points (5, 5) and (1, 1) Question 2: Find the distance between the points P(2 x, 7 x) and Q( 2 x, 4 x) where x 0. Question
Recitation (1.1) Question 1: Find a point on the y-axis that is equidistant from the points (5, 5) and (1, 1) Question 2: Find the distance between the points P(2 x, 7 x) and Q( 2 x, 4 x) where x 0. Question
West Haven Public Schools Unit Planning Organizer
 West Haven Public Schools Unit Planning Organizer Subject: Circles and Other Conic Sections Grade 10 Unit: Five Pacing: 4 weeks + 1 week Essential Question(s): 1. What is the relationship between angles
West Haven Public Schools Unit Planning Organizer Subject: Circles and Other Conic Sections Grade 10 Unit: Five Pacing: 4 weeks + 1 week Essential Question(s): 1. What is the relationship between angles
Key competencies (student abilities)
 Year 9 Mathematics Cambridge IGCSE Mathematics is accepted by universities and employers as proof of mathematical knowledge and understanding. Successful Cambridge IGCSE Mathematics candidates gain lifelong
Year 9 Mathematics Cambridge IGCSE Mathematics is accepted by universities and employers as proof of mathematical knowledge and understanding. Successful Cambridge IGCSE Mathematics candidates gain lifelong
ARCS An ARC is any unbroken part of the circumference of a circle. It is named using its ENDPOINTS.
 ARCS An ARC is any unbroken part of the circumference of a circle. It is named using its ENDPOINTS. A B X Z Y A MINOR arc is LESS than 1/2 way around the circle. A MAJOR arc is MORE than 1/2 way around
ARCS An ARC is any unbroken part of the circumference of a circle. It is named using its ENDPOINTS. A B X Z Y A MINOR arc is LESS than 1/2 way around the circle. A MAJOR arc is MORE than 1/2 way around
VKR Classes TIME BOUND TESTS 1-7 Target JEE ADVANCED For Class XI VKR Classes, C , Indra Vihar, Kota. Mob. No
 VKR Classes TIME BOUND TESTS -7 Target JEE ADVANCED For Class XI VKR Classes, C-9-0, Indra Vihar, Kota. Mob. No. 9890605 Single Choice Question : PRACTICE TEST-. The smallest integer greater than log +
VKR Classes TIME BOUND TESTS -7 Target JEE ADVANCED For Class XI VKR Classes, C-9-0, Indra Vihar, Kota. Mob. No. 9890605 Single Choice Question : PRACTICE TEST-. The smallest integer greater than log +
Assignment. Riding a Ferris Wheel Introduction to Circles. 1. For each term, name all of the components of circle Y that are examples of the term.
 ssignment ssignment for Lesson.1 Name Date Riding a Ferris Wheel Introduction to ircles 1. For each term, name all of the components of circle Y that are examples of the term. G R Y O T M a. hord GM, R,
ssignment ssignment for Lesson.1 Name Date Riding a Ferris Wheel Introduction to ircles 1. For each term, name all of the components of circle Y that are examples of the term. G R Y O T M a. hord GM, R,
Time : 2 Hours (Pages 3) Max. Marks : 40. Q.1. Solve the following : (Any 5) 5 In PQR, m Q = 90º, m P = 30º, m R = 60º. If PR = 8 cm, find QR.
 Q.P. SET CODE Q.1. Solve the following : (ny 5) 5 (i) (ii) In PQR, m Q 90º, m P 0º, m R 60º. If PR 8 cm, find QR. O is the centre of the circle. If m C 80º, the find m (arc C) and m (arc C). Seat No. 01
Q.P. SET CODE Q.1. Solve the following : (ny 5) 5 (i) (ii) In PQR, m Q 90º, m P 0º, m R 60º. If PR 8 cm, find QR. O is the centre of the circle. If m C 80º, the find m (arc C) and m (arc C). Seat No. 01
10.3 Start Thinking Warm Up Cumulative Review Warm Up
 10.3 tart hinking etermine if the statement is always true, sometimes true, or never true. plain your reasoning. 1. chord is a diameter. 2. diameter is a chord. 3. chord and a radius have the same measure.
10.3 tart hinking etermine if the statement is always true, sometimes true, or never true. plain your reasoning. 1. chord is a diameter. 2. diameter is a chord. 3. chord and a radius have the same measure.
Intermediate Math Circles Wednesday October Problem Set 3
 The CETRE for EDUCTI in MTHEMTICS and CMPUTIG Intermediate Math Circles Wednesday ctober 24 2012 Problem Set 3.. Unless otherwise stated, any point labelled is assumed to represent the centre of the circle.
The CETRE for EDUCTI in MTHEMTICS and CMPUTIG Intermediate Math Circles Wednesday ctober 24 2012 Problem Set 3.. Unless otherwise stated, any point labelled is assumed to represent the centre of the circle.
CBSE Class X Mathematics Board Paper 2019 All India Set 3 Time: 3 hours Total Marks: 80
 CBSE Class X Mathematics Board Paper 2019 All India Set 3 Time: 3 hours Total Marks: 80 General Instructions: (i) All questions are compulsory. (ii) The question paper consists of 30 questions divided
CBSE Class X Mathematics Board Paper 2019 All India Set 3 Time: 3 hours Total Marks: 80 General Instructions: (i) All questions are compulsory. (ii) The question paper consists of 30 questions divided
MT - w A.P. SET CODE MT - w - MATHEMATICS (71) GEOMETRY- SET - A (E) Time : 2 Hours Preliminary Model Answer Paper Max.
 .P. SET CODE.. Solve NY FIVE of the following : (i) ( BE) ( BD) ( BE) ( BD) BE D 6 9 MT - w 07 00 - MT - w - MTHEMTICS (7) GEOMETRY- (E) Time : Hours Preliminary Model nswer Paper Max. Marks : 40 [Triangles
.P. SET CODE.. Solve NY FIVE of the following : (i) ( BE) ( BD) ( BE) ( BD) BE D 6 9 MT - w 07 00 - MT - w - MTHEMTICS (7) GEOMETRY- (E) Time : Hours Preliminary Model nswer Paper Max. Marks : 40 [Triangles
Class X Delhi Math Set-3 Section A
 Class X Delhi Math Set-3 Section A 1. The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30. The distance of the car from the base of the tower (in m.) is:
Class X Delhi Math Set-3 Section A 1. The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30. The distance of the car from the base of the tower (in m.) is:
