arxiv: v2 [hep-ph] 2 Apr 2019
|
|
|
- Hilary Eaton
- 5 years ago
- Views:
Transcription
1 MITP/ arxiv: v2 [hep-ph] 2 Apr 2019 Two-loop master integrals for the mixed QCD-electroweak corrections for H b b through a Ht t-coupling Ekta Chaubey and Stefan Weinzierl PRISMA Cluster of Excellence, Institut für Physik, Johannes Gutenberg-Universität Mainz, D Mainz, Germany Abstract We present the two-loop master integrals relevant to the O(αα s )-corrections to the decay H b b through a Ht t-coupling. We keep the full dependence on the heavy particle masses, but neglect the b-quark mass. The occurring square roots can be rationalised and the result is expressed in terms of multiple polylogarithms.
2 1 Introduction The precise determination of the properties of the Higgs boson is now a central pillar of the experimental programs at the LHC. As the Higgs boson decays predominately to b b, the partial width for this decay is of central importance [1]. This raises immediately the question, how precise can we predict this partial width within the Standard Model from theory? This requires the computation of quantum corrections. The state-of-the-art for the partial decay width for H b b is as follows: In massless QCD the corrections are known to O(α 4 s) [2]. Keeping the mass dependence, QCD corrections are known to O(α 3 s ) [3 5]. The QCD calculation of order O(α2 s ) for the decay H b b through a Ht t-coupling has become available quite recently [6]. Two-loop QED corrections and mixed QED-QCD corrections have been considered in [7]. For the mixed electroweak-qcd corrections to the decay H b b of order O(αα s ) the leading term in an expansion in m 2 H /m2 t has been obtained in [8, 9]. This has been improved by including systematically more terms in [10]. As far as the two-loop electroweak corrections of order O(α 2 ) are concerned only the leading term in an expansion in m 2 H /m2 t is known [11, 12]. In recent years, there has been a substantial progress in our abilities to compute Feynman integrals, and Feynman integrals which previously could only be calculated approximatively come into reach. In this article we present the two-loop master integrals relevant to the O(αα s )-corrections to the decay H b b through a Ht t-coupling. We keep the full dependence on the heavy particle masses (m t, m H and m W ), but neglect the b-quark mass. In Higgs and top physics there are two-loop Feynman integrals related to elliptic curves [13 17]. One might fear that we are in a similar situation here. To some relief this is not the case. All master integrals can be expressed entirely in terms of multiple polylogarithm. The difficulty of these integrals is entirely due to the required simultaneous rationalisation of two square roots. Large parts of the calculation are based on by now standard techniques: We first derive a system of differential equations for the master integrals [18 28], using integration-by-parts identities [29, 30] and the Laporta algorithm [31]. We then bring the system of differential equations into an ε-form [24]. This will introduce two square roots. It turns out that the square roots can be rationalised simultaneously with the methods of [32]. This is the essential new ingredient of our calculation. The resulting system of differential equations involves only dlog-forms and can be solved in terms of multiple polylogarithms. We are able to express all master integrals in terms of multiple polylogarithms with an alphabet consisting of 13 letters. This paper is organised as follows: In the next section we introduce our notation. In particular we define the kinematic variables which will rationalise the square roots. In section 3 we define the master integrals, for which the system of differential equations is in ε-form. The system of differential equations is presented in section 4. The analytic results for the master integrals are given in section 5. In addition, section 6 gives numerical results for the most interesting case p 2 = m 2 H. Finally, our conclusions are contained in section 7. The appendix shows for all master integrals the corresponding Feynman diagrams and describes the content of the supplementary electronic file attached to the arxiv version of this article. 2
3 G A G B G C G D G E Figure 1: Examples of Feynman diagrams contributing to the mixed O(αα s )-corrections to the decay H b b through a Ht t-coupling. The Higgs boson is denoted by a dashed line, a top quark by a green line, a bottom quark with a black line and a gluon by a curly line. Particles with mass m W are drawn with a wavy line. 2 Notation We are interested in the mixed O(αα s )-corrections to the decay H b b through a Ht t-coupling. Examples of Feynman diagrams are shown in fig. 1. Not shown are diagrams whose master integrals are related to the master integrals of the diagrams of fig. 1 by symmetry. We will neglect the b-quark mass. However, we will treat the dependence on the top quark mass m t, the W-boson mass m W and the momentum p of the Higgs boson exactly. For an on-shell Higgs-boson we have p 2 = m 2 H. For the two-loop contributions to the Higgs decay we have two independent external momenta p 1 and p 2, which label the momenta of b-quark and b-quark, respectively. With two independent loop momenta we thus have seven linearly independent scalar products. For each of the four Feynman diagrams G A -G D we introduce an auxiliary topology with seven propagators. These are shown in fig. 2. The master integrals related to diagram G E are a subset of the master integrals related to diagram G A (and likewise a subset of the master integrals related to diagram G D ). We consider the integrals I X ν 1 ν 2 ν 3 ν 4 ν 5 ν 6 ν 7 = e 2γ Eε ( µ 2) ν D d D k 1 iπ D 2 d D k 2 iπ D 2 7 j=1 ( P X j 1 ) ν j, X {A,B,C,D}, (1) where D=4 2ε denotes the number of space-time dimensions, γ E denotes the Euler-Mascheroni constant, µ is an arbitrary scale introduced to render the Feynman integral dimensionless, and the 3
4 p 1 p 1 p 1 p p 2 p 2 p 2 p 2 T A 2 6 T B p 1 3 p 12 p 12 7 p 1 p p 2 4 p 2 p 2 T C 2 6 T D 3 6 Figure 2: Auxiliary diagrams for the two planar vertex corrections, the non-planar vertex correction and topology D. The internal masses of the propagators are encoded by the colour of the propagators: massless (black), m t (green), m W (red). 4
5 quantity ν is defined by ν = 7 ν j. (2) j=1 The inverse propagators P X j are defined as follows: Topology A: P A 1 = k2 1 + m2 t, PA 2 = (k 1 p 1 p 2 ) 2 + m 2 t, PA 3 = (k 1+ k 2 ) 2, P A 4 = k2 2 + m2 t, PA 5 = (k 2+ p 1 ) 2 + m 2 W, PA 6 = (k 2+ p 1 + p 2 ) 2 + m 2 t, P A 7 = (k 1 p 1 ) 2 + m 2 t. (3) Topology B: Topology C: Topology D: P B 1 = k2 1 + m2 t, PB 2 = (k 1 p 1 p 2 ) 2 + m 2 t, PB 3 = (k 1+ k 2 ) 2 + m 2 W, P B 4 = k2 2, PB 5 = (k 2+ p 1 ) 2, P B 6 = (k 2+ p 1 + p 2 ) 2, P B 7 = (k 1 p 1 ) 2 + m 2 t. (4) P C 1 = k2 1 + m2 t, PC 2 = (k 1 p 1 p 2 ) 2 + m 2 t, PC 3 = (k 1+ k 2 ) 2, P C 4 = (k 1+ k 2 p 1 ) 2, P C 5 = k2 2 + m2 W, PC 6 = (k 2+ p 2 ) 2 + m 2 t, P C 7 = (k 1 p 1 ) 2 + m 2 t. (5) P D 1 = k2 1 + m2 t, PD 2 = (k 1 p 1 p 2 ) 2 + m 2 t, PD 3 = (k 1 p 1 ) 2 + m 2 W, P D 4 = (k 1+ k 2 ) 2 + m 2 t, PD 5 = k2 2, PD 6 = (k 2+ p 1 ) 2, P D 7 = (k 2 + p 1 + p 2 ) 2. (6) For all topologies our conventions are such that we are interested in the integrals with ν 7 0. The Feynman parameter representations for the four topologies are given by I X ν 1 ν 2 ν 3 ν 4 ν 5 ν 6 ν 7 = e 2γ Eε Γ(ν D) 7 j=1 Γ(ν j ) σ ( 7 x ν j 1 j j=1 ) ν U 2 3 D ω, (7) X F ν D X where the integration is over σ = { } [x 1 :... : x 7 ] RP 6 x i 0. (8) 5
6 The differential form ω is given by ω = 7 j=1 ( 1) j 1 x j dx 1... dx j... dx 7, (9) where the hat indicates that the corresponding term is omitted. The graph polynomials are given by U A = (x 1 + x 2 + x 7 )(x 4 + x 5 + x 6 )+x 3 (x 1 + x 2 + x 4 + x 5 + x 6 + x 7 ), ( p 2) F A = [x 1 x 2 (x 3 + x 4 + x 5 + x 6 )+x 4 x 6 (x 1 + x 2 + x 3 + x 7 )+x 3 (x 1 x 6 + x 2 x 4 )] µ 2 [ +U A (x 1 + x 2 + x 4 + x 6 + x 7 ) m2 t µ 2 + x m 2 ] W 5 µ 2, U B = (x 1 + x 2 + x 7 )(x 4 + x 5 + x 6 )+x 3 (x 1 + x 2 + x 4 + x 5 + x 6 + x 7 ), ( p 2) F B = [x 1 x 2 (x 3 + x 4 + x 5 + x 6 )+x 4 x 6 (x 1 + x 2 + x 3 + x 7 )+x 3 (x 1 x 6 + x 2 x 4 )] [ +U B (x 1 + x 2 + x 7 ) m2 t µ 2 + x 3 mw 2 µ 2 U C = (x 1 + x 2 + x 7 )(x 5 + x 6 )+(x 3 + x 4 )(x 1 + x 2 + x 5 + x 6 + x 7 ), ( p 2) F C = [x 1 x 2 (x 3 + x 4 + x 5 + x 6 )+x 1 x 4 x 6 + x 2 x 3 x 5 x 3 x 6 x 7 ] [ +U C (x 1 + x 2 + x 6 + x 7 ) m2 t µ 2 + x 5 ], mw 2 µ 2 U D = (x 1 + x 2 + x 3 )(x 5 + x 6 + x 7 )+x 4 (x 1 + x 2 + x 3 + x 5 + x 6 + x 7 ), ( p 2) F D = [x 1 x 2 (x 4 + x 5 + x 6 + x 7 )+x 5 x 7 (x 1 + x 2 + x 3 + x 4 )+x 4 (x 1 x 7 + x 2 x 5 )] ], [ +U D (x 1 + x 2 + x 4 ) m2 t µ 2 + x m 2 ] W 3 µ 2. (10) Let us introduce an operator i +, which raises the power of the propagator i by one, e.g. 1 + I X ν 1 ν 2 ν 3 ν 4 ν 5 ν 6 ν 7 = I X (ν 1 +1)ν 2 ν 3 ν 4 ν 5 ν 6 ν 7. (11) In addition we define two operators D ±, which shift the dimension of space-time by two through The dimensional shift relations read [33, 34] D ± I X ν 1 ν 2 ν 3 ν 4 ν 5 ν 6 ν 7 (D) = I X ν 1 ν 2 ν 3 ν 4 ν 5 ν 6 ν 7 (D±2). (12) D I X ν 1 ν 2 ν 3 ν 4 ν 5 ν 6 ν 7 (D) = U X ( ν1 1 +,ν 2 2 +,ν 3 3 +,ν 4 4 +,ν 5 5 +,ν 6 6 +,ν 7 7 +) I X ν 1 ν 2 ν 3 ν 4 ν 5 ν 6 ν 7 (D). 6 µ 2 µ 2 µ 2 (13)
7 In the following we will set µ 2 = m 2 t. (14) After setting µ 2 = m 2 t the master integrals depend kinematically on two dimensionless quantities. A naive choice is v = p2 mt 2, w = m2 W mt 2, (15) with p = p 1 + p 2. However, with this choice we will encounter square roots. In particular, the square roots v(4 v) and λ(v,w,1) (16) will occur. The Källen function is defined by λ(x,y,z) = x 2 + y 2 + z 2 2xy 2yz 2zx. (17) In order to rationalise the square roots we introduce dimensionless quantities x and y through p 2 m 2 t = v = (1 x)2, x m 2 W m 2 t = w = (1 y+2xy)(x 2y+xy) x(1 y 2. (18) ) The first transformation is standard and has occurred in many places before, the second one is easily obtained with the methods of ref. [32]. The Feynman integrals are then functions of x,y and the dimensional regularisation parameter ε. The inverse transformations are given by x = 1 2 ( 2 v ) v(4 v), y = λ(v,w,1) v(4 v), (19) 1 w+2v such that x=0 corresponds to v= and y=0 corresponds to w=1. Let us also note that the point (v,w) = (0,1) is blown up in (x,y)-space to the hypersurface x = 1. This motivates our final change of coordinates and we introduce x = 1 x. (20) 3 Master integrals For the reduction to master integrals we use the programs Reduze [35], Kira [36] or Fire [37] combined with LiteRed [38, 39]. Each topology involves a certain number of master integrals. This number is shown in table 1 and corresponds to the number of master integrals if we just consider one topology in isolation. Of course, the various topologies share some master integrals and the final number of master integral which we have to compute is lower. We have the following relations I A µ00ν000 = I C µ0000ν0 = I D µ00ν000, 7
8 Topology Number of master integrals A 18 B 15 C 31 D 14 Table 1: The number of master integrals for a given topology. I A µ000ν00 = I B µ0ν0000 = I C µ000ν00 = I D 00νµ000, I A µν0ρ000 = I C µν000ρ0 = I D µν0ρ000, I A µν00ρ00 = I B µνρ0000 = I C µν00ρ00, I A 0µνρ000 = I C µ00ν0ρ0 = I D 0µ0ρν00, I B 0µνρ000 = I C 0µρ0ν00, I A µ0ν0ρ00 = I B µ0ρν000 = I C µ0ν0ρ00 = I D 00ρµν00, I A µ00νρσ0 = I D νσρµ000, I B µνρσ000 = I C µνσ0ρ00, I C µνρ00σ0 = I D µν0σ0ρ0, I A µνρ0σ00 = I B µνσ0ρ00 = I C µν0ρσ00, I A 0µνρσ00 = I C µ00νσρ00 = ID 0ρσµν00, I A µνρσκ00 = IC µν0ρκσ0, I B µνρσκ00 = IC µνσκρ00, I C µ0νρσκ0 = ID 0κσµνρ0. (21) In total we have to consider 39 master integrals, which are grouped into 25 blocks such that one block corresponds to one sub-topology. Some of the master integrals are taken as integrals in D 2 = 2 2ε space-time dimensions. Of course, with the help of the dimensional shift relations in eq. (13) they are easily expressed as (longer) linear combinations of master integrals in D=4 2ε space-time dimensions. A system of master integrals is given by J 1 = ε 2 D I A , J 2 = ε 2 D I A (, 1 x J 3 = ε 2 2 ) D I A 2x, ( 1 x J 4 = ε 2 2 ) D I A 2x, J 5 = 1 2 ε2 v D I B , 8
9 J 6 = 1 2 ε2 v D I B, ( 1 x J 7 = ε 2 2 ) D I A 2x , J 8 = ε 2 D I( 1) A, J 9 = ε 2(1 x)( 1+x 2y+y 2 + 2xy+xy 2) x(1 y 2 D I B ), J 10 = ε 2[ ] D I( 1) B (1 w)d I B, J 11 = 2ε 2 D I B 0111( 1)00 2ε2 D I B , J 12 = ε 2 (1 w) D I A , J 13 = ε 2 ( 1 x 2 ) 2 4x 2 D I A , J 14 = ε 2(1 x)3 (1+x) 4x 2 D I B, J 15 = ε 3 (1 ε)v I A (, 1 x J 16 = ε 2 2 ) [ (1 w) D I B x D I B ], J 17 = ε 3 v I C, J 18 = ε 3 v I C (, 1 x J 19 = ε 2 2 ) x J 20 = ε 3 v I A, [ (1 2ε) I C ε IC J 21 = ε 3 v I A, J 22 = 2ε 2 (1 x) [ (1 2ε)(1+x) I A x(1+w) ε(x w) IA ε(1 x+2w) IA ] 2 (1+x) D I A, J 23 = 2ε 3 v I A , J 24 = 2ε 3 v I A , J 25 = 2ε 3 v I C , J 26 = 2ε 3 v I C , J 27 = ε 3(1 x)2 x(1+x) J 28 = 2ε 3 (1 2ε)v I B , J 29 = 2ε 3 v(1 w) I A , ], [ (1 2ε)(1 x) I A (1 ε) IA ], 9
10 J 30 ( ) = 2ε 3 v I A I A, J 31 = 4ε 3 (1 x)2 [ (1 x 2 ) x(1+x 2 I A ) (1+w)IA IA IA IA ] I A 2IA , J 32 = 4ε 4 v I B , J 33 = 2ε 3 v(1 w) I C (, ) J 34 = 2ε 3 vw I C + IC , J 35 = 2ε 3 v(1 w) I C, J 36 = 4ε 3 (1 x)2 [ (1 x 2 ) x(1+x 2 I C ) (1+w)IC w IC (1 w)ic ] +2I C + IC IC IC , J 37 = 2ε 4 v I C , J 38 = ε 3 vw I D , J 39 = 4ε 4(1 x)2( 1 x+x 2 xw ) x 2 I C (22) 4 The system of differential equations Let us set J =(J 1,...,J 39 ) T for the vector of master integrals. In this basis the system of differential equations is in ε-form [24]. We have d J = εa J, (23) where the matrix A is independent of ε. Let us first describe the singularities of the system of differential equations. The singularities are on hypersurfaces and each hypersurface is defined by a polynomial in x and y. There are sixteen polynomials, which are given by p 1 = x, p 2 p 3 = x 1, = x+1, p 4 = y, p 5 p 6 p 7 p 8 p 9 = y 1, = y+1, = xy+x y+1, = xy+x 2y, = 2xy y+1, 10
11 p 10 p 11 p 12 p 13 p 14 p 15 = xy 2 + 2xy 2y 2 + x+2y, = xy 2 + 2xy+y 2 + x 2y+1, = xy 2 + 2xy y 2 + x+2y 1, = 2xy 2 + 2xy y 2 + 2y 1, = 2xy 2 + 2xy 3y 2 + 2y+1, = 3xy 2 + 2xy 2y 2 x+2y, p 16 = 3xy 2 + 2xy 3y 2 x+2y+1. (24) We note that the polynomials p k are maximally of degree 3. The highest degree in the variable y is two, the highest degree in the variable x is one. The entries of the matrix A are Q-linear combinations of dlog-forms of these polynomials: A i j = 16 c i jk d ln(p k (x,y)), c i jk Q. (25) k=1 We find that the matrix A contains only fifteen Q-independent linear combinations of dlog-forms. A basis for these is given by ω 1 = ds = 2d ln p 2 d ln p 1, s ds ω 2 = s 4mt 2 = 2d ln p 3 d ln p 1, ds ω 3 = s ( 4mt 2 s ) = d ln p 1, ω 4 = dm2 W m 2 W = d ln p 8 + d ln p 9 d ln p 5 d ln p 6 d ln p 1, dm 2 W ω 5 = mw 2 = d ln p 7 d ln p 5 d ln p 6 + d ln p 4 + d ln p 2 d ln p 1, m2 t ω 6 = d ln ( s+mw 2 mt) 2 = d ln p16 d ln p 5 d ln p 6 + d ln p 2 d ln p 1, ω 7 = d ln ( s mw 2 + t) m2 = d ln p12 d ln p 5 d ln p 6 + d ln p 2 d ln p 1, ω 8 = 1 (sm 2 d ln W 2 +( mt 2 ) 2 ) m2 W = 1 2 d ln p d ln p 14 d ln p 5 d ln p 6 + d ln p 2 d ln p 1, ω 9 = 1 ( (2m 2 d ln 2 t mw) 2 ( s+ m 2 t mw 2 ) 2 ) ω 10 = 1 2 d ln p d ln p 10 d ln p 5 d ln p 6 + d ln p 2 d ln p 1, = 1 2 d ln( λ ( s,mw,m 2 t 2 )) = d ln p 11 d ln p 5 d ln p 6 + d ln p 2 d ln p 1, 11
12 ω 11 = 1 2 d ln p d ln p 14, ω 12 = 1 2 d ln p d ln p 10, ω 13 = 1 2 d ln p d ln p 8, ω 14 = 1 2 d ln p d ln p 5, ω 15 = d ln p d ln p d ln p 5. (26) The entries of A are therefore of the form A i j = 15 c i jk ω k, c i jk Q. (27) k=1 By a rescaling of the master integrals with constant factors we may actually achieve c i jk Z. (28) For our choice of basis of master integrals J we have c i jk Z. Equivalently, we may express the matrix A as A = 15 k=1 C k ω k, (29) where the entries of the matrices C k are integer numbers. The matrix A is given in the supplementary electronic file attached to the arxiv version of this article. On specific hypersurfaces the differential forms simplify considerably. On the hypersurface y=0 (i.e. for the case m W = m t ) the differential forms reduce to a linear combination of dx x, dx x 1, dx x+1. (30) On the hypersurface x = 0 (i.e. for the case p 2 ) the differential forms reduce to a linear combination of dy y, dy y 1, dy y+1, dy y (31) On the hypersurface x=1 (i.e. for the case p 2 = 0 and m 2 W = m2 t ) the differential forms reduce to a linear combination of dy y, dy y 1, dy y+1, 2ydy y 2 + 1, 2(y 2)dy y 2 4y 1, 2(y+2)dy y 2 + 4y 1. (32) The derivative of the master integrals is given by the product of the matrix A with the vector J: d J = εa J. (33) 12
13 The right-hand side vanishes if J is in the kernel of A. This is what happens on the hypersurface x=1: Although A 0 we have J = 0. (34) y x=1 It follows that the master integrals are constant on the hypersurface x=1. This is a significant simplification for solving the differential equations. 5 Analytical results The analytic result for the master integrals at a point (x,y) is obtained from the value of the master integrals at a boundary point (x i,y i ) by integrating the system of differential equations along a path from (x i,y i ) to (x,y). The result does not depend on the chosen path, but only on the homotopy class of the path. For the case at hand we have several significant simplification: 1. All master integrals are constant on the hypersurface x=1 (corresponding to p 2 = 0 and mw 2 = m2 t ) and we may take the values of the master integrals on this hypersurface as boundary values. We therefore have a boundary line. 2. It is then sufficient to integrate the differential equation along a straight line from (1,y) to (x,y) with y = const. The polynomials p 1 -p 3 and p 7 -p 16 are all linear in x (the polynomials p 4 -p 6 don t contribute along y=const), avoiding the need to factorise higher-order polynomials in x. 3. The boundary values on the hypersurface x = 1 are particularly simple: 35 out of the 39 master integrals vanish on this hypersurface, the four non-vanishing master integrals are products of one-loop integrals. Since all integration kernels are dlog-forms, the result can be expressed in terms of multiple polylogarithms. Multiple polylogarithms are defined for l k 0 by [40 43] We have G(l 1,...,l k ;z) = z G(l 1,l 2,...,l k ;z) = 0 dz 1 z 1 l 1 z 0 z 1 0 dz 2 z 2 l 2... z k 1 0 dz k z k l k. (35) dz 1 z 1 l 1 G(l 2,...,l k ;z 1 ). (36) We define G(0,...,0;z) with k zeros for l 1 to l k to be G(0,...,0;z) = 1 k! (lnz)k. (37) 13
14 This permits us to allow trailing zeros in the sequence(l 1,...,l k ) by defining the function G with trailing zeros via eq. (36) and eq. (37). For l k 0 we have the scaling relation Let us introduce the short-hand notation G(l 1,...,l k ;z) = G(λl 1,...,λl k ;λz). (38) G m1,...,m k (l 1,...,l k ;z) = G(0,...,0,l }{{} 1,...,l k 1,0...,0,l }{{} k ;z), (39) m 1 1 m k 1 where all l j for j = 1,...,k are assumed to be non-zero. The sum representation of multiple polylogarithms is defined by Li m1,...,m k (x 1,...,x k ) = n 1 >n 2 >...>n k >0 x n xnk k, (40) n m 1 1 n m k k and related to the integral representation by ( ) 1 Li m1,...,m k (x 1,...,x k ) = ( 1) k 1 1 G m1,...,m k,,..., ;1, x 1 x 1 x 2 x 1...x k G m1,...,m k (l 1,...,l k ;z) = ( 1) k Li m1,...,m k ( z l 1, l 1 l 2,..., l k 1 l k ). (41) The master integrals J 1, J 2, J 5 and J 6 are products of one-loop integrals and rather simple. They are given by J 1 = e 2γ E ε (Γ(1+ε)) 2, J 2 = e 2γ E ε (Γ(1+ε)) 2 w ε, J 5 = e 2γ E ε (Γ(1+ε))2 (Γ(1 ε)) 2 Γ(1 2ε) J 6 = e 2γ E ε (Γ(1+ε))2 (Γ(1 ε)) 2 Γ(1 2ε) ( v) ε, ( v) ε w ε. (42) These are the only master integrals, which do not vanish on the hypersurface x = 1. All other master integrals vanish on the hypersurface x = 1. This fully specifies the boundary conditions on the line(x,y)=(1,y). Note that the integrals J 5 and J 6 have logarithmic singularities at x=1. For the integration in (x,y)-space from (1,y) to (x,y) it is better to change variables from x to x = 1 x. We therefore integrate in (x,y)-space from (0,y) to (x,y), where y is treated as a parameter. This integration gives multiple polylogarithms of the form where the letters l 1,..., l k are from the alphabet G ( l 1,...,l k ;x ), (43) A = { 0,1,2,x 7,x 8,x 9,x 10,x 11,x 12,x 13,x 14,x 15,x 16}. (44) 14
15 The non-trivial letters x 7 -x 16 are given by x 7 = 2 1+y, x 8 = 1 y 1+y, x 9 = 1+y 2y, ( 1+y 2 ) x 10 = 1+4y y2 (1+y) 2, x 11 = 2 (1+y) 2, x 13 = 1 4y y2 2y(1+y), x 14 = 1+4y y2 2y(1+y), x 12 = 4y (1+y) 2, x 15 = 1 4y y2 (1+y)(1 3y), x 16 = 4y (1+y)(1 3y). (45) For all basis integrals we write J k = ε j J ( j) k. (46) j=0 The quantities J ( j) k are given for 1 k 39 and 0 j 4 in the supplementary electronic file attached to the arxiv version of this article. To give an example, let us show the first non-vanishing term of the most complicated integral, the non-planar vertex correction J 39. We find J (3) 39 = 8G( 0,1,1;x ) 4G ( 0,1,x 8;x ) 4G ( 0,x 8,1;x ) + 4G ( 0,x 8,x 9;x ) + 4G ( 0,x 9,x 8;x ) 8G ( 1,2,1;x ) + 8G ( 1,x 15,1;x ) 4G ( 1,x 15,x 8 ;x ) 4G ( 1,x 15,x 9 ;x ) 16G ( 1,x 7,1;x ) + 8G ( 1,x 7,x 8 ;x ) + 12G ( 1,x 7,x 9 ;x ) + 4G ( 1,x 8,1;x ) 4G ( 1,x 8,x 9 ;x ) 4G ( 1,x 9,x 8 ;x ) + 8G ( x 14,2,1;x ) 8G ( x 14,x 15,1;x ) +4G ( x 14,x 15,x 8;x ) + 4G ( x 14,x 15,x 9;x ) + 16G ( x 14,x 7,1;x ) 8G ( x 14,x 7,x 8;x ) 12G ( x 14,x 7,x 9 ;x ) 4G ( x 14,x 8,1;x ) + 4G ( x 14,x 8,x 9 ;x ) + 4G ( x 14,x 9,x 8 ;x ) +8G ( x 15,1,1;x ) + 4G ( x 15,1,x 8 ;x ) 8G ( x 15,2,1;x ) + 4G ( x 15,x 14,x 8 ;x ) +4G ( x 15,x 14,x 9;x ) + 4G ( x 15,x 7,1;x ) 12G ( x 15,x 7,x 8;x ) 8G ( x 15,x 7,x 9;x ) 4G ( x 15,x 8,1;x ) + 4G ( x 15,x 8,x 9 ;x ) + 4G ( x 15,x 9,x 8 ;x ) 8G ( x 7,1,1;x ) +4G ( x 7,1,x 8 ;x ) + 4G ( x 7,x 8,1;x ) 4G ( x 7,x 8,x 9 ;x ) 4G ( x 7,x 9,x 8 ;x ). (47) 6 Numerical results Of particular interest are numerical results for p 2 = m 2 H. (48) Since p 2 > 0, we are not in the Euclidean region. Feynman s i0-prescription instructs us to take a small imaginary part into account: p 2 p 2 + i0. This selects the correct branches for the two square roots v(4 v) and λ(v,w,1). With m W = GeV, m H = GeV, m t = GeV (49) 15
16 we obtain for the variables x and y x = i, y = i. (50) The values of the master integrals at this point are given to 8 digits in table 2. They are easily ε 0 ε 1 ε 2 ε 3 ε 4 J J J i i i i J i i i i J i i i i J i i i i J i i i i J J i i i i J J J J J i i i i J J i i i i J J J i i i i J J J i i i J J J J J i i J i i J J J i i J J J J J i i J J J Table 2: Numerical results for the first five terms of the ε-expansion of the master integrals J 1 -J 39 at the kinematic point s=m 2 H. computed to arbitrary precision by evaluating the multiple polylogarithms with the help of GiNaC [44, 45]. In addition we verified the first few digits at various kinematic points with the help of the programssector_decomposition [46] andpysecdec [47, 48]. 16
17 7 Conclusions In this paper we presented the two-loop master integrals relevant to the O(αα s )-corrections to the decay H b b through a Ht t-coupling. We kept the exact dependence of the masses of the heavy particles (m W and m t ) and the momentum p 2 of the Higgs boson, but neglected the b-quark mass. All master integrals are expressed in terms of multiple polylogarithms with an alphabet of 13 letters. They can be evaluated to arbitrary precision with the help of the GiNaC-library. For the special case p 2 = m 2 H we presented the numerical values. Acknowledgements This work has been supported by the Cluster of Excellence Precision Physics, Fundamental Interactions, and Structure of Matter (PRISMA+ EXC 2118/1) funded by the German Research Foundation (DFG) within the German Excellence Strategy (Project ID ). S.W. would like to thank the Institute for Theoretical Studies in Zurich for hospitality, where part of this work was carried out. The Feynman diagrams in this article have been made with the programaxodraw [49]. A Master topologies In this appendix we show in tables 3-6 the diagrams of all master topologies. J 1 J 2 Figure 3: Master topologies (part 1). 17
18 J 3 J 4 J 5 J 6 J 7 J 8 J 9 J 11 J 12 J 13 Figure 4: Master topologies (part 2). 18
19 J 14 J 15 J 16 J 17 J 19 J 20 J 22 J 23 J 24 J 25 J 26 J 27 Figure 5: Master topologies (part 3). 19
20 J 28 J 29 J 31 J 32 J 33 J 36 J 37 J 38 J 39 Figure 6: Master topologies (part 4). 20
21 B Supplementary material Attached to the arxiv version of this article is an electronic file in ASCII format with Maple syntax, defining the quantities A, J. The matrixaappears in the differential equation d J = εa J. (51) The entries of the matrix A are Z-linear combinations of ω 1,..., ω 15, defined in eq. (26). These differential forms are denoted by omega_1,...,omega_15. The vector J contains the results for the master integrals up to order ε 4 in terms of multiple polylogarithms. The variable ε is denoted byeps, ζ 2, ζ 3, ζ 4 by zeta_2,zeta_3,zeta_4, respectively. For the notation of multiple polylogarithms we given an example: G(x 7,x 8,1;x ) is denoted by References Glog([xp7,xp8,1],xp). [1] G. P. Lepage, P. B. Mackenzie, and M. E. Peskin, (2014), arxiv: [2] P. A. Baikov, K. G. Chetyrkin, and J. H. Kühn, Phys. Rev. Lett. 96, (2006), arxiv:hep-ph/ [3] K. G. Chetyrkin and A. Kwiatkowski, Nucl. Phys. B461, 3 (1996), arxiv:hep-ph/ [4] K. G. Chetyrkin, J. H. Kühn, and M. Steinhauser, Nucl. Phys. B505, 40 (1997), arxiv:hep-ph/ [5] K. G. Chetyrkin and M. Steinhauser, Phys. Lett. B408, 320 (1997), arxiv:hep-ph/ [6] A. Primo, G. Sasso, G. Somogyi, and F. Tramontano, Phys. Rev. D99, (2019), arxiv: [7] A. L. Kataev, JETP Lett. 66, 327 (1997), arxiv:hep-ph/ [8] A. Kwiatkowski and M. Steinhauser, Phys. Lett. B338, 66 (1994), arxiv:hep-ph/ , [Erratum: Phys. Lett.B342,455(1995)]. [9] B. A. Kniehl and M. Spira, Nucl. Phys. B432, 39 (1994), arxiv:hep-ph/ [10] L. Mihaila, B. Schmidt, and M. Steinhauser, Phys. Lett. B751, 442 (2015), arxiv: [11] M. Butenschön, F. Fugel, and B. A. Kniehl, Phys. Rev. Lett. 98, (2007), arxiv:hep-ph/ [12] M. Butenschön, F. Fugel, and B. A. Kniehl, Nucl. Phys. B772, 25 (2007), arxiv:hep-ph/ [13] R. Bonciani et al., JHEP 12, 096 (2016), arxiv: [14] A. von Manteuffel and L. Tancredi, JHEP 06, 127 (2017), arxiv:
22 [15] B. Mistlberger, JHEP 05, 028 (2018), arxiv: [16] L. Adams, E. Chaubey, and S. Weinzierl, Phys. Rev. Lett. 121, (2018), arxiv: [17] L. Adams, E. Chaubey, and S. Weinzierl, JHEP 10, 206 (2018), arxiv: [18] A. V. Kotikov, Phys. Lett. B254, 158 (1991). [19] A. V. Kotikov, Phys. Lett. B267, 123 (1991). [20] E. Remiddi, Nuovo Cim. A110, 1435 (1997), hep-th/ [21] T. Gehrmann and E. Remiddi, Nucl. Phys. B580, 485 (2000), hep-ph/ [22] M. Argeri and P. Mastrolia, Int. J. Mod. Phys. A22, 4375 (2007), arxiv: [23] S. Müller-Stach, S. Weinzierl, and R. Zayadeh, Commun.Math.Phys. 326, 237 (2014), arxiv: [24] J. M. Henn, Phys. Rev. Lett. 110, (2013), arxiv: [25] J. M. Henn, J. Phys. A48, (2015), arxiv: [26] J. Ablinger et al., Comput. Phys. Commun. 202, 33 (2016), arxiv: [27] L. Adams, E. Chaubey, and S. Weinzierl, Phys. Rev. Lett. 118, (2017), arxiv: [28] J. Bosma, K. J. Larsen, and Y. Zhang, Phys. Rev. D97, (2018), arxiv: [29] F. V. Tkachov, Phys. Lett. B100, 65 (1981). [30] K. G. Chetyrkin and F. V. Tkachov, Nucl. Phys. B192, 159 (1981). [31] S. Laporta, Int. J. Mod. Phys. A15, 5087 (2000), hep-ph/ [32] M. Besier, D. Van Straten, and S. Weinzierl, (2018), arxiv: [33] O. V. Tarasov, Phys. Rev. D54, 6479 (1996), hep-th/ [34] O. V. Tarasov, Nucl. Phys. B502, 455 (1997), hep-ph/ [35] A. von Manteuffel and C. Studerus, (2012), arxiv: [36] P. Maierhöfer, J. Usovitsch, and P. Uwer, Comput. Phys. Commun. 230, 99 (2018), arxiv: [37] A. V. Smirnov, Comput. Phys. Commun. 189, 182 (2015), arxiv: [38] R. N. Lee, (2012), arxiv: [39] R. N. Lee, J. Phys. Conf. Ser. 523, (2014), arxiv: [40] A. B. Goncharov, Math. Res. Lett. 5, 497 (1998). [41] A. B. Goncharov, (2001), math.ag/ [42] J. M. Borwein, D. M. Bradley, D. J. Broadhurst, and P. Lisonek, Trans. Amer. Math. Soc. 353:3, 907 (2001), math.ca/ [43] S. Moch, P. Uwer, and S. Weinzierl, J. Math. Phys. 43, 3363 (2002), hep-ph/ [44] C. Bauer, A. Frink, and R. Kreckel, J. Symbolic Computation 33, 1 (2002), cs.sc/ [45] J. Vollinga and S. Weinzierl, Comput. Phys. Commun. 167, 177 (2005), hep-ph/ [46] C. Bogner and S. Weinzierl, Comput. Phys. Commun. 178, 596 (2008), arxiv: [47] S. Borowka et al., Comput. Phys. Commun. 222, 313 (2018), arxiv: [48] S. Borowka et al., (2018), arxiv: [49] J. A. M. Vermaseren, Comput. Phys. Commun. 83, 45 (1994). 22
One-Mass Two-Loop Master Integrals for Mixed
 One-Mass Two-Loop Master Integrals for Mixed α s -Electroweak Drell-Yan Production work ongoing with Andreas von Manteuffel The PRISMA Cluster of Excellence and Institute of Physics Johannes Gutenberg
One-Mass Two-Loop Master Integrals for Mixed α s -Electroweak Drell-Yan Production work ongoing with Andreas von Manteuffel The PRISMA Cluster of Excellence and Institute of Physics Johannes Gutenberg
Functions associated to scattering amplitudes. Stefan Weinzierl
 Functions associated to scattering amplitudes Stefan Weinzierl Institut für Physik, Universität Mainz I: Periodic functions and periods II: III: Differential equations The two-loop sun-rise diagramm in
Functions associated to scattering amplitudes Stefan Weinzierl Institut für Physik, Universität Mainz I: Periodic functions and periods II: III: Differential equations The two-loop sun-rise diagramm in
Schematic Project of PhD Thesis: Two-Loop QCD Corrections with the Differential Equations Method
 Schematic Project of PhD Thesis: Two-Loop QCD Corrections with the Differential Equations Method Matteo Becchetti Supervisor Roberto Bonciani University of Rome La Sapienza 24/01/2017 1 The subject of
Schematic Project of PhD Thesis: Two-Loop QCD Corrections with the Differential Equations Method Matteo Becchetti Supervisor Roberto Bonciani University of Rome La Sapienza 24/01/2017 1 The subject of
Multiloop integrals in dimensional regularization made simple
 Multiloop integrals in dimensional regularization made simple Johannes M. Henn Institute for Advanced Study based on PRL 110 (2013) [arxiv:1304.1806], JHEP 1307 (2013) 128 [arxiv:1306.2799] with A. V.
Multiloop integrals in dimensional regularization made simple Johannes M. Henn Institute for Advanced Study based on PRL 110 (2013) [arxiv:1304.1806], JHEP 1307 (2013) 128 [arxiv:1306.2799] with A. V.
arxiv: v2 [hep-ph] 4 Jun 2018
![arxiv: v2 [hep-ph] 4 Jun 2018 arxiv: v2 [hep-ph] 4 Jun 2018](/thumbs/81/82655817.jpg) Prepared for submission to JHEP Evaluating elliptic master integrals at special kinematic values: using differential equations and their solutions via expansions near singular points arxiv:1805.00227v2
Prepared for submission to JHEP Evaluating elliptic master integrals at special kinematic values: using differential equations and their solutions via expansions near singular points arxiv:1805.00227v2
arxiv:hep-ph/ v1 18 Nov 1996
 TTP96-55 1 MPI/PhT/96-122 hep-ph/9611354 November 1996 arxiv:hep-ph/9611354v1 18 Nov 1996 AUTOMATIC COMPUTATION OF THREE-LOOP TWO-POINT FUNCTIONS IN LARGE MOMENTUM EXPANSION K.G. Chetyrkin a,b, R. Harlander
TTP96-55 1 MPI/PhT/96-122 hep-ph/9611354 November 1996 arxiv:hep-ph/9611354v1 18 Nov 1996 AUTOMATIC COMPUTATION OF THREE-LOOP TWO-POINT FUNCTIONS IN LARGE MOMENTUM EXPANSION K.G. Chetyrkin a,b, R. Harlander
Systems of differential equations for Feynman Integrals; Schouten identities and canonical bases.
 Systems of differential equations for Feynman Integrals; Schouten identities and canonical bases. Lorenzo Tancredi TTP, KIT - Karlsruhe Bologna, 18 Novembre 2014 Based on collaboration with Thomas Gehrmann,
Systems of differential equations for Feynman Integrals; Schouten identities and canonical bases. Lorenzo Tancredi TTP, KIT - Karlsruhe Bologna, 18 Novembre 2014 Based on collaboration with Thomas Gehrmann,
Exploring the function space of Feynman integrals. Stefan Weinzierl
 Exploring the function space of Feynman integrals Stefan Weinzierl Institut für Physik, Universität Mainz Mathematics intro: Physics intro: Part I: Part II: Periodic functions and periods Precision calculations
Exploring the function space of Feynman integrals Stefan Weinzierl Institut für Physik, Universität Mainz Mathematics intro: Physics intro: Part I: Part II: Periodic functions and periods Precision calculations
From Tensor Integral to IBP
 From Tensor Integral to IBP Mohammad Assadsolimani, in collaboration with P. Kant, B. Tausk and P. Uwer 11. Sep. 2012 Mohammad Assadsolimani From Tensor Integral to IBP 1 Contents Motivation NNLO Tensor
From Tensor Integral to IBP Mohammad Assadsolimani, in collaboration with P. Kant, B. Tausk and P. Uwer 11. Sep. 2012 Mohammad Assadsolimani From Tensor Integral to IBP 1 Contents Motivation NNLO Tensor
Reduction to Master Integrals. V.A. Smirnov Atrani, September 30 October 05, 2013 p.1
 Reduction to Master Integrals V.A. Smirnov Atrani, September 30 October 05, 2013 p.1 Reduction to Master Integrals IBP (integration by parts) V.A. Smirnov Atrani, September 30 October 05, 2013 p.1 Reduction
Reduction to Master Integrals V.A. Smirnov Atrani, September 30 October 05, 2013 p.1 Reduction to Master Integrals IBP (integration by parts) V.A. Smirnov Atrani, September 30 October 05, 2013 p.1 Reduction
PoS(DIS2017)295. Hadronic Higgs boson decay at order α 4 s and α 5 s
 Institut für Theoretische Teilchenphysik, Karlsruhe Institute of Technology (KIT) 7618 Karlsruhe, Germany E-mail: joshua.davies@kit.edu Matthias Steinhauser Institut für Theoretische Teilchenphysik, Karlsruhe
Institut für Theoretische Teilchenphysik, Karlsruhe Institute of Technology (KIT) 7618 Karlsruhe, Germany E-mail: joshua.davies@kit.edu Matthias Steinhauser Institut für Theoretische Teilchenphysik, Karlsruhe
Non-planar two-loop Feynman integrals contributing to Higgs plus jet production
 Non-planar two-loop Feynman integrals contributing to Higgs plus jet production Institute for Theoretical Particle Physics (TTP), Karlsruhe Institute of Technology Engesserstraße 7, D-76128 Karlsruhe,
Non-planar two-loop Feynman integrals contributing to Higgs plus jet production Institute for Theoretical Particle Physics (TTP), Karlsruhe Institute of Technology Engesserstraße 7, D-76128 Karlsruhe,
Multiloop scattering amplitudes in the LHC Era
 Multiloop scattering amplitudes in the LHC Era Francesco Moriello Based on arxiv:1609.06685 In collaboration with: R. Bonciani, V. Del Duca, H. Frellesvig, J.M. Henn, V. Smirnov October 26, 2016 Outline
Multiloop scattering amplitudes in the LHC Era Francesco Moriello Based on arxiv:1609.06685 In collaboration with: R. Bonciani, V. Del Duca, H. Frellesvig, J.M. Henn, V. Smirnov October 26, 2016 Outline
arxiv: v2 [hep-th] 7 Jul 2016
![arxiv: v2 [hep-th] 7 Jul 2016 arxiv: v2 [hep-th] 7 Jul 2016](/thumbs/92/108002000.jpg) Integration-by-parts reductions from unitarity cuts and algebraic geometry arxiv:1606.09447v [hep-th] 7 Jul 016 Institute for Theoretical Physics, ETH Zürich, 8093 Zürich, Switzerland E-mail: Kasper.Larsen@phys.ethz.ch
Integration-by-parts reductions from unitarity cuts and algebraic geometry arxiv:1606.09447v [hep-th] 7 Jul 016 Institute for Theoretical Physics, ETH Zürich, 8093 Zürich, Switzerland E-mail: Kasper.Larsen@phys.ethz.ch
Evaluating multiloop Feynman integrals by Mellin-Barnes representation
 April 7, 004 Loops&Legs 04 Evaluating multiloop Feynman integrals by Mellin-Barnes representation V.A. Smirnov Nuclear Physics Institute of Moscow State University Mellin-Barnes representation as a tool
April 7, 004 Loops&Legs 04 Evaluating multiloop Feynman integrals by Mellin-Barnes representation V.A. Smirnov Nuclear Physics Institute of Moscow State University Mellin-Barnes representation as a tool
arxiv:hep-lat/ v1 30 Sep 2005
 September 2005 Applying Gröbner Bases to Solve Reduction Problems for Feynman Integrals arxiv:hep-lat/0509187v1 30 Sep 2005 A.V. Smirnov 1 Mechanical and Mathematical Department and Scientific Research
September 2005 Applying Gröbner Bases to Solve Reduction Problems for Feynman Integrals arxiv:hep-lat/0509187v1 30 Sep 2005 A.V. Smirnov 1 Mechanical and Mathematical Department and Scientific Research
Single mass scale diagrams: construction of a basis for the ε-expansion.
 BI-TP 99/4 Single mass scale diagrams: construction of a basis for the ε-expansion. J. Fleischer a 1, M. Yu. Kalmykov a,b 2 a b Fakultät für Physik, Universität Bielefeld, D-615 Bielefeld, Germany BLTP,
BI-TP 99/4 Single mass scale diagrams: construction of a basis for the ε-expansion. J. Fleischer a 1, M. Yu. Kalmykov a,b 2 a b Fakultät für Physik, Universität Bielefeld, D-615 Bielefeld, Germany BLTP,
arxiv: v1 [hep-ph] 30 Dec 2015
![arxiv: v1 [hep-ph] 30 Dec 2015 arxiv: v1 [hep-ph] 30 Dec 2015](/thumbs/94/118068708.jpg) June 3, 8 Derivation of functional equations for Feynman integrals from algebraic relations arxiv:5.94v [hep-ph] 3 Dec 5 O.V. Tarasov II. Institut für Theoretische Physik, Universität Hamburg, Luruper
June 3, 8 Derivation of functional equations for Feynman integrals from algebraic relations arxiv:5.94v [hep-ph] 3 Dec 5 O.V. Tarasov II. Institut für Theoretische Physik, Universität Hamburg, Luruper
Two loop O N f s 2 corrections to the decay width of the Higgs boson to two massive fermions
 PHYSICAL REVIEW D VOLUME 53, NUMBER 9 1 MAY 1996 Two loop O N f s corrections to the decay width of the Higgs boson to two massive fermions K Melnikov Institut für Physik, THEP, Johannes Gutenberg Universität,
PHYSICAL REVIEW D VOLUME 53, NUMBER 9 1 MAY 1996 Two loop O N f s corrections to the decay width of the Higgs boson to two massive fermions K Melnikov Institut für Physik, THEP, Johannes Gutenberg Universität,
Reduction of Feynman integrals to master integrals
 Reduction of Feynman integrals to master integrals A.V. Smirnov Scientific Research Computing Center of Moscow State University A.V. Smirnov ACAT 2007 p.1 Reduction problem for Feynman integrals A review
Reduction of Feynman integrals to master integrals A.V. Smirnov Scientific Research Computing Center of Moscow State University A.V. Smirnov ACAT 2007 p.1 Reduction problem for Feynman integrals A review
arxiv: v2 [hep-ph] 12 Jul 2017
![arxiv: v2 [hep-ph] 12 Jul 2017 arxiv: v2 [hep-ph] 12 Jul 2017](/thumbs/72/67823954.jpg) MaPhy-AvH/7-5 MITP/7-38 arxiv:75.895v [hep-ph] Jul 7 Analytic continuation and numerical evaluation of the kite integral and the equal mass sunrise integral Christian Bogner a, Armin Schweitzer a and Stefan
MaPhy-AvH/7-5 MITP/7-38 arxiv:75.895v [hep-ph] Jul 7 Analytic continuation and numerical evaluation of the kite integral and the equal mass sunrise integral Christian Bogner a, Armin Schweitzer a and Stefan
NNLO antenna subtraction with two hadronic initial states
 NNLO antenna subtraction with two hadronic initial states Institut für Theoretische Physik, Universität Zürich, Winterthurerstr. 190, 8057 Zürich, Switzerland E-mail: radja@physik.uzh.ch Aude Gehrmann-De
NNLO antenna subtraction with two hadronic initial states Institut für Theoretische Physik, Universität Zürich, Winterthurerstr. 190, 8057 Zürich, Switzerland E-mail: radja@physik.uzh.ch Aude Gehrmann-De
Feynman integrals and multiple polylogarithms. Stefan Weinzierl
 Feynman integrals and multiple polylogarithms Stefan Weinzierl Universität Mainz I. Basic techniques II. Nested sums and iterated integrals III. Multiple Polylogarithms IV. Applications The need for precision
Feynman integrals and multiple polylogarithms Stefan Weinzierl Universität Mainz I. Basic techniques II. Nested sums and iterated integrals III. Multiple Polylogarithms IV. Applications The need for precision
The Pentabox Master Integrals with the Simplified Differential Equations approach
 The Pentabox Master Integrals with the Simplified Differential Equations approach Costas G. Papadopoulos INPP, NCSR Demokritos Zurich, August 25, 2016 C.G.Papadopoulos (INPP) 5box QCD@LHC 2016 1 / 36 Introduction
The Pentabox Master Integrals with the Simplified Differential Equations approach Costas G. Papadopoulos INPP, NCSR Demokritos Zurich, August 25, 2016 C.G.Papadopoulos (INPP) 5box QCD@LHC 2016 1 / 36 Introduction
Evaluating double and triple (?) boxes
 Evaluating double and triple (?) boxes V.A. Smirnov a hep-ph/0209295 September 2002 a Nuclear Physics Institute of Moscow State University, Moscow 9992, Russia A brief review of recent results on analytical
Evaluating double and triple (?) boxes V.A. Smirnov a hep-ph/0209295 September 2002 a Nuclear Physics Institute of Moscow State University, Moscow 9992, Russia A brief review of recent results on analytical
Toward a Precision Standard Model Theory of the Higgs Boson Couplings
 Toward a Precision Standard Model Theory of the Higgs Boson Couplings M. E. Peskin Gunion-fest March 2014 describing work with P. Lepage, P. Mackenzie Ellis, Gunion, Haber, Roszkowski, Zwirner, PR D 39,
Toward a Precision Standard Model Theory of the Higgs Boson Couplings M. E. Peskin Gunion-fest March 2014 describing work with P. Lepage, P. Mackenzie Ellis, Gunion, Haber, Roszkowski, Zwirner, PR D 39,
Forcer: a FORM program for 4-loop massless propagators
 Forcer: a FORM program for 4-loop massless propagators, a B. Ruijl ab and J.A.M. Vermaseren a a Nikhef Theory Group, Science Park 105, 1098 XG Amsterdam, The Netherlands b Leiden Centre of Data Science,
Forcer: a FORM program for 4-loop massless propagators, a B. Ruijl ab and J.A.M. Vermaseren a a Nikhef Theory Group, Science Park 105, 1098 XG Amsterdam, The Netherlands b Leiden Centre of Data Science,
Two-loop QCD Corrections to the Heavy Quark Form Factors p.1
 Two-loop QCD Corrections to the Heavy Quark Form Factors Thomas Gehrmann Universität Zürich UNIVERSITAS TURICENSIS MDCCC XXXIII Snowmass Linear Collider Worksho005 Two-loop QCD Corrections to the Heavy
Two-loop QCD Corrections to the Heavy Quark Form Factors Thomas Gehrmann Universität Zürich UNIVERSITAS TURICENSIS MDCCC XXXIII Snowmass Linear Collider Worksho005 Two-loop QCD Corrections to the Heavy
arxiv: v2 [hep-ph] 20 Jul 2014
![arxiv: v2 [hep-ph] 20 Jul 2014 arxiv: v2 [hep-ph] 20 Jul 2014](/thumbs/89/98127046.jpg) arxiv:407.67v [hep-ph] 0 Jul 04 Mass-corrections to double-higgs production & TopoID Jonathan Grigo and Institut für Theoretische Teilchenphysik, Karlsruhe Institute of Technology (KIT) E-mail: jonathan.grigo@kit.edu,
arxiv:407.67v [hep-ph] 0 Jul 04 Mass-corrections to double-higgs production & TopoID Jonathan Grigo and Institut für Theoretische Teilchenphysik, Karlsruhe Institute of Technology (KIT) E-mail: jonathan.grigo@kit.edu,
A numerical test of differential equations for one- and two-loop sunrise diagrams using configuration space techniques
 Eur. Phys. J. C 7:85 DOI.4/epjc/s5--85-z Special Article - Tools for Experiment and Theory A numerical test of differential equations for one- and two-loop sunrise diagrams using configuration space techniques
Eur. Phys. J. C 7:85 DOI.4/epjc/s5--85-z Special Article - Tools for Experiment and Theory A numerical test of differential equations for one- and two-loop sunrise diagrams using configuration space techniques
Numerical Evaluation of Multi-loop Integrals
 Numerical Evaluation of Multi-loop Integrals Sophia Borowka MPI for Physics, Munich In collaboration with G. Heinrich Based on arxiv:124.4152 [hep-ph] HP 8 :Workshop on High Precision for Hard Processes,
Numerical Evaluation of Multi-loop Integrals Sophia Borowka MPI for Physics, Munich In collaboration with G. Heinrich Based on arxiv:124.4152 [hep-ph] HP 8 :Workshop on High Precision for Hard Processes,
Precision Calculations to Top- and Bottom-Yukawa Couplings within the SM and BSM
 Precision Calculations to Top- and Bottom-Yukawa Couplings within the SM and BSM Institut for Theoretical Physics, University of Heidelberg, 69117 Heidelberg, Germany E-mail: mihaila@thphys.uni-heidelberg.de
Precision Calculations to Top- and Bottom-Yukawa Couplings within the SM and BSM Institut for Theoretical Physics, University of Heidelberg, 69117 Heidelberg, Germany E-mail: mihaila@thphys.uni-heidelberg.de
Numerical Evaluation of Multi-loop Integrals
 Numerical Evaluation of Multi-loop Integrals Sophia Borowka MPI for Physics, Munich In collaboration with: J. Carter and G. Heinrich Based on arxiv:124.4152 [hep-ph] http://secdec.hepforge.org DESY-HU
Numerical Evaluation of Multi-loop Integrals Sophia Borowka MPI for Physics, Munich In collaboration with: J. Carter and G. Heinrich Based on arxiv:124.4152 [hep-ph] http://secdec.hepforge.org DESY-HU
HIGH ENERGY BEHAVIOUR OF FORM FACTORS
 HIGH ENERGY BEHAVIOUR OF FORM FACTORS Taushif Ahmed Johannes Gutenberg University Mainz Germany Skype Seminar IIT Hyderabad May 10, 018 With Johannes Henn & Matthias Steinhauser Ref: JHEP 1706 (017) 15
HIGH ENERGY BEHAVIOUR OF FORM FACTORS Taushif Ahmed Johannes Gutenberg University Mainz Germany Skype Seminar IIT Hyderabad May 10, 018 With Johannes Henn & Matthias Steinhauser Ref: JHEP 1706 (017) 15
Simplified differential equations approach for the calculation of multi-loop integrals
 Simplified differential equations approach for the calculation of multi-loop integrals Chris Wever (N.C.S.R. Demokritos) 1 C. Papadopoulos [arxiv: 1401.6057 [hep-ph]] C. Papadopoulos, D. Tommasini, C.
Simplified differential equations approach for the calculation of multi-loop integrals Chris Wever (N.C.S.R. Demokritos) 1 C. Papadopoulos [arxiv: 1401.6057 [hep-ph]] C. Papadopoulos, D. Tommasini, C.
Hopf algebra structures in particle physics
 EPJ manuscript No. will be inserted by the editor) Hopf algebra structures in particle physics Stefan Weinzierl a Max-Planck-Institut für Physik Werner-Heisenberg-Institut), Föhringer Ring 6, D-80805 München,
EPJ manuscript No. will be inserted by the editor) Hopf algebra structures in particle physics Stefan Weinzierl a Max-Planck-Institut für Physik Werner-Heisenberg-Institut), Föhringer Ring 6, D-80805 München,
NNLO antenna subtraction with one hadronic initial state
 antenna subtraction with one hadronic initial state Alejandro Daleo, Aude Gehrmann-De Ridder Institute for Theoretical Physics, ETH Zürich E-mail: adaleo@phys.ethz.ch, gehra@phys.ethz.ch Thomas Gehrmann,
antenna subtraction with one hadronic initial state Alejandro Daleo, Aude Gehrmann-De Ridder Institute for Theoretical Physics, ETH Zürich E-mail: adaleo@phys.ethz.ch, gehra@phys.ethz.ch Thomas Gehrmann,
Two-loop self-energy master integrals on shell
 BI-TP 99/1 Two-loop self-energy master integrals on shell J. Fleischer 1, M. Yu. Kalmykov and A. V. Kotikov 3 Fakultät für Physik, Universität Bielefeld, D-33615 Bielefeld 1, Germany Abstract Analytic
BI-TP 99/1 Two-loop self-energy master integrals on shell J. Fleischer 1, M. Yu. Kalmykov and A. V. Kotikov 3 Fakultät für Physik, Universität Bielefeld, D-33615 Bielefeld 1, Germany Abstract Analytic
The rare decay H Zγ in perturbative QCD
 The rare decay H Zγ in perturbative QCD [arxiv: hep-ph/1505.00561] Thomas Gehrmann, Sam Guns & Dominik Kara June 15, 2015 RADCOR 2015 AND LOOPFEST XIV - UNIVERSITY OF CALIFORNIA, LOS ANGELES Z Z H g q
The rare decay H Zγ in perturbative QCD [arxiv: hep-ph/1505.00561] Thomas Gehrmann, Sam Guns & Dominik Kara June 15, 2015 RADCOR 2015 AND LOOPFEST XIV - UNIVERSITY OF CALIFORNIA, LOS ANGELES Z Z H g q
Two-loop Remainder Functions in N = 4 SYM
 Two-loop Remainder Functions in N = 4 SYM Claude Duhr Institut für theoretische Physik, ETH Zürich, Wolfgang-Paulistr. 27, CH-8093, Switzerland E-mail: duhrc@itp.phys.ethz.ch 1 Introduction Over the last
Two-loop Remainder Functions in N = 4 SYM Claude Duhr Institut für theoretische Physik, ETH Zürich, Wolfgang-Paulistr. 27, CH-8093, Switzerland E-mail: duhrc@itp.phys.ethz.ch 1 Introduction Over the last
K. Melnikov 1. Institut fur Physik, THEP, Johannes Gutenberg Universitat, Abstract
 MZ-TH-95-0 November 995 Two loopo(n f s )corrections to the decay width of the Higgs boson to two massive fermions. K. Melnikov Institut fur Physik, THEP, Johannes Gutenberg Universitat, Staudinger Weg
MZ-TH-95-0 November 995 Two loopo(n f s )corrections to the decay width of the Higgs boson to two massive fermions. K. Melnikov Institut fur Physik, THEP, Johannes Gutenberg Universitat, Staudinger Weg
arxiv: v3 [hep-ph] 20 Apr 2017
![arxiv: v3 [hep-ph] 20 Apr 2017 arxiv: v3 [hep-ph] 20 Apr 2017](/thumbs/76/73111934.jpg) MITP/14-76 A quasi-finite basis for multi-loop Feynman integrals arxiv:1411.7392v3 [hep-ph] 2 Apr 217 Andreas von Manteuffel, a Erik Panzer, b, c and Robert M. Schabinger a a PRISMA Cluster of Excellence
MITP/14-76 A quasi-finite basis for multi-loop Feynman integrals arxiv:1411.7392v3 [hep-ph] 2 Apr 217 Andreas von Manteuffel, a Erik Panzer, b, c and Robert M. Schabinger a a PRISMA Cluster of Excellence
FIRE4, LiteRed and accompanying tools to solve integration by parts relations
 Prepared for submission to JHEP HU-EP-13/04 HU-Mathematik:05-2013 FIRE4, LiteRed and accompanying tools to solve integration by parts relations Alexander V. Smirnov a Vladimir A. Smirnov b,c a Scientific
Prepared for submission to JHEP HU-EP-13/04 HU-Mathematik:05-2013 FIRE4, LiteRed and accompanying tools to solve integration by parts relations Alexander V. Smirnov a Vladimir A. Smirnov b,c a Scientific
Differential Equations for Feynman Integrals
 for Feynman Integrals Ulrich Schubert Max-Planck-Institut für Physik Föhringer Ring 6, München January 18, 2015 based on work with M. Argeri, S. Di Vita, P. Mastrolia, E. Mirabella, J. Schlenk, L. Tancredi,
for Feynman Integrals Ulrich Schubert Max-Planck-Institut für Physik Föhringer Ring 6, München January 18, 2015 based on work with M. Argeri, S. Di Vita, P. Mastrolia, E. Mirabella, J. Schlenk, L. Tancredi,
arxiv: v2 [hep-th] 1 Aug 2018
![arxiv: v2 [hep-th] 1 Aug 2018 arxiv: v2 [hep-th] 1 Aug 2018](/thumbs/87/96944118.jpg) Differential equations for loop integrals in Baikov representation Jorrit Bosma 1 Kasper J Larsen and Yang Zhang 1 3 1 ETH Zürich Wolfang-Pauli-Strasse 7 893 Zürich Switzerland School of Physics and Astronomy
Differential equations for loop integrals in Baikov representation Jorrit Bosma 1 Kasper J Larsen and Yang Zhang 1 3 1 ETH Zürich Wolfang-Pauli-Strasse 7 893 Zürich Switzerland School of Physics and Astronomy
arxiv: v1 [hep-ph] 28 Dec 2018
![arxiv: v1 [hep-ph] 28 Dec 2018 arxiv: v1 [hep-ph] 28 Dec 2018](/thumbs/92/110903335.jpg) MPP-208-06 All master integrals for three-jet production at NNLO D. Chicherin a, T. Gehrmann b, J. M. Henn a, P. Wasser c, Y. Zhang a, S. Zoia a a Max-Planck-Institut für Physik, Werner-Heisenberg-Institut,
MPP-208-06 All master integrals for three-jet production at NNLO D. Chicherin a, T. Gehrmann b, J. M. Henn a, P. Wasser c, Y. Zhang a, S. Zoia a a Max-Planck-Institut für Physik, Werner-Heisenberg-Institut,
Numerical multi-loop calculations: tools and applications
 Journal of Physics: Conference Series PAPER OPEN ACCESS Numerical multi-loop calculations: tools and applications To cite this article: S. Borowka et al 2016 J. Phys.: Conf. Ser. 762 012073 Related content
Journal of Physics: Conference Series PAPER OPEN ACCESS Numerical multi-loop calculations: tools and applications To cite this article: S. Borowka et al 2016 J. Phys.: Conf. Ser. 762 012073 Related content
Multiple polylogarithms and Feynman integrals
 Multiple polylogarithms and Feynman integrals Erik Panzer Institute des Hautes E tudes Scientifiques Amplitudes 215 July 7th ETH/University of Zu rich Topics 1 hyperlogarithms & iterated integrals 2 multiple
Multiple polylogarithms and Feynman integrals Erik Panzer Institute des Hautes E tudes Scientifiques Amplitudes 215 July 7th ETH/University of Zu rich Topics 1 hyperlogarithms & iterated integrals 2 multiple
arxiv:hep-ph/ v1 28 Mar 2006
 DESY-06-0 SFB/CPP-06- Hypergeometric representation of the two-loop equal mass sunrise diagram arxiv:hep-ph/0607v 8 Mar 006 O.V. Tarasov Deutsches Elektronen - Synchrotron DESY Platanenallee 6, D-578 Zeuthen,
DESY-06-0 SFB/CPP-06- Hypergeometric representation of the two-loop equal mass sunrise diagram arxiv:hep-ph/0607v 8 Mar 006 O.V. Tarasov Deutsches Elektronen - Synchrotron DESY Platanenallee 6, D-578 Zeuthen,
Master integrals without subdivergences
 Master integrals without subdivergences Joint work with Andreas von Manteuffel and Robert Schabinger Erik Panzer 1 (CNRS, ERC grant 257638) Institute des Hautes Études Scientifiques 35 Route de Chartres
Master integrals without subdivergences Joint work with Andreas von Manteuffel and Robert Schabinger Erik Panzer 1 (CNRS, ERC grant 257638) Institute des Hautes Études Scientifiques 35 Route de Chartres
The Pentabox Master Integrals with the Simplified Differential Equations approach
 Prepared for submission to JHEP TTP15-042 The Pentabox Master Integrals with the Simplified Differential Equations approach Costas G. Papadopoulos ab Damiano Tommasini a and Christopher Wever ac a Institute
Prepared for submission to JHEP TTP15-042 The Pentabox Master Integrals with the Simplified Differential Equations approach Costas G. Papadopoulos ab Damiano Tommasini a and Christopher Wever ac a Institute
Feynman integrals as Periods
 Feynman integrals as Periods Pierre Vanhove Amplitudes 2017, Higgs Center, Edinburgh, UK based on [arxiv:1309.5865], [arxiv:1406.2664], [arxiv:1601.08181] Spencer Bloch, Matt Kerr Pierre Vanhove (IPhT)
Feynman integrals as Periods Pierre Vanhove Amplitudes 2017, Higgs Center, Edinburgh, UK based on [arxiv:1309.5865], [arxiv:1406.2664], [arxiv:1601.08181] Spencer Bloch, Matt Kerr Pierre Vanhove (IPhT)
Multiple polylogarithms and Feynman integrals
 Multiple polylogarithms and Feynman integrals Erik Panzer Institute des Hautes E tudes Scientifiques Amplitudes 215 July 7th ETH/University of Zu rich Topics 1 hyperlogarithms & iterated integrals 2 multiple
Multiple polylogarithms and Feynman integrals Erik Panzer Institute des Hautes E tudes Scientifiques Amplitudes 215 July 7th ETH/University of Zu rich Topics 1 hyperlogarithms & iterated integrals 2 multiple
Hypergeometric representation of the two-loop equal mass sunrise diagram
 Physics Letters B 68 6 95 wwwelseviercom/locate/physletb Hypergeometric representation of the two-loop equal mass sunrise diagram OV Tarasov Deutsches Elektronen-Synchrotron DESY Platanenallee 6 D-578
Physics Letters B 68 6 95 wwwelseviercom/locate/physletb Hypergeometric representation of the two-loop equal mass sunrise diagram OV Tarasov Deutsches Elektronen-Synchrotron DESY Platanenallee 6 D-578
The Higgs pt distribution
 The Higgs pt distribution Chris Wever (TUM) In collaboration with: F. Caola, K. Kudashkin, J. Lindert, K. Melnikov, P. Monni, L. Tancredi GGI: Amplitudes in the LHC era, Florence 16 Oktober, 2018 Outline
The Higgs pt distribution Chris Wever (TUM) In collaboration with: F. Caola, K. Kudashkin, J. Lindert, K. Melnikov, P. Monni, L. Tancredi GGI: Amplitudes in the LHC era, Florence 16 Oktober, 2018 Outline
Two-loop Heavy Fermion Corrections to Bhabha Scattering
 Two-loop Heavy Fermion Corrections to Bhabha Scattering S. Actis 1, M. Czakon 2, J. Gluza 3 and T. Riemann 1 1 Deutsches Elektronen-Synchrotron DESY Platanenallee 6, D 15738 Zeuthen, Germany 2 Institut
Two-loop Heavy Fermion Corrections to Bhabha Scattering S. Actis 1, M. Czakon 2, J. Gluza 3 and T. Riemann 1 1 Deutsches Elektronen-Synchrotron DESY Platanenallee 6, D 15738 Zeuthen, Germany 2 Institut
Calculating four-loop massless propagators with Forcer
 Calculating four-loop massless propagators with Forcer Takahiro Ueda Nikhef, The Netherlands Collaboration with: Ben Ruijl and Jos Vermaseren 18 Jan. 2016 ACAT2016, UTFSM, Valparaíso 1 / 30 Contents Introduction
Calculating four-loop massless propagators with Forcer Takahiro Ueda Nikhef, The Netherlands Collaboration with: Ben Ruijl and Jos Vermaseren 18 Jan. 2016 ACAT2016, UTFSM, Valparaíso 1 / 30 Contents Introduction
INP MSU 96-34/441 hep-ph/ October 1996 Some techniques for calculating two-loop diagrams 1 Andrei I. Davydychev Institute for Nuclear Physics,
 INP MSU 96-34/441 hep-ph/9610510 October 1996 Some techniques for calculating two-loop diagrams 1 Andrei I. Davydychev Institute for Nuclear Physics, Moscow State University, 119899 Moscow, Russia Abstract
INP MSU 96-34/441 hep-ph/9610510 October 1996 Some techniques for calculating two-loop diagrams 1 Andrei I. Davydychev Institute for Nuclear Physics, Moscow State University, 119899 Moscow, Russia Abstract
Colour octet potential to three loops
 SFB/CPP-13-54 TTP13-8 Colour octet potential to three loops Chihaya Anzai a), Mario Prausa a), Alexander V. Smirnov b), Vladimir A. Smirnov c), Matthias Steinhauser a) a) Institut für Theoretische Teilchenphysik,
SFB/CPP-13-54 TTP13-8 Colour octet potential to three loops Chihaya Anzai a), Mario Prausa a), Alexander V. Smirnov b), Vladimir A. Smirnov c), Matthias Steinhauser a) a) Institut für Theoretische Teilchenphysik,
arxiv:hep-ph/ v2 2 Feb 1998
 BI-TP 97/53, hep-ph/9711487 to appear in 15 March 1998 issue of Phys. Rev. D (Rapid Comm.) Improvement of the method of diagonal Padé approximants for perturbative series in gauge theories arxiv:hep-ph/9711487v2
BI-TP 97/53, hep-ph/9711487 to appear in 15 March 1998 issue of Phys. Rev. D (Rapid Comm.) Improvement of the method of diagonal Padé approximants for perturbative series in gauge theories arxiv:hep-ph/9711487v2
Unitarity, Dispersion Relations, Cutkosky s Cutting Rules
 Unitarity, Dispersion Relations, Cutkosky s Cutting Rules 04.06.0 For more information about unitarity, dispersion relations, and Cutkosky s cutting rules, consult Peskin& Schröder, or rather Le Bellac.
Unitarity, Dispersion Relations, Cutkosky s Cutting Rules 04.06.0 For more information about unitarity, dispersion relations, and Cutkosky s cutting rules, consult Peskin& Schröder, or rather Le Bellac.
Two-loop massive fermionic operator matrix elements and intial state QED corrections to e + e γ /Z
 Two-loop massive fermionic operator matrix elements and intial state QED corrections to e + e γ /Z J. Blümlein, a ab and W. van Neerven c a DESY, Zeuthen, Platanenalle 6, D-173 Zeuthen, Germany. b Departamento
Two-loop massive fermionic operator matrix elements and intial state QED corrections to e + e γ /Z J. Blümlein, a ab and W. van Neerven c a DESY, Zeuthen, Platanenalle 6, D-173 Zeuthen, Germany. b Departamento
arxiv: v2 [hep-ph] 23 Jan 2013
![arxiv: v2 [hep-ph] 23 Jan 2013 arxiv: v2 [hep-ph] 23 Jan 2013](/thumbs/93/113359617.jpg) MITP/13-009 January 2013 The decays of on-shell and off-shell polarized gauge bosons into massive uark pairs at NLO QCD 1 S. Groote a, J.G. Körner b and P. Tuvike a arxiv:1301.5217v2 hep-ph] 23 Jan 2013
MITP/13-009 January 2013 The decays of on-shell and off-shell polarized gauge bosons into massive uark pairs at NLO QCD 1 S. Groote a, J.G. Körner b and P. Tuvike a arxiv:1301.5217v2 hep-ph] 23 Jan 2013
Two-loop corrections to t t production in the gluon channel. Matteo Capozi Sapienza University of Rome
 Two-loop corrections to t t production in the gluon channel Matteo Capozi Sapienza University of Rome November 7, 2016 Top quark With a mass of m t = 172.44 ± 0.13(stat) ± 0.47(syst)GeV, the top quark
Two-loop corrections to t t production in the gluon channel Matteo Capozi Sapienza University of Rome November 7, 2016 Top quark With a mass of m t = 172.44 ± 0.13(stat) ± 0.47(syst)GeV, the top quark
Numerical multi-loop calculations with SecDec
 Journal of Physics: Conference Series OPEN ACCESS Numerical multi-loop calculations with SecDec To cite this article: Sophia Borowka and Gudrun Heinrich 214 J. Phys.: Conf. Ser. 523 1248 View the article
Journal of Physics: Conference Series OPEN ACCESS Numerical multi-loop calculations with SecDec To cite this article: Sophia Borowka and Gudrun Heinrich 214 J. Phys.: Conf. Ser. 523 1248 View the article
Higgs boson production at the LHC: NNLO partonic cross sections through order ǫ and convolutions with splitting functions to N 3 LO
 SFB/CPP-12-93 TTP12-45 LPN12-127 Higgs boson production at the LHC: NNLO partonic cross sections through order ǫ and convolutions with splitting functions to N 3 LO Maik Höschele, Jens Hoff, Aleey Pak,
SFB/CPP-12-93 TTP12-45 LPN12-127 Higgs boson production at the LHC: NNLO partonic cross sections through order ǫ and convolutions with splitting functions to N 3 LO Maik Höschele, Jens Hoff, Aleey Pak,
Simplified differential equations approach for NNLO calculations
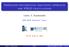 Simplified differential equations approach for NNLO calculations Costas. G. Papadopoulos INPP, NCSR Demokritos, Athens UCLA, June 19, 2015 Costas. G. Papadopoulos NNLO Radcor-Loopfest, LA, 2015 1 / 39
Simplified differential equations approach for NNLO calculations Costas. G. Papadopoulos INPP, NCSR Demokritos, Athens UCLA, June 19, 2015 Costas. G. Papadopoulos NNLO Radcor-Loopfest, LA, 2015 1 / 39
arxiv: v2 [hep-ph] 25 Sep 2018
![arxiv: v2 [hep-ph] 25 Sep 2018 arxiv: v2 [hep-ph] 25 Sep 2018](/thumbs/88/115472931.jpg) Applications of integrand reduction to two-loop five-point scattering amplitudes in QCD arxiv:1807.09709v2 [hep-ph] 25 Sep 2018 Institute for Particle Physics Phenomenology, Department of Physics, Durham
Applications of integrand reduction to two-loop five-point scattering amplitudes in QCD arxiv:1807.09709v2 [hep-ph] 25 Sep 2018 Institute for Particle Physics Phenomenology, Department of Physics, Durham
Bare Higgs mass and potential at ultraviolet cutoff
 Bare Higgs mass and potential at ultraviolet cutoff Yuta Hamada and Hikaru Kawai Department of Physics, Kyoto University, Kyoto 606-850, Japan Kin-ya Oda Department of Physics, Osaka University, Osaka
Bare Higgs mass and potential at ultraviolet cutoff Yuta Hamada and Hikaru Kawai Department of Physics, Kyoto University, Kyoto 606-850, Japan Kin-ya Oda Department of Physics, Osaka University, Osaka
Generalizations of polylogarithms for Feynman integrals
 Journal of Physics: Conference Series PAPER OPEN ACCESS Generalizations of polylogarithms for Feynman integrals To cite this article: Christian Bogner 6 J. Phys.: Conf. Ser. 76 67 View the article online
Journal of Physics: Conference Series PAPER OPEN ACCESS Generalizations of polylogarithms for Feynman integrals To cite this article: Christian Bogner 6 J. Phys.: Conf. Ser. 76 67 View the article online
arxiv: v2 [hep-ph] 18 Nov 2009
![arxiv: v2 [hep-ph] 18 Nov 2009 arxiv: v2 [hep-ph] 18 Nov 2009](/thumbs/91/107559014.jpg) Space-time dimensionality D as complex variable: calculating loop integrals using dimensional recurrence relation and analytical properties with respect to D. arxiv:0911.05v [hep-ph] 18 Nov 009 R.N. Lee
Space-time dimensionality D as complex variable: calculating loop integrals using dimensional recurrence relation and analytical properties with respect to D. arxiv:0911.05v [hep-ph] 18 Nov 009 R.N. Lee
PSEUDO SCALAR FORM FACTORS AT 3-LOOP QCD. Taushif Ahmed Institute of Mathematical Sciences, India March 22, 2016
 PSEUDO SCALAR FORM FACTORS AT 3-LOOP QCD Taushif Ahmed Institute of Mathematical Sciences, India March, 016 PROLOGUE: SM & MSSM SM Complex scalar doublet (4 DOF) 3 DOF transform into longitudinal modes
PSEUDO SCALAR FORM FACTORS AT 3-LOOP QCD Taushif Ahmed Institute of Mathematical Sciences, India March, 016 PROLOGUE: SM & MSSM SM Complex scalar doublet (4 DOF) 3 DOF transform into longitudinal modes
arxiv: v1 [hep-lat] 22 Oct 2013
![arxiv: v1 [hep-lat] 22 Oct 2013 arxiv: v1 [hep-lat] 22 Oct 2013](/thumbs/93/114143203.jpg) Renormalization of the momentum density on the lattice using shifted boundary conditions arxiv:1310.6075v1 [hep-lat] 22 Oct 2013 Daniel Robaina PRISMA Cluster of Excellence, Institut für Kernphysik, Johannes
Renormalization of the momentum density on the lattice using shifted boundary conditions arxiv:1310.6075v1 [hep-lat] 22 Oct 2013 Daniel Robaina PRISMA Cluster of Excellence, Institut für Kernphysik, Johannes
TVID: Three-loop Vacuum Integrals from Dispersion relations
 TVID: Three-loop Vacuum Integrals from Dispersion relations Stefan Bauberger, Ayres Freitas Hochschule für Philosophie, Philosophische Fakultät S.J., Kaulbachstr. 3, 80539 München, Germany Pittsburgh Particle-physics
TVID: Three-loop Vacuum Integrals from Dispersion relations Stefan Bauberger, Ayres Freitas Hochschule für Philosophie, Philosophische Fakultät S.J., Kaulbachstr. 3, 80539 München, Germany Pittsburgh Particle-physics
A magic connection between massive and massless diagrams. Department of Physics, University of Bergen, Allegaten 55, N-5007 Bergen, Norway
 University of Bergen, Department of Physics Scientific/Technical Report No.995-7 ISSN 8-696 MZ-TH{95-4 hep-ph/9544 April 995 A magic connection between massive and massless diagrams A.I. Davydychev a;
University of Bergen, Department of Physics Scientific/Technical Report No.995-7 ISSN 8-696 MZ-TH{95-4 hep-ph/9544 April 995 A magic connection between massive and massless diagrams A.I. Davydychev a;
arxiv: v1 [hep-ph] 20 Jan 2012
![arxiv: v1 [hep-ph] 20 Jan 2012 arxiv: v1 [hep-ph] 20 Jan 2012](/thumbs/94/118313158.jpg) ZU-TH 01/12 MZ-TH/12-03 BI-TP 2012/02 Reduze 2 Distributed Feynman Integral Reduction arxiv:1201.4330v1 [hep-ph] 20 Jan 2012 A. von Manteuffel, a,b C. Studerus c a Institut für Theoretische Physik, Universität
ZU-TH 01/12 MZ-TH/12-03 BI-TP 2012/02 Reduze 2 Distributed Feynman Integral Reduction arxiv:1201.4330v1 [hep-ph] 20 Jan 2012 A. von Manteuffel, a,b C. Studerus c a Institut für Theoretische Physik, Universität
Computing of Charged Current DIS at three loops
 Computing of Charged Current DIS at three loops Mikhail Rogal Mikhail.Rogal@desy.de DESY, Zeuthen, Germany ACAT 2007, Amsterdam, Netherlands, April 23-28, 2007 Computing of Charged CurrentDIS at three
Computing of Charged Current DIS at three loops Mikhail Rogal Mikhail.Rogal@desy.de DESY, Zeuthen, Germany ACAT 2007, Amsterdam, Netherlands, April 23-28, 2007 Computing of Charged CurrentDIS at three
Numerical Evaluation of Loop Integrals
 Numerical Evaluation of Loop Integrals Institut für Theoretische Physik Universität Zürich Tsukuba, April 22 nd 2006 In collaboration with Babis Anastasiou Rationale (Why do we need complicated loop amplitudes?)
Numerical Evaluation of Loop Integrals Institut für Theoretische Physik Universität Zürich Tsukuba, April 22 nd 2006 In collaboration with Babis Anastasiou Rationale (Why do we need complicated loop amplitudes?)
arxiv: v1 [hep-ph] 22 Sep 2016
![arxiv: v1 [hep-ph] 22 Sep 2016 arxiv: v1 [hep-ph] 22 Sep 2016](/thumbs/77/75758952.jpg) TTP16-037 arxiv:1609.06786v1 [hep-ph] 22 Sep 2016 Five-loop massive tadpoles Thomas Luthe Institut für Theoretische Teilchenphysik, Karlsruhe Institute of Technology, Karlsruhe, Germany E-mail: thomas.luthe@kit.edu
TTP16-037 arxiv:1609.06786v1 [hep-ph] 22 Sep 2016 Five-loop massive tadpoles Thomas Luthe Institut für Theoretische Teilchenphysik, Karlsruhe Institute of Technology, Karlsruhe, Germany E-mail: thomas.luthe@kit.edu
Electroweak accuracy in V-pair production at the LHC
 Electroweak accuracy in V-pair production at the LHC Anastasiya Bierweiler Karlsruhe Institute of Technology (KIT), Institut für Theoretische Teilchenphysik, D-7628 Karlsruhe, Germany E-mail: nastya@particle.uni-karlsruhe.de
Electroweak accuracy in V-pair production at the LHC Anastasiya Bierweiler Karlsruhe Institute of Technology (KIT), Institut für Theoretische Teilchenphysik, D-7628 Karlsruhe, Germany E-mail: nastya@particle.uni-karlsruhe.de
Asymptotic Expansions of Feynman Integrals on the Mass Shell in Momenta and Masses
 Asymptotic Expansions of Feynman Integrals on the Mass Shell in Momenta and Masses arxiv:hep-ph/9708423v 2 Aug 997 V.A. Smirnov Nuclear Physics Institute of Moscow State University Moscow 9899, Russia
Asymptotic Expansions of Feynman Integrals on the Mass Shell in Momenta and Masses arxiv:hep-ph/9708423v 2 Aug 997 V.A. Smirnov Nuclear Physics Institute of Moscow State University Moscow 9899, Russia
arxiv:hep-ph/ v1 21 Jan 1998
 TARCER - A Mathematica program for the reduction of two-loop propagator integrals R. Mertig arxiv:hep-ph/980383v Jan 998 Abstract Mertig Research & Consulting, Kruislaan 49, NL-098 VA Amsterdam, The Netherlands
TARCER - A Mathematica program for the reduction of two-loop propagator integrals R. Mertig arxiv:hep-ph/980383v Jan 998 Abstract Mertig Research & Consulting, Kruislaan 49, NL-098 VA Amsterdam, The Netherlands
Anomalous dimensions and splitting functions beyond the next-to-next-to-leading order
 Anomalous dimensions and splitting functions beyond the next-to-next-to-leading order Department of Mathematical Sciences, University of Liverpool, Liverpool L69 3BX, UK E-mail: Andreas.Vogt@liverpool.ac.uk
Anomalous dimensions and splitting functions beyond the next-to-next-to-leading order Department of Mathematical Sciences, University of Liverpool, Liverpool L69 3BX, UK E-mail: Andreas.Vogt@liverpool.ac.uk
Schouten identities for Feynman graph amplitudes; The Master Integrals for the two-loop massive sunrise graph
 Available online at www.sciencedirect.com ScienceDirect Nuclear Physics B 880 0 33 377 www.elsevier.com/locate/nuclphysb Schouten identities for Feynman graph amplitudes; The Master Integrals for the two-loop
Available online at www.sciencedirect.com ScienceDirect Nuclear Physics B 880 0 33 377 www.elsevier.com/locate/nuclphysb Schouten identities for Feynman graph amplitudes; The Master Integrals for the two-loop
Dipole subtraction with random polarisations
 , Christopher Schwan, Stefan Weinzierl PRISMA Cluster of Excellence, Johannes Gutenberg University, Mainz goetz@uni-mainz.de schwan@uni-mainz.de stefanw@thep.physik.uni-mainz.de In this talk, we discuss
, Christopher Schwan, Stefan Weinzierl PRISMA Cluster of Excellence, Johannes Gutenberg University, Mainz goetz@uni-mainz.de schwan@uni-mainz.de stefanw@thep.physik.uni-mainz.de In this talk, we discuss
Feynman Integrals, Regulators and Elliptic Polylogarithms
 Feynman Integrals, Regulators and Elliptic Polylogarithms Pierre Vanhove Automorphic Forms, Lie Algebras and String Theory March 5, 2014 based on [arxiv:1309.5865] and work in progress Spencer Bloch, Matt
Feynman Integrals, Regulators and Elliptic Polylogarithms Pierre Vanhove Automorphic Forms, Lie Algebras and String Theory March 5, 2014 based on [arxiv:1309.5865] and work in progress Spencer Bloch, Matt
arxiv: v1 [hep-ph] 28 Jul 2017
![arxiv: v1 [hep-ph] 28 Jul 2017 arxiv: v1 [hep-ph] 28 Jul 2017](/thumbs/80/80942710.jpg) with Calibrated Uncertainty arxiv:1707.09404v1 [hep-ph] 28 Jul 2017 Departamento de Física Teórica Instituto de Física Universidad Nacional Autónoma de México Apartado Postal 20 364, México CDMX 01000,
with Calibrated Uncertainty arxiv:1707.09404v1 [hep-ph] 28 Jul 2017 Departamento de Física Teórica Instituto de Física Universidad Nacional Autónoma de México Apartado Postal 20 364, México CDMX 01000,
Towards improved predictions for electroweak vector boson pair production at the LHC
 Towards improved predictions for electroweak vector boson pair production at the LHC Kirill Melnikov TTP KIT Based on collaboration with M. Dowling, F. Caola, J. Henn, A. Smirnov, V. Smirnov Outline 1)
Towards improved predictions for electroweak vector boson pair production at the LHC Kirill Melnikov TTP KIT Based on collaboration with M. Dowling, F. Caola, J. Henn, A. Smirnov, V. Smirnov Outline 1)
Analytical expressions of 3 and 4-loop sunrise Feynman integrals and 4-dimensional lattice integrals
 3 September 8 Analytical expressions of 3 and 4-loop sunrise Feynman integrals and 4-dimensional lattice integrals arxiv:83.7v3 [hep-ph] Mar 8 S. Laporta Museo Storico della Fisica e Centro Studi e Ricerche
3 September 8 Analytical expressions of 3 and 4-loop sunrise Feynman integrals and 4-dimensional lattice integrals arxiv:83.7v3 [hep-ph] Mar 8 S. Laporta Museo Storico della Fisica e Centro Studi e Ricerche
Numerical evaluation of multi-loop integrals
 Max-Planck-Institut für Physik, München, Germany E-mail: sjahn@mpp.mpg.de We present updates on the development of pyse CDE C, a toolbox to numerically evaluate parameter integrals in the context of dimensional
Max-Planck-Institut für Physik, München, Germany E-mail: sjahn@mpp.mpg.de We present updates on the development of pyse CDE C, a toolbox to numerically evaluate parameter integrals in the context of dimensional
arxiv: v1 [hep-th] 22 Dec 2017
![arxiv: v1 [hep-th] 22 Dec 2017 arxiv: v1 [hep-th] 22 Dec 2017](/thumbs/76/73496231.jpg) arxiv:1712.08541v1 [hep-th] 22 Dec 2017 DESY 17-225, DO-TH 17/37 Special functions, transcendentals and their numerics arxiv:yymmdd.xxxxx Jakob Ablinger a, Johannes Blümlein b, Mark Round a,b, and Carsten
arxiv:1712.08541v1 [hep-th] 22 Dec 2017 DESY 17-225, DO-TH 17/37 Special functions, transcendentals and their numerics arxiv:yymmdd.xxxxx Jakob Ablinger a, Johannes Blümlein b, Mark Round a,b, and Carsten
Outline Motivations for ILC: e + e γ/z q qg LHC: pp l + l + jet (q q l + l g + qg l + l q + qg l + l q) Existing literature The complete EW one-loop c
 Complete electroweak corrections to e + e 3 jets C.M. Carloni Calame INFN & University of Southampton Workshop LC08: e + e Physics at TeV scale September 22-25, 2008 in collaboration with S. Moretti, F.
Complete electroweak corrections to e + e 3 jets C.M. Carloni Calame INFN & University of Southampton Workshop LC08: e + e Physics at TeV scale September 22-25, 2008 in collaboration with S. Moretti, F.
gg! hh in the high energy limit
 gg! hh in the high energy limit Go Mishima Karlsruhe Institute of Technology (KIT), TTP in collaboration with Matthias Steinhauser, Joshua Davies, David Wellmann work in progress gg! hh : previous works
gg! hh in the high energy limit Go Mishima Karlsruhe Institute of Technology (KIT), TTP in collaboration with Matthias Steinhauser, Joshua Davies, David Wellmann work in progress gg! hh : previous works
Single Higgs production at LHC as a probe for an anomalous Higgs self coupling
 Single Higgs production at LHC as a probe for an anomalous Higgs self coupling Brookhaven National Laboratory E-mail: pgiardino@bnl.gov We explore the possibility of probing the trilinear Higgs self coupling
Single Higgs production at LHC as a probe for an anomalous Higgs self coupling Brookhaven National Laboratory E-mail: pgiardino@bnl.gov We explore the possibility of probing the trilinear Higgs self coupling
arxiv: v1 [hep-th] 10 Apr 2014
![arxiv: v1 [hep-th] 10 Apr 2014 arxiv: v1 [hep-th] 10 Apr 2014](/thumbs/87/96193264.jpg) Prepared for submission to JHEP Iterative structure of finite loop integrals arxiv:404.2922v [hep-th] 0 Apr 204 Simon Caron-Huot a,b Johannes M. Henn a a Institute for Advanced Study, Princeton, NJ 08540,
Prepared for submission to JHEP Iterative structure of finite loop integrals arxiv:404.2922v [hep-th] 0 Apr 204 Simon Caron-Huot a,b Johannes M. Henn a a Institute for Advanced Study, Princeton, NJ 08540,
General amplitude of the n vertex one-loop process in a strong magnetic field
 Yaroslavl State University Preprint YARU-HE-0/09 hep-ph/01009 arxiv:hep-ph/01009v 1 Mar 003 General amplitude of the n vertex one-loop process in a strong magnetic field A. V. Kuznetsov, N. V. Mikheev,
Yaroslavl State University Preprint YARU-HE-0/09 hep-ph/01009 arxiv:hep-ph/01009v 1 Mar 003 General amplitude of the n vertex one-loop process in a strong magnetic field A. V. Kuznetsov, N. V. Mikheev,
HyperInt - exact integration with hyperlogarithms
 HyperInt - exact integration with hyperlogarithms Erik Panzer erikpanzer@ihes.fr (CNRS, ERC grant 257638, F. Brown) Institute des Hautes Études Scientifiques 35 Route de Chartres 9144 Bures-sur-Yvette
HyperInt - exact integration with hyperlogarithms Erik Panzer erikpanzer@ihes.fr (CNRS, ERC grant 257638, F. Brown) Institute des Hautes Études Scientifiques 35 Route de Chartres 9144 Bures-sur-Yvette
arxiv: v1 [hep-ph] 27 Aug 2009
![arxiv: v1 [hep-ph] 27 Aug 2009 arxiv: v1 [hep-ph] 27 Aug 2009](/thumbs/88/116124978.jpg) arxiv:0908.3969v1 [hep-ph] 27 Au 2009 QCD-electroweak effects and a new prediction for His production in luon fusion process Institut für Theoretische Physik, Universität Zürich, Winterthurerstr. 190,
arxiv:0908.3969v1 [hep-ph] 27 Au 2009 QCD-electroweak effects and a new prediction for His production in luon fusion process Institut für Theoretische Physik, Universität Zürich, Winterthurerstr. 190,
arxiv:hep-ph/ v1 29 Aug 2006
 IPPP/6/59 August 26 arxiv:hep-ph/6837v1 29 Aug 26 Third-order QCD results on form factors and coefficient functions A. Vogt a, S. Moch b and J.A.M. Vermaseren c a IPPP, Physics Department, Durham University,
IPPP/6/59 August 26 arxiv:hep-ph/6837v1 29 Aug 26 Third-order QCD results on form factors and coefficient functions A. Vogt a, S. Moch b and J.A.M. Vermaseren c a IPPP, Physics Department, Durham University,
arxiv:hep-ph/ v3 2 Mar 1999
 MZ-TH/98-47 hep-ph/9811482 November 1998 arxiv:hep-ph/9811482v3 2 Mar 1999 Polarized top decay into polarized W t( ) W( )+b at O(α s ) M. Fischer, S. Groote, J.G. Körner and M.C. Mauser Institut für Physik,
MZ-TH/98-47 hep-ph/9811482 November 1998 arxiv:hep-ph/9811482v3 2 Mar 1999 Polarized top decay into polarized W t( ) W( )+b at O(α s ) M. Fischer, S. Groote, J.G. Körner and M.C. Mauser Institut für Physik,
