Background Transfer Function (4A) Young Won Lim 4/20/15
|
|
|
- Valentine Skinner
- 5 years ago
- Views:
Transcription
1 Background (4A) 4/2/15
2 Copyrght (c) Young W. Lm. Permsson s granted to copy, dstrbute and/or modfy ths document under the terms of the GNU Free Documentaton Lcense, Verson 1.2 or any later verson publshed by the Free Software Foundaton; wth no Invarant Sectons, no Front-Cover Texts, and no Back-Cover Texts. A copy of the lcense s ncluded n the secton enttled "GNU Free Documentaton Lcense". Please send correctons (or suggestons) to youngwlm@hotmal.com. Ths document was produced by usng OpenOffce and Octave. 4/2/15
3 Vald Interval of ZIR & ZSR IVPs y ' ' + P(x) y ' + Q(x) y = f (x) y = y h + y p < t < y ( ) = y y ' ( ) = y 1 y ( ) = y h ( ) + y p ( ) = y + = y y ' ( ) = y h '( ) + y p '( ) = y 1 + = y 1 y ' ' + P(x) y ' + Q(x) y = y ( ) = y y ' ( ) = y 1 y h Nonzero Intal Condtons Zero Input Response Response due to the ntal condtons y ' ' + P(x) y ' + Q(x) y = f (x) y ( ) = y ' ( ) = y h + y p Zero Intal Condtons Zero State Response Response due to the forcng functon f 3 4/2/15
4 ZIR & ZSR y ' ' + 3 y ' + 2 y = x (t ) y ( ) = k 1, y '( ) = k 2 (s s + 2)Y (s) = k 1 s+k 2 +3 k 1 + X (s) [s 2 Y (s) s y ( ) y '( )]+3 [s Y (s) y( )]+2 Y (s)=x (s) Y (s) = k 1 s+k 2 +3 k 1 (s+1)(s+2) + X (s) (s+1)(s+2) Zero Input Response x (t) = Zero State Response y ( ) =, y ' ( ) = Y (s) = s+5 (s+1)(s+2) Y (s) = X (s) (s+1)(s+2) x (t) = e + t 1 = +4 (s+1) 3 1 (s+2) = (s+2) (s+1) (s 1) y = 4 e t 3 e 2t y = 1 2 e t e 2 t e+t 4 4/2/15
5 y ' ' + 3 y ' + 2 y = x (t ) y ( ) = k 1, y '( ) = k 2 (s s + 2)Y (s) = k 1 s+k 2 +3 k 1 + X (s) [s 2 Y (s) s y ( ) y '( )]+3 [s Y (s) y( )]+2 Y (s)=x (s) Y (s) = k 1 s+k 2 +3 k 1 (s+1)(s+2) + X (s) (s+1)(s+2) Zero State Response y ( ) =, y ' ( ) = Y (s) = X (s) (s+1)(s+2) Y (s) X (s) = 1 (s+1)(s+2) 5 4/2/15
6 & Impulse Response y ' ' + 3 y ' + 2 y = x (t ) y ( ) = k 1, y '( ) = k 2 (s s + 2)Y (s) = k 1 s+k 2 +3 k 1 + X (s) [s 2 Y (s) s y ( ) y '( )]+3 [s Y (s) y( )]+2 Y (s)=x (s) Y (s) = k 1 s+k 2 +3 k 1 (s+1)(s+2) + X (s) (s+1)(s+2) Y (s) X (s) = H (s) Zero State Response y ( ) =, y ' ( ) = Y (s) = H (s) X (s) y (t) = h(t) x (t) Y (s) = X (s) (s+1)(s+2) H (s) Transfer Functon h(t) Impulse Response Y (s) X (s) = 1 (s+1)(s+2) 6 4/2/15
7 and an ODE d N y(t) d N 1 y(t ) +a d t N 1 d t N 1 d y(t) d M x(t ) + +a N 1 +a d t N y(t) = b d t +b M 1 d M 1 x(t ) d t M 1 d x(t) + +b N 1 +b d t N x(t) (s N +a 1 s N 1 + +a N 1 s+a N ) Y (s) = (b s M +b 1 s M 1 + +b N 1 s+b N ) X (s) H (s) = Y (s) X (s) = (b s M +b 1 s M 1 + +b N 1 s+b N ) (s N +a 1 s N 1 + +a N 1 s+a N ) (D N +a 1 D N 1 + +a N 1 D+a N ) y (t ) = (b D M +b 1 D M 1 + +b N 1 D+b N ) x(t) Q(D) = (D N +a 1 D N 1 + +a N 1 D+a N ) P( D) = (b D M +b 1 D M 1 + +b N 1 D+b N ) Q(s) = (s N +a 1 s N 1 + +a N 1 s+a N ) P(s) = (b s M +b 1 s M 1 + +b N 1 s+b N ) Q(s) Y (s) = P(s) X (s) H (s) = Y (s) X (s) = P(s) Q( s) 7 4/2/15
8 Everlastng Exponental Inputs Causal Exponental Inputs 8 4/2/15
9 Exponental and Snusod Functons exponental functon e st = e σ t + ω t (s = σ + ω) snusod functon e ζ t = e ω t (ζ = ω) = e σ t (cos(ωt) + sn(ω t)) R{s} < (σ < ) R{s}= (σ = ) R{s} > (σ > ) 9 4/2/15
10 Everlastng & Causal Functon exponental functon snusod functon (s = σ + ω) (ζ = ω) everlastng exponental functon everlastng snusod functon appled at t = appled at t = e st e ζ t causal exponental functon causal snusod functon appled at t = appled at t = e st u(t) e ζ t u(t) 1 4/2/15
11 Snusodal Inputs and States everlastng snusod functon causal snusod functon state at t = = state at t = + contnuous state between t = & + zero state at t = non-zero state at t = + contnuous states possble dscontnuty forced ZSR t = t = + t = t = + non-causal ZIR + ZSR natural + forced ZIR + ZSR natural + forced nput appled at t = - lm t nput appled y p at t = h(t) {e ζ t u(t )} 11 4/2/15
12 States at t= + and t= nput appled at t = - contnuous ntal condtons e ζ t y () ( ) y (1) ( ) y (2) ( ) y () ( + ) y (1) ( + ) y (2) ( + ) forced Steady State Response nput appled at t = may be dscontnuous non-zero condtons at tme + created by the causal sgnal e ζ t u(t) y () ( + ) y (1) ( + ) y (2) ( + ) ZSR Zero State Response 12 4/2/15
13 Steady State and Zero State Responses non-causal h(t) {e ζ t } lm t [ {e ζt }] e ζ t nput appled at t = - natural K e λ t + βe ζt forced = βe ζ t = lm t y p (t) Steady State Response nput appled at t = e ζ t u(t) zero condtons ZIR ZSR c e λ t + h(t) {e ζ t u(t )} K e λ t + βe ζ t Zero State Response natural forced 13 4/2/15
14 Steady State Responses h(t) {e ζ t } lm t [ {e ζt }] lm t [ {e ζt }] natural K e λ t + βe ζt forced = βe ζ t = lm t y p (t) lm t βe ζ t = β e ζ t = lm t y p (t) Steady State Response zero condtons ZIR ZSR c e λ t + h(t) {e ζ t u(t )} Zero State Response h(t) can contan mode terms whch approach to zero lm t [ {e ζ t u(t)}] natural K e λ t + βe ζ t forced lm t [ natural K e λ t + β e ζ t ] forced = βe ζ t = lm t y p (t ) for a pure magnary ζ 14 4/2/15
15 Total Response to an everlastng exponental nput nput appled at t = - non-causal e s t H (s)e s t y (t) = e s t + = h(τ)e s(t τ) d τ + = e s t = e s t H (s) h(τ)e s τ d τ = (t < ) convoluton works for non-causal nput x(t) also But causal system s assumed + H (s) = h(τ)e s τ d τ H (s) 15 4/2/15
16 Total Response to an everlastng exponental nput (b, b 1,, b N 1, b N ) (1, a 1,, a N 1, a N ) Q(D) y(t) = P( D) x(t) Q( D)[ x(t)] = P( D) x(t) Q( D)[e s t H (s)] = P(D )e st H (s)q( D)e s t = P(D)e st D r e st = dr d t r es t = s r e st Q(D)e s t = Q (s)e s t P( D)e s t = P(s)e s t H (s)q( s)e s t = P(s)e st H (s) = P(s) Q(s) 16 4/2/15
17 Forced Response to a causal exponental nput nput appled at t = ZIR ZSR e ζ t u(t) natural c e λ t + h(t) {e ζ t u(t )} K e λ t + βe ζt forced y (t) = natural forced K e λ t + βe ζ t (t > ) Steady State Response lm t y p (t) = βe ζ t Y (s) = K (s λ ) + H (ζ) X (ζ) Transent Response {y(t ) lm t y p (t)} = K e λ t For a forced response For a steady response any complex ζ a pure magnary ζ 17 4/2/15
18 Forced Response to a causal exponental nput (b, b 1,, b N 1, b N ) (1, a 1,, a N 1, a N ) Q( D) y(t) = P( D)x(t) Q(D)[βe ζ t ] = P(D)e ζ t βq( D)e ζ t = P( D)e ζ t D r e ζ t = dr d t r eζt = ζ r e ζ t Q( D)e ζ t = Q(ζ)e ζ t P( D)e ζ t = P(ζ)e ζ t ζ : NOT a characterstc mode β = P(ζ) Q(ζ) 18 4/2/15
19 Defntons Q( D) y(t) = P( D) x(t) nput appled at t = - zero ntal condtons ZSR Q(s) Y (s) = P(s) X (s) δ(t ) H (s) = Y (s) X (s) = P(s) Q( s) e s t H (s)e s t ZSR Transfer functon (s-doman) H (s) = Y (s) X (s) Transfer functon (t-doman) H (s) = [ y (t ) x(t ) ]x(t )=e st Polynomals of Dfferental Equaton Laplace Transform of h(t) H (s) = P(s) Q(s) (b, b 1,, b N 1, b N ) (1, a 1,, a N 1, a N ) + H (s) = h(τ)e s τ d τ 19 4/2/15
20 Everlastng Exponental Total Response nput appled at t = - δ(t ) (1, a 1,, a N 1, a N ) e s t (b, b 1,, b N 1, b N ) H (s)e s t ZSR for a gven s = ζ ZSR y (t) = H (ζ)e ζ t < t < + y (t) = H (ζ)x (t) x(t ) = e ζ t Y (s) = H (s) X (s) 2 4/2/15
21 Causal Exponental Total Response nput appled at t = ZIR ZSR δ(t) e ζ t (1, a 1,, a N 1, a N ) (b, b 1,, b N 1, b N ) y y (1) y (N 1) natural c e λ t + h(t) K e λ t + βe ζ t forced steady state natural forced for a gven s = ζ y (t) = K e λ t + H (ζ)e ζ t t y (t) = K e λ t + H (ζ)x(t) x (t) = e ζ t Y (s) = K (s λ ) + H (s) X (s) 21 4/2/15
22 Specal cases of H(s) s = σ+ j ω nput appled at t = - general cases σ = e s t H (s) e s t R {e j ω t } e j ω t H ( j ω) e j ω t restrcted cases cos(ωt ) H ( j ω) cos(ωt) 22 4/2/15
23 Frequency Response Laplace Transform of h(t) Fourer Transform of h(t) + H (s) = h(τ)e s τ d τ s = σ+ j ω + H ( j ω) = h(τ)e j ω τ d τ s = j ω Polynomals of Dfferental Equaton Polynomals of Dfferental Equaton H (s) = P(s) Q(s) s = σ+ j ω H ( j ω) = P( j ω) Q( j ω) s = j ω Transfer functon (t-doman) Frequency response (t-doman) H (s) = [ y (t ) x(t ) ]x(t )=e st s = σ+ j ω H ( j ω) = [ y (t ) x(t ) ]x (t )=e jω t s = j ω Transfer functon (s-doman) Frequency response (ω-doman) H (s) = Y (s) X (s) s = σ+ j ω H ( j ω) = Y ( j ω) X ( j ω) s = j ω 23 4/2/15
24 & Frequency Response nput appled at t = - δ(t ) e s t zero ntal condtons (1, a 1,, a N 1, a N ) (b, b 1,, b N 1, b N ) H (s)e s t nput appled at t = - δ(t ) e j ω t zero ntal condtons (1, a 1,, a N 1, a N ) (b, b 1,, b N 1, b N ) H ( j ω)e j ω t y (t) = e s t s = σ+ j ω y (t) = e j ω t s = j ω + = h(τ)e s(t τ) d τ + = h(τ)e j ω(t τ) d τ + = e s t h(τ)e s τ d τ = (t < ) + = e j ω t h(τ)e j ω τ d τ = (t < ) = e s t H (s) = e j ω t H ( j ω) + H (s) = h(τ)e s τ d τ Transfer functon + H ( j ω) = h(τ)e j ω τ d τ Frequency response 24 4/2/15
25 Total Response to everlastng snusodal nputs e + j ω t H (+ j ω)e + j ω t = H (+ j ω) e + j arg{h (+ j ω)} e + j ω t e j ω t H ( j ω)e j ω t = H ( j ω) e + j arg{h ( j ω)} e j ω t e + j ω t + e j ω t H (+ j ω) e [+ j ω t +arg{h (+ j ω)}] [ j ω t+arg{h ( j ω)}] + H ( j ω) e = H (+ j ω) {e [+ j ω t +arg {H (+ j ω)}] + e [ j ω t arg{h (+ j ω)}] } 2 cos(ω t) H ( j ω) 2cos(ω t+arg {H ( j ω)}) A cos(ωt +α) A H ( j ω) cos(ωt +α+arg{h ( j ω)}) A sn (ω t+α) A H ( j ω) sn (ω t+α+arg {H ( j ω)}) 25 4/2/15
26 Snusodal Steady State Response (1) nput appled at t = δ(t) e ζ t (1, a 1,, a N 1, a N ) (b, b 1,, b N 1, b N ) h(t) natural K e λ t + βe ζt forced nput appled at t = - δ(t ) e s t zero ntal condtons (1, a 1,, a N 1, a N ) (b, b 1,, b N 1, b N ) H (s)e s t total response steady state response natural forced forced y (t) = K e λ t + H (ζ)e ζ t t y ss (t) = H (ζ)e ζ t t y (t) = K e λ t + H (ζ)x(t) x(t) = e ζ t y ss (t) = H (ζ) x(t ) x (t) = e ζ t Y (s) = K (s λ ) + H (s) X (s) Y ss (s) = H (s) X (s) 26 4/2/15
27 Snusodal Steady State Response (2) nput appled at t = ZIR ZSR δ(t) e ζ t (1, a 1,, a N 1, a N ) (b, b 1,, b N 1, b N ) y y (1) y (N 1) natural c e λ t + h(t) K e λ t + βe ζt forced steady state response x(t) = A y ss (t ) = H () A e t (N 1) y ξ = = A H () y y (1) x(t) = A e j ωt ξ = j ω y y (1) y (N 1) y ss (t ) = H ( j ω) A e jωt = A H ( j ω) e jω x(t) = A cos(ωt ) y y (1) y ss (t ) = H ( j ω) A cos(ωt ) (N 1) ξ = j ω y = A H ( j ω) cos(ω t) 27 4/2/15
28 Snusodal Steady State Response (3) y ss (t ) = H () A e t = A H () x(t) = A ξ = nput appled at t = ZIR ZSR δ(t) e ζ t (1, a 1,, a N 1, a N ) (b, b 1,, b N 1, b N ) y y (1) y (N 1) natural c e λ t + h(t) K e λ t + βe ζ t forced steady state response steady state response Forced response Forced response steady state response y ss (t ) = H ( j ω) A cos(ωt ) x(t) = A cos(ωt ) = A H ( j ω) cos(ω t) ξ = j ω 28 4/2/15
29 Frequency Response y ss (t ) = H ( j ω) A cos(ωt ) x(t) = A cos(ωt ) = A H ( j ω) cos(ω t) ξ = j ω ω 1 ω 1 ω 2 ω 3 ω 1 ω 2 ω 2 ω 3 ω /2/15
30 Transent Response y ss (t ) = H () A e t = A H () x(t) = A ξ = Natural + Forced response transent response /2/15
31 Frequency Response n Control Theory (1) A 2 +B 2 cos(ωt θ) G(s) ( ) G( j ω) A 2 +B 2 cos(ω t θ+arg {G( j ω)}) A cos(ωt)+b sn(ωt ) A cos(ωt)+b sn(ωt ) = A 2 +B 2 [ A cos(ωt )+ B sn(ω A 2 + B 2 A 2 + B t)] 2 = A 2 +B 2 [cos(θ)cos(ωt)+sn(θ)sn(ωt )] = A 2 +B 2 cos(θ ωt ) = A 2 +B 2 cos(ωt θ) = A 2 + B 2 cos(ωt θ) cos(θ) = sn(θ) = A A 2 +B 2 B A 2 +B /2/15
32 Frequency Response n Control Theory (2) A 2 +B 2 cos(ωt θ) G(s) G( j ω) A 2 +B 2 cos(ω( t θ+arg {G( j ω)}) ) A cos(ωt)+b sn(ωt ) = A 2 +B 2 cos(ωt θ) A s s 2 +ω + B ω 2 s 2 +ω 2 = A s+b ω s 2 +ω 2 Y (s) = A s+b ω s 2 +ω 2 G(s) = A s+b ω (s+ j ω)(s j ω) G(s) = K 1 s+ j ω + K 2 s j ω + F( s) Partal Fracton [ K 1 = A s+b ω [ (s+ j = A s+b ω s 2 +ω 2 (s j ω) ω)g(s)]s= j G(s) = ω ]s= j ω A jω+b ω 2 jω G ( j ω) = 1 ( A+ j B)G( j ω) 2 [ K 2 = A s+b ω [ (s j = A s+b ω s 2 +ω 2 (s+ j ω) ω)g(s)]s=+ G(s) = A j ω+b ω j ω ]s=+ j ω +2 j ω G(+ j ω) = 1 ( A j B)G(+ j ω) /2/15
33 Frequency Response n Control Theory (3) A 2 +B 2 cos(ωt θ) G(s) G( j ω) A 2 +B 2 cos(ω( t θ+arg {G( j ω)}) ) Y (s) = K 1 s+ j ω + K 2 s j ω + F( s) K 1 = 1 2 ( A+ j B)G( j ω) K 2 = 1 ( A j B)G(+ j ω) 2 A± j B = A 2 + B 2[ A A 2 +B 2 ± j = A 2 +B 2 [cos θ ± j sn θ ] = A 2 + B 2 e ± j θ B ] A 2 +B 2 Stable System e p e σ lm t f (t ) = lm s system modes p <, σ < s F (s) = Ignore F (s) Y ss (s) = K 1 s+ j ω + K 2 s j ω K 1 = 1 2 A2 +B 2 e + jθ G( j ω) K 2 = 1 2 A 2 +B 2 e j θ G ( j ω) 33 4/2/15
34 Frequency Response n Control Theory (4) A 2 +B 2 cos(ωt θ) G(s) G( j ω) A 2 +B 2 cos(ω( t θ+arg {G( j ω)}) ) Y ss (s) = K 1 s+ j ω + K 2 s j ω = 1 2 ( A + j B)G( j ω) 1 s+ j ω ( A j B)G(+ j ω) 1 s j ω = 1 2 A 2 +B 2 e + jθ G( j ω) 1 s+ j ω + 1 A 2 +B 2 e jθ 1 G(+ j ω) 2 s j ω A 2 +B 2 y ss (t ) = [G( j ω)e jωt e + jθ 2 + G(+ j ω)e + jωt e jθ ] A 2 +B 2 = [G(+ j ω)e j(ωt θ) 2 + G(+ j ω)e + j( ωt θ) ] = A 2 +B 2 R{G(+ j ω) e + j(ωt θ) } = A 2 +B 2 G(+ j ω) cos(ωt θ+arg{g(+ j ω)}) 34 4/2/15
35 Impulse Response h(t) 35 4/2/15
36 References [1] [2] J.H. McClellan, et al., Sgnal Processng Frst, Pearson Prentce Hall, 23 [3] M. J. Roberts, Fundamentals of Sgnals and Systems [4] S. J. Orfands, Introducton to Sgnal Processng [5] B. P. Lath, Sgnals and Systems 4/2/15
CLTI System Response (4A) Young Won Lim 4/11/15
 CLTI System Response (4A) Copyright (c) 2011-2015 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2
CLTI System Response (4A) Copyright (c) 2011-2015 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2
Background LTI Systems (4A) Young Won Lim 4/20/15
 Background LTI Systems (4A) Copyright (c) 2014-2015 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2
Background LTI Systems (4A) Copyright (c) 2014-2015 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2
Phasor Young Won Lim 05/19/2015
 Phasor Copyright (c) 2009-2015 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version
Phasor Copyright (c) 2009-2015 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version
Digital Signal Processing
 Dgtal Sgnal Processng Dscrete-tme System Analyss Manar Mohasen Offce: F8 Emal: manar.subh@ut.ac.r School of IT Engneerng Revew of Precedent Class Contnuous Sgnal The value of the sgnal s avalable over
Dgtal Sgnal Processng Dscrete-tme System Analyss Manar Mohasen Offce: F8 Emal: manar.subh@ut.ac.r School of IT Engneerng Revew of Precedent Class Contnuous Sgnal The value of the sgnal s avalable over
Propagating Wave (1B)
 Wave (1B) 3-D Wave Copyright (c) 2011 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later
Wave (1B) 3-D Wave Copyright (c) 2011 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later
Group Delay and Phase Delay (1A) Young Won Lim 7/19/12
 Group Delay and Phase Delay (A) 7/9/2 Copyright (c) 2 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2
Group Delay and Phase Delay (A) 7/9/2 Copyright (c) 2 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2
CLTI Differential Equations (3A) Young Won Lim 6/4/15
 CLTI Differential Equations (3A) Copyright (c) 2011-2015 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version
CLTI Differential Equations (3A) Copyright (c) 2011-2015 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version
Signals and Spectra (1A) Young Won Lim 11/26/12
 Signals and Spectra (A) Copyright (c) 202 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2 or any later
Signals and Spectra (A) Copyright (c) 202 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2 or any later
Fourier Analysis Overview (0B)
 CTFS: Continuous Time Fourier Series CTFT: Continuous Time Fourier Transform DTFS: Fourier Series DTFT: Fourier Transform DFT: Discrete Fourier Transform Copyright (c) 2009-2016 Young W. Lim. Permission
CTFS: Continuous Time Fourier Series CTFT: Continuous Time Fourier Transform DTFS: Fourier Series DTFT: Fourier Transform DFT: Discrete Fourier Transform Copyright (c) 2009-2016 Young W. Lim. Permission
CT Rectangular Function Pairs (5B)
 C Rectangular Function Pairs (5B) Continuous ime Rect Function Pairs Copyright (c) 009-013 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU
C Rectangular Function Pairs (5B) Continuous ime Rect Function Pairs Copyright (c) 009-013 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU
EE 3054: Signals, Systems, and Transforms Summer It is observed of some continuous-time LTI system that the input signal.
 EE 34: Signals, Systems, and Transforms Summer 7 Test No notes, closed book. Show your work. Simplify your answers. 3. It is observed of some continuous-time LTI system that the input signal = 3 u(t) produces
EE 34: Signals, Systems, and Transforms Summer 7 Test No notes, closed book. Show your work. Simplify your answers. 3. It is observed of some continuous-time LTI system that the input signal = 3 u(t) produces
Root Locus (2A) Young Won Lim 10/15/14
 Root Locus (2A Copyright (c 2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version
Root Locus (2A Copyright (c 2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version
Designing Information Devices and Systems II Spring 2018 J. Roychowdhury and M. Maharbiz Discussion 3A
 EECS 16B Desgnng Informaton Devces and Systems II Sprng 018 J. Roychowdhury and M. Maharbz Dscusson 3A 1 Phasors We consder snusodal voltages and currents of a specfc form: where, Voltage vt) = V 0 cosωt
EECS 16B Desgnng Informaton Devces and Systems II Sprng 018 J. Roychowdhury and M. Maharbz Dscusson 3A 1 Phasors We consder snusodal voltages and currents of a specfc form: where, Voltage vt) = V 0 cosωt
Fourier Analysis Overview (0A)
 CTFS: Fourier Series CTFT: Fourier Transform DTFS: Fourier Series DTFT: Fourier Transform DFT: Discrete Fourier Transform Copyright (c) 2011-2016 Young W. Lim. Permission is granted to copy, distribute
CTFS: Fourier Series CTFT: Fourier Transform DTFS: Fourier Series DTFT: Fourier Transform DFT: Discrete Fourier Transform Copyright (c) 2011-2016 Young W. Lim. Permission is granted to copy, distribute
Digital Signal Octave Codes (0A)
 Digital Signal Periodic Conditions Copyright (c) 2009-2017 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version
Digital Signal Periodic Conditions Copyright (c) 2009-2017 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version
CT Correlation (2A) Young Won Lim 9/9/14
 CT Correlation (2A) Copyright (c) 200-204 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2 or any later
CT Correlation (2A) Copyright (c) 200-204 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2 or any later
Fourier Analysis Overview (0A)
 CTFS: Fourier Series CTFT: Fourier Transform DTFS: Fourier Series DTFT: Fourier Transform DFT: Discrete Fourier Transform Copyright (c) 2011-2016 Young W. Lim. Permission is granted to copy, distribute
CTFS: Fourier Series CTFT: Fourier Transform DTFS: Fourier Series DTFT: Fourier Transform DFT: Discrete Fourier Transform Copyright (c) 2011-2016 Young W. Lim. Permission is granted to copy, distribute
Explanations and Discussion of Some Laplace Methods: Transfer Functions and Frequency Response. Y(s) = b 1
 Engs 22 p. 1 Explanations Discussion of Some Laplace Methods: Transfer Functions Frequency Response I. Anatomy of Differential Equations in the S-Domain Parts of the s-domain solution. We will consider
Engs 22 p. 1 Explanations Discussion of Some Laplace Methods: Transfer Functions Frequency Response I. Anatomy of Differential Equations in the S-Domain Parts of the s-domain solution. We will consider
Time Response Analysis (Part II)
 Time Response Analysis (Part II). A critically damped, continuous-time, second order system, when sampled, will have (in Z domain) (a) A simple pole (b) Double pole on real axis (c) Double pole on imaginary
Time Response Analysis (Part II). A critically damped, continuous-time, second order system, when sampled, will have (in Z domain) (a) A simple pole (b) Double pole on real axis (c) Double pole on imaginary
Modeling of Dynamic Systems
 Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
Digital Signal Octave Codes (0A)
 Digital Signal Periodic Conditions Copyright (c) 2009-2017 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version
Digital Signal Periodic Conditions Copyright (c) 2009-2017 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version
General CORDIC Description (1A)
 General CORDIC Description (1A) Copyright (c) 2010, 2011, 2012 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License,
General CORDIC Description (1A) Copyright (c) 2010, 2011, 2012 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License,
Group & Phase Velocities (2A)
 (2A) 1-D Copyright (c) 2011 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published
(2A) 1-D Copyright (c) 2011 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published
Continuous Time Markov Chain
 Contnuous Tme Markov Chan Hu Jn Department of Electroncs and Communcaton Engneerng Hanyang Unversty ERICA Campus Contents Contnuous tme Markov Chan (CTMC) Propertes of sojourn tme Relatons Transton probablty
Contnuous Tme Markov Chan Hu Jn Department of Electroncs and Communcaton Engneerng Hanyang Unversty ERICA Campus Contents Contnuous tme Markov Chan (CTMC) Propertes of sojourn tme Relatons Transton probablty
Digital Signal Octave Codes (0A)
 Digital Signal Periodic Conditions Copyright (c) 2009-207 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2
Digital Signal Periodic Conditions Copyright (c) 2009-207 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2
Transfer Functions. Convenient representation of a linear, dynamic model. A transfer function (TF) relates one input and one output: ( ) system
 Transfer Functons Convenent representaton of a lnear, dynamc model. A transfer functon (TF) relates one nput and one output: x t X s y t system Y s The followng termnology s used: x y nput output forcng
Transfer Functons Convenent representaton of a lnear, dynamc model. A transfer functon (TF) relates one nput and one output: x t X s y t system Y s The followng termnology s used: x y nput output forcng
Chapter 2 Problem Solutions 2.1 R v = Peak diode current i d (max) = R 1 K 0.6 I 0 I 0
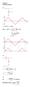 Chapter Problem Solutons. K γ.6, r f Ω For v, v.6 r + f ( 9.4) +. v 9..6 9.. v v v v v T ln and S v T ln S v v.3 8snωt (a) vs 3.33snωt 6 3.33 Peak dode current d (max) (b) P v s (max) 3.3 (c) T o π vo(
Chapter Problem Solutons. K γ.6, r f Ω For v, v.6 r + f ( 9.4) +. v 9..6 9.. v v v v v T ln and S v T ln S v v.3 8snωt (a) vs 3.33snωt 6 3.33 Peak dode current d (max) (b) P v s (max) 3.3 (c) T o π vo(
Digital Signal Octave Codes (0A)
 Digital Signal Periodic Conditions Copyright (c) 2009-207 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2
Digital Signal Periodic Conditions Copyright (c) 2009-207 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2
ECE301 Fall, 2006 Exam 1 Soluation October 7, Name: Score: / Consider the system described by the differential equation
 ECE301 Fall, 2006 Exam 1 Soluation October 7, 2006 1 Name: Score: /100 You must show all of your work for full credit. Calculators may NOT be used. 1. Consider the system described by the differential
ECE301 Fall, 2006 Exam 1 Soluation October 7, 2006 1 Name: Score: /100 You must show all of your work for full credit. Calculators may NOT be used. 1. Consider the system described by the differential
(b) i(t) for t 0. (c) υ 1 (t) and υ 2 (t) for t 0. Solution: υ 2 (0 ) = I 0 R 1 = = 10 V. υ 1 (0 ) = 0. (Given).
 Problem 5.37 Pror to t =, capactor C 1 n the crcut of Fg. P5.37 was uncharged. For I = 5 ma, R 1 = 2 kω, = 5 kω, C 1 = 3 µf, and C 2 = 6 µf, determne: (a) The equvalent crcut nvolvng the capactors for
Problem 5.37 Pror to t =, capactor C 1 n the crcut of Fg. P5.37 was uncharged. For I = 5 ma, R 1 = 2 kω, = 5 kω, C 1 = 3 µf, and C 2 = 6 µf, determne: (a) The equvalent crcut nvolvng the capactors for
Module 3 LOSSY IMAGE COMPRESSION SYSTEMS. Version 2 ECE IIT, Kharagpur
 Module 3 LOSSY IMAGE COMPRESSION SYSTEMS Verson ECE IIT, Kharagpur Lesson 6 Theory of Quantzaton Verson ECE IIT, Kharagpur Instructonal Objectves At the end of ths lesson, the students should be able to:
Module 3 LOSSY IMAGE COMPRESSION SYSTEMS Verson ECE IIT, Kharagpur Lesson 6 Theory of Quantzaton Verson ECE IIT, Kharagpur Instructonal Objectves At the end of ths lesson, the students should be able to:
Modelli Clamfim Equazione del Calore Lezione ottobre 2014
 CLAMFIM Bologna Modell 1 @ Clamfm Equazone del Calore Lezone 17 15 ottobre 2014 professor Danele Rtell danele.rtell@unbo.t 1/24? Convoluton The convoluton of two functons g(t) and f(t) s the functon (g
CLAMFIM Bologna Modell 1 @ Clamfm Equazone del Calore Lezone 17 15 ottobre 2014 professor Danele Rtell danele.rtell@unbo.t 1/24? Convoluton The convoluton of two functons g(t) and f(t) s the functon (g
Digital Signal Octave Codes (0A)
 Digital Signal Periodic Conditions Copyright (c) 2009-207 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2
Digital Signal Periodic Conditions Copyright (c) 2009-207 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2
EE Homework 12 - Solutions. 1. The transfer function of the system is given to be H(s) = s j j
 EE3054 - Homework 2 - Solutions. The transfer function of the system is given to be H(s) = s 2 +3s+3. Decomposing into partial fractions, H(s) = 0.5774j s +.5 0.866j + 0.5774j s +.5 + 0.866j. () (a) The
EE3054 - Homework 2 - Solutions. The transfer function of the system is given to be H(s) = s 2 +3s+3. Decomposing into partial fractions, H(s) = 0.5774j s +.5 0.866j + 0.5774j s +.5 + 0.866j. () (a) The
Down-Sampling (4B) Young Won Lim 11/15/12
 Down-Sampling (B) /5/ Copyright (c) 9,, Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version. or any later
Down-Sampling (B) /5/ Copyright (c) 9,, Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version. or any later
Hilbert Inner Product Space (2B) Young Won Lim 2/7/12
 Hilbert nner Product Space (2B) Copyright (c) 2009-2011 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version
Hilbert nner Product Space (2B) Copyright (c) 2009-2011 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version
Up-Sampling (5B) Young Won Lim 11/15/12
 Up-Sampling (5B) Copyright (c) 9,, Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version. or any later version
Up-Sampling (5B) Copyright (c) 9,, Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version. or any later version
Discrete Time Rect Function(4B)
 Discrete Time Rect Function(4B) Discrete Time Rect Functions Copyright (c) 29-23 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation
Discrete Time Rect Function(4B) Discrete Time Rect Functions Copyright (c) 29-23 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation
Capacitor and Inductor
 Capacitor and Inductor Copyright (c) 2015 2017 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Capacitor and Inductor Copyright (c) 2015 2017 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Capacitor and Inductor
 Capacitor and Inductor Copyright (c) 2015 2017 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Capacitor and Inductor Copyright (c) 2015 2017 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Introduction to Antennas & Arrays
 Introducton to Antennas & Arrays Antenna transton regon (structure) between guded eaves (.e. coaxal cable) and free space waves. On transmsson, antenna accepts energy from TL and radates t nto space. J.D.
Introducton to Antennas & Arrays Antenna transton regon (structure) between guded eaves (.e. coaxal cable) and free space waves. On transmsson, antenna accepts energy from TL and radates t nto space. J.D.
Digital Signal Octave Codes (0A)
 Digital Signal Periodic Conditions Copyright (c) 2009-207 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2
Digital Signal Periodic Conditions Copyright (c) 2009-207 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2
THE HARTLEY TRANSFORM IN A FINITE FIELD
 THE HARTLEY TRANSFORM IN A FINITE FIELD R. M. Campello de Souza H. M. de Olvera A. N. Kauffman CODEC - Grupo de Pesusas em Comuncações Departamento de Eletrônca e Sstemas - CTG - UFPE C.P. 78 57-97 Recfe
THE HARTLEY TRANSFORM IN A FINITE FIELD R. M. Campello de Souza H. M. de Olvera A. N. Kauffman CODEC - Grupo de Pesusas em Comuncações Departamento de Eletrônca e Sstemas - CTG - UFPE C.P. 78 57-97 Recfe
ENGIN 211, Engineering Math. Laplace Transforms
 ENGIN 211, Engineering Math Laplace Transforms 1 Why Laplace Transform? Laplace transform converts a function in the time domain to its frequency domain. It is a powerful, systematic method in solving
ENGIN 211, Engineering Math Laplace Transforms 1 Why Laplace Transform? Laplace transform converts a function in the time domain to its frequency domain. It is a powerful, systematic method in solving
Background ODEs (2A) Young Won Lim 3/7/15
 Background ODEs (2A) Copyright (c) 2014-2015 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any
Background ODEs (2A) Copyright (c) 2014-2015 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any
Definitions of the Laplace Transform (1A) Young Won Lim 1/31/15
 Definitions of the Laplace Transform (A) Copyright (c) 24 Young W. Lim. Permission is granted to copy, distriute and/or modify this document under the terms of the GNU Free Documentation License, Version.2
Definitions of the Laplace Transform (A) Copyright (c) 24 Young W. Lim. Permission is granted to copy, distriute and/or modify this document under the terms of the GNU Free Documentation License, Version.2
Spectra (2A) Young Won Lim 11/8/12
 Spectra (A) /8/ Copyright (c) 0 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version. or any later version
Spectra (A) /8/ Copyright (c) 0 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version. or any later version
6. Stochastic processes (2)
 Contents Markov processes Brth-death processes Lect6.ppt S-38.45 - Introducton to Teletraffc Theory Sprng 5 Markov process Consder a contnuous-tme and dscrete-state stochastc process X(t) wth state space
Contents Markov processes Brth-death processes Lect6.ppt S-38.45 - Introducton to Teletraffc Theory Sprng 5 Markov process Consder a contnuous-tme and dscrete-state stochastc process X(t) wth state space
6. Stochastic processes (2)
 6. Stochastc processes () Lect6.ppt S-38.45 - Introducton to Teletraffc Theory Sprng 5 6. Stochastc processes () Contents Markov processes Brth-death processes 6. Stochastc processes () Markov process
6. Stochastc processes () Lect6.ppt S-38.45 - Introducton to Teletraffc Theory Sprng 5 6. Stochastc processes () Contents Markov processes Brth-death processes 6. Stochastc processes () Markov process
Hongyi Miao, College of Science, Nanjing Forestry University, Nanjing ,China. (Received 20 June 2013, accepted 11 March 2014) I)ϕ (k)
 ISSN 1749-3889 (prnt), 1749-3897 (onlne) Internatonal Journal of Nonlnear Scence Vol.17(2014) No.2,pp.188-192 Modfed Block Jacob-Davdson Method for Solvng Large Sparse Egenproblems Hongy Mao, College of
ISSN 1749-3889 (prnt), 1749-3897 (onlne) Internatonal Journal of Nonlnear Scence Vol.17(2014) No.2,pp.188-192 Modfed Block Jacob-Davdson Method for Solvng Large Sparse Egenproblems Hongy Mao, College of
Newton s Method for One - Dimensional Optimization - Theory
 Numercal Methods Newton s Method for One - Dmensonal Optmzaton - Theory For more detals on ths topc Go to Clck on Keyword Clck on Newton s Method for One- Dmensonal Optmzaton You are free to Share to copy,
Numercal Methods Newton s Method for One - Dmensonal Optmzaton - Theory For more detals on ths topc Go to Clck on Keyword Clck on Newton s Method for One- Dmensonal Optmzaton You are free to Share to copy,
Analysis of Discrete Time Queues (Section 4.6)
 Analyss of Dscrete Tme Queues (Secton 4.6) Copyrght 2002, Sanjay K. Bose Tme axs dvded nto slots slot slot boundares Arrvals can only occur at slot boundares Servce to a job can only start at a slot boundary
Analyss of Dscrete Tme Queues (Secton 4.6) Copyrght 2002, Sanjay K. Bose Tme axs dvded nto slots slot slot boundares Arrvals can only occur at slot boundares Servce to a job can only start at a slot boundary
LTI Systems (Continuous & Discrete) - Basics
 LTI Systems (Continuous & Discrete) - Basics 1. A system with an input x(t) and output y(t) is described by the relation: y(t) = t. x(t). This system is (a) linear and time-invariant (b) linear and time-varying
LTI Systems (Continuous & Discrete) - Basics 1. A system with an input x(t) and output y(t) is described by the relation: y(t) = t. x(t). This system is (a) linear and time-invariant (b) linear and time-varying
Note 10. Modeling and Simulation of Dynamic Systems
 Lecture Notes of ME 475: Introducton to Mechatroncs Note 0 Modelng and Smulaton of Dynamc Systems Department of Mechancal Engneerng, Unversty Of Saskatchewan, 57 Campus Drve, Saskatoon, SK S7N 5A9, Canada
Lecture Notes of ME 475: Introducton to Mechatroncs Note 0 Modelng and Smulaton of Dynamc Systems Department of Mechancal Engneerng, Unversty Of Saskatchewan, 57 Campus Drve, Saskatoon, SK S7N 5A9, Canada
CITY UNIVERSITY LONDON. MSc in Information Engineering DIGITAL SIGNAL PROCESSING EPM746
 No: CITY UNIVERSITY LONDON MSc in Information Engineering DIGITAL SIGNAL PROCESSING EPM746 Date: 19 May 2004 Time: 09:00-11:00 Attempt Three out of FIVE questions, at least One question from PART B PART
No: CITY UNIVERSITY LONDON MSc in Information Engineering DIGITAL SIGNAL PROCESSING EPM746 Date: 19 May 2004 Time: 09:00-11:00 Attempt Three out of FIVE questions, at least One question from PART B PART
Chapter 4 The Wave Equation
 Chapter 4 The Wave Equaton Another classcal example of a hyperbolc PDE s a wave equaton. The wave equaton s a second-order lnear hyperbolc PDE that descrbes the propagaton of a varety of waves, such as
Chapter 4 The Wave Equaton Another classcal example of a hyperbolc PDE s a wave equaton. The wave equaton s a second-order lnear hyperbolc PDE that descrbes the propagaton of a varety of waves, such as
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
Numerical Solution of Ordinary Differential Equations
 Numercal Methods (CENG 00) CHAPTER-VI Numercal Soluton of Ordnar Dfferental Equatons 6 Introducton Dfferental equatons are equatons composed of an unknown functon and ts dervatves The followng are examples
Numercal Methods (CENG 00) CHAPTER-VI Numercal Soluton of Ordnar Dfferental Equatons 6 Introducton Dfferental equatons are equatons composed of an unknown functon and ts dervatves The followng are examples
Definition of the Laplace transform. 0 x(t)e st dt
 Definition of the Laplace transform Bilateral Laplace Transform: X(s) = x(t)e st dt Unilateral (or one-sided) Laplace Transform: X(s) = 0 x(t)e st dt ECE352 1 Definition of the Laplace transform (cont.)
Definition of the Laplace transform Bilateral Laplace Transform: X(s) = x(t)e st dt Unilateral (or one-sided) Laplace Transform: X(s) = 0 x(t)e st dt ECE352 1 Definition of the Laplace transform (cont.)
DFT Frequency (9A) Each Row of the DFT Matrix. Young Won Lim 7/31/10
 DFT Frequency (9A) Each ow of the DFT Matrix Copyright (c) 2009, 2010 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GU Free Documentation License,
DFT Frequency (9A) Each ow of the DFT Matrix Copyright (c) 2009, 2010 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GU Free Documentation License,
Higher Order ODE's, (3A)
 Higher Order ODE's, (3A) Initial Value Problems, and Boundary Value Problems Copyright (c) 2011-2015 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms
Higher Order ODE's, (3A) Initial Value Problems, and Boundary Value Problems Copyright (c) 2011-2015 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms
Lab 3: Poles, Zeros, and Time/Frequency Domain Response
 ECEN 33 Linear Systems Spring 2 2-- P. Mathys Lab 3: Poles, Zeros, and Time/Frequency Domain Response of CT Systems Introduction Systems that are used for signal processing are very often characterized
ECEN 33 Linear Systems Spring 2 2-- P. Mathys Lab 3: Poles, Zeros, and Time/Frequency Domain Response of CT Systems Introduction Systems that are used for signal processing are very often characterized
Group Velocity and Phase Velocity (1A) Young Won Lim 5/26/12
 Group Velocity and Phase Velocity (1A) Copyright (c) 211 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version
Group Velocity and Phase Velocity (1A) Copyright (c) 211 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version
( ) = ( ) + ( 0) ) ( )
 EETOMAGNETI OMPATIBIITY HANDBOOK 1 hapter 9: Transent Behavor n the Tme Doman 9.1 Desgn a crcut usng reasonable values for the components that s capable of provdng a tme delay of 100 ms to a dgtal sgnal.
EETOMAGNETI OMPATIBIITY HANDBOOK 1 hapter 9: Transent Behavor n the Tme Doman 9.1 Desgn a crcut usng reasonable values for the components that s capable of provdng a tme delay of 100 ms to a dgtal sgnal.
Multi-dimensional Central Limit Argument
 Mult-dmensonal Central Lmt Argument Outlne t as Consder d random proceses t, t,. Defne the sum process t t t t () t (); t () t are d to (), t () t 0 () t tme () t () t t t As, ( t) becomes a Gaussan random
Mult-dmensonal Central Lmt Argument Outlne t as Consder d random proceses t, t,. Defne the sum process t t t t () t (); t () t are d to (), t () t 0 () t tme () t () t t t As, ( t) becomes a Gaussan random
NON-LINEAR CONVOLUTION: A NEW APPROACH FOR THE AURALIZATION OF DISTORTING SYSTEMS
 NON-LINEAR CONVOLUTION: A NEW APPROAC FOR TE AURALIZATION OF DISTORTING SYSTEMS Angelo Farna, Alberto Belln and Enrco Armellon Industral Engneerng Dept., Unversty of Parma, Va delle Scenze 8/A Parma, 00
NON-LINEAR CONVOLUTION: A NEW APPROAC FOR TE AURALIZATION OF DISTORTING SYSTEMS Angelo Farna, Alberto Belln and Enrco Armellon Industral Engneerng Dept., Unversty of Parma, Va delle Scenze 8/A Parma, 00
The Tangential Force Distribution on Inner Cylinder of Power Law Fluid Flowing in Eccentric Annuli with the Inner Cylinder Reciprocating Axially
 Open Journal of Flud Dynamcs, 2015, 5, 183-187 Publshed Onlne June 2015 n ScRes. http://www.scrp.org/journal/ojfd http://dx.do.org/10.4236/ojfd.2015.52020 The Tangental Force Dstrbuton on Inner Cylnder
Open Journal of Flud Dynamcs, 2015, 5, 183-187 Publshed Onlne June 2015 n ScRes. http://www.scrp.org/journal/ojfd http://dx.do.org/10.4236/ojfd.2015.52020 The Tangental Force Dstrbuton on Inner Cylnder
Differentiating Gaussian Processes
 Dfferentatng Gaussan Processes Andrew McHutchon Aprl 17, 013 1 Frst Order Dervatve of the Posteror Mean The posteror mean of a GP s gven by, f = x, X KX, X 1 y x, X α 1 Only the x, X term depends on the
Dfferentatng Gaussan Processes Andrew McHutchon Aprl 17, 013 1 Frst Order Dervatve of the Posteror Mean The posteror mean of a GP s gven by, f = x, X KX, X 1 y x, X α 1 Only the x, X term depends on the
GEORGIA INSTITUTE OF TECHNOLOGY SCHOOL of ELECTRICAL & COMPUTER ENGINEERING FINAL EXAM. COURSE: ECE 3084A (Prof. Michaels)
 GEORGIA INSTITUTE OF TECHNOLOGY SCHOOL of ELECTRICAL & COMPUTER ENGINEERING FINAL EXAM DATE: 30-Apr-14 COURSE: ECE 3084A (Prof. Michaels) NAME: STUDENT #: LAST, FIRST Write your name on the front page
GEORGIA INSTITUTE OF TECHNOLOGY SCHOOL of ELECTRICAL & COMPUTER ENGINEERING FINAL EXAM DATE: 30-Apr-14 COURSE: ECE 3084A (Prof. Michaels) NAME: STUDENT #: LAST, FIRST Write your name on the front page
Modelli Clamfim Equazioni differenziali 22 settembre 2016
 CLAMFIM Bologna Modell 1 @ Clamfm Equazon dfferenzal 22 settembre 2016 professor Danele Rtell danele.rtell@unbo.t 1/22? Ordnary Dfferental Equatons A dfferental equaton s an equaton that defnes a relatonshp
CLAMFIM Bologna Modell 1 @ Clamfm Equazon dfferenzal 22 settembre 2016 professor Danele Rtell danele.rtell@unbo.t 1/22? Ordnary Dfferental Equatons A dfferental equaton s an equaton that defnes a relatonshp
Introduction. - The Second Lyapunov Method. - The First Lyapunov Method
 Stablty Analyss A. Khak Sedgh Control Systems Group Faculty of Electrcal and Computer Engneerng K. N. Toos Unversty of Technology February 2009 1 Introducton Stablty s the most promnent characterstc of
Stablty Analyss A. Khak Sedgh Control Systems Group Faculty of Electrcal and Computer Engneerng K. N. Toos Unversty of Technology February 2009 1 Introducton Stablty s the most promnent characterstc of
Appendix B. The Finite Difference Scheme
 140 APPENDIXES Appendx B. The Fnte Dfference Scheme In ths appendx we present numercal technques whch are used to approxmate solutons of system 3.1 3.3. A comprehensve treatment of theoretcal and mplementaton
140 APPENDIXES Appendx B. The Fnte Dfference Scheme In ths appendx we present numercal technques whch are used to approxmate solutons of system 3.1 3.3. A comprehensve treatment of theoretcal and mplementaton
ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EQUATION
 Advanced Mathematcal Models & Applcatons Vol.3, No.3, 2018, pp.215-222 ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EUATION
Advanced Mathematcal Models & Applcatons Vol.3, No.3, 2018, pp.215-222 ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EUATION
Lecture 5: Linear Systems. Transfer functions. Frequency Domain Analysis. Basic Control Design.
 ISS0031 Modeling and Identification Lecture 5: Linear Systems. Transfer functions. Frequency Domain Analysis. Basic Control Design. Aleksei Tepljakov, Ph.D. September 30, 2015 Linear Dynamic Systems Definition
ISS0031 Modeling and Identification Lecture 5: Linear Systems. Transfer functions. Frequency Domain Analysis. Basic Control Design. Aleksei Tepljakov, Ph.D. September 30, 2015 Linear Dynamic Systems Definition
Down-Sampling (4B) Young Won Lim 10/25/12
 Down-Sampling (4B) /5/ Copyright (c) 9,, Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version. or any later
Down-Sampling (4B) /5/ Copyright (c) 9,, Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version. or any later
Line Integrals (4A) Line Integral Path Independence. Young Won Lim 10/22/12
 Line Integrals (4A Line Integral Path Independence Copyright (c 2012 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License,
Line Integrals (4A Line Integral Path Independence Copyright (c 2012 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License,
MAXIMAL INVARIANT SUBSPACES AND OBSERVABILITY OF MULTIDIMENSIONAL SYSTEMS. PART 2: THE ALGORITHM
 U.P.B. Sc. Bull., Seres A, Vol. 80, Iss. 1, 2018 ISSN 1223-7027 MAXIMAL INVARIANT SUBSPACES AND OBSERVABILITY OF MULTIDIMENSIONAL SYSTEMS. PART 2: THE ALGORITHM Valeru Prepelţă 1, Tberu Vaslache 2 The
U.P.B. Sc. Bull., Seres A, Vol. 80, Iss. 1, 2018 ISSN 1223-7027 MAXIMAL INVARIANT SUBSPACES AND OBSERVABILITY OF MULTIDIMENSIONAL SYSTEMS. PART 2: THE ALGORITHM Valeru Prepelţă 1, Tberu Vaslache 2 The
Δ x. u(x,t) Fig. Schematic view of elastic bar undergoing axial motions
 ME67 - Handout 4 Vbratons of Contnuous Systems Axal vbratons of elastc bars The fgure shows a unform elastc bar of length and cross secton A. The bar materal propertes are ts densty ρ and elastc modulus
ME67 - Handout 4 Vbratons of Contnuous Systems Axal vbratons of elastc bars The fgure shows a unform elastc bar of length and cross secton A. The bar materal propertes are ts densty ρ and elastc modulus
Signal Functions (0B)
 Signal Functions (0B) Signal Functions Copyright (c) 2009-203 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License,
Signal Functions (0B) Signal Functions Copyright (c) 2009-203 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License,
Δ x. u(x,t) Fig. Schematic view of elastic bar undergoing axial motions
 ME67 - Handout 4 Vbratons of Contnuous Systems Axal vbratons of elastc bars The fgure shows a unform elastc bar of length and cross secton A. The bar materal propertes are ts densty ρ and elastc modulus
ME67 - Handout 4 Vbratons of Contnuous Systems Axal vbratons of elastc bars The fgure shows a unform elastc bar of length and cross secton A. The bar materal propertes are ts densty ρ and elastc modulus
Electrical Circuits II (ECE233b)
 Electrcal Crcuts (ECE33b SteadyState Power Analyss Anests Dounas The Unersty of Western Ontaro Faculty of Engneerng Scence SteadyState Power Analyss (t AC crcut: The steady state oltage and current can
Electrcal Crcuts (ECE33b SteadyState Power Analyss Anests Dounas The Unersty of Western Ontaro Faculty of Engneerng Scence SteadyState Power Analyss (t AC crcut: The steady state oltage and current can
Dispersion (3A) 1-D Dispersion. Young W. Lim 10/15/13
 1-D Dispersion Copyright (c) 013. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1. or any later version published
1-D Dispersion Copyright (c) 013. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1. or any later version published
First and Second Order Circuits. Claudio Talarico, Gonzaga University Spring 2015
 First and Second Order Circuits Claudio Talarico, Gonzaga University Spring 2015 Capacitors and Inductors intuition: bucket of charge q = Cv i = C dv dt Resist change of voltage DC open circuit Store voltage
First and Second Order Circuits Claudio Talarico, Gonzaga University Spring 2015 Capacitors and Inductors intuition: bucket of charge q = Cv i = C dv dt Resist change of voltage DC open circuit Store voltage
Discrete Time Rect Function(4B)
 Discrete Time Rect Function(4B) Discrete Time Rect Functions Copyright (c) 29-213 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation
Discrete Time Rect Function(4B) Discrete Time Rect Functions Copyright (c) 29-213 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation
2.161 Signal Processing: Continuous and Discrete Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 2.6 Signal Processing: Continuous and Discrete Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS
MIT OpenCourseWare http://ocw.mit.edu 2.6 Signal Processing: Continuous and Discrete Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS
Degenerate PT. ψ φ λψ. When two zeroth order states are degenerate (or near degenerate), cannot use simple PT.
 Degenerate PT When two zeroth order states are degenerate (or near degenerate), cannot use smple PT. Degenerate PT desgned to deal wth such cases Suppose the energy level of nterest s r fold degenerate
Degenerate PT When two zeroth order states are degenerate (or near degenerate), cannot use smple PT. Degenerate PT desgned to deal wth such cases Suppose the energy level of nterest s r fold degenerate
Advanced Analog Building Blocks. Prof. Dr. Peter Fischer, Dr. Wei Shen, Dr. Albert Comerma, Dr. Johannes Schemmel, etc
 Advanced Analog Building Blocks Prof. Dr. Peter Fischer, Dr. Wei Shen, Dr. Albert Comerma, Dr. Johannes Schemmel, etc 1 Topics 1. S domain and Laplace Transform Zeros and Poles 2. Basic and Advanced current
Advanced Analog Building Blocks Prof. Dr. Peter Fischer, Dr. Wei Shen, Dr. Albert Comerma, Dr. Johannes Schemmel, etc 1 Topics 1. S domain and Laplace Transform Zeros and Poles 2. Basic and Advanced current
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
The equation of motion of a dynamical system is given by a set of differential equations. That is (1)
 Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Chapter 5 Frequency Domain Analysis of Systems
 Chapter 5 Frequency Domain Analysis of Systems CT, LTI Systems Consider the following CT LTI system: xt () ht () yt () Assumption: the impulse response h(t) is absolutely integrable, i.e., ht ( ) dt< (this
Chapter 5 Frequency Domain Analysis of Systems CT, LTI Systems Consider the following CT LTI system: xt () ht () yt () Assumption: the impulse response h(t) is absolutely integrable, i.e., ht ( ) dt< (this
( ) [ ( k) ( k) ( x) ( ) ( ) ( ) [ ] ξ [ ] [ ] [ ] ( )( ) i ( ) ( )( ) 2! ( ) = ( ) 3 Interpolation. Polynomial Approximation.
![( ) [ ( k) ( k) ( x) ( ) ( ) ( ) [ ] ξ [ ] [ ] [ ] ( )( ) i ( ) ( )( ) 2! ( ) = ( ) 3 Interpolation. Polynomial Approximation. ( ) [ ( k) ( k) ( x) ( ) ( ) ( ) [ ] ξ [ ] [ ] [ ] ( )( ) i ( ) ( )( ) 2! ( ) = ( ) 3 Interpolation. Polynomial Approximation.](/thumbs/84/90601477.jpg) 3 Interpolaton {( y } Gven:,,,,,, [ ] Fnd: y for some Mn, Ma Polynomal Appromaton Theorem (Weerstrass Appromaton Theorem --- estence ε [ ab] f( P( , then there ests a polynomal
3 Interpolaton {( y } Gven:,,,,,, [ ] Fnd: y for some Mn, Ma Polynomal Appromaton Theorem (Weerstrass Appromaton Theorem --- estence ε [ ab] f( P( , then there ests a polynomal
Capacitor Young Won Lim 06/22/2017
 Capacitor Copyright (c) 2011 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version
Capacitor Copyright (c) 2011 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version
Chapter 4: Root Finding
 Chapter 4: Root Fndng Startng values Closed nterval methods (roots are search wthn an nterval o Bsecton Open methods (no nterval o Fxed Pont o Newton-Raphson o Secant Method Repeated roots Zeros of Hgher-Dmensonal
Chapter 4: Root Fndng Startng values Closed nterval methods (roots are search wthn an nterval o Bsecton Open methods (no nterval o Fxed Pont o Newton-Raphson o Secant Method Repeated roots Zeros of Hgher-Dmensonal
Higher Order ODE's (3A) Young Won Lim 7/7/14
 Higher Order ODE's (3A) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Higher Order ODE's (3A) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
DECOUPLING THEORY HW2
 8.8 DECOUPLIG THEORY HW2 DOGHAO WAG DATE:OCT. 3 207 Problem We shall start by reformulatng the problem. Denote by δ S n the delta functon that s evenly dstrbuted at the n ) dmensonal unt sphere. As a temporal
8.8 DECOUPLIG THEORY HW2 DOGHAO WAG DATE:OCT. 3 207 Problem We shall start by reformulatng the problem. Denote by δ S n the delta functon that s evenly dstrbuted at the n ) dmensonal unt sphere. As a temporal
Raktim Bhattacharya. . AERO 422: Active Controls for Aerospace Vehicles. Dynamic Response
 .. AERO 422: Active Controls for Aerospace Vehicles Dynamic Response Raktim Bhattacharya Laboratory For Uncertainty Quantification Aerospace Engineering, Texas A&M University. . Previous Class...........
.. AERO 422: Active Controls for Aerospace Vehicles Dynamic Response Raktim Bhattacharya Laboratory For Uncertainty Quantification Aerospace Engineering, Texas A&M University. . Previous Class...........
Capacitor in an AC circuit
 Capacitor in an AC circuit Copyright (c) 2011 2017 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2
Capacitor in an AC circuit Copyright (c) 2011 2017 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2
Modelli Clamfim Integrali Multipli 7 ottobre 2015
 CLAMFIM Bologna Modell 1 @ Clamfm Integral Multpl 7 ottobre 2015 professor Danele Rtell danele.rtell@unbo.t 1/30? roduct of σ-algebras Let (Ω 1, A 1, µ 1 ), (Ω 2, A 2, µ 2 ) two measure spaces. ut Ω :=
CLAMFIM Bologna Modell 1 @ Clamfm Integral Multpl 7 ottobre 2015 professor Danele Rtell danele.rtell@unbo.t 1/30? roduct of σ-algebras Let (Ω 1, A 1, µ 1 ), (Ω 2, A 2, µ 2 ) two measure spaces. ut Ω :=
Lecture 2: Numerical Methods for Differentiations and Integrations
 Numercal Smulaton of Space Plasmas (I [AP-4036] Lecture 2 by Lng-Hsao Lyu March, 2018 Lecture 2: Numercal Methods for Dfferentatons and Integratons As we have dscussed n Lecture 1 that numercal smulaton
Numercal Smulaton of Space Plasmas (I [AP-4036] Lecture 2 by Lng-Hsao Lyu March, 2018 Lecture 2: Numercal Methods for Dfferentatons and Integratons As we have dscussed n Lecture 1 that numercal smulaton
November 5, 2002 SE 180: Earthquake Engineering SE 180. Final Project
 SE 8 Fnal Project Story Shear Frame u m Gven: u m L L m L L EI ω ω Solve for m Story Bendng Beam u u m L m L Gven: m L L EI ω ω Solve for m 3 3 Story Shear Frame u 3 m 3 Gven: L 3 m m L L L 3 EI ω ω ω
SE 8 Fnal Project Story Shear Frame u m Gven: u m L L m L L EI ω ω Solve for m Story Bendng Beam u u m L m L Gven: m L L EI ω ω Solve for m 3 3 Story Shear Frame u 3 m 3 Gven: L 3 m m L L L 3 EI ω ω ω
