Appendix 2 Complex Analysis
|
|
|
- Cynthia Pitts
- 5 years ago
- Views:
Transcription
1 Appendix Complex Analsis This section is intended to review several important theorems and definitions from complex analsis. Analtic function Let f be a complex variable function of a complex value, i.e. f : The derivative of f at = x+ iis defined b f ( ) ' = lim h ( + ) ( ) f h f h where h=δ x+ iδ is a complex number. Note the difference between this definition of derivative and the definition of derivative for real-valued functions. Namel, in the real case, the limit is from left and right onl. But in the complex plan h can approach ero from various direction as show in the figure. Definition: A function f ( ) defined on an open set D is said to be analtic on D, if f '( ) exists and is continuous for all in D. Moreover, if ( ) we sa f ( ) is entire. Example: Here are some examples of analtic functions.. f ( ) = is analtic and f '( ) =.. For an polnomial n n f ( ) = an + an + + a + a is analtic, and we have n- n- f '( ) = nan + ( n-) an + + a + a 3. The function e is define b It is eas to show that - x+ i x e = e = e (cos + isin ). e is analtic and ( e )' = e f is analtic on all of, A function f ( ) can be expressed in the form of real and the imaginar parts:
2 For example, for f ( ) = ² we have ( ) = ( + ) = ( ) + ( ) f f x i u x, iv x,. where ( ) = ( + ) f f x i = ( x+ i)² = x² ² + xi ( ) iv( x ) = u x, +,. (, ) = ² ² and v( x ) u x x, = x Notice that ux = v and u = -vx These last equations are called Cauch-Riemann equation, and all analtic function satisfies them. Theorem (Cauch-Riemann criterion) The function ( ) (, ) (, ) f = u x + v x i is analtic in an open set D if and onl if the partial derivatives are continuous and satisf the Cauch-Riemann equations u = v and u = v x x In this case ( ) (, ) (, ) (, ) (, ) f = ux x + vx x i = v x u x i. The Figure illustrates the proof of the Cauch-Riemann equations. = + iδ x x = + Δx Figure Figure
3 Example Here is how the Cauch-Riemann equations are used to determine if a function is analtic.. f ( ) = ². So f ( x+ i) = ( x+ i) ² = x² ² + xi, hence ( ) and v( x, ) = x. You can easil check that u = x= v and. f ( ) =. So f ( x+ i) = x i, hence u( x, ) Contour Integral x u x, = x² ², u = = vx, and so it follows that f is analtic. = x, and v( x, ) =. You can easil check that u = = v, and so it follows that f is not analtic. x Before we can discuss integral of complex function, we need to define curves in the complex plane. Definition A complex-valued function of a real variable f ( t) continuous on [ ab, ] if. f () t exists and is continuous for all but finitel man points in ( ab ). At an discontinuous point c ( a, b). Both lim f ( t) and lim f () t and are finite. + t c 3. At the endpoints, lim f ( t) and lim f ( t) + t a t b f t is smooth or continuousl differentiable on [, ] () t are both continuous on [ ab, ]. The function () f is said to be piecewise t c exist and are finite.,. ab if f () t and exist Definition A path or a contour is a continuous piecewise smooth curve () t closed interval [ ab, ]. over a The figure illustrates a path (or contour). 3
4 Recall the definition of the Riemann integral over an interval [ ab, ]. If map [ ab, ] is defined on [ ab, ]. The contour integral of f on is the on [ ab, ]. as in the following definition. into is a path then f Riemann integral of f Definition Suppose that is a path over a closed interval [ ab, ] and that f is a continuous complex-valued function defined on the graph of. The contour integral of f on is given b b f ( d ) = f ( ( t)) '( t) dt a Definition. Let a and b be points in the region D, and and are paths in D joining a to b. is continuousl deformable into relative to D if we can continuousl move over while keeping the ends fixed without leaving D.. Let and be closed paths in D. is continuousl deformable into relative to D if we can continuousl move to overlap in both position and direction without leaving D. The figures illustrate the deformation of a path and a closed path. 4
5 Cauch's Theorem and its Consequences Cauch's theorem tells us that the integral of different path is the same as long as the paths are deformable into each other. Theorem (Cauch's Theorem) Let f be an analtic function in a region D and α and β be points in D.. If and are two paths joining α to β in D, and if is continuousl deformable into relative to D, then f ( d ) = f( d ). If and are closed paths in D, and if is continuousl deformable into relative to D, then f ( d ) = f( d ) Example Here are some examples of using Cauch's Theorem to evaluate line integrals.. Let f ( ) = ². Since f is analtic on and inside the curve in Figure below. It follows from Cauch's Theorem that f( ) d = f =. The curves and in Figure below are deformable into each other without passing through the singularit at, it follows that. Let ( ) f ( d ) = f( d ) f =. The curves and in Figure 3 below are not deformable into each other without passing through the singularit at, Cauch's theorem gives no information about the relative value of these integrals. In fact, 3. Let ( ) f ( d ) f( d ) 5
6 Im Im Im Re Re Re Figure Figure Figure 3 The consequences of Cauch s theorem help us to develop most important integral formulas. Cauch's theorem tells us that the value of an analtic function of f at point inside a curve is completel determined b its values on. This is quite a surprising propert of analtic function. Theorem (Cauch's integral formula) Suppose that f is analtic inside and on a simple closed path C with positive orientation. If is an point inside C, then f ( ζ ) f ( ) = dζ πi ζ C Theorem (Liouville's theorem) If f is entire and bounded, the f is constant. Theorem (Identit Principle) Suppose f ( ) and g( ) be analtic on a region D, and suppose that { n} is an infinite sequence of distinct points in D converging to in D. If f ( ) = g( ) for all n, then f ( ) = g( ) for all in D. n n 6
NATIONAL UNIVERSITY OF SINGAPORE Department of Mathematics MA4247 Complex Analysis II Lecture Notes Part I
 NATIONAL UNIVERSITY OF SINGAPORE Department of Mathematics MA4247 Comple Analsis II Lecture Notes Part I Chapter 1 Preliminar results/review of Comple Analsis I These are more detailed notes for the results
NATIONAL UNIVERSITY OF SINGAPORE Department of Mathematics MA4247 Comple Analsis II Lecture Notes Part I Chapter 1 Preliminar results/review of Comple Analsis I These are more detailed notes for the results
Lecture 4. Properties of Logarithmic Function (Contd ) y Log z tan constant x. It follows that
 Lecture 4 Properties of Logarithmic Function (Contd ) Since, Logln iarg u Re Log ln( ) v Im Log tan constant It follows that u v, u v This shows that Re Logand Im Log are (i) continuous in C { :Re 0,Im
Lecture 4 Properties of Logarithmic Function (Contd ) Since, Logln iarg u Re Log ln( ) v Im Log tan constant It follows that u v, u v This shows that Re Logand Im Log are (i) continuous in C { :Re 0,Im
L-FUNCTIONS AND THE RIEMANN HYPOTHESIS. 1 n s
 L-FUNCTIONS AND THE RIEMANN HYPOTHESIS KEITH CONRAD (.). The zeta-function and Dirichlet L-functions For real s >, the infinite series n converges b the integral test. We want to use this series when s
L-FUNCTIONS AND THE RIEMANN HYPOTHESIS KEITH CONRAD (.). The zeta-function and Dirichlet L-functions For real s >, the infinite series n converges b the integral test. We want to use this series when s
MATH 417 Homework 2 Instructor: D. Cabrera Due June 23. v = e x sin y
 MATH 47 Homework Instructor: D. Cabrera Due June under the trans-. Find and sketch the image of the rectangle 0 < x
MATH 47 Homework Instructor: D. Cabrera Due June under the trans-. Find and sketch the image of the rectangle 0 < x
Part D. Complex Analysis
 Part D. Comple Analsis Chapter 3. Comple Numbers and Functions. Man engineering problems ma be treated and solved b using comple numbers and comple functions. First, comple numbers and the comple plane
Part D. Comple Analsis Chapter 3. Comple Numbers and Functions. Man engineering problems ma be treated and solved b using comple numbers and comple functions. First, comple numbers and the comple plane
Notes 7 Analytic Continuation
 ECE 6382 Fall 27 David R. Jackson Notes 7 Analtic Continuation Notes are from D. R. Wilton, Dept. of ECE Analtic Continuation of Functions We define analtic continuation as the process of continuing a
ECE 6382 Fall 27 David R. Jackson Notes 7 Analtic Continuation Notes are from D. R. Wilton, Dept. of ECE Analtic Continuation of Functions We define analtic continuation as the process of continuing a
Harmonic functions, Poisson kernels
 June 17, 16 Harmonic functions, Poisson kernels Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/complex/notes 14-15/8c harmonic.pdf]
June 17, 16 Harmonic functions, Poisson kernels Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/complex/notes 14-15/8c harmonic.pdf]
Topic 3 Notes Jeremy Orloff
 Topic 3 Notes Jerem Orloff 3 Line integrals and auch s theorem 3.1 Introduction The basic theme here is that comple line integrals will mirror much of what we ve seen for multivariable calculus line integrals.
Topic 3 Notes Jerem Orloff 3 Line integrals and auch s theorem 3.1 Introduction The basic theme here is that comple line integrals will mirror much of what we ve seen for multivariable calculus line integrals.
3.1 Graphing Quadratic Functions. Quadratic functions are of the form.
 3.1 Graphing Quadratic Functions A. Quadratic Functions Completing the Square Quadratic functions are of the form. 3. It is easiest to graph quadratic functions when the are in the form using transformations.
3.1 Graphing Quadratic Functions A. Quadratic Functions Completing the Square Quadratic functions are of the form. 3. It is easiest to graph quadratic functions when the are in the form using transformations.
Math 20 Spring 2005 Final Exam Practice Problems (Set 2)
 Math 2 Spring 2 Final Eam Practice Problems (Set 2) 1. Find the etreme values of f(, ) = 2 2 + 3 2 4 on the region {(, ) 2 + 2 16}. 2. Allocation of Funds: A new editor has been allotted $6, to spend on
Math 2 Spring 2 Final Eam Practice Problems (Set 2) 1. Find the etreme values of f(, ) = 2 2 + 3 2 4 on the region {(, ) 2 + 2 16}. 2. Allocation of Funds: A new editor has been allotted $6, to spend on
One-Dimensional Dynamics
 One-Dimensional Dnamics We aim to characterize the dnamics completel describe the phase portrait) of the one-dimensional autonomous differential equation Before proceeding we worr about 1.1) having a solution.
One-Dimensional Dnamics We aim to characterize the dnamics completel describe the phase portrait) of the one-dimensional autonomous differential equation Before proceeding we worr about 1.1) having a solution.
Limits and Continuous Functions. 2.2 Introduction to Limits. We first interpret limits loosely. We write. lim f(x) = L
 2 Limits and Continuous Functions 2.2 Introduction to Limits We first interpret limits loosel. We write lim f() = L and sa the limit of f() as approaches c, equals L if we can make the values of f() arbitraril
2 Limits and Continuous Functions 2.2 Introduction to Limits We first interpret limits loosel. We write lim f() = L and sa the limit of f() as approaches c, equals L if we can make the values of f() arbitraril
Spotlight on the Extended Method of Frobenius
 113 Spotlight on the Extended Method of Frobenius See Sections 11.1 and 11.2 for the model of an aging spring. Reference: Section 11.4 and SPOTLIGHT ON BESSEL FUNCTIONS. Bessel functions of the first kind
113 Spotlight on the Extended Method of Frobenius See Sections 11.1 and 11.2 for the model of an aging spring. Reference: Section 11.4 and SPOTLIGHT ON BESSEL FUNCTIONS. Bessel functions of the first kind
10.5 Graphs of the Trigonometric Functions
 790 Foundations of Trigonometr 0.5 Graphs of the Trigonometric Functions In this section, we return to our discussion of the circular (trigonometric functions as functions of real numbers and pick up where
790 Foundations of Trigonometr 0.5 Graphs of the Trigonometric Functions In this section, we return to our discussion of the circular (trigonometric functions as functions of real numbers and pick up where
Physics of Tsunamis. This is an article from my home page: Ole Witt-Hansen 2011 (2016)
 Phsics of Tsunamis This is an article from m home page: www.olewitthansen.dk Ole Witt-Hansen 11 (16) Contents 1. Constructing a differential equation for the Tsunami wave...1. The velocit of propagation
Phsics of Tsunamis This is an article from m home page: www.olewitthansen.dk Ole Witt-Hansen 11 (16) Contents 1. Constructing a differential equation for the Tsunami wave...1. The velocit of propagation
4 Inverse function theorem
 Tel Aviv Universit, 2013/14 Analsis-III,IV 53 4 Inverse function theorem 4a What is the problem................ 53 4b Simple observations before the theorem..... 54 4c The theorem.....................
Tel Aviv Universit, 2013/14 Analsis-III,IV 53 4 Inverse function theorem 4a What is the problem................ 53 4b Simple observations before the theorem..... 54 4c The theorem.....................
+ b n sin 2πnt. dt. However, we have also seen that, using Euler s Formula, trigonometric functions can be written in a complex exponential form,
 4 omple Analsis He is not a true man of science who does not bring some smpath to his studies, and epect to learn something b behavior as well as b application. It is childish to rest in the discover of
4 omple Analsis He is not a true man of science who does not bring some smpath to his studies, and epect to learn something b behavior as well as b application. It is childish to rest in the discover of
Section 1.2: A Catalog of Functions
 Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
Asymptotics at regular singular points
 Ma 7, 2011 Asmptotics at regular singular points Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ Introduction 1. Examples 2. Regular singular points 3. Regular singular points at infinit
Ma 7, 2011 Asmptotics at regular singular points Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ Introduction 1. Examples 2. Regular singular points 3. Regular singular points at infinit
Complex Variables. For ECON 397 Macroeconometrics Steve Cunningham
 Comple Variables For ECON 397 Macroeconometrics Steve Cnningham Open Disks or Neighborhoods Deinition. The set o all points which satis the ineqalit
Comple Variables For ECON 397 Macroeconometrics Steve Cnningham Open Disks or Neighborhoods Deinition. The set o all points which satis the ineqalit
Math 421 Midterm 2 review questions
 Math 42 Midterm 2 review questions Paul Hacking November 7, 205 () Let U be an open set and f : U a continuous function. Let be a smooth curve contained in U, with endpoints α and β, oriented from α to
Math 42 Midterm 2 review questions Paul Hacking November 7, 205 () Let U be an open set and f : U a continuous function. Let be a smooth curve contained in U, with endpoints α and β, oriented from α to
ECE Spring Prof. David R. Jackson ECE Dept. Notes 33
 ECE 6341 Spring 16 Prof. David R. Jackson ECE Dept. Notes 33 1 Complex Integral: Steepest-Descent Method Ω g z I f z e dz Ω = C This is an extension of Laplace s method to treat integrals in the complex
ECE 6341 Spring 16 Prof. David R. Jackson ECE Dept. Notes 33 1 Complex Integral: Steepest-Descent Method Ω g z I f z e dz Ω = C This is an extension of Laplace s method to treat integrals in the complex
The Central Limit Theorem for Free Additive Convolution
 journal of functional analsis 140, 359380 (1996) article no. 0112 The Central Limit Theorem for Free Additive Convolution Vittorino Pata*, - Dipartimento di Elettronica per l'automazione, Universita di
journal of functional analsis 140, 359380 (1996) article no. 0112 The Central Limit Theorem for Free Additive Convolution Vittorino Pata*, - Dipartimento di Elettronica per l'automazione, Universita di
You don't have to be a mathematician to have a feel for numbers. John Forbes Nash, Jr.
 Course Title: Real Analsis Course Code: MTH3 Course instructor: Dr. Atiq ur Rehman Class: MSc-II Course URL: www.mathcit.org/atiq/fa5-mth3 You don't have to be a mathematician to have a feel for numbers.
Course Title: Real Analsis Course Code: MTH3 Course instructor: Dr. Atiq ur Rehman Class: MSc-II Course URL: www.mathcit.org/atiq/fa5-mth3 You don't have to be a mathematician to have a feel for numbers.
10.2 The Unit Circle: Cosine and Sine
 0. The Unit Circle: Cosine and Sine 77 0. The Unit Circle: Cosine and Sine In Section 0.., we introduced circular motion and derived a formula which describes the linear velocit of an object moving on
0. The Unit Circle: Cosine and Sine 77 0. The Unit Circle: Cosine and Sine In Section 0.., we introduced circular motion and derived a formula which describes the linear velocit of an object moving on
Fritz Hörmann MATH 316: Complex Analysis Fall 2010 Solutions to exercise sheet 2
 Fritz Hörmann MATH 316: Complex Analsis Fall 2010 Solutions to exercise sheet 2 1 Möbius transformations: Prove that (a the group of Möbius transformations Aut(Ĉ acts transitivel on the set of circles
Fritz Hörmann MATH 316: Complex Analsis Fall 2010 Solutions to exercise sheet 2 1 Möbius transformations: Prove that (a the group of Möbius transformations Aut(Ĉ acts transitivel on the set of circles
Chapter 3: Three faces of the derivative. Overview
 Overview We alread saw an algebraic wa of thinking about a derivative. Geometric: zooming into a line Analtic: continuit and rational functions Computational: approimations with computers 3. The geometric
Overview We alread saw an algebraic wa of thinking about a derivative. Geometric: zooming into a line Analtic: continuit and rational functions Computational: approimations with computers 3. The geometric
Syllabus: for Complex variables
 EE-2020, Spring 2009 p. 1/42 Syllabus: for omplex variables 1. Midterm, (4/27). 2. Introduction to Numerical PDE (4/30): [Ref.num]. 3. omplex variables: [Textbook]h.13-h.18. omplex numbers and functions,
EE-2020, Spring 2009 p. 1/42 Syllabus: for omplex variables 1. Midterm, (4/27). 2. Introduction to Numerical PDE (4/30): [Ref.num]. 3. omplex variables: [Textbook]h.13-h.18. omplex numbers and functions,
8 Complex Representations of Functions
 8 omple Representations of Functions He is not a true man of science who does not bring some smpath to his studies, and epect to learn something b behavior as well as b application. It is childish to rest
8 omple Representations of Functions He is not a true man of science who does not bring some smpath to his studies, and epect to learn something b behavior as well as b application. It is childish to rest
MA30056: Complex Analysis. Revision: Checklist & Previous Exam Questions I
 MA30056: Complex Analysis Revision: Checklist & Previous Exam Questions I Given z C and r > 0, define B r (z) and B r (z). Define what it means for a subset A C to be open/closed. If M A C, when is M said
MA30056: Complex Analysis Revision: Checklist & Previous Exam Questions I Given z C and r > 0, define B r (z) and B r (z). Define what it means for a subset A C to be open/closed. If M A C, when is M said
David M. Bressoud Macalester College, St. Paul, Minnesota Given at Allegheny College, Oct. 23, 2003
 David M. Bressoud Macalester College, St. Paul, Minnesota Given at Allegheny College, Oct. 23, 2003 The Fundamental Theorem of Calculus:. If F' ( x)= f ( x), then " f ( x) dx = F( b)! F( a). b a 2. d dx
David M. Bressoud Macalester College, St. Paul, Minnesota Given at Allegheny College, Oct. 23, 2003 The Fundamental Theorem of Calculus:. If F' ( x)= f ( x), then " f ( x) dx = F( b)! F( a). b a 2. d dx
Law of Sines, Law of Cosines, Heron s Formula:
 PreAP Math Analsis nd Semester Review Law of Sines, Law of Cosines, Heron s Formula:. Determine how man solutions the triangle has and eplain our reasoning. (FIND YOUR FLOW CHART) a. A = 4, a = 4 ards,
PreAP Math Analsis nd Semester Review Law of Sines, Law of Cosines, Heron s Formula:. Determine how man solutions the triangle has and eplain our reasoning. (FIND YOUR FLOW CHART) a. A = 4, a = 4 ards,
(z 0 ) = lim. = lim. = f. Similarly along a vertical line, we fix x = x 0 and vary y. Setting z = x 0 + iy, we get. = lim. = i f
 . Holomorphic Harmonic Functions Basic notation. Considering C as R, with coordinates x y, z = x + iy denotes the stard complex coordinate, in the usual way. Definition.1. Let f : U C be a complex valued
. Holomorphic Harmonic Functions Basic notation. Considering C as R, with coordinates x y, z = x + iy denotes the stard complex coordinate, in the usual way. Definition.1. Let f : U C be a complex valued
Time-Frequency Analysis: Fourier Transforms and Wavelets
 Chapter 4 Time-Frequenc Analsis: Fourier Transforms and Wavelets 4. Basics of Fourier Series 4.. Introduction Joseph Fourier (768-83) who gave his name to Fourier series, was not the first to use Fourier
Chapter 4 Time-Frequenc Analsis: Fourier Transforms and Wavelets 4. Basics of Fourier Series 4.. Introduction Joseph Fourier (768-83) who gave his name to Fourier series, was not the first to use Fourier
APPENDIXES. B Coordinate Geometry and Lines C. D Trigonometry E F. G The Logarithm Defined as an Integral H Complex Numbers I
 APPENDIXES A Numbers, Inequalities, and Absolute Values B Coordinate Geometr and Lines C Graphs of Second-Degree Equations D Trigonometr E F Sigma Notation Proofs of Theorems G The Logarithm Defined as
APPENDIXES A Numbers, Inequalities, and Absolute Values B Coordinate Geometr and Lines C Graphs of Second-Degree Equations D Trigonometr E F Sigma Notation Proofs of Theorems G The Logarithm Defined as
Examples of the Fourier Theorem (Sect. 10.3). The Fourier Theorem: Continuous case.
 s of the Fourier Theorem (Sect. 1.3. The Fourier Theorem: Continuous case. : Using the Fourier Theorem. The Fourier Theorem: Piecewise continuous case. : Using the Fourier Theorem. The Fourier Theorem:
s of the Fourier Theorem (Sect. 1.3. The Fourier Theorem: Continuous case. : Using the Fourier Theorem. The Fourier Theorem: Piecewise continuous case. : Using the Fourier Theorem. The Fourier Theorem:
MEMORIAL UNIVERSITY OF NEWFOUNDLAND
 MEMORIAL UNIVERSITY OF NEWFOUNDLAND DEPARTMENT OF MATHEMATICS AND STATISTICS Volumes Math 11 Winter 17 SOLUTIONS 1. (a) i. The axis of smmetr is a horizontal line, so we integrate with respect to x. The
MEMORIAL UNIVERSITY OF NEWFOUNDLAND DEPARTMENT OF MATHEMATICS AND STATISTICS Volumes Math 11 Winter 17 SOLUTIONS 1. (a) i. The axis of smmetr is a horizontal line, so we integrate with respect to x. The
(2.5) 1. Solve the following compound inequality and graph the solution set.
 Intermediate Algebra Practice Final Math 0 (7 th ed.) (Ch. -) (.5). Solve the following compound inequalit and graph the solution set. 0 and and > or or (.7). Solve the following absolute value inequalities.
Intermediate Algebra Practice Final Math 0 (7 th ed.) (Ch. -) (.5). Solve the following compound inequalit and graph the solution set. 0 and and > or or (.7). Solve the following absolute value inequalities.
Time-Frequency Analysis: Fourier Transforms and Wavelets
 Chapter 4 Time-Frequenc Analsis: Fourier Transforms and Wavelets 4. Basics of Fourier Series 4.. Introduction Joseph Fourier (768-83) who gave his name to Fourier series, was not the first to use Fourier
Chapter 4 Time-Frequenc Analsis: Fourier Transforms and Wavelets 4. Basics of Fourier Series 4.. Introduction Joseph Fourier (768-83) who gave his name to Fourier series, was not the first to use Fourier
Week 3 September 5-7.
 MA322 Weekl topics and quiz preparations Week 3 September 5-7. Topics These are alread partl covered in lectures. We collect the details for convenience.. Solutions of homogeneous equations AX =. 2. Using
MA322 Weekl topics and quiz preparations Week 3 September 5-7. Topics These are alread partl covered in lectures. We collect the details for convenience.. Solutions of homogeneous equations AX =. 2. Using
3.2 Differentiability; Tangent planes; differentials
 4 Chapter 3 Draft October 23, 2009 3.2 Differentiabilit; Tangent planes; differentials Overview: In this section, differentiabilit is defined in terms of linear approximation. A function is differentiable
4 Chapter 3 Draft October 23, 2009 3.2 Differentiabilit; Tangent planes; differentials Overview: In this section, differentiabilit is defined in terms of linear approximation. A function is differentiable
Vector Fields. Field (II) Field (V)
 Math 1a Vector Fields 1. Match the following vector fields to the pictures, below. Eplain our reasoning. (Notice that in some of the pictures all of the vectors have been uniforml scaled so that the picture
Math 1a Vector Fields 1. Match the following vector fields to the pictures, below. Eplain our reasoning. (Notice that in some of the pictures all of the vectors have been uniforml scaled so that the picture
3.7 InveRSe FUnCTIOnS
 CHAPTER functions learning ObjeCTIveS In this section, ou will: Verif inverse functions. Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
CHAPTER functions learning ObjeCTIveS In this section, ou will: Verif inverse functions. Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
Analysis Comprehensive Exam, January 2011 Instructions: Do as many problems as you can. You should attempt to answer completely some questions in both
 Analysis Comprehensive Exam, January 2011 Instructions: Do as many problems as you can. You should attempt to answer completely some questions in both real and complex analysis. You have 3 hours. Real
Analysis Comprehensive Exam, January 2011 Instructions: Do as many problems as you can. You should attempt to answer completely some questions in both real and complex analysis. You have 3 hours. Real
Complex Variables Notes for Math 703. Updated Fall Anton R. Schep
 Complex Variables Notes for Math 703. Updated Fall 20 Anton R. Schep CHAPTER Holomorphic (or Analytic) Functions. Definitions and elementary properties In complex analysis we study functions f : S C,
Complex Variables Notes for Math 703. Updated Fall 20 Anton R. Schep CHAPTER Holomorphic (or Analytic) Functions. Definitions and elementary properties In complex analysis we study functions f : S C,
Review for Exam #3 MATH 3200
 Review for Exam #3 MATH 3 Lodwick/Kawai You will have hrs. to complete Exam #3. There will be one full problem from Laplace Transform with the unit step function. There will be linear algebra, but hopefull,
Review for Exam #3 MATH 3 Lodwick/Kawai You will have hrs. to complete Exam #3. There will be one full problem from Laplace Transform with the unit step function. There will be linear algebra, but hopefull,
INTEGRATION WORKSHOP 2004 COMPLEX ANALYSIS EXERCISES
 INTEGRATION WORKSHOP 2004 COMPLEX ANALYSIS EXERCISES PHILIP FOTH 1. Cauchy s Formula and Cauchy s Theorem 1. Suppose that γ is a piecewise smooth positively ( counterclockwise ) oriented simple closed
INTEGRATION WORKSHOP 2004 COMPLEX ANALYSIS EXERCISES PHILIP FOTH 1. Cauchy s Formula and Cauchy s Theorem 1. Suppose that γ is a piecewise smooth positively ( counterclockwise ) oriented simple closed
Solving Quadratic Equations by Graphs and Factoring
 Solving Quadratic Equations b Graphs and Factoring Algebra Unit: 05 Lesson: 0 Consider the equation - 8 + 15 = 0. Show (numericall) that = 5 is a solution. There is also another solution to the equation.
Solving Quadratic Equations b Graphs and Factoring Algebra Unit: 05 Lesson: 0 Consider the equation - 8 + 15 = 0. Show (numericall) that = 5 is a solution. There is also another solution to the equation.
Chapter 13. Overview. The Quadratic Formula. Overview. The Quadratic Formula. The Quadratic Formula. Lewinter & Widulski 1. The Quadratic Formula
 Chapter 13 Overview Some More Math Before You Go The Quadratic Formula The iscriminant Multiplication of Binomials F.O.I.L. Factoring Zero factor propert Graphing Parabolas The Ais of Smmetr, Verte and
Chapter 13 Overview Some More Math Before You Go The Quadratic Formula The iscriminant Multiplication of Binomials F.O.I.L. Factoring Zero factor propert Graphing Parabolas The Ais of Smmetr, Verte and
Section 3.1. ; X = (0, 1]. (i) f : R R R, f (x, y) = x y
![Section 3.1. ; X = (0, 1]. (i) f : R R R, f (x, y) = x y Section 3.1. ; X = (0, 1]. (i) f : R R R, f (x, y) = x y](/thumbs/83/88503328.jpg) Paul J. Bruillard MATH 0.970 Problem Set 6 An Introduction to Abstract Mathematics R. Bond and W. Keane Section 3.1: 3b,c,e,i, 4bd, 6, 9, 15, 16, 18c,e, 19a, 0, 1b Section 3.: 1f,i, e, 6, 1e,f,h, 13e,
Paul J. Bruillard MATH 0.970 Problem Set 6 An Introduction to Abstract Mathematics R. Bond and W. Keane Section 3.1: 3b,c,e,i, 4bd, 6, 9, 15, 16, 18c,e, 19a, 0, 1b Section 3.: 1f,i, e, 6, 1e,f,h, 13e,
18.02 Review Jeremy Orloff. 1 Review of multivariable calculus (18.02) constructs
 18.02 eview Jerem Orloff 1 eview of multivariable calculus (18.02) constructs 1.1 Introduction These notes are a terse summar of what we ll need from multivariable calculus. If, after reading these, some
18.02 eview Jerem Orloff 1 eview of multivariable calculus (18.02) constructs 1.1 Introduction These notes are a terse summar of what we ll need from multivariable calculus. If, after reading these, some
Polynomial Functions and their Graphs
 College Algebra - MAT 11 Page: 1 Copright 009 Killoran Polnomial Functions and their Graphs Polnomial Functions have the general form: p./ D a n n C a n 1 n 1 C C a C a 1 C a 0 And the all share a common
College Algebra - MAT 11 Page: 1 Copright 009 Killoran Polnomial Functions and their Graphs Polnomial Functions have the general form: p./ D a n n C a n 1 n 1 C C a C a 1 C a 0 And the all share a common
Complex Analysis. Travis Dirle. December 4, 2016
 Complex Analysis 2 Complex Analysis Travis Dirle December 4, 2016 2 Contents 1 Complex Numbers and Functions 1 2 Power Series 3 3 Analytic Functions 7 4 Logarithms and Branches 13 5 Complex Integration
Complex Analysis 2 Complex Analysis Travis Dirle December 4, 2016 2 Contents 1 Complex Numbers and Functions 1 2 Power Series 3 3 Analytic Functions 7 4 Logarithms and Branches 13 5 Complex Integration
Introduction to Differential Equations. National Chiao Tung University Chun-Jen Tsai 9/14/2011
 Introduction to Differential Equations National Chiao Tung Universit Chun-Jen Tsai 9/14/011 Differential Equations Definition: An equation containing the derivatives of one or more dependent variables,
Introduction to Differential Equations National Chiao Tung Universit Chun-Jen Tsai 9/14/011 Differential Equations Definition: An equation containing the derivatives of one or more dependent variables,
MATH 722, COMPLEX ANALYSIS, SPRING 2009 PART 5
 MATH 722, COMPLEX ANALYSIS, SPRING 2009 PART 5.. The Arzela-Ascoli Theorem.. The Riemann mapping theorem Let X be a metric space, and let F be a family of continuous complex-valued functions on X. We have
MATH 722, COMPLEX ANALYSIS, SPRING 2009 PART 5.. The Arzela-Ascoli Theorem.. The Riemann mapping theorem Let X be a metric space, and let F be a family of continuous complex-valued functions on X. We have
Integration in the Complex Plane (Zill & Wright Chapter 18)
 Integration in the omplex Plane Zill & Wright hapter 18) 116-4-: omplex Variables Fall 11 ontents 1 ontour Integrals 1.1 Definition and Properties............................. 1. Evaluation.....................................
Integration in the omplex Plane Zill & Wright hapter 18) 116-4-: omplex Variables Fall 11 ontents 1 ontour Integrals 1.1 Definition and Properties............................. 1. Evaluation.....................................
MAT389 Fall 2016, Problem Set 2
 MAT389 Fall 2016, Problem Set 2 Circles in the Riemann sphere Recall that the Riemann sphere is defined as the set Let P be the plane defined b Σ = { (a, b, c) R 3 a 2 + b 2 + c 2 = 1 } P = { (a, b, c)
MAT389 Fall 2016, Problem Set 2 Circles in the Riemann sphere Recall that the Riemann sphere is defined as the set Let P be the plane defined b Σ = { (a, b, c) R 3 a 2 + b 2 + c 2 = 1 } P = { (a, b, c)
CHAPTER 80 NUMERICAL METHODS FOR FIRST-ORDER DIFFERENTIAL EQUATIONS
 CHAPTER 8 NUMERICAL METHODS FOR FIRST-ORDER DIFFERENTIAL EQUATIONS EXERCISE 33 Page 834. Use Euler s method to obtain a numerical solution of the differential equation d d 3, with the initial conditions
CHAPTER 8 NUMERICAL METHODS FOR FIRST-ORDER DIFFERENTIAL EQUATIONS EXERCISE 33 Page 834. Use Euler s method to obtain a numerical solution of the differential equation d d 3, with the initial conditions
Polynomial and Rational Functions
 Name Date Chapter Polnomial and Rational Functions Section.1 Quadratic Functions Objective: In this lesson ou learned how to sketch and analze graphs of quadratic functions. Important Vocabular Define
Name Date Chapter Polnomial and Rational Functions Section.1 Quadratic Functions Objective: In this lesson ou learned how to sketch and analze graphs of quadratic functions. Important Vocabular Define
Integration. 5.1 Antiderivatives and Indefinite Integration. Suppose that f(x) = 5x 4. Can we find a function F (x) whose derivative is f(x)?
 5 Integration 5. Antiderivatives and Indefinite Integration Suppose that f() = 5 4. Can we find a function F () whose derivative is f()? Definition. A function F is an antiderivative of f on an interval
5 Integration 5. Antiderivatives and Indefinite Integration Suppose that f() = 5 4. Can we find a function F () whose derivative is f()? Definition. A function F is an antiderivative of f on an interval
Linear Transformations
 inear Transformations 6 The main objects of stud in an course in linear algebra are linear functions: Definition A function : V! W is linear if V and W are vector spaces and (ru + sv) r(u)+s(v) for all
inear Transformations 6 The main objects of stud in an course in linear algebra are linear functions: Definition A function : V! W is linear if V and W are vector spaces and (ru + sv) r(u)+s(v) for all
3 Polynomial and Rational Functions
 3 Polnomial and Rational Functions 3.1 Quadratic Functions and Models 3.2 Polnomial Functions and Their Graphs 3.3 Dividing Polnomials 3.4 Real Zeros of Polnomials 3.5 Comple Zeros and the Fundamental
3 Polnomial and Rational Functions 3.1 Quadratic Functions and Models 3.2 Polnomial Functions and Their Graphs 3.3 Dividing Polnomials 3.4 Real Zeros of Polnomials 3.5 Comple Zeros and the Fundamental
z = 1 2 x 3 4 y + 3 y dt
 Exact First Order Differential Equations This Lecture covers material in Section 2.6. A first order differential equations is exact if it can be written in the form M(x, ) + N(x, ) d dx = 0, where M =
Exact First Order Differential Equations This Lecture covers material in Section 2.6. A first order differential equations is exact if it can be written in the form M(x, ) + N(x, ) d dx = 0, where M =
Boundary layers in a two-point boundary value problem with fractional derivatives
 Boundary layers in a two-point boundary value problem with fractional derivatives J.L. Gracia and M. Stynes Institute of Mathematics and Applications (IUMA) and Department of Applied Mathematics, University
Boundary layers in a two-point boundary value problem with fractional derivatives J.L. Gracia and M. Stynes Institute of Mathematics and Applications (IUMA) and Department of Applied Mathematics, University
MATH College Algebra Review for Test 2
 MATH 4 - College Algebra Review for Test Sections. and.. For f (x) = x + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the axis of
MATH 4 - College Algebra Review for Test Sections. and.. For f (x) = x + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the axis of
2.1 Evaluate and Graph Polynomial
 2. Evaluate and Graph Polnomial Functions Georgia Performance Standard(s) MM3Ab, MM3Ac, MM3Ad Your Notes Goal p Evaluate and graph polnomial functions. VOCABULARY Polnomial Polnomial function Degree of
2. Evaluate and Graph Polnomial Functions Georgia Performance Standard(s) MM3Ab, MM3Ac, MM3Ad Your Notes Goal p Evaluate and graph polnomial functions. VOCABULARY Polnomial Polnomial function Degree of
summation of series: sommerfeld-watson transformation
 Phsics 2400 Spring 207 summation of series: sommerfeld-watson transformation spring semester 207 http://www.phs.uconn.edu/ rozman/courses/p2400_7s/ Last modified: Ma 3, 207 Sommerfeld-Watson transformation,
Phsics 2400 Spring 207 summation of series: sommerfeld-watson transformation spring semester 207 http://www.phs.uconn.edu/ rozman/courses/p2400_7s/ Last modified: Ma 3, 207 Sommerfeld-Watson transformation,
In this chapter a student has to learn the Concept of adjoint of a matrix. Inverse of a matrix. Rank of a matrix and methods finding these.
 MATRICES UNIT STRUCTURE.0 Objectives. Introduction. Definitions. Illustrative eamples.4 Rank of matri.5 Canonical form or Normal form.6 Normal form PAQ.7 Let Us Sum Up.8 Unit End Eercise.0 OBJECTIVES In
MATRICES UNIT STRUCTURE.0 Objectives. Introduction. Definitions. Illustrative eamples.4 Rank of matri.5 Canonical form or Normal form.6 Normal form PAQ.7 Let Us Sum Up.8 Unit End Eercise.0 OBJECTIVES In
MAT 1275: Introduction to Mathematical Analysis. Graphs and Simplest Equations for Basic Trigonometric Functions. y=sin( x) Function
 MAT 275: Introduction to Mathematical Analsis Dr. A. Rozenblum Graphs and Simplest Equations for Basic Trigonometric Functions We consider here three basic functions: sine, cosine and tangent. For them,
MAT 275: Introduction to Mathematical Analsis Dr. A. Rozenblum Graphs and Simplest Equations for Basic Trigonometric Functions We consider here three basic functions: sine, cosine and tangent. For them,
Math 312 Fall 2013 Final Exam Solutions (2 + i)(i + 1) = (i 1)(i + 1) = 2i i2 + i. i 2 1
 . (a) We have 2 + i i Math 32 Fall 203 Final Exam Solutions (2 + i)(i + ) (i )(i + ) 2i + 2 + i2 + i i 2 3i + 2 2 3 2 i.. (b) Note that + i 2e iπ/4 so that Arg( + i) π/4. This implies 2 log 2 + π 4 i..
. (a) We have 2 + i i Math 32 Fall 203 Final Exam Solutions (2 + i)(i + ) (i )(i + ) 2i + 2 + i2 + i i 2 3i + 2 2 3 2 i.. (b) Note that + i 2e iπ/4 so that Arg( + i) π/4. This implies 2 log 2 + π 4 i..
Differential Equations of First Order. Separable Differential Equations. Euler s Method
 Calculus 2 Lia Vas Differential Equations of First Order. Separable Differential Equations. Euler s Method A differential equation is an equation in unknown function that contains one or more derivatives
Calculus 2 Lia Vas Differential Equations of First Order. Separable Differential Equations. Euler s Method A differential equation is an equation in unknown function that contains one or more derivatives
Ch 3 Alg 2 Note Sheet.doc 3.1 Graphing Systems of Equations
 Ch 3 Alg Note Sheet.doc 3.1 Graphing Sstems of Equations Sstems of Linear Equations A sstem of equations is a set of two or more equations that use the same variables. If the graph of each equation =.4
Ch 3 Alg Note Sheet.doc 3.1 Graphing Sstems of Equations Sstems of Linear Equations A sstem of equations is a set of two or more equations that use the same variables. If the graph of each equation =.4
v t t t t a t v t d dt t t t t t 23.61
 SECTION 4. MAXIMUM AND MINIMUM VALUES 285 The values of f at the endpoints are f 0 0 and f 2 2 6.28 Comparing these four numbers and using the Closed Interval Method, we see that the absolute minimum value
SECTION 4. MAXIMUM AND MINIMUM VALUES 285 The values of f at the endpoints are f 0 0 and f 2 2 6.28 Comparing these four numbers and using the Closed Interval Method, we see that the absolute minimum value
Complex Variables. Cathal Ormond
 Complex Variables Cathal Ormond Contents 1 Introduction 3 1.1 Definition: Polar Form.............................. 3 1.2 Definition: Length................................ 3 1.3 Definitions.....................................
Complex Variables Cathal Ormond Contents 1 Introduction 3 1.1 Definition: Polar Form.............................. 3 1.2 Definition: Length................................ 3 1.3 Definitions.....................................
. Then Φ is a diffeomorphism from (0, ) onto (0, 1)
 1 + 5..0: uv i Set F s, t s α 1 t β 1 e s+t and Φu, v. Then Φ is a u1 v diffeomorphism from 0, 0, 1 onto 0,, and JΦu, v u. Hence, ΓαΓβ F s, t dsdt F Φu, vjφu, v dudv 0, 0, 0,1 u α+β 1 e u v α 1 1 v β 1
1 + 5..0: uv i Set F s, t s α 1 t β 1 e s+t and Φu, v. Then Φ is a u1 v diffeomorphism from 0, 0, 1 onto 0,, and JΦu, v u. Hence, ΓαΓβ F s, t dsdt F Φu, vjφu, v dudv 0, 0, 0,1 u α+β 1 e u v α 1 1 v β 1
f(x) = 2x 2 + 2x - 4
 4-1 Graphing Quadratic Functions What You ll Learn Scan the tet under the Now heading. List two things ou will learn about in the lesson. 1. Active Vocabular 2. New Vocabular Label each bo with the terms
4-1 Graphing Quadratic Functions What You ll Learn Scan the tet under the Now heading. List two things ou will learn about in the lesson. 1. Active Vocabular 2. New Vocabular Label each bo with the terms
2.5. Infinite Limits and Vertical Asymptotes. Infinite Limits
 . Infinite Limits and Vertical Asmptotes. Infinite Limits and Vertical Asmptotes In this section we etend the concept of it to infinite its, which are not its as before, but rather an entirel new use of
. Infinite Limits and Vertical Asmptotes. Infinite Limits and Vertical Asmptotes In this section we etend the concept of it to infinite its, which are not its as before, but rather an entirel new use of
MTH 3102 Complex Variables Final Exam May 1, :30pm-5:30pm, Skurla Hall, Room 106
 Name (Last name, First name): MTH 32 Complex Variables Final Exam May, 27 3:3pm-5:3pm, Skurla Hall, Room 6 Exam Instructions: You have hour & 5 minutes to complete the exam. There are a total of problems.
Name (Last name, First name): MTH 32 Complex Variables Final Exam May, 27 3:3pm-5:3pm, Skurla Hall, Room 6 Exam Instructions: You have hour & 5 minutes to complete the exam. There are a total of problems.
Marcinkiewicz Interpolation Theorem by Daniel Baczkowski
 1 Introduction Marcinkiewicz Interpolation Theorem b Daniel Baczkowski Let (, µ be a measure space. Let M denote the collection of all extended real valued µ-measurable functions on. Also, let M denote
1 Introduction Marcinkiewicz Interpolation Theorem b Daniel Baczkowski Let (, µ be a measure space. Let M denote the collection of all extended real valued µ-measurable functions on. Also, let M denote
MA123, Chapter 8: Idea of the Integral (pp , Gootman)
 MA13, Chapter 8: Idea of the Integral (pp. 155-187, Gootman) Chapter Goals: Understand the relationship between the area under a curve and the definite integral. Understand the relationship between velocit
MA13, Chapter 8: Idea of the Integral (pp. 155-187, Gootman) Chapter Goals: Understand the relationship between the area under a curve and the definite integral. Understand the relationship between velocit
Complex Integration Line Integral in the Complex Plane CHAPTER 14
 HAPTER 14 omplex Integration hapter 13 laid the groundwork for the study of complex analysis, covered complex numbers in the complex plane, limits, and differentiation, and introduced the most important
HAPTER 14 omplex Integration hapter 13 laid the groundwork for the study of complex analysis, covered complex numbers in the complex plane, limits, and differentiation, and introduced the most important
MA3111S COMPLEX ANALYSIS I
 MA3111S COMPLEX ANALYSIS I 1. The Algebra of Complex Numbers A complex number is an expression of the form a + ib, where a and b are real numbers. a is called the real part of a + ib and b the imaginary
MA3111S COMPLEX ANALYSIS I 1. The Algebra of Complex Numbers A complex number is an expression of the form a + ib, where a and b are real numbers. a is called the real part of a + ib and b the imaginary
SOME PROPERTIES OF CONJUGATE HARMONIC FUNCTIONS IN A HALF-SPACE
 SOME PROPERTIES OF CONJUGATE HARMONIC FUNCTIONS IN A HALF-SPACE ANATOLY RYABOGIN AND DMITRY RYABOGIN Abstract. We prove a multi-dimensional analog of the Theorem of Hard and Littlewood about the logarithmic
SOME PROPERTIES OF CONJUGATE HARMONIC FUNCTIONS IN A HALF-SPACE ANATOLY RYABOGIN AND DMITRY RYABOGIN Abstract. We prove a multi-dimensional analog of the Theorem of Hard and Littlewood about the logarithmic
Flows and Connectivity
 Chapter 4 Flows and Connectivit 4. Network Flows Capacit Networks A network N is a connected weighted loopless graph (G,w) with two specified vertices and, called the source and the sink, respectivel,
Chapter 4 Flows and Connectivit 4. Network Flows Capacit Networks A network N is a connected weighted loopless graph (G,w) with two specified vertices and, called the source and the sink, respectivel,
Green s Theorem Jeremy Orloff
 Green s Theorem Jerem Orloff Line integrals and Green s theorem. Vector Fields Vector notation. In 8.4 we will mostl use the notation (v) = (a, b) for vectors. The other common notation (v) = ai + bj runs
Green s Theorem Jerem Orloff Line integrals and Green s theorem. Vector Fields Vector notation. In 8.4 we will mostl use the notation (v) = (a, b) for vectors. The other common notation (v) = ai + bj runs
Review of Multi-Calculus (Study Guide for Spivak s CHAPTER ONE TO THREE)
 Review of Multi-Calculus (Study Guide for Spivak s CHPTER ONE TO THREE) This material is for June 9 to 16 (Monday to Monday) Chapter I: Functions on R n Dot product and norm for vectors in R n : Let X
Review of Multi-Calculus (Study Guide for Spivak s CHPTER ONE TO THREE) This material is for June 9 to 16 (Monday to Monday) Chapter I: Functions on R n Dot product and norm for vectors in R n : Let X
SEPARABLE EQUATIONS 2.2
 46 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 4. Chemical Reactions When certain kinds of chemicals are combined, the rate at which the new compound is formed is modeled b the autonomous differential equation
46 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 4. Chemical Reactions When certain kinds of chemicals are combined, the rate at which the new compound is formed is modeled b the autonomous differential equation
Two Dimensional Linear Systems of ODEs
 34 CHAPTER 3 Two Dimensional Linear Sstems of ODEs A first-der, autonomous, homogeneous linear sstem of two ODEs has the fm x t ax + b, t cx + d where a, b, c, d are real constants The matrix fm is 31
34 CHAPTER 3 Two Dimensional Linear Sstems of ODEs A first-der, autonomous, homogeneous linear sstem of two ODEs has the fm x t ax + b, t cx + d where a, b, c, d are real constants The matrix fm is 31
Chapter 8 Notes SN AA U2C8
 Chapter 8 Notes SN AA U2C8 Name Period Section 8-: Eploring Eponential Models Section 8-2: Properties of Eponential Functions In Chapter 7, we used properties of eponents to determine roots and some of
Chapter 8 Notes SN AA U2C8 Name Period Section 8-: Eploring Eponential Models Section 8-2: Properties of Eponential Functions In Chapter 7, we used properties of eponents to determine roots and some of
We saw in Section 5.1 that a limit of the form. arises when we compute an area.
 INTEGRALS 5 INTEGRALS Equation 1 We saw in Section 5.1 that a limit of the form n lim f ( x *) x n i 1 i lim[ f ( x *) x f ( x *) x... f ( x *) x] n 1 2 arises when we compute an area. n We also saw that
INTEGRALS 5 INTEGRALS Equation 1 We saw in Section 5.1 that a limit of the form n lim f ( x *) x n i 1 i lim[ f ( x *) x f ( x *) x... f ( x *) x] n 1 2 arises when we compute an area. n We also saw that
Definition: div Let n, d 0. We define ndiv d as the least integer quotient obtained when n is divided by d. That is if
 Section 5. Congruence Arithmetic A number of computer languages have built-in functions that compute the quotient and remainder of division. Definition: div Let n, d 0. We define ndiv d as the least integer
Section 5. Congruence Arithmetic A number of computer languages have built-in functions that compute the quotient and remainder of division. Definition: div Let n, d 0. We define ndiv d as the least integer
Part IB Complex Methods
 Part IB Complex Methods Based on lectures by R. E. Hunt Notes taken by Dexter Chua Lent 26 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Part IB Complex Methods Based on lectures by R. E. Hunt Notes taken by Dexter Chua Lent 26 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Algebra II Practice Semester Exam Specification Sheet
 Algebra II Practice Semester Exam Specification Sheet 1. Properties of real numbers. Procedure (write procedure or process) 3. Concept development/linkage. Theorem/factual knowledge (of theorems and rules)
Algebra II Practice Semester Exam Specification Sheet 1. Properties of real numbers. Procedure (write procedure or process) 3. Concept development/linkage. Theorem/factual knowledge (of theorems and rules)
Complex Functions (1A) Young Won Lim 2/22/14
 Complex Functions (1A) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Complex Functions (1A) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
5.6 RATIOnAl FUnCTIOnS. Using Arrow notation. learning ObjeCTIveS
 CHAPTER PolNomiAl ANd rational functions learning ObjeCTIveS In this section, ou will: Use arrow notation. Solve applied problems involving rational functions. Find the domains of rational functions. Identif
CHAPTER PolNomiAl ANd rational functions learning ObjeCTIveS In this section, ou will: Use arrow notation. Solve applied problems involving rational functions. Find the domains of rational functions. Identif
2.5 CONTINUITY. a x. Notice that Definition l implicitly requires three things if f is continuous at a:
 SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
(z + n) 2. n=0. 2 (z + 2) (z + n). 2 We d like to compute this as an integral. To this end, we d like a function with residues
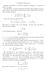 8. Stirling Formula Stirling s Formula is a classical formula to compute n! accurately when n is large. We will derive a version of Stirling s formula using complex analysis and residues. Recall the formula
8. Stirling Formula Stirling s Formula is a classical formula to compute n! accurately when n is large. We will derive a version of Stirling s formula using complex analysis and residues. Recall the formula
BACKWARD FOKKER-PLANCK EQUATION FOR DETERMINATION OF MODEL PREDICTABILITY WITH UNCERTAIN INITIAL ERRORS
 BACKWARD FOKKER-PLANCK EQUATION FOR DETERMINATION OF MODEL PREDICTABILITY WITH UNCERTAIN INITIAL ERRORS. INTRODUCTION It is widel recognized that uncertaint in atmospheric and oceanic models can be traced
BACKWARD FOKKER-PLANCK EQUATION FOR DETERMINATION OF MODEL PREDICTABILITY WITH UNCERTAIN INITIAL ERRORS. INTRODUCTION It is widel recognized that uncertaint in atmospheric and oceanic models can be traced
AB.Q103.NOTES: Chapter 2.4, 3.1, 3.2 LESSON 1. Discovering the derivative at x = a: Slopes of secants and tangents to a curve
 AB.Q103.NOTES: Chapter 2.4, 3.1, 3.2 LESSON 1 Discovering the derivative at x = a: Slopes of secants and tangents to a curve 1 1. Instantaneous rate of change versus average rate of change Equation of
AB.Q103.NOTES: Chapter 2.4, 3.1, 3.2 LESSON 1 Discovering the derivative at x = a: Slopes of secants and tangents to a curve 1 1. Instantaneous rate of change versus average rate of change Equation of
Local Maximums and Local Minimums of Functions. f(x, y) has a local minimum at the point (x 0, y 0 ) if f(x 0, y 0 ) f(x, y) for
 Local Extrema Previousl we have taken the partial derivative of a function f(x, ). But those partial derivatives were themselves functions and so we can take their partial derivatives. Local Maximums and
Local Extrema Previousl we have taken the partial derivative of a function f(x, ). But those partial derivatives were themselves functions and so we can take their partial derivatives. Local Maximums and
