Automated Selection of Optimal Gaussian Fits to Arbitrary Functions in Electronic Structure Theory

Transcription

1 Autoted Seleton of Optl Gussn Fts to Artrry Funtons n Eletron Struture Theory CLAUDINE C. TAZARTES, 1 CHRISTOPHER R. ANDERSON, 1 EMILY A. CARTER 2 1 Deprtent of Mthets, Unversty of Clforn, Los Angeles, Clforn Deprtent of Chestry nd Bohestry, Unversty of Clforn, Los Angeles, Clforn, Reeved 13 Noveer 1997; epted 26 Mrh 1998 ABSTRACT: We present ethod of fttng rtrry funtons to lner ontons of Gussns. In prtulr, we dsuss n dptton of Prony s ethod, or seprton of exponentls, whh llows us to utotlly selet pproprte exponents for these Gussns. We then pply ths tehnque to the seleton of delsng sets for pseudospetrl eletron orrelton ethods. We show tht t n suessfully hoose funtons tht generlly prove the ury of pseudospetrl orrelton energes whle redung the sze of the delsng set hosen John Wley & Sons, In. J Coput Che 19: , 1998 Keywords: Gussn fts; Prony s ethod; pseudospetrl ethods; eletron orrelton; lsng error Introduton I n theoretrl hestry nd physs, one frequently enounters proles n whh one wshes to ft funtons to lner ontons of Gussns Že.g., delsng funtons n pseudospetrl ethods, 1 fttng of the densty n den- 2, 3 sty funtonl theory DFT ethods, fttng Correspondene to: E. A. Crter; e-l: e@he.ul.edu Contrt grnt sponsor: Offe of Nvl Reserh produts of ss funtons to uxlry ss sets, 4 5 fttng of pseudopotentls 7.. However, deternng pproprte exponents for these Gussns n e dffult. The de pursued n ths rtle onssts of desgnng utot proedures to selet suh exponents. Our tehnque s sed on Prony s ethod, or the seprton of exponentls; lthough ths ethod s desgned to ft funtons to deyng exponentls, hnge of vrles llows us to nsted do the fttng to Gussns. We frst desre ths ethod n generl ters nd then show ( ) Journl of Coputtonl Chestry, Vol. 19, No. 11, John Wley & Sons, In. CCC / 98 /

2 GAUSSIAN FITS TO ARBITRARY FUNCTIONS how t n e used n spef pplton: fndng delsng funtons n pseudospetrl eletron orrelton ethods. Work y Fresner 8 suggested tht ss funton representtons of the one-eletron wve funtons y e oned wth grd-sed representtons Ž the pseudospetrl ethod.. On grd, the Coulo opertor n e represented s sprse trx; to pply the Coulo opertor, we trnsfor the wve funton to grd Ž physl. spe representton, pply the opertor on the grd, nd then trnsfor k to spetrl Žoeff- ent. spe. Ths pproh redues the slng of the two-eletron ntegrl lultons fro K 4 to roughly K 3, where K s the nuer of ss funtons. The trnsforton fro physl nto spetrl spe produes oponents outsde the orgnl ss set, the so-lled lsng ters The strtegy proposed y Fresner to redue lsng effets s to dd nuer of delsng funtons to the orgnl ss set; the role of these delsng funtons s to opleent the ss set n urtely pturng the ehvor of the funtons ourrng n the lulton to ke ther trnsfortons ore urte. However, t s not ler how est to hoose these delsng funtons. In ths work, we dsuss the developent of systet ens of hoosng pproprte delsng sets nd nuerl pproxtons to the relevnt ntegrls; the de s tht n dequte representton of the oponents outsde the spn of the orgnl ss set wll nze the error nurred n the trnsforton etween grd nd ss funton representtons. We hoose sutle delsng sets y studyng the grd-sed qunttes tht re to e trnsfored k nto spetrl spe nd y fttng the to to-entered, Crtesn Gussns v ethod lled seprton of exponentls. The Gussns resultng fro the ft Ž or, rther, soe verge or suset of the. re used s our delsng sets. In ddton to the developent of the ehns for pkng delsng funtons, we explore the pplton of ths tehnque to eletron orrelton lultons for severl oleules. These oputtons not only llustrte the usefulness of our ethod y ther fvorle oprson to prevously pulshed results, ut lso re rul n gudng the developent of generl thetl proedure tht n e used for other ppltons. Fttng Funton to Gussns The generl nture of the pproxton prole s s follows: Suppose tht we hve rel-vlued funton yž,,.. We would lke to ft y to lner onton of Gussns. If yž,,. hs strong rdl dependene nd wek Ž,. dependene, then t s resonle to onsder fttng y to funtons of the for y Ae. 1 2 Of ourse, ths, dependene y not e known pror, ut t y e sertned through oputtonl tests, s ws done n ref. 11. SEPARATION OF EXPONENTIALS The hllenge s to selet pproprte oeffents A nd exponents. Ths s prole of spetrl estton, nd vrety of ethods exst 12 for fttng dsrete dt to lner ontons x of exponentls e. ŽWe wll dsuss the djustent needed to ft to Gussns e x 2 n lter seton.. One prtulrly sutle tehnque for fttng eqully sped dt ponts to dped exponentls s Prony s ethod. 12 Prony s ethod s known to e senstve to nose, ut euse our dsrete dt re deterned y nuerl evlutons of funtons, the nose level s neglgle, nd Prony s ethod works stsftorly. The de ehnd Prony s ethod s s follows: f Ž dsretzed. funton yž x. looks lke 1 x 2 x x y x Ae A e A e, then, just s lner sus of exponentls stsfy onstnt-oeffent lner dfferentl equtons, y stsfes lner, onstnt-oeffent dfferene equton, nd the re dentfed fro solutons of the dfferene equton yž x. yž x h. yž x h Ž 2. Speflly, suppose tht we re gven set of 2 dt ponts Ž x, y., y yž x., where the x JOURNAL OF COMPUTATIONAL CHEMISTRY 1301

3 TAZARTES, ANDERSON, AND CARTER re equsped y h: x x h 1. 1 We wnt our y vlues to stsfy eq. Ž. 2, nd tkng 1, we n generte syste of lner equtons for the renng : 0y1 1y2 1y y 1, 0y2 1y3 1y 1 y 2,... 0y 1y 1 1y2 1 y 2. We now hve n trx equton for the oeffents, Y y, Ž 3. where Y s the trx of y vlues suh tht YŽ, j. y j 1; nd y re vetors of length, where Ž. nd yž. y. Thus, we o- tn y solvng the trx equton gven n eq. Ž. 3. One we hve the, we n onstrut solutons to the dfferene equton, eq. Ž. 2, y ssung solutons of the for of eq. Ž. 1, tht s, jx jžx h. 0 j 1 j ž / ž / j 1 j 1 jžx h. Aje 0, ž / j 1 1x 1kh Ae 1 e ž k / k 0 A e A e ž / ž k / 2 x 2kh 2 k k 0 A e e x kh Ae e 0. k 0 Ths yelds n th degree polynol equton, where 2 0, e j h j nd,,..., re the roots of eq. Ž These roots n e found usng stndrd egenvlue ethods. 13 These ethods ke use of the ft tht the egenvlues of n trx A re the roots of the hrterst polynol P x det A I, where I s the dentty trx nd det denotes deternnt. Thus, to fnd the roots of the polynol gven n eq. Ž. 4, we use the ft tht the hrterst polynol of the opnon trx, A , s equvlent to eq. Ž. 4. Thus, y fndng the egenvlues of A, we re fndng the roots of eq. Ž. 4. One we hve the j, we n fnd the exponents j trvlly fro 1 lnž. j j. h If we lso wnt to deterne the oeffents A, we n generte lner syste of equtons for the y requrng tht the y e of the for of eq. Ž. 1: Ae 1x 1 A e 2 x 1 A e x 1 y, Ae 1x 2 A e 2 x 2 A e x 2 y, Ae 1x 2 A e 2 x 2 A e x 2 y Note tht ths s n overdeterned syste, EA y, 5 where E s the 2 trx desred y EŽ, j. e x j, A s the vetor of length suh tht A Ž. A, nd y s the vetor of length 2 suh tht y Ž. y.we n solve ths syste n the lest squres sense ether y dretly usng sngulr vlue deoposton on the overdeterned syste or y solvng the norl equtons usng, e.g., Gussn elnton wth pvotng : E T EA E T y. REDUCING SYSTEM SIZE In order to redue the syste sze Žnd hene redue the order of the polynol whose roots we ust fnd., we use the tehnque proposed y Lnzos. 14 We do not use onseutve vlues of y 1302 VOL. 19, NO. 11

4 GAUSSIAN FITS TO ARBITRARY FUNCTIONS n eq. Ž. 3. Insted, we dvde the dt nto groups nd use the su of the ordntes n eh group s our y. For exple, suppose tht we hve 60 dt ponts nd we wnt to use 5 exponentls n our fttng proedure. We n seprte these nto 2 10 groups of 6 vlues eh. The su of the 6 vlues n eh of these 10 groups gves us 10 new vlues, y, whh we n use n eq. Ž. 3. For our dt sets, the lner syste Ž. 3 s not very lrge nd we solve the syste usng Gussn elnton Ž wth pvotng.. For lrger systes, the spel struture of Y Žwth rerrngeent of 15 the rows, t s Toepltz trx. n e exploted nd ore effent solvers re vlle. 13,15 FITTING TO GAUSSIANS Our tsk s to fnd funtons of the for y Ae, j 1 x 2 j j whh re Gussns nsted of dped exponentls. To pply the tehnque desred ove, we sply ft exponentls to the dt Ž t, y., where the t re equsped nd Thus, s requred. y yž x., t x 2. jt jx 2 j j j 1 j 1 y Ae Ae, Applton: Delsng n Pseudospetrl Eletron Correlton Methods We used the fttng proedure desred ove to systetlly selet delsng funtons 9 n pseudospetrl eletron orrelton ethods. A oputtonl oponent of these ethods s to nuerlly evlute the two-eletron ntegrls: Ž. ² j J : j Ž. r Ž. r Ž r. Ž r. j k l HH drdr, 3 3 r r Ž r. Ž r. k l J Ž. r H dr. 3 r r 6 We wll frst desre the pseudospetrl pproxton to two-eletron ntegrls nd how ths pproxton leds to lsng errors. We wll then dsuss how to selet delsng funtons, the purpose of whh s to redue lsng effets. We wll lt our dsusson to tretent of the Coulo opertor J ; the exhnge opertor n e treted slrly. TWO REPRESENTATIONS OF In pseudospetrl ethods, we ke use of two dfferent representtons of the one-eletron ortl. One of the s ss funton representton, K n n 1, Ž 7. where the n re set of known ss funtons. We tke the to e norlzed, to-entered Crtesn Gussns. The other representton we use s physl, or grd-sed representton, frst proposed y Fresner; 8 thus, we ntrodue set of G grd ponts, r, r,...,r 3, 1 2 G nd G K olloton trx R of ss funtons evluted t these grd ponts; tht s, n n RŽ g, n. Ž r.. Ž 8. Then the grd-sed verson of n e wrtten s or n Ž r 1. Ž r 2. Ž r G. g R, 9 where s vetor of oeffents,...,. 1 K PSEUDOSPECTRAL TWO-ELECTRON INTEGRALS AND NEED FOR DEALIASING Ž. ² The two-eletron ntegrl j J : j y e thought of s projeton of the funton J onto the ss set 4 K. Ths ens tht j n n 1 JOURNAL OF COMPUTATIONAL CHEMISTRY 1303

5 TAZARTES, ANDERSON, AND CARTER Ž. the funton r J Ž. j r n e expressed s lner onton of the n, wth soe oeff- ents P, so tht the Žj. nj y e wrtten s follows: K Ž. Ž. Ž. j nj n n 1 r J r P r, K Ž. ² : ² : j nj n n 1 j J P. 10 We would lke to use pseudospetrl pproxtons to the two-eletron ntegrls Ž j.. Thus, we defne n nner produt, ² : w, wth sso- ted weghts w g, g 1,...,G: G ² f y: fž r. yž r. w. w g g g g 1 Pseudospetrl pproxtons to the Ž j. re otned y replng one of the nlytl ntegr- 3 tons over n Ž j. see eq. Ž. 7 wth nuerl pproxton: Ž. ² j J : w j G Ž. r Ž. k l r Ž r. Ž r. g j g wgh dr. 3 r r g 1 We ntrodue the followng notton, Thus, we n wrte f J. j, k, l j Ž j. ² f : ² f :. j, k, l j, k, l g w 11 The suess of the pseudospetrl ethod depends on our lty to opute nuerl nner produts urtely. The fj, k, l re projeted onto the spe spnned y the n, ut they y ontn oponents not n ths spe tht n ontnte the ² f : j, k, l w. These re lled lsng ters. To llustrte tht there s ndeed n ury prole, we show pseudospetrl seond-order Møller Plesset perturton theory Ž MP2. lultons 16 n Tle I for etylene on three dfferent grd szes Žorse, edu, nd fne PSGVB v grds.. Es s the spetrl MP2 orrelton energy e., ll ntegrls re lulted nlytlly., nd Eps s the MP2 orrelton energy lulted usng nuerl pproxtons. We pont out here tht these results were otned usng strght nuerl qudrture s seen TABLE I. Sple Nuerl Qudrture MP2 Clultons on Dfferent Grd Szes for C H G** Bss Sets for C H ( K =40 ) 2 2 ; E = hrtrees s No. Grd E E s Grd Ponts E ( hrtrees) ( hrtrees) ps d ps Corse e-03 Medu e-03 Fne e-04 ( ) See eq. 11 nd Appendx A. Spetrl MP2 orrelton energy. Pseudospetrl MP2 orrelton energy. d ( ) Dfferene n solute vlue etween spetrl nd pseudospetrl MP2 orrelton energes. n eq. Ž 11., s opposed to the ore urte pproh used y Mrtnez nd Crter. 16 See Appendx A for ore detls. We see tht s we refne the grd, the pseudospetrl orrelton energes eoe ore urte; to get to wthn 1 hrtree of the spetrl results, we need to use fne grds where G K 2. However, the pseudospetrl pproxton s dvntgeous only f G K 2. 8 Thus, we ust ke djustents to our nuerl pproxtons so tht we otn suffent ury n the nner produts wthout usng suh fne grds. DEALIASING FUNCTIONS To ddress the proles wth our nner produt rule, let us onsder the physl spe projeton of f J onto 4 K : j, k, l j n n 1 K j, k, l g nj n g n 1 f r P r, K ² : w ² : j, k, l nj n w n 1 f P. To otn ury n the ² f : j, k, l we need to ensure the ury of the ² : n w, ut we lso need to ensure tht ² : w s urte for opo- nents of f 4 j, k, l outsde the spn of n n 1 K. Suppose, then, tht we hve funtons suh tht 4 K 4 L j, k, l Ž n n 1 1. f spn, VOL. 19, NO. 11

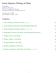
6 GAUSSIAN FITS TO ARBITRARY FUNCTIONS Then 18 K ² : f w P ² : j, k, l nj n w n 1 L D ² :. 1 j If ² : nd ² : n w w re urte to wthn soe eptle tolerne, then ² f : j, k, l w wll lso e suffently urte. Thus, our tsk s twofold: we need to fnd funtons Ž lled delsng funtons. tht wll opleent our orgnl ss funtons n y properly pturng the ehvor of the f j, k, l. Then, one we hve the, we ust nze the errors de n oputng ² n : w nd ² : w; to do so, we ust defne nd pose soe onstrnts on ² : w. In the se wy tht spe- lzed qudrture rules re desgned to work for ertn lsses of funtons, we wll redefne our qudrture rule so tht t s urte speflly for the types of nner produts we wnt to opute. In ths rtle we re onerned nly wth the seleton of delsng funtons, nd we turn our ttenton to ths prole n the next seton. A desrpton of the qudrture rule tht we used for ll results presented elow s gven n Appendx A. Choosng Delsng Funtons We now dsuss the tehnque we use to hoose our delsng funtons. As dsussed n the prevous seton, we need to pk delsng funtons tht wll suppleent our orgnl ss funtons n properly pturng the ehvor of the f j, k, l. Thus, we need to pk our so tht the fj, k, l n e well represented y the set of funtons 4 K, 4 L It therefore sees resonle to ft the fj, k, l to set of funtons nd use these s our delsng funtons. Rngnld et l. 1 nd Fresner 9 propose tht the delsng funtons e of the se for s the to ortls Ž.e., to-entered norlzed Crtesn Gussns.. Ths flttes the oputton of ertn neessry nner produts Ž² : n, ² :; see Appendx A. ; lso, s we shll see shortly, n ost ses the fj, k, l funtons tht we re tryng to pture roughly the ehvor of j n the rdl dreton. Thus, to-entered norlzed Crtesn Gussns see lke re- w sonle hoe for the. However, we ust pk exponents for these Gussns. To ths end, we ft the fj, k, l to lner on- tons of Gussns usng the proedure outlned n n erler seton. In ths wy, we n dentfy funtons tht dequtely represent the fj, k, l nd use these funtons Ž or soe suset of the. s our. Theoretlly, we ft only the rdl oponent of the f. Ž j, k, l In tulty, the fj, k, l re not relly seprle, ut we found tht the ngulr oponents hve lttle effet on the overll fttng proedure. 11 In prtulr, n lultons on C 2H 2 nd C 2H 4 tht tested how the ngulr oponents ffeted the MP2 energy, we found vrtons n the optl delsng exponents of up to 11%; ut these resulted n vrtons n the MP2 energy of, n the worst se, 76 hrtree.. Also, for splty, we only ft the f j, k, k, whh seeed to well represent the entre set of f j, k, l. MODEL PROBLEM: HYDROGEN ATOM We enter our hydrogen to nd ts ss funtons Ž we use the 6 31G** sets. t the orgn nd hoose our grd ponts to e of the for r Ž 0, 0, z. g g, where the z g re postve nd ther squres, t g, re evenly sped: t z 2, g g g 0.08 z 4 ohr, h t t 0.27 Ž G 60.. g 1 g We then do the fttng of the f j, k, k. There re fve funtons n the ss set Žtwo s funtons, nd one eh of p, p, p. x y z, ut px py 0 every- where on our grd; thus, there re only three possle hoes for j. There re four possle hoes for Ž kk k euse J s the se for p nd p. x y,sowe re fttng 12 fj, k, k funtons. We found tht fve Gussns usully provdes us wth good ft; n ost ses, usng fewer thn fve Gussns does not gve us n urte enough ft to the f j, k, k, nd usng ore thn fve does not pprely nrese the ury of the ft. Moreover, usng lrge nuers of funtons nreses the syste sze n eqs. Ž. 3 nd Ž. 5 nd nreses the hnes of genertng ll-ondtoned systes. However, n soe nstnes ore thn fve Gussns y e needed to otn resonle fts to the f j, k, k. 11 We lso pont out tht, for gven f j, k, k, usng dfferent nuers of Gussns wll yeld dfferent exponents. JOURNAL OF COMPUTATIONAL CHEMISTRY 1305

7 TAZARTES, ANDERSON, AND CARTER funton, hs exponent 1.1. Thus, when hoosng exponents for s-type funtons, we wll gnore the ns n the rnge; when hoosng exponents for p-type funtons, we wll gnore the ns n the rnge. Ottng those exponents tht re n the se n s ss funtons, we use s our s funtons wth exponents 1.33 nd 2.93 Žwe onsder 4.12 n outler; nludng t or not n our vergng de no dfferene. nd p funtons wth exponents 0.56 nd Note tht for lrger exponents we hoose lrger n wdths Žs the exponents get lrger, the orrespondng Gussns look ore nd ore lke; see Tle II.. FIGURE 1. Exponents for hydrogen to fttng. In the se tht we re urrently dsussng, the hydrogen to, we ft eh fj, k, k to fve Guss- ns, gvng us totl of 60 exponents fro whh to hoose Ž see Fg. 1.. We do not wnt to use ll of these exponents, euse there re ny of the nd ny of the re slr. Thus, we group our exponents nto ns of vryng wdths nd tke verges over eh of these ns to otn exponents for our. Note tht we re relly only fttng to s funtons Ž.e., funtons of the for r e 2.; however, we found t useful to lso nlude Ž r 2 r 2 r p funtons.e., xe, ye, ze 2.. We found tht nludng d-type funtons does not prove our results for orrelton energes of n group oleules. It s lkely tht suh funtons wll e needed for trnston etl ontnng oleules, ut ths s eyond the sope of the present work. We ot fro the seleton proess those exponents tht re lose to exponents lredy n the ss set. For exple, we note 24 vlues n the rnge nd 2 s n s-type funton wth exponent Slrly, there re 22 funtons n the rnge nd 5, p-type ss DEALIASING SETS FOR LARGER SYSTEMS Now suppose tht we wnt to fnd delsng sets for use n oleules ontnng ore thn one type of to. Then we need to ft fj, k, k funtons where the j funton s entered t one nuleus nd the k funton s entered t nother. In Fgures 2 nd 3 we show soe plots of f j, k, k funtons: typl se nd se n whh the shpe of fj, k, k devtes notely fro tht of j, respetvely. In oth ses, j s tght on- trted s-type funton Ž sx ontrted Gussns. fro the 6 31G** hydrogen set. In Fgure 2 the k funtons elong to the 6 31G** hydrogen set, nd n Fgure 3 the k funtons elong to the 6 31G** ron set. Fgure 4 shows j y tself. We n see tht, n ost ses, the fj, k, k roughly follows the ehvor of j, exept n Fgure 3; for k 1 fro the ron ss set Ž ontrted, tght s funton., J kk s lrge nd hs pronouned pek ner the ron enter; t would pper fro these fgures tht ths pek s not opletely elnted y the hydrogen j funton. Thus, euse the fj, k, k usully look roughly lke Crtesn Gussns entered t the j funton s nuleus, we ft the fj, k, k to get orre- spondng to the j ss funtons. For exple, f we wnt for hydrogen n oleule tht lso ontns ron, we use the hydrogen ss funtons s our j funtons nd TABLE II. Sus of Exponents for Hydrogen Ato Fttng No. Exponents Su Averge VOL. 19, NO. 11

8 GAUSSIAN FITS TO ARBITRARY FUNCTIONS FIGURE 2. f : j = 1 on H ( ontrted s funton ) 1, k, k ; k = 1, 2, 3, nd 5 on H. FIGURE 4. 1 s funton ). for hydrogen 6 31G** set ( ontrted the ron funtons s our k funtons. We enter the hydrogen to t Ž 0, 0, 0. nd the ron to on the postve z xs t the desred dstne fro Ž 0, 0, 0.. We then ft the fj, k, k nd pool the result- ng exponents together wth those fro the sngle hydrogen to fttng. We n now verge over the pproprte ns to otn delsng funtons for hydrogen. To get delsng funtons for r- FIGURE 3. f : j = 1 on H ( ontrted s funton ) 1, k, k ; k =1 3, 5 7, 9, 10, nd on C. on, we sply reverse the roles nd postons of the ron nd hydrogen tos n the proedure ove. Soe delsng sets for dfferent ontons of tos re gven n Appendx B. Note tht our delsng sets re opletely deterned y the orgnl ss sets nd re not grd dependent Ž.e., we do not use ny nforton out the grds tht wll eventully e used n the pseudospetrl lultons.. We re urrently nvestgtng how dependent the fttng proess s on our hoe of nterto dstnes. For exple, we would lke to know f the fttng proedure yelds the se exponents for tos X nd Y whether these tos re, sy, 1 or 2 A prt. If the fttng proedure s not ffeted y dstnes etween tos, then we n use the proedure to opute exponents for whhever ontons of tos we lke, therey retng lrry of exponents tht re vlle for use wth ny syste. So, for spef oleule, we sply extrt fro the lrry those exponents tht we need, pool the together s desred n the exple ove, nd run the vergng ode to otn delsng funtons pproprte for tht oleule. If the fttng proedure s ffeted y dstnes etween tos, then we n stll rete the exponent lrry desred ove; however, t wll e ore oplex, euse we wll hve exponents not only for dfferent ontons of tos, ut lso for dfferent dstnes etween tos. Thus, JOURNAL OF COMPUTATIONAL CHEMISTRY 1307

9 TAZARTES, ANDERSON, AND CARTER when we re extrtng exponents fro the lrry nd poolng the together for vergng, we ust ke sure tht we re seletng those exponents ost pproprte to the dstnes wthn our oleule. For ovous resons, ths s less thn desrle. Prelnry tests ndte tht nterto dstnes see to hve lttle pt on the exponents otned, ut ore tests re needed to see f ths s generlly true. In the frst row of Tle III our j funtons re ll hydrogen 6 31G** ss funtons nd our k funtons re ron nd hydrogen 6 31G** ss funtons; we show the verge exponents when the hydrogen nd ron tos re A prt nd when they re A Ž pproxtely twe the prevous dstne. prt. 19 The seond row s slr, wth the j funtons re now on ron nd the k funtons on oth hydrogen nd ron. ŽSee Tle B.II n Appendx B for few pseudospetrl orrelton energes oprng the funtons fro Tle III.. We see tht the results fro the two sets re nerly dentl. Ths ponts to our sets eng trnsferle Ž.e., t does not pper tht we need to run the fttng proedure for ny dfferent nterto dstnes.. TABLE III. Averge Exponents for Hydrogen nd Cron for Dfferent Interto Dstnes. Dstne 1: A Dstne 2: A Hydrogen 0.58, 1.35, 2.77, , 1.27, 2.92, 4.12 Cron 0.56, 1.41, 3.23, , 1.45, 3.11, 8.47 We lso pont out here tht the fnl hoe of exponents n e senstve to our hoe of n szes. We experented wth vrous shees Že.g., ottng ny exponents wthn set tolerne fro ss funton exponent., ut the proedure outlned ove worked est for our purposes. Results We now present pseudospetrl orrelton energes for two dfferent types of lultons, MP2 nd sngle nd doule extton onfgurton nterton Ž SDCI., n Tles IV VI usng the new delsng funton sets gven n Tle B.InAp- pendx B. We opre our pseudospetrl results to orrespondng spetrl lultons, s well s to prevously pulshed pseudospetrl results 16 n whh PSGVB v1.00 delsng sets were used. In ll ses, we use the PSGVB v1.00 grds. The pseudospetrl qunttes were lulted usng odes desred n refs. 10 nd 11. The sets fro Tle B.I used n eh oleule re those tht est orrespond to the onton of tos n tht oleule; for exple, n HCN we used the hydrogen-ron-ntrogen delsng set for hydrogen, the ron-hydrogen-ntrogen delsng set for ron, nd the ntrogen-ronhydrogen set for ntrogen Žsee Appendx B for noenlture explnton.. The sets soetes look very slr Že.g., the ron-hydrogen set does not look pprely dfferent fro the ron-hydrogen-ntrogen set.; susttuton of one set for nother y led to only slghtly less urte pseudospetrl results Žsee Tle B.III n Appendx B., ut ths lso needs to e studed ore refully TABLE IV. Errors n Pseudospetrl MP2 Correlton Energes ( Medu Grds ). Moleule E E E E Prevous Error d,16 s ps s ps HF e e-04 H2O e e-04 HCN e e-04 CH e e CH e e-04 Ethylene oxde e e-03 CH e e-03 Glyne e e-03 Spetrl MP2 orrelton energy ( hrtrees ). Pseudospetrl MP2 orrelton energy ( hrtrees) usng new sets. Dfferene ( n solute vlue) etween spetrl nd pseudospetrl MP2 orrelton energes ( hrtrees ). d ( ) 17 Pseudospetrl MP2 orrelton energy error hrtrees usng delsng funton sets due to Rngnld et l VOL. 19, NO. 11

10 GAUSSIAN FITS TO ARBITRARY FUNCTIONS TABLE V. Errors n Pseudospetrl SDCI Totl Energes ( Corse Grds ). Moleule E E E E Prevous Error d,10,11 s ps s ps H2O e e-04 HCN e e-04 CH e e CH e e CH e e-04 Ethylene oxde e e-04 CH e e-04 Glyne e e-05 Spetrl SDCI totl energy ( hrtrees ). Pseudospetrl SDCI totl energy ( hrtrees) usng new sets. Dfferene ( n solute vlue) etween spetrl nd pseudospetrl SDCI totl energes ( hrtrees ). d ( ) 17 Pseudospetrl SDCI totl energy error hrtrees usng delsng funton sets due to Rngnld et l. efore we n sy nythng onlusve out the pt of n to s envronent on our hoe of. These prelnry results, lke those we o tned n studyng the effet of nterto dstnes on the fttng proedure, see to pont to trnsferlty of the. The ode used to do the fttng nd vergng ws orgnlly wrtten n MATLAB, 11 lthough we now lso hve C verson of ths ode. 11 For ore nforton on PSGVB, see ref. 17. The pseudospetrl MP2 lultons n Tle IV were done usng 6 31G** ss sets on the edu grds. It s evdent tht, n ost ses, our results re s urte, or ore urte, thn those prevously otned. Thus, ths new ens of hoosng the does eet ury requreents. Tles V nd VI present pseudospetrl SDCI lultons on orse nd edu grds, respetvely. On orse grds, our results re roughly the se s those prevously pulshed. 10 On edu grds, our SDCI results show etter ury thn those usng the PSGVB Q trx Ždefned n Appendx A. wth delsng sets developed y Rng- 17 nld et l. for self-onsstent feld Ž SCF. lultons. We lso note rked proveent over our own SDCI orse grd results. Our sets were desgned speflly for use wth the 6 31G** ss sets, though the fttng proedure n e used for ny other type of Gussn ss set. In ft, we lso ft the Dunnng Huzng 19, 20 9s5p 3s2 p sets. However, they were not desgned wth ny prtulr grd n nd. We would then hope tht s grd hoes prove, so should the perforne of our Ž s exhted n the oprson of the two sets of SDCI results.. Soe dvntges of usng these new sets re s follows. Frst, n our seleton ethod we tret the TABLE VI. Errors n Pseudospetrl SDCI Totl Energes ( Medu Grds ). Moleule E E E E Prevous Error d s ps s ps H2O e e-04 HCN e e-05 CH e e CH e e CH e e-04 Ethylene oxde e e-05 CH e e-04 Glyne e e-04 Spetrl SDCI totl energy ( hrtrees ). Pseudospetrl SDCI totl energy ( hrtrees) usng new sets. Dfferene ( n solute vlue) etween spetrl nd pseudospetrl SDCI totl energes ( hrtrees ). d ( ) 17 Pseudospetrl SDCI totl energy error hrtrees usng delsng funton sets due to Rngnld et l. JOURNAL OF COMPUTATIONAL CHEMISTRY 1309

11 TAZARTES, ANDERSON, AND CARTER lsng prole expltly: lsng ters pper when we projet the f 4 j, k, l onto the 1 K, nd we ddress ths prole dretly y usng systet proess to deterne pproprte delsng funtons. Seond, our sets re ore opt Ž8 12 delsng funtons per to s opposed to roughly 30 delsng funtons per to n the PSGVB v1.00 sets. nd ontn only s nd p funtons. However, ths y e due to the ft tht t s uh eser to nuerlly estte the uh sller orrelton energes thn the lrge SCF energes tht Fresner s sets were desgned to reprodue. Indeed, whle our sets perfor well for oputng orrelton energes, we fnd tht they do not lwys provde us wth urte SCF energes or wth urte Fok tres for ensung orrelton energy lultons. Even when the SCF energes re eptle Žerrors on the order of 1 hrtree., the resultng pseudospetrl Fok tres do not perfor well n orrelton energy lultons. ŽMP2 lultons, for nstne, frequently do not onverge when these Fok tres re used.. Ths s kn to the oservton y Mrtnez nd Crter 10, 21 tht sller grds n e used n orrelton energy lultons, even though they yeld very poor SCF totl energes when used n SCF lultons. In the se wy we n get wy wth sller nd less oplex delsng sets for orrelton energy lultons thn for SCF lultons. Thus, we envson heper orrelton ethods y usng sller grds nd delsng funton sets thn re eployed for SCF lultons. Sury We dsussed the seprton of exponentls ethod of fttng Ž dsrete. funton to lner ontons of deyng exponentls nd showed how the ethod ould e slghtly ltered nsted to represent funton s lner onton of Gussns. Then we dsussed the pplton of ths ethod to pseudospetrl eletron orrelton energes. In prtulr, we wnted to opute nuerl pproxtons to the two-eletron ntegrls Ž j.. Thus, we defned the funton f j, k, l J, so tht Ž j. ² f : j j, k, l. We ntro- dued nuerl nner produt, ² : w,top- proxte the ² f : e., ² f : ² j, k, l j, k, l f :.. In oputng these nner produts nuer- j, k, l w lly, we re projetng the fj, k, l onto the spe spnned y the orgnl ss set 4 nn 1 K ; however, the fj, k, l y ontn oponents outsde the org- nl ss set. Thus, t sees resonle to ntrodue suppleentry set of funtons, lled delsng funtons, to opleent our ss set to dequtely represent the fj, k, l on the grd. We then explned tht y usng pproprte delsng funtons nd djustng our qudrture rule to e urte for the spef types of nner produts we need Ž see Appendx A., we ould sustntlly prove the ury of pseudospetrl eletron orrelton energes. To deterne pproprte delsng funtons, we ppled the seprton of exponentls tehnque to fttng the funtons tht we wsh to kk represent: the f r r J Ž r. j, k, k g j g g. We used ertn ontons of the Gussns resultng fro the ft s our delsng sets, ddng n hgher ngulr oentu funtons for proved ury. Our proedure hs worked well n oth MP2 nd SDCI lultons. We were le to heve results slr to, or etter thn, those prevously otned wth the PSGVB v1.00 delsng sets. We lso sw n the se of the SDCI lultons tht the perforne of our delsng sets proved onsderly s grds were refned. Thus, we expet tht s grds re proved, our delsng sets should produe ore urte results. Our delsng sets re opt, grd ndependent, nd produe results generlly t ore urte thn those n refs. 10 nd 16; lso, we expltly nd systetlly ddress the ssue of lsng y fttng speflly those funtons tht we seek to represent n grd spe. However, we ust pont out tht the fnl hoe of delsng funton exponents n e senstve to n wdth n our vergng proedure, s well s to the envronent; t y lso e senstve to nternuler dstnes, soethng tht we re urrently nvestgtng. Intl results do not show uh senstvty to nterto dstnes, ut ore testng wll e requred efore we n onlude tht ths s generlly true. Seprton of exponentls n potentlly e ppled to other ethods n quntu hestry s well. For exple, n Vhtrs et l. s uxlry ss set expnson pproh, 4 they propose tht produts of Gussn ss funtons e expnded s lner ontons of Gussns, Ž. Ž. j r r C, Ž 12. j 1310 VOL. 19, NO. 11

12 GAUSSIAN FITS TO ARBITRARY FUNCTIONS where the re ss funtons nd the re Crtesn Gussns Žnot neessrly to entered.. Here, the two-eletron ntegrls ould ulttely e oputed nlytlly y usng the expnsons n eq. Ž 12., ut the expnson tself ould e deterned usng the seprton of exponentls proedure. The resultng ntegrls ould then e used, for nstne, n spetrl eletron orrelton lultons. Another potentl pplton s n DFT. 2, 3 Here, we need to opute qunttes of the for ² 4 3, :, Ž 13. where s the eletron densty. The eletron densty s often ftted to n uxlry ss of Gussns, whh ould e ft y the proedure desred n ths work. Thus, we hope tht n ddton to provng pseudospetrl eletron orrelton ethods, the fttng proedures presented here n e used to enhne other ethods n quntu hestry, s desred n the two exples ove, s well s n other res of sene. Aknowledgents E.A.C. nd C.R.A. re grteful to the Offe of Nvl Reserh for support of ths work. We thnk j Rhrd Fresner for provdng us wth pseudospetrl Hrtree Fok ode. C.C.T. thnks Todd Mrtnez nd Gregg Reynolds for helpful dsussons nd Al Sepehr for runnng soe senstvty tests. Appendx A: Q Opertor Suppose tht we hve set of. We ust djust ² : w so tht ² : w nd ² : n n w re urte: G ² : Ž r. Ž r. w ² :, n w n g g g n g 1 G ² : Ž r. Ž r. w ² :. n w n g g g n g 1 In trx for, T R w R S, Ž A.1. K GG GG Ž K L. K Ž K L. where the letters underneth the tres denote the trx densons. R nd S re extended versons of the olloton trx nd the overlp trx, respetvely. R Ž r. Ž r. Ž r. Ž r. 1 1 K L 1, Ž r. Ž r. Ž r. Ž r. S 1 G K G 1 G L G ² : ² : ² : ² : K L ² : ² : ² : ² : K 1 K K K 1 K L. However, eq. A.1 s usully not stsfed, exept perhps n the se of very sll systes. To solve ths prole, Rngnld et l. 1 nd Fresner 9 ntrodued new opertor, Q to redefne the nner produt: 1 T T Q PS Ž R wr. R w, where S s the Ž K L. Ž K L. overlp trx Ž nludng ll eleents of the for ² :. nd P s the K Ž K L. projeton trx whose top K K seton s the K K dentty trx nd whose renng eleents re ll 0. Thus, the K G trx Q s suh tht QR S. In ths wy, the qudrture rule s fored to e urte for the spef types of nner produts n whh we re nterested. We generte our verson of Q y solvng the followng underdeterned syste for Q: 1 2 Qw R S. K G G Ž K L. K Ž K L. JOURNAL OF COMPUTATIONAL CHEMISTRY 1311

13 TAZARTES, ANDERSON, AND CARTER We fnd Q y solvng the trx equton T 1 2 T T R w Q S, A.2 13, 15 usng sngulr vlue deoposton. We now use ths Q nsted of R T w 1 2 n ll of our nuerl nner produts, so the pseudospetrl two-eletron ntegrls re ² f : j, k, l G w 1 2 g Q, g w g, g J r R g, j. A.3 g 1 To test these dfferent wys of defnng our qudrture rules, we dd seres of MP2 lultons on the PSGVB v1.00 edu grds, usng dfferent opertor A n eh se to defne our nner produt rule: G 1 2 g g 1 j A, g J r w g, g R g, j. In Tle A.1, we see tht when A R T w 1 2 Žths s wht we en y strght nuerl qudrture., Eps s not very urte nd our p- proxton to the ² : e., entres of S. n s poor. By lettng A Q s solved for n eq. Ž A.2. wth no delsng funtons, we prove our ² n : w ut Eps tully worsens. We eleve tht ths s euse the weghts wg used n strght nuerl qudrture re supposed to e pproprte for rod lss of funtons, wheres Q s desgned only to ensure urte overlp ntegrls wthout ny regrd to the projeton of the f j, k, l. However, when A Q wth our new delsng funton set, we otn very urte result n E nd our ² : ps n w re lso urte. Thus, t would pper tht usng oth ondtons on Q s wht helps prove results etter ft to S nd etter jo of pturng the ehvor of fj, k, l on the grd. TABLE A.I. E for C H ( Medu Grds: G = 754, K =40 ). ps 2 2 Opertor A E E E S Aw R 2 1/ 2 ps s ps T 1/ 2 Rw e e-01 Q e e-04 Q, { } e e-04 =1 Pseudospetrl MP2 orrelton energy ( hrtrees ). Dfferene ( n solute vlue) etween spetrl nd pseudospetrl MP2 orrelton energes ( hrtrees ). For n N N trx M, M 2 s the squre root of the ( ) T xu n solute vlue egenvlue of MM. Appendx B: Delsng Sets for 6 31G** Bss Sets Tle B.I lsts the pseudospetrl 6 31G** sets for dfferent ontons of tos. The to t whh the re entered s lsted frst, nd ny other tos re pled long the postve z xs t the desred dstne fro the frst to. We ple the long the postve z xs euse the z vrle represents rdl dstne, nd thus we defne t to lwys e postve. For exple, the hydrogen-ron-oxygen set re the entered on the hydrogen to when there re hydrogen, ron, nd oxygen tos n the oleule. Fgure B.1 shows how we postoned these tos durng the fttng proedure. ŽOf ourse, ths s not how they re postoned n the susequent energy lultons.. None of the re ontrted, so we lst no ontrton oeffents. The dstnes etween tos re gven n Angstros. We hose our nterto dstnes to e the se s those used y 10, 16 Mrtnez nd Crter. Tle B.II shows pseudospetrl MP2 orrelton energes usng sets otned fro two seprte fttngs, s desred n n erler seton. In the frst fttng, we set the dstne etween the hydrogen nd ron tos to e A; n the seond fttng, we set the dstne etween the hydrogen nd ron tos to e A. The resultng exponents re shown n Tle III. The results n Tle B.II show tht the two sets yeld slr MP2 energes. ŽNote tht the errors n the thrd olun of Tle B.II re the se s those n the fourth olun of Tle IV.. We note here tht the exponents for gven to s delsng set do vry wth tht to s envronent; however, n ost ses, the exponents do not vry y uh. For exple, the ron exponents n the Cron set re not very dfferent fro those n the Cron-Hydrogen set. In Tle B.III we show soe MP2 energes for dfferent sets. Coned sets refer to those sets whh tke nto ount the to s envronent wthn the oleule for exple, the Ntrogen-Cron-Hydrogen set. Sngle to sets re those n whh only sngle to s used to fnd exponents for exple, the Hydrogen set. Thus the errors n the thrd olun of Tle B.III re the se s those n the fourth olun of Tle IV. Whle further testng wll e needed, the results fro Tles B.II nd B.III do suggest the possl VOL. 19, NO. 11

14 GAUSSIAN FITS TO ARBITRARY FUNCTIONS TABLE B.I. Delsng Sets for 6 31G** Bss Sets. Funton Atos ( Dstnes) Type Exponents Hydrogen s 1.33, 2.93 p 0.56, 2.93 Hydrogen-Cron s 1.35, 2.77 ( H C = A ) p 0.58, 2.77 Hydrogen-Oxygen s 1.39, 3.18 ( H O = A ) p 0.59, 3.18 Hydrogen-Fluorne s 1.40, 2.89 ( H F = 0.91 A ) p 0.52, 2.89 Hydrogen-Cron-Oxygen s 1.38, 3.05 (H C = A, p 0.59, 3.05 H O = A ) Hydrogen-Cron-Ntrogen s 1.33, 3.02 (H C = A, p 0.48, 3.02 H N = A ) H C N O ( H O = A, s 1.35, 3.10 H C = A, p 0.51, 3.10 H N = A ) Cron s 1.46, 3.16, 9.02 p 1.46, 3.16, 9.02 Cron-Hydrogen s 1.41, 3.23, 8.94 ( C O = A ) p 1.41, 3.23, 8.94 Cron-Hydrogen-Oxygen s 1.34, 3.28, 8.70 (C H = A, p 1.34, 3.28, 8.70 C O = A ) Cron-Hydrogen-Ntrogen s 1.43, 3.16, 8.58 (C O = A, p 1.43, 3.16, 8.58 C N = A ) C H N O ( C H = A, s 1.37, 3.23, 8.97 C N = A, p 1.37, 3.23, 8.97 C O = A ) Oxygen-Hydrogen s 2.78, 6.23, ( O H = A ) p 2.78, 6.23, Oxygen-Cron-Hydrogen s 2.88, 6.12, (O C = A, p 2.88, 6.12, O H = A ) Ntrogen s 1.38, 3.67, 9.14 p 1.38, 3.67, 9.14 Ntrogen-Cron-Hydrogen s 1.37, 3.61, (N H = A, p 1.37, 3.61, N C = A ) Fluorne-Hydrogen s 2.92, 7.55, ( F H = 0.91 A ) p 2.92, 7.55, FIGURE B.1. Postons of tos used for fttng proedure ( hydrogen-ron-oxygen set ). TABLE B.II. Errors n Pseudospetrl MP2 Correlton Energes ( Medu Grds) for Dfferent Interto Dstne Delsng Sets. E E E E s ps s ps Moleule E ( Dstne 1 ) ( Dstne 2 ) s CH e e-05 CH e e-04 CH e e-03 Spetrl MP2 orrelton energy ( hrtrees ). Dfferene ( n solute vlue) etween spetrl nd pseudospetrl MP2 orrelton energes ( hrtrees) usng Dstne 1 ( H C = A ). Dfferene ( n solute vlue) etween spetrl nd pseudospetrl MP2 orrelton energes ( hrtrees) usng Dstne 2 ( H C = A ). TABLE B.III. Errors n Pseudospetrl MP2 Correlton Energes ( Medu Grds) for Dfferent Ato Envronent Delsng Sets. E E E E s ps s ps ( Coned ( Sngle Ato Moleule E Sets) Sets) s CH e e-05 CH e e-04 HCN e e-04 Spetrl MP2 orrelton energy ( hrtrees ). Dfferene ( n solute vlue) etween spetrl nd pseudospetrl MP2 orrelton energes ( hrtrees) usng oned sets. Dfferene ( n solute vlue) etween spetrl nd pseudospetrl MP2 orrelton energes ( hrtrees) usng sngle to sets. JOURNAL OF COMPUTATIONAL CHEMISTRY 1313

15 TAZARTES, ANDERSON, AND CARTER ty of onstrutng delsng sets whh do not strongly depend on the envronent of gven to wthn oleule. Referenes 1. M. N. Rngnld, M. Belhdj, nd R. A. Fresner, J. Che. Phys. 93, 3397 Ž B. I. Dunlp, J. W. D. Connolly, nd J. R. Sn, J. Che. Phys. 71, 3396 Ž H. Sle nd R. H. Felton, J. Che. Phys. 62, 1122 Ž O. Vhtrs, J. Allof, nd M. W. Feyeresen, Che. Phys. Lett. 213, 514 Ž A. K. Rppe, T. A. Sedley, nd W. A. Goddrd III, J. Phys. Che. 85, 1662 Ž G. B. Bhelet, D. R. Hnn, nd M. Shluter, Phys. Rev. B, 26, 4199 Ž W. R. Wdt nd P. J. Hy, J. Che. Phys. 82, 284 Ž R. A. Fresner, Che. Phys. Lett. 116, 39 Ž R. A. Fresner, J. Che. Phys. 85, 1462 Ž T. J. Mrtnez, Ph.D. thess, UCLA, C. C. Tzrtes, Ph.D. thess, UCLA, S. L. Mrple, Jr., Dgtl Spetrl Anlyss wth Appltons, Prente Hll, Englewood Clffs, NJ, W. H. Press, S. A. Teukolsky, W. T. Vetterlng, nd B. P. Flnnery, Nuerl Repes n C, Crdge Unversty Press, New York, C. Lnzos, Appled Anlyss, Dover, New York, 1988, p G. Golu nd C. Vn Lon, Mtrx Coputtons, Johns Hopkns Unversty Press, Bltore, MD, T. J. Mrtnez nd E. A. Crter, J. Che. Phys. 100, 3631 Ž M. N. Rngnld, J. M. Lnglos, B. H. Greeley, T. V. Russo, R. P. Muller, B. Mrten, Y. Won, R. E. Donnelly, Jr., W.T. Pollrd, G. H. Mller, W. A. Goddrd III, nd R. A. Fresner, PS-GVB v1.00, Shrodnger, In. New York, T. J. Mrtnez nd E. A. Crter, n Modern Eletron Struture Theory Prt II, vol. 2, D. R. Yrkony, Ed., Advned Seres n Physl Chestry, World Sentf, Sngpore, 1995, p A. Sepehr, C. C. Tzrtes, nd E. A. Crter, unpulshed results. 20. T. H. Dunnng, Jr., J. Che. Phys. 53, 2823 Ž T. J. Mrtnez nd E. A. Crter, J. Che. Phys. 102, 7564 Ž VOL. 19, NO. 11