Research Article Boltzmann s Six-Moment One-Dimensional Nonlinear System Equations with the Maxwell-Auzhan Boundary Conditions
|
|
|
- Doreen Gardner
- 5 years ago
- Views:
Transcription
1 Hndw Publshng Corporon Journl of Appled Mhemcs Volume 216, Arcle ID , 8 pges hp://dx.do.org/1.1155/216/ Reserch Arcle Bolzmnn s Sx-Momen One-Dmensonl Nonlner Sysem Equons wh he Mxwell-Auzhn Boundry Condons A. Skbekov 1 nd Y. Auzhn 2 1 Reserch Lborory Appled Modelng Ol nd Gs Felds, Kzkh-Brsh Techncl Unversy, 59 Tole B Sree, Almy 5, Kzkhsn 2 Al-Frb Kzkh Nonl Unversy, 71 Al-Frb Avenue, Almy 54, Kzkhsn Correspondence should be ddressed o A. Skbekov;.skbekov@kbu.kz Receved 2 Februry 216; Revsed 1 June 216; Acceped 5 June 216 Acdemc Edor: Peer G. L. Lech Copyrgh 216 A. Skbekov nd Y. Auzhn. Ths s n open ccess rcle dsrbued under he Creve Commons Arbuon Lcense, whch perms unresrced use, dsrbuon, nd reproducon n ny medum, provded he orgnl work s properly ced. We prove exsence nd unqueness of he soluon of he problem wh nl nd Mxwell-Auzhn boundry condons for nonsonry nonlner one-dmensonl Bolzmnn s sx-momen sysem equons n spce of funcons connuous n me nd summble n squre by spl vrble. In order o obn pror esmon of he nl nd boundry vlue problem for nonsonry nonlner one-dmensonl Bolzmnn s sx-momen sysem equons we ge he negrl equly nd hen use he sphercl represenon of vecor. Then we obn he nl vlue problem for Rcc equon. We hve mnged o obn prculr soluon of hs equon n n explc form. 1. Inroducon In cse of one-om gs ny mcroscopc sysem durng process of s evoluon o n equlbrum se psses 3 sges: nl rnson perod, descrbed n erms of full funcon of sysem dsrbuon; he knec perod, by mens of oneprl dsrbuon funcon; nd he hydrodynmc perod, by mens of fve frs momens of he dsrbuon funcon. In knec regme he behvor of rrefed gs n spce of me nd velocy s descrbed by Bolzmnn s equon. I s known fromgsdynmcshnmosofheencouneredproblems here s no need o use deled mcroscopc gs descrpon wh help of he dsrbuon funcon. Therefore s nurl o look for less deled descrpon usng mcroscopc hydrodynmc vrbles (densy, hydrodynmc velocy, emperure, ec.). As hese vrbles re defned n erms of momens of he dsrbuon funcon, we re fced wh he problemofnlyznghevrousmomensofbolzmnn s equon. Noe h Bolzmnn s momen equons re nermede beween Bolzmnn (knec heory) nd hydrodynmc levels of descrpon of se of he rrefed gs nd form clss of nonlner prl dfferenl equons. Exsence of such clss of equons ws noced by Grd [1, 2] n He obned he momen sysem by expndng he prcle dsrbuon funcon n Herme polynomls ner he locl Mxwell dsrbuon. Grd used Cresn coordnes of veloces nd Grd s momen sysem conned s coeffcens such unknown hydrodynmc chrcerscs lke densy, emperure, verge speed, nd so forh. Formulon of boundry condons for Grd s sysem s lmos mpossble, s he chrcersc equons for vrous pproxmons of Grd s hyperbolc sysem conn unknown prmeers lke densy, emperure, nd verge speed. However, 13- nd 2-momen Grd equons re wdely used n solvng mny problems of he knec heory of gses nd plsm. Bolzmnn s equon s equvlen o n nfne sysem of dfferenl equons relve o he momens of he prcle dsrbuon funcon n he complee sysem of egenfuncons of lnerzed operor. As rule we lm sudy by fne momen sysem of equons becuse solvng nfne sysem of equons does no seem o be possble. Fne sysem of momen equons for specfc sk wh cern degree of ccurcy replces Bolzmnn s equon. I s necessry, lso roughly, o replce he boundry condons for he prcle dsrbuon funcon by number of mcroscopc condons for he momens; h s, here rses he problem of boundry condons for fne sysem of
2 2 Journl of Appled Mhemcs equons h pproxme he mcroscopc boundry condons for Bolzmnn s equon. The queson of boundry condons for fne sysem of momen equons cn be dvded no wo prs: how mny condons mus be mposed nd how hey should be prepred. From mcroscopc boundry condons for Bolzmnn s equon here cn be obned n nfne se of boundry condons for ech ype of decomposon. However, he number of boundry condons s deermned no by he number of momen equons; h s, s mpossble, for exmple, o ke s mny boundry condons s equons, lhough he number of momen equons ffecs he number of boundry condons. In ddon, he boundry condons mus be conssen wh he momen equons nd he resulng problem mus be correc. Boundry condon problems rse n he followng sks: (1) momen boundry condons n rrefed gs slp-flow problems; (2) defnon of boundry condons on he surfces of sremlned rrefed gs; (3) predcon erospce erodynmc chrcerscs of rcrf very hgh speeds nd hgh ludes nd so forh. In work [3] we hve obned he momen sysem whch dffers from Grd s sysem of equons. We used sphercl velocy coordnes nd decomposed he dsrbuon funcon no seres of egenfuncons of he lnerzed collson operor [4, 5], whch s he produc of Sonne polynomls nd sphercl funcons. The resulng sysem of equons, whch correspond o he prl sum of seres nd whch we clled Bolzmnn s momen sysem of equons, s nonlner hyperbolc sysem n relon o he momens of he prcles dsrbuon funcon. The srucure of Bolzmnn s momen sysem of equons correspondsohesrucureofbolzmnn sequon;nmely, he dfferenl pr of he resulng sysem s lner n relon o he momens of he dsrbuon funcon nd nonlnery s ncluded s momens of collson negrl [6]. The lnery of dfferenl pr of Bolzmnn s momen sysem of equons smplfes he sk of formulon of he boundry condons. In work [3] homogeneous boundry condon for prcles dsrbuon funcon ws pproxmed nd proved he correcness of nl nd boundry vlue problem for nonlner nonsonry Bolzmnn s momen sysem of equons n hree-dmensonl spce. In work [7] he nl nd boundry vlue problem for one-dmensonl nonsonry Bolzmnn s equon wh boundry condons of Mxwell ws pproxmed by correspondng problem for Bolzmnn s momen sysem of equons. The boundry condons for Bolzmnn s momen sysem of equons were clled Mxwell-Auzhn condons. In work [8] sysemc nonperurbve dervon of herrchy of closed sysems of momen equons correspondng o ny clsscl heory hs been presened. Ths pper s fundmenl work where closed sysems of momen equons descrbe rnson regme. Moreover, hydrodynmcl model s used o descrbe chrge rnspor n generc compound semconducor. Compound semconducors hve found wde use n he mcroelecronc ndusry.theevoluonequonformcroscopcvrbless obned by kng momens of he rnspor equon [9 13]. The sudy of vrous problems for Bolzmnn s momen sysem of equons s n mporn nd cul sk n he heory of rrefed gs nd oher pplcons of he momen sysem equons. The correcness of nl nd boundry problems for Bolzmnn s momen sysem of equons wh Mxwell-Auzhn boundry condons s beng suded for he frs me. 2. Exsence nd Unqueness of he Soluons of Inl nd Boundry Vlue Problem for Sx-Momen One-Dmensonl Bolzmnn s Sysem of Equons wh Mxwell-Auzhn Boundry Condons In hs secon we prove he exsence nd unqueness of soluons of he nl nd boundry vlue problem for sx-momen one-dmensonl Bolzmnn s sysem of equons wh Mxwell-Auzhn boundry condons n spce of funcons, connuous n me nd summble n squre by spl vrble. Noe h he heorem of he exsence of globl soluon n me of he nl nd boundry vlue problem for 3-dmensonl nonlner Bolzmnn s equon wh boundry condons of Mxwell s proved n work [14]. We wre n n expnded form sysem of one-dmensonl Bolzmnn s momen equons n he kh pproxmon, whch corresponds o decomposon of he prcle dsrbuon funcon by egenfuncons of he lnerzed collson operor f nl + 1 α x [l ( 2 (n+l+1/2) (2l 1)(2l + 1) f n,l 2 (n+1) (2l 1)(2l + 1) f n+1,l)+(l+1) ( 2 (n+l+1/2) (2l + 1)(2l + 3) f n,l+1 2n (2l + 1)(2l + 3) f n,l+1)] = I nl, 2n+l=,1,...,k, where he momens I nl of nonlner collson operor re expressed hrough coeffcens of Tlm nd Klebsh-Gordon [15, 16] nd hve he form I nl = N 3 L 3 n 3 l 3 : l nl : l N 3 L 3 n 3 l 3 :l n 1 l 1 n 2 l 2 :l ( l 1l 2 l )(σ l 3 σ ) f n1 l 1 f n2 l 2, where N 3 L 3 n 3 l 3 :l n 1 l 1 n 2 l 2 :l re generlzed coeffcens of Tlm, (l 1 l 2 /l) re Klebsh-Gordon coeffcens, α = 1/ Rθ s he consn, R s Bolzmnn s consn, nd θ s he del gs emperure. (1) (2)
3 Journl of Appled Mhemcs 3 For generlzed coeffcens of Tlm here exss ble [15] for ech vlue of qunum number ξ = 2n + l from o 6. Moreover, here s progrm on IBM for clculon of generlzed coeffcens of Tlm. If n (1) 2n + l kes vlues from o 3, we ge Bolzmnn s momen sysem equons n he hrd pproxmon. We wre n n expnded form: f 2 f + 1 f 1 α x =, + 1 α x ( 2 3 f f f 11) =J 2, f 1 f α x ( 2 3 f f 11) =, + 1 α x (f f f 1) =, f α x 5 f 2 =J 3, f α x ( f f 1) =J 11, x (, ), >, (3) (Aw +Bu ) x= = 1 β (Aw+ Bu + ) x= where (1 β) η F, [, T], αβ π (Aw Bu ) x= = 1 β (Aw+ +Bu + ) x= A= 1 α ( + 2 ( 3 (1 β) η F, [, T], αβ π B= 1 ( α π 1 ( 3 J 1 (u, w) =(,J 2,), ), ) ) 3 2 ) (6) (7) (8) where f =f (, x) nd f 1 =f 1 (,x),...,f 11 =f 11 (, x) re he momens of he prcle dsrbuon funcon; J 2 = (σ 2 σ )(f f 2 f 2 1 / 3)/2, J 3 = (1/4)(σ 3 +3σ 1 4σ )f f 3 +(1/4 5)(2σ 1 +σ 3σ 3 )f 1 f 2,ndJ 11 = (σ 1 σ )(f f 11 + (1/2) 5/3f 1 f 1 ( 2/ 15)f 1 f 2 ) re momens of he collson negrl, where σ, σ 1, σ 2,ndσ 3 re he Fourer coeffcens of he cross secon expnson by he Legendre polynomls. The frs, hrd, nd fourh equons of sysem (3) correspond o mss conservon lw, momenum conservon lw, nd energy conservon lw, respecvely. We sudy he correcness of nl nd boundry vlue problem for sx-momen one-dmensonl Bolzmnn s sysem equons A J 2 (u, w) =(,J 3,J 11 ), u=(f,f 2,f 1 ), w = (f 1,f 3,f 11 ), F=( 1 4 2, 1 8 6, ). s he rnspose mrx; B s he posve defne mrx; u (x) = (f (x), f 2 (x), f 1 (x)) nd w (x) = (f 1 (x), f 3 (x), f 11 (x)) re gven nl vecor-funcons; w +,u + re vecor momens of fllng o he boundry prcle dsrbuon funcon; w,u re vecor momens of reflecng from he boundry prcle dsrbuon funcon. Equon (4) s vecor mrx form of sysem equons (3). I s possble o check hrough drec clculons h u +A w x =J 1 (u, w) w u +A x =J 2 (u, w), u = =u (x), w = =w (x), (, T], x (, ), x [, ], (4) (5) de A 1 = de ( A A ) =, (9) nd mrx A 1 hs hree posve nd he sme number of negve nonzero egenvlues. From (6)-(7) follows h he number of boundry condons on he lef nd rgh ends of nervl (, ) s equl o he number of posve nd negve egenvlues of he mrx A 1. Thus sysem (4) s symmerc hyperbolc nonlner prl dfferenl equons sysem. Le us show h J 2
4 4 Journl of Appled Mhemcs s sgn-nondefned squre form. I s esy o check h f f 2 (f 2 1 / 3) = (CU, U),whereU = (u, w) nd C= ( 1. (1) 3 ) ( ) Egenvlues of mrx C re /2, / 3,,,,nd1/2. Therefore J 2 s sgn-nondefned squre form. Smlrly, we cn show h J 3 nd J 11 re lso sgn-nondefned squre forms. For problem (4) (7) he followng heorem kes plce. Theorem 1. If U =(u (x), w (x)) L 2 [, ],henproblem (4) (7) hs unque soluon n domn [, ] [, T] belongng o he spce C([, T]; L 2 [, ]);moreover U L 2 [,] r 1 C[,T] C 1 ( U L 2 [,] r 1 ()), (11) where C 1 s consn ndependen from U nd T M( U L 2 [,] r 1 ()) ), r 1 () s he prculr soluon of Rcc equon (15) n n explc form. Proof. Le U L 2 [, ]. Le us prove esmon (11). We mulply he frs equon n sysem (4) by u nd he second equon by w nd perform negron from o : 1 d 2 d [(u, u) + (w, w)] dx + [(A w u x,u)+(a, w)] dx x = [(J 1,u)+(J 2,w)]dx. Afer negron by prs we ge 1 d 2 d [(u, u) + (w, w)] dx + (u,aw ) x= (u,aw ) = x= [(J 1,u)+(J 2,w)]dx. (12) (13) Tkng no ccoun boundry condons (6)-(7) we rewre equly (13) n he followng form: 1 d 2 d [(u, u) + (w, w)] dx + (Bu,u ) x= +(F 1,u ) x= = [(J 1 (u, w),u)+(j 2 (u, w),w)]dx, (14) where F 1 = ((1 β)η/αβ π)f. Le us use he sphercl represenon [17] of vecor U(, x) = r()ω(, x), whereω(, x) = (ω 1 (, x), ω 2 (, x)), r() = U(, ) L 2 [,], nd ω L 2 [,] = 1.Furhermore ssume h ω(, x) C 2 [, T],wherehevlueofTwedefne below. Subsung he vlues u = r()ω 1 (, x) nd w = r()ω 2 (, x) no (14) we hve h where dr d +rp() =r2 Q () f(), (15) P () = (Bω 1,ω 1 ) x= +(Bω 1,ω 1 ) x= + 1 β [(Aω+ 2,ω 1 ) x= +(Bω+ 1,ω 1 ) x= + (Bω + 1,ω 1 ) x= (Aω+ 2,ω 1 ) x= ], Q () = [(J 1 (ω 1,ω 2 ),ω 1 )+(J 2 (ω 1,ω 2 ),ω 2 )] dx, f () = (F 1,ω 1 ) x= + (F 1,ω 1 ) x=. Le us sudy (15) wh n nl condon (16) r () = U = U L 2 [,]. (17) Le r 1 () be prculr soluon of Rcc equon (15). Then he generl soluon of (15) hs he form r () =r 1 () + exp ( (2Q (τ) r 1 (τ) P(τ))dτ)[C Q (τ) τ exp ( (2Q (ξ) r 1 (ξ) P(ξ))dξ)dτ]. (18) +(Bu,u ) x= 1 β ((Aw+ Bu + ),u ) x= + 1 β ((Aw+ +Bu + ),u ) x= +(F 1,u ) x= Hence, kng no consderon nl condon (17) we obn
5 Journl of Appled Mhemcs 5 r () =r 1 () + exp ( 1 (2Q (τ) r 1 (τ) P(τ))dτ)[ U r 1 () τ Q (τ) exp ( (2Q (ξ) r 1 (ξ) P(ξ))dξ)dτ]. (19) If R() Q(τ) exp( τ(2q(ξ)r 1(ξ) P(ξ))dξ)dτ, hen he second erm of r() s bounded [, + ) under he condon h dfference U r 1 () s posve. Furher we suppose dfference U r 1 () s posve number. Le R() >. We denoe by T 1 he momen of me whch 1 U r 1 () T 1 =. τ Q (τ) exp ( (2Q (ξ) r 1 (ξ) P(ξ))dξ)dτ (2) Then r() r 1 () s bounded [, T], wheret<t 1 nd T 1 M(1/( U r 1 ())). Anlyzngsrucureofr 1 () (see (31)) from equly (2) we obn Q() > for ny [,T]. Now we found one prculr soluon of (15). The nonlner Rcc equon cn lwys be reduced o secondorder lner ordnry dfferenl equon [18] where y +f 1 () y +f 2 () y=, (21) y () = exp ( Q (τ) r (τ) dτ), f 1 () = Q () P () Q (), Q () f 2 () =Q() f (). (22) Soluon of hs equon wll led o soluon of r() = y /yq() of he orgnl Rcc equon. By subsuon y () =z() exp ( 1 2 f 1 (τ) dτ) (23) wewre(21)nhefollowngform[18]: z () +() z () =, (24) where () = f 2 () (1/2)f 1 () (1/4)f2 1 (). If nsed of f 1 () nd f 2 () we subsue vlues from (22), hen we ge () =Qf() 2(Q2 P Q Q+Q 2 )+(QP Q ) 2 4Q 2. In work [19] ws proven h funcon z () =1+ k=1 (25) b k () (26) s he soluon of (24), where b 1 () = b k () = ξ (τ) dτ dξ, ξ (τ) b k (τ) dτ dξ (27) nd he seres on he rgh hnd sde of (26) unformly converge. Then y=(1+ k=1 b k ()) exp ( 1 2 f 1 (τ) dτ), r 1 () = y yq = z () (1/2) z () f 1 () z () Q () s prculr soluon of Rcc equon (15). Snce z () =,vlueof r 1 () = z () (1/2) z () f 1 () z () Q () (28) = f 1 () 2Q (). (29) Now nsed of f 1 () we subsue s vlue P() Q ()/Q() nd ge r 1 () = (P()Q() Q ())/2Q 2 (). The vlue of Q() wh =s Q () = ((J 1 (ω 1,ω 2 ),ω 1 )+(J 2 (ω 1,ω 2 ),ω 2 )) dx = (3) >, snce Q() > for ny [, T]. An expnson form of he funcon r 1 () = 1 Q () [ 1 z () + Q () P () Q () ]. 2Q () (τ) z (τ) dτ (31) I s no dffcul o prove usng mmede subsuon h funcon r 1 () ssfes Rcc equon (15). From equly (19) we obn Hence r () r 1 () C( U r 1 ()). (32) U (, ) L 2 [,] r 1 () C( U r 1 ()), U L 2 [,] r 1 C[,T] C( U r 1 ()). (33)
6 6 Journl of Appled Mhemcs We ke s nervl of he soluon of problem (15) (17) segmen [; 1/( U r 1 ())], snce he negrnd Q(τ) exp( τ (2Q(ξ)r 1(ξ) P(ξ))dξ) s bounded. Hence [, T] (where T T 1 ) pror esmon (11) kes plce. Now we prove he exsence of soluon for (4) (7) usng Glerkn mehod. Le {V l (x)} l=1 be bss n spce L2 [, ], where he dmenson of vecor V l (x) s equl o he dmenson of vecor U.Forechm we defne n pproxme soluon U m of (4) (7) s follows: U m = m =1 c m () V (x), (34) (( U m U +A m 1 x ),V (x))dx = (J (U m ),V (x))dx, =1, m, (, T], (35) U m = =U m (x), x R, (36) (Aw m Bu m ) x= = 1 β (Aw+ m ±Bu+ m ) x=± ± (1 β) η αβ π F, (37) where U m s he orhogonl proecon n L 2 of he funcon U on he subspce, spnned by V 1,...,V m, J(U m )=(J 1 (u m,w m ),J 2 (u m,w m )). (38) We represen V (x) n form V (x) = (V (1), V(2) ),where +(F 1 +(F 1 ) x= ] = ((A V(2) (J ( ) +(F x= 1 ) x= x, V(1) m =1 V(1) )+(A c m V ),V )dx, x, V(2) )) dx} =1, m, (, T] (4) c m () =d m, = 1, m, (41) where d m s he h componen of U m. We mulply (35) by c m () nd sum over from 1 o m: (( U m U +A m 1 x ),U m)dx = (J (U m ),U m )dx. (42) Wh help of he bove shown rgumens we now prove h r m () s bounded n some me nervl [, T m ],where U m (, x) = r m ()ω m (, x), T m M(( U m r m1 ()) ), T m T m,nd V (1) =(V 1, V 2, V 3 ), V (2) =(V 4, V 5, V 6 ). (39) U m L 2 [,] r m1 C[,T] C 2 ( U L 2 [,] r 1 ()), (43) The coeffcens c m () re deermned from he equons m =1 { dc m d +(BV (1) +(BV (1) (V, V )dx+c m [(BV (1) + 1 β ((AV+(2) 1 β ((AV+(2) + 1 β ((AV+(2) 1 β (AV+(2) ) x= +(BV (1) ) x= +BV +(1) BV +(1) +BV +(1) BV +(1) ),V (1) ) x= ),V (1) ) x= ),V (1) ) x= ) x= ) x= ) +(F x= 1 ) x= where C 2 s consn nd ndependen from m nd r m1 () s prculr soluon of Rcc equon bou r m (). Problem (4)-(41) represens Cuchy problem for he ordnry sysem of dfferenl equons. Exsence of he soluon of problem (4)-(41) follows from heory of ordnry sysem of dfferenl equons (Pcrd s exsence nd unqueness heorem) [2]. Hence he exsence of he soluon of problem (34) (37) follows. Thus, ccordng o esmon (43) he sequence {U m r m1 } of pproxme soluons of problem (5) (7) s unformly bounded n funcon spce C([, T]; L 2 [, ]).Moreover,he homogeneous sysem of equons τe + (1/α)Aξ wh respec o τ, ξ hs only rvl soluon. Then follows from resuls n [21] h U m r m1 U r 1 s week n C([, T]; L 2 [, ]) nd J(U m, ) J(U)s week n C([, T]; L 2 [, ]) s m. Furher cn be shown wh sndrd mehods h lm elemen s wek soluon of problem (5) (7). The unqueness of soluon of problem (5) (7) s proved by conrdcon. Le problem (5) (7) hve wo dfferen soluons u 1,w 1 nd u 2,w 2. We denoe hem gn by u=u 1 u 2
7 Journl of Appled Mhemcs 7 nd w=w 1 w 2. Then wh respec o new vlues of u nd w we obn he followng problem: u +A w x =J 1 (u 1,w 1 ) J 1 (u 2,w 2 ) w u +A x =J 2 (u 1,w 1 ) J 2 (u 2,w 2 ), u = =, w = =, (Aw +Bu ) x= = 1 β (Aw+ Bu + ) x=, x (, ) (44) (45) (Aw Bu ) x= = 1 β (Aw+ +Bu + ) x=. (46) We prove h soluon of problem (44) (46) s rvl. Hence he unqueness of he soluon of problem (5) (7) follows. Usng he mehod whch ws menoned before we ge (see equly (14)) 1 d 2 d [(u, u) + (w, w)] dx + (Bu,u ) x= +(Bu,u ) x= 1 β ((Aw+ Bu + ),u ) x= + 1 β ((Aw+ +Bu + ),u ) x= = [((J 1 (u 1,w 1 ) J 1 (u 2,w 2 )), u) +((J 2 (u 1,w 1 ) J 2 (u 2,w 2 )), w)] dx. (47) Le us rnsform he negrnd on he rgh sde of he equly s ((J 1 (u 1,w 1 ) J 1 (u 2,w 2 )), u) = σ 2 σ 2 [(f,1 f 2,1 f2 1,1 3 ) (f,2f 2,2 f2 1,2 3 )] (f 2,1 f 2,2 )= σ 2 σ [(f 2,1 f 2,1 f,2 f 2,2 ) 1 3 (f2 1,1 f2 1,2 )] (f 2,1 f 2,2 ) = σ 2 σ 2 [(f,1 f,2 )f 2,1 +f,2 (f 2,1 f 2,2 ) 1 3 (f 1,1 f 1,2 )(f 1,1 +f 1,2 )] (f 2,1 f 2,2 ); ((J 2 (u 1,w 1 ) J 2 (u 2,w 2 )), u) = ((J 3 (u 1,w 1 ) J 3 (u 2,w 2 )), (f 3,1 f 3,2 )) + ((J 11 (u 1,w 1 ) J 11 (u 2,w 2 )), (f 11,1 f 11,2 )) = ( 1 4 (σ 3 +3σ 1 4σ )[(f,1 f,2 )f 3,1 +f,2 (f 3,1 f 3,2 )] (2σ 1 +σ 3σ 3 )[(f 1,1 f 1,2 )f 2,1 +f 1,2 (f 2,1 f 2,2 )]) (f 3,1 f 3,2 )+(σ 1 σ ) ((f,1 f,2 )f 11,1 +f,2 (f 11,1 f 11,2 ) [(f 1,1 f 1,2 )f 1,1 +f 1,2 (f 1,1 f 1,2 )] 2 15 [(f 1,1 f 1,2 )f 2,1 +f 1,2 (f 2,1 f 2,2 )]) (f 11,1 f 11,2 ). (48) Once gn we use sphercl represenon of u=r()w 1 (, x) nd w=r()w 2 (, x), wherer() = U(, ) L 2 [,]. Then concernng r() we obn new nl vlue problem dr d +rp() =r2 Q 1 (), (49) r () =, (5) where P() hshesmevluesn(15)nd Q 1 () = σ 2 σ 2 [(ω,1 ω,2 )ω 2,1 +ω,2 (ω 2,1 ω 2,2 ) 1 3 (ω 1,1 ω 1,2 )(ω 1,1 +ω 1,2 )] (ω 2,1 ω 2,2 )dx+ 1 4 (σ 3 +3σ 1 4σ ) [(ω,1 ω,2 )ω 3,1 ++ω,2 (ω 3,1 ω 3,2 )] (ω 3,1 ω 3,2 )dx (2σ 1 +σ 3σ 3 ) [(ω 1,1 ω 1,2 )ω 2,1 +ω 1,2 (ω 2,1 ω 2,2 )] (ω 3,1 ω 3,2 )dx+(σ 1 σ ) [(ω,1 ω,2 )ω 11,1 +ω,2 (ω 11,1 ω 11,2 )+ 1 2
8 8 Journl of Appled Mhemcs 5 2 [(ω 1,1 ω 1,2 )ω 1,1 +ω 1,2 (ω 1,1 ω 1,2 )] 2 15 [(ω 1,1 ω 1,2 )ω 2,1 +ω 1,2 (ω 2,1 ω 2,2 )] (ω 11,1 ω 11,2 )] dx. The generl soluon of (49) s r () = exp ( P (τ) dτ) [C τ Q 1 (τ) exp ( P (ξ) dξ) dτ]. (51) (52) Soluon of (49), whch s ssfyng homogeneous condon (5), s rvl; h s, r() =. Hence, U C([,T];L 2 [,]) = nd u 1 =u 2 nd w 1 =w 2. The heorem s proved. Compeng Ineress The uhors declre h hey hve no compeng neress. References [1] H. Grd, On he knec heory of rrefed gses, Communcons on Pure nd Appled Mhemcs,vol.2,no.4,pp , [2] H. Grd, Prncple of he knec heory of gses, n Thermodynmcs of Gses,vol.12ofHndbuch der Physk, pp , Sprnger, Berln, Germny, [3] A. Skbekov, Inl-Boundry Vlue Problems for he Bolzmnn s Momen Sysem Equons Gylym, Almy,22. [4] C. Cercgnn, Theory nd Applcon of he Bolzmnn Equon, Insuo d Memc, Mlno, Ily, [5] M. N. Kogn, Dynmc of Rrefed Gs,Nuk,Moscow,Russ, [6] K. Kumr, Polynoml expnsons n knec heory of gses, Annls of Physcs,vol.37,no.1,pp ,1966. [7] A. Skbekov nd Y. Auzhn, Boundry condons for he onedmensonl nonlner nonsonry Bolzmnn s momen sysem equons, Journl of Mhemcl Physcs, vol.55, Arcle ID 12357, 214. [8] C. D. Levermore, Momen closure herrches for knec heores, Journl of Sscl Physcs,vol.83,no.5-6,pp , [9] G. Mscl nd V. Romno, A hydrodynmcl model for holes n slcon semconducors: he cse of non-prbolc wrped bnds, Mhemcl nd Compuer Modellng, vol.53,no.1-2, pp , 211. [1] G. Mscl nd V. Romno, A non prbolc hydrodynmcl subbnd model for semconducors bsed on he mxmum enropy prncple, Mhemcl nd Compuer Modellng,vol. 55, no. 3-4, pp , 212. [11] V. D. Cmol nd V. Romno, 2DEG-3DEG chrge rnspor model for MOSFET bsed on he mxmum enropy prncple, SIAMJournlonAppledMhemcs,vol.73,no.4,pp , 213. [12] G. Alì, G. Mscl, V. Romno, nd R. C. Torcso, A hydrodynmcl model for covlen semconducors wh generlzed energy dsperson relon, Europen Journl of Appled Mhemcs,vol.25,no.2,pp ,214. [13] V. D. Cmol nd V. Romno, Hydrodynmcl model for chrge rnspor n grphene, JournlofSsclPhyscs, vol. 157, no. 6, pp , 214. [14] S. Mschler, Knec equons wh Mxwell boundry condons, Annles Scenfques de l Ecole Normle Supereure, vol. 43,no.5,pp ,21. [15] V.G.NeudchnndU.F.Smrnov,Nucleon Assocon of Esy Kernel,Nuk,Moscow,Russ,1969. [16] M. Moshnsky, The Hrmonc Oscllor n Modern Physcs: from Aoms o Qurks,196. [17] S. I. Pokhozhev, On n pproch o nonlner equon, Dokldy Akdem Nuk SSSR,vol.247,pp ,1979. [18] E. Kmke, Dfferenlglechungen Lösungsmehoden und Lösungen, I. Gewohulche Dfferenlglechungen, B.G.Teubner, Lepzg, Germny, [19] A. Tungrov nd D. K. Akhmed-Zk, Cuchy problem for one clss of ordnry dfferenl equons, Inernonl Journl of Mhemcl Anlyss, vol.6,no.14,pp , 212. [2] M. Tenenbum nd H. Pollrd, Ordnry Dfferenl Equons, HrperndRow,NewYork,NY,USA,1963. [21] L. Trr, Compensed compcness nd pplcons o prl dfferenl equons, n Proceedngs of he Non-Lner Anlyss nd Mechncs, Hero-W Symposum, R.J.Knops, Ed., vol. 4 of Reserch Noes n Mh,pp ,1979.
9 Advnces n Operons Reserch Hndw Publshng Corporon hp:// Volume 214 Advnces n Decson Scences Hndw Publshng Corporon hp:// Volume 214 Journl of Appled Mhemcs Algebr Hndw Publshng Corporon hp:// Hndw Publshng Corporon hp:// Volume 214 Journl of Probbly nd Sscs Volume 214 The Scenfc World Journl Hndw Publshng Corporon hp:// Hndw Publshng Corporon hp:// Volume 214 Inernonl Journl of Dfferenl Equons Hndw Publshng Corporon hp:// Volume 214 Volume 214 Subm your mnuscrps hp:// Inernonl Journl of Advnces n Combnorcs Hndw Publshng Corporon hp:// Mhemcl Physcs Hndw Publshng Corporon hp:// Volume 214 Journl of Complex Anlyss Hndw Publshng Corporon hp:// Volume 214 Inernonl Journl of Mhemcs nd Mhemcl Scences Mhemcl Problems n Engneerng Journl of Mhemcs Hndw Publshng Corporon hp:// Volume 214 Hndw Publshng Corporon hp:// Volume 214 Volume 214 Hndw Publshng Corporon hp:// Volume 214 Dscree Mhemcs Journl of Volume 214 Hndw Publshng Corporon hp:// Dscree Dynmcs n Nure nd Socey Journl of Funcon Spces Hndw Publshng Corporon hp:// Absrc nd Appled Anlyss Volume 214 Hndw Publshng Corporon hp:// Volume 214 Hndw Publshng Corporon hp:// Volume 214 Inernonl Journl of Journl of Sochsc Anlyss Opmzon Hndw Publshng Corporon hp:// Hndw Publshng Corporon hp:// Volume 214 Volume 214
Research Article Oscillatory Criteria for Higher Order Functional Differential Equations with Damping
 Journl of Funcon Spces nd Applcons Volume 2013, Arcle ID 968356, 5 pges hp://dx.do.org/10.1155/2013/968356 Reserch Arcle Oscllory Crer for Hgher Order Funconl Dfferenl Equons wh Dmpng Pegung Wng 1 nd H
Journl of Funcon Spces nd Applcons Volume 2013, Arcle ID 968356, 5 pges hp://dx.do.org/10.1155/2013/968356 Reserch Arcle Oscllory Crer for Hgher Order Funconl Dfferenl Equons wh Dmpng Pegung Wng 1 nd H
THE EXISTENCE OF SOLUTIONS FOR A CLASS OF IMPULSIVE FRACTIONAL Q-DIFFERENCE EQUATIONS
 Europen Journl of Mhemcs nd Compuer Scence Vol 4 No, 7 SSN 59-995 THE EXSTENCE OF SOLUTONS FOR A CLASS OF MPULSVE FRACTONAL Q-DFFERENCE EQUATONS Shuyun Wn, Yu Tng, Q GE Deprmen of Mhemcs, Ynbn Unversy,
Europen Journl of Mhemcs nd Compuer Scence Vol 4 No, 7 SSN 59-995 THE EXSTENCE OF SOLUTONS FOR A CLASS OF MPULSVE FRACTONAL Q-DFFERENCE EQUATONS Shuyun Wn, Yu Tng, Q GE Deprmen of Mhemcs, Ynbn Unversy,
Jordan Journal of Physics
 Volume, Number, 00. pp. 47-54 RTICLE Jordn Journl of Physcs Frconl Cnoncl Qunzon of he Free Elecromgnec Lgrngn ensy E. K. Jrd, R. S. w b nd J. M. Khlfeh eprmen of Physcs, Unversy of Jordn, 94 mmn, Jordn.
Volume, Number, 00. pp. 47-54 RTICLE Jordn Journl of Physcs Frconl Cnoncl Qunzon of he Free Elecromgnec Lgrngn ensy E. K. Jrd, R. S. w b nd J. M. Khlfeh eprmen of Physcs, Unversy of Jordn, 94 mmn, Jordn.
Supporting information How to concatenate the local attractors of subnetworks in the HPFP
 n Effcen lgorh for Idenfyng Prry Phenoype rcors of Lrge-Scle Boolen Newor Sng-Mo Choo nd Kwng-Hyun Cho Depren of Mhecs Unversy of Ulsn Ulsn 446 Republc of Kore Depren of Bo nd Brn Engneerng Kore dvnced
n Effcen lgorh for Idenfyng Prry Phenoype rcors of Lrge-Scle Boolen Newor Sng-Mo Choo nd Kwng-Hyun Cho Depren of Mhecs Unversy of Ulsn Ulsn 446 Republc of Kore Depren of Bo nd Brn Engneerng Kore dvnced
On One Analytic Method of. Constructing Program Controls
 Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
ANOTHER CATEGORY OF THE STOCHASTIC DEPENDENCE FOR ECONOMETRIC MODELING OF TIME SERIES DATA
 Tn Corn DOSESCU Ph D Dre Cner Chrsn Unversy Buchres Consnn RAISCHI PhD Depren of Mhecs The Buchres Acdey of Econoc Sudes ANOTHER CATEGORY OF THE STOCHASTIC DEPENDENCE FOR ECONOMETRIC MODELING OF TIME SERIES
Tn Corn DOSESCU Ph D Dre Cner Chrsn Unversy Buchres Consnn RAISCHI PhD Depren of Mhecs The Buchres Acdey of Econoc Sudes ANOTHER CATEGORY OF THE STOCHASTIC DEPENDENCE FOR ECONOMETRIC MODELING OF TIME SERIES
A NEW INTERPRETATION OF INTERVAL-VALUED FUZZY INTERIOR IDEALS OF ORDERED SEMIGROUPS
 ScInLhore),7),9-37,4 ISSN 3-536; CODEN: SINTE 8 9 A NEW INTERPRETATION O INTERVAL-VALUED UZZY INTERIOR IDEALS O ORDERED SEMIGROUPS Hdy Ullh Khn, b, Nor Hnz Srmn, Asghr Khn c nd z Muhmmd Khn d Deprmen of
ScInLhore),7),9-37,4 ISSN 3-536; CODEN: SINTE 8 9 A NEW INTERPRETATION O INTERVAL-VALUED UZZY INTERIOR IDEALS O ORDERED SEMIGROUPS Hdy Ullh Khn, b, Nor Hnz Srmn, Asghr Khn c nd z Muhmmd Khn d Deprmen of
Research Article The General Solution of Impulsive Systems with Caputo-Hadamard Fractional Derivative of Order
 Hndw Publhng Corporon Mhemcl Problem n Engneerng Volume 06, Arcle ID 8080, 0 pge hp://dx.do.org/0.55/06/8080 Reerch Arcle The Generl Soluon of Impulve Syem wh Cpuo-Hdmrd Frconl Dervve of Order q C (R(q)
Hndw Publhng Corporon Mhemcl Problem n Engneerng Volume 06, Arcle ID 8080, 0 pge hp://dx.do.org/0.55/06/8080 Reerch Arcle The Generl Soluon of Impulve Syem wh Cpuo-Hdmrd Frconl Dervve of Order q C (R(q)
Origin Destination Transportation Models: Methods
 In Jr. of Mhemcl Scences & Applcons Vol. 2, No. 2, My 2012 Copyrgh Mnd Reder Publcons ISSN No: 2230-9888 www.journlshub.com Orgn Desnon rnsporon Models: Mehods Jyo Gup nd 1 N H. Shh Deprmen of Mhemcs,
In Jr. of Mhemcl Scences & Applcons Vol. 2, No. 2, My 2012 Copyrgh Mnd Reder Publcons ISSN No: 2230-9888 www.journlshub.com Orgn Desnon rnsporon Models: Mehods Jyo Gup nd 1 N H. Shh Deprmen of Mhemcs,
NUMERICAL SOLUTION OF THIN FILM EQUATION IN A CLASS OF DISCONTINUOUS FUNCTIONS
 Eropen Scenfc Jornl Ags 5 /SPECAL/ eon SSN: 857 788 Prn e - SSN 857-74 NMERCAL SOLON OF HN FLM EQAON N A CLASS OF DSCONNOS FNCONS Bn Snsoysl Assoc Prof Mr Rslov Prof Beyen nversy Deprmen of Memcs n Compng
Eropen Scenfc Jornl Ags 5 /SPECAL/ eon SSN: 857 788 Prn e - SSN 857-74 NMERCAL SOLON OF HN FLM EQAON N A CLASS OF DSCONNOS FNCONS Bn Snsoysl Assoc Prof Mr Rslov Prof Beyen nversy Deprmen of Memcs n Compng
Hidden Markov Model. a ij. Observation : O1,O2,... States in time : q1, q2,... All states : s1, s2,..., sn
 Hdden Mrkov Model S S servon : 2... Ses n me : 2... All ses : s s2... s 2 3 2 3 2 Hdden Mrkov Model Con d Dscree Mrkov Model 2 z k s s s s s s Degree Mrkov Model Hdden Mrkov Model Con d : rnson roly from
Hdden Mrkov Model S S servon : 2... Ses n me : 2... All ses : s s2... s 2 3 2 3 2 Hdden Mrkov Model Con d Dscree Mrkov Model 2 z k s s s s s s Degree Mrkov Model Hdden Mrkov Model Con d : rnson roly from
MODEL SOLUTIONS TO IIT JEE ADVANCED 2014
 MODEL SOLUTIONS TO IIT JEE ADVANCED Pper II Code PART I 6 7 8 9 B A A C D B D C C B 6 C B D D C A 7 8 9 C A B D. Rhc(Z ). Cu M. ZM Secon I K Z 8 Cu hc W mu hc 8 W + KE hc W + KE W + KE W + KE W + KE (KE
MODEL SOLUTIONS TO IIT JEE ADVANCED Pper II Code PART I 6 7 8 9 B A A C D B D C C B 6 C B D D C A 7 8 9 C A B D. Rhc(Z ). Cu M. ZM Secon I K Z 8 Cu hc W mu hc 8 W + KE hc W + KE W + KE W + KE W + KE (KE
Approximate Analytic Solution of (2+1) - Dimensional Zakharov-Kuznetsov(Zk) Equations Using Homotopy
 Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
ON THE DYNAMICS AND THERMODYNAMICS OF SMALL MARKOW-TYPE MATERIAL SYSTEMS
 ON THE DYNAMICS AND THERMODYNAMICS OF SMALL MARKOW-TYPE MATERIAL SYSTEMS Andrzej Trzęsows Deprmen of Theory of Connuous Med, Insue of Fundmenl Technologcl Reserch, Polsh Acdemy of Scences, Pwńsego 5B,
ON THE DYNAMICS AND THERMODYNAMICS OF SMALL MARKOW-TYPE MATERIAL SYSTEMS Andrzej Trzęsows Deprmen of Theory of Connuous Med, Insue of Fundmenl Technologcl Reserch, Polsh Acdemy of Scences, Pwńsego 5B,
The Characterization of Jones Polynomial. for Some Knots
 Inernon Mhemc Forum,, 8, no, 9 - The Chrceron of Jones Poynom for Some Knos Mur Cncn Yuuncu Y Ünversy, Fcuy of rs nd Scences Mhemcs Deprmen, 8, n, Turkey m_cencen@yhoocom İsm Yr Non Educon Mnsry, 8, n,
Inernon Mhemc Forum,, 8, no, 9 - The Chrceron of Jones Poynom for Some Knos Mur Cncn Yuuncu Y Ünversy, Fcuy of rs nd Scences Mhemcs Deprmen, 8, n, Turkey m_cencen@yhoocom İsm Yr Non Educon Mnsry, 8, n,
Lecture 4: Trunking Theory and Grade of Service (GOS)
 Lecure 4: Trunkng Theory nd Grde of Servce GOS 4.. Mn Problems nd Defnons n Trunkng nd GOS Mn Problems n Subscrber Servce: lmed rdo specrum # of chnnels; mny users. Prncple of Servce: Defnon: Serve user
Lecure 4: Trunkng Theory nd Grde of Servce GOS 4.. Mn Problems nd Defnons n Trunkng nd GOS Mn Problems n Subscrber Servce: lmed rdo specrum # of chnnels; mny users. Prncple of Servce: Defnon: Serve user
Solution in semi infinite diffusion couples (error function analysis)
 Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
II The Z Transform. Topics to be covered. 1. Introduction. 2. The Z transform. 3. Z transforms of elementary functions
 II The Z Trnsfor Tocs o e covered. Inroducon. The Z rnsfor 3. Z rnsfors of eleenry funcons 4. Proeres nd Theory of rnsfor 5. The nverse rnsfor 6. Z rnsfor for solvng dfference equons II. Inroducon The
II The Z Trnsfor Tocs o e covered. Inroducon. The Z rnsfor 3. Z rnsfors of eleenry funcons 4. Proeres nd Theory of rnsfor 5. The nverse rnsfor 6. Z rnsfor for solvng dfference equons II. Inroducon The
GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS. Youngwoo Ahn and Kitae Kim
 Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
To Possibilities of Solution of Differential Equation of Logistic Function
 Arnold Dávd, Frnše Peller, Rená Vooroosová To Possbles of Soluon of Dfferenl Equon of Logsc Funcon Arcle Info: Receved 6 My Acceped June UDC 7 Recommended con: Dávd, A., Peller, F., Vooroosová, R. ().
Arnold Dávd, Frnše Peller, Rená Vooroosová To Possbles of Soluon of Dfferenl Equon of Logsc Funcon Arcle Info: Receved 6 My Acceped June UDC 7 Recommended con: Dávd, A., Peller, F., Vooroosová, R. ().
M. Y. Adamu Mathematical Sciences Programme, AbubakarTafawaBalewa University, Bauchi, Nigeria
 IOSR Journal of Mahemacs (IOSR-JM e-issn: 78-578, p-issn: 9-765X. Volume 0, Issue 4 Ver. IV (Jul-Aug. 04, PP 40-44 Mulple SolonSoluons for a (+-dmensonalhroa-sasuma shallow waer wave equaon UsngPanlevé-Bӓclund
IOSR Journal of Mahemacs (IOSR-JM e-issn: 78-578, p-issn: 9-765X. Volume 0, Issue 4 Ver. IV (Jul-Aug. 04, PP 40-44 Mulple SolonSoluons for a (+-dmensonalhroa-sasuma shallow waer wave equaon UsngPanlevé-Bӓclund
( ) () we define the interaction representation by the unitary transformation () = ()
 Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
Existence and Uniqueness Results for Random Impulsive Integro-Differential Equation
 Global Journal of Pure and Appled Mahemacs. ISSN 973-768 Volume 4, Number 6 (8), pp. 89-87 Research Inda Publcaons hp://www.rpublcaon.com Exsence and Unqueness Resuls for Random Impulsve Inegro-Dfferenal
Global Journal of Pure and Appled Mahemacs. ISSN 973-768 Volume 4, Number 6 (8), pp. 89-87 Research Inda Publcaons hp://www.rpublcaon.com Exsence and Unqueness Resuls for Random Impulsve Inegro-Dfferenal
Dynamic Team Decision Theory. EECS 558 Project Shrutivandana Sharma and David Shuman December 10, 2005
 Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
Let s treat the problem of the response of a system to an applied external force. Again,
 Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Stability Analysis for VAR systems. )', a VAR model of order p (VAR(p)) can be written as:
 Sbl Anlss for VAR ssems For se of n me seres vrbles (,,, n ', VAR model of order p (VAR(p n be wren s: ( A + A + + Ap p + u where he A s re (nxn oeffen mres nd u ( u, u,, un ' s n unobservble d zero men
Sbl Anlss for VAR ssems For se of n me seres vrbles (,,, n ', VAR model of order p (VAR(p n be wren s: ( A + A + + Ap p + u where he A s re (nxn oeffen mres nd u ( u, u,, un ' s n unobservble d zero men
Notes on the stability of dynamic systems and the use of Eigen Values.
 Noes on he sabl of dnamc ssems and he use of Egen Values. Source: Macro II course noes, Dr. Davd Bessler s Tme Seres course noes, zarads (999) Ineremporal Macroeconomcs chaper 4 & Techncal ppend, and Hamlon
Noes on he sabl of dnamc ssems and he use of Egen Values. Source: Macro II course noes, Dr. Davd Bessler s Tme Seres course noes, zarads (999) Ineremporal Macroeconomcs chaper 4 & Techncal ppend, and Hamlon
HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD
 Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
Advanced Electromechanical Systems (ELE 847)
 (ELE 847) Dr. Smr ouro-rener Topc 1.4: DC moor speed conrol Torono, 2009 Moor Speed Conrol (open loop conrol) Consder he followng crcu dgrm n V n V bn T1 T 5 T3 V dc r L AA e r f L FF f o V f V cn T 4
(ELE 847) Dr. Smr ouro-rener Topc 1.4: DC moor speed conrol Torono, 2009 Moor Speed Conrol (open loop conrol) Consder he followng crcu dgrm n V n V bn T1 T 5 T3 V dc r L AA e r f L FF f o V f V cn T 4
Rotations.
 oons j.lbb@phscs.o.c.uk To s summ Fmes of efeence Invnce une nsfomons oon of wve funcon: -funcons Eule s ngles Emple: e e - - Angul momenum s oon geneo Genec nslons n Noehe s heoem Fmes of efeence Conse
oons j.lbb@phscs.o.c.uk To s summ Fmes of efeence Invnce une nsfomons oon of wve funcon: -funcons Eule s ngles Emple: e e - - Angul momenum s oon geneo Genec nslons n Noehe s heoem Fmes of efeence Conse
Chapter Lagrangian Interpolation
 Chaper 5.4 agrangan Inerpolaon Afer readng hs chaper you should be able o:. dere agrangan mehod of nerpolaon. sole problems usng agrangan mehod of nerpolaon and. use agrangan nerpolans o fnd deraes and
Chaper 5.4 agrangan Inerpolaon Afer readng hs chaper you should be able o:. dere agrangan mehod of nerpolaon. sole problems usng agrangan mehod of nerpolaon and. use agrangan nerpolans o fnd deraes and
[ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5
![[ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5 [ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5](/thumbs/85/92299540.jpg) TPG460 Reservor Smulaon 08 page of 5 DISCRETIZATIO OF THE FOW EQUATIOS As we already have seen, fne dfference appromaons of he paral dervaves appearng n he flow equaons may be obaned from Taylor seres
TPG460 Reservor Smulaon 08 page of 5 DISCRETIZATIO OF THE FOW EQUATIOS As we already have seen, fne dfference appromaons of he paral dervaves appearng n he flow equaons may be obaned from Taylor seres
BLOWUPS IN GAUGE AND CONSTRAINT MODES. Bernd Reimann, AEI in collaboration with M. Alcubierre, ICN (Mexico)
 BLOWUPS IN GAUGE AND CONSTRAINT MODES Bernd Remnn, AEI n ollboron M. Aluberre, ICN (Mexo) Jen, Jnury 30, 006 1 Tops Pologes ( soks nd bloups ) n sysems of PDEs Te soure rer for vodng bloups Evoluon Sysem:
BLOWUPS IN GAUGE AND CONSTRAINT MODES Bernd Remnn, AEI n ollboron M. Aluberre, ICN (Mexo) Jen, Jnury 30, 006 1 Tops Pologes ( soks nd bloups ) n sysems of PDEs Te soure rer for vodng bloups Evoluon Sysem:
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
1.B Appendix to Chapter 1
 Secon.B.B Append o Chper.B. The Ordnr Clcl Here re led ome mporn concep rom he ordnr clcl. The Dervve Conder ncon o one ndependen vrble. The dervve o dened b d d lm lm.b. where he ncremen n de o n ncremen
Secon.B.B Append o Chper.B. The Ordnr Clcl Here re led ome mporn concep rom he ordnr clcl. The Dervve Conder ncon o one ndependen vrble. The dervve o dened b d d lm lm.b. where he ncremen n de o n ncremen
CH.3. COMPATIBILITY EQUATIONS. Continuum Mechanics Course (MMC) - ETSECCPB - UPC
 CH.3. COMPATIBILITY EQUATIONS Connuum Mechancs Course (MMC) - ETSECCPB - UPC Overvew Compably Condons Compably Equaons of a Poenal Vecor Feld Compably Condons for Infnesmal Srans Inegraon of he Infnesmal
CH.3. COMPATIBILITY EQUATIONS Connuum Mechancs Course (MMC) - ETSECCPB - UPC Overvew Compably Condons Compably Equaons of a Poenal Vecor Feld Compably Condons for Infnesmal Srans Inegraon of he Infnesmal
Numerical Simulations of Femtosecond Pulse. Propagation in Photonic Crystal Fibers. Comparative Study of the S-SSFM and RK4IP
 Appled Mhemcl Scences Vol. 6 1 no. 117 5841 585 Numercl Smulons of Femosecond Pulse Propgon n Phoonc Crysl Fbers Comprve Sudy of he S-SSFM nd RK4IP Mourd Mhboub Scences Fculy Unversy of Tlemcen BP.119
Appled Mhemcl Scences Vol. 6 1 no. 117 5841 585 Numercl Smulons of Femosecond Pulse Propgon n Phoonc Crysl Fbers Comprve Sudy of he S-SSFM nd RK4IP Mourd Mhboub Scences Fculy Unversy of Tlemcen BP.119
V.Abramov - FURTHER ANALYSIS OF CONFIDENCE INTERVALS FOR LARGE CLIENT/SERVER COMPUTER NETWORKS
 R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION
 S19 A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION by Xaojun YANG a,b, Yugu YANG a*, Carlo CATTANI c, and Mngzheng ZHU b a Sae Key Laboraory for Geomechancs and Deep Underground Engneerng, Chna Unversy
S19 A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION by Xaojun YANG a,b, Yugu YANG a*, Carlo CATTANI c, and Mngzheng ZHU b a Sae Key Laboraory for Geomechancs and Deep Underground Engneerng, Chna Unversy
Ordinary Differential Equations in Neuroscience with Matlab examples. Aim 1- Gain understanding of how to set up and solve ODE s
 Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
Simplified Variance Estimation for Three-Stage Random Sampling
 Deprmen of ppled Sscs Johnnes Kepler Unversy Lnz IFS Reserch Pper Seres 04-67 Smplfed rnce Esmon for Three-Sge Rndom Smplng ndres Quember Ocober 04 Smplfed rnce Esmon for Three-Sge Rndom Smplng ndres Quember
Deprmen of ppled Sscs Johnnes Kepler Unversy Lnz IFS Reserch Pper Seres 04-67 Smplfed rnce Esmon for Three-Sge Rndom Smplng ndres Quember Ocober 04 Smplfed rnce Esmon for Three-Sge Rndom Smplng ndres Quember
Power Series Solutions for Nonlinear Systems. of Partial Differential Equations
 Appled Mhemcl Scences, Vol. 6, 1, no. 14, 5147-5159 Power Seres Soluons for Nonlner Sysems of Prl Dfferenl Equons Amen S. Nuser Jordn Unversy of Scence nd Technology P. O. Bo 33, Irbd, 11, Jordn nuser@us.edu.o
Appled Mhemcl Scences, Vol. 6, 1, no. 14, 5147-5159 Power Seres Soluons for Nonlner Sysems of Prl Dfferenl Equons Amen S. Nuser Jordn Unversy of Scence nd Technology P. O. Bo 33, Irbd, 11, Jordn nuser@us.edu.o
Survival Analysis and Reliability. A Note on the Mean Residual Life Function of a Parallel System
 Communcaons n Sascs Theory and Mehods, 34: 475 484, 2005 Copyrgh Taylor & Francs, Inc. ISSN: 0361-0926 prn/1532-415x onlne DOI: 10.1081/STA-200047430 Survval Analyss and Relably A Noe on he Mean Resdual
Communcaons n Sascs Theory and Mehods, 34: 475 484, 2005 Copyrgh Taylor & Francs, Inc. ISSN: 0361-0926 prn/1532-415x onlne DOI: 10.1081/STA-200047430 Survval Analyss and Relably A Noe on he Mean Resdual
 ISSN 075-7 : (7) 0 007 C ( ), E-l: ssolos@glco FPGA LUT FPGA EM : FPGA, LUT, EM,,, () FPGA (feldprogrble ge rrs) [, ] () [], () [] () [5] [6] FPGA LUT (Look-Up-Tbles) EM (Ebedded Meor locks) [7, 8] LUT
ISSN 075-7 : (7) 0 007 C ( ), E-l: ssolos@glco FPGA LUT FPGA EM : FPGA, LUT, EM,,, () FPGA (feldprogrble ge rrs) [, ] () [], () [] () [5] [6] FPGA LUT (Look-Up-Tbles) EM (Ebedded Meor locks) [7, 8] LUT
Multi-load Optimal Design of Burner-inner-liner Under Performance Index Constraint by Second-Order Polynomial Taylor Series Method
 , 0005 (06) DOI: 0.05/ mecconf/06700005 ICMI 06 Mul-lod Opml Desgn of Burner-nner-lner Under Performnce Index Consrn by Second-Order Polynoml ylor Seres Mehod U Goqo, Wong Chun Nm, Zheng Mn nd ng Kongzheng
, 0005 (06) DOI: 0.05/ mecconf/06700005 ICMI 06 Mul-lod Opml Desgn of Burner-nner-lner Under Performnce Index Consrn by Second-Order Polynoml ylor Seres Mehod U Goqo, Wong Chun Nm, Zheng Mn nd ng Kongzheng
John Geweke a and Gianni Amisano b a Departments of Economics and Statistics, University of Iowa, USA b European Central Bank, Frankfurt, Germany
 Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
Interval Estimation. Consider a random variable X with a mean of X. Let X be distributed as X X
 ECON 37: Ecoomercs Hypohess Tesg Iervl Esmo Wh we hve doe so fr s o udersd how we c ob esmors of ecoomcs reloshp we wsh o sudy. The queso s how comforble re we wh our esmors? We frs exme how o produce
ECON 37: Ecoomercs Hypohess Tesg Iervl Esmo Wh we hve doe so fr s o udersd how we c ob esmors of ecoomcs reloshp we wsh o sudy. The queso s how comforble re we wh our esmors? We frs exme how o produce
Macroscopic quantum effects generated by the acoustic wave in a molecular magnet
 Cudnovsky-Fes-09034 Mcroscopc qunum effecs genered by e cousc wve n moleculr mgne Gwng-Hee Km ejong Unv., Kore Eugene M. Cudnovksy Lemn College, CUNY Acknowledgemens D. A. Grnn Lemn College, CUNY Oulne
Cudnovsky-Fes-09034 Mcroscopc qunum effecs genered by e cousc wve n moleculr mgne Gwng-Hee Km ejong Unv., Kore Eugene M. Cudnovksy Lemn College, CUNY Acknowledgemens D. A. Grnn Lemn College, CUNY Oulne
W. B. Vasantha Kandasamy Florentin Smarandache NEUTROSOPHIC BILINEAR ALGEBRAS AND THEIR GENERALIZATIONS
 W. B. Vsnh Kndsmy Florenn Smrndche NEUTROSOPHIC BILINEAR ALGEBRAS AND THEIR GENERALIZATIONS Svensk fyskrkve Sockholm, Sweden 00 Svensk fyskrkve (Swedsh physcs rchve) s publsher regsered wh he Royl Nonl
W. B. Vsnh Kndsmy Florenn Smrndche NEUTROSOPHIC BILINEAR ALGEBRAS AND THEIR GENERALIZATIONS Svensk fyskrkve Sockholm, Sweden 00 Svensk fyskrkve (Swedsh physcs rchve) s publsher regsered wh he Royl Nonl
EEM 486: Computer Architecture
 EEM 486: Compuer Archecure Lecure 4 ALU EEM 486 MIPS Arhmec Insrucons R-ype I-ype Insrucon Exmpe Menng Commen dd dd $,$2,$3 $ = $2 + $3 sub sub $,$2,$3 $ = $2 - $3 3 opernds; overfow deeced 3 opernds;
EEM 486: Compuer Archecure Lecure 4 ALU EEM 486 MIPS Arhmec Insrucons R-ype I-ype Insrucon Exmpe Menng Commen dd dd $,$2,$3 $ = $2 + $3 sub sub $,$2,$3 $ = $2 - $3 3 opernds; overfow deeced 3 opernds;
An improved statistical disclosure attack
 In J Grnulr Compung, Rough Ses nd Inellgen Sysems, Vol X, No Y, xxxx An mproved sscl dsclosure c Bn Tng* Deprmen of Compuer Scence, Clforn Se Unversy Domnguez Hlls, Crson, CA, USA Eml: bng@csudhedu *Correspondng
In J Grnulr Compung, Rough Ses nd Inellgen Sysems, Vol X, No Y, xxxx An mproved sscl dsclosure c Bn Tng* Deprmen of Compuer Scence, Clforn Se Unversy Domnguez Hlls, Crson, CA, USA Eml: bng@csudhedu *Correspondng
Linear Response Theory: The connection between QFT and experiments
 Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
OPERATOR-VALUED KERNEL RECURSIVE LEAST SQUARES ALGORITHM
 3rd Europen Sgnl Processng Conference EUSIPCO OPERATOR-VALUED KERNEL RECURSIVE LEAST SQUARES ALGORITM P. O. Amblrd GIPSAlb/CNRS UMR 583 Unversé de Grenoble Grenoble, Frnce. Kdr LIF/CNRS UMR 779 Ax-Mrselle
3rd Europen Sgnl Processng Conference EUSIPCO OPERATOR-VALUED KERNEL RECURSIVE LEAST SQUARES ALGORITM P. O. Amblrd GIPSAlb/CNRS UMR 583 Unversé de Grenoble Grenoble, Frnce. Kdr LIF/CNRS UMR 779 Ax-Mrselle
Track Properities of Normal Chain
 In. J. Conemp. Mah. Scences, Vol. 8, 213, no. 4, 163-171 HIKARI Ld, www.m-har.com rac Propes of Normal Chan L Chen School of Mahemacs and Sascs, Zhengzhou Normal Unversy Zhengzhou Cy, Hennan Provnce, 4544,
In. J. Conemp. Mah. Scences, Vol. 8, 213, no. 4, 163-171 HIKARI Ld, www.m-har.com rac Propes of Normal Chan L Chen School of Mahemacs and Sascs, Zhengzhou Normal Unversy Zhengzhou Cy, Hennan Provnce, 4544,
10. A.C CIRCUITS. Theoretically current grows to maximum value after infinite time. But practically it grows to maximum after 5τ. Decay of current :
 . A. IUITS Synopss : GOWTH OF UNT IN IUIT : d. When swch S s closed a =; = d. A me, curren = e 3. The consan / has dmensons of me and s called he nducve me consan ( τ ) of he crcu. 4. = τ; =.63, n one
. A. IUITS Synopss : GOWTH OF UNT IN IUIT : d. When swch S s closed a =; = d. A me, curren = e 3. The consan / has dmensons of me and s called he nducve me consan ( τ ) of he crcu. 4. = τ; =.63, n one
HERMITE SERIES SOLUTIONS OF LINEAR FREDHOLM INTEGRAL EQUATIONS
 Mhemcl nd Compuonl Applcons, Vol 6, o, pp 97-56, Assocon fo Scenfc Resech ERMITE SERIES SOLUTIOS OF LIEAR FREDOLM ITEGRAL EQUATIOS Slh Ylçınbş nd Müge Angül Depmen of Mhemcs, Fcul of Scence nd As, Cell
Mhemcl nd Compuonl Applcons, Vol 6, o, pp 97-56, Assocon fo Scenfc Resech ERMITE SERIES SOLUTIOS OF LIEAR FREDOLM ITEGRAL EQUATIOS Slh Ylçınbş nd Müge Angül Depmen of Mhemcs, Fcul of Scence nd As, Cell
SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β
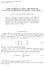 SARAJEVO JOURNAL OF MATHEMATICS Vol.3 (15) (2007), 137 143 SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β M. A. K. BAIG AND RAYEES AHMAD DAR Absrac. In hs paper, we propose
SARAJEVO JOURNAL OF MATHEMATICS Vol.3 (15) (2007), 137 143 SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β M. A. K. BAIG AND RAYEES AHMAD DAR Absrac. In hs paper, we propose
Query Data With Fuzzy Information In Object- Oriented Databases An Approach The Semantic Neighborhood Of Hedge Algebras
 (IJCSIS) Inernonl Journl of Compuer Scence nd Informon Secury, Vol 9, No 5, My 20 Query D Wh Fuzzy Informon In Obec- Orened Dbses An Approch The Semnc Neghborhood Of edge Algebrs Don Vn Thng Kore-VeNm
(IJCSIS) Inernonl Journl of Compuer Scence nd Informon Secury, Vol 9, No 5, My 20 Query D Wh Fuzzy Informon In Obec- Orened Dbses An Approch The Semnc Neghborhood Of edge Algebrs Don Vn Thng Kore-VeNm
Principle Component Analysis
 Prncple Component Anlyss Jng Go SUNY Bufflo Why Dmensonlty Reducton? We hve too mny dmensons o reson bout or obtn nsghts from o vsulze oo much nose n the dt Need to reduce them to smller set of fctors
Prncple Component Anlyss Jng Go SUNY Bufflo Why Dmensonlty Reducton? We hve too mny dmensons o reson bout or obtn nsghts from o vsulze oo much nose n the dt Need to reduce them to smller set of fctors
Privacy-Preserving Bayesian Network Parameter Learning
 4h WSEAS In. Conf. on COMUTATIONAL INTELLIGENCE, MAN-MACHINE SYSTEMS nd CYBERNETICS Mm, Flord, USA, November 7-9, 005 pp46-5) rvcy-reservng Byesn Nework rmeer Lernng JIANJIE MA. SIVAUMAR School of EECS,
4h WSEAS In. Conf. on COMUTATIONAL INTELLIGENCE, MAN-MACHINE SYSTEMS nd CYBERNETICS Mm, Flord, USA, November 7-9, 005 pp46-5) rvcy-reservng Byesn Nework rmeer Lernng JIANJIE MA. SIVAUMAR School of EECS,
P R = P 0. The system is shown on the next figure:
 TPG460 Reservor Smulaon 08 page of INTRODUCTION TO RESERVOIR SIMULATION Analycal and numercal soluons of smple one-dmensonal, one-phase flow equaons As an nroducon o reservor smulaon, we wll revew he smples
TPG460 Reservor Smulaon 08 page of INTRODUCTION TO RESERVOIR SIMULATION Analycal and numercal soluons of smple one-dmensonal, one-phase flow equaons As an nroducon o reservor smulaon, we wll revew he smples
THE PREDICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS
 THE PREICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS INTROUCTION The wo dmensonal paral dfferenal equaons of second order can be used for he smulaon of compeve envronmen n busness The arcle presens he
THE PREICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS INTROUCTION The wo dmensonal paral dfferenal equaons of second order can be used for he smulaon of compeve envronmen n busness The arcle presens he
Should Exact Index Numbers have Standard Errors? Theory and Application to Asian Growth
 Should Exac Index umbers have Sandard Errors? Theory and Applcaon o Asan Growh Rober C. Feensra Marshall B. Rensdorf ovember 003 Proof of Proposon APPEDIX () Frs, we wll derve he convenonal Sao-Vara prce
Should Exac Index umbers have Sandard Errors? Theory and Applcaon o Asan Growh Rober C. Feensra Marshall B. Rensdorf ovember 003 Proof of Proposon APPEDIX () Frs, we wll derve he convenonal Sao-Vara prce
Scattering at an Interface: Oblique Incidence
 Course Insrucor Dr. Raymond C. Rumpf Offce: A 337 Phone: (915) 747 6958 E Mal: rcrumpf@uep.edu EE 4347 Appled Elecromagnecs Topc 3g Scaerng a an Inerface: Oblque Incdence Scaerng These Oblque noes may
Course Insrucor Dr. Raymond C. Rumpf Offce: A 337 Phone: (915) 747 6958 E Mal: rcrumpf@uep.edu EE 4347 Appled Elecromagnecs Topc 3g Scaerng a an Inerface: Oblque Incdence Scaerng These Oblque noes may
Lecture 18: The Laplace Transform (See Sections and 14.7 in Boas)
 Lecure 8: The Lalace Transform (See Secons 88- and 47 n Boas) Recall ha our bg-cure goal s he analyss of he dfferenal equaon, ax bx cx F, where we emloy varous exansons for he drvng funcon F deendng on
Lecure 8: The Lalace Transform (See Secons 88- and 47 n Boas) Recall ha our bg-cure goal s he analyss of he dfferenal equaon, ax bx cx F, where we emloy varous exansons for he drvng funcon F deendng on
Lecture 2 M/G/1 queues. M/G/1-queue
 Lecure M/G/ queues M/G/-queue Posson arrval process Arbrary servce me dsrbuon Sngle server To deermne he sae of he sysem a me, we mus now The number of cusomers n he sysems N() Tme ha he cusomer currenly
Lecure M/G/ queues M/G/-queue Posson arrval process Arbrary servce me dsrbuon Sngle server To deermne he sae of he sysem a me, we mus now The number of cusomers n he sysems N() Tme ha he cusomer currenly
2.1 Constitutive Theory
 Secon.. Consuve Theory.. Consuve Equaons Governng Equaons The equaons governng he behavour of maerals are (n he spaal form) dρ v & ρ + ρdv v = + ρ = Conservaon of Mass (..a) d x σ j dv dvσ + b = ρ v& +
Secon.. Consuve Theory.. Consuve Equaons Governng Equaons The equaons governng he behavour of maerals are (n he spaal form) dρ v & ρ + ρdv v = + ρ = Conservaon of Mass (..a) d x σ j dv dvσ + b = ρ v& +
Motion Feature Extraction Scheme for Content-based Video Retrieval
 oon Feure Exrcon Scheme for Conen-bsed Vdeo Rerevl Chun Wu *, Yuwen He, L Zho, Yuzhuo Zhong Deprmen of Compuer Scence nd Technology, Tsnghu Unversy, Bejng 100084, Chn ABSTRACT Ths pper proposes he exrcon
oon Feure Exrcon Scheme for Conen-bsed Vdeo Rerevl Chun Wu *, Yuwen He, L Zho, Yuzhuo Zhong Deprmen of Compuer Scence nd Technology, Tsnghu Unversy, Bejng 100084, Chn ABSTRACT Ths pper proposes he exrcon
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
. The geometric multiplicity is dim[ker( λi. number of linearly independent eigenvectors associated with this eigenvalue.
 Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
Comparison of Differences between Power Means 1
 In. Journal of Mah. Analyss, Vol. 7, 203, no., 5-55 Comparson of Dfferences beween Power Means Chang-An Tan, Guanghua Sh and Fe Zuo College of Mahemacs and Informaon Scence Henan Normal Unversy, 453007,
In. Journal of Mah. Analyss, Vol. 7, 203, no., 5-55 Comparson of Dfferences beween Power Means Chang-An Tan, Guanghua Sh and Fe Zuo College of Mahemacs and Informaon Scence Henan Normal Unversy, 453007,
Lump Solutions to a Jimbo-Miwa Like Equations
 Lump Soluons o Jmbo-Mw Lke Equons Hrun-Or-Roshd * M. Zulkr Al b Deprmen o Mhemcs Pbn Unvers o Scence nd Technolog Bngldesh b Deprmen o Mhemcs Rjshh Unvers Bngldesh * Eml: hrunorroshdmd@gml.com Absrc A
Lump Soluons o Jmbo-Mw Lke Equons Hrun-Or-Roshd * M. Zulkr Al b Deprmen o Mhemcs Pbn Unvers o Scence nd Technolog Bngldesh b Deprmen o Mhemcs Rjshh Unvers Bngldesh * Eml: hrunorroshdmd@gml.com Absrc A
Electromagnetic Transient Simulation of Large Power Transformer Internal Fault
 Inernonl Conference on Advnces n Energy nd Envronmenl Scence (ICAEES 5) Elecromgnec Trnsen Smulon of rge Power Trnsformer Inernl Ful Jun u,, Shwu Xo,, Qngsen Sun,c, Huxng Wng,d nd e Yng,e School of Elecrcl
Inernonl Conference on Advnces n Energy nd Envronmenl Scence (ICAEES 5) Elecromgnec Trnsen Smulon of rge Power Trnsformer Inernl Ful Jun u,, Shwu Xo,, Qngsen Sun,c, Huxng Wng,d nd e Yng,e School of Elecrcl
. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.
![. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue. . The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.](/thumbs/78/77822798.jpg) Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
Background and Motivation: Importance of Pressure Measurements
 Imornce of Pressre Mesremens: Pressre s rmry concern for mny engneerng lcons e.g. lf nd form drg. Cvon : Pressre s of fndmenl mornce n ndersndng nd modelng cvon. Trblence: Velocy-Pressre-Grden ensor whch
Imornce of Pressre Mesremens: Pressre s rmry concern for mny engneerng lcons e.g. lf nd form drg. Cvon : Pressre s of fndmenl mornce n ndersndng nd modelng cvon. Trblence: Velocy-Pressre-Grden ensor whch
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
Convergence of Singular Integral Operators in Weighted Lebesgue Spaces
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
New M-Estimator Objective Function. in Simultaneous Equations Model. (A Comparative Study)
 Inernaonal Mahemacal Forum, Vol. 8, 3, no., 7 - HIKARI Ld, www.m-hkar.com hp://dx.do.org/.988/mf.3.3488 New M-Esmaor Objecve Funcon n Smulaneous Equaons Model (A Comparave Sudy) Ahmed H. Youssef Professor
Inernaonal Mahemacal Forum, Vol. 8, 3, no., 7 - HIKARI Ld, www.m-hkar.com hp://dx.do.org/.988/mf.3.3488 New M-Esmaor Objecve Funcon n Smulaneous Equaons Model (A Comparave Sudy) Ahmed H. Youssef Professor
2/20/2013. EE 101 Midterm 2 Review
 //3 EE Mderm eew //3 Volage-mplfer Model The npu ressance s he equalen ressance see when lookng no he npu ermnals of he amplfer. o s he oupu ressance. I causes he oupu olage o decrease as he load ressance
//3 EE Mderm eew //3 Volage-mplfer Model The npu ressance s he equalen ressance see when lookng no he npu ermnals of he amplfer. o s he oupu ressance. I causes he oupu olage o decrease as he load ressance
Review: Transformations. Transformations - Viewing. Transformations - Modeling. world CAMERA OBJECT WORLD CSE 681 CSE 681 CSE 681 CSE 681
 Revew: Trnsforons Trnsforons Modelng rnsforons buld cople odels b posonng (rnsforng sple coponens relve o ech oher ewng rnsforons plcng vrul cer n he world rnsforon fro world coordnes o cer coordnes Perspecve
Revew: Trnsforons Trnsforons Modelng rnsforons buld cople odels b posonng (rnsforng sple coponens relve o ech oher ewng rnsforons plcng vrul cer n he world rnsforon fro world coordnes o cer coordnes Perspecve
FTCS Solution to the Heat Equation
 FTCS Soluon o he Hea Equaon ME 448/548 Noes Gerald Reckenwald Porland Sae Unversy Deparmen of Mechancal Engneerng gerry@pdxedu ME 448/548: FTCS Soluon o he Hea Equaon Overvew Use he forward fne d erence
FTCS Soluon o he Hea Equaon ME 448/548 Noes Gerald Reckenwald Porland Sae Unversy Deparmen of Mechancal Engneerng gerry@pdxedu ME 448/548: FTCS Soluon o he Hea Equaon Overvew Use he forward fne d erence
( ) [ ] MAP Decision Rule
![( ) [ ] MAP Decision Rule ( ) [ ] MAP Decision Rule](/thumbs/82/84970741.jpg) Announcemens Bayes Decson Theory wh Normal Dsrbuons HW0 due oday HW o be assgned soon Proec descrpon posed Bomercs CSE 90 Lecure 4 CSE90, Sprng 04 CSE90, Sprng 04 Key Probables 4 ω class label X feaure
Announcemens Bayes Decson Theory wh Normal Dsrbuons HW0 due oday HW o be assgned soon Proec descrpon posed Bomercs CSE 90 Lecure 4 CSE90, Sprng 04 CSE90, Sprng 04 Key Probables 4 ω class label X feaure
Method of upper lower solutions for nonlinear system of fractional differential equations and applications
 Malaya Journal of Maemak, Vol. 6, No. 3, 467-472, 218 hps://do.org/1.26637/mjm63/1 Mehod of upper lower soluons for nonlnear sysem of fraconal dfferenal equaons and applcaons D.B. Dhagude1 *, N.B. Jadhav2
Malaya Journal of Maemak, Vol. 6, No. 3, 467-472, 218 hps://do.org/1.26637/mjm63/1 Mehod of upper lower soluons for nonlnear sysem of fraconal dfferenal equaons and applcaons D.B. Dhagude1 *, N.B. Jadhav2
Software Reliability Growth Models Incorporating Fault Dependency with Various Debugging Time Lags
 Sofwre Relbly Growh Models Incorporng Ful Dependency wh Vrous Debuggng Tme Lgs Chn-Yu Hung 1 Chu-T Ln 1 Sy-Yen Kuo Mchel R. Lyu 3 nd Chun-Chng Sue 4 1 Deprmen of Compuer Scence Nonl Tsng Hu Unversy Hsnchu
Sofwre Relbly Growh Models Incorporng Ful Dependency wh Vrous Debuggng Tme Lgs Chn-Yu Hung 1 Chu-T Ln 1 Sy-Yen Kuo Mchel R. Lyu 3 nd Chun-Chng Sue 4 1 Deprmen of Compuer Scence Nonl Tsng Hu Unversy Hsnchu
Applied Statistics Qualifier Examination
 Appled Sttstcs Qulfer Exmnton Qul_june_8 Fll 8 Instructons: () The exmnton contns 4 Questons. You re to nswer 3 out of 4 of them. () You my use ny books nd clss notes tht you mght fnd helpful n solvng
Appled Sttstcs Qulfer Exmnton Qul_june_8 Fll 8 Instructons: () The exmnton contns 4 Questons. You re to nswer 3 out of 4 of them. () You my use ny books nd clss notes tht you mght fnd helpful n solvng
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 0 Canoncal Transformaons (Chaper 9) Wha We Dd Las Tme Hamlon s Prncple n he Hamlonan formalsm Dervaon was smple δi δ Addonal end-pon consrans pq H( q, p, ) d 0 δ q ( ) δq ( ) δ
Mechancs Physcs 5 Lecure 0 Canoncal Transformaons (Chaper 9) Wha We Dd Las Tme Hamlon s Prncple n he Hamlonan formalsm Dervaon was smple δi δ Addonal end-pon consrans pq H( q, p, ) d 0 δ q ( ) δq ( ) δ
Relative controllability of nonlinear systems with delays in control
 Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
How about the more general "linear" scalar functions of scalars (i.e., a 1st degree polynomial of the following form with a constant term )?
 lmcd Lnear ransformaon of a vecor he deas presened here are que general hey go beyond he radonal mar-vecor ype seen n lnear algebra Furhermore, hey do no deal wh bass and are equally vald for any se of
lmcd Lnear ransformaon of a vecor he deas presened here are que general hey go beyond he radonal mar-vecor ype seen n lnear algebra Furhermore, hey do no deal wh bass and are equally vald for any se of
Katholieke Universiteit Leuven Department of Computer Science
 Updte Rules for Weghted Non-negtve FH*G Fctorzton Peter Peers Phlp Dutré Report CW 440, Aprl 006 Ktholeke Unverstet Leuven Deprtment of Computer Scence Celestjnenln 00A B-3001 Heverlee (Belgum) Updte Rules
Updte Rules for Weghted Non-negtve FH*G Fctorzton Peter Peers Phlp Dutré Report CW 440, Aprl 006 Ktholeke Unverstet Leuven Deprtment of Computer Scence Celestjnenln 00A B-3001 Heverlee (Belgum) Updte Rules
Existence of Time Periodic Solutions for the Ginzburg-Landau Equations. model of superconductivity
 Journal of Mahemacal Analyss and Applcaons 3, 3944 999 Arcle ID jmaa.999.683, avalable onlne a hp:www.dealbrary.com on Exsence of me Perodc Soluons for he Gnzburg-Landau Equaons of Superconducvy Bxang
Journal of Mahemacal Analyss and Applcaons 3, 3944 999 Arcle ID jmaa.999.683, avalable onlne a hp:www.dealbrary.com on Exsence of me Perodc Soluons for he Gnzburg-Landau Equaons of Superconducvy Bxang
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
Motion in Two Dimensions
 Phys 1 Chaper 4 Moon n Two Dmensons adzyubenko@csub.edu hp://www.csub.edu/~adzyubenko 005, 014 A. Dzyubenko 004 Brooks/Cole 1 Dsplacemen as a Vecor The poson of an objec s descrbed by s poson ecor, r The
Phys 1 Chaper 4 Moon n Two Dmensons adzyubenko@csub.edu hp://www.csub.edu/~adzyubenko 005, 014 A. Dzyubenko 004 Brooks/Cole 1 Dsplacemen as a Vecor The poson of an objec s descrbed by s poson ecor, r The
Chapter 2: Evaluative Feedback
 Chper 2: Evluive Feedbck Evluing cions vs. insrucing by giving correc cions Pure evluive feedbck depends olly on he cion ken. Pure insrucive feedbck depends no ll on he cion ken. Supervised lerning is
Chper 2: Evluive Feedbck Evluing cions vs. insrucing by giving correc cions Pure evluive feedbck depends olly on he cion ken. Pure insrucive feedbck depends no ll on he cion ken. Supervised lerning is
Online Supplement for Dynamic Multi-Technology. Production-Inventory Problem with Emissions Trading
 Onlne Supplemen for Dynamc Mul-Technology Producon-Invenory Problem wh Emssons Tradng by We Zhang Zhongsheng Hua Yu Xa and Baofeng Huo Proof of Lemma For any ( qr ) Θ s easy o verfy ha he lnear programmng
Onlne Supplemen for Dynamc Mul-Technology Producon-Invenory Problem wh Emssons Tradng by We Zhang Zhongsheng Hua Yu Xa and Baofeng Huo Proof of Lemma For any ( qr ) Θ s easy o verfy ha he lnear programmng
Fractional Quantum Field Theory on Multifractals Sets
 Amercn J. of Engneerng nd Appled Scences 4 (): 33-4, 2 ISSN 94-72 2 Scence Publcons Frconl Qunum Feld Theory on Mulfrcls Ses El-Nbuls Ahmd Rm Deprmen of Nucler nd Energy Engneerng, Cheju Nonl Unversy,
Amercn J. of Engneerng nd Appled Scences 4 (): 33-4, 2 ISSN 94-72 2 Scence Publcons Frconl Qunum Feld Theory on Mulfrcls Ses El-Nbuls Ahmd Rm Deprmen of Nucler nd Energy Engneerng, Cheju Nonl Unversy,
CHOVER-TYPE LAWS OF THE ITERATED LOGARITHM FOR WEIGHTED SUMS OF ρ -MIXING SEQUENCES
 CHOVER-TYPE LAWS OF THE ITERATED LOGARITHM FOR WEIGHTED SUMS OF ρ -MIXING SEQUENCES GUANG-HUI CAI Receved 24 September 2004; Revsed 3 My 2005; Accepted 3 My 2005 To derve Bum-Ktz-type result, we estblsh
CHOVER-TYPE LAWS OF THE ITERATED LOGARITHM FOR WEIGHTED SUMS OF ρ -MIXING SEQUENCES GUANG-HUI CAI Receved 24 September 2004; Revsed 3 My 2005; Accepted 3 My 2005 To derve Bum-Ktz-type result, we estblsh
MODELLING AND EXPERIMENTAL ANALYSIS OF MOTORCYCLE DYNAMICS USING MATLAB
 MODELLING AND EXPERIMENTAL ANALYSIS OF MOTORCYCLE DYNAMICS USING MATLAB P. Florn, P. Vrání, R. Čermá Fculy of Mechncl Engneerng, Unversy of Wes Bohem Asrc The frs pr of hs pper s devoed o mhemcl modellng
MODELLING AND EXPERIMENTAL ANALYSIS OF MOTORCYCLE DYNAMICS USING MATLAB P. Florn, P. Vrání, R. Čermá Fculy of Mechncl Engneerng, Unversy of Wes Bohem Asrc The frs pr of hs pper s devoed o mhemcl modellng
Epistemic Game Theory: Online Appendix
 Epsemc Game Theory: Onlne Appendx Edde Dekel Lucano Pomao Marcano Snscalch July 18, 2014 Prelmnares Fx a fne ype srucure T I, S, T, β I and a probably µ S T. Le T µ I, S, T µ, βµ I be a ype srucure ha
Epsemc Game Theory: Onlne Appendx Edde Dekel Lucano Pomao Marcano Snscalch July 18, 2014 Prelmnares Fx a fne ype srucure T I, S, T, β I and a probably µ S T. Le T µ I, S, T µ, βµ I be a ype srucure ha
Lecture 9: Dynamic Properties
 Shor Course on Molecular Dynamcs Smulaon Lecure 9: Dynamc Properes Professor A. Marn Purdue Unversy Hgh Level Course Oulne 1. MD Bascs. Poenal Energy Funcons 3. Inegraon Algorhms 4. Temperaure Conrol 5.
Shor Course on Molecular Dynamcs Smulaon Lecure 9: Dynamc Properes Professor A. Marn Purdue Unversy Hgh Level Course Oulne 1. MD Bascs. Poenal Energy Funcons 3. Inegraon Algorhms 4. Temperaure Conrol 5.
