Integrable billiards, Poncelet-Darboux grids and Kowalevski top
|
|
|
- Lucas Spencer
- 6 years ago
- Views:
Transcription
1 Integrable billiards, Poncelet-Darboux grids and Kowalevski top Vladimir Dragović Math. Phys. Group, University of Lisbon Lisbon-Austin conference University of Texas, Austin, 3 April 2010
2 Contents 1 Sophie s world 2 Billiard within ellipse 3 Generalization of the Darboux theorem 4 Higher-dimensional generalization of the Darboux theorem 5 A new view on the Kowalevski top 6 Kowalevski top and Buchstaber-Novikov multi-valued groups
3 Sophie s world Софья Васильевна Ковалевская,
4 Sophie s world: the story of the history of integrability Acta Mathematica, 1889
5 Addition Theorems sin(x + y) = sinx cos y + cos x sin y cos(x + y) = cos x cos y sin x sin y sn(x + y) = cn (x + y) = snx cny dny + sny cn x dnx 1 k 2 sn 2 x sn 2 y cnx cn y snx sny dnx dn y 1 k 2 sn 2 x sn 2 y (x + y) = (x) (y) ( (x) ) (y) 2 (x) (y)
6 The Quantum Yang-Baxter Equation R 12 (t 1 t 2,h)R 13 (t 1,h)R 23 (t 2,h) = R 23 (t 2,h)(R 13 (t 1,h)R 12 (t 1 t 2,h) R ij (t,h) : V V V V V V t spectral parameter h Planck constant
7 The Euler-Chasles correspondence E : ax 2 y 2 + b(x 2 y + xy 2 ) + c(x 2 + y 2 ) + 2dxy + e(x + y) + f = 0
8 The Euler-Chasles correspondence The Euler equation dx p4 (x) ± dy p4 (y) = 0 Poncelet theorem for triangles
9 Elliptical Billiard
10 Billiard within ellipse A trajectory of a billirad within an ellipse is a polygonal line with vertices on the ellipse, such that successive edges satisfy the billiard reflection law: the edges form equal angles with the to the ellipse at the common vertex.
11 Focal property of ellipses
12 Focal property of ellipses
13 Caustics of billiard trajectories
14 Poncelet theorem (Jean Victor Poncelet, 1813.) Let C and D be two given conics in the plane. Suppose there exists a closed polygonal line inscribed in C and circumscribed about D. Then, there are infinitely many such polygonal lines and all of them have the same number of edges. Moreover, every point of the conic C is a vertex of one of these lines.
15 Mechanical interpretation of the Poncelet theorem Let us consider closed trajectory of billiard system within ellipse E. Then every billiard trajectory within E, which has the same caustic as the given closed one, is also closed. Moreover, all these trajectories are closed with the same number of reflections at E.
16 Nonperiodic billiard trajectories
17 Generalization of the Darboux theorem Тheorem [V. D., M. Radnović (2008)] Let E be an ellipse in E 2 and (a m ) m Z, (b m ) m Z be two sequences of the segments of billiard trajectories E, sharing the same caustic. Then all the points a m b m (m Z) belong to one conic K, confocal with E.
18 Moreover, under the additional assumption that the caustic is an ellipse, we have: if both trajectories are winding in the same direction about the caustic, then K is also an ellipse; if the trajectories are winding in opposite directions, then K is a hyperbola.
19 For a hyperbola as a caustic, it holds: if segments a m, b m intersect the long axis of E in the same direction, then K is a hyperbola, otherwise it is an ellipse.
20 Grids in arbitrary dimension Тheorem [V. D., M. Radnović (2008)] Let (a m ) m Z, (b m ) m Z be two sequences of the segments of billiard trajectories within the ellipsoid E in E d, sharing the same d 1 caustics. Suppose the pair (a 0,b 0 ) is s-skew, and that by the sequence of reflections on quadrics Q 1,..., Q s+1 the minimal billiard trajectory connecting a 0 to b 0 is realized. Then, each pair (a m,b m ) is s-skew, and the minimal billiard trajectory connecting these two lines is determined by the sequence of reflections on the same quadrics Q 1,...,Q s+1.
21 Кandinsky, Grid 1923.
22 Pencil of conics Two conics and tangential pencil C 1 : a 0 w a 2w a 4w a 3w 2 w 3 + 2a 5 w 1 w 3 + 2a 1 w 1 w 2 = 0 C 2 : w 2 2 4w 1w 3 = 0 Coordinate pencil F(s,z 1,z 2,z 3 ) := det M(s,z 1,z 2,z 3 ) = 0 M(s,z 1,z 2,z 3 ) = F := H + Ks + Ls 2 = 0 0 z 1 z 2 z 3 z 1 a 0 a 1 a 5 2s z 2 a 1 a 2 + s a 3 z 3 a 5 2s a 3 a 4
23 Darboux coordinates t C2 (l 0 ) : z 1 l 2 0 2z 2 l 0 + z 3 = 0 ẑ 1 l 2 2ẑ 2 l + ẑ 3 = 0 ẑ 1 = 1, ẑ 2 = x 1 + x 2, ẑ 3 = x 1 x 2 2 F(s, x 1,x 2 ) = L(x 1,x 2 )s 2 + K(x 1,x 2 )s + H(x 1,x 2 ) H(x 1, x 2 ) = (a 2 1 a 0a 2 )x 2 1 x2 2 + (a 0a 3 a 5 a 1 )x 1 x 2 (x 1 + x 2 ) + (a5 2 a 0 a 4 )(x1 2 + x2) 2 + (2(a 5 a 2 a 1 a 3 ) (a2 5 a 0 a 4 )x 1 x 2 + (a 1 a 4 a 3 a 5 ))(x 1 + x 2 ) + a3 2 a 2a 4 K(x 1, x 2 ) = a 0 x1 2 x a 1x 1 x 2 (x 1 + x 2 ) a 5 (x1 2 + x2 2 ) 4a 2x 1 x 2 + 2a 3 (x 1 + x 2 ) a 4 L(x 1, x 2 ) = (x 1 x 2 ) 2
24 Тheorem [V. D. (2009)] (i) There exists a polynomial P = P(x) such that the discriminant of the polynomial F in s as a polynomial in variables x 1 and x 2 separates the variables: D s (F)(x 1,x 2 ) = P(x 1 )P(x 2 ). (1) (ii) There exists a polynomial J = J(s) such that the discriminant of the polynomial F in x 2 as a polynomial in variables x 1 and s separates the variables: D x2 (F)(s,x 1 ) = J(s)P(x 1 ). (2) Due to the symmetry between x 1 and x 2 the last statement remains valid after exchanging the places of x 1 and x 2.
25 Lemma Given a polynomial S = S(x,y,z) of the second degree in each of its variables in the form: S(x,y,z) = A(y,z)x 2 + 2B(y,z)x + C(y,z). If there are polynomials P 1 and P 2 of the fourth degree such that B(y,z) 2 A(y,z)C(y,z) = P 1 (y)p 2 (z), (3) then there exists a polynomial f such that D y S(x,z) = f (x)p 2 (z), D z S(x,y) = f (x)p 1 (y).
26 Gauge equivalence Gauge transformations x a 1x + b 1 c 1 x + d 1 y a 2y + b 2 c 2 y + d 2 z a 3z + b 3 c 3 z + d 3
27 Discriminantly separable polynomials definition For a polynomial F(x 1,...,x n ) we say that it is discriminantly separable if there exist polynomials f i (x i ) such that for every i = 1,...,n D xi F(x 1,..., ˆx i,...,x n ) = j i f j (x j ). It is symmetrically discriminantly separable if f 2 = f 3 = = f n, while it is strongly discriminatly separable if f 1 = f 2 = f 3 = = f n. It is weakly discriminantly separable if there exist polynomials f j i (x i) such that for every i = 1,...,n D xi F(x 1,..., ˆx i,...,x n ) = j i f i j (x j ).
28 Тheorem [V. D. (2009)] Given a polynomial F(s,x 1,x 2 ) of the second degree in each of the variables s,x 1,x 2 of the form F = s 2 A(x 1,x 2 ) + 2B(x 1,x 2 )s + C(x 1,x 2 ). Denote by T B 2 AC a 5 5 matrix such that (B 2 AC)(x 1,x 2 ) = 5 5 j=1 i=1 T ij B 2 AC xi 1 1 x j 1 2. Then, polynomial F is discriminantly separable if and only if rank T B 2 AC = 1.
29 Geometric interpretation of the Kowalevski fundamental equation Q(w,x 1,x 2 ) := (x 1 x 2 ) 2 w 2 2R(x 1,x 2 )w R 1 (x 1,x 2 ) = 0 R(x 1,x 2 ) = x 2 1x l 1 x 1 x 2 + 2lc(x 1 + x 2 ) + c 2 k 2 R 1 (x 1,x 2 ) = 6l 1 x 2 1x 2 2 (c 2 k 2 )(x 1 + x 2 ) 2 4clx 1 x 2 (x 1 + x 2 ) + 6l 1 (c 2 k 2 ) 4c 2 l 2 a 0 = 2 a 1 = 0 a 5 = 0 a 2 = 3l 1 a 3 = 2cl a 4 = 2(c 2 k 2 )
30 Geometric interpretation of the Kowalevski fundamental equation Тhеоrem [V. D. (2009)] The Kowalevski fundamental equation represents a point pencil of conics given by their tangential equations Ĉ 1 : 2w l 1w (c2 k 2 )w 2 3 4clw 2w 3 = 0; C 2 : w 2 2 4w 1w 3 = 0. The Kowalevski variables w,x 1,x 2 in this geometric settings are the pencil parameter, and the Darboux coordinates with respect to the conic C 2 respectively.
31 Multi-valued Buchstaber-Novikov groups n-valued group on X m : X X (X) n, m(x,y) = x y = [z 1,...,z n ] (X) n symmetric n-th power of X Associativity Equality of two n 2 -sets: [x (y z) 1,...,x (y z) n ] и [(x y) 1 z,...,(x y) n z] for every triplet (x,y,z) X 3. Unity e e x = x e = [x,...,x] for each x X. Inverse inv : X X e inv(x) x, e x inv(x) for each x X.
32 Multi-valued Buchstaber-Novikov groups Action of n-valued group X on the set Y Two n 2 -multi-subsets in Y : φ : X Y (Y ) n φ(x,y) = x y x 1 (x 2 y) и (x 1 x 2 ) y are equal for every triplet x 1,x 2 X, y Y. Additionally, we assume: for each y Y. e y = [y,...,y]
33 Two-valued group on CP 1 The equation of a pencil F(s,x 1,x 2 ) = 0 Isomorphic elliptic curves Γ 1 : y 2 = P(x) deg P = 4 Γ 2 : t 2 = J(s) deg J = 3 Canonical equation of the curve Γ 2 Γ 2 : t 2 = J (s) = 4s 3 g 2 s g 3 Birational morphism of curves ψ : Γ 2 Γ 1 Induced by fractional-linear mapping ˆψ which maps zeros of the polynomial J and to the four zeros of the polynomial P.
34 Two-valued group on CP 1 There is a group structure on the cubic Γ 2. Together with its subgroup Z 2, it defines the standrad two-valued group structure on CP 1 : [ ( ) t1 t 2 ( ) ] 2 t1 + t 2 2 s 1 c s 2 = s 1 s 2 +, s 1 s 2 +, 2(s 1 s 2 ) 2(s 1 s 2 ) where t i = J (s i ), i = 1,2. Тheorem [V. D. (2009)] The general pencil equation after fractional-linear transformations F(s, ˆψ 1 (x 1 ), ˆψ 1 (x 2 )) = 0 defines the two valued coset group structure (Γ 2, Z 2 ).
35 i Γ1 i Γ1 id id Γ 1 Γ 1 C C ϕ 1 ϕ 2 C C i Γ1 i Γ1 m CP 1 C CP 1 C ψ 1 ψ 1 id C 4 Γ 1 Γ 1 C Γ 2 Γ 2 C i a i a m p 1 p 1 id ˆψ 1 ˆψ 1 id p 1 p 1 id m 2 CP 2 f m c τ c CP 2 C/
36 Two-valued group CP 1 Тhеоrem [V. D. (2009)] Associativity conditions for the group structure of the two-valued coset group (Γ 2, Z 2 ) and for its action on Γ 1 are equivalent to the great Poncelet theorem for a triangle.
37 Experimental Math Other n-valued groups p 3 = s s 3 Dp 3 = y 2 x 2 (x y) 2. p 4 = s s 2 1s s s 1 s 3 Dp 4 = y 3 x 3 (x y) 2 (y + 4x) 2 (4y + x) 2. p 5 = s s 2 1s s 2 s 3 Dp 5 = y 4 x 4 (x y) 4 ( y 2 11xy + x 2 ) 2 ( y xy + x 2 ) 2.
38 References 1. V. Dragović, Geometrization and Generalization of the Ko walevski top, arxiv: , to appear in Comm. Math. Phys. 2. V. Dragović, M. Radnović Integrable Billiards and Quadrics Russian Math. Surveys, 2010, Vol. 65, no. 2 p V. Dragović, Marden theorem and Poncelet-Darboux curves arxiv: (2008) 4. V. Dragović, Multi-valued hyperelliptic continued fractions of generalized Halphen type, IMRN (2009) arxiv: V. Dragović, M. Radnović, Hyperelliptic Jacobians as Billiard Algebra of Pencils of Quadrics: Beyond Poncelet Porisms, Advances in Mathematics, 219 (2008) V. Dragović, M. Radnović, Geometry of integrable billiards and pencils of quadrics, Journal de Mathématiques Pures et Appliquées 85 (2006)
Hyperelliptic Jacobians as billiard algebra of pencils of quadrics: Beyond Poncelet porisms
 Advances in Mathematics 219 (2008) 1577 1607 www.elsevier.com/locate/aim Hyperelliptic Jacobians as billiard algebra of pencils of quadrics: Beyond Poncelet porisms Vladimir Dragović, Milena Radnović Mathematical
Advances in Mathematics 219 (2008) 1577 1607 www.elsevier.com/locate/aim Hyperelliptic Jacobians as billiard algebra of pencils of quadrics: Beyond Poncelet porisms Vladimir Dragović, Milena Radnović Mathematical
March Algebra 2 Question 1. March Algebra 2 Question 1
 March Algebra 2 Question 1 If the statement is always true for the domain, assign that part a 3. If it is sometimes true, assign it a 2. If it is never true, assign it a 1. Your answer for this question
March Algebra 2 Question 1 If the statement is always true for the domain, assign that part a 3. If it is sometimes true, assign it a 2. If it is never true, assign it a 1. Your answer for this question
An Elementary Proof of Poncelet s Theorem
 An Elementary Proof of Poncelet s Theorem (on the occasion to its bicentennial) Lorenz Halbeisen (University of Zürich) Norbert Hungerbühler (ETH Zürich) Abstract We present an elementary proof of Poncelet
An Elementary Proof of Poncelet s Theorem (on the occasion to its bicentennial) Lorenz Halbeisen (University of Zürich) Norbert Hungerbühler (ETH Zürich) Abstract We present an elementary proof of Poncelet
Rational Distance Sets on Conic Sections
 Rational Distance Sets on Conic Sections Megan D Ly Loyola Marymount Shawn E Tsosie UMASS Amherst July 010 Lyda P Urresta Union College Abstract Leonhard Euler noted that there exists an infinite set of
Rational Distance Sets on Conic Sections Megan D Ly Loyola Marymount Shawn E Tsosie UMASS Amherst July 010 Lyda P Urresta Union College Abstract Leonhard Euler noted that there exists an infinite set of
Periods of Pseudo-Integrable Billiards
 Arnold Math J. (2015) 1:69 73 DOI 10.1007/s40598-014-0004-0 PROBLEM CONTRIBUTION Periods of Pseudo-Integrable Billiards Vladimir Dragović Milena Radnović Received: 10 November 2014 / Accepted: 26 December
Arnold Math J. (2015) 1:69 73 DOI 10.1007/s40598-014-0004-0 PROBLEM CONTRIBUTION Periods of Pseudo-Integrable Billiards Vladimir Dragović Milena Radnović Received: 10 November 2014 / Accepted: 26 December
A NOTE ON BILLIARD SYSTEMS IN FINSLER PLANE WITH ELLIPTIC INDICATRICES. Milena Radnović
 PUBLICATIONS DE L INSTITUT MATHÉMATIQUE Nouvelle série, tome 74(88) (2003), 97 101 A NOTE ON BILLIARD SYSTEMS IN FINSLER PLANE WITH ELLIPTIC INDICATRICES Milena Radnović Communicated by Rade Živaljević
PUBLICATIONS DE L INSTITUT MATHÉMATIQUE Nouvelle série, tome 74(88) (2003), 97 101 A NOTE ON BILLIARD SYSTEMS IN FINSLER PLANE WITH ELLIPTIC INDICATRICES Milena Radnović Communicated by Rade Živaljević
The Poncelet grid and the billiard in an ellipse
 arxiv:math/0511009v1 [math.dg] 1 Nov 2005 The Poncelet grid and the billiard in an ellipse Mark Levi and Serge Tabachnikov Department of Mathematics, Penn State University University Park, PA 16802, USA
arxiv:math/0511009v1 [math.dg] 1 Nov 2005 The Poncelet grid and the billiard in an ellipse Mark Levi and Serge Tabachnikov Department of Mathematics, Penn State University University Park, PA 16802, USA
Conjugate conics and closed chains of Poncelet polygons
 Mitt. Math. Ges. Hamburg?? (????), 1 0 Conjugate conics and closed chains of Poncelet polygons Lorenz Halbeisen Department of Mathematics, ETH Zentrum, Rämistrasse 101, 8092 Zürich, Switzerland Norbert
Mitt. Math. Ges. Hamburg?? (????), 1 0 Conjugate conics and closed chains of Poncelet polygons Lorenz Halbeisen Department of Mathematics, ETH Zentrum, Rämistrasse 101, 8092 Zürich, Switzerland Norbert
Some Recent Generalizations of the Classical Rigid Body Systems
 Arnold Math J. (2016) 2:511 578 DOI 10.1007/s40598-016-0054-6 RESEARCH EXPOSITION Some Recent Generalizations of the Classical Rigid Body Systems Vladimir Dragović 1,2 Borislav Gajić 2 Received: 20 November
Arnold Math J. (2016) 2:511 578 DOI 10.1007/s40598-016-0054-6 RESEARCH EXPOSITION Some Recent Generalizations of the Classical Rigid Body Systems Vladimir Dragović 1,2 Borislav Gajić 2 Received: 20 November
Roots and Coefficients Polynomials Preliminary Maths Extension 1
 Preliminary Maths Extension Question If, and are the roots of x 5x x 0, find the following. (d) (e) Question If p, q and r are the roots of x x x 4 0, evaluate the following. pq r pq qr rp p q q r r p
Preliminary Maths Extension Question If, and are the roots of x 5x x 0, find the following. (d) (e) Question If p, q and r are the roots of x x x 4 0, evaluate the following. pq r pq qr rp p q q r r p
Structure of elliptic curves and addition laws
 Structure of elliptic curves and addition laws David R. Kohel Institut de Mathématiques de Luminy Barcelona 9 September 2010 Elliptic curve models We are interested in explicit projective models of elliptic
Structure of elliptic curves and addition laws David R. Kohel Institut de Mathématiques de Luminy Barcelona 9 September 2010 Elliptic curve models We are interested in explicit projective models of elliptic
Geometry of integrable billiards and pencils of quadrics
 J. Math. Pures Appl. 85 (2006) 758 790 www.elsevier.com/locate/matpur Geometry of integrable billiards and pencils of quadrics Vladimir Dragović a, Milena Radnović a,b, a Mathematical Institute SANU, Kneza
J. Math. Pures Appl. 85 (2006) 758 790 www.elsevier.com/locate/matpur Geometry of integrable billiards and pencils of quadrics Vladimir Dragović a, Milena Radnović a,b, a Mathematical Institute SANU, Kneza
Chapter 12 Review Vector. MATH 126 (Section 9.5) Vector and Scalar The University of Kansas 1 / 30
 Chapter 12 Review Vector MATH 126 (Section 9.5) Vector and Scalar The University of Kansas 1 / 30 iclicker 1: Let v = PQ where P = ( 2, 5) and Q = (1, 2). Which of the following vectors with the given
Chapter 12 Review Vector MATH 126 (Section 9.5) Vector and Scalar The University of Kansas 1 / 30 iclicker 1: Let v = PQ where P = ( 2, 5) and Q = (1, 2). Which of the following vectors with the given
x 3y 2z = 6 1.2) 2x 4y 3z = 8 3x + 6y + 8z = 5 x + 3y 2z + 5t = 4 1.5) 2x + 8y z + 9t = 9 3x + 5y 12z + 17t = 7
 Linear Algebra and its Applications-Lab 1 1) Use Gaussian elimination to solve the following systems x 1 + x 2 2x 3 + 4x 4 = 5 1.1) 2x 1 + 2x 2 3x 3 + x 4 = 3 3x 1 + 3x 2 4x 3 2x 4 = 1 x + y + 2z = 4 1.4)
Linear Algebra and its Applications-Lab 1 1) Use Gaussian elimination to solve the following systems x 1 + x 2 2x 3 + 4x 4 = 5 1.1) 2x 1 + 2x 2 3x 3 + x 4 = 3 3x 1 + 3x 2 4x 3 2x 4 = 1 x + y + 2z = 4 1.4)
TEST CODE: MMA (Objective type) 2015 SYLLABUS
 TEST CODE: MMA (Objective type) 2015 SYLLABUS Analytical Reasoning Algebra Arithmetic, geometric and harmonic progression. Continued fractions. Elementary combinatorics: Permutations and combinations,
TEST CODE: MMA (Objective type) 2015 SYLLABUS Analytical Reasoning Algebra Arithmetic, geometric and harmonic progression. Continued fractions. Elementary combinatorics: Permutations and combinations,
1. Projective geometry
 1. Projective geometry Homogeneous representation of points and lines in D space D projective space Points at infinity and the line at infinity Conics and dual conics Projective transformation Hierarchy
1. Projective geometry Homogeneous representation of points and lines in D space D projective space Points at infinity and the line at infinity Conics and dual conics Projective transformation Hierarchy
TEST CODE: MIII (Objective type) 2010 SYLLABUS
 TEST CODE: MIII (Objective type) 200 SYLLABUS Algebra Permutations and combinations. Binomial theorem. Theory of equations. Inequalities. Complex numbers and De Moivre s theorem. Elementary set theory.
TEST CODE: MIII (Objective type) 200 SYLLABUS Algebra Permutations and combinations. Binomial theorem. Theory of equations. Inequalities. Complex numbers and De Moivre s theorem. Elementary set theory.
Things You Should Know Coming Into Calc I
 Things You Should Know Coming Into Calc I Algebraic Rules, Properties, Formulas, Ideas and Processes: 1) Rules and Properties of Exponents. Let x and y be positive real numbers, let a and b represent real
Things You Should Know Coming Into Calc I Algebraic Rules, Properties, Formulas, Ideas and Processes: 1) Rules and Properties of Exponents. Let x and y be positive real numbers, let a and b represent real
Exercise Sheet 7 - Solutions
 Algebraic Geometry D-MATH, FS 2016 Prof. Pandharipande Exercise Sheet 7 - Solutions 1. Prove that the Zariski tangent space at the point [S] Gr(r, V ) is canonically isomorphic to S V/S (or equivalently
Algebraic Geometry D-MATH, FS 2016 Prof. Pandharipande Exercise Sheet 7 - Solutions 1. Prove that the Zariski tangent space at the point [S] Gr(r, V ) is canonically isomorphic to S V/S (or equivalently
On Cayley conditions for billiards inside ellipsoids
 London Mathematical Society Nonlinearity Nonlinearity 27 (2014) 1003 1028 doi:10.1088/0951-7715/27/5/1003 On Cayley conditions for billiards inside ellipsoids Rafael Ramírez-Ros Departament de Matemàtica
London Mathematical Society Nonlinearity Nonlinearity 27 (2014) 1003 1028 doi:10.1088/0951-7715/27/5/1003 On Cayley conditions for billiards inside ellipsoids Rafael Ramírez-Ros Departament de Matemàtica
Dynamical billiards 1
 Dynamical billiards 1 Vladimir Georgiev, Irena Georgieva, Veneta Nedyalkova 1 Short introduction Dynamical billiard is a dynamical system corresponding to the inertial motion of a point mass within a region
Dynamical billiards 1 Vladimir Georgiev, Irena Georgieva, Veneta Nedyalkova 1 Short introduction Dynamical billiard is a dynamical system corresponding to the inertial motion of a point mass within a region
, a 1. , a 2. ,..., a n
 CHAPTER Points to Remember :. Let x be a variable, n be a positive integer and a 0, a, a,..., a n be constants. Then n f ( x) a x a x... a x a, is called a polynomial in variable x. n n n 0 POLNOMIALS.
CHAPTER Points to Remember :. Let x be a variable, n be a positive integer and a 0, a, a,..., a n be constants. Then n f ( x) a x a x... a x a, is called a polynomial in variable x. n n n 0 POLNOMIALS.
Local properties of plane algebraic curves
 Chapter 7 Local properties of plane algebraic curves Throughout this chapter let K be an algebraically closed field of characteristic zero, and as usual let A (K) be embedded into P (K) by identifying
Chapter 7 Local properties of plane algebraic curves Throughout this chapter let K be an algebraically closed field of characteristic zero, and as usual let A (K) be embedded into P (K) by identifying
Week Quadratic forms. Principal axes theorem. Text reference: this material corresponds to parts of sections 5.5, 8.2,
 Math 051 W008 Margo Kondratieva Week 10-11 Quadratic forms Principal axes theorem Text reference: this material corresponds to parts of sections 55, 8, 83 89 Section 41 Motivation and introduction Consider
Math 051 W008 Margo Kondratieva Week 10-11 Quadratic forms Principal axes theorem Text reference: this material corresponds to parts of sections 55, 8, 83 89 Section 41 Motivation and introduction Consider
b n x n + b n 1 x n b 1 x + b 0
 Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Dr. Sophie Marques. MAM1020S Tutorial 8 August Divide. 1. 6x 2 + x 15 by 3x + 5. Solution: Do a long division show your work.
 Dr. Sophie Marques MAM100S Tutorial 8 August 017 1. Divide 1. 6x + x 15 by 3x + 5. 6x + x 15 = (x 3)(3x + 5) + 0. 1a 4 17a 3 + 9a + 7a 6 by 3a 1a 4 17a 3 + 9a + 7a 6 = (4a 3 3a + a + 3)(3a ) + 0 3. 1a
Dr. Sophie Marques MAM100S Tutorial 8 August 017 1. Divide 1. 6x + x 15 by 3x + 5. 6x + x 15 = (x 3)(3x + 5) + 0. 1a 4 17a 3 + 9a + 7a 6 by 3a 1a 4 17a 3 + 9a + 7a 6 = (4a 3 3a + a + 3)(3a ) + 0 3. 1a
NATIONAL INSTITUTE OF HOTEL MANAGEMENT, KOLKATA BUSINESS MATHEMATICS 3 rd Semester
 NATIONAL INSTITUTE OF HOTEL MANAGEMENT, KOLKATA BUSINESS MATHEMATICS 3 rd Semester Choose (tick) the appropriate from the following options given below. 1. Find the number of subsets of a set {x : x is
NATIONAL INSTITUTE OF HOTEL MANAGEMENT, KOLKATA BUSINESS MATHEMATICS 3 rd Semester Choose (tick) the appropriate from the following options given below. 1. Find the number of subsets of a set {x : x is
Linear DifferentiaL Equation
 Linear DifferentiaL Equation Massoud Malek The set F of all complex-valued functions is known to be a vector space of infinite dimension. Solutions to any linear differential equations, form a subspace
Linear DifferentiaL Equation Massoud Malek The set F of all complex-valued functions is known to be a vector space of infinite dimension. Solutions to any linear differential equations, form a subspace
MATH 369 Linear Algebra
 Assignment # Problem # A father and his two sons are together 00 years old. The father is twice as old as his older son and 30 years older than his younger son. How old is each person? Problem # 2 Determine
Assignment # Problem # A father and his two sons are together 00 years old. The father is twice as old as his older son and 30 years older than his younger son. How old is each person? Problem # 2 Determine
Quadratic families of elliptic curves and degree 1 conic bundles
 Quadratic families of elliptic curves and degree 1 conic bundles János Kollár Princeton University joint with Massimiliano Mella Elliptic curves E := ( y 2 = a 3 x 3 + a 2 x 2 + a 1 x + a 0 ) A 2 xy Major
Quadratic families of elliptic curves and degree 1 conic bundles János Kollár Princeton University joint with Massimiliano Mella Elliptic curves E := ( y 2 = a 3 x 3 + a 2 x 2 + a 1 x + a 0 ) A 2 xy Major
1. Let r, s, t, v be the homogeneous relations defined on the set M = {2, 3, 4, 5, 6} by
 Seminar 1 1. Which ones of the usual symbols of addition, subtraction, multiplication and division define an operation (composition law) on the numerical sets N, Z, Q, R, C? 2. Let A = {a 1, a 2, a 3 }.
Seminar 1 1. Which ones of the usual symbols of addition, subtraction, multiplication and division define an operation (composition law) on the numerical sets N, Z, Q, R, C? 2. Let A = {a 1, a 2, a 3 }.
Poncelet s porism and periodic triangles in ellipse 1
 Poncelet s porism and periodic triangles in ellipse 1 Vladimir Georgiev, Veneta Nedyalkova 1 Small historical introduction One of the most important and beautiful theorems in projective geometry is that
Poncelet s porism and periodic triangles in ellipse 1 Vladimir Georgiev, Veneta Nedyalkova 1 Small historical introduction One of the most important and beautiful theorems in projective geometry is that
Rotation of Axes. By: OpenStaxCollege
 Rotation of Axes By: OpenStaxCollege As we have seen, conic sections are formed when a plane intersects two right circular cones aligned tip to tip and extending infinitely far in opposite directions,
Rotation of Axes By: OpenStaxCollege As we have seen, conic sections are formed when a plane intersects two right circular cones aligned tip to tip and extending infinitely far in opposite directions,
QUESTION BANK ON. CONIC SECTION (Parabola, Ellipse & Hyperbola)
 QUESTION BANK ON CONIC SECTION (Parabola, Ellipse & Hyperbola) Question bank on Parabola, Ellipse & Hyperbola Select the correct alternative : (Only one is correct) Q. Two mutually perpendicular tangents
QUESTION BANK ON CONIC SECTION (Parabola, Ellipse & Hyperbola) Question bank on Parabola, Ellipse & Hyperbola Select the correct alternative : (Only one is correct) Q. Two mutually perpendicular tangents
Solutions 2017 AB Exam
 1. Solve for x : x 2 = 4 x. Solutions 2017 AB Exam Texas A&M High School Math Contest October 21, 2017 ANSWER: x = 3 Solution: x 2 = 4 x x 2 = 16 8x + x 2 x 2 9x + 18 = 0 (x 6)(x 3) = 0 x = 6, 3 but x
1. Solve for x : x 2 = 4 x. Solutions 2017 AB Exam Texas A&M High School Math Contest October 21, 2017 ANSWER: x = 3 Solution: x 2 = 4 x x 2 = 16 8x + x 2 x 2 9x + 18 = 0 (x 6)(x 3) = 0 x = 6, 3 but x
2. A die is rolled 3 times, the probability of getting a number larger than the previous number each time is
 . If P(A) = x, P = 2x, P(A B) = 2, P ( A B) = 2 3, then the value of x is (A) 5 8 5 36 6 36 36 2. A die is rolled 3 times, the probability of getting a number larger than the previous number each time
. If P(A) = x, P = 2x, P(A B) = 2, P ( A B) = 2 3, then the value of x is (A) 5 8 5 36 6 36 36 2. A die is rolled 3 times, the probability of getting a number larger than the previous number each time
2.3. VECTOR SPACES 25
 2.3. VECTOR SPACES 25 2.3 Vector Spaces MATH 294 FALL 982 PRELIM # 3a 2.3. Let C[, ] denote the space of continuous functions defined on the interval [,] (i.e. f(x) is a member of C[, ] if f(x) is continuous
2.3. VECTOR SPACES 25 2.3 Vector Spaces MATH 294 FALL 982 PRELIM # 3a 2.3. Let C[, ] denote the space of continuous functions defined on the interval [,] (i.e. f(x) is a member of C[, ] if f(x) is continuous
8. Diagonalization.
 8. Diagonalization 8.1. Matrix Representations of Linear Transformations Matrix of A Linear Operator with Respect to A Basis We know that every linear transformation T: R n R m has an associated standard
8. Diagonalization 8.1. Matrix Representations of Linear Transformations Matrix of A Linear Operator with Respect to A Basis We know that every linear transformation T: R n R m has an associated standard
A Mathematical Trivium
 A Mathematical Trivium V.I. Arnold 1991 1. Sketch the graph of the derivative and the graph of the integral of a function given by a freehand graph. 2. Find the limit lim x 0 sin tan x tan sin x arcsin
A Mathematical Trivium V.I. Arnold 1991 1. Sketch the graph of the derivative and the graph of the integral of a function given by a freehand graph. 2. Find the limit lim x 0 sin tan x tan sin x arcsin
Note: Final Exam is at 10:45 on Tuesday, 5/3/11 (This is the Final Exam time reserved for our labs). From Practice Test I
 MA Practice Final Answers in Red 4/8/ and 4/9/ Name Note: Final Exam is at :45 on Tuesday, 5// (This is the Final Exam time reserved for our labs). From Practice Test I Consider the integral 5 x dx. Sketch
MA Practice Final Answers in Red 4/8/ and 4/9/ Name Note: Final Exam is at :45 on Tuesday, 5// (This is the Final Exam time reserved for our labs). From Practice Test I Consider the integral 5 x dx. Sketch
CHAPTER 2 POLYNOMIALS KEY POINTS
 CHAPTER POLYNOMIALS KEY POINTS 1. Polynomials of degrees 1, and 3 are called linear, quadratic and cubic polynomials respectively.. A quadratic polynomial in x with real coefficient is of the form a x
CHAPTER POLYNOMIALS KEY POINTS 1. Polynomials of degrees 1, and 3 are called linear, quadratic and cubic polynomials respectively.. A quadratic polynomial in x with real coefficient is of the form a x
Practice problems for first midterm, Spring 98
 Practice problems for first midterm, Spring 98 midterm to be held Wednesday, February 25, 1998, in class Dave Bayer, Modern Algebra All rings are assumed to be commutative with identity, as in our text.
Practice problems for first midterm, Spring 98 midterm to be held Wednesday, February 25, 1998, in class Dave Bayer, Modern Algebra All rings are assumed to be commutative with identity, as in our text.
A normal form for elliptic curves in characteristic 2
 A normal form for elliptic curves in characteristic 2 David R. Kohel Institut de Mathématiques de Luminy Arithmetic, Geometry, Cryptography et Coding Theory 2011 CIRM, Luminy, 15 March 2011 Edwards model
A normal form for elliptic curves in characteristic 2 David R. Kohel Institut de Mathématiques de Luminy Arithmetic, Geometry, Cryptography et Coding Theory 2011 CIRM, Luminy, 15 March 2011 Edwards model
1) The line has a slope of ) The line passes through (2, 11) and. 6) r(x) = x + 4. From memory match each equation with its graph.
 Review Test 2 Math 1314 Name Write an equation of the line satisfying the given conditions. Write the answer in standard form. 1) The line has a slope of - 2 7 and contains the point (3, 1). Use the point-slope
Review Test 2 Math 1314 Name Write an equation of the line satisfying the given conditions. Write the answer in standard form. 1) The line has a slope of - 2 7 and contains the point (3, 1). Use the point-slope
Introduction to conic sections. Author: Eduard Ortega
 Introduction to conic sections Author: Eduard Ortega 1 Introduction A conic is a two-dimensional figure created by the intersection of a plane and a right circular cone. All conics can be written in terms
Introduction to conic sections Author: Eduard Ortega 1 Introduction A conic is a two-dimensional figure created by the intersection of a plane and a right circular cone. All conics can be written in terms
Math 1060 Linear Algebra Homework Exercises 1 1. Find the complete solutions (if any!) to each of the following systems of simultaneous equations:
 Homework Exercises 1 1 Find the complete solutions (if any!) to each of the following systems of simultaneous equations: (i) x 4y + 3z = 2 3x 11y + 13z = 3 2x 9y + 2z = 7 x 2y + 6z = 2 (ii) x 4y + 3z =
Homework Exercises 1 1 Find the complete solutions (if any!) to each of the following systems of simultaneous equations: (i) x 4y + 3z = 2 3x 11y + 13z = 3 2x 9y + 2z = 7 x 2y + 6z = 2 (ii) x 4y + 3z =
D-MATH Algebraic Geometry FS 2018 Prof. Emmanuel Kowalski. Solutions Sheet 1. Classical Varieties
 D-MATH Algebraic Geometry FS 2018 Prof. Emmanuel Kowalski Solutions Sheet 1 Classical Varieties Let K be an algebraically closed field. All algebraic sets below are defined over K, unless specified otherwise.
D-MATH Algebraic Geometry FS 2018 Prof. Emmanuel Kowalski Solutions Sheet 1 Classical Varieties Let K be an algebraically closed field. All algebraic sets below are defined over K, unless specified otherwise.
Reading Mathematical Expressions & Arithmetic Operations Expression Reads Note
 Math 001 - Term 171 Reading Mathematical Expressions & Arithmetic Operations Expression Reads Note x A x belongs to A,x is in A Between an element and a set. A B A is a subset of B Between two sets. φ
Math 001 - Term 171 Reading Mathematical Expressions & Arithmetic Operations Expression Reads Note x A x belongs to A,x is in A Between an element and a set. A B A is a subset of B Between two sets. φ
Elliptic Functions. Introduction
 Elliptic Functions Introduction 1 0.1 What is an elliptic function Elliptic function = Doubly periodic meromorphic function on C. Too simple object? Indeed, in most of modern textbooks on the complex analysis,
Elliptic Functions Introduction 1 0.1 What is an elliptic function Elliptic function = Doubly periodic meromorphic function on C. Too simple object? Indeed, in most of modern textbooks on the complex analysis,
Points of Finite Order
 Points of Finite Order Alex Tao 23 June 2008 1 Points of Order Two and Three If G is a group with respect to multiplication and g is an element of G then the order of g is the minimum positive integer
Points of Finite Order Alex Tao 23 June 2008 1 Points of Order Two and Three If G is a group with respect to multiplication and g is an element of G then the order of g is the minimum positive integer
Explicit Computations of the Frozen Boundaries of Rhombus Tilings of Polygonal Domains
 Explicit Computations of the Frozen Boundaries of Rhombus Tilings of Polygonal Domains Arthur Azvolinsky Council Rock High School South February 12, 2016 Abstract Consider a polygonal domain Ω drawn on
Explicit Computations of the Frozen Boundaries of Rhombus Tilings of Polygonal Domains Arthur Azvolinsky Council Rock High School South February 12, 2016 Abstract Consider a polygonal domain Ω drawn on
Calabi-Yau Geometry and Mirror Symmetry Conference. Cheol-Hyun Cho (Seoul National Univ.) (based on a joint work with Hansol Hong and Siu-Cheong Lau)
 Calabi-Yau Geometry and Mirror Symmetry Conference Cheol-Hyun Cho (Seoul National Univ.) (based on a joint work with Hansol Hong and Siu-Cheong Lau) Mirror Symmetry between two spaces Mirror symmetry explains
Calabi-Yau Geometry and Mirror Symmetry Conference Cheol-Hyun Cho (Seoul National Univ.) (based on a joint work with Hansol Hong and Siu-Cheong Lau) Mirror Symmetry between two spaces Mirror symmetry explains
1. Group Theory Permutations.
 1.1. Permutations. 1. Group Theory Problem 1.1. Let G be a subgroup of S n of index 2. Show that G = A n. Problem 1.2. Find two elements of S 7 that have the same order but are not conjugate. Let π S 7
1.1. Permutations. 1. Group Theory Problem 1.1. Let G be a subgroup of S n of index 2. Show that G = A n. Problem 1.2. Find two elements of S 7 that have the same order but are not conjugate. Let π S 7
1. The positive zero of y = x 2 + 2x 3/5 is, to the nearest tenth, equal to
 SAT II - Math Level Test #0 Solution SAT II - Math Level Test No. 1. The positive zero of y = x + x 3/5 is, to the nearest tenth, equal to (A) 0.8 (B) 0.7 + 1.1i (C) 0.7 (D) 0.3 (E). 3 b b 4ac Using Quadratic
SAT II - Math Level Test #0 Solution SAT II - Math Level Test No. 1. The positive zero of y = x + x 3/5 is, to the nearest tenth, equal to (A) 0.8 (B) 0.7 + 1.1i (C) 0.7 (D) 0.3 (E). 3 b b 4ac Using Quadratic
Module Two: Differential Calculus(continued) synopsis of results and problems (student copy)
 Module Two: Differential Calculus(continued) synopsis of results and problems (student copy) Srikanth K S 1 Syllabus Taylor s and Maclaurin s theorems for function of one variable(statement only)- problems.
Module Two: Differential Calculus(continued) synopsis of results and problems (student copy) Srikanth K S 1 Syllabus Taylor s and Maclaurin s theorems for function of one variable(statement only)- problems.
MATH 423 Linear Algebra II Lecture 3: Subspaces of vector spaces. Review of complex numbers. Vector space over a field.
 MATH 423 Linear Algebra II Lecture 3: Subspaces of vector spaces. Review of complex numbers. Vector space over a field. Vector space A vector space is a set V equipped with two operations, addition V V
MATH 423 Linear Algebra II Lecture 3: Subspaces of vector spaces. Review of complex numbers. Vector space over a field. Vector space A vector space is a set V equipped with two operations, addition V V
MTH310 EXAM 2 REVIEW
 MTH310 EXAM 2 REVIEW SA LI 4.1 Polynomial Arithmetic and the Division Algorithm A. Polynomial Arithmetic *Polynomial Rings If R is a ring, then there exists a ring T containing an element x that is not
MTH310 EXAM 2 REVIEW SA LI 4.1 Polynomial Arithmetic and the Division Algorithm A. Polynomial Arithmetic *Polynomial Rings If R is a ring, then there exists a ring T containing an element x that is not
Some elliptic curves from the real world
 Some elliptic curves from the real world Bas Edixhoven Universiteit Leiden 2015/06/18 mathematics colloquium Luxembourg and the conference Frontiers in Serre s modularity conjecture Bas Edixhoven (Universiteit
Some elliptic curves from the real world Bas Edixhoven Universiteit Leiden 2015/06/18 mathematics colloquium Luxembourg and the conference Frontiers in Serre s modularity conjecture Bas Edixhoven (Universiteit
Introduction to Arithmetic Geometry
 Introduction to Arithmetic Geometry 18.782 Andrew V. Sutherland September 5, 2013 What is arithmetic geometry? Arithmetic geometry applies the techniques of algebraic geometry to problems in number theory
Introduction to Arithmetic Geometry 18.782 Andrew V. Sutherland September 5, 2013 What is arithmetic geometry? Arithmetic geometry applies the techniques of algebraic geometry to problems in number theory
Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra
 Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra D. R. Wilkins Contents 3 Topics in Commutative Algebra 2 3.1 Rings and Fields......................... 2 3.2 Ideals...............................
Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra D. R. Wilkins Contents 3 Topics in Commutative Algebra 2 3.1 Rings and Fields......................... 2 3.2 Ideals...............................
A Simple Proof of Poncelet s Theorem (on the Occasion of Its Bicentennial)
 A Simple Proof of Poncelet s Theorem (on the Occasion of Its Bicentennial) Lorenz Halbeisen and Norbert Hungerbühler Abstract. We present a proof of Poncelet s theorem in the real projective plane which
A Simple Proof of Poncelet s Theorem (on the Occasion of Its Bicentennial) Lorenz Halbeisen and Norbert Hungerbühler Abstract. We present a proof of Poncelet s theorem in the real projective plane which
Electromagnetism HW 1 math review
 Electromagnetism HW math review Problems -5 due Mon 7th Sep, 6- due Mon 4th Sep Exercise. The Levi-Civita symbol, ɛ ijk, also known as the completely antisymmetric rank-3 tensor, has the following properties:
Electromagnetism HW math review Problems -5 due Mon 7th Sep, 6- due Mon 4th Sep Exercise. The Levi-Civita symbol, ɛ ijk, also known as the completely antisymmetric rank-3 tensor, has the following properties:
Review for the Final Exam
 Calculus 3 Lia Vas Review for the Final Exam. Sequences. Determine whether the following sequences are convergent or divergent. If they are convergent, find their limits. (a) a n = ( 2 ) n (b) a n = n+
Calculus 3 Lia Vas Review for the Final Exam. Sequences. Determine whether the following sequences are convergent or divergent. If they are convergent, find their limits. (a) a n = ( 2 ) n (b) a n = n+
Transweb Educational Services Pvt. Ltd Tel:
 . An aeroplane flying at a constant speed, parallel to the horizontal ground, km above it, is observed at an elevation of 6º from a point on the ground. If, after five seconds, its elevation from the same
. An aeroplane flying at a constant speed, parallel to the horizontal ground, km above it, is observed at an elevation of 6º from a point on the ground. If, after five seconds, its elevation from the same
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 31 OCTOBER 2018
 SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY OCTOBER 8 Mark Scheme: Each part of Question is worth marks which are awarded solely for the correct answer. Each
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY OCTOBER 8 Mark Scheme: Each part of Question is worth marks which are awarded solely for the correct answer. Each
Polynomials 6c Classifying the Zeros of a Polynomial Functions
 Polynomials 6c Classifying the Zeros of a Polynomial Functions Standards: A APR.2, A APR.3, F IF.7c, N CN.9 Learning Target(s): How many zeros does a polynomial have? How can we find all the exact zeros
Polynomials 6c Classifying the Zeros of a Polynomial Functions Standards: A APR.2, A APR.3, F IF.7c, N CN.9 Learning Target(s): How many zeros does a polynomial have? How can we find all the exact zeros
MATH32062 Notes. 1 Affine algebraic varieties. 1.1 Definition of affine algebraic varieties
 MATH32062 Notes 1 Affine algebraic varieties 1.1 Definition of affine algebraic varieties We want to define an algebraic variety as the solution set of a collection of polynomial equations, or equivalently,
MATH32062 Notes 1 Affine algebraic varieties 1.1 Definition of affine algebraic varieties We want to define an algebraic variety as the solution set of a collection of polynomial equations, or equivalently,
b = 2, c = 3, we get x = 0.3 for the positive root. Ans. (D) x 2-2x - 8 < 0, or (x - 4)(x + 2) < 0, Therefore -2 < x < 4 Ans. (C)
 SAT II - Math Level 2 Test #02 Solution 1. The positive zero of y = x 2 + 2x is, to the nearest tenth, equal to (A) 0.8 (B) 0.7 + 1.1i (C) 0.7 (D) 0.3 (E) 2.2 ± Using Quadratic formula, x =, with a = 1,
SAT II - Math Level 2 Test #02 Solution 1. The positive zero of y = x 2 + 2x is, to the nearest tenth, equal to (A) 0.8 (B) 0.7 + 1.1i (C) 0.7 (D) 0.3 (E) 2.2 ± Using Quadratic formula, x =, with a = 1,
On complete degenerations of surfaces with ordinary singularities in
 Home Search Collections Journals About Contact us My IOPscience On complete degenerations of surfaces with ordinary singularities in This article has been downloaded from IOPscience. Please scroll down
Home Search Collections Journals About Contact us My IOPscience On complete degenerations of surfaces with ordinary singularities in This article has been downloaded from IOPscience. Please scroll down
Polytechnic Institute of NYU MA 2132 Final Practice Answers Fall 2012
 Polytechnic Institute of NYU MA Final Practice Answers Fall Studying from past or sample exams is NOT recommended. If you do, it should be only AFTER you know how to do all of the homework and worksheet
Polytechnic Institute of NYU MA Final Practice Answers Fall Studying from past or sample exams is NOT recommended. If you do, it should be only AFTER you know how to do all of the homework and worksheet
PolynomialExponential Equations in Two Variables
 journal of number theory 62, 428438 (1997) article no. NT972058 PolynomialExponential Equations in Two Variables Scott D. Ahlgren* Department of Mathematics, University of Colorado, Boulder, Campus Box
journal of number theory 62, 428438 (1997) article no. NT972058 PolynomialExponential Equations in Two Variables Scott D. Ahlgren* Department of Mathematics, University of Colorado, Boulder, Campus Box
INTRODUCTION TO ELLIPTIC CURVES
 INTRODUCTION TO ELLIPTIC CURVES MATILDE LALÍN Abstract. These notes correspond to a mini-course taught by the author during the program Two Weeks at Waterloo - A Summer School for Women in Math. Please
INTRODUCTION TO ELLIPTIC CURVES MATILDE LALÍN Abstract. These notes correspond to a mini-course taught by the author during the program Two Weeks at Waterloo - A Summer School for Women in Math. Please
M GENERAL MATHEMATICS -2- Dr. Tariq A. AlFadhel 1 Solution of the First Mid-Term Exam First semester H
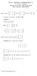 M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
LECTURE 5, FRIDAY
 LECTURE 5, FRIDAY 20.02.04 FRANZ LEMMERMEYER Before we start with the arithmetic of elliptic curves, let us talk a little bit about multiplicities, tangents, and singular points. 1. Tangents How do we
LECTURE 5, FRIDAY 20.02.04 FRANZ LEMMERMEYER Before we start with the arithmetic of elliptic curves, let us talk a little bit about multiplicities, tangents, and singular points. 1. Tangents How do we
Elliptic Curves and Mordell s Theorem
 Elliptic Curves and Mordell s Theorem Aurash Vatan, Andrew Yao MIT PRIMES December 16, 2017 Diophantine Equations Definition (Diophantine Equations) Diophantine Equations are polynomials of two or more
Elliptic Curves and Mordell s Theorem Aurash Vatan, Andrew Yao MIT PRIMES December 16, 2017 Diophantine Equations Definition (Diophantine Equations) Diophantine Equations are polynomials of two or more
. (a) Express [ ] as a non-trivial linear combination of u = [ ], v = [ ] and w =[ ], if possible. Otherwise, give your comments. (b) Express +8x+9x a
![. (a) Express [ ] as a non-trivial linear combination of u = [ ], v = [ ] and w =[ ], if possible. Otherwise, give your comments. (b) Express +8x+9x a . (a) Express [ ] as a non-trivial linear combination of u = [ ], v = [ ] and w =[ ], if possible. Otherwise, give your comments. (b) Express +8x+9x a](/thumbs/89/99588281.jpg) TE Linear Algebra and Numerical Methods Tutorial Set : Two Hours. (a) Show that the product AA T is a symmetric matrix. (b) Show that any square matrix A can be written as the sum of a symmetric matrix
TE Linear Algebra and Numerical Methods Tutorial Set : Two Hours. (a) Show that the product AA T is a symmetric matrix. (b) Show that any square matrix A can be written as the sum of a symmetric matrix
Linear Algebra: Matrix Eigenvalue Problems
 CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
FAIRFIELD COUNTY MATH LEAGUE (FCML) Match 4 Round 1 Arithmetic: Basic Statistics
 Match 4 Round 1 Arithmetic: Basic Statistics 1.) 6.4.) 14706.) 85 1.)The geometric mean of the numbers x 1, x, x n is defined to be n x 1 x...x n. What is the positive difference between the arithmetic
Match 4 Round 1 Arithmetic: Basic Statistics 1.) 6.4.) 14706.) 85 1.)The geometric mean of the numbers x 1, x, x n is defined to be n x 1 x...x n. What is the positive difference between the arithmetic
Calculus I (Math 241) (In Progress)
 Calculus I (Math 241) (In Progress) The following is a collection of Calculus I (Math 241) problems. Students may expect that their final exam is comprised, more or less, of one problem from each section,
Calculus I (Math 241) (In Progress) The following is a collection of Calculus I (Math 241) problems. Students may expect that their final exam is comprised, more or less, of one problem from each section,
PROJECTIVE GEOMETRY. Contents
 PROJECTIVE GEOMETRY Abstract. Projective geometry Contents 5. Geometric constructions, projective transformations, transitivity on triples, projective pl 1. Ceva, Menelaus 1 2. Desargues theorem, Pappus
PROJECTIVE GEOMETRY Abstract. Projective geometry Contents 5. Geometric constructions, projective transformations, transitivity on triples, projective pl 1. Ceva, Menelaus 1 2. Desargues theorem, Pappus
MATH 431 PART 2: POLYNOMIAL RINGS AND FACTORIZATION
 MATH 431 PART 2: POLYNOMIAL RINGS AND FACTORIZATION 1. Polynomial rings (review) Definition 1. A polynomial f(x) with coefficients in a ring R is n f(x) = a i x i = a 0 + a 1 x + a 2 x 2 + + a n x n i=0
MATH 431 PART 2: POLYNOMIAL RINGS AND FACTORIZATION 1. Polynomial rings (review) Definition 1. A polynomial f(x) with coefficients in a ring R is n f(x) = a i x i = a 0 + a 1 x + a 2 x 2 + + a n x n i=0
The Distance Formula. The Midpoint Formula
 Math 120 Intermediate Algebra Sec 9.1: Distance Midpoint Formulas The Distance Formula The distance between two points P 1 = (x 1, y 1 ) P 2 = (x 1, y 1 ), denoted by d(p 1, P 2 ), is d(p 1, P 2 ) = (x
Math 120 Intermediate Algebra Sec 9.1: Distance Midpoint Formulas The Distance Formula The distance between two points P 1 = (x 1, y 1 ) P 2 = (x 1, y 1 ), denoted by d(p 1, P 2 ), is d(p 1, P 2 ) = (x
Finite affine planes in projective spaces
 Finite affine planes in projective spaces J. A.Thas H. Van Maldeghem Ghent University, Belgium {jat,hvm}@cage.ugent.be Abstract We classify all representations of an arbitrary affine plane A of order q
Finite affine planes in projective spaces J. A.Thas H. Van Maldeghem Ghent University, Belgium {jat,hvm}@cage.ugent.be Abstract We classify all representations of an arbitrary affine plane A of order q
Solutions to Exam 2, Math 10560
 Solutions to Exam, Math 6. Which of the following expressions gives the partial fraction decomposition of the function x + x + f(x = (x (x (x +? Solution: Notice that (x is not an irreducile factor. If
Solutions to Exam, Math 6. Which of the following expressions gives the partial fraction decomposition of the function x + x + f(x = (x (x (x +? Solution: Notice that (x is not an irreducile factor. If
MATH 101A: ALGEBRA I, PART D: GALOIS THEORY 11
 MATH 101A: ALGEBRA I, PART D: GALOIS THEORY 11 3. Examples I did some examples and explained the theory at the same time. 3.1. roots of unity. Let L = Q(ζ) where ζ = e 2πi/5 is a primitive 5th root of
MATH 101A: ALGEBRA I, PART D: GALOIS THEORY 11 3. Examples I did some examples and explained the theory at the same time. 3.1. roots of unity. Let L = Q(ζ) where ζ = e 2πi/5 is a primitive 5th root of
Basic Definitions: Group, subgroup, order of a group, order of an element, Abelian, center, centralizer, identity, inverse, closed.
 Math 546 Review Exam 2 NOTE: An (*) at the end of a line indicates that you will not be asked for the proof of that specific item on the exam But you should still understand the idea and be able to apply
Math 546 Review Exam 2 NOTE: An (*) at the end of a line indicates that you will not be asked for the proof of that specific item on the exam But you should still understand the idea and be able to apply
3. Which of these numbers does not belong to the set of solutions of the inequality 4
 Math Field Day Exam 08 Page. The number is equal to b) c) d) e). Consider the equation 0. The slope of this line is / b) / c) / d) / e) None listed.. Which of these numbers does not belong to the set of
Math Field Day Exam 08 Page. The number is equal to b) c) d) e). Consider the equation 0. The slope of this line is / b) / c) / d) / e) None listed.. Which of these numbers does not belong to the set of
Section IV.23. Factorizations of Polynomials over a Field
 IV.23 Factorizations of Polynomials 1 Section IV.23. Factorizations of Polynomials over a Field Note. Our experience with classical algebra tells us that finding the zeros of a polynomial is equivalent
IV.23 Factorizations of Polynomials 1 Section IV.23. Factorizations of Polynomials over a Field Note. Our experience with classical algebra tells us that finding the zeros of a polynomial is equivalent
Chapter 4: Interpolation and Approximation. October 28, 2005
 Chapter 4: Interpolation and Approximation October 28, 2005 Outline 1 2.4 Linear Interpolation 2 4.1 Lagrange Interpolation 3 4.2 Newton Interpolation and Divided Differences 4 4.3 Interpolation Error
Chapter 4: Interpolation and Approximation October 28, 2005 Outline 1 2.4 Linear Interpolation 2 4.1 Lagrange Interpolation 3 4.2 Newton Interpolation and Divided Differences 4 4.3 Interpolation Error
Math 4377/6308 Advanced Linear Algebra I Dr. Vaughn Climenhaga, PGH 651A HOMEWORK 3
 Math 4377/6308 Advanced Linear Algebra I Dr. Vaughn Climenhaga, PGH 651A Fall 2013 HOMEWORK 3 Due 4pm Wednesday, September 11. You will be graded not only on the correctness of your answers but also on
Math 4377/6308 Advanced Linear Algebra I Dr. Vaughn Climenhaga, PGH 651A Fall 2013 HOMEWORK 3 Due 4pm Wednesday, September 11. You will be graded not only on the correctness of your answers but also on
Classification of cubics up to affine transformations
 Classification of cubics up to affine transformations Mehdi Nadjafikah and Ahmad-Reza Forough Abstract. Classification of cubics (that is, third order planar curves in the R 2 ) up to certain transformations
Classification of cubics up to affine transformations Mehdi Nadjafikah and Ahmad-Reza Forough Abstract. Classification of cubics (that is, third order planar curves in the R 2 ) up to certain transformations
1. Use the properties of exponents to simplify the following expression, writing your answer with only positive exponents.
 Math120 - Precalculus. Final Review. Fall, 2011 Prepared by Dr. P. Babaali 1 Algebra 1. Use the properties of exponents to simplify the following expression, writing your answer with only positive exponents.
Math120 - Precalculus. Final Review. Fall, 2011 Prepared by Dr. P. Babaali 1 Algebra 1. Use the properties of exponents to simplify the following expression, writing your answer with only positive exponents.
1. Let g(x) and h(x) be polynomials with real coefficients such that
 1. Let g(x) and h(x) be polynomials with real coefficients such that g(x)(x 2 3x + 2) = h(x)(x 2 + 3x + 2) and f(x) = g(x)h(x) + (x 4 5x 2 + 4). Prove that f(x) has at least four real roots. 2. Let M be
1. Let g(x) and h(x) be polynomials with real coefficients such that g(x)(x 2 3x + 2) = h(x)(x 2 + 3x + 2) and f(x) = g(x)h(x) + (x 4 5x 2 + 4). Prove that f(x) has at least four real roots. 2. Let M be
Elliptic Curves and Public Key Cryptography
 Elliptic Curves and Public Key Cryptography Jeff Achter January 7, 2011 1 Introduction to Elliptic Curves 1.1 Diophantine equations Many classical problems in number theory have the following form: Let
Elliptic Curves and Public Key Cryptography Jeff Achter January 7, 2011 1 Introduction to Elliptic Curves 1.1 Diophantine equations Many classical problems in number theory have the following form: Let
Solving Systems of Linear Equations. Classification by Number of Solutions
 Solving Systems of Linear Equations Case 1: One Solution Case : No Solution Case 3: Infinite Solutions Independent System Inconsistent System Dependent System x = 4 y = Classification by Number of Solutions
Solving Systems of Linear Equations Case 1: One Solution Case : No Solution Case 3: Infinite Solutions Independent System Inconsistent System Dependent System x = 4 y = Classification by Number of Solutions
Linear Algebra Lecture Notes-I
 Linear Algebra Lecture Notes-I Vikas Bist Department of Mathematics Panjab University, Chandigarh-6004 email: bistvikas@gmail.com Last revised on February 9, 208 This text is based on the lectures delivered
Linear Algebra Lecture Notes-I Vikas Bist Department of Mathematics Panjab University, Chandigarh-6004 email: bistvikas@gmail.com Last revised on February 9, 208 This text is based on the lectures delivered
Acta Mathematica Academiae Paedagogicae Nyíregyháziensis 26 (2010), ISSN
 Acta Mathematica Academiae Paedagogicae Nyíregyháziensis 6 (010), 359 375 www.emis.de/journals ISSN 1786-0091 EXAMPLES AND NOTES ON GENERALIZED CONICS AND THEIR APPLICATIONS Á NAGY AND CS. VINCZE Abstract.
Acta Mathematica Academiae Paedagogicae Nyíregyháziensis 6 (010), 359 375 www.emis.de/journals ISSN 1786-0091 EXAMPLES AND NOTES ON GENERALIZED CONICS AND THEIR APPLICATIONS Á NAGY AND CS. VINCZE Abstract.
3. Identify and find the general solution of each of the following first order differential equations.
 Final Exam MATH 33, Sample Questions. Fall 7. y = Cx 3 3 is the general solution of a differential equation. Find the equation. Answer: y = 3y + 9 xy. y = C x + C x is the general solution of a differential
Final Exam MATH 33, Sample Questions. Fall 7. y = Cx 3 3 is the general solution of a differential equation. Find the equation. Answer: y = 3y + 9 xy. y = C x + C x is the general solution of a differential
Given the table of values, determine the equation
 3.1 Properties of Quadratic Functions Recall: Standard Form f(x) = ax 2 + bx + c Factored Form f(x) = a(x r)(x s) Vertex Form f(x) = a(x h) 2 + k Given the table of values, determine the equation x y 1
3.1 Properties of Quadratic Functions Recall: Standard Form f(x) = ax 2 + bx + c Factored Form f(x) = a(x r)(x s) Vertex Form f(x) = a(x h) 2 + k Given the table of values, determine the equation x y 1
King Fahd University of Petroleum and Minerals Prep-Year Math Program Math Term 161 Recitation (R1, R2)
 Math 001 - Term 161 Recitation (R1, R) Question 1: How many rational and irrational numbers are possible between 0 and 1? (a) 1 (b) Finite (c) 0 (d) Infinite (e) Question : A will contain how many elements
Math 001 - Term 161 Recitation (R1, R) Question 1: How many rational and irrational numbers are possible between 0 and 1? (a) 1 (b) Finite (c) 0 (d) Infinite (e) Question : A will contain how many elements
