1. THE MOMENTUM EQUATIONS FOR SYNOPTIC-SCALE FLOW IN THE ROTATING COORDINATE SYSTEM
|
|
|
- Berniece Byrd
- 5 years ago
- Views:
Transcription
1 NOTES FO THE THEOY OF WKD 35. THE MOMENTUM EQUATIONS FO SYNOPTIC-SCALE FLOW IN THE OTATING COODINATE SYSTEM Scalin o the momentm eqations or snotic scale circlation (>000km dimension) reslted in the elimination o relatiel small terms to ield the olloin eqations: i - direction : d sin (.) j - direction : d sin (.) k - direction : (hdrostatic aroimation) (.3) These terms reresent orces on a nit mass (m=) o the atmoshere: d ) Acceleration orces:, ) Coriolis orces:, d here sin 3) Pressre radient orces:,, ) Grait orce: The horiontal eqations (.) and (.) ma also be ritten in ector ormat: d i d j i j sin i sin j i j i j d (i j) ( i j) ( i j)
2 Let the horiontal ind be (i j). Thereore, or the last terms on the riht ( i j) k i 0 j 0 k 0 and let i j The momentm eqation or horiontal lo ma then be ritten as: d k (.)
3 . NATUAL COODINATES The natral coordinate sstem is a coordinate sstem ith orthoonal (indeendent or erendiclar to each other) nit ectors, n and k that makes it easier to describe horiontal cred lo in the atmoshere. The nit ectors are orientated in sch a a that oints toards the direction o lo (here horiontal lo), n oints 90 o toards the let o the direction o lo ( ) and k ards (90 o to the horiontal lane o lo). The coordinates ill ollo the cratre lo as illstrated in ire. O B D C Q s n A P Fire In natral coordinates the horiontal elocit ector hich oints toards the direction o lo ( -direction) ma be ritten as (.) 3
4 here is the horiontal ind seed. The horiontal ind seed, hich is deined to be ositie, ma be eressed as ds (.) here s is a increment o the cre olloed b a arcel o air moin in the horiontal lane. It is imortant to note that is rearded as ositie ( > 0) i n oints toards the centre o the circle ormed b the cratre lo, and is neatie ( < 0) i n oints aa rom the centre o the circle ormed b the cratre lo. 3. THE MOMENTUM EQUATIONS IN NATUAL COODINATES For alication in natral coordinates the horiontal momentm eqation (eqation (.)) needs to be conerted to natral coordinates. Acceleration term o eqation (.): d B alin the rodct rle o dierentiation, eqation (.), hich reresents the horiontal acceleration (orce er nit mass) that ollos the motion, becomes: d d d (3.) The second art o the second term on the riht hand side o eqation (3.) ma be ritten in a more aroriate a. We start b
5 d d ds ds (3.) Let s irst look at the irst art on the riht hand side o eqation (3.). I e consider a small increment dislacement PQ in ire, e ma assme that, hich in realit orms a cre, is close to the lenth o CD, and that oints in the same direction o nit ector n. In eneral the arch lenth o a comlete circle (circmerence) is eqal to meanin that the arc lenth o PQ and CD is s and, resectiel. Note that becase is a nit ector it ollos that. It thereore ollos that s d ds lim s0 s d ds n (3.3) Secondl, accordin to eqation (.) the second art on the riht hand side o eqation ds (3.) ma be ritten as Eqation (3.) ma no be ritten as d n and b relacin this back into eqation (3.) the acceleration in natral coordinates becomes d d n (3.) 5
6 Pressre radient term o eqation (.): In the horiontal lane ressre radient orce can thereore be ritten as: n in the natral coordinate sstem and the s n n (3.5) s n Coriolis term o eqation (.): k Accordin to eqation (.) and thereor k. The cross rodct o nit ectors k and ields the nit ector in the direction o n (riht hand rle). The Coriolis term then becomes k 0 n 0 0 k 0 n (3.6) From eqations (3.), (3.5) and (3.6), the horiontal momentm eqation (.) ma no be ritten in terms o natral coordinates d n n n (3.7) s n Comonents o eqation (3.7) in the and n directions are - direction : d (3.8) s 6
7 n - direction : (3.9) n These to eqations orm the basis rom here e ill inestiate the roerties o dierent tes o snotic-scale circlation in the atmoshere.. SUMMAY OF CONDITIONS FO NATUAL COODINATES Condition d 0 in eqation (3.8). s The eqation alies or lo in the direction o moement ( ). We are considerin lo alon isobars, meanin that ressre ill not chane oer the ininitesimal dislacement s. The seed is constant olloin the motion. Condition The soltion or in eqation (3.9) is alas ositie. Condition 3 is rearded as ositie (>0) i n oints toards the centre o the circle ormed b the cratre lo, and is neatie (<0) i n oints aa rom the centre o the circle ormed b the cratre lo. Condition The nit ector n oints 90 o toards the let o the direction o lo ( ) 7
8 5. GEOSTOPHIC FLOW For eostrohic lo ( ) condition in section alies. Note that the eostrohic ind is deined as a ind here the ressre radient orce is in balance ith (or eqal to) the Coriolis orce, and thereore here the centrietal orce is inored ( 0 ) in eqation (3.9). n is not an eact soltion o eqation (3.9) since the centrietal orce is inored, and condition does thereore not al ( miht be ositie or neatie). The eostrohic lo describes constant motion (no acceleration) in a straiht line since the to orces actin on the motion are eqal and thereore. The Coriolis arameter ( sin ) is alas neatie in the Sothern Hemishere. It is thereore onl the ressre radient alon the n -direction that can chane. I the ressre radient is ositie, mst be ositie (riht belo), and i the ressre radient is neatie, mst be neatie (let belo). H = hih ressre; L = lo ressre. L n 0 n H H n 0 n L 8
9 6. INETIAL FLOW For inertial lo the ressre ield is niorm (isobaric srace), and thereore here the ressre radient orce is inored ( 0 ) in eqation (3.9). n mst be ositie (condition ), and is alas neatie in the Sothern Hemishere. The onl otion is that mst be ositie to ield a ositie. Accordin to condition 3 is ositie (>0) i n oints toards the centre o the circle ormed b the cratre lo. Inertial lo is alas anti-cclonic or conter-clockise in the Sothern Hemishere. This te o lo does not oten occr in the atmoshere. n 9
10 7. CYCLOSTOPHIC FLOW For cclostrohic lo the Coriolis orce is deined as small and can be inored. This miht haen i the horiontal scale o the circlation is small (tornado) or in eqatorial reions here the Coriolis orce is ero, and thereore here the Coriolis orce is inored ( 0 ) in eqation 3.9. n mst be real and non-neatie and thereore mst be ositie. This ill onl n be tre i >0 and the ressre radient neatie, or i <0 and the ressre radient ositie. is rearded as ositie and constant. > 0 and 0 n < 0 and 0 n L n L n For cclostrohic lo circlation can either be clockise or conter-clockise arond a lo-ressre sstem in the Sothern Hemishere. 0
11 8. GADIENT FLOW For radient lo e sole b sin all three terms in eqation (3.9). The radient ind is thereore a three-a balance beteen the Coriolis orce, the ressre radient orce and the centrial orce in the horiontal lane and thereore n Since the eqation or radient ind takes accont o the centrial orce, the radient ind is a better aroimation o the actal ind than is the eostrohic assmtion. The radient ind eqation (3.9) ma be rearraned to orm the olloin qadratic eqation: n 0 ith soltions (or roots) (8.) n mst be ositie and real (eression nder the root mst be ositie). Not all the mathematical ossible roots in eqation (8.) ill corresond to hsicall ossible soltions. While is neatie in the Sothern Hemishere and is constant, and the ressre radient in the n -direction miht be neatie or ositie. We hae the olloin eiht otions - (a) to (h):
12 > 0 < 0 0 n 0 n (a) : hsicall ossible (c) : hsicall ossible (b) : hsicall ossible (d) : hsicall imossible (e) : hsicall ossible () : hsicall imossible () : hsicall imossible (h) : hsicall imossible Otions (a) and (b) Ste : Dra the circlation sstem The olloin to conditions reslt in conter-clockise lo arond a H n hih (anti-cclone) 0 ( n oints toards centre) 0 n (Hih ressre in centre) Ste : Ealate the term otside the root o eqation (8.) > 0 since > 0 and < 0. I e add this ositie term to the ositie root one ill alas obtain a ositie ale or. Otion (a) is thereore hsicall ossible. Otion (b) needs some rther inestiation.
13 Ste 3: Ealate the terms nder the root o eqation (8.) > 0 hile n > 0 and thereore take the sqare root n bt e are interested in the neatie root n add n both sides to obtain in (8.) n bt < 0 and > 0 > 0 is thereore hsicall ossible Otions (c) and (d) Ste : Dra the circlation sstem The olloin to conditions reslt in clockise lo arond a lo (cclone) 0 ( n oints aa rom centre) 0 n (Lo ressre in centre) L n Ste : Ealate the term otside the root o eqation (8.) < 0 since < 0 and < 0. I e add this neatie term to the neatie root one ill alas obtain a neatie ale or. Otion (d) is thereore hsicall imossible. Otion (c) needs some rther inestiation. 3
14 Ste 3: Ealate the terms nder the root o eqation (8.) > 0 hile n < 0 and thereore n take the sqare root n add both sides to obtain in (8.) n bt < 0 and < 0 > 0 is thereore hsicall ossible
15 Otions (e) and () Ste : Dra the circlation sstem The olloin to conditions reslt in conter-clockise lo arond a lo (cclone) L n 0 ( n oints toards centre) 0 n (Lo ressre in centre) Ste : Ealate the term otside the root o eqation (8.) > 0 since > 0 and < 0. I e add this ositie term to the ositie root one ill alas obtain a ositie ale or. Otion (e) is thereore hsicall ossible. Otion () needs some rther inestiation. Ste 3: Ealate the terms nder the root o eqation (8.) > 0 hile n < 0 and thereore take the sqare root n bt e are interested in the neatie root n add n both sides to obtain in (8.) n bt < 0 and > 0 < 0 is thereore hsicall imossible 5
16 Otions () and (h) Ste : Dra the circlation sstem The olloin to conditions reslt in clockise lo arond a hih (anti-cclone) H n 0 ( n oints aa rom centre) 0 n (Hih ressre in centre) Ste : Ealate the term otside the root o eqation (8.) < 0 since < 0 and < 0. I e add this neatie term to the neatie root one ill alas obtain a neatie ale or. Otion (h) is thereore hsicall imossible. Otion () needs some rther inestiation. Ste 3: Ealate the terms nder the root o eqation (8.) > 0 hile n > 0 and thereore take the sqare root n add n both sides to obtain in (8.) n bt < 0 and < 0 < 0 is thereore hsicall imossible 6
17 9. FINITE DIFFEENCE METHODS TO CALCULATE WINDS Consider the eostrohic ind eqations, as discssed in section 5, bt in this case or snotic lo in the OTATING COODINATE SYSTEM (see eqations (.) and (.)): i - direction : j - direction : sin sin (9.) (9.) From eqations (9.), the eostrohic ind comonent in the i direction ( ais: est to east) and j direction ( ais: soth to north) becomes: (9.3) sin Geostrohic ind comonent in the -direction : sin (9.) The term sin can be easil soled since and are constants and the latitde () is knon. The to deriaties, hoeer, are not that eas to sole. Meteoroloical data is oten roided in the orm o rid ields, here rid oints are arraned alon latitde () and lonitde () lines ith interal distances o and., i,, j, On sch a rid ield, artial deriaties in the and directions ma be nmericall estimated b sin the olloin inite dierence method: 7
18 : West East. The ble circles reresent 3 rid oints (,, 3 ) in the -direction alon latitde and lonitdes,, 3. The ressre ales at the 3 rid oints are,, 3. The distance beteen the rid oints is. We assme that lim 0 And thereore 3 (9.5) Where, on the sherical Earth: r cos ( ) r cos ( 3 ) : North Soth 8
19 The ble circles reresent 3 rid oints (,, 3 ) in the -direction alon lonitde and latetdes,, 3. The ressre ales at the 3 rid oints are,, 3. The distance beteen the rid oints is. We assme that lim 0 And thereore 3 (9.6) Where, on the sherical Earth: r( ) r( 3 ) EXECISE 9. Consider the olloin ressre ale rid ield on the srace o the Earth ith Pressre: 990 hpa Pressre: 989 hpa Pressre: 988 hpa 7 o Pressre: 989 hpa Pressre: 988 hpa Pressre: 987 hpa 8 o Pressre: 988 hpa Pressre: 987 hpa Pressre: 986 hpa 0 o E o o E 9 o S Calclate and at the black circle. 9
20 EXECISE A O Soth Pelican 00 Harbor hpa Paradise Island O hpa 998 hpa.00 O.50 O.00 O O Consider an Island (Paradise Island) somehere in the Paciic Ocean. Shis in the icinit o the Island hae measred the ressre at each one o the rid oint at a ien time. The ressre at Pelican Island Harbor is also knon as 000 hpa. A shi, not ar rom the Island, asked or ermission to enter the harbor. It ma be daneros or shis to enter the harbor i the reailin inds are too stron ( > ms - ) Yo are in chare o Pelican harbor, and the onl inormation aailable are the ressre ales at the ien rid oints. Yo also hae the olloin constants aailable: adis o the earth: a = m Earth s anlar seed o rotation: = rad.s - Standard sea-leel densit o air: O =.5 k. m -3 PLEASE ANSWE THE FOLLOWING QUESTIONS:. The shi is crrentl at rid oint A. Determine the aroimated distance beteen the shi and Pelican Harbor (in kilometers).. Dra the 00hPa, 000 hpa and 999hPa isobars on the ma (dra the aroimated direction o ind lo beteen these isobars b assmin the ind is eostrohic). 3. Write don an eression or the eostrohic ind in the - and - directions. 0
21 . Use the eqations in 3 to calclate the eostrohic ind seed and direction at Pelican Harbor and dra the ind ector on the ma. Wold it be sae or the shi to enter the harbor? BACKGOUND Beore e calclate the distance beteen the harbor and shi, e irst need to eress the - and - comonents o distances on the sherical srace o the Earth in terms o lonitde () and latitde (). emember that e are not dealin ith a lat srace! To do that e consider the circmerence o a circle namel r circmerence = anle radis = r and thereore = r Accordin to this e ma rite and on the sherical srace o the Earth as: = r = = r cos() here r is the radis o the Earth s. ANSWE FO QUESTION D A shi = r harbor C = r cos() B We kno that: r = = = 0.5 o
22 These to anle increments mst be in radiance. To conert rom derees to radiance, e se the olloin: = 80 o rad = rad = 0.5 = First calclate and : r cos (line CB) = ( ) cos(-35)( ) = ( )(0.855)( ) = meters = 5.5 km r (line AB) = ( )( ) = meters = 55.6 km (AC) = (CB) + (AB) = (5535.6) + ( ) = ( ) + ( ) = and thereore AC = meters = 7.9 km ANSWE FO QUESTION In the Sothern Hemishere, lare-scale ind circlation is clockise arond loressre sstems and conter-clockise arond hih-ressre sstems. The eostrohic lo is arallel to the isobars (lines o eqal ressre measred in hpa thick lines in the diaram). The ind ector shold thereore oint toards the northeast (as indicated b black arros in the diaram). This eercise miht be a a to eri that or inal calclated eostrohic ind oints in the aroriate direction.
23 Hiher ressres 000 A O Soth 00 Harbor hpa Paradise Island Loer hpa 998 hpa ressres.00 O West Pelican.50 O West.00 O West O Soth O Soth ANSWE FO QUESTION 3 Geostrohic ind in the -direction (ointin rom est to east): sin sin Geostrohic ind in the -direction (ointin rom soth to north): sin sin ANSWE FO QUESTION We irst calclate the constant term sin hich occrs in both the - and - direction eostrohic ind eqations at latitde = 35.5 o S. sin (.5)()(7.90 From QUESTION e kno that )(sin 35.5)
24 ()(5535.6) 907.m ()( ) 77.m I e consider the ressre dierences (radients) across these distances in the - and - directions, e can calclate the deriaties in the eostrohic ind eqations o QUESTION 3 (remember that ressre on the ma is ien in the nit hpa, and mst be conerted to Pa or calclations: hpa=00pa): We no relace all the reslts aboe in the eostrohic ind eqations o QUESTION 3 Geostrohic ind comonent in the -direction: sin.0370 ( ) 7.35m. s Geostrohic ind comonent in the -direction: sin.0370 ( ).7m. s The manitde o the total eostrohic ind seed is thereore: (7.35)(7.35) (.7)(.7) 7.37ms 98.5kmh Note that the ind direction is alas ien as an anle that oriinates rom the North ais, and is ositie clockise rom the North ais. The ector that is ormed b this anle indicates the direction FOM hich the ind blos. For or roblem, this is illstrated as ollos here is the anle o the ind ector rom the North ais:
25 North () East () sin o rom here This anle allo or the ind to blo in the estimated directions indicated in QUESTION here e hae considered lo arond hih and lo ressre sstems. Hoeer, ind direction is alas measred rom here the ind blos, in other ords: The ind direction is ( 80) ( ) o 9.3 A ind ith direction 9.3 o bloin at a seed o 7.37 m.s - old be too stron and it is thereore not sae or the shi to enter the harbor. 5
26 0. THEMAL WIND The thermal ind describes chane (ertical ind shear) o the eostrohic ind ith altitde in the resence o a horiontal temeratre radient. The thermal ind thereore occrs in areas here one inds stee temeratre radient on horiontal leels in the ertical - here on constant ressre leels. A tical eamle is a olar ront here arm air rom the troics meets ith cold olar air. Isobar - line o constant ressre (or eamle the 500 hpa line) Area o temeratre radient (olar ront) Isoterm - line o constant temeratre A B ertical heiht Cold air Warm air Soth North Consider a ertical cross section in the atmoshere ith a cold air mass on the let and a armer air mass on the riht. The isotherms, and thereore also isobars, ill lit to a hiher altitde oer the arm air mass that ill reslt in a isotherm, and isobar, sloe in the area o temeratre radient. A horiontal temeratre and ressre radient ill thereore aear oer the horiontal area AB. This temeratre and ressre radient ill reslt in airlo (or inds). The horiontal inds ma be aroimated as eostroic inds, meanin that the Coriolis and Pressre radient orces are in balance. The horiontal lo ill thereore be in a direction that is aroimatel arallel to the isobars in the area o temeratre radient. Instead o considerin inds oer the horiontal area AB e ill rather analse inds on CONSTANT PESSUE leels - remember that a horiontal temeratre radient ill still occr oer a constant ressre leel - or eamle the 500 hpa leel. We ill 6
27 thereore derie an eression or the chane (ertical ind shear) eostrohic ind on dierent constant ressre leels rom the srace o the Earth ards into the atmoshere as a reslt o a horiontal temeratre radient oer these leels. Scalin o the horiontal momentm eqations or snotic scale circlation (>000km dimension) reslted in the elimination o relatiel small terms to ield eqations (.) and (.). When makin the eostrohic assmtion (Coriolis Force = Pressre Gradient Force; d d 0 ), it ollos that: i - orce comonents : (0.) j - orce comonents: here sin (0.) Since the thermal ind has to do ith a ertical ind shear e also need to incororate the ertical atmosheric eqation or hdrostatic eqation (.3): k - direction : (0.3) In eqations (0.), (0.) and (0.3) ressre is a ariable that chanes oer,, and sraces. Since e ant to ork on constant ressre leels, e need to relace the crrent deriaties that elain chane oer constant altitdes () ith deriaties that elain chane oer constant ressre () leels. In a sstem here (,,,t) are indeendent coordinates one ma rite (the ootnotes denote constant and sraces): 7
28 8 t t t t Since (,,,t) are indeendent coordinates in the -sstem and since ressre does not chane in the and directions in the -sstem, these eqations become 0 and thereore 0 and thereore relace eqation (0.3) hich are eressions here the deriaties on constant altitdes () are reritten in terms o deriaties on constant ressres (). elace these reslts into eqations (0.) and (0.) (0.) (0.5)
29 9 hich ield eqations here the deriaties are ealated ith ressre held constant (on constant ressre leels in the ertical). Since e are interested in the ertical ind shear o the eostrohic ind on dierent constant ressre leels in the ertical, e dierentiate eqations (0.) and (0.5) ith resect to : since is not a nction o and since is continos. From eqation (9.3) ollos that: and i is continos and T e obtain T Thereore T T T ln T T T ln since is constant and since is constant in the and directions as deined (ootnote denote constant ressre). In ector orm the aboe ma be ritten as j T i T j) i ( ln i ) j i ( and j T i T T T T 0 0 k j i T k
30 e end ith the THEMAL WIND EQUATION ln k T (0.6) Hoeer, eqation (0.6) is actall a relationshi or the ertical eostroic ind shear or the chane o the eostrohic ind ith resect to ln in the ertical. Strictl seakin the THEMAL WIND reers to the ector dierence beteen the eostrohic inds at to constant ressre leels. This becomes obios i e interate eqation (0.6) beteen ressre leels 0 and. () (0) 0 k () (0) T ln k T (ln ln 0) here T is the aerae temeratre beteen 0 and This ields an eqation or the THEMAL WIND T () (0) ln k T (0.7) 0 Interretation o eqation (0.7) I can be shon that the thickness o the laer beteen ressres 0 and is roortional to the aerae temeratre T beteen these to laers. The armer the atmoshere, the thicker the laer ill become. The thermal ind eqation is an etremel sel dianostic tool or hiher latitdes. It ma be sed to check data o the obsered ind and temeratre or consistenc, or it ma be also be sed to estimate the mean horiontal temeratre adection in a laer. 30
31 Since the temeratre radient in ire 0. is alas erendiclar to the isotherms, the cross rodct in eqation 0.7 indicates that the thermal ind ector ill alas arallel to the isotherms (line o constant temeratre) ointin let in the Sothern Hemishere here the cold air is soth and the armer air is north. As illstrated in Fire 0., a eostrohic ind that trns conter clockise ith heiht (backs) is associated ith cold air adection (cold air lo in the direction o the srace eostrohic ind). Clockise trnin (eerin) o the eostrohic ind ith heiht imlies arm air adection in the laer. It is thereore ossible to estimate the horiontal temeratre adection at a ien location solel rom data on the ertical roile o the inds. The eostrohic ind at an leel in the atmoshere can also be calclated i the srace eostrohic ind and the mean horiontal temeratre radient are knon. (a) Warm T o +T T T 0 T o Cold T o -T (b) Warm T o +T 0 T T o T Fire 0. T o -T Cold elationshi beteen trnin o the eostrohic ind and temeratre adection (a) conter clockise ind direction shit ith heiht (backs) and (b) clockise ind direction shit ith heiht (eerin) 3
32 3. CICULATION AND OTICITY Additional notes on the hsical meanin o orticit ill be roided (not or eam roses) Circlation and orticit are to rimar measres o rotation in a lid. Circlation, hich is a scalar interal qantit, is a macroscoic measre o rotation or a inite area o the lid. orticit, hoeer, is a ector ield that ies a microscoic measre o the rotation at an oint in the lid. In this section e ill ocs on orticit, since it is a concet commonl sed in meteorolo to determine the deree o rotation in the atmoshere. The relatie orticit is deined as the crl o the relatie elocit, in other ords elocit as eerienced in a rotatin coordinate sstem on the Earth. The ector o relatie orticit ma thereore be ritten as: k j i U For snotic scale circlation e onl consider the ertical ( k ) comonent, hich describes chanes on the horiontal leel. elatie orticit thereore becomes: U k (.) For snotic scale motion, the orticit eqation o the atmoshere can be deried sin the aroimated horiontal momentm eqations (.) and (.). The deriaties in eqations (.) and (.) ma be ritten in terms o artial deriaties to ield: t (.) t here sin (.3) Dierentiate eqation (.) ith resect to and eqation (.3) ith resect to t (.) t (.5) a c b d e
33 33 The olloin ste is to sbtract eqation (.) rom eqation (.5). We ill do that searatel or each set o terms (terms a to ). Terms a: t t t t t relace eqation (.) t (.6) Terms b: relace eqation (.) (.7) Terms c: Similar to Terms b ollos (.8)
34 3 Terms d: relace eqation (.) (.9) Terms e: ) ( ) (.. (.0) Terms : (Note: The Coriolis arameter is a nction o onl - soth-north direction) () ()
35 35 bt 0 (.) B ttin terms a to in eqations (.6) to (.) toether e et t and ith some minor simliications ) ( t (.) I e assme that Coriolis () is onl a nction o it ollos that t 0 0 t 0 ) ( d hich is eqal to the let hand side o eqation (0.). Eqation (.) thereore becomes ) ( ) ( d (.3) to orm the orticit eqation. Eqation (.3) states that the rate o chane o the absolte orticit (orticit as ieed rom sace - addition o that contains the anlar seed) olloin the motion is ien b the sm o three terms on the riht, called the dierence term, the tiltin or tistin term and the solenoidal term, resectiel.
The Vorticity Equation
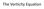 The Vorticit Eqation Potential orticit Circlation theorem is reall good Circlation theorem imlies a consered qantit dp dt 0 P g 2 PV or barotroic lid General orm o Ertel s otential orticit: P g const Consider
The Vorticit Eqation Potential orticit Circlation theorem is reall good Circlation theorem imlies a consered qantit dp dt 0 P g 2 PV or barotroic lid General orm o Ertel s otential orticit: P g const Consider
Rossby waves (waves in vorticity)
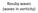 Rossb waes (waes in orticit) Stationar (toograhicall orced) waes NCEP Reanalsis Z500 Janar mean 2 3 Vorticit eqation z w z w z w t 2 1 Change in relatie (ertical comonent o) orticit at a oint, Adection
Rossb waes (waes in orticit) Stationar (toograhicall orced) waes NCEP Reanalsis Z500 Janar mean 2 3 Vorticit eqation z w z w z w t 2 1 Change in relatie (ertical comonent o) orticit at a oint, Adection
Dynamics of the Atmosphere 11:670:324. Class Time: Tuesdays and Fridays 9:15-10:35
 Dnamics o the Atmosphere 11:67:34 Class Time: Tesdas and Fridas 9:15-1:35 Instrctors: Dr. Anthon J. Broccoli (ENR 9) broccoli@ensci.rtgers.ed 73-93-98 6 Dr. Benjamin Lintner (ENR 5) lintner@ensci.rtgers.ed
Dnamics o the Atmosphere 11:67:34 Class Time: Tesdas and Fridas 9:15-1:35 Instrctors: Dr. Anthon J. Broccoli (ENR 9) broccoli@ensci.rtgers.ed 73-93-98 6 Dr. Benjamin Lintner (ENR 5) lintner@ensci.rtgers.ed
SUBJECT:ENGINEERING MATHEMATICS-I SUBJECT CODE :SMT1101 UNIT III FUNCTIONS OF SEVERAL VARIABLES. Jacobians
 SUBJECT:ENGINEERING MATHEMATICS-I SUBJECT CODE :SMT0 UNIT III FUNCTIONS OF SEVERAL VARIABLES Jacobians Changing ariable is something e come across er oten in Integration There are man reasons or changing
SUBJECT:ENGINEERING MATHEMATICS-I SUBJECT CODE :SMT0 UNIT III FUNCTIONS OF SEVERAL VARIABLES Jacobians Changing ariable is something e come across er oten in Integration There are man reasons or changing
The homework problem (pucks_on_ice) illustrates several important points:
 Ekman laers, friction & eostrohic flow The homework roblem (ucks_on_ice) illustrates several imortant oints: 1. Particles move erendicular to the alied force, to the riht in the northern hemishere, to
Ekman laers, friction & eostrohic flow The homework roblem (ucks_on_ice) illustrates several imortant oints: 1. Particles move erendicular to the alied force, to the riht in the northern hemishere, to
Derivation of the basic equations of fluid flows. No. Conservation of mass of a solute (applies to non-sinking particles at low concentration).
 Deriation of the basic eqations of flid flos. No article in the flid at this stage (net eek). Conseration of mass of the flid. Conseration of mass of a solte (alies to non-sinking articles at lo concentration).
Deriation of the basic eqations of flid flos. No article in the flid at this stage (net eek). Conseration of mass of the flid. Conseration of mass of a solte (alies to non-sinking articles at lo concentration).
Lecture 5. Differential Analysis of Fluid Flow Navier-Stockes equation
 Lectre 5 Differential Analsis of Flid Flo Naier-Stockes eqation Differential analsis of Flid Flo The aim: to rodce differential eqation describing the motion of flid in detail Flid Element Kinematics An
Lectre 5 Differential Analsis of Flid Flo Naier-Stockes eqation Differential analsis of Flid Flo The aim: to rodce differential eqation describing the motion of flid in detail Flid Element Kinematics An
LECTURE NOTES - VI. Prof. Dr. Atıl BULU
 LECTURE NOTES - VI «FLUID MECHANICS» Istanbl Technical Uniersit College of Ciil Engineering Ciil Engineering Deartment Hdralics Diision CHAPTER 6 TWO-DIMENSIONAL IDEAL FLOW 6. INTRODUCTION An ideal flid
LECTURE NOTES - VI «FLUID MECHANICS» Istanbl Technical Uniersit College of Ciil Engineering Ciil Engineering Deartment Hdralics Diision CHAPTER 6 TWO-DIMENSIONAL IDEAL FLOW 6. INTRODUCTION An ideal flid
Linear Strain Triangle and other types of 2D elements. By S. Ziaei Rad
 Linear Strain Triangle and other tpes o D elements B S. Ziaei Rad Linear Strain Triangle (LST or T6 This element is also called qadratic trianglar element. Qadratic Trianglar Element Linear Strain Triangle
Linear Strain Triangle and other tpes o D elements B S. Ziaei Rad Linear Strain Triangle (LST or T6 This element is also called qadratic trianglar element. Qadratic Trianglar Element Linear Strain Triangle
Synoptic Meteorology I. Some Thermodynamic Concepts
 Synotic Meteoroloy I Some hermodynamic Concets Geootential Heiht Geootential Heiht (h): the otential enery of a nit mass lifted from srface to. Φ d 0 -Since constant in the trooshere, we can write Φ Δ
Synotic Meteoroloy I Some hermodynamic Concets Geootential Heiht Geootential Heiht (h): the otential enery of a nit mass lifted from srface to. Φ d 0 -Since constant in the trooshere, we can write Φ Δ
Concept of Stress at a Point
 Washkeic College of Engineering Section : STRONG FORMULATION Concept of Stress at a Point Consider a point ithin an arbitraril loaded deformable bod Define Normal Stress Shear Stress lim A Fn A lim A FS
Washkeic College of Engineering Section : STRONG FORMULATION Concept of Stress at a Point Consider a point ithin an arbitraril loaded deformable bod Define Normal Stress Shear Stress lim A Fn A lim A FS
STATIC, STAGNATION, AND DYNAMIC PRESSURES
 STATIC, STAGNATION, AND DYNAMIC PRESSURES Bernolli eqation is g constant In this eqation is called static ressre, becase it is the ressre that wold be measred by an instrment that is static with resect
STATIC, STAGNATION, AND DYNAMIC PRESSURES Bernolli eqation is g constant In this eqation is called static ressre, becase it is the ressre that wold be measred by an instrment that is static with resect
Viscous Dissipation and Heat Absorption effect on Natural Convection Flow with Uniform Surface Temperature along a Vertical Wavy Surface
 Aailable at htt://am.ed/aam Al. Al. Math. ISSN: 93-966 Alications and Alied Mathematics: An International Jornal (AAM) Secial Isse No. (Ma 6),. 8 8th International Mathematics Conference, March,, IUB Cams,
Aailable at htt://am.ed/aam Al. Al. Math. ISSN: 93-966 Alications and Alied Mathematics: An International Jornal (AAM) Secial Isse No. (Ma 6),. 8 8th International Mathematics Conference, March,, IUB Cams,
Synoptic Meterorology I. Some Thermodynamic Concepts
 Synotic Meteroroloy I Some hermoynamic Concets Geootential Heiht Geootential Heiht (h): the otential enery of a nit mass lifte from srface to. Φ 0 -Since constant in the trooshere, we can write Φ m m m
Synotic Meteroroloy I Some hermoynamic Concets Geootential Heiht Geootential Heiht (h): the otential enery of a nit mass lifte from srface to. Φ 0 -Since constant in the trooshere, we can write Φ m m m
Synoptic Meteorology I: The Geostrophic Approximation. 30 September, 7 October 2014
 The Equations of Motion Synotic Meteorology I: The Geostrohic Aroimation 30 Setember, 7 October 2014 In their most general form, and resented without formal derivation, the equations of motion alicable
The Equations of Motion Synotic Meteorology I: The Geostrohic Aroimation 30 Setember, 7 October 2014 In their most general form, and resented without formal derivation, the equations of motion alicable
3. Several Random Variables
 . Several Random Variables. To Random Variables. Conditional Probabilit--Revisited. Statistical Independence.4 Correlation beteen Random Variables Standardied (or ero mean normalied) random variables.5
. Several Random Variables. To Random Variables. Conditional Probabilit--Revisited. Statistical Independence.4 Correlation beteen Random Variables Standardied (or ero mean normalied) random variables.5
Homework 1. System dynamics can be expressed in nonlinear state-space form as
 Hoework arane s eqation and soe iortant systes This Hoework irst ives an eale o indin the dynaics o a certain canonical syste, then asks yo to do the sae or two other canonical systes odelin Physical Systes
Hoework arane s eqation and soe iortant systes This Hoework irst ives an eale o indin the dynaics o a certain canonical syste, then asks yo to do the sae or two other canonical systes odelin Physical Systes
Velocity and Accceleration in Different Coordinate system
 Velocity & cceleration in different coordinate system Chapter Velocity and ccceleration in Different Coordinate system In physics basic laws are first introdced for a point partile and then laws are etended
Velocity & cceleration in different coordinate system Chapter Velocity and ccceleration in Different Coordinate system In physics basic laws are first introdced for a point partile and then laws are etended
EE2 Mathematics : Functions of Multiple Variables
 EE2 Mathematics : Fnctions of Mltiple Variables http://www2.imperial.ac.k/ nsjones These notes are not identical word-for-word with m lectres which will be gien on the blackboard. Some of these notes ma
EE2 Mathematics : Fnctions of Mltiple Variables http://www2.imperial.ac.k/ nsjones These notes are not identical word-for-word with m lectres which will be gien on the blackboard. Some of these notes ma
Integration of Basic Functions. Session 7 : 9/23 1
 Integration o Basic Fnctions Session 7 : 9/3 Antiderivation Integration Deinition: Taking the antiderivative, or integral, o some nction F(), reslts in the nction () i ()F() Pt simply: i yo take the integral
Integration o Basic Fnctions Session 7 : 9/3 Antiderivation Integration Deinition: Taking the antiderivative, or integral, o some nction F(), reslts in the nction () i ()F() Pt simply: i yo take the integral
Comments on Vertical Vorticity Advection
 Comments on Vertical Vorticity Advection It shold be fairly intitive that ositive maima in vertical vorticity are associated with cyclones, and ths ositive cyclonic vorticity advection might be a sefl
Comments on Vertical Vorticity Advection It shold be fairly intitive that ositive maima in vertical vorticity are associated with cyclones, and ths ositive cyclonic vorticity advection might be a sefl
Fluid Dynamics. Type of Flows Continuity Equation Bernoulli Equation Steady Flow Energy Equation Applications of Bernoulli Equation
 Tye of Flows Continity Eqation Bernolli Eqation Steady Flow Energy Eqation Alications of Bernolli Eqation Flid Dynamics Streamlines Lines having the direction of the flid velocity Flids cannot cross a
Tye of Flows Continity Eqation Bernolli Eqation Steady Flow Energy Eqation Alications of Bernolli Eqation Flid Dynamics Streamlines Lines having the direction of the flid velocity Flids cannot cross a
1 The space of linear transformations from R n to R m :
 Math 540 Spring 20 Notes #4 Higher deriaties, Taylor s theorem The space of linear transformations from R n to R m We hae discssed linear transformations mapping R n to R m We can add sch linear transformations
Math 540 Spring 20 Notes #4 Higher deriaties, Taylor s theorem The space of linear transformations from R n to R m We hae discssed linear transformations mapping R n to R m We can add sch linear transformations
Propagation of error for multivariable function
 Proagation o error or mltiariable nction No consider a mltiariable nction (,,, ). I measrements o,,,. All hae ncertaint,,,., ho ill this aect the ncertaint o the nction? L tet) o (Eqation (3.8) ± L ),...,,
Proagation o error or mltiariable nction No consider a mltiariable nction (,,, ). I measrements o,,,. All hae ncertaint,,,., ho ill this aect the ncertaint o the nction? L tet) o (Eqation (3.8) ± L ),...,,
Introduction to Convection
 Chater 6 Introdction to Conection he Conection Bondar aer Velocit Bondar aer A coneqence o ico eect aociated with relatie motion between a lid and a race A region between the race and the ree tream whoe
Chater 6 Introdction to Conection he Conection Bondar aer Velocit Bondar aer A coneqence o ico eect aociated with relatie motion between a lid and a race A region between the race and the ree tream whoe
1 such that v k g. v g. u g
 Mesoscale Meteoroloy: Quasi-Geostrohic Theory 4, 6 February 7 Wait this is a mesoscale class why do we care about a tenet o synotic meteoroloy?? On the synotic-scale, scale analysis o the orcin terms in
Mesoscale Meteoroloy: Quasi-Geostrohic Theory 4, 6 February 7 Wait this is a mesoscale class why do we care about a tenet o synotic meteoroloy?? On the synotic-scale, scale analysis o the orcin terms in
Chapter 6 Momentum Transfer in an External Laminar Boundary Layer
 6. Similarit Soltions Chapter 6 Momentm Transfer in an Eternal Laminar Bondar Laer Consider a laminar incompressible bondar laer with constant properties. Assme the flow is stead and two-dimensional aligned
6. Similarit Soltions Chapter 6 Momentm Transfer in an Eternal Laminar Bondar Laer Consider a laminar incompressible bondar laer with constant properties. Assme the flow is stead and two-dimensional aligned
Primary dependent variable is fluid velocity vector V = V ( r ); where r is the position vector
 Chapter 4: Flids Kinematics 4. Velocit and Description Methods Primar dependent ariable is flid elocit ector V V ( r ); where r is the position ector If V is known then pressre and forces can be determined
Chapter 4: Flids Kinematics 4. Velocit and Description Methods Primar dependent ariable is flid elocit ector V V ( r ); where r is the position ector If V is known then pressre and forces can be determined
Module 4. Analysis of Statically Indeterminate Structures by the Direct Stiffness Method. Version 2 CE IIT, Kharagpur
 Modle Analysis of Statically Indeterminate Strctres by the Direct Stiffness Method Version CE IIT, Kharagr Lesson The Direct Stiffness Method: Trss Analysis (Contined) Version CE IIT, Kharagr Instrctional
Modle Analysis of Statically Indeterminate Strctres by the Direct Stiffness Method Version CE IIT, Kharagr Lesson The Direct Stiffness Method: Trss Analysis (Contined) Version CE IIT, Kharagr Instrctional
Place value and fractions. Explanation and worked examples We read this number as two hundred and fifty-six point nine one.
 3 3 Place vale and ractions Exlanation and worked examles Level Yo shold know and nderstand which digit o a nmer shows the nmer o: ten thosands 0 000 thosands 000 hndreds 00 tens 0 nits As well as the
3 3 Place vale and ractions Exlanation and worked examles Level Yo shold know and nderstand which digit o a nmer shows the nmer o: ten thosands 0 000 thosands 000 hndreds 00 tens 0 nits As well as the
MAT389 Fall 2016, Problem Set 6
 MAT389 Fall 016, Problem Set 6 Trigonometric and hperbolic fnctions 6.1 Show that e iz = cos z + i sin z for eer comple nmber z. Hint: start from the right-hand side and work or wa towards the left-hand
MAT389 Fall 016, Problem Set 6 Trigonometric and hperbolic fnctions 6.1 Show that e iz = cos z + i sin z for eer comple nmber z. Hint: start from the right-hand side and work or wa towards the left-hand
Complex Variables. For ECON 397 Macroeconometrics Steve Cunningham
 Comple Variables For ECON 397 Macroeconometrics Steve Cnningham Open Disks or Neighborhoods Deinition. The set o all points which satis the ineqalit
Comple Variables For ECON 397 Macroeconometrics Steve Cnningham Open Disks or Neighborhoods Deinition. The set o all points which satis the ineqalit
EFFECT OF DIMENSIONLESS NUMBER ON NATURAL CONVECTION IN AN OPEN SQUARE CAVITY HAVING PARTIALLY HEATED SQUARE CYLINDER
 Proceedings of the International Conference on echanical Engineering ICE) 8- December Dhaka Bangladesh ICE-TH- EFFECT OF DIEIOE BER O TR COECTIO I OPE QRE CIT HIG PRTI HETED QRE CIDER ohammed asir ddin
Proceedings of the International Conference on echanical Engineering ICE) 8- December Dhaka Bangladesh ICE-TH- EFFECT OF DIEIOE BER O TR COECTIO I OPE QRE CIT HIG PRTI HETED QRE CIDER ohammed asir ddin
Numerical Simulation of Density Currents over a Slope under the Condition of Cooling Period in Lake Biwa
 Nmerical Simlation of Densit Crrents oer a Slope nder the Condition of Cooling Period in Lake Bia Takashi Hosoda Professor, Department of Urban Management, Koto Uniersit, C1-3-65, Kotodai-Katsra, Nishiko-k,
Nmerical Simlation of Densit Crrents oer a Slope nder the Condition of Cooling Period in Lake Bia Takashi Hosoda Professor, Department of Urban Management, Koto Uniersit, C1-3-65, Kotodai-Katsra, Nishiko-k,
m = Average Rate of Change (Secant Slope) Example:
 Average Rate o Change Secant Slope Deinition: The average change secant slope o a nction over a particlar interval [a, b] or [a, ]. Eample: What is the average rate o change o the nction over the interval
Average Rate o Change Secant Slope Deinition: The average change secant slope o a nction over a particlar interval [a, b] or [a, ]. Eample: What is the average rate o change o the nction over the interval
Net Force on a Body Completely in a Fluid. Natural Convection Heat Transfer. Net Buoyancy Force and Temperature
 Natral Conection eat ranfer Net Force on a Bo Comletel in a Fli he net force alie to a bo comletel bmere in a fli i Bo F W F net bo bo boanc V bo fli fli V V bo bo W F boanc Fli q he bo can be a blk of
Natral Conection eat ranfer Net Force on a Bo Comletel in a Fli he net force alie to a bo comletel bmere in a fli i Bo F W F net bo bo boanc V bo fli fli V V bo bo W F boanc Fli q he bo can be a blk of
ATM The thermal wind Fall, 2016 Fovell
 ATM 316 - The thermal wind Fall, 2016 Fovell Reca and isobaric coordinates We have seen that for the synotic time and sace scales, the three leading terms in the horizontal equations of motion are du dt
ATM 316 - The thermal wind Fall, 2016 Fovell Reca and isobaric coordinates We have seen that for the synotic time and sace scales, the three leading terms in the horizontal equations of motion are du dt
Lesson 81: The Cross Product of Vectors
 Lesson 8: The Cross Prodct of Vectors IBHL - SANTOWSKI In this lesson yo will learn how to find the cross prodct of two ectors how to find an orthogonal ector to a plane defined by two ectors how to find
Lesson 8: The Cross Prodct of Vectors IBHL - SANTOWSKI In this lesson yo will learn how to find the cross prodct of two ectors how to find an orthogonal ector to a plane defined by two ectors how to find
Section 7.4: Integration of Rational Functions by Partial Fractions
 Section 7.4: Integration of Rational Fnctions by Partial Fractions This is abot as complicated as it gets. The Method of Partial Fractions Ecept for a few very special cases, crrently we have no way to
Section 7.4: Integration of Rational Fnctions by Partial Fractions This is abot as complicated as it gets. The Method of Partial Fractions Ecept for a few very special cases, crrently we have no way to
Correlations for Nusselt Number in Free Convection from an Isothermal Inclined Square Plate by a Numerical Simulation
 American Jornal of Mechanics and Applications 5; : 8-8 Pblished online Ma 4, 5 http://sciencepblishinggropcom/j/ajma doi: 648/jajma5 ISSN: 76-65 Print; ISSN: 76-6 Online Correlations for Nsselt Nmber in
American Jornal of Mechanics and Applications 5; : 8-8 Pblished online Ma 4, 5 http://sciencepblishinggropcom/j/ajma doi: 648/jajma5 ISSN: 76-65 Print; ISSN: 76-6 Online Correlations for Nsselt Nmber in
Profit Maximization. Beattie, Taylor, and Watts Sections: 3.1b-c, 3.2c, , 5.2a-d
 Proit Maimization Beattie Talor and Watts Sections:.b-c.c 4.-4. 5.a-d Agenda Generalized Proit Maimization Proit Maimization ith One Inut and One Outut Proit Maimization ith To Inuts and One Outut Proit
Proit Maimization Beattie Talor and Watts Sections:.b-c.c 4.-4. 5.a-d Agenda Generalized Proit Maimization Proit Maimization ith One Inut and One Outut Proit Maimization ith To Inuts and One Outut Proit
Chapter 9 Flow over Immersed Bodies
 57:00 Mechanics o Flids and Transport Processes Chapter 9 Proessor Fred Stern Fall 01 1 Chapter 9 Flow over Immersed Bodies Flid lows are broadly categorized: 1. Internal lows sch as dcts/pipes, trbomachinery,
57:00 Mechanics o Flids and Transport Processes Chapter 9 Proessor Fred Stern Fall 01 1 Chapter 9 Flow over Immersed Bodies Flid lows are broadly categorized: 1. Internal lows sch as dcts/pipes, trbomachinery,
Chapter 8: MULTIPLE CONTINUOUS RANDOM VARIABLES
 Charles Boncelet Probabilit Statistics and Random Signals" Oord Uniersit Press 06. ISBN: 978-0-9-0005-0 Chapter 8: MULTIPLE CONTINUOUS RANDOM VARIABLES Sections 8. Joint Densities and Distribution unctions
Charles Boncelet Probabilit Statistics and Random Signals" Oord Uniersit Press 06. ISBN: 978-0-9-0005-0 Chapter 8: MULTIPLE CONTINUOUS RANDOM VARIABLES Sections 8. Joint Densities and Distribution unctions
FFTs in Graphics and Vision. Rotational and Reflective Symmetry Detection
 FFTs in Grahics and Vision Rotational and Relectie Symmetry Detection Outline Reresentation Theory Symmetry Detection Rotational Symmetry Relectie Symmetry Reresentation Theory Recall: A rou is a set o
FFTs in Grahics and Vision Rotational and Relectie Symmetry Detection Outline Reresentation Theory Symmetry Detection Rotational Symmetry Relectie Symmetry Reresentation Theory Recall: A rou is a set o
Ch.1: Basics of Shallow Water Fluid
 AOS611Chapter1,/16/16,Z.Li 1 Sec. 1.1: Basic Eqations 1. Shallow Water Eqations on a Sphere Ch.1: Basics of Shallow Water Flid We start with the shallow water flid of a homogeneos densit and focs on the
AOS611Chapter1,/16/16,Z.Li 1 Sec. 1.1: Basic Eqations 1. Shallow Water Eqations on a Sphere Ch.1: Basics of Shallow Water Flid We start with the shallow water flid of a homogeneos densit and focs on the
GEF2500 GEOPHYSICAL FLUID MECHANICS
 GEF5 GEOPHYSICAL FLUID MECHANICS Jan Erik H. Weber Deartment of Geosciences Section for Meteorolog and Oceanograh Uniersit of Oslo. E-mail: j.e.weber@geo.uio.no Blindern Januar 3 Contents. FLUID MECHANICS
GEF5 GEOPHYSICAL FLUID MECHANICS Jan Erik H. Weber Deartment of Geosciences Section for Meteorolog and Oceanograh Uniersit of Oslo. E-mail: j.e.weber@geo.uio.no Blindern Januar 3 Contents. FLUID MECHANICS
The Faraday Induction Law and Field Transformations in Special Relativity
 Apeiron, ol. 10, No., April 003 118 The Farada Indction Law and Field Transformations in Special Relatiit Aleander L. Kholmetskii Department of Phsics, elars State Uniersit, 4, F. Skorina Aene, 0080 Minsk
Apeiron, ol. 10, No., April 003 118 The Farada Indction Law and Field Transformations in Special Relatiit Aleander L. Kholmetskii Department of Phsics, elars State Uniersit, 4, F. Skorina Aene, 0080 Minsk
MHD Heat and Mass Transfer Forced Convection Flow Along a Stretching Sheet with Heat Generation, Radiation and Viscous Dissipation
 Dhaka Univ. J. Sci. 59(): -8, (July) MHD Heat and Mass Transer Forced onvection Flo Along a Stretching Sheet ith Heat Generation, Radiation and Viscous Dissiation M. A. Samad, Sajid Ahmed and Md. Motaleb
Dhaka Univ. J. Sci. 59(): -8, (July) MHD Heat and Mass Transer Forced onvection Flo Along a Stretching Sheet ith Heat Generation, Radiation and Viscous Dissiation M. A. Samad, Sajid Ahmed and Md. Motaleb
Non-Linear Squeezing Flow of Casson Fluid. between Parallel Plates
 International Jornal o Matematical Analsis Vol. 9 5 no. 5 - HIKAI Ltd www.m-ikari.com tt://d.doi.org/.988/ijma.5.49 Non-Linear Sqeezing Flow o Casson Flid between Parallel Plates S. Ganes C. K. Kirbasankar
International Jornal o Matematical Analsis Vol. 9 5 no. 5 - HIKAI Ltd www.m-ikari.com tt://d.doi.org/.988/ijma.5.49 Non-Linear Sqeezing Flow o Casson Flid between Parallel Plates S. Ganes C. K. Kirbasankar
Vectors in Rn un. This definition of norm is an extension of the Pythagorean Theorem. Consider the vector u = (5, 8) in R 2
 MATH 307 Vectors in Rn Dr. Neal, WKU Matrices of dimension 1 n can be thoght of as coordinates, or ectors, in n- dimensional space R n. We can perform special calclations on these ectors. In particlar,
MATH 307 Vectors in Rn Dr. Neal, WKU Matrices of dimension 1 n can be thoght of as coordinates, or ectors, in n- dimensional space R n. We can perform special calclations on these ectors. In particlar,
Ground Rules. PC1221 Fundamentals of Physics I. Position and Displacement. Average Velocity. Lectures 7 and 8 Motion in Two Dimensions
 PC11 Fndamentals of Physics I Lectres 7 and 8 Motion in Two Dimensions A/Prof Tay Sen Chan 1 Grond Rles Switch off yor handphone and paer Switch off yor laptop compter and keep it No talkin while lectre
PC11 Fndamentals of Physics I Lectres 7 and 8 Motion in Two Dimensions A/Prof Tay Sen Chan 1 Grond Rles Switch off yor handphone and paer Switch off yor laptop compter and keep it No talkin while lectre
7. Two Random Variables
 7. Two Random Variables In man eeriments the observations are eressible not as a single quantit but as a amil o quantities. or eamle to record the height and weight o each erson in a communit or the number
7. Two Random Variables In man eeriments the observations are eressible not as a single quantit but as a amil o quantities. or eamle to record the height and weight o each erson in a communit or the number
Change of Variables. (f T) JT. f = U
 Change of Variables 4-5-8 The change of ariables formla for mltiple integrals is like -sbstittion for single-ariable integrals. I ll gie the general change of ariables formla first, and consider specific
Change of Variables 4-5-8 The change of ariables formla for mltiple integrals is like -sbstittion for single-ariable integrals. I ll gie the general change of ariables formla first, and consider specific
4 Primitive Equations
 4 Primitive Eqations 4.1 Spherical coordinates 4.1.1 Usefl identities We now introdce the special case of spherical coordinates: (,, r) (longitde, latitde, radial distance from Earth s center), with 0
4 Primitive Eqations 4.1 Spherical coordinates 4.1.1 Usefl identities We now introdce the special case of spherical coordinates: (,, r) (longitde, latitde, radial distance from Earth s center), with 0
CE 2313 / MAE 2312 Mechanics of Materials. Examination III
 E 1 / E 1 ecanics of aterials Eamination ril 6, 7 Name: Tere are 4 numered rolems on tis eam. Te relatie eigt of eac rolem is roided in arenteses immediatel after te rolem numer. Time ed for te eam is
E 1 / E 1 ecanics of aterials Eamination ril 6, 7 Name: Tere are 4 numered rolems on tis eam. Te relatie eigt of eac rolem is roided in arenteses immediatel after te rolem numer. Time ed for te eam is
ATMS 310 The Vorticity Equation. The Vorticity Equation describes the factors that can alter the magnitude of the absolute vorticity with time.
 ATMS 30 The Vorici Eqaion The Vorici Eqaion describes he acors ha can aler he magnide o he absole orici ih ime. Vorici Eqaion in Caresian Coordinaes The (,,,) orm is deried rom he rimiie horional eqaions
ATMS 30 The Vorici Eqaion The Vorici Eqaion describes he acors ha can aler he magnide o he absole orici ih ime. Vorici Eqaion in Caresian Coordinaes The (,,,) orm is deried rom he rimiie horional eqaions
A Proposed Method for Reliability Analysis in Higher Dimension
 A Proposed Method or Reliabilit Analsis in Higher Dimension S Kadr Abstract In this paper a new method is proposed to ealate the reliabilit o stochastic mechanical sstems This techniqe is based on the
A Proposed Method or Reliabilit Analsis in Higher Dimension S Kadr Abstract In this paper a new method is proposed to ealate the reliabilit o stochastic mechanical sstems This techniqe is based on the
3.3 Operations With Vectors, Linear Combinations
 Operations With Vectors, Linear Combinations Performance Criteria: (d) Mltiply ectors by scalars and add ectors, algebraically Find linear combinations of ectors algebraically (e) Illstrate the parallelogram
Operations With Vectors, Linear Combinations Performance Criteria: (d) Mltiply ectors by scalars and add ectors, algebraically Find linear combinations of ectors algebraically (e) Illstrate the parallelogram
5 th Smosium on Integrating CF and Exeriments in Aerodnamics (Integration 0) 3-5 October 0 JAXA Chofu Aerosace Center, Toko, Jaan rag and Lift Predict
 5th Smosium on Integrating CF and Exeriments in Aerodnamics (Integration 0) 45 5 th Smosium on Integrating CF and Exeriments in Aerodnamics (Integration 0) 3-5 October 0 JAXA Chofu Aerosace Center, Toko,
5th Smosium on Integrating CF and Exeriments in Aerodnamics (Integration 0) 45 5 th Smosium on Integrating CF and Exeriments in Aerodnamics (Integration 0) 3-5 October 0 JAXA Chofu Aerosace Center, Toko,
Multiplication and division. Explanation and worked examples. First, we ll look at work you should know at this level.
 x Mltilication and division Exlanation and worked examles Level First, we ll look at work yo shold know at this level. Work ot these mltilication and division sms: a) ) 96 c) 8 d) 6 Soltions: a) 9 6 Yo
x Mltilication and division Exlanation and worked examles Level First, we ll look at work yo shold know at this level. Work ot these mltilication and division sms: a) ) 96 c) 8 d) 6 Soltions: a) 9 6 Yo
Get the frictional force from the normal force. Use dynamics to get the normal force.
 . L F n µ k L =00 t µ k = 0.60 = 0 o = 050 lb F n +y +x x = sin y = cos = µf n Is the initial elocity o the car reater than 30 mph? Approach: Use conseration o enery. System: car Initial time: beore you
. L F n µ k L =00 t µ k = 0.60 = 0 o = 050 lb F n +y +x x = sin y = cos = µf n Is the initial elocity o the car reater than 30 mph? Approach: Use conseration o enery. System: car Initial time: beore you
Node-voltage method using virtual current sources technique for special cases
 Node-oltage method using irtual current sources technique for secial cases George E. Chatzarakis and Marina D. Tortoreli Electrical and Electronics Engineering Deartments, School of Pedagogical and Technological
Node-oltage method using irtual current sources technique for secial cases George E. Chatzarakis and Marina D. Tortoreli Electrical and Electronics Engineering Deartments, School of Pedagogical and Technological
ECE Notes 4 Functions of a Complex Variable as Mappings. Fall 2017 David R. Jackson. Notes are adapted from D. R. Wilton, Dept.
 ECE 638 Fall 017 Daid R. Jackson Notes 4 Fnctions of a Comple Variable as Mappings Notes are adapted from D. R. Wilton, Dept. of ECE 1 A Fnction of a Comple Variable as a Mapping A fnction of a comple
ECE 638 Fall 017 Daid R. Jackson Notes 4 Fnctions of a Comple Variable as Mappings Notes are adapted from D. R. Wilton, Dept. of ECE 1 A Fnction of a Comple Variable as a Mapping A fnction of a comple
An example of Lagrangian for a non-holonomic system
 Uniersit of North Georgia Nighthaks Open Institutional Repositor Facult Publications Department of Mathematics 9-9-05 An eample of Lagrangian for a non-holonomic sstem Piotr W. Hebda Uniersit of North
Uniersit of North Georgia Nighthaks Open Institutional Repositor Facult Publications Department of Mathematics 9-9-05 An eample of Lagrangian for a non-holonomic sstem Piotr W. Hebda Uniersit of North
0.1 Practical Guide - Surface Integrals. C (0,0,c) A (0,b,0) A (a,0,0)
 . Practical Guide - urface Integrals urface integral,means to integrate over a surface. We begin with the stud of surfaces. The easiest wa is to give as man familiar eamles as ossible ) a lane surface
. Practical Guide - urface Integrals urface integral,means to integrate over a surface. We begin with the stud of surfaces. The easiest wa is to give as man familiar eamles as ossible ) a lane surface
Math 263 Assignment #3 Solutions. 1. A function z = f(x, y) is called harmonic if it satisfies Laplace s equation:
 Math 263 Assignment #3 Soltions 1. A fnction z f(x, ) is called harmonic if it satisfies Laplace s eqation: 2 + 2 z 2 0 Determine whether or not the following are harmonic. (a) z x 2 + 2. We se the one-variable
Math 263 Assignment #3 Soltions 1. A fnction z f(x, ) is called harmonic if it satisfies Laplace s eqation: 2 + 2 z 2 0 Determine whether or not the following are harmonic. (a) z x 2 + 2. We se the one-variable
The. Consortium. Continuum Mechanics. Original notes by Professor Mike Gunn, South Bank University, London, UK Produced by the CRISP Consortium Ltd
 The C R I S P Consortium Continuum Mechanics Original notes b Professor Mike Gunn, South Bank Universit, London, UK Produced b the CRISP Consortium Ltd THOR OF STRSSS In a three dimensional loaded bod,
The C R I S P Consortium Continuum Mechanics Original notes b Professor Mike Gunn, South Bank Universit, London, UK Produced b the CRISP Consortium Ltd THOR OF STRSSS In a three dimensional loaded bod,
Boundary layer develops in the flow direction, δ = δ (x) τ
 58:68 Trblent Flos Handot: Bondar Laers Differences to Trblent Channel Flo Bondar laer develops in the flo direction, not knon a priori Oter part of the flo consists of interittent trblent/non-trblent
58:68 Trblent Flos Handot: Bondar Laers Differences to Trblent Channel Flo Bondar laer develops in the flo direction, not knon a priori Oter part of the flo consists of interittent trblent/non-trblent
Where: Where: f Wave s frequency (Hz) c Speed of light ( ms -1 ) Wavelength (m)
 in a direction to both of the fields as shown in Figure 1. In wave model, the electromagnetic radiation is commonly associated with wavelength and frequency, exressed mathematically as: c f...(1) f Wave
in a direction to both of the fields as shown in Figure 1. In wave model, the electromagnetic radiation is commonly associated with wavelength and frequency, exressed mathematically as: c f...(1) f Wave
P6.5 (a) static friction. v r. = r ( 30.0 cm )( 980 cm s ) P6.15 Let the tension at the lowest point be T.
 Q65 The speed chanes The tanential orce component causes tanential acceleration Q69 I would not accept that statement or two reasons First, to be beyond the pull o raity, one would hae to be ininitely
Q65 The speed chanes The tanential orce component causes tanential acceleration Q69 I would not accept that statement or two reasons First, to be beyond the pull o raity, one would hae to be ininitely
λ. It is usually positive; if it is zero then the constraint is not binding.
 hater 4 Utilit Maimization and hoice rational consmer chooses his most referred bndle of commodities from the set of feasible choices to consme The rocess of obtaining this otimal bndle is called tilit-maimization
hater 4 Utilit Maimization and hoice rational consmer chooses his most referred bndle of commodities from the set of feasible choices to consme The rocess of obtaining this otimal bndle is called tilit-maimization
Q2. The velocity field in a fluid flow is given by
 Kinematics of Flid Q. Choose the correct anser (i) streamline is a line (a) hich is along the path of a particle (b) dran normal to the elocit ector at an point (c) sch that the streamlines diide the passage
Kinematics of Flid Q. Choose the correct anser (i) streamline is a line (a) hich is along the path of a particle (b) dran normal to the elocit ector at an point (c) sch that the streamlines diide the passage
= ( 2) = p 5.
 MATH 0 Exam (Version ) Solutions Setember, 00 S. F. Ellermeyer Name Instructions. Your work on this exam will be raded accordin to two criteria: mathematical correctness clarity of resentation. In other
MATH 0 Exam (Version ) Solutions Setember, 00 S. F. Ellermeyer Name Instructions. Your work on this exam will be raded accordin to two criteria: mathematical correctness clarity of resentation. In other
Department of Economics. Issn Discussion paper 32/09. Optimal Interest Rate Rules Under One-Sided Output and Inflation Targets *
 Deartment of Economics Issn 44-549 Discssion aer 3/9 Otimal Interest Rate Rles Under One-Sided Ott and Inflation Targets * Peter J. Stem Abstract: We inestigate the deriation of otimal interest rate rles
Deartment of Economics Issn 44-549 Discssion aer 3/9 Otimal Interest Rate Rles Under One-Sided Ott and Inflation Targets * Peter J. Stem Abstract: We inestigate the deriation of otimal interest rate rles
Reaction-Diusion Systems with. 1-Homogeneous Non-linearity. Matthias Buger. Mathematisches Institut der Justus-Liebig-Universitat Gieen
 Reaction-Dision Systems ith 1-Homogeneos Non-linearity Matthias Bger Mathematisches Institt der Jsts-Liebig-Uniersitat Gieen Arndtstrae 2, D-35392 Gieen, Germany Abstract We describe the dynamics of a
Reaction-Dision Systems ith 1-Homogeneos Non-linearity Matthias Bger Mathematisches Institt der Jsts-Liebig-Uniersitat Gieen Arndtstrae 2, D-35392 Gieen, Germany Abstract We describe the dynamics of a
Chapter 2 Introduction to the Stiffness (Displacement) Method. The Stiffness (Displacement) Method
 CIVL 7/87 Chater - The Stiffness Method / Chater Introdction to the Stiffness (Dislacement) Method Learning Objectives To define the stiffness matrix To derive the stiffness matrix for a sring element
CIVL 7/87 Chater - The Stiffness Method / Chater Introdction to the Stiffness (Dislacement) Method Learning Objectives To define the stiffness matrix To derive the stiffness matrix for a sring element
2 The Bhaduri-Marglin model
 The Bhaduri-Marglin model n this chapter the basics o the Bhaduri-Marglin model ill be discussed. Doing so, attention ill be directed on hich eatures o the model ill hae to be altered hen endogeniing labor
The Bhaduri-Marglin model n this chapter the basics o the Bhaduri-Marglin model ill be discussed. Doing so, attention ill be directed on hich eatures o the model ill hae to be altered hen endogeniing labor
Notes on Optical Pumping Procedure & Theory
 Notes on Otical Puming Procedure & Theory Pre-lab 1. Why is the exeriment called otical uming? What is umed? 2. What is the exerimental signature of having cancelled all magnetic fields in the samle cell?
Notes on Otical Puming Procedure & Theory Pre-lab 1. Why is the exeriment called otical uming? What is umed? 2. What is the exerimental signature of having cancelled all magnetic fields in the samle cell?
Final Examination, MEA 443 Fall 2003, Lackmann
 Place an X here to count it double! Name: Final Eamination, MEA 443 Fall 003, Lackmann If ou wish to have the final eam count double, and dro our lowest score in an of the three semester eams, mark an
Place an X here to count it double! Name: Final Eamination, MEA 443 Fall 003, Lackmann If ou wish to have the final eam count double, and dro our lowest score in an of the three semester eams, mark an
Turbulence and boundary layers
 Trblence and bondary layers Weather and trblence Big whorls hae little whorls which feed on the elocity; and little whorls hae lesser whorls and so on to iscosity Lewis Fry Richardson Momentm eqations
Trblence and bondary layers Weather and trblence Big whorls hae little whorls which feed on the elocity; and little whorls hae lesser whorls and so on to iscosity Lewis Fry Richardson Momentm eqations
u P(t) = P(x,y) r v t=0 4/4/2006 Motion ( F.Robilliard) 1
 y g j P(t) P(,y) r t0 i 4/4/006 Motion ( F.Robilliard) 1 Motion: We stdy in detail three cases of motion: 1. Motion in one dimension with constant acceleration niform linear motion.. Motion in two dimensions
y g j P(t) P(,y) r t0 i 4/4/006 Motion ( F.Robilliard) 1 Motion: We stdy in detail three cases of motion: 1. Motion in one dimension with constant acceleration niform linear motion.. Motion in two dimensions
Math Review. Week 1, Wed Jan 10
 Uniersity of British Colbia CPSC 4 Coter Grahics Jan-Ar 007 Taara Mnzner Math Reiew Week, Wed Jan 0 htt://www.grad.cs.bc.ca/~cs4/vjan007 News sign sheet with nae, eail, rogra Reiew: Coter Grahics Defined
Uniersity of British Colbia CPSC 4 Coter Grahics Jan-Ar 007 Taara Mnzner Math Reiew Week, Wed Jan 0 htt://www.grad.cs.bc.ca/~cs4/vjan007 News sign sheet with nae, eail, rogra Reiew: Coter Grahics Defined
Inertial and gravitational mass in relativistic mechanics
 Träge nd schere Masse in der Relativitätsmechanik Ann. Phs. (Leipig) (4) 4 (1913) 856-878. Inertial and gravitational mass in relativistic mechanics B Gnnar Nordstrøm Translated b D. H. Delphenich In several
Träge nd schere Masse in der Relativitätsmechanik Ann. Phs. (Leipig) (4) 4 (1913) 856-878. Inertial and gravitational mass in relativistic mechanics B Gnnar Nordstrøm Translated b D. H. Delphenich In several
Equivalence between transition systems. Modal logic and first order logic. In pictures: forth condition. Bisimilation. In pictures: back condition
 odal logic and first order logic odal logic: local ie of the strctre ( here can I get by folloing links from here ). First order logic: global ie of the strctre (can see eerything, qantifiers do not follo
odal logic and first order logic odal logic: local ie of the strctre ( here can I get by folloing links from here ). First order logic: global ie of the strctre (can see eerything, qantifiers do not follo
10.2 Solving Quadratic Equations by Completing the Square
 . Solving Qadratic Eqations b Completing the Sqare Consider the eqation ( ) We can see clearl that the soltions are However, What if the eqation was given to s in standard form, that is 6 How wold we go
. Solving Qadratic Eqations b Completing the Sqare Consider the eqation ( ) We can see clearl that the soltions are However, What if the eqation was given to s in standard form, that is 6 How wold we go
Synoptic Meteorology I: Kinematic Properties. 23, 28 October 2014
 Soptic Meteorolo I: Kiematic Properties 3, 8 October 4 What is the Wid? Qalitatiel, we derstad the wid as bei a relectio o the air s (three-dimesioal) motio. Beore we proceed, howeer, it is worthwhile
Soptic Meteorolo I: Kiematic Properties 3, 8 October 4 What is the Wid? Qalitatiel, we derstad the wid as bei a relectio o the air s (three-dimesioal) motio. Beore we proceed, howeer, it is worthwhile
SECTION 6.7. The Dot Product. Preview Exercises. 754 Chapter 6 Additional Topics in Trigonometry. 7 w u 7 2 =?. 7 v 77w7
 754 Chapter 6 Additional Topics in Trigonometry 115. Yo ant to fly yor small plane de north, bt there is a 75-kilometer ind bloing from est to east. a. Find the direction angle for here yo shold head the
754 Chapter 6 Additional Topics in Trigonometry 115. Yo ant to fly yor small plane de north, bt there is a 75-kilometer ind bloing from est to east. a. Find the direction angle for here yo shold head the
OPTIMAL INTEREST RATE RULES UNDER ONE-SIDED OUTPUT AND INFLATION TARGETS. Peter J. Stemp
 OPTIMAL INTEREST RATE RULES UNDER ONE-SIDED OUTPUT AND INFLATION TARGETS b Peter J. Stem Deartment of Economics Monash Uniersit PO Box 197, Calfield East Victoria, 3145 Astralia email: eter.stem@bseco.monash.ed.a
OPTIMAL INTEREST RATE RULES UNDER ONE-SIDED OUTPUT AND INFLATION TARGETS b Peter J. Stem Deartment of Economics Monash Uniersit PO Box 197, Calfield East Victoria, 3145 Astralia email: eter.stem@bseco.monash.ed.a
Numerical Methods: Structured vs. unstructured grids. General Introduction: Why numerical methods? Numerical methods and their fields of application
 Numerical Methods: Structured vs. unstructured grids The goals o this course General : Why numerical methods? Numerical methods and their ields o alication Review o inite dierences Goals: Understanding
Numerical Methods: Structured vs. unstructured grids The goals o this course General : Why numerical methods? Numerical methods and their ields o alication Review o inite dierences Goals: Understanding
Elio Sacco. Dipartimento di Ingegneria Civile e Meccanica Università di Cassino e LM
 Elio Sacco Diartimento di Ingegneria Civile e Meccanica Università di Cassino e LM 1D erect elastolastic resonse OA elastic resonse AB nonlinear resonse, constant stress BC elastic nloading CB elastic
Elio Sacco Diartimento di Ingegneria Civile e Meccanica Università di Cassino e LM 1D erect elastolastic resonse OA elastic resonse AB nonlinear resonse, constant stress BC elastic nloading CB elastic
Higher Maths A1.3 Recurrence Relations - Revision
 Higher Maths A Recrrence Relations - Revision This revision pack covers the skills at Unit Assessment exam level or Recrrence Relations so yo can evalate yor learning o this otcome It is important that
Higher Maths A Recrrence Relations - Revision This revision pack covers the skills at Unit Assessment exam level or Recrrence Relations so yo can evalate yor learning o this otcome It is important that
Graphs and Networks Lecture 5. PageRank. Lecturer: Daniel A. Spielman September 20, 2007
 Graphs and Networks Lectre 5 PageRank Lectrer: Daniel A. Spielman September 20, 2007 5.1 Intro to PageRank PageRank, the algorithm reportedly sed by Google, assigns a nmerical rank to eery web page. More
Graphs and Networks Lectre 5 PageRank Lectrer: Daniel A. Spielman September 20, 2007 5.1 Intro to PageRank PageRank, the algorithm reportedly sed by Google, assigns a nmerical rank to eery web page. More
Bertrand s Theorem. October 8, µr 2 + V (r) 0 = dv eff dr. 3 + dv. f (r 0 )
 Bertrand s Theorem October 8, Circlar orbits The eective potential, V e = has a minimm or maximm at r i and only i so we mst have = dv e L µr + V r = L µ 3 + dv = L µ 3 r r = L µ 3 At this radis, there
Bertrand s Theorem October 8, Circlar orbits The eective potential, V e = has a minimm or maximm at r i and only i so we mst have = dv e L µr + V r = L µ 3 + dv = L µ 3 r r = L µ 3 At this radis, there
Program Burn Algorithms Based on Detonation Shock Dynamics
 Program Brn Algorithms Based on Detonation Shock Dynamics Discrete Aroimations of Detonation Flows with Discontinos Front Models J. B. Bdzil, D. S. Stewart and T. L. Jackson DX-division, Los Alamos National
Program Brn Algorithms Based on Detonation Shock Dynamics Discrete Aroimations of Detonation Flows with Discontinos Front Models J. B. Bdzil, D. S. Stewart and T. L. Jackson DX-division, Los Alamos National
called the potential flow, and function φ is called the velocity potential.
 J. Szantr Lectre No. 3 Potential flows 1 If the flid flow is irrotational, i.e. everwhere or almost everwhere in the field of flow there is rot 0 it means that there eists a scalar fnction ϕ,, z), sch
J. Szantr Lectre No. 3 Potential flows 1 If the flid flow is irrotational, i.e. everwhere or almost everwhere in the field of flow there is rot 0 it means that there eists a scalar fnction ϕ,, z), sch
Chapter 3. Systems of Linear Equations: Geometry
 Chapter 3 Systems of Linear Equations: Geometry Motiation We ant to think about the algebra in linear algebra (systems of equations and their solution sets) in terms of geometry (points, lines, planes,
Chapter 3 Systems of Linear Equations: Geometry Motiation We ant to think about the algebra in linear algebra (systems of equations and their solution sets) in terms of geometry (points, lines, planes,
The Dot Product
 The Dot Product 1-9-017 If = ( 1,, 3 ) and = ( 1,, 3 ) are ectors, the dot product of and is defined algebraically as = 1 1 + + 3 3. Example. (a) Compute the dot product (,3, 7) ( 3,,0). (b) Compute the
The Dot Product 1-9-017 If = ( 1,, 3 ) and = ( 1,, 3 ) are ectors, the dot product of and is defined algebraically as = 1 1 + + 3 3. Example. (a) Compute the dot product (,3, 7) ( 3,,0). (b) Compute the
Change of Variables. f(x, y) da = (1) If the transformation T hasn t already been given, come up with the transformation to use.
 MATH 2Q Spring 26 Daid Nichols Change of Variables Change of ariables in mltiple integrals is complicated, bt it can be broken down into steps as follows. The starting point is a doble integral in & y.
MATH 2Q Spring 26 Daid Nichols Change of Variables Change of ariables in mltiple integrals is complicated, bt it can be broken down into steps as follows. The starting point is a doble integral in & y.
The Cross Product of Two Vectors in Space DEFINITION. Cross Product. u * v = s ƒ u ƒƒv ƒ sin ud n
 12.4 The Cross Prodct 873 12.4 The Cross Prodct In stdying lines in the plane, when we needed to describe how a line was tilting, we sed the notions of slope and angle of inclination. In space, we want
12.4 The Cross Prodct 873 12.4 The Cross Prodct In stdying lines in the plane, when we needed to describe how a line was tilting, we sed the notions of slope and angle of inclination. In space, we want
Numerical Investigation of Natural Convection Heat Transfer from Square Cylinder in an Enclosed Enclosure Filled with Nanofluids
 Rochester Institte o echnolog RI Scholar Works Articles 0-3-0 Nmerical Inestigation o Natral Conection Heat ranser rom Sqare Clinder in an Enclosed Enclosre Filled with Nanolids Ghalib Kahwaji Rochester
Rochester Institte o echnolog RI Scholar Works Articles 0-3-0 Nmerical Inestigation o Natral Conection Heat ranser rom Sqare Clinder in an Enclosed Enclosre Filled with Nanolids Ghalib Kahwaji Rochester
