Notes on the Fourier Transform
|
|
|
- Ashley Stewart
- 5 years ago
- Views:
Transcription
1 BE/EECS 56 6 FT Note Note on the Fourier Tranform Definition. The Fourier Tranform FT relate a function to it frequenc omain equivalent. The FT of a function i efine b the Fourier integral: G F{ } e iπ for R. There are a variet of eitence criteria an the FT oen t eit for all function. For eample the function co/ ha an infinite number of ocillation a an the FT integral can t be evaluate. If the FT oe eit then there i an invere FT relationhip: iπ F { G } G e Uniquene: Given the eitence of the invere FT it follow that if the FT eit it mut be unique. That i for a function form a unique pair with it FT: G Caveat. An eception to the uniquene propert i a cla of function calle male or null function. An eample i the continuou function f {. Thi function an other like it have the ame Fourier tranform a f : F. Thu the uniquene eit onl for a function plu or minu arbitrar null function. In practice thee function are not realizable energle an thu for the purpoe of thi cla we will aume that the FT i unique. Alternate FT Definition. In the above erivation the i the frequenc parameter. There i another common FT efinition that ue a raian frequenc parameter ω: iω G ω F{ } e G ω / π with an invere FT of: g F G ω ω G ω e i { } ω π Unit. If ha unit of Q then will have unit of ccle/q or Q -. Pleae note that uner our efinition of the FT thi i not an angular frequenc with unit of raian/q but jut plain Q -. Pleae alo keep in min that i the ine of variation for eample we can have repreent a velocit that varie a a function of patial location. The function ha unit cm/ but ha unit cm an G ha unit of cm/ but ha unit of cm -. Eample: Time econ Ditance cm Temporal Frequenc - Hz ccle/ Spatial Frequenc cm - ccle/cm
2 BE/EECS 56 6 FT Note Smmetr Definition. We firt ecompoe ome function in to even an o component e an o repectivel a follow: e o [ + ] [ ] thu e + o an e e an o o A function i Hermitian Smmetric Conjugate Smmetric if: Re{ } e an Im{ } o thu e + io g * Smmetr Propertie of the FT. There are everal relate propertie:. If i real then G i Hermitian mmetric e.g. G G*-.. If i real an even G i real an even. 3. If i real an o G i imaginar an o. 4. If i real G can be efine trictl b non-negative frequencie. 5. If i imaginar then G i Anti-Hermitian mmetric e.g. G -G*-. Proof of. G e iπ [ e + o [coπ i in π] co i evenin i o e co π + e + o i o co π i o i e in π i e o in π E + i io co i even in in i o i - o E io E + io G * Q.E.D. Comment. One intereting conequence of the mmetr propertie i that if i real the onl one-half of the Fourier tranform i necear to pecif the function thi follow from propert. above. ore pecificall i trictl etermine b G for all non-negative frequencie.
3 BE/EECS 56 6 FT Note 3 Comment on negative frequencie. Conier a real-value ignal imagine a voltage on a wire or the oun preure againt our earrum the Fourier tranform of thee i completel pecifie b the non-negative frequencie e.g. G- G*. We can argue that we have the concept of a frequenc ocillation/econ but it oen t reall make phical ene to talk about poitive or negative frequencie. In thi cae we coul argue that the having poitive an negative frequencie i merel a mathematical convenience. Are there cae where negative frequencie have meaning? Conier the bit in a rill it can turn clockwie or counter clockwie an ifferent rotational rate. Here poitive an negative frequencie have phical meaning the irection of rotation. A we hall ee there are cae in meical imaging where thi itinction i important for eample the magnetic moment in RI i a cae where the ign inicate the irection of preceion. Convolution Definition. The convolution operator i efine a: The convolution operator commute: g * h h - g * h h h h * - The elta function δ. The Dirac elta or implue function i a mathematical contruct that i infinitel high in amplitue infinitel hort in uration an ha unit area: δ { an δ ot propertie of δ can eit onl in a limiting cae e.g. a a equence of function δ or uner an integral. Some important propertie of δ : g n - δ with continuou at δ a a with continuou at a δ a a with continuou at F{ δ } Delta function propertie. Firt two are technicall onl efine uner the integral but we ll till talk about them. Similarit tretching δ a δ a Prouct/Sifting δ a a δ a Sifting δ a a 3
4 BE/EECS 56 6 FT Note 4 Convolution * δ δ * * δ a δ a * a Fourier Tranform Theorem. There are man Fourier tranform propertie an theorem. Thi i a partial lit. Aume that F { } G F { h } H an that a an b are contant: Linearit F { a + bh } ag + bh Similarit tretching Shift F { a} G a a F{ a} G e iπa Convolution F { * h } G H Prouct F { h } G * H Comple oulation F i π g e } G { oulation F{ coπ } [ G + G + ] Raleigh Power F{ inπ } G h * G [ G G ] i + Cro Power g H * Ai Reveral F{ } G Comple Conjugation F{ g * } G * Autocorrelation F { * g * } G G * G Revere Relationhip F{ G } Differentiation { } iπg F oment i F{ } G π DC Value G Some common FT pair: g G δ δ coπ [ δ + δ + ] inπ rect { inc triangle { < < [ δ δ ] i + inπ inc π rect inc 4
5 BE/EECS 56 6 FT Note 5 gn { e π e π < iπ e + π e for > ; otherwie iπ + π J π comb rect / π comb The comb function comb. The ampling or comb function i a train of elta function: n comb δ n The Fourier tranform of comb i: F { comb } comb Proof. iπn F{ comb } F δ n e F n n The RHS of the above epreion can be viewe a the eponential Fourier erie repreentation of a perioic function F with perio an α n for all n. Recall the Fourier erie epreion are: F iπn α e whereα F e. n n iπn Now let G rectf one perio of F an thu α n F e iπn G e n iπn m F G m. Now oberve that F { G } One function that atifie thi relationhip i G δ. Thu one poible Fourier tranform of comb i: F δ m comb m B uniquene of the Fourier tranform thi i the unique Fourier tranform of comb. n 5
6 BE/EECS 56 6 FT Note 6 Sampling an replication b comb. The comb function can be ue to ample or etract value of a continuou function. Sampling with perio can be one a: n δ n δ n n n. comb δ n n B the tretching an ifting propertie of the elta function. A function can be replicate with perio b convolving with a comb function: n [ * δ n ] [ * n ] *comb δ n B the tretching an convolution propertie of the elta function. n n Sampling Theor. When manipulating real object in a computer we mut firt ample the continuou omain object into a icretize verion that the computer can hanle. A ecribe above we can ample a function at frequenc f / uing the comb function: n g comb n δ n. The Fourier tranform i: G G * comb G * G * m m δ m G mf δ m mf Thu ampling in one omain lea to replication of the pectrum in the other omain. The pectrum i perioic with perio f. Tpicall onl frequencie le than f / can be repreente in the icrete omain ignal. An component that lie outie of thi pectral region f f / reult in aliaing the mi-aignment of pectral information. / G Original Spectrum G Replicate Spectra -f/ Aliaing f/ 6
7 BE/EECS 56 6 FT Note 7 The Whittaker-Shannon ampling theorem tate that a ban limite function with maimum frequenc ma can be full repreente b a icrete time equivalent provie the ampling frequenc atifie the Nquit ampling criterion: f ma If thi i the cae then the original pectrum can be etracte b filtering an b uniquene of the FT the original ignal can be recontructe. To recontruct the original ignal we appl a recontruction filter H rect / f rect : Gˆ G H G rect G if there i no aliaing In the omain thi reult in inc interpolation: ˆ g * inc n n δ n *inc n inc If the Nquit criterion i met then g ˆ. n n gn Info from all ample contribute to thi point D Linear Stem Conier a tem S[. ] with an input function f an an output or repone function S[f]. Thi tem i linear if an onl if: S [ α f + βf ] αs[ f ] + βs[ f ] αg + βg for all α β f an f. ore generall the uperpoition of an arbitrar et of input function will iel a net repone that i the uperpoition of repone to each input function alone. 7
8 BE/EECS 56 6 FT Note 8 Aitionall if an input i cale e.g. b α then the output will alo be cale b the ame amount. Bae on the ifting propertie of the elta function we know that f f δ f * δ which i the uperpoition of an infinite number of weighte an hifte elta function. Bae on linearit the output of thi tem S[f] i: g S f δ f S[ δ ] The tem operate on function of an f i a contant caling factor. S[δ- ] i a pecial function know a the impule repone an can i efine a: [ δ ] h ; S i the repone to an impule locate at an g f h ; i known a the uperpoition integral. Thi repreentation for the output i vali for an linear tem. Now conier a tem that i hift invariant or time invariant for function of time. We efine a tem a being hift invariant if an onl if: -a S[f-a] for all g an a. For linear hift invariant tem the impule repone can be written a: The uperpoition integral then become: [ δ ] h ; h h ; S f h f * h the convolution of the input function with the impule repone h. For linear hift invariant tem or linear time-invariant tem onl we can then conier the Fourier omain equivalent: G FH Where H i known a the tranfer function or tem pectral repone. 8
9 BE/EECS 56 6 FT Note 9 Note on the D Fourier Tranform Definition. The D Fourier Tranform FT relate a function to it frequenc omain equivalent. The FT of a function i efine b the D Fourier integral: G u v There i alo an invere FT relationhip: i π u+ v F{ } e i π u+ v F { G u v} G u. v e uv Uniquene: Given the eitence of the invere FT it follow that if the FT eit it mut be unique. That i for a function form a unique pair with it FT: G u v Given to me b a tuent I m ure I houl cite where thi came from but I on t know if ou know pleae tell me D FT in Polar Coorinate. We conier a pecial cae where the functional form of i eparable in polar coorinate that i rθ g R rg Θ θ. Since g Θ θ i perioic in θ it ha a Fourier erie repreentation: It can be hown that F inθ Θ θ a n e. n g inθ n inφ { g r e } i e D R πg R r J n πrρ rr where the part uner the integral in known a the Hankel tranform of orer n an J n i the n th orer Beel function of the firt kin: 9
10 BE/EECS 56 6 FT Note J π Derivation of the Hankel tranform relationhip relie on e D FT in polar form i: π i ainϕ nϕ n a e ϕ. π n inφ { g R r gθ θ } an i e n e iπ u+ v iπrρ co θ φ G ρ φ F πg r J πrρ rr For the pecial cae of circular mmetr of g that i rθ g R r then: G ρ φ G ρ π g R r J πrρ rr R which i alo a circularl mmetric function. The invere relationhip i the ame: g R r π G ρ J πrρ ρρ n. Thu the Smmetr Propertie of the FT. If i real then Guv i Hermitian Smmetric that i Guv G*-u-v. If i real an even that i -- then Guv i alo real an even. Finall a ecribe above if we have a real an circularl mmetric function rθ g R r the Gρφ Gρ a real an circularl mmetric function. The elta function δ. The elta function in two i equal the to prouct of two D elta function δ δ δ. In a manner imilar to the D elta function the D elta function ha the following efinition: an δ { an δ otherwie ot propertie of δ can be erive from the D elta function. There i alo a polar coorinate verion of the D elta function: δ δ r / πr.
11 BE/EECS 56 6 FT Note Fourier Tranform Theorem. Let a an b are non-zero contant an F{} Guv an F{h} Huv. Linearit F { a + bh } ag u v + bh u v agnification F { g a b } u v iπ ua+ vb Shift { } ab G F a b G u v e iπ a+ b Comple oulation F{ e } G u a v b Convolution/ultiplication { ** h } a b ** h h F G u v H u v Separabilit F { h } G u v ** H u v g g F{ } F D { g } F D { g } Power G u G v G u v uv h * Ai Reveral F { } G * u v Some common D FT pair: g G u v δ u v δ a b i π ua+ e δ vb πr e co rect π π e e coπ πρ π u πv e e e δ u + δ u + δ v G u v H * u v uv π [ ] rect δ uinc v rect a rect b u v inc inc r rect r { r > ab J πρ jinc ρ a ρ r r J circ r rect { πρ 4jincρ r > ρ r comb combcomb ρ b combuv combucombv
12 BE/EECS 56 6 FT Note The comb function in D comb. The D ampling or comb function i efine a combcombcomb an ha the D FT F{comb} combuv. Formall the D comb function i efine a: n m comb δ n m In a manner imilar to the D cae we can prove that Fourier tranform of the D comb function i alo a D comb function a given in the above table. Sampling Theor in D. In a manner imilar to ampling in D ampling in D can be moele a multipling a function time the D comb function. With ample pacing of an in the an irection the ample function i: g comb δ n m n m n m δ n m n m δ n m n m The icrete omain equivalent i g nm n m g n m. In the Fourier omain the reult i: G u v G u v ** comb u v G u v ** n m n m G u δ u Thu ampling in one omain lea to replication of the pectrum in the other omain. Spacing of the replicate pectra i //. The Whittaker-Shannon ampling theorem in D tate that a ban limite function with maimum frequencie ma an ma can be full repreente b a icrete time equivalent provie the ampling frequenc atifie the Nquit ampling criterion: an n n v ma Uner thee circumtance there i no pectral overlap or aliaing the original pectrum an b uniquene of the FT the original ignal can be recontructe. v To recontruct the original ignal we appl a recontruction filter H u v rect urect v. Gˆ u v G u v H u v G u vrect urect v m ma m G u v if there i no aliaing
13 BE/EECS 56 6 FT Note 3 In the omain thi correpon to inc interpolation in D inc gˆ g ** inc inc inπ : π n m δ n m n m **inc n m inc n m inc n n inc inc m m n m g n m inc The lat line emontrate how the original continuou ignal can be retrieve from the icrete ample verion of. 3
14 BE/EECS 56 6 FT Note 4 Eample of Fourier Tranform: D ata in Low patial freq High patial freq image omain ata image omain ata image omain D ata in Low patial freq High patial freq Fourier omain ata Fourier omain ata Fourier omain 4
15 BE/EECS 56 6 FT Note 5 5
16 BE/EECS 56 6 FT Note 6 6
17 BE/EECS 56 6 FT Note 7 rectrec Guv incuincv caling magnification propert caling magnification propert hifting propert moulation Image AbFourier RealFourier ImaFourier 7
18 BE/EECS 56 6 FT Note 8 incinc Guv recturectv ampling pattern with Δ Δ In the Fourier tranform we have the replication pattern with pacing /Δ /Δ ampling pattern with Δ < Δ In the Fourier tranform we have the replication pattern with pacing /Δ > /Δ ampling pattern with Δ << Δ Thi ha aliaing in the v irection Image Data Fourier Data 8
19 BE/EECS 56 6 FT Note 9 Aliaing in the Spatial Domain.5 unit -.75 unit - In thi eample the frequenc i wept from a.5 to.75 ccle/unit itance a goe from -5 to 5. At location zero the frequenc i.5 ccle/unit. In the upper plot we ee the original ignal. In the lower plot the ignal i ample with a pace in of Δ unit f unit - which mean that all frequencie higher than f /.5 unit - anthing to the right of will be aliae. Inee a the frequenc continue to go higher the apparent frequenc get lower. The apparent frequenc i f f i where f i i the local frequenc. In the econ eample below we eten thi to two imenion. Here we have a linear variation of frequencie in both an that i the component of the frequencie varie from.5 to.75 ccle/unit an the component of the frequencie varie from.5 to.75 ccle/unit. The upper image i the original ignal an the lower image i the ignal ample at Δ Δ unit. The ahe line mark the +/-.5 unit - line the correpon the Nquit limit. Onl the pectral component in the central bo can be repreente. In the attache pectral plot the blue ot correpon to elta function of the true frequencie. The green ot are the pectral replicant in the cae of ampling. Onl the upper left quarant ha no aliaing. The upper left an lower right appear to have the ame frequenc but the latter i aliae. The upper right an lower left alo appear to have the ame frequenc but from ifferent aliaing mechanim aliaing of the component an -component repectivel. 9
20 BE/EECS 56 6 FT Note v v u u v v u u v v u u v v u u
21 BE/EECS 56 6 FT Note D Linear Stem Conier an imaging tem with an input image I that goe through ome tem S[. ] an prouce an output image I e.g. I S[I ]. Several propertie that we are interete in are: Linearit which a two part uperpoition an caling. Thu a tem i linear if an onl if: S[ α + βh ] αs[ ] + βs[ h ] For a linear tem we can efine an impule repone a the output of a tem for an impule locate at poition : h ; S[ δ ] an in general we can efine the output given ome input image I uing the uperpoition integral: I I h ; Space Invariance. A tem i pace invariant if an onl if: I -a-b S[I -a-b] for all a b an I. Alternatel a tem i pace invariant if an onl if the impule repone can be epree in term of the hift of the elta function: h S[ δ ]. Thu h S[ δ ] i all that i neee to pecif the tem. The uperpoition integral become: I I h I ** h where ** inicate D convolution.
22 BE/EECS 56 6 FT Note Eample of a D Imaging Stem. Here we conier a pinhole imaging tem: I thi tem linear? Auming that the aperture i open or cloe an that light alwa travel in traight line through the hole then e the tem i linear. We houl then be able to etermine the impule repone. Let firt conier two ifferent magnification factor one for the object an one for the pinhole aperture. For object magnification we imagine the pinhole in infinitel mall: For a hift of in the input we will get a hift of input ource magnification term a b. a b in the output plane. Thu we efine an a Conier then a tem for a elta function at poition : h ; S[ δ ] Cδ where the elta function appear cale b C an at location. I thi tem pace invariant? No the above epreion cannot be written a a function of an. Now given an input image I we can till etermine the output image uing the uperpoition integral remember the tem i till linear:
23 BE/EECS 56 6 FT Note 3 3 ; I C I C I C h I I δ δ The output i a cale an magnifie verion of the input image. For the pinhole magnification imagine that the pinhole ha a raiu of R then the raiu in output plane woul be R a a + b ieling an aperture magnification function of a b a m +. Now uppoe we ha ome aperture function a thi will now be magnifie in the output plane. Thu the impule repone will take on a form imilar to: ; m m Ca h an the ouput image will take on the form: ** m m a I C m m a I C m m a I C I Here the output image i the convolution of the cale an magnifie verion of the input image an the pinhole function. Though thi tem i not pace invariant we were can till able to write the output in the form of a convolution though not a convolution of the input image but with a magnifie verion of the input image.
Notes on the Fourier Transform
 BE/EECS 56 FT Note Note on the Fourier Trnfor Definition. The Fourier Trnfor FT relte function to it frequenc oin equivlent. The FT of function i efine b the Fourier integrl: G F{ } iπ e for R. There re
BE/EECS 56 FT Note Note on the Fourier Trnfor Definition. The Fourier Trnfor FT relte function to it frequenc oin equivlent. The FT of function i efine b the Fourier integrl: G F{ } iπ e for R. There re
Notes on the Fourier Transform
 BE/EECS 56 4 FT Note Note on the Fourier Trnfor Definition. The Fourier Trnfor FT relte function to it frequenc oin equivlent. The FT of function i efine b the Fourier integrl: G F{ } e iπ for R. There
BE/EECS 56 4 FT Note Note on the Fourier Trnfor Definition. The Fourier Trnfor FT relte function to it frequenc oin equivlent. The FT of function i efine b the Fourier integrl: G F{ } e iπ for R. There
Chapter 2 Sampling and Quantization. In order to investigate sampling and quantization, the difference between analog
 Chapter Sampling and Quantization.1 Analog and Digital Signal In order to invetigate ampling and quantization, the difference between analog and digital ignal mut be undertood. Analog ignal conit of continuou
Chapter Sampling and Quantization.1 Analog and Digital Signal In order to invetigate ampling and quantization, the difference between analog and digital ignal mut be undertood. Analog ignal conit of continuou
Sampling and the Discrete Fourier Transform
 Sampling and the Dicrete Fourier Tranform Sampling Method Sampling i mot commonly done with two device, the ample-and-hold (S/H) and the analog-to-digital-converter (ADC) The S/H acquire a CT ignal at
Sampling and the Dicrete Fourier Tranform Sampling Method Sampling i mot commonly done with two device, the ample-and-hold (S/H) and the analog-to-digital-converter (ADC) The S/H acquire a CT ignal at
Position. If the particle is at point (x, y, z) on the curved path s shown in Fig a,then its location is defined by the position vector
 34 C HAPTER 1 KINEMATICS OF A PARTICLE 1 1.5 Curvilinear Motion: Rectangular Component Occaionall the motion of a particle can bet be decribed along a path that can be epreed in term of it,, coordinate.
34 C HAPTER 1 KINEMATICS OF A PARTICLE 1 1.5 Curvilinear Motion: Rectangular Component Occaionall the motion of a particle can bet be decribed along a path that can be epreed in term of it,, coordinate.
Spring 2014 EE 445S Real-Time Digital Signal Processing Laboratory. Homework #0 Solutions on Review of Signals and Systems Material
 Spring 4 EE 445S Real-Time Digital Signal Proceing Laboratory Prof. Evan Homework # Solution on Review of Signal and Sytem Material Problem.. Continuou-Time Sinuoidal Generation. In practice, we cannot
Spring 4 EE 445S Real-Time Digital Signal Proceing Laboratory Prof. Evan Homework # Solution on Review of Signal and Sytem Material Problem.. Continuou-Time Sinuoidal Generation. In practice, we cannot
EE 477 Digital Signal Processing. 4 Sampling; Discrete-Time
 EE 477 Digital Signal Proceing 4 Sampling; Dicrete-Time Sampling a Continuou Signal Obtain a equence of ignal ample uing a periodic intantaneou ampler: x [ n] = x( nt ) Often plot dicrete ignal a dot or
EE 477 Digital Signal Proceing 4 Sampling; Dicrete-Time Sampling a Continuou Signal Obtain a equence of ignal ample uing a periodic intantaneou ampler: x [ n] = x( nt ) Often plot dicrete ignal a dot or
LTV System Modelling
 Helinki Univerit of Technolog S-72.333 Potgraduate Coure in Radiocommunication Fall 2000 LTV Stem Modelling Heikki Lorentz Sonera Entrum O heikki.lorentz@onera.fi Januar 23 rd 200 Content. Introduction
Helinki Univerit of Technolog S-72.333 Potgraduate Coure in Radiocommunication Fall 2000 LTV Stem Modelling Heikki Lorentz Sonera Entrum O heikki.lorentz@onera.fi Januar 23 rd 200 Content. Introduction
System models. We look at LTI systems for the time being Time domain models
 Stem moel We look at LTI tem for the time being Time omain moel High orer orinar ifferential equation moel Contain onl input variable, output variable, their erivative, an contant parameter Proper: highet
Stem moel We look at LTI tem for the time being Time omain moel High orer orinar ifferential equation moel Contain onl input variable, output variable, their erivative, an contant parameter Proper: highet
Roadmap for Discrete-Time Signal Processing
 EE 4G Note: Chapter 8 Continuou-time Signal co(πf Roadmap for Dicrete-ime Signal Proceing.5 -.5 -..4.6.8..4.6.8 Dicrete-time Signal (Section 8.).5 -.5 -..4.6.8..4.6.8 Sampling Period econd (or ampling
EE 4G Note: Chapter 8 Continuou-time Signal co(πf Roadmap for Dicrete-ime Signal Proceing.5 -.5 -..4.6.8..4.6.8 Dicrete-time Signal (Section 8.).5 -.5 -..4.6.8..4.6.8 Sampling Period econd (or ampling
Chapter 3 : Transfer Functions Block Diagrams Signal Flow Graphs
 Chapter 3 : Tranfer Function Block Diagram Signal Flow Graph 3.. Tranfer Function 3.. Block Diagram of Control Sytem 3.3. Signal Flow Graph 3.4. Maon Gain Formula 3.5. Example 3.6. Block Diagram to Signal
Chapter 3 : Tranfer Function Block Diagram Signal Flow Graph 3.. Tranfer Function 3.. Block Diagram of Control Sytem 3.3. Signal Flow Graph 3.4. Maon Gain Formula 3.5. Example 3.6. Block Diagram to Signal
p. (The electron is a point particle with radius r = 0.)
 - pin ½ Recall that in the H-atom olution, we howed that the fact that the wavefunction Ψ(r) i ingle-valued require that the angular momentum quantum nbr be integer: l = 0,,.. However, operator algebra
- pin ½ Recall that in the H-atom olution, we howed that the fact that the wavefunction Ψ(r) i ingle-valued require that the angular momentum quantum nbr be integer: l = 0,,.. However, operator algebra
2.0 ANALYTICAL MODELS OF THERMAL EXCHANGES IN THE PYRANOMETER
 2.0 ANAYTICA MODE OF THERMA EXCHANGE IN THE PYRANOMETER In Chapter 1, it wa etablihe that a better unertaning of the thermal exchange within the intrument i neceary to efine the quantitie proucing an offet.
2.0 ANAYTICA MODE OF THERMA EXCHANGE IN THE PYRANOMETER In Chapter 1, it wa etablihe that a better unertaning of the thermal exchange within the intrument i neceary to efine the quantitie proucing an offet.
SAMPLING. Sampling is the acquisition of a continuous signal at discrete time intervals and is a fundamental concept in real-time signal processing.
 SAMPLING Sampling i the acquiition of a continuou ignal at dicrete time interval and i a fundamental concept in real-time ignal proceing. he actual ampling operation can alo be defined by the figure belo
SAMPLING Sampling i the acquiition of a continuou ignal at dicrete time interval and i a fundamental concept in real-time ignal proceing. he actual ampling operation can alo be defined by the figure belo
Chapter 2: Problem Solutions
 Chapter 2: Solution Dicrete Time Proceing of Continuou Time Signal Sampling à 2.. : Conider a inuoidal ignal and let u ample it at a frequency F 2kHz. xt 3co000t 0. a) Determine and expreion for the ampled
Chapter 2: Solution Dicrete Time Proceing of Continuou Time Signal Sampling à 2.. : Conider a inuoidal ignal and let u ample it at a frequency F 2kHz. xt 3co000t 0. a) Determine and expreion for the ampled
Adelic Modular Forms
 Aelic Moular Form October 3, 20 Motivation Hecke theory i concerne with a family of finite-imenional vector pace S k (N, χ), inexe by weight, level, an character. The Hecke operator on uch pace alreay
Aelic Moular Form October 3, 20 Motivation Hecke theory i concerne with a family of finite-imenional vector pace S k (N, χ), inexe by weight, level, an character. The Hecke operator on uch pace alreay
Chapter 4: Applications of Fourier Representations. Chih-Wei Liu
 Chapter 4: Application of Fourier Repreentation Chih-Wei Liu Outline Introduction Fourier ranform of Periodic Signal Convolution/Multiplication with Non-Periodic Signal Fourier ranform of Dicrete-ime Signal
Chapter 4: Application of Fourier Repreentation Chih-Wei Liu Outline Introduction Fourier ranform of Periodic Signal Convolution/Multiplication with Non-Periodic Signal Fourier ranform of Dicrete-ime Signal
ON ITERATIVE FEEDBACK TUNING AND DISTURBANCE REJECTION USING SIMPLE NOISE MODELS. Bo Wahlberg
 ON ITERATIVE FEEDBACK TUNING AND DISTURBANCE REJECTION USING SIMPLE NOISE MODELS Bo Wahlberg S3 Automatic Control, KTH, SE 100 44 Stockholm, Sween. Email: bo.wahlberg@3.kth.e Abtract: The objective of
ON ITERATIVE FEEDBACK TUNING AND DISTURBANCE REJECTION USING SIMPLE NOISE MODELS Bo Wahlberg S3 Automatic Control, KTH, SE 100 44 Stockholm, Sween. Email: bo.wahlberg@3.kth.e Abtract: The objective of
into a discrete time function. Recall that the table of Laplace/z-transforms is constructed by (i) selecting to get
 Lecture 25 Introduction to Some Matlab c2d Code in Relation to Sampled Sytem here are many way to convert a continuou time function, { h( t) ; t [0, )} into a dicrete time function { h ( k) ; k {0,,, }}
Lecture 25 Introduction to Some Matlab c2d Code in Relation to Sampled Sytem here are many way to convert a continuou time function, { h( t) ; t [0, )} into a dicrete time function { h ( k) ; k {0,,, }}
Computed Tomography Notes, Part 1. The equation that governs the image intensity in projection imaging is:
 Noll 6 CT Notes : Page Compute Tomograph Notes Part Challenges with Projection X-ra Sstems The equation that governs the image intensit in projection imaging is: z I I ep μ z Projection -ra sstems are
Noll 6 CT Notes : Page Compute Tomograph Notes Part Challenges with Projection X-ra Sstems The equation that governs the image intensit in projection imaging is: z I I ep μ z Projection -ra sstems are
SIMON FRASER UNIVERSITY School of Engineering Science ENSC 320 Electric Circuits II. Solutions to Assignment 3 February 2005.
 SIMON FRASER UNIVERSITY School of Engineering Science ENSC 320 Electric Circuit II Solution to Aignment 3 February 2005. Initial Condition Source 0 V battery witch flip at t 0 find i 3 (t) Component value:
SIMON FRASER UNIVERSITY School of Engineering Science ENSC 320 Electric Circuit II Solution to Aignment 3 February 2005. Initial Condition Source 0 V battery witch flip at t 0 find i 3 (t) Component value:
ERTH403/HYD503, NM Tech Fall 2006
 ERTH43/HYD53, NM Tech Fall 6 Variation from normal rawown hyrograph Unconfine aquifer figure from Krueman an e Rier (99) Variation from normal rawown hyrograph Unconfine aquifer Early time: when pumping
ERTH43/HYD53, NM Tech Fall 6 Variation from normal rawown hyrograph Unconfine aquifer figure from Krueman an e Rier (99) Variation from normal rawown hyrograph Unconfine aquifer Early time: when pumping
Design of Digital Filters
 Deign of Digital Filter Paley-Wiener Theorem [ ] ( ) If h n i a caual energy ignal, then ln H e dω< B where B i a finite upper bound. One implication of the Paley-Wiener theorem i that a tranfer function
Deign of Digital Filter Paley-Wiener Theorem [ ] ( ) If h n i a caual energy ignal, then ln H e dω< B where B i a finite upper bound. One implication of the Paley-Wiener theorem i that a tranfer function
Moment of Inertia of an Equilateral Triangle with Pivot at one Vertex
 oment of nertia of an Equilateral Triangle with Pivot at one Vertex There are two wa (at leat) to derive the expreion f an equilateral triangle that i rotated about one vertex, and ll how ou both here.
oment of nertia of an Equilateral Triangle with Pivot at one Vertex There are two wa (at leat) to derive the expreion f an equilateral triangle that i rotated about one vertex, and ll how ou both here.
Medical Imaging. Transmission Measurement
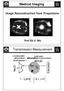 Medical Imaging Image Recontruction from Projection Prof Ed X. Wu Tranmiion Meaurement ( meaurable unknown attenuation, aborption cro-ection hadowgram ) I(ϕ,ξ) µ(x,) I = I o exp A(x, )dl L X-ra ource X-Ra
Medical Imaging Image Recontruction from Projection Prof Ed X. Wu Tranmiion Meaurement ( meaurable unknown attenuation, aborption cro-ection hadowgram ) I(ϕ,ξ) µ(x,) I = I o exp A(x, )dl L X-ra ource X-Ra
Module: 8 Lecture: 1
 Moule: 8 Lecture: 1 Energy iipate by amping Uually amping i preent in all ocillatory ytem. It effect i to remove energy from the ytem. Energy in a vibrating ytem i either iipate into heat oun or raiate
Moule: 8 Lecture: 1 Energy iipate by amping Uually amping i preent in all ocillatory ytem. It effect i to remove energy from the ytem. Energy in a vibrating ytem i either iipate into heat oun or raiate
Introduction to Laplace Transform Techniques in Circuit Analysis
 Unit 6 Introduction to Laplace Tranform Technique in Circuit Analyi In thi unit we conider the application of Laplace Tranform to circuit analyi. A relevant dicuion of the one-ided Laplace tranform i found
Unit 6 Introduction to Laplace Tranform Technique in Circuit Analyi In thi unit we conider the application of Laplace Tranform to circuit analyi. A relevant dicuion of the one-ided Laplace tranform i found
Question 1 Equivalent Circuits
 MAE 40 inear ircuit Fall 2007 Final Intruction ) Thi exam i open book You may ue whatever written material you chooe, including your cla note and textbook You may ue a hand calculator with no communication
MAE 40 inear ircuit Fall 2007 Final Intruction ) Thi exam i open book You may ue whatever written material you chooe, including your cla note and textbook You may ue a hand calculator with no communication
Computed Tomography Notes, Part 1. The equation that governs the image intensity in projection imaging is:
 Noll 3 CT Notes : Page Compute Tomograph Notes Part Challenges with Projection X-ra Sstems The equation that governs the image intensit in projection imaging is: z I I ep µ z Projection -ra sstems are
Noll 3 CT Notes : Page Compute Tomograph Notes Part Challenges with Projection X-ra Sstems The equation that governs the image intensit in projection imaging is: z I I ep µ z Projection -ra sstems are
Lecture 2: The z-transform
 5-59- Control Sytem II FS 28 Lecture 2: The -Tranform From the Laplace Tranform to the tranform The Laplace tranform i an integral tranform which take a function of a real variable t to a function of a
5-59- Control Sytem II FS 28 Lecture 2: The -Tranform From the Laplace Tranform to the tranform The Laplace tranform i an integral tranform which take a function of a real variable t to a function of a
Advanced Digital Signal Processing. Stationary/nonstationary signals. Time-Frequency Analysis... Some nonstationary signals. Time-Frequency Analysis
 Advanced Digital ignal Proceing Prof. Nizamettin AYDIN naydin@yildiz.edu.tr Time-Frequency Analyi http://www.yildiz.edu.tr/~naydin 2 tationary/nontationary ignal Time-Frequency Analyi Fourier Tranform
Advanced Digital ignal Proceing Prof. Nizamettin AYDIN naydin@yildiz.edu.tr Time-Frequency Analyi http://www.yildiz.edu.tr/~naydin 2 tationary/nontationary ignal Time-Frequency Analyi Fourier Tranform
Fourier Series And Transforms
 Chapter Fourier Serie And ranform. Fourier Serie A function that i defined and quare-integrable over an interval, [,], and i then periodically extended over the entire real line can be expreed a an infinite
Chapter Fourier Serie And ranform. Fourier Serie A function that i defined and quare-integrable over an interval, [,], and i then periodically extended over the entire real line can be expreed a an infinite
Practice Problems - Week #7 Laplace - Step Functions, DE Solutions Solutions
 For Quetion -6, rewrite the piecewie function uing tep function, ketch their graph, and find F () = Lf(t). 0 0 < t < 2. f(t) = (t 2 4) 2 < t In tep-function form, f(t) = u 2 (t 2 4) The graph i the olid
For Quetion -6, rewrite the piecewie function uing tep function, ketch their graph, and find F () = Lf(t). 0 0 < t < 2. f(t) = (t 2 4) 2 < t In tep-function form, f(t) = u 2 (t 2 4) The graph i the olid
Digital Control System
 Digital Control Sytem Summary # he -tranform play an important role in digital control and dicrete ignal proceing. he -tranform i defined a F () f(k) k () A. Example Conider the following equence: f(k)
Digital Control Sytem Summary # he -tranform play an important role in digital control and dicrete ignal proceing. he -tranform i defined a F () f(k) k () A. Example Conider the following equence: f(k)
5.5 Sampling. The Connection Between: Continuous Time & Discrete Time
 5.5 Sampling he Connection Between: Continuou ime & Dicrete ime Warning: I don t really like how the book cover thi! It i not that it i wrong it jut ail to make the correct connection between the mathematic
5.5 Sampling he Connection Between: Continuou ime & Dicrete ime Warning: I don t really like how the book cover thi! It i not that it i wrong it jut ail to make the correct connection between the mathematic
11.2 Stability. A gain element is an active device. One potential problem with every active circuit is its stability
 5/7/2007 11_2 tability 1/2 112 tability eading Aignment: pp 542-548 A gain element i an active device One potential problem with every active circuit i it tability HO: TABIITY Jim tile The Univ of Kana
5/7/2007 11_2 tability 1/2 112 tability eading Aignment: pp 542-548 A gain element i an active device One potential problem with every active circuit i it tability HO: TABIITY Jim tile The Univ of Kana
Bogoliubov Transformation in Classical Mechanics
 Bogoliubov Tranformation in Claical Mechanic Canonical Tranformation Suppoe we have a et of complex canonical variable, {a j }, and would like to conider another et of variable, {b }, b b ({a j }). How
Bogoliubov Tranformation in Claical Mechanic Canonical Tranformation Suppoe we have a et of complex canonical variable, {a j }, and would like to conider another et of variable, {b }, b b ({a j }). How
ANSWERS TO MA1506 TUTORIAL 7. Question 1. (a) We shall use the following s-shifting property: L(f(t)) = F (s) L(e ct f(t)) = F (s c)
 ANSWERS O MA56 UORIAL 7 Quetion. a) We hall ue the following -Shifting property: Lft)) = F ) Le ct ft)) = F c) Lt 2 ) = 2 3 ue Ltn ) = n! Lt 2 e 3t ) = Le 3t t 2 ) = n+ 2 + 3) 3 b) Here u denote the Unit
ANSWERS O MA56 UORIAL 7 Quetion. a) We hall ue the following -Shifting property: Lft)) = F ) Le ct ft)) = F c) Lt 2 ) = 2 3 ue Ltn ) = n! Lt 2 e 3t ) = Le 3t t 2 ) = n+ 2 + 3) 3 b) Here u denote the Unit
Given the following circuit with unknown initial capacitor voltage v(0): X(s) Immediately, we know that the transfer function H(s) is
 EE 4G Note: Chapter 6 Intructor: Cheung More about ZSR and ZIR. Finding unknown initial condition: Given the following circuit with unknown initial capacitor voltage v0: F v0/ / Input xt 0Ω Output yt -
EE 4G Note: Chapter 6 Intructor: Cheung More about ZSR and ZIR. Finding unknown initial condition: Given the following circuit with unknown initial capacitor voltage v0: F v0/ / Input xt 0Ω Output yt -
Physics 741 Graduate Quantum Mechanics 1 Solutions to Final Exam, Fall 2014
 Phyic 7 Graduate Quantum Mechanic Solution to inal Eam all 0 Each quetion i worth 5 point with point for each part marked eparately Some poibly ueful formula appear at the end of the tet In four dimenion
Phyic 7 Graduate Quantum Mechanic Solution to inal Eam all 0 Each quetion i worth 5 point with point for each part marked eparately Some poibly ueful formula appear at the end of the tet In four dimenion
Department of Mechanical Engineering Massachusetts Institute of Technology Modeling, Dynamics and Control III Spring 2002
 Department of Mechanical Engineering Maachuett Intitute of Technology 2.010 Modeling, Dynamic and Control III Spring 2002 SOLUTIONS: Problem Set # 10 Problem 1 Etimating tranfer function from Bode Plot.
Department of Mechanical Engineering Maachuett Intitute of Technology 2.010 Modeling, Dynamic and Control III Spring 2002 SOLUTIONS: Problem Set # 10 Problem 1 Etimating tranfer function from Bode Plot.
0 of the same magnitude. If we don t use an OA and ignore any damping, the CTF is
 1 4. Image Simulation Influence of C Spherical aberration break the ymmetry that would otherwie exit between overfocu and underfocu. One reult i that the fringe in the FT of the CTF are generally farther
1 4. Image Simulation Influence of C Spherical aberration break the ymmetry that would otherwie exit between overfocu and underfocu. One reult i that the fringe in the FT of the CTF are generally farther
Symmetry Lecture 9. 1 Gellmann-Nishijima relation
 Symmetry Lecture 9 1 Gellmann-Nihijima relation In the lat lecture we found that the Gell-mann and Nihijima relation related Baryon number, charge, and the third component of iopin. Q = [(1/2)B + T 3 ]
Symmetry Lecture 9 1 Gellmann-Nihijima relation In the lat lecture we found that the Gell-mann and Nihijima relation related Baryon number, charge, and the third component of iopin. Q = [(1/2)B + T 3 ]
Lecture #9 Continuous time filter
 Lecture #9 Continuou time filter Oliver Faut December 5, 2006 Content Review. Motivation......................................... 2 2 Filter pecification 2 2. Low pa..........................................
Lecture #9 Continuou time filter Oliver Faut December 5, 2006 Content Review. Motivation......................................... 2 2 Filter pecification 2 2. Low pa..........................................
Properties of Z-transform Transform 1 Linearity a
 Midterm 3 (Fall 6 of EEG:. Thi midterm conit of eight ingle-ided page. The firt three page contain variou table followed by FOUR eam quetion and one etra workheet. You can tear out any page but make ure
Midterm 3 (Fall 6 of EEG:. Thi midterm conit of eight ingle-ided page. The firt three page contain variou table followed by FOUR eam quetion and one etra workheet. You can tear out any page but make ure
( ) ( ) ω = X x t e dt
 The Laplace Tranform The Laplace Tranform generalize the Fourier Traform for the entire complex plane For an ignal x(t) the pectrum, or it Fourier tranform i (if it exit): t X x t e dt ω = For the ame
The Laplace Tranform The Laplace Tranform generalize the Fourier Traform for the entire complex plane For an ignal x(t) the pectrum, or it Fourier tranform i (if it exit): t X x t e dt ω = For the ame
EXERCISES FOR SECTION 6.3
 y 6. Secon-Orer Equation 499.58 4 t EXERCISES FOR SECTION 6.. We ue integration by part twice to compute Lin ωt Firt, letting u in ωt an v e t t,weget Lin ωt in ωt e t e t lim b in ωt e t t. in ωt ω e
y 6. Secon-Orer Equation 499.58 4 t EXERCISES FOR SECTION 6.. We ue integration by part twice to compute Lin ωt Firt, letting u in ωt an v e t t,weget Lin ωt in ωt e t e t lim b in ωt e t t. in ωt ω e
Social Studies 201 Notes for March 18, 2005
 1 Social Studie 201 Note for March 18, 2005 Etimation of a mean, mall ample ize Section 8.4, p. 501. When a reearcher ha only a mall ample ize available, the central limit theorem doe not apply to the
1 Social Studie 201 Note for March 18, 2005 Etimation of a mean, mall ample ize Section 8.4, p. 501. When a reearcher ha only a mall ample ize available, the central limit theorem doe not apply to the
7.2 INVERSE TRANSFORMS AND TRANSFORMS OF DERIVATIVES 281
 72 INVERSE TRANSFORMS AND TRANSFORMS OF DERIVATIVES 28 and i 2 Show how Euler formula (page 33) can then be ued to deduce the reult a ( a) 2 b 2 {e at co bt} {e at in bt} b ( a) 2 b 2 5 Under what condition
72 INVERSE TRANSFORMS AND TRANSFORMS OF DERIVATIVES 28 and i 2 Show how Euler formula (page 33) can then be ued to deduce the reult a ( a) 2 b 2 {e at co bt} {e at in bt} b ( a) 2 b 2 5 Under what condition
SIMON FRASER UNIVERSITY School of Engineering Science ENSC 320 Electric Circuits II. R 4 := 100 kohm
 SIMON FRASER UNIVERSITY School of Engineering Science ENSC 320 Electric Circuit II Solution to Aignment 3 February 2003. Cacaded Op Amp [DC&L, problem 4.29] An ideal op amp ha an output impedance of zero,
SIMON FRASER UNIVERSITY School of Engineering Science ENSC 320 Electric Circuit II Solution to Aignment 3 February 2003. Cacaded Op Amp [DC&L, problem 4.29] An ideal op amp ha an output impedance of zero,
Design By Emulation (Indirect Method)
 Deign By Emulation (Indirect Method he baic trategy here i, that Given a continuou tranfer function, it i required to find the bet dicrete equivalent uch that the ignal produced by paing an input ignal
Deign By Emulation (Indirect Method he baic trategy here i, that Given a continuou tranfer function, it i required to find the bet dicrete equivalent uch that the ignal produced by paing an input ignal
R. W. Erickson. Department of Electrical, Computer, and Energy Engineering University of Colorado, Boulder
 R. W. Erickon Department of Electrical, Computer, and Energy Engineering Univerity of Colorado, Boulder Cloed-loop buck converter example: Section 9.5.4 In ECEN 5797, we ued the CCM mall ignal model to
R. W. Erickon Department of Electrical, Computer, and Energy Engineering Univerity of Colorado, Boulder Cloed-loop buck converter example: Section 9.5.4 In ECEN 5797, we ued the CCM mall ignal model to
EE 508 Lecture 16. Filter Transformations. Lowpass to Bandpass Lowpass to Highpass Lowpass to Band-reject
 EE 508 Lecture 6 Filter Tranformation Lowpa to Bandpa Lowpa to Highpa Lowpa to Band-reject Review from Lat Time Theorem: If the perimeter variation and contact reitance are neglected, the tandard deviation
EE 508 Lecture 6 Filter Tranformation Lowpa to Bandpa Lowpa to Highpa Lowpa to Band-reject Review from Lat Time Theorem: If the perimeter variation and contact reitance are neglected, the tandard deviation
Introduction to Mechanism Design
 5 1 Introuction to Mechanim Deign 1.1 Dominant trategie an Nah equilibria In the previou lecture we have een example of game that amit everal Nah equilibria. Moreover, ome of thee equilibria correpon to
5 1 Introuction to Mechanim Deign 1.1 Dominant trategie an Nah equilibria In the previou lecture we have een example of game that amit everal Nah equilibria. Moreover, ome of thee equilibria correpon to
EE Control Systems LECTURE 6
 Copyright FL Lewi 999 All right reerved EE - Control Sytem LECTURE 6 Updated: Sunday, February, 999 BLOCK DIAGRAM AND MASON'S FORMULA A linear time-invariant (LTI) ytem can be repreented in many way, including:
Copyright FL Lewi 999 All right reerved EE - Control Sytem LECTURE 6 Updated: Sunday, February, 999 BLOCK DIAGRAM AND MASON'S FORMULA A linear time-invariant (LTI) ytem can be repreented in many way, including:
3. In an interaction between two objects, each object exerts a force on the other. These forces are equal in magnitude and opposite in direction.
 Lecture quiz toda. Small change to webite. Problem 4.30 the peed o the elevator i poitive even though it i decending. The WebAign anwer i wrong. ewton Law o Motion (page 9-99) 1. An object velocit vector
Lecture quiz toda. Small change to webite. Problem 4.30 the peed o the elevator i poitive even though it i decending. The WebAign anwer i wrong. ewton Law o Motion (page 9-99) 1. An object velocit vector
EE/ME/AE324: Dynamical Systems. Chapter 8: Transfer Function Analysis
 EE/ME/AE34: Dynamical Sytem Chapter 8: Tranfer Function Analyi The Sytem Tranfer Function Conider the ytem decribed by the nth-order I/O eqn.: ( n) ( n 1) ( m) y + a y + + a y = b u + + bu n 1 0 m 0 Taking
EE/ME/AE34: Dynamical Sytem Chapter 8: Tranfer Function Analyi The Sytem Tranfer Function Conider the ytem decribed by the nth-order I/O eqn.: ( n) ( n 1) ( m) y + a y + + a y = b u + + bu n 1 0 m 0 Taking
Learning Multiplicative Interactions
 CSC2535 2011 Lecture 6a Learning Multiplicative Interaction Geoffrey Hinton Two different meaning of multiplicative If we take two denity model and multiply together their probability ditribution at each
CSC2535 2011 Lecture 6a Learning Multiplicative Interaction Geoffrey Hinton Two different meaning of multiplicative If we take two denity model and multiply together their probability ditribution at each
Lecture 17: Analytic Functions and Integrals (See Chapter 14 in Boas)
 Lecture 7: Analytic Function and Integral (See Chapter 4 in Boa) Thi i a good point to take a brief detour and expand on our previou dicuion of complex variable and complex function of complex variable.
Lecture 7: Analytic Function and Integral (See Chapter 4 in Boa) Thi i a good point to take a brief detour and expand on our previou dicuion of complex variable and complex function of complex variable.
Lecture 10 Filtering: Applied Concepts
 Lecture Filtering: Applied Concept In the previou two lecture, you have learned about finite-impule-repone (FIR) and infinite-impule-repone (IIR) filter. In thee lecture, we introduced the concept of filtering
Lecture Filtering: Applied Concept In the previou two lecture, you have learned about finite-impule-repone (FIR) and infinite-impule-repone (IIR) filter. In thee lecture, we introduced the concept of filtering
Nuclear and Particle Physics - Lecture 16 Neutral kaon decays and oscillations
 1 Introction Nclear an Particle Phyic - Lectre 16 Netral kaon ecay an ocillation e have alreay een that the netral kaon will have em-leptonic an haronic ecay. However, they alo exhibit the phenomenon of
1 Introction Nclear an Particle Phyic - Lectre 16 Netral kaon ecay an ocillation e have alreay een that the netral kaon will have em-leptonic an haronic ecay. However, they alo exhibit the phenomenon of
Quadratic Log-Aesthetic Curves
 Quadratic Log-Aethetic Curve Norimaa Yohida[0000-000-8889-0949] and Takafumi Saito[0000-000-583-596X] Nihon Univerit, norimaa@acm.org Toko Univerit of Agriculture and Technolog, taito@cc.tuat.ac.jp ABSTRACT
Quadratic Log-Aethetic Curve Norimaa Yohida[0000-000-8889-0949] and Takafumi Saito[0000-000-583-596X] Nihon Univerit, norimaa@acm.org Toko Univerit of Agriculture and Technolog, taito@cc.tuat.ac.jp ABSTRACT
Unit #6 - Families of Functions, Taylor Polynomials, l Hopital s Rule
 Unit # - Families of Functions, Taylor Polynomials, l Hopital s Rule Some problems an solutions selecte or aapte from Hughes-Hallett Calculus. Critical Points. Consier the function f) = 54 +. b) a) Fin
Unit # - Families of Functions, Taylor Polynomials, l Hopital s Rule Some problems an solutions selecte or aapte from Hughes-Hallett Calculus. Critical Points. Consier the function f) = 54 +. b) a) Fin
1 Parity. 2 Time reversal. Even. Odd. Symmetry Lecture 9
 Even Odd Symmetry Lecture 9 1 Parity The normal mode of a tring have either even or odd ymmetry. Thi alo occur for tationary tate in Quantum Mechanic. The tranformation i called partiy. We previouly found
Even Odd Symmetry Lecture 9 1 Parity The normal mode of a tring have either even or odd ymmetry. Thi alo occur for tationary tate in Quantum Mechanic. The tranformation i called partiy. We previouly found
MAE140 Linear Circuits Fall 2012 Final, December 13th
 MAE40 Linear Circuit Fall 202 Final, December 3th Intruction. Thi exam i open book. You may ue whatever written material you chooe, including your cla note and textbook. You may ue a hand calculator with
MAE40 Linear Circuit Fall 202 Final, December 3th Intruction. Thi exam i open book. You may ue whatever written material you chooe, including your cla note and textbook. You may ue a hand calculator with
Lecture 8: Period Finding: Simon s Problem over Z N
 Quantum Computation (CMU 8-859BB, Fall 205) Lecture 8: Period Finding: Simon Problem over Z October 5, 205 Lecturer: John Wright Scribe: icola Rech Problem A mentioned previouly, period finding i a rephraing
Quantum Computation (CMU 8-859BB, Fall 205) Lecture 8: Period Finding: Simon Problem over Z October 5, 205 Lecturer: John Wright Scribe: icola Rech Problem A mentioned previouly, period finding i a rephraing
Lecture 1b. Differential operators and orthogonal coordinates. Partial derivatives. Divergence and divergence theorem. Gradient. A y. + A y y dy. 1b.
 b. Partial erivatives Lecture b Differential operators an orthogonal coorinates Recall from our calculus courses that the erivative of a function can be efine as f ()=lim 0 or using the central ifference
b. Partial erivatives Lecture b Differential operators an orthogonal coorinates Recall from our calculus courses that the erivative of a function can be efine as f ()=lim 0 or using the central ifference
Laplace Transformation
 Univerity of Technology Electromechanical Department Energy Branch Advance Mathematic Laplace Tranformation nd Cla Lecture 6 Page of 7 Laplace Tranformation Definition Suppoe that f(t) i a piecewie continuou
Univerity of Technology Electromechanical Department Energy Branch Advance Mathematic Laplace Tranformation nd Cla Lecture 6 Page of 7 Laplace Tranformation Definition Suppoe that f(t) i a piecewie continuou
Week 3 Statistics for bioinformatics and escience
 Week 3 Statitic for bioinformatic and escience Line Skotte 28. november 2008 2.9.3-4) In thi eercie we conider microrna data from Human and Moue. The data et repreent 685 independent realiation of the
Week 3 Statitic for bioinformatic and escience Line Skotte 28. november 2008 2.9.3-4) In thi eercie we conider microrna data from Human and Moue. The data et repreent 685 independent realiation of the
Lecture 15 - Current. A Puzzle... Advanced Section: Image Charge for Spheres. Image Charge for a Grounded Spherical Shell
 Lecture 15 - Current Puzzle... Suppoe an infinite grounded conducting plane lie at z = 0. charge q i located at a height h above the conducting plane. Show in three different way that the potential below
Lecture 15 - Current Puzzle... Suppoe an infinite grounded conducting plane lie at z = 0. charge q i located at a height h above the conducting plane. Show in three different way that the potential below
Fourier Transforms of Functions on the Continuous Domain
 Chapter Fourier Tranform of Function on the Continuou Domain. Introduction The baic concept of pectral analyi through Fourier tranform typically are developed for function on a one-dimenional domain where
Chapter Fourier Tranform of Function on the Continuou Domain. Introduction The baic concept of pectral analyi through Fourier tranform typically are developed for function on a one-dimenional domain where
Performance Evaluation of Acoustic Scene Classification Using DNN-GMM and Frame-Concatenated Acoustic Features
 Proceeing of APSIPA Annual Summit an Conference 2017 Performance Evaluation of Acoutic Scene Claification Uing NN-GMM an Frame-Concatenate Acoutic Feature Gen Takahahi, Takehi Yamaa, Nobutaka Ono an Shoji
Proceeing of APSIPA Annual Summit an Conference 2017 Performance Evaluation of Acoutic Scene Claification Uing NN-GMM an Frame-Concatenate Acoutic Feature Gen Takahahi, Takehi Yamaa, Nobutaka Ono an Shoji
Nonlinear Single-Particle Dynamics in High Energy Accelerators
 Nonlinear Single-Particle Dynamic in High Energy Accelerator Part 6: Canonical Perturbation Theory Nonlinear Single-Particle Dynamic in High Energy Accelerator Thi coure conit of eight lecture: 1. Introduction
Nonlinear Single-Particle Dynamic in High Energy Accelerator Part 6: Canonical Perturbation Theory Nonlinear Single-Particle Dynamic in High Energy Accelerator Thi coure conit of eight lecture: 1. Introduction
What lies between Δx E, which represents the steam valve, and ΔP M, which is the mechanical power into the synchronous machine?
 A 2.0 Introduction In the lat et of note, we developed a model of the peed governing mechanim, which i given below: xˆ K ( Pˆ ˆ) E () In thee note, we want to extend thi model o that it relate the actual
A 2.0 Introduction In the lat et of note, we developed a model of the peed governing mechanim, which i given below: xˆ K ( Pˆ ˆ) E () In thee note, we want to extend thi model o that it relate the actual
DESIGN OF CONTROLLERS FOR STABLE AND UNSTABLE SYSTEMS WITH TIME DELAY
 DESIGN OF CONTROLLERS FOR STABLE AND UNSTABLE SYSTEMS WITH TIME DELAY P. Dotál, V. Bobál Department of Proce Control, Facult of Technolog, Toma Bata Univerit in Zlín Nám. T. G. Maarka 75, 76 7 Zlín, Czech
DESIGN OF CONTROLLERS FOR STABLE AND UNSTABLE SYSTEMS WITH TIME DELAY P. Dotál, V. Bobál Department of Proce Control, Facult of Technolog, Toma Bata Univerit in Zlín Nám. T. G. Maarka 75, 76 7 Zlín, Czech
Example: Amplifier Distortion
 4/6/2011 Example Amplifier Ditortion 1/9 Example: Amplifier Ditortion Recall thi circuit from a previou handout: 15.0 R C =5 K v ( t) = v ( t) o R B =5 K β = 100 _ vi( t ) 58. R E =5 K CUS We found that
4/6/2011 Example Amplifier Ditortion 1/9 Example: Amplifier Ditortion Recall thi circuit from a previou handout: 15.0 R C =5 K v ( t) = v ( t) o R B =5 K β = 100 _ vi( t ) 58. R E =5 K CUS We found that
RaneNote BESSEL FILTER CROSSOVER
 RaneNote BESSEL FILTER CROSSOVER A Beel Filter Croover, and It Relation to Other Croover Beel Function Phae Shift Group Delay Beel, 3dB Down Introduction One of the way that a croover may be contructed
RaneNote BESSEL FILTER CROSSOVER A Beel Filter Croover, and It Relation to Other Croover Beel Function Phae Shift Group Delay Beel, 3dB Down Introduction One of the way that a croover may be contructed
USPAS Course on Recirculated and Energy Recovered Linear Accelerators
 USPAS Coure on Recirculated and Energy Recovered Linear Accelerator G. A. Krafft and L. Merminga Jefferon Lab I. Bazarov Cornell Lecture 6 7 March 005 Lecture Outline. Invariant Ellipe Generated by a Unimodular
USPAS Coure on Recirculated and Energy Recovered Linear Accelerator G. A. Krafft and L. Merminga Jefferon Lab I. Bazarov Cornell Lecture 6 7 March 005 Lecture Outline. Invariant Ellipe Generated by a Unimodular
Compensation of backlash effects in an Electrical Actuator
 1 Compenation of backlah effect in an Electrical Actuator R. Merzouki, J. C. Caiou an N. M Siri LaboratoireeRobotiqueeVeraille 10-12, avenue e l Europe 78140 Vélizy e-mail: merzouki@robot.uvq.fr Abtract
1 Compenation of backlah effect in an Electrical Actuator R. Merzouki, J. C. Caiou an N. M Siri LaboratoireeRobotiqueeVeraille 10-12, avenue e l Europe 78140 Vélizy e-mail: merzouki@robot.uvq.fr Abtract
PHYSICS 151 Notes for Online Lecture 2.3
 PHYSICS 151 Note for Online Lecture.3 riction: The baic fact of acrocopic (everda) friction are: 1) rictional force depend on the two aterial that are liding pat each other. bo liding over a waed floor
PHYSICS 151 Note for Online Lecture.3 riction: The baic fact of acrocopic (everda) friction are: 1) rictional force depend on the two aterial that are liding pat each other. bo liding over a waed floor
Assessment Schedule 2017 Scholarship Physics (93103)
 Scholarhip Phyic (93103) 201 page 1 of 5 Aement Schedule 201 Scholarhip Phyic (93103) Evidence Statement Q Evidence 1-4 mark 5-6 mark -8 mark ONE (a)(i) Due to the motion of the ource, there are compreion
Scholarhip Phyic (93103) 201 page 1 of 5 Aement Schedule 201 Scholarhip Phyic (93103) Evidence Statement Q Evidence 1-4 mark 5-6 mark -8 mark ONE (a)(i) Due to the motion of the ource, there are compreion
The Laplace Transform
 The Laplace Tranform Prof. Siripong Potiuk Pierre Simon De Laplace 749-827 French Atronomer and Mathematician Laplace Tranform An extenion of the CT Fourier tranform to allow analyi of broader cla of CT
The Laplace Tranform Prof. Siripong Potiuk Pierre Simon De Laplace 749-827 French Atronomer and Mathematician Laplace Tranform An extenion of the CT Fourier tranform to allow analyi of broader cla of CT
THE THERMOELASTIC SQUARE
 HE HERMOELASIC SQUARE A mnemonic for remembering thermodynamic identitie he tate of a material i the collection of variable uch a tre, train, temperature, entropy. A variable i a tate variable if it integral
HE HERMOELASIC SQUARE A mnemonic for remembering thermodynamic identitie he tate of a material i the collection of variable uch a tre, train, temperature, entropy. A variable i a tate variable if it integral
Solutions. Digital Control Systems ( ) 120 minutes examination time + 15 minutes reading time at the beginning of the exam
 BSc - Sample Examination Digital Control Sytem (5-588-) Prof. L. Guzzella Solution Exam Duration: Number of Quetion: Rating: Permitted aid: minute examination time + 5 minute reading time at the beginning
BSc - Sample Examination Digital Control Sytem (5-588-) Prof. L. Guzzella Solution Exam Duration: Number of Quetion: Rating: Permitted aid: minute examination time + 5 minute reading time at the beginning
4-4 E-field Calculations using Coulomb s Law
 1/21/24 ection 4_4 -field calculation uing Coulomb Law blank.doc 1/1 4-4 -field Calculation uing Coulomb Law Reading Aignment: pp. 9-98 1. xample: The Uniform, Infinite Line Charge 2. xample: The Uniform
1/21/24 ection 4_4 -field calculation uing Coulomb Law blank.doc 1/1 4-4 -field Calculation uing Coulomb Law Reading Aignment: pp. 9-98 1. xample: The Uniform, Infinite Line Charge 2. xample: The Uniform
Rapidly convergent representations for 2D and 3D Green s functions for a linear periodic array of dipole sources
 Rapily convergent repreentation for D an reen function for a linear perioic array of ipole ource Derek Van Oren an Vitaliy Lomakin Department of Electrical an Computer Engineering, Univerity of California,
Rapily convergent repreentation for D an reen function for a linear perioic array of ipole ource Derek Van Oren an Vitaliy Lomakin Department of Electrical an Computer Engineering, Univerity of California,
Digital Control System
 Digital Control Sytem - A D D A Micro ADC DAC Proceor Correction Element Proce Clock Meaurement A: Analog D: Digital Continuou Controller and Digital Control Rt - c Plant yt Continuou Controller Digital
Digital Control Sytem - A D D A Micro ADC DAC Proceor Correction Element Proce Clock Meaurement A: Analog D: Digital Continuou Controller and Digital Control Rt - c Plant yt Continuou Controller Digital
Adder Circuits Ivor Page 1
 Adder Circuit Adder Circuit Ivor Page 4. The Ripple Carr Adder The ripple carr adder i probabl the implet parallel binar adder. It i made up of k full-adder tage, where each full-adder can be convenientl
Adder Circuit Adder Circuit Ivor Page 4. The Ripple Carr Adder The ripple carr adder i probabl the implet parallel binar adder. It i made up of k full-adder tage, where each full-adder can be convenientl
Reading assignment: In this chapter we will cover Sections Definition and the Laplace transform of simple functions
 Chapter 4 Laplace Tranform 4 Introduction Reading aignment: In thi chapter we will cover Section 4 45 4 Definition and the Laplace tranform of imple function Given f, a function of time, with value f(t
Chapter 4 Laplace Tranform 4 Introduction Reading aignment: In thi chapter we will cover Section 4 45 4 Definition and the Laplace tranform of imple function Given f, a function of time, with value f(t
Control Systems Engineering ( Chapter 7. Steady-State Errors ) Prof. Kwang-Chun Ho Tel: Fax:
 Control Sytem Engineering ( Chapter 7. Steady-State Error Prof. Kwang-Chun Ho kwangho@hanung.ac.kr Tel: 0-760-453 Fax:0-760-4435 Introduction In thi leon, you will learn the following : How to find the
Control Sytem Engineering ( Chapter 7. Steady-State Error Prof. Kwang-Chun Ho kwangho@hanung.ac.kr Tel: 0-760-453 Fax:0-760-4435 Introduction In thi leon, you will learn the following : How to find the
online learning Unit Workbook 4 RLC Transients
 online learning Pearon BTC Higher National in lectrical and lectronic ngineering (QCF) Unit 5: lectrical & lectronic Principle Unit Workbook 4 in a erie of 4 for thi unit Learning Outcome: RLC Tranient
online learning Pearon BTC Higher National in lectrical and lectronic ngineering (QCF) Unit 5: lectrical & lectronic Principle Unit Workbook 4 in a erie of 4 for thi unit Learning Outcome: RLC Tranient
Exam 1 Solutions. +4q +2q. +2q +2q
 PHY6 9-8-6 Exam Solution y 4 3 6 x. A central particle of charge 3 i urrounded by a hexagonal array of other charged particle (>). The length of a ide i, and charge are placed at each corner. (a) [6 point]
PHY6 9-8-6 Exam Solution y 4 3 6 x. A central particle of charge 3 i urrounded by a hexagonal array of other charged particle (>). The length of a ide i, and charge are placed at each corner. (a) [6 point]
ELECTROMAGNETIC WAVES AND PHOTONS
 CHAPTER ELECTROMAGNETIC WAVES AND PHOTONS Problem.1 Find the magnitude and direction of the induced electric field of Example.1 at r = 5.00 cm if the magnetic field change at a contant rate from 0.500
CHAPTER ELECTROMAGNETIC WAVES AND PHOTONS Problem.1 Find the magnitude and direction of the induced electric field of Example.1 at r = 5.00 cm if the magnetic field change at a contant rate from 0.500
ME 375 EXAM #1 Tuesday February 21, 2006
 ME 375 EXAM #1 Tueday February 1, 006 Diviion Adam 11:30 / Savran :30 (circle one) Name Intruction (1) Thi i a cloed book examination, but you are allowed one 8.5x11 crib heet. () You have one hour to
ME 375 EXAM #1 Tueday February 1, 006 Diviion Adam 11:30 / Savran :30 (circle one) Name Intruction (1) Thi i a cloed book examination, but you are allowed one 8.5x11 crib heet. () You have one hour to
Correction for Simple System Example and Notes on Laplace Transforms / Deviation Variables ECHE 550 Fall 2002
 Correction for Simple Sytem Example and Note on Laplace Tranform / Deviation Variable ECHE 55 Fall 22 Conider a tank draining from an initial height of h o at time t =. With no flow into the tank (F in
Correction for Simple Sytem Example and Note on Laplace Tranform / Deviation Variable ECHE 55 Fall 22 Conider a tank draining from an initial height of h o at time t =. With no flow into the tank (F in
Chapter 4. The Laplace Transform Method
 Chapter 4. The Laplace Tranform Method The Laplace Tranform i a tranformation, meaning that it change a function into a new function. Actually, it i a linear tranformation, becaue it convert a linear combination
Chapter 4. The Laplace Tranform Method The Laplace Tranform i a tranformation, meaning that it change a function into a new function. Actually, it i a linear tranformation, becaue it convert a linear combination
Pulsed Magnet Crimping
 Puled Magnet Crimping Fred Niell 4/5/00 1 Magnetic Crimping Magnetoforming i a metal fabrication technique that ha been in ue for everal decade. A large capacitor bank i ued to tore energy that i ued to
Puled Magnet Crimping Fred Niell 4/5/00 1 Magnetic Crimping Magnetoforming i a metal fabrication technique that ha been in ue for everal decade. A large capacitor bank i ued to tore energy that i ued to
Reading assignment: In this chapter we will cover Sections Definition and the Laplace transform of simple functions
 Chapter 4 Laplace Tranform 4 Introduction Reading aignment: In thi chapter we will cover Section 4 45 4 Definition and the Laplace tranform of imple function Given f, a function of time, with value f(t
Chapter 4 Laplace Tranform 4 Introduction Reading aignment: In thi chapter we will cover Section 4 45 4 Definition and the Laplace tranform of imple function Given f, a function of time, with value f(t
SMALL-SIGNAL STABILITY ASSESSMENT OF THE EUROPEAN POWER SYSTEM BASED ON ADVANCED NEURAL NETWORK METHOD
 SMALL-SIGNAL STABILITY ASSESSMENT OF THE EUROPEAN POWER SYSTEM BASED ON ADVANCED NEURAL NETWORK METHOD S.P. Teeuwen, I. Erlich U. Bachmann Univerity of Duiburg, Germany Department of Electrical Power Sytem
SMALL-SIGNAL STABILITY ASSESSMENT OF THE EUROPEAN POWER SYSTEM BASED ON ADVANCED NEURAL NETWORK METHOD S.P. Teeuwen, I. Erlich U. Bachmann Univerity of Duiburg, Germany Department of Electrical Power Sytem
Linearteam tech paper. The analysis of fourth-order state variable filter and it s application to Linkwitz- Riley filters
 Linearteam tech paper The analyi of fourth-order tate variable filter and it application to Linkwitz- iley filter Janne honen 5.. TBLE OF CONTENTS. NTOCTON.... FOTH-OE LNWTZ-LEY (L TNSFE FNCTON.... TNSFE
Linearteam tech paper The analyi of fourth-order tate variable filter and it application to Linkwitz- iley filter Janne honen 5.. TBLE OF CONTENTS. NTOCTON.... FOTH-OE LNWTZ-LEY (L TNSFE FNCTON.... TNSFE
