1 Heat Equation Dirichlet Boundary Conditions
|
|
|
- Angel Woods
- 5 years ago
- Views:
Transcription
1 Chapter 3 Heat Exampes in Rectanges Heat Equation Dirichet Boundary Conditions u t (x, t) = ku xx (x, t), < x <, t > (.) u(, t) =, u(, t) = u(x, ) = f(x). Separate Variabes Look for simpe soutions in the form u(x, t) = ϕ(x)ψ(t). Substituting into (.) and dividing both sides by ϕ(x)ψ(t) gives ψ (t) kψ(t) = ϕ (x) ϕ(x) Since the eft side is independent of x and the right side is independent of t, it foows that the expression must be a constant: ψ (t) kψ(t) = ϕ (x) ϕ(x) = λ. We seek to find a possibe constants λ and the corresponding nonzero functions ϕ and ψ. We obtain The soution of the second equation is ϕ λϕ =, ψ kλψ =. ψ(t) = Ce kλt (.) where C is an arbitrary constant. Furthermore, the boundary conditions give ϕ()ψ(t) =, ϕ()ψ(t) = for a t. Since ψ(t) is not identicay zero we obtain the desired eigenvaue probem ϕ (x) λϕ(x) =, ϕ() =, ϕ() =. (.3). Find Eigenvaues and Eignevectors The next main step is to find the eigenvaues and eigenfunctions from (.3). There are, in genera, three cases: (a) If λ = then ϕ(x) = ax + b so appying the boundary conditions we get Zero is not an eigenvaue. = ϕ() = b, = ϕ() = a a = b =.
2 (b) If λ = µ > then Appying the boundary conditions we have ϕ(x) = a cosh(µx) + b sinh(µx). = ϕ() = a a = = ϕ() = b sinh(µ) b =. Therefore, there are no positive eigenvaues. Consider the foowing aternative argument: If ϕ (x) = λϕ(x) then mutipying by ϕ we have ϕ(x)ϕ (x) = λϕ(x). Integrate this expression from x = to x =. We have λ ϕ(x) = Since ϕ() = ϕ() = we concude ϕ(x)ϕ (x) = λ = ϕ (x) ϕ(x) and we see that λ must be ess than or equa to zero. (c) So, finay, consider λ = µ so that Appying the boundary conditions we have ϕ(x) = a cos(µx) + b sin(µx). ϕ (x) + ϕ(x)ϕ (x). = ϕ() = a a = = ϕ() = b sin(µ). From this we concude sin(µ) = which impies µ =. So we have eigenfunctions b n sin( x) and we choose the constant b n so that and therefore ϕ n (x) = b n = ( λ n = µ n = ), ϕn (x) = From (.) we aso have the associated functions ψ n (t) = e kλnt. sin(x), n =,,. (.4) 3. Write Forma Sum From the above considerations we can concude that for any integer N and constants {c n } N n= N u N (x, t) = c n ψ n (t)ϕ n (x). satisfies the differentia equation in (.) and the boundary conditions.
3 4. Use Fourier Series to Find Coefficients The ony probem remaining is to somehow pick the constants b n so that the initia condition u(x, ) = f(x) is satisfied. To do this we consider what we earned from Fourier series. In particuar we ook for u as an infinite sum and we try to find {c n } satisfying u(x, t) = c n e kλnt ϕ n (x) f(x) = u(x, ) = c n ϕ n (x) But this nothing more than a Sine expansion of the function ϕ on the interva (, ). c n = f(x)ϕ n (x). (.5) Exampe.. As an expicit ( exampe for the initia condition consider =, k = / and f(x) = x( x). ) Let us reca that = which in this case reduces to. c n = = = [ x( x) sin (x) ( ) cos (x) x( x) x( x) cos(x) + ( x) cos(x) = = [ = () ( ) sin (x) ( x) ( x) sin(x) sin(x) = () ( ) sin (x) [ cos(x) = [ ( ) n () 3 We arrive at the soution u(x, t) = 4 π 3 [ ( ) n n 3 e n π t/ sin (x). (.6) where x( x) = 4 π 3 [ ( ) n n 3 sin (x). 3
4 As an exampe with N = 3 we have x( x) 8 ( sin(πx) + sin(3πx) ). π 3 7 In the foowing figure we pot the eft and right hand side of the above x Finay we pot the approximate soution at times t =, t =, t =, t = 3 u(x, t) = 4 3 [ ( ) n e nπt/ sin (x). π 3 n x Heat Equation Neumann Boundary Conditions u t (x, t) = u xx (x, t), < x <, t > (.7) u x (, t) =, u x (, t) = u(x, ) = f(x) 4
5 . Separate Variabes Look for simpe soutions in the form u(x, t) = ϕ(x)ψ(t). Substituting into (.7) and dividing both sides by ϕ(x)ψ(t) gives ψ (t) ψ(t) = ϕ (x) ϕ(x) Since the eft side is independent of x and the right side is independent of t, it foows that the expression must be a constant: ψ (t) ψ(t) = ϕ (x) ϕ(x) = λ. We seek to find a possibe constants λ and the corresponding nonzero functions ϕ and ψ. We obtain The soution of the second equation is ϕ λϕ =, ψ λψ =. ψ(t) = Ce λt (.8) where C is an arbitrary constant. Furthermore, the boundary conditions give ϕ ()ψ(t) =, ϕ ()ψ(t) = for a t. Since ψ(t) is not identicay zero we obtain the desired eigenvaue probem ϕ (x) λϕ(x) =, ϕ () =, ϕ () =. (.9). Find Eigenvaues and Eignevectors The next main step is to find the eigenvaues and eigenfunctions from (.9). There are, in genera, three cases: (a) If λ = then ϕ(x) = ax + b so appying the boundary conditions we get = ϕ () = a, = ϕ () = a a =. Notice that b is sti an arbitrary constant. We concude that λ = is an eigenvaue with normaized eigenfunction ϕ (x) = /. (b) If λ = µ > then and Appying the boundary conditions we have ϕ(x) = a cosh(µx) + b sinh(µx) ϕ (x) = aµ sinh(µx) + bµ cosh(µx). = ϕ () = bµ b = = ϕ () = aµ sinh(µ) a =. Therefore, there are no positive eigenvaues. Consider the foowing aternative argument: If ϕ (x) = λϕ(x) then mutipying by ϕ we have ϕ(x)ϕ (x) = λϕ(x). Integrate this expression from x = to x =. We have λ ϕ(x) = ϕ(x)ϕ (x) = ϕ (x) + ϕ(x)ϕ (x). 5
6 Since ϕ () = ϕ () = we concude λ = ϕ (x) ϕ(x) and we see that λ must be ess than or equa to zero ( zero ony if ϕ = ). (c) So, finay, consider λ = µ so that and Appying the boundary conditions we have ϕ(x) = a cos(µx) + b sin(µx) ϕ (x) = aµ sin(µx) + bµ cos(µx). = ϕ () = bµ b = = ϕ () = aµ sin(µ). From this we concude sin(µ) = which impies µ =. So we have eigenfunctions a n cos( x) and we choose the constant a n so that and therefore ϕ n (x) = a n = ( ) λ n = µ n =, ϕn (x) = cos(x), n =,,.. (.) From (.8) we aso have the associated functions ψ n (t) = e λnt. 3. Write Forma Infinite Sum From the above considerations we can concude that for any integer N and constants {a n } N n= N u n (x, t) = c ϕ + c n ψ n (t)ϕ n (x) satisfies the differentia equation in (.7) and the boundary conditions. 4. Use Fourier Series to Find Coefficients The ony probem remaining is to somehow pick the constants a n so that the initia condition u(x, ) = f(x) is satisfied. To do this we consider what we earned from Fourier series. In particuar we ook for u as an infinite sum u(x, t) = c ϕ + c n e λnt ϕ n (x) and we try to find {a n } satisfying ϕ(x) = u(x, ) = c ϕ + c n ϕ n (x). But this nothing more than a Cosine expansion of the function ϕ on the interva (, ). Our work on Fourier series showed us that c n = 6 f(x)ϕ n (x). (.)
7 As an expicit exampe for the initia condition consider = (so ϕ (x) = ) and f(x) = x( x). In this case (.) becomes We have c n = f(x)ϕ n (x). and for n > c = f(x)ϕ (x) = [ x = x3 = 3 6. x( x) c n = = = [ ϕ(x) cos (x) = ( ) sin (x) x( x) x( x) sin (x) x( x) cos (x) ( x) sin (x) ( ) cos (x) = ( x) [ cos (x) = ( x) cos (x) ( ) = [ cos () = () (( )n + ) = (), n even, n odd. In order to eiminate the odd terms in the expansion we introduce a new index, k by n = k where k =,,. So finay we arrive at the soution u(x, t) = 6 π k= k e 4k πt cos(kπx). (.) As an exampe with N = 4 we have x( x) 6 π ( 4 7 ) cos(kπx). k
8 Notice that as t the infinite sum converges to zero uniformy in x. Indeed, πt k e 4k cos(kπx) t e 4π k = π 6 e 4πt. k= So the soution converges to a nonzero steady state temperature which is exacty the average vaue of the initia temperature distribution. im u(x, t) = t 6 = f(x). In the foowing figure we pot the eft and right hand side of the above. k= x Finay we pot the approximate soution at times t =, t = /, t = /, t = 3/ x 8
9 . Heat Equation Dirichet-Neumann Boundary Conditions u t (x, t) = u xx (x, t), < x <, t > u(, t) =, u x (, t) = u(x, ) = f(x) Appy Separation of Variabes to obtain the Sturm-Liouvie probem for {λ n, ϕ n (x)}. Find Eigenvaues and Eignevectors The next main step is to find the eigenvaues and eigenfunctions. There are, in genera, three cases:. If λ = then ϕ(x) = ax + b so appying the boundary conditions we get Zero is not an eigenvaue.. If λ = µ > then and Appying the boundary conditions we have = ϕ() = b, = ϕ () = a a = b =. ϕ(x) = a cosh(µx) + b sinh(µx) ϕ (x) = aµ sinh(µx) + bµ cosh(µx). = ϕ () = aµ a = = ϕ () = bµ cosh(µ) b =. Therefore, there are no positive eigenvaues. Consider the foowing aternative argument: If ϕ (x) = λϕ(x) then mutipying by ϕ we have ϕ(x)ϕ (x) = λϕ(x). Integrate this expression from x = to x =. We have λ ϕ(x) = ϕ(x)ϕ (x) = Since ϕ() = ϕ () = we concude λ = ϕ (x) ϕ(x) and we see that λ must be ess than or equa to zero. 3. So, finay, consider λ = µ so that and Appying the boundary conditions we have ϕ(x) = a cos(µx) + b sin(µx) ϕ (x) = aµ sin(µx) + bµ cos(µx). ϕ (x) + ϕ(x)ϕ (x). = ϕ() = aµ a = = ϕ () = bµ cos(µ). 9
10 From this we concude cos(µ) = which impies µ = (n )π So we have eigenfunctions b n sin( x) and we choose the constant b n so that and therefore ϕ n (x) = b n = ( ) (n )π λ n = µ n =, ϕ n (x) = From (.) we aso have the associated functions ψ n (t) = e λnt. sin(x), n =,,. (.3) Write Forma Infinite Sum From the above considerations we can concude that for any integer N and constants {b n } N n= N u n (x, t) = c n ψ n (t)ϕ n (x). satisfies the heat equation and the boundary conditions. Use Fourier Series to Find Coefficients The ony probem remaining is to somehow pick the constants c n so that the initia condition u(x, ) = f(x) is satisfied. To do this we consider what we earned from Fourier series. In particuar we ook for u as an infinite sum and we try to find {b n } satisfying u(x, t) = c n e λnt ϕ n (x) f(x) = u(x, ) = c n ϕ n (x). But this nothing more than a Sine type expansion of the function ϕ on the interva (, ) and we have f(x) = c n = c n ϕ n (x). f(x)ϕ n (x). (.4) As an expicit exampe et = so that ϕ n (x) = ( ) sin( x) and for the initia condition consider (n )π f(x) = x. Let us reca that =
11 c n = = = [ ϕ(x)ϕ n (x) = ( x cos (µ ) nx) x cos(x) + = [ cos() + sin(µ nx) µ n = [ cos((n )π/) + = 4 ( ) n+ (n ) π x sin ( x) cos( x) sin((n )π/) µ n We arrive at the soution u(x, t) = 8 π ( ) n+ (n ) eλnt sin ( x). (.5)
4 1-D Boundary Value Problems Heat Equation
 4 -D Boundary Vaue Probems Heat Equation The main purpose of this chapter is to study boundary vaue probems for the heat equation on a finite rod a x b. u t (x, t = ku xx (x, t, a < x < b, t > u(x, = ϕ(x
4 -D Boundary Vaue Probems Heat Equation The main purpose of this chapter is to study boundary vaue probems for the heat equation on a finite rod a x b. u t (x, t = ku xx (x, t, a < x < b, t > u(x, = ϕ(x
1 Wave Equation on Finite Interval
 1 Wave Equation on Finite Interval 1.1 Wave Equation Dirichlet Boundary Conditions u tt (x, t) = c u xx (x, t), < x < l, t > (1.1) u(, t) =, u(l, t) = u(x, ) = f(x) u t (x, ) = g(x) First we present the
1 Wave Equation on Finite Interval 1.1 Wave Equation Dirichlet Boundary Conditions u tt (x, t) = c u xx (x, t), < x < l, t > (1.1) u(, t) =, u(l, t) = u(x, ) = f(x) u t (x, ) = g(x) First we present the
Wave Equation Dirichlet Boundary Conditions
 Wave Equation Dirichet Boundary Conditions u tt x, t = c u xx x, t, < x 1 u, t =, u, t = ux, = fx u t x, = gx Look for simpe soutions in the form ux, t = XxT t Substituting into 13 and dividing
Wave Equation Dirichet Boundary Conditions u tt x, t = c u xx x, t, < x 1 u, t =, u, t = ux, = fx u t x, = gx Look for simpe soutions in the form ux, t = XxT t Substituting into 13 and dividing
Math 220B - Summer 2003 Homework 1 Solutions
 Math 0B - Summer 003 Homework Soutions Consider the eigenvaue probem { X = λx 0 < x < X satisfies symmetric BCs x = 0, Suppose f(x)f (x) x=b x=a 0 for a rea-vaued functions f(x) which satisfy the boundary
Math 0B - Summer 003 Homework Soutions Consider the eigenvaue probem { X = λx 0 < x < X satisfies symmetric BCs x = 0, Suppose f(x)f (x) x=b x=a 0 for a rea-vaued functions f(x) which satisfy the boundary
14 Separation of Variables Method
 14 Separation of Variabes Method Consider, for exampe, the Dirichet probem u t = Du xx < x u(x, ) = f(x) < x < u(, t) = = u(, t) t > Let u(x, t) = T (t)φ(x); now substitute into the equation: dt
14 Separation of Variabes Method Consider, for exampe, the Dirichet probem u t = Du xx < x u(x, ) = f(x) < x < u(, t) = = u(, t) t > Let u(x, t) = T (t)φ(x); now substitute into the equation: dt
Strauss PDEs 2e: Section Exercise 2 Page 1 of 12. For problem (1), complete the calculation of the series in case j(t) = 0 and h(t) = e t.
 Strauss PDEs e: Section 5.6 - Exercise Page 1 of 1 Exercise For probem (1, compete the cacuation of the series in case j(t = and h(t = e t. Soution With j(t = and h(t = e t, probem (1 on page 147 becomes
Strauss PDEs e: Section 5.6 - Exercise Page 1 of 1 Exercise For probem (1, compete the cacuation of the series in case j(t = and h(t = e t. Soution With j(t = and h(t = e t, probem (1 on page 147 becomes
Lecture Notes for Math 251: ODE and PDE. Lecture 32: 10.2 Fourier Series
 Lecture Notes for Math 251: ODE and PDE. Lecture 32: 1.2 Fourier Series Shawn D. Ryan Spring 212 Last Time: We studied the heat equation and the method of Separation of Variabes. We then used Separation
Lecture Notes for Math 251: ODE and PDE. Lecture 32: 1.2 Fourier Series Shawn D. Ryan Spring 212 Last Time: We studied the heat equation and the method of Separation of Variabes. We then used Separation
Homework #04 Answers and Hints (MATH4052 Partial Differential Equations)
 Homework #4 Answers and Hints (MATH452 Partia Differentia Equations) Probem 1 (Page 89, Q2) Consider a meta rod ( < x < ), insuated aong its sides but not at its ends, which is initiay at temperature =
Homework #4 Answers and Hints (MATH452 Partia Differentia Equations) Probem 1 (Page 89, Q2) Consider a meta rod ( < x < ), insuated aong its sides but not at its ends, which is initiay at temperature =
MATH 172: MOTIVATION FOR FOURIER SERIES: SEPARATION OF VARIABLES
 MATH 172: MOTIVATION FOR FOURIER SERIES: SEPARATION OF VARIABLES Separation of variabes is a method to sove certain PDEs which have a warped product structure. First, on R n, a inear PDE of order m is
MATH 172: MOTIVATION FOR FOURIER SERIES: SEPARATION OF VARIABLES Separation of variabes is a method to sove certain PDEs which have a warped product structure. First, on R n, a inear PDE of order m is
Math 124B January 31, 2012
 Math 124B January 31, 212 Viktor Grigoryan 7 Inhomogeneous boundary vaue probems Having studied the theory of Fourier series, with which we successfuy soved boundary vaue probems for the homogeneous heat
Math 124B January 31, 212 Viktor Grigoryan 7 Inhomogeneous boundary vaue probems Having studied the theory of Fourier series, with which we successfuy soved boundary vaue probems for the homogeneous heat
Assignment 7 Due Tuessday, March 29, 2016
 Math 45 / AMCS 55 Dr. DeTurck Assignment 7 Due Tuessday, March 9, 6 Topics for this week Convergence of Fourier series; Lapace s equation and harmonic functions: basic properties, compuations on rectanges
Math 45 / AMCS 55 Dr. DeTurck Assignment 7 Due Tuessday, March 9, 6 Topics for this week Convergence of Fourier series; Lapace s equation and harmonic functions: basic properties, compuations on rectanges
Math 124B January 17, 2012
 Math 124B January 17, 212 Viktor Grigoryan 3 Fu Fourier series We saw in previous ectures how the Dirichet and Neumann boundary conditions ead to respectivey sine and cosine Fourier series of the initia
Math 124B January 17, 212 Viktor Grigoryan 3 Fu Fourier series We saw in previous ectures how the Dirichet and Neumann boundary conditions ead to respectivey sine and cosine Fourier series of the initia
MA 201: Partial Differential Equations Lecture - 10
 MA 201: Partia Differentia Equations Lecture - 10 Separation of Variabes, One dimensiona Wave Equation Initia Boundary Vaue Probem (IBVP) Reca: A physica probem governed by a PDE may contain both boundary
MA 201: Partia Differentia Equations Lecture - 10 Separation of Variabes, One dimensiona Wave Equation Initia Boundary Vaue Probem (IBVP) Reca: A physica probem governed by a PDE may contain both boundary
4 Separation of Variables
 4 Separation of Variabes In this chapter we describe a cassica technique for constructing forma soutions to inear boundary vaue probems. The soution of three cassica (paraboic, hyperboic and eiptic) PDE
4 Separation of Variabes In this chapter we describe a cassica technique for constructing forma soutions to inear boundary vaue probems. The soution of three cassica (paraboic, hyperboic and eiptic) PDE
Lecture Notes 4: Fourier Series and PDE s
 Lecture Notes 4: Fourier Series and PDE s 1. Periodic Functions A function fx defined on R is caed a periodic function if there exists a number T > such that fx + T = fx, x R. 1.1 The smaest number T for
Lecture Notes 4: Fourier Series and PDE s 1. Periodic Functions A function fx defined on R is caed a periodic function if there exists a number T > such that fx + T = fx, x R. 1.1 The smaest number T for
6 Non-homogeneous Heat Problems
 6 Non-homogeneous Heat Problems Up to this point all the problems we have considered for the heat or wave equation we what we call homogeneous problems. This means that for an interval < x < l the problems
6 Non-homogeneous Heat Problems Up to this point all the problems we have considered for the heat or wave equation we what we call homogeneous problems. This means that for an interval < x < l the problems
MA 201: Partial Differential Equations Lecture - 11
 MA 201: Partia Differentia Equations Lecture - 11 Heat Equation Heat conduction in a thin rod The IBVP under consideration consists of: The governing equation: u t = αu xx, (1) where α is the therma diffusivity.
MA 201: Partia Differentia Equations Lecture - 11 Heat Equation Heat conduction in a thin rod The IBVP under consideration consists of: The governing equation: u t = αu xx, (1) where α is the therma diffusivity.
6 Wave Equation on an Interval: Separation of Variables
 6 Wave Equation on an Interva: Separation of Variabes 6.1 Dirichet Boundary Conditions Ref: Strauss, Chapter 4 We now use the separation of variabes technique to study the wave equation on a finite interva.
6 Wave Equation on an Interva: Separation of Variabes 6.1 Dirichet Boundary Conditions Ref: Strauss, Chapter 4 We now use the separation of variabes technique to study the wave equation on a finite interva.
Strauss PDEs 2e: Section Exercise 1 Page 1 of 7
 Strauss PDEs 2e: Section 4.3 - Exercise 1 Page 1 of 7 Exercise 1 Find the eigenvaues graphicay for the boundary conditions X(0) = 0, X () + ax() = 0. Assume that a 0. Soution The aim here is to determine
Strauss PDEs 2e: Section 4.3 - Exercise 1 Page 1 of 7 Exercise 1 Find the eigenvaues graphicay for the boundary conditions X(0) = 0, X () + ax() = 0. Assume that a 0. Soution The aim here is to determine
Section 12.6: Non-homogeneous Problems
 Section 12.6: Non-homogeneous Problems 1 Introduction Up to this point all the problems we have considered are we what we call homogeneous problems. This means that for an interval < x < l the problems
Section 12.6: Non-homogeneous Problems 1 Introduction Up to this point all the problems we have considered are we what we call homogeneous problems. This means that for an interval < x < l the problems
1D Heat Propagation Problems
 Chapter 1 1D Heat Propagation Probems If the ambient space of the heat conduction has ony one dimension, the Fourier equation reduces to the foowing for an homogeneous body cρ T t = T λ 2 + Q, 1.1) x2
Chapter 1 1D Heat Propagation Probems If the ambient space of the heat conduction has ony one dimension, the Fourier equation reduces to the foowing for an homogeneous body cρ T t = T λ 2 + Q, 1.1) x2
Fourier Series. 10 (D3.9) Find the Cesàro sum of the series. 11 (D3.9) Let a and b be real numbers. Under what conditions does a series of the form
 Exercises Fourier Anaysis MMG70, Autumn 007 The exercises are taken from: Version: Monday October, 007 DXY Section XY of H F Davis, Fourier Series and orthogona functions EÖ Some exercises from earier
Exercises Fourier Anaysis MMG70, Autumn 007 The exercises are taken from: Version: Monday October, 007 DXY Section XY of H F Davis, Fourier Series and orthogona functions EÖ Some exercises from earier
David Eigen. MA112 Final Paper. May 10, 2002
 David Eigen MA112 Fina Paper May 1, 22 The Schrodinger equation describes the position of an eectron as a wave. The wave function Ψ(t, x is interpreted as a probabiity density for the position of the eectron.
David Eigen MA112 Fina Paper May 1, 22 The Schrodinger equation describes the position of an eectron as a wave. The wave function Ψ(t, x is interpreted as a probabiity density for the position of the eectron.
Assignment Number 3 Solutions
 Math 4354, Assigmet Number 3 Solutios 1. u t (x, t) = u xx (x, t), < x (1) u(, t) =, u(, t) = u(x, ) = x ( 1) +1 u(x, t) = e t si(x). () =1 Solutio: Look for simple solutios i the form u(x, t) =
Math 4354, Assigmet Number 3 Solutios 1. u t (x, t) = u xx (x, t), < x (1) u(, t) =, u(, t) = u(x, ) = x ( 1) +1 u(x, t) = e t si(x). () =1 Solutio: Look for simple solutios i the form u(x, t) =
Lecture Notes for Math 251: ODE and PDE. Lecture 34: 10.7 Wave Equation and Vibrations of an Elastic String
 ecture Notes for Math 251: ODE and PDE. ecture 3: 1.7 Wave Equation and Vibrations of an Eastic String Shawn D. Ryan Spring 212 ast Time: We studied other Heat Equation probems with various other boundary
ecture Notes for Math 251: ODE and PDE. ecture 3: 1.7 Wave Equation and Vibrations of an Eastic String Shawn D. Ryan Spring 212 ast Time: We studied other Heat Equation probems with various other boundary
Chapter 5. Wave equation. 5.1 Physical derivation
 Chapter 5 Wave equation In this chapter, we discuss the wave equation u tt a 2 u = f, (5.1) where a > is a constant. We wi discover that soutions of the wave equation behave in a different way comparing
Chapter 5 Wave equation In this chapter, we discuss the wave equation u tt a 2 u = f, (5.1) where a > is a constant. We wi discover that soutions of the wave equation behave in a different way comparing
Week 5 Lectures, Math 6451, Tanveer
 Week 5 Lectures, Math 651, Tanveer 1 Separation of variabe method The method of separation of variabe is a suitabe technique for determining soutions to inear PDEs, usuay with constant coefficients, when
Week 5 Lectures, Math 651, Tanveer 1 Separation of variabe method The method of separation of variabe is a suitabe technique for determining soutions to inear PDEs, usuay with constant coefficients, when
Course 2BA1, Section 11: Periodic Functions and Fourier Series
 Course BA, 8 9 Section : Periodic Functions and Fourier Series David R. Wikins Copyright c David R. Wikins 9 Contents Periodic Functions and Fourier Series 74. Fourier Series of Even and Odd Functions...........
Course BA, 8 9 Section : Periodic Functions and Fourier Series David R. Wikins Copyright c David R. Wikins 9 Contents Periodic Functions and Fourier Series 74. Fourier Series of Even and Odd Functions...........
SEMINAR 2. PENDULUMS. V = mgl cos θ. (2) L = T V = 1 2 ml2 θ2 + mgl cos θ, (3) d dt ml2 θ2 + mgl sin θ = 0, (4) θ + g l
 Probem 7. Simpe Penduum SEMINAR. PENDULUMS A simpe penduum means a mass m suspended by a string weightess rigid rod of ength so that it can swing in a pane. The y-axis is directed down, x-axis is directed
Probem 7. Simpe Penduum SEMINAR. PENDULUMS A simpe penduum means a mass m suspended by a string weightess rigid rod of ength so that it can swing in a pane. The y-axis is directed down, x-axis is directed
Fourier series. Part - A
 Fourier series Part - A 1.Define Dirichet s conditions Ans: A function defined in c x c + can be expanded as an infinite trigonometric series of the form a + a n cos nx n 1 + b n sin nx, provided i) f
Fourier series Part - A 1.Define Dirichet s conditions Ans: A function defined in c x c + can be expanded as an infinite trigonometric series of the form a + a n cos nx n 1 + b n sin nx, provided i) f
C. Fourier Sine Series Overview
 12 PHILIP D. LOEWEN C. Fourier Sine Series Overview Let some constant > be given. The symboic form of the FSS Eigenvaue probem combines an ordinary differentia equation (ODE) on the interva (, ) with a
12 PHILIP D. LOEWEN C. Fourier Sine Series Overview Let some constant > be given. The symboic form of the FSS Eigenvaue probem combines an ordinary differentia equation (ODE) on the interva (, ) with a
2M2. Fourier Series Prof Bill Lionheart
 M. Fourier Series Prof Bi Lionheart 1. The Fourier series of the periodic function f(x) with period has the form f(x) = a 0 + ( a n cos πnx + b n sin πnx ). Here the rea numbers a n, b n are caed the Fourier
M. Fourier Series Prof Bi Lionheart 1. The Fourier series of the periodic function f(x) with period has the form f(x) = a 0 + ( a n cos πnx + b n sin πnx ). Here the rea numbers a n, b n are caed the Fourier
Higher dimensional PDEs and multidimensional eigenvalue problems
 Higher dimensiona PEs and mutidimensiona eigenvaue probems 1 Probems with three independent variabes Consider the prototypica equations u t = u (iffusion) u tt = u (W ave) u zz = u (Lapace) where u = u
Higher dimensiona PEs and mutidimensiona eigenvaue probems 1 Probems with three independent variabes Consider the prototypica equations u t = u (iffusion) u tt = u (W ave) u zz = u (Lapace) where u = u
Lecture Notes for Math 251: ODE and PDE. Lecture 30: 10.1 Two-Point Boundary Value Problems
 Lecture Notes for Math 251: ODE and PDE. Lecture 30: 10.1 Two-Point Boundary Value Problems Shawn D. Ryan Spring 2012 Last Time: We finished Chapter 9: Nonlinear Differential Equations and Stability. Now
Lecture Notes for Math 251: ODE and PDE. Lecture 30: 10.1 Two-Point Boundary Value Problems Shawn D. Ryan Spring 2012 Last Time: We finished Chapter 9: Nonlinear Differential Equations and Stability. Now
Transforms and Boundary Value Problems
 Transforms and Boundary Vaue Probems (For B.Tech Students (Third/Fourth/Fifth Semester Soved University Questions Papers Prepared by Dr. V. SUVITHA Department of Mathematics, SRMIST Kattankuathur 6. CONTENTS
Transforms and Boundary Vaue Probems (For B.Tech Students (Third/Fourth/Fifth Semester Soved University Questions Papers Prepared by Dr. V. SUVITHA Department of Mathematics, SRMIST Kattankuathur 6. CONTENTS
Week 6 Lectures, Math 6451, Tanveer
 Fourier Series Week 6 Lectures, Math 645, Tanveer In the context of separation of variabe to find soutions of PDEs, we encountered or and in other cases f(x = f(x = a 0 + f(x = a 0 + b n sin nπx { a n
Fourier Series Week 6 Lectures, Math 645, Tanveer In the context of separation of variabe to find soutions of PDEs, we encountered or and in other cases f(x = f(x = a 0 + f(x = a 0 + b n sin nπx { a n
FOURIER SERIES ON ANY INTERVAL
 FOURIER SERIES ON ANY INTERVAL Overview We have spent considerabe time earning how to compute Fourier series for functions that have a period of 2p on the interva (-p,p). We have aso seen how Fourier series
FOURIER SERIES ON ANY INTERVAL Overview We have spent considerabe time earning how to compute Fourier series for functions that have a period of 2p on the interva (-p,p). We have aso seen how Fourier series
Separation of Variables and a Spherical Shell with Surface Charge
 Separation of Variabes and a Spherica She with Surface Charge In cass we worked out the eectrostatic potentia due to a spherica she of radius R with a surface charge density σθ = σ cos θ. This cacuation
Separation of Variabes and a Spherica She with Surface Charge In cass we worked out the eectrostatic potentia due to a spherica she of radius R with a surface charge density σθ = σ cos θ. This cacuation
Introduction to Simulation - Lecture 13. Convergence of Multistep Methods. Jacob White. Thanks to Deepak Ramaswamy, Michal Rewienski, and Karen Veroy
 Introduction to Simuation - Lecture 13 Convergence of Mutistep Methods Jacob White Thans to Deepa Ramaswamy, Micha Rewiensi, and Karen Veroy Outine Sma Timestep issues for Mutistep Methods Loca truncation
Introduction to Simuation - Lecture 13 Convergence of Mutistep Methods Jacob White Thans to Deepa Ramaswamy, Micha Rewiensi, and Karen Veroy Outine Sma Timestep issues for Mutistep Methods Loca truncation
11.1 One-dimensional Helmholtz Equation
 Chapter Green s Functions. One-dimensiona Hemhotz Equation Suppose we have a string driven by an externa force, periodic with frequency ω. The differentia equation here f is some prescribed function) 2
Chapter Green s Functions. One-dimensiona Hemhotz Equation Suppose we have a string driven by an externa force, periodic with frequency ω. The differentia equation here f is some prescribed function) 2
Mat 1501 lecture notes, penultimate installment
 Mat 1501 ecture notes, penutimate instament 1. bounded variation: functions of a singe variabe optiona) I beieve that we wi not actuay use the materia in this section the point is mainy to motivate the
Mat 1501 ecture notes, penutimate instament 1. bounded variation: functions of a singe variabe optiona) I beieve that we wi not actuay use the materia in this section the point is mainy to motivate the
Math 201 Assignment #11
 Math 21 Assignment #11 Problem 1 (1.5 2) Find a formal solution to the given initial-boundary value problem. = 2 u x, < x < π, t > 2 u(, t) = u(π, t) =, t > u(x, ) = x 2, < x < π Problem 2 (1.5 5) Find
Math 21 Assignment #11 Problem 1 (1.5 2) Find a formal solution to the given initial-boundary value problem. = 2 u x, < x < π, t > 2 u(, t) = u(π, t) =, t > u(x, ) = x 2, < x < π Problem 2 (1.5 5) Find
u(x) s.t. px w x 0 Denote the solution to this problem by ˆx(p, x). In order to obtain ˆx we may simply solve the standard problem max x 0
 Bocconi University PhD in Economics - Microeconomics I Prof M Messner Probem Set 4 - Soution Probem : If an individua has an endowment instead of a monetary income his weath depends on price eves In particuar,
Bocconi University PhD in Economics - Microeconomics I Prof M Messner Probem Set 4 - Soution Probem : If an individua has an endowment instead of a monetary income his weath depends on price eves In particuar,
Math Assignment 14
 Math 2280 - Assignment 14 Dylan Zwick Spring 2014 Section 9.5-1, 3, 5, 7, 9 Section 9.6-1, 3, 5, 7, 14 Section 9.7-1, 2, 3, 4 1 Section 9.5 - Heat Conduction and Separation of Variables 9.5.1 - Solve the
Math 2280 - Assignment 14 Dylan Zwick Spring 2014 Section 9.5-1, 3, 5, 7, 9 Section 9.6-1, 3, 5, 7, 14 Section 9.7-1, 2, 3, 4 1 Section 9.5 - Heat Conduction and Separation of Variables 9.5.1 - Solve the
ODE Homework 2. Since M y N x, the equation is not exact. 2. Determine whether the following equation is exact. If it is exact, M y N x 1 x.
 ODE Homework.6. Exact Equations and Integrating Factors 1. Determine whether the foowing equation is exact. If it is exact, find the soution pe x sin qdx p3x e x sin qd 0 [.6 #8] So. Let Mpx, q e x sin,
ODE Homework.6. Exact Equations and Integrating Factors 1. Determine whether the foowing equation is exact. If it is exact, find the soution pe x sin qdx p3x e x sin qd 0 [.6 #8] So. Let Mpx, q e x sin,
Problem set 6 The Perron Frobenius theorem.
 Probem set 6 The Perron Frobenius theorem. Math 22a4 Oct 2 204, Due Oct.28 In a future probem set I want to discuss some criteria which aow us to concude that that the ground state of a sef-adjoint operator
Probem set 6 The Perron Frobenius theorem. Math 22a4 Oct 2 204, Due Oct.28 In a future probem set I want to discuss some criteria which aow us to concude that that the ground state of a sef-adjoint operator
Examples of the Fourier Theorem (Sect. 10.3). The Fourier Theorem: Continuous case.
 s of the Fourier Theorem (Sect. 1.3. The Fourier Theorem: Continuous case. : Using the Fourier Theorem. The Fourier Theorem: Piecewise continuous case. : Using the Fourier Theorem. The Fourier Theorem:
s of the Fourier Theorem (Sect. 1.3. The Fourier Theorem: Continuous case. : Using the Fourier Theorem. The Fourier Theorem: Piecewise continuous case. : Using the Fourier Theorem. The Fourier Theorem:
Fourier Series in Complex notation. cos(x) = eix + e ix 2. A n cos + B n sin l. i 2 B n. e inx=l + A n + ib n 2 8. ( 0 m 6= n. C n = 1 2l.
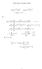 Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
Legendre Polynomials - Lecture 8
 Legendre Poynomias - Lecture 8 Introduction In spherica coordinates the separation of variabes for the function of the poar ange resuts in Legendre s equation when the soution is independent of the azimutha
Legendre Poynomias - Lecture 8 Introduction In spherica coordinates the separation of variabes for the function of the poar ange resuts in Legendre s equation when the soution is independent of the azimutha
Physics 505 Fall 2007 Homework Assignment #5 Solutions. Textbook problems: Ch. 3: 3.13, 3.17, 3.26, 3.27
 Physics 55 Fa 7 Homework Assignment #5 Soutions Textook proems: Ch. 3: 3.3, 3.7, 3.6, 3.7 3.3 Sove for the potentia in Proem 3., using the appropriate Green function otained in the text, and verify that
Physics 55 Fa 7 Homework Assignment #5 Soutions Textook proems: Ch. 3: 3.3, 3.7, 3.6, 3.7 3.3 Sove for the potentia in Proem 3., using the appropriate Green function otained in the text, and verify that
Midterm 2: Sample solutions Math 118A, Fall 2013
 Midterm 2: Sample solutions Math 118A, Fall 213 1. Find all separated solutions u(r,t = F(rG(t of the radially symmetric heat equation u t = k ( r u. r r r Solve for G(t explicitly. Write down an ODE for
Midterm 2: Sample solutions Math 118A, Fall 213 1. Find all separated solutions u(r,t = F(rG(t of the radially symmetric heat equation u t = k ( r u. r r r Solve for G(t explicitly. Write down an ODE for
1 2-D Second Order Equations: Separation of Variables
 Chpter 12 PDEs in Rectngles 1 2-D Second Order Equtions: Seprtion of Vribles 1. A second order liner prtil differentil eqution in two vribles x nd y is A 2 u x + B 2 u 2 x y + C 2 u y + D u 2 x + E u +
Chpter 12 PDEs in Rectngles 1 2-D Second Order Equtions: Seprtion of Vribles 1. A second order liner prtil differentil eqution in two vribles x nd y is A 2 u x + B 2 u 2 x y + C 2 u y + D u 2 x + E u +
Suggested Solution to Assignment 5
 MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
Introduction to Simulation - Lecture 14. Multistep Methods II. Jacob White. Thanks to Deepak Ramaswamy, Michal Rewienski, and Karen Veroy
 Introduction to Simuation - Lecture 14 Mutistep Methods II Jacob White Thans to Deepa Ramaswamy, Micha Rewiensi, and Karen Veroy Outine Sma Timestep issues for Mutistep Methods Reminder about LTE minimization
Introduction to Simuation - Lecture 14 Mutistep Methods II Jacob White Thans to Deepa Ramaswamy, Micha Rewiensi, and Karen Veroy Outine Sma Timestep issues for Mutistep Methods Reminder about LTE minimization
Lecture notes. May 2, 2017
 Lecture notes May, 7 Preface These are ecture notes for MATH 47: Partia differentia equations with the soe purpose of providing reading materia for topics covered in the ectures of the cass. Severa exampes
Lecture notes May, 7 Preface These are ecture notes for MATH 47: Partia differentia equations with the soe purpose of providing reading materia for topics covered in the ectures of the cass. Severa exampes
Steepest Descent Adaptation of Min-Max Fuzzy If-Then Rules 1
 Steepest Descent Adaptation of Min-Max Fuzzy If-Then Rues 1 R.J. Marks II, S. Oh, P. Arabshahi Λ, T.P. Caude, J.J. Choi, B.G. Song Λ Λ Dept. of Eectrica Engineering Boeing Computer Services University
Steepest Descent Adaptation of Min-Max Fuzzy If-Then Rues 1 R.J. Marks II, S. Oh, P. Arabshahi Λ, T.P. Caude, J.J. Choi, B.G. Song Λ Λ Dept. of Eectrica Engineering Boeing Computer Services University
Find the Fourier series of the odd-periodic extension of the function f (x) = 1 for x ( 1, 0). Solution: The Fourier series is.
 Review for Final Exam. Monday /09, :45-:45pm in CC-403. Exam is cumulative, -4 problems. 5 grading attempts per problem. Problems similar to homeworks. Integration and LT tables provided. No notes, no
Review for Final Exam. Monday /09, :45-:45pm in CC-403. Exam is cumulative, -4 problems. 5 grading attempts per problem. Problems similar to homeworks. Integration and LT tables provided. No notes, no
221B Lecture Notes Notes on Spherical Bessel Functions
 Definitions B Lecture Notes Notes on Spherica Besse Functions We woud ike to sove the free Schrödinger equation [ h d r R(r) = h k R(r). () m r dr r m R(r) is the radia wave function ψ( x) = R(r)Y m (θ,
Definitions B Lecture Notes Notes on Spherica Besse Functions We woud ike to sove the free Schrödinger equation [ h d r R(r) = h k R(r). () m r dr r m R(r) is the radia wave function ψ( x) = R(r)Y m (θ,
Methods for Ordinary Differential Equations. Jacob White
 Introduction to Simuation - Lecture 12 for Ordinary Differentia Equations Jacob White Thanks to Deepak Ramaswamy, Jaime Peraire, Micha Rewienski, and Karen Veroy Outine Initia Vaue probem exampes Signa
Introduction to Simuation - Lecture 12 for Ordinary Differentia Equations Jacob White Thanks to Deepak Ramaswamy, Jaime Peraire, Micha Rewienski, and Karen Veroy Outine Initia Vaue probem exampes Signa
Physics 116C Helmholtz s and Laplace s Equations in Spherical Polar Coordinates: Spherical Harmonics and Spherical Bessel Functions
 Physics 116C Hemhotz s an Lapace s Equations in Spherica Poar Coorinates: Spherica Harmonics an Spherica Besse Functions Peter Young Date: October 28, 2013) I. HELMHOLTZ S EQUATION As iscusse in cass,
Physics 116C Hemhotz s an Lapace s Equations in Spherica Poar Coorinates: Spherica Harmonics an Spherica Besse Functions Peter Young Date: October 28, 2013) I. HELMHOLTZ S EQUATION As iscusse in cass,
LECTURE NOTES 8 THE TRACELESS SYMMETRIC TENSOR EXPANSION AND STANDARD SPHERICAL HARMONICS
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Eectromagnetism II October, 202 Prof. Aan Guth LECTURE NOTES 8 THE TRACELESS SYMMETRIC TENSOR EXPANSION AND STANDARD SPHERICAL HARMONICS
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Eectromagnetism II October, 202 Prof. Aan Guth LECTURE NOTES 8 THE TRACELESS SYMMETRIC TENSOR EXPANSION AND STANDARD SPHERICAL HARMONICS
NOISE-INDUCED STABILIZATION OF STOCHASTIC DIFFERENTIAL EQUATIONS
 NOISE-INDUCED STABILIZATION OF STOCHASTIC DIFFERENTIAL EQUATIONS TONY ALLEN, EMILY GEBHARDT, AND ADAM KLUBALL 3 ADVISOR: DR. TIFFANY KOLBA 4 Abstract. The phenomenon of noise-induced stabiization occurs
NOISE-INDUCED STABILIZATION OF STOCHASTIC DIFFERENTIAL EQUATIONS TONY ALLEN, EMILY GEBHARDT, AND ADAM KLUBALL 3 ADVISOR: DR. TIFFANY KOLBA 4 Abstract. The phenomenon of noise-induced stabiization occurs
$, (2.1) n="# #. (2.2)
 Chapter. Eectrostatic II Notes: Most of the materia presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartoo, Chap... Mathematica Considerations.. The Fourier series and the Fourier
Chapter. Eectrostatic II Notes: Most of the materia presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartoo, Chap... Mathematica Considerations.. The Fourier series and the Fourier
Radiation Fields. Lecture 12
 Radiation Fieds Lecture 12 1 Mutipoe expansion Separate Maxwe s equations into two sets of equations, each set separatey invoving either the eectric or the magnetic fied. After remova of the time dependence
Radiation Fieds Lecture 12 1 Mutipoe expansion Separate Maxwe s equations into two sets of equations, each set separatey invoving either the eectric or the magnetic fied. After remova of the time dependence
EXISTENCE OF SOLUTIONS FOR ONE-DIMENSIONAL WAVE EQUATIONS WITH NONLOCAL CONDITIONS
 Eectronic Journa of Differentia Equations, Vo. 21(21), No. 76, pp. 1 8. ISSN: 172-6691. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu (ogin: ftp) EXISTENCE OF SOLUTIONS
Eectronic Journa of Differentia Equations, Vo. 21(21), No. 76, pp. 1 8. ISSN: 172-6691. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu (ogin: ftp) EXISTENCE OF SOLUTIONS
Physics 235 Chapter 8. Chapter 8 Central-Force Motion
 Physics 35 Chapter 8 Chapter 8 Centra-Force Motion In this Chapter we wi use the theory we have discussed in Chapter 6 and 7 and appy it to very important probems in physics, in which we study the motion
Physics 35 Chapter 8 Chapter 8 Centra-Force Motion In this Chapter we wi use the theory we have discussed in Chapter 6 and 7 and appy it to very important probems in physics, in which we study the motion
MATH 425, HOMEWORK 5, SOLUTIONS
 MATH 425, HOMEWORK 5, SOLUTIONS Exercise (Uniqueness for the heat equation on R) Suppose that the functions u, u 2 : R x R t R solve: t u k 2 xu = 0, x R, t > 0 u (x, 0) = φ(x), x R and t u 2 k 2 xu 2
MATH 425, HOMEWORK 5, SOLUTIONS Exercise (Uniqueness for the heat equation on R) Suppose that the functions u, u 2 : R x R t R solve: t u k 2 xu = 0, x R, t > 0 u (x, 0) = φ(x), x R and t u 2 k 2 xu 2
More Scattering: the Partial Wave Expansion
 More Scattering: the Partia Wave Expansion Michae Fower /7/8 Pane Waves and Partia Waves We are considering the soution to Schrödinger s equation for scattering of an incoming pane wave in the z-direction
More Scattering: the Partia Wave Expansion Michae Fower /7/8 Pane Waves and Partia Waves We are considering the soution to Schrödinger s equation for scattering of an incoming pane wave in the z-direction
Integrating Factor Methods as Exponential Integrators
 Integrating Factor Methods as Exponentia Integrators Borisav V. Minchev Department of Mathematica Science, NTNU, 7491 Trondheim, Norway Borko.Minchev@ii.uib.no Abstract. Recenty a ot of effort has been
Integrating Factor Methods as Exponentia Integrators Borisav V. Minchev Department of Mathematica Science, NTNU, 7491 Trondheim, Norway Borko.Minchev@ii.uib.no Abstract. Recenty a ot of effort has been
Partial differential equations (ACM30220)
 (ACM3. A pot on a stove has a handle of length that can be modelled as a rod with diffusion constant D. The equation for the temperature in the rod is u t Du xx < x
(ACM3. A pot on a stove has a handle of length that can be modelled as a rod with diffusion constant D. The equation for the temperature in the rod is u t Du xx < x
A Brief Introduction to Markov Chains and Hidden Markov Models
 A Brief Introduction to Markov Chains and Hidden Markov Modes Aen B MacKenzie Notes for December 1, 3, &8, 2015 Discrete-Time Markov Chains You may reca that when we first introduced random processes,
A Brief Introduction to Markov Chains and Hidden Markov Modes Aen B MacKenzie Notes for December 1, 3, &8, 2015 Discrete-Time Markov Chains You may reca that when we first introduced random processes,
Lecture 6: Moderately Large Deflection Theory of Beams
 Structura Mechanics 2.8 Lecture 6 Semester Yr Lecture 6: Moderatey Large Defection Theory of Beams 6.1 Genera Formuation Compare to the cassica theory of beams with infinitesima deformation, the moderatey
Structura Mechanics 2.8 Lecture 6 Semester Yr Lecture 6: Moderatey Large Defection Theory of Beams 6.1 Genera Formuation Compare to the cassica theory of beams with infinitesima deformation, the moderatey
(f) is called a nearly holomorphic modular form of weight k + 2r as in [5].
![(f) is called a nearly holomorphic modular form of weight k + 2r as in [5]. (f) is called a nearly holomorphic modular form of weight k + 2r as in [5].](/thumbs/77/75192090.jpg) PRODUCTS OF NEARLY HOLOMORPHIC EIGENFORMS JEFFREY BEYERL, KEVIN JAMES, CATHERINE TRENTACOSTE, AND HUI XUE Abstract. We prove that the product of two neary hoomorphic Hece eigenforms is again a Hece eigenform
PRODUCTS OF NEARLY HOLOMORPHIC EIGENFORMS JEFFREY BEYERL, KEVIN JAMES, CATHERINE TRENTACOSTE, AND HUI XUE Abstract. We prove that the product of two neary hoomorphic Hece eigenforms is again a Hece eigenform
The One-Dimensional Heat Equation
 The One-Dimensional Heat Equation R. C. Trinity University Partial Differential Equations February 24, 2015 Introduction The heat equation Goal: Model heat (thermal energy) flow in a one-dimensional object
The One-Dimensional Heat Equation R. C. Trinity University Partial Differential Equations February 24, 2015 Introduction The heat equation Goal: Model heat (thermal energy) flow in a one-dimensional object
Review Sol. of More Long Answer Questions
 Review Sol. of More Long Answer Questions 1. Solve the integro-differential equation t y (t) e t v y(v)dv = t; y()=. (1) Solution. The key is to recognize the convolution: t e t v y(v) dv = e t y. () Now
Review Sol. of More Long Answer Questions 1. Solve the integro-differential equation t y (t) e t v y(v)dv = t; y()=. (1) Solution. The key is to recognize the convolution: t e t v y(v) dv = e t y. () Now
WMS. MA250 Introduction to Partial Differential Equations. Revision Guide. Written by Matthew Hutton and David McCormick
 WMS MA25 Introduction to Partia Differentia Equations Revision Guide Written by Matthew Hutton and David McCormick WMS ii MA25 Introduction to Partia Differentia Equations Contents Introduction 1 1 First-Order
WMS MA25 Introduction to Partia Differentia Equations Revision Guide Written by Matthew Hutton and David McCormick WMS ii MA25 Introduction to Partia Differentia Equations Contents Introduction 1 1 First-Order
arxiv: v1 [math.fa] 23 Aug 2018
![arxiv: v1 [math.fa] 23 Aug 2018 arxiv: v1 [math.fa] 23 Aug 2018](/thumbs/84/89702159.jpg) An Exact Upper Bound on the L p Lebesgue Constant and The -Rényi Entropy Power Inequaity for Integer Vaued Random Variabes arxiv:808.0773v [math.fa] 3 Aug 08 Peng Xu, Mokshay Madiman, James Mebourne Abstract
An Exact Upper Bound on the L p Lebesgue Constant and The -Rényi Entropy Power Inequaity for Integer Vaued Random Variabes arxiv:808.0773v [math.fa] 3 Aug 08 Peng Xu, Mokshay Madiman, James Mebourne Abstract
Haar Decomposition and Reconstruction Algorithms
 Jim Lambers MAT 773 Fa Semester 018-19 Lecture 15 and 16 Notes These notes correspond to Sections 4.3 and 4.4 in the text. Haar Decomposition and Reconstruction Agorithms Decomposition Suppose we approximate
Jim Lambers MAT 773 Fa Semester 018-19 Lecture 15 and 16 Notes These notes correspond to Sections 4.3 and 4.4 in the text. Haar Decomposition and Reconstruction Agorithms Decomposition Suppose we approximate
b n n=1 a n cos nx (3) n=1
 Fourier Anaysis The Fourier series First some terminoogy: a function f(x) is periodic if f(x ) = f(x) for a x for some, if is the smaest such number, it is caed the period of f(x). It is even if f( x)
Fourier Anaysis The Fourier series First some terminoogy: a function f(x) is periodic if f(x ) = f(x) for a x for some, if is the smaest such number, it is caed the period of f(x). It is even if f( x)
CS229 Lecture notes. Andrew Ng
 CS229 Lecture notes Andrew Ng Part IX The EM agorithm In the previous set of notes, we taked about the EM agorithm as appied to fitting a mixture of Gaussians. In this set of notes, we give a broader view
CS229 Lecture notes Andrew Ng Part IX The EM agorithm In the previous set of notes, we taked about the EM agorithm as appied to fitting a mixture of Gaussians. In this set of notes, we give a broader view
Ch 10.1: Two Point Boundary Value Problems
 Ch 10.1: Two Point Boundary Value Problems In many important physical problems there are two or more independent variables, so the corresponding mathematical models involve partial differential equations.
Ch 10.1: Two Point Boundary Value Problems In many important physical problems there are two or more independent variables, so the corresponding mathematical models involve partial differential equations.
Ma 221 Eigenvalues and Fourier Series
 Ma Eigenvalues and Fourier Series Eigenvalue and Eigenfunction Examples Example Find the eigenvalues and eigenfunctions for y y 47 y y y5 Solution: The characteristic equation is r r 47 so r 44 447 6 Thus
Ma Eigenvalues and Fourier Series Eigenvalue and Eigenfunction Examples Example Find the eigenvalues and eigenfunctions for y y 47 y y y5 Solution: The characteristic equation is r r 47 so r 44 447 6 Thus
Solutions to Exercises 8.1
 Section 8. Partial Differential Equations in Physics and Engineering 67 Solutions to Exercises 8.. u xx +u xy u is a second order, linear, and homogeneous partial differential equation. u x (,y) is linear
Section 8. Partial Differential Equations in Physics and Engineering 67 Solutions to Exercises 8.. u xx +u xy u is a second order, linear, and homogeneous partial differential equation. u x (,y) is linear
Scott Cohen. November 10, Abstract. The method of Block Cyclic Reduction (BCR) is described in the context of
 ycic Reduction Scott ohen November, 99 bstract The method of ock ycic Reduction (R) is described in the context of soving Poisson's equation with Dirichet boundary conditions The numerica instabiityof
ycic Reduction Scott ohen November, 99 bstract The method of ock ycic Reduction (R) is described in the context of soving Poisson's equation with Dirichet boundary conditions The numerica instabiityof
Method of Separation of Variables
 MODUE 5: HEAT EQUATION 11 ecture 3 Method of Separation of Variables Separation of variables is one of the oldest technique for solving initial-boundary value problems (IBVP) and applies to problems, where
MODUE 5: HEAT EQUATION 11 ecture 3 Method of Separation of Variables Separation of variables is one of the oldest technique for solving initial-boundary value problems (IBVP) and applies to problems, where
# Points Score Total 100
 Name: PennID: Math 241 Make-Up Final Exam January 19, 2016 Instructions: Turn off and put away your cell phone. Please write your Name and PennID on the top of this page. Please sign and date the pledge
Name: PennID: Math 241 Make-Up Final Exam January 19, 2016 Instructions: Turn off and put away your cell phone. Please write your Name and PennID on the top of this page. Please sign and date the pledge
LECTURE 19: SEPARATION OF VARIABLES, HEAT CONDUCTION IN A ROD
 ECTURE 19: SEPARATION OF VARIABES, HEAT CONDUCTION IN A ROD The idea of separation of variables is simple: in order to solve a partial differential equation in u(x, t), we ask, is it possible to find a
ECTURE 19: SEPARATION OF VARIABES, HEAT CONDUCTION IN A ROD The idea of separation of variables is simple: in order to solve a partial differential equation in u(x, t), we ask, is it possible to find a
V.B The Cluster Expansion
 V.B The Custer Expansion For short range interactions, speciay with a hard core, it is much better to repace the expansion parameter V( q ) by f( q ) = exp ( βv( q )), which is obtained by summing over
V.B The Custer Expansion For short range interactions, speciay with a hard core, it is much better to repace the expansion parameter V( q ) by f( q ) = exp ( βv( q )), which is obtained by summing over
Vibrations of Structures
 Vibrations of Structures Modue I: Vibrations of Strings and Bars Lesson : The Initia Vaue Probem Contents:. Introduction. Moda Expansion Theorem 3. Initia Vaue Probem: Exampes 4. Lapace Transform Method
Vibrations of Structures Modue I: Vibrations of Strings and Bars Lesson : The Initia Vaue Probem Contents:. Introduction. Moda Expansion Theorem 3. Initia Vaue Probem: Exampes 4. Lapace Transform Method
Physics 250 Green s functions for ordinary differential equations
 Physics 25 Green s functions for ordinary differential equations Peter Young November 25, 27 Homogeneous Equations We have already discussed second order linear homogeneous differential equations, which
Physics 25 Green s functions for ordinary differential equations Peter Young November 25, 27 Homogeneous Equations We have already discussed second order linear homogeneous differential equations, which
BALANCING REGULAR MATRIX PENCILS
 BALANCING REGULAR MATRIX PENCILS DAMIEN LEMONNIER AND PAUL VAN DOOREN Abstract. In this paper we present a new diagona baancing technique for reguar matrix pencis λb A, which aims at reducing the sensitivity
BALANCING REGULAR MATRIX PENCILS DAMIEN LEMONNIER AND PAUL VAN DOOREN Abstract. In this paper we present a new diagona baancing technique for reguar matrix pencis λb A, which aims at reducing the sensitivity
A NOTE ON QUASI-STATIONARY DISTRIBUTIONS OF BIRTH-DEATH PROCESSES AND THE SIS LOGISTIC EPIDEMIC
 (January 8, 2003) A NOTE ON QUASI-STATIONARY DISTRIBUTIONS OF BIRTH-DEATH PROCESSES AND THE SIS LOGISTIC EPIDEMIC DAMIAN CLANCY, University of Liverpoo PHILIP K. POLLETT, University of Queensand Abstract
(January 8, 2003) A NOTE ON QUASI-STATIONARY DISTRIBUTIONS OF BIRTH-DEATH PROCESSES AND THE SIS LOGISTIC EPIDEMIC DAMIAN CLANCY, University of Liverpoo PHILIP K. POLLETT, University of Queensand Abstract
FRST Multivariate Statistics. Multivariate Discriminant Analysis (MDA)
 1 FRST 531 -- Mutivariate Statistics Mutivariate Discriminant Anaysis (MDA) Purpose: 1. To predict which group (Y) an observation beongs to based on the characteristics of p predictor (X) variabes, using
1 FRST 531 -- Mutivariate Statistics Mutivariate Discriminant Anaysis (MDA) Purpose: 1. To predict which group (Y) an observation beongs to based on the characteristics of p predictor (X) variabes, using
Lemma 1. Suppose K S is a compact subset and I α is a covering of K. There is a finite subcollection {I j } such that
 2 Singuar Integras We start with a very usefu covering emma. Lemma. Suppose K S is a compact subset and I α is a covering of K. There is a finite subcoection {I j } such that. {I j } are disjoint. 2. The
2 Singuar Integras We start with a very usefu covering emma. Lemma. Suppose K S is a compact subset and I α is a covering of K. There is a finite subcoection {I j } such that. {I j } are disjoint. 2. The
SCHOOL OF MATHEMATICS AND STATISTICS. Mathematics II (Materials) Section A. Find the general solution of the equation
 Data provided: Formua Sheet MAS250 SCHOOL OF MATHEMATICS AND STATISTICS Mathematics II (Materias Autumn Semester 204 5 2 hours Marks wi be awarded for answers to a questions in Section A, and for your
Data provided: Formua Sheet MAS250 SCHOOL OF MATHEMATICS AND STATISTICS Mathematics II (Materias Autumn Semester 204 5 2 hours Marks wi be awarded for answers to a questions in Section A, and for your
Solving the Heat Equation (Sect. 10.5).
 Solving the Heat Equation Sect. 1.5. Review: The Stationary Heat Equation. The Heat Equation. The Initial-Boundary Value Problem. The separation of variables method. An example of separation of variables.
Solving the Heat Equation Sect. 1.5. Review: The Stationary Heat Equation. The Heat Equation. The Initial-Boundary Value Problem. The separation of variables method. An example of separation of variables.
Some Measures for Asymmetry of Distributions
 Some Measures for Asymmetry of Distributions Georgi N. Boshnakov First version: 31 January 2006 Research Report No. 5, 2006, Probabiity and Statistics Group Schoo of Mathematics, The University of Manchester
Some Measures for Asymmetry of Distributions Georgi N. Boshnakov First version: 31 January 2006 Research Report No. 5, 2006, Probabiity and Statistics Group Schoo of Mathematics, The University of Manchester
MARKOV CHAINS AND MARKOV DECISION THEORY. Contents
 MARKOV CHAINS AND MARKOV DECISION THEORY ARINDRIMA DATTA Abstract. In this paper, we begin with a forma introduction to probabiity and expain the concept of random variabes and stochastic processes. After
MARKOV CHAINS AND MARKOV DECISION THEORY ARINDRIMA DATTA Abstract. In this paper, we begin with a forma introduction to probabiity and expain the concept of random variabes and stochastic processes. After
MAS 315 Waves 1 of 8 Answers to Examples Sheet 1. To solve the three problems, we use the methods of 1.3 (with necessary changes in notation).
 MAS 35 Waves of 8 Answers to Exampes Sheet. From.) and.5), the genera soution of φ xx = c φ yy is φ = fx cy) + gx + cy). Put c = : the genera soution of φ xx = φ yy is therefore φ = fx y) + gx + y) ) To
MAS 35 Waves of 8 Answers to Exampes Sheet. From.) and.5), the genera soution of φ xx = c φ yy is φ = fx cy) + gx + cy). Put c = : the genera soution of φ xx = φ yy is therefore φ = fx y) + gx + y) ) To
BASIC NOTIONS AND RESULTS IN TOPOLOGY. 1. Metric spaces. Sets with finite diameter are called bounded sets. For x X and r > 0 the set
 BASIC NOTIONS AND RESULTS IN TOPOLOGY 1. Metric spaces A metric on a set X is a map d : X X R + with the properties: d(x, y) 0 and d(x, y) = 0 x = y, d(x, y) = d(y, x), d(x, y) d(x, z) + d(z, y), for a
BASIC NOTIONS AND RESULTS IN TOPOLOGY 1. Metric spaces A metric on a set X is a map d : X X R + with the properties: d(x, y) 0 and d(x, y) = 0 x = y, d(x, y) = d(y, x), d(x, y) d(x, z) + d(z, y), for a
