OLSO. Online Learning and Stochastic Optimization. Yoram Singer August 10, Google Research
|
|
|
- Evangeline Carroll
- 5 years ago
- Views:
Transcription
1 OLSO Online Learning and Stochastic Optimization Yoram Singer August 10, 2016 Google Research
2 References Introduction to Online Convex Optimization, Elad Hazan, Princeton University Online Learning and Online Convex Optimization, Shai Shalev-Shwartz, Hebrew University 1
3 Why Convex in Non-Convex World? Building blocks for solving non-convex problem Better understanding of properties of convex & non-convex problems Algorithms for convex problems work well in non-convex settings 2
4 A Gentle Start
5 Using Experts Advice: The Consistent Algorithm We consult with n weather forecasters h 1,..., h n One of the forecasters is always correct in her forecasts On day t forecaster j predicts: h j (x t ) = temp(lima) 25 c [+1 or -1] We keep a list of forecasters who have been Consistent On day t + 1 we choose a forecaster from list for prediction By end of day t + 1 if y t+1 h i (x t ) remove i from list 3
6 The Consistent Algorithm V 1 = [n] = {1,..., n} For t = 1, 2,..., T,... : Pick i V t and predict ŷ t+1 = h i (x t ) If ŷ t+1 y t+1 then V t+1 V t {i} else V t+1 V t Analysis There is one perfect forecaster. In the worst case all erroneous forecasters will be selected once and then get discarded. Thus Consistent is going to make at most n 1 mistakes. 4
7 Using Experts Advice: Halving Algorithm We can suffer much smaller number of errors by forming a consensus. In the following we use y t, ŷ t { 1, +1}. V 1 = [n] = {1,..., n} For t = 1, 2,..., T,... : ( ) Set ŷ t = sign h i (x t ) (majority vote) i V t V t+1 V t {i : h i (x t ) y t } 5
8 The Halving Algorithm Claim Halving is going to make at most log 2 (n) mistakes. Proof Whenever Halving makes a prediction error on round t, at least half of the forecasters in V t are wrong. Therefore, on the next round V t+1 is at most half the size of V t. Rounds without a prediction mistake may or may not reduce the size of V t but we do not care. 6
9 Neat, but... What if a single consistent predictor does not exist? Claim Assume that the experts are deterministic and master which combines their predictions deterministically. The number of mistakes made by the best expert is at most T/2 while the master algorithm makes T mistakes. Proof Assume that there are 2 experts such that one always predicts +1 while the other always 1. The master algorithm makes a deterministic prediction ŷ t and then an adversary sets y t = ŷ t. Therefore, one of the experts makes at most T/2 mistakes while the master is always mistaken. 7
10 Notation Scalars: a, b, c,..., i, j, k Column vectors: x, w, u, Standard vector space R d with inner-product w, v = w v = w v = j w jv j Matrices: A, B, C,..., (except for T ) Eigen values of A: λ max (A) = def λ 1 (A) λ 2 (A)... λ d (A) = def λ min (A) Trace of A: Tr (A) = def i,i A i,i = i λ i(a) PSD: A 0 w : w A w 0 λ d (A) 0 Condition number of A: λ max (A)/λ min (A) 8
11 Conventions Input dimension: d Number of examples: m Step number / iteration index: t Number of iterations: T 9
12 Concepts in Convex Analysis
13 Convex Sets A set Ω R d is convex if for any vectors u, v Ω, the line segment from u to v is in Ω, α [0, 1] : αu + (1 α)v Ω non-convex convex 10
14 Convex Functions Let Ω be a convex set. A function f : Ω R is convex if for every u, v Ω and α [0, 1], f (αu + (1 α)v) αf (u) + (1 α)f (v) f (v) αf (u) + (1 α)f (v) f (u) f (αu + (1 α)v) u αu + (1 α)v v 11
15 Local Minimum Global Minimum (Proof) Let B(u, r) = {v : v u r} f (u) local minimum r > 0 s.t. v B(u, r) : f (v) f (u) For any v (not necessarily in B), α > 0 such that u + α(v u) B(u, r) and therefore f (u) f (u + α(v u)) Since f is convex f (u + α(v u)) = f (αv + (1 α)u) (1 α)f (u) + αf (v) Therefore, f (u) (1 α)f (u) + αf (v) f (u) f (v) Since it holds for all v, f (u) is also a global minimum of f. 12
16 Gradients or What Lies Beneath? Gradient of f at w: f (w) = ( f (w) w 1,..., ) f (w) w d f is convex & differentiable: u f (u) f (w) + f (w), u w f (w) f (u) f (w) + u w, f (w) w u 13
17 Subgradients v is sub-gradient of f at w if u, f (u) f (w) + v, u w Differential set, f (w), is the set of subgradients of f at w Lemma: f is convex iff for every w, f (w) f (w) f (u) f (w) + u w, v w u 14
18 Lipschitzness, Strong Convexity, & Smoothness Function f : Ω R is ρ-lipschitz if w 1, w 2 Ω, f (w 1 ) f (w 2 ) ρ w 1 w 2 15
19 Lipschitzness, Strong Convexity, & Smoothness Function f : Ω R is α-strongly-convex if f (w) f (u) + f (u) (w u) + α 2 w u 2 16
20 Lipschitzness, Strong Convexity, & Smoothness Function f : Ω R is β-smooth f (w) f (u) + f (u) (w u) + β 2 w u 2 which is equivalent to Lipschitz condition of the gradients f (w) f (v) β w v f is twice differentiable, strong-convexity & smoothness imply w : αi 2 f (w) βi f is γ-well-conditioned where γ = α β 1 (condition number) 17
21 Strong Convexity & Smoothness f (u) + f (u) (w u) + β 2 w u 2 f (w) f (u) + f (u) (w u) + α 2 w u 2 18
22 Projection Onto Convex Set Projection of u onto Ω: P Ω (u) arg min w u w Ω Theorem (Pythagoras, 500 BC) Let Ω R d be a convex set, u R d, & w = P Ω (u). Then for any v Ω we have u v w v. Unconstrained minimzation: f (w) = 0 w arg min u R n f (u) Theorem (Karush-Kuhn-Tucker) Let Ω R d be a convex set, w arg min w Ω f (w). If f is convex, then for any u Ω we have f (w ) (u w ) 0. 19
23 KKT Theorem - Illustration Ω u Constrained Optimum w* - f(w*) Unconstrained Optimum 20
24 Deterministic Gradient Descent
25 Gradient Descent Algorithm (Basic) Input: f, T, initial point w 1 Ω, step sizes {η t } Loop: For t = 1 to T Gradient Stepping: w t+1 w t η t f (w t ) Optional Projection: w t+1 P Ω (w t+1 ) 21
26 ( ) t 2 2α t 22 Convergence of GD Theorem Let f (w) be γ-well-conditioned (α s.c. & β smooth) and set η t = 1 β. Then, unconstrained gradient descent converges exponentially fast, f (w t ) f (w ) e γt Proof From strong convexity, f (y) f (x) + f (x) (y x) + α x y 2 { 2 min f (x) + f (x) (z x) + α } z 2 x z 2 = f (x) 1 f (x) 2 [Setting: 2α z = x 1/α f (x)] def def t = f (w t ), t = f (w t ) f (w ), x w t, y w :
27 Convergence of GD (cont.) t+1 t = f (w t+1 ) f (w t ) t (w t+1 w t ) + β 2 w t+1 w t 2 β-smoothness = η t t 2 + β 2 η2 t t 2 GD step = 1 2β t 2 α β t η t = 1 β From ( ) t+1 t (1 α/β) 1 (1 γ) t 1 e γt 23
28 What if f is not strongly-convex? Suppose that f (w) = log ( 1 + exp( w x) ) Prove that f is not strongly-convex when z = w x R Smooth f by adding a quadratic term f (w) = f (w) + α/2 w 2 Use GD (with or without domain constraint) as before Lemma Let w = arg min w f (w), then b s.t. w b 2f (0)/ α 24
29 Obtaining Strong-Convexity by Smothering Thm. Assume f is β-smooth and set α = β log(t) b 2 t. Then, ( ) β log(t) t = O t Proof outline (Complete Details) Properties: f is α + β smooth α stronly convex γ = α/( α + β) well conditioned Progress: t (f ) t ( f ) + αb 2 Recursion: as before Note O ( β t ) can be obtained via direct analysis 25
30 GD For General Convex Functions Rates of Convergence General 1 T α-strongly-convex 1 αt β-smooth β T γ-well-conditioned e γt 26
31 Convex Learning & Optimization
32 Convex Losses Convex loss function denoted l(w, z) : l : Z R + Restriction: w Ω R d Linear Regression Z = R d R, l(w, (x, y)) = ( w x y ) 2 Logistic Regression Z = R d { 1, +1}, l(w, (x, y)) = log ( 1 + exp( yw x) ) Hinge Loss (SVM) Z = R d { 1, +1}, l(w, (x, y)) = [ 1 yw x ] + where [z] + = max{z, 0} 27
33 Predicting Using Experts Advice Consistent & Halving combined the predictions of individual experts, Z = { 1, +1} d { 1, +1} Domain Ω of w is not convex, Ω = {0, 1} d Loss is 0 1 loss, l(w, (x, y)) = 1 [ sign(w x) y ] Finding w which minimizes 0 1 loss over a sequence of examples is NP-hard 28
34 Why do Consistent and Halving work? Paradigm Online Learning and Optimization Loss Relaxation Replace 0 1 with Hinge loss l hinge l y w, x Covexify Domain Ω = {0, 1} d [0, 1] d 29
35 Convex Learning Problem (Ω, Z, l) is termed convex-learning if Ω is convex and l(w, z) is convex in w Ω for all z Z Prove linear / logistic regression & SVM employ convex losses Example z i induces a convex function f i : Ω R + f i (w) = def l(w, z i ) Empirical Risk Minimization (aka Batch Learning ) min w Ω 1 m m i=1 1 l(w, z i ) = min w Ω m m f i (w) i=1 30
36 Regret
37 Online Learning or Online Convex Optimization Example arrive one at a time Initialization choose w 1 Ω On each round t: Loss: f t (w t ) Update: w t+1 T Ω (w t, f t ( )) Focus on updates T which are gradient-based 31
38 Regret Bound Model regret T = T t=1 f t (w t ) min w Ω T f t (w) t=1 Online learning w 1 w 2... w t... Compared to fixed w T = arg min w Ω t=1 f t(w) Does not make distribution assumptions on f t ( ) Pessimistic - w is minimizer in hindsight and holds for all T 32
39 Why OL & OCO? Simple to describe Simple to analyze Coupling between algorithm & analysis OCO Stochastic Optimization & Generalization 33
40 Online Gradient Descent
41 Online Gradient def Convention: t = f t (w t ) = f (w) w=wt Input: Domain Ω, step sizes {η t } Initialize: w 1 Ω For t = 1,..., T do:. Predict using w t. Suffer loss f t (w t ). Update w t+1 w t η t t. Project w t+1 P Ω (w t+1 ) t Output: w T = 1 T w s (SGM) s=1 34
42 GD vs. SG vs. SG with Averaging 35
43 Analysis of Online Gradient Descent Assumptions: f t ( ) are ρ-lipschitz, max w Ω w w r, t : η t = η Pythagoras to the rescue, w t+1 w 2 = P Ω (w t η t ) w 2 w t η t w 2 w t+1 w 2 w t w 2 + η 2 t 2 2η t (w t w ) 2 t (w t w ) w t w 2 w t+1 w 2 η + ηρ 2 Next we sum over t and telescope the summands... 36
44 Analysis of Online Gradient Descent (cont.) T t=1 t (w t w ) 1 ( w1 w 2 w T +1 w 2) T ηρ 2 + 2η }{{} 2 r 2 Choosing η = r/ρ T we get, T t (w t w ) rρ T From convexity, Regret bound, t=1 f t (w t ) f t (w ) t (w t w ) regret T = T (f t (w t ) f t (w )) rρ T t=1 37
45 Properties of Online Gradient Descent Infinite Horizon By setting η = r/ρ t obtain t 1 : regret t 3rρ T /2 If f t ( ) are α-strongly convex, the regret of SG with η t = 1 αt regret t ρ (1 + log(t)) 2α Lower Bound! Algorithms for online convex optimization incur Ω ( rρ T ) regret in worst case, even when f t ( ) are generated from an i.i.d distribution 38
46 Regret Vs. Convergence Regret Bound for α-strongly convex is O (log(t )/α) Convergence Rate for α-strongly convex is O (1/αT )) Next we discuss how Online Gradient Descent can be converted to Stochastic Gradient Method for empirical risk minimization yielding approximation error of O(log(T )/T ) Slower Convergence factor of log(t ) Two Sets of Parameters Much Faster Iterates w t & 1 t O(1) vs. m s t w s 39
47 Stochastic Gradient Method
48 Stochastic Gradient Method Define f (w) = 1 m i l(w, z i) i l(w, z i ) is a stochastic estimate of f (w) where i chosen with probability 1 m Linearity of expectation, E[ i ] = f and E[ i 2 ] ρ 2 Theorem E [f ( w T )] min f (w) + 3rρ w Ω 2 }{{ T } =regret T 40
49 Exercise Time Prove of disprove: Hinge & logistic losses are strong convex Find: strong convexity & Lipschitz constants for logistic loss when x b Derive: projection algorithm onto Ω = {w w r} Generate: synthetic data m = d = 1000 ( w, x i N 0, 1/ ) di w P K (w) for r = 1/2 d y i = sign((w ) x i ) y i y i w.p
50 Coding Time Implement: GD, OGD, and SGM for logistic regression Implement: projection onto Ω Run: all algorithms Check: convergence and regret bounds by comparing w T & w T to w (in term of losses) Repeat: for hinge loss (Pegasos) 42
Logarithmic Regret Algorithms for Strongly Convex Repeated Games
 Logarithmic Regret Algorithms for Strongly Convex Repeated Games Shai Shalev-Shwartz 1 and Yoram Singer 1,2 1 School of Computer Sci & Eng, The Hebrew University, Jerusalem 91904, Israel 2 Google Inc 1600
Logarithmic Regret Algorithms for Strongly Convex Repeated Games Shai Shalev-Shwartz 1 and Yoram Singer 1,2 1 School of Computer Sci & Eng, The Hebrew University, Jerusalem 91904, Israel 2 Google Inc 1600
Lecture 16: Perceptron and Exponential Weights Algorithm
 EECS 598-005: Theoretical Foundations of Machine Learning Fall 2015 Lecture 16: Perceptron and Exponential Weights Algorithm Lecturer: Jacob Abernethy Scribes: Yue Wang, Editors: Weiqing Yu and Andrew
EECS 598-005: Theoretical Foundations of Machine Learning Fall 2015 Lecture 16: Perceptron and Exponential Weights Algorithm Lecturer: Jacob Abernethy Scribes: Yue Wang, Editors: Weiqing Yu and Andrew
Full-information Online Learning
 Introduction Expert Advice OCO LM A DA NANJING UNIVERSITY Full-information Lijun Zhang Nanjing University, China June 2, 2017 Outline Introduction Expert Advice OCO 1 Introduction Definitions Regret 2
Introduction Expert Advice OCO LM A DA NANJING UNIVERSITY Full-information Lijun Zhang Nanjing University, China June 2, 2017 Outline Introduction Expert Advice OCO 1 Introduction Definitions Regret 2
Littlestone s Dimension and Online Learnability
 Littlestone s Dimension and Online Learnability Shai Shalev-Shwartz Toyota Technological Institute at Chicago The Hebrew University Talk at UCSD workshop, February, 2009 Joint work with Shai Ben-David
Littlestone s Dimension and Online Learnability Shai Shalev-Shwartz Toyota Technological Institute at Chicago The Hebrew University Talk at UCSD workshop, February, 2009 Joint work with Shai Ben-David
Tutorial: PART 1. Online Convex Optimization, A Game- Theoretic Approach to Learning.
 Tutorial: PART 1 Online Convex Optimization, A Game- Theoretic Approach to Learning http://www.cs.princeton.edu/~ehazan/tutorial/tutorial.htm Elad Hazan Princeton University Satyen Kale Yahoo Research
Tutorial: PART 1 Online Convex Optimization, A Game- Theoretic Approach to Learning http://www.cs.princeton.edu/~ehazan/tutorial/tutorial.htm Elad Hazan Princeton University Satyen Kale Yahoo Research
Online Convex Optimization
 Advanced Course in Machine Learning Spring 2010 Online Convex Optimization Handouts are jointly prepared by Shie Mannor and Shai Shalev-Shwartz A convex repeated game is a two players game that is performed
Advanced Course in Machine Learning Spring 2010 Online Convex Optimization Handouts are jointly prepared by Shie Mannor and Shai Shalev-Shwartz A convex repeated game is a two players game that is performed
Machine Learning. Support Vector Machines. Fabio Vandin November 20, 2017
 Machine Learning Support Vector Machines Fabio Vandin November 20, 2017 1 Classification and Margin Consider a classification problem with two classes: instance set X = R d label set Y = { 1, 1}. Training
Machine Learning Support Vector Machines Fabio Vandin November 20, 2017 1 Classification and Margin Consider a classification problem with two classes: instance set X = R d label set Y = { 1, 1}. Training
Online Convex Optimization. Gautam Goel, Milan Cvitkovic, and Ellen Feldman CS 159 4/5/2016
 Online Convex Optimization Gautam Goel, Milan Cvitkovic, and Ellen Feldman CS 159 4/5/2016 The General Setting The General Setting (Cover) Given only the above, learning isn't always possible Some Natural
Online Convex Optimization Gautam Goel, Milan Cvitkovic, and Ellen Feldman CS 159 4/5/2016 The General Setting The General Setting (Cover) Given only the above, learning isn't always possible Some Natural
Making Gradient Descent Optimal for Strongly Convex Stochastic Optimization
 Making Gradient Descent Optimal for Strongly Convex Stochastic Optimization Alexander Rakhlin University of Pennsylvania Ohad Shamir Microsoft Research New England Karthik Sridharan University of Pennsylvania
Making Gradient Descent Optimal for Strongly Convex Stochastic Optimization Alexander Rakhlin University of Pennsylvania Ohad Shamir Microsoft Research New England Karthik Sridharan University of Pennsylvania
Learnability, Stability, Regularization and Strong Convexity
 Learnability, Stability, Regularization and Strong Convexity Nati Srebro Shai Shalev-Shwartz HUJI Ohad Shamir Weizmann Karthik Sridharan Cornell Ambuj Tewari Michigan Toyota Technological Institute Chicago
Learnability, Stability, Regularization and Strong Convexity Nati Srebro Shai Shalev-Shwartz HUJI Ohad Shamir Weizmann Karthik Sridharan Cornell Ambuj Tewari Michigan Toyota Technological Institute Chicago
On the Generalization Ability of Online Strongly Convex Programming Algorithms
 On the Generalization Ability of Online Strongly Convex Programming Algorithms Sham M. Kakade I Chicago Chicago, IL 60637 sham@tti-c.org Ambuj ewari I Chicago Chicago, IL 60637 tewari@tti-c.org Abstract
On the Generalization Ability of Online Strongly Convex Programming Algorithms Sham M. Kakade I Chicago Chicago, IL 60637 sham@tti-c.org Ambuj ewari I Chicago Chicago, IL 60637 tewari@tti-c.org Abstract
Statistical Machine Learning II Spring 2017, Learning Theory, Lecture 4
 Statistical Machine Learning II Spring 07, Learning Theory, Lecture 4 Jean Honorio jhonorio@purdue.edu Deterministic Optimization For brevity, everywhere differentiable functions will be called smooth.
Statistical Machine Learning II Spring 07, Learning Theory, Lecture 4 Jean Honorio jhonorio@purdue.edu Deterministic Optimization For brevity, everywhere differentiable functions will be called smooth.
Large-scale Stochastic Optimization
 Large-scale Stochastic Optimization 11-741/641/441 (Spring 2016) Hanxiao Liu hanxiaol@cs.cmu.edu March 24, 2016 1 / 22 Outline 1. Gradient Descent (GD) 2. Stochastic Gradient Descent (SGD) Formulation
Large-scale Stochastic Optimization 11-741/641/441 (Spring 2016) Hanxiao Liu hanxiaol@cs.cmu.edu March 24, 2016 1 / 22 Outline 1. Gradient Descent (GD) 2. Stochastic Gradient Descent (SGD) Formulation
Big Data Analytics: Optimization and Randomization
 Big Data Analytics: Optimization and Randomization Tianbao Yang Tutorial@ACML 2015 Hong Kong Department of Computer Science, The University of Iowa, IA, USA Nov. 20, 2015 Yang Tutorial for ACML 15 Nov.
Big Data Analytics: Optimization and Randomization Tianbao Yang Tutorial@ACML 2015 Hong Kong Department of Computer Science, The University of Iowa, IA, USA Nov. 20, 2015 Yang Tutorial for ACML 15 Nov.
Optimistic Rates Nati Srebro
 Optimistic Rates Nati Srebro Based on work with Karthik Sridharan and Ambuj Tewari Examples based on work with Andy Cotter, Elad Hazan, Tomer Koren, Percy Liang, Shai Shalev-Shwartz, Ohad Shamir, Karthik
Optimistic Rates Nati Srebro Based on work with Karthik Sridharan and Ambuj Tewari Examples based on work with Andy Cotter, Elad Hazan, Tomer Koren, Percy Liang, Shai Shalev-Shwartz, Ohad Shamir, Karthik
Accelerating Stochastic Optimization
 Accelerating Stochastic Optimization Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem and Mobileye Master Class at Tel-Aviv, Tel-Aviv University, November 2014 Shalev-Shwartz
Accelerating Stochastic Optimization Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem and Mobileye Master Class at Tel-Aviv, Tel-Aviv University, November 2014 Shalev-Shwartz
Tutorial: PART 2. Optimization for Machine Learning. Elad Hazan Princeton University. + help from Sanjeev Arora & Yoram Singer
 Tutorial: PART 2 Optimization for Machine Learning Elad Hazan Princeton University + help from Sanjeev Arora & Yoram Singer Agenda 1. Learning as mathematical optimization Stochastic optimization, ERM,
Tutorial: PART 2 Optimization for Machine Learning Elad Hazan Princeton University + help from Sanjeev Arora & Yoram Singer Agenda 1. Learning as mathematical optimization Stochastic optimization, ERM,
Online Learning and Online Convex Optimization
 Online Learning and Online Convex Optimization Nicolò Cesa-Bianchi Università degli Studi di Milano N. Cesa-Bianchi (UNIMI) Online Learning 1 / 49 Summary 1 My beautiful regret 2 A supposedly fun game
Online Learning and Online Convex Optimization Nicolò Cesa-Bianchi Università degli Studi di Milano N. Cesa-Bianchi (UNIMI) Online Learning 1 / 49 Summary 1 My beautiful regret 2 A supposedly fun game
Online Learning with Experts & Multiplicative Weights Algorithms
 Online Learning with Experts & Multiplicative Weights Algorithms CS 159 lecture #2 Stephan Zheng April 1, 2016 Caltech Table of contents 1. Online Learning with Experts With a perfect expert Without perfect
Online Learning with Experts & Multiplicative Weights Algorithms CS 159 lecture #2 Stephan Zheng April 1, 2016 Caltech Table of contents 1. Online Learning with Experts With a perfect expert Without perfect
Tutorial: PART 2. Online Convex Optimization, A Game- Theoretic Approach to Learning
 Tutorial: PART 2 Online Convex Optimization, A Game- Theoretic Approach to Learning Elad Hazan Princeton University Satyen Kale Yahoo Research Exploiting curvature: logarithmic regret Logarithmic regret
Tutorial: PART 2 Online Convex Optimization, A Game- Theoretic Approach to Learning Elad Hazan Princeton University Satyen Kale Yahoo Research Exploiting curvature: logarithmic regret Logarithmic regret
Linear smoother. ŷ = S y. where s ij = s ij (x) e.g. s ij = diag(l i (x))
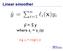 Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
Notes on AdaGrad. Joseph Perla 2014
 Notes on AdaGrad Joseph Perla 2014 1 Introduction Stochastic Gradient Descent (SGD) is a common online learning algorithm for optimizing convex (and often non-convex) functions in machine learning today.
Notes on AdaGrad Joseph Perla 2014 1 Introduction Stochastic Gradient Descent (SGD) is a common online learning algorithm for optimizing convex (and often non-convex) functions in machine learning today.
Computational and Statistical Learning Theory
 Computational and Statistical Learning Theory TTIC 31120 Prof. Nati Srebro Lecture 17: Stochastic Optimization Part II: Realizable vs Agnostic Rates Part III: Nearest Neighbor Classification Stochastic
Computational and Statistical Learning Theory TTIC 31120 Prof. Nati Srebro Lecture 17: Stochastic Optimization Part II: Realizable vs Agnostic Rates Part III: Nearest Neighbor Classification Stochastic
Warm up: risk prediction with logistic regression
 Warm up: risk prediction with logistic regression Boss gives you a bunch of data on loans defaulting or not: {(x i,y i )} n i= x i 2 R d, y i 2 {, } You model the data as: P (Y = y x, w) = + exp( yw T
Warm up: risk prediction with logistic regression Boss gives you a bunch of data on loans defaulting or not: {(x i,y i )} n i= x i 2 R d, y i 2 {, } You model the data as: P (Y = y x, w) = + exp( yw T
Online Passive-Aggressive Algorithms
 Online Passive-Aggressive Algorithms Koby Crammer Ofer Dekel Shai Shalev-Shwartz Yoram Singer School of Computer Science & Engineering The Hebrew University, Jerusalem 91904, Israel {kobics,oferd,shais,singer}@cs.huji.ac.il
Online Passive-Aggressive Algorithms Koby Crammer Ofer Dekel Shai Shalev-Shwartz Yoram Singer School of Computer Science & Engineering The Hebrew University, Jerusalem 91904, Israel {kobics,oferd,shais,singer}@cs.huji.ac.il
Adaptive Gradient Methods AdaGrad / Adam. Machine Learning for Big Data CSE547/STAT548, University of Washington Sham Kakade
 Adaptive Gradient Methods AdaGrad / Adam Machine Learning for Big Data CSE547/STAT548, University of Washington Sham Kakade 1 Announcements: HW3 posted Dual coordinate ascent (some review of SGD and random
Adaptive Gradient Methods AdaGrad / Adam Machine Learning for Big Data CSE547/STAT548, University of Washington Sham Kakade 1 Announcements: HW3 posted Dual coordinate ascent (some review of SGD and random
15-859E: Advanced Algorithms CMU, Spring 2015 Lecture #16: Gradient Descent February 18, 2015
 5-859E: Advanced Algorithms CMU, Spring 205 Lecture #6: Gradient Descent February 8, 205 Lecturer: Anupam Gupta Scribe: Guru Guruganesh In this lecture, we will study the gradient descent algorithm and
5-859E: Advanced Algorithms CMU, Spring 205 Lecture #6: Gradient Descent February 8, 205 Lecturer: Anupam Gupta Scribe: Guru Guruganesh In this lecture, we will study the gradient descent algorithm and
Course Notes for EE227C (Spring 2018): Convex Optimization and Approximation
 Course Notes for EE7C (Spring 08): Convex Optimization and Approximation Instructor: Moritz Hardt Email: hardt+ee7c@berkeley.edu Graduate Instructor: Max Simchowitz Email: msimchow+ee7c@berkeley.edu October
Course Notes for EE7C (Spring 08): Convex Optimization and Approximation Instructor: Moritz Hardt Email: hardt+ee7c@berkeley.edu Graduate Instructor: Max Simchowitz Email: msimchow+ee7c@berkeley.edu October
ECS171: Machine Learning
 ECS171: Machine Learning Lecture 4: Optimization (LFD 3.3, SGD) Cho-Jui Hsieh UC Davis Jan 22, 2018 Gradient descent Optimization Goal: find the minimizer of a function min f (w) w For now we assume f
ECS171: Machine Learning Lecture 4: Optimization (LFD 3.3, SGD) Cho-Jui Hsieh UC Davis Jan 22, 2018 Gradient descent Optimization Goal: find the minimizer of a function min f (w) w For now we assume f
Adaptive Online Gradient Descent
 University of Pennsylvania ScholarlyCommons Statistics Papers Wharton Faculty Research 6-4-2007 Adaptive Online Gradient Descent Peter Bartlett Elad Hazan Alexander Rakhlin University of Pennsylvania Follow
University of Pennsylvania ScholarlyCommons Statistics Papers Wharton Faculty Research 6-4-2007 Adaptive Online Gradient Descent Peter Bartlett Elad Hazan Alexander Rakhlin University of Pennsylvania Follow
On the tradeoff between computational complexity and sample complexity in learning
 On the tradeoff between computational complexity and sample complexity in learning Shai Shalev-Shwartz School of Computer Science and Engineering The Hebrew University of Jerusalem Joint work with Sham
On the tradeoff between computational complexity and sample complexity in learning Shai Shalev-Shwartz School of Computer Science and Engineering The Hebrew University of Jerusalem Joint work with Sham
Learning Methods for Online Prediction Problems. Peter Bartlett Statistics and EECS UC Berkeley
 Learning Methods for Online Prediction Problems Peter Bartlett Statistics and EECS UC Berkeley Course Synopsis A finite comparison class: A = {1,..., m}. 1. Prediction with expert advice. 2. With perfect
Learning Methods for Online Prediction Problems Peter Bartlett Statistics and EECS UC Berkeley Course Synopsis A finite comparison class: A = {1,..., m}. 1. Prediction with expert advice. 2. With perfect
Support vector machines Lecture 4
 Support vector machines Lecture 4 David Sontag New York University Slides adapted from Luke Zettlemoyer, Vibhav Gogate, and Carlos Guestrin Q: What does the Perceptron mistake bound tell us? Theorem: The
Support vector machines Lecture 4 David Sontag New York University Slides adapted from Luke Zettlemoyer, Vibhav Gogate, and Carlos Guestrin Q: What does the Perceptron mistake bound tell us? Theorem: The
Ad Placement Strategies
 Case Study : Estimating Click Probabilities Intro Logistic Regression Gradient Descent + SGD AdaGrad Machine Learning for Big Data CSE547/STAT548, University of Washington Emily Fox January 7 th, 04 Ad
Case Study : Estimating Click Probabilities Intro Logistic Regression Gradient Descent + SGD AdaGrad Machine Learning for Big Data CSE547/STAT548, University of Washington Emily Fox January 7 th, 04 Ad
Online Learning. Jordan Boyd-Graber. University of Colorado Boulder LECTURE 21. Slides adapted from Mohri
 Online Learning Jordan Boyd-Graber University of Colorado Boulder LECTURE 21 Slides adapted from Mohri Jordan Boyd-Graber Boulder Online Learning 1 of 31 Motivation PAC learning: distribution fixed over
Online Learning Jordan Boyd-Graber University of Colorado Boulder LECTURE 21 Slides adapted from Mohri Jordan Boyd-Graber Boulder Online Learning 1 of 31 Motivation PAC learning: distribution fixed over
No-Regret Algorithms for Unconstrained Online Convex Optimization
 No-Regret Algorithms for Unconstrained Online Convex Optimization Matthew Streeter Duolingo, Inc. Pittsburgh, PA 153 matt@duolingo.com H. Brendan McMahan Google, Inc. Seattle, WA 98103 mcmahan@google.com
No-Regret Algorithms for Unconstrained Online Convex Optimization Matthew Streeter Duolingo, Inc. Pittsburgh, PA 153 matt@duolingo.com H. Brendan McMahan Google, Inc. Seattle, WA 98103 mcmahan@google.com
Online Passive-Aggressive Algorithms
 Online Passive-Aggressive Algorithms Koby Crammer Ofer Dekel Shai Shalev-Shwartz Yoram Singer School of Computer Science & Engineering The Hebrew University, Jerusalem 91904, Israel {kobics,oferd,shais,singer}@cs.huji.ac.il
Online Passive-Aggressive Algorithms Koby Crammer Ofer Dekel Shai Shalev-Shwartz Yoram Singer School of Computer Science & Engineering The Hebrew University, Jerusalem 91904, Israel {kobics,oferd,shais,singer}@cs.huji.ac.il
Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers)
 Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers) Solution only depends on a small subset of training
Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers) Solution only depends on a small subset of training
Machine Learning for NLP
 Machine Learning for NLP Linear Models Joakim Nivre Uppsala University Department of Linguistics and Philology Slides adapted from Ryan McDonald, Google Research Machine Learning for NLP 1(26) Outline
Machine Learning for NLP Linear Models Joakim Nivre Uppsala University Department of Linguistics and Philology Slides adapted from Ryan McDonald, Google Research Machine Learning for NLP 1(26) Outline
Trade-Offs in Distributed Learning and Optimization
 Trade-Offs in Distributed Learning and Optimization Ohad Shamir Weizmann Institute of Science Includes joint works with Yossi Arjevani, Nathan Srebro and Tong Zhang IHES Workshop March 2016 Distributed
Trade-Offs in Distributed Learning and Optimization Ohad Shamir Weizmann Institute of Science Includes joint works with Yossi Arjevani, Nathan Srebro and Tong Zhang IHES Workshop March 2016 Distributed
Support Vector Machine
 Andrea Passerini passerini@disi.unitn.it Machine Learning Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers)
Andrea Passerini passerini@disi.unitn.it Machine Learning Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers)
Towards stability and optimality in stochastic gradient descent
 Towards stability and optimality in stochastic gradient descent Panos Toulis, Dustin Tran and Edoardo M. Airoldi August 26, 2016 Discussion by Ikenna Odinaka Duke University Outline Introduction 1 Introduction
Towards stability and optimality in stochastic gradient descent Panos Toulis, Dustin Tran and Edoardo M. Airoldi August 26, 2016 Discussion by Ikenna Odinaka Duke University Outline Introduction 1 Introduction
Distributed online optimization over jointly connected digraphs
 Distributed online optimization over jointly connected digraphs David Mateos-Núñez Jorge Cortés University of California, San Diego {dmateosn,cortes}@ucsd.edu Southern California Optimization Day UC San
Distributed online optimization over jointly connected digraphs David Mateos-Núñez Jorge Cortés University of California, San Diego {dmateosn,cortes}@ucsd.edu Southern California Optimization Day UC San
Classification Logistic Regression
 Announcements: Classification Logistic Regression Machine Learning CSE546 Sham Kakade University of Washington HW due on Friday. Today: Review: sub-gradients,lasso Logistic Regression October 3, 26 Sham
Announcements: Classification Logistic Regression Machine Learning CSE546 Sham Kakade University of Washington HW due on Friday. Today: Review: sub-gradients,lasso Logistic Regression October 3, 26 Sham
Linear & nonlinear classifiers
 Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1394 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1394 1 / 34 Table
Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1394 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1394 1 / 34 Table
Stochastic Optimization Algorithms Beyond SG
 Stochastic Optimization Algorithms Beyond SG Frank E. Curtis 1, Lehigh University involving joint work with Léon Bottou, Facebook AI Research Jorge Nocedal, Northwestern University Optimization Methods
Stochastic Optimization Algorithms Beyond SG Frank E. Curtis 1, Lehigh University involving joint work with Léon Bottou, Facebook AI Research Jorge Nocedal, Northwestern University Optimization Methods
Contents. 1 Introduction. 1.1 History of Optimization ALG-ML SEMINAR LISSA: LINEAR TIME SECOND-ORDER STOCHASTIC ALGORITHM FEBRUARY 23, 2016
 ALG-ML SEMINAR LISSA: LINEAR TIME SECOND-ORDER STOCHASTIC ALGORITHM FEBRUARY 23, 2016 LECTURERS: NAMAN AGARWAL AND BRIAN BULLINS SCRIBE: KIRAN VODRAHALLI Contents 1 Introduction 1 1.1 History of Optimization.....................................
ALG-ML SEMINAR LISSA: LINEAR TIME SECOND-ORDER STOCHASTIC ALGORITHM FEBRUARY 23, 2016 LECTURERS: NAMAN AGARWAL AND BRIAN BULLINS SCRIBE: KIRAN VODRAHALLI Contents 1 Introduction 1 1.1 History of Optimization.....................................
1 Overview. 2 Learning from Experts. 2.1 Defining a meaningful benchmark. AM 221: Advanced Optimization Spring 2016
 AM 1: Advanced Optimization Spring 016 Prof. Yaron Singer Lecture 11 March 3rd 1 Overview In this lecture we will introduce the notion of online convex optimization. This is an extremely useful framework
AM 1: Advanced Optimization Spring 016 Prof. Yaron Singer Lecture 11 March 3rd 1 Overview In this lecture we will introduce the notion of online convex optimization. This is an extremely useful framework
Logistic Regression Logistic
 Case Study 1: Estimating Click Probabilities L2 Regularization for Logistic Regression Machine Learning/Statistics for Big Data CSE599C1/STAT592, University of Washington Carlos Guestrin January 10 th,
Case Study 1: Estimating Click Probabilities L2 Regularization for Logistic Regression Machine Learning/Statistics for Big Data CSE599C1/STAT592, University of Washington Carlos Guestrin January 10 th,
Optimal and Adaptive Online Learning
 Optimal and Adaptive Online Learning Haipeng Luo Advisor: Robert Schapire Computer Science Department Princeton University Examples of Online Learning (a) Spam detection 2 / 34 Examples of Online Learning
Optimal and Adaptive Online Learning Haipeng Luo Advisor: Robert Schapire Computer Science Department Princeton University Examples of Online Learning (a) Spam detection 2 / 34 Examples of Online Learning
Online Learning and Sequential Decision Making
 Online Learning and Sequential Decision Making Emilie Kaufmann CNRS & CRIStAL, Inria SequeL, emilie.kaufmann@univ-lille.fr Research School, ENS Lyon, Novembre 12-13th 2018 Emilie Kaufmann Online Learning
Online Learning and Sequential Decision Making Emilie Kaufmann CNRS & CRIStAL, Inria SequeL, emilie.kaufmann@univ-lille.fr Research School, ENS Lyon, Novembre 12-13th 2018 Emilie Kaufmann Online Learning
Convex Optimization Lecture 16
 Convex Optimization Lecture 16 Today: Projected Gradient Descent Conditional Gradient Descent Stochastic Gradient Descent Random Coordinate Descent Recall: Gradient Descent (Steepest Descent w.r.t Euclidean
Convex Optimization Lecture 16 Today: Projected Gradient Descent Conditional Gradient Descent Stochastic Gradient Descent Random Coordinate Descent Recall: Gradient Descent (Steepest Descent w.r.t Euclidean
Online Learning Summer School Copenhagen 2015 Lecture 1
 Online Learning Summer School Copenhagen 2015 Lecture 1 Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem Online Learning Shai Shalev-Shwartz (Hebrew U) OLSS Lecture
Online Learning Summer School Copenhagen 2015 Lecture 1 Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem Online Learning Shai Shalev-Shwartz (Hebrew U) OLSS Lecture
Lecture 5: Linear models for classification. Logistic regression. Gradient Descent. Second-order methods.
 Lecture 5: Linear models for classification. Logistic regression. Gradient Descent. Second-order methods. Linear models for classification Logistic regression Gradient descent and second-order methods
Lecture 5: Linear models for classification. Logistic regression. Gradient Descent. Second-order methods. Linear models for classification Logistic regression Gradient descent and second-order methods
Adaptive Gradient Methods AdaGrad / Adam
 Case Study 1: Estimating Click Probabilities Adaptive Gradient Methods AdaGrad / Adam Machine Learning for Big Data CSE547/STAT548, University of Washington Sham Kakade 1 The Problem with GD (and SGD)
Case Study 1: Estimating Click Probabilities Adaptive Gradient Methods AdaGrad / Adam Machine Learning for Big Data CSE547/STAT548, University of Washington Sham Kakade 1 The Problem with GD (and SGD)
Lecture 23: Online convex optimization Online convex optimization: generalization of several algorithms
 EECS 598-005: heoretical Foundations of Machine Learning Fall 2015 Lecture 23: Online convex optimization Lecturer: Jacob Abernethy Scribes: Vikas Dhiman Disclaimer: hese notes have not been subjected
EECS 598-005: heoretical Foundations of Machine Learning Fall 2015 Lecture 23: Online convex optimization Lecturer: Jacob Abernethy Scribes: Vikas Dhiman Disclaimer: hese notes have not been subjected
Introduction to Machine Learning (67577) Lecture 7
 Introduction to Machine Learning (67577) Lecture 7 Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem Solving Convex Problems using SGD and RLM Shai Shalev-Shwartz (Hebrew
Introduction to Machine Learning (67577) Lecture 7 Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem Solving Convex Problems using SGD and RLM Shai Shalev-Shwartz (Hebrew
Convergence rate of SGD
 Convergence rate of SGD heorem: (see Nemirovski et al 09 from readings) Let f be a strongly convex stochastic function Assume gradient of f is Lipschitz continuous and bounded hen, for step sizes: he expected
Convergence rate of SGD heorem: (see Nemirovski et al 09 from readings) Let f be a strongly convex stochastic function Assume gradient of f is Lipschitz continuous and bounded hen, for step sizes: he expected
Warm up. Regrade requests submitted directly in Gradescope, do not instructors.
 Warm up Regrade requests submitted directly in Gradescope, do not email instructors. 1 float in NumPy = 8 bytes 10 6 2 20 bytes = 1 MB 10 9 2 30 bytes = 1 GB For each block compute the memory required
Warm up Regrade requests submitted directly in Gradescope, do not email instructors. 1 float in NumPy = 8 bytes 10 6 2 20 bytes = 1 MB 10 9 2 30 bytes = 1 GB For each block compute the memory required
Online Manifold Regularization: A New Learning Setting and Empirical Study
 Online Manifold Regularization: A New Learning Setting and Empirical Study Andrew B. Goldberg 1, Ming Li 2, Xiaojin Zhu 1 1 Computer Sciences, University of Wisconsin Madison, USA. {goldberg,jerryzhu}@cs.wisc.edu
Online Manifold Regularization: A New Learning Setting and Empirical Study Andrew B. Goldberg 1, Ming Li 2, Xiaojin Zhu 1 1 Computer Sciences, University of Wisconsin Madison, USA. {goldberg,jerryzhu}@cs.wisc.edu
Stochastic and Adversarial Online Learning without Hyperparameters
 Stochastic and Adversarial Online Learning without Hyperparameters Ashok Cutkosky Department of Computer Science Stanford University ashokc@cs.stanford.edu Kwabena Boahen Department of Bioengineering Stanford
Stochastic and Adversarial Online Learning without Hyperparameters Ashok Cutkosky Department of Computer Science Stanford University ashokc@cs.stanford.edu Kwabena Boahen Department of Bioengineering Stanford
Stochastic Subgradient Method
 Stochastic Subgradient Method Lingjie Weng, Yutian Chen Bren School of Information and Computer Science UC Irvine Subgradient Recall basic inequality for convex differentiable f : f y f x + f x T (y x)
Stochastic Subgradient Method Lingjie Weng, Yutian Chen Bren School of Information and Computer Science UC Irvine Subgradient Recall basic inequality for convex differentiable f : f y f x + f x T (y x)
Exponentiated Gradient Descent
 CSE599s, Spring 01, Online Learning Lecture 10-04/6/01 Lecturer: Ofer Dekel Exponentiated Gradient Descent Scribe: Albert Yu 1 Introduction In this lecture we review norms, dual norms, strong convexity,
CSE599s, Spring 01, Online Learning Lecture 10-04/6/01 Lecturer: Ofer Dekel Exponentiated Gradient Descent Scribe: Albert Yu 1 Introduction In this lecture we review norms, dual norms, strong convexity,
Logistic Regression. Stochastic Gradient Descent
 Tutorial 8 CPSC 340 Logistic Regression Stochastic Gradient Descent Logistic Regression Model A discriminative probabilistic model for classification e.g. spam filtering Let x R d be input and y { 1, 1}
Tutorial 8 CPSC 340 Logistic Regression Stochastic Gradient Descent Logistic Regression Model A discriminative probabilistic model for classification e.g. spam filtering Let x R d be input and y { 1, 1}
Machine Learning. Support Vector Machines. Manfred Huber
 Machine Learning Support Vector Machines Manfred Huber 2015 1 Support Vector Machines Both logistic regression and linear discriminant analysis learn a linear discriminant function to separate the data
Machine Learning Support Vector Machines Manfred Huber 2015 1 Support Vector Machines Both logistic regression and linear discriminant analysis learn a linear discriminant function to separate the data
Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm. Lecturer: Sanjeev Arora
 princeton univ. F 13 cos 521: Advanced Algorithm Design Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm Lecturer: Sanjeev Arora Scribe: (Today s notes below are
princeton univ. F 13 cos 521: Advanced Algorithm Design Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm Lecturer: Sanjeev Arora Scribe: (Today s notes below are
Machine Learning in the Data Revolution Era
 Machine Learning in the Data Revolution Era Shai Shalev-Shwartz School of Computer Science and Engineering The Hebrew University of Jerusalem Machine Learning Seminar Series, Google & University of Waterloo,
Machine Learning in the Data Revolution Era Shai Shalev-Shwartz School of Computer Science and Engineering The Hebrew University of Jerusalem Machine Learning Seminar Series, Google & University of Waterloo,
Agnostic Online learnability
 Technical Report TTIC-TR-2008-2 October 2008 Agnostic Online learnability Shai Shalev-Shwartz Toyota Technological Institute Chicago shai@tti-c.org ABSTRACT We study a fundamental question. What classes
Technical Report TTIC-TR-2008-2 October 2008 Agnostic Online learnability Shai Shalev-Shwartz Toyota Technological Institute Chicago shai@tti-c.org ABSTRACT We study a fundamental question. What classes
Optimizing Nonconvex Finite Sums by a Proximal Primal-Dual Method
 Optimizing Nonconvex Finite Sums by a Proximal Primal-Dual Method Davood Hajinezhad Iowa State University Davood Hajinezhad Optimizing Nonconvex Finite Sums by a Proximal Primal-Dual Method 1 / 35 Co-Authors
Optimizing Nonconvex Finite Sums by a Proximal Primal-Dual Method Davood Hajinezhad Iowa State University Davood Hajinezhad Optimizing Nonconvex Finite Sums by a Proximal Primal-Dual Method 1 / 35 Co-Authors
Fast Stochastic Optimization Algorithms for ML
 Fast Stochastic Optimization Algorithms for ML Aaditya Ramdas April 20, 205 This lecture is about efficient algorithms for minimizing finite sums min w R d n i= f i (w) or min w R d n f i (w) + λ 2 w 2
Fast Stochastic Optimization Algorithms for ML Aaditya Ramdas April 20, 205 This lecture is about efficient algorithms for minimizing finite sums min w R d n i= f i (w) or min w R d n f i (w) + λ 2 w 2
Lecture 9: Large Margin Classifiers. Linear Support Vector Machines
 Lecture 9: Large Margin Classifiers. Linear Support Vector Machines Perceptrons Definition Perceptron learning rule Convergence Margin & max margin classifiers (Linear) support vector machines Formulation
Lecture 9: Large Margin Classifiers. Linear Support Vector Machines Perceptrons Definition Perceptron learning rule Convergence Margin & max margin classifiers (Linear) support vector machines Formulation
Foundations of Machine Learning On-Line Learning. Mehryar Mohri Courant Institute and Google Research
 Foundations of Machine Learning On-Line Learning Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu Motivation PAC learning: distribution fixed over time (training and test). IID assumption.
Foundations of Machine Learning On-Line Learning Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu Motivation PAC learning: distribution fixed over time (training and test). IID assumption.
Convex Repeated Games and Fenchel Duality
 Convex Repeated Games and Fenchel Duality Shai Shalev-Shwartz 1 and Yoram Singer 1,2 1 School of Computer Sci. & Eng., he Hebrew University, Jerusalem 91904, Israel 2 Google Inc. 1600 Amphitheater Parkway,
Convex Repeated Games and Fenchel Duality Shai Shalev-Shwartz 1 and Yoram Singer 1,2 1 School of Computer Sci. & Eng., he Hebrew University, Jerusalem 91904, Israel 2 Google Inc. 1600 Amphitheater Parkway,
Linear & nonlinear classifiers
 Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1396 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1396 1 / 44 Table
Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1396 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1396 1 / 44 Table
Mini-Batch Primal and Dual Methods for SVMs
 Mini-Batch Primal and Dual Methods for SVMs Peter Richtárik School of Mathematics The University of Edinburgh Coauthors: M. Takáč (Edinburgh), A. Bijral and N. Srebro (both TTI at Chicago) arxiv:1303.2314
Mini-Batch Primal and Dual Methods for SVMs Peter Richtárik School of Mathematics The University of Edinburgh Coauthors: M. Takáč (Edinburgh), A. Bijral and N. Srebro (both TTI at Chicago) arxiv:1303.2314
Simultaneous Model Selection and Optimization through Parameter-free Stochastic Learning
 Simultaneous Model Selection and Optimization through Parameter-free Stochastic Learning Francesco Orabona Yahoo! Labs New York, USA francesco@orabona.com Abstract Stochastic gradient descent algorithms
Simultaneous Model Selection and Optimization through Parameter-free Stochastic Learning Francesco Orabona Yahoo! Labs New York, USA francesco@orabona.com Abstract Stochastic gradient descent algorithms
0.1 Motivating example: weighted majority algorithm
 princeton univ. F 16 cos 521: Advanced Algorithm Design Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm Lecturer: Sanjeev Arora Scribe: Sanjeev Arora (Today s notes
princeton univ. F 16 cos 521: Advanced Algorithm Design Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm Lecturer: Sanjeev Arora Scribe: Sanjeev Arora (Today s notes
Empirical Risk Minimization Algorithms
 Empirical Risk Minimization Algorithms Tirgul 2 Part I November 2016 Reminder Domain set, X : the set of objects that we wish to label. Label set, Y : the set of possible labels. A prediction rule, h:
Empirical Risk Minimization Algorithms Tirgul 2 Part I November 2016 Reminder Domain set, X : the set of objects that we wish to label. Label set, Y : the set of possible labels. A prediction rule, h:
Adaptive Subgradient Methods for Online Learning and Stochastic Optimization John Duchi, Elad Hanzan, Yoram Singer
 Adaptive Subgradient Methods for Online Learning and Stochastic Optimization John Duchi, Elad Hanzan, Yoram Singer Vicente L. Malave February 23, 2011 Outline Notation minimize a number of functions φ
Adaptive Subgradient Methods for Online Learning and Stochastic Optimization John Duchi, Elad Hanzan, Yoram Singer Vicente L. Malave February 23, 2011 Outline Notation minimize a number of functions φ
Composite Objective Mirror Descent
 Composite Objective Mirror Descent John C. Duchi 1,3 Shai Shalev-Shwartz 2 Yoram Singer 3 Ambuj Tewari 4 1 University of California, Berkeley 2 Hebrew University of Jerusalem, Israel 3 Google Research
Composite Objective Mirror Descent John C. Duchi 1,3 Shai Shalev-Shwartz 2 Yoram Singer 3 Ambuj Tewari 4 1 University of California, Berkeley 2 Hebrew University of Jerusalem, Israel 3 Google Research
STA141C: Big Data & High Performance Statistical Computing
 STA141C: Big Data & High Performance Statistical Computing Lecture 8: Optimization Cho-Jui Hsieh UC Davis May 9, 2017 Optimization Numerical Optimization Numerical Optimization: min X f (X ) Can be applied
STA141C: Big Data & High Performance Statistical Computing Lecture 8: Optimization Cho-Jui Hsieh UC Davis May 9, 2017 Optimization Numerical Optimization Numerical Optimization: min X f (X ) Can be applied
Distributed online optimization over jointly connected digraphs
 Distributed online optimization over jointly connected digraphs David Mateos-Núñez Jorge Cortés University of California, San Diego {dmateosn,cortes}@ucsd.edu Mathematical Theory of Networks and Systems
Distributed online optimization over jointly connected digraphs David Mateos-Núñez Jorge Cortés University of California, San Diego {dmateosn,cortes}@ucsd.edu Mathematical Theory of Networks and Systems
The Online Approach to Machine Learning
 The Online Approach to Machine Learning Nicolò Cesa-Bianchi Università degli Studi di Milano N. Cesa-Bianchi (UNIMI) Online Approach to ML 1 / 53 Summary 1 My beautiful regret 2 A supposedly fun game I
The Online Approach to Machine Learning Nicolò Cesa-Bianchi Università degli Studi di Milano N. Cesa-Bianchi (UNIMI) Online Approach to ML 1 / 53 Summary 1 My beautiful regret 2 A supposedly fun game I
A survey: The convex optimization approach to regret minimization
 A survey: The convex optimization approach to regret minimization Elad Hazan September 10, 2009 WORKING DRAFT Abstract A well studied and general setting for prediction and decision making is regret minimization
A survey: The convex optimization approach to regret minimization Elad Hazan September 10, 2009 WORKING DRAFT Abstract A well studied and general setting for prediction and decision making is regret minimization
Machine Learning A Geometric Approach
 Machine Learning A Geometric Approach CIML book Chap 7.7 Linear Classification: Support Vector Machines (SVM) Professor Liang Huang some slides from Alex Smola (CMU) Linear Separator Ham Spam From Perceptron
Machine Learning A Geometric Approach CIML book Chap 7.7 Linear Classification: Support Vector Machines (SVM) Professor Liang Huang some slides from Alex Smola (CMU) Linear Separator Ham Spam From Perceptron
ECS289: Scalable Machine Learning
 ECS289: Scalable Machine Learning Cho-Jui Hsieh UC Davis Sept 29, 2016 Outline Convex vs Nonconvex Functions Coordinate Descent Gradient Descent Newton s method Stochastic Gradient Descent Numerical Optimization
ECS289: Scalable Machine Learning Cho-Jui Hsieh UC Davis Sept 29, 2016 Outline Convex vs Nonconvex Functions Coordinate Descent Gradient Descent Newton s method Stochastic Gradient Descent Numerical Optimization
Lecture 14 : Online Learning, Stochastic Gradient Descent, Perceptron
 CS446: Machine Learning, Fall 2017 Lecture 14 : Online Learning, Stochastic Gradient Descent, Perceptron Lecturer: Sanmi Koyejo Scribe: Ke Wang, Oct. 24th, 2017 Agenda Recap: SVM and Hinge loss, Representer
CS446: Machine Learning, Fall 2017 Lecture 14 : Online Learning, Stochastic Gradient Descent, Perceptron Lecturer: Sanmi Koyejo Scribe: Ke Wang, Oct. 24th, 2017 Agenda Recap: SVM and Hinge loss, Representer
A Second-order Bound with Excess Losses
 A Second-order Bound with Excess Losses Pierre Gaillard 12 Gilles Stoltz 2 Tim van Erven 3 1 EDF R&D, Clamart, France 2 GREGHEC: HEC Paris CNRS, Jouy-en-Josas, France 3 Leiden University, the Netherlands
A Second-order Bound with Excess Losses Pierre Gaillard 12 Gilles Stoltz 2 Tim van Erven 3 1 EDF R&D, Clamart, France 2 GREGHEC: HEC Paris CNRS, Jouy-en-Josas, France 3 Leiden University, the Netherlands
Adaptive Online Learning in Dynamic Environments
 Adaptive Online Learning in Dynamic Environments Lijun Zhang, Shiyin Lu, Zhi-Hua Zhou National Key Laboratory for Novel Software Technology Nanjing University, Nanjing 210023, China {zhanglj, lusy, zhouzh}@lamda.nju.edu.cn
Adaptive Online Learning in Dynamic Environments Lijun Zhang, Shiyin Lu, Zhi-Hua Zhou National Key Laboratory for Novel Software Technology Nanjing University, Nanjing 210023, China {zhanglj, lusy, zhouzh}@lamda.nju.edu.cn
Lecture 2 - Learning Binary & Multi-class Classifiers from Labelled Training Data
 Lecture 2 - Learning Binary & Multi-class Classifiers from Labelled Training Data DD2424 March 23, 2017 Binary classification problem given labelled training data Have labelled training examples? Given
Lecture 2 - Learning Binary & Multi-class Classifiers from Labelled Training Data DD2424 March 23, 2017 Binary classification problem given labelled training data Have labelled training examples? Given
The FTRL Algorithm with Strongly Convex Regularizers
 CSE599s, Spring 202, Online Learning Lecture 8-04/9/202 The FTRL Algorithm with Strongly Convex Regularizers Lecturer: Brandan McMahan Scribe: Tamara Bonaci Introduction In the last lecture, we talked
CSE599s, Spring 202, Online Learning Lecture 8-04/9/202 The FTRL Algorithm with Strongly Convex Regularizers Lecturer: Brandan McMahan Scribe: Tamara Bonaci Introduction In the last lecture, we talked
Convex Optimization Algorithms for Machine Learning in 10 Slides
 Convex Optimization Algorithms for Machine Learning in 10 Slides Presenter: Jul. 15. 2015 Outline 1 Quadratic Problem Linear System 2 Smooth Problem Newton-CG 3 Composite Problem Proximal-Newton-CD 4 Non-smooth,
Convex Optimization Algorithms for Machine Learning in 10 Slides Presenter: Jul. 15. 2015 Outline 1 Quadratic Problem Linear System 2 Smooth Problem Newton-CG 3 Composite Problem Proximal-Newton-CD 4 Non-smooth,
Empirical Risk Minimization
 Empirical Risk Minimization Fabrice Rossi SAMM Université Paris 1 Panthéon Sorbonne 2018 Outline Introduction PAC learning ERM in practice 2 General setting Data X the input space and Y the output space
Empirical Risk Minimization Fabrice Rossi SAMM Université Paris 1 Panthéon Sorbonne 2018 Outline Introduction PAC learning ERM in practice 2 General setting Data X the input space and Y the output space
An Evolving Gradient Resampling Method for Machine Learning. Jorge Nocedal
 An Evolving Gradient Resampling Method for Machine Learning Jorge Nocedal Northwestern University NIPS, Montreal 2015 1 Collaborators Figen Oztoprak Stefan Solntsev Richard Byrd 2 Outline 1. How to improve
An Evolving Gradient Resampling Method for Machine Learning Jorge Nocedal Northwestern University NIPS, Montreal 2015 1 Collaborators Figen Oztoprak Stefan Solntsev Richard Byrd 2 Outline 1. How to improve
Sub-Sampled Newton Methods
 Sub-Sampled Newton Methods F. Roosta-Khorasani and M. W. Mahoney ICSI and Dept of Statistics, UC Berkeley February 2016 F. Roosta-Khorasani and M. W. Mahoney (UCB) Sub-Sampled Newton Methods Feb 2016 1
Sub-Sampled Newton Methods F. Roosta-Khorasani and M. W. Mahoney ICSI and Dept of Statistics, UC Berkeley February 2016 F. Roosta-Khorasani and M. W. Mahoney (UCB) Sub-Sampled Newton Methods Feb 2016 1
1 Review of Winnow Algorithm
 COS 511: Theoretical Machine Learning Lecturer: Rob Schapire Lecture # 17 Scribe: Xingyuan Fang, Ethan April 9th, 2013 1 Review of Winnow Algorithm We have studied Winnow algorithm in Algorithm 1. Algorithm
COS 511: Theoretical Machine Learning Lecturer: Rob Schapire Lecture # 17 Scribe: Xingyuan Fang, Ethan April 9th, 2013 1 Review of Winnow Algorithm We have studied Winnow algorithm in Algorithm 1. Algorithm
arxiv: v4 [math.oc] 5 Jan 2016
![arxiv: v4 [math.oc] 5 Jan 2016 arxiv: v4 [math.oc] 5 Jan 2016](/thumbs/76/73387413.jpg) Restarted SGD: Beating SGD without Smoothness and/or Strong Convexity arxiv:151.03107v4 [math.oc] 5 Jan 016 Tianbao Yang, Qihang Lin Department of Computer Science Department of Management Sciences The
Restarted SGD: Beating SGD without Smoothness and/or Strong Convexity arxiv:151.03107v4 [math.oc] 5 Jan 016 Tianbao Yang, Qihang Lin Department of Computer Science Department of Management Sciences The
Bregman Divergence and Mirror Descent
 Bregman Divergence and Mirror Descent Bregman Divergence Motivation Generalize squared Euclidean distance to a class of distances that all share similar properties Lots of applications in machine learning,
Bregman Divergence and Mirror Descent Bregman Divergence Motivation Generalize squared Euclidean distance to a class of distances that all share similar properties Lots of applications in machine learning,
Stochastic gradient methods for machine learning
 Stochastic gradient methods for machine learning Francis Bach INRIA - Ecole Normale Supérieure, Paris, France Joint work with Eric Moulines, Nicolas Le Roux and Mark Schmidt - September 2012 Context Machine
Stochastic gradient methods for machine learning Francis Bach INRIA - Ecole Normale Supérieure, Paris, France Joint work with Eric Moulines, Nicolas Le Roux and Mark Schmidt - September 2012 Context Machine
Non-negative Matrix Factorization via accelerated Projected Gradient Descent
 Non-negative Matrix Factorization via accelerated Projected Gradient Descent Andersen Ang Mathématique et recherche opérationnelle UMONS, Belgium Email: manshun.ang@umons.ac.be Homepage: angms.science
Non-negative Matrix Factorization via accelerated Projected Gradient Descent Andersen Ang Mathématique et recherche opérationnelle UMONS, Belgium Email: manshun.ang@umons.ac.be Homepage: angms.science
