Machine Learning. Support Vector Machines. Fabio Vandin November 20, 2017
|
|
|
- Myron Anderson
- 5 years ago
- Views:
Transcription
1 Machine Learning Support Vector Machines Fabio Vandin November 20,
2 Classification and Margin Consider a classification problem with two classes: instance set X = R d label set Y = { 1, 1}. Training data: S = ((x 1, y 1 ),..., (x m, y m )) Hypothesis set H = halfspaces Assumption: data is linearly separable there exist a halfspace that perfectly classify the training set In general: multiple separating hyperplanes: which one is the best choice? 2
3 Classification and Margin The last one seems the best choice, since it can tolerate more noise. Informally, for a given separating halfspace we define its margin as its minimum distance to an example in the training set S. Intuition: best separating hyperplane is the one with largest margin. How do we find it? 3
4 Linearly Separable Training Set Training set S = ((x 1, y 1 ),..., (x m, y m )) is linearly separable if there exists a halfspace (w, b) such that y i = sign( w, x i + b) for all i = 1,..., m. Equivalent to: i = 1,..., m : y i ( w, x i + b) > 0 Informally: margin of a separating hyperplane is its minimum distance to an example in the training set S 4
5 Separating Hyperplane and Margin Given hyperplane defined by L = {v : w, v + b = 0}, and given x, the distance of x to L is d(x, L) = min{ x v : v L} Claim: if w = 1 then d(x, L) = w, x + b (Proof: Claim 15.1 [UML]) 5
6 Margin and Support Vectors The margin of a separating hyperplane is the distance of the closest example in training set to it. If w = 1 the margin is: min w, x i + b i {1,...,m} The closest examples are called support vectors 6
7 Support Vector Machine (SVM) Hard-SVM: seek for the separating hyperplane with largest margin (only for linearly separable data) Computational problem: arg max (w,b): w =1 subject to i : y i ( w, x i + b) > 0 min w, x i + b i {1,...,m} Equivalent formulation (due to separability assumption): arg max (w,b): w =1 min y i( w, x i + b) i {1,...,m} 7
8 Hard-SVM: Quadratic Programming Formulation input: (x 1, y 1 ),..., (x m, y m ) solve: (w 0, b 0 ) = arg min (w,b) w 2 subject to i : y i ( w, x i + b) 1 output: ŵ = w 0 w 0, ˆb = b 0 w 0 How do we get a solution? Quadratic optimization problem: objective is convex quadratic function, constraints are linear inequalities Quadratic Programming solvers! Proposition The output of algorithm above is a solution to the Equivalent Formulation in the previous slide. Proof: on the board and in the book (Lemma 15.2 [UML]) 8
9 Equivalent Formulation and Support Vectors Equivalent formulation (homogeneous halfspaces): assume first component of x X is 1, then w 0 = min w w 2 subject to i : y i w, x i 1 Support Vectors = vectors at minimum distance from w 0 The support vectors are the only ones that matter for defining w 0! Proposition Let w 0 be as above. Let I = {i : w 0, x = 1}. Then there exist coefficients α 1,..., α m such that w 0 = i I α i x i Support vectors = {x i : i I } Note: Solving Hard-SVM is equivalent to find α i for i = 1,..., m, and α i 0 only for support vectors 9
10 Soft-SVM 10 Hard-SVM works if data is linearly separable. What if data is not linearly separable? soft-svm Idea: modify constraints of Hard-SVM to allow for some violation, but take into account violations into objective function
11 Hard-SVM constraints: Soft-SVM Constraints y i ( w, x i + b) 1 Soft-SVM constraints: slack variables: ξ 1,..., ξ m 0 vector ξ for each i = 1,..., m: y i ( w, x i + b) 1 ξ i ξ i : how much constraint y i ( w, x i + b) 1 is violated Soft-SVM minimizes combinations of norm of w average of ξ i Tradeoff among two terms is controlled by a parameter λ R, λ > 0 11
12 Soft-SVM: Optimization Problem 12 input: (x 1, y 1 ),..., (x m, y m ), parameter λ > 0 solve: ( ) min λ w ξ i w,b,ξ m subject to i : y i ( w, x i + b) 1 ξ i and ξ i 0 output: w, b Equivalent formulation: consider the hinge loss l hinge ((w, b), (x, y)) = max{0, 1 y( w, x + b)} Given (w, b) and a training S, the empirical risk L hinge S ((w, b)) is L hinge S ((w, b)) = 1 l hinge ((w, b), (x i, y i )) m
13 Soft-SVM: solve Soft-SVM as RLM min w,b,ξ ( λ w m ) ξ i subject to i : y i ( w, x i + b) 1 ξ i and ξ i 0 Equivalent formulation with hinge loss: that is min w,b ( min w,b λ w m ( λ w 2 + L hinge S (w, b) ) ) l hinge ((w, b), (x i, y i )) Note: λ w 2 : l 2 regularization L hinge S (w, b): empirical risk for hinge loss 13
14 Soft-SVM: Solution 14 We need to solve: ( How? min w,b λ w m ) l hinge ((w, b), (x i, y i )) standard solvers for optimization problems Stochastic Gradient Descent
15 Gradient Descent 15 General approach for minimizing a differentiable convex function f (w) Let f : R d R be a differentiable function Definition The gradient f (w) of f at w = (w 1,..., w d ) is ( ) f (w) f (w) f (w) =,..., w 1 w d Intuition: the gradient points in the direction of the greatest rate of increase of f around w
16 Let η R, η > 0 be a parameter. Gradient Descent (GD) algorithm: w (0) 0; for t 0 to T 1 do w (t+1) w (t) η f (w (t) ); return w = 1 T T t=1 w(t) ; Notes: output vector could also be w (T ) or arg min t {1,...,T } f (w (t) ) returning w is useful for nondifferentiable functions (using subgradients instead of gradients...) and for stochastic gradient descent... Guarantees: Let f be convex and ρ-lipschitz continuos; let w arg min w: w B f (w). Then for every ɛ > 0, to find w such that f ( w) f (w ) ɛ it is sufficient to run the GD algorithm for T B 2 ρ 2 /ɛ 2 iterations. 16
17 Stochastic Gradient Descent (SGD) 17 Idea: instead of using exactly the gradient, we take a (random) vector with expected value equal to the gradient direction. SGD algorithm: w (0) 0; for t 1 to T do choose v t at random from a distribution such that E[v t w (t) ] f (w (t) ); w (t+1) w (t) ηv t ; return w = 1 T T t=1 w(t) ;
18 Guarantees: Let f be convex and ρ-lipschitz continuos; let w arg min w: w B f (w). Then for every ɛ > 0, to find w such that E[f ( w)] f (w ) ɛ it is sufficient to run the SGD algorithm for T B 2 ρ 2 /ɛ 2 iterations. 18
19 19 Why should we use SGD instead of GD? Question: when do we use GD in the first place? Answer: for example to find w that minimizes L S (w) That is f (w) = L S (w) f (w) depends on all pairs (x i, y i ) S, i = 1,..., m: may require long time to compute it! What about SGD? We need to pick v t such that E[v t w (t) ] f (w (t) ): how? Pick a random (x i, y i ) pick v t l(w (t), (x i, y i )): satisfies the requirement! requires much less computation than GD Analogously we can use SGD for regularized losses, etc.
20 We want to solve min w SGD for Solving Soft-SVM ( λ 2 w m ) max{0, 1 y w, x i } Note: it s standard to add a 1 2 some computations. in the regularization to simplify Algorithm: θ (1) 0 ; for t 1 to T do let w (t) 1 λt θ(t) ; choose i uniformly at random from {1,..., m}; if y i w (t), x i < 1 then θ (t+1) θ (t) + y i x i ; else θ (t+1) θ (t) ; return w = 1 T T t=1 w(t) ; 20
21 Duality We now present (Hard-)SVM in a different way which is very useful for kernels We want to solve w 0 = min w 1 2 w 2 subject to i : y i w, x i 1 Define Note that g(w) = g(w) = max α R m :α 0 α i (1 y i w, x i ) { 0 if i : y i w, x i 1 + otherwise Then the problem above can be rewritten as: ( ) 1 min w 2 w 2 + g(w) 21
22 ( ) 1 min w 2 w 2 + g(w) Rerranging a bit the terms we obtain the equivalent problem: ( ) 1 min max w α R m :α 0 2 w 2 + α i (1 y i w, x i ) One can prove that min w max α R m :α 0 ( 1 2 w 2 + ( = max min 1 α R m :α 0 w 2 w 2 + ) α i (1 y i w, x i ) ) α i (1 y i w, x i ) Note: the result above is called strong duality 22
23 23 We therefore define the dual problem ( ) max min 1 α R m :α 0 w 2 w 2 + α i (1 y i w, x i ) Note: once α is fixed the optimization with respect to w is unconstrained the objective is differentiable at the optimum the gradient is equal to 0: w α i y i x i = 0 w = α i y i x i Replacing in the dual problem we get: max 1 2 m α α R m :α 0 2 i y i x i + α i 1 y i α j y j x j, x i j=1
24 24 max α R m :α α 2 i y i x i + α i m 1 y i α j y j x j, x i j=1 rearranging we get the problem: max α i 1 α R m :α 0 2 α i α j y i y j x j, x i j=1 Note: solution is the vector α which defines the support vectors {x i : α i 0} dual problem requires only to compute inner products x j, x i, does not need to consider x i by itself
CSC 411 Lecture 17: Support Vector Machine
 CSC 411 Lecture 17: Support Vector Machine Ethan Fetaya, James Lucas and Emad Andrews University of Toronto CSC411 Lec17 1 / 1 Today Max-margin classification SVM Hard SVM Duality Soft SVM CSC411 Lec17
CSC 411 Lecture 17: Support Vector Machine Ethan Fetaya, James Lucas and Emad Andrews University of Toronto CSC411 Lec17 1 / 1 Today Max-margin classification SVM Hard SVM Duality Soft SVM CSC411 Lec17
Support Vector Machines for Classification and Regression. 1 Linearly Separable Data: Hard Margin SVMs
 E0 270 Machine Learning Lecture 5 (Jan 22, 203) Support Vector Machines for Classification and Regression Lecturer: Shivani Agarwal Disclaimer: These notes are a brief summary of the topics covered in
E0 270 Machine Learning Lecture 5 (Jan 22, 203) Support Vector Machines for Classification and Regression Lecturer: Shivani Agarwal Disclaimer: These notes are a brief summary of the topics covered in
Kernelized Perceptron Support Vector Machines
 Kernelized Perceptron Support Vector Machines Emily Fox University of Washington February 13, 2017 What is the perceptron optimizing? 1 The perceptron algorithm [Rosenblatt 58, 62] Classification setting:
Kernelized Perceptron Support Vector Machines Emily Fox University of Washington February 13, 2017 What is the perceptron optimizing? 1 The perceptron algorithm [Rosenblatt 58, 62] Classification setting:
Support Vector Machines for Classification and Regression
 CIS 520: Machine Learning Oct 04, 207 Support Vector Machines for Classification and Regression Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may
CIS 520: Machine Learning Oct 04, 207 Support Vector Machines for Classification and Regression Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may
Lecture 14 : Online Learning, Stochastic Gradient Descent, Perceptron
 CS446: Machine Learning, Fall 2017 Lecture 14 : Online Learning, Stochastic Gradient Descent, Perceptron Lecturer: Sanmi Koyejo Scribe: Ke Wang, Oct. 24th, 2017 Agenda Recap: SVM and Hinge loss, Representer
CS446: Machine Learning, Fall 2017 Lecture 14 : Online Learning, Stochastic Gradient Descent, Perceptron Lecturer: Sanmi Koyejo Scribe: Ke Wang, Oct. 24th, 2017 Agenda Recap: SVM and Hinge loss, Representer
Topics we covered. Machine Learning. Statistics. Optimization. Systems! Basics of probability Tail bounds Density Estimation Exponential Families
 Midterm Review Topics we covered Machine Learning Optimization Basics of optimization Convexity Unconstrained: GD, SGD Constrained: Lagrange, KKT Duality Linear Methods Perceptrons Support Vector Machines
Midterm Review Topics we covered Machine Learning Optimization Basics of optimization Convexity Unconstrained: GD, SGD Constrained: Lagrange, KKT Duality Linear Methods Perceptrons Support Vector Machines
Machine Learning Basics Lecture 4: SVM I. Princeton University COS 495 Instructor: Yingyu Liang
 Machine Learning Basics Lecture 4: SVM I Princeton University COS 495 Instructor: Yingyu Liang Review: machine learning basics Math formulation Given training data x i, y i : 1 i n i.i.d. from distribution
Machine Learning Basics Lecture 4: SVM I Princeton University COS 495 Instructor: Yingyu Liang Review: machine learning basics Math formulation Given training data x i, y i : 1 i n i.i.d. from distribution
Support vector machines Lecture 4
 Support vector machines Lecture 4 David Sontag New York University Slides adapted from Luke Zettlemoyer, Vibhav Gogate, and Carlos Guestrin Q: What does the Perceptron mistake bound tell us? Theorem: The
Support vector machines Lecture 4 David Sontag New York University Slides adapted from Luke Zettlemoyer, Vibhav Gogate, and Carlos Guestrin Q: What does the Perceptron mistake bound tell us? Theorem: The
Machine Learning And Applications: Supervised Learning-SVM
 Machine Learning And Applications: Supervised Learning-SVM Raphaël Bournhonesque École Normale Supérieure de Lyon, Lyon, France raphael.bournhonesque@ens-lyon.fr 1 Supervised vs unsupervised learning Machine
Machine Learning And Applications: Supervised Learning-SVM Raphaël Bournhonesque École Normale Supérieure de Lyon, Lyon, France raphael.bournhonesque@ens-lyon.fr 1 Supervised vs unsupervised learning Machine
Lecture Support Vector Machine (SVM) Classifiers
 Introduction to Machine Learning Lecturer: Amir Globerson Lecture 6 Fall Semester Scribe: Yishay Mansour 6.1 Support Vector Machine (SVM) Classifiers Classification is one of the most important tasks in
Introduction to Machine Learning Lecturer: Amir Globerson Lecture 6 Fall Semester Scribe: Yishay Mansour 6.1 Support Vector Machine (SVM) Classifiers Classification is one of the most important tasks in
Machine Learning. Support Vector Machines. Manfred Huber
 Machine Learning Support Vector Machines Manfred Huber 2015 1 Support Vector Machines Both logistic regression and linear discriminant analysis learn a linear discriminant function to separate the data
Machine Learning Support Vector Machines Manfred Huber 2015 1 Support Vector Machines Both logistic regression and linear discriminant analysis learn a linear discriminant function to separate the data
Outline. Basic concepts: SVM and kernels SVM primal/dual problems. Chih-Jen Lin (National Taiwan Univ.) 1 / 22
 Outline Basic concepts: SVM and kernels SVM primal/dual problems Chih-Jen Lin (National Taiwan Univ.) 1 / 22 Outline Basic concepts: SVM and kernels Basic concepts: SVM and kernels SVM primal/dual problems
Outline Basic concepts: SVM and kernels SVM primal/dual problems Chih-Jen Lin (National Taiwan Univ.) 1 / 22 Outline Basic concepts: SVM and kernels Basic concepts: SVM and kernels SVM primal/dual problems
Support Vector Machines, Kernel SVM
 Support Vector Machines, Kernel SVM Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 27, 2017 1 / 40 Outline 1 Administration 2 Review of last lecture 3 SVM
Support Vector Machines, Kernel SVM Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 27, 2017 1 / 40 Outline 1 Administration 2 Review of last lecture 3 SVM
MLCC 2017 Regularization Networks I: Linear Models
 MLCC 2017 Regularization Networks I: Linear Models Lorenzo Rosasco UNIGE-MIT-IIT June 27, 2017 About this class We introduce a class of learning algorithms based on Tikhonov regularization We study computational
MLCC 2017 Regularization Networks I: Linear Models Lorenzo Rosasco UNIGE-MIT-IIT June 27, 2017 About this class We introduce a class of learning algorithms based on Tikhonov regularization We study computational
Machine Learning. Linear Models. Fabio Vandin October 10, 2017
 Machine Learning Linear Models Fabio Vandin October 10, 2017 1 Linear Predictors and Affine Functions Consider X = R d Affine functions: L d = {h w,b : w R d, b R} where ( d ) h w,b (x) = w, x + b = w
Machine Learning Linear Models Fabio Vandin October 10, 2017 1 Linear Predictors and Affine Functions Consider X = R d Affine functions: L d = {h w,b : w R d, b R} where ( d ) h w,b (x) = w, x + b = w
Announcements - Homework
 Announcements - Homework Homework 1 is graded, please collect at end of lecture Homework 2 due today Homework 3 out soon (watch email) Ques 1 midterm review HW1 score distribution 40 HW1 total score 35
Announcements - Homework Homework 1 is graded, please collect at end of lecture Homework 2 due today Homework 3 out soon (watch email) Ques 1 midterm review HW1 score distribution 40 HW1 total score 35
Machine Learning. Linear Models. Fabio Vandin October 10, 2017
 Machine Learning Linear Models Fabio Vandin October 10, 2017 1 Linear Predictors and Affine Functions Consider X = R d Affine functions: L d = {h w,b : w R d, b R} where ( d ) h w,b (x) = w, x + b = w
Machine Learning Linear Models Fabio Vandin October 10, 2017 1 Linear Predictors and Affine Functions Consider X = R d Affine functions: L d = {h w,b : w R d, b R} where ( d ) h w,b (x) = w, x + b = w
Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers)
 Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers) Solution only depends on a small subset of training
Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers) Solution only depends on a small subset of training
Support Vector Machine
 Andrea Passerini passerini@disi.unitn.it Machine Learning Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers)
Andrea Passerini passerini@disi.unitn.it Machine Learning Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers)
Support Vector Machines: Training with Stochastic Gradient Descent. Machine Learning Fall 2017
 Support Vector Machines: Training with Stochastic Gradient Descent Machine Learning Fall 2017 1 Support vector machines Training by maximizing margin The SVM objective Solving the SVM optimization problem
Support Vector Machines: Training with Stochastic Gradient Descent Machine Learning Fall 2017 1 Support vector machines Training by maximizing margin The SVM objective Solving the SVM optimization problem
Dan Roth 461C, 3401 Walnut
 CIS 519/419 Applied Machine Learning www.seas.upenn.edu/~cis519 Dan Roth danroth@seas.upenn.edu http://www.cis.upenn.edu/~danroth/ 461C, 3401 Walnut Slides were created by Dan Roth (for CIS519/419 at Penn
CIS 519/419 Applied Machine Learning www.seas.upenn.edu/~cis519 Dan Roth danroth@seas.upenn.edu http://www.cis.upenn.edu/~danroth/ 461C, 3401 Walnut Slides were created by Dan Roth (for CIS519/419 at Penn
Introduction to Machine Learning (67577) Lecture 7
 Introduction to Machine Learning (67577) Lecture 7 Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem Solving Convex Problems using SGD and RLM Shai Shalev-Shwartz (Hebrew
Introduction to Machine Learning (67577) Lecture 7 Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem Solving Convex Problems using SGD and RLM Shai Shalev-Shwartz (Hebrew
Machine Learning A Geometric Approach
 Machine Learning A Geometric Approach CIML book Chap 7.7 Linear Classification: Support Vector Machines (SVM) Professor Liang Huang some slides from Alex Smola (CMU) Linear Separator Ham Spam From Perceptron
Machine Learning A Geometric Approach CIML book Chap 7.7 Linear Classification: Support Vector Machines (SVM) Professor Liang Huang some slides from Alex Smola (CMU) Linear Separator Ham Spam From Perceptron
Mark your answers ON THE EXAM ITSELF. If you are not sure of your answer you may wish to provide a brief explanation.
 CS 189 Spring 2015 Introduction to Machine Learning Midterm You have 80 minutes for the exam. The exam is closed book, closed notes except your one-page crib sheet. No calculators or electronic items.
CS 189 Spring 2015 Introduction to Machine Learning Midterm You have 80 minutes for the exam. The exam is closed book, closed notes except your one-page crib sheet. No calculators or electronic items.
Binary Classification / Perceptron
 Binary Classification / Perceptron Nicholas Ruozzi University of Texas at Dallas Slides adapted from David Sontag and Vibhav Gogate Supervised Learning Input: x 1, y 1,, (x n, y n ) x i is the i th data
Binary Classification / Perceptron Nicholas Ruozzi University of Texas at Dallas Slides adapted from David Sontag and Vibhav Gogate Supervised Learning Input: x 1, y 1,, (x n, y n ) x i is the i th data
Stochastic Subgradient Method
 Stochastic Subgradient Method Lingjie Weng, Yutian Chen Bren School of Information and Computer Science UC Irvine Subgradient Recall basic inequality for convex differentiable f : f y f x + f x T (y x)
Stochastic Subgradient Method Lingjie Weng, Yutian Chen Bren School of Information and Computer Science UC Irvine Subgradient Recall basic inequality for convex differentiable f : f y f x + f x T (y x)
CS6375: Machine Learning Gautam Kunapuli. Support Vector Machines
 Gautam Kunapuli Example: Text Categorization Example: Develop a model to classify news stories into various categories based on their content. sports politics Use the bag-of-words representation for this
Gautam Kunapuli Example: Text Categorization Example: Develop a model to classify news stories into various categories based on their content. sports politics Use the bag-of-words representation for this
Support Vector Machine (SVM) & Kernel CE-717: Machine Learning Sharif University of Technology. M. Soleymani Fall 2012
 Support Vector Machine (SVM) & Kernel CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Linear classifier Which classifier? x 2 x 1 2 Linear classifier Margin concept x 2
Support Vector Machine (SVM) & Kernel CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Linear classifier Which classifier? x 2 x 1 2 Linear classifier Margin concept x 2
Support Vector Machines
 EE 17/7AT: Optimization Models in Engineering Section 11/1 - April 014 Support Vector Machines Lecturer: Arturo Fernandez Scribe: Arturo Fernandez 1 Support Vector Machines Revisited 1.1 Strictly) Separable
EE 17/7AT: Optimization Models in Engineering Section 11/1 - April 014 Support Vector Machines Lecturer: Arturo Fernandez Scribe: Arturo Fernandez 1 Support Vector Machines Revisited 1.1 Strictly) Separable
Machine Learning. Regularization and Feature Selection. Fabio Vandin November 14, 2017
 Machine Learning Regularization and Feature Selection Fabio Vandin November 14, 2017 1 Regularized Loss Minimization Assume h is defined by a vector w = (w 1,..., w d ) T R d (e.g., linear models) Regularization
Machine Learning Regularization and Feature Selection Fabio Vandin November 14, 2017 1 Regularized Loss Minimization Assume h is defined by a vector w = (w 1,..., w d ) T R d (e.g., linear models) Regularization
ICS-E4030 Kernel Methods in Machine Learning
 ICS-E4030 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 28. September, 2016 Juho Rousu 28. September, 2016 1 / 38 Convex optimization Convex optimisation This
ICS-E4030 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 28. September, 2016 Juho Rousu 28. September, 2016 1 / 38 Convex optimization Convex optimisation This
Cheng Soon Ong & Christian Walder. Canberra February June 2018
 Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 Outlines Overview Introduction Linear Algebra Probability Linear Regression
Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 Outlines Overview Introduction Linear Algebra Probability Linear Regression
10701 Recitation 5 Duality and SVM. Ahmed Hefny
 10701 Recitation 5 Duality and SVM Ahmed Hefny Outline Langrangian and Duality The Lagrangian Duality Eamples Support Vector Machines Primal Formulation Dual Formulation Soft Margin and Hinge Loss Lagrangian
10701 Recitation 5 Duality and SVM Ahmed Hefny Outline Langrangian and Duality The Lagrangian Duality Eamples Support Vector Machines Primal Formulation Dual Formulation Soft Margin and Hinge Loss Lagrangian
A short introduction to supervised learning, with applications to cancer pathway analysis Dr. Christina Leslie
 A short introduction to supervised learning, with applications to cancer pathway analysis Dr. Christina Leslie Computational Biology Program Memorial Sloan-Kettering Cancer Center http://cbio.mskcc.org/leslielab
A short introduction to supervised learning, with applications to cancer pathway analysis Dr. Christina Leslie Computational Biology Program Memorial Sloan-Kettering Cancer Center http://cbio.mskcc.org/leslielab
Machine Learning. Regularization and Feature Selection. Fabio Vandin November 13, 2017
 Machine Learning Regularization and Feature Selection Fabio Vandin November 13, 2017 1 Learning Model A: learning algorithm for a machine learning task S: m i.i.d. pairs z i = (x i, y i ), i = 1,..., m,
Machine Learning Regularization and Feature Selection Fabio Vandin November 13, 2017 1 Learning Model A: learning algorithm for a machine learning task S: m i.i.d. pairs z i = (x i, y i ), i = 1,..., m,
Warm up: risk prediction with logistic regression
 Warm up: risk prediction with logistic regression Boss gives you a bunch of data on loans defaulting or not: {(x i,y i )} n i= x i 2 R d, y i 2 {, } You model the data as: P (Y = y x, w) = + exp( yw T
Warm up: risk prediction with logistic regression Boss gives you a bunch of data on loans defaulting or not: {(x i,y i )} n i= x i 2 R d, y i 2 {, } You model the data as: P (Y = y x, w) = + exp( yw T
Support Vector Machines
 Wien, June, 2010 Paul Hofmarcher, Stefan Theussl, WU Wien Hofmarcher/Theussl SVM 1/21 Linear Separable Separating Hyperplanes Non-Linear Separable Soft-Margin Hyperplanes Hofmarcher/Theussl SVM 2/21 (SVM)
Wien, June, 2010 Paul Hofmarcher, Stefan Theussl, WU Wien Hofmarcher/Theussl SVM 1/21 Linear Separable Separating Hyperplanes Non-Linear Separable Soft-Margin Hyperplanes Hofmarcher/Theussl SVM 2/21 (SVM)
SVMs: Non-Separable Data, Convex Surrogate Loss, Multi-Class Classification, Kernels
 SVMs: Non-Separable Data, Convex Surrogate Loss, Multi-Class Classification, Kernels Karl Stratos June 21, 2018 1 / 33 Tangent: Some Loose Ends in Logistic Regression Polynomial feature expansion in logistic
SVMs: Non-Separable Data, Convex Surrogate Loss, Multi-Class Classification, Kernels Karl Stratos June 21, 2018 1 / 33 Tangent: Some Loose Ends in Logistic Regression Polynomial feature expansion in logistic
Discriminative Models
 No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
ECS171: Machine Learning
 ECS171: Machine Learning Lecture 4: Optimization (LFD 3.3, SGD) Cho-Jui Hsieh UC Davis Jan 22, 2018 Gradient descent Optimization Goal: find the minimizer of a function min f (w) w For now we assume f
ECS171: Machine Learning Lecture 4: Optimization (LFD 3.3, SGD) Cho-Jui Hsieh UC Davis Jan 22, 2018 Gradient descent Optimization Goal: find the minimizer of a function min f (w) w For now we assume f
Max Margin-Classifier
 Max Margin-Classifier Oliver Schulte - CMPT 726 Bishop PRML Ch. 7 Outline Maximum Margin Criterion Math Maximizing the Margin Non-Separable Data Kernels and Non-linear Mappings Where does the maximization
Max Margin-Classifier Oliver Schulte - CMPT 726 Bishop PRML Ch. 7 Outline Maximum Margin Criterion Math Maximizing the Margin Non-Separable Data Kernels and Non-linear Mappings Where does the maximization
Cutting Plane Training of Structural SVM
 Cutting Plane Training of Structural SVM Seth Neel University of Pennsylvania sethneel@wharton.upenn.edu September 28, 2017 Seth Neel (Penn) Short title September 28, 2017 1 / 33 Overview Structural SVMs
Cutting Plane Training of Structural SVM Seth Neel University of Pennsylvania sethneel@wharton.upenn.edu September 28, 2017 Seth Neel (Penn) Short title September 28, 2017 1 / 33 Overview Structural SVMs
Introduction to Support Vector Machines
 Introduction to Support Vector Machines Shivani Agarwal Support Vector Machines (SVMs) Algorithm for learning linear classifiers Motivated by idea of maximizing margin Efficient extension to non-linear
Introduction to Support Vector Machines Shivani Agarwal Support Vector Machines (SVMs) Algorithm for learning linear classifiers Motivated by idea of maximizing margin Efficient extension to non-linear
The Lagrangian L : R d R m R r R is an (easier to optimize) lower bound on the original problem:
 HT05: SC4 Statistical Data Mining and Machine Learning Dino Sejdinovic Department of Statistics Oxford Convex Optimization and slides based on Arthur Gretton s Advanced Topics in Machine Learning course
HT05: SC4 Statistical Data Mining and Machine Learning Dino Sejdinovic Department of Statistics Oxford Convex Optimization and slides based on Arthur Gretton s Advanced Topics in Machine Learning course
Support Vector Machine (SVM) and Kernel Methods
 Support Vector Machine (SVM) and Kernel Methods CE-717: Machine Learning Sharif University of Technology Fall 2014 Soleymani Outline Margin concept Hard-Margin SVM Soft-Margin SVM Dual Problems of Hard-Margin
Support Vector Machine (SVM) and Kernel Methods CE-717: Machine Learning Sharif University of Technology Fall 2014 Soleymani Outline Margin concept Hard-Margin SVM Soft-Margin SVM Dual Problems of Hard-Margin
Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers)
 Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers) Solution only depends on a small subset of training
Support vector machines In a nutshell Linear classifiers selecting hyperplane maximizing separation margin between classes (large margin classifiers) Solution only depends on a small subset of training
Support Vector Machines. Machine Learning Fall 2017
 Support Vector Machines Machine Learning Fall 2017 1 Where are we? Learning algorithms Decision Trees Perceptron AdaBoost 2 Where are we? Learning algorithms Decision Trees Perceptron AdaBoost Produce
Support Vector Machines Machine Learning Fall 2017 1 Where are we? Learning algorithms Decision Trees Perceptron AdaBoost 2 Where are we? Learning algorithms Decision Trees Perceptron AdaBoost Produce
Linear smoother. ŷ = S y. where s ij = s ij (x) e.g. s ij = diag(l i (x))
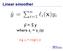 Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
CS-E4830 Kernel Methods in Machine Learning
 CS-E4830 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 27. September, 2017 Juho Rousu 27. September, 2017 1 / 45 Convex optimization Convex optimisation This
CS-E4830 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 27. September, 2017 Juho Rousu 27. September, 2017 1 / 45 Convex optimization Convex optimisation This
Machine Learning 4771
 Machine Learning 477 Instructor: Tony Jebara Topic 5 Generalization Guarantees VC-Dimension Nearest Neighbor Classification (infinite VC dimension) Structural Risk Minimization Support Vector Machines
Machine Learning 477 Instructor: Tony Jebara Topic 5 Generalization Guarantees VC-Dimension Nearest Neighbor Classification (infinite VC dimension) Structural Risk Minimization Support Vector Machines
Support Vector Machines
 Support Vector Machines Ryan M. Rifkin Google, Inc. 2008 Plan Regularization derivation of SVMs Geometric derivation of SVMs Optimality, Duality and Large Scale SVMs The Regularization Setting (Again)
Support Vector Machines Ryan M. Rifkin Google, Inc. 2008 Plan Regularization derivation of SVMs Geometric derivation of SVMs Optimality, Duality and Large Scale SVMs The Regularization Setting (Again)
Computational and Statistical Learning Theory
 Computational and Statistical Learning Theory TTIC 31120 Prof. Nati Srebro Lecture 17: Stochastic Optimization Part II: Realizable vs Agnostic Rates Part III: Nearest Neighbor Classification Stochastic
Computational and Statistical Learning Theory TTIC 31120 Prof. Nati Srebro Lecture 17: Stochastic Optimization Part II: Realizable vs Agnostic Rates Part III: Nearest Neighbor Classification Stochastic
CSE 417T: Introduction to Machine Learning. Lecture 11: Review. Henry Chai 10/02/18
 CSE 417T: Introduction to Machine Learning Lecture 11: Review Henry Chai 10/02/18 Unknown Target Function!: # % Training data Formal Setup & = ( ), + ),, ( -, + - Learning Algorithm 2 Hypothesis Set H
CSE 417T: Introduction to Machine Learning Lecture 11: Review Henry Chai 10/02/18 Unknown Target Function!: # % Training data Formal Setup & = ( ), + ),, ( -, + - Learning Algorithm 2 Hypothesis Set H
Jeff Howbert Introduction to Machine Learning Winter
 Classification / Regression Support Vector Machines Jeff Howbert Introduction to Machine Learning Winter 2012 1 Topics SVM classifiers for linearly separable classes SVM classifiers for non-linearly separable
Classification / Regression Support Vector Machines Jeff Howbert Introduction to Machine Learning Winter 2012 1 Topics SVM classifiers for linearly separable classes SVM classifiers for non-linearly separable
Optimization in the Big Data Regime 2: SVRG & Tradeoffs in Large Scale Learning. Sham M. Kakade
 Optimization in the Big Data Regime 2: SVRG & Tradeoffs in Large Scale Learning. Sham M. Kakade Machine Learning for Big Data CSE547/STAT548 University of Washington S. M. Kakade (UW) Optimization for
Optimization in the Big Data Regime 2: SVRG & Tradeoffs in Large Scale Learning. Sham M. Kakade Machine Learning for Big Data CSE547/STAT548 University of Washington S. M. Kakade (UW) Optimization for
Kernels. Machine Learning CSE446 Carlos Guestrin University of Washington. October 28, Carlos Guestrin
 Kernels Machine Learning CSE446 Carlos Guestrin University of Washington October 28, 2013 Carlos Guestrin 2005-2013 1 Linear Separability: More formally, Using Margin Data linearly separable, if there
Kernels Machine Learning CSE446 Carlos Guestrin University of Washington October 28, 2013 Carlos Guestrin 2005-2013 1 Linear Separability: More formally, Using Margin Data linearly separable, if there
Support Vector Machines: Maximum Margin Classifiers
 Support Vector Machines: Maximum Margin Classifiers Machine Learning and Pattern Recognition: September 16, 2008 Piotr Mirowski Based on slides by Sumit Chopra and Fu-Jie Huang 1 Outline What is behind
Support Vector Machines: Maximum Margin Classifiers Machine Learning and Pattern Recognition: September 16, 2008 Piotr Mirowski Based on slides by Sumit Chopra and Fu-Jie Huang 1 Outline What is behind
Stochastic Optimization with Variance Reduction for Infinite Datasets with Finite Sum Structure
 Stochastic Optimization with Variance Reduction for Infinite Datasets with Finite Sum Structure Alberto Bietti Julien Mairal Inria Grenoble (Thoth) March 21, 2017 Alberto Bietti Stochastic MISO March 21,
Stochastic Optimization with Variance Reduction for Infinite Datasets with Finite Sum Structure Alberto Bietti Julien Mairal Inria Grenoble (Thoth) March 21, 2017 Alberto Bietti Stochastic MISO March 21,
Support Vector Machines and Kernel Methods
 2018 CS420 Machine Learning, Lecture 3 Hangout from Prof. Andrew Ng. http://cs229.stanford.edu/notes/cs229-notes3.pdf Support Vector Machines and Kernel Methods Weinan Zhang Shanghai Jiao Tong University
2018 CS420 Machine Learning, Lecture 3 Hangout from Prof. Andrew Ng. http://cs229.stanford.edu/notes/cs229-notes3.pdf Support Vector Machines and Kernel Methods Weinan Zhang Shanghai Jiao Tong University
Discriminative Models
 No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
HOMEWORK 4: SVMS AND KERNELS
 HOMEWORK 4: SVMS AND KERNELS CMU 060: MACHINE LEARNING (FALL 206) OUT: Sep. 26, 206 DUE: 5:30 pm, Oct. 05, 206 TAs: Simon Shaolei Du, Tianshu Ren, Hsiao-Yu Fish Tung Instructions Homework Submission: Submit
HOMEWORK 4: SVMS AND KERNELS CMU 060: MACHINE LEARNING (FALL 206) OUT: Sep. 26, 206 DUE: 5:30 pm, Oct. 05, 206 TAs: Simon Shaolei Du, Tianshu Ren, Hsiao-Yu Fish Tung Instructions Homework Submission: Submit
Pattern Recognition 2018 Support Vector Machines
 Pattern Recognition 2018 Support Vector Machines Ad Feelders Universiteit Utrecht Ad Feelders ( Universiteit Utrecht ) Pattern Recognition 1 / 48 Support Vector Machines Ad Feelders ( Universiteit Utrecht
Pattern Recognition 2018 Support Vector Machines Ad Feelders Universiteit Utrecht Ad Feelders ( Universiteit Utrecht ) Pattern Recognition 1 / 48 Support Vector Machines Ad Feelders ( Universiteit Utrecht
Support Vector Machine for Classification and Regression
 Support Vector Machine for Classification and Regression Ahlame Douzal AMA-LIG, Université Joseph Fourier Master 2R - MOSIG (2013) November 25, 2013 Loss function, Separating Hyperplanes, Canonical Hyperplan
Support Vector Machine for Classification and Regression Ahlame Douzal AMA-LIG, Université Joseph Fourier Master 2R - MOSIG (2013) November 25, 2013 Loss function, Separating Hyperplanes, Canonical Hyperplan
Statistical Machine Learning from Data
 Samy Bengio Statistical Machine Learning from Data 1 Statistical Machine Learning from Data Support Vector Machines Samy Bengio IDIAP Research Institute, Martigny, Switzerland, and Ecole Polytechnique
Samy Bengio Statistical Machine Learning from Data 1 Statistical Machine Learning from Data Support Vector Machines Samy Bengio IDIAP Research Institute, Martigny, Switzerland, and Ecole Polytechnique
Lecture 9: Large Margin Classifiers. Linear Support Vector Machines
 Lecture 9: Large Margin Classifiers. Linear Support Vector Machines Perceptrons Definition Perceptron learning rule Convergence Margin & max margin classifiers (Linear) support vector machines Formulation
Lecture 9: Large Margin Classifiers. Linear Support Vector Machines Perceptrons Definition Perceptron learning rule Convergence Margin & max margin classifiers (Linear) support vector machines Formulation
Learning by constraints and SVMs (2)
 Statistical Techniques in Robotics (16-831, F12) Lecture#14 (Wednesday ctober 17) Learning by constraints and SVMs (2) Lecturer: Drew Bagnell Scribe: Albert Wu 1 1 Support Vector Ranking Machine pening
Statistical Techniques in Robotics (16-831, F12) Lecture#14 (Wednesday ctober 17) Learning by constraints and SVMs (2) Lecturer: Drew Bagnell Scribe: Albert Wu 1 1 Support Vector Ranking Machine pening
Convex Optimization and Support Vector Machine
 Convex Optimization and Support Vector Machine Problem 0. Consider a two-class classification problem. The training data is L n = {(x 1, t 1 ),..., (x n, t n )}, where each t i { 1, 1} and x i R p. We
Convex Optimization and Support Vector Machine Problem 0. Consider a two-class classification problem. The training data is L n = {(x 1, t 1 ),..., (x n, t n )}, where each t i { 1, 1} and x i R p. We
Big Data Analytics: Optimization and Randomization
 Big Data Analytics: Optimization and Randomization Tianbao Yang Tutorial@ACML 2015 Hong Kong Department of Computer Science, The University of Iowa, IA, USA Nov. 20, 2015 Yang Tutorial for ACML 15 Nov.
Big Data Analytics: Optimization and Randomization Tianbao Yang Tutorial@ACML 2015 Hong Kong Department of Computer Science, The University of Iowa, IA, USA Nov. 20, 2015 Yang Tutorial for ACML 15 Nov.
Lecture 2 - Learning Binary & Multi-class Classifiers from Labelled Training Data
 Lecture 2 - Learning Binary & Multi-class Classifiers from Labelled Training Data DD2424 March 23, 2017 Binary classification problem given labelled training data Have labelled training examples? Given
Lecture 2 - Learning Binary & Multi-class Classifiers from Labelled Training Data DD2424 March 23, 2017 Binary classification problem given labelled training data Have labelled training examples? Given
Lecture Notes on Support Vector Machine
 Lecture Notes on Support Vector Machine Feng Li fli@sdu.edu.cn Shandong University, China 1 Hyperplane and Margin In a n-dimensional space, a hyper plane is defined by ω T x + b = 0 (1) where ω R n is
Lecture Notes on Support Vector Machine Feng Li fli@sdu.edu.cn Shandong University, China 1 Hyperplane and Margin In a n-dimensional space, a hyper plane is defined by ω T x + b = 0 (1) where ω R n is
Support Vector Machines
 Two SVM tutorials linked in class website (please, read both): High-level presentation with applications (Hearst 1998) Detailed tutorial (Burges 1998) Support Vector Machines Machine Learning 10701/15781
Two SVM tutorials linked in class website (please, read both): High-level presentation with applications (Hearst 1998) Detailed tutorial (Burges 1998) Support Vector Machines Machine Learning 10701/15781
Support Vector Machines
 Support Vector Machines Le Song Machine Learning I CSE 6740, Fall 2013 Naïve Bayes classifier Still use Bayes decision rule for classification P y x = P x y P y P x But assume p x y = 1 is fully factorized
Support Vector Machines Le Song Machine Learning I CSE 6740, Fall 2013 Naïve Bayes classifier Still use Bayes decision rule for classification P y x = P x y P y P x But assume p x y = 1 is fully factorized
Convex Optimization Lecture 16
 Convex Optimization Lecture 16 Today: Projected Gradient Descent Conditional Gradient Descent Stochastic Gradient Descent Random Coordinate Descent Recall: Gradient Descent (Steepest Descent w.r.t Euclidean
Convex Optimization Lecture 16 Today: Projected Gradient Descent Conditional Gradient Descent Stochastic Gradient Descent Random Coordinate Descent Recall: Gradient Descent (Steepest Descent w.r.t Euclidean
Support Vector Machine (SVM) and Kernel Methods
 Support Vector Machine (SVM) and Kernel Methods CE-717: Machine Learning Sharif University of Technology Fall 2015 Soleymani Outline Margin concept Hard-Margin SVM Soft-Margin SVM Dual Problems of Hard-Margin
Support Vector Machine (SVM) and Kernel Methods CE-717: Machine Learning Sharif University of Technology Fall 2015 Soleymani Outline Margin concept Hard-Margin SVM Soft-Margin SVM Dual Problems of Hard-Margin
Machine Learning for NLP
 Machine Learning for NLP Linear Models Joakim Nivre Uppsala University Department of Linguistics and Philology Slides adapted from Ryan McDonald, Google Research Machine Learning for NLP 1(26) Outline
Machine Learning for NLP Linear Models Joakim Nivre Uppsala University Department of Linguistics and Philology Slides adapted from Ryan McDonald, Google Research Machine Learning for NLP 1(26) Outline
Support Vector Machine (continued)
 Support Vector Machine continued) Overlapping class distribution: In practice the class-conditional distributions may overlap, so that the training data points are no longer linearly separable. We need
Support Vector Machine continued) Overlapping class distribution: In practice the class-conditional distributions may overlap, so that the training data points are no longer linearly separable. We need
Machine Learning. Model Selection and Validation. Fabio Vandin November 7, 2017
 Machine Learning Model Selection and Validation Fabio Vandin November 7, 2017 1 Model Selection When we have to solve a machine learning task: there are different algorithms/classes algorithms have parameters
Machine Learning Model Selection and Validation Fabio Vandin November 7, 2017 1 Model Selection When we have to solve a machine learning task: there are different algorithms/classes algorithms have parameters
Support Vector Machine
 Support Vector Machine Kernel: Kernel is defined as a function returning the inner product between the images of the two arguments k(x 1, x 2 ) = ϕ(x 1 ), ϕ(x 2 ) k(x 1, x 2 ) = k(x 2, x 1 ) modularity-
Support Vector Machine Kernel: Kernel is defined as a function returning the inner product between the images of the two arguments k(x 1, x 2 ) = ϕ(x 1 ), ϕ(x 2 ) k(x 1, x 2 ) = k(x 2, x 1 ) modularity-
Mehryar Mohri Foundations of Machine Learning Courant Institute of Mathematical Sciences Homework assignment 3 April 5, 2013 Due: April 19, 2013
 Mehryar Mohri Foundations of Machine Learning Courant Institute of Mathematical Sciences Homework assignment 3 April 5, 2013 Due: April 19, 2013 A. Kernels 1. Let X be a finite set. Show that the kernel
Mehryar Mohri Foundations of Machine Learning Courant Institute of Mathematical Sciences Homework assignment 3 April 5, 2013 Due: April 19, 2013 A. Kernels 1. Let X be a finite set. Show that the kernel
Support Vector Machines
 Support Vector Machines Bingyu Wang, Virgil Pavlu March 30, 2015 based on notes by Andrew Ng. 1 What s SVM The original SVM algorithm was invented by Vladimir N. Vapnik 1 and the current standard incarnation
Support Vector Machines Bingyu Wang, Virgil Pavlu March 30, 2015 based on notes by Andrew Ng. 1 What s SVM The original SVM algorithm was invented by Vladimir N. Vapnik 1 and the current standard incarnation
Support Vector Machine
 Support Vector Machine Fabrice Rossi SAMM Université Paris 1 Panthéon Sorbonne 2018 Outline Linear Support Vector Machine Kernelized SVM Kernels 2 From ERM to RLM Empirical Risk Minimization in the binary
Support Vector Machine Fabrice Rossi SAMM Université Paris 1 Panthéon Sorbonne 2018 Outline Linear Support Vector Machine Kernelized SVM Kernels 2 From ERM to RLM Empirical Risk Minimization in the binary
Machine Learning Support Vector Machines. Prof. Matteo Matteucci
 Machine Learning Support Vector Machines Prof. Matteo Matteucci Discriminative vs. Generative Approaches 2 o Generative approach: we derived the classifier from some generative hypothesis about the way
Machine Learning Support Vector Machines Prof. Matteo Matteucci Discriminative vs. Generative Approaches 2 o Generative approach: we derived the classifier from some generative hypothesis about the way
Multisurface Proximal Support Vector Machine Classification via Generalized Eigenvalues
 Multisurface Proximal Support Vector Machine Classification via Generalized Eigenvalues O. L. Mangasarian and E. W. Wild Presented by: Jun Fang Multisurface Proximal Support Vector Machine Classification
Multisurface Proximal Support Vector Machine Classification via Generalized Eigenvalues O. L. Mangasarian and E. W. Wild Presented by: Jun Fang Multisurface Proximal Support Vector Machine Classification
Linear Models. min. i=1... m. i=1...m
 6 Linear Models A hyperplane in a space H endowed with a dot product is described by the set {x H w x + b = 0} (6.) where w H and b R. Such a hyperplane naturally divides H into two half-spaces: {x H w
6 Linear Models A hyperplane in a space H endowed with a dot product is described by the set {x H w x + b = 0} (6.) where w H and b R. Such a hyperplane naturally divides H into two half-spaces: {x H w
Accelerating Stochastic Optimization
 Accelerating Stochastic Optimization Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem and Mobileye Master Class at Tel-Aviv, Tel-Aviv University, November 2014 Shalev-Shwartz
Accelerating Stochastic Optimization Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem and Mobileye Master Class at Tel-Aviv, Tel-Aviv University, November 2014 Shalev-Shwartz
Coordinate Descent and Ascent Methods
 Coordinate Descent and Ascent Methods Julie Nutini Machine Learning Reading Group November 3 rd, 2015 1 / 22 Projected-Gradient Methods Motivation Rewrite non-smooth problem as smooth constrained problem:
Coordinate Descent and Ascent Methods Julie Nutini Machine Learning Reading Group November 3 rd, 2015 1 / 22 Projected-Gradient Methods Motivation Rewrite non-smooth problem as smooth constrained problem:
Machine Learning Lecture 6 Note
 Machine Learning Lecture 6 Note Compiled by Abhi Ashutosh, Daniel Chen, and Yijun Xiao February 16, 2016 1 Pegasos Algorithm The Pegasos Algorithm looks very similar to the Perceptron Algorithm. In fact,
Machine Learning Lecture 6 Note Compiled by Abhi Ashutosh, Daniel Chen, and Yijun Xiao February 16, 2016 1 Pegasos Algorithm The Pegasos Algorithm looks very similar to the Perceptron Algorithm. In fact,
10-701/ Machine Learning - Midterm Exam, Fall 2010
 10-701/15-781 Machine Learning - Midterm Exam, Fall 2010 Aarti Singh Carnegie Mellon University 1. Personal info: Name: Andrew account: E-mail address: 2. There should be 15 numbered pages in this exam
10-701/15-781 Machine Learning - Midterm Exam, Fall 2010 Aarti Singh Carnegie Mellon University 1. Personal info: Name: Andrew account: E-mail address: 2. There should be 15 numbered pages in this exam
STA141C: Big Data & High Performance Statistical Computing
 STA141C: Big Data & High Performance Statistical Computing Lecture 8: Optimization Cho-Jui Hsieh UC Davis May 9, 2017 Optimization Numerical Optimization Numerical Optimization: min X f (X ) Can be applied
STA141C: Big Data & High Performance Statistical Computing Lecture 8: Optimization Cho-Jui Hsieh UC Davis May 9, 2017 Optimization Numerical Optimization Numerical Optimization: min X f (X ) Can be applied
Statistical Machine Learning II Spring 2017, Learning Theory, Lecture 4
 Statistical Machine Learning II Spring 07, Learning Theory, Lecture 4 Jean Honorio jhonorio@purdue.edu Deterministic Optimization For brevity, everywhere differentiable functions will be called smooth.
Statistical Machine Learning II Spring 07, Learning Theory, Lecture 4 Jean Honorio jhonorio@purdue.edu Deterministic Optimization For brevity, everywhere differentiable functions will be called smooth.
Linear classifiers Lecture 3
 Linear classifiers Lecture 3 David Sontag New York University Slides adapted from Luke Zettlemoyer, Vibhav Gogate, and Carlos Guestrin ML Methodology Data: labeled instances, e.g. emails marked spam/ham
Linear classifiers Lecture 3 David Sontag New York University Slides adapted from Luke Zettlemoyer, Vibhav Gogate, and Carlos Guestrin ML Methodology Data: labeled instances, e.g. emails marked spam/ham
Kernel Machines. Pradeep Ravikumar Co-instructor: Manuela Veloso. Machine Learning
 Kernel Machines Pradeep Ravikumar Co-instructor: Manuela Veloso Machine Learning 10-701 SVM linearly separable case n training points (x 1,, x n ) d features x j is a d-dimensional vector Primal problem:
Kernel Machines Pradeep Ravikumar Co-instructor: Manuela Veloso Machine Learning 10-701 SVM linearly separable case n training points (x 1,, x n ) d features x j is a d-dimensional vector Primal problem:
Accelerate Subgradient Methods
 Accelerate Subgradient Methods Tianbao Yang Department of Computer Science The University of Iowa Contributors: students Yi Xu, Yan Yan and colleague Qihang Lin Yang (CS@Uiowa) Accelerate Subgradient Methods
Accelerate Subgradient Methods Tianbao Yang Department of Computer Science The University of Iowa Contributors: students Yi Xu, Yan Yan and colleague Qihang Lin Yang (CS@Uiowa) Accelerate Subgradient Methods
Linear & nonlinear classifiers
 Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1394 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1394 1 / 34 Table
Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1394 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1394 1 / 34 Table
Introduction to Support Vector Machines
 Introduction to Support Vector Machines Hsuan-Tien Lin Learning Systems Group, California Institute of Technology Talk in NTU EE/CS Speech Lab, November 16, 2005 H.-T. Lin (Learning Systems Group) Introduction
Introduction to Support Vector Machines Hsuan-Tien Lin Learning Systems Group, California Institute of Technology Talk in NTU EE/CS Speech Lab, November 16, 2005 H.-T. Lin (Learning Systems Group) Introduction
Support Vector Machines.
 Support Vector Machines www.cs.wisc.edu/~dpage 1 Goals for the lecture you should understand the following concepts the margin slack variables the linear support vector machine nonlinear SVMs the kernel
Support Vector Machines www.cs.wisc.edu/~dpage 1 Goals for the lecture you should understand the following concepts the margin slack variables the linear support vector machine nonlinear SVMs the kernel
Polyhedral Computation. Linear Classifiers & the SVM
 Polyhedral Computation Linear Classifiers & the SVM mcuturi@i.kyoto-u.ac.jp Nov 26 2010 1 Statistical Inference Statistical: useful to study random systems... Mutations, environmental changes etc. life
Polyhedral Computation Linear Classifiers & the SVM mcuturi@i.kyoto-u.ac.jp Nov 26 2010 1 Statistical Inference Statistical: useful to study random systems... Mutations, environmental changes etc. life
Machine Learning and Data Mining. Support Vector Machines. Kalev Kask
 Machine Learning and Data Mining Support Vector Machines Kalev Kask Linear classifiers Which decision boundary is better? Both have zero training error (perfect training accuracy) But, one of them seems
Machine Learning and Data Mining Support Vector Machines Kalev Kask Linear classifiers Which decision boundary is better? Both have zero training error (perfect training accuracy) But, one of them seems
Linear, threshold units. Linear Discriminant Functions and Support Vector Machines. Biometrics CSE 190 Lecture 11. X i : inputs W i : weights
 Linear Discriminant Functions and Support Vector Machines Linear, threshold units CSE19, Winter 11 Biometrics CSE 19 Lecture 11 1 X i : inputs W i : weights θ : threshold 3 4 5 1 6 7 Courtesy of University
Linear Discriminant Functions and Support Vector Machines Linear, threshold units CSE19, Winter 11 Biometrics CSE 19 Lecture 11 1 X i : inputs W i : weights θ : threshold 3 4 5 1 6 7 Courtesy of University
Statistical Pattern Recognition
 Statistical Pattern Recognition Support Vector Machine (SVM) Hamid R. Rabiee Hadi Asheri, Jafar Muhammadi, Nima Pourdamghani Spring 2013 http://ce.sharif.edu/courses/91-92/2/ce725-1/ Agenda Introduction
Statistical Pattern Recognition Support Vector Machine (SVM) Hamid R. Rabiee Hadi Asheri, Jafar Muhammadi, Nima Pourdamghani Spring 2013 http://ce.sharif.edu/courses/91-92/2/ce725-1/ Agenda Introduction
