> Y ~ X1 + X2. The tilde character separates the response variable from the explanatory variables. So in essence we fit the model
|
|
|
- Adela McLaughlin
- 5 years ago
- Views:
Transcription
1 Regression Analysis Regression analysis is one of the most important topics in Statistical theory. In the sequel this widely known methodology will be used with S-Plus by means of formulae for models. Models in S-Plus A formula is an S-PLUS expression that specifies the form of a model in terms of the variables involved. For example, to specify that Y is a linear combination of two predictors X1 and X2, you use the following formula: > Y ~ X1 + X2 The tilde character separates the response variable from the explanatory variables. So in essence we fit the model Y = β 0 + β 1 X1 + β 2 X2. A formula always implicitly includes an intercept term (β 0 ) in the above formula). You can, however, remove the intercept term by specifying the model with 1 as an explicit predictor: > Y ~ -1 + X1 + X2 Similarly, you can explicitly include an intercept with a + 1. When you specify categorical variables (factors, ordered factors, or categories) as predictors in the formulas, the modelling functions fit a coefficient for each level of the variable. For example, to model salary as a linear model of age (continuous) and gender (factor) you specify it as follows: > salary ~ age + gender However, a different parameter is fitted for each of the two levels of gender. This is equivalent to fitting two dummy variables, one for males and one for females. Thus, you need not create and specify dummy variables in the model. Here are the main expressions: Y X: Y is modeled as X 1
2 X1+X2: Include both X1 and X2 in the model X1-X2: Include all of X1 except what is in X2 in the model X1:X2; The interaction between X1 and X2 X1*X2 full model X1 + X2 + X1 : X2 The next sections put these applies these concepts to a multiple linear regression model. A Multiple Regression Model The data set consists of a sample of black cherry trees. These were cut down measurements made on the diameter (in inches) height (in feet) and volume (in cubic feet). The purpose of collecting these data was to provide a way of predicting the volume of timber in trees from their height and diameter measurements, using a regression model. Diameter Height Volume Table 1: The first six observations from the data set Here the dependent variable is continuous and the initial model considered is the usual linear regression one, having the general form y = β 0 + β 1 x β p x p + ɛ where y is the response variable, x 1,..., x p a set of explanatory variables, and ɛ a residual term. We estimate β s by least squares assuming that the residual term is normally distributed with mean 0 and constant variance σ 2. For n observations on the response and explanatory variables the model may be written concisely as E(y) = Xβ A formal analysis in S-Plus uses the function lm() as outlined below: trees.fit <- lm(volume~ Diameter+Height, trees) > trees.fit Call: lm(formula = Volume ~ Diameter + Height, data = trees) 2
3 Coefficients: (Intercept) Diameter Height Degrees of freedom: 31 total; 28 residual Residual standard error: > trees.res <- residuals(trees.fit) #obtain the residuals > trees.prd <- predict(trees.fit) #obtain the predicted values These results suggest that the regression coefficients for both Diameter and Height are significantly different from zero, and that about 95% of the variance ( the value given by R 2 ) in volume can attributed to two explanatory variables. The next stage in the analysis should be an examination of the residuals from the model, that is the differences between the observed and fitted (predicted) values of the response. The most useful plots are the following: 1. A plot of the residuals against explanatory variable in the model. The presence of a curvilinear relationship, for example, may suggest a higher order term, perhaps a quadratic should be added to the model (Figure 1). 2. A plot of the residuals against predicted values of the response variable. If the variance of the response appears to increase with predicted value, a transformation of the response may be in order (Figure 2). 3. A normal probability plot of the residuals. After all systematic variation has been removed from the data, the residuals should look like a sample from the normal distribution. That is a plot of the ordered residuals against the expected order statistics from a normal distribution (Figure 3). We are going to work with the standardized residuals which are defined by r i = y i ŷ i s 1 h ii where h ii are the diagonal elements of the matrix: H = X(X X) 1 X. > s <- summary(trees.fit)$sigma #obtain an estimator of sigma > h <- lm.influence(trees.fit)$hat #obtain the diagonal elements of H > trees.res <- trees.res/(s*sqrt(1-h)) # redefine the residuals so that # they are standardized. > par(mfrow=c(2,1)) # obtain the plots of regressors vs # standardized residuals > plot(trees[,"diameter"], trees.res, xlab="diameter", ylab="std. Residuals") > abline(h=0, lty=2) > title("std. Residuals versus Diameter") 3
4 > plot(trees[,"height"], trees.res, xlab="height", ylab="std. Residuals") > abline(h=0, lty=2) > title("std. Residuals versus Height") > par(mfrow=c(1,1)) #plots of residuals vs predicted values > plot(trees.prd, trees.res, xlab="predicted Volume", ylab="std. Residuals") > abline(h=0,lty=2) > title("std. Residuals vs Fitted Values") > qqnorm(trees.res,ylab="std. Residuals") #qqnorm of the residuals > qqline(trees.res) > title("normal Plot of Std. Residuals") Std. Residuals versus Diameter Std. Residuals Diameter Std. Residuals versus Height Std. Residuals Height Figure 1: Standardized residuals plotted against values of explanatory variables 4
5 Std. Residuals vs Fitted Values Std. Residuals Predicted Volume Figure 2: Standardized residuals plotted against fitted values of response variables. Normal Plot of Std. Residuals Std. Residuals Quantiles of Standard Normal Figure 3: Normal plot of standardized residuals. 5
6 The plots involving Diameter and the fitted values both show some evidence that a quadratic term may be needed in the model. The interpretation of the normal probability plot is often unclear, particularly with small samples. Examination of the plot indicates that the residuals show little departure from normality. The hat matrix, H, is also helpful in identifying strange or peculiar data points, those having unusually large potential effect on the regression. Such points are indicated by relatively high values in the appropriate position in the diagonal of H. The maximum value of any diagonal element is 1. Technically these points are referred as having high leverage (Figure 4). > h <- lm.influence(trees.fit)$hat > h [1] [5] [9] [13] [17] [21] [25] [29] > plot(1:31,h, type="n", xlab="l", ylab="diagonal of Hat Matrix") > abline(h=mean(h)) > segments(1:31, h, 1:31, mean(h)) Diagonal of Hat Matrix l Figure 4: Leverage plot. Here there seem to be no obvious problem points which might be unduly affecting the estimation process. The leverage values are relatively low. 6
7 Returning now to the evidence from the residual plots, a new model involving a quadratic term in Diameter might now be considered. > trees1.fit <- lm(volume~diameter+i(diameter*diameter)+height, trees) > trees1.fit Call: lm(formula = Volume ~ Diameter + I(Diameter * Diameter) + Height, data = trees) Coefficients: (Intercept) Diameter I(Diameter * Diameter) Height Degrees of freedom: 31 total; 27 residual Residual standard error: > summary(trees1.fit) Call: lm(formula = Volume ~ Diameter + I(Diameter * Diameter) + Height, data = trees) Residuals: Min 1Q Median 3Q Max Coefficients: Value Std. Error t value Pr(> t ) (Intercept) Diameter I(Diameter * Diameter) Height Residual standard error: on 27 degrees of freedom Multiple R-Squared: F-statistic: on 3 and 27 degrees of freedom, the p-value is 0 Correlation of Coefficients: Diameter I(Diameter * Diameter) (Intercept) Diameter I(Diameter * Diameter) Height The new residual plots are not shown but they can be obtained as before. It turns out that the plot involving diameter has now lost the structure it had previously and the other plots look satisfactory. Although the results indicate that the regression coefficients of both height and diameter are significantly different from zero, it is often useful to explore a number of models in an attempt to find the simplest and adequately describe the data. Essentially, this involves adding or deleting terms from an existing model and assessing the effect of the change. 7
8 For example, for the models which involves diameter and height we get by deleting one variable at a time: > attach(trees) > trees.drop1 <- drop1(trees.fit) #dropping terms sequentially > trees.drop1 Single term deletions Model: Volume ~ Diameter + Height Df Sum of Sq RSS Cp <none> Diameter Height Sums of squares due to the deleted terms and residuals sums of squares for the reduced model are given. Here their value indicate the great importance of diameter in the model. The opposite approach starts from a model and adds on terms. > trees0.fit <- lm(volume~1) #model with constant term > trees.add1 <- add1(trees0.fit,~ Height+Diameter) #add sequentially terms > trees.add1 Single term additions Model: Volume ~ 1 Df Sum of Sq RSS Cp <none> Height Diameter The results are shown above. The terms are the same as before, but now correspond to adding particular variables. As a final note the function predict() can be used to obtain predicted values for a model. 8
SCHOOL OF MATHEMATICS AND STATISTICS Autumn Semester
 RESTRICTED OPEN BOOK EXAMINATION (Not to be removed from the examination hall) Data provided: "Statistics Tables" by H.R. Neave PAS 371 SCHOOL OF MATHEMATICS AND STATISTICS Autumn Semester 2008 9 Linear
RESTRICTED OPEN BOOK EXAMINATION (Not to be removed from the examination hall) Data provided: "Statistics Tables" by H.R. Neave PAS 371 SCHOOL OF MATHEMATICS AND STATISTICS Autumn Semester 2008 9 Linear
14 Multiple Linear Regression
 B.Sc./Cert./M.Sc. Qualif. - Statistics: Theory and Practice 14 Multiple Linear Regression 14.1 The multiple linear regression model In simple linear regression, the response variable y is expressed in
B.Sc./Cert./M.Sc. Qualif. - Statistics: Theory and Practice 14 Multiple Linear Regression 14.1 The multiple linear regression model In simple linear regression, the response variable y is expressed in
UNIVERSITY OF MASSACHUSETTS. Department of Mathematics and Statistics. Basic Exam - Applied Statistics. Tuesday, January 17, 2017
 UNIVERSITY OF MASSACHUSETTS Department of Mathematics and Statistics Basic Exam - Applied Statistics Tuesday, January 17, 2017 Work all problems 60 points are needed to pass at the Masters Level and 75
UNIVERSITY OF MASSACHUSETTS Department of Mathematics and Statistics Basic Exam - Applied Statistics Tuesday, January 17, 2017 Work all problems 60 points are needed to pass at the Masters Level and 75
22s:152 Applied Linear Regression
 22s:152 Applied Linear Regression Chapter 7: Dummy Variable Regression So far, we ve only considered quantitative variables in our models. We can integrate categorical predictors by constructing artificial
22s:152 Applied Linear Regression Chapter 7: Dummy Variable Regression So far, we ve only considered quantitative variables in our models. We can integrate categorical predictors by constructing artificial
Analytics 512: Homework # 2 Tim Ahn February 9, 2016
 Analytics 512: Homework # 2 Tim Ahn February 9, 2016 Chapter 3 Problem 1 (# 3) Suppose we have a data set with five predictors, X 1 = GP A, X 2 = IQ, X 3 = Gender (1 for Female and 0 for Male), X 4 = Interaction
Analytics 512: Homework # 2 Tim Ahn February 9, 2016 Chapter 3 Problem 1 (# 3) Suppose we have a data set with five predictors, X 1 = GP A, X 2 = IQ, X 3 = Gender (1 for Female and 0 for Male), X 4 = Interaction
ST430 Exam 2 Solutions
 ST430 Exam 2 Solutions Date: November 9, 2015 Name: Guideline: You may use one-page (front and back of a standard A4 paper) of notes. No laptop or textbook are permitted but you may use a calculator. Giving
ST430 Exam 2 Solutions Date: November 9, 2015 Name: Guideline: You may use one-page (front and back of a standard A4 paper) of notes. No laptop or textbook are permitted but you may use a calculator. Giving
Lecture 4 Multiple linear regression
 Lecture 4 Multiple linear regression BIOST 515 January 15, 2004 Outline 1 Motivation for the multiple regression model Multiple regression in matrix notation Least squares estimation of model parameters
Lecture 4 Multiple linear regression BIOST 515 January 15, 2004 Outline 1 Motivation for the multiple regression model Multiple regression in matrix notation Least squares estimation of model parameters
Linear Modelling: Simple Regression
 Linear Modelling: Simple Regression 10 th of Ma 2018 R. Nicholls / D.-L. Couturier / M. Fernandes Introduction: ANOVA Used for testing hpotheses regarding differences between groups Considers the variation
Linear Modelling: Simple Regression 10 th of Ma 2018 R. Nicholls / D.-L. Couturier / M. Fernandes Introduction: ANOVA Used for testing hpotheses regarding differences between groups Considers the variation
Statistics - Lecture Three. Linear Models. Charlotte Wickham 1.
 Statistics - Lecture Three Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Linear Models 1. The Theory 2. Practical Use 3. How to do it in R 4. An example 5. Extensions
Statistics - Lecture Three Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Linear Models 1. The Theory 2. Practical Use 3. How to do it in R 4. An example 5. Extensions
Leverage. the response is in line with the other values, or the high leverage has caused the fitted model to be pulled toward the observed response.
 Leverage Some cases have high leverage, the potential to greatly affect the fit. These cases are outliers in the space of predictors. Often the residuals for these cases are not large because the response
Leverage Some cases have high leverage, the potential to greatly affect the fit. These cases are outliers in the space of predictors. Often the residuals for these cases are not large because the response
Inference for Regression
 Inference for Regression Section 9.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 13b - 3339 Cathy Poliak, Ph.D. cathy@math.uh.edu
Inference for Regression Section 9.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 13b - 3339 Cathy Poliak, Ph.D. cathy@math.uh.edu
SCHOOL OF MATHEMATICS AND STATISTICS
 SHOOL OF MATHEMATIS AND STATISTIS Linear Models Autumn Semester 2015 16 2 hours Marks will be awarded for your best three answers. RESTRITED OPEN BOOK EXAMINATION andidates may bring to the examination
SHOOL OF MATHEMATIS AND STATISTIS Linear Models Autumn Semester 2015 16 2 hours Marks will be awarded for your best three answers. RESTRITED OPEN BOOK EXAMINATION andidates may bring to the examination
> modlyq <- lm(ly poly(x,2,raw=true)) > summary(modlyq) Call: lm(formula = ly poly(x, 2, raw = TRUE))
 School of Mathematical Sciences MTH5120 Statistical Modelling I Tutorial 4 Solutions The first two models were looked at last week and both had flaws. The output for the third model with log y and a quadratic
School of Mathematical Sciences MTH5120 Statistical Modelling I Tutorial 4 Solutions The first two models were looked at last week and both had flaws. The output for the third model with log y and a quadratic
ST430 Exam 1 with Answers
 ST430 Exam 1 with Answers Date: October 5, 2015 Name: Guideline: You may use one-page (front and back of a standard A4 paper) of notes. No laptop or textook are permitted but you may use a calculator.
ST430 Exam 1 with Answers Date: October 5, 2015 Name: Guideline: You may use one-page (front and back of a standard A4 paper) of notes. No laptop or textook are permitted but you may use a calculator.
Linear Regression. In this lecture we will study a particular type of regression model: the linear regression model
 1 Linear Regression 2 Linear Regression In this lecture we will study a particular type of regression model: the linear regression model We will first consider the case of the model with one predictor
1 Linear Regression 2 Linear Regression In this lecture we will study a particular type of regression model: the linear regression model We will first consider the case of the model with one predictor
Regression. Marc H. Mehlman University of New Haven
 Regression Marc H. Mehlman marcmehlman@yahoo.com University of New Haven the statistician knows that in nature there never was a normal distribution, there never was a straight line, yet with normal and
Regression Marc H. Mehlman marcmehlman@yahoo.com University of New Haven the statistician knows that in nature there never was a normal distribution, there never was a straight line, yet with normal and
Example: Poisondata. 22s:152 Applied Linear Regression. Chapter 8: ANOVA
 s:5 Applied Linear Regression Chapter 8: ANOVA Two-way ANOVA Used to compare populations means when the populations are classified by two factors (or categorical variables) For example sex and occupation
s:5 Applied Linear Regression Chapter 8: ANOVA Two-way ANOVA Used to compare populations means when the populations are classified by two factors (or categorical variables) For example sex and occupation
General Linear Model (Chapter 4)
 General Linear Model (Chapter 4) Outcome variable is considered continuous Simple linear regression Scatterplots OLS is BLUE under basic assumptions MSE estimates residual variance testing regression coefficients
General Linear Model (Chapter 4) Outcome variable is considered continuous Simple linear regression Scatterplots OLS is BLUE under basic assumptions MSE estimates residual variance testing regression coefficients
13 Simple Linear Regression
 B.Sc./Cert./M.Sc. Qualif. - Statistics: Theory and Practice 3 Simple Linear Regression 3. An industrial example A study was undertaken to determine the effect of stirring rate on the amount of impurity
B.Sc./Cert./M.Sc. Qualif. - Statistics: Theory and Practice 3 Simple Linear Regression 3. An industrial example A study was undertaken to determine the effect of stirring rate on the amount of impurity
Data Analysis 1 LINEAR REGRESSION. Chapter 03
 Data Analysis 1 LINEAR REGRESSION Chapter 03 Data Analysis 2 Outline The Linear Regression Model Least Squares Fit Measures of Fit Inference in Regression Other Considerations in Regression Model Qualitative
Data Analysis 1 LINEAR REGRESSION Chapter 03 Data Analysis 2 Outline The Linear Regression Model Least Squares Fit Measures of Fit Inference in Regression Other Considerations in Regression Model Qualitative
Lecture 18: Simple Linear Regression
 Lecture 18: Simple Linear Regression BIOS 553 Department of Biostatistics University of Michigan Fall 2004 The Correlation Coefficient: r The correlation coefficient (r) is a number that measures the strength
Lecture 18: Simple Linear Regression BIOS 553 Department of Biostatistics University of Michigan Fall 2004 The Correlation Coefficient: r The correlation coefficient (r) is a number that measures the strength
22s:152 Applied Linear Regression. Take random samples from each of m populations.
 22s:152 Applied Linear Regression Chapter 8: ANOVA NOTE: We will meet in the lab on Monday October 10. One-way ANOVA Focuses on testing for differences among group means. Take random samples from each
22s:152 Applied Linear Regression Chapter 8: ANOVA NOTE: We will meet in the lab on Monday October 10. One-way ANOVA Focuses on testing for differences among group means. Take random samples from each
1 Multiple Regression
 1 Multiple Regression In this section, we extend the linear model to the case of several quantitative explanatory variables. There are many issues involved in this problem and this section serves only
1 Multiple Regression In this section, we extend the linear model to the case of several quantitative explanatory variables. There are many issues involved in this problem and this section serves only
Comparing Nested Models
 Comparing Nested Models ST 370 Two regression models are called nested if one contains all the predictors of the other, and some additional predictors. For example, the first-order model in two independent
Comparing Nested Models ST 370 Two regression models are called nested if one contains all the predictors of the other, and some additional predictors. For example, the first-order model in two independent
Biostatistics 380 Multiple Regression 1. Multiple Regression
 Biostatistics 0 Multiple Regression ORIGIN 0 Multiple Regression Multiple Regression is an extension of the technique of linear regression to describe the relationship between a single dependent (response)
Biostatistics 0 Multiple Regression ORIGIN 0 Multiple Regression Multiple Regression is an extension of the technique of linear regression to describe the relationship between a single dependent (response)
Stat 401B Final Exam Fall 2015
 Stat 401B Final Exam Fall 015 I have neither given nor received unauthorized assistance on this exam. Name Signed Date Name Printed ATTENTION! Incorrect numerical answers unaccompanied by supporting reasoning
Stat 401B Final Exam Fall 015 I have neither given nor received unauthorized assistance on this exam. Name Signed Date Name Printed ATTENTION! Incorrect numerical answers unaccompanied by supporting reasoning
Business Statistics. Tommaso Proietti. Linear Regression. DEF - Università di Roma 'Tor Vergata'
 Business Statistics Tommaso Proietti DEF - Università di Roma 'Tor Vergata' Linear Regression Specication Let Y be a univariate quantitative response variable. We model Y as follows: Y = f(x) + ε where
Business Statistics Tommaso Proietti DEF - Università di Roma 'Tor Vergata' Linear Regression Specication Let Y be a univariate quantitative response variable. We model Y as follows: Y = f(x) + ε where
Multiple Regression Examples
 Multiple Regression Examples Example: Tree data. we have seen that a simple linear regression of usable volume on diameter at chest height is not suitable, but that a quadratic model y = β 0 + β 1 x +
Multiple Regression Examples Example: Tree data. we have seen that a simple linear regression of usable volume on diameter at chest height is not suitable, but that a quadratic model y = β 0 + β 1 x +
Example: 1982 State SAT Scores (First year state by state data available)
 Lecture 11 Review Section 3.5 from last Monday (on board) Overview of today s example (on board) Section 3.6, Continued: Nested F tests, review on board first Section 3.4: Interaction for quantitative
Lecture 11 Review Section 3.5 from last Monday (on board) Overview of today s example (on board) Section 3.6, Continued: Nested F tests, review on board first Section 3.4: Interaction for quantitative
Stat 5102 Final Exam May 14, 2015
 Stat 5102 Final Exam May 14, 2015 Name Student ID The exam is closed book and closed notes. You may use three 8 1 11 2 sheets of paper with formulas, etc. You may also use the handouts on brand name distributions
Stat 5102 Final Exam May 14, 2015 Name Student ID The exam is closed book and closed notes. You may use three 8 1 11 2 sheets of paper with formulas, etc. You may also use the handouts on brand name distributions
MODELS WITHOUT AN INTERCEPT
 Consider the balanced two factor design MODELS WITHOUT AN INTERCEPT Factor A 3 levels, indexed j 0, 1, 2; Factor B 5 levels, indexed l 0, 1, 2, 3, 4; n jl 4 replicate observations for each factor level
Consider the balanced two factor design MODELS WITHOUT AN INTERCEPT Factor A 3 levels, indexed j 0, 1, 2; Factor B 5 levels, indexed l 0, 1, 2, 3, 4; n jl 4 replicate observations for each factor level
Introduction to Linear Regression Rebecca C. Steorts September 15, 2015
 Introduction to Linear Regression Rebecca C. Steorts September 15, 2015 Today (Re-)Introduction to linear models and the model space What is linear regression Basic properties of linear regression Using
Introduction to Linear Regression Rebecca C. Steorts September 15, 2015 Today (Re-)Introduction to linear models and the model space What is linear regression Basic properties of linear regression Using
Multiple Regression: Example
 Multiple Regression: Example Cobb-Douglas Production Function The Cobb-Douglas production function for observed economic data i = 1,..., n may be expressed as where O i is output l i is labour input c
Multiple Regression: Example Cobb-Douglas Production Function The Cobb-Douglas production function for observed economic data i = 1,..., n may be expressed as where O i is output l i is labour input c
Tests of Linear Restrictions
 Tests of Linear Restrictions 1. Linear Restricted in Regression Models In this tutorial, we consider tests on general linear restrictions on regression coefficients. In other tutorials, we examine some
Tests of Linear Restrictions 1. Linear Restricted in Regression Models In this tutorial, we consider tests on general linear restrictions on regression coefficients. In other tutorials, we examine some
Lecture 4: Regression Analysis
 Lecture 4: Regression Analysis 1 Regression Regression is a multivariate analysis, i.e., we are interested in relationship between several variables. For corporate audience, it is sufficient to show correlation.
Lecture 4: Regression Analysis 1 Regression Regression is a multivariate analysis, i.e., we are interested in relationship between several variables. For corporate audience, it is sufficient to show correlation.
Ch 3: Multiple Linear Regression
 Ch 3: Multiple Linear Regression 1. Multiple Linear Regression Model Multiple regression model has more than one regressor. For example, we have one response variable and two regressor variables: 1. delivery
Ch 3: Multiple Linear Regression 1. Multiple Linear Regression Model Multiple regression model has more than one regressor. For example, we have one response variable and two regressor variables: 1. delivery
Chapter 13. Multiple Regression and Model Building
 Chapter 13 Multiple Regression and Model Building Multiple Regression Models The General Multiple Regression Model y x x x 0 1 1 2 2... k k y is the dependent variable x, x,..., x 1 2 k the model are the
Chapter 13 Multiple Regression and Model Building Multiple Regression Models The General Multiple Regression Model y x x x 0 1 1 2 2... k k y is the dependent variable x, x,..., x 1 2 k the model are the
MATH 644: Regression Analysis Methods
 MATH 644: Regression Analysis Methods FINAL EXAM Fall, 2012 INSTRUCTIONS TO STUDENTS: 1. This test contains SIX questions. It comprises ELEVEN printed pages. 2. Answer ALL questions for a total of 100
MATH 644: Regression Analysis Methods FINAL EXAM Fall, 2012 INSTRUCTIONS TO STUDENTS: 1. This test contains SIX questions. It comprises ELEVEN printed pages. 2. Answer ALL questions for a total of 100
STK4900/ Lecture 3. Program
 STK4900/9900 - Lecture 3 Program 1. Multiple regression: Data structure and basic questions 2. The multiple linear regression model 3. Categorical predictors 4. Planned experiments and observational studies
STK4900/9900 - Lecture 3 Program 1. Multiple regression: Data structure and basic questions 2. The multiple linear regression model 3. Categorical predictors 4. Planned experiments and observational studies
Dealing with Heteroskedasticity
 Dealing with Heteroskedasticity James H. Steiger Department of Psychology and Human Development Vanderbilt University James H. Steiger (Vanderbilt University) Dealing with Heteroskedasticity 1 / 27 Dealing
Dealing with Heteroskedasticity James H. Steiger Department of Psychology and Human Development Vanderbilt University James H. Steiger (Vanderbilt University) Dealing with Heteroskedasticity 1 / 27 Dealing
POLSCI 702 Non-Normality and Heteroskedasticity
 Goals of this Lecture POLSCI 702 Non-Normality and Heteroskedasticity Dave Armstrong University of Wisconsin Milwaukee Department of Political Science e: armstrod@uwm.edu w: www.quantoid.net/uwm702.html
Goals of this Lecture POLSCI 702 Non-Normality and Heteroskedasticity Dave Armstrong University of Wisconsin Milwaukee Department of Political Science e: armstrod@uwm.edu w: www.quantoid.net/uwm702.html
Math 423/533: The Main Theoretical Topics
 Math 423/533: The Main Theoretical Topics Notation sample size n, data index i number of predictors, p (p = 2 for simple linear regression) y i : response for individual i x i = (x i1,..., x ip ) (1 p)
Math 423/533: The Main Theoretical Topics Notation sample size n, data index i number of predictors, p (p = 2 for simple linear regression) y i : response for individual i x i = (x i1,..., x ip ) (1 p)
1.) Fit the full model, i.e., allow for separate regression lines (different slopes and intercepts) for each species
 Lecture notes 2/22/2000 Dummy variables and extra SS F-test Page 1 Crab claw size and closing force. Problem 7.25, 10.9, and 10.10 Regression for all species at once, i.e., include dummy variables for
Lecture notes 2/22/2000 Dummy variables and extra SS F-test Page 1 Crab claw size and closing force. Problem 7.25, 10.9, and 10.10 Regression for all species at once, i.e., include dummy variables for
22s:152 Applied Linear Regression. There are a couple commonly used models for a one-way ANOVA with m groups. Chapter 8: ANOVA
 22s:152 Applied Linear Regression Chapter 8: ANOVA NOTE: We will meet in the lab on Monday October 10. One-way ANOVA Focuses on testing for differences among group means. Take random samples from each
22s:152 Applied Linear Regression Chapter 8: ANOVA NOTE: We will meet in the lab on Monday October 10. One-way ANOVA Focuses on testing for differences among group means. Take random samples from each
Lecture 1: Linear Models and Applications
 Lecture 1: Linear Models and Applications Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction to linear models Exploratory data analysis (EDA) Estimation
Lecture 1: Linear Models and Applications Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction to linear models Exploratory data analysis (EDA) Estimation
Lecture 2. The Simple Linear Regression Model: Matrix Approach
 Lecture 2 The Simple Linear Regression Model: Matrix Approach Matrix algebra Matrix representation of simple linear regression model 1 Vectors and Matrices Where it is necessary to consider a distribution
Lecture 2 The Simple Linear Regression Model: Matrix Approach Matrix algebra Matrix representation of simple linear regression model 1 Vectors and Matrices Where it is necessary to consider a distribution
Need for Several Predictor Variables
 Multiple regression One of the most widely used tools in statistical analysis Matrix expressions for multiple regression are the same as for simple linear regression Need for Several Predictor Variables
Multiple regression One of the most widely used tools in statistical analysis Matrix expressions for multiple regression are the same as for simple linear regression Need for Several Predictor Variables
STATISTICS 174: APPLIED STATISTICS FINAL EXAM DECEMBER 10, 2002
 Time allowed: 3 HOURS. STATISTICS 174: APPLIED STATISTICS FINAL EXAM DECEMBER 10, 2002 This is an open book exam: all course notes and the text are allowed, and you are expected to use your own calculator.
Time allowed: 3 HOURS. STATISTICS 174: APPLIED STATISTICS FINAL EXAM DECEMBER 10, 2002 This is an open book exam: all course notes and the text are allowed, and you are expected to use your own calculator.
Lecture 2. Simple linear regression
 Lecture 2. Simple linear regression Jesper Rydén Department of Mathematics, Uppsala University jesper@math.uu.se Regression and Analysis of Variance autumn 2014 Overview of lecture Introduction, short
Lecture 2. Simple linear regression Jesper Rydén Department of Mathematics, Uppsala University jesper@math.uu.se Regression and Analysis of Variance autumn 2014 Overview of lecture Introduction, short
Correlation and simple linear regression S5
 Basic medical statistics for clinical and eperimental research Correlation and simple linear regression S5 Katarzyna Jóźwiak k.jozwiak@nki.nl November 15, 2017 1/41 Introduction Eample: Brain size and
Basic medical statistics for clinical and eperimental research Correlation and simple linear regression S5 Katarzyna Jóźwiak k.jozwiak@nki.nl November 15, 2017 1/41 Introduction Eample: Brain size and
Lecture 6 Multiple Linear Regression, cont.
 Lecture 6 Multiple Linear Regression, cont. BIOST 515 January 22, 2004 BIOST 515, Lecture 6 Testing general linear hypotheses Suppose we are interested in testing linear combinations of the regression
Lecture 6 Multiple Linear Regression, cont. BIOST 515 January 22, 2004 BIOST 515, Lecture 6 Testing general linear hypotheses Suppose we are interested in testing linear combinations of the regression
Categorical Predictor Variables
 Categorical Predictor Variables We often wish to use categorical (or qualitative) variables as covariates in a regression model. For binary variables (taking on only 2 values, e.g. sex), it is relatively
Categorical Predictor Variables We often wish to use categorical (or qualitative) variables as covariates in a regression model. For binary variables (taking on only 2 values, e.g. sex), it is relatively
Chapter 3: Multiple Regression. August 14, 2018
 Chapter 3: Multiple Regression August 14, 2018 1 The multiple linear regression model The model y = β 0 +β 1 x 1 + +β k x k +ǫ (1) is called a multiple linear regression model with k regressors. The parametersβ
Chapter 3: Multiple Regression August 14, 2018 1 The multiple linear regression model The model y = β 0 +β 1 x 1 + +β k x k +ǫ (1) is called a multiple linear regression model with k regressors. The parametersβ
Announcements: You can turn in homework until 6pm, slot on wall across from 2202 Bren. Make sure you use the correct slot! (Stats 8, closest to wall)
 Announcements: You can turn in homework until 6pm, slot on wall across from 2202 Bren. Make sure you use the correct slot! (Stats 8, closest to wall) We will cover Chs. 5 and 6 first, then 3 and 4. Mon,
Announcements: You can turn in homework until 6pm, slot on wall across from 2202 Bren. Make sure you use the correct slot! (Stats 8, closest to wall) We will cover Chs. 5 and 6 first, then 3 and 4. Mon,
CAS MA575 Linear Models
 CAS MA575 Linear Models Boston University, Fall 2013 Midterm Exam (Correction) Instructor: Cedric Ginestet Date: 22 Oct 2013. Maximal Score: 200pts. Please Note: You will only be graded on work and answers
CAS MA575 Linear Models Boston University, Fall 2013 Midterm Exam (Correction) Instructor: Cedric Ginestet Date: 22 Oct 2013. Maximal Score: 200pts. Please Note: You will only be graded on work and answers
Multiple Linear Regression
 Multiple Linear Regression ST 430/514 Recall: a regression model describes how a dependent variable (or response) Y is affected, on average, by one or more independent variables (or factors, or covariates).
Multiple Linear Regression ST 430/514 Recall: a regression model describes how a dependent variable (or response) Y is affected, on average, by one or more independent variables (or factors, or covariates).
Density Temp vs Ratio. temp
 Temp Ratio Density 0.00 0.02 0.04 0.06 0.08 0.10 0.12 Density 0.0 0.2 0.4 0.6 0.8 1.0 1. (a) 170 175 180 185 temp 1.0 1.5 2.0 2.5 3.0 ratio The histogram shows that the temperature measures have two peaks,
Temp Ratio Density 0.00 0.02 0.04 0.06 0.08 0.10 0.12 Density 0.0 0.2 0.4 0.6 0.8 1.0 1. (a) 170 175 180 185 temp 1.0 1.5 2.0 2.5 3.0 ratio The histogram shows that the temperature measures have two peaks,
Inference. ME104: Linear Regression Analysis Kenneth Benoit. August 15, August 15, 2012 Lecture 3 Multiple linear regression 1 1 / 58
 Inference ME104: Linear Regression Analysis Kenneth Benoit August 15, 2012 August 15, 2012 Lecture 3 Multiple linear regression 1 1 / 58 Stata output resvisited. reg votes1st spend_total incumb minister
Inference ME104: Linear Regression Analysis Kenneth Benoit August 15, 2012 August 15, 2012 Lecture 3 Multiple linear regression 1 1 / 58 Stata output resvisited. reg votes1st spend_total incumb minister
Simple Linear Regression
 Simple Linear Regression September 24, 2008 Reading HH 8, GIll 4 Simple Linear Regression p.1/20 Problem Data: Observe pairs (Y i,x i ),i = 1,...n Response or dependent variable Y Predictor or independent
Simple Linear Regression September 24, 2008 Reading HH 8, GIll 4 Simple Linear Regression p.1/20 Problem Data: Observe pairs (Y i,x i ),i = 1,...n Response or dependent variable Y Predictor or independent
Correlation and Regression
 Correlation and Regression Marc H. Mehlman marcmehlman@yahoo.com University of New Haven All models are wrong. Some models are useful. George Box the statistician knows that in nature there never was a
Correlation and Regression Marc H. Mehlman marcmehlman@yahoo.com University of New Haven All models are wrong. Some models are useful. George Box the statistician knows that in nature there never was a
Linear Regression Model. Badr Missaoui
 Linear Regression Model Badr Missaoui Introduction What is this course about? It is a course on applied statistics. It comprises 2 hours lectures each week and 1 hour lab sessions/tutorials. We will focus
Linear Regression Model Badr Missaoui Introduction What is this course about? It is a course on applied statistics. It comprises 2 hours lectures each week and 1 hour lab sessions/tutorials. We will focus
Unit 6 - Introduction to linear regression
 Unit 6 - Introduction to linear regression Suggested reading: OpenIntro Statistics, Chapter 7 Suggested exercises: Part 1 - Relationship between two numerical variables: 7.7, 7.9, 7.11, 7.13, 7.15, 7.25,
Unit 6 - Introduction to linear regression Suggested reading: OpenIntro Statistics, Chapter 7 Suggested exercises: Part 1 - Relationship between two numerical variables: 7.7, 7.9, 7.11, 7.13, 7.15, 7.25,
Analysis of variance. Gilles Guillot. September 30, Gilles Guillot September 30, / 29
 Analysis of variance Gilles Guillot gigu@dtu.dk September 30, 2013 Gilles Guillot (gigu@dtu.dk) September 30, 2013 1 / 29 1 Introductory example 2 One-way ANOVA 3 Two-way ANOVA 4 Two-way ANOVA with interactions
Analysis of variance Gilles Guillot gigu@dtu.dk September 30, 2013 Gilles Guillot (gigu@dtu.dk) September 30, 2013 1 / 29 1 Introductory example 2 One-way ANOVA 3 Two-way ANOVA 4 Two-way ANOVA with interactions
Regression and Models with Multiple Factors. Ch. 17, 18
 Regression and Models with Multiple Factors Ch. 17, 18 Mass 15 20 25 Scatter Plot 70 75 80 Snout-Vent Length Mass 15 20 25 Linear Regression 70 75 80 Snout-Vent Length Least-squares The method of least
Regression and Models with Multiple Factors Ch. 17, 18 Mass 15 20 25 Scatter Plot 70 75 80 Snout-Vent Length Mass 15 20 25 Linear Regression 70 75 80 Snout-Vent Length Least-squares The method of least
Chaper 5: Matrix Approach to Simple Linear Regression. Matrix: A m by n matrix B is a grid of numbers with m rows and n columns. B = b 11 b m1 ...
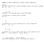 Chaper 5: Matrix Approach to Simple Linear Regression Matrix: A m by n matrix B is a grid of numbers with m rows and n columns B = b 11 b 1n b m1 b mn Element b ik is from the ith row and kth column A
Chaper 5: Matrix Approach to Simple Linear Regression Matrix: A m by n matrix B is a grid of numbers with m rows and n columns B = b 11 b 1n b m1 b mn Element b ik is from the ith row and kth column A
MATH 423/533 - ASSIGNMENT 4 SOLUTIONS
 MATH 423/533 - ASSIGNMENT 4 SOLUTIONS INTRODUCTION This assignment concerns the use of factor predictors in linear regression modelling, and focusses on models with two factors X 1 and X 2 with M 1 and
MATH 423/533 - ASSIGNMENT 4 SOLUTIONS INTRODUCTION This assignment concerns the use of factor predictors in linear regression modelling, and focusses on models with two factors X 1 and X 2 with M 1 and
lm statistics Chris Parrish
 lm statistics Chris Parrish 2017-04-01 Contents s e and R 2 1 experiment1................................................. 2 experiment2................................................. 3 experiment3.................................................
lm statistics Chris Parrish 2017-04-01 Contents s e and R 2 1 experiment1................................................. 2 experiment2................................................. 3 experiment3.................................................
Handling Categorical Predictors: ANOVA
 Handling Categorical Predictors: ANOVA 1/33 I Hate Lines! When we think of experiments, we think of manipulating categories Control, Treatment 1, Treatment 2 Models with Categorical Predictors still reflect
Handling Categorical Predictors: ANOVA 1/33 I Hate Lines! When we think of experiments, we think of manipulating categories Control, Treatment 1, Treatment 2 Models with Categorical Predictors still reflect
STAT 3022 Spring 2007
 Simple Linear Regression Example These commands reproduce what we did in class. You should enter these in R and see what they do. Start by typing > set.seed(42) to reset the random number generator so
Simple Linear Regression Example These commands reproduce what we did in class. You should enter these in R and see what they do. Start by typing > set.seed(42) to reset the random number generator so
Regression Analysis for Data Containing Outliers and High Leverage Points
 Alabama Journal of Mathematics 39 (2015) ISSN 2373-0404 Regression Analysis for Data Containing Outliers and High Leverage Points Asim Kumer Dey Department of Mathematics Lamar University Md. Amir Hossain
Alabama Journal of Mathematics 39 (2015) ISSN 2373-0404 Regression Analysis for Data Containing Outliers and High Leverage Points Asim Kumer Dey Department of Mathematics Lamar University Md. Amir Hossain
Nature vs. nurture? Lecture 18 - Regression: Inference, Outliers, and Intervals. Regression Output. Conditions for inference.
 Understanding regression output from software Nature vs. nurture? Lecture 18 - Regression: Inference, Outliers, and Intervals In 1966 Cyril Burt published a paper called The genetic determination of differences
Understanding regression output from software Nature vs. nurture? Lecture 18 - Regression: Inference, Outliers, and Intervals In 1966 Cyril Burt published a paper called The genetic determination of differences
Regression. Bret Hanlon and Bret Larget. December 8 15, Department of Statistics University of Wisconsin Madison.
 Regression Bret Hanlon and Bret Larget Department of Statistics University of Wisconsin Madison December 8 15, 2011 Regression 1 / 55 Example Case Study The proportion of blackness in a male lion s nose
Regression Bret Hanlon and Bret Larget Department of Statistics University of Wisconsin Madison December 8 15, 2011 Regression 1 / 55 Example Case Study The proportion of blackness in a male lion s nose
Activity #12: More regression topics: LOWESS; polynomial, nonlinear, robust, quantile; ANOVA as regression
 Activity #12: More regression topics: LOWESS; polynomial, nonlinear, robust, quantile; ANOVA as regression Scenario: 31 counts (over a 30-second period) were recorded from a Geiger counter at a nuclear
Activity #12: More regression topics: LOWESS; polynomial, nonlinear, robust, quantile; ANOVA as regression Scenario: 31 counts (over a 30-second period) were recorded from a Geiger counter at a nuclear
Matrices and vectors A matrix is a rectangular array of numbers. Here s an example: A =
 Matrices and vectors A matrix is a rectangular array of numbers Here s an example: 23 14 17 A = 225 0 2 This matrix has dimensions 2 3 The number of rows is first, then the number of columns We can write
Matrices and vectors A matrix is a rectangular array of numbers Here s an example: 23 14 17 A = 225 0 2 This matrix has dimensions 2 3 The number of rows is first, then the number of columns We can write
Unit 6 - Simple linear regression
 Sta 101: Data Analysis and Statistical Inference Dr. Çetinkaya-Rundel Unit 6 - Simple linear regression LO 1. Define the explanatory variable as the independent variable (predictor), and the response variable
Sta 101: Data Analysis and Statistical Inference Dr. Çetinkaya-Rundel Unit 6 - Simple linear regression LO 1. Define the explanatory variable as the independent variable (predictor), and the response variable
Homework1 Yang Sun 2017/9/11
 Homework1 Yang Sun 2017/9/11 1. Describe data According to the data description, the response variable is AmountSpent; the predictors are, Age, Gender, OwnHome, Married, Location, Salary, Children, History,
Homework1 Yang Sun 2017/9/11 1. Describe data According to the data description, the response variable is AmountSpent; the predictors are, Age, Gender, OwnHome, Married, Location, Salary, Children, History,
SCHOOL OF MATHEMATICS AND STATISTICS
 RESTRICTED OPEN BOOK EXAMINATION (Not to be removed from the examination hall) Data provided: Statistics Tables by H.R. Neave MAS5052 SCHOOL OF MATHEMATICS AND STATISTICS Basic Statistics Spring Semester
RESTRICTED OPEN BOOK EXAMINATION (Not to be removed from the examination hall) Data provided: Statistics Tables by H.R. Neave MAS5052 SCHOOL OF MATHEMATICS AND STATISTICS Basic Statistics Spring Semester
27. SIMPLE LINEAR REGRESSION II
 27. SIMPLE LINEAR REGRESSION II The Model In linear regression analysis, we assume that the relationship between X and Y is linear. This does not mean, however, that Y can be perfectly predicted from X.
27. SIMPLE LINEAR REGRESSION II The Model In linear regression analysis, we assume that the relationship between X and Y is linear. This does not mean, however, that Y can be perfectly predicted from X.
Modeling kid s test scores (revisited) Lecture 20 - Model Selection. Model output. Backward-elimination
 Modeling kid s test scores (revisited) Lecture 20 - Model Selection Sta102 / BME102 Colin Rundel November 17, 2014 Predicting cognitive test scores of three- and four-year-old children using characteristics
Modeling kid s test scores (revisited) Lecture 20 - Model Selection Sta102 / BME102 Colin Rundel November 17, 2014 Predicting cognitive test scores of three- and four-year-old children using characteristics
STAT 572 Assignment 5 - Answers Due: March 2, 2007
 1. The file glue.txt contains a data set with the results of an experiment on the dry sheer strength (in pounds per square inch) of birch plywood, bonded with 5 different resin glues A, B, C, D, and E.
1. The file glue.txt contains a data set with the results of an experiment on the dry sheer strength (in pounds per square inch) of birch plywood, bonded with 5 different resin glues A, B, C, D, and E.
Consider fitting a model using ordinary least squares (OLS) regression:
 Example 1: Mating Success of African Elephants In this study, 41 male African elephants were followed over a period of 8 years. The age of the elephant at the beginning of the study and the number of successful
Example 1: Mating Success of African Elephants In this study, 41 male African elephants were followed over a period of 8 years. The age of the elephant at the beginning of the study and the number of successful
BANA 7046 Data Mining I Lecture 2. Linear Regression, Model Assessment, and Cross-validation 1
 BANA 7046 Data Mining I Lecture 2. Linear Regression, Model Assessment, and Cross-validation 1 Shaobo Li University of Cincinnati 1 Partially based on Hastie, et al. (2009) ESL, and James, et al. (2013)
BANA 7046 Data Mining I Lecture 2. Linear Regression, Model Assessment, and Cross-validation 1 Shaobo Li University of Cincinnati 1 Partially based on Hastie, et al. (2009) ESL, and James, et al. (2013)
x 21 x 22 x 23 f X 1 X 2 X 3 ε
 Chapter 2 Estimation 2.1 Example Let s start with an example. Suppose that Y is the fuel consumption of a particular model of car in m.p.g. Suppose that the predictors are 1. X 1 the weight of the car
Chapter 2 Estimation 2.1 Example Let s start with an example. Suppose that Y is the fuel consumption of a particular model of car in m.p.g. Suppose that the predictors are 1. X 1 the weight of the car
y i s 2 X 1 n i 1 1. Show that the least squares estimators can be written as n xx i x i 1 ns 2 X i 1 n ` px xqx i x i 1 pδ ij 1 n px i xq x j x
 Question 1 Suppose that we have data Let x 1 n x i px 1, y 1 q,..., px n, y n q. ȳ 1 n y i s 2 X 1 n px i xq 2 Throughout this question, we assume that the simple linear model is correct. We also assume
Question 1 Suppose that we have data Let x 1 n x i px 1, y 1 q,..., px n, y n q. ȳ 1 n y i s 2 X 1 n px i xq 2 Throughout this question, we assume that the simple linear model is correct. We also assume
Multiple Predictor Variables: ANOVA
 Multiple Predictor Variables: ANOVA 1/32 Linear Models with Many Predictors Multiple regression has many predictors BUT - so did 1-way ANOVA if treatments had 2 levels What if there are multiple treatment
Multiple Predictor Variables: ANOVA 1/32 Linear Models with Many Predictors Multiple regression has many predictors BUT - so did 1-way ANOVA if treatments had 2 levels What if there are multiple treatment
Swarthmore Honors Exam 2015: Statistics
 Swarthmore Honors Exam 2015: Statistics 1 Swarthmore Honors Exam 2015: Statistics John W. Emerson, Yale University NAME: Instructions: This is a closed-book three-hour exam having 7 questions. You may
Swarthmore Honors Exam 2015: Statistics 1 Swarthmore Honors Exam 2015: Statistics John W. Emerson, Yale University NAME: Instructions: This is a closed-book three-hour exam having 7 questions. You may
6.1 Introduction. Regression Model:
 6.1 Introduction Regression Model: y = Xβ + ɛ Assumptions: 1. The relationship between y and the predictors is linear. 2. The noise term has zero mean. ɛ 3. All ε s have the same variance σ 2. 4. The ε
6.1 Introduction Regression Model: y = Xβ + ɛ Assumptions: 1. The relationship between y and the predictors is linear. 2. The noise term has zero mean. ɛ 3. All ε s have the same variance σ 2. 4. The ε
Final Exam - Solutions
 Ecn 102 - Analysis of Economic Data University of California - Davis March 19, 2010 Instructor: John Parman Final Exam - Solutions You have until 5:30pm to complete this exam. Please remember to put your
Ecn 102 - Analysis of Economic Data University of California - Davis March 19, 2010 Instructor: John Parman Final Exam - Solutions You have until 5:30pm to complete this exam. Please remember to put your
( ), which of the coefficients would end
 Discussion Sheet 29.7.9 Qualitative Variables We have devoted most of our attention in multiple regression to quantitative or numerical variables. MR models can become more useful and complex when we consider
Discussion Sheet 29.7.9 Qualitative Variables We have devoted most of our attention in multiple regression to quantitative or numerical variables. MR models can become more useful and complex when we consider
Bivariate data analysis
 Bivariate data analysis Categorical data - creating data set Upload the following data set to R Commander sex female male male male male female female male female female eye black black blue green green
Bivariate data analysis Categorical data - creating data set Upload the following data set to R Commander sex female male male male male female female male female female eye black black blue green green
36-707: Regression Analysis Homework Solutions. Homework 3
 36-707: Regression Analysis Homework Solutions Homework 3 Fall 2012 Problem 1 Y i = βx i + ɛ i, i {1, 2,..., n}. (a) Find the LS estimator of β: RSS = Σ n i=1(y i βx i ) 2 RSS β = Σ n i=1( 2X i )(Y i βx
36-707: Regression Analysis Homework Solutions Homework 3 Fall 2012 Problem 1 Y i = βx i + ɛ i, i {1, 2,..., n}. (a) Find the LS estimator of β: RSS = Σ n i=1(y i βx i ) 2 RSS β = Σ n i=1( 2X i )(Y i βx
STAT 571A Advanced Statistical Regression Analysis. Chapter 8 NOTES Quantitative and Qualitative Predictors for MLR
 STAT 571A Advanced Statistical Regression Analysis Chapter 8 NOTES Quantitative and Qualitative Predictors for MLR 2015 University of Arizona Statistics GIDP. All rights reserved, except where previous
STAT 571A Advanced Statistical Regression Analysis Chapter 8 NOTES Quantitative and Qualitative Predictors for MLR 2015 University of Arizona Statistics GIDP. All rights reserved, except where previous
MATH Notebook 4 Spring 2018
 MATH448001 Notebook 4 Spring 2018 prepared by Professor Jenny Baglivo c Copyright 2010 2018 by Jenny A. Baglivo. All Rights Reserved. 4 MATH448001 Notebook 4 3 4.1 Simple Linear Model.................................
MATH448001 Notebook 4 Spring 2018 prepared by Professor Jenny Baglivo c Copyright 2010 2018 by Jenny A. Baglivo. All Rights Reserved. 4 MATH448001 Notebook 4 3 4.1 Simple Linear Model.................................
Applied Regression Analysis
 Applied Regression Analysis Chapter 3 Multiple Linear Regression Hongcheng Li April, 6, 2013 Recall simple linear regression 1 Recall simple linear regression 2 Parameter Estimation 3 Interpretations of
Applied Regression Analysis Chapter 3 Multiple Linear Regression Hongcheng Li April, 6, 2013 Recall simple linear regression 1 Recall simple linear regression 2 Parameter Estimation 3 Interpretations of
Topic 14: Inference in Multiple Regression
 Topic 14: Inference in Multiple Regression Outline Review multiple linear regression Inference of regression coefficients Application to book example Inference of mean Application to book example Inference
Topic 14: Inference in Multiple Regression Outline Review multiple linear regression Inference of regression coefficients Application to book example Inference of mean Application to book example Inference
School of Mathematical Sciences. Question 1
 School of Mathematical Sciences MTH5120 Statistical Modelling I Practical 8 and Assignment 7 Solutions Question 1 Figure 1: The residual plots do not contradict the model assumptions of normality, constant
School of Mathematical Sciences MTH5120 Statistical Modelling I Practical 8 and Assignment 7 Solutions Question 1 Figure 1: The residual plots do not contradict the model assumptions of normality, constant
6. Multiple Linear Regression
 6. Multiple Linear Regression SLR: 1 predictor X, MLR: more than 1 predictor Example data set: Y i = #points scored by UF football team in game i X i1 = #games won by opponent in their last 10 games X
6. Multiple Linear Regression SLR: 1 predictor X, MLR: more than 1 predictor Example data set: Y i = #points scored by UF football team in game i X i1 = #games won by opponent in their last 10 games X
INTRODUCING LINEAR REGRESSION MODELS Response or Dependent variable y
 INTRODUCING LINEAR REGRESSION MODELS Response or Dependent variable y Predictor or Independent variable x Model with error: for i = 1,..., n, y i = α + βx i + ε i ε i : independent errors (sampling, measurement,
INTRODUCING LINEAR REGRESSION MODELS Response or Dependent variable y Predictor or Independent variable x Model with error: for i = 1,..., n, y i = α + βx i + ε i ε i : independent errors (sampling, measurement,
Lab 3 A Quick Introduction to Multiple Linear Regression Psychology The Multiple Linear Regression Model
 Lab 3 A Quick Introduction to Multiple Linear Regression Psychology 310 Instructions.Work through the lab, saving the output as you go. You will be submitting your assignment as an R Markdown document.
Lab 3 A Quick Introduction to Multiple Linear Regression Psychology 310 Instructions.Work through the lab, saving the output as you go. You will be submitting your assignment as an R Markdown document.
Coefficient of Determination
 Coefficient of Determination ST 430/514 The coefficient of determination, R 2, is defined as before: R 2 = 1 SS E (yi ŷ i ) = 1 2 SS yy (yi ȳ) 2 The interpretation of R 2 is still the fraction of variance
Coefficient of Determination ST 430/514 The coefficient of determination, R 2, is defined as before: R 2 = 1 SS E (yi ŷ i ) = 1 2 SS yy (yi ȳ) 2 The interpretation of R 2 is still the fraction of variance
