Gauss Quadrature Rule of Integration
|
|
|
- Maximillian Edwards
- 5 years ago
- Views:
Transcription
1 Guss Qudrture Rule o Integrtion Mjor: All Engineering Mjors Authors: Autr Kw, Chrlie Brker Trnsorming Numeril Methods Edution or STEM Undergrdutes /0/00
2 Guss Qudrture Rule o Integrtion
3 Wht is Integrtion? Integrtion The proess o mesuring the re under urve. y )d ) I )d Where: ) is the integrnd lower limit o integrtion upper limit o integrtion
4 Two-Point Gussin Qudrture Rule 4
5 5 Bsis o the Gussin Qudrture Rule Previously, the Trpezoidl Rule ws developed y the method o undetermined oeiients. The result o tht development is summrized elow. ) ) ) ) ) d
6 Bsis o the Gussin Qudrture Rule The two-point Guss Qudrture Rule is n etension o the Trpezoidl Rule pproimtion where the rguments o the untion re not predetermined s nd ut s unknowns nd. In the two-point Guss Qudrture Rule, the integrl is pproimted s I )d ) ) 6
7 7 Bsis o the Gussin Qudrture Rule The our unknowns,, nd re ound y ssuming tht the ormul gives et results or integrting generl third order polynomil,. ) 0 Hene ) d )d )
8 8 Bsis o the Gussin Qudrture Rule It ollows tht ) ) 0 0 )d Equting Equtions the two previous two epressions yield ) ) ) 0 0 ) ) ) ) 0
9 9 Bsis o the Gussin Qudrture Rule Sine the onstnts 0,,, re ritrry 4 4 4
10 0 Bsis o Guss Qudrture The previous our simultneous nonliner Equtions hve only one eptle solution,
11 Bsis o Guss Qudrture Hene Two-Point Gussin Qudrture Rule ) ) ) d
12 Higher Point Gussin Qudrture Formuls
13 Higher Point Gussin Qudrture Formuls ) ) ) ) d is lled the three-point Guss Qudrture Rule. The oeiients,, nd, nd the untionl rguments,, nd re lulted y ssuming the ormul gives et epressions or ) d Generl n-point rules would pproimte the integrl ) ) ) )d n n integrting ith order polynomil
14 Arguments nd Weighing Ftors or n-point Guss Qudrture Formuls In hndooks, oeiients nd rguments given or n-point Guss Qudrture Rule re given or integrls g )d n i s shown in Tle. i g i ) Tle : Weighting tors nd untion rguments used in Guss Qudrture Formuls. Points Weighting Ftors Funtion Arguments
15 Arguments nd Weighing Ftors or n-point Guss Qudrture Formuls Tle ont.) : Weighting tors nd untion rguments used in Guss Qudrture Formuls. Points Weighting Ftors Funtion Arguments
16 Arguments nd Weighing Ftors or n-point Guss Qudrture So i the tle is given or g Formuls )d integrls, how does one solve )d? The nswer lies in tht ny integrl with limits o [, ] n e onverted into n integrl with limits [,] mt Let I, then t I then t, Suh tht: 6 m
17 Arguments nd Weighing Ftors or n-point Guss Qudrture Formuls Then Hene t d dt Sustituting our vlues o, nd d into the integrl gives us ) d t dt 7
18 Emple For n integrl Rule. )d, derive the one-point Gussin Qudrture Solution The one-point Gussin Qudrture Rule is )d ) 8
19 Solution The two unknowns, nd re ound y ssuming tht the ormul gives et results or integrting generl irst order polynomil, ) 0. ) d ) 0 d 0 0 ) 9
20 Solution It ollows tht ) ) d Equting Equtions, the two previous two epressions yield 0 ) 0 ) 0 ) ) 0 0
21 Bsis o the Gussin Qudrture Rule Sine the onstnts 0, nd re ritrry giving
22 Solution Hene One-Point Gussin Qudrture Rule ) d ) )
23 Emple ) Use two-point Guss Qudrture Rule to pproimte the distne overed y roket rom t8 to t0 s given y ln 9. 8t dt t ) Find the true error, E t or prt ). ) Also, ind the solute reltive true error, or prt ).
24 Solution First, hnge the limits o integrtion rom [8,0] to [-,] y previous reltions s ollows 0 t )dt d 9) d 4
25 Solution ont) Net, get weighting tors nd untion rgument vlues rom Tle or the two point rule,
26 Solution ont.) Now we n use the Guss Qudrture ormul 9) d 9) 9) ) 9) ) 9) ) ) ) ) m 6
27 Solution ont) sine ) 000ln ) ) ) 000ln ) )
28 Solution ont) ) The true error, t ) E t E, is True Vlue Approimte Vlue m The solute reltive true error, t, is Et vlue 06.4m) t 00% %
29 Additionl Resoures For ll resoures on this topi suh s digitl udiovisul letures, primers, tetook hpters, multiple-hoie tests, worksheets in MATLAB, MATHEMATICA, MthCd nd MAPLE, logs, relted physil prolems, plese visit drture.html
30 THE END
Gauss Quadrature Rule of Integration
 Guss Qudrture Rule o Integrtion Computer Engineering Mjors Authors: Autr Kw, Chrlie Brker http://numerilmethods.eng.us.edu Trnsorming Numeril Methods Edution or STEM Undergrdutes /0/00 http://numerilmethods.eng.us.edu
Guss Qudrture Rule o Integrtion Computer Engineering Mjors Authors: Autr Kw, Chrlie Brker http://numerilmethods.eng.us.edu Trnsorming Numeril Methods Edution or STEM Undergrdutes /0/00 http://numerilmethods.eng.us.edu
Chapter Gauss Quadrature Rule of Integration
 Chpter 7. Guss Qudrture Rule o Integrtion Ater reding this hpter, you should e le to:. derive the Guss qudrture method or integrtion nd e le to use it to solve prolems, nd. use Guss qudrture method to
Chpter 7. Guss Qudrture Rule o Integrtion Ater reding this hpter, you should e le to:. derive the Guss qudrture method or integrtion nd e le to use it to solve prolems, nd. use Guss qudrture method to
Simpson s 1/3 rd Rule of Integration
 Simpso s 1/3 rd Rule o Itegrtio Mjor: All Egieerig Mjors Authors: Autr Kw, Chrlie Brker Trsormig Numericl Methods Eductio or STEM Udergrdutes 1/10/010 1 Simpso s 1/3 rd Rule o Itegrtio Wht is Itegrtio?
Simpso s 1/3 rd Rule o Itegrtio Mjor: All Egieerig Mjors Authors: Autr Kw, Chrlie Brker Trsormig Numericl Methods Eductio or STEM Udergrdutes 1/10/010 1 Simpso s 1/3 rd Rule o Itegrtio Wht is Itegrtio?
Trapezoidal Rule of Integration
 Trpezoidl Rule o Itegrtio Mjor: All Egieerig Mjors Authors: Autr Kw, Chrlie Brker Trsormig Numericl Methods Eductio or STEM Udergrdutes /0/200 Trpezoidl Rule o Itegrtio Wht is Itegrtio Itegrtio: The process
Trpezoidl Rule o Itegrtio Mjor: All Egieerig Mjors Authors: Autr Kw, Chrlie Brker Trsormig Numericl Methods Eductio or STEM Udergrdutes /0/200 Trpezoidl Rule o Itegrtio Wht is Itegrtio Itegrtio: The process
Trapezoidal Rule of Integration
 Trpezoidl Rule o Itegrtio Civil Egieerig Mjors Authors: Autr Kw, Chrlie Brker http://umericlmethods.eg.us.edu Trsormig Numericl Methods Eductio or STEM Udergrdutes /0/00 http://umericlmethods.eg.us.edu
Trpezoidl Rule o Itegrtio Civil Egieerig Mjors Authors: Autr Kw, Chrlie Brker http://umericlmethods.eg.us.edu Trsormig Numericl Methods Eductio or STEM Udergrdutes /0/00 http://umericlmethods.eg.us.edu
Numerical Methods. Lecture 5. Numerical integration. dr hab. inż. Katarzyna Zakrzewska, prof. AGH. Numerical Methods lecture 5 1
 Numeril Methods Leture 5. Numeril itegrtio dr h. iż. Ktrzy Zkrzewsk, pro. AGH Numeril Methods leture 5 Outlie Trpezoidl rule Multi-segmet trpezoidl rule Rihrdso etrpoltio Romerg's method Simpso's rule
Numeril Methods Leture 5. Numeril itegrtio dr h. iż. Ktrzy Zkrzewsk, pro. AGH Numeril Methods leture 5 Outlie Trpezoidl rule Multi-segmet trpezoidl rule Rihrdso etrpoltio Romerg's method Simpso's rule
Calculus Cheat Sheet. Integrals Definitions. where F( x ) is an anti-derivative of f ( x ). Fundamental Theorem of Calculus. dx = f x dx g x dx
 Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Chapter 3 Single Random Variables and Probability Distributions (Part 2)
 Chpter 3 Single Rndom Vriles nd Proilit Distriutions (Prt ) Contents Wht is Rndom Vrile? Proilit Distriution Functions Cumultive Distriution Function Proilit Densit Function Common Rndom Vriles nd their
Chpter 3 Single Rndom Vriles nd Proilit Distriutions (Prt ) Contents Wht is Rndom Vrile? Proilit Distriution Functions Cumultive Distriution Function Proilit Densit Function Common Rndom Vriles nd their
Calculus AB. For a function f(x), the derivative would be f '(
 lculus AB Derivtive Formuls Derivtive Nottion: For function f(), the derivtive would e f '( ) Leiniz's Nottion: For the derivtive of y in terms of, we write d For the second derivtive using Leiniz's Nottion:
lculus AB Derivtive Formuls Derivtive Nottion: For function f(), the derivtive would e f '( ) Leiniz's Nottion: For the derivtive of y in terms of, we write d For the second derivtive using Leiniz's Nottion:
Time in Seconds Speed in ft/sec (a) Sketch a possible graph for this function.
 4. Are under Curve A cr is trveling so tht its speed is never decresing during 1-second intervl. The speed t vrious moments in time is listed in the tle elow. Time in Seconds 3 6 9 1 Speed in t/sec 3 37
4. Are under Curve A cr is trveling so tht its speed is never decresing during 1-second intervl. The speed t vrious moments in time is listed in the tle elow. Time in Seconds 3 6 9 1 Speed in t/sec 3 37
Integration. antidifferentiation
 9 Integrtion 9A Antidifferentition 9B Integrtion of e, sin ( ) nd os ( ) 9C Integrtion reognition 9D Approimting res enlosed funtions 9E The fundmentl theorem of integrl lulus 9F Signed res 9G Further
9 Integrtion 9A Antidifferentition 9B Integrtion of e, sin ( ) nd os ( ) 9C Integrtion reognition 9D Approimting res enlosed funtions 9E The fundmentl theorem of integrl lulus 9F Signed res 9G Further
] dx (3) = [15x] 2 0
![] dx (3) = [15x] 2 0 ] dx (3) = [15x] 2 0](/thumbs/80/81916477.jpg) Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
The Trapezoidal Rule
 _.qd // : PM Pge 9 SECTION. Numericl Integrtion 9 f Section. The re of the region cn e pproimted using four trpezoids. Figure. = f( ) f( ) n The re of the first trpezoid is f f n. Figure. = Numericl Integrtion
_.qd // : PM Pge 9 SECTION. Numericl Integrtion 9 f Section. The re of the region cn e pproimted using four trpezoids. Figure. = f( ) f( ) n The re of the first trpezoid is f f n. Figure. = Numericl Integrtion
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
Review Exercises for Chapter 4
 _R.qd // : PM Pge CHAPTER Integrtion Review Eercises for Chpter In Eercises nd, use the grph of to sketch grph of f. To print n enlrged cop of the grph, go to the wesite www.mthgrphs.com... In Eercises
_R.qd // : PM Pge CHAPTER Integrtion Review Eercises for Chpter In Eercises nd, use the grph of to sketch grph of f. To print n enlrged cop of the grph, go to the wesite www.mthgrphs.com... In Eercises
University of Sioux Falls. MAT204/205 Calculus I/II
 University of Sioux Flls MAT204/205 Clulus I/II Conepts ddressed: Clulus Textook: Thoms Clulus, 11 th ed., Weir, Hss, Giordno 1. Use stndrd differentition nd integrtion tehniques. Differentition tehniques
University of Sioux Flls MAT204/205 Clulus I/II Conepts ddressed: Clulus Textook: Thoms Clulus, 11 th ed., Weir, Hss, Giordno 1. Use stndrd differentition nd integrtion tehniques. Differentition tehniques
Numbers and indices. 1.1 Fractions. GCSE C Example 1. Handy hint. Key point
 GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
Polynomial Approximations for the Natural Logarithm and Arctangent Functions. Math 230
 Polynomil Approimtions for the Nturl Logrithm nd Arctngent Functions Mth 23 You recll from first semester clculus how one cn use the derivtive to find n eqution for the tngent line to function t given
Polynomil Approimtions for the Nturl Logrithm nd Arctngent Functions Mth 23 You recll from first semester clculus how one cn use the derivtive to find n eqution for the tngent line to function t given
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
2 b. , a. area is S= 2π xds. Again, understand where these formulas came from (pages ).
 AP Clculus BC Review Chpter 8 Prt nd Chpter 9 Things to Know nd Be Ale to Do Know everything from the first prt of Chpter 8 Given n integrnd figure out how to ntidifferentite it using ny of the following
AP Clculus BC Review Chpter 8 Prt nd Chpter 9 Things to Know nd Be Ale to Do Know everything from the first prt of Chpter 8 Given n integrnd figure out how to ntidifferentite it using ny of the following
CHAPTER 6b. NUMERICAL INTERPOLATION
 CHAPTER 6. NUMERICAL INTERPOLATION A. J. Clrk School o Engineering Deprtment o Civil nd Environmentl Engineering y Dr. Irhim A. Asskk Spring ENCE - Computtion s in Civil Engineering II Deprtment o Civil
CHAPTER 6. NUMERICAL INTERPOLATION A. J. Clrk School o Engineering Deprtment o Civil nd Environmentl Engineering y Dr. Irhim A. Asskk Spring ENCE - Computtion s in Civil Engineering II Deprtment o Civil
COSC 3361 Numerical Analysis I Numerical Integration and Differentiation (III) - Gauss Quadrature and Adaptive Quadrature
 COSC 336 Numericl Anlysis I Numericl Integrtion nd Dierentition III - Guss Qudrture nd Adptive Qudrture Edgr Griel Fll 5 COSC 336 Numericl Anlysis I Edgr Griel Summry o the lst lecture I For pproximting
COSC 336 Numericl Anlysis I Numericl Integrtion nd Dierentition III - Guss Qudrture nd Adptive Qudrture Edgr Griel Fll 5 COSC 336 Numericl Anlysis I Edgr Griel Summry o the lst lecture I For pproximting
MA10207B: ANALYSIS SECOND SEMESTER OUTLINE NOTES
 MA10207B: ANALYSIS SECOND SEMESTER OUTLINE NOTES CHARLIE COLLIER UNIVERSITY OF BATH These notes hve been typeset by Chrlie Collier nd re bsed on the leture notes by Adrin Hill nd Thoms Cottrell. These
MA10207B: ANALYSIS SECOND SEMESTER OUTLINE NOTES CHARLIE COLLIER UNIVERSITY OF BATH These notes hve been typeset by Chrlie Collier nd re bsed on the leture notes by Adrin Hill nd Thoms Cottrell. These
50 AMC Lectures Problem Book 2 (36) Substitution Method
 0 AMC Letures Prolem Book Sustitution Metho PROBLEMS Prolem : Solve for rel : 9 + 99 + 9 = Prolem : Solve for rel : 0 9 8 8 Prolem : Show tht if 8 Prolem : Show tht + + if rel numers,, n stisf + + = Prolem
0 AMC Letures Prolem Book Sustitution Metho PROBLEMS Prolem : Solve for rel : 9 + 99 + 9 = Prolem : Solve for rel : 0 9 8 8 Prolem : Show tht if 8 Prolem : Show tht + + if rel numers,, n stisf + + = Prolem
The practical version
 Roerto s Notes on Integrl Clculus Chpter 4: Definite integrls nd the FTC Section 7 The Fundmentl Theorem of Clculus: The prcticl version Wht you need to know lredy: The theoreticl version of the FTC. Wht
Roerto s Notes on Integrl Clculus Chpter 4: Definite integrls nd the FTC Section 7 The Fundmentl Theorem of Clculus: The prcticl version Wht you need to know lredy: The theoreticl version of the FTC. Wht
For a, b, c, d positive if a b and. ac bd. Reciprocal relations for a and b positive. If a > b then a ab > b. then
 Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
MAT 403 NOTES 4. f + f =
 MAT 403 NOTES 4 1. Fundmentl Theorem o Clulus We will proo more generl version o the FTC thn the textook. But just like the textook, we strt with the ollowing proposition. Let R[, ] e the set o Riemnn
MAT 403 NOTES 4 1. Fundmentl Theorem o Clulus We will proo more generl version o the FTC thn the textook. But just like the textook, we strt with the ollowing proposition. Let R[, ] e the set o Riemnn
Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx
![Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx](/thumbs/79/79316452.jpg) Fill in the Blnks for the Big Topis in Chpter 5: The Definite Integrl Estimting n integrl using Riemnn sum:. The Left rule uses the left endpoint of eh suintervl.. The Right rule uses the right endpoint
Fill in the Blnks for the Big Topis in Chpter 5: The Definite Integrl Estimting n integrl using Riemnn sum:. The Left rule uses the left endpoint of eh suintervl.. The Right rule uses the right endpoint
September 13 Homework Solutions
 College of Engineering nd Computer Science Mechnicl Engineering Deprtment Mechnicl Engineering 5A Seminr in Engineering Anlysis Fll Ticket: 5966 Instructor: Lrry Cretto Septemer Homework Solutions. Are
College of Engineering nd Computer Science Mechnicl Engineering Deprtment Mechnicl Engineering 5A Seminr in Engineering Anlysis Fll Ticket: 5966 Instructor: Lrry Cretto Septemer Homework Solutions. Are
Chapter Direct Method of Interpolation More Examples Electrical Engineering
 Chpter. Direct Method of Interpoltion More Emples Electricl Engineering Emple hermistors re used to mesure the temperture of bodies. hermistors re bsed on mterils chnge in resistnce with temperture. o
Chpter. Direct Method of Interpoltion More Emples Electricl Engineering Emple hermistors re used to mesure the temperture of bodies. hermistors re bsed on mterils chnge in resistnce with temperture. o
MA Exam 2 Study Guide, Fall u n du (or the integral of linear combinations
 LESSON 0 Chpter 7.2 Trigonometric Integrls. Bsic trig integrls you should know. sin = cos + C cos = sin + C sec 2 = tn + C sec tn = sec + C csc 2 = cot + C csc cot = csc + C MA 6200 Em 2 Study Guide, Fll
LESSON 0 Chpter 7.2 Trigonometric Integrls. Bsic trig integrls you should know. sin = cos + C cos = sin + C sec 2 = tn + C sec tn = sec + C csc 2 = cot + C csc cot = csc + C MA 6200 Em 2 Study Guide, Fll
Goals: Determine how to calculate the area described by a function. Define the definite integral. Explore the relationship between the definite
 Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Polynomials. Polynomials. Curriculum Ready ACMNA:
 Polynomils Polynomils Curriulum Redy ACMNA: 66 www.mthletis.om Polynomils POLYNOMIALS A polynomil is mthemtil expression with one vrile whose powers re neither negtive nor frtions. The power in eh expression
Polynomils Polynomils Curriulum Redy ACMNA: 66 www.mthletis.om Polynomils POLYNOMIALS A polynomil is mthemtil expression with one vrile whose powers re neither negtive nor frtions. The power in eh expression
Core 2 Logarithms and exponentials. Section 1: Introduction to logarithms
 Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
AP CALCULUS Test #6: Unit #6 Basic Integration and Applications
 AP CALCULUS Test #6: Unit #6 Bsi Integrtion nd Applitions A GRAPHING CALCULATOR IS REQUIRED FOR SOME PROBLEMS OR PARTS OF PROBLEMS IN THIS PART OF THE EXAMINATION. () The ext numeril vlue of the orret
AP CALCULUS Test #6: Unit #6 Bsi Integrtion nd Applitions A GRAPHING CALCULATOR IS REQUIRED FOR SOME PROBLEMS OR PARTS OF PROBLEMS IN THIS PART OF THE EXAMINATION. () The ext numeril vlue of the orret
Logarithms LOGARITHMS.
 Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Improper Integrals. Introduction. Type 1: Improper Integrals on Infinite Intervals. When we defined the definite integral.
 Improper Integrls Introduction When we defined the definite integrl f d we ssumed tht f ws continuous on [, ] where [, ] ws finite, closed intervl There re t lest two wys this definition cn fil to e stisfied:
Improper Integrls Introduction When we defined the definite integrl f d we ssumed tht f ws continuous on [, ] where [, ] ws finite, closed intervl There re t lest two wys this definition cn fil to e stisfied:
Section 4: Integration ECO4112F 2011
 Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
Autar Kaw Benjamin Rigsby. Transforming Numerical Methods Education for STEM Undergraduates
 Autr Kw Bejmi Rigsby http://m.mthforcollege.com Trsformig Numericl Methods Eductio for STEM Udergrdutes http://m.mthforcollege.com . solve set of simulteous lier equtios usig Nïve Guss elimitio,. ler the
Autr Kw Bejmi Rigsby http://m.mthforcollege.com Trsformig Numericl Methods Eductio for STEM Udergrdutes http://m.mthforcollege.com . solve set of simulteous lier equtios usig Nïve Guss elimitio,. ler the
Quadrature Rules for Evaluation of Hyper Singular Integrals
 Applied Mthemticl Sciences, Vol., 01, no. 117, 539-55 HIKARI Ltd, www.m-hikri.com http://d.doi.org/10.19/ms.01.75 Qudrture Rules or Evlution o Hyper Singulr Integrls Prsnt Kumr Mohnty Deprtment o Mthemtics
Applied Mthemticl Sciences, Vol., 01, no. 117, 539-55 HIKARI Ltd, www.m-hikri.com http://d.doi.org/10.19/ms.01.75 Qudrture Rules or Evlution o Hyper Singulr Integrls Prsnt Kumr Mohnty Deprtment o Mthemtics
4.6 Numerical Integration
 .6 Numericl Integrtion 5.6 Numericl Integrtion Approimte definite integrl using the Trpezoidl Rule. Approimte definite integrl using Simpson s Rule. Anlze the pproimte errors in the Trpezoidl Rule nd Simpson
.6 Numericl Integrtion 5.6 Numericl Integrtion Approimte definite integrl using the Trpezoidl Rule. Approimte definite integrl using Simpson s Rule. Anlze the pproimte errors in the Trpezoidl Rule nd Simpson
Chapter 6 Techniques of Integration
 MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
8.3 THE HYPERBOLA OBJECTIVES
 8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
The Ellipse. is larger than the other.
 The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
Lecture 14: Quadrature
 Lecture 14: Qudrture This lecture is concerned with the evlution of integrls fx)dx 1) over finite intervl [, b] The integrnd fx) is ssumed to be rel-vlues nd smooth The pproximtion of n integrl by numericl
Lecture 14: Qudrture This lecture is concerned with the evlution of integrls fx)dx 1) over finite intervl [, b] The integrnd fx) is ssumed to be rel-vlues nd smooth The pproximtion of n integrl by numericl
Review of Gaussian Quadrature method
 Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
On the Scale factor of the Universe and Redshift.
 On the Sle ftor of the Universe nd Redshift. J. M. unter. john@grvity.uk.om ABSTRACT It is proposed tht there hs been longstnding misunderstnding of the reltionship between sle ftor of the universe nd
On the Sle ftor of the Universe nd Redshift. J. M. unter. john@grvity.uk.om ABSTRACT It is proposed tht there hs been longstnding misunderstnding of the reltionship between sle ftor of the universe nd
Generalization of 2-Corner Frequency Source Models Used in SMSIM
 Generliztion o 2-Corner Frequeny Soure Models Used in SMSIM Dvid M. Boore 26 Mrh 213, orreted Figure 1 nd 2 legends on 5 April 213, dditionl smll orretions on 29 My 213 Mny o the soure spetr models ville
Generliztion o 2-Corner Frequeny Soure Models Used in SMSIM Dvid M. Boore 26 Mrh 213, orreted Figure 1 nd 2 legends on 5 April 213, dditionl smll orretions on 29 My 213 Mny o the soure spetr models ville
Construction of Gauss Quadrature Rules
 Jim Lmbers MAT 772 Fll Semester 2010-11 Lecture 15 Notes These notes correspond to Sections 10.2 nd 10.3 in the text. Construction of Guss Qudrture Rules Previously, we lerned tht Newton-Cotes qudrture
Jim Lmbers MAT 772 Fll Semester 2010-11 Lecture 15 Notes These notes correspond to Sections 10.2 nd 10.3 in the text. Construction of Guss Qudrture Rules Previously, we lerned tht Newton-Cotes qudrture
Chapter 9 Definite Integrals
 Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
More Properties of the Riemann Integral
 More Properties of the Riemnn Integrl Jmes K. Peterson Deprtment of Biologil Sienes nd Deprtment of Mthemtil Sienes Clemson University Februry 15, 2018 Outline More Riemnn Integrl Properties The Fundmentl
More Properties of the Riemnn Integrl Jmes K. Peterson Deprtment of Biologil Sienes nd Deprtment of Mthemtil Sienes Clemson University Februry 15, 2018 Outline More Riemnn Integrl Properties The Fundmentl
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
Chapter 6 Notes, Larson/Hostetler 3e
 Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
APPM 1360 Exam 2 Spring 2016
 APPM 6 Em Spring 6. 8 pts, 7 pts ech For ech of the following prts, let f + nd g 4. For prts, b, nd c, set up, but do not evlute, the integrl needed to find the requested informtion. The volume of the
APPM 6 Em Spring 6. 8 pts, 7 pts ech For ech of the following prts, let f + nd g 4. For prts, b, nd c, set up, but do not evlute, the integrl needed to find the requested informtion. The volume of the
The Double Integral. The Riemann sum of a function f (x; y) over this partition of [a; b] [c; d] is. f (r j ; t k ) x j y k
![The Double Integral. The Riemann sum of a function f (x; y) over this partition of [a; b] [c; d] is. f (r j ; t k ) x j y k The Double Integral. The Riemann sum of a function f (x; y) over this partition of [a; b] [c; d] is. f (r j ; t k ) x j y k](/thumbs/86/94790710.jpg) The Double Integrl De nition of the Integrl Iterted integrls re used primrily s tool for omputing double integrls, where double integrl is n integrl of f (; y) over region : In this setion, we de ne double
The Double Integrl De nition of the Integrl Iterted integrls re used primrily s tool for omputing double integrls, where double integrl is n integrl of f (; y) over region : In this setion, we de ne double
H (2a, a) (u 2a) 2 (E) Show that u v 4a. Explain why this implies that u v 4a, with equality if and only u a if u v 2a.
 Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
HOMEWORK SOLUTIONS MATH 1910 Sections 7.9, 8.1 Fall 2016
 HOMEWORK SOLUTIONS MATH 9 Sections 7.9, 8. Fll 6 Problem 7.9.33 Show tht for ny constnts M,, nd, the function yt) = )) t ) M + tnh stisfies the logistic eqution: y SOLUTION. Let Then nd Finlly, y = y M
HOMEWORK SOLUTIONS MATH 9 Sections 7.9, 8. Fll 6 Problem 7.9.33 Show tht for ny constnts M,, nd, the function yt) = )) t ) M + tnh stisfies the logistic eqution: y SOLUTION. Let Then nd Finlly, y = y M
Lecture 6: Singular Integrals, Open Quadrature rules, and Gauss Quadrature
 Lecture notes on Vritionl nd Approximte Methods in Applied Mthemtics - A Peirce UBC Lecture 6: Singulr Integrls, Open Qudrture rules, nd Guss Qudrture (Compiled 6 August 7) In this lecture we discuss the
Lecture notes on Vritionl nd Approximte Methods in Applied Mthemtics - A Peirce UBC Lecture 6: Singulr Integrls, Open Qudrture rules, nd Guss Qudrture (Compiled 6 August 7) In this lecture we discuss the
Calculus AB Section I Part A A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAMINATION
 lculus Section I Prt LULTOR MY NOT US ON THIS PRT OF TH XMINTION In this test: Unless otherwise specified, the domin of function f is ssumed to e the set of ll rel numers for which f () is rel numer..
lculus Section I Prt LULTOR MY NOT US ON THIS PRT OF TH XMINTION In this test: Unless otherwise specified, the domin of function f is ssumed to e the set of ll rel numers for which f () is rel numer..
Solutions to Assignment 1
 MTHE 237 Fll 2015 Solutions to Assignment 1 Problem 1 Find the order of the differentil eqution: t d3 y dt 3 +t2 y = os(t. Is the differentil eqution liner? Is the eqution homogeneous? b Repet the bove
MTHE 237 Fll 2015 Solutions to Assignment 1 Problem 1 Find the order of the differentil eqution: t d3 y dt 3 +t2 y = os(t. Is the differentil eqution liner? Is the eqution homogeneous? b Repet the bove
Solids of Revolution
 Solis of Revolution Solis of revolution re rete tking n re n revolving it roun n is of rottion. There re two methos to etermine the volume of the soli of revolution: the isk metho n the shell metho. Disk
Solis of Revolution Solis of revolution re rete tking n re n revolving it roun n is of rottion. There re two methos to etermine the volume of the soli of revolution: the isk metho n the shell metho. Disk
AP Calculus AB Unit 4 Assessment
 Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
CAAM 453 NUMERICAL ANALYSIS I Examination There are four questions, plus a bonus. Do not look at them until you begin the exam.
 Exmintion 1 Posted 23 October 2002. Due no lter thn 5pm on Mondy, 28 October 2002. Instructions: 1. Time limit: 3 uninterrupted hours. 2. There re four questions, plus bonus. Do not look t them until you
Exmintion 1 Posted 23 October 2002. Due no lter thn 5pm on Mondy, 28 October 2002. Instructions: 1. Time limit: 3 uninterrupted hours. 2. There re four questions, plus bonus. Do not look t them until you
The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a).
![The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a). The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a).](/thumbs/78/77467690.jpg) The Fundmentl Theorems of Clculus Mth 4, Section 0, Spring 009 We now know enough bout definite integrls to give precise formultions of the Fundmentl Theorems of Clculus. We will lso look t some bsic emples
The Fundmentl Theorems of Clculus Mth 4, Section 0, Spring 009 We now know enough bout definite integrls to give precise formultions of the Fundmentl Theorems of Clculus. We will lso look t some bsic emples
MATH 409 Advanced Calculus I Lecture 22: Improper Riemann integrals.
 MATH 409 Advned Clulus I Leture 22: Improper Riemnn integrls. Improper Riemnn integrl If funtion f : [,b] R is integrble on [,b], then the funtion F(x) = x f(t)dt is well defined nd ontinuous on [,b].
MATH 409 Advned Clulus I Leture 22: Improper Riemnn integrls. Improper Riemnn integrl If funtion f : [,b] R is integrble on [,b], then the funtion F(x) = x f(t)dt is well defined nd ontinuous on [,b].
The Trapezoidal Rule
 SECTION. Numericl Integrtion 9 f Section. The re of the region cn e pproimted using four trpezoids. Figure. = f( ) f( ) n The re of the first trpezoid is f f n. Figure. = Numericl Integrtion Approimte
SECTION. Numericl Integrtion 9 f Section. The re of the region cn e pproimted using four trpezoids. Figure. = f( ) f( ) n The re of the first trpezoid is f f n. Figure. = Numericl Integrtion Approimte
LINEAR ALGEBRA APPLIED
 5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
Fundamental Theorem of Calculus
 Fundmentl Theorem of Clculus Recll tht if f is nonnegtive nd continuous on [, ], then the re under its grph etween nd is the definite integrl A= f() d Now, for in the intervl [, ], let A() e the re under
Fundmentl Theorem of Clculus Recll tht if f is nonnegtive nd continuous on [, ], then the re under its grph etween nd is the definite integrl A= f() d Now, for in the intervl [, ], let A() e the re under
DOING PHYSICS WITH MATLAB MATHEMATICAL ROUTINES
 DOIG PHYSICS WITH MATLAB MATHEMATICAL ROUTIES COMPUTATIO OF OE-DIMESIOAL ITEGRALS In Cooper School of Physics, University of Sydney in.cooper@sydney.edu.u DOWLOAD DIRECTORY FOR MATLAB SCRIPTS mth_integrtion_1d.m
DOIG PHYSICS WITH MATLAB MATHEMATICAL ROUTIES COMPUTATIO OF OE-DIMESIOAL ITEGRALS In Cooper School of Physics, University of Sydney in.cooper@sydney.edu.u DOWLOAD DIRECTORY FOR MATLAB SCRIPTS mth_integrtion_1d.m
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Mat 210 Updated on April 28, 2013
 Mt Brief Clculus Mt Updted on April 8, Alger: m n / / m n m n / mn n m n m n n ( ) ( )( ) n terms n n n n n n ( )( ) Common denomintor: ( ) ( )( ) ( )( ) ( )( ) ( )( ) Prctice prolems: Simplify using common
Mt Brief Clculus Mt Updted on April 8, Alger: m n / / m n m n / mn n m n m n n ( ) ( )( ) n terms n n n n n n ( )( ) Common denomintor: ( ) ( )( ) ( )( ) ( )( ) ( )( ) Prctice prolems: Simplify using common
First Semester Review Calculus BC
 First Semester Review lculus. Wht is the coordinte of the point of inflection on the grph of Multiple hoice: No lcultor y 3 3 5 4? 5 0 0 3 5 0. The grph of piecewise-liner function f, for 4, is shown below.
First Semester Review lculus. Wht is the coordinte of the point of inflection on the grph of Multiple hoice: No lcultor y 3 3 5 4? 5 0 0 3 5 0. The grph of piecewise-liner function f, for 4, is shown below.
are coplanar. ˆ ˆ ˆ and iˆ
 SML QUSTION Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor ii The question pper onsists of 6 questions divided into three Setions, B nd C iii Question No
SML QUSTION Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor ii The question pper onsists of 6 questions divided into three Setions, B nd C iii Question No
Section 4.4. Green s Theorem
 The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
Lecture Summaries for Multivariable Integral Calculus M52B
 These leture summries my lso be viewed online by liking the L ion t the top right of ny leture sreen. Leture Summries for Multivrible Integrl Clulus M52B Chpter nd setion numbers refer to the 6th edition.
These leture summries my lso be viewed online by liking the L ion t the top right of ny leture sreen. Leture Summries for Multivrible Integrl Clulus M52B Chpter nd setion numbers refer to the 6th edition.
Numerical Differentiation and Integration
 Numerl Deretto d Itegrto Overvew Numerl Deretto Newto-Cotes Itegrto Formuls Trpezodl rule Smpso s Rules Guss Qudrture Cheyshev s ormul Numerl Deretto Forwrd te dvded deree Bkwrd te dvded deree Ceter te
Numerl Deretto d Itegrto Overvew Numerl Deretto Newto-Cotes Itegrto Formuls Trpezodl rule Smpso s Rules Guss Qudrture Cheyshev s ormul Numerl Deretto Forwrd te dvded deree Bkwrd te dvded deree Ceter te
Chapter Direct Method of Interpolation More Examples Civil Engineering
 Chpter 5. Direct Method of Interpoltion More Exmples Civil Engineering Exmple o mximie ctch of bss in lke, it is suggested to throw the line to the depth of the thermocline. he chrcteristic feture of this
Chpter 5. Direct Method of Interpoltion More Exmples Civil Engineering Exmple o mximie ctch of bss in lke, it is suggested to throw the line to the depth of the thermocline. he chrcteristic feture of this
Section 7.1 Area of a Region Between Two Curves
 Section 7.1 Are of Region Between Two Curves White Bord Chllenge The circle elow is inscried into squre: Clcultor 0 cm Wht is the shded re? 400 100 85.841cm White Bord Chllenge Find the re of the region
Section 7.1 Are of Region Between Two Curves White Bord Chllenge The circle elow is inscried into squre: Clcultor 0 cm Wht is the shded re? 400 100 85.841cm White Bord Chllenge Find the re of the region
1 Part II: Numerical Integration
 Mth 4 Lb 1 Prt II: Numericl Integrtion This section includes severl techniques for getting pproimte numericl vlues for definite integrls without using ntiderivtives. Mthemticll, ect nswers re preferble
Mth 4 Lb 1 Prt II: Numericl Integrtion This section includes severl techniques for getting pproimte numericl vlues for definite integrls without using ntiderivtives. Mthemticll, ect nswers re preferble
Solving Radical Equations
 Solving dil Equtions Equtions with dils: A rdil eqution is n eqution in whih vrible ppers in one or more rdinds. Some emples o rdil equtions re: Solution o dil Eqution: The solution o rdil eqution is the
Solving dil Equtions Equtions with dils: A rdil eqution is n eqution in whih vrible ppers in one or more rdinds. Some emples o rdil equtions re: Solution o dil Eqution: The solution o rdil eqution is the
Math 131. Numerical Integration Larson Section 4.6
 Mth. Numericl Integrtion Lrson Section. This section looks t couple of methods for pproimting definite integrls numericlly. The gol is to get good pproimtion of the definite integrl in problems where n
Mth. Numericl Integrtion Lrson Section. This section looks t couple of methods for pproimting definite integrls numericlly. The gol is to get good pproimtion of the definite integrl in problems where n
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
INTEGRATION. 1 Integrals of Complex Valued functions of a REAL variable
 INTEGRATION NOTE: These notes re supposed to supplement Chpter 4 of the online textbook. 1 Integrls of Complex Vlued funtions of REAL vrible If I is n intervl in R (for exmple I = [, b] or I = (, b)) nd
INTEGRATION NOTE: These notes re supposed to supplement Chpter 4 of the online textbook. 1 Integrls of Complex Vlued funtions of REAL vrible If I is n intervl in R (for exmple I = [, b] or I = (, b)) nd
Applications of Definite Integral
 Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
B.Sc. in Mathematics (Ordinary)
 R48/0 DUBLIN INSTITUTE OF TECHNOLOGY KEVIN STREET, DUBLIN 8 B.Sc. in Mthemtics (Ordinry) SUPPLEMENTAL EXAMINATIONS 01 Numericl Methods Dr. D. Mckey Dr. C. Hills Dr. E.A. Cox Full mrks for complete nswers
R48/0 DUBLIN INSTITUTE OF TECHNOLOGY KEVIN STREET, DUBLIN 8 B.Sc. in Mthemtics (Ordinry) SUPPLEMENTAL EXAMINATIONS 01 Numericl Methods Dr. D. Mckey Dr. C. Hills Dr. E.A. Cox Full mrks for complete nswers
T b a(f) [f ] +. P b a(f) = Conclude that if f is in AC then it is the difference of two monotone absolutely continuous functions.
![T b a(f) [f ] +. P b a(f) = Conclude that if f is in AC then it is the difference of two monotone absolutely continuous functions. T b a(f) [f ] +. P b a(f) = Conclude that if f is in AC then it is the difference of two monotone absolutely continuous functions.](/thumbs/78/77085178.jpg) Rel Vribles, Fll 2014 Problem set 5 Solution suggestions Exerise 1. Let f be bsolutely ontinuous on [, b] Show tht nd T b (f) P b (f) f (x) dx [f ] +. Conlude tht if f is in AC then it is the differene
Rel Vribles, Fll 2014 Problem set 5 Solution suggestions Exerise 1. Let f be bsolutely ontinuous on [, b] Show tht nd T b (f) P b (f) f (x) dx [f ] +. Conlude tht if f is in AC then it is the differene
Mathematics Number: Logarithms
 plce of mind F A C U L T Y O F E D U C A T I O N Deprtment of Curriculum nd Pedgogy Mthemtics Numer: Logrithms Science nd Mthemtics Eduction Reserch Group Supported y UBC Teching nd Lerning Enhncement
plce of mind F A C U L T Y O F E D U C A T I O N Deprtment of Curriculum nd Pedgogy Mthemtics Numer: Logrithms Science nd Mthemtics Eduction Reserch Group Supported y UBC Teching nd Lerning Enhncement
Lecture 1 - Introduction and Basic Facts about PDEs
 * 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
* 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
Type 2: Improper Integrals with Infinite Discontinuities
 mth imroer integrls: tye 6 Tye : Imroer Integrls with Infinite Disontinuities A seond wy tht funtion n fil to be integrble in the ordinry sense is tht it my hve n infinite disontinuity (vertil symtote)
mth imroer integrls: tye 6 Tye : Imroer Integrls with Infinite Disontinuities A seond wy tht funtion n fil to be integrble in the ordinry sense is tht it my hve n infinite disontinuity (vertil symtote)
Do the one-dimensional kinetic energy and momentum operators commute? If not, what operator does their commutator represent?
 1 Problem 1 Do the one-dimensionl kinetic energy nd momentum opertors commute? If not, wht opertor does their commuttor represent? KE ˆ h m d ˆP i h d 1.1 Solution This question requires clculting the
1 Problem 1 Do the one-dimensionl kinetic energy nd momentum opertors commute? If not, wht opertor does their commuttor represent? KE ˆ h m d ˆP i h d 1.1 Solution This question requires clculting the
1 This question is about mean bond enthalpies and their use in the calculation of enthalpy changes.
 1 This question is out men ond enthlpies nd their use in the lultion of enthlpy hnges. Define men ond enthlpy s pplied to hlorine. Explin why the enthlpy of tomistion of hlorine is extly hlf the men ond
1 This question is out men ond enthlpies nd their use in the lultion of enthlpy hnges. Define men ond enthlpy s pplied to hlorine. Explin why the enthlpy of tomistion of hlorine is extly hlf the men ond
METHODS OF APPROXIMATING THE RIEMANN INTEGRALS AND APPLICATIONS
 Journl of Young Scientist Volume III 5 ISSN 44-8; ISSN CD-ROM 44-9; ISSN Online 44-5; ISSN-L 44 8 METHODS OF APPROXIMATING THE RIEMANN INTEGRALS AND APPLICATIONS An ALEXANDRU Scientific Coordintor: Assist
Journl of Young Scientist Volume III 5 ISSN 44-8; ISSN CD-ROM 44-9; ISSN Online 44-5; ISSN-L 44 8 METHODS OF APPROXIMATING THE RIEMANN INTEGRALS AND APPLICATIONS An ALEXANDRU Scientific Coordintor: Assist
Math 259 Winter Solutions to Homework #9
 Mth 59 Winter 9 Solutions to Homework #9 Prolems from Pges 658-659 (Section.8). Given f(, y, z) = + y + z nd the constrint g(, y, z) = + y + z =, the three equtions tht we get y setting up the Lgrnge multiplier
Mth 59 Winter 9 Solutions to Homework #9 Prolems from Pges 658-659 (Section.8). Given f(, y, z) = + y + z nd the constrint g(, y, z) = + y + z =, the three equtions tht we get y setting up the Lgrnge multiplier
Chapter 8.2: The Integral
 Chpter 8.: The Integrl You cn think of Clculus s doule-wide triler. In one width of it lives differentil clculus. In the other hlf lives wht is clled integrl clculus. We hve lredy eplored few rooms in
Chpter 8.: The Integrl You cn think of Clculus s doule-wide triler. In one width of it lives differentil clculus. In the other hlf lives wht is clled integrl clculus. We hve lredy eplored few rooms in
7.8 IMPROPER INTEGRALS
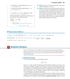 7.8 Improper Integrls 547 the grph of g psses through the points (, ), (, ), nd (, ); the grph of g psses through the points (, ), ( 3, 3 ), nd ( 4, 4 );... the grph of g n/ psses through the points (
7.8 Improper Integrls 547 the grph of g psses through the points (, ), (, ), nd (, ); the grph of g psses through the points (, ), ( 3, 3 ), nd ( 4, 4 );... the grph of g n/ psses through the points (
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
MATH Final Review
 MATH 1591 - Finl Review November 20, 2005 1 Evlution of Limits 1. the ε δ definition of limit. 2. properties of limits. 3. how to use the diret substitution to find limit. 4. how to use the dividing out
MATH 1591 - Finl Review November 20, 2005 1 Evlution of Limits 1. the ε δ definition of limit. 2. properties of limits. 3. how to use the diret substitution to find limit. 4. how to use the dividing out
5.1 How do we Measure Distance Traveled given Velocity? Student Notes
 . How do we Mesure Distnce Trveled given Velocity? Student Notes EX ) The tle contins velocities of moving cr in ft/sec for time t in seconds: time (sec) 3 velocity (ft/sec) 3 A) Lel the x-xis & y-xis
. How do we Mesure Distnce Trveled given Velocity? Student Notes EX ) The tle contins velocities of moving cr in ft/sec for time t in seconds: time (sec) 3 velocity (ft/sec) 3 A) Lel the x-xis & y-xis
