UC Berkeley UC Berkeley Previously Published Works
|
|
|
- Shannon Park
- 6 years ago
- Views:
Transcription
1 UC Berkeley UC Berkeley Previously Published Works Title Global well-posedness for the Maxwell-Klein-Gordon equation in 4+1 dimensions: Small energy Permalink Journal Duke Mathematical Journal, 164(6) ISSN Authors Krieger, J Sterbenz, J Tataru, D Publication Date DOI / Peer reviewed escholarship.org Powered by the California Digital Library University of California
2 GLOBAL WELL-POSEDNESS FOR THE MAXWELL-KLEIN GORDON EQUATION IN 4+1 DIMENSIONS. SMALL ENERGY. JOACHIM KRIEGER, JACOB STERBENZ, AND DANIEL TATARU arxiv: v1 [math.ap] 15 Nov 2012 Abstract. We prove that the critical Maxwell-Klein Gordon equation on R 4+1 is globally well-posed for smooth initial data which are small in the energy. This reduces the problem of global regularity for large, smooth initial data to precluding concentration of energy. 1. Introduction Let R 4+1 be the five dimensional Minkowski space equipped with the standard Lorentzian metric g = diag(1, 1, 1, 1, 1). Denote by φ : R 4+1 C a scalar function, and by A α : R 4+1 R, α = 1...,4, a real valued connection form, interpreted as taking values in isu(1). Introducing the curvature tensor as well as the covariant derivative F αβ := α A β β A α D α φ := ( α +ia α )φ the Maxwell-Klein Gordon system are the Euler-Lagrange equations associated with the formal Lagrangian action functional 1 L(A α,φ) := 1 (1 2 R 2 D αφd α φ+ 1 4 F αβf αβ) dxdt; 4+1 here we are using the standard convention for raising indices. Introducing the covariant wave operator A := D α D α we can write the Maxwell-Klein Gordon system in the following form (1) β F αβ = J α := I(φD α φ), A φ = 0 One key feature of this system is the underlying Gauge invariance, which is manifested by the fact that if (A α,φ) is a solution, then so is (A α α χ,e iχ φ). This allows us to impose an The first author was partially supported by the Swiss National Science Foundation. The second author was partially supported by the NSF grant DMS The third author was partially supported by the NSF grant DMS and by the Simons Foundation. The first author would like to express his thanks to the University of California, Berkeley, for hosting him during the summer 2011 and The Lagrangianbelow should also contain a mass term, which we chooseto neglect here; thus the system under consideration might be more aptly named the Maxwell-scalar field system. For historical reasons we have chosen to retain the Maxwell-Klein Gordon terminology. 1
3 additional Gauge condition, and we shall henceforth impose the Coulomb Gauge condition which requires 4 (2) j A j = 0 The MKG-CG system can be written explicitly in the following form (3a) (3b) (3c) (3d) j=1 A i = P i J x A φ = 0 A 0 = J 0 t A 0 = i J i, where the operator P denotes the Leray projection onto divergence free vector fields, P = I 1 The last equation (3d) is a consequence of (3c) due to the divergence free condition on the moments α J α = 0, which in turn follows from (3b). However, it plays a role in the sequel so it is added here for convenience. Here it is assumed that the data A j (0, ) satisfy the vanishing divergence relation (2). We remark that given an arbitrary finite energy data set for the MKG problem, one can find a gauge equivalent data set of comparable size which satisfies the Coulomb gauge condition. This argument only involves solving linear elliptic pde s, and is omitted. The key question now is to decide whether a family of data (A,φ)[0] := (A α (0, ), t A α (0, ),φ(0, ), t φ(0, )) which satisfy the compatibility conditions required by the two equations for A 0 above can be extended to a global-in-time solution for the Maxwell-Klein-Gordon system. The key for deciding this question is the criticality character of the system. Note that the energy E(A,φ) := R 4 (1 4 Fαβ D α φ 2) dx 2 α,β is preserved under the flow (1), and in our 4+1-dimensional setting it is also invariant under the natural scaling φ(t,x) λφ(λt,λx), A α (t,x) λa(λt,λx) This means the 4+1-MKG system is energy critical, and in recent years a general approach to the large data Cauchy problem associated with energy critical wave equations has emerged. The first key step in this approach consists in establishing an essentially optimal global wellposedness result for data which are small in the energy norm, which is usually the optimal small-data global well-posedness result achievable. In this paper, we set out to prove this for the dimensional Maxwell-Klein-Gordon system. Theorem 1. a) Let (A,φ)[0] be a C Coulomb data set satisfying (4) E(A,φ) < ǫ for a sufficiently small universal constant ǫ > 0. Then the system (1) admits a unique global smooth solution (A,φ) on R 4+1 with these data. 2 α
4 b) In addition, the data to solution operator extends continuously 2 on the set (4) to a map Ḣ 1 (R 4 ) L 2 (R 4 ) (A,φ)[0] (A,φ) C(R;Ḣ1 (R 4 )) Ċ1 (R,L 2 (R 4 )) We remark that the same result holds in all higher dimensions for small data in the scale invariant space Ḣ n 2 1 Ḣ n 2 2. This has already been known in dimensions n 6, see [21]. We have chosen to restrict our exposition to the more difficult case n = 4 in order to keep the notations simple, but our analysis easily carries over to dimension n = 5. On the other hand, we do not know whether a similar result holds in dimension n = 3. Before explaining some more details of our approach, we recall here earlier developments on this problem, and how our approach relates to these. Considering the case of general spatial dimension n and denoting the critical Sobolev exponent by s c = n 1 (thus s 2 c = 1 for n = 4, corresponding to the energy), a global regularity result for data which are smooth and small in was established in dimensions n 6 in the work [21] which served as inspiration Ḣsc to the present work. We note in passing that a result analogous to [21] was established in [18] for the Yang-Mills system in dimensions n 6, and the present work most likely also admits a corresponding analogue for the dimensional Yang-Mills problem. The global regularity question for the physically relevant n = 3 case of the Yang-Mills problem had been established earlier in the groundbreaking work [6]. Observe that this problem is energy sub-critical. In the context of MKG, the result [21] had been preceded by a number of works which aimed at improving the local wellposedness of MKG in the n = 3 case, beginning with [9], followed by [5], and more recently [19]; the latter in particular established an essentially optimal local well-posedness result by exploiting a subtle cancellation feature of MKG, which also plays a role in the present work. We also mention the recent result [8] which establishes global regularity for energy sub-critical data in the n = 3 case, in the spirit of earlier work by Bourgain [3]. In the higher dimensional case n 4, an essentially optimal local well-posedness result for a model problem closely related to MKG was obtained in [14]. This model problem does not display the crucial cancellation feature of the precise MKG-system which enable us here to go all the way to the critical exponent and global regularity. We mention also that essentially optimal local well-posedness for the exact MKG-system was obtained in [17]. Finally, the recent work [24] established global regularity of equations of MKG-type with data small in a weighted but scaling invariant Besov type space, in the case n = 4. The present paper follows a similar strategy as [21] : one observes that the spatial Gauge connection components A j, j = 1,2,3, which are governed by the first equation (3a), may in fact be decomposed into a free wave part and an inhomogeneous term (the second term in the Duhamel formula for A) which in fact obeys a better l 1 -Besov type bound (while energy corresponds to l 2 ) A j = A free j +A nonlin j This is important for handling the key difficulty of the MKG-system, which is the equation for φ, i. e. the second equation (3b). In fact, we shall verify that the contribution of the term A nonlin tothedifficult magneticinteractionterm2ia j j φin the low-high frequencyinteraction case can be suitably bounded when combined with the term 2iA 0 t φ, an observation coming from [19]. However, the contribution of the free term A free to the magnetic interaction term 2 here the continuity is locally in time 3
5 is nonperturbative and cannot be handled in this manner. Thus, following the example set in [21], we retain this term into the covariant wave operator 3 A free. More precisely, we shall define a suitable paradifferential wave operator p A which incorporates the leading part of A free while relegating the rest to the source terms on the right. The key novelty of this paper then is the development of a functional calculus, involving in particular X s,b -type as well as atomic null-frame spaces developed in other contexts, for solutions of the general inhomogeneous covariant wave equation p A = f This refined functional calculus is necessary to control the nonlinear interaction terms, which become significantly more delicate in the critical dimension than in the setting studied in [21]. In particular, the Strichartz norms themselves appear far from sufficient to handle the present situation. The above covariant wave equation will be solved by means of a suitable approximate parametrix, and we show that this parametrix satisfies many of the same bounds as the usual free wave parametrix, in particular encompassing refined square sum type microlocalized Strichartz norms as well as null-frame spaces. We expect the calculus developed here to be of fundamental importance in other contexts, such as the regularity question of the critical Yang-Mills system and related problems from mathematical physics. 2. Technical preliminaries Throughout the sequel we shall rely on Littlewood-Paley calculus, both in space as well as space-time. In particular, we constantly invoke the standard Littlewood-Paley localizers P k, k Z, which are defined by P k f = χ( ξ 2 k)ˆf(ξ) for functions f defined on R 4. Here χ is a smooth bump function, supported on [ 1,4], which 4 satisfies the key condition k Z χ( ξ ) = 1 if ξ > 0. To measure proximity of the space-time 2 k Fourier support to the light cone, we use the concept of modulation. Thus we introduce the multipliers Q j, j Z, via Q j f(τ,ξ) = χ( τ ξ )ˆf(τ,ξ) 2 j with the same χ as before, whereˆin this context denotes the space-time Fourier transform. We then refer to 2 j as the modulation of the function. On occasion we shall also use multipliers S l, which restrict the space-time frequency to size 2 l. These multipliers allow us to introduce a variety of norms. In particular, for any p [1, ), we set for any norm S F lps := ( Pk F p S k Z We also have the following X s,b -type norms, applied to functions localized to spatial frequency 2 k : F X s,r := 2 sk( [ p 2 rj Qj F ] p )1 p L 2, p [1, ), t,x j Z )1 p 3 Here we set A free 0 = 0. 4
6 with the obvious analogue F X s,r := 2sk sup k Z2 rj Qj F L 2 t,x For more refined norms, we shall also have to use multipliers Pl ω, which localize the homogeneous variable ξ to caps ω S 3 of diameter 2 l, by means of smooth cutoffs. In these ξ situations, we shall assume that for each l a uniformly (in l) finitely overlapping covering of S 3 by caps ω has been chosen with appropriate cutoffs subordinate to these caps. Similar comments apply to the multipliers P C l which localize to rectangular boxes and will be defined below. k Given a norm S with corresponding space S, we denote by S k the space of functions in S which are localized to frequency 2 k. Furthermore, we denote by S k,± the subspace of functions in S k with Fourier support in the half-space τ >< 0, with τ the Fourier variable dual to t. 3. Function Spaces There are three function spaces we work with: N, N, and S. These are set up to that their dyadic subspaces N k, N k, and S k satisfy the following relations: (5) N k = L 1 (L 2 )+X 0, 1 2 1, X 0,1 2 1 S k N k, Then define: F 2 N = k P k F 2 N k. We also define S k by u S = u Nk + u L L 2 k On occasion we need to separate the two characteristic cones {τ = ± ξ }. Thus we define N k,±, N k = N k,+ N k, S k,±, S k = S k,+ +S k, Nk,±, Nk = Nk,+ +Nk, Our space S k scales like L 2 free waves, and is defined by: where: φ 2 S k = φ 2 S str k + φ 2 S ang k (6) Sk str = 1 2 (1 q +4 r 2)k L q (L r ), φ 2 q +3/2 r 3 S ang 4 k + φ 2 X 0,1 2 = sup l<0, ω P ω l Q <k+2l φ 2 S ω k (l), The angular sector norms Sk ω (l) are essentially the same as in the wave maps context, see e.g. [27], and defined shortly. Our space of solutions scales like free waves with Ḣ1 data, with a high modulational gain as in [25]. Thus we set: (7) φ 2 S 1 = k t,x P k φ 2 S k + φ 2 l 1 L 2 (Ḣ 1 2). 5
7 For later reference, we shall also use the norms φ S N := N 1 t,x φ S 1, N 2 Returning to Sk ω (l), we define these as usual except that we need to add additional square information over smaller radially directed blocks C k (l ) dimensions 2 k (2 k +l ) 3 with appropriate dyadic gains. First define: φ PW ± ω (l) = inf φ= φ ω φ NE = sup ω ω ω 2 l φ ω / ω φ L ω (L 2 ω ), L 2 ±ω (L (±ω ) ) dω, where the norms are with respect to l ± ω = t ± ω x and the transverse variable, while / ω denotes spatial differentiation in the (l + ω) plane. Now set: (8) φ 2 S ω k (l) = φ 2 S str k + sup k k,l k φ 2 NE +2 3k ± k+2l k +l C k+l k (l ) Q ± φ 2 PW ω (l) ( P Ck (l )φ 2 S +2 2k P k str Ck (l )φ 2 NE +2 2k k P Ck (l )φ 2 L 2 (L ) +2 3(k +l ) ± ) Q ± P Ck (l )φ 2. PWω (l) We remark that an important feature of these norms is that the time-like oriented L 2 (L ) block norm gains dyadically from the length of C k (l ) in the radial direction, while the null oriented L 2 ω(l ω ) norms gain from the size of C k (l ) in the angular direction. We also remark that a useful feature of this setup is: (9) ( P Ck P k φ 2 L 2 (L ) C k )1 2 2 k k P k φ S ang k X 0,1 2 where C k are a finitely overlapping set of cubes of side length 2 k. This follows by splitting P k φ = Q <k P k φ+q k P k φ and using the Sk( ω 1 2 (k k) ) norm for the first term and the X 0,1 2 norm and Bernstein s inequality for the second. Next we describe some auxiliary spaces of L 1 (L ) which will be useful for decomposing the non-linearity. The first is for the hyperbolic part of the solution: φ Z hyp = k P k φ Z hyp k, φ 2 Z hyp k = sup l<c ω, 2 l P ω l Q k+2lφ 2 L 1 (L ). Note that as defined this space already scales like Ḣ1 free waves. In addition, note the following useful embedding which is a direct consequence of Bernstein s inequality: (10) 1 l 1 L 1 (L 2 ) Z hyp. The second is for the elliptic part of the solution: A Z ell = k j A L j<k+c Q 1 (L ), A Z ell = k P k A Z ell k We remark that the only purpose of this last norm is to handle sums over Q j in product estimates involving A in L 1 (L ). 6.
8 Finally, thefunctionspaces fora 0 aremuch easier todescribe asthea 0 equation iselliptic: We also have the derivative norms A 0 2 Y 1 = x,ta 0 2 L L 2 + A 0 2 L 2 tḣ 3 2 x + t A 0 2 L 2 tḣ 1 2 x. A 0 Y N := N 1 t,x A 0 Y 1, N 2 4. Decomposing the non-linearity; Statement and use of the core multilinear estimates Recalling the definition of the currents J α = I(φD α φ) we write the MKG-CG system again here as: (11a) (11b) (11c) A i = P i J x, A φ = 0, A 0 = J 0, This system will be solved iteratively using the following scheme. We initialize A (1) i = A free i, A (1) 0 = 0, φ (1) = φ free, where A free i and φ free solve the flat wave equation with initial data A i [0], respectively φ[0]. Given A α (m), φ α (m) and their associated currents J α (m), we define the next iteration via the equations (12a) (12b) (12c) A (m+1) i A (m)φ (m+1) = 0, = P i J (m) x, A (m+1) 0 = J (m) 0, with the same initial data A i [0], respectively φ[0]. Assuming small energy for the initial data A i [0] and φ[0] as in (4), we will prove that this Picard type iteration converges in the space S 1. Our starting point is the linear bound (13) A (1) x S 1 + φ(1) S 1 C 0 ǫ Then we will inductively establish the bound (14) A (m+1) x A (m) x l 1 S 1 + φ(m+1) φ (m) S 1 + A (m+1) 0 A (m) 0 Y 1 (Cǫ ) m for a universal constant C 2C 0. Assuming this holds, passing to the limit as n we obtain a Coulomb solution (A,φ) to the MKG equation which satisfies the bound (15) A nonlin x l 1 S 1 + φ S 1 + A 0 Y 1 ǫ The same argument proves uniqueness. If two solutions (A (0),φ (0) ) and (A (1),φ (1) ) have the same Cauchy data for A x, then the same A free x is used for both. Thus applying the same series of estimates in this section to the difference of the two exact solutions rather than two approximate solutions we obtain the bound (16) A (0) x A (1) x l 1 S 1 + φ(0) φ (1) S 1 + A (0) 0 A (1) 0 Y 1 φ (0) [0] φ (1) [0] Ḣ1 L 2 7
9 This bound proves both uniqueness and Lipschitz dependence of the solution with respect to φ[0]. The continuous dependence with respect to A x [0] is a more delicate issue and will be explained in section 5. The estimate (14)(m) will follow from (14)(< m). Summing up (14)(< m) and (13), we can easily add to our induction hypothesis the bound (17) A (n) x A free x l 1 S 1 + φ(n) S 1 + A (n) 0 Y 1 2C 0ǫ, n m provided that ǫ is small enough. A simple but very useful observation is that, since all iterated φ (m) solve covariant wave equations, it follows that the associated moments are divergence free, D α J α (m) = 0. Then, differentiating the equation (12c), we obtain (18) t A (m+1) 0 = i J (m) i which will be used to estimate the high modulations of A 0. This is the reason why we have completely avoided using φ (m) in (12b), even though some of the terms in there will be treated perturbatively. A second fact to keep in mind is that while in terms of formulas this is a one step iteration, in terms of estimates this is really a two step iteration. Precisely, in order to obtain good bounds for φ (m+1) we will need to reiterate bad portions of A α in terms of φ (m 1) (but not A (m 1) ). All this is explained in detail below. To decompose the non-linearity, the following device will be useful. If M(D t,x,d t,y ) is any bilinear operator we set: H k M(φ,ψ) = Q j P k M(Q <j C φ,q <j C ψ), j<k+c H k M(φ,ψ) = j<k+c Q <j C M(Q j P k φ,q <j C ψ), Now we describe the function spaces and multilinear estimates for each iterative piece of the non-linearity. In this Section we only state the main estimates, and reduce them to appropriate dyadic bounds. These will be proved later in the paper Estimates for the A i. We split the spatial potentials into homogeneous and inhomogeneous parts with respect to t = 0 as follows, A (m) i = A free i + A nonlin,(m) i where the second part solves the linear equation (19) A nonlin,(m+1) ( ) i = P i φ (m) x φ (m) + φ (m) 2 A x (m), A nonlin i [0] = 0 In order to establish the l 1 S 1 bound in the first term of (14) it suffices to work directly with this equation. However, A (m) also appears in the φ (m+1) equation (12b), and in order to be able to treat its contribution perturbatively there we also need to control its Z hyp norm (see the subsection below devoted to φ). This works for the most part, but there is a part of A nonlin,(m) i which requires a more delicate treatment, which is: = (20) HA nonlin,(m) i k,k i : k<min{, } C 8 1 H k P i (φ (m 1) x φ (m 1) ).
10 For the good part of A nonlin,(m) i we will establish the difference bound (21) (A nonlin,(n) i HA nonlin,(n) i as well as the summed estimate (22) A nonlin,(n) i ) (A nonlin,(n 1) i HA nonlin,(n 1) i ) Z hyp (Cǫ ) n 1, 3 n m+1 HA nonlin,(n) i Z hyp C 2 0ǫ 2, 2 n m+1 On the other hand the bad part HA nonlin,(m) i will be considered later in combination with the similar part of A 0. As seen above, we need estimates not only for the equation (19), but also for differences of two consecutive iterations. Thus we are led to consider a more general equation of the form ), B nonlin i [0] = 0. (23) B i = P i ( φ (1) x φ (2) +φ (3) φ (4) A (1) i and its corresponding bad part, (24) HB i = Then we will show: k,k i : k<min{, } C 1 H k P i (φ (1) x φ (2) ). Proposition 4.1. One has the following iterative estimates for the functions B i and HB i defined above: (25) (26) B i l 1 S 1 φ(1) S 1 φ (2) S 1 + A (1) i S 1 φ (3) S 1 φ (4) S 1, B i HB i Z hyp φ (1) S 1 φ (2) S 1. In combination with our induction hypothesis, the estimate (25) leads to the l 1 S 1 bound for the first term in (14). Similarly, the estimate (26) yields the Z hyp bounds for the good part of A nonlin,(m) i in (21) and (22). Decomposition of the proof of estimates (25) and (26). For estimate (25) we begin with the high modulational bounds: (27) φ (1) t,x φ (2) l 1 L 2 (Ḣ 1 2) φ (1) S 1 φ (2) S 1, (28) φ (3) φ (4) φ (5) l 1 L 2 (Ḣ 1 2) φ (3) S 1 φ (4) S 1 φ (5) S 1. Next, for the cubic terms in A nonlin i both (25) and (26) follow once we can show: (29) φ (3) φ (4) φ (5) l 1 L 1 (L 2 ) φ (3) S 1 φ (4) S 1 φ (5) S 1. Returning to the quadratic part, we employ the notation: which allows us to write: N ij (φ (1),φ (2) ) = i φ (1) j φ (2) j φ (1) i φ (2), (30) P j (φ (1) x φ (2) ) = 1 i N ij (φ (1),φ (2) ). Then for the quadratic part of (25) it suffices to show: (31) x 1 N(φ (1),φ (2) ) l 1 N φ (1) S 1 φ (2) S 1, 9
11 where N denotes any instance of the N ij. Finally, making an analogous definition to (24) for each term in (30) we need to show: (32) (I H) x 1 N(φ (1),φ (2) ) Z hyp φ (1) S 1 φ (2) S Estimates for A 0 and t A 0. The estimates for temporal potentials are analogous to those above, but using instead the equations (12c) and (18). In expanded form these are written as A (m+1) 0 = I(φ (m) t φ(m) ) A (m) 0 φ (m) 2 t A (m+1) 0 = i I(φ (m) i φ(m) ) i (A (m) i φ (m) 2 ) In a first approximation, from A (m) 0 we isolate to output of bilinear high high low interactions, namely A (m+1),hh 0 = k,k i : k<min{, } C 1 P k (φ (m) t φ (m) ). To bring the analysis to the same level as in the case of the A j s, in analogy with (20), we also define the component HA (m+1) 0 of A (m+1),hh 0, (33) HA (m+1) 0 = 1 H k (φ (m) t φ (m) ). k,k i : k<min{, } C In addition to the estimates included in (14), we also need the some similar bounds for A (m+1),hh) as well as bounds for the good differences for 3 n m+1: (34) A (n),hh 0 A (n 1),hh 0 l 1 L 2 (Ḣ 3 2) (Cǫ)n 1 (A (n) 0 A (n),hh 0 ) (A (n 1) 0 A (n 1),hh 0 ) l 1 L 1 (L ) (Cǫ) n 1 (HA (n) 0 A (n),hh 0 ) (HA (n 1) 0 A (n 1),hh 0 ) Z ell (Cǫ) n 1 Passing to differences we arrive at a system of equations with multilinear inhomogeneities of the form: (35) (36) As above we write: respectively B 0 = φ (1) t φ (2) +φ (3) φ (4) A (1) 0, t B 0 = x ( φ (1) x φ (2) +φ (3) φ (4) A (1) i B hh 0 = (37) HB 0 = Then we will show: k,k i : k<min{, } C k,k i : k<min{, } C 10 P k (φ (1) t φ (2) ). ). 1 H k (φ (1) t φ (2) ).
12 Proposition 4.2. One has the following estimates for B 0 and t B 0 defined above: (38) (39) (40) (41) (42) t,x B 0 L (L 2 ) φ (1) S 1 φ (2) S 1 + A (1) α L (Ḣ1 ) φ(3) S 1 φ (4) S 1, (B 0,B hh 0 ) l 1 L 2 (Ḣ 3 2) t B 0 l 1 L 2 (Ḣ 1 2) φ (1) S 1 φ (2) S 1 + A (1) 0 L 2 (Ḣ 3 2) φ(3) S 1 φ (4) S 1, φ (1) S 1 φ (2) S 1 + A (1) i S 1 φ (3) S 1 φ (4) S 1, B 0 B hh 0 l 1 L 1 (L ) φ (1) S 1 φ (2) S 1 + A (1) 0 L 2 (Ḣ 3 2) φ(3) S 1 φ (4) S 1, B hh 0 HB 0 Z ell φ (1) S 1 φ (2) S 1. The bound for the last term in (14) follows from (38), (39) and (40). The three bounds in (34) are consequences of (39), (41) and (42). Outline of proof of estimates (39) (41). Estimate (38) follows from Sobolev s embedding, while the proofs of (39) and (40) either follow immediately from (27) and (28) above, or in the case of A hh 0 from the estimates used to produce those bounds. Estimate (41) follows from similar considerations. In detail, the estimates (38) - (41) will be proved in subsection 4.4. On the other hand (42) is more microlocal in nature and follows from calculations similar to those in the proof of (32) listed above. It will be proved as a consequence of Theorem 12.2 below Estimates for φ. We now turn to the heart of the matter, which is the covariant wave equation (18) for φ (m+1). This cannot be viewed as an equation of type φ = perturbative, and therein lies the difficulty. To address this issue we identify the nonperturbative part, and add it to the main operator to obtain a paradifferential type magnetic d Alembertian. Precisely, we define the leading order paradifferential approximation to the covariant A equation using only the free part A free i (43) p A = 2i k of A (m) i, which is independent of n: P <k C A free,j P k j, Fortunately, this operator does not depend on m. Then the equation for φ (m+1) takes the form (44) p A φ(m+1) = M(A (m),φ (m+1) ) where M(A (m),φ (m+1) ) is given by (45) M(A (m),φ (m+1) ) = 2i ( A (m),α α φ (m+1) k P <k C A free,j j P k φ (m+1)) ( i t A (m) 0 φ (m+1) +A (m),α A (m) α φ(m+1)) := M 1 (A (m),φ (m+1) )+M 2 (A (m),φ (m+1) ) We further write M 1 = N +N 0 where N contains the terms of the form A j j φ and N 0 contains the terms of the form A 0 0 φ. We remark that N exhibits a null structure. Indeed, using the divergence free character of A i we write: A j = i 1 F ij, F ij = i A j j A i, 11
13 so that: N(A x,φ) = A i i φ = 1 N ij ( i 1 A j,φ). 2 From here on we take the last expression as the definition of N. This will allow us to retain the null form while discarding the divergence free condition on finer decompositions of A x. Now the idea is to first produce a parametrix for p A, and then to estimate the right hand side of (44) perturbatively. The linear estimate for the magnetic wave operator p A is one of the key points of the paper, and has the following form: Theorem 4.3 (Linear estimates for φ). Let p A be the paradifferential gauge-covariant wave operator defined on line (43), and suppose that A free = 0 with A free [0] Ḣ1 L2 ǫ. If ǫ is sufficiently small then we have: (46) φ S 1 φ[0] Ḣ1 L 2 + p A φ N l 1 L 2 (Ḣ 1 2). Section 6 is devoted to the proof of this result. In order to solve the equation (44) it remains to estimate the the right hand side of (44), (47) M(A (m),φ (m+1) ) N L 2 (Ḣ 1 2) ǫ φ (m+1) S 1 which is applied with φ = φ (m). In order to estimate the difference φ (m+1) φ (m) we need in addition to show that (48) M(A (m),φ) M(A (m 1),φ) N L 2 (Ḣ 1 2) (Cǫ)m 1 φ S which is then applied to φ = φ (m). To prove (47) and (48) we peel off some easier cases before we arrive at the heart of the matter. Step 1:(The M 2 term.) For this it suffices to have the following estimates: (49) (50) t A 0 φ l 1 L 2 (Ḣ 1 2) L 1 (L 2 ) t A 0 L 2 (Ḣ 2) L 1 φ (L 2 ) S 1, A (1) 0 A (2) 0 φ l A (i) 1 L 2 (Ḣ 1 2) L 1 (L 2 ) 0 L 2 (Ḣ 3 φ 2) L (Ḣ1 ) S 1. i<j i=1,2 which are proved using only global Strichartz type bounds and Sobolev embeddings. Step 2:(High modulation bounds for M 1 ) To establish the L 2 2) (Ḣ 1 bound for M 1 we use (27) and the following two estimates: (51) (52) k P <k C A free i x P k φ L 2 (Ḣ 1 2) A 0 t φ l 1 L 2 (Ḣ 1 2) A free i S 1 φ S 1, A 0 L 2 (Ḣ 3 2) φ S 1. It remains to prove the N bounds for M 1. At first we separately consider N and N 0. Step 3:(Peeling off the good parts of N) The first step will be to show that we can restrict our attention to low high interactions in N. For this we define the component N lowhi by N lowhi (A x,φ) = k N(P <k C A i,p k φ), To estimate the difference N N lowhi we will prove the null form estimate (53) N(A x,φ) N lowhi (A x,φ) N A x S 1 φ S 1. 12
14 We remark that once this is done, the free part A free x has been taken care of and will no longer appear. For the low-high interactions in N we still have the null structure to use, but the balance of frequencies is unfavourable. For the most part we can still bound N lowhi via a null form bilinear S 1 S 1 estimate; the exception to this is the case of high low low modulation interactions. We group these in an expression denoted by H N lowhi, which is given by H N lowhi (A j,φ) = k,k : k <k C H k N(A j,p k φ), For the difference we will prove the bilinear null form estimate (54) N lowhi (A x,φ) H N lowhi (A x,φ) N A (1) i l 1 S 1 φ(1) S 1, in the last section of the paper. The high low low modulation interactions contained in H N lowhi can no longer be estimated using the S 1 norm of A x, instead we need the stronger Z hyp norm. This leads us to introduce the expression H N lowhi (HA x,φ) In view of the estimates (26), (22) and (21), the N bound for the expression H N lowhi (A x (m),φ) H N lowhi (HA x (m 1),φ), as well as the corresponding differences, is a consequence of the following (55) H N lowhi (A x,φ) N A x Z hyp φ S 1. After peeling all the good contributions, the only part of N which has not been estimated so far is H N lowhi (HA (m) x,φ (m+1) ) Step 4:(Peeling off the good parts of N 0 ) The arguments here follow the same lines as before. However, since A 0 solves an elliptic equation, a larger portion of all cases can be treated in a direct fashion via Strichartz estimates and Sobolev embeddings, which leaves less in terms of bilinear estimates to be proved later. Recall that N 0 (A 0,φ) = A 0 t φ. Modifying slightly the setup before we set N lowhi 0 (A 0,φ) = k Then the difference is estimated via N 0 (P <k C Q <k C A 0,P k φ), (56) N 0 (A 0,φ) N lowhi 0 (A 0,φ) L 1 L 2 A 0 Y 1 φ S The extra step we can take in the case of N 0 is to replace A (n) 0 by A (n),hh 0. By (39) and the second part of (34) the difference is estimated using (57) N lowhi 0 (A 0,φ) N lowhi 0 (A hh 0,φ) L 1 L 2 A 0 A hh 0 l 1 L 1 L φ S The last two steps are similar to the case of A x. First we introduce H N lowhi 0 (A hh 0,φ) = k,k : k <k C 13 H k N(Ahh 0,P kφ),
15 In view of (39) and the first part of (34), the corresponding differences are estimated using (58) N lowhi 0 (A hh 0,φ) H N lowhi 0 (A hh 0,φ) N A hh 0 l 1 L 2 (Ḣ 3 2) φ S 1, Finally, replace this by H N lowhi 0 (HA 0,φ). By (42) and the third part of (34) for the difference it suffices to have the estimate (59) H N0 lowhi (A hh 0,φ) H N0 lowhi (HA 0,φ) N A (1),hh 0 HA (1) 0 Z ell φ (1) S 1. After peeling all the good contributions, the only part of N 0 which has not been estimated so far is H N0 lowhi (HA (m) 0,φ (m+1) ) Step 5:(Reduction of the remaining terms to quadrilinear null form bounds) So far we have one portion of N and one portion of N 0 left to estimate. We collect the two together in the expression Here we recall that HA (m) x R (n+1) = H N lowhi 0 (HA (m) x,φ (m+1) )+H N lowhi (HA (m) 0,φ (m+1) ) and HA (m) 0 are bilinear expressions in φ (m 1). The key idea is that there is a cancellation that occurs between the two terms above, which is why they need to be treated together rather than separately. The trilinear estimate that needs to be proved in this case for the trilinear expression is R(φ (1),φ (2),φ (3) ) = H N lowhi 0 (HA x (φ (1),φ (2) ),φ (3) )+H N lowhi (HA 0 (φ (1),φ (2) ),φ 3 ) (60) R(φ (1),φ (2),φ (3) ) N φ (1) S 1 φ (2) S 1 φ (3) S 1, Expanding everything into φ (i), and performing some algebraic manipulations 4 we have: where (61) (62) (63) R(φ (1),φ (2),φ (3) ) = Q 1 Q 2 Q 3, Q 1 = H ( 1 H(φ (1) α φ (2) ) α φ (3)), Q 2 = H ( 1 1 t α H(φ (1) α φ (2) ) t φ (3)), Q 3 = H ( 1 1 α i H(φ (1) i φ (2) ) α φ (3)). For each of these we prove (60) separately, which concludes our estimates for M quad Proof of the L p product estimates. Before continuing with the main thrust of the paper, we pause here to dispense with the easiest cases of the multilinear estimates listed above. These are (27), (28), (29), (38), (39), (40), (41), (51), (52), (57), (49), and (50). For the most part these can be broken down into the following estimates, which are immediate consequences of Hölder s and Bernstein s inequalitites: Lemma 4.4 (Core generic product estimates). One has the following dyadic bounds: (64) P k (A k1 φ k2 ) L 1 (L 2 ) 2 δ(k max{k i}) 2 δ A k1 L 2 (Ḣ 1 2) φ L 2 (Ẇ6,1 6), (65) P k (φ (1) φ (2) ) L 2 (Ḣ 1 2) 2 δ(k max{k i}) 2 δ φ (1) L (L 2 ) φ (2) L 2 (Ẇ6,1 6), 4 See the Appendix for a calculation done without the clutter of abstract index notation. 14
16 (66) S 1 L 2 (Ẇ6,1 6 ). Proof of estimate (27). This follows at once from summing over (65) and the inclusion: Proof of estimate (28). This follows from the inclusion S 1 S 1 L (L 2 ), a simple consequence of energy estimates and Ḣ1 L 4, and then summing over (65). Proof of estimate (29). This follows from summing over (64) after using (66) and the bilinear embedding: (67) B B L 2 (Ḣ 1 2 ), B = L 2 (Ẇ6,1 6 ) L (Ḣ1 ). This last estimate is a straightforward application of trichotomy, putting the high frequency term in the energy norm. The standard details are left to the reader. Proof of estimate (38). This is immediate from Sobolev embeddings involving L 4,L 4 3,L 2. Proof of estimates (39), (40), (51), and (52). These follow from (65) as in estimates (27) and (28) above. We use: (68) L 2 (Ḣ 3 2 ) L 2 (Ẇ6,1 6 ), as a replacement for (66) when necessary. Proof of estimate (41). First notice that the desired bound for the cubic terms follows from (64) and estimates similar to those above, and 1 l 1 L 1 (L 2 ) l 1 L 1 (L ). On the other hand, for the quadratic term one has: P k (φ (1) t φ (2) ) L 1 (L ) φ (1) L 2 (Ẇ6,1 6) tφ (1) L 2 (Ẇ6,1 6). when k = max{k i }+O(1). Proof of estimate (49). This is again an immediate consequence of (64), (65), and (66) Proof of estimate (50). For the L 2 (Ḣ 1 2) we can use (65) once we place the product of A 0 in L (L 2 ) via Ḣ1 L 4. On the other hand the L 1 (L 2 ) estimate comes from (64) and using (67) for the produce of A 0 and (66) for φ. Proof of estimate (56). First decompose: where: (69) A 0 t φ N lowhi 0 (A 0,φ) = T 1 +T 2, T 1 = k P k C A 0 t φ k, T 2 = P <k C Q >k C A 0 t φ k We ll show each of T i L 1 (L 2 ). For T 1 this follows from (64) and using: P k C A 0 L 2 (Ḣ 1 2) k 2 k P k A 0 L 2 (Ḣ 3 2), tφ k L 2 (Ẇ 6,1 6) 15 2 k φ k S 1.
17 The bound for T 2 is similar except we use: P <k C Q k C A 0 L 2 (Ḣ 1 2) 2 k t A 0 L 2 (Ḣ 1 2). The bound for T 2 L 1 L 2 follows from (41), placing the second factor in L (L 2 ). Proof of estimate (57). This follows from (41) by placing again the second factor in L (L 2 ). We remark that at this point we have reduced the proof of our main Theorem 1 to the demonstration of the linear estimates in Theorem 4.3 in Section 6, and then proving the multilinear estimates (31), (32), (42), (53), (54), (55), (58), (59), and finally (60) for each of the expressions (61) (63). These bounds are dealt with in the last section of the paper. 5. Higher regularity and continuous dependence In the previous section we have constructed solutions which are small in S 1 for all small energy data. Here we complete the proof of Theorem 1 by discusing the remaining issues, namely higher regularity and continuous dependence. The ideas here are fairly standard, and in particular closely resemble the similar proof for wave maps, see [30]. For that reason we merely outline the arguments that follow Higher regularity. The goal here is to establish the bound (70) A nonlin x l 1 S N + φ S N + A 0 Y N (A x [0],φ[0]) ḢN ḢN 1 for all small energy data MKG solutions. This is done by a standard iterative procedure, and we explain here how to obtain bounds on x A x, x A 0, x φ. In fact, this is accomplished by using the same estimates as before. Commencing with A x,a 0, recall that we have A nonlin,(m+1) i = P i ( φ (m) x φ (m) + φ (m) 2 A (m) x whence we see that A nonlin,(m+1) i satisfies a wave equation whose source term is a multilinear expression like theonefor A nonlin,(m+1) i but withonefactorφ (m) ora x (m) replaced by x φ (m), respectively x A x (m). Using the same multilinear estimates as before, one then concludes that x A nonlin,(m+1) i x A nonlin,(m) i l (Cǫ 1 S 1 ) m, (1 H) x A nonlin,(m+1) i (1 H) x A nonlin,(m) i Z hyp (Cǫ ) m with implicit constant depending on x φ[0, ] Ḣ1 L 2+ xa i [0] Ḣ1 L2. A similar argument applies to x A 0, x t A 0. It remains to bound x φ (m+1). Here we recall (44) which leads to p A φ(m+1) = M(A (m),φ (m+1) ), p A ( xφ (m+1) ) = x M(A (m),φ (m+1) )+2i k x P <k C A free,j P k j φ (m+1) From (131), we find with < C x P k1 A free,j j P k2 φ (m+1) N 2 δ P k1 A free,j S 1 x P k2 φ (m+1) S 1, 16 )
18 from which we easily infer 2i x P <k C A free,j P k j φ (m+1) N A free x S 1 x φ S 1 On the other hand, the term k x M(A (m),φ (m+1) ) is again a multilinear expression in φ (k),a (k), x φ (k), x A (k), k {m,m 1}, with at most one derivative factor in each monomial. Thus the multilinear estimates from above apply Frequency envelope bounds. TheS 1 bounds forthesmall datasolutionscanbesupplemented with corresponding frequency envelope bounds in a standard manner. Precisely, suppose that {c k } is a Ḣ1 L 2 frequency envelope for the data, in the sense that (71) P k (A x [0],φ[0]) Ḣ1 L 2 c k, (A x [0],φ[0]) Ḣ1 L 2 c k l 2 ǫ 1 Assume also that {c k } is slowly varying, c k /c j 2 δ j k, δ 1 Then we have a similar bound for the solutions, (72) P k A nonlin x S 1 c 2 k, P kφ S 1 + P k A 0 Y 1 c k The proof of these bounds is a straightforward consequence of the estimates in the previous section, since we have off-diagonal decay in all of our multilinear estimates Weak Lipschitz dependence on data. While establishing Lipschitz dependence on data in the energy norm would be desirable, this does not seem to hold because of the free wave component of the magnetic wave equation. Instead, we have a weaker bound for the difference of two solutions (A (1) x,φ (1) ) and (A (2) x,φ (2) ), of the form (73) A (1) x A(2) x S 1 δ+ φ(1) φ (2) ) S 1 δ+ A (1) 0 A(2) 0 Y 1 δ (A(1) x A(2) x,φ(1) (2) φ )[0] Ḣ1 δ Ḣ δ for small positive δ. This is equivalent to a similar bound for the linearized equation. All the components of the nonlinearity for which we have off-diagonal decay in the multilinear estimates cause no difficulty, and impose no sign restriction on δ. The only difficulty arises in the paradifferential magnetic wave equation p A φ = 0 Denoting by(b, ψ) the corresponding linearized variables, we are led to consider the equation p A ψ = k B j,<k j φ k where B is an H 1 δ free wave. By the bilinear estimate (54), for the right hand side we have the bound B j,<k j φ k N δ B[0] Ḣ1 δ Ḣ δ φ S 1, δ > 0 k which leads to the desired linearized bound ψ S 1 δ ψ[0] Ḣ1 δ Ḣ δ + B[0] Ḣ1 δ Ḣ φ δ S 1, δ > 0 17
19 5.4. Approximation by smooth solutions. Consider a small energy Coulomb initial data (A x,ψ)[0] and its regularizations (A x (m),ψ (m) )[0] = P <m (A x,ψ)[0]. Denote by (A x,φ), respectively (A x (m),ψ (m) ) the corresponding solutions. Our aim here is to prove the following: Lemma 2. Let {c k } be a slowly varying frequency envelope for (A x,ψ)[0] in the energy norm Ḣ 1 L 2. Then (74) (A (m) x A x,ψ (m) ψ) 2 S 1 k>mc 2 k The proof of the lemma is straightforward, by using (73) to bound the fequencies less tham m for the difference, and by using (72) for the higher frequencies of each of the terms Continuous dependence. Given a convergent sequence of small data (A k x,ψ k )[0] (A x,ψ)[0] in Ḣ1 L 2, we consider their frequency envelopes {c k,m } respectively c k in l 2. Due to the above convergence, it follows that (75) lim c k,m 2 = 0, uniformly in k m 0 m>m 0 We consider the corresponding regularized data (Ax k,(m),ψ k,(m) )[0] and the corresponding solutions (A k,(m),ψ k,(m) ). By the relation (75) and (74) it follows that (A k,(m),ψ k,(m) ) (A k,ψ k ) in S 1, uniformly in k On the other hand by the well-posedness theory for smooth data we have the convergence (A k,(m),ψ k,(m) ) (A (m),ψ (m) ) in H N loc Combining the two we obtain the desired local in time convergence (A k,ψ k ) (A,ψ) in S 1 loc. 6. Renormalization In what follows we work with the selfadjoint paradifferential covariant wave operator (76) p A = 2i k A j <k C jp k Here x A = 0 are Coulomb gauge potentials which solve the free wave equation A = 0. Our first goal is to prove estimates and construct a parametrix for the frequency localized evolution (77) p A φ = f, (φ(0),φ t(0)) = (g,h) with all functions φ, f, g, h localized at frequency 1. In general A 0, so one cannot in addition have da = 0; in other words the derivative interaction cannot be removed via a physical space gauge transformation. The situation changes drastically if one views the gauge potentials as pseudo-differential operators. This stems from the fact that when viewed microlocally all connections have zero curvature, because they contain only one component for each fixed direction in phase space. To write the gauge interaction in terms of a potential we need to solve: A ξ = τψ t +ξψ x. 18
20 This is impossible, but if we further restrict ourselves to the region where τ ± ξ, we are left with the exact solution: A ξ = dψ ± ( ξ,ξ), Here ψ ± are real valued and ψ ± (t,x,ξ) = L ω ± 1 ω (A ω). ω = ξ ξ, Lω ± = t ±ω x, ω = (ω x ) 2, Also we have used the relation L ω + Lω = + ω. As defined ψ + is associated to the upper cone {τ = ξ } and ψ is associated to the lower cone {τ = ξ }. Quantizing this, one can write the reduced covariant wave equation approximately as: p A 2i( α ψ ± )(t,x,d) α, ±τ > 0. which suggests that one should be be able to remove the gauge interaction through the pseudodifferential conjugation: p A e iψ ± (t,x,d) e iψ ± (D,y,s) ±τ > 0. Applying this algorithm directly does not work well for two reasons. First, the symbol we obtainisnotlocalizedatfrequency 1. Secondly, thesymbolψdefinedaboveistoosingular due to degeneracy of the operator 1 ; this corresponds exactly to parallel frequencies in A ω and φ. To remedy the latter issue we take advantage of the fact that in the bilinear null form estimates there is a small angle gain. This allows us to tightly cut off the small angle interactions between A and φ in the construction of Ψ, though not uniformly with respect to the A frequencies. Precisely, we define the dyadic portions of ψ by (78) ψ k,± (t,x,ξ) = L ω ± 1 ω (Π ω >δk A k ω) Then the full ψ s are defined by ψ ± := ψ <0,± For the renormalization we will use frequency localized versions of e ±iψ ±, namely the operators e iψ ± <0 (t,x,d), e iψ ± <0 (D,y,s) Here we use P(x,D) for the left quantization, and P(D,y) for the right quantization. Also the subscript < 0 stands for the space-time frequency localization at frequencies 1. Our main goal now is to show that the renormalizations are compatible with the S and N spaces. Below we use the notation and analogously for p A <k. p A <0 := 2iA j < C jp 0 19
21 Theorem 3. The frequency localized renormalization operators have the following mapping properties with Z {N 0,L 2,N 0 }: (79) (80) (81) e iψ ± (82) (83) e iψ ± e ±iψ± <0 (t,x,d) : Z Z, t e ±iψ ± <0 (t,x,d) : Z Z, <0 (t,x,d)e iψ ± <0 (D,y,s) I : Z ǫz, <0 (t,x,d) p A <0 e iψ ± <0 (t,x,d) : N 0,± ǫn 0,±. e iψ ± <0 (t,x,d) : S 0 S 0, The above theorem allows us to construct an approximate solution for (76) as follows: φ app = 1 e iψ ± <0 (t,x,d) 1 2 D e±it D e iψ ± <0 (D,y,0)( D g±h) ± (84) +e iψ ± <0 (t,x,d) 1 D K± e ±iψ ± <0 (D,y,s)f where represents the solution to K ± f(t) = t 0 e ±i(t s) D f(s)ds ( t i D )u = f, u(0) = 0 Here if we drop the e ±iφ ± operators we simply have the expression of the exact solution for the constant coefficient wave equation. Thus the idea is that these operators approximately conjugate the covariant wave flow to the constant coefficient wave flow. Theorem 4. Assume that f,g,h are localized at frequency 1, and also that f is localized at modulation 1. Then φ app is an approximate solution for p A <0 φ = f, φ(0) = (f,g), in the sense that (85) φ app S0 f N0 + g L 2 + h L 2 and (86) φ app [0] (g,h) L 2 + p A <0 φ app f N0 f N0 + g L 2 + h L 2 We remark that φ app constructed above has the same localization at frequency 1 and modulation 1. We also remark that the actual parametrix construction only requires the estimates (79)-(83), but yields a weaker form of (85) with S 0 replaced by N0. Then the estimate (83) serves to provide the additional S 0 regularity. An easy consequence of this is the following Theorem 5. For all f N and (g,h) Ḣ1 L 2 the solution to the paradifferential covariant wave equation (77) is defined globally and satisfies (87) φ S 1 f N l 1 L 2Ḣ g Ḣ 1 + h L 2 Again, using only (79)-(83) suffices but yields a weaker form of (85) with S replaced by N. For the remainder of the section we use Theorem 3 to prove Theorems 4, 5. The proof of Theorem 3 is completed in Sections 8, 9, after some preliminaries in Section 7. 20
22 Proof of Theorem 4. The estimate (85) follows directly by concatenating (79) and (83). It remains to consider (86). We begin with the initial data. For the position we have φ app (0) g = 1 e iψ ± <0 (0,x,D) 1 2 D eiψ ± <0 (D,y,0)( D g±h) g ± = 1 [ e iψ ± <0 (0,x,D) 1 2 D eiψ ± <0 (D,y,0) 1 ] ( D g±h) D ± and we can apply the L 2 version of (81). For the velocity we have t φ app (0) h = 1 ±e iψ ± <0 (0,x,D)e iψ ± <0 (D,y,0)( D g±h) h 2 ± ± +[ t e iψ ± <0 ](0,x,D) 1 D eiψ ± <0 (D,y,0)( D g±h)+ +e iψ ± <0 (0,x,D) 1 D [ te iψ ± <0 ](D,y,0)( D g±h) ±e iψ ± <0 (0,x,D)e iψ ± <0 (D,y,0)f(0) The first line is rewritten as 1 [ ] e iψ ± <0 (0,x,D)e iψ ± <0 (D,y,0) 1 (± D g +h) 2 and then we can use (81). For the second and third lines we use (80). Finally, for the last line we use (81) twice, along with the bound f(0) L 2 f N0 derived by Bernstein s inequality due to the unit modulation localization of f. Lastly, we consider the error estimate. We have p A <0 φ app f = ± [ p A <0 e iψ ± <0 (t,x,d) e iψ ± <0 (t,x,d) ]φ ± ± 1 2 e iψ ± <0 (t,x,d) D t ± D e iψ ± <0 (D,y,s)f f D = ± [ p A <0 e iψ ± <0 (t,x,d) e iψ ± <0 (t,x,d) ]φ ± where [e iψ ± <0 (t,x,d)e iψ ± <0 (D,y,s) 1]f ± [ 1 2 [e iψ ± <0 (t,x,d) 1 D eiψ ± <0 (D,y,s) 1 D ] tf +e iψ ± <0 (t,x,d) 1 D [ te iψ ± <0 ](D,y,s))]f] φ ± = 1 D [e±it D e iψ ± <0 (D,y,0)( D g±h)+k± e ±iψ ± <0 (D,y,s)] 21
23 Forthefirstlineweboundφ ± inn ± via(79)and 1 estimates, andthenusetheconjugation bound (82). For the second and third we use (81) in N. Finally for the fourth line we use (80) in N. Proof of Theorem 5. Consider first the frequency localized problems (with k referring to spatial frequency) p A <k φ k = f k, φ k (0) = (g k,h k ), k Z We solve each of these approximately and re-assemble the solutions φ app,k to the full approximate solution φ app = k φ app,k. We cannot immediately apply the preceding theorem, since we make no further assumption on the space-time Fourier support of the source f. To remedy this, we split where f hyp k f k = f hyp k +f ell k, is supported in the region τ ξ 2 k.then we solve the two problems p A <k φ 1 k = fhyp k, p A <k φ 2 k = fell k approximately, the first by using the previous theorem, the second by neglecting the magnetic term 2iA j <k jφ 2 k. We then solve the second equation by division by the symbol, i. e. we set (from now on k = 0 by scaling invariance and we omit the subscripts) φ 2 := 1 f ell where the operator 1 is defined by multiplication with the bound φ 2 S0 f ell N0 is immediate, and we reduce to solving the problem p A <0 φ 1 = f hyp, φ 1 (0) = (g,h) 1 f ell (0) 1 τ 2 ξ 2 on the Fourier side. Then which we do by invoking Theorem 4. It remains to control the additional error generated by our approximate solution φ 2, which is 2iA j <0 j φ 2 This is estimated by 2iA j <0 j φ 2 L 1 t L 2 x L 2Ḣ 1 2 Aj <0 L 2 t L x φ2 L 2 t,x L t L2 x fell N0 It follows that our approximate solution φ app = k φ app,k satisfies the conditions p A φ app f N l 1 L 2Ḣ φ app(0) (g,h) Ḣ1 L 2 f N l 1 L 2Ḣ (g,h) Ḣ 1 L 2 Also, observe that the preceding Theorem 4 implies φ app S 1 f N l 1 L 2Ḣ (g,h) Ḣ 1 L 2 The proof is now completed by simple iterative application of the preceding to the successive errors. 22
24 7. Decomposable Spaces and Some Symbol Bounds 7.1. Review of the Basic Decomposable Calculus. First we discuss the notion of decomposable function spaces and estimates. Recall that a zero homogeneous symbol c(t, x; ξ) is said to be in decomposable L q (L r ) if c = θ c(θ), θ 2 N, and: (88) c (θ) ) <, Dθ (L q t (Lr x ) where: ( 10n (89) c (θ) ( ) = Dθ L q t (Lr x ) θ k=0 φ sup ω b φ θ (θ ξ) k c (θ) 2 L r x )1 2 L q t Hereb φ θ (ξ)denotes acutoff onasolidangularsector ξ ξ 1 φ θ forafixed φ S n 1, and the sum is taken over a uniformly finitely overlapping collection. We define b DL q (L r ) as the infimum over all sums (88). In [18] it is shown that the following Hölder type inequality holds: (90) m b i DL q (L r ) i=1 m i=1 b i DL qi(l ri), (q 1,r 1 ) = i. (q 1 i,r 1 i ). In the sequel we only need a special case of decompositions provided in terms of these norms: Lemma 7.1 (Decomposability Lemma). Let A(t, x; D) be any pseudodifferential operator with symbol a(t,x;ξ). Suppose A satisfies the fixed time bound: (91) sup A(t,x;D) L 2 L 2 1. t Then for any symbol c(t,x;ξ) DL q (L r ) one has the space-time bounds: (92) (ac)(t,x;d) L q 1L 2 L q 2(L r 2) c DL q (L r ), 1 q q = 1 q 2, r = 1 r 2, 1 q 1,q 2,q,r,r 2 Proof. Due to the l 1 summation over θ in (88) it suffices to consider the case c = c θ for a fixed θ. We further decompose c θ (t,x,ξ) = φ c φ θ (t,x,ξ), cφ θ (t,x,ξ) := bφ θ (ξ)c(θ) (t,x,ξ) By (89) each c φ θ is supported in an angle θ sector, and it is smooth on the scale of its support. Thus by a Fourier series decomposition we can separate variables and represent c φ θ (t,x,ξ) = j>0 d φ,j θ (t,x)eφ,j θ (ξ), where d φ,j θ (t,x) L r j N x 10n b φ θ (θ ξ) k c (θ) L r x, k=0 23 e φ,j θ 1
25 Due to the rapid decay with respect to j it suffices to consider the contribution to c φ θ coming from a single j, say j = 1. Then c θ has the form c θ = φ d φ θ (t,x)eφ θ (ξ), where (93) d φ θ L q 1, t l2 φ Lr x eφ θ 1 Then we can represent (ac)(t,x,d)u = d φ θ (t,x) A(t,x,D)eφ θ (D)u φ The second factor above inherits the L 2 norm from u due to (91) and the square summation in ω due to the sector decomposition. Thus A(t,x,D)e φ θ (D)u L q 1 t l 2 ωl 2 x u L 2 The estimate for (ac)(t, x, D)u follows by combining the last bound with (93) A Decomposable Calculus for Pseudodifferential Products. In the sequel it will also be useful for us treat estimates for products of operators in a modular way. Recall that if a(x,ξ) and b(x,ξ) are symbols, then a r b r (ab) r i( x a ξ b) r. This formula is not exact, but it leads to an estimate: Lemma 7.2 (Decomposable product calculus). Let a(x, ξ) and b(x, ξ) be smooth symbols. Then: (94) a r b r (ab) r L r (L 2 ) L q (L 2 ) ( x a) r L r (L 2 ) L p 1(L 2 ) ξ b D1 L p 2(L ) where q 1 = p 1 i. Furthermore, if b = b(ξ) is a smooth compactly supported multiplier, then for any two translation invariant spaces X,Y one has: (95) a r b r (ab) r X Y ( x a) r X Y. Proof. Toprovethefirstestimate(94)wewritethekernelK(x,y)ofthedifferencea r b r (ab) r as follows: K(x,y) = c n R 3n e i(x z) ξ e i(z y) η a(z,ξ) ( b(y,η) b(y,ξ) ) dzdξdη 1 = c n e i(x z) ξ e i(z y) η a(z,ξ) ξ b ( y,sη+(1 s)ξ ) (η ξ)dzdξdηds, 0 R 3n 1 = c n i e i(x z) ξ e i(z y) η x a(z,ξ) ξ b ( y,sη+(1 s)ξ ) dzdξdηds, 0 R 3n 1 1 (96) = i T (2π) n (s 1)Ξ x a r (x,d)t sξ ξ b(,ξ)dsdξ, 0 R n where we have used Fourier inversion: ξ b ( y,sη+(1 s)ξ ) 1 = e i(sη+(1 s)ξ) Ξ (2π) n ξ b(y,ξ)dξ. R n 24
The Chern-Simons-Schrödinger equation
 The Chern-Simons-Schrödinger equation Low regularity local wellposedness Baoping Liu, Paul Smith, Daniel Tataru University of California, Berkeley July 16, 2012 Paul Smith (UC Berkeley) Chern-Simons-Schrödinger
The Chern-Simons-Schrödinger equation Low regularity local wellposedness Baoping Liu, Paul Smith, Daniel Tataru University of California, Berkeley July 16, 2012 Paul Smith (UC Berkeley) Chern-Simons-Schrödinger
A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS
 A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS DAN-ANDREI GEBA Abstract. We obtain a sharp local well-posedness result for an equation of wave maps type with variable coefficients.
A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS DAN-ANDREI GEBA Abstract. We obtain a sharp local well-posedness result for an equation of wave maps type with variable coefficients.
DISPERSIVE ESTIMATES FOR WAVE EQUATIONS WITH ROUGH COEFFICIENTS
 DISPERSIVE ESTIMATES FOR WAVE EQUATIONS WITH ROUGH COEFFICIENTS DANIEL TATARU AND DAN-ANDREI GEBA Abstract. We obtain a multiscale wave packet representation for the fundamental solution of the wave equation
DISPERSIVE ESTIMATES FOR WAVE EQUATIONS WITH ROUGH COEFFICIENTS DANIEL TATARU AND DAN-ANDREI GEBA Abstract. We obtain a multiscale wave packet representation for the fundamental solution of the wave equation
Simple Examples on Rectangular Domains
 84 Chapter 5 Simple Examples on Rectangular Domains In this chapter we consider simple elliptic boundary value problems in rectangular domains in R 2 or R 3 ; our prototype example is the Poisson equation
84 Chapter 5 Simple Examples on Rectangular Domains In this chapter we consider simple elliptic boundary value problems in rectangular domains in R 2 or R 3 ; our prototype example is the Poisson equation
2 A Model, Harmonic Map, Problem
 ELLIPTIC SYSTEMS JOHN E. HUTCHINSON Department of Mathematics School of Mathematical Sciences, A.N.U. 1 Introduction Elliptic equations model the behaviour of scalar quantities u, such as temperature or
ELLIPTIC SYSTEMS JOHN E. HUTCHINSON Department of Mathematics School of Mathematical Sciences, A.N.U. 1 Introduction Elliptic equations model the behaviour of scalar quantities u, such as temperature or
RANDOM PROPERTIES BENOIT PAUSADER
 RANDOM PROPERTIES BENOIT PAUSADER. Quasilinear problems In general, one consider the following trichotomy for nonlinear PDEs: A semilinear problem is a problem where the highest-order terms appears linearly
RANDOM PROPERTIES BENOIT PAUSADER. Quasilinear problems In general, one consider the following trichotomy for nonlinear PDEs: A semilinear problem is a problem where the highest-order terms appears linearly
Euler Equations: local existence
 Euler Equations: local existence Mat 529, Lesson 2. 1 Active scalars formulation We start with a lemma. Lemma 1. Assume that w is a magnetization variable, i.e. t w + u w + ( u) w = 0. If u = Pw then u
Euler Equations: local existence Mat 529, Lesson 2. 1 Active scalars formulation We start with a lemma. Lemma 1. Assume that w is a magnetization variable, i.e. t w + u w + ( u) w = 0. If u = Pw then u
A COUNTEREXAMPLE TO AN ENDPOINT BILINEAR STRICHARTZ INEQUALITY TERENCE TAO. t L x (R R2 ) f L 2 x (R2 )
 Electronic Journal of Differential Equations, Vol. 2006(2006), No. 5, pp. 6. ISSN: 072-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) A COUNTEREXAMPLE
Electronic Journal of Differential Equations, Vol. 2006(2006), No. 5, pp. 6. ISSN: 072-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) A COUNTEREXAMPLE
Dispersive Equations and Nonlinear Waves
 Herbert Koch Daniel Tataru Monica Vi an Dispersive Equations and Nonlinear Waves Generalized Korteweg-de Vries, Nonlinear Schrodinger, Wave and Schrodinger Maps ^ Birkhauser Contents Preface xi Nonlinear
Herbert Koch Daniel Tataru Monica Vi an Dispersive Equations and Nonlinear Waves Generalized Korteweg-de Vries, Nonlinear Schrodinger, Wave and Schrodinger Maps ^ Birkhauser Contents Preface xi Nonlinear
arxiv: v1 [math.ap] 1 May 2017
![arxiv: v1 [math.ap] 1 May 2017 arxiv: v1 [math.ap] 1 May 2017](/thumbs/92/108638608.jpg) LOW REGULARITY LOCAL WELL-POSEDNESS FOR THE (N+1)-DIMENSIONAL MAXWELL-KLEIN-GORDON EQUATIONS IN LORENZ GAUGE arxiv:1705.00599v1 [math.ap] 1 May 017 HARTMUT PECHER FACHBEREICH MATHEMATIK UND NATURWISSENSCHAFTEN
LOW REGULARITY LOCAL WELL-POSEDNESS FOR THE (N+1)-DIMENSIONAL MAXWELL-KLEIN-GORDON EQUATIONS IN LORENZ GAUGE arxiv:1705.00599v1 [math.ap] 1 May 017 HARTMUT PECHER FACHBEREICH MATHEMATIK UND NATURWISSENSCHAFTEN
Chapter One. The Calderón-Zygmund Theory I: Ellipticity
 Chapter One The Calderón-Zygmund Theory I: Ellipticity Our story begins with a classical situation: convolution with homogeneous, Calderón- Zygmund ( kernels on R n. Let S n 1 R n denote the unit sphere
Chapter One The Calderón-Zygmund Theory I: Ellipticity Our story begins with a classical situation: convolution with homogeneous, Calderón- Zygmund ( kernels on R n. Let S n 1 R n denote the unit sphere
MATH 205C: STATIONARY PHASE LEMMA
 MATH 205C: STATIONARY PHASE LEMMA For ω, consider an integral of the form I(ω) = e iωf(x) u(x) dx, where u Cc (R n ) complex valued, with support in a compact set K, and f C (R n ) real valued. Thus, I(ω)
MATH 205C: STATIONARY PHASE LEMMA For ω, consider an integral of the form I(ω) = e iωf(x) u(x) dx, where u Cc (R n ) complex valued, with support in a compact set K, and f C (R n ) real valued. Thus, I(ω)
A LOWER BOUND ON BLOWUP RATES FOR THE 3D INCOMPRESSIBLE EULER EQUATION AND A SINGLE EXPONENTIAL BEALE-KATO-MAJDA ESTIMATE. 1.
 A LOWER BOUND ON BLOWUP RATES FOR THE 3D INCOMPRESSIBLE EULER EQUATION AND A SINGLE EXPONENTIAL BEALE-KATO-MAJDA ESTIMATE THOMAS CHEN AND NATAŠA PAVLOVIĆ Abstract. We prove a Beale-Kato-Majda criterion
A LOWER BOUND ON BLOWUP RATES FOR THE 3D INCOMPRESSIBLE EULER EQUATION AND A SINGLE EXPONENTIAL BEALE-KATO-MAJDA ESTIMATE THOMAS CHEN AND NATAŠA PAVLOVIĆ Abstract. We prove a Beale-Kato-Majda criterion
arxiv: v1 [math.ap] 20 Nov 2007
![arxiv: v1 [math.ap] 20 Nov 2007 arxiv: v1 [math.ap] 20 Nov 2007](/thumbs/79/79495062.jpg) Long range scattering for the Maxwell-Schrödinger system with arbitrarily large asymptotic data arxiv:0711.3100v1 [math.ap] 20 Nov 2007 J. Ginibre Laboratoire de Physique Théorique Université de Paris
Long range scattering for the Maxwell-Schrödinger system with arbitrarily large asymptotic data arxiv:0711.3100v1 [math.ap] 20 Nov 2007 J. Ginibre Laboratoire de Physique Théorique Université de Paris
JUHA KINNUNEN. Harmonic Analysis
 JUHA KINNUNEN Harmonic Analysis Department of Mathematics and Systems Analysis, Aalto University 27 Contents Calderón-Zygmund decomposition. Dyadic subcubes of a cube.........................2 Dyadic cubes
JUHA KINNUNEN Harmonic Analysis Department of Mathematics and Systems Analysis, Aalto University 27 Contents Calderón-Zygmund decomposition. Dyadic subcubes of a cube.........................2 Dyadic cubes
L. Levaggi A. Tabacco WAVELETS ON THE INTERVAL AND RELATED TOPICS
 Rend. Sem. Mat. Univ. Pol. Torino Vol. 57, 1999) L. Levaggi A. Tabacco WAVELETS ON THE INTERVAL AND RELATED TOPICS Abstract. We use an abstract framework to obtain a multilevel decomposition of a variety
Rend. Sem. Mat. Univ. Pol. Torino Vol. 57, 1999) L. Levaggi A. Tabacco WAVELETS ON THE INTERVAL AND RELATED TOPICS Abstract. We use an abstract framework to obtain a multilevel decomposition of a variety
INSTANTON MODULI AND COMPACTIFICATION MATTHEW MAHOWALD
 INSTANTON MODULI AND COMPACTIFICATION MATTHEW MAHOWALD () Instanton (definition) (2) ADHM construction (3) Compactification. Instantons.. Notation. Throughout this talk, we will use the following notation:
INSTANTON MODULI AND COMPACTIFICATION MATTHEW MAHOWALD () Instanton (definition) (2) ADHM construction (3) Compactification. Instantons.. Notation. Throughout this talk, we will use the following notation:
arxiv:math/ v1 [math.ap] 24 Apr 2003
![arxiv:math/ v1 [math.ap] 24 Apr 2003 arxiv:math/ v1 [math.ap] 24 Apr 2003](/thumbs/95/122489725.jpg) ICM 2002 Vol. III 1 3 arxiv:math/0304397v1 [math.ap] 24 Apr 2003 Nonlinear Wave Equations Daniel Tataru Abstract The analysis of nonlinear wave equations has experienced a dramatic growth in the last ten
ICM 2002 Vol. III 1 3 arxiv:math/0304397v1 [math.ap] 24 Apr 2003 Nonlinear Wave Equations Daniel Tataru Abstract The analysis of nonlinear wave equations has experienced a dramatic growth in the last ten
Global well-posedness for KdV in Sobolev spaces of negative index
 Electronic Journal of Differential Equations, Vol. (), No. 6, pp. 7. ISSN: 7-669. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu (login: ftp) Global well-posedness for
Electronic Journal of Differential Equations, Vol. (), No. 6, pp. 7. ISSN: 7-669. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu (login: ftp) Global well-posedness for
MODIFIED SCATTERING FOR THE BOSON STAR EQUATION 1. INTRODUCTION
 MODIFIED SCATTERING FOR THE BOSON STAR EQUATION FABIO PUSATERI ABSTRACT We consider the question of scattering for the boson star equation in three space dimensions This is a semi-relativistic Klein-Gordon
MODIFIED SCATTERING FOR THE BOSON STAR EQUATION FABIO PUSATERI ABSTRACT We consider the question of scattering for the boson star equation in three space dimensions This is a semi-relativistic Klein-Gordon
SCALE INVARIANT FOURIER RESTRICTION TO A HYPERBOLIC SURFACE
 SCALE INVARIANT FOURIER RESTRICTION TO A HYPERBOLIC SURFACE BETSY STOVALL Abstract. This result sharpens the bilinear to linear deduction of Lee and Vargas for extension estimates on the hyperbolic paraboloid
SCALE INVARIANT FOURIER RESTRICTION TO A HYPERBOLIC SURFACE BETSY STOVALL Abstract. This result sharpens the bilinear to linear deduction of Lee and Vargas for extension estimates on the hyperbolic paraboloid
SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY
 SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY S. IBRAHIM, M. MAJDOUB, N. MASMOUDI, AND K. NAKANISHI Abstract. We investigate existence and asymptotic completeness of the wave operators
SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY S. IBRAHIM, M. MAJDOUB, N. MASMOUDI, AND K. NAKANISHI Abstract. We investigate existence and asymptotic completeness of the wave operators
Sobolev spaces. May 18
 Sobolev spaces May 18 2015 1 Weak derivatives The purpose of these notes is to give a very basic introduction to Sobolev spaces. More extensive treatments can e.g. be found in the classical references
Sobolev spaces May 18 2015 1 Weak derivatives The purpose of these notes is to give a very basic introduction to Sobolev spaces. More extensive treatments can e.g. be found in the classical references
Piecewise Smooth Solutions to the Burgers-Hilbert Equation
 Piecewise Smooth Solutions to the Burgers-Hilbert Equation Alberto Bressan and Tianyou Zhang Department of Mathematics, Penn State University, University Park, Pa 68, USA e-mails: bressan@mathpsuedu, zhang
Piecewise Smooth Solutions to the Burgers-Hilbert Equation Alberto Bressan and Tianyou Zhang Department of Mathematics, Penn State University, University Park, Pa 68, USA e-mails: bressan@mathpsuedu, zhang
The NLS on product spaces and applications
 October 2014, Orsay The NLS on product spaces and applications Nikolay Tzvetkov Cergy-Pontoise University based on joint work with Zaher Hani, Benoit Pausader and Nicola Visciglia A basic result Consider
October 2014, Orsay The NLS on product spaces and applications Nikolay Tzvetkov Cergy-Pontoise University based on joint work with Zaher Hani, Benoit Pausader and Nicola Visciglia A basic result Consider
Energy method for wave equations
 Energy method for wave equations Willie Wong Based on commit 5dfb7e5 of 2017-11-06 13:29 Abstract We give an elementary discussion of the energy method (and particularly the vector field method) in the
Energy method for wave equations Willie Wong Based on commit 5dfb7e5 of 2017-11-06 13:29 Abstract We give an elementary discussion of the energy method (and particularly the vector field method) in the
ALMOST OPTIMAL LOCAL WELL-POSEDNESS FOR THE (3+1)-DIMENSIONAL MAXWELL KLEIN GORDON EQUATIONS
 JOURNAL OF THE AMERICAN MATHEMATICAL SOCIETY Volume 7, Number, Pages 97 359 S 0894-03470300445-4 Article electronically published on November 3, 003 ALMOST OPTIMAL LOCAL WELL-POSEDNESS FOR THE 3+-DIMENSIONAL
JOURNAL OF THE AMERICAN MATHEMATICAL SOCIETY Volume 7, Number, Pages 97 359 S 0894-03470300445-4 Article electronically published on November 3, 003 ALMOST OPTIMAL LOCAL WELL-POSEDNESS FOR THE 3+-DIMENSIONAL
LECTURE 3 Functional spaces on manifolds
 LECTURE 3 Functional spaces on manifolds The aim of this section is to introduce Sobolev spaces on manifolds (or on vector bundles over manifolds). These will be the Banach spaces of sections we were after
LECTURE 3 Functional spaces on manifolds The aim of this section is to introduce Sobolev spaces on manifolds (or on vector bundles over manifolds). These will be the Banach spaces of sections we were after
Functional Analysis. Franck Sueur Metric spaces Definitions Completeness Compactness Separability...
 Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
A new class of pseudodifferential operators with mixed homogenities
 A new class of pseudodifferential operators with mixed homogenities Po-Lam Yung University of Oxford Jan 20, 2014 Introduction Given a smooth distribution of hyperplanes on R N (or more generally on a
A new class of pseudodifferential operators with mixed homogenities Po-Lam Yung University of Oxford Jan 20, 2014 Introduction Given a smooth distribution of hyperplanes on R N (or more generally on a
Overview of normed linear spaces
 20 Chapter 2 Overview of normed linear spaces Starting from this chapter, we begin examining linear spaces with at least one extra structure (topology or geometry). We assume linearity; this is a natural
20 Chapter 2 Overview of normed linear spaces Starting from this chapter, we begin examining linear spaces with at least one extra structure (topology or geometry). We assume linearity; this is a natural
On the local existence for an active scalar equation in critical regularity setting
 On the local existence for an active scalar equation in critical regularity setting Walter Rusin Department of Mathematics, Oklahoma State University, Stillwater, OK 7478 Fei Wang Department of Mathematics,
On the local existence for an active scalar equation in critical regularity setting Walter Rusin Department of Mathematics, Oklahoma State University, Stillwater, OK 7478 Fei Wang Department of Mathematics,
Strauss conjecture for nontrapping obstacles
 Chengbo Wang Joint work with: Hart Smith, Christopher Sogge Department of Mathematics Johns Hopkins University Baltimore, Maryland 21218 wangcbo@jhu.edu November 3, 2010 1 Problem and Background Problem
Chengbo Wang Joint work with: Hart Smith, Christopher Sogge Department of Mathematics Johns Hopkins University Baltimore, Maryland 21218 wangcbo@jhu.edu November 3, 2010 1 Problem and Background Problem
ALMOST CONSERVATION LAWS AND GLOBAL ROUGH SOLUTIONS TO A NONLINEAR SCHRÖDINGER EQUATION
 ALMOST CONSERVATION LAWS AND GLOBAL ROUGH SOLUTIONS TO A NONLINEAR SCHRÖDINGER EQUATION J. COLLIANDER, M. KEEL, G. STAFFILANI, H. TAKAOKA, AND T. TAO Abstract. We prove an almost conservation law to obtain
ALMOST CONSERVATION LAWS AND GLOBAL ROUGH SOLUTIONS TO A NONLINEAR SCHRÖDINGER EQUATION J. COLLIANDER, M. KEEL, G. STAFFILANI, H. TAKAOKA, AND T. TAO Abstract. We prove an almost conservation law to obtain
Overview of the proof of the Bounded L 2 Curvature Conjecture. Sergiu Klainerman Igor Rodnianski Jeremie Szeftel
 Overview of the proof of the Bounded L 2 Curvature Conjecture Sergiu Klainerman Igor Rodnianski Jeremie Szeftel Department of Mathematics, Princeton University, Princeton NJ 8544 E-mail address: seri@math.princeton.edu
Overview of the proof of the Bounded L 2 Curvature Conjecture Sergiu Klainerman Igor Rodnianski Jeremie Szeftel Department of Mathematics, Princeton University, Princeton NJ 8544 E-mail address: seri@math.princeton.edu
Eigenvalues and Eigenfunctions of the Laplacian
 The Waterloo Mathematics Review 23 Eigenvalues and Eigenfunctions of the Laplacian Mihai Nica University of Waterloo mcnica@uwaterloo.ca Abstract: The problem of determining the eigenvalues and eigenvectors
The Waterloo Mathematics Review 23 Eigenvalues and Eigenfunctions of the Laplacian Mihai Nica University of Waterloo mcnica@uwaterloo.ca Abstract: The problem of determining the eigenvalues and eigenvectors
LECTURE 1: SOURCES OF ERRORS MATHEMATICAL TOOLS A PRIORI ERROR ESTIMATES. Sergey Korotov,
 LECTURE 1: SOURCES OF ERRORS MATHEMATICAL TOOLS A PRIORI ERROR ESTIMATES Sergey Korotov, Institute of Mathematics Helsinki University of Technology, Finland Academy of Finland 1 Main Problem in Mathematical
LECTURE 1: SOURCES OF ERRORS MATHEMATICAL TOOLS A PRIORI ERROR ESTIMATES Sergey Korotov, Institute of Mathematics Helsinki University of Technology, Finland Academy of Finland 1 Main Problem in Mathematical
THE WAVE MAPS EQUATION. 1. The equations Let us begin with the Laplace equation, R n
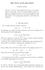 THE WAVE MAPS EQUATION DANIEL TATARU Abstract. The wave maps equation has become a very popular topic in recent years. The aim of these expository notes is to present a non-technical survey of the ideas
THE WAVE MAPS EQUATION DANIEL TATARU Abstract. The wave maps equation has become a very popular topic in recent years. The aim of these expository notes is to present a non-technical survey of the ideas
Scalar curvature and the Thurston norm
 Scalar curvature and the Thurston norm P. B. Kronheimer 1 andt.s.mrowka 2 Harvard University, CAMBRIDGE MA 02138 Massachusetts Institute of Technology, CAMBRIDGE MA 02139 1. Introduction Let Y be a closed,
Scalar curvature and the Thurston norm P. B. Kronheimer 1 andt.s.mrowka 2 Harvard University, CAMBRIDGE MA 02138 Massachusetts Institute of Technology, CAMBRIDGE MA 02139 1. Introduction Let Y be a closed,
Multiscale Frame-based Kernels for Image Registration
 Multiscale Frame-based Kernels for Image Registration Ming Zhen, Tan National University of Singapore 22 July, 16 Ming Zhen, Tan (National University of Singapore) Multiscale Frame-based Kernels for Image
Multiscale Frame-based Kernels for Image Registration Ming Zhen, Tan National University of Singapore 22 July, 16 Ming Zhen, Tan (National University of Singapore) Multiscale Frame-based Kernels for Image
arxiv: v3 [math.ap] 10 Oct 2014
![arxiv: v3 [math.ap] 10 Oct 2014 arxiv: v3 [math.ap] 10 Oct 2014](/thumbs/82/85678438.jpg) THE BOUNDED L 2 CURVATURE CONJECTURE arxiv:1204.1767v3 [math.ap] 10 Oct 2014 SERGIU KLAINERMAN, IGOR RODNIANSKI, AND JEREMIE SZEFTEL Abstract. This is the main paper in a sequence in which we give a complete
THE BOUNDED L 2 CURVATURE CONJECTURE arxiv:1204.1767v3 [math.ap] 10 Oct 2014 SERGIU KLAINERMAN, IGOR RODNIANSKI, AND JEREMIE SZEFTEL Abstract. This is the main paper in a sequence in which we give a complete
2. Function spaces and approximation
 2.1 2. Function spaces and approximation 2.1. The space of test functions. Notation and prerequisites are collected in Appendix A. Let Ω be an open subset of R n. The space C0 (Ω), consisting of the C
2.1 2. Function spaces and approximation 2.1. The space of test functions. Notation and prerequisites are collected in Appendix A. Let Ω be an open subset of R n. The space C0 (Ω), consisting of the C
at time t, in dimension d. The index i varies in a countable set I. We call configuration the family, denoted generically by Φ: U (x i (t) x j (t))
 Notations In this chapter we investigate infinite systems of interacting particles subject to Newtonian dynamics Each particle is characterized by its position an velocity x i t, v i t R d R d at time
Notations In this chapter we investigate infinite systems of interacting particles subject to Newtonian dynamics Each particle is characterized by its position an velocity x i t, v i t R d R d at time
NONLINEAR PROPAGATION OF WAVE PACKETS. Ritsumeikan University, and 22
 NONLINEAR PROPAGATION OF WAVE PACKETS CLOTILDE FERMANIAN KAMMERER Ritsumeikan University, 21-1 - 21 and 22 Our aim in this lecture is to explain the proof of a recent Theorem obtained in collaboration
NONLINEAR PROPAGATION OF WAVE PACKETS CLOTILDE FERMANIAN KAMMERER Ritsumeikan University, 21-1 - 21 and 22 Our aim in this lecture is to explain the proof of a recent Theorem obtained in collaboration
POINTWISE BOUNDS ON QUASIMODES OF SEMICLASSICAL SCHRÖDINGER OPERATORS IN DIMENSION TWO
 POINTWISE BOUNDS ON QUASIMODES OF SEMICLASSICAL SCHRÖDINGER OPERATORS IN DIMENSION TWO HART F. SMITH AND MACIEJ ZWORSKI Abstract. We prove optimal pointwise bounds on quasimodes of semiclassical Schrödinger
POINTWISE BOUNDS ON QUASIMODES OF SEMICLASSICAL SCHRÖDINGER OPERATORS IN DIMENSION TWO HART F. SMITH AND MACIEJ ZWORSKI Abstract. We prove optimal pointwise bounds on quasimodes of semiclassical Schrödinger
Appendix A Functional Analysis
 Appendix A Functional Analysis A.1 Metric Spaces, Banach Spaces, and Hilbert Spaces Definition A.1. Metric space. Let X be a set. A map d : X X R is called metric on X if for all x,y,z X it is i) d(x,y)
Appendix A Functional Analysis A.1 Metric Spaces, Banach Spaces, and Hilbert Spaces Definition A.1. Metric space. Let X be a set. A map d : X X R is called metric on X if for all x,y,z X it is i) d(x,y)
CUTOFF RESOLVENT ESTIMATES AND THE SEMILINEAR SCHRÖDINGER EQUATION
 CUTOFF RESOLVENT ESTIMATES AND THE SEMILINEAR SCHRÖDINGER EQUATION HANS CHRISTIANSON Abstract. This paper shows how abstract resolvent estimates imply local smoothing for solutions to the Schrödinger equation.
CUTOFF RESOLVENT ESTIMATES AND THE SEMILINEAR SCHRÖDINGER EQUATION HANS CHRISTIANSON Abstract. This paper shows how abstract resolvent estimates imply local smoothing for solutions to the Schrödinger equation.
Some physical space heuristics for Strichartz estimates
 Some physical space heuristics for Strichartz estimates Felipe Hernandez July 30, 2014 SPUR Final Paper, Summer 2014 Mentor Chenjie Fan Project suggested by Gigliola Staffilani Abstract This note records
Some physical space heuristics for Strichartz estimates Felipe Hernandez July 30, 2014 SPUR Final Paper, Summer 2014 Mentor Chenjie Fan Project suggested by Gigliola Staffilani Abstract This note records
On the quantum theory of rotating electrons
 Zur Quantentheorie des rotierenden Elektrons Zeit. f. Phys. 8 (98) 85-867. On the quantum theory of rotating electrons By Friedrich Möglich in Berlin-Lichterfelde. (Received on April 98.) Translated by
Zur Quantentheorie des rotierenden Elektrons Zeit. f. Phys. 8 (98) 85-867. On the quantum theory of rotating electrons By Friedrich Möglich in Berlin-Lichterfelde. (Received on April 98.) Translated by
Decoupling of modes for the elastic wave equation in media of limited smoothness
 Decoupling of modes for the elastic wave equation in media of limited smoothness Valeriy Brytik 1 Maarten V. de Hoop 1 Hart F. Smith Gunther Uhlmann September, 1 1 Center for Computational and Applied
Decoupling of modes for the elastic wave equation in media of limited smoothness Valeriy Brytik 1 Maarten V. de Hoop 1 Hart F. Smith Gunther Uhlmann September, 1 1 Center for Computational and Applied
2tdt 1 y = t2 + C y = which implies C = 1 and the solution is y = 1
 Lectures - Week 11 General First Order ODEs & Numerical Methods for IVPs In general, nonlinear problems are much more difficult to solve than linear ones. Unfortunately many phenomena exhibit nonlinear
Lectures - Week 11 General First Order ODEs & Numerical Methods for IVPs In general, nonlinear problems are much more difficult to solve than linear ones. Unfortunately many phenomena exhibit nonlinear
arxiv: v1 [math.ap] 17 May 2017
![arxiv: v1 [math.ap] 17 May 2017 arxiv: v1 [math.ap] 17 May 2017](/thumbs/81/83547596.jpg) ON A HOMOGENIZATION PROBLEM arxiv:1705.06174v1 [math.ap] 17 May 2017 J. BOURGAIN Abstract. We study a homogenization question for a stochastic divergence type operator. 1. Introduction and Statement Let
ON A HOMOGENIZATION PROBLEM arxiv:1705.06174v1 [math.ap] 17 May 2017 J. BOURGAIN Abstract. We study a homogenization question for a stochastic divergence type operator. 1. Introduction and Statement Let
Propagating terraces and the dynamics of front-like solutions of reaction-diffusion equations on R
 Propagating terraces and the dynamics of front-like solutions of reaction-diffusion equations on R P. Poláčik School of Mathematics, University of Minnesota Minneapolis, MN 55455 Abstract We consider semilinear
Propagating terraces and the dynamics of front-like solutions of reaction-diffusion equations on R P. Poláčik School of Mathematics, University of Minnesota Minneapolis, MN 55455 Abstract We consider semilinear
i=1 α i. Given an m-times continuously
 1 Fundamentals 1.1 Classification and characteristics Let Ω R d, d N, d 2, be an open set and α = (α 1,, α d ) T N d 0, N 0 := N {0}, a multiindex with α := d i=1 α i. Given an m-times continuously differentiable
1 Fundamentals 1.1 Classification and characteristics Let Ω R d, d N, d 2, be an open set and α = (α 1,, α d ) T N d 0, N 0 := N {0}, a multiindex with α := d i=1 α i. Given an m-times continuously differentiable
Existence theorems for some nonlinear hyperbolic equations on a waveguide
 Existence theorems for some nonlinear hyperbolic equations on a waveguide by Ann C. Stewart A dissertation submitted to the Johns Hopkins University in conformity with the requirements for the degree of
Existence theorems for some nonlinear hyperbolic equations on a waveguide by Ann C. Stewart A dissertation submitted to the Johns Hopkins University in conformity with the requirements for the degree of
5 Constructions of connections
 [under construction] 5 Constructions of connections 5.1 Connections on manifolds and the Levi-Civita theorem We start with a bit of terminology. A connection on the tangent bundle T M M of a manifold M
[under construction] 5 Constructions of connections 5.1 Connections on manifolds and the Levi-Civita theorem We start with a bit of terminology. A connection on the tangent bundle T M M of a manifold M
Fourier Transform & Sobolev Spaces
 Fourier Transform & Sobolev Spaces Michael Reiter, Arthur Schuster Summer Term 2008 Abstract We introduce the concept of weak derivative that allows us to define new interesting Hilbert spaces the Sobolev
Fourier Transform & Sobolev Spaces Michael Reiter, Arthur Schuster Summer Term 2008 Abstract We introduce the concept of weak derivative that allows us to define new interesting Hilbert spaces the Sobolev
Null Cones to Infinity, Curvature Flux, and Bondi Mass
 Null Cones to Infinity, Curvature Flux, and Bondi Mass Arick Shao (joint work with Spyros Alexakis) University of Toronto May 22, 2013 Arick Shao (University of Toronto) Null Cones to Infinity May 22,
Null Cones to Infinity, Curvature Flux, and Bondi Mass Arick Shao (joint work with Spyros Alexakis) University of Toronto May 22, 2013 Arick Shao (University of Toronto) Null Cones to Infinity May 22,
Brane Gravity from Bulk Vector Field
 Brane Gravity from Bulk Vector Field Merab Gogberashvili Andronikashvili Institute of Physics, 6 Tamarashvili Str., Tbilisi 380077, Georgia E-mail: gogber@hotmail.com September 7, 00 Abstract It is shown
Brane Gravity from Bulk Vector Field Merab Gogberashvili Andronikashvili Institute of Physics, 6 Tamarashvili Str., Tbilisi 380077, Georgia E-mail: gogber@hotmail.com September 7, 00 Abstract It is shown
Large data local solutions for the derivative NLS equation
 J. Eur. Math. Soc. 1, 957 985 c European Mathematical Society 8 Ioan Bejenaru Daniel Tataru Large data local solutions for the derivative NLS equation Received May 9, 7 Abstract. We consider the derivative
J. Eur. Math. Soc. 1, 957 985 c European Mathematical Society 8 Ioan Bejenaru Daniel Tataru Large data local solutions for the derivative NLS equation Received May 9, 7 Abstract. We consider the derivative
CALCULUS ON MANIFOLDS. 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M =
 CALCULUS ON MANIFOLDS 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M = a M T am, called the tangent bundle, is itself a smooth manifold, dim T M = 2n. Example 1.
CALCULUS ON MANIFOLDS 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M = a M T am, called the tangent bundle, is itself a smooth manifold, dim T M = 2n. Example 1.
On m-accretive Schrödinger operators in L p -spaces on manifolds of bounded geometry
 On m-accretive Schrödinger operators in L p -spaces on manifolds of bounded geometry Ognjen Milatovic Department of Mathematics and Statistics University of North Florida Jacksonville, FL 32224 USA. Abstract
On m-accretive Schrödinger operators in L p -spaces on manifolds of bounded geometry Ognjen Milatovic Department of Mathematics and Statistics University of North Florida Jacksonville, FL 32224 USA. Abstract
Notes. 1 Fourier transform and L p spaces. March 9, For a function in f L 1 (R n ) define the Fourier transform. ˆf(ξ) = f(x)e 2πi x,ξ dx.
 Notes March 9, 27 1 Fourier transform and L p spaces For a function in f L 1 (R n ) define the Fourier transform ˆf(ξ) = f(x)e 2πi x,ξ dx. Properties R n 1. f g = ˆfĝ 2. δλ (f)(ξ) = ˆf(λξ), where δ λ f(x)
Notes March 9, 27 1 Fourier transform and L p spaces For a function in f L 1 (R n ) define the Fourier transform ˆf(ξ) = f(x)e 2πi x,ξ dx. Properties R n 1. f g = ˆfĝ 2. δλ (f)(ξ) = ˆf(λξ), where δ λ f(x)
Wave equation on manifolds and finite speed of propagation
 Wave equation on manifolds and finite speed of propagation Ethan Y. Jaffe Let M be a Riemannian manifold (without boundary), and let be the (negative of) the Laplace-Beltrami operator. In this note, we
Wave equation on manifolds and finite speed of propagation Ethan Y. Jaffe Let M be a Riemannian manifold (without boundary), and let be the (negative of) the Laplace-Beltrami operator. In this note, we
A Sharpened Hausdorff-Young Inequality
 A Sharpened Hausdorff-Young Inequality Michael Christ University of California, Berkeley IPAM Workshop Kakeya Problem, Restriction Problem, Sum-Product Theory and perhaps more May 5, 2014 Hausdorff-Young
A Sharpened Hausdorff-Young Inequality Michael Christ University of California, Berkeley IPAM Workshop Kakeya Problem, Restriction Problem, Sum-Product Theory and perhaps more May 5, 2014 Hausdorff-Young
ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS
 Bendikov, A. and Saloff-Coste, L. Osaka J. Math. 4 (5), 677 7 ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS ALEXANDER BENDIKOV and LAURENT SALOFF-COSTE (Received March 4, 4)
Bendikov, A. and Saloff-Coste, L. Osaka J. Math. 4 (5), 677 7 ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS ALEXANDER BENDIKOV and LAURENT SALOFF-COSTE (Received March 4, 4)
Covariant Formulation of Electrodynamics
 Chapter 7. Covariant Formulation of Electrodynamics Notes: Most of the material presented in this chapter is taken from Jackson, Chap. 11, and Rybicki and Lightman, Chap. 4. Starting with this chapter,
Chapter 7. Covariant Formulation of Electrodynamics Notes: Most of the material presented in this chapter is taken from Jackson, Chap. 11, and Rybicki and Lightman, Chap. 4. Starting with this chapter,
The Helically Reduced Wave Equation as a Symmetric Positive System
 Utah State University DigitalCommons@USU All Physics Faculty Publications Physics 2003 The Helically Reduced Wave Equation as a Symmetric Positive System Charles G. Torre Utah State University Follow this
Utah State University DigitalCommons@USU All Physics Faculty Publications Physics 2003 The Helically Reduced Wave Equation as a Symmetric Positive System Charles G. Torre Utah State University Follow this
The Bounded L 2 curvature conjecture in general relativity
 The Bounded L 2 curvature conjecture in general relativity Jérémie Szeftel Département de Mathématiques et Applications, Ecole Normale Supérieure (Joint work with Sergiu Klainerman and Igor Rodnianski)
The Bounded L 2 curvature conjecture in general relativity Jérémie Szeftel Département de Mathématiques et Applications, Ecole Normale Supérieure (Joint work with Sergiu Klainerman and Igor Rodnianski)
ON THE UNIQUENESS OF SOLUTIONS TO THE GROSS-PITAEVSKII HIERARCHY. 1. Introduction
 ON THE UNIQUENESS OF SOLUTIONS TO THE GROSS-PITAEVSKII HIERARCHY SERGIU KLAINERMAN AND MATEI MACHEDON Abstract. The purpose of this note is to give a new proof of uniqueness of the Gross- Pitaevskii hierarchy,
ON THE UNIQUENESS OF SOLUTIONS TO THE GROSS-PITAEVSKII HIERARCHY SERGIU KLAINERMAN AND MATEI MACHEDON Abstract. The purpose of this note is to give a new proof of uniqueness of the Gross- Pitaevskii hierarchy,
The initial value problem for non-linear Schrödinger equations
 The initial value problem for non-linear Schrödinger equations LUIS VEGA Universidad del País Vasco Euskal Herriko Unibertsitatea ICM MADRID 2006 1 In this talk I shall present some work done in collaboration
The initial value problem for non-linear Schrödinger equations LUIS VEGA Universidad del País Vasco Euskal Herriko Unibertsitatea ICM MADRID 2006 1 In this talk I shall present some work done in collaboration
2. Duality and tensor products. In class, we saw how to define a natural map V1 V2 (V 1 V 2 ) satisfying
 Math 396. Isomorphisms and tensor products In this handout, we work out some examples of isomorphisms involving tensor products of vector spaces. The three basic principles are: (i) to construct maps involving
Math 396. Isomorphisms and tensor products In this handout, we work out some examples of isomorphisms involving tensor products of vector spaces. The three basic principles are: (i) to construct maps involving
CONVERGENCE THEORY. G. ALLAIRE CMAP, Ecole Polytechnique. 1. Maximum principle. 2. Oscillating test function. 3. Two-scale convergence
 1 CONVERGENCE THEOR G. ALLAIRE CMAP, Ecole Polytechnique 1. Maximum principle 2. Oscillating test function 3. Two-scale convergence 4. Application to homogenization 5. General theory H-convergence) 6.
1 CONVERGENCE THEOR G. ALLAIRE CMAP, Ecole Polytechnique 1. Maximum principle 2. Oscillating test function 3. Two-scale convergence 4. Application to homogenization 5. General theory H-convergence) 6.
8 Singular Integral Operators and L p -Regularity Theory
 8 Singular Integral Operators and L p -Regularity Theory 8. Motivation See hand-written notes! 8.2 Mikhlin Multiplier Theorem Recall that the Fourier transformation F and the inverse Fourier transformation
8 Singular Integral Operators and L p -Regularity Theory 8. Motivation See hand-written notes! 8.2 Mikhlin Multiplier Theorem Recall that the Fourier transformation F and the inverse Fourier transformation
7 Curvature of a connection
 [under construction] 7 Curvature of a connection 7.1 Theorema Egregium Consider the derivation equations for a hypersurface in R n+1. We are mostly interested in the case n = 2, but shall start from the
[under construction] 7 Curvature of a connection 7.1 Theorema Egregium Consider the derivation equations for a hypersurface in R n+1. We are mostly interested in the case n = 2, but shall start from the
CONDITIONAL GLOBAL REGULARITY OF SCHRÖDINGER MAPS: SUBTHRESHOLD DISPERSED ENERGY arxiv: v2 [math.ap] 8 Jun 2012
![CONDITIONAL GLOBAL REGULARITY OF SCHRÖDINGER MAPS: SUBTHRESHOLD DISPERSED ENERGY arxiv: v2 [math.ap] 8 Jun 2012 CONDITIONAL GLOBAL REGULARITY OF SCHRÖDINGER MAPS: SUBTHRESHOLD DISPERSED ENERGY arxiv: v2 [math.ap] 8 Jun 2012](/thumbs/86/94410892.jpg) CONDITIONAL GLOBAL REGULARITY OF SCHRÖDINGER MAPS: SUBTHRESHOLD DISPERSED ENERGY arxiv:112.448v2 [math.ap] 8 Jun 212 PAUL SMITH Abstract. We consider the Schrödinger map initial value problem { tϕ = ϕ
CONDITIONAL GLOBAL REGULARITY OF SCHRÖDINGER MAPS: SUBTHRESHOLD DISPERSED ENERGY arxiv:112.448v2 [math.ap] 8 Jun 212 PAUL SMITH Abstract. We consider the Schrödinger map initial value problem { tϕ = ϕ
8.821 F2008 Lecture 12: Boundary of AdS; Poincaré patch; wave equation in AdS
 8.821 F2008 Lecture 12: Boundary of AdS; Poincaré patch; wave equation in AdS Lecturer: McGreevy Scribe: Francesco D Eramo October 16, 2008 Today: 1. the boundary of AdS 2. Poincaré patch 3. motivate boundary
8.821 F2008 Lecture 12: Boundary of AdS; Poincaré patch; wave equation in AdS Lecturer: McGreevy Scribe: Francesco D Eramo October 16, 2008 Today: 1. the boundary of AdS 2. Poincaré patch 3. motivate boundary
Putzer s Algorithm. Norman Lebovitz. September 8, 2016
 Putzer s Algorithm Norman Lebovitz September 8, 2016 1 Putzer s algorithm The differential equation dx = Ax, (1) dt where A is an n n matrix of constants, possesses the fundamental matrix solution exp(at),
Putzer s Algorithm Norman Lebovitz September 8, 2016 1 Putzer s algorithm The differential equation dx = Ax, (1) dt where A is an n n matrix of constants, possesses the fundamental matrix solution exp(at),
Metric Spaces and Topology
 Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
S chauder Theory. x 2. = log( x 1 + x 2 ) + 1 ( x 1 + x 2 ) 2. ( 5) x 1 + x 2 x 1 + x 2. 2 = 2 x 1. x 1 x 2. 1 x 1.
 Sep. 1 9 Intuitively, the solution u to the Poisson equation S chauder Theory u = f 1 should have better regularity than the right hand side f. In particular one expects u to be twice more differentiable
Sep. 1 9 Intuitively, the solution u to the Poisson equation S chauder Theory u = f 1 should have better regularity than the right hand side f. In particular one expects u to be twice more differentiable
Week 1, solution to exercise 2
 Week 1, solution to exercise 2 I. THE ACTION FOR CLASSICAL ELECTRODYNAMICS A. Maxwell s equations in relativistic form Maxwell s equations in vacuum and in natural units (c = 1) are, E=ρ, B t E=j (inhomogeneous),
Week 1, solution to exercise 2 I. THE ACTION FOR CLASSICAL ELECTRODYNAMICS A. Maxwell s equations in relativistic form Maxwell s equations in vacuum and in natural units (c = 1) are, E=ρ, B t E=j (inhomogeneous),
Analysis in weighted spaces : preliminary version
 Analysis in weighted spaces : preliminary version Frank Pacard To cite this version: Frank Pacard. Analysis in weighted spaces : preliminary version. 3rd cycle. Téhéran (Iran, 2006, pp.75.
Analysis in weighted spaces : preliminary version Frank Pacard To cite this version: Frank Pacard. Analysis in weighted spaces : preliminary version. 3rd cycle. Téhéran (Iran, 2006, pp.75.
A brief introduction to Semi-Riemannian geometry and general relativity. Hans Ringström
 A brief introduction to Semi-Riemannian geometry and general relativity Hans Ringström May 5, 2015 2 Contents 1 Scalar product spaces 1 1.1 Scalar products...................................... 1 1.2 Orthonormal
A brief introduction to Semi-Riemannian geometry and general relativity Hans Ringström May 5, 2015 2 Contents 1 Scalar product spaces 1 1.1 Scalar products...................................... 1 1.2 Orthonormal
RIGIDITY OF STATIONARY BLACK HOLES WITH SMALL ANGULAR MOMENTUM ON THE HORIZON
 RIGIDITY OF STATIONARY BLACK HOLES WITH SMALL ANGULAR MOMENTUM ON THE HORIZON S. ALEXAKIS, A. D. IONESCU, AND S. KLAINERMAN Abstract. We prove a black hole rigidity result for slowly rotating stationary
RIGIDITY OF STATIONARY BLACK HOLES WITH SMALL ANGULAR MOMENTUM ON THE HORIZON S. ALEXAKIS, A. D. IONESCU, AND S. KLAINERMAN Abstract. We prove a black hole rigidity result for slowly rotating stationary
Spanning and Independence Properties of Finite Frames
 Chapter 1 Spanning and Independence Properties of Finite Frames Peter G. Casazza and Darrin Speegle Abstract The fundamental notion of frame theory is redundancy. It is this property which makes frames
Chapter 1 Spanning and Independence Properties of Finite Frames Peter G. Casazza and Darrin Speegle Abstract The fundamental notion of frame theory is redundancy. It is this property which makes frames
Here we used the multiindex notation:
 Mathematics Department Stanford University Math 51H Distributions Distributions first arose in solving partial differential equations by duality arguments; a later related benefit was that one could always
Mathematics Department Stanford University Math 51H Distributions Distributions first arose in solving partial differential equations by duality arguments; a later related benefit was that one could always
Lipschitz p-convex and q-concave maps
 Lipschitz p-convex and q-concave maps J. Alejandro Chávez-Domínguez Instituto de Ciencias Matemáticas, CSIC-UAM-UCM-UC3M, Madrid and Department of Mathematics, University of Texas at Austin Conference
Lipschitz p-convex and q-concave maps J. Alejandro Chávez-Domínguez Instituto de Ciencias Matemáticas, CSIC-UAM-UCM-UC3M, Madrid and Department of Mathematics, University of Texas at Austin Conference
Part V. 17 Introduction: What are measures and why measurable sets. Lebesgue Integration Theory
 Part V 7 Introduction: What are measures and why measurable sets Lebesgue Integration Theory Definition 7. (Preliminary). A measure on a set is a function :2 [ ] such that. () = 2. If { } = is a finite
Part V 7 Introduction: What are measures and why measurable sets Lebesgue Integration Theory Definition 7. (Preliminary). A measure on a set is a function :2 [ ] such that. () = 2. If { } = is a finite
Optimal Transportation. Nonlinear Partial Differential Equations
 Optimal Transportation and Nonlinear Partial Differential Equations Neil S. Trudinger Centre of Mathematics and its Applications Australian National University 26th Brazilian Mathematical Colloquium 2007
Optimal Transportation and Nonlinear Partial Differential Equations Neil S. Trudinger Centre of Mathematics and its Applications Australian National University 26th Brazilian Mathematical Colloquium 2007
A survey on l 2 decoupling
 A survey on l 2 decoupling Po-Lam Yung 1 The Chinese University of Hong Kong January 31, 2018 1 Research partially supported by HKRGC grant 14313716, and by CUHK direct grants 4053220, 4441563 Introduction
A survey on l 2 decoupling Po-Lam Yung 1 The Chinese University of Hong Kong January 31, 2018 1 Research partially supported by HKRGC grant 14313716, and by CUHK direct grants 4053220, 4441563 Introduction
FACTORIZATION OF SECOND-ORDER STRICTLY HYPERBOLIC OPERATORS WITH LOGARITHMIC SLOW SCALE COEFFICIENTS AND GENERALIZED MICROLOCAL APPROXIMATIONS
 Electronic Journal of Differential Equations, Vol. 28 28, No. 42, pp. 49. ISSN: 72-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu FACTORIZATION OF SECOND-ORDER STRICTLY HYPERBOLIC OPERATORS
Electronic Journal of Differential Equations, Vol. 28 28, No. 42, pp. 49. ISSN: 72-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu FACTORIZATION OF SECOND-ORDER STRICTLY HYPERBOLIC OPERATORS
A PHYSICAL SPACE PROOF OF THE BILINEAR STRICHARTZ AND LOCAL SMOOTHING ESTIMATES FOR THE SCHRÖDINGER EQUATION
 A PHYSICAL SPACE PROOF OF THE BILINEAR STRICHARTZ AND LOCAL SMOOTHING ESTIMATES FOR THE SCHRÖDINGER EQUATION TERENCE TAO Abstract. Let d 1, and let u, v : R R d C be Schwartz space solutions to the Schrödinger
A PHYSICAL SPACE PROOF OF THE BILINEAR STRICHARTZ AND LOCAL SMOOTHING ESTIMATES FOR THE SCHRÖDINGER EQUATION TERENCE TAO Abstract. Let d 1, and let u, v : R R d C be Schwartz space solutions to the Schrödinger
Chapter Four Gelfond s Solution of Hilbert s Seventh Problem (Revised January 2, 2011)
 Chapter Four Gelfond s Solution of Hilbert s Seventh Problem (Revised January 2, 2011) Before we consider Gelfond s, and then Schneider s, complete solutions to Hilbert s seventh problem let s look back
Chapter Four Gelfond s Solution of Hilbert s Seventh Problem (Revised January 2, 2011) Before we consider Gelfond s, and then Schneider s, complete solutions to Hilbert s seventh problem let s look back
Riemannian Curvature Functionals: Lecture I
 Riemannian Curvature Functionals: Lecture I Jeff Viaclovsky Park City athematics Institute July 16, 2013 Overview of lectures The goal of these lectures is to gain an understanding of critical points of
Riemannian Curvature Functionals: Lecture I Jeff Viaclovsky Park City athematics Institute July 16, 2013 Overview of lectures The goal of these lectures is to gain an understanding of critical points of
Duality of multiparameter Hardy spaces H p on spaces of homogeneous type
 Duality of multiparameter Hardy spaces H p on spaces of homogeneous type Yongsheng Han, Ji Li, and Guozhen Lu Department of Mathematics Vanderbilt University Nashville, TN Internet Analysis Seminar 2012
Duality of multiparameter Hardy spaces H p on spaces of homogeneous type Yongsheng Han, Ji Li, and Guozhen Lu Department of Mathematics Vanderbilt University Nashville, TN Internet Analysis Seminar 2012
Littlewood-Paley theory
 Chapitre 6 Littlewood-Paley theory Introduction The purpose of this chapter is the introduction by this theory which is nothing but a precise way of counting derivatives using the localization in the frequency
Chapitre 6 Littlewood-Paley theory Introduction The purpose of this chapter is the introduction by this theory which is nothing but a precise way of counting derivatives using the localization in the frequency
Attempts at relativistic QM
 Attempts at relativistic QM based on S-1 A proper description of particle physics should incorporate both quantum mechanics and special relativity. However historically combining quantum mechanics and
Attempts at relativistic QM based on S-1 A proper description of particle physics should incorporate both quantum mechanics and special relativity. However historically combining quantum mechanics and
FOURIER INVERSION. an additive character in each of its arguments. The Fourier transform of f is
 FOURIER INVERSION 1. The Fourier Transform and the Inverse Fourier Transform Consider functions f, g : R n C, and consider the bilinear, symmetric function ψ : R n R n C, ψ(, ) = ep(2πi ), an additive
FOURIER INVERSION 1. The Fourier Transform and the Inverse Fourier Transform Consider functions f, g : R n C, and consider the bilinear, symmetric function ψ : R n R n C, ψ(, ) = ep(2πi ), an additive
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND First Printing, 99 Chapter LINEAR EQUATIONS Introduction to linear equations A linear equation in n unknowns x,
ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND First Printing, 99 Chapter LINEAR EQUATIONS Introduction to linear equations A linear equation in n unknowns x,
