A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS
|
|
|
- Hilary Riley
- 5 years ago
- Views:
Transcription
1 A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS DAN-ANDREI GEBA Abstract. We obtain a sharp local well-posedness result for an equation of wave maps type with variable coefficients. The proof relies on a recent construction ([2]) of curved versions for X spaces. 1. Introduction In this paper we study the low regularity well-posedness for a variable coefficient wave maps type equation. This can be viewed as a continuation of recent work ([2]) that investigated the same question in the general class of quadratic nonlinear wave equations on curved background. A function u : R 1+n M, from the Minkowski space-time into a Riemannian manifold (M, h), is called a wave map if it is a critical point for the Lagrangian L(u) = < u, u > dt dx where R 1+n < u, u > = h JK α u J α u K in local coordinates on M, with t = t and x = x 1. The associated Euler- Lagrange equation has the simplified form: (1) u I = Γ I JK(u) Q 0 (u J, u K ) where = α α = t 2 + is the wave operator, u = (u 1, u 2,..., u N ), Γ I JK are the Christoffel symbols of M in the local chart, N = dim M and Q 0 is the null form n (2) Q 0 (v, w) = α v α w = t v t w + i v i w The initial value problem for (1) in R n+1, subject to the initial data (3) u(0, x) = u 0 (x), t u(0, x) = u 1 (x) is known to be locally well-posed for i=1 (u 0, u 1 ) H s (R n ) H s 1 (R n ), s > n 2 This range is optimal and it was obtained in a series of papers by Klainerman- Machedon [4] (n 4), Klainerman-Selberg [8] (n 2), and Keel-Tao [3] (n = 1). 1 Throughout this paper we assume the standard convention on summation. 1
2 2 DAN-ANDREI GEBA These results should be compared with the ones for general quadratic semilinear wave equations (Ponce-Sideris [10], Foschi -Klainerman [1], Tataru [14]) (4) u = q ij (u) i u j u in which the Cauchy problem is known to be locally well-posed for { n (5) s > max 2, n + 5 } 4 The gap in regularity between the two equations, noticeable only for dimensions 2 n 4, has to do with the improved cancellation properties of Q 0. In loose terms, the null form damps the parallel interactions of the two functions, but preserves the transverse ones. One can see this by looking at its Fourier symbol (6) Q0 (τ, ξ, σ, η) = τσ ξ η = ( (τ + σ) 2 ξ + η 2) (τ 2 ξ 2 ) (σ 2 η 2 ) which vanishes if both (τ, ξ) and (σ, η) are on the cone and collinear. For a better motivation of our problem, let us consider also the associated quasilinear wave equation (7) g(u) u = q ij (u) i u j u with g = g ij i j (the summation occurs from 0 to n and the index 0 stands for the time variable). To insure hyperbolicity, we assume that the matrix g ij has signature (1, n) and the time level sets {x 0 = const} are space-like (i.e., g 00 > 0). For simplicity, we take g Sharp local well-posedness holds for (7) only in the and dimensional cases (Smith-Tataru [12], Lindblad [9]; see also the results of Klainerman- Rodnianski [5], [6], [7], for Einstein vacuum equations). For higher dimensions, it is not known yet whether the range (5) applies to (7) too, or if one needs to impose additional conditions on s. A first step in answering this question was taken in [2], where the related semilinear problem on a curved background (8) g u = q ij (u) i u j u was investigated. It was shown that for metrics satisfying 2 g L 2 t L x 2, the Cauchy problem for (8) is locally well-posed in H s (R 4 ) H s 1 (R 4 ), s > 9 4 matching the above range, (5). In this article we consider the variable coefficient version of (1), namely (9) g u I = Γ I JK(u) Q g 0 (uj, u K ) where the corresponding null form Q g 0 is defined as (10) Q g 0 (u, v) = gαβ α u β v = 1 2 ( g(uv) u g v v g u) We are able to prove that in certain dimensions, under reasonable regularity conditions for the metric g, the local well-posedness theories for (1) and (9) coincide: 2 We make the convention in the sequel that L p L q = L p t Lq x, while L p = L p t,x, with the exception of fixed time estimates.
3 A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS3 Theorem 1.1. Let 3 n 5 and assume 2 g L 2 L. The Cauchy problem associated to (9) is locally well-posed in H s (R n ) H s 1 (R n ) for s > n 2. Remark 1.2. The hypothesis on the regularity of the metric g is related to the fact that, for both (8) and(9), we have to control X norms, which are in fact L 2 L 2 norms. A typical cross term to estimate is 2 g u L 2 L 2 2 g L 2 L u L L 2 One needs to compare this with the optimal regularity, 2 g L 1 L (Tataru [15]), required for the wave operator g to have the full range of Strichartz exponents. It is interesting to note that these regularities infer that g is global Lipschitz. Remark 1.3. The more challenging case of dimension n = 2 is current work in progress, and will be addressed in a subsequent paper. An argument based only on techniques contained in this article yields local well-posedness of the initial value problem in H s (R 2 ) for s > The proof of Theorem 1.1 is based, as it is usually the case for these problems, on a fixed point argument that exhibits a considerable amount of similarities with the one in [2]. To be precise, all that is needed new for (9), in comparison to (8), is one new estimate and several extensions of previous ones to different settings. Due to (10), and modulo the standard reduction to the case of small initial data and time interval set to [ 1, 1], our result can be inferred from the following set of inequalities: (11) S(u 0, u 1 ) X (u 0, u 1 ) Hs H s 1 (12) 1 H X H Y (13) (14) (15) (16) g g u Y u X u v X u X v X Γ(u) X C( u L )(1 + u 5 X) u w Y u X w Y where C = C( u L ) is a constant that depends solely on the dimension n and u L, X and Y are suitably chosen Banach spaces, while S(u 0, u 1 ) and 1 g are respectively the homogeneous and inhomogeneous solution operators (17) (18) g S(u 0, u 1 ) = 0, S(u 0, u 1 )(0) = u 0, t S(u 0, u 1 )(0) = u 1 g ( 1 g H) = H, ( 1 g H)(0) = 0, t ( 1 g H)(0) = 0 Remark The new estimate which is needed in our analysis, but was absent in the one for equation (8), is (13). 2. Based on (10), (13), (14), and (16), one can infer immediately that Q g 0 (u, v) Y u X v X This is the variable coefficient version of a certain null-form estimate of Klainerman- Machedon, which has been previously obtained by Sogge [13], Sogge-Smith [11], and Tataru [16], under various regularity assumptions for the metric g. Remark (11)-(12) have already been proved in [2], in the context of our problem (i.e., for 3 n 5). 2. [2] contains the proof of (14)-(16) for the 4+1 dimensional case; here we extend them to 3 + 1, respectively dimensions.
4 4 DAN-ANDREI GEBA In the next section, for completeness, we will reintroduce the notations, definitions, and results from [2] that will be needed in our analysis, while in the last section, we will discuss the estimates mentioned in the above remarks. 2. Curved X spaces: definitions, notations and properties We introduce first the Banach spaces that will be used in our argument: (19) X = X Y = X s 1,θ 1 where Definition 2.1. (Definition 2.1 in [2]) For 0 < θ < 1 and s R, X is the space of functions u L 2 ( 1, 1; H s (R n )) for which (20) u 2 X = inf { with, d taking dyadic values and u 2 ; u = X } S u < (21) u X = s d θ u L 2 + s 1 d θ 1 g< u L 2 We define negative index spaces by setting, again for 0 < θ < 1 and s R, the X s 1,θ 1 norm to equal { f 2 X = inf f s 1,θ L 2 H + f s 1 2 ; X (22) } f = f 0 + g< S f < Remark 2.2. S, S < and S are the usual multipliers associated with a Littlewood- Paley decomposition. All but one frequency localizations are with respect to the spatial variables (i.e., S = S (D x )). The exception is the localization of the metric g, which is truncated using space-time multipliers. For this to work, we extend g to have similar properties in all of R n+1. In this case, S = S (D t,x ). We start by recording Lemma 2.3. (Lemma 2.4 in [2]) The following estimate holds: (23) s 1 d θ S u L 2 + s 1 d θ 1 g< S u L 2 u X This result allows us to replace the X norm in the Definition 2.1 by (24) u = s 1 d θ u X L 2 + s 1 d θ 1 g< u L 2 and to assume, without any restriction in generality, that the functions u and f, appearing in the above definition, are localized at frequency. The presence of the gradient in this new, equivalent norm, is easier to handle in the context of the wave equation. An immediate consequence of this is the following
5 A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS5 Lemma 2.4. (Corollary 2.8 in [2]) For θ > 0 the following energy inequality takes place (25) s 1 d θ 1 2 S u L L 2 S u X As a result, for θ > 1 2 : (26) u L H s + u t L H s 1 u X The next important issue to address is the truncation in frequency of the metric g. This is achieved by Lemma 2.5. (Lemma 2.9 in [2]) If S is a spatial multiplier with slightly larger support (i.e. S S = S ), 0 s 3, and the metric g has regularity 2 g L 2 L, the following fixed time estimate is true: (27) 2(s 1) S (g > u)(t) 2 L 2 (M( 2 g L x )(t)) 2 u(t) 2 H s 2 =1 with M being the maximal function with respect to time. The dual estimate also holds: (28) g > (t) S f (t) 2 H 2(1 s) f 2 s (t) 2 L 2 =1 As it turns out, the results listed so far are the only tools needed to prove the estimates for the homogeneous and inhomogeneous solution operators (i.e., (11) and (12)). We are left to investigate (13)-(16). To go further, one needs to identify the link between the X spaces of positive and negative indices: =1 Lemma 2.6. (Lemma 2.13 in [2]) For 0 < θ < 1 2 we have the following duality relation (29) X s, θ = (X + L 2 H s+θ ) The next natural step is to relate the X spaces to spaces relevant to Strichartz estimates. We have the following: Lemma 2.7. (Corollary 3.2 in [2]) a) For θ > 0 and (σ, p, q) verifying we have σ = n p + n q, 2 p + n 1 q n 1, 2 p, 2 q < 2 (30) S u L p L q 1 s σ d 1 2 θ u X If additionally θ > 1 2 then (31) S u L p L q 1 s σ u X b) If instead 2 p + n 1 n 1 q 2
6 6 DAN-ANDREI GEBA then (32) S u L p L q 1 1 s σ+ 2 ( 2 p + n 1 q n 1 2 ) d 1 2 θ 1 2 ( 2 p + n 1 q n 1 2 ) u X Remark 2.8. In the above embeddings, one can use also the index q =. We will rely in particular on the triplets ( n 1,, ) ( n, 2, ) 2 2 noting that for n = 3 and (σ, p, q) = ( 1, 2, ), one loses in the previous bounds either a ln or ɛ, with ɛ > 0 arbitrary small. However, this loss is harmless because it is covered by the strict inequalities imposed on the exponents. Therefore we can ignore it. For a finer analysis, that is needed in the last section, we introduce also the norm (see section 3 in [2]) { d } d (33) u 2 X = inf u h 2 X ; u = u h u 2 X,<d,h For d = we use instead the notation X. A straightforward calculation yields { } (34) u 2 X = inf S u 2 X ; u = S u =1 In this new context, for θ > 0 and (σ, p, q) as in part a) of Lemma 2.7, we also have (Corollary 3.4 in [2]): =1 (35) S u L p L q 1 s σ max{1, d 1 2 θ } u X,<d Finally, we make the following Remark 2.9. All the results mentioned in this section are proved in [2], independent of dimension n. 3. Conclusion: Proof of the estimates (13)-(16) We start by proving (13), which, as mentioned in the first section, is one of the novelties of this paper, being specifically needed for our problem, (9): Proposition 3.1. For θ > 1 2 and 0 s 3, the following mapping holds: (36) g : X X s 1,θ 1 Proof. We use the decomposition (37) u = S u = S u with u = =1 d=1 u
7 A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS7 Then one can write g u = g> S u + =1 Using Definition 2.1, Lemma 2.5, and (26), we can infer g< S u g u 2 X s 1,θ 1 g> S u 2 L 2 H + s 1 =1 u 2 X S u 2 L H + s 1 u 2 X u 2 X =1 For (14)-(16), at this moment, our arguments for 3 + 1, respectively dimensions do not stray far from the dimensional proof, given in [2]. This is why we discuss here only the relevant differences and the corresponding numerology. A key ingredient of this analysis is to have good X control on bilinear structures that involve functions localized at different frequencies. The 4+1 dimensional case is handled by lemmas 3.5 and 3.6 in [2]. Another contribution of our paper is that it optimizes that argument (i.e., we obtain improved bounds for some estimates), allowing for these results to be written in a more compact form. Lemma 3.2. Let θ > 0 and n 3. i) The following estimates hold (38) (39) (40) (41) n+3 tt S u L2 L 2 s d 1 2 θ u X { n+3 tt S u L2 L 2 s max 1, d 1 2 θ} u X,<d ii) For µ d, we have S µ v S u ( } S X µ v L + min {d 1 S µ v L, d 1 2 Sµ v L 2 L + iii) For µ, we have S µ v S u X,µ + 1 d ) 1 2 tt S µ v L2 L S u X { µ n 2 s max 1, µ 1 θ} 2 S µ v S u X X µ ( S µ v L + max { + max µ θ 2, µ 3 2 { } µ θ 1, µ 1 2 S µ v L 2 L + } tt S µ v L 2 L ) S u X,<µ µ n 1 2 +θ s max { 1, µ 1 2θ} S µ v X µ S u X,<µ Proof. The main tools used in this proof are the energy estimate (25) and the embeddings contained in Lemma 2.7. For (38) and (39), we combine (30) and (35) with the observation, based on g 00 1, that ( tt g< )S S (40) and (41) have similar arguments. The strategy is to estimate the L 2 norm of the cross terms arising from Leibnitz s rule either by a L L 2 L 2 L product or
8 8 DAN-ANDREI GEBA a L 2 L 2 L L one. We focus on (41). The first two cross terms can be estimated directly, using (35): s 1 µ θ S µ v S u L 2 max{µθ, µ 1 2 } S µ v L2 L S u X,<µ s 1 µ θ S µ v S u L 2 max{µ θ, µ 1 2 } Sµ v L2 L S u X,<µ More delicate terms appear when g< acts on the product S µ vs u. The first two are easier to estimate than the one involving g< S µ v: s 1 µ θ 1 S µ v g< S u L 2 s 1 µ θ 1 g < S µ v S u L 2 S µ v L S u X,<µ For the last term, let us consider the decomposition µ u = as in the definition of the s 1 µ θ 1 g< (S µ v) S u L 2 max{µ θ 1, µ 1 2 } Sµ v L2 L S u X,<µ u h X,<µ spaces. We can infer as follows s 1 µ θ 1 ( tt S µ v L2 L + µ S µv L2 L ) S u L L 2 ( µ ) 1 µθ 1 ( tts µ v L2 L + µ S µv L2 L ) ( ) 2 1 µ 1 2 h 2θ 1 2s h 2θ 1 S u h 2 L L 2 µθ 1 max { 1, µ 1 2 θ} ( tt S µ v L 2 L + µ S µv L 2 L ) ( µ which is obviously the right bound. We are now ready to prove the remaining main estimates: Proposition 3.3. Let n 3 and 1 2 < θ < s n 1 2. Then: (42) (43) (44) u v X u X v X u w X s 1,θ 1 u X w X s 1,θ 1 Γ(u) X C( u L )(1 + u 5 X ) Proof. We use decompositions identical with the ones in (37): u = S u = S u, v = It follows that uv = =1 µ=1 1=1 2=1 S µ (S 1 u 1 S 2 v 2 ) S u h 2 X,h S v = S v The nontrivial interactions in the above sum are only when 1 2 µ or max{ 1, 2 } µ. These are handled by using (40) and (41) to claim =1 ) 1 2
9 A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS9 (45) (46) S u S v X µ,µ µs+θ 2 n+3 S u S µ v µ 2 X 2 2s u X µ n 1+2θ 2s v µ 2 X µ d=1 v X u 2 X It turns out that this is all that is needed to infer (42) (see also Proposition 3.7 in [2]). Using the duality relation (29) and the fact that s > n 2, one can reduce (43) to X X 1 s,1 θ X 1 s,1 θ + L 2 H 2 s θ which is then treated by considering decompositions as above. In this case, there are three possible interactions, one of which requiring a different analysis than the one of Proposition 3.8 in [2]. This is the term S µ (S u S v ) which needs to be estimated in the space L 2 H 2 s θ. For n 4, (35) allows us to show that S u S v L 2 L n 1 S u n 2 2(n 1) S v 2(n 1) L 4 L n 2 L 4 L n 2 θ 1+ 1 n 1 u v X X1 s,1 θ Sobolev embeddings can then be used to obtain S µ (S u S v ) L2 H 2 s θ n(n 3) µ2 s θ+ 2(n 1) θ 1+ 1 n 1 u X which agrees with the numerology included in the hypothesis. The case n = 3 is a little more delicate and we need (32) to infer S u S v L 2 L 2 1+2ɛ S u L4 L 4 1 4ɛ S v L4 L 4 1+8ɛ ɛ u v X X1 s,1 θ Again by Sobolev embeddings we can conclude that v X1 s,1 θ S µ (S u S v ) L 2 H 2 s θ µ2 s θ+3ɛ ɛ u v X X1 s,1 θ The proof of (44) follows the same lines as the one in Proposition 3.9 from [2]. Acknowledgement I am grateful to Daniel Tataru for suggesting this problem and for many stimulating discussions. Also, I would like to thank the referee for many helpful suggestions. References 1. Damiano Foschi and Sergiu Klainerman, Bilinear space-time estimates for homogeneous wave equations, Ann. Sci. École Norm. Sup. (4) 33 (2000), no. 2, MR MR (2001g:35145) 2. Dan-Andrei Geba and Daniel Tataru, Gradient NLW on curved background in dimensions, Internat. Math. Res. Notices 2008 (2008), rnn Markus Keel and Terence Tao, Local and global well-posedness of wave maps on R 1+1 for rough data, Internat. Math. Res. Notices (1998), no. 21, MR MR (99k:58180)
10 10 DAN-ANDREI GEBA 4. S. Klainerman and M. Machedon, Smoothing estimates for null forms and applications, Duke Math. J. 81 (1995), no. 1, (1996), A celebration of John F. Nash, Jr. MR MR (97h:35022) 5. Sergiu Klainerman and Igor Rodnianski, Rough solutions of the Einstein vacuum equations, C. R. Math. Acad. Sci. Paris 334 (2002), no. 2, MR MR (2002m:58047) 6., Ricci defects of microlocalized Einstein metrics, J. Hyperbolic Differ. Equ. 1 (2004), no. 1, MR MR (2005f:58048) 7., The causal structure of microlocalized rough Einstein metrics, Ann. of Math. (2) 161 (2005), no. 3, MR MR Sergiu Klainerman and Sigmund Selberg, Remark on the optimal regularity for equations of wave maps type, Comm. Partial Differential Equations 22 (1997), no. 5-6, MR MR (99c:35163) 9. Hans Lindblad, Counterexamples to local existence for quasilinear wave equations, Math. Res. Lett. 5 (1998), no. 5, MR MR (2000a:35171) 10. Gustavo Ponce and Thomas C. Sideris, Local regularity of nonlinear wave equations in three space dimensions, Comm. Partial Differential Equations 18 (1993), no. 1-2, MR MR (95a:35092) 11. Hart F. Smith and Christopher D. Sogge, Null form estimates for (1/2, 1/2) symbols and local existence for a quasilinear Dirichlet-wave equation, Ann. Sci. École Norm. Sup. (4) 33 (2000), no. 4, MR MR (2002j:35194) 12. Hart F. Smith and Daniel Tataru, Sharp local well-posedness results for the nonlinear wave equation, Ann. of Math. (2) 162 (2005), no. 1, MR MR Christopher D. Sogge, On local existence for nonlinear wave equations satisfying variable coefficient null conditions, Comm. Partial Differential Equations 18 (1993), no. 11, MR MR (94m:35199) 14. Daniel Tataru, On the equation u = u 2 in dimensions, Math. Res. Lett. 6 (1999), no. 5-6, MR MR (2001k:35219) 15., Strichartz estimates for second order hyperbolic operators with nonsmooth coefficients. III, J. Amer. Math. Soc. 15 (2002), no. 2, (electronic). MR MR (2003a:35120) 16., Null form estimates for second order hyperbolic operators with rough coefficients, Harmonic analysis at Mount Holyoke (South Hadley, MA, 2001), Contemp. Math., vol. 320, Amer. Math. Soc., Providence, RI, 2003, pp MR MR (2004d:35177) Department of Mathematics, Hylan Building, University of Rochester, Rochester, NY 14627
arxiv:math/ v1 [math.ap] 24 Apr 2003
![arxiv:math/ v1 [math.ap] 24 Apr 2003 arxiv:math/ v1 [math.ap] 24 Apr 2003](/thumbs/95/122489725.jpg) ICM 2002 Vol. III 1 3 arxiv:math/0304397v1 [math.ap] 24 Apr 2003 Nonlinear Wave Equations Daniel Tataru Abstract The analysis of nonlinear wave equations has experienced a dramatic growth in the last ten
ICM 2002 Vol. III 1 3 arxiv:math/0304397v1 [math.ap] 24 Apr 2003 Nonlinear Wave Equations Daniel Tataru Abstract The analysis of nonlinear wave equations has experienced a dramatic growth in the last ten
The Bounded L 2 curvature conjecture in general relativity
 The Bounded L 2 curvature conjecture in general relativity Jérémie Szeftel Département de Mathématiques et Applications, Ecole Normale Supérieure (Joint work with Sergiu Klainerman and Igor Rodnianski)
The Bounded L 2 curvature conjecture in general relativity Jérémie Szeftel Département de Mathématiques et Applications, Ecole Normale Supérieure (Joint work with Sergiu Klainerman and Igor Rodnianski)
A COUNTEREXAMPLE TO AN ENDPOINT BILINEAR STRICHARTZ INEQUALITY TERENCE TAO. t L x (R R2 ) f L 2 x (R2 )
 Electronic Journal of Differential Equations, Vol. 2006(2006), No. 5, pp. 6. ISSN: 072-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) A COUNTEREXAMPLE
Electronic Journal of Differential Equations, Vol. 2006(2006), No. 5, pp. 6. ISSN: 072-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) A COUNTEREXAMPLE
Strichartz Estimates for the Schrödinger Equation in Exterior Domains
 Strichartz Estimates for the Schrödinger Equation in University of New Mexico May 14, 2010 Joint work with: Hart Smith (University of Washington) Christopher Sogge (Johns Hopkins University) The Schrödinger
Strichartz Estimates for the Schrödinger Equation in University of New Mexico May 14, 2010 Joint work with: Hart Smith (University of Washington) Christopher Sogge (Johns Hopkins University) The Schrödinger
Strauss conjecture for nontrapping obstacles
 Chengbo Wang Joint work with: Hart Smith, Christopher Sogge Department of Mathematics Johns Hopkins University Baltimore, Maryland 21218 wangcbo@jhu.edu November 3, 2010 1 Problem and Background Problem
Chengbo Wang Joint work with: Hart Smith, Christopher Sogge Department of Mathematics Johns Hopkins University Baltimore, Maryland 21218 wangcbo@jhu.edu November 3, 2010 1 Problem and Background Problem
A PHYSICAL SPACE PROOF OF THE BILINEAR STRICHARTZ AND LOCAL SMOOTHING ESTIMATES FOR THE SCHRÖDINGER EQUATION
 A PHYSICAL SPACE PROOF OF THE BILINEAR STRICHARTZ AND LOCAL SMOOTHING ESTIMATES FOR THE SCHRÖDINGER EQUATION TERENCE TAO Abstract. Let d 1, and let u, v : R R d C be Schwartz space solutions to the Schrödinger
A PHYSICAL SPACE PROOF OF THE BILINEAR STRICHARTZ AND LOCAL SMOOTHING ESTIMATES FOR THE SCHRÖDINGER EQUATION TERENCE TAO Abstract. Let d 1, and let u, v : R R d C be Schwartz space solutions to the Schrödinger
DISPERSIVE ESTIMATES FOR WAVE EQUATIONS WITH ROUGH COEFFICIENTS
 DISPERSIVE ESTIMATES FOR WAVE EQUATIONS WITH ROUGH COEFFICIENTS DANIEL TATARU AND DAN-ANDREI GEBA Abstract. We obtain a multiscale wave packet representation for the fundamental solution of the wave equation
DISPERSIVE ESTIMATES FOR WAVE EQUATIONS WITH ROUGH COEFFICIENTS DANIEL TATARU AND DAN-ANDREI GEBA Abstract. We obtain a multiscale wave packet representation for the fundamental solution of the wave equation
THE WAVE MAPS EQUATION. 1. The equations Let us begin with the Laplace equation, R n
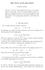 THE WAVE MAPS EQUATION DANIEL TATARU Abstract. The wave maps equation has become a very popular topic in recent years. The aim of these expository notes is to present a non-technical survey of the ideas
THE WAVE MAPS EQUATION DANIEL TATARU Abstract. The wave maps equation has become a very popular topic in recent years. The aim of these expository notes is to present a non-technical survey of the ideas
Global well-posedness for KdV in Sobolev spaces of negative index
 Electronic Journal of Differential Equations, Vol. (), No. 6, pp. 7. ISSN: 7-669. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu (login: ftp) Global well-posedness for
Electronic Journal of Differential Equations, Vol. (), No. 6, pp. 7. ISSN: 7-669. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu (login: ftp) Global well-posedness for
Lectures on Non-Linear Wave Equations
 Lectures on Non-Linear Wave Equations Second Edition Christopher D. Sogge Department of Mathematics Johns Hopkins University International Press www.intlpress.com Lectures on Non-Linear Wave Equations,
Lectures on Non-Linear Wave Equations Second Edition Christopher D. Sogge Department of Mathematics Johns Hopkins University International Press www.intlpress.com Lectures on Non-Linear Wave Equations,
A SHORT PROOF OF THE COIFMAN-MEYER MULTILINEAR THEOREM
 A SHORT PROOF OF THE COIFMAN-MEYER MULTILINEAR THEOREM CAMIL MUSCALU, JILL PIPHER, TERENCE TAO, AND CHRISTOPH THIELE Abstract. We give a short proof of the well known Coifman-Meyer theorem on multilinear
A SHORT PROOF OF THE COIFMAN-MEYER MULTILINEAR THEOREM CAMIL MUSCALU, JILL PIPHER, TERENCE TAO, AND CHRISTOPH THIELE Abstract. We give a short proof of the well known Coifman-Meyer theorem on multilinear
Recent developments on the global behavior to critical nonlinear dispersive equations. Carlos E. Kenig
 Recent developments on the global behavior to critical nonlinear dispersive equations Carlos E. Kenig In the last 25 years or so, there has been considerable interest in the study of non-linear partial
Recent developments on the global behavior to critical nonlinear dispersive equations Carlos E. Kenig In the last 25 years or so, there has been considerable interest in the study of non-linear partial
ON STRICHARTZ ESTIMATES FOR SCHRÖDINGER OPERATORS IN COMPACT MANIFOLDS WITH BOUNDARY. 1. Introduction
 ON STRICHARTZ ESTIMATES FOR SCHRÖDINGER OPERATORS IN COMPACT MANIFOLDS WITH BOUNDARY MATTHEW D. BLAIR, HART F. SMITH, AND CHRISTOPHER D. SOGGE 1. Introduction Let (M, g) be a Riemannian manifold of dimension
ON STRICHARTZ ESTIMATES FOR SCHRÖDINGER OPERATORS IN COMPACT MANIFOLDS WITH BOUNDARY MATTHEW D. BLAIR, HART F. SMITH, AND CHRISTOPHER D. SOGGE 1. Introduction Let (M, g) be a Riemannian manifold of dimension
CUTOFF RESOLVENT ESTIMATES AND THE SEMILINEAR SCHRÖDINGER EQUATION
 CUTOFF RESOLVENT ESTIMATES AND THE SEMILINEAR SCHRÖDINGER EQUATION HANS CHRISTIANSON Abstract. This paper shows how abstract resolvent estimates imply local smoothing for solutions to the Schrödinger equation.
CUTOFF RESOLVENT ESTIMATES AND THE SEMILINEAR SCHRÖDINGER EQUATION HANS CHRISTIANSON Abstract. This paper shows how abstract resolvent estimates imply local smoothing for solutions to the Schrödinger equation.
arxiv: v1 [math.ap] 1 May 2017
![arxiv: v1 [math.ap] 1 May 2017 arxiv: v1 [math.ap] 1 May 2017](/thumbs/92/108638608.jpg) LOW REGULARITY LOCAL WELL-POSEDNESS FOR THE (N+1)-DIMENSIONAL MAXWELL-KLEIN-GORDON EQUATIONS IN LORENZ GAUGE arxiv:1705.00599v1 [math.ap] 1 May 017 HARTMUT PECHER FACHBEREICH MATHEMATIK UND NATURWISSENSCHAFTEN
LOW REGULARITY LOCAL WELL-POSEDNESS FOR THE (N+1)-DIMENSIONAL MAXWELL-KLEIN-GORDON EQUATIONS IN LORENZ GAUGE arxiv:1705.00599v1 [math.ap] 1 May 017 HARTMUT PECHER FACHBEREICH MATHEMATIK UND NATURWISSENSCHAFTEN
Overview of the proof of the Bounded L 2 Curvature Conjecture. Sergiu Klainerman Igor Rodnianski Jeremie Szeftel
 Overview of the proof of the Bounded L 2 Curvature Conjecture Sergiu Klainerman Igor Rodnianski Jeremie Szeftel Department of Mathematics, Princeton University, Princeton NJ 8544 E-mail address: seri@math.princeton.edu
Overview of the proof of the Bounded L 2 Curvature Conjecture Sergiu Klainerman Igor Rodnianski Jeremie Szeftel Department of Mathematics, Princeton University, Princeton NJ 8544 E-mail address: seri@math.princeton.edu
ON THE FOLIATION OF SPACE-TIME BY CONSTANT MEAN CURVATURE HYPERSURFACES
 ON THE FOLIATION OF SPACE-TIME BY CONSTANT MEAN CURVATURE HYPERSURFACES CLAUS GERHARDT Abstract. We prove that the mean curvature τ of the slices given by a constant mean curvature foliation can be used
ON THE FOLIATION OF SPACE-TIME BY CONSTANT MEAN CURVATURE HYPERSURFACES CLAUS GERHARDT Abstract. We prove that the mean curvature τ of the slices given by a constant mean curvature foliation can be used
Lp Bounds for Spectral Clusters. Compact Manifolds with Boundary
 on Compact Manifolds with Boundary Department of Mathematics University of Washington, Seattle Hangzhou Conference on Harmonic Analysis and PDE s (M, g) = compact 2-d Riemannian manifold g = Laplacian
on Compact Manifolds with Boundary Department of Mathematics University of Washington, Seattle Hangzhou Conference on Harmonic Analysis and PDE s (M, g) = compact 2-d Riemannian manifold g = Laplacian
Piecewise Smooth Solutions to the Burgers-Hilbert Equation
 Piecewise Smooth Solutions to the Burgers-Hilbert Equation Alberto Bressan and Tianyou Zhang Department of Mathematics, Penn State University, University Park, Pa 68, USA e-mails: bressan@mathpsuedu, zhang
Piecewise Smooth Solutions to the Burgers-Hilbert Equation Alberto Bressan and Tianyou Zhang Department of Mathematics, Penn State University, University Park, Pa 68, USA e-mails: bressan@mathpsuedu, zhang
STRICHARTZ ESTIMATES FOR THE WAVE EQUATION ON MANIFOLDS WITH BOUNDARY. 1. Introduction
 STRICHARTZ ESTIMATES FOR THE WAVE EQUATION ON MANIFOLDS WITH BOUNDARY MATTHEW D. BLAIR, HART F. SMITH, AND CHRISTOPHER D. SOGGE. Introduction Let (M, g) be a Riemannian manifold of dimension n. Strichartz
STRICHARTZ ESTIMATES FOR THE WAVE EQUATION ON MANIFOLDS WITH BOUNDARY MATTHEW D. BLAIR, HART F. SMITH, AND CHRISTOPHER D. SOGGE. Introduction Let (M, g) be a Riemannian manifold of dimension n. Strichartz
Four-Fermion Interaction Approximation of the Intermediate Vector Boson Model
 Four-Fermion Interaction Approximation of the Intermediate Vector Boson odel Yoshio Tsutsumi Department of athematics, Kyoto University, Kyoto 66-852, JAPAN 1 Introduction In this note, we consider the
Four-Fermion Interaction Approximation of the Intermediate Vector Boson odel Yoshio Tsutsumi Department of athematics, Kyoto University, Kyoto 66-852, JAPAN 1 Introduction In this note, we consider the
arxiv: v3 [math.ap] 10 Oct 2014
![arxiv: v3 [math.ap] 10 Oct 2014 arxiv: v3 [math.ap] 10 Oct 2014](/thumbs/82/85678438.jpg) THE BOUNDED L 2 CURVATURE CONJECTURE arxiv:1204.1767v3 [math.ap] 10 Oct 2014 SERGIU KLAINERMAN, IGOR RODNIANSKI, AND JEREMIE SZEFTEL Abstract. This is the main paper in a sequence in which we give a complete
THE BOUNDED L 2 CURVATURE CONJECTURE arxiv:1204.1767v3 [math.ap] 10 Oct 2014 SERGIU KLAINERMAN, IGOR RODNIANSKI, AND JEREMIE SZEFTEL Abstract. This is the main paper in a sequence in which we give a complete
DISPERSIVE EQUATIONS: A SURVEY
 DISPERSIVE EQUATIONS: A SURVEY GIGLIOLA STAFFILANI 1. Introduction These notes were written as a guideline for a short talk; hence, the references and the statements of the theorems are often not given
DISPERSIVE EQUATIONS: A SURVEY GIGLIOLA STAFFILANI 1. Introduction These notes were written as a guideline for a short talk; hence, the references and the statements of the theorems are often not given
Existence theorems for some nonlinear hyperbolic equations on a waveguide
 Existence theorems for some nonlinear hyperbolic equations on a waveguide by Ann C. Stewart A dissertation submitted to the Johns Hopkins University in conformity with the requirements for the degree of
Existence theorems for some nonlinear hyperbolic equations on a waveguide by Ann C. Stewart A dissertation submitted to the Johns Hopkins University in conformity with the requirements for the degree of
ON THE UNIQUENESS OF SOLUTIONS TO THE GROSS-PITAEVSKII HIERARCHY. 1. Introduction
 ON THE UNIQUENESS OF SOLUTIONS TO THE GROSS-PITAEVSKII HIERARCHY SERGIU KLAINERMAN AND MATEI MACHEDON Abstract. The purpose of this note is to give a new proof of uniqueness of the Gross- Pitaevskii hierarchy,
ON THE UNIQUENESS OF SOLUTIONS TO THE GROSS-PITAEVSKII HIERARCHY SERGIU KLAINERMAN AND MATEI MACHEDON Abstract. The purpose of this note is to give a new proof of uniqueness of the Gross- Pitaevskii hierarchy,
DETERMINATION OF THE BLOW-UP RATE FOR THE SEMILINEAR WAVE EQUATION
 DETERMINATION OF THE LOW-UP RATE FOR THE SEMILINEAR WAVE EQUATION y FRANK MERLE and HATEM ZAAG Abstract. In this paper, we find the optimal blow-up rate for the semilinear wave equation with a power nonlinearity.
DETERMINATION OF THE LOW-UP RATE FOR THE SEMILINEAR WAVE EQUATION y FRANK MERLE and HATEM ZAAG Abstract. In this paper, we find the optimal blow-up rate for the semilinear wave equation with a power nonlinearity.
A LOWER BOUND ON BLOWUP RATES FOR THE 3D INCOMPRESSIBLE EULER EQUATION AND A SINGLE EXPONENTIAL BEALE-KATO-MAJDA ESTIMATE. 1.
 A LOWER BOUND ON BLOWUP RATES FOR THE 3D INCOMPRESSIBLE EULER EQUATION AND A SINGLE EXPONENTIAL BEALE-KATO-MAJDA ESTIMATE THOMAS CHEN AND NATAŠA PAVLOVIĆ Abstract. We prove a Beale-Kato-Majda criterion
A LOWER BOUND ON BLOWUP RATES FOR THE 3D INCOMPRESSIBLE EULER EQUATION AND A SINGLE EXPONENTIAL BEALE-KATO-MAJDA ESTIMATE THOMAS CHEN AND NATAŠA PAVLOVIĆ Abstract. We prove a Beale-Kato-Majda criterion
arxiv:math/ v1 [math.ap] 28 Oct 2005
![arxiv:math/ v1 [math.ap] 28 Oct 2005 arxiv:math/ v1 [math.ap] 28 Oct 2005](/thumbs/72/66322244.jpg) arxiv:math/050643v [math.ap] 28 Oct 2005 A remark on asymptotic completeness for the critical nonlinear Klein-Gordon equation Hans Lindblad and Avy Soffer University of California at San Diego and Rutgers
arxiv:math/050643v [math.ap] 28 Oct 2005 A remark on asymptotic completeness for the critical nonlinear Klein-Gordon equation Hans Lindblad and Avy Soffer University of California at San Diego and Rutgers
Strauss conjecture on asymptotically Euclidean manifolds
 Strauss conjecture on asymptotically Euclidean manifolds Xin Yu (Joint with Chengbo Wang) Department of Mathematics, Johns Hopkins University Baltimore, Maryland 21218 xinyu@jhu.edu Mar 12-Mar 13, 2010
Strauss conjecture on asymptotically Euclidean manifolds Xin Yu (Joint with Chengbo Wang) Department of Mathematics, Johns Hopkins University Baltimore, Maryland 21218 xinyu@jhu.edu Mar 12-Mar 13, 2010
ALMOST CONSERVATION LAWS AND GLOBAL ROUGH SOLUTIONS TO A NONLINEAR SCHRÖDINGER EQUATION
 ALMOST CONSERVATION LAWS AND GLOBAL ROUGH SOLUTIONS TO A NONLINEAR SCHRÖDINGER EQUATION J. COLLIANDER, M. KEEL, G. STAFFILANI, H. TAKAOKA, AND T. TAO Abstract. We prove an almost conservation law to obtain
ALMOST CONSERVATION LAWS AND GLOBAL ROUGH SOLUTIONS TO A NONLINEAR SCHRÖDINGER EQUATION J. COLLIANDER, M. KEEL, G. STAFFILANI, H. TAKAOKA, AND T. TAO Abstract. We prove an almost conservation law to obtain
Mathematical Research Letters 5, (1998) COUNTEREXAMPLES TO LOCAL EXISTENCE FOR QUASILINEAR WAVE EQUATIONS. Hans Lindblad
 Mathematical Research Letters 5, 65 622 1998) COUNTEREXAMPLES TO LOCAL EXISTENCE FOR QUASILINEAR WAVE EQUATIONS Hans Lindblad 1. Introduction and themain argument In this paper, we study quasilinear wave
Mathematical Research Letters 5, 65 622 1998) COUNTEREXAMPLES TO LOCAL EXISTENCE FOR QUASILINEAR WAVE EQUATIONS Hans Lindblad 1. Introduction and themain argument In this paper, we study quasilinear wave
Well-posedness for the Fourth-order Schrödinger Equations with Quadratic Nonlinearity
 Well-posedness for the Fourth-order Schrödinger Equations with Quadratic Nonlinearity Jiqiang Zheng The Graduate School of China Academy of Engineering Physics P. O. Box 20, Beijing, China, 00088 (zhengjiqiang@gmail.com)
Well-posedness for the Fourth-order Schrödinger Equations with Quadratic Nonlinearity Jiqiang Zheng The Graduate School of China Academy of Engineering Physics P. O. Box 20, Beijing, China, 00088 (zhengjiqiang@gmail.com)
A RELATIONSHIP BETWEEN THE DIRICHLET AND REGULARITY PROBLEMS FOR ELLIPTIC EQUATIONS. Zhongwei Shen
 A RELATIONSHIP BETWEEN THE DIRICHLET AND REGULARITY PROBLEMS FOR ELLIPTIC EQUATIONS Zhongwei Shen Abstract. Let L = diva be a real, symmetric second order elliptic operator with bounded measurable coefficients.
A RELATIONSHIP BETWEEN THE DIRICHLET AND REGULARITY PROBLEMS FOR ELLIPTIC EQUATIONS Zhongwei Shen Abstract. Let L = diva be a real, symmetric second order elliptic operator with bounded measurable coefficients.
The NLS on product spaces and applications
 October 2014, Orsay The NLS on product spaces and applications Nikolay Tzvetkov Cergy-Pontoise University based on joint work with Zaher Hani, Benoit Pausader and Nicola Visciglia A basic result Consider
October 2014, Orsay The NLS on product spaces and applications Nikolay Tzvetkov Cergy-Pontoise University based on joint work with Zaher Hani, Benoit Pausader and Nicola Visciglia A basic result Consider
Euler Equations: local existence
 Euler Equations: local existence Mat 529, Lesson 2. 1 Active scalars formulation We start with a lemma. Lemma 1. Assume that w is a magnetization variable, i.e. t w + u w + ( u) w = 0. If u = Pw then u
Euler Equations: local existence Mat 529, Lesson 2. 1 Active scalars formulation We start with a lemma. Lemma 1. Assume that w is a magnetization variable, i.e. t w + u w + ( u) w = 0. If u = Pw then u
Inégalités de dispersion via le semi-groupe de la chaleur
 Inégalités de dispersion via le semi-groupe de la chaleur Valentin Samoyeau, Advisor: Frédéric Bernicot. Laboratoire de Mathématiques Jean Leray, Université de Nantes January 28, 2016 1 Introduction Schrödinger
Inégalités de dispersion via le semi-groupe de la chaleur Valentin Samoyeau, Advisor: Frédéric Bernicot. Laboratoire de Mathématiques Jean Leray, Université de Nantes January 28, 2016 1 Introduction Schrödinger
NONTRIVIAL SOLUTIONS FOR SUPERQUADRATIC NONAUTONOMOUS PERIODIC SYSTEMS. Shouchuan Hu Nikolas S. Papageorgiou. 1. Introduction
 Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 34, 29, 327 338 NONTRIVIAL SOLUTIONS FOR SUPERQUADRATIC NONAUTONOMOUS PERIODIC SYSTEMS Shouchuan Hu Nikolas S. Papageorgiou
Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 34, 29, 327 338 NONTRIVIAL SOLUTIONS FOR SUPERQUADRATIC NONAUTONOMOUS PERIODIC SYSTEMS Shouchuan Hu Nikolas S. Papageorgiou
A non-strictly hyperbolic system for the Einstein equations with arbitrary lapse and shift
 IFP-UNC-518 TAR-UNC-054 gr-qc/9607006 A non-strictly hyperbolic system for the Einstein equations with arbitrary lapse and shift Andrew Abrahams, Arlen Anderson, Yvonne Choquet-Bruhat[*] and James W. York,
IFP-UNC-518 TAR-UNC-054 gr-qc/9607006 A non-strictly hyperbolic system for the Einstein equations with arbitrary lapse and shift Andrew Abrahams, Arlen Anderson, Yvonne Choquet-Bruhat[*] and James W. York,
Large data local solutions for the derivative NLS equation
 J. Eur. Math. Soc. 1, 957 985 c European Mathematical Society 8 Ioan Bejenaru Daniel Tataru Large data local solutions for the derivative NLS equation Received May 9, 7 Abstract. We consider the derivative
J. Eur. Math. Soc. 1, 957 985 c European Mathematical Society 8 Ioan Bejenaru Daniel Tataru Large data local solutions for the derivative NLS equation Received May 9, 7 Abstract. We consider the derivative
TADAHIRO OH 0, 3 8 (T R), (1.5) The result in [2] is in fact stated for time-periodic functions: 0, 1 3 (T 2 ). (1.4)
![TADAHIRO OH 0, 3 8 (T R), (1.5) The result in [2] is in fact stated for time-periodic functions: 0, 1 3 (T 2 ). (1.4) TADAHIRO OH 0, 3 8 (T R), (1.5) The result in [2] is in fact stated for time-periodic functions: 0, 1 3 (T 2 ). (1.4)](/thumbs/95/125089959.jpg) PERIODIC L 4 -STRICHARTZ ESTIMATE FOR KDV TADAHIRO OH 1. Introduction In [], Bourgain proved global well-posedness of the periodic KdV in L T): u t + u xxx + uu x 0, x, t) T R. 1.1) The key ingredient
PERIODIC L 4 -STRICHARTZ ESTIMATE FOR KDV TADAHIRO OH 1. Introduction In [], Bourgain proved global well-posedness of the periodic KdV in L T): u t + u xxx + uu x 0, x, t) T R. 1.1) The key ingredient
Sharp Sobolev Strichartz estimates for the free Schrödinger propagator
 Sharp Sobolev Strichartz estimates for the free Schrödinger propagator Neal Bez, Chris Jeavons and Nikolaos Pattakos Abstract. We consider gaussian extremisability of sharp linear Sobolev Strichartz estimates
Sharp Sobolev Strichartz estimates for the free Schrödinger propagator Neal Bez, Chris Jeavons and Nikolaos Pattakos Abstract. We consider gaussian extremisability of sharp linear Sobolev Strichartz estimates
SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY
 SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY S. IBRAHIM, M. MAJDOUB, N. MASMOUDI, AND K. NAKANISHI Abstract. We investigate existence and asymptotic completeness of the wave operators
SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY S. IBRAHIM, M. MAJDOUB, N. MASMOUDI, AND K. NAKANISHI Abstract. We investigate existence and asymptotic completeness of the wave operators
EXISTENCE RESULTS FOR QUASILINEAR HEMIVARIATIONAL INEQUALITIES AT RESONANCE. Leszek Gasiński
 DISCRETE AND CONTINUOUS Website: www.aimsciences.org DYNAMICAL SYSTEMS SUPPLEMENT 2007 pp. 409 418 EXISTENCE RESULTS FOR QUASILINEAR HEMIVARIATIONAL INEQUALITIES AT RESONANCE Leszek Gasiński Jagiellonian
DISCRETE AND CONTINUOUS Website: www.aimsciences.org DYNAMICAL SYSTEMS SUPPLEMENT 2007 pp. 409 418 EXISTENCE RESULTS FOR QUASILINEAR HEMIVARIATIONAL INEQUALITIES AT RESONANCE Leszek Gasiński Jagiellonian
Sharp estimates for a class of hyperbolic pseudo-differential equations
 Results in Math., 41 (2002), 361-368. Sharp estimates for a class of hyperbolic pseudo-differential equations Michael Ruzhansky Abstract In this paper we consider the Cauchy problem for a class of hyperbolic
Results in Math., 41 (2002), 361-368. Sharp estimates for a class of hyperbolic pseudo-differential equations Michael Ruzhansky Abstract In this paper we consider the Cauchy problem for a class of hyperbolic
Strichartz Estimates in Domains
 Department of Mathematics Johns Hopkins University April 15, 2010 Wave equation on Riemannian manifold (M, g) Cauchy problem: 2 t u(t, x) gu(t, x) =0 u(0, x) =f (x), t u(0, x) =g(x) Strichartz estimates:
Department of Mathematics Johns Hopkins University April 15, 2010 Wave equation on Riemannian manifold (M, g) Cauchy problem: 2 t u(t, x) gu(t, x) =0 u(0, x) =f (x), t u(0, x) =g(x) Strichartz estimates:
Notes. 1 Fourier transform and L p spaces. March 9, For a function in f L 1 (R n ) define the Fourier transform. ˆf(ξ) = f(x)e 2πi x,ξ dx.
 Notes March 9, 27 1 Fourier transform and L p spaces For a function in f L 1 (R n ) define the Fourier transform ˆf(ξ) = f(x)e 2πi x,ξ dx. Properties R n 1. f g = ˆfĝ 2. δλ (f)(ξ) = ˆf(λξ), where δ λ f(x)
Notes March 9, 27 1 Fourier transform and L p spaces For a function in f L 1 (R n ) define the Fourier transform ˆf(ξ) = f(x)e 2πi x,ξ dx. Properties R n 1. f g = ˆfĝ 2. δλ (f)(ξ) = ˆf(λξ), where δ λ f(x)
Some physical space heuristics for Strichartz estimates
 Some physical space heuristics for Strichartz estimates Felipe Hernandez July 30, 2014 SPUR Final Paper, Summer 2014 Mentor Chenjie Fan Project suggested by Gigliola Staffilani Abstract This note records
Some physical space heuristics for Strichartz estimates Felipe Hernandez July 30, 2014 SPUR Final Paper, Summer 2014 Mentor Chenjie Fan Project suggested by Gigliola Staffilani Abstract This note records
STOKES PROBLEM WITH SEVERAL TYPES OF BOUNDARY CONDITIONS IN AN EXTERIOR DOMAIN
 Electronic Journal of Differential Equations, Vol. 2013 2013, No. 196, pp. 1 28. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu STOKES PROBLEM
Electronic Journal of Differential Equations, Vol. 2013 2013, No. 196, pp. 1 28. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu STOKES PROBLEM
Global well-posedness for semi-linear Wave and Schrödinger equations. Slim Ibrahim
 Global well-posedness for semi-linear Wave and Schrödinger equations Slim Ibrahim McMaster University, Hamilton ON University of Calgary, April 27th, 2006 1 1 Introduction Nonlinear Wave equation: ( 2
Global well-posedness for semi-linear Wave and Schrödinger equations Slim Ibrahim McMaster University, Hamilton ON University of Calgary, April 27th, 2006 1 1 Introduction Nonlinear Wave equation: ( 2
The Helically Reduced Wave Equation as a Symmetric Positive System
 Utah State University DigitalCommons@USU All Physics Faculty Publications Physics 2003 The Helically Reduced Wave Equation as a Symmetric Positive System Charles G. Torre Utah State University Follow this
Utah State University DigitalCommons@USU All Physics Faculty Publications Physics 2003 The Helically Reduced Wave Equation as a Symmetric Positive System Charles G. Torre Utah State University Follow this
NULL CONDITION FOR SEMILINEAR WAVE EQUATION WITH VARIABLE COEFFICIENTS. Fabio Catalano
 Serdica Math J 25 (999), 32-34 NULL CONDITION FOR SEMILINEAR WAVE EQUATION WITH VARIABLE COEFFICIENTS Fabio Catalano Communicated by V Petkov Abstract In this work we analyse the nonlinear Cauchy problem
Serdica Math J 25 (999), 32-34 NULL CONDITION FOR SEMILINEAR WAVE EQUATION WITH VARIABLE COEFFICIENTS Fabio Catalano Communicated by V Petkov Abstract In this work we analyse the nonlinear Cauchy problem
INTEGRABILITY OF SUPERHARMONIC FUNCTIONS IN A JOHN DOMAIN. Hiroaki Aikawa
 INTEGRABILITY OF SUPERHARMONIC FUNCTIONS IN A OHN OMAIN Hiroaki Aikawa Abstract. The integrability of positive erharmonic functions on a bounded fat ohn domain is established. No exterior conditions are
INTEGRABILITY OF SUPERHARMONIC FUNCTIONS IN A OHN OMAIN Hiroaki Aikawa Abstract. The integrability of positive erharmonic functions on a bounded fat ohn domain is established. No exterior conditions are
Geometry and the Kato square root problem
 Geometry and the Kato square root problem Lashi Bandara Centre for Mathematics and its Applications Australian National University 29 July 2014 Geometric Analysis Seminar Beijing International Center for
Geometry and the Kato square root problem Lashi Bandara Centre for Mathematics and its Applications Australian National University 29 July 2014 Geometric Analysis Seminar Beijing International Center for
i=1 α i. Given an m-times continuously
 1 Fundamentals 1.1 Classification and characteristics Let Ω R d, d N, d 2, be an open set and α = (α 1,, α d ) T N d 0, N 0 := N {0}, a multiindex with α := d i=1 α i. Given an m-times continuously differentiable
1 Fundamentals 1.1 Classification and characteristics Let Ω R d, d N, d 2, be an open set and α = (α 1,, α d ) T N d 0, N 0 := N {0}, a multiindex with α := d i=1 α i. Given an m-times continuously differentiable
Dispersive Equations and Hyperbolic Orbits
 Dispersive Equations and Hyperbolic Orbits H. Christianson Department of Mathematics University of California, Berkeley 4/16/07 The Johns Hopkins University Outline 1 Introduction 3 Applications 2 Main
Dispersive Equations and Hyperbolic Orbits H. Christianson Department of Mathematics University of California, Berkeley 4/16/07 The Johns Hopkins University Outline 1 Introduction 3 Applications 2 Main
GLOBAL EXISTENCE FOR THE ONE-DIMENSIONAL SEMILINEAR TRICOMI-TYPE EQUATIONS
 GLOBAL EXISTENCE FOR THE ONE-DIMENSIONAL SEMILINEAR TRICOMI-TYPE EQUATIONS ANAHIT GALSTYAN The Tricomi equation u tt tu xx = 0 is a linear partial differential operator of mixed type. (For t > 0, the Tricomi
GLOBAL EXISTENCE FOR THE ONE-DIMENSIONAL SEMILINEAR TRICOMI-TYPE EQUATIONS ANAHIT GALSTYAN The Tricomi equation u tt tu xx = 0 is a linear partial differential operator of mixed type. (For t > 0, the Tricomi
Curriculum Vitae for Hart Smith - Updated April, 2016
 Curriculum Vitae for Hart Smith - Updated April, 2016 Education Princeton University, 1984 1988. Ph.D. in Mathematics, January, 1989. Thesis supervisor: E. M. Stein. Thesis title: The subelliptic oblique
Curriculum Vitae for Hart Smith - Updated April, 2016 Education Princeton University, 1984 1988. Ph.D. in Mathematics, January, 1989. Thesis supervisor: E. M. Stein. Thesis title: The subelliptic oblique
ALMOST OPTIMAL LOCAL WELL-POSEDNESS FOR THE (3+1)-DIMENSIONAL MAXWELL KLEIN GORDON EQUATIONS
 JOURNAL OF THE AMERICAN MATHEMATICAL SOCIETY Volume 7, Number, Pages 97 359 S 0894-03470300445-4 Article electronically published on November 3, 003 ALMOST OPTIMAL LOCAL WELL-POSEDNESS FOR THE 3+-DIMENSIONAL
JOURNAL OF THE AMERICAN MATHEMATICAL SOCIETY Volume 7, Number, Pages 97 359 S 0894-03470300445-4 Article electronically published on November 3, 003 ALMOST OPTIMAL LOCAL WELL-POSEDNESS FOR THE 3+-DIMENSIONAL
Decouplings and applications
 April 27, 2018 Let Ξ be a collection of frequency points ξ on some curved, compact manifold S of diameter 1 in R n (e.g. the unit sphere S n 1 ) Let B R = B(c, R) be a ball with radius R 1. Let also a
April 27, 2018 Let Ξ be a collection of frequency points ξ on some curved, compact manifold S of diameter 1 in R n (e.g. the unit sphere S n 1 ) Let B R = B(c, R) be a ball with radius R 1. Let also a
POINTWISE BOUNDS ON QUASIMODES OF SEMICLASSICAL SCHRÖDINGER OPERATORS IN DIMENSION TWO
 POINTWISE BOUNDS ON QUASIMODES OF SEMICLASSICAL SCHRÖDINGER OPERATORS IN DIMENSION TWO HART F. SMITH AND MACIEJ ZWORSKI Abstract. We prove optimal pointwise bounds on quasimodes of semiclassical Schrödinger
POINTWISE BOUNDS ON QUASIMODES OF SEMICLASSICAL SCHRÖDINGER OPERATORS IN DIMENSION TWO HART F. SMITH AND MACIEJ ZWORSKI Abstract. We prove optimal pointwise bounds on quasimodes of semiclassical Schrödinger
The Chern-Simons-Schrödinger equation
 The Chern-Simons-Schrödinger equation Low regularity local wellposedness Baoping Liu, Paul Smith, Daniel Tataru University of California, Berkeley July 16, 2012 Paul Smith (UC Berkeley) Chern-Simons-Schrödinger
The Chern-Simons-Schrödinger equation Low regularity local wellposedness Baoping Liu, Paul Smith, Daniel Tataru University of California, Berkeley July 16, 2012 Paul Smith (UC Berkeley) Chern-Simons-Schrödinger
Scientific Computing WS 2018/2019. Lecture 15. Jürgen Fuhrmann Lecture 15 Slide 1
 Scientific Computing WS 2018/2019 Lecture 15 Jürgen Fuhrmann juergen.fuhrmann@wias-berlin.de Lecture 15 Slide 1 Lecture 15 Slide 2 Problems with strong formulation Writing the PDE with divergence and gradient
Scientific Computing WS 2018/2019 Lecture 15 Jürgen Fuhrmann juergen.fuhrmann@wias-berlin.de Lecture 15 Slide 1 Lecture 15 Slide 2 Problems with strong formulation Writing the PDE with divergence and gradient
arxiv: v1 [math.ap] 28 Jun 2011
![arxiv: v1 [math.ap] 28 Jun 2011 arxiv: v1 [math.ap] 28 Jun 2011](/thumbs/85/92110193.jpg) GLOBAL WELL-POSEDNESS AND SCATTERING FOR SKYRME WAVE MAPS arxiv:1106.5750v1 [math.ap] 28 Jun 2011 DAN-ANDREI GEBA, KENJI NAKANISHI, AND SARADA G. RAJEEV Abstract. We study equivariant solutions for two
GLOBAL WELL-POSEDNESS AND SCATTERING FOR SKYRME WAVE MAPS arxiv:1106.5750v1 [math.ap] 28 Jun 2011 DAN-ANDREI GEBA, KENJI NAKANISHI, AND SARADA G. RAJEEV Abstract. We study equivariant solutions for two
Dispersive Equations and Nonlinear Waves
 Herbert Koch Daniel Tataru Monica Vi an Dispersive Equations and Nonlinear Waves Generalized Korteweg-de Vries, Nonlinear Schrodinger, Wave and Schrodinger Maps ^ Birkhauser Contents Preface xi Nonlinear
Herbert Koch Daniel Tataru Monica Vi an Dispersive Equations and Nonlinear Waves Generalized Korteweg-de Vries, Nonlinear Schrodinger, Wave and Schrodinger Maps ^ Birkhauser Contents Preface xi Nonlinear
COMPARISON PRINCIPLES FOR CONSTRAINED SUBHARMONICS PH.D. COURSE - SPRING 2019 UNIVERSITÀ DI MILANO
 COMPARISON PRINCIPLES FOR CONSTRAINED SUBHARMONICS PH.D. COURSE - SPRING 2019 UNIVERSITÀ DI MILANO KEVIN R. PAYNE 1. Introduction Constant coefficient differential inequalities and inclusions, constraint
COMPARISON PRINCIPLES FOR CONSTRAINED SUBHARMONICS PH.D. COURSE - SPRING 2019 UNIVERSITÀ DI MILANO KEVIN R. PAYNE 1. Introduction Constant coefficient differential inequalities and inclusions, constraint
Regularity results for the Dirac-Klein-Gordon equations
 Achenef Tesfahun Temesgen Regularity results for the Dirac-Klein-Gordon equations Thesis for the degree of Philosophiae Doctor Trondheim, January 2009 Norwegian University of Science and Technology Faculty
Achenef Tesfahun Temesgen Regularity results for the Dirac-Klein-Gordon equations Thesis for the degree of Philosophiae Doctor Trondheim, January 2009 Norwegian University of Science and Technology Faculty
ANALYTIC SMOOTHING EFFECT FOR NONLI TitleSCHRÖDINGER EQUATION IN TWO SPACE DIMENSIONS. Citation Osaka Journal of Mathematics.
 ANALYTIC SMOOTHING EFFECT FOR NONLI TitleSCHRÖDINGER EQUATION IN TWO SPACE DIMENSIONS Author(s) Hoshino, Gaku; Ozawa, Tohru Citation Osaka Journal of Mathematics. 51(3) Issue 014-07 Date Text Version publisher
ANALYTIC SMOOTHING EFFECT FOR NONLI TitleSCHRÖDINGER EQUATION IN TWO SPACE DIMENSIONS Author(s) Hoshino, Gaku; Ozawa, Tohru Citation Osaka Journal of Mathematics. 51(3) Issue 014-07 Date Text Version publisher
LIST OF PUBLICATIONS. Mu-Tao Wang. March 2017
 LIST OF PUBLICATIONS Mu-Tao Wang Publications March 2017 1. (with P.-K. Hung, J. Keller) Linear stability of Schwarzschild spacetime: the Cauchy problem of metric coefficients. arxiv: 1702.02843v2 2. (with
LIST OF PUBLICATIONS Mu-Tao Wang Publications March 2017 1. (with P.-K. Hung, J. Keller) Linear stability of Schwarzschild spacetime: the Cauchy problem of metric coefficients. arxiv: 1702.02843v2 2. (with
BLOWUP THEORY FOR THE CRITICAL NONLINEAR SCHRÖDINGER EQUATIONS REVISITED
 BLOWUP THEORY FOR THE CRITICAL NONLINEAR SCHRÖDINGER EQUATIONS REVISITED TAOUFIK HMIDI AND SAHBI KERAANI Abstract. In this note we prove a refined version of compactness lemma adapted to the blowup analysis
BLOWUP THEORY FOR THE CRITICAL NONLINEAR SCHRÖDINGER EQUATIONS REVISITED TAOUFIK HMIDI AND SAHBI KERAANI Abstract. In this note we prove a refined version of compactness lemma adapted to the blowup analysis
Classical Fourier Analysis
 Loukas Grafakos Classical Fourier Analysis Second Edition 4y Springer 1 IP Spaces and Interpolation 1 1.1 V and Weak IP 1 1.1.1 The Distribution Function 2 1.1.2 Convergence in Measure 5 1.1.3 A First
Loukas Grafakos Classical Fourier Analysis Second Edition 4y Springer 1 IP Spaces and Interpolation 1 1.1 V and Weak IP 1 1.1.1 The Distribution Function 2 1.1.2 Convergence in Measure 5 1.1.3 A First
Decoupling of modes for the elastic wave equation in media of limited smoothness
 Decoupling of modes for the elastic wave equation in media of limited smoothness Valeriy Brytik 1 Maarten V. de Hoop 1 Hart F. Smith Gunther Uhlmann September, 1 1 Center for Computational and Applied
Decoupling of modes for the elastic wave equation in media of limited smoothness Valeriy Brytik 1 Maarten V. de Hoop 1 Hart F. Smith Gunther Uhlmann September, 1 1 Center for Computational and Applied
2 A Model, Harmonic Map, Problem
 ELLIPTIC SYSTEMS JOHN E. HUTCHINSON Department of Mathematics School of Mathematical Sciences, A.N.U. 1 Introduction Elliptic equations model the behaviour of scalar quantities u, such as temperature or
ELLIPTIC SYSTEMS JOHN E. HUTCHINSON Department of Mathematics School of Mathematical Sciences, A.N.U. 1 Introduction Elliptic equations model the behaviour of scalar quantities u, such as temperature or
arxiv:math/ v2 [math.ap] 8 Jun 2006
![arxiv:math/ v2 [math.ap] 8 Jun 2006 arxiv:math/ v2 [math.ap] 8 Jun 2006](/thumbs/73/68662045.jpg) LOW REGULARITY GLOBAL WELL-POSEDNESS FOR THE KLEIN-GORDON-SCHRÖDINGER SYSTEM WITH THE HIGHER ORDER YUKAWA COUPLING arxiv:math/0606079v [math.ap] 8 Jun 006 Changxing Miao Institute of Applied Physics and
LOW REGULARITY GLOBAL WELL-POSEDNESS FOR THE KLEIN-GORDON-SCHRÖDINGER SYSTEM WITH THE HIGHER ORDER YUKAWA COUPLING arxiv:math/0606079v [math.ap] 8 Jun 006 Changxing Miao Institute of Applied Physics and
ATTRACTORS FOR SEMILINEAR PARABOLIC PROBLEMS WITH DIRICHLET BOUNDARY CONDITIONS IN VARYING DOMAINS. Emerson A. M. de Abreu Alexandre N.
 ATTRACTORS FOR SEMILINEAR PARABOLIC PROBLEMS WITH DIRICHLET BOUNDARY CONDITIONS IN VARYING DOMAINS Emerson A. M. de Abreu Alexandre N. Carvalho Abstract Under fairly general conditions one can prove that
ATTRACTORS FOR SEMILINEAR PARABOLIC PROBLEMS WITH DIRICHLET BOUNDARY CONDITIONS IN VARYING DOMAINS Emerson A. M. de Abreu Alexandre N. Carvalho Abstract Under fairly general conditions one can prove that
RANDOM PROPERTIES BENOIT PAUSADER
 RANDOM PROPERTIES BENOIT PAUSADER. Quasilinear problems In general, one consider the following trichotomy for nonlinear PDEs: A semilinear problem is a problem where the highest-order terms appears linearly
RANDOM PROPERTIES BENOIT PAUSADER. Quasilinear problems In general, one consider the following trichotomy for nonlinear PDEs: A semilinear problem is a problem where the highest-order terms appears linearly
The Kato square root problem on vector bundles with generalised bounded geometry
 The Kato square root problem on vector bundles with generalised bounded geometry Lashi Bandara (Joint work with Alan McIntosh, ANU) Centre for Mathematics and its Applications Australian National University
The Kato square root problem on vector bundles with generalised bounded geometry Lashi Bandara (Joint work with Alan McIntosh, ANU) Centre for Mathematics and its Applications Australian National University
Energy method for wave equations
 Energy method for wave equations Willie Wong Based on commit 5dfb7e5 of 2017-11-06 13:29 Abstract We give an elementary discussion of the energy method (and particularly the vector field method) in the
Energy method for wave equations Willie Wong Based on commit 5dfb7e5 of 2017-11-06 13:29 Abstract We give an elementary discussion of the energy method (and particularly the vector field method) in the
The Kato square root problem on vector bundles with generalised bounded geometry
 The Kato square root problem on vector bundles with generalised bounded geometry Lashi Bandara (Joint work with Alan McIntosh, ANU) Centre for Mathematics and its Applications Australian National University
The Kato square root problem on vector bundles with generalised bounded geometry Lashi Bandara (Joint work with Alan McIntosh, ANU) Centre for Mathematics and its Applications Australian National University
Riemannian Curvature Functionals: Lecture I
 Riemannian Curvature Functionals: Lecture I Jeff Viaclovsky Park City athematics Institute July 16, 2013 Overview of lectures The goal of these lectures is to gain an understanding of critical points of
Riemannian Curvature Functionals: Lecture I Jeff Viaclovsky Park City athematics Institute July 16, 2013 Overview of lectures The goal of these lectures is to gain an understanding of critical points of
The Stability of the Irrotational Euler-Einstein System with a Positive Cosmological Constant
 The Stability of the Irrotational Euler-Einstein System with a Positive Cosmological Constant Jared Speck & Igor Rodnianski jspeck@math.princeton.edu University of Cambridge & Princeton University October
The Stability of the Irrotational Euler-Einstein System with a Positive Cosmological Constant Jared Speck & Igor Rodnianski jspeck@math.princeton.edu University of Cambridge & Princeton University October
MAXIMIZERS FOR THE STRICHARTZ AND THE SOBOLEV-STRICHARTZ INEQUALITIES FOR THE SCHRÖDINGER EQUATION
 Electronic Journal of Differential Euations, Vol. 9(9), No. 3, pp. 1 13. ISSN: 17-6691. UR: http://ede.math.tstate.edu or http://ede.math.unt.edu ftp ede.math.tstate.edu (login: ftp) MAXIMIZERS FOR THE
Electronic Journal of Differential Euations, Vol. 9(9), No. 3, pp. 1 13. ISSN: 17-6691. UR: http://ede.math.tstate.edu or http://ede.math.unt.edu ftp ede.math.tstate.edu (login: ftp) MAXIMIZERS FOR THE
Duality of multiparameter Hardy spaces H p on spaces of homogeneous type
 Duality of multiparameter Hardy spaces H p on spaces of homogeneous type Yongsheng Han, Ji Li, and Guozhen Lu Department of Mathematics Vanderbilt University Nashville, TN Internet Analysis Seminar 2012
Duality of multiparameter Hardy spaces H p on spaces of homogeneous type Yongsheng Han, Ji Li, and Guozhen Lu Department of Mathematics Vanderbilt University Nashville, TN Internet Analysis Seminar 2012
A NASH-MOSER THEOREM WITH NEAR-MINIMAL HYPOTHESIS
 A NASH-MOSER THEOREM WITH NEAR-MINIMAL HYPOTHESIS J. W. NEUBERGER Abstract. A proof of a Nash-Moser type inverse function theorem is given under substantially weaker hypothesis than previously known. Our
A NASH-MOSER THEOREM WITH NEAR-MINIMAL HYPOTHESIS J. W. NEUBERGER Abstract. A proof of a Nash-Moser type inverse function theorem is given under substantially weaker hypothesis than previously known. Our
Wave operators with non-lipschitz coefficients: energy and observability estimates
 Wave operators with non-lipschitz coefficients: energy and observability estimates Institut de Mathématiques de Jussieu-Paris Rive Gauche UNIVERSITÉ PARIS DIDEROT PARIS 7 JOURNÉE JEUNES CONTRÔLEURS 2014
Wave operators with non-lipschitz coefficients: energy and observability estimates Institut de Mathématiques de Jussieu-Paris Rive Gauche UNIVERSITÉ PARIS DIDEROT PARIS 7 JOURNÉE JEUNES CONTRÔLEURS 2014
ABSOLUTE CONTINUITY OF FOLIATIONS
 ABSOLUTE CONTINUITY OF FOLIATIONS C. PUGH, M. VIANA, A. WILKINSON 1. Introduction In what follows, U is an open neighborhood in a compact Riemannian manifold M, and F is a local foliation of U. By this
ABSOLUTE CONTINUITY OF FOLIATIONS C. PUGH, M. VIANA, A. WILKINSON 1. Introduction In what follows, U is an open neighborhood in a compact Riemannian manifold M, and F is a local foliation of U. By this
MULTIPLE SOLUTIONS FOR THE p-laplace EQUATION WITH NONLINEAR BOUNDARY CONDITIONS
 Electronic Journal of Differential Equations, Vol. 2006(2006), No. 37, pp. 1 7. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) MULTIPLE
Electronic Journal of Differential Equations, Vol. 2006(2006), No. 37, pp. 1 7. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) MULTIPLE
Sobolev regularity for the Monge-Ampère equation, with application to the semigeostrophic equations
 Sobolev regularity for the Monge-Ampère equation, with application to the semigeostrophic equations Alessio Figalli Abstract In this note we review some recent results on the Sobolev regularity of solutions
Sobolev regularity for the Monge-Ampère equation, with application to the semigeostrophic equations Alessio Figalli Abstract In this note we review some recent results on the Sobolev regularity of solutions
Geometric Methods in Hyperbolic PDEs
 Geometric Methods in Hyperbolic PDEs Jared Speck jspeck@math.princeton.edu Department of Mathematics Princeton University January 24, 2011 Unifying mathematical themes Many physical phenomena are modeled
Geometric Methods in Hyperbolic PDEs Jared Speck jspeck@math.princeton.edu Department of Mathematics Princeton University January 24, 2011 Unifying mathematical themes Many physical phenomena are modeled
SYMMETRY OF POSITIVE SOLUTIONS OF SOME NONLINEAR EQUATIONS. M. Grossi S. Kesavan F. Pacella M. Ramaswamy. 1. Introduction
 Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 12, 1998, 47 59 SYMMETRY OF POSITIVE SOLUTIONS OF SOME NONLINEAR EQUATIONS M. Grossi S. Kesavan F. Pacella M. Ramaswamy
Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 12, 1998, 47 59 SYMMETRY OF POSITIVE SOLUTIONS OF SOME NONLINEAR EQUATIONS M. Grossi S. Kesavan F. Pacella M. Ramaswamy
Energy transfer model and large periodic boundary value problem for the quintic NLS
 Energy transfer model and large periodic boundary value problem for the quintic NS Hideo Takaoka Department of Mathematics, Kobe University 1 ntroduction This note is based on a talk given at the conference
Energy transfer model and large periodic boundary value problem for the quintic NS Hideo Takaoka Department of Mathematics, Kobe University 1 ntroduction This note is based on a talk given at the conference
On Estimates of Biharmonic Functions on Lipschitz and Convex Domains
 The Journal of Geometric Analysis Volume 16, Number 4, 2006 On Estimates of Biharmonic Functions on Lipschitz and Convex Domains By Zhongwei Shen ABSTRACT. Using Maz ya type integral identities with power
The Journal of Geometric Analysis Volume 16, Number 4, 2006 On Estimates of Biharmonic Functions on Lipschitz and Convex Domains By Zhongwei Shen ABSTRACT. Using Maz ya type integral identities with power
RIGIDITY OF STATIONARY BLACK HOLES WITH SMALL ANGULAR MOMENTUM ON THE HORIZON
 RIGIDITY OF STATIONARY BLACK HOLES WITH SMALL ANGULAR MOMENTUM ON THE HORIZON S. ALEXAKIS, A. D. IONESCU, AND S. KLAINERMAN Abstract. We prove a black hole rigidity result for slowly rotating stationary
RIGIDITY OF STATIONARY BLACK HOLES WITH SMALL ANGULAR MOMENTUM ON THE HORIZON S. ALEXAKIS, A. D. IONESCU, AND S. KLAINERMAN Abstract. We prove a black hole rigidity result for slowly rotating stationary
Analytic families of multilinear operators
 Analytic families of multilinear operators Mieczysław Mastyło Adam Mickiewicz University in Poznań Nonlinar Functional Analysis Valencia 17-20 October 2017 Based on a joint work with Loukas Grafakos M.
Analytic families of multilinear operators Mieczysław Mastyło Adam Mickiewicz University in Poznań Nonlinar Functional Analysis Valencia 17-20 October 2017 Based on a joint work with Loukas Grafakos M.
Strichartz estimates for the Schrödinger equation on polygonal domains
 estimates for the Schrödinger equation on Joint work with Matt Blair (UNM), G. Austin Ford (Northwestern U) and Sebastian Herr (U Bonn and U Düsseldorf)... With a discussion of previous work with Andrew
estimates for the Schrödinger equation on Joint work with Matt Blair (UNM), G. Austin Ford (Northwestern U) and Sebastian Herr (U Bonn and U Düsseldorf)... With a discussion of previous work with Andrew
MAXIMAL AVERAGE ALONG VARIABLE LINES. 1. Introduction
 MAXIMAL AVERAGE ALONG VARIABLE LINES JOONIL KIM Abstract. We prove the L p boundedness of the maximal operator associated with a family of lines l x = {(x, x 2) t(, a(x )) : t [0, )} when a is a positive
MAXIMAL AVERAGE ALONG VARIABLE LINES JOONIL KIM Abstract. We prove the L p boundedness of the maximal operator associated with a family of lines l x = {(x, x 2) t(, a(x )) : t [0, )} when a is a positive
Geometry and the Kato square root problem
 Geometry and the Kato square root problem Lashi Bandara Centre for Mathematics and its Applications Australian National University 7 June 2013 Geometric Analysis Seminar University of Wollongong Lashi
Geometry and the Kato square root problem Lashi Bandara Centre for Mathematics and its Applications Australian National University 7 June 2013 Geometric Analysis Seminar University of Wollongong Lashi
Global stability problems in General Relativity
 Global stability problems in General Relativity Peter Hintz with András Vasy Murramarang March 21, 2018 Einstein vacuum equations Ric(g) + Λg = 0. g: Lorentzian metric (+ ) on 4-manifold M Λ R: cosmological
Global stability problems in General Relativity Peter Hintz with András Vasy Murramarang March 21, 2018 Einstein vacuum equations Ric(g) + Λg = 0. g: Lorentzian metric (+ ) on 4-manifold M Λ R: cosmological
Existence of Positive Solutions to a Nonlinear Biharmonic Equation
 International Mathematical Forum, 3, 2008, no. 40, 1959-1964 Existence of Positive Solutions to a Nonlinear Biharmonic Equation S. H. Al Hashimi Department of Chemical Engineering The Petroleum Institute,
International Mathematical Forum, 3, 2008, no. 40, 1959-1964 Existence of Positive Solutions to a Nonlinear Biharmonic Equation S. H. Al Hashimi Department of Chemical Engineering The Petroleum Institute,
A BILINEAR ESTIMATE WITH APPLICATIONS TO THE KdV EQUATION
 JOURNAL OF THE AMERICAN MATHEMATICAL SOCIETY Volume 9, Number 2, April 996 A BILINEAR ESTIMATE WITH APPLICATIONS TO THE KdV EQUATION CARLOS E. KENIG, GUSTAVO PONCE, AND LUIS VEGA. Introduction In this
JOURNAL OF THE AMERICAN MATHEMATICAL SOCIETY Volume 9, Number 2, April 996 A BILINEAR ESTIMATE WITH APPLICATIONS TO THE KdV EQUATION CARLOS E. KENIG, GUSTAVO PONCE, AND LUIS VEGA. Introduction In this
