SBS Chapter 2: Limits & continuity
|
|
|
- Jody Lindsey
- 6 years ago
- Views:
Transcription
1 SBS Chapter 2: Limits & continuity (SBS 2.1) Limit of a function Consider a free falling body with no air resistance. Falls approximately s(t) = 16t 2 feet in t seconds. We already know how to nd the average velocity over an interval of time. Now we want to know instantaneous velocity at t = 2 seconds, for example. We can express this as a limit. Compute the average velocity over a smaller and smaller time interval near t = 2 seconds.
2 Start with v as the average velocity over the interval 1.9 t 2. distance traveled v = elapsed time s(2) s(1.9) = = 16(2)2 16(1.9) = 62.4 ft/s
3 We can make similar computations with smaller and smaller intervals from above or below t = 2. From below: Interval [1.9,2] [1.99,2] [1.999,2] Length Ave. velocity From above: Interval [2,2.0001] [2,2.001] [2,2.01] Length Ave. velocity Average velocity seems to be approaching 64 as we make the time intervals smaller. So we expect the instantaneous velocity at t = 2 will be 64.
4 Average velocity of the falling body over time interval 2 t 2 + h is s t = s(2 + h) s(2) (2 + h) 2 = 16(2 + h)2 16(2) 2. h Think of h as a small number, so (2,2 + h) is a small interval above 2. In this example, the average velocity has a limiting value of 64 as the length h of the time interval tends to zero. We write: 16(2 + h) 2 16(2) 2 lim h 0 h = 64.
5 Informal limit denition: The notation lim x c f (x) = L means: the function values f (x) can be made arbitrarily close to a unique number L by choosing x suciently close to c (but not equal to c). Other notation: Also written as f (x) L as x c
6 Limit example: Evaluate (by table) 2 x + 1 x 2 L = lim x 0 x 2 x f(x) undef Table pattern suggests that the limit L is Note that we can have a limit of 0.25 as f (x) 0 even thought f (0) itself is undened. Be careful with calculators (or computers) and subtracting very small numbers! Can introduce errors.
7 One-Sided Limits Right-hand limit: lim = L x c + if we can make f (x) arbitrarily close to L by choosing x suciently close to c on a small interval (c,b) immediately to the right of c. Left-hand limit: lim = L x c if we can make f (x) arbitrarily close to L by choosing x suciently close to c on a small interval (a,c) immediately to the left of c.
8 Theorem. (One-sided limit theorem) The two-sided limit lim x c f (x) exists i the two onesided limits exist and are equal. Furthermore, if lim f (x) = L = lim f (x), x c x c + then lim f (x) = L x c
9 Note that the limit does not depend on how the function behaves exactly at c. The function does not even have to be dened at x = c!
10 Example: consider 3 examples with same limit f (x) = x2 1 { x 1 x 2 1 g(x) = x 1, x 1 1, x = 1 h(x) = x + 1
11 Limits do not always exist: If the limit of the function f fails to exist, f (x) is said to diverge as x c. The function may grow arbitrarily large (or small) as x c E.g., lim x 0 1 x 2 A function f that increases or decreases without bound as x approaches c is said to tend to innity as x c. lim f (x) = + x c lim f (x) = x c if f increases without bound if f decreases without bound The function may oscillate as x c E.g., lim x 0 sin 1 x divergence by oscillation
12 Formal denition of a limit (epsilon-delta denition): Denition. The limit statement: lim f (x) = L x c means that for each number ε > 0 there corresponds a number δ > 0 such that f (x) L < ε whenever 0 < x c < δ. In other words: If the distance between x and c is small enough, then the distance between f (x) and L is also small. If x is in (c,c + δ) or (c δ,c), then f (x) must be in the interval (L ε, L + ε).
13 If the limit exists, can aways nd a value of δ that makes the ε band as narrow as I ask it to be. If I can't always nd such a δ, the limit does not exist.
14 Example. (ε δ proof) Show that lim x 1 (5x 3) = 2. Need to show that for any ε, we can nd a δ so that whenever 0 < x 1 < δ, we also have f (x) 2 < ε.
15 Algebraic computation of limits (SBS 2.2) Basic properties and rules for limits: For any real number c, suppose f and g both have limits as x c, and let k be a constant: Constant rule: Limit of x rule: limk = k x c limx = c x c
16 Multiple rule: lim[k f (x)] = k lim f (x) x c x c Sum rule: lim[ f (x)+g(x)] = lim f (x)+limg(x) x c x c x c Dierence rule: lim x c [ f (x) g(x)] = lim x c f (x) lim x c g(x)
17 Product rule: lim f (x)g(x) = (lim f (x))(limg(x)) x c x c x c Quotient rule: Power rule: lim x c ( ) f (x) g(x) = lim x c f (x) lim x c g(x) if lim x c g(x) 0 lim( f (x) n ) = x c ( ) n lim f (x) x c for n rational and limit on right exists
18 Limit of a polynomial: If P is a polynomial function, then limp(x) = P(c) x c Proof: use rst 5 rules.
19 Limit of a rational function: If Q is a rational function Q(x) = P(x) then D(x) P(c) limq(x) = x c D(c) provided lim x c D(x) 0 Proof: use Quotient Rule and Limit of a Polynomial rule.
20 Limits of trigonometric functions: If c is any number in the domain of the given function, then lim(cosx) = cosc x c lim(secx) = secc x c lim(sinx) = sinc x c lim(cscx) = cscc x c lim(tanx) = tanc x c lim(cotx) = cotc x c
21 Examples of limits: sometimes need to manipulate function to nd the limit Fractional reduction x 2 + x 2 lim x 1 x 2 x Note that f (1) is undened. But the limit still exists as x 1.
22 Rationalization lim x 0 x x 2 =? x x 2 = ( ) ( ) x x x 2 x One of the most common tricks in math is multiplying by a clever choice of 1
23 Piecewise functions lim f (x) = x 2 { x 2 + 1, x 2 2x + 1 x > 2 For a limit at the break, need to check left and right limits and see if they are equal.
24 Squeeze Rule Theorem. (Squeeze rule, a.k.a. sandwich theorem) If g(x) f (x) h(x) for all x in an open interval about c (but not necessarily including c), and if limg(x) = limh(x) = L, x c x c then lim f (x) = L. x c
25 Example: use Squeeze rule to prove: lim xsin x 0 ( ) 1 x = 0 Can't use product rule since 2nd limit diverges (by oscillation).
26 For proof, recall a a a and sin 1 x 1 for all x 0:
27 Some special limits (can prove with squeeze rule - see textbook) sinx lim x 0 x = 1 cosx 1 lim x 0 x = 0 (memorize these for now - we'll have a better way of doing them later)
28 Continuity (SBS 2.3) Intuitively, continuity means without jumps or breaks. Formal denition: Denition. A function f is continuous at a point x = c if the following three conditions are all satised: 1. f (c) is dened 2. lim x c f (x) exists 3. lim x c f (x) = f (c) A function that is not continuous at c is said to have a discontinuity at that point.
29 The key idea of continuity is that if x is close to c, then f (x) is close to f (c). Examples: f (x) = x2 1 { x 1 x 2 1 g(x) = x 1, x 1 4, x = 1 h(x) = x + 1 All three have a limit of 2 as x 1, but only h(x) is continuous at x = 1.
30 Some common discontinuity examples: jumps holes, poles, hole: lim x c f (x) exists, but f (c) not dened lim x c f (x) exists, f (c) dened, but f (c) lim x c f (x) jump: left limit not equal to right limit pole: f (c) dened, but either left or right limit ±
31 Continuity Theorem Theorem. If f is a polynomial, rational function, power function, trigonometric function, or an inverse trigonometric function, then f is continuous at any number x = c for which f (c) is dened (i.e., f is continuous at each x in its domain).
32 Theorem. If functions f and g are continuous at x = c, then the following functions are also continuous at x = c: Scalar multiple: k f (x) for any const k Sum and dierence: f (x) + g(x) and f (x) g(x) Product: Quotient: f (x) g(x) f (x) g(x) provided g(c) 0 Composition: f g(x) provided g cont at c and f cont at g(c)
33 Theorem. (Composition Limit Rule) If lim x c g(x) = L and f is continuous at L, then lim x c f [g(x)] = f (L). I.e., lim f [g(x)] = f x c [ ] limg(x) x c = f (L) Applies similarly to left and right limits. Idea is that the limit of a continuous function is the function of the limiting value.
34 Continuity from the left and right: Denition. The function f is continuous from the right at a i lim f (x) = f (a) x a + The function f is continuous from the left at b i lim f (x) = f (b) x b I.e., continuous from the right at a i 1. f (a) is dened 2. lim x c+ f (x) exists 3. lim x c + f (x) = f (a) (Similarly for left continuity.)
35 Continuity on an interval: Denition. The function f is continuous on the open interval (a,b) if it is continuous at each number in the interval. (Note that the end points are not in the interval.) If f is continuous on (a,b) and continuous from the right at a, then f is continuous on the half-open interval [a, b). If f is continuous on (a,b) and continuous from the left at b, then f is continuous on the half-open interval (a, b]. If f is continuous on (a, b), continuous from the right at a, and continuous from the left at b, then f is continuous on the closed interval [a, b].
36 Checking continuity at suspicious points Often, there are only a few points in the domain where a discontinuity may occur. We call such points suspicious points: where the dening rule for f changes (e.g., piecewise dened functions, absolute values) where substitution of x = c causes division by 0 Example of checking suspicious points: f (x) = { 2x + 5, x > 2 15 x 2, x 2
37 Intermediate Value Theorem Theorem. (Intermediate Value Theorem) If f is a continuous function on the closed interval [a, b] and L is some number strictly between f (a) and f (b), then there exists at least one number c on the open interval (a,b) such that f (c) = L. In other words: if f is a continuous function on [a, b] then f (x) must take on all values between f (a) and f (b).
38 Important special case of the Intermediate Value Theorem: Theorem. (Root location theorem) If f is continuous on the closed interval [a, b] and if f (a) and f (b) have opposite algebraic signs, then f (c) = 0 for at least one number c on the open interval (a,b).
39 Example: Show that f (x) = sinx x + 1 has a root on the interval ( π 2,π): Proof: f (x) is continuous on the interval [ π 2,π] (no suspicious points; it's continuous on whole real line). f ( π 2 ) = 1 π = 2 π 2 > 0 f (π) = 0 π + 1 < 0
40 (i.e., L = 0 is strictly between f ( π 2 ) and f (π)) Therefore f (x) has at least one root in ( π 2,π) by Root location theorem (or by Intermediate Value Theorem)
41 Exponentials and Logarithms (SBS 2.4) Recall that we can already dene b x number x: for any rational For natural (counting) numbers n, we have b n = b b b b (n factors). If b 0, then b 0 = 1, and b n = 1 b n. If b > 0, then b 1/n = n b. If m, n are integers and m/n is a reduced fraction, then b m/n = (b 1/n ) m = n b m. These steps work us up from counting numbers to any rational number m n. We now want to extend the idea to all real numbers.
42 Completeness of the reals For any real number x there is a sequence r n of rational numbers such that x = lim x r n. That is, for any ε > 0 there is a number N such that n > N x r n < ε. As n gets bigger and bigger, r n to the real number x. gets closer and closer This means that we can approximate any real number to any degree of accuracy by a rational number.
43 Exponential functions Denition. Let x be a real number and let r n be a sequence of rational numbers such that x = lim x r n. Then the exponential function with base b, b > 0 (b 1), is given by b x = lim n b r n b is called the base and x is the exponent. [Do not confuse these with power functions f (x) = x p. Here the variable is in the exponent. In a power function, it is in the base.]
44 Properties of the exponential function Let x and y be any real numbers, and let a and b be positive real numbers. Equality rule: Inequality rules: Product rule: Quotient rule: Power rules: If b 1, then b x = b y i x = y If x > y and b > 1, then b x > b y If x > y and 0 < b < 1, then b x < b y b x b y = b x+y b x b y = b x y (b x ) y = b xy ; (ab) x = a x b x ; ( a b )x = ax b x
45 Graphical properties: The exponential function f (x) = b x is continuous for all real numbers x. b x > 0 The graph is always rising for b > 1 and always falling for 0 < b < 1.
46
47
48 Example of working with exponentials: 3 x2 x = 9 3 x2 x = 3 2 x 2 x = 2 (equality rule) x 2 x 2 = 0 (x 2)(x + 1) = 0 x = 2, 1
49 Logarithmic functions y = b x (b > 0, b 1) is monotonic, so the exponential has an inverse. If b > 0 and b 1, the logarithm of x to the base b is the function y = log b x that satises b y = x. y = log b x means b y = x Note that since b y = x, this means that we can only take the logarithm of positive numbers. I.e., the domain of the logarithm (which is the range of the exponential) is (0, ).
50 Properties of the logarithmic function Let x and y be real numbers, and assume b > 0 and b 1. Equality rule: log b x = log b y if and only if x = y Inequality rules: Product rule: Quotient rule: Power rule: Inversion rules: If x > y and b > 1, then log b x > log b y If x > y and 0 < b < 1, then log b x < log b y log b (xy) = log b x + log b y log b ( x y ) = log b x log b y log b x p = plog b x for any real number p b log b x = x and log b b x = x Special values: log b b = 1 and log b 1 = 0
51 y = log 2 (x)
52 Examples: solve for x log x 16 = 2 log 3 x + log 3 (2x + 1) = 1
53 Natural exponential and natural logarithm ( e = lim ) n n n e Notation: exp(x) = e x is the natural exponential Natural Logarithm is the log base e, log e x, and is often written lnx Common Logarithm is the log base 10, log 10 x, and is written logx Beware: the notation logx is often used to represent whichever base is the standard base in a particular eld (or a particular course).
54 But lnx always means the Natural Logarithm. In this class, logx or log 10 x will always mean the common logarithm and lnx or log e x will mean the natural logarithm. For any other base we write log b x.
55 Basic properties of the natural logarithm: (logarithm base e) ln1 = 0 lne = log e e = 1 e lnx = x for all x > 0 lne y = y for all y b y = e ylnb for any b > 0 (b 1)
56 Theorem. (Change of base theorem) for any b > 0 (b 1). log b x = lnx lnb Important, for example, for taking logarithms on a calculator or in many software packages, which often only do common and natural logarithms.
57 Example: Find N such that e N = 10 2x :
58 Example: an object moves along a straight line such that after t seconds, its velocity is given by v(t) = 10log 5 t + 3log 2 t in ft/sec. How long will it take for the velocity to reach 20 ft/sec?
59 What is so natural about the natural log? Many important growth (and decay) processes are described in terms of natural exponentials and logarithms. For example, Can be used to describe some types of biological colony growth e.g., exponential growth of E. Coli bacteria Describes continuous compound interest (see examples in 2.4) Newton's law of cooling (see problem 69 in 2.4) Many other applications such as disease propagation, radioactive decay...
60 Example: Exponential growth The population of a particular bacterial colony at time t minutes is P(t): P(t) = P 0 e kt where P 0 is the initial population and k is a positive constant. If the colony begins with 5000 individuals and has a population of 7000 after 20 minutes, what is the constant k, and what will the population be after 30 minutes?
61 Example: continuous compounding interest If D dollars are compounded n times per year at an annual interest rate r, then the Future Value after t years is ( A(t) = D 1 + r ) nt n If the compounding interest is continuous, the Future Value is A(t) = De rt
December Exam Summary
 December Exam Summary 1 Lines and Distances 1.1 List of Concepts Distance between two numbers on the real number line or on the Cartesian Plane. Increments. If A = (a 1, a 2 ) and B = (b 1, b 2 ), then
December Exam Summary 1 Lines and Distances 1.1 List of Concepts Distance between two numbers on the real number line or on the Cartesian Plane. Increments. If A = (a 1, a 2 ) and B = (b 1, b 2 ), then
Calculus I. George Voutsadakis 1. LSSU Math 151. Lake Superior State University. 1 Mathematics and Computer Science
 Calculus I George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 151 George Voutsadakis (LSSU) Calculus I November 2014 1 / 67 Outline 1 Limits Limits, Rates
Calculus I George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 151 George Voutsadakis (LSSU) Calculus I November 2014 1 / 67 Outline 1 Limits Limits, Rates
Calculus I Exam 1 Review Fall 2016
 Problem 1: Decide whether the following statements are true or false: (a) If f, g are differentiable, then d d x (f g) = f g. (b) If a function is continuous, then it is differentiable. (c) If a function
Problem 1: Decide whether the following statements are true or false: (a) If f, g are differentiable, then d d x (f g) = f g. (b) If a function is continuous, then it is differentiable. (c) If a function
Topics from Algebra and Pre-Calculus. (Key contains solved problems)
 Topics from Algebra and Pre-Calculus (Key contains solved problems) Note: The purpose of this packet is to give you a review of basic skills. You are asked not to use the calculator, except on p. (8) and
Topics from Algebra and Pre-Calculus (Key contains solved problems) Note: The purpose of this packet is to give you a review of basic skills. You are asked not to use the calculator, except on p. (8) and
Section 1.4 Tangents and Velocity
 Math 132 Tangents and Velocity Section 1.4 Section 1.4 Tangents and Velocity Tangent Lines A tangent line to a curve is a line that just touches the curve. In terms of a circle, the definition is very
Math 132 Tangents and Velocity Section 1.4 Section 1.4 Tangents and Velocity Tangent Lines A tangent line to a curve is a line that just touches the curve. In terms of a circle, the definition is very
Transformations of Functions and Exponential Functions January 24, / 35
 Exponential Functions January 24, 2017 Exponential Functions January 24, 2017 1 / 35 Review of Section 1.2 Reminder: Week-in-Review, Help Sessions, Oce Hours Mathematical Models Linear Regression Function
Exponential Functions January 24, 2017 Exponential Functions January 24, 2017 1 / 35 Review of Section 1.2 Reminder: Week-in-Review, Help Sessions, Oce Hours Mathematical Models Linear Regression Function
7.1 Exponential Functions
 7.1 Exponential Functions 1. What is 16 3/2? Definition of Exponential Functions Question. What is 2 2? Theorem. To evaluate a b, when b is irrational (so b is not a fraction of integers), we approximate
7.1 Exponential Functions 1. What is 16 3/2? Definition of Exponential Functions Question. What is 2 2? Theorem. To evaluate a b, when b is irrational (so b is not a fraction of integers), we approximate
DRAFT - Math 101 Lecture Note - Dr. Said Algarni
 2 Limits 2.1 The Tangent Problems The word tangent is derived from the Latin word tangens, which means touching. A tangent line to a curve is a line that touches the curve and a secant line is a line that
2 Limits 2.1 The Tangent Problems The word tangent is derived from the Latin word tangens, which means touching. A tangent line to a curve is a line that touches the curve and a secant line is a line that
Calculus I. 1. Limits and Continuity
 2301107 Calculus I 1. Limits and Continuity Outline 1.1. Limits 1.1.1 Motivation:Tangent 1.1.2 Limit of a function 1.1.3 Limit laws 1.1.4 Mathematical definition of a it 1.1.5 Infinite it 1.1. Continuity
2301107 Calculus I 1. Limits and Continuity Outline 1.1. Limits 1.1.1 Motivation:Tangent 1.1.2 Limit of a function 1.1.3 Limit laws 1.1.4 Mathematical definition of a it 1.1.5 Infinite it 1.1. Continuity
1 Functions, Graphs and Limits
 1 Functions, Graphs and Limits 1.1 The Cartesian Plane In this course we will be dealing a lot with the Cartesian plane (also called the xy-plane), so this section should serve as a review of it and its
1 Functions, Graphs and Limits 1.1 The Cartesian Plane In this course we will be dealing a lot with the Cartesian plane (also called the xy-plane), so this section should serve as a review of it and its
ter. on Can we get a still better result? Yes, by making the rectangles still smaller. As we make the rectangles smaller and smaller, the
 Area and Tangent Problem Calculus is motivated by two main problems. The first is the area problem. It is a well known result that the area of a rectangle with length l and width w is given by A = wl.
Area and Tangent Problem Calculus is motivated by two main problems. The first is the area problem. It is a well known result that the area of a rectangle with length l and width w is given by A = wl.
UNIT 3: DERIVATIVES STUDY GUIDE
 Calculus I UNIT 3: Derivatives REVIEW Name: Date: UNIT 3: DERIVATIVES STUDY GUIDE Section 1: Section 2: Limit Definition (Derivative as the Slope of the Tangent Line) Calculating Rates of Change (Average
Calculus I UNIT 3: Derivatives REVIEW Name: Date: UNIT 3: DERIVATIVES STUDY GUIDE Section 1: Section 2: Limit Definition (Derivative as the Slope of the Tangent Line) Calculating Rates of Change (Average
MATH 151 Engineering Mathematics I
 MATH 151 Engineering Mathematics I Fall 2018, WEEK 3 JoungDong Kim Week 3 Section 2.3, 2.5, 2.6, Calculating Limits Using the Limit Laws, Continuity, Limits at Infinity; Horizontal Asymptotes. Section
MATH 151 Engineering Mathematics I Fall 2018, WEEK 3 JoungDong Kim Week 3 Section 2.3, 2.5, 2.6, Calculating Limits Using the Limit Laws, Continuity, Limits at Infinity; Horizontal Asymptotes. Section
Calculus. Weijiu Liu. Department of Mathematics University of Central Arkansas 201 Donaghey Avenue, Conway, AR 72035, USA
 Calculus Weijiu Liu Department of Mathematics University of Central Arkansas 201 Donaghey Avenue, Conway, AR 72035, USA 1 Opening Welcome to your Calculus I class! My name is Weijiu Liu. I will guide you
Calculus Weijiu Liu Department of Mathematics University of Central Arkansas 201 Donaghey Avenue, Conway, AR 72035, USA 1 Opening Welcome to your Calculus I class! My name is Weijiu Liu. I will guide you
function independent dependent domain range graph of the function The Vertical Line Test
 Functions A quantity y is a function of another quantity x if there is some rule (an algebraic equation, a graph, a table, or as an English description) by which a unique value is assigned to y by a corresponding
Functions A quantity y is a function of another quantity x if there is some rule (an algebraic equation, a graph, a table, or as an English description) by which a unique value is assigned to y by a corresponding
1.5 Inverse Trigonometric Functions
 1.5 Inverse Trigonometric Functions Remember that only one-to-one functions have inverses. So, in order to find the inverse functions for sine, cosine, and tangent, we must restrict their domains to intervals
1.5 Inverse Trigonometric Functions Remember that only one-to-one functions have inverses. So, in order to find the inverse functions for sine, cosine, and tangent, we must restrict their domains to intervals
Math 261 Calculus I. Test 1 Study Guide. Name. Decide whether the limit exists. If it exists, find its value. 1) lim x 1. f(x) 2) lim x -1/2 f(x)
 Math 261 Calculus I Test 1 Study Guide Name Decide whether the it exists. If it exists, find its value. 1) x 1 f(x) 2) x -1/2 f(x) Complete the table and use the result to find the indicated it. 3) If
Math 261 Calculus I Test 1 Study Guide Name Decide whether the it exists. If it exists, find its value. 1) x 1 f(x) 2) x -1/2 f(x) Complete the table and use the result to find the indicated it. 3) If
2.1 Limits, Rates of Change and Slopes of Tangent Lines
 2.1 Limits, Rates of Change and Slopes of Tangent Lines (1) Average rate of change of y f x over an interval x 0,x 1 : f x 1 f x 0 x 1 x 0 Instantaneous rate of change of f x at x x 0 : f x lim 1 f x 0
2.1 Limits, Rates of Change and Slopes of Tangent Lines (1) Average rate of change of y f x over an interval x 0,x 1 : f x 1 f x 0 x 1 x 0 Instantaneous rate of change of f x at x x 0 : f x lim 1 f x 0
2.6 Logarithmic Functions. Inverse Functions. Question: What is the relationship between f(x) = x 2 and g(x) = x?
 Inverse Functions Question: What is the relationship between f(x) = x 3 and g(x) = 3 x? Question: What is the relationship between f(x) = x 2 and g(x) = x? Definition (One-to-One Function) A function f
Inverse Functions Question: What is the relationship between f(x) = x 3 and g(x) = 3 x? Question: What is the relationship between f(x) = x 2 and g(x) = x? Definition (One-to-One Function) A function f
Limits and Continuity
 Limits and Continuity MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After this lesson we will be able to: Determine the left-hand and right-hand limits
Limits and Continuity MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After this lesson we will be able to: Determine the left-hand and right-hand limits
The function graphed below is continuous everywhere. The function graphed below is NOT continuous everywhere, it is discontinuous at x 2 and
 Section 1.4 Continuity A function is a continuous at a point if its graph has no gaps, holes, breaks or jumps at that point. If a function is not continuous at a point, then we say it is discontinuous
Section 1.4 Continuity A function is a continuous at a point if its graph has no gaps, holes, breaks or jumps at that point. If a function is not continuous at a point, then we say it is discontinuous
Chapter 1: Limits and Continuity
 Chapter 1: Limits and Continuity Winter 2015 Department of Mathematics Hong Kong Baptist University 1/69 1.1 Examples where limits arise Calculus has two basic procedures: differentiation and integration.
Chapter 1: Limits and Continuity Winter 2015 Department of Mathematics Hong Kong Baptist University 1/69 1.1 Examples where limits arise Calculus has two basic procedures: differentiation and integration.
MAC Module 8. Exponential and Logarithmic Functions I. Learning Objectives. - Exponential Functions - Logarithmic Functions
 MAC 1105 Module 8 Exponential and Logarithmic Functions I Learning Objectives Upon completing this module, you should be able to: 1. Distinguish between linear and exponential growth. 2. Model data with
MAC 1105 Module 8 Exponential and Logarithmic Functions I Learning Objectives Upon completing this module, you should be able to: 1. Distinguish between linear and exponential growth. 2. Model data with
MAC Module 8 Exponential and Logarithmic Functions I. Rev.S08
 MAC 1105 Module 8 Exponential and Logarithmic Functions I Learning Objectives Upon completing this module, you should be able to: 1. Distinguish between linear and exponential growth. 2. Model data with
MAC 1105 Module 8 Exponential and Logarithmic Functions I Learning Objectives Upon completing this module, you should be able to: 1. Distinguish between linear and exponential growth. 2. Model data with
Infinite series, improper integrals, and Taylor series
 Chapter 2 Infinite series, improper integrals, and Taylor series 2. Introduction to series In studying calculus, we have explored a variety of functions. Among the most basic are polynomials, i.e. functions
Chapter 2 Infinite series, improper integrals, and Taylor series 2. Introduction to series In studying calculus, we have explored a variety of functions. Among the most basic are polynomials, i.e. functions
The main way we switch from pre-calc. to calc. is the use of a limit process. Calculus is a "limit machine".
 A Preview of Calculus Limits and Their Properties Objectives: Understand what calculus is and how it compares with precalculus. Understand that the tangent line problem is basic to calculus. Understand
A Preview of Calculus Limits and Their Properties Objectives: Understand what calculus is and how it compares with precalculus. Understand that the tangent line problem is basic to calculus. Understand
7.1. Calculus of inverse functions. Text Section 7.1 Exercise:
 Contents 7. Inverse functions 1 7.1. Calculus of inverse functions 2 7.2. Derivatives of exponential function 4 7.3. Logarithmic function 6 7.4. Derivatives of logarithmic functions 7 7.5. Exponential
Contents 7. Inverse functions 1 7.1. Calculus of inverse functions 2 7.2. Derivatives of exponential function 4 7.3. Logarithmic function 6 7.4. Derivatives of logarithmic functions 7 7.5. Exponential
MATH 1902: Mathematics for the Physical Sciences I
 MATH 1902: Mathematics for the Physical Sciences I Dr Dana Mackey School of Mathematical Sciences Room A305 A Email: Dana.Mackey@dit.ie Dana Mackey (DIT) MATH 1902 1 / 46 Module content/assessment Functions
MATH 1902: Mathematics for the Physical Sciences I Dr Dana Mackey School of Mathematical Sciences Room A305 A Email: Dana.Mackey@dit.ie Dana Mackey (DIT) MATH 1902 1 / 46 Module content/assessment Functions
Chapter 2: Functions, Limits and Continuity
 Chapter 2: Functions, Limits and Continuity Functions Limits Continuity Chapter 2: Functions, Limits and Continuity 1 Functions Functions are the major tools for describing the real world in mathematical
Chapter 2: Functions, Limits and Continuity Functions Limits Continuity Chapter 2: Functions, Limits and Continuity 1 Functions Functions are the major tools for describing the real world in mathematical
MATH 409 Advanced Calculus I Lecture 11: More on continuous functions.
 MATH 409 Advanced Calculus I Lecture 11: More on continuous functions. Continuity Definition. Given a set E R, a function f : E R, and a point c E, the function f is continuous at c if for any ε > 0 there
MATH 409 Advanced Calculus I Lecture 11: More on continuous functions. Continuity Definition. Given a set E R, a function f : E R, and a point c E, the function f is continuous at c if for any ε > 0 there
2.1 The derivative. Rates of change. m sec = y f (a + h) f (a)
 2.1 The derivative Rates of change 1 The slope of a secant line is m sec = y f (b) f (a) = x b a and represents the average rate of change over [a, b]. Letting b = a + h, we can express the slope of the
2.1 The derivative Rates of change 1 The slope of a secant line is m sec = y f (b) f (a) = x b a and represents the average rate of change over [a, b]. Letting b = a + h, we can express the slope of the
Continuity, Intermediate Value Theorem (2.4)
 Continuity, Intermediate Value Theorem (2.4) Xiannan Li Kansas State University January 29th, 2017 Intuitive Definition: A function f(x) is continuous at a if you can draw the graph of y = f(x) without
Continuity, Intermediate Value Theorem (2.4) Xiannan Li Kansas State University January 29th, 2017 Intuitive Definition: A function f(x) is continuous at a if you can draw the graph of y = f(x) without
10 Exponential and Logarithmic Functions
 10 Exponential and Logarithmic Functions Concepts: Rules of Exponents Exponential Functions Power Functions vs. Exponential Functions The Definition of an Exponential Function Graphing Exponential Functions
10 Exponential and Logarithmic Functions Concepts: Rules of Exponents Exponential Functions Power Functions vs. Exponential Functions The Definition of an Exponential Function Graphing Exponential Functions
Limits of Functions (a, L)
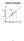 Limits of Functions f(x) (a, L) L f(x) x a x x 20 Informal Definition: If the values of can be made as close to as we like by taking values of sufficiently close to [but not equal to ] then we write or
Limits of Functions f(x) (a, L) L f(x) x a x x 20 Informal Definition: If the values of can be made as close to as we like by taking values of sufficiently close to [but not equal to ] then we write or
2.2 The Limit of a Function
 2.2 The Limit of a Function Introductory Example: Consider the function f(x) = x is near 0. x f(x) x f(x) 1 3.7320508 1 4.236068 0.5 3.8708287 0.5 4.1213203 0.1 3.9748418 0.1 4.0248457 0.05 3.9874607 0.05
2.2 The Limit of a Function Introductory Example: Consider the function f(x) = x is near 0. x f(x) x f(x) 1 3.7320508 1 4.236068 0.5 3.8708287 0.5 4.1213203 0.1 3.9748418 0.1 4.0248457 0.05 3.9874607 0.05
1. Use the properties of exponents to simplify the following expression, writing your answer with only positive exponents.
 Math120 - Precalculus. Final Review. Fall, 2011 Prepared by Dr. P. Babaali 1 Algebra 1. Use the properties of exponents to simplify the following expression, writing your answer with only positive exponents.
Math120 - Precalculus. Final Review. Fall, 2011 Prepared by Dr. P. Babaali 1 Algebra 1. Use the properties of exponents to simplify the following expression, writing your answer with only positive exponents.
Week 1: need to know. November 14, / 20
 Week 1: need to know How to find domains and ranges, operations on functions (addition, subtraction, multiplication, division, composition), behaviors of functions (even/odd/ increasing/decreasing), library
Week 1: need to know How to find domains and ranges, operations on functions (addition, subtraction, multiplication, division, composition), behaviors of functions (even/odd/ increasing/decreasing), library
The final is cumulative, but with more emphasis on chapters 3 and 4. There will be two parts.
 Math 141 Review for Final The final is cumulative, but with more emphasis on chapters 3 and 4. There will be two parts. Part 1 (no calculator) graphing (polynomial, rational, linear, exponential, and logarithmic
Math 141 Review for Final The final is cumulative, but with more emphasis on chapters 3 and 4. There will be two parts. Part 1 (no calculator) graphing (polynomial, rational, linear, exponential, and logarithmic
Advanced Mathematics Unit 2 Limits and Continuity
 Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics Unit 2 Limits and Continuity
 Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Calculus. Central role in much of modern science Physics, especially kinematics and electrodynamics Economics, engineering, medicine, chemistry, etc.
 Calculus Calculus - the study of change, as related to functions Formally co-developed around the 1660 s by Newton and Leibniz Two main branches - differential and integral Central role in much of modern
Calculus Calculus - the study of change, as related to functions Formally co-developed around the 1660 s by Newton and Leibniz Two main branches - differential and integral Central role in much of modern
AP Calculus Summer Prep
 AP Calculus Summer Prep Topics from Algebra and Pre-Calculus (Solutions are on the Answer Key on the Last Pages) The purpose of this packet is to give you a review of basic skills. You are asked to have
AP Calculus Summer Prep Topics from Algebra and Pre-Calculus (Solutions are on the Answer Key on the Last Pages) The purpose of this packet is to give you a review of basic skills. You are asked to have
3.1 Day 1: The Derivative of a Function
 A P Calculus 3.1 Day 1: The Derivative of a Function I CAN DEFINE A DERIVATIVE AND UNDERSTAND ITS NOTATION. Last chapter we learned to find the slope of a tangent line to a point on a graph by using a
A P Calculus 3.1 Day 1: The Derivative of a Function I CAN DEFINE A DERIVATIVE AND UNDERSTAND ITS NOTATION. Last chapter we learned to find the slope of a tangent line to a point on a graph by using a
College Algebra Notes
 Metropolitan Community College Contents Introduction 2 Unit 1 3 Rational Expressions........................................... 3 Quadratic Equations........................................... 9 Polynomial,
Metropolitan Community College Contents Introduction 2 Unit 1 3 Rational Expressions........................................... 3 Quadratic Equations........................................... 9 Polynomial,
, find the value(s) of a and b which make f differentiable at bx 2 + x if x 2 x = 2 or explain why no such values exist.
 Math 171 Exam II Summary Sheet and Sample Stuff (NOTE: The questions posed here are not necessarily a guarantee of the type of questions which will be on Exam II. This is a sampling of questions I have
Math 171 Exam II Summary Sheet and Sample Stuff (NOTE: The questions posed here are not necessarily a guarantee of the type of questions which will be on Exam II. This is a sampling of questions I have
Continuity and One-Sided Limits. By Tuesday J. Johnson
 Continuity and One-Sided Limits By Tuesday J. Johnson Suggested Review Topics Algebra skills reviews suggested: Evaluating functions Rationalizing numerators and/or denominators Trigonometric skills reviews
Continuity and One-Sided Limits By Tuesday J. Johnson Suggested Review Topics Algebra skills reviews suggested: Evaluating functions Rationalizing numerators and/or denominators Trigonometric skills reviews
Welcome to AP Calculus!!!
 Welcome to AP Calculus!!! In preparation for next year, you need to complete this summer packet. This packet reviews & expands upon the concepts you studied in Algebra II and Pre-calculus. Make sure you
Welcome to AP Calculus!!! In preparation for next year, you need to complete this summer packet. This packet reviews & expands upon the concepts you studied in Algebra II and Pre-calculus. Make sure you
This Week. Professor Christopher Hoffman Math 124
 This Week Sections 2.1-2.3,2.5,2.6 First homework due Tuesday night at 11:30 p.m. Average and instantaneous velocity worksheet Tuesday available at http://www.math.washington.edu/ m124/ (under week 2)
This Week Sections 2.1-2.3,2.5,2.6 First homework due Tuesday night at 11:30 p.m. Average and instantaneous velocity worksheet Tuesday available at http://www.math.washington.edu/ m124/ (under week 2)
Example. Determine the inverse of the given function (if it exists). f(x) = 3
 Example. Determine the inverse of the given function (if it exists). f(x) = g(x) = p x + x We know want to look at two di erent types of functions, called logarithmic functions and exponential functions.
Example. Determine the inverse of the given function (if it exists). f(x) = g(x) = p x + x We know want to look at two di erent types of functions, called logarithmic functions and exponential functions.
Calculus (Math 1A) Lecture 4
 Calculus (Math 1A) Lecture 4 Vivek Shende August 31, 2017 Hello and welcome to class! Last time We discussed shifting, stretching, and composition. Today We finish discussing composition, then discuss
Calculus (Math 1A) Lecture 4 Vivek Shende August 31, 2017 Hello and welcome to class! Last time We discussed shifting, stretching, and composition. Today We finish discussing composition, then discuss
MAT137 Calculus! Lecture 5
 MAT137 Calculus! Lecture 5 Today: 2.5 The Pinching Theorem; 2.5 Trigonometric Limits. 2.6 Two Basic Theorems. 3.1 The Derivative Next: 3.2-3.6 DIfferentiation Rules Deadline to notify us if you have a
MAT137 Calculus! Lecture 5 Today: 2.5 The Pinching Theorem; 2.5 Trigonometric Limits. 2.6 Two Basic Theorems. 3.1 The Derivative Next: 3.2-3.6 DIfferentiation Rules Deadline to notify us if you have a
Composition of Functions
 Math 120 Intermediate Algebra Sec 9.1: Composite and Inverse Functions Composition of Functions The composite function f g, the composition of f and g, is defined as (f g)(x) = f(g(x)). Recall that a function
Math 120 Intermediate Algebra Sec 9.1: Composite and Inverse Functions Composition of Functions The composite function f g, the composition of f and g, is defined as (f g)(x) = f(g(x)). Recall that a function
Internet Mat117 Formulas and Concepts. d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. ( x 1 + x 2 2., y 1 + y 2. (x h) 2 + (y k) 2 = r 2. m = y 2 y 1 x 2 x 1
 Internet Mat117 Formulas and Concepts 1. The distance between the points A(x 1, y 1 ) and B(x 2, y 2 ) in the plane is d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. 2. The midpoint of the line segment from A(x
Internet Mat117 Formulas and Concepts 1. The distance between the points A(x 1, y 1 ) and B(x 2, y 2 ) in the plane is d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. 2. The midpoint of the line segment from A(x
Calculus (Math 1A) Lecture 4
 Calculus (Math 1A) Lecture 4 Vivek Shende August 30, 2017 Hello and welcome to class! Hello and welcome to class! Last time Hello and welcome to class! Last time We discussed shifting, stretching, and
Calculus (Math 1A) Lecture 4 Vivek Shende August 30, 2017 Hello and welcome to class! Hello and welcome to class! Last time Hello and welcome to class! Last time We discussed shifting, stretching, and
Topic Subtopics Essential Knowledge (EK)
 Unit/ Unit 1 Limits [BEAN] 1.1 Limits Graphically Define a limit (y value a function approaches) One sided limits. Easy if it s continuous. Tricky if there s a discontinuity. EK 1.1A1: Given a function,
Unit/ Unit 1 Limits [BEAN] 1.1 Limits Graphically Define a limit (y value a function approaches) One sided limits. Easy if it s continuous. Tricky if there s a discontinuity. EK 1.1A1: Given a function,
3 Algebraic Methods. we can differentiate both sides implicitly to obtain a differential equation involving x and y:
 3 Algebraic Methods b The first appearance of the equation E Mc 2 in Einstein s handwritten notes. So far, the only general class of differential equations that we know how to solve are directly integrable
3 Algebraic Methods b The first appearance of the equation E Mc 2 in Einstein s handwritten notes. So far, the only general class of differential equations that we know how to solve are directly integrable
Continuity. To handle complicated functions, particularly those for which we have a reasonable formula or formulas, we need a more precise definition.
 Continuity Intuitively, a function is continuous if its graph can be traced on paper in one motion without lifting the pencil from the paper. Thus the graph has no tears or holes. To handle complicated
Continuity Intuitively, a function is continuous if its graph can be traced on paper in one motion without lifting the pencil from the paper. Thus the graph has no tears or holes. To handle complicated
Chapter 6: Exponential and Logarithmic Functions
 Section 6.1: Algebra and Composition of Functions #1-9: Let f(x) = 2x + 3 and g(x) = 3 x. Find each function. 1) (f + g)(x) 2) (g f)(x) 3) (f/g)(x) 4) ( )( ) 5) ( g/f)(x) 6) ( )( ) 7) ( )( ) 8) (g+f)(x)
Section 6.1: Algebra and Composition of Functions #1-9: Let f(x) = 2x + 3 and g(x) = 3 x. Find each function. 1) (f + g)(x) 2) (g f)(x) 3) (f/g)(x) 4) ( )( ) 5) ( g/f)(x) 6) ( )( ) 7) ( )( ) 8) (g+f)(x)
We are going to discuss what it means for a sequence to converge in three stages: First, we define what it means for a sequence to converge to zero
 Chapter Limits of Sequences Calculus Student: lim s n = 0 means the s n are getting closer and closer to zero but never gets there. Instructor: ARGHHHHH! Exercise. Think of a better response for the instructor.
Chapter Limits of Sequences Calculus Student: lim s n = 0 means the s n are getting closer and closer to zero but never gets there. Instructor: ARGHHHHH! Exercise. Think of a better response for the instructor.
Objectives List. Important Students should expect test questions that require a synthesis of these objectives.
 MATH 1040 - of One Variable, Part I Textbook 1: : Algebra and Trigonometry for ET. 4 th edition by Brent, Muller Textbook 2:. Early Transcendentals, 3 rd edition by Briggs, Cochran, Gillett, Schulz s List
MATH 1040 - of One Variable, Part I Textbook 1: : Algebra and Trigonometry for ET. 4 th edition by Brent, Muller Textbook 2:. Early Transcendentals, 3 rd edition by Briggs, Cochran, Gillett, Schulz s List
Please print the following information in case your scan sheet is misplaced:
 MATH 1100 Common Final Exam FALL 010 December 10, 010 Please print the following information in case your scan sheet is misplaced: Name: Instructor: Student ID: Section/Time: The exam consists of 40 multiple
MATH 1100 Common Final Exam FALL 010 December 10, 010 Please print the following information in case your scan sheet is misplaced: Name: Instructor: Student ID: Section/Time: The exam consists of 40 multiple
1 + lim. n n+1. f(x) = x + 1, x 1. and we check that f is increasing, instead. Using the quotient rule, we easily find that. 1 (x + 1) 1 x (x + 1) 2 =
 Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
8. Limit Laws. lim(f g)(x) = lim f(x) lim g(x), (x) = lim x a f(x) g lim x a g(x)
 8. Limit Laws 8.1. Basic Limit Laws. If f and g are two functions and we know the it of each of them at a given point a, then we can easily compute the it at a of their sum, difference, product, constant
8. Limit Laws 8.1. Basic Limit Laws. If f and g are two functions and we know the it of each of them at a given point a, then we can easily compute the it at a of their sum, difference, product, constant
TEXT AND OTHER MATERIALS:
 1. TEXT AND OTHER MATERIALS: Check Learning Resources in shared class files Calculus Wiki-book: https://en.wikibooks.org/wiki/calculus (Main Reference e-book) Paul s Online Math Notes: http://tutorial.math.lamar.edu
1. TEXT AND OTHER MATERIALS: Check Learning Resources in shared class files Calculus Wiki-book: https://en.wikibooks.org/wiki/calculus (Main Reference e-book) Paul s Online Math Notes: http://tutorial.math.lamar.edu
Sec 4.1 Limits, Informally. When we calculated f (x), we first started with the difference quotient. f(x + h) f(x) h
 1 Sec 4.1 Limits, Informally When we calculated f (x), we first started with the difference quotient f(x + h) f(x) h and made h small. In other words, f (x) is the number f(x+h) f(x) approaches as h gets
1 Sec 4.1 Limits, Informally When we calculated f (x), we first started with the difference quotient f(x + h) f(x) h and made h small. In other words, f (x) is the number f(x+h) f(x) approaches as h gets
Chapter 1 Functions and Limits
 Contents Chapter 1 Functions and Limits Motivation to Chapter 1 2 4 Tangent and Velocity Problems 3 4.1 VIDEO - Secant Lines, Average Rate of Change, and Applications......................... 3 4.2 VIDEO
Contents Chapter 1 Functions and Limits Motivation to Chapter 1 2 4 Tangent and Velocity Problems 3 4.1 VIDEO - Secant Lines, Average Rate of Change, and Applications......................... 3 4.2 VIDEO
MATH 3A FINAL REVIEW
 MATH 3A FINAL REVIEW Guidelines to taking the nal exam You must show your work very clearly You will receive no credit if we do not understand what you are doing 2 You must cross out any incorrect work
MATH 3A FINAL REVIEW Guidelines to taking the nal exam You must show your work very clearly You will receive no credit if we do not understand what you are doing 2 You must cross out any incorrect work
Rational Exponents. Polynomial function of degree n: with leading coefficient,, with maximum number of turning points is given by (n-1)
 Useful Fact Sheet Final Exam Interval, Set Builder Notation (a,b) = {x a
Useful Fact Sheet Final Exam Interval, Set Builder Notation (a,b) = {x a
Math 106 Calculus 1 Topics for first exam
 Chapter 2: Limits and Continuity Rates of change and its: Math 06 Calculus Topics for first exam Limit of a function f at a point a = the value the function should take at the point = the value that the
Chapter 2: Limits and Continuity Rates of change and its: Math 06 Calculus Topics for first exam Limit of a function f at a point a = the value the function should take at the point = the value that the
Math 0031, Final Exam Study Guide December 7, 2015
 Math 0031, Final Exam Study Guide December 7, 2015 Chapter 1. Equations of a line: (a) Standard Form: A y + B x = C. (b) Point-slope Form: y y 0 = m (x x 0 ), where m is the slope and (x 0, y 0 ) is a
Math 0031, Final Exam Study Guide December 7, 2015 Chapter 1. Equations of a line: (a) Standard Form: A y + B x = C. (b) Point-slope Form: y y 0 = m (x x 0 ), where m is the slope and (x 0, y 0 ) is a
MATH1013 Calculus I. Revision 1
 MATH1013 Calculus I Revision 1 Edmund Y. M. Chiang Department of Mathematics Hong Kong University of Science & Technology November 27, 2014 2013 1 Based on Briggs, Cochran and Gillett: Calculus for Scientists
MATH1013 Calculus I Revision 1 Edmund Y. M. Chiang Department of Mathematics Hong Kong University of Science & Technology November 27, 2014 2013 1 Based on Briggs, Cochran and Gillett: Calculus for Scientists
MATH 100 and MATH 180 Learning Objectives Session 2010W Term 1 (Sep Dec 2010)
 Course Prerequisites MATH 100 and MATH 180 Learning Objectives Session 2010W Term 1 (Sep Dec 2010) As a prerequisite to this course, students are required to have a reasonable mastery of precalculus mathematics
Course Prerequisites MATH 100 and MATH 180 Learning Objectives Session 2010W Term 1 (Sep Dec 2010) As a prerequisite to this course, students are required to have a reasonable mastery of precalculus mathematics
Teacher: Mr. Chafayay. Name: Class & Block : Date: ID: A. 3 Which function is represented by the graph?
 Teacher: Mr hafayay Name: lass & lock : ate: I: Midterm Exam Math III H Multiple hoice Identify the choice that best completes the statement or answers the question Which function is represented by the
Teacher: Mr hafayay Name: lass & lock : ate: I: Midterm Exam Math III H Multiple hoice Identify the choice that best completes the statement or answers the question Which function is represented by the
Chapter 2. Limits and Continuity. 2.1 Rates of change and Tangents to Curves. The average Rate of change of y = f(x) with respect to x over the
 Chapter 2 Limits and Continuity 2.1 Rates of change and Tangents to Curves Definition 2.1.1 : interval [x 1, x 2 ] is The average Rate of change of y = f(x) with respect to x over the y x = f(x 2) f(x
Chapter 2 Limits and Continuity 2.1 Rates of change and Tangents to Curves Definition 2.1.1 : interval [x 1, x 2 ] is The average Rate of change of y = f(x) with respect to x over the y x = f(x 2) f(x
Exponential and Logarithmic Functions
 Exponential and Logarithmic Functions Learning Targets 1. I can evaluate, analyze, and graph exponential functions. 2. I can solve problems involving exponential growth & decay. 3. I can evaluate expressions
Exponential and Logarithmic Functions Learning Targets 1. I can evaluate, analyze, and graph exponential functions. 2. I can solve problems involving exponential growth & decay. 3. I can evaluate expressions
Review questions for Math 111 final. Please SHOW your WORK to receive full credit Final Test is based on 150 points
 Please SHOW your WORK to receive full credit Final Test is based on 150 points 1. True or False questions (17 pts) a. Common Logarithmic functions cross the y axis at (0,1) b. A square matrix has as many
Please SHOW your WORK to receive full credit Final Test is based on 150 points 1. True or False questions (17 pts) a. Common Logarithmic functions cross the y axis at (0,1) b. A square matrix has as many
REQUIRED MATHEMATICAL SKILLS FOR ENTERING CADETS
 REQUIRED MATHEMATICAL SKILLS FOR ENTERING CADETS The Department of Applied Mathematics administers a Math Placement test to assess fundamental skills in mathematics that are necessary to begin the study
REQUIRED MATHEMATICAL SKILLS FOR ENTERING CADETS The Department of Applied Mathematics administers a Math Placement test to assess fundamental skills in mathematics that are necessary to begin the study
INTERNET MAT 117 Review Problems. (1) Let us consider the circle with equation. (b) Find the center and the radius of the circle given above.
 INTERNET MAT 117 Review Problems (1) Let us consider the circle with equation x 2 + y 2 + 2x + 3y + 3 4 = 0. (a) Find the standard form of the equation of the circle given above. (b) Find the center and
INTERNET MAT 117 Review Problems (1) Let us consider the circle with equation x 2 + y 2 + 2x + 3y + 3 4 = 0. (a) Find the standard form of the equation of the circle given above. (b) Find the center and
2.1 Quadratic Functions
 Date:.1 Quadratic Functions Precalculus Notes: Unit Polynomial Functions Objective: The student will sketch the graph of a quadratic equation. The student will write the equation of a quadratic function.
Date:.1 Quadratic Functions Precalculus Notes: Unit Polynomial Functions Objective: The student will sketch the graph of a quadratic equation. The student will write the equation of a quadratic function.
1 Functions and Graphs
 1 Functions and Graphs 1.1 Functions Cartesian Coordinate System A Cartesian or rectangular coordinate system is formed by the intersection of a horizontal real number line, usually called the x axis,
1 Functions and Graphs 1.1 Functions Cartesian Coordinate System A Cartesian or rectangular coordinate system is formed by the intersection of a horizontal real number line, usually called the x axis,
3 Inequalities Absolute Values Inequalities and Intervals... 4
 Contents 1 Real Numbers, Exponents, and Radicals 2 1.1 Rationalizing the Denominator................................... 2 1.2 Factoring Polynomials........................................ 2 1.3 Algebraic
Contents 1 Real Numbers, Exponents, and Radicals 2 1.1 Rationalizing the Denominator................................... 2 1.2 Factoring Polynomials........................................ 2 1.3 Algebraic
HW#1. Unit 4B Logarithmic Functions HW #1. 1) Which of the following is equivalent to y=log7 x? (1) y =x 7 (3) x = 7 y (2) x =y 7 (4) y =x 1/7
 HW#1 Name Unit 4B Logarithmic Functions HW #1 Algebra II Mrs. Dailey 1) Which of the following is equivalent to y=log7 x? (1) y =x 7 (3) x = 7 y (2) x =y 7 (4) y =x 1/7 2) If the graph of y =6 x is reflected
HW#1 Name Unit 4B Logarithmic Functions HW #1 Algebra II Mrs. Dailey 1) Which of the following is equivalent to y=log7 x? (1) y =x 7 (3) x = 7 y (2) x =y 7 (4) y =x 1/7 2) If the graph of y =6 x is reflected
MATH 1040 Objectives List
 MATH 1040 Objectives List Textbook: Calculus, Early Transcendentals, 7th edition, James Stewart Students should expect test questions that require synthesis of these objectives. Unit 1 WebAssign problems
MATH 1040 Objectives List Textbook: Calculus, Early Transcendentals, 7th edition, James Stewart Students should expect test questions that require synthesis of these objectives. Unit 1 WebAssign problems
Review for Cumulative Test 2
 Review for Cumulative Test We will have our second course-wide cumulative test on Tuesday February 9 th or Wednesday February 10 th, covering from the beginning of the course up to section 4.3 in our textbook.
Review for Cumulative Test We will have our second course-wide cumulative test on Tuesday February 9 th or Wednesday February 10 th, covering from the beginning of the course up to section 4.3 in our textbook.
Continuity. MATH 161 Calculus I. J. Robert Buchanan. Fall Department of Mathematics
 Continuity MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Fall 2017 Intuitive Idea A process or an item can be described as continuous if it exists without interruption. The mathematical
Continuity MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Fall 2017 Intuitive Idea A process or an item can be described as continuous if it exists without interruption. The mathematical
Chapter 3: Derivatives
 Name: Date: Period: AP Calc AB Mr. Mellina Chapter 3: Derivatives Sections: v 2.4 Rates of Change & Tangent Lines v 3.1 Derivative of a Function v 3.2 Differentiability v 3.3 Rules for Differentiation
Name: Date: Period: AP Calc AB Mr. Mellina Chapter 3: Derivatives Sections: v 2.4 Rates of Change & Tangent Lines v 3.1 Derivative of a Function v 3.2 Differentiability v 3.3 Rules for Differentiation
Final Exam Review Exercise Set A, Math 1551, Fall 2017
 Final Exam Review Exercise Set A, Math 1551, Fall 2017 This review set gives a list of topics that we explored throughout this course, as well as a few practice problems at the end of the document. A complete
Final Exam Review Exercise Set A, Math 1551, Fall 2017 This review set gives a list of topics that we explored throughout this course, as well as a few practice problems at the end of the document. A complete
Practice Questions for Final Exam - Math 1060Q - Fall 2014
 Practice Questions for Final Exam - Math 1060Q - Fall 01 Before anyone asks, the final exam is cumulative. It will consist of about 50% problems on exponential and logarithmic functions, 5% problems on
Practice Questions for Final Exam - Math 1060Q - Fall 01 Before anyone asks, the final exam is cumulative. It will consist of about 50% problems on exponential and logarithmic functions, 5% problems on
Exponential Growth (Doubling Time)
 Exponential Growth (Doubling Time) 4 Exponential Growth (Doubling Time) Suppose we start with a single bacterium, which divides every hour. After one hour we have 2 bacteria, after two hours we have 2
Exponential Growth (Doubling Time) 4 Exponential Growth (Doubling Time) Suppose we start with a single bacterium, which divides every hour. After one hour we have 2 bacteria, after two hours we have 2
Chapter Product Rule and Quotient Rule for Derivatives
 Chapter 3.3 - Product Rule and Quotient Rule for Derivatives Theorem 3.6: The Product Rule If f(x) and g(x) are differentiable at any x then Example: The Product Rule. Find the derivatives: Example: The
Chapter 3.3 - Product Rule and Quotient Rule for Derivatives Theorem 3.6: The Product Rule If f(x) and g(x) are differentiable at any x then Example: The Product Rule. Find the derivatives: Example: The
Internet Mat117 Formulas and Concepts. d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2., y 1 + y 2. ( x 1 + x 2 2
 Internet Mat117 Formulas and Concepts 1. The distance between the points A(x 1, y 1 ) and B(x 2, y 2 ) in the plane is d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. 2. The midpoint of the line segment from A(x
Internet Mat117 Formulas and Concepts 1. The distance between the points A(x 1, y 1 ) and B(x 2, y 2 ) in the plane is d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. 2. The midpoint of the line segment from A(x
MATH 1910 Limits Numerically and Graphically Introduction to Limits does not exist DNE DOES does not Finding Limits Numerically
 MATH 90 - Limits Numerically and Graphically Introduction to Limits The concept of a limit is our doorway to calculus. This lecture will explain what the limit of a function is and how we can find such
MATH 90 - Limits Numerically and Graphically Introduction to Limits The concept of a limit is our doorway to calculus. This lecture will explain what the limit of a function is and how we can find such
f( x) f( y). Functions which are not one-to-one are often called many-to-one. Take the domain and the range to both be all the real numbers:
 I. UNIVARIATE CALCULUS Given two sets X and Y, a function is a rule that associates each member of X with exactly one member of Y. That is, some x goes in, and some y comes out. These notations are used
I. UNIVARIATE CALCULUS Given two sets X and Y, a function is a rule that associates each member of X with exactly one member of Y. That is, some x goes in, and some y comes out. These notations are used
Preliminaries Lectures. Dr. Abdulla Eid. Department of Mathematics MATHS 101: Calculus I
 Preliminaries 2 1 2 Lectures Department of Mathematics http://www.abdullaeid.net/maths101 MATHS 101: Calculus I (University of Bahrain) Prelim 1 / 35 Pre Calculus MATHS 101: Calculus MATHS 101 is all about
Preliminaries 2 1 2 Lectures Department of Mathematics http://www.abdullaeid.net/maths101 MATHS 101: Calculus I (University of Bahrain) Prelim 1 / 35 Pre Calculus MATHS 101: Calculus MATHS 101 is all about
Part 2 Continuous functions and their properties
 Part 2 Continuous functions and their properties 2.1 Definition Definition A function f is continuous at a R if, and only if, that is lim f (x) = f (a), x a ε > 0, δ > 0, x, x a < δ f (x) f (a) < ε. Notice
Part 2 Continuous functions and their properties 2.1 Definition Definition A function f is continuous at a R if, and only if, that is lim f (x) = f (a), x a ε > 0, δ > 0, x, x a < δ f (x) f (a) < ε. Notice
Chapter 2: Limits & Continuity
 Name: Date: Period: AP Calc AB Mr. Mellina Chapter 2: Limits & Continuity Sections: v 2.1 Rates of Change of Limits v 2.2 Limits Involving Infinity v 2.3 Continuity v 2.4 Rates of Change and Tangent Lines
Name: Date: Period: AP Calc AB Mr. Mellina Chapter 2: Limits & Continuity Sections: v 2.1 Rates of Change of Limits v 2.2 Limits Involving Infinity v 2.3 Continuity v 2.4 Rates of Change and Tangent Lines
Exp, Log, Poly Functions Quarter 3 Review Name
 Exp, Log, Poly Functions Quarter 3 Review Name Textbook problems for practice: p. 285-293; p. 293 #9-14, p. 294-5 #1-34, 49-52, 55,56, 57; p. 297-321 logs; p. 280-1 #11-84 *Blood Alcohol, Bungee-from binder
Exp, Log, Poly Functions Quarter 3 Review Name Textbook problems for practice: p. 285-293; p. 293 #9-14, p. 294-5 #1-34, 49-52, 55,56, 57; p. 297-321 logs; p. 280-1 #11-84 *Blood Alcohol, Bungee-from binder
Solutions to Math 41 First Exam October 15, 2013
 Solutions to Math 41 First Exam October 15, 2013 1. (16 points) Find each of the following its, with justification. If the it does not exist, explain why. If there is an infinite it, then explain whether
Solutions to Math 41 First Exam October 15, 2013 1. (16 points) Find each of the following its, with justification. If the it does not exist, explain why. If there is an infinite it, then explain whether
Chapter 7: Techniques of Integration
 Chapter 7: Techniques of Integration MATH 206-01: Calculus II Department of Mathematics University of Louisville last corrected September 14, 2013 1 / 43 Chapter 7: Techniques of Integration 7.1. Integration
Chapter 7: Techniques of Integration MATH 206-01: Calculus II Department of Mathematics University of Louisville last corrected September 14, 2013 1 / 43 Chapter 7: Techniques of Integration 7.1. Integration
f(x) = d(x) q(x) + r(x).
 Section 5.4: Dividing Polynomials 1. The division algorithm states, given a polynomial dividend, f(x), and non-zero polynomial divisor, d(x), where the degree of d(x) is less than or equal to the degree
Section 5.4: Dividing Polynomials 1. The division algorithm states, given a polynomial dividend, f(x), and non-zero polynomial divisor, d(x), where the degree of d(x) is less than or equal to the degree
