2.2 The Limit of a Function
|
|
|
- Tiffany Chapman
- 6 years ago
- Views:
Transcription
1 2.2 The Limit of a Function Introductory Example: Consider the function f(x) = x is near 0. x f(x) x f(x) x x+4 2. Examine the values of the function when We can see that as the values of x get closer to 0 from both sides, the values of f(x) are getting closer to 4. x This is written mathematically as: = 4 x 0 x+4 2 We write f(x) = L x a read as the it of f(x) as x approaches a is L if we can make the values of f(x) arbitrarily close to L (as close to L as we want) by letting x get closer and closer to a, but not equal to a. 0 Note that f(0) is undefined in the above example since f(0) = = 0 0. When dealing with its, we are examining values as x approaches a, but not equal to a. We ll see later that the value of the function at a may or may not equal the value of the it. For all three figures below: Left-Handed Limit: x a f(x) Right-Handed Limit: x a +f(x) The it exists if and only if the left-handed and right-handed its both exist and are equal. x a f(x) = L if and only if = L and x a f(x) x a +f(x) = L 1
2 1 Infinite Limits: Calculate x 0 x 2 x f(x) x f(x) , , , 000, , 000, , 000, , 000, 000 We can see that as the values of x approach 0 from both sides, that f(x) gets larger and larger without 1 bound. In this case, we say that x 0 x 2 =. 1 Example: Calculate x 0 + x, x x 0 1 1, and x 0 x Definition: The line x = a is a vertical asymptote if the it from the left, right, or both is or. Example: Consider the graph of f below. Find the indicated its. x 4 f(x) x 4 +f(x) f(x) x 4 x 2 f(x) x 2 +f(x) f(x) x f(x) x 1 4 f(x) x 6 2 x 3 +f(x) x 3 f(x) f(x) x f(x) x What are the vertical asymptotes of f(x)? 8 2
3 Asymptotes vs Holes When the it of a function at x = a is of the form nonzero 0, then there is a vertical asymptote at x = a. Why? When the it of a function at x = a is of the form 0 0 we say the it is indeterminate. Two things could be happening. There is either a vertical asymptote or a hole in the graph at x = a. If after using algebra the it simplifies to nonzero 0, then there is a vertical asymptote. If the it simplifies to a number, then there is a hole. Find all vertical asymptotes of the function f(x) = at all such values of x. x 2 x 2 6x+8 and calculate the left and right-hand its Calculate the following its: x 1 x 5 x+5 x 1 x 5 + x+5 x 1 x 5 x+5 x 3 x 3 (x 6)(x 3) 2 3
4 2.3 Calculating Limits Using the Limit Laws Limit Laws: Also found on pp of your textbook. Suppose f(x) and g(x) exist and that c is x a x a any constant. Then: 1. x a (f(x)±g(x)) = x a f(x)± x a g(x) 2. x a cf(x) = c x a f(x) 3. x a f(x)g(x) = x a f(x) x a g(x) f(x) 4. x a g(x) = f(x) x a g(x) x a 5. x a (f(x)) n = provided that x a g(x) 0 ( ) n f(x) x a 6. x a n f(x) = n x a f(x). If n is even, then we must have that x a f(x) > 0 In particular, 7. x a c = c 8. x a x = a 9. x a x n = a n Given that x 3 f(x) = 16, calculate x 3 (x 2 4)f(x) f(x)+x+2 If f is a polynomial or rational function and a is in the domain of f, then x a f(x) = f(a). x 2 (3x2 +5x+1) 4 4
5 We saw in the previous section what happens when only the it of the denominator is 0. There is an infinite it which yields a vertical asymptote. If the its of both the numerator AND denominator are 0, the it is indeterminate, so you must USE ALGEBRA to determine the it. Some methods are expanding, factoring, or multiplying by the conjugate of a radical. x 2 x 12 x 4 x 2 16 (h 4) 2 16 h 0 h t 2 t 2 (t 2) 3 x 1 x+3 2 x 1 5
6 For vector functions, if r(t) =< f(t),g(t) >, then r(t) = f(t),g(t) t a t a t a provided the its of the component functions exist. 2(t 2) 1 2 t Calculate r(t), where r(t) =, t 3 t 3 t 3 9 t(t 3) Find a number a so that the following it exists and then find the value of the it. x 2 +ax+a+5 x 3 (x+3)(x 5) 6
7 Let f(x) = x if x < 0 x 2 if 0 x < 2 8 x if 2 x < 5 2 if x = 5 x 2 if x > 5 Calculate x 0 f(x), x 2 f(x), and x 5 f(x) or explain why the it does not exist. { Recall the definition of the absolute value function: x = Calculate x 0 x 2 +x x or explain why the it does not exist. 7
8 Calculate x 3 x 3 6 2x or explain why the it does not exist. Squeeze Theorem: If g(x) h(x) f(x) for all x in an interval that contains a (except possibly at a) and g(x) = f(x) = L x a x a then x a h(x) = L Example: If 4x 2 f(x) x 2 +2 for 0 x 3, find x 2 f(x). ) Example: Find x sin( 2 1 x 0 x. 8
9 2.5 Continuity In Section 2.3 we saw that the it as x approaches a can sometimes be found by evaluating the function at a. If this is the case, then the function is continuous. Definition: A function is continuous at a number a if f(x) = f(a) x a Otherwise, we say the function is discontinuous at a, or that there is a discontinuity at a. In order for a function to be continuous at a number a: (1) f(a) must be defined. So a function will NOT be continuous anywhere it is undefined. (2) x a f(x) must exist. (The left-handed and right-handed its must both equal the same value.) (3) x a f(x) = f(a) Examples of discontinuities: Holes, vertical asymptotes, and jumps. A hole in a graph is also referred to as a removable discontinuity because if we wanted to, we could just redefine the function at that point to make it continuous. Removable discontinuities occur where the it exists at a (left and right its are equal), but is not equal to f(a). A vertical asymptote is referred to as an infinite discontinuity. A jump in the graph is referred to as a jump discontinuity. Jumps occur where the its from the left and right exist, but are not equal. 9
10 A function is continuous from the left at a number a if = f(a) and continuous from the x a f(x) right if x a +f(x) = f(a). A function is continuous if and only if it is continuous from both the right and the left. Examples: Determine where the functions below are discontinuous. State the type of discontinuity and explain why mathematically using its. Is the function continuous from the left or right there? (1) f(x) = x2 25 x 5 (2) f(x) = (x+3)(x 2) (x 2) 3 (3) f(x) = { x 2 4 if x 1 x+1 if x > 1 Fact: All polynomials are continuous everywhere! Fact: A rational function is continuous wherever it is defined, i.e. where the denominator is not 0. 10
11 2x 1 if x < 4 (4) f(x) = 6 if x = 4 x 2 9 if x > 4 (5) f(x) = 3x+1 if x < 2 x 2 5 x 1 if 2 x 3 x 3 25 x 2 if x > 3 What values of a and b would make the following function continuous everywhere? What are the values of f(x) and f(x)? x 3 x 1 ax 2 +bx+1 if x 3 x f(x) = 2 +6x 7 if 3 < x < 1 x 1 4x+a+2b if x 1 11
12 If f and g are continuous at a and c is any constant, then the functions f +g, f g, cf, fg, and f g (where g(a) 0) are all continuous functions. The Intermediate Value Theorem: Suppose f is continuous on the closed interval [a, b] and let N be any number strictly between f(a) and f(b). Then there exists a number c in (a,b) such that f(c) = N. Example: Show that the equation x 3 +2x+2 = 0 has a root (solution) on the interval (1,2). Example: If f(x) = x 4 x 3 +3x 2 +2, show that there is a number c so that f(c) = 3. 12
1.5 Inverse Trigonometric Functions
 1.5 Inverse Trigonometric Functions Remember that only one-to-one functions have inverses. So, in order to find the inverse functions for sine, cosine, and tangent, we must restrict their domains to intervals
1.5 Inverse Trigonometric Functions Remember that only one-to-one functions have inverses. So, in order to find the inverse functions for sine, cosine, and tangent, we must restrict their domains to intervals
2.4 The Precise Definition of a Limit
 2.4 The Precise Definition of a Limit Reminders/Remarks: x 4 < 3 means that the distance between x and 4 is less than 3. In other words, x lies strictly between 1 and 7. So, x a < δ means that the distance
2.4 The Precise Definition of a Limit Reminders/Remarks: x 4 < 3 means that the distance between x and 4 is less than 3. In other words, x lies strictly between 1 and 7. So, x a < δ means that the distance
MATH 151 Engineering Mathematics I
 MATH 151 Engineering Mathematics I Fall 2018, WEEK 3 JoungDong Kim Week 3 Section 2.3, 2.5, 2.6, Calculating Limits Using the Limit Laws, Continuity, Limits at Infinity; Horizontal Asymptotes. Section
MATH 151 Engineering Mathematics I Fall 2018, WEEK 3 JoungDong Kim Week 3 Section 2.3, 2.5, 2.6, Calculating Limits Using the Limit Laws, Continuity, Limits at Infinity; Horizontal Asymptotes. Section
Chapter 2. Limits and Continuity. 2.1 Rates of change and Tangents to Curves. The average Rate of change of y = f(x) with respect to x over the
 Chapter 2 Limits and Continuity 2.1 Rates of change and Tangents to Curves Definition 2.1.1 : interval [x 1, x 2 ] is The average Rate of change of y = f(x) with respect to x over the y x = f(x 2) f(x
Chapter 2 Limits and Continuity 2.1 Rates of change and Tangents to Curves Definition 2.1.1 : interval [x 1, x 2 ] is The average Rate of change of y = f(x) with respect to x over the y x = f(x 2) f(x
CH 2: Limits and Derivatives
 2 The tangent and velocity problems CH 2: Limits and Derivatives the tangent line to a curve at a point P, is the line that has the same slope as the curve at that point P, ie the slope of the tangent
2 The tangent and velocity problems CH 2: Limits and Derivatives the tangent line to a curve at a point P, is the line that has the same slope as the curve at that point P, ie the slope of the tangent
ter. on Can we get a still better result? Yes, by making the rectangles still smaller. As we make the rectangles smaller and smaller, the
 Area and Tangent Problem Calculus is motivated by two main problems. The first is the area problem. It is a well known result that the area of a rectangle with length l and width w is given by A = wl.
Area and Tangent Problem Calculus is motivated by two main problems. The first is the area problem. It is a well known result that the area of a rectangle with length l and width w is given by A = wl.
MATH 151 Engineering Mathematics I
 MATH 151 Engineering Mathematics I Spring 2018, WEEK 3 JoungDong Kim Week 3 Section 2.5, 2.6, 2.7, Continuity, Limits at Infinity; Horizontal Asymptotes, Derivatives and Rates of Change. Section 2.5 Continuity
MATH 151 Engineering Mathematics I Spring 2018, WEEK 3 JoungDong Kim Week 3 Section 2.5, 2.6, 2.7, Continuity, Limits at Infinity; Horizontal Asymptotes, Derivatives and Rates of Change. Section 2.5 Continuity
The function graphed below is continuous everywhere. The function graphed below is NOT continuous everywhere, it is discontinuous at x 2 and
 Section 1.4 Continuity A function is a continuous at a point if its graph has no gaps, holes, breaks or jumps at that point. If a function is not continuous at a point, then we say it is discontinuous
Section 1.4 Continuity A function is a continuous at a point if its graph has no gaps, holes, breaks or jumps at that point. If a function is not continuous at a point, then we say it is discontinuous
1.3 Limits and Continuity
 .3 Limits and Continuity.3. Limits Problem 8. What will happen to the functional values of as x gets closer and closer to 2? f(x) = Solution. We can evaluate f(x) using x values nearer and nearer to 2
.3 Limits and Continuity.3. Limits Problem 8. What will happen to the functional values of as x gets closer and closer to 2? f(x) = Solution. We can evaluate f(x) using x values nearer and nearer to 2
Chapter 1 Functions and Limits
 Contents Chapter 1 Functions and Limits Motivation to Chapter 1 2 4 Tangent and Velocity Problems 3 4.1 VIDEO - Secant Lines, Average Rate of Change, and Applications......................... 3 4.2 VIDEO
Contents Chapter 1 Functions and Limits Motivation to Chapter 1 2 4 Tangent and Velocity Problems 3 4.1 VIDEO - Secant Lines, Average Rate of Change, and Applications......................... 3 4.2 VIDEO
Continuity. MATH 161 Calculus I. J. Robert Buchanan. Fall Department of Mathematics
 Continuity MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Fall 2017 Intuitive Idea A process or an item can be described as continuous if it exists without interruption. The mathematical
Continuity MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Fall 2017 Intuitive Idea A process or an item can be described as continuous if it exists without interruption. The mathematical
Calculus I Exam 1 Review Fall 2016
 Problem 1: Decide whether the following statements are true or false: (a) If f, g are differentiable, then d d x (f g) = f g. (b) If a function is continuous, then it is differentiable. (c) If a function
Problem 1: Decide whether the following statements are true or false: (a) If f, g are differentiable, then d d x (f g) = f g. (b) If a function is continuous, then it is differentiable. (c) If a function
Section 1.4 Tangents and Velocity
 Math 132 Tangents and Velocity Section 1.4 Section 1.4 Tangents and Velocity Tangent Lines A tangent line to a curve is a line that just touches the curve. In terms of a circle, the definition is very
Math 132 Tangents and Velocity Section 1.4 Section 1.4 Tangents and Velocity Tangent Lines A tangent line to a curve is a line that just touches the curve. In terms of a circle, the definition is very
Chapter 2: Functions, Limits and Continuity
 Chapter 2: Functions, Limits and Continuity Functions Limits Continuity Chapter 2: Functions, Limits and Continuity 1 Functions Functions are the major tools for describing the real world in mathematical
Chapter 2: Functions, Limits and Continuity Functions Limits Continuity Chapter 2: Functions, Limits and Continuity 1 Functions Functions are the major tools for describing the real world in mathematical
Limits and Continuity
 Limits and Continuity Philippe B. Laval Kennesaw State University January 2, 2005 Contents Abstract Notes and practice problems on its and continuity. Limits 2. Introduction... 2.2 Theory:... 2.2. GraphicalMethod...
Limits and Continuity Philippe B. Laval Kennesaw State University January 2, 2005 Contents Abstract Notes and practice problems on its and continuity. Limits 2. Introduction... 2.2 Theory:... 2.2. GraphicalMethod...
LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS
 LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS RECALL: VERTICAL ASYMPTOTES Remember that for a rational function, vertical asymptotes occur at values of x = a which have infinite its (either positive or
LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS RECALL: VERTICAL ASYMPTOTES Remember that for a rational function, vertical asymptotes occur at values of x = a which have infinite its (either positive or
DRAFT - Math 101 Lecture Note - Dr. Said Algarni
 2 Limits 2.1 The Tangent Problems The word tangent is derived from the Latin word tangens, which means touching. A tangent line to a curve is a line that touches the curve and a secant line is a line that
2 Limits 2.1 The Tangent Problems The word tangent is derived from the Latin word tangens, which means touching. A tangent line to a curve is a line that touches the curve and a secant line is a line that
2.1 The Tangent and Velocity Problems
 2.1 The Tangent and Velocity Problems Tangents What is a tangent? Tangent lines and Secant lines Estimating slopes from discrete data: Example: 1. A tank holds 1000 gallons of water, which drains from
2.1 The Tangent and Velocity Problems Tangents What is a tangent? Tangent lines and Secant lines Estimating slopes from discrete data: Example: 1. A tank holds 1000 gallons of water, which drains from
1.10 Continuity Brian E. Veitch
 1.10 Continuity Definition 1.5. A function is continuous at x = a if 1. f(a) exists 2. lim x a f(x) exists 3. lim x a f(x) = f(a) If any of these conditions fail, f is discontinuous. Note: From algebra
1.10 Continuity Definition 1.5. A function is continuous at x = a if 1. f(a) exists 2. lim x a f(x) exists 3. lim x a f(x) = f(a) If any of these conditions fail, f is discontinuous. Note: From algebra
Induction, sequences, limits and continuity
 Induction, sequences, limits and continuity Material covered: eclass notes on induction, Chapter 11, Section 1 and Chapter 2, Sections 2.2-2.5 Induction Principle of mathematical induction: Let P(n) be
Induction, sequences, limits and continuity Material covered: eclass notes on induction, Chapter 11, Section 1 and Chapter 2, Sections 2.2-2.5 Induction Principle of mathematical induction: Let P(n) be
Continuity and One-Sided Limits. By Tuesday J. Johnson
 Continuity and One-Sided Limits By Tuesday J. Johnson Suggested Review Topics Algebra skills reviews suggested: Evaluating functions Rationalizing numerators and/or denominators Trigonometric skills reviews
Continuity and One-Sided Limits By Tuesday J. Johnson Suggested Review Topics Algebra skills reviews suggested: Evaluating functions Rationalizing numerators and/or denominators Trigonometric skills reviews
Calculus I. George Voutsadakis 1. LSSU Math 151. Lake Superior State University. 1 Mathematics and Computer Science
 Calculus I George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 151 George Voutsadakis (LSSU) Calculus I November 2014 1 / 67 Outline 1 Limits Limits, Rates
Calculus I George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 151 George Voutsadakis (LSSU) Calculus I November 2014 1 / 67 Outline 1 Limits Limits, Rates
Calculus I. 1. Limits and Continuity
 2301107 Calculus I 1. Limits and Continuity Outline 1.1. Limits 1.1.1 Motivation:Tangent 1.1.2 Limit of a function 1.1.3 Limit laws 1.1.4 Mathematical definition of a it 1.1.5 Infinite it 1.1. Continuity
2301107 Calculus I 1. Limits and Continuity Outline 1.1. Limits 1.1.1 Motivation:Tangent 1.1.2 Limit of a function 1.1.3 Limit laws 1.1.4 Mathematical definition of a it 1.1.5 Infinite it 1.1. Continuity
Limits and Continuity
 Limits and Continuity MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After this lesson we will be able to: Determine the left-hand and right-hand limits
Limits and Continuity MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After this lesson we will be able to: Determine the left-hand and right-hand limits
6.1 Polynomial Functions
 6.1 Polynomial Functions Definition. A polynomial function is any function p(x) of the form p(x) = p n x n + p n 1 x n 1 + + p 2 x 2 + p 1 x + p 0 where all of the exponents are non-negative integers and
6.1 Polynomial Functions Definition. A polynomial function is any function p(x) of the form p(x) = p n x n + p n 1 x n 1 + + p 2 x 2 + p 1 x + p 0 where all of the exponents are non-negative integers and
Math 115 Spring 11 Written Homework 10 Solutions
 Math 5 Spring Written Homework 0 Solutions. For following its, state what indeterminate form the its are in and evaluate the its. (a) 3x 4x 4 x x 8 Solution: This is in indeterminate form 0. Algebraically,
Math 5 Spring Written Homework 0 Solutions. For following its, state what indeterminate form the its are in and evaluate the its. (a) 3x 4x 4 x x 8 Solution: This is in indeterminate form 0. Algebraically,
Math 473: Practice Problems for Test 1, Fall 2011, SOLUTIONS
 Math 473: Practice Problems for Test 1, Fall 011, SOLUTIONS Show your work: 1. (a) Compute the Taylor polynomials P n (x) for f(x) = sin x and x 0 = 0. Solution: Compute f(x) = sin x, f (x) = cos x, f
Math 473: Practice Problems for Test 1, Fall 011, SOLUTIONS Show your work: 1. (a) Compute the Taylor polynomials P n (x) for f(x) = sin x and x 0 = 0. Solution: Compute f(x) = sin x, f (x) = cos x, f
Continuity. To handle complicated functions, particularly those for which we have a reasonable formula or formulas, we need a more precise definition.
 Continuity Intuitively, a function is continuous if its graph can be traced on paper in one motion without lifting the pencil from the paper. Thus the graph has no tears or holes. To handle complicated
Continuity Intuitively, a function is continuous if its graph can be traced on paper in one motion without lifting the pencil from the paper. Thus the graph has no tears or holes. To handle complicated
This Week. Professor Christopher Hoffman Math 124
 This Week Sections 2.1-2.3,2.5,2.6 First homework due Tuesday night at 11:30 p.m. Average and instantaneous velocity worksheet Tuesday available at http://www.math.washington.edu/ m124/ (under week 2)
This Week Sections 2.1-2.3,2.5,2.6 First homework due Tuesday night at 11:30 p.m. Average and instantaneous velocity worksheet Tuesday available at http://www.math.washington.edu/ m124/ (under week 2)
Advanced Mathematics Unit 2 Limits and Continuity
 Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics Unit 2 Limits and Continuity
 Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
2. If the values for f(x) can be made as close as we like to L by choosing arbitrarily large. lim
 Limits at Infinity and Horizontal Asymptotes As we prepare to practice graphing functions, we should consider one last piece of information about a function that will be helpful in drawing its graph the
Limits at Infinity and Horizontal Asymptotes As we prepare to practice graphing functions, we should consider one last piece of information about a function that will be helpful in drawing its graph the
and lim lim 6. The Squeeze Theorem
 Limits (day 3) Things we ll go over today 1. Limits of the form 0 0 (continued) 2. Limits of piecewise functions 3. Limits involving absolute values 4. Limits of compositions of functions 5. Limits similar
Limits (day 3) Things we ll go over today 1. Limits of the form 0 0 (continued) 2. Limits of piecewise functions 3. Limits involving absolute values 4. Limits of compositions of functions 5. Limits similar
Homework for Section 1.4, Continuity and One sided Limits. Study 1.4, # 1 21, 27, 31, 37 41, 45 53, 61, 69, 87, 91, 93. Class Notes: Prof. G.
 GOAL: 1. Understand definition of continuity at a point. 2. Evaluate functions for continuity at a point, and on open and closed intervals 3. Understand the Intermediate Value Theorum (IVT) Homework for
GOAL: 1. Understand definition of continuity at a point. 2. Evaluate functions for continuity at a point, and on open and closed intervals 3. Understand the Intermediate Value Theorum (IVT) Homework for
Section 1.2 Combining Functions; Shifting and Scaling Graphs. (a) Function addition: Given two functions f and g we define the sum of f and g as
 Section 1.2 Combining Functions; Shifting and Scaling Graphs We will get new functions from the ones we know. Tow functions f and g can be combined to form new functions by function addition, substraction,
Section 1.2 Combining Functions; Shifting and Scaling Graphs We will get new functions from the ones we know. Tow functions f and g can be combined to form new functions by function addition, substraction,
Limits and Their Properties
 Chapter 1 Limits and Their Properties Course Number Section 1.1 A Preview of Calculus Objective: In this lesson you learned how calculus compares with precalculus. I. What is Calculus? (Pages 42 44) Calculus
Chapter 1 Limits and Their Properties Course Number Section 1.1 A Preview of Calculus Objective: In this lesson you learned how calculus compares with precalculus. I. What is Calculus? (Pages 42 44) Calculus
Infinite Limits. Infinite Limits. Infinite Limits. Previously, we discussed the limits of rational functions with the indeterminate form 0/0.
 Infinite Limits Return to Table of Contents Infinite Limits Infinite Limits Previously, we discussed the limits of rational functions with the indeterminate form 0/0. Now we will consider rational functions
Infinite Limits Return to Table of Contents Infinite Limits Infinite Limits Previously, we discussed the limits of rational functions with the indeterminate form 0/0. Now we will consider rational functions
Limits of Functions (a, L)
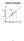 Limits of Functions f(x) (a, L) L f(x) x a x x 20 Informal Definition: If the values of can be made as close to as we like by taking values of sufficiently close to [but not equal to ] then we write or
Limits of Functions f(x) (a, L) L f(x) x a x x 20 Informal Definition: If the values of can be made as close to as we like by taking values of sufficiently close to [but not equal to ] then we write or
Continuity, Intermediate Value Theorem (2.4)
 Continuity, Intermediate Value Theorem (2.4) Xiannan Li Kansas State University January 29th, 2017 Intuitive Definition: A function f(x) is continuous at a if you can draw the graph of y = f(x) without
Continuity, Intermediate Value Theorem (2.4) Xiannan Li Kansas State University January 29th, 2017 Intuitive Definition: A function f(x) is continuous at a if you can draw the graph of y = f(x) without
Limit. Chapter Introduction
 Chapter 9 Limit Limit is the foundation of calculus that it is so useful to understand more complicating chapters of calculus. Besides, Mathematics has black hole scenarios (dividing by zero, going to
Chapter 9 Limit Limit is the foundation of calculus that it is so useful to understand more complicating chapters of calculus. Besides, Mathematics has black hole scenarios (dividing by zero, going to
Polynomial and Rational Functions. Chapter 3
 Polynomial and Rational Functions Chapter 3 Quadratic Functions and Models Section 3.1 Quadratic Functions Quadratic function: Function of the form f(x) = ax 2 + bx + c (a, b and c real numbers, a 0) -30
Polynomial and Rational Functions Chapter 3 Quadratic Functions and Models Section 3.1 Quadratic Functions Quadratic function: Function of the form f(x) = ax 2 + bx + c (a, b and c real numbers, a 0) -30
THS Step By Step Calculus Chapter 1
 Name: Class Period: Throughout this packet there will be blanks you are epected to fill in prior to coming to class. This packet follows your Larson Tetbook. Do NOT throw away! Keep in 3 ring binder until
Name: Class Period: Throughout this packet there will be blanks you are epected to fill in prior to coming to class. This packet follows your Larson Tetbook. Do NOT throw away! Keep in 3 ring binder until
O.K. But what if the chicken didn t have access to a teleporter.
 The intermediate value theorem, and performing algebra on its. This is a dual topic lecture. : The Intermediate value theorem First we should remember what it means to be a continuous function: A function
The intermediate value theorem, and performing algebra on its. This is a dual topic lecture. : The Intermediate value theorem First we should remember what it means to be a continuous function: A function
e x = 1 + x + x2 2! + x3 If the function f(x) can be written as a power series on an interval I, then the power series is of the form
 Taylor Series Given a function f(x), we would like to be able to find a power series that represents the function. For example, in the last section we noted that we can represent e x by the power series
Taylor Series Given a function f(x), we would like to be able to find a power series that represents the function. For example, in the last section we noted that we can represent e x by the power series
x y More precisely, this equation means that given any ε > 0, there exists some δ > 0 such that
 Chapter 2 Limits and continuity 21 The definition of a it Definition 21 (ε-δ definition) Let f be a function and y R a fixed number Take x to be a point which approaches y without being equal to y If there
Chapter 2 Limits and continuity 21 The definition of a it Definition 21 (ε-δ definition) Let f be a function and y R a fixed number Take x to be a point which approaches y without being equal to y If there
Continuity. Chapter 4
 Chapter 4 Continuity Throughout this chapter D is a nonempty subset of the real numbers. We recall the definition of a function. Definition 4.1. A function from D into R, denoted f : D R, is a subset of
Chapter 4 Continuity Throughout this chapter D is a nonempty subset of the real numbers. We recall the definition of a function. Definition 4.1. A function from D into R, denoted f : D R, is a subset of
Continuity. The Continuity Equation The equation that defines continuity at a point is called the Continuity Equation.
 Continuity A function is continuous at a particular x location when you can draw it through that location without picking up your pencil. To describe this mathematically, we have to use limits. Recall
Continuity A function is continuous at a particular x location when you can draw it through that location without picking up your pencil. To describe this mathematically, we have to use limits. Recall
Last week we looked at limits generally, and at finding limits using substitution.
 Math 1314 ONLINE Week 4 Notes Lesson 4 Limits (continued) Last week we looked at limits generally, and at finding limits using substitution. Indeterminate Forms What do you do when substitution gives you
Math 1314 ONLINE Week 4 Notes Lesson 4 Limits (continued) Last week we looked at limits generally, and at finding limits using substitution. Indeterminate Forms What do you do when substitution gives you
Chapter 1 Limits and Their Properties
 Chapter 1 Limits and Their Properties Calculus: Chapter P Section P.2, P.3 Chapter P (briefly) WARM-UP 1. Evaluate: cot 6 2. Find the domain of the function: f( x) 3x 3 2 x 4 g f ( x) f ( x) x 5 3. Find
Chapter 1 Limits and Their Properties Calculus: Chapter P Section P.2, P.3 Chapter P (briefly) WARM-UP 1. Evaluate: cot 6 2. Find the domain of the function: f( x) 3x 3 2 x 4 g f ( x) f ( x) x 5 3. Find
MATH 113: ELEMENTARY CALCULUS
 MATH 3: ELEMENTARY CALCULUS Please check www.ualberta.ca/ zhiyongz for notes updation! 6. Rates of Change and Limits A fundamental philosophical truth is that everything changes. In physics, the change
MATH 3: ELEMENTARY CALCULUS Please check www.ualberta.ca/ zhiyongz for notes updation! 6. Rates of Change and Limits A fundamental philosophical truth is that everything changes. In physics, the change
8. Limit Laws. lim(f g)(x) = lim f(x) lim g(x), (x) = lim x a f(x) g lim x a g(x)
 8. Limit Laws 8.1. Basic Limit Laws. If f and g are two functions and we know the it of each of them at a given point a, then we can easily compute the it at a of their sum, difference, product, constant
8. Limit Laws 8.1. Basic Limit Laws. If f and g are two functions and we know the it of each of them at a given point a, then we can easily compute the it at a of their sum, difference, product, constant
Mathematic 108, Fall 2015: Solutions to assignment #7
 Mathematic 08, Fall 05: Solutions to assignment #7 Problem # Suppose f is a function with f continuous on the open interval I and so that f has a local maximum at both x = a and x = b for a, b I with a
Mathematic 08, Fall 05: Solutions to assignment #7 Problem # Suppose f is a function with f continuous on the open interval I and so that f has a local maximum at both x = a and x = b for a, b I with a
Integer-Valued Polynomials
 Integer-Valued Polynomials LA Math Circle High School II Dillon Zhi October 11, 2015 1 Introduction Some polynomials take integer values p(x) for all integers x. The obvious examples are the ones where
Integer-Valued Polynomials LA Math Circle High School II Dillon Zhi October 11, 2015 1 Introduction Some polynomials take integer values p(x) for all integers x. The obvious examples are the ones where
Section 2: Limits and Continuity
 Chapter 2 The Derivative Business Calculus 79 Section 2: Limits and Continuity In the last section, we saw that as the interval over which we calculated got smaller, the secant slopes approached the tangent
Chapter 2 The Derivative Business Calculus 79 Section 2: Limits and Continuity In the last section, we saw that as the interval over which we calculated got smaller, the secant slopes approached the tangent
College Algebra Notes
 Metropolitan Community College Contents Introduction 2 Unit 1 3 Rational Expressions........................................... 3 Quadratic Equations........................................... 9 Polynomial,
Metropolitan Community College Contents Introduction 2 Unit 1 3 Rational Expressions........................................... 3 Quadratic Equations........................................... 9 Polynomial,
Do now as a warm up: Is there some number a, such that this limit exists? If so, find the value of a and find the limit. If not, explain why not.
 Do now as a warm up: Is there some number a, such that this limit exists? If so, find the value of a and find the limit. If not, explain why not. 1 Continuity and One Sided Limits To say that a function
Do now as a warm up: Is there some number a, such that this limit exists? If so, find the value of a and find the limit. If not, explain why not. 1 Continuity and One Sided Limits To say that a function
1.3 Limits and Continuity
 40 CHAPTER 1. RATES OF CHANGE AND THE DERIVATIVE 1.3 Limits and Continuity Despite the fact that we have placed all of the proofs of the theorems from this section in the Technical Matters section, Section
40 CHAPTER 1. RATES OF CHANGE AND THE DERIVATIVE 1.3 Limits and Continuity Despite the fact that we have placed all of the proofs of the theorems from this section in the Technical Matters section, Section
Solutions to Math 41 First Exam October 15, 2013
 Solutions to Math 41 First Exam October 15, 2013 1. (16 points) Find each of the following its, with justification. If the it does not exist, explain why. If there is an infinite it, then explain whether
Solutions to Math 41 First Exam October 15, 2013 1. (16 points) Find each of the following its, with justification. If the it does not exist, explain why. If there is an infinite it, then explain whether
Infinite Limits. By Tuesday J. Johnson
 Infinite Limits By Tuesday J. Johnson Suggested Review Topics Algebra skills reviews suggested: Evaluating functions Graphing functions Working with inequalities Working with absolute values Trigonometric
Infinite Limits By Tuesday J. Johnson Suggested Review Topics Algebra skills reviews suggested: Evaluating functions Graphing functions Working with inequalities Working with absolute values Trigonometric
Math 261 Calculus I. Test 1 Study Guide. Name. Decide whether the limit exists. If it exists, find its value. 1) lim x 1. f(x) 2) lim x -1/2 f(x)
 Math 261 Calculus I Test 1 Study Guide Name Decide whether the it exists. If it exists, find its value. 1) x 1 f(x) 2) x -1/2 f(x) Complete the table and use the result to find the indicated it. 3) If
Math 261 Calculus I Test 1 Study Guide Name Decide whether the it exists. If it exists, find its value. 1) x 1 f(x) 2) x -1/2 f(x) Complete the table and use the result to find the indicated it. 3) If
MATH 114 Calculus Notes on Chapter 2 (Limits) (pages 60-? in Stewart)
 Still under construction. MATH 114 Calculus Notes on Chapter 2 (Limits) (pages 60-? in Stewart) As seen in A Preview of Calculus, the concept of it underlies the various branches of calculus. Hence we
Still under construction. MATH 114 Calculus Notes on Chapter 2 (Limits) (pages 60-? in Stewart) As seen in A Preview of Calculus, the concept of it underlies the various branches of calculus. Hence we
UNIT 3. Rational Functions Limits at Infinity (Horizontal and Slant Asymptotes) Infinite Limits (Vertical Asymptotes) Graphing Rational Functions
 UNIT 3 Rational Functions Limits at Infinity (Horizontal and Slant Asymptotes) Infinite Limits (Vertical Asymptotes) Graphing Rational Functions Recall From Unit Rational Functions f() is a rational function
UNIT 3 Rational Functions Limits at Infinity (Horizontal and Slant Asymptotes) Infinite Limits (Vertical Asymptotes) Graphing Rational Functions Recall From Unit Rational Functions f() is a rational function
Lecture 3 (Limits and Derivatives)
 Lecture 3 (Limits and Derivatives) Continuity In the previous lecture we saw that very often the limit of a function as is just. When this is the case we say that is continuous at a. Definition: A function
Lecture 3 (Limits and Derivatives) Continuity In the previous lecture we saw that very often the limit of a function as is just. When this is the case we say that is continuous at a. Definition: A function
Continuity at a Point
 Continuity at a Point When we eplored the limit of f() as approaches c, the emphasis was on the function values close to = c rather than what happens to the function at = c. We will now consider the following
Continuity at a Point When we eplored the limit of f() as approaches c, the emphasis was on the function values close to = c rather than what happens to the function at = c. We will now consider the following
MATH 409 Advanced Calculus I Lecture 16: Mean value theorem. Taylor s formula.
 MATH 409 Advanced Calculus I Lecture 16: Mean value theorem. Taylor s formula. Points of local extremum Let f : E R be a function defined on a set E R. Definition. We say that f attains a local maximum
MATH 409 Advanced Calculus I Lecture 16: Mean value theorem. Taylor s formula. Points of local extremum Let f : E R be a function defined on a set E R. Definition. We say that f attains a local maximum
Section Properties of Rational Expressions
 88 Section. - Properties of Rational Expressions Recall that a rational number is any number that can be written as the ratio of two integers where the integer in the denominator cannot be. Rational Numbers:
88 Section. - Properties of Rational Expressions Recall that a rational number is any number that can be written as the ratio of two integers where the integer in the denominator cannot be. Rational Numbers:
MTH4100 Calculus I. Lecture notes for Week 4. Thomas Calculus, Sections 2.4 to 2.6. Rainer Klages
 MTH4100 Calculus I Lecture notes for Week 4 Thomas Calculus, Sections 2.4 to 2.6 Rainer Klages School of Mathematical Sciences Queen Mary University of London Autumn 2009 One-sided its and its at infinity
MTH4100 Calculus I Lecture notes for Week 4 Thomas Calculus, Sections 2.4 to 2.6 Rainer Klages School of Mathematical Sciences Queen Mary University of London Autumn 2009 One-sided its and its at infinity
Intermediate Algebra. Gregg Waterman Oregon Institute of Technology
 Intermediate Algebra Gregg Waterman Oregon Institute of Technology c 017 Gregg Waterman This work is licensed under the Creative Commons Attribution 4.0 International license. The essence of the license
Intermediate Algebra Gregg Waterman Oregon Institute of Technology c 017 Gregg Waterman This work is licensed under the Creative Commons Attribution 4.0 International license. The essence of the license
Continuity. Chapter 4
 Chapter 4 Continuity Throughout this chapter D is a nonempty subset of the real numbers. We recall the definition of a function. Definition 4.1. A function from D into R, denoted f : D R, is a subset of
Chapter 4 Continuity Throughout this chapter D is a nonempty subset of the real numbers. We recall the definition of a function. Definition 4.1. A function from D into R, denoted f : D R, is a subset of
Review: Limits of Functions - 10/7/16
 Review: Limits of Functions - 10/7/16 1 Right and Left Hand Limits Definition 1.0.1 We write lim a f() = L to mean that the function f() approaches L as approaches a from the left. We call this the left
Review: Limits of Functions - 10/7/16 1 Right and Left Hand Limits Definition 1.0.1 We write lim a f() = L to mean that the function f() approaches L as approaches a from the left. We call this the left
Math 1120 Calculus, sections 3 and 10 Test 1
 October 3, 206 Name The problems count as marked The total number of points available is 7 Throughout this test, show your work This is an amalgamation of the tests from sections 3 and 0 (0 points) Find
October 3, 206 Name The problems count as marked The total number of points available is 7 Throughout this test, show your work This is an amalgamation of the tests from sections 3 and 0 (0 points) Find
2.1 The Tangent and Velocity Problems
 2.1 The Tangent and Velocity Problems Ex: When you jump off a swing, where do you go? Ex: Can you approximate this line with another nearby? How would you get a better approximation? Ex: A cardiac monitor
2.1 The Tangent and Velocity Problems Ex: When you jump off a swing, where do you go? Ex: Can you approximate this line with another nearby? How would you get a better approximation? Ex: A cardiac monitor
Unit 1 PreCalculus Review & Limits
 1 Unit 1 PreCalculus Review & Limits Factoring: Remove common factors first Terms - Difference of Squares a b a b a b - Sum of Cubes ( )( ) a b a b a ab b 3 3 - Difference of Cubes a b a b a ab b 3 3 3
1 Unit 1 PreCalculus Review & Limits Factoring: Remove common factors first Terms - Difference of Squares a b a b a b - Sum of Cubes ( )( ) a b a b a ab b 3 3 - Difference of Cubes a b a b a ab b 3 3 3
Chapter 1: Limits and Continuity
 Chapter 1: Limits and Continuity Winter 2015 Department of Mathematics Hong Kong Baptist University 1/69 1.1 Examples where limits arise Calculus has two basic procedures: differentiation and integration.
Chapter 1: Limits and Continuity Winter 2015 Department of Mathematics Hong Kong Baptist University 1/69 1.1 Examples where limits arise Calculus has two basic procedures: differentiation and integration.
October 27, 2018 MAT186 Week 3 Justin Ko. We use the following notation to describe the limiting behavior of functions.
 October 27, 208 MAT86 Week 3 Justin Ko Limits. Intuitive Definitions of Limits We use the following notation to describe the iting behavior of functions.. (Limit of a Function A it is written as f( = L
October 27, 208 MAT86 Week 3 Justin Ko Limits. Intuitive Definitions of Limits We use the following notation to describe the iting behavior of functions.. (Limit of a Function A it is written as f( = L
CHAPTER 3: CONTINUITY ON R 3.1 TWO SIDED LIMITS
 CHAPTER 3: CONTINUITY ON R 3.1 TWO SIDED LIMITS DEFINITION. Let a R and let I be an open interval contains a, and let f be a real function defined everywhere except possibly at a. Then f(x) is said to
CHAPTER 3: CONTINUITY ON R 3.1 TWO SIDED LIMITS DEFINITION. Let a R and let I be an open interval contains a, and let f be a real function defined everywhere except possibly at a. Then f(x) is said to
1) If f x symmetric about what? (Box in one:) (2 points) the x-axis the y-axis the origin none of these
 QUIZ ON CHAPTERS AND - SOLUTIONS REVIEW / LIMITS AND CONTINUITY; MATH 50 FALL 06 KUNIYUKI 05 POINTS TOTAL, BUT 00 POINTS = 00% = x /, then the graph of y = f ( x) in the usual (Cartesian) xy-plane is )
QUIZ ON CHAPTERS AND - SOLUTIONS REVIEW / LIMITS AND CONTINUITY; MATH 50 FALL 06 KUNIYUKI 05 POINTS TOTAL, BUT 00 POINTS = 00% = x /, then the graph of y = f ( x) in the usual (Cartesian) xy-plane is )
Determine whether the formula determines y as a function of x. If not, explain. Is there a way to look at a graph and determine if it's a function?
 1.2 Functions and Their Properties Name: Objectives: Students will be able to represent functions numerically, algebraically, and graphically, determine the domain and range for functions, and analyze
1.2 Functions and Their Properties Name: Objectives: Students will be able to represent functions numerically, algebraically, and graphically, determine the domain and range for functions, and analyze
Limits Student Study Session
 Teacher Notes Limits Student Study Session Solving limits: The vast majority of limits questions can be solved by using one of four techniques: SUBSTITUTING, FACTORING, CONJUGATING, or by INSPECTING A
Teacher Notes Limits Student Study Session Solving limits: The vast majority of limits questions can be solved by using one of four techniques: SUBSTITUTING, FACTORING, CONJUGATING, or by INSPECTING A
THE LIMIT PROCESS (AN INTUITIVE INTRODUCTION)
 The Limit Process THE LIMIT PROCESS (AN INTUITIVE INTRODUCTION) We could begin by saying that limits are important in calculus, but that would be a major understatement. Without limits, calculus would
The Limit Process THE LIMIT PROCESS (AN INTUITIVE INTRODUCTION) We could begin by saying that limits are important in calculus, but that would be a major understatement. Without limits, calculus would
Math 117: Honours Calculus I Fall, 2002 List of Theorems. a n k b k. k. Theorem 2.1 (Convergent Bounded) A convergent sequence is bounded.
 Math 117: Honours Calculus I Fall, 2002 List of Theorems Theorem 1.1 (Binomial Theorem) For all n N, (a + b) n = n k=0 ( ) n a n k b k. k Theorem 2.1 (Convergent Bounded) A convergent sequence is bounded.
Math 117: Honours Calculus I Fall, 2002 List of Theorems Theorem 1.1 (Binomial Theorem) For all n N, (a + b) n = n k=0 ( ) n a n k b k. k Theorem 2.1 (Convergent Bounded) A convergent sequence is bounded.
MATH 409 Advanced Calculus I Lecture 11: More on continuous functions.
 MATH 409 Advanced Calculus I Lecture 11: More on continuous functions. Continuity Definition. Given a set E R, a function f : E R, and a point c E, the function f is continuous at c if for any ε > 0 there
MATH 409 Advanced Calculus I Lecture 11: More on continuous functions. Continuity Definition. Given a set E R, a function f : E R, and a point c E, the function f is continuous at c if for any ε > 0 there
Topic 3 Outline. What is a Limit? Calculating Limits Infinite Limits Limits at Infinity Continuity. 1 Limits and Continuity
 Topic 3 Outline 1 Limits and Continuity What is a Limit? Calculating Limits Infinite Limits Limits at Infinity Continuity D. Kalajdzievska (University of Manitoba) Math 1520 Fall 2015 1 / 27 Topic 3 Learning
Topic 3 Outline 1 Limits and Continuity What is a Limit? Calculating Limits Infinite Limits Limits at Infinity Continuity D. Kalajdzievska (University of Manitoba) Math 1520 Fall 2015 1 / 27 Topic 3 Learning
MATH 151 Engineering Mathematics I
 MATH 151 Engineering Mathematics I Fall, 2016, WEEK 4 JoungDong Kim Week4 Section 2.6, 2.7, 3.1 Limits at infinity, Velocity, Differentiation Section 2.6 Limits at Infinity; Horizontal Asymptotes Definition.
MATH 151 Engineering Mathematics I Fall, 2016, WEEK 4 JoungDong Kim Week4 Section 2.6, 2.7, 3.1 Limits at infinity, Velocity, Differentiation Section 2.6 Limits at Infinity; Horizontal Asymptotes Definition.
1.1 Introduction to Limits
 Chapter 1 LIMITS 1.1 Introduction to Limits Why Limit? Suppose that an object steadily moves forward, with s(t) denotes the position at time t. The average speed over the interval [1,2] is The average
Chapter 1 LIMITS 1.1 Introduction to Limits Why Limit? Suppose that an object steadily moves forward, with s(t) denotes the position at time t. The average speed over the interval [1,2] is The average
Limits at Infinity. Horizontal Asymptotes. Definition (Limits at Infinity) Horizontal Asymptotes
 Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
B553 Lecture 1: Calculus Review
 B553 Lecture 1: Calculus Review Kris Hauser January 10, 2012 This course requires a familiarity with basic calculus, some multivariate calculus, linear algebra, and some basic notions of metric topology.
B553 Lecture 1: Calculus Review Kris Hauser January 10, 2012 This course requires a familiarity with basic calculus, some multivariate calculus, linear algebra, and some basic notions of metric topology.
Section 2.6: Continuity
 Section 2.6: Continuity Problem 1 (a) Let f(x) = x 1 x 2 5x. Then f(2) = 1 6 and f(6) = 5, but there is no value of c between 2 6 and 6 for which f(c) = 0. Does this fact violate the Intermediate Value
Section 2.6: Continuity Problem 1 (a) Let f(x) = x 1 x 2 5x. Then f(2) = 1 6 and f(6) = 5, but there is no value of c between 2 6 and 6 for which f(c) = 0. Does this fact violate the Intermediate Value
Pre-Calculus Mathematics Limit Process Calculus
 NOTES : LIMITS AND DERIVATIVES Name: Date: Period: Mrs. Nguyen s Initial: LESSON.1 THE TANGENT AND VELOCITY PROBLEMS Pre-Calculus Mathematics Limit Process Calculus The type of it that is used to find
NOTES : LIMITS AND DERIVATIVES Name: Date: Period: Mrs. Nguyen s Initial: LESSON.1 THE TANGENT AND VELOCITY PROBLEMS Pre-Calculus Mathematics Limit Process Calculus The type of it that is used to find
Practice Test - Chapter 2
 Graph and analyze each function. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing. 1. f (x) = 0.25x 3 Evaluate the function for several
Graph and analyze each function. Describe the domain, range, intercepts, end behavior, continuity, and where the function is increasing or decreasing. 1. f (x) = 0.25x 3 Evaluate the function for several
Limits, Continuity, and the Derivative
 Unit #2 : Limits, Continuity, and the Derivative Goals: Study and define continuity Review limits Introduce the derivative as the limit of a difference quotient Discuss the derivative as a rate of change
Unit #2 : Limits, Continuity, and the Derivative Goals: Study and define continuity Review limits Introduce the derivative as the limit of a difference quotient Discuss the derivative as a rate of change
Exam 1. (2x + 1) 2 9. lim. (rearranging) (x 1 implies x 1, thus x 1 0
 Department of Mathematical Sciences Instructor: Daiva Pucinskaite Calculus I January 28, 2016 Name: Exam 1 1. Evaluate the it x 1 (2x + 1) 2 9. x 1 (2x + 1) 2 9 4x 2 + 4x + 1 9 = 4x 2 + 4x 8 = 4(x 1)(x
Department of Mathematical Sciences Instructor: Daiva Pucinskaite Calculus I January 28, 2016 Name: Exam 1 1. Evaluate the it x 1 (2x + 1) 2 9. x 1 (2x + 1) 2 9 4x 2 + 4x + 1 9 = 4x 2 + 4x 8 = 4(x 1)(x
PreCalculus Notes. MAT 129 Chapter 5: Polynomial and Rational Functions. David J. Gisch. Department of Mathematics Des Moines Area Community College
 PreCalculus Notes MAT 129 Chapter 5: Polynomial and Rational Functions David J. Gisch Department of Mathematics Des Moines Area Community College September 2, 2011 1 Chapter 5 Section 5.1: Polynomial Functions
PreCalculus Notes MAT 129 Chapter 5: Polynomial and Rational Functions David J. Gisch Department of Mathematics Des Moines Area Community College September 2, 2011 1 Chapter 5 Section 5.1: Polynomial Functions
Lecture Notes for Math 1000
 Lecture Notes for Math 1000 Dr. Xiang-Sheng Wang Memorial University of Newfoundland Office: HH-2016, Phone: 864-4321 Office hours: 13:00-15:00 Wednesday, 12:00-13:00 Friday Email: swang@mun.ca Course
Lecture Notes for Math 1000 Dr. Xiang-Sheng Wang Memorial University of Newfoundland Office: HH-2016, Phone: 864-4321 Office hours: 13:00-15:00 Wednesday, 12:00-13:00 Friday Email: swang@mun.ca Course
1.1 Limits and Continuity. Precise definition of a limit and limit laws. Squeeze Theorem. Intermediate Value Theorem. Extreme Value Theorem.
 STATE EXAM MATHEMATICS Variant A ANSWERS AND SOLUTIONS 1 1.1 Limits and Continuity. Precise definition of a limit and limit laws. Squeeze Theorem. Intermediate Value Theorem. Extreme Value Theorem. Definition
STATE EXAM MATHEMATICS Variant A ANSWERS AND SOLUTIONS 1 1.1 Limits and Continuity. Precise definition of a limit and limit laws. Squeeze Theorem. Intermediate Value Theorem. Extreme Value Theorem. Definition
Math Section Bekki George: 08/28/18. University of Houston. Bekki George (UH) Math /28/18 1 / 37
 Math 1431 Section 14616 Bekki George: bekki@math.uh.edu University of Houston 08/28/18 Bekki George (UH) Math 1431 08/28/18 1 / 37 Office Hours: Tuesdays and Thursdays 12:30-2pm (also available by appointment)
Math 1431 Section 14616 Bekki George: bekki@math.uh.edu University of Houston 08/28/18 Bekki George (UH) Math 1431 08/28/18 1 / 37 Office Hours: Tuesdays and Thursdays 12:30-2pm (also available by appointment)
MATH CALCULUS I 1.5: Continuity
 MATH 12002 - CALCULUS I 1.5: Continuity Professor Donald L. White Department of Mathematical Sciences Kent State University D.L. White (Kent State University) 1 / 12 Definition of Continuity Intuitively,
MATH 12002 - CALCULUS I 1.5: Continuity Professor Donald L. White Department of Mathematical Sciences Kent State University D.L. White (Kent State University) 1 / 12 Definition of Continuity Intuitively,
(x + 3)(x 1) lim(x + 3) = 4. lim. (x 2)( x ) = (x 2)(x + 2) x + 2 x = 4. dt (t2 + 1) = 1 2 (t2 + 1) 1 t. f(x) = lim 3x = 6,
 Math 140 MT1 Sample C Solutions Tyrone Crisp 1 (B): First try direct substitution: you get 0. So try to cancel common factors. We have 0 x 2 + 2x 3 = x 1 and so the it as x 1 is equal to (x + 3)(x 1),
Math 140 MT1 Sample C Solutions Tyrone Crisp 1 (B): First try direct substitution: you get 0. So try to cancel common factors. We have 0 x 2 + 2x 3 = x 1 and so the it as x 1 is equal to (x + 3)(x 1),
AP Calculus AB. Limits & Continuity.
 1 AP Calculus AB Limits & Continuity 2015 10 20 www.njctl.org 2 Table of Contents click on the topic to go to that section Introduction The Tangent Line Problem Definition of a Limit and Graphical Approach
1 AP Calculus AB Limits & Continuity 2015 10 20 www.njctl.org 2 Table of Contents click on the topic to go to that section Introduction The Tangent Line Problem Definition of a Limit and Graphical Approach
Rational Functions. Elementary Functions. Algebra with mixed fractions. Algebra with mixed fractions
 Rational Functions A rational function f (x) is a function which is the ratio of two polynomials, that is, Part 2, Polynomials Lecture 26a, Rational Functions f (x) = where and are polynomials Dr Ken W
Rational Functions A rational function f (x) is a function which is the ratio of two polynomials, that is, Part 2, Polynomials Lecture 26a, Rational Functions f (x) = where and are polynomials Dr Ken W
