Math 544, Exam 2 Information.
|
|
|
- Darleen Hodges
- 6 years ago
- Views:
Transcription
1 Math 544, Exam 2 Information. 10/12/10, LC 115, 2:00-3:15. Exam 2 will be based on: Sections 1.7, 1.9, 3.2, 3.3, 3.4; The corresponding assigned homework problems (see boylan/sccourses/544fa10/544.html) At minimum, you need to understand how to do the homework problems. Lecture notes: 9/16-10/7. Topic List (not necessarily comprehensive): You will need to know: theorems, results, and definitions from class. 1.7: Linear independence and non-singular matrices. You will need to know/identify the following terms: Linear combination of vectors. Linear dependence of a set of vectors; linear independence of a set of vectors. Let S = { v 1,..., v n } R m. The set S is linearly independent the vector equation x 1 v x n v n = 0 x 1 has only the trivial solution x =. x n = 0. Conversely, S is linearly dependent the vector equation has a non-trivial solution x 0. The vector equation can be written in matrix form as A x = ( v 1 v n ) x = 0, where the vectors in S form the columns of A Mat n n (R). Only sets of vectors can be linearly dependent/linearly independent. It does not make sense to speak of matrices or systems of equations being linearly dependent/independent. Notes: 1. Any set of vectors S with 0 S is linearly dependent. 2. Suppose that v 0. Then { v} is linearly independent. 3. Two vectors are linearly dependent if and only if they are scalar multiples of each other.
2 Singular matrices; non-singular matrices. Let A Mat n n (R). The A is non-singular the equation A x = 0 has only the trivial solution, x = 0. Conversely, A is singular this equation has a non-trivial solution x 0. Only square matrices can be singular/non-singular. It does not make sense to speak of a system of equations or a set of vectors as being singular/non-singular. Note: Similarly, only systems of linear equations can consistent/inconsistent. It does not make sense to speak of matrices or sets of vectors as being consistent/inconsistent. Theorem. Suppose that S = { v 1,..., v n } R m with m < n. dependent set. Then S is a linearly Facts: Let A and B Mat n n (R). 1. AB is non-singular if and only if A and B are non-singular. 2. AB is singular if and only if one (or both) of A and B is singular. 1.9: Matrix inverses and their properties. Matrix inverses. A matrix A Mat n n (R) is invertible if and only if there exists B Mat n n (R) with BA = I n = AB. We say that B is the inverse of A, and we write B = A Only square matrices are allowed to be invertible. 2. Suppose that A Mat n n (R) is invertible. Then the inverse, A 1, is unique. Theorem. Let A Mat n n. Then the following conditions on A are equivalent. A is non-singular. A x = 0 has only the trivial solution, x = 0. The columns of A are a linearly independent set of vectors. For all b R n, A x = b has a unique solution. A is invertible. A is row-equivalent to I n. Facts: Suppose that A Mat n n (R) is invertible. To compute A 1, form the augmented matrix (A I n ) Mat n 2n (R). Apply the Gauss- Jordan algorithm to convert it to its reduced echelon form, (I n A 1 ). For all b R n, the system A x = b is consistent (i.e., it has a solution); the unique solution is x = A 1 b. 2
3 Theorem. Suppose that A, B Mat n n (R) are invertible. Then we have 1. (A 1 ) 1 = A. 2. (AB) 1 = B 1 A 1. (Note: (AB) 1 = A 1 B 1 AB = BA.) 3. Let k 0 in R. Then we have (ka) 1 = 1 k A (A T ) 1 = (A 1 ) T. ( ) a b Proposition. Let Mat c d 2 2 (R). Then we have ad bc = 0 = A is not invertible. ad bc 0 = A is invertible. 3.2: Vector space properties of R n. Vector space. A vector space is a collection of objects called vectors and a collection of constants called scalars together with the operations of vector addition (+) and scalar multiplication ( ) which satisfy the following axioms: Two closure axioms: closure under + and. Four addition axioms: associativity, identity, inverses, commutativity. Four scalar multiplication axioms: associativity, distributivity, identity. Subspace. Suppose that V is a vector space. A subset W V is a subspace of V if and only if W is itself a vector space (with the same scalars, addition, and multiplication as V ). 1. Let V be a vector space. Then { 0} and V are subspaces of V. These are the trivial subspaces of V. 2. The non-trivial subspaces of R 2 are lines through the origin; the non-trivial subspaces of R 3 are lines through the origin and planes through the origin. Theorem. Let V be a vector space, and let W V. Then W is a subspace of V if and only if W satisfies the following three axioms: 1. { 0} W. 2. For all x, y W, we have x + y W. 3. For all a R and for all x W, we have a x W. Note: One can combine axioms 2 and 3: for all a R and for all x, y W, we have a x + y W. Question: How does one determine whether a subset W of a vector space V is a subspace? To show that W is a subspace, you need to verify the three subspace axioms. To show that W is not a subspace, it suffices to provide a simple numerical example in which one of the axioms is violated. 3
4 Note: If a subset W of a vector space V is defined by a system of linear homogeneous equations satisfied by the coordinates of vectors in W, then it is a subspace. Facts: Suppose that U and V are subspaces of R n. Then we have: 1. U + V = { u + v : u U, v V } is always a subspace of R n. 2. U V is always a subspace of R n. 3. U V is not generally a subspace of R n. 3.3: Subspaces. Span. The span of a set S = { v 1,..., v r } R n is the set Span(S) = {all linear combinations of vectors in S} = { y = a 1 v a r v r : a 1,..., a r R} R n. Examples. Let v 0. Then Span{ v} is a line through the origin in the direction of v. Let u, v be non-zero vectors in R n. Then u Span{ v} if and only if u and v determine the same line. Theorem. Suppose that S = { v 1,..., v r } R n. Then Span(S) is a subspace of R n. Let A Mat m n (R). Important subspaces associated to A are: The null space of A is Null(A) = { x R n : A x = 0}. It is a subspace of R n. The range of A is Range(A) = { y R m : there exists x R n such that A x = y}. It is a subspace of R m. The column space of A is Col(A) = Span{columns of A}. It is a subspace of R m. The row space of A is Row(A) = Span{rows of A}. It is a subspace of R n. Theorem. Suppose that A Mat m n (R). Then we have Range(A) = Col(A) = Row(A T ) R m. Theorem. Suppose that A, B Mat m n (R) are row-equivalent. Then we have Row(A) = Row(B). Problem: Given a matrix A Mat m n (R), give a basis (algebraic description) of the important subspaces associated to A. 3.4: Bases. A set of vectors S spans a subspace W of a vector space V if and only if Span(S) = W. Theorem. Suppose that Span(S) = W. 1. Suppose that S is linearly dependent. Then there exists T S with T < S for which Span(T ) = W. 4
5 2. Suppose that S is linearly independent. Then no set T with T < S has Span(T ) = W. Basis. Let W { 0} be a subspace of R n. Then a subset S W is a basis if and only if 1. S is linearly independent. 2. Span(S) = W. Note: Bases are not unique. Given a matrix A Mat m n (R), compute bases for Null(A), Range(A), Col(A), and Row(A). To do this, you first compute the reduced echelon form of A. Call it B. Row(A): The nonzero rows of B form a basis for Row(A). Col(A): The columns of B with the leading 1 s correspond to the columns of A which form a basis. Range(A): Since the range and column space of A agree, you compute Range(A) just as you would Col(A). Null(A): Null(A) is the set of solutions to the homogenous system A x = 0. Therefore, begin by solving A x = 0. Convert your solution to vector form. i.e., write your solution as Null(A) = Span(S). Verify that the vectors in S are linearly independent (which is usually easy to do and requires little or no justification). Theorem. Suppose that B is a basis for a subspace W or R n. Then every vector x W is expressible as linear combination of vectors from B in a unique way. 5
MATH 2331 Linear Algebra. Section 2.1 Matrix Operations. Definition: A : m n, B : n p. Example: Compute AB, if possible.
 MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
Row Space, Column Space, and Nullspace
 Row Space, Column Space, and Nullspace MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Introduction Every matrix has associated with it three vector spaces: row space
Row Space, Column Space, and Nullspace MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Introduction Every matrix has associated with it three vector spaces: row space
Solutions to Homework 5 - Math 3410
 Solutions to Homework 5 - Math 34 (Page 57: # 489) Determine whether the following vectors in R 4 are linearly dependent or independent: (a) (, 2, 3, ), (3, 7,, 2), (, 3, 7, 4) Solution From x(, 2, 3,
Solutions to Homework 5 - Math 34 (Page 57: # 489) Determine whether the following vectors in R 4 are linearly dependent or independent: (a) (, 2, 3, ), (3, 7,, 2), (, 3, 7, 4) Solution From x(, 2, 3,
The definition of a vector space (V, +, )
 The definition of a vector space (V, +, ) 1. For any u and v in V, u + v is also in V. 2. For any u and v in V, u + v = v + u. 3. For any u, v, w in V, u + ( v + w) = ( u + v) + w. 4. There is an element
The definition of a vector space (V, +, ) 1. For any u and v in V, u + v is also in V. 2. For any u and v in V, u + v = v + u. 3. For any u, v, w in V, u + ( v + w) = ( u + v) + w. 4. There is an element
Review Notes for Linear Algebra True or False Last Updated: February 22, 2010
 Review Notes for Linear Algebra True or False Last Updated: February 22, 2010 Chapter 4 [ Vector Spaces 4.1 If {v 1,v 2,,v n } and {w 1,w 2,,w n } are linearly independent, then {v 1 +w 1,v 2 +w 2,,v n
Review Notes for Linear Algebra True or False Last Updated: February 22, 2010 Chapter 4 [ Vector Spaces 4.1 If {v 1,v 2,,v n } and {w 1,w 2,,w n } are linearly independent, then {v 1 +w 1,v 2 +w 2,,v n
MATH 300, Second Exam REVIEW SOLUTIONS. NOTE: You may use a calculator for this exam- You only need something that will perform basic arithmetic.
 MATH 300, Second Exam REVIEW SOLUTIONS NOTE: You may use a calculator for this exam- You only need something that will perform basic arithmetic. [ ] [ ] 2 2. Let u = and v =, Let S be the parallelegram
MATH 300, Second Exam REVIEW SOLUTIONS NOTE: You may use a calculator for this exam- You only need something that will perform basic arithmetic. [ ] [ ] 2 2. Let u = and v =, Let S be the parallelegram
Review Notes for Midterm #2
 Review Notes for Midterm #2 Joris Vankerschaver This version: Nov. 2, 200 Abstract This is a summary of the basic definitions and results that we discussed during class. Whenever a proof is provided, I
Review Notes for Midterm #2 Joris Vankerschaver This version: Nov. 2, 200 Abstract This is a summary of the basic definitions and results that we discussed during class. Whenever a proof is provided, I
Math 2174: Practice Midterm 1
 Math 74: Practice Midterm Show your work and explain your reasoning as appropriate. No calculators. One page of handwritten notes is allowed for the exam, as well as one blank page of scratch paper.. Consider
Math 74: Practice Midterm Show your work and explain your reasoning as appropriate. No calculators. One page of handwritten notes is allowed for the exam, as well as one blank page of scratch paper.. Consider
Chapter 3. Directions: For questions 1-11 mark each statement True or False. Justify each answer.
 Chapter 3 Directions: For questions 1-11 mark each statement True or False. Justify each answer. 1. (True False) Asking whether the linear system corresponding to an augmented matrix [ a 1 a 2 a 3 b ]
Chapter 3 Directions: For questions 1-11 mark each statement True or False. Justify each answer. 1. (True False) Asking whether the linear system corresponding to an augmented matrix [ a 1 a 2 a 3 b ]
If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined
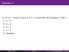 Question 1 If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined Quang T. Bach Math 18 October 18, 2017 1 / 17 Question 2 1 2 Let A = 3 4 1 2 3
Question 1 If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined Quang T. Bach Math 18 October 18, 2017 1 / 17 Question 2 1 2 Let A = 3 4 1 2 3
Math 369 Exam #2 Practice Problem Solutions
 Math 369 Exam #2 Practice Problem Solutions 2 5. Is { 2, 3, 8 } a basis for R 3? Answer: No, it is not. To show that it is not a basis, it suffices to show that this is not a linearly independent set.
Math 369 Exam #2 Practice Problem Solutions 2 5. Is { 2, 3, 8 } a basis for R 3? Answer: No, it is not. To show that it is not a basis, it suffices to show that this is not a linearly independent set.
2. Every linear system with the same number of equations as unknowns has a unique solution.
 1. For matrices A, B, C, A + B = A + C if and only if A = B. 2. Every linear system with the same number of equations as unknowns has a unique solution. 3. Every linear system with the same number of equations
1. For matrices A, B, C, A + B = A + C if and only if A = B. 2. Every linear system with the same number of equations as unknowns has a unique solution. 3. Every linear system with the same number of equations
Lecture 22: Section 4.7
 Lecture 22: Section 47 Shuanglin Shao December 2, 213 Row Space, Column Space, and Null Space Definition For an m n, a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn, the vectors r 1 = [ a 11 a 12 a 1n
Lecture 22: Section 47 Shuanglin Shao December 2, 213 Row Space, Column Space, and Null Space Definition For an m n, a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn, the vectors r 1 = [ a 11 a 12 a 1n
Practice Final Exam. Solutions.
 MATH Applied Linear Algebra December 6, 8 Practice Final Exam Solutions Find the standard matrix f the linear transfmation T : R R such that T, T, T Solution: Easy to see that the transfmation T can be
MATH Applied Linear Algebra December 6, 8 Practice Final Exam Solutions Find the standard matrix f the linear transfmation T : R R such that T, T, T Solution: Easy to see that the transfmation T can be
Kevin James. MTHSC 3110 Section 4.3 Linear Independence in Vector Sp
 MTHSC 3 Section 4.3 Linear Independence in Vector Spaces; Bases Definition Let V be a vector space and let { v. v 2,..., v p } V. If the only solution to the equation x v + x 2 v 2 + + x p v p = is the
MTHSC 3 Section 4.3 Linear Independence in Vector Spaces; Bases Definition Let V be a vector space and let { v. v 2,..., v p } V. If the only solution to the equation x v + x 2 v 2 + + x p v p = is the
MATH 152 Exam 1-Solutions 135 pts. Write your answers on separate paper. You do not need to copy the questions. Show your work!!!
 MATH Exam -Solutions pts Write your answers on separate paper. You do not need to copy the questions. Show your work!!!. ( pts) Find the reduced row echelon form of the matrix Solution : 4 4 6 4 4 R R
MATH Exam -Solutions pts Write your answers on separate paper. You do not need to copy the questions. Show your work!!!. ( pts) Find the reduced row echelon form of the matrix Solution : 4 4 6 4 4 R R
Midterm #2 Solutions
 Naneh Apkarian Math F Winter Midterm # Solutions Here is a solution key for the second midterm. The solutions presented here are more complete and thorough than your responses needed to be - in order to
Naneh Apkarian Math F Winter Midterm # Solutions Here is a solution key for the second midterm. The solutions presented here are more complete and thorough than your responses needed to be - in order to
Family Feud Review. Linear Algebra. October 22, 2013
 Review Linear Algebra October 22, 2013 Question 1 Let A and B be matrices. If AB is a 4 7 matrix, then determine the dimensions of A and B if A has 19 columns. Answer 1 Answer A is a 4 19 matrix, while
Review Linear Algebra October 22, 2013 Question 1 Let A and B be matrices. If AB is a 4 7 matrix, then determine the dimensions of A and B if A has 19 columns. Answer 1 Answer A is a 4 19 matrix, while
1 Last time: inverses
 MATH Linear algebra (Fall 8) Lecture 8 Last time: inverses The following all mean the same thing for a function f : X Y : f is invertible f is one-to-one and onto 3 For each b Y there is exactly one a
MATH Linear algebra (Fall 8) Lecture 8 Last time: inverses The following all mean the same thing for a function f : X Y : f is invertible f is one-to-one and onto 3 For each b Y there is exactly one a
MATH 2030: ASSIGNMENT 4 SOLUTIONS
 MATH 23: ASSIGNMENT 4 SOLUTIONS More on the LU factorization Q.: pg 96, q 24. Find the P t LU factorization of the matrix 2 A = 3 2 2 A.. By interchanging row and row 4 we get a matrix that may be easily
MATH 23: ASSIGNMENT 4 SOLUTIONS More on the LU factorization Q.: pg 96, q 24. Find the P t LU factorization of the matrix 2 A = 3 2 2 A.. By interchanging row and row 4 we get a matrix that may be easily
Math 102, Winter 2009, Homework 7
 Math 2, Winter 29, Homework 7 () Find the standard matrix of the linear transformation T : R 3 R 3 obtained by reflection through the plane x + z = followed by a rotation about the positive x-axes by 6
Math 2, Winter 29, Homework 7 () Find the standard matrix of the linear transformation T : R 3 R 3 obtained by reflection through the plane x + z = followed by a rotation about the positive x-axes by 6
Chapter 1. Vectors, Matrices, and Linear Spaces
 1.6 Homogeneous Systems, Subspaces and Bases 1 Chapter 1. Vectors, Matrices, and Linear Spaces 1.6. Homogeneous Systems, Subspaces and Bases Note. In this section we explore the structure of the solution
1.6 Homogeneous Systems, Subspaces and Bases 1 Chapter 1. Vectors, Matrices, and Linear Spaces 1.6. Homogeneous Systems, Subspaces and Bases Note. In this section we explore the structure of the solution
Math 123, Week 5: Linear Independence, Basis, and Matrix Spaces. Section 1: Linear Independence
 Math 123, Week 5: Linear Independence, Basis, and Matrix Spaces Section 1: Linear Independence Recall that every row on the left-hand side of the coefficient matrix of a linear system A x = b which could
Math 123, Week 5: Linear Independence, Basis, and Matrix Spaces Section 1: Linear Independence Recall that every row on the left-hand side of the coefficient matrix of a linear system A x = b which could
LINEAR ALGEBRA REVIEW
 LINEAR ALGEBRA REVIEW SPENCER BECKER-KAHN Basic Definitions Domain and Codomain. Let f : X Y be any function. This notation means that X is the domain of f and Y is the codomain of f. This means that for
LINEAR ALGEBRA REVIEW SPENCER BECKER-KAHN Basic Definitions Domain and Codomain. Let f : X Y be any function. This notation means that X is the domain of f and Y is the codomain of f. This means that for
2018 Fall 2210Q Section 013 Midterm Exam II Solution
 08 Fall 0Q Section 0 Midterm Exam II Solution True or False questions points 0 0 points) ) Let A be an n n matrix. If the equation Ax b has at least one solution for each b R n, then the solution is unique
08 Fall 0Q Section 0 Midterm Exam II Solution True or False questions points 0 0 points) ) Let A be an n n matrix. If the equation Ax b has at least one solution for each b R n, then the solution is unique
(c)
 1. Find the reduced echelon form of the matrix 1 1 5 1 8 5. 1 1 1 (a) 3 1 3 0 1 3 1 (b) 0 0 1 (c) 3 0 0 1 0 (d) 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 (e) 1 0 5 0 0 1 3 0 0 0 0 Solution. 1 1 1 1 1 1 1 1
1. Find the reduced echelon form of the matrix 1 1 5 1 8 5. 1 1 1 (a) 3 1 3 0 1 3 1 (b) 0 0 1 (c) 3 0 0 1 0 (d) 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 (e) 1 0 5 0 0 1 3 0 0 0 0 Solution. 1 1 1 1 1 1 1 1
Math 314H EXAM I. 1. (28 points) The row reduced echelon form of the augmented matrix for the system. is the matrix
 Math 34H EXAM I Do all of the problems below. Point values for each of the problems are adjacent to the problem number. Calculators may be used to check your answer but not to arrive at your answer. That
Math 34H EXAM I Do all of the problems below. Point values for each of the problems are adjacent to the problem number. Calculators may be used to check your answer but not to arrive at your answer. That
Dr. Abdulla Eid. Section 4.2 Subspaces. Dr. Abdulla Eid. MATHS 211: Linear Algebra. College of Science
 Section 4.2 Subspaces College of Science MATHS 211: Linear Algebra (University of Bahrain) Subspaces 1 / 42 Goal: 1 Define subspaces. 2 Subspace test. 3 Linear Combination of elements. 4 Subspace generated
Section 4.2 Subspaces College of Science MATHS 211: Linear Algebra (University of Bahrain) Subspaces 1 / 42 Goal: 1 Define subspaces. 2 Subspace test. 3 Linear Combination of elements. 4 Subspace generated
Math 3191 Applied Linear Algebra
 Math 9 Applied Linear Algebra Lecture : Null and Column Spaces Stephen Billups University of Colorado at Denver Math 9Applied Linear Algebra p./8 Announcements Study Guide posted HWK posted Math 9Applied
Math 9 Applied Linear Algebra Lecture : Null and Column Spaces Stephen Billups University of Colorado at Denver Math 9Applied Linear Algebra p./8 Announcements Study Guide posted HWK posted Math 9Applied
Lecture 6: Spanning Set & Linear Independency
 Lecture 6: Elif Tan Ankara University Elif Tan (Ankara University) Lecture 6 / 0 Definition (Linear Combination) Let v, v 2,..., v k be vectors in (V,, ) a vector space. A vector v V is called a linear
Lecture 6: Elif Tan Ankara University Elif Tan (Ankara University) Lecture 6 / 0 Definition (Linear Combination) Let v, v 2,..., v k be vectors in (V,, ) a vector space. A vector v V is called a linear
MATH 304 Linear Algebra Lecture 10: Linear independence. Wronskian.
 MATH 304 Linear Algebra Lecture 10: Linear independence. Wronskian. Spanning set Let S be a subset of a vector space V. Definition. The span of the set S is the smallest subspace W V that contains S. If
MATH 304 Linear Algebra Lecture 10: Linear independence. Wronskian. Spanning set Let S be a subset of a vector space V. Definition. The span of the set S is the smallest subspace W V that contains S. If
MTH 362: Advanced Engineering Mathematics
 MTH 362: Advanced Engineering Mathematics Lecture 5 Jonathan A. Chávez Casillas 1 1 University of Rhode Island Department of Mathematics September 26, 2017 1 Linear Independence and Dependence of Vectors
MTH 362: Advanced Engineering Mathematics Lecture 5 Jonathan A. Chávez Casillas 1 1 University of Rhode Island Department of Mathematics September 26, 2017 1 Linear Independence and Dependence of Vectors
MATH 1120 (LINEAR ALGEBRA 1), FINAL EXAM FALL 2011 SOLUTIONS TO PRACTICE VERSION
 MATH (LINEAR ALGEBRA ) FINAL EXAM FALL SOLUTIONS TO PRACTICE VERSION Problem (a) For each matrix below (i) find a basis for its column space (ii) find a basis for its row space (iii) determine whether
MATH (LINEAR ALGEBRA ) FINAL EXAM FALL SOLUTIONS TO PRACTICE VERSION Problem (a) For each matrix below (i) find a basis for its column space (ii) find a basis for its row space (iii) determine whether
Lecture 3q Bases for Row(A), Col(A), and Null(A) (pages )
 Lecture 3q Bases for Row(A), Col(A), and Null(A) (pages 57-6) Recall that the basis for a subspace S is a set of vectors that both spans S and is linearly independent. Moreover, we saw in section 2.3 that
Lecture 3q Bases for Row(A), Col(A), and Null(A) (pages 57-6) Recall that the basis for a subspace S is a set of vectors that both spans S and is linearly independent. Moreover, we saw in section 2.3 that
Math 221 Midterm Fall 2017 Section 104 Dijana Kreso
 The University of British Columbia Midterm October 5, 017 Group B Math 1: Matrix Algebra Section 104 (Dijana Kreso) Last Name: Student Number: First Name: Section: Format: 50 min long exam. Total: 5 marks.
The University of British Columbia Midterm October 5, 017 Group B Math 1: Matrix Algebra Section 104 (Dijana Kreso) Last Name: Student Number: First Name: Section: Format: 50 min long exam. Total: 5 marks.
3.4 Elementary Matrices and Matrix Inverse
 Math 220: Summer 2015 3.4 Elementary Matrices and Matrix Inverse A n n elementary matrix is a matrix which is obtained from the n n identity matrix I n n by a single elementary row operation. Elementary
Math 220: Summer 2015 3.4 Elementary Matrices and Matrix Inverse A n n elementary matrix is a matrix which is obtained from the n n identity matrix I n n by a single elementary row operation. Elementary
Math 4A Notes. Written by Victoria Kala Last updated June 11, 2017
 Math 4A Notes Written by Victoria Kala vtkala@math.ucsb.edu Last updated June 11, 2017 Systems of Linear Equations A linear equation is an equation that can be written in the form a 1 x 1 + a 2 x 2 +...
Math 4A Notes Written by Victoria Kala vtkala@math.ucsb.edu Last updated June 11, 2017 Systems of Linear Equations A linear equation is an equation that can be written in the form a 1 x 1 + a 2 x 2 +...
Math 313 Chapter 5 Review
 Math 313 Chapter 5 Review Howard Anton, 9th Edition May 2010 Do NOT write on me! Contents 1 5.1 Real Vector Spaces 2 2 5.2 Subspaces 3 3 5.3 Linear Independence 4 4 5.4 Basis and Dimension 5 5 5.5 Row
Math 313 Chapter 5 Review Howard Anton, 9th Edition May 2010 Do NOT write on me! Contents 1 5.1 Real Vector Spaces 2 2 5.2 Subspaces 3 3 5.3 Linear Independence 4 4 5.4 Basis and Dimension 5 5 5.5 Row
(b) The nonzero rows of R form a basis of the row space. Thus, a basis is [ ], [ ], [ ]
![(b) The nonzero rows of R form a basis of the row space. Thus, a basis is [ ], [ ], [ ] (b) The nonzero rows of R form a basis of the row space. Thus, a basis is [ ], [ ], [ ]](/thumbs/71/65565758.jpg) Exam will be on Monday, October 6, 27. The syllabus for Exam 2 consists of Sections Two.III., Two.III.2, Two.III.3, Three.I, and Three.II. You should know the main definitions, results and computational
Exam will be on Monday, October 6, 27. The syllabus for Exam 2 consists of Sections Two.III., Two.III.2, Two.III.3, Three.I, and Three.II. You should know the main definitions, results and computational
MATH 213 Linear Algebra and ODEs Spring 2015 Study Sheet for Midterm Exam. Topics
 MATH 213 Linear Algebra and ODEs Spring 2015 Study Sheet for Midterm Exam This study sheet will not be allowed during the test Books and notes will not be allowed during the test Calculators and cell phones
MATH 213 Linear Algebra and ODEs Spring 2015 Study Sheet for Midterm Exam This study sheet will not be allowed during the test Books and notes will not be allowed during the test Calculators and cell phones
Inverting Matrices. 1 Properties of Transpose. 2 Matrix Algebra. P. Danziger 3.2, 3.3
 3., 3.3 Inverting Matrices P. Danziger 1 Properties of Transpose Transpose has higher precedence than multiplication and addition, so AB T A ( B T and A + B T A + ( B T As opposed to the bracketed expressions
3., 3.3 Inverting Matrices P. Danziger 1 Properties of Transpose Transpose has higher precedence than multiplication and addition, so AB T A ( B T and A + B T A + ( B T As opposed to the bracketed expressions
Linear Algebra Practice Problems
 Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
Math 415 Exam I. Name: Student ID: Calculators, books and notes are not allowed!
 Math 415 Exam I Calculators, books and notes are not allowed! Name: Student ID: Score: Math 415 Exam I (20pts) 1. Let A be a square matrix satisfying A 2 = 2A. Find the determinant of A. Sol. From A 2
Math 415 Exam I Calculators, books and notes are not allowed! Name: Student ID: Score: Math 415 Exam I (20pts) 1. Let A be a square matrix satisfying A 2 = 2A. Find the determinant of A. Sol. From A 2
Math 3C Lecture 20. John Douglas Moore
 Math 3C Lecture 20 John Douglas Moore May 18, 2009 TENTATIVE FORMULA I Midterm I: 20% Midterm II: 20% Homework: 10% Quizzes: 10% Final: 40% TENTATIVE FORMULA II Higher of two midterms: 30% Homework: 10%
Math 3C Lecture 20 John Douglas Moore May 18, 2009 TENTATIVE FORMULA I Midterm I: 20% Midterm II: 20% Homework: 10% Quizzes: 10% Final: 40% TENTATIVE FORMULA II Higher of two midterms: 30% Homework: 10%
6. The scalar multiple of u by c, denoted by c u is (also) in V. (closure under scalar multiplication)
 Definition: A subspace of a vector space V is a subset H of V which is itself a vector space with respect to the addition and scalar multiplication in V. As soon as one verifies a), b), c) below for H,
Definition: A subspace of a vector space V is a subset H of V which is itself a vector space with respect to the addition and scalar multiplication in V. As soon as one verifies a), b), c) below for H,
Chapter 7. Linear Algebra: Matrices, Vectors,
 Chapter 7. Linear Algebra: Matrices, Vectors, Determinants. Linear Systems Linear algebra includes the theory and application of linear systems of equations, linear transformations, and eigenvalue problems.
Chapter 7. Linear Algebra: Matrices, Vectors, Determinants. Linear Systems Linear algebra includes the theory and application of linear systems of equations, linear transformations, and eigenvalue problems.
b for the linear system x 1 + x 2 + a 2 x 3 = a x 1 + x 3 = 3 x 1 + x 2 + 9x 3 = 3 ] 1 1 a 2 a
![b for the linear system x 1 + x 2 + a 2 x 3 = a x 1 + x 3 = 3 x 1 + x 2 + 9x 3 = 3 ] 1 1 a 2 a b for the linear system x 1 + x 2 + a 2 x 3 = a x 1 + x 3 = 3 x 1 + x 2 + 9x 3 = 3 ] 1 1 a 2 a](/thumbs/71/65559666.jpg) Practice Exercises for Exam Exam will be on Monday, September 8, 7. The syllabus for Exam consists of Sections One.I, One.III, Two.I, and Two.II. You should know the main definitions, results and computational
Practice Exercises for Exam Exam will be on Monday, September 8, 7. The syllabus for Exam consists of Sections One.I, One.III, Two.I, and Two.II. You should know the main definitions, results and computational
SUMMARY OF MATH 1600
 SUMMARY OF MATH 1600 Note: The following list is intended as a study guide for the final exam. It is a continuation of the study guide for the midterm. It does not claim to be a comprehensive list. You
SUMMARY OF MATH 1600 Note: The following list is intended as a study guide for the final exam. It is a continuation of the study guide for the midterm. It does not claim to be a comprehensive list. You
PRACTICE PROBLEMS FOR THE FINAL
 PRACTICE PROBLEMS FOR THE FINAL Here are a slew of practice problems for the final culled from old exams:. Let P be the vector space of polynomials of degree at most. Let B = {, (t ), t + t }. (a) Show
PRACTICE PROBLEMS FOR THE FINAL Here are a slew of practice problems for the final culled from old exams:. Let P be the vector space of polynomials of degree at most. Let B = {, (t ), t + t }. (a) Show
NAME MATH 304 Examination 2 Page 1
 NAME MATH 4 Examination 2 Page. [8 points (a) Find the following determinant. However, use only properties of determinants, without calculating directly (that is without expanding along a column or row
NAME MATH 4 Examination 2 Page. [8 points (a) Find the following determinant. However, use only properties of determinants, without calculating directly (that is without expanding along a column or row
Chapter 2 Notes, Linear Algebra 5e Lay
 Contents.1 Operations with Matrices..................................1.1 Addition and Subtraction.............................1. Multiplication by a scalar............................ 3.1.3 Multiplication
Contents.1 Operations with Matrices..................................1.1 Addition and Subtraction.............................1. Multiplication by a scalar............................ 3.1.3 Multiplication
Math 313 Chapter 1 Review
 Math 313 Chapter 1 Review Howard Anton, 9th Edition May 2010 Do NOT write on me! Contents 1 1.1 Introduction to Systems of Linear Equations 2 2 1.2 Gaussian Elimination 3 3 1.3 Matrices and Matrix Operations
Math 313 Chapter 1 Review Howard Anton, 9th Edition May 2010 Do NOT write on me! Contents 1 1.1 Introduction to Systems of Linear Equations 2 2 1.2 Gaussian Elimination 3 3 1.3 Matrices and Matrix Operations
Math 54 HW 4 solutions
 Math 54 HW 4 solutions 2.2. Section 2.2 (a) False: Recall that performing a series of elementary row operations A is equivalent to multiplying A by a series of elementary matrices. Suppose that E,...,
Math 54 HW 4 solutions 2.2. Section 2.2 (a) False: Recall that performing a series of elementary row operations A is equivalent to multiplying A by a series of elementary matrices. Suppose that E,...,
MATH 323 Linear Algebra Lecture 12: Basis of a vector space (continued). Rank and nullity of a matrix.
 MATH 323 Linear Algebra Lecture 12: Basis of a vector space (continued). Rank and nullity of a matrix. Basis Definition. Let V be a vector space. A linearly independent spanning set for V is called a basis.
MATH 323 Linear Algebra Lecture 12: Basis of a vector space (continued). Rank and nullity of a matrix. Basis Definition. Let V be a vector space. A linearly independent spanning set for V is called a basis.
Math 22 Fall 2018 Midterm 2
 Math 22 Fall 218 Midterm 2 October 23, 218 NAME: SECTION (check one box): Section 1 (S. Allen 12:5) Section 2 (A. Babei 2:1) Instructions: 1. Write your name legibly on this page, and indicate your section
Math 22 Fall 218 Midterm 2 October 23, 218 NAME: SECTION (check one box): Section 1 (S. Allen 12:5) Section 2 (A. Babei 2:1) Instructions: 1. Write your name legibly on this page, and indicate your section
SECTION 3.3. PROBLEM 22. The null space of a matrix A is: N(A) = {X : AX = 0}. Here are the calculations of AX for X = a,b,c,d, and e. =
 SECTION 3.3. PROBLEM. The null space of a matrix A is: N(A) {X : AX }. Here are the calculations of AX for X a,b,c,d, and e. Aa [ ][ ] 3 3 [ ][ ] Ac 3 3 [ ] 3 3 [ ] 4+4 6+6 Ae [ ], Ab [ ][ ] 3 3 3 [ ]
SECTION 3.3. PROBLEM. The null space of a matrix A is: N(A) {X : AX }. Here are the calculations of AX for X a,b,c,d, and e. Aa [ ][ ] 3 3 [ ][ ] Ac 3 3 [ ] 3 3 [ ] 4+4 6+6 Ae [ ], Ab [ ][ ] 3 3 3 [ ]
Math 308 Discussion Problems #4 Chapter 4 (after 4.3)
 Math 38 Discussion Problems #4 Chapter 4 (after 4.3) () (after 4.) Let S be a plane in R 3 passing through the origin, so that S is a two-dimensional subspace of R 3. Say that a linear transformation T
Math 38 Discussion Problems #4 Chapter 4 (after 4.3) () (after 4.) Let S be a plane in R 3 passing through the origin, so that S is a two-dimensional subspace of R 3. Say that a linear transformation T
MAT 242 CHAPTER 4: SUBSPACES OF R n
 MAT 242 CHAPTER 4: SUBSPACES OF R n JOHN QUIGG 1. Subspaces Recall that R n is the set of n 1 matrices, also called vectors, and satisfies the following properties: x + y = y + x x + (y + z) = (x + y)
MAT 242 CHAPTER 4: SUBSPACES OF R n JOHN QUIGG 1. Subspaces Recall that R n is the set of n 1 matrices, also called vectors, and satisfies the following properties: x + y = y + x x + (y + z) = (x + y)
Linear Algebra Exam 1 Spring 2007
 Linear Algebra Exam 1 Spring 2007 March 15, 2007 Name: SOLUTION KEY (Total 55 points, plus 5 more for Pledged Assignment.) Honor Code Statement: Directions: Complete all problems. Justify all answers/solutions.
Linear Algebra Exam 1 Spring 2007 March 15, 2007 Name: SOLUTION KEY (Total 55 points, plus 5 more for Pledged Assignment.) Honor Code Statement: Directions: Complete all problems. Justify all answers/solutions.
Find the solution set of 2x 3y = 5. Answer: We solve for x = (5 + 3y)/2. Hence the solution space consists of all vectors of the form
 Math 2 Homework #7 March 4, 2 7.3.3. Find the solution set of 2x 3y = 5. Answer: We solve for x = (5 + 3y/2. Hence the solution space consists of all vectors of the form ( ( ( ( x (5 + 3y/2 5/2 3/2 x =
Math 2 Homework #7 March 4, 2 7.3.3. Find the solution set of 2x 3y = 5. Answer: We solve for x = (5 + 3y/2. Hence the solution space consists of all vectors of the form ( ( ( ( x (5 + 3y/2 5/2 3/2 x =
Math Linear algebra, Spring Semester Dan Abramovich
 Math 52 0 - Linear algebra, Spring Semester 2012-2013 Dan Abramovich Fields. We learned to work with fields of numbers in school: Q = fractions of integers R = all real numbers, represented by infinite
Math 52 0 - Linear algebra, Spring Semester 2012-2013 Dan Abramovich Fields. We learned to work with fields of numbers in school: Q = fractions of integers R = all real numbers, represented by infinite
Math 2030 Assignment 5 Solutions
 Math 030 Assignment 5 Solutions Question 1: Which of the following sets of vectors are linearly independent? If the set is linear dependent, find a linear dependence relation for the vectors (a) {(1, 0,
Math 030 Assignment 5 Solutions Question 1: Which of the following sets of vectors are linearly independent? If the set is linear dependent, find a linear dependence relation for the vectors (a) {(1, 0,
MATH 20F: LINEAR ALGEBRA LECTURE B00 (T. KEMP)
 MATH 20F: LINEAR ALGEBRA LECTURE B00 (T KEMP) Definition 01 If T (x) = Ax is a linear transformation from R n to R m then Nul (T ) = {x R n : T (x) = 0} = Nul (A) Ran (T ) = {Ax R m : x R n } = {b R m
MATH 20F: LINEAR ALGEBRA LECTURE B00 (T KEMP) Definition 01 If T (x) = Ax is a linear transformation from R n to R m then Nul (T ) = {x R n : T (x) = 0} = Nul (A) Ran (T ) = {Ax R m : x R n } = {b R m
Math 4377/6308 Advanced Linear Algebra
 2. Linear Transformations Math 4377/638 Advanced Linear Algebra 2. Linear Transformations, Null Spaces and Ranges Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu math.uh.edu/
2. Linear Transformations Math 4377/638 Advanced Linear Algebra 2. Linear Transformations, Null Spaces and Ranges Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu math.uh.edu/
Sept. 26, 2013 Math 3312 sec 003 Fall 2013
 Sept. 26, 2013 Math 3312 sec 003 Fall 2013 Section 4.1: Vector Spaces and Subspaces Definition A vector space is a nonempty set V of objects called vectors together with two operations called vector addition
Sept. 26, 2013 Math 3312 sec 003 Fall 2013 Section 4.1: Vector Spaces and Subspaces Definition A vector space is a nonempty set V of objects called vectors together with two operations called vector addition
MATH 240 Spring, Chapter 1: Linear Equations and Matrices
 MATH 240 Spring, 2006 Chapter Summaries for Kolman / Hill, Elementary Linear Algebra, 8th Ed. Sections 1.1 1.6, 2.1 2.2, 3.2 3.8, 4.3 4.5, 5.1 5.3, 5.5, 6.1 6.5, 7.1 7.2, 7.4 DEFINITIONS Chapter 1: Linear
MATH 240 Spring, 2006 Chapter Summaries for Kolman / Hill, Elementary Linear Algebra, 8th Ed. Sections 1.1 1.6, 2.1 2.2, 3.2 3.8, 4.3 4.5, 5.1 5.3, 5.5, 6.1 6.5, 7.1 7.2, 7.4 DEFINITIONS Chapter 1: Linear
Lecture 13: Row and column spaces
 Spring 2018 UW-Madison Lecture 13: Row and column spaces 1 The column space of a matrix 1.1 Definition The column space of matrix A denoted as Col(A) is the space consisting of all linear combinations
Spring 2018 UW-Madison Lecture 13: Row and column spaces 1 The column space of a matrix 1.1 Definition The column space of matrix A denoted as Col(A) is the space consisting of all linear combinations
1 Systems of equations
 Highlights from linear algebra David Milovich, Math 2 TA for sections -6 November, 28 Systems of equations A leading entry in a matrix is the first (leftmost) nonzero entry of a row. For example, the leading
Highlights from linear algebra David Milovich, Math 2 TA for sections -6 November, 28 Systems of equations A leading entry in a matrix is the first (leftmost) nonzero entry of a row. For example, the leading
Worksheet for Lecture 15 (due October 23) Section 4.3 Linearly Independent Sets; Bases
 Worksheet for Lecture 5 (due October 23) Name: Section 4.3 Linearly Independent Sets; Bases Definition An indexed set {v,..., v n } in a vector space V is linearly dependent if there is a linear relation
Worksheet for Lecture 5 (due October 23) Name: Section 4.3 Linearly Independent Sets; Bases Definition An indexed set {v,..., v n } in a vector space V is linearly dependent if there is a linear relation
7.6 The Inverse of a Square Matrix
 7.6 The Inverse of a Square Matrix Copyright Cengage Learning. All rights reserved. What You Should Learn Verify that two matrices are inverses of each other. Use Gauss-Jordan elimination to find inverses
7.6 The Inverse of a Square Matrix Copyright Cengage Learning. All rights reserved. What You Should Learn Verify that two matrices are inverses of each other. Use Gauss-Jordan elimination to find inverses
Fall 2016 MATH*1160 Final Exam
 Fall 2016 MATH*1160 Final Exam Last name: (PRINT) First name: Student #: Instructor: M. R. Garvie Dec 16, 2016 INSTRUCTIONS: 1. The exam is 2 hours long. Do NOT start until instructed. You may use blank
Fall 2016 MATH*1160 Final Exam Last name: (PRINT) First name: Student #: Instructor: M. R. Garvie Dec 16, 2016 INSTRUCTIONS: 1. The exam is 2 hours long. Do NOT start until instructed. You may use blank
Study Guide for Linear Algebra Exam 2
 Study Guide for Linear Algebra Exam 2 Term Vector Space Definition A Vector Space is a nonempty set V of objects, on which are defined two operations, called addition and multiplication by scalars (real
Study Guide for Linear Algebra Exam 2 Term Vector Space Definition A Vector Space is a nonempty set V of objects, on which are defined two operations, called addition and multiplication by scalars (real
Vector space and subspace
 Vector space and subspace Math 112, week 8 Goals: Vector space, subspace, span. Null space, column space. Linearly independent, bases. Suggested Textbook Readings: Sections 4.1, 4.2, 4.3 Week 8: Vector
Vector space and subspace Math 112, week 8 Goals: Vector space, subspace, span. Null space, column space. Linearly independent, bases. Suggested Textbook Readings: Sections 4.1, 4.2, 4.3 Week 8: Vector
ORIE 6300 Mathematical Programming I August 25, Recitation 1
 ORIE 6300 Mathematical Programming I August 25, 2016 Lecturer: Calvin Wylie Recitation 1 Scribe: Mateo Díaz 1 Linear Algebra Review 1 1.1 Independence, Spanning, and Dimension Definition 1 A (usually infinite)
ORIE 6300 Mathematical Programming I August 25, 2016 Lecturer: Calvin Wylie Recitation 1 Scribe: Mateo Díaz 1 Linear Algebra Review 1 1.1 Independence, Spanning, and Dimension Definition 1 A (usually infinite)
Homework 11/Solutions. (Section 6.8 Exercise 3). Which pairs of the following vector spaces are isomorphic?
 MTH 9-4 Linear Algebra I F Section Exercises 6.8,4,5 7.,b 7.,, Homework /Solutions (Section 6.8 Exercise ). Which pairs of the following vector spaces are isomorphic? R 7, R, M(, ), M(, 4), M(4, ), P 6,
MTH 9-4 Linear Algebra I F Section Exercises 6.8,4,5 7.,b 7.,, Homework /Solutions (Section 6.8 Exercise ). Which pairs of the following vector spaces are isomorphic? R 7, R, M(, ), M(, 4), M(4, ), P 6,
Math 54. Selected Solutions for Week 5
 Math 54. Selected Solutions for Week 5 Section 4. (Page 94) 8. Consider the following two systems of equations: 5x + x 3x 3 = 5x + x 3x 3 = 9x + x + 5x 3 = 4x + x 6x 3 = 9 9x + x + 5x 3 = 5 4x + x 6x 3
Math 54. Selected Solutions for Week 5 Section 4. (Page 94) 8. Consider the following two systems of equations: 5x + x 3x 3 = 5x + x 3x 3 = 9x + x + 5x 3 = 4x + x 6x 3 = 9 9x + x + 5x 3 = 5 4x + x 6x 3
YORK UNIVERSITY. Faculty of Science Department of Mathematics and Statistics MATH M Test #1. July 11, 2013 Solutions
 YORK UNIVERSITY Faculty of Science Department of Mathematics and Statistics MATH 222 3. M Test # July, 23 Solutions. For each statement indicate whether it is always TRUE or sometimes FALSE. Note: For
YORK UNIVERSITY Faculty of Science Department of Mathematics and Statistics MATH 222 3. M Test # July, 23 Solutions. For each statement indicate whether it is always TRUE or sometimes FALSE. Note: For
1. What is the determinant of the following matrix? a 1 a 2 4a 3 2a 2 b 1 b 2 4b 3 2b c 1. = 4, then det
 What is the determinant of the following matrix? 3 4 3 4 3 4 4 3 A 0 B 8 C 55 D 0 E 60 If det a a a 3 b b b 3 c c c 3 = 4, then det a a 4a 3 a b b 4b 3 b c c c 3 c = A 8 B 6 C 4 D E 3 Let A be an n n matrix
What is the determinant of the following matrix? 3 4 3 4 3 4 4 3 A 0 B 8 C 55 D 0 E 60 If det a a a 3 b b b 3 c c c 3 = 4, then det a a 4a 3 a b b 4b 3 b c c c 3 c = A 8 B 6 C 4 D E 3 Let A be an n n matrix
Problem 1: Solving a linear equation
 Math 38 Practice Final Exam ANSWERS Page Problem : Solving a linear equation Given matrix A = 2 2 3 7 4 and vector y = 5 8 9. (a) Solve Ax = y (if the equation is consistent) and write the general solution
Math 38 Practice Final Exam ANSWERS Page Problem : Solving a linear equation Given matrix A = 2 2 3 7 4 and vector y = 5 8 9. (a) Solve Ax = y (if the equation is consistent) and write the general solution
LECTURES 14/15: LINEAR INDEPENDENCE AND BASES
 LECTURES 14/15: LINEAR INDEPENDENCE AND BASES MA1111: LINEAR ALGEBRA I, MICHAELMAS 2016 1. Linear Independence We have seen in examples of span sets of vectors that sometimes adding additional vectors
LECTURES 14/15: LINEAR INDEPENDENCE AND BASES MA1111: LINEAR ALGEBRA I, MICHAELMAS 2016 1. Linear Independence We have seen in examples of span sets of vectors that sometimes adding additional vectors
Math 290, Midterm II-key
 Math 290, Midterm II-key Name (Print): (first) Signature: (last) The following rules apply: There are a total of 20 points on this 50 minutes exam. This contains 7 pages (including this cover page) and
Math 290, Midterm II-key Name (Print): (first) Signature: (last) The following rules apply: There are a total of 20 points on this 50 minutes exam. This contains 7 pages (including this cover page) and
Math 54 First Midterm Exam, Prof. Srivastava September 23, 2016, 4:10pm 5:00pm, 155 Dwinelle Hall.
 Math 54 First Midterm Exam, Prof Srivastava September 23, 26, 4:pm 5:pm, 55 Dwinelle Hall Name: SID: Instructions: Write all answers in the provided space This exam includes two pages of scratch paper,
Math 54 First Midterm Exam, Prof Srivastava September 23, 26, 4:pm 5:pm, 55 Dwinelle Hall Name: SID: Instructions: Write all answers in the provided space This exam includes two pages of scratch paper,
Math Linear Algebra Final Exam Review Sheet
 Math 15-1 Linear Algebra Final Exam Review Sheet Vector Operations Vector addition is a component-wise operation. Two vectors v and w may be added together as long as they contain the same number n of
Math 15-1 Linear Algebra Final Exam Review Sheet Vector Operations Vector addition is a component-wise operation. Two vectors v and w may be added together as long as they contain the same number n of
Chapter 3. Vector spaces
 Chapter 3. Vector spaces Lecture notes for MA1111 P. Karageorgis pete@maths.tcd.ie 1/22 Linear combinations Suppose that v 1,v 2,...,v n and v are vectors in R m. Definition 3.1 Linear combination We say
Chapter 3. Vector spaces Lecture notes for MA1111 P. Karageorgis pete@maths.tcd.ie 1/22 Linear combinations Suppose that v 1,v 2,...,v n and v are vectors in R m. Definition 3.1 Linear combination We say
1. Determine by inspection which of the following sets of vectors is linearly independent. 3 3.
 1. Determine by inspection which of the following sets of vectors is linearly independent. (a) (d) 1, 3 4, 1 { [ [,, 1 1] 3]} (b) 1, 4 5, (c) 3 6 (e) 1, 3, 4 4 3 1 4 Solution. The answer is (a): v 1 is
1. Determine by inspection which of the following sets of vectors is linearly independent. (a) (d) 1, 3 4, 1 { [ [,, 1 1] 3]} (b) 1, 4 5, (c) 3 6 (e) 1, 3, 4 4 3 1 4 Solution. The answer is (a): v 1 is
Linear Independence. Linear Algebra MATH Linear Algebra LI or LD Chapter 1, Section 7 1 / 1
 Linear Independence Linear Algebra MATH 76 Linear Algebra LI or LD Chapter, Section 7 / Linear Combinations and Span Suppose s, s,..., s p are scalars and v, v,..., v p are vectors (all in the same space
Linear Independence Linear Algebra MATH 76 Linear Algebra LI or LD Chapter, Section 7 / Linear Combinations and Span Suppose s, s,..., s p are scalars and v, v,..., v p are vectors (all in the same space
MATH 1553, SPRING 2018 SAMPLE MIDTERM 2 (VERSION B), 1.7 THROUGH 2.9
 MATH 155, SPRING 218 SAMPLE MIDTERM 2 (VERSION B), 1.7 THROUGH 2.9 Name Section 1 2 4 5 Total Please read all instructions carefully before beginning. Each problem is worth 1 points. The maximum score
MATH 155, SPRING 218 SAMPLE MIDTERM 2 (VERSION B), 1.7 THROUGH 2.9 Name Section 1 2 4 5 Total Please read all instructions carefully before beginning. Each problem is worth 1 points. The maximum score
Math 2114 Common Final Exam May 13, 2015 Form A
 Math 4 Common Final Exam May 3, 5 Form A Instructions: Using a # pencil only, write your name and your instructor s name in the blanks provided. Write your student ID number and your CRN in the blanks
Math 4 Common Final Exam May 3, 5 Form A Instructions: Using a # pencil only, write your name and your instructor s name in the blanks provided. Write your student ID number and your CRN in the blanks
ICS 6N Computational Linear Algebra Vector Space
 ICS 6N Computational Linear Algebra Vector Space Xiaohui Xie University of California, Irvine xhx@uci.edu Xiaohui Xie (UCI) ICS 6N 1 / 24 Vector Space Definition: A vector space is a non empty set V of
ICS 6N Computational Linear Algebra Vector Space Xiaohui Xie University of California, Irvine xhx@uci.edu Xiaohui Xie (UCI) ICS 6N 1 / 24 Vector Space Definition: A vector space is a non empty set V of
The scope of the midterm exam is up to and includes Section 2.1 in the textbook (homework sets 1-4). Below we highlight some of the important items.
 AMS 10: Review for the Midterm Exam The scope of the midterm exam is up to and includes Section 2.1 in the textbook (homework sets 1-4). Below we highlight some of the important items. Complex numbers
AMS 10: Review for the Midterm Exam The scope of the midterm exam is up to and includes Section 2.1 in the textbook (homework sets 1-4). Below we highlight some of the important items. Complex numbers
GENERAL VECTOR SPACES AND SUBSPACES [4.1]
![GENERAL VECTOR SPACES AND SUBSPACES [4.1] GENERAL VECTOR SPACES AND SUBSPACES [4.1]](/thumbs/79/79367558.jpg) GENERAL VECTOR SPACES AND SUBSPACES [4.1] General vector spaces So far we have seen special spaces of vectors of n dimensions denoted by R n. It is possible to define more general vector spaces A vector
GENERAL VECTOR SPACES AND SUBSPACES [4.1] General vector spaces So far we have seen special spaces of vectors of n dimensions denoted by R n. It is possible to define more general vector spaces A vector
Lecture 14: Orthogonality and general vector spaces. 2 Orthogonal vectors, spaces and matrices
 Lecture 14: Orthogonality and general vector spaces 1 Symmetric matrices Recall the definition of transpose A T in Lecture note 9. Definition 1.1. If a square matrix S satisfies then we say S is a symmetric
Lecture 14: Orthogonality and general vector spaces 1 Symmetric matrices Recall the definition of transpose A T in Lecture note 9. Definition 1.1. If a square matrix S satisfies then we say S is a symmetric
Midterm 1 Review. Written by Victoria Kala SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015
 Midterm 1 Review Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015 Summary This Midterm Review contains notes on sections 1.1 1.5 and 1.7 in your
Midterm 1 Review Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015 Summary This Midterm Review contains notes on sections 1.1 1.5 and 1.7 in your
Math 308 Practice Final Exam Page and vector y =
 Math 308 Practice Final Exam Page Problem : Solving a linear equation 2 0 2 5 Given matrix A = 3 7 0 0 and vector y = 8. 4 0 0 9 (a) Solve Ax = y (if the equation is consistent) and write the general solution
Math 308 Practice Final Exam Page Problem : Solving a linear equation 2 0 2 5 Given matrix A = 3 7 0 0 and vector y = 8. 4 0 0 9 (a) Solve Ax = y (if the equation is consistent) and write the general solution
Elementary maths for GMT
 Elementary maths for GMT Linear Algebra Part 2: Matrices, Elimination and Determinant m n matrices The system of m linear equations in n variables x 1, x 2,, x n a 11 x 1 + a 12 x 2 + + a 1n x n = b 1
Elementary maths for GMT Linear Algebra Part 2: Matrices, Elimination and Determinant m n matrices The system of m linear equations in n variables x 1, x 2,, x n a 11 x 1 + a 12 x 2 + + a 1n x n = b 1
Lecture 03. Math 22 Summer 2017 Section 2 June 26, 2017
 Lecture 03 Math 22 Summer 2017 Section 2 June 26, 2017 Just for today (10 minutes) Review row reduction algorithm (40 minutes) 1.3 (15 minutes) Classwork Review row reduction algorithm Review row reduction
Lecture 03 Math 22 Summer 2017 Section 2 June 26, 2017 Just for today (10 minutes) Review row reduction algorithm (40 minutes) 1.3 (15 minutes) Classwork Review row reduction algorithm Review row reduction
MTH501- Linear Algebra MCQS MIDTERM EXAMINATION ~ LIBRIANSMINE ~
 MTH501- Linear Algebra MCQS MIDTERM EXAMINATION ~ LIBRIANSMINE ~ Question No: 1 (Marks: 1) If for a linear transformation the equation T(x) =0 has only the trivial solution then T is One-to-one Onto Question
MTH501- Linear Algebra MCQS MIDTERM EXAMINATION ~ LIBRIANSMINE ~ Question No: 1 (Marks: 1) If for a linear transformation the equation T(x) =0 has only the trivial solution then T is One-to-one Onto Question
Linear Algebra I Lecture 8
 Linear Algebra I Lecture 8 Xi Chen 1 1 University of Alberta January 25, 2019 Outline 1 2 Gauss-Jordan Elimination Given a system of linear equations f 1 (x 1, x 2,..., x n ) = 0 f 2 (x 1, x 2,..., x n
Linear Algebra I Lecture 8 Xi Chen 1 1 University of Alberta January 25, 2019 Outline 1 2 Gauss-Jordan Elimination Given a system of linear equations f 1 (x 1, x 2,..., x n ) = 0 f 2 (x 1, x 2,..., x n
What is on this week. 1 Vector spaces (continued) 1.1 Null space and Column Space of a matrix
 Professor Joana Amorim, jamorim@bu.edu What is on this week Vector spaces (continued). Null space and Column Space of a matrix............................. Null Space...........................................2
Professor Joana Amorim, jamorim@bu.edu What is on this week Vector spaces (continued). Null space and Column Space of a matrix............................. Null Space...........................................2
Math 3108: Linear Algebra
 Math 3108: Linear Algebra Instructor: Jason Murphy Department of Mathematics and Statistics Missouri University of Science and Technology 1 / 323 Contents. Chapter 1. Slides 3 70 Chapter 2. Slides 71 118
Math 3108: Linear Algebra Instructor: Jason Murphy Department of Mathematics and Statistics Missouri University of Science and Technology 1 / 323 Contents. Chapter 1. Slides 3 70 Chapter 2. Slides 71 118
