Overview. Regular Languages. Finite Automata. A finite automaton. Startstate : q Acceptstate : q. Transitions
|
|
|
- Crystal Simon
- 6 years ago
- Views:
Transcription
1 Overvew Regulr Lnguges Andres Krwth & Mlte Helmert Determnstc fnte utomt Regulr lnguges Nondetermnstc fnte utomt Closure oertons Regulr exressons Nonregulr lnguges The umng lemm 2 Fnte Automt A fnte utomton An ntutve exmle : suermrket door controller Fgure.4 Formlly front d door rer d To vew of n utomtc door Prolstc counterrts exst Mrkov chns, Byesn nets, etc. Not n ths course rer oth nether closed Trnston tle for the utomtc door controler: closed oen front nether nether closed closed oen front oen oen front rer oth Stte dgrm for the utomtc door controler rer closed oen oth closed oen 3 q, Sttes : q, q, q 2 3 Strtstte : q Accetstte : q Trnstons Outut : ccet or reject 2 q 3 A fnte utomton s 5-tule ( Q, Σ, δ, q, F). Qs fnte set of sttes 2. Σ s fnte set, the lhet 3. δ : Q Σ Qs the trnston functon 4. q Q s the strt stte o 5. F Qs the set of ccet sttes 4
2 q q 3 As the lnguge of mchne M we wrte LM ( ) = A A= { w wcontns t lest one nd n even numer of s follows the lst } Descre M Q= { q, q, q } 2 3 Σ= {,} δ defned y q strt stte F = { q } q q q q q q q q q 2 q Stte dgrm of the two-stte fnte utomton M 2 q Stte dgrm of the two-stte fnte utomton M Other exmles Another exmle 7,8,9 A generlston : A s the lnguge of ll strngs where the sum of the numers s multle of excet tht the sum s reset to whenever the symol reset ers Automton B =. Q = { q,..., q } 2. Σ ={,,2, reset } 3. δ ( q,) = q j δ ( q,) = q where k = ( j+ ) mod j δ ( q, 2) = q where k = ( j+ 2) mod j δ ( q, reset ) = q j k j k 4. q Q s strt nd ccet stte o 7 8
3 Forml defnton of comutton Desgnng fnte utomt Let M e fnte utomton ( Q, Σ, δ, q, F) Let w= w... w e strng over Σ M ccets wf sequence of sttes r,..., r exsts n Q such tht. r δ ( r, w ) = r for ll =,..., n 3. r F n = q n n Desgn utomton for lnguge consstng of nry strngs wth n odd numer of s Desgn frst sttes Then trnstons q even Strt stte nd ccet sttes q odd M recognzes lnguge Af A= { w M ccets w} A lnguge s regulr f some fnte utomton recognzes t. 9 Another exmle Another exmle Desgn n utomton to recognze the lnguge of nry strngs contnng the strng s sustrng We hve four ossltes:. we hven t seen ny symol of the ttern yet, or 2. we hve seen, or 3. we hve seen, or 4. we hve seen the ttern Desgn n utomton to recognze the lnguge of nry strngs contnng the strng s sustrng We hve four ossltes:. we hven t seen ny symol of the ttern yet, or 2. we hve seen, or 3. we hve seen, or 4. we hve seen the ttern q q, q q 2
4 The Regulr Oertons Regulr lnguges re closed under Let A nd B e lnguges We defne : Unon : A B= { x x A or x B} Conctenton : Ao B= { xy x A nd y B} Str : A = { xx2... xn n nd ech x A} note: lwys A A set S s closed under n oerton of lyng oon elements of S yelds elements of S. Exmle: multlcton on nturl numers Counterexmle :dvson of nturl numers Exmle A = { good, d} B = { oy, grl} A B= { good, d, oy, grl} Ao B = { goodoy, goodgrl, doy, dgrl} Theorem.2 The clss of the regulr lnguges s closed under the unon oerton. In other words, f A nd A re regulr lnguges, so s A A 2 2 A = {, good, d, goodgood, goodd, dgood, dd, goodgoodgood, goodgoodd,...} 4 5 Proof.2 (y constructon) Let M recognze A, where M = (Q, Σ, δ,q,f ), nd M recognze A, where M = (Q, Σδ,,q,F ) Construct M to recognze A A, where M = (Q, Σ,δ, q,f ). { }. Q = (r,r ) r Q nd r Q Ths set s the Crtesn roduct of sets Q nd Q (wrtten Q Q ) It s the set of ll rs of sttes, the frst from Q nd the second from Q Σ, the lhet, s the sme s n M nd M. The theorem remns true f they hve dfferent lhets, Σ nd Σ. We would then modfy the roof to let Σ = Σ Σ δ, the trnston functon, s defned s follows. For ech (r,r ) Q nd ech Σ, let δ(( r,r ), ) = ( δ ( r, ), δ ( r, )) Hence δ gets stte of M (whch ctully s r of sttes from M nd M ), together wth n nut symol, nd returns M's next stte. 4. q s the r (q,q ) F M M2 5. s the set of rs n whch ether memer s n ccet stte of nd. We cn wrte t s F = {(r,r ) r F or r F } Ths exresson s the sme s F = (F Q ) (Q F ) Note tht t s not the sme s F = F F. Wht would tht gve us? 6 7
5 Exmle M wth L(M ) = {w w contns }, q M = ( Q, Σ, δ, q, F) constructed from M = ( Q, Σ, δ, q, F) nd M = ( Q, Σ, δ, q, F ) Defne. Q= {( r, r ) r Q nd r Q } 2. Σ=Σ Σ δ(( r, r ), ) = ( δ ( r, ), δ ( r, )) q = ( q, q ) 2 5. F = {( r, r ) r F or r F } M 2 wth L(M 2 ) = {w w contns t lest two s}, 2 3 Theorem.3 The clss of the regulr lnguges s closed under the conctenton oerton. In other words, f A nd A re regulr lnguges, so s A o A Non determnstc fnte utomt Determnstc versus non determnstc comutton Determnstc One successor stte trnstons not llowed Non determnstc Severl successor sttes ossle trnstons ossle Fgure 5,,, q q 3 q 4 2 2
6 Another NFA,, q, q 3 q 4 q q Inut: w = q q 3 q q 3 q q 3 q 4 q q 3 q 4 q 4 q q 3 q 4 q Nondetermnstc fnte utomton Exmle A nondetermnstc fnte utomton s 5-tule ( Q, Σ, δ, q, F). Qs fnte set of sttes 2. Σ s fnte set, the lhet 3. δ : Q Σ P( Q) s the trnston functon 4. q Q s the strt stte o 5. F Qs the set of ccet sttes Σ ncludes P( Q) the owerset of Q,,, q q 3 q 4. Q= { q, q, q, q } Σ = {,} 3. δ s gven s: q { q} { q, q } {} 2 q { q } {} { q } q {} { q } {} 3 4 q { q } { q } {} q s the strt stte 5. F = { q }
7 Forml defnton of comutton Every NFA hs n equvlent DFA Let M e nondetermnstc fnte utomton ( Q, Σ, δ, q, F) Let w= w... w e strng over Σ n M ccets wf sequence of sttes r,..., r exsts n Q such tht. r = q 2. r δ ( r, w ) for ll =,..., n r n F n Equvlence NFA nd DFA Proof: Theorem.9 Two mchnes re equvlent f they recognze the sme lnguge Theorem.9 Every nondetermnstc fnte utomton hs n equvlent fnte utomton Let N = (Q, Σ, δ,q,f ) e the NFA recognzng some lnguge A. Construct DFA M recognzng A. Frst we consder the eser cse wheren N hs no rrows. The rrows re tken nto ccount lter. Corollry.2 A lnguge s regulr f nd onl y f some nondetermnstc fnte utomton recognzes t
8 Proof: Theorem.9 (cont.) Proof: Theorem.9 (cont.) ' ' Construct M = (Q', Σ, δ,q,f').. Q' = P(Q ). Every stte of M s set of sttes of N. (Recll tht P(Q) s the ower set of Q). 2. For R Q' nd Σ let δ '(R,) = {q Q q δ(r,) for some r R}. If R s stte of M, t s lso set of sttes of N. When M reds symol n stte R, t shows where tkes ech stte n R. Becuse ech stte leds to to set of sttes, we tke the unon of ll these sets. Alterntvly we wrte: 3. q = {q }. ' U δ '( R, ) = δ( r, ). r R M strts n the stte corresondng to the collecton contnng just the strt stte of N. 4. F' = {R Q' R contns n ccet stte of N }. The mchne M ccets f one of the ossle sttes tht N could e n t ths ont s n ccet stte. Now for the rrows one needs to set u n extr t of notton. For ny stte R of M we defne E(R) to e the collecton of sttes tht cn e reched from R y gong only long rrows, ncludng the memers of R themselves. Formlly, for R Q let E( R ) = { q q cn e reched from R y trvelng long or more rrows }. The trnston functon of M s then modfed to tke nt o ccount ll sttes tht cn e reched y gong long rrows fter every ste. Relcng δ(r,) y E( δ(r, )) cheves ths. Thus δ '( R, ) = { q Q q E( δ( r, )) for some r R }. Addtonlly the strt stte of M hs to e modfed to cter for ll ossle sttes tht cn e reched from the strt stte of N long the rrows. Chngng q to e E({q }) cheves ths effect. ' We hve now comleted the constructon of the DFA M tht smultes the NFA N. 3 3 An exmle An exmle The resultng DFA The resultng DFA fter removng redundnt sttes 32 33
9 Closure under the regulr oertons Proof de Theorem.2/.22 The clss of the regulr lnguges s closed under the unon oerton. In other words, f A nd A re regulr lnguges, so s A A 2 2 Theorem.23 The clss of the regulr lnguges s closed under the conctenton oerton. Theorem.2/.22 The clss of the regulr lnguges s closed under the unon oerton. In other words, f A nd A re regulr lnguges, so s A A 2 2 Theorem.24 The clss of the regulr lnguges s closed under the str oerton Proof.2/.22 Proof de Let N = (Q, Σ, δ,q,f ) recognze A, nd N = (Q, Σ, δ,q,f ) recognze A Construct N = (Q, Σ, δ,q,f ) to recognze A A. 2 Theorem.23 The clss of the regulr lnguges s closed under the conctenton oerton.. Q = {q } Q Q. 2 The sttes of N re ll the sttes of N nd N, wth the ddton of new strt stte q. 2. The stte q s the strt stte of N. 3. The ccet sttes F = F F. 2 2 The ccet sttes of N re ll the ccet sttes of N nd N. Tht wy N ccets f ether N ccets or N ccets Defne δ so tht for ny q Q nd ny Σ, δ(q,) q Q δ2(q,) q Q2 δ (q,) = {q,} q= q nd = q = q nd
10 Proof.23 Proof de Let N = (Q, Σ, δ,q,f ) recognze A, nd N = (Q, Σ, δ,q,f ) recognze A Construct N = (Q, Σ, δ,q,f ) to recognze A o A. 2 2 Theorem.24 The clss of the regulr lnguges s closed under the str oerton.. Q = Q Q. 2 The sttes of N re ll the sttes of N nd N The stte q s the sme s the strt stte of N. 3. The ccet sttes F re the sme s the ccet sttes of N Defne δ so tht for ny q Q nd ny Σ, δ(q,) q Q nd q F δ (q,) q F nd δ (q,) = δ (q,) {q 2} q = F nd = δ (q,) q Q Proof.24 Regulr exressons Let N = (Q, Σ, δ,q,f ) recognze A. Construct N = (Q, Σ, δ,q,f ) recognze A.. Q = {q } Q. The sttes of N re the sttes of N lus new strt stte. 2. The stte q s the new strt stte. 3. F = {q } F The ccet sttes re the old ccet sttes lus the new strt stte. 4. Defne δ so tht for ny q Q nd ny Σ, δ(q,) q Q nd q F δ (q,) q F nd δ (q,) = δ (q,) {q } q F nd = {q } q= q nd = q = q nd Defnton Sy tht R s regulr exresson f R s. for some n the lhet Σ, 2., 3., 4. (R R ), where R nd R re regulr exressons, (R o R ), where R nd R re regulr exressons, or R, where Rs regulr exresson. 4 4
11 RE Exmles RE Exmles (cont.) In the followng exmles we ssume tht the lhet Σ s {,}.. = {w whs exctly sngle }. 2. Σ Σ = {w w hs t lest one }. 3. Σ Σ = { w w contns the strng s sustrng }. 4. ( ΣΣ) = {w w s strng of even length }. 5. ( ΣΣΣ ) = {w the length of w s multle of three }. 6. = {, }. 7. Σ Σ = { w w strts nd ends wth the sme symol }. 8. ( )( ) =. The exresson descres the lnguge {, }, so the conctenton oerton dds ether or efore every strng n. 9. ( )( ) = {,,,}.. =. Conctentng the emty set to ny set yelds the emty set.. = { }. The str oerton uts together ny numer of strngs from the lnguge to get strng n the result. If the lnguge s emty, the str oerton cn ut together strng, gvng only the emty strng. R = R Ro = R R Ro R R Alctons Equvlence RE nd NFA Desgn of comlers { +,, }( DD DD. D D. DD ) where D = {,...,9} Theorem.28 A lnguge s regulr f nd only f some regulr exresson descres t Proof through : wk, gre, v n unx (serch for strngs) Perl, Python, or Jv rogrmmng lnguges Bonformtcs So clled motfs (tterns occurrng n sequences, e.g. rotens) Lemm.29 If lnguge s descred y some regulr exresson, then t s regulr Lemm.32 If lnguge s regulr, then t s descred y some regulr exresson 44 45
12 Proof for Lemm.29 (cont.) Proof for Lemm.29 (cont.) 2. R =. Then L(R) = { }, nd the followng NFA recognzes L(R). 3. R =. Then L(R) =, nd the followng NFA recognzes L(R). Formlly, N = ({q }, Σ, δ,q,{q }), where δ (r,) = for ny r nd. Formlly, N = ({q}, Σ, δ,q, ), where δ (r,) = for ny r nd Proof for Lemm.29 (cont.) Exmle.3 4. R= R R R= Ro R R = R. For the lst three cses we use the constructons gven n the roofs tht the clss of regulr lnguges s closed under the regulr oertons. In other words, we construct the NFA for R from the NFAs for R nd R (or just R n cse 6) nd the rorte closure constructon. 2 We convert the regulr exresson ( ) to n NFA n sequence of stges. We uld u from the smllest suexressons to lrger suexressons untl we hve n NFA for the orgnl exresson, s shown n the followng dgrm. Note tht ths rocedure generlly doesn't gve the NFA wth the fewest sttes! 49 5
13 Exmle: NFA for: ( ) Exercse: NFA for: ( ) : : : : : ( ) ( ) 5 52 Exmle: NFA for: ( ) (cont.) : Lemm.32 If lnguge s regulr, then t s descred y some regulr exresson ( ): Two stes DFA nto GNFA (generlzed nondetermnstc fnte utomton) Convert GNFA nto regulr exresson 53 54
14 GNFAs Formlly Lels re regulr exressons Two sttes q nd r re connected n oth drectons (fully connected) Exceton : One drecton only Strt stte (extng trnston rrows) Accet stte (only one!) (only ncomng trnston rrows) q strt Ø () q ccet 55 A generlzed nondetermnstc fnte utomton s 5-tule ( Q, Σ, δ, q, q ). Qs fnte set of sttes 2. Σ s fnte set, the lhet 3. δ : ( Q { q }) ( Q { q }) R s the trnston functon ccet 4. q Q s the strt stte strt strt 56 strt ccet 5. qccet Q the ccet stte A GNFA ccets w= w... wk where ech w Σ f sequence of sttes r,..., r exsts n Q such tht. r 2. r k = q = q strt ccet 3. for ll =,..., n, we h ve tht w L( R) where R = δ ( r, r) n Convert DFA nto GNFA Convert GNFA nto regulr exresson Add new strt stte, wth rrow to old strt stte Add new ccet stte, wth rrows from old ccet sttes If ny rrows hve multle lels nd, relce y Add rrows wth lel etween sttes where necessry (:etween sttes tht hd no rrows efore) 3 stte DFA 5 stte GNFA 4 stte GNFA Regulr Exresson 2 stte GNFA 3 stte GNFA 57 58
15 Rng of sttes Convert(G) Relce one stte y the corresondng RE R 4 q R q R r 3 R 2 (R )(R 2 ) ) (R 3 ) R 4 q Convert( G ) :. Let k e the numer of sttes of G. 2. If k = 2, then G must consst of strt stte, n ccet stte, nd sngle rrow connectong them nd leled wth regulr exresson R. Return the exresson R. 3. If k > 2, we select ny stte q Q dfferent from q nd q nd let G' e the GNFA (Q', Σδ, ',q,q ), where strt r strt ccet ccet Q' = Q { q }, nd for ny q Q' {q } nd ny q Q' {q } let r ccet j strt δ '(q,q ) = (R )(R )(R ) (R ), j 3 4 for R =δ (q,q ),R =δ (q,q ),R =δ (q,q ), nd R =δ(q,q ). r 2 r r 3 r j 4 j 4. Comute Convert( G') nd return ths vlue Exmle Another Exmle R q R 4 q r R 2 R 3 q (R )(R 2 ) (R 3 ) R 4 DFA: 2 3 GNFA: s 2 3 R 2: R : R : R 2: 2 s ( ) s ( ) 3 3 ( ) ( ) ( ) ( ) R 3: s (( ) )(( ) ( ) )(( ) ( ) ) ( ) 6 63
16 Inducton Proof Inducton Proof (cont.) R 4 q (R )(R 2 ) (R 3 ) R 4 q R q r R 2 R 2 Clm For ny GNFA G, Convert( G ) s equvlent to G. We rove ths clm y nducton on k, the numer of sttes of the GNFA. Bss: Prove the clm true for k = 2 sttes. If G hs only two sttes, t cn hve only sngle rrow, whch goes from the strt stte to the ccet stte. The regulr exresson lel on ths rrow descres ll the strngs tht llow G to get to the ccet stte. Hence ths exresson s equvlent to G. Inducton ste: Assume tht the clm s true for k sttes nd use ths ssumton to rove tht the clm s true for k sttes. Frst we show tht G nd G' recognze the sme lnguge. Suose tht G ccets n nut w. Then n n ccetng rnch of the comutton G enters sequence of sttes q,q,q,q,...,q. strt 2 3 ccet If none of them s the removed stte q, clerly G' lso ccets w. The reson s tht ech of the new regulr exressons lelng the rrows of G' contns the old regulr exresson s rt of unon. r 64 R 4 q (R )(R 2 ) (R 3 ) R 4 q R q r R 2 R 2 If q does er, removng ech run of consecutve q sttes r forms n ccetng comutton for G'. The sttes q nd q rcketng run hve new regulr exresson on the rrow etween them tht descres ll strngs tkng q to q v q on G. So G' ccets w. j r For the other drecton, suose tht G' ccets n nut w. As ech rrow etween ny two sttes q nd q n G' descres the collecton of strngs tkng q to q n G, ether drectly or v q,g must lso j r ccet wthus G nd G' re equvlent. The nducton hyothess sttes tht when the lorthm clls tself recursvely on nut G', the result s regulr exresson tht s equvlent to G' ecuse G' hs k sttes. Hence the regulr exresson lso s equvlent to G, nd the lgorthm s roved correct. Ths concludes the roof of Clm.34, Lemm.32, nd theorem j r j Nonregulr Lnguges The umng lemm Fnte Automt hve fnte memory Are the followng lnguges regulr? n n B= { n } C = { w whs n equl numer of s nd s} D= { w whs n equl numer of occurences of nd } Mthemtcl roof necessry If A s regulr lnguge, then there s numer (the umng length), where, f s s ny strng n A of length t lest then s my e dvded nto three eces s = xyz such tht. for ech, xy z A 2. y > 3. xy Note from 2: y 66 67
17 Proof Ide Proof: Pumng Lemm Let M e DFA recognzng A. Assgn to e the numer of sttes n M. Show tht strng s, wth length t lest, cnerokenntoxyz. Pgeonhole rncle Now rove tht ll three condtons re met Let M = (Q, Σ, δ, q, F) e DFA recognzng A nd Q =. Let s = s s 2...s n e strng n A, wth s = n, nd n Let r =r,...,r n+ e the sequence of sttes tht M enters for s, so r + = δ(r,s ) wth n. r,...,r n+ = n+, n+ +. Amoung the frst + elements n r, there must e r j nd r l eng the sme stte q m, wth j l. As r l occurs n the frst + sttes: l +. Let x = s...s j-, y = s j...s l- nd z = s l...s n : s x tkes M from r to r j, y from r j to r l, nd z from r l to r n+, eng n ccet stte, M must ccet xy z for wth j l, y > wth l +, xy Pumng Lemm (cont.) Nonregulr lnguges exmles Use umng lemm to rove tht lnguge A s not regulr:. Assume tht A s regulr (Proof y contrdcton) 2. use the lemm to gurntee the exstence of, such tht strngs of length or greter cn e umed 3. fnd strng s of A, wth s tht cnnot e umed 4. demonstrte tht s cnnot e umed usng ll dfferent wys of dvdng s nto x,y, nd z (usng condton 3. s here very useful ) 5. the exstence of s contrdcts the ssumton, therefore A s not regulr lnguge B n n = { n } Choose s = for s :. for ech, xy z A 2. y > 3. xy If would now only consder condton2, then we would hve tht:. strng y conssts only of s 2. strng y conssts only of s 3. strng y conssts of oth s nd s 7 7
18 C = { w whs n equl numer of s nd s} Exmle lnguge B gn Choose s = Would seem ossle wthout condton 3! However, condton 3 of lemm sttes xy Thus y conssts of s only Then xyyz C Choc e of s crucl. Consder s = () Alterntve roof : B s nonregulr If C were C = B regulr, then regulr Regulr lnguges closed under ntersecton for s :. for ech, xy z A 2. y > 3. xy n n B= { n } Choose s = condton 3 of lemm sttes xy Thus y conssts of s only Then xyyz B for s :. for ech, xy z A 2. y > 3. xy F = { ww w {,}} D 2 n = { n> } Choose s = Condton 3 of lemm sttes xy Thus y conssts of s only Then xyyz F would not work, s t cn e umed! for s :. for ech, xy z A 2. y > 3. xy Choose s = 2 Perfect squres :,,4,9,6,25,36,49,... Consder + xy z xy z nd xyz xy z + Prove tht for lrge : nd cnnot oth e erfect squres, whch should e true ccordng to umng lemm. Therefore, D s not regulr lnguge Proof: 2 Let m= n = xy z 2 2 Then: ( ) 2 2 n+ n = n+ = m+ Choose y < 2 m+ = 2 xy z + Indeed, oserve 2 4 ; let then: y s = = <2 y = + 2 xy z + for s :. for ech, xy z A 2. y > 3. xy 74 75
19 j E = { w where > j} Exmle Exm Queston for s :. for ech, xy z A 2. y > 3. xy + Choose s = Condton 3 of lemm sttes xy Thus y conssts of s only Then xy z F for s :. for ech, xy z A 2. y > 3. xy Q: Use the umng lemm to rove tht L = { k j : k,j nd k 2j} s not regulr. A: Assume tht L = { k j : k,j nd k 2j} s regulr. Let e the umng length of L. The umng lemm sttes tht for ny strng s L of t lest length, there exst strng x,y, nd z such tht s = xyz, xy, y >, nd for ll : xy z L. Choose s = 2. Becuse s L nd s =3, we otn from the umng lemm the strngs x,y, nd z wth the ove roertes. As s = xyz, xy, nd s egns wth 2 zeros, one cn see tht xy cn only consst of zeros. If we um s down,.e. select =, the strng xy z = xz = 2- y. As xz hs ones, nd y >, xz hs fewer thn 2 zeros. Hence xz L CONTRADICTION. Therfore L s not regulr! Exmle Exm Queston for s :. for ech, xy z A 2. y > 3. xy Summry Q: Use the umng lemm to rove tht L = { k j : k,j nd k 2j} s not regulr. A: Assume tht L = { k j : k,j nd k 2j} s regulr. Let e the umng length of L. The umng lemm sttes tht for ny strng s L of t lest length, there exst strng x,y, nd z such tht s = xyz, xy, y >, nd for ll : xy z L. Choose s = 2. Becuse s L nd s =3, we otn from the umng lemm the strngs x,y, nd z wth the ove roertes. As s = xyz, xy, nd s egns wth 2 zeros, one cn see tht xy cn only consst of zeros. If we um s down,.e. select =, the strng xy z = xz = 2- y. Determnstc fnte utomt Regulr lnguges Nondetermnstc fnte utomt Closure oertons Regulr exressons Nonregulr lnguges The umng lemm As xz hs ones, nd y >, xz hs fewer thn 2 zeros. Hence xz L CONTRADICTION. Therfore L s not regulr! 78 79
Theory of Computation Regular Languages. (NTU EE) Regular Languages Fall / 38
 Theory of Computtion Regulr Lnguges (NTU EE) Regulr Lnguges Fll 2017 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of Finite Automt A finite utomton hs finite set of control
Theory of Computtion Regulr Lnguges (NTU EE) Regulr Lnguges Fll 2017 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of Finite Automt A finite utomton hs finite set of control
Theory of Computation Regular Languages
 Theory of Computtion Regulr Lnguges Bow-Yw Wng Acdemi Sinic Spring 2012 Bow-Yw Wng (Acdemi Sinic) Regulr Lnguges Spring 2012 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of
Theory of Computtion Regulr Lnguges Bow-Yw Wng Acdemi Sinic Spring 2012 Bow-Yw Wng (Acdemi Sinic) Regulr Lnguges Spring 2012 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of
acs-04: Regular Languages Regular Languages Andreas Karwath & Malte Helmert Informatik Theorie II (A) WS2009/10
 Regular Languages Andreas Karwath & Malte Helmert 1 Overview Deterministic finite automata Regular languages Nondeterministic finite automata Closure operations Regular expressions Nonregular languages
Regular Languages Andreas Karwath & Malte Helmert 1 Overview Deterministic finite automata Regular languages Nondeterministic finite automata Closure operations Regular expressions Nonregular languages
CHAPTER 1 Regular Languages. Contents
 Finite Automt (FA or DFA) CHAPTE 1 egulr Lnguges Contents definitions, exmples, designing, regulr opertions Non-deterministic Finite Automt (NFA) definitions, euivlence of NFAs nd DFAs, closure under regulr
Finite Automt (FA or DFA) CHAPTE 1 egulr Lnguges Contents definitions, exmples, designing, regulr opertions Non-deterministic Finite Automt (NFA) definitions, euivlence of NFAs nd DFAs, closure under regulr
AUTOMATA AND LANGUAGES. Definition 1.5: Finite Automaton
 25. Finite Automt AUTOMATA AND LANGUAGES A system of computtion tht only hs finite numer of possile sttes cn e modeled using finite utomton A finite utomton is often illustrted s stte digrm d d d. d q
25. Finite Automt AUTOMATA AND LANGUAGES A system of computtion tht only hs finite numer of possile sttes cn e modeled using finite utomton A finite utomton is often illustrted s stte digrm d d d. d q
CHAPTER 1 Regular Languages. Contents. definitions, examples, designing, regular operations. Non-deterministic Finite Automata (NFA)
 Finite Automt (FA or DFA) CHAPTER Regulr Lnguges Contents definitions, exmples, designing, regulr opertions Non-deterministic Finite Automt (NFA) definitions, equivlence of NFAs DFAs, closure under regulr
Finite Automt (FA or DFA) CHAPTER Regulr Lnguges Contents definitions, exmples, designing, regulr opertions Non-deterministic Finite Automt (NFA) definitions, equivlence of NFAs DFAs, closure under regulr
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY. FLAC (15-453) - Spring L. Blum
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY THE PUMPING LEMMA FOR REGULAR LANGUAGES nd REGULAR EXPRESSIONS TUESDAY Jn 21 WHICH OF THESE ARE REGULAR? B = {0 n 1 n n 0} C = { w w hs equl numer of
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY THE PUMPING LEMMA FOR REGULAR LANGUAGES nd REGULAR EXPRESSIONS TUESDAY Jn 21 WHICH OF THESE ARE REGULAR? B = {0 n 1 n n 0} C = { w w hs equl numer of
Chapter Five: Nondeterministic Finite Automata. Formal Language, chapter 5, slide 1
 Chpter Five: Nondeterministic Finite Automt Forml Lnguge, chpter 5, slide 1 1 A DFA hs exctly one trnsition from every stte on every symol in the lphet. By relxing this requirement we get relted ut more
Chpter Five: Nondeterministic Finite Automt Forml Lnguge, chpter 5, slide 1 1 A DFA hs exctly one trnsition from every stte on every symol in the lphet. By relxing this requirement we get relted ut more
Lecture 08: Feb. 08, 2019
 4CS4-6:Theory of Computtion(Closure on Reg. Lngs., regex to NDFA, DFA to regex) Prof. K.R. Chowdhry Lecture 08: Fe. 08, 2019 : Professor of CS Disclimer: These notes hve not een sujected to the usul scrutiny
4CS4-6:Theory of Computtion(Closure on Reg. Lngs., regex to NDFA, DFA to regex) Prof. K.R. Chowdhry Lecture 08: Fe. 08, 2019 : Professor of CS Disclimer: These notes hve not een sujected to the usul scrutiny
CISC 4090 Theory of Computation
 9/6/28 Stereotypicl computer CISC 49 Theory of Computtion Finite stte mchines & Regulr lnguges Professor Dniel Leeds dleeds@fordhm.edu JMH 332 Centrl processing unit (CPU) performs ll the instructions
9/6/28 Stereotypicl computer CISC 49 Theory of Computtion Finite stte mchines & Regulr lnguges Professor Dniel Leeds dleeds@fordhm.edu JMH 332 Centrl processing unit (CPU) performs ll the instructions
CMPSCI 250: Introduction to Computation. Lecture #31: What DFA s Can and Can t Do David Mix Barrington 9 April 2014
 CMPSCI 250: Introduction to Computtion Lecture #31: Wht DFA s Cn nd Cn t Do Dvid Mix Brrington 9 April 2014 Wht DFA s Cn nd Cn t Do Deterministic Finite Automt Forml Definition of DFA s Exmples of DFA
CMPSCI 250: Introduction to Computtion Lecture #31: Wht DFA s Cn nd Cn t Do Dvid Mix Brrington 9 April 2014 Wht DFA s Cn nd Cn t Do Deterministic Finite Automt Forml Definition of DFA s Exmples of DFA
Homework 4. 0 ε 0. (00) ε 0 ε 0 (00) (11) CS 341: Foundations of Computer Science II Prof. Marvin Nakayama
 CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 4 1. UsetheproceduredescriedinLemm1.55toconverttheregulrexpression(((00) (11)) 01) into n NFA. Answer: 0 0 1 1 00 0 0 11 1 1 01 0 1 (00)
CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 4 1. UsetheproceduredescriedinLemm1.55toconverttheregulrexpression(((00) (11)) 01) into n NFA. Answer: 0 0 1 1 00 0 0 11 1 1 01 0 1 (00)
1.3 Regular Expressions
 56 1.3 Regulr xpressions These hve n importnt role in describing ptterns in serching for strings in mny pplictions (e.g. wk, grep, Perl,...) All regulr expressions of lphbet re 1.Ønd re regulr expressions,
56 1.3 Regulr xpressions These hve n importnt role in describing ptterns in serching for strings in mny pplictions (e.g. wk, grep, Perl,...) All regulr expressions of lphbet re 1.Ønd re regulr expressions,
Minimal DFA. minimal DFA for L starting from any other
 Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
1. For each of the following theorems, give a two or three sentence sketch of how the proof goes or why it is not true.
 York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
5. (±±) Λ = fw j w is string of even lengthg [ 00 = f11,00g 7. (11 [ 00)± Λ = fw j w egins with either 11 or 00g 8. (0 [ ffl)1 Λ = 01 Λ [ 1 Λ 9.
 Regulr Expressions, Pumping Lemm, Right Liner Grmmrs Ling 106 Mrch 25, 2002 1 Regulr Expressions A regulr expression descries or genertes lnguge: it is kind of shorthnd for listing the memers of lnguge.
Regulr Expressions, Pumping Lemm, Right Liner Grmmrs Ling 106 Mrch 25, 2002 1 Regulr Expressions A regulr expression descries or genertes lnguge: it is kind of shorthnd for listing the memers of lnguge.
NFAs and Regular Expressions. NFA-ε, continued. Recall. Last class: Today: Fun:
 CMPU 240 Lnguge Theory nd Computtion Spring 2019 NFAs nd Regulr Expressions Lst clss: Introduced nondeterministic finite utomt with -trnsitions Tody: Prove n NFA- is no more powerful thn n NFA Introduce
CMPU 240 Lnguge Theory nd Computtion Spring 2019 NFAs nd Regulr Expressions Lst clss: Introduced nondeterministic finite utomt with -trnsitions Tody: Prove n NFA- is no more powerful thn n NFA Introduce
Finite Automata. Informatics 2A: Lecture 3. John Longley. 22 September School of Informatics University of Edinburgh
 Lnguges nd Automt Finite Automt Informtics 2A: Lecture 3 John Longley School of Informtics University of Edinburgh jrl@inf.ed.c.uk 22 September 2017 1 / 30 Lnguges nd Automt 1 Lnguges nd Automt Wht is
Lnguges nd Automt Finite Automt Informtics 2A: Lecture 3 John Longley School of Informtics University of Edinburgh jrl@inf.ed.c.uk 22 September 2017 1 / 30 Lnguges nd Automt 1 Lnguges nd Automt Wht is
Regular Language. Nonregular Languages The Pumping Lemma. The pumping lemma. Regular Language. The pumping lemma. Infinitely long words 3/17/15
 Regulr Lnguge Nonregulr Lnguges The Pumping Lemm Models of Comput=on Chpter 10 Recll, tht ny lnguge tht cn e descried y regulr expression is clled regulr lnguge In this lecture we will prove tht not ll
Regulr Lnguge Nonregulr Lnguges The Pumping Lemm Models of Comput=on Chpter 10 Recll, tht ny lnguge tht cn e descried y regulr expression is clled regulr lnguge In this lecture we will prove tht not ll
1 Nondeterministic Finite Automata
 1 Nondeterministic Finite Automt Suppose in life, whenever you hd choice, you could try oth possiilities nd live your life. At the end, you would go ck nd choose the one tht worked out the est. Then you
1 Nondeterministic Finite Automt Suppose in life, whenever you hd choice, you could try oth possiilities nd live your life. At the end, you would go ck nd choose the one tht worked out the est. Then you
Regular expressions, Finite Automata, transition graphs are all the same!!
 CSI 3104 /Winter 2011: Introduction to Forml Lnguges Chpter 7: Kleene s Theorem Chpter 7: Kleene s Theorem Regulr expressions, Finite Automt, trnsition grphs re ll the sme!! Dr. Neji Zgui CSI3104-W11 1
CSI 3104 /Winter 2011: Introduction to Forml Lnguges Chpter 7: Kleene s Theorem Chpter 7: Kleene s Theorem Regulr expressions, Finite Automt, trnsition grphs re ll the sme!! Dr. Neji Zgui CSI3104-W11 1
Non-deterministic Finite Automata
 Non-deterministic Finite Automt Eliminting non-determinism Rdoud University Nijmegen Non-deterministic Finite Automt H. Geuvers nd T. vn Lrhoven Institute for Computing nd Informtion Sciences Intelligent
Non-deterministic Finite Automt Eliminting non-determinism Rdoud University Nijmegen Non-deterministic Finite Automt H. Geuvers nd T. vn Lrhoven Institute for Computing nd Informtion Sciences Intelligent
Harvard University Computer Science 121 Midterm October 23, 2012
 Hrvrd University Computer Science 121 Midterm Octoer 23, 2012 This is closed-ook exmintion. You my use ny result from lecture, Sipser, prolem sets, or section, s long s you quote it clerly. The lphet is
Hrvrd University Computer Science 121 Midterm Octoer 23, 2012 This is closed-ook exmintion. You my use ny result from lecture, Sipser, prolem sets, or section, s long s you quote it clerly. The lphet is
The Schur-Cohn Algorithm
 Modelng, Estmton nd Otml Flterng n Sgnl Processng Mohmed Njm Coyrght 8, ISTE Ltd. Aendx F The Schur-Cohn Algorthm In ths endx, our m s to resent the Schur-Cohn lgorthm [] whch s often used s crteron for
Modelng, Estmton nd Otml Flterng n Sgnl Processng Mohmed Njm Coyrght 8, ISTE Ltd. Aendx F The Schur-Cohn Algorthm In ths endx, our m s to resent the Schur-Cohn lgorthm [] whch s often used s crteron for
GNFA GNFA GNFA GNFA GNFA
 DFA RE NFA DFA -NFA REX GNFA Definition GNFA A generlize noneterministic finite utomton (GNFA) is grph whose eges re lele y regulr expressions, with unique strt stte with in-egree, n unique finl stte with
DFA RE NFA DFA -NFA REX GNFA Definition GNFA A generlize noneterministic finite utomton (GNFA) is grph whose eges re lele y regulr expressions, with unique strt stte with in-egree, n unique finl stte with
Finite Automata-cont d
 Automt Theory nd Forml Lnguges Professor Leslie Lnder Lecture # 6 Finite Automt-cont d The Pumping Lemm WEB SITE: http://ingwe.inghmton.edu/ ~lnder/cs573.html Septemer 18, 2000 Exmple 1 Consider L = {ww
Automt Theory nd Forml Lnguges Professor Leslie Lnder Lecture # 6 Finite Automt-cont d The Pumping Lemm WEB SITE: http://ingwe.inghmton.edu/ ~lnder/cs573.html Septemer 18, 2000 Exmple 1 Consider L = {ww
Designing finite automata II
 Designing finite utomt II Prolem: Design DFA A such tht L(A) consists of ll strings of nd which re of length 3n, for n = 0, 1, 2, (1) Determine wht to rememer out the input string Assign stte to ech of
Designing finite utomt II Prolem: Design DFA A such tht L(A) consists of ll strings of nd which re of length 3n, for n = 0, 1, 2, (1) Determine wht to rememer out the input string Assign stte to ech of
Homework 3 Solutions
 CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 3 Solutions 1. Give NFAs with the specified numer of sttes recognizing ech of the following lnguges. In ll cses, the lphet is Σ = {,1}.
CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 3 Solutions 1. Give NFAs with the specified numer of sttes recognizing ech of the following lnguges. In ll cses, the lphet is Σ = {,1}.
Nondeterminism and Nodeterministic Automata
 Nondeterminism nd Nodeterministic Automt 61 Nondeterminism nd Nondeterministic Automt The computtionl mchine models tht we lerned in the clss re deterministic in the sense tht the next move is uniquely
Nondeterminism nd Nodeterministic Automt 61 Nondeterminism nd Nondeterministic Automt The computtionl mchine models tht we lerned in the clss re deterministic in the sense tht the next move is uniquely
Quadratic reciprocity
 Qudrtic recirocity Frncisc Bozgn Los Angeles Mth Circle Octoer 8, 01 1 Qudrtic Recirocity nd Legendre Symol In the eginning of this lecture, we recll some sic knowledge out modulr rithmetic: Definition
Qudrtic recirocity Frncisc Bozgn Los Angeles Mth Circle Octoer 8, 01 1 Qudrtic Recirocity nd Legendre Symol In the eginning of this lecture, we recll some sic knowledge out modulr rithmetic: Definition
CS:4330 Theory of Computation Spring Regular Languages. Equivalences between Finite automata and REs. Haniel Barbosa
 CS:4330 Theory of Computtion Spring 208 Regulr Lnguges Equivlences between Finite utomt nd REs Hniel Brbos Redings for this lecture Chpter of [Sipser 996], 3rd edition. Section.3. Finite utomt nd regulr
CS:4330 Theory of Computtion Spring 208 Regulr Lnguges Equivlences between Finite utomt nd REs Hniel Brbos Redings for this lecture Chpter of [Sipser 996], 3rd edition. Section.3. Finite utomt nd regulr
1.4 Nonregular Languages
 74 1.4 Nonregulr Lnguges The number of forml lnguges over ny lphbet (= decision/recognition problems) is uncountble On the other hnd, the number of regulr expressions (= strings) is countble Hence, ll
74 1.4 Nonregulr Lnguges The number of forml lnguges over ny lphbet (= decision/recognition problems) is uncountble On the other hnd, the number of regulr expressions (= strings) is countble Hence, ll
Nondeterminism. Nondeterministic Finite Automata. Example: Moves on a Chessboard. Nondeterminism (2) Example: Chessboard (2) Formal NFA
 Nondeterminism Nondeterministic Finite Automt Nondeterminism Subset Construction A nondeterministic finite utomton hs the bility to be in severl sttes t once. Trnsitions from stte on n input symbol cn
Nondeterminism Nondeterministic Finite Automt Nondeterminism Subset Construction A nondeterministic finite utomton hs the bility to be in severl sttes t once. Trnsitions from stte on n input symbol cn
I. Theory of Automata II. Theory of Formal Languages III. Theory of Turing Machines
 CI 3104 /Winter 2011: Introduction to Forml Lnguges Chter 13: Grmmticl Formt Chter 13: Grmmticl Formt I. Theory of Automt II. Theory of Forml Lnguges III. Theory of Turing Mchines Dr. Neji Zgui CI3104-W11
CI 3104 /Winter 2011: Introduction to Forml Lnguges Chter 13: Grmmticl Formt Chter 13: Grmmticl Formt I. Theory of Automt II. Theory of Forml Lnguges III. Theory of Turing Mchines Dr. Neji Zgui CI3104-W11
Convert the NFA into DFA
 Convert the NF into F For ech NF we cn find F ccepting the sme lnguge. The numer of sttes of the F could e exponentil in the numer of sttes of the NF, ut in prctice this worst cse occurs rrely. lgorithm:
Convert the NF into F For ech NF we cn find F ccepting the sme lnguge. The numer of sttes of the F could e exponentil in the numer of sttes of the NF, ut in prctice this worst cse occurs rrely. lgorithm:
Grammar. Languages. Content 5/10/16. Automata and Languages. Regular Languages. Regular Languages
 5//6 Grmmr Automt nd Lnguges Regulr Grmmr Context-free Grmmr Context-sensitive Grmmr Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Regulr Lnguges Context Free Lnguges Context Sensitive
5//6 Grmmr Automt nd Lnguges Regulr Grmmr Context-free Grmmr Context-sensitive Grmmr Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Regulr Lnguges Context Free Lnguges Context Sensitive
Lecture 09: Myhill-Nerode Theorem
 CS 373: Theory of Computtion Mdhusudn Prthsrthy Lecture 09: Myhill-Nerode Theorem 16 Ferury 2010 In this lecture, we will see tht every lnguge hs unique miniml DFA We will see this fct from two perspectives
CS 373: Theory of Computtion Mdhusudn Prthsrthy Lecture 09: Myhill-Nerode Theorem 16 Ferury 2010 In this lecture, we will see tht every lnguge hs unique miniml DFA We will see this fct from two perspectives
Previously on GLT. Basic technologies. Lexical analysis. Basic technologies ASF+SDF. Concepts of programming languages
 Prevously on GLT Generc Lnguge Technology: Bsc technologes Pro.dr. Mrk vn den Brnd ASF+SDF syntx descrptons semntc descrptons: type checkng nlyss trnsormtons t so to s Concepts o progrmmng lnguges syntctc
Prevously on GLT Generc Lnguge Technology: Bsc technologes Pro.dr. Mrk vn den Brnd ASF+SDF syntx descrptons semntc descrptons: type checkng nlyss trnsormtons t so to s Concepts o progrmmng lnguges syntctc
CMSC 330: Organization of Programming Languages
 CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 CMSC 330 1 Types of Finite Automt Deterministic Finite Automt (DFA) Exctly one sequence of steps for ech string All exmples so fr Nondeterministic
CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 CMSC 330 1 Types of Finite Automt Deterministic Finite Automt (DFA) Exctly one sequence of steps for ech string All exmples so fr Nondeterministic
CS 301. Lecture 04 Regular Expressions. Stephen Checkoway. January 29, 2018
 CS 301 Lecture 04 Regulr Expressions Stephen Checkowy Jnury 29, 2018 1 / 35 Review from lst time NFA N = (Q, Σ, δ, q 0, F ) where δ Q Σ P (Q) mps stte nd n lphet symol (or ) to set of sttes We run n NFA
CS 301 Lecture 04 Regulr Expressions Stephen Checkowy Jnury 29, 2018 1 / 35 Review from lst time NFA N = (Q, Σ, δ, q 0, F ) where δ Q Σ P (Q) mps stte nd n lphet symol (or ) to set of sttes We run n NFA
Finite Automata. Informatics 2A: Lecture 3. Mary Cryan. 21 September School of Informatics University of Edinburgh
 Finite Automt Informtics 2A: Lecture 3 Mry Cryn School of Informtics University of Edinburgh mcryn@inf.ed.c.uk 21 September 2018 1 / 30 Lnguges nd Automt Wht is lnguge? Finite utomt: recp Some forml definitions
Finite Automt Informtics 2A: Lecture 3 Mry Cryn School of Informtics University of Edinburgh mcryn@inf.ed.c.uk 21 September 2018 1 / 30 Lnguges nd Automt Wht is lnguge? Finite utomt: recp Some forml definitions
First Midterm Examination
 Çnky University Deprtment of Computer Engineering 203-204 Fll Semester First Midterm Exmintion ) Design DFA for ll strings over the lphet Σ = {,, c} in which there is no, no nd no cc. 2) Wht lnguge does
Çnky University Deprtment of Computer Engineering 203-204 Fll Semester First Midterm Exmintion ) Design DFA for ll strings over the lphet Σ = {,, c} in which there is no, no nd no cc. 2) Wht lnguge does
Non-deterministic Finite Automata
 Non-deterministic Finite Automt From Regulr Expressions to NFA- Eliminting non-determinism Rdoud University Nijmegen Non-deterministic Finite Automt H. Geuvers nd J. Rot Institute for Computing nd Informtion
Non-deterministic Finite Automt From Regulr Expressions to NFA- Eliminting non-determinism Rdoud University Nijmegen Non-deterministic Finite Automt H. Geuvers nd J. Rot Institute for Computing nd Informtion
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
CS 311 Homework 3 due 16:30, Thursday, 14 th October 2010
 CS 311 Homework 3 due 16:30, Thursdy, 14 th Octoer 2010 Homework must e sumitted on pper, in clss. Question 1. [15 pts.; 5 pts. ech] Drw stte digrms for NFAs recognizing the following lnguges:. L = {w
CS 311 Homework 3 due 16:30, Thursdy, 14 th Octoer 2010 Homework must e sumitted on pper, in clss. Question 1. [15 pts.; 5 pts. ech] Drw stte digrms for NFAs recognizing the following lnguges:. L = {w
Non-Deterministic Finite Automata. Fall 2018 Costas Busch - RPI 1
 Non-Deterministic Finite Automt Fll 2018 Costs Busch - RPI 1 Nondeterministic Finite Automton (NFA) Alphbet ={} q q2 1 q 0 q 3 Fll 2018 Costs Busch - RPI 2 Nondeterministic Finite Automton (NFA) Alphbet
Non-Deterministic Finite Automt Fll 2018 Costs Busch - RPI 1 Nondeterministic Finite Automton (NFA) Alphbet ={} q q2 1 q 0 q 3 Fll 2018 Costs Busch - RPI 2 Nondeterministic Finite Automton (NFA) Alphbet
Homework Solution - Set 5 Due: Friday 10/03/08
 CE 96 Introduction to the Theory of Computtion ll 2008 Homework olution - et 5 Due: ridy 10/0/08 1. Textook, Pge 86, Exercise 1.21. () 1 2 Add new strt stte nd finl stte. Mke originl finl stte non-finl.
CE 96 Introduction to the Theory of Computtion ll 2008 Homework olution - et 5 Due: ridy 10/0/08 1. Textook, Pge 86, Exercise 1.21. () 1 2 Add new strt stte nd finl stte. Mke originl finl stte non-finl.
Types of Finite Automata. CMSC 330: Organization of Programming Languages. Comparing DFAs and NFAs. NFA for (a b)*abb.
 CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
1 From NFA to regular expression
 Note 1: How to convert DFA/NFA to regulr expression Version: 1.0 S/EE 374, Fll 2017 Septemer 11, 2017 In this note, we show tht ny DFA cn e converted into regulr expression. Our construction would work
Note 1: How to convert DFA/NFA to regulr expression Version: 1.0 S/EE 374, Fll 2017 Septemer 11, 2017 In this note, we show tht ny DFA cn e converted into regulr expression. Our construction would work
Assignment 1 Automata, Languages, and Computability. 1 Finite State Automata and Regular Languages
 Deprtment of Computer Science, Austrlin Ntionl University COMP2600 Forml Methods for Softwre Engineering Semester 2, 206 Assignment Automt, Lnguges, nd Computility Smple Solutions Finite Stte Automt nd
Deprtment of Computer Science, Austrlin Ntionl University COMP2600 Forml Methods for Softwre Engineering Semester 2, 206 Assignment Automt, Lnguges, nd Computility Smple Solutions Finite Stte Automt nd
Deterministic Finite Automata
 Finite Automt Deterministic Finite Automt H. Geuvers nd J. Rot Institute for Computing nd Informtion Sciences Version: fll 2016 J. Rot Version: fll 2016 Tlen en Automten 1 / 21 Outline Finite Automt Finite
Finite Automt Deterministic Finite Automt H. Geuvers nd J. Rot Institute for Computing nd Informtion Sciences Version: fll 2016 J. Rot Version: fll 2016 Tlen en Automten 1 / 21 Outline Finite Automt Finite
Types of Finite Automata. CMSC 330: Organization of Programming Languages. Comparing DFAs and NFAs. Comparing DFAs and NFAs (cont.) Finite Automata 2
 CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
Talen en Automaten Test 1, Mon 7 th Dec, h45 17h30
 Tlen en Automten Test 1, Mon 7 th Dec, 2015 15h45 17h30 This test consists of four exercises over 5 pges. Explin your pproch, nd write your nswer to ech exercise on seprte pge. You cn score mximum of 100
Tlen en Automten Test 1, Mon 7 th Dec, 2015 15h45 17h30 This test consists of four exercises over 5 pges. Explin your pproch, nd write your nswer to ech exercise on seprte pge. You cn score mximum of 100
Formal Languages and Automata
 Moile Computing nd Softwre Engineering p. 1/5 Forml Lnguges nd Automt Chpter 2 Finite Automt Chun-Ming Liu cmliu@csie.ntut.edu.tw Deprtment of Computer Science nd Informtion Engineering Ntionl Tipei University
Moile Computing nd Softwre Engineering p. 1/5 Forml Lnguges nd Automt Chpter 2 Finite Automt Chun-Ming Liu cmliu@csie.ntut.edu.tw Deprtment of Computer Science nd Informtion Engineering Ntionl Tipei University
Let's start with an example:
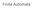 Finite Automt Let's strt with n exmple: Here you see leled circles tht re sttes, nd leled rrows tht re trnsitions. One of the sttes is mrked "strt". One of the sttes hs doule circle; this is terminl stte
Finite Automt Let's strt with n exmple: Here you see leled circles tht re sttes, nd leled rrows tht re trnsitions. One of the sttes is mrked "strt". One of the sttes hs doule circle; this is terminl stte
State Minimization for DFAs
 Stte Minimiztion for DFAs Red K & S 2.7 Do Homework 10. Consider: Stte Minimiztion 4 5 Is this miniml mchine? Step (1): Get rid of unrechle sttes. Stte Minimiztion 6, Stte is unrechle. Step (2): Get rid
Stte Minimiztion for DFAs Red K & S 2.7 Do Homework 10. Consider: Stte Minimiztion 4 5 Is this miniml mchine? Step (1): Get rid of unrechle sttes. Stte Minimiztion 6, Stte is unrechle. Step (2): Get rid
Fundamentals of Computer Science
 Fundmentls of Computer Science Chpter 3: NFA nd DFA equivlence Regulr expressions Henrik Björklund Umeå University Jnury 23, 2014 NFA nd DFA equivlence As we shll see, it turns out tht NFA nd DFA re equivlent,
Fundmentls of Computer Science Chpter 3: NFA nd DFA equivlence Regulr expressions Henrik Björklund Umeå University Jnury 23, 2014 NFA nd DFA equivlence As we shll see, it turns out tht NFA nd DFA re equivlent,
Name Ima Sample ASU ID
 Nme Im Smple ASU ID 2468024680 CSE 355 Test 1, Fll 2016 30 Septemer 2016, 8:35-9:25.m., LSA 191 Regrding of Midterms If you elieve tht your grde hs not een dded up correctly, return the entire pper to
Nme Im Smple ASU ID 2468024680 CSE 355 Test 1, Fll 2016 30 Septemer 2016, 8:35-9:25.m., LSA 191 Regrding of Midterms If you elieve tht your grde hs not een dded up correctly, return the entire pper to
Proof that if Voting is Perfect in One Dimension, then the First. Eigenvector Extracted from the Double-Centered Transformed
 Proof tht f Votng s Perfect n One Dmenson, then the Frst Egenvector Extrcted from the Doule-Centered Trnsformed Agreement Score Mtrx hs the Sme Rn Orderng s the True Dt Keth T Poole Unversty of Houston
Proof tht f Votng s Perfect n One Dmenson, then the Frst Egenvector Extrcted from the Doule-Centered Trnsformed Agreement Score Mtrx hs the Sme Rn Orderng s the True Dt Keth T Poole Unversty of Houston
Regular Expressions (RE) Regular Expressions (RE) Regular Expressions (RE) Regular Expressions (RE) Kleene-*
 Regulr Expressions (RE) Regulr Expressions (RE) Empty set F A RE denotes the empty set Opertion Nottion Lnguge UNIX Empty string A RE denotes the set {} Alterntion R +r L(r ) L(r ) r r Symol Alterntion
Regulr Expressions (RE) Regulr Expressions (RE) Empty set F A RE denotes the empty set Opertion Nottion Lnguge UNIX Empty string A RE denotes the set {} Alterntion R +r L(r ) L(r ) r r Symol Alterntion
More on automata. Michael George. March 24 April 7, 2014
 More on utomt Michel George Mrch 24 April 7, 2014 1 Automt constructions Now tht we hve forml model of mchine, it is useful to mke some generl constructions. 1.1 DFA Union / Product construction Suppose
More on utomt Michel George Mrch 24 April 7, 2014 1 Automt constructions Now tht we hve forml model of mchine, it is useful to mke some generl constructions. 1.1 DFA Union / Product construction Suppose
Worked out examples Finite Automata
 Worked out exmples Finite Automt Exmple Design Finite Stte Automton which reds inry string nd ccepts only those tht end with. Since we re in the topic of Non Deterministic Finite Automt (NFA), we will
Worked out exmples Finite Automt Exmple Design Finite Stte Automton which reds inry string nd ccepts only those tht end with. Since we re in the topic of Non Deterministic Finite Automt (NFA), we will
12.1 Nondeterminism Nondeterministic Finite Automata. a a b ε. CS125 Lecture 12 Fall 2016
 CS125 Lecture 12 Fll 2016 12.1 Nondeterminism The ide of nondeterministic computtions is to llow our lgorithms to mke guesses, nd only require tht they ccept when the guesses re correct. For exmple, simple
CS125 Lecture 12 Fll 2016 12.1 Nondeterminism The ide of nondeterministic computtions is to llow our lgorithms to mke guesses, nd only require tht they ccept when the guesses re correct. For exmple, simple
NFAs continued, Closure Properties of Regular Languages
 Algorithms & Models of Computtion CS/ECE 374, Fll 2017 NFAs continued, Closure Properties of Regulr Lnguges Lecture 5 Tuesdy, Septemer 12, 2017 Sriel Hr-Peled (UIUC) CS374 1 Fll 2017 1 / 31 Regulr Lnguges,
Algorithms & Models of Computtion CS/ECE 374, Fll 2017 NFAs continued, Closure Properties of Regulr Lnguges Lecture 5 Tuesdy, Septemer 12, 2017 Sriel Hr-Peled (UIUC) CS374 1 Fll 2017 1 / 31 Regulr Lnguges,
Bases for Vector Spaces
 Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
First Midterm Examination
 24-25 Fll Semester First Midterm Exmintion ) Give the stte digrm of DFA tht recognizes the lnguge A over lphet Σ = {, } where A = {w w contins or } 2) The following DFA recognizes the lnguge B over lphet
24-25 Fll Semester First Midterm Exmintion ) Give the stte digrm of DFA tht recognizes the lnguge A over lphet Σ = {, } where A = {w w contins or } 2) The following DFA recognizes the lnguge B over lphet
Intermediate Math Circles Wednesday, November 14, 2018 Finite Automata II. Nickolas Rollick a b b. a b 4
 Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
QUADRATIC RESIDUES MATH 372. FALL INSTRUCTOR: PROFESSOR AITKEN
 QUADRATIC RESIDUES MATH 37 FALL 005 INSTRUCTOR: PROFESSOR AITKEN When is n integer sure modulo? When does udrtic eution hve roots modulo? These re the uestions tht will concern us in this hndout 1 The
QUADRATIC RESIDUES MATH 37 FALL 005 INSTRUCTOR: PROFESSOR AITKEN When is n integer sure modulo? When does udrtic eution hve roots modulo? These re the uestions tht will concern us in this hndout 1 The
Some Theory of Computation Exercises Week 1
 Some Theory of Computtion Exercises Week 1 Section 1 Deterministic Finite Automt Question 1.3 d d d d u q 1 q 2 q 3 q 4 q 5 d u u u u Question 1.4 Prt c - {w w hs even s nd one or two s} First we sk whether
Some Theory of Computtion Exercises Week 1 Section 1 Deterministic Finite Automt Question 1.3 d d d d u q 1 q 2 q 3 q 4 q 5 d u u u u Question 1.4 Prt c - {w w hs even s nd one or two s} First we sk whether
NFA DFA Example 3 CMSC 330: Organization of Programming Languages. Equivalence of DFAs and NFAs. Equivalence of DFAs and NFAs (cont.
 NFA DFA Exmple 3 CMSC 330: Orgniztion of Progrmming Lnguges NFA {B,D,E {A,E {C,D {E Finite Automt, con't. R = { {A,E, {B,D,E, {C,D, {E 2 Equivlence of DFAs nd NFAs Any string from {A to either {D or {CD
NFA DFA Exmple 3 CMSC 330: Orgniztion of Progrmming Lnguges NFA {B,D,E {A,E {C,D {E Finite Automt, con't. R = { {A,E, {B,D,E, {C,D, {E 2 Equivlence of DFAs nd NFAs Any string from {A to either {D or {CD
Converting Regular Expressions to Discrete Finite Automata: A Tutorial
 Converting Regulr Expressions to Discrete Finite Automt: A Tutoril Dvid Christinsen 2013-01-03 This is tutoril on how to convert regulr expressions to nondeterministic finite utomt (NFA) nd how to convert
Converting Regulr Expressions to Discrete Finite Automt: A Tutoril Dvid Christinsen 2013-01-03 This is tutoril on how to convert regulr expressions to nondeterministic finite utomt (NFA) nd how to convert
CS103 Handout 32 Fall 2016 November 11, 2016 Problem Set 7
 CS103 Hndout 32 Fll 2016 Novemer 11, 2016 Prolem Set 7 Wht cn you do with regulr expressions? Wht re the limits of regulr lnguges? On this prolem set, you'll find out! As lwys, plese feel free to drop
CS103 Hndout 32 Fll 2016 Novemer 11, 2016 Prolem Set 7 Wht cn you do with regulr expressions? Wht re the limits of regulr lnguges? On this prolem set, you'll find out! As lwys, plese feel free to drop
Formal languages, automata, and theory of computation
 Mälrdlen University TEN1 DVA337 2015 School of Innovtion, Design nd Engineering Forml lnguges, utomt, nd theory of computtion Thursdy, Novemer 5, 14:10-18:30 Techer: Dniel Hedin, phone 021-107052 The exm
Mälrdlen University TEN1 DVA337 2015 School of Innovtion, Design nd Engineering Forml lnguges, utomt, nd theory of computtion Thursdy, Novemer 5, 14:10-18:30 Techer: Dniel Hedin, phone 021-107052 The exm
Chapter 4 Regular Grammar and Regular Sets. (Solutions / Hints)
 C K Ngpl Forml Lnguges nd utomt Theory Chpter 4 Regulr Grmmr nd Regulr ets (olutions / Hints) ol. (),,,,,,,,,,,,,,,,,,,,,,,,,, (),, (c) c c, c c, c, c, c c, c, c, c, c, c, c, c c,c, c, c, c, c, c, c, c,
C K Ngpl Forml Lnguges nd utomt Theory Chpter 4 Regulr Grmmr nd Regulr ets (olutions / Hints) ol. (),,,,,,,,,,,,,,,,,,,,,,,,,, (),, (c) c c, c c, c, c, c c, c, c, c, c, c, c, c c,c, c, c, c, c, c, c, c,
Coalgebra, Lecture 15: Equations for Deterministic Automata
 Colger, Lecture 15: Equtions for Deterministic Automt Julin Slmnc (nd Jurrin Rot) Decemer 19, 2016 In this lecture, we will study the concept of equtions for deterministic utomt. The notes re self contined
Colger, Lecture 15: Equtions for Deterministic Automt Julin Slmnc (nd Jurrin Rot) Decemer 19, 2016 In this lecture, we will study the concept of equtions for deterministic utomt. The notes re self contined
3 Regular expressions
 3 Regulr expressions Given n lphet Σ lnguge is set of words L Σ. So fr we were le to descrie lnguges either y using set theory (i.e. enumertion or comprehension) or y n utomton. In this section we shll
3 Regulr expressions Given n lphet Σ lnguge is set of words L Σ. So fr we were le to descrie lnguges either y using set theory (i.e. enumertion or comprehension) or y n utomton. In this section we shll
NFAs continued, Closure Properties of Regular Languages
 lgorithms & Models of omputtion S/EE 374, Spring 209 NFs continued, losure Properties of Regulr Lnguges Lecture 5 Tuesdy, Jnury 29, 209 Regulr Lnguges, DFs, NFs Lnguges ccepted y DFs, NFs, nd regulr expressions
lgorithms & Models of omputtion S/EE 374, Spring 209 NFs continued, losure Properties of Regulr Lnguges Lecture 5 Tuesdy, Jnury 29, 209 Regulr Lnguges, DFs, NFs Lnguges ccepted y DFs, NFs, nd regulr expressions
2.4 Linear Inequalities and Interval Notation
 .4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
.4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
Non Deterministic Automata. Linz: Nondeterministic Finite Accepters, page 51
 Non Deterministic Automt Linz: Nondeterministic Finite Accepters, pge 51 1 Nondeterministic Finite Accepter (NFA) Alphbet ={} q 1 q2 q 0 q 3 2 Nondeterministic Finite Accepter (NFA) Alphbet ={} Two choices
Non Deterministic Automt Linz: Nondeterministic Finite Accepters, pge 51 1 Nondeterministic Finite Accepter (NFA) Alphbet ={} q 1 q2 q 0 q 3 2 Nondeterministic Finite Accepter (NFA) Alphbet ={} Two choices
Finite state automata
 Finite stte utomt Lecture 2 Model-Checking Finite-Stte Systems (untimed systems) Finite grhs with lels on edges/nodes set of nodes (sttes) set of edges (trnsitions) set of lels (lhet) Finite Automt, CTL,
Finite stte utomt Lecture 2 Model-Checking Finite-Stte Systems (untimed systems) Finite grhs with lels on edges/nodes set of nodes (sttes) set of edges (trnsitions) set of lels (lhet) Finite Automt, CTL,
CSCI 340: Computational Models. Kleene s Theorem. Department of Computer Science
 CSCI 340: Computtionl Models Kleene s Theorem Chpter 7 Deprtment of Computer Science Unifiction In 1954, Kleene presented (nd proved) theorem which (in our version) sttes tht if lnguge cn e defined y ny
CSCI 340: Computtionl Models Kleene s Theorem Chpter 7 Deprtment of Computer Science Unifiction In 1954, Kleene presented (nd proved) theorem which (in our version) sttes tht if lnguge cn e defined y ny
Finite-State Automata: Recap
 Finite-Stte Automt: Recp Deepk D Souz Deprtment of Computer Science nd Automtion Indin Institute of Science, Bnglore. 09 August 2016 Outline 1 Introduction 2 Forml Definitions nd Nottion 3 Closure under
Finite-Stte Automt: Recp Deepk D Souz Deprtment of Computer Science nd Automtion Indin Institute of Science, Bnglore. 09 August 2016 Outline 1 Introduction 2 Forml Definitions nd Nottion 3 Closure under
Chapter Newton-Raphson Method of Solving a Nonlinear Equation
 Chpter.4 Newton-Rphson Method of Solvng Nonlner Equton After redng ths chpter, you should be ble to:. derve the Newton-Rphson method formul,. develop the lgorthm of the Newton-Rphson method,. use the Newton-Rphson
Chpter.4 Newton-Rphson Method of Solvng Nonlner Equton After redng ths chpter, you should be ble to:. derve the Newton-Rphson method formul,. develop the lgorthm of the Newton-Rphson method,. use the Newton-Rphson
Farey Fractions. Rickard Fernström. U.U.D.M. Project Report 2017:24. Department of Mathematics Uppsala University
 U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
Partially Observable Systems. 1 Partially Observable Markov Decision Process (POMDP) Formalism
 CS294-40 Lernng for Rootcs nd Control Lecture 10-9/30/2008 Lecturer: Peter Aeel Prtlly Oservle Systems Scre: Dvd Nchum Lecture outlne POMDP formlsm Pont-sed vlue terton Glol methods: polytree, enumerton,
CS294-40 Lernng for Rootcs nd Control Lecture 10-9/30/2008 Lecturer: Peter Aeel Prtlly Oservle Systems Scre: Dvd Nchum Lecture outlne POMDP formlsm Pont-sed vlue terton Glol methods: polytree, enumerton,
1. For each of the following theorems, give a two or three sentence sketch of how the proof goes or why it is not true.
 York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
INTRODUCTION TO COMPLEX NUMBERS
 INTRODUCTION TO COMPLEX NUMBERS The numers -4, -3, -, -1, 0, 1,, 3, 4 represent the negtve nd postve rel numers termed ntegers. As one frst lerns n mddle school they cn e thought of s unt dstnce spced
INTRODUCTION TO COMPLEX NUMBERS The numers -4, -3, -, -1, 0, 1,, 3, 4 represent the negtve nd postve rel numers termed ntegers. As one frst lerns n mddle school they cn e thought of s unt dstnce spced
CSE396 Prelim I Answer Key Spring 2017
 Nme nd St.ID#: CSE96 Prelim I Answer Key Spring 2017 (1) (24 pts.) Define A to e the lnguge of strings x {, } such tht x either egins with or ends with, ut not oth. Design DFA M such tht L(M) = A. A node-rc
Nme nd St.ID#: CSE96 Prelim I Answer Key Spring 2017 (1) (24 pts.) Define A to e the lnguge of strings x {, } such tht x either egins with or ends with, ut not oth. Design DFA M such tht L(M) = A. A node-rc
Today s Topics Automata and Languages
 Tody s Topics Automt nd Lnguges Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn DFA to Regulr Expression GFNA DFAèGNFA GNFA è RE DFA è RE Exmples 2 DFA è RE NFA DFA -NFA REX GNFA 3 Definition
Tody s Topics Automt nd Lnguges Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn DFA to Regulr Expression GFNA DFAèGNFA GNFA è RE DFA è RE Exmples 2 DFA è RE NFA DFA -NFA REX GNFA 3 Definition
Automata and Languages
 Automt nd Lnguges Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Tody s Topics DFA to Regulr Expression GFNA DFAèGNFA GNFA è RE DFA è RE Exmples 2 DFA è RE NFA DFA -NFA REX GNFA 3 Definition
Automt nd Lnguges Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Tody s Topics DFA to Regulr Expression GFNA DFAèGNFA GNFA è RE DFA è RE Exmples 2 DFA è RE NFA DFA -NFA REX GNFA 3 Definition
CS103B Handout 18 Winter 2007 February 28, 2007 Finite Automata
 CS103B ndout 18 Winter 2007 Ferury 28, 2007 Finite Automt Initil text y Mggie Johnson. Introduction Severl childrens gmes fit the following description: Pieces re set up on plying ord; dice re thrown or
CS103B ndout 18 Winter 2007 Ferury 28, 2007 Finite Automt Initil text y Mggie Johnson. Introduction Severl childrens gmes fit the following description: Pieces re set up on plying ord; dice re thrown or
Anatomy of a Deterministic Finite Automaton. Deterministic Finite Automata. A machine so simple that you can understand it in less than one minute
 Victor Admchik Dnny Sletor Gret Theoreticl Ides In Computer Science CS 5-25 Spring 2 Lecture 2 Mr 3, 2 Crnegie Mellon University Deterministic Finite Automt Finite Automt A mchine so simple tht you cn
Victor Admchik Dnny Sletor Gret Theoreticl Ides In Computer Science CS 5-25 Spring 2 Lecture 2 Mr 3, 2 Crnegie Mellon University Deterministic Finite Automt Finite Automt A mchine so simple tht you cn
Language Processors F29LP2, Lecture 5
 Lnguge Pocessos F29LP2, Lectue 5 Jmie Gy Feuy 2, 2014 1 / 1 Nondeteministic Finite Automt (NFA) NFA genelise deteministic finite utomt (DFA). They llow sevel (0, 1, o moe thn 1) outgoing tnsitions with
Lnguge Pocessos F29LP2, Lectue 5 Jmie Gy Feuy 2, 2014 1 / 1 Nondeteministic Finite Automt (NFA) NFA genelise deteministic finite utomt (DFA). They llow sevel (0, 1, o moe thn 1) outgoing tnsitions with
Non-Deterministic Finite Automata
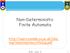 Non-Deterministic Finite Automt http://users.comlb.ox.c.uk/luke. ong/teching/moc/nf2up.pdf 1 Nondeterministic Finite Automton (NFA) Alphbet ={} q1 q2 2 Alphbet ={} Two choices q1 q2 3 Alphbet ={} Two choices
Non-Deterministic Finite Automt http://users.comlb.ox.c.uk/luke. ong/teching/moc/nf2up.pdf 1 Nondeterministic Finite Automton (NFA) Alphbet ={} q1 q2 2 Alphbet ={} Two choices q1 q2 3 Alphbet ={} Two choices
CS 275 Automata and Formal Language Theory
 CS 275 utomt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Prolem (II) Chpter II.5.: Properties of Context Free Grmmrs (14) nton Setzer (Bsed on ook drft y J. V. Tucker nd K. Stephenson)
CS 275 utomt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Prolem (II) Chpter II.5.: Properties of Context Free Grmmrs (14) nton Setzer (Bsed on ook drft y J. V. Tucker nd K. Stephenson)
Rank One Update And the Google Matrix by Al Bernstein Signal Science, LLC
 Introducton Rnk One Updte And the Google Mtrx y Al Bernsten Sgnl Scence, LLC www.sgnlscence.net here re two dfferent wys to perform mtrx multplctons. he frst uses dot product formulton nd the second uses
Introducton Rnk One Updte And the Google Mtrx y Al Bernsten Sgnl Scence, LLC www.sgnlscence.net here re two dfferent wys to perform mtrx multplctons. he frst uses dot product formulton nd the second uses
12.1 Nondeterminism Nondeterministic Finite Automata. a a b ε. CS125 Lecture 12 Fall 2014
 CS125 Lecture 12 Fll 2014 12.1 Nondeterminism The ide of nondeterministic computtions is to llow our lgorithms to mke guesses, nd only require tht they ccept when the guesses re correct. For exmple, simple
CS125 Lecture 12 Fll 2014 12.1 Nondeterminism The ide of nondeterministic computtions is to llow our lgorithms to mke guesses, nd only require tht they ccept when the guesses re correct. For exmple, simple
Two Coefficients of the Dyson Product
 Two Coeffcents of the Dyson Product rxv:07.460v mth.co 7 Nov 007 Lun Lv, Guoce Xn, nd Yue Zhou 3,,3 Center for Combntorcs, LPMC TJKLC Nnk Unversty, Tnjn 30007, P.R. Chn lvlun@cfc.nnk.edu.cn gn@nnk.edu.cn
Two Coeffcents of the Dyson Product rxv:07.460v mth.co 7 Nov 007 Lun Lv, Guoce Xn, nd Yue Zhou 3,,3 Center for Combntorcs, LPMC TJKLC Nnk Unversty, Tnjn 30007, P.R. Chn lvlun@cfc.nnk.edu.cn gn@nnk.edu.cn
Formal Methods in Software Engineering
 Forml Methods in Softwre Engineering Lecture 09 orgniztionl issues Prof. Dr. Joel Greenyer Decemer 9, 2014 Written Exm The written exm will tke plce on Mrch 4 th, 2015 The exm will tke 60 minutes nd strt
Forml Methods in Softwre Engineering Lecture 09 orgniztionl issues Prof. Dr. Joel Greenyer Decemer 9, 2014 Written Exm The written exm will tke plce on Mrch 4 th, 2015 The exm will tke 60 minutes nd strt
Duke Math Meet
 Duke Mth Meet 01-14 Power Round Qudrtic Residues nd Prime Numers For integers nd, we write to indicte tht evenly divides, nd to indicte tht does not divide For exmle, 4 nd 4 Let e rime numer An integer
Duke Mth Meet 01-14 Power Round Qudrtic Residues nd Prime Numers For integers nd, we write to indicte tht evenly divides, nd to indicte tht does not divide For exmle, 4 nd 4 Let e rime numer An integer
