Computational Fluid Dynamics
|
|
|
- Felicity Cole
- 6 years ago
- Views:
Transcription
1 Nir-toks Introdction Mrch, 00 Introdction to oltion of Nir- toks qtion Lrr Crtto Mchnicl nginring 69 Compttionl Flid Dnmics Mrch, 00 Homork for Mrch Donlod th cl orkbook from th cors b sit for th smpl conction problm ith cll.5 hos rslts for Cntrl nd Upind on sprt orkshts Add similr orkshts to gt rslts for Hbrid, or L, nd QUICK Add rror rslts for ths lgorithms to th rror chrt An qstions? Otlin Ri finit-olm conction Cntrl, pind, por l, QUICK, TVD Fls diffsion oling th Nir-toks qtions Approchs Grids rssr trms nd th nd for stggrd grids Drition of momntm qtions Ri Algorithm roprtis Consrti schms consr proprtis in finit diffrnc qtions Rqirs it fl from on fc to b sm s inpt fl in djcnt cll Trnsporti schms h corrct blnc btn diffsion nd conction Accrc nd schms tht h good trnction rror 4 Ri Algorithm roprtis II Limit on cofficint mgnitd for itrtion schms bonddnss Absolt l of digonl cofficint mst b grtr thn th sm of bsolt ls of ll othr cofficints For simpl qtions hr Dfrrd corrction sprts cofficints into to prts Adjstmnt ls lcs prt rmod from djstd cofficints into sorc trm 5 Ri Conction Trms td qtion ith conction nd diffsion trms in on dimnsion td continit qtion in on dimnsion d d Appl finit olm pproch to intgrt smll olm d dv d d d Γ d dv d d d d Γ d d 0 d d dv 0 d 6 M 69 Compttionl Flid Dnmics
2 Nir-toks Introdction Mrch, 00 F Ri Intgrtd D Constnt r rslt Dfin F nd D Γ/δ F D D Diffrnt pprochs for φ nd φ Cntrl diffrnc, pind, hbrid, porl, QUICK, TVD All gt rltions mong nighbor nods Thr nods for ll bt QUICK 0 pcil trtmnt for bondr nods 7 Ri mpl roblm Constnt,, nd Γ ith φ φ 0 t 0 nd φ φ L t L d d d d d d Γ d d d Γ d d d ct soltion blo ith plot on nt slid 0 L 0 Γ L Γ L/Γ cll δ/γ F/D ξ - ξ0/ξ L - ξ0 ct oltion Ri Cntrl Diffrnc Hr δ, nd Γ r constnts F F F D D Γ / δ D D D F F F lft right Bondr conditions t 0 nd L F F D D F D lft F F D N D N D F right 0 Ri Upind Diffrncs Compttionl formls D m F,0 D m F,0 F F Lft bondr D m F,0 F F lft Right bondr D F F right m F,0 Ri Hbrid Diffrnc Compttionl Formls F F m F, D,0 m F, D, 0 F F Lft bondr m[ D, D F ] F F lft Right bondr [ D, D F ] m F F right M 69 Compttionl Flid Dnmics
3 Nir-toks Introdction Mrch, 00 Ri or L Compttions 5 D m[ 0, ] m[ F,0] F F D m 0, m F,0 F Lft bondr: gt ith D D F F lft Right bondr : gt ith D D 5 [ ] [ ] D F F right F D Ri QUICK QUICK formls for cntrl nod inol fi nods instd of thr α 0 αf F αf αf D αf 6 α F α F α F D α if F > 0 nd α if F > 0 α 4 0 if F < 0 nd α 0 if F < 0 6 Ri QUICK II Bondr formls drition in tt Assm F > 0 nd F > 0 First nod from lft F cond nod from lft 4 D F F D D F 4 F F lft 7 F D F D F F F lft Lst nod F D 6F D on right N N F F D F N 5 N Ri TVD Algorithms Totl Vrition Diminishing schms Dsignd to mintin both ccrc nd stbilit ith no nphsicl iggls Considr st of diffrnt diffrncing schms for φ ith positi locit ork origintd in trnsint gs dnmics Ltr modifictions to gnrl CFD Bsd on s of limitr fnctions tht r pplid to conntionl formls Dfrrd corrction rqird in itrtion 6 Ri TVD Algorithms II Gnrl form is φ φ Corrction Corrction cn ls b rittn s corrction ψ/ tims φ φ Corrction fnction ψ dpnds on φ φ /φ φ r φ φ ψrφ φ / For scond-ordr ccrc nd TVD For 0 < r, r ψr r For r, ψr r For r >, ψr 7 ψ r 0 Conction chms r UD r LUD QUICK CD condordr TVD Ar M 69 Compttionl Flid Dnmics
4 Nir-toks Introdction Mrch, 00 M 69 Compttionl Flid Dnmics 4 TVD Fl Limitrs r ψr Vn Lr Vn Albd min-mod URB UMIT 0 Fls Diffsion Upind diffrncing css rrors similr to hing diffsion cofficint tht is too lrg Css smring of rslts spcill noticbl in flos ith shrp grdints nd shock s ffct is rdcd if flo is lignd ith grid not ls possibl to do this Diffrnt from rtificl diffsion Nir-toks qtions Continit nd -momntm 0 t t Δ κ B -momntm qtion t Δ κ B -momntm qtion t Δ κ B 4 Nir-toks qtions Continit nd momntm qtions Up to no h bn ssming tht th locit fild s knon nd cold find th gnrl ribl, φ This bckgrond is ncssr for soling Nir-toks, bt no h to sol for φ,, nd This gis st of nonlinr qtions.g., φ bcoms for -momntm
5 Nir-toks Introdction Mrch, 00 Nir-toks qtions II H to find to sol nonlinr qtions Bsic pproch rqirs otr itrtion procss Assm ls for,, nd Us ths ls to compt th conction/diffsion cofficints, N, tc. ol finit diffrnc forms of th Nir- toks qtions for n ls of,, nd sing ths old, N, tc. 5 Nir-toks qtions III Onc n ls of,, nd r knon pdt, N, tc. itrt gin Considr std-stt flos no nd trnsint flos ltr om trnsint mthods cn s nonlinr trms t old tim stp to gt n ls for, N, tc. For std flos th itrtions on th nonlinr trms bcoms prt of th orll itrtion procss 6 Finding rssr nd Dnsit For comprssibl flos sol continit nd momntm for dnsit,,, nd Gt prssr from qtion of stt.g., p RT for comprssibl flos For incomprssibl flos find,,, nd p to stisf thr momntm qtions nd continit Dnsit is n inpt prmtr or dpnds on ribls othr thn locl prssr 7 Incomprssibl Flos Mch nmbr is lo < ~0. Dnsit.g., p/rt m dpnd on mn, bt not locl prssr Cn h qtions lik 0 βt for hr β //T Dnsit m b constnt, bt nd not b for incomprssibl flos Frnc flos good mpl of this Bsic id is tht dnsit dos not dpnd on locl prssr Nir-toks roblms Comprssibl flos ol continit nd momntm for thr locit componnts nd dnsit Gt prssr from qtion of stt Incomprssibl flos Mch nmbr is lo Dnsit is problm inpt, oftn rltd to tmprtr m or m not b constnt ol continit nd momntm for thr locit componnts nd prssr 9 Th td D roblm Continit nd momntn qtions H nd dirction conction-diffsion No h sorc trm nd prssr grdint 0 0 M 69 Compttionl Flid Dnmics 5
6 Nir-toks Introdction Mrch, 00 Th roblm ith rssr Considr th momntm qtion for th locit componnt t point p p p cond-ordr prssion for prssr grdint t δ ith this prssion th locit t is not ffctd b th prssr t Also chckrbord pttrn of prssr old compt s ro prssr grdint Th tggrd Grid roblm ith prssr s first rcognid b Hrlo nd lch in 965 Thir soltion, commonl dptd for CFD ntil th 990s: th stggrd grid If th prssr p ij is th prssr t i, j thn ij is l t i δ/, j nd ij is l t i, j δ/ Coloctd ribls no sd, bt tts still introdc stggrd grid tggrd Grid II tggrd Grid III N n s N n s n s, φ loctions loction of loction of ht is i,j nottion for stggrd grid? Cn contin to s N,,,, n, s,,, n, n, s, s, tc. For nmbring in finit-olm formls cn s i,j s p coordint, i/,j s coordint nd i,j/ s coordint Tt ss I,J nd i,j coordint schm i I δ nd j J δ p, othr φ ls nd proprtis, Γ t Vlocit loctions nd Ij 4 Δ tggrd Grid IV I- i I i I J I-j Ij j I-J I-j - Ij - Δ J - j J-, φ loctions loction of loction of 5 Finit Volm qtions tnd prios rslts for on dimnsion to to dimnsions Cn s n of th diffrnc mthods discssd for conction nd diffsion H for fcs, n,, s,, in D Appl sm rltions to gt cofficints N,,, nd, sing F nd D Γ/δ for ch fc As bfor N ΔF Hr ΔF F n F s F F 6 M 69 Compttionl Flid Dnmics 6
7 Nir-toks Introdction Mrch, 00 Finit Volm qtions II Intgrtion of prssr trms p p dv I J A I I I ΔV I p p A p p Δ ΔV I J p dv p p p I J j p p A p p Δ Ij Ij J J J I J J i j A i Ij Finit Volm qtions III H similr qtions for nd b rprsnts intgrtd sorc trm Not tht K cofficints r from nod to nod nd r diffrnt for nd N i J p p A b N NIj I j I j Ij Ij pij pij AIj b N Ij Ij 7 Control Volm for fc Control Volm for fc i-j I-J I-j I-j - Ij Ij - qtions for fc t Fl J F F I J i I J Γ D i i 9 J i-j I-J I-j I-j - Ij Ij - qtions for fc t I-J Fl J F F I J I J i I J ΓI J D i i 40 J Control Volm for n fc Control Volm for s fc i-j I-J I-j I-j - D Ij Ij - ΓI J n qtions for n fc t j FIj FI j Fn Ij Γ 4 I J I J I J J Γ J I j Γ 4 i-j I-J I-j I-j - D Ij Ij qtions for n fc t j FIj FI j Fs Ij I J I J I - ΓI J ΓI J Γ s 4 J J Γ 4 M 69 Compttionl Flid Dnmics 7
8 Nir-toks Introdction Mrch, 00 hr to Nt H similr qtions to gi rios F nd D trms for control olm Gt finit olm rprsnttion of continit b intgrtion or control olm cntrd bot p s bstitt finit diffrnc momntm qtions into finit diffrnc continit qtion to gt finit diffrnc qtion for prssr Dlop soltion procdr for,, p 4 M 69 Compttionl Flid Dnmics
Modern Channel Coding
Modrn Chnnl Coding Ingmr Lnd & Joss Sir Lctr 4: EXIT Chrts ACoRN Smmr School 27 Itrti Dcoding How dos th mtl informtion ol in n itrti dcoding lgorithm? W h lrnd tht it is possibl to optimiz LDPC cods so
Figure 1: Schematic of a fluid element used for deriving the energy equation.
Driation of th Enrg Eation ME 7710 Enironmntal Flid Dnamics Spring 01 This driation follos closl from Bird, Start and Lightfoot (1960) bt has bn tndd to incld radiation and phas chang. W can rit th 1 st
Integration Continued. Integration by Parts Solving Definite Integrals: Area Under a Curve Improper Integrals
Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
INTEGRALS. Chapter 7. d dx. 7.1 Overview Let d dx F (x) = f (x). Then, we write f ( x)
Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
Assignment 5-6 For Problems 1-4, find a general solution of each differential equation. *Solve for y in Problems 2 and 4.
Empl 6: Lt rprsnt th mss, in ponds, of rdioctiv lmnt whos hlf-lif is 4000 rs. If thr r 00 ponds of th lmnt in n inctiv min, how mch will still rmin in 000 rs? Eprss or nswr to or mor dciml plc ccrc. 4
ME 522 PRINCIPLES OF ROBOTICS. FIRST MIDTERM EXAMINATION April 19, M. Kemal Özgören
ME 522 PINCIPLES OF OBOTICS FIST MIDTEM EXAMINATION April 9, 202 Nm Lst Nm M. Kml Özgörn 2 4 60 40 40 0 80 250 USEFUL FOMULAS cos( ) cos cos sin sin sin( ) sin cos cos sin sin y/ r, cos x/ r, r 0 tn 2(
Instructions for Section 1
Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
TMMI37, vt2, Lecture 8; Introductory 2-dimensional elastostatics; cont.
Lctr 8; ntrodctor 2-dimnsional lastostatics; cont. (modifid 23--3) ntrodctor 2-dimnsional lastostatics; cont. W will now contin or std of 2-dim. lastostatics, and focs on a somwhat mor adancd lmnt thn
Lecture 11 Waves in Periodic Potentials Today: Questions you should be able to address after today s lecture:
Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
Theory of Spatial Problems
Chpt 7 ho of Sptil Polms 7. Diffntil tions of iliim (-D) Z Y X Inol si nknon stss componnts:. 7- 7. Stt of Stss t Point t n sfc ith otd noml N th sfc componnts ltd to (dtmind ) th 6 stss componnts X N
TOPIC 5: INTEGRATION
TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
Ch 1.2: Solutions of Some Differential Equations
Ch 1.2: Solutions of Som Diffrntil Equtions Rcll th fr fll nd owl/mic diffrntil qutions: v 9.8.2v, p.5 p 45 Ths qutions hv th gnrl form y' = y - b W cn us mthods of clculus to solv diffrntil qutions of
Multiple-Choice Test Introduction to Partial Differential Equations COMPLETE SOLUTION SET
Mltipl-Choic Tst Introdction to Partial Diffrntial Eqations COMPLETE SOLUTION SET 1. A partial diffrntial qation has (A on indpndnt variabl (B two or mor indpndnt variabls (C mor than on dpndnt variabl
Casson Flow of MHD Fluid Moving. Steadily with Constant Velocity
Alid atmatical Scincs Vol. 9 5 no. 3 53-58 HIKAI Ltd www.m-ikari.com tt:d.doi.org.988ams.5.553 Casson Flow of HD Flid oing Stadil wit Constant Vlocit Y. Immanl Baji Pll and C. K. Kirbasankar 3 3 Dartmnt
This Week. Computer Graphics. Introduction. Introduction. Graphics Maths by Example. Graphics Maths by Example
This Wk Computr Grphics Vctors nd Oprtions Vctor Arithmtic Gomtric Concpts Points, Lins nd Plns Eploiting Dot Products CSC 470 Computr Grphics 1 CSC 470 Computr Grphics 2 Introduction Introduction Wh do
Minimum Spanning Trees
Minimum Spnning Trs Minimum Spnning Trs Problm A town hs st of houss nd st of rods A rod conncts nd only houss A rod conncting houss u nd v hs rpir cost w(u, v) Gol: Rpir nough (nd no mor) rods such tht:
CIVL 8/ D Boundary Value Problems - Rectangular Elements 1/7
CIVL / -D Boundr Vlu Prolms - Rctngulr Elmnts / RECANGULAR ELEMENS - In som pplictions, it m mor dsirl to us n lmntl rprsnttion of th domin tht hs four sids, ithr rctngulr or qudriltrl in shp. Considr
The Derivative of the Natural Logarithmic Function. Derivative of the Natural Exponential Function. Let u be a differentiable function of x.
Th Ntrl Logrithmic n Eponntil Fnctions: : Diffrntition n Intgrtion Objctiv: Fin rivtivs of fnctions involving th ntrl logrithmic fnction. Th Drivtiv of th Ntrl Logrithmic Fnction Lt b iffrntibl fnction
Winter 2016 COMP-250: Introduction to Computer Science. Lecture 23, April 5, 2016
Wintr 2016 COMP-250: Introduction to Computr Scinc Lctur 23, April 5, 2016 Commnt out input siz 2) Writ ny lgorithm tht runs in tim Θ(n 2 log 2 n) in wors cs. Explin why this is its running tim. I don
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 8: Effect of a Vertical Field on Tokamak Equilibrium
.65, MHD Thory of usion Systms Prof. ridrg Lctur 8: Effct of Vrticl ild on Tokmk Equilirium Toroidl orc lnc y Mns of Vrticl ild. Lt us riw why th rticl fild is imortnt. 3. or ry short tims, th cuum chmr
1 Isoparametric Concept
UNIVERSITY OF CALIFORNIA BERKELEY Dpartmnt of Civil Enginring Spring 06 Structural Enginring, Mchanics and Matrials Profssor: S. Govindj Nots on D isoparamtric lmnts Isoparamtric Concpt Th isoparamtric
u x v x dx u x v x v x u x dx d u x v x u x v x dx u x v x dx Integration by Parts Formula
7. Intgration by Parts Each drivativ formula givs ris to a corrsponding intgral formula, as w v sn many tims. Th drivativ product rul yilds a vry usful intgration tchniqu calld intgration by parts. Starting
Image Enhancement in the Spatial Domain
s=tr Eampl PR3.: Eponntials of th form -ar a a positi constant ar sfl for constrcting smooth gra-ll transformation fnctions. Constrct th transformation fnctions haing th gnral shaps shown in th following
ME469A Numerical Methods for Fluid Mechanics
ME469A Numrical Mthods for Fluid Mchanics Handout #5 Gianluca Iaccarino Finit Volum Mthods Last tim w introducd th FV mthod as a discrtization tchniqu applid to th intgral form of th govrning quations
Chapter 16. 1) is a particular point on the graph of the function. 1. y, where x y 1
Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
Multi-Section Coupled Line Couplers
/0/009 MultiSction Coupld Lin Couplrs /8 Multi-Sction Coupld Lin Couplrs W cn dd multipl coupld lins in sris to incrs couplr ndwidth. Figur 7.5 (p. 6) An N-sction coupld lin l W typiclly dsign th couplr
CHAPTER 12. Finite-Volume (control-volume) Method-Introduction
CHAPR 12 Finit-Volum (control-volum) Mthod-Introduction 12-1 Introduction (1) In dvloing ht hs bcom knon s th finit-volum mthod, th consrvtion rincils r lid to fixd rgion in sc knon s control volum, r
Errata for Second Edition, First Printing
Errt for Scond Edition, First Printing pg 68, lin 1: z=.67 should b z=.44 pg 1: Eqution (.63) should rd B( R) = x= R = θ ( x R) p( x) R 1 x= [1 G( x)] = θp( R) + ( θ R)[1 G( R)] pg 15, problm 6: dmnd of
Engineering 323 Beautiful HW #13 Page 1 of 6 Brown Problem 5-12
Enginring Bautiful HW #1 Pag 1 of 6 5.1 Two componnts of a minicomputr hav th following joint pdf for thir usful liftims X and Y: = x(1+ x and y othrwis a. What is th probability that th liftim X of th
We are looking for ways to compute the integral of a function f(x), f(x)dx.
INTEGRATION TECHNIQUES Introdction We re looking for wys to compte the integrl of fnction f(x), f(x)dx. To pt it simply, wht we need to do is find fnction F (x) sch tht F (x) = f(x). Then if the integrl
Chapter 11 Calculation of
Chtr 11 Clcultion of th Flow Fild OUTLINE 11-1 Nd for Scil Procdur 11-2 Som Rltd Difficultis 11-3 A Rmdy : Th stggrd Grid 11-4 Th Momntum Equtions 11-5 Th Prssur nd Vlocity Corrctions 11-6 Th Prssur-Corrction
Derivation of Eigenvalue Matrix Equations
Drivation of Eignvalu Matrix Equations h scalar wav quations ar φ φ η + ( k + 0ξ η β ) φ 0 x y x pq ε r r whr for E mod E, 1, y pq φ φ x 1 1 ε r nr (4 36) for E mod H,, 1 x η η ξ ξ n [ N ] { } i i i 1
4. THE SCALAR-TRANSPORT EQUATION SPRING 2018
. TH SCALAR-TRANSORT QUATION SRING 8. Control-volum nottion. Th stdy-stt -d dvction-diffusion qution.3 Discrtising diffusion. Discrtising th sourc trm.5 Th mtrix qution.6 Discrtising dvction (prt ).7 xtnsion
COMPUTATIONAL NUCLEAR THERMAL HYDRAULICS
COMPUTTIONL NUCLER THERML HYDRULICS Cho, Hyoung Kyu Dpartmnt of Nuclar Enginring Soul National Univrsity CHPTER4. THE FINITE VOLUME METHOD FOR DIFFUSION PROBLEMS 2 Tabl of Contnts Chaptr 1 Chaptr 2 Chaptr
Errata for Second Edition, First Printing
Errt for Scond Edition, First Printing pg 68, lin 1: z=.67 should b z=.44 pg 71: Eqution (.3) should rd B( R) = θ R 1 x= [1 G( x)] pg 1: Eqution (.63) should rd B( R) = x= R = θ ( x R) p( x) R 1 x= [1
COMP108 Algorithmic Foundations
Grdy mthods Prudn Wong http://www.s.liv..uk/~pwong/thing/omp108/01617 Coin Chng Prolm Suppos w hv 3 typs of oins 10p 0p 50p Minimum numr of oins to mk 0.8, 1.0, 1.? Grdy mthod Lrning outoms Undrstnd wht
Miscellaneous open problems in the Regular Boundary Collocation approach
Miscllnous opn problms in th Rgulr Boundry Colloction pproch A. P. Zilińsi Crcow Univrsity of chnology Institut of Mchin Dsign pz@mch.p.du.pl rfftz / MFS Confrnc ohsiung iwn 5-8 Mrch 0 Bsic formultions
spring from 1 cm to 2 cm is given by
Problem [8 pts] Tre or Flse. Give brief explntion or exmple to jstify yor nswer. ) [ pts] Given solid generted by revolving region bot the line x, if we re sing the shell method to compte its volme, then
SUMMER 17 EXAMINATION
(ISO/IEC - 7-5 Crtifid) SUMMER 7 EXAMINATION Modl wr jct Cod: Important Instructions to aminrs: ) Th answrs should b amind by ky words and not as word-to-word as givn in th modl answr schm. ) Th modl answr
Functions and Graphs 1. (a) (b) (c) (f) (e) (d) 2. (a) (b) (c) (d)
Functions nd Grps. () () (c) - - - O - - - O - - - O - - - - (d) () (f) - - O - 7 6 - - O - -7-6 - - - - - O. () () (c) (d) - - - O - O - O - - O - -. () G() f() + f( ), G(-) f( ) + f(), G() G( ) nd G()
Differential Equations
UNIT I Diffrntial Equations.0 INTRODUCTION W li in a world of intrrlatd changing ntitis. Th locit of a falling bod changs with distanc, th position of th arth changs with tim, th ara of a circl changs
UNIT # 08 (PART - I)
. r. d[h d[h.5 7.5 mol L S d[o d[so UNIT # 8 (PRT - I CHEMICL INETICS EXERCISE # 6. d[ x [ x [ x. r [X[C ' [X [[B r '[ [B [C. r [NO [Cl. d[so d[h.5 5 mol L S d[nh d[nh. 5. 6. r [ [B r [x [y r' [x [y r'
Higher order derivatives
Robrto s Nots on Diffrntial Calculus Chaptr 4: Basic diffrntiation ruls Sction 7 Highr ordr drivativs What you nd to know alrady: Basic diffrntiation ruls. What you can larn hr: How to rpat th procss of
Interactive Simulation of Elasto-Plastic Materials using the Finite Element Method
Otline Interctie Simltion of Elsto-Plstic Mterils sing the Finite Element Method Moie Mtthis Müller Seminr Wintersemester FEM s. Mss-Spring he Mtri StticDnmic Deformtion Continm Mechnics nd FEM Strin nd
Last time: introduced our first computational model the DFA.
Lctur 7 Homwork #7: 2.2.1, 2.2.2, 2.2.3 (hnd in c nd d), Misc: Givn: M, NFA Prov: (q,xy) * (p,y) iff (q,x) * (p,) (follow proof don in clss tody) Lst tim: introducd our first computtionl modl th DFA. Tody
Optimizing LTS-Simulation Algorithm
Optimizing LTS-ltion Algorithm MEMICS 09 Lkáš Holík 1, Jiří Šimáček 1,2 emil: {holik,isimcek}@fit.tbr.cz, simcek@img.fr 1 FIT BUT, Božetěcho 2, 61266 Brno, Czech Repblic 2 VERIMAG, UJF, 2.. de Vignte,
Higher-Order Discrete Calculus Methods
Highr-Ordr Discrt Calculus Mthods J. Blair Prot V. Subramanian Ralistic Practical, Cost-ctiv, Physically Accurat Paralll, Moving Msh, Complx Gomtry, Slid 1 Contxt Discrt Calculus Mthods Finit Dirnc Mimtic
Fourier Transforms and the Wave Equation. Key Mathematics: More Fourier transform theory, especially as applied to solving the wave equation.
Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
The Matrix Exponential
Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
u 3 = u 3 (x 1, x 2, x 3 )
Lctur 23: Curvilinar Coordinats (RHB 8.0 It is oftn convnint to work with variabls othr than th Cartsian coordinats x i ( = x, y, z. For xampl in Lctur 5 w mt sphrical polar and cylindrical polar coordinats.
Fundamentals of Continuum Mechanics. Seoul National University Graphics & Media Lab
Fndmntls of Contnm Mchncs Sol Ntonl Unvrsty Grphcs & Md Lb Th Rodmp of Contnm Mchncs Strss Trnsformton Strn Trnsformton Strss Tnsor Strn T + T ++ T Strss-Strn Rltonshp Strn Enrgy FEM Formlton Lt s Stdy
COHORT MBA. Exponential function. MATH review (part2) by Lucian Mitroiu. The LOG and EXP functions. Properties: e e. lim.
MTH rviw part b Lucian Mitroiu Th LOG and EXP functions Th ponntial function p : R, dfind as Proprtis: lim > lim p Eponntial function Y 8 6 - -8-6 - - X Th natural logarithm function ln in US- log: function
Analysis of Convection-Diffusion Problems at Various Peclet Numbers Using Finite Volume and Finite Difference Schemes Anand Shukla
Mathmatical Thory and Modling.iist.org ISSN 4-5804 (apr) ISSN 5-05 (Onlin) Vol., No.6, 01-Slctd from Intrnational Confrnc on Rcnt Trnds in Applid Scincs ith nginring Applications Analysis of Convction-iffusion
PH427/PH527: Periodic systems Spring Overview of the PH427 website (syllabus, assignments etc.) 2. Coupled oscillations.
Dy : Mondy 5 inuts. Ovrviw of th PH47 wsit (syllus, ssignnts tc.). Coupld oscilltions W gin with sss coupld y Hook's Lw springs nd find th possil longitudinl) otion of such syst. W ll xtnd this to finit
Collisions between electrons and ions
DRAFT 1 Collisions btwn lctrons and ions Flix I. Parra Rudolf Pirls Cntr for Thortical Physics, Unirsity of Oxford, Oxford OX1 NP, UK This rsion is of 8 May 217 1. Introduction Th Fokkr-Planck collision
Limits Indeterminate Forms and L Hospital s Rule
Limits Indtrmint Forms nd L Hospitl s Rul I Indtrmint Form o th Tp W hv prviousl studid its with th indtrmint orm s shown in th ollowin mpls: Empl : Empl : tn [Not: W us th ivn it ] Empl : 8 h 8 [Not:
The Matrix Exponential
Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Addition of angular momentum
Addition of angular momntum April, 0 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat th
Why is a E&M nature of light not sufficient to explain experiments?
1 Th wird world of photons Why is a E&M natur of light not sufficint to xplain xprimnts? Do photons xist? Som quantum proprtis of photons 2 Black body radiation Stfan s law: Enrgy/ ara/ tim = Win s displacmnt
Exp-function method to solve the nonlinear dispersive K(m,n) equations
From th SlctdWork of Ji-Hn H 8 Exp-fnction mthod to olv th nonlinr dipriv K(mn qtion Xin-Wi Zho Yi-Xin Wn Ji-Hn H Dongh Univrity Avilbl t: http://work.bpr.com/ji_hn_h/9/ Frnd Pblihing Ho Ltd. Intrntionl
Elementary Linear Algebra
Elementry Liner Algebr Anton & Rorres, 9 th Edition Lectre Set Chpter : Vectors in -Spce nd -Spce Chpter Content Introdction to Vectors (Geometric Norm of Vector; Vector Arithmetic Dot Prodct; Projections
Computer Vision. Fourier Analysis. Computer Science Tripos Part II. Dr Christopher Town. Fourier Analysis. Fourier Analysis
Comptr Vision Comptr Scinc Tripos Part II Dr Christophr Town orir Analsis An imag can b rprsntd b a linar combination of basis fnctions: In th cas of 2D orir analsis: orir Analsis orir Analsis Th transform
ANALYSIS IN THE FREQUENCY DOMAIN
ANALYSIS IN THE FREQUENCY DOMAIN SPECTRAL DENSITY Dfinition Th spctral dnsit of a S.S.P. t also calld th spctrum of t is dfind as: + { γ }. jτ γ τ F τ τ In othr words, of th covarianc function. is dfind
Minimum Spanning Trees
Mnmum Spnnng Trs Spnnng Tr A tr (.., connctd, cyclc grph) whch contns ll th vrtcs of th grph Mnmum Spnnng Tr Spnnng tr wth th mnmum sum of wghts 1 1 Spnnng forst If grph s not connctd, thn thr s spnnng
2F1120 Spektrala transformer för Media Solutions to Steiglitz, Chapter 1
F110 Spktrala transformr för Mdia Solutions to Stiglitz, Chaptr 1 Prfac This documnt contains solutions to slctd problms from Kn Stiglitz s book: A Digital Signal Procssing Primr publishd by Addison-Wsly.
Section 3: Antiderivatives of Formulas
Chptr Th Intgrl Appli Clculus 96 Sction : Antirivtivs of Formuls Now w cn put th is of rs n ntirivtivs togthr to gt wy of vluting finit intgrls tht is ct n oftn sy. To vlut finit intgrl f(t) t, w cn fin
Sec 2.3 Modeling with First Order Equations
Sc.3 Modling with First Ordr Equations Mathmatical modls charactriz physical systms, oftn using diffrntial quations. Modl Construction: Translating physical situation into mathmatical trms. Clarly stat
CSE 373: AVL trees. Warmup: Warmup. Interlude: Exploring the balance invariant. AVL Trees: Invariants. AVL tree invariants review
rmup CSE 7: AVL trs rmup: ht is n invrint? Mihl L Friy, Jn 9, 0 ht r th AVL tr invrints, xtly? Disuss with your nighor. AVL Trs: Invrints Intrlu: Exploring th ln invrint Cor i: xtr invrint to BSTs tht
(a) v 1. v a. v i. v s. (b)
Outlin RETIMING Struturl optimiztion mthods. Gionni D Mihli Stnford Unirsity Rtiming. { Modling. { Rtiming for minimum dly. { Rtiming for minimum r. Synhronous Logi Ntwork Synhronous Logi Ntwork Synhronous
Electricity and Magnetism Electric Dipole Continuous Distribution of Charge
Electricit nd Mgnetism Electric Dipole Continos Distribtion of Chrge Ln heridn De Anz College Jn 16, 2018 Lst time electric field lines electric field from point chrge net electric field from mn chrges
Abstract Interpretation: concrete and abstract semantics
Abstract Intrprtation: concrt and abstract smantics Concrt smantics W considr a vry tiny languag that manags arithmtic oprations on intgrs valus. Th (concrt) smantics of th languags cab b dfind by th funzcion
Continuous Random Variables: Basics
Continuous Rndom Vrils: Bsics Brlin Chn Dprtmnt o Computr Scinc & Inormtion Enginring Ntionl Tiwn Norml Univrsit Rrnc: - D.. Brtss, J. N. Tsitsilis, Introduction to roilit, Sctions 3.-3.3 Continuous Rndom
Sara Godoy del Olmo Calculation of contaminated soil volumes : Geostatistics applied to a hydrocarbons spill Lac Megantic Case
wwwnvisol-canadaca Sara Godoy dl Olmo Calculation of contaminatd soil volums : Gostatistics applid to a hydrocarbons spill Lac Mgantic Cas Gostatistics: study of a PH contamination CONTEXT OF THE STUDY
Vowel package manual
Vwl pckg mnl FUKUI R Grdt Schl f Hmnts nd Sclgy Unvrsty f Tky 28 ctbr 2001 1 Drwng vwl dgrms 1.1 Th vwl nvrnmnt Th gnrl frmt f th vwl nvrnmnt s s fllws. [ptn(,ptn,)] cmmnds fr npttng vwls ptns nd cmmnds
3.4 Repeated Roots; Reduction of Order
3.4 Rpd Roos; Rducion of Ordr Rcll our nd ordr linr homognous ODE b c 0 whr, b nd c r consns. Assuming n xponnil soluion lds o chrcrisic quion: r r br c 0 Qudric formul or fcoring ilds wo soluions, r &
Reflections on a mismatched transmission line Reflections.doc (4/1/00) Introduction The transmission line equations are given by
Reflections on a mismatched transmission line Reflections.doc (4/1/00) Introdction The transmission line eqations are given by, I z, t V z t l z t I z, t V z, t c z t (1) (2) Where, c is the per-nit-length
Dealing with quantitative data and problem solving life is a story problem! Attacking Quantitative Problems
Daling with quantitati data and problm soling lif is a story problm! A larg portion of scinc inols quantitati data that has both alu and units. Units can sa your butt! Nd handl on mtric prfixs Dimnsional
CBSE 2015 FOREIGN EXAMINATION
CBSE 05 FOREIGN EXAMINATION (Sris SSO Cod No 65//F, 65//F, 65//F : Forign Rgion) Not tht ll th sts hv sm qustions Onl thir squnc of pprnc is diffrnt M Mrks : 00 Tim Allowd : Hours SECTION A Q0 Find th
CSE303 - Introduction to the Theory of Computing Sample Solutions for Exercises on Finite Automata
CSE303 - Introduction to th Thory of Computing Smpl Solutions for Exrciss on Finit Automt Exrcis 2.1.1 A dtrministic finit utomton M ccpts th mpty string (i.., L(M)) if nd only if its initil stt is finl
Finite Element Models for Steady Flows of Viscous Incompressible Fluids
Finit Elmnt Modls for Stad Flows of Viscous Incomprssibl Fluids Rad: Chaptr 10 JN Rdd CONTENTS Govrning Equations of Flows of Incomprssibl Fluids Mid (Vlocit-Prssur) Finit Elmnt Modl Pnalt Function Mthod
ME 321 Kinematics and Dynamics of Machines S. Lambert Winter 2002
3.4 Forc Analysis of Linkas An undrstandin of forc analysis of linkas is rquird to: Dtrmin th raction forcs on pins, tc. as a consqunc of a spcifid motion (don t undrstimat th sinificanc of dynamic or
PHA 5127 Answers Homework 2 Fall 2001
PH 5127 nswrs Homwork 2 Fall 2001 OK, bfor you rad th answrs, many of you spnt a lot of tim on this homwork. Plas, nxt tim if you hav qustions plas com talk/ask us. Thr is no nd to suffr (wll a littl suffring
Phys 344 Lect 17 March 16 th,
Phs 344 Lct 7 March 6 th, 7 Fri. 3/ 6 C.8.-.8.7, S. B. Gaussian, 6.3-.5 quipartion, Mawll HW7 S. 3,36, 4 B.,,3 Mon. 3/9 Wd. 3/ Fri. 3/3 S 6.5-7 Partition Function S A.5 Q.M. Background: Bos and Frmi S
VII. Quantum Entanglement
VII. Quantum Entanglmnt Quantum ntanglmnt is a uniqu stat of quantum suprposition. It has bn studid mainly from a scintific intrst as an vidnc of quantum mchanics. Rcntly, it is also bing studid as a basic
Math 61 : Discrete Structures Final Exam Instructor: Ciprian Manolescu. You have 180 minutes.
Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
Self-Adjointness and Its Relationship to Quantum Mechanics. Ronald I. Frank 2016
Ronald I. Frank 06 Adjoint https://n.wikipdia.org/wiki/adjoint In gnral thr is an oprator and a procss that dfin its adjoint *. It is thn slf-adjoint if *. Innr product spac https://n.wikipdia.org/wiki/innr_product_spac
High Energy Physics. Lecture 5 The Passage of Particles through Matter
High Enrgy Physics Lctur 5 Th Passag of Particls through Mattr 1 Introduction In prvious lcturs w hav sn xampls of tracks lft by chargd particls in passing through mattr. Such tracks provid som of th most
Weighted Residual Methods
Weighted Resil Methods Formltion of FEM Model Direct Method Formltion of FEM Model Vritionl Method Weighted Resils Severl pproches cn e sed to trnsform the phsicl formltion of prolem to its finite element
Derivation of Electron-Electron Interaction Terms in the Multi-Electron Hamiltonian
Drivation of Elctron-Elctron Intraction Trms in th Multi-Elctron Hamiltonian Erica Smith Octobr 1, 010 1 Introduction Th Hamiltonian for a multi-lctron atom with n lctrons is drivd by Itoh (1965) by accounting
, between the vertical lines x a and x b. Given a demand curve, having price as a function of quantity, p f (x) at height k is the curve f ( x,
Clculus for Businss nd Socil Scincs - Prof D Yun Finl Em Rviw vrsion 5/9/7 Chck wbsit for ny postd typos nd updts Pls rport ny typos This rviw sht contins summris of nw topics only (This rviw sht dos hv
( ) Geometric Operations and Morphing. Geometric Transformation. Forward v.s. Inverse Mapping. I (x,y ) Image Processing - Lesson 4 IDC-CG 1
Img Procssing - Lsson 4 Gomtric Oprtions nd Morphing Gomtric Trnsformtion Oprtions dpnd on Pil s Coordints. Contt fr. Indpndnt of pil vlus. f f (, ) (, ) ( f (, ), f ( ) ) I(, ) I', (,) (, ) I(,) I (,
EECE 301 Signals & Systems Prof. Mark Fowler
EECE 301 Signals & Systms Prof. Mark Fowlr ot St #21 D-T Signals: Rlation btwn DFT, DTFT, & CTFT 1/16 W can us th DFT to implmnt numrical FT procssing This nabls us to numrically analyz a signal to find
Difference -Analytical Method of The One-Dimensional Convection-Diffusion Equation
Diffrnc -Analytical Mthod of Th On-Dimnsional Convction-Diffusion Equation Dalabav Umurdin Dpartmnt mathmatic modlling, Univrsity of orld Economy and Diplomacy, Uzbistan Abstract. An analytical diffrncing
The van der Waals interaction 1 D. E. Soper 2 University of Oregon 20 April 2012
Th van dr Waals intraction D. E. Sopr 2 Univrsity of Orgon 20 pril 202 Th van dr Waals intraction is discussd in Chaptr 5 of J. J. Sakurai, Modrn Quantum Mchanics. Hr I tak a look at it in a littl mor
I. The Connection between Spectroscopy and Quantum Mechanics
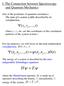I. Th Connction twn Spctroscopy nd Quntum Mchnics On of th postults of quntum mchnics: Th stt of systm is fully dscrid y its wvfunction, Ψ( r1, r,..., t) whr r 1, r, tc. r th coordints of th constitunt
Linear Non-Gaussian Structural Equation Models
IMPS 8, Durham, NH Linar Non-Gaussian Structural Equation Modls Shohi Shimizu, Patrik Hoyr and Aapo Hyvarinn Osaka Univrsity, Japan Univrsity of Hlsinki, Finland Abstract Linar Structural Equation Modling
MA 262, Spring 2018, Final exam Version 01 (Green)
MA 262, Spring 218, Final xam Vrsion 1 (Grn) INSTRUCTIONS 1. Switch off your phon upon ntring th xam room. 2. Do not opn th xam booklt until you ar instructd to do so. 3. Bfor you opn th booklt, fill in
Lecture 4. Conic section
Lctur 4 Conic sction Conic sctions r locus of points whr distncs from fixd point nd fixd lin r in constnt rtio. Conic sctions in D r curvs which r locus of points whor position vctor r stisfis r r. whr
Introduction - the economics of incomplete information
Introdction - th conomics of incomplt information Backgrond: Noclassical thory of labor spply: No nmploymnt, individals ithr mployd or nonparticipants. Altrnativs: Job sarch Workrs hav incomplt info on
Section 14.3 Arc Length and Curvature
Section 4.3 Arc Length nd Curvture Clculus on Curves in Spce In this section, we ly the foundtions for describing the movement of n object in spce.. Vector Function Bsics In Clc, formul for rc length in