Quadratic Function. Parabola. Parent quadratic function. Vertex. Axis of Symmetry
|
|
|
- Florence Holt
- 6 years ago
- Views:
Transcription
1 Name: Chapter 10: Quadratic Equations and Functions Section 10.1: Graph = a + c Quadratic Function Parabola Parent quadratic function Verte Ais of Smmetr Parent Function =
2 Eample 1: Make a table, graph and compare the graphs of = 3 and = = Compared to = Vertical: Stretch or Shrink Reflection: Yes or No Translation: Up or Down or Neither Domain: Range: Eample : Make a table, graph and compare the graphs of 1 4 and = Compared to = Vertical: Stretch or Shrink Reflection: Yes or No Translation: Up or Down or Neither Domain: Range:
3 Eample 3: Make a table, graph and compare the graphs of 1 and = Compared to = Vertical: Stretch or Shrink Reflection: Yes or No Translation: Up or Down or Neither Domain: Range: Eample 4: Make a table, graph and compare the graphs of = and = = Compared to = Vertical: Stretch or Shrink Reflection: Yes or No Translation: Up or Down or Neither 3 Domain: Range:
4 Section 10.: Graph = a + b + c PROPERTIES OF THE GRAPH OF A QUADRATIC FUNCTION To graph a parabola in the form = a + b + c : Step 1: Determine if the parabola opens up or down. If the a-value is, it opens. If the a-value is, it opens. Step : Find the ais of smmetr (the mirror of the parabola). Step 3: Find and plot the verte (middle point of the parabola). Step 4: Find more points on the graph b getting the calculator table. Plot the points. (Center the verte) Verte Other Important Information About Parabolas Minimum value Maimum value -Intercept Roots 4
5 Eample 1: Graph = Step 1: Determine whether the parabola opens up or down Step : Find and draw the ais of smmetr: Step 3: Find and plot the verte. Step 4: Find more points on the graph. Choose -values less than and greater than the verte. Verte Eample : Graph = Step 1: Determine whether the parabola opens up or down Step : Find and draw the ais of smmetr: Step 3: Find and plot the verte. Step 4: Find more points on the graph. Choose -values less than and greater than the verte. 5 Verte
6 Eample 3: Graph = Step 1: Determine whether the parabola opens up or down Step : Find and draw the ais of smmetr: Step 3: Find and plot the verte. Step 4: Find more points on the graph. Choose -values less than and greater than the verte. Verte Eample 4: The cables between two telephone poles can be modeled b the equation = , where and are measured in feet. To the nearest foot, what is the height of the cable above the ground at its lowest point? 6
7 10. Etension Eploration Each group will receive a quadratic equation to eamine. You will create a poster with the following information. If there are onl three group members, one person should do the tasks for group members #1 and #4. Group Member #1 Determine a = b = c = Does the parabola open up or down? b Determine the ais of smmetr: a Group Member # Enter the equation into the calculator Create a table verte Group Member #3 Graph the equation Identif the -intercepts Group Member #4 Solve the equation b factoring When ou re done, put a star or circle our Factored form Solutions X-intercepts 10. Etension Poster Summar Equation Factored Form Solutions -intercepts = = = 8 = = = = 4 = Wh is the factored form referred to as intercept form? What is the relationship between the solutions of the equation and the -intercepts? 7
8 Etension 10.: Graph Quadratic Functions in Intercept Form GRAPH OF INTERCEPT FORM: = a( p)( q) Step 1: Find the -intercepts b setting the factors equal to zero. Step : The Ais of Smmetr is halfwa between the roots. Step 3: Find and plot the verte. Opens Up if a-value is. Opens Down if a-value is. Eample 1: Graph = -( + 1)( 5) Step 1: Identif and plot the -intercepts Step : Find and draw the ais of smmetr: Step 3: Find and plot the verte. 8
9 Eample : Graph = ( + 1)( 3) Step 1: Identif and plot the -intercepts Step : Find and draw the ais of smmetr: Step 3: Find and plot the verte. Eample 3: = 8 Step 1: Rewrite the quadratic function in intercept form. Step : Identif and plot the -intercepts Step 3: Find and draw the ais of smmetr: Step 4: Find and plot the verte. 9
10 Section 10.3: Solve Quadratic Equations b Graphing NUMBER OF SOLUTIONS OF A QUADRATIC EQUATION Two Solutions One Solution No Solutions (Unfactorable) Eample 1: Solve + 4 = 5 b graphing. Step 1: Put equation into standard form. Step : Plug equation into calculator. Locate the intercepts ( = 0) and center the verte. Verte Step 3: Factor and solve the equation to check our roots. 10
11 Eample : Solve 4 = -4 b graphing. Step 1: Put equation into standard form. Step : Plug equation into calculator. Locate the intercepts ( = 0) and center the verte. Verte Step 3: Factor and solve the equation to check our roots. Eample 3: Solve + 8 = b graphing. Step 1: Put equation into standard form. Step : Plug equation into calculator. Locate the intercepts ( = 0) and center the verte. Verte Step 3: Factor and solve the equation to check our roots. 11
12 Section 10.4: Use Square Roots to solve Quadratic Equations Step 1: Get the squared term all b itself on one side of the equal sign. = (number) Step : To undo the square term, we have to do the inverse, which is to. If the (number) is positive, ou will have solution(s). (number) If the (number) is zero, ou will have solution(s). 0 If the (number) is negative, ou will have solution(s). Ø Step 3: Solve the remaining equations for the variable (if necessar). Eample 1: Solve the Equation. a. z 5 = 4 b. 5k = 9 c = 3 d. 6g + 1 = 19 e. 5( + 1) = 30 f. 3(m 4) = 1 1
13 Eample : During an ice hocke game, a remote-controlled blimp flies above the crowd and drops a numbered table-tennis ball. The number of the ball corresponds to a prize. Use the information in the diagram to find the amount of time that the ball is in the air. Eample 3: You drop our glasses from a balcon 18 feet above our den on to a table that is 3 feet above the ground. How long are our glasses in the air? 13
14 Section 10.5 Solve Quadratic Equations b Completing the Square Use a bo to square the binomial. 1. ( + 3). ( + 4) 3. ( 7) What patterns do ou notice? Complete the Square: How can we reverse the procedure? Find the number that completes the square = ( + ) = ( - ) = ( + ) 4. + = ( - ) Let s Practice! Find the value of c such that each epression is a perfect square trinomial. Then write the epression as the square of a binomial c 6. r 4r + c 7. p 30p + c 14
15 Completing the Square Step 1: Put the epression into this form: + b + = (number) or b + = (number) Step : To fill in the blank, take half of b, square it and add it to both sides. + b + b b = (number) + or b + b = (number) + b Step 3: Factor the left side into a perfect square, simplif the right side. Step 4: Square root both sides to solve for. Eample 1: Solve the quadratic equation a. + 6 = -5 b. r 8r = 9 c. + 6 = 7 d. d 4 = 5d 15
16 Eample : Solve the equation b completing the square. a. 4m 16m + 8 = 0 b. 5s + 60s + 15 = 0 c = 0 d. k + 0k = 8 Eample 5: You are designing a herb garden with a uniform border of ornamental grass around it as shown below. Your design includes 1 square feet for the herb garden. Find the width of the grass border to the nearest inch. 16 ft 6 ft 16 6 ft
17 Section 10.5 Etension: Graph Quadratic Functions in Verte Form Sometimes quadratic functions are written: = a( h) + k This form of a quadratic is known as VERTEX FORM. Let s see if we can figure out wh. 1. = ( 3) + 4 Rewrite the given equation in standard form: = a + b + c. = ( + 1) Rewrite the given equation in standard form: = a + b + c Graph the equation b finding the ais of smmetr and creating a table. Graph the equation b finding the ais of smmetr and creating a table. verte verte 17
18 3. = -( + ) 3 Rewrite the given equation in standard form: = a + b + c 4. = ( + 3) + 1 Rewrite the given equation in standard form: = a + b + c Graph the equation b finding the ais of smmetr and creating a table. Graph the equation b finding the ais of smmetr and creating a table. verte verte Wh do ou think = a( h) + k is called verte form? 18
19 h Verte Form k a Verte: Ais of Smmetr: Up if: Down if: Eample 1: Graph a quadratic function in verte form = -( + ) + 3 Step 1: Identif the values of a, h, and k. Step : Identif and draw the ais of smmetr. Step 3: Find and plot the verte (h, k). Step 4: Find more points on the graph. Choose -values less than and greater than the verte. Verte 19
20 Eample : Write the function in verte form (complete the square) and graph the function. = Step 1: Write the function in verte form b completing the square. Step : Identif the values of a, h, and k. Step 3: Identif and draw the ais of smmetr. Step 4: Find and plot the verte (h, k). Step 5: Find more points on the graph. Choose -values less than and greater than the verte. Verte 0
21 Eample 3: Write the function in verte form (complete the square) and graph the function. a. = Step 1: Write the function in verte form b completing the square. Step : Identif the values of a, h, and k. Step 3: Identif and draw the ais of smmetr. Step 4: Find and plot the verte (h, k). Step 5: Find more points on the graph. Choose -values less than and greater than the verte. 1 Verte
22 Section 10.6: Solve Quadratic Equations b the Quadratic Formula The Quadratic Formula Used to solve quadratics equations in standard form. Standard Form: Quadratic Formula: b b 4ac a b c 0 a Eample 1: Use the quadratic formula to solve a. 5 = 3 b. + 7 = 9 c. 3 1 =
23 Eample : A crabbing net is thrown from a bridge, which is 35 feet above the water. If the net s initial velocit is 10 feet per second, how long will it take the net to hit the water? Eample 3: For the period , the number of book titles published b a small publishing compan can be modeled b the function = , where is the number of ears since In what ear did the compan publish 80 books? 3
24 Section 10.7: Interpret the Discriminant Discriminant Can determine how man solutions a quadratic equation has. b b 4ac a USING THE DISCRIMINANT OF a + b + c = 0 Value of the discriminant Number of solutions Graph of = a + b + c = 0 4
25 Eample 1: Find the discriminant and determine the number of solutions a. 3 = 0 b = -5 c. - 9 = 6 d. 3 + = 0 e = 0 f. + = 1 5
26 Section 10.8: Compare Linear, Eponential, and Quadratic Models Linear Function Eponential Function Quadratic Function = = = Eample 1: Use a graph to tell whether the ordered pairs represent a linear function, an eponential function, or a quadratic function. a. (-, 7), (-1, 1), (0, -1), (1, 1), (, 7) b. (-, 4), (-1,), (0, 1), (1, ½), (, ¼) 6
27 Differences and ratios in a table Linear equation Eponential function Quadratic Function Eample : Use differences or ratios to tell whether the table of values represents a linear function, an eponential function, or a quadratic function. Then write the equation for the function a b c
28 Eample 3: The table shows the cost to run an as in a magazine. Tell whether the data can be modeled b a linear function, an eponential function, or a quadratic function. Then write the equation for the function. Number of lines, Total cost, 4 $ $1.5 6 $ $ $ $19.65 Eample 4: The table shows the distance a clock s pendulum swings after certain amounts of time. Tell whether the data can be modeled b a linear function, an eponential function, or a quadratic function. Then write the equation for the function. Time in seconds, Distance in feet,
7.2 Connecting Intercepts and Linear Factors
 Name Class Date 7.2 Connecting Intercepts and Linear Factors Essential Question: How are -intercepts of a quadratic function and its linear factors related? Resource Locker Eplore Connecting Factors and
Name Class Date 7.2 Connecting Intercepts and Linear Factors Essential Question: How are -intercepts of a quadratic function and its linear factors related? Resource Locker Eplore Connecting Factors and
Writing Quadratic Functions in Standard Form
 Chapter Summar Ke Terms standard form (general form) of a quadratic function (.1) parabola (.1) leading coefficient (.) second differences (.) vertical motion model (.3) zeros (.3) interval (.3) open interval
Chapter Summar Ke Terms standard form (general form) of a quadratic function (.1) parabola (.1) leading coefficient (.) second differences (.) vertical motion model (.3) zeros (.3) interval (.3) open interval
20.2 Connecting Intercepts and Linear Factors
 Name Class Date 20.2 Connecting Intercepts and Linear Factors Essential Question: How are -intercepts of a quadratic function and its linear factors related? Resource Locker Eplore Connecting Factors and
Name Class Date 20.2 Connecting Intercepts and Linear Factors Essential Question: How are -intercepts of a quadratic function and its linear factors related? Resource Locker Eplore Connecting Factors and
6.3 Interpreting Vertex Form and Standard Form
 Name Class Date 6.3 Interpreting Verte Form and Standard Form Essential Question: How can ou change the verte form of a quadratic function to standard form? Resource Locker Eplore Identifing Quadratic
Name Class Date 6.3 Interpreting Verte Form and Standard Form Essential Question: How can ou change the verte form of a quadratic function to standard form? Resource Locker Eplore Identifing Quadratic
Name Class Date. Deriving the Standard-Form Equation of a Parabola
 Name Class Date 1. Parabolas Essential Question: How is the distance formula connected with deriving equations for both vertical and horizontal parabolas? Eplore Deriving the Standard-Form Equation of
Name Class Date 1. Parabolas Essential Question: How is the distance formula connected with deriving equations for both vertical and horizontal parabolas? Eplore Deriving the Standard-Form Equation of
Quadratic Functions Objective: To be able to graph a quadratic function and identify the vertex and the roots.
 Name: Quadratic Functions Objective: To be able to graph a quadratic function and identif the verte and the roots. Period: Quadratic Function Function of degree. Usuall in the form: We are now going to
Name: Quadratic Functions Objective: To be able to graph a quadratic function and identif the verte and the roots. Period: Quadratic Function Function of degree. Usuall in the form: We are now going to
Mth 95 Module 4 Chapter 8 Spring Review - Solving quadratic equations using the quadratic formula
 Mth 95 Module 4 Chapter 8 Spring 04 Review - Solving quadratic equations using the quadratic formula Write the quadratic formula. The NUMBER of REAL and COMPLEX SOLUTIONS to a quadratic equation ( a b
Mth 95 Module 4 Chapter 8 Spring 04 Review - Solving quadratic equations using the quadratic formula Write the quadratic formula. The NUMBER of REAL and COMPLEX SOLUTIONS to a quadratic equation ( a b
Maintaining Mathematical Proficiency
 Chapter Maintaining Mathematical Proficienc Find the -intercept of the graph of the linear equation. 1. = + 3. = 3 + 5 3. = 10 75. = ( 9) 5. 7( 10) = +. 5 + 15 = 0 Find the distance between the two points.
Chapter Maintaining Mathematical Proficienc Find the -intercept of the graph of the linear equation. 1. = + 3. = 3 + 5 3. = 10 75. = ( 9) 5. 7( 10) = +. 5 + 15 = 0 Find the distance between the two points.
Chapter 5 Smartboard Notes
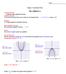 Name Chapter 5 Smartboard Notes 10.1 Graph ax 2 + c Learning Outcome To graph simple quadratic functions Quadratic function A non linear function that can be written in the standard form y = ax 2 + bx
Name Chapter 5 Smartboard Notes 10.1 Graph ax 2 + c Learning Outcome To graph simple quadratic functions Quadratic function A non linear function that can be written in the standard form y = ax 2 + bx
= x. Algebra II Notes Quadratic Functions Unit Graphing Quadratic Functions. Math Background
 Algebra II Notes Quadratic Functions Unit 3.1 3. Graphing Quadratic Functions Math Background Previousl, ou Identified and graphed linear functions Applied transformations to parent functions Graphed quadratic
Algebra II Notes Quadratic Functions Unit 3.1 3. Graphing Quadratic Functions Math Background Previousl, ou Identified and graphed linear functions Applied transformations to parent functions Graphed quadratic
Chapter 9 Notes Alg. 1H 9-A1 (Lesson 9-3) Solving Quadratic Equations by Finding the Square Root and Completing the Square
 Chapter Notes Alg. H -A (Lesson -) Solving Quadratic Equations b Finding the Square Root and Completing the Square p. *Calculator Find the Square Root: take the square root of. E: Solve b finding square
Chapter Notes Alg. H -A (Lesson -) Solving Quadratic Equations b Finding the Square Root and Completing the Square p. *Calculator Find the Square Root: take the square root of. E: Solve b finding square
3.1 Graph Quadratic Functions
 3. Graph Quadratic Functions in Standard Form Georgia Performance Standard(s) MMA3b, MMA3c Goal p Use intervals of increase and decrease to understand average rates of change of quadratic functions. Your
3. Graph Quadratic Functions in Standard Form Georgia Performance Standard(s) MMA3b, MMA3c Goal p Use intervals of increase and decrease to understand average rates of change of quadratic functions. Your
Maintaining Mathematical Proficiency
 Name Date Chapter 8 Maintaining Mathematical Proficienc Graph the linear equation. 1. = 5. = + 3 3. 1 = + 3. = + Evaluate the epression when =. 5. + 8. + 3 7. 3 8. 5 + 8 9. 8 10. 5 + 3 11. + + 1. 3 + +
Name Date Chapter 8 Maintaining Mathematical Proficienc Graph the linear equation. 1. = 5. = + 3 3. 1 = + 3. = + Evaluate the epression when =. 5. + 8. + 3 7. 3 8. 5 + 8 9. 8 10. 5 + 3 11. + + 1. 3 + +
A. B. C. D. Quadratics Practice Test. Question 1. Select the graph of the quadratic function. g (x ) = 1 3 x 2. 3/8/2018 Print Assignment
 Question 1. Select the graph of the quadratic function. g (x ) = 1 3 x 2 C. D. https://my.hrw.com/wwtb2/viewer/printall_vs23.html?umk5tfdnj31tcldd29v4nnzkclztk3w8q6wgvr262aca0a5fsymn1tfv8j1vs4qotwclvofjr8xhs0cldd29v4
Question 1. Select the graph of the quadratic function. g (x ) = 1 3 x 2 C. D. https://my.hrw.com/wwtb2/viewer/printall_vs23.html?umk5tfdnj31tcldd29v4nnzkclztk3w8q6wgvr262aca0a5fsymn1tfv8j1vs4qotwclvofjr8xhs0cldd29v4
Fair Game Review. Chapter 8. Graph the linear equation. Big Ideas Math Algebra Record and Practice Journal
 Name Date Chapter Graph the linear equation. Fair Game Review. =. = +. =. =. = +. = + Copright Big Ideas Learning, LLC Big Ideas Math Algebra Name Date Chapter Fair Game Review (continued) Evaluate the
Name Date Chapter Graph the linear equation. Fair Game Review. =. = +. =. =. = +. = + Copright Big Ideas Learning, LLC Big Ideas Math Algebra Name Date Chapter Fair Game Review (continued) Evaluate the
x Radical Sign: Radicand: the number beneath the radical sign
 Sllabus Objective: 9.4 The student will solve quadratic equations using graphic and algebraic techniques to include the quadratic formula, square roots, factoring, completing the square, and graphing.
Sllabus Objective: 9.4 The student will solve quadratic equations using graphic and algebraic techniques to include the quadratic formula, square roots, factoring, completing the square, and graphing.
6.1 Solving Quadratic Equations by Graphing Algebra 2
 10.1 Solving Quadratic Equations b Graphing Algebra Goal 1: Write functions in quadratic form Goal : Graph quadratic functions Goal 3: Solve quadratic equations b graphing. Quadratic Function: Eample 1:
10.1 Solving Quadratic Equations b Graphing Algebra Goal 1: Write functions in quadratic form Goal : Graph quadratic functions Goal 3: Solve quadratic equations b graphing. Quadratic Function: Eample 1:
Unit 2 Notes Packet on Quadratic Functions and Factoring
 Name: Period: Unit Notes Packet on Quadratic Functions and Factoring Notes #: Graphing quadratic equations in standard form, verte form, and intercept form. A. Intro to Graphs of Quadratic Equations: a
Name: Period: Unit Notes Packet on Quadratic Functions and Factoring Notes #: Graphing quadratic equations in standard form, verte form, and intercept form. A. Intro to Graphs of Quadratic Equations: a
Lesson Goals. Unit 4 Polynomial/Rational Functions Quadratic Functions (Chap 0.3) Family of Quadratic Functions. Parabolas
 Unit 4 Polnomial/Rational Functions Quadratic Functions (Chap 0.3) William (Bill) Finch Lesson Goals When ou have completed this lesson ou will: Graph and analze the graphs of quadratic functions. Solve
Unit 4 Polnomial/Rational Functions Quadratic Functions (Chap 0.3) William (Bill) Finch Lesson Goals When ou have completed this lesson ou will: Graph and analze the graphs of quadratic functions. Solve
2 nd Semester Final Exam Review Block Date
 Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. Identif the verte and ais of smmetr. 1 (10-1) 1. (10-1). 3 (10-) 3. 4 7 (10-) 4. 3 6 4 (10-1) 5. Predict
Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. Identif the verte and ais of smmetr. 1 (10-1) 1. (10-1). 3 (10-) 3. 4 7 (10-) 4. 3 6 4 (10-1) 5. Predict
Final Exam Review Part 2 #1 Page 1 / 21
 Final Eam Review Part #1 Intermediate Algebra / MAT 135 Spring 017 Master ( Master Templates) Student Name/ID: v 1. Solve for, where is a real number. v v + 1 + =. Solve for, where is a real number. +
Final Eam Review Part #1 Intermediate Algebra / MAT 135 Spring 017 Master ( Master Templates) Student Name/ID: v 1. Solve for, where is a real number. v v + 1 + =. Solve for, where is a real number. +
MAT 1033C -- Martin-Gay Intermediate Algebra Chapter 8 (8.1, 8.2, 8.5, 8.6) Practice for the Exam
 MAT 33C -- Martin-Ga Intermediate Algebra Chapter 8 (8.1 8. 8. 8.6) Practice for the Eam Name Date Da/Time: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
MAT 33C -- Martin-Ga Intermediate Algebra Chapter 8 (8.1 8. 8. 8.6) Practice for the Eam Name Date Da/Time: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
Chapter 5: Quadratic Equations and Functions 5.1 Modeling Data With Quadratic Functions Quadratic Functions and Their Graphs
 Ch 5 Alg Note Sheet Ke Chapter 5: Quadratic Equations and Functions 5.1 Modeling Data With Quadratic Functions Quadratic Functions and Their Graphs Definition: Standard Form of a Quadratic Function The
Ch 5 Alg Note Sheet Ke Chapter 5: Quadratic Equations and Functions 5.1 Modeling Data With Quadratic Functions Quadratic Functions and Their Graphs Definition: Standard Form of a Quadratic Function The
REVIEW KEY VOCABULARY REVIEW EXAMPLES AND EXERCISES
 Etra Eample. Graph.. 6. 7. (, ) (, ) REVIEW KEY VOCABULARY quadratic function, p. 6 standard form of a quadratic function, p. 6 parabola, p. 6 verte, p. 6 ais of smmetr, p. 6 minimum, maimum value, p.
Etra Eample. Graph.. 6. 7. (, ) (, ) REVIEW KEY VOCABULARY quadratic function, p. 6 standard form of a quadratic function, p. 6 parabola, p. 6 verte, p. 6 ais of smmetr, p. 6 minimum, maimum value, p.
f(x) = 2x 2 + 2x - 4
 4-1 Graphing Quadratic Functions What You ll Learn Scan the tet under the Now heading. List two things ou will learn about in the lesson. 1. Active Vocabular 2. New Vocabular Label each bo with the terms
4-1 Graphing Quadratic Functions What You ll Learn Scan the tet under the Now heading. List two things ou will learn about in the lesson. 1. Active Vocabular 2. New Vocabular Label each bo with the terms
Properties of the Graph of a Quadratic Function. has a vertex with an x-coordinate of 2 b } 2a
 0.2 Graph 5 a 2 b c Before You graphed simple quadratic functions. Now You will graph general quadratic functions. Wh? So ou can investigate a cable s height, as in Eample 4. Ke Vocabular minimum value
0.2 Graph 5 a 2 b c Before You graphed simple quadratic functions. Now You will graph general quadratic functions. Wh? So ou can investigate a cable s height, as in Eample 4. Ke Vocabular minimum value
2 nd Semester Final Exam Review Block Date
 Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. 1 (10-1) 1. (10-1). (10-1) 3. (10-1) 4. 3 Graph each function. Identif the verte, ais of smmetr, and
Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. 1 (10-1) 1. (10-1). (10-1) 3. (10-1) 4. 3 Graph each function. Identif the verte, ais of smmetr, and
Ready To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions
 Read To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions Find these vocabular words in Lesson 5-1 and the Multilingual Glossar. Vocabular quadratic function parabola verte
Read To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions Find these vocabular words in Lesson 5-1 and the Multilingual Glossar. Vocabular quadratic function parabola verte
9-1. The Function with Equation y = ax 2. Vocabulary. Graphing y = x 2. Lesson
 Chapter 9 Lesson 9-1 The Function with Equation = a BIG IDEA The graph of an quadratic function with equation = a, with a 0, is a parabola with verte at the origin. Vocabular parabola refl ection-smmetric
Chapter 9 Lesson 9-1 The Function with Equation = a BIG IDEA The graph of an quadratic function with equation = a, with a 0, is a parabola with verte at the origin. Vocabular parabola refl ection-smmetric
Unit 10 - Graphing Quadratic Functions
 Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
First Semester Final Review NON-Graphing Calculator
 Algebra First Semester Final Review NON-Graphing Calculator Name:. 1. Find the slope of the line passing through the points ( 5, ) and ( 3, 7).. Find the slope-intercept equation of the line passing through
Algebra First Semester Final Review NON-Graphing Calculator Name:. 1. Find the slope of the line passing through the points ( 5, ) and ( 3, 7).. Find the slope-intercept equation of the line passing through
4. exponential decay; 20% 9.1 Practice A found square root instead of cube root 16 =
 9.. eponential deca; 0% 9. Practice A.. 7. 7.. 6. 9. 0 7.. 9. 0. found square root instead of cube root 6 = = = 9. = 7, 9. =,.. 7n 7n. 96. =, 97. =, 9. linear function: = + 0 99. quadratic function: =
9.. eponential deca; 0% 9. Practice A.. 7. 7.. 6. 9. 0 7.. 9. 0. found square root instead of cube root 6 = = = 9. = 7, 9. =,.. 7n 7n. 96. =, 97. =, 9. linear function: = + 0 99. quadratic function: =
PRACTICE FINAL EXAM. 3. Solve: 3x 8 < 7. Write your answer using interval notation. Graph your solution on the number line.
 MAC 1105 PRACTICE FINAL EXAM College Algebra *Note: this eam is provided as practice onl. It was based on a book previousl used for this course. You should not onl stud these problems in preparing for
MAC 1105 PRACTICE FINAL EXAM College Algebra *Note: this eam is provided as practice onl. It was based on a book previousl used for this course. You should not onl stud these problems in preparing for
4.2 Parabolas. Explore Deriving the Standard-Form Equation. Houghton Mifflin Harcourt Publishing Company. (x - p) 2 + y 2 = (x + p) 2
 COMMON CORE. d Locker d LESSON Parabolas Common Core Math Standards The student is epected to: COMMON CORE A-CED.A. Create equations in two or more variables to represent relationships between quantities;
COMMON CORE. d Locker d LESSON Parabolas Common Core Math Standards The student is epected to: COMMON CORE A-CED.A. Create equations in two or more variables to represent relationships between quantities;
MATH 60 Review Problems for Final Exam
 MATH 60 Review Problems for Final Eam Scientific Calculators Onl - Graphing Calculators Not Allowed NO CLASS NOTES PERMITTED Evaluate the epression for the given values. m 1) m + 3 for m = 3 2) m 2 - n2
MATH 60 Review Problems for Final Eam Scientific Calculators Onl - Graphing Calculators Not Allowed NO CLASS NOTES PERMITTED Evaluate the epression for the given values. m 1) m + 3 for m = 3 2) m 2 - n2
Skills Practice Skills Practice for Lesson 3.1
 Skills Practice Skills Practice for Lesson. Name Date Lots and Projectiles Introduction to Quadratic Functions Vocabular Define each term in our own words.. quadratic function. vertical motion Problem
Skills Practice Skills Practice for Lesson. Name Date Lots and Projectiles Introduction to Quadratic Functions Vocabular Define each term in our own words.. quadratic function. vertical motion Problem
Algebra 1 Unit 9 Quadratic Equations
 Algebra 1 Unit 9 Quadratic Equations Part 1 Name: Period: Date Name of Lesson Notes Tuesda 4/4 Wednesda 4/5 Thursda 4/6 Frida 4/7 Monda 4/10 Tuesda 4/11 Wednesda 4/12 Thursda 4/13 Frida 4/14 Da 1- Quadratic
Algebra 1 Unit 9 Quadratic Equations Part 1 Name: Period: Date Name of Lesson Notes Tuesda 4/4 Wednesda 4/5 Thursda 4/6 Frida 4/7 Monda 4/10 Tuesda 4/11 Wednesda 4/12 Thursda 4/13 Frida 4/14 Da 1- Quadratic
Name Class Date. Solving by Graphing and Algebraically
 Name Class Date 16-4 Nonlinear Sstems Going Deeper Essential question: How can ou solve a sstem of equations when one equation is linear and the other is quadratic? To estimate the solution to a sstem
Name Class Date 16-4 Nonlinear Sstems Going Deeper Essential question: How can ou solve a sstem of equations when one equation is linear and the other is quadratic? To estimate the solution to a sstem
Skills Practice Skills Practice for Lesson 1.1
 Skills Practice Skills Practice for Lesson. Name Date Lots and Projectiles Introduction to Quadratic Functions Vocabular Give an eample of each term.. quadratic function 9 0. vertical motion equation s
Skills Practice Skills Practice for Lesson. Name Date Lots and Projectiles Introduction to Quadratic Functions Vocabular Give an eample of each term.. quadratic function 9 0. vertical motion equation s
Fair Game Review. Chapter 9. Find the square root(s) ± Find the side length of the square. 7. Simplify Simplify 63.
 Name Date Chapter 9 Find the square root(s). Fair Game Review... 9. ±. Find the side length of the square.. s. s s Area = 9 ft s Area = 0. m 7. Simplif 0. 8. Simplif. 9. Simplif 08. 0. Simplif 88. Copright
Name Date Chapter 9 Find the square root(s). Fair Game Review... 9. ±. Find the side length of the square.. s. s s Area = 9 ft s Area = 0. m 7. Simplif 0. 8. Simplif. 9. Simplif 08. 0. Simplif 88. Copright
TRANSFORMATIONS OF f(x) = x Example 1
 TRANSFORMATIONS OF f() = 2 2.1.1 2.1.2 Students investigate the general equation for a famil of quadratic functions, discovering was to shift and change the graphs. Additionall, the learn how to graph
TRANSFORMATIONS OF f() = 2 2.1.1 2.1.2 Students investigate the general equation for a famil of quadratic functions, discovering was to shift and change the graphs. Additionall, the learn how to graph
Answers Investigation 2
 Applications 1. a. Square Side Area 4 16 2 6 36 7 49 64 9 1 10 100 11 121 Rectangle Length Width Area 0 0 9 1 9 10 2 20 11 3 33 12 4 4 13 6 14 6 4 1 7 10 b. (See Figure 1.) c. The graph and the table both
Applications 1. a. Square Side Area 4 16 2 6 36 7 49 64 9 1 10 100 11 121 Rectangle Length Width Area 0 0 9 1 9 10 2 20 11 3 33 12 4 4 13 6 14 6 4 1 7 10 b. (See Figure 1.) c. The graph and the table both
Chapter 18 Quadratic Function 2
 Chapter 18 Quadratic Function Completed Square Form 1 Consider this special set of numbers - the square numbers or the set of perfect squares. 4 = = 9 = 3 = 16 = 4 = 5 = 5 = Numbers like 5, 11, 15 are
Chapter 18 Quadratic Function Completed Square Form 1 Consider this special set of numbers - the square numbers or the set of perfect squares. 4 = = 9 = 3 = 16 = 4 = 5 = 5 = Numbers like 5, 11, 15 are
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Math 2 Stud Guide-Chapters 8 and 9 Name Date: Time: MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find all square roots of the number. ) 600 9,
Math 2 Stud Guide-Chapters 8 and 9 Name Date: Time: MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find all square roots of the number. ) 600 9,
ALGEBRA 1 CP FINAL EXAM REVIEW
 ALGEBRA CP FINAL EXAM REVIEW Alg CP Sem Eam Review 0 () Page of 8 Chapter 8: Eponents. Write in rational eponent notation. 7. Write in radical notation. Simplif the epression.. 00.. 6 6. 7 7. 6 6 8. 8
ALGEBRA CP FINAL EXAM REVIEW Alg CP Sem Eam Review 0 () Page of 8 Chapter 8: Eponents. Write in rational eponent notation. 7. Write in radical notation. Simplif the epression.. 00.. 6 6. 7 7. 6 6 8. 8
Review 5 Symbolic Graphical Interplay Name 5.1 Key Features on Graphs Per Date
 3 1. Graph the function y = + 3. 4 a. Circle the -intercept. b. Place an on the y-intercept.. Given the linear function with slope ½ and a y-intercept of -: Draw a line on the coordinate grid to graph
3 1. Graph the function y = + 3. 4 a. Circle the -intercept. b. Place an on the y-intercept.. Given the linear function with slope ½ and a y-intercept of -: Draw a line on the coordinate grid to graph
Unit 5 Test: 9.1 Quadratic Graphs and Their Properties
 Unit 5 Test: 9.1 Quadratic Graphs and Their Properties Quadratic Equation: (Also called PARABOLAS) 1. of the STANDARD form y = ax 2 + bx + c 2. a, b, c are all real numbers and a 0 3. Always have an x
Unit 5 Test: 9.1 Quadratic Graphs and Their Properties Quadratic Equation: (Also called PARABOLAS) 1. of the STANDARD form y = ax 2 + bx + c 2. a, b, c are all real numbers and a 0 3. Always have an x
Algebra II Notes Unit Five: Quadratic Functions. Syllabus Objectives: 5.1 The student will graph quadratic functions with and without technology.
 Sllabus Objectives:.1 The student will graph quadratic functions with and without technolog. Quadratic Function: a function that can be written in the form are real numbers Parabola: the U-shaped graph
Sllabus Objectives:.1 The student will graph quadratic functions with and without technolog. Quadratic Function: a function that can be written in the form are real numbers Parabola: the U-shaped graph
9.1. Solving Quadratic Equations. Investigation: Rocket Science CONDENSED LESSON
 CONDENSED LESSON 9.1 Solving Quadratic Equations In this lesson you will look at quadratic functions that model projectile motion use tables and graphs to approimate solutions to quadratic equations solve
CONDENSED LESSON 9.1 Solving Quadratic Equations In this lesson you will look at quadratic functions that model projectile motion use tables and graphs to approimate solutions to quadratic equations solve
Algebra 2 Semester Exam Review
 Algebra Semester Eam Review 7 Graph the numbers,,,, and 0 on a number line Identif the propert shown rs rs r when r and s Evaluate What is the value of k k when k? Simplif the epression 7 7 Solve the equation
Algebra Semester Eam Review 7 Graph the numbers,,,, and 0 on a number line Identif the propert shown rs rs r when r and s Evaluate What is the value of k k when k? Simplif the epression 7 7 Solve the equation
Algebra 2 Unit 2 Practice
 Algebra Unit Practice LESSON 7-1 1. Consider a rectangle that has a perimeter of 80 cm. a. Write a function A(l) that represents the area of the rectangle with length l.. A rectangle has a perimeter of
Algebra Unit Practice LESSON 7-1 1. Consider a rectangle that has a perimeter of 80 cm. a. Write a function A(l) that represents the area of the rectangle with length l.. A rectangle has a perimeter of
Nonlinear Systems. No solution One solution Two solutions. Solve the system by graphing. Check your answer.
 8-10 Nonlinear Sstems CC.9-1.A.REI.7 Solve a simple sstem consisting of a linear equation and a quadratic equation in two variables algebraicall and graphicall. Objective Solve sstems of equations in two
8-10 Nonlinear Sstems CC.9-1.A.REI.7 Solve a simple sstem consisting of a linear equation and a quadratic equation in two variables algebraicall and graphicall. Objective Solve sstems of equations in two
Additional Factoring Examples:
 Honors Algebra -3 Solving Quadratic Equations by Graphing and Factoring Learning Targets 1. I can solve quadratic equations by graphing. I can solve quadratic equations by factoring 3. I can write a quadratic
Honors Algebra -3 Solving Quadratic Equations by Graphing and Factoring Learning Targets 1. I can solve quadratic equations by graphing. I can solve quadratic equations by factoring 3. I can write a quadratic
College Algebra ~ Review for Test 2 Sections
 College Algebra ~ Review for Test Sections. -. Use the given graphs of = a + b to solve the inequalit. Write the solution set in interval notation. ) - + 9 8 7 6 (, ) - - - - 6 7 8 - Solve the inequalit
College Algebra ~ Review for Test Sections. -. Use the given graphs of = a + b to solve the inequalit. Write the solution set in interval notation. ) - + 9 8 7 6 (, ) - - - - 6 7 8 - Solve the inequalit
Mini-Lecture 8.1 Solving Quadratic Equations by Completing the Square
 Mini-Lecture 8.1 Solving Quadratic Equations b Completing the Square Learning Objectives: 1. Use the square root propert to solve quadratic equations.. Solve quadratic equations b completing the square.
Mini-Lecture 8.1 Solving Quadratic Equations b Completing the Square Learning Objectives: 1. Use the square root propert to solve quadratic equations.. Solve quadratic equations b completing the square.
Section 5.5 Complex Numbers
 Name: Period: Section 5.5 Comple Numbers Objective(s): Perform operations with comple numbers. Essential Question: Tell whether the statement is true or false, and justify your answer. Every comple number
Name: Period: Section 5.5 Comple Numbers Objective(s): Perform operations with comple numbers. Essential Question: Tell whether the statement is true or false, and justify your answer. Every comple number
Ch 5 Alg 2 L2 Note Sheet Key Do Activity 1 on your Ch 5 Activity Sheet.
 Ch Alg L Note Sheet Ke Do Activit 1 on our Ch Activit Sheet. Chapter : Quadratic Equations and Functions.1 Modeling Data With Quadratic Functions You had three forms for linear equations, ou will have
Ch Alg L Note Sheet Ke Do Activit 1 on our Ch Activit Sheet. Chapter : Quadratic Equations and Functions.1 Modeling Data With Quadratic Functions You had three forms for linear equations, ou will have
Mth Quadratic functions and quadratic equations
 Mth 0 - Quadratic functions and quadratic equations Name Find the product. 1) 8a3(2a3 + 2 + 12a) 2) ( + 4)( + 6) 3) (3p - 1)(9p2 + 3p + 1) 4) (32 + 4-4)(2-3 + 3) ) (4a - 7)2 Factor completel. 6) 92-4 7)
Mth 0 - Quadratic functions and quadratic equations Name Find the product. 1) 8a3(2a3 + 2 + 12a) 2) ( + 4)( + 6) 3) (3p - 1)(9p2 + 3p + 1) 4) (32 + 4-4)(2-3 + 3) ) (4a - 7)2 Factor completel. 6) 92-4 7)
Graph the linear system and estimate the solution. Then check the solution algebraically.
 (Chapters and ) A. Linear Sstems (pp. 6 0). Solve a Sstem b Graphing Vocabular Solution For a sstem of linear equations in two variables, an ordered pair (x, ) that satisfies each equation. Consistent
(Chapters and ) A. Linear Sstems (pp. 6 0). Solve a Sstem b Graphing Vocabular Solution For a sstem of linear equations in two variables, an ordered pair (x, ) that satisfies each equation. Consistent
Answers. Chapter Warm Up. Sample answer: The graph of h is a translation. 3 units right of the parent linear function.
 Chapter. Start Thinking As the string V gets wider, the points on the string move closer to the -ais. This activit mimics a vertical shrink of a parabola... Warm Up.. Sample answer: The graph of f is a
Chapter. Start Thinking As the string V gets wider, the points on the string move closer to the -ais. This activit mimics a vertical shrink of a parabola... Warm Up.. Sample answer: The graph of f is a
LESSON #24 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
Name Class Date. Understanding How to Graph g(x) = a(x - h ) 2 + k
 Name Class Date - Transforming Quadratic Functions Going Deeper Essential question: How can ou obtain the graph of g() = a( h ) + k from the graph of f () =? 1 F-BF..3 ENGAGE Understanding How to Graph
Name Class Date - Transforming Quadratic Functions Going Deeper Essential question: How can ou obtain the graph of g() = a( h ) + k from the graph of f () =? 1 F-BF..3 ENGAGE Understanding How to Graph
Reteaching (continued)
 Quadratic Functions and Transformations If a, the graph is a stretch or compression of the parent function b a factor of 0 a 0. 0 0 0 0 0 a a 7 The graph is a vertical The graph is a vertical compression
Quadratic Functions and Transformations If a, the graph is a stretch or compression of the parent function b a factor of 0 a 0. 0 0 0 0 0 a a 7 The graph is a vertical The graph is a vertical compression
Answers. Chapter Start Thinking Sample answer: y-intercept: 8 5. x x
 . ( 7, ) 9. (, 9 ) 0. (, 7). no solution. (, 7). no solution. no solution. ( 7, ). infinitel man solutions 7. (, 7 ). infinitel man solutions 9. (, 9) 70. 9a + a + 7. b b + 9 7. c + 90c + 7. 9d d + 7.
. ( 7, ) 9. (, 9 ) 0. (, 7). no solution. (, 7). no solution. no solution. ( 7, ). infinitel man solutions 7. (, 7 ). infinitel man solutions 9. (, 9) 70. 9a + a + 7. b b + 9 7. c + 90c + 7. 9d d + 7.
Lesson 10.1 Solving Quadratic Equations
 Lesson 10.1 Solving Quadratic Equations 1. Sketch the graph of a quadratic equation with each set of conditions. a. One -intercept and all nonnegative y-values b. The verte in the third quadrant and no
Lesson 10.1 Solving Quadratic Equations 1. Sketch the graph of a quadratic equation with each set of conditions. a. One -intercept and all nonnegative y-values b. The verte in the third quadrant and no
Lesson 7.1 Polynomial Degree and Finite Differences
 Lesson 7.1 Polnomial Degree and Finite Differences 1. Identif the degree of each polnomial. a. 1 b. 0. 1. 3. 3 c. 0 16 0. Determine which of the epressions are polnomials. For each polnomial, state its
Lesson 7.1 Polnomial Degree and Finite Differences 1. Identif the degree of each polnomial. a. 1 b. 0. 1. 3. 3 c. 0 16 0. Determine which of the epressions are polnomials. For each polnomial, state its
Graphing Calculator Computations 2
 Graphing Calculator Computations A) Write the graphing calculator notation and B) Evaluate each epression. 4 1) 15 43 8 e) 15 - -4 * 3^ + 8 ^ 4/ - 1) ) 5 ) 8 3 3) 3 4 1 8 3) 7 9 4) 1 3 5 4) 5) 5 5) 6)
Graphing Calculator Computations A) Write the graphing calculator notation and B) Evaluate each epression. 4 1) 15 43 8 e) 15 - -4 * 3^ + 8 ^ 4/ - 1) ) 5 ) 8 3 3) 3 4 1 8 3) 7 9 4) 1 3 5 4) 5) 5 5) 6)
3.1-Quadratic Functions & Inequalities
 3.1-Quadratic Functions & Inequalities Quadratic Functions: Quadratic functions are polnomial functions of the form also be written in the form f ( ) a( h) k. f ( ) a b c. A quadratic function ma Verte
3.1-Quadratic Functions & Inequalities Quadratic Functions: Quadratic functions are polnomial functions of the form also be written in the form f ( ) a( h) k. f ( ) a b c. A quadratic function ma Verte
Answers. Investigation 2. ACE Assignment Choices. Applications. Problem 2.5. Problem 2.1. Problem 2.2. Problem 2.3. Problem 2.4
 Answers Investigation ACE Assignment Choices Problem. Core, Problem. Core, Other Applications ; Connections, 3; unassigned choices from previous problems Problem.3 Core Other Connections, ; unassigned
Answers Investigation ACE Assignment Choices Problem. Core, Problem. Core, Other Applications ; Connections, 3; unassigned choices from previous problems Problem.3 Core Other Connections, ; unassigned
Using Intercept Form
 8.5 Using Intercept Form Essential Question What are some of the characteristics of the graph of f () = a( p)( q)? Using Zeros to Write Functions Work with a partner. Each graph represents a function of
8.5 Using Intercept Form Essential Question What are some of the characteristics of the graph of f () = a( p)( q)? Using Zeros to Write Functions Work with a partner. Each graph represents a function of
Quadratic Graphs and Their Properties
 - Think About a Plan Quadratic Graphs and Their Properties Physics In a physics class demonstration, a ball is dropped from the roof of a building, feet above the ground. The height h (in feet) of the
- Think About a Plan Quadratic Graphs and Their Properties Physics In a physics class demonstration, a ball is dropped from the roof of a building, feet above the ground. The height h (in feet) of the
Advanced Algebra 2 Final Review Packet KG Page 1 of Find the slope of the line passing through (3, -1) and (6, 4).
 Advanced Algebra Final Review Packet KG 0 Page of 8. Evaluate (7 ) 0 when and. 7 7. Solve the equation.. Solve the equation.. Solve the equation. 6. An awards dinner costs $ plus $ for each person making
Advanced Algebra Final Review Packet KG 0 Page of 8. Evaluate (7 ) 0 when and. 7 7. Solve the equation.. Solve the equation.. Solve the equation. 6. An awards dinner costs $ plus $ for each person making
MAT135 Review for Test 4 Dugopolski Sections 7.5, 7.6, 8.1, 8.2, 8.3, 8.4
 Sections 7.5, 7.6, 8.1, 8., 8., 8.4 1. Use the discriminant to determine the number and type(s) of solutions for 4x 8x 4 0. One real solution B. One complex solution Two real solutions Two complex solutions.
Sections 7.5, 7.6, 8.1, 8., 8., 8.4 1. Use the discriminant to determine the number and type(s) of solutions for 4x 8x 4 0. One real solution B. One complex solution Two real solutions Two complex solutions.
Math 0210 Common Final Review Questions (2 5 i)(2 5 i )
 Math 0 Common Final Review Questions In problems 1 6, perform the indicated operations and simplif if necessar. 1. ( 8)(4) ( )(9) 4 7 4 6( ). 18 6 8. ( i) ( 1 4 i ) 4. (8 i ). ( 9 i)( 7 i) 6. ( i)( i )
Math 0 Common Final Review Questions In problems 1 6, perform the indicated operations and simplif if necessar. 1. ( 8)(4) ( )(9) 4 7 4 6( ). 18 6 8. ( i) ( 1 4 i ) 4. (8 i ). ( 9 i)( 7 i) 6. ( i)( i )
Honors Algebra 2 ~ Spring 2014 Name 1 Unit 3: Quadratic Functions and Equations
 Honors Algebra ~ Spring Name Unit : Quadratic Functions and Equations NC Objectives Covered:. Define and compute with comple numbers. Operate with algebraic epressions (polnomial, rational, comple fractions)
Honors Algebra ~ Spring Name Unit : Quadratic Functions and Equations NC Objectives Covered:. Define and compute with comple numbers. Operate with algebraic epressions (polnomial, rational, comple fractions)
Learning Targets: Standard Form: Quadratic Function. Parabola. Vertex Max/Min. x-coordinate of vertex Axis of symmetry. y-intercept.
 Name: Hour: Algebra A Lesson:.1 Graphing Quadratic Functions Learning Targets: Term Picture/Formula In your own words: Quadratic Function Standard Form: Parabola Verte Ma/Min -coordinate of verte Ais of
Name: Hour: Algebra A Lesson:.1 Graphing Quadratic Functions Learning Targets: Term Picture/Formula In your own words: Quadratic Function Standard Form: Parabola Verte Ma/Min -coordinate of verte Ais of
Quadratics in Vertex Form Unit 1
 1 U n i t 1 11C Date: Name: Tentative TEST date Quadratics in Verte Form Unit 1 Reflect previous TEST mark, Overall mark now. Looking back, what can ou improve upon? Learning Goals/Success Criteria Use
1 U n i t 1 11C Date: Name: Tentative TEST date Quadratics in Verte Form Unit 1 Reflect previous TEST mark, Overall mark now. Looking back, what can ou improve upon? Learning Goals/Success Criteria Use
Unit 4 Practice Problem ANSWERS
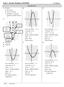 Unit Practice Problem ANSWERS SECTION.1A 1) Parabola ) a. Root, Zeros b. Ais of smmetr c. Substitute = 0 into the equation to find the value of. -int 6) 7 6 1 - - - - -1-1 1 - - - - -6-7 - ) ) Maimum )
Unit Practice Problem ANSWERS SECTION.1A 1) Parabola ) a. Root, Zeros b. Ais of smmetr c. Substitute = 0 into the equation to find the value of. -int 6) 7 6 1 - - - - -1-1 1 - - - - -6-7 - ) ) Maimum )
Algebra Final Exam Review Packet
 Algebra 1 00 Final Eam Review Packet UNIT 1 EXPONENTS / RADICALS Eponents Degree of a monomial: Add the degrees of all the in the monomial together. o Eample - Find the degree of 5 7 yz Degree of a polynomial:
Algebra 1 00 Final Eam Review Packet UNIT 1 EXPONENTS / RADICALS Eponents Degree of a monomial: Add the degrees of all the in the monomial together. o Eample - Find the degree of 5 7 yz Degree of a polynomial:
7.1 Connecting Intercepts and Zeros
 Locker LESSON 7. Connecting Intercepts and Zeros Common Core Math Standards The student is epected to: F-IF.7a Graph linear and quadratic functions and show intercepts, maima, and minima. Also A-REI.,
Locker LESSON 7. Connecting Intercepts and Zeros Common Core Math Standards The student is epected to: F-IF.7a Graph linear and quadratic functions and show intercepts, maima, and minima. Also A-REI.,
Chapters 8 & 9 Review for Final
 Math 203 - Intermediate Algebra Professor Valdez Chapters 8 & 9 Review for Final SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Solve the formula for
Math 203 - Intermediate Algebra Professor Valdez Chapters 8 & 9 Review for Final SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Solve the formula for
For questions 5-8, solve each inequality and graph the solution set. You must show work for full credit. (2 pts each)
 Alg Midterm Review Practice Level 1 C 1. Find the opposite and the reciprocal of 0. a. 0, 1 b. 0, 1 0 0 c. 0, 1 0 d. 0, 1 0 For questions -, insert , or = to make the sentence true. (1pt each) A. 5
Alg Midterm Review Practice Level 1 C 1. Find the opposite and the reciprocal of 0. a. 0, 1 b. 0, 1 0 0 c. 0, 1 0 d. 0, 1 0 For questions -, insert , or = to make the sentence true. (1pt each) A. 5
c) domain {x R, x 3}, range {y R}
 Answers Chapter 1 Functions 1.1 Functions, Domain, and Range 1. a) Yes, no vertical line will pass through more than one point. b) No, an vertical line between = 6 and = 6 will pass through two points..
Answers Chapter 1 Functions 1.1 Functions, Domain, and Range 1. a) Yes, no vertical line will pass through more than one point. b) No, an vertical line between = 6 and = 6 will pass through two points..
Study Guide and Intervention
 6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
Self- assessment 1010 (Intermediate Algebra)
 Self- assessment (Intermediate Algebra) If ou can work these problems using a scientific calculator, ou should have sufficient knowledge to demonstrate master of Intermediate Algebra and to succeed in
Self- assessment (Intermediate Algebra) If ou can work these problems using a scientific calculator, ou should have sufficient knowledge to demonstrate master of Intermediate Algebra and to succeed in
QUADRATIC FUNCTION REVIEW
 Name: Date: QUADRATIC FUNCTION REVIEW Linear and eponential functions are used throughout mathematics and science due to their simplicit and applicabilit. Quadratic functions comprise another ver important
Name: Date: QUADRATIC FUNCTION REVIEW Linear and eponential functions are used throughout mathematics and science due to their simplicit and applicabilit. Quadratic functions comprise another ver important
Final Exam Review Part 2 #4
 Final Eam Review Part # Intermediate Algebra / MAT 135 Fall 01 Master (Prof. Fleischner) Student Name/ID: 1. Solve for, where is a real number. + = 8. Solve for, where is a real number. 9 1 = 3. Solve
Final Eam Review Part # Intermediate Algebra / MAT 135 Fall 01 Master (Prof. Fleischner) Student Name/ID: 1. Solve for, where is a real number. + = 8. Solve for, where is a real number. 9 1 = 3. Solve
Final Exam Review Part 2 #4
 Final Eam Review Part # Intermediate Algebra / MAT 135 Fall 01 Master (Prof. Fleischner) Student Name/ID: 1. Solve for, where is a real number. + =. Solve for, where is a real number. 9 1 = 3. Solve for,
Final Eam Review Part # Intermediate Algebra / MAT 135 Fall 01 Master (Prof. Fleischner) Student Name/ID: 1. Solve for, where is a real number. + =. Solve for, where is a real number. 9 1 = 3. Solve for,
MATH College Algebra Review for Test 2
 MATH 4 - College Algebra Review for Test Sections. and.. For f (x) = x + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the axis of
MATH 4 - College Algebra Review for Test Sections. and.. For f (x) = x + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the axis of
a. plotting points in Cartesian coordinates (Grade 9 and 10), b. using a graphing calculator such as the TI-83 Graphing Calculator,
 GRADE PRE-CALCULUS UNIT C: QUADRATIC FUNCTIONS CLASS NOTES FRAME. After linear functions, = m + b, and their graph the Quadratic Functions are the net most important equation or function. The Quadratic
GRADE PRE-CALCULUS UNIT C: QUADRATIC FUNCTIONS CLASS NOTES FRAME. After linear functions, = m + b, and their graph the Quadratic Functions are the net most important equation or function. The Quadratic
MATH College Algebra Review for Test 2
 MATH 34 - College Algebra Review for Test 2 Sections 3. and 3.2. For f (x) = x 2 + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the
MATH 34 - College Algebra Review for Test 2 Sections 3. and 3.2. For f (x) = x 2 + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the
MATH 91 Final Study Package Name
 MATH 91 Final Stud Package Name Solve the sstem b the substitution method. If there is no solution or an infinite number of solutions, so state. Use set notation to epress the solution set. 1) - = 1 1)
MATH 91 Final Stud Package Name Solve the sstem b the substitution method. If there is no solution or an infinite number of solutions, so state. Use set notation to epress the solution set. 1) - = 1 1)
Review of Essential Skills and Knowledge
 Review of Essential Skills and Knowledge R Eponent Laws...50 R Epanding and Simplifing Polnomial Epressions...5 R 3 Factoring Polnomial Epressions...5 R Working with Rational Epressions...55 R 5 Slope
Review of Essential Skills and Knowledge R Eponent Laws...50 R Epanding and Simplifing Polnomial Epressions...5 R 3 Factoring Polnomial Epressions...5 R Working with Rational Epressions...55 R 5 Slope
Name Class Date. Quadratic Functions and Transformations. 4 6 x
 - Quadratic Functions and Transformations For Eercises, choose the correct letter.. What is the verte of the function 53()? D (, ) (, ) (, ) (, ). Which is the graph of the function f ()5(3) 5? F 6 6 O
- Quadratic Functions and Transformations For Eercises, choose the correct letter.. What is the verte of the function 53()? D (, ) (, ) (, ) (, ). Which is the graph of the function f ()5(3) 5? F 6 6 O
Characteristics of Quadratic Functions
 . Characteristics of Quadratic Functions Essential Question What tpe of smmetr does the graph of f() = a( h) + k have and how can ou describe this smmetr? Parabolas and Smmetr Work with a partner. a. Complete
. Characteristics of Quadratic Functions Essential Question What tpe of smmetr does the graph of f() = a( h) + k have and how can ou describe this smmetr? Parabolas and Smmetr Work with a partner. a. Complete
3.1. Shape and Structure Forms of Quadratic Functions ESSENTIAL IDEAS TEXAS ESSENTIAL KNOWLEDGE AND SKILLS FOR MATHEMATICS 169A
 Shape and Structure Forms of Quadratic Functions.1 LEARNING GOALS KEY TERMS In this lesson, ou will: Match a quadratic function with its corresponding graph. Identif ke characteristics of quadratic functions
Shape and Structure Forms of Quadratic Functions.1 LEARNING GOALS KEY TERMS In this lesson, ou will: Match a quadratic function with its corresponding graph. Identif ke characteristics of quadratic functions
2 variables. is the same value as the solution of. 1 variable. You can use similar reasoning to solve quadratic equations. Work with a partner.
 9. b Graphing Essential Question How can ou use a graph to solve a quadratic equation in one variable? Based on what ou learned about the -intercepts of a graph in Section., it follows that the -intercept
9. b Graphing Essential Question How can ou use a graph to solve a quadratic equation in one variable? Based on what ou learned about the -intercepts of a graph in Section., it follows that the -intercept
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question
 Midterm Review 0 Precalculu Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question ) A graph of a function g is shown below. Find g(0). (-, ) (-, 0) - -
Midterm Review 0 Precalculu Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question ) A graph of a function g is shown below. Find g(0). (-, ) (-, 0) - -
Instructor: Imelda Valencia Course: A3 Honors Pre Calculus
 Student: Date: Instructor: Imelda Valencia Course: A3 Honors Pre Calculus 01 017 Assignment: Summer Homework for those who will be taking FOCA 017 01 onl available until Sept. 15 1. Write the epression
Student: Date: Instructor: Imelda Valencia Course: A3 Honors Pre Calculus 01 017 Assignment: Summer Homework for those who will be taking FOCA 017 01 onl available until Sept. 15 1. Write the epression
Solving Linear-Quadratic Systems
 36 LESSON Solving Linear-Quadratic Sstems UNDERSTAND A sstem of two or more equations can include linear and nonlinear equations. In a linear-quadratic sstem, there is one linear equation and one quadratic
36 LESSON Solving Linear-Quadratic Sstems UNDERSTAND A sstem of two or more equations can include linear and nonlinear equations. In a linear-quadratic sstem, there is one linear equation and one quadratic
