Honors Algebra 2 ~ Spring 2014 Name 1 Unit 3: Quadratic Functions and Equations
|
|
|
- Pearl Gregory
- 6 years ago
- Views:
Transcription
1 Honors Algebra ~ Spring Name Unit : Quadratic Functions and Equations NC Objectives Covered:. Define and compute with comple numbers. Operate with algebraic epressions (polnomial, rational, comple fractions) to solve problems. Use quadratic functions and inequalities to model and solve problems. a. Solve using graphs. b. Interpret the constants and coefficients in the contet of the problem. Da Date Lesson Assignment Tues. Feb. 5 Intro to Parabolas/Transformations Discover Education Activit(computer lab) Handout Packet p. Wed. Feb. 6 Summar of Transformations(notepacket p. ) Standard Form to Verte Form Verte Form to Standard Form, Applications Packet p. Thurs. Feb. 7 Quadratic Regression What do ou know about Factoring? Packet p. Fri. Feb. 8 Factoring: GCF, Grouping, Trinomials, Difference of Squares Packet p. 5 5 Monda March * Quiz on Sections Solving Quadratic Equations b Factoring Packet p. 6 6 Tues. March ACT Solving Quadratic Equations b Factoring and Graphing Packet p. 7 7 Wed. March 5 Review of Radicals Comple Numbers Brochure Project : Packet p. 8 EVEN 8 Thurs. March 6 Comple Numbers Solve b taking the square root Packet p. 9 #-7 odd, #-8 9 Fri. March 7 REVIEW Quiz on das 7-9 Work on Brochure Project Mon. March Complete the Square/Station Activit Packet p. Tues. March Discriminant Quadratic Formula Handout Wed. March Solving Quadratic Inequalities and Quadratic Sstems Packet p. &
2 Honors Algebra ~ Spring Name Thurs. March Review/Quadratic Applications Packet p. & 5 Fri. March Quadratic Functions TEST Packet p. 7 & 8 Finish Brochure Project Mon. March 7 BROCHURE PROJECT DUE!! Homework Grade: ******************************************************************* Homework Da Part : Identif the verte, the ais of smmetr, the maimum or minimum value, and the domain and range of each parabola. ) ) 5 ) Verte Verte Verte AOS: AOS: AOS: ma/min value ma/min value ma/min domain domain domain range range range Part : Describe how to transform the parent function to the graph of each function below. ) ( ) ) ( ) ) ( ) ) ( ) +5 5).5 + 6).( ) - Part
3 Honors Algebra ~ Spring Name Homework Da Write in Standard Form. Identif the verte and -intercept.. = ( ) +. = -( ) 6. = -( + ) 8. = ( 8) + 5. = -( + 7) 6. =.( 5.) + Determine whether the equations in each pair are equivalent. 7. = ( ) 7 8. = ( + ) + 8 = + = 6 + Match each equation with the correct statement. 9. = a. The verte is at (, ).. = ( ) + b. The -intercept is 5.. = ( 5) + c. The -intercept is.. = d. The verte is at (5, ).. The Galleria, in BCE Place in Toronto, has man beautiful parabolic arches. One of the arches can be modeled b the function = -.5( 6.8) + 6. The -ais represents the floor in the Galleria and the -ais represents the height above the floor. Distances are in meters. a. Write the function in standard form. b. What is the height of the arch at its center? c. The -intercept represents the lowest point at one side of the base of an arch. What is this height?. The height, h, of a baseball thrown off a bridge can be modeled b the equation h = -5(t ) + where the height is measured in meters and t is the time in seconds since the ball was thrown. a. How high was the ball thrown? b. How long did the ball take to reach its highest point?
4 Honors Algebra ~ Spring Name. A to rocket is shot upward from ground level. The table shows the height of the rocket at different times. Time(seconds) Height(feet) a. Find a quadratic model for this data. b. Use the model to estimate the height of the rocket after.5 seconds.. Suppose ou are tossing an apple up to a friend on a third-stor balcon. After t seconds, the height of the apple in feet is given b h 6t 8.t.96. Your friend catches the apple just as it reaches its highest point. How long does the apple take to reach our friend, and at what height above the ground does our friend catch it?. the barber s profit p each week depends on his charge c per haircut. It is modeled b the equation p c c 7. What price should he charge for the largest profit?. A skating ring manager finds that revenue R based on an hourl fee F for sakting is represented b the function R 8F F. What hourl fee will produce maimum revenues? 5. The path of a baseball after it has been hit is modeled b the function h. d d, where h is the height in feet of the baseball and d is the distance in feet the baseball is from home plate. What is the maimum height reached b the baseball? How far is the baseball from home plate when it reaches its maimum height? 6. A lighting fiture manufacturer has dail production costs of C.5n n 8, Where C is the total cost in dollars and n is the number of light fitures produced. How man fitures should be produced to ield a minimum cost? 7. Find a quadratic model for the data. Use 98 as ear. Price of First-Class Stamp Year Price(Cents) a. What is the quadratic model? b. Describe a reasonable domain and range for our model. (Hint: This is a real situation.) c. Predict when the cost of a stamp will be 5 cents. Is this valid? Wh or wh not?
5 Honors Algebra ~ Spring Name 5 Factoring Practice a a b + ab b k 8k z z c + c c k + k. a a + ad d. - 5 REVIEW: Part A: For each function, the verte of the function s graph is given. Find a and b.. a b 7; (, ). a b 5; (, ). a b 8; (, ). a b ; (,) Part B:. The equation for the motion of a projectile fired straight up at an initial velocit of 6 ft/s is h = 6t - 6t, where h is the height in feet and t is the time in seconds. Find the time the projectile needs to reach its highest point. How high it will go?
6 Honors Algebra ~ Spring Name 6 Factor each polnomial
7 Honors Algebra ~ Spring Name 7 Solving Quadratic Equations Solve each equation b factoring = =. n + 5 = n. 9z = z 5. 7 = 6. c = c w - 5w + 6 = 8. d + d + 5 = 9. 5v + 9v + 6 =. j + 6 = j. 6k = 5. m - 8m = 5m. 6e = 5e + 6e. 9 = 6p Solve each equation b graphing. Round each answer to two decimal places
8 Honors Algebra ~ Spring Name 8 Simplifing Epressions Containing Comple Numbers
9 Honors Algebra ~ Spring Name 9 Simplifing Epressions Containing Comple Numbers Continued Find the value of m and n for which equation is true. ) 8 5i m ni ) ( m n) ( m n) i 5 5i ) (m 5 n) ( m) i i ) ( n) ( m n) i 8 i Solving using square roots. 5) n 5 6) n 8 8 7) 8b 7 9 8) 85
10 Honors Algebra ~ Spring Name Completing the square: Homework da Solve each equation b completing the square. Give the eact answer.. a a. v 6v 65. p 6 p. n 8n r r 6. a a 8 7. m m k k 6. p p 6. m m. 7p 8p 5 Part : Find the value of k that would make the left side of each equation a perfect square trinomial.. k 5. k. k 6. 9 k 5. k 8 6. k
11 Honors Algebra ~ Spring Name Homework Da : Completing the square Solve each quadratic b completing the square. Give the eact answer Part : Solve b factoring, completing the square, or taking the square root ( )
12 Honors Algebra ~ Spring Name Quadratic Applications. A smoke jumper jumps from a plane that is 7 feet above the ground. The function = gives a jumper s height in feet after seconds. a. How long is the jumper in free fall if the parachute opens at ft? b. How long is the jumper in free fall if the parachute opens at 9 ft?. You want to epand the garden below b planting a border of flowers. The border will have the same width around the entire garden. The flowers ou bought will fill an area of 76 ft. How wide should the border be? ft 6 6. One side of a rectangular garden is d less than the other side. The area of the garden is 6 d. Find the dimensions of the garden.. An electronics compan has a new line of portable radios with CD plaers. Their research suggests that the dail sales s for the new product can be modeled b s = -p + p +, where p is the price of each unit. a. Find the verte of the function. b. What is the maimum dail sales total for the new product? c. What price should the compan charge to make this profit? 5. The shape of the Gatewa Arch in St. Louis is a catenar curve, which closel resembles a parabola. The function closel models the shape of the arch, where is the 5 height in feet and is the horizontal distance from the base of the left side of the arch in feet. a. Graph the function and find its verte. b. What is the maimum height of the arch? c. What is the width of the arch at the base?
13 Honors Algebra ~ Spring Name Graphing Quadratic Inequalities Solving Quadratic Inequalities Solve each inequalit. -- >. -+6 < z z 8. t < >
14 Honors Algebra ~ Spring Name. A ball is thrown straight up with an initial velocit of 56 feet per second. The height of the ball t seconds after it is thrown is given b the formula h(t) = 56t 6t. a. What is the height of the ball after second? b. What is its maimum height? c. After how man seconds will it return to the ground? d. When will the ball be 5 feet above the ground?. An object is thrown upward into the air with an initial velocit of 8 feet per second. The formula h(t) = 8t 6t gives its height above the ground after t seconds. a. What is the height after seconds? b. What is the maimum height reached? c. For how man seconds will the object be in the air?. A baseball is projected upward from the top of a 8 foot tall building with an initial velocit of 8 feet per second. The distance s of the baseball from the ground at an time t, in seconds, is given b the equation s = -6t + 8t + 8. a. Find the time it takes for the baseball to strike the ground. b. What is the baseball s maimum height?. A rocket is shot upward such that it s height in feet, h, is given as h = 6t 5t, where t is the number of seconds since liftoff. a. Approimate the length of time the rocket is above feet. b. When will the rocket hit the ground? Use the formula h( t ) vt 6t where h(t) is the height of an object in feet, v is the object's initial velocit in feet per second, and t is the time in seconds. 5. An arrow is shot upward with a velocit of 6 feet per second. Ignoring the height of the archer, how long after the arrow is released does it hit the ground? 6. A tennis ball is hit upward with a velocit of 8 feet per second. Ignoring the height of the tennis plaer, how long does it take for the ball to fall to the ground?
15 Honors Algebra ~ Spring Name 5 Review Sheet: Unit. The following function represents the height, h, of a rocket t seconds after it is launched: h = - (t.5) +. When does the rocket reach its maimum height?. Bob wants to fence in his backard using his house as one side of the fence. He has 5 ft of fencing available. Find the dimensions of the fence needed to maimize the area.. The function h = -6t + 5t + represents the height of a ball t seconds after it is thrown. Could it hit a kite fling feet in the air?. A ball is thrown up in the air with an initial velocit of 56 feet per second. The height of the ball t seconds after it is thrown is given b the formula h(t) = 56t 6t. What is the maimum height of the ball? When does it return to the ground? 5. Solve 7 - > 6. Solve Solve using an method: + = 8. Solve using an method = 9. State the discriminant and nature of roots: - 7. State the discriminant and nature of roots: -. Solve: 8. Simplif: ( 5 i) ( i) (5 6 i ). Simplif: i 9 i. Simplif: 5. Simplif: ( 5 i)( 6 i ) 6. Simplif: ( i ) 7. Simplif: 7 i i 8. A rectangular garden contains ft and has a walk of uniform width surrounding it. If the entire area, including the walk, is ft ft., how wide is the sidewalk? Factor Completel: 9) a a a ) ) m m 6 ) m m 7 ) 6 Find the verte and ais of smmetr: ) 7 5) 7 6) ( ) 7) Write the equation of a parabola that has a verte at the origin and passes through the point (, -6). 8) Write the equation of a parabola that has a verte at (, -7), and passes through (,-9). 9) Describe how the parabola ( ) is shifted/different from.
16 Honors Algebra ~ Spring Name 6 Answers to Review Sheet. Ma at.5 sec.. dimensions: 87.5 ft 75 ft. no (graphs do not intersect). Ma height: 9 ft., and returns to the ground after.5 seconds 5. 5 or and 8. 5 i 9. discriminant = -8, so imaginar roots. discriminant =, so real rational root. i. 6-i i. 8. i i 6. 6i 7. 7 i 8. foot 9. ( a )( a ). 8( )( ). (m+)(m-). (m-)(m+7). ( )( )( ). V=(, ); a of s: = 5. V=(.75, -6.5); a of s: = V=(,); a of s: = ( ) 7 9. more narrow, left, up
17 Honors Algebra ~ Spring Name 7 Cumulative Review Units -. The attendance at a ball game was people. Student tickets cost $ and adult tickets cost $. $,5 was collected in ticket sales. Which sstem models the situation if s is the number of students and a is the number of a is the number of adults? A. s = a B. s = a C. s + a = D. s + a = (s + a) =,5,5(s + a) = s + a =,5 s + a =,5. What sstem describes this graph below? (tick marks are one unit apart) A. B. C. D.. Which of the following is FALSE? A. C. is the identit matri. B. D.. What is the solution of X has no inverse. is the identit matri for addition. 5? 6 A. 5 B. 5 C. 5 D. 5 E Which product does not eist? A. B. C. D Solve the formula for h. A ( b b ) h 7. A factor can produce products, and, with a profit of P = The Production of can eceed b no more than units. Also, production is limited b the Constraint. What production levels ield maimum profit? A. =, = B. =, = C. =, = D. =, = 6 8. What is the value of 7? A. B. 9 C. -9 D. -
18 Honors Algebra ~ Spring Name 8 a 6 6 b a 9. What are the values of a,b, and c if? 7 c 7 c A. a = -, b = 8, c = B. a = -, b =, c = C. a =, b = 8, c = - D. a = -, b =, c = -. What does z equal in the solution of the sstem z 8 z 7? z. What is the solution of in the sstem 6 5?. Write the equation of a line with slope 5 and passes through (, 9) in slope-intercept form.. For a campaign, a compan gave awa 5, tos to children. Tos and cost the compan $.9 and $.98, respectivel. The compan spent $5,6. How man of to did the give awa? A. 9 B., C., D.,. Two pickup trucks have capacities of ¼ and ½ ton. The made a total of 8 round trips to haul 7 ½ tons of crushed rock to a job site. Which matri equation could be used to determine how man round trips each truck made? A B. 5. The Coast Guard flies a rescue out of Elizabeth Cit to Hatteras in the middle of a Nor easter. It takes them one hour with a headwind to fl one hundred miles to get there and thirt minutes to fl back. How fast was the wind and how fast was the plane in still air? 6. What is the equation of the graph of an absolute function that opens down with verte (,) and passes Through the point (6,)? A. B. C. D. 7. Solve. A. B. C. or D. or 8. What is i ( i) ( i) written as a comple number in standard form? C D A. 6i B. 6i C. i D. i 9. Which quadratic function has a verte of (-,) and passes through the point (,9)? A. B. C. D Solve A. 6 B. 6 C. D.
MAT 1033C -- Martin-Gay Intermediate Algebra Chapter 8 (8.1, 8.2, 8.5, 8.6) Practice for the Exam
 MAT 33C -- Martin-Ga Intermediate Algebra Chapter 8 (8.1 8. 8. 8.6) Practice for the Eam Name Date Da/Time: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
MAT 33C -- Martin-Ga Intermediate Algebra Chapter 8 (8.1 8. 8. 8.6) Practice for the Eam Name Date Da/Time: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
3.1 Graph Quadratic Functions
 3. Graph Quadratic Functions in Standard Form Georgia Performance Standard(s) MMA3b, MMA3c Goal p Use intervals of increase and decrease to understand average rates of change of quadratic functions. Your
3. Graph Quadratic Functions in Standard Form Georgia Performance Standard(s) MMA3b, MMA3c Goal p Use intervals of increase and decrease to understand average rates of change of quadratic functions. Your
Mini-Lecture 8.1 Solving Quadratic Equations by Completing the Square
 Mini-Lecture 8.1 Solving Quadratic Equations b Completing the Square Learning Objectives: 1. Use the square root propert to solve quadratic equations.. Solve quadratic equations b completing the square.
Mini-Lecture 8.1 Solving Quadratic Equations b Completing the Square Learning Objectives: 1. Use the square root propert to solve quadratic equations.. Solve quadratic equations b completing the square.
Name Class Date. Quadratic Functions and Transformations. 4 6 x
 - Quadratic Functions and Transformations For Eercises, choose the correct letter.. What is the verte of the function 53()? D (, ) (, ) (, ) (, ). Which is the graph of the function f ()5(3) 5? F 6 6 O
- Quadratic Functions and Transformations For Eercises, choose the correct letter.. What is the verte of the function 53()? D (, ) (, ) (, ) (, ). Which is the graph of the function f ()5(3) 5? F 6 6 O
Mth 95 Module 4 Chapter 8 Spring Review - Solving quadratic equations using the quadratic formula
 Mth 95 Module 4 Chapter 8 Spring 04 Review - Solving quadratic equations using the quadratic formula Write the quadratic formula. The NUMBER of REAL and COMPLEX SOLUTIONS to a quadratic equation ( a b
Mth 95 Module 4 Chapter 8 Spring 04 Review - Solving quadratic equations using the quadratic formula Write the quadratic formula. The NUMBER of REAL and COMPLEX SOLUTIONS to a quadratic equation ( a b
PRACTICE FINAL EXAM. 3. Solve: 3x 8 < 7. Write your answer using interval notation. Graph your solution on the number line.
 MAC 1105 PRACTICE FINAL EXAM College Algebra *Note: this eam is provided as practice onl. It was based on a book previousl used for this course. You should not onl stud these problems in preparing for
MAC 1105 PRACTICE FINAL EXAM College Algebra *Note: this eam is provided as practice onl. It was based on a book previousl used for this course. You should not onl stud these problems in preparing for
Advanced Algebra 2 Final Review Packet KG Page 1 of Find the slope of the line passing through (3, -1) and (6, 4).
 Advanced Algebra Final Review Packet KG 0 Page of 8. Evaluate (7 ) 0 when and. 7 7. Solve the equation.. Solve the equation.. Solve the equation. 6. An awards dinner costs $ plus $ for each person making
Advanced Algebra Final Review Packet KG 0 Page of 8. Evaluate (7 ) 0 when and. 7 7. Solve the equation.. Solve the equation.. Solve the equation. 6. An awards dinner costs $ plus $ for each person making
3.1-Quadratic Functions & Inequalities
 3.1-Quadratic Functions & Inequalities Quadratic Functions: Quadratic functions are polnomial functions of the form also be written in the form f ( ) a( h) k. f ( ) a b c. A quadratic function ma Verte
3.1-Quadratic Functions & Inequalities Quadratic Functions: Quadratic functions are polnomial functions of the form also be written in the form f ( ) a( h) k. f ( ) a b c. A quadratic function ma Verte
f(x) Determine whether each function has a maximum or minimum value, and find that value. Then state the domain and range of the function.
 NAME DATE PERID 4-1 Practice Graphing Quadratic Functions Complete parts a c for each quadratic function. a. Find the -intercept, the equation of the ais of smmetr, and the -coordinate of the verte. b.
NAME DATE PERID 4-1 Practice Graphing Quadratic Functions Complete parts a c for each quadratic function. a. Find the -intercept, the equation of the ais of smmetr, and the -coordinate of the verte. b.
MATH 115: Review for Chapter 3
 MATH : Review for Chapter Can ou use the Zero-Product Propert to solve quadratic equations b factoring? () Solve each equation b factoring. 6 7 8 + = + ( ) = 8 7p ( p ) p ( p) = = c = c = + Can ou solve
MATH : Review for Chapter Can ou use the Zero-Product Propert to solve quadratic equations b factoring? () Solve each equation b factoring. 6 7 8 + = + ( ) = 8 7p ( p ) p ( p) = = c = c = + Can ou solve
Study Guide and Intervention
 6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
Unit 2 Notes Packet on Quadratic Functions and Factoring
 Name: Period: Unit Notes Packet on Quadratic Functions and Factoring Notes #: Graphing quadratic equations in standard form, verte form, and intercept form. A. Intro to Graphs of Quadratic Equations: a
Name: Period: Unit Notes Packet on Quadratic Functions and Factoring Notes #: Graphing quadratic equations in standard form, verte form, and intercept form. A. Intro to Graphs of Quadratic Equations: a
Solving Linear-Quadratic Systems
 36 LESSON Solving Linear-Quadratic Sstems UNDERSTAND A sstem of two or more equations can include linear and nonlinear equations. In a linear-quadratic sstem, there is one linear equation and one quadratic
36 LESSON Solving Linear-Quadratic Sstems UNDERSTAND A sstem of two or more equations can include linear and nonlinear equations. In a linear-quadratic sstem, there is one linear equation and one quadratic
Copyrighted by Gabriel Tang B.Ed., B.Sc. Page 1.
 Chapter : Linear and Quadratic Functions Chapter : Linear and Quadratic Functions -: Points and Lines Sstem of Linear Equations: - two or more linear equations on the same coordinate grid. Solution of
Chapter : Linear and Quadratic Functions Chapter : Linear and Quadratic Functions -: Points and Lines Sstem of Linear Equations: - two or more linear equations on the same coordinate grid. Solution of
Essential Question How can you use a quadratic function to model a real-life situation?
 3. TEXAS ESSENTIAL KNOWLEDGE AND SKILLS A..A A..E A..A A..B A..C Modeling with Quadratic Functions Essential Question How can ou use a quadratic function to model a real-life situation? Work with a partner.
3. TEXAS ESSENTIAL KNOWLEDGE AND SKILLS A..A A..E A..A A..B A..C Modeling with Quadratic Functions Essential Question How can ou use a quadratic function to model a real-life situation? Work with a partner.
TEST REVIEW QUADRATICS EQUATIONS Name: 2. Which of the following statements is true about the graph of the function?
 Chapter MATHEMATICS 00 TEST REVIEW QUADRATICS EQUATIONS Name:. Which equation does not represent a quadratic function?. Which of the following statements is true about the graph of the function? it has
Chapter MATHEMATICS 00 TEST REVIEW QUADRATICS EQUATIONS Name:. Which equation does not represent a quadratic function?. Which of the following statements is true about the graph of the function? it has
Final Exam Review Part 2 #1 Page 1 / 21
 Final Eam Review Part #1 Intermediate Algebra / MAT 135 Spring 017 Master ( Master Templates) Student Name/ID: v 1. Solve for, where is a real number. v v + 1 + =. Solve for, where is a real number. +
Final Eam Review Part #1 Intermediate Algebra / MAT 135 Spring 017 Master ( Master Templates) Student Name/ID: v 1. Solve for, where is a real number. v v + 1 + =. Solve for, where is a real number. +
Algebra 2 Unit 2 Practice
 Algebra Unit Practice LESSON 7-1 1. Consider a rectangle that has a perimeter of 80 cm. a. Write a function A(l) that represents the area of the rectangle with length l.. A rectangle has a perimeter of
Algebra Unit Practice LESSON 7-1 1. Consider a rectangle that has a perimeter of 80 cm. a. Write a function A(l) that represents the area of the rectangle with length l.. A rectangle has a perimeter of
Algebra 1 Unit 9 Quadratic Equations
 Algebra 1 Unit 9 Quadratic Equations Part 1 Name: Period: Date Name of Lesson Notes Tuesda 4/4 Wednesda 4/5 Thursda 4/6 Frida 4/7 Monda 4/10 Tuesda 4/11 Wednesda 4/12 Thursda 4/13 Frida 4/14 Da 1- Quadratic
Algebra 1 Unit 9 Quadratic Equations Part 1 Name: Period: Date Name of Lesson Notes Tuesda 4/4 Wednesda 4/5 Thursda 4/6 Frida 4/7 Monda 4/10 Tuesda 4/11 Wednesda 4/12 Thursda 4/13 Frida 4/14 Da 1- Quadratic
6.1 Solving Quadratic Equations by Graphing Algebra 2
 10.1 Solving Quadratic Equations b Graphing Algebra Goal 1: Write functions in quadratic form Goal : Graph quadratic functions Goal 3: Solve quadratic equations b graphing. Quadratic Function: Eample 1:
10.1 Solving Quadratic Equations b Graphing Algebra Goal 1: Write functions in quadratic form Goal : Graph quadratic functions Goal 3: Solve quadratic equations b graphing. Quadratic Function: Eample 1:
Chapter 8 Vocabulary Check
 28 CHAPTER 8 Quadratic Equations and Functions d. What is the level of methane emissions for that ear? (Use our rounded answer from part (c).) (Round this answer to 2 decimals places.) Use a graphing calculator
28 CHAPTER 8 Quadratic Equations and Functions d. What is the level of methane emissions for that ear? (Use our rounded answer from part (c).) (Round this answer to 2 decimals places.) Use a graphing calculator
Additional Factoring Examples:
 Honors Algebra -3 Solving Quadratic Equations by Graphing and Factoring Learning Targets 1. I can solve quadratic equations by graphing. I can solve quadratic equations by factoring 3. I can write a quadratic
Honors Algebra -3 Solving Quadratic Equations by Graphing and Factoring Learning Targets 1. I can solve quadratic equations by graphing. I can solve quadratic equations by factoring 3. I can write a quadratic
Fair Game Review. Chapter 9. Find the square root(s) ± Find the side length of the square. 7. Simplify Simplify 63.
 Name Date Chapter 9 Find the square root(s). Fair Game Review... 9. ±. Find the side length of the square.. s. s s Area = 9 ft s Area = 0. m 7. Simplif 0. 8. Simplif. 9. Simplif 08. 0. Simplif 88. Copright
Name Date Chapter 9 Find the square root(s). Fair Game Review... 9. ±. Find the side length of the square.. s. s s Area = 9 ft s Area = 0. m 7. Simplif 0. 8. Simplif. 9. Simplif 08. 0. Simplif 88. Copright
Polynomial and Rational Functions
 Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of work b Horia Varlan;
Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of work b Horia Varlan;
Algebra 2 Semester Exam Review
 Algebra Semester Eam Review 7 Graph the numbers,,,, and 0 on a number line Identif the propert shown rs rs r when r and s Evaluate What is the value of k k when k? Simplif the epression 7 7 Solve the equation
Algebra Semester Eam Review 7 Graph the numbers,,,, and 0 on a number line Identif the propert shown rs rs r when r and s Evaluate What is the value of k k when k? Simplif the epression 7 7 Solve the equation
Mth Quadratic functions and quadratic equations
 Mth 0 - Quadratic functions and quadratic equations Name Find the product. 1) 8a3(2a3 + 2 + 12a) 2) ( + 4)( + 6) 3) (3p - 1)(9p2 + 3p + 1) 4) (32 + 4-4)(2-3 + 3) ) (4a - 7)2 Factor completel. 6) 92-4 7)
Mth 0 - Quadratic functions and quadratic equations Name Find the product. 1) 8a3(2a3 + 2 + 12a) 2) ( + 4)( + 6) 3) (3p - 1)(9p2 + 3p + 1) 4) (32 + 4-4)(2-3 + 3) ) (4a - 7)2 Factor completel. 6) 92-4 7)
2 nd Semester Final Exam Review Block Date
 Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. Identif the verte and ais of smmetr. 1 (10-1) 1. (10-1). 3 (10-) 3. 4 7 (10-) 4. 3 6 4 (10-1) 5. Predict
Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. Identif the verte and ais of smmetr. 1 (10-1) 1. (10-1). 3 (10-) 3. 4 7 (10-) 4. 3 6 4 (10-1) 5. Predict
Ready To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions
 Read To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions Find these vocabular words in Lesson 5-1 and the Multilingual Glossar. Vocabular quadratic function parabola verte
Read To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions Find these vocabular words in Lesson 5-1 and the Multilingual Glossar. Vocabular quadratic function parabola verte
APPLIED ALGEBRA II SEMESTER 1 EXAM ITEM SPECIFICATION SHEET & KEY
 APPLIED ALGEBRA II SEMESTER 1 EXAM ITEM SPECIFICATION SHEET & KEY Constructed Response # Objective Sllabus Objective NV State Standard 1 Graph a polnomial function. 1.1.7.1 Analze graphs of polnomial functions
APPLIED ALGEBRA II SEMESTER 1 EXAM ITEM SPECIFICATION SHEET & KEY Constructed Response # Objective Sllabus Objective NV State Standard 1 Graph a polnomial function. 1.1.7.1 Analze graphs of polnomial functions
(TPP #3) Test Preparation Practice. Algebra Holt Algebra 1. Name Date Class
 Test Preparation Practice Algebra 1 Solve each problem. Choose the best answer for each question and record our answer on the Student Answer Sheet. Figures are not drawn to scale 1. Jack budgets $35 for
Test Preparation Practice Algebra 1 Solve each problem. Choose the best answer for each question and record our answer on the Student Answer Sheet. Figures are not drawn to scale 1. Jack budgets $35 for
Algebra II Notes Unit Five: Quadratic Functions. Syllabus Objectives: 5.1 The student will graph quadratic functions with and without technology.
 Sllabus Objectives:.1 The student will graph quadratic functions with and without technolog. Quadratic Function: a function that can be written in the form are real numbers Parabola: the U-shaped graph
Sllabus Objectives:.1 The student will graph quadratic functions with and without technolog. Quadratic Function: a function that can be written in the form are real numbers Parabola: the U-shaped graph
Answers. Chapter Warm Up. Sample answer: The graph of h is a translation. 3 units right of the parent linear function.
 Chapter. Start Thinking As the string V gets wider, the points on the string move closer to the -ais. This activit mimics a vertical shrink of a parabola... Warm Up.. Sample answer: The graph of f is a
Chapter. Start Thinking As the string V gets wider, the points on the string move closer to the -ais. This activit mimics a vertical shrink of a parabola... Warm Up.. Sample answer: The graph of f is a
Self- assessment 1010 (Intermediate Algebra)
 Self- assessment (Intermediate Algebra) If ou can work these problems using a scientific calculator, ou should have sufficient knowledge to demonstrate master of Intermediate Algebra and to succeed in
Self- assessment (Intermediate Algebra) If ou can work these problems using a scientific calculator, ou should have sufficient knowledge to demonstrate master of Intermediate Algebra and to succeed in
7.2 Connecting Intercepts and Linear Factors
 Name Class Date 7.2 Connecting Intercepts and Linear Factors Essential Question: How are -intercepts of a quadratic function and its linear factors related? Resource Locker Eplore Connecting Factors and
Name Class Date 7.2 Connecting Intercepts and Linear Factors Essential Question: How are -intercepts of a quadratic function and its linear factors related? Resource Locker Eplore Connecting Factors and
College Algebra ~ Review for Test 2 Sections
 College Algebra ~ Review for Test Sections. -. Find a point-slope form for the equation of the line satisfing the conditions. ) a) Slope -, passing through (7, ) b) Passing through (-, -8) and (-, ) Write
College Algebra ~ Review for Test Sections. -. Find a point-slope form for the equation of the line satisfing the conditions. ) a) Slope -, passing through (7, ) b) Passing through (-, -8) and (-, ) Write
20.2 Connecting Intercepts and Linear Factors
 Name Class Date 20.2 Connecting Intercepts and Linear Factors Essential Question: How are -intercepts of a quadratic function and its linear factors related? Resource Locker Eplore Connecting Factors and
Name Class Date 20.2 Connecting Intercepts and Linear Factors Essential Question: How are -intercepts of a quadratic function and its linear factors related? Resource Locker Eplore Connecting Factors and
Quadratic Function. Parabola. Parent quadratic function. Vertex. Axis of Symmetry
 Name: Chapter 10: Quadratic Equations and Functions Section 10.1: Graph = a + c Quadratic Function Parabola Parent quadratic function Verte Ais of Smmetr Parent Function = - -1 0 1 1 Eample 1: Make a table,
Name: Chapter 10: Quadratic Equations and Functions Section 10.1: Graph = a + c Quadratic Function Parabola Parent quadratic function Verte Ais of Smmetr Parent Function = - -1 0 1 1 Eample 1: Make a table,
Graph Quadratic Functions in Standard Form
 TEKS 4. 2A.4.A, 2A.4.B, 2A.6.B, 2A.8.A Graph Quadratic Functions in Standard Form Before You graphed linear functions. Now You will graph quadratic functions. Wh? So ou can model sports revenue, as in
TEKS 4. 2A.4.A, 2A.4.B, 2A.6.B, 2A.8.A Graph Quadratic Functions in Standard Form Before You graphed linear functions. Now You will graph quadratic functions. Wh? So ou can model sports revenue, as in
Lesson 7.1 Polynomial Degree and Finite Differences
 Lesson 7.1 Polnomial Degree and Finite Differences 1. Identif the degree of each polnomial. a. 1 b. 0. 1. 3. 3 c. 0 16 0. Determine which of the epressions are polnomials. For each polnomial, state its
Lesson 7.1 Polnomial Degree and Finite Differences 1. Identif the degree of each polnomial. a. 1 b. 0. 1. 3. 3 c. 0 16 0. Determine which of the epressions are polnomials. For each polnomial, state its
College Algebra ~ Review for Test 2 Sections
 College Algebra ~ Review for Test Sections. -. Use the given graphs of = a + b to solve the inequalit. Write the solution set in interval notation. ) - + 9 8 7 6 (, ) - - - - 6 7 8 - Solve the inequalit
College Algebra ~ Review for Test Sections. -. Use the given graphs of = a + b to solve the inequalit. Write the solution set in interval notation. ) - + 9 8 7 6 (, ) - - - - 6 7 8 - Solve the inequalit
Characteristics of Quadratic Functions
 . Characteristics of Quadratic Functions Essential Question What tpe of smmetr does the graph of f() = a( h) + k have and how can ou describe this smmetr? Parabolas and Smmetr Work with a partner. a. Complete
. Characteristics of Quadratic Functions Essential Question What tpe of smmetr does the graph of f() = a( h) + k have and how can ou describe this smmetr? Parabolas and Smmetr Work with a partner. a. Complete
Shape and Structure. Forms of Quadratic Functions. Lesson 2.1 Assignment
 Lesson.1 Assignment Name Date Shape and Structure Forms of Quadratic Functions 1. Analze the graph of the quadratic function. a. The standard form of a quadratic function is f() 5 a 1 b 1 c. What possible
Lesson.1 Assignment Name Date Shape and Structure Forms of Quadratic Functions 1. Analze the graph of the quadratic function. a. The standard form of a quadratic function is f() 5 a 1 b 1 c. What possible
2 nd Semester Final Exam Review Block Date
 Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. 1 (10-1) 1. (10-1). (10-1) 3. (10-1) 4. 3 Graph each function. Identif the verte, ais of smmetr, and
Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. 1 (10-1) 1. (10-1). (10-1) 3. (10-1) 4. 3 Graph each function. Identif the verte, ais of smmetr, and
3 Polynomial and Rational Functions
 3 Polnomial and Rational Functions 3.1 Quadratic Functions and Models 3.2 Polnomial Functions and Their Graphs 3.3 Dividing Polnomials 3.4 Real Zeros of Polnomials 3.5 Comple Zeros and the Fundamental
3 Polnomial and Rational Functions 3.1 Quadratic Functions and Models 3.2 Polnomial Functions and Their Graphs 3.3 Dividing Polnomials 3.4 Real Zeros of Polnomials 3.5 Comple Zeros and the Fundamental
Write each expression in terms of i : Add: (3 4i) (5 7i) (3 5) ( 4 7)i. 8 3i. Subtract: (3 4i) (5 7i) (3 4i) ( 5 7i) Find each product:
 7_Ch09_online 7// 0:7 AM Page 9-0 9-0 CHAPTER 9 Quadratic Equations SECTION 9. Comple Numbers DEFINITIONS AND CONCEPTS EXAMPLES The imaginar number i is defined as Write each epression in terms of i :
7_Ch09_online 7// 0:7 AM Page 9-0 9-0 CHAPTER 9 Quadratic Equations SECTION 9. Comple Numbers DEFINITIONS AND CONCEPTS EXAMPLES The imaginar number i is defined as Write each epression in terms of i :
PreCalculus. Ocean Township High School Mathematics Department
 PreCalculus Summer Assignment Name Period Date Ocean Township High School Mathematics Department These are important topics from previous courses that ou must be comfortable doing before ou can be successful
PreCalculus Summer Assignment Name Period Date Ocean Township High School Mathematics Department These are important topics from previous courses that ou must be comfortable doing before ou can be successful
Lesson 9.1 Using the Distance Formula
 Lesson. Using the Distance Formula. Find the eact distance between each pair of points. a. (0, 0) and (, ) b. (0, 0) and (7, ) c. (, 8) and (, ) d. (, ) and (, 7) e. (, 7) and (8, ) f. (8, ) and (, 0)
Lesson. Using the Distance Formula. Find the eact distance between each pair of points. a. (0, 0) and (, ) b. (0, 0) and (7, ) c. (, 8) and (, ) d. (, ) and (, 7) e. (, 7) and (8, ) f. (8, ) and (, 0)
Properties of the Graph of a Quadratic Function. has a vertex with an x-coordinate of 2 b } 2a
 0.2 Graph 5 a 2 b c Before You graphed simple quadratic functions. Now You will graph general quadratic functions. Wh? So ou can investigate a cable s height, as in Eample 4. Ke Vocabular minimum value
0.2 Graph 5 a 2 b c Before You graphed simple quadratic functions. Now You will graph general quadratic functions. Wh? So ou can investigate a cable s height, as in Eample 4. Ke Vocabular minimum value
REVIEW PACKET FOR END OF COURSE EXAM
 Math H REVIEW PACKET FOR END OF COURSE EXAM DO NOT WRITE ON PACKET! Do on binder paper, show support work. On this packet leave all fractional answers in improper fractional form (ecept where appropriate
Math H REVIEW PACKET FOR END OF COURSE EXAM DO NOT WRITE ON PACKET! Do on binder paper, show support work. On this packet leave all fractional answers in improper fractional form (ecept where appropriate
Mathematics 2201 Midterm Exam Review
 Mathematics 0 Midterm Eam Review Chapter : Radicals Chapter 6: Quadratic Functions Chapter 7: Quadratic Equations. Evaluate: 6 8 (A) (B) (C) (D). Epress as an entire radical. (A) (B) (C) (D). What is the
Mathematics 0 Midterm Eam Review Chapter : Radicals Chapter 6: Quadratic Functions Chapter 7: Quadratic Equations. Evaluate: 6 8 (A) (B) (C) (D). Epress as an entire radical. (A) (B) (C) (D). What is the
Honors Math 2 Unit 1 Test #2 Review 1
 Honors Math Unit 1 Test # Review 1 Test Review & Study Guide Modeling with Quadratics Show ALL work for credit! Use etra paper, if needed. Factor Completely: 1. Factor 8 15. Factor 11 4 3. Factor 1 4.
Honors Math Unit 1 Test # Review 1 Test Review & Study Guide Modeling with Quadratics Show ALL work for credit! Use etra paper, if needed. Factor Completely: 1. Factor 8 15. Factor 11 4 3. Factor 1 4.
Unit 4 Practice Problem ANSWERS
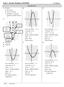 Unit Practice Problem ANSWERS SECTION.1A 1) Parabola ) a. Root, Zeros b. Ais of smmetr c. Substitute = 0 into the equation to find the value of. -int 6) 7 6 1 - - - - -1-1 1 - - - - -6-7 - ) ) Maimum )
Unit Practice Problem ANSWERS SECTION.1A 1) Parabola ) a. Root, Zeros b. Ais of smmetr c. Substitute = 0 into the equation to find the value of. -int 6) 7 6 1 - - - - -1-1 1 - - - - -6-7 - ) ) Maimum )
5. Determine the discriminant for each and describe the nature of the roots.
 4. Quadratic Equations Notes Day 1 1. Solve by factoring: a. 3 16 1 b. 3 c. 8 0 d. 9 18 0. Quadratic Formula: The roots of a quadratic equation of the form A + B + C = 0 with a 0 are given by the following
4. Quadratic Equations Notes Day 1 1. Solve by factoring: a. 3 16 1 b. 3 c. 8 0 d. 9 18 0. Quadratic Formula: The roots of a quadratic equation of the form A + B + C = 0 with a 0 are given by the following
Maintaining Mathematical Proficiency
 Chapter Maintaining Mathematical Proficienc Find the -intercept of the graph of the linear equation. 1. = + 3. = 3 + 5 3. = 10 75. = ( 9) 5. 7( 10) = +. 5 + 15 = 0 Find the distance between the two points.
Chapter Maintaining Mathematical Proficienc Find the -intercept of the graph of the linear equation. 1. = + 3. = 3 + 5 3. = 10 75. = ( 9) 5. 7( 10) = +. 5 + 15 = 0 Find the distance between the two points.
9 (0, 3) and solve equations to earn full credit.
 Math 0 Intermediate Algebra II Final Eam Review Page of Instructions: (6, ) Use our own paper for the review questions. For the final eam, show all work on the eam. (-6, ) This is an algebra class do not
Math 0 Intermediate Algebra II Final Eam Review Page of Instructions: (6, ) Use our own paper for the review questions. For the final eam, show all work on the eam. (-6, ) This is an algebra class do not
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question
 Midterm Review 0 Precalculu Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question ) A graph of a function g is shown below. Find g(0). (-, ) (-, 0) - -
Midterm Review 0 Precalculu Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question ) A graph of a function g is shown below. Find g(0). (-, ) (-, 0) - -
MAT 116 Final Exam Review
 MAT 116 Final Eam Review 1. Determine the equation for the line described, writing the answer in slope-intercept form. The line is parallel to = 8 and passes through ( 1,9). The line is perpendicular to
MAT 116 Final Eam Review 1. Determine the equation for the line described, writing the answer in slope-intercept form. The line is parallel to = 8 and passes through ( 1,9). The line is perpendicular to
MATH College Algebra Review for Test 2
 MATH 4 - College Algebra Review for Test Sections. and.. For f (x) = x + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the axis of
MATH 4 - College Algebra Review for Test Sections. and.. For f (x) = x + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the axis of
REVIEW KEY VOCABULARY REVIEW EXAMPLES AND EXERCISES
 Etra Eample. Graph.. 6. 7. (, ) (, ) REVIEW KEY VOCABULARY quadratic function, p. 6 standard form of a quadratic function, p. 6 parabola, p. 6 verte, p. 6 ais of smmetr, p. 6 minimum, maimum value, p.
Etra Eample. Graph.. 6. 7. (, ) (, ) REVIEW KEY VOCABULARY quadratic function, p. 6 standard form of a quadratic function, p. 6 parabola, p. 6 verte, p. 6 ais of smmetr, p. 6 minimum, maimum value, p.
3 2 (C) 1 (D) 2 (E) 2. Math 112 Fall 2017 Midterm 2 Review Problems Page 1. Let. . Use these functions to answer the next two questions.
 Math Fall 07 Midterm Review Problems Page Let f and g. Evaluate and simplify f g. Use these functions to answer the net two questions.. (B) (E) None of these f g. Evaluate and simplify. (B) (E). Consider
Math Fall 07 Midterm Review Problems Page Let f and g. Evaluate and simplify f g. Use these functions to answer the net two questions.. (B) (E) None of these f g. Evaluate and simplify. (B) (E). Consider
Chapter 2 Polynomial, Power, and Rational Functions
 Section. Linear and Quadratic Functions and Modeling 6 Chapter Polnomial, Power, and Rational Functions Section. Linear and Quadratic Functions and Modeling Eploration. $000 per ear.. The equation will
Section. Linear and Quadratic Functions and Modeling 6 Chapter Polnomial, Power, and Rational Functions Section. Linear and Quadratic Functions and Modeling Eploration. $000 per ear.. The equation will
MATH 91 Final Study Package Name
 MATH 91 Final Stud Package Name Solve the sstem b the substitution method. If there is no solution or an infinite number of solutions, so state. Use set notation to epress the solution set. 1) - = 1 1)
MATH 91 Final Stud Package Name Solve the sstem b the substitution method. If there is no solution or an infinite number of solutions, so state. Use set notation to epress the solution set. 1) - = 1 1)
Mathematics 2201 Midterm Exam Review
 Mathematics 0 Midterm Eam Review Chapter : Radicals Chapter : Quadratic Functions Chapter 7: Quadratic Equations. Evaluate: 8 (A) (B) (C) (D). Epress as an entire radical. (A) (B) (C) (D). What is the
Mathematics 0 Midterm Eam Review Chapter : Radicals Chapter : Quadratic Functions Chapter 7: Quadratic Equations. Evaluate: 8 (A) (B) (C) (D). Epress as an entire radical. (A) (B) (C) (D). What is the
Name Class Date. Solving by Graphing and Algebraically
 Name Class Date 16-4 Nonlinear Sstems Going Deeper Essential question: How can ou solve a sstem of equations when one equation is linear and the other is quadratic? To estimate the solution to a sstem
Name Class Date 16-4 Nonlinear Sstems Going Deeper Essential question: How can ou solve a sstem of equations when one equation is linear and the other is quadratic? To estimate the solution to a sstem
d. 2x 3 7x 2 5x 2 2x 2 3x 1 x 2x 3 3x 2 1x 2 4x 2 6x 2 3. a. x 5 x x 2 5x 5 5x 25 b. x 4 2x 2x 2 8x 3 3x 12 c. x 6 x x 2 6x 6 6x 36
 Vertices: (.8, 5.), (.37, 3.563), (.6, 0.980), (5.373, 6.66), (.8, 7.88), (.95,.) Graph the equation for an value of P (the second graph shows the circle with P 5) and imagine increasing the value of P,
Vertices: (.8, 5.), (.37, 3.563), (.6, 0.980), (5.373, 6.66), (.8, 7.88), (.95,.) Graph the equation for an value of P (the second graph shows the circle with P 5) and imagine increasing the value of P,
Summary, Review, and Test
 Summar, Review, and Test 79 56. Galileo s telescope brought about revolutionar changes in astronom. A comparable leap in our abilit to observe the universe took place as a result of the Hubble Space Telescope.
Summar, Review, and Test 79 56. Galileo s telescope brought about revolutionar changes in astronom. A comparable leap in our abilit to observe the universe took place as a result of the Hubble Space Telescope.
Math 20-1 Year End Review
 M0- Year End Review.docx Name: Math 0- Year End Review hapter Sequences & Series... Pages hapter Trigonometr... Pages hapters & Quadratic Functions & Equations... Pages hapter Radicals... Pages hapter
M0- Year End Review.docx Name: Math 0- Year End Review hapter Sequences & Series... Pages hapter Trigonometr... Pages hapters & Quadratic Functions & Equations... Pages hapter Radicals... Pages hapter
Math 112 Spring 2018 Midterm 2 Review Problems Page 1
 Math Spring 08 Midterm Review Problems Page Note: Certain eam questions have been more challenging for students. Questions marked (***) are similar to those challenging eam questions. Let f and g. (***)
Math Spring 08 Midterm Review Problems Page Note: Certain eam questions have been more challenging for students. Questions marked (***) are similar to those challenging eam questions. Let f and g. (***)
First Semester Final Review NON-Graphing Calculator
 Algebra First Semester Final Review NON-Graphing Calculator Name:. 1. Find the slope of the line passing through the points ( 5, ) and ( 3, 7).. Find the slope-intercept equation of the line passing through
Algebra First Semester Final Review NON-Graphing Calculator Name:. 1. Find the slope of the line passing through the points ( 5, ) and ( 3, 7).. Find the slope-intercept equation of the line passing through
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 Spring 0 Math 08 Eam Preparation Ch Dressler Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Solve the quadratic equation b the square root propert.
Spring 0 Math 08 Eam Preparation Ch Dressler Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Solve the quadratic equation b the square root propert.
 Eam Name algebra final eam review147 aam032020181t4highschool www.alvarezmathhelp.com MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the equation.
Eam Name algebra final eam review147 aam032020181t4highschool www.alvarezmathhelp.com MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the equation.
Fair Game Review. Chapter 8. Graph the linear equation. Big Ideas Math Algebra Record and Practice Journal
 Name Date Chapter Graph the linear equation. Fair Game Review. =. = +. =. =. = +. = + Copright Big Ideas Learning, LLC Big Ideas Math Algebra Name Date Chapter Fair Game Review (continued) Evaluate the
Name Date Chapter Graph the linear equation. Fair Game Review. =. = +. =. =. = +. = + Copright Big Ideas Learning, LLC Big Ideas Math Algebra Name Date Chapter Fair Game Review (continued) Evaluate the
Final Exam Review Part 2 #4
 Final Eam Review Part # Intermediate Algebra / MAT 135 Fall 01 Master (Prof. Fleischner) Student Name/ID: 1. Solve for, where is a real number. + = 8. Solve for, where is a real number. 9 1 = 3. Solve
Final Eam Review Part # Intermediate Algebra / MAT 135 Fall 01 Master (Prof. Fleischner) Student Name/ID: 1. Solve for, where is a real number. + = 8. Solve for, where is a real number. 9 1 = 3. Solve
Final Exam Review Part 2 #4
 Final Eam Review Part # Intermediate Algebra / MAT 135 Fall 01 Master (Prof. Fleischner) Student Name/ID: 1. Solve for, where is a real number. + =. Solve for, where is a real number. 9 1 = 3. Solve for,
Final Eam Review Part # Intermediate Algebra / MAT 135 Fall 01 Master (Prof. Fleischner) Student Name/ID: 1. Solve for, where is a real number. + =. Solve for, where is a real number. 9 1 = 3. Solve for,
Unit 3. Expressions and Equations. 118 Jordan School District
 Unit 3 Epressions and Equations 118 Unit 3 Cluster 1 (A.SSE.): Interpret the Structure of Epressions Cluster 1: Interpret the structure of epressions 3.1. Recognize functions that are quadratic in nature
Unit 3 Epressions and Equations 118 Unit 3 Cluster 1 (A.SSE.): Interpret the Structure of Epressions Cluster 1: Interpret the structure of epressions 3.1. Recognize functions that are quadratic in nature
Name Period Date. Practice FINAL EXAM Intro to Calculus (50 points) Show all work on separate sheet of paper for full credit!
 Name Period Date Practice FINAL EXAM Intro to Calculus (0 points) Show all work on separate sheet of paper for full credit! ) Evaluate the algebraic epression for the given value or values of the variable(s).
Name Period Date Practice FINAL EXAM Intro to Calculus (0 points) Show all work on separate sheet of paper for full credit! ) Evaluate the algebraic epression for the given value or values of the variable(s).
5. 2. The solution set is 7 6 i, 7 x. Since b = 20, add
 Chapter : Quadratic Equations and Functions Chapter Review Eercises... 5 8 6 8 The solution set is 8, 8. 5 5 5 5 5 5 The solution set is 5,5. Rationalize the denominator. 6 The solution set is. 8 8 9 6
Chapter : Quadratic Equations and Functions Chapter Review Eercises... 5 8 6 8 The solution set is 8, 8. 5 5 5 5 5 5 The solution set is 5,5. Rationalize the denominator. 6 The solution set is. 8 8 9 6
C H A P T E R 3 Polynomial Functions
 C H A P T E R Polnomial Functions Section. Quadratic Functions and Models............. 9 Section. Polnomial Functions of Higher Degree......... Section. Polnomial and Snthetic Division............ 8 Section.
C H A P T E R Polnomial Functions Section. Quadratic Functions and Models............. 9 Section. Polnomial Functions of Higher Degree......... Section. Polnomial and Snthetic Division............ 8 Section.
SECTION 3.1: Quadratic Functions
 SECTION 3.: Quadratic Functions Objectives Graph and Analyze Quadratic Functions in Standard and Verte Form Identify the Verte, Ais of Symmetry, and Intercepts of a Quadratic Function Find the Maimum or
SECTION 3.: Quadratic Functions Objectives Graph and Analyze Quadratic Functions in Standard and Verte Form Identify the Verte, Ais of Symmetry, and Intercepts of a Quadratic Function Find the Maimum or
Chapter 5: Quadratic Equations and Functions 5.1 Modeling Data With Quadratic Functions Quadratic Functions and Their Graphs
 Ch 5 Alg Note Sheet Ke Chapter 5: Quadratic Equations and Functions 5.1 Modeling Data With Quadratic Functions Quadratic Functions and Their Graphs Definition: Standard Form of a Quadratic Function The
Ch 5 Alg Note Sheet Ke Chapter 5: Quadratic Equations and Functions 5.1 Modeling Data With Quadratic Functions Quadratic Functions and Their Graphs Definition: Standard Form of a Quadratic Function The
Nonlinear Systems. No solution One solution Two solutions. Solve the system by graphing. Check your answer.
 8-10 Nonlinear Sstems CC.9-1.A.REI.7 Solve a simple sstem consisting of a linear equation and a quadratic equation in two variables algebraicall and graphicall. Objective Solve sstems of equations in two
8-10 Nonlinear Sstems CC.9-1.A.REI.7 Solve a simple sstem consisting of a linear equation and a quadratic equation in two variables algebraicall and graphicall. Objective Solve sstems of equations in two
Chapters 8 & 9 Review for Final
 Math 203 - Intermediate Algebra Professor Valdez Chapters 8 & 9 Review for Final SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Solve the formula for
Math 203 - Intermediate Algebra Professor Valdez Chapters 8 & 9 Review for Final SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Solve the formula for
Unit 10 - Graphing Quadratic Functions
 Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
indicates that a student should be able to complete this item without a
 The semester A eamination for Honors Algebra will consist of two parts. Part 1 will be selected response on which a calculator will NOT be allowed. Part will be short answer on which a calculator will
The semester A eamination for Honors Algebra will consist of two parts. Part 1 will be selected response on which a calculator will NOT be allowed. Part will be short answer on which a calculator will
Final Exam Review Spring a. Is this a quadratic? 2 a. Is this a quadratic? b. EXPLAIN why or why not. b. EXPLAIN why or why not!!
 Final Exam Review Spring 01-013 Name Module 4 Fill in the charts below. x x -6 0 Change in 0 0 Change in -3 1 1-1 4 5 0 9 3 10 16 4 17 5 5 5 6 6 36 6 37 1 Is this a quadratic? Is this a quadratic? b. EXPLAIN
Final Exam Review Spring 01-013 Name Module 4 Fill in the charts below. x x -6 0 Change in 0 0 Change in -3 1 1-1 4 5 0 9 3 10 16 4 17 5 5 5 6 6 36 6 37 1 Is this a quadratic? Is this a quadratic? b. EXPLAIN
Month Price Month Price January February March April May June. July August September October November December
 . Gas prices at a local gas station for the year 999000 are as follows: Month Price Month Price January February March pril May June.7.36.40.5.38.34 July ugust September October November ecember.30.43.5.58.65.69
. Gas prices at a local gas station for the year 999000 are as follows: Month Price Month Price January February March pril May June.7.36.40.5.38.34 July ugust September October November ecember.30.43.5.58.65.69
HAlgebra 2: Unit 7: Chapter 9 Spring Day Date Lesson Assignment. Section 9.1: Direct, Inverse, & Joint Variation Classwork: Packet p.
 HAlgebra : Unit 7: Chapter Spring 0 Name RATIONAL FUNCTIONS. NC Objectives:.0 Operate with algebraic epressions (polynomial, rational, comple fractions) to solve problems..0 Model and solve problems using
HAlgebra : Unit 7: Chapter Spring 0 Name RATIONAL FUNCTIONS. NC Objectives:.0 Operate with algebraic epressions (polynomial, rational, comple fractions) to solve problems..0 Model and solve problems using
MATH College Algebra Review for Test 2
 MATH 34 - College Algebra Review for Test 2 Sections 3. and 3.2. For f (x) = x 2 + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the
MATH 34 - College Algebra Review for Test 2 Sections 3. and 3.2. For f (x) = x 2 + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the
Graph is a parabola that opens up if a 7 0 and opens down if a 6 0. a - 2a, fa - b. 2a bb
 238 CHAPTER 3 Polynomial and Rational Functions Chapter Review Things to Know Quadratic function (pp. 150 157) f12 = a 2 + b + c Graph is a parabola that opens up if a 7 0 and opens down if a 6 0. Verte:
238 CHAPTER 3 Polynomial and Rational Functions Chapter Review Things to Know Quadratic function (pp. 150 157) f12 = a 2 + b + c Graph is a parabola that opens up if a 7 0 and opens down if a 6 0. Verte:
LESSON #28 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #8 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #8 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
Algebra 2 Honors Summer Packet 2018
 Algebra Honors Summer Packet 018 Solving Linear Equations with Fractional Coefficients For these problems, ou should be able to: A) determine the LCD when given two or more fractions B) solve a linear
Algebra Honors Summer Packet 018 Solving Linear Equations with Fractional Coefficients For these problems, ou should be able to: A) determine the LCD when given two or more fractions B) solve a linear
1. Without the use of your calculator, evaluate each of the following quadratic functions for the specified input values. (c) ( )
 Name: Date: QUADRATIC FUNCTION REVIEW FLUENCY Algebra II 1. Without the use of our calculator, evaluate each of the following quadratic functions for the specified input values. (a) g( x) g g ( 5) ( 3)
Name: Date: QUADRATIC FUNCTION REVIEW FLUENCY Algebra II 1. Without the use of our calculator, evaluate each of the following quadratic functions for the specified input values. (a) g( x) g g ( 5) ( 3)
Section 7.1 Solving Quadratic Equations by Graphing. Solving Quadratic Equations by Graphing
 Unit III Quadratic Equations 1 Section 7.1 Solving Quadratic Equations by Graphing Goal: Solving Quadratic Equations by Graphing Investigating Solutions to Quadratic Equations Eample: A missile fired from
Unit III Quadratic Equations 1 Section 7.1 Solving Quadratic Equations by Graphing Goal: Solving Quadratic Equations by Graphing Investigating Solutions to Quadratic Equations Eample: A missile fired from
Review for Intermediate Algebra (MATD 0390) Final Exam Oct 2009
 Review for Intermediate Algebra (MATD 090) Final Eam Oct 009 Students are epected to know all relevant formulas, including: All special factoring formulas Equation of a circle All formulas for linear equations
Review for Intermediate Algebra (MATD 090) Final Eam Oct 009 Students are epected to know all relevant formulas, including: All special factoring formulas Equation of a circle All formulas for linear equations
[ ] 4. Math 70 Intermediate Algebra II Final Exam Review Page 1 of 19. Instructions:
![[ ] 4. Math 70 Intermediate Algebra II Final Exam Review Page 1 of 19. Instructions: [ ] 4. Math 70 Intermediate Algebra II Final Exam Review Page 1 of 19. Instructions:](/thumbs/80/81204581.jpg) Math Intermediate Algebra II Final Eam Review Page of 9 Instructions: Use our own paper for the review questions. For the final eam, show all work on the eam. This is an algebra class do not guess! Write
Math Intermediate Algebra II Final Eam Review Page of 9 Instructions: Use our own paper for the review questions. For the final eam, show all work on the eam. This is an algebra class do not guess! Write
Ch 5 Alg 2 L2 Note Sheet Key Do Activity 1 on your Ch 5 Activity Sheet.
 Ch Alg L Note Sheet Ke Do Activit 1 on our Ch Activit Sheet. Chapter : Quadratic Equations and Functions.1 Modeling Data With Quadratic Functions You had three forms for linear equations, ou will have
Ch Alg L Note Sheet Ke Do Activit 1 on our Ch Activit Sheet. Chapter : Quadratic Equations and Functions.1 Modeling Data With Quadratic Functions You had three forms for linear equations, ou will have
Lesson Master 9-1B. REPRESENTATIONS Objective G. Questions on SPUR Objectives. 1. Let f(x) = 1. a. What are the coordinates of the vertex?
 Back to Lesson 9-9-B REPRESENTATIONS Objective G. Let f() =. a. What are the coordinates of the verte? b. Is the verte a minimum or a maimum? c. Complete the table of values below. 3 0 3 f() d. Graph the
Back to Lesson 9-9-B REPRESENTATIONS Objective G. Let f() =. a. What are the coordinates of the verte? b. Is the verte a minimum or a maimum? c. Complete the table of values below. 3 0 3 f() d. Graph the
More applications of quadratic functions
 Algebra More applications of quadratic functions Name: There are many applications of quadratic functions in the real world. We have already considered applications for which we were given formulas and
Algebra More applications of quadratic functions Name: There are many applications of quadratic functions in the real world. We have already considered applications for which we were given formulas and
4 B. 4 D. 4 F. 3. How can you use the graph of a quadratic equation to determine the number of real solutions of the equation?
 3.1 Solving Quadratic Equations COMMON CORE Learning Standards HSA-SSE.A. HSA-REI.B.b HSF-IF.C.8a Essential Question Essential Question How can ou use the graph of a quadratic equation to determine the
3.1 Solving Quadratic Equations COMMON CORE Learning Standards HSA-SSE.A. HSA-REI.B.b HSF-IF.C.8a Essential Question Essential Question How can ou use the graph of a quadratic equation to determine the
x Radical Sign: Radicand: the number beneath the radical sign
 Sllabus Objective: 9.4 The student will solve quadratic equations using graphic and algebraic techniques to include the quadratic formula, square roots, factoring, completing the square, and graphing.
Sllabus Objective: 9.4 The student will solve quadratic equations using graphic and algebraic techniques to include the quadratic formula, square roots, factoring, completing the square, and graphing.
