Mth 95 Module 4 Chapter 8 Spring Review - Solving quadratic equations using the quadratic formula
|
|
|
- James Atkinson
- 6 years ago
- Views:
Transcription
1 Mth 95 Module 4 Chapter 8 Spring 04 Review - Solving quadratic equations using the quadratic formula Write the quadratic formula. The NUMBER of REAL and COMPLEX SOLUTIONS to a quadratic equation ( a b c 0) can be determined b evaluating the discriminant, b 4ac, the radicand in the quadratic formula. If b 4ac > 0, then there are TWO REAL solutions. If b 4ac = 0, then there is ONE REAL solution. If b 4ac < 0, then there are NO REAL solutions. Instead there are TWO imaginar solutions. Use the discriminant to determine the number of real or imaginar solutions for each equation Solving Quadratic Equations b Square Root and/or Completing the Square A quadratic equation is a degree equation that can be written in the standard form as where a, b, and c are real numbers and Which of the following are quadratic equations? 44 8 e) 57 ( ) f ) 7 Remember the Square Root Propert: If b is a real number and if a b, then a b. Use square root to solve each equation over the set of Comple Numbers. First isolate or the binomial squared, and then take the square root on both sides of the equation
2 Mth 95 Module 4 Chapter 8 Spring 04 ( 4) 5 ( ) 0 Applications: Height of a Free-falling Object Neglecting air resistance, the distance s(t) in feet traveled b an object freel falling is given b s( t) 6t, where t is the number of seconds elapsed How long would it take a pebble to hit the water if dropped off a bridge 00 feet above? A flower pot is knocked off the window sill of a nd stor apartment. The sill is 0 feet above the ground. How long will it take to hit the ground? Solving Quadratic Equations b Completing the Square What does a perfect square trinomial look like? Remember the square of a binomial creates a perfect square trinomial. ( ) ( 5) When a is one, the value of c in a perfect square trinomial can be found b squaring half of b, the coefficient of. Complete each perfect square trinomial. 0 7 Fill in the correct c to make each of the following a perfect square trinomial and then write it b as a binomial squared. Remember c
3 Mth 95 Module 4 Chapter 8 Spring 04 Steps in Completing the Square for ) Isolate the quadratic and linear terms ) If a, it is necessar to divide the equation b the coefficient of the quadratic term, a. (step not needed). ) Divide the coefficient of b and square it. Add this result to BOTH SIDES of the equation. 4) Factor the perfect square trinomial. 5 5) Take the square root of both sides ) Isolate. 5 (eact answers) = or = (approimate answers) Solve the follow quadratic equations where a =, b completel the square Eample of Completing the Square where a. Solve for : 5 0 ) Isolate the quadratic and linear terms 5 ) If necessar, when a, divide the equation b the coefficient of the quadratic term ) Divide the coefficient of b and square it Add this result to BOTH SIDES of the equation 6 6 4) Factor the perfect square trinomial 5 7 5) Take the square root of both sides 6) Isolate
4 Mth 95 Module 4 Chapter 8 Spring 04 Solve the following quadratic equations b completing the square. + 7 = = 0 Another Application Simple interest is used when loans are made. It uses the formula I = prt. Most investments are computed with compound interest. In this case, the interest is accrued on both the principal and the interest. It produces an eponential growth function. The formula used for the total amount of mone when the interest is compounded annuall is: AP( r ) t where P is the principal, r is the annual rate, t is the amount of time in ears and A is the amount of mone at the end of t ears. Find the amount of mone in an account that has $500 invested at 6%, compounded annuall for ears. Find the interest rate, r, if $600 compounded annuall grows to $764 in ears. Review: Evaluate the discriminant for each quadratic equation and tell how man real solutions or comple solutions there are
5 Mth 95 Module 4 Chapter 8 Spring 04 Use the completing the square and/or the square root propert to solve each equation. Simplif completel. Give solutions in eact form, no decimals. Use a + bi form where appropriate The Quadratic Formula The quadratic formula can be derived from the standard form of a quadratic equation b completing the square. a b c 0 Standard form, a 0 a b c Isolate quadratic and linear terms. b c a a Divide each term b a. b b b c a a a a b b c 4a a 4a a 4a b b 4ac a 4a 4a b b 4ac Divide the coefficient of the linear term b, square it, and add the result to both sides of the equation. Factor the perfect square trinomial on the left side. Take the square root of both sides. Simplif. Simplif. Isolate and simplif again. a a a a b b 4ac b b 4ac a Use the quadratic formula to find the real solutions (-intercepts) of each equation. You ma check our solution(s) b graphing each equation on our calculator and finding the -intercepts. Give the eact solution and a decimal approimation rounded to two decimal places where appropriate. In the case of comple solutions, write them in standard form
6 Mth 95 Module 4 Chapter 8 Spring 04 Use Completing the Square AND the Quadratic Formula to solve the following. Make sure our answers match!: Applications Use the Pthagorean Theorem to find the distance saved b cutting across the lawn. The sidewalks meet at a right angle. One leg of the sidewalk is feet longer than the other. The path across the lawn measures 0 feet. How man feet are saved b the cut off instead of going around on the sidewalk? 6
7 Mth 95 Module 4 Chapter 8 Spring 04 Bob has a picture that is 8 centimeters longer than it is wide. The area of the picture is 900 square centimeters. What are the length and width of his picture? Give our answer in a complete sentence with our dimensions rounded to the nearest tenth of a centimeter. Suppose that a stone is thrown upward with an initial velocit of 44 feet per second (0 miles per hour) and is released 4 feet above the ground. Its height (h) in feet after t seconds is given b the model. h( t) 6t 44t 4 a) When does the stone reach a height of feet? Approimate that time to the nearest tenth of a second if it is not eact. b) After how man seconds does the stone hit the ground? Approimate that time to the nearest tenth of a second if it is not eact. 7
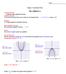
8 Mth 95 Module 4 Chapter 8 Spring Quadratic Functions and Their Graphs A QUADRATIC function can be written in the form f a b c, where a, b, and c are real numbers and a 0. The graph of a quadratic function is called a PARABOLA. The VERTEX is the lowest point on a parabola that opens UPWARD or the highest point on a parabola that opens DOWNWARD. Graph f. Label it. Name the verte. To determine when the graph is increasing and decreasing, walk along the -ais, left to right. The graph is increasing when.the graph is decreasing when. The ais of smmetr (AOS) is the vertical line What is f()? f( )? Use our calculator to help sketch graphs of the following on the above set of aes. 4 5 Basic Transformations of Graphs in the form = a When a > 0, the graph of When a < 0, the graph of a is a parabola that OPENS. a is a parabola that OPENS. As the value a increases, the parabola becomes. For a, is the graph is than =. As the value a decreases, the parabola becomes. For 0 a, the graph is than =. For all graphs of the form a, the verte is, and the ais of smmetr is. 8
9 Mth 95 Module 4 Chapter 8 Spring 04 Quadratics of the form: f ( ) a k Use our calculator to help sketch graphs of the following on the same set of aes Basic Transformations of Graphs in the form = a + k For all graphs a k, the verte is. If k is positive, the graph shifted k units. If k is negative, the graph shifted k units. The ais of smmetr is. Quadratics of the form: f ( ) ( h) Use our calculator to help sketch graphs of the following on the same set of aes. 4 ( ) ( 4) ( ) Basic Transformations of Graphs in the form f ( ) ( h). The graph has the same shape as and the verte is. If h is positive, the graph shifted to the h units. If h is negative, the graph shifted to the h units. The ais of smmetr is. 9
10 Mth 95 Module 4 Chapter 8 Spring 04 Quadratics of the form: f ( ) ( h) k Use our calculator to help sketch graphs of the following on the same set of aes. ( ) ( ) Label each verte. Sketch and label each ais of smmetr (AOS). Basic Transformations of Graphs in the form f ( ) ( h) k, The graph has the same shape as and the verte is. The ais of smmetr is the vertical line.. Summarize the VERTICAL and HORIZONTAL translations of the parabola in terms of h and k. Write each equation in the formf ( ) ( h) k. Identif each verte. 4 Verte Form of a Parabola: f ( ) a( h) k The verte form of a parabola with verte hk, is a h k, where a is a constant and a 0. When a > 0, the parabola opens. When a < 0, the parabola opens. For a, is the graph is than =. For 0 a, the graph is than =. The ais of smmetr is the vertical line. 0
11 Mth 95 Module 4 Chapter 8 Spring 04 Graph the following: f ( ) 5 Label the verte. Sketch and label the ais of smmetr (AOS). Graph the following: f ( ) ( ) 4 Label the verte. Sketch and label the ais of smmetr (AOS). Sec Further Graphing of Quadratic Functions The verte is not obvious when the quadratic equation is written in standard form, but we can find the verte using the following formula. b The -coordinate of the graph a b c, a 0, is given b. a b To find the -coordinate, substitute the -value into the equation, i.e. find f a. Using the above formulas, find the verte for f ( ) -intercept -coordinate -coordinate Verte Ais of Smmetr Parabola opens
12 Mth 95 Module 4 Chapter 8 Spring 04 g 5 6 Complete the following steps to help ou graph Using the above formulas, find the verte -coordinate -coordinate Verte -intercept Parabola opens Use factoring, completing the square, or the quadratic formula to algebraicall find an -intercepts that are real numbers, -intercept(s) g 5 6. Now graph Indicate the verte and the ais of smmetr. Find the verte and an or intercepts to help ou graph the following equations. Indicate the verte and the ais of smmetr on our graphs. f Verte Ais of smmetr -intercept Parabola opens -intercept(s)
Chapter 8 Vocabulary Check
 28 CHAPTER 8 Quadratic Equations and Functions d. What is the level of methane emissions for that ear? (Use our rounded answer from part (c).) (Round this answer to 2 decimals places.) Use a graphing calculator
28 CHAPTER 8 Quadratic Equations and Functions d. What is the level of methane emissions for that ear? (Use our rounded answer from part (c).) (Round this answer to 2 decimals places.) Use a graphing calculator
Mth Quadratic functions and quadratic equations
 Mth 0 - Quadratic functions and quadratic equations Name Find the product. 1) 8a3(2a3 + 2 + 12a) 2) ( + 4)( + 6) 3) (3p - 1)(9p2 + 3p + 1) 4) (32 + 4-4)(2-3 + 3) ) (4a - 7)2 Factor completel. 6) 92-4 7)
Mth 0 - Quadratic functions and quadratic equations Name Find the product. 1) 8a3(2a3 + 2 + 12a) 2) ( + 4)( + 6) 3) (3p - 1)(9p2 + 3p + 1) 4) (32 + 4-4)(2-3 + 3) ) (4a - 7)2 Factor completel. 6) 92-4 7)
Self- assessment 1010 (Intermediate Algebra)
 Self- assessment (Intermediate Algebra) If ou can work these problems using a scientific calculator, ou should have sufficient knowledge to demonstrate master of Intermediate Algebra and to succeed in
Self- assessment (Intermediate Algebra) If ou can work these problems using a scientific calculator, ou should have sufficient knowledge to demonstrate master of Intermediate Algebra and to succeed in
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Math 2 Stud Guide-Chapters 8 and 9 Name Date: Time: MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find all square roots of the number. ) 600 9,
Math 2 Stud Guide-Chapters 8 and 9 Name Date: Time: MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find all square roots of the number. ) 600 9,
Unit 2 Notes Packet on Quadratic Functions and Factoring
 Name: Period: Unit Notes Packet on Quadratic Functions and Factoring Notes #: Graphing quadratic equations in standard form, verte form, and intercept form. A. Intro to Graphs of Quadratic Equations: a
Name: Period: Unit Notes Packet on Quadratic Functions and Factoring Notes #: Graphing quadratic equations in standard form, verte form, and intercept form. A. Intro to Graphs of Quadratic Equations: a
Quadratic Function. Parabola. Parent quadratic function. Vertex. Axis of Symmetry
 Name: Chapter 10: Quadratic Equations and Functions Section 10.1: Graph = a + c Quadratic Function Parabola Parent quadratic function Verte Ais of Smmetr Parent Function = - -1 0 1 1 Eample 1: Make a table,
Name: Chapter 10: Quadratic Equations and Functions Section 10.1: Graph = a + c Quadratic Function Parabola Parent quadratic function Verte Ais of Smmetr Parent Function = - -1 0 1 1 Eample 1: Make a table,
REVIEW KEY VOCABULARY REVIEW EXAMPLES AND EXERCISES
 Etra Eample. Graph.. 6. 7. (, ) (, ) REVIEW KEY VOCABULARY quadratic function, p. 6 standard form of a quadratic function, p. 6 parabola, p. 6 verte, p. 6 ais of smmetr, p. 6 minimum, maimum value, p.
Etra Eample. Graph.. 6. 7. (, ) (, ) REVIEW KEY VOCABULARY quadratic function, p. 6 standard form of a quadratic function, p. 6 parabola, p. 6 verte, p. 6 ais of smmetr, p. 6 minimum, maimum value, p.
MAT 1033C -- Martin-Gay Intermediate Algebra Chapter 8 (8.1, 8.2, 8.5, 8.6) Practice for the Exam
 MAT 33C -- Martin-Ga Intermediate Algebra Chapter 8 (8.1 8. 8. 8.6) Practice for the Eam Name Date Da/Time: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
MAT 33C -- Martin-Ga Intermediate Algebra Chapter 8 (8.1 8. 8. 8.6) Practice for the Eam Name Date Da/Time: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
MATH 91 Final Study Package Name
 MATH 91 Final Stud Package Name Solve the sstem b the substitution method. If there is no solution or an infinite number of solutions, so state. Use set notation to epress the solution set. 1) - = 1 1)
MATH 91 Final Stud Package Name Solve the sstem b the substitution method. If there is no solution or an infinite number of solutions, so state. Use set notation to epress the solution set. 1) - = 1 1)
Chapter 9 Notes Alg. 1H 9-A1 (Lesson 9-3) Solving Quadratic Equations by Finding the Square Root and Completing the Square
 Chapter Notes Alg. H -A (Lesson -) Solving Quadratic Equations b Finding the Square Root and Completing the Square p. *Calculator Find the Square Root: take the square root of. E: Solve b finding square
Chapter Notes Alg. H -A (Lesson -) Solving Quadratic Equations b Finding the Square Root and Completing the Square p. *Calculator Find the Square Root: take the square root of. E: Solve b finding square
2 nd Semester Final Exam Review Block Date
 Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. Identif the verte and ais of smmetr. 1 (10-1) 1. (10-1). 3 (10-) 3. 4 7 (10-) 4. 3 6 4 (10-1) 5. Predict
Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. Identif the verte and ais of smmetr. 1 (10-1) 1. (10-1). 3 (10-) 3. 4 7 (10-) 4. 3 6 4 (10-1) 5. Predict
Vertex form of a quadratic equation
 Verte form of a quadratic equation Nikos Apostolakis Spring 017 Recall 1. Last time we looked at the graphs of quadratic equations in two variables. The upshot was that the graph of the equation: k = a(
Verte form of a quadratic equation Nikos Apostolakis Spring 017 Recall 1. Last time we looked at the graphs of quadratic equations in two variables. The upshot was that the graph of the equation: k = a(
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 Spring 0 Math 08 Eam Preparation Ch Dressler Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Solve the quadratic equation b the square root propert.
Spring 0 Math 08 Eam Preparation Ch Dressler Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Solve the quadratic equation b the square root propert.
Math 0210 Common Final Review Questions (2 5 i)(2 5 i )
 Math 0 Common Final Review Questions In problems 1 6, perform the indicated operations and simplif if necessar. 1. ( 8)(4) ( )(9) 4 7 4 6( ). 18 6 8. ( i) ( 1 4 i ) 4. (8 i ). ( 9 i)( 7 i) 6. ( i)( i )
Math 0 Common Final Review Questions In problems 1 6, perform the indicated operations and simplif if necessar. 1. ( 8)(4) ( )(9) 4 7 4 6( ). 18 6 8. ( i) ( 1 4 i ) 4. (8 i ). ( 9 i)( 7 i) 6. ( i)( i )
Mini-Lecture 8.1 Solving Quadratic Equations by Completing the Square
 Mini-Lecture 8.1 Solving Quadratic Equations b Completing the Square Learning Objectives: 1. Use the square root propert to solve quadratic equations.. Solve quadratic equations b completing the square.
Mini-Lecture 8.1 Solving Quadratic Equations b Completing the Square Learning Objectives: 1. Use the square root propert to solve quadratic equations.. Solve quadratic equations b completing the square.
Write each expression in terms of i : Add: (3 4i) (5 7i) (3 5) ( 4 7)i. 8 3i. Subtract: (3 4i) (5 7i) (3 4i) ( 5 7i) Find each product:
 7_Ch09_online 7// 0:7 AM Page 9-0 9-0 CHAPTER 9 Quadratic Equations SECTION 9. Comple Numbers DEFINITIONS AND CONCEPTS EXAMPLES The imaginar number i is defined as Write each epression in terms of i :
7_Ch09_online 7// 0:7 AM Page 9-0 9-0 CHAPTER 9 Quadratic Equations SECTION 9. Comple Numbers DEFINITIONS AND CONCEPTS EXAMPLES The imaginar number i is defined as Write each epression in terms of i :
2 nd Semester Final Exam Review Block Date
 Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. 1 (10-1) 1. (10-1). (10-1) 3. (10-1) 4. 3 Graph each function. Identif the verte, ais of smmetr, and
Algebra 1B Name nd Semester Final Eam Review Block Date Calculator NOT Allowed Graph each function. 1 (10-1) 1. (10-1). (10-1) 3. (10-1) 4. 3 Graph each function. Identif the verte, ais of smmetr, and
Name Class Date. Solving by Graphing and Algebraically
 Name Class Date 16-4 Nonlinear Sstems Going Deeper Essential question: How can ou solve a sstem of equations when one equation is linear and the other is quadratic? To estimate the solution to a sstem
Name Class Date 16-4 Nonlinear Sstems Going Deeper Essential question: How can ou solve a sstem of equations when one equation is linear and the other is quadratic? To estimate the solution to a sstem
 Test # 33 QUESTIONS MATH131 091700 COLLEGE ALGEBRA Name atfm131bli www.alvarezmathhelp.com website MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Test # 33 QUESTIONS MATH131 091700 COLLEGE ALGEBRA Name atfm131bli www.alvarezmathhelp.com website MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
f(x) Determine whether each function has a maximum or minimum value, and find that value. Then state the domain and range of the function.
 NAME DATE PERID 4-1 Practice Graphing Quadratic Functions Complete parts a c for each quadratic function. a. Find the -intercept, the equation of the ais of smmetr, and the -coordinate of the verte. b.
NAME DATE PERID 4-1 Practice Graphing Quadratic Functions Complete parts a c for each quadratic function. a. Find the -intercept, the equation of the ais of smmetr, and the -coordinate of the verte. b.
Final Exam Review Part 2 #1 Page 1 / 21
 Final Eam Review Part #1 Intermediate Algebra / MAT 135 Spring 017 Master ( Master Templates) Student Name/ID: v 1. Solve for, where is a real number. v v + 1 + =. Solve for, where is a real number. +
Final Eam Review Part #1 Intermediate Algebra / MAT 135 Spring 017 Master ( Master Templates) Student Name/ID: v 1. Solve for, where is a real number. v v + 1 + =. Solve for, where is a real number. +
Mathematics 10 Page 1 of 7 The Quadratic Function (Vertex Form): Translations. and axis of symmetry is at x a.
 Mathematics 10 Page 1 of 7 Verte form of Quadratic Relations The epression a p q defines a quadratic relation called the verte form with a horizontal translation of p units and vertical translation of
Mathematics 10 Page 1 of 7 Verte form of Quadratic Relations The epression a p q defines a quadratic relation called the verte form with a horizontal translation of p units and vertical translation of
Chapter 5: Quadratic Equations and Functions 5.1 Modeling Data With Quadratic Functions Quadratic Functions and Their Graphs
 Ch 5 Alg Note Sheet Ke Chapter 5: Quadratic Equations and Functions 5.1 Modeling Data With Quadratic Functions Quadratic Functions and Their Graphs Definition: Standard Form of a Quadratic Function The
Ch 5 Alg Note Sheet Ke Chapter 5: Quadratic Equations and Functions 5.1 Modeling Data With Quadratic Functions Quadratic Functions and Their Graphs Definition: Standard Form of a Quadratic Function The
Study Guide and Intervention
 6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
Chapters 8 & 9 Review for Final
 Math 203 - Intermediate Algebra Professor Valdez Chapters 8 & 9 Review for Final SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Solve the formula for
Math 203 - Intermediate Algebra Professor Valdez Chapters 8 & 9 Review for Final SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Solve the formula for
Instructor: Imelda Valencia Course: A3 Honors Pre Calculus
 Student: Date: Instructor: Imelda Valencia Course: A3 Honors Pre Calculus 01 017 Assignment: Summer Homework for those who will be taking FOCA 017 01 onl available until Sept. 15 1. Write the epression
Student: Date: Instructor: Imelda Valencia Course: A3 Honors Pre Calculus 01 017 Assignment: Summer Homework for those who will be taking FOCA 017 01 onl available until Sept. 15 1. Write the epression
math0320 FALL interactmath sections developmental mathematics sullivan 1e
 Eam final eam review 180 plus 234 TSI questions for intermediate algebra m032000 013014 NEW Name www.alvarezmathhelp.com math0320 FALL 201 1400 interactmath sections developmental mathematics sullivan
Eam final eam review 180 plus 234 TSI questions for intermediate algebra m032000 013014 NEW Name www.alvarezmathhelp.com math0320 FALL 201 1400 interactmath sections developmental mathematics sullivan
Algebra II Unit #2 4.6 NOTES: Solving Quadratic Equations (More Methods) Block:
 Algebra II Unit # Name: 4.6 NOTES: Solving Quadratic Equations (More Methods) Block: (A) Background Skills - Simplifying Radicals To simplify a radical that is not a perfect square: 50 8 300 7 7 98 (B)
Algebra II Unit # Name: 4.6 NOTES: Solving Quadratic Equations (More Methods) Block: (A) Background Skills - Simplifying Radicals To simplify a radical that is not a perfect square: 50 8 300 7 7 98 (B)
MATH College Algebra Review for Test 2
 MATH 4 - College Algebra Review for Test Sections. and.. For f (x) = x + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the axis of
MATH 4 - College Algebra Review for Test Sections. and.. For f (x) = x + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the axis of
College Algebra ~ Review for Test 2 Sections
 College Algebra ~ Review for Test Sections. -. Find a point-slope form for the equation of the line satisfing the conditions. ) a) Slope -, passing through (7, ) b) Passing through (-, -8) and (-, ) Write
College Algebra ~ Review for Test Sections. -. Find a point-slope form for the equation of the line satisfing the conditions. ) a) Slope -, passing through (7, ) b) Passing through (-, -8) and (-, ) Write
Algebra II Notes Unit Five: Quadratic Functions. Syllabus Objectives: 5.1 The student will graph quadratic functions with and without technology.
 Sllabus Objectives:.1 The student will graph quadratic functions with and without technolog. Quadratic Function: a function that can be written in the form are real numbers Parabola: the U-shaped graph
Sllabus Objectives:.1 The student will graph quadratic functions with and without technolog. Quadratic Function: a function that can be written in the form are real numbers Parabola: the U-shaped graph
Last modified Spring 2016
 Math 00 Final Review Questions In problems 6, perform the indicated operations and simplif if necessar.. 8 6 8. 7 6. ( i) ( 4 i) 4. (8 i). ( 9 i)( 7 i) 6. ( i)( i) In problems 7-, solve the following applications.
Math 00 Final Review Questions In problems 6, perform the indicated operations and simplif if necessar.. 8 6 8. 7 6. ( i) ( 4 i) 4. (8 i). ( 9 i)( 7 i) 6. ( i)( i) In problems 7-, solve the following applications.
x Radical Sign: Radicand: the number beneath the radical sign
 Sllabus Objective: 9.4 The student will solve quadratic equations using graphic and algebraic techniques to include the quadratic formula, square roots, factoring, completing the square, and graphing.
Sllabus Objective: 9.4 The student will solve quadratic equations using graphic and algebraic techniques to include the quadratic formula, square roots, factoring, completing the square, and graphing.
math FALL developmental mathematics sullivan 1e
 TSIpractice eam review 1 131 180 plus 34 TSI questions for elementar and intermediate algebra m0300004301 aaa Name www.alvarezmathhelp.com math0300004301 FALL 01 100 interactmath developmental mathematics
TSIpractice eam review 1 131 180 plus 34 TSI questions for elementar and intermediate algebra m0300004301 aaa Name www.alvarezmathhelp.com math0300004301 FALL 01 100 interactmath developmental mathematics
1. Without the use of your calculator, evaluate each of the following quadratic functions for the specified input values. (c) ( )
 Name: Date: QUADRATIC FUNCTION REVIEW FLUENCY Algebra II 1. Without the use of our calculator, evaluate each of the following quadratic functions for the specified input values. (a) g( x) g g ( 5) ( 3)
Name: Date: QUADRATIC FUNCTION REVIEW FLUENCY Algebra II 1. Without the use of our calculator, evaluate each of the following quadratic functions for the specified input values. (a) g( x) g g ( 5) ( 3)
Lesson 7.1 Polynomial Degree and Finite Differences
 Lesson 7.1 Polnomial Degree and Finite Differences 1. Identif the degree of each polnomial. a. 1 b. 0. 1. 3. 3 c. 0 16 0. Determine which of the epressions are polnomials. For each polnomial, state its
Lesson 7.1 Polnomial Degree and Finite Differences 1. Identif the degree of each polnomial. a. 1 b. 0. 1. 3. 3 c. 0 16 0. Determine which of the epressions are polnomials. For each polnomial, state its
Ch 5 Alg 2 L2 Note Sheet Key Do Activity 1 on your Ch 5 Activity Sheet.
 Ch Alg L Note Sheet Ke Do Activit 1 on our Ch Activit Sheet. Chapter : Quadratic Equations and Functions.1 Modeling Data With Quadratic Functions You had three forms for linear equations, ou will have
Ch Alg L Note Sheet Ke Do Activit 1 on our Ch Activit Sheet. Chapter : Quadratic Equations and Functions.1 Modeling Data With Quadratic Functions You had three forms for linear equations, ou will have
Algebra 1 Unit 9 Quadratic Equations
 Algebra 1 Unit 9 Quadratic Equations Part 1 Name: Period: Date Name of Lesson Notes Tuesda 4/4 Wednesda 4/5 Thursda 4/6 Frida 4/7 Monda 4/10 Tuesda 4/11 Wednesda 4/12 Thursda 4/13 Frida 4/14 Da 1- Quadratic
Algebra 1 Unit 9 Quadratic Equations Part 1 Name: Period: Date Name of Lesson Notes Tuesda 4/4 Wednesda 4/5 Thursda 4/6 Frida 4/7 Monda 4/10 Tuesda 4/11 Wednesda 4/12 Thursda 4/13 Frida 4/14 Da 1- Quadratic
3.1 Graphing Quadratic Functions. Quadratic functions are of the form.
 3.1 Graphing Quadratic Functions A. Quadratic Functions Completing the Square Quadratic functions are of the form. 3. It is easiest to graph quadratic functions when the are in the form using transformations.
3.1 Graphing Quadratic Functions A. Quadratic Functions Completing the Square Quadratic functions are of the form. 3. It is easiest to graph quadratic functions when the are in the form using transformations.
College Algebra ~ Review for Test 2 Sections
 College Algebra ~ Review for Test Sections. -. Use the given graphs of = a + b to solve the inequalit. Write the solution set in interval notation. ) - + 9 8 7 6 (, ) - - - - 6 7 8 - Solve the inequalit
College Algebra ~ Review for Test Sections. -. Use the given graphs of = a + b to solve the inequalit. Write the solution set in interval notation. ) - + 9 8 7 6 (, ) - - - - 6 7 8 - Solve the inequalit
Honors Algebra 2 ~ Spring 2014 Name 1 Unit 3: Quadratic Functions and Equations
 Honors Algebra ~ Spring Name Unit : Quadratic Functions and Equations NC Objectives Covered:. Define and compute with comple numbers. Operate with algebraic epressions (polnomial, rational, comple fractions)
Honors Algebra ~ Spring Name Unit : Quadratic Functions and Equations NC Objectives Covered:. Define and compute with comple numbers. Operate with algebraic epressions (polnomial, rational, comple fractions)
Algebra 2 Unit 2 Practice
 Algebra Unit Practice LESSON 7-1 1. Consider a rectangle that has a perimeter of 80 cm. a. Write a function A(l) that represents the area of the rectangle with length l.. A rectangle has a perimeter of
Algebra Unit Practice LESSON 7-1 1. Consider a rectangle that has a perimeter of 80 cm. a. Write a function A(l) that represents the area of the rectangle with length l.. A rectangle has a perimeter of
Baruch College MTH 1030 Sample Final B Form 0809 PAGE 1
 Baruch College MTH 00 Sample Final B Form 0809 PAGE MTH 00 SAMPLE FINAL B BARUCH COLLEGE DEPARTMENT OF MATHEMATICS SPRING 00 PART I (NO PARTIAL CREDIT, NO CALCULATORS ALLOWED). ON THE FINAL EXAM, THERE
Baruch College MTH 00 Sample Final B Form 0809 PAGE MTH 00 SAMPLE FINAL B BARUCH COLLEGE DEPARTMENT OF MATHEMATICS SPRING 00 PART I (NO PARTIAL CREDIT, NO CALCULATORS ALLOWED). ON THE FINAL EXAM, THERE
Ready To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions
 Read To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions Find these vocabular words in Lesson 5-1 and the Multilingual Glossar. Vocabular quadratic function parabola verte
Read To Go On? Skills Intervention 5-1 Using Transformations to Graph Quadratic Functions Find these vocabular words in Lesson 5-1 and the Multilingual Glossar. Vocabular quadratic function parabola verte
First Semester Final Review NON-Graphing Calculator
 Algebra First Semester Final Review NON-Graphing Calculator Name:. 1. Find the slope of the line passing through the points ( 5, ) and ( 3, 7).. Find the slope-intercept equation of the line passing through
Algebra First Semester Final Review NON-Graphing Calculator Name:. 1. Find the slope of the line passing through the points ( 5, ) and ( 3, 7).. Find the slope-intercept equation of the line passing through
3.1 Graph Quadratic Functions
 3. Graph Quadratic Functions in Standard Form Georgia Performance Standard(s) MMA3b, MMA3c Goal p Use intervals of increase and decrease to understand average rates of change of quadratic functions. Your
3. Graph Quadratic Functions in Standard Form Georgia Performance Standard(s) MMA3b, MMA3c Goal p Use intervals of increase and decrease to understand average rates of change of quadratic functions. Your
Skills Practice Skills Practice for Lesson 3.1
 Skills Practice Skills Practice for Lesson. Name Date Lots and Projectiles Introduction to Quadratic Functions Vocabular Define each term in our own words.. quadratic function. vertical motion Problem
Skills Practice Skills Practice for Lesson. Name Date Lots and Projectiles Introduction to Quadratic Functions Vocabular Define each term in our own words.. quadratic function. vertical motion Problem
Quadratic Functions Objective: To be able to graph a quadratic function and identify the vertex and the roots.
 Name: Quadratic Functions Objective: To be able to graph a quadratic function and identif the verte and the roots. Period: Quadratic Function Function of degree. Usuall in the form: We are now going to
Name: Quadratic Functions Objective: To be able to graph a quadratic function and identif the verte and the roots. Period: Quadratic Function Function of degree. Usuall in the form: We are now going to
Math 100 Final Exam Review
 Math 0 Final Eam Review Name The problems included in this review involve the important concepts covered this semester. Work in groups of 4. If our group gets stuck on a problem, let our instructor know.
Math 0 Final Eam Review Name The problems included in this review involve the important concepts covered this semester. Work in groups of 4. If our group gets stuck on a problem, let our instructor know.
Math 103 Final Exam Review Problems Rockville Campus Fall 2006
 Math Final Eam Review Problems Rockville Campus Fall. Define a. relation b. function. For each graph below, eplain why it is or is not a function. a. b. c. d.. Given + y = a. Find the -intercept. b. Find
Math Final Eam Review Problems Rockville Campus Fall. Define a. relation b. function. For each graph below, eplain why it is or is not a function. a. b. c. d.. Given + y = a. Find the -intercept. b. Find
Chapter 13. Overview. The Quadratic Formula. Overview. The Quadratic Formula. The Quadratic Formula. Lewinter & Widulski 1. The Quadratic Formula
 Chapter 13 Overview Some More Math Before You Go The Quadratic Formula The iscriminant Multiplication of Binomials F.O.I.L. Factoring Zero factor propert Graphing Parabolas The Ais of Smmetr, Verte and
Chapter 13 Overview Some More Math Before You Go The Quadratic Formula The iscriminant Multiplication of Binomials F.O.I.L. Factoring Zero factor propert Graphing Parabolas The Ais of Smmetr, Verte and
Lesson 4.1 Exercises, pages
 Lesson 4.1 Eercises, pages 57 61 When approimating answers, round to the nearest tenth. A 4. Identify the y-intercept of the graph of each quadratic function. a) y = - 1 + 5-1 b) y = 3-14 + 5 Use mental
Lesson 4.1 Eercises, pages 57 61 When approimating answers, round to the nearest tenth. A 4. Identify the y-intercept of the graph of each quadratic function. a) y = - 1 + 5-1 b) y = 3-14 + 5 Use mental
Graph the linear system and estimate the solution. Then check the solution algebraically.
 (Chapters and ) A. Linear Sstems (pp. 6 0). Solve a Sstem b Graphing Vocabular Solution For a sstem of linear equations in two variables, an ordered pair (x, ) that satisfies each equation. Consistent
(Chapters and ) A. Linear Sstems (pp. 6 0). Solve a Sstem b Graphing Vocabular Solution For a sstem of linear equations in two variables, an ordered pair (x, ) that satisfies each equation. Consistent
Chapter 8 Notes SN AA U2C8
 Chapter 8 Notes SN AA U2C8 Name Period Section 8-: Eploring Eponential Models Section 8-2: Properties of Eponential Functions In Chapter 7, we used properties of eponents to determine roots and some of
Chapter 8 Notes SN AA U2C8 Name Period Section 8-: Eploring Eponential Models Section 8-2: Properties of Eponential Functions In Chapter 7, we used properties of eponents to determine roots and some of
Chapter 12 and 13 Math 125 Practice set Note: the actual test differs. Given f(x) and g(x), find the indicated composition and
 Chapter 1 and 13 Math 1 Practice set Note: the actual test differs. Given f() and g(), find the indicated composition. 1) f() = - ; g() = 3 + Find (f g)(). Determine whether the function is one-to-one.
Chapter 1 and 13 Math 1 Practice set Note: the actual test differs. Given f() and g(), find the indicated composition. 1) f() = - ; g() = 3 + Find (f g)(). Determine whether the function is one-to-one.
Glossary. Also available at BigIdeasMath.com: multi-language glossary vocabulary flash cards. An equation that contains an absolute value expression
 Glossar This student friendl glossar is designed to be a reference for ke vocabular, properties, and mathematical terms. Several of the entries include a short eample to aid our understanding of important
Glossar This student friendl glossar is designed to be a reference for ke vocabular, properties, and mathematical terms. Several of the entries include a short eample to aid our understanding of important
8.2 Solving Quadratic Equations by the Quadratic Formula
 Section 8. Solving Quadratic Equations by the Quadratic Formula 85 8. Solving Quadratic Equations by the Quadratic Formula S Solve Quadratic Equations by Using the Quadratic Formula. Determine the Number
Section 8. Solving Quadratic Equations by the Quadratic Formula 85 8. Solving Quadratic Equations by the Quadratic Formula S Solve Quadratic Equations by Using the Quadratic Formula. Determine the Number
C)not a function. B) function domain: {-3, 2, 4, 6} range: {-7, 4, 2, -1}
 Name Spring Semester Final Review (Dual) Precalculus MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Determine whether the relation represents a function.
Name Spring Semester Final Review (Dual) Precalculus MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Determine whether the relation represents a function.
Nonlinear Systems. No solution One solution Two solutions. Solve the system by graphing. Check your answer.
 8-10 Nonlinear Sstems CC.9-1.A.REI.7 Solve a simple sstem consisting of a linear equation and a quadratic equation in two variables algebraicall and graphicall. Objective Solve sstems of equations in two
8-10 Nonlinear Sstems CC.9-1.A.REI.7 Solve a simple sstem consisting of a linear equation and a quadratic equation in two variables algebraicall and graphicall. Objective Solve sstems of equations in two
Algebra 2 Semester Exam Review
 Algebra Semester Eam Review 7 Graph the numbers,,,, and 0 on a number line Identif the propert shown rs rs r when r and s Evaluate What is the value of k k when k? Simplif the epression 7 7 Solve the equation
Algebra Semester Eam Review 7 Graph the numbers,,,, and 0 on a number line Identif the propert shown rs rs r when r and s Evaluate What is the value of k k when k? Simplif the epression 7 7 Solve the equation
SHOW ALL OF YOUR WORK.
 Algebra Semester Practice Final 0 3 6.) r 5r 9 9r 9 0r 8 0r 8 9r Name SHOW ALL OF YOUR WORK..) 3c d 8 8 9c d 9c d 8 6 6c d 6c d 3.) 5 9 5 5 0 0 35.) 5 6 6 5.) 6.) 3 z 3 3 5 0 36 z z 3 5 5 z 3 5 9 z 3.)
Algebra Semester Practice Final 0 3 6.) r 5r 9 9r 9 0r 8 0r 8 9r Name SHOW ALL OF YOUR WORK..) 3c d 8 8 9c d 9c d 8 6 6c d 6c d 3.) 5 9 5 5 0 0 35.) 5 6 6 5.) 6.) 3 z 3 3 5 0 36 z z 3 5 5 z 3 5 9 z 3.)
MAT 116 Final Exam Review
 MAT 116 Final Eam Review 1. Determine the equation for the line described, writing the answer in slope-intercept form. The line is parallel to = 8 and passes through ( 1,9). The line is perpendicular to
MAT 116 Final Eam Review 1. Determine the equation for the line described, writing the answer in slope-intercept form. The line is parallel to = 8 and passes through ( 1,9). The line is perpendicular to
Unit 10 - Graphing Quadratic Functions
 Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
MATH College Algebra Review for Test 2
 MATH 34 - College Algebra Review for Test 2 Sections 3. and 3.2. For f (x) = x 2 + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the
MATH 34 - College Algebra Review for Test 2 Sections 3. and 3.2. For f (x) = x 2 + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the
review math0410 (1-174) and math 0320 ( ) aafinm mg
 Eam Name review math04 (1-174) and math 0320 (17-243) 03201700aafinm0424300 mg MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Simplif. 1) 7 2-3 A)
Eam Name review math04 (1-174) and math 0320 (17-243) 03201700aafinm0424300 mg MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Simplif. 1) 7 2-3 A)
Advanced Algebra 2 Final Review Packet KG Page 1 of Find the slope of the line passing through (3, -1) and (6, 4).
 Advanced Algebra Final Review Packet KG 0 Page of 8. Evaluate (7 ) 0 when and. 7 7. Solve the equation.. Solve the equation.. Solve the equation. 6. An awards dinner costs $ plus $ for each person making
Advanced Algebra Final Review Packet KG 0 Page of 8. Evaluate (7 ) 0 when and. 7 7. Solve the equation.. Solve the equation.. Solve the equation. 6. An awards dinner costs $ plus $ for each person making
 Test #4 33 QUESTIONS MATH1314 09281700 COLLEGE ALGEBRA Name atfm1314bli28 www.alvarezmathhelp.com website SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
Test #4 33 QUESTIONS MATH1314 09281700 COLLEGE ALGEBRA Name atfm1314bli28 www.alvarezmathhelp.com website SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
Math 100 Final Exam Review
 Math 0 Final Eam Review Name The problems included in this review involve the important concepts covered this semester. Work in groups of 4. If our group gets stuck on a problem, let our instructor know.
Math 0 Final Eam Review Name The problems included in this review involve the important concepts covered this semester. Work in groups of 4. If our group gets stuck on a problem, let our instructor know.
ALGEBRA 1 CP FINAL EXAM REVIEW
 ALGEBRA CP FINAL EXAM REVIEW Alg CP Sem Eam Review 0 () Page of 8 Chapter 8: Eponents. Write in rational eponent notation. 7. Write in radical notation. Simplif the epression.. 00.. 6 6. 7 7. 6 6 8. 8
ALGEBRA CP FINAL EXAM REVIEW Alg CP Sem Eam Review 0 () Page of 8 Chapter 8: Eponents. Write in rational eponent notation. 7. Write in radical notation. Simplif the epression.. 00.. 6 6. 7 7. 6 6 8. 8
MATH 115: Final Exam Review. Can you find the distance between two points and the midpoint of a line segment? (1.1)
 MATH : Final Eam Review Can ou find the distance between two points and the midpoint of a line segment? (.) () Consider the points A (,) and ( 6, ) B. (a) Find the distance between A and B. (b) Find the
MATH : Final Eam Review Can ou find the distance between two points and the midpoint of a line segment? (.) () Consider the points A (,) and ( 6, ) B. (a) Find the distance between A and B. (b) Find the
f(x) = 2x 2 + 2x - 4
 4-1 Graphing Quadratic Functions What You ll Learn Scan the tet under the Now heading. List two things ou will learn about in the lesson. 1. Active Vocabular 2. New Vocabular Label each bo with the terms
4-1 Graphing Quadratic Functions What You ll Learn Scan the tet under the Now heading. List two things ou will learn about in the lesson. 1. Active Vocabular 2. New Vocabular Label each bo with the terms
Writing Quadratic Functions in Standard Form
 Chapter Summar Ke Terms standard form (general form) of a quadratic function (.1) parabola (.1) leading coefficient (.) second differences (.) vertical motion model (.3) zeros (.3) interval (.3) open interval
Chapter Summar Ke Terms standard form (general form) of a quadratic function (.1) parabola (.1) leading coefficient (.) second differences (.) vertical motion model (.3) zeros (.3) interval (.3) open interval
QUADRATIC FUNCTION REVIEW
 Name: Date: QUADRATIC FUNCTION REVIEW Linear and eponential functions are used throughout mathematics and science due to their simplicit and applicabilit. Quadratic functions comprise another ver important
Name: Date: QUADRATIC FUNCTION REVIEW Linear and eponential functions are used throughout mathematics and science due to their simplicit and applicabilit. Quadratic functions comprise another ver important
Practice A ( 1, 3 ( 0, 1. Match the function with its graph. 3 x. Explain how the graph of g can be obtained from the graph of f. 5 x.
 8. Practice A For use with pages 65 7 Match the function with its graph.. f. f.. f 5. f 6. f f Lesson 8. A. B. C. (, 6) (0, ) (, ) (0, ) ( 0, ) (, ) D. E. F. (0, ) (, 6) ( 0, ) (, ) (, ) (0, ) Eplain how
8. Practice A For use with pages 65 7 Match the function with its graph.. f. f.. f 5. f 6. f f Lesson 8. A. B. C. (, 6) (0, ) (, ) (0, ) ( 0, ) (, ) D. E. F. (0, ) (, 6) ( 0, ) (, ) (, ) (0, ) Eplain how
Skills Practice Skills Practice for Lesson 1.1
 Skills Practice Skills Practice for Lesson. Name Date Lots and Projectiles Introduction to Quadratic Functions Vocabular Give an eample of each term.. quadratic function 9 0. vertical motion equation s
Skills Practice Skills Practice for Lesson. Name Date Lots and Projectiles Introduction to Quadratic Functions Vocabular Give an eample of each term.. quadratic function 9 0. vertical motion equation s
LESSON #24 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
LESSON #28 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #8 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #8 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
2 variables. is the same value as the solution of. 1 variable. You can use similar reasoning to solve quadratic equations. Work with a partner.
 9. b Graphing Essential Question How can ou use a graph to solve a quadratic equation in one variable? Based on what ou learned about the -intercepts of a graph in Section., it follows that the -intercept
9. b Graphing Essential Question How can ou use a graph to solve a quadratic equation in one variable? Based on what ou learned about the -intercepts of a graph in Section., it follows that the -intercept
Graphing Quadratic Functions 9.1
 Quadratic Functions - Graphing Quadratic Functions 9.1 f ( x) = a x + b x + c (also called standard form). The graph of quadratic functions is called a parabola. Axis of Symmetry a central line which makes
Quadratic Functions - Graphing Quadratic Functions 9.1 f ( x) = a x + b x + c (also called standard form). The graph of quadratic functions is called a parabola. Axis of Symmetry a central line which makes
Solving Quadratic Equations
 9 Solving Quadratic Equations 9. Properties of Radicals 9. Solving Quadratic Equations b Graphing 9. Solving Quadratic Equations Using Square Roots 9. Solving Quadratic Equations b Completing the Square
9 Solving Quadratic Equations 9. Properties of Radicals 9. Solving Quadratic Equations b Graphing 9. Solving Quadratic Equations Using Square Roots 9. Solving Quadratic Equations b Completing the Square
The speed the speed of light is 30,000,000,000 m/s. Write this number in scientific notation.
 Chapter 1 Section 1.1 Scientific Notation Powers of Ten 1 1 1.1.1.1.1 Standard Scientific Notation N n where 1 N and n is an integers Eamples of numbers in scientific notation. 8.17 11 Using Scientific
Chapter 1 Section 1.1 Scientific Notation Powers of Ten 1 1 1.1.1.1.1 Standard Scientific Notation N n where 1 N and n is an integers Eamples of numbers in scientific notation. 8.17 11 Using Scientific
= x. Algebra II Notes Quadratic Functions Unit Graphing Quadratic Functions. Math Background
 Algebra II Notes Quadratic Functions Unit 3.1 3. Graphing Quadratic Functions Math Background Previousl, ou Identified and graphed linear functions Applied transformations to parent functions Graphed quadratic
Algebra II Notes Quadratic Functions Unit 3.1 3. Graphing Quadratic Functions Math Background Previousl, ou Identified and graphed linear functions Applied transformations to parent functions Graphed quadratic
Additional Exercises 10.1 Form I Solving Quadratic Equations by the Square Root Property
 Additional Exercises 10.1 Form I Solving Quadratic Equations by the Square Root Property Solve the quadratic equation by the square root property. If possible, simplify radicals or rationalize denominators.
Additional Exercises 10.1 Form I Solving Quadratic Equations by the Square Root Property Solve the quadratic equation by the square root property. If possible, simplify radicals or rationalize denominators.
 Eam Name algebra final eam review147 aam032020181t4highschool www.alvarezmathhelp.com MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the equation.
Eam Name algebra final eam review147 aam032020181t4highschool www.alvarezmathhelp.com MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the equation.
Maintaining Mathematical Proficiency
 Name Date Chapter 8 Maintaining Mathematical Proficienc Graph the linear equation. 1. = 5. = + 3 3. 1 = + 3. = + Evaluate the epression when =. 5. + 8. + 3 7. 3 8. 5 + 8 9. 8 10. 5 + 3 11. + + 1. 3 + +
Name Date Chapter 8 Maintaining Mathematical Proficienc Graph the linear equation. 1. = 5. = + 3 3. 1 = + 3. = + Evaluate the epression when =. 5. + 8. + 3 7. 3 8. 5 + 8 9. 8 10. 5 + 3 11. + + 1. 3 + +
Chapter 5 Smartboard Notes
 Name Chapter 5 Smartboard Notes 10.1 Graph ax 2 + c Learning Outcome To graph simple quadratic functions Quadratic function A non linear function that can be written in the standard form y = ax 2 + bx
Name Chapter 5 Smartboard Notes 10.1 Graph ax 2 + c Learning Outcome To graph simple quadratic functions Quadratic function A non linear function that can be written in the standard form y = ax 2 + bx
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 Practice for the Final Eam MAC 1 Sullivan Version 1 (2007) SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Find the distance d(p1, P2) between the points
Practice for the Final Eam MAC 1 Sullivan Version 1 (2007) SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Find the distance d(p1, P2) between the points
Fair Game Review. Chapter 9. Find the square root(s) ± Find the side length of the square. 7. Simplify Simplify 63.
 Name Date Chapter 9 Find the square root(s). Fair Game Review... 9. ±. Find the side length of the square.. s. s s Area = 9 ft s Area = 0. m 7. Simplif 0. 8. Simplif. 9. Simplif 08. 0. Simplif 88. Copright
Name Date Chapter 9 Find the square root(s). Fair Game Review... 9. ±. Find the side length of the square.. s. s s Area = 9 ft s Area = 0. m 7. Simplif 0. 8. Simplif. 9. Simplif 08. 0. Simplif 88. Copright
Quadratic Functions and Equations
 Quadratic Functions and Equations Quadratic Graphs and Their Properties Objective: To graph quadratic functions of the form y = ax 2 and y = ax 2 + c. Objectives I can identify a vertex. I can grapy y
Quadratic Functions and Equations Quadratic Graphs and Their Properties Objective: To graph quadratic functions of the form y = ax 2 and y = ax 2 + c. Objectives I can identify a vertex. I can grapy y
Chapter 4. Introduction to Mathematical Modeling. Types of Modeling. 1) Linear Modeling 2) Quadratic Modeling 3) Exponential Modeling
 Chapter 4 Introduction to Mathematical Modeling Tpes of Modeling 1) Linear Modeling ) Quadratic Modeling ) Eponential Modeling Each tpe of modeling in mathematics is determined b the graph of equation
Chapter 4 Introduction to Mathematical Modeling Tpes of Modeling 1) Linear Modeling ) Quadratic Modeling ) Eponential Modeling Each tpe of modeling in mathematics is determined b the graph of equation
Lesson 5.1 Exponential Functions
 Lesson.1 Eponential Functions 1. Evaluate each function at the given value. Round to four decimal places if necessar. a. r (t) 2(1 0.0) t, t 8 b. j() 9.(1 0.09), 10 2. Record the net three terms for each
Lesson.1 Eponential Functions 1. Evaluate each function at the given value. Round to four decimal places if necessar. a. r (t) 2(1 0.0) t, t 8 b. j() 9.(1 0.09), 10 2. Record the net three terms for each
Math125 Exam 5 Review Name. Do the following as indicated.
 Math Eam Review Name Do the following as indicated. For the given functions f and g, find the requested function. ) f() = - 6; g() = 9 Find (f - g)(). ) ) f() = 33 + ; g() = - Find (f g)(). 3) f() = ;
Math Eam Review Name Do the following as indicated. For the given functions f and g, find the requested function. ) f() = - 6; g() = 9 Find (f - g)(). ) ) f() = 33 + ; g() = - Find (f g)(). 3) f() = ;
20.2 Connecting Intercepts and Linear Factors
 Name Class Date 20.2 Connecting Intercepts and Linear Factors Essential Question: How are -intercepts of a quadratic function and its linear factors related? Resource Locker Eplore Connecting Factors and
Name Class Date 20.2 Connecting Intercepts and Linear Factors Essential Question: How are -intercepts of a quadratic function and its linear factors related? Resource Locker Eplore Connecting Factors and
Name: Period: SM Starter on Reading Quadratic Graph. This graph and equation represent the path of an object being thrown.
 SM Name: Period: 7.5 Starter on Reading Quadratic Graph This graph and equation represent the path of an object being thrown. 1. What is the -ais measuring?. What is the y-ais measuring? 3. What are the
SM Name: Period: 7.5 Starter on Reading Quadratic Graph This graph and equation represent the path of an object being thrown. 1. What is the -ais measuring?. What is the y-ais measuring? 3. What are the
Lesson 9.1 Using the Distance Formula
 Lesson. Using the Distance Formula. Find the eact distance between each pair of points. a. (0, 0) and (, ) b. (0, 0) and (7, ) c. (, 8) and (, ) d. (, ) and (, 7) e. (, 7) and (8, ) f. (8, ) and (, 0)
Lesson. Using the Distance Formula. Find the eact distance between each pair of points. a. (0, 0) and (, ) b. (0, 0) and (7, ) c. (, 8) and (, ) d. (, ) and (, 7) e. (, 7) and (8, ) f. (8, ) and (, 0)
Graphs and Solutions for Quadratic Equations
 Format y = a + b + c where a 0 Graphs and Solutions for Quadratic Equations Graphing a quadratic equation creates a parabola. If a is positive, the parabola opens up or is called a smiley face. If a is
Format y = a + b + c where a 0 Graphs and Solutions for Quadratic Equations Graphing a quadratic equation creates a parabola. If a is positive, the parabola opens up or is called a smiley face. If a is
MAT135 Review for Test 4 Dugopolski Sections 7.5, 7.6, 8.1, 8.2, 8.3, 8.4
 Sections 7.5, 7.6, 8.1, 8., 8., 8.4 1. Use the discriminant to determine the number and type(s) of solutions for 4x 8x 4 0. One real solution B. One complex solution Two real solutions Two complex solutions.
Sections 7.5, 7.6, 8.1, 8., 8., 8.4 1. Use the discriminant to determine the number and type(s) of solutions for 4x 8x 4 0. One real solution B. One complex solution Two real solutions Two complex solutions.
TO THE STUDENT: To best prepare for Test 4, do all the problems on separate paper. The answers are given at the end of the review sheet.
 MATH TEST 4 REVIEW TO THE STUDENT: To best prepare for Test 4, do all the problems on separate paper. The answers are given at the end of the review sheet. PART NON-CALCULATOR DIRECTIONS: The problems
MATH TEST 4 REVIEW TO THE STUDENT: To best prepare for Test 4, do all the problems on separate paper. The answers are given at the end of the review sheet. PART NON-CALCULATOR DIRECTIONS: The problems
Algebra Final Exam Review Packet
 Algebra 1 00 Final Eam Review Packet UNIT 1 EXPONENTS / RADICALS Eponents Degree of a monomial: Add the degrees of all the in the monomial together. o Eample - Find the degree of 5 7 yz Degree of a polynomial:
Algebra 1 00 Final Eam Review Packet UNIT 1 EXPONENTS / RADICALS Eponents Degree of a monomial: Add the degrees of all the in the monomial together. o Eample - Find the degree of 5 7 yz Degree of a polynomial:
6.3 Interpreting Vertex Form and Standard Form
 Name Class Date 6.3 Interpreting Verte Form and Standard Form Essential Question: How can ou change the verte form of a quadratic function to standard form? Resource Locker Eplore Identifing Quadratic
Name Class Date 6.3 Interpreting Verte Form and Standard Form Essential Question: How can ou change the verte form of a quadratic function to standard form? Resource Locker Eplore Identifing Quadratic
