Physics 506 Winter 2008 Homework Assignment #4 Solutions. Textbook problems: Ch. 9: 9.6, 9.11, 9.16, 9.17
|
|
|
- Thomasina Goodman
- 6 years ago
- Views:
Transcription
1 Physics 56 Winter 28 Homework Assignment #4 Solutions Textbook problems: Ch. 9: 9.6, 9., 9.6, a) Starting from the general expression (9.2) for A and the corresponding expression for Φ, expand both R = x x and t = t R/c to first order in x /r to obtain the electric dipole potentials for arbitrary time variation Φ( x, t) = [ 4πɛ r 2 n p ret + cr n p ] ret t A( x, t) = µ p ret 4πr t where p ret = p(t = t r/c) is the dipole moment evaluated at the retarded time measured from the origin. We start with the scalar potential, which is given by Φ( x ) = 4πɛ We now use the expansion as well as t = t x x c ρ( x, t x x /c) x x d 3 x () x x r ˆn x t r c + ˆn x c = t ret + ˆn x where t ret = t r/c. Since ρ is a function of time t, we make the expansion c ρ( x, t ) = ρ( x ˆn x ρ( x, t ret ), t ret ) + c t ˆn x ρ ret = ρ ret + + c t + As a result, the expansion of () becomes Φ( x ) = [ 4πɛ r = 4πɛ r ( ρ ret + ˆn x r ρ ret + ) ρ ret c t ( r p ret + ) ] p ret + c t [ Q + ˆn ] + d 3 x
2 where we have used the expressions for charge and electric dipole moment Q = ρ ret d 3 x, p ret = x ρ ret d 3 x Note that, by charge conservation, Q is independent of time, so the subscript Q ret is superfluous. Dropping the static Coulomb potential (which does not radiate) then gives Φ( x ) [ 4πɛ r 2 ˆn p ret + cr ˆn p ] ret (2) t For the vector potential, the expansion is even simpler. We only need to keep the lowest order behavior A( x ) = µ J( x, t x x /c) 4π x x d 3 x = µ [ Jret + ] d 3 x 4πr Using integration by parts, we note that x J ret i d 3 x = i x J ret j d 3 x = x i( J ret ) d 3 x = j x ρ ret i t d3 x = p ret i t Hence A( x ) µ p ret 4πr t (3) b) Calculate the dipole electric and magnetic fields directly from these potentials and show that B( x, t) = µ [ 4π cr 2 n p ret ] t c 2 r n 2 p ret t 2 E( x, t) = {( + r ) [ ] 3 n( n pret ) p ret 4πɛ c t r 3 + ( )} c 2 r n n 2 p ret t 2 For the magnetic field, we use B = A, where the vector potential is given by (3). It is important to note that the electric dipole p ret in (3) is actually a function of retarded time p ret = p(t r/c) Application of the chain rule then gives p ret r = c p ret t Since r = ˆn, the magnetic field turns out to be B = µ ( ) 4π p ret = µ ( r t 4π ˆn p ret r 2 t cr 2 ) p ret t 2 (4)
3 The expression for the electric field is a bit more involved. Using (2) and (3), we obtain E = Φ A t = ( x 4πɛ r 3 p ret + x cr 2 p ) ret µ 2 p ret t 4πr t 2 = [ pret 4πɛ r 3 3 x( x p ret) r 5 x ( cr 4 x p ) ret + p ret t cr 2 t 2 x ( cr 4 x p ) ret x ( )] t c 2 r 3 x 2 p ret t 2 2 p ret 4πɛ c 2 r t 2 = [ pret 3ˆn(ˆn p ret ) 4πɛ r 3 + cr 2 t ( p ret 3ˆn(ˆn p ret )) + 2 ] c 2 r t 2 ( p ret ˆn(ˆn p ret )) = [( + r ) 3ˆn(ˆn pret ) p ret 4πɛ c t r 3 + ( )] c 2 r ˆn ˆn 2 p ret t 2 (5) c) Show explicitly how you can go back and forth between these results and the harmonic fields of (9.8) by the substitutions iω / t and pe ikr iωt p ret (t ). Making the substitution p ret pe ikr and t iω the magnetic field (4) becomes H = ( 4π ˆn r 2 ( iω) p ) cr ( ω2 ) p e ikr = ω2 4πcr (ˆn p ) ( c iωr while the electric field (5) becomes E = [ ( + r 4πɛ [ e ikr = 4πɛ ) ( e ikr = ck2 (ˆn p )eikr ) 4π r ikr c ( iω) ) 3ˆn(ˆn p ) p r 3 + ] c 2 r ( ω2 )ˆn (ˆn p ) ] eikr ( ikr)(3ˆn(ˆn p ) p ) k2 ˆn (ˆn p ) r3 r To go in the other direction, we simply read these equations backwards. e ikr
4 9. Three charges are located along the z axis, a charge +2q at the origin, and charges q at z = ±a cos ωt. Determine the lowest nonvanishing multipole moments, the angular distribution of radiation, and the total power radiated. Assume that ka. We start by specifying the charge and current densities ρ = q[2δ(z) δ(z a cos ωt) δ(z + a cos ωt)]δ(x)δ(y) J = ẑqaω sin ωt[δ(z a cos ωt) δ(z + a cos ωt)]δ(x)δ(y) (6) It should be clear that these moving charges do not directly correspond to time harmonic sources of the form ρe iωt, Je iωt Thus we must use some of the techniques discussed in problem 9. in Fourier decomposing the source charge and current distributions. Essentially we find it easiest to take the approach of 9.a, which is to compute the time-dependent multipole moments first before Fourier decomposing in frequency. Assuming that ka, we may directly compute the first few multipole moments. Working with Cartesian tensors, we have p(t) = x ρ d 3 x = q(a cos ωt a cos ωt) = and m(t) = 2 x J d 3 x = In fact, all magnetic multipole moments vanish since the charges are undergoing linear motion. The electric quadrupole moment is non-vanishing, however Q ij (t) = (3x i x j r 2 δ ij )ρ(t) d 3 x = qa 2 cos 2 ωt(3δ i3 δ j3 δ ij ) The non-vanishing moments are then Q 33 (t) = 2Q (t) = 2Q 22 (t) = 4qa 2 cos 2 ωt Note that this may be written as Q 33 (t) = 2qa 2 [ + cos(2ωt)] = R[ 2qa 2 ( + e 2iωt )] Since the zero frequency term does not radiate, this indicates that we may assume a harmonic quadrupole moment Q 33 = 2Q = 2Q 22 = 2qa 2 (7)
5 which oscillates with angular frequency 2ω. The angular distribution of radiation is then given by dω = c2 Z k 6 52π 2 Q 33 2 sin 2 θ cos 2 θ = Z q 2 28π 2 (ck)2 (ka) 4 sin 2 θ cos 2 θ Using ck = 2ω (since the harmonic frequency is 2ω), we find dω = Z q 2 ω 2 32π 2 (ka)4 sin 2 θ cos 2 θ (8) Integrating this over the solid angle gives a total power P = Z q 2 ω 2 6π (ka)4 (9) Alternatively, we may apply the multipole expansion formalism to write down all multipole coefficients. Using the ka approximation, these expansion coefficients are given by a E (l, m) ckl+2 l + Q lm i(2l + )!! l () a M (l, m) ikl+2 l + M lm (2l + )!! l where Q lm = r l Ylmρ d 3 x, M lm = l + r l Y lm ( r J ) d 3 x To proceed, we convert the charge and current densities (6) to spherical coordinates ρ = q ( ) δ(r) δ(r a cos ωt)[δ(cos θ ) + δ(cos θ + )] 2πr 2 J = ˆr qaω sin ωt δ(r a cos ωt)[δ(cos θ ) + δ(cos θ + )] 2πr2 For the magnetic multipoles, we see that since J ˆr the cross product vanishes, r J =. Thus all magnetic multipoles vanish a M (l, m) = We are thus left with the electric multipoles Q lm (t) = q r l Y 2π lm( δ(r) δ(r a cos ωt) [δ(cos θ ) + δ(cos θ + )] ) drd cos θdφ ( = qδ m, 2δl, Y [Yl(, ) + Yl(π, )](a cos ωt) l)
6 Using then gives Y = 2l + 4π, [Y l(, ) + Y l (π, )] = 4π [P l() + P l ( )] 2l + Q l (t) = 2q 4π (a cos ωt)l l = 2, 4, 6,... A Fourier decomposition gives both positive and negative frequency modes 2l + ( a ) l ( Q l (t) = 2q e iωt + e iωt) l 4π 2 2l + ( a ) l l ( ) l = 2q e i(l 2k)ωt l = 2, 4, 6,... 4π 2 k k= However, since the real part of e ±inωt does not care about the sign of inωt we may group such terms together to eliminate negative frequencies 2l + ( a ) l Q l (t) = 4q R 4π 2 2 ( ) l + ( l/2 n=2,4,...,l l (l n)/2 ) e inωt where l = 2, 4, 6,.... Note that the zero frequency mode does not radiate, and hence may be ignored. In general, the l-th mode radiates at frequencies lω, (l 2)ω, (l 4)ω,.... The lowest non-vanishing moment is the electric quadrupole moment Q 2 = qa 2 5 4π and its harmonic frequency is 2ω. Note, in particular, that this agrees with (7) when converted to a Cartesian tensor. Using (), this yields a multipole coefficient a E (2, ) = iqk(ck)(ka) 2 () 2π We now turn to the angular distribution of the radiation. For a pure multipole of order (l, m), the angular distribution of radiated power is (l, m) dω = Z 2k 2 l(l + ) a(l, m) 2[ 2 (l m)(l + m + ) Y l,m (l + m)(l m + ) Y l,m 2 + m 2 Y lm 2]
7 This simplifies considerably for m = (l, ) dω = Z 2k 2 a(l, ) 2 Y l, 2 Since the lowest multipole is the electric quadrupole, we substitute in l = 2 and m = to obtain dω = Z 2k 2 a E(2, ) 2 5 8π sin2 θ cos 2 θ (2) Using () then gives dω = Z q 2 28π 2 (ck)2 (ka) 4 sin 2 θ cos 2 θ = Z q 2 ω 2 32π 2 (ka)4 sin 2 θ cos 2 θ Note that we have used ck = 2ω, since the harmonic frequency is 2ω. The total radiated power is given by P = Z 2k 2 [ a E (l, m) 2 + a M (l, m) 2 ] l,m For the electric quadrupole, this gives P = Z 2k 2 a E(2, ) 2 = Z q 2 ω 2 6π (ka)4 (3) The next non-vanishing multipole would be l = 4, which radiates at frequencies 2ω and 4ω. However, this will be subdominant, so long as ka. Note that the angular distribution (2) and the total radiated power (3) agree with those found earlier, namely (8) and (9). 9.6 A thin linear antenna of length d is excited in such a way that the sinusoidal current makes a full wavelength of oscillation as shown in the figure. a) Calculate exactly the power radiated per unit solid angle and plot the angular distribution of radiation. Note that the current flows in opposite directions in the top and bottom half of this antenna. As a result, we may write the source current density as J(z) = ẑi sin(kz)δ(x)δ(y)θ(d/2 z ) (4) where k = 2π d In the radiation zone, the vector potential is given by A( x ) = µ e ikr J( x )e ikˆn x d 3 x 4π r = ẑ µ I 4π e ikr d/2 r d/2 sin(kz)e ikz cos θ dz
8 Since the source current is odd under z z, this integral may be written as A = ẑ iµ I 4π = ẑ iµ I 4π = ẑ iµ I 4π e ikr d/2 r e ikr d/2 r e ikr kr 2 sin(kz) sin(kz cos θ) dz [cos(( cos θ)kz) cos(( + cos θ)kz)] dz [ cos θ sin(( cos θ)kz) sin(( + cos θ)kz) + cos θ = ẑ iµ I e ikr sin(π cos θ) 2π kr sin 2 θ In the radiation zone, the magnetic field is H = ik ˆn A µ = ˆφ I e ikr sin(π cos θ) 2π r sin θ where we have used ˆn ẑ ˆr ẑ = ˆφ sin θ. This gives rise to a radiated power dω = Z r 2 2 H 2 = Z I 2 sin 2 (π cos θ) 8π 2 sin 2 θ This looks almost (but not quite) like a quadrupole pattern. z ] d/2 (5) b) Determine the total power radiated and find a numerical value for the radiation resistance. The total radiated power is given by integrating the angular distribution over the solid angle P = Z I 2 8π 2 2π sin 2 (π cos θ) cos 2 θ d cos θ = Z I 2 sin 2 (πx) 4π x 2 dx Z I π
9 Comparing this with P = 2 R rad I 2 gives a radiation resistance R rad = Z 2π.557 = 93.4 Ω (6) 9.7 Treat the linear antenna of Problem 9.6 by the multipole expansion method. a) Calculate the multipole moments (electric dipole, magnetic dipole, and electric quadrupole) exactly and in the long-wavelength approximation. In order to calculate the exact multipole moments, we must use the full multipole expansion method. For a current source without intrinsic magnetization, this involves computing the electric and magnetic multipole coefficients k 2 a E (l, m) = i l(l + ) k 2 a M (l, m) = i l(l + ) [ Ylm cρ ] r [rj l(kr)] + ik( r J )j l (kr) d 3 x Y lm ( r J )j l (kr) d 3 x (7) However, we may begin with the long-wavelength approximation. In this case, the first few moments are given by the standard expressions p = x ρ d 3 x, m = 2 x J d 3 x and Q ij = (3x i x j r 2 δ ij )ρ d 3 x Although the length of the antenna is equal to the wavelength (so that the longwavelength expansion is not particularly valid), we may still see what we get. Using the current density (4), we obtain a charge density ρ = iω J = dj iω dz = ii c cos(kz)δ(x)δ(y)θ(d/2 z ) where we used ω = ck. The electric dipole moment is then p = x ρ d 3 x = ẑ ii c d/2 d/2 z cos(kz) dz = Of course, a simple symmetry argument under z z demonstrates that this electric dipole must vanish. The magnetic dipole moment also vanishes since m = 2 x J d 3 x = I 2 d/2 d/2 z [ẑ sin(kz)] dz =
10 We are left with an electric quadrupole moment Q ij = (3x i x j r 2 δ ij )ρ d 3 x = ii d/2 [3(zδ i3 )(zδ j3 ) z 2 δ ij ] cos(kz) dz c The only non-vanishing moments are d/2 Q 33 = 2Q = 2Q 22 = 2iI c The integral is straightforward, and the result is d/2 d/2 z 2 cos(kz) dz Q 33 = 2Q = 2Q 22 = 8πiI ck 3 (8) This is of course for the long-wavelength approximation. In order to compute the exact multipole moments, we must go back to the expressions for a E (l, m) and a M (l, m) given in (7). Since these multipole coefficients are given as spherical quantities, it is convenient to convert the rectangular coordinate expressions for J and ρ into spherical coordinates ρ = ii 2πr 2 cos(kr)[δ(cos θ ) + δ(cos θ + )] c (9) I J = ˆr 2πr 2 sin(kr)[δ(cos θ ) + δ(cos θ + )] where we have dropped the step function Θ(d/2 r) for simplicity of notation. (We will of course limit the r integration to the range < r < d/2.) Since in (7) we need expressions for r J and r J, we compute r J = I sin(kr)[δ(cos θ ) + δ(cos θ + )] 2πr r J = The vanishing of the cross product immediately indicates that all magnetic multipole coefficients vanish a M (l, m) = This is consistent with the vanishing of the magnetic dipole moment found above in the long-wavelength approximation. For the electric multipoles, we have ( a E (l, m) = k2 I Y lm l(l + ) 2πr 2 cos(kr) ) r [rj l(kr)] kr sin(kr)j l (kr) = k2 I l(l + ) Ylm 2π r [δ(cos θ ) + δ(cos θ + )]r 2 drd cos θdφ ( ) r cos(kr)j l (kr) [δ(cos θ ) + δ(cos θ + )]drd cos θdφ = k2 I [ ] d/2 δ m, [Yl(, ) + Yl(π, )] r cos(kr)j l (kr) l(l + ) = 2π 2 I d l(l + ) δ m,[y l(, ) + Y l(π, )]j l (π)
11 where in the last line we have used k = 2π/d. Noting that 2l + Y l (θ, φ) = 4π P l(cos θ) and that P l () = and P l ( ) = ( ) l, we see that Y l(, ) + Y l(π, ) = Hence the non-vanishing electric multipoles are a E (l, m) = 2πI d 2l + 4π { 2 l even l odd (2l + )π l(l + ) j l(π)δ m, (l even) Taking into account the vanishing of all a M (l, m), we see that of the electric dipole, magnetic dipole, and electric quadrupole moments, only the latter is nonvanishing. Using j 2 (π) = 3/π 2, we find explicitly electric quadrupole: a E (2, ) = I d 3 π 3.9I d (exact) (2) We may also consider the long-wavelength approximation in the formalism of a E (l, m) and a M (l, m). In this case, we write the approximate versions of (7) as where Q lm = a E (l, m) ckl+2 l + i(2l + )!! l a M (l, m) ikl+2 l + (2l + )!! l r l Ylmρ d 3 x, M lm = l + Q lm M lm r l Y lm ( r J ) d 3 x Since r J =, we see that the magnetic moments vanish regardless of whether the long-wavelength approximation is taken or not. For the electric moments, we use (9) to obtain Q lm = ii c 2πr 2 cos(kr)rl Ylm[δ(cos θ ) + δ(cos θ + )]r 2 drd cos θdφ d/2 = ii c δ m,[yl(, ) + Yl(π, )] r l cos(kr)dr = 2iI 2l + d/2 c 4π δ m, r l cos(kr)dr (l even) = 2iI 2l + π ck l+ 4π δ m, x l cos x dx (l even)
12 so that I 4π(l + )(2l + ) π a E (l, m) δ m, x l cos x dx d(2l + )!! l (l even) For l = 2, we use π x2 cos x dx = 2π to obtain electric quadrupole: a E (2, ) = I d 8π I d (long λ approx) (2) Note that this amplitude is larger than the exact expression (2). Of course, this approximation is not to be trusted, since the size of the antenna is equal to one whole wavelength. b) Compare the shape of the angular distribution of radiated power for the lowest nonvanishing multipole with the exact distribution of Problem 9.6. The lowest multipole is the electric quadrupole. Using the simple multipole expansion in the long-wavelength approximation, the angular distribution is dω = c2 Z k 6 52π 2 Q 2 sin 2 θ cos 2 θ = Z I 2 8π 2 π2 sin 2 θ cos 2 θ (22) where Q = Q 33 = 2Q = 2Q 22 is given in (8). This is plotted in black, and may be compared with the exact distribution (5), plotted in green in using the same scale z This shows that the angular distribution is similar to but not exactly the same as the exact one. Perhaps more importantly, however, the long-wavelength approximation seriously overestimates the radiated power.
13 We now turn to the exact quadrupole result of (2). For a pure multipole of order (l, m), the angular distribution of radiated power is (l, m) dω = Z 2k 2 l(l + ) a(l, m) 2[ 2 (l m)(l + m + ) Y l,m (l + m)(l m + ) Y l,m 2 + m 2 Y lm 2] For the electric quadrupole (l = 2, m = ), this simplifies to the expression given in (2) dω = Z 2k 2 a E(2, ) 2 5 8π sin2 θ cos 2 θ Using the exact calculation of a E (2, ) from (2) gives dω = Z I 2 8π 2 ( ) 2 5 sin 2 θ cos 2 θ 2π This is plotted in black, and may be compared with the exact distribution (5), plotted in green in using the same scale z Note that, from (2), the approximate value of a E (2, ) in the long-wavelength approximation is given by a approx E (2, ) = 2π2 5 aexact E (2, ).36 a exact E (2, ) Hence the long-wavelength approximation would give an overestimate of the quadrupole radiated power approx dω = Z I 2 8π 2 π2 sin 2 θ cos 2 θ
14 Furthermore, this expression is identical to (22), as it ought to be (since the long-wavelength expansion is physically the same, regardless of whether we use Cartesian or spherical multipole tensors). c) Determine the total power radiated for the lowest multipole and the corresponding radiation resistance using both multipole moments from part a. Compare with Problem 9.6b. Is there a paradox here? In terms of the multipole expansion coefficients, the total radiated power is given by P = Z 2k 2 [ a E (l, m) 2 + a M (l, m) 2 ] (23) l,m which is a sum of squares without interference. (Of course, interference still shows up in the angular distribution.) Using the exact quadrupole factor (2), the total power radiated for the lowest multipole is P = Z 2k 2 a E(2, ) 2 = Z I 2 5 4π 3 R rad = 9.2 Ω which is around 2% less than the exact result for the total power radiated in all modes, (6). This shows that here the quadrupole really is the dominant mode. Note that, if we had used the long-wavelength approximation (22), we would have found instead P = Z I 2 2π sin 2 θ cos 2 θ d cos θ = Z I 2 π 8 5 R rad = 58 Ω This radiated power (and radiation resistance) is larger than the exact expression of (6). Since the multipoles add incoherently in (23), the power cannot be reduced to the exact value of (6). However, this is not a paradox, since the long-wavelength approximation is invalid for the present case. In particular, this approximation involves the quasi-static source multipole moments Q lm = r l Y lmρ d 3 x (24) However, for an extended source, different charges (and currents) in different regions of the source may add destructively and reduce the true strength of the multipole coefficient compared to the approximate value obtained from (24).
EM radiation - Lecture 14
 EM radiation - Lecture 14 1 Review Begin with a review of the potentials, fields, and Poynting vector for a point charge in accelerated motion. The retarded potential forms are given below. The source
EM radiation - Lecture 14 1 Review Begin with a review of the potentials, fields, and Poynting vector for a point charge in accelerated motion. The retarded potential forms are given below. The source
where ω 0 is the angular frequency of rotation. Using this, we first examine the time-dependent multipole moments
 9. A common textbook example of a adiating system (see Poblem 9.2) is a configuation of chages fixed elative to each othe but in otation. The chage density is obviously a function of time, but it is not
9. A common textbook example of a adiating system (see Poblem 9.2) is a configuation of chages fixed elative to each othe but in otation. The chage density is obviously a function of time, but it is not
Module I: Electromagnetic waves
 Module I: Electromagnetic waves Lectures 10-11: Multipole radiation Amol Dighe TIFR, Mumbai Outline 1 Multipole expansion 2 Electric dipole radiation 3 Magnetic dipole and electric quadrupole radiation
Module I: Electromagnetic waves Lectures 10-11: Multipole radiation Amol Dighe TIFR, Mumbai Outline 1 Multipole expansion 2 Electric dipole radiation 3 Magnetic dipole and electric quadrupole radiation
Module I: Electromagnetic waves
 Module I: Electromagnetic waves Lecture 9: EM radiation Amol Dighe Outline 1 Electric and magnetic fields: radiation components 2 Energy carried by radiation 3 Radiation from antennas Coming up... 1 Electric
Module I: Electromagnetic waves Lecture 9: EM radiation Amol Dighe Outline 1 Electric and magnetic fields: radiation components 2 Energy carried by radiation 3 Radiation from antennas Coming up... 1 Electric
Electrodynamics II: Lecture 9
 Electrodynamics II: Lecture 9 Multipole radiation Amol Dighe Sep 14, 2011 Outline 1 Multipole expansion 2 Electric dipole radiation 3 Magnetic dipole and electric quadrupole radiation Outline 1 Multipole
Electrodynamics II: Lecture 9 Multipole radiation Amol Dighe Sep 14, 2011 Outline 1 Multipole expansion 2 Electric dipole radiation 3 Magnetic dipole and electric quadrupole radiation Outline 1 Multipole
Multipole Fields in the Vacuum Gauge. June 26, 2016
 Multipole Fields in the Vacuum Gauge June 26, 2016 Whatever you call them rubber bands, or Poincaré stresses, or something else there have to be other forces in nature to make a consistent theory of this
Multipole Fields in the Vacuum Gauge June 26, 2016 Whatever you call them rubber bands, or Poincaré stresses, or something else there have to be other forces in nature to make a consistent theory of this
Multipole Expansion for Radiation;Vector Spherical Harmonics
 Multipole Expansion for Radiation;Vector Spherical Harmonics Michael Dine Department of Physics University of California, Santa Cruz February 2013 We seek a more systematic treatment of the multipole expansion
Multipole Expansion for Radiation;Vector Spherical Harmonics Michael Dine Department of Physics University of California, Santa Cruz February 2013 We seek a more systematic treatment of the multipole expansion
Scattering. 1 Classical scattering of a charged particle (Rutherford Scattering)
 Scattering 1 Classical scattering of a charged particle (Rutherford Scattering) Begin by considering radiation when charged particles collide. The classical scattering equation for this process is called
Scattering 1 Classical scattering of a charged particle (Rutherford Scattering) Begin by considering radiation when charged particles collide. The classical scattering equation for this process is called
Multipole moments. November 9, 2015
 Multipole moments November 9, 5 The far field expansion Suppose we have a localized charge distribution, confined to a region near the origin with r < R. Then for values of r > R, the electric field must
Multipole moments November 9, 5 The far field expansion Suppose we have a localized charge distribution, confined to a region near the origin with r < R. Then for values of r > R, the electric field must
G( x x, t) = 1 (2π) 3. d 3 k e k2 t/µσ e i k ( x x ) A( k, t)e k x d 3 k. A( x, t) = 1
 Physics 505 Fall 2005 Homework Assignment #10 Solutions Textbook problems: Ch. 6: 6.3, 6.4, 6.14, 6.18 6.3 The homogeneous diffusion equation (5.160) for the vector potential for quasi-static fields in
Physics 505 Fall 2005 Homework Assignment #10 Solutions Textbook problems: Ch. 6: 6.3, 6.4, 6.14, 6.18 6.3 The homogeneous diffusion equation (5.160) for the vector potential for quasi-static fields in
Spring /2/ pts 1 point per minute
 Physics 519 MIDTERM Name: Spring 014 6//14 80 pts 1 point per minute Exam procedures. Please write your name above. Please sit away from other students. If you have a question about the exam, please ask.
Physics 519 MIDTERM Name: Spring 014 6//14 80 pts 1 point per minute Exam procedures. Please write your name above. Please sit away from other students. If you have a question about the exam, please ask.
University of Illinois at Chicago Department of Physics. Electricity and Magnetism PhD Qualifying Examination
 University of Illinois at Chicago Department of Physics Electricity and Magnetism PhD Qualifying Examination January 8, 216 (Friday) 9: am - 12: noon Full credit can be achieved from completely correct
University of Illinois at Chicago Department of Physics Electricity and Magnetism PhD Qualifying Examination January 8, 216 (Friday) 9: am - 12: noon Full credit can be achieved from completely correct
Quantization of the E-M field
 April 6, 20 Lecture XXVI Quantization of the E-M field 2.0. Electric quadrupole transition If E transitions are forbidden by selection rules, then we consider the next term in the expansion of the spatial
April 6, 20 Lecture XXVI Quantization of the E-M field 2.0. Electric quadrupole transition If E transitions are forbidden by selection rules, then we consider the next term in the expansion of the spatial
Phys. 506 Electricity and Magnetism Winter 2004 Prof. G. Raithel Problem Set 5 Total 40 Points. 1. Problem Points
 Phys. 56 Electricity and Magnetism Winter 4 Prof. G. Raithel Problem Set 5 Total 4 Points. Problem. Points The partial-wave analysis presented in Chapter.4 applied to the case of a perfectly conducting
Phys. 56 Electricity and Magnetism Winter 4 Prof. G. Raithel Problem Set 5 Total 4 Points. Problem. Points The partial-wave analysis presented in Chapter.4 applied to the case of a perfectly conducting
FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 2017
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II November 5, 207 Prof. Alan Guth FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 207 A few items below are marked
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II November 5, 207 Prof. Alan Guth FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 207 A few items below are marked
Physics 505 Fall Homework Assignment #9 Solutions
 Physics 55 Fall 25 Textbook problems: Ch. 5: 5.2, 5.22, 5.26 Ch. 6: 6.1 Homework Assignment #9 olutions 5.2 a) tarting from the force equation (5.12) and the fact that a magnetization M inside a volume
Physics 55 Fall 25 Textbook problems: Ch. 5: 5.2, 5.22, 5.26 Ch. 6: 6.1 Homework Assignment #9 olutions 5.2 a) tarting from the force equation (5.12) and the fact that a magnetization M inside a volume
Lecture 10 February 25, 2010
 Lecture 10 February 5, 010 Last time we discussed a small scatterer at origin. Interesting effects come from many small scatterers occupying a region of size d large compared to λ. The scatterer j at position
Lecture 10 February 5, 010 Last time we discussed a small scatterer at origin. Interesting effects come from many small scatterers occupying a region of size d large compared to λ. The scatterer j at position
Short Wire Antennas: A Simplified Approach Part I: Scaling Arguments. Dan Dobkin version 1.0 July 8, 2005
 Short Wire Antennas: A Simplified Approach Part I: Scaling Arguments Dan Dobkin version 1.0 July 8, 2005 0. Introduction: How does a wire dipole antenna work? How do we find the resistance and the reactance?
Short Wire Antennas: A Simplified Approach Part I: Scaling Arguments Dan Dobkin version 1.0 July 8, 2005 0. Introduction: How does a wire dipole antenna work? How do we find the resistance and the reactance?
Scattering. March 20, 2016
 Scattering March 0, 06 The scattering of waves of any kind, by a compact object, has applications on all scales, from the scattering of light from the early universe by intervening galaxies, to the scattering
Scattering March 0, 06 The scattering of waves of any kind, by a compact object, has applications on all scales, from the scattering of light from the early universe by intervening galaxies, to the scattering
Review of Fundamental Equations Supplementary notes on Section 1.2 and 1.3
 Review of Fundamental Equations Supplementary notes on Section. and.3 Introduction of the velocity potential: irrotational motion: ω = u = identity in the vector analysis: ϕ u = ϕ Basic conservation principles:
Review of Fundamental Equations Supplementary notes on Section. and.3 Introduction of the velocity potential: irrotational motion: ω = u = identity in the vector analysis: ϕ u = ϕ Basic conservation principles:
Physics 505 Fall 2005 Homework Assignment #8 Solutions
 Physics 55 Fall 5 Homework Assignment #8 Solutions Textbook problems: Ch. 5: 5., 5.4, 5.7, 5.9 5. A circular current loop of radius a carrying a current I lies in the x-y plane with its center at the origin.
Physics 55 Fall 5 Homework Assignment #8 Solutions Textbook problems: Ch. 5: 5., 5.4, 5.7, 5.9 5. A circular current loop of radius a carrying a current I lies in the x-y plane with its center at the origin.
2nd Year Electromagnetism 2012:.Exam Practice
 2nd Year Electromagnetism 2012:.Exam Practice These are sample questions of the type of question that will be set in the exam. They haven t been checked the way exam questions are checked so there may
2nd Year Electromagnetism 2012:.Exam Practice These are sample questions of the type of question that will be set in the exam. They haven t been checked the way exam questions are checked so there may
Expansion of 1/r potential in Legendre polynomials
 Expansion of 1/r potential in Legendre polynomials In electrostatics and gravitation, we see scalar potentials of the form V = K d Take d = R r = R 2 2Rr cos θ + r 2 = R 1 2 r R cos θ + r R )2 Use h =
Expansion of 1/r potential in Legendre polynomials In electrostatics and gravitation, we see scalar potentials of the form V = K d Take d = R r = R 2 2Rr cos θ + r 2 = R 1 2 r R cos θ + r R )2 Use h =
The Helmholtz theorem at last!
 Problem. The Helmholtz theorem at last! Recall in class the Helmholtz theorem that says that if if E =0 then E can be written as E = φ () if B =0 then B can be written as B = A (2) (a) Let n be a unit
Problem. The Helmholtz theorem at last! Recall in class the Helmholtz theorem that says that if if E =0 then E can be written as E = φ () if B =0 then B can be written as B = A (2) (a) Let n be a unit
(b) For the system in question, the electric field E, the displacement D, and the polarization P = D ɛ 0 E are as follows. r2 0 inside the sphere,
 PHY 35 K. Solutions for the second midterm exam. Problem 1: a The boundary conditions at the oil-air interface are air side E oil side = E and D air side oil side = D = E air side oil side = ɛ = 1+χ E.
PHY 35 K. Solutions for the second midterm exam. Problem 1: a The boundary conditions at the oil-air interface are air side E oil side = E and D air side oil side = D = E air side oil side = ɛ = 1+χ E.
So far we have derived two electrostatic equations E = 0 (6.2) B = 0 (6.3) which are to be modified due to Faraday s observation,
 Chapter 6 Maxwell Equations 6.1 Maxwell equations So far we have derived two electrostatic equations and two magnetostatics equations E = ρ ɛ 0 (6.1) E = 0 (6.2) B = 0 (6.3) B = µ 0 J (6.4) which are to
Chapter 6 Maxwell Equations 6.1 Maxwell equations So far we have derived two electrostatic equations and two magnetostatics equations E = ρ ɛ 0 (6.1) E = 0 (6.2) B = 0 (6.3) B = µ 0 J (6.4) which are to
Jackson 6.4 Homework Problem Solution Dr. Christopher S. Baird University of Massachusetts Lowell
 Jackson 6.4 Homework Problem Solution Dr. Christopher S. Baird University of Massachusetts Lowell PROBLEM: A uniformly magnetized and conducting sphere of radius R and total magnetic moment m = 4πMR 3
Jackson 6.4 Homework Problem Solution Dr. Christopher S. Baird University of Massachusetts Lowell PROBLEM: A uniformly magnetized and conducting sphere of radius R and total magnetic moment m = 4πMR 3
11 Radiation in Non-relativistic Systems
 Radiation in Non-relativisti Systems. Basi equations This first setion will NOT make a non-relativisti approximation, but will examine the far field limit. (a) We wrote down the wave equations in the ovariant
Radiation in Non-relativisti Systems. Basi equations This first setion will NOT make a non-relativisti approximation, but will examine the far field limit. (a) We wrote down the wave equations in the ovariant
Physics 506 Winter 2004
 Physics 506 Winter 004 G. Raithel January 6, 004 Disclaimer: The purpose of these notes is to provide you with a general list of topics that were covered in class. The notes are not a substitute for reading
Physics 506 Winter 004 G. Raithel January 6, 004 Disclaimer: The purpose of these notes is to provide you with a general list of topics that were covered in class. The notes are not a substitute for reading
Phys 4322 Final Exam - Solution May 12, 2015
 Phys 4322 Final Exam - Solution May 12, 2015 You may NOT use any book or notes other than that supplied with this test. You will have 3 hours to finish. DO YOUR OWN WORK. Express your answers clearly and
Phys 4322 Final Exam - Solution May 12, 2015 You may NOT use any book or notes other than that supplied with this test. You will have 3 hours to finish. DO YOUR OWN WORK. Express your answers clearly and
Lecture 8 February 18, 2010
 Sources of Eectromagnetic Fieds Lecture 8 February 18, 2010 We now start to discuss radiation in free space. We wi reorder the materia of Chapter 9, bringing sections 6 7 up front. We wi aso cover some
Sources of Eectromagnetic Fieds Lecture 8 February 18, 2010 We now start to discuss radiation in free space. We wi reorder the materia of Chapter 9, bringing sections 6 7 up front. We wi aso cover some
Department of Physics IIT Kanpur, Semester II,
 Department of Physics IIT Kanpur, Semester II, 7-8 PHYA: Physics II Solution # 4 Instructors: AKJ & SC Solution 4.: Force with image charges (Griffiths rd ed. Prob.6 As far as force is concerned, this
Department of Physics IIT Kanpur, Semester II, 7-8 PHYA: Physics II Solution # 4 Instructors: AKJ & SC Solution 4.: Force with image charges (Griffiths rd ed. Prob.6 As far as force is concerned, this
Homework Assignment 4 Solution Set
 Homework Assignment 4 Solution Set PHYCS 442 7 February, 24 Problem (Griffiths 2.37 If the plates are sufficiently large the field near them does not depend on d. The field between the plates is zero (the
Homework Assignment 4 Solution Set PHYCS 442 7 February, 24 Problem (Griffiths 2.37 If the plates are sufficiently large the field near them does not depend on d. The field between the plates is zero (the
EM waves: energy, resonators. Scalar wave equation Maxwell equations to the EM wave equation A simple linear resonator Energy in EM waves 3D waves
 EM waves: energy, resonators Scalar wave equation Maxwell equations to the EM wave equation A simple linear resonator Energy in EM waves 3D waves Simple scalar wave equation 2 nd order PDE 2 z 2 ψ (z,t)
EM waves: energy, resonators Scalar wave equation Maxwell equations to the EM wave equation A simple linear resonator Energy in EM waves 3D waves Simple scalar wave equation 2 nd order PDE 2 z 2 ψ (z,t)
Phys. 505 Electricity and Magnetism Fall 2003 Prof. G. Raithel Problem Set 1
 Phys. 505 Electricity and Magnetism Fall 2003 Prof. G. Raithel Problem Set Problem.3 a): By symmetry, the solution must be of the form ρ(x) = ρ(r) = Qδ(r R)f, with a constant f to be specified by the condition
Phys. 505 Electricity and Magnetism Fall 2003 Prof. G. Raithel Problem Set Problem.3 a): By symmetry, the solution must be of the form ρ(x) = ρ(r) = Qδ(r R)f, with a constant f to be specified by the condition
Homework 7-8 Solutions. Problems
 Homework 7-8 Solutions Problems 26 A rhombus is a parallelogram with opposite sides of equal length Let us form a rhombus using vectors v 1 and v 2 as two adjacent sides, with v 1 = v 2 The diagonals of
Homework 7-8 Solutions Problems 26 A rhombus is a parallelogram with opposite sides of equal length Let us form a rhombus using vectors v 1 and v 2 as two adjacent sides, with v 1 = v 2 The diagonals of
Notes: Most of the material presented in this chapter is taken from Jackson, Chap. 2, 3, and 4, and Di Bartolo, Chap. 2. 2π nx i a. ( ) = G n.
 Chapter. Electrostatic II Notes: Most of the material presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartolo, Chap... Mathematical Considerations.. The Fourier series and the Fourier
Chapter. Electrostatic II Notes: Most of the material presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartolo, Chap... Mathematical Considerations.. The Fourier series and the Fourier
d 1 µ 2 Θ = 0. (4.1) consider first the case of m = 0 where there is no azimuthal dependence on the angle φ.
 4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
Phys. 506 Electricity and Magnetism Winter 2004 Prof. G. Raithel Problem Set 4 Total 40 Points. 1. Problem Points
 Phys. 56 Electricity nd Mgnetism Winter Prof. G. Rithel Problem Set Totl Points. Problem 9. Points ). In the long-wvelength limit, in the source nd its immedite vicinity electro- nd mgnetosttic equtions
Phys. 56 Electricity nd Mgnetism Winter Prof. G. Rithel Problem Set Totl Points. Problem 9. Points ). In the long-wvelength limit, in the source nd its immedite vicinity electro- nd mgnetosttic equtions
Electromagnetism Answers to Problem Set 8 Spring Jackson Prob. 4.1: Multipole expansion for various charge distributions
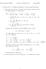 Electromagnetism 76 Answers to Problem Set 8 Spring 6. Jackson Prob. 4.: Multipole expansion for various charge distributions (a) In the first case, we have 4 charges in the xy plane at distance a from
Electromagnetism 76 Answers to Problem Set 8 Spring 6. Jackson Prob. 4.: Multipole expansion for various charge distributions (a) In the first case, we have 4 charges in the xy plane at distance a from
Electrodynamics Exam Solutions
 Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Electrodynamics Exam Solutions Name: FS 215 Prof. C. Anastasiou Student number: Exercise 1 2 3 4 Total Max. points 15 15 15 15 6 Points Visum 1 Visum 2 The exam lasts 18 minutes. Start every new exercise
Fiber Optics. Equivalently θ < θ max = cos 1 (n 0 /n 1 ). This is geometrical optics. Needs λ a. Two kinds of fibers:
 Waves can be guided not only by conductors, but by dielectrics. Fiber optics cable of silica has nr varying with radius. Simplest: core radius a with n = n 1, surrounded radius b with n = n 0 < n 1. Total
Waves can be guided not only by conductors, but by dielectrics. Fiber optics cable of silica has nr varying with radius. Simplest: core radius a with n = n 1, surrounded radius b with n = n 0 < n 1. Total
Electromagnetic Theory I
 Electromagnetic Theory I Final Examination 18 December 2009, 12:30-2:30 pm Instructions: Answer the following 10 questions, each of which is worth 10 points. Explain your reasoning in each case. Use SI
Electromagnetic Theory I Final Examination 18 December 2009, 12:30-2:30 pm Instructions: Answer the following 10 questions, each of which is worth 10 points. Explain your reasoning in each case. Use SI
RADIATION OF ELECTROMAGNETIC WAVES
 Chapter RADIATION OF ELECTROMAGNETIC WAVES. Introduction We know that a charge q creates the Coulomb field given by E c 4πɛ 0 q r 2 e r, but a stationary charge cannot radiate electromagnetic waves which
Chapter RADIATION OF ELECTROMAGNETIC WAVES. Introduction We know that a charge q creates the Coulomb field given by E c 4πɛ 0 q r 2 e r, but a stationary charge cannot radiate electromagnetic waves which
Chapter 11. Radiation. How accelerating charges and changing currents produce electromagnetic waves, how they radiate.
 Chapter 11. Radiation How accelerating charges and changing currents produce electromagnetic waves, how they radiate. 11.1.1 What is Radiation? Assume a radiation source is localized near the origin. Total
Chapter 11. Radiation How accelerating charges and changing currents produce electromagnetic waves, how they radiate. 11.1.1 What is Radiation? Assume a radiation source is localized near the origin. Total
Optical Lattices. Chapter Polarization
 Chapter Optical Lattices Abstract In this chapter we give details of the atomic physics that underlies the Bose- Hubbard model used to describe ultracold atoms in optical lattices. We show how the AC-Stark
Chapter Optical Lattices Abstract In this chapter we give details of the atomic physics that underlies the Bose- Hubbard model used to describe ultracold atoms in optical lattices. We show how the AC-Stark
Magnetostatics and the vector potential
 Magnetostatics and the vector potential December 8, 2015 1 The divergence of the magnetic field Starting with the general form of the Biot-Savart law, B (x 0 ) we take the divergence of both sides with
Magnetostatics and the vector potential December 8, 2015 1 The divergence of the magnetic field Starting with the general form of the Biot-Savart law, B (x 0 ) we take the divergence of both sides with
Angular Momentum and Conservation Laws in Classical Electrodynamics
 UPTEC F09 017 Examensarbete 30 hp Februari 2009 Angular Momentum and Conservation Laws in Classical Electrodynamics Johan Lindberg Abstract Angular Momentum and Conservation Laws in Classical Electrodynamics
UPTEC F09 017 Examensarbete 30 hp Februari 2009 Angular Momentum and Conservation Laws in Classical Electrodynamics Johan Lindberg Abstract Angular Momentum and Conservation Laws in Classical Electrodynamics
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics Spring 2014 Practice Problem Set 11 Solutions
 MASSACHUSES INSIUE OF ECHNOLOGY Department of Physics 8 Spring 4 Practice Problem Set Solutions Problem : Electromagnetic Waves and the Poynting Vector We have been studying one particular class of electric
MASSACHUSES INSIUE OF ECHNOLOGY Department of Physics 8 Spring 4 Practice Problem Set Solutions Problem : Electromagnetic Waves and the Poynting Vector We have been studying one particular class of electric
Spherical Waves, Radiator Groups
 Waves, Radiator Groups ELEC-E5610 Acoustics and the Physics of Sound, Lecture 10 Archontis Politis Department of Signal Processing and Acoustics Aalto University School of Electrical Engineering November
Waves, Radiator Groups ELEC-E5610 Acoustics and the Physics of Sound, Lecture 10 Archontis Politis Department of Signal Processing and Acoustics Aalto University School of Electrical Engineering November
(a) Show that electric field and magnetic field have units (force)/area or energy/volume.
 Problem. Units (a) how that electric field and magnetic field have units (force)/area or energy/volume. (b) A rule of thumb that you may need in the lab is that coaxial cable has a capcitance of 2 pf/foot.
Problem. Units (a) how that electric field and magnetic field have units (force)/area or energy/volume. (b) A rule of thumb that you may need in the lab is that coaxial cable has a capcitance of 2 pf/foot.
Electrodynamics I Midterm - Part A - Closed Book KSU 2005/10/17 Electro Dynamic
 Electrodynamics I Midterm - Part A - Closed Book KSU 5//7 Name Electro Dynamic. () Write Gauss Law in differential form. E( r) =ρ( r)/ɛ, or D = ρ, E= electricfield,ρ=volume charge density, ɛ =permittivity
Electrodynamics I Midterm - Part A - Closed Book KSU 5//7 Name Electro Dynamic. () Write Gauss Law in differential form. E( r) =ρ( r)/ɛ, or D = ρ, E= electricfield,ρ=volume charge density, ɛ =permittivity
1 (2n)! (-1)n (θ) 2n
 Complex Numbers and Algebra The real numbers are complete for the operations addition, subtraction, multiplication, and division, or more suggestively, for the operations of addition and multiplication
Complex Numbers and Algebra The real numbers are complete for the operations addition, subtraction, multiplication, and division, or more suggestively, for the operations of addition and multiplication
(a) Write down the total Hamiltonian of this system, including the spin degree of freedom of the electron, but neglecting spin-orbit interactions.
 1. Quantum Mechanics (Spring 2007) Consider a hydrogen atom in a weak uniform magnetic field B = Bê z. (a) Write down the total Hamiltonian of this system, including the spin degree of freedom of the electron,
1. Quantum Mechanics (Spring 2007) Consider a hydrogen atom in a weak uniform magnetic field B = Bê z. (a) Write down the total Hamiltonian of this system, including the spin degree of freedom of the electron,
3.2 Numerical Methods for Antenna Analysis
 ECEn 665: Antennas and Propagation for Wireless Communications 43 3.2 Numerical Methods for Antenna Analysis The sinusoidal current model for a dipole antenna is convenient because antenna parameters can
ECEn 665: Antennas and Propagation for Wireless Communications 43 3.2 Numerical Methods for Antenna Analysis The sinusoidal current model for a dipole antenna is convenient because antenna parameters can
2.3 Oscillation. The harmonic oscillator equation is the differential equation. d 2 y dt 2 r y (r > 0). Its solutions have the form
 2. Oscillation So far, we have used differential equations to describe functions that grow or decay over time. The next most common behavior for a function is to oscillate, meaning that it increases and
2. Oscillation So far, we have used differential equations to describe functions that grow or decay over time. The next most common behavior for a function is to oscillate, meaning that it increases and
Guided waves - Lecture 11
 Guided waves - Lecture 11 1 Wave equations in a rectangular wave guide Suppose EM waves are contained within the cavity of a long conducting pipe. To simplify the geometry, consider a pipe of rectangular
Guided waves - Lecture 11 1 Wave equations in a rectangular wave guide Suppose EM waves are contained within the cavity of a long conducting pipe. To simplify the geometry, consider a pipe of rectangular
Physics 511 Spring 2000
 Physics 511 Spring 2000 Problem Set #8: Due Friday April 7, 2000 Read: Notes on Multipole Radiation, Jackson Third Ed. Chap. 6.3-6.4, 9.1-9.4, Low 4.1-4.6 Problem 1. Electromagnetic radiation in one dimension
Physics 511 Spring 2000 Problem Set #8: Due Friday April 7, 2000 Read: Notes on Multipole Radiation, Jackson Third Ed. Chap. 6.3-6.4, 9.1-9.4, Low 4.1-4.6 Problem 1. Electromagnetic radiation in one dimension
Classical Field Theory: Electrostatics-Magnetostatics
 Classical Field Theory: Electrostatics-Magnetostatics April 27, 2010 1 1 J.D.Jackson, Classical Electrodynamics, 2nd Edition, Section 1-5 Electrostatics The behavior of an electrostatic field can be described
Classical Field Theory: Electrostatics-Magnetostatics April 27, 2010 1 1 J.D.Jackson, Classical Electrodynamics, 2nd Edition, Section 1-5 Electrostatics The behavior of an electrostatic field can be described
Theory of Electromagnetic Fields
 Theory of Electromagnetic Fields Andrzej Wolski University of Liverpool, and the Cockcroft Institute, UK Abstract We discuss the theory of electromagnetic fields, with an emphasis on aspects relevant to
Theory of Electromagnetic Fields Andrzej Wolski University of Liverpool, and the Cockcroft Institute, UK Abstract We discuss the theory of electromagnetic fields, with an emphasis on aspects relevant to
Non-stationary States and Electric Dipole Transitions
 Pre-Lab Lecture II Non-stationary States and Electric Dipole Transitions You will recall that the wavefunction for any system is calculated in general from the time-dependent Schrödinger equation ĤΨ(x,t)=i
Pre-Lab Lecture II Non-stationary States and Electric Dipole Transitions You will recall that the wavefunction for any system is calculated in general from the time-dependent Schrödinger equation ĤΨ(x,t)=i
Physics 214 Final Exam Solutions Winter 2017
 Physics 14 Final Exam Solutions Winter 017 1 An electron of charge e and mass m moves in a plane perpendicular to a uniform magnetic field B If the energy loss by radiation is neglected, the orbit is a
Physics 14 Final Exam Solutions Winter 017 1 An electron of charge e and mass m moves in a plane perpendicular to a uniform magnetic field B If the energy loss by radiation is neglected, the orbit is a
Electromagnetic Theory
 Summary: Electromagnetic Theory Maxwell s equations EM Potentials Equations of motion of particles in electromagnetic fields Green s functions Lienard-Weichert potentials Spectral distribution of electromagnetic
Summary: Electromagnetic Theory Maxwell s equations EM Potentials Equations of motion of particles in electromagnetic fields Green s functions Lienard-Weichert potentials Spectral distribution of electromagnetic
Physics 214 Midterm Exam Solutions Winter 2017
 Physics 14 Midterm Exam Solutions Winter 017 1. A linearly polarized electromagnetic wave, polarized in the ˆx direction, is traveling in the ẑ-direction in a dielectric medium of refractive index n 1.
Physics 14 Midterm Exam Solutions Winter 017 1. A linearly polarized electromagnetic wave, polarized in the ˆx direction, is traveling in the ẑ-direction in a dielectric medium of refractive index n 1.
Let b be the distance of closest approach between the trajectory of the center of the moving ball and the center of the stationary one.
 Scattering Classical model As a model for the classical approach to collision, consider the case of a billiard ball colliding with a stationary one. The scattering direction quite clearly depends rather
Scattering Classical model As a model for the classical approach to collision, consider the case of a billiard ball colliding with a stationary one. The scattering direction quite clearly depends rather
Solutions to exam : 1FA352 Quantum Mechanics 10 hp 1
 Solutions to exam 6--6: FA35 Quantum Mechanics hp Problem (4 p): (a) Define the concept of unitary operator and show that the operator e ipa/ is unitary (p is the momentum operator in one dimension) (b)
Solutions to exam 6--6: FA35 Quantum Mechanics hp Problem (4 p): (a) Define the concept of unitary operator and show that the operator e ipa/ is unitary (p is the momentum operator in one dimension) (b)
Electromagnetism Answers to Problem Set 9 Spring 2006
 Electromagnetism 70006 Answers to Problem et 9 pring 006. Jackson Prob. 5.: Reformulate the Biot-avart law in terms of the solid angle subtended at the point of observation by the current-carrying circuit.
Electromagnetism 70006 Answers to Problem et 9 pring 006. Jackson Prob. 5.: Reformulate the Biot-avart law in terms of the solid angle subtended at the point of observation by the current-carrying circuit.
Physics 139B Solutions to Homework Set 5 Fall 2009
 Physics 39B Solutions to Homework Set 5 Fall 9 Liboff, problem 35 on pages 749 75 A one-dimensional harmonic oscillator of charge-to-mass ratio e/m, and spring constant K oscillates parallel to the x-axis
Physics 39B Solutions to Homework Set 5 Fall 9 Liboff, problem 35 on pages 749 75 A one-dimensional harmonic oscillator of charge-to-mass ratio e/m, and spring constant K oscillates parallel to the x-axis
Maxwell s equations for electrostatics
 Maxwell s equations for electrostatics October 6, 5 The differential form of Gauss s law Starting from the integral form of Gauss s law, we treat the charge as a continuous distribution, ρ x. Then, letting
Maxwell s equations for electrostatics October 6, 5 The differential form of Gauss s law Starting from the integral form of Gauss s law, we treat the charge as a continuous distribution, ρ x. Then, letting
Problem Set #4: 4.1,4.7,4.9 (Due Monday, March 25th)
 Chapter 4 Multipoles, Dielectrics Problem Set #4: 4.,4.7,4.9 (Due Monday, March 5th 4. Multipole expansion Consider a localized distribution of charges described by ρ(x contained entirely in a sphere of
Chapter 4 Multipoles, Dielectrics Problem Set #4: 4.,4.7,4.9 (Due Monday, March 5th 4. Multipole expansion Consider a localized distribution of charges described by ρ(x contained entirely in a sphere of
Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Electro Dynamic
 Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Name Electro Dynamic Instructions: Use SI units. Short answers! No derivations here, just state your responses clearly. 1. (2) Write an
Electrodynamics I Final Exam - Part A - Closed Book KSU 2005/12/12 Name Electro Dynamic Instructions: Use SI units. Short answers! No derivations here, just state your responses clearly. 1. (2) Write an
Classical electric dipole radiation
 B Classical electric dipole radiation In Chapter a classical model was used to describe the scattering of X-rays by electrons. The equation relating the strength of the radiated to incident X-ray electric
B Classical electric dipole radiation In Chapter a classical model was used to describe the scattering of X-rays by electrons. The equation relating the strength of the radiated to incident X-ray electric
221B Lecture Notes Scattering Theory II
 22B Lecture Notes Scattering Theory II Born Approximation Lippmann Schwinger equation ψ = φ + V ψ, () E H 0 + iɛ is an exact equation for the scattering problem, but it still is an equation to be solved
22B Lecture Notes Scattering Theory II Born Approximation Lippmann Schwinger equation ψ = φ + V ψ, () E H 0 + iɛ is an exact equation for the scattering problem, but it still is an equation to be solved
ψ s a ˆn a s b ˆn b ψ Hint: Because the state is spherically symmetric the answer can depend only on the angle between the two directions.
 1. Quantum Mechanics (Fall 2004) Two spin-half particles are in a state with total spin zero. Let ˆn a and ˆn b be unit vectors in two arbitrary directions. Calculate the expectation value of the product
1. Quantum Mechanics (Fall 2004) Two spin-half particles are in a state with total spin zero. Let ˆn a and ˆn b be unit vectors in two arbitrary directions. Calculate the expectation value of the product
r,t r R Z j ³ 0 1 4π² 0 r,t) = 4π
 5.4 Lienard-Wiechert Potential and Consequent Fields 5.4.1 Potential and Fields (chapter 10) Lienard-Wiechert potential In the previous section, we studied the radiation from an electric dipole, a λ/2
5.4 Lienard-Wiechert Potential and Consequent Fields 5.4.1 Potential and Fields (chapter 10) Lienard-Wiechert potential In the previous section, we studied the radiation from an electric dipole, a λ/2
r 2. (5) This agrees of course with the traditional multipole way of writing it: for an axial point dipole at the coordinate origin
 1. A Digression on Dipoles From the perspective of potential theory, the dipole represents the point source obtained by allowing two point charges of opposite sign to approach each other, in such a way
1. A Digression on Dipoles From the perspective of potential theory, the dipole represents the point source obtained by allowing two point charges of opposite sign to approach each other, in such a way
Physics 221B Spring 2018 Notes 34 The Photoelectric Effect
 Copyright c 2018 by Robert G. Littlejohn Physics 221B Spring 2018 Notes 34 The Photoelectric Effect 1. Introduction In these notes we consider the ejection of an atomic electron by an incident photon,
Copyright c 2018 by Robert G. Littlejohn Physics 221B Spring 2018 Notes 34 The Photoelectric Effect 1. Introduction In these notes we consider the ejection of an atomic electron by an incident photon,
Scattering cross-section (µm 2 )
 Supplementary Figures Scattering cross-section (µm 2 ).16.14.12.1.8.6.4.2 Total scattering Electric dipole, a E (1,1) Magnetic dipole, a M (1,1) Magnetic quardupole, a M (2,1). 44 48 52 56 Wavelength (nm)
Supplementary Figures Scattering cross-section (µm 2 ).16.14.12.1.8.6.4.2 Total scattering Electric dipole, a E (1,1) Magnetic dipole, a M (1,1) Magnetic quardupole, a M (2,1). 44 48 52 56 Wavelength (nm)
KIPMU Set 1: CMB Statistics. Wayne Hu
 KIPMU Set 1: CMB Statistics Wayne Hu CMB Blackbody COBE FIRAS spectral measurement. yellblackbody spectrum. T = 2.725K giving Ω γ h 2 = 2.471 10 5 12 GHz 200 400 600 10 B ν ( 10 5 ) 8 6 4 error 50 2 0
KIPMU Set 1: CMB Statistics Wayne Hu CMB Blackbody COBE FIRAS spectral measurement. yellblackbody spectrum. T = 2.725K giving Ω γ h 2 = 2.471 10 5 12 GHz 200 400 600 10 B ν ( 10 5 ) 8 6 4 error 50 2 0
( ) /, so that we can ignore all
 Physics 531: Atomic Physics Problem Set #5 Due Wednesday, November 2, 2011 Problem 1: The ac-stark effect Suppose an atom is perturbed by a monochromatic electric field oscillating at frequency ω L E(t)
Physics 531: Atomic Physics Problem Set #5 Due Wednesday, November 2, 2011 Problem 1: The ac-stark effect Suppose an atom is perturbed by a monochromatic electric field oscillating at frequency ω L E(t)
Physics 505 Fall 2005 Homework Assignment #7 Solutions
 Physics 505 Fall 005 Homework Assignment #7 Solutions Textbook problems: Ch. 4: 4.10 Ch. 5: 5.3, 5.6, 5.7 4.10 Two concentric conducting spheres of inner and outer radii a and b, respectively, carry charges
Physics 505 Fall 005 Homework Assignment #7 Solutions Textbook problems: Ch. 4: 4.10 Ch. 5: 5.3, 5.6, 5.7 4.10 Two concentric conducting spheres of inner and outer radii a and b, respectively, carry charges
CHAPTER 11 RADIATION 4/13/2017. Outlines. 1. Electric Dipole radiation. 2. Magnetic Dipole Radiation. 3. Point Charge. 4. Synchrotron Radiation
 CHAPTER 11 RADIATION Outlines 1. Electric Dipole radiation 2. Magnetic Dipole Radiation 3. Point Charge Lee Chow Department of Physics University of Central Florida Orlando, FL 32816 4. Synchrotron Radiation
CHAPTER 11 RADIATION Outlines 1. Electric Dipole radiation 2. Magnetic Dipole Radiation 3. Point Charge Lee Chow Department of Physics University of Central Florida Orlando, FL 32816 4. Synchrotron Radiation
Physics 504, Spring 2010 Electricity and Magnetism
 Resonant cavities do not need to be cylindrical, of course. The surface of the Earth R E 6400 m the ionosphere R = R E + h, h 100 m form concentric spheres which are sufficiently good conductors to form
Resonant cavities do not need to be cylindrical, of course. The surface of the Earth R E 6400 m the ionosphere R = R E + h, h 100 m form concentric spheres which are sufficiently good conductors to form
Generation of EM waves
 Generation of EM waves Susan Lea Spring 015 1 The Green s funtion In Lorentz gauge, we obtained the wave equation: A 4π J 1 The orresponding Green s funtion for the problem satisfies the simpler differential
Generation of EM waves Susan Lea Spring 015 1 The Green s funtion In Lorentz gauge, we obtained the wave equation: A 4π J 1 The orresponding Green s funtion for the problem satisfies the simpler differential
University of Illinois at Chicago Department of Physics
 University of Illinois at Chicago Department of Physics Electromagnetism Qualifying Examination January 4, 2017 9.00 am - 12.00 pm Full credit can be achieved from completely correct answers to 4 questions.
University of Illinois at Chicago Department of Physics Electromagnetism Qualifying Examination January 4, 2017 9.00 am - 12.00 pm Full credit can be achieved from completely correct answers to 4 questions.
Quantum Mechanics II
 Quantum Mechanics II Prof. Boris Altshuler April, 20 Lecture 2. Scattering Theory Reviewed Remember what we have covered so far for scattering theory. We separated the Hamiltonian similar to the way in
Quantum Mechanics II Prof. Boris Altshuler April, 20 Lecture 2. Scattering Theory Reviewed Remember what we have covered so far for scattering theory. We separated the Hamiltonian similar to the way in
z = x + iy ; x, y R rectangular or Cartesian form z = re iθ ; r, θ R polar form. (1)
 11 Complex numbers Read: Boas Ch. Represent an arb. complex number z C in one of two ways: z = x + iy ; x, y R rectangular or Cartesian form z = re iθ ; r, θ R polar form. (1) Here i is 1, engineers call
11 Complex numbers Read: Boas Ch. Represent an arb. complex number z C in one of two ways: z = x + iy ; x, y R rectangular or Cartesian form z = re iθ ; r, θ R polar form. (1) Here i is 1, engineers call
(b) Show that the charged induced on the hemisphere is: Q = E o a 2 3π (1)
 Problem. Defects This problem will study defects in parallel plate capacitors. A parallel plate capacitor has area, A, and separation, D, and is maintained at the potential difference, V = E o D. There
Problem. Defects This problem will study defects in parallel plate capacitors. A parallel plate capacitor has area, A, and separation, D, and is maintained at the potential difference, V = E o D. There
Multipole Radiation. February 29, The electromagnetic field of an isolated, oscillating source
 Multipole Radiation Febuay 29, 26 The electomagnetic field of an isolated, oscillating souce Conside a localized, oscillating souce, located in othewise empty space. We know that the solution fo the vecto
Multipole Radiation Febuay 29, 26 The electomagnetic field of an isolated, oscillating souce Conside a localized, oscillating souce, located in othewise empty space. We know that the solution fo the vecto
Classical Mechanics Comprehensive Exam
 Name: Student ID: Classical Mechanics Comprehensive Exam Spring 2018 You may use any intermediate results in the textbook. No electronic devices (calculator, computer, cell phone etc) are allowed. For
Name: Student ID: Classical Mechanics Comprehensive Exam Spring 2018 You may use any intermediate results in the textbook. No electronic devices (calculator, computer, cell phone etc) are allowed. For
Chapter 10: Sinusoidal Steady-State Analysis
 Chapter 10: Sinusoidal Steady-State Analysis 1 Objectives : sinusoidal functions Impedance use phasors to determine the forced response of a circuit subjected to sinusoidal excitation Apply techniques
Chapter 10: Sinusoidal Steady-State Analysis 1 Objectives : sinusoidal functions Impedance use phasors to determine the forced response of a circuit subjected to sinusoidal excitation Apply techniques
Green s function for the wave equation
 Green s function for the wave equation Non-relativistic case January 2018 1 The wave equations In the Lorentz Gauge, the wave equations for the potentials are (Notes 1 eqns 44 and 43): 1 2 2 2 2 0 (1)
Green s function for the wave equation Non-relativistic case January 2018 1 The wave equations In the Lorentz Gauge, the wave equations for the potentials are (Notes 1 eqns 44 and 43): 1 2 2 2 2 0 (1)
The Helmholtz Decomposition and the Coulomb Gauge
 The Helmholtz Decomposition and the Coulomb Gauge 1 Problem Kirk T. McDonald Joseph Henry Laboratories, Princeton University, Princeton, NJ 08544 (April 17, 2008; updated February 7, 2015 Helmholtz showed
The Helmholtz Decomposition and the Coulomb Gauge 1 Problem Kirk T. McDonald Joseph Henry Laboratories, Princeton University, Princeton, NJ 08544 (April 17, 2008; updated February 7, 2015 Helmholtz showed
(a) Determine the general solution for φ(ρ) near ρ = 0 for arbitary values E. (b) Show that the regular solution at ρ = 0 has the series expansion
 Problem 1. Curious Wave Functions The eigenfunctions of a D7 brane in a curved geometry lead to the following eigenvalue equation of the Sturm Liouville type ρ ρ 3 ρ φ n (ρ) = E n w(ρ)φ n (ρ) w(ρ) = where
Problem 1. Curious Wave Functions The eigenfunctions of a D7 brane in a curved geometry lead to the following eigenvalue equation of the Sturm Liouville type ρ ρ 3 ρ φ n (ρ) = E n w(ρ)φ n (ρ) w(ρ) = where
Question 1: Spherical Pendulum
 Question 1: Spherical Pendulum Consider a two-dimensional pendulum of length l with mass M at its end. It is easiest to use spherical coordinates centered at the pivot since the magnitude of the position
Question 1: Spherical Pendulum Consider a two-dimensional pendulum of length l with mass M at its end. It is easiest to use spherical coordinates centered at the pivot since the magnitude of the position
Radiation Damping. 1 Introduction to the Abraham-Lorentz equation
 Radiation Damping Lecture 18 1 Introduction to the Abraham-Lorentz equation Classically, a charged particle radiates energy if it is accelerated. We have previously obtained the Larmor expression for the
Radiation Damping Lecture 18 1 Introduction to the Abraham-Lorentz equation Classically, a charged particle radiates energy if it is accelerated. We have previously obtained the Larmor expression for the
The 3 dimensional Schrödinger Equation
 Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Radiation Fields. Lecture 12
 Radiation Fieds Lecture 12 1 Mutipoe expansion Separate Maxwe s equations into two sets of equations, each set separatey invoving either the eectric or the magnetic fied. After remova of the time dependence
Radiation Fieds Lecture 12 1 Mutipoe expansion Separate Maxwe s equations into two sets of equations, each set separatey invoving either the eectric or the magnetic fied. After remova of the time dependence
Wave Phenomena Physics 15c. Lecture 17 EM Waves in Matter
 Wave Phenomena Physics 15c Lecture 17 EM Waves in Matter What We Did Last Time Reviewed reflection and refraction Total internal reflection is more subtle than it looks Imaginary waves extend a few beyond
Wave Phenomena Physics 15c Lecture 17 EM Waves in Matter What We Did Last Time Reviewed reflection and refraction Total internal reflection is more subtle than it looks Imaginary waves extend a few beyond
Lecture X: External fields and generation of gravitational waves
 Lecture X: External fields and generation of gravitational waves Christopher M. Hirata Caltech M/C 350-17, Pasadena CA 91125, USA (Dated: November 12, 2012) I. OVEVIEW Having examined weak field gravity
Lecture X: External fields and generation of gravitational waves Christopher M. Hirata Caltech M/C 350-17, Pasadena CA 91125, USA (Dated: November 12, 2012) I. OVEVIEW Having examined weak field gravity
