Harmonic Oscillator with raising and lowering operators. We write the Schrödinger equation for the harmonic oscillator in one dimension as follows:
|
|
|
- Blake Wright
- 6 years ago
- Views:
Transcription
1 We write the Schrödinger equation for the harmonic oscillator in one dimension as follows: H ˆ! = "!2 d 2! + 1 2µ dx 2 2 kx 2! = E! T ˆ = "! 2 2µ d 2 dx 2 V ˆ = 1 2 kx 2 H ˆ = ˆ T + ˆ V (1) where µ is the reduced mass and k is the force constant of the oscillator. We would rather use algebra than calculus to solve this problem. If we utilize operator algebra, we can find an alternative way to solve the problem that uses only algebra. First, let k = µ! 2 where µ = reduced mass ( µ = m 1 m 2 m 1 + m 2 ) and ω is the frequency of the oscillation. This is a standard substitution from classical physics. With this substitution, the Schrödinger equation becomes:!! 2 d 2 " = E! µ2 2µ dx 2 2 x2 Dividing both sides by!! 2 )" (2) ( 2µ yields: d 2! = µ 2 " 2 x 2 dx 2 2µE! 2! 2 )! (3) ( Now we let! = µ" 2µE and! = and substitute back into equation (3) so that the!! 2 Schrödinger equation becomes: d 2 dx 2! = " 2 x 2 ( )! (4) To simplify, we transform from the variable x, to a new variable ξ where! = "x or x =! " (5) d! = "dx or dx = d! " (6) Now we transform the Schrödinger equation into this new variable:
2 d! dx = d! d" d" dx = d! d" (via the chain rule) (7) and d 2! dx 2 = d dx d! d" d" ( = d dx dx ) d! ( = ) d d! ( = ) d d! d" ( = ) d 2! (8) d" dx d" d" d" dx d" 2 This makes it possible for us to change equation (4) to the variable ξ: d 2! = " d 2! = " 2 2 dx 2 d 2 ( " ) * +! = (" 2 x 2 )! d 2! = 2 ) d 2 "*! (9) If we substitute the values we defined for α and β, we find that! " = 2µE! 2 µ! = 2E! which we will call =! " (10) λ is a dimensionless number that compares two energies. We can think of! = as an " index that will be a measure of state and energy (as we will see). λ will start to seem like a quantum number of sorts. Now equation (9) becomes: d 2! d" 2 = " 2 ( )! or d 2! d" 2 " 2! =! (11) The left hand side of equation (11) is an operator equation, nearly the Hamiltonian, and right hand side looks like an eigenvalue. Thus, equation (11) is an eigenvalue problem waiting to be solved. It is easier if we regroup and multiply by negative one:! 2 " d 2 d! 2 () = *) (12)
3 The left side of equation (12) looks like it should be able to be factored if we wanted. That is what we often do with algebra so let us try remember that we are now dealing with operator algebra and operators do not necessarily commute. If the expression were not operators, we could just write down: a 2 x 2! b 2 y 2 = ( a! b) ( a + b) but if we try that we find:! " d d! (! + d d! () =! " d d! (!) + d) ( d! =! 2 ) "! d) d! + d ( d!!) ) " d 2 ) d! 2 =! 2 ) "! d) d! d! d) +) +! d! d! " d 2 ) d! 2 =! 2 ) "! d) d) +) +! d! d! " d 2 ) d! 2 =! 2 ) +) " d 2 ) d! 2 =! 2 +1" d 2 d! 2 () which is almost, but not quite what we wanted. If we do it in the opposite order, we get:! " d d! (! + d d! () =! 2 "1" d 2 d! 2 () (14) Note well that we did not get the same answer when we reversed the order. That is because we are dealing with operators and apparently ξ and d do not commute, that is, d! "!, d d! ( 0. This is not entirely unexpected as ξ is a modified position operator while d is a modified momentum operator. We know that position and momentum do not d! commute so it is not surprising that order should matter for the factorization. We also note that the factorizations did not work. We wanted equation (12) but we got:! 2 "1" d 2 d! 2 () and! 2 +1" d 2 d! 2 () (13)
4 However, we notice, that if we add these two expressions, we get almost what we wanted:! 2 "1" d 2 d! 2 ()! 2 +1" d 2 d! 2 () + 2! 2 " d 2 d! 2 () (15) Equation (15) is just equation (12) times 2 so we have to divide by 2 to get what we wanted. If we divide both factors by 2, we get: 1 2! 2 "1" d 2 d! 2 () + 1 2! 2 +1" d 2 d! 2 () =! 2 " d 2 d! 2 () = *) Now we go back to the factored forms of equations (13) and (14) and distribute the additional factors of 1/2 over the factored operators: 1 2! " d ( d! 1 2! + d ( d! 1 2! + d () = 1 d! 2! 2 "1" d 2 d! 2 () = (* "1)) 1 2! " d () = 1 d! 2! 2 +1" d 2 d! 2 () = (* +1)) Notice that the eigenvalue we got from each equation either adds one to or subtracts one from our index, λ. We will make a definition for the factors: 1 2! " d ( = 1 d! 2! + d ( = (16) d! Then, 1 2! " d ( d! 1 2! + d ( d! and 1 2! + d () = ˆ a ) = (* "1)) d! 1 2! " d () = ) = (* +1)) d! (17)
5 ! 2 " d 2 () = ( 2 +1)) d! 2 = ( 2 "1)) (18) We can rewrite equations (18) in terms of and ˆ a! = 1 2 (" 1)!! = 1 2 (" +1)! (19) The most amazing thing is that the expressions in equations (19), are still the original, unmultiplied, unapproximated Schrödinger equation that we set out to solve in equation (1). The only difference is that it is transformed into different variables, into operator form. Now we manipulate this operator form; combine the operator forms in equations (18) to get: ( 2 +1)! = (" 1)! ( 2 1)! = (" +1)! 2(! )" =!2" 20 or (! )" =!" ˆ a " = (!1)" 21 " = ( +1)" Careful perusal of equation 20 reveals that, while the separate terms do not present an eigenvalue problem for the wavefunction ψ, the combination! ˆ a ( ) does. In ( a! ˆ a ) =!1 or [, ] =!1 ; these operators do not commute (so we cannot addition, ˆ measure them simultaneously.)
6 So what exactly are and? We can find out by letting them operate on ψ. First let us define a new operator (it will become transparent why as we use it): N ˆ = (22) What the properties of N ˆ? We can look at the commutator with and [ N ˆ, ] = N ˆ! N ˆ = ˆ a! ( ) ˆ = ˆ a! +1 a = ˆ a!! =! [ N ˆ, ] =! Similarly, [ N ˆ, ] = N ˆ! N ˆ =! =! (!1) = ˆ [ N ˆ, ] = ˆ =! + ˆ a a a (23) (24) Let us take ψ n to be an eigenfunction of the operator ˆ N. We will assume that it is normalized to make our lives easier. Then: ˆ N = n (25) What happens if we allow or to operate on ψ n? If we do it with N ˆ we can get an idea: N ˆ = (" + N ˆ ) ( ) = " + n = ("1 + n ) = ( n "1) = ( n "1) (26)
7 From equations (26), it appears that has the property of turning ψ n into ψ n-1 because we know that the eigenvalue for N ˆ must be n. In order to get an eigenvalue of n-1, N ˆ must operate on ψ n-1. N ˆ = n N ˆ "1 = n "1"1 and N ˆ so ˆ a "1 = n "1 ˆ a (27) Therefore, we call the lowering operator. Similarly, is a raising operator, that is, it changes ψ n into ψ n+1 What happens if we allow ˆ a to operate on ψ 0, the lowest energy state? ˆ a! 0 = 0 (28) because you cannot go any lower than the lowest state. If we then try to raise the state we get:! 0 =! 0 = 0 = 0 What does this mean? We know from the equations in (19) that! = 1 2 (" 1)!! 0 = 1 2 (" 1)! 0 This means that when we raise the lowered lowest state, it must be ˆ a! 0 = 1 2 (" 1)! 0 = 0 (29)
8 Because we know that neither ψ 0 nor 1/2 are zero, then the only way to get zero is for (λ 1) to be equal to zero for the minimum level and thus the smallest value that λ can have is λ 0 =1. Remember, λ is not just an index, it is given in equation number (10) and is a ratio of energies! = " = 2E! and! 0 = 2E 0! = 1 (30) E 0 =! 2 which means that the lowest energy of the harmonic oscillator is not zero, it is a finite positive value. This energy is commonly known as the zero point energy. It follows that the energy levels of the harmonic oscillator are given by:! E n = n + 1! where n=0, 1, 2, 3, (31) " 2 Now we see that and make it possible for us to change from level to level in the harmonic oscillator potential well. For example:! 7 "! 6 and! 7 "! 8 However, we do not know the equality here, only the proportionality. Neither do we have a good physical feel for what and really are. Let us return to the definition of and from equation (16) and substitute back in for ξ = 1 " 2! + d d! = 1 " 2 = 1 " 2! * d d! = 1 " 2 ( x + 1 d ( dx = ( " 2 x + 1 d = µ) " x ˆ + ( dx 2! ( x * 1 d = ( " ( dx 2 x * 1 d = µ) " x ˆ * ( dx 2! i µ) ˆ p x i µ) ˆ p x (32) where p ˆ x =! i d dx or d dx = i! ˆ p x
9 Now we can define ˆ x and ˆ p x in terms of ˆ a and ˆ a : x ˆ = 1 a 2! ˆ + and ( ) (33) ˆ p x = µ! i 1 a 2" ˆ ˆ ( a ) (34) Now we can use equations (33) and (34) to regain the Schrödinger equation again: = 1 " 2! + d d! = = µ) " x 2! ˆ 2 (! µ) (!2 d 2 µ 2 ) 2 dx 2 and 1 " 2! ( d d! = µ) " x 2! ˆ 2 +! µ) (! 2 d 2 µ 2 ) 2 dx 2 1 " 2! ( d = 1 " d! 2! 2 (1( d 2 d! 3 1 " 2! + d d! = 1 " 2! 2 +1( d 2 d! 3 (35) As before, these are almost what we want but not quite because they have an extra term. However, if we combine them linearly, we get: + ˆ a = µ! 2! x ˆ 2 "! µ! "!2 d 2 µ 2! 2 dx 2 ( + µ! 2! x ˆ 2 +! µ! "!2 d 2 µ 2! 2 dx 2 ( = µ!! x ˆ 2 "!2 d 2 µ 2! 2 dx 2 ( Multiplying both sides by!! and dividing by 2 we get:!! + 2 ˆ H =!! 2 ( ) =!! 2 ( + ˆ a ) µ! x ˆ 2 "! 2 d 2! µ 2! 2 dx 2 ( = "!2 d 2 2µ dx µ!2 x ˆ 2 = H ˆ (36) which is the same thing that we started with for ˆ H in equation (1). If we return to our definitions and derivation in equation 21, then we see that
10 = ˆ a +1 ˆ H =!! 2 ( + ˆ a ) =!! 2 (( +1 ) + ) =!! 2 2ˆ a +1 ( ) =!! ˆ " a =!! " N ˆ so, we see that H ˆ =!" N ˆ H ˆ =!" N ˆ + 1 2! n =!" n = E n E n =!" n This means that N ˆ is an operator that is closely related to H ˆ ; in fact, N ˆ is essentially equivalent to H ˆ save a few constants. N ˆ tells us in which level of the harmonic oscillator the system is found. This may seem like a trivial result but it is the same as solving a lot of differential equations and yields insight into the system. We call N ˆ the number operator. The final thing that we need to do is to figure out exactly what the raising and lowering operators do to the system. We know (38) " 1 and " +1 or = c lower 1 and = c raise +1 What are c lower and c raise? Knowing that the solution to the harmonic oscillator must form an orthonormal set of eigenfunctions, we can write: 37 = 1 "1 "1 = = 1 and have an adjoint relation with each other, that is, = implies that (39) and ˆ a = ˆ a. This * = "1 c lower c lower "1 (40) because when the raising operator operates on the wavefunction to the left, it operates as its adjoint or as the lowering operator. but ˆ a ˆ a = ˆ N = n = n = n (41)
11 This suggests that * c lower c lower = n 2 If c lower is real, then c lower = n or c lower = n, and ˆ a = n "1 (42) In a similar fashion, ˆ a = n (43) Final note: While this derivation may seem tedious and incomprehensible, you will see when we do problems to predict infrared transitions or perturbation theory problems, that it makes solving the harmonic oscillator incredibly tractable.
Harmonic Oscillator I
 Physics 34 Lecture 7 Harmonic Oscillator I Lecture 7 Physics 34 Quantum Mechanics I Monday, February th, 008 We can manipulate operators, to a certain extent, as we would algebraic expressions. By considering
Physics 34 Lecture 7 Harmonic Oscillator I Lecture 7 Physics 34 Quantum Mechanics I Monday, February th, 008 We can manipulate operators, to a certain extent, as we would algebraic expressions. By considering
The Sommerfeld Polynomial Method: Harmonic Oscillator Example
 Chemistry 460 Fall 2017 Dr. Jean M. Standard October 2, 2017 The Sommerfeld Polynomial Method: Harmonic Oscillator Example Scaling the Harmonic Oscillator Equation Recall the basic definitions of the harmonic
Chemistry 460 Fall 2017 Dr. Jean M. Standard October 2, 2017 The Sommerfeld Polynomial Method: Harmonic Oscillator Example Scaling the Harmonic Oscillator Equation Recall the basic definitions of the harmonic
Lecture 12. The harmonic oscillator
 Lecture 12 The harmonic oscillator 107 108 LECTURE 12. THE HARMONIC OSCILLATOR 12.1 Introduction In this chapter, we are going to find explicitly the eigenfunctions and eigenvalues for the time-independent
Lecture 12 The harmonic oscillator 107 108 LECTURE 12. THE HARMONIC OSCILLATOR 12.1 Introduction In this chapter, we are going to find explicitly the eigenfunctions and eigenvalues for the time-independent
Simple Harmonic Oscillator
 Classical harmonic oscillator Linear force acting on a particle (Hooke s law): F =!kx From Newton s law: F = ma = m d x dt =!kx " d x dt + # x = 0, # = k / m Position and momentum solutions oscillate in
Classical harmonic oscillator Linear force acting on a particle (Hooke s law): F =!kx From Newton s law: F = ma = m d x dt =!kx " d x dt + # x = 0, # = k / m Position and momentum solutions oscillate in
Reading: Mathchapters F and G, MQ - Ch. 7-8, Lecture notes on hydrogen atom.
 Chemistry 356 017: Problem set No. 6; Reading: Mathchapters F and G, MQ - Ch. 7-8, Lecture notes on hydrogen atom. The H atom involves spherical coordinates and angular momentum, which leads to the shapes
Chemistry 356 017: Problem set No. 6; Reading: Mathchapters F and G, MQ - Ch. 7-8, Lecture notes on hydrogen atom. The H atom involves spherical coordinates and angular momentum, which leads to the shapes
Total Angular Momentum for Hydrogen
 Physics 4 Lecture 7 Total Angular Momentum for Hydrogen Lecture 7 Physics 4 Quantum Mechanics I Friday, April th, 008 We have the Hydrogen Hamiltonian for central potential φ(r), we can write: H r = p
Physics 4 Lecture 7 Total Angular Momentum for Hydrogen Lecture 7 Physics 4 Quantum Mechanics I Friday, April th, 008 We have the Hydrogen Hamiltonian for central potential φ(r), we can write: H r = p
Quantum Mechanics II
 Quantum Mechanics II Prof. Boris Altshuler March 8, 011 1 Lecture 19 1.1 Second Quantization Recall our results from simple harmonic oscillator. We know the Hamiltonian very well so no need to repeat here.
Quantum Mechanics II Prof. Boris Altshuler March 8, 011 1 Lecture 19 1.1 Second Quantization Recall our results from simple harmonic oscillator. We know the Hamiltonian very well so no need to repeat here.
Basic Quantum Mechanics Prof. Ajoy Ghatak Department of Physics Indian Institute of Technology, Delhi
 Basic Quantum Mechanics Prof. Ajoy Ghatak Department of Physics Indian Institute of Technology, Delhi Module No. # 07 Bra-Ket Algebra and Linear Harmonic Oscillator II Lecture No. # 02 Dirac s Bra and
Basic Quantum Mechanics Prof. Ajoy Ghatak Department of Physics Indian Institute of Technology, Delhi Module No. # 07 Bra-Ket Algebra and Linear Harmonic Oscillator II Lecture No. # 02 Dirac s Bra and
Page 404. Lecture 22: Simple Harmonic Oscillator: Energy Basis Date Given: 2008/11/19 Date Revised: 2008/11/19
 Page 404 Lecture : Simple Harmonic Oscillator: Energy Basis Date Given: 008/11/19 Date Revised: 008/11/19 Coordinate Basis Section 6. The One-Dimensional Simple Harmonic Oscillator: Coordinate Basis Page
Page 404 Lecture : Simple Harmonic Oscillator: Energy Basis Date Given: 008/11/19 Date Revised: 008/11/19 Coordinate Basis Section 6. The One-Dimensional Simple Harmonic Oscillator: Coordinate Basis Page
Dimensional analysis
 Dimensional analysis Calvin W. Johnson September 9, 04 Dimensional analysis Dimensional analysis is a powerful and important tool in calculations. In fact, you should make it a habit to automatically use
Dimensional analysis Calvin W. Johnson September 9, 04 Dimensional analysis Dimensional analysis is a powerful and important tool in calculations. In fact, you should make it a habit to automatically use
Minimal coupling and Berry s phase
 Phys460.nb 63 5 Minimal coupling Berry s phase Q: For charged quantum particles (e.g. electrons), if we apply an E&M field (E or B), the particle will feel the field. How do we consider the effect E B
Phys460.nb 63 5 Minimal coupling Berry s phase Q: For charged quantum particles (e.g. electrons), if we apply an E&M field (E or B), the particle will feel the field. How do we consider the effect E B
For a system with more than one electron, we can t solve the Schrödinger Eq. exactly. We must develop methods of approximation, such as
 VARIATIO METHOD For a system with more than one electron, we can t solve the Schrödinger Eq. exactly. We must develop methods of approximation, such as Variation Method Perturbation Theory Combination
VARIATIO METHOD For a system with more than one electron, we can t solve the Schrödinger Eq. exactly. We must develop methods of approximation, such as Variation Method Perturbation Theory Combination
If electrons moved in simple orbits, p and x could be determined, but this violates the Heisenberg Uncertainty Principle.
 CHEM 2060 Lecture 18: Particle in a Box L18-1 Atomic Orbitals If electrons moved in simple orbits, p and x could be determined, but this violates the Heisenberg Uncertainty Principle. We can only talk
CHEM 2060 Lecture 18: Particle in a Box L18-1 Atomic Orbitals If electrons moved in simple orbits, p and x could be determined, but this violates the Heisenberg Uncertainty Principle. We can only talk
Linear Algebra in Hilbert Space
 Physics 342 Lecture 16 Linear Algebra in Hilbert Space Lecture 16 Physics 342 Quantum Mechanics I Monday, March 1st, 2010 We have seen the importance of the plane wave solutions to the potentialfree Schrödinger
Physics 342 Lecture 16 Linear Algebra in Hilbert Space Lecture 16 Physics 342 Quantum Mechanics I Monday, March 1st, 2010 We have seen the importance of the plane wave solutions to the potentialfree Schrödinger
Physics 137A Quantum Mechanics Fall 2012 Midterm II - Solutions
 Physics 37A Quantum Mechanics Fall 0 Midterm II - Solutions These are the solutions to the exam given to Lecture Problem [5 points] Consider a particle with mass m charge q in a simple harmonic oscillator
Physics 37A Quantum Mechanics Fall 0 Midterm II - Solutions These are the solutions to the exam given to Lecture Problem [5 points] Consider a particle with mass m charge q in a simple harmonic oscillator
2. As we shall see, we choose to write in terms of σ x because ( X ) 2 = σ 2 x.
 Section 5.1 Simple One-Dimensional Problems: The Free Particle Page 9 The Free Particle Gaussian Wave Packets The Gaussian wave packet initial state is one of the few states for which both the { x } and
Section 5.1 Simple One-Dimensional Problems: The Free Particle Page 9 The Free Particle Gaussian Wave Packets The Gaussian wave packet initial state is one of the few states for which both the { x } and
Ch 125a Problem Set 1
 Ch 5a Problem Set Due Monday, Oct 5, 05, am Problem : Bra-ket notation (Dirac notation) Bra-ket notation is a standard and convenient way to describe quantum state vectors For example, φ is an abstract
Ch 5a Problem Set Due Monday, Oct 5, 05, am Problem : Bra-ket notation (Dirac notation) Bra-ket notation is a standard and convenient way to describe quantum state vectors For example, φ is an abstract
Second Quantization Method for Bosons
 Second Quantization Method for Bosons Hartree-Fock-based methods cannot describe the effects of the classical image potential (cf. fig. 1) because HF is a mean-field theory. DFF-LDA is not able either
Second Quantization Method for Bosons Hartree-Fock-based methods cannot describe the effects of the classical image potential (cf. fig. 1) because HF is a mean-field theory. DFF-LDA is not able either
How to Use Calculus Like a Physicist
 How to Use Calculus Like a Physicist Physics A300 Fall 2004 The purpose of these notes is to make contact between the abstract descriptions you may have seen in your calculus classes and the applications
How to Use Calculus Like a Physicist Physics A300 Fall 2004 The purpose of these notes is to make contact between the abstract descriptions you may have seen in your calculus classes and the applications
Brief review of Quantum Mechanics (QM)
 Brief review of Quantum Mechanics (QM) Note: This is a collection of several formulae and facts that we will use throughout the course. It is by no means a complete discussion of QM, nor will I attempt
Brief review of Quantum Mechanics (QM) Note: This is a collection of several formulae and facts that we will use throughout the course. It is by no means a complete discussion of QM, nor will I attempt
Physics 342 Lecture 17. Midterm I Recap. Lecture 17. Physics 342 Quantum Mechanics I
 Physics 342 Lecture 17 Midterm I Recap Lecture 17 Physics 342 Quantum Mechanics I Monday, March 1th, 28 17.1 Introduction In the context of the first midterm, there are a few points I d like to make about
Physics 342 Lecture 17 Midterm I Recap Lecture 17 Physics 342 Quantum Mechanics I Monday, March 1th, 28 17.1 Introduction In the context of the first midterm, there are a few points I d like to make about
Lecture #5: Begin Quantum Mechanics: Free Particle and Particle in a 1D Box
 561 Fall 017 Lecture #5 page 1 Last time: Lecture #5: Begin Quantum Mechanics: Free Particle and Particle in a 1D Box 1-D Wave equation u x = 1 u v t * u(x,t): displacements as function of x,t * nd -order:
561 Fall 017 Lecture #5 page 1 Last time: Lecture #5: Begin Quantum Mechanics: Free Particle and Particle in a 1D Box 1-D Wave equation u x = 1 u v t * u(x,t): displacements as function of x,t * nd -order:
Problems and Multiple Choice Questions
 Problems and Multiple Choice Questions 1. A momentum operator in one dimension is 2. A position operator in 3 dimensions is 3. A kinetic energy operator in 1 dimension is 4. If two operator commute, a)
Problems and Multiple Choice Questions 1. A momentum operator in one dimension is 2. A position operator in 3 dimensions is 3. A kinetic energy operator in 1 dimension is 4. If two operator commute, a)
ECE 487 Lecture 6 : Time-Dependent Quantum Mechanics I Class Outline:
 ECE 487 Lecture 6 : Time-Dependent Quantum Mechanics I Class Outline: Time-Dependent Schrödinger Equation Solutions to thetime-dependent Schrödinger Equation Expansion of Energy Eigenstates Things you
ECE 487 Lecture 6 : Time-Dependent Quantum Mechanics I Class Outline: Time-Dependent Schrödinger Equation Solutions to thetime-dependent Schrödinger Equation Expansion of Energy Eigenstates Things you
Properties of Commutators and Schroedinger Operators and Applications to Quantum Computing
 International Journal of Engineering and Advanced Research Technology (IJEART) Properties of Commutators and Schroedinger Operators and Applications to Quantum Computing N. B. Okelo Abstract In this paper
International Journal of Engineering and Advanced Research Technology (IJEART) Properties of Commutators and Schroedinger Operators and Applications to Quantum Computing N. B. Okelo Abstract In this paper
Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Spring Semester 2006 Christopher J. Cramer. Lecture 9, February 8, 2006
 Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Spring Semester 2006 Christopher J. Cramer Lecture 9, February 8, 2006 The Harmonic Oscillator Consider a diatomic molecule. Such a molecule
Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Spring Semester 2006 Christopher J. Cramer Lecture 9, February 8, 2006 The Harmonic Oscillator Consider a diatomic molecule. Such a molecule
SYDE 112, LECTURE 7: Integration by Parts
 SYDE 112, LECTURE 7: Integration by Parts 1 Integration By Parts Consider trying to take the integral of xe x dx. We could try to find a substitution but would quickly grow frustrated there is no substitution
SYDE 112, LECTURE 7: Integration by Parts 1 Integration By Parts Consider trying to take the integral of xe x dx. We could try to find a substitution but would quickly grow frustrated there is no substitution
The Simple Harmonic Oscillator
 The Simple Harmonic Oscillator Asaf Pe er 1 November 4, 215 This part of the course is based on Refs [1] [3] 1 Introduction We return now to the study of a 1-d stationary problem: that of the simple harmonic
The Simple Harmonic Oscillator Asaf Pe er 1 November 4, 215 This part of the course is based on Refs [1] [3] 1 Introduction We return now to the study of a 1-d stationary problem: that of the simple harmonic
Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Fall Semester 2006 Christopher J. Cramer. Lecture 5, January 27, 2006
 Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Fall Semester 2006 Christopher J. Cramer Lecture 5, January 27, 2006 Solved Homework (Homework for grading is also due today) We are told
Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Fall Semester 2006 Christopher J. Cramer Lecture 5, January 27, 2006 Solved Homework (Homework for grading is also due today) We are told
P3317 HW from Lecture and Recitation 7
 P3317 HW from Lecture 1+13 and Recitation 7 Due Oct 16, 018 Problem 1. Separation of variables Suppose we have two masses that can move in 1D. They are attached by a spring, yielding a Hamiltonian where
P3317 HW from Lecture 1+13 and Recitation 7 Due Oct 16, 018 Problem 1. Separation of variables Suppose we have two masses that can move in 1D. They are attached by a spring, yielding a Hamiltonian where
We can instead solve the problem algebraically by introducing up and down ladder operators b + and b
 Physics 17c: Statistical Mechanics Second Quantization Ladder Operators in the SHO It is useful to first review the use of ladder operators in the simple harmonic oscillator. Here I present the bare bones
Physics 17c: Statistical Mechanics Second Quantization Ladder Operators in the SHO It is useful to first review the use of ladder operators in the simple harmonic oscillator. Here I present the bare bones
Sample Quantum Chemistry Exam 2 Solutions
 Chemistry 46 Fall 7 Dr. Jean M. Standard Name SAMPE EXAM Sample Quantum Chemistry Exam Solutions.) ( points) Answer the following questions by selecting the correct answer from the choices provided. a.)
Chemistry 46 Fall 7 Dr. Jean M. Standard Name SAMPE EXAM Sample Quantum Chemistry Exam Solutions.) ( points) Answer the following questions by selecting the correct answer from the choices provided. a.)
3. Quantum Mechanics in 3D
 3. Quantum Mechanics in 3D 3.1 Introduction Last time, we derived the time dependent Schrödinger equation, starting from three basic postulates: 1) The time evolution of a state can be expressed as a unitary
3. Quantum Mechanics in 3D 3.1 Introduction Last time, we derived the time dependent Schrödinger equation, starting from three basic postulates: 1) The time evolution of a state can be expressed as a unitary
Chm 331 Fall 2015, Exercise Set 4 NMR Review Problems
 Chm 331 Fall 015, Exercise Set 4 NMR Review Problems Mr. Linck Version.0. Compiled December 1, 015 at 11:04:44 4.1 Diagonal Matrix Elements for the nmr H 0 Find the diagonal matrix elements for H 0 (the
Chm 331 Fall 015, Exercise Set 4 NMR Review Problems Mr. Linck Version.0. Compiled December 1, 015 at 11:04:44 4.1 Diagonal Matrix Elements for the nmr H 0 Find the diagonal matrix elements for H 0 (the
Quantum Mechanics-I Prof. Dr. S. Lakshmi Bala Department of Physics Indian Institute of Technology, Madras. Lecture - 21 Square-Integrable Functions
 Quantum Mechanics-I Prof. Dr. S. Lakshmi Bala Department of Physics Indian Institute of Technology, Madras Lecture - 21 Square-Integrable Functions (Refer Slide Time: 00:06) (Refer Slide Time: 00:14) We
Quantum Mechanics-I Prof. Dr. S. Lakshmi Bala Department of Physics Indian Institute of Technology, Madras Lecture - 21 Square-Integrable Functions (Refer Slide Time: 00:06) (Refer Slide Time: 00:14) We
The Schroedinger equation
 The Schroedinger equation After Planck, Einstein, Bohr, de Broglie, and many others (but before Born), the time was ripe for a complete theory that could be applied to any problem involving nano-scale
The Schroedinger equation After Planck, Einstein, Bohr, de Broglie, and many others (but before Born), the time was ripe for a complete theory that could be applied to any problem involving nano-scale
E = hν light = hc λ = ( J s)( m/s) m = ev J = ev
 Problem The ionization potential tells us how much energy we need to use to remove an electron, so we know that any energy left afterwards will be the kinetic energy of the ejected electron. So first we
Problem The ionization potential tells us how much energy we need to use to remove an electron, so we know that any energy left afterwards will be the kinetic energy of the ejected electron. So first we
Addition of Angular Momenta
 Addition of Angular Momenta What we have so far considered to be an exact solution for the many electron problem, should really be called exact non-relativistic solution. A relativistic treatment is needed
Addition of Angular Momenta What we have so far considered to be an exact solution for the many electron problem, should really be called exact non-relativistic solution. A relativistic treatment is needed
( ) in the interaction picture arises only
 Physics 606, Quantum Mechanics, Final Exam NAME 1 Atomic transitions due to time-dependent electric field Consider a hydrogen atom which is in its ground state for t < 0 For t > 0 it is subjected to a
Physics 606, Quantum Mechanics, Final Exam NAME 1 Atomic transitions due to time-dependent electric field Consider a hydrogen atom which is in its ground state for t < 0 For t > 0 it is subjected to a
Creation and Destruction Operators and Coherent States
 Creation and Destruction Operators and Coherent States WKB Method for Ground State Wave Function state harmonic oscillator wave function, We first rewrite the ground < x 0 >= ( π h )1/4 exp( x2 a 2 h )
Creation and Destruction Operators and Coherent States WKB Method for Ground State Wave Function state harmonic oscillator wave function, We first rewrite the ground < x 0 >= ( π h )1/4 exp( x2 a 2 h )
Statistical Interpretation
 Physics 342 Lecture 15 Statistical Interpretation Lecture 15 Physics 342 Quantum Mechanics I Friday, February 29th, 2008 Quantum mechanics is a theory of probability densities given that we now have an
Physics 342 Lecture 15 Statistical Interpretation Lecture 15 Physics 342 Quantum Mechanics I Friday, February 29th, 2008 Quantum mechanics is a theory of probability densities given that we now have an
20 The Hydrogen Atom. Ze2 r R (20.1) H( r, R) = h2 2m 2 r h2 2M 2 R
 20 The Hydrogen Atom 1. We want to solve the time independent Schrödinger Equation for the hydrogen atom. 2. There are two particles in the system, an electron and a nucleus, and so we can write the Hamiltonian
20 The Hydrogen Atom 1. We want to solve the time independent Schrödinger Equation for the hydrogen atom. 2. There are two particles in the system, an electron and a nucleus, and so we can write the Hamiltonian
Unit 9 Study Sheet Rational Expressions and Types of Equations
 Algebraic Fractions: Unit 9 Study Sheet Rational Expressions and Types of Equations Simplifying Algebraic Fractions: To simplify an algebraic fraction means to reduce it to lowest terms. This is done by
Algebraic Fractions: Unit 9 Study Sheet Rational Expressions and Types of Equations Simplifying Algebraic Fractions: To simplify an algebraic fraction means to reduce it to lowest terms. This is done by
Physics 342 Lecture 26. Angular Momentum. Lecture 26. Physics 342 Quantum Mechanics I
 Physics 342 Lecture 26 Angular Momentum Lecture 26 Physics 342 Quantum Mechanics I Friday, April 2nd, 2010 We know how to obtain the energy of Hydrogen using the Hamiltonian operator but given a particular
Physics 342 Lecture 26 Angular Momentum Lecture 26 Physics 342 Quantum Mechanics I Friday, April 2nd, 2010 We know how to obtain the energy of Hydrogen using the Hamiltonian operator but given a particular
ECE 487 Lecture 5 : Foundations of Quantum Mechanics IV Class Outline:
 ECE 487 Lecture 5 : Foundations of Quantum Mechanics IV Class Outline: Linearly Varying Potential Triangular Potential Well Time-Dependent Schrödinger Equation Things you should know when you leave Key
ECE 487 Lecture 5 : Foundations of Quantum Mechanics IV Class Outline: Linearly Varying Potential Triangular Potential Well Time-Dependent Schrödinger Equation Things you should know when you leave Key
Physics 202 Laboratory 5. Linear Algebra 1. Laboratory 5. Physics 202 Laboratory
 Physics 202 Laboratory 5 Linear Algebra Laboratory 5 Physics 202 Laboratory We close our whirlwind tour of numerical methods by advertising some elements of (numerical) linear algebra. There are three
Physics 202 Laboratory 5 Linear Algebra Laboratory 5 Physics 202 Laboratory We close our whirlwind tour of numerical methods by advertising some elements of (numerical) linear algebra. There are three
base 2 4 The EXPONENT tells you how many times to write the base as a factor. Evaluate the following expressions in standard notation.
 EXPONENTIALS Exponential is a number written with an exponent. The rules for exponents make computing with very large or very small numbers easier. Students will come across exponentials in geometric sequences
EXPONENTIALS Exponential is a number written with an exponent. The rules for exponents make computing with very large or very small numbers easier. Students will come across exponentials in geometric sequences
Problem 1: A 3-D Spherical Well(10 Points)
 Problem : A 3-D Spherical Well( Points) For this problem, consider a particle of mass m in a three-dimensional spherical potential well, V (r), given as, V = r a/2 V = W r > a/2. with W >. All of the following
Problem : A 3-D Spherical Well( Points) For this problem, consider a particle of mass m in a three-dimensional spherical potential well, V (r), given as, V = r a/2 V = W r > a/2. with W >. All of the following
MODELING MATTER AT NANOSCALES. 4. Introduction to quantum treatments Outline of the principles and the method of quantum mechanics
 MODELING MATTER AT NANOSCALES 4. Introduction to quantum treatments 4.01. Outline of the principles and the method of quantum mechanics 1 Why quantum mechanics? Physics and sizes in universe Knowledge
MODELING MATTER AT NANOSCALES 4. Introduction to quantum treatments 4.01. Outline of the principles and the method of quantum mechanics 1 Why quantum mechanics? Physics and sizes in universe Knowledge
Quantum Theory and Group Representations
 Quantum Theory and Group Representations Peter Woit Columbia University LaGuardia Community College, November 1, 2017 Queensborough Community College, November 15, 2017 Peter Woit (Columbia University)
Quantum Theory and Group Representations Peter Woit Columbia University LaGuardia Community College, November 1, 2017 Queensborough Community College, November 15, 2017 Peter Woit (Columbia University)
The energy of the emitted light (photons) is given by the difference in energy between the initial and final states of hydrogen atom.
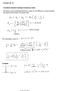 Lecture 20-21 Page 1 Lectures 20-21 Transitions between hydrogen stationary states The energy of the emitted light (photons) is given by the difference in energy between the initial and final states of
Lecture 20-21 Page 1 Lectures 20-21 Transitions between hydrogen stationary states The energy of the emitted light (photons) is given by the difference in energy between the initial and final states of
26 Group Theory Basics
 26 Group Theory Basics 1. Reference: Group Theory and Quantum Mechanics by Michael Tinkham. 2. We said earlier that we will go looking for the set of operators that commute with the molecular Hamiltonian.
26 Group Theory Basics 1. Reference: Group Theory and Quantum Mechanics by Michael Tinkham. 2. We said earlier that we will go looking for the set of operators that commute with the molecular Hamiltonian.
Extending the Number System
 Analytical Geometry Extending the Number System Extending the Number System Remember how you learned numbers? You probably started counting objects in your house as a toddler. You learned to count to ten
Analytical Geometry Extending the Number System Extending the Number System Remember how you learned numbers? You probably started counting objects in your house as a toddler. You learned to count to ten
Joel Broida UCSD Fall 2009 Phys 130B QM II. Homework Set 4
 Joel Broida UCSD Fall 009 Phys 130B QM II Homework Set 4 1. Consider the particle-in-a-box problem but with a delta function potential H (x) = αδ(x l/) at the center (with α = const): H = αδ(x l/) 0 l/
Joel Broida UCSD Fall 009 Phys 130B QM II Homework Set 4 1. Consider the particle-in-a-box problem but with a delta function potential H (x) = αδ(x l/) at the center (with α = const): H = αδ(x l/) 0 l/
The Harmonic Oscillator: Zero Point Energy and Tunneling
 The Harmonic Oscillator: Zero Point Energy and Tunneling Lecture Objectives: 1. To introduce simple harmonic oscillator model using elementary classical mechanics.. To write down the Schrodinger equation
The Harmonic Oscillator: Zero Point Energy and Tunneling Lecture Objectives: 1. To introduce simple harmonic oscillator model using elementary classical mechanics.. To write down the Schrodinger equation
Physical Chemistry II Exam 2 Solutions
 Chemistry 362 Spring 208 Dr Jean M Standard March 9, 208 Name KEY Physical Chemistry II Exam 2 Solutions ) (4 points) The harmonic vibrational frequency (in wavenumbers) of LiH is 4057 cm Based upon this
Chemistry 362 Spring 208 Dr Jean M Standard March 9, 208 Name KEY Physical Chemistry II Exam 2 Solutions ) (4 points) The harmonic vibrational frequency (in wavenumbers) of LiH is 4057 cm Based upon this
Harmonic Oscillator. Robert B. Griffiths Version of 5 December Notation 1. 3 Position and Momentum Representations of Number Eigenstates 2
 qmd5 Harmonic Oscillator Robert B. Griffiths Version of 5 December 0 Contents Notation Eigenstates of the Number Operator N 3 Position and Momentum Representations of Number Eigenstates 4 Coherent States
qmd5 Harmonic Oscillator Robert B. Griffiths Version of 5 December 0 Contents Notation Eigenstates of the Number Operator N 3 Position and Momentum Representations of Number Eigenstates 4 Coherent States
1 Commutators (10 pts)
 Final Exam Solutions 37A Fall 0 I. Siddiqi / E. Dodds Commutators 0 pts) ) Consider the operator  = Ĵx Ĵ y + ĴyĴx where J i represents the total angular momentum in the ith direction. a) Express both
Final Exam Solutions 37A Fall 0 I. Siddiqi / E. Dodds Commutators 0 pts) ) Consider the operator  = Ĵx Ĵ y + ĴyĴx where J i represents the total angular momentum in the ith direction. a) Express both
P3317 HW from Lecture and Recitation 10
 P3317 HW from Lecture 18+19 and Recitation 10 Due Nov 6, 2018 Problem 1. Equipartition Note: This is a problem from classical statistical mechanics. We will need the answer for the next few problems, and
P3317 HW from Lecture 18+19 and Recitation 10 Due Nov 6, 2018 Problem 1. Equipartition Note: This is a problem from classical statistical mechanics. We will need the answer for the next few problems, and
Physics 505 Homework No. 1 Solutions S1-1
 Physics 505 Homework No s S- Some Preliminaries Assume A and B are Hermitian operators (a) Show that (AB) B A dx φ ABψ dx (A φ) Bψ dx (B (A φ)) ψ dx (B A φ) ψ End (b) Show that AB [A, B]/2+{A, B}/2 where
Physics 505 Homework No s S- Some Preliminaries Assume A and B are Hermitian operators (a) Show that (AB) B A dx φ ABψ dx (A φ) Bψ dx (B (A φ)) ψ dx (B A φ) ψ End (b) Show that AB [A, B]/2+{A, B}/2 where
Chemistry 532 Problem Set 7 Spring 2012 Solutions
 Chemistry 53 Problem Set 7 Spring 01 Solutions 1. The study of the time-independent Schrödinger equation for a one-dimensional particle subject to the potential function leads to the differential equation
Chemistry 53 Problem Set 7 Spring 01 Solutions 1. The study of the time-independent Schrödinger equation for a one-dimensional particle subject to the potential function leads to the differential equation
The Hamiltonian and the Schrödinger equation Consider time evolution from t to t + ɛ. As before, we expand in powers of ɛ; we have. H(t) + O(ɛ 2 ).
 Lecture 12 Relevant sections in text: 2.1 The Hamiltonian and the Schrödinger equation Consider time evolution from t to t + ɛ. As before, we expand in powers of ɛ; we have U(t + ɛ, t) = I + ɛ ( īh ) H(t)
Lecture 12 Relevant sections in text: 2.1 The Hamiltonian and the Schrödinger equation Consider time evolution from t to t + ɛ. As before, we expand in powers of ɛ; we have U(t + ɛ, t) = I + ɛ ( īh ) H(t)
8.04 Spring 2013 March 12, 2013 Problem 1. (10 points) The Probability Current
 Prolem Set 5 Solutions 8.04 Spring 03 March, 03 Prolem. (0 points) The Proaility Current We wish to prove that dp a = J(a, t) J(, t). () dt Since P a (t) is the proaility of finding the particle in the
Prolem Set 5 Solutions 8.04 Spring 03 March, 03 Prolem. (0 points) The Proaility Current We wish to prove that dp a = J(a, t) J(, t). () dt Since P a (t) is the proaility of finding the particle in the
How NMR Works Section I
 How NMR Works ------- Section I by Shaoxiong Wu 02-20-2010 During the NMR course I use classic energy levels and vector model to explain simple NMR pulse sequences and spectra. It is limited, however,
How NMR Works ------- Section I by Shaoxiong Wu 02-20-2010 During the NMR course I use classic energy levels and vector model to explain simple NMR pulse sequences and spectra. It is limited, however,
Lecture-XXVI. Time-Independent Schrodinger Equation
 Lecture-XXVI Time-Independent Schrodinger Equation Time Independent Schrodinger Equation: The time-dependent Schrodinger equation: Assume that V is independent of time t. In that case the Schrodinger equation
Lecture-XXVI Time-Independent Schrodinger Equation Time Independent Schrodinger Equation: The time-dependent Schrodinger equation: Assume that V is independent of time t. In that case the Schrodinger equation
Consistent Histories. Chapter Chain Operators and Weights
 Chapter 10 Consistent Histories 10.1 Chain Operators and Weights The previous chapter showed how the Born rule can be used to assign probabilities to a sample space of histories based upon an initial state
Chapter 10 Consistent Histories 10.1 Chain Operators and Weights The previous chapter showed how the Born rule can be used to assign probabilities to a sample space of histories based upon an initial state
df(x) = h(x) dx Chemistry 4531 Mathematical Preliminaries Spring 2009 I. A Primer on Differential Equations Order of differential equation
 Chemistry 4531 Mathematical Preliminaries Spring 009 I. A Primer on Differential Equations Order of differential equation Linearity of differential equation Partial vs. Ordinary Differential Equations
Chemistry 4531 Mathematical Preliminaries Spring 009 I. A Primer on Differential Equations Order of differential equation Linearity of differential equation Partial vs. Ordinary Differential Equations
in terms of the classical frequency, ω = , puts the classical Hamiltonian in the form H = p2 2m + mω2 x 2
 One of the most important problems in quantum mechanics is the simple harmonic oscillator, in part because its properties are directly applicable to field theory. The treatment in Dirac notation is particularly
One of the most important problems in quantum mechanics is the simple harmonic oscillator, in part because its properties are directly applicable to field theory. The treatment in Dirac notation is particularly
α β β α β β 0 β α 0 0 0
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Chemistry 5.6 Quantum Mechanics Fall 03 Problem Set #7 Reading Assignment: McQuarrie 9.-9.5, 0.-0.5,Matlab and Linear Algebra Handouts ( = Easier = More
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Chemistry 5.6 Quantum Mechanics Fall 03 Problem Set #7 Reading Assignment: McQuarrie 9.-9.5, 0.-0.5,Matlab and Linear Algebra Handouts ( = Easier = More
6.4 Division of Polynomials. (Long Division and Synthetic Division)
 6.4 Division of Polynomials (Long Division and Synthetic Division) When we combine fractions that have a common denominator, we just add or subtract the numerators and then keep the common denominator
6.4 Division of Polynomials (Long Division and Synthetic Division) When we combine fractions that have a common denominator, we just add or subtract the numerators and then keep the common denominator
Physics 221A Fall 2017 Notes 27 The Variational Method
 Copyright c 2018 by Robert G. Littlejohn Physics 221A Fall 2017 Notes 27 The Variational Method 1. Introduction Very few realistic problems in quantum mechanics are exactly solvable, so approximation methods
Copyright c 2018 by Robert G. Littlejohn Physics 221A Fall 2017 Notes 27 The Variational Method 1. Introduction Very few realistic problems in quantum mechanics are exactly solvable, so approximation methods
Qualifying Exam. Aug Part II. Please use blank paper for your work do not write on problems sheets!
 Qualifying Exam Aug. 2015 Part II Please use blank paper for your work do not write on problems sheets! Solve only one problem from each of the four sections Mechanics, Quantum Mechanics, Statistical Physics
Qualifying Exam Aug. 2015 Part II Please use blank paper for your work do not write on problems sheets! Solve only one problem from each of the four sections Mechanics, Quantum Mechanics, Statistical Physics
Quantum Physics Notes-7 Operators, Observables, Understanding QM. Notes 6 Quantum Physics F2005 1
 Quantum Physics 2005 Notes-7 Operators, Observables, Understanding QM Notes 6 Quantum Physics F2005 A summary of this section This section of notes is a brief overview of the ideas in chapters 0-2 of Morrison.
Quantum Physics 2005 Notes-7 Operators, Observables, Understanding QM Notes 6 Quantum Physics F2005 A summary of this section This section of notes is a brief overview of the ideas in chapters 0-2 of Morrison.
Continuous quantum states, Particle on a line and Uncertainty relations
 Continuous quantum states, Particle on a line and Uncertainty relations So far we have considered k-level (discrete) quantum systems. Now we turn our attention to continuous quantum systems, such as a
Continuous quantum states, Particle on a line and Uncertainty relations So far we have considered k-level (discrete) quantum systems. Now we turn our attention to continuous quantum systems, such as a
Introduction to Quantum Mechanics (Prelude to Nuclear Shell Model) Heisenberg Uncertainty Principle In the microscopic world,
 Introduction to Quantum Mechanics (Prelude to Nuclear Shell Model) Heisenberg Uncertainty Principle In the microscopic world, x p h π If you try to specify/measure the exact position of a particle you
Introduction to Quantum Mechanics (Prelude to Nuclear Shell Model) Heisenberg Uncertainty Principle In the microscopic world, x p h π If you try to specify/measure the exact position of a particle you
0. Introduction 1 0. INTRODUCTION
 0. Introduction 1 0. INTRODUCTION In a very rough sketch we explain what algebraic geometry is about and what it can be used for. We stress the many correlations with other fields of research, such as
0. Introduction 1 0. INTRODUCTION In a very rough sketch we explain what algebraic geometry is about and what it can be used for. We stress the many correlations with other fields of research, such as
BASICS OF QUANTUM MECHANICS. Reading: QM Course packet Ch 5
 BASICS OF QUANTUM MECHANICS 1 Reading: QM Course packet Ch 5 Interesting things happen when electrons are confined to small regions of space (few nm). For one thing, they can behave as if they are in an
BASICS OF QUANTUM MECHANICS 1 Reading: QM Course packet Ch 5 Interesting things happen when electrons are confined to small regions of space (few nm). For one thing, they can behave as if they are in an
1. Quantum Mechanics, Cohen Tannoudji, Chapters Linear Algebra, Schaum Series 3. Quantum Chemistry Ch. 6
 Lecture # Today s Program 1. Recap: Classical States, Hamiltonians and time evolution. First postulate The description of a state of a system. 3. Second postulate physical quantities. 4. Linear operators.
Lecture # Today s Program 1. Recap: Classical States, Hamiltonians and time evolution. First postulate The description of a state of a system. 3. Second postulate physical quantities. 4. Linear operators.
Quantum Mechanics Solutions. λ i λ j v j v j v i v i.
 Quantum Mechanics Solutions 1. (a) If H has an orthonormal basis consisting of the eigenvectors { v i } of A with eigenvalues λ i C, then A can be written in terms of its spectral decomposition as A =
Quantum Mechanics Solutions 1. (a) If H has an orthonormal basis consisting of the eigenvectors { v i } of A with eigenvalues λ i C, then A can be written in terms of its spectral decomposition as A =
Problem Set 6: Workbook on Operators, and Dirac Notation Solution
 Moern Physics: Home work 5 Due ate: 0 March. 014 Problem Set 6: Workbook on Operators, an Dirac Notation Solution 1. nswer 1: a The cat is being escribe by the state, ψ >= ea > If we try to observe it
Moern Physics: Home work 5 Due ate: 0 March. 014 Problem Set 6: Workbook on Operators, an Dirac Notation Solution 1. nswer 1: a The cat is being escribe by the state, ψ >= ea > If we try to observe it
Harmonic Oscillator Eigenvalues and Eigenfunctions
 Chemistry 46 Fall 217 Dr. Jean M. Standard October 4, 217 Harmonic Oscillator Eigenvalues and Eigenfunctions The Quantum Mechanical Harmonic Oscillator The quantum mechanical harmonic oscillator in one
Chemistry 46 Fall 217 Dr. Jean M. Standard October 4, 217 Harmonic Oscillator Eigenvalues and Eigenfunctions The Quantum Mechanical Harmonic Oscillator The quantum mechanical harmonic oscillator in one
Consequently, the exact eigenfunctions of the Hamiltonian are also eigenfunctions of the two spin operators
 VI. SPIN-ADAPTED CONFIGURATIONS A. Preliminary Considerations We have described the spin of a single electron by the two spin functions α(ω) α and β(ω) β. In this Sect. we will discuss spin in more detail
VI. SPIN-ADAPTED CONFIGURATIONS A. Preliminary Considerations We have described the spin of a single electron by the two spin functions α(ω) α and β(ω) β. In this Sect. we will discuss spin in more detail
Solving Linear Equations (in one variable)
 Solving Linear Equations (in one variable) In Chapter of my Elementary Algebra text you are introduced to solving linear equations. The main idea presented throughout Sections.1. is that you need to isolate
Solving Linear Equations (in one variable) In Chapter of my Elementary Algebra text you are introduced to solving linear equations. The main idea presented throughout Sections.1. is that you need to isolate
ECE 501b Homework #4 Due: 10/22/2012
 1. Game Strategy: Consider a multiplayer boardgame that takes place on the following board and with the following rules: 7 8 9 10 6 11 5 12 4 3 2 1 The board contains six squares that are property (the
1. Game Strategy: Consider a multiplayer boardgame that takes place on the following board and with the following rules: 7 8 9 10 6 11 5 12 4 3 2 1 The board contains six squares that are property (the
Lecture 5: Harmonic oscillator, Morse Oscillator, 1D Rigid Rotor
 Lecture 5: Harmonic oscillator, Morse Oscillator, 1D Rigid Rotor It turns out that the boundary condition of the wavefunction going to zero at infinity is sufficient to quantize the value of energy that
Lecture 5: Harmonic oscillator, Morse Oscillator, 1D Rigid Rotor It turns out that the boundary condition of the wavefunction going to zero at infinity is sufficient to quantize the value of energy that
Section 4.6 Negative Exponents
 Section 4.6 Negative Exponents INTRODUCTION In order to understand negative exponents the main topic of this section we need to make sure we understand the meaning of the reciprocal of a number. Reciprocals
Section 4.6 Negative Exponents INTRODUCTION In order to understand negative exponents the main topic of this section we need to make sure we understand the meaning of the reciprocal of a number. Reciprocals
Physics 70007, Fall 2009 Answers to Final Exam
 Physics 70007, Fall 009 Answers to Final Exam December 17, 009 1. Quantum mechanical pictures a Demonstrate that if the commutation relation [A, B] ic is valid in any of the three Schrodinger, Heisenberg,
Physics 70007, Fall 009 Answers to Final Exam December 17, 009 1. Quantum mechanical pictures a Demonstrate that if the commutation relation [A, B] ic is valid in any of the three Schrodinger, Heisenberg,
Page 1. These are all fairly simple functions in that wherever the variable appears it is by itself. What about functions like the following, ( ) ( )
 Chain Rule Page We ve taken a lot of derivatives over the course of the last few sections. However, if you look back they have all been functions similar to the following kinds of functions. 0 w ( ( tan
Chain Rule Page We ve taken a lot of derivatives over the course of the last few sections. However, if you look back they have all been functions similar to the following kinds of functions. 0 w ( ( tan
+E v(t) H(t) = v(t) E where v(t) is real and where v 0 for t ±.
 . Brick in a Square Well REMEMBER: THIS PROBLEM AND THOSE BELOW SHOULD NOT BE HANDED IN. THEY WILL NOT BE GRADED. THEY ARE INTENDED AS A STUDY GUIDE TO HELP YOU UNDERSTAND TIME DEPENDENT PERTURBATION THEORY
. Brick in a Square Well REMEMBER: THIS PROBLEM AND THOSE BELOW SHOULD NOT BE HANDED IN. THEY WILL NOT BE GRADED. THEY ARE INTENDED AS A STUDY GUIDE TO HELP YOU UNDERSTAND TIME DEPENDENT PERTURBATION THEORY
Perturbation Theory 1
 Perturbation Theory 1 1 Expansion of Complete System Let s take a look of an expansion for the function in terms of the complete system : (1) In general, this expansion is possible for any complete set.
Perturbation Theory 1 1 Expansion of Complete System Let s take a look of an expansion for the function in terms of the complete system : (1) In general, this expansion is possible for any complete set.
Introduction to Quantum Mechanics PVK - Solutions. Nicolas Lanzetti
 Introduction to Quantum Mechanics PVK - Solutions Nicolas Lanzetti lnicolas@student.ethz.ch 1 Contents 1 The Wave Function and the Schrödinger Equation 3 1.1 Quick Checks......................................
Introduction to Quantum Mechanics PVK - Solutions Nicolas Lanzetti lnicolas@student.ethz.ch 1 Contents 1 The Wave Function and the Schrödinger Equation 3 1.1 Quick Checks......................................
Section 9 Variational Method. Page 492
 Section 9 Variational Method Page 492 Page 493 Lecture 27: The Variational Method Date Given: 2008/12/03 Date Revised: 2008/12/03 Derivation Section 9.1 Variational Method: Derivation Page 494 Motivation
Section 9 Variational Method Page 492 Page 493 Lecture 27: The Variational Method Date Given: 2008/12/03 Date Revised: 2008/12/03 Derivation Section 9.1 Variational Method: Derivation Page 494 Motivation
The Particle in a Box
 Page 324 Lecture 17: Relation of Particle in a Box Eigenstates to Position and Momentum Eigenstates General Considerations on Bound States and Quantization Continuity Equation for Probability Date Given:
Page 324 Lecture 17: Relation of Particle in a Box Eigenstates to Position and Momentum Eigenstates General Considerations on Bound States and Quantization Continuity Equation for Probability Date Given:
Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Spring Semester 2006 Christopher J. Cramer. Lecture 8, February 3, 2006 & L "
 Chem 352/452 Physical Chemistry II (Quantum Mechanics) 3 Credits Spring Semester 26 Christopher J. Cramer Lecture 8, February 3, 26 Solved Homework (Homework for grading is also due today) Evaluate
Chem 352/452 Physical Chemistry II (Quantum Mechanics) 3 Credits Spring Semester 26 Christopher J. Cramer Lecture 8, February 3, 26 Solved Homework (Homework for grading is also due today) Evaluate
Lecture Notes 2: Review of Quantum Mechanics
 Quantum Field Theory for Leg Spinners 18/10/10 Lecture Notes 2: Review of Quantum Mechanics Lecturer: Prakash Panangaden Scribe: Jakub Závodný This lecture will briefly review some of the basic concepts
Quantum Field Theory for Leg Spinners 18/10/10 Lecture Notes 2: Review of Quantum Mechanics Lecturer: Prakash Panangaden Scribe: Jakub Závodný This lecture will briefly review some of the basic concepts
Time-Independent Perturbation Theory
 4 Phys46.nb Time-Independent Perturbation Theory.. Overview... General question Assuming that we have a Hamiltonian, H = H + λ H (.) where λ is a very small real number. The eigenstates of the Hamiltonian
4 Phys46.nb Time-Independent Perturbation Theory.. Overview... General question Assuming that we have a Hamiltonian, H = H + λ H (.) where λ is a very small real number. The eigenstates of the Hamiltonian
Lecture #8: Quantum Mechanical Harmonic Oscillator
 5.61 Fall, 013 Lecture #8 Page 1 Last time Lecture #8: Quantum Mechanical Harmonic Oscillator Classical Mechanical Harmonic Oscillator * V(x) = 1 kx (leading term in power series expansion of most V(x)
5.61 Fall, 013 Lecture #8 Page 1 Last time Lecture #8: Quantum Mechanical Harmonic Oscillator Classical Mechanical Harmonic Oscillator * V(x) = 1 kx (leading term in power series expansion of most V(x)
Vibrations and Rotations of Diatomic Molecules
 Chapter 6 Vibrations and Rotations of Diatomic Molecules With the electronic part of the problem treated in the previous chapter, the nuclear motion shall occupy our attention in this one. In many ways
Chapter 6 Vibrations and Rotations of Diatomic Molecules With the electronic part of the problem treated in the previous chapter, the nuclear motion shall occupy our attention in this one. In many ways
Getting Started with Communications Engineering
 1 Linear algebra is the algebra of linear equations: the term linear being used in the same sense as in linear functions, such as: which is the equation of a straight line. y ax c (0.1) Of course, if we
1 Linear algebra is the algebra of linear equations: the term linear being used in the same sense as in linear functions, such as: which is the equation of a straight line. y ax c (0.1) Of course, if we
CHAPTER 6 Quantum Mechanics II
 CHAPTER 6 Quantum Mechanics II 6.1 6.2 6.3 6.4 6.5 6.6 6.7 The Schrödinger Wave Equation Expectation Values Infinite Square-Well Potential Finite Square-Well Potential Three-Dimensional Infinite-Potential
CHAPTER 6 Quantum Mechanics II 6.1 6.2 6.3 6.4 6.5 6.6 6.7 The Schrödinger Wave Equation Expectation Values Infinite Square-Well Potential Finite Square-Well Potential Three-Dimensional Infinite-Potential
