PolyGamma Functions of Negative Order
|
|
|
- Bryce Walton
- 6 years ago
- Views:
Transcription
1 Carnegie Mellon University Research CMU Computer Science Department School of Computer Science -998 PolyGamma Functions of Negative Order Victor S. Adamchik Carnegie Mellon University Follow this and additional works at: This Article is brought to you for free and open access by the School of Computer Science at Research CMU. It has been accepted for inclusion in Computer Science Department by an authorized administrator of Research CMU. For more information, please contact research-showcase@andrew.cmu.edu.
2 PolyGamma Functions of Negative Order VICTOR S. ADAMCHIK January, 998 Abstract Liouville's fractional integration is used to dene polygamma functions (n) (z) for negative integer n. It's shown that such (n) (z) can be represented in a closed form by means of the rst derivatives of the Hurwitz Zeta function. Relations to the Barnes G-function and generalized Glaisher's constants are also discussed. Introduction The idea to dene the polygamma function () (z) for every complex via Liouville's fractional integration operator is quite natural and was around for a while (see Ross (974) and Grossman (976)). However, for arbitrary negative integer the closed form of () (z) was not developed yet - the only two particular cases =, and =,3 have been studied (see Gosper (997)). It is the purpose of this note is to consider (,n) (z) = (n, )! (z, t) n, log,(t) dt; <(z) > () when n is an arbitrary positive integer, and present (,n) (z) in terms of the Bernoulli numbers and polynomials, the harmonic numbers and rst derivatives of the Zeta function. Our approach is based on the following
3 series representation of log,( + z): log,( + z) =(, ) z, log +z +, z log z + sin(z), (k +) k= z k+ k + () Replacing log,( + z) in () by (), upon inverting the order of summation and integration, we thus observe that the essential part of this approach depends on whether or not we are able to evaluate series involving the Riemann Zeta function. We will propose here a specic technique (for more details see Adamchik and Srivastava (998)) dealing with Zeta series and show that generally the latter can be expressed in terms of derivatives of the Hurwitz function (s; a) with respect to its rst argument. Furthermore, we will show that when s is negative odd and a is rational a =,,,,, 3 and then 6 (s; a) can be always simplied to less transcendental functions, like the polygamma function and the Riemann Zeta function. In case of negative s we will understand the Hurwitz function, usually dened by the series (s; a) = n= (n + a) s <(s) > ; <(a) > (3) as the analytic continuation, provided by the Fourier expansion (see Magnus et al (966)): (s; a) =() s,,(, s) n= n s, sin(ns + s) (4) <(s) < ; <a Series involving the Zeta function Let us consider the general quantity S= k= f(k) (k +;a) (5)
4 where the function f(k) behaves at innity like O( (,)k ). Replacing the Zeta k function in (5) by the integral representation (s; a) =,(s) Z t s, e,at dt; <(s) > ; <(a) > (6), e,t and interchanging the order of summation and integration, we obtain S= Z e,at F (t) dt; (7), e,t where the function F (t) is a generating function of f(k) F (t)= k= f(k) tk k! Thus, the problem of summation has been reduced to integration. Though, the integral (7) looks terribly complicated and hopeless for symbolic integration, the point is that we don't wanttoevaluate the integral (7), but reduce it again to the integral reprezentation (6). It is easy to see that if the generating function F (t) is a combination of the power, exponential, trigonometric or hyperbolic functions then the integral (7) is a combination of Zeta functions and their derivatives, and thus so is the sum (5). In other words, with this approach we are staying in the same class of functions - sums involving the Zeta function are expressible in Zeta functions. Next we will provide a couple of examples demonstrating this technique. Consider In view of (x) = k= k k + (k), x k (s), =(s; ) = Z t s, e,t,(s) e t, dt upon inverting the order of summation and integration, which can be justied by the absolute convergence of the series and the integral involved, we nd that Z e,t dt k (xt) k (x) = e t, t (k +),(k) k= 3
5 The inner sum is a combination of power series of the exponential function k= k (xt) k (k +),(k) = tx, tx + etx t x, tx + Now we need to substitute this into the above integral and integrate the whole expression term by term. Unfortunately, we cannot do that since each integral does not pass the convergency test at t =. To avoid this obstacle we multiply the whole expression by t and then integrate each term. We thus obtain (x) = lim!,( +)( +;, x) x +,() (;, x), x,(, ) (, ;, x),( +)( +; ), + x Evaluating the limit, we nally arrive at,(, ) (, ; ) (x) = 3, x + (;, x) x, (,) + (;, x)+ (,;, x) x x where is the Euler-Mascheroni constant and denotes the derivative of (s; z) with respect to the rst parameter. As we will see later, for some rational x the sum (x) can be further simplied. For example, if x = 4, then ( 4 )= , 8, ( + ) G, 9 (,) + log( 7,( 7 4 ) 64 p ) where G is Catalan's constant. If x =, 3, then (, 3 )= p 3 + 4p 3,( 6 + log(7 3 ) 64 p )+ x! (8) 36 (4, 3 p 3 ) ( 3 )+4 (,) All these bring us to another interesting topic: for what values of x the above expression (8) can be simplied to less transcendental functions? It is well-known that (;x)= (x) (,) =, log A 4
6 (;x) = log(,(x) p ) where A is Glaisher`s constant (see Finch (996)) (also known as the Glaisher- Kinkelin constant). But what is (,;x)? Or more general (,n, ;x);n=; ; :::? 3 Derivatives of the Hurwitz Zeta function From Lerch's transformation formula (see Bateman et al. (953)): (z; s; v) =iz,v () s,,(, s) e, is e,iv ;, s; log(z) i, e i( s +v) e iv ;, s;, log(z) putting v =,s =, s and z = e ix it follows, that (s;, x)+e is (s; x) = e is () s,(s) Li,s (e ix ); where we assume that < x < and s is real. Dierentiating this functional equation with respect to s, setting s to,n, where n is a positve integer, we obtain Proposition Let n be a positive integer and < x <, then (,n; x)+(,) n (,n;, x) =i B n+(x) n + in + e, i n! () n Li n+ (e ix ); (9) where B n (x) are Bernoulli polynomials, and Li n (x) is the polylogarithm function. Taking into account the multiplication property of the Zeta function X (s; k z) =k,s k, i= s; z + i k and the proposition, we easily derive the following representations (,; )=log 6 44, p 3 + ( 8 p (,) 5 3 )
7 (,3; log )=,3 6 59, 7 log p 3, ( 384 p (,3) (,; 4 )= G 4, 8 (,) (,3; 4 )=,log , ( 4 ) 48 3, 7 8 (,3) (,; 3 )=,log 3 7, 8 p 3 + ( p, 3 3 (,) (,3; 3 )=log p 3, ( 43 p, (,3) Similar formulas can be obtained for (,n; x) when n is odd and x =, 6,,,, 3 and 5. For additional formulas of this kind I refer you to the papers Adamchik (997), and Miller and Adamchik (998). 4 Negapolygammas In the second section dealing with zeta sums we mentioned Glaisher's constant A. First this transcendent was studied by Glaisher (see Glaisher (877)). He found the following integral representation log A =, log(5 6 ) 36 Let us consider a more general integral and show that Z q log,(z) dz = Z q (, q) q + 3 Z 3 ) 3 ) 3 ) log,(z) dz log,(z) dz () + q log(), (,) + (,;q) () The proof is based on the series representation (). Integrating each term of it with respect to z and taking into account the identity k=, (k +) (k +)(k +) qk+ =(,) q, (,)+ (,;,q)+ (,; +q) 6
8 (that can be easily deduced by using the idea described in the second section), we prove (). The formula () rst was obtained in Gosper (997). The integral () can be envisaged from another point of view. It is known that the polygamma function is dened by (n) (z) log,(z) () for positive integer n. However, using Liouville's fractional integration and dierentiation operator we can extend the above denition for negative integer n. Thus, for n =, and n =, it follows immediately that and (,) (z) = log,(z) (,) (z) = log,(t)dt respectively. This means that the integral () is actually a "negapolygamma" of the second order (the term was proposed by B. Gosper). Generally, if we agree on that the bottom limit of integration is zero, we can dene polygammas of the negative order as it follows (,n) (z) = (n, )! (z, t) n, log,(t) dt; <(z) > (3) As a matter of fact, using the series representation () for log,( + z), the integral (3) can be evaluated in a closed form Proposition Let n be apositive integer and <(z) >, then n! (,n) (z) = n log() zn,, B n (z)h n, + n (, n; z), n, X i= n i! (,i)(n, i) z n,i, + bx n c i= (4) n!b i H i, z n,i where B n and B n (z) are Bernoulli numbers and polynomials, and H n are harmonic numbers. i 7
9 Here are some particular cases: (,) (z) = (, z) z + z log(), (,) + (,;z) (,3) (z) =, z 4 (6z, 9z +)+ z 4 log(), (,), z (,) + (,;z) More formulas: (,3) () = log A + 4 log() (,3) ( )= log A + 6 log(), 7 8 (,) (,3) ( 3 )+ (,3) ( 3 ) = log A log(), 3 9 (,) If we integrate both sides of the equation (4) with respect to z from to z, we obtain the following recurrence relation for (,n; z) Corollary Let n be a positive integer and <(z) >, then n (, n; x) dx = B n+, B n+ (z) n (n +) 4. Integrals with Polygamma Functions, (,n)+ (,n; z) (5) From the denition (), using simple integration by parts, we can express the integral x n in terms of negapolygammas. We have (x) dx (,) (z) =z (,) (z), (,3) (z) =z (,) (z), z and more generally, x n (x) dx =(,) n n! (,) (z)+ nx k= x (x) dx x (x) dx (,) k (k,n,) (z) zk k! (6) Thus, taking into account the representation (4) of negapolygammas, we obtain 8
10 Proposition 3 Let n be a nonnegative integer and <(z) >, then x n (x) dx =(,) n, (,n)+ (,)n n + B n+ H n,! nx (,) k n z n,k k k + B k+(z)h k + k= nx k= (,) k n k! z n,k (,k; z) (7) 4. Barnes G-functon Choi et al. (995) considered a class of series involving the Zeta function that can be evaluated by means of the double Gamma function G (see Barnes (899)) and their integrals. If we apply our technique described in the second section to those sums we get results in terms of the Hurwitz functions. To compare both approaches we need to establish a connection between the Barnes G-function and the derivatives of the Hurwitz function. The G- function and are related to each other by log G(z +), z log,(z) = (,), (,;z) (8) The identity pops up immediately from Alexeiewsky's theorem (see Barnes (899)) and the formula (). Integrating both sides of (8) with respect to z, in view of formulas (4) and (5), we obtain the following (presumably new) representation log G(x +)dx = z (, z ) + z 4 log()+ z (,) + (,;z) + (,), (,;z) (9) 5 Generalized Glaisher's constants In 933 L. Bendersky (see Bendersky (933) or Finch (996)) considered the limit log A k = lim n! nx m= m k log m, p(n; k)! ; () 9
11 where p(n; k) = nk log n + nk+ k + log n, + k + k! kx j= " n k,j B j+ log n +(, k,j ) (j + )! (k, j)! and k is the Kronecker symbol. He found that log A = log() kx i= # k, i + and log A =, (,) = log A and for the next three values he gave their numerical approximations. However, it turns out that all A k can be expressed in terms of derivatives of the Zeta function, by using the asymptotic expansion of the Hurwitz Zeta function (see Magnus et al (966)): X (z; ) =,z z, +,z m, + B j,(z +j, ),j,z+ +O(,m,z, ) (j)!,(z) j= () when jj!and j arg j <. Dierentiating () with respect to z and setting z to, and,, for example, we have and (,;)=, 4 + log, +! +O( ) ()! (,;)=, log 6, + 3 +O( 3 ) (3) Now, taking into account the analytical property of the Hurwitz function, the sum in () is nx m= m k log m = (,k; n +), (,k)
12 Therefore, applying asymptotic expansions of the derivatives of the Hurwitz functions to (), we nd that log A =, (,) Generally, log A 3 =, 7, (,3) log A 4 =, (,4) Proposition 4 Let k be a nonnegative integer, then the generalized Glaisher constants A k are of the form log A k = B k+ H k k +, (,k) (4) where B n are Bernoulli numbers and H n are harmonic numbers. References [] Adamchik,V. S., Srivastava,H. M. (998) Some Series of the Zeta and Related Functions. Analysis (accepted for publication). [] Adamchik V. S.,(997), A Class of Logarithmic Integrals, Proc. of IS- SAC'97, {8. [3] Adamchik, V.S., Srivastava, H.M. (998),Some Series of the Zeta and Related Functions. Analysis, accepted for publication. [4] Barnes,E. W. (899), The Theory of G-function, Quart. J. Math, 3, [5] Bateman,H., Erdelyi,A. (953) Higher Transcendental Functions, Vol., McGraw-Hill. [6] Bendersky, L. (933), Sur la function gamma generalisee, Acta Math, 6, [7] Choi,J., Srivastava,H. M, Quine,J. R. (995), Some Series Involving the Zeta Function, Bull. Austral. Math. Soc., 5,
13 [8] Finch, S. (996), Glaisher-Kinkelin Constant, In HTML essay at URL, constant/glshkn/glshkn.html. [9] Glaisher,J. W. L. (877), On a Numerical Continued Product, Messenger of Math., 6, [] Gosper,R. W. (997), R m 6 n log,(z)dz, InSpecial Functions, q-series and 4 related topics, Amer. Math. Soc. Vol. 4. [] Magnus,W., Oberhettinger,F., Soni,R. P. (966), Formulas and Theorems for the Special Functions of Mathematical Physics, Springer-Verlag. [] Miller,J., Adamchik, V.S. (998), Derivatives of the Hurwitz Zeta Function for Rational Arguments, J. Symb. Comput., to appear. [3] Ross, B.. (974), Problem 6, Amer. Math. Monthly, 8,. [4] Grossman, N.. (976), Polygamma Functions of Arbitrary Order, SIAM J. Math. Anal., 7,
rama.tex; 21/03/2011; 0:37; p.1
 rama.tex; /03/0; 0:37; p. Multiple Gamma Function and Its Application to Computation of Series and Products V. S. Adamchik Department of Computer Science, Carnegie Mellon University, Pittsburgh, USA Abstract.
rama.tex; /03/0; 0:37; p. Multiple Gamma Function and Its Application to Computation of Series and Products V. S. Adamchik Department of Computer Science, Carnegie Mellon University, Pittsburgh, USA Abstract.
arxiv:math/ v1 [math.ca] 8 Aug 2003
![arxiv:math/ v1 [math.ca] 8 Aug 2003 arxiv:math/ v1 [math.ca] 8 Aug 2003](/thumbs/73/69290084.jpg) arxiv:math/886v [math.ca] 8 Aug CONTRIBUTIONS TO THE THEORY OF THE BARNES FUNCTION V. S. ADAMCHIK Abstract. This paper presents a family of new integral representations and asymptotic series of the multiple
arxiv:math/886v [math.ca] 8 Aug CONTRIBUTIONS TO THE THEORY OF THE BARNES FUNCTION V. S. ADAMCHIK Abstract. This paper presents a family of new integral representations and asymptotic series of the multiple
J. CHOI, AND H. M. SRIVASTAVA, AND V. S. ADAMCHIK We begin by recalling the Barnes G-function (=G = being the so-called double Gamma function) which h
 MULTIPLE GAMMA AND RELATED FUNCTIONS Junesang Choi, H. M. Srivastava, and V. S. Adamchik Abstract. The authors give several new (and potentially useful) relationships between the multiple Gamma functions
MULTIPLE GAMMA AND RELATED FUNCTIONS Junesang Choi, H. M. Srivastava, and V. S. Adamchik Abstract. The authors give several new (and potentially useful) relationships between the multiple Gamma functions
Polyexponentials. Khristo N. Boyadzhiev Ohio Northern University Departnment of Mathematics Ada, OH
 Polyexponentials Khristo N. Boyadzhiev Ohio Northern University Departnment of Mathematics Ada, OH 45810 k-boyadzhiev@onu.edu 1. Introduction. The polylogarithmic function [15] (1.1) and the more general
Polyexponentials Khristo N. Boyadzhiev Ohio Northern University Departnment of Mathematics Ada, OH 45810 k-boyadzhiev@onu.edu 1. Introduction. The polylogarithmic function [15] (1.1) and the more general
ON THE TAYLOR COEFFICIENTS OF THE HURWITZ ZETA FUNCTION
 ON THE TAYLOR COEFFICIENTS OF THE HURWITZ ZETA FUNCTION Khristo N. Boyadzhiev Department of Mathematics, Ohio Northern University, Ada, Ohio, 45810 k-boyadzhiev@onu.edu Abstract. We find a representation
ON THE TAYLOR COEFFICIENTS OF THE HURWITZ ZETA FUNCTION Khristo N. Boyadzhiev Department of Mathematics, Ohio Northern University, Ada, Ohio, 45810 k-boyadzhiev@onu.edu Abstract. We find a representation
The Riemann and Hurwitz zeta functions, Apery s constant and new rational series representations involving ζ(2k)
 The Riemann and Hurwitz zeta functions, Apery s constant and new rational series representations involving ζ(k) Cezar Lupu 1 1 Department of Mathematics University of Pittsburgh Pittsburgh, PA, USA Algebra,
The Riemann and Hurwitz zeta functions, Apery s constant and new rational series representations involving ζ(k) Cezar Lupu 1 1 Department of Mathematics University of Pittsburgh Pittsburgh, PA, USA Algebra,
Analytic Aspects of the Riemann Zeta and Multiple Zeta Values
 Analytic Aspects of the Riemann Zeta and Multiple Zeta Values Cezar Lupu Department of Mathematics University of Pittsburgh Pittsburgh, PA, USA PhD Thesis Overview, October 26th, 207, Pittsburgh, PA Outline
Analytic Aspects of the Riemann Zeta and Multiple Zeta Values Cezar Lupu Department of Mathematics University of Pittsburgh Pittsburgh, PA, USA PhD Thesis Overview, October 26th, 207, Pittsburgh, PA Outline
arxiv: v2 [math.nt] 19 Apr 2017
![arxiv: v2 [math.nt] 19 Apr 2017 arxiv: v2 [math.nt] 19 Apr 2017](/thumbs/87/95682745.jpg) Evaluation of Log-tangent Integrals by series involving ζn + BY Lahoucine Elaissaoui And Zine El Abidine Guennoun arxiv:6.74v [math.nt] 9 Apr 7 Mohammed V University in Rabat Faculty of Sciences Department
Evaluation of Log-tangent Integrals by series involving ζn + BY Lahoucine Elaissaoui And Zine El Abidine Guennoun arxiv:6.74v [math.nt] 9 Apr 7 Mohammed V University in Rabat Faculty of Sciences Department
Quadratic Transformations of Hypergeometric Function and Series with Harmonic Numbers
 Quadratic Transformations of Hypergeometric Function and Series with Harmonic Numbers Martin Nicholson In this brief note, we show how to apply Kummer s and other quadratic transformation formulas for
Quadratic Transformations of Hypergeometric Function and Series with Harmonic Numbers Martin Nicholson In this brief note, we show how to apply Kummer s and other quadratic transformation formulas for
Integral representations for the Dirichlet L-functions and their expansions in Meixner-Pollaczek polynomials and rising factorials
 Integral representations for the Dirichlet L-functions and their expansions in Meixner-Pollaczek polynomials and rising factorials A. Kuznetsov Dept. of Mathematical Sciences University of New Brunswick
Integral representations for the Dirichlet L-functions and their expansions in Meixner-Pollaczek polynomials and rising factorials A. Kuznetsov Dept. of Mathematical Sciences University of New Brunswick
Generating and characteristic functions. Generating and Characteristic Functions. Probability generating function. Probability generating function
 Generating and characteristic functions Generating and Characteristic Functions September 3, 03 Probability generating function Moment generating function Power series expansion Characteristic function
Generating and characteristic functions Generating and Characteristic Functions September 3, 03 Probability generating function Moment generating function Power series expansion Characteristic function
#A08 INTEGERS 9 (2009), ON ASYMPTOTIC CONSTANTS RELATED TO PRODUCTS OF BERNOULLI NUMBERS AND FACTORIALS
 #A08 INTEGERS 9 009), 83-06 ON ASYMPTOTIC CONSTANTS RELATED TO PRODUCTS OF BERNOULLI NUMBERS AND FACTORIALS Bernd C. Kellner Mathematisches Institut, Universität Göttingen, Bunsenstr. 3-5, 37073 Göttingen,
#A08 INTEGERS 9 009), 83-06 ON ASYMPTOTIC CONSTANTS RELATED TO PRODUCTS OF BERNOULLI NUMBERS AND FACTORIALS Bernd C. Kellner Mathematisches Institut, Universität Göttingen, Bunsenstr. 3-5, 37073 Göttingen,
1. Prove the following properties satisfied by the gamma function: 4 n n!
 Math 205A: Complex Analysis, Winter 208 Homework Problem Set #6 February 20, 208. Prove the following properties satisfied by the gamma function: (a) Values at half-integers: Γ ( n + 2 (b) The duplication
Math 205A: Complex Analysis, Winter 208 Homework Problem Set #6 February 20, 208. Prove the following properties satisfied by the gamma function: (a) Values at half-integers: Γ ( n + 2 (b) The duplication
B n (x) zn n! n=0. E n (x) zn n! n=0
 UDC 517.9 Q.-M. Luo Chongqing Normal Univ., China) q-apostol EULER POLYNOMIALS AND q-alternating SUMS* q-полiноми АПОСТОЛА ЕЙЛЕРА ТА q-знакозмiннi СУМИ We establish the basic properties generating functions
UDC 517.9 Q.-M. Luo Chongqing Normal Univ., China) q-apostol EULER POLYNOMIALS AND q-alternating SUMS* q-полiноми АПОСТОЛА ЕЙЛЕРА ТА q-знакозмiннi СУМИ We establish the basic properties generating functions
A Note about the Pochhammer Symbol
 Mathematica Moravica Vol. 12-1 (2008), 37 42 A Note about the Pochhammer Symbol Aleksandar Petoević Abstract. In this paper we give elementary proofs of the generating functions for the Pochhammer symbol
Mathematica Moravica Vol. 12-1 (2008), 37 42 A Note about the Pochhammer Symbol Aleksandar Petoević Abstract. In this paper we give elementary proofs of the generating functions for the Pochhammer symbol
The Generating Functions for Pochhammer
 The Generating Functions for Pochhammer Symbol { }, n N Aleksandar Petoević University of Novi Sad Teacher Training Faculty, Department of Mathematics Podgorička 4, 25000 Sombor SERBIA and MONTENEGRO Email
The Generating Functions for Pochhammer Symbol { }, n N Aleksandar Petoević University of Novi Sad Teacher Training Faculty, Department of Mathematics Podgorička 4, 25000 Sombor SERBIA and MONTENEGRO Email
Bernoulli Numbers and their Applications
 Bernoulli Numbers and their Applications James B Silva Abstract The Bernoulli numbers are a set of numbers that were discovered by Jacob Bernoulli (654-75). This set of numbers holds a deep relationship
Bernoulli Numbers and their Applications James B Silva Abstract The Bernoulli numbers are a set of numbers that were discovered by Jacob Bernoulli (654-75). This set of numbers holds a deep relationship
of Classical Constants Philippe Flajolet and Ilan Vardi February 24, 1996 Many mathematical constants are expressed as slowly convergent sums
 Zeta Function Expansions of Classical Constants Philippe Flajolet and Ilan Vardi February 24, 996 Many mathematical constants are expressed as slowly convergent sums of the form C = f( ) () n n2a for some
Zeta Function Expansions of Classical Constants Philippe Flajolet and Ilan Vardi February 24, 996 Many mathematical constants are expressed as slowly convergent sums of the form C = f( ) () n n2a for some
arxiv: v6 [math.nt] 12 Sep 2017
![arxiv: v6 [math.nt] 12 Sep 2017 arxiv: v6 [math.nt] 12 Sep 2017](/thumbs/89/100965697.jpg) Counterexamples to the conjectured transcendence of /α) k, its closed-form summation and extensions to polygamma functions and zeta series arxiv:09.44v6 [math.nt] Sep 07 F. M. S. Lima Institute of Physics,
Counterexamples to the conjectured transcendence of /α) k, its closed-form summation and extensions to polygamma functions and zeta series arxiv:09.44v6 [math.nt] Sep 07 F. M. S. Lima Institute of Physics,
Asymptotics of Integrals of. Hermite Polynomials
 Applied Mathematical Sciences, Vol. 4, 010, no. 61, 04-056 Asymptotics of Integrals of Hermite Polynomials R. B. Paris Division of Complex Systems University of Abertay Dundee Dundee DD1 1HG, UK R.Paris@abertay.ac.uk
Applied Mathematical Sciences, Vol. 4, 010, no. 61, 04-056 Asymptotics of Integrals of Hermite Polynomials R. B. Paris Division of Complex Systems University of Abertay Dundee Dundee DD1 1HG, UK R.Paris@abertay.ac.uk
CONGRUENCES FOR BERNOULLI - LUCAS SUMS
 CONGRUENCES FOR BERNOULLI - LUCAS SUMS PAUL THOMAS YOUNG Abstract. We give strong congruences for sums of the form N BnVn+1 where Bn denotes the Bernoulli number and V n denotes a Lucas sequence of the
CONGRUENCES FOR BERNOULLI - LUCAS SUMS PAUL THOMAS YOUNG Abstract. We give strong congruences for sums of the form N BnVn+1 where Bn denotes the Bernoulli number and V n denotes a Lucas sequence of the
On the stirling expansion into negative powers of a triangular number
 MATHEMATICAL COMMUNICATIONS 359 Math. Commun., Vol. 5, No. 2, pp. 359-364 200) On the stirling expansion into negative powers of a triangular number Cristinel Mortici, Department of Mathematics, Valahia
MATHEMATICAL COMMUNICATIONS 359 Math. Commun., Vol. 5, No. 2, pp. 359-364 200) On the stirling expansion into negative powers of a triangular number Cristinel Mortici, Department of Mathematics, Valahia
Convergence of sequences and series
 Convergence of sequences and series A sequence f is a map from N the positive integers to a set. We often write the map outputs as f n rather than f(n). Often we just list the outputs in order and leave
Convergence of sequences and series A sequence f is a map from N the positive integers to a set. We often write the map outputs as f n rather than f(n). Often we just list the outputs in order and leave
COMPLETE MONOTONICITIES OF FUNCTIONS INVOLVING THE GAMMA AND DIGAMMA FUNCTIONS. 1. Introduction
 COMPLETE MONOTONICITIES OF FUNCTIONS INVOLVING THE GAMMA AND DIGAMMA FUNCTIONS FENG QI AND BAI-NI GUO Abstract. In the article, the completely monotonic results of the functions [Γ( + 1)] 1/, [Γ(+α+1)]1/(+α),
COMPLETE MONOTONICITIES OF FUNCTIONS INVOLVING THE GAMMA AND DIGAMMA FUNCTIONS FENG QI AND BAI-NI GUO Abstract. In the article, the completely monotonic results of the functions [Γ( + 1)] 1/, [Γ(+α+1)]1/(+α),
Explicit formulas for computing Bernoulli numbers of the second kind and Stirling numbers of the first kind
 Filomat 28:2 (24), 39 327 DOI.2298/FIL4239O Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Explicit formulas for computing Bernoulli
Filomat 28:2 (24), 39 327 DOI.2298/FIL4239O Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Explicit formulas for computing Bernoulli
Sums of Products of Bernoulli Numbers*
 journal of number theory 60, 234 (996) article no. 00 Sums of Products of Bernoulli Numbers* Karl Dilcher Department of Mathematics, Statistics, and Computing Science, Dalhousie University, Halifax, Nova
journal of number theory 60, 234 (996) article no. 00 Sums of Products of Bernoulli Numbers* Karl Dilcher Department of Mathematics, Statistics, and Computing Science, Dalhousie University, Halifax, Nova
Research Article Operator Representation of Fermi-Dirac and Bose-Einstein Integral Functions with Applications
 Hindawi Publishing Corporation International Journal of Mathematics and Mathematical Sciences Volume 2007, Article ID 80515, 9 pages doi:10.1155/2007/80515 Research Article Operator Representation of Fermi-Dirac
Hindawi Publishing Corporation International Journal of Mathematics and Mathematical Sciences Volume 2007, Article ID 80515, 9 pages doi:10.1155/2007/80515 Research Article Operator Representation of Fermi-Dirac
MOMENTS OF HYPERGEOMETRIC HURWITZ ZETA FUNCTIONS
 MOMENTS OF HYPERGEOMETRIC HURWITZ ZETA FUNCTIONS ABDUL HASSEN AND HIEU D. NGUYEN Abstract. This paper investigates a generalization the classical Hurwitz zeta function. It is shown that many of the properties
MOMENTS OF HYPERGEOMETRIC HURWITZ ZETA FUNCTIONS ABDUL HASSEN AND HIEU D. NGUYEN Abstract. This paper investigates a generalization the classical Hurwitz zeta function. It is shown that many of the properties
This ODE arises in many physical systems that we shall investigate. + ( + 1)u = 0. (λ + s)x λ + s + ( + 1) a λ. (s + 1)(s + 2) a 0
 Legendre equation This ODE arises in many physical systems that we shall investigate We choose We then have Substitution gives ( x 2 ) d 2 u du 2x 2 dx dx + ( + )u u x s a λ x λ a du dx λ a λ (λ + s)x
Legendre equation This ODE arises in many physical systems that we shall investigate We choose We then have Substitution gives ( x 2 ) d 2 u du 2x 2 dx dx + ( + )u u x s a λ x λ a du dx λ a λ (λ + s)x
arxiv: v1 [math.ca] 4 Apr 2016
![arxiv: v1 [math.ca] 4 Apr 2016 arxiv: v1 [math.ca] 4 Apr 2016](/thumbs/81/83127487.jpg) The Fourier series of the log-barnes function István Mező Department of Mathematics, Nanjing University of Information Science and Technology, No.29 Ningliu Rd, Pukou, Nanjing, Jiangsu, P. R. China arxiv:64.753v
The Fourier series of the log-barnes function István Mező Department of Mathematics, Nanjing University of Information Science and Technology, No.29 Ningliu Rd, Pukou, Nanjing, Jiangsu, P. R. China arxiv:64.753v
Introductions to ExpIntegralEi
 Introductions to ExpIntegralEi Introduction to the exponential integrals General The exponential-type integrals have a long history. After the early developments of differential calculus, mathematicians
Introductions to ExpIntegralEi Introduction to the exponential integrals General The exponential-type integrals have a long history. After the early developments of differential calculus, mathematicians
Existence of a Limit on a Dense Set, and. Construction of Continuous Functions on Special Sets
 Existence of a Limit on a Dense Set, and Construction of Continuous Functions on Special Sets REU 2012 Recap: Definitions Definition Given a real-valued function f, the limit of f exists at a point c R
Existence of a Limit on a Dense Set, and Construction of Continuous Functions on Special Sets REU 2012 Recap: Definitions Definition Given a real-valued function f, the limit of f exists at a point c R
Chebyshev coordinates and Salem numbers
 Chebyshev coordinates and Salem numbers S.Capparelli and A. Del Fra arxiv:181.11869v1 [math.co] 31 Dec 018 January 1, 019 Abstract By expressing polynomials in the basis of Chebyshev polynomials, certain
Chebyshev coordinates and Salem numbers S.Capparelli and A. Del Fra arxiv:181.11869v1 [math.co] 31 Dec 018 January 1, 019 Abstract By expressing polynomials in the basis of Chebyshev polynomials, certain
20 ZIAD ZAHREDDINE For some interesting relationships between these two types of stability: Routh- Hurwitz for continuous-time and Schur-Cohn for disc
 SOOCHOW JOURNAL OF MATHEMATICS Volume 25, No. 1, pp. 19-28, January 1999 ON SOME PROPERTIES OF HURWITZ POLYNOMIALS WITH APPLICATION TO STABILITY THEORY BY ZIAD ZAHREDDINE Abstract. Necessary as well as
SOOCHOW JOURNAL OF MATHEMATICS Volume 25, No. 1, pp. 19-28, January 1999 ON SOME PROPERTIES OF HURWITZ POLYNOMIALS WITH APPLICATION TO STABILITY THEORY BY ZIAD ZAHREDDINE Abstract. Necessary as well as
Yunhi Cho and Young-One Kim
 Bull. Korean Math. Soc. 41 (2004), No. 1, pp. 27 43 ANALYTIC PROPERTIES OF THE LIMITS OF THE EVEN AND ODD HYPERPOWER SEQUENCES Yunhi Cho Young-One Kim Dedicated to the memory of the late professor Eulyong
Bull. Korean Math. Soc. 41 (2004), No. 1, pp. 27 43 ANALYTIC PROPERTIES OF THE LIMITS OF THE EVEN AND ODD HYPERPOWER SEQUENCES Yunhi Cho Young-One Kim Dedicated to the memory of the late professor Eulyong
Beukers integrals and Apéry s recurrences
 2 3 47 6 23 Journal of Integer Sequences, Vol. 8 (25), Article 5.. Beukers integrals and Apéry s recurrences Lalit Jain Faculty of Mathematics University of Waterloo Waterloo, Ontario N2L 3G CANADA lkjain@uwaterloo.ca
2 3 47 6 23 Journal of Integer Sequences, Vol. 8 (25), Article 5.. Beukers integrals and Apéry s recurrences Lalit Jain Faculty of Mathematics University of Waterloo Waterloo, Ontario N2L 3G CANADA lkjain@uwaterloo.ca
Analogues for Bessel Functions of the Christoffel-Darboux Identity
 Analogues for Bessel Functions of the Christoffel-Darboux Identity Mark Tygert Research Report YALEU/DCS/RR-1351 March 30, 2006 Abstract We derive analogues for Bessel functions of what is known as the
Analogues for Bessel Functions of the Christoffel-Darboux Identity Mark Tygert Research Report YALEU/DCS/RR-1351 March 30, 2006 Abstract We derive analogues for Bessel functions of what is known as the
Limits at Infinity. Horizontal Asymptotes. Definition (Limits at Infinity) Horizontal Asymptotes
 Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
arxiv: v1 [math.nt] 13 Jun 2016
![arxiv: v1 [math.nt] 13 Jun 2016 arxiv: v1 [math.nt] 13 Jun 2016](/thumbs/71/66185300.jpg) arxiv:606.03837v [math.nt] 3 Jun 206 Identities on the k-ary Lyndon words related to a family of zeta functions Irem Kucukoglu,a and Yilmaz Simsek,b a ikucukoglu@akdeniz.edu.tr b ysimsek@akdeniz.edu.tr
arxiv:606.03837v [math.nt] 3 Jun 206 Identities on the k-ary Lyndon words related to a family of zeta functions Irem Kucukoglu,a and Yilmaz Simsek,b a ikucukoglu@akdeniz.edu.tr b ysimsek@akdeniz.edu.tr
Chapter 11. Taylor Series. Josef Leydold Mathematical Methods WS 2018/19 11 Taylor Series 1 / 27
 Chapter 11 Taylor Series Josef Leydold Mathematical Methods WS 2018/19 11 Taylor Series 1 / 27 First-Order Approximation We want to approximate function f by some simple function. Best possible approximation
Chapter 11 Taylor Series Josef Leydold Mathematical Methods WS 2018/19 11 Taylor Series 1 / 27 First-Order Approximation We want to approximate function f by some simple function. Best possible approximation
HYPERGEOMETRIC BERNOULLI POLYNOMIALS AND APPELL SEQUENCES
 HYPERGEOMETRIC BERNOULLI POLYNOMIALS AND APPELL SEQUENCES ABDUL HASSEN AND HIEU D. NGUYEN Abstract. There are two analytic approaches to Bernoulli polynomials B n(x): either by way of the generating function
HYPERGEOMETRIC BERNOULLI POLYNOMIALS AND APPELL SEQUENCES ABDUL HASSEN AND HIEU D. NGUYEN Abstract. There are two analytic approaches to Bernoulli polynomials B n(x): either by way of the generating function
8 Singular Integral Operators and L p -Regularity Theory
 8 Singular Integral Operators and L p -Regularity Theory 8. Motivation See hand-written notes! 8.2 Mikhlin Multiplier Theorem Recall that the Fourier transformation F and the inverse Fourier transformation
8 Singular Integral Operators and L p -Regularity Theory 8. Motivation See hand-written notes! 8.2 Mikhlin Multiplier Theorem Recall that the Fourier transformation F and the inverse Fourier transformation
1. Introduction Interest in this project began with curiosity about the Laplace transform of the Digamma function, e as ψ(s + 1)ds,
 ON THE LAPLACE TRANSFORM OF THE PSI FUNCTION M. LAWRENCE GLASSER AND DANTE MANNA Abstract. Guided by numerical experimentation, we have been able to prove that Z 8 / x x + ln dx = γ + ln) [cosx)] and to
ON THE LAPLACE TRANSFORM OF THE PSI FUNCTION M. LAWRENCE GLASSER AND DANTE MANNA Abstract. Guided by numerical experimentation, we have been able to prove that Z 8 / x x + ln dx = γ + ln) [cosx)] and to
Applications of Fourier Series and Zeta Functions to Genocchi Polynomials
 Appl. Math. Inf. Sci., No. 5, 95-955 (8) 95 Applied Mathematics & Information Sciences An International Journal http://d.doi.org/.8576/amis/58 Applications of Fourier Series Zeta Functions to Genocchi
Appl. Math. Inf. Sci., No. 5, 95-955 (8) 95 Applied Mathematics & Information Sciences An International Journal http://d.doi.org/.8576/amis/58 Applications of Fourier Series Zeta Functions to Genocchi
Sums of arctangents and some formulas of Ramanujan
 SCIENTIA Series A: Mathematical Sciences, Vol. 11 (2005), 13 24 Universidad Técnica Federico Santa María Valparaíso, Chile ISSN 0716-8446 c Universidad Técnica Federico Santa María 2005 Sums of arctangents
SCIENTIA Series A: Mathematical Sciences, Vol. 11 (2005), 13 24 Universidad Técnica Federico Santa María Valparaíso, Chile ISSN 0716-8446 c Universidad Técnica Federico Santa María 2005 Sums of arctangents
VALUES OF THE LEGENDRE CHI AND HURWITZ ZETA FUNCTIONS AT RATIONAL ARGUMENTS
 MATHEMATICS OF COMPUTATION Volume 68, Number 228, Pages 1623 1630 S 0025-5718(99)01091-1 Article electronically published on May 17, 1999 VALUES OF THE LEGENDRE CHI AND HURWITZ ZETA FUNCTIONS AT RATIONAL
MATHEMATICS OF COMPUTATION Volume 68, Number 228, Pages 1623 1630 S 0025-5718(99)01091-1 Article electronically published on May 17, 1999 VALUES OF THE LEGENDRE CHI AND HURWITZ ZETA FUNCTIONS AT RATIONAL
Inequalities for logarithmic and exponential functions
 General Mathematics Vol. 12, No. 2 (24), 47 52 Inequalities for logarithmic and exponential functions Eugen Constantinescu Abstract In [1] it was announced the precise inequality : for x 1 4 ( ) ( ) 12x
General Mathematics Vol. 12, No. 2 (24), 47 52 Inequalities for logarithmic and exponential functions Eugen Constantinescu Abstract In [1] it was announced the precise inequality : for x 1 4 ( ) ( ) 12x
On reaching head-to-tail ratios for balanced and unbalanced coins
 Journal of Statistical Planning and Inference 0 (00) 0 0 www.elsevier.com/locate/jspi On reaching head-to-tail ratios for balanced and unbalanced coins Tamas Lengyel Department of Mathematics, Occidental
Journal of Statistical Planning and Inference 0 (00) 0 0 www.elsevier.com/locate/jspi On reaching head-to-tail ratios for balanced and unbalanced coins Tamas Lengyel Department of Mathematics, Occidental
On integral representations of q-gamma and q beta functions
 On integral representations of -gamma and beta functions arxiv:math/3232v [math.qa] 4 Feb 23 Alberto De Sole, Victor G. Kac Department of Mathematics, MIT 77 Massachusetts Avenue, Cambridge, MA 239, USA
On integral representations of -gamma and beta functions arxiv:math/3232v [math.qa] 4 Feb 23 Alberto De Sole, Victor G. Kac Department of Mathematics, MIT 77 Massachusetts Avenue, Cambridge, MA 239, USA
arxiv: v1 [math.ca] 17 Feb 2017
![arxiv: v1 [math.ca] 17 Feb 2017 arxiv: v1 [math.ca] 17 Feb 2017](/thumbs/90/103282277.jpg) GENERALIZED STIELTJES CONSTANTS AND INTEGRALS INVOLVING THE LOG-LOG FUNCTION: KUMMER S THEOREM IN ACTION OMRAN KOUBA arxiv:7549v [mathca] 7 Feb 7 Abstract In this note, we recall Kummer s Fourier series
GENERALIZED STIELTJES CONSTANTS AND INTEGRALS INVOLVING THE LOG-LOG FUNCTION: KUMMER S THEOREM IN ACTION OMRAN KOUBA arxiv:7549v [mathca] 7 Feb 7 Abstract In this note, we recall Kummer s Fourier series
ASYMPTOTIC ESTIMATES FOR APOSTOL-BERNOULLI AND APOSTOL-EULER POLYNOMIALS
 ASYMPTOTIC ESTIMATES FOR APOSTOL-BERNOULLI AND APOSTOL-EULER POLYNOMIALS LUIS M. NAVAS, FRANCISCO J. RUIZ, AND JUAN L. VARONA Abstract. We analyze the asymptotic behavior of the Apostol-Bernoulli polynomials
ASYMPTOTIC ESTIMATES FOR APOSTOL-BERNOULLI AND APOSTOL-EULER POLYNOMIALS LUIS M. NAVAS, FRANCISCO J. RUIZ, AND JUAN L. VARONA Abstract. We analyze the asymptotic behavior of the Apostol-Bernoulli polynomials
Bernoulli Polynomials
 Chapter 4 Bernoulli Polynomials 4. Bernoulli Numbers The generating function for the Bernoulli numbers is x e x = n= B n n! xn. (4.) That is, we are to expand the left-hand side of this equation in powers
Chapter 4 Bernoulli Polynomials 4. Bernoulli Numbers The generating function for the Bernoulli numbers is x e x = n= B n n! xn. (4.) That is, we are to expand the left-hand side of this equation in powers
Sharp inequalities and complete monotonicity for the Wallis ratio
 Sharp inequalities and complete monotonicity for the Wallis ratio Cristinel Mortici Abstract The aim of this paper is to prove the complete monotonicity of a class of functions arising from Kazarinoff
Sharp inequalities and complete monotonicity for the Wallis ratio Cristinel Mortici Abstract The aim of this paper is to prove the complete monotonicity of a class of functions arising from Kazarinoff
An improper integral and an infinite series
 An improper integral and an infinite series A. Baltimore one of the old cities in the United States Yue Kwok Choy In summer of 2010, I had great time visiting my daughter, Wendy, who is living in a small
An improper integral and an infinite series A. Baltimore one of the old cities in the United States Yue Kwok Choy In summer of 2010, I had great time visiting my daughter, Wendy, who is living in a small
Lecture 2: Review of Prerequisites. Table of contents
 Math 348 Fall 217 Lecture 2: Review of Prerequisites Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams. In this
Math 348 Fall 217 Lecture 2: Review of Prerequisites Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams. In this
Approximation theory
 Approximation theory Xiaojing Ye, Math & Stat, Georgia State University Spring 2019 Numerical Analysis II Xiaojing Ye, Math & Stat, Georgia State University 1 1 1.3 6 8.8 2 3.5 7 10.1 Least 3squares 4.2
Approximation theory Xiaojing Ye, Math & Stat, Georgia State University Spring 2019 Numerical Analysis II Xiaojing Ye, Math & Stat, Georgia State University 1 1 1.3 6 8.8 2 3.5 7 10.1 Least 3squares 4.2
The evaluation of integrals of Bessel functions via G-function identities
 The evaluation of integrals of Bessel functions via G-function identities Victor Adamchik Wolfram earch Inc., 1 Trade Center Dr., Champaign, IL 6182, USA Abstract A few transformations are presented for
The evaluation of integrals of Bessel functions via G-function identities Victor Adamchik Wolfram earch Inc., 1 Trade Center Dr., Champaign, IL 6182, USA Abstract A few transformations are presented for
IDENTITIES ABOUT INFINITE SERIES CONTAINING HYPERBOLIC FUNCTIONS AND TRIGONOMETRIC FUNCTIONS. Sung-Geun Lim
 Korean J. Math. 19 (2011), No. 4, pp. 465 480 IDENTITIES ABOUT INFINITE SERIES CONTAINING HYPERBOLIC FUNCTIONS AND TRIGONOMETRIC FUNCTIONS Sung-Geun Lim Abstract. B. C. Berndt established many identities
Korean J. Math. 19 (2011), No. 4, pp. 465 480 IDENTITIES ABOUT INFINITE SERIES CONTAINING HYPERBOLIC FUNCTIONS AND TRIGONOMETRIC FUNCTIONS Sung-Geun Lim Abstract. B. C. Berndt established many identities
ON EVALUATION OF RIEMANN ZETA FUNCTION ζ(s) 1. Introduction. It is well-known that the Riemann Zeta function defined by. ζ(s) = n s, R(s) > 1 (2)
 ON EVALUATION OF RIEMANN ZETA FUNCTION ζ(s) QIU-MING LUO, BAI-NI GUO, AND FENG QI Abstract. In this paper, by using Fourier series theory, several summing formulae for Riemann Zeta function ζ(s) and Dirichlet
ON EVALUATION OF RIEMANN ZETA FUNCTION ζ(s) QIU-MING LUO, BAI-NI GUO, AND FENG QI Abstract. In this paper, by using Fourier series theory, several summing formulae for Riemann Zeta function ζ(s) and Dirichlet
n f(k) k=1 means to evaluate the function f(k) at k = 1, 2,..., n and add up the results. In other words: n f(k) = f(1) + f(2) f(n). 1 = 2n 2.
 Handout on induction and written assignment 1. MA113 Calculus I Spring 2007 Why study mathematical induction? For many students, mathematical induction is an unfamiliar topic. Nonetheless, this is an important
Handout on induction and written assignment 1. MA113 Calculus I Spring 2007 Why study mathematical induction? For many students, mathematical induction is an unfamiliar topic. Nonetheless, this is an important
FRACTIONAL HYPERGEOMETRIC ZETA FUNCTIONS
 FRACTIONAL HYPERGEOMETRIC ZETA FUNCTIONS HUNDUMA LEGESSE GELETA, ABDULKADIR HASSEN Both authors would like to dedicate this in fond memory of Marvin Knopp. Knop was the most humble and exemplary teacher
FRACTIONAL HYPERGEOMETRIC ZETA FUNCTIONS HUNDUMA LEGESSE GELETA, ABDULKADIR HASSEN Both authors would like to dedicate this in fond memory of Marvin Knopp. Knop was the most humble and exemplary teacher
The Continuing Story of Zeta
 The Continuing Story of Zeta Graham Everest, Christian Röttger and Tom Ward November 3, 2006. EULER S GHOST. We can only guess at the number of careers in mathematics which have been launched by the sheer
The Continuing Story of Zeta Graham Everest, Christian Röttger and Tom Ward November 3, 2006. EULER S GHOST. We can only guess at the number of careers in mathematics which have been launched by the sheer
1 Review of di erential calculus
 Review of di erential calculus This chapter presents the main elements of di erential calculus needed in probability theory. Often, students taking a course on probability theory have problems with concepts
Review of di erential calculus This chapter presents the main elements of di erential calculus needed in probability theory. Often, students taking a course on probability theory have problems with concepts
Chapter 1. Functions 1.1. Functions and Their Graphs
 1.1 Functions and Their Graphs 1 Chapter 1. Functions 1.1. Functions and Their Graphs Note. We start by assuming that you are familiar with the idea of a set and the set theoretic symbol ( an element of
1.1 Functions and Their Graphs 1 Chapter 1. Functions 1.1. Functions and Their Graphs Note. We start by assuming that you are familiar with the idea of a set and the set theoretic symbol ( an element of
Euler s Formula for.2n/
 Euler s Formula for.2n/ Timothy W. Jones January 28, 208 Abstract In this article we derive a formula for zeta(2) and zeta(2n). Introduction In this paper we derive from scratch k 2 D 2 6 () and k 2p D.
Euler s Formula for.2n/ Timothy W. Jones January 28, 208 Abstract In this article we derive a formula for zeta(2) and zeta(2n). Introduction In this paper we derive from scratch k 2 D 2 6 () and k 2p D.
UNIVERSITY OF CAMBRIDGE
 UNIVERSITY OF CAMBRIDGE DOWNING COLLEGE MATHEMATICS FOR ECONOMISTS WORKBOOK This workbook is intended for students coming to Downing College Cambridge to study Economics 2018/ 19 1 Introduction Mathematics
UNIVERSITY OF CAMBRIDGE DOWNING COLLEGE MATHEMATICS FOR ECONOMISTS WORKBOOK This workbook is intended for students coming to Downing College Cambridge to study Economics 2018/ 19 1 Introduction Mathematics
RECENT RESULTS ON STIELTJES CONSTANTS ADDENDUM TO HIGHER DERIVATIVES OF THE HURWITZ ZETA FUNCTION. 1. Introduction
 RECENT RESULTS ON STIELTJES CONSTANTS ADDENDUM TO HIGHER DERIVATIVES OF THE HURWITZ ZETA FUNCTION DOMINIC LANPHIER. Introduction Much recent significant wor on the arithmetic and analytic properties of
RECENT RESULTS ON STIELTJES CONSTANTS ADDENDUM TO HIGHER DERIVATIVES OF THE HURWITZ ZETA FUNCTION DOMINIC LANPHIER. Introduction Much recent significant wor on the arithmetic and analytic properties of
arxiv:math/ v1 [math.ca] 8 Nov 2003
![arxiv:math/ v1 [math.ca] 8 Nov 2003 arxiv:math/ v1 [math.ca] 8 Nov 2003](/thumbs/89/100985604.jpg) arxiv:math/0311126v1 [math.ca] 8 Nov 2003 PARTIAL SUMS OF HYPERGEOMETRIC SERIES OF UNIT ARGUMENT 1 WOLFGANG BÜHRING Abstract. The asymptotic behaviour of partial sums of generalized hypergeometric series
arxiv:math/0311126v1 [math.ca] 8 Nov 2003 PARTIAL SUMS OF HYPERGEOMETRIC SERIES OF UNIT ARGUMENT 1 WOLFGANG BÜHRING Abstract. The asymptotic behaviour of partial sums of generalized hypergeometric series
Some applications of the Hermite matrix polynomials series expansions 1
 Journal of Computational and Applied Mathematics 99 (1998) 105 117 Some applications of the Hermite matrix polynomials series expansions 1 Emilio Defez, Lucas Jodar Departamento de Matematica Aplicada,
Journal of Computational and Applied Mathematics 99 (1998) 105 117 Some applications of the Hermite matrix polynomials series expansions 1 Emilio Defez, Lucas Jodar Departamento de Matematica Aplicada,
Mathematics 324 Riemann Zeta Function August 5, 2005
 Mathematics 324 Riemann Zeta Function August 5, 25 In this note we give an introduction to the Riemann zeta function, which connects the ideas of real analysis with the arithmetic of the integers. Define
Mathematics 324 Riemann Zeta Function August 5, 25 In this note we give an introduction to the Riemann zeta function, which connects the ideas of real analysis with the arithmetic of the integers. Define
Certain Dual Series Equations Involving Generalized Laguerre Polynomials
 International Journal of Computational and Applied Mathematics. ISSN 1819-4966 Volume 11, Number 1 (2016), pp. 55-59 Research India Publications http://www.ripublication.com Certain Dual Series Equations
International Journal of Computational and Applied Mathematics. ISSN 1819-4966 Volume 11, Number 1 (2016), pp. 55-59 Research India Publications http://www.ripublication.com Certain Dual Series Equations
Yet another failed attempt to prove the Irrationality of ζ(5)
 Yet another failed attempt to prove the Irrationality of ζ5 Abstract Introduction The irrationality of the values of the Riemann zeta function at even integers has been known since Euler. However, for
Yet another failed attempt to prove the Irrationality of ζ5 Abstract Introduction The irrationality of the values of the Riemann zeta function at even integers has been known since Euler. However, for
Newton, Fermat, and Exactly Realizable Sequences
 1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 8 (2005), Article 05.1.2 Newton, Fermat, and Exactly Realizable Sequences Bau-Sen Du Institute of Mathematics Academia Sinica Taipei 115 TAIWAN mabsdu@sinica.edu.tw
1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 8 (2005), Article 05.1.2 Newton, Fermat, and Exactly Realizable Sequences Bau-Sen Du Institute of Mathematics Academia Sinica Taipei 115 TAIWAN mabsdu@sinica.edu.tw
Phase Calculations for Planar Partition Polynomials
 Phase Calculations for Planar Partition Polynomials Robert Boyer and Daniel Parry Abstract. In the study of the asymptotic behavior of polynomials from partition theory, the determination of their leading
Phase Calculations for Planar Partition Polynomials Robert Boyer and Daniel Parry Abstract. In the study of the asymptotic behavior of polynomials from partition theory, the determination of their leading
Math 421 Midterm 2 review questions
 Math 42 Midterm 2 review questions Paul Hacking November 7, 205 () Let U be an open set and f : U a continuous function. Let be a smooth curve contained in U, with endpoints α and β, oriented from α to
Math 42 Midterm 2 review questions Paul Hacking November 7, 205 () Let U be an open set and f : U a continuous function. Let be a smooth curve contained in U, with endpoints α and β, oriented from α to
Computing the Principal Branch of log-gamma
 Computing the Principal Branch of log-gamma by D.E.G. Hare Symbolic Computation Group Department of Computer Science University of Waterloo Waterloo, Canada Revised: August 11, 1994 Abstract The log-gamma
Computing the Principal Branch of log-gamma by D.E.G. Hare Symbolic Computation Group Department of Computer Science University of Waterloo Waterloo, Canada Revised: August 11, 1994 Abstract The log-gamma
Splitting Fields for Characteristic Polynomials of Matrices with Entries in a Finite Field.
 Splitting Fields for Characteristic Polynomials of Matrices with Entries in a Finite Field. Eric Schmutz Mathematics Department, Drexel University,Philadelphia, Pennsylvania, 19104. Abstract Let M n be
Splitting Fields for Characteristic Polynomials of Matrices with Entries in a Finite Field. Eric Schmutz Mathematics Department, Drexel University,Philadelphia, Pennsylvania, 19104. Abstract Let M n be
THE RIEMANN ZETA FUNCTION (s; a) := n= (n + a) s (R(s) > ; a 6= ; ; ; :::) ; (.) can indeed be extended meromorphically to the whole complex s-plane e
 SOME DEFINITE INTEGRALS ASSOCIATED WITH THE RIEMANN ZETA FUNCTION H.M. Srivastava Department of Mathematics Statistics University of Victoria Victoria, British Columbia V8W P4, Canada E-Mail: harimsri@math.uvic.ca
SOME DEFINITE INTEGRALS ASSOCIATED WITH THE RIEMANN ZETA FUNCTION H.M. Srivastava Department of Mathematics Statistics University of Victoria Victoria, British Columbia V8W P4, Canada E-Mail: harimsri@math.uvic.ca
On Tornheim's double series
 ACTA ARITHMETICA LXXV.2 (1996) On Tornheim's double series JAMES G. HUARD (Buffalo, N.Y.), KENNETH S. WILLIAMS (Ottawa, Ont.) and ZHANG NAN-YUE (Beijing) 1. Introduction. We call the double infinite series
ACTA ARITHMETICA LXXV.2 (1996) On Tornheim's double series JAMES G. HUARD (Buffalo, N.Y.), KENNETH S. WILLIAMS (Ottawa, Ont.) and ZHANG NAN-YUE (Beijing) 1. Introduction. We call the double infinite series
Math 229: Introduction to Analytic Number Theory Čebyšev (and von Mangoldt and Stirling)
 ath 9: Introduction to Analytic Number Theory Čebyšev (and von angoldt and Stirling) Before investigating ζ(s) and L(s, χ) as functions of a complex variable, we give another elementary approach to estimating
ath 9: Introduction to Analytic Number Theory Čebyšev (and von angoldt and Stirling) Before investigating ζ(s) and L(s, χ) as functions of a complex variable, we give another elementary approach to estimating
P -adic root separation for quadratic and cubic polynomials
 P -adic root separation for quadratic and cubic polynomials Tomislav Pejković Abstract We study p-adic root separation for quadratic and cubic polynomials with integer coefficients. The quadratic and reducible
P -adic root separation for quadratic and cubic polynomials Tomislav Pejković Abstract We study p-adic root separation for quadratic and cubic polynomials with integer coefficients. The quadratic and reducible
A Subrecursive Refinement of FTA. of the Fundamental Theorem of Algebra
 A Subrecursive Refinement of the Fundamental Theorem of Algebra P. Peshev D. Skordev Faculty of Mathematics and Computer Science University of Sofia Computability in Europe, 2006 Outline Introduction 1
A Subrecursive Refinement of the Fundamental Theorem of Algebra P. Peshev D. Skordev Faculty of Mathematics and Computer Science University of Sofia Computability in Europe, 2006 Outline Introduction 1
FUNCTIONAL SEQUENTIAL AND TRIGONOMETRIC SUMMABILITY OF REAL AND COMPLEX FUNCTIONS
 International Journal of Analysis Applications ISSN 91-8639 Volume 15, Number (17), -8 DOI: 1.894/91-8639-15-17- FUNCTIONAL SEQUENTIAL AND TRIGONOMETRIC SUMMABILITY OF REAL AND COMPLEX FUNCTIONS M.H. HOOSHMAND
International Journal of Analysis Applications ISSN 91-8639 Volume 15, Number (17), -8 DOI: 1.894/91-8639-15-17- FUNCTIONAL SEQUENTIAL AND TRIGONOMETRIC SUMMABILITY OF REAL AND COMPLEX FUNCTIONS M.H. HOOSHMAND
Investigating Geometric and Exponential Polynomials with Euler-Seidel Matrices
 1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 14 (2011), Article 11.4.6 Investigating Geometric and Exponential Polynomials with Euler-Seidel Matrices Ayhan Dil and Veli Kurt Department of Mathematics
1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 14 (2011), Article 11.4.6 Investigating Geometric and Exponential Polynomials with Euler-Seidel Matrices Ayhan Dil and Veli Kurt Department of Mathematics
Spurious Chaotic Solutions of Dierential. Equations. Sigitas Keras. September Department of Applied Mathematics and Theoretical Physics
 UNIVERSITY OF CAMBRIDGE Numerical Analysis Reports Spurious Chaotic Solutions of Dierential Equations Sigitas Keras DAMTP 994/NA6 September 994 Department of Applied Mathematics and Theoretical Physics
UNIVERSITY OF CAMBRIDGE Numerical Analysis Reports Spurious Chaotic Solutions of Dierential Equations Sigitas Keras DAMTP 994/NA6 September 994 Department of Applied Mathematics and Theoretical Physics
UNIFORM BOUNDS FOR BESSEL FUNCTIONS
 Journal of Applied Analysis Vol. 1, No. 1 (006), pp. 83 91 UNIFORM BOUNDS FOR BESSEL FUNCTIONS I. KRASIKOV Received October 8, 001 and, in revised form, July 6, 004 Abstract. For ν > 1/ and x real we shall
Journal of Applied Analysis Vol. 1, No. 1 (006), pp. 83 91 UNIFORM BOUNDS FOR BESSEL FUNCTIONS I. KRASIKOV Received October 8, 001 and, in revised form, July 6, 004 Abstract. For ν > 1/ and x real we shall
List of mathematical functions
 List of mathematical functions From Wikipedia, the free encyclopedia In mathematics, a function or groups of functions are important enough to deserve their own names. This is a listing of articles which
List of mathematical functions From Wikipedia, the free encyclopedia In mathematics, a function or groups of functions are important enough to deserve their own names. This is a listing of articles which
Automatic Sequences and Transcendence of Real Numbers
 Automatic Sequences and Transcendence of Real Numbers Wu Guohua School of Physical and Mathematical Sciences Nanyang Technological University Sendai Logic School, Tohoku University 28 Jan, 2016 Numbers
Automatic Sequences and Transcendence of Real Numbers Wu Guohua School of Physical and Mathematical Sciences Nanyang Technological University Sendai Logic School, Tohoku University 28 Jan, 2016 Numbers
On the Natural Logarithm Function and its Applications
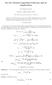 On the Natral Logarithm Fnction and its Applications By Edigles Gedes Febrary 4, 8 at March 7, 5 We love him, becase he rst loved s. - I John 4:9 Abstract. In present article, we create new integral representations
On the Natral Logarithm Fnction and its Applications By Edigles Gedes Febrary 4, 8 at March 7, 5 We love him, becase he rst loved s. - I John 4:9 Abstract. In present article, we create new integral representations
Bernstein-Szegö Inequalities in Reproducing Kernel Hilbert Spaces ABSTRACT 1. INTRODUCTION
 Malaysian Journal of Mathematical Sciences 6(2): 25-36 (202) Bernstein-Szegö Inequalities in Reproducing Kernel Hilbert Spaces Noli N. Reyes and Rosalio G. Artes Institute of Mathematics, University of
Malaysian Journal of Mathematical Sciences 6(2): 25-36 (202) Bernstein-Szegö Inequalities in Reproducing Kernel Hilbert Spaces Noli N. Reyes and Rosalio G. Artes Institute of Mathematics, University of
arxiv: v1 [math.ca] 10 Dec 2017
![arxiv: v1 [math.ca] 10 Dec 2017 arxiv: v1 [math.ca] 10 Dec 2017](/thumbs/94/120119353.jpg) ON THE HIGHER DERIVATIVES OF THE INVERSE TANGENT FUNCTION MOHAMED AMINE BOUTICHE AND MOURAD RAHMANI arxiv:1710351v1 [mathca] 10 Dec 017 Abstract In this paper, we find explicit formulas for higher order
ON THE HIGHER DERIVATIVES OF THE INVERSE TANGENT FUNCTION MOHAMED AMINE BOUTICHE AND MOURAD RAHMANI arxiv:1710351v1 [mathca] 10 Dec 017 Abstract In this paper, we find explicit formulas for higher order
arxiv: v2 [math.nt] 4 Jun 2016
![arxiv: v2 [math.nt] 4 Jun 2016 arxiv: v2 [math.nt] 4 Jun 2016](/thumbs/89/100982161.jpg) ON THE p-adic VALUATION OF STIRLING NUMBERS OF THE FIRST KIND PAOLO LEONETTI AND CARLO SANNA arxiv:605.07424v2 [math.nt] 4 Jun 206 Abstract. For all integers n k, define H(n, k) := /(i i k ), where the
ON THE p-adic VALUATION OF STIRLING NUMBERS OF THE FIRST KIND PAOLO LEONETTI AND CARLO SANNA arxiv:605.07424v2 [math.nt] 4 Jun 206 Abstract. For all integers n k, define H(n, k) := /(i i k ), where the
On Tornheim s double series
 ACTA ARITHMETICA LXXV.2 (1996 On Tornheim s double series by James G. Huard (Buffalo, N.Y., Kenneth S. Williams (Ottawa, Ont. and Zhang Nan-Yue (Beijing 1. Introduction. We call the double infinite series
ACTA ARITHMETICA LXXV.2 (1996 On Tornheim s double series by James G. Huard (Buffalo, N.Y., Kenneth S. Williams (Ottawa, Ont. and Zhang Nan-Yue (Beijing 1. Introduction. We call the double infinite series
Formulas for Factorial N
 mathematics of computation volume 39, number 160 october 1982, pages 655-662 Formulas for Factorial N By Francis J. Murray Abstract. Burnside's and Stirling's formulas for factorial N are special cases
mathematics of computation volume 39, number 160 october 1982, pages 655-662 Formulas for Factorial N By Francis J. Murray Abstract. Burnside's and Stirling's formulas for factorial N are special cases
NORMAL NUMBERS AND UNIFORM DISTRIBUTION (WEEKS 1-3) OPEN PROBLEMS IN NUMBER THEORY SPRING 2018, TEL AVIV UNIVERSITY
 ORMAL UMBERS AD UIFORM DISTRIBUTIO WEEKS -3 OPE PROBLEMS I UMBER THEORY SPRIG 28, TEL AVIV UIVERSITY Contents.. ormal numbers.2. Un-natural examples 2.3. ormality and uniform distribution 2.4. Weyl s criterion
ORMAL UMBERS AD UIFORM DISTRIBUTIO WEEKS -3 OPE PROBLEMS I UMBER THEORY SPRIG 28, TEL AVIV UIVERSITY Contents.. ormal numbers.2. Un-natural examples 2.3. ormality and uniform distribution 2.4. Weyl s criterion
A TALE OF TWO CONFORMALLY INVARIANT METRICS
 A TALE OF TWO CONFORMALLY INVARIANT METRICS H. S. BEAR AND WAYNE SMITH Abstract. The Harnack metric is a conformally invariant metric defined in quite general domains that coincides with the hyperbolic
A TALE OF TWO CONFORMALLY INVARIANT METRICS H. S. BEAR AND WAYNE SMITH Abstract. The Harnack metric is a conformally invariant metric defined in quite general domains that coincides with the hyperbolic
Congruences involving Bernoulli and Euler numbers Zhi-Hong Sun
 The aer will aear in Journal of Nuber Theory. Congruences involving Bernoulli Euler nubers Zhi-Hong Sun Deartent of Matheatics, Huaiyin Teachers College, Huaian, Jiangsu 300, PR China Received January
The aer will aear in Journal of Nuber Theory. Congruences involving Bernoulli Euler nubers Zhi-Hong Sun Deartent of Matheatics, Huaiyin Teachers College, Huaian, Jiangsu 300, PR China Received January
Coecient bounds for certain subclasses of analytic functions of complex order
 Hacettepe Journal of Mathematics and Statistics Volume 45 (4) (2016), 1015 1022 Coecient bounds for certain subclasses of analytic functions of complex order Serap Bulut Abstract In this paper, we introduce
Hacettepe Journal of Mathematics and Statistics Volume 45 (4) (2016), 1015 1022 Coecient bounds for certain subclasses of analytic functions of complex order Serap Bulut Abstract In this paper, we introduce
On Computably Enumerable Sets over Function Fields
 On Computably Enumerable Sets over Function Fields Alexandra Shlapentokh East Carolina University Joint Meetings 2017 Atlanta January 2017 Some History Outline 1 Some History A Question and the Answer
On Computably Enumerable Sets over Function Fields Alexandra Shlapentokh East Carolina University Joint Meetings 2017 Atlanta January 2017 Some History Outline 1 Some History A Question and the Answer
1 + lim. n n+1. f(x) = x + 1, x 1. and we check that f is increasing, instead. Using the quotient rule, we easily find that. 1 (x + 1) 1 x (x + 1) 2 =
 Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
