Discrete Time Sliding Mode Flow Controllers for Connection-Oriented Networks with Lossy Links
|
|
|
- Alannah Thompson
- 6 years ago
- Views:
Transcription
1 BULGARIAN ACADEMY OF SCIENCES CYBERNEICS AND INFORMAION ECHNOLOGIES Volume 3, No Sofi 3 Prit ISSN: 3-97; Olie ISSN: DOI:.478/it-3-9 Disrete ime Slidig Mode Flow Cotrollers for Coetio-Orieted Networks with Lossy Liks Adrze Brtoszewiz, Piotr Leśiewski Istitute of Automti Cotrol, ehil Uiversity of Łódź, 8/ Stefowskiego St., 9-94 Łódź, Pold Emils: drze.brtoszewiz@p.lodz.pl piotr.lesiewski@gmil.om Abstrt: I this pper we propose two disrete-time slidig mode flow otrollers for multisoure oetio-orieted etworks. Eh oetio i the osidered etworks is hrterized by time dely d pket loss rtio. he proposed otrollers tke dvtge of ppropritely desiged slidig hyperples, whih esure the losed-loop system stbility d fiite-time error overgee to zero. Moreover, the proposed otrollers esure full utiliztio of the bottleek lik vilble bdwidth, gurtee bouded trsmissio rtes, d elimite the risk of buffer overflow i the bottleek ode. Sie the primry otroller my led to exessive vlues of the trsmissio rte t the begiig of the otrol proess, the modified otroller is desiged usig the oept of the rehig lw, whih helps the removig of the udesirble effet. Keywords: Cogestio otrol, slidig mode otrol, disrete time systems.. Itrodutio I oetio-orieted ommuitio etworks the dt uits, set by soures pss through series of itermedite odes before rehig their destitios. If itermedite ode due to limited dt flow rte of its outgoig lik ot pss o ll the dt it reeives, the ogestio ours. Cosequetly, i order to mximize the throughput d miimize the queuig delys d itter i moder ommuitio etworks, ogestio otrol lgorithms re pplied. he mi diffiulty i pproprite ogestio otrol lgorithm desig is used by the lrge propgtio delys i the etworks. he delys re ievitble sie iformtio 7
2 bout the ogestio t speifi ode must be dispthed to ll soures trsmittig dt through this ode, i order to eble dustmet of the soure trsmissio rtes, d this tio does ot ffet the ogested ode immeditely, but oly with dely usully lled Roud rip ime (R). he problem of ogestio otrol i the oetio-orieted ommuitio etworks hs bee studied i my ppers (see for exmple [,, 5, 6]) d extesive review of the ppers be foud i the reet moogrph []. Furthermore, due to the robustess of the Slidig Mode (SM) otrol [7], vrious types of SM ogestio otrollers hve bee proposed. I [3] SM otroller with stte preditor ws used, d the mximum dely, eessry for the system stbility hs bee estblished. A fuzzy otroller ombiig the dvtges of lier d termil SM ws proposed i [4] for simplified dely-free etwork model. For DiffServ etwork dptive SM otroller (usig the bksteppig proedure) for model whih eglets the feedbk ltey ws preseted i []. O the other hd, for DiffServ etwork with dely, the seod order SM tehique hs bee pplied i [] i order to redue the htterig of the otrol sigl. I [] the problem of fir (i the mx-mi sese) dt rte distributio mog the soures is osidered. A biry ogestio sigl is used to otrol the dt output of the soures d the lysis of this lgorithm is performed for dely-free system. All otrollers preseted i the foremetioed publitios re desiged i the otiuous time domi. However, it is evidet tht y flow otrol lgorithm for dt trsmissio etwork must be implemeted s digitl otroller. herefore, i the followig works disrete-time pproh to the problem of the dt flow otrol ws used. A SM otroller ws preseted i [8], but the result of this pper ws derived without osiderig the system delys. I [9] it is show tht y mx-mi fir system with stble symmetri Jobi mtrix mitis symptoti stbility uder rbitrry diretiol delys. his mes tht if the otroller is desiged so tht the system hs symmetri Jobi mtrix, its stbility be exmied bsed o the orrespodig udelyed system. A dedbet SM otroller for multi-soure etworks with priori kow roud trip times is preseted i [3] d i [7] LQ optiml SM otroller for sigle-soure etworks is proposed. he sme pproh is the exteded for multi-soure etworks i [8], d i [9], similr optiml flow otroller is desiged for multisoure etworks with the roud trip times whih my hge durig the otrol proess. I most ppers published up to ow, oly pket losses due to bottleek lik buffer overflows re osidered, d the ourree of lossy liks i the etwork is egleted. Sie i rel etworks trsmissio losses re ievitble, i this pper we preset disrete-time slidig mode otrollers [, 4, 5, 6, ] for multisoure etworks, i whih pkets re lost durig the trsmissio proess.. Network model We osider oetio-orieted ommuitio etwork whih osists of persistet dt soures, itermedite odes d dt destitios. We ssume tht 8
3 ll oetios pss through sigle bottleek ode. he totl mout of dt to be set (represeted by u) by ll of the soures is determied by otroller pled t the bottleek ode. We ssume tht this mout is distributed mog the oetios by y higher-level lgorithm. Eh oetio p reeives γ p of the totl rte, where γ p, d m p= γ = wher p e m is the umber of soures. I this wy the flow otrol d the totl rte distributio re deoupled. he blok digrm of the etwork is show i Fig.. Eh sigl γ p u rehes soure p fter bkwrd dely b p. he soure the seds the requested mout of dt, whih is pssed from ode ode util it rehes the bottleek queue fter the forwrd dely f p. Fig.. he etwork model he roud trip time of eh oetio the dely betwee geertig the sigl by the otroller, d the momet whe the requested dt from soure p rrives t the bottleek ode, be expressed s sum of the bkwrd d forwrd propgtio delys () R p = b p + f p. It is ssumed, tht durig the trsmissio some peretge of dt pkets re lost, so tht oly α p γ p u dt pkets from the soure p rrive t the buffer, where α p (, for p =,,..., m. We ssume tht eh R p is multiple of the disretiztio period, i.e., R p = m R p. Furthermore, y(k) deotes the bottleek queue legth t the time istt k. he mout of the dt whih my leve the bottleek ode t time k is modeled s priori ukow futio of time d(k). he mximum vlue of d(k) is represeted by d mx. he mout of dt tully levig the buffer t time k is deoted by h(k). For y k () h k d k d. mx ( ) ( ) It is ssumed thtt the buffer is empty prior to the dt trsmissio proess, i.e., y(k < ) =, dd tht the first otrol sigl is geerted t k =, i.e., u(k < ) =. he queue legth for y k be lulted from the followig expressio 9
4 (3) y( k) = αγ p pu( p) h( ) m k k R. p= = = o simplify the model we represet ll oetios with equl roud trip times s sigle oetio. he mout of dt tht will rrive t the buffer from this oetio is equl to i u, where = α γ, i =,,, d i p p pm : Rp = i = mx(m Rp ) +. Obviously, if o oetio hs the roud trip time i, the the orrespodig oeffiiet i equls zero. Now we rewrite (3) s follows: k k (4) y( k) = u ( i) h( ) i = = he etwork be desribed i the stte spe s x ( k + ) = Ax( k) + bu( k) + oh( k), (5) y( k) = q x( k), where x(k) = [x (k) x (k) x (k)] is the stte vetor d y(k) = x (k) is the queue legth. he stte vribles exept x re the delyed vlues of the otrol sigl, i.e. (6) xi ( k ) = u ( k + i ), i =,,. A is stte mtrix, (7) Α =, d b, o, d q re vetors (8) b= o= q =. Altertively, the stte spe equtio be writte s follows: x ( k + ) = x( k) + x( k) + x3( k) + + x( k) h( k) x ( k + ) = x3( k) (9), x ( k + ) = x( k) x ( k + ) = u( k).
5 with the output sigl y(k) = x (k). he desired stte of the system is deoted by x d = [x d x d x d ]. he first stte vrible x d is the demd queue legth, d further i the pper it is represeted by x d. It be otied from (9) tht for h(k) = ll other ompoets of the demd stte vetor re equl to zero. 3. Proposed otrol strtegy Further i the pper we pply the etwork model preseted i the previous setio to desig two slidig mode ogestio otrollers: lssil ded-bet otroller d its rehig lw bsed extesio. 3.. Primry slidig mode otroller I this setio the flow otrol lgorithms for the desribed etwork re desiged d essetil properties of the lgorithms re proved. For the purpose of the otroller desig we ssume h(k) = d we itrodue slidig hyperple desribed by equtio () s( k) = e ( k) =, where vetor = [ ] stisfies b. he losed-loop system error is deoted by e(k) = x d x(k). Substitutig (5) ito e[(k + )] = we obti the followig otrol lw () u( k) ( b) x Ax ( k) = d, with the pplitio of this otrol sigl, the losed-loop system stte mtrix hs the form A = [ b( b) ]A. he hrteristi polyomil of this mtrix be foud s () det + = z + z, ( zi A ) z z whih leds to the oditio. A disrete-time system is symptotilly stble if d oly if ll its eigevlues re loted iside uit irle. Furthermore, i order to esure error overgee to zero i fiite time, the hrteristi polyomil () hs to stisfy (3) det ( zi A ) = z. Oe esily fid tht (3) is stisfied with the followig vetor =, i (4) i = for i =,,. = Substitutig (7) d (8) ito () we obti
6 (5) ( ) u k xd x k = ( ) ( ) x x k x k d i i = = = ( ) u ( k ) i + i. = his ompletes the desig of the primry flow otrol lgorithm for the osidered etwork. Further i this setio, importt properties of the proposed lgorithm will be disussed. Let us first otie tht the mout of dt to be set t the iitil otrol istt is xd (6) u( ) =. Next we determie the reltio betwee the utilized bdwidth d the trsmissio rte geerted by the otroller. his reltio is stted i the followig lemm. Lemm. If the proposed otroller is pplied, the its output sigl for y k > is give by (7) u( k) = h ( k ). = P r o o f: From (4), for y i = 3,,, we obti (8). i = i + + i he usig (8) d (5) we get u ( k + ) = xd x ( k ) ixi ( k ) u( k) + + = (9) = xd x ( k ) ixi ( k ) + + xd x ( k ) ixi ( k ) h( k ) h ( k ). = = his equtio hs bee derived ssumig k. If we ssume k > we rewrite it to be idetil to (7). his eds the proof. = =
7 Remrk. Beuse h(k), d mx for y k, d (, this lemm with (6) imply tht the vlue of the otrol sigl is lwys oegtive d upper-bouded. Further importt properties of the proposed otroller re give i the followig two theorems. heorem. With the pplitio of the proposed otrol lgorithm the queue legth ever exeeds its demd vlue. P r o o f: rsformig (5) we obti () x x ( k) u( k) u ( k i ) = + +. d i Sie i for i (, ), usig Remrk we olude tht the right hd side of () is oegtive, whih implies tht x (k) x d for y k. his eds the proof. heorem. If the proposed otroller is pplied d the demd queue legth stisfies iequlity () x d > ( ) i i+ dmx, = the the queue legth is stritly positive for y k > mx(m Rp ) +. Proof: We observe, tht u(k < ) =. his llows us to rewrite (4) for k > mx(m Rp ) + s k k y( k) = iu ( i) h( ) = = = i k k = iu ( i) + u i ( ) + i u ( i) h( ) = = = i+ = k k x d = i + i u ( i) h( ) = = i+ = () = k i k = xd + i h( ) h( ) = = = = k i h( ) i ( i+ ) dmx = k i x d = = = = xd + >. 3
8 his eds the proof. his theorem shows tht if oditio () is stisfied, the the queue legth is stritly greter th zero for y k > mx(m Rp ) + whih implies tht the vilble bdwidth is fully used. 3.. Rehig lw bsed slidig mode otroller A disdvtge of the slidig mode otroller preseted i the previous hpter is the lrge vlue of the otrol sigl t the iitil time istt. herefore, i this subsetio we itrodue rehig lw bsed otrol strtegy i order to miimize this effet. he properties of the modified strtegy re the formulted d proved. I order to desig the modified otroller, we dpt the rehig lw proposed i [6]. It be formulted i the followig wy (3) s ( k + ) s( k) = φ s( k), where φ[s(k)] = mi[ s(k), δ]sg[s(k)] d δ >.With this lw pplied to the ded-bet type otroller like the oe proposed i the previous subsetio the system represettive poit is gurteed to reh the hyperple s(k) = mootoilly i fiite umber of steps. Equtio (3) be ltertively expressed s follows (4) s ( ) k = e( k ) + f ( k ), where s (k) is ew slidig vrible, vetor is give by (4) d futio f(k) is defied s follows f ( k ) = f ( ) sg{ ( ) } for, (5) k + δ s k k < k f ( k ) = for k k. We ssume, tht s () =, whih results i the followig oditio (6) f ( ) = e ( ) = x d = xd. I this wy the represettive poit will move towrds the origil slidig hyperple desribed by (), tti it fter k, d remi o it fterwrds. Now we will determie the reltio betwee the desig prmeter δ d the time istt k. From (5) we obti (7) f ( k ) = f ( ) + δ( k ) sg s( ) = xd + δ ( k ). If f(k ) =, the f[(k )] δ. From this reltio it follows tht x (8) d k =, δ where futio ξ deotes the smllest iteger greter th its rgumet ξ. his shows how the hoie of prmeter δ ffets the time istt whe the represettive poit rehes the slidig hyperple. With the pplitio of the proposed rehig lw, the otrol sigl be derived by substitutig (5) ito equtio e[(k + )] + f[(k + )] =. his leds to (9) u( k) = ( b) { x ( k) + f ( k + ) d Ax } 4 Substitutig (7), (8) d (4) ito (9) we obti.
9 (3) u( k) = xd x ( k) i xi( k) + f ( k ). + his ompletes the desig of the rehig lw bsed otrol strtegy. Further i this setio, we stte d prove importt properties of the proposed strtegy. Lemm shows tht the otrol sigl is lwys oegtive d upper bouded. heorems 3 d 4 (logous to heorems d ) show tht the queue legth ever exeeds its demd vlue d tht fter some iitil time the queue legth is lwys stritly positive, whih mes tht the vilble bdwidth is fully used. Lemm. If the desiged slidig mode otroller is pplied, the its output for y k stisfies h ( k ) + f ( k + ) f ( k) (3) u( k) =. Proof: he proof is similr to the proof of Lemm. We rewrite (3) s u( k) = xd x ( k) ixi ( k) + f ( k ) u ( k ) + = = xd x ( k ) ixi ( k ) + f ( k ) + + (3) xd x ( k ) i xi ( k ) f ( k) + = h ( k ) + f ( k + ) f ( k) =. = = = his eds the proof. Remrk. We otie tht f(k) is o-deresig, h(k), d (,. From this it follows, tht the otrol sigl is lwys oegtive. Furthermore h(k) d mx, d mx{f[(k + )] f(k)} = δ. his mes tht the otrol sigl is lwys upper-bouded, i.e., dm x + δ (33) u( k) for y k. By pproprite hoie of futio f(k) we obtied ostt upper boud o the otrol sigl, whih is prtil for pplitio i rel etwork. heorem 3. If the proposed otrol strtegy is pplied, the the queue legth ever exeeds its demd vlue. Proof: Usig (6) we trsform (3) d obti = 5
10 (34) 6 d ( ) x x k ( ) = u k + = = ( ) ( ) iu k + i f k +. Futio f(k) is lwys smller th or equl to zero, >, d from = Remrk the otrol sigl is lwys oegtive. his mes, tht the right hd x k x d eds the proof. side of equtio (34) is oegtive, whih gives ( ) d heorem 4. If the proposed otrol lgorithm is pplied, d the demd queue legth stisfies the followig oditio (35) x d > i ( + ) i = the for y k > k + mx(m Rp ) + the queue legth is stritly greter th zero. P r o o f: Usig (3) d reltio u(k < ) =, we rewrite (4) for y k > k + mx(m Rp ) + s follows: (36) his eds the proof. ( ) ( ) d mx k k { i } ( ) y k = u i h = = = k k = i u ( i) h( ) = = i = k i h ( ) f ( ) f ( ) k = i + + h ( ) = = = r r r= r= k i h ( ) ( ) k =+ i f h ( ) = = = r r= k i k = xd + i h( ) h( ) = = = r r= k ( ) ( ) = =, i h i i+ dmx = k i = xd x. d
11 his theorem shows tht if the demd queue legth stisfies the sme oditio s for the bsi versio of the ded-bet slidig mode otroller, the the queue legth is stritly greter th zero for y k > k + mx(m Rp ) +, whih implies tht the vilble bdwidth is fully used. 4. Simultio exmples I order to verify the properties of the proposed flow otrol strtegy, omputer simultios of the etwork with 4 dt soures were performed. As stted i Setio, we ssume tht the distributio of dt rte mog the oetios is performed by some higher-level lgorithm. he disretistio period is seleted s ms. he prmeters of the oetios re show i ble. ble. Lik prmeters i the simulted etwork p 3 4 m Rp b p, ms 3 5 γ p α p Beuse mx(m Rp ) = 9, we get =. Aordig to Setio, the stte spe etwork model prmeters re: =, =.98, 3 =, 4 =.97, 5 =, 6 =.38, 7 =, 8 =, 9 =.86. he mximum vilble bdwidth of the bottleek ode is d mx = 3 kb. Aordig to heorems d 4 i order to esure full bdwidth utiliztio, the demd queue legth must be greter th 97 kb for both proposed otrollers. herefore, the demd queue legth hs bee hose s kb. he vilble bdwidth hges rpidly from low to high vlues, whih reflets the most dverse possible oditios i the etwork. he vilble bdwidth is show i Fig.. For the rehig lw bsed slidig mode otroller, prmeter δ hs bee hose s 35 kb, whih ordig to (8) gives k = 6. Fig.. Avilble bdwidth Fig. 3 shows the bottleek lik queue legth whe the primry ded-bet otroller is pplied. We otie from the figure tht the queue legth ever exeeds its demd vlue, d fter the iitil time derived i heorem it is lwys stritly positive. herefore, there is o risk of buffer overflow, d full bdwidth 7
12 utiliztio is esured. he vlue of the otrol sigl d the mout of dt levig the buffer re show i Fig. 4. he vlue of the otrol sigl t the first time istt is equl to 8. kb. As oe see from the figure, the otrol sigl is lwys stritly positive d upper bouded. he trsmissio rtes of idividul soures with the pplitio of the bsi otrol strtegy re show i Fig. 5. Fig. 3. Queue legth with pplitio of the primry slidig mode otroller Fig. 4. Amout of dt levig the buffer d the otrol sigl with pplitio of the primry slidig mode otroller 8 Fig. 5. rsmissio rtes of idividul soures i the etwork with the primry slidig mode otroller
13 Figs 6, 7 d 8 preset the simultio results obtied for the rehig lw bsed slidig mode otroller. Fig. 6 shows the queue legth i the bottleek lik buffer. It be see from the figure, tht the queue ever exeeds its demd vlue d fter the iitil time predited by heorem 4, it is lwys stritly positive. Fig. 7 shows the mout of dt levig the buffer d the vlue of the otrol sigl. Comprig Figs 4 d 7 oe otie, tht the itrodutio of the rehig lw sigifitly redues the mximum vlue of the otrol sigl t the begiig of the dt trsmissio proess. he trsmissio rtes of idividul soures re show i Fig. 8. Fig. 6. Queue legth with pplitio of the rehig lw bsed slidig mode otroller Fig. 7. he mout of dt levig the buffer d the otrol sigl with pplitio of the rehig lw bsed otroller Fig. 8. rsmissio rtes of idividul soures i the etwork with the rehig lw bsed slidig mode otroller 9
14 5. Colusios I this pper two disrete time slidig mode flow otrollers for oetioorieted etworks with multiple oetios hve bee preseted. he possible losses durig the trsmissio hve bee expliitly tke ito out i desigig the slidig hyperple. he first lgorithm hs bee desiged to esure fiite-time error overgee. he it hs bee modified by itroduig rehig lw to redue the mximum vlue of the otrol sigl t the begiig of the dt trsmissio. It hs bee proved tht the flow rtes geerted by both otrol lgorithms re lwys oegtive d upper-bouded. Furthermore, both proposed otrollers esure full bottleek bdwidth osumptio d elimite the risk of buffer overflow. Akowledgemet: his work hs bee performed i the frmework of Proet Optiml Slidig Mode Cotrol of ime Dely Systems, fied by the Ntiol Siee Cetre of Pold Deisio No DEC //B/S7/ Referees. Bdyopdhyy, B., S. Jrdh. Disrete-ime Slidig Mode Cotrol: A Multirte Output Feedbk Approh. Berli, Heidelberg, Spriger-Verlg, 6.. B r t o s z e w i z, A. Nolier Flow Cotrol Strtegies for Coetio-Orieted Commuitio Networks. I: IEE Proeedigs o Cotrol heory d Applitios, Vol. 53, 6, Brtoszewiz, A., J. Ż u k. Disrete ime Slidig Mode Flow Cotroller for Multi-Soure Sigle-Bottleek Coetio-Orieted Commuitio Networks. Jourl of Vibrtio d Cotrol, Vol. 5, 9, No, F u r u t, K. Slidig Mode Cotrol of Disrete System. Systems & Cotrol Letters, Vol. 4, 99, G o, W., Y. W g, A. H o m i f. Disrete-ime Vrible Struture Cotrol Systems. IEEE rstios o Idustril Eletrois, Vol. 4, 995, G o l o, G., Ć. Milosvlević. Robust Disrete-ime Chtterig Free Slidig Mode Cotrol. Systems & Cotrol Letters, Vol. 4,, I g i u k, P., A. B r t o s z e w i z. Lier Qudrti Optiml Disrete-ime Slidig-Mode Cotroller for Coetio-Orieted Commuitio Networks. IEEE rstios o Idustril Eletrois, Vol. 55, 8, Igiuk, P., A. Brtoszewiz. Lier Qudrti Optiml Slidig Mode Flow Cotrol for Coetio-Orieted Commuitio Networks. Itertiol Jourl of Robust d Nolier Cotrol, Vol. 9, 9, I g i u k, P., A. B r t o s z e w i z. Disrete-ime Slidig-Mode Cogestio Cotrol i Multisoure Commuitio Networks with ime-vryig Dely. IEEE rstios o Cotrol Systems ehology, Vol. 9,, I g i u k, P., A. B r t o s z e w i z. Cogestio Cotrol i Dt rsmissio Networks Slidig Mode d Other Desigs. Lodo, Spriger-Verlg,.. J g t h, S., J. l l u r i. Preditive Cogestio Cotrol of AM Networks: Multiple Soures/Sigle Buffer Serio. Automti, Vol. 38,, J i, J., W. H. W g, M. P l i s w m i. A Simple Frmework of Utility Mx-Mi Flow Cotrol usig Slidig Mode Approh. IEEE Commuitio Letters, Vol. 3, 9,
15 3. J i g, Y., L. H e, G. M. D i m i r o v s k i, H. Z h u. Robust Stbiliztio of Stte d Iput Dely for Ative Queue Mgemet Algorithm. I: Pro. of the Ameri Cotrol Coferee, 7, J i g, Y., N. Y u, Z. K o g, G. M. D i m i r o v s k i. Ative Queue Mgemet Algorithm Bsed o Fuzzy Slidig Model Cotroller. I: Pro. of 7th IFAC World Cogress, 8, Lberteux, K., C. Rohrs, P. Atsklis. A Prtil Cotroller for Expliit Rte Cogestio Cotrol. IEEE rstios o Automti Cotrol, Vol. 47,, L e g l i z, I., F. K m o u. A Rte-Bsed Flow Cotrol Method for ABR Servie i AM Networks. Computer Networks, Vol. 34,, U t k i, V. Vrible Struture Systems with Slidig Modes. IEEE rstios o Automti Cotrol, Vol., 977, Y, M.,. D. Kolemisevsk-Gugulovsk, Y. Jig, G. M. Dimirovski. Robust Disrete-ime Slidig-Mode Cotrol Algorithm for CP Networks Cogestio Cotrol. I: Pro ELSIKS, 7, Y g, M., Y. J i g, G. M. D i m i r o v s k i, N. Z h g. Stbility d Performe Alysis of Cogestio Cotrol Algorithm for Networks. I: Pro. of 46th IEEE Coferee Deisio d Cotrol, New Orles, USA, 7, Y u, X., B. W g, X. L i. Computer-Cotrolled Vrible Struture Systems: he Stte of the Art. IEEE rstios o Idustril Iformtis, Vol. 8,, Z h g, N., M. Y g, Y. J i g, S. Z h g. Cogestio Cotrol for DiffServ Network usig Seod-Order Slidig Mode Cotrol. IEEE rstios o Idustril Eletrois, Vol. 56, 9, Z h e g, X., N. Z h g, G. M. D i m i r o v s k i, Y. J i g. Adptive Slidig Mode Cogestio Cotrol for DiffServ Network. I: Pro. of 7th IFAC World Cogress, 8,
CS 331 Design and Analysis of Algorithms. -- Divide and Conquer. Dr. Daisy Tang
 CS 33 Desig d Alysis of Algorithms -- Divide d Coquer Dr. Disy Tg Divide-Ad-Coquer Geerl ide: Divide problem ito subproblems of the sme id; solve subproblems usig the sme pproh, d ombie prtil solutios,
CS 33 Desig d Alysis of Algorithms -- Divide d Coquer Dr. Disy Tg Divide-Ad-Coquer Geerl ide: Divide problem ito subproblems of the sme id; solve subproblems usig the sme pproh, d ombie prtil solutios,
Riemann Integral Oct 31, such that
 Riem Itegrl Ot 31, 2007 Itegrtio of Step Futios A prtitio P of [, ] is olletio {x k } k=0 suh tht = x 0 < x 1 < < x 1 < x =. More suitly, prtitio is fiite suset of [, ] otiig d. It is helpful to thik of
Riem Itegrl Ot 31, 2007 Itegrtio of Step Futios A prtitio P of [, ] is olletio {x k } k=0 suh tht = x 0 < x 1 < < x 1 < x =. More suitly, prtitio is fiite suset of [, ] otiig d. It is helpful to thik of
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS. Assoc. Prof. Dr. Burak Kelleci. Spring 2018
 DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Assoc. Prof. Dr. Bur Kelleci Sprig 8 OUTLINE The Z-Trsform The Regio of covergece for the Z-trsform The Iverse Z-Trsform Geometric
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Assoc. Prof. Dr. Bur Kelleci Sprig 8 OUTLINE The Z-Trsform The Regio of covergece for the Z-trsform The Iverse Z-Trsform Geometric
AN DIGITAL FILTER DESIGN SCHEME BASED ON MATRIX TRANSFORMATION
 Jourl of heoretil d Applied Iformtio ehology 5 th November. Vol. 5 No. 5 - JAI & LLS. All rights reserved. ISSN: 99-865 www.jtit.org E-ISSN: 87-95 AN DIGIAL FILER DESIGN SCHEME BASED ON MARIX RANSFORMAION
Jourl of heoretil d Applied Iformtio ehology 5 th November. Vol. 5 No. 5 - JAI & LLS. All rights reserved. ISSN: 99-865 www.jtit.org E-ISSN: 87-95 AN DIGIAL FILER DESIGN SCHEME BASED ON MARIX RANSFORMAION
MATH 104: INTRODUCTORY ANALYSIS SPRING 2008/09 PROBLEM SET 10 SOLUTIONS. f m. and. f m = 0. and x i = a + i. a + i. a + n 2. n(n + 1) = a(b a) +
 MATH 04: INTRODUCTORY ANALYSIS SPRING 008/09 PROBLEM SET 0 SOLUTIONS Throughout this problem set, B[, b] will deote the set of ll rel-vlued futios bouded o [, b], C[, b] the set of ll rel-vlued futios
MATH 04: INTRODUCTORY ANALYSIS SPRING 008/09 PROBLEM SET 0 SOLUTIONS Throughout this problem set, B[, b] will deote the set of ll rel-vlued futios bouded o [, b], C[, b] the set of ll rel-vlued futios
MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS. and x i = a + i. i + n(n + 1)(2n + 1) + 2a. (b a)3 6n 2
 MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS 6.9: Let f(x) { x 2 if x Q [, b], 0 if x (R \ Q) [, b], where > 0. Prove tht b. Solutio. Let P { x 0 < x 1 < < x b} be regulr prtitio
MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS 6.9: Let f(x) { x 2 if x Q [, b], 0 if x (R \ Q) [, b], where > 0. Prove tht b. Solutio. Let P { x 0 < x 1 < < x b} be regulr prtitio
Air Compressor Driving with Synchronous Motors at Optimal Parameters
 Iuliu Petri, Adri Vleti Petri AALELE UIVERSITĂłII EFTIMIE MURGU REŞIłA AUL XVII, R., 010, ISS 1453-7397 Air Compressor Drivig with Syhroous Motors t Optiml Prmeters I this pper method of optiml ompestio
Iuliu Petri, Adri Vleti Petri AALELE UIVERSITĂłII EFTIMIE MURGU REŞIłA AUL XVII, R., 010, ISS 1453-7397 Air Compressor Drivig with Syhroous Motors t Optiml Prmeters I this pper method of optiml ompestio
Convergence rates of approximate sums of Riemann integrals
 Jourl of Approximtio Theory 6 (9 477 49 www.elsevier.com/locte/jt Covergece rtes of pproximte sums of Riem itegrls Hiroyuki Tski Grdute School of Pure d Applied Sciece, Uiversity of Tsukub, Tsukub Ibrki
Jourl of Approximtio Theory 6 (9 477 49 www.elsevier.com/locte/jt Covergece rtes of pproximte sums of Riem itegrls Hiroyuki Tski Grdute School of Pure d Applied Sciece, Uiversity of Tsukub, Tsukub Ibrki
Neighborhoods of Certain Class of Analytic Functions of Complex Order with Negative Coefficients
 Ge Mth Notes Vol 2 No Jury 20 pp 86-97 ISSN 229-784; Copyriht ICSRS Publitio 20 wwwi-srsor Avilble free olie t http://wwwemi Neihborhoods of Certi Clss of Alyti Futios of Complex Order with Netive Coeffiiets
Ge Mth Notes Vol 2 No Jury 20 pp 86-97 ISSN 229-784; Copyriht ICSRS Publitio 20 wwwi-srsor Avilble free olie t http://wwwemi Neihborhoods of Certi Clss of Alyti Futios of Complex Order with Netive Coeffiiets
Introduction of Fourier Series to First Year Undergraduate Engineering Students
 Itertiol Jourl of Adved Reserh i Computer Egieerig & Tehology (IJARCET) Volume 3 Issue 4, April 4 Itrodutio of Fourier Series to First Yer Udergrdute Egieerig Studets Pwr Tejkumr Dtttry, Hiremth Suresh
Itertiol Jourl of Adved Reserh i Computer Egieerig & Tehology (IJARCET) Volume 3 Issue 4, April 4 Itrodutio of Fourier Series to First Yer Udergrdute Egieerig Studets Pwr Tejkumr Dtttry, Hiremth Suresh
EXPONENTS AND LOGARITHMS
 978--07-6- Mthemtis Stdrd Level for IB Diplom Eerpt EXPONENTS AND LOGARITHMS WHAT YOU NEED TO KNOW The rules of epoets: m = m+ m = m ( m ) = m m m = = () = The reltioship etwee epoets d rithms: = g where
978--07-6- Mthemtis Stdrd Level for IB Diplom Eerpt EXPONENTS AND LOGARITHMS WHAT YOU NEED TO KNOW The rules of epoets: m = m+ m = m ( m ) = m m m = = () = The reltioship etwee epoets d rithms: = g where
Thomas J. Osler Mathematics Department Rowan University Glassboro NJ Introduction
 Ot 0 006 Euler s little summtio formul d speil vlues of te zet futio Toms J Osler temtis Deprtmet Row Uiversity Glssboro J 0608 Osler@rowedu Itrodutio I tis ote we preset elemetry metod of determiig vlues
Ot 0 006 Euler s little summtio formul d speil vlues of te zet futio Toms J Osler temtis Deprtmet Row Uiversity Glssboro J 0608 Osler@rowedu Itrodutio I tis ote we preset elemetry metod of determiig vlues
SPH3UW Unit 7.5 Snell s Law Page 1 of Total Internal Reflection occurs when the incoming refraction angle is
 SPH3UW Uit 7.5 Sell s Lw Pge 1 of 7 Notes Physis Tool ox Refrtio is the hge i diretio of wve due to hge i its speed. This is most ommoly see whe wve psses from oe medium to other. Idex of refrtio lso lled
SPH3UW Uit 7.5 Sell s Lw Pge 1 of 7 Notes Physis Tool ox Refrtio is the hge i diretio of wve due to hge i its speed. This is most ommoly see whe wve psses from oe medium to other. Idex of refrtio lso lled
Frequency-domain Characteristics of Discrete-time LTI Systems
 requecy-domi Chrcteristics of Discrete-time LTI Systems Prof. Siripog Potisuk LTI System descriptio Previous bsis fuctio: uit smple or DT impulse The iput sequece is represeted s lier combitio of shifted
requecy-domi Chrcteristics of Discrete-time LTI Systems Prof. Siripog Potisuk LTI System descriptio Previous bsis fuctio: uit smple or DT impulse The iput sequece is represeted s lier combitio of shifted
Modified Farey Trees and Pythagorean Triples
 Modified Frey Trees d Pythgore Triples By Shi-ihi Kty Deprtet of Mthetil Siees, Fulty of Itegrted Arts d Siees, The Uiversity of Tokushi, Tokushi 0-0, JAPAN e-il ddress : kty@istokushi-ujp Abstrt I 6,
Modified Frey Trees d Pythgore Triples By Shi-ihi Kty Deprtet of Mthetil Siees, Fulty of Itegrted Arts d Siees, The Uiversity of Tokushi, Tokushi 0-0, JAPAN e-il ddress : kty@istokushi-ujp Abstrt I 6,
Waves in dielectric media. Waveguiding: χ (r ) Wave equation in linear non-dispersive homogenous and isotropic media
 Wves i dieletri medi d wveguides Setio 5. I this leture, we will osider the properties of wves whose propgtio is govered by both the diffrtio d ofiemet proesses. The wveguides re result of the ble betwee
Wves i dieletri medi d wveguides Setio 5. I this leture, we will osider the properties of wves whose propgtio is govered by both the diffrtio d ofiemet proesses. The wveguides re result of the ble betwee
Project 3: Using Identities to Rewrite Expressions
 MAT 5 Projet 3: Usig Idetities to Rewrite Expressios Wldis I lger, equtios tht desrie properties or ptters re ofte lled idetities. Idetities desrie expressio e repled with equl or equivlet expressio tht
MAT 5 Projet 3: Usig Idetities to Rewrite Expressios Wldis I lger, equtios tht desrie properties or ptters re ofte lled idetities. Idetities desrie expressio e repled with equl or equivlet expressio tht
Convergence rates of approximate sums of Riemann integrals
 Covergece rtes of pproximte sums of Riem itegrls Hiroyuki Tski Grdute School of Pure d Applied Sciece, Uiversity of Tsuku Tsuku Irki 5-857 Jp tski@mth.tsuku.c.jp Keywords : covergece rte; Riem sum; Riem
Covergece rtes of pproximte sums of Riem itegrls Hiroyuki Tski Grdute School of Pure d Applied Sciece, Uiversity of Tsuku Tsuku Irki 5-857 Jp tski@mth.tsuku.c.jp Keywords : covergece rte; Riem sum; Riem
Numerical Methods. Lecture 5. Numerical integration. dr hab. inż. Katarzyna Zakrzewska, prof. AGH. Numerical Methods lecture 5 1
 Numeril Methods Leture 5. Numeril itegrtio dr h. iż. Ktrzy Zkrzewsk, pro. AGH Numeril Methods leture 5 Outlie Trpezoidl rule Multi-segmet trpezoidl rule Rihrdso etrpoltio Romerg's method Simpso's rule
Numeril Methods Leture 5. Numeril itegrtio dr h. iż. Ktrzy Zkrzewsk, pro. AGH Numeril Methods leture 5 Outlie Trpezoidl rule Multi-segmet trpezoidl rule Rihrdso etrpoltio Romerg's method Simpso's rule
Chapter 2. LOGARITHMS
 Chpter. LOGARITHMS Dte: - 009 A. INTRODUCTION At the lst hpter, you hve studied bout Idies d Surds. Now you re omig to Logrithms. Logrithm is ivers of idies form. So Logrithms, Idies, d Surds hve strog
Chpter. LOGARITHMS Dte: - 009 A. INTRODUCTION At the lst hpter, you hve studied bout Idies d Surds. Now you re omig to Logrithms. Logrithm is ivers of idies form. So Logrithms, Idies, d Surds hve strog
THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK SUMMER EXAMINATION 2005 FIRST ENGINEERING
 OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK SUMMER EXAMINATION 2005 FIRST ENGINEERING MATHEMATICS MA008 Clculus d Lier
OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK SUMMER EXAMINATION 2005 FIRST ENGINEERING MATHEMATICS MA008 Clculus d Lier
1/16/2013. Overview. 05-Three Phase Analysis Text: Three Phase. Three-Phase Voltages. Benefits of Three-Phase Systems.
 oltge () 1/16/21 Overview 5Three Phse Alysis Text: 2.4 2.7 ECEGR 451 Power Systems ThreePhse Soures Delt d Y Coetios ThreePhse Lods ThreePhse Power ThreePhse Alysis PerPhse Alysis Dr. Louie 2 ThreePhse
oltge () 1/16/21 Overview 5Three Phse Alysis Text: 2.4 2.7 ECEGR 451 Power Systems ThreePhse Soures Delt d Y Coetios ThreePhse Lods ThreePhse Power ThreePhse Alysis PerPhse Alysis Dr. Louie 2 ThreePhse
=> PARALLEL INTERCONNECTION. Basic Properties LTI Systems. The Commutative Property. Convolution. The Commutative Property. The Distributive Property
 Lier Time-Ivrit Bsic Properties LTI The Commuttive Property The Distributive Property The Associtive Property Ti -6.4 / Chpter Covolutio y ] x ] ] x ]* ] x ] ] y] y ( t ) + x( τ ) h( t τ ) dτ x( t) * h(
Lier Time-Ivrit Bsic Properties LTI The Commuttive Property The Distributive Property The Associtive Property Ti -6.4 / Chpter Covolutio y ] x ] ] x ]* ] x ] ] y] y ( t ) + x( τ ) h( t τ ) dτ x( t) * h(
Error-free compression
 Error-free compressio Useful i pplictio where o loss of iformtio is tolerble. This mybe due to ccurcy requiremets, legl requiremets, or less th perfect qulity of origil imge. Compressio c be chieved by
Error-free compressio Useful i pplictio where o loss of iformtio is tolerble. This mybe due to ccurcy requiremets, legl requiremets, or less th perfect qulity of origil imge. Compressio c be chieved by
Section 11.5 Notes Page Partial Fraction Decomposition. . You will get: +. Therefore we come to the following: x x
 Setio Notes Pge Prtil Frtio Deompositio Suppose we were sked to write the followig s sigle frtio: We would eed to get ommo deomitors: You will get: Distributig o top will give you: 8 This simplifies to:
Setio Notes Pge Prtil Frtio Deompositio Suppose we were sked to write the followig s sigle frtio: We would eed to get ommo deomitors: You will get: Distributig o top will give you: 8 This simplifies to:
MA123, Chapter 9: Computing some integrals (pp )
 MA13, Chpter 9: Computig some itegrls (pp. 189-05) Dte: Chpter Gols: Uderstd how to use bsic summtio formuls to evlute more complex sums. Uderstd how to compute its of rtiol fuctios t ifiity. Uderstd how
MA13, Chpter 9: Computig some itegrls (pp. 189-05) Dte: Chpter Gols: Uderstd how to use bsic summtio formuls to evlute more complex sums. Uderstd how to compute its of rtiol fuctios t ifiity. Uderstd how
Observer Design with Reduced Measurement Information
 Observer Desig with Redued Measuremet Iformatio I pratie all the states aot be measured so that SVF aot be used Istead oly a redued set of measuremets give by y = x + Du p is available where y( R We assume
Observer Desig with Redued Measuremet Iformatio I pratie all the states aot be measured so that SVF aot be used Istead oly a redued set of measuremets give by y = x + Du p is available where y( R We assume
B. Examples 1. Finite Sums finite sums are an example of Riemann Sums in which each subinterval has the same length and the same x i
 Mth 06 Clculus Sec. 5.: The Defiite Itegrl I. Riem Sums A. Def : Give y=f(x):. Let f e defied o closed itervl[,].. Prtitio [,] ito suitervls[x (i-),x i ] of legth Δx i = x i -x (i-). Let P deote the prtitio
Mth 06 Clculus Sec. 5.: The Defiite Itegrl I. Riem Sums A. Def : Give y=f(x):. Let f e defied o closed itervl[,].. Prtitio [,] ito suitervls[x (i-),x i ] of legth Δx i = x i -x (i-). Let P deote the prtitio
Review of the Riemann Integral
 Chpter 1 Review of the Riem Itegrl This chpter provides quick review of the bsic properties of the Riem itegrl. 1.0 Itegrls d Riem Sums Defiitio 1.0.1. Let [, b] be fiite, closed itervl. A prtitio P of
Chpter 1 Review of the Riem Itegrl This chpter provides quick review of the bsic properties of the Riem itegrl. 1.0 Itegrls d Riem Sums Defiitio 1.0.1. Let [, b] be fiite, closed itervl. A prtitio P of
FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES. To a 2π-periodic function f(x) we will associate a trigonometric series. a n cos(nx) + b n sin(nx),
 FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES To -periodic fuctio f() we will ssocite trigoometric series + cos() + b si(), or i terms of the epoetil e i, series of the form c e i. Z For most of the
FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES To -periodic fuctio f() we will ssocite trigoometric series + cos() + b si(), or i terms of the epoetil e i, series of the form c e i. Z For most of the
1. (25 points) Use the limit definition of the definite integral and the sum formulas to compute. [1 x + x2
 Mth 3, Clculus II Fil Exm Solutios. (5 poits) Use the limit defiitio of the defiite itegrl d the sum formuls to compute 3 x + x. Check your swer by usig the Fudmetl Theorem of Clculus. Solutio: The limit
Mth 3, Clculus II Fil Exm Solutios. (5 poits) Use the limit defiitio of the defiite itegrl d the sum formuls to compute 3 x + x. Check your swer by usig the Fudmetl Theorem of Clculus. Solutio: The limit
Data Compression Techniques (Spring 2012) Model Solutions for Exercise 4
 58487 Dt Compressio Tehiques (Sprig 0) Moel Solutios for Exerise 4 If you hve y fee or orretios, plese ott jro.lo t s.helsii.fi.. Prolem: Let T = Σ = {,,, }. Eoe T usig ptive Huffm oig. Solutio: R 4 U
58487 Dt Compressio Tehiques (Sprig 0) Moel Solutios for Exerise 4 If you hve y fee or orretios, plese ott jro.lo t s.helsii.fi.. Prolem: Let T = Σ = {,,, }. Eoe T usig ptive Huffm oig. Solutio: R 4 U
a f(x)dx is divergent.
 Mth 250 Exm 2 review. Thursdy Mrh 5. Brig TI 30 lultor but NO NOTES. Emphsis o setios 5.5, 6., 6.2, 6.3, 3.7, 6.6, 8., 8.2, 8.3, prt of 8.4; HW- 2; Q-. Kow for trig futios tht 0.707 2/2 d 0.866 3/2. From
Mth 250 Exm 2 review. Thursdy Mrh 5. Brig TI 30 lultor but NO NOTES. Emphsis o setios 5.5, 6., 6.2, 6.3, 3.7, 6.6, 8., 8.2, 8.3, prt of 8.4; HW- 2; Q-. Kow for trig futios tht 0.707 2/2 d 0.866 3/2. From
Section 6.3: Geometric Sequences
 40 Chpter 6 Sectio 6.: Geometric Sequeces My jobs offer ul cost-of-livig icrese to keep slries cosistet with ifltio. Suppose, for exmple, recet college grdute fids positio s sles mger erig ul slry of $6,000.
40 Chpter 6 Sectio 6.: Geometric Sequeces My jobs offer ul cost-of-livig icrese to keep slries cosistet with ifltio. Suppose, for exmple, recet college grdute fids positio s sles mger erig ul slry of $6,000.
Ch. 12 Linear Bayesian Estimators
 h. Lier Byesi stimtors Itrodutio I hpter we sw: the MMS estimtor tkes simple form whe d re joitly Gussi it is lier d used oly the st d d order momets (mes d ovries). Without the Gussi ssumptio, the Geerl
h. Lier Byesi stimtors Itrodutio I hpter we sw: the MMS estimtor tkes simple form whe d re joitly Gussi it is lier d used oly the st d d order momets (mes d ovries). Without the Gussi ssumptio, the Geerl
lecture 16: Introduction to Least Squares Approximation
 97 lecture 16: Itroductio to Lest Squres Approximtio.4 Lest squres pproximtio The miimx criterio is ituitive objective for pproximtig fuctio. However, i my cses it is more ppelig (for both computtio d
97 lecture 16: Itroductio to Lest Squres Approximtio.4 Lest squres pproximtio The miimx criterio is ituitive objective for pproximtig fuctio. However, i my cses it is more ppelig (for both computtio d
0 otherwise. sin( nx)sin( kx) 0 otherwise. cos( nx) sin( kx) dx 0 for all integers n, k.
 . Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric
. Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric
ROUTH-HURWITZ CRITERION
 Automti Cotrol Sytem, Deprtmet of Mehtroi Egieerig, Germ Jordi Uiverity Routh-Hurwitz Criterio ite.google.om/ite/ziydmoud 7 ROUTH-HURWITZ CRITERION The Routh-Hurwitz riterio i lytil proedure for determiig
Automti Cotrol Sytem, Deprtmet of Mehtroi Egieerig, Germ Jordi Uiverity Routh-Hurwitz Criterio ite.google.om/ite/ziydmoud 7 ROUTH-HURWITZ CRITERION The Routh-Hurwitz riterio i lytil proedure for determiig
MTH 146 Class 16 Notes
 MTH 46 Clss 6 Notes 0.4- Cotiued Motivtio: We ow cosider the rc legth of polr curve. Suppose we wish to fid the legth of polr curve curve i terms of prmetric equtios s: r f where b. We c view the cos si
MTH 46 Clss 6 Notes 0.4- Cotiued Motivtio: We ow cosider the rc legth of polr curve. Suppose we wish to fid the legth of polr curve curve i terms of prmetric equtios s: r f where b. We c view the cos si
Hypergeometric Functions and Lucas Numbers
 IOSR Jourl of Mthetis (IOSR-JM) ISSN: 78-78. Volue Issue (Sep-Ot. ) PP - Hypergeoetri utios d us Nuers P. Rjhow At Kur Bor Deprtet of Mthetis Guhti Uiversity Guwhti-78Idi Astrt: The i purpose of this pper
IOSR Jourl of Mthetis (IOSR-JM) ISSN: 78-78. Volue Issue (Sep-Ot. ) PP - Hypergeoetri utios d us Nuers P. Rjhow At Kur Bor Deprtet of Mthetis Guhti Uiversity Guwhti-78Idi Astrt: The i purpose of this pper
[ 20 ] 1. Inequality exists only between two real numbers (not complex numbers). 2. If a be any real number then one and only one of there hold.
![[ 20 ] 1. Inequality exists only between two real numbers (not complex numbers). 2. If a be any real number then one and only one of there hold. [ 20 ] 1. Inequality exists only between two real numbers (not complex numbers). 2. If a be any real number then one and only one of there hold.](/thumbs/78/77732161.jpg) [ 0 ]. Iequlity eists oly betwee two rel umbers (ot comple umbers).. If be y rel umber the oe d oly oe of there hold.. If, b 0 the b 0, b 0.. (i) b if b 0 (ii) (iii) (iv) b if b b if either b or b b if
[ 0 ]. Iequlity eists oly betwee two rel umbers (ot comple umbers).. If be y rel umber the oe d oly oe of there hold.. If, b 0 the b 0, b 0.. (i) b if b 0 (ii) (iii) (iv) b if b b if either b or b b if
Fatigue life analysis of the plate structure with random vibro-acoustic loading
 INTER-NOISE 16 Ftigue life lysis of the plte struture with rdom vibro-ousti lodig Go Zhg 1 ; Hubig Jig 1 Istitute of Systems Egieerig, Chi Ademy of Egieerig Physis,Miyg Chi Istitute of Systems Egieerig,
INTER-NOISE 16 Ftigue life lysis of the plte struture with rdom vibro-ousti lodig Go Zhg 1 ; Hubig Jig 1 Istitute of Systems Egieerig, Chi Ademy of Egieerig Physis,Miyg Chi Istitute of Systems Egieerig,
1.3 Continuous Functions and Riemann Sums
 mth riem sums, prt 0 Cotiuous Fuctios d Riem Sums I Exmple we sw tht lim Lower() = lim Upper() for the fuctio!! f (x) = + x o [0, ] This is o ccidet It is exmple of the followig theorem THEOREM Let f be
mth riem sums, prt 0 Cotiuous Fuctios d Riem Sums I Exmple we sw tht lim Lower() = lim Upper() for the fuctio!! f (x) = + x o [0, ] This is o ccidet It is exmple of the followig theorem THEOREM Let f be
A GENERALIZATION OF GAUSS THEOREM ON QUADRATIC FORMS
 A GENERALIZATION OF GAU THEOREM ON QUADRATIC FORM Nicole I Brtu d Adi N Cret Deprtmet of Mth - Criov Uiversity, Romi ABTRACT A origil result cocerig the extesio of Guss s theorem from the theory of biry
A GENERALIZATION OF GAU THEOREM ON QUADRATIC FORM Nicole I Brtu d Adi N Cret Deprtmet of Mth - Criov Uiversity, Romi ABTRACT A origil result cocerig the extesio of Guss s theorem from the theory of biry
ON n-fold FILTERS IN BL-ALGEBRAS
 Jourl of Alger Numer Theor: Adves d Applitios Volume 2 Numer 29 Pges 27-42 ON -FOLD FILTERS IN BL-ALGEBRAS M. SHIRVANI-GHADIKOLAI A. MOUSSAVI A. KORDI 2 d A. AHMADI 2 Deprtmet of Mthemtis Trit Modres Uiversit
Jourl of Alger Numer Theor: Adves d Applitios Volume 2 Numer 29 Pges 27-42 ON -FOLD FILTERS IN BL-ALGEBRAS M. SHIRVANI-GHADIKOLAI A. MOUSSAVI A. KORDI 2 d A. AHMADI 2 Deprtmet of Mthemtis Trit Modres Uiversit
Section IV.6: The Master Method and Applications
 Sectio IV.6: The Mster Method d Applictios Defiitio IV.6.1: A fuctio f is symptoticlly positive if d oly if there exists rel umer such tht f(x) > for ll x >. A cosequece of this defiitio is tht fuctio
Sectio IV.6: The Mster Method d Applictios Defiitio IV.6.1: A fuctio f is symptoticlly positive if d oly if there exists rel umer such tht f(x) > for ll x >. A cosequece of this defiitio is tht fuctio
Surds, Indices, and Logarithms Radical
 MAT 6 Surds, Idices, d Logrithms Rdicl Defiitio of the Rdicl For ll rel, y > 0, d ll itegers > 0, y if d oly if y where is the ide is the rdicl is the rdicd. Surds A umber which c be epressed s frctio
MAT 6 Surds, Idices, d Logrithms Rdicl Defiitio of the Rdicl For ll rel, y > 0, d ll itegers > 0, y if d oly if y where is the ide is the rdicl is the rdicd. Surds A umber which c be epressed s frctio
Similar idea to multiplication in N, C. Divide and conquer approach provides unexpected improvements. Naïve matrix multiplication
 Next. Covered bsics of simple desig techique (Divided-coquer) Ch. of the text.. Next, Strsse s lgorithm. Lter: more desig d coquer lgorithms: MergeSort. Solvig recurreces d the Mster Theorem. Similr ide
Next. Covered bsics of simple desig techique (Divided-coquer) Ch. of the text.. Next, Strsse s lgorithm. Lter: more desig d coquer lgorithms: MergeSort. Solvig recurreces d the Mster Theorem. Similr ide
INFINITE SERIES. ,... having infinite number of terms is called infinite sequence and its indicated sum, i.e., a 1
 Appedix A.. Itroductio As discussed i the Chpter 9 o Sequeces d Series, sequece,,...,,... hvig ifiite umber of terms is clled ifiite sequece d its idicted sum, i.e., + + +... + +... is clled ifite series
Appedix A.. Itroductio As discussed i the Chpter 9 o Sequeces d Series, sequece,,...,,... hvig ifiite umber of terms is clled ifiite sequece d its idicted sum, i.e., + + +... + +... is clled ifite series
Dynamics of Structures
 UNION Dymis of Strutures Prt Zbigiew Wójii Je Grosel Projet o-fied by Europe Uio withi Europe Soil Fud UNION Mtries Defiitio of mtri mtri is set of umbers or lgebri epressios rrged i retgulr form with
UNION Dymis of Strutures Prt Zbigiew Wójii Je Grosel Projet o-fied by Europe Uio withi Europe Soil Fud UNION Mtries Defiitio of mtri mtri is set of umbers or lgebri epressios rrged i retgulr form with
NOP 10 * * * * + NOP NOP + < TIME 1 TIME 2 TIME 3 TIME 4 NOP
 Outlie SCHEDULING The schedulig problem. cgiovi De Micheli Schedulig without costrits. Stford Uiversity Schedulig uder timig costrits. { Reltive schedulig. Schedulig uder resource costrits. { The ILP model.
Outlie SCHEDULING The schedulig problem. cgiovi De Micheli Schedulig without costrits. Stford Uiversity Schedulig uder timig costrits. { Reltive schedulig. Schedulig uder resource costrits. { The ILP model.
Definite Integral. The Left and Right Sums
 Clculus Li Vs Defiite Itegrl. The Left d Right Sums The defiite itegrl rises from the questio of fidig the re betwee give curve d x-xis o itervl. The re uder curve c be esily clculted if the curve is give
Clculus Li Vs Defiite Itegrl. The Left d Right Sums The defiite itegrl rises from the questio of fidig the re betwee give curve d x-xis o itervl. The re uder curve c be esily clculted if the curve is give
CH 19 SOLVING FORMULAS
 1 CH 19 SOLVING FORMULAS INTRODUCTION S olvig equtios suh s 2 + 7 20 is oviousl the orerstoe of lger. But i siee, usiess, d omputers it is lso eessr to solve equtios tht might hve vriet of letters i them.
1 CH 19 SOLVING FORMULAS INTRODUCTION S olvig equtios suh s 2 + 7 20 is oviousl the orerstoe of lger. But i siee, usiess, d omputers it is lso eessr to solve equtios tht might hve vriet of letters i them.
Taylor Polynomials. The Tangent Line. (a, f (a)) and has the same slope as the curve y = f (x) at that point. It is the best
 Tylor Polyomils Let f () = e d let p() = 1 + + 1 + 1 6 3 Without usig clcultor, evlute f (1) d p(1) Ok, I m still witig With little effort it is possible to evlute p(1) = 1 + 1 + 1 (144) + 6 1 (178) =
Tylor Polyomils Let f () = e d let p() = 1 + + 1 + 1 6 3 Without usig clcultor, evlute f (1) d p(1) Ok, I m still witig With little effort it is possible to evlute p(1) = 1 + 1 + 1 (144) + 6 1 (178) =
Radix-2/4 Streamlined Real Factor FFT Algorithms
 SHAIK QADEER et l: RADIX-/ STREAMLIED REAL FACTOR FFT ALGORITHMS Rdix-/ Stremlied Rel Ftor FFT Algorithms Shi Qdeer () Mohmmed Zfr Ali Kh () d Syed A. Sttr () () Deprtmet of Eletril d Eletrois egieerig
SHAIK QADEER et l: RADIX-/ STREAMLIED REAL FACTOR FFT ALGORITHMS Rdix-/ Stremlied Rel Ftor FFT Algorithms Shi Qdeer () Mohmmed Zfr Ali Kh () d Syed A. Sttr () () Deprtmet of Eletril d Eletrois egieerig
CH 20 SOLVING FORMULAS
 CH 20 SOLVING FORMULAS 179 Itrodutio S olvig equtios suh s 2 + 7 20 is oviousl the orerstoe of lger. But i siee, usiess, d omputers it is lso eessr to solve equtios tht might hve vriet of letters i them.
CH 20 SOLVING FORMULAS 179 Itrodutio S olvig equtios suh s 2 + 7 20 is oviousl the orerstoe of lger. But i siee, usiess, d omputers it is lso eessr to solve equtios tht might hve vriet of letters i them.
Chapter 5. The Riemann Integral. 5.1 The Riemann integral Partitions and lower and upper integrals. Note: 1.5 lectures
 Chpter 5 The Riem Itegrl 5.1 The Riem itegrl Note: 1.5 lectures We ow get to the fudmetl cocept of itegrtio. There is ofte cofusio mog studets of clculus betwee itegrl d tiderivtive. The itegrl is (iformlly)
Chpter 5 The Riem Itegrl 5.1 The Riem itegrl Note: 1.5 lectures We ow get to the fudmetl cocept of itegrtio. There is ofte cofusio mog studets of clculus betwee itegrl d tiderivtive. The itegrl is (iformlly)
PROGRESSIONS AND SERIES
 PROGRESSIONS AND SERIES A sequece is lso clled progressio. We ow study three importt types of sequeces: () The Arithmetic Progressio, () The Geometric Progressio, () The Hrmoic Progressio. Arithmetic Progressio.
PROGRESSIONS AND SERIES A sequece is lso clled progressio. We ow study three importt types of sequeces: () The Arithmetic Progressio, () The Geometric Progressio, () The Hrmoic Progressio. Arithmetic Progressio.
POWER SERIES R. E. SHOWALTER
 POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise
POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise
Module B3 3.1 Sinusoidal steady-state analysis (single-phase), a review 3.2 Three-phase analysis. Kirtley
 Module B.1 Siusoidl stedy-stte lysis (sigle-phse), review.2 Three-phse lysis Kirtley Chpter 2: AC Voltge, Curret d Power 2.1 Soures d Power 2.2 Resistors, Idutors, d Cpitors Chpter 4: Polyphse systems
Module B.1 Siusoidl stedy-stte lysis (sigle-phse), review.2 Three-phse lysis Kirtley Chpter 2: AC Voltge, Curret d Power 2.1 Soures d Power 2.2 Resistors, Idutors, d Cpitors Chpter 4: Polyphse systems
Power Series Solutions to Generalized Abel Integral Equations
 Itertiol Jourl of Mthemtics d Computtiol Sciece Vol., No. 5, 5, pp. 5-54 http://www.isciece.org/jourl/ijmcs Power Series Solutios to Geerlized Abel Itegrl Equtios Rufi Abdulli * Deprtmet of Physics d Mthemtics,
Itertiol Jourl of Mthemtics d Computtiol Sciece Vol., No. 5, 5, pp. 5-54 http://www.isciece.org/jourl/ijmcs Power Series Solutios to Geerlized Abel Itegrl Equtios Rufi Abdulli * Deprtmet of Physics d Mthemtics,
Chapter 11 Design of State Variable Feedback Systems
 Chpter Desig of Stte Vrible Feedbck Systems This chpter dels with the desig of cotrollers utilizig stte feedbck We will cosider three mjor subjects: Cotrollbility d observbility d the the procedure for
Chpter Desig of Stte Vrible Feedbck Systems This chpter dels with the desig of cotrollers utilizig stte feedbck We will cosider three mjor subjects: Cotrollbility d observbility d the the procedure for
Remarks: (a) The Dirac delta is the function zero on the domain R {0}.
 Sectio Objective(s): The Dirc s Delt. Mi Properties. Applictios. The Impulse Respose Fuctio. 4.4.. The Dirc Delt. 4.4. Geerlized Sources Defiitio 4.4.. The Dirc delt geerlized fuctio is the limit δ(t)
Sectio Objective(s): The Dirc s Delt. Mi Properties. Applictios. The Impulse Respose Fuctio. 4.4.. The Dirc Delt. 4.4. Geerlized Sources Defiitio 4.4.. The Dirc delt geerlized fuctio is the limit δ(t)
Statistics for Financial Engineering Session 1: Linear Algebra Review March 18 th, 2006
 Sttistics for Ficil Egieerig Sessio : Lier Algebr Review rch 8 th, 6 Topics Itroductio to trices trix opertios Determits d Crmer s rule Eigevlues d Eigevectors Quiz The cotet of Sessio my be fmilir to
Sttistics for Ficil Egieerig Sessio : Lier Algebr Review rch 8 th, 6 Topics Itroductio to trices trix opertios Determits d Crmer s rule Eigevlues d Eigevectors Quiz The cotet of Sessio my be fmilir to
Solution of the exam in TMA4212 Monday 23rd May 2013 Time: 9:00 13:00
 Norwegi Uiversity of Sciece d Techology Deprtmet of Mthemticl Scieces Cotct durig the exm: Ele Celledoi, tlf. 735 93541 Pge 1 of 7 of the exm i TMA4212 Mody 23rd My 2013 Time: 9:00 13:00 Allowed ids: Approved
Norwegi Uiversity of Sciece d Techology Deprtmet of Mthemticl Scieces Cotct durig the exm: Ele Celledoi, tlf. 735 93541 Pge 1 of 7 of the exm i TMA4212 Mody 23rd My 2013 Time: 9:00 13:00 Allowed ids: Approved
Approximations of Definite Integrals
 Approximtios of Defiite Itegrls So fr we hve relied o tiderivtives to evlute res uder curves, work doe by vrible force, volumes of revolutio, etc. More precisely, wheever we hve hd to evlute defiite itegrl
Approximtios of Defiite Itegrls So fr we hve relied o tiderivtives to evlute res uder curves, work doe by vrible force, volumes of revolutio, etc. More precisely, wheever we hve hd to evlute defiite itegrl
2.1.1 Definition The Z-transform of a sequence x [n] is simply defined as (2.1) X re x k re x k r
![2.1.1 Definition The Z-transform of a sequence x [n] is simply defined as (2.1) X re x k re x k r 2.1.1 Definition The Z-transform of a sequence x [n] is simply defined as (2.1) X re x k re x k r](/thumbs/82/85448174.jpg) Z-Trsforms. INTRODUCTION TO Z-TRANSFORM The Z-trsform is coveiet d vluble tool for represetig, lyig d desigig discrete-time sigls d systems. It plys similr role i discrete-time systems to tht which Lplce
Z-Trsforms. INTRODUCTION TO Z-TRANSFORM The Z-trsform is coveiet d vluble tool for represetig, lyig d desigig discrete-time sigls d systems. It plys similr role i discrete-time systems to tht which Lplce
On AP-Henstock Integrals of Interval-Valued. Functions and Fuzzy-Number-Valued Functions.
 Applied Mthemtis, 206, 7, 2285-2295 http://www.sirp.org/jourl/m ISSN Olie: 252-7393 ISSN Prit: 252-7385 O AP-Hestok Itegrls of Itervl-Vlued Futios d Fuzzy-Numer-Vlued Futios Muwy Elsheikh Hmid *, Alshikh
Applied Mthemtis, 206, 7, 2285-2295 http://www.sirp.org/jourl/m ISSN Olie: 252-7393 ISSN Prit: 252-7385 O AP-Hestok Itegrls of Itervl-Vlued Futios d Fuzzy-Numer-Vlued Futios Muwy Elsheikh Hmid *, Alshikh
8.3 Sequences & Series: Convergence & Divergence
 8.3 Sequeces & Series: Covergece & Divergece A sequece is simply list of thigs geerted by rule More formlly, sequece is fuctio whose domi is the set of positive itegers, or turl umbers,,,3,. The rge of
8.3 Sequeces & Series: Covergece & Divergece A sequece is simply list of thigs geerted by rule More formlly, sequece is fuctio whose domi is the set of positive itegers, or turl umbers,,,3,. The rge of
Infinite Series Sequences: terms nth term Listing Terms of a Sequence 2 n recursively defined n+1 Pattern Recognition for Sequences Ex:
 Ifiite Series Sequeces: A sequece i defied s fuctio whose domi is the set of positive itegers. Usully it s esier to deote sequece i subscript form rther th fuctio ottio.,, 3, re the terms of the sequece
Ifiite Series Sequeces: A sequece i defied s fuctio whose domi is the set of positive itegers. Usully it s esier to deote sequece i subscript form rther th fuctio ottio.,, 3, re the terms of the sequece
Addendum. Addendum. Vector Review. Department of Computer Science and Engineering 1-1
 Addedum Addedum Vetor Review Deprtmet of Computer Siee d Egieerig - Coordite Systems Right hded oordite system Addedum y z Deprtmet of Computer Siee d Egieerig - -3 Deprtmet of Computer Siee d Egieerig
Addedum Addedum Vetor Review Deprtmet of Computer Siee d Egieerig - Coordite Systems Right hded oordite system Addedum y z Deprtmet of Computer Siee d Egieerig - -3 Deprtmet of Computer Siee d Egieerig
Introduction to Matrix Algebra
 Itrodutio to Mtri Alger George H Olso, Ph D Dotorl Progrm i Edutiol Ledership Applhi Stte Uiversit Septemer Wht is mtri? Dimesios d order of mtri A p q dimesioed mtri is p (rows) q (olums) rr of umers,
Itrodutio to Mtri Alger George H Olso, Ph D Dotorl Progrm i Edutiol Ledership Applhi Stte Uiversit Septemer Wht is mtri? Dimesios d order of mtri A p q dimesioed mtri is p (rows) q (olums) rr of umers,
z line a) Draw the single phase equivalent circuit. b) Calculate I BC.
 ECE 2260 F 08 HW 7 prob 4 solutio EX: V gyb' b' b B V gyc' c' c C = 101 0 V = 1 + j0.2 Ω V gyb' = 101 120 V = 6 + j0. Ω V gyc' = 101 +120 V z LΔ = 9 j1.5 Ω ) Drw the sigle phse equivlet circuit. b) Clculte
ECE 2260 F 08 HW 7 prob 4 solutio EX: V gyb' b' b B V gyc' c' c C = 101 0 V = 1 + j0.2 Ω V gyb' = 101 120 V = 6 + j0. Ω V gyc' = 101 +120 V z LΔ = 9 j1.5 Ω ) Drw the sigle phse equivlet circuit. b) Clculte
Chapter 7 Infinite Series
 MA Ifiite Series Asst.Prof.Dr.Supree Liswdi Chpter 7 Ifiite Series Sectio 7. Sequece A sequece c be thought of s list of umbers writte i defiite order:,,...,,... 2 The umber is clled the first term, 2
MA Ifiite Series Asst.Prof.Dr.Supree Liswdi Chpter 7 Ifiite Series Sectio 7. Sequece A sequece c be thought of s list of umbers writte i defiite order:,,...,,... 2 The umber is clled the first term, 2
Gauss Elimination, Gauss-Jordan Elimination and Gauss Seidel Iteration Method: Performance Comparison using MAT LAB
 Itertiol Jourl of Egieerig Tehology Siee d Reserh www.ietsr.om ISSN 394 3386 Volume 4, Issue 0 Otober 07 Guss Elimitio, Guss-Jord Elimitio d Guss Seidel Itertio Method: Performe Compriso usig MAT LAB *Dr.
Itertiol Jourl of Egieerig Tehology Siee d Reserh www.ietsr.om ISSN 394 3386 Volume 4, Issue 0 Otober 07 Guss Elimitio, Guss-Jord Elimitio d Guss Seidel Itertio Method: Performe Compriso usig MAT LAB *Dr.
( ) 2 3 ( ) I. Order of operations II. Scientific Notation. Simplify. Write answers in scientific notation. III.
 Assessmet Ceter Elemetry Alger Study Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d otet of questios o the Aupler Elemetry Alger test. Reviewig these smples will give
Assessmet Ceter Elemetry Alger Study Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d otet of questios o the Aupler Elemetry Alger test. Reviewig these smples will give
Certain sufficient conditions on N, p n, q n k summability of orthogonal series
 Avilble olie t www.tjs.com J. Nolier Sci. Appl. 7 014, 7 77 Reserch Article Certi sufficiet coditios o N, p, k summbility of orthogol series Xhevt Z. Krsiqi Deprtmet of Mthemtics d Iformtics, Fculty of
Avilble olie t www.tjs.com J. Nolier Sci. Appl. 7 014, 7 77 Reserch Article Certi sufficiet coditios o N, p, k summbility of orthogol series Xhevt Z. Krsiqi Deprtmet of Mthemtics d Iformtics, Fculty of
Accuplacer Elementary Algebra Study Guide
 Testig Ceter Studet Suess Ceter Aupler Elemetry Alger Study Guide The followig smple questios re similr to the formt d otet of questios o the Aupler Elemetry Alger test. Reviewig these smples will give
Testig Ceter Studet Suess Ceter Aupler Elemetry Alger Study Guide The followig smple questios re similr to the formt d otet of questios o the Aupler Elemetry Alger test. Reviewig these smples will give
Riemann Integration. Chapter 1
 Mesure, Itegrtio & Rel Alysis. Prelimiry editio. 8 July 2018. 2018 Sheldo Axler 1 Chpter 1 Riem Itegrtio This chpter reviews Riem itegrtio. Riem itegrtio uses rectgles to pproximte res uder grphs. This
Mesure, Itegrtio & Rel Alysis. Prelimiry editio. 8 July 2018. 2018 Sheldo Axler 1 Chpter 1 Riem Itegrtio This chpter reviews Riem itegrtio. Riem itegrtio uses rectgles to pproximte res uder grphs. This
The Weierstrass Approximation Theorem
 The Weierstrss Approximtio Theorem Jmes K. Peterso Deprtmet of Biologicl Scieces d Deprtmet of Mthemticl Scieces Clemso Uiversity Februry 26, 2018 Outlie The Wierstrss Approximtio Theorem MtLb Implemettio
The Weierstrss Approximtio Theorem Jmes K. Peterso Deprtmet of Biologicl Scieces d Deprtmet of Mthemticl Scieces Clemso Uiversity Februry 26, 2018 Outlie The Wierstrss Approximtio Theorem MtLb Implemettio
10.5 Power Series. In this section, we are going to start talking about power series. A power series is a series of the form
 0.5 Power Series I the lst three sectios, we ve spet most of tht time tlkig bout how to determie if series is coverget or ot. Now it is time to strt lookig t some specific kids of series d we will evetully
0.5 Power Series I the lst three sectios, we ve spet most of tht time tlkig bout how to determie if series is coverget or ot. Now it is time to strt lookig t some specific kids of series d we will evetully
Merge Sort. Outline and Reading. Divide-and-Conquer. Divide-and-conquer paradigm ( 4.1.1) Merge-sort ( 4.1.1)
 Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 Merge Sort versio 1.3 1 Outlie d Redig Divide-d-coquer prdigm ( 4.1.1 Merge-sort ( 4.1.1 Algorithm Mergig two sorted sequeces Merge-sort tree
Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 Merge Sort versio 1.3 1 Outlie d Redig Divide-d-coquer prdigm ( 4.1.1 Merge-sort ( 4.1.1 Algorithm Mergig two sorted sequeces Merge-sort tree
Autar Kaw Benjamin Rigsby. Transforming Numerical Methods Education for STEM Undergraduates
 Autr Kw Bejmi Rigsby http://m.mthforcollege.com Trsformig Numericl Methods Eductio for STEM Udergrdutes http://m.mthforcollege.com . solve set of simulteous lier equtios usig Nïve Guss elimitio,. ler the
Autr Kw Bejmi Rigsby http://m.mthforcollege.com Trsformig Numericl Methods Eductio for STEM Udergrdutes http://m.mthforcollege.com . solve set of simulteous lier equtios usig Nïve Guss elimitio,. ler the
Closed Newton-Cotes Integration
 Closed Newto-Cotes Itegrtio Jmes Keeslig This documet will discuss Newto-Cotes Itegrtio. Other methods of umericl itegrtio will be discussed i other posts. The other methods will iclude the Trpezoidl Rule,
Closed Newto-Cotes Itegrtio Jmes Keeslig This documet will discuss Newto-Cotes Itegrtio. Other methods of umericl itegrtio will be discussed i other posts. The other methods will iclude the Trpezoidl Rule,
( a n ) converges or diverges.
 Chpter Ifiite Series Pge of Sectio E Rtio Test Chpter : Ifiite Series By the ed of this sectio you will be ble to uderstd the proof of the rtio test test series for covergece by pplyig the rtio test pprecite
Chpter Ifiite Series Pge of Sectio E Rtio Test Chpter : Ifiite Series By the ed of this sectio you will be ble to uderstd the proof of the rtio test test series for covergece by pplyig the rtio test pprecite
BC Calculus Review Sheet
 BC Clculus Review Sheet Whe you see the words. 1. Fid the re of the ubouded regio represeted by the itegrl (sometimes 1 f ( ) clled horizotl improper itegrl). This is wht you thik of doig.... Fid the re
BC Clculus Review Sheet Whe you see the words. 1. Fid the re of the ubouded regio represeted by the itegrl (sometimes 1 f ( ) clled horizotl improper itegrl). This is wht you thik of doig.... Fid the re
EXERCISE a a a 5. + a 15 NEETIIT.COM
 - Dowlod our droid App. Sigle choice Type Questios EXERCISE -. The first term of A.P. of cosecutive iteger is p +. The sum of (p + ) terms of this series c be expressed s () (p + ) () (p + ) (p + ) ()
- Dowlod our droid App. Sigle choice Type Questios EXERCISE -. The first term of A.P. of cosecutive iteger is p +. The sum of (p + ) terms of this series c be expressed s () (p + ) () (p + ) (p + ) ()
Chapter 10: The Z-Transform Adapted from: Lecture notes from MIT, Binghamton University Dr. Hamid R. Rabiee Fall 2013
 Sigls & Systems Chpter 0: The Z-Trsform Adpted from: Lecture otes from MIT, Bighmto Uiversity Dr. Hmid R. Rbiee Fll 03 Lecture 5 Chpter 0 Lecture 6 Chpter 0 Outlie Itroductio to the -Trsform Properties
Sigls & Systems Chpter 0: The Z-Trsform Adpted from: Lecture otes from MIT, Bighmto Uiversity Dr. Hmid R. Rbiee Fll 03 Lecture 5 Chpter 0 Lecture 6 Chpter 0 Outlie Itroductio to the -Trsform Properties
Laws of Integral Indices
 A Lws of Itegrl Idices A. Positive Itegrl Idices I, is clled the se, is clled the idex lso clled the expoet. mes times.... Exmple Simplify 5 6 c Solutio 8 5 6 c 6 Exmple Simplify Solutio The results i
A Lws of Itegrl Idices A. Positive Itegrl Idices I, is clled the se, is clled the idex lso clled the expoet. mes times.... Exmple Simplify 5 6 c Solutio 8 5 6 c 6 Exmple Simplify Solutio The results i
Module 4. Signal Representation and Baseband Processing. Version 2 ECE IIT, Kharagpur
 Module 4 Sigl Represettio d Bsed Processig Versio ECE IIT, Khrgpur Lesso 5 Orthogolity Versio ECE IIT, Khrgpur Ater redig this lesso, you will ler out Bsic cocept o orthogolity d orthoormlity; Strum -
Module 4 Sigl Represettio d Bsed Processig Versio ECE IIT, Khrgpur Lesso 5 Orthogolity Versio ECE IIT, Khrgpur Ater redig this lesso, you will ler out Bsic cocept o orthogolity d orthoormlity; Strum -
Section 2.2. Matrix Multiplication
 Mtri Alger Mtri Multiplitio Setio.. Mtri Multiplitio Mtri multiplitio is little more omplite th mtri itio or slr multiplitio. If A is the prout A of A is the ompute s follow: m mtri, the is k mtri, 9 m
Mtri Alger Mtri Multiplitio Setio.. Mtri Multiplitio Mtri multiplitio is little more omplite th mtri itio or slr multiplitio. If A is the prout A of A is the ompute s follow: m mtri, the is k mtri, 9 m
Chapter System of Equations
 hpter 4.5 System of Equtios After redig th chpter, you should be ble to:. setup simulteous lier equtios i mtrix form d vice-vers,. uderstd the cocept of the iverse of mtrix, 3. kow the differece betwee
hpter 4.5 System of Equtios After redig th chpter, you should be ble to:. setup simulteous lier equtios i mtrix form d vice-vers,. uderstd the cocept of the iverse of mtrix, 3. kow the differece betwee
Linford 1. Kyle Linford. Math 211. Honors Project. Theorems to Analyze: Theorem 2.4 The Limit of a Function Involving a Radical (A4)
 Liford 1 Kyle Liford Mth 211 Hoors Project Theorems to Alyze: Theorem 2.4 The Limit of Fuctio Ivolvig Rdicl (A4) Theorem 2.8 The Squeeze Theorem (A5) Theorem 2.9 The Limit of Si(x)/x = 1 (p. 85) Theorem
Liford 1 Kyle Liford Mth 211 Hoors Project Theorems to Alyze: Theorem 2.4 The Limit of Fuctio Ivolvig Rdicl (A4) Theorem 2.8 The Squeeze Theorem (A5) Theorem 2.9 The Limit of Si(x)/x = 1 (p. 85) Theorem
DIGITAL SIGNAL PROCESSING LECTURE 5
 DIGITAL SIGNAL PROCESSING LECTURE 5 Fll K8-5 th Semester Thir Muhmmd tmuhmmd_7@yhoo.com Cotet d Figures re from Discrete-Time Sigl Processig, e by Oppeheim, Shfer, d Buck, 999- Pretice Hll Ic. The -Trsform
DIGITAL SIGNAL PROCESSING LECTURE 5 Fll K8-5 th Semester Thir Muhmmd tmuhmmd_7@yhoo.com Cotet d Figures re from Discrete-Time Sigl Processig, e by Oppeheim, Shfer, d Buck, 999- Pretice Hll Ic. The -Trsform
Double Sums of Binomial Coefficients
 Itertiol Mthemticl Forum, 3, 008, o. 3, 50-5 Double Sums of Biomil Coefficiets Athoy Sofo School of Computer Sciece d Mthemtics Victori Uiversity, PO Box 448 Melboure, VIC 800, Austrli thoy.sofo@vu.edu.u
Itertiol Mthemticl Forum, 3, 008, o. 3, 50-5 Double Sums of Biomil Coefficiets Athoy Sofo School of Computer Sciece d Mthemtics Victori Uiversity, PO Box 448 Melboure, VIC 800, Austrli thoy.sofo@vu.edu.u
PEPERIKSAAN PERCUBAAN SPM TAHUN 2007 ADDITIONAL MATHEMATICS. Form Five. Paper 2. Two hours and thirty minutes
 SULIT 347/ 347/ Form Five Additiol Mthemtics Pper September 007 ½ hours PEPERIKSAAN PERCUBAAN SPM TAHUN 007 ADDITIONAL MATHEMATICS Form Five Pper Two hours d thirty miutes DO NOT OPEN THIS QUESTION PAPER
SULIT 347/ 347/ Form Five Additiol Mthemtics Pper September 007 ½ hours PEPERIKSAAN PERCUBAAN SPM TAHUN 007 ADDITIONAL MATHEMATICS Form Five Pper Two hours d thirty miutes DO NOT OPEN THIS QUESTION PAPER
Reversing the Arithmetic mean Geometric mean inequality
 Reversig the Arithmetic me Geometric me iequlity Tie Lm Nguye Abstrct I this pper we discuss some iequlities which re obtied by ddig o-egtive expressio to oe of the sides of the AM-GM iequlity I this wy
Reversig the Arithmetic me Geometric me iequlity Tie Lm Nguye Abstrct I this pper we discuss some iequlities which re obtied by ddig o-egtive expressio to oe of the sides of the AM-GM iequlity I this wy
Let. Then. k n. And. Φ npq. npq. ε 2. Φ npq npq. npq. = ε. k will be very close to p. If n is large enough, the ratio n
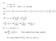 Let The m ( ) ( + ) where > very smll { } { ( ) ( + ) } Ad + + { } Φ Φ Φ Φ Φ Let, the Φ( ) lim This is lled thelw of lrge umbers If is lrge eough, the rtio will be very lose to. Exmle -Tossig oi times.
Let The m ( ) ( + ) where > very smll { } { ( ) ( + ) } Ad + + { } Φ Φ Φ Φ Φ Let, the Φ( ) lim This is lled thelw of lrge umbers If is lrge eough, the rtio will be very lose to. Exmle -Tossig oi times.
ELG4156 Design of State Variable Feedback Systems
 ELG456 Desig of Stte Vrible Feedbck Systems This chpter dels with the desig of cotrollers utilizig stte feedbck We will cosider three mjor subjects: Cotrollbility d observbility d the the procedure for
ELG456 Desig of Stte Vrible Feedbck Systems This chpter dels with the desig of cotrollers utilizig stte feedbck We will cosider three mjor subjects: Cotrollbility d observbility d the the procedure for
Fig. 1. I a. V ag I c. I n. V cg. Z n Z Y. I b. V bg
 ymmetricl Compoets equece impedces Although the followig focuses o lods, the results pply eqully well to lies, or lies d lods. Red these otes together with sectios.6 d.9 of text. Cosider the -coected lced
ymmetricl Compoets equece impedces Although the followig focuses o lods, the results pply eqully well to lies, or lies d lods. Red these otes together with sectios.6 d.9 of text. Cosider the -coected lced
