Radix-2/4 Streamlined Real Factor FFT Algorithms
|
|
|
- Poppy Chapman
- 5 years ago
- Views:
Transcription
1 SHAIK QADEER et l: RADIX-/ STREAMLIED REAL FACTOR FFT ALGORITHMS Rdix-/ Stremlied Rel Ftor FFT Algorithms Shi Qdeer () Mohmmed Zfr Ali Kh () d Syed A. Sttr () () Deprtmet of Eletril d Eletrois egieerig MJ College of Egieerig Hyderbd Idi {emil:hqbei@gmil.om} () Deprtmet of Eletril egieerig Idi Istitute of Tehology Hyderbd Idi {emil: zfr@iith..i} () Deprtmet of Eletrois d ommuitio egieerig RITS Hyderbd Idi {emil: syedbdulsttr965@gmil.om } Abstrt I this pper three Rel Ftor FFT lgorithms re preseted. Two of them re bsed o Rdix- d oe o Rdix-. The omputtiol omplexity of Rdix- d Rdix- is show s order log d log respetively ulie ~ ~ their stdrd outerprts ~ 5log d ~ log. Moreover the proposed lgorithms lso require fewer multiplitios th their stdrd FFTs. e the show tht the fixed poit implemettio of 'rel ftor' FFT be modified with uique slig proedure so tht its oise to sigl rtio (SR) is lower th the SR of stdrd FFT. Filly implemettio issues re preseted whih verify the suitbility of the proposed 'rel ftor' FFT's. Keywords - Disrete Fourier Trsform () Deimtio i frequey (DIF) Fst Fourier Trsform (FFT) d rel-ftor FFT I. ITRODUCTIO The Disrete Fourier trsform () is mog the most fudmetl opertio i digitl sigl proessig [7 9]. he osiderig the lterte implemettios the FFT/IFFT lgorithm should be hose eepig i view the exeutio speed hrdwre omplexity flexibility d preisio [ 9]. Most of the bove metioed prmeters deped o the ext out of rithmeti opertios (rel dditios d multiplitios) herei lled flops (flotigpoit opertio) required for of give size whih remis itriguig usolved mthemtil questio. Amog the umerous developmets tht followed Cooley d Tuey's [] origil otributio re the iogrd Fourier trsform lgorithm (FTA) [] d the rel ftor lgorithms [ ] for redutio i the order of the multiplitive omplexity. However both FTA d 'relftor' FFT did ot meet expettios oe implemeted s the umber of dditios (d dt trsfers) lso mtter i the implemettio. I dditio Rder d Breer's 'rel ftor' FFT s re ill-oditioed i.e. "smll omputtiol errors led to lrge output errors"[] due to the lrge vlues tht the twiddle ftor te. I this pper the solutios for both the problems of Rder d Breer's 'rel ftor' FFT lgorithm is preseted. e first show tht the rithmeti omplexity (Multiplitios plus dditios lso ow s the 'Flop out') of the Rder d Breer's 'rel ftor' FFT be redued to bout ~ log whih is less th the rithmeti omplexity of Cooley-Tuey rdix- FFT the orrespodig Rdix- is lso disussed whih tes ~ log whih is gi lesser th its outerprt. It is the show tht the modified 'rel ftor' FFT is free from ill-oditios s the mgitude of ll the twiddle ftors is less th d hee hs lower SR th rdix- Cooley- Tuey FFT. As result the proposed FFT is more suitble s it requires oly hlf the umber of rel multiplitios. The rest of the pper is orgized s follows: I setio II modified DIT versio of Rder d Breer Rdix- FFT tht requires ~ 5log flops is first preseted i subsetio II-A. I subsetio II-B we derive the orrespodig rdix- DIF FFT. I subsetio II-C it is show tht the flop out be further redued to ~ log. otbly this is the best ow flop out tht be hieved by rdix- FFT. I subsetio II-D equivlet Rdix- FFT lgorithm is overed. e the preset i setio III implemettio issues of rel ftor FFT bsed o the rdix- FFTs developed i this pper d olusios re give i setio IV. II. E FFT I this setio we first modify Rder d Breer DIT FFT tht requires ~ 5log flops. The orrespodig DIF versio is derived d the lgorithm is further modified so tht the flop out is redued dow to ~ log. Filly similr rdix- DIF FFT lgorithm is lso derived. DOI.5/IJSSST...6. ISS: 7-x olie 7- prit
2 SHAIK QADEER et l: RADIX-/ STREAMLIED REAL FACTOR FFT ALGORITHMS A. DIT versio of Rder d Breer FFT: The essee of Rder d Breer's DIT FFT is s follows: Let { } deotes -poit of the sequee of = M i.e. { }= / { }. The rdix- DIT FFT is give by A B.. D () where =exp (-/) d the /-poit sequees re defied s b = = d {B }= / {b } d {D }= / {d }. ote tht for -poit sequee if the idex is greter th we ssume mod. Sie i geerl D d re both omplex i ture the bsi butterfly opertio idited i () requires '' rel multiplitios d '' rel dditios. Rder d Breer itrodued the followig sequee [] d d q.. () where q d. It follows tht () be rewritte s m m A B C A / B C d A B s & / where { }= / { }. d s(x) is the oset of x. If we hge the sig to plus i the defiitio of the the oeffiiet of i () is /se(/) where se(x) is set of x. I either se () requires rel multiplitios d rel dditios. But this is t the expese of more dditios to fid q d from b. Therefore totl rel dditios (A()) will be A()=++=5. The rel multiplitios (M()) re give by M()= d the totl flop out (T()) is give by T()=~ 6log. To further redue the rithmeti omplexity here we modify s C d d.. It follows tht () is still vlid with the exeptio tht is defied s C 5 Deote P( ) s the the DIT omputtio for the ew lgorithm is shemtilly represeted for =6 is show i Figure. The rithmeti omplexity of this DIT FFT will beome T( ) 5 log due to the redutio i the umber of dditio to ompute usig () isted of (). ote tht the differee betwee Rder d Breer's FFT d our proposed FFT is i the omputtio of C. I Rder d Breer's FFT C q is dded to ll whih requires '(-)' rel dditios while i our versio C is diretly omputed usig (5) whih requires '(-) rel dditios. B. Derivtio of DIF versio of ew FFT Aordig to the priiple of DIF FFT the eve d odd oeffiiets re give by A.. (6) A.. (7) Fig. The deompositio of poit ito two DIT Rdix- FFT lgorithm for =6. - poit s of ew Fig. The deompositio of poit ito two - poit s for ew DIF Rdix- FFT lgorithm for =6. DOI.5/IJSSST...6. ISS: 7-x olie 7- prit
3 SHAIK QADEER et l: RADIX-/ STREAMLIED REAL FACTOR FFT ALGORITHMS To elimite the omplex multiplitio ftor from (7) we defie the sequee { } s ( ).. () where δ() is uit impulse futio. Equtio () be simplified s (9) s..( ) () Applyig / poit o both sides of () we get.. where (). The Rdix- DIF omputtio for the ew lgorithm is shemtilly represeted for =6 is show i Figure. The umber of multiplitios be lulted from (). For eh vlue of '' '' rel multiplitios re eeded d the totl umber of rel multiplitios with give two / -poits s is (-). Therefore the totl umber of rel multiplitios for -poit is give by M( ) if M( ) if Solvig () by repeted substitutios we hve M ( ) log The umber of rel dditios give two /-poits s is lulted s follows (/) rel dditios for evlutig (6) for =../-. (/+)rel dditios for evlutig () for =../-. (/)rel dditios for evlutig () for =../-. It follows tht T( ) A( ) if A( ) if Solvig () by repeted substitutios we hve A( ) log () () () (5) The totl flop out is the give by 5 log. Importtly the DIF versio of the FFT preseted i sub setio II-A d II-B requires the sme umber of omputtios (rel dds + rel multiplies) s orml Rdix- DIT or DIF FFT while requirig lesser multiplies. Also s ompred to DIT versio of Rder d Breer's FFT the modified DIT show i subsetio II-A d DIF i II-B requires fewer rel dditios. C. Modified DIF versio of ew FFT I this sub setio we show tht the omputtiol omplexity be redued dow further. If we dd to () the for = (/) s( / ) (6) Fig. the deompositio of poit ito two - poit s for ew modified DIF Rdix- FFT lgorithm for =6. Ad rest of the sequee { } = /- / +.. /- is give by (9)-(). Equtio () for this se modifies to C C for evevlues of A (7) C C otherwise The DIF omputtio for the ew lgorithm is shemtilly represeted for =6 re show i Figure DOI.5/IJSSST...6. ISS: 7-x olie 7- prit
4 SHAIK QADEER et l: RADIX-/ STREAMLIED REAL FACTOR FFT ALGORITHMS DOI.5/IJSSST...6. ISS: 7-x olie 7- prit d Figure. ith these substitutios it is obvious tht the umbers of rel multiplitios re sme. However s ompred to the sub setio II-A d II-B the umber of rel dditios re redued by /-. Aordigly the umber of rel dditios is give by 7 if if ) A( ) A( () Solvig () by repeted substitutios we hve log ) ( A 7 (9) The totl flop out is give by log ) ( T. Importtly flop out of this Rdix- FFT is less th y other Rdix- FFTs (iludig stdrd DIT d DIF Rdix- FFTs). D. ew Rdix- DIF FFT: Aordig to the priiple of Rdix- DIF FFT the eve d odd oeffiiets re give by for.. To elimite the omplex multiplitio ftor from () we similrly defie the sequee { } s.. ( ) where δ() is uit impulse futio. Equtio () be simplified s Fig.. The omplete i ple omputtio digrm of ew DIF Rdix- FFT lgorithm for = / s Applyig / poit o both sides of () we get 6.. A where d As i subsetio II-C if we dd to (5) the for =/ s Ad for the rest of the sequee { } = /- / + /- is give by (5). Equtio (6) for this se modifies to
5 SHAIK QADEER et l: RADIX-/ STREAMLIED REAL FACTOR FFT ALGORITHMS C A C C for evevlues of C otherwise Methods M() T() Stdrd log 5log Rdix- RB-FFT log 6log Proposed log Rdix- log Stdrd log Rdix- log Proposed Rdix- log log (7) oly Rdix- DIF d other be similrly obtied [ d 5]). The oise to sigl rtio (SR) of Rder d Breer's lgorithm is ow to be very poor beuse of the lrge vlues of s []. Aordigly we first modify the rel ftor FFT for fixed poit implemettio i setio III-A to elimite the problem of ill omputtio; the we disussed the remiig implemettio issues i III-B d expeted exeutio times is give i setio III-C. A. Modifitio to rel ftor FFT for fixed poit implemettio To elimite the problem of ill-oditioed we proposed slig method to (9)-() s Tble I. Computtiol Complexity of vrious FFT's Deote P( ) s the the DIF omputtio for the ew lgorithm is shemtilly represeted for =6 is show i Figure. The totl dditio for eh butterfly will be A( ) d totl multiplitio will be M ( ). Hee the totl flop outs T( ) 6 per butterfly. The ost of the ew Rdix- FFT lgorithm ow be represeted by the followig reurree igorig otrivil multiplitios: T( ) T 6 6 if if Solvig () by repeted substitutios we hve () T( ) log (.) E. Compriso of omputtiol Complexity of vrious FFT lgorithms: The omputtiol omplexity ompriso for Rdix- / FFTs is give i Tble. I (ote tht RF-FFT mes Rel Ftor while RB-FFT mes Rder d Breer's FFT). Observe tht the ew DIF versio of modified rel ftor FFT preseted i setio II requires ot oly lesser multiplitios but lso the totl flop outs (T ()). III. IMPLEMETATIO ISSUES OF PROPOSED FFT I this setio we osider the implemettio issues of 'rel ftor' FFTs preseted i setio II (ote tht we over here ĉ l s ĉ l l.. where l is hose suh tht s(/) l+. It follows tht s(/)/ l+ for ll. This modifitio esures tht the rel multiplitio ftors re less th. Applyig o both sides of () with this modifitio we get l Ĉ Ĉ ĉ A.. () where Ĉ ĉ d ĉ ( ) ĉ. The purely imgiry twiddle ftor is ow give by P( ) s. A similr lgorithm with purely l rel twiddle ftor be similrly developed. ote tht i both the ses P(). The dvtge of the preseted fixed poit lgorithm be observed from () wherei the effet of lrge vlues of s(θ) hs bee ptured i l d the effetive preisio t the output is l+b bits [6 ]. A. I-ple omputtio of proposed FFT lgorithm: Figure 5 shows the i-ple omputtio digrm of the proposed rel ftor FFT whih implemets (6) through (7) for =. It is observed tht Prt-I of lgorithm is similr to Cooley-Tuey's rdix- DIF FFT lgorithms [] exept the twiddle ftor 'P( )' whih is defied erlier (but ot show i lgorithm ). Oe butterfly opertio is performed o pir of omplex umber ( b) to produe (A B) there is o eed to sve the iput pir ( b) exept the first vlue of vetor '' s show i Figure 5. Hee we store the results (A B) i the sme lotios s ( b). 9 DOI.5/IJSSST ISS: 7-x olie 7- prit
6 SHAIK QADEER et l: RADIX-/ STREAMLIED REAL FACTOR FFT ALGORITHMS Cosequetly we require fixed umber of storge registers i order to store the results (ote tht is omplex umber) of the omputtios t eh stge. Sie storge lotios re used throughout the omputtio of the -Poit we sy tht the omputtios re doe i-ple. A seod observtio is eed of dt shufflig (DS) i Prt-II of proposed lgorithm. TABLE II. Expeted Exeutio time of FFT vrits for Rdix- = υ S.o Problem Legth C-T i m se Proposed RDIF i m se Proposed RDIF i m se log log log.5.5*.5* *ote tht our lgorithms wors for >. IV. COCLUSIO I this pper we hve show tht the rithmeti omplexity of rel ftor FFTs is sigifitly less th tht of stdrd FFT. e hve show tht these FFTs hve sigifit dvtge ompred to orrespodig stdrd FFTs. he it omes to fixed poit implemettio s it hs lower umber of oise soures (rel multiplitios) d hee lower SR. This lgorithm is of prtil importe s Rdix-/ FFTs re geerlly preferred i ASIC implemettio d for softwre defied rdio (ogitive rdio) pplitios due to ese of re-ofigurbility. Over ll these ftors re i fvor of rel ftor FFTs. However the disdvtge is dditiol memory storge of C required for eh stge. But s the ost of memory is deresig storge my ot be sigifit ftor. A prt of this pper ws preseted t EUSIPCO []. There is eed of dt deimtio fter eh dditiol dditio s show i Figure 6 s t the ed of Prt-I the order of dt of our lgorithm is bit reversed. e defie this deimtio of dt s DS. The DS eeded for = is show i Figure 6. Observe tht '' DS opertios re required for =. I geerl if the DS opertios re required to ompute -poit FFT. ote tht the umber of times dt deimtios/shufflig re eeded i the omputtio of usig C-T FFT is. Hee the omputtio requiremet for both DS d Bit reversed opertios re equl. B. Expeted Exeutio Time of Vrious FFT lgorithms: To help thigs i perspetive it is istrutive to see the differees i opertio outs i terms of expeted exeutio times []. The bove expeted times re lulted by osiderig the se of TMSC5 DSP proessor whose speed of opertio is 5s (MIPS) for proposed Rdix- FFT. Assumig tht both multiplitio d dditio tes sme time we get the results s show i bove Tble II. Fig. 5 I-Ple omputtio digrm for = of the Proposed Rel Ftor FFT lgorithm. () () () (6) () (5) () (7) Dt shufflig Bit Reversed Order () () () (6) () () (5) (7) Dt shufflig A () A () A () A () A () A (5) A (6) A(7) turl Order Fig.6 Shufflig of Dt d bit reversl DOI.5/IJSSST ISS: 7-x olie 7- prit
7 SHAIK QADEER et l: RADIX-/ STREAMLIED REAL FACTOR FFT ALGORITHMS REFERECES [] J.. Cooley d J.. Tuey A lgorithm for the mhiecomputtio of the omplex Fourier series Mth. Computtio vol. 9 pp. 97 Apr [] S. iogrd O omputig the disrete Fourier trsform Pro. t. Ad. Si. USA Vol. 7 April 976 pp [] C. M. Rder d. M. Breer A ew priiple for fst Fourier trsformtio IEEE Trs. Aoust. Speeh Sigl Proessig vol. pp [] K.M. Cho d G.C. Temes Rel-ftor FFT lgorithms Pro.ICASSP 7 Tuls UK April 97 pp [5] A. V. Oppeheim d C. J. eistei Effets of fiite registerlegth i digitl filterig d the fst Fourier trsform Pro. of IEEE. 97 pp [6] T. Tr B. Liu Fixed-poit fst Fourier trsform error lysis IEEE Trs. o ASSP 976 vol.(6) pp [7]. M. Getlem d G. Sde Fst Fourier trsform for fu d profit i 966 Fll Joit Corput. Cof. AFIPS Pro.v ol. 9. ew Yor: Sprt pp [] de Lowdermil d Fred Hrris Fiite Arithmeti Cosidertios for the FFT Implemeted i FPGA-Bsed EmbeddedProessors i Sytheti Istrumets I IEEE Istrumettio d Mesuremet Mgzie August 7. [9].-H. Chg d T. guye O the Fixed-Poit Aury Alysis of FFT Algorithms IEEE Trstios O Sig Proessig Vol. 56 o. pp Otober. [] P. D. elh A fixed poit fst Fourier trsform error lysis IEEE Trs. Audio Eletrooust. vol. AU-7 pp Jue 969. [] A. V. Oppeheim d R. Shfer Digitl Sigl Proessig.Perso Edutio. [] Sit Mitr Digitl Sigl Proessig: A Computer Approh rd editio Chpter MGrw- Hill 6. [] Eleor Chu d Al George Iside the FFT Bl Box: Seril d Prllel FFT lgorithms Pge o. Appedix A CRC Press. [] M.Z.A. Kh d Shi Qdeer Stremlied Rel Ftor EUSIPCO AlborgDemrAugust-7. [5] J.G. Prois d D.G. Molis"Digitl Sigl ProessigPriiplesAlgortihmsd pplitios"perso rd Editio. DOI.5/IJSSST ISS: 7-x olie 7- prit
CS 331 Design and Analysis of Algorithms. -- Divide and Conquer. Dr. Daisy Tang
 CS 33 Desig d Alysis of Algorithms -- Divide d Coquer Dr. Disy Tg Divide-Ad-Coquer Geerl ide: Divide problem ito subproblems of the sme id; solve subproblems usig the sme pproh, d ombie prtil solutios,
CS 33 Desig d Alysis of Algorithms -- Divide d Coquer Dr. Disy Tg Divide-Ad-Coquer Geerl ide: Divide problem ito subproblems of the sme id; solve subproblems usig the sme pproh, d ombie prtil solutios,
Introduction to Matrix Algebra
 Itrodutio to Mtri Alger George H Olso, Ph D Dotorl Progrm i Edutiol Ledership Applhi Stte Uiversit Septemer Wht is mtri? Dimesios d order of mtri A p q dimesioed mtri is p (rows) q (olums) rr of umers,
Itrodutio to Mtri Alger George H Olso, Ph D Dotorl Progrm i Edutiol Ledership Applhi Stte Uiversit Septemer Wht is mtri? Dimesios d order of mtri A p q dimesioed mtri is p (rows) q (olums) rr of umers,
Section 11.5 Notes Page Partial Fraction Decomposition. . You will get: +. Therefore we come to the following: x x
 Setio Notes Pge Prtil Frtio Deompositio Suppose we were sked to write the followig s sigle frtio: We would eed to get ommo deomitors: You will get: Distributig o top will give you: 8 This simplifies to:
Setio Notes Pge Prtil Frtio Deompositio Suppose we were sked to write the followig s sigle frtio: We would eed to get ommo deomitors: You will get: Distributig o top will give you: 8 This simplifies to:
Addendum. Addendum. Vector Review. Department of Computer Science and Engineering 1-1
 Addedum Addedum Vetor Review Deprtmet of Computer Siee d Egieerig - Coordite Systems Right hded oordite system Addedum y z Deprtmet of Computer Siee d Egieerig - -3 Deprtmet of Computer Siee d Egieerig
Addedum Addedum Vetor Review Deprtmet of Computer Siee d Egieerig - Coordite Systems Right hded oordite system Addedum y z Deprtmet of Computer Siee d Egieerig - -3 Deprtmet of Computer Siee d Egieerig
Chapter 2. LOGARITHMS
 Chpter. LOGARITHMS Dte: - 009 A. INTRODUCTION At the lst hpter, you hve studied bout Idies d Surds. Now you re omig to Logrithms. Logrithm is ivers of idies form. So Logrithms, Idies, d Surds hve strog
Chpter. LOGARITHMS Dte: - 009 A. INTRODUCTION At the lst hpter, you hve studied bout Idies d Surds. Now you re omig to Logrithms. Logrithm is ivers of idies form. So Logrithms, Idies, d Surds hve strog
0 otherwise. sin( nx)sin( kx) 0 otherwise. cos( nx) sin( kx) dx 0 for all integers n, k.
 . Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric
. Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric
Riemann Integral Oct 31, such that
 Riem Itegrl Ot 31, 2007 Itegrtio of Step Futios A prtitio P of [, ] is olletio {x k } k=0 suh tht = x 0 < x 1 < < x 1 < x =. More suitly, prtitio is fiite suset of [, ] otiig d. It is helpful to thik of
Riem Itegrl Ot 31, 2007 Itegrtio of Step Futios A prtitio P of [, ] is olletio {x k } k=0 suh tht = x 0 < x 1 < < x 1 < x =. More suitly, prtitio is fiite suset of [, ] otiig d. It is helpful to thik of
Data Compression Techniques (Spring 2012) Model Solutions for Exercise 4
 58487 Dt Compressio Tehiques (Sprig 0) Moel Solutios for Exerise 4 If you hve y fee or orretios, plese ott jro.lo t s.helsii.fi.. Prolem: Let T = Σ = {,,, }. Eoe T usig ptive Huffm oig. Solutio: R 4 U
58487 Dt Compressio Tehiques (Sprig 0) Moel Solutios for Exerise 4 If you hve y fee or orretios, plese ott jro.lo t s.helsii.fi.. Prolem: Let T = Σ = {,,, }. Eoe T usig ptive Huffm oig. Solutio: R 4 U
AN DIGITAL FILTER DESIGN SCHEME BASED ON MATRIX TRANSFORMATION
 Jourl of heoretil d Applied Iformtio ehology 5 th November. Vol. 5 No. 5 - JAI & LLS. All rights reserved. ISSN: 99-865 www.jtit.org E-ISSN: 87-95 AN DIGIAL FILER DESIGN SCHEME BASED ON MARIX RANSFORMAION
Jourl of heoretil d Applied Iformtio ehology 5 th November. Vol. 5 No. 5 - JAI & LLS. All rights reserved. ISSN: 99-865 www.jtit.org E-ISSN: 87-95 AN DIGIAL FILER DESIGN SCHEME BASED ON MARIX RANSFORMAION
Fast Fourier Transform 1) Legendre s Interpolation 2) Vandermonde Matrix 3) Roots of Unity 4) Polynomial Evaluation
 Algorithm Desig d Alsis Victor Admchi CS 5-45 Sprig 4 Lecture 3 J 7, 4 Cregie Mello Uiversit Outlie Fst Fourier Trsform ) Legedre s Iterpoltio ) Vdermode Mtri 3) Roots of Uit 4) Polomil Evlutio Guss (777
Algorithm Desig d Alsis Victor Admchi CS 5-45 Sprig 4 Lecture 3 J 7, 4 Cregie Mello Uiversit Outlie Fst Fourier Trsform ) Legedre s Iterpoltio ) Vdermode Mtri 3) Roots of Uit 4) Polomil Evlutio Guss (777
Accuplacer Elementary Algebra Study Guide
 Testig Ceter Studet Suess Ceter Aupler Elemetry Alger Study Guide The followig smple questios re similr to the formt d otet of questios o the Aupler Elemetry Alger test. Reviewig these smples will give
Testig Ceter Studet Suess Ceter Aupler Elemetry Alger Study Guide The followig smple questios re similr to the formt d otet of questios o the Aupler Elemetry Alger test. Reviewig these smples will give
MATH 104: INTRODUCTORY ANALYSIS SPRING 2008/09 PROBLEM SET 10 SOLUTIONS. f m. and. f m = 0. and x i = a + i. a + i. a + n 2. n(n + 1) = a(b a) +
 MATH 04: INTRODUCTORY ANALYSIS SPRING 008/09 PROBLEM SET 0 SOLUTIONS Throughout this problem set, B[, b] will deote the set of ll rel-vlued futios bouded o [, b], C[, b] the set of ll rel-vlued futios
MATH 04: INTRODUCTORY ANALYSIS SPRING 008/09 PROBLEM SET 0 SOLUTIONS Throughout this problem set, B[, b] will deote the set of ll rel-vlued futios bouded o [, b], C[, b] the set of ll rel-vlued futios
Project 3: Using Identities to Rewrite Expressions
 MAT 5 Projet 3: Usig Idetities to Rewrite Expressios Wldis I lger, equtios tht desrie properties or ptters re ofte lled idetities. Idetities desrie expressio e repled with equl or equivlet expressio tht
MAT 5 Projet 3: Usig Idetities to Rewrite Expressios Wldis I lger, equtios tht desrie properties or ptters re ofte lled idetities. Idetities desrie expressio e repled with equl or equivlet expressio tht
a f(x)dx is divergent.
 Mth 250 Exm 2 review. Thursdy Mrh 5. Brig TI 30 lultor but NO NOTES. Emphsis o setios 5.5, 6., 6.2, 6.3, 3.7, 6.6, 8., 8.2, 8.3, prt of 8.4; HW- 2; Q-. Kow for trig futios tht 0.707 2/2 d 0.866 3/2. From
Mth 250 Exm 2 review. Thursdy Mrh 5. Brig TI 30 lultor but NO NOTES. Emphsis o setios 5.5, 6., 6.2, 6.3, 3.7, 6.6, 8., 8.2, 8.3, prt of 8.4; HW- 2; Q-. Kow for trig futios tht 0.707 2/2 d 0.866 3/2. From
SPH3UW Unit 7.5 Snell s Law Page 1 of Total Internal Reflection occurs when the incoming refraction angle is
 SPH3UW Uit 7.5 Sell s Lw Pge 1 of 7 Notes Physis Tool ox Refrtio is the hge i diretio of wve due to hge i its speed. This is most ommoly see whe wve psses from oe medium to other. Idex of refrtio lso lled
SPH3UW Uit 7.5 Sell s Lw Pge 1 of 7 Notes Physis Tool ox Refrtio is the hge i diretio of wve due to hge i its speed. This is most ommoly see whe wve psses from oe medium to other. Idex of refrtio lso lled
Introduction of Fourier Series to First Year Undergraduate Engineering Students
 Itertiol Jourl of Adved Reserh i Computer Egieerig & Tehology (IJARCET) Volume 3 Issue 4, April 4 Itrodutio of Fourier Series to First Yer Udergrdute Egieerig Studets Pwr Tejkumr Dtttry, Hiremth Suresh
Itertiol Jourl of Adved Reserh i Computer Egieerig & Tehology (IJARCET) Volume 3 Issue 4, April 4 Itrodutio of Fourier Series to First Yer Udergrdute Egieerig Studets Pwr Tejkumr Dtttry, Hiremth Suresh
( ) 2 3 ( ) I. Order of operations II. Scientific Notation. Simplify. Write answers in scientific notation. III.
 Assessmet Ceter Elemetry Alger Study Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d otet of questios o the Aupler Elemetry Alger test. Reviewig these smples will give
Assessmet Ceter Elemetry Alger Study Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d otet of questios o the Aupler Elemetry Alger test. Reviewig these smples will give
1. (25 points) Use the limit definition of the definite integral and the sum formulas to compute. [1 x + x2
 Mth 3, Clculus II Fil Exm Solutios. (5 poits) Use the limit defiitio of the defiite itegrl d the sum formuls to compute 3 x + x. Check your swer by usig the Fudmetl Theorem of Clculus. Solutio: The limit
Mth 3, Clculus II Fil Exm Solutios. (5 poits) Use the limit defiitio of the defiite itegrl d the sum formuls to compute 3 x + x. Check your swer by usig the Fudmetl Theorem of Clculus. Solutio: The limit
Merge Sort. Outline and Reading. Divide-and-Conquer. Divide-and-conquer paradigm ( 4.1.1) Merge-sort ( 4.1.1)
 Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 Merge Sort versio 1.3 1 Outlie d Redig Divide-d-coquer prdigm ( 4.1.1 Merge-sort ( 4.1.1 Algorithm Mergig two sorted sequeces Merge-sort tree
Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 Merge Sort versio 1.3 1 Outlie d Redig Divide-d-coquer prdigm ( 4.1.1 Merge-sort ( 4.1.1 Algorithm Mergig two sorted sequeces Merge-sort tree
Dynamics of Structures
 UNION Dymis of Strutures Prt Zbigiew Wójii Je Grosel Projet o-fied by Europe Uio withi Europe Soil Fud UNION Mtries Defiitio of mtri mtri is set of umbers or lgebri epressios rrged i retgulr form with
UNION Dymis of Strutures Prt Zbigiew Wójii Je Grosel Projet o-fied by Europe Uio withi Europe Soil Fud UNION Mtries Defiitio of mtri mtri is set of umbers or lgebri epressios rrged i retgulr form with
MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS. and x i = a + i. i + n(n + 1)(2n + 1) + 2a. (b a)3 6n 2
 MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS 6.9: Let f(x) { x 2 if x Q [, b], 0 if x (R \ Q) [, b], where > 0. Prove tht b. Solutio. Let P { x 0 < x 1 < < x b} be regulr prtitio
MATH 104: INTRODUCTORY ANALYSIS SPRING 2009/10 PROBLEM SET 8 SOLUTIONS 6.9: Let f(x) { x 2 if x Q [, b], 0 if x (R \ Q) [, b], where > 0. Prove tht b. Solutio. Let P { x 0 < x 1 < < x b} be regulr prtitio
CH 19 SOLVING FORMULAS
 1 CH 19 SOLVING FORMULAS INTRODUCTION S olvig equtios suh s 2 + 7 20 is oviousl the orerstoe of lger. But i siee, usiess, d omputers it is lso eessr to solve equtios tht might hve vriet of letters i them.
1 CH 19 SOLVING FORMULAS INTRODUCTION S olvig equtios suh s 2 + 7 20 is oviousl the orerstoe of lger. But i siee, usiess, d omputers it is lso eessr to solve equtios tht might hve vriet of letters i them.
ROUTH-HURWITZ CRITERION
 Automti Cotrol Sytem, Deprtmet of Mehtroi Egieerig, Germ Jordi Uiverity Routh-Hurwitz Criterio ite.google.om/ite/ziydmoud 7 ROUTH-HURWITZ CRITERION The Routh-Hurwitz riterio i lytil proedure for determiig
Automti Cotrol Sytem, Deprtmet of Mehtroi Egieerig, Germ Jordi Uiverity Routh-Hurwitz Criterio ite.google.om/ite/ziydmoud 7 ROUTH-HURWITZ CRITERION The Routh-Hurwitz riterio i lytil proedure for determiig
MTH 146 Class 16 Notes
 MTH 46 Clss 6 Notes 0.4- Cotiued Motivtio: We ow cosider the rc legth of polr curve. Suppose we wish to fid the legth of polr curve curve i terms of prmetric equtios s: r f where b. We c view the cos si
MTH 46 Clss 6 Notes 0.4- Cotiued Motivtio: We ow cosider the rc legth of polr curve. Suppose we wish to fid the legth of polr curve curve i terms of prmetric equtios s: r f where b. We c view the cos si
Linear Programming. Preliminaries
 Lier Progrmmig Prelimiries Optimiztio ethods: 3L Objectives To itroduce lier progrmmig problems (LPP To discuss the stdrd d coicl form of LPP To discuss elemetry opertio for lier set of equtios Optimiztio
Lier Progrmmig Prelimiries Optimiztio ethods: 3L Objectives To itroduce lier progrmmig problems (LPP To discuss the stdrd d coicl form of LPP To discuss elemetry opertio for lier set of equtios Optimiztio
Neighborhoods of Certain Class of Analytic Functions of Complex Order with Negative Coefficients
 Ge Mth Notes Vol 2 No Jury 20 pp 86-97 ISSN 229-784; Copyriht ICSRS Publitio 20 wwwi-srsor Avilble free olie t http://wwwemi Neihborhoods of Certi Clss of Alyti Futios of Complex Order with Netive Coeffiiets
Ge Mth Notes Vol 2 No Jury 20 pp 86-97 ISSN 229-784; Copyriht ICSRS Publitio 20 wwwi-srsor Avilble free olie t http://wwwemi Neihborhoods of Certi Clss of Alyti Futios of Complex Order with Netive Coeffiiets
12.2 The Definite Integrals (5.2)
 Course: Aelerted Egieerig Clulus I Istrutor: Mihel Medvisky. The Defiite Itegrls 5. Def: Let fx e defied o itervl [,]. Divide [,] ito suitervls of equl width Δx, so x, x + Δx, x + jδx, x. Let x j j e ritrry
Course: Aelerted Egieerig Clulus I Istrutor: Mihel Medvisky. The Defiite Itegrls 5. Def: Let fx e defied o itervl [,]. Divide [,] ito suitervls of equl width Δx, so x, x + Δx, x + jδx, x. Let x j j e ritrry
INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
 Mthemtics Revisio Guides Itegrtig Trig, Log d Ep Fuctios Pge of MK HOME TUITION Mthemtics Revisio Guides Level: AS / A Level AQA : C Edecel: C OCR: C OCR MEI: C INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
Mthemtics Revisio Guides Itegrtig Trig, Log d Ep Fuctios Pge of MK HOME TUITION Mthemtics Revisio Guides Level: AS / A Level AQA : C Edecel: C OCR: C OCR MEI: C INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
POWER SERIES R. E. SHOWALTER
 POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise
POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise
( a n ) converges or diverges.
 Chpter Ifiite Series Pge of Sectio E Rtio Test Chpter : Ifiite Series By the ed of this sectio you will be ble to uderstd the proof of the rtio test test series for covergece by pplyig the rtio test pprecite
Chpter Ifiite Series Pge of Sectio E Rtio Test Chpter : Ifiite Series By the ed of this sectio you will be ble to uderstd the proof of the rtio test test series for covergece by pplyig the rtio test pprecite
FREE Download Study Package from website: &
 FREE Dolod Study Pkge from esite:.tekolsses.om &.MthsBySuhg.om Get Solutio of These Pkges & Ler y Video Tutorils o.mthsbysuhg.om SHORT REVISION. Defiitio : Retgulr rry of m umers. Ulike determits it hs
FREE Dolod Study Pkge from esite:.tekolsses.om &.MthsBySuhg.om Get Solutio of These Pkges & Ler y Video Tutorils o.mthsbysuhg.om SHORT REVISION. Defiitio : Retgulr rry of m umers. Ulike determits it hs
Ch. 12 Linear Bayesian Estimators
 h. Lier Byesi stimtors Itrodutio I hpter we sw: the MMS estimtor tkes simple form whe d re joitly Gussi it is lier d used oly the st d d order momets (mes d ovries). Without the Gussi ssumptio, the Geerl
h. Lier Byesi stimtors Itrodutio I hpter we sw: the MMS estimtor tkes simple form whe d re joitly Gussi it is lier d used oly the st d d order momets (mes d ovries). Without the Gussi ssumptio, the Geerl
EXPONENTS AND LOGARITHMS
 978--07-6- Mthemtis Stdrd Level for IB Diplom Eerpt EXPONENTS AND LOGARITHMS WHAT YOU NEED TO KNOW The rules of epoets: m = m+ m = m ( m ) = m m m = = () = The reltioship etwee epoets d rithms: = g where
978--07-6- Mthemtis Stdrd Level for IB Diplom Eerpt EXPONENTS AND LOGARITHMS WHAT YOU NEED TO KNOW The rules of epoets: m = m+ m = m ( m ) = m m m = = () = The reltioship etwee epoets d rithms: = g where
CH 20 SOLVING FORMULAS
 CH 20 SOLVING FORMULAS 179 Itrodutio S olvig equtios suh s 2 + 7 20 is oviousl the orerstoe of lger. But i siee, usiess, d omputers it is lso eessr to solve equtios tht might hve vriet of letters i them.
CH 20 SOLVING FORMULAS 179 Itrodutio S olvig equtios suh s 2 + 7 20 is oviousl the orerstoe of lger. But i siee, usiess, d omputers it is lso eessr to solve equtios tht might hve vriet of letters i them.
Digital Signal Processing. Homework 2 Solution. Due Monday 4 October Following the method on page 38, the difference equation
 Digital Sigal Proessig Homework Solutio Due Moda 4 Otober 00. Problem.4 Followig the method o page, the differee equatio [] (/4[-] + (/[-] x[-] has oeffiiets a0, a -/4, a /, ad b. For these oeffiiets A(z
Digital Sigal Proessig Homework Solutio Due Moda 4 Otober 00. Problem.4 Followig the method o page, the differee equatio [] (/4[-] + (/[-] x[-] has oeffiiets a0, a -/4, a /, ad b. For these oeffiiets A(z
Review of the Riemann Integral
 Chpter 1 Review of the Riem Itegrl This chpter provides quick review of the bsic properties of the Riem itegrl. 1.0 Itegrls d Riem Sums Defiitio 1.0.1. Let [, b] be fiite, closed itervl. A prtitio P of
Chpter 1 Review of the Riem Itegrl This chpter provides quick review of the bsic properties of the Riem itegrl. 1.0 Itegrls d Riem Sums Defiitio 1.0.1. Let [, b] be fiite, closed itervl. A prtitio P of
Bernoulli Numbers. n(n+1) = n(n+1)(2n+1) = n(n 1) 2
 Beroulli Numbers Beroulli umbers are amed after the great Swiss mathematiia Jaob Beroulli5-705 who used these umbers i the power-sum problem. The power-sum problem is to fid a formula for the sum of the
Beroulli Numbers Beroulli umbers are amed after the great Swiss mathematiia Jaob Beroulli5-705 who used these umbers i the power-sum problem. The power-sum problem is to fid a formula for the sum of the
Exponents and Radical
 Expoets d Rdil Rule : If the root is eve d iside the rdil is egtive, the the swer is o rel umber, meig tht If is eve d is egtive, the Beuse rel umber multiplied eve times by itself will be lwys positive.
Expoets d Rdil Rule : If the root is eve d iside the rdil is egtive, the the swer is o rel umber, meig tht If is eve d is egtive, the Beuse rel umber multiplied eve times by itself will be lwys positive.
INTEGRAL SOLUTIONS OF THE TERNARY CUBIC EQUATION
 Itertiol Reserch Jourl of Egieerig d Techology IRJET) e-issn: 9-006 Volume: 04 Issue: Mr -017 www.irjet.et p-issn: 9-007 INTEGRL SOLUTIONS OF THE TERNRY CUBIC EQUTION y ) 4y y ) 97z G.Jki 1, C.Sry,* ssistt
Itertiol Reserch Jourl of Egieerig d Techology IRJET) e-issn: 9-006 Volume: 04 Issue: Mr -017 www.irjet.et p-issn: 9-007 INTEGRL SOLUTIONS OF THE TERNRY CUBIC EQUTION y ) 4y y ) 97z G.Jki 1, C.Sry,* ssistt
Gauss Elimination, Gauss-Jordan Elimination and Gauss Seidel Iteration Method: Performance Comparison using MAT LAB
 Itertiol Jourl of Egieerig Tehology Siee d Reserh www.ietsr.om ISSN 394 3386 Volume 4, Issue 0 Otober 07 Guss Elimitio, Guss-Jord Elimitio d Guss Seidel Itertio Method: Performe Compriso usig MAT LAB *Dr.
Itertiol Jourl of Egieerig Tehology Siee d Reserh www.ietsr.om ISSN 394 3386 Volume 4, Issue 0 Otober 07 Guss Elimitio, Guss-Jord Elimitio d Guss Seidel Itertio Method: Performe Compriso usig MAT LAB *Dr.
Introduction to Algorithms 6.046J/18.401J
 Itrodutio to Algorithms.04J/8.40J The divide-d-oquer desig prdigm. Divide the problem (iste) ito subproblems.. Coquer the subproblems by solvig them reursively. 3. Combie subproblem solutios. Leture 3
Itrodutio to Algorithms.04J/8.40J The divide-d-oquer desig prdigm. Divide the problem (iste) ito subproblems.. Coquer the subproblems by solvig them reursively. 3. Combie subproblem solutios. Leture 3
2.1.1 Definition The Z-transform of a sequence x [n] is simply defined as (2.1) X re x k re x k r
![2.1.1 Definition The Z-transform of a sequence x [n] is simply defined as (2.1) X re x k re x k r 2.1.1 Definition The Z-transform of a sequence x [n] is simply defined as (2.1) X re x k re x k r](/thumbs/82/85448174.jpg) Z-Trsforms. INTRODUCTION TO Z-TRANSFORM The Z-trsform is coveiet d vluble tool for represetig, lyig d desigig discrete-time sigls d systems. It plys similr role i discrete-time systems to tht which Lplce
Z-Trsforms. INTRODUCTION TO Z-TRANSFORM The Z-trsform is coveiet d vluble tool for represetig, lyig d desigig discrete-time sigls d systems. It plys similr role i discrete-time systems to tht which Lplce
ECE 102 Engineering Computation
 ECE Egieerig Computtio Phillip Wog Mth Review Vetor Bsis Mtri Bsis System of Lier Equtios Summtio Symol is the symol for summtio. Emple: N k N... 9 k k k k k the, If e e e f e f k Vetor Bsis A vetor is
ECE Egieerig Computtio Phillip Wog Mth Review Vetor Bsis Mtri Bsis System of Lier Equtios Summtio Symol is the symol for summtio. Emple: N k N... 9 k k k k k the, If e e e f e f k Vetor Bsis A vetor is
THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK SUMMER EXAMINATION 2005 FIRST ENGINEERING
 OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK SUMMER EXAMINATION 2005 FIRST ENGINEERING MATHEMATICS MA008 Clculus d Lier
OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK SUMMER EXAMINATION 2005 FIRST ENGINEERING MATHEMATICS MA008 Clculus d Lier
After the completion of this section the student. V.4.2. Power Series Solution. V.4.3. The Method of Frobenius. V.4.4. Taylor Series Solution
 Chapter V ODE V.4 Power Series Solutio Otober, 8 385 V.4 Power Series Solutio Objetives: After the ompletio of this setio the studet - should reall the power series solutio of a liear ODE with variable
Chapter V ODE V.4 Power Series Solutio Otober, 8 385 V.4 Power Series Solutio Objetives: After the ompletio of this setio the studet - should reall the power series solutio of a liear ODE with variable
Numbers (Part I) -- Solutions
 Ley College -- For AMATYC SML Mth Competitio Cochig Sessios v.., [/7/00] sme s /6/009 versio, with presettio improvemets Numbers Prt I) -- Solutios. The equtio b c 008 hs solutio i which, b, c re distict
Ley College -- For AMATYC SML Mth Competitio Cochig Sessios v.., [/7/00] sme s /6/009 versio, with presettio improvemets Numbers Prt I) -- Solutios. The equtio b c 008 hs solutio i which, b, c re distict
z line a) Draw the single phase equivalent circuit. b) Calculate I BC.
 ECE 2260 F 08 HW 7 prob 4 solutio EX: V gyb' b' b B V gyc' c' c C = 101 0 V = 1 + j0.2 Ω V gyb' = 101 120 V = 6 + j0. Ω V gyc' = 101 +120 V z LΔ = 9 j1.5 Ω ) Drw the sigle phse equivlet circuit. b) Clculte
ECE 2260 F 08 HW 7 prob 4 solutio EX: V gyb' b' b B V gyc' c' c C = 101 0 V = 1 + j0.2 Ω V gyb' = 101 120 V = 6 + j0. Ω V gyc' = 101 +120 V z LΔ = 9 j1.5 Ω ) Drw the sigle phse equivlet circuit. b) Clculte
Observer Design with Reduced Measurement Information
 Observer Desig with Redued Measuremet Iformatio I pratie all the states aot be measured so that SVF aot be used Istead oly a redued set of measuremets give by y = x + Du p is available where y( R We assume
Observer Desig with Redued Measuremet Iformatio I pratie all the states aot be measured so that SVF aot be used Istead oly a redued set of measuremets give by y = x + Du p is available where y( R We assume
Vectors. Vectors in Plane ( 2
 Vectors Vectors i Ple ( ) The ide bout vector is to represet directiol force Tht mes tht every vector should hve two compoets directio (directiol slope) d mgitude (the legth) I the ple we preset vector
Vectors Vectors i Ple ( ) The ide bout vector is to represet directiol force Tht mes tht every vector should hve two compoets directio (directiol slope) d mgitude (the legth) I the ple we preset vector
1.3 Continuous Functions and Riemann Sums
 mth riem sums, prt 0 Cotiuous Fuctios d Riem Sums I Exmple we sw tht lim Lower() = lim Upper() for the fuctio!! f (x) = + x o [0, ] This is o ccidet It is exmple of the followig theorem THEOREM Let f be
mth riem sums, prt 0 Cotiuous Fuctios d Riem Sums I Exmple we sw tht lim Lower() = lim Upper() for the fuctio!! f (x) = + x o [0, ] This is o ccidet It is exmple of the followig theorem THEOREM Let f be
Schrödinger Equation Via Laplace-Beltrami Operator
 IOSR Jourl of Mthemtics (IOSR-JM) e-issn: 78-578, p-issn: 39-765X. Volume 3, Issue 6 Ver. III (Nov. - Dec. 7), PP 9-95 www.iosrjourls.org Schrödiger Equtio Vi Lplce-Beltrmi Opertor Esi İ Eskitşçioğlu,
IOSR Jourl of Mthemtics (IOSR-JM) e-issn: 78-578, p-issn: 39-765X. Volume 3, Issue 6 Ver. III (Nov. - Dec. 7), PP 9-95 www.iosrjourls.org Schrödiger Equtio Vi Lplce-Beltrmi Opertor Esi İ Eskitşçioğlu,
Chapter 5. The Riemann Integral. 5.1 The Riemann integral Partitions and lower and upper integrals. Note: 1.5 lectures
 Chpter 5 The Riem Itegrl 5.1 The Riem itegrl Note: 1.5 lectures We ow get to the fudmetl cocept of itegrtio. There is ofte cofusio mog studets of clculus betwee itegrl d tiderivtive. The itegrl is (iformlly)
Chpter 5 The Riem Itegrl 5.1 The Riem itegrl Note: 1.5 lectures We ow get to the fudmetl cocept of itegrtio. There is ofte cofusio mog studets of clculus betwee itegrl d tiderivtive. The itegrl is (iformlly)
PROGRESSIONS AND SERIES
 PROGRESSIONS AND SERIES A sequece is lso clled progressio. We ow study three importt types of sequeces: () The Arithmetic Progressio, () The Geometric Progressio, () The Hrmoic Progressio. Arithmetic Progressio.
PROGRESSIONS AND SERIES A sequece is lso clled progressio. We ow study three importt types of sequeces: () The Arithmetic Progressio, () The Geometric Progressio, () The Hrmoic Progressio. Arithmetic Progressio.
LEVEL I. ,... if it is known that a 1
 LEVEL I Fid the sum of first terms of the AP, if it is kow tht + 5 + 0 + 5 + 0 + = 5 The iterior gles of polygo re i rithmetic progressio The smllest gle is 0 d the commo differece is 5 Fid the umber of
LEVEL I Fid the sum of first terms of the AP, if it is kow tht + 5 + 0 + 5 + 0 + = 5 The iterior gles of polygo re i rithmetic progressio The smllest gle is 0 d the commo differece is 5 Fid the umber of
A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD
 Diol Bgoo () A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD I. Itroductio The first seprtio of vribles (see pplictios to Newto s equtios) is ver useful method
Diol Bgoo () A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD I. Itroductio The first seprtio of vribles (see pplictios to Newto s equtios) is ver useful method
Chapter 10: The Z-Transform Adapted from: Lecture notes from MIT, Binghamton University Dr. Hamid R. Rabiee Fall 2013
 Sigls & Systems Chpter 0: The Z-Trsform Adpted from: Lecture otes from MIT, Bighmto Uiversity Dr. Hmid R. Rbiee Fll 03 Lecture 5 Chpter 0 Lecture 6 Chpter 0 Outlie Itroductio to the -Trsform Properties
Sigls & Systems Chpter 0: The Z-Trsform Adpted from: Lecture otes from MIT, Bighmto Uiversity Dr. Hmid R. Rbiee Fll 03 Lecture 5 Chpter 0 Lecture 6 Chpter 0 Outlie Itroductio to the -Trsform Properties
Chapter System of Equations
 hpter 4.5 System of Equtios After redig th chpter, you should be ble to:. setup simulteous lier equtios i mtrix form d vice-vers,. uderstd the cocept of the iverse of mtrix, 3. kow the differece betwee
hpter 4.5 System of Equtios After redig th chpter, you should be ble to:. setup simulteous lier equtios i mtrix form d vice-vers,. uderstd the cocept of the iverse of mtrix, 3. kow the differece betwee
( ) k ( ) 1 T n 1 x = xk. Geometric series obtained directly from the definition. = 1 1 x. See also Scalars 9.1 ADV-1: lim n.
 Sclrs-9.0-ADV- Algebric Tricks d Where Tylor Polyomils Come From 207.04.07 A.docx Pge of Algebric tricks ivolvig x. You c use lgebric tricks to simplify workig with the Tylor polyomils of certi fuctios..
Sclrs-9.0-ADV- Algebric Tricks d Where Tylor Polyomils Come From 207.04.07 A.docx Pge of Algebric tricks ivolvig x. You c use lgebric tricks to simplify workig with the Tylor polyomils of certi fuctios..
Numerical Methods. Lecture 5. Numerical integration. dr hab. inż. Katarzyna Zakrzewska, prof. AGH. Numerical Methods lecture 5 1
 Numeril Methods Leture 5. Numeril itegrtio dr h. iż. Ktrzy Zkrzewsk, pro. AGH Numeril Methods leture 5 Outlie Trpezoidl rule Multi-segmet trpezoidl rule Rihrdso etrpoltio Romerg's method Simpso's rule
Numeril Methods Leture 5. Numeril itegrtio dr h. iż. Ktrzy Zkrzewsk, pro. AGH Numeril Methods leture 5 Outlie Trpezoidl rule Multi-segmet trpezoidl rule Rihrdso etrpoltio Romerg's method Simpso's rule
Graphing Review Part 3: Polynomials
 Grphig Review Prt : Polomils Prbols Recll, tht the grph of f ( ) is prbol. It is eve fuctio, hece it is smmetric bout the bout the -is. This mes tht f ( ) f ( ). Its grph is show below. The poit ( 0,0)
Grphig Review Prt : Polomils Prbols Recll, tht the grph of f ( ) is prbol. It is eve fuctio, hece it is smmetric bout the bout the -is. This mes tht f ( ) f ( ). Its grph is show below. The poit ( 0,0)
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS. Assoc. Prof. Dr. Burak Kelleci. Spring 2018
 DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Assoc. Prof. Dr. Bur Kelleci Sprig 8 OUTLINE The Z-Trsform The Regio of covergece for the Z-trsform The Iverse Z-Trsform Geometric
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Assoc. Prof. Dr. Bur Kelleci Sprig 8 OUTLINE The Z-Trsform The Regio of covergece for the Z-trsform The Iverse Z-Trsform Geometric
Numerical Solutions of Fredholm Integral Equations Using Bernstein Polynomials
 Numericl Solutios of Fredholm Itegrl Equtios Usig erstei Polyomils A. Shiri, M. S. Islm Istitute of Nturl Scieces, Uited Itertiol Uiversity, Dhk-, gldesh Deprtmet of Mthemtics, Uiversity of Dhk, Dhk-,
Numericl Solutios of Fredholm Itegrl Equtios Usig erstei Polyomils A. Shiri, M. S. Islm Istitute of Nturl Scieces, Uited Itertiol Uiversity, Dhk-, gldesh Deprtmet of Mthemtics, Uiversity of Dhk, Dhk-,
1/16/2013. Overview. 05-Three Phase Analysis Text: Three Phase. Three-Phase Voltages. Benefits of Three-Phase Systems.
 oltge () 1/16/21 Overview 5Three Phse Alysis Text: 2.4 2.7 ECEGR 451 Power Systems ThreePhse Soures Delt d Y Coetios ThreePhse Lods ThreePhse Power ThreePhse Alysis PerPhse Alysis Dr. Louie 2 ThreePhse
oltge () 1/16/21 Overview 5Three Phse Alysis Text: 2.4 2.7 ECEGR 451 Power Systems ThreePhse Soures Delt d Y Coetios ThreePhse Lods ThreePhse Power ThreePhse Alysis PerPhse Alysis Dr. Louie 2 ThreePhse
Let. Then. k n. And. Φ npq. npq. ε 2. Φ npq npq. npq. = ε. k will be very close to p. If n is large enough, the ratio n
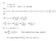 Let The m ( ) ( + ) where > very smll { } { ( ) ( + ) } Ad + + { } Φ Φ Φ Φ Φ Let, the Φ( ) lim This is lled thelw of lrge umbers If is lrge eough, the rtio will be very lose to. Exmle -Tossig oi times.
Let The m ( ) ( + ) where > very smll { } { ( ) ( + ) } Ad + + { } Φ Φ Φ Φ Φ Let, the Φ( ) lim This is lled thelw of lrge umbers If is lrge eough, the rtio will be very lose to. Exmle -Tossig oi times.
Modified Farey Trees and Pythagorean Triples
 Modified Frey Trees d Pythgore Triples By Shi-ihi Kty Deprtet of Mthetil Siees, Fulty of Itegrted Arts d Siees, The Uiversity of Tokushi, Tokushi 0-0, JAPAN e-il ddress : kty@istokushi-ujp Abstrt I 6,
Modified Frey Trees d Pythgore Triples By Shi-ihi Kty Deprtet of Mthetil Siees, Fulty of Itegrted Arts d Siees, The Uiversity of Tokushi, Tokushi 0-0, JAPAN e-il ddress : kty@istokushi-ujp Abstrt I 6,
MA123, Chapter 9: Computing some integrals (pp )
 MA13, Chpter 9: Computig some itegrls (pp. 189-05) Dte: Chpter Gols: Uderstd how to use bsic summtio formuls to evlute more complex sums. Uderstd how to compute its of rtiol fuctios t ifiity. Uderstd how
MA13, Chpter 9: Computig some itegrls (pp. 189-05) Dte: Chpter Gols: Uderstd how to use bsic summtio formuls to evlute more complex sums. Uderstd how to compute its of rtiol fuctios t ifiity. Uderstd how
Content: Essential Calculus, Early Transcendentals, James Stewart, 2007 Chapter 1: Functions and Limits., in a set B.
 Review Sheet: Chpter Cotet: Essetil Clculus, Erly Trscedetls, Jmes Stewrt, 007 Chpter : Fuctios d Limits Cocepts, Defiitios, Lws, Theorems: A fuctio, f, is rule tht ssigs to ech elemet i set A ectly oe
Review Sheet: Chpter Cotet: Essetil Clculus, Erly Trscedetls, Jmes Stewrt, 007 Chpter : Fuctios d Limits Cocepts, Defiitios, Lws, Theorems: A fuctio, f, is rule tht ssigs to ech elemet i set A ectly oe
INFINITE SERIES. ,... having infinite number of terms is called infinite sequence and its indicated sum, i.e., a 1
 Appedix A.. Itroductio As discussed i the Chpter 9 o Sequeces d Series, sequece,,...,,... hvig ifiite umber of terms is clled ifiite sequece d its idicted sum, i.e., + + +... + +... is clled ifite series
Appedix A.. Itroductio As discussed i the Chpter 9 o Sequeces d Series, sequece,,...,,... hvig ifiite umber of terms is clled ifiite sequece d its idicted sum, i.e., + + +... + +... is clled ifite series
B. Examples 1. Finite Sums finite sums are an example of Riemann Sums in which each subinterval has the same length and the same x i
 Mth 06 Clculus Sec. 5.: The Defiite Itegrl I. Riem Sums A. Def : Give y=f(x):. Let f e defied o closed itervl[,].. Prtitio [,] ito suitervls[x (i-),x i ] of legth Δx i = x i -x (i-). Let P deote the prtitio
Mth 06 Clculus Sec. 5.: The Defiite Itegrl I. Riem Sums A. Def : Give y=f(x):. Let f e defied o closed itervl[,].. Prtitio [,] ito suitervls[x (i-),x i ] of legth Δx i = x i -x (i-). Let P deote the prtitio
Discrete-Time Signals & Systems
 Chpter 2 Discrete-Time Sigls & Systems 清大電機系林嘉文 cwli@ee.thu.edu.tw 03-57352 Discrete-Time Sigls Sigls re represeted s sequeces of umbers, clled smples Smple vlue of typicl sigl or sequece deoted s x =
Chpter 2 Discrete-Time Sigls & Systems 清大電機系林嘉文 cwli@ee.thu.edu.tw 03-57352 Discrete-Time Sigls Sigls re represeted s sequeces of umbers, clled smples Smple vlue of typicl sigl or sequece deoted s x =
Section 2.2. Matrix Multiplication
 Mtri Alger Mtri Multiplitio Setio.. Mtri Multiplitio Mtri multiplitio is little more omplite th mtri itio or slr multiplitio. If A is the prout A of A is the ompute s follow: m mtri, the is k mtri, 9 m
Mtri Alger Mtri Multiplitio Setio.. Mtri Multiplitio Mtri multiplitio is little more omplite th mtri itio or slr multiplitio. If A is the prout A of A is the ompute s follow: m mtri, the is k mtri, 9 m
ENGR 3861 Digital Logic Boolean Algebra. Fall 2007
 ENGR 386 Digitl Logi Boole Alger Fll 007 Boole Alger A two vlued lgeri system Iveted y George Boole i 854 Very similr to the lger tht you lredy kow Sme opertios ivolved dditio sutrtio multiplitio Repled
ENGR 386 Digitl Logi Boole Alger Fll 007 Boole Alger A two vlued lgeri system Iveted y George Boole i 854 Very similr to the lger tht you lredy kow Sme opertios ivolved dditio sutrtio multiplitio Repled
Unit 1. Extending the Number System. 2 Jordan School District
 Uit Etedig the Number System Jord School District Uit Cluster (N.RN. & N.RN.): Etedig Properties of Epoets Cluster : Etedig properties of epoets.. Defie rtiol epoets d eted the properties of iteger epoets
Uit Etedig the Number System Jord School District Uit Cluster (N.RN. & N.RN.): Etedig Properties of Epoets Cluster : Etedig properties of epoets.. Defie rtiol epoets d eted the properties of iteger epoets
DIGITAL SIGNAL PROCESSING LECTURE 5
 DIGITAL SIGNAL PROCESSING LECTURE 5 Fll K8-5 th Semester Thir Muhmmd tmuhmmd_7@yhoo.com Cotet d Figures re from Discrete-Time Sigl Processig, e by Oppeheim, Shfer, d Buck, 999- Pretice Hll Ic. The -Trsform
DIGITAL SIGNAL PROCESSING LECTURE 5 Fll K8-5 th Semester Thir Muhmmd tmuhmmd_7@yhoo.com Cotet d Figures re from Discrete-Time Sigl Processig, e by Oppeheim, Shfer, d Buck, 999- Pretice Hll Ic. The -Trsform
 n. A Very Interesting Example + + = d. + x3. + 5x4. math 131 power series, part ii 7. One of the first power series we examined was. 2!
 mth power series, prt ii 7 A Very Iterestig Emple Oe of the first power series we emied ws! + +! + + +!! + I Emple 58 we used the rtio test to show tht the itervl of covergece ws (, ) Sice the series coverges
mth power series, prt ii 7 A Very Iterestig Emple Oe of the first power series we emied ws! + +! + + +!! + I Emple 58 we used the rtio test to show tht the itervl of covergece ws (, ) Sice the series coverges
Certain sufficient conditions on N, p n, q n k summability of orthogonal series
 Avilble olie t www.tjs.com J. Nolier Sci. Appl. 7 014, 7 77 Reserch Article Certi sufficiet coditios o N, p, k summbility of orthogol series Xhevt Z. Krsiqi Deprtmet of Mthemtics d Iformtics, Fculty of
Avilble olie t www.tjs.com J. Nolier Sci. Appl. 7 014, 7 77 Reserch Article Certi sufficiet coditios o N, p, k summbility of orthogol series Xhevt Z. Krsiqi Deprtmet of Mthemtics d Iformtics, Fculty of
Frequency-domain Characteristics of Discrete-time LTI Systems
 requecy-domi Chrcteristics of Discrete-time LTI Systems Prof. Siripog Potisuk LTI System descriptio Previous bsis fuctio: uit smple or DT impulse The iput sequece is represeted s lier combitio of shifted
requecy-domi Chrcteristics of Discrete-time LTI Systems Prof. Siripog Potisuk LTI System descriptio Previous bsis fuctio: uit smple or DT impulse The iput sequece is represeted s lier combitio of shifted
=> PARALLEL INTERCONNECTION. Basic Properties LTI Systems. The Commutative Property. Convolution. The Commutative Property. The Distributive Property
 Lier Time-Ivrit Bsic Properties LTI The Commuttive Property The Distributive Property The Associtive Property Ti -6.4 / Chpter Covolutio y ] x ] ] x ]* ] x ] ] y] y ( t ) + x( τ ) h( t τ ) dτ x( t) * h(
Lier Time-Ivrit Bsic Properties LTI The Commuttive Property The Distributive Property The Associtive Property Ti -6.4 / Chpter Covolutio y ] x ] ] x ]* ] x ] ] y] y ( t ) + x( τ ) h( t τ ) dτ x( t) * h(
EXERCISE a a a 5. + a 15 NEETIIT.COM
 - Dowlod our droid App. Sigle choice Type Questios EXERCISE -. The first term of A.P. of cosecutive iteger is p +. The sum of (p + ) terms of this series c be expressed s () (p + ) () (p + ) (p + ) ()
- Dowlod our droid App. Sigle choice Type Questios EXERCISE -. The first term of A.P. of cosecutive iteger is p +. The sum of (p + ) terms of this series c be expressed s () (p + ) () (p + ) (p + ) ()
SOLUTION OF DIFFERENTIAL EQUATION FOR THE EULER-BERNOULLI BEAM
 Jourl of Applied Mthemtics d Computtiol Mechics () 57-6 SOUION O DIERENIA EQUAION OR HE EUER-ERNOUI EAM Izbel Zmorsk Istitute of Mthemtics Czestochow Uiversit of echolog Częstochow Pold izbel.zmorsk@im.pcz.pl
Jourl of Applied Mthemtics d Computtiol Mechics () 57-6 SOUION O DIERENIA EQUAION OR HE EUER-ERNOUI EAM Izbel Zmorsk Istitute of Mthemtics Czestochow Uiversit of echolog Częstochow Pold izbel.zmorsk@im.pcz.pl
MATRIX ALGEBRA, Systems Linear Equations
 MATRIX ALGEBRA, Systes Lier Equtios Now we chge to the LINEAR ALGEBRA perspective o vectors d trices to reforulte systes of lier equtios. If you fid the discussio i ters of geerl d gets lost i geerlity,
MATRIX ALGEBRA, Systes Lier Equtios Now we chge to the LINEAR ALGEBRA perspective o vectors d trices to reforulte systes of lier equtios. If you fid the discussio i ters of geerl d gets lost i geerlity,
ON n-fold FILTERS IN BL-ALGEBRAS
 Jourl of Alger Numer Theor: Adves d Applitios Volume 2 Numer 29 Pges 27-42 ON -FOLD FILTERS IN BL-ALGEBRAS M. SHIRVANI-GHADIKOLAI A. MOUSSAVI A. KORDI 2 d A. AHMADI 2 Deprtmet of Mthemtis Trit Modres Uiversit
Jourl of Alger Numer Theor: Adves d Applitios Volume 2 Numer 29 Pges 27-42 ON -FOLD FILTERS IN BL-ALGEBRAS M. SHIRVANI-GHADIKOLAI A. MOUSSAVI A. KORDI 2 d A. AHMADI 2 Deprtmet of Mthemtis Trit Modres Uiversit
SUTCLIFFE S NOTES: CALCULUS 2 SWOKOWSKI S CHAPTER 11
 UTCLIFFE NOTE: CALCULU WOKOWKI CHAPTER Ifiite eries Coverget or Diverget eries Cosider the sequece If we form the ifiite sum 0, 00, 000, 0 00 000, we hve wht is clled ifiite series We wt to fid the sum
UTCLIFFE NOTE: CALCULU WOKOWKI CHAPTER Ifiite eries Coverget or Diverget eries Cosider the sequece If we form the ifiite sum 0, 00, 000, 0 00 000, we hve wht is clled ifiite series We wt to fid the sum
Introduction to mathematical Statistics
 More ttistics tutoril t wwwdumblittledoctorcom Itroductio to mthemticl ttistics Chpter 7 ypothesis Testig Exmple (ull hypothesis) : the verge height is 5 8 or more ( : μ 5'8" ) (ltertive hypothesis) :
More ttistics tutoril t wwwdumblittledoctorcom Itroductio to mthemticl ttistics Chpter 7 ypothesis Testig Exmple (ull hypothesis) : the verge height is 5 8 or more ( : μ 5'8" ) (ltertive hypothesis) :
Lincoln Land Community College Placement and Testing Office
 Licol Ld Commuity College Plcemet d Testig Office Elemetry Algebr Study Guide for the ACCUPLACER (CPT) A totl of questios re dmiistered i this test. The first type ivolves opertios with itegers d rtiol
Licol Ld Commuity College Plcemet d Testig Office Elemetry Algebr Study Guide for the ACCUPLACER (CPT) A totl of questios re dmiistered i this test. The first type ivolves opertios with itegers d rtiol
Limit of a function:
 - Limit of fuctio: We sy tht f ( ) eists d is equl with (rel) umer L if f( ) gets s close s we wt to L if is close eough to (This defiitio c e geerlized for L y syig tht f( ) ecomes s lrge (or s lrge egtive
- Limit of fuctio: We sy tht f ( ) eists d is equl with (rel) umer L if f( ) gets s close s we wt to L if is close eough to (This defiitio c e geerlized for L y syig tht f( ) ecomes s lrge (or s lrge egtive
Error-free compression
 Error-free compressio Useful i pplictio where o loss of iformtio is tolerble. This mybe due to ccurcy requiremets, legl requiremets, or less th perfect qulity of origil imge. Compressio c be chieved by
Error-free compressio Useful i pplictio where o loss of iformtio is tolerble. This mybe due to ccurcy requiremets, legl requiremets, or less th perfect qulity of origil imge. Compressio c be chieved by
Student Success Center Elementary Algebra Study Guide for the ACCUPLACER (CPT)
 Studet Success Ceter Elemetry Algebr Study Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d cotet of questios o the Accuplcer Elemetry Algebr test. Reviewig these smples
Studet Success Ceter Elemetry Algebr Study Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d cotet of questios o the Accuplcer Elemetry Algebr test. Reviewig these smples
Northwest High School s Algebra 2
 Northwest High School s Algebr Summer Review Pcket 0 DUE August 8, 0 Studet Nme This pcket hs bee desiged to help ou review vrious mthemticl topics tht will be ecessr for our success i Algebr. Istructios:
Northwest High School s Algebr Summer Review Pcket 0 DUE August 8, 0 Studet Nme This pcket hs bee desiged to help ou review vrious mthemticl topics tht will be ecessr for our success i Algebr. Istructios:
Chapter 10: The Z-Transform Adapted from: Lecture notes from MIT, Binghamton University Hamid R. Rabiee Arman Sepehr Fall 2010
 Sigls & Systems Chpter 0: The Z-Trsform Adpted from: Lecture otes from MIT, Bighmto Uiversity Hmid R. Riee Arm Sepehr Fll 00 Lecture 5 Chpter 0 Outlie Itroductio to the -Trsform Properties of the ROC of
Sigls & Systems Chpter 0: The Z-Trsform Adpted from: Lecture otes from MIT, Bighmto Uiversity Hmid R. Riee Arm Sepehr Fll 00 Lecture 5 Chpter 0 Outlie Itroductio to the -Trsform Properties of the ROC of
M3P14 EXAMPLE SHEET 1 SOLUTIONS
 M3P14 EXAMPLE SHEET 1 SOLUTIONS 1. Show tht for, b, d itegers, we hve (d, db) = d(, b). Sice (, b) divides both d b, d(, b) divides both d d db, d hece divides (d, db). O the other hd, there exist m d
M3P14 EXAMPLE SHEET 1 SOLUTIONS 1. Show tht for, b, d itegers, we hve (d, db) = d(, b). Sice (, b) divides both d b, d(, b) divides both d d db, d hece divides (d, db). O the other hd, there exist m d
National Quali cations AHEXEMPLAR PAPER ONLY
 Ntiol Quli ctios AHEXEMPLAR PAPER ONLY EP/AH/0 Mthemtics Dte Not pplicble Durtio hours Totl mrks 00 Attempt ALL questios. You my use clcultor. Full credit will be give oly to solutios which coti pproprite
Ntiol Quli ctios AHEXEMPLAR PAPER ONLY EP/AH/0 Mthemtics Dte Not pplicble Durtio hours Totl mrks 00 Attempt ALL questios. You my use clcultor. Full credit will be give oly to solutios which coti pproprite
Section 6.3: Geometric Sequences
 40 Chpter 6 Sectio 6.: Geometric Sequeces My jobs offer ul cost-of-livig icrese to keep slries cosistet with ifltio. Suppose, for exmple, recet college grdute fids positio s sles mger erig ul slry of $6,000.
40 Chpter 6 Sectio 6.: Geometric Sequeces My jobs offer ul cost-of-livig icrese to keep slries cosistet with ifltio. Suppose, for exmple, recet college grdute fids positio s sles mger erig ul slry of $6,000.
Chapter 7 Infinite Series
 MA Ifiite Series Asst.Prof.Dr.Supree Liswdi Chpter 7 Ifiite Series Sectio 7. Sequece A sequece c be thought of s list of umbers writte i defiite order:,,...,,... 2 The umber is clled the first term, 2
MA Ifiite Series Asst.Prof.Dr.Supree Liswdi Chpter 7 Ifiite Series Sectio 7. Sequece A sequece c be thought of s list of umbers writte i defiite order:,,...,,... 2 The umber is clled the first term, 2
Autar Kaw Benjamin Rigsby. Transforming Numerical Methods Education for STEM Undergraduates
 Autr Kw Bejmi Rigsby http://m.mthforcollege.com Trsformig Numericl Methods Eductio for STEM Udergrdutes http://m.mthforcollege.com . solve set of simulteous lier equtios usig Nïve Guss elimitio,. ler the
Autr Kw Bejmi Rigsby http://m.mthforcollege.com Trsformig Numericl Methods Eductio for STEM Udergrdutes http://m.mthforcollege.com . solve set of simulteous lier equtios usig Nïve Guss elimitio,. ler the
Review of Sections
 Review of Sectios.-.6 Mrch 24, 204 Abstrct This is the set of otes tht reviews the mi ides from Chpter coverig sequeces d series. The specific sectios tht we covered re s follows:.: Sequces..2: Series,
Review of Sectios.-.6 Mrch 24, 204 Abstrct This is the set of otes tht reviews the mi ides from Chpter coverig sequeces d series. The specific sectios tht we covered re s follows:.: Sequces..2: Series,
FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES. To a 2π-periodic function f(x) we will associate a trigonometric series. a n cos(nx) + b n sin(nx),
 FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES To -periodic fuctio f() we will ssocite trigoometric series + cos() + b si(), or i terms of the epoetil e i, series of the form c e i. Z For most of the
FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES To -periodic fuctio f() we will ssocite trigoometric series + cos() + b si(), or i terms of the epoetil e i, series of the form c e i. Z For most of the
Thomas J. Osler Mathematics Department Rowan University Glassboro NJ Introduction
 Ot 0 006 Euler s little summtio formul d speil vlues of te zet futio Toms J Osler temtis Deprtmet Row Uiversity Glssboro J 0608 Osler@rowedu Itrodutio I tis ote we preset elemetry metod of determiig vlues
Ot 0 006 Euler s little summtio formul d speil vlues of te zet futio Toms J Osler temtis Deprtmet Row Uiversity Glssboro J 0608 Osler@rowedu Itrodutio I tis ote we preset elemetry metod of determiig vlues
Inference on One Population Mean Hypothesis Testing
 Iferece o Oe Popultio Me ypothesis Testig Scerio 1. Whe the popultio is orml, d the popultio vrice is kow i. i. d. Dt : X 1, X,, X ~ N(, ypothesis test, for istce: Exmple: : : : : : 5'7" (ull hypothesis:
Iferece o Oe Popultio Me ypothesis Testig Scerio 1. Whe the popultio is orml, d the popultio vrice is kow i. i. d. Dt : X 1, X,, X ~ N(, ypothesis test, for istce: Exmple: : : : : : 5'7" (ull hypothesis:
Chapter Real Numbers
 Chpter. - Rel Numbers Itegers: coutig umbers, zero, d the egtive of the coutig umbers. ex: {,-3, -, -,,,, 3, } Rtiol Numbers: quotiets of two itegers with ozero deomitor; termitig or repetig decimls. ex:
Chpter. - Rel Numbers Itegers: coutig umbers, zero, d the egtive of the coutig umbers. ex: {,-3, -, -,,,, 3, } Rtiol Numbers: quotiets of two itegers with ozero deomitor; termitig or repetig decimls. ex:
