Discretization-Optimization Methods for Optimal Control Problems
|
|
|
- Imogen Rich
- 6 years ago
- Views:
Transcription
1 Proceedigs of the 5th WSEAS It Cof o SIMULAION MODELING AND OPIMIZAION Corfu Greece August (pp399-46) Discretizatio-Optiizatio Methods for Optia Cotro Probes ION CHRYSSOVERGHI Departet of Matheatics Schoo of Appied Matheatics ad Physics Natioa echica Uiversity of Athes Zografou Capus 578 Athes GREECE Abstract: - We cosider a optia cotro probe described by oiear ordiary differetia equatios with cotro ad state costraits Sice this probe ay have o cassica soutios it is aso foruated i reaxed for he cassica cotro probe is the discretized by usig the ipicit idpoit schee for state approxiatio whie the cotros are approxiated by piecewise costat cassica oes We first study the behavior i the iit of properties of discrete optiaity ad of discrete adissibiity ad extreaity We the appy a peaized gradiet proectio ethod to each discrete cassica probe ad aso a correspodig progressivey refiig discretizatio-optiizatio ethod to the cotiuous cassica probe thus reducig coputig tie ad eory We show that accuuatio poits of sequeces geerated by these ethods are adissibe ad extrea for the correspodig discrete or cotiuous cassica or reaxed probe For ocovex probes whose soutios are o-cassica we show that we ca appy the above ethods to the probe foruated i the Gareidze for Fiay uerica exapes are give Key-Words: - Optia cotro discretizatio idpoit schee piecewise costat cotros peaized gradiet proectio ethod reaxed cotros Itroductio I this paper we propose discretizatio-optiizatio ethods geeratig cassica cotros istead of reaxed cotros (see [] [] [5]) for sovig optia cotro probes ad study their behavior i the iit i the fraewors of cassica ad reaxatio theories We cosider a optia cotro probe described by oiear ordiary differetia equatios with cotro ad ed-poit state costraits ad ed-poit cost Sice this probe ay have o cassica soutios it is aso foruated i reaxed for he cassica cotro probe is the discretized by usig ipicit idpoit schees for state ad adoit approxiatio the idpoit itegratio rue for approxiatio of the itegras ivoved i the derivatives of fuctioas whie the cotros are approxiated by piecewise costat cassica oes We first give various ecessary coditios for optiaity for the cotiuous cassica ad reaxed probes ad for the discrete probe Next we show that strog accuuatio poits i L of sequeces of optia (resp adissibe ad extrea) discrete cotros are optia (resp adissibe ad weay extrea) for the cotiuous cassica probe ad that reaxed accuuatio poits of sequeces of optia (resp adissibe ad extrea) discrete cotros are optia (resp adissibe ad weay extrea) for the cotiuous reaxed probe We the appy a peaized gradiet proectio ethod to each discrete cassica probe ad aso a correspodig ixed discretizatiooptiizatio ethod to the cotiuous cassica probe that progressivey refies the discretizatio durig the iteratios thus reducig coputig tie ad eory especiay for arge systes We prove that accuuatio poits of sequeces geerated by the fixed discretizatio ethod are adissibe ad extrea for each discrete probe ad that strog cassica (resp reaxed) accuuatio poits of sequeces of discrete cotros geerated by the progressivey refiig ethod are adissibe ad weay extrea for the cotiuous cassica (resp reaxed) probe For ocovex probes whose soutios are o-cassica we show that we ca appy the above ethods to the probe foruated i the Gareidze for Usig a stadard procedure the coputed Gareidze cotros ca the be approxiated by cassica oes Fiay uerica exapes are give Probes ivovig poitwise state costraits have bee studied i [4] [5] For various discretizatio ad optiizatio ethods i optia cotro see [-7] [9] [] ad refereces there
2 Proceedigs of the 5th WSEAS It Cof o SIMULAION MODELING AND OPIMIZAION Corfu Greece August (pp399-46) he cotiuous probes Cosider the foowig optia cotro probe he state equatio is give by the differetia syste y'( t) = f( t y( t) w( t)) for aa t I : = [ ] d y() = y yt ( ) the costraits o the cotro w are wt () U for aa t I ' where U is a copact subset of d the costraits o the state y: = yw are G( w): = g( y( )) = G( w): = g( y( )) where the vector fuctios g g tae vaues i respectivey ad the cost fuctioa to be iiized is G( w) : = g( y( )) We defie the set of cassica cotros by d ' W : = { w: I U w easurabe} L ( I ) ad the set of reaxed cotros (for the reevat theory see [] ad [8]) by R: = { r: I M( U) r weay easurabe} Lw ( I M( U)) L( I C( U))* where M ( U ) (resp M( U )) is the set of Rado (resp probabiity) easures o U he set W (resp R ) is edowed with the reative strog (resp wea star) topoogy ad R is covex etrizabe ad copact If each cassica cotro w( ) is idetified with its associated Dirac reaxed cotro r(): = δ w() the W ay be cosidered as a subset of R ad W is thus dese i R For a give fuctio φ BIU ( ; ) where B is the set of Caratheodory fuctios i the sese of Warga [] ad r R we use the sipified otatio φ( trt ()): = φ( turt ) ()( du) U We ca ow defie the reaxed probe he state equatio is y'( t) = f( t y( t) r( t)) for aa t I y() = y with y: = yr the cotro costrait is r R ad the state costraits ad cost are defied as i the cassica probe but with w repaced by r accordig to the above otatio We deote by the Eucidea or i We suppose i the seque that the fuctio f d is defied o I U easurabe for yu fixed cotiuous for t fixed ad satisfies f ( t y u) ψ() t + β y d for every ( t y u) I U with ψ L ( I) β f ( t y u) f( t y u) L y y for every ( t y y u) I d U heore For every reaxed (or cassica as W R) cotro r R the state equatio has a uique absoutey cotiuous soutio y: = yr Moreover there exists a costat b such that y b for every cotro r R r Let B deote the cosed ba i d with ceter ad radius b defied i heore We suppose ow i additio that the fuctios g = are cotiuous o B heore he appigs G : W(resp R) = are cotiuous o W (resp R ) If the reaxed probe is feasibe the it has a soutio Note that i the cassica probe we have y'( t) f( t y( t) U) (veocity set) whie i the reaxed oe y'( t) co[ f( t y( t) U)] he cassica probe ay have o cassica soutio ad because W R we have i geera c : = i G ( r) if G ( w) : = c R costraits o r costraits o w where the equaity hods i particuar if there are o state costraits sice W is dese i R Usuay uerica ethods sighty vioate the state costraits; so approxiatig a optia reaxed cotro by a reaxed or a cassica oe hece the reaxed optia cost c R is ot a drawbac i practice (see [] p 48) Note aso that approxiatig sequeces of cassica cotros ay coverge to reaxed oes I order to state the various ecessary coditios for optiaity we suppose i additio that the fuctios f f y f u are defied o I B' U' where B ' (resp U ' ) is a ope set cotaiig B (resp U ) easurabe o I for fixed ( yu ) B U cotiuous o B U for fixed t I ad such that f ( t y u) ξ () t f ( tyu ) η() t y for every ( t y u) I B U with ξη L( I) ad that the fuctios g g y = are defied o B ' ad cotiuous o B u W
3 Proceedigs of the 5th WSEAS It Cof o SIMULAION MODELING AND OPIMIZAION Corfu Greece August (pp399-46) heore 3 (i) If U is covex the for ww ' W the directioa derivative of the appig G = defied o W is give by G ( w+ α( w' w)) G ( w) DG ( ' ): i w w w = + α α = z ( t ) f ( t y ( t u ) w ( t ))[ w '( t ) w ( t )] dt where y: = yw ad the adoit state z : = z a row w vector fuctio ( = ) or a atrix fuctio ( = ) is defied by the iear adoit equatio z '( t) = z ( t) f ( t y( t) w( t)) for aa t I y z( ) = gy( y( )) with y: = yw where the cotros are cosidered as cassica oes (ii) For rr ' R the directioa derivative of the appig G = defied o R is give by G ( r+ α( r' r)) G ( r) DG ( ' ): i r r r = + α α = z () t f ( t y () t r '() t r ()) t dt where y: = yr ad the reaxed adoit z : = z is r defied by the iear reaxed adoit equatio z '( t) = z( t) fy( t y( t) r( t)) for aa t I z( ) = gy( y( )) with y: = yr (iii) he appigs ( ww ') a DG ( ww ' w) (resp( rr') a DG ( rr' r) ) = are cotiuous o W W (resp R R ) heore 4 (i) If U is covex ad the cotro w W is optia for the cassica probe the w is weay extrea cassica ie there exist utipiers λ λ λ with λ λ () = = λ DG ( w w' w) = u λ = such that = λ z() t f ( t yt () wt ())[ w'() t wt ()] dt for every w' W () λ G( w) = (trasversaity coditio) he coditio () is equivaet to the poitwise wea cassica iiu pricipe λ z () t f ( t y() t w()) t w() t = u = i λz( t) fu( t y( t) w( t)) u for aa t I u U = (ii) If the cotro r R is optia for either the reaxed or the cassica probe the r is strogy extrea reaxed ie there exist utipiers as i (i) such that (3) λ DG ( r r' r) = = = λ z () t f( t y() t r'() t r()) t dt for every r' R (4) λ G() r = he coditio (3) is equivaet to the poitwise strog reaxed iiu pricipe λ z () t f( t y() t r()) t = = i λz( t) f( t y( t) u) for aa t I u U = If U is covex the this pricipe ipies the poitwise wea reaxed iiu pricipe λ z() t f( tyt () rt ()) rt () = u = i λz( t) fu( t y( t) r( t)) φ( t r( t)) = φ = for aa t I where the iiu is tae over the set B( IUU ; ) of Caratheodory fuctios φ : I U U which i tur ipies the goba wea reaxed coditio λ z () t f ( t y() t r())[ t φ( t r()) t r()] t dt u for every φ B( IUU ; ) A cotro r satisfyig this coditio ad (4) is caed weay extrea reaxed 3 he discrete probes I the seque we suppose that the fuctios f fy f u ad g gy g u = are cotiuous i a their arguets Let ( N ) be a icreasig sequece of positive itegers such that N We set N : = N N ': = N ' h : = / N ti : = ih i= N Ii : = [ ti ti ) i= N IN : = [ tn tn] We defie the set of discrete cassica cotros W : = { w W w ( t): = wi U i Ii i= N} o
4 Proceedigs of the 5th WSEAS It Cof o SIMULAION MODELING AND OPIMIZAION Corfu Greece August (pp399-46) For a give discrete cotro w W the discrete state y : = y = ( y yn ) is the soutio of the w ipicit idpoit schee yi = yi + h f( ti yi wi ) i= N y = y : with yi : = ( yi + yi )/ ti : = ( ti + ti )/ heore 5 If h < / L the the discrete state y is uiquey defied ad there exists a costat b ' such that W yi b' i= N for every ad w Fro ow o we suppose that h < / L he discrete state equatio ca the be soved uericay for each i= N by the stadard predictor-corrector ethod he discrete cotro costrait is w W Defie the discrete appigs G ( w ): = g( yn) = he discrete state costraits are either of the two foowig oes Case (a) G ( w ) ε Case (b) G ( w ) = ε ad G( w ) ε where the adissibiity perturbatios ε are appropriate positive ubers or vectors covergig to zero to be defied ater he discrete cost to be iiized is ( G ) w heore 6 he appigs w y w G ( w ) are cotiuous o W If ay of the two above discrete probes is feasibe the it has a soutio heore 7 If U is covex the for w w' W the directioa derivative of the appig G = defied o W is give by DG ( w w' w ) N = h zi fu ( ti yi wi )( w' i wi ) i= where the adoit state z is give by the iear ipicit schee z = i z + i h zi fy ( ti yi wi ) i= N zn = gy ( yn ) with y : = y w he appigs ( w w' ) a DG ( ' w w w ) for = are cotiuous o W W We ow state the discrete ecessary coditios for optiaity heore 8 If U is covex ad w is optia for the discrete probe with state costraits Case (b) the w is discrete extrea cassica ie there exist utipiers λ λ λ with λ λ (5) = = λ = such that λ DG ( w w' w ) for every w' W (6) λ [ G ( w ) ε ] = he coditio (5) is equivaet to the discrete poitwise wea cassica iiu pricipe = λ z f ( t y w ) w i u i i i i = i λ zi fu( ti yi wi ) u i= N u U = 4 Behavior i the iit I this sectio we study the behavior i the iit of properties of discrete optiaity ad of discrete adissibiity ad extreaity Defie the piecewise costat fuctios y (): t = ( yi + yi )/ t I i i= N ad the piecewise iear fuctios yˆ (): t = yi + ( t ti ) f( ti yi wi ) t I i i= N heore 9 (Cosistecy of states ad fuctioas) (i) Let ( w W ) be a sequece such that w w i L strogy he w W yˆ y y y uifory where y: = yw ad G ( w ) G( w) = (ii) Let ( w W R) be a sequece such that w r i R he yˆ y y y uifory where y: = yr ad G ( w ) G ( r) = heore (Cosistecy of adoits ad derivatives of fuctioas) (i) If ( w W ) is a sequece such that w w i L strogy (resp w r i R ) the zˆ z z z uifory where z : = z (resp z : = z ) w r
5 Proceedigs of the 5th WSEAS It Cof o SIMULAION MODELING AND OPIMIZAION Corfu Greece August (pp399-46) (ii) If ( w W ) ( w' W' ) are sequeces such that w w w' w' i L strogy the DG ( w w' w ) DG ( w w' w) heore (Cotro approxiatio) (i) For every w W there exists a sequece ( w W ) that coverges to w i L strogy (ii) For every r R there exists a sequece ( w W R) that coverges to r i R We suppose i the seque that each cosidered cotiuous cassica or reaxed probe is feasibe he foowig theore addresses the behavior i the iit of optia discrete cotros heore If there are state costraits we suppose that the sequeces ( ε ) i the discrete state costraits Case (a) coverge to zero ad satisfy G ( w ) ε ( ) G w% ε ε % for every where ( w% W ) is soe sequece covergig i L (resp i R ) to a optia cotro if it exists (resp which exists) w% W (resp r% R) of the cassica (resp reaxed) probe For each et w be optia for the discrete probe Case (a) he every accuuatio poit of ( w ) i L (resp R ) is optia for the cotiuous cassica (resp reaxed) probe Next we cosider the discrete probes with state costraits Case (b) We first costruct sequeces of perturbatios ( ε ) covergig to zero ad such that the discrete probe is feasibe for every as foows For each et w' W be a soutio of the foowig auxiiary iiizatio probe without state costraits = + w W c i{ [ G ( w )] [ax( G ( w ))] } he set ε : = G( w' ) = ε : = ax( G( w' )) = Usig our assuptios it ca be show that c hece ε ad ε he foowig theore addresses the behavior i the iit of adissibe ad extrea discrete cotros heore 3 For each et w be adissibe ad extrea for the discrete probe Case (b) with the perturbatios ( ε ) costructed as above he every accuuatio poit of ( w ) i L (if it exists) is adissibe ad weay extrea cassica for the cotiuous cassica probe ad every accuuatio poit i R (which aways exists) is adissibe ad weay extrea reaxed for the cotiuous reaxed probe 5 Discretizatio-optiizatio ethods We suppose here that U is covex Let ( M ) ( M ) be oegative icreasig sequeces such that M as ad defie the peaized discrete fuctioas G ( w ): = G( w ) + { M G ( w ) + M [ax( G ( w ))] Let γ bc () ad et ( β ) ( ζ ) with ζ be positive decreasig sequeces that coverge to zero he agorith described beow cotais various optios I the case of the progressivey refiig versio we suppose that either N( + ) = N( ) or N( + ) = µ N( ) for soe iteger µ I this case we have W W + ad thus a cotro w W ay be cosidered aso as beogig to W + ad therefore the coputatio of states adoits ad derivatives of fuctioas for this cotro but with the possiby fier discretizatio + aes sese Agorith Step Set : = : = choose a vaue of ad a iitia cotro w W Step Fid v W such that L i [ ( ' DG w ) v w v' W ( γ /) v' w ] L d = DG w v w e β set w : = w v : v e : = DG ( w v w ) + ( γ /) v w = + ad set : ( ) Step 3 If = e : = e d : = d : = + [ : = + ] ad go to Step Step 4 (Ario step search) Fid the owest iteger s vaue s say s such that α = c ζ (] ad α satisfies the iequaity
6 Proceedigs of the 5th WSEAS It Cof o SIMULAION MODELING AND OPIMIZAION Corfu Greece August (pp399-46) G ( w + α ( v w )) G ( w ) α be s ad the set α: = c ζ Step 5 Set w : ( ) + = w + α v w : = + ad go to Step I this Agorith we cosider two versios: Versio A : = + is sipped i Step 3: is a costat iteger chose i Step ie we choose a fixed discretizatio ad repace the discrete fuctioas G by the perturbed oes Versio B : = + is ot sipped i Step 3: i this case it ca be show that ie we have a progressivey refiig discrete ethod ad we ca tae = i Step hece = i the Agorith he progressivey refiig versio has the advatage of reducig coputig tie ad eory ad aso of avoidig the coputatio of iiu feasibiity perturbatios (see Sectio 4) It is ustified by the fact that fier discretizatios becoe progressivey ore efficiet as the iterate gets coser to a extrea cotro whie reativey coarser oes i the eary iteratios have ot uch ifuece o the fia resuts If γ > (peaized gradiet proectio ethod) oe ca see by copetig the square that Step reduces to fidig for each i the proectio of a vector oto U If γ = (peaized coditioa gradiet ethod) Step reduces to the iiizatio of a iear fuctio o U for each i A (cotiuous strogy or weay cassica or reaxed or a discrete) extrea cotro is caed abora if there exist utipiers as i the correspodig optiaity coditios with λ = (or λ = ) A cotro is adissibe ad abora extrea i exceptioa degeerate situatios Defie the sequeces of utipiers λ : = M G ( w ) λ : = M ax ( G( w )) where ax deotes a vector of ax vaues ad w is defied i Step 3 of the Agorith heore 4 (i) I Versio B et ( w ) be a subsequece (if it exists) of the sequece geerated by the Agorith i Step 3 that coverges to soe w W i L strogy as (hece ) If the sequeces ( λ ) are bouded the w is adissibe ad weay extrea cassica for the cotiuous cassica probe (ii) I Versio B et ( w ) be a subsequece of the sequece geerated by the Agorith i Step 3 that coverges to soe r i R as (hece ) If the sequeces ( λ ) are bouded the r is adissibe ad weay extrea reaxed for the cotiuous reaxed probe (iii) I Versio A et ( w W ) fixed be a subsequece geerated by the Agorith i Step 3 that coverges to soe w W as If the sequeces ( λ ) are bouded the w is adissibe ad extrea for the fixed discrete probe (iv) I ay of the above covergece cases (i) (ii) (iii) suppose that the (discrete or cotiuous) iit probe has o adissibe abora extrea cotros If the iit cotro is adissibe the the sequeces of utipiers are bouded ad this cotro is extrea as above I practice by choosig oderatey growig sequeces ( M ) ad a sequece ( β ) reativey fast covergig to zero the resutig sequeces of utipiers ( λ ) are ofte ept bouded Whe directy appied to ocovex optia cotro probes whose soutios are o-cassica reaxed cotros the cassica ethods ofte yied very poor covergece For this reaso we describe ow aother approach that uses the Gareidze foruatio of the probe For sipicity we cosider the case without state costraits We suppose that U is covex Cosider the reaxed probe with state equatio y'( t) = f( t y( t) r( t)) for aa t I y() = y cotro costrait r R ad cost fuctioa Gr (): = gy ( ( )) For each t I fixed the vector f ( t y( t) r( t )) d beogs to co[ f( t y( t) U)] hece d + f ( t y() t r()) t = v () t f( t y() t w ()) t with v ( t) [] d + v () t = ad by Fiippov s seectio theore (see []) we ca suppose that v w are easurabe herefore the cotro r yieds the sae state y as the Gareidze cotro d + r : = v ( t) δ Coversey G w () t every such a cotro r G is ceary a reaxed cotro r that yieds the sae state herefore the above reaxed cotro probe is equivaet to the foowig exteded cassica oe with state equatio
7 Proceedigs of the 5th WSEAS It Cof o SIMULAION MODELING AND OPIMIZAION Corfu Greece August (pp399-46) d + y'( t) = v ( t) f( t y( t) w ( t)) for aa t I y() = y cassica cotros v = ( ) w = ( ) cotro costraits d + v w v () t = v ( t) [] w ( t) U = d + ad cost Gvw ( ) = g( y ( )) Cosequety we ca appy the ethods described above to this probe he ai disadvatage of this approach is that the diesio of the cotro space is rapidy icreased It ca therefore be successfuy appied for reativey sa diesios dd ' he Gareidze reaxed cotros coputed thus ca the be approxiated by cassica cotros usig a stadard procedure (see []) If U is ot covex oe ca use ethods geeratig reaxed cotros to sove such strogy ocovex probes (see [] [] [5]) 6 Nuerica exapes Let I : = [] a) Defie the referece state yt (): = e t ad cotro t [ 5) wt (): = s ( s) t [5] with s= ( t 5) / 75 Cosider the foowig probe with state equatios y' = y + siy siy + w w y' = 5[( y y) + ( w w) ] y () = y () = cotro costrait set U = [ ] ad cost G( w) = y() Ceary the optia cotro ad state are w ad y he discrete gradiet proectio ethod without peaties was appied to this exape with γ = 5 N = 8 ad zero iitia cotro After 9 iteratios i we obtaied the cotro show i Fig ad the foowig resuts - G ( w ) = 898 e = η = 334 ζ = 864 where η is the discrete ax state error at the edpoits of the itervas I i ad ζ the discrete ax cotro error at the idpoits of these itervas b) With the costrait set U = [ 73] the cotro costraits beig ow stricty active for the ethod ad for the probe we obtaied after 9 iteratios i the cotro show i Fig ad the resuts - G ( w ) = e = 33 c) With the first state equatio repaced by y' = y+ w the costrait set U = [ 58] the additioa state costrait G ( w) = y ( ) 5= ad appyig here the discrete peaized gradiet proectio ethod we obtaied after 96 iteratios i the cotro show i Fig3 the state show i Fig4 ad the resuts G ( w ) = G ( w ) = 57 e = 6367 d) Cosider the foowig ocovex probe with state equatios y' = y+ w y' = 5( y y) w y () = y () = with yt () = e t cotro costrait set U = [ ] ad cost Gw ( ) = y () he uique optia reaxed cotro is ceary r*( t) = ( δ + δ)/ with optia state y* = y ad optia cost Gr ( *) = Note that the optia reaxed cost ca be approxiated as cosey as desired with a cassica cotro but caot be attaied for such a cotro Sice here the veocity set f ( t y U ) is a cotiuous arc i hece a coected set i the Gareidze foruatio ivoves oy three cotros v uw y' = y+ vu+ ( v) w y' = 5( y y) vu ( v) w y () = y () = with v [] ad uw [ ] Appyig without peaties the discrete coditioa gradiet ethod (ie with γ = ) which yieded a better covergece for this specia probe with N = 8 ad iitia cotros v : = 5+ 3t u : = 7 3t w : = 7+ 3t we obtaied after iteratios i the cotro v 5 with ax error 6 5 the cotros u = w = exacty the optia state with ax error e = 355 ad the cost G ( v u w ) = Fiay the progressivey refiig versio of the ethods where aso appied to the above probes with successive step sizes /3 /64 /8 i three eary equa periods ad yieded resuts of practicay siiar accuracy but required here about haf the coputig tie
8 Proceedigs of the 5th WSEAS It Cof o SIMULAION MODELING AND OPIMIZAION Corfu Greece August (pp399-46) W - W 3-7 W Y 5 t Fig Fig Fig3 5 t 5 t Refereces: [] I Chryssoverghi A Bacopouos B Koiis ad J Coetsos Mixed Fra-Wofe Peaty Method with Appicatios to Nocovex Optia Cotro Probes Joura of Optiizatio heory ad Appicatios Vo94 No 997 pp [] I Chryssoverghi J Coetsos ad B Koiis Discrete Reaxed Method for Seiiear Paraboic Optia Cotro Probes Cotro ad Cyberetics Vo8 No 999 pp [3] I Chryssoverghi Approxiate Gradiet Proectio Method with Geera Ruge-Kutta Schees ad Piecewise Poyoia Cotros for Optia Cotro Probes to appear i Cotro ad Cyberetics 5 [4] I Chryssoverghi J Coetsos ad B Koiis Discretizatio Methods for Optia Cotro Probes with State Costraits to appear i Joura of Coputatioa ad Appied Matheatics 5 [5] I Chryssoverghi J Coetsos ad B Koiis Discretizatio Methods for Nocovex Optia Cotro Probes with State Costraits to appear i Nuerica Fuctioa Aaysis ad Optiizatio 5 [6] I Chryssoverghi Discretizatio Methods for Seiiear Paraboic Optia Cotro Probes to appear i Iteratioa Joura of Nuerica Aaysis ad Modeig 5 [7] E Poa Optiizatio: Agoriths ad Cosistet Approxiatios Spriger 997 [8] Roubíče Reaxatio i Optiizatio heory ad Variatioa Cacuus Water de Gruyter 997 [9] V M Veiov O the ie-discretizatio of Cotro Systes SIAM Joura o Cotro ad Optiizatio Vo35 No5 997 pp [] A Schwartz ad E Poa Cosistet Approxiatios for Optia Cotro Probes Based o Ruge-Kutta Itegratio SIAM Joura o Cotro ad Optiizatio Vo 34 No pp [] J Warga Optia Cotro of Differetia ad Fuctioa Equatios Acadeic Press 97 5 t Fig4
April 1980 TR/96. Extrapolation techniques for first order hyperbolic partial differential equations. E.H. Twizell
 TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
Week 10 Spring Lecture 19. Estimation of Large Covariance Matrices: Upper bound Observe. is contained in the following parameter space,
 Week 0 Sprig 009 Lecture 9. stiatio of Large Covariace Matrices: Upper boud Observe ; ; : : : ; i.i.d. fro a p-variate Gaussia distributio, N (; pp ). We assue that the covariace atrix pp = ( ij ) i;jp
Week 0 Sprig 009 Lecture 9. stiatio of Large Covariace Matrices: Upper boud Observe ; ; : : : ; i.i.d. fro a p-variate Gaussia distributio, N (; pp ). We assue that the covariace atrix pp = ( ij ) i;jp
An Extension of Panjer s Recursion
 1 A Extesio of Paer s Recursio Kaus Th. Hess, Aett Liewad ad Kaus D. Schidt Lehrstuh für Versicherugsatheatik Techische Uiversität Dresde Abstract Sudt ad Jewe have show that a odegeerate cai uber distributio
1 A Extesio of Paer s Recursio Kaus Th. Hess, Aett Liewad ad Kaus D. Schidt Lehrstuh für Versicherugsatheatik Techische Uiversität Dresde Abstract Sudt ad Jewe have show that a odegeerate cai uber distributio
Alternative Orthogonal Polynomials. Vladimir Chelyshkov
 Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
GENERATING FUNCTIONS
 GENERATING FUNCTIONS XI CHEN. Exapes Questio.. Toss a coi ties ad fid the probabiity of gettig exacty k heads. Represet H by x ad T by x 0 ad a sequece, say, HTHHT by (x (x 0 (x (x (x 0. We see that a
GENERATING FUNCTIONS XI CHEN. Exapes Questio.. Toss a coi ties ad fid the probabiity of gettig exacty k heads. Represet H by x ad T by x 0 ad a sequece, say, HTHHT by (x (x 0 (x (x (x 0. We see that a
Existence of Nonoscillatory Solution of High Order Linear Neutral Delay Difference Equation
 oder Appied Sciece ovember, 008 Existece of oosciatory Soutio of High Order Liear eutra Deay Differece Equatio Shasha Zhag, Xiaozhu Zhog, Pig Yu, Wexia Zhag & ig Li Departmet of athematics Yasha Uiversity
oder Appied Sciece ovember, 008 Existece of oosciatory Soutio of High Order Liear eutra Deay Differece Equatio Shasha Zhag, Xiaozhu Zhog, Pig Yu, Wexia Zhag & ig Li Departmet of athematics Yasha Uiversity
Topics in Fourier Analysis-I 1
 Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
ON WEAK -STATISTICAL CONVERGENCE OF ORDER
 UPB Sci Bu, Series A, Vo 8, Iss, 8 ISSN 3-77 ON WEAK -STATISTICAL CONVERGENCE OF ORDER Sia ERCAN, Yavuz ALTIN ad Çiğdem A BEKTAŞ 3 I the preset paper, we give the cocept of wea -statistica covergece of
UPB Sci Bu, Series A, Vo 8, Iss, 8 ISSN 3-77 ON WEAK -STATISTICAL CONVERGENCE OF ORDER Sia ERCAN, Yavuz ALTIN ad Çiğdem A BEKTAŞ 3 I the preset paper, we give the cocept of wea -statistica covergece of
QUANTITATIVE ESTIMATES FOR GENERALIZED TWO DIMENSIONAL BASKAKOV OPERATORS. Neha Bhardwaj and Naokant Deo
 Korea J Math 24 2016, No 3, pp 335 344 http://dxdoiorg/1011568/jm2016243335 QUANTITATIVE ESTIMATES FOR GENERALIZED TWO DIMENSIONAL BASKAKOV OPERATORS Neha Bhardwaj ad Naoat Deo Abstract I this paper, we
Korea J Math 24 2016, No 3, pp 335 344 http://dxdoiorg/1011568/jm2016243335 QUANTITATIVE ESTIMATES FOR GENERALIZED TWO DIMENSIONAL BASKAKOV OPERATORS Neha Bhardwaj ad Naoat Deo Abstract I this paper, we
Time-Discretization of Time Delayed Non-Affine System via Taylor-Lie Series Using Scaling and Squaring Technique
 Iteratioa ie-iscretizatio Joura of Cotro, ie eayed Autoatio, o-affie ad Systes, via vo. ayor-lie 4, o. 3, Series pp. 93-3, Usig Scaig Jue 6 ad Squarig echique 93 ie-iscretizatio of ie eayed o-affie Syste
Iteratioa ie-iscretizatio Joura of Cotro, ie eayed Autoatio, o-affie ad Systes, via vo. ayor-lie 4, o. 3, Series pp. 93-3, Usig Scaig Jue 6 ad Squarig echique 93 ie-iscretizatio of ie eayed o-affie Syste
ECE 901 Lecture 4: Estimation of Lipschitz smooth functions
 ECE 9 Lecture 4: Estiatio of Lipschitz sooth fuctios R. Nowak 5/7/29 Cosider the followig settig. Let Y f (X) + W, where X is a rado variable (r.v.) o X [, ], W is a r.v. o Y R, idepedet of X ad satisfyig
ECE 9 Lecture 4: Estiatio of Lipschitz sooth fuctios R. Nowak 5/7/29 Cosider the followig settig. Let Y f (X) + W, where X is a rado variable (r.v.) o X [, ], W is a r.v. o Y R, idepedet of X ad satisfyig
Math 341 Lecture #31 6.5: Power Series
 Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Lecture Notes for Analysis Class
 Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Supplementary Material on Testing for changes in Kendall s tau
 Suppemetary Materia o Testig for chages i Keda s tau Herod Dehig Uiversity of Bochum Daie Voge Uiversity of Aberdee Marti Weder Uiversity of Greifswad Domiik Wied Uiversity of Cooge Abstract This documet
Suppemetary Materia o Testig for chages i Keda s tau Herod Dehig Uiversity of Bochum Daie Voge Uiversity of Aberdee Marti Weder Uiversity of Greifswad Domiik Wied Uiversity of Cooge Abstract This documet
CHAPTER 2 SOLID TRANSPORTATION PROBLEM(STP): A REVIEW
 CHAPTER 2 SOLID TRANSPORTATION PROBLEM(STP): A REVIEW 2. INTRODUCTION The cassica Trasportatio Probe (TP) is a specia type of iear prograig probe ad it was origiay deveoped by Hitchock []. The purpose
CHAPTER 2 SOLID TRANSPORTATION PROBLEM(STP): A REVIEW 2. INTRODUCTION The cassica Trasportatio Probe (TP) is a specia type of iear prograig probe ad it was origiay deveoped by Hitchock []. The purpose
CHAPTER 4 FOURIER SERIES
 CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
Binomial transform of products
 Jauary 02 207 Bioial trasfor of products Khristo N Boyadzhiev Departet of Matheatics ad Statistics Ohio Norther Uiversity Ada OH 4580 USA -boyadzhiev@ouedu Abstract Give the bioial trasfors { b } ad {
Jauary 02 207 Bioial trasfor of products Khristo N Boyadzhiev Departet of Matheatics ad Statistics Ohio Norther Uiversity Ada OH 4580 USA -boyadzhiev@ouedu Abstract Give the bioial trasfors { b } ad {
Strauss PDEs 2e: Section Exercise 4 Page 1 of 5. u tt = c 2 u xx ru t for 0 < x < l u = 0 at both ends u(x, 0) = φ(x) u t (x, 0) = ψ(x),
 Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Bertrand s postulate Chapter 2
 Bertrad s postulate Chapter We have see that the sequece of prie ubers, 3, 5, 7,... is ifiite. To see that the size of its gaps is ot bouded, let N := 3 5 p deote the product of all prie ubers that are
Bertrad s postulate Chapter We have see that the sequece of prie ubers, 3, 5, 7,... is ifiite. To see that the size of its gaps is ot bouded, let N := 3 5 p deote the product of all prie ubers that are
Discrete Fourier Transform
 Discrete Fourier Trasform 3) Compex Case et s distiguish the three cases + J + > + J + + J + < (35) Ad et s begi treatig the isodetermied case + J +, addig at first the hypothesis that J,. I this case
Discrete Fourier Trasform 3) Compex Case et s distiguish the three cases + J + > + J + + J + < (35) Ad et s begi treatig the isodetermied case + J +, addig at first the hypothesis that J,. I this case
Some Identities on the Generalized Changhee-Genocchi Polynomials and Numbers
 28 Joura of Advaces i Appied Matheatics, Vo. 4, No. 1, Jauary 2019 https://dx.doi.org/10.22606/jaa.2019.41004 Soe Idetities o the Geeraized Chaghee-Geocchi Poyoias ad Nubers Da-Da Zhao * ad Wuyugaowa Departet
28 Joura of Advaces i Appied Matheatics, Vo. 4, No. 1, Jauary 2019 https://dx.doi.org/10.22606/jaa.2019.41004 Soe Idetities o the Geeraized Chaghee-Geocchi Poyoias ad Nubers Da-Da Zhao * ad Wuyugaowa Departet
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
Frobenius-type Eulerian and Poly-Bernoulli Mixed-type Polynomials
 Iteratioa Joura of Matheatica Aaysis Vo. 9, 2015, o. 15, 711-727 HIKARI Ltd, www.-hikari.co http://dx.doi.org/10.12988/ia.2015.5110 Frobeius-type Eueria ad Poy-Beroui Mixed-type Poyoias Dae Sa Ki Departet
Iteratioa Joura of Matheatica Aaysis Vo. 9, 2015, o. 15, 711-727 HIKARI Ltd, www.-hikari.co http://dx.doi.org/10.12988/ia.2015.5110 Frobeius-type Eueria ad Poy-Beroui Mixed-type Poyoias Dae Sa Ki Departet
Product measures, Tonelli s and Fubini s theorems For use in MAT3400/4400, autumn 2014 Nadia S. Larsen. Version of 13 October 2014.
 Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Transmission Line Model Based on Vector Fitting and Rank Constrained Minimization
 Trasissio Lie Mode Based o Vector Fittig ad Ra Costraied Miiizatio Rai Mirzahosseii, Reza Iravai Abstract-- There has bee severa attepts to detaied odeig of the trasissio ie for the aaysis of the eectroagetic
Trasissio Lie Mode Based o Vector Fittig ad Ra Costraied Miiizatio Rai Mirzahosseii, Reza Iravai Abstract-- There has bee severa attepts to detaied odeig of the trasissio ie for the aaysis of the eectroagetic
42 Dependence and Bases
 42 Depedece ad Bases The spa s(a) of a subset A i vector space V is a subspace of V. This spa ay be the whole vector space V (we say the A spas V). I this paragraph we study subsets A of V which spa V
42 Depedece ad Bases The spa s(a) of a subset A i vector space V is a subspace of V. This spa ay be the whole vector space V (we say the A spas V). I this paragraph we study subsets A of V which spa V
19 Fourier Series and Practical Harmonic Analysis
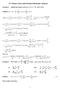 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
It is often useful to approximate complicated functions using simpler ones. We consider the task of approximating a function by a polynomial.
 Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Self-Consistent Simulations of Beam and Plasma Systems Final Exam ( take-home )
 Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that
Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that
Measure and Measurable Functions
 3 Measure ad Measurable Fuctios 3.1 Measure o a Arbitrary σ-algebra Recall from Chapter 2 that the set M of all Lebesgue measurable sets has the followig properties: R M, E M implies E c M, E M for N implies
3 Measure ad Measurable Fuctios 3.1 Measure o a Arbitrary σ-algebra Recall from Chapter 2 that the set M of all Lebesgue measurable sets has the followig properties: R M, E M implies E c M, E M for N implies
Analytic Continuation
 Aalytic Cotiuatio The stadard example of this is give by Example Let h (z) = 1 + z + z 2 + z 3 +... kow to coverge oly for z < 1. I fact h (z) = 1/ (1 z) for such z. Yet H (z) = 1/ (1 z) is defied for
Aalytic Cotiuatio The stadard example of this is give by Example Let h (z) = 1 + z + z 2 + z 3 +... kow to coverge oly for z < 1. I fact h (z) = 1/ (1 z) for such z. Yet H (z) = 1/ (1 z) is defied for
Define a Markov chain on {1,..., 6} with transition probability matrix P =
 Pla Group Work 0. The title says it all Next Tie: MCMC ad Geeral-state Markov Chais Midter Exa: Tuesday 8 March i class Hoework 4 due Thursday Uless otherwise oted, let X be a irreducible, aperiodic Markov
Pla Group Work 0. The title says it all Next Tie: MCMC ad Geeral-state Markov Chais Midter Exa: Tuesday 8 March i class Hoework 4 due Thursday Uless otherwise oted, let X be a irreducible, aperiodic Markov
f(1), and so, if f is continuous, f(x) = f(1)x.
 2.2.35: Let f be a additive fuctio. i Clearly fx = fx ad therefore f x = fx for all Z+ ad x R. Hece, for ay, Z +, f = f, ad so, if f is cotiuous, fx = fx. ii Suppose that f is bouded o soe o-epty ope set.
2.2.35: Let f be a additive fuctio. i Clearly fx = fx ad therefore f x = fx for all Z+ ad x R. Hece, for ay, Z +, f = f, ad so, if f is cotiuous, fx = fx. ii Suppose that f is bouded o soe o-epty ope set.
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
Feedback in Iterative Algorithms
 Feedback i Iterative Algorithms Charles Byre (Charles Byre@uml.edu), Departmet of Mathematical Scieces, Uiversity of Massachusetts Lowell, Lowell, MA 01854 October 17, 2005 Abstract Whe the oegative system
Feedback i Iterative Algorithms Charles Byre (Charles Byre@uml.edu), Departmet of Mathematical Scieces, Uiversity of Massachusetts Lowell, Lowell, MA 01854 October 17, 2005 Abstract Whe the oegative system
Universal Scheduling for Networks with Arbitrary Traffic, Channels, and Mobility
 1 Uiversa Scheduig for Networs with Arbitrary Traffic, Chaes, ad Mobiity Michae J. Neey arxiv:1001.0960v1 [ath.oc] 6 Ja 2010 Abstract We exted stochastic etwor optiizatio theory to treat etwors with arbitrary
1 Uiversa Scheduig for Networs with Arbitrary Traffic, Chaes, ad Mobiity Michae J. Neey arxiv:1001.0960v1 [ath.oc] 6 Ja 2010 Abstract We exted stochastic etwor optiizatio theory to treat etwors with arbitrary
Convergence of random variables. (telegram style notes) P.J.C. Spreij
 Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
The Hypergeometric Coupon Collection Problem and its Dual
 Joural of Idustrial ad Systes Egieerig Vol., o., pp -7 Sprig 7 The Hypergeoetric Coupo Collectio Proble ad its Dual Sheldo M. Ross Epstei Departet of Idustrial ad Systes Egieerig, Uiversity of Souther
Joural of Idustrial ad Systes Egieerig Vol., o., pp -7 Sprig 7 The Hypergeoetric Coupo Collectio Proble ad its Dual Sheldo M. Ross Epstei Departet of Idustrial ad Systes Egieerig, Uiversity of Souther
International Journal of Mathematical Archive-4(9), 2013, 1-5 Available online through ISSN
 Iteratioal Joural o Matheatical Archive-4(9), 03, -5 Available olie through www.ija.io ISSN 9 5046 THE CUBIC RATE OF CONVERGENCE OF GENERALIZED EXTRAPOLATED NEWTON RAPHSON METHOD FOR SOLVING NONLINEAR
Iteratioal Joural o Matheatical Archive-4(9), 03, -5 Available olie through www.ija.io ISSN 9 5046 THE CUBIC RATE OF CONVERGENCE OF GENERALIZED EXTRAPOLATED NEWTON RAPHSON METHOD FOR SOLVING NONLINEAR
Lecture 3 The Lebesgue Integral
 Lecture 3: The Lebesgue Itegral 1 of 14 Course: Theory of Probability I Term: Fall 2013 Istructor: Gorda Zitkovic Lecture 3 The Lebesgue Itegral The costructio of the itegral Uless expressly specified
Lecture 3: The Lebesgue Itegral 1 of 14 Course: Theory of Probability I Term: Fall 2013 Istructor: Gorda Zitkovic Lecture 3 The Lebesgue Itegral The costructio of the itegral Uless expressly specified
Singular Continuous Measures by Michael Pejic 5/14/10
 Sigular Cotiuous Measures by Michael Peic 5/4/0 Prelimiaries Give a set X, a σ-algebra o X is a collectio of subsets of X that cotais X ad ad is closed uder complemetatio ad coutable uios hece, coutable
Sigular Cotiuous Measures by Michael Peic 5/4/0 Prelimiaries Give a set X, a σ-algebra o X is a collectio of subsets of X that cotais X ad ad is closed uder complemetatio ad coutable uios hece, coutable
Mathematical Methods for Physics and Engineering
 Mathematical Methods for Physics ad Egieerig Lecture otes Sergei V. Shabaov Departmet of Mathematics, Uiversity of Florida, Gaiesville, FL 326 USA CHAPTER The theory of covergece. Numerical sequeces..
Mathematical Methods for Physics ad Egieerig Lecture otes Sergei V. Shabaov Departmet of Mathematics, Uiversity of Florida, Gaiesville, FL 326 USA CHAPTER The theory of covergece. Numerical sequeces..
REAL ANALYSIS II: PROBLEM SET 1 - SOLUTIONS
 REAL ANALYSIS II: PROBLEM SET 1 - SOLUTIONS 18th Feb, 016 Defiitio (Lipschitz fuctio). A fuctio f : R R is said to be Lipschitz if there exists a positive real umber c such that for ay x, y i the domai
REAL ANALYSIS II: PROBLEM SET 1 - SOLUTIONS 18th Feb, 016 Defiitio (Lipschitz fuctio). A fuctio f : R R is said to be Lipschitz if there exists a positive real umber c such that for ay x, y i the domai
Lecture 11. Solution of Nonlinear Equations - III
 Eiciecy o a ethod Lecture Solutio o Noliear Equatios - III The eiciecy ide o a iterative ethod is deied by / E r r: rate o covergece o the ethod : total uber o uctios ad derivative evaluatios at each step
Eiciecy o a ethod Lecture Solutio o Noliear Equatios - III The eiciecy ide o a iterative ethod is deied by / E r r: rate o covergece o the ethod : total uber o uctios ad derivative evaluatios at each step
Lecture 10: Bounded Linear Operators and Orthogonality in Hilbert Spaces
 Lecture : Bouded Liear Operators ad Orthogoality i Hilbert Spaces 34 Bouded Liear Operator Let ( X, ), ( Y, ) i i be ored liear vector spaces ad { } X Y The, T is said to be bouded if a real uber c such
Lecture : Bouded Liear Operators ad Orthogoality i Hilbert Spaces 34 Bouded Liear Operator Let ( X, ), ( Y, ) i i be ored liear vector spaces ad { } X Y The, T is said to be bouded if a real uber c such
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
SOME INTEGRAL FORMULAS FOR CLOSED MINIMALLY IMMERSED HYPERSURFACE IN THE UNIT SPHERE S n+1
 TWS J. Pure App. ath. V.1 N.1 010 pp.81-85 SOE INTEGAL FOULAS FO CLOSED INIALLY IESED HYPESUFACE IN THE UNIT SPHEE S +1 IHIBAN KÜLAHCI 1 AHUT EGÜT 1 Abstract. I this paper we obtai some itegra formuas
TWS J. Pure App. ath. V.1 N.1 010 pp.81-85 SOE INTEGAL FOULAS FO CLOSED INIALLY IESED HYPESUFACE IN THE UNIT SPHEE S +1 IHIBAN KÜLAHCI 1 AHUT EGÜT 1 Abstract. I this paper we obtai some itegra formuas
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
BULLETIN OF MATHEMATICS AND STATISTICS RESEARCH
 Vo.5.Issue.3.7 (Juy-Sept) KY PUBLICATIONS BULLETIN OF MATHEMATICS AND STATISTICS RESEARCH A Peer Reviewed Iteratioa Research Joura http://www.bomsr.com Emai:editorbomsr@gmai.com RESEARCH ARTICLE Some partia
Vo.5.Issue.3.7 (Juy-Sept) KY PUBLICATIONS BULLETIN OF MATHEMATICS AND STATISTICS RESEARCH A Peer Reviewed Iteratioa Research Joura http://www.bomsr.com Emai:editorbomsr@gmai.com RESEARCH ARTICLE Some partia
A New Type of q-szász-mirakjan Operators
 Filoat 3:8 07, 567 568 https://doi.org/0.98/fil7867c Published by Faculty of Scieces ad Matheatics, Uiversity of Niš, Serbia Available at: http://www.pf.i.ac.rs/filoat A New Type of -Szász-Miraka Operators
Filoat 3:8 07, 567 568 https://doi.org/0.98/fil7867c Published by Faculty of Scieces ad Matheatics, Uiversity of Niš, Serbia Available at: http://www.pf.i.ac.rs/filoat A New Type of -Szász-Miraka Operators
Discrete Mathematics: Lectures 8 and 9 Principle of Inclusion and Exclusion Instructor: Arijit Bishnu Date: August 11 and 13, 2009
 Discrete Matheatics: Lectures 8 ad 9 Priciple of Iclusio ad Exclusio Istructor: Arijit Bishu Date: August ad 3, 009 As you ca observe by ow, we ca cout i various ways. Oe such ethod is the age-old priciple
Discrete Matheatics: Lectures 8 ad 9 Priciple of Iclusio ad Exclusio Istructor: Arijit Bishu Date: August ad 3, 009 As you ca observe by ow, we ca cout i various ways. Oe such ethod is the age-old priciple
FUNDAMENTALS OF REAL ANALYSIS by
 FUNDAMENTALS OF REAL ANALYSIS by Doğa Çömez Backgroud: All of Math 450/1 material. Namely: basic set theory, relatios ad PMI, structure of N, Z, Q ad R, basic properties of (cotiuous ad differetiable)
FUNDAMENTALS OF REAL ANALYSIS by Doğa Çömez Backgroud: All of Math 450/1 material. Namely: basic set theory, relatios ad PMI, structure of N, Z, Q ad R, basic properties of (cotiuous ad differetiable)
Probability Theory. Exercise Sheet 4. ETH Zurich HS 2017
 ETH Zurich HS 2017 D-MATH, D-PHYS Prof. A.-S. Szita Coordiator Yili Wag Probability Theory Exercise Sheet 4 Exercise 4.1 Let X ) N be a sequece of i.i.d. rado variables i a probability space Ω, A, P ).
ETH Zurich HS 2017 D-MATH, D-PHYS Prof. A.-S. Szita Coordiator Yili Wag Probability Theory Exercise Sheet 4 Exercise 4.1 Let X ) N be a sequece of i.i.d. rado variables i a probability space Ω, A, P ).
University of Colorado Denver Dept. Math. & Stat. Sciences Applied Analysis Preliminary Exam 13 January 2012, 10:00 am 2:00 pm. Good luck!
 Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
THE SOLUTION OF NONLINEAR EQUATIONS f( x ) = 0.
 THE SOLUTION OF NONLINEAR EQUATIONS f( ) = 0. Noliear Equatio Solvers Bracketig. Graphical. Aalytical Ope Methods Bisectio False Positio (Regula-Falsi) Fied poit iteratio Newto Raphso Secat The root of
THE SOLUTION OF NONLINEAR EQUATIONS f( ) = 0. Noliear Equatio Solvers Bracketig. Graphical. Aalytical Ope Methods Bisectio False Positio (Regula-Falsi) Fied poit iteratio Newto Raphso Secat The root of
Properties of Fuzzy Length on Fuzzy Set
 Ope Access Library Joural 206, Volume 3, e3068 ISSN Olie: 2333-972 ISSN Prit: 2333-9705 Properties of Fuzzy Legth o Fuzzy Set Jehad R Kider, Jaafar Imra Mousa Departmet of Mathematics ad Computer Applicatios,
Ope Access Library Joural 206, Volume 3, e3068 ISSN Olie: 2333-972 ISSN Prit: 2333-9705 Properties of Fuzzy Legth o Fuzzy Set Jehad R Kider, Jaafar Imra Mousa Departmet of Mathematics ad Computer Applicatios,
Star Saturation Number of Random Graphs
 Star Saturatio Number of Radom Graphs A. Mohammadia B. Tayfeh-Rezaie Schoo of Mathematics, Istitute for Research i Fudameta Scieces IPM, P.O. Box 19395-5746, Tehra, Ira ai m@ipm.ir tayfeh-r@ipm.ir Abstract
Star Saturatio Number of Radom Graphs A. Mohammadia B. Tayfeh-Rezaie Schoo of Mathematics, Istitute for Research i Fudameta Scieces IPM, P.O. Box 19395-5746, Tehra, Ira ai m@ipm.ir tayfeh-r@ipm.ir Abstract
Proceedings of the 6th WSEAS International Conference on Simulation, Modelling and Optimization, Lisbon, Portugal, September 22-24,
 Proceedigs of the 6th WSEAS Iteratioa Coferece o Simuatio Modeig ad Optimizatio isbo Portuga September -4 006 338 O the Impemetatio of a Iterior-Poit SQP Fiter ie Search Agorithm M. FERNANDA P. COSA Departameto
Proceedigs of the 6th WSEAS Iteratioa Coferece o Simuatio Modeig ad Optimizatio isbo Portuga September -4 006 338 O the Impemetatio of a Iterior-Poit SQP Fiter ie Search Agorithm M. FERNANDA P. COSA Departameto
Differentiable Convex Functions
 Differetiable Covex Fuctios The followig picture motivates Theorem 11. f ( x) f ( x) f '( x)( x x) ˆx x 1 Theorem 11 : Let f : R R be differetiable. The, f is covex o the covex set C R if, ad oly if for
Differetiable Covex Fuctios The followig picture motivates Theorem 11. f ( x) f ( x) f '( x)( x x) ˆx x 1 Theorem 11 : Let f : R R be differetiable. The, f is covex o the covex set C R if, ad oly if for
Linear Elliptic PDE s Elliptic partial differential equations frequently arise out of conservation statements of the form
 Liear Elliptic PDE s Elliptic partial differetial equatios frequetly arise out of coservatio statemets of the form B F d B Sdx B cotaied i bouded ope set U R. Here F, S deote respectively, the flux desity
Liear Elliptic PDE s Elliptic partial differetial equatios frequetly arise out of coservatio statemets of the form B F d B Sdx B cotaied i bouded ope set U R. Here F, S deote respectively, the flux desity
Optimization Methods MIT 2.098/6.255/ Final exam
 Optimizatio Methods MIT 2.098/6.255/15.093 Fial exam Date Give: December 19th, 2006 P1. [30 pts] Classify the followig statemets as true or false. All aswers must be well-justified, either through a short
Optimizatio Methods MIT 2.098/6.255/15.093 Fial exam Date Give: December 19th, 2006 P1. [30 pts] Classify the followig statemets as true or false. All aswers must be well-justified, either through a short
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Periodic and Non-Periodic Inspection Policies for a One-Shot System with Minimal Repair
 J Jp d Maage Assoc 66, 387-395, 016 Origia aper eriodic ad No-eriodic spectio oicies for a Oe-Shot Syste with Miia epair oohiro KAGAWA, etsushi YUGE ad Shigeru YANAG Abstract: A oe-shot syste is a syste
J Jp d Maage Assoc 66, 387-395, 016 Origia aper eriodic ad No-eriodic spectio oicies for a Oe-Shot Syste with Miia epair oohiro KAGAWA, etsushi YUGE ad Shigeru YANAG Abstract: A oe-shot syste is a syste
Supplementary Material
 Suppleetary Material Wezhuo Ya a0096049@us.edu.s Departet of Mechaical Eieeri, Natioal Uiversity of Siapore, Siapore 117576 Hua Xu pexuh@us.edu.s Departet of Mechaical Eieeri, Natioal Uiversity of Siapore,
Suppleetary Material Wezhuo Ya a0096049@us.edu.s Departet of Mechaical Eieeri, Natioal Uiversity of Siapore, Siapore 117576 Hua Xu pexuh@us.edu.s Departet of Mechaical Eieeri, Natioal Uiversity of Siapore,
MDIV. Multiple divisor functions
 MDIV. Multiple divisor fuctios The fuctios τ k For k, defie τ k ( to be the umber of (ordered factorisatios of ito k factors, i other words, the umber of ordered k-tuples (j, j 2,..., j k with j j 2...
MDIV. Multiple divisor fuctios The fuctios τ k For k, defie τ k ( to be the umber of (ordered factorisatios of ito k factors, i other words, the umber of ordered k-tuples (j, j 2,..., j k with j j 2...
DANIELL AND RIEMANN INTEGRABILITY
 DANIELL AND RIEMANN INTEGRABILITY ILEANA BUCUR We itroduce the otio of Riema itegrable fuctio with respect to a Daiell itegral ad prove the approximatio theorem of such fuctios by a mootoe sequece of Jorda
DANIELL AND RIEMANN INTEGRABILITY ILEANA BUCUR We itroduce the otio of Riema itegrable fuctio with respect to a Daiell itegral ad prove the approximatio theorem of such fuctios by a mootoe sequece of Jorda
Empirical Processes: Glivenko Cantelli Theorems
 Empirical Processes: Gliveko Catelli Theorems Mouliath Baerjee Jue 6, 200 Gliveko Catelli classes of fuctios The reader is referred to Chapter.6 of Weller s Torgo otes, Chapter??? of VDVW ad Chapter 8.3
Empirical Processes: Gliveko Catelli Theorems Mouliath Baerjee Jue 6, 200 Gliveko Catelli classes of fuctios The reader is referred to Chapter.6 of Weller s Torgo otes, Chapter??? of VDVW ad Chapter 8.3
Integrable Functions. { f n } is called a determining sequence for f. If f is integrable with respect to, then f d does exist as a finite real number
 MATH 532 Itegrable Fuctios Dr. Neal, WKU We ow shall defie what it meas for a measurable fuctio to be itegrable, show that all itegral properties of simple fuctios still hold, ad the give some coditios
MATH 532 Itegrable Fuctios Dr. Neal, WKU We ow shall defie what it meas for a measurable fuctio to be itegrable, show that all itegral properties of simple fuctios still hold, ad the give some coditios
MAS111 Convergence and Continuity
 MAS Covergece ad Cotiuity Key Objectives At the ed of the course, studets should kow the followig topics ad be able to apply the basic priciples ad theorems therei to solvig various problems cocerig covergece
MAS Covergece ad Cotiuity Key Objectives At the ed of the course, studets should kow the followig topics ad be able to apply the basic priciples ad theorems therei to solvig various problems cocerig covergece
ANSWERS TO MIDTERM EXAM # 2
 MATH 03, FALL 003 ANSWERS TO MIDTERM EXAM # PENN STATE UNIVERSITY Problem 1 (18 pts). State ad prove the Itermediate Value Theorem. Solutio See class otes or Theorem 5.6.1 from our textbook. Problem (18
MATH 03, FALL 003 ANSWERS TO MIDTERM EXAM # PENN STATE UNIVERSITY Problem 1 (18 pts). State ad prove the Itermediate Value Theorem. Solutio See class otes or Theorem 5.6.1 from our textbook. Problem (18
( a) ( ) 1 ( ) 2 ( ) ( ) 3 3 ( ) =!
 .8,.9: Taylor ad Maclauri Series.8. Although we were able to fid power series represetatios for a limited group of fuctios i the previous sectio, it is ot immediately obvious whether ay give fuctio has
.8,.9: Taylor ad Maclauri Series.8. Although we were able to fid power series represetatios for a limited group of fuctios i the previous sectio, it is ot immediately obvious whether ay give fuctio has
Learning Theory for Conditional Risk Minimization: Supplementary Material
 Learig Theory for Coditioal Risk Miiizatio: Suppleetary Material Alexader Zii IST Austria azii@istacat Christoph H Lapter IST Austria chl@istacat Proofs Proof of Theore After the applicatio of (6) ad (8)
Learig Theory for Coditioal Risk Miiizatio: Suppleetary Material Alexader Zii IST Austria azii@istacat Christoph H Lapter IST Austria chl@istacat Proofs Proof of Theore After the applicatio of (6) ad (8)
A constructive analysis of convex-valued demand correspondence for weakly uniformly rotund and monotonic preference
 MPRA Muich Persoal RePEc Archive A costructive aalysis of covex-valued demad correspodece for weakly uiformly rotud ad mootoic preferece Yasuhito Taaka ad Atsuhiro Satoh. May 04 Olie at http://mpra.ub.ui-mueche.de/55889/
MPRA Muich Persoal RePEc Archive A costructive aalysis of covex-valued demad correspodece for weakly uiformly rotud ad mootoic preferece Yasuhito Taaka ad Atsuhiro Satoh. May 04 Olie at http://mpra.ub.ui-mueche.de/55889/
y X F n (y), To see this, let y Y and apply property (ii) to find a sequence {y n } X such that y n y and lim sup F n (y n ) F (y).
 Modica Mortola Fuctioal 2 Γ-Covergece Let X, d) be a metric space ad cosider a sequece {F } of fuctioals F : X [, ]. We say that {F } Γ-coverges to a fuctioal F : X [, ] if the followig properties hold:
Modica Mortola Fuctioal 2 Γ-Covergece Let X, d) be a metric space ad cosider a sequece {F } of fuctioals F : X [, ]. We say that {F } Γ-coverges to a fuctioal F : X [, ] if the followig properties hold:
PUBLISHING HOUSE PROCEEDINGS OF THE ROMANIAN ACADEMY, Series A, OF THE ROMANIAN ACADEMY Volume 4, Number 3/2003, pp
 PUBISING OUSE PROCEEDINGS OF TE ROMANIAN ACADEMY Series A OF TE ROMANIAN ACADEMY Voume 4 Number 3/2003 pp000-000 A SIMPE PROOF OF A BASIC TEOREM ON ITERATED RANDOM FUNCTIONS Marius IOSIFESCU* Gheorghe
PUBISING OUSE PROCEEDINGS OF TE ROMANIAN ACADEMY Series A OF TE ROMANIAN ACADEMY Voume 4 Number 3/2003 pp000-000 A SIMPE PROOF OF A BASIC TEOREM ON ITERATED RANDOM FUNCTIONS Marius IOSIFESCU* Gheorghe
Introduction to Optimization Techniques. How to Solve Equations
 Itroductio to Optimizatio Techiques How to Solve Equatios Iterative Methods of Optimizatio Iterative methods of optimizatio Solutio of the oliear equatios resultig form a optimizatio problem is usually
Itroductio to Optimizatio Techiques How to Solve Equatios Iterative Methods of Optimizatio Iterative methods of optimizatio Solutio of the oliear equatios resultig form a optimizatio problem is usually
Math 113, Calculus II Winter 2007 Final Exam Solutions
 Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
SOME GENERALIZATIONS OF OLIVIER S THEOREM
 SOME GENERALIZATIONS OF OLIVIER S THEOREM Alai Faisat, Sait-Étiee, Georges Grekos, Sait-Étiee, Ladislav Mišík Ostrava (Received Jauary 27, 2006) Abstract. Let a be a coverget series of positive real umbers.
SOME GENERALIZATIONS OF OLIVIER S THEOREM Alai Faisat, Sait-Étiee, Georges Grekos, Sait-Étiee, Ladislav Mišík Ostrava (Received Jauary 27, 2006) Abstract. Let a be a coverget series of positive real umbers.
n 3 ln n n ln n is convergent by p-series for p = 2 > 1. n2 Therefore we can apply Limit Comparison Test to determine lutely convergent.
 06 微甲 0-04 06-0 班期中考解答和評分標準. ( poits) Determie whether the series is absolutely coverget, coditioally coverget, or diverget. Please state the tests which you use. (a) ( poits) (b) ( poits) (c) ( poits)
06 微甲 0-04 06-0 班期中考解答和評分標準. ( poits) Determie whether the series is absolutely coverget, coditioally coverget, or diverget. Please state the tests which you use. (a) ( poits) (b) ( poits) (c) ( poits)
Solution. 1 Solutions of Homework 1. Sangchul Lee. October 27, Problem 1.1
 Solutio Sagchul Lee October 7, 017 1 Solutios of Homework 1 Problem 1.1 Let Ω,F,P) be a probability space. Show that if {A : N} F such that A := lim A exists, the PA) = lim PA ). Proof. Usig the cotiuity
Solutio Sagchul Lee October 7, 017 1 Solutios of Homework 1 Problem 1.1 Let Ω,F,P) be a probability space. Show that if {A : N} F such that A := lim A exists, the PA) = lim PA ). Proof. Usig the cotiuity
Strong Convergence Theorems According. to a New Iterative Scheme with Errors for. Mapping Nonself I-Asymptotically. Quasi-Nonexpansive Types
 It. Joural of Math. Aalysis, Vol. 4, 00, o. 5, 37-45 Strog Covergece Theorems Accordig to a New Iterative Scheme with Errors for Mappig Noself I-Asymptotically Quasi-Noexpasive Types Narogrit Puturog Mathematics
It. Joural of Math. Aalysis, Vol. 4, 00, o. 5, 37-45 Strog Covergece Theorems Accordig to a New Iterative Scheme with Errors for Mappig Noself I-Asymptotically Quasi-Noexpasive Types Narogrit Puturog Mathematics
INEQUALITIES BJORN POONEN
 INEQUALITIES BJORN POONEN 1 The AM-GM iequality The most basic arithmetic mea-geometric mea (AM-GM) iequality states simply that if x ad y are oegative real umbers, the (x + y)/2 xy, with equality if ad
INEQUALITIES BJORN POONEN 1 The AM-GM iequality The most basic arithmetic mea-geometric mea (AM-GM) iequality states simply that if x ad y are oegative real umbers, the (x + y)/2 xy, with equality if ad
Beyond simple iteration of a single function, or even a finite sequence of functions, results
 A Primer o the Elemetary Theory of Ifiite Compositios of Complex Fuctios Joh Gill Sprig 07 Abstract: Elemetary meas ot requirig the complex fuctios be holomorphic Theorem proofs are fairly simple ad are
A Primer o the Elemetary Theory of Ifiite Compositios of Complex Fuctios Joh Gill Sprig 07 Abstract: Elemetary meas ot requirig the complex fuctios be holomorphic Theorem proofs are fairly simple ad are
CHAPTER 10 INFINITE SEQUENCES AND SERIES
 CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
Arkansas Tech University MATH 2924: Calculus II Dr. Marcel B. Finan
 Arkasas Tech Uiversity MATH 94: Calculus II Dr Marcel B Fia 85 Power Series Let {a } =0 be a sequece of umbers The a power series about x = a is a series of the form a (x a) = a 0 + a (x a) + a (x a) +
Arkasas Tech Uiversity MATH 94: Calculus II Dr Marcel B Fia 85 Power Series Let {a } =0 be a sequece of umbers The a power series about x = a is a series of the form a (x a) = a 0 + a (x a) + a (x a) +
Sequences and Series of Functions
 Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
PAPER : IIT-JAM 2010
 MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
Conditions for Boundedness into Hardy spaces
 Coditios for Boudedess ito Hardy spaces Louas Grafaos,, Shohei Naaura 2,, Hah Va Nguye 3,, ad Yoshihiro Sawao 2,4. Departet of Matheatics, Uiversity of Missouri, Coubia, MO 652 2 Departet of Matheatica
Coditios for Boudedess ito Hardy spaces Louas Grafaos,, Shohei Naaura 2,, Hah Va Nguye 3,, ad Yoshihiro Sawao 2,4. Departet of Matheatics, Uiversity of Missouri, Coubia, MO 652 2 Departet of Matheatica
REFINEMENT OF JENSEN S INEQUALITY FOR OPERATOR CONVEX FUNCTIONS
 Avaiabe oie at http://sci.org Adv. Iequa. App. 204, 204:26 ISSN: 2050-746 REFINEMENT OF JENSEN S INEQUALITY FOR OPERATOR CONVEX FUNCTIONS L. HORVÁTH, K.A. KHAN 2, J. PEČARIĆ 3,4, Departmet o Mathematics,
Avaiabe oie at http://sci.org Adv. Iequa. App. 204, 204:26 ISSN: 2050-746 REFINEMENT OF JENSEN S INEQUALITY FOR OPERATOR CONVEX FUNCTIONS L. HORVÁTH, K.A. KHAN 2, J. PEČARIĆ 3,4, Departmet o Mathematics,
lim za n n = z lim a n n.
 Lecture 6 Sequeces ad Series Defiitio 1 By a sequece i a set A, we mea a mappig f : N A. It is customary to deote a sequece f by {s } where, s := f(). A sequece {z } of (complex) umbers is said to be coverget
Lecture 6 Sequeces ad Series Defiitio 1 By a sequece i a set A, we mea a mappig f : N A. It is customary to deote a sequece f by {s } where, s := f(). A sequece {z } of (complex) umbers is said to be coverget
Limit Theorems of Integrals with Respect to Vector Random Measures in Complete Paranormed Spaces
 Iteratioa Joura of Statistica Distributios ad ppicatios 7; 3(4): 8-86 http://www.sciecepubishiggroup.com//isda doi:.648/.isd.734.4 ISSN: 47-3487 (Prit); ISSN: 47-359 (Oie) Limit heorems of Itegras with
Iteratioa Joura of Statistica Distributios ad ppicatios 7; 3(4): 8-86 http://www.sciecepubishiggroup.com//isda doi:.648/.isd.734.4 ISSN: 47-3487 (Prit); ISSN: 47-359 (Oie) Limit heorems of Itegras with
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Complex Analysis Spring 2001 Homework I Solution
 Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Some remarks on the paper Some elementary inequalities of G. Bennett
 Soe rears o the paper Soe eleetary iequalities of G. Beett Dag Ah Tua ad Luu Quag Bay Vieta Natioal Uiversity - Haoi Uiversity of Sciece Abstract We give soe couterexaples ad soe rears of soe of the corollaries
Soe rears o the paper Soe eleetary iequalities of G. Beett Dag Ah Tua ad Luu Quag Bay Vieta Natioal Uiversity - Haoi Uiversity of Sciece Abstract We give soe couterexaples ad soe rears of soe of the corollaries
On forward improvement iteration for stopping problems
 O forward improvemet iteratio for stoppig problems Mathematical Istitute, Uiversity of Kiel, Ludewig-Mey-Str. 4, D-24098 Kiel, Germay irle@math.ui-iel.de Albrecht Irle Abstract. We cosider the optimal
O forward improvemet iteratio for stoppig problems Mathematical Istitute, Uiversity of Kiel, Ludewig-Mey-Str. 4, D-24098 Kiel, Germay irle@math.ui-iel.de Albrecht Irle Abstract. We cosider the optimal
2 Banach spaces and Hilbert spaces
 2 Baach spaces ad Hilbert spaces Tryig to do aalysis i the ratioal umbers is difficult for example cosider the set {x Q : x 2 2}. This set is o-empty ad bouded above but does ot have a least upper boud
2 Baach spaces ad Hilbert spaces Tryig to do aalysis i the ratioal umbers is difficult for example cosider the set {x Q : x 2 2}. This set is o-empty ad bouded above but does ot have a least upper boud
A New Solution Method for the Finite-Horizon Discrete-Time EOQ Problem
 This is the Pre-Published Versio. A New Solutio Method for the Fiite-Horizo Discrete-Time EOQ Problem Chug-Lu Li Departmet of Logistics The Hog Kog Polytechic Uiversity Hug Hom, Kowloo, Hog Kog Phoe: +852-2766-7410
This is the Pre-Published Versio. A New Solutio Method for the Fiite-Horizo Discrete-Time EOQ Problem Chug-Lu Li Departmet of Logistics The Hog Kog Polytechic Uiversity Hug Hom, Kowloo, Hog Kog Phoe: +852-2766-7410
