arxiv: v1 [math-ph] 28 Mar 2019
|
|
|
- Beverly Miller
- 5 years ago
- Views:
Transcription
1 ITEP-TH-07 /19 The Dynamical equations for gln m E. Dotsenko 1,2,3 1 - Institute for Theoretical and Experimental Physics, Moscow, , Russia 2 - Moscow Institute of physics and Technology, Dolgoprudny, Russia 3 - Skolkovo Institute of Science and Technology, Moscow, Russia edotsenko95@gmail.com arxiv: v1 math-ph 28 Mar 2019 Astract In this note we propose a compatile set of equations which commutes with the Knizhnik- Zamolodchikov equations ased on the gln m symmetry algera and estalish the Matsuo- Cherednik correspondence for them. 1 Introduction There is a relation etween the solutions of the quantum Knizhnik-Zamolodchikov equaitons qkz for short and the spectral prolem of quantum systems Calogero-Moser type, proposed in 3 and later in 4, 5. The recent discussion of this correspondence 15, 11 was originated in the quantum-classical correspondence 13, 12. It was shown in 1 and generalized in 6, that for twisted KZ equations, ased on simple finite dimensional Lie algera g, there is a compatile set of equations with respect to twist parameters, which commutes with KZ. This set of equations was called Dynamical equaitons. The joint system could e viewed as a vector analogue of the ispectral prolem of 2. In fact they are related through the Matsuo-Cherednik map MC for revity: if one has a solution of joint system of KZ and Dynamical equations, then one can cook-up the solution of the ispectral prolem for the corresponding system of Calogero-Moser type. For the proof one can consult with 17 section 7, 18 and 14. It is worth to mention that in 7 the KZ and Dynamical equations were defined for a wide class of algeras and it will e very interesting to study the MC map in this generality. Integrale systems with Z/2Z graded symmetry algeras mostly of type A were studied in many papers, for example one can consult with 16. Also recently superchains were emedded in the context of the Bethe/Gauge correspondence in 8. And, maye, it might e interesting to derive the Dynamical equations, proposed in this note using approach of 7. The outline of the work is the following: in the section 2 we will proof compatiility of the proposed Dynamical equations and in the section 3 we will estalish the MC map. The generalization of the proposed equations to the difference case as well as issues aout the monodromy we will leave for the future work 10 Acknowledgements The author was enefited from the dicussions with B. Feigin, A. Zarodin, A. Zotov and N. Slavnov. Also the author is grateful to P. Etingof for the reference 9. This work was supported y the RFBR grant. 1
2 2 The Dynamical equations Let z C k \ i<j z i z j and λ C nm \ i<j λ i λ j. Let V k i1 Cn m e the tensor product of the vector representations of gln m. And let Ψ : z, λ V e the flat section, namely κ zi c λ c e i cc j, i P ij z i z j Ψ 0, 1 where graded permutation P ij a, 1p e i a ej a and pa is a parity fuction, defined in the Appendix. e j a is the generator of gln m which non-trivially acts only in the ith tensor component of V as matrix unit in some asis see Appendix. Theorem 2.1. The following system of equations is compatile and commute with 1 κ a j z j e j aa 1 pe ae a E aa λ a λ, a Ψ 0, 2 where E a E a k j1 ej a. Proof. Let us prove first, that 2 is compatile system. For showing this one has to check that the following commutator vanishes κ a j z j e j aa 1 pce ace ca E aa,κ λ a λ c c, a l There are three types of terms z l e l 1 pde de d E λ λ d d, 3 1 a, 1 pde de d E 1 pce ace ca E aa, λ λ d λ a λ c d, c, a 1 pae ae a E 1 pe ae a E aa λ λ a 2 λ a λ 2 The last equation holds due to relations j 1pa λ a z j e j aa, 1 pde de d E λ λ d d, j z j E a e j a ej a E a The last equation is true due to 31 1 pce ace ca E aa, λ a λ c c, a l 1p λ a j z l e l z j e j a E a E a e j a pce ace ca E aa, 1 pde de d E λ a λ c λ λ d c, a d, 1 pe ae a, 1 pce ce c E ac E ca, E ce c λ ac λ c c, a, 1 pce ace ca, 1 pae ae a 1 pap E a E a, E ae a λ a λ a 6 2
3 A short calculation shows that the last commutator vanishes. Let us focus on the middle row in the aove expression, which is more complicated. To prove that it is zero one has to consider the following four cases pa p 0, pc 1 E a E a, E ce c E ace a E c E c E a E ca pa pc 0, p 1 E a E a, E ce c E ace a E c E c E a E ca p pc 1, pa 0 E a E a, E ce c E ace a E c E c E a E a E ac E ca, E ce c E ac E ca, E ae a λ ac λ c E ace a E c E c E a E ca λ ac λ c E ace a E c E c E a E ca E ac E ca, E ce c E ac E ca, E ae a λ ac λ c E ace a E c E c E a E ca λ ac λ c pa p 1, pc 0 E a E a, E ce c E ace a E c E c E a E ca E ace a E c E c E a E ca E ac E ca, E ce c E ac E ca, E ae a λ ac λ c E ace a E c E c E a E ca λ ac λ c E ace a E c E c E a E ca E ac E ca, E ce c E ac E ca, E ae a λ ac λ c E ace a E c E c E a E ca λ ac λ c E ace a E c E c E a E ca The two cases where parities of a, and c are equal are not considered ecause the three corresponding generators of the gln m are osonic. From the aove computation one sees that the system 2 is compatile and the first part of the theorem is proven. Now let us show that systems 1 and 2 are compatile. Again one needs to check that the following commutator vanishes κ zi c λ c e i cc j, i P ij z i z j,κ a j z j e j aa 1 pe ae a E aa λ a λ, a Let is consider the most complicated parts of the aove commutator λ c e cc i, 1 pe ae a E aa λ c a, a 1 p e i a E a E a e i, a a ei j, i P ij z ij, j z j e j aa a E a E a e i a 12 3
4 2. P ij, 1 pe ae a E aa 13 z i z j λ a λ j, i, a Indeed one has to check that Simple calculation shows that this is true. 3 The Matsuo-Cherednik map In this section we fix k nm in the definition of V. P ij,e a E a 14 Theorem 3.1. The following covectors provide the Matsuo-Cherednik map for Dynamical equations 2 Ω 0 e 1... e nm P σ, 15a σ S nm Ω 1 e 1... e nm 1 sgnσ P σ, 15 σ S nm where P σ P si1...p sil, where P sij is a permutation, that corresponds to the reflection s ij and σ s i1 s i2...s il is a reduced decomposition. Because P sij satisfy raid relation the element P σ is correctly defined. The appearance of 15 is a property of V1 on which we are projecting the Dynamical equation. The V1 V is a suspace, such that E aa V1 1 for all a nm. Such condition is consistent with equations 1 and 2 ecause the Cartan generators commute with them. And presumaly one can not consider the other weight suspaces different to V1, ecasue the symmetry etween z s and λ s is roken. Now let us prove a simple and useful Lemma 3.2. The covectors 15a and 15 are eigenvectors of the following operators where i 0,1. E a E a E aa Ω i 1 pi Ω i, 16 Proof. One can consider vectors Ω i and prove for them the analogue properties 16. Let us consider the symmetrized vector as an example E a E a E aa Ω 0 σ S nm P σ E a E a E aa e 1... e nm, 17 thanks to 14. A simple computation shows that E a E a E aa e 1... e nm 1 p P a e 1... e nm. 18 Then applying to the result the symmetrizer, or skew symmetrizer one otains16 immediately. Now we are ready to proof the follwoing 4
5 Theorem 3.3. Let Ψ e the solution of joint system 1, 2 with values in V1, than mn κ 2 1 i nm κ 1 Ω i Ψ λ 2 z a1 a 2 i Ω i Ψ, 19a a i1 mn κ 2 1 i nm κ 1 Ω i Ψ z 2 λ a 2 i Ω i Ψ, 19 where i 0,1 a1 a Proof. The first equation was proven in 11, so we are to proof the second.let D a e the a th dynamical operator. So now we are consider the following sum i1 Ω i n κ 2 λ 2 a { n z i e i aa, 1 pe ae a E aa } λ a λ a n Da 2 Ψ Ω a1 a1 i,a1 2 z i e aa i 1 ppc E a E a E aa E ac E ca E aa λ i a λ λ a λ c c a κ 1 p E a E a E aa E a E a E aa 2 Ψ, λ a λ 2 a 20 where the 2 was used. After using 16 and the identity c a expression simplifies to 1 λ a λ λ a λ c 0 the aove nm Ω i κ 2 2 λ 2 a a1 nm { i,a1 z i e i aa, a 1 pe ae a E aa } λ a λ i z 2 i a κ 1 i 1 Ψ 21 λ a λ 2 To prove the theorem one has to show, that nm Ω i { z i e aa i, 1 pe ae a E aa } Ψ 22 λ i,a1 a λ a In fact one has to prove, that for any distinct a and nm nm Ω i { z i e aa i, 1p E a E a E aa } { z i e i, 1pa E a E a E } 23 i1 After opening the rackets one otains the following n n Ω i z i e aa i 1p E a E a E aa 1 i Ω i z i e i aa Ω i i1 n i1 i1 z i e i 1pa E a E a E 1 i Ω i i1 n i1 z i e i. 24 One can write the projectors 15a, 15 in the following form Ω i e a1... e i a... e j... e anm f i a 1,...,a nm. a 1... a nm 25 5
6 where the functions f i are generalizations of the sign function of the ordinary permutation to the graded case. Let us set i 0 and consider the most non-trivial case pa 0, p 1 explicitly n j, i i1 nm i1 {a i a,a j } j, i {a i a,a j } e a1... e a i... e j... e anm f 0 a 1,...,a nm z i 1 p E a E a E aa 1 e a1... e i... e j a... e amn 1 k {i,j} pak e σ1... e a i... e j... e anm f 0 a 1,...,a,...,,...,a nm where {a i a,a j } a 1... a a mn and k {i,j} means, that summation runs over all k, that lies in the interval strictly etween i and j. Then the second line gives the following z i, 26 nm i1 j, i {a i,a j a} e a1... e i a... ej... e amn 1 k {i,j} pa k e σ1... e i... e a l... e anm f 0 a 1,...,,...,a,...,a nm z i. 27 Because of 16 one has the following relation f 0 a 1,...,a,...,,...,a nm 1 k {i,j} pa k f 0 a 1,...,,...,a,...,a nm. From which one sees that difference 24 vanishes. The other cases of parity of a and as well as other value of i considered similarly. 4 Summary To conclude we have proved the compatiility of proposed system of Dynamical equations and its commutativity with twisted KZ equations. The structure of the formula 2 is very much like in 1, ut not quite ecause of fermionic roots. It will e interesting to generalize the work of 6 to the Lie superalgera case as well as compute the monodromy of the proposed Dynamical equations. It will e addressed elsewhere Appendix Here we give a rief summary of some definitions of the Lie superalgera gln m Let J {1,...nm} and let p : J {0,1} { pa 0, a n,osons, pa 1, a > nfermions. 28 The gln m algera is generated y e a where a, J with the following relations e a e cd 1 pe ape cd e cd e a δ c e ad 1 pe ape cd δ da e c, 29 6
7 where pe a papmod The product of the superalgera representations is defined in such a way, that for operators, which has definite parity, and acting non-trivially only in the i th and j th component of the tensor product the following holds A i B j 1 papb B j A i. 31 In the C n m there is a asis e a such that e a e c δ c e a, meaning that e a are just matrix units. Let x,y C n m with definite px and py then the graded permutation acts as follows References P 12 x y 1 pxpy y x Felder, G., Markov, Y., Tarasov, V., Varchenko, A Differential equations compatile with KZ equations. Mathematical Physics, Analysis and Geometry, 32, Duistermaat, J. J., Grünaum, F. A Differential equations in the spectral parameter. Communications in mathematical physics, 1032, Matsuo, A Integrale connections related to zonal spherical functions. Inventiones mathematicae, 1101, Cherednik, I Integration of quantum many-ody prolems y affine Knizhnik- Zamolodchikov equations. Advances in Mathematics, 1061, Mimachi, K A solution to quantum Knizhnik-Zamolodchikov equations and its application to eigenvalue prolems of the Macdonald type. Duke mathematical journal, 853, Etingof, P., Varchenko, A Dynamical Weyl groups and applications. Advances in Mathematics, 1671, Okounkov, A., Smirnov, A Quantum difference equation for Nakajima varieties. arxiv preprint arxiv: Nekrasov, N Superspin chains and supersymmetric gauge theories. arxiv preprint arxiv: Geer, N Etingof Kazhdan quantization of Lie superialgeras. Advances in Mathematics, 2071, Dotsenko, E. in preparation 11 Grekov, A., Zarodin, A., Zotov, A Supersymmetric extension of qkz-ruijsenaars correspondence. Nuclear Physics B, 939, Gorsky, A., Zarodin, A., Zotov, A Spectrum of quantum transfer matrices via classical many-ody systems. Journal of High Energy Physics, 20141, Nekrasov, N., Rosly, A., Shatashvili, S Daroux coordinates, Yang-Yang functional, and gauge theory. Nuclear Physics B-Proceedings Supplements, 2161, Braverman, A., Maulik, D., Okounkov, A Quantum cohomology of the Springer resolution. Advances in Mathematics, 2271,
8 15 Zarodin, A., Zotov, A QKZ Ruijsenaars correspondence revisited. Nuclear Physics B, 922, Belliard, S., Ragoucy, E The nested Bethe ansatz for all closed spin chains. Journal of Physics A: Mathematical and Theoretical, 4129, Laredo, V. T The trigonometric Casimir connection of a simple Lie algera. Journal of Algera, 3291, van Meer, M., Stokman, J Doule affine Hecke algeras and ispectral quantum Knizhnik Zamolodchikov equations. International Mathematics Research Notices, 20106,
Baxter Q-operators and tau-function for quantum integrable spin chains
 Baxter Q-operators and tau-function for quantum integrable spin chains Zengo Tsuboi Institut für Mathematik und Institut für Physik, Humboldt-Universität zu Berlin This is based on the following papers.
Baxter Q-operators and tau-function for quantum integrable spin chains Zengo Tsuboi Institut für Mathematik und Institut für Physik, Humboldt-Universität zu Berlin This is based on the following papers.
Knizhnik-Zamolodchikov type equations for the root system B and Capelli central elements
 Journal of Physics: Conference Series OPEN ACCESS Knizhnik-Zamolodchikov type equations for the root system B and Capelli central elements To cite this article: D V Artamonov and V A Golubeva 2014 J. Phys.:
Journal of Physics: Conference Series OPEN ACCESS Knizhnik-Zamolodchikov type equations for the root system B and Capelli central elements To cite this article: D V Artamonov and V A Golubeva 2014 J. Phys.:
KZ-Calogero correspondence revisited
 ITEP-TH-03/7 KZ-Caloero correspondence revisited A. Zabrodin A. Zotov arxiv:70.06074v2 [math-ph] 30 Mar 207 January 207 Abstract We discuss the correspondence between the Knizhnik-Zamolodchikov equations
ITEP-TH-03/7 KZ-Caloero correspondence revisited A. Zabrodin A. Zotov arxiv:70.06074v2 [math-ph] 30 Mar 207 January 207 Abstract We discuss the correspondence between the Knizhnik-Zamolodchikov equations
arxiv: v1 [math.qa] 15 Apr 2019
![arxiv: v1 [math.qa] 15 Apr 2019 arxiv: v1 [math.qa] 15 Apr 2019](/thumbs/96/129195555.jpg) DUALITY FOR KNIZHNIK-ZAMOLODCHIKOV AND DYNAMICAL OPERATORS V.TARASOV AND F.UVAROV arxiv:1904.07309v1 [math.qa] 15 Apr 2019 Department of Mathematical Sciences, Indiana University Purdue University Indianapolis
DUALITY FOR KNIZHNIK-ZAMOLODCHIKOV AND DYNAMICAL OPERATORS V.TARASOV AND F.UVAROV arxiv:1904.07309v1 [math.qa] 15 Apr 2019 Department of Mathematical Sciences, Indiana University Purdue University Indianapolis
Список публикаций Зотов Андрей Владимирович
 Список публикаций Зотов Андрей Владимирович С сайта Математического института им. В.А. Стеклова РАН http://www.mi.ras.ru/index.php?c=pubs&id=20736&showmode=years&showall=show&l=0 2018 1. I. Sechin, A.
Список публикаций Зотов Андрей Владимирович С сайта Математического института им. В.А. Стеклова РАН http://www.mi.ras.ru/index.php?c=pubs&id=20736&showmode=years&showall=show&l=0 2018 1. I. Sechin, A.
What elliptic cohomology might have to do with other generalized Schubert calculi
 What elliptic cohomology might have to do with other generalized Schubert calculi Gufang Zhao University of Massachusetts Amherst Equivariant generalized Schubert calculus and its applications Apr. 28,
What elliptic cohomology might have to do with other generalized Schubert calculi Gufang Zhao University of Massachusetts Amherst Equivariant generalized Schubert calculus and its applications Apr. 28,
Representation theory of SU(2), density operators, purification Michael Walter, University of Amsterdam
 Symmetry and Quantum Information Feruary 6, 018 Representation theory of S(), density operators, purification Lecture 7 Michael Walter, niversity of Amsterdam Last week, we learned the asic concepts of
Symmetry and Quantum Information Feruary 6, 018 Representation theory of S(), density operators, purification Lecture 7 Michael Walter, niversity of Amsterdam Last week, we learned the asic concepts of
Extended Conformal Symmetry and Recursion Formulae for Nekrasov Partition Function
 CFT and integrability in memorial of Alexei Zamolodchikov Sogan University, Seoul December 2013 Extended Conformal Symmetry and Recursion Formulae for Nekrasov Partition Function Yutaka Matsuo (U. Tokyo)
CFT and integrability in memorial of Alexei Zamolodchikov Sogan University, Seoul December 2013 Extended Conformal Symmetry and Recursion Formulae for Nekrasov Partition Function Yutaka Matsuo (U. Tokyo)
SU(N) representations
 Appendix C SU(N) representations The group SU(N) has N 2 1 generators t a which form the asis of a Lie algera defined y the commutator relations in (A.2). The group has rank N 1 so there are N 1 Casimir
Appendix C SU(N) representations The group SU(N) has N 2 1 generators t a which form the asis of a Lie algera defined y the commutator relations in (A.2). The group has rank N 1 so there are N 1 Casimir
EE201/MSE207 Lecture 10 Angular momentum
 EE20/MSE207 Lecture 0 Angular momentum (A lot of mathematics; I will try to explain as simple as possile) Classical mechanics r L = r p (angular momentum) Quantum mechanics The same, ut p x = iħ x p =
EE20/MSE207 Lecture 0 Angular momentum (A lot of mathematics; I will try to explain as simple as possile) Classical mechanics r L = r p (angular momentum) Quantum mechanics The same, ut p x = iħ x p =
Quivers. Virginia, Lonardo, Tiago and Eloy UNICAMP. 28 July 2006
 Quivers Virginia, Lonardo, Tiago and Eloy UNICAMP 28 July 2006 1 Introduction This is our project Throughout this paper, k will indicate an algeraically closed field of characteristic 0 2 Quivers 21 asic
Quivers Virginia, Lonardo, Tiago and Eloy UNICAMP 28 July 2006 1 Introduction This is our project Throughout this paper, k will indicate an algeraically closed field of characteristic 0 2 Quivers 21 asic
Difference Equations and Highest Weight Modules of U q [sl(n)]
![Difference Equations and Highest Weight Modules of U q [sl(n)] Difference Equations and Highest Weight Modules of U q [sl(n)]](/thumbs/75/72831271.jpg) arxiv:math/9805089v1 [math.qa] 20 May 1998 Difference Equations and Highest Weight Modules of U q [sl(n)] A. Zapletal 1,2 Institut für Theoretische Physik Freie Universität Berlin, Arnimallee 14, 14195
arxiv:math/9805089v1 [math.qa] 20 May 1998 Difference Equations and Highest Weight Modules of U q [sl(n)] A. Zapletal 1,2 Institut für Theoretische Physik Freie Universität Berlin, Arnimallee 14, 14195
1 2 2 Circulant Matrices
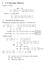 Circulant Matrices General matrix a c d Ax x ax + cx x x + dx General circulant matrix a x ax + x a x x + ax. Evaluating the Eigenvalues Find eigenvalues and eigenvectors of general circulant matrix: a
Circulant Matrices General matrix a c d Ax x ax + cx x x + dx General circulant matrix a x ax + x a x x + ax. Evaluating the Eigenvalues Find eigenvalues and eigenvectors of general circulant matrix: a
New worlds for Lie Theory. math.columbia.edu/~okounkov/icm.pdf
 New worlds for Lie Theory math.columbia.edu/~okounkov/icm.pdf Lie groups, continuous symmetries, etc. are among the main building blocks of mathematics and mathematical physics Since its birth, Lie theory
New worlds for Lie Theory math.columbia.edu/~okounkov/icm.pdf Lie groups, continuous symmetries, etc. are among the main building blocks of mathematics and mathematical physics Since its birth, Lie theory
Baker-Akhiezer functions and configurations of hyperplanes
 Baker-Akhiezer functions and configurations of hyperplanes Alexander Veselov, Loughborough University ENIGMA conference on Geometry and Integrability, Obergurgl, December 2008 Plan BA function related
Baker-Akhiezer functions and configurations of hyperplanes Alexander Veselov, Loughborough University ENIGMA conference on Geometry and Integrability, Obergurgl, December 2008 Plan BA function related
R-matrices, affine quantum groups and applications
 R-matrices, affine quantum groups and applications From a mini-course given by David Hernandez at Erwin Schrödinger Institute in January 2017 Abstract R-matrices are solutions of the quantum Yang-Baxter
R-matrices, affine quantum groups and applications From a mini-course given by David Hernandez at Erwin Schrödinger Institute in January 2017 Abstract R-matrices are solutions of the quantum Yang-Baxter
Vertex Algebras and Algebraic Curves
 Mathematical Surveys and Monographs Volume 88 Vertex Algebras and Algebraic Curves Edward Frenkei David Ben-Zvi American Mathematical Society Contents Preface xi Introduction 1 Chapter 1. Definition of
Mathematical Surveys and Monographs Volume 88 Vertex Algebras and Algebraic Curves Edward Frenkei David Ben-Zvi American Mathematical Society Contents Preface xi Introduction 1 Chapter 1. Definition of
arxiv:math/ v1 [math.qa] 26 Oct 2006
![arxiv:math/ v1 [math.qa] 26 Oct 2006 arxiv:math/ v1 [math.qa] 26 Oct 2006](/thumbs/75/71823066.jpg) A GENERALIZATION OF THE CAPELLI IDENTITY arxiv:math/0610799v1 [math.qa] 26 Oct 2006 E. MUKHIN, V. TARASOV, AND A. VARCHENKO Abstract. We prove a generalization of the Capelli identity. As an application
A GENERALIZATION OF THE CAPELLI IDENTITY arxiv:math/0610799v1 [math.qa] 26 Oct 2006 E. MUKHIN, V. TARASOV, AND A. VARCHENKO Abstract. We prove a generalization of the Capelli identity. As an application
Deformed Richardson-Gaudin model
 Deformed Richardson-Gaudin model P Kulish 1, A Stolin and L H Johannesson 1 St. Petersburg Department of Stelov Mathematical Institute, Russian Academy of Sciences Fontana 7, 19103 St. Petersburg, Russia
Deformed Richardson-Gaudin model P Kulish 1, A Stolin and L H Johannesson 1 St. Petersburg Department of Stelov Mathematical Institute, Russian Academy of Sciences Fontana 7, 19103 St. Petersburg, Russia
arxiv:math/ v1 [math.qa] 5 Nov 2002
![arxiv:math/ v1 [math.qa] 5 Nov 2002 arxiv:math/ v1 [math.qa] 5 Nov 2002](/thumbs/88/116829103.jpg) A new quantum analog of the Brauer algebra arxiv:math/0211082v1 [math.qa] 5 Nov 2002 A. I. Molev School of Mathematics and Statistics University of Sydney, NSW 2006, Australia alexm@ maths.usyd.edu.au
A new quantum analog of the Brauer algebra arxiv:math/0211082v1 [math.qa] 5 Nov 2002 A. I. Molev School of Mathematics and Statistics University of Sydney, NSW 2006, Australia alexm@ maths.usyd.edu.au
Markov Chains, Stochastic Processes, and Matrix Decompositions
 Markov Chains, Stochastic Processes, and Matrix Decompositions 5 May 2014 Outline 1 Markov Chains Outline 1 Markov Chains 2 Introduction Perron-Frobenius Matrix Decompositions and Markov Chains Spectral
Markov Chains, Stochastic Processes, and Matrix Decompositions 5 May 2014 Outline 1 Markov Chains Outline 1 Markov Chains 2 Introduction Perron-Frobenius Matrix Decompositions and Markov Chains Spectral
10 Lorentz Group and Special Relativity
 Physics 129 Lecture 16 Caltech, 02/27/18 Reference: Jones, Groups, Representations, and Physics, Chapter 10. 10 Lorentz Group and Special Relativity Special relativity says, physics laws should look the
Physics 129 Lecture 16 Caltech, 02/27/18 Reference: Jones, Groups, Representations, and Physics, Chapter 10. 10 Lorentz Group and Special Relativity Special relativity says, physics laws should look the
Introduction to the Mathematics of the XY -Spin Chain
 Introduction to the Mathematics of the XY -Spin Chain Günter Stolz June 9, 2014 Abstract In the following we present an introduction to the mathematical theory of the XY spin chain. The importance of this
Introduction to the Mathematics of the XY -Spin Chain Günter Stolz June 9, 2014 Abstract In the following we present an introduction to the mathematical theory of the XY spin chain. The importance of this
Fluctuations of interacting particle systems
 Stat Phys Page 1 Fluctuations of interacting particle systems Ivan Corwin (Columbia University) Stat Phys Page 2 Interacting particle systems & ASEP In one dimension these model mass transport, traffic,
Stat Phys Page 1 Fluctuations of interacting particle systems Ivan Corwin (Columbia University) Stat Phys Page 2 Interacting particle systems & ASEP In one dimension these model mass transport, traffic,
Schedule of the Lectures
 Schedule of the Lectures Wednesday, December 13 All lectures will be held in room Waaier 4 of building 12 called Waaier. 09.30 10.00 Registration, Coffee and Tea 10.00 10.05 Welcome and Opening 10.05 11.05
Schedule of the Lectures Wednesday, December 13 All lectures will be held in room Waaier 4 of building 12 called Waaier. 09.30 10.00 Registration, Coffee and Tea 10.00 10.05 Welcome and Opening 10.05 11.05
ARTIN/Integrable Systems Workshop. Programme
 ARTIN/Integrable Systems Workshop University of Glasgow, Department of Mathematics, Room 516 23-24 April, 2010 Programme Friday, 23.04.2010 2:00 3:00 V. Dotsenko Compatible associative products and trees
ARTIN/Integrable Systems Workshop University of Glasgow, Department of Mathematics, Room 516 23-24 April, 2010 Programme Friday, 23.04.2010 2:00 3:00 V. Dotsenko Compatible associative products and trees
BRST and Dirac Cohomology
 BRST and Dirac Cohomology Peter Woit Columbia University Dartmouth Math Dept., October 23, 2008 Peter Woit (Columbia University) BRST and Dirac Cohomology October 2008 1 / 23 Outline 1 Introduction 2 Representation
BRST and Dirac Cohomology Peter Woit Columbia University Dartmouth Math Dept., October 23, 2008 Peter Woit (Columbia University) BRST and Dirac Cohomology October 2008 1 / 23 Outline 1 Introduction 2 Representation
RESEARCH STATEMENT NOAH WHITE
 RESEARCH STATEMENT NOAH WHITE 1. Introduction My research centres on connections between representation theory and algebraic geometry which give meaning to, or are inspired by, interesting combinatorial
RESEARCH STATEMENT NOAH WHITE 1. Introduction My research centres on connections between representation theory and algebraic geometry which give meaning to, or are inspired by, interesting combinatorial
Signatures of Multiplicity Spaces in Tensor Products of sl 2 and U q (sl 2 ) Representations, and Applications
 Signatures of Multiplicity Spaces in Tensor Products of sl and U (sl Representations, and Applications Shashwat Kishore Abstract We study multiplicity space signatures in tensor products of sl and U (sl
Signatures of Multiplicity Spaces in Tensor Products of sl and U (sl Representations, and Applications Shashwat Kishore Abstract We study multiplicity space signatures in tensor products of sl and U (sl
Part III Symmetries, Fields and Particles
 Part III Symmetries, Fields and Particles Theorems Based on lectures by N. Dorey Notes taken by Dexter Chua Michaelmas 2016 These notes are not endorsed by the lecturers, and I have modified them (often
Part III Symmetries, Fields and Particles Theorems Based on lectures by N. Dorey Notes taken by Dexter Chua Michaelmas 2016 These notes are not endorsed by the lecturers, and I have modified them (often
Bethe states and separation of variables for SU(N) Heisenberg spin chain
 Bethe states and separation of variables for SU(N) Heisenberg spin chain Nikolay Gromov King s College London & PNPI based on 1610.08032 [NG, F. Levkovich-Maslyuk, G. Sizov] Below: FLM = F. Levkovich-Maslyuk
Bethe states and separation of variables for SU(N) Heisenberg spin chain Nikolay Gromov King s College London & PNPI based on 1610.08032 [NG, F. Levkovich-Maslyuk, G. Sizov] Below: FLM = F. Levkovich-Maslyuk
Classical Geometry of Quantum Integrability and Gauge Theory. Nikita Nekrasov IHES
 Classical Geometry of Quantum Integrability and Gauge Theory Nikita Nekrasov IHES This is a work on experimental theoretical physics In collaboration with Alexei Rosly (ITEP) and Samson Shatashvili (HMI
Classical Geometry of Quantum Integrability and Gauge Theory Nikita Nekrasov IHES This is a work on experimental theoretical physics In collaboration with Alexei Rosly (ITEP) and Samson Shatashvili (HMI
Quantum integrable systems and non-skew-symmetric classical r-matrices. T. Skrypnyk
 Quantum integrable systems and non-skew-symmetric classical r-matrices. T. Skrypnyk Universita degli studi di Milano Bicocca, Milano, Italy and Bogolyubov Institute for Theoretical Physics, Kyiv, Ukraine
Quantum integrable systems and non-skew-symmetric classical r-matrices. T. Skrypnyk Universita degli studi di Milano Bicocca, Milano, Italy and Bogolyubov Institute for Theoretical Physics, Kyiv, Ukraine
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
FUSION PROCEDURE FOR THE BRAUER ALGEBRA
 FUSION PROCEDURE FOR THE BRAUER ALGEBRA A. P. ISAEV AND A. I. MOLEV Abstract. We show that all primitive idempotents for the Brauer algebra B n ω can be found by evaluating a rational function in several
FUSION PROCEDURE FOR THE BRAUER ALGEBRA A. P. ISAEV AND A. I. MOLEV Abstract. We show that all primitive idempotents for the Brauer algebra B n ω can be found by evaluating a rational function in several
Affine Gaudin models
 Affine Gaudin models Sylvain Lacroix Laboratoire de Physique, ENS de Lyon RAQIS 18, Annecy September 10th, 2018 [SL, Magro, Vicedo, 1703.01951] [SL, Vicedo, Young, 1804.01480, 1804.06751] Introduction
Affine Gaudin models Sylvain Lacroix Laboratoire de Physique, ENS de Lyon RAQIS 18, Annecy September 10th, 2018 [SL, Magro, Vicedo, 1703.01951] [SL, Vicedo, Young, 1804.01480, 1804.06751] Introduction
Algebraic Spectral Relations forelliptic Quantum Calogero-MoserProblems
 Journal of Nonlinear Mathematical Physics 1999, V.6, N 3, 263{268. Letter Algebraic Spectral Relations forelliptic Quantum Calogero-MoserProblems L.A. KHODARINOVA yz and I.A. PRIKHODSKY z y Wessex Institute
Journal of Nonlinear Mathematical Physics 1999, V.6, N 3, 263{268. Letter Algebraic Spectral Relations forelliptic Quantum Calogero-MoserProblems L.A. KHODARINOVA yz and I.A. PRIKHODSKY z y Wessex Institute
arxiv:q-alg/ v1 14 Feb 1997
 arxiv:q-alg/97009v 4 Feb 997 On q-clebsch Gordan Rules and the Spinon Character Formulas for Affine C ) Algebra Yasuhiko Yamada Department of Mathematics Kyushu University September 8, 07 Abstract A q-analog
arxiv:q-alg/97009v 4 Feb 997 On q-clebsch Gordan Rules and the Spinon Character Formulas for Affine C ) Algebra Yasuhiko Yamada Department of Mathematics Kyushu University September 8, 07 Abstract A q-analog
arxiv:math-ph/ v1 29 Dec 1999
 On the classical R-matrix of the degenerate Calogero-Moser models L. Fehér and B.G. Pusztai arxiv:math-ph/9912021v1 29 Dec 1999 Department of Theoretical Physics, József Attila University Tisza Lajos krt
On the classical R-matrix of the degenerate Calogero-Moser models L. Fehér and B.G. Pusztai arxiv:math-ph/9912021v1 29 Dec 1999 Department of Theoretical Physics, József Attila University Tisza Lajos krt
Tetrahedron equation and quantum R matrices for q-oscillator representations
 Tetrahedron equation and quantum R matrices for q-oscillator representations Atsuo Kuniba University of Tokyo 17 July 2014, Group30@Ghent University Joint work with Masato Okado Tetrahedron equation R
Tetrahedron equation and quantum R matrices for q-oscillator representations Atsuo Kuniba University of Tokyo 17 July 2014, Group30@Ghent University Joint work with Masato Okado Tetrahedron equation R
THE QUANTUM CONNECTION
 THE QUANTUM CONNECTION MICHAEL VISCARDI Review of quantum cohomology Genus 0 Gromov-Witten invariants Let X be a smooth projective variety over C, and H 2 (X, Z) an effective curve class Let M 0,n (X,
THE QUANTUM CONNECTION MICHAEL VISCARDI Review of quantum cohomology Genus 0 Gromov-Witten invariants Let X be a smooth projective variety over C, and H 2 (X, Z) an effective curve class Let M 0,n (X,
On the singular elements of a semisimple Lie algebra and the generalized Amitsur-Levitski Theorem
 On the singular elements of a semisimple Lie algebra and the generalized Amitsur-Levitski Theorem Bertram Kostant, MIT Conference on Representations of Reductive Groups Salt Lake City, Utah July 10, 2013
On the singular elements of a semisimple Lie algebra and the generalized Amitsur-Levitski Theorem Bertram Kostant, MIT Conference on Representations of Reductive Groups Salt Lake City, Utah July 10, 2013
The Waring rank of the Vandermonde determinant
 The Waring rank of the Vandermonde determinant Alexander Woo (U. Idaho) joint work with Zach Teitler(Boise State) SIAM Conference on Applied Algebraic Geometry, August 3, 2014 Waring rank Given a polynomial
The Waring rank of the Vandermonde determinant Alexander Woo (U. Idaho) joint work with Zach Teitler(Boise State) SIAM Conference on Applied Algebraic Geometry, August 3, 2014 Waring rank Given a polynomial
Zhedanov's algebra AW(3) and the double affine Hecke algebra in the rank one case: II: The spherical subalgebra Koornwinder, T.H.
 UvA-DARE Digital Academic Repository Zhedanov's algebra AW3 and the double affine Hecke algebra in the rank one case: II: The spherical subalgebra Koornwinder, T.H. Published in: Symmetry, Integrability
UvA-DARE Digital Academic Repository Zhedanov's algebra AW3 and the double affine Hecke algebra in the rank one case: II: The spherical subalgebra Koornwinder, T.H. Published in: Symmetry, Integrability
Definition 9.1. The scheme µ 1 (O)/G is called the Hamiltonian reduction of M with respect to G along O. We will denote by R(M, G, O).
 9. Calogero-Moser spaces 9.1. Hamiltonian reduction along an orbit. Let M be an affine algebraic variety and G a reductive algebraic group. Suppose M is Poisson and the action of G preserves the Poisson
9. Calogero-Moser spaces 9.1. Hamiltonian reduction along an orbit. Let M be an affine algebraic variety and G a reductive algebraic group. Suppose M is Poisson and the action of G preserves the Poisson
arxiv: v1 [math-ph] 28 Aug 2008
![arxiv: v1 [math-ph] 28 Aug 2008 arxiv: v1 [math-ph] 28 Aug 2008](/thumbs/80/82097480.jpg) arxiv:0808.3875v1 [math-ph] 28 Aug 2008 On a Hamiltonian form of an elliptic spin Ruijsenaars-Schneider system 1 Introduction F.Soloviev May 27, 2018 An elliptic Ruijenaars-Schneider (RS) model [1] is
arxiv:0808.3875v1 [math-ph] 28 Aug 2008 On a Hamiltonian form of an elliptic spin Ruijsenaars-Schneider system 1 Introduction F.Soloviev May 27, 2018 An elliptic Ruijenaars-Schneider (RS) model [1] is
arxiv: v2 [math-ph] 14 Jul 2014
![arxiv: v2 [math-ph] 14 Jul 2014 arxiv: v2 [math-ph] 14 Jul 2014](/thumbs/87/96898919.jpg) ITP-UU-14/14 SPIN-14/12 Reflection algebra and functional equations arxiv:1405.4281v2 [math-ph] 14 Jul 2014 W. Galleas and J. Lamers Institute for Theoretical Physics and Spinoza Institute, Utrecht University,
ITP-UU-14/14 SPIN-14/12 Reflection algebra and functional equations arxiv:1405.4281v2 [math-ph] 14 Jul 2014 W. Galleas and J. Lamers Institute for Theoretical Physics and Spinoza Institute, Utrecht University,
L. Fehér, KFKI RMKI Budapest and University of Szeged Spin Calogero models and dynamical r-matrices
 L. Fehér, KFKI RMKI Budapest and University of Szeged Spin Calogero models and dynamical r-matrices Integrable systems of Calogero (Moser, Sutherland, Olshanetsky- Perelomov, Gibbons-Hermsen, Ruijsenaars-Schneider)
L. Fehér, KFKI RMKI Budapest and University of Szeged Spin Calogero models and dynamical r-matrices Integrable systems of Calogero (Moser, Sutherland, Olshanetsky- Perelomov, Gibbons-Hermsen, Ruijsenaars-Schneider)
1 The postulates of quantum mechanics
 1 The postulates of quantum mechanics The postulates of quantum mechanics were derived after a long process of trial and error. These postulates provide a connection between the physical world and the
1 The postulates of quantum mechanics The postulates of quantum mechanics were derived after a long process of trial and error. These postulates provide a connection between the physical world and the
arxiv:hep-th/ Jan 95
 Exact Solution of Long-Range Interacting Spin Chains with Boundaries SPhT/95/003 arxiv:hep-th/9501044 1 Jan 95 D. Bernard*, V. Pasquier and D. Serban Service de Physique Théorique y, CE Saclay, 91191 Gif-sur-Yvette,
Exact Solution of Long-Range Interacting Spin Chains with Boundaries SPhT/95/003 arxiv:hep-th/9501044 1 Jan 95 D. Bernard*, V. Pasquier and D. Serban Service de Physique Théorique y, CE Saclay, 91191 Gif-sur-Yvette,
COMBINATORICS OF RATIONAL FUNCTIONS AND POINCARÉ-BIRKHOFF-WITT EXPANSIONS OF THE CANONICAL U(n )-VALUED DIFFERENTIAL FORM
 COMBINATORICS OF RATIONAL FUNCTIONS AND POINCARÉ-BIRKHOFF-WITT EXPANSIONS OF THE CANONICAL Un -VALUED DIFFERENTIAL FORM R. RIMÁNYI, L. STEVENS, AND A. VARCHENKO Abstract. We study the canonical Un -valued
COMBINATORICS OF RATIONAL FUNCTIONS AND POINCARÉ-BIRKHOFF-WITT EXPANSIONS OF THE CANONICAL Un -VALUED DIFFERENTIAL FORM R. RIMÁNYI, L. STEVENS, AND A. VARCHENKO Abstract. We study the canonical Un -valued
Generators of affine W-algebras
 1 Generators of affine W-algebras Alexander Molev University of Sydney 2 The W-algebras first appeared as certain symmetry algebras in conformal field theory. 2 The W-algebras first appeared as certain
1 Generators of affine W-algebras Alexander Molev University of Sydney 2 The W-algebras first appeared as certain symmetry algebras in conformal field theory. 2 The W-algebras first appeared as certain
arxiv:hep-th/ v1 14 Jan 1997
 Transformation of second-class into first-class constraints in supersymmetric theories arxiv:hep-th/9701058v1 14 Jan 1997 J. Barcelos-Neto and W. Oliveira Instituto de Física Universidade Federal do Rio
Transformation of second-class into first-class constraints in supersymmetric theories arxiv:hep-th/9701058v1 14 Jan 1997 J. Barcelos-Neto and W. Oliveira Instituto de Física Universidade Federal do Rio
MIURA OPERS AND CRITICAL POINTS OF MASTER FUNCTIONS arxiv:math/ v2 [math.qa] 12 Oct 2004
![MIURA OPERS AND CRITICAL POINTS OF MASTER FUNCTIONS arxiv:math/ v2 [math.qa] 12 Oct 2004 MIURA OPERS AND CRITICAL POINTS OF MASTER FUNCTIONS arxiv:math/ v2 [math.qa] 12 Oct 2004](/thumbs/96/129245953.jpg) MIURA OPERS AND CRITICAL POINTS OF MASTER FUNCTIONS arxiv:math/03406v [math.qa] Oct 004 EVGENY MUKHIN, AND ALEXANDER VARCHENKO, Abstract. Critical points of a master function associated to a simple Lie
MIURA OPERS AND CRITICAL POINTS OF MASTER FUNCTIONS arxiv:math/03406v [math.qa] Oct 004 EVGENY MUKHIN, AND ALEXANDER VARCHENKO, Abstract. Critical points of a master function associated to a simple Lie
Some multilinear algebra
 Some multilinear algera Multilinear forms Let V e a finite dimensional R-vector space, dim V n. For k P N 0, we denote y T k V the vector space of k-linear forms Then T 1 V V and, y convention, T 0 V R.
Some multilinear algera Multilinear forms Let V e a finite dimensional R-vector space, dim V n. For k P N 0, we denote y T k V the vector space of k-linear forms Then T 1 V V and, y convention, T 0 V R.
Lectures on Quantum Groups
 Lectures in Mathematical Physics Lectures on Quantum Groups Pavel Etingof and Olivier Schiffinann Second Edition International Press * s. c *''.. \ir.ik,!.'..... Contents Introduction ix 1 Poisson algebras
Lectures in Mathematical Physics Lectures on Quantum Groups Pavel Etingof and Olivier Schiffinann Second Edition International Press * s. c *''.. \ir.ik,!.'..... Contents Introduction ix 1 Poisson algebras
Dispersionless integrable systems in 3D and Einstein-Weyl geometry. Eugene Ferapontov
 Dispersionless integrable systems in 3D and Einstein-Weyl geometry Eugene Ferapontov Department of Mathematical Sciences, Loughborough University, UK E.V.Ferapontov@lboro.ac.uk Based on joint work with
Dispersionless integrable systems in 3D and Einstein-Weyl geometry Eugene Ferapontov Department of Mathematical Sciences, Loughborough University, UK E.V.Ferapontov@lboro.ac.uk Based on joint work with
On generalisations of Calogero-Moser-Sutherland quantum problem and WDVV equations
 On generalisations of Calogero-Moser-Sutherland quantum problem and WDVV equations June 18, 2002 A.P.Veselov Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire,
On generalisations of Calogero-Moser-Sutherland quantum problem and WDVV equations June 18, 2002 A.P.Veselov Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire,
Spectral dualities in XXZ spin chains and five dimensional gauge theories
 FIAN/TD-12/13 ITEP-TH-24/13 Spectral dualities in XXZ spin chains and five dimensional gauge theories A. Mironov a,b, A. Morozov a, B. Runov a,d, Y. Zenkevich a,c, A. Zotov a,d,e a ITEP, Moscow, Russia
FIAN/TD-12/13 ITEP-TH-24/13 Spectral dualities in XXZ spin chains and five dimensional gauge theories A. Mironov a,b, A. Morozov a, B. Runov a,d, Y. Zenkevich a,c, A. Zotov a,d,e a ITEP, Moscow, Russia
Propagation of multiplicity-free property for holomorphic vector bundles
 Propagation of multiplicity-free property for holomorphic vector undles Toshiyuki KOBAYASHI Research Institute for Mathematical Sciences Kyoto University E-mail address: toshi@kurims.kyoto-u.ac.jp Astract
Propagation of multiplicity-free property for holomorphic vector undles Toshiyuki KOBAYASHI Research Institute for Mathematical Sciences Kyoto University E-mail address: toshi@kurims.kyoto-u.ac.jp Astract
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
A matrix over a field F is a rectangular array of elements from F. The symbol
 Chapter MATRICES Matrix arithmetic A matrix over a field F is a rectangular array of elements from F The symbol M m n (F ) denotes the collection of all m n matrices over F Matrices will usually be denoted
Chapter MATRICES Matrix arithmetic A matrix over a field F is a rectangular array of elements from F The symbol M m n (F ) denotes the collection of all m n matrices over F Matrices will usually be denoted
U(N) Matrix Difference Equations and a Nested Bethe Ansatz
 U(N) Matrix Difference Equations and a Nested Bethe Ansatz arxiv:hep-th/9611006v1 1 Nov 1996 H. Babujian 1,2,3, M. Karowski 4 and A. Zapletal 5,6 Institut für Theoretische Physik Freie Universität Berlin,
U(N) Matrix Difference Equations and a Nested Bethe Ansatz arxiv:hep-th/9611006v1 1 Nov 1996 H. Babujian 1,2,3, M. Karowski 4 and A. Zapletal 5,6 Institut für Theoretische Physik Freie Universität Berlin,
Langlands duality from modular duality
 Langlands duality from modular duality Jörg Teschner DESY Hamburg Motivation There is an interesting class of N = 2, SU(2) gauge theories G C associated to a Riemann surface C (Gaiotto), in particular
Langlands duality from modular duality Jörg Teschner DESY Hamburg Motivation There is an interesting class of N = 2, SU(2) gauge theories G C associated to a Riemann surface C (Gaiotto), in particular
(1.1) In particular, ψ( q 1, m 1 ; ; q N, m N ) 2 is the probability to find the first particle
 Chapter 1 Identical particles 1.1 Distinguishable particles The Hilbert space of N has to be a subspace H = N n=1h n. Observables Ân of the n-th particle are self-adjoint operators of the form 1 1 1 1
Chapter 1 Identical particles 1.1 Distinguishable particles The Hilbert space of N has to be a subspace H = N n=1h n. Observables Ân of the n-th particle are self-adjoint operators of the form 1 1 1 1
Deformed Richardson-Gaudin model
 Home Search Collections Journals About Contact us My IOPscience Deformed Richardson-Gaudin model This content has been downloaded from IOPscience. Please scroll down to see the full text. View the table
Home Search Collections Journals About Contact us My IOPscience Deformed Richardson-Gaudin model This content has been downloaded from IOPscience. Please scroll down to see the full text. View the table
Specialized Macdonald polynomials, quantum K-theory, and Kirillov-Reshetikhin crystals
 Specialized Macdonald polynomials, quantum K-theory, and Kirillov-Reshetikhin crystals Cristian Lenart Max-Planck-Institut für Mathematik, Bonn State University of New York at Albany Geometry Seminar,
Specialized Macdonald polynomials, quantum K-theory, and Kirillov-Reshetikhin crystals Cristian Lenart Max-Planck-Institut für Mathematik, Bonn State University of New York at Albany Geometry Seminar,
LECTURE III Asymmetric Simple Exclusion Process: Bethe Ansatz Approach to the Kolmogorov Equations. Craig A. Tracy UC Davis
 LECTURE III Asymmetric Simple Exclusion Process: Bethe Ansatz Approach to the Kolmogorov Equations Craig A. Tracy UC Davis Bielefeld, August 2013 ASEP on Integer Lattice q p suppressed both suppressed
LECTURE III Asymmetric Simple Exclusion Process: Bethe Ansatz Approach to the Kolmogorov Equations Craig A. Tracy UC Davis Bielefeld, August 2013 ASEP on Integer Lattice q p suppressed both suppressed
Hendrik De Bie. Hong Kong, March 2011
 A Ghent University (joint work with B. Ørsted, P. Somberg and V. Soucek) Hong Kong, March 2011 A Classical FT New realizations of sl 2 in harmonic analysis A Outline Classical FT New realizations of sl
A Ghent University (joint work with B. Ørsted, P. Somberg and V. Soucek) Hong Kong, March 2011 A Classical FT New realizations of sl 2 in harmonic analysis A Outline Classical FT New realizations of sl
Topological Phases in One Dimension
 Topological Phases in One Dimension Lukasz Fidkowski and Alexei Kitaev arxiv:1008.4138 Topological phases in 2 dimensions: - Integer quantum Hall effect - quantized σ xy - robust chiral edge modes - Fractional
Topological Phases in One Dimension Lukasz Fidkowski and Alexei Kitaev arxiv:1008.4138 Topological phases in 2 dimensions: - Integer quantum Hall effect - quantized σ xy - robust chiral edge modes - Fractional
arxiv:math/ v2 [math.qa] 10 Jan 2003
![arxiv:math/ v2 [math.qa] 10 Jan 2003 arxiv:math/ v2 [math.qa] 10 Jan 2003](/thumbs/86/94411626.jpg) R-matrix presentation for (super) Yangians Y(g) D. Arnaudon a, J. Avan b, N. Crampé a, L. Frappat ac, E. Ragoucy a arxiv:math/0111325v2 [math.qa] 10 Jan 2003 a Laboratoire d Annecy-le-Vieux de Physique
R-matrix presentation for (super) Yangians Y(g) D. Arnaudon a, J. Avan b, N. Crampé a, L. Frappat ac, E. Ragoucy a arxiv:math/0111325v2 [math.qa] 10 Jan 2003 a Laboratoire d Annecy-le-Vieux de Physique
The XYZ spin chain/8-vertex model with quasi-periodic boundary conditions Exact solution by Separation of Variables
 The XYZ spin chain/8-vertex model with quasi-periodic boundary conditions Exact solution by Separation of Variables Véronique TERRAS CNRS & Université Paris Sud, France Workshop: Beyond integrability.
The XYZ spin chain/8-vertex model with quasi-periodic boundary conditions Exact solution by Separation of Variables Véronique TERRAS CNRS & Université Paris Sud, France Workshop: Beyond integrability.
Ph12b Solution Set 4
 Ph Solution Set 4 Feruary 5, 00 The state ψ S un E is transforme to p ψ S un E + p a 0 S γ E + S η E Since γ E an η E aren t mutually orthogonal, we can t use this equation irectly to compute the new ensity
Ph Solution Set 4 Feruary 5, 00 The state ψ S un E is transforme to p ψ S un E + p a 0 S γ E + S η E Since γ E an η E aren t mutually orthogonal, we can t use this equation irectly to compute the new ensity
ADMISSIBLE W -GRAPHS. John R. Stembridge
 ADMISSIBLE W -GRAPHS John R. Stemridge jrs@umich.edu Contents. General W -Graphs. Admissile W -Graphs 3. The Agenda 4. The Admissile Cells in Rank 5. Cominatorial Characterization 6 3 6 5 4 5 36 5 3 4
ADMISSIBLE W -GRAPHS John R. Stemridge jrs@umich.edu Contents. General W -Graphs. Admissile W -Graphs 3. The Agenda 4. The Admissile Cells in Rank 5. Cominatorial Characterization 6 3 6 5 4 5 36 5 3 4
58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that
![58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that 58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that](/thumbs/86/94310732.jpg) 786 CAPTER 12 VECTORS AND TE GEOETRY OF SPACE 0, 0, 1, and 1, 1, 1 as shown in the figure. Then the centroid is. ( 1 2, 1 2, 1 2 ) ] x z C 54. If c a a, where a,, and c are all nonzero vectors, show that
786 CAPTER 12 VECTORS AND TE GEOETRY OF SPACE 0, 0, 1, and 1, 1, 1 as shown in the figure. Then the centroid is. ( 1 2, 1 2, 1 2 ) ] x z C 54. If c a a, where a,, and c are all nonzero vectors, show that
Perron Frobenius Theory
 Perron Frobenius Theory Oskar Perron Georg Frobenius (1880 1975) (1849 1917) Stefan Güttel Perron Frobenius Theory 1 / 10 Positive and Nonnegative Matrices Let A, B R m n. A B if a ij b ij i, j, A > B
Perron Frobenius Theory Oskar Perron Georg Frobenius (1880 1975) (1849 1917) Stefan Güttel Perron Frobenius Theory 1 / 10 Positive and Nonnegative Matrices Let A, B R m n. A B if a ij b ij i, j, A > B
Construction of wedge-local nets of observables through Longo-Witten endomorphisms
 Construction of wedge-local nets of observables through Longo-Witten endomorphisms Yoh Tanimoto (arxiv:1107.2629, work in progress with M. Bischoff) Department of Mathematics, University of Rome Tor Vergata
Construction of wedge-local nets of observables through Longo-Witten endomorphisms Yoh Tanimoto (arxiv:1107.2629, work in progress with M. Bischoff) Department of Mathematics, University of Rome Tor Vergata
Spectral action, scale anomaly. and the Higgs-Dilaton potential
 Spectral action, scale anomaly and the Higgs-Dilaton potential Fedele Lizzi Università di Napoli Federico II Work in collaboration with A.A. Andrianov (St. Petersburg) and M.A. Kurkov (Napoli) JHEP 1005:057,2010
Spectral action, scale anomaly and the Higgs-Dilaton potential Fedele Lizzi Università di Napoli Federico II Work in collaboration with A.A. Andrianov (St. Petersburg) and M.A. Kurkov (Napoli) JHEP 1005:057,2010
Determinants of generalized binary band matrices
 Determinants of generalized inary and matrices Dmitry Efimov arxiv:17005655v1 [mathra] 18 Fe 017 Department of Mathematics, Komi Science Centre UrD RAS, Syktyvkar, Russia Astract Under inary matrices we
Determinants of generalized inary and matrices Dmitry Efimov arxiv:17005655v1 [mathra] 18 Fe 017 Department of Mathematics, Komi Science Centre UrD RAS, Syktyvkar, Russia Astract Under inary matrices we
Part I. Many-Body Systems and Classical Field Theory
 Part I. Many-Body Systems and Classical Field Theory 1. Classical and Quantum Mechanics of Particle Systems 3 1.1 Introduction. 3 1.2 Classical Mechanics of Mass Points 4 1.3 Quantum Mechanics: The Harmonic
Part I. Many-Body Systems and Classical Field Theory 1. Classical and Quantum Mechanics of Particle Systems 3 1.1 Introduction. 3 1.2 Classical Mechanics of Mass Points 4 1.3 Quantum Mechanics: The Harmonic
arxiv: v1 [nlin.si] 24 May 2017
![arxiv: v1 [nlin.si] 24 May 2017 arxiv: v1 [nlin.si] 24 May 2017](/thumbs/93/113600722.jpg) Boundary Algebraic Bethe Ansatz for a nineteen vertex model with U q osp ) ) ] symmetry arxiv:1705.08953v1 nlin.si] 4 May 017 R. S. Vieira E-mail: rsvieira@df.ufscar.br Universidade Federal de São Carlos,
Boundary Algebraic Bethe Ansatz for a nineteen vertex model with U q osp ) ) ] symmetry arxiv:1705.08953v1 nlin.si] 4 May 017 R. S. Vieira E-mail: rsvieira@df.ufscar.br Universidade Federal de São Carlos,
arxiv: v1 [math-ph] 24 Dec 2013
![arxiv: v1 [math-ph] 24 Dec 2013 arxiv: v1 [math-ph] 24 Dec 2013](/thumbs/95/124403329.jpg) ITP-UU-13/32 SPIN-13/24 Twisted Heisenberg chain and the six-vertex model with DWBC arxiv:1312.6817v1 [math-ph] 24 Dec 2013 W. Galleas Institute for Theoretical Physics and Spinoza Institute, Utrecht University,
ITP-UU-13/32 SPIN-13/24 Twisted Heisenberg chain and the six-vertex model with DWBC arxiv:1312.6817v1 [math-ph] 24 Dec 2013 W. Galleas Institute for Theoretical Physics and Spinoza Institute, Utrecht University,
A Recursion and a Combinatorial Formula for Jack Polynomials
 A Recursion and a Combinatorial Formula for Jack Polynomials Friedrich Knop & Siddhartha Sahi* Department of Mathematics, Rutgers University, New Brunswick NJ 08903, USA 1. Introduction The Jack polynomials
A Recursion and a Combinatorial Formula for Jack Polynomials Friedrich Knop & Siddhartha Sahi* Department of Mathematics, Rutgers University, New Brunswick NJ 08903, USA 1. Introduction The Jack polynomials
1 Electrons on a lattice, with noisy electric field
 IHES-P/05/34 XXIII Solvay Conference Mathematical structures: On string theory applications in condensed matter physics. Topological strings and two dimensional electrons Prepared comment by Nikita Nekrasov
IHES-P/05/34 XXIII Solvay Conference Mathematical structures: On string theory applications in condensed matter physics. Topological strings and two dimensional electrons Prepared comment by Nikita Nekrasov
Poisson structure on moduli of flat connections on Riemann surfaces and r-matrix
 Poisson structure on moduli of flat connections on Riemann surfaces and r-matrix arxiv:math/9802054v2 [math.qa] 18 Feb 1998 V.V.Fock and A.A.Rosly Institute of Theoretical and Experimental Physics, B.Cheremushkinskaya
Poisson structure on moduli of flat connections on Riemann surfaces and r-matrix arxiv:math/9802054v2 [math.qa] 18 Feb 1998 V.V.Fock and A.A.Rosly Institute of Theoretical and Experimental Physics, B.Cheremushkinskaya
Semigroup Quantum Spin Chains
 Semigroup Quantum Spin Chains Pramod Padmanabhan Center for Physics of Complex Systems Institute for Basic Science, Korea 12th July, 2018 Based on work done with D. Texeira, D. Trancanelli ; F. Sugino
Semigroup Quantum Spin Chains Pramod Padmanabhan Center for Physics of Complex Systems Institute for Basic Science, Korea 12th July, 2018 Based on work done with D. Texeira, D. Trancanelli ; F. Sugino
Representation of Lie Groups and Special Functions
 Representation of Lie Groups and Special Functions Recent Advances by N. Ja. Vilenkint formerly of The Correspondence Pedagogical Institute, Moscow, Russia and A.U. Klimyk Institute for Theoretical Physics,
Representation of Lie Groups and Special Functions Recent Advances by N. Ja. Vilenkint formerly of The Correspondence Pedagogical Institute, Moscow, Russia and A.U. Klimyk Institute for Theoretical Physics,
Kac-Moody Algebras. Ana Ros Camacho June 28, 2010
 Kac-Moody Algebras Ana Ros Camacho June 28, 2010 Abstract Talk for the seminar on Cohomology of Lie algebras, under the supervision of J-Prof. Christoph Wockel Contents 1 Motivation 1 2 Prerequisites 1
Kac-Moody Algebras Ana Ros Camacho June 28, 2010 Abstract Talk for the seminar on Cohomology of Lie algebras, under the supervision of J-Prof. Christoph Wockel Contents 1 Motivation 1 2 Prerequisites 1
Curriculum Vitae. Department of Mathematics, UC Berkeley 970 Evans Hall, Berkeley, CA
 Personal Information Official Name: Transliteration used in papers: Mailing Address: E-mail: Semen Artamonov Semeon Arthamonov Department of Mathematics, UC Berkeley 970 Evans Hall, Berkeley, CA 94720
Personal Information Official Name: Transliteration used in papers: Mailing Address: E-mail: Semen Artamonov Semeon Arthamonov Department of Mathematics, UC Berkeley 970 Evans Hall, Berkeley, CA 94720
Combinatorial bases for representations. of the Lie superalgebra gl m n
 Combinatorial bases for representations of the Lie superalgebra gl m n Alexander Molev University of Sydney Gelfand Tsetlin bases for gln Gelfand Tsetlin bases for gl n Finite-dimensional irreducible representations
Combinatorial bases for representations of the Lie superalgebra gl m n Alexander Molev University of Sydney Gelfand Tsetlin bases for gln Gelfand Tsetlin bases for gl n Finite-dimensional irreducible representations
Quantum Phase Transitions
 1 Davis, September 19, 2011 Quantum Phase Transitions A VIGRE 1 Research Focus Group, Fall 2011 Spring 2012 Bruno Nachtergaele See the RFG webpage for more information: http://wwwmathucdavisedu/~bxn/rfg_quantum_
1 Davis, September 19, 2011 Quantum Phase Transitions A VIGRE 1 Research Focus Group, Fall 2011 Spring 2012 Bruno Nachtergaele See the RFG webpage for more information: http://wwwmathucdavisedu/~bxn/rfg_quantum_
arxiv:quant-ph/ v1 3 Apr 2001
 Kronecer product/direct product/tensor product in Quantum Theory arxiv:quant-ph/0104019v1 3 Apr 2001 Z. S. Sazonova Physics Department, Moscow Automobile and Road Construction Institute (Technical University),
Kronecer product/direct product/tensor product in Quantum Theory arxiv:quant-ph/0104019v1 3 Apr 2001 Z. S. Sazonova Physics Department, Moscow Automobile and Road Construction Institute (Technical University),
3.14. The model of Haldane on a honeycomb lattice
 4 Phys60.n..7. Marginal case: 4 t Dirac points at k=(,). Not an insulator. No topological index...8. case IV: 4 t All the four special points has z 0. We just use u I for the whole BZ. No singularity.
4 Phys60.n..7. Marginal case: 4 t Dirac points at k=(,). Not an insulator. No topological index...8. case IV: 4 t All the four special points has z 0. We just use u I for the whole BZ. No singularity.
Highest-weight Theory: Verma Modules
 Highest-weight Theory: Verma Modules Math G4344, Spring 2012 We will now turn to the problem of classifying and constructing all finitedimensional representations of a complex semi-simple Lie algebra (or,
Highest-weight Theory: Verma Modules Math G4344, Spring 2012 We will now turn to the problem of classifying and constructing all finitedimensional representations of a complex semi-simple Lie algebra (or,
CV of Dr. Takeo Kojima
 CV of Dr. Takeo Kojima Name: Takeo Kojima Affiliation: Position: Professor Date Prepared: May 30, 2017 Day and Place of Birth: March 22, 1969, Japan Education March 1992 : B.S. Kyoto University, School
CV of Dr. Takeo Kojima Name: Takeo Kojima Affiliation: Position: Professor Date Prepared: May 30, 2017 Day and Place of Birth: March 22, 1969, Japan Education March 1992 : B.S. Kyoto University, School
45. The Parallelogram Law states that. product of a and b is the vector a b a 2 b 3 a 3 b 2, a 3 b 1 a 1 b 3, a 1 b 2 a 2 b 1. a c. a 1. b 1.
 SECTION 10.4 THE CROSS PRODUCT 537 42. Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular. 43.
SECTION 10.4 THE CROSS PRODUCT 537 42. Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular. 43.
Fock space representations of twisted affine Lie algebras
 Fock space representations of twisted affine Lie algebras Gen KUROKI Mathematical Institute, Tohoku University, Sendai JAPAN June 9, 2010 0. Introduction Fock space representations of Wakimoto type for
Fock space representations of twisted affine Lie algebras Gen KUROKI Mathematical Institute, Tohoku University, Sendai JAPAN June 9, 2010 0. Introduction Fock space representations of Wakimoto type for
arxiv:math/ v1 [math.qa] 11 Dec 2002
![arxiv:math/ v1 [math.qa] 11 Dec 2002 arxiv:math/ v1 [math.qa] 11 Dec 2002](/thumbs/88/116295678.jpg) arxiv:math/055v [math.qa] Dec 00 MULTIPLICATION FORMULAS FOR THE ELLIPTIC GAMMA FUNCTION GIOVANNI FELDER AND ALEXANDER VARCHENKO, Departement Mathematik, ETH-Zentrum, 809 Zürich, Switzerland felder@math.ethz.ch
arxiv:math/055v [math.qa] Dec 00 MULTIPLICATION FORMULAS FOR THE ELLIPTIC GAMMA FUNCTION GIOVANNI FELDER AND ALEXANDER VARCHENKO, Departement Mathematik, ETH-Zentrum, 809 Zürich, Switzerland felder@math.ethz.ch
Automorphic Equivalence Within Gapped Phases
 1 Harvard University May 18, 2011 Automorphic Equivalence Within Gapped Phases Robert Sims University of Arizona based on joint work with Sven Bachmann, Spyridon Michalakis, and Bruno Nachtergaele 2 Outline:
1 Harvard University May 18, 2011 Automorphic Equivalence Within Gapped Phases Robert Sims University of Arizona based on joint work with Sven Bachmann, Spyridon Michalakis, and Bruno Nachtergaele 2 Outline:
Free Field Representation for the Classical Limit of Quantum Affine Algebra
 IASSNS-HEP-92/62 RU-92/37 Free Field Representation for the Classical Limit of Quantum Affine Algebra Sergei Lukyanov Department of Physics and Astronomy Rutgers University,Piscataway, NJ 08855-049 Samson
IASSNS-HEP-92/62 RU-92/37 Free Field Representation for the Classical Limit of Quantum Affine Algebra Sergei Lukyanov Department of Physics and Astronomy Rutgers University,Piscataway, NJ 08855-049 Samson
