TKM II: Equation of motion technique - Anderson model and screening (RPA)
|
|
|
- Gervais Bond
- 5 years ago
- Views:
Transcription
1 TKM II: Equation of motion technique - Anderson model and screening RPA Dr. Jens Michelsen Contents 1 Preliminaries: Bands etc 2 2 Anderson s model for magnetic impurities Single level coupled to continuum Short on analytical continuation Full Anderson Model Self-consistency: Formation of local magnetic moment Screening effects in metals Dielectric response Non-interacting case Lindhard function Limits Interacting system - RPA approximation Plasma oscillations Screened potential Diagrammatic representation of the mean-field approximations Anderson model without on-site interaction Anderson model with on-site interaction RPA
2 1 Preliminaries: Bands etc Let us consider the non-interacting Hamiltonian in second quantized form H 0 = d 3 r [ ] p ˆψ σr 2 V 2m µ + V r ˆψ σ r 1 σ where V r is a periodic crystal potential. The eigenfunctions φ nkσ r = u n rχ σ e ik r of the single-particle Hamiltonian are characterized by band index n, crystal momentum k 1st B.Z. and spin index σ. The energy spectrum is separated into bands ɛ nk. If ɛ F = µt = 0 crosses one of the bands the material is a metal and the band is referred to as conduction band. The bandwidth is defined as D n = max[ɛ nk ] min[ɛ nk ]. The field operator can be expanded in the complete set of eigenstates ˆψ σ r = φ nkσ rĉ nkσ 2 nk The Hamiltonian in this basis takes the form H 0 = nkσ ɛ nk ĉ nkσĉnkσ 3 For metals it is common to restrict oneself to the conduction band and adopt an effective mass approximation φ nkσ r 1 k 1.B.Z. V e ik r χ σ k unrestricted m m nkσ ɛ 4 nkĉ nkσĉnkσ kσ ɛ kĉ kσĉkσ We will, however, for the following discussion of the Anderson Model, assume that the spectrum has a certain bandwidth D. The single particle Matsubara thermal Green s function is given by G σσ rτ, r τ = T τ ˆψσ r, τ ˆψ σ r, τ 5 where ˆψ σ r, τ = e H0τ ˆψσ re H0τ, ˆψ σ r, τ = e H0τ ˆψ σ re H0τ 6 It is usually easier to work with the GF in momentum space which is related to the GF in position space through G kσ,k σ τ, τ = T τ ĉ kσ τĉ k σ τ 7 G σσ rτ, r τ = 1 T τ ĉ V kσ τĉ k σ τ e ik r ik r χ σ χ σ k,k = 1 8 G kσ,k V σ τ, τ e ik r ik r χ σ χ σ k,k If the system is invariant under spin-rotational symmetry, then the GF in Eq. 5 will be proportional to δ σσ, and if we have translational periodic invariance in space the GF s will only 2
3 depend on the relative coordinate r r. Finally, if the Hamiltonian does not explicitly depend on imaginary time τ, the GF will depend only on the relative coordinates τ τ. Thus under these conditions we may restrict ourselves to Single particle GF Fermions G k,σ τ = T τ ĉ kσ τĉ kσ 0 9 The single particle Matsubara thermal Green s function is defined as G k,σ τ = T τ ĉ kσ τĉ kσ 0 = [ Θτ ĉ kσ τĉ kσ 0 Θ τ ĉ kσ 0ĉ kσ τ ] 10 with We note, in particular that ĉ k τ = e τh ĉ k e τh, ĉ k τ = eτh ĉ k e τh, 11 G kσ 0 = n kσ 12 The retarded and advanced GFs are obtained by analytical continuation of the Fouriertransform G R kσω = G kσ ω + iδ, G A kσω = G kσ ω iδ 13 The momentum- and spin resolved spectral function is given by A kσ ω = i [ G R kσω G A kσω ] = 2ImG R kσω 14 For a non-interacting system, H = H 0 = k ξ kĉ kσĉkσ, with ξ k = ɛ k µ, we have ĉ kσ τ = e ξ kτ ĉ kσ, ĉ kσ τ = eξ kτ ĉ kσ. 15 The Matsubara GF s can then be explicitly written as [ ] G 0,kσ τ = Θτ1 n F ɛ k Θ τn F ɛ k e ξ kτ 16 The unperturbed GF satisfies the equation of motion or in frequency domain τ ξ k G 0,kσ τ = δτ 17 iω n ξ k G 0,kσ iω n = 1 18 which yields 1 G 0,kσ iω n = 19 iω n ξ k Exercise: Check that G 0,kσ τ = 1 β ω n G 0,kσ iω n e iωnτ. The spectral density for the unperturbed system is given by A 0,kσ ω = 2πδω ξ k 20 3
4 2 Anderson s model for magnetic impurities The Anderson model has been used to describe the appearance of a magnetic moment of impurities of certain magnetic ions embedded in a non-magnetic host metal. It has also been used in the description of coulomb blockade in quantum dots. It is a natural starting point to describe the Kondo effect in both metals and quantum dots. The host metal is described as indicated above, i.e. by an effective mass Hamiltonian describing the conduction band. The impurity atoms are assumed to have only one spin-degenerate state in the active shell usually the d-shell, hence the subsequent notation d for the impurity states. The system is described in the eigenbasis of the individual Hamiltonians of the metal and the impurity atoms, φ kσ r and φ dσ r, with corresponding energies and creation-/annihilation operators ξ k = ɛ k µ, ĉ kσ, ĉ kσ, ξ d = ɛ d µ, ĉ dσ, ĉ dσ 21 Once the impurity atoms are embedded into the metal, the crystal- and impurity potentials are perturbed and the basis φ kσ, φ dσ is no longer an eigen-basis of the full single particle Hamiltonian. Expanding the field-operators in this eigen-basis then does no longer lead to a diagonal form but will include overlaps between the states of the conduction band and the states of the impurities. These terms are usually called hopping terms and describe a probability amplitude of transitions from the impurity atoms to the conduction band and vice versa. Furthermore, because of the highly localized wave functions at the impurity atom, the Coulomb interaction is much stronger between electrons occupying these states. Consequently, there is an additional energy cost associated with having both spin-degenerate impurity states occupied. This is modeled by a so-called on-site interaction with characteristic energy U. The full Hamiltonian of this model is then given by H = H c + H t + H d + H U 22 where H c = k,σ ξ k ĉ kσĉkσ,, H d = σ ξ d ĉ dσĉdσ 23 describe the individual unperturbed Hamiltonians of the conduction band and the impurity atom and H t = t k ĉ kσĉdσ + t kĉ dσĉkσ 24 kσ kσ describes the hopping between the two subsystems. Finally the last term H U = U ˆn ˆn 25 describes the on-site Coulomb interaction. The d-electron energy ɛ d is below the chemical potential i.e. ξ d < 0 and from the kinetic energy point of view it is favorable to fill the orbital by two electrons. However, this costs potential energy U, which is not possible if 2ɛ d + U > 2µ i.e. if 2ξ d + U > 0. Single occupancy of the atom would appear to lead, quite naturally, to a magnetic moment since only one of the spin-degenerate states must be occupied. On the other hand, the hopping between the impurity states and the conduction band implies that the direction of the spin may fluctuate strongly, and average out. The efficiency of such processes depends on the strength of the hopping. But strong hopping also increases the energy the contribution H t to the Hamiltonian so there is a trade-off between on-site interaction and hopping. 4
5 It will turn out, that for certain values of the parameters it is energetically favorable for the system to have a magnetic moment and thus minimizing the on-site interaction energy while for other values there is no magnetic moment. 2.1 Single level coupled to continuum To get a better feel for the system let us first consider only the effect of the hopping between the impurity states and the conduction band states and, for the time being, neglect the on-site interaction. H = H c + H t + H d 26 The operators obey the equations of motion τ ĉ dσ τ = [H, ĉ dσ τ] = ξ d ĉ dσ τ t kĉ kσ k 27 τ ĉ kσ τ = [H, ĉ kσ τ] = ξ k ĉ kσ τ t k ĉ dσ Analogous to the conduction band Green s functions, we define the GF of the impurity states G dσ τ = T τ ĉ dσ τĉ dσ 0 28 This GF obeys the equation of motion τ ξ d G dσ τ = δτ τ k = δτ τ + k t k T τ ĉ kσ τĉ dσ 0 t kf kσ τ 29 where we also defined This GF satisfies the equation of motion F kσ τ = T τ ĉ kσ τĉ dσ τ ξ k F kσ τ = t k G dσ τ 31 This gives us a system of coupled equations which in Fourier-space can be written iω n ξ d G dσ iω n = 1 + t kf kσ iω n k iω n ξ k F kσ iω n = t k G dσ iω n 32 Using G 1 0,kσ iω n = iω n ξ k we can write the second equation in the form Inserting into the first gets us F kσ iω n = G 0,kσ iω n t k G dσ iω n 33 G dσ iω n = G 0,dσ iω n + G 0,dσ iω n k t kg 0,kσ iω n t k G dσ iω n 34 5
6 If we define Σ σ iω n = k t k 2 G 0,kσ iω n 35 we have with the solution for G dσ iω n : G dσ iω n = G 0,dσ iω n + G 0,dσ iω n Σ σ iω n G dσ iω n 36 1 G dσ iω n = G 1 0,dσ iω n + Σ σ iω n = 1 iω n ξ d + Σ σ iω n We have Σ σ iω n = t k 2 G 0,kσ iω n = t k 2 38 iω n ξ k k k Let us assume that t k and ξ k both only depend on k = k such that Σ σ iω n = t k 2 d 3 k t k 2 = V iω n ξ k 2π 3 = V iω n ξ k 2π 2 dkk 2 t k 2 iω n ξ k k = dξ Nξ t kξ 2 39 iω n ξ dξ ξ = π iω n ξ where ξ = πnξ t kξ 2 is the hybridization energy and the density of states Nξ is defined such that 1 V Nξ = 1 2π 2 k 2 dk = νξ 40 dξ k=kξ Note: Here we distinguish between the density of states Nξ and the density of states per unit volume νξ compare dimensions. To simplify matters, let us assume that the chemical potential lies in the middle of the gap and thus ξ [ D, D] where D is the bandwidth. We also assume that the hybridization energy is constant across the band ξ =. We then have Σiω n = π Short on analytical continuation D D [ ] 1 dξ iω n ξ = ln iωn + D iω n D Note lnz = lnre iϕ = lnr + ln e iϕ = lnr + iϕ, not periodic w.r.t. ϕ such that even though z = re iϕ and z = re iϕ+2π represent the same complex number, the logarithm does not give the same result. lnz is a multivalued function in the complex plane. To avoid this problem a principal branch is chosen as ϕ π, π and a branch cut is introduced at Rez, 0. The logarithm is discontinuous across this branch cut and the function is analytic everywhere else. For a complex number with an infinitesimally small imaginary part, z = x ± iδ, δ > 0, we have that the absolute value is r x and that the phase is always either ϕ ±πθ x { ln x, x > 0 lnx ± iδ ln x + iπθ x = 42 ln x ± iπ, x <
7 D 0 D D 0 D D 0 D D 0 D Figure 1: Left: Real part of Σz. Right: Imaginary part of Σz. Thus we have Σω ± iδ = [ ] lnω ± iδ + D lnω ± iδ D π = [ ] ln ω + D ln ω D ± iπθ ω D iπθ ω + D π = π ln ω + D ω D iθd ω 43 We note that for ω D we have ln ω + D/ω D ω/d 0 Having G R dσ ω = G dσω + iδ we can write the spectral function A dσ ω = 2ImG R ω = ω ξ d Figure 2: Effect of hybridization between d electron orbitals and conduction band. 2.2 Full Anderson Model Let us now attack the full model H = H c + H t + H d + H U 45 7
8 The equation of motion of the operators is given by τ ĉ dσ τ = ξ d ĉ dσ τ t kĉ kσ + [H U, ĉ dσ tτ] k 46 τ ĉ kσ τ = ξ k ĉ kσ τ t k ĉ dσ which is the same as before except for the extra term [ ] [H U, ĉ dσ τ] = U ˆn d τˆn d τ, ĉ dσ τ = U ˆn d, σ τĉ dσ τ 47 which follows from [ˆn d σ τ, ĉ dσ τ] = 0 and [ˆn dσ τ, ĉ dσ τ] = ĉ dσ τ. We then have for the GFs τ ξ d G dσ τ = δτ + k τ ξ k F kσ τ = t k G dσ τ t kf kσ τ U T τ ˆn d, σ τĉ dσ τĉ dσ 0 48 The last term of the top equation complicates the equation of motion as we need also the equation of motion of the two particle GF, which in turn depends on the three-particle GF etc. The straight forward route would be to perform perturbation theory. This, however, is only meaningful for weak interaction, and can not directly cover non-perturbative effects such as bound states and the appearance of local moments which we are interested in here. Instead we make a so-called mean-field approximation: T τ ˆn d, σ τĉ dσ τĉ dσ 0 = ĉ d, σ τĉ d, σ τĉ dσ τĉ dσ 0 T τ ĉ d, σ τĉ d, σ τ T τ ĉ dσ τĉ dσ 0 = ˆn d, σ G dσ τ 49 The equation of motion of the GFs are then in Fourier space given by using from now on the notation n σ = ˆn dσ iω n ξ d Un σ G dσ iω n = 1 + t kf kσ iω n k iω n ξ k F kσ iω n = t k G dσ iω n 50 Solving again for the second one and inserting into the first one we get G dσ iω n = 1 iω n ξ d Un σ + Σiω n 51 With the same approximations as in the previous section we find A dσ ω = ω ξ d Un σ
9 2.3 Self-consistency: Formation of local magnetic moment Using the relationship derived from the Lehmann-representation dω dω n σ = 2π n F ωaω = 2π n F ω ω ξ d Un σ we obtain a self-consistency equation. At T = 0, i.e. n F ω = Θ ω, we get 1 n σ = π arctan ξd + Un σ 54 or using cot π 2 arctanx = x cotπn σ = ξ d + Un σ Introducing the total occupation N = n + n and the magnetization M = n n we may write this as N = 1 ξd + U 2 N σm arccot π σ 56 M = 1 ξd + U 2 N σm σarccot π σ Note that there is always a solution with M = 0 since the second equation of 56 is trivially satisfied. The total occupation is then given by N = 2n where n is the occupation of one of the levels and given by 55 with index σ removed. It is useful to consider a special case where the states are half-filled on average. To find the condition for we set n = 1/2 and get the condition Half-filling, N = 1: ξ d = U 2, for M = 0, i.e. n = n σ = The interesting thing about the Anderson model is, however, the existence of a solution with finite magnetization. To see that such a solution exists, let us try to find the condition for complete magnetization 2 M = 1 which implies also that N = M = 1. Effectively this means that only one state is occupied and the other is empty. Inserting this condition into 56 and adding/subtracting the two equations we get ξd ξd + U π = arccot, 0 = arccot 58 Using the half-filling condition from before ξ d = U/2 the left and right equations become the same and lead to the condition ξ d = U = cotπ = Using the indefinite integral g dx x a 2 +g 2 2 Note that M [ 1, 1] since n σ 0, 1 = arctan a x g 9
10 This result should not be surprising since if the on-site interaction is infinitely strong compared to hybridization only one of the states should be occupied and processes where the electron occupying this state is exchanged with an electron from the conduction band are suppressed. To find the critical values of the parameters for a finite magnetization we may linearize the left hand side of Eq. 56 by using arccota + bx = arccota bx 1+a 2 + Ox2 to obtain N 2 π arccot ξd + U 2 N M 1 π ξd + U 2 N 2 U M 60 Thus, using again the half-filling condition ξ d = U/2 we get N = 1 from the first equation while the second equation requires, for non-zero M, the following condition to be satisfied U = π 61 which is the critical value for the ratio of interaction strength versus hybridization in order to form a local moment. M π U Figure 3: Top figures: Spectral density on x-axis, Energy on y-axis. Left: U = = 0. Middle: U < π. Right: U > π. Bottom: Magnetic moment as a function of U/. 10
11 3 Screening effects in metals The electric potential φr, t in a system can be separated into two parts, the externally applied potential φ ext r, t, as well as an induced potential φ ind r, t. φr, t = φ ext r, t + φ ind r, t 62 In the absence of an externally applied electric potential a system at equilibrium has a vanishing electric potential 3 φr, t = φ ind r, t = 0 63 The induced electric potential is related to the induced charge through the Poisson equation 2 φ ind r, t = 1 ρ ind r, t φr, t = d 3 r V c r r ρ ind r, t 64 ɛ 0 where V c r r = 1 4πɛ 0 1 r r is the Coulomb interaction. At equilibrium the charge density from the electrons is cancelled over macroscopic distances by the charge density of the ions, i.e. at equilibrium we have charge neutrality and ρ ind r, t = 0. The induced charge ρ ind is due to an induced displacement of the electron density δnr, t. In the linear response regime, the induced charge density can be written as ρ ind r, t = d 3 r dt χ R rt, r t φ ext r, t 66 where χ R is known as the polarizability function. 3.1 Dielectric response The relationship between the external potential and the total potential defines the dielectric function ε φ ext r, t = d 3 r dt εrt, r t φr, t 67 Usually it is more interesting/useful to talk about the inverse relationship φr, t = d 3 r dt ε 1 rt, r t φ ext r, t 68 Using the definitions from the previous section we can write this as ε 1 rt, r t = δr r δt t + d 3 r V c r r χ R r t, r t In principle it only needs to be constant, but such a potential is not observable since the electro-magnetic field depends on the gradient and time derivative of the potential - Gauge invariance 11
12 Translational invariance For a translationally invariant system the polarizability depends only on the relative coordinates χ R rt, r t = χ R r r ; t t and therefore so does the dielectric function and its inverse. It then makes sense to talk about the Fourier transformed quantities which are related through φk, ω = ɛ 1 k, ωφ ext k, ω 70 with the dielectric function being related to the polarizability ε 1 k, ω = 1 + V c kχ R k, ω 71 Using E ext k, ω = ikφ ext k, ω together with the continuity equation iωρk, ω + ik jk, ω = 0 we can obtain a relationship to the conductivity defined through or jk, ω = σk, ωe ext k, ω ɛ 1 k, ω = 1 i k2 σk, ω 72 ω σk, ω = iω k 2 V ckχ R k, ω 73 In a quantum mechanical system the coupling to the electric potential is described by adding a perturbation H ext = d 3 rˆρr, tφ ext r, t = e d 3 r ˆψ r, tψr, tφ ext r, t 74 to the Hamiltonian. Note: in this section we shall neglect spin, which only leads to a factor of two in the end-result. The linear response is then written as ρr, t = i d 3 r dt Θt t [ˆρr, t, ˆρr, t ] φ ext r t 75 which identifies the polarizability function χ R rt, r t = iθt t [ˆρr, t, ˆρr, t ] 76 In the basis of φ k r = 1 V e ik r the density can be written as and we have ˆρr, t = e ĉ k V tĉ k te ik k r = e ĉ k V tĉ te iq r k+q 77 kk kq χ R rt, r t = iθt t e2 V 2 [ĉ k tĉ k+q t, ĉ k t ĉ k +q t ] e iq r e iq r 78 kk qq 12
13 For a translationally invariant system the response function should only depend on the relative coordinate r r, which means that q = q. Introducing the notation ˆρ q t = e k ĉ k tĉ k+q t 79 we have or in momentum space χ R r r ; t = iθt 1 V 2 [ˆρ q t, ˆρ q 0] e iq r r q 80 χ R q; t = iθt 1 V [ˆρ qt, ˆρ q 0] 81 In the following sections we shall try to evaluate this response function by first deriving the Fourier transform of the corresponding imaginary time GF χq, iω n = β 0 dτχk, τe iωnτ, χk, τ = 1 V T τ ˆρ q τˆρ q 0 82 and then performing an analytical continuation to obtain the retarded GF χ R k, ω, i.e. the polarizability function. 3.2 Non-interacting case We start by investigating the non-interacting case where the unperturbed Hamiltonian is given by H 0 = k ξ k ĉ kĉk 83 and the equation of motion of the operators is τ ĉ k τ = [H, ĉ k ] = ξ k ĉ k τ τ ĉ k τ = [H, ĉ k ] = ξ kĉ k τ 84 It is useful to rewrite the two-particle GF as the index 0 denotes non-interacting where from now on setting e = 1 for notational brevity χ 0 q, τ = 1 χ 0 k, q, τ, 85 V k χ 0 k, q; τ = T τ ĉ k τĉ k+q τˆρ q0 86 It is then useful to investigate the time derivative τ ĉ k τĉ k+q τ = [H 0, ĉ k τĉ k+q τ] = ξ k+q ξ k ĉ k τĉ k+q τ 87 The equation of motion of the two-particle GF is then given by remember to take into account the discontinuity due to the time ordering τ ξ k+q ξ k χk, q; τ = δτ [ĉ kĉk+q, ˆρ q] 88 13
14 The commutator on the right hand side is [ĉ kĉk+q, ˆρ q] = ĉ kĉk ĉ k+qĉk+q = n F ξ k n F ξ k+q 89 In Fourier space the equation of motion then becomes iω n ξ k+q ξ k χ 0 k, q; iω n = n F ξ k n F ξ k+q 90 or The polarizability function is then given by χ 0 k, q; iω n = n F ξ k n F ξ k+q iω n ξ k+q ξ k χ R 0 q, ω = χ 0 q, ω + iδ = 1 V k n F ξ k n F ξ k+q ω + iδ ξ k+q ξ k The right hand side of this equation is known as the Lindhard function Lindhard function The Lindhard function can be evaluated exactly but for most purposes it is sufficient to consider the low wave-length approximation ξ k+q ξ k + q v k with v k = k ξ k, which leads to χ R 0 q, ω = d 3 k n F ξ k n F ξ k+q 2π 3 ω + iδ ξ k+q ξ k d 3 k 2π 3 q v k ω + iδ q v k dn F dɛ 93 The imaginary part of the response is given by Imχ R d 3 k 0 q, ω = 2π 3 q v kπδω q v k dn F dɛ 1 ω k2 F dcos θδω qv F cos θ 4πv F 1 = ω kf 2 Θ ω v F q v F q 4πv F ω = πν0 2v F q Θ ω v F q 94 We may use the Kramers-Kronig relation to obtain the real part [ Reχ R 0 q, ω = ν0 1 ω ] 2v F q ln ω + v F q ω v F q 95 with ν0 = k F m/2π 2. 14
15 Figure 4: Absorbtion imaginary part of χ R 0 q, ω at T = 0 derived from full Lindhard-function. Dashed line indicating ω = qv F Limits For ω = 0 static polarizability - compressibility we get Imχ R 0 q, 0 = 0 and χ R 0 q, 0 = Reχ R 0 q, 0 = ν0. For small v F q/ω the imaginary part of the polarizability goes to zero and for the real part we get to second order using ln 1+x 1 x = 2x + 2x3 /3 + Ox 4 χ R 0 q, ω = Reχ R 0 q, ω ν vf q 2 = ν0 ω 3 vf q 2 n = ω m q 2 ω 2 96 where we used the mean electron density n = d 3 k 2π n 3 F ξ k = 1 4πk 3 2π 3 F 3 = 1 k 3 2π 2 F 3 = ν0 3 mv2 F. This result could have been obtained more directly by expanding the integrand to first nonvanishing order in q to get χ R d 3 k q v k 2 0 q, ω 2π 3 ω 2 dn F = n q 2 97 dɛ m ω 2 Note: First order expansion in q cancels for isotropic medium. 3.4 Interacting system - RPA approximation In this section we extend our analysis to the case of interacting electrons by adding the interaction Hamiltonian H int = 1 d 3 rd 3 r 2 ˆψ r ˆψr V c r r ˆψr ˆψr 98 15
16 where V c r r is again the Coulomb interaction vertex. In momentum space the Hamiltonian takes the form H int = 1 V c qĉ 2V k+qĉ k qĉk ĉ k 99 kk,q 0 The equation of motion of the operator ĉ k τĉ k+q τ is then given by τ ĉ k τĉ k+q τ = [H 0, ĉ k τĉ k+q τ] + [H int, ĉ k τĉ k+q τ] 100 The first term is the same as before, while the last term is [H int, ĉ k τĉ k+q τ] = 1 2V k,q 0 { V q ĉ k+q ĉ k qĉk ĉ k+q + ĉ k +q ĉ k q ĉ k+q ĉ k ĉ k +q ĉ kĉk+q+q ĉ k ĉ kĉ k q ĉ k ĉ k+q q } 101 We now apply what is known as the Random Phase Approximation, consisting in replacing pairs of operators by their expectation values. In essence this is also a type of mean-field approximation. The procedure requires us to take all the pairings between annihilation- and creation operators. For instance we get for the first term ĉ k+q ĉ k qĉk ĉ k+q ĉ k+q ĉ k+q ĉ k qĉk + ĉ k+q ĉ k+q ĉ k qĉk = ĉ k+q ĉ k+q n F ξ k δ q,0 + n F ξ k δ q,q ĉ k qĉk 102 Doing this for all terms and summing over q leads to [H int, ĉ 1 k τĉ k+q τ] = V cq n F ξ k+q n F ξ k ĉ k qĉk 103 V k Collecting everything we then get τ ξ k+q ξ k χk, q; τ = n F ξ k n F ξ k+q 1 + V q 1 χk, q; τ V k which in Fourier space becomes iω n ξ k+q ξ k χk, q; iω n = n F ξ k n F ξ k+q 1 + V c q 1 χk, q; iω n V k Using the previous result for the non-interacting response χ 0 k, q; iω n we can write χk, q; iω n = χ 0 k, q; iω n 1 + V c q 1 χk, q; iω n V k Summing over k we get χq, iω n = χ 0 q, iω n 1 + V c qχq; iω n
17 Solving for χq, iω n yields χq, iω n = χ 0 q, iω n 1 V c qχ 0 q, iω n Since we have the analytical continuation of χ R 0 q, ω we can insert this into the expression for 3.5 Plasma oscillations χ R q, ω = 108 χ R 0 q, ω 1 V c qχ R 0 q, ω 109 Inserting the expression for the polarizability in the RPA approximation into the definition of the dielectric function we have ε 1 V c k, ω 1 k, ω = V c kχ R 0 k, ωχr 0 k, ω = 1 V c kχ R 0 k, ω 110 or inversely Thus we can write the polarizability as εk, ω = 1 V c kχ R 0 k, ω. 111 χ R k, ω = χr 0 k, ω εk, ω 112 which can be interpreted as a screened response to the external potential with the inverse of the dielectric function representing the screening. For very small k we have χ R 0 k, ω = n k 2 m ω. Then there exists a zero of the dielectric function at 2 ω = ω p =. This zero indicates a resonance associated with plasma oscillations. e 2 n ɛ 0m 3.6 Screened potential Alternatively, we can write where ε 1 k, ω = 1 + V c k, ω 1 V c kχ R 0 k, ωχr 0 k, ω = 1 + Ṽckχ R 0 k, ω 113 Ṽ c k, ω = V ck 1 V ckχ R 0 k,ω = V ck εk, ω represents a screened Coulomb interaction. For ω = 0 we have χ R 0 k, 0 = ν0, and thus Ṽ c k, 0 = V c k 1 + ν0v c k = 1 = ɛ 0 k ν0 ɛ 0 k ɛ 0 k 2 + κ 2 where κ = ɛ 1 0 ν0 is the Thomas-Fermi screening length. The Fourier transform of this interaction gives a short range interaction Ṽ c r r = e κ r r 4πɛ 0 r r
18 Figure 5: Absorbtion as calculated by imaginary part of χ R 0 q, ω at T = 0 together with the plasma mode ωq = ω p + 3 v F 10 ωp q 2. 4 Diagrammatic representation of the mean-field approximations 4.1 Anderson model without on-site interaction Recall that the GF equation for the Anderson Model in the absence of on-site interaction can be written as G dσ iω n = G 0,dσ iω n + G 0,dσ iω n t kg 0,kσ iω n t k G dσ iω n 116 This may be expressed diagrammatically by introducing the following representations of the propagators G dσ =, G 0,dσ =, G 0,kσ = 117 and the vertices k t k =, t k = 118 It is then easy to see that the diagrammatic representation of the Anderson model without on-site interaction is given by = By inserting this equation into itself we can generate an infinite series of diagrams. Needless to say, it is a big advantage to sum up these diagrams up by defining Σ = = k t kg 0,kσ t k 120 which justifies the use of the term self-energy for this object. 18
19 4.2 Anderson model with on-site interaction When we include on-site interaction in the Anderson model we also need to include the corresponding diagrams. To identify which diagrams are kept within the approximations used in this text, let us first look at the case when the hopping is absent, t k = 0. The equation of motion can then be written on the form Here n σ = G dσ τ = 0 = 1 β the vertex G dσ iω n = G 0,dσ iω n + G 0,dσ iω n [Un σ ] G dσ iω n 121 ω n G dσ iω n e iωn0. Using the diagrammatical representation of U = 122 The term Un dσ can then be represented by a tadpole diagram Un dσ = 123 and the equation of motion for the Greens function is given by = If we include also hopping we may write [ G dσ iω n = G 0,dσ iω n + G 0,dσ iω n Un σ + k t kg 0,kσ iω n t k ] G dσ iω n or where = = + = Σ tot 126 Note that since the tadpole diagram contains the full propagator the self-energy has to be evaluated self-consistently together with the Dyson equation. 4.3 RPA We write the unperturbed polarizability χ 0 χ 0 =
20 while we write the full response function as χ = 128 Using the equation of motion for the polarizability which we can represent diagrammatically as χq, iω n = χ 0 q, iω n + χ 0 q, iω n V c qχq; iω n 129 = If we use diagrammatic representation Ṽ c =, V c = 131 for the screened- and unscreened Coulomb potential and rewrite the equation for the screened potential as Ṽ c q, ω = V c q + V c qχ 0 q, ωṽcq, ω, which we can represent as =
Green s functions: calculation methods
 M. A. Gusmão IF-UFRGS 1 FIP161 Text 13 Green s functions: calculation methods Equations of motion One of the usual methods for evaluating Green s functions starts by writing an equation of motion for the
M. A. Gusmão IF-UFRGS 1 FIP161 Text 13 Green s functions: calculation methods Equations of motion One of the usual methods for evaluating Green s functions starts by writing an equation of motion for the
Preface Introduction to the electron liquid
 Table of Preface page xvii 1 Introduction to the electron liquid 1 1.1 A tale of many electrons 1 1.2 Where the electrons roam: physical realizations of the electron liquid 5 1.2.1 Three dimensions 5 1.2.2
Table of Preface page xvii 1 Introduction to the electron liquid 1 1.1 A tale of many electrons 1 1.2 Where the electrons roam: physical realizations of the electron liquid 5 1.2.1 Three dimensions 5 1.2.2
Quantum Cluster Methods (CPT/CDMFT)
 Quantum Cluster Methods (CPT/CDMFT) David Sénéchal Département de physique Université de Sherbrooke Sherbrooke (Québec) Canada Autumn School on Correlated Electrons Forschungszentrum Jülich, Sept. 24,
Quantum Cluster Methods (CPT/CDMFT) David Sénéchal Département de physique Université de Sherbrooke Sherbrooke (Québec) Canada Autumn School on Correlated Electrons Forschungszentrum Jülich, Sept. 24,
RPA in infinite systems
 RPA in infinite systems Translational invariance leads to conservation of the total momentum, in other words excited states with different total momentum don t mix So polarization propagator diagonal in
RPA in infinite systems Translational invariance leads to conservation of the total momentum, in other words excited states with different total momentum don t mix So polarization propagator diagonal in
QUANTUM FIELD THEORY IN CONDENSED MATTER PHYSICS. Wolfgang Belzig
 QUANTUM FIELD THEORY IN CONDENSED MATTER PHYSICS Wolfgang Belzig FORMAL MATTERS Wahlpflichtfach 4h lecture + 2h exercise Lecture: Mon & Thu, 10-12, P603 Tutorial: Mon, 14-16 (P912) or 16-18 (P712) 50%
QUANTUM FIELD THEORY IN CONDENSED MATTER PHYSICS Wolfgang Belzig FORMAL MATTERS Wahlpflichtfach 4h lecture + 2h exercise Lecture: Mon & Thu, 10-12, P603 Tutorial: Mon, 14-16 (P912) or 16-18 (P712) 50%
561 F 2005 Lecture 14 1
 56 F 2005 Lecture 4 56 Fall 2005 Lecture 4 Green s Functions at Finite Temperature: Matsubara Formalism Following Mahan Ch. 3. Recall from T=0 formalism In terms of the exact hamiltonian H the Green s
56 F 2005 Lecture 4 56 Fall 2005 Lecture 4 Green s Functions at Finite Temperature: Matsubara Formalism Following Mahan Ch. 3. Recall from T=0 formalism In terms of the exact hamiltonian H the Green s
v(r i r j ) = h(r i )+ 1 N
 Chapter 1 Hartree-Fock Theory 1.1 Formalism For N electrons in an external potential V ext (r), the many-electron Hamiltonian can be written as follows: N H = [ p i i=1 m +V ext(r i )]+ 1 N N v(r i r j
Chapter 1 Hartree-Fock Theory 1.1 Formalism For N electrons in an external potential V ext (r), the many-electron Hamiltonian can be written as follows: N H = [ p i i=1 m +V ext(r i )]+ 1 N N v(r i r j
Lecture 1: The Equilibrium Green Function Method
 Lecture 1: The Equilibrium Green Function Method Mark Jarrell April 27, 2011 Contents 1 Why Green functions? 2 2 Different types of Green functions 4 2.1 Retarded, advanced, time ordered and Matsubara
Lecture 1: The Equilibrium Green Function Method Mark Jarrell April 27, 2011 Contents 1 Why Green functions? 2 2 Different types of Green functions 4 2.1 Retarded, advanced, time ordered and Matsubara
Examination paper for TFY4210 Quantum theory of many-particle systems
 Department of Physics Examination paper for TFY4210 Quantum theory of many-particle systems Academic contact during examination: Associate Professor John Ove Fjærestad Phone: 97 94 00 36 Examination date:
Department of Physics Examination paper for TFY4210 Quantum theory of many-particle systems Academic contact during examination: Associate Professor John Ove Fjærestad Phone: 97 94 00 36 Examination date:
Green Functions in Many Body Quantum Mechanics
 Green Functions in Many Body Quantum Mechanics NOTE This section contains some advanced material, intended to give a brief introduction to methods used in many body quantum mechanics. The material at the
Green Functions in Many Body Quantum Mechanics NOTE This section contains some advanced material, intended to give a brief introduction to methods used in many body quantum mechanics. The material at the
5. Superconductivity. R(T) = 0 for T < T c, R(T) = R 0 +at 2 +bt 5, B = H+4πM = 0,
 5. Superconductivity In this chapter we shall introduce the fundamental experimental facts about superconductors and present a summary of the derivation of the BSC theory (Bardeen Cooper and Schrieffer).
5. Superconductivity In this chapter we shall introduce the fundamental experimental facts about superconductors and present a summary of the derivation of the BSC theory (Bardeen Cooper and Schrieffer).
2.1 Green Functions in Quantum Mechanics
 Chapter 2 Green Functions and Observables 2.1 Green Functions in Quantum Mechanics We will be interested in studying the properties of the ground state of a quantum mechanical many particle system. We
Chapter 2 Green Functions and Observables 2.1 Green Functions in Quantum Mechanics We will be interested in studying the properties of the ground state of a quantum mechanical many particle system. We
A theoretical study of the single-molecule transistor
 A theoretical study of the single-molecule transistor B. C. Friesen Department of Physics, Oklahoma Baptist University, Shawnee, OK 74804 J. K. Ingersent Department of Physics, University of Florida, Gainesville,
A theoretical study of the single-molecule transistor B. C. Friesen Department of Physics, Oklahoma Baptist University, Shawnee, OK 74804 J. K. Ingersent Department of Physics, University of Florida, Gainesville,
Quantization of Scalar Field
 Quantization of Scalar Field Wei Wang 2017.10.12 Wei Wang(SJTU) Lectures on QFT 2017.10.12 1 / 41 Contents 1 From classical theory to quantum theory 2 Quantization of real scalar field 3 Quantization of
Quantization of Scalar Field Wei Wang 2017.10.12 Wei Wang(SJTU) Lectures on QFT 2017.10.12 1 / 41 Contents 1 From classical theory to quantum theory 2 Quantization of real scalar field 3 Quantization of
Time dependent perturbation theory 1 D. E. Soper 2 University of Oregon 11 May 2012
 Time dependent perturbation theory D. E. Soper University of Oregon May 0 offer here some background for Chapter 5 of J. J. Sakurai, Modern Quantum Mechanics. The problem Let the hamiltonian for a system
Time dependent perturbation theory D. E. Soper University of Oregon May 0 offer here some background for Chapter 5 of J. J. Sakurai, Modern Quantum Mechanics. The problem Let the hamiltonian for a system
Quantum Physics III (8.06) Spring 2008 Final Exam Solutions
 Quantum Physics III (8.6) Spring 8 Final Exam Solutions May 19, 8 1. Short answer questions (35 points) (a) ( points) α 4 mc (b) ( points) µ B B, where µ B = e m (c) (3 points) In the variational ansatz,
Quantum Physics III (8.6) Spring 8 Final Exam Solutions May 19, 8 1. Short answer questions (35 points) (a) ( points) α 4 mc (b) ( points) µ B B, where µ B = e m (c) (3 points) In the variational ansatz,
Symmetry of the Dielectric Tensor
 Symmetry of the Dielectric Tensor Curtis R. Menyuk June 11, 2010 In this note, I derive the symmetry of the dielectric tensor in two ways. The derivations are taken from Landau and Lifshitz s Statistical
Symmetry of the Dielectric Tensor Curtis R. Menyuk June 11, 2010 In this note, I derive the symmetry of the dielectric tensor in two ways. The derivations are taken from Landau and Lifshitz s Statistical
Basis 4 ] = Integration of s(t) has been performed numerically by an adaptive quadrature algorithm. Discretization in the ɛ space
![Basis 4 ] = Integration of s(t) has been performed numerically by an adaptive quadrature algorithm. Discretization in the ɛ space Basis 4 ] = Integration of s(t) has been performed numerically by an adaptive quadrature algorithm. Discretization in the ɛ space](/thumbs/92/110829637.jpg) 1 [NPHYS-007-06-00643] SUPPLEMENTARY MATERIAL for Spinons and triplons in spatially anisotropic frustrated antiferromagnets by Masanori Kohno, Oleg A. Starykh, and Leon Balents Basis The two-spinon states
1 [NPHYS-007-06-00643] SUPPLEMENTARY MATERIAL for Spinons and triplons in spatially anisotropic frustrated antiferromagnets by Masanori Kohno, Oleg A. Starykh, and Leon Balents Basis The two-spinon states
LS coupling. 2 2 n + H s o + H h f + H B. (1) 2m
 LS coupling 1 The big picture We start from the Hamiltonian of an atomic system: H = [ ] 2 2 n Ze2 1 + 1 e 2 1 + H s o + H h f + H B. (1) 2m n e 4πɛ 0 r n 2 4πɛ 0 r nm n,m Here n runs pver the electrons,
LS coupling 1 The big picture We start from the Hamiltonian of an atomic system: H = [ ] 2 2 n Ze2 1 + 1 e 2 1 + H s o + H h f + H B. (1) 2m n e 4πɛ 0 r n 2 4πɛ 0 r nm n,m Here n runs pver the electrons,
Solution of the Anderson impurity model via the functional renormalization group
 Solution of the Anderson impurity model via the functional renormalization group Simon Streib, Aldo Isidori, and Peter Kopietz Institut für Theoretische Physik, Goethe-Universität Frankfurt Meeting DFG-Forschergruppe
Solution of the Anderson impurity model via the functional renormalization group Simon Streib, Aldo Isidori, and Peter Kopietz Institut für Theoretische Physik, Goethe-Universität Frankfurt Meeting DFG-Forschergruppe
Unitarity, Dispersion Relations, Cutkosky s Cutting Rules
 Unitarity, Dispersion Relations, Cutkosky s Cutting Rules 04.06.0 For more information about unitarity, dispersion relations, and Cutkosky s cutting rules, consult Peskin& Schröder, or rather Le Bellac.
Unitarity, Dispersion Relations, Cutkosky s Cutting Rules 04.06.0 For more information about unitarity, dispersion relations, and Cutkosky s cutting rules, consult Peskin& Schröder, or rather Le Bellac.
Microscopic Properties of BCS Superconductors (cont.)
 PHYS598 A.J.Leggett Lecture 8 Microscopic Properties of BCS Superconductors (cont.) 1 Microscopic Properties of BCS Superconductors (cont.) References: Tinkham, ch. 3, sections 7 9 In last lecture, examined
PHYS598 A.J.Leggett Lecture 8 Microscopic Properties of BCS Superconductors (cont.) 1 Microscopic Properties of BCS Superconductors (cont.) References: Tinkham, ch. 3, sections 7 9 In last lecture, examined
16. GAUGE THEORY AND THE CREATION OF PHOTONS
 6. GAUGE THEORY AD THE CREATIO OF PHOTOS In the previous chapter the existence of a gauge theory allowed the electromagnetic field to be described in an invariant manner. Although the existence of this
6. GAUGE THEORY AD THE CREATIO OF PHOTOS In the previous chapter the existence of a gauge theory allowed the electromagnetic field to be described in an invariant manner. Although the existence of this
Transport Coefficients of the Anderson Model via the numerical renormalization group
 Transport Coefficients of the Anderson Model via the numerical renormalization group T. A. Costi 1, A. C. Hewson 1 and V. Zlatić 2 1 Department of Mathematics, Imperial College, London SW7 2BZ, UK 2 Institute
Transport Coefficients of the Anderson Model via the numerical renormalization group T. A. Costi 1, A. C. Hewson 1 and V. Zlatić 2 1 Department of Mathematics, Imperial College, London SW7 2BZ, UK 2 Institute
Supplementary Figure 3: Interaction effects in the proposed state preparation with Bloch oscillations. The numerical results are obtained by
 Supplementary Figure : Bandstructure of the spin-dependent hexagonal lattice. The lattice depth used here is V 0 = E rec, E rec the single photon recoil energy. In a and b, we choose the spin dependence
Supplementary Figure : Bandstructure of the spin-dependent hexagonal lattice. The lattice depth used here is V 0 = E rec, E rec the single photon recoil energy. In a and b, we choose the spin dependence
1 Fluctuations of the number of particles in a Bose-Einstein condensate
 Exam of Quantum Fluids M1 ICFP 217-218 Alice Sinatra and Alexander Evrard The exam consists of two independant exercises. The duration is 3 hours. 1 Fluctuations of the number of particles in a Bose-Einstein
Exam of Quantum Fluids M1 ICFP 217-218 Alice Sinatra and Alexander Evrard The exam consists of two independant exercises. The duration is 3 hours. 1 Fluctuations of the number of particles in a Bose-Einstein
Summary Sec. 1.6: The dielectric function of jellium in the RPA
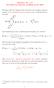 Summary Sec 6: The dielectric function of jellium in the RPA Starting with the diagram that describes the simplest approximation of a polarisation insertion into a bare Coulomb interaction line and translating
Summary Sec 6: The dielectric function of jellium in the RPA Starting with the diagram that describes the simplest approximation of a polarisation insertion into a bare Coulomb interaction line and translating
Lecture notes for QFT I (662)
 Preprint typeset in JHEP style - PAPER VERSION Lecture notes for QFT I (66) Martin Kruczenski Department of Physics, Purdue University, 55 Northwestern Avenue, W. Lafayette, IN 47907-036. E-mail: markru@purdue.edu
Preprint typeset in JHEP style - PAPER VERSION Lecture notes for QFT I (66) Martin Kruczenski Department of Physics, Purdue University, 55 Northwestern Avenue, W. Lafayette, IN 47907-036. E-mail: markru@purdue.edu
Quantum statistics: properties of the Fermi-Dirac distribution.
 Statistical Mechanics Phys54 Fall 26 Lecture #11 Anthony J. Leggett Department of Physics, UIUC Quantum statistics: properties of the Fermi-Dirac distribution. In the last lecture we discussed the properties
Statistical Mechanics Phys54 Fall 26 Lecture #11 Anthony J. Leggett Department of Physics, UIUC Quantum statistics: properties of the Fermi-Dirac distribution. In the last lecture we discussed the properties
Many-Body Problems and Quantum Field Theory
 Philippe A. Martin Francois Rothen Many-Body Problems and Quantum Field Theory An Introduction Translated by Steven Goldfarb, Andrew Jordan and Samuel Leach Second Edition With 102 Figures, 7 Tables and
Philippe A. Martin Francois Rothen Many-Body Problems and Quantum Field Theory An Introduction Translated by Steven Goldfarb, Andrew Jordan and Samuel Leach Second Edition With 102 Figures, 7 Tables and
a = ( a σ )( b σ ) = a b + iσ ( a b) mω 2! x + i 1 2! x i 1 2m!ω p, a = mω 2m!ω p Physics 624, Quantum II -- Final Exam
 Physics 624, Quantum II -- Final Exam Please show all your work on the separate sheets provided (and be sure to include your name). You are graded on your work on those pages, with partial credit where
Physics 624, Quantum II -- Final Exam Please show all your work on the separate sheets provided (and be sure to include your name). You are graded on your work on those pages, with partial credit where
Electrons in a periodic potential
 Chapter 3 Electrons in a periodic potential 3.1 Bloch s theorem. We consider in this chapter electrons under the influence of a static, periodic potential V (x), i.e. such that it fulfills V (x) = V (x
Chapter 3 Electrons in a periodic potential 3.1 Bloch s theorem. We consider in this chapter electrons under the influence of a static, periodic potential V (x), i.e. such that it fulfills V (x) = V (x
Phys460.nb Back to our example. on the same quantum state. i.e., if we have initial condition (5.241) ψ(t = 0) = χ n (t = 0)
 Phys46.nb 89 on the same quantum state. i.e., if we have initial condition ψ(t ) χ n (t ) (5.41) then at later time ψ(t) e i ϕ(t) χ n (t) (5.4) This phase ϕ contains two parts ϕ(t) - E n(t) t + ϕ B (t)
Phys46.nb 89 on the same quantum state. i.e., if we have initial condition ψ(t ) χ n (t ) (5.41) then at later time ψ(t) e i ϕ(t) χ n (t) (5.4) This phase ϕ contains two parts ϕ(t) - E n(t) t + ϕ B (t)
P3317 HW from Lecture 15 and Recitation 8
 P3317 HW from Lecture 15 and Recitation 8 Due Oct 23, 218 Problem 1. Variational Energy of Helium Here we will estimate the ground state energy of Helium. Helium has two electrons circling around a nucleus
P3317 HW from Lecture 15 and Recitation 8 Due Oct 23, 218 Problem 1. Variational Energy of Helium Here we will estimate the ground state energy of Helium. Helium has two electrons circling around a nucleus
Optical Lattices. Chapter Polarization
 Chapter Optical Lattices Abstract In this chapter we give details of the atomic physics that underlies the Bose- Hubbard model used to describe ultracold atoms in optical lattices. We show how the AC-Stark
Chapter Optical Lattices Abstract In this chapter we give details of the atomic physics that underlies the Bose- Hubbard model used to describe ultracold atoms in optical lattices. We show how the AC-Stark
Lecture 20: Effective field theory for the Bose- Hubbard model
 Lecture 20: Effective field theory for the Bose- Hubbard model In the previous lecture, we have sketched the expected phase diagram of the Bose-Hubbard model, and introduced a mean-field treatment that
Lecture 20: Effective field theory for the Bose- Hubbard model In the previous lecture, we have sketched the expected phase diagram of the Bose-Hubbard model, and introduced a mean-field treatment that
Fermi liquid theory Can we apply the free fermion approximation to a real metal? Phys540.nb Strong interaction vs.
 Phys540.nb 7 Fermi liquid theory.. Can we apply the free fermion approximation to a real metal? Can we ignore interactions in a real metal? Experiments says yes (free fermion models work very well), but
Phys540.nb 7 Fermi liquid theory.. Can we apply the free fermion approximation to a real metal? Can we ignore interactions in a real metal? Experiments says yes (free fermion models work very well), but
Part III: Impurities in Luttinger liquids
 Functional RG for interacting fermions... Part III: Impurities in Luttinger liquids 1. Luttinger liquids 2. Impurity effects 3. Microscopic model 4. Flow equations 5. Results S. Andergassen, T. Enss (Stuttgart)
Functional RG for interacting fermions... Part III: Impurities in Luttinger liquids 1. Luttinger liquids 2. Impurity effects 3. Microscopic model 4. Flow equations 5. Results S. Andergassen, T. Enss (Stuttgart)
A Brief Introduction to Linear Response Theory with Examples in Electromagnetic Response
 A Brief Introduction to Linear Response Theory with Examples in Electromagnetic Response Robert Van Wesep May 3, 2013 In order to gain information about any physical system, it is necessary to probe the
A Brief Introduction to Linear Response Theory with Examples in Electromagnetic Response Robert Van Wesep May 3, 2013 In order to gain information about any physical system, it is necessary to probe the
Interacting Fermi Gases
 Interacting Fermi Gases Mike Hermele (Dated: February 11, 010) Notes on Interacting Fermi Gas for Physics 7450, Spring 010 I. FERMI GAS WITH DELTA-FUNCTION INTERACTION Since it is easier to illustrate
Interacting Fermi Gases Mike Hermele (Dated: February 11, 010) Notes on Interacting Fermi Gas for Physics 7450, Spring 010 I. FERMI GAS WITH DELTA-FUNCTION INTERACTION Since it is easier to illustrate
The properties of an ideal Fermi gas are strongly determined by the Pauli principle. We shall consider the limit:
 Chapter 13 Ideal Fermi gas The properties of an ideal Fermi gas are strongly determined by the Pauli principle. We shall consider the limit: k B T µ, βµ 1, which defines the degenerate Fermi gas. In this
Chapter 13 Ideal Fermi gas The properties of an ideal Fermi gas are strongly determined by the Pauli principle. We shall consider the limit: k B T µ, βµ 1, which defines the degenerate Fermi gas. In this
Landau-Fermi liquid theory
 Landau-Fermi liquid theory Shreyas Patankar Chennai Mathematical Institute Abstract We study the basic properties of Landau s theory of a system of interacting fermions (a Fermi liquid). The main feature
Landau-Fermi liquid theory Shreyas Patankar Chennai Mathematical Institute Abstract We study the basic properties of Landau s theory of a system of interacting fermions (a Fermi liquid). The main feature
GW quasiparticle energies
 Chapter 4 GW quasiparticle energies Density functional theory provides a good description of ground state properties by mapping the problem of interacting electrons onto a KS system of independent particles
Chapter 4 GW quasiparticle energies Density functional theory provides a good description of ground state properties by mapping the problem of interacting electrons onto a KS system of independent particles
Quantum Physics III (8.06) Spring 2007 FINAL EXAMINATION Monday May 21, 9:00 am You have 3 hours.
 Quantum Physics III (8.06) Spring 2007 FINAL EXAMINATION Monday May 21, 9:00 am You have 3 hours. There are 10 problems, totalling 180 points. Do all problems. Answer all problems in the white books provided.
Quantum Physics III (8.06) Spring 2007 FINAL EXAMINATION Monday May 21, 9:00 am You have 3 hours. There are 10 problems, totalling 180 points. Do all problems. Answer all problems in the white books provided.
Local moment approach to the multi - orbital single impurity Anderson and Hubbard models
 Local moment approach to the multi - orbital single impurity Anderson and Hubbard models Anna Kauch Institute of Theoretical Physics Warsaw University PIPT/Les Houches Summer School on Quantum Magnetism
Local moment approach to the multi - orbital single impurity Anderson and Hubbard models Anna Kauch Institute of Theoretical Physics Warsaw University PIPT/Les Houches Summer School on Quantum Magnetism
Collective Effects. Equilibrium and Nonequilibrium Physics
 Collective Effects in Equilibrium and Nonequilibrium Physics: Lecture 3, 3 March 2006 Collective Effects in Equilibrium and Nonequilibrium Physics Website: http://cncs.bnu.edu.cn/mccross/course/ Caltech
Collective Effects in Equilibrium and Nonequilibrium Physics: Lecture 3, 3 March 2006 Collective Effects in Equilibrium and Nonequilibrium Physics Website: http://cncs.bnu.edu.cn/mccross/course/ Caltech
2. The interaction between an electron gas and the potential field is given by
 68A. Solutions to Exercises II. April 5. Carry out a Hubbard Stratonovich transformation for the following interaction Hamiltonians, factorizing the terms in brackets, and write one or two sentences interpreting
68A. Solutions to Exercises II. April 5. Carry out a Hubbard Stratonovich transformation for the following interaction Hamiltonians, factorizing the terms in brackets, and write one or two sentences interpreting
Quantum Transport through Coulomb-Blockade Systems
 Quantum Transport through Coulomb-Blockade Systems Björn Kubala Institut für Theoretische Physik III Ruhr-Universität Bochum COQUSY6 p.1 Overview Motivation Single-electron box/transistor Coupled single-electron
Quantum Transport through Coulomb-Blockade Systems Björn Kubala Institut für Theoretische Physik III Ruhr-Universität Bochum COQUSY6 p.1 Overview Motivation Single-electron box/transistor Coupled single-electron
where β = 1, H = H µn (3.3) If the Hamiltonian has no explicit time dependence, the Greens functions are homogeneous in time:
 3. Greens functions 3.1 Matsubara method In the solid state theory class, Greens functions were introduced as response functions; they can be used to determine the quasiparticle density of states. They
3. Greens functions 3.1 Matsubara method In the solid state theory class, Greens functions were introduced as response functions; they can be used to determine the quasiparticle density of states. They
Physics 218. Quantum Field Theory. Professor Dine. Green s Functions and S Matrices from the Operator (Hamiltonian) Viewpoint
 Physics 28. Quantum Field Theory. Professor Dine Green s Functions and S Matrices from the Operator (Hamiltonian) Viewpoint Field Theory in a Box Consider a real scalar field, with lagrangian L = 2 ( µφ)
Physics 28. Quantum Field Theory. Professor Dine Green s Functions and S Matrices from the Operator (Hamiltonian) Viewpoint Field Theory in a Box Consider a real scalar field, with lagrangian L = 2 ( µφ)
FREE ELECTRON LASER THEORY USING TWO TIMES GREEN FUNCTION FORMALISM HIROSHI TAKAHASHI. Brookhaven Natioanal Laboratory Upton New York, 11973
 FREE ELECTRON LASER THEORY USING TWO TIMES GREEN FUNCTION FORMALISM HIROSHI TAKAHASHI Brookhaven Natioanal Laboratory Upton New York, 11973 In this paper, we present a quatum theory for free electron laser
FREE ELECTRON LASER THEORY USING TWO TIMES GREEN FUNCTION FORMALISM HIROSHI TAKAHASHI Brookhaven Natioanal Laboratory Upton New York, 11973 In this paper, we present a quatum theory for free electron laser
Theory of Many-Particle Systems
 Theory of Many-Particle Systems Lecture notes for P654, Cornell University, spring 2005. c Piet Brouwer, 2005. Permission is granted to print and copy these notes, if ept together with the title page and
Theory of Many-Particle Systems Lecture notes for P654, Cornell University, spring 2005. c Piet Brouwer, 2005. Permission is granted to print and copy these notes, if ept together with the title page and
Causality. but that does not mean it is local in time, for = 1. Let us write ɛ(ω) = ɛ 0 [1 + χ e (ω)] in terms of the electric susceptibility.
![Causality. but that does not mean it is local in time, for = 1. Let us write ɛ(ω) = ɛ 0 [1 + χ e (ω)] in terms of the electric susceptibility. Causality. but that does not mean it is local in time, for = 1. Let us write ɛ(ω) = ɛ 0 [1 + χ e (ω)] in terms of the electric susceptibility.](/thumbs/86/93789482.jpg) We have seen that the issue of how ɛ, µ n depend on ω raises questions about causality: Can signals travel faster than c, or even backwards in time? It is very often useful to assume that polarization
We have seen that the issue of how ɛ, µ n depend on ω raises questions about causality: Can signals travel faster than c, or even backwards in time? It is very often useful to assume that polarization
Magnetism at finite temperature: molecular field, phase transitions
 Magnetism at finite temperature: molecular field, phase transitions -The Heisenberg model in molecular field approximation: ferro, antiferromagnetism. Ordering temperature; thermodynamics - Mean field
Magnetism at finite temperature: molecular field, phase transitions -The Heisenberg model in molecular field approximation: ferro, antiferromagnetism. Ordering temperature; thermodynamics - Mean field
Summary of Mattuck Chapters 16 and 17
 Summary of Mattuck Chapters 16 and 17 Tomas Petersson Växjö university 2008-02-05 1 Phonons form a Many-Body Viewpoint Hamiltonian for coupled Einstein phonons Definition of Einstein phonon propagator
Summary of Mattuck Chapters 16 and 17 Tomas Petersson Växjö university 2008-02-05 1 Phonons form a Many-Body Viewpoint Hamiltonian for coupled Einstein phonons Definition of Einstein phonon propagator
The 3 dimensional Schrödinger Equation
 Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
V. ELECTRON GAS, RANDOM PHASE APPROXIMATION
 V. ELECTRON GAS, RANDOM PHASE APPROXIMATION Marus Holzmann LPMMC, Maison de Magistère, Grenoble, and LPTMC, Jussieu, Paris marus@lptl.jussieu.fr http://www.lptl.jussieu.fr/users/marus/cours.html (Dated:
V. ELECTRON GAS, RANDOM PHASE APPROXIMATION Marus Holzmann LPMMC, Maison de Magistère, Grenoble, and LPTMC, Jussieu, Paris marus@lptl.jussieu.fr http://www.lptl.jussieu.fr/users/marus/cours.html (Dated:
Lecture 4 Recap: normal metals and the clectron-phonon interaction *
 Phys. 598SC Fall 2015 Prof. A. J. Leggett Lecture 4 Recap: normal metals and the clectron-phonon interaction * 1. Normal metals: Sommerfeld-Bloch picture 2. Screening 3. Fermi liquid theory 4. Electron-phonon
Phys. 598SC Fall 2015 Prof. A. J. Leggett Lecture 4 Recap: normal metals and the clectron-phonon interaction * 1. Normal metals: Sommerfeld-Bloch picture 2. Screening 3. Fermi liquid theory 4. Electron-phonon
Phonons (Classical theory)
 Phonons (Classical theory) (Read Kittel ch. 4) Classical theory. Consider propagation of elastic waves in cubic crystal, along [00], [0], or [] directions. Entire plane vibrates in phase in these directions
Phonons (Classical theory) (Read Kittel ch. 4) Classical theory. Consider propagation of elastic waves in cubic crystal, along [00], [0], or [] directions. Entire plane vibrates in phase in these directions
Condensed matter theory Lecture notes and problem sets 2012/2013
 Condensed matter theory Lecture notes and problem sets 2012/2013 Dmitri Ivanov Recommended books and lecture notes: [AM] N. W. Ashcroft and N. D. Mermin, Solid State Physics. [Mar] M. P. Marder, Condensed
Condensed matter theory Lecture notes and problem sets 2012/2013 Dmitri Ivanov Recommended books and lecture notes: [AM] N. W. Ashcroft and N. D. Mermin, Solid State Physics. [Mar] M. P. Marder, Condensed
Lecture notes on many-body theory
 Lecture notes on many-body theory Michele Fabrizio updated to 203, but still work in progress!! All comments are most welcome! Contents Landau-Fermi-liquid theory: Phenomenology 5. The Landau energy functional
Lecture notes on many-body theory Michele Fabrizio updated to 203, but still work in progress!! All comments are most welcome! Contents Landau-Fermi-liquid theory: Phenomenology 5. The Landau energy functional
The Quantum Theory of Finite-Temperature Fields: An Introduction. Florian Divotgey. Johann Wolfgang Goethe Universität Frankfurt am Main
 he Quantum heory of Finite-emperature Fields: An Introduction Florian Divotgey Johann Wolfgang Goethe Universität Franfurt am Main Fachbereich Physi Institut für heoretische Physi 1..16 Outline 1 he Free
he Quantum heory of Finite-emperature Fields: An Introduction Florian Divotgey Johann Wolfgang Goethe Universität Franfurt am Main Fachbereich Physi Institut für heoretische Physi 1..16 Outline 1 he Free
Physics 139B Solutions to Homework Set 4 Fall 2009
 Physics 139B Solutions to Homework Set 4 Fall 9 1. Liboff, problem 1.16 on page 594 595. Consider an atom whose electrons are L S coupled so that the good quantum numbers are j l s m j and eigenstates
Physics 139B Solutions to Homework Set 4 Fall 9 1. Liboff, problem 1.16 on page 594 595. Consider an atom whose electrons are L S coupled so that the good quantum numbers are j l s m j and eigenstates
Electronic structure of correlated electron systems. Lecture 2
 Electronic structure of correlated electron systems Lecture 2 Band Structure approach vs atomic Band structure Delocalized Bloch states Fill up states with electrons starting from the lowest energy No
Electronic structure of correlated electron systems Lecture 2 Band Structure approach vs atomic Band structure Delocalized Bloch states Fill up states with electrons starting from the lowest energy No
2.1 Calculation of the ground state energy via path integral
 Chapter 2 Instantons in Quantum Mechanics Before describing the instantons and their effects in non-abelian gauge theories, it is instructive to become familiar with the relevant ideas in the context of
Chapter 2 Instantons in Quantum Mechanics Before describing the instantons and their effects in non-abelian gauge theories, it is instructive to become familiar with the relevant ideas in the context of
M. A. Gusmão IF-UFRGS
 M. A. Gusmão IF-UFRGS - 217 1 FIP164-217/2 Text 9 Mean-field approximation - II Heisenberg Hamiltonian in wave-vector space As we saw in Text 8, the uniform susceptibility does not diverge in the case
M. A. Gusmão IF-UFRGS - 217 1 FIP164-217/2 Text 9 Mean-field approximation - II Heisenberg Hamiltonian in wave-vector space As we saw in Text 8, the uniform susceptibility does not diverge in the case
SECOND QUANTIZATION. Lecture notes with course Quantum Theory
 SECOND QUANTIZATION Lecture notes with course Quantum Theory Dr. P.J.H. Denteneer Fall 2008 2 SECOND QUANTIZATION 1. Introduction and history 3 2. The N-boson system 4 3. The many-boson system 5 4. Identical
SECOND QUANTIZATION Lecture notes with course Quantum Theory Dr. P.J.H. Denteneer Fall 2008 2 SECOND QUANTIZATION 1. Introduction and history 3 2. The N-boson system 4 3. The many-boson system 5 4. Identical
Physics 127c: Statistical Mechanics. Weakly Interacting Fermi Gas. The Electron Gas
 Physics 7c: Statistical Mechanics Wealy Interacting Fermi Gas Unlie the Boson case, there is usually no ualitative change in behavior going from the noninteracting to the wealy interacting Fermi gas for
Physics 7c: Statistical Mechanics Wealy Interacting Fermi Gas Unlie the Boson case, there is usually no ualitative change in behavior going from the noninteracting to the wealy interacting Fermi gas for
Introduction to Green functions and many-body perturbation theory
 Introduction to Green functions and many-body perturbation theory Last updated 10 April 2014 Contents 1 Motivation 2 1.1 Connection to experiments............................ 2 1.2 Divergences in the standard
Introduction to Green functions and many-body perturbation theory Last updated 10 April 2014 Contents 1 Motivation 2 1.1 Connection to experiments............................ 2 1.2 Divergences in the standard
2. The Schrödinger equation for one-particle problems. 5. Atoms and the periodic table of chemical elements
 1 Historical introduction The Schrödinger equation for one-particle problems 3 Mathematical tools for quantum chemistry 4 The postulates of quantum mechanics 5 Atoms and the periodic table of chemical
1 Historical introduction The Schrödinger equation for one-particle problems 3 Mathematical tools for quantum chemistry 4 The postulates of quantum mechanics 5 Atoms and the periodic table of chemical
Lecture 6 Photons, electrons and other quanta. EECS Winter 2006 Nanophotonics and Nano-scale Fabrication P.C.Ku
 Lecture 6 Photons, electrons and other quanta EECS 598-002 Winter 2006 Nanophotonics and Nano-scale Fabrication P.C.Ku From classical to quantum theory In the beginning of the 20 th century, experiments
Lecture 6 Photons, electrons and other quanta EECS 598-002 Winter 2006 Nanophotonics and Nano-scale Fabrication P.C.Ku From classical to quantum theory In the beginning of the 20 th century, experiments
Lecture 4: Basic elements of band theory
 Phys 769 Selected Topics in Condensed Matter Physics Summer 010 Lecture 4: Basic elements of band theory Lecturer: Anthony J. Leggett TA: Bill Coish 1 Introduction Most matter, in particular most insulating
Phys 769 Selected Topics in Condensed Matter Physics Summer 010 Lecture 4: Basic elements of band theory Lecturer: Anthony J. Leggett TA: Bill Coish 1 Introduction Most matter, in particular most insulating
Lorentz invariant scattering cross section and phase space
 Chapter 3 Lorentz invariant scattering cross section and phase space In particle physics, there are basically two observable quantities : Decay rates, Scattering cross-sections. Decay: p p 2 i a f p n
Chapter 3 Lorentz invariant scattering cross section and phase space In particle physics, there are basically two observable quantities : Decay rates, Scattering cross-sections. Decay: p p 2 i a f p n
Chapter 5. The electron liquid (Last version: 28 September 2011) Contents
 Chapter 5 The electron liuid (Last version: 8 September ) Contents 5. The jellium model....................... 3 5. The random-phase approximation (RPA)......... 33 5.. Dielectric function and density-density
Chapter 5 The electron liuid (Last version: 8 September ) Contents 5. The jellium model....................... 3 5. The random-phase approximation (RPA)......... 33 5.. Dielectric function and density-density
PG5295 Muitos Corpos 1 Electronic Transport in Quantum dots 2 Kondo effect: Intro/theory. 3 Kondo effect in nanostructures
 PG5295 Muitos Corpos 1 Electronic Transport in Quantum dots 2 Kondo effect: Intro/theory. 3 Kondo effect in nanostructures Prof. Luis Gregório Dias DFMT PG5295 Muitos Corpos 1 Electronic Transport in Quantum
PG5295 Muitos Corpos 1 Electronic Transport in Quantum dots 2 Kondo effect: Intro/theory. 3 Kondo effect in nanostructures Prof. Luis Gregório Dias DFMT PG5295 Muitos Corpos 1 Electronic Transport in Quantum
Assignment 8. Tyler Shendruk December 7, 2010
 Assignment 8 Tyler Shendruk December 7, 21 1 Kadar Ch. 6 Problem 8 We have a density operator ˆρ. Recall that classically we would have some probability density p(t) for being in a certain state (position
Assignment 8 Tyler Shendruk December 7, 21 1 Kadar Ch. 6 Problem 8 We have a density operator ˆρ. Recall that classically we would have some probability density p(t) for being in a certain state (position
For the magnetic field B called magnetic induction (unfortunately) M called magnetization is the induced field H called magnetic field H =
 To review, in our original presentation of Maxwell s equations, ρ all J all represented all charges, both free bound. Upon separating them, free from bound, we have (dropping quadripole terms): For the
To review, in our original presentation of Maxwell s equations, ρ all J all represented all charges, both free bound. Upon separating them, free from bound, we have (dropping quadripole terms): For the
Quantum phase transition and conductivity of parallel quantum dots with a moderate Coulomb interaction
 Journal of Physics: Conference Series PAPER OPEN ACCESS Quantum phase transition and conductivity of parallel quantum dots with a moderate Coulomb interaction To cite this article: V S Protsenko and A
Journal of Physics: Conference Series PAPER OPEN ACCESS Quantum phase transition and conductivity of parallel quantum dots with a moderate Coulomb interaction To cite this article: V S Protsenko and A
Classical field theory 2012 (NS-364B) Feynman propagator
 Classical field theory 212 (NS-364B Feynman propagator 1. Introduction States in quantum mechanics in Schrödinger picture evolve as ( Ψt = Û(t,t Ψt, Û(t,t = T exp ı t dt Ĥ(t, (1 t where Û(t,t denotes the
Classical field theory 212 (NS-364B Feynman propagator 1. Introduction States in quantum mechanics in Schrödinger picture evolve as ( Ψt = Û(t,t Ψt, Û(t,t = T exp ı t dt Ĥ(t, (1 t where Û(t,t denotes the
Monday, April 13. Today: equation of motion method (EOM) Dyson equation and Self-energy. Many-Body Green s Functions
 Monday, April 13 Today: equation of motion method (EOM) Dyson equation and Self-energy Unperturbed propagator Take a system of non interacting fermions The unperturbed propagator is: ( ) or Unperturbed
Monday, April 13 Today: equation of motion method (EOM) Dyson equation and Self-energy Unperturbed propagator Take a system of non interacting fermions The unperturbed propagator is: ( ) or Unperturbed
3. Greens functions. H = H 0 + V t. V t = ˆBF t. e βh. ρ 0 ρ t. 3.1 Introduction
 3. Greens functions 3.1 Introduction Greens functions appear naturally as response functions, i.e. as answers to the function how a quantum mechanical system responds to an external perturbation, like
3. Greens functions 3.1 Introduction Greens functions appear naturally as response functions, i.e. as answers to the function how a quantum mechanical system responds to an external perturbation, like
NANOSCALE SCIENCE & TECHNOLOGY
 . NANOSCALE SCIENCE & TECHNOLOGY V Two-Level Quantum Systems (Qubits) Lecture notes 5 5. Qubit description Quantum bit (qubit) is an elementary unit of a quantum computer. Similar to classical computers,
. NANOSCALE SCIENCE & TECHNOLOGY V Two-Level Quantum Systems (Qubits) Lecture notes 5 5. Qubit description Quantum bit (qubit) is an elementary unit of a quantum computer. Similar to classical computers,
Microscopic-Macroscopic connection. Silvana Botti
 relating experiment and theory European Theoretical Spectroscopy Facility (ETSF) CNRS - Laboratoire des Solides Irradiés Ecole Polytechnique, Palaiseau - France Temporary Address: Centre for Computational
relating experiment and theory European Theoretical Spectroscopy Facility (ETSF) CNRS - Laboratoire des Solides Irradiés Ecole Polytechnique, Palaiseau - France Temporary Address: Centre for Computational
Quantum Theory of Matter
 Quantum Theory of Matter Revision Lecture Derek Lee Imperial College London May 2006 Outline 1 Exam and Revision 2 Quantum Theory of Matter Microscopic theory 3 Summary Outline 1 Exam and Revision 2 Quantum
Quantum Theory of Matter Revision Lecture Derek Lee Imperial College London May 2006 Outline 1 Exam and Revision 2 Quantum Theory of Matter Microscopic theory 3 Summary Outline 1 Exam and Revision 2 Quantum
A. Field theoretical methods for the partition function, perturbative expansions
 IV. QUANTUM FIELD THEORY, GREEN S FUNCTION, AND PERTURBATION THEORY Markus Holzmann LPMMC, Maison de Magistère, Grenoble, and LPTMC, Jussieu, Paris markus@lptl.jussieu.fr http://www.lptl.jussieu.fr/users/markus
IV. QUANTUM FIELD THEORY, GREEN S FUNCTION, AND PERTURBATION THEORY Markus Holzmann LPMMC, Maison de Magistère, Grenoble, and LPTMC, Jussieu, Paris markus@lptl.jussieu.fr http://www.lptl.jussieu.fr/users/markus
Topological Kondo Insulators!
 Topological Kondo Insulators! Maxim Dzero, University of Maryland Collaborators: Kai Sun, University of Maryland Victor Galitski, University of Maryland Piers Coleman, Rutgers University Main idea Kondo
Topological Kondo Insulators! Maxim Dzero, University of Maryland Collaborators: Kai Sun, University of Maryland Victor Galitski, University of Maryland Piers Coleman, Rutgers University Main idea Kondo
1. Electricity and Magnetism (Fall 1995, Part 1) A metal sphere has a radius R and a charge Q.
 1. Electricity and Magnetism (Fall 1995, Part 1) A metal sphere has a radius R and a charge Q. (a) Compute the electric part of the Maxwell stress tensor T ij (r) = 1 {E i E j 12 } 4π E2 δ ij both inside
1. Electricity and Magnetism (Fall 1995, Part 1) A metal sphere has a radius R and a charge Q. (a) Compute the electric part of the Maxwell stress tensor T ij (r) = 1 {E i E j 12 } 4π E2 δ ij both inside
2 Electronic structure theory
 Electronic structure theory. Generalities.. Born-Oppenheimer approximation revisited In Sec..3 (lecture 3) the Born-Oppenheimer approximation was introduced (see also, for instance, [Tannor.]). We are
Electronic structure theory. Generalities.. Born-Oppenheimer approximation revisited In Sec..3 (lecture 3) the Born-Oppenheimer approximation was introduced (see also, for instance, [Tannor.]). We are
Lecture 6. Fermion Pairing. WS2010/11: Introduction to Nuclear and Particle Physics
 Lecture 6 Fermion Pairing WS2010/11: Introduction to Nuclear and Particle Physics Experimental indications for Cooper-Pairing Solid state physics: Pairing of electrons near the Fermi surface with antiparallel
Lecture 6 Fermion Pairing WS2010/11: Introduction to Nuclear and Particle Physics Experimental indications for Cooper-Pairing Solid state physics: Pairing of electrons near the Fermi surface with antiparallel
w2dynamics : operation and applications
 w2dynamics : operation and applications Giorgio Sangiovanni ERC Kick-off Meeting, 2.9.2013 Hackers Nico Parragh (Uni Wü) Markus Wallerberger (TU) Patrik Gunacker (TU) Andreas Hausoel (Uni Wü) A solver
w2dynamics : operation and applications Giorgio Sangiovanni ERC Kick-off Meeting, 2.9.2013 Hackers Nico Parragh (Uni Wü) Markus Wallerberger (TU) Patrik Gunacker (TU) Andreas Hausoel (Uni Wü) A solver
An imbalanced Fermi gas in 1 + ɛ dimensions. Andrew J. A. James A. Lamacraft
 An imbalanced Fermi gas in 1 + ɛ dimensions Andrew J. A. James A. Lamacraft 2009 Quantum Liquids Interactions and statistics (indistinguishability) Some examples: 4 He 3 He Electrons in a metal Ultracold
An imbalanced Fermi gas in 1 + ɛ dimensions Andrew J. A. James A. Lamacraft 2009 Quantum Liquids Interactions and statistics (indistinguishability) Some examples: 4 He 3 He Electrons in a metal Ultracold
Figure 6.1: Schematic representation of the resistivity of a metal with a transition to a superconducting phase at T c.
 Chapter 6 Superconductivity Before we start with the theoretical treatment of superconductivity, we review some of the characteristic experimental facts, in order to gain an overall picture of this striking
Chapter 6 Superconductivity Before we start with the theoretical treatment of superconductivity, we review some of the characteristic experimental facts, in order to gain an overall picture of this striking
Finite Temperature Field Theory
 Finite Temperature Field Theory Dietrich Bödeker, Universität Bielefeld 1. Thermodynamics (better: thermo-statics) (a) Imaginary time formalism (b) free energy: scalar particles, resummation i. pedestrian
Finite Temperature Field Theory Dietrich Bödeker, Universität Bielefeld 1. Thermodynamics (better: thermo-statics) (a) Imaginary time formalism (b) free energy: scalar particles, resummation i. pedestrian
MODEL WITH SPIN; CHARGE AND SPIN EXCITATIONS 57
 56 BOSONIZATION Note that there seems to be some arbitrariness in the above expressions in terms of the bosonic fields since by anticommuting two fermionic fields one can introduce a minus sine and thus
56 BOSONIZATION Note that there seems to be some arbitrariness in the above expressions in terms of the bosonic fields since by anticommuting two fermionic fields one can introduce a minus sine and thus
QFT Perturbation Theory
 QFT Perturbation Theory Ling-Fong Li (Institute) Slide_04 1 / 43 Interaction Theory As an illustration, take electromagnetic interaction. Lagrangian density is The combination L = ψ (x ) γ µ ( i µ ea µ
QFT Perturbation Theory Ling-Fong Li (Institute) Slide_04 1 / 43 Interaction Theory As an illustration, take electromagnetic interaction. Lagrangian density is The combination L = ψ (x ) γ µ ( i µ ea µ
Properties of the S-matrix
 Properties of the S-matrix In this chapter we specify the kinematics, define the normalisation of amplitudes and cross sections and establish the basic formalism used throughout. All mathematical functions
Properties of the S-matrix In this chapter we specify the kinematics, define the normalisation of amplitudes and cross sections and establish the basic formalism used throughout. All mathematical functions
7. Response functions
 7. Response functions 7.1 Random Phase Approximation The truncation of the equation of motion for the Greens function with the Hartree Foc mean field approximation transforms the Hamiltonian into an effective
7. Response functions 7.1 Random Phase Approximation The truncation of the equation of motion for the Greens function with the Hartree Foc mean field approximation transforms the Hamiltonian into an effective
Chapter 4. Fermi-liquid theory (Last version: 29 September 2011) Contents
 Chapter 4 Fermi-liquid theory (Last version: 29 September 2011) Contents 4.1 The quasi-particle concept.................. 270 4.1.1 Landau energy functional E[n]............... 273 4.1.2 Stability of the
Chapter 4 Fermi-liquid theory (Last version: 29 September 2011) Contents 4.1 The quasi-particle concept.................. 270 4.1.1 Landau energy functional E[n]............... 273 4.1.2 Stability of the
Summary Sec. 1.3: The interacting Green s function Feynman diagrams
 Summary Sec. 1.3: The interacting Green s function Feynman diagrams From Sec. 1.2.1: Remember the most important properties of the one-particle Green s function for non-interacting electrons: G 0 αβ(r,
Summary Sec. 1.3: The interacting Green s function Feynman diagrams From Sec. 1.2.1: Remember the most important properties of the one-particle Green s function for non-interacting electrons: G 0 αβ(r,
Non-relativistic scattering
 Non-relativistic scattering Contents Scattering theory 2. Scattering amplitudes......................... 3.2 The Born approximation........................ 5 2 Virtual Particles 5 3 The Yukawa Potential
Non-relativistic scattering Contents Scattering theory 2. Scattering amplitudes......................... 3.2 The Born approximation........................ 5 2 Virtual Particles 5 3 The Yukawa Potential
