Chapter 4. Fermi-liquid theory (Last version: 29 September 2011) Contents
|
|
|
- June Rogers
- 5 years ago
- Views:
Transcription
1 Chapter 4 Fermi-liquid theory (Last version: 29 September 2011) Contents 4.1 The quasi-particle concept Landau energy functional E[n] Stability of the ground state Effective mass Thermodynamics Specific heat Compressibility Spin susceptibility Non-equilibrium properties Kinetic equation Conservation laws Collective modes Response functions Multi-pair excitations Microscopic basis of Fermi-liquid theory Quasi-particles Thermodynamic potential Ω[n] Quantum Boltzmann equation Ward identities for the Fermi liquid Response to external fields Luttinger theorem Fermi-liquid theory and renormalization group One of the main goals of this book is to introduce the theoretical methods necessary to study (strongly) correlated quantum systems. This chapter is devoted to a class of fermion systems known as Landau Fermi liquids or merely Fermi liquids that can be understood without resorting to sophisticated many-body techniques. The Fermiliquid paradigm describes not only the low-energy behavior of electrons in metals but also Fermi systems such as He 3, nuclear matter, or ultracold fermion gases. In a Fermi liquid, the elementary excitations (quasi-particles and quasi-holes) are in direct correspondence with the (particle or hole) excitations of the ideal Fermi gas; 269
2 270 Chapter 4. Fermi-liquid theory they carry the same quantum numbers and satisfy the Fermi-Dirac statistics. 1,2 This correspondence can be made explicit by means of an adiabatic switching-on of the interactions. The quasi-particles and quasi-holes determine both the low-temperature thermodynamics and the response of the system to macroscopic perturbations. In a very elegant phenomenological theory [1, 2, 3], Landau has shown that the low-energy behavior of the system can be expressed in terms of a few unknown parameters (the Landau parameters) that depend on the interactions between quasi-particles. In the first part of the chapter (Secs. 4.1, 4.2 and 4.3), we review the main aspects of Landau Fermi-liquid theory starting from the quasi-particle concept. We mainly consider neutral Fermi liquids. 3 In the second part (Sec. 4.4), we discuss the microscopic underpinning of Fermi-liquid theory. We conclude the chapter by a discussion of Fermi-liquid theory in the framework of the renormalization group (Sec. 4.5). 4.1 The quasi-particle concept Landau Fermi-liquid theory relies on the assumption that the low-lying eigenstates of the ideal Fermi gas continuously evolve into eigenstates of the real system as the interaction is adiabatically switched on. The quasi-particle concept, which is the starting point of Fermi-liquid theory, is a direct consequence of this assumption. Before discussing this concept in detail, it should be noted that the adiabatic continuity assumption is quite restrictive and there are a number of cases where it is obviously violated. For instance, in a superconductor and more generally whenever an instability of the Fermi surface leads to a broken symmetry state the ground state is not related in any direct way to any one state of the free Fermi gas but rather to a coherent superposition of a large number of states. Fermi-liquid theory can also break down without the occurrence of a broken symmetry state as in the 1D interacting fermion gas. The ideal Fermi gas Let us start with the ideal Fermi gas and for simplicity consider a three-dimensional isotropic system. The eigenstates are antisymmetric combinations of plane waves, and a state of the system is fully determined by the momentum distribution function n kσ giving the number of particles with momentum k and spin σ. The ground state corresponds to the distribution function n 0 k = Θ(k F k ) where the Fermi momentum k F is related to the mean particle density n = 1 V Θ(k F k ) = 2 d 3 k (2π) 3 Θ(k F k ) = k3 F 3π 2 (4.1) 1 Generally, the term quasi-particles refers to the elementary excitations whatever their relation to the bare particles. In the Fermi-liquid theory context, it has a narrower sense as explained in section The Fermi-liquid theory elucidates the success of the ideal Fermi gas model in explaining some physical properties of electrons in metals despite the importance of the Coulomb interaction at metallic densities (this latter point is discussed in detail in chapter 5). 3 The electromagnetic response of charged systems was the subject of section 3.4. The electron liquid will be studied in chapter 5 within the framework of the random-phase approximation.
3 4.1 The quasi-particle concept 271 (the sum over σ gives a factor of 2). The ground state energy is given by E 0 = k k F 0 ɛk = 3 5 nɛ0 F V, (4.2) where ɛ 0 k = k2 /2m is the free fermion dispersion and ɛ 0 F = k2 F /2m = µ(t = 0) the Fermi energy. Low-lying excited states are defined by their distribution function The change in the total energy corresponding to δn kσ is n kσ = n 0 k + δn kσ. (4.3) δe[δn] = E[n] E 0 = ɛ 0 kδn kσ. (4.4) We denote by n {n kσ } the momentum distribution function (not to be confused with the mean particle density). The particle energy can be defined as the functional derivative of the total energy with respect to the momentum distribution function n kσ, ɛ 0 k = δe[n] δn kσ. (4.5) The particle group velocity and the Fermi velocity are obtained from v k = k ɛ 0 k, v F = v k kf = ɛ0 k k = k F kf m, (4.6) respectively. Near the Fermi surface k = k F, one can therefore write the dispersion law as ɛ 0 k = ɛ 0 F + v F ( k k F ) + O ( ( k k F ) 2). (4.7) An elementary excitation corresponds to a particle added to or removed from the ground state. Any excited eigenstate of the system can be constructed by creating a certain number of these elementary particle or hole excitations. Since the latter are non-interacting, the total energy δe of the excited state is simply the sum of the particle and hole excitation energies [Eq. (4.4)]. The interacting Fermi liquid According to the central hypothesis of Landau Fermi-liquid theory, any state of the ideal Fermi gas, characterized by a momentum distribution function n kσ = n 0 k +δn kσ, generates an eigenstate of the interacting system as the interactions are switched on. This eigenstate can therefore be labeled by the distribution function n kσ. For reasons given below, this distribution function is referred to as the quasi-particle distribution function of the interacting Fermi liquid. As we shall see in section 4.4.1, it differs from and should not be confused with the momentum distribution ψ σ(k) ψ σ (k) of the interacting system.
4 272 Chapter 4. Fermi-liquid theory For reasons of symmetry, the Fermi surface of the interacting (isotropic) system is spherical. 4 Basic to Fermi-liquid theory is the fact that the volume of the Fermi surface is not changed by interactions (Luttinger theorem, derived in section 4.4.6) so that the Fermi momentum k F of the interacting system is the same as that of the ideal gas. The ground state of the interacting system is then generated adiabatically from that of the ideal gas. 5 Let us now add a particle with momentum k ( k > k F ) and spin σ to the ground state of the ideal gas. According to the adiabatic continuity assumption, as the interaction is slowly turned on we generate an (excited) eigenstate of the interacting system. However, because of the interactions the state under study is damped and acquires a finite life-time. Central to Fermi-liquid theory is the fact that the life-time becomes larger and larger at low energy ( k k F ). This property is a consequence of the Pauli principle which makes interactions ineffective near the Fermi surface (Sec ). 6 Thus, the state obtained by adding a low-lying ( k k F ) particle to the non-interacting Fermi sea evolves into a quasi-eigenstate of the interacting system, which is referred to as a quasi-particle. Similarly, one can define a quasi-hole by removing a particle with momentum k k F from the non-interacting Fermi sea. Since the total momentum and spin are conserved, quasi-particles and quasi-holes can be labeled by the same quantum numbers as in the non-interacting case, namely the momentum k and the spin projection σ along a given axis. As the bare particles, they carry charge e < 0 (quasi-particles) and e > 0 (quasi-holes). Near the Fermi surface, the quasi-particle dispersion can be expanded as ɛ k = ɛ kf + v F ( k k F ) + O ( ( k k F ) 2), v F = k F m, (4.8) which defines the (renormalized) Fermi velocity v F and the effective mass m. ɛ F = µ(t = 0) is the Fermi energy. The quasi-particle group velocity is defined by v k = k ɛ k v F k for k k F. (4.9) At the Fermi level, the density of quasi-particle states (per spin) N (ξ) = V 1 k δ(ξ ξ k ) takes the value N (0) = m k F 2π 2. (4.10) The only difference with the case of the ideal Fermi gas is that the mass is replaced by the effective mass. A generic low-lying excited state of the ideal Fermi gas, defined by its momentum distribution function n kσ n 0 k, can be constructed by combining particle and hole 4 Note that at this stage we have not rigorously defined the Fermi surface of an interacting system; this will be done in section This is not true in anisotropic systems, where in general interactions deform the Fermi surface. The ground state then follows adiabatically from an excited state of the non-interacting system. 6 This result can be obtained from a simple phase space argument. Consider the process where a particle above the Fermi sea ( k > k F ) is scattered into the state k + q ( k + q > k F ) by creating a particle-hole pair (k, k q) ( k < k F and k q > k F ). Because of energy conservation, ω = ɛ k+q ɛ k = ɛ k q+ɛ k < 0, the phase phase available for this scattering process is proportional to ( k k F ) 2. This result can be seen by evaluating the integral d 3 k d 3 qδ(ɛ k+q + ɛ k q ɛ k + ɛ k ) where the momenta satisfied the above mentioned constraints. Higher-order processes, involving multi-pair excitations, are more strongly suppressed as the corresponding phase space is smaller.
5 4.1 The quasi-particle concept 273 excitations. As the interaction is switched on, it evolves into a quasi-eigenstate of the interacting system characterized by the quasi-particle distribution function n kσ. 7,8 Because of the one-to-one correspondence between particle (or hole) excitations in the ideal Fermi gas and quasi-particle excitations in the Fermi liquid, quasi-particles follow the Fermi-Dirac statistics. Since the concept of quasi-particles refers only to low-lying excited states, δn kσ = n kσ n 0 k should be appreciable only in the vicinity of the Fermi surface. More precisely, for the notion of quasi-particles (or quasi-holes) to make sense, their life-time τ k and excitation energy ξ k = ɛ k µ should satisfy 1 τ k ξ k, (4.11) since 1/ ξ k is the minimum time required to observe (or create with an external field) the quasi-particle. We shall see in section that in a three-dimensional Fermi liquid 6 1 = O ( ( k k F ) 2) τ k (4.12) at zero temperature, so that the condition (4.11) is satisfied in the vicinity of the Fermi surface (recall that ξ k = O( k k F )). Suppose that the interaction is switched on within a characteristic time η 1 : Ĥ int (t) = Ĥint(t = 0)e ηt. Quasi-particles can be observed if their life-time is larger than η 1 and 1/ ξ k smaller than η 1, i.e. 1 τ k η ξ k. (4.13) When condition (4.11) is fulfilled, it is possible to satisfy the inequality (4.13). It should be emphasized that quasi-particle and quasi-hole excitations are not necessarily the only elementary excitations in the interacting system. The adiabatic continuity hypothesis does not exclude the possibility of other elementary excitations of the real system which disappear when the interaction is reduced to zero. These states correspond to collective excitations and emerge naturally in Landau Fermiliquid theory (Sec. 4.3) Landau energy functional E[n] In the interacting Fermi liquid, the change in energy due a change δn = n n 0 in the distribution function reads δe[δn] = ɛ k δn kσ (4.14) to first order in δn. Here ɛ k is the energy of a single quasi-particle added to the ground state of the system (as defined in the preceding section by (4.8)). According 7 Note that the term quasi-particle often refers both to quasi-particles and/or quasi-holes. We shall explicitely distinguish between quasi-particles ( k > k F ) and quasi-holes ( k < k F ) only when necessary. 8 If the system is anisotropic in spin space and the spin projection not a good quantum number, the quasi-particle distribution function n kσσ becomes a matrix in spin space.
6 274 Chapter 4. Fermi-liquid theory to (4.14), there is no interaction between quasi-particles or quasi-holes, since the total energy is simply additive. This suggests to push (4.14) one step further, δe[δn] = ɛ k δn kσ + 1 2V f σσ (k, k )δn kσ δn k σ. (4.15) k,k,σ,σ The quadratic term in (4.15) is due to the interactions between quasi-particles. The Landau function f is defined as the second-order functional derivative of the total energy, 1 V f σσ (k, k ) = δ(2) E[n] δn kσ δn k (4.16) σ n=n 0, and is therefore symmetric under the exchange (k, σ) (k, σ ). In the grand-canonical ensemble at T = 0, the relevant thermodynamic potential is Ω(T = 0) = E µn, where N = n kσ is the total number of quasiparticles (see below). Its variation is given by δe[δn] µδn[δn] = (ɛ k µ)δn kσ + 1 2V f σσ (k, k )δn kσ δn k σ. (4.17) k,k,σ,σ Suppose that δn kσ is appreciable only for k k F δ. Then both terms in (4.17) are of order δ 2, which shows the need to push the expansion in δn to second order. The quasi-particle energy ɛ k is defined as the variation of the total energy of the system due to the introduction of this quasi-particle. Mathematically, this means that ɛ k is given by the functional derivative of E[n] with respect to the distribution function n kσ, ɛ k = δe[n] = ɛ k + 1 f σσ (k, k )δn k δn kσ V σ. (4.18) k,σ Thus the quasi-particle energy ɛ k ɛ k [δn] depends on the distribution δn kσ = n kσ n 0 k of quasi-particles present in the system; it coincides with ɛ k only when δn = 0. In an isotropic liquid, spin rotation invariance ensures that ɛ k is independent of σ. Equation (4.18) gives the quasi-particle energy change coming from the average field due to the other quasi-particles. This mean-field-like description is characteristic of Landau Fermi-liquid theory. It also shows up in the RPA form of the response functions (Sec ). Landau parameters The Landau function f plays a crucial role in Fermi-liquid theory. Spin rotation invariance implies that it can be written in terms of a spin symmetric and a spin anti-symmetric part, f σσ (k, k ) = f s (k, k ) + σσ f a (k, k ). (4.19) Furthermore, for states near the Fermi surface one can set k = k = k F f σσ (k, k ) depends only on the angle θ between k F = k F k and k F = k k F, so that f σσ (k, k ) = f σσ (k F, k F ) = f s (θ) + σσ f a (θ), (4.20)
7 4.1 The quasi-particle concept 275 where the functions f s (θ) and f a (θ) can be expanded in Legendre polynomials, f s,a (θ) = l=0 π f s,a l P l (cos θ), f s,a dω l = (2l + 1) 0 4π f s,a (θ)p l (cos θ) (4.21) (dω = dϕdθ sin θ denotes the elementary solid angle in the direction (ϕ, θ)). It is convenient to introduce dimensionless parameters the Landau parameters by multiplying f s,a l by the density of states at the Fermi level, F s,a l = 2N (0)f s,a l (4.22) (recall that N (ξ) is the quasi-particle density of states per spin and 2N (ξ) the total density of states). Entropy and thermodynamic potential Since quasi-particles obey the Fermi-Dirac statistics, their entropy takes the form S[n] = [n kσ ln n kσ + (1 n kσ ) ln(1 n kσ )]. (4.23) The thermodynamic potential is given by Ω[n] = E[n] µn[n] T S[n], (4.24) where N[n] = n kσ is the total quasi-particle number. The equilibrium distribution function n { n kσ } is obtained from the stationarity condition δω[n]/δn kσ = 0, where n kσ = n F ( ξ k ), (4.25) ɛ k = δe[n] = ɛ k + 1 f σσ (k, k ) ( nk σ δn kσ n V ) n0 k σ k,σ (4.26) is the quasi-particle energy corresponding to the equilibrium distribution n. If we expand Ω[n] about its equilibrium value, we obtain 9 Ω[ n + δn] Ω[ n] = 1 2 k,k,σ,σ [ δ σ,σ δ k,k n F ( ξ k ) + 1 ] V f σσ (k, k ) δn kσ δn k σ (4.27) to lowest order in δn. There is no linear term since Ω[n] is stationary for n = n. Equation (4.27) shows that the f function can also be defined from the thermodynamic potential, 1 V f σσ (k, k ) = δ σ,σ δ k,k n F ( ξ k ) + δ(2) Ω[n]. (4.28) δn kσ δn k σ n This relation will be used in section to obtain a microscopic definition of the Landau function. 9 δ The first term in the rhs of (4.27) comes from (2) S[n] = δ k,k n δ σ,σ δ k,k δ σ,σ β/n F ( ξ k ). δn kσ δn k σ n kσ (1 n kσ ) =
8 276 Chapter 4. Fermi-liquid theory Stability of the ground state Because of the thermal factor 1/n F ( ξ k ) in (4.27), small variations of the thermodynamic potential are due to quasi-particle excitations lying in the thermal broadening of the Fermi surface ( ξ k T ). When T 0, these excitations have vanishing energies and can be viewed as resulting from a displacement (that can depend on spin) of the Fermi surface. Suppose that in the direction k, the Fermi momentum k F varies by an infinitesimal amount u σ (k) for spin-σ particles. This induces a change δn kσ = lim u σ(k) 0 { n F [ ξ k v F u σ (k)] n F ( ξ k ) = v F n F ( ξ k )u σ (k) = v F δ(ξ k )u σ (k) (T 0) (4.29) in the distribution function. We have used ɛ k ɛ k and n F (x) δ(x) when T 0. The corresponding variation of the thermodynamic potential reads δω[u] = V v 2 F N (0) dωk 4π { σ,σ δ σ,σ dωk 4π u2 σ(k) dωk 4π F σσ (k F, k F )u σ (k)u σ (k ) } } (4.30) in the limit T 0. dωk denotes the elementary solid angle in the direction of k. To proceed further, we expand u σ (k) in spherical harmonics, u σ (k) = u s (k) + σu a (k) = l l=0 m= l (u s lm + σu a lm) Y m l (k), (4.31) where u s,a l, m = ( 1)m u s,a lm since u σ (k) is real. Using the addition theorem and other standard properties of spherical harmonics, we obtain δω[u] = V v 2 F N (0) 4π l l=0 m= l [ u slm (1 2 + F l s ) + u alm (1 2 + F a )] l. (4.32) 2l + 1 2l + 1 The stability of the spherical Fermi surface requires δω[u] to be positive for any deformation u σ (k), i.e. F s l > 2l 1, F a l > 2l 1. (4.33) The instabilities occurring when the conditions (4.33) are violated are known as Pomeranchuk instabilities Effective mass The current carried by a quasi-particle, as well as its effective mass, can be obtained by considering the system from a reference frame moving at a velocity v = q/m with respect to the laboratory frame. In the moving frame, the Hamiltonian is Ĥ = Ĥ P v + O(v2 ), (4.34)
9 4.1 The quasi-particle concept 277 where M is the total mass, and P the total momentum measured with respect to the laboratory frame (Sec ). Since the momentum coincides with the current in a translation invariant system, J = P m = 1 E m v = E v=0 q, (4.35) q=0 where E is the energy in the moving frame. Let us consider the state corresponding to a quasi-particle of momentum k (in the laboratory frame) added to the ground state. The current in that state is simply j k = k m. (4.36) The current can also be calculated by considering the same physical state in the moving frame, where the quasi-particle has momentum k q and the ground state is a shifted Fermi sea: n k = n 0 k+q. Since equation (4.15) is valid in any Galilean reference frame, the quasi-particle energy in the moving frame reads 10 ɛ k q = ɛ k q + 1 V f σσ (k, k )[n 0 k +q n 0 k ], (4.37) k,σ so that the current j k measured in the laboratory frame carried by a quasi-particle of momentum k is j k = ɛ k q q = k ɛ k 1 f σσ (k, k ) k n 0 k q=0 V k,σ = vk + 1 f σσ (k, k )vk V δ(ξ k ). (4.38) k,σ The first term in (4.38) can be seen as the contribution of a localized wave packet containing one extra particle and moving with the group velocity vk (in a picture where we see the quasi-particle as a localized excitation). The second term is a drag current that comes from the interaction of the moving wave packet with the surrounding fluid. Near the Fermi surface, where ξ k vf ( k k F ) and vk v k, F equation (4.38) gives j k = vf k [ 1 + 2N dωk ] ( (0) 4π f s (θ) cos θ = vf k 1 + F 1 s ). (4.39) 3 By comparing (4.36) and (4.39), we obtain m m = 1 + F s 1 3. (4.40) Depending on the sign of F s 1, the effective mass can be larger or smaller than the bare mass. When F s 1 < 3, the effective mass is negative and the system unstable since quasi-particle excitations across the Fermi surface are energetically favorable. This is a special case of Pomeranchuk instabilities [Eqs. (4.33)]. 10 Note that k should not be shifted in the Landau function since the interaction between particles is velocity independent.
10 278 Chapter 4. Fermi-liquid theory 4.2 Thermodynamics In this section, we show how to obtain the thermodynamics quantities from the Landau energy functional E[n] Specific heat The specific heat is defined by C V = E T, (4.41) V,N where E = E(T = 0) + ɛ k δn kσ + 1 2V f σσ (k, k k,k σ,σ )δn kσ δn k σ (4.42) and δn kσ = n F ( ɛ k ) n 0 k. If we neglect the interactions between quasi-particles, then C V = V 2π2 3 N (0)T = V m k F T (4.43) 3 (T 0) is simply the specific heat of non-interacting fermions with mass m. The interaction term in (4.42) is O(T 4 ), since d k k 2 δn kσ = O(T 2 ) in the grand-canonical ensemble, and can be neglected. Clearly, this conclusion will not change if we consider the O(T 2 ) shift of the chemical potential necessary to keep the total number of particles constant Compressibility The isothermal compressibility is defined as κ = 1 V V P = 1 n T,N n 2 µ (4.44) T (Sec. 3.3), so that what we need to calculate is n/ µ. A variation in the density n = kf 3 /3π2 is equivalent to a variation of the Fermi momentum k F : k F / n = π 2 /kf 2. When k F varies, the quasi-particle distribution also varies, so that the change in the chemical potential µ = ɛ kf is given by µ n = ɛ k F k F k F n + 1 V k,σ f σσ (k F, k ) n k σ k F k F n. (4.45) Using ɛ kf / k F = v F = k F /m and n kσ / k F = δ(k F k ) (T = 0), we obtain µ [v n = π2 kf 2 F + σ d3 k ] (2π) 3 f σσ (k F, k )δ(k F k ) = π2 kf 2 [vf + 2N (0)vF f0 s ] = 1 + F 0 s 2N (0), (4.46) 11 If we approximate f σσ (k, k ) by f σσ (k F, k F ), then the interacting term in (4.42) vanishes in the canonical ensemble (N fixed) where 1 V k δn kσ = (2π 2 ) 1 d k k 2 δn kσ = 0.
11 4.2 Thermodynamics 279 and in turn n 2 κ = 2N (0) 1 + F0 s. (4.47) The interactions between quasi-particles lead to a renormalization by a factor 1/(1 + F0 s ) of the naive result 2N (0) obtained from the compressibility of the ideal Fermi gas by the mere replacement m m. Again, we note that the stability of the system requires F0 s > 1 in agreement with (4.33). Equation (4.47) yields the macroscopic sound velocity 1 c s = = v ( ) F 1 + F s 1/2 ( 0 κnm F1 s/3 = v F [(1 + F0 s ) 1 + F s )] 1/2 1 (4.48) 3 3 (see Eq. (3.112)). In the absence of interaction, we recover the sound velocity v F / 3 of the ideal Fermi gas Spin susceptibility In the presence of a magnetic field B = Bẑ, the energy ɛ kσ is shifted by σ 2 gµ BB, where µ B is the Bohr magneton. A spin-σ quasi-particle being an eigenstate of Ŝz with eigenvalue σ/2, the Landé factor g = 2 coincides with that of the bare particle. Since the field displaces the Fermi surface and changes the quasi-particle distribution, the quasi-particle energy becomes ɛ kσ = ɛ k + σ 2 gµ BB + 1 f σσ (k, k )δn k V σ. (4.49) k,σ The new (spin-dependent) Fermi surface is defined by ɛ kf, = ɛ kf, = µ, 12 i.e. where ɛ kf + gµ BB V k,σ f σ (k F, k )δn k σ = ɛ kf gµ BB V f σ (k F, k )δn k σ, (4.50) k,σ δn kσ = Θ(k F + δk F σ k ) Θ(k F k ) = δk F σ v F δ(ξ k ) (4.51) (δk F σ = k F σ k F ) to leading order in B. Using ɛ kf σ = ɛ kf +vf δk F σ, equation (4.50) gives vf (δk F δk F ) = gµ BB 1 + F0 a. (4.52) The magnetization per unit volume is given by M = 1 2V gµ B = ( gµb 2 (δn k δn k ) = 1 2 gµ BN (0)vF (δk F δk F ) k ) 2 2N (0) 1 + F0 a B. (4.53) 12 Since δµ cannot depend on the direction of B, it is at least of order B 2 and the chemical potential is constant to leading order in B.
12 280 Chapter 4. Fermi-liquid theory This yields the spin susceptibility χ = M ( B = gµb 2 Stability against ferromagnetism requires F a 0 > 1. ) 2 2N (0) 1 + F0 a. (4.54) 4.3 Non-equilibrium properties The Landau energy function δe[δn] enables to compute the thermodynamic properties of the Fermi liquid but does not contain any information about the quasi-particle dynamics. To study the latter, one has to extend the definition of δe to non-equilibrium states. When physical properties vary only on macroscopic scales ( k 1 F ), one can adopt a semiclassical description and define a local quasi-particle distribution function n kσ (r, t) giving the density of quasi-particles with momentum k and spin σ in the vicinity of point r at time t. By analogy with (4.15), we define the time-dependent functional δe[δn, t] = d 3 rɛ k δn kσ (r, t) + 1 2V k,k,σ,σ d 3 rd 3 r f σσ (k, k ; r r )δn kσ (r, t)δn k σ (r, t). (4.55) For a homogeneous system, ɛ k is independent of the spin σ and position r of the quasiparticle. The interaction is assumed to be instantaneous in time and short-range in space. f σσ (k, k ; r r ) then decreases rapidly in space and we can approximate δn k σ (r, t) by δn k σ (r, t) in (4.55). This leads to δe[δn, t] = d 3 rɛ k δn kσ (x) + 1 d 3 rf σσ (k, k )δn kσ (x)δn k σ (x), (4.56) 2V k,k,σ,σ where f σσ (k, k ) = d 3 r f σσ (k, k ; r r ) and x = (r, t) Kinetic equation To obtain the equation governing the quasi-particle dynamics, we consider the timedependent quasi-particle energy ɛ kσ (x) = δe[n, t] δn kσ (x) = ɛ k + 1 V f σσ (k, k )δn k σ (x) (4.57) k,σ as a quasi-classical Hamiltonian. This assumption leads to the equations of motion t r = k ɛ kσ (x), t k = r ɛ kσ (x). (4.58)
13 4.3 Non-equilibrium properties 281 The time evolution of the quasi-particle distribution is then governed by the usual Boltzmann equation 13 dn kσ (x) dt = t n kσ (x) k n kσ (x) r ɛ kσ (x) + r n kσ (x) k ɛ kσ (x) = I[n kσ (x)], (4.59) where the collision integral I[n kσ (x)] = t n kσ (x) coll takes into account the collisions between particles. To first order in δn kσ (x) = n kσ (x) n 0 k, t δn kσ (x) k n 0 k r ɛ kσ (x) + r δn kσ (x) k ɛ k = I[n kσ (x)], (4.60) so that we finally obtain t δn kσ (x) + vk r δn kσ (x) + 1 f σσ (k, k ) r δn k V σ (x) v kδ(ξ k ) = I[n kσ (x)]. (4.61) k,σ Note that this equation involves only states near the Fermi surface where the quasiparticle concept is valid Conservation laws Particle number conservation Since the collisions conserve the total number of particles, dn kσ (x) dt = I[n kσ (x)] = 0. (4.62) Making use of (4.59), this equation can be written as the continuity equation t n(x)+ j(x) = 0, where n(x) = 1 n kσ (x) (4.63) V is the particle density at point r and time t and j(x) = 1 V n kσ (x) k ɛ kσ (x) (4.64) the current density. To linear order in δn, we obtain j(x) = 1 [ δn kσ (x) vk + 1 ] f σσ (k, k )vk V V δ(ξ k ) k,σ = 1 δn kσ (x)j V k, (4.65) where j k is the current carried by a quasi-particle of momentum k [Eqs. (4.36,4.38)]. 13 See, for instance, N. W. Ashcroft and N. D. Mermin, Solid State Physics, chapter 16 (Saunders College Publishing, 1976).
14 282 Chapter 4. Fermi-liquid theory Momentum conservation Similarly, by multiplying (4.59) by k i and summing over k and σ, we obtain t g i (x) + 1 [ ( k i n kσ (x) ɛ ) kσ(x) ( n kσ (x) ɛ )] kσ(x) = 0, (4.66) V r j k j k j r j where,j g(x) = 1 V kn kσ (x) (4.67) is the momentum density. Again, from momentum conservation in collisions, the collision term does not appear in (4.66). By integrating by part, we rewrite the last term of (4.66) as 1 n kσ (x) ɛ kσ(x) = 1 [ ( nkσ (x) ɛ kσ (x) ) n ] kσ(x) ɛ kσ (x) V r i V r i r i = 1 V r i [n kσ (x) ɛ kσ (x)] 1 V where we have used (4.18). From (4.66,4.68), we deduce the equation E r i, (4.68) t g i (x) + j rj Π ij (x) = 0, (4.69) where Π ij (x) = 1 V k i n kσ (x) ɛ kσ(x) k j + δ i,j [ 1 V n kσ (x) ɛ kσ (x) E ] V (4.70) is the momentum-current tensor. To linear order in δn, Π ij (x) = 1 [ k i δn kσ (x) + δ(ξ k ) 1 ] f σσ (k, k )δn k V V σ (x) vkj. (4.71) k,σ Energy conservation Last, we obtain the expression of the energy current by multiplying (4.59) by ɛ kσ and summing over k and σ, t E + 1 [ ( ɛ kσ (x) n kσ (x) ɛ ) kσ(x) ( n kσ (x) ɛ )] kσ(x) = 0, (4.72) V r i k i k i r i where,i t E = 1 V δe δn kσ (x) tn kσ (x) = 1 V ɛ kσ (x) t n kσ (x). (4.73) is the time derivative of the energy. Integrating by part the last term in (4.72), we obtain t E + j E (x) = 0, (4.74)
15 4.3 Non-equilibrium properties 283 where the energy current is given by j E (x) = 1 V ɛ kσ (x)n kσ (x) k ɛ kσ (x). (4.75) To linear order in δn, j E (x) = 1 V ɛ k [ δn kσ (x) + δ(ξ k ) 1 V ] f σσ (k, k )δn k σ (x) vk. (4.76) k,σ Collective modes A collective mode with momentum q and frequency ω is a coherent superposition of quasi-particle quasi-hole pair excitations. When q 0, the quasi-particles (holes) excitations have vanishing energy and the collective mode can be seen as a timedependent displacement u σ (k)e i(q r ωt) + c.c. of the Fermi surface. Generalizing (4.29), we therefore consider δn kσ (x) = v F δ(ξ k )u σ (k)e i(q r ωt) + c.c. (4.77) (Note that u σ (k) is now complex.) As before we expand u σ (k) in spherical harmonics [Eq. (4.31)] and choose q as the polar axis. Since δn kσ (x) satisfies the kinetic equation (4.61), we have (cos θ s)u ν (k) + cos θ dωk 4π F ν (k, k )u ν (k ) = I[u] (4.78) (ν = s, a), where s = ω/vf q and θ is the angle between k and q. Using standard properties of the spherical harmonics, we obtain (cos θ s) l l=0 m= l u ν lmyl m (k) + cos θ l=0 F ν l 2l + 1 l m= l u ν lmy m l (k) = I[u]. (4.79) A set of equations for the u ν lm s can be obtained multiplying (4.79) by dωky m l (k). One readily sees that m is a good quantum number (but l is not) if one ignores the collision term. The longitudinal mode m = 0 is particular as it is the only one to involve density fluctuations. Indeed, we have δn(x) = 2N (0)vF dωk 4π us (k)e i(q r ωt) + c.c. = N (0)vF u s 00 e i(q r ωt) + c.c. π = k2 F 2π 5/2 us 00e i(q r ωt) + c.c. (4.80)
16 284 Chapter 4. Fermi-liquid theory Figure 4.1: Dispersion ω = c 0 q of an undamped zero-sound mode (c 0 > vf ). The shaded area shows the continuum of particle-hole excitations. After straightforward manipulations, one finds that in the mode m = 0 the current is longitudinal and takes the form j(x) = qn (0)vF 2 u s 10 (1 + F s ) 1 e i(q r ωt) + c.c. 3π 3 Zero sound k 3 F = q 2 3π 5/2 m us 10e i(q r ωt) + c.c. (4.81) Let us consider the longitudinal mode m = 0 in the frequency range ωτ 1 where the collision term I[n kσ ] δn kσ /τ can be neglected with respect to t δn kσ (x). τ is a characteristic quasi-particle collision time. We shall see later that τ 1/T 2 at low temperatures (Sec ). We further assume that f σσ (k, k ) = f s 0. For a solution where both spin states oscillate in phase (sound mode: u a = 0), equation (4.78) gives the solution of which is 1 F s 0 (cos θ s)u s (k) + F0 s cos θ dωk 4π us (k ) = 0, (4.82) = dω 4π u s cos θ (k) = const s + iη cos θ, cos θ s + iη cos θ = 1 + s 2 ln ( s + iη + 1 s + iη 1 ). (4.83) We have added to the real frequency s an infinitesimal imaginary part iη = i0 +, which amounts to switching the collective fluctuations adiabatically. This makes the logarithm in (4.83) well defined even when s 1. As when considering a retarded response function (Sec ), one can allow s to take complex values and interpret the imaginary part of ω as the inverse life-time of the collective mode. For a repulsive interaction F0 s > 0, s is real and larger then unity. The limiting cases are s 1 + 2e 2/F s 0 2 for F0 s 0, s (F0 s /3) 1/2 for F0 s (4.84).
17 4.3 Non-equilibrium properties 285 Figure 4.2: Fermi surface deformations in the zero-sound and first-sound modes for a constant interaction f σσ (k, k ) = f s 0. The dashed lines show the equilibrium Fermi surface. In the first-sound mode, the Fermi surface keeps its spherical shape. The solution corresponds to an undamped mode known as the zero-sound mode propagating at the velocity c 0 = ω/ q = svf larger than v F (Fig. 4.1). The corresponding Fermi surface deformation is shown in figure 4.2. In practice, the collisions between particles will give a finite life-time to the zero-sound mode. In the limit ωτ 1, this effect is however negligible and the main source of damping comes from multi-pair excitations (Sec ). For moderate attractive interactions, 1 < F0 s < 0, one can numerically verify that s is complex and satisfies R(s) < 1 and I(s) < 0, corresponding to a damped zero-sound mode. From (4.83), it is clear that the imaginary part of s is due to the interaction of the collective mode with quasi-hole quasi-particle pair excitations. When ω = ɛ k+q ɛ k vf q cos θ, the interaction is resonant and gives rise to a damping of the collective mode (known as Landau damping). The collective mode has then a short life-time and does not represent a well-defined excitation of the system. Last, for F0 s < 1, there are two purely imaginary solutions. Substituting s = iα into (4.83), one finds 1 F s 0 = 1 + i ( ) 1 + iα ( 2 α ln = 1 α γ π ), (4.85) iα 1 2 where γ ] π, π] is defined by 1 + iα = 1 + α 2 e iγ and 1 + iα = 1 + α 2 e i(π γ). Since tan γ = α, we eventually obtain 1 F s 0 ( = 1 α arctan α π ) ( ) 1 = 1 + α arctan. (4.86) 2 α For F0 s < 1, this equation possesses two real solutions of opposite signs. One of these (α > 0, i.e. I(ω) > 0) corresponds to an unstable collective mode. This instability, characterized by divergent density fluctuations, also shows up in the negative compressibility [Eq. (4.47)]. It should be noted that the zero-sound mode exists only in neutral Fermi liquids. In a charged system, it is replaced by a plasmon mode as discussed in section We shall come back to this point in section
18 286 Chapter 4. Fermi-liquid theory Figure 4.3: Velocities of the zero- and first-sound modes when f σσ (k, k ) = f s 0. For F s 0, c s c 0 v F (F s 0 /3) 1/2. First sound Since the Fermi surface relaxes towards its equilibrium position within a characteristic time τ, in the hydrodynamic regime ωτ 1 the displacement u σ (k) of the Fermi surface is expected to be extremely small. In fact, this is true of all components u s lm except u s 00 and u s 10 whose fluctuations (and return to equilibrium) are constrained by the conservation of particle number [Eqs. (4.80,4.81)]. Thus, the sound propagation in the hydrodynamic regime can be studied by retaining only the hydrodynamic components u s 00 and u s 10 (which are not affected by the collisions). With Y0 0 (k) = 1/2 π and Y1 0 (k) = cos θ 3Y0 0 (k), the kinetic equation then becomes (cos θ s) ( ) ( u s 00 + u s 10 3 cos θ + cos θ F0 s u s 00 + F 1 s ) u s 10 cos θ = 0. (4.87) 3 Multiplying this equation by dωky 0 0 (k) and dωky 1 0 (k), we deduce su s 00 us 10 (1 + F s ) 1 = 0, 3 3 u s 00 (1 + F s 0 ) s 3u s 10 = 0. (4.88) The first of these equations is nothing else but the continuity equation t n(x) + j(x) = 0 in the longitudinal mode m = 0 [Eqs. (4.80,4.81)]. The second one can be identified with (4.69). 14 They admit a solution if s 2 = ω2 (vf = 1 ( q)2 3 (1 + F 0 s ) 1 + F 1 s ) 1/2, (4.89) 3 which agrees with the macroscopic sound velocity c s obtained from the compressibility by the usual hydrodynamic arguments [Eq. (4.48)]. The solution reads [ u s (k) = us ( ) 1 + F s 1/2 3 0 π 1 + F1 s/3 cos θ]. (4.90) 14 In the hydrodynamic mode m = 0 (where only u s 00 and us 10 are considered), the momentum current tensor Π ij = δ i,j Π is diagonal with Π(x) = 1 3 π N (0)k F vf 2 u s 00 (1 + F 0 s)ei(q r ωt) + c.c. The second of equations (4.88) can be rewritten as m tj(x) + Π(x) = 0.
19 4.3 Non-equilibrium properties 287 The Fermi surface keeps its spherical shape but its center oscillates about the origin in momentum space (hence the cos θ term in (4.90)). It is instructive to compare the zero- and first-sound modes within the simple model where f σσ (k, k ) = f s 0. In the limit F s 0, the sound velocity of the two modes tend to the same value v F (F s 0 /3) 1/2 (Fig. 4.3), while the Fermi surface deformation takes the simple form u s (k) cos θ. An example of transverse mode Let us consider the transverse mode m = 1 where u σ (k) = l=1 u s l,m=1y 1 l (k) u s (θ)e iϕ. (4.91) There are no density fluctuations in this mode [see Eq. (4.80)]. Making use of (4.65), one easily finds that the current is transverse ( q) and circularly polarized, j(x) = j 0 [x cos(q r ωt) ŷ sin(q r ωt)], (4.92) with j 0 a constant depending on u s (θ) and F s (θ). In the collisionless regime, the kinetic equation (4.78) then gives dω (cos θ s)u s (θ)e iϕ + cos θ 4π F s (Ω, Ω )u s (θ )e iϕ = 0. (4.93) In the following, we assume that only F0 s and F1 s are non-zero, i.e. F s (α) = F0 s + F1 s cos α (α is the angle between Ω and Ω ). Using cos α = cos θ cos θ +sin θ sin θ cos(ϕ ϕ ), we obtain so that 4 F s 1 = (cos θ s)u s (θ) + F s 1 4 π 0 cos θ sin θ π 0 dθ sin 2 (θ )u s (θ ) = 0, (4.94) u s cos θ sin θ (θ, ϕ) = const s + iη cos θ eiϕ, (4.95) dθ sin3 θ cos θ s + iη cos θ = s2 + s(1 s 2 ) ln ( s + iη + 1 s + iη 1 ). (4.96) As previously, we have added an infinitesimal imaginary part to the frequency ω. A real solution must satisfy s > 1. Since the rhs of (4.96) is maximum at s = 1 where it takes the value 2/3, a real solution is possible only if F s 1 > 6. The interaction between quasi-particles must be quite strong for the mode m = 1 to propagate. For F s 1 6, the collective mode mixes with quasi-particle quasi-hole pair excitations and is not a well-defined excitation of the system any more. Spin-wave modes Until now we have only considered spin symmetric solutions (u a = 0) corresponding to density oscillations (sound modes). We could repeat the same discussion for spin
20 288 Chapter 4. Fermi-liquid theory antisymmetric solutions (u a 0) corresponding to spin density oscillations. The spin collective modes are similar to their charge counterparts but involve the spin antisymmetric Landau parameters F a instead of F s. For instance, for F0 a > 0, one finds a spin zero-sound mode analogous to the (charge) zero-sound mode Response functions In this section, we compute the density-density and current-current response functions in the long-wavelength low-energy limit. To this end we consider the quasi-classical Hamiltonian ɛ kσ (x) + φ(x) e k A(x). (4.97) m For a neutral Fermi liquid, φ and ea should be considered as fictitious external fields introduced in order to derive the response functions; in a charged system they correspond to the usual scalar and vector potential. The linearized kinetic equation now reads t δn kσ (x) + vk r δn kσ (x) + 1 f σσ (k, k ) r δn k σ V (x) v kδ(ξ k ) k,σ + δ(ξ k )vk [φ(x) e ] m k A(x) = I[n kσ (x)]. (4.98) Following the analysis of section 4.3.2, we can verify that the conservation of particle number implies the continuity equation t n(x) + J(x) = 0, where the current J(x) = j(x) ne m A(x), includes the usual diamagnetic part. j(x) = 1 V Density-density response function in the collisionless regime We first consider the response to a scalar potential potential k m δn kσ(x) (4.99) φ(x) = φ(q, ω)e i[q r (ω+iη)t] + c.c. (4.100) in the regime ωτ 1 where collisions can be neglected. We use (4.77) valid for q 0 and write the induced density as δn(x) = 1 V δn(q, ω) = 1 V δn kσ (x) = δn(q, ω)e i[q r (ω+iη)t] + c.c., vf δ(ξ k )u σ (k) = 2N (0)vF dωk 4π us (k). (4.101) As shown in section 3.3, the linear response to the external field is determined by the density-density response function, δn(q, ω) = χ R nn(q, ω)φ(q, ω) (4.102)
21 4.3 Non-equilibrium properties 289 (note the minus sign). Without the collision terms, the kinetic equation gives (ω + iη v k q)u σ (k) v k q 1 V k,σ f σσ (k, k )δ(ξ k )u σ (k ) = v k q φ(q, ω) vf. (4.103) In the absence of interactions, equation (4.103) gives δn(q, ω) = χ 0R nn(q, ω)φ(q, ω), where χ 0R nn(q, ω) = 2 vk q V ω + iη v k k qδ(ξ k) [ = 2N (0) 1 s ( )] s + iη ln (4.104) s + iη 1 (s = ω/vf q ) is the non-interacting density-density response function. Equation (4.104) agrees with the direct evaluation of the density-density correlation function of the ideal Fermi gas in the limit q 0 [Eq. (3.73)]. It is difficult to solve (4.103) in the general case. Assuming that f σσ (k, k ) = f0 s, we find χ R χ 0R nn(q, ω) = nn(q, ω) 1 + f0 sχ0r nn(q, ω). (4.105) The density-density response function possesses a pole for 1 + f0 s χ 0R nn(q, ω) = 0, which is precisely the equation determining the zero-sound frequency obtained previously [Eq. (4.83)]. Such a pole (for ω real) exists only for a repulsive interaction (f0 s > 0). More generally, the density excitation spectrum can be obtained from the imaginary part of the response function or, equivalently, the structure factor S nn (q, ω; T = 0) = 2Θ(ω)I[χ R nn(q, ω)] = 2Θ(ω)χ nn(q, ω) (Sec ). In the non-interacting case Snn(q, 0 ω) = ω 2πN(0) v F q = m2 π 0 otherwise. ω q if 0 ω v F q, (4.106) In the interacting case, there are two possible contributions to the structure factor χ 0 nn (q, ω) S nn (q, ω) = 2Θ(ω) ( 1 + f s 0 R[χ 0R nn(q, ω)] ) 2 ( + f s 0 χ 0 nn (q, ω) ) 2. (4.107) The first one is due to a non-vanishing χ 0 nn and comes from the quasi-particle quasihole excitations. These are quite similar to the particle-hole excitations of the noninteracting system and give a continuous excitation spectrum for ω v F q.15 When f s 0 > 0, there is a second contribution due to the pole of χ R nn(q, ω) at the (real) zerosound frequency ω = c 0 q. For ω near c 0 q, χ R 1 1 nn(q, ω) ω + iη c 0 q f0 s2 ω χ 0R, nn(q, ω) ω=c0 q χ π nn(q, ω) = f0 s2 ω χ 0R δ(ω c 0 q ). nn(q, ω) ω=c0 q (4.108) 15 Note that m = m and vf = v F in the simple model (f σσ (k, k ) = f0 s ) we are considering here.
22 290 Chapter 4. Fermi-liquid theory Figure 4.4: Structure factors S 0 nn(q, ω) and S nn (q, ω) obtained within the Landau Fermi-liquid theory for f s (k, k ) = f s 0 and q k F. Thus the zero-sound mode gives a delta peak contribution to the structure factor S nn (q, ω) (Fig. 4.4). When 1 < F0 s < 0, the zero-sound mode strongly couples to the quasi-particle quasi-hole pair excitations (Landau damping) and is not a well defined excitation of the interacting Fermi liquid; it appears as a pole of χ R nn(q, ω) at a complex frequency. In the structure factor S nn (q, ω), it manifests itself as a broad resonance, characteristic of a damped collective mode, located at the frequency ω defined by 1 + f0 s R[χ 0R nn(q, ω)] = 0 (ω < vf q ). We have already pointed out that the zero-sound mode exists only in a neutral Fermi liquid. In the presence of long-range Coulomb interactions, it is convenient to write the density-density response function as in (3.124). Its poles then appear as zeros of the longitudinal dielectric function ɛ R (q, ω) = 1 + e2 ɛ 0 q 2 ΠR nn(q, ω), (4.109) where Π R nn is the irreducible part of the density-density response function (Sec ). The simplest approximation amounts to approximating Π nn by the density-density response function of the neutral (i.e. without the long-range Coulomb interaction) system. Making use of χ R nn(q, ω) χ 0R nn(q, ω) 2N (0)vF 2 q 2 3ω 2 = nq2 mω 2 for ω v F q, (4.110) where χ nn denotes the density-density response function of the neutral system [Eq. (4.105)], we obtain ɛ R (q, ω) 1 ω2 p ω 2 for ω v F q, (4.111) where ω p = (ne 2 /ɛ 0 m) 1/2 is the plasma frequency (Sec. 3.4). ɛ R (q, ω) possesses a pole at ω = ω p. We conclude that the zero-sound mode of the neutral Fermi liquid has been replaced by the plasmon mode of the charged Fermi liquid. Density-density response function in the hydrodynamic regime We have shown earlier that in the regime ωτ 1, the effect of collisions is to suppress all components u s lm except the hydrodynamic variables us 00 and u s 10. The kinetic
23 4.3 Non-equilibrium properties 291 equation (4.103) then reduces to [ ] (ω + iη vk q) u s 00Y0 0 (k) + u s 10Y1 0 (k) [ vk q F0 s u s 00Y0 0 (k) + F 1 s ] 3 Y 1 0 (k) = v k q vf φ(q, ω). (4.112) Multiplying this equation by dωky 0 0 (k) and dωky 1 0 (k), we obtain (ω + iη)u s 00 vf q us 10 (1 + F s ) 1 = 0, 3 3 v F q u s 00(1 + F s 0 ) (ω + iη) 3u s 10 = 2 π q φ(q, ω). (4.113) From (4.101), δn(q, ω) = π 1/2 N (0)v F us 00, we deduce and χ R nq 2 /m nn(q, ω) = (ω + iη) 2 c 2 sq 2 (4.114) S nn (q, ω) = Θ(ω) πn mc s q δ(ω c s q ). (4.115) The structure factor exhibits a single delta peak at the first-sound frequency c s q. The quasi-particle quasi-hole pair excitations have been washed out by collisions. Remarkably, the structure factor (4.115) satisfies the f-sum rule (3.107) and the compressibility sum rule (3.112), namely 0 0 dω π ωs nn(q, ω) = nq2 m, dω S nn (q, ω) = n π ω mc 2. s (4.116) This shows that the Landau theory, in spite of being a low-energy theory, describes all excitations of the system in the hydrodynamic regime. At finite temperature, one should in principle include the coupling between mass and energy density fluctuations. The latter give rise to a thermal diffusive mode ω = id T q 2 (D T is the thermal diffusion coefficient), which contributes a term proportional to [ D T q 2 ] I iω + D T q 2 = ωd T q 2 ω 2 + DT 2 (4.117) q4 to the structure factor. Since its spectral weight extends to infinity, the diffusive mode broadens the first-sound delta peak at ω = c s q. It can be shown that the weight of the diffusive part is of order 1 C p /C v and is therefore negligible at very low temperatures [4]. Current-current response function In this section, we compute the transverse current-current response function and the conductivity in the collisionless regime. We take A(x) = A(q, ω)e i[q r (ω+iη)t] + c.c. (4.118)
24 292 Chapter 4. Fermi-liquid theory and q ẑ. We write the induced paramagnetic current as j(x) = 1 V j(q, ω) = 1 V k m δn kσ(x) = j(q, ω)e i[q r (ω+iη)t] + c.c. k m v F δ(ξ k )u σ (k) = 3n m dωk 4π ku s (k). (4.119) The linear response to the potential is given by the current-current response function, J µ (q, ω) = µ [ χ R j µj µ (q, ω) + n m δ µ,µ ] ea µ (q, ω) (4.120) (see Sec ). Without the collision term, the kinetic equation gives (ω + iη v k q)u σ (k) v k q 1 V k,σ f σσ (k, k )δ(ξ k )u σ (k ) = e mvf (vk q)k A(q, ω). (4.121) In the absence of interaction, equation (4.121) gives j µ (q, ω) = µ χ0r j (q, ω)a µj µ µ (q, ω) where χ 0R j µj µ (q, ω) = 2 V vk δ(ξ k ) q k µ k µ ω + iη vk q m 2 (4.122) k is the non-interacting (paramagnetic) current-current response function. To evaluate the transverse response, we take µ = µ = x, χ 0R (q, ω) = 2 V vk δ(ξ k ) q kx 2 ω + iη vk q m 2 = 3 4 k nm I(s + iη), (4.123) m2 where s = ω/vf q and I(x) = π 0 dθ sin3 θ cos θ x cos θ = x2 + x(1 x 2 ) ln ( ) x + 1. (4.124) x 1 In order to solve (4.121) in the interacting case, we assume that f σσ (k, k ) = f s 0 + f s 1 cos(α) (α is the angle between k and k ). After some algebra, one finds χ R (q, ω) = 1 + F s 1 3+F s 1 χ 0R (q, ω) m n χ0r (q, ω) = χ0r (q, ω) 1 F 1 s 4 I(s + iη). (4.125) The transverse current-current correlation function possesses a pole for 1 F s 1 4 I(s + iη) = 0. We recover the equation (4.96) determining the frequency of the transverse mode m = 1.
25 4.3 Non-equilibrium properties 293 The preceding results enable us to calculate the response to the (local) electromagnetic field in a charged Fermi liquid. 16 The transverse conductivity is defined by e 2 [ σ (q, ω) = χ R i(ω + iη) (q, ω) n ] (4.126) m (see Sec ). Using χ 0R (0, ω) = 0, we obtain σ (0, ω) σ(0, ω) = i ne 2 ω + iη m, (4.127) which is the expected result for a translation invariant system (Sec ). Making use of χ 0R (q, ω) = n ( m 1 + i 3 ) 4 πs + O(s 2 ), (4.128) we obtain the static transverse conductivity σ (q, 0) = 3π 4 ne 2 k F q, (4.129) a result that does not depend on the mass of the particles. The transverse mode m = 1 which appears as a pole of χ R (q, ω) when F 1 s > 6 [Eq. (4.96)] is modified by the coupling to the electromagnetic field. The dispersion of the transverse modes of the electron system coupled to the electromagnetic field is obtained from (3.163). Solving this equation together with (4.125), one finds that the transverse excitations of the neutral system that appear as a pole of χ R are little affected by the coupling to the electromagnetic field for q ω p /c l (c l is the velocity of light). But at low frequency, when q ω p /c l, the transverse mode disappears in the continuum of particle-hole excitations (see figure 3.9 and the discussion in section 3.4.2) Multi-pair excitations The preceeding study of the response functions χ R nn(q, ω) and χ R (q, ω) shows that the Landau theory describes single-pair excitations and collective modes but does not take into account multi-pair excitations. In an interacting Fermi liquid, a single quasiparticle quasi-hole pair excitation can decay into multiple excited pairs. In other words focusing on the density-density response function the density operator n(q) couples the ground state to excited states with an arbitrary number of quasi-particle quasi-hole pairs. In this section, we briefly discuss to what extent the multi-pair excitations are expected to affect the structure factor S nn (q, ω). For a thorough analysis, we refer to Refs. [4, 5]. When q k F, the excitation energy ω = ɛ k+q ɛ k of a single pair is necessarily small since the Pauli principle requires k < k F and k + q > k F (Fig. 4.5). Energy conservation imposes ɛ k and ɛ k+q to be within ω of the Fermi surface. The density 16 The Landau theory gives a transverse current-current response function χ R (q, 0) lim q 0 χ R (q, 0) which is independent of q; χr (q, 0) is obtained from (4.123) and (4.125) with s = 0. As a result, the Landau theory does not describe the orbital diamagnetism of the charged Fermi liquid (Sec ).
V. FERMI LIQUID THEORY
 V. FERMI LIQUID THEORY Markus Holzmann LPMMC, Maison de Magistère, Grenoble, and LPTMC, Jussieu, Paris markus@lptl.jussieu.fr http://www.lptl.jussieu.fr/users/markus/cours.html (Dated: March 30, 2010)
V. FERMI LIQUID THEORY Markus Holzmann LPMMC, Maison de Magistère, Grenoble, and LPTMC, Jussieu, Paris markus@lptl.jussieu.fr http://www.lptl.jussieu.fr/users/markus/cours.html (Dated: March 30, 2010)
Preface Introduction to the electron liquid
 Table of Preface page xvii 1 Introduction to the electron liquid 1 1.1 A tale of many electrons 1 1.2 Where the electrons roam: physical realizations of the electron liquid 5 1.2.1 Three dimensions 5 1.2.2
Table of Preface page xvii 1 Introduction to the electron liquid 1 1.1 A tale of many electrons 1 1.2 Where the electrons roam: physical realizations of the electron liquid 5 1.2.1 Three dimensions 5 1.2.2
Landau s Fermi Liquid Theory
 Thors Hans Hansson Stockholm University Outline 1 Fermi Liquids Why, What, and How? Why Fermi liquids? What is a Fermi liquids? Fermi Liquids How? 2 Landau s Phenomenological Approach The free Fermi gas
Thors Hans Hansson Stockholm University Outline 1 Fermi Liquids Why, What, and How? Why Fermi liquids? What is a Fermi liquids? Fermi Liquids How? 2 Landau s Phenomenological Approach The free Fermi gas
Fermi Liquid and BCS Phase Transition
 Fermi Liquid and BCS Phase Transition Yu, Zhenhua November 2, 25 Abstract Landau fermi liquid theory is introduced as a successful theory describing the low energy properties of most fermi systems. Besides
Fermi Liquid and BCS Phase Transition Yu, Zhenhua November 2, 25 Abstract Landau fermi liquid theory is introduced as a successful theory describing the low energy properties of most fermi systems. Besides
J10M.1 - Rod on a Rail (M93M.2)
 Part I - Mechanics J10M.1 - Rod on a Rail (M93M.2) J10M.1 - Rod on a Rail (M93M.2) s α l θ g z x A uniform rod of length l and mass m moves in the x-z plane. One end of the rod is suspended from a straight
Part I - Mechanics J10M.1 - Rod on a Rail (M93M.2) J10M.1 - Rod on a Rail (M93M.2) s α l θ g z x A uniform rod of length l and mass m moves in the x-z plane. One end of the rod is suspended from a straight
Lecture notes on many-body theory
 Lecture notes on many-body theory Michele Fabrizio updated to 203, but still work in progress!! All comments are most welcome! Contents Landau-Fermi-liquid theory: Phenomenology 5. The Landau energy functional
Lecture notes on many-body theory Michele Fabrizio updated to 203, but still work in progress!! All comments are most welcome! Contents Landau-Fermi-liquid theory: Phenomenology 5. The Landau energy functional
Condensed matter theory Lecture notes and problem sets 2012/2013
 Condensed matter theory Lecture notes and problem sets 2012/2013 Dmitri Ivanov Recommended books and lecture notes: [AM] N. W. Ashcroft and N. D. Mermin, Solid State Physics. [Mar] M. P. Marder, Condensed
Condensed matter theory Lecture notes and problem sets 2012/2013 Dmitri Ivanov Recommended books and lecture notes: [AM] N. W. Ashcroft and N. D. Mermin, Solid State Physics. [Mar] M. P. Marder, Condensed
Week 5-6: Lectures The Charged Scalar Field
 Notes for Phys. 610, 2011. These summaries are meant to be informal, and are subject to revision, elaboration and correction. They will be based on material covered in class, but may differ from it by
Notes for Phys. 610, 2011. These summaries are meant to be informal, and are subject to revision, elaboration and correction. They will be based on material covered in class, but may differ from it by
The properties of an ideal Fermi gas are strongly determined by the Pauli principle. We shall consider the limit:
 Chapter 13 Ideal Fermi gas The properties of an ideal Fermi gas are strongly determined by the Pauli principle. We shall consider the limit: k B T µ, βµ 1, which defines the degenerate Fermi gas. In this
Chapter 13 Ideal Fermi gas The properties of an ideal Fermi gas are strongly determined by the Pauli principle. We shall consider the limit: k B T µ, βµ 1, which defines the degenerate Fermi gas. In this
Landau-Fermi liquid theory
 Landau-Fermi liquid theory Shreyas Patankar Chennai Mathematical Institute Abstract We study the basic properties of Landau s theory of a system of interacting fermions (a Fermi liquid). The main feature
Landau-Fermi liquid theory Shreyas Patankar Chennai Mathematical Institute Abstract We study the basic properties of Landau s theory of a system of interacting fermions (a Fermi liquid). The main feature
QUALIFYING EXAMINATION, Part 1. 2:00 PM 5:00 PM, Thursday September 3, 2009
 QUALIFYING EXAMINATION, Part 1 2:00 PM 5:00 PM, Thursday September 3, 2009 Attempt all parts of all four problems. Please begin your answer to each problem on a separate sheet, write your 3 digit code
QUALIFYING EXAMINATION, Part 1 2:00 PM 5:00 PM, Thursday September 3, 2009 Attempt all parts of all four problems. Please begin your answer to each problem on a separate sheet, write your 3 digit code
Microscopic Properties of BCS Superconductors (cont.)
 PHYS598 A.J.Leggett Lecture 8 Microscopic Properties of BCS Superconductors (cont.) 1 Microscopic Properties of BCS Superconductors (cont.) References: Tinkham, ch. 3, sections 7 9 In last lecture, examined
PHYS598 A.J.Leggett Lecture 8 Microscopic Properties of BCS Superconductors (cont.) 1 Microscopic Properties of BCS Superconductors (cont.) References: Tinkham, ch. 3, sections 7 9 In last lecture, examined
ɛ(k) = h2 k 2 2m, k F = (3π 2 n) 1/3
 4D-XY Quantum Criticality in Underdoped High-T c cuprates M. Franz University of British Columbia franz@physics.ubc.ca February 22, 2005 In collaboration with: A.P. Iyengar (theory) D.P. Broun, D.A. Bonn
4D-XY Quantum Criticality in Underdoped High-T c cuprates M. Franz University of British Columbia franz@physics.ubc.ca February 22, 2005 In collaboration with: A.P. Iyengar (theory) D.P. Broun, D.A. Bonn
The 3 dimensional Schrödinger Equation
 Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Identical Particles. Bosons and Fermions
 Identical Particles Bosons and Fermions In Quantum Mechanics there is no difference between particles and fields. The objects which we refer to as fields in classical physics (electromagnetic field, field
Identical Particles Bosons and Fermions In Quantum Mechanics there is no difference between particles and fields. The objects which we refer to as fields in classical physics (electromagnetic field, field
Collective behavior, from particles to fields
 978-0-51-87341-3 - Statistical Physics of Fields 1 Collective behavior, from particles to fields 1.1 Introduction One of the most successful aspects of physics in the twentieth century was revealing the
978-0-51-87341-3 - Statistical Physics of Fields 1 Collective behavior, from particles to fields 1.1 Introduction One of the most successful aspects of physics in the twentieth century was revealing the
Landau Bogolubov Energy Spectrum of Superconductors
 Landau Bogolubov Energy Spectrum of Superconductors L.N. Tsintsadze 1 and N.L. Tsintsadze 1,2 1. Department of Plasma Physics, E. Andronikashvili Institute of Physics, Tbilisi 0128, Georgia 2. Faculty
Landau Bogolubov Energy Spectrum of Superconductors L.N. Tsintsadze 1 and N.L. Tsintsadze 1,2 1. Department of Plasma Physics, E. Andronikashvili Institute of Physics, Tbilisi 0128, Georgia 2. Faculty
Lecture 4 Recap: normal metals and the clectron-phonon interaction *
 Phys. 598SC Fall 2015 Prof. A. J. Leggett Lecture 4 Recap: normal metals and the clectron-phonon interaction * 1. Normal metals: Sommerfeld-Bloch picture 2. Screening 3. Fermi liquid theory 4. Electron-phonon
Phys. 598SC Fall 2015 Prof. A. J. Leggett Lecture 4 Recap: normal metals and the clectron-phonon interaction * 1. Normal metals: Sommerfeld-Bloch picture 2. Screening 3. Fermi liquid theory 4. Electron-phonon
Collective Effects. Equilibrium and Nonequilibrium Physics
 Collective Effects in Equilibrium and Nonequilibrium Physics: Lecture 3, 3 March 2006 Collective Effects in Equilibrium and Nonequilibrium Physics Website: http://cncs.bnu.edu.cn/mccross/course/ Caltech
Collective Effects in Equilibrium and Nonequilibrium Physics: Lecture 3, 3 March 2006 Collective Effects in Equilibrium and Nonequilibrium Physics Website: http://cncs.bnu.edu.cn/mccross/course/ Caltech
Waves in plasma. Denis Gialis
 Waves in plasma Denis Gialis This is a short introduction on waves in a non-relativistic plasma. We will consider a plasma of electrons and protons which is fully ionized, nonrelativistic and homogeneous.
Waves in plasma Denis Gialis This is a short introduction on waves in a non-relativistic plasma. We will consider a plasma of electrons and protons which is fully ionized, nonrelativistic and homogeneous.
CHAPTER 1. SPECIAL RELATIVITY AND QUANTUM MECHANICS
 CHAPTER 1. SPECIAL RELATIVITY AND QUANTUM MECHANICS 1.1 PARTICLES AND FIELDS The two great structures of theoretical physics, the theory of special relativity and quantum mechanics, have been combined
CHAPTER 1. SPECIAL RELATIVITY AND QUANTUM MECHANICS 1.1 PARTICLES AND FIELDS The two great structures of theoretical physics, the theory of special relativity and quantum mechanics, have been combined
The Quantum Heisenberg Ferromagnet
 The Quantum Heisenberg Ferromagnet Soon after Schrödinger discovered the wave equation of quantum mechanics, Heisenberg and Dirac developed the first successful quantum theory of ferromagnetism W. Heisenberg,
The Quantum Heisenberg Ferromagnet Soon after Schrödinger discovered the wave equation of quantum mechanics, Heisenberg and Dirac developed the first successful quantum theory of ferromagnetism W. Heisenberg,
Quantum statistics: properties of the Fermi-Dirac distribution.
 Statistical Mechanics Phys54 Fall 26 Lecture #11 Anthony J. Leggett Department of Physics, UIUC Quantum statistics: properties of the Fermi-Dirac distribution. In the last lecture we discussed the properties
Statistical Mechanics Phys54 Fall 26 Lecture #11 Anthony J. Leggett Department of Physics, UIUC Quantum statistics: properties of the Fermi-Dirac distribution. In the last lecture we discussed the properties
Grand Canonical Formalism
 Grand Canonical Formalism Grand Canonical Ensebmle For the gases of ideal Bosons and Fermions each single-particle mode behaves almost like an independent subsystem, with the only reservation that the
Grand Canonical Formalism Grand Canonical Ensebmle For the gases of ideal Bosons and Fermions each single-particle mode behaves almost like an independent subsystem, with the only reservation that the
Phys 622 Problems Chapter 5
 1 Phys 622 Problems Chapter 5 Problem 1 The correct basis set of perturbation theory Consider the relativistic correction to the electron-nucleus interaction H LS = α L S, also known as the spin-orbit
1 Phys 622 Problems Chapter 5 Problem 1 The correct basis set of perturbation theory Consider the relativistic correction to the electron-nucleus interaction H LS = α L S, also known as the spin-orbit
Electrons in a periodic potential
 Chapter 3 Electrons in a periodic potential 3.1 Bloch s theorem. We consider in this chapter electrons under the influence of a static, periodic potential V (x), i.e. such that it fulfills V (x) = V (x
Chapter 3 Electrons in a periodic potential 3.1 Bloch s theorem. We consider in this chapter electrons under the influence of a static, periodic potential V (x), i.e. such that it fulfills V (x) = V (x
List of Comprehensive Exams Topics
 List of Comprehensive Exams Topics Mechanics 1. Basic Mechanics Newton s laws and conservation laws, the virial theorem 2. The Lagrangian and Hamiltonian Formalism The Lagrange formalism and the principle
List of Comprehensive Exams Topics Mechanics 1. Basic Mechanics Newton s laws and conservation laws, the virial theorem 2. The Lagrangian and Hamiltonian Formalism The Lagrange formalism and the principle
The Superfluid Phase s of Helium 3
 The Superfluid Phase s of Helium 3 DIETER VOLLHARD T Rheinisch-Westfälische Technische Hochschule Aachen, Federal Republic of German y PETER WÖLFL E Universität Karlsruhe Federal Republic of Germany PREFACE
The Superfluid Phase s of Helium 3 DIETER VOLLHARD T Rheinisch-Westfälische Technische Hochschule Aachen, Federal Republic of German y PETER WÖLFL E Universität Karlsruhe Federal Republic of Germany PREFACE
arxiv: v1 [cond-mat.mes-hall] 26 Sep 2013
![arxiv: v1 [cond-mat.mes-hall] 26 Sep 2013 arxiv: v1 [cond-mat.mes-hall] 26 Sep 2013](/thumbs/83/88173709.jpg) Berry phase and the unconventional quantum Hall effect in graphene Jiamin Xue Microelectronic Research Center, The University arxiv:1309.6714v1 [cond-mat.mes-hall] 26 Sep 2013 of Texas at Austin, Austin,
Berry phase and the unconventional quantum Hall effect in graphene Jiamin Xue Microelectronic Research Center, The University arxiv:1309.6714v1 [cond-mat.mes-hall] 26 Sep 2013 of Texas at Austin, Austin,
Fermi liquid theory Can we apply the free fermion approximation to a real metal? Phys540.nb Strong interaction vs.
 Phys540.nb 7 Fermi liquid theory.. Can we apply the free fermion approximation to a real metal? Can we ignore interactions in a real metal? Experiments says yes (free fermion models work very well), but
Phys540.nb 7 Fermi liquid theory.. Can we apply the free fermion approximation to a real metal? Can we ignore interactions in a real metal? Experiments says yes (free fermion models work very well), but
NANOSCALE SCIENCE & TECHNOLOGY
 . NANOSCALE SCIENCE & TECHNOLOGY V Two-Level Quantum Systems (Qubits) Lecture notes 5 5. Qubit description Quantum bit (qubit) is an elementary unit of a quantum computer. Similar to classical computers,
. NANOSCALE SCIENCE & TECHNOLOGY V Two-Level Quantum Systems (Qubits) Lecture notes 5 5. Qubit description Quantum bit (qubit) is an elementary unit of a quantum computer. Similar to classical computers,
Lecture 20: Effective field theory for the Bose- Hubbard model
 Lecture 20: Effective field theory for the Bose- Hubbard model In the previous lecture, we have sketched the expected phase diagram of the Bose-Hubbard model, and introduced a mean-field treatment that
Lecture 20: Effective field theory for the Bose- Hubbard model In the previous lecture, we have sketched the expected phase diagram of the Bose-Hubbard model, and introduced a mean-field treatment that
Time dependent perturbation theory 1 D. E. Soper 2 University of Oregon 11 May 2012
 Time dependent perturbation theory D. E. Soper University of Oregon May 0 offer here some background for Chapter 5 of J. J. Sakurai, Modern Quantum Mechanics. The problem Let the hamiltonian for a system
Time dependent perturbation theory D. E. Soper University of Oregon May 0 offer here some background for Chapter 5 of J. J. Sakurai, Modern Quantum Mechanics. The problem Let the hamiltonian for a system
Landau-Fermi liquid theory
 Landau- 1 Chennai Mathematical Institute April 25, 2011 1 Final year project under Prof. K. Narayan, CMI Interacting fermion system I Basic properties of metals (heat capacity, susceptibility,...) were
Landau- 1 Chennai Mathematical Institute April 25, 2011 1 Final year project under Prof. K. Narayan, CMI Interacting fermion system I Basic properties of metals (heat capacity, susceptibility,...) were
Lecture 6. Fermion Pairing. WS2010/11: Introduction to Nuclear and Particle Physics
 Lecture 6 Fermion Pairing WS2010/11: Introduction to Nuclear and Particle Physics Experimental indications for Cooper-Pairing Solid state physics: Pairing of electrons near the Fermi surface with antiparallel
Lecture 6 Fermion Pairing WS2010/11: Introduction to Nuclear and Particle Physics Experimental indications for Cooper-Pairing Solid state physics: Pairing of electrons near the Fermi surface with antiparallel
1.1 Quantum mechanics of one particle
 1 Second quantization 1.1 Quantum mechanics of one particle In quantum mechanics the physical state of a particle is described in terms of a ket Ψ. This ket belongs to a Hilbert space which is nothing
1 Second quantization 1.1 Quantum mechanics of one particle In quantum mechanics the physical state of a particle is described in terms of a ket Ψ. This ket belongs to a Hilbert space which is nothing
Basis 4 ] = Integration of s(t) has been performed numerically by an adaptive quadrature algorithm. Discretization in the ɛ space
![Basis 4 ] = Integration of s(t) has been performed numerically by an adaptive quadrature algorithm. Discretization in the ɛ space Basis 4 ] = Integration of s(t) has been performed numerically by an adaptive quadrature algorithm. Discretization in the ɛ space](/thumbs/92/110829637.jpg) 1 [NPHYS-007-06-00643] SUPPLEMENTARY MATERIAL for Spinons and triplons in spatially anisotropic frustrated antiferromagnets by Masanori Kohno, Oleg A. Starykh, and Leon Balents Basis The two-spinon states
1 [NPHYS-007-06-00643] SUPPLEMENTARY MATERIAL for Spinons and triplons in spatially anisotropic frustrated antiferromagnets by Masanori Kohno, Oleg A. Starykh, and Leon Balents Basis The two-spinon states
PHYSICS 219 Homework 2 Due in class, Wednesday May 3. Makeup lectures on Friday May 12 and 19, usual time. Location will be ISB 231 or 235.
 PHYSICS 219 Homework 2 Due in class, Wednesday May 3 Note: Makeup lectures on Friday May 12 and 19, usual time. Location will be ISB 231 or 235. No lecture: May 8 (I m away at a meeting) and May 29 (holiday).
PHYSICS 219 Homework 2 Due in class, Wednesday May 3 Note: Makeup lectures on Friday May 12 and 19, usual time. Location will be ISB 231 or 235. No lecture: May 8 (I m away at a meeting) and May 29 (holiday).
Physics 221A Fall 1996 Notes 13 Spins in Magnetic Fields
 Physics 221A Fall 1996 Notes 13 Spins in Magnetic Fields A nice illustration of rotation operator methods which is also important physically is the problem of spins in magnetic fields. The earliest experiments
Physics 221A Fall 1996 Notes 13 Spins in Magnetic Fields A nice illustration of rotation operator methods which is also important physically is the problem of spins in magnetic fields. The earliest experiments
Statistical Mechanics
 Franz Schwabl Statistical Mechanics Translated by William Brewer Second Edition With 202 Figures, 26 Tables, and 195 Problems 4u Springer Table of Contents 1. Basic Principles 1 1.1 Introduction 1 1.2
Franz Schwabl Statistical Mechanics Translated by William Brewer Second Edition With 202 Figures, 26 Tables, and 195 Problems 4u Springer Table of Contents 1. Basic Principles 1 1.1 Introduction 1 1.2
(a) Write down the total Hamiltonian of this system, including the spin degree of freedom of the electron, but neglecting spin-orbit interactions.
 1. Quantum Mechanics (Spring 2007) Consider a hydrogen atom in a weak uniform magnetic field B = Bê z. (a) Write down the total Hamiltonian of this system, including the spin degree of freedom of the electron,
1. Quantum Mechanics (Spring 2007) Consider a hydrogen atom in a weak uniform magnetic field B = Bê z. (a) Write down the total Hamiltonian of this system, including the spin degree of freedom of the electron,
Second Quantization: Quantum Fields
 Second Quantization: Quantum Fields Bosons and Fermions Let X j stand for the coordinate and spin subscript (if any) of the j-th particle, so that the vector of state Ψ of N particles has the form Ψ Ψ(X
Second Quantization: Quantum Fields Bosons and Fermions Let X j stand for the coordinate and spin subscript (if any) of the j-th particle, so that the vector of state Ψ of N particles has the form Ψ Ψ(X
3.5 The random-phase approximation
 154 3. LINEAR RESPONSE THEORY 3.5 The random-phase approximation Earlier in this chapter, we have demonstrated that many experimentally observable properties of solids can be expressed in terms of two-particle
154 3. LINEAR RESPONSE THEORY 3.5 The random-phase approximation Earlier in this chapter, we have demonstrated that many experimentally observable properties of solids can be expressed in terms of two-particle
The Simple Harmonic Oscillator
 The Simple Harmonic Oscillator Asaf Pe er 1 November 4, 215 This part of the course is based on Refs [1] [3] 1 Introduction We return now to the study of a 1-d stationary problem: that of the simple harmonic
The Simple Harmonic Oscillator Asaf Pe er 1 November 4, 215 This part of the course is based on Refs [1] [3] 1 Introduction We return now to the study of a 1-d stationary problem: that of the simple harmonic
MACROSCOPIC VARIABLES, THERMAL EQUILIBRIUM. Contents AND BOLTZMANN ENTROPY. 1 Macroscopic Variables 3. 2 Local quantities and Hydrodynamics fields 4
 MACROSCOPIC VARIABLES, THERMAL EQUILIBRIUM AND BOLTZMANN ENTROPY Contents 1 Macroscopic Variables 3 2 Local quantities and Hydrodynamics fields 4 3 Coarse-graining 6 4 Thermal equilibrium 9 5 Two systems
MACROSCOPIC VARIABLES, THERMAL EQUILIBRIUM AND BOLTZMANN ENTROPY Contents 1 Macroscopic Variables 3 2 Local quantities and Hydrodynamics fields 4 3 Coarse-graining 6 4 Thermal equilibrium 9 5 Two systems
Macroscopic dielectric theory
 Macroscopic dielectric theory Maxwellʼs equations E = 1 c E =4πρ B t B = 4π c J + 1 c B = E t In a medium it is convenient to explicitly introduce induced charges and currents E = 1 B c t D =4πρ H = 4π
Macroscopic dielectric theory Maxwellʼs equations E = 1 c E =4πρ B t B = 4π c J + 1 c B = E t In a medium it is convenient to explicitly introduce induced charges and currents E = 1 B c t D =4πρ H = 4π
J07M.1 - Ball on a Turntable
 Part I - Mechanics J07M.1 - Ball on a Turntable J07M.1 - Ball on a Turntable ẑ Ω A spherically symmetric ball of mass m, moment of inertia I about any axis through its center, and radius a, rolls without
Part I - Mechanics J07M.1 - Ball on a Turntable J07M.1 - Ball on a Turntable ẑ Ω A spherically symmetric ball of mass m, moment of inertia I about any axis through its center, and radius a, rolls without
We already came across a form of indistinguishably in the canonical partition function: V N Q =
 Bosons en fermions Indistinguishability We already came across a form of indistinguishably in the canonical partition function: for distinguishable particles Q = Λ 3N βe p r, r 2,..., r N ))dτ dτ 2...
Bosons en fermions Indistinguishability We already came across a form of indistinguishably in the canonical partition function: for distinguishable particles Q = Λ 3N βe p r, r 2,..., r N ))dτ dτ 2...
The nature of superfluidity in the cold atomic unitary Fermi gas
 The nature of superfluidity in the cold atomic unitary Fermi gas Introduction Yoram Alhassid (Yale University) Finite-temperature auxiliary-field Monte Carlo (AFMC) method The trapped unitary Fermi gas
The nature of superfluidity in the cold atomic unitary Fermi gas Introduction Yoram Alhassid (Yale University) Finite-temperature auxiliary-field Monte Carlo (AFMC) method The trapped unitary Fermi gas
B2.III Revision notes: quantum physics
 B.III Revision notes: quantum physics Dr D.M.Lucas, TT 0 These notes give a summary of most of the Quantum part of this course, to complement Prof. Ewart s notes on Atomic Structure, and Prof. Hooker s
B.III Revision notes: quantum physics Dr D.M.Lucas, TT 0 These notes give a summary of most of the Quantum part of this course, to complement Prof. Ewart s notes on Atomic Structure, and Prof. Hooker s
ψ s a ˆn a s b ˆn b ψ Hint: Because the state is spherically symmetric the answer can depend only on the angle between the two directions.
 1. Quantum Mechanics (Fall 2004) Two spin-half particles are in a state with total spin zero. Let ˆn a and ˆn b be unit vectors in two arbitrary directions. Calculate the expectation value of the product
1. Quantum Mechanics (Fall 2004) Two spin-half particles are in a state with total spin zero. Let ˆn a and ˆn b be unit vectors in two arbitrary directions. Calculate the expectation value of the product
CHAPTER 4. Cluster expansions
 CHAPTER 4 Cluster expansions The method of cluster expansions allows to write the grand-canonical thermodynamic potential as a convergent perturbation series, where the small parameter is related to the
CHAPTER 4 Cluster expansions The method of cluster expansions allows to write the grand-canonical thermodynamic potential as a convergent perturbation series, where the small parameter is related to the
Physics 127c: Statistical Mechanics. Weakly Interacting Fermi Gas. The Electron Gas
 Physics 7c: Statistical Mechanics Wealy Interacting Fermi Gas Unlie the Boson case, there is usually no ualitative change in behavior going from the noninteracting to the wealy interacting Fermi gas for
Physics 7c: Statistical Mechanics Wealy Interacting Fermi Gas Unlie the Boson case, there is usually no ualitative change in behavior going from the noninteracting to the wealy interacting Fermi gas for
Linear and Nonlinear Oscillators (Lecture 2)
 Linear and Nonlinear Oscillators (Lecture 2) January 25, 2016 7/441 Lecture outline A simple model of a linear oscillator lies in the foundation of many physical phenomena in accelerator dynamics. A typical
Linear and Nonlinear Oscillators (Lecture 2) January 25, 2016 7/441 Lecture outline A simple model of a linear oscillator lies in the foundation of many physical phenomena in accelerator dynamics. A typical
Physics 127a: Class Notes
 Physics 127a: Class Notes Lecture 15: Statistical Mechanics of Superfluidity Elementary excitations/quasiparticles In general, it is hard to list the energy eigenstates, needed to calculate the statistical
Physics 127a: Class Notes Lecture 15: Statistical Mechanics of Superfluidity Elementary excitations/quasiparticles In general, it is hard to list the energy eigenstates, needed to calculate the statistical
Attempts at relativistic QM
 Attempts at relativistic QM based on S-1 A proper description of particle physics should incorporate both quantum mechanics and special relativity. However historically combining quantum mechanics and
Attempts at relativistic QM based on S-1 A proper description of particle physics should incorporate both quantum mechanics and special relativity. However historically combining quantum mechanics and
The Euler Equation of Gas-Dynamics
 The Euler Equation of Gas-Dynamics A. Mignone October 24, 217 In this lecture we study some properties of the Euler equations of gasdynamics, + (u) = ( ) u + u u + p = a p + u p + γp u = where, p and u
The Euler Equation of Gas-Dynamics A. Mignone October 24, 217 In this lecture we study some properties of the Euler equations of gasdynamics, + (u) = ( ) u + u u + p = a p + u p + γp u = where, p and u
P3317 HW from Lecture 15 and Recitation 8
 P3317 HW from Lecture 15 and Recitation 8 Due Oct 23, 218 Problem 1. Variational Energy of Helium Here we will estimate the ground state energy of Helium. Helium has two electrons circling around a nucleus
P3317 HW from Lecture 15 and Recitation 8 Due Oct 23, 218 Problem 1. Variational Energy of Helium Here we will estimate the ground state energy of Helium. Helium has two electrons circling around a nucleus
Strongly correlated systems in atomic and condensed matter physics. Lecture notes for Physics 284 by Eugene Demler Harvard University
 Strongly correlated systems in atomic and condensed matter physics Lecture notes for Physics 284 by Eugene Demler Harvard University January 25, 2011 2 Chapter 12 Collective modes in interacting Fermi
Strongly correlated systems in atomic and condensed matter physics Lecture notes for Physics 284 by Eugene Demler Harvard University January 25, 2011 2 Chapter 12 Collective modes in interacting Fermi
Phase Synchronization
 Phase Synchronization Lecture by: Zhibin Guo Notes by: Xiang Fan May 10, 2016 1 Introduction For any mode or fluctuation, we always have where S(x, t) is phase. If a mode amplitude satisfies ϕ k = ϕ k
Phase Synchronization Lecture by: Zhibin Guo Notes by: Xiang Fan May 10, 2016 1 Introduction For any mode or fluctuation, we always have where S(x, t) is phase. If a mode amplitude satisfies ϕ k = ϕ k
Lecture 3: Fermi-liquid theory. 1 General considerations concerning condensed matter
 Phys 769 Selected Topics in Condensed Matter Physics Summer 200 Lecture 3: Fermi-liquid theory Lecturer: Anthony J. Leggett TA: Bill Coish General considerations concerning condensed matter (NB: Ultracold
Phys 769 Selected Topics in Condensed Matter Physics Summer 200 Lecture 3: Fermi-liquid theory Lecturer: Anthony J. Leggett TA: Bill Coish General considerations concerning condensed matter (NB: Ultracold
RPA in infinite systems
 RPA in infinite systems Translational invariance leads to conservation of the total momentum, in other words excited states with different total momentum don t mix So polarization propagator diagonal in
RPA in infinite systems Translational invariance leads to conservation of the total momentum, in other words excited states with different total momentum don t mix So polarization propagator diagonal in
1 Fluctuations of the number of particles in a Bose-Einstein condensate
 Exam of Quantum Fluids M1 ICFP 217-218 Alice Sinatra and Alexander Evrard The exam consists of two independant exercises. The duration is 3 hours. 1 Fluctuations of the number of particles in a Bose-Einstein
Exam of Quantum Fluids M1 ICFP 217-218 Alice Sinatra and Alexander Evrard The exam consists of two independant exercises. The duration is 3 hours. 1 Fluctuations of the number of particles in a Bose-Einstein
Magnets, 1D quantum system, and quantum Phase transitions
 134 Phys620.nb 10 Magnets, 1D quantum system, and quantum Phase transitions In 1D, fermions can be mapped into bosons, and vice versa. 10.1. magnetization and frustrated magnets (in any dimensions) Consider
134 Phys620.nb 10 Magnets, 1D quantum system, and quantum Phase transitions In 1D, fermions can be mapped into bosons, and vice versa. 10.1. magnetization and frustrated magnets (in any dimensions) Consider
Elastic Scattering. R = m 1r 1 + m 2 r 2 m 1 + m 2. is the center of mass which is known to move with a constant velocity (see previous lectures):
 Elastic Scattering In this section we will consider a problem of scattering of two particles obeying Newtonian mechanics. The problem of scattering can be viewed as a truncated version of dynamic problem
Elastic Scattering In this section we will consider a problem of scattering of two particles obeying Newtonian mechanics. The problem of scattering can be viewed as a truncated version of dynamic problem
+ 1. which gives the expected number of Fermions in energy state ɛ. The expected number of Fermions in energy range ɛ to ɛ + dɛ is then dn = n s g s
 Chapter 8 Fermi Systems 8.1 The Perfect Fermi Gas In this chapter, we study a gas of non-interacting, elementary Fermi particles. Since the particles are non-interacting, the potential energy is zero,
Chapter 8 Fermi Systems 8.1 The Perfect Fermi Gas In this chapter, we study a gas of non-interacting, elementary Fermi particles. Since the particles are non-interacting, the potential energy is zero,
Coupling of Angular Momenta Isospin Nucleon-Nucleon Interaction
 Lecture 5 Coupling of Angular Momenta Isospin Nucleon-Nucleon Interaction WS0/3: Introduction to Nuclear and Particle Physics,, Part I I. Angular Momentum Operator Rotation R(θ): in polar coordinates the
Lecture 5 Coupling of Angular Momenta Isospin Nucleon-Nucleon Interaction WS0/3: Introduction to Nuclear and Particle Physics,, Part I I. Angular Momentum Operator Rotation R(θ): in polar coordinates the
Lecture Models for heavy-ion collisions (Part III): transport models. SS2016: Dynamical models for relativistic heavy-ion collisions
 Lecture Models for heavy-ion collisions (Part III: transport models SS06: Dynamical models for relativistic heavy-ion collisions Quantum mechanical description of the many-body system Dynamics of heavy-ion
Lecture Models for heavy-ion collisions (Part III: transport models SS06: Dynamical models for relativistic heavy-ion collisions Quantum mechanical description of the many-body system Dynamics of heavy-ion
3.3 Energy absorption and the Green function
 142 3. LINEAR RESPONSE THEORY 3.3 Energy absorption and the Green function In this section, we first present a calculation of the energy transferred to the system by the external perturbation H 1 = Âf(t)
142 3. LINEAR RESPONSE THEORY 3.3 Energy absorption and the Green function In this section, we first present a calculation of the energy transferred to the system by the external perturbation H 1 = Âf(t)
Quantum Phase Transitions
 Quantum Phase Transitions Subir Sachdev Department of Physics Yale University P.O. Box 208120, New Haven, CT 06520-8120 USA E-mail: subir.sachdev@yale.edu May 19, 2004 To appear in Encyclopedia of Mathematical
Quantum Phase Transitions Subir Sachdev Department of Physics Yale University P.O. Box 208120, New Haven, CT 06520-8120 USA E-mail: subir.sachdev@yale.edu May 19, 2004 To appear in Encyclopedia of Mathematical
Plasmas as fluids. S.M.Lea. January 2007
 Plasmas as fluids S.M.Lea January 2007 So far we have considered a plasma as a set of non intereacting particles, each following its own path in the electric and magnetic fields. Now we want to consider
Plasmas as fluids S.M.Lea January 2007 So far we have considered a plasma as a set of non intereacting particles, each following its own path in the electric and magnetic fields. Now we want to consider
Green Functions in Many Body Quantum Mechanics
 Green Functions in Many Body Quantum Mechanics NOTE This section contains some advanced material, intended to give a brief introduction to methods used in many body quantum mechanics. The material at the
Green Functions in Many Body Quantum Mechanics NOTE This section contains some advanced material, intended to give a brief introduction to methods used in many body quantum mechanics. The material at the
9.1 System in contact with a heat reservoir
 Chapter 9 Canonical ensemble 9. System in contact with a heat reservoir We consider a small system A characterized by E, V and N in thermal interaction with a heat reservoir A 2 characterized by E 2, V
Chapter 9 Canonical ensemble 9. System in contact with a heat reservoir We consider a small system A characterized by E, V and N in thermal interaction with a heat reservoir A 2 characterized by E 2, V
in-medium pair wave functions the Cooper pair wave function the superconducting order parameter anomalous averages of the field operators
 (by A. A. Shanenko) in-medium wave functions in-medium pair-wave functions and spatial pair particle correlations momentum condensation and ODLRO (off-diagonal long range order) U(1) symmetry breaking
(by A. A. Shanenko) in-medium wave functions in-medium pair-wave functions and spatial pair particle correlations momentum condensation and ODLRO (off-diagonal long range order) U(1) symmetry breaking
5. Superconductivity. R(T) = 0 for T < T c, R(T) = R 0 +at 2 +bt 5, B = H+4πM = 0,
 5. Superconductivity In this chapter we shall introduce the fundamental experimental facts about superconductors and present a summary of the derivation of the BSC theory (Bardeen Cooper and Schrieffer).
5. Superconductivity In this chapter we shall introduce the fundamental experimental facts about superconductors and present a summary of the derivation of the BSC theory (Bardeen Cooper and Schrieffer).
Joint Entrance Examination for Postgraduate Courses in Physics EUF
 Joint Entrance Examination for Postgraduate Courses in Physics EUF For the first semester 2014 Part 1 15 October 2013 Instructions: DO NOT WRITE YOUR NAME ON THE TEST. It should be identified only by your
Joint Entrance Examination for Postgraduate Courses in Physics EUF For the first semester 2014 Part 1 15 October 2013 Instructions: DO NOT WRITE YOUR NAME ON THE TEST. It should be identified only by your
Physics 4022 Notes on Density Matrices
 Physics 40 Notes on Density Matrices Definition: For a system in a definite normalized state ψ > the density matrix ρ is ρ = ψ >< ψ 1) From Eq 1 it is obvious that in the basis defined by ψ > and other
Physics 40 Notes on Density Matrices Definition: For a system in a definite normalized state ψ > the density matrix ρ is ρ = ψ >< ψ 1) From Eq 1 it is obvious that in the basis defined by ψ > and other
Relativistic magnetotransport in graphene
 Relativistic magnetotransport in graphene Markus Müller in collaboration with Lars Fritz (Harvard) Subir Sachdev (Harvard) Jörg Schmalian (Iowa) Landau Memorial Conference June 6, 008 Outline Relativistic
Relativistic magnetotransport in graphene Markus Müller in collaboration with Lars Fritz (Harvard) Subir Sachdev (Harvard) Jörg Schmalian (Iowa) Landau Memorial Conference June 6, 008 Outline Relativistic
8.333: Statistical Mechanics I Problem Set # 5 Due: 11/22/13 Interacting particles & Quantum ensembles
 8.333: Statistical Mechanics I Problem Set # 5 Due: 11/22/13 Interacting particles & Quantum ensembles 1. Surfactant condensation: N surfactant molecules are added to the surface of water over an area
8.333: Statistical Mechanics I Problem Set # 5 Due: 11/22/13 Interacting particles & Quantum ensembles 1. Surfactant condensation: N surfactant molecules are added to the surface of water over an area
Multi-Electron Atoms II
 Multi-Electron Atoms II LS Coupling The basic idea of LS coupling or Russell-Saunders coupling is to assume that spin-orbit effects are small, and can be neglected to a first approximation. If there is
Multi-Electron Atoms II LS Coupling The basic idea of LS coupling or Russell-Saunders coupling is to assume that spin-orbit effects are small, and can be neglected to a first approximation. If there is
Luigi Paolasini
 Luigi Paolasini paolasini@esrf.fr LECTURE 7: Magnetic excitations - Phase transitions and the Landau mean-field theory. - Heisenberg and Ising models. - Magnetic excitations. External parameter, as for
Luigi Paolasini paolasini@esrf.fr LECTURE 7: Magnetic excitations - Phase transitions and the Landau mean-field theory. - Heisenberg and Ising models. - Magnetic excitations. External parameter, as for
Phonons and lattice dynamics
 Chapter Phonons and lattice dynamics. Vibration modes of a cluster Consider a cluster or a molecule formed of an assembly of atoms bound due to a specific potential. First, the structure must be relaxed
Chapter Phonons and lattice dynamics. Vibration modes of a cluster Consider a cluster or a molecule formed of an assembly of atoms bound due to a specific potential. First, the structure must be relaxed
III.H Zeroth Order Hydrodynamics
 III.H Zeroth Order Hydrodynamics As a first approximation, we shall assume that in local equilibrium, the density f 1 at each point in space can be represented as in eq.(iii.56), i.e. [ ] p m q, t)) f
III.H Zeroth Order Hydrodynamics As a first approximation, we shall assume that in local equilibrium, the density f 1 at each point in space can be represented as in eq.(iii.56), i.e. [ ] p m q, t)) f
Physics 139B Solutions to Homework Set 4 Fall 2009
 Physics 139B Solutions to Homework Set 4 Fall 9 1. Liboff, problem 1.16 on page 594 595. Consider an atom whose electrons are L S coupled so that the good quantum numbers are j l s m j and eigenstates
Physics 139B Solutions to Homework Set 4 Fall 9 1. Liboff, problem 1.16 on page 594 595. Consider an atom whose electrons are L S coupled so that the good quantum numbers are j l s m j and eigenstates
129 Lecture Notes More on Dirac Equation
 19 Lecture Notes More on Dirac Equation 1 Ultra-relativistic Limit We have solved the Diraction in the Lecture Notes on Relativistic Quantum Mechanics, and saw that the upper lower two components are large
19 Lecture Notes More on Dirac Equation 1 Ultra-relativistic Limit We have solved the Diraction in the Lecture Notes on Relativistic Quantum Mechanics, and saw that the upper lower two components are large
Summary Sec. 1.6: The dielectric function of jellium in the RPA
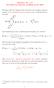 Summary Sec 6: The dielectric function of jellium in the RPA Starting with the diagram that describes the simplest approximation of a polarisation insertion into a bare Coulomb interaction line and translating
Summary Sec 6: The dielectric function of jellium in the RPA Starting with the diagram that describes the simplest approximation of a polarisation insertion into a bare Coulomb interaction line and translating
Concepts for Specific Heat
 Concepts for Specific Heat Andreas Wacker 1 Mathematical Physics, Lund University August 17, 018 1 Introduction These notes shall briefly explain general results for the internal energy and the specific
Concepts for Specific Heat Andreas Wacker 1 Mathematical Physics, Lund University August 17, 018 1 Introduction These notes shall briefly explain general results for the internal energy and the specific
Landau Theory of Fermi Liquids : Equilibrium Properties
 Quantum Liquids LECTURE I-II Landau Theory of Fermi Liquids : Phenomenology and Microscopic Foundations LECTURE III Superfluidity. Bogoliubov theory. Bose-Einstein condensation. LECTURE IV Luttinger Liquids.
Quantum Liquids LECTURE I-II Landau Theory of Fermi Liquids : Phenomenology and Microscopic Foundations LECTURE III Superfluidity. Bogoliubov theory. Bose-Einstein condensation. LECTURE IV Luttinger Liquids.
2 Canonical quantization
 Phys540.nb 7 Canonical quantization.1. Lagrangian mechanics and canonical quantization Q: How do we quantize a general system?.1.1.lagrangian Lagrangian mechanics is a reformulation of classical mechanics.
Phys540.nb 7 Canonical quantization.1. Lagrangian mechanics and canonical quantization Q: How do we quantize a general system?.1.1.lagrangian Lagrangian mechanics is a reformulation of classical mechanics.
Quantum Theory of Matter
 Quantum Theory of Matter Revision Lecture Derek Lee Imperial College London May 2006 Outline 1 Exam and Revision 2 Quantum Theory of Matter Microscopic theory 3 Summary Outline 1 Exam and Revision 2 Quantum
Quantum Theory of Matter Revision Lecture Derek Lee Imperial College London May 2006 Outline 1 Exam and Revision 2 Quantum Theory of Matter Microscopic theory 3 Summary Outline 1 Exam and Revision 2 Quantum
LOCAL MOMENTS NEAR THE METAL-INSULATOR TRANSITION
 LOCAL MOMENTS NEAR THE METAL-INSULATOR TRANSITION Subir Sachdev Center for Theoretical Physics, P.O. Box 6666 Yale University, New Haven, CT 06511 This paper reviews recent progress in understanding the
LOCAL MOMENTS NEAR THE METAL-INSULATOR TRANSITION Subir Sachdev Center for Theoretical Physics, P.O. Box 6666 Yale University, New Haven, CT 06511 This paper reviews recent progress in understanding the
Donoghue, Golowich, Holstein Chapter 4, 6
 1 Week 7: Non linear sigma models and pion lagrangians Reading material from the books Burgess-Moore, Chapter 9.3 Donoghue, Golowich, Holstein Chapter 4, 6 Weinberg, Chap. 19 1 Goldstone boson lagrangians
1 Week 7: Non linear sigma models and pion lagrangians Reading material from the books Burgess-Moore, Chapter 9.3 Donoghue, Golowich, Holstein Chapter 4, 6 Weinberg, Chap. 19 1 Goldstone boson lagrangians
Lecture notes for QFT I (662)
 Preprint typeset in JHEP style - PAPER VERSION Lecture notes for QFT I (66) Martin Kruczenski Department of Physics, Purdue University, 55 Northwestern Avenue, W. Lafayette, IN 47907-036. E-mail: markru@purdue.edu
Preprint typeset in JHEP style - PAPER VERSION Lecture notes for QFT I (66) Martin Kruczenski Department of Physics, Purdue University, 55 Northwestern Avenue, W. Lafayette, IN 47907-036. E-mail: markru@purdue.edu
Phase transitions and critical phenomena
 Phase transitions and critical phenomena Classification of phase transitions. Discontinous (st order) transitions Summary week -5 st derivatives of thermodynamic potentials jump discontinously, e.g. (
Phase transitions and critical phenomena Classification of phase transitions. Discontinous (st order) transitions Summary week -5 st derivatives of thermodynamic potentials jump discontinously, e.g. (
8 Quantized Interaction of Light and Matter
 8 Quantized Interaction of Light and Matter 8.1 Dressed States Before we start with a fully quantized description of matter and light we would like to discuss the evolution of a two-level atom interacting
8 Quantized Interaction of Light and Matter 8.1 Dressed States Before we start with a fully quantized description of matter and light we would like to discuss the evolution of a two-level atom interacting
Optical Lattices. Chapter Polarization
 Chapter Optical Lattices Abstract In this chapter we give details of the atomic physics that underlies the Bose- Hubbard model used to describe ultracold atoms in optical lattices. We show how the AC-Stark
Chapter Optical Lattices Abstract In this chapter we give details of the atomic physics that underlies the Bose- Hubbard model used to describe ultracold atoms in optical lattices. We show how the AC-Stark
Macroscopic plasma description
 Macroscopic plasma description Macroscopic plasma theories are fluid theories at different levels single fluid (magnetohydrodynamics MHD) two-fluid (multifluid, separate equations for electron and ion
Macroscopic plasma description Macroscopic plasma theories are fluid theories at different levels single fluid (magnetohydrodynamics MHD) two-fluid (multifluid, separate equations for electron and ion
Likewise, any operator, including the most generic Hamiltonian, can be written in this basis as H11 H
 Finite Dimensional systems/ilbert space Finite dimensional systems form an important sub-class of degrees of freedom in the physical world To begin with, they describe angular momenta with fixed modulus
Finite Dimensional systems/ilbert space Finite dimensional systems form an important sub-class of degrees of freedom in the physical world To begin with, they describe angular momenta with fixed modulus
Hydrodynamics and QCD Critical Point in Magnetic Field
 Hydrodynamics and QCD Critical Point in Magnetic Field University of Illinois at Chicago May 25, 2018 INT Workshop Multi Scale Problems Using Effective Field Theories Reference: Phys.Rev. D97 (2018) no.5,
Hydrodynamics and QCD Critical Point in Magnetic Field University of Illinois at Chicago May 25, 2018 INT Workshop Multi Scale Problems Using Effective Field Theories Reference: Phys.Rev. D97 (2018) no.5,
(i) T, p, N Gibbs free energy G (ii) T, p, µ no thermodynamic potential, since T, p, µ are not independent of each other (iii) S, p, N Enthalpy H
 Solutions exam 2 roblem 1 a Which of those quantities defines a thermodynamic potential Why? 2 points i T, p, N Gibbs free energy G ii T, p, µ no thermodynamic potential, since T, p, µ are not independent
Solutions exam 2 roblem 1 a Which of those quantities defines a thermodynamic potential Why? 2 points i T, p, N Gibbs free energy G ii T, p, µ no thermodynamic potential, since T, p, µ are not independent
