Nonlinear ion-acoustic solitons in a magnetized quantum plasma with arbitrary degeneracy of electrons. Abstract
|
|
|
- Nicholas Julius Glenn
- 5 years ago
- Views:
Transcription
1 Nonlinear ion-acoustic solitons in a magnetized quantum plasma with arbitrary degeneracy of electrons Fernando Haas Physics Institute, Federal University of Rio Grande do Sul, CEP , Av. Bento Gonçalves 9500, Porto Alegre, RS, Brazil Shahzad Mahmood Theoretical Physics Division TPD, PINSTECH, P. O. Nilore Islamabad 44000, Pakistan Abstract Nonlinear ion-acoustic waves are analyzed in a non-relativistic magnetized quantum plasma with arbitrary degeneracy of electrons. Quantum statistics is taken into account by means of the equation of state for ideal fermions at arbitrary temperature. Quantum diffraction is described by a modified Bohm potential consistent with finite temperature quantum kinetic theory in the long wavelength limit. The dispersion relation of the obliquely propagating electrostatic waves in magnetized quantum plasma with arbitrary degeneracy of electrons is obtained. Using the reductive perturbation method, the corresponding Zakharov-Kuznetsov equation is derived, describing obliquely propagating two-dimensional ion-acoustic solitons in a magnetized quantum plasma with degenerate electrons having arbitrary electron temperature. It is found that in the dilute plasma case only electrostatic potential hump structures are possible, while in dense quantum plasma in principle both hump and dip soliton structures are obtainable, depending on the electron plasma density and its temperature. The results are validated by comparison with the quantum hydrodynamic model including electron inertia and magnetization effects. Suitable physical parameters for observations are identified. PACS numbers: 5.35.Fp, 5.35.Sb, Db, Jn 1
2 I. INTRODUCTION The ion-acoustic wave, which is the fundamental low frequency mode of plasma physics, is a prime focus of many current studies of localized electrostatic disturbances in laboratory, space and astrophysical plasmas. The study of ion-acoustic waves has also gained its importance in quantum plasmas to understand electrostatic wave propagation in microscopic scales. During the last decade, there has been a renewed interest to study collective wave phenomenon in quantum plasma, motivated by applications in semiconductors [1], high intensity laser-plasma experiments [ 4] and high density astrophysical plasmas such as in the interior of massive planets and white dwarfs, neutron stars or magnetars [5 7]. The quantum or degeneracy effects appears in plasmas when the de Broglie wavelength associated with the charged carriers becomes of the order of the inter-particle distances. The quantum effects in plasmas are more frequently due to electrons, which are lighter than ions, and it includes both Pauli s exclusion principle for half spin particles and Heisenberg s uncertainty principle, due to wave like nature of the particles. Quantum ion-acoustic waves in unmagnetized dense plasma have been investigated using quantum hydrodynamic models [8]. In quantum hydrodynamics, the momentum equation for degenerate electrons contains a pressure term compatible with a Fermi-Dirac distribution function, while the Bohm potential term is included to account for quantum diffraction [9 11]. Later on the quantum hydrodynamics model for plasmas was extended to include magnetic fields, with the associated quantum magnetohydrodynamics theory developed and discussed in connection to astrophysical dense plasmas [1]. Quantum Trivelpiece-Gould modes in a dense magnetized quantum plasma were derived [13]. The exchange effects on low frequency excitations in plasma have been discussed [14], using a modified Vlasov equation incorporating the exchange interaction [15, 16]. The Zakharov-Kuznetsov ZK equation was derived in 1974, to study nonlinear propagation of ion-acoustic waves in magnetized plasmas [17]-[19]. The ZK equation is a multidimensional extension of the well-known Korteweg-de Vries equation for studying solitons or single pulse structures. In the degenerate magnetized plasma case, the cold Fermi electron gas assumption has been applied in the derivation of the appropriate ZK equation [0 ], restricted to the fully degenerate case of negligible thermodynamic temperature in comparison to the Fermi temperature.
3 Linear ion-acoustic and electron Langmuir waves in a plasma with arbitrary degeneracy of electrons were studied using quantum kinetic theory [3]. The nonlinear theory of the isothermal ion-acoustic waves in degenerate unmagnetized electron plasmas was investigated [4]. The ranges of the phase velocities of the periodic ion-acoustic waves and the soliton speed were determined in degenerate plasma, but ignoring quantum diffraction effects. Also nonlinear Langmuir waves in a dense plasma with arbitrary degeneracy of electrons in the absence as well as in the presence of quantum diffraction effects in the model have been studied [5]. Eliasson and Shukla [6] derived certain nonlinear quantum electron fluid equation by taking into account the moments of the Wigner equation and using the Fermi-Dirac distribution function for electrons with arbitrary temperature. The relativistic description of localized wavepackets in electrostatic plasma [7] as well as the associated ZK equation for dense relativistic plasma [8] were obtained, in the limit of negligible thermodynamic temperature. Recently, the hydrodynamic equations for ion-acoustic excitations in electrostatic quantum plasma with arbitrary degeneracy were put forward [9]. The purpose of the present communication is to achieve a notable generalization of this work, obtaining the corresponding fluid theory for quantum magnetized ion-acoustic waves MIAWs, both in the linear and nonlinear realms. The extension has a definite interest since magnetized degenerate plasmas are ubiquitous in astrophysics as well as in laboratory [30]. Specifically, it is of fundamental interest to access the nonlinear aspects of quantum MIAWs, which is a more accessible trend using hydrodynamic methods. The manuscript is organized in the following way. In Section II, the set of dynamic equations or studying ion-acoustic waves in magnetized quantum plasmas with arbitrary degeneracy of electrons is presented. In Section III, the dispersion relation of the obliquely propagating electrostatic linear waves in magnetized quantum plasma with arbitrary degeneracy of electrons is obtained. The limiting cases of waves parallel or perpendicular to the the magnetic field are discussed, as well as the strongly magnetized ions limit. Section IV describes the modifications of the linear dispersion relation due to the inclusion of electron inertia and magnetization effects. Section V shows that the fluid theory is the limit case of quantum kinetic theory in the long wavelength limit, as it should be. In Section VI, using reductive perturbation methods, the ZK equation for two dimensional propagation of nonlinear ion-acoustic waves is derived for a magnetized degenerate electrons plasma with arbitrary temperature. The soliton solution is presented. Section VII illustrates the re- 3
4 sults, using suitable plasma parameters for observations, within the applicability range of the model. Section VIII contains the summary of the conclusions. Finally, Appendix A has a more detailed derivation of the static electronic response from quantum kinetic theory, necessary in Section VI. II. DYNAMIC EQUATIONS FOR MAGNETIZED QUANTUM FLUIDS Consider a quantum electron-ion plasma with arbitrary degeneracy of electrons, embedded in an external magnetic field B 0 = B 0ˆx directed along the x-axis. In principle, the electrostatic wave is assumed to propagate obliquely to the external magnetic field in the xy-plane i.e., = x, y, 0. In order to study the quantum MIAWs the ions are taken to be inertial, while electrons are assumed to be inertialess. The set of dynamic equations for MIAWs in a quantum plasma with arbitrary degeneracy of electrons is described as follows. The ion continuity equation is given by n i t + x n iu ix + y n iu iy = 0, 1 while the ion momentum equations in component form are u ix + u ix t x + u iy y u iy + u ix t x + u iy u iy = e ϕ y m i u iz + u ix t x + u iy y u ix = e m i ϕ x, y + ω ciu iz, 3 u iz = ω ci u iy. 4 The momentum equation for the inertialess quantum electron fluid is 0 = p [ ] + e ϕ + α 1 n e 6m e ne x + ne. 5 y The Poisson equation is written as x + y ϕ = e ε 0 n e n i, 6 where ϕ is the electrostatic potential. The ion fluid density and velocity are represented by n i and u i = u ix, u iy, u iz respectively, while n e is the electron fluid density. Also, m e and m i are the electron and ion masses, e is the electronic charge, ε 0 is the vacuum permittivity, is the reduced Planck s constant and ω ci = eb 0 /m i is the ion cyclotron frequency. In 4
5 equilibrium, we have n e0 = n i0 n 0. The electron s fluid pressure p = pn e is specified by a barotropic equation of state which is given below. The last term on the right hand side of the momentum equation 5 for electrons is the quantum force, which arises from the Bohm potential, giving rise to quantum diffraction or tunneling effects due to the wave like nature of the charged particles. The dimensionless quantity α is selected in order to fit the kinetic linear dispersion relation in the long wavelength limit, in a Fermi-Dirac equilibrium, as shown in the continuation. Quantum effects on ions are ignored in view of their large mass in comparison to electrons. In addition, temperature effects on ions are disregarded. Finally, to avoid too much complexity and to focus on the interplay between degeneracy and quantum recoil, exchange effects are also ignored. The equation of state can be obtained from the moments of a local Fermi-Dirac distribution function [9, 31] of an ideal Fermi gas and reads where β = κ B T 1, κ B chemical potential, satisfying p = n e β Li 5/ e βµ Li 3/ e βµ, 7 is the Boltzmann constant, T is the temperature and µ is the Li 3/ e βµ n e = n 0. 8 Li 3/ e βµ 0 The equilibrium chemical potential µ 0 is related to the equilibrium density n 0 through n 0 Li 3/ e βµ 0 βme π 3/ = where the quantity A was defined for later convenience. me 3 = A, 9 π Equations 7 and 8 contain the polylogarithm function Li ν z with index ν, which for ν > 0 can be defined [3] as Li ν z = 1 Γν 0 s ν 1 ds, ν > e s /z where Γν is the gamma function. For ν < 0 one applies Li ν z = z Li ν+1 z 11 z as many times as necessary, where ν + 1 > 0. The numerical coefficient α appearing in the Bohm potential term in Eq. 5 has been derived from finite-temperature quantum kinetic theory for low-frequency electrostatic excitations in [9], α = Li 3/ e βµ 0 Li 1/ e βµ 0 [Li 1/ e βµ 0 ], 1 5
6 expressed as a function of the equilibrium fugacity z = expβµ 0. The treatment of [9] considered non-magnetized plasmas, but in Section V it is proved that Eq. 1 applies to MIAWs too. As discussed in [9], in the classical limit z 1 one has α 1, while in the full degenerate limit z 1 one has α 1/3. The same behavior is seen for α as a function of the chemical potential, as depicted in Fig. 1, showing a transition zone from classical to dense regimes Α Α Μ 0 ev FIG. 1: Coefficient α from Eq. 1, as a function of the chemical potential µ 0. Solid line: T = 4000 K. Doted line: T = 6000 K. Dashed line: T = 8000 K. It happens [33] that the finite-temperature quantum hydrodynamic equations using α from Eq. 1 are consistent with the results from orbital free density functional theory [34, 35]. III. LINEAR WAVES In order to find the dispersion relation for electrostatic wave in a magnetized quantum plasma with arbitrary degeneracy of electrons, we linearize the system of equations 1-6 by considering n i = n 0 + n i1, n e = n 0 + n e1, u ix = u ix1, u iy = u iy1, u iz = u iz1, ϕ = ϕ 1, 13 6
7 inducing a correction µ = µ 0 + µ 1, where the subscript 1 denotes the first order quantities. In particular, using the expansion of the polylogarithm function to first order, i.e., Li ν e βµ 0+µ 1 = Li ν e βµ 0 + βµ 1 Li ν 1 e βµ 0, 14 and considering plane wave perturbations exp[ik x x + k y y ωt], the result is 1 + χ i ω, k + χ e 0, k = 0, 15 where the ionic and electronic susceptibilities are respectively given by χ i ω, k = ω piω ωci cos θ ω ω ωci, 16 [ ] 1 dp χ e 0, k = ωpe k + α k 4 1, 17 m e dn e 0 1m e where ω pj = n 0 e /m j ε 0 for j = i, e and k = k cos θ, sin θ, 0. Due to the neglect of electrons inertia, only the static electronic susceptibility χ e 0, k is necessary. There is no loss of generality in assuming waves in the xy plane, due to the cylindrical geometry around the x axis. The dispersion relation 15 develops as a quadratic equation for ω whose solution is ω = 1 [ ω0 + ωci 18 1/ ] ± ω0 + ωci 4ω0ω ci cos θ, where ω 0 was already obtained [9] in the case of unmagnetized quantum ion-acoustic waves, ω 0 = c sk [1 + H kλ D /4] 1 + kλ D + H kλ D 4 /4. 19 In Eq. 19 one has the ion-acoustic speed c s which follows from c s = 1 dp = κ BT m i dn e 0 m i Li 3/ e βµ0, Li 1/ e βµ 0 0 the generalized electronic screening length λ D from λ D = c s ω pi = κ BT m e ω pe as well as the quantum diffraction parameter H specified by Li 3/ e βµ 0 Li 1/ e βµ 0, 1 H = β ω pe Li 1/ e βµ 0 1/. 3 Li 3/ e βµ 0 7
8 In the dilute plasma limit e βµ 0 1, implying Li ν e βµ 0 e βµ 0, one has c s κb T/m i, λ D = κ B T/m e ω pe, which respectively are the more traditional ion-acoustic speed and Debye length, and H β ω pe / 3. On the other hand, in the fully degenerate case e βµ 0 1, using Li ν e βµ 0 βµ 0 ν /Γν+1 one has µ 0 E F = 3π n 0 /3 /m e, which is the Fermi energy, and c s /3E F /m i, λ D = E F /3m e ωpe, which are respectively the quantum ion-acoustic speed and the Thomas-Fermi screening length, and H 1/ ω pe /E F. The dispersion relation 18 is formally the same as for classical magnetized plasma [36, 37], provided the fully quantum ion-acoustic frequency ω 0 is replaced by its purely classical counterpart. As apparent from the dispersion relation 15, ions are responsible for providing inertia effects, while electrons are responsible for kinetic energy arising from the standard, thermodynamic temperature and/or Fermi pressure and quantum diffraction is represented by the parameter H. It is convenient to rewrite Eq. using Eq. 9, yielding H = α F 3 βme c Li 1/ e βµ 0, 3 π where α F = e /4πε 0 c 1/137 is the fine structure constant. Obviously the theory is non-relativistic, in spite of the appearance of the rest energy m e c in Eq. 3. For a fixed temperature, H is a simple function of the fugacity z = expβµ 0, as shown in Fig. below. It is seen that the pure wave like quantum effects are enhanced for larger densities and fugacities up to z 3.03, while for larger degeneracy the quantum statistical effects prevail showing that the quantum force becomes less effective in denser systems, in view of Pauli s exclusion principle. Therefore for dilute systems H increases with the density and decreases with temperature, while for fully degenerate systems the leading order behavior shows a decreasing of H for an increasing density. The positive sign in Eq. 18 corresponds to fast electrostatic waves, and a negative sign corresponds to slow electrostatic waves in a magnetized plasma. The effect of degeneracy for arbitrary angle θ is not entirely straightforward to identify, due to the somehow involved expression 18. However, in practical applications it is likely to have ω 0 ω ci, so that the fast mode becomes ω ω0 + ωci sin θ while the slow mode becomes ω ωci cos θ. Since quantum effects are present only on ω0 ωci, it happens that the fast wave has an angular dependence appearing as a correction, while the slow wave is strongly angle dependent, but not so influenced by quantum effects. As an example, consider hydrogen 8
9 0.6 H H z FIG. : Quantum diffraction parameter defined in Eq. 3, as a function of the equilibrium fugacity z = e βµ 0, and normalized to H 0 = [α F /3βm e c /π 1/ ] 1/. plasma with an ambient magnetic field B 0 = 10 3 T, yielding the ion cyclotron frequency ω ci = rad/s. For solid-density plasma with T = 10 6 K, n 0 = m 3 and a wave-number k = π 10 9 m 1, one has ω 0 = rad/s ω ci. These parameters are in accordance with the more detailed validity conditions discussed in Section VII. In addition, some significant limiting cases are described below. A. Wave propagation parallel to the magnetic field Considering θ = 0 in Eq. 18, one has either ω = ω ci the ion cyclotron frequency or ω = ω 0. The later has already been discussed in [9]. In the limit kλ D 1 one has ω 0 c s k, where the ion-acoustic speed contains only quantum degeneracy effects as seen from Eq. 0. B. Wave propagation perpendicular to the magnetic field Considering θ = π/ in Eq. 18, one has a vanishing solution ω = 0 as well as a quantum modified electrostatic ion cyclotron wave given by ω = ω ci + ω 0. 9
10 C. Strongly magnetized ions For completeness we consider the strongly magnetized ions case. If ω ci ω 0 one has the fast mode and the slow mode ω = ω ci [ 1 + ω 0 sin θ + ω4 0 sin θ + O ωci 4 ωci 4 ω = ω 0 cos θ [ 1 ω 0 sin θ + O ωci ] 6 ω0, 4 ω ci ] 4 ω0. 5 ω ci IV. ELECTRON INERTIA AND MAGNETIZATION EFFECTS In the purely classical case, the conditions of applicability of the model are well-known [18, 19]. In the quantum case, it is interesting to include electron inertia and magnetization effects, to measure the limitations of Eq. 15. In this context one adds to Eqs. 1-4 and 6 the electron continuity equation n e t + x n eu ex + y n eu ey = 0, 6 and replace Eq. 5 by m e ue t + u e u e = p n e e ϕ + u e B 0 [ + α 1 6m e ne x + ne ], 7 y where u e = u ex, u ey, u ez is the electron fluid velocity. Proceeding as in Section III and also supposing linear perturbations where u e = u e1, the result is 1 + χ i ω, k + χ e ω, k = 0, 8 where the ionic susceptibility is still given by Eq. 16 and ωpeω ωce cos θ χ e ω, k = ω 4 k vt k + ω ceω + k vt kω ce cos θ, 9 where ω ce = eb 0 /m e is the electron cyclotron frequency and vt k = 1 dp + α k. 30 m e dn e 1m e 0 10
11 It is not the purpose of this work to develop the full consequences of the dispersion relation 8, but it is useful to observe that in the formal limit ω 0 the electron response 9 regains the static electronic response χ e 0, k given by Eq. 17. Moreover, by inspection of Eq. 9 it is found that such a limit is attended for a warm electron fluid, where k vt k ω ce so that the electrons magnetization could be disregarded, and k vt k ω, which is attainable for low frequency excitations. In addition, notice that v T k from Eq. 30 depends not only on pressure but also on quantum diffraction effects. On the other hand, ions are assumed to be cold and non-quantum enough. V. COMPARISON TO KINETIC THEORY The results from hydrodynamics should agree with kinetic theory in the long wavelength limit. Therefore it is necessary to compare the ionic and electronic responses found from kinetic theory, to the susceptibilities shown in Eqs. 16 and 17. Since ions are safely assumed as classical in most cases, their particle distribution function f i = f i r, v, t satisfy Vlasov s equation, which presently is [ t + v + e ] ϕ + v B 0 f i = m i v On the other hand, the quantum nature of electrons deserves the use of the quantum Vlasov equation satisfied by the electronic Wigner quasi-distribution f e = f e r, v, t, f e t + v f e ie me 3 3 π ds dv ime v v s exp [ ϕ r + s, t ϕ r s ], t f e r, v, t = 0. All integrals run from to, unless otherwise stated. Moreover, under the same assumption as before, namely large electron thermal and quantum statistical and diffraction effects, the magnetic force on electrons was omitted in Eq. 3. The scalar potential is self-consistently determined by Poisson s equation, x + ϕ = eε0 f y e dv f i dv, 33 where we are taking spatial variations in the xy-plane only. 11
12 Proceeding as in Section III, assuming plane wave perturbations exp[ik x x + k y y ωt] around isotropic in velocities equilibria, the dispersion relation 1 + χ i ω, k + χ e ω, k = 0 is easily derived. Disregarding the negligibly small Landau damping of MIAWs in the case of cold ions, it is found [38, 39] that the ionic susceptibility from kinetic theory coincides with the fluid expression 16. On the other hand, for low frequency waves, the static limit χ e 0, k is sufficient for electrons, reading χ e 0, k = e dv ε 0 k k v [ F v k F v+ k ], 34 m e m e where the principal value of the integral is understood if necessary and where the equilibrium electronic Wigner function is f e = F v. Consider a Fermi-Dirac equilibrium, F v = A 1 + e βm ev / µ 0, v = v, 35 where the normalization constant A is given in Eq. 9, assuring that F v dv = n 0. It turns out that the right-hand side of Eq. 34 can be evaluated as a power series of the quantum recoil q = β/m e k/, supposed to be a small quantity for long wavelengths and/or sufficiently large electronic temperature: χ e 0, k = βm e ω pe π Li3/ zk [Γ + Γ + Γ = 1 3 Li 1/ z q 1 Li 1/ z + 3 ] Li 3/ z q βm e ω pe π Li3/ zk q j j=0 Γ 1 j Li 1/ j z j + 1, 36 where z = e βµ 0. The derivation is detailed in the Appendix A. The expression 36 is exact, as long as the series converges. Moreover, it coincides with the static limit of Eq. 9 of [40], where only the leading Oq quantum recoil correction was calculated. 1
13 For the sake of comparison, the hydrodynamic result from Eq. 17 can be rewritten as χ e 0, k = βm eωpeli 1/ z Li 3/ zk βm e ω pe = Li 3/ zk + Oq q 3 Li 1/ z 1 Li 1/ z Li 1/ z q 3 Li 1/ z, 37 which coincides with Eq. 36 in the long wavelength limit, in view of Γ1/ = π, Γ 1/ = π. This completes the justification of α in Eq. 1 in the magnetized case. VI. ZAKHAROV-KUZNETSOV EQUATION FOR ARBITRARY DEGENERACY In order to derive the ZK equation for obliquely propagating MIAWs in arbitrary degenerate plasma, it is convenient to make use of normalized quantities. The dispersion relation 18 suggests the use of the dimensionless variables x, ỹ = x, y/λ D, t = ω pi t, ũ ix, ũ iy, ũ iz = u ix, u iy, u iz /c s as well as ϕ = eϕ/m i c s, ñ j = n j /n 0, where j = e, i. Equations 1-6 are then written as ũ iy t + ũ ix ñ i t + x ñ iũ ix + ỹ ñ iũ iy = 0, 38 + ũ ix x + ũ iy ũ ix = ϕ ỹ x, 39 t ũ ix ũ iz t x + ũ iy ỹ ũ ix + ũ iy = ϕ x + ũ iy ỹ ỹ + Ωũ iz, 40 ũ iz = Ωũ iy, 41 0 = ϕ Li 1/ e βµ 0 Li 1/ e βµ ñ e [ ] + H 1 ñe x + ñe, 4 ỹ x + ϕ = ñ ỹ e ñ i, 43 where Ω = ω ci /ω pi has been defined and where = / x, / ỹ, 0, while Eq. 8 becomes ñ e = Li 3/ e βµ Li 3/ e βµ
14 In the following calculations, for brevity the tilde sign used for defining normalized quantities will be omitted. In order to find a nonlinear evolution equation describing the magnetized plasma, the stretching of the independent variables x, y and t is defined under the assumption of strong magnetization as follows [41 44], X = ε 1/ x V 0 t, Y = ε 1/ y, τ = ε 3/ t, 45 where ε is a formal small expansion parameter and V 0 is the phase velocity of the wave, to be determined later on. The perturbed quantities can be expanded in powers of ε as follows, n j = 1 + εn j1 + ε n j +..., j = e, i, 46 u ix = εu x1 + ε u x + ε 3 u x3..., 47 u i = ε 3/ u 1 + ε u + ε 5/ u 3..., = y, z, 48 ϕ = εϕ 1 + ε ϕ +..., 49 µ = µ 0 + εµ 1 + ε µ In the present model, the ion velocity components u iy, u iz in the perpendicular to the magnetic field directions are taken as higher order perturbations compared to the parallel component u ix since in the presence of a strong magnetic field, the plasma is anisotropic so that the ion gyro-motion becomes a higher order effect. The lowest ε order terms ε 3/ from the set of equations 38-4 give The velocity u z1 appears in Eq. 53 due to the E B drift. V 0 n i1 X + u x1 X = 0, 51 u x1 V 0 X = ϕ 1 X, 5 u z1 = 1 ϕ 1 Ω Y, 53 Ωu y1 = 0, 54 ϕ 1 X = n e1 X. 55 The lowest ε order terms ε from equations 43 and 44 give n i1 = n e1 = Li 1/ e βµ 0 Li 3/ e βµ 0 βµ
15 Solving the system 51-56, we get V 0 = ±1. We set V 0 = 1 the normalized phase velocity of the MIAW without loss of generality. Collecting the next higher order terms of the ion continuity ε 5/ and of the X, Y and Z components of the ion momentum equations ε 5/, ε, ε, and after a rearrangement, we find n i1 τ n i X + u x u x1 τ X + X n i1u x1 + u y Y = 0, 57 X u x1 = ϕ X, 58 u x X + u x1 u y1 X = Ωu z, 59 u z1 X = Ωu y. 60 Using Eq. 56 and the next higher order terms ε 5/ from the equations of motion of the inertialess degenerate electrons in the X and Y directions, we get n e X = ϕ X + αn n e1 e1 X + H 3 4 X + 3 X and n e Y = ϕ Y + αn n e1 e1 Y + H 4 Y where α has been defined in equation 1. Y n e1 61 X + 3 n Y 3 e1, 6 Now collecting the ε order terms from Poisson s equation, we have X + ϕ Y 1 = n e n i, 63 while the next higher terms from Eqs. 57, 58 and 60 give n i X = n i1 τ + X n i1u x1 + 1 Ω + u x1 τ + u x1 uz1 Y X u x1 X + ϕ X. 64 Differentiating Eq. 63 with respect to X and using Eqs. 61 and 64 together with n i1 = n e1 = u x1 = ϕ 1, u z1 = 1/Ω ϕ 1 / Y, it is finally possible to write the ZK equation for obliquely propagating quantum MIAWs in terms of ϕ 1 φ, φ φ + Aφ τ X + B φ X X + C φ = Y 15
16 The nonlinearity coefficient A and the dispersion coefficients B and C in the parallel and perpendicular directions of the magnetic field, respectively, are defined as A = 1 3 α, 66 B = 1 1 H, 67 4 C = 1 1Ω H In the purely classical limit the nonlinearity and dispersion coefficients become A = 1, B = 1/ and C = 1/ 1 + 1/Ω in agreement with Refs. [17, 43, 44] treating MIAWs in a classical electron-ion plasma. In addition, the ZK equation for fully degenerate plasma will have A = 4/3 and H = 1/ ω pe /E F in the coefficients B, C. The associated fully degenerate ZK equation does not matches the results from Refs. [0 ], after comparison using physical dimensional and non-stretched coordinates, restricted to the case of electronion plasmas. Note that the ZK equations from the previous works do not match the purely classical result. Provided l xb + l yc 0, the soliton solution of the ZK equation 65 for obliquely propagating MIAWs is given by φ = φ 0 sech η/w, 69 where φ 0 = 3u 0 /Al x is the height and where W = 4l x lxb + lyc/u 0 is the width of the soliton in terms of the stretched coordinates. The polarity of the soliton depends on the sign of φ 0. The transformed coordinate η in the co-moving frame is defined as η = l x X + l y Y u 0 τ, where u 0 0 is the speed of the nonlinear pulse and where l x > 0 and l y are direction cosines, so that l x + l y = 1. To obtain localized structures, decaying boundary conditions as η ± were applied. Following the habitual usage the terminology soliton is applied to the solitary wave 69, although the ZK equation does not belong to the class of completely integrable evolution equations. The dispersion effects arising from the combination of charge separation and finite ion Larmor radius balances the nonlinearity in the system to form the soliton. Defining δv = εu 0 /l x, in the laboratory frame the solution reads φ = 3 δv { 1/ 1 δv A sech lxb + lyc ]} [l x x V 0 + δv t + l y y
17 It is apparent that V 0 + δv corresponds to the velocity at which travels the intersection between a plane of constant phase and a field line, down the same field line [4]. From Eq. 70 the width L of the soliton in the laboratory frame is l x B + l 1/ 1/ yc L = = 1 H δv δv 4 + l y 71 Ω From this expression one concludes that while in the non-quantum H = 0 limit necessarily δv > 0 bright soliton propagating at supersonic speed, in the quantum case one has the theoretical possibility of δv < 0 dark soliton propagating at subsonic speed, provided H /4 > 1 + l y/ω. It is interesting to single out the different quantum effects in the soliton 70. amplitude/dip of bright/dark solitons is inversely proportional to A, which depends only on quantum degeneracy and not on quantum diffraction. More degenerate systems produce a smaller α - as seen e.g. from Fig. 1 - and hence a bigger A. Therefore the soliton amplitude/dip decreases with the degeneracy. On the other hand, from the width 71 one find the dependence on the quantum diffraction parameter H which is also dependent on the degeneracy degree shown in Fig. 3 below. For semiclassical bright solitons δv > 0 one has L decreasing with quantum effects, while for quantum, dark solitons δv < 0 one has L increasing with quantum effects. L The V ly 1 V 0 1 ly V 0 H 4 FIG. 3: Squared width of the localized structure as shown in Eq. 71, as a function of the quantum diffraction parameter H. In unmagnetized quantum plasmas, by construction the term 1/Ω does not appears. In this case when H = the corresponding Korteweg-de Vries KdV equation collapses to 17
18 the Burger s equation, producing an ion-acoustic shock wave structure instead of a soliton [8]. In the magnetized case, a further possibility happens when C = 0, or, equivalently, 1 + 1/Ω = H /4, which is not allowed in the classical limit H 0. When C = 0, from Eq. 65 one has φ τ + Aφ φ X 1 Ω 3 φ X 3 = 0, 7 which transforms to the KdV equation in its standard form by means of φ φ, X X, τ τ. Therefore, in this particular situation the problem becomes completely integrable. Finally, if B = 0, it means that 1 H /4 = 0 due to which C = 1/Ω, so that Eq. 65 becomes φ τ + Aφ φ X + 1 Ω X φ = 0, 73 Y This is a KdV-like equation having perpendicular to the magnetic field dispersion effects, due to the obliquely propagating MIAW. Regarding the ranges of validity of the parameters A, B and C in Eqs , first we observe that from Eq. 1 one has 1/3 < α < 1, so that 1 < A < 4/3. In addition, since H from Eq. 3 can in principle attain any non-negative value, B and C are not positive definite. However, strictly speaking, very large values of H are associated with strongly coupling effects which can have a large impact on soliton propagation, to be addressed in a separate extended theory. Only in such generalized framework one could be able to make more precise statements on pure quantum soliton existence or non-existence. Nevertheless, significant values of H are certainly physically acceptable, as found from the present treatment. These issues are best discussed in the following Section. VII. APPLICATIONS It is important to discuss the validity domain of the general theory devised in the last Sections. Moreover, it is highly desirable to offer precise physical parameters where the predicted linear and nonlinear waves could be searched in practice. Obviously, the theory is more relevant in the intermediate regimes, where the thermal and Fermi temperatures are not significantly different. Otherwise, the fully degenerate or dilute limits could be 18
19 sufficiently accurate. Therefore, in this Section frequently we assume T = T F, 74 where T F = E F /κ B is the electrons Fermi temperature. To start, consider the normalization condition 9, which can be expressed [6] as Li 3/ z = 4 3 π βe F 3/, 75 where z = expβµ 0. For equal thermal and Fermi temperatures, βe F = 1, which from Eq. 75 gives the equilibrium fugacity z = 0.98 and from Eq. 1 a parameter α = 0.80, definitely in the intermediate dilute-degenerate situation as explicitly seen e.g. in Fig. 1. Besides quantum degeneracy, quantum diffraction effects can also provide qualitatively new aspects as found e.g. in the extra dispersion of linear waves in Section III and the modified width of the solitons in Section VI. Therefore it would be interesting to investigate systems with a large parameter H. However, realistically speaking it is not possible to increase H without limits, which would enter the strongly coupled plasma regime, not included in the present formalism. For instance, the ideal Fermi gas equation of state for electrons would be unappropriated. Therefore, it is necessary to analyze the coupling parameter g for electrons, which can be defined [45] as g = l/a, where e l = 1πε 0 κ B T n 0 Λ 3 T Li 5/ z 76 is a generalized Landau length involving the thermal de Broglie wavelength Λ T = [π /m e κ B T ] 1/, and a = 4πn 0 /3 1/3 is the Wigner-Seitz radius. In the dilute case, one has e /4πε 0 l = 3/κ B T, so that l would be the classical distance of closest approach in a binary collision, for average kinetic energy. The general expression 76 accounts for the degeneracy effects on the mean kinetic energy. A few calculations yield g = α F βme c 3 3 [Li 3/ z] /3, 77 π 1/3 Li 5/ z an expression similar to the one for H in Eq. 3. Hence, it is legitimate to suspect that the indiscriminate increase of quantum diffraction gives rise to nonideality effects such as dynamical screening and bound states [45]. Incidentally Eq. 77 agrees with Eq. 16 of [9], found from related but different methods. 19
20 The resemblance between the coupling and quantum diffraction parameters is confirmed in Fig. 4 below, which can be compared to Fig. for H. Moreover, it is apparent in Fig. 5, that we have H < 0.5 for the whole span of degeneracy regimes, as far as g < 1. Strictly speaking, the dark soliton, shock wave and the completely integrable case associated to the KdV equation 7 are therefore outside the validity domain of the model, since they need large values of quantum diffraction parameter H. Nevertheless, the influence of the wave nature of the electrons can still provide important corrections by its own, at least for reasonable values of H, as is obvious, for instance, in the width of the ZK soliton in Eq g g z FIG. 4: Coupling parameter defined in Eq. 77, as a function of the equilibrium fugacity z = e βµ 0, and normalized to g 0 = α F βme c /[33 π 1/3 ]. The behavior of the parameters g, H can be summarized in Fig. 6, for T = T F considering hydrogen plasma parameters. We observe that g < 1 for n 0 > m 3, or E F > 5.11 ev, which starts becoming realizable for typical densities in solid-density plasmas [46, 47]. It is necessary to discuss additional points about the validity conditions of the model. Both the static electronic response and long wavelength and hence fluid assumptions are collected in Eq. 7 of [9], reproduced here for convenience, k min 3m e c s and k ω pi c s k max. 78 For hydrogen plasma and T = T F, from Eq. 78 one has k max > k min for n 0 < m 3. The later condition is safely satisfied for non-relativistic plasma. At such high 0
21 H g z FIG. 5: Ratio between the diffraction parameter H from Eq. 3 and the coupling parameter g from Eq. 77, as a function of the equilibrium fugacity z = e βµ g, H E F ev FIG. 6: Upper, dotted curve: coupling parameter g from Eq. 77; lower, dashed curve: quantum diffraction parameter H from Eq. 3, as a function of the electronic Fermi energy E F in ev, for hydrogen plasma and the intermediate dilute-degenerate regime where T = T F. densities available in compact astrophysical objects like white dwarfs and neutron stars, the Fermi momentum becomes comparable to m e c, asking for a relativistic treatment. Strictly speaking, the first inequality in Eq. 78 could be removed, but in this case the quantum recoil would be less significant. In this case, only quantum degeneracy effects would be relevant. In terms of the wavelength λ, Eq. 78 yields a suitable range λ min = π/k max λ 1
22 λ max = π/k min, shown in Fig. 7, in the nanometric scale from extreme ultraviolet to soft X-rays Λ nm 4 3 Λ max Λ min E F ev FIG. 7: Upper, dotted curve: maximum wavelength λ max ; lower, dashed curve: minimal wavelength λ min, consistent with Eq. 78, as a function of the electronic Fermi energy E F in ev, for hydrogen plasma and the intermediate dilute-degenerate regime where T = T F. As discussed in Section IV, the model also assumes that the pressure effects are significantly larger than magnetic field effects regarding electrons, or k v T k ω ce. In the worse case where k k min, the quantum diffraction is typically a correction in the expression 30 for v T k. We then find for T = T F. ω ce E F 3 me m i 1/ Li 3/ z Li 1/ z 0.10, 79 The condition 79, which is easier to satisfy for larger densities, is safely satisfied except for very strong magnetic fields. For instance, for E F 10 ev, we just need B kt. Ions have been assumed to be cold, classical and ideal disregarding strong ion coupling effects. Denoting T i as the ionic temperature, when T F T i the MIAW phase speed becomes much larger than the ionic thermal speed, justifying the cold ions assumption. On the other hand, there is the need of a small ionic coupling parameter g i. For a non-degenerate ionic fluid we then [45] have g i = e 4πε 0 a 1 3κB T i 1. 80
23 Otherwise one would have a ionic liquid or even an ionic crystal, as is believed to happens for g i 17 in an one-component plasma [48]. The joint requirements of cold and nonstrongly coupled ions is represented in Fig. 8 below, where the allowable region is between the straight lines T i = T F, g i = 1. A minimal number density n 0 = m 3 is found to be necessary, which again is accessible for typical solid-density plasmas log 10 T I K T i T F g i log 10 n 0 m 3 FIG. 8: Cold and weakly coupled ions are below the upper, dotted straight line where the ionic temperature T i equals the electronic Fermi temperature T F and above the lower, dashed straight line where the ionic coupling parameter g i = 1. For the sake of illustration, consider the bright soliton solution from Eq. 70, for parameters representative of solid-density plasmas, namely, n 0 = m 3, H = 0.10, g = 0. and T = T F = K. In this case the allowable wavenumbers satisfy 0.4 nm < λ < 1.85 nm, the ionic temperatures are in the range K < T i < K and the magnetic field should have a strength B 0 < T. The soliton is shown in Fig. 9, where B 0 = 10 3 T, l x = l y = / and δv = VIII. SUMMARY The main results of the work are the dispersion relation 18 and the ZK equation 65, both of which describe quantum MIAWs in the linear and nonlinear regimes, respectively, allowing for arbitrary electrons degeneracy degree. The results significantly generalize the previous literature, restricted to either dilute Maxwell-Boltzmann or fully degenerate plas- 3
24 φ x V 0 V t L y L FIG. 9: The two dimensional profile of the MIAW hump soliton structure 70 moving with supersonic speed in the laboratory frame, using normalized coordinates. Parameters: n 0 = m 3, H = 0.10, g = 0., T = T F = K, B 0 = 10 3 T, l x = l y = / and δv = 0.10 mas. The conditions for applications are investigated in depth, pointing the importance of the findings, for e.g. magnetized solid-density plasma. While the physical parameters were more focused on hydrogen plasma in the intermediate dilute-degenerate limit where T = T F, adaptation to fully ionized electron-ion cases with atomic number Z 1 and arbitrary temperatures is not difficult at all. With minor remarks, the whole parametric analysis of Section VII also applies to the unmagnetized case. It is hoped that the detailed assessment of physical parameters thus developed, will incentive experimental and observational verifications of linear and nonlinear quantum ion-acoustic waves, both in laboratory and nature, considering a large span of degeneracy regimes. A possibly important next step is the rigorous non ad hoc incorporation of exchange-correlation effects, which are beyond the reach of the present communication. Acknowledgments FH acknowledges CNPq Conselho Nacional de Desenvolvimento Científico e Tecnológico for financial support. 4
25 APPENDIX A: DERIVATION OF EQ. 36 From Eqs. 34 and 35 one has χ e 0, k [ ] = Ae 1 dv ε 0 k k v + k /m e 1 k v k /m e expβm e v //z [ ] = πae 1 dv ε 0 k kv + k /m e 1 kv k /m e 0 v dv 1 + exp[βm e v +, A1 v /]/z where v = v k/k + v, k v = 0, z = expβµ 0 and all integrals consider the principal value sense. Performing the v integral, considering the expression of A in Eq. 9 and applying a simple change of variables we get χ e 0, k = βm e ωpe 4 π Li 3/ zqk [ ln 1 + ze s+q ln ds s 1 + ze s q], A where q = β/m e k/. Expanding in powers of the quantum recoil one has ln 1 + ze s+q ln 1 + ze s q A3 = 4q gs + q 3! g s + q4 5! giv s + Oq 6, where gs s/[1 + exps /z]. At this point notice that the possible divergence at s = 0 in the integral A was explicitly removed. After integrating by parts, it is found that χ e 0, k = βm eωpez ds π Li3/ zk z + e s q 3 + 4q ds e s A4 z + e s ds e s e s z + Oq 6. z + e s 3 5
26 From Eqs. 10 and 11, each term on the right hand side of A4 can be evaluated in terms of polylogarithms. For instance, Li 1/ z = z ds, π z + e s 0 Li 1/ z = z ds e s π z + e s, A5 Li 3/ z = 0 z π 0 ds e s z e s z + e s 3, clearly related to the integrals in expression A4. In this way Eq. 36, which is also independently confirmed by numerical evaluation, is proved. [1] P. A. Markowich, C. A. Ringhofer and C. Schmeiser, Semiconductor Equations Springer- Verlag, Vienna, [] M. Marklund and P.K. Shukla, Rev. Mod. Phys. 78, [3] S. H. Glenzer, O. L. Landen, P. Neumayer, R. W. Lee, K. Widmann, S. W. Pollaine, R. J. Wallace, G. Gregori, A. Höll, T. Bornath, R. Thiele, V. Schwarz, W.-D. Kraeft and R. Redmer, Phys. Rev. Lett. 98, [4] J. E. Cross, B. Reville and G. Gregori, Astrophys. J. 795, [5] M. Opher, L. O. Silva, D. E. Dauger, V. K. Decyk and J. M. Dawson, Phys. Plasmas 8, [6] G. Chabrier, D. Saumon and A. Y. Potekhin, J. Phys. A: Math. Gen. 39, [7] A. K. Harding and D. Lai, Rep. Prog. Phys. 69, [8] F. Haas, L. G. Garcia, J. Goedert and G. Manfredi, Phys. Plasmas 10, [9] F. Haas, Quantum Plasmas: an Hydrodynamic Approach Springer, New York, 011. [10] R. E. Wyatt, Quantum Dynamics with Trajectories: Introduction to Quantum Hydrodynamics Springer, New York, 005. [11] P. K. Shukla and B. Eliasson, Physics-Uspekhi 53, [1] F. Haas, Phys. Plasmas 1, [13] H. Terças, J. T. Mendonca and P. K. Shukla, Phys. Plasmas 15, [14] J. Zamanian, M. Marklund and G. Brodin, Phys. Rev. E 88, [15] J. Zamanian, M. Marklund and G. Brodin, Eur. Phys. J. D 69,
27 [16] R. Ekman, J. Zamanian and G. Brodin, Phys. Rev. E 9, [17] V. Zakharov and E. Kuznetsov, Sov. Phys. JETP 39, [18] E. Infeld and G. Rowlands, Nonlinear Waves, Solitons and Chaos Cambridge University Press, Cambridge, 000 [19] E. W. Laedke and K. H. Spatschek, Phys. Rev. Lett. 47, [0] R. Sabry, W. M. Moslem, F. Haas. S. Ali and P.K. Shukla, Phys. Plasmas 15, [1] W. M. Moslem, S. Ali, P. K. Shukla, X. Y. Tang and G. Rowlands, Phys. Plasmas 14, [] S. A. Khan and W. Masood, Phys. Plasmas 15, [3] N. Maafa, Phys. Scripta 48, [4] A. E. Dubinov, A. A. Dubinova and M. A. Sazokin, J. Commun. Tech. Elec. 55, [5] A. E. Dubinov and I. N. Kitaev, Phys. Plasmas 1, [6] B. Eliasson and P. K. Shukla, Phys. Scripta 78, [7] M. McKerr, F. Haas and I. Kourakis, Phys. Rev. E 90, [8] E. E. Behery, F. Haas and I. Kourakis, Phys Rev. E 93, [9] F. Haas and S. Mahmood, Phys. Rev. E 9, [30] V. E. Fortov, Extreme States of Matter on Earth and in the Cosmos Springer, Berlin, 011. [31] R. K. Pathria and P. D. Beale, Statistical Mechanics-3rd Edition Elsevier, New York USA, 011. [3] L. Lewin, Polylogarithms and Associated Functions North Holland, New York, [33] B. Eliasson and M. Akbari-Moghanjoughi, Finite temperature static charge screening in quantum plasmas, accepted for publication in Phys. Lett. A 016, DOI /j.physleta [34] L. G. Stanton and M. S. Murillo, Phys. Rev. E 91, [35] L. G. Stanton, M. S. Murillo, Phys. Rev. E 91, E 015. [36] T. E. Stringer, J. Nucl. Energy Part C 5, [37] E. Witt and W. Lotko, Phys. Fluids 6, [38] K. N. Stepanov, Soviet Phys. JETP 8, [39] A. I. Akhiezer, I. A. Akhiezer, R. V. Polovin, A. G. Sitenko and K. N. Stepanov, Plasma Electrodynamics - vol. I Pergamon, Oxford, [40] D. B. Melrose and A. Mushtaq, Phys. Rev. E 8,
28 [41] I. Kourakis, W. M. Moslem, U. M. Abdelsalam, R. Sabry and P. K. Shukla, Plasma Fusion Res. 4, [4] R. L. Mace and M. A. Hellberg, Phys. Plasmas 8, [43] E. Infeld, J. Plasma Phys. 33, [44] E. W. Laedke and K. H. Spatschek, Phys. Fluids 5, [45] D. Kremp, M. Schlanges and W.-D. Kraeft, Quantum Statistics of Nonideal Plasmas Springer- Verlag, Berlin-Heidelberg, 005. [46] M. Tatarakis, I. Watts, F. N. Beg, E. L. Clark, A. E. Dangor, A. Gopal, M. G. Haines, P. A. Norreys, U. Wagner, M.-S. Wei, M. Zepf and K. Krushelnick, Nature 415, [47] U. Wagner, M. Tatarakis, A. Gopal, F. N. Beg, E. L. Clark, A. E. Dangor, R. G. Evans, M. G. Haines, S. P. D. Mangles, P. A. Norreys, M.-S. Wei, M. Zepf and K. Krushelnick, Phys. Rev. E 70, [48] M. S. Murillo, Phys. Plasmas 11,
Modeling of relativistic ion-acoustic waves in ultra-degenerate plasmas
 Under consideration for publication in J. Plasma Phys. 1 Modeling of relativistic ion-acoustic waves in ultra-degenerate plasmas Fernando Haas, Physics Institute, Federal University of Rio Grande do Sul,
Under consideration for publication in J. Plasma Phys. 1 Modeling of relativistic ion-acoustic waves in ultra-degenerate plasmas Fernando Haas, Physics Institute, Federal University of Rio Grande do Sul,
arxiv:physics/ v1 [physics.plasm-ph] 26 Oct 2004
![arxiv:physics/ v1 [physics.plasm-ph] 26 Oct 2004 arxiv:physics/ v1 [physics.plasm-ph] 26 Oct 2004](/thumbs/92/107928568.jpg) Modified Zakharov equations for plasmas with a quantum correction arxiv:physics/0410251v1 [physics.plasm-ph] 26 Oct 2004 L. G. Garcia, F. Haas, L. P. L. de Oliveira and J. Goedert Universidade do Vale
Modified Zakharov equations for plasmas with a quantum correction arxiv:physics/0410251v1 [physics.plasm-ph] 26 Oct 2004 L. G. Garcia, F. Haas, L. P. L. de Oliveira and J. Goedert Universidade do Vale
Springer Series on. atomic, optical, and plasma physics 65
 Springer Series on atomic, optical, and plasma physics 65 Springer Series on atomic, optical, and plasma physics The Springer Series on Atomic, Optical, and Plasma Physics covers in a comprehensive manner
Springer Series on atomic, optical, and plasma physics 65 Springer Series on atomic, optical, and plasma physics The Springer Series on Atomic, Optical, and Plasma Physics covers in a comprehensive manner
Waves in plasma. Denis Gialis
 Waves in plasma Denis Gialis This is a short introduction on waves in a non-relativistic plasma. We will consider a plasma of electrons and protons which is fully ionized, nonrelativistic and homogeneous.
Waves in plasma Denis Gialis This is a short introduction on waves in a non-relativistic plasma. We will consider a plasma of electrons and protons which is fully ionized, nonrelativistic and homogeneous.
arxiv:physics/ v1 31 Oct 2006
 Nonlinear wave interactions in quantum magnetoplasmas P. K. Shukla and S. Ali Institut für Theoretische Physik IV and Centre for Plasma Science and Astrophysics, Fakultät für Physik und Astronomie, Ruhr
Nonlinear wave interactions in quantum magnetoplasmas P. K. Shukla and S. Ali Institut für Theoretische Physik IV and Centre for Plasma Science and Astrophysics, Fakultät für Physik und Astronomie, Ruhr
Nonlinear electrostatic structures in unmagnetized pair-ion (fullerene) plasmas
 Nonlinear electrostatic structures in unmagnetized pair-ion (fullerene) plasmas S. Mahmood Theoretical Plasma Physics Division, PINSTECH Islamabad Collaborators: H. Saleem National Center for Physics,
Nonlinear electrostatic structures in unmagnetized pair-ion (fullerene) plasmas S. Mahmood Theoretical Plasma Physics Division, PINSTECH Islamabad Collaborators: H. Saleem National Center for Physics,
Nonlinear Excitations in Strongly-Coupled Fermi-Dirac Plasmas. Abstract
 Nonlinear Excitations in Strongly-Coupled Fermi-Dirac Plasmas M. Akbari-Moghanjoughi Azarbaijan University of Tarbiat Moallem, Faculty of Sciences, Department of Physics, 51745-406, Tabriz, Iran (Dated:
Nonlinear Excitations in Strongly-Coupled Fermi-Dirac Plasmas M. Akbari-Moghanjoughi Azarbaijan University of Tarbiat Moallem, Faculty of Sciences, Department of Physics, 51745-406, Tabriz, Iran (Dated:
Dust acoustic solitary and shock waves in strongly coupled dusty plasmas with nonthermal ions
 PRAMANA c Indian Academy of Sciences Vol. 73, No. 5 journal of November 2009 physics pp. 913 926 Dust acoustic solitary and shock waves in strongly coupled dusty plasmas with nonthermal ions HAMID REZA
PRAMANA c Indian Academy of Sciences Vol. 73, No. 5 journal of November 2009 physics pp. 913 926 Dust acoustic solitary and shock waves in strongly coupled dusty plasmas with nonthermal ions HAMID REZA
arxiv:quant-ph/ v1 4 Apr 2006
 New low frequency oscillations in quantum dusty plasmas L. Stenflo, P. K. Shukla, and M. Marklund Department of Physics, Umeå University, SE 901 87 Umeå, Sweden Abstract The existence of two new low-frequency
New low frequency oscillations in quantum dusty plasmas L. Stenflo, P. K. Shukla, and M. Marklund Department of Physics, Umeå University, SE 901 87 Umeå, Sweden Abstract The existence of two new low-frequency
Computational Solutions for the Korteweg devries Equation in Warm Plasma
 COMPUTATIONAL METHODS IN SCIENCE AND TECHNOLOGY 16(1, 13-18 (1 Computational Solutions for the Korteweg devries Equation in Warm Plasma E.K. El-Shewy*, H.G. Abdelwahed, H.M. Abd-El-Hamid. Theoretical Physics
COMPUTATIONAL METHODS IN SCIENCE AND TECHNOLOGY 16(1, 13-18 (1 Computational Solutions for the Korteweg devries Equation in Warm Plasma E.K. El-Shewy*, H.G. Abdelwahed, H.M. Abd-El-Hamid. Theoretical Physics
2/8/16 Dispersive Media, Lecture 5 - Thomas Johnson 1. Waves in plasmas. T. Johnson
 2/8/16 Dispersive Media, Lecture 5 - Thomas Johnson 1 Waves in plasmas T. Johnson Introduction to plasma physics Magneto-Hydro Dynamics, MHD Plasmas without magnetic fields Cold plasmas Transverse waves
2/8/16 Dispersive Media, Lecture 5 - Thomas Johnson 1 Waves in plasmas T. Johnson Introduction to plasma physics Magneto-Hydro Dynamics, MHD Plasmas without magnetic fields Cold plasmas Transverse waves
Effect of Positive Dust on Non-linear Properties of Ion-acoustic Waves
 Effect of Positive Dust on Non-linear Properties of Ion-acoustic Waves Sanjit Kumar Paul Department of Basic Sciences and Humanities, University of Asia Pacific,Green Road, Dhaka-1215, Bangladesh. Abstract-The
Effect of Positive Dust on Non-linear Properties of Ion-acoustic Waves Sanjit Kumar Paul Department of Basic Sciences and Humanities, University of Asia Pacific,Green Road, Dhaka-1215, Bangladesh. Abstract-The
Dispersive Media, Lecture 7 - Thomas Johnson 1. Waves in plasmas. T. Johnson
 2017-02-14 Dispersive Media, Lecture 7 - Thomas Johnson 1 Waves in plasmas T. Johnson Introduction to plasmas as a coupled system Magneto-Hydro Dynamics, MHD Plasmas without magnetic fields Cold plasmas
2017-02-14 Dispersive Media, Lecture 7 - Thomas Johnson 1 Waves in plasmas T. Johnson Introduction to plasmas as a coupled system Magneto-Hydro Dynamics, MHD Plasmas without magnetic fields Cold plasmas
Relativistic Degeneracy Effect on Propagation of Arbitrary Amplitude Ion-Acoustic Solitons in Thomas-Fermi Plasmas
 Relativistic Degeneracy Effect on Propagation of Arbitrary Amplitude Ion-Acoustic Solitons in Thomas-Fermi Plasmas Abdolrasoul ESFANDYARI-KALEJAHI, Massoud AKBARI-MOGHANJOUGHI and Ehsan SABERIAN Department
Relativistic Degeneracy Effect on Propagation of Arbitrary Amplitude Ion-Acoustic Solitons in Thomas-Fermi Plasmas Abdolrasoul ESFANDYARI-KALEJAHI, Massoud AKBARI-MOGHANJOUGHI and Ehsan SABERIAN Department
Self-gravitating Envelope Solitons in a Degenerate Quantum Plasma System
 Advances in Astrophysics, Vol. 3, No. 4, November 18 https://dx.doi.org/1.66/adap.18.345 57 Self-gravitating Envelope Solitons in a Degenerate Quantum Plasma System N. Ahmed, N. A. Chowdhury, A. Mannan
Advances in Astrophysics, Vol. 3, No. 4, November 18 https://dx.doi.org/1.66/adap.18.345 57 Self-gravitating Envelope Solitons in a Degenerate Quantum Plasma System N. Ahmed, N. A. Chowdhury, A. Mannan
COMPRESSIVE AND RAREFACTIVE DUST-ACOUSTIC SOLITARY STRUCTURES IN A MAGNETIZED TWO-ION-TEMPERATURE DUSTY PLASMA. 1. Introduction
 COMPRESSIVE AND RAREFACTIVE DUST-ACOUSTIC SOLITARY STRUCTURES IN A MAGNETIZED TWO-ION-TEMPERATURE DUSTY PLASMA A.A. MAMUN Department of Physics, Jahangirnagar University, Savar, Dhaka, Bangladesh E-mail:
COMPRESSIVE AND RAREFACTIVE DUST-ACOUSTIC SOLITARY STRUCTURES IN A MAGNETIZED TWO-ION-TEMPERATURE DUSTY PLASMA A.A. MAMUN Department of Physics, Jahangirnagar University, Savar, Dhaka, Bangladesh E-mail:
(2008) 74 (5) ISSN
 Eliasson, Bengt and Shukla, Padma (008) Ion solitary waves in a dense quantum plasma. Journal of Plasma Physics, 74 (5). pp. 581-584. ISSN 00-3778, http://dx.doi.org/10.1017/s0037780800737x This version
Eliasson, Bengt and Shukla, Padma (008) Ion solitary waves in a dense quantum plasma. Journal of Plasma Physics, 74 (5). pp. 581-584. ISSN 00-3778, http://dx.doi.org/10.1017/s0037780800737x This version
Two-scale numerical solution of the electromagnetic two-fluid plasma-maxwell equations: Shock and soliton simulation
 Mathematics and Computers in Simulation 76 (2007) 3 7 Two-scale numerical solution of the electromagnetic two-fluid plasma-maxwell equations: Shock and soliton simulation S. Baboolal a,, R. Bharuthram
Mathematics and Computers in Simulation 76 (2007) 3 7 Two-scale numerical solution of the electromagnetic two-fluid plasma-maxwell equations: Shock and soliton simulation S. Baboolal a,, R. Bharuthram
Collisionless Shocks and the Earth s Bow Shock
 Collisionless Shocks and the Earth s Bow Shock Jean-Luc Thiffeault AST 381 Gas Dynamics 17 November 1994 1 Introduction The mean free path for particle collisions in the solar wind at the boundary of the
Collisionless Shocks and the Earth s Bow Shock Jean-Luc Thiffeault AST 381 Gas Dynamics 17 November 1994 1 Introduction The mean free path for particle collisions in the solar wind at the boundary of the
Stable Propagating Waves and Wake Fields in Relativistic Electromagnetic Plasma
 Commun. Theor. Phys. (Beijing, China) 49 (2008) pp. 753 758 c Chinese Physical Society Vol. 49, No. 3, March 15, 2008 Stable Propagating Waves and Wake Fields in Relativistic Electromagnetic Plasma XIE
Commun. Theor. Phys. (Beijing, China) 49 (2008) pp. 753 758 c Chinese Physical Society Vol. 49, No. 3, March 15, 2008 Stable Propagating Waves and Wake Fields in Relativistic Electromagnetic Plasma XIE
The ideal Maxwellian plasma
 The ideal Maxwellian plasma Dr. L. Conde Departamento de Física Aplicada. E.T.S. Ingenieros Aeronáuticos Universidad Politécnica de Madrid Plasmas are,... The plasma state of matter may be defined as a
The ideal Maxwellian plasma Dr. L. Conde Departamento de Física Aplicada. E.T.S. Ingenieros Aeronáuticos Universidad Politécnica de Madrid Plasmas are,... The plasma state of matter may be defined as a
Energy mode distribution: an analysis of the ratio of anti-stokes to Stokes amplitudes generated by a pair of counterpropagating Langmuir waves.
 Energy mode distribution: an analysis of the ratio of anti-stokes to Stokes amplitudes generated by a pair of counterpropagating Langmuir waves. Fernando J. R. Simões Júnior a, M. Virgínia Alves a, Felipe
Energy mode distribution: an analysis of the ratio of anti-stokes to Stokes amplitudes generated by a pair of counterpropagating Langmuir waves. Fernando J. R. Simões Júnior a, M. Virgínia Alves a, Felipe
Influence of Generalized (r, q) Distribution Function on Electrostatic Waves
 Commun. Theor. Phys. (Beijing, China) 45 (2006) pp. 550 554 c International Academic Publishers Vol. 45, No. 3, March 15, 2006 Influence of Generalized (r, q) istribution Function on Electrostatic Waves
Commun. Theor. Phys. (Beijing, China) 45 (2006) pp. 550 554 c International Academic Publishers Vol. 45, No. 3, March 15, 2006 Influence of Generalized (r, q) istribution Function on Electrostatic Waves
Introduction. Chapter Plasma: definitions
 Chapter 1 Introduction 1.1 Plasma: definitions A plasma is a quasi-neutral gas of charged and neutral particles which exhibits collective behaviour. An equivalent, alternative definition: A plasma is a
Chapter 1 Introduction 1.1 Plasma: definitions A plasma is a quasi-neutral gas of charged and neutral particles which exhibits collective behaviour. An equivalent, alternative definition: A plasma is a
Neutrino effective charge in a dense Fermi plasma
 Physics Letters B 657 (007) 154 158 www.elsevier.com/locate/physletb Neutrino effective charge in a dense Fermi plasma L.A. Rios a,, P.K. Shukla a,a.serbeto b a Fakultät für Physik und Astronomie, Institut
Physics Letters B 657 (007) 154 158 www.elsevier.com/locate/physletb Neutrino effective charge in a dense Fermi plasma L.A. Rios a,, P.K. Shukla a,a.serbeto b a Fakultät für Physik und Astronomie, Institut
The properties of an ideal Fermi gas are strongly determined by the Pauli principle. We shall consider the limit:
 Chapter 13 Ideal Fermi gas The properties of an ideal Fermi gas are strongly determined by the Pauli principle. We shall consider the limit: k B T µ, βµ 1, which defines the degenerate Fermi gas. In this
Chapter 13 Ideal Fermi gas The properties of an ideal Fermi gas are strongly determined by the Pauli principle. We shall consider the limit: k B T µ, βµ 1, which defines the degenerate Fermi gas. In this
Soliton propagation in an inhomogeneous plasma at critical density of negative ions: Effects of gyratory and thermal motions of ions
 PHYSICS OF PLASMAS 14, 102110 2007 Soliton propagation in an inhomogeneous plasma at critical density of negative ions: Effects of gyratory and thermal motions of ions Hitendra K. Malik and Shigeo Kawata
PHYSICS OF PLASMAS 14, 102110 2007 Soliton propagation in an inhomogeneous plasma at critical density of negative ions: Effects of gyratory and thermal motions of ions Hitendra K. Malik and Shigeo Kawata
Chapter 3. Head-on collision of ion acoustic solitary waves in electron-positron-ion plasma with superthermal electrons and positrons.
 Chapter 3 Head-on collision of ion acoustic solitary waves in electron-positron-ion plasma with superthermal electrons and positrons. 73 3.1 Introduction The study of linear and nonlinear wave propagation
Chapter 3 Head-on collision of ion acoustic solitary waves in electron-positron-ion plasma with superthermal electrons and positrons. 73 3.1 Introduction The study of linear and nonlinear wave propagation
Effects of Spin Quantum Force in Magnetized Quantum Plasma
 Commun. Theor. Phys. 56 (011 769 773 Vol. 56, No. 4, October 15, 011 Effects of Spin Quantum Force in Magnetized Quantum Plasma YANG Xiu-Feng ( ô, JIANG Hong (, QI Xue-Hong (, and DUAN Wen-Shan ( College
Commun. Theor. Phys. 56 (011 769 773 Vol. 56, No. 4, October 15, 011 Effects of Spin Quantum Force in Magnetized Quantum Plasma YANG Xiu-Feng ( ô, JIANG Hong (, QI Xue-Hong (, and DUAN Wen-Shan ( College
Landau Bogolubov Energy Spectrum of Superconductors
 Landau Bogolubov Energy Spectrum of Superconductors L.N. Tsintsadze 1 and N.L. Tsintsadze 1,2 1. Department of Plasma Physics, E. Andronikashvili Institute of Physics, Tbilisi 0128, Georgia 2. Faculty
Landau Bogolubov Energy Spectrum of Superconductors L.N. Tsintsadze 1 and N.L. Tsintsadze 1,2 1. Department of Plasma Physics, E. Andronikashvili Institute of Physics, Tbilisi 0128, Georgia 2. Faculty
Bose-Einstein Condensation and Intermediate State of the. Photon Gas. Abstract
 Bose-Einstein Condensation and Intermediate State of the Photon Gas Levan N. Tsintsadze Venture Business Laboratory, Hiroshima University, Higashi-Hiroshima, Japan (July 19, 2002) Abstract Possibility
Bose-Einstein Condensation and Intermediate State of the Photon Gas Levan N. Tsintsadze Venture Business Laboratory, Hiroshima University, Higashi-Hiroshima, Japan (July 19, 2002) Abstract Possibility
Anisotropic electron distribution functions and the transition between the Weibel and the whistler instabilities
 Anisotropic electron distribution functions and the transition between the Weibel and the whistler instabilities F. Pegoraro, L. Palodhi, F. Califano 5 th INTERNATIONAL CONFERENCE ON THE FRONTIERS OF PLASMA
Anisotropic electron distribution functions and the transition between the Weibel and the whistler instabilities F. Pegoraro, L. Palodhi, F. Califano 5 th INTERNATIONAL CONFERENCE ON THE FRONTIERS OF PLASMA
Simulation results for magnetized plasmas
 Chapter 4 Simulation results for magnetized plasmas In this chapter, we consider the dust charge fluctuation mode and lower hybrid wave damping in a magnetized plasma. Also, we consider plasma instabilities
Chapter 4 Simulation results for magnetized plasmas In this chapter, we consider the dust charge fluctuation mode and lower hybrid wave damping in a magnetized plasma. Also, we consider plasma instabilities
EXPLODING BOSE-EINSTEIN CONDENSATES AND COLLAPSING NEUTRON STARS DRIVEN BY CRITICAL MAGNETIC FIELDS
 EXPLODING BOSE-EINSTEIN CONDENSATES AND COLLAPSING NEUTRON STARS DRIVEN BY CRITICAL MAGNETIC FIELDS H. PÉREZ ROJAS, A. PÉREZ MARTíNEZ Instituto de Cibernética, Matemática y Física, 10400 La Habana, Cuba
EXPLODING BOSE-EINSTEIN CONDENSATES AND COLLAPSING NEUTRON STARS DRIVEN BY CRITICAL MAGNETIC FIELDS H. PÉREZ ROJAS, A. PÉREZ MARTíNEZ Instituto de Cibernética, Matemática y Física, 10400 La Habana, Cuba
arxiv: v1 [physics.plasm-ph] 15 Dec 2017
![arxiv: v1 [physics.plasm-ph] 15 Dec 2017 arxiv: v1 [physics.plasm-ph] 15 Dec 2017](/thumbs/73/69084727.jpg) Neutrino magnetohydrodynamics Fernando Haas and Kellen Alves Pascoal Instituto de Física, Universidade Federal do Rio Grande do Sul, arxiv:1712.05640v1 [physics.plasm-ph] 15 Dec 2017 Av. Bento Gonçalves
Neutrino magnetohydrodynamics Fernando Haas and Kellen Alves Pascoal Instituto de Física, Universidade Federal do Rio Grande do Sul, arxiv:1712.05640v1 [physics.plasm-ph] 15 Dec 2017 Av. Bento Gonçalves
arxiv: v1 [physics.plasm-ph] 11 Jun 2012
![arxiv: v1 [physics.plasm-ph] 11 Jun 2012 arxiv: v1 [physics.plasm-ph] 11 Jun 2012](/thumbs/93/111994657.jpg) Quantum effects in beam-plasma instabilities A. Bret 1, 2 and F. Haas 3 1 ETSI Industriales, Universidad de Castilla-La Mancha, 13071 Ciudad Real, Spain 2 Instituto de Investigaciones Energeticas y Aplicaciones
Quantum effects in beam-plasma instabilities A. Bret 1, 2 and F. Haas 3 1 ETSI Industriales, Universidad de Castilla-La Mancha, 13071 Ciudad Real, Spain 2 Instituto de Investigaciones Energeticas y Aplicaciones
Plasma waves in the fluid picture I
 Plasma waves in the fluid picture I Langmuir oscillations and waves Ion-acoustic waves Debye length Ordinary electromagnetic waves General wave equation General dispersion equation Dielectric response
Plasma waves in the fluid picture I Langmuir oscillations and waves Ion-acoustic waves Debye length Ordinary electromagnetic waves General wave equation General dispersion equation Dielectric response
Quantum effects on Rayleigh Taylor instability in magnetized plasma
 Quantum effects on Rayleigh Taylor instability in magnetized plasma Jintao Cao, 1 Haijun Ren, 1 Zhengwei Wu, 1,,a and Paul K. Chu 1 CAS Key Laboratory of Basic Plasma Physics, University of Science and
Quantum effects on Rayleigh Taylor instability in magnetized plasma Jintao Cao, 1 Haijun Ren, 1 Zhengwei Wu, 1,,a and Paul K. Chu 1 CAS Key Laboratory of Basic Plasma Physics, University of Science and
Solution for Problem Set 19-20
 Solution for Problem Set 19-0 compiled by Dan Grin and Nate Bode) April 16, 009 A 19.4 Ion Acoustic Waves [by Xinkai Wu 00] a) The derivation of these equations is trivial, so we omit it here. b) Write
Solution for Problem Set 19-0 compiled by Dan Grin and Nate Bode) April 16, 009 A 19.4 Ion Acoustic Waves [by Xinkai Wu 00] a) The derivation of these equations is trivial, so we omit it here. b) Write
Energy and momentum losses in the process of neutrino scattering on plasma electrons with the presence of a magnetic field.
 Energy and momentum losses in the process of neutrino scattering on plasma electrons with the presence of a magnetic field. Nickolay V. Mikheev and Elena N. Narynskaya Division of Theoretical Physics,
Energy and momentum losses in the process of neutrino scattering on plasma electrons with the presence of a magnetic field. Nickolay V. Mikheev and Elena N. Narynskaya Division of Theoretical Physics,
List of Comprehensive Exams Topics
 List of Comprehensive Exams Topics Mechanics 1. Basic Mechanics Newton s laws and conservation laws, the virial theorem 2. The Lagrangian and Hamiltonian Formalism The Lagrange formalism and the principle
List of Comprehensive Exams Topics Mechanics 1. Basic Mechanics Newton s laws and conservation laws, the virial theorem 2. The Lagrangian and Hamiltonian Formalism The Lagrange formalism and the principle
Dr. A A Mamun Professor of Physics Jahangirnagar University Dhaka, Bangladesh
 SOLITARY AND SHOCK WAVES IN DUSTY PLASMAS Dr. A A Mamun Professor of Physics Jahangirnagar University Dhaka, Bangladesh OUTLINE Introduction Static Dust: DIA Waves DIA Solitary Waves DIA Shock Waves Mobile
SOLITARY AND SHOCK WAVES IN DUSTY PLASMAS Dr. A A Mamun Professor of Physics Jahangirnagar University Dhaka, Bangladesh OUTLINE Introduction Static Dust: DIA Waves DIA Solitary Waves DIA Shock Waves Mobile
Face-to-face interaction of multisolitons in spin-1/2 quantum plasma
 Pramana J. Phys. (2017) 88: 18 DOI 10.1007/s12043-016-1313-8 c Indian Academy of Sciences Face-to-face interaction of multisolitons in spin-1/2 quantum plasma KAUSHIK ROY 1,, SOURAV CHOUDHURY 2, PRASANTA
Pramana J. Phys. (2017) 88: 18 DOI 10.1007/s12043-016-1313-8 c Indian Academy of Sciences Face-to-face interaction of multisolitons in spin-1/2 quantum plasma KAUSHIK ROY 1,, SOURAV CHOUDHURY 2, PRASANTA
arxiv: v1 [physics.plasm-ph] 3 Aug 2017
![arxiv: v1 [physics.plasm-ph] 3 Aug 2017 arxiv: v1 [physics.plasm-ph] 3 Aug 2017](/thumbs/89/100953502.jpg) Generation of Low Frequency Plasma Waves After Wave-Breaking Prabal Singh Verma CNRS/Université d Aix-Marseille Centre saint Jérôme, case, F-97 Marseille cedex, France arxiv:78.99v [physics.plasm-ph] Aug
Generation of Low Frequency Plasma Waves After Wave-Breaking Prabal Singh Verma CNRS/Université d Aix-Marseille Centre saint Jérôme, case, F-97 Marseille cedex, France arxiv:78.99v [physics.plasm-ph] Aug
Fluid equations, magnetohydrodynamics
 Fluid equations, magnetohydrodynamics Multi-fluid theory Equation of state Single-fluid theory Generalised Ohm s law Magnetic tension and plasma beta Stationarity and equilibria Validity of magnetohydrodynamics
Fluid equations, magnetohydrodynamics Multi-fluid theory Equation of state Single-fluid theory Generalised Ohm s law Magnetic tension and plasma beta Stationarity and equilibria Validity of magnetohydrodynamics
Chapter 14. Ideal Bose gas Equation of state
 Chapter 14 Ideal Bose gas In this chapter, we shall study the thermodynamic properties of a gas of non-interacting bosons. We will show that the symmetrization of the wavefunction due to the indistinguishability
Chapter 14 Ideal Bose gas In this chapter, we shall study the thermodynamic properties of a gas of non-interacting bosons. We will show that the symmetrization of the wavefunction due to the indistinguishability
arxiv: v1 [physics.plasm-ph] 14 Dec 2017
![arxiv: v1 [physics.plasm-ph] 14 Dec 2017 arxiv: v1 [physics.plasm-ph] 14 Dec 2017](/thumbs/74/70893560.jpg) Collisional Effects, Ion-Acoustic Waves and Neutrino Oscillations Fernando Haas and Kellen Alves Pascoal Instituto de Física, Universidade Federal do Rio Grande do Sul, arxiv:1712.05345v1 [physics.plasm-ph]
Collisional Effects, Ion-Acoustic Waves and Neutrino Oscillations Fernando Haas and Kellen Alves Pascoal Instituto de Física, Universidade Federal do Rio Grande do Sul, arxiv:1712.05345v1 [physics.plasm-ph]
Lecture 4 Recap: normal metals and the clectron-phonon interaction *
 Phys. 598SC Fall 2015 Prof. A. J. Leggett Lecture 4 Recap: normal metals and the clectron-phonon interaction * 1. Normal metals: Sommerfeld-Bloch picture 2. Screening 3. Fermi liquid theory 4. Electron-phonon
Phys. 598SC Fall 2015 Prof. A. J. Leggett Lecture 4 Recap: normal metals and the clectron-phonon interaction * 1. Normal metals: Sommerfeld-Bloch picture 2. Screening 3. Fermi liquid theory 4. Electron-phonon
Nonlinear low-frequency collisional quantum Buneman instability
 arxiv:6.89v [physics.plasm-ph] Jun Nonliar low-frequency collisional quantum Buman instability F. Haas Departamento de Física, Universidade Federal do Paraná, 83-99, Curitiba, Paraná, Brazil A. Bret ETSI
arxiv:6.89v [physics.plasm-ph] Jun Nonliar low-frequency collisional quantum Buman instability F. Haas Departamento de Física, Universidade Federal do Paraná, 83-99, Curitiba, Paraná, Brazil A. Bret ETSI
Instabilities and propagation of neutrino magnetohydrodynamic waves in arbitrary direction. Abstract
 Instabilities and propagation of neutrino magnetohydrodynamic waves in arbitrary direction Fernando Haas and Kellen Alves Pascoal arxiv:171.0538v1 [physics.plasm-ph] 1 Dec 017 Instituto de Física, Universidade
Instabilities and propagation of neutrino magnetohydrodynamic waves in arbitrary direction Fernando Haas and Kellen Alves Pascoal arxiv:171.0538v1 [physics.plasm-ph] 1 Dec 017 Instituto de Física, Universidade
Nonlinear Waves, Solitons and Chaos
 Nonlinear Waves, Solitons and Chaos Eryk Infeld Institute for Nuclear Studies, Warsaw George Rowlands Department of Physics, University of Warwick 2nd edition CAMBRIDGE UNIVERSITY PRESS Contents Foreword
Nonlinear Waves, Solitons and Chaos Eryk Infeld Institute for Nuclear Studies, Warsaw George Rowlands Department of Physics, University of Warwick 2nd edition CAMBRIDGE UNIVERSITY PRESS Contents Foreword
Fermi energy of electrons in neutron stars with strong magnetic field and magnetars
 EPJ Web of Conferences 109, 07003 (2016) DOI: 10.1051/ epjconf/ 201610907003 C Owned by the authors, published by EDP Sciences, 2016 Fermi energy of electrons in neutron stars with strong magnetic field
EPJ Web of Conferences 109, 07003 (2016) DOI: 10.1051/ epjconf/ 201610907003 C Owned by the authors, published by EDP Sciences, 2016 Fermi energy of electrons in neutron stars with strong magnetic field
Plasma Astrophysics Chapter 1: Basic Concepts of Plasma. Yosuke Mizuno Institute of Astronomy National Tsing-Hua University
 Plasma Astrophysics Chapter 1: Basic Concepts of Plasma Yosuke Mizuno Institute of Astronomy National Tsing-Hua University What is a Plasma? A plasma is a quasi-neutral gas consisting of positive and negative
Plasma Astrophysics Chapter 1: Basic Concepts of Plasma Yosuke Mizuno Institute of Astronomy National Tsing-Hua University What is a Plasma? A plasma is a quasi-neutral gas consisting of positive and negative
Non-Linear Plasma Wave Decay to Longer Wavelength
 Non-Linear Plasma Wave Decay to Longer Wavelength F. Anderegg 1, a), M. Affolter 1, A. Ashourvan 1, D.H.E. Dubin 1, F. Valentini 2 and C.F. Driscoll 1 1 University of California San Diego Physics Department
Non-Linear Plasma Wave Decay to Longer Wavelength F. Anderegg 1, a), M. Affolter 1, A. Ashourvan 1, D.H.E. Dubin 1, F. Valentini 2 and C.F. Driscoll 1 1 University of California San Diego Physics Department
Whistler oscillitons revisited: the role of charge neutrality?
 Nonlinear Processes in Geophysics 004 11: 447 45 SRef-ID: 1607-7946/npg/004-11-447 Nonlinear Processes in Geophysics European Geosciences Union 004 Whistler oscillitons revisited: the role of charge neutrality?
Nonlinear Processes in Geophysics 004 11: 447 45 SRef-ID: 1607-7946/npg/004-11-447 Nonlinear Processes in Geophysics European Geosciences Union 004 Whistler oscillitons revisited: the role of charge neutrality?
Relativistic magnetohydrodynamics. Abstract
 Relativistic magnetohydrodynamics R. D. Hazeltine and S. M. Mahajan Institute for Fusion Studies, The University of Texas, Austin, Texas 78712 (October 19, 2000) Abstract The lowest-order description of
Relativistic magnetohydrodynamics R. D. Hazeltine and S. M. Mahajan Institute for Fusion Studies, The University of Texas, Austin, Texas 78712 (October 19, 2000) Abstract The lowest-order description of
We are IntechOpen, the world s leading publisher of Open Access books Built by scientists, for scientists. International authors and editors
 We are IntechOpen, the world s leading publisher of Open Access books Built by scientists, for scientists,900 116,000 10M Open access books available International authors and editors Downloads Our authors
We are IntechOpen, the world s leading publisher of Open Access books Built by scientists, for scientists,900 116,000 10M Open access books available International authors and editors Downloads Our authors
The Physics of Fluids and Plasmas
 The Physics of Fluids and Plasmas An Introduction for Astrophysicists ARNAB RAI CHOUDHURI CAMBRIDGE UNIVERSITY PRESS Preface Acknowledgements xiii xvii Introduction 1 1. 3 1.1 Fluids and plasmas in the
The Physics of Fluids and Plasmas An Introduction for Astrophysicists ARNAB RAI CHOUDHURI CAMBRIDGE UNIVERSITY PRESS Preface Acknowledgements xiii xvii Introduction 1 1. 3 1.1 Fluids and plasmas in the
The de Haas van Alphen Oscillation in Two-Dimensional QED at Finite Temperature and Density
 Commun. Theor. Phys. (Beijing, China) 35 (21) pp. 673 678 c International Academic Publishers Vol. 35, No. 6, June 15, 21 The de Haas van Alphen Oscillation in Two-Dimensional QED at Finite Temperature
Commun. Theor. Phys. (Beijing, China) 35 (21) pp. 673 678 c International Academic Publishers Vol. 35, No. 6, June 15, 21 The de Haas van Alphen Oscillation in Two-Dimensional QED at Finite Temperature
Computers and Mathematics with Applications. Stability analysis for Zakharov Kuznetsov equation of weakly nonlinear ion-acoustic waves in a plasma
 Computers and Mathematics with Applications 67 () 7 8 Contents lists available at ScienceDirect Computers and Mathematics with Applications journal homepage: www.elsevier.com/locate/camwa Stability analysis
Computers and Mathematics with Applications 67 () 7 8 Contents lists available at ScienceDirect Computers and Mathematics with Applications journal homepage: www.elsevier.com/locate/camwa Stability analysis
ELECTROSTATIC ION-CYCLOTRON WAVES DRIVEN BY PARALLEL VELOCITY SHEAR
 1 ELECTROSTATIC ION-CYCLOTRON WAVES DRIVEN BY PARALLEL VELOCITY SHEAR R. L. Merlino Department of Physics and Astronomy University of Iowa Iowa City, IA 52242 December 21, 2001 ABSTRACT Using a fluid treatment,
1 ELECTROSTATIC ION-CYCLOTRON WAVES DRIVEN BY PARALLEL VELOCITY SHEAR R. L. Merlino Department of Physics and Astronomy University of Iowa Iowa City, IA 52242 December 21, 2001 ABSTRACT Using a fluid treatment,
arxiv: v2 [nlin.ps] 14 Aug 2016
![arxiv: v2 [nlin.ps] 14 Aug 2016 arxiv: v2 [nlin.ps] 14 Aug 2016](/thumbs/74/70318692.jpg) arxiv:1605.05726v2 [nlin.ps] 14 Aug 2016 Stability of ion acoustic nonlinear waves and solitons in magnetized plasmas Piotr Goldstein and Eryk Infeld Theoretical Physics Division, National Centre for Nuclear
arxiv:1605.05726v2 [nlin.ps] 14 Aug 2016 Stability of ion acoustic nonlinear waves and solitons in magnetized plasmas Piotr Goldstein and Eryk Infeld Theoretical Physics Division, National Centre for Nuclear
PHY 140A: Solid State Physics. Solution to Homework #7
 PHY 14A: Solid State Physics Solution to Homework #7 Xun Jia 1 December 5, 26 1 Email: jiaxun@physics.ucla.edu Fall 26 Physics 14A c Xun Jia (December 5, 26) Problem #1 Static magnetoconductivity tensor.
PHY 14A: Solid State Physics Solution to Homework #7 Xun Jia 1 December 5, 26 1 Email: jiaxun@physics.ucla.edu Fall 26 Physics 14A c Xun Jia (December 5, 26) Problem #1 Static magnetoconductivity tensor.
A Model for Periodic Nonlinear Electric Field Structures in Space Plasmas
 Commun. Theor. Phys. (Beijing, China) 52 (2009) pp. 149 154 c Chinese Physical Society and IOP Publishing Ltd Vol. 52, No. 1, July 15, 2009 A Model for Periodic Nonlinear Electric Field Structures in Space
Commun. Theor. Phys. (Beijing, China) 52 (2009) pp. 149 154 c Chinese Physical Society and IOP Publishing Ltd Vol. 52, No. 1, July 15, 2009 A Model for Periodic Nonlinear Electric Field Structures in Space
Effects of ion temperature on electrostatic solitary structures in nonthermal plasmas
 PHYSICAL REVIEW E VOLUME 55, NUMBER FEBRUARY 1997 Effects of ion temperature on electrostatic solitary structures in nonthermal plasmas A. A. Mamun Department of Physics, Jahangirnagar University, Savar,
PHYSICAL REVIEW E VOLUME 55, NUMBER FEBRUARY 1997 Effects of ion temperature on electrostatic solitary structures in nonthermal plasmas A. A. Mamun Department of Physics, Jahangirnagar University, Savar,
Homogeneous Bianisotropic Medium, Dissipation and the Non-constancy of Speed of Light in Vacuum for Different Galilean Reference Systems
 Progress In Electromagnetics Research Symposium Proceedings, Cambridge, USA, July 5 8, 2010 489 Homogeneous Bianisotropic Medium, Dissipation and the Non-constancy of Speed of Light in Vacuum for Different
Progress In Electromagnetics Research Symposium Proceedings, Cambridge, USA, July 5 8, 2010 489 Homogeneous Bianisotropic Medium, Dissipation and the Non-constancy of Speed of Light in Vacuum for Different
Plasmas as fluids. S.M.Lea. January 2007
 Plasmas as fluids S.M.Lea January 2007 So far we have considered a plasma as a set of non intereacting particles, each following its own path in the electric and magnetic fields. Now we want to consider
Plasmas as fluids S.M.Lea January 2007 So far we have considered a plasma as a set of non intereacting particles, each following its own path in the electric and magnetic fields. Now we want to consider
26. Non-linear effects in plasma
 Phys780: Plasma Physics Lecture 26. Non-linear effects. Collisionless shocks.. 1 26. Non-linear effects in plasma Collisionless shocks ([1], p.405-421, [6], p.237-245, 249-254; [4], p.429-440) Collisionless
Phys780: Plasma Physics Lecture 26. Non-linear effects. Collisionless shocks.. 1 26. Non-linear effects in plasma Collisionless shocks ([1], p.405-421, [6], p.237-245, 249-254; [4], p.429-440) Collisionless
The First Principle Calculation of Green Kubo Formula with the Two-Time Ensemble Technique
 Commun. Theor. Phys. (Beijing, China 35 (2 pp. 42 46 c International Academic Publishers Vol. 35, No. 4, April 5, 2 The First Principle Calculation of Green Kubo Formula with the Two-Time Ensemble Technique
Commun. Theor. Phys. (Beijing, China 35 (2 pp. 42 46 c International Academic Publishers Vol. 35, No. 4, April 5, 2 The First Principle Calculation of Green Kubo Formula with the Two-Time Ensemble Technique
Chapter 9 WAVES IN COLD MAGNETIZED PLASMA. 9.1 Introduction. 9.2 The Wave Equation
 Chapter 9 WAVES IN COLD MAGNETIZED PLASMA 9.1 Introduction For this treatment, we will regard the plasma as a cold magnetofluid with an associated dielectric constant. We then derive a wave equation using
Chapter 9 WAVES IN COLD MAGNETIZED PLASMA 9.1 Introduction For this treatment, we will regard the plasma as a cold magnetofluid with an associated dielectric constant. We then derive a wave equation using
PHYSICS OF HOT DENSE PLASMAS
 Chapter 6 PHYSICS OF HOT DENSE PLASMAS 10 26 10 24 Solar Center Electron density (e/cm 3 ) 10 22 10 20 10 18 10 16 10 14 10 12 High pressure arcs Chromosphere Discharge plasmas Solar interior Nd (nω) laserproduced
Chapter 6 PHYSICS OF HOT DENSE PLASMAS 10 26 10 24 Solar Center Electron density (e/cm 3 ) 10 22 10 20 10 18 10 16 10 14 10 12 High pressure arcs Chromosphere Discharge plasmas Solar interior Nd (nω) laserproduced
J10M.1 - Rod on a Rail (M93M.2)
 Part I - Mechanics J10M.1 - Rod on a Rail (M93M.2) J10M.1 - Rod on a Rail (M93M.2) s α l θ g z x A uniform rod of length l and mass m moves in the x-z plane. One end of the rod is suspended from a straight
Part I - Mechanics J10M.1 - Rod on a Rail (M93M.2) J10M.1 - Rod on a Rail (M93M.2) s α l θ g z x A uniform rod of length l and mass m moves in the x-z plane. One end of the rod is suspended from a straight
curriculum vitae Post-Doc Fellowship, School of Physics university of sydney NSW 2006 Australia ( ) with Prof. D. B.
 curriculum vitae Prof. Dr. Mushtaq Ahmad Nationality: Charsadda (Pakistan) Personal Data Current address for correspondence: Department of Physics, Abdul Wali Khan University Mardan KPK, Pakistan; Tel:
curriculum vitae Prof. Dr. Mushtaq Ahmad Nationality: Charsadda (Pakistan) Personal Data Current address for correspondence: Department of Physics, Abdul Wali Khan University Mardan KPK, Pakistan; Tel:
Gyrokinetic simulations of magnetic fusion plasmas
 Gyrokinetic simulations of magnetic fusion plasmas Tutorial 2 Virginie Grandgirard CEA/DSM/IRFM, Association Euratom-CEA, Cadarache, 13108 St Paul-lez-Durance, France. email: virginie.grandgirard@cea.fr
Gyrokinetic simulations of magnetic fusion plasmas Tutorial 2 Virginie Grandgirard CEA/DSM/IRFM, Association Euratom-CEA, Cadarache, 13108 St Paul-lez-Durance, France. email: virginie.grandgirard@cea.fr
Australian Journal of Physics
 CSIRO PUBLISHING Australian Journal of Physics Volume 50, 1997 CSIRO Australia 1997 A journal for the publication of original research in all branches of physics www.publish.csiro.au/journals/ajp All enquiries
CSIRO PUBLISHING Australian Journal of Physics Volume 50, 1997 CSIRO Australia 1997 A journal for the publication of original research in all branches of physics www.publish.csiro.au/journals/ajp All enquiries
13.1 Ion Acoustic Soliton and Shock Wave
 13 Nonlinear Waves In linear theory, the wave amplitude is assumed to be sufficiently small to ignore contributions of terms of second order and higher (ie, nonlinear terms) in wave amplitude In such a
13 Nonlinear Waves In linear theory, the wave amplitude is assumed to be sufficiently small to ignore contributions of terms of second order and higher (ie, nonlinear terms) in wave amplitude In such a
Chemical potential and internal energy of the noninteracting Fermi gas in fractional-dimensional space
 PRAMANA c Indian Academy of Sciences Vol. 75, No. 3 journal of September 2010 physics pp. 393 402 Chemical potential and internal energy of the noninteracting Fermi gas in fractional-dimensional space
PRAMANA c Indian Academy of Sciences Vol. 75, No. 3 journal of September 2010 physics pp. 393 402 Chemical potential and internal energy of the noninteracting Fermi gas in fractional-dimensional space
Two-stage Rydberg charge exchange in a strong magnetic field
 Two-stage Rydberg charge exchange in a strong magnetic field M. L. Wall, C. S. Norton, and F. Robicheaux Department of Physics, Auburn University, Auburn, Alabama 36849-5311, USA Received 21 June 2005;
Two-stage Rydberg charge exchange in a strong magnetic field M. L. Wall, C. S. Norton, and F. Robicheaux Department of Physics, Auburn University, Auburn, Alabama 36849-5311, USA Received 21 June 2005;
2m 2 Ze2. , where δ. ) 2 l,n is the quantum defect (of order one but larger
 PHYS 402, Atomic and Molecular Physics Spring 2017, final exam, solutions 1. Hydrogenic atom energies: Consider a hydrogenic atom or ion with nuclear charge Z and the usual quantum states φ nlm. (a) (2
PHYS 402, Atomic and Molecular Physics Spring 2017, final exam, solutions 1. Hydrogenic atom energies: Consider a hydrogenic atom or ion with nuclear charge Z and the usual quantum states φ nlm. (a) (2
Characteristic Behavior of Ion Acoustic Wave in A dusty Plasma
 Characteristic Behavior of Ion Acoustic Wave in A dusty Plasma M. K. Jassim Department of physics College of Education Iben AL-Haitham University of Baghdad Abstract In this research we make an attempt
Characteristic Behavior of Ion Acoustic Wave in A dusty Plasma M. K. Jassim Department of physics College of Education Iben AL-Haitham University of Baghdad Abstract In this research we make an attempt
Space Plasma Physics Thomas Wiegelmann, 2012
 Space Plasma Physics Thomas Wiegelmann, 2012 1. Basic Plasma Physics concepts 2. Overview about solar system plasmas Plasma Models 3. Single particle motion, Test particle model 4. Statistic description
Space Plasma Physics Thomas Wiegelmann, 2012 1. Basic Plasma Physics concepts 2. Overview about solar system plasmas Plasma Models 3. Single particle motion, Test particle model 4. Statistic description
Simple examples of MHD equilibria
 Department of Physics Seminar. grade: Nuclear engineering Simple examples of MHD equilibria Author: Ingrid Vavtar Mentor: prof. ddr. Tomaž Gyergyek Ljubljana, 017 Summary: In this seminar paper I will
Department of Physics Seminar. grade: Nuclear engineering Simple examples of MHD equilibria Author: Ingrid Vavtar Mentor: prof. ddr. Tomaž Gyergyek Ljubljana, 017 Summary: In this seminar paper I will
Cluster fusion in a high magnetic field
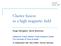 Santa Fe July 28, 2009 Cluster fusion in a high magnetic field Roger Bengtson, Boris Breizman Institute for Fusion Studies, Fusion Research Center The University of Texas at Austin In collaboration with:
Santa Fe July 28, 2009 Cluster fusion in a high magnetic field Roger Bengtson, Boris Breizman Institute for Fusion Studies, Fusion Research Center The University of Texas at Austin In collaboration with:
Lagrangian formulation for neutrino plasma interactions
 PHYSICS OF PLASMAS VOLUME 6, NUMBER 4 APRIL 1999 Lagrangian formulation for neutrino plasma interactions Alain J. Brizard and Jonathan S. Wurtele Department of Physics, University of California and Lawrence
PHYSICS OF PLASMAS VOLUME 6, NUMBER 4 APRIL 1999 Lagrangian formulation for neutrino plasma interactions Alain J. Brizard and Jonathan S. Wurtele Department of Physics, University of California and Lawrence
Production of Over-dense Plasmas by Launching. 2.45GHz Electron Cyclotron Waves in a Helical Device
 Production of Over-dense Plasmas by Launching 2.45GHz Electron Cyclotron Waves in a Helical Device R. Ikeda a, M. Takeuchi a, T. Ito a, K. Toi b, C. Suzuki b, G. Matsunaga c, S. Okamura b, and CHS Group
Production of Over-dense Plasmas by Launching 2.45GHz Electron Cyclotron Waves in a Helical Device R. Ikeda a, M. Takeuchi a, T. Ito a, K. Toi b, C. Suzuki b, G. Matsunaga c, S. Okamura b, and CHS Group
A Zero Field Monte Carlo Algorithm Accounting for the Pauli Exclusion Principle
 A Zero Field Monte Carlo Algorithm Accounting for the Pauli Exclusion Principle Sergey Smirnov, Hans Kosina, Mihail Nedjalkov, and Siegfried Selberherr Institute for Microelectronics, TU-Vienna, Gusshausstrasse
A Zero Field Monte Carlo Algorithm Accounting for the Pauli Exclusion Principle Sergey Smirnov, Hans Kosina, Mihail Nedjalkov, and Siegfried Selberherr Institute for Microelectronics, TU-Vienna, Gusshausstrasse
Fundamentals of wave kinetic theory
 Fundamentals of wave kinetic theory Introduction to the subject Perturbation theory of electrostatic fluctuations Landau damping - mathematics Physics of Landau damping Unmagnetized plasma waves The plasma
Fundamentals of wave kinetic theory Introduction to the subject Perturbation theory of electrostatic fluctuations Landau damping - mathematics Physics of Landau damping Unmagnetized plasma waves The plasma
5. Systems in contact with a thermal bath
 5. Systems in contact with a thermal bath So far, isolated systems (micro-canonical methods) 5.1 Constant number of particles:kittel&kroemer Chap. 3 Boltzmann factor Partition function (canonical methods)
5. Systems in contact with a thermal bath So far, isolated systems (micro-canonical methods) 5.1 Constant number of particles:kittel&kroemer Chap. 3 Boltzmann factor Partition function (canonical methods)
Do atomic electrons stay bound in changing plasma environment?
 Do atomic electrons stay bound in changing plasma environment? T. N. Chang 1 and T. K. Fang 2 1 Department of Physics and Astronomy, University of Southern California, Los Angeles, CA 90089-0484, U.S.A.
Do atomic electrons stay bound in changing plasma environment? T. N. Chang 1 and T. K. Fang 2 1 Department of Physics and Astronomy, University of Southern California, Los Angeles, CA 90089-0484, U.S.A.
J. Astrophys. Astr., Vol. 36, No. 4, December 2015, pp
 Review J. Astrophys. Astr., Vol. 36, No. 4, December 2015, pp. 635 642 Inverse Bremsstrahlung in Astrophysical Plasmas: The Absorption Coefficients and Gaunt Factors A. A. Mihajlov, V. A. Srećković & N.
Review J. Astrophys. Astr., Vol. 36, No. 4, December 2015, pp. 635 642 Inverse Bremsstrahlung in Astrophysical Plasmas: The Absorption Coefficients and Gaunt Factors A. A. Mihajlov, V. A. Srećković & N.
Electronic Structure of Atoms. Chapter 6
 Electronic Structure of Atoms Chapter 6 Electronic Structure of Atoms 1. The Wave Nature of Light All waves have: a) characteristic wavelength, λ b) amplitude, A Electronic Structure of Atoms 1. The Wave
Electronic Structure of Atoms Chapter 6 Electronic Structure of Atoms 1. The Wave Nature of Light All waves have: a) characteristic wavelength, λ b) amplitude, A Electronic Structure of Atoms 1. The Wave
Quantum Physics II (8.05) Fall 2002 Outline
 Quantum Physics II (8.05) Fall 2002 Outline 1. General structure of quantum mechanics. 8.04 was based primarily on wave mechanics. We review that foundation with the intent to build a more formal basis
Quantum Physics II (8.05) Fall 2002 Outline 1. General structure of quantum mechanics. 8.04 was based primarily on wave mechanics. We review that foundation with the intent to build a more formal basis
Dust density waves: ion flows and finite temperature effects
 Dust density waves: ion flows and finite temperature effects Edward Thomas, Jr. Physics Department, Auburn University This work is supported by National Science Foundation and the US Department of Energy
Dust density waves: ion flows and finite temperature effects Edward Thomas, Jr. Physics Department, Auburn University This work is supported by National Science Foundation and the US Department of Energy
SOLID STATE PHYSICS. Second Edition. John Wiley & Sons. J. R. Hook H. E. Hall. Department of Physics, University of Manchester
 SOLID STATE PHYSICS Second Edition J. R. Hook H. E. Hall Department of Physics, University of Manchester John Wiley & Sons CHICHESTER NEW YORK BRISBANE TORONTO SINGAPORE Contents Flow diagram Inside front
SOLID STATE PHYSICS Second Edition J. R. Hook H. E. Hall Department of Physics, University of Manchester John Wiley & Sons CHICHESTER NEW YORK BRISBANE TORONTO SINGAPORE Contents Flow diagram Inside front
[variable] = units (or dimension) of variable.
![[variable] = units (or dimension) of variable. [variable] = units (or dimension) of variable.](/thumbs/95/122609291.jpg) Dimensional Analysis Zoe Wyatt wyatt.zoe@gmail.com with help from Emanuel Malek Understanding units usually makes physics much easier to understand. It also gives a good method of checking if an answer
Dimensional Analysis Zoe Wyatt wyatt.zoe@gmail.com with help from Emanuel Malek Understanding units usually makes physics much easier to understand. It also gives a good method of checking if an answer
Suppression of Radiation Excitation in Focusing Environment * Abstract
 SLAC PUB 7369 December 996 Suppression of Radiation Excitation in Focusing Environment * Zhirong Huang and Ronald D. Ruth Stanford Linear Accelerator Center Stanford University Stanford, CA 94309 Abstract
SLAC PUB 7369 December 996 Suppression of Radiation Excitation in Focusing Environment * Zhirong Huang and Ronald D. Ruth Stanford Linear Accelerator Center Stanford University Stanford, CA 94309 Abstract
Part VIII. Interaction with Solids
 I with Part VIII I with Solids 214 / 273 vs. long pulse is I with Traditional i physics (ICF ns lasers): heating and creation of long scale-length plasmas Laser reflected at critical density surface Fast
I with Part VIII I with Solids 214 / 273 vs. long pulse is I with Traditional i physics (ICF ns lasers): heating and creation of long scale-length plasmas Laser reflected at critical density surface Fast
J07M.1 - Ball on a Turntable
 Part I - Mechanics J07M.1 - Ball on a Turntable J07M.1 - Ball on a Turntable ẑ Ω A spherically symmetric ball of mass m, moment of inertia I about any axis through its center, and radius a, rolls without
Part I - Mechanics J07M.1 - Ball on a Turntable J07M.1 - Ball on a Turntable ẑ Ω A spherically symmetric ball of mass m, moment of inertia I about any axis through its center, and radius a, rolls without
APPENDIX Z. USEFUL FORMULAS 1. Appendix Z. Useful Formulas. DRAFT 13:41 June 30, 2006 c J.D Callen, Fundamentals of Plasma Physics
 APPENDIX Z. USEFUL FORMULAS 1 Appendix Z Useful Formulas APPENDIX Z. USEFUL FORMULAS 2 Key Vector Relations A B = B A, A B = B A, A A = 0, A B C) = A B) C A B C) = B A C) C A B), bac-cab rule A B) C D)
APPENDIX Z. USEFUL FORMULAS 1 Appendix Z Useful Formulas APPENDIX Z. USEFUL FORMULAS 2 Key Vector Relations A B = B A, A B = B A, A A = 0, A B C) = A B) C A B C) = B A C) C A B), bac-cab rule A B) C D)
Magnetohydrodynamic waves in a plasma
 Department of Physics Seminar 1b Magnetohydrodynamic waves in a plasma Author: Janez Kokalj Advisor: prof. dr. Tomaž Gyergyek Petelinje, April 2016 Abstract Plasma can sustain different wave phenomena.
Department of Physics Seminar 1b Magnetohydrodynamic waves in a plasma Author: Janez Kokalj Advisor: prof. dr. Tomaž Gyergyek Petelinje, April 2016 Abstract Plasma can sustain different wave phenomena.
